Изобретение относится к области связи, в частности к радиотехническим беспроводным коммуникационным системам, а более конкретно к способам обработки сигналов в адаптивных антенных решетках (АР).
Адаптивные антенны (в иностранной литературе иногда «смарт-антенна») - это такой тип антенных систем, параметры которых изменяются автоматически с целью обеспечения наилучшего условия приема полезного сигнала на фоне изменяющихся мешающих внешних воздействий [1-3].
Основными элементами адаптивной антенны являются: антенная решетка, диаграммообразующая схема и блок адаптивного управления диаграммой направленности (ДН) [3]. Сигналы, принятые отдельными антеннами системы, проходят через устройства, регулирующие их амплитуду и фазу, и складываются в сумматоре, каждый со своим весовым коэффициентом (w1, w2, wn). Блок адаптивного управления ДН осуществляет подстройку весовых коэффициентов в диаграммообразующей схеме. В адаптивном процессоре, в свою очередь, выделяют процессор сигнала и устройство, реализующее процедуру управления. Для каждой антенны при заданной сигнально-помеховой обстановке существует оптимальный вектор весовых коэффициентов (Wопт) (ВВК), однозначно связанный с формируемой ДН АР [1-3].
Одной из главных характеристик адаптивной АР, определяющих качество обработки сигналов, является вид и параметры адаптивной процедуры формирования ВВК. Поскольку характер принимаемых сигналов и направление прихода заранее обычно неизвестны, адаптивный процессор должен автоматически подстраиваться к любым изменениям условий приема сигналов. Основной задачей адаптивного процессора является подстройка весовых коэффициентов, при которых оптимизируется определенный критерий эффективности, и формируется требуемая ДН АР.
Адаптивный процессор осуществляет подстройку ВВК для каждого элемента АР. Изменение ВВК от исходного значения до оптимального может происходить по различным траекториям, вид которых зависит от многих факторов, в первую очередь, от выбранного критерия качества адаптации и метода поиска экстремума.
Известны различные технические решения с градиентными способами обработки разнородных входных параметров.
Так, известен патент РФ на изобретение №2325044 (МПК G06K 9/46, опубл. 20.05.2008) «Градиентный способ выделения контуров объектов на матрице полутонового растрового изображения». Градиентный способ выделения контуров объектов на матрице полутонового растрового изображения заключается в том, что для всех пикселей растрового изображения по заранее выбранному способу вычисляют норму или квадрат нормы градиента изменения их яркости, затем на новой черно-белой монохромной матрице черным цветом на белом фоне выделяют все элементы, у которых значение нормы или квадрата нормы градиента больше некоторого порогового значения, а в качестве контуров объектов на монохромной матрице принимают связные конфигурации элементов черного цвета. Для выбранного способа вычисления градиента экспериментально определяют коэффициент, затем рассчитывают пороговое значение квадрата нормы градиента как произведение данного коэффициента на сумму квадратов средних величин модулей изменения яркости соседних пикселей по строкам и столбцам, у которых значения превышают общие средние уровни ненулевых изменений соответственно по строкам и столбцам, а среди связных конфигураций элементов черного цвета на монохромной матрице сразу отбрасывают конфигурации, у которых число входящих элементов менее 5-7 элементов, для оставшихся конфигураций вычисляют среднюю степень соседства - частное от деления суммы по всем элементам конфигурации соседних с ним элементов на сумму элементов в конфигурации, причем те конфигурации, у которых средняя степень соседства менее 3, отбрасывают, как погрешности распознавания, а оставшиеся принимают в качестве искомых контуров объектов.
Известен градиентный способ выделения контуров объектов на матрице полутонового растрового изображения [Андреев А.Л. Автоматизированные телевизионные системы наблюдения. Часть П. Арифметико-логические основы и алгоритмы. Уч. пособие. СПб, СПбГУИТМО, 2005, с. 35-38. http://window.edu.ru/window/library], заключающийся в том, что для всех пикселей растрового изображения по заранее выбранному способу вычисляется норма или квадрат нормы градиента изменения их яркости, затем на новой черно-белой монохромной матрице черным цветом на белом фоне выделяют все элементы, у которых значение нормы или квадрата нормы градиента больше некоторого порогового значения, а в качестве контуров объектов на монохромной матрице принимают связные конфигурации элементов черного цвета.
Патент РФ на изобретение №2695417 (МПК G06K 9/48, опубл. 23.07.2019) «Способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях». Способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях, при котором формируют две матрицы и компонент градиента яркости в каждой точке изображения, определяют модуль градиента яркости в каждой точке изображения, формируют контуры объекта путем порогового преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента для которых в соответствующих координатах изображения превышает порог преобразования. Перед формированием матриц и компонент градиента яркости с учетом уровня зашумленности изображения выбирают коэффициент сглаживания и вычисляют коэффициенты сглаживающих кубических В-сплайнов вдоль каждой строки и каждого столбца изображения, а две матрицы и компонент градиента яркости в каждой точке изображения формируют путем суммирования сглаживающих параболических В-сплайнов с найденными ранее коэффициентами сглаживающих кубических В-сплайнов для строк и столбцов соответственно.
Известен способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях (патент РФ №2648954, МПК G06K 9/48, опубл. 15.08.2017), заключающийся в том, что сначала вычисляют прямое вейвлет-преобразование строк и столбцов цифрового полутонового изображения, а затем формируют две матрицы и компонент градиента яркости в каждой точке изображения путем обратного вейвлет преобразования, в котором в качестве ядра преобразования используют аналитические функции, описывающие производные используемых вейвлетов обратного преобразования по соответствующим координатам. После этого определяют модуль градиента яркости в каждой точке изображения, и формируют контуры объекта путем порогового преобразования модуля градиента яркости, в процессе которого на новой белой матрице черным цветом выделяют элементы, модуль градиента, для которых в соответствующих координатах изображения превышает порог преобразования.
Недостатком является то, что вычисление прямого вейвлет-преобразования строк и столбцов цифрового полутонового изображения требует больших вычислительных затрат. Кроме того, известный способ демонстрирует слабую устойчивость к воздействию импульсных помех.
Одним их наиболее распространенных способов обработки разнородных входных параметров адаптивных АР в радиотехнических беспроводных коммуникационных системах является способ оптимального по критерию минимума среднеквадратической ошибки (МСКО) между принимаемым и эталонным (опорным) сигналом [1-3]. Для осуществления нормальной работы контура адаптации, возникает задача задания или выделения опорного сигнала, наиболее близкого, например, в какой-либо метрике к полезному, что решается либо использованием способов синхронизации, либо выделением опорного сигнала из полезного, в случае, если полезный сигнал имеет сложную структуру (такие решения известны для фазоманипулированных сигналов псевдослучайными последовательностями, сигналов с псевдослучайной перестройкой рабочей частоты и некоторых других) [4].
В способе МСКО реализовано рекуррентное вычисление оценок ВВК  . Вектор w находится в результате решения оптимизационной задачи - поиска минимума целевой функции F1(k, w), зависящей от времени. Для поиска минимума функции F1(k, w) наиболее часто используют градиентный метод (метод наискорейшего спуска) - итерационную процедуру, определяющую траекторию пошагового приближения к минимуму, где шагам итерации соответствуют моменты дискретного времени к. На каждом шаге итерации оценивается вектор
. Вектор w находится в результате решения оптимизационной задачи - поиска минимума целевой функции F1(k, w), зависящей от времени. Для поиска минимума функции F1(k, w) наиболее часто используют градиентный метод (метод наискорейшего спуска) - итерационную процедуру, определяющую траекторию пошагового приближения к минимуму, где шагам итерации соответствуют моменты дискретного времени к. На каждом шаге итерации оценивается вектор  , смещаемый относительно вектора
, смещаемый относительно вектора 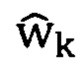 на величину, пропорциональную градиенту функции F1(k, w) в точке k.
на величину, пропорциональную градиенту функции F1(k, w) в точке k.
Известный способ с использованием итерационной процедуры вычисления оценок параметров АР по критерию МСКО включает следующие шаги:
шаг 1 - присвоить k=0 и задать начальные значения оценок параметров АР 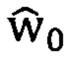 ;
;
шаг 2 - вычислить значения выходного сигнала yk и сигнала ошибки
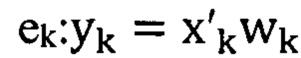 ; ek=dk - yk;
; ek=dk - yk;
шаг 3 - обновить оценки параметров  ;
;
шаг 4 - присвоить k=k+1;
шаг 5 - повторить процедуру вычисления оценок параметров АР: перейти на шаг 2-4.
Несмотря на простоту известного способа, анализ сходимости оценок параметров 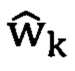 к оптимальным параметрам wopt, получаемым из винеровского решения [1-3], сводится к выбору величины шага адаптации μ, гарантирующему сходимость результатов. Под сходимостью в известном способе понимается приближение значений оценок параметров
к оптимальным параметрам wopt, получаемым из винеровского решения [1-3], сводится к выбору величины шага адаптации μ, гарантирующему сходимость результатов. Под сходимостью в известном способе понимается приближение значений оценок параметров 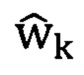 к значениям wopt. В процессе адаптации они будут флюктуировать относительно значений wopt, хаотично приближаясь к ним, но никогда не достигнут этих значений, даже при k → ∞. Поэтому, при выборе шага адаптации μ анализируется сходимость средних (математических ожиданий) и средних квадратов (дисперсий) значений вектора
к значениям wopt. В процессе адаптации они будут флюктуировать относительно значений wopt, хаотично приближаясь к ним, но никогда не достигнут этих значений, даже при k → ∞. Поэтому, при выборе шага адаптации μ анализируется сходимость средних (математических ожиданий) и средних квадратов (дисперсий) значений вектора 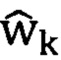 , которые сводятся к соответствующим значениям вектора wopt. В первом случае, говорят о сходимости в среднем, а во втором - в среднем квадрате. В режиме дисперсии сигнала ошибки АР с процедурой МСКО будет больше минимального достижимого в фильтре Винера, т.к. значения вектора
, которые сводятся к соответствующим значениям вектора wopt. В первом случае, говорят о сходимости в среднем, а во втором - в среднем квадрате. В режиме дисперсии сигнала ошибки АР с процедурой МСКО будет больше минимального достижимого в фильтре Винера, т.к. значения вектора  не достигают значений вектора wopt, и ее значение будет зависеть от шага адаптации. Поэтому, шаг адаптации выбирается из компромиссных соображений: чем больше μ, тем выше скорость сходимости; чем больше μ., тем больше дисперсия сигнала ошибки (по сравнению с фильтром Винера). Обычно значение μ равняется половине максимального шага 1/NP. В случае если мощность сигнала Р невозможно оценить заранее, или оно меняется в процессе обработки сигнала, применяют нормированную процедуру МСКО (NLMS) с шагом адаптации, нормированным к входному. Процедура NLMS имеет меньший уровень средней ошибки по сравнению с обыкновенной процедурой МСКО.
не достигают значений вектора wopt, и ее значение будет зависеть от шага адаптации. Поэтому, шаг адаптации выбирается из компромиссных соображений: чем больше μ, тем выше скорость сходимости; чем больше μ., тем больше дисперсия сигнала ошибки (по сравнению с фильтром Винера). Обычно значение μ равняется половине максимального шага 1/NP. В случае если мощность сигнала Р невозможно оценить заранее, или оно меняется в процессе обработки сигнала, применяют нормированную процедуру МСКО (NLMS) с шагом адаптации, нормированным к входному. Процедура NLMS имеет меньший уровень средней ошибки по сравнению с обыкновенной процедурой МСКО.
Техническая проблема в рассматриваемой сфере заключается в низкой скорости сходимости процедуры адаптации АР. В предлагаемом решении названная проблема решается за счет уменьшения итераций, требуемых для сходимости процедуры к установившемуся состоянию. Для этого в градиентной процедуре адаптации вводится переменный вектор коэффициентов усиления, зависящий от коэффициента забывания.
Технический результат предлагаемого решения состоит в увеличении скорости сходимости процедуры адаптации антенной решетки за счет уменьшения итераций.
Достигается технический результат тем, что в предлагаемом способе адаптации антенной решетки градиентной процедурой с переменным шагом, в котором определенным образом выбираются начальные условия для градиентной процедуры в виде нулевых значений весового вектора и единичной мгновенной оценки матрицы входных сигналов, с последующим итерационным вычислением выходного сигнала, сигнала ошибки, коэффициента усиления линейного рекуррентного фильтра, согласно изобретению, введен переменный вектор коэффициентов усиления, зависящий от коэффициента забывания, учитывающий предшествующие отсчеты входного сигнала в критерии с экспоненциально уменьшаемым весом. Кроме того, вычисляется мгновенное значение оценки матрицы входных сигналов и весового вектора, определяющего мгновенную диаграмму направленности антенной решетки, с учетом выбираемого из условия принадлежности к диапазону от нуля до единицы коэффициента забывания, при вычислении коэффициента усиления и мгновенного значения оценки матрицы входных сигналов.
В способе, реализующим процедуру RLS (Recursive Least Squares, рекурсивный способ по критерию наименьших квадратов), являющимся наиболее близким к предлагаемому способу, соответственно, принятом за прототип [5, с. 478-484], реализуется рекуррентное вычисление оптимальных параметров весовых коэффициентов Wk в установившемся режиме. В качестве наилучшего приближения выходного сигнала yk к образцовому dk используется минимум суммы квадратов сигнал ошибки ek
 ,
,
где L - длина входного сигнала Xk, w - вектор весовых коэффициентов. Вектор w находится в результате решения оптимизационной задачи - поиска минимума целевой функции F2(W), не зависящей от времени:
 .
.
Минимум функции F2(w) достигается при равенстве нулю частных производных по всем wn в момент времени k. Их совокупность можно записать в виде системы линейных алгебраических уравнений следующего вида:
 .
.
Заменим n на m вне скобок и разделим обе части равенства на 2:
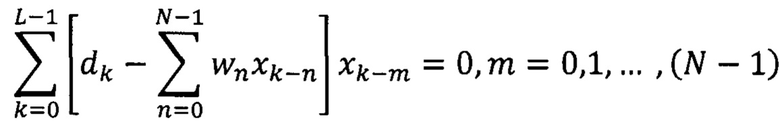 .
.
После переноса суммы с неизвестными параметрами wn в левую часть и изменения порядка суммирования получим:
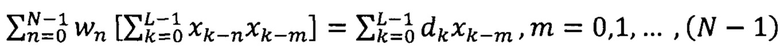 .
.
Полагая начальные условия нулевыми (Xk-n=0, k - n < 0), запишем (*) в матричном виде левую часть:

и аналогично правую:
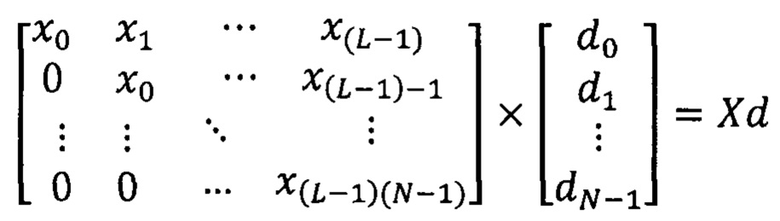
Тогда:

Определим значение вектора wk в момент времени k:
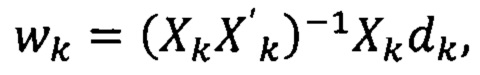
где матрица Xk и вектор dk вычисляются на текущем интервале [0; k]. Для следующего момента времени (k+1):
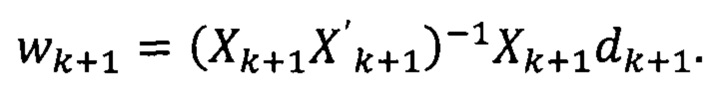
В этом случае в матрице Xk появится дополнительный столбец xk+1:

В векторе dk - дополнительный элемент dk+1, это позволяет установить рекуррентную связь произведения Xk+1X'k+1 с произведением XkX'k:

а также рекуррентную связь произведения Xk+1dk+1 с произведением Xkdk:
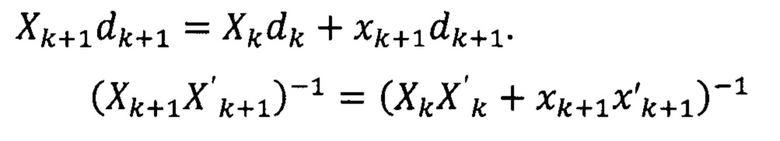
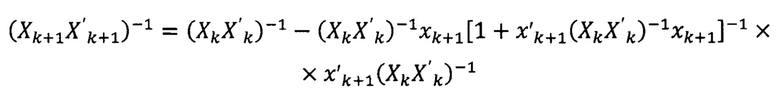
Введем переменную:
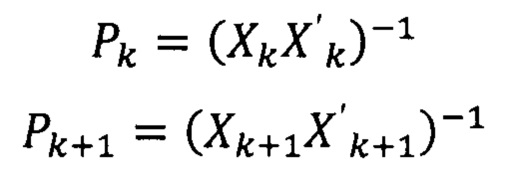
Тогда с учетом новой переменной:

Результатом выполнения операций в квадратных скобках будет скаляр, для которого операция обращения соответствует возведению в минус первую степень:
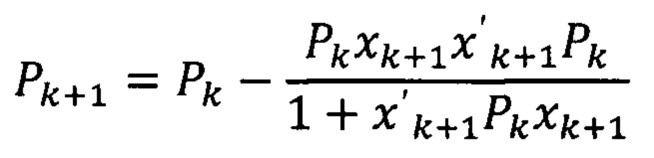
С учетом обозначения Pk+1:

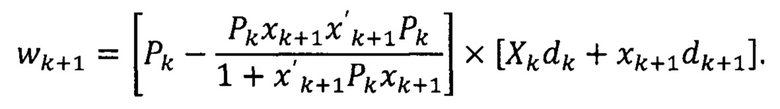
С учетом wk=PkXkdk:

Выражение в квадратных скобках является сигналом ошибки ek+1:
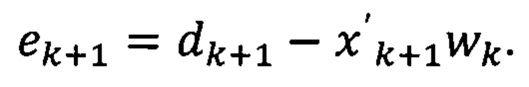
Множитель перед этим сигналом представляет собой вектор коэффициентов усиления:

Тогда рекуррентную формулу в процедуре RLS можно представить в виде:

Процедура RLS включает в себя следующие шаги:
1. Задать начальные (обычно нулевые) значения параметров АР (W-1).
2. Задать начальные значения элементам матрицы Р-1. Рекомендуется использовать единичную матрицу.
3. Присвоить k=0.
4. Вычислить значения выходного сигнала yk и сигнала ошибки ek:

5. Вычислить значение вектора коэффициентов усиления Kk:
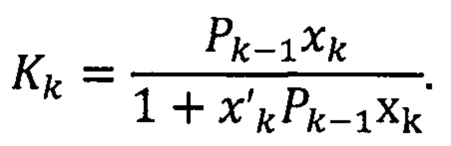
6. Обновить матрицу Pk с учетом вектора весовых коэффициентов:
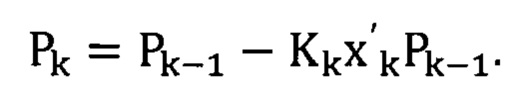
7. Обновить значение вектора весовых коэффициентов Wk:

8. Присвоить k=k+1.
9. Повторить пп. 4 - 8.
С помощью предлагаемого способа, известный критерий модифицируем, добавив в него коэффициент забывания λ, выбираемый из диапазона 0<λ≤1, что позволяет учитывать предшествующие отсчеты входного сигнала в критерии с экспоненциально уменьшаемым весом:

Тогда:
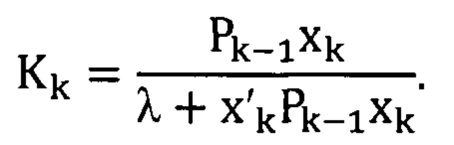

Способ адаптации антенной решетки градиентной процедурой с переменным шагом состоит в том, что определенным образом выбираются начальные условия для градиентной процедуры в виде нулевых значений весового вектора и единичной мгновенной оценки матрицы входных сигналов, с последующим итерационным вычислением выходного сигнала, сигнала ошибки, коэффициента усиления линейного рекуррентного фильтра. Введен переменный вектор коэффициентов усиления, зависящий от коэффициента забывания, учитывающий предшествующие отсчеты входного сигнала в критерии с экспоненциально уменьшаемым весом, кроме того вычисляется мгновенное значение оценки матрицы входных сигналов и весового вектора, определяющего мгновенную диаграмму направленности антенной решетки, с учетом выбираемого из условия принадлежности к диапазону от нуля до единицы коэффициента забывания, при вычислении коэффициента усиления и мгновенного значения оценки матрицы входных сигналов.
Предлагаемый способ поясняется графическим материалом, представленным на фиг. 1-3, из которых видно, что процедура RLS, согласно предлагаемому способу, обеспечивает более быструю сходимость результатов, по сравнению с классической, однако имеет большую дисперсию сигнала ошибки, поэтому коэффициент забывания λ выбирается из компромиссных решений:
- при увеличении λ, дисперсия шума уменьшается, а при предельном значении λ=1 модифицированная процедура сводится к классической;
- при уменьшении λ увеличивается скорость сходимости результатов.
Таким образом, с помощью предлагаемого способа достигается уменьшение, практически в два раза, количества итераций, обеспечивающих сходимость результатов, что позволяет использовать способ адаптации антенной решетки градиентной процедурой с переменным шагом в условиях быстро изменяющейся сигнально-помеховой обстановки в радиотехнических системах передачи информации, с увеличенной скоростью сходимости процедуры адаптации антенной решетки.
Литература
1. Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки. Введение в теорию. - М.: Радио и связь, 1986. - 448 с.
2. Уидроу Б., Стирнз С. Адаптивная обработка сигналов. - М.: Радио и связь, 1989. - 440 с.
3. Пистолькорс А.А., Литвинов О.С. Введение в теорию адаптивных антенн - М.: Наука, 1991. - 200 с.
4. Джиган В.И. Адаптивная фильтрация сигналов: теория и алгоритмы. - М.: Техносфера, 2013. - 528 с.
5. Солонина А.И. Цифровая обработка сигналов в зеркале Matlab. СПб.: БХВ. 2018.



Изобретение относится к области связи, в частности к радиотехническим беспроводным коммуникационным системам, а более конкретно к способам обработки сигналов в адаптивных антенных решетках (АР). Способ адаптации антенной решетки градиентной процедурой с переменным шагом состоит в том, что определенным образом выбирают начальные условия для градиентной процедуры в виде нулевых значений весового вектора и единичной мгновенной оценки матрицы входных сигналов, в последующем итерационно вычисляют значение выходного сигнала, сигнала ошибки, коэффициента усиления линейного рекуррентного фильтра. Введен переменный вектор коэффициентов усиления, зависящий от коэффициента забывания, учитывающий предшествующие отсчеты входного сигнала в критерии с экспоненциально уменьшаемым весом, кроме того, вычисляют мгновенное значение оценки матрицы входных сигналов и весового вектора, определяющего мгновенную диаграмму направленности антенной решетки, с учетом выбираемого из условия принадлежности к диапазону от нуля до единицы коэффициента забывания при вычислении коэффициента усиления и мгновенного значения оценки матрицы входных сигналов. Технический результат предлагаемого решения состоит в увеличении скорости сходимости процедуры адаптации антенной решетки за счет уменьшения итераций. 3 ил.
Способ адаптации антенной решетки градиентной процедурой с переменным шагом, в котором определенным образом выбирают начальные условия для градиентной процедуры в виде нулевых значений весового вектора и единичной мгновенной оценки матрицы входных сигналов с последующим итерационным вычислением значений выходного сигнала, сигнала ошибки, коэффициента усиления линейного рекуррентного фильтра,
отличающийся тем, что введен переменный вектор коэффициентов усиления, зависящий от коэффициента забывания, учитывающий предшествующие отсчеты входного сигнала в критерии с экспоненциально уменьшаемым весом, кроме того вычисляют мгновенное значение оценки матрицы входных сигналов и весового вектора, определяющего мгновенную диаграмму направленности антенной решетки, с учетом выбираемого из условия принадлежности к диапазону от нуля до единицы коэффициента забывания при вычислении коэффициента усиления и мгновенного значения оценки матрицы входных сигналов.
| RU 94039019 A1, 10.09.1996 | |||
| Статья: "МЕТОДИКА ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ ОБРАБОТКИ И ЕЕ РЕАЛИЗАЦИИ В АДАПТИВНЫХ АНТЕННЫХ РЕШЕТКАХ", Известия ТулГУ | |||
| Технические науки | |||
| Способ восстановления спиралей из вольфрамовой проволоки для электрических ламп накаливания, наполненных газом | 1924 |
|
SU2020A1 |
| Вып | |||
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
| Способ помехоустойчивого градиентного выделения контуров объектов на цифровых полутоновых изображениях | 2018 |
|
RU2695417C1 |
| Статья: МОДЕЛИРОВАНИЕ ГРАДИЕНТНОГО АЛГОРИТМА АДАПТАЦИИ АНТЕННОЙ РЕШЁТКИ В СРЕДЕ MATLAB", Радиотехнические и телекоммуникационные системы, | |||
Авторы
Даты
2023-01-23—Публикация
2021-12-14—Подача