Изобретение относится к системам пассивной радиолокации наблюдения за поверхностью и неподвижными объектами на поверхности на базе многоканальных (с антенными решетками) и сканирующих радиотеплолокаторов.
При получении изображений поверхности и неподвижных объектов на поверхности на базе бортовых радиотеплолокационных станций (РТЛС) миллиметрового диапазона формируется матрица радиотеплолокационного изображения (РТЛИ) в системе координат угла места и азимута. Элементами матрицы являются амплитуды сигналов излучения, выделенные в тракте первичной обработки РТЛС. Для повышения разрешающей способности по угловым координатам полученной матрицы РТЛИ (матрицы измерений) применяются методы восстановления изображений, например [1]. Однако восстановленное двумерное РТЛИ не дает информации о дальности до элементов поверхности, изображение которой получено, а также о высоте рельефа или объектов на поверхности. Это затрудняет решение ряда тактических задач и снижает безопасность маловысотных полетов. В связи с этим возникает актуальная проблема формирования трехмерного РТЛИ.
Известен способ формирования двумерного радиолокационного изображения (РЛИ) [2] в элементах разрешения дальности, который позволяет получить и трехмерное РЛИ по совокупности изображений, найденных в элементах дальности. Однако в РТЛС отсутствуют элементы разрешения дальности, и требуется иной подход к формированию трехмерного РТЛИ.
Известен способ измерения дальности до воздушного объекта в РТЛС [3, с.157-161], основанный на одновременном принятии сигнала излучения двумя пространственно-разнесенными антеннами, а также интерферометрический способ измерения дальности до движущегося воздушного объекта. Однако эти способы не позволяют измерить дальность до неподвижного объекта на поверхности и, соответственно, не позволяют получить трехмерное РТЛИ поверхности. Кроме того, они обладают низкой точностью измерения дальности и не предлагают способов уменьшения ошибок измерения.
Наиболее близким по технической сущности является способ формирования двумерного РЛИ поверхности с повышенной разрешающей способностью по угловым координатам [2], который заключается в восстановлении матрицы изображения в заданном диапазоне (или элементе разрешения) дальности и в силу этого применим для формирования двумерного РТЛИ. Способ сводится к следующим операциям:
1. В q-x приемных элементах антенной решетки или q-x каналах сканирующей по углу места (по i) и азимуту (по j) антенны измеряются амплитуды отраженных сигналов 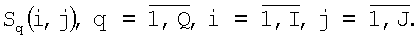
2. Относительно каждого i,j-го элемента 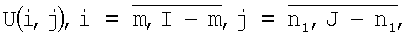 искомой матрицы изображения U строится плавающее окно ограниченного размера (2m+1)x(2n+1) по ширине M×N-диаграммы направленности (ДН) антенны (на уровне 0,5 мощности): M×N=(2m+1)x(2n+1).
искомой матрицы изображения U строится плавающее окно ограниченного размера (2m+1)x(2n+1) по ширине M×N-диаграммы направленности (ДН) антенны (на уровне 0,5 мощности): M×N=(2m+1)x(2n+1).
3. Амплитуды сигналов Sq (i+i1, j+j1), взятые в этом окне, суммируют по i1 и j1 с весовыми коэффициентами ωq (i+i1, j+j1), расчет которых осуществляют заранее по определенной методике. В результате получают оценку
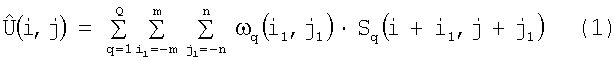
искомого изображения в центральном элементе окна, которому соответствует наибольшая точность оценивания.
4. Полученные по совокупности i,j оценки 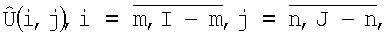 располагают в составе (I-2m)×(J-2n)-матрицы
располагают в составе (I-2m)×(J-2n)-матрицы 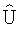 , которая представляет восстановленное изображение в i,j-x синтезированных элементах разрешения по азимуту и углу места, размеры которых в несколько раз меньше ширины ДН.
, которая представляет восстановленное изображение в i,j-x синтезированных элементах разрешения по азимуту и углу места, размеры которых в несколько раз меньше ширины ДН.
5. По совокупности элементов дальности формируют трехмерное РЛИ поверхности.
6. Способ предложен для случая Q=2 и обобщается на случай Q>2. Точность оценивания (восстановления РЛИ) возрастает с увеличением числа Q. При числе каналов, большем, чем число оцениваемых амплитуд (Q>MN в антенной решетке), точность оценивания элементов в окне становится равномерной, и оцениванию подлежат все элементы окна по формуле
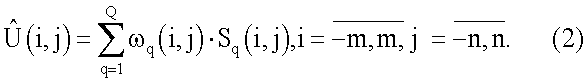
При этом отпадает необходимость поэлементного сканирования антенны, и сканирование I×J-зоны обзора осуществляется со смещением на ширину ДН по азимуту и углу места, что увеличивает быстродействие получения РЛИ. При этом формируется I×J-матрица 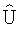 РЛИ зоны обзора.
РЛИ зоны обзора.
7. Операции (1), (2) могут выполняться в векторно-матричной форме:
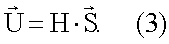
Здесь для (1): 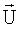 - (I-2m)(J-2n)-вектор-столбец оценок (1) амплитуд поля отражения; Н - (I-2m)(J-2n)×Q(I-2m)(J-2n)-матрица весовых коэффициентов ω;
- (I-2m)(J-2n)-вектор-столбец оценок (1) амплитуд поля отражения; Н - (I-2m)(J-2n)×Q(I-2m)(J-2n)-матрица весовых коэффициентов ω;
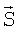 - Q(I-2m)(J-2n)-вектор-столбец измерений S.
- Q(I-2m)(J-2n)-вектор-столбец измерений S.
Для (2): 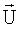 - IJ-вектор-столбец оценок (2); Н - IJ×QK-матрица весовых коэффициентов;
- IJ-вектор-столбец оценок (2); Н - IJ×QK-матрица весовых коэффициентов; 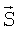 - QK-вектор-столбец измерений; К - число сканирований на ширину ДН в зоне обзора.
- QK-вектор-столбец измерений; К - число сканирований на ширину ДН в зоне обзора.
Применительно к РТЛС под элементом дальности понимается диапазон дальности в зоне обзора. Поэтому РТЛИ, в отличие от РЛИ, для фиксированного положения РТЛС в пространстве получается двумерным в координатах угол места - азимут.
Отсюда следует, что указанный способ применительно к РТЛС обладает следующим существенным недостатком. Он не позволяет измерить дальность до элемента поверхности (или неподвижного объекта на поверхности), без которой невозможно сформировать трехмерное РТЛИ. Устранение указанного недостатка требует изменений режима наблюдения за поверхностью и способа обработки результатов измерения.
Технический результат направлен на устранение указанного недостатка, то есть на формирование трехмерного РТЛИ.
Технический результат предлагаемого технического решения достигается тем, что способ формирования трехмерного изображения поверхности на базе бортовых РТЛС, при облете носителем РТЛС контролируемого участка поверхности, заключается в том, что при наблюдении за поверхностью с помощью Q-элементной антенной решетки или сканирующей Q-канальной антенны в дискретный момент времени t1 линию визирования антенны направляют на контролируемый участок поверхности и измеряют в q-x каналах 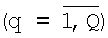 значения амплитуд приемных сигналов, прошедших операции первичной обработки, из этих амплитуд формируют Q-вектор - столбец измерений S, который умножают справа на IJ×Q-матрицу весовых коэффициентов Н, вычисляемую заранее, и получают IJ-вектор-столбец оценок
значения амплитуд приемных сигналов, прошедших операции первичной обработки, из этих амплитуд формируют Q-вектор - столбец измерений S, который умножают справа на IJ×Q-матрицу весовых коэффициентов Н, вычисляемую заранее, и получают IJ-вектор-столбец оценок 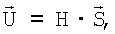 элементы которого разворачивают в матрицу
элементы которого разворачивают в матрицу 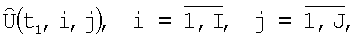 восстановленного на момент времени t1 амплитудного изображения участка поверхности с разрешением по углу места по i и азимуту - по j, отличается тем, что для формирования трехмерного изображения по истечении времени Δt облета носителем РТЛС контролируемого участка поверхности в момент t2 формируется вторая матрица изображения
восстановленного на момент времени t1 амплитудного изображения участка поверхности с разрешением по углу места по i и азимуту - по j, отличается тем, что для формирования трехмерного изображения по истечении времени Δt облета носителем РТЛС контролируемого участка поверхности в момент t2 формируется вторая матрица изображения 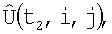 a координаты x1, y1 центра каждого i,j-го элемента матрицы
a координаты x1, y1 центра каждого i,j-го элемента матрицы 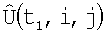 , взятые в антенной системе координат x,y,z, на основе данных навигационной системы об углах поворота осей ox, oy, oz и смещении носителя РТЛС относительно положения в момент t1 экстраполируют на момент времени t2 в координаты
, взятые в антенной системе координат x,y,z, на основе данных навигационной системы об углах поворота осей ox, oy, oz и смещении носителя РТЛС относительно положения в момент t1 экстраполируют на момент времени t2 в координаты 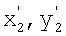 и округляют до ближайших элементов дискретизации i',j', в результате чего получают экстраполированную матрицу изображения
и округляют до ближайших элементов дискретизации i',j', в результате чего получают экстраполированную матрицу изображения 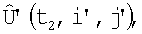 положение которой относительно
положение которой относительно 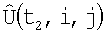 корректируют с помощью корреляционно-экстремального метода совмещения кадров, который компенсирует ошибки измерения навигационной системы, и устанавливают соответствие между элементами матриц
корректируют с помощью корреляционно-экстремального метода совмещения кадров, который компенсирует ошибки измерения навигационной системы, и устанавливают соответствие между элементами матриц 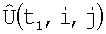 и
и 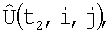 затем для каждой пары соответствующих элементов двух матриц, угловые координаты которых дают направление на один и тот же элемент поверхности, вычисляют координаты единичных векторов
затем для каждой пары соответствующих элементов двух матриц, угловые координаты которых дают направление на один и тот же элемент поверхности, вычисляют координаты единичных векторов 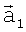 и
и 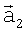 , направленных на i,j-й элемент поверхности, которые вместе с вектором перемещения
, направленных на i,j-й элемент поверхности, которые вместе с вектором перемещения 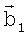 носителя относительно положения в момент t1 образуют треугольник, по углам α и β которого, найденным с помощью скалярного произведения векторов
носителя относительно положения в момент t1 образуют треугольник, по углам α и β которого, найденным с помощью скалярного произведения векторов 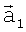 ,
, 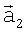 , и
, и 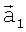 ,
,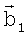 , вычисляют дальности до i,j-го элемента поверхности по формулам
, вычисляют дальности до i,j-го элемента поверхности по формулам
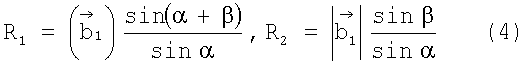
и запоминают их в матрицах R(t1,i,j) и R(t2,i,j), указанные операции повторяют в последовательности моментов времени tµ, µ=1,2,…,L, а найденные значения  и Rµ(tµ,i,j) усредняют во времени t, что компенсирует ошибки измерения и округления до элементов дискретизации, в результате к моменту tL формируют две усредненные матрицы:
и Rµ(tµ,i,j) усредняют во времени t, что компенсирует ошибки измерения и округления до элементов дискретизации, в результате к моменту tL формируют две усредненные матрицы:  и
и 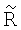 L(i,j), затем среди усредненных дальностей
L(i,j), затем среди усредненных дальностей 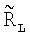 (i,j) находят максимальную дальность по i,j и заполняют матрицу высот рельефа и объектов на поверхности:
(i,j) находят максимальную дальность по i,j и заполняют матрицу высот рельефа и объектов на поверхности:
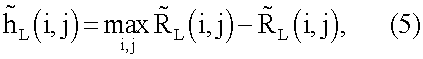
найденные таким образом матрицы 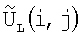 и
и 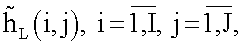 представляют трехмерное изображение поверхности, которое выводится на экран.
представляют трехмерное изображение поверхности, которое выводится на экран.
Алгоритмически способ осуществляется следующим образом.
1. В каждый дискретный момент времени tµ,µ=1,2,…,L, формируются двумерные РТЛИ 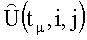 в соответствии с алгоритмами (1), (2) или (3).
в соответствии с алгоритмами (1), (2) или (3).
2. Координаты х1,у1 центра каждого i,j-гo элемента матрицы 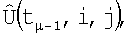 взятые в антенной системе координат x,y,z, на основе навигационных данных об углах поворота осей ox, oy, oz и параллельном смещении носителя РТЛС пересчитываются (экстраполируются) на момент времени tµ в координаты
взятые в антенной системе координат x,y,z, на основе навигационных данных об углах поворота осей ox, oy, oz и параллельном смещении носителя РТЛС пересчитываются (экстраполируются) на момент времени tµ в координаты 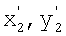 и округляются до ближайших элементов дискретизации i',j'.
и округляются до ближайших элементов дискретизации i',j'.
3. Если i',j' попадают в поле матрицы 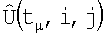 , то i,j-e амплитуды
, то i,j-e амплитуды 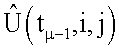 переписываются в соответствующие i',j'-е элементы экстраполированной матрицы
переписываются в соответствующие i',j'-е элементы экстраполированной матрицы 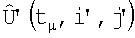 . Установленное соответствие между i,j и i',j'запоминается. Иначе фиксируется непопадание i',j'.
. Установленное соответствие между i,j и i',j'запоминается. Иначе фиксируется непопадание i',j'.
4. Для компенсации ошибок навигационной системы положение 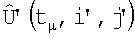 относительно
относительно 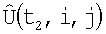 корректируется корреляционо-экстремальным методом, и устанавливается соответствие между элементами матриц
корректируется корреляционо-экстремальным методом, и устанавливается соответствие между элементами матриц 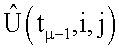 и
и 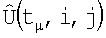 . Изменения запоминаются.
. Изменения запоминаются.
5. Для каждой пары соответствующих элементов матриц 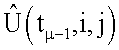 и
и 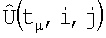 , угловые координаты которых дают направление на один и тот же элемент поверхности, вычисляются координаты единичных векторов
, угловые координаты которых дают направление на один и тот же элемент поверхности, вычисляются координаты единичных векторов 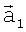 и
и 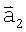 , направленных на i,j-й элемент поверхности, которые вместе с вектором перемещения
, направленных на i,j-й элемент поверхности, которые вместе с вектором перемещения 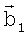 носителя относительно положения в момент t1 образуют треугольник.
носителя относительно положения в момент t1 образуют треугольник.
6. С помощью скалярного произведения векторов 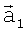 ,
, 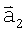 и
и 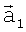 ,
, 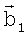 находятся углы α, β в треугольнике и по формуле (4) вычисляется дальность до i,j-гo элемента поверхности, которая запоминается в матрице R(tµ,i,j).
находятся углы α, β в треугольнике и по формуле (4) вычисляется дальность до i,j-гo элемента поверхности, которая запоминается в матрице R(tµ,i,j).
7. Операции п.п.1-6 повторяются в последовательности моментов времени tµ, а найденные значения 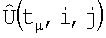 и
и
Rµ(tµ,i,j) усредняются во времени t. В результате к моменту tL формируются две матрицы: 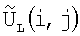 и
и 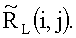 .
.
8. В момент tL заполняется матрица относительных высот рельефа и объектов на поверхности 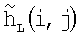 :
:
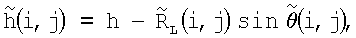
где h - высота объекта-носителя РТЛС на момент tL; 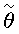 (i, j) - запомненные и усредненные вместе с дальностями значения углов места i,j-x лучей.
(i, j) - запомненные и усредненные вместе с дальностями значения углов места i,j-x лучей.
При вычислении 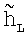 (i,j) можно использовать формулу (5), которая позволяет судить о высоте по относительному удалению элементов поверхности от наблюдателя и не требует запоминания θ(i, j).
(i,j) можно использовать формулу (5), которая позволяет судить о высоте по относительному удалению элементов поверхности от наблюдателя и не требует запоминания θ(i, j).
9. Найденные матрицы 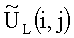 и
и 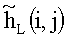 представляют трехмерное изображение поверхности, которое выводится на экран индикатора.
представляют трехмерное изображение поверхности, которое выводится на экран индикатора.
10. Для расширения зоны обзора в каждый момент времени tµ дополнительно осуществляется сканирование антенны со смещением линии визирования на ширину ДН по азимуту и углу места в промежуточные k-е моменты времени, tµk,
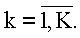 Полученные блочные матрицы обрабатываются в соответствии с п.п.1-9. Для устранения динамических ошибок предусматривается промежуточный пересчет координат.
Полученные блочные матрицы обрабатываются в соответствии с п.п.1-9. Для устранения динамических ошибок предусматривается промежуточный пересчет координат.
Математические модели и методы, положенные в основу способа, сводятся к следующему. При использовании многоканальной антенной системы в виде решетки из Q расположенным определенным образом элементов [4] приемный сигнал S(t) попадает одновременно в q-e приемные каналы 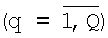 и подвергается в них узкополосной фильтрации. В результате спектральной обработки в каждом q-м канале в дискретный µ-й момент времени tµ,
и подвергается в них узкополосной фильтрации. В результате спектральной обработки в каждом q-м канале в дискретный µ-й момент времени tµ, 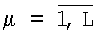 , выделяется комплексная амплитуда сигнала
, выделяется комплексная амплитуда сигнала 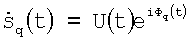 с амплитудой U(t), которая характеризует интенсивность поля излучения по ширине диаграммы направленности (ДН) q-гo приемного элемента антенны (на уровне 0,5 мощности), и фазой Фq(t), которая включает в себя детерминированную составляющую, зависящую от расположения q-гo элемента в антенне, и аддитивную случайную составляющую. В области совместного действия всех q-x ДН справедлива следующая дискретная модель измерений:
с амплитудой U(t), которая характеризует интенсивность поля излучения по ширине диаграммы направленности (ДН) q-гo приемного элемента антенны (на уровне 0,5 мощности), и фазой Фq(t), которая включает в себя детерминированную составляющую, зависящую от расположения q-гo элемента в антенне, и аддитивную случайную составляющую. В области совместного действия всех q-x ДН справедлива следующая дискретная модель измерений:
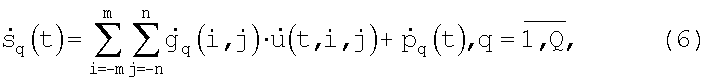
где суммирование ведется от центра антенны (линии визирования) по i,j-м элементам дискретизации угла места 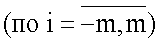 и азимута
и азимута 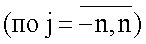 угломерной области размера M×N=(2m+1)×(2n+1) в системе координат носителя РТЛС;
угломерной области размера M×N=(2m+1)×(2n+1) в системе координат носителя РТЛС; 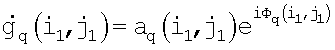 - нормированные комплексные коэффициенты ДН q-гo канала, известные фазы которых Фq(i,j) описывают свойство приемных элементов и включают в себя известный фазовый сдвиг (запаздывание) при приеме отраженного сигнала с i,j-гo углового направления q-м приемным элементом по отношению к фазовому центру антенны;
- нормированные комплексные коэффициенты ДН q-гo канала, известные фазы которых Фq(i,j) описывают свойство приемных элементов и включают в себя известный фазовый сдвиг (запаздывание) при приеме отраженного сигнала с i,j-гo углового направления q-м приемным элементом по отношению к фазовому центру антенны; 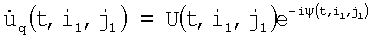 - полезная i,j-я составляющая сигнала
- полезная i,j-я составляющая сигнала  q(t) с амплитудой U(t,i,j), несущей информацию о поле излучения в i,j-м элементе дискретизации, и случайной фазой ψ(t,i,j), равномерно распределенной на
q(t) с амплитудой U(t,i,j), несущей информацию о поле излучения в i,j-м элементе дискретизации, и случайной фазой ψ(t,i,j), равномерно распределенной на 
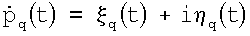 - нормальная помеха: ξ,η∈N(0,
- нормальная помеха: ξ,η∈N(0,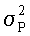 ).
).
В векторно-матричной форме модель измерений (1) принимает вид:
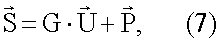
где 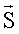 - Q-вектор-столбец комплексных измерений (1)
- Q-вектор-столбец комплексных измерений (1) 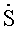 q(t), взятых по совокупности q (
q(t), взятых по совокупности q (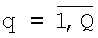 ); G - Q×MN-матрица комплексных коэффициентов ДН
); G - Q×MN-матрица комплексных коэффициентов ДН 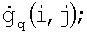
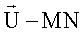 - вектор-столбец искомых комплексных параметров поля излучения
- вектор-столбец искомых комплексных параметров поля излучения 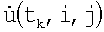 , свернутых построчно в
, свернутых построчно в 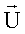 ;
; 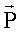 - Q-вектор-столбец помех.
- Q-вектор-столбец помех.
Если коэффициенты ДН 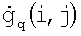 в (6) описываются функцией с разделенными переменными:
в (6) описываются функцией с разделенными переменными: 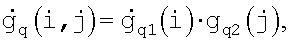 , то модель измерений для матричной антенной решетки с приемными q,k-ми элементами
, то модель измерений для матричной антенной решетки с приемными q,k-ми элементами 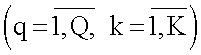 представляется в матричной форме:
представляется в матричной форме:
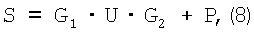
где S - Q×K-матрица q,k-x измерений 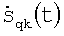 , расположенных в q-x строках и k-х столбцах; G1- Q×M-матрица q,i-x коэффициентов ДН
, расположенных в q-x строках и k-х столбцах; G1- Q×M-матрица q,i-x коэффициентов ДН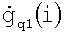 ; U - M×N-матрица i,j-x искомых комплексных амплитуд поля излучения
; U - M×N-матрица i,j-x искомых комплексных амплитуд поля излучения 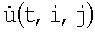 ; G2 - N×K-матрица j,k-x коэффициентов ДНА
; G2 - N×K-матрица j,k-x коэффициентов ДНА 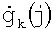 ; Р - Q×K-матрица
; Р - Q×K-матрица 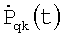 .
.
Носитель РТЛС находится в самолетной прямоугольной системе координат, центр которой совмещен с центром носителя, ось OY совпадает с вектором скорости 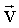 движения носителя, а ось ОХ расположена в плоскости правого крыла. Антенна в момент времени t1 находится в прямоугольной системе координат O1X1Y1Z1, а в момент t2 - в системе O2X2Y2Z2, которые расположены определенным образом относительно самолетной системы. Оси O1Z1 и O2Z2 представляют линию визирования антенны. Так как между самолетной и антенной системами существует известная связь, то ограничимся рассмотрением одной антенной системы во времени t. При движении объекта носителя РТЛС на промежутке [t1,t2] осуществляется поворот осей О1Х1, O1Y1 и O1Z1 на углы α, β, γ (тангаж, крен, курс), а точка O1 получает приращения параллельного переноса Δx, Δy, Δz.
движения носителя, а ось ОХ расположена в плоскости правого крыла. Антенна в момент времени t1 находится в прямоугольной системе координат O1X1Y1Z1, а в момент t2 - в системе O2X2Y2Z2, которые расположены определенным образом относительно самолетной системы. Оси O1Z1 и O2Z2 представляют линию визирования антенны. Так как между самолетной и антенной системами существует известная связь, то ограничимся рассмотрением одной антенной системы во времени t. При движении объекта носителя РТЛС на промежутке [t1,t2] осуществляется поворот осей О1Х1, O1Y1 и O1Z1 на углы α, β, γ (тангаж, крен, курс), а точка O1 получает приращения параллельного переноса Δx, Δy, Δz.
Метод измерения дальности в РТЛС заключается в следующем. Пусть в момент времени t1 из точки O1 в сторону точки А, расположенной на поверхности, направлен i,j-й луч, положение которого определяется углом места θi, отсчитываемым от плоскости O1X1Z1, и азимутом φj, отсчитываемым от оси O1Z1. По этому лучу идет в направлении антенны i,j-я составляющая 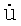 (t, i, j) излучаемого сигнала. Строится единичный вектор
(t, i, j) излучаемого сигнала. Строится единичный вектор 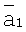 - орт вектора
- орт вектора 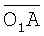 , направленный по лучу к точке А, и запишем его координаты в прямоугольной системе O1X1Y1Z1:
, направленный по лучу к точке А, и запишем его координаты в прямоугольной системе O1X1Y1Z1:
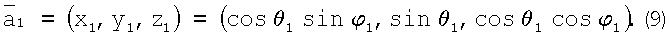
Пересчитываются координаты вектора 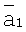 в систему координат O2X2Y2Z2 в соответствии с формулами поворота осей и параллельного переноса:
в систему координат O2X2Y2Z2 в соответствии с формулами поворота осей и параллельного переноса:
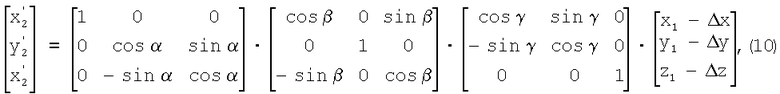
полагая в (10) для свободных векторов приращения параллельного переноса, равными нулю: Δх=Δу=Δz=0. Получается вектор 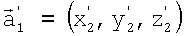 .
.
В текущий момент t2 в системе координат O2X2Y2Z2 строится вектор 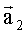 - орт вектора
- орт вектора 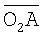 , направленный к той же точке А на поверхности:
, направленный к той же точке А на поверхности:
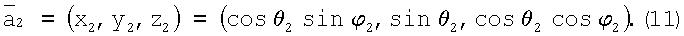
В системе координат O2X2Y2Z2 рассматриваются три вектора: 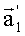 ,
, 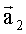 и вектор перемещения носителя
и вектор перемещения носителя 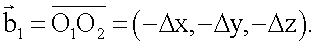 Если измерения координат векторов выполнены без ошибок, то три вектора
Если измерения координат векторов выполнены без ошибок, то три вектора 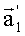 ,
, 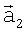 и
и 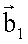 оказываются в одной плоскости и на них строится треугольник АО1О2, стороны которого О1А и О2А равны дальностям R1 и R2 до точки А.
оказываются в одной плоскости и на них строится треугольник АО1О2, стороны которого О1А и О2А равны дальностям R1 и R2 до точки А.
С помощью скалярного произведения находятся косинусы внутренних углов треугольника α1,β1,γ1(γ1=π-α1-β1), и по теореме синусов определяются дальности:
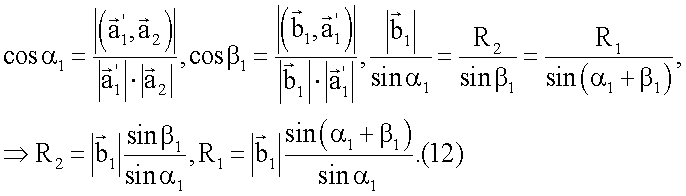 ,
,
Такие расчеты повторяются для нескольких моментов времени t1,t2,…,tL при наблюдении А из разных положений носителя РТЛС. В результате определяется последовательность измерений дальности R1,R2,…,RL. Так как реальные измерения углов поворота и координат векторов содержат ошибки, то с целью сглаживания этих ошибок найденные оценки дальности усредняются на момент времени tL: 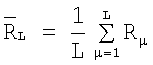 .
.
При малых значениях α1 решение (12) может быть неустойчивым, поэтому оценивание дальности следует производить при достаточно больших перемещениях носителя  .
.
В вычислительном плане возможны некоторые упрощения. При малых углах φ1, θ1 (в пределах ДН) векторы (9), (11) приближенно можно определить:
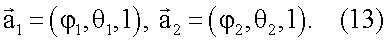
При малых углах поворота упрощается формула (10):
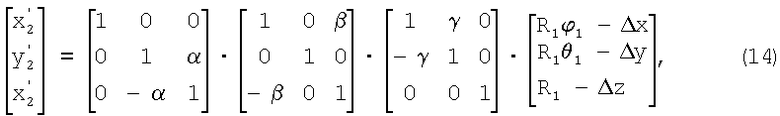
где для векторов полагается Δх=Δy=Δz=0.
Исследование потенциальной возможности измерения высоты объекта сводится к следующему. Пусть объект высотой h находится на поверхности в точке А, принадлежащей элементу дискретизации прямоугольной сетки координат. Носитель РТЛС движется по курсу в сторону точки А, наблюдая ее в момент времени t под некоторым углом места θ к горизонтальной линии движения, при азимуте φ=0. Обозначим точками А и В вершину и основание объекта, точкой О - положение носителя РТЛС, удаленного от точек А и В на RA=ОА и RB=OB. Точка А наблюдается из точки О под углом θA, точка В - под углом θB.
Разность этих углов Δθ=θB-θA представляет разрешающую способность РТЛС по углу места, необходимую для обнаружения объекта высотой h.
Из треугольника ОАВ по теореме синусов устанавливается:
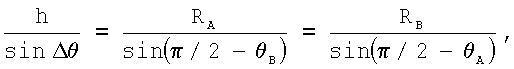
откуда при малых Δθ, θ=θA≈θB и R=RA≈RB получается зависимость:
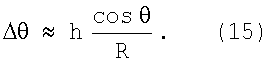
Из (15) следует, например, что при наблюдении РТЛС объекта высотой h=5 м под углом θ=π/3 на расстоянии R=1000 м требуется разрешающая способность по углу места Δθ=0,0025рад или 0,14°. Это означает, что при ширине ДА в 1° требуется повысить разрешающую способность РТЛС не менее чем в 7 раз. При этом высоту объекта целесообразно измерять в режиме его облета на малой высоте, то есть при наблюдении под малым углом θ.
Методы повышения разрешающей способности РТЛС по угловым координатам основаны на восстановлении изображений по методике [3]. Решение задачи восстановления сводится к нахождению оценки 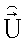 вектора
вектора 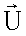 в (8) по методу наименьших квадратов (МНК):
в (8) по методу наименьших квадратов (МНК):
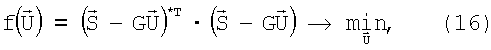
где *Т - символ комплексного сопряжения и транспонирования. После дифференцирования скалярной функции (16) по вектору 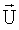 :
:
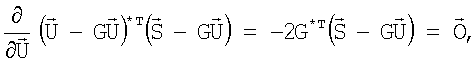
где 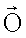 - нулевой вектор-столбец, получается следующий результат:
- нулевой вектор-столбец, получается следующий результат:
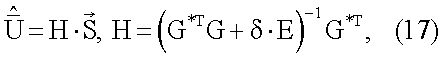
где Н - матрица комплексных весовых коэффициентов; Е - единичная матрица; δ - комплексный параметр регуляризации, необходимый для обращения матрицы G*TG в тех случаях, когда число измерительных каналов Q меньше числа оцениваемых параметров MN.
В качестве оценок амплитуд поля излучения U(t, i, j) берутся модули элементов вектора 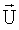 , которые для вывода на экран построчно располагаются в составе M×N-матрицы
, которые для вывода на экран построчно располагаются в составе M×N-матрицы 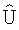 с элементами
с элементами 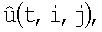
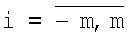 ,
, 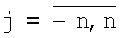 . Матрица
. Матрица 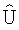 представляет восстановленное в дискретный момент времени t в пределах ширины ДН амплитудное изображение поверхности с повышенной в несколько раз разрешающей способностью по углам. Для расширения зоны обзора осуществляется построчное сканирование антенны со смещением линии визирования на ширину ДН.
представляет восстановленное в дискретный момент времени t в пределах ширины ДН амплитудное изображение поверхности с повышенной в несколько раз разрешающей способностью по углам. Для расширения зоны обзора осуществляется построчное сканирование антенны со смещением линии визирования на ширину ДН.
Для модели измерений (8) задача восстановления заключается в оптимальном оценивании матрицы U на основе матрицы измерений S, связанной с U уравнением (8). Решение задачи по критерию МНК сводится к минимизации следа tr матрицы F взятием производной по U:
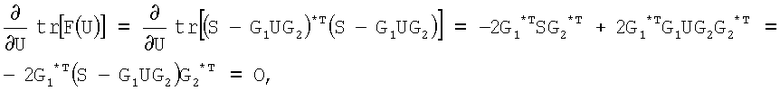
где О - нулевая матрица. Отсюда:
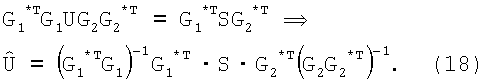
Для реализации (18) применяется двухэтапная процедура:
1. 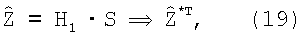
2. 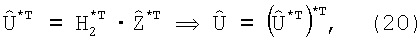
где матрицы весовых коэффициентов вычисляются заранее с использованием процедур обращения матриц:
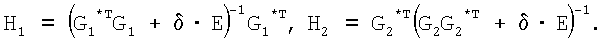
Как показывают результаты расчета количества операций, алгоритм (19), (20) в вычислительном плане имеет значительно более высокое быстродействие по сравнению с алгоритмом (17) за счет использования матричной формы и меньшего размера матриц G1, G2 в сравнении с матрицей G в (17).
Для уменьшение влияния ошибок измерения на точность формирования РТЛИ предлагается следующий метод. Пусть в последовательности моментов времени t1,t2,…,tL получены матрицы амплитудного изображения участка поверхности 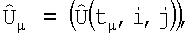
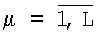 , в режиме его облета носителем РТЛС. Если линия визирования антенны в каждый µ-й момент направлена на один и тот объект (ориентир) поверхности, то в случае отсутствия ошибок пересчета координат i,j-e элементы матриц будут соответствовать одним и тем же элементам поверхности. В действительности носитель РТЛС смещается относительно ориентиров случайным образом, и изображение поверхности движется в матрице изображения. Кроме того, ошибки измерения дают ошибки пересчета координат, что приводит к искажению РТИ. Возникает проблема уменьшения влияния ошибок измерения на точность формирования РТИ в условиях движущегося изображения. Указанная проблема решается методами корреляционно-экстремального совмещения соседних кадров и пространственно-временной фильтрации [5] следующим образом:
, в режиме его облета носителем РТЛС. Если линия визирования антенны в каждый µ-й момент направлена на один и тот объект (ориентир) поверхности, то в случае отсутствия ошибок пересчета координат i,j-e элементы матриц будут соответствовать одним и тем же элементам поверхности. В действительности носитель РТЛС смещается относительно ориентиров случайным образом, и изображение поверхности движется в матрице изображения. Кроме того, ошибки измерения дают ошибки пересчета координат, что приводит к искажению РТИ. Возникает проблема уменьшения влияния ошибок измерения на точность формирования РТИ в условиях движущегося изображения. Указанная проблема решается методами корреляционно-экстремального совмещения соседних кадров и пространственно-временной фильтрации [5] следующим образом:
1. Пусть в момент t1 получена матрица 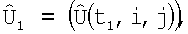 которая ставится в соответствие матрице
которая ставится в соответствие матрице 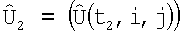 . На основе данных навигационной системы о движении объекта носителя РТЛС (измерений углов поворота α, β, γ и смещений
. На основе данных навигационной системы о движении объекта носителя РТЛС (измерений углов поворота α, β, γ и смещений 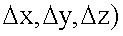 координаты центра х1, у1 каждого i,j-гo элемента матрицы
координаты центра х1, у1 каждого i,j-гo элемента матрицы 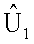 в соответствии с формулами (10), (14), учитывающими α, β, γ и
в соответствии с формулами (10), (14), учитывающими α, β, γ и 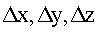 , пересчитываются (экстраполируются) на момент t2, то есть находятся экстраполированные значения координат
, пересчитываются (экстраполируются) на момент t2, то есть находятся экстраполированные значения координат 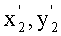 и соответствующие им номера i',j', при этом z1 в (10), (14) полагается равным нулю (плоское изображение), а координата
и соответствующие им номера i',j', при этом z1 в (10), (14) полагается равным нулю (плоское изображение), а координата 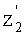 не используется. Значения элементов матрицы
не используется. Значения элементов матрицы 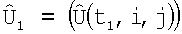 переписываются в матрицу экстраполированного изображения
переписываются в матрицу экстраполированного изображения 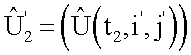 по всем элементам i',j', координаты которых попадают в поле 2-го кадра
по всем элементам i',j', координаты которых попадают в поле 2-го кадра  , в противном случае для i',j' фиксируются пропуски.
, в противном случае для i',j' фиксируются пропуски.
2. Рассматривается центральная часть матрицы 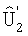 - область D, в которой пропуски заведомо отсутствуют. Даются приращения координатам i,j по всем элементам матрицы
- область D, в которой пропуски заведомо отсутствуют. Даются приращения координатам i,j по всем элементам матрицы 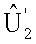 в области D на малое число элементов дискретизации
в области D на малое число элементов дискретизации 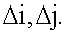 Оптимальные значения
Оптимальные значения 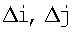 определяются критерием близости двух изображений:
определяются критерием близости двух изображений: 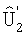 и
и  , например:
, например:
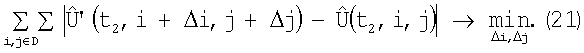
3. На основе найденных значений Δi, Δj корректируются экстраполированные номера i', j'. Тем самым устанавливается более точное соответствие между элементами соседних матриц РТИ в смысле принадлежности каждой пары этих элементов одному и тому же элементу поверхности и, как следствие, уменьшается влияние ошибок измерения на пересчет координат и определение координат векторов 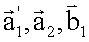 при вычислении дальностей R1, R2 в (12), вследствие чего повышается точность формирования РТЛИ.
при вычислении дальностей R1, R2 в (12), вследствие чего повышается точность формирования РТЛИ.
4. Амплитуды соответствующих элементов соседних кадров усредняются во времени t с помощью известных рекуррентных фильтров [5]. При усреднении сглаживаются ошибки измерения и повышается отношение сигнал-шум, что приводит к повышению разрешающей способности РТИ по угловым координатам и качеству изображения.
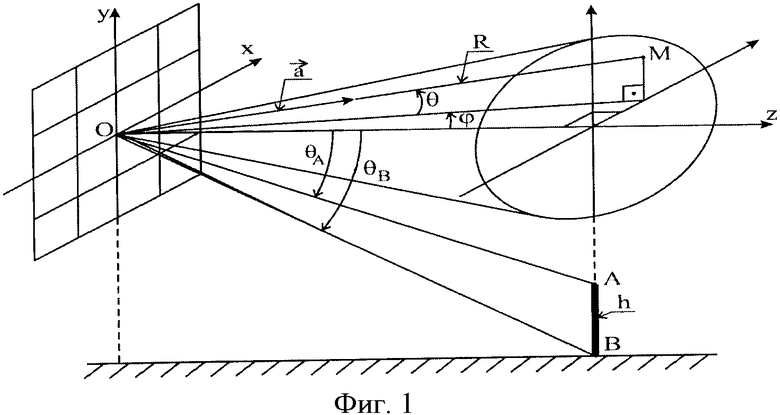
Иллюстрации к способу даны на фиг.1 и 2. На фиг.1 показана антенная система координат, использованная в формулах (9)-(11) при определении координат вектора 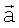 (на фиг.1 вектор
(на фиг.1 вектор 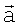 направлен в сторону точки М). Здесь же показаны углы места θA и θB при исследовании возможности измерения высоты h объекта АВ на поверхности в соответствии с (15).
направлен в сторону точки М). Здесь же показаны углы места θA и θB при исследовании возможности измерения высоты h объекта АВ на поверхности в соответствии с (15).
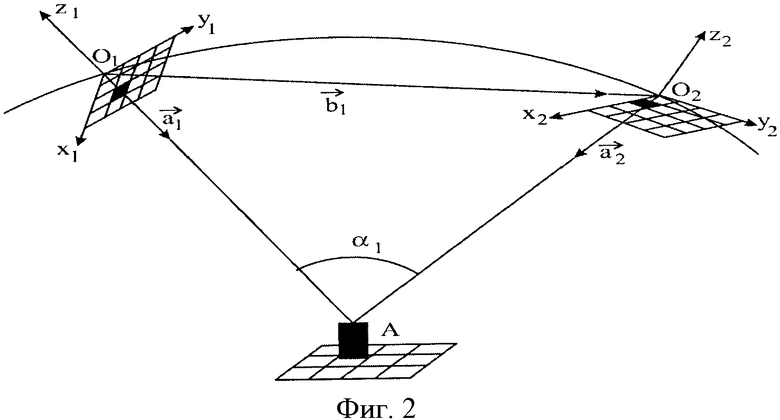
На фиг.2 показано движение РТЛС по траектории облета участка поверхности, на котором расположен высотный объект. В двух соседних матрицах РТИ отмечены (зачернены) элементы, между которыми установлено соответствие: они дают координаты векторов 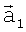 и
и 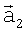 , направленных на объект. На векторах
, направленных на объект. На векторах  ,
,  и векторе перемещения
и векторе перемещения  построен треугольник АО1O2, по углам которого определяются дальности R1 и R2.
построен треугольник АО1O2, по углам которого определяются дальности R1 и R2.
Предложенный способ позволяет формировать трехмерные изображения поверхности и неподвижных объектов на поверхности в системах пассивной радиолокации при облете носителем РТЛС поверхности на малой дальности в условиях отсутствия оптической видимости, что повышает безопасность маловысотных полетов. Способ применим также для измерения дальности и высоты объектов на поверхности в оптических системах.
Источники информации
1. Пирогов Ю.А., Тимановский А.Л. Сверхразрешение в системах пассивного радиовидения миллиметрового диапазона. // Радиотехника. 2006, № 3. С.14-19.
2. Патент RU 2292060 C1. Способ наблюдения за воздушными объектами и поверхностью на базе бортовой РЛС. / В.К.Клочко. МПК: G01S 13/02. Приоритет 28.06.2005. Опубл., 20.01. 2007. Бюл. № 2.
3. Николаев А.Г., Перцов С.В. Радиотеплолокация. М.: Сов. радио, 1964. 335 с.
4. Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки: Введение в теорию. / Пер. с англ. М.: Радио и связь, 1986. 448 с.
5. Баклицкий В.К., Юрьев А.Н. Корреляционно-экстремальные методы навигации. М.: Радио и связь, 1982. 256 с.
6. Клочко В.К. Методы оптимального восстановления радиолокационных изображений поверхности. // Автометрия. 2005. Т.41. № 6. С.62-73.
Изобретение относится к системам пассивной радиолокации наблюдения за поверхностью и неподвижными объектами на поверхности на базе многоканальных и сканирующих радиотеплолокаторов. Достигаемый технический результат заключается в обеспечении формирования трехмерного изображения поверхности. Заявленный способ заключается в том, что в дискретные моменты времени обзора формируют матрицы амплитудных изображений контролируемого участка поверхности с разрешением по угловым координатам, с помощью пересчета координат и совмещения соседних кадров изображения устанавливают соответствие между элементами матриц и по углам между векторами измеряют дальности до соответствующих элементов поверхности, полученные результаты усредняют во времени и получают трехмерное изображение в виде матрицы амплитуд и матрицы высот рельефа поверхности. 2 ил.
Способ формирования трехмерного изображения поверхности на базе бортовых радиотеплолокационных станций (РТЛС) при облете носителем РТЛС контролируемого участка поверхности, заключающийся в том, что при наблюдении за поверхностью с помощью Q-элементной антенной решетки или сканирующей Q-канальной антенны в дискретный момент времени t1 линию визирования антенны направляют на контролируемый участок поверхности и измеряют в q-x каналах 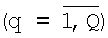 значения амплитуд приемных сигналов, прошедших операции первичной обработки, из этих амплитуд формируют Q-вектор-столбец измерений
значения амплитуд приемных сигналов, прошедших операции первичной обработки, из этих амплитуд формируют Q-вектор-столбец измерений 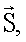 который умножают справа на IJ·Q-матрицу весовых коэффициентов Н, вычисляемую заранее, и получают IJ-вектор-столбец оценок
который умножают справа на IJ·Q-матрицу весовых коэффициентов Н, вычисляемую заранее, и получают IJ-вектор-столбец оценок 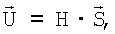 , элементы которого разворачивают в матрицу
, элементы которого разворачивают в матрицу 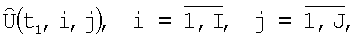 , восстановленного на момент времени t1 амплитудного изображения участка поверхности с разрешением по углу места i и азимуту по j, отличающийся тем, что для формирования трехмерного изображения по истечении времени Δt облета носителем РТЛС контролируемого участка поверхности в момент t2 формируется вторая матрица изображения
, восстановленного на момент времени t1 амплитудного изображения участка поверхности с разрешением по углу места i и азимуту по j, отличающийся тем, что для формирования трехмерного изображения по истечении времени Δt облета носителем РТЛС контролируемого участка поверхности в момент t2 формируется вторая матрица изображения 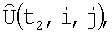 а координаты х1,у1 центра каждого i, j-го элемента матрицы
а координаты х1,у1 центра каждого i, j-го элемента матрицы 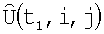 , взятые в антенной системе координат x,y,z, на основе данных навигационной системы об углах поворота осей ox, oy, oz и смещении носителя РТЛС относительно положения в момент t1 экстраполируют на момент времени t2 в координагы
, взятые в антенной системе координат x,y,z, на основе данных навигационной системы об углах поворота осей ox, oy, oz и смещении носителя РТЛС относительно положения в момент t1 экстраполируют на момент времени t2 в координагы 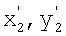 и округляют до ближайших элементов дискретизации i',j', в результате чего получают экстраполированную матрицу изображения
и округляют до ближайших элементов дискретизации i',j', в результате чего получают экстраполированную матрицу изображения 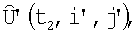 положение которой относительно
положение которой относительно 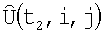 корректируют с помощью корреляционно-экстремального метода совмещения кадров, который компенсирует ошибки измерения навигационной системы и устанавливает соответствие между элементами матриц
корректируют с помощью корреляционно-экстремального метода совмещения кадров, который компенсирует ошибки измерения навигационной системы и устанавливает соответствие между элементами матриц 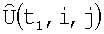 и
и 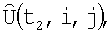 затем для каждой пары соответствующих элементов двух матриц, угловые координаты которых дают направление на один и тот же элемент поверхности, вычисляют координаты единичных векторов
затем для каждой пары соответствующих элементов двух матриц, угловые координаты которых дают направление на один и тот же элемент поверхности, вычисляют координаты единичных векторов 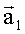 и
и 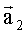 , направленных на i,j-й элемент поверхности, которые вместе с вектором перемещения
, направленных на i,j-й элемент поверхности, которые вместе с вектором перемещения 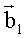 , носителя относительно положения в момент t1 образуют треугольник, по углам α и β которого, найденным с помощью скалярного произведения векторов
, носителя относительно положения в момент t1 образуют треугольник, по углам α и β которого, найденным с помощью скалярного произведения векторов 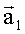 ,
, 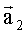 , и
, и 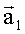 ,
,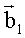 , вычисляют дальности до i,j-го элемента поверхности по формулам
, вычисляют дальности до i,j-го элемента поверхности по формулам
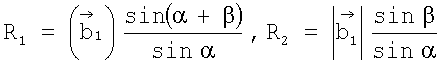
и запоминают их в матрицах R(t1,i,j) и R(t2,i,j), указанные операции повторяют в последовательности моментов времени tµ, µ=1,2,…,L, а найденные значения 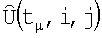
и Rµ(tµ,i,j) усредняют во времени t, что компенсирует ошибки измерения и округления до элементов дискретизации, в результате к моменту tL формируют две усредненные матрицы: 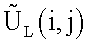 и
и 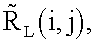 затем среди усредненных дальностей
затем среди усредненных дальностей 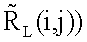 находят максимальную дальность по i,j и заполняют матрицу высот рельефа и объектов на поверхности:
находят максимальную дальность по i,j и заполняют матрицу высот рельефа и объектов на поверхности:
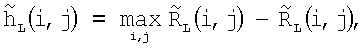
найденные таким образом матрицы 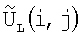 и
и 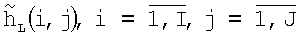 , представляют трехмерное изображение поверхности, которое выводится на экран.
, представляют трехмерное изображение поверхности, которое выводится на экран.
| СПОСОБ НАБЛЮДЕНИЯ ЗА ВОЗДУШНЫМИ ОБЪЕКТАМИ И ПОВЕРХНОСТЬЮ НА БАЗЕ БОРТОВОЙ РЛС | 2005 |
|
RU2292060C1 |
| СПОСОБ ПОЛУЧЕНИЯ ТРЕХМЕРНОГО РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ ПОВЕРХНОСТИ | 2005 |
|
RU2290663C1 |
| СПОСОБ ПОВЫШЕНИЯ РАДИОЛОКАЦИОННОГО РАЗРЕШЕНИЯ, СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ И СПОСОБ ДИСТАНЦИОННОГО ВЫЯВЛЕНИЯ СИСТЕМОЙ МАЛОРАЗМЕРНЫХ ОБЪЕКТОВ | 2004 |
|
RU2265866C1 |
| US 5442364 A, 15.08.1995 | |||
| US 5329286 A, 12.07.1994 | |||
| Устройство для получения потока сыпучих материалов с заданной плотностью | 1977 |
|
SU690315A1 |
| US 5896098 A, 20.04.1999. | |||
Даты
2009-09-27—Публикация
2008-04-07—Подача