Изобретение относится к устройствам различного назначения, преобразующим энергию вращающегося вала установки в поступательное движение корпуса этой же установки.
Из уровня техники известны различные технические решения, в которых описаны способы и устройства, преобразующие один вид энергии в другой. Известны устройства, когда энергия одного вида преобразуется в поступательное движение корпуса самого устройства. Так, например, известен патент, в котором описан способ и устройство преобразования энергии ветра в электроэнергию, которая используется для передвижения платформы с мобильным генератором [1].
Сравнительно недавно стали известны способы и устройства, преобразовывающие энергию вращающего вала в поступательное движение корпуса, в котором вал размещен [2]. Суть этого преобразования энергии заключается в том, что каким-либо образом, например от электроэнергии солнечных батарей, придают вращение валу устройства и затем различными путями преобразуют энергию вращающегося вала в поступательное движение корпуса, в котором установлен вал. Причем этот корпус может иметь поступательное движение самостоятельно или, установленный на любом виде транспорта, придавать движение последнему.
Наиболее близким к заявленному изобретению и принятому за прототип является так называемый инерцоид Толчина [3]. Это устройство содержит в корпусе установки вал вращения, на котором жестко закреплен стержень с неподвижным грузом и устройство, передающее энергию вращающегося рычага с грузом на пульсатор. Последний в свою очередь прикреплен к корпусу через гибкую связь в виде пружины. При вращении энергия вращающегося вала и укрепленных на нем рычага и груза передается импульсами корпусу установки через пульсатор и гибкую связь в виде пружины. К корпусу присоединены колеса, в результате чего при вращении вала происходит неравномерное поступательное передвижение устройства.
Устройство представляет довольно сложную конструкцию, движется рывками и имеет малый коэффициент преобразования энергии вращающегося вала в поступательное движение устройства. В этой связи была поставлена техническая задача разработать способ и создать устройство, в которых бы решалась задача преобразования энергии вращающегося вала устройства в его поступательное движение более плавно, с более простым конструктивным решением и с большим эффектом преобразования одного вида энергии в другой.
Решение этой технической задачи отражено в заявляемом изобретении «Способ преобразования кинетической энергии вращающегося вала установки в поступательное движение ее корпуса и устройство для осуществления способа».
Существо заявляемых способа и устройства представлено на графических материалах и фотографиях. На фиг.1 представлена схема устройства, раскрывающего предложенный способ преобразования кинетической энергии вращающегося вала установки в поступательное движение ее корпуса; на фиг.2 - кинематическая схема работы установки; на фиг.3 - схема сил, действующих на пульсатор во время работы установки; на фиг.4 - схема сил, действующих на груз и вращающийся вал установки; на фиг.5 - положение векторов сил в пространстве, действующих на груз и вращающийся вал установки; на фиг.6 - диаграмма изменения коэффициента преобразования силы, действующей на корпус установки при ее работе; на фиг.7 - схема изменения сил, действующих на вращающийся вал установки; на фиг.8 - диаграмма изменения коэффициента преобразования при малых значениях угла отклонения гибкой связи; на фиг.9 - схема сил в системе координат, действующих на установку; на фиг.10 - схема изменения соотношения сил, действующих на корпус установки; на фиг 11 - диаграмма изменения сил тяги от угловой скорости вращения вала установки; на фиг.12 - устройство преобразования кинетической энергии вращающегося вала в поступательное движение корпуса; на фиг.13 - общий вид действующей модели заявленного устройства.
Представленная на фиг.1 схема устройства, раскрывающего предложенный способ преобразования кинетической энергии вращающегося вала установки в поступательное движение ее корпуса, включает корпус 1 с массой М, в котором размещен вал вращения 2, стержень 3, жестко закрепленный на валу вращения 2, груз 4 массой m1, укрепленный на стержне 3 с возможностью свободного перемещения, пульсатор 5, установленный на корпусе 1, и гибкая связь 6, охватывающая с натягом вал вращения 2, груз 4 и пульсатор 5. Кроме того, приведены величины: Fи - сила инерции; Та и Тв - силы действия в ветвях гибкой связи 5; Rc - сила сопротивления; d - расстояние по осям вала вращения 2 и пульсатора 5; R - расстояние по осям вала вращения 2 и груза 4; А - точка нахождения вала вращения 2; В - точка нахождения груза 4; ω - угловая скорость.
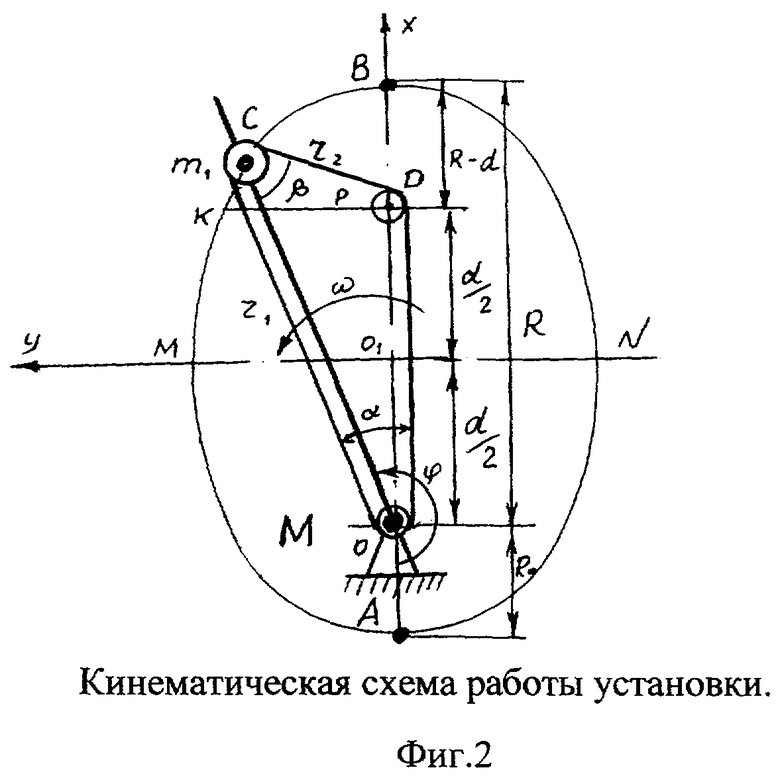
Представленная на фиг.2 кинематическая схема работы установки включает обозначения: X и Y - оси координат; О, D и С - оси соответственно вала вращения 2, пульсатора 5 и груза 4; точки А, В и С - отметки нахождения груза 4 на эллипсе во время вращения вала 2; d - расстояние между осью вращения вала 2 и осью пульсатора 5; Fи - сила инерции; Та - сила действия; Rc - сила сопротивления; F - движущая сила; ω - угловая скорость; α и β - углы между гибкой связью, охватывающей при вращении вал вращения 2 и груз 4.
Предложенный способ преобразования кинетической энергии вращающегося вала 2 установки, представленной на фиг.1, в поступательное движение ее корпуса 1 реализуется следующим образом. Каким-либо образом (в изобретении не раскрывается) придают вращение валу 2 установки и одновременно с валом 2 происходит вращение стержня 3 вместе с грузом 4. Вследствие свободного перемещения груза 4 на стержне 3 происходит натяжение гибкой связи 6 и передача по ней кинетической энергии вращающихся стержня 3 и груза 4 пульсатору 5. На фиг.2 раскрывается процесс преобразования кинетической энергии вращающегося вала 2 в поступательное движение корпуса 1 установки. При каждом обороте стержня 3 с грузом 4 гибкая связь 6 будет передавать импульс силы валу вращения 2 и через него на корпус 1. Если силы действия гибкой связи 6 на корпус 1 будут превышать силу сопротивления (Та>Rc), а в точке размещения груза 4 не превышать силу инерции (Тв<Fи), то в результате такого взаимодействия возникает движущая сила установки, равная F=Та-Rc. Гибкая связь 6 выполняет роль преобразователя сил и обеспечивает заданную траекторию движения груза 4 с массой m1. Подвижной груз 4 под действием вращающегося вала 2 и гибкой связи 6 совершает сложное движение по эллипсу. Уравнение траектории движения груза 4 с массой m1 в полярных координатах имеет вид
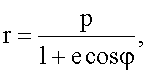
где е - эксцентриситет, равный O1D/О1В;
р - параметр эллипса - длина отрезка перпендикуляра, восстановленного в фокусе эллипса к его большой оси, до его пересечения с траекторией.
По условиям эллипса р=α(1-е2), где α - большая полуось эллипса, т.е.
α=AO1=BO1=R-0,5 d.
Тогда
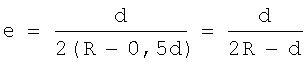
Р=(R-0,5d)(1-e2).
После подстановки значений эксцентриситета и параметра эллипса в уравнение траектории и простых алгебраических преобразований получим
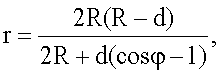
где R - радиус ротора,
d - плечо пульсатора - расстояние от оси вращения ротора до упора,
φ - полярный угол, φ=180°+α, где
α - угол эффективного импульса сил.
Так как по условиям эллипса алгебраическая сумма радиус-векторов r1 и r2 равна большой оси, то r1+r2=2R-d.
Тогда
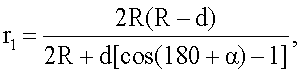
r2=2R-d-r1.
Последние формулы определяют основные геометрические параметры установки и являются основой для дальнейшего расчета ее динамических характеристик.
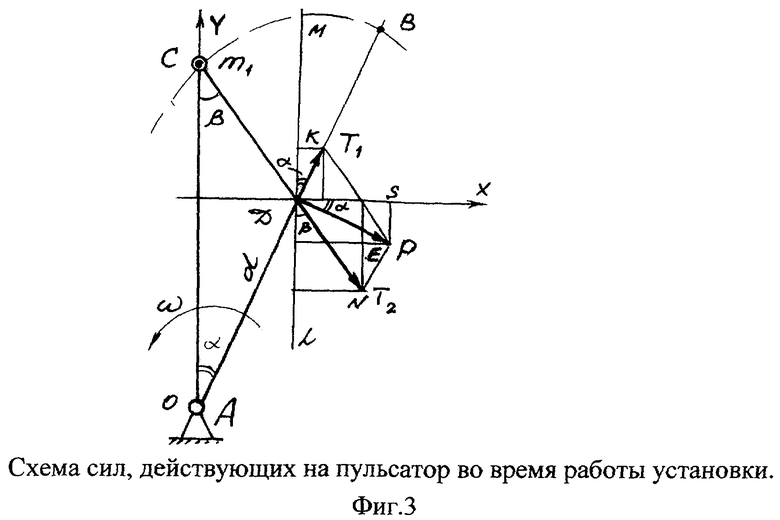
Гибкая связь 6 является одним из основных элементов заявленного способа. Ее назначение заключается в преобразовании действующей на нее внешней силы Р и передаче импульсов сил как грузу 4 с массой m1, так и корпусу 1 установки с массой М в заданном направлении. При вращении стержня 3 гибкая связь 6 постоянно взаимодействует с подвижной массой m1 и при каждом обороте кратковременно воспринимает силу реакции пульсатора 5, сталкиваясь с ним набегающей гибкой связью 6 в точке D, как это представлено на фиг.3.
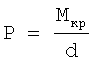 ,
,
где Мкр - крутящий момент,
d - плечо - расстояние от оси вращения до точки D.
Для определения сил натяжения гибкой связи 6 разложим силу Р на две составляющие T1 и Т2 вдоль ветвей нити OD и CD и определим их проекции на координатные оси Х и Y.
Проведем через точку D линию ML параллельно оси Y. Так как ∠MDK=∠COD=∠EDS=α и ∠LDN=∠OCD=В, то проекции сил
на оси Х и Y составят:
По теореме о сложении сил имеем:
Решая полученную систему уравнений относительно T1 и T2, находим
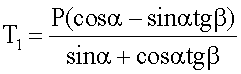
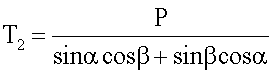
Выражая силу Р через крутящий момент Мкр и плечо d пульсатора 5, получим
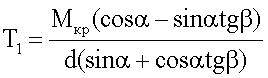
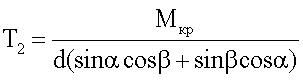
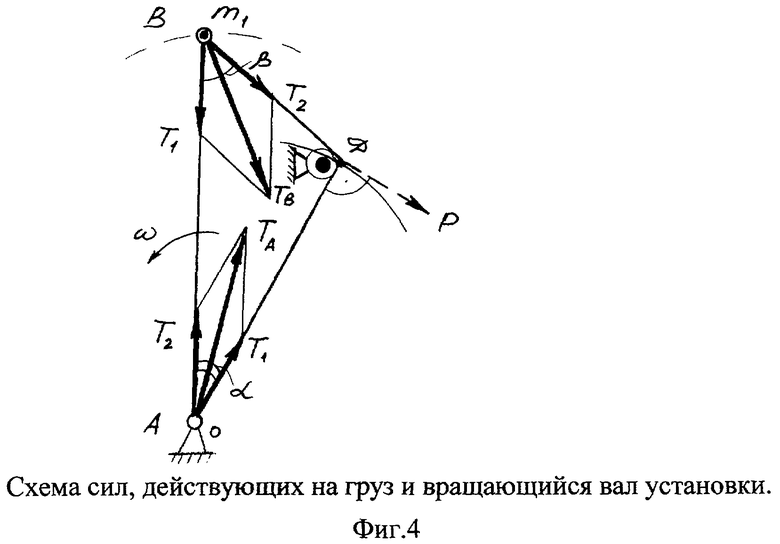
Зная силы натяжения гибкой связи 6, определим ее действие на подвижную массу m1 и М. Для этого перенесем силы Т1 и Т2 вдоль линии их действия в точки А и В соответственно, как это представлено на фиг.4.
Материальные точки А и В являются шарнирными опорами и, в момент импульса силы Р, гибкая связь 6 действует на них также, как трос в подвижных блоках, стремясь их сблизить. Таким образом, в момент столкновения гибкой связи 6 с пульсатором 5 на точки А и В действуют векторные суммы сил T1 и Т2, значения которых определяются по правилу параллелограмма
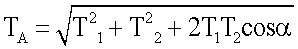
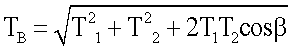
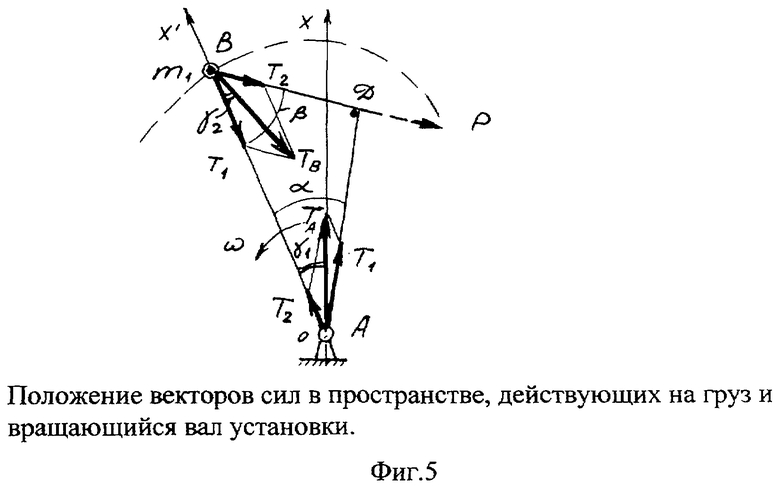
Для определения положений векторов Та и Тв в пространстве проведем координатную ось Х вдоль линии действия вектора Та, как это представлено на фиг.5.
Через ось вращения вала 2 (точка А) и подвижную массу m1 (точка В) проведем подвижную координатную ось X', связанную с вращающимся стержнем 3. Тогда положение вектора Та определится углом γ1 между осями Х и X', а вектора Тв - углом γ2 между вектором Тв и осью X'. Угол γ1 определяется из условия равенства сумм проекций сил T1 и Т2 и проекций их равнодействующей Та на ось Х'
TAcosγ1=T1cosα+T2
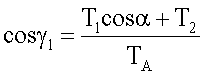
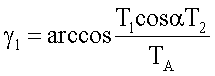
Аналогично находим угол γ2
ТВcosγ2=T1+Т2cosβ
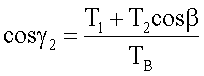
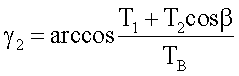
Силы натяжения гибкой связи 6 Т1 и Т2 не являются постоянными величинами, действуют импульсивно и с поворотом стержня 3 изменяются в больших пределах в течение малого промежутка времени t.
При равномерном вращении стержня 3 (ω=const, ε=0) в момент столкновения гибкой связи 6 с пульсатором 5 сила Р всегда постоянна и по величине, и по направлению. Но ее составляющие Т1 и Т2 изменяются в зависимости от положения ветвей гибкой связи 6. С увеличением угла α силы Т1 и Т2 уменьшаются до нуля (α=180°).
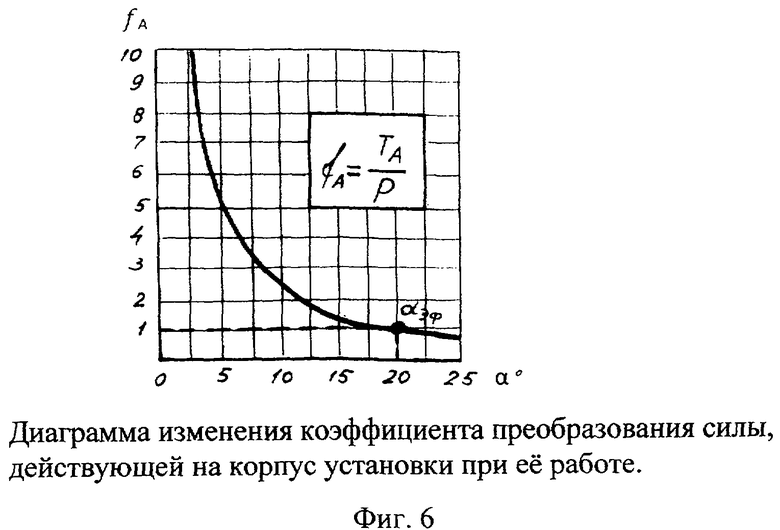
Поэтому эффективным углом действия импульса силы Р следует считать наибольшее значение угла α, при котором гибкая связь 6 преобразует силу Р на входе в равную ей по величине силу действия Та на корпус 1. Эта зависимость представлена на диаграмме на фиг.6. В этом случае коэффициент преобразования fA должен быть равным единице
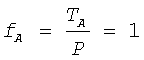
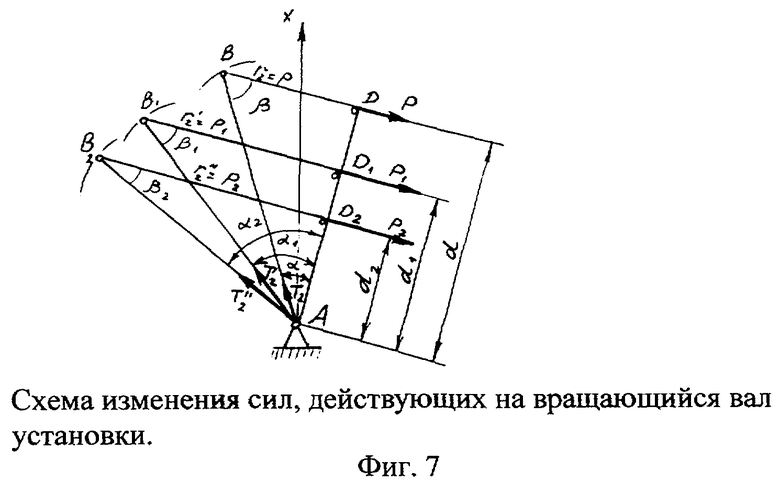
Такое положение гибкой связи происходит при каждом обороте стержня 3, когда малый радиус-вектор r2 совпадает с параметром эллипса р(r2=Р) и составляющая Т2 становится равной силе Р, а Т1=0. Эта зависимость представлена на фиг.7. Предельное значение угла α зависит от конструктивной схемы установки (параметров R и d) и в общем случае определяется по формуле
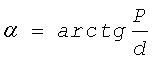 ,
,
где р - параметр траектории,
d - плечо пульсатора.
Угол β определяется из треугольника ABD по заданному углу α по теореме синусов
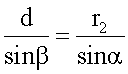
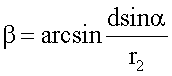
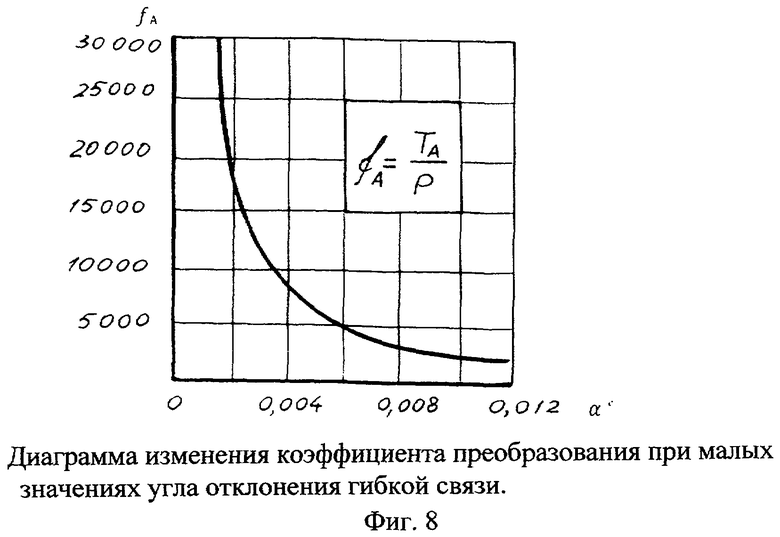
Малые значения угла α(α<0,1°), когда коэффициент преобразования стремится к бесконечности, как показано на фиг.8, а переменные силы действуют мгновенно, учитывать в практических инженерных расчетах очень сложно. Это вопрос специального исследования на уровне микро и нанотехнологий. Поэтому при определении основных характеристик рассматриваемой установки следует принимать средние значения сил Т1 и Т2, действующих в секторе предельного угла α, а следовательно, и средние значения коэффициентов преобразования равными
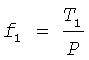
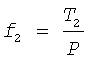
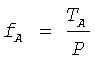
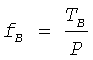
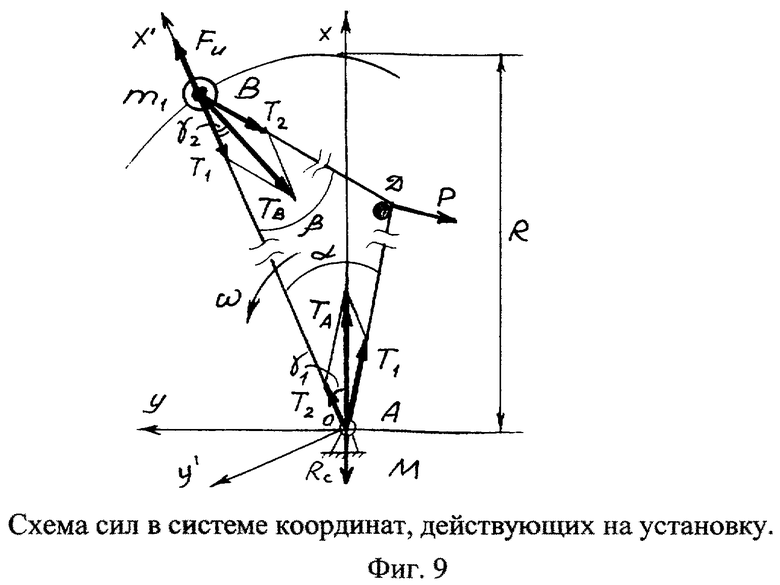
Теперь рассмотрим условия равновесия активных сил, действующих на рассматриваемую установку, целенаправленное изменение которых приводит корпус 1 в поступательное движение. На фиг.9 представлена схема сил в системе координат, действующих на установку. Выделим из системы движущие материальные точки А (ось вала вращения 2) и В (груз 4 с массой m1) и по принципу Даламбера представим уравнения их равновесия в проекциях на координатные оси Х и Х' при равномерном вращении вала 2 и вместе с ним стержня 3 (ω=const, ε=0).
Так как Fи=m1ω2 R=TВcosγ2, то пороговое значение угловой скорости ротора выражается формулой
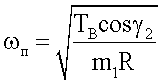
Пороговая частота вращения
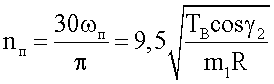
Следовательно, для уравновешивания сил в точке В необходимо приложить со стороны гибкой связи такую силу Тв, проекция которой на ось Х была бы равна центробежной силе инерции Fи. Это условие имеет важное значение для дальнейшего расчета рассматриваемой установки, так как позволяет определить минимальную (пороговую) угловую скорость вращения стержня 3, при которой устанавливается динамическое равновесие подвижной массы m1.
Присоединим к действующим на точку В внешним силам T1 и Т2 силу инерции подвижной массы Fи и определим сумму проекций этих сил на подвижную ось X'
Fи-T1-T2cosβ=0
Отсюда
Fи=TВcosγ2,
так как Fиx'=Fи, T1x'=-T1, T2x'=-T2cosβ,
Tвх'=T1x'+Т2х'=-TВcosγ2.
Условие динамического равновесия точки А, взаимодействующей непосредственно с корпусом 1, определяется равенством силы действия Та гибкой связи 6 и силы инерции покоя Rс корпуса 1 установки (силы сопротивления движению).
Линии действия этих сил проходят по оси Х и поэтому
ТА-RC=0
ТА=RC
Следовательно, динамическое равновесие установки относительно координатной оси X, совпадающей с направлением движения корпуса 1, достигается при условиях:
Fи=Tвcosγ2
ТА=RC.
Пороговое значение окружной силы Р, соответствующее пороговой угловой скорости стержня 3, можно определять по коэффициентам преобразования и силам Та и Тв
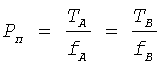 .
.
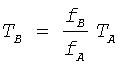 .
.
Преобразовывая приведенные выше уравнения, имеем
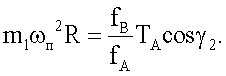
Так как ТА=RC, то
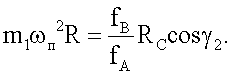
Отсюда находим взаимосвязь силы сопротивления движению корпуса 1 с основными параметрами заявленной установки
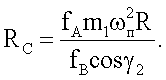
С увеличением оборотов стержня 3 (ω>ωп) условие равновесия будет нарушено и корпус 1 установки изменит свое положение, так как получит поступательное движение в пространстве.
С увеличением скорости вращения стержня 3 происходит изменение соотношений действующих на корпус 1 сил, и корпус 1 установки выходит из состояния динамического равновесия:
Fи≥TВcosγ2
ТА>RC.
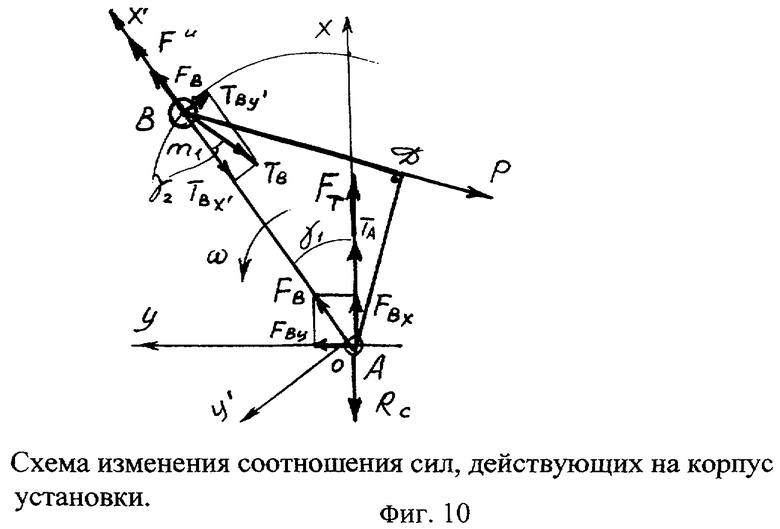
На фиг.10 представлена схема изменения соотношения сил, действующих на корпус 1 установки. Вектор силы тяги FТ является равнодействующей составляющих сил Fи, Тв и Та, действующих в направлении оси X.
Перенесем силу F=Fи-Твх' вдоль линии ее действия в точку А и разложим на составляющие по осям Х и Y.
Тогда
Fвх=FBcosγ1
или Fвх=(FИ-TBcosY2)cosγ1.
Суммируя силы TA и FBX, получим уравнение силы тяги установки:
FT=TA+Fвх
FT=TA+(FИ-TBcosγ1)cosγ1.
Последняя формула связывает все основные параметры заявляемой установки и является основным уравнением при расчете динамических характеристик.
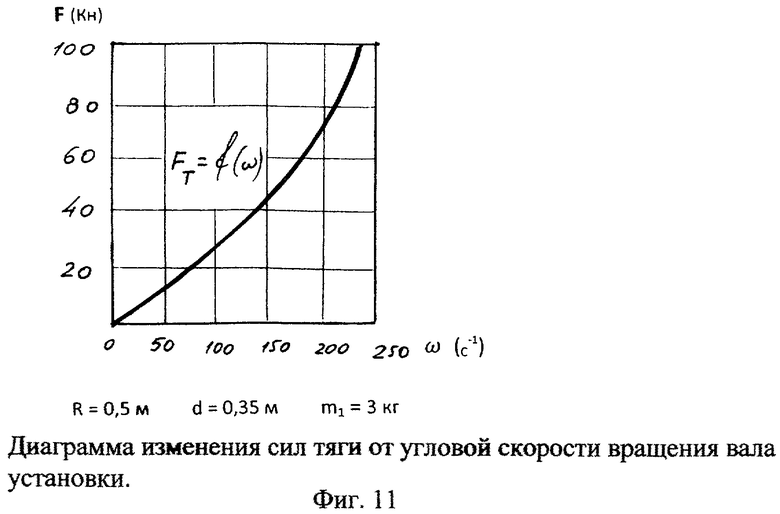
Сила тяги зависит от угловой скорости вращающегося стержня 3 и эта зависимость представлена на фиг.11. Сила тяги при соответствующей мощности, передаваемой валу вращения 2, может достигать значительных величин. Если сила тяги превышает силу сопротивления движению корпуса 1 установки (Fт>Rc), то создается движущая сила F, которая и приводит корпус 1 в поступательное движение:
F=TA+(Fи-Tвcosγ2)cosγ1-RС.
Сила сопротивления Rс определяется известными методами в зависимости от назначения устройства и сферы его применения. При трогании с места по поверхности следует определять силу трения покоя, применяя статический коэффициент трения. При движении в сплошной воздушной или водной среде необходимо определять силу аэродинамического или гидродинамического сопротивления, так как в этом случае сила сопротивления зависит от скорости движения устройства.
При определении динамических характеристик заявленной установки следует учитывать, что движущая сила действует на установку импульсивно в зависимости от частоты вращения стержня 3. Интенсивность действия движущей силы (k) определяется числом столкновений гибкой связи 6 с пульсатором 5 в единицу времени по зависимости
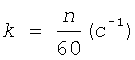 .
.
Продолжительность действия импульса зависит от угла α и частоты вращения:
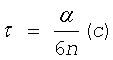 .
.
Тогда элементарный импульс движущей силы составит
ΔS=Fτ,
который при равномерном вращении стержня 3 (ω=const, ε=0) является величиной постоянной. Поэтому суммарный импульс за некоторый промежуток времени t определится как произведение элементарного импульса ΔS на число столкновений гибкой связи 6 с пульсатором 5:
ΣS=ΔSkt.
Скорость движения корпуса 1 определяется согласно теореме об изменении количества движения по зависимости:
M(V-V0)=ΣS,
где М - масса объекта,
V0 - начальная скорость,
V - конечная скорость,
ΣS - суммарный импульс.
Потребная мощность заявляемой установки определяется при максимальной угловой скорости стержня 3 и соответствующим ей значением окружной силы
N=PMAXdωМАХ.
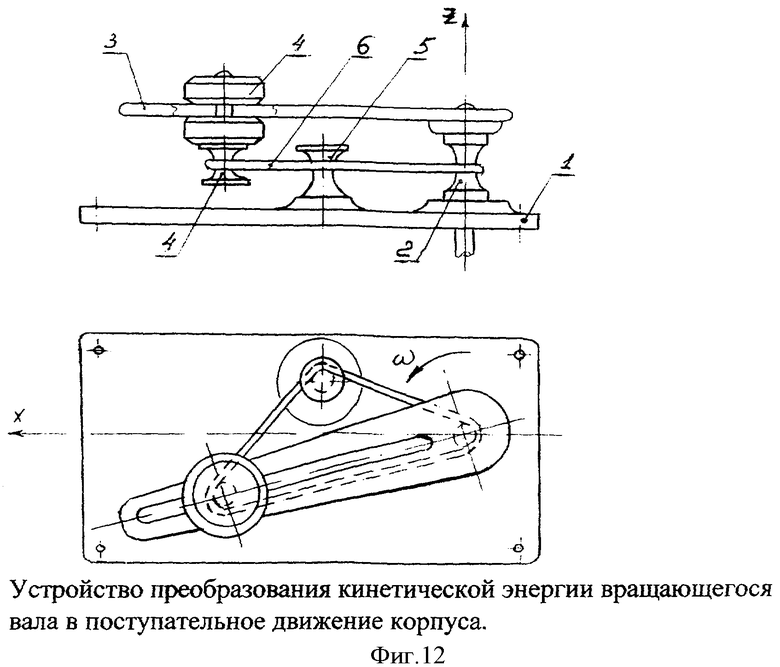
На фиг.12 представлено устройство преобразования кинетической энергии вращающего вала в поступательное движение корпуса. Установка содержит корпус 1, в котором расположен вал вращения 2. На валу 2 жестко укреплен стержень 3, в прорези которого свободно перемещается груз 4. На корпусе 1 укреплен пульсатор 5. В одной плоскости вал вращения 2, груз и пульсатор 5 охватывает гибкая связь 6, которая размещена в выточках указанных предметов. Причем оси вала вращения 2, груза 4 и пульсатора 5 расположены параллельно.
Устройство преобразования кинетической энергии вращающегося вала установки в поступательное движение ее корпуса, представленное на фиг.12, работает следующим образом. Каким-либо способом (в изобретении не раскрывается) придают вращение валу 2, размещенному в корпусе 1. Вместе с валом вращения 2 получают вращение стержень 3 и расположенный в прорези стержня 3 груз 4. В одной плоскости по выточкам на валу вращения 2, пульсаторе 5 и грузе 4 размещена гибкая связь 6, которая охватывает эти элементы установки во время вращения вала 2. Груз 4, свободно перемещаемый в прорези, во время своего вращения вместе со стержнем 3 описывает кривую в виде эллипса и при этом кинетическая энергия груза 4 импульсами передается через гибкую связь 6 валу вращения 2. Причем груз 4 свободно перемещается в прорези стержня 3, не ударяясь о ее концевые участки. Вследствие того, что кинетическая энергия вращающегося груза 4 передается корпусу 1, он приобретает поступательное движение. Причем с увеличением частоты вращения поступательное движение становится более равномерным.
Источники информации
1. US 7105440 ВВ, F01C 13/00, 2004.
2. Нурбей Гулиа. Алфизики XX века, рис.2. «Техника-молодежи», №8, 1986. Электронная версия: НиТ. Текущие публикации, 1997.
3. Шипов Г.И. Теория физического вакуума в популярном изложении, раздел «Инерциоид Толчина», рис.47, 49. М., 2002.
Изобретение относится к устройствам, преобразующим энергию вращающегося вала установки в поступательное движение установки по поверхности. Устройство включает корпус, в котором размещен вал вращения, а также установленный на корпусе пульсатор. На валу вращения жестко закреплен стержень, на котором укреплен груз с возможностью свободного перемещения по стержню. Гибкая связь охватывает вал вращения, груз и пульсатор. Решение направлено на обеспечение плавного перемещения установки и упрощение конструкции. 2 н.п. ф-лы, 13 ил.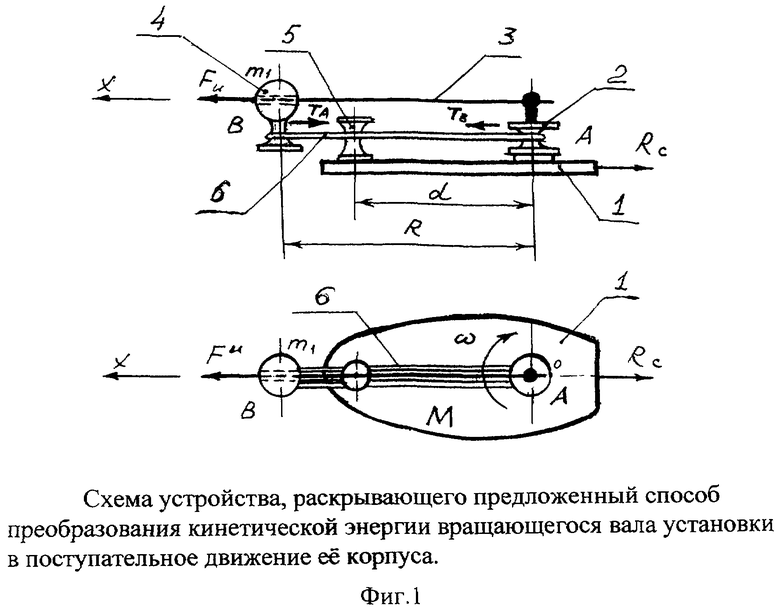
1. Способ преобразования кинетической энергии вала вращения установки в поступательное движение ее корпуса по поверхности, включающий вращение стержня, жестко закрепленного на валу вращения перпендикулярно его оси, размещение на стержне груза и передачу кинетической энергии вращающегося груза корпусу установки через гибкую связь, отличающийся тем, что груз устанавливают на стержне с возможностью его свободного перемещения на стержне, пульсатор укрепляют на корпусе установки, а гибкой связью охватывают в одной плоскости вал вращения, груз и пульсатор.
2. Устройство преобразования кинетической энергии вала вращения установки в поступательное движение его корпуса по поверхности, содержащее корпус, размещенный в нем вал вращения, стержень, закрепленный на валу вращения, пульсатор, укрепленный на корпусе, гибкую связь между корпусом и грузом, отличающееся тем, что гибкая связь выполнена в виде кольцевой нити, пульсатор укреплен на корпусе, груз размещен на стержне с возможностью свободного перемещения на стержне, при этом гибкая связь охватывает в одной плоскости вал, груз и пульсатор, оси которых параллельны.
| ШИПОВ Г.И | |||
| Теория физического вакуума в популярном изложении, раздел «Инерциоид Толчина», рис.47, 49 | |||
| - М., 2002 | |||
| RU 2001115911 A, 10.06.2003 | |||
| RU 2000116592 A, 27.04.2002. |
Авторы
Даты
2011-01-10—Публикация
2009-04-28—Подача