Изобретение относится к локационной технике и может быть использовано в тренажерах подготовки операторов локационных станций, а также для функционально-диагностического контроля локационных систем.
Известен способ имитации траекторий движения воздушных объектов [1], который осуществляется путем ручного ввода начальных полярных координат объекта в виде пеленга П0, дальности d0, курса kоб и начальной скорости νоб и последующего автоматического формирования траектории движения в виде отрезка прямой, исходящего из точки (П0; d0) в направлении kоб. Сигнал к началу маневра (поворота) поступает синхронно с вводом нового курса движения kоб и скорости объекта νоб к моменту выхода на новый курс. В результате выполняется имитация поворота путем сопряжения двух прямолинейных разнонаправленных участков движения дугой окружности, радиус которой определяется скоростью изменения курса ωк, которая также задается в момент начала маневра.
Данный способ осуществляется в известном устройстве тренажера (фиг.1) операторов РЛС [1], содержащем пульт преподавателя 1, предназначенный для набора параметров движения объекта в виде цифровых кодов, первый выход которого соединен с первым входом преобразователя координат 2, предназначенного для вычисления текущих координат при имитации движения воздушного объекта, а второй выход - с первым входом сглаживающего блока 3, превращающего скачки курса и скорости движущегося объекта в плавное движение по дуге окружности, второй вход которого соединен с первым выходом преобразователя координат 2, выход сглаживающего блока 3 соединен со вторым входом преобразователя координат 2; второй выход преобразователя координат 2 соединен со входом пульта оператора 4 со встроенным выносным панорамным индикатором для слежения и вычисления координат объекта.
Известному способу присущи следующие два основных недостатка. С одной стороны, это нереальная имитация траектории движения с учетом кинематики маневра воздушного объекта, когда объект (его пилот) испытывает мгновенное воздействие перегрузки вследствие скачка центробежной силы Fц=mυ2/R (m и υ - соответственно масса и скорость воздушного объекта), который неизбежно возникает при переходе с траектории движения по прямой с радиусом кривизны R→∞ на траекторию движения с конечным радиусом Rокр. С другой стороны, имитируемая траектория является плоскостной кривой, все точки которой расположены на некоторой условно заданной высоте над поверхностью земли, что не характерно для реальных полетов воздушных объектов в трехмерном пространстве.
Недостатком устройства тренажера является также приблизительное задание значений параметров движения по переходной кривой и ограниченные точностные возможности наложения на первичную радиолокационную обстановку вторичной имитируемой информации.
Целью изобретения является расширение функциональных возможностей устройства имитации траекторий движения воздушных объектов с расчетом на формирование наиболее реалистичной трассы полета в трехмерном воздушном пространстве без скачков скорости и ускорения, а также обеспечение более эффективного функционально-диагностического контроля аппаратуры РЛС, повышение качества подготовки операторов.
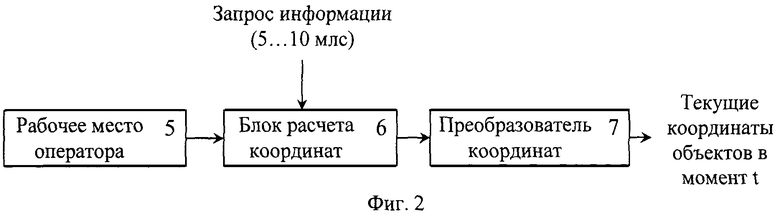
Поставленная цель достигается тем, что в способе и устройстве имитации траекторий движения воздушных объектов предлагается путем ручного ввода задавать координаты опорных точек траектории движения с указанием скоростей полета в этих точках и автоматически производить расчет уравнений движения по трем координатам x(t), y(t), z(t) и скорости ϑ(t) непосредственно после ввода исходных данных на рабочем месте оператора 5 (которое заменяет пульт преподавателя), выполненном на основе PC-подобного персонального компьютера, затем передавать коэффициенты указанных уравнений движения в блок расчета координат 6 (который заменяет сглаживающий блок), реализованный в виде модуля ADP24PCI на основе сигнального процессора 1892ВМ2Т производства ГУП НПЦ «ЭЛВИС», вход которого соединен с выходом рабочего места оператора 5 (фиг.2), а в последствии в нем в ответ на запрос информации о текущем положении объекта, поступающий через интерфейс внешних запросов, вычислять его декартовы координаты и конвертировать их в полярную систему в преобразователе координат 7, вход которого соединен с выходом блока расчета координат 6, а выход служит выходом устройства, путем подстановки параметра времени t в уравнения движения, соответствующие преодолеваемому в момент t участку траектории, а для этого предлагается представлять траекторию движения воздушного объекта состоящей из элементарных сегментов в виде отрезков прямых, сопряжение которых при значении угла между ними φ<90° производится с исключением скачков скорости и ускорения согласующими участками в виде дуги окружности и двух сегментов кубических парабол, на которых радиус кривизны Rк плавно меняется от бесконечного в точках стыка с прямолинейными участками до радиуса согласования Rc в точках стыка с участком в виде дуги окружности или с исключением участка в виде дуги окружности при значении угла между согласуемыми отрезками прямых φ≥90°.
На начальном участке переходной кривой траектория сопряжения отрезков прямых воспроизводится сегментом кубической параболы y=х3/6q с радиусом кривизны
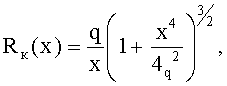 обеспечивающим плавный (без скачков скорости и ускорения) переход с прямолинейного участка при х=0 и Rк=∞ на начало второго участка с минимальным радиусом кривизны Rк=Rmin.
обеспечивающим плавный (без скачков скорости и ускорения) переход с прямолинейного участка при х=0 и Rк=∞ на начало второго участка с минимальным радиусом кривизны Rк=Rmin.
При значении угла между двумя отрезками прямых, определяющих направление прямолинейных движений, φ<90° траектория сопряжения двух отрезков прямых последовательно делится на три участка: сегмент кубической параболы, участок дуги окружности с радиусом Rmin и третий участок в виде сегмента кубической параболы с плавным изменением радиуса кривизны Rк от значения Rк=Rmin до Rк=∞. При φ≥90° траектория сопряжения двух отрезков прямых состоит из двух сегментов кубических парабол с плавным уменьшением для первого сегмента радиуса кривизны Rк от значения Rк=∞ до Rc=Rк в точке стыка и последующим увеличением для второго сегмента Rк от значения Rc до Rк=∞.
На фиг.1 представлена структурная схема устройства имитации траекторий движения (прототипа), состоящего из пульта преподавателя 1, преобразователя координат 2, сглаживающего блока 3 и пульта оператора 4.
На фиг.2 представлена структурная схема заявляемого устройства, состоящая из рабочего места оператора 5, блока расчета координат 6 и преобразователя координат 7.
Принцип работы заявляемого способа и устройства может быть показан следующим образом.
Оператор выбирает из функционального меню на рабочем месте преподавателя режим создания файла имитируемой воздушной обстановки и задает траекторию движения воздушных объектов с помощью «мыши» и клавиатуры. Один из вариантов реализации функционального меню приведен в [2; 3].
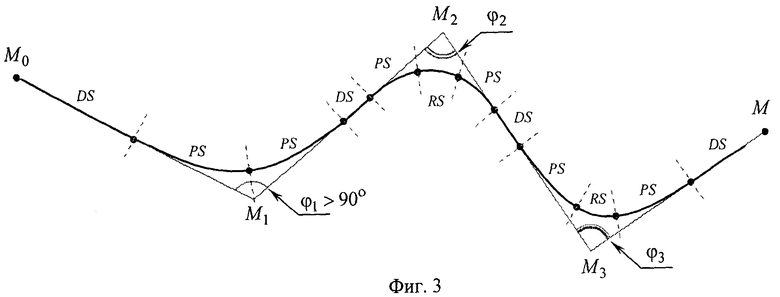
Траектория движения воздушного объекта рассматривается как участок плавной (без изломов) пространственной кривой, протяженный во времени с момента начала движения T0 до момента его завершения TL, образующийся при фиксации координат объекта в каждый момент времени при отсутствии в его движении скачков скорости и ускорения. Такая кривая задается набором опорных вершин {Mn(xn, yn, zn)} ломаной линии, очерчивающей траекторию движения объекта (фиг.3) [4].
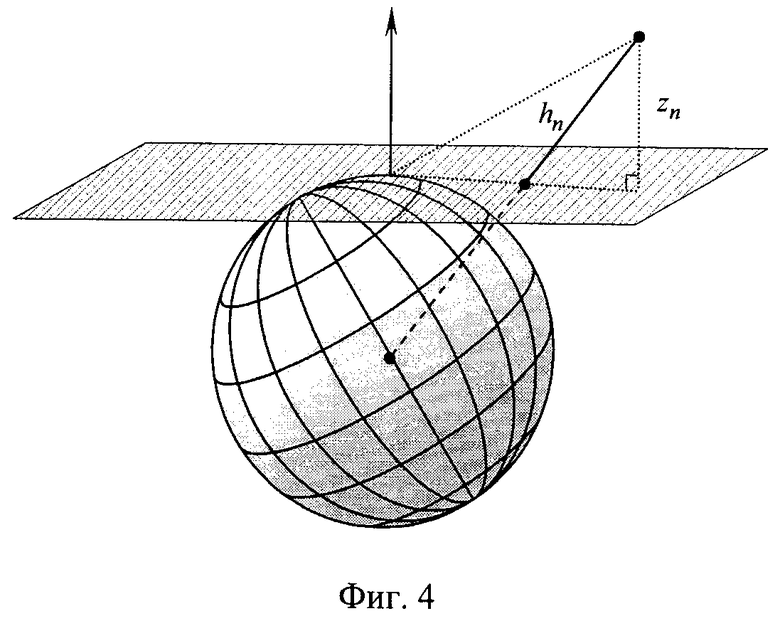
Ввод точек Mn осуществляется в естественном для оператора виде {Mn(xn, yn, hn)}, когда в качестве третьей координаты выступает высота hn воздушного объекта над поверхностью Земли (фиг.4).
Последующий расчет кинематики движения выполняется с использованием прямоугольной системы координат, в которой оси OX, OY и OZ попарно перпендикулярны и величина zn выражается через высоту hn следующим образом:
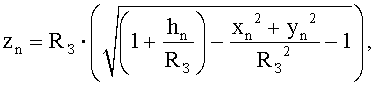
где 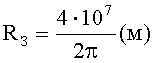 - радиус Земли.
- радиус Земли.
Величины xn и yn также задаются оператором относительно поверхности Земли, однако не подвергаются преобразованиям вследствие их незначительного несоответствия координатам в выбранной прямоугольной системе XYZ.
Для каждой точки Mn задается не только ее пространственное положение относительно некоторой выбранной прямоугольной системы координат (центром которой может случить антенна РЛС), но также и значение линейной скорости движения объекта νn. Траектория движения объекта повторяет опорную ломаную линию, совпадая с ней лишь в центральных участках отрезков MnMn+1. Излом опорной линии должен быть сглажен путем правильного подбора трассы маневра, учитывающей максимальную переносимую пилотом перегрузку. Вследствие этого, воздушный объект никогда не окажется ни в одной из точек Mn, за исключением первой и последней. Поэтому величина νn трактуется как скорость, которую имеет объект в момент выхода с переходной кривой на прямолинейный участок MnMn+1.
Заявляемое устройство осуществляет расчет координат (х, y, z) положения объекта в заданный момент времени t∈[Т0; TL] и формирует на выходе сигналы, соответствующие значениям координат.
С этой целью траектория движения представляется состоящей из отрезков прямых линий и участков маневрирования (фиг.3), таких что каждый участок маневрирования может быть адекватно представлен совокупностью двух ветвей кубической параболы, сопряженных между собой дугой окружности (если угол φn между направлениями 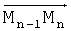 и
и 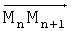 острый) или совмещенных непосредственно (если угол φn прямой или тупой).
острый) или совмещенных непосредственно (если угол φn прямой или тупой).
Таким образом, вся траектория делится на смежные сегменты трех типов: прямолинейные (DS), параболические (PS) и круговые (RS). Чередование сегментов происходит, как правило, циклически в порядке: К→DS→PS→RS→PS→К, однако в некоторых конкретных случаях сегменты DS и RS могут исключаться. При этом выбор граничных точек сегментов производится так, чтобы обеспечить плавную линию движения объекта без скачков скорости и ускорения.
Для каждого из трех типов сегментов траектории сформулирован закон движения, позволяющий определить пространственное положение объекта, а также его радиальную скорость в заданный момент времени t. Каждый из трех законов применим только для своего типа сегмента и имеет в своей математической записи как постоянные во времени коэффициенты, так и параметры, зависящие от t. Поэтому перед расчетом положения объекта на траектории в рамках данного сегмента постоянные коэффициенты вычисляются на рабочем месте оператора 5 и заносятся в память ЭВМ. Такая операция проводится для каждого сегмента, в результате чего формируется основная расчетная таблица.
где Tн и Tк - моменты времени начала и окончания движения объекта по сегменту, которые позволяют идентифицировать именно тот сегмент, по которому перемещается объект в момент времени t;
ω - угловая скорость;
ε - угловое ускорение.
Величины ω и ε определены только для криволинейных сегментов траектории.
Для расчета радиальной скорости и координат объекта в заданный момент времени знание величин, взятых из столбца таблицы, для которого выполняется условие Tн≤t<Тк, является достаточным.
2. Расчетные формулы для определения координат объекта в заданный момент времени t
2.1 Прямолинейные сегменты траектории
Для прямолинейных сегментов расчет текущих значений координат и радиальной скорости выполняется по формулам:

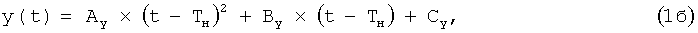
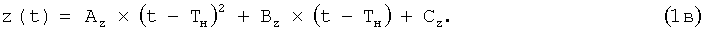
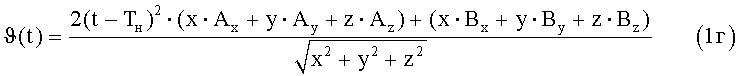
Значения коэффициентов таблицы 1 для формул (1a)-(1г) принимаются следующими:

Здесь:
Δx01=xn-xn-1, Δy01=yn-yn-1, Δz01=zn-zn-1- расстояние от точки Mn-1 до точки Mn в проекции на оси х, y и z соответственно.
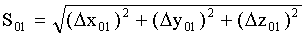 - расстояние от точки Mn-1 до точки Mn.
- расстояние от точки Mn-1 до точки Mn.
Аналогично:
Δx02=xn+1-xn, Δy02=yn+1-yn, Δz02=zn+1-zn - расстояние от точки Mn до точки Mn+1 в проекции на оси х, y и z соответственно.
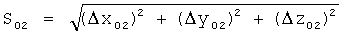 - расстояние от точки Mn до точки Mn+1.
- расстояние от точки Mn до точки Mn+1.
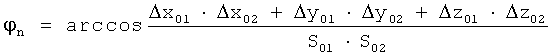 - угол между направлениями движения.
- угол между направлениями движения.
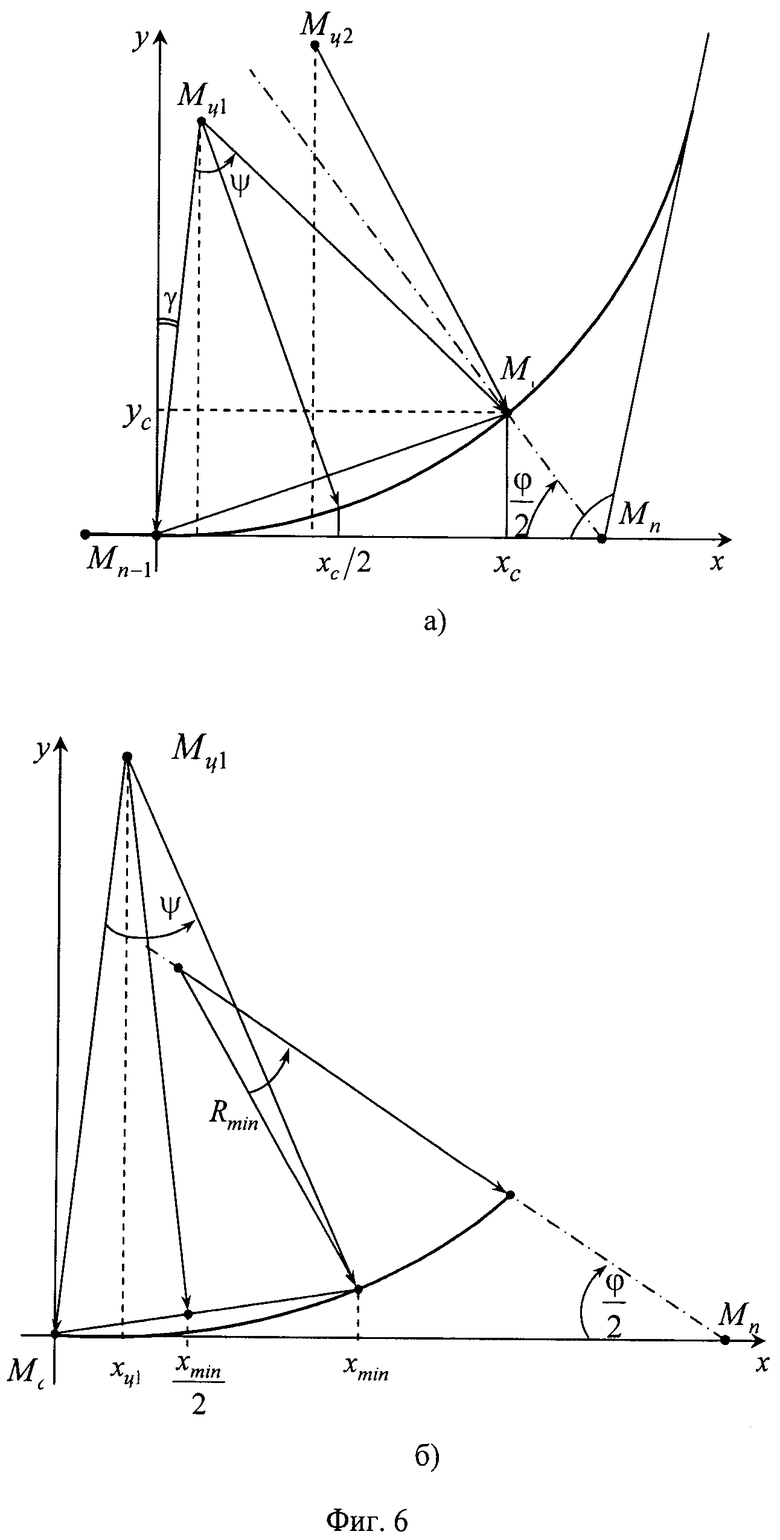
Величины  и Rmin определяются в зависимости от характера переходной кривой на предшествующем участке поворота (соответствующем т. Mn-1) и влияют на вид траектории, огибающей точку Mn. Поскольку отрезок ломаной линии Mn-1Mn является для двух рассматриваемых участков общим и длина его ограничена, радиус кривизны поворота (с учетом максимальной переносимой перегрузки) вблизи т. Mn подбирается таким, что точка начала переходной кривой
и Rmin определяются в зависимости от характера переходной кривой на предшествующем участке поворота (соответствующем т. Mn-1) и влияют на вид траектории, огибающей точку Mn. Поскольку отрезок ломаной линии Mn-1Mn является для двух рассматриваемых участков общим и длина его ограничена, радиус кривизны поворота (с учетом максимальной переносимой перегрузки) вблизи т. Mn подбирается таким, что точка начала переходной кривой 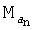 не заходит за точку
не заходит за точку 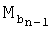 и не оказывается ближе нее к вершине Mn-1 (см. фиг.5).
и не оказывается ближе нее к вершине Mn-1 (см. фиг.5).
Во избежание разрыва траектории расчет производится следующим образом. Сначала определяется максимальная скорость из двух заданных номинальных скоростей в точках Mn-1 и Mn: ϑmax=max(ϑn-1, ϑn). Затем выбирается номинальный (комфортный) уровень перегрузки, выраженный в числе ускорений свободного падения, например nц_ном=0,1, и вычисляется минимальный радиус кривизны поворота по формуле:
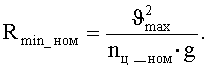
Номинальному значению минимального радиуса кривизны соответствует величина 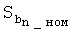 :
:
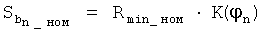
При значении Sb, равном 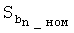 , возможна ситуация, проиллюстрированная фиг.5б. Для ее исключения осуществляется проверка условий:
, возможна ситуация, проиллюстрированная фиг.5б. Для ее исключения осуществляется проверка условий:
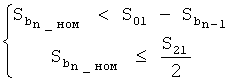 .
.
Если оба условия выполняются, то Rmin и Sb принимаются равными Rmin_ном и 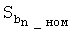 соответственно, иначе расчет производится следующим образом:
соответственно, иначе расчет производится следующим образом:
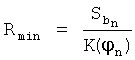 ,
,
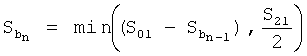 .
.
Резервирование участка отрезка 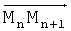 длиной S21/2 позволяет получить заявленный результат. Если в ходе дальнейших вычислений окажется, что поворот на опорной точке Mn+1 задан более крутым и для его осуществления требуется участок
длиной S21/2 позволяет получить заявленный результат. Если в ходе дальнейших вычислений окажется, что поворот на опорной точке Mn+1 задан более крутым и для его осуществления требуется участок 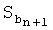 , больший чем S21/2, то в этом случае недостаток пространства для маневра компенсируется более резким поворотом с увеличением перегрузки.
, больший чем S21/2, то в этом случае недостаток пространства для маневра компенсируется более резким поворотом с увеличением перегрузки.
Величина K(φn), использованная при расчете 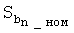 , показывает расстояние от точки Mn до ближайшего края прямолинейного отрезка движения, выраженное в числе Rmin.
, показывает расстояние от точки Mn до ближайшего края прямолинейного отрезка движения, выраженное в числе Rmin.
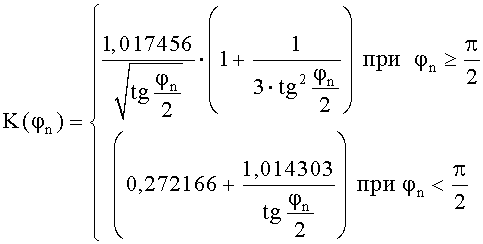
2.2 Переходная кривая
На участке траектории от точки  до точки
до точки 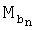 при каждой вершине Mn опорной ломаной линии объект движется по переходной кривой. Она, как было условлено, может быть представлена совокупностью двух ветвей параболы, которые стыкуются между собой при φn≥90°, а при φn<90° - совмещаются посредством дуги окружности. При движении объекта по сегменту кубической параболы воспроизведение текущих значений координат в функции времени производится замещением дуги кубической параболы дугой окружности, совмещенной с ней в трех точках, с представлением значений координаты x через параметрическое представление координаты x(t) окружности и выражением значений координаты y(t) через координату x(t) в соответствии с уравнением кубической параболы. На фиг.6 представлены оба вида сопряжения: двухсегментное (а) и трехсегментное (б).
при каждой вершине Mn опорной ломаной линии объект движется по переходной кривой. Она, как было условлено, может быть представлена совокупностью двух ветвей параболы, которые стыкуются между собой при φn≥90°, а при φn<90° - совмещаются посредством дуги окружности. При движении объекта по сегменту кубической параболы воспроизведение текущих значений координат в функции времени производится замещением дуги кубической параболы дугой окружности, совмещенной с ней в трех точках, с представлением значений координаты x через параметрическое представление координаты x(t) окружности и выражением значений координаты y(t) через координату x(t) в соответствии с уравнением кубической параболы. На фиг.6 представлены оба вида сопряжения: двухсегментное (а) и трехсегментное (б).
В обоих случаях переходная кривая симметрична относительно биссектрисы угла φn и не образует изломов в точках совмещения сегментов.
Расчет кинематики движения объекта на параболическом участке траектории осуществляется путем замены ветки параболы дугой окружности, которая совмещается с параболой в крайних точках и посередине. Однако перерасчет координат происходит таким образом, что объект не отклоняется от заданной параболой траектории. Такой результат достигается путем расчета координаты x положения объекта на круговой траектории и последующей ее подстановкой в выражение для вычисления координаты у принадлежащей параболе точки.
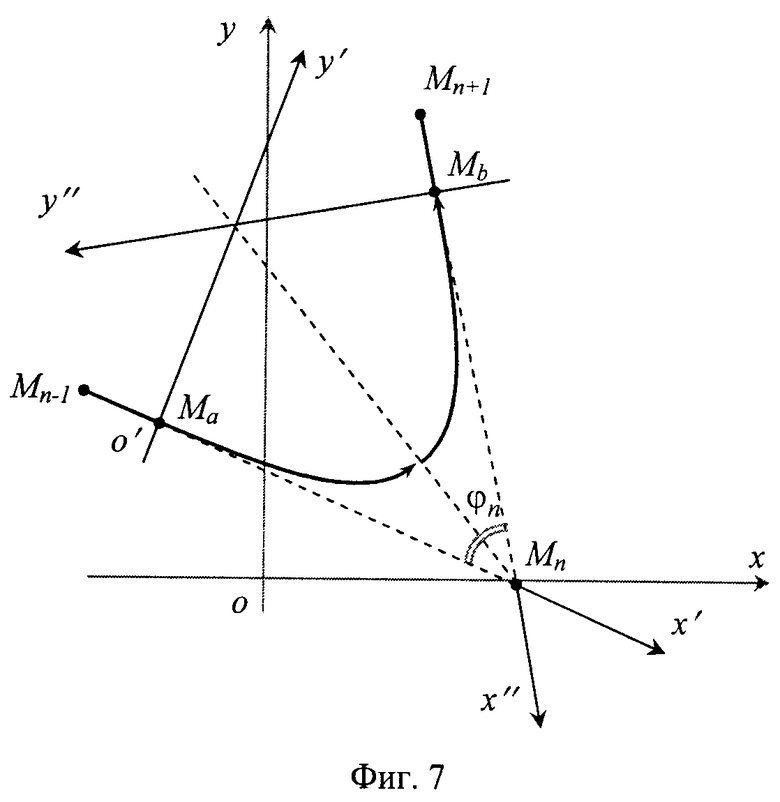
Расчет движения объекта на каждом таком сегменте осуществляется в локальной, связанной с ним системе координат. Эта система выбирается для целого участка маневра (поворота) с прилегающими к траектории виража участками прямолинейного движения.
Переходная кривая лежит в плоскости Mn-1MnMn+1, и естественную систему координат, в которой переходная кривая имеет простейший вид, составляют ось O'X', совпадающая с вектором 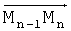 и перпендикулярная ей ось O'Y', направленная в сторону движения объекта (фиг.7). Началом координат служит точка Ma, в которой начинается переход на криволинейный участок.
и перпендикулярная ей ось O'Y', направленная в сторону движения объекта (фиг.7). Началом координат служит точка Ma, в которой начинается переход на криволинейный участок.
Траектория движения, рассчитанная в локальной системе координат, затем переводится в единые для всей траектории координаты (система XYZ, в которой заданы опорные точки). Для этого рассчитываются коэффициенты преобразования координат (направляющие косинусы осей). Для начального участка переходной кривой (до биссектрисы угла φn):

Для расчета движения по конечному участку переходной кривой (за биссектрисой угла φn) этот фрагмент траектории подвергается дополнительным аффинным преобразованиям, поэтому коэффициенты преобразования координат для него другие:

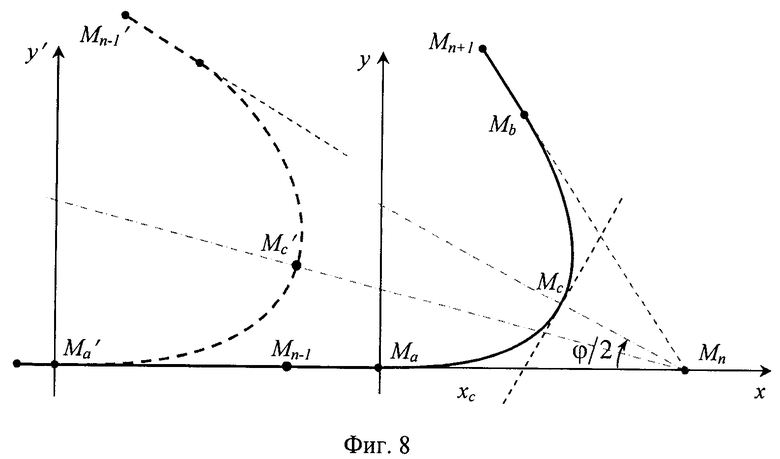
2.2.1 Круговые сегменты
Круговой сегмент добавляется в переходную кривую при малых углах поворота (φn<90°) для того, чтобы не допустить значительное удаление от вершины Mn точки стыка Mc двух параболических сегментов (фиг.8).
Движение по круговому сегменту рассчитывается по формулам:
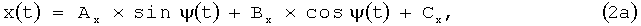
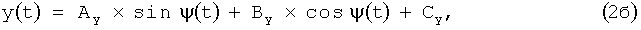
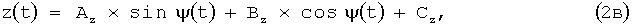
где

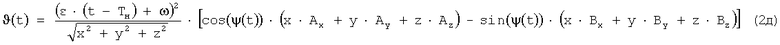
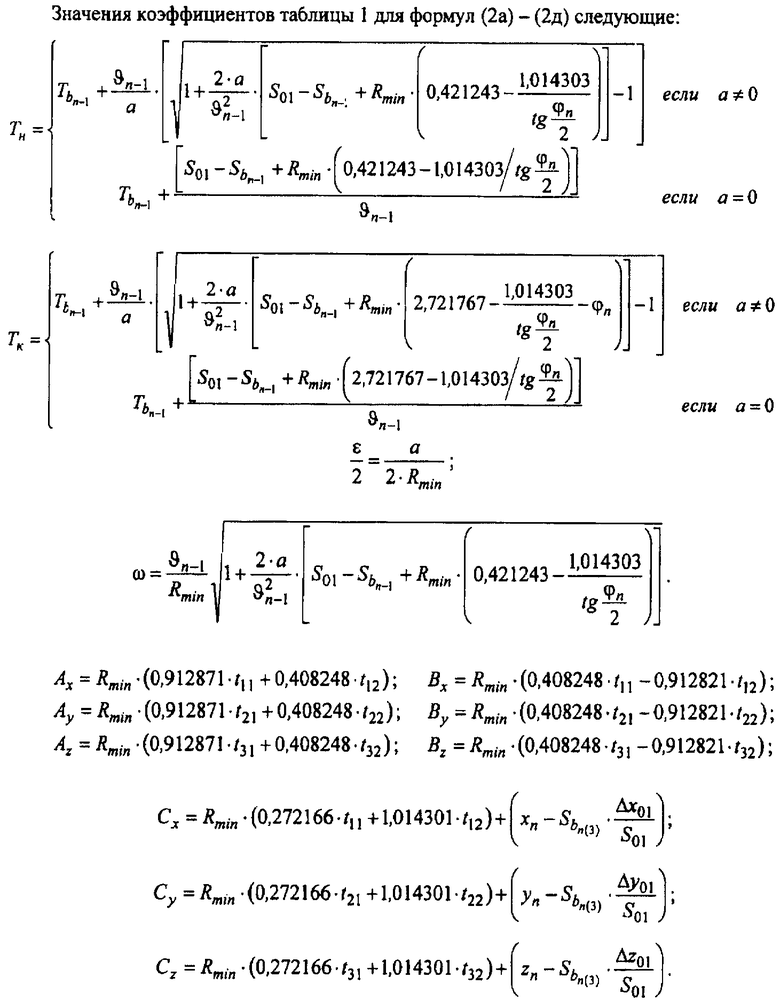
Значения используемых коэффициентов те же, что и для прямолинейного участка.
2.2.2 Параболические сегменты
Для параболических сегментов применяются следующие расчетные формулы:
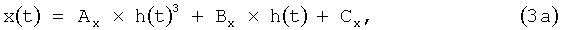
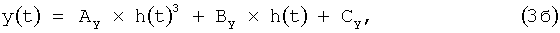

где
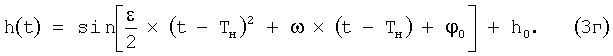
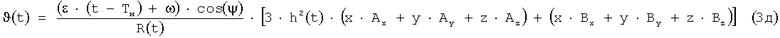
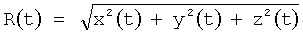
Значения коэффициентов для параболических участков различаются для начального и конечного участка переходной кривой, а также зависят от метода ее построения (двух- или трехсегментный).


Для φn≥90° определены следующие вспомогательные величины:
- отношение радиуса окружности, замещающей кубическую параболу, к минимальному радиусу кривизны Rmin:
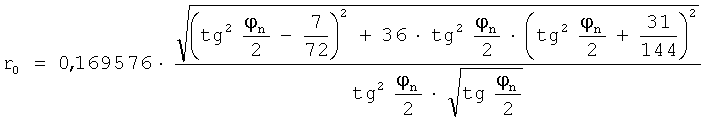 ;
;
- максимальное перемещение по параболе:
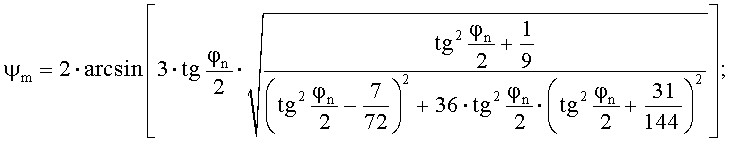
- угол между осью O'Y' и радиус-вектором от центра замещающей окружности до точки выхода на переходную кривую (Ma):

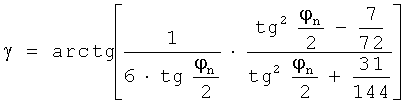 .
.

Расчет кинематики движения сопровождается проверкой перегрузок, которые неизбежно возникают при перемещении объекта по криволинейному участку траектории (будь то круговой или параболический сегмент). Для этого вычисляется максимальное центростремительное ускорение:
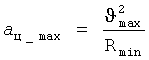 .
.
Для вычисления линейного ускорения рассчитывается общий пройденный путь по траектории, огибающей вершину Mn (переходная кривая и предшествующий ей участок прямолинейного движения):

где
 .
.
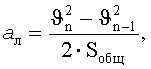
Испытываемая объектом совокупная перегрузка рассчитывается по формуле:
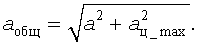 .
.
Если a общ<8g, то расчет продолжается, иначе трасса (вершина Mn) бракуется.
В момент перехода устройства в режим вычисления координат коэффициенты таблицы 1, рассчитанные на рабочем месте оператора 5, передаются в блок расчета координат 6, реализующий вычисления по формулам (1а)-(1г), (2а)-(2д), (3а)-(3д) с подстановкой в них параметра времени t. Запросы на расчет координат поступают в блок расчета координат 6 через интерфейс канала передачи информации с интервалом 5-10 млс.
На выход устройства поступают координаты, переведенные преобразователем координат 7 в полярную систему, полюсом которой является установка РЛС, а отсчет угла ведется, например, от направления на север. Расчет осуществляется в соответствии с выражениями:
дальность: ;
;
азимут (отсчет от направления на север по часовой стрелке):
 ,
,
где:
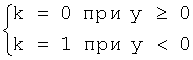 ,
,
φ(t)=φ(t)+2π при φ(t)<0;
угол места (отсчет от горизонтали):
 ,
, 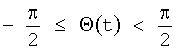 .
.
Литература
1. АС №991479 СССР. Тренажер оператора локационных станций. А.В.Гусев. Опубл. 1983 Бюл. №3.
2. Чекушкин В.В., Юрин О.В., Булкин В.В. Реализация вычислительных процессов в информационно-измерительных системах: Монография. Муром: Изд.-полиграфический центр МИ ВлГУ. 2005 - 158 с.
3. Юрин О.В., Чекушкин В.В., Дударев В.А. Автоматизированная система управления радиолокационным комплексом. Приборы и системы. Управление. Контроль. Диагностика 2004, №1, с.18-21.
4. Свидетельство о гос. регистрации программы для ЭВМ №2009611848 от 09.04.2009 «Программа сглаживания траекторий движения воздушных объектов для радиолокационных систем управления (Trajectory)». Заявка №2009610537 от 16.02.2009.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ имитации траекторий движения объектов | 2015 |
|
RU2617144C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ АЭРОБАЛЛИСТИЧЕСКОГО ЛЕТАТЕЛЬНОГО АППАРАТА ПО ЗАДАННОЙ ПРОСТРАНСТВЕННОЙ ТРАЕКТОРИИ | 2013 |
|
RU2571567C2 |
| СПОСОБ И УСТРОЙСТВО ИМИТАЦИИ РАДИОЛОКАЦИОННОЙ ИНФОРМАЦИИ | 2011 |
|
RU2489753C2 |
| ОСЕВОЙ ВЕНТИЛЯТОР | 1999 |
|
RU2208711C2 |
| Отвод трубопровода для транспортировки многофазного потока | 2023 |
|
RU2814319C1 |
| УСТРОЙСТВО ДЛЯ ПЕРЕМЕЩЕНИЯ ЛЕНТЫ ЛЬНА | 2010 |
|
RU2425482C1 |
| ОСЕВОЙ ВЕНТИЛЯТОР | 1999 |
|
RU2208712C2 |
| СПОСОБ НЕПРЕРЫВНОЙ РАЗЛИВКИ МЕТАЛЛИЧЕСКИХ ЗАГОТОВОК И УСТАНОВКА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2229957C2 |
| СПОСОБ ИЗГОТОВЛЕНИЯ КРИВОЛИНЕЙНОЙ СПИЦЫ СЕТЧАТОЙ СТРУКТУРЫ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ И КРИВОЛИНЕЙНАЯ СПИЦА СЕТЧАТОЙ СТРУКТУРЫ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ | 2011 |
|
RU2481237C1 |
| СПОСОБ ЗАДАНИЯ ТРАЕКТОРИИ И РЕЖИМОВ ДВИЖЕНИЯ СУДНА | 2014 |
|
RU2550236C1 |

Изобретение относится к области приборостроения и может быть использовано в тренажерах подготовки операторов локационных станций. Технический результат - расширение функциональных возможностей. Для достижения данного результата траектория движения воздушного объекта представляется состоящей из разнонаправленных отрезков прямолинейного движения и переходных кривых. Каждая из кривых состоит из двух ветвей кубической параболы, сопряженных между собой дугой окружности или совмещенных непосредственно. Задание траектории осуществляется путем ввода координат узловых точек опорной ломаной линии, очерчивающей траекторию движения воздушного объекта. На начальном участке переходной кривой траектория сопряжения отрезков прямых воспроизводится сегментом кубической параболы с радиусом кривизны, обеспечивающим плавный (без скачков скорости и ускорения) переход с прямолинейного участка на начало второго участка с минимальным радиусом кривизны. 5 з.п. ф-лы, 8 ил.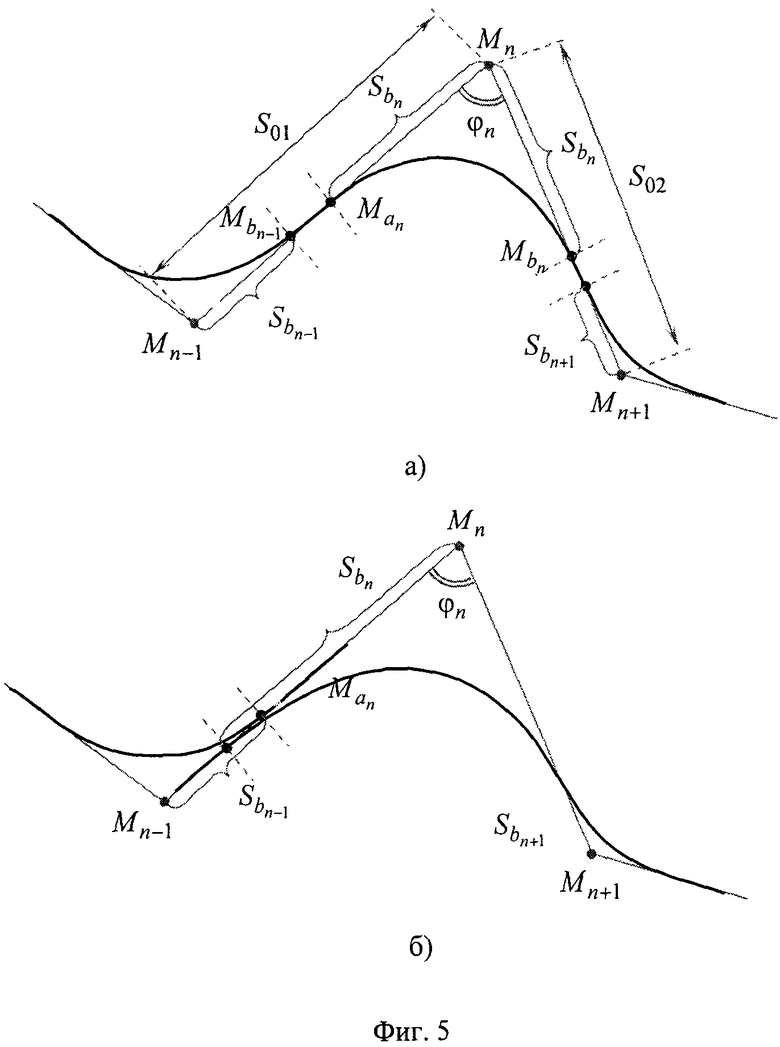
1. Способ имитации траекторий движения воздушных объектов путем ручного ввода начальных полярных координат объекта в виде пеленга П0, дальности d0, курса kоб, начальной скорости vоб и последующего автоматического формирования траектории движения в виде отрезка прямой, исходящего из точки (П0; d0) в направлении kоб, до момента поступления сигнала к началу маневра (поворота), синхронного со вводом нового курса движения kоб и скорости объекта vоб к моменту выхода на новый курс, с имитацией маневра (поворота) путем сопряжения двух прямолинейных разнонаправленных участков движения дугой окружности, радиус которой определяется скоростью изменения курса ωk, которая также задается в момент начала маневра, отличающийся тем, что имитация траекторий движения объектов осуществляется путем ручного ввода координат опорных точек траектории движения с указанием скоростей полета в этих точках и автоматического расчета уравнений движения по трем координатам x(t), y(t), z(t) и скорости v(t) непосредственно после ввода исходных данных на рабочем месте оператора с последующей передачей коэффициентов указанных уравнений в блок расчета координат, в котором в ответ на запрос информации о текущем положении объекта вычисляются его декартовы координаты путем подстановки параметра времени t в уравнения движения, соответствующие преодолеваемому в момент t участку траектории, для чего траектория движения воздушного объекта представляется состоящей из элементарных сегментов в виде отрезков прямых, сопряжение которых при значении угла между ними φ<90° производится с исключением скачков скорости и ускорения согласующими участками в виде дуги окружности и двух сегментов кубических парабол, на которых радиус кривизны Rк плавно меняется от бесконечного в точках стыка с прямолинейными участками до радиуса согласования Rc в точках стыка с участком в виде дуги окружности или с исключением участка в виде дуги окружности при значении угла между согласуемыми отрезками прямых φ≥90°, вычисленные в блоке расчета координат декартовы координаты воздушного объекта в момент времени t конвертируются затем в полярные в преобразователе координат.
2. Способ по п.1, отличающийся тем, что на начальном участке переходной кривой траектория сопряжения отрезков прямых воспроизводится сегментом кубической параболы y=x3/6q с радиусом кривизны 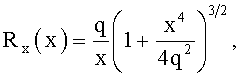 обеспечивающим плавный (без скачков скорости и ускорения) переход с прямолинейного участка при х=0 и Rk=∞ на начало второго участка с минимальным радиусом кривизны Rк=Rmin.
обеспечивающим плавный (без скачков скорости и ускорения) переход с прямолинейного участка при х=0 и Rk=∞ на начало второго участка с минимальным радиусом кривизны Rк=Rmin.
3. Способ по п.1, отличающийся тем, что при значении угла между двумя отрезками прямых, определяющих направление прямолинейных движений, φ<90° траектория сопряжения двух отрезков прямых последовательно делится на три участка: сегмент кубической параболы, участок дуги окружности с радиусом Rmin, и третий участок в виде сегмента кубической параболы с плавным изменением радиуса кривизны Rк от значения Rк=Rmin до Rк=∞.
4. Способ по п.1, отличающийся тем, что при значении угла между двумя отрезками прямых, определяющих направление прямолинейных движений, φ≥90° траектория сопряжения двух отрезков прямых состоит из двух сегментов кубических парабол с плавным уменьшением для первого сегмента радиуса кривизны Rк от значения Rк=∞ до Rc=Rк в точке стыка и последующим увеличением для второго сегмента Rк от значения Rc до Rк=∞.
5. Способ по п.1, отличающийся тем, что для воспроизведения траектории движения по дуге окружности в функции времени t в прямоугольной системе координат текущие значения координат объекта представляются параметрическими уравнениями дуги окружности в функции времени.
6. Способ по п.1, отличающийся тем, что при движении объекта по сегменту кубической параболы воспроизведение текущих значений координат в функции времени производится замещением дуги кубической параболы дугой окружности, совмещенной с ней в трех точках, с представлением значений координаты x через параметрическое представление координаты x(t) окружности и выражением значений координаты y(t) через координату x(t) в соответствии с уравнением кубической параболы.
| Устройство для имитации положения цели в пространстве | 1976 |
|
SU636659A1 |
| Тренажер оператора локационных станций | 1981 |
|
SU991479A1 |
| US 4599070 A, 08.07.1986 | |||
| Тренажерные системы | |||
| ШУКШУНОВ В.Е., БАКУЛОВ Ю.А., ГРГОРЕНКО В.Н | |||
| и др | |||
| - М.: Машиностроение, 1981, с.20, 46, 99 | |||
| US 6000942 А, 14.12.1999 | |||
| ТРЕНАЖЕР ВОЗДУШНОГО БОЯ | 2005 |
|
RU2297674C2 |
| ЮРИН О.В., ЧЕКУШКИН В.В., ДУДАРЕВ В.А | |||
| Автоматизированная система управления радиолокационным комплексом. | |||
Авторы
Даты
2011-05-20—Публикация
2009-06-01—Подача