Изобретение относится к области судовождения, в частности к системам автоматического управления движением судна.
Способ может использоваться в электронных картографических навигационно-информационных системах для задания программной траектории и режимов движения при автоматическом или интеллектуальном управлении судна.
По требованиям Резолюции ИМО А. 893 (21) разработка плана рейса или перехода, а также непрерывный контроль за движением судна очень важны для обеспечения безопасности человеческой жизни на море, надлежащего судовождения и защиты морской окружающей среды. Результатом планирования перехода является детализированная программа, на основе которой и обеспечивается безопасное плавание судна.
Известны расчетные методы задания траектории судна, в которых раздельно задаются прямолинейные и криволинейные участки пути. Прямолинейные участки пути задаются отрезками прямых линий. В работе [1] криволинейные участки аппроксимируются дугами кривых постоянного радиуса (окружностями). В работе [2] криволинейные участки пути аппроксимируются дугами эллипса. Известен способ задания траектории движения судна [3], в котором криволинейные участки пути задаются полиномами Бернштейна (кривая Безье).
К недостаткам этих способов относится использование не единообразных выражений для задания траектории и невозможность обеспечения точной проводки судна при автоматическом или интеллектуальном управлении по заданной траектории. Это объясняется тем, что в данных способах пренебрегают следующими важными физико-математическими принципами формирования траектории движения:
1. За путевые точки (точки перекладки руля, изменения частоты вращения движителя и т.п.), по определению расположенные на пути судна, принимаются точки пересечения прямолинейных отрезков, которые могут не располагаться в пределах судоходной части.
2. В траектории не учитываются все силовые воздействия (изменение частоты вращения движителя; подруливающего устройства; работа буксиров и т.п.).
3. Движение судна задается без угла дрейфа и сноса и режимов их изменений.
4. Полагается, что в процессе поворота курс судна изменяется равномерно.
5. В точках сопряжения прямых линий с дугами окружностей, эллипсов (точках начала и конца поворота) имеются разрывы в первой и второй производных.
6. В криволинейной части траектории не учитывается изменение радиуса кривизны (коэффициента касания).
7. В расчет не принимается одержание поворота судна (местоположение, величина и время перекладки руля на противоположный борт).
За прототип принят способ задания траектории судна, описанный в работах [4, 5]. Способ заключается в представлении траектории движения судна функциями, аппроксимирующими градиенты и изменения компонентов вектора перемещения точки управления судна (курс, скорость и угол дрейфа) в зависимости от пройденного судном расстояния по траектории. Эти зависимости представляются выражениями:
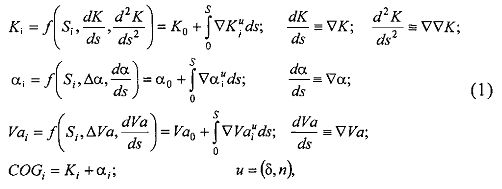
где K - истинный курс судна, град; i - индекс текущего значения; S - расстояние, пройденное по траектории, м; 0 - индекс начального значения; dV, dK, dα - приращения скорости, курса, угла дрейфа соответственно; u - индекс управляющего воздействия; Δ, ∇ - знаки приращений и градиентов соответствующих параметров; α - угол дрейфа, град; Va - скорость судна, относительно грунта, м/с; COG - направление вектора перемещения центра тяжести (ЦТ) судна относительно грунта, град; δ - угол перекладки руля, град; n - частота вращения винта, об/мин.
Согласно работе [5] выражения, связывающие изменения компонентов градиента вектора перемещения от силовых воздействий, предлагаются в форме, удобной для решения задач построения траектории судна:
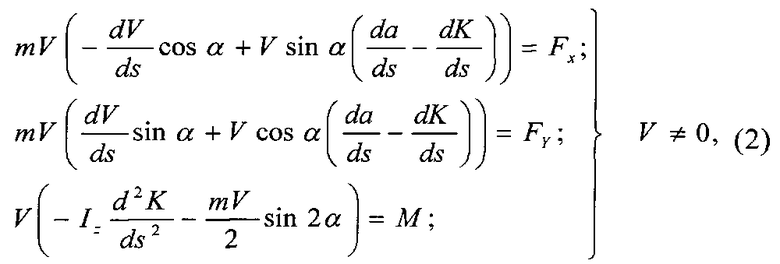
где m - масса судна, кг; V - скорость судна относительно воды, м/с; Fx, Fy - сумма проекций сил, действующих на судно, по осям X, Y соответственно, N; Iz - момент инерции судна относительно вертикальной оси, кг/м2; М - суммарный момент сил относительно начала координат, N м.
В качестве функций, аппроксимирующих согласованные программные изменения градиентов и изменений компонентов вектора перемещения точки управления судна (курс, угол дрейфа, скорость), используются сигмоподобные функции с изменяемыми коэффициентами кривизны (наклона), см. фиг. 1, фиг. 2, фиг. 3, фиг. 4:

где max - индекс максимальной величины параметра при силовом воздействии; in - индекс начального значения соответствующего параметра; Su - расстояние до точки перегиба сигмоподобной функции, м; ΔSu - поправка, учитывающая смещение функции из начальных условий маневра, м; mn - индекс значения параметра, в средней точке переходного периода маневра; R - множитель, определяющий изменение коэффициента наклона сигмоподобной функции; KP - соответствующий кинематический параметр; Km - коэффициент, определяющий значение коэффициента наклона сигмоподобной функции после приложения силового воздействия, м.
Для установления причинно-следственных связей изменения кинематических параметров (коэффициентов выражений (1), (3), (4)) от силовых воздействий (перекладок руля, изменения частоты вращения движителя) по выражениям (2) в работе [4] предлагается единообразный подход на основе сигмоподобной функции:
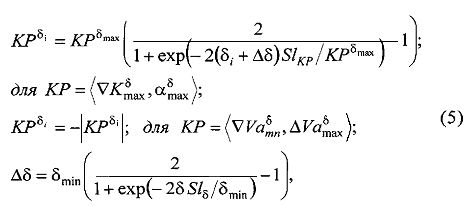
где Sl - коэффициенты, соответствующие углу наклона аппроксимирующей функции в окрестности незначительных по величине перекладок руля; min - индекс, соответствующий наименьшему значению соответствующего параметра.
Недостатком рассмотренного способа задания траектории движения судна (прототипа) является то, что в способе не учитываются изменения радиусов кривизны выражений (3), в зависимости от различий в силовых воздействиях.
Целью предлагаемого способа задания траектории и режимов движения судна является повышение безопасности судовождения в стесненных, портовых водах.
Для достижения указанной цели в способе задания траектории и режимов движения судна, заключающемся в том, что траектория движения представляется сигмоподобными функциями с изменяемыми (переменными) коэффициентами кривизны, задаваемыми выражениями:
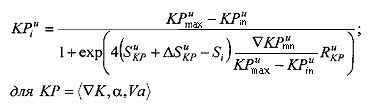
которые аппроксимируют градиенты и изменения компонентов вектора перемещения точки управления судна (курс, скорость и угол дрейфа) в зависимости от пройденного судном расстояния по траектории, согласно изобретению в систему аппроксимирующих сигмоподобных выражений подставляется сумма экспоненциальных зависимостей, см. фиг. 5:
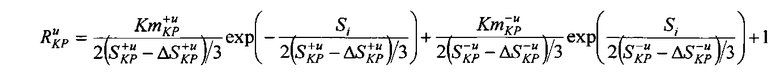
это позволяет учитывать изменения кинематических параметров движения судна вследствие изменения величины силового воздействия, рассчитываемого по выражению:
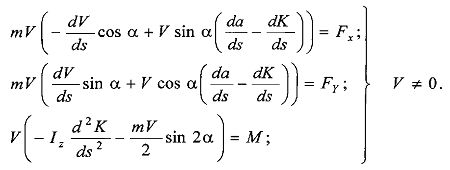
Технический результат предлагаемого изобретения заключается в детализации принципов аппроксимации кинематических параметров движения судна вследствие различий в силовых воздействиях и основывается на принципах выполнения маневров судна в стесненных и портовых водах и вариантах получения итоговой кривой (траектории движения).
Технический результат обеспечивается тем, что траектория и режимы движения судна представляется сигмоподобными функциями с изменяемыми (переменными) коэффициентами кривизны, задаваемыми выражениями:
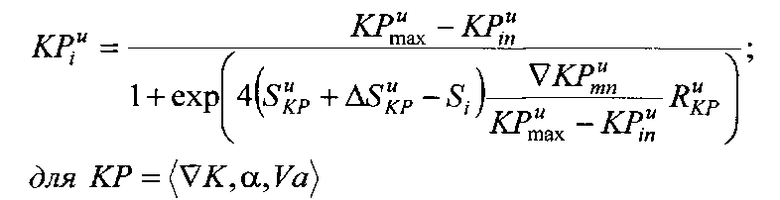
эти выражения аппроксимируют градиенты и изменения компонентов вектора перемещения точки управления судна (курс, скорость и угол дрейфа) в зависимости от пройденного судном расстояния по траектории, причем в аппроксимирующих выражениях радиус кривизны задается суммой экспоненциальных зависимостей:
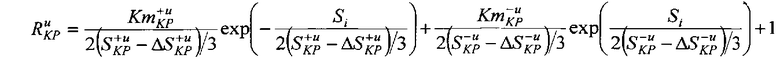
это позволяет учитывать изменения кинематических параметров движения судна и их градиентов вследствие изменения величины силового воздействия, где: KP - соответствующий кинематический параметр; K - истинный курс, град; i - индекс текущего значения; S - пройденное расстояние, м; Δ, ∇ - знаки приращений и градиентов соответствующих KP; α - угол дрейфа, град; Va - скорость относительно грунта, м/с; max - индекс максимальной величины KP при силовом воздействии; in - индекс начального значения соответствующего KP; Su - расстояние до точки перегиба сигмоподобной функции, м; ΔSu - поправка, учитывающая смещение функции из начальных условий маневра, м; mn - индекс значения KP, в средней точке переходного периода маневра; R - множитель, определяющий изменение коэффициента наклона сигмоподобной функции; Km - коэффициент, определяющий значение коэффициента наклона сигмоподобной функции после приложения силового воздействия, м.
Сущность изобретения состоит в том, что для решения поставленной задачи коэффициент кривизны сигмоподобной функции в выражении (3) задается в зависимости от различий в силовых воздействиях.
Для учета изменений в кинематических параметрах движения судна вследствие силового воздействия (типовые маневры судна: циркуляция и разгон) используются выражения (2) с коэффициентом кривизны, получаемым по выражению (4).
Для учета изменений в кинематических параметрах движения судна вследствие изменения величины силового воздействия (в практическом судовождении маневры одерживание и пассивное торможение) применяются аппроксимирующие выражения (2) с коэффициентами кривизны, соответствующими сумме экспоненциальных выражений.
Для учета изменений в кинематических параметрах движения вследствие изменения направления силового воздействия применяется сумма выражений (2) с коэффициентами кривизны, получаемыми по выражению (4), причем каждое аппроксимирующее выражение (2), соответствующее силовому воздействию (например, перекладке руля), смещается по траектории в точки изменения направлений силовых воздействий, а количество суммируемых выражений (аппроксимирующих выражений) соответствует общему количеству перекладок руля (числу смены направлений силового воздействия).
Заявленное изобретение отличается от прототипа тем, что радиус кривизны выражений, аппроксимирующих кинематические параметры движения, задается суммой экспоненциальных зависимостей, что позволяет точнее задавать траекторию и режимы движения судна.
Сущность изобретения поясняется графическими материалами, где показаны:
Фиг. 1. Аппроксимация градиента курса судна на циркуляции: 1 - экспериментальные данные; 2 - аппроксимация сигмоподобной функцией с переменным множителем R по выражению (4); 3 - установившийся период маневра; 4 - силовое воздействие (точка перекладки руля).
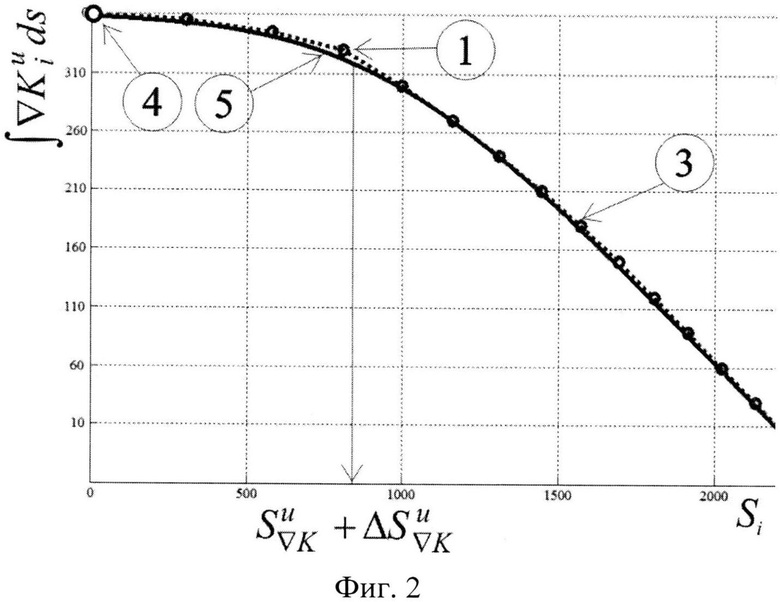
Фиг. 2. Аппроксимация курса судна на циркуляции: 1 - экспериментальные данные; 3 - установившийся период маневра; 4 - силовое воздействие (точка перекладки руля); 5 - результаты аппроксимации.
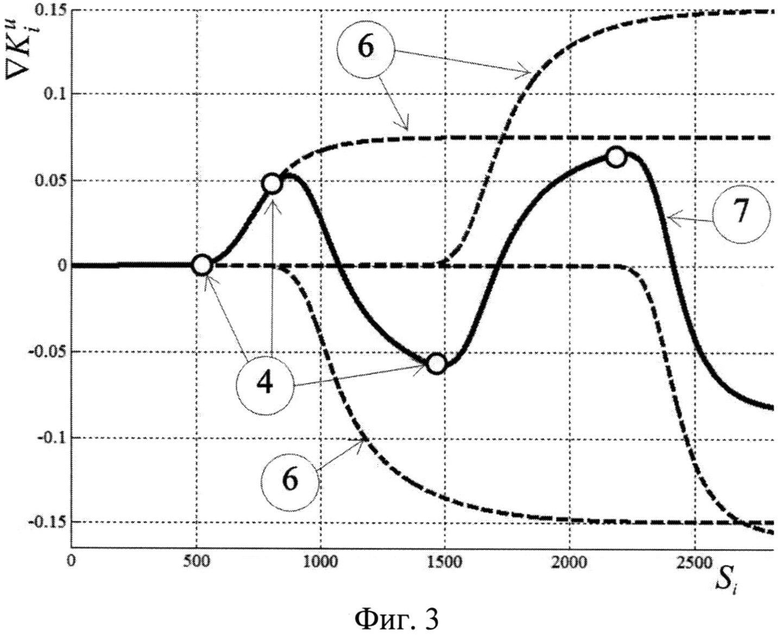
Фиг. 3. Изменение градиента курса судна при маневре «Зиг-Заг»: 4 - силовое воздействие (точка перекладки руля); 6 - аппроксимация градиента курса при различных перекладках руля; 7 - модель градиента курса при маневре «Зиг-Заг».
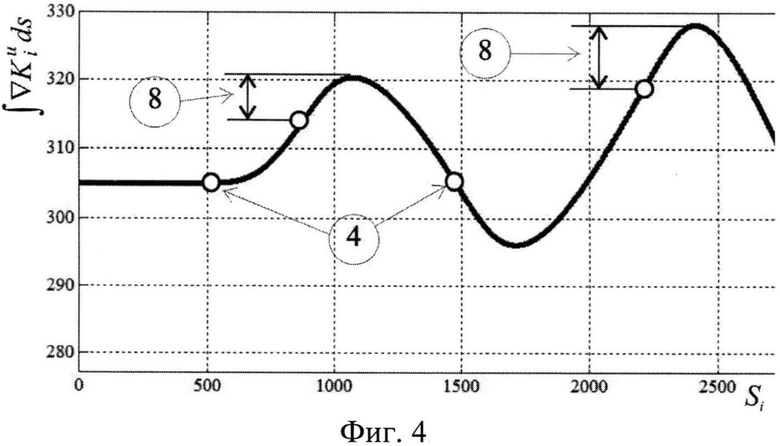
Фиг. 4. Изменение курса судна при маневре «Зиг-Заг»: 4 - силовое воздействие (точка перекладки руля); 8 - угол зарыскивания.
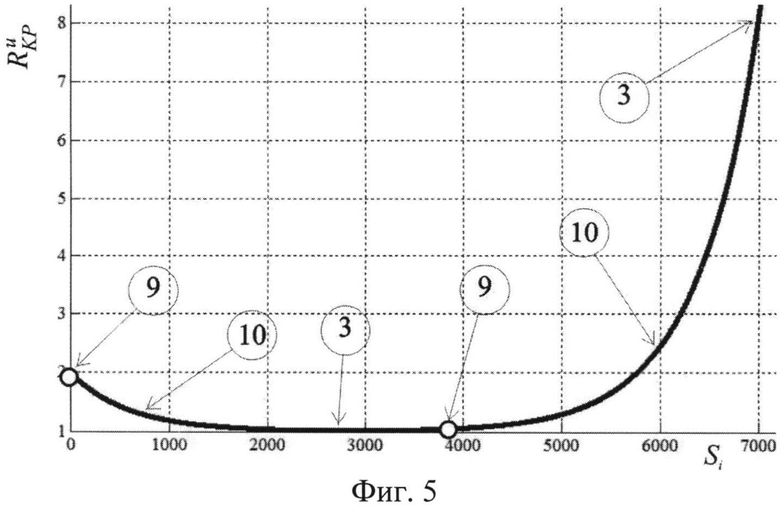
Фиг. 5. Изменение множителя R (коэффициента кривизны) по сумме экспоненциальных выражений: 3 - установившийся период маневра; 9 - точка изменения величины силового воздействия; 10 - изменение множителя R на неустановившемся периоде маневра.
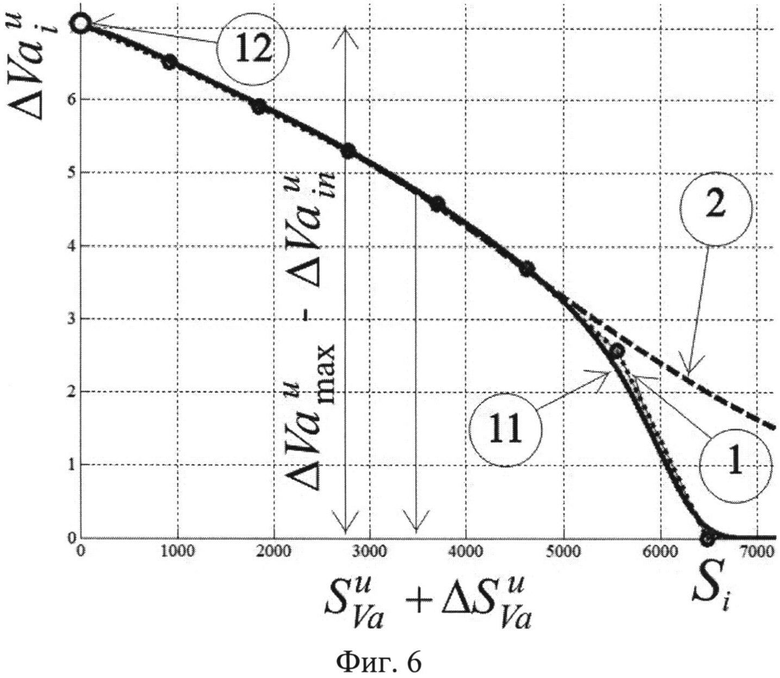
Фиг. 6. Изменение скорости судна при пассивном торможении: 1 - экспериментальные данные; 2 - аппроксимация сигмоподобной функцией с переменным множителем R по выражению (4); 11 - результаты аппроксимации выражением (3) с множителем R по сумме экспоненциальных выражений; 12 - точка уменьшения величины силового воздействия (остановки главного движителя).
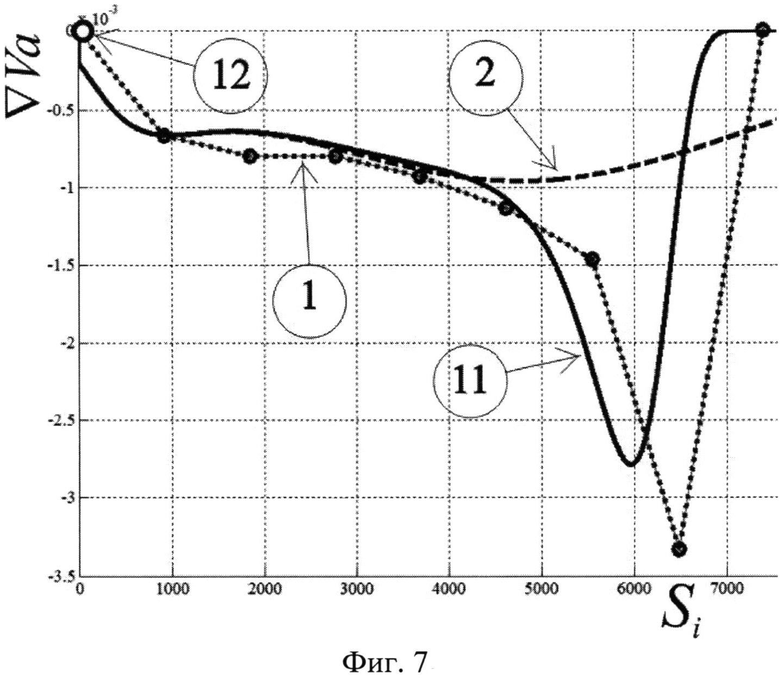
Фиг. 7. Изменение градиента скорости судна при пассивном торможении: 1 - экспериментальные данные; 2 - аппроксимация сигмоподобной функцией с переменным множителем R по выражению (4); 11 - результаты аппроксимации выражением (3) с множителем R по сумме экспоненциальных выражений; 12 - точка уменьшения величины силового воздействия (остановки главного движителя).
Фиг. 6, 7 демонстрируют сравнительное моделирование изменения кинематического параметра скорость судна и его градиента вследствие уменьшения величины силового воздействия (уменьшения оборотов главного движителя). По оси ординат указаны: на фиг. 6 - изменение скорости судна, на фиг. 7 - градиент скорости судна. По осям абсцисс - расстояние, пройденное судном по траектории. Пунктирная линия 1 показывает экспериментальные данные, полученные при «пассивном» торможении судна. Пунктирной линией 2 показаны результаты моделирования с использованием аппроксимирующих выражений (3) и переменных коэффициентов кривизны, полученных по сумме экспоненциальных выражений. Сплошная линия 11 соответствует результатам математического моделирования по аппроксимирующим выражениям (3) к переменными коэффициентами кривизны по выражениям (4). Как видно из фиг. 6, 7, использование коэффициента кривизны, полученного по сумме экспоненциальных выражений, позволяет точнее моделировать изменение кинематического параметра скорость судна и его градиента при уменьшении величины силового воздействия (уменьшения оборотов главного движителя).
Положительный эффект предлагаемого изобретения заключается в том, что в отличие от других известных аналогичных решений учтены требования, налагаемые на свойства кривых, используемых при аппроксимации движения:
- координаты точек на траектории и их изменение лежат в пределах физических ограничений маневрирования, учитывающих возможность торможения/разгона или смены направления движения;
- допустимая траектория учитывает динамику судна и исполнительных устройств (винт, перо руля), т.е. дважды непрерывно-дифференцируема;
- учтены ограничения на максимальную кривизну траектории, соответствующую предельным перекладкам руля; максимальной мощности движителя и подруливающего устройства; упору, создаваемому буксирами;
- траектории отхода/подхода судна от/к причалу, в общем случае, направленная от/к причалу задается углом дрейфа, курсом и режимами их изменений.
Использование предлагаемого изобретения повысит качество проработки маршрута судна, безопасность и эффективность выполнения маневров в стесненных водах.
Источники информации
1. Вагущенко Л.Л., Цымбал Н.Н. Системы автоматического управления движением судна.- Одесса: Латстар, 2002. - 310 с. (аналог).
2. Васьков А.А. Формирование траектории движения судна // Изв. Вузов. Сев. -Кавказ. регион. Техн. Науки. Спецвып. Проблемы водного транспорта. 2004. Ч. 1. - С. 14-16. (аналог).
3. Довгоброд Г.М. Использование параметрической аппроксимации при планировании траекторий движения аппаратов // Изв. ВУЗов. Приборостроение. 2009. - Т. 52, №9. - С. 11-17. (аналог).
4. Мироненко А.А. Модель программного движения судна в стесненных водах // Мехатроника, автоматизация, управление. 2013, №. 2. - С. 65-70. (прототип).
5. Mironenko A. Formalization of navigational environment and vessel′s motion // Proceedings of the 1 st International Conference of Black Sea Association of Maritime Institutions (BSAMI) - Actual problems of marine shipping. Novorossiysk, Russia 25-27 June 2013. pp. 26-34 (прототип).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АВТОМАТИЧЕСКОЙ ПРОВОДКИ СУДНА | 2021 |
|
RU2759068C1 |
| Способ отслеживания запланированного маршрута морского подвижного объекта | 2018 |
|
RU2703338C1 |
| СПОСОБ УПРАВЛЕНИЯ ПРОГРАММНЫМИ ДВИЖЕНИЯМИ СУДНА ПО ТРАЕКТОРИИ | 2015 |
|
RU2596202C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ТРАЕКТОРИИ ПЕРЕВОДА СУДНА НА НОВЫЙ КУРС | 2012 |
|
RU2491509C1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ ПРОВОДКИ СУДНА | 2012 |
|
RU2501708C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ТРАЕКТОРИИ ПЕРЕВОДА СУДНА НА ПАРАЛЛЕЛЬНЫЙ КУРС С СОБЛЮДЕНИЕМ ОГРАНИЧЕНИЙ НА ДИАПАЗОН ИЗМЕНЕНИЯ СИГНАЛА УПРАВЛЕНИЯ | 2012 |
|
RU2515006C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГИДРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДВИЖЕНИЯ СУДНА | 2010 |
|
RU2442718C1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ ПРОВОДКИ СУДОВ | 2005 |
|
RU2277495C1 |
| Способ управления движением судна при маневре | 1987 |
|
SU1633378A1 |
| Способ управления движением судна | 1982 |
|
SU1066896A1 |
Изобретение относится к области судовождения, а именно к системам автоматического управления движением судна. Для задания траектории и режима движения судна представляют сигмоподобные функции с изменяемыми коэффициентами кривизны и задаваемыми выражениями. Сигмоподобные функции аппроксимируют градиенты и изменения компонентов вектора, перемещения точки управления судна в зависимости от пройденного судном расстояния по траектории. В аппроксимирующих выражениях радиус кривизны задается суммой экспоненциальных зависимостей и позволяет учитывать изменения кинематических параметров движения судна и их градиентов вследствие изменения величины силового воздействия. Достигается повышение безопасности судовождения в стесненных портовых водах. 7 ил.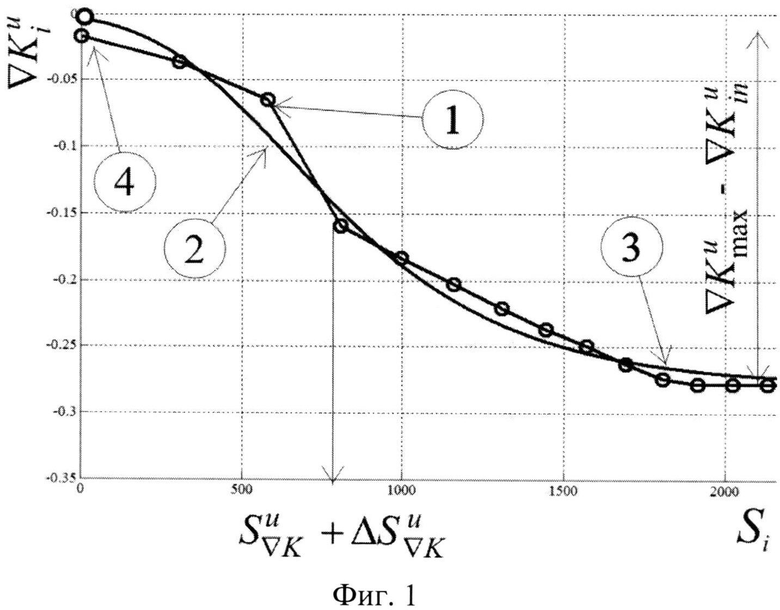
Способ задания траектории и режимов движения судна, заключающийся в том, что траектория движения судна представляется сигмоподобными функциями с изменяемыми (переменными) коэффициентами кривизны, задаваемыми выражениями:
KP
u i
= KP
u max
-KP
u in
/1 + exp (4(S
u KP
+ ∆S
u KP
- S
i
))/((∇KP
u mn
/KP
u max
- KP
u in
) R
u KP
); (1)
для KP = ‹∇K, α, Vα›,
которые аппроксимируют градиенты и изменения компонентов вектора перемещения точки управления судна (курс, скорость и угол дрейфа) в зависимости от пройденного судном расстояния по траектории, отличающийся тем, что в аппроксимирующих выражениях радиус кривизны задается суммой экспоненциальных зависимостей:
R
u KP
= (Km
+u KP
/((2(S
+u KP
- ∆S
+u KP
))/3))exp(-(S
i
/((2(S
+u KP
- ∆S
+u KP
))/3)) +
+ (Km
-u KP
/((2(S
-u KP
- ∆S
-u KP
)/3))exp(S
i
/((2(S
-u KP
- ∆S
-u KP
))/3))+1 (2)
что позволяет учитывать изменения кинематических параметров движения судна и их градиентов вследствие изменения величины силового воздействия, где KP - соответствующий кинематический параметр; К - истинный курс, град; i - индекс текущего значения; S - пройденное расстояние, м; ∆, ∇ - знаки приращений и градиентов, соответствующих KP; α - угол дрейфа, град; Va - скорость относительно грунта, м/с; max - индекс максимальной величины KP при силовом воздействии; in - индекс начального значения соответствующего KP; Su - расстояние до точки перегиба сигмоподобной функции, м; ∆Su - поправка, учитывающая смещение функции из начальных условий маневра, м; mn - индекс значения KP, в средней точке переходного периода маневра; R - множитель, определяющий изменение коэффициента наклона сигмоподобной функции; Km - коэффициент, определяющий значение коэффициента наклона сигмоподобной функции после приложения силового воздействия, м.
| СПОСОБ АВТОМАТИЧЕСКОЙ ПРОВОДКИ СУДНА | 2012 |
|
RU2501708C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГИДРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДВИЖЕНИЯ СУДНА | 2010 |
|
RU2442718C1 |
| Устройство для сборки и формования покрышек пневматических шин | 1987 |
|
SU1511137A2 |
Авторы
Даты
2015-05-10—Публикация
2014-02-18—Подача