Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области информационной безопасности телекоммуникационных систем, в частности может быть использовано в криптографических системах с открытым распределением ключей для формирования общего ключа шифрования и аутентификации удаленных абонентов.
Известен способ формирования ключа шифрования у абонентов конфиденциального сеанса связи, включающий преобразование случайного многоразрядного двоичного числа, называемого временной отметкой и определяемого по моменту времени, например по моменту времени начала сеанса связи, по заранее оговоренному криптографическому алгоритму под управлением секретного ключа, которым абоненты обмениваются предварительно по защищенному каналу связи [Иванов М.А. Криптография. М.: КУДИЦ-ОБРАЗ, 2001, - с.197-198]. Недостатком этого способа формирования ключа шифрования является необходимость передачи секретного ключа по защищенному каналу связи, который является дорогостоящим элементом систем секретной связи.
Также известен способ формирования ключей шифрования путем многократного последовательного модифицирования секретного ключа в соответствии с алгоритмом одностороннего преобразования [Иванов М.А. Криптография. М.: КУДИЦ-ОБРАЗ, 2001, - с.205]. Недостатком известного способа формирования ключа шифрования является то, что при компрометации текущего ключа компрометируются все последующие ключи шифрования.
Также известен способ формирования общего секретного ключа двух удаленных абонентов с использованием открытых каналов связи, описанный в книге [Молдовян Н.А., Молдовян А.А., Еремеев М.А. Криптография: от примитивов к синтезу алгоритмов. - СПб, БХВ-Петербург, 2004, - 436 с. - см. с.408 и с.412-413]. Способ-аналог заключается в выполнении следующей последовательности действий:
1. У первого абонента формируют открытый ключ (ОК) в виде двух многоразрядных двоичных чисел (МДЧ) первого n и второго α (здесь и далее по тексту описания под МДЧ следует понимать электромагнитный сигнал в двоичной цифровой форме, в котором общее число битов и порядок их следования отражает некоторое двоичное число1) (1 Толкование терминов, используемых в описании, приведено в Приложении 1), для чего
генерируют первый m и второй q вспомогательные простые множители в виде МДЧ, а первое МДЧ n ОК вычисляют как произведение n=mq;
вычисляют функцию Эйлера φ(n) от первого МДЧ n ОК по формуле φ(n)=(m-1)(q-1);
генерируют второе МДЧ α ОК, являющееся взаимно простым со значением функции Эйлера φ(n) (пара МДЧ n и α образует ОК);
вычисляют секретное МДЧ γ=α-1 mod φ(n), при котором выполняется условие γα mod φ(n)=1.
2. Передают ОК, т.е. пару МДЧ p и α, второму абоненту, например, по телекоммуникационным сетям.
3. У второго абонента генерируют секретный ключ К и формируют образ секретного ключа в виде МДЧ r, путем его вычисления по формуле r=Кα mod n.
4. Передают получателю информации образ ключа r.
5. У получателя информации вычисляют ключ шифрования T по формуле К=rγ mod n.
При таком способе оказывается возможным открытое распределение ключей, т.е. без использования защищенных каналов связи, что снижает затраты на обеспечение информационной безопасности.
Однако известный способ имеет недостаток - относительно большое время, необходимое для формирования общего секретного ключа шифрования, что связано с необходимостью выполнения большого объема вычислений у получателя информации, обусловленного большой разрядностью МДЧ γ примерно равной разрядности первого МДЧ n ОК, которую для достижения требуемой криптостойкости выбирают в пределах 1024-2048 бит.
Также известен способ формирования ключа шифрования, предложенный в патенте Российской Федерации №2286022 и заключающийся в следующей последовательности действий:
у получателя информации (первого абонента) формируют ОК в виде первого р и второго α МДЧ, разрядность каждого из которых выбирается равной не менее 1024 бит.
передают ОК отправителю информации (второму абоненту),
у отправителя информации формируют образ ключа шифрования в виде МДЧ r и передают его получателю информации;
у получателя информации по образу ключа шифрования r вычисляют ключ шифрования в виде МДЧ К.
Недостатком известного способа является относительно большой размер ОК, который равен суммарной разрядности чисел α и р.
Наиболее близким по своей технической сущности к заявленному является известный способ формирования общего секретного ключа шифрования двух удаленных абонентов с использованием открытых каналов связи, описанный в книге [Молдовян Н.А., Молдовян А.А. Введение в криптосистемы с открытым ключом. - СПб, БХВ-Петербург, 2005, - 286 с. - см. с.104-105]. Ближайший способ-аналог (прототип) включает следующие действия:
1. Генерируют конечную группу Г, включающую множество целых чисел {1, 2, …, р-1}, над которыми в качестве групповой операции задана операция умножения по модулю р, где р - простое МДЧ, имеющее разрядность не менее 1024 бит. Для этого генерируют простое МДЧ p требуемой разрядности.
2. Формируют общий для обоих абонентов элемент Z конечной группы Г, представляющий собой МДЧ Z∈{1, 2, …, p-1}, относящееся к показателю р-1 по модулю р.
3. У первого абонента генерируют ОК в виде элемента Y1 конечной группы Г, для чего генерируют его личный секретный ключ в виде случайно сгенерированного МДЧ х1 и вычисляют Y1 по формуле  .
.
4. Открытый ключ Y1 передают по открытому каналу второму абоненту.
5. У второго абонента генерируют ОК в виде элемента Y2 конечной группы Г, для чего генерируют его личный секретный ключ в виде МДЧ х2 и вычисляют Y2 по формуле 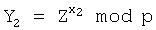 .
.
6. Открытый ключ Y2 передают по открытому каналу первому абоненту.
7. У первого абонента формируют общий секретный ключ в виде элемента К конечной группы Г путем его вычисления по формуле 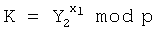 .
.
8. У второго абонента формируют общий секретный ключ в виде элемента К конечной группы Г путем его вычисления по формуле 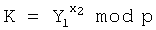 .
.
Недостатком ближайшего аналога является относительно высокая сложность процедуры формирования общего секретного ключа шифрования К, связанная с тем, что общий секретный ключ шифрования К вычисляют путем возведения по модулю МДЧ p ОК одного абонента в большую целочисленную степень, равную личному секретному ключу другого абонента.
Целью изобретения является разработка способа формирования ключа шифрования, обеспечивающего уменьшение времени, необходимого для формирования ключа шифрования за счет снижения объема вычислений по формированию ключа шифрования при сохранении требуемой его криптостойкости.
Кроме того, заявленное техническое решение расширяет арсенал средств данного назначения.
Поставленная цель достигается тем, что в известном способе формирования общего секретного ключа двух удаленных абонентов, заключающемся в том, что генерируют конечную группу Г, формируют общий элемент Z конечной группы Г, у первого абонента генерируют его личный секретный ключ и его ОК в виде элемента Y1 конечной группы Г, передают ОК первого абонента Y1 второму абоненту, у второго абонента генерируют его личный секретный ключ и его ОК в виде элемента Y2 конечной группы Г, передают ОК второго абонента Y2 первому абоненту, у первого абонента формируют общий секретный ключ в виде элемента К конечной группы Г в зависимости от ОК второго абонента Y2 и личного секретного ключа первого абонента, а у второго абонента формируют общий секретный ключ в виде элемента К конечной группы Г в зависимости от OK первого абонента Y1 и личного секретного ключа второго абонента, новым в заявленном изобретении является то, что формируют дополнительный общий элемент G конечной группы Г, такой что выполняется неравенство 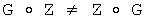 , у первого абонента генерируют его личный секретный ключ в виде двух многоразрядных двоичных чисел х1 и w1 и формируют его OK Y1 путем генерации элементов X1 и W1 конечной группы Г по формулам
, у первого абонента генерируют его личный секретный ключ в виде двух многоразрядных двоичных чисел х1 и w1 и формируют его OK Y1 путем генерации элементов X1 и W1 конечной группы Г по формулам 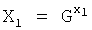 и
и 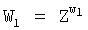 и генерации открытого ключа Y1 по формуле
и генерации открытого ключа Y1 по формуле 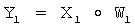 , где знак
, где знак  обозначает групповую операцию конечной группы Г, у второго абонента генерируют его личный секретный ключ в виде двух многоразрядных двоичных чисел x1 и w2 и формируют ОК Y2 второго абонента путем генерации элементов Х2 и W2 конечной группы Г по формулам
обозначает групповую операцию конечной группы Г, у второго абонента генерируют его личный секретный ключ в виде двух многоразрядных двоичных чисел x1 и w2 и формируют ОК Y2 второго абонента путем генерации элементов Х2 и W2 конечной группы Г по формулам 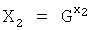 и
и  и генерации открытого ключа Y2 по формуле
и генерации открытого ключа Y2 по формуле 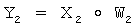 , причем в качестве конечной группы Г используют некоммутативную конечную группу.
, причем в качестве конечной группы Г используют некоммутативную конечную группу.
Некоммутативную конечную группу Г можно сформировать, используя способ задания мультипликативных групп векторов, предложенный в работе [Молдовяну П.А., Дернова Е.С., Молдовян Д.Н. Синтез конечных расширенных полей для криптографических приложений // Вопросы защиты информации. 2008. №3(82). С.2-7]. Примеры задания некоммутативных групп векторов с операцией умножения векторов, обладающей относительно низкой сложностью, приведены ниже. Благодаря сравнительно низкой сложности операции векторного умножения и возможности ее эффективного распараллеливания обеспечивается существенное уменьшение времени формирования общего секретного ключа двух удаленных абонентов.
Новым является также и то, что у первого абонента формируют общий секретный ключ К по формуле 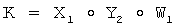 , где
, где 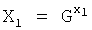 и
и 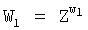 , у второго абонента формируют общий секретный ключ К по формуле
, у второго абонента формируют общий секретный ключ К по формуле 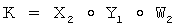 , где
, где 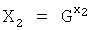 и
и  .
.
Благодаря использованию только двух групповых операций при формировании общего секретного ключа К обеспечивается дальнейшее уменьшение времени, затрачиваемого на эту процедуру.
Новым является также и то, что в качестве некоммутативной конечной группы Г используют некоммутативную конечную группу четырехмерных векторов.
Использование некоммутативной конечной группы четырехмерных векторов упрощает программную реализацию заявленного способа формирования общего секретного ключа двух удаленных абонентов.
Новым является также и то, что в качестве некоммутативной конечной группы Г используют некоммутативную конечную группу шестимерных векторов.
Использование некоммутативной конечной группы шестимерных векторов расширяет варианты реализации заявленного способа, обеспечивающие существенное уменьшение времени генерации общего секретного ключа двух удаленных абонентов.
Новым является также и то, что в качестве некоммутативной конечной группы Г используют некоммутативную конечную группу матриц.
Использование некоммутативных конечных групп матриц расширяет арсенал средств программной и аппаратной реализации заявленного способа формирования общего секретного ключа двух удаленных абонентов.
Изобретательский замысел заявленного нового технического решения состоит в применении некоммутативных конечных групп, в которых в общем случае результат выполнения групповой операции зависит от порядка расположения элементов группы, над которыми выполняется групповая операция. Благодаря этому уравнения вида 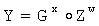 с неизвестными значениями МДЧ х и w, в которых элементы G и Z некоммутативной конечной группы Г имеют достаточно большое простое значение порядка и удовлетворяют условию
с неизвестными значениями МДЧ х и w, в которых элементы G и Z некоммутативной конечной группы Г имеют достаточно большое простое значение порядка и удовлетворяют условию 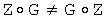 , являются трудно решаемыми. Это позволяет формировать OK Y абонента в зависимости от его секретного ключа, представляющего пару МДЧ х и w, по формуле
, являются трудно решаемыми. Это позволяет формировать OK Y абонента в зависимости от его секретного ключа, представляющего пару МДЧ х и w, по формуле 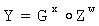 обеспечивая достаточно высокую криптографическую стойкость открытого ключа. По известным значениям Y, G и Z вычислительно неосуществимо нахождение пары МДЧ (х, w), если значение порядка элементов G и Z равно простому МДЧ разрядность которого равна 80 бит и более. При этом каждая пара удаленных абонентов, формирующих свои ОК по формуле
обеспечивая достаточно высокую криптографическую стойкость открытого ключа. По известным значениям Y, G и Z вычислительно неосуществимо нахождение пары МДЧ (х, w), если значение порядка элементов G и Z равно простому МДЧ разрядность которого равна 80 бит и более. При этом каждая пара удаленных абонентов, формирующих свои ОК по формуле 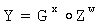 может сформировать один и тот же элемент К группы Г, который может служить в качестве общего секретного ключа, без того, чтобы обмениваться своими личными секретными ключами.
может сформировать один и тот же элемент К группы Г, который может служить в качестве общего секретного ключа, без того, чтобы обмениваться своими личными секретными ключами.
Это можно реализовать следующим путем. Каждый из двух удаленных абонентов генерирует свой секретный ключ в виде пары случайных МДЧ (х, w) и формирует свой ОК Y по формуле 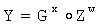 ,
,
Действительно, первый абонент генерирует свой личный секретный ключ в виде пары МДЧ (х1, w1) и свой ОК 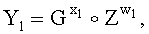 второй абонент генерирует свой личный секретный ключ в виде пары МДЧ (х2, w2) и свой ОК
второй абонент генерирует свой личный секретный ключ в виде пары МДЧ (х2, w2) и свой ОК 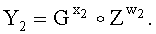 По открытому каналу связи OK Y1 первого абонента передается второму абоненту, а ОК Y2 второго абонента передается первому абоненту. Первый абонент вычисляет общий секретный ключ по формуле
По открытому каналу связи OK Y1 первого абонента передается второму абоненту, а ОК Y2 второго абонента передается первому абоненту. Первый абонент вычисляет общий секретный ключ по формуле
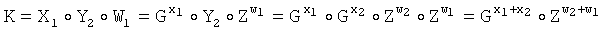 ,
,
а второй - по формуле
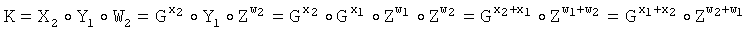 .
.
Сравнение правых частей последних двух выражений показывает, что первый и второй абоненты формируют одно и то же секретное значение К. В силу некоммутативности группы Г ее элемент К не может быть вычислен, используя значения открытых ключей Y1 и Y2, поскольку из условия 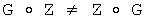 следует
следует 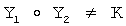 и
и 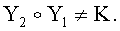 Это дает возможность использовать K в качестве общего секретного ключа двух удаленных абонентов.
Это дает возможность использовать K в качестве общего секретного ключа двух удаленных абонентов.
Рассмотрим примеры генерации некоммутативных конечных трупп и конкретные примеры реализации заявленного способа формирования общего секретного ключа двух удаленных абонентов.
Пример 1: Генерация некоммутативных конечных групп векторов.
Рассмотрим упорядоченные наборы МДЧ {а1, а2, …, am), каждое из которых не превосходит некоторого выбранного простого МДЧ р. Такой набор называется вектором, а МДЧ а1, a2, …, am - координатами вектора, значение m≥2 - это размерность вектора, равная числу координат в векторе. Координаты представляют собой МДЧ, принадлежащие множеству МДЧ {1, 2, …, р-1}, где p - заданное простое МДЧ, над которыми определены операции сложения и умножения по модулю p. Другой формой записи векторов является его запись в виде суммы одномерных векторов, называемых компонентами вектора, каждый из которых представляет собой координату вектора с приписанным к ней формальным базисным вектором. Обозначим формальные базисные вектора строчными латинскими буквами е, i, j и т.д. В последней записи очередность записи компонентов вектора не имеет значения, например, вектора Z1=523425е+3676785i+53453453j и Z2=3676785i+523425е+53453453j, где е, i, j - формальные базисные вектора, в которых координатами являются МДЧ, рассматриваются как равные, т.е. Z1=Z2. Операция умножения векторов определяется как перемножение всех компонентов векторов-сомножителей, с учетом того, что возникающие при этом произведения формальных базисных векторов, заменяются по некоторой специфицированной таблице одним базисным вектором или однокомпонентным вектором, после чего все координаты, приписанные одному и тому же базисному вектору, складываются по модулю р. Указанная таблица умножения базисных векторов (ТУБВ) для случая векторов размерности m=3 имеет, например, вид таблицы 1, которая определяет следующее правило подстановки базисных векторов:
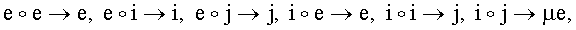
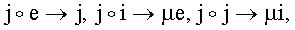
где µ - заданное МДЧ, принадлежащее множеству МДЧ {1, 2, …, р-1}.
Например, пусть Z1=а1е+b1i+c1j и Z2=а2е+b2i+c2j, тогда операция умножения векторов Z1 и Z2 (обозначим ее знаком «∘») выполняется следующим образом:
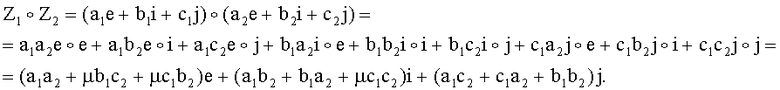

Поскольку каждая координата вектора принимает не более р различных значений, то множество векторов для конечного значения размерности является конечным. При соответствующем задании ТУБВ операция умножения векторов будет обладать свойством ассоциативности. Тогда все обратимые вектора, т.е. вектора, для которых существуют обратные значения, будут образовывать конечную группу. При этом, если ассоциативная операция умножения векторов будет некоммутативной, то сгенерированная группа векторов будет некоммутативной.
Некоммутативная конечная группа четырехмерных векторов вида Z=ае+bi+сj+dk может быть сгенерирована путем выбора простого МДЧ р и выбора ТУБВ, представленной таблицей 2. Единичным элементом данной некоммутативной конечной группы является вектор Е=1е+0i+0j+0k=(1, 0, 0, 0). Генерация различных вариантов некоммутативных конечных групп четырехмерных векторов осуществляется генерацией различных значений простого МДЧ р и различных конкретных значений коэффициентов µ и ε.
Некоммутативная конечная группа шестимерных векторов вида Z=ае+bi+сj+dk+gu+hv может быть сгенерирована путем выбора простого МДЧ p и выбора ТУБВ, представленной таблицей 3. Единичным элементом данной некоммутативной конечной группы является вектор Е=1е+0i+0j+0k+0u+0v=(1, 0, 0, 0, 0, 0). Генерация различных вариантов некоммутативных конечных групп шестимерных векторов осуществляется генерацией различных значений простого МДЧ и различных конкретных значений коэффициента µ.

В рассматриваемых ниже частных вариантах реализации заявленного способа генерируется некоммутативная конечная группа Г четырехмерных векторов (пример 2) и некоммутативная конечная группа Г шестимерных векторов (пример 3). При этом использовано простое МДЧ р с искусственно уменьшенной разрядностью для более компактной записи примеров. В реальных применениях разрядность МДЧ р следует выбирать равной 80 бит и более для обеспечения достаточной криптостойкости заявленного способа формирования общего секретного ключа двух удаленных абонентов.

По аналогии с приводимыми ниже примерами могут быть реализованы различные варианты заявленного способа, в котором используются некоммутативные конечные группы шестимерных векторов, некоммутативные конечные группы векторов других размерностей, а также некоммутативные конечные группы другой природы, например некоммутативные конечные группы невырожденных матриц с групповой операцией матричного умножения.
Пример 2: Реализация заявленного способа по пп.1, 2 и 3 формулы изобретения (ФИ).
1. Генерируют некоммутативную конечную группу Г в виде некоммутативной конечной группы четырехмерных векторов, для чего
1.1) генерируют простое МДЧ р=96472531979077;
1.2) генерируют ТУБВ в виде таблицы 2, где ε=17 и µ=101.
2. Формируют общий элемент Z конечной группы Г в виде вектора Z=(66775182990061, 57229319875485, 73063284932254, 90523737617977), имеющего порядок q=48236265989539.
3. Формируют дополнительный общий элемент G конечной группы Г в виде вектора
G=(67768610658596, 11099045903591, 90612186435040, 64725430944719), имеющего порядок q=48236265989539, такого, что выполняется условие 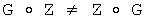 :
:
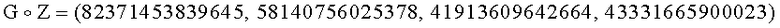
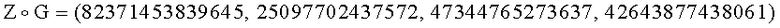
4. У первого абонента генерируют ОК в виде элемента Y1 конечной группы Г, для чего
4.1) генерируют личный секретный ключ первого абонента в виде двух МДЧ x1 и w1: x1=291530213 и w1=184575638;
4.2) генерируют вспомогательные элементы Х1 и W1 конечной группы Г, вычисляемые по формулам 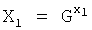 и
и 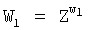 :
:
X1=(84502868072367, 45061080384352, 88410340821553, 6796543925148) и
W1=(83201061049747, 56946323430001, 94408459431543, 56465842605117).
4.3) генерируют OK Y1 по формуле 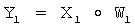 :
:
Y1=(5260066628221, 28021131636428, 8616109554186, 9125388823068)
5. У второго абонента генерируют OK в виде элемента Y2 конечной группы Г, для чего
5.1) генерируют личный секретный ключ первого абонента в виде двух МДЧ x2 и w2: х2=3597143917 и w2=5198742547351;
5.2) генерируют вспомогательные элементы Х2 и W2 конечной группы Г, вычисляемые по формулам 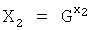 и
и 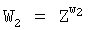 :
:
Х2=(47663039913656, 63812898287270, 22649891867007, 14607248085466) и
W2=(95381228206449, 55656910307297, 92238180220573, 72264168884538).
5.3) генерируют ОК Y2 по формуле 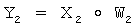 :
:
Y2=(86420244212282, 21998306006685, 25228720958331, 1637998552883).
6. Передают ОК первого абонента второму абоненту.
7. Передают ОК второго абонента первому абоненту.
8. У первого абонента формируют общий секретный ключ в виде элемента К конечной группы Г в зависимости от ОК второго абонента и личного секретного ключа первого абонента, для чего
8.1) формируют элемент R1 конечной группы Г путем выполнения групповой операции над элементом Х1 конечной группы Г и ОК Y2 второго абонента, т.е. по формуле 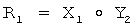 , где
, где 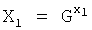 :
:
R1=(60350034043042, 52559132338546, 42094869982047, 36982368622803);
8.2) формируют общий секретный ключ двух удаленных абонентов путем выполнения групповой операции над элементами R1 и W1 конечной группы Г, т.е. по формуле 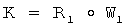 , где
, где 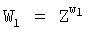 :
:
К=(17647586018660, 93791888231477, 10397382443771, 27375886739329).
9. У второго абонента формируют общий секретный ключ в виде элемента К конечной группы Г в зависимости от ОК первого абонента и личного секретного ключа второго абонента, для чего
9.1) формируют элемент R2 конечной группы Г путем выполнения групповой операции над элементом Х2 конечной группы Г и OK Y1 первого абонента, т.е. по формуле 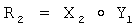 , где
, где 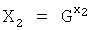 :
:
R2=(3993969809188, 73978638578996, 90701364574612, 16771893687435);
9.2) формируют общий секретный ключ путем выполнения групповой операции над элементами R2 и W2 конечной группы Г, т.е. по формуле 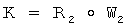 , где
, где 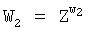 :
:
К=(17647586018660, 93791888231477, 10397382443771, 27375886739329).
В результате выполненных действий у первого и второго абонентов сформирован один и тот же секретный ключ, который в явном виде не передавался по открытому каналу. Для постороннего субъекта, перехватывающего значения открытых ключей Y1 и Y2, передаваемых по каналу связи абонентов, вычисление секретного ключа К вычислительно неосуществимо на практике при выборе достаточно большой разрядности МДЧ p. В случае некоммутативных конечных групп четырехмерных векторов заявленный способ формирования общего секретного ключа двух удаленных абонентов обеспечивает достаточную стойкость при выборе простого МДЧ p размером 80 бит и более. Одна операция умножения векторов, являющаяся групповой операцией в рассмотренных вариантах реализации заявленного способа по примеру 2, требует выполнения не более 22 операций умножения по модулю р. Уменьшение времени формирования общего секретного ключа в заявленном способе по сравнению со способами аналогами обеспечивается тем, что 1) при формировании общего секретного ключа выполняется меньшее количество групповых операций, 2) в некоммутативных группах четырехмерных векторов вычисления ведутся по простому модулю, разрядность которого примерно в 12,8 раз меньше разрядности простого модуля в способах-аналогах и 3) время выполнения операции умножения по модулю пропорционально квадрату разрядности модуля. В способе-прототипе для формирования общего секретного ключа двух удаленных абонентов используется операция возведения в степень МДЧ разрядность которого составляет не менее 160 бит. Эта операция реализуется путем выполнения 1,5·160 операций умножения по модулю 1024-битового числа. При обеспечении того же уровня криптостойкости в вариантах реализации заявленного способа по примеру 2 используется 80-битовое простое число р и при формировании общего секретного ключа двух удаленных абонентов выполняются только две операции умножения четырехмерных векторов, что требует выполнения не более 44 операций умножения по модулю 80-битового числа. В результате время формирования общего секретного ключа двух удаленных абонентов уменьшается в 12,82·1,5·160/44>800 раз по сравнению со способом-прототипом. Рассмотренные варианты реализации заявленного способа формирования общего секретного ключа двух удаленных абонентов обеспечивает уменьшение времени формирования общего секретного ключа по сравнению с ближайшим способом-аналогом даже при выборе размера МДЧ p, равного 2048 бит, что позволяет существенно повышать криптостойкость, сохраняя относительно малое время формирования общего секретного ключа (в 200 раз меньшее по сравнению со способом-прототипом).
Пример 3: Реализация заявленного способа по пп.1, 2 и 4 ФИ.
1. Генерируют некоммутативную конечную группу Г в виде некоммутативной конечной группы шестимерных векторов, для чего
1.1) генерируют простое МДЧ p=719806693;
1.2) генерируют ТУБВ в виде таблицы 3, где µ=41.
2. Формируют общий элемент Z конечной группы Г в виде вектора Z=(184287476, 503858799, 430553268, 505201319, 108610231, 426908987), имеющего порядок q=359903347.
3. Формируют дополнительный общий элемент G конечной группы Г в виде вектора
G=(650284701, 635481592, 1221589, 83103512, 164916961, 624411725), имеющего порядок q=359903347, такого, что выполняется условие 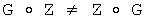 :
:
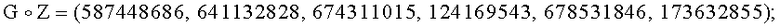
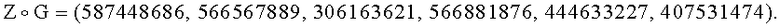
4. У первого абонента генерируют ОК в виде элемента Y1 конечной группы Г, для чего
4.1) генерируют личный секретный ключ первого абонента в виде двух МДЧ x1 и w1: x1=5215727 и w1=3147638;
4.2) генерируют вспомогательные элементы Х1 и W1 конечной группы Г, вычисляемые по формулам 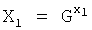 и
и 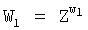 :
:
Х1=(122370970, 675677594, 424973984, 338961808, 439461946, 157973778) и
W1=(89160942, 468303175, 228602915, 22900603, 451159123, 179486629).
4.3) генерируют ОК первого абонента по формуле 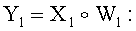
Y1=(117822156, 306068694, 660884618, 472660074, 591023716, 10960822).
5. У второго абонента генерируют ОК в виде элемента Y2 конечной группы Г, для чего
5.1) генерируют личный секретный ключ второго абонента в виде двух МДЧ x2 и w2: x2=70159139 и w2=95325137;
5.2) генерируют вспомогательные элементы Х2 и W2 конечной группы Г, вычисляемые по формулам 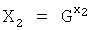 и
и  :
:
Х2=(410116946, 669208031, 416482098, 353923257, 51135937, 258553811) и
W2=(481225381, 413601702, 375271544, 650740140, 422833000, 535555006).
4.3) генерируют ОК второго абонента по формуле 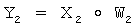 :
:
Y2=(400073232, 498454785, 99068895, 122283013, 528743046, 510797109).
6. Передают ОК первого абонента второму абоненту.
7. Передают ОК второго абонента первому абоненту.
8. У первого абонента формируют общий секретный ключ в виде элемента К конечной группы Г в зависимости от ОК второго абонента и личного секретного ключа первого абонента, для чего
8.1) формируют элемент R1 конечной группы Г путем выполнения групповой операции над элементом Х1 конечной группы Г и ОК Y2 второго абонента, т.е. путем умножения вектора X1 на вектор Y2, т.е. 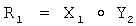 , где
, где 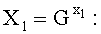
R1=(353841441, 405715910, 442902339, 590995137, 295757663, 70207590);
8.2) выполняют групповую операцию над элементами R1 и W1 конечной группы Г, т.е. умножают вектор R1 на вектор W1, т.е. 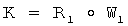 , где
, где 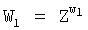 :
:
К=(20630241, 154350895, 408651245, 156804553, 29291380, 669885073).
9. У второго абонента формируют общий секретный ключ в виде элемента К конечной группы Г в зависимости от ОК первого абонента и личного секретного ключа второго абонента, для чего
9.1) формируют элемент R2 конечной группы Г путем выполнения групповой операции над элементом Х2 конечной группы Г и OK Y1 первого абонента, т.е. путем умножения вектора X2 на вектор Y1, т.е. 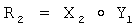 , где
, где 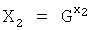 :
:
R2=(660581862, 616263706, 196498673, 626851007, 552903793, 226127732);
9.2) выполняют групповую операцию над элементами R2 и W2 конечной группы Г, т.е. умножают вектор R2, на вектор W2, т.е. 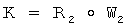 , где
, где  :
:
К=(20630241, 154350895, 408651245, 156804553, 29291380, 669885073).
В результате выполненных действий у первого и второго абонентов сформирован один и тот же секретный ключ, который в явном виде не передавался по открытому каналу. Формирование общего секретного ключа требует выполнения двух операций умножения шестимерных векторов, каждое из которых требует выполнения не более 45 операций умножения по модулю МДЧ p. Данный вариант реализации заявленного способа формирования общего секретного ключа двух удаленных абонентов обеспечивает достаточную криптостойкость при выборе простого МДЧ p размером 80 бит и более, при этом он обеспечивает уменьшение времени формирования общего секретного ключа в 12,82·1,5·160/90>400 раз по сравнению с ближайшим способом-аналогом.
Пример 4: Реализация заявленного способа по пп.1, 2 и 5 ФИ.
В качестве некоммутативной конечной группы Г можно использовать некоммутативную конечную группу матриц с операцией матричного умножения, которая является ассоциативной и некоммутативной, в качестве групповой операции. Поскольку операция умножения матриц (матричное умножение) является некоммутативной, то конечные группы матриц являются некоммутативными группами. Примеры генерация различных вариантов конечных групп матриц размера n×n, где n=2, 3, 4, 5… - натуральное число, приведены в патентах РФ №2369972 и №2369973, а также в работе [Дернова B.C., Костина А.А., Молдовяну П.А. Конечные группы матриц как примитив алгоритмов цифровой подписи // Вопросы защиты информации. 2008. №3(82). С.8-12]. При реализации заявленного способа формирования общего секретного ключа двух удаленных абонентов с использованием конечных групп матриц время формирования общего секретного ключа равно времени выполнения двух операций матричного умножения, для выполнения которых требуется осуществить не более n3 операций умножения по модулю простого числа р, размер которого для обеспечения требуемой криптостойкости выбирается равным 160/n бит. Расчет показывает, что по сравнению со способом-прототипом при использовании конечных групп матриц заявленный способ обеспечивает уменьшение времени формирования общего секретного ключа двух удаленных абонентов примерно в 2000 раз (для n=2), 700 раз (для n=3), 500 раз (для n=4), 400 раз (для n=5), 100 раз (для n=11). Значительное уменьшение времени формирования общего секретного ключа двух удаленных абонентов обеспечивается применением матриц размером n×n при n=2, 3, …, 101. То есть конечные группы матриц составляют широкий арсенал некоммутативных групп для реализации заявленного способа формирования общего секретного ключа двух удаленных абонентов.
Приведенные примеры и математическое обоснование показывают, что заявленный способ формирования общего секретного ключа двух удаленных абонентов работает корректно, технически реализуем и позволяет достичь сформулированного технического результата.
Приложение 1
Толкование терминов, используемых в описании заявки
1. Двоичный цифровой электромагнитный сигнал - последовательность битов в виде нулей и единиц.
2. Параметры двоичного цифрового электромагнитного сигнала: разрядность и порядок следования единичных и нулевых битов.
3. Разрядность двоичного цифрового электромагнитного сигнала - общее число его единичных и нулевых битов, например число 10011 является 5-разрядным.
4. Битовая строка - двоичный цифровой электромагнитный сигнал, представляемый в виде конечной последовательности цифр «0» и «1».
5. Личный секретный ключ - двоичный цифровой электромагнитный сигнал, используемый для формирования открытого ключа пользователя (абонента) телекоммуникационной системы. Секретный ключ представляется, например, в двоичном виде как последовательность цифр «0» и «1».
6. Открытый ключ - битовая строка, параметры которой зависят от личного секретного ключа. Открытый ключ вычисляется по секретному как значение функции, вычислимой в одну сторону, которая делает практически неосуществимым вычисление секретного ключа по открытому ключу.
7. Общий секретный ключ - двоичный цифровой электромагнитный сигнал, используемый двумя или более абонентами для зашифрования информации, передаваемой по открытым каналам в виде шифр текста, и расшифрования принимаемой информации.
8. Многоразрядное двоичное число (МДЧ) - двоичный цифровой электромагнитный сигнал, интерпретируемый как двоичное число и представляемый в виде последовательности цифр «0» и «1».
9. Алгебраическая структура - это множество математических элементов, некоторой природы. В качестве математических элементов могут выступать, например многочлены, МДЧ, пары МДЧ, пары многочленов, тройки МДЧ, тройки многочленов, матрицы МДЧ, матрицы многочленов и т.д., над которыми заданы математические действия (операции). Математически алгебраическая структура определяется путем задания конкретного множества математических элементов и одной или нескольких операций, выполняемых над элементами.
10. Элемент алгебраической структуры - это одна битовая строка или набор из нескольких битовых строк, над которыми определена алгебраическая операция. При определении конкретного типа алгебраической структуры определяются операции над элементами алгебраической структуры, которые указывают однозначно правила интерпретации и преобразования битовых строк, представляющих эти элементы. Реализуемые в вычислительных устройствах преобразования битовых строк соответствуют операциям, выполняемым над элементами заданной алгебраической структуры.
11. Группа - это алгебраическая структура (т.е. множество элементов различной природы), над элементами которой определена одна операция, которая при заданной операции обладает следующим набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является также элемент этой же структуры, существует единичный элемент такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Детальное описание групп дано в книгах [А.Г.Курош. Теория групп. - М.: изд-во «Наука», 1967, - 648 с.] и [М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп. - М.: изд-во «Наука. Физматлит», 1996, - 287 с.].
12. Групповая операция - это операция, определенная над элементами группы.
13. Операция возведения в степень в группе. Обычно в группе определяют операцию возведения в степень, которая является производной от групповой операции. Возведение в степень в группе - это многократное выполнение групповой операции над одним и тем же элементом. Например, для элемента группы а и натурального числа n по определению имеем 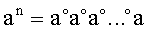 (n раз), где «
(n раз), где « » обозначает групповую операцию. Существуют алгоритмы быстрого возведения в большую целочисленную степень (см., например, с.17-18 в книге [Молдовян Н.А. Практикум по криптосистемам с открытым ключом. - СПб, БХВ-Петербург, 2007, - 298 с.]). Один из таких методов использует последовательное возведении в квадрат текущего результата. Возведение в степень, имеющую двоичную разрядность u, выполняется за 1,5·u групповых операций. При использовании методов быстрого возведения в степень возведение, например, в степень 18446744073709551616=264 требует выполнения около 1,5·64=96 групповых операций.
» обозначает групповую операцию. Существуют алгоритмы быстрого возведения в большую целочисленную степень (см., например, с.17-18 в книге [Молдовян Н.А. Практикум по криптосистемам с открытым ключом. - СПб, БХВ-Петербург, 2007, - 298 с.]). Один из таких методов использует последовательное возведении в квадрат текущего результата. Возведение в степень, имеющую двоичную разрядность u, выполняется за 1,5·u групповых операций. При использовании методов быстрого возведения в степень возведение, например, в степень 18446744073709551616=264 требует выполнения около 1,5·64=96 групповых операций.
14. Единичный элемент группы Г - это такой элемент, что при выполнении операции над ним и другим произвольным элементом Z группы Г результатом является элемент Z, т.е. для любого Z∈Г имеем 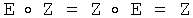 , где Е - единичный элемент группы (Знак принадлежности «∈» используется для обозначения принадлежности элемента Z группе Г.)
, где Е - единичный элемент группы (Знак принадлежности «∈» используется для обозначения принадлежности элемента Z группе Г.)
15. Порядком элемента Z группы Г называется наименьшее натуральное число q, такое что Zq=Е, где Е - единичный элемент группы Г.
16. Обратный элемент по отношению к заданному элементу Z группы Г - некоторый элемент группы Г, обозначаемый как Z-1, такой что 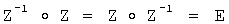 , где Е - единичный элемент группы Г.
, где Е - единичный элемент группы Г.
17. Некоммутативная группа - это группа с некоммутативной групповой операцией, т.е. с групповой операцией, для которой в общем случае результат ее действия над двумя элементами группы зависит от их расстановки относительно знака групповой операции, например для двух элементов Z1∈Г и Z2∈Г в общем случае имеет место следующее неравенство 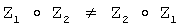 .
.
18. Конечная группа - это группа, содержащая конечное число элементов.
19. Вектор - это набор из двух или более МДЧ, называемых координатами вектора. Число координат вектора называется размерностью вектора.
20. Операция векторного умножения - это операция умножения двух векторов, являющаяся групповой операцией в конечной группе векторов.
Изобретение относится к области электросвязи, а именно к способу защиты информации, передаваемой по открытым каналам телекоммуникационных систем. Техническим результатом является уменьшение времени формирования общего секретного ключа (СК) удаленных абонентов. Технический результат достигается тем, что: формируют общие элементы Z и G некоммутативной конечной группы Г, такие, что 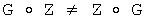 , у первого абонента генерируют его личный СК в виде двух многоразрядных двоичных чисел (МДЧ) x1 и w1, генерируют элементы
, у первого абонента генерируют его личный СК в виде двух многоразрядных двоичных чисел (МДЧ) x1 и w1, генерируют элементы 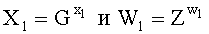 группы Г и формируют открытый ключ (ОК) первого абонента в виде элемента Y1 группы Г по формуле
группы Г и формируют открытый ключ (ОК) первого абонента в виде элемента Y1 группы Г по формуле 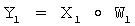 , где знак
, где знак  обозначает групповую операцию группы Г, передают Y1 второму абоненту, у второго абонента генерируют его личный СК в виде двух МДЧ x2 и w2, генерируют элементы
обозначает групповую операцию группы Г, передают Y1 второму абоненту, у второго абонента генерируют его личный СК в виде двух МДЧ x2 и w2, генерируют элементы 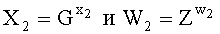 группы Г и формируют ОК второго абонента в виде элемента Y2 группы Г по формуле
группы Г и формируют ОК второго абонента в виде элемента Y2 группы Г по формуле 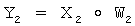 , передают его первому абоненту, у первого абонента формируют общий СК в виде элемента К группы Г в зависимости от Y2 и СК первого абонента, а у второго абонента формируют общий СК в виде элемента К группы Г в зависимости от Y1 и СК второго абонента. 4 з.п. ф-лы, 3 табл.
, передают его первому абоненту, у первого абонента формируют общий СК в виде элемента К группы Г в зависимости от Y2 и СК первого абонента, а у второго абонента формируют общий СК в виде элемента К группы Г в зависимости от Y1 и СК второго абонента. 4 з.п. ф-лы, 3 табл.
1. Способ формирования общего секретного ключа двух удаленных абонентов телекоммуникационной системы, заключающийся в том, что генерируют конечную группу Г, формируют общий элемент Z конечной группы Г, у первого абонента генерируют его личный секретный ключ и его открытый ключ в виде элемента Y1 конечной группы Г, передают открытый ключ Y1 первого абонента второму абоненту, у второго абонента генерируют его личный секретный ключ и его открытый ключ в виде элемента Y2 конечной группы Г, передают открытый ключ Y2 второго абонента первому абоненту, у первого абонента формируют общий секретный ключ в виде элемента К конечной группы Г в зависимости от открытого ключа Y2 второго абонента и личного секретного ключа первого абонента, а у второго абонента формируют общий секретный ключ в виде элемента К конечной группы Г в зависимости от открытого ключа Y1 первого абонента и личного секретного ключа второго абонента, отличающийся тем, что формируют дополнительный общий элемент G конечной группы Г, такой, что выполняется неравенство 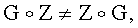 у первого абонента генерируют его личный секретный ключ в виде двух многоразрядных двоичных чисел x1 и w1 и формируют его открытый ключ Y1 путем генерации элементов X1 и W1 конечной группы Г по формулам
у первого абонента генерируют его личный секретный ключ в виде двух многоразрядных двоичных чисел x1 и w1 и формируют его открытый ключ Y1 путем генерации элементов X1 и W1 конечной группы Г по формулам 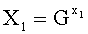 и
и 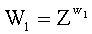 и генерации открытого ключа Y1 по формуле
и генерации открытого ключа Y1 по формуле 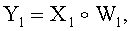 где знак
где знак  обозначает групповую операцию конечной группы Г, у второго абонента генерируют его личный секретный ключ в виде двух многоразрядных двоичных чисел x2 и w2 и формируют открытый ключ Y2 второго абонента путем генерации элементов Х2 и W2 конечной группы Г по формулам
обозначает групповую операцию конечной группы Г, у второго абонента генерируют его личный секретный ключ в виде двух многоразрядных двоичных чисел x2 и w2 и формируют открытый ключ Y2 второго абонента путем генерации элементов Х2 и W2 конечной группы Г по формулам  и
и 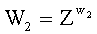 и генерации открытого ключа Y2 по формуле
и генерации открытого ключа Y2 по формуле 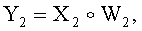 причем в качестве конечной труппы Г используют некоммутативную конечную группу.
причем в качестве конечной труппы Г используют некоммутативную конечную группу.
2. Способ по п.1, отличающийся тем, что у первого абонента формируют общий секретный ключ К по формуле 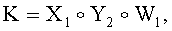 где
где 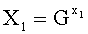 и
и 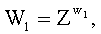 у второго абонента формируют общий секретный ключ К по формуле
у второго абонента формируют общий секретный ключ К по формуле 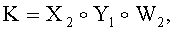 где
где  и
и 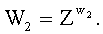
3. Способ по п.1 или 2, отличающийся тем, что в качестве некоммутативной конечной группы Г используют некоммутативную конечную группу четырехмерных векторов.
4. Способ по п.1 или 2, отличающийся тем, что в качестве некоммутативной конечной группы Г используют некоммутативную конечную группу шестимерных векторов.
5. Способ по п.1 или 2, отличающийся тем, что в качестве некоммутативной конечной группы Г используют некоммутативную конечную группу матриц.
| US 2004156498 A1, 12.08.2004 | |||
| WO 03013052 A1, 13.02.2003 | |||
| 0 |
|
SU191368A1 | |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ | 2005 |
|
RU2286022C1 |
| СПОСОБ ОБМЕНА КРИПТОГРАФИЧЕСКИМИ КЛЮЧАМИ МЕЖДУ КОМПЬЮТЕРНЫМ БЛОКОМ ПОЛЬЗОВАТЕЛЯ И СЕТЕВЫМ КОМПЬЮТЕРНЫМ БЛОКОМ | 1996 |
|
RU2175465C2 |
| US 2005002532 A1, 06.01.2005 | |||
| Молдовян Н.А и др | |||
| Введение в криптосистемы с открытым ключом | |||
| - СПб.: БХВ-Петербург, 2005. | |||
Авторы
Даты
2011-06-10—Публикация
2009-10-28—Подача