Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов аутентификации электронных сообщений, передаваемых по телекоммуникационным сетям и сетям ЭВМ, и может быть использовано в системах передачи электронных сообщений (документов), заверенных электронной цифровой подписью (ЭЦП), представленной, например, в виде многоразрядного двоичного числа (МДЧ) или набора МДЧ. Здесь и далее под МДЧ понимается электромагнитный сигнал в двоичной цифровой форме, параметрами которого являются: число битов и порядок следования их единичных и нулевых значений 1). (1) толкование используемых в описании терминов приведено в Приложении 1.)
Известен способ формирования и проверки ЭЦП, предложенный в статье [Rivest R., Shamir A., Adleman A. A method for Obtaining Digital Signatures and Public-Key Cryptosystems // Communication of the ACM. 1978. V. 21. No. 2. P. 120-126], детально описанный также и в книге [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - СПб, БХВ-Петербург, 2010. - с. 63-64]. Известный способ заключается в следующей последовательности действий:
генерируют секретный ключ в виде трех МДЧ р, q и d, причем р и q являются простыми числами,
формируют открытый ключ (n, е) в виде пары МДЧ n и е, где n - число, представляющее собой произведение двух простых МДЧ р и q, и е - МДЧ, удовлетворяющее условию ed=1 mod (р-1)(q-1), принимают электронный документ (ЭД), представленный МДЧ М;
в зависимости от значения М и значения секретного ключа формируют ЭЦП в виде МДЧ S=Md mod n;
в зависимости от открытого ключа и от ЭД М выполняют процедуру верификации ЭЦП, включающую вычисление МДЧ М' по формуле М'=Se mod n и сравнение МДЧ М' и М;
если М'=М, то делают вывод о подлинности ЭЦП, а если М'≠М, то делают вывод о ложности ЭЦП.
Недостатком известного способа является относительно большой размер ЭЦП и необходимость увеличения размера ЭЦП при разработке новых более эффективных методов разложения числа n на множители или при росте производительности современных вычислительных устройств. Это объясняется тем, что стойкость ЭЦП в этом способе определяется сложностью разложения модуля n на множители р и q.
Известен также способ формирования и проверки подлинности ЭЦП Эль-Гамаля, описанный в статье [ElGamal Т. A public key cryptosystem and a signature scheme based on discrete logarithms // IEEE Transactions on Information Theory, 1985, vol. IT-31, no. 4, pp. 469-472.] и в книге [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - СПб, БХВ-Петербург, 2010. - с. 79], который включает следующие действия:
формируют простое МДЧ р и двоичное число G, являющееся первообразным корнем по модулю р, генерируют секретный ключ в виде МДЧ х, в зависимости от секретного ключа формируют открытый ключ в виде МДЧ Y=Gx mod р, принимают ЭД, представленный в виде МДЧ М, в зависимости от М и секретного ключа формируют ЭЦП в виде двух МДЧ S и R;
осуществляют процедуру проверки подлинности ЭЦП, включающую вычисление двух контрольных параметров с использованием исходных МДЧ р, G, Y, М и S путем возведения МДЧ G, Y, R в дискретную степень по модулю р и сравнение вычисленных контрольных параметров;
при совпадении значений контрольных параметров делают вывод о подлинности ЭЦП.
Недостатком данного способа также является относительно большой размер ЭЦП. Это объясняется тем, что для получения приемлемого уровня стойкости требуется использовать 2048-битное МДЧ р, а значения элементов ЭЦП S и R вычисляют путем выполнения арифметических операций по модулю р - 1 и по модулю р, соответственно, т.е. каждое из МДЧ S и R имеет разрядность около 2048 бит.
Известен также способ формирования и проверки ЭЦП, предложенный в статье [Schnorr С.P. Efficient signature generation by smart cards // J. Cryptology. 1991. V. 4. No. 3. P. 161-174] и описанный также и в книге [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - СПб, БХВ-Петербург, 2010. - с. 83]. Известный способ заключается в следующей последовательности действий:
формируют простое МДЧ р, такое что р=Nq+1, где q - простое МДЧ;
формируют простое МДЧ a, такое что а≠1 и aq mod р=1;
методом генерации случайной равновероятной последовательности формируют секретный ключ в виде МДЧ х;
формируют открытый ключ в виде МДЧ у по формуле у=ax mod р;
принимают ЭД, представленный МДЧ М;
формируют ЭЦП в виде пары МДЧ (е, s), для чего генерируют случайное МДЧ t, формируют МДЧ R по формуле R=at mod р, формируют МДЧ е=ƒH(M||R), где ƒH - некоторая специфицированная хэш-функция, значение которой имеет фиксированную длину (обычно от 160 бит до 512 бит), независимо от размера аргумента, т.е. от размера битовой строки M||R, и знак || обозначает операцию присоединения (конкатенации) двух битовых строк М и R, а затем формируют МДЧ s по формуле s=(t-ex) mod q;
формируют контрольное МДЧ е', для чего генерируют МДЧ R' по формуле R'=asye mod р и формируют МДЧ е'=ƒ(M||R');
сравнивают сформированное контрольное МДЧ е'и МДЧ е;
при совпадении параметров сравниваемых МДЧ е' и е делают вывод о подлинности ЭЦП.
Недостатком этого способа, основанного на вычислительно трудности решения задачи дискретного логарифмирования (вычисление неизвестного х из уравнения у=ax mod р при заданных значениях у, а и р), является то, что он не обеспечивает стойкости к квантовым атакам, т.е. к атакам с использованием квантовых компьютеров, для которых известны эффективные полиномиальные алгоритмы решения задачи дискретного логарифмирования и задачи факторизации (см. статью [Shor P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on quantum computer // SIAM Journal of Computing. 1997. V. 26. P. 1484-1509]).
Наиболее близким по своей технической сущности к заявленному является известный постквантовый способ формирования и проверки подлинности ЭЦП, предлагаемый в статье [Moldovyan N.A., Moldovyan A.A. Candidate for practical post-quantum signature scheme // Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2020. Т. 16. Вып. 4. С. 455-461. https://doi.org/10.21638/11701/spbu10.2020.410], согласно которому
генерируют четырехмерную конечную некоммутативную ассоциативную алгебру путем генерации простого числа p=2q+1, где q - 256-битное простое число, и формирования таблицы умножения базисных векторов, задающих некоммутативную ассоциативную операцию умножения четырехмерных векторов, координатами которых являются элементы простого конечного поля GF(p), т.е. числа из множества {0, 1, 2…, р-1};
генерируют секретный ключ в виде набора четырехмерных векторов G, Q, J, А1, А2, В1, В2, W и МДЧ х и w, удовлетворяющих условиям GQ=QG, JG=GJ, A2=A1Qw, А1В1≠В1А1, A1G≠GA1, B1G≠GB1, А2В2≠В2А2, A2G≠GA2 и B2G≠GB2;
по секретному ключу формируют открытый ключ в виде набора четырехмерных векторов U1, Y1, Z1, U2, Y2 и Z2, вычисляемых по формулам U1=A1GxB1-1, Y1=B1GB1-1, Z1=B1QA1-1, U2=A2JxB2-1, Y2=B2JB2-1, Z2=B2QA2-1;
принимают ЭД, представленный многоразрядной битовой строкой М;
в зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП в виде двух МДЧ е и s и четырехмерного вектора S, для чего генерируют случайное МДЧ k<q и случайный четырехмерный вектор K, вычисляют векторы R1 и R2 по формулам R1=A1GkK и R2=A2JkW-1K, вычисляют значение хэш-функции ƒH от ЭД М и присоединенных к нему векторов R1 и R2, т.е. вычисляют значение МДЧ е=ƒH(M||R1||R2), где знак || обозначает операцию конкатенации (присоединения), вычисляют МДЧ s как решение квадратного уравнения es2+xs=k mod q, вычисляют вектор S по формуле S=A1Q-sK;
в зависимости от открытого ключа, принятого ЭД и ЭЦП выполняют процедуру верификации ЭЦП, включающую выполнение операций, операндами которых являются элементы открытого ключа, элементы ЭЦП и МДЧ, зависящее от элементов ЭЦП е и s (а именно МДЧ, равное произведению es), причем в ходе выполнения процедуры верификации ЭЦП осуществляют вычисление двух контрольных векторов R1' и R2' по формулам R1'=(U1Y1esZ1)sS и R2'=(U2Y2esZ2)sS (дублирования операций возведения в степень МДЧ при одинаковых значениях степени es и s необходимо для устранения возможности подделки ЭЦП с использованием вектора S в качестве подгоночного параметра) и вычисление значения хэш-функции ƒH от ЭД и присоединенных к нему векторов R1' и R2', т.е. вычисление контрольного МДЧ eK=ƒH(M, R1', R2'), после чего сравнивают контрольное МДЧ eK и МДЧ е;
формируют результат по проверке подлинности ЭЦП, а именно, при выполнении равенства eK=е делают вывод о том, что ЭЦП является подлинной, а при выполнении неравенства eK≠е делают вывод о том, что ЭЦП является ложной.
Недостатком ближайшего аналога является относительно невысокая производительность процедур генерации и верификации ЭЦП. Этот недостаток связан со сравнительно большой разрядностью используемых простых МДЧ р и q, обусловленной тем, что в основу стойкости ближайшего аналога положена вычислительная сложность скрытой задачи дискретного логарифмирования [Молдовян А.А., Молдовян Д.Н. Постквантовая схема ЭЦП на основе скрытой задачи дискретного логарифмирования в четырехмерной конечной алгебре // Вопросы защиты информации. 2019. №2. С. 18-22.]. При этом дополнительное снижение производительности указанных процедур обусловлено тем, что с вероятностью 0,5 процедура генерации ЭЦП должна выполняться повторно, пока не будут получены случайные значения е и k, при которых квадратное уравнение es2+xs=k mod q с неизвестным значением s будет иметь решения, а в процедуре верификации ЭЦП используются четыре операции возведения в степень.
Целью изобретения является разработка постквантового способа формирования и проверки подлинности ЭЦП, заверяющей ЭД, который обеспечивает существенное повышение производительности процедур генерации и верификации ЭЦП за счет того, что обеспечивается возможность использования (в качестве алгебраического носителя) конечной некоммутативной ассоциативной алгебры, заданной над полем GF(p), где р=2q+1 с простым МДЧ q, разрядность которого существенно меньше 256 бит, при обеспечении высокой стойкости к квантовым атакам, достигаемой тем, что в основу заявленного способа ставится вычислительная трудность решения системы из многих квадратных уравнений с многими неизвестными, т.е. вычислительная трудность задачи, для решения которой квантовый компьютер является неэффективным [Shuaiting Q., Wenbao H., Yifa Li, Luyao J. Construction of Extended Multivariate Public Key Cryptosystems // International Journal of Network Security. 2016. Vol. 18. N. 1. P. 60-67] (см. также [Jintai D., Dieter S. Multivariable Public Key Cryptosystems (2004) https://eprint.iacr.org/2004/350.pdf]). При этом обеспечивается возможность использования в качестве алгебраического носителя m-мерных конечных некоммутативных ассоциативных алгебр, заданных над полем GF(2z) характеристики два, в которых операция умножения имеет существенно более низкую вычислительную сложность по сравнению со случаем использования алгебр, заданных над простым полем GF(p) при одинаковой разрядности МДЧ 2z и р. Кроме того, устраняется вероятность повторного выполнения процедуры генерации ЭЦП и обеспечивается возможность выполнения процедуры верификации ЭЦП, включающей менее четырех операций возведения в степень МДЧ.
Поставленная цель достигается тем, что в известном постквантовом способе формирования и проверки подлинности ЭЦП, заверяющей ЭД, заключающемся в том, что
генерируют m-мерную конечную некоммутативную ассоциативную алгебру, где m≥4, генерируют секретный ключ, включающий набор m-мерных векторов в качестве своих элементов, по секретному ключу формируют открытый ключ в виде набора m-мерных векторов, принимают ЭД, представленный многоразрядной битовой строкой М, в зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП, включающую m-мерный вектор S, в зависимости от открытого ключа, принятого ЭД М и ЭЦП выполняют процедуру верификации ЭЦП, включающую выполнение операций умножения m-мерных векторов, возведения m-мерных векторов в степень МДЧ и сравнения, и формируют результат по проверке подлинности ЭЦП,
новым является то, что выполняют процедуру верификации ЭЦП, включающую осуществление операций по математической формуле в виде равенства с k≥2 вхождениями m-мерного вектора S.
Выполнение процедуры верификации ЭЦП, включающую выполнение операций по математической формуле в виде равенства с k≥2 вхождениями m-мерного вектора S в качестве множителя, записанной над конечной некоммутативной алгеброй, обусловливает то, что постквантовая стойкость заявленного способа основывается на вычислительной трудности решения систем из многих квадратных уравнений с многими неизвестными, благодаря чему при заданном уровне стойкости могут быть использованы простые МДЧ р и q с существенно меньшим значением разрядности, что приводит к существенному возрастанию производительности процедур формирования и верификации ЭЦП. При этом обеспечивается защита от подделки ЭЦП с использованием m-мерного вектора S в качестве подгоночного параметра без дублирования операций возведения в степень МДЧ при одинаковом значении степени, за счет чего дополнительно повышается производительность процедуры верификации ЭЦП.
Новым является также и то, что генерируют секретный ключ в виде набора m-мерных векторов А, В, D, G, Н, Gx, Gu и Hw, МДЧ х, w и u путем генерации случайных многоразрядных двоичных чисел х, w и u и случайных m-мерных векторов А, В, D, G и Н, удовлетворяющих условиям АВ≠ВА, AD≠DA, AG≠GA, DB≠BD, BG≠GB, DG≠GD и GH=HG, и вычисления m-мерных векторов Gx, Gu и Hw по формулам Gx=Gx, Gu=Gu и Hw=Hw, формируют открытый ключ в виде набора m-мерных векторов Y1, Z1, Y2, Z2 и Р путем выполнения вычислении по формулам Y1=AGB, Z1=DHA-1, Y2=AHwB, Z2=DGxA-1 и P=AGuHA-1, в зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП в виде m-мерного вектора S, выполняют процедуру верификации ЭЦП, включающую генерацию в зависимости от принятого ЭД М многоразрядных двоичных чисел h1, h2, и h3, выполнение вычислений по формуле 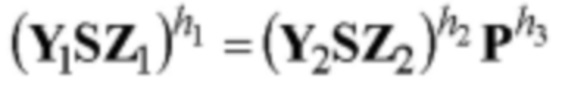 с k=2 вхождениями m-мерного вектора S, реализуемых как вычисление контрольных m-мерных векторов
с k=2 вхождениями m-мерного вектора S, реализуемых как вычисление контрольных m-мерных векторов 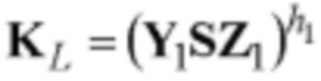 и
и 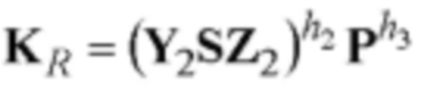 и сравнение контрольных m-мерных векторов KL и KR, и формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если KL=KR, или о ложности ЭЦП, если KL≠KR.
и сравнение контрольных m-мерных векторов KL и KR, и формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если KL=KR, или о ложности ЭЦП, если KL≠KR.
Новым является также и то, что генерируют секретный ключ в виде набора m-мерных векторов А, В, D, G, Н, Gx, Hw, Gi и Hj путем генерации случайных многоразрядных двоичных чисел х, w, i, и j и случайных m-мерных векторов А, В, D, F, G и Н, где порядок векторов равен простому МДЧ q, удовлетворяющих условиям АВ≠ВА, AD≠DA, AF≠FA, AG≠GA, BD≠DB, ≠FB, BG≠GB, DF≠FD, DG≠GD, FG≠GF и GH=HG, и вычисления m-мерных векторов Gx, Hw, Gi и Hj по формулам Gx=Gx, Hw=Hw, Gj=Gj и Hi=Hi, формируют открытый ключ в виде набора m-мерных векторов Y1, Z1, Y2, Z2, Y3 и Z3 путем выполнения вычислений по формулам Y1=AGB, Z1=DHA-1, Y2=FHwB, Z2=DGxF-1, Y3=AHiD-1 и Z3=B-1GjF-1, формируют ЭЦП в виде МДЧ е и m-мерного вектора S, для чего генерируют случайные МДЧ k и t, вычисляют вектор R=AGkHtF-1 и МДЧ е=e1||e2=ƒH(М||R), где ƒH - коллизионно стойкая хэш-функция и е1 и е2 - МДЧ, имеющее одинаковую разрядность, вычисляют МДЧ n и d по формулам  и
и 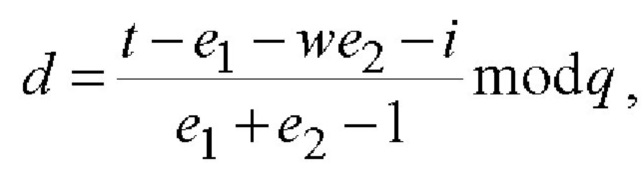 вычисляют вектор S по формуле S=B-lGnHdD-1, выполняют процедуру верификации ЭЦП, включающую вычисление контрольного m-мерного вектора RK по формуле
вычисляют вектор S по формуле S=B-lGnHdD-1, выполняют процедуру верификации ЭЦП, включающую вычисление контрольного m-мерного вектора RK по формуле 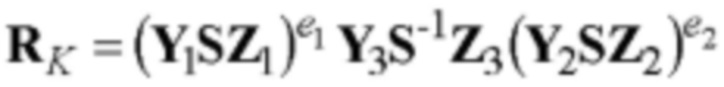 с k=3 вхождениями m-мерного вектора S, вычисление контрольного МДЧ eK=ƒH(M||RK) и сравнение МДЧ eK и е, и формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если eK=е, или о ложности ЭЦП, если eK≠е.
с k=3 вхождениями m-мерного вектора S, вычисление контрольного МДЧ eK=ƒH(M||RK) и сравнение МДЧ eK и е, и формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если eK=е, или о ложности ЭЦП, если eK≠е.
Новым является также и то, что генерируют секретный ключ в виде набора m-мерных векторов А, В, G, Gx и Н путем генерации случайного МДЧ х и случайных m-мерных векторов А, В, G и Н, где порядок векторов равен простому МДЧ q, удовлетворяющих условиям АВ≠ВА, AG≠GA, BG≠GB и GH=HG, и вычисления m-мерного вектора Gx по формуле Gx=Gx, формируют открытый ключ в виде набора m-мерных векторов Y, Z и U путем выполнения вычислений по формулам Y=AGB, Z=AGxB, U=АНВ, в зависимости от принятого ЭД М и секретного ключа формируют ЭЦП в виде МДЧ е и m-мерного вектора S, выполняют процедуру верификации ЭЦП, включающую вычисление контрольного m-мерного вектора RK по формуле 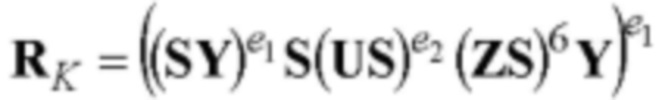 с k=4 вхождениями m-мерного вектора S и вычисление контрольного МДЧ eK=ƒH(M||RK), сравнение МДЧ eK и е, и формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если eK=е, или о ложности ЭЦП, если eK≠е.
с k=4 вхождениями m-мерного вектора S и вычисление контрольного МДЧ eK=ƒH(M||RK), сравнение МДЧ eK и е, и формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если eK=е, или о ложности ЭЦП, если eK≠е.
Возможность вычисления m-мерного вектора S, удовлетворяющего математической формуле в виде равенства с многократным (k≥2) вхождением m-мерного вектора S, записанного над КНАА с некоммутативной операцией умножения, обеспечивается за счет того, что знание секретного ключа, связанного с открытым ключом, позволяет свести равенство, записанное над КНАА, к равенству, записанному над некоторой скрытой (секретной) коммутативной группой, содержащейся в КНАА. При этом такое сведение требует использования секретных векторов (являющихся элементами секретного ключа), поэтому подделка ЭЦП (формирование ЭЦП без знания секретного ключа) требует вычисления векторов, удовлетворяющих совокупности векторных уравнений, задаваемых совокупностью математических формул, по которым вычисляется открытый ключ по секретному ключу, и перестановочностью секретных векторов, выбираемых из скрытой коммутативной группы. При этом возникающие векторные уравнения содержат произведения пар неизвестных векторов, т.е. они являются квадратными. Таким образом, подделка ЭЦП требует решения систем квадратных векторных уравнений, которые сводятся к решению систем из многих квадратных уравнений с многими неизвестными, записанными над конечным полем, над которым задана КНАА, используемая в качестве алгебраического носителя для реализации конкретного варианта заявленного способа. Использование квантового компьютера для решения таких систем уравнений является малоэффективным, что обеспечивает постквантовую стойкость заявленного способа.
В заявленном способе важным является k-кратное вхождение вектора S в метематическую формулу в виде равенства, задающую совокупность и очередность выполняемых операций умножения и возведения в степень. Также важным является использование некоммутативной конечной ассоциативной алгебры. Именно свойство некоммутативности операции умножения устраняет возможность упрощения формулы с двумя и более вхождениями вектора S и сведения ее к формуле с однократным вхождением вектора S в виде множителя Sb, где b - некоторое МДЧ. В случае использования коммутативных ассоциативных алгебр для реализации заявленного способа указанное сведение легко осуществляется, поэтому для реализации заявленного способа требуется использовать некоммутативные конечные ассоциативные алгебры в качестве алгебраического носителя заявленного способа. Свойство ассоциативности обеспечивает возможность быстрого выполнения операции возведения в степень МДЧ с разрядностью до 500 бит и более.
В заявленном постквантовом способе формирования и проверки подлинности ЭЦП, заверяющей ЭД, генерируют m-мерную конечную некоммутативную ассоциативную алгебру (КНАА) путем генерации параметров, определяющих множество m-мерных векторов как элементов КНАА и операцию умножения векторов. Под термином «m-мерная конечная алгебра» понимается m-мерное конечное векторное пространство, в котором дополнительно к операции сложения векторов определена операция умножения векторов, обладающая свойствами замкнутости и дистрибутивности слева и справа относительно операции сложения. Пусть дано m-мерное векторное пространство, которое задано над некоторым конечным полем  . Для реализации заявленного способа в качестве поля
. Для реализации заявленного способа в качестве поля  можно использовать, например, простое конечное поле GF(p) или поле GF(2z), являющееся расширением степени z двоичного поля GF(2). Некоторый m-мерный вектор А будем записывать в виде упорядоченного набора элементов поля
можно использовать, например, простое конечное поле GF(p) или поле GF(2z), являющееся расширением степени z двоичного поля GF(2). Некоторый m-мерный вектор А будем записывать в виде упорядоченного набора элементов поля 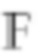 , называемых координатами вектора: А=(a0, a1, …, am-1). В некоторых случаях более удобным является представление вектора в виде следующей суммы
, называемых координатами вектора: А=(a0, a1, …, am-1). В некоторых случаях более удобным является представление вектора в виде следующей суммы 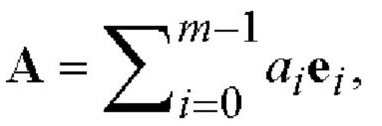 где ei - формальные базисные векторы; aiei - одномерные компоненты вектора А; ai ∈
где ei - формальные базисные векторы; aiei - одномерные компоненты вектора А; ai ∈ 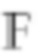 - координаты вектора; выражение aiei может быть рассмотрено как умножение скаляра ai на вектор ei. Векторное пространство (см. с. 12 в книге [Кострикин А.И. Введение в алгебру. Ч. 2. Линейная алгебра. - М., ФИЗМАТЛИТ, 2001. - 367 с.]) с дополнительно заданной операцией умножения произвольной пары векторов, дистрибутивной слева и справа относительно операции сложения и обладающей свойством замкнутости, называется алгеброй.
- координаты вектора; выражение aiei может быть рассмотрено как умножение скаляра ai на вектор ei. Векторное пространство (см. с. 12 в книге [Кострикин А.И. Введение в алгебру. Ч. 2. Линейная алгебра. - М., ФИЗМАТЛИТ, 2001. - 367 с.]) с дополнительно заданной операцией умножения произвольной пары векторов, дистрибутивной слева и справа относительно операции сложения и обладающей свойством замкнутости, называется алгеброй.
Операция умножения векторов 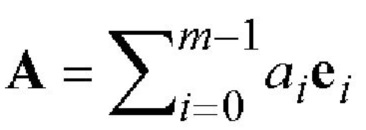 и
и 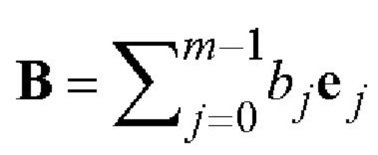 определяется как перемножение каждой компоненты вектора А с каждой компонентой вектора В, выполняемое в соответствии со следующей формулой:
определяется как перемножение каждой компоненты вектора А с каждой компонентой вектора В, выполняемое в соответствии со следующей формулой:
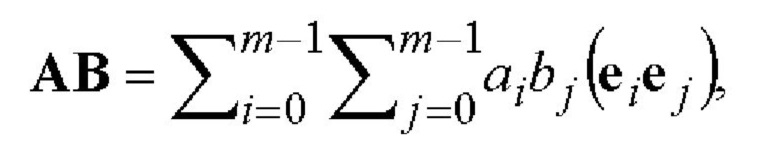
в которой координаты умножаются как элементы поля  и все произведения пар базисных векторов заменяются на однокомпонентные векторы. А именно, каждое из произведений eiej заменяется на некоторый вектор λeh, выбираемый из специально разработанной таблицы умножения базисных векторов (ТУБВ). В случае λ=1 в ТУБВ указывается базисный вектор eh. Если значение λ не равно единице поля
и все произведения пар базисных векторов заменяются на однокомпонентные векторы. А именно, каждое из произведений eiej заменяется на некоторый вектор λeh, выбираемый из специально разработанной таблицы умножения базисных векторов (ТУБВ). В случае λ=1 в ТУБВ указывается базисный вектор eh. Если значение λ не равно единице поля  , то оно называется структурной константой. Выбор значений λeh осуществляется следующим образом. В произведении eiej первый (левый) операнд указывает строку, а второй (правый) - столбец, на пересечение которых получаем ячейку, содержащую требуемое значение λeh.
, то оно называется структурной константой. Выбор значений λeh осуществляется следующим образом. В произведении eiej первый (левый) операнд указывает строку, а второй (правый) - столбец, на пересечение которых получаем ячейку, содержащую требуемое значение λeh.
Для задания ассоциативной алгебры разрабатывается ТУБВ, которая определяет операцию умножения, обладающую свойством ассоциативности, т.е. такую операцию умножения, для которой для всевозможных троек векторов А, В и С имеет место следующее равенство:
(АВ)С=А(ВС).
В случае, если равенство АВ=ВА выполняется для произвольной пары векторов А и В, операция умножения и задаваемая алгебра называются коммутативной, в противном случае - некоммутативной. В последнем случае имеем КНАА. Свойство ассоциативности умножения обеспечивается, если ТУБВ, по которой задается операция умножения векторов, для всех возможных троек базисных векторов ei, ej и ek обеспечивает выполнимость равенства (eiej)ek=ei(ejek).
Для четных значений размерности m>2 разработаны различные частные ТУБВ, задающие m-мерные КНАА, содержащие некоторый вектор Е, для которого выполняется условие EV=VE=V для каждого вектора V. Вектор Е называется глобальной двухсторонней единицей. Для элементов КНАА с глобальной единицей вводится понятие обратимости. Обратимым называется вектор V, для которого существует обратный вектор, обозначаемый как V-1, для которого выполняется условие VV-1=V-1V=Е. Обратный вектор легко вычисляется путем решения векторного уравнения VX=Е с неизвестным вектором X, которое, используя ТУБВ, сводится к решению системы из m линейных уравнений с m неизвестными (координатами вектора X) в конечном поле 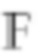 .
.
Следует различать операцию умножения векторов, для которой оба операнда являются векторами, и операцию скалярного умножения вектора, для которой одним операндом является элемент поля 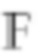 , а вторым - вектор. Например, скалярное умножение вектора V на скаляр σ ∈
, а вторым - вектор. Например, скалярное умножение вектора V на скаляр σ ∈ 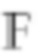 может быть выполнено как умножение каждой координаты вектора V на σ. Этот же результат будет получен, если выполнить умножение векторов V и σЕ, поэтому векторы вида σЕ при всевозможных значениях σ ∈
может быть выполнено как умножение каждой координаты вектора V на σ. Этот же результат будет получен, если выполнить умножение векторов V и σЕ, поэтому векторы вида σЕ при всевозможных значениях σ ∈ 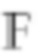 будем называть скалярными векторами.
будем называть скалярными векторами.
В статье [Молдовян Д.Н. Задание шестимерных алгебр как носителей криптосхем, основанных на скрытой задаче дискретного логарифмирования // Вопросы защиты информации. 2021. №1. С. 26-32. DOI: 10.52190/2073-2600_2021_1_26] рассмотрены разреженные ТУБВ, представленные в таблицах 1-4, которые задают различные четырехмерные КНАА. Задание операции умножения по прореженным ТУБВ обеспечивает существенное снижение вычислительной сложности операции умножения векторов, а значит и операции возведения в степень. Еще один вариант задания четырехмерной КНАА в виде табл. 5 представлен в статье [Moldovyan A.A., Moldovyan N.A. Post-quantum signature algorithms based on the hidden discrete logarithm problem // Computer Science Journal of Moldova. 2018. Vol. 26, N. 3(78). P. 301-313].
В статье [N.A. Moldovyan, Unified Method for Defining Finite Associative Algebras of Arbitrary Even Dimensions, Quasigroups and Related Systems. 2018. vol. 26, no. 2. P. 263-270] предложен унифицированный способ задания КНАА произвольных четных размерностей m>4, используя который легко построить ТУБВ для шестимерной (табл. 6) и восьмимерной (табл. 7) КНАА.
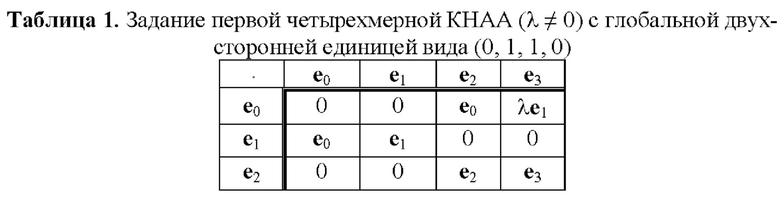

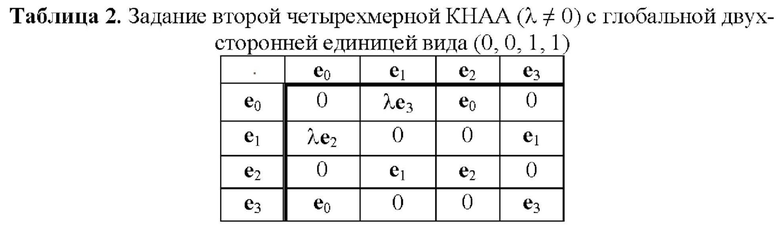
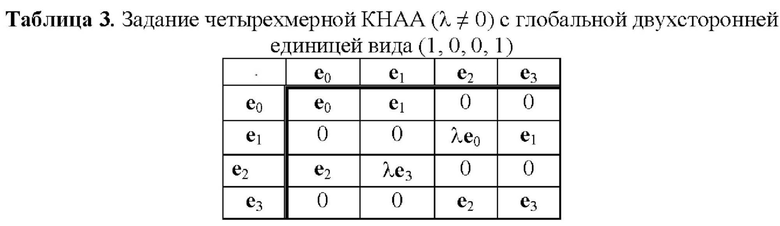
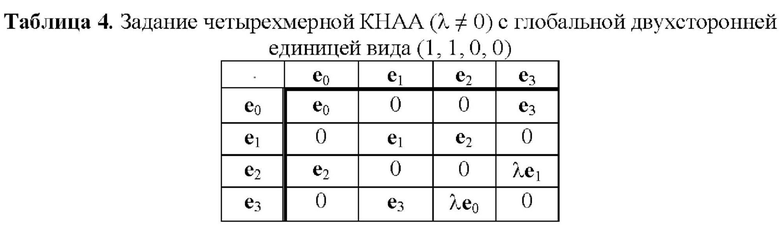

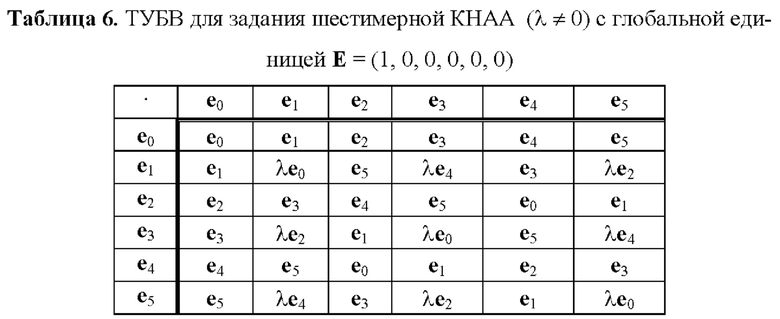
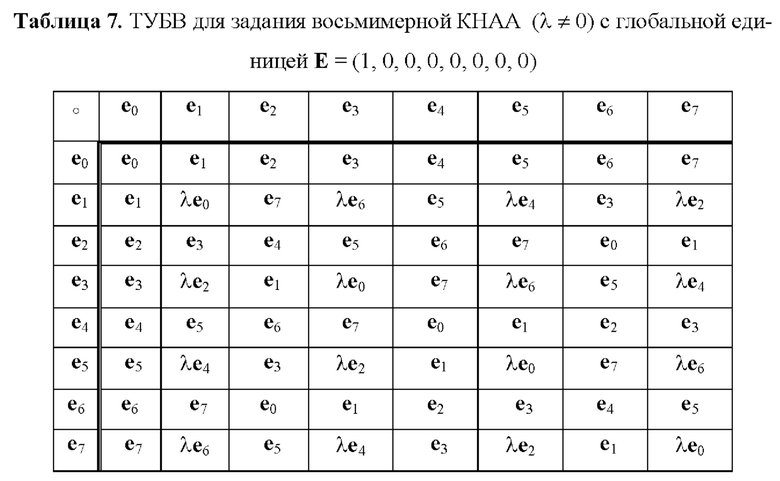
Каждая из табл. 1-7 может быть использована для задания КНАА над простым конечным полем GF(p) или конечным полем GF(2z). В первом случае координатами векторов являются элементы множества МДЧ {0, 1, 2, …, р-1} и при выполнении операции векторного умножения над координатами выполняются операции сложения и умножения по модулю р. Во втором случае координатами векторов являются элементы множества всех двоичных многочленов степени z-1, которые записываются в виде всевозможных z-битовых строк, и при выполнении операции векторного умножения над координатами выполняются операции побитового сложения по модулю два и умножения по модулю неприводимого двоичного многочлена степени z.
В заявленном способе генерируют секретный ключ, включающий набор m-мерных векторов, часть из которых являются попарно перестановочными. Для генерации этих элементов секретного ключа, например, генерируют базис <G, Н>, формирующий коммутативную примарную группу порядка q2, в который включены два вектора G и Н, порядок каждого из которых равен простому МДЧ q. При задании КНАА над полем GF(p) наличие в КНАА большого числа таких групп обеспечивается использованием простого МДЧ р вида р=2q+1, где q - также постое МДЧ. Например, генерируются следующие простые МДЧ q, которые задают генерацию простых МДЧ р=2q+1:
1) 80-битное МДЧ q=1041260943259690172052821,
2) 96-битное МДЧ q=71907494709617529358502495579,
3) 128-битное МДЧ q=304643710790881018612993287215112007979;
4) 160-битное МДЧ q=1443420272407352009010766274913970921515428178119.
5) 192-битное МДЧ q=5261472747218403390125581496192701306697287924851078249233.
При задании КНАА над полем GF(2z), представляющим собой расширение степени z двоичного поля GF(2), следует учитывать, что порядок мультипликативной группы поля GF(2z) равен МДЧ q=2z-1, КНАА содержит большое число коммутативных групп, каждая из которых генерируется базисом <G, Н>, включающим два вектора порядка q, и имеет порядок q2. Получение МДЧ q, являющимся простым числом, обеспечивается выбором z, равной степени Мерсенна, при которой МДЧ q=2z-1 является простым. Например, следующие степени z задают генерацию простых МДЧ q=2z-1:
1) при z=89 имеем q=618970019642690137449562111,
2) при z=107 имеем q=162259276829213363391578010288127,
3) при z=127 имеем q=170141183460469231731687303715884105727,
4) при z=521 имеем q=6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151,
5) при z=607 имеем q=531137992816767098689588206552468627329593117727031923199444138200403559860852242739162502265229285668889329486246501015346579337652707239409519978766587351943831270835393219031728127.
Для этих значений степени расширения z в поле GF(2z) операцию умножения целесообразно задать по модулю следующих неприводимых двоичных многочленов δ(x)=х89+х38+1 (z=89), δ(х)=х107+х9+х7+х4+1 (z=107), δ(х)=х127+х+1 (z=127), δ(х)=х521+х32+1 (z=521) и δ(х)=х607+х105+1 (z=607), для которых операция умножения в поле GF(2z), а значит и операция умножения векторов в КНАА, заданной над полем GF(2z), имеет сравнительно низкую вычислительную сложность. Таблица неприводимых двоичных трехчленов и пятичленов до степени 10000 приведена, например, на сайте [Table of Low-Weight Binary Irreducible Polynomials // https://www.hpl.hp.com/techreports/98/HPL-98-135.pdf]. Для разработки стойких постквантовых алгоритмов ЭЦП по заявленному способу, достаточно использование неприводимых двоичных многочленов степени z≤1000.
Как в случае использования КНАА, заданных над полем CF(p), где простое МДЧ р=2q+1 при простом МДЧ q, так и в случае использования КНАА, заданных над полем GF(2z), где z - степень Мерсенна, для генерации базиса <G, Н> случайной группы с двухмерной цикличностью, содержащейся в КНАА и имеющей порядок q2, может быть использована процедура, включающая следующие действия:
1. Сгенерировать случайный обратимый вектор N и вычислить вектор L=N2.
2. Если Lq=Е и L≠λE для всех значений λ ∈  (т.е. если L не является скалярным вектором), то перейти к шагу 3, иначе перейти к шагу 1.
(т.е. если L не является скалярным вектором), то перейти к шагу 3, иначе перейти к шагу 1.
3. Сгенерировать случайное значение β ∈  , отличное от нуля и единицы поля
, отличное от нуля и единицы поля 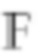 , такое, что β2 также не равно единице поля
, такое, что β2 также не равно единице поля 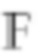 .
.
4. Сгенерировать случайное целое число k(0<k<q)
5. Вычислить вектор Н=β2Lk.
6. Выдать в качестве базиса <G, Н> случайной группы с двухмерной цикличностью два вектора G=L и Н.
Стойкость заявленного постквантового способа формирования и проверки подлинности ЭЦП, заверяющей ЭД, к атакам с использованием обычных и квантовых компьютеров обеспечивается тем, что вычисление секретного ключа по открытому ключу связано с решением системы из многих квадратных уравнений (заданных в поле 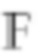 ) с многими неизвестными, для чего применение квантового компьютера не является эффективным. Заданный уровень стойкости заявленного способа обеспечивается выбором размерности генерируемой КНАА m≥4 и достаточно большой разрядности |q| простого МДЧ q. При этом выбор значений m и |q| согласовывается между собой и с требуемым уровнем стойкости, выражаемым как значение двоичного логарифма L от минимального числа операций, которые необходимо выполнить для подделки ЭЦП. Например, для заданного уровня L-битной стойкости значения m и |q| могут быть выбраны из условия m|q|≥4L.
) с многими неизвестными, для чего применение квантового компьютера не является эффективным. Заданный уровень стойкости заявленного способа обеспечивается выбором размерности генерируемой КНАА m≥4 и достаточно большой разрядности |q| простого МДЧ q. При этом выбор значений m и |q| согласовывается между собой и с требуемым уровнем стойкости, выражаемым как значение двоичного логарифма L от минимального числа операций, которые необходимо выполнить для подделки ЭЦП. Например, для заданного уровня L-битной стойкости значения m и |q| могут быть выбраны из условия m|q|≥4L.
Рассмотрим конкретные примеры реализации заявленного способа.
Пример 1. Случай реализации заявленного способа, иллюстрирующий пп. 1 и 2 формулы изобретения. В данном примере выполняется следующая последовательность действий:
1. Генерируют четырехмерную КНАА, для чего
1.1) генерируют простое МДЧ р=2q+1, где q - 128-битное простое МДЧ;
1.2) генерируют ТУБВ, задающую некоммутативную ассоциативную операцию умножения четырехмерных векторов, заданных над полем GF(p), например, путем копирования табл. 1 и задания значения λ=2.
2. Генерируют секретный ключ, включающий набор четырехмерных векторов А, В, D, G, Н, Gx, Gu и Hw и МДЧ х, w и u в качестве своих элементов, для чего
2.1) генерируют два случайных четырехмерных вектора G и Н порядка образующих базис <G, Н> коммутативной группы порядка q2, обладающей двухмерной цикличностью;
2.2) генерируют случайные МДЧ х (1 х<q), w (1 w<q) и u (1 u<q) и вычисляют четырехмерные векторы Gx, Gu и Hw по формулам Gx=Gx, Gu=Gu и Hw=Hw (очевидно, что векторы G, Н, Gx, Gu и Hw являются попарно перестановочными как принадлежащие коммутативной группе, генерируемой базисом <G, Н>);
2.3) генерируют случайные обратимые четырехмерные векторы А, В и D, удовлетворяющие условиям АВ≠ВА, AD≠DA, AG≠GA, DB≠BD, BG≠GB, DG≠GD.
3. Формируют открытый ключ в виде набора четырехмерных векторов Y1, Z1, Y2, Z2 и Р, для чего осуществляют вычисления по следующим формулам Y1=AGB, Z1=DHA-1, Y2=AHwB, Z2=DGxA-1 и P=AGuHA-1.
4. Принимают ЭД, представленный многоразрядной битовой строкой М.
5. В зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП в виде четырехмерного вектора S, для чего
5.1) используя некоторую специфицированную 384-битную хэш-функцию ƒH, вычисляют МДЧ h=h1||h2||h3=ƒH(М), где хэш-значение h представлено как конкатенация трех 128-битных МДЧ h1, h2 и h3;
5.2) вычисляют МДЧ n и d по следующим двум формулам:
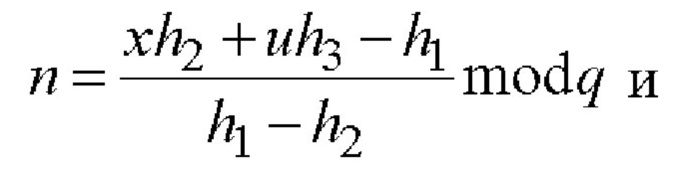
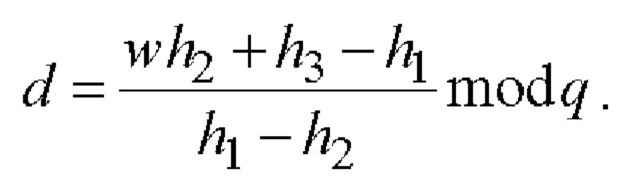
5.3) вычисляют ЭЦП в виде четырехмерного вектора S по формуле S=B-1GnHdD-1.
6. В зависимости от открытого ключа, принятого ЭД и ЭЦП выполняют процедуру верификации ЭЦП, для чего
6.1) вычисляют МДЧ h=h1||h2||h3=ƒH(М), где 384-битное значение хэш-функции h представлено как конкатенация трех 128-битных МДЧ h1, h2 и h3;
6.2) осуществляют вычисления по формуле 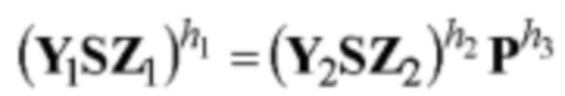 с двумя (k=2) вхождениями четырехмерного вектора S и тремя операциями возведения в степень МДЧ, реализуемые как вычисление контрольных m-мерных векторов
с двумя (k=2) вхождениями четырехмерного вектора S и тремя операциями возведения в степень МДЧ, реализуемые как вычисление контрольных m-мерных векторов 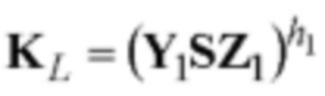 и
и 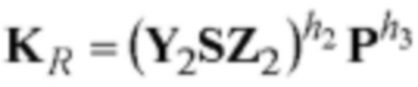 и сравнение контрольных m-мерных векторов KL и KR.
и сравнение контрольных m-мерных векторов KL и KR.
7. Формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если KL=KR, или о ложности ЭЦП, если KL≠KR.
Легко видеть, что вычисление секретного ключа по открытому ключу связано с решением системы из 9 квадратных векторных уравнений с 8 неизвестными, заданной над четырехмерной КНАА, заданной по табл. 1 при значении λ=2. Указанная система векторных уравнений сводится к системе из 36 квадратных уравнений с 32 неизвестными, заданной над полем GF(p) со 129-битным порядком. Это определяет постквантовую стойкость данного частного примера реализации заявленного способа.
Корректность данного примера реализации заявленного способа доказывается путем демонстрации того, что корректно сформированная ЭЦП в соответствии с шагом 5 проходит процедуру верификации ЭЦП, выполняемую на шаге 6, как подлинная ЭЦП. Действительно пусть четырехмерный вектор S составляет ЭЦП, сформированную в полном соответствии с действиями, предписанным шагом 5 примера 1. Тогда имеем такое доказательство корректности:
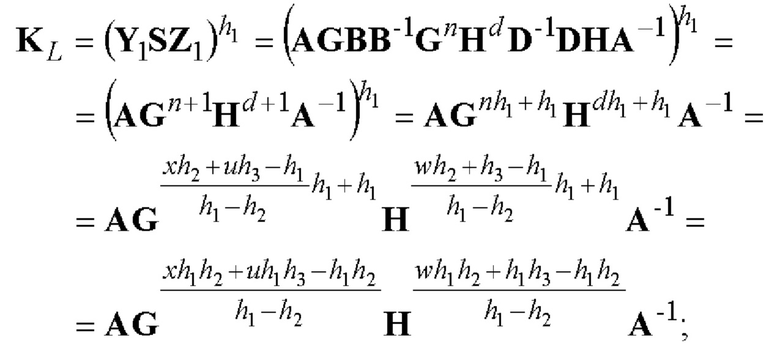
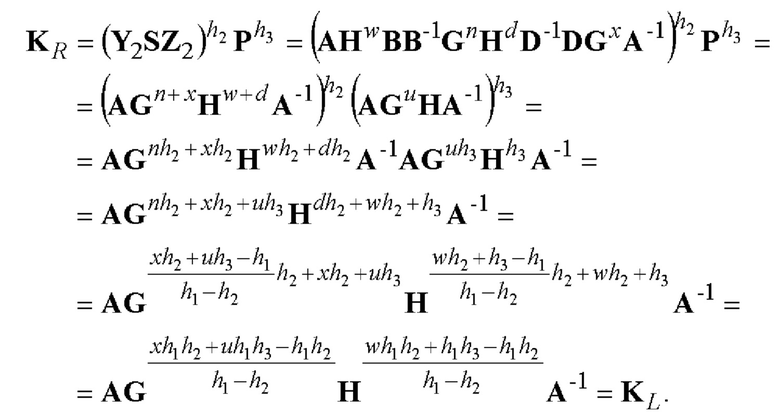
Поскольку выполняется равенство KL=KR, то правильно сгенерированная ЭЦП проходит процедуру верификации как подлинная ЭЦП, т.е. пример 1, представляющий частный вариант реализации заявленного способа, работает корректно.
Другие модификации рассмотренного примера 1 могут быть получены при использовании вместо КНАА, заданной над полем GF(p) со 129-битной характеристикой р по табл. 1, одного из следующих алгебраических носителей:
-- шестимерной КНАА, заданной над полем GF(p) со 97-битной характеристикой р (при простом 96-битном МДЧ q=71907494709617529358502495579) по табл. 6;
-- четырехмерной КНАА, заданной по табл. 2 над полем GF(2z) со степенью расширения z=127, при которой имеем простое МДЧ q=2z-1==170141183460469231731687303715884105727;
-- восьмимерной КНАА, заданной по табл. 7 над полем GF(p) с 81-битной характеристикой р (при простом 80-битном МДЧ q=1041260943259690172052821).
Возможны и другие модификации примера 1 с заданием КНАА различных размерностей, причем по различным ТУБВ для каждого значения размерности. При этом практический интерес представляет 1) задание КНАА над простым конечным полем GF(p) и 2) задание КНАА над конечным полем GF(2z)
Пример 2. Случай реализации заявленного способа, иллюстрирующий пп. 1 и 3 формулы изобретения. В данном примере выполняется следующая последовательность действий:
1. Генерируют шестимерную КНАА, для чего
1.1) генерируют простое МДЧ z=107, при котором МДЧ 2z-1=q является простым (q=162259276829213363391578010288127);
1.2) генерируют неприводимый двоичный многочлен степени z=107, например, двоичный многочлен δ(х)=х107+х9+х1+х4+1;
1.3) генерируют ТУБВ, задающую некоммутативную ассоциативную операцию умножения шестимерных векторов, заданных над полем GF(2z) с операцией умножения по модулю неприводимого двоичного многочлена δ(х)=х101+х9+х7+х4+1, например, путем копирования табл. 6, и задания структурной константы λ, равной единице поля GF(2z), т.е. λ=1.
2. Генерируют секретный ключ, включающий набор шестимерных векторов А, В, D, F, G, Н, Gx, Hw, Gj и Hi - и МДЧ х, w, i и j в качестве своих элементов, для чего
2.1) генерируют два случайных шестимерных вектора G и Н порядка q, образующих базис <G, Н> коммутативной группы порядка q2, обладающей двухмерной цикличностью;
2.2) генерируют случайные шестимерные обратимые векторы А, В, D, F порядка которые удовлетворяют условиям АВ≠ВА, AD≠DA, AF≠FA, AG≠GA, BD≠DB, BF≠FB, BG≠GB, DF≠FD, DG≠GD, FG≠GF;
2.3) генерируют случайные МДЧ х (1<х<q), w (1<w<q), i (1<i<q) и j (1<j<q) и вычисляют шестимерные векторы Gx, Gj, Hw и Hi по формулам Gx=Gx, Gj=Gj, Hw=Hw и Hi=Hi (очевидно, что векторы G, Н, Gx, Gj, Hw и Hi являются попарно перестановочными как принадлежащие коммутативной группе, генерируемой базисом <G, Н>).
3. Формируют открытый ключ в виде набора шестимерных векторов Y1, Z1, Y2, Z2, Y3 и Z3, для чего осуществляют вычисления по следующим формулам Y1=AGB, Z1=DHA-1, Y2=FHwB, Z2=DGxF-1, Y3=AHiD-1 и Z3=В-1GjF-1
4. Принимают ЭД, представленный многоразрядной битовой строкой М.
5. В зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП в виде МДЧ е и шестимерного вектора S в качестве своих элементов, для чего
5.1) генерируют случайные целые числа k и t, удовлетворяющие условиям 1<k<q и 1<t<q, и вычисляют вектор R=AGkHtF-1;
5.2) используя некоторую коллизионно стойкую 256-битную хэш-функцию ƒH, вычисляют МДЧ е=е1||е2=ƒH(M||R), где хэш-значение е представлено как конкатенация двух 128-битных МДЧ е1 и е2;
5.3) вычисляют МДЧ n и d по следующим двум формулам:
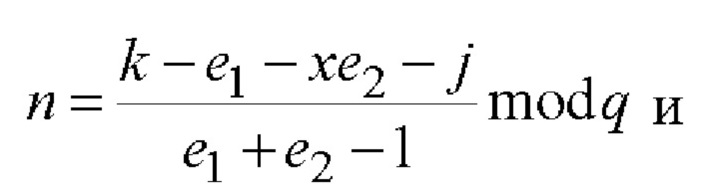
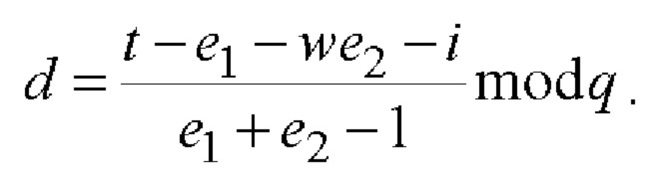
5.4) вычисляют шестимерный вектор S по формуле S=B-1GnHdD-1.
6. В зависимости от открытого ключа, принятого ЭД и ЭЦП выполняют процедуру верификации ЭЦП, для чего
6.1) вычисляют контрольный шестимерный вектор RK по математической формуле в виде равенства 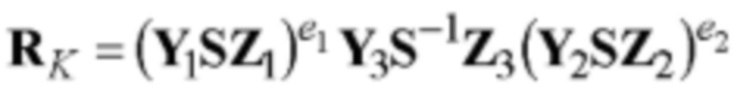 с k=3 вхождениями шестимерного вектора S и двумя операциями возведения в степень МДЧ;
с k=3 вхождениями шестимерного вектора S и двумя операциями возведения в степень МДЧ;
6.2) вычисляют контрольное МДЧ eK=ƒH(М||RK);
6.3) сравнивают контрольное МДЧ eK и МДЧ е.
7. Формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если eK=е, или о ложности ЭЦП, если eK≠е.
Постквантовая стойкость данного частного примера реализации заявленного способа обеспечивается тем, что вычисление секретного ключа по открытому ключу связано с решением системы из 11 квадратных векторных уравнений с 10 неизвестными, заданной над использованной шестимерной КНАА. Указанная система векторных уравнений сводится к системе из 66 квадратных уравнений с 60 неизвестными, заданной над полем GF(2z) со 107-битной степенью расширения двоичного поля GF(2). Использование поля GF(2z) вместо поля GF(p) обеспечивает повышение производительности и снижение схемотехнической сложности аппаратной реализации заявленного способа. Доказательство корректности работы заявленного способа по примеру 2 выполняется следующим образом:
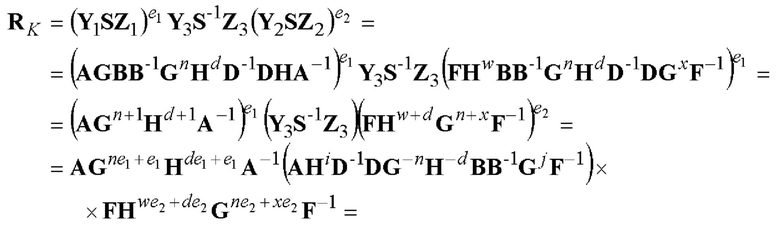
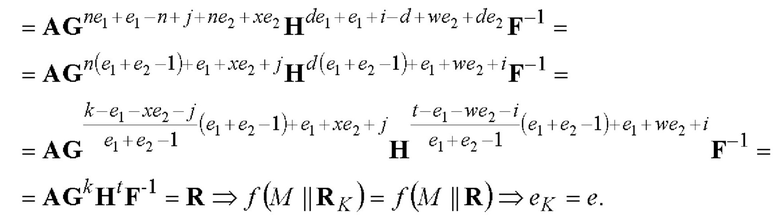
Пример 3. Случай реализации заявленного способа, иллюстрирующий пп. 1 и 4 формулы изобретения. В данном примере выполняется следующая последовательность действий:
1. Генерируют шестимерную КНАА, для чего
1.1) генерируют простое МДЧ z=127, при котором МДЧ 2z-1 = q является простым (q=170141183460469231731687303715884105727);
1.2) генерируют неприводимый двоичный многочлен степени z=121, например, двоичный многочлен δ(х)=х127+х+1;
1.3) генерируют ТУБВ, задающую некоммутативную ассоциативную операцию умножения шестимерных векторов, заданных над полем GF(2z) с операцией умножения по модулю неприводимого двоичного многочлена δ(х)=х127+х+1, например, путем копирования табл. 6 и задания структурной константы λ, равной единице поля GF(2z), т.е. λ=1;
2. Генерируют секретный ключ, включающий набор шестимерных векторов А, В, G, Gx и Н и МДЧ х в качестве своих элементов, для чего
2.1) генерируют два случайных шестимерных вектора G и Н порядка q, образующих базис <G, Н> коммутативной группы порядка q2, обладающей двухмерной цикличностью;
2.2) генерируют случайные шестимерные обратимые векторы А и В порядка q, которые удовлетворяют условиям АВ≠ВА, AG≠GA и BG≠GB;
2.3) генерируют случайное МДЧ х (1<x<q) и вычисляют шестимерный вектор Gx по формуле Gx=Gx (очевидно, что векторы G, Н и Gx являются попарно перестановочными как принадлежащие коммутативной группе, генерируемой базисом <G, Н>).
3. Формируют открытый ключ в виде набора шестимерных векторов Y, Z и U, для чего осуществляют вычисления по следующим формулам Y=AGB, Z=AGxB и U=АНВ
4. Принимают ЭД, представленный многоразрядной битовой строкой М.
5. В зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП в виде МДЧ е и шестимерного вектора S в качестве своих элементов, для чего
5.1) генерируют случайные целые числа k и t, удовлетворяющие условиям 1<k<q и 1<t<q, и вычисляют вектор R=В-1GkHtB;
5.2) используя некоторую коллизионно стойкую 256-битную хэш-функцию ƒH, вычисляют МДЧ е=e1||e2=ƒH(М||R), где хэш-значение е представлено как конкатенация двух 128-битных МДЧ е1 и е2;
5.3) вычисляют МДЧ n и d по следующим двум формулам:
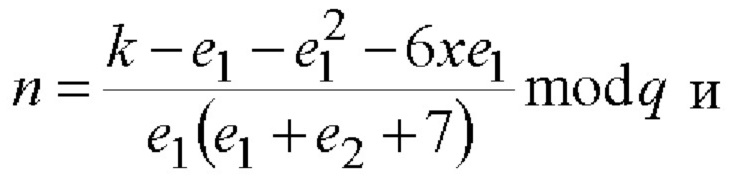
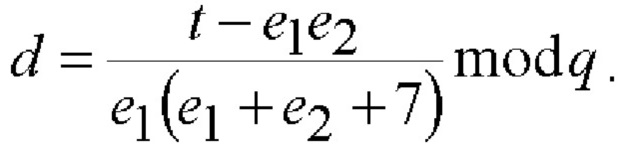
5.4) вычисляют шестимерный вектор S по формуле S=B-1GnHdA-1.
6. В зависимости от открытого ключа, принятого ЭД и ЭЦП выполняют процедуру верификации ЭЦП, для чего
6.1) вычисляют контрольный шестимерный вектор RK по математической формуле в виде равенства 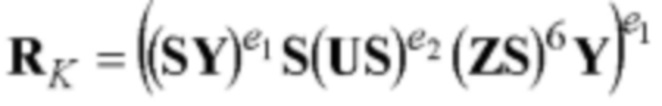 с k=4 вхождениями шестимерного вектора S и тремя операциями возведения в степень МДЧ (возведение в степень 6 несущественно влияет на вычислительную сложность вычисления правой части равенства);
с k=4 вхождениями шестимерного вектора S и тремя операциями возведения в степень МДЧ (возведение в степень 6 несущественно влияет на вычислительную сложность вычисления правой части равенства);
6.2) вычисляют контрольное МДЧ eK=ƒH(М||RK);
6.3) сравнивают МДЧ eK и е.
7. Формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если eK=е, или о ложности ЭЦП, если eK≠е.
Постквантовая стойкость данного частного примера реализации заявленного способа обеспечивается тем, что вычисление секретного ключа по открытому ключу связано с решением системы из следующих 5 квадратных векторных уравнений с 5 неизвестными А, В-1, G, Gx и Н:
YB-1=AG, ZB-1=AGx, UB-1=АН, GGx=GxG, GH=HG.
Указанная система векторных уравнений сводится к системе из 30 квадратных уравнений с 30 неизвестными, заданной над полем GF(2z) со 127-битной степенью расширения двоичного поля. Доказательство корректности работы частного варианта реализации заявленного способа по примеру 3 выполняется, учитывая формулы для вычисления МДЧ n и d (см. шаг 5.3)), следующим образом:
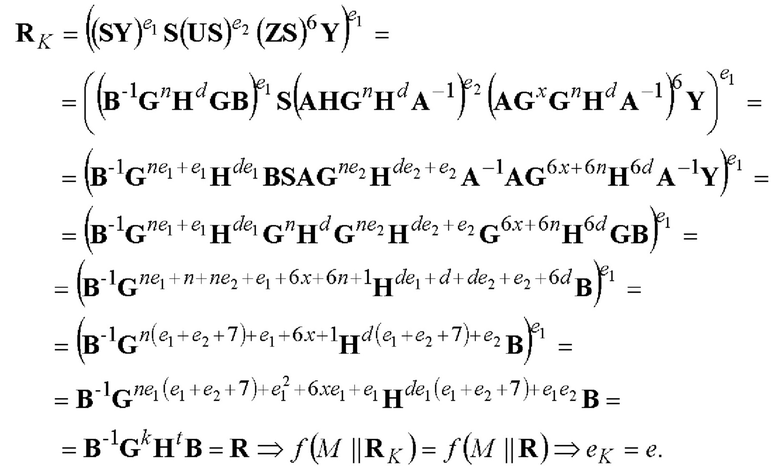
Пример 4. Случай реализации заявленного способа, иллюстрирующий п. 1 формулы изобретения. В данном примере выполняется следующая последовательность действий:
1. Генерируют четырехмерную КНАА, для чего
1.1) генерируют простое МДЧ p=2q+1, где q - 192-битное простое МДЧ, а именно, q=5261472747218403390125581496192701306697287924851078249233;
1.2) генерируют ТУБВ, задающую некоммутативную ассоциативную операцию умножения четырехмерных векторов, заданных над полем GF(p), например, путем копирования табл. 5 и задания значения λ=2.
2. Генерируют секретный ключ, включающий набор четырехмерных векторов А, В, F, G, Н, Gx, Hw, Gj и Hi и МДЧ х, w, i, и j в качестве своих элементов, для чего
2.1) генерируют два случайных четырехмерных вектора G и Н порядка q, образующих базис <G, Н> коммутативной группы порядка q, обладающей двухмерной цикличностью;
2.2) генерируют случайные четырехмерные обратимые векторы А, В, F порядка q, которые удовлетворяют условиям АВ≠ВА, AF≠FA, AG≠GA, BF≠FB, BG≠GB, FG≠GF;
2.3) генерируют случайные МДЧ х (1 х<q), w (1 w<q), i (1<i<q), и j (1<j<q) и вычисляют четырехмерные векторы Gx, Gj, Hw и Hi по формулам Gx=Gx, Gj=Gj, Hw=Hw и Hi=Hi (очевидно, что векторы G, Н, Gx, Gj, Hw и Hi являются попарно перестановочными как принадлежащие коммутативной группе, генерируемой базисом <G, Н>).
3. Формируют открытый ключ в виде набора четырехмерных векторов Y1, Z1, Y2, Z2, Y3 и Z3, для чего осуществляют вычисления по следующим формулам Y1=AGB-1, Z1=BHA-1, Y2=FHwB-1, Z2=BGxF-1, Y3=AHiB-1 и Z3=BGiF-1.
4. Принимают ЭД, представленный многоразрядной битовой строкой М.
5. В зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП в виде МДЧ е и четырехмерного вектора S в качестве своих элементов, для чего
5.1) генерируют случайные целые числа k и t, удовлетворяющие условиям 1<k<q и 1<t<q, и вычисляют вектор R=AGkHtF-1;
5.2) используя некоторую коллизионно стойкую 384-битную хэш-функцию ƒH, вычисляют МДЧ е=e1||e2||e3=ƒH(М||R), где хэш-значение е представлено как конкатенация трех 128-битных МДЧ е1, е2 и е3;
5.3) вычисляют МДЧ n и d по следующим двум формулам:
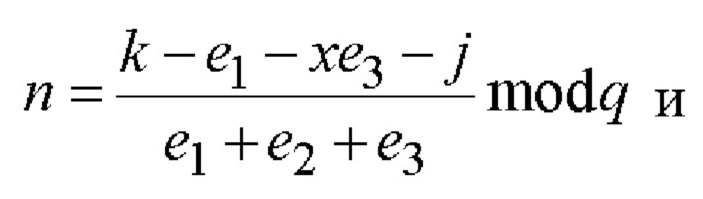
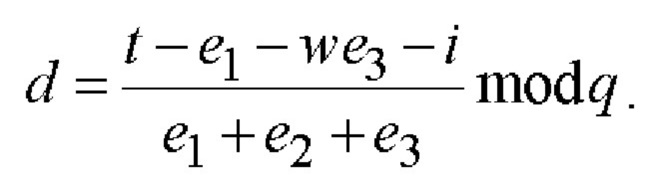
5.4) вычисляют шестимерный вектор S по формуле S=BGnHdB-1.
6. В зависимости от открытого ключа, принятого ЭД и ЭЦП выполняют процедуру верификации ЭЦП, для чего
6.1) вычисляют контрольный четырехмерный вектор RK по математической формуле в виде равенства 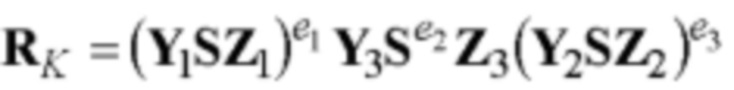 с k=3 вхождениями четырехмерного вектора S и тремя операциями возведения в степень МДЧ;
с k=3 вхождениями четырехмерного вектора S и тремя операциями возведения в степень МДЧ;
6.2) вычисляют контрольное МДЧ eK=ƒH(M||RK);
6.3) сравнивают контрольное МДЧ eK и МДЧ е.
7. Формируют результат по проверке подлинности ЭЦП в виде вывода о подлинности ЭЦП, если eK=е, или о ложности ЭЦП, если eK≠е.
Постквантовая стойкость данного частного примера реализации заявленного способа обеспечивается тем, что вычисление секретного ключа по открытому ключу связано с решением системы из 11 квадратных векторных уравнений с 9 неизвестными, заданной над использованной шестимерной КНАА. Указанная система векторных уравнений сводится к системе из 44 уравнений с 36 неизвестными, заданной над полем GF(p), порядок которого равен 192-битному простому числу. Доказательство корректности работы заявленного способа по примеру 4 выполняется следующим образом:
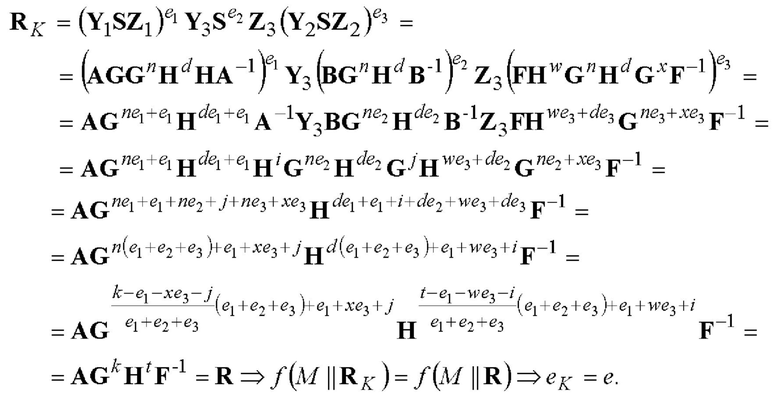
В приведенных выше примерах конкретных вариантов реализации заявленного способа даны математические доказательства корректности этих вариантов реализаций заявленного постквантового способа формирования и проверки ЭЦП, заверяющей ЭД.
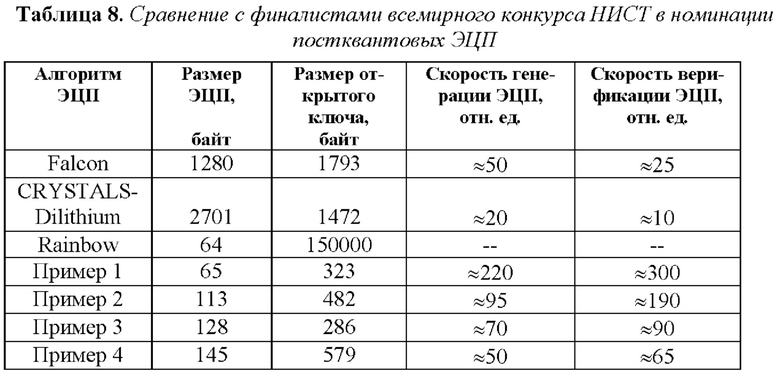
Таким образом, показано, что заявляемый способ может быть положен в основу стойких постквантовых алгоритмов ЭЦП, обеспечивающих сравнительно высокую производительности устройств и программ формирования и проверки подлинности ЭЦП. При этом решается проблема разработки практичных постквантовых алгоритмов ЭЦП с малыми размерами ЭЦП и открытого ключа, которая, судя по текущим итогам всемирного конкурса, объявленного на период 2017-2024 гг. Национальным институтом стандартов и технологий США (НИСТ), по разработке постквантовых двухключевых алгоритмов открытого согласования ключа и постквантовых алгоритмов ЭЦП [Federal Register. Announcing Request for Nominations for Public-Key Post-Quantum Cryptographic Algorithms. Available at: https://www.gpo.gov/fdsys/pkg/FR-2016-12-20/pdf/2016-30615.pdf], в настоящее время является открытой [Moody, D. 2021. NIST Status Update on the 3rd Round // https://csrc.nist.gov/CSRC/media/Presentations/status-update-on-the-3rd-round/images-media/session-1-moody-nist-round-3-update.pdf]. В табл. 8 приведено сравнение размеров открытого ключа и ЭЦП в алгоритмах, составленных по заявленному способу, и в финалистах (алгоритмы Falcon, CRYSTALS-Dilithium, Rainbow) конкурса НИСТ в номинации постквантовых алгоритмов ЭЦП [Round 3 Finalists: Public-key Encryption and Key-establishment Algorithms https://csrc.nist.gov/projects/post-quantum-crvptographv/round-3-submissions!.
Приведенные примеры и математическое обоснование показывают, что предлагаемый постквантовый способ формирования и проверки подлинности ЭЦП, заверяющей ЭД, работает корректно, обеспечивает стойкость к квантовым атакам, технически реализуем и позволяет достичь сформулированного технического результата.
Приложение 1
Толкование терминов, используемых в описании заявки
1. Двоичный цифровой электромагнитный сигнал - электромагнитный сигнал, задающий последовательность битов в виде нулей и единиц, обрабатываемую в электронных устройствах вычислительных и информационно-коммуникационных сетей и систем.
2. Параметры двоичного цифрового электромагнитного сигнала - разрядность и порядок следования сигналов, передающих единичные и нулевые биты.
3. Разрядность двоичного цифрового электромагнитного сигнала - общее число его единичных и нулевых битов, например, число 10011 является 5-разрядным.
4. Многоразрядная битовая строка - электромагнитный сигнал в двоичной цифровой форме, параметрами которого являются: число битов и порядок следования их единичных и нулевых значений.
5. Многоразрядное двоичное число (МДЧ) - многоразрядная битовая строка, интерпретируемая как двоичное число.
6. Многоразрядный двоичный многочлен (МДМ) - многоразрядная битовая строка, интерпретируемая как двоичный многочлен, записанный в виде упорядоченной последовательности его коэффициентов.
7. Электронная цифровая подпись (ЭЦП) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от подписанного электронного документа и от секретного ключа. Проверка подлинности ЭЦП осуществляют с помощью открытого ключа, который зависит от секретного ключа.
8. Электронный документ (ЭД) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от исходного документа и способа его преобразования к электронному виду.
9. Хэш-функция ƒH - функция, значение которой используется как криптографическая контрольная сумма, вычисляемая от электронных документов и сообщений и обладающая свойствами трудной обратимости и практической невозможности формирования двух различных сообщений или документов, обладающих одинаковым значением хэш-функции. Второе свойство называется коллизионной стойкостью. Входным значением (аргументом) хэш-функции является электронное сообщение или электронный документ произвольного размера, а выходное значение (значение хэш-функции) имеет фиксированный размер от 160 до 512 бит. Хэш-функция задается в виде алгоритма, описывающего последовательность действий, выполняемых над аргументом, результатом которых является значение хэш-функции.
10. Векторы размерности m (m-мерные векторы) - упорядоченные наборы из m многоразрядных битовых строк, например, из m МДЧ, образующие множество наборов, над которым задана одна или несколько алгебраических операций, обладающих свойством замкнутости. Множество m-мерных векторов, над которым заданы операции сложения векторов и умножения скаляра на вектор, обладающие свойством замкнутости, коммутативности и ассоциативности, называется m-мерным векторным пространством [Кострикин А.И. Введение в алгебру. Ч. 2. Линейная алгебра. - М., ФИЗМАТЛИТ, 2001. - 367 с.; см. с. 12].
11. Конечная m-мерная алгебра - это коечное в m-мерное векторное пространство с дополнительно определенной операцией векторного умножения всевозможных пар m-мерных векторов, обладающей свойствами замкнутости и дистрибутивности слева и справа относительно операции сложения.
12. Некоммутативная ассоциативная алгебра - алгебра, в которой операция умножения обладает свойствами некоммутативности и ассоциативности, т.е. в общем случае выполняется неравенство АВ≠ВА и равенство (АВ)С=А(ВС), где А, В и С - векторы, являющиеся элементами алгебры.
13. Секретный ключ - двоичный цифровой электромагнитный сигнал, используемый для формирования ЭЦП к заданному электронному документу. Секретный ключ представляется, например, в двоичном виде как МДЧ (последовательность битов «0» и «1»), набор МДЧ, вектор, набор векторов, набор МДЧ и векторов.
14. Открытый ключ - двоичный цифровой электромагнитный сигнал, параметры которого зависят от секретного ключа и который предназначен для проверки подлинности цифровой электронной подписи.
15. Хэш-функция от электронного документа - двоичный цифровой электромагнитный сигнал, параметры которого зависят от электронного документа и выбранного метода ее вычисления. В системах ЭЦП считается, что хэш-функция однозначно представляет ЭД, поскольку используемые хэш-функции удовлетворяют требованию коллизионной стойкости, которое означает вычислительную невозможность нахождения двух различных ЭД, которым соответствует одно и то же значение хэш-функции.
16. Операция возведения вектора А в дискретную степень МДЧ е - это операция е-кратного умножения вектора на себя: Ае=АА…А (е раз). Благодаря существованию алгоритма быстрого возведения в степень, основанного на процедуре последовательного возведения в квадрат (см., например, [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - СПб, БХВ-Петербург, 2010. - с. 56]), возведение в t-разрядную степень е вектора А может быть осуществлено путем выполнения в среднем 1,5t векторных умножений, что на современных ЭВМ реализуется за малые доли секунды для разрядностей t=100, t=1000 и более. Свойство ассоциативности операции умножения лежит в основе корректности работы алгоритма быстрого возведения в степень.
17. Порядок q вектора А - это минимальное из чисел γ, для которых выполняется условие Аγ=Е, т.е. q=min{γ: Аγ=Е}, где Е - единичный вектор.
18. Группа - это алгебраическая структура (т.е. множество математических элементов различной природы), над элементами которой задана некоторая операция и они обладают заданным набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является также элемент этой же структуры, существует нейтральный элемент ε такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а; каждый элемент обратим, т.е. для любого элемента а существует элемент а-1, такой, что выполняется равенство аа-1=ε. Детальное описание групп дано в книгах [А.Г. Курош. Теория групп. - М., изд-во «Наука», 1967. - 648 с.] и [М.И. Каргаполов, Ю.И. Мерзляков. Основы теории групп. - М., изд-во «Наука. Физматлит», 1996. - 287 с.]. Операция определенная над элементами группы называется групповой операцией.
19. Циклическая группа - это группа, каждый элемент которой может быть представлен в виде g=an для некоторого натурального значения n, где а - элемент данной группы, называемый генератором или образующим элементом циклической группы. Степень n означает, что над элементом а выполняются n последовательных операций, т.е. выполняются вычисления по формуле an=а°а°а°…°а (n раз), где «°» обозначает операцию, определенную над элементами группы.
20. Группа с двухмерной цикличностью - это конечная коммутативная группа, каждый элемент g которой может быть представлен в виде g=anbd при некоторых натуральных значениях n и d, где а и b - элементы группы, имеющие одинаковое значение порядка. Элементы а и b называются образующими группы.
21. Базис группы - минимальный набор образующих группы, например, базис группы с двухмерной цикличностью включает два образующих элемента группы а и b одного порядка и обозначается как <а, b>.
22. Операнд - элемент алгебраической структуры, над которым выполняется операция.
23. Параметр операции - МДЧ, используемое как значение степени операции возведения вектора в степень.
24. Неприводимый двоичный многочлен степени z - двоичный многочлен степени z, который непредставим в виде произведения двоичных многочленов степеней, меньших, чем z.
25. Конечное поле GF(2z) - множество всех двоичных многочленов, степень которых не превышает значения z-1, для которых определена операция сложения как сложение по модулю 2 всех коэффициентов многочленов-операндов при одинаковых степенях переменной и операция умножения по модулю неприводимого двоичного многочлена степени z, включая нулевой двоичный многочлен 0 (нулевой элемент поля GF(2z)) и единичный двоичный многочлен 1 (единица поля GF(2z)). Различные варианты полей GF(2z) различаются операцией умножения, конкретный тип которой определяется заданием конкретного неприводимого двоичного многочлена. Существует большое число различных неприводимых многочленов степени z>10. Для технических приложений полей GF(2z) представляют интерес поля с умножением задаваемым по модулю неприводимого многочлена с тремя (трехчлены) и пятью (пятичлены) ненулевыми коэффициентами. Выбор таких неприводимых двоичных многочленов обеспечивает существенное снижение вычислительной сложности операции умножения в поле GF(2z). Элементы поля GF(2z) записываются в виде битовых строк длины z, в которых каждый 1-й бит равен значению коэффициента при i-й степени переменной х, т.е. коэффициент при xi в записи двоичного многочлена в виде суммы kz-1xz-1+…+kixi+…+k2x2+k1x+k0, где коэффициенты ki имеют значение 1 или 0. Слагаемые с нулевым значением коэффициента ki опускаются в записи двоичного многочлена как суммы степеней переменной х, но присутствуют в записи двоичного многочлена в виде битовой строки kz-1ki…k2k1k0.
26. Операция конкатенации (операция присоединения), обозначаемая знаком «||» - операция объединения двух битовых строк в единую битовую строку, длина (разрядность) которой равна сумме длин (разрядностей) исходных двух битовых строк, например, 10101||0001=101010001.
27. Таблица умножения базисных векторов (ТУБВ) - таблица, по которой задают результат умножения всех возможных упорядоченных пар базисных векторов, причем такой результат задается в виде однокомпонентного вектора, т.е. базисного вектора, умноженного на скаляр.
28. Примарная группа - группа порядок которой равен простому числу или степени простого числа.
Изобретение относится к способам проверки электронной подписи (ЭЦП). Технический результат – повышение производительности постквантовых алгоритмов ЭЦП без снижения уровня их стойкости. Постквантовый способ формирования и проверки подлинности ЭЦП: генерируют m-мерную конечную некоммутативную ассоциативную алгебру, где m≥4, генерируют секретный ключ, включающий набор m-мерных векторов в качестве своих элементов, по которому формируют открытый ключ в виде набора m-мерных векторов, принимают электронный документ, представленный многоразрядной битовой строкой M, в зависимости от принятого электронного документа и от значения секретного ключа формируют ЭЦП, включающую m-мерный вектор S, в зависимости от открытого ключа, принятого электронного документа M и ЭЦП выполняют процедуру верификации ЭЦП, включающую выполнение операций умножения m-мерных векторов, возведения m-мерных векторов в степень многоразрядного двоичного числа и сравнения, и формируют результат по проверке подлинности электронной цифровой подписи, отличающийся тем, что выполняют процедуру верификации ЭЦП, включающую осуществление операций по математической формуле в виде равенства с k≥2 вхождениями m-мерного вектора S. 8 табл.
Постквантовый способ формирования и проверки подлинности электронной цифровой подписи, заверяющей электронный документ, заключающийся в том, что генерируют m-мерную конечную некоммутативную ассоциативную алгебру, где m ≥ 4, генерируют секретный ключ, включающий набор m-мерных векторов в качестве своих элементов, по секретному ключу формируют открытый ключ в виде набора m-мерных векторов, принимают электронный документ, представленный многоразрядной битовой строкой M, в зависимости от принятого электронного документа и от значения секретного ключа формируют электронную цифровую подпись, включающую m-мерный вектор S, в зависимости от открытого ключа, принятого электронного документа M и электронной цифровой подписи выполняют процедуру верификации электронной цифровой подписи, включающую выполнение операций умножения m-мерных векторов, возведения m-мерных векторов в степень многоразрядного двоичного числа и сравнения, и формируют результат по проверке подлинности электронной цифровой подписи, отличающийся тем, что генерируют секретный ключ в виде набора m-мерных векторов A, B, D, F, G, H, Gx, Hw, Gj и Hi путем генерации случайных многоразрядных двоичных чисел x, w, i, и j и случайных m-мерных векторов A, B, D, F, G и H, где порядок векторов G и H равен простому многоразрядному двоичному числу q, удовлетворяющих условиям AB # BA, AD # DA, AF # FA, AG # GA, BD # DB, BF # FB, BG # GB, DF # FD, DG # GD, FG # GF и GH = HG, и вычисления m-мерных векторов Gx, Hw, Gj и Hi по формулам Gx = Gx, Hw = Hw, Gj = Gj и Hi = Hi, формируют открытый ключ в виде набора m-мерных векторов Y1, Z1, Y2, Z2, Y3 и Z3 путем выполнения вычислений по формулам Y1 = AGB, Z1 = DHA-1, Y2 = FHwB, Z2 = DGxF-1, Y3 = AHiD-1 и Z3 = B-1GjF-1, формируют электронную цифровую подпись в виде многоразрядного двоичного числа e и m-мерного вектора S, для чего генерируют случайные многоразрядные двоичные числа k и t, вычисляют вектор R = AGkHtF-1 и многоразрядное двоичное число e = e1||e2 = fH(M||R), где fH – коллизионно-стойкая хэш-функция и e1 и e2 – многоразрядные двоичные числа, имеющее одинаковую разрядность, вычисляют многоразрядные двоичные числа n и d по формулам  и
и 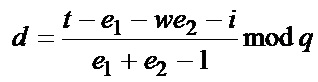 , вычисляют вектор S по формуле S = B-1GnHdD-1, выполняют процедуру верификации электронной цифровой подписи, включающую вычисление контрольного m-мерного вектора RK по формуле
, вычисляют вектор S по формуле S = B-1GnHdD-1, выполняют процедуру верификации электронной цифровой подписи, включающую вычисление контрольного m-мерного вектора RK по формуле 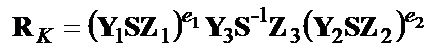 с k=3 вхождениями m-мерного вектора S, вычисление контрольного многоразрядного двоичного числа eK = fH(M||RK) и сравнение многоразрядных двоичных чисел eK и e, и формируют результат по проверке подлинности электронной цифровой подписи в виде вывода о подлинности электронной цифровой подписи, если eK = e, или о ложности электронной цифровой подписи, если eK # e.
с k=3 вхождениями m-мерного вектора S, вычисление контрольного многоразрядного двоичного числа eK = fH(M||RK) и сравнение многоразрядных двоичных чисел eK и e, и формируют результат по проверке подлинности электронной цифровой подписи в виде вывода о подлинности электронной цифровой подписи, если eK = e, или о ложности электронной цифровой подписи, если eK # e.
| CN 102164032 A, 24.08.2011 | |||
| JP 2020052393 A, 02.04.2020 | |||
| Токарный резец | 1924 |
|
SU2016A1 |
| СПОСОБ ГЕНЕРАЦИИ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2392736C1 |
| статья Moldovyan, Nikolay A | |||
| и др | |||
| "Candidate for practical post-quantum signature scheme" опубл | |||
| Способ восстановления спиралей из вольфрамовой проволоки для электрических ламп накаливания, наполненных газом | 1924 |
|
SU2020A1 |
Авторы
Даты
2023-12-12—Публикация
2022-02-24—Подача