Изобретение относится к криптографии и защите информации от несанкционированного доступа, может применяться для быстрой генерации случайных чисел с высокой степенью статистического соответствия закону равномерного распределения и качеством непредсказуемости таких последовательностей.
Известен способ генерации случайных чисел [1]. Способ генерации случайных чисел с использованием n-разрядного регистра сдвига с обратной связью, разрядом которого выбран q-ичный символ (q=2l, l=8, 16 бит), в цепях обратной связи осуществляют не менее трех двухпараметрических операций над q-ичными символами на основе случайных таблиц замены Тк, каждая из которых содержит 2l неповторяющихся значений двоичных комбинаций длиной l, начальное заполнение регистра сдвига с обратной связью и таблиц случайной замены выполняют от физического датчика случайных чисел неповторяющимися значениями случайных чисел, для чего сравнивают очередное значение случайного числа с ранее записанными значениями случайных чисел, при совпадении нового значения числа с любым из ранее записанных новое значение отбрасывают, при несовпадении - записывают в очередной разряд регистра сдвига и очередную строку таблицы замены, для генерации очередного случайного числа выбирают пять значений, указывающих номера разрядов регистра сдвига, первая и вторая пары значений указывают номера разрядов регистра сдвига для выполнения соответственно первой и второй операций, операндами третьей операции являются результаты выполнения первых двух операций, операндами которых являются значения q-ичных символов, записанные в данном такте в разрядах регистра сдвига с указанными номерами, для выполнения всех операций находят в используемой таблице Тк значение первого операнда и считывают из таблицы Тк значение, которое отстоит на число строк используемой таблицы Тк, совпадающее с двоичным значением второго операнда, результат выполнения третьей операции, являющийся очередным результатом генерации, записывают в последний выбранный разряд регистра сдвига, после чего производят сдвиг содержимого регистра сдвига на один q-ичный разряд.
Существенным недостатком данного способа являются значительно худшие статистические свойства генерируемой псевдослучайной последовательности по сравнению с белым шумом из-за периодичности псевдослучайной последовательности, на основе которой построен способ.
Задача, на решение которой направлено данное изобретение, заключается в улучшении статистических свойств генерируемой последовательности за счет устранения периодичности.
Техническим результатом заявляемого изобретения является генерация последовательности чисел более случайных, чем в прототипе, близкой по характеристикам к белому шуму [6, стр.172-180].
Указанный технический результат достигается тем, что в известном способе генерации случайных чисел, заключающемся в начальном заполнении таблицы случайной замены, выполняемом от физического датчика случайных чисел неповторяющимися значениями случайных чисел, для чего сравнивают очередное значение случайного числа с ранее записанными значениями случайных чисел, отбрасывают новое значение при совпадении нового значения числа с любым из ранее записанных, записывают в очередную ячейку таблицы замены - при несовпадении, согласно изобретению значения случайных чисел skn, записанные в k-й строке n-го столбца таблицы случайной замены, используют как n-й параметр рn k-й броуновской частицы qk, где k=1,…, K, причем K - количество броуновских частиц, а n=3,…, N, причем N - количество параметров броуновских частиц, при этом параметры р1 и р2 используют как координаты в двумерном пространстве xk, yk, а параметр р3 - как угол вектора движения φk броуновской частицы qk, причем координаты xk, yk частицы qk такие, что qk располагается внутри области моделирования броуновского движения А, а угол вектора движения φk∈[0; 2π] рад; имитируют движение броуновских частиц qk внутри области А путем периодического пересчета через промежуток времени Δt параметров pn броуновских частиц qk в соответствии с законами движения броуновских частиц в замкнутом пространстве с абсолютно упругими соударениями частиц между собой и со стенками области моделирования броуновского движения, с последующим сохранением пересчитанных параметров pn броуновских частиц qk в виде числа skn таблицы случайной замены; выделяют внутри области моделирования броуновского движения А область А', представляющей собой совокупность всех точек области А, в которых может находиться центр любой броуновской частицы; разбивают выделенную область А' на М равных по площади кусочков, причем М≥2, из которых выбирают ключевые кусочки ai при этом i=1,…, I, где I - количество разрядов генерируемого случайного числа, причем 2≤I≤М; формируют значение i-го двоичного разряда очередного I-разрядного случайного двоичного числа Z путем анализа наличия центров броуновских частиц в ключевом кусочке ai выделенной области А', присваивают i-му двоичному разряду числа Z значение 1, если в ключевом кусочке ai находится центр хотя бы одной броуновской частицы, присваивают i-му двоичному разряду числа Z значение 0 в противном случае, возвращают сформированное I-разрядное случайное двоичное число Z.
Эти отличительные признаки по сравнению с прототипом позволяют сделать вывод о соответствии заявляемого технического решения критерию "новизна".
Сущность изобретения заключается в следующем. Движение броуновских частиц является случайным и имеет плоский ("белый") спектр мощности (2, стр.199). За счет имитации в предлагаемом способе броуновского движения спектр мощности генерируемых чисел близок к спектру мощности "белого" шума. При этом генерируемая последовательность будет тем ближе по своим статистическим свойствам к "белому" шуму, чем точнее будут определяться координаты движения броуновских частиц. Координаты могут быть дробными и рассчитываться с любой необходимой точностью.
В предлагаемом способе генерации случайных чисел перечисленная совокупность существенных признаков в указанном порядке обеспечивает генерацию последовательности чисел с хорошими статистическими свойствами, близкими к свойствам "белого" шума.
Именно новое свойство совокупности признаков, приводящих к генерации более случайных чисел за счет имитации броуновского движения частиц, позволяет сделать вывод о соответствии предлагаемого технического решения критерию "изобретательский уровень".
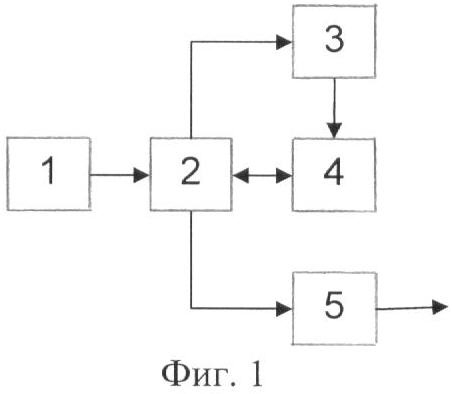
Предлагаемый способ генерации случайных чисел может быть реализован с помощью ЭВМ и вычислительного устройства, структура которых представлена на фиг.1, где обозначено:
блок 1 - физический датчик случайных чисел;
блок 2 - запоминающее устройство (таблица случайной замены);
блок 3 - тактовый генератор (таймер);
блок 4 - вычислительное устройство;
блок 5 - устройство чтения случайных чисел.
Назначение блоков понятно из их названия.
Для простоты описания работы устройства будем использовать следующие условия и ограничения:
- в качестве области моделирования броуновского движения используют прямоугольную область;
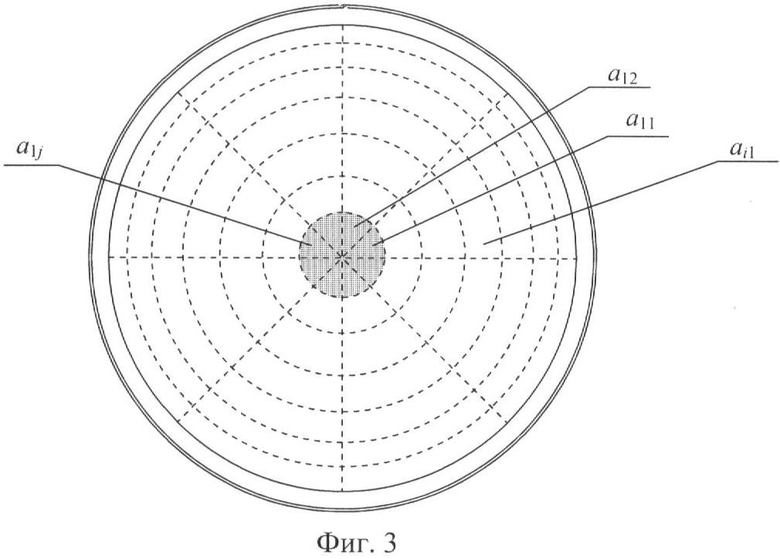
- таблица случайной замены в каждой строке содержит координаты в двумерном пространстве xk, yk и угол вектора движения φk броуновских частиц qk, где 1≤k≤K, K - количество броуновских частиц, причем r≤xk≤L-r, r≤yk≤Н-r; xk, yk - действительные числа, где L и Н - соответственно длина и высота прямоугольной области моделирования броуновского движения, r - радиус броуновской частицы, 0≤φk<2π рад (фиг.2);
- внутри области моделирования броуновского движения размера L×H выделяют область А размером (L-2·r)×(H-2·r), при этом центр области моделирования броуновского движения совпадает с центром выделенной области А;
- выделенную область А разбивают на 2n равных строк и 2n равных столбцов, где n - натуральное число, причем каждая ячейка aij, где i=1…2n - количество строк, j=1…2n - количество столбцов выделенной области А имеет размеры l×h, где l=(L-2·r)/2n, h=(H-2·r)/2n.
Осуществляют начальное заполнение таблицы случайной замены 2 от физического датчика случайных чисел 1 неповторяющимися значениями случайных чисел, для чего сравнивают очередное значение случайного числа с ранее записанными значениями случайных чисел, отбрасывают новое значение при совпадении нового значения числа с любым из ранее записанных, записывают в очередную ячейку таблицы замены - при несовпадении. После заполнения таблицы случайной замены передают сигнал инициализации работы устройства на блок 3. С блока 3 поступают тактовые сигналы на вычислительное устройство 4, которое при поступлении очередного тактового сигнала осуществляет пересчет изменяемых параметров xk, yk и φk всех броуновских частиц. С помощью блока 5 считывают очередное двоичное 2n-разрядное случайное двоичное число Z путем анализа наличия броуновских частиц, например, в первой строке выделенной области А следующим образом: присваивают j-му двоичному разряду числа Z значение 1, если в ячейке a1j находится хотя бы одна броуновская частица, то есть существует хотя бы одна броуновская частица qk такая, что ее координаты удовлетворяют условиям r+(j-1)·l≤xk<r+j·l, r+(j-l)·h≤yk<r+j·h, в противном случае присваивают j-му двоичному разряду числа Z значение 0.
Для улучшения статистических свойств генерируемой случайной последовательности можно использовать:
- считывание случайных чисел из произвольной строки или столбца таблицы;
- в качестве дополнительных параметров броуновских частиц qk, хранимых в таблице случайной замены и учитываемых при имитации движения: радиусы rk, массы mk и скорости движения νk броуновских частиц, где 1≤k≤K, K - количество броуновских частиц;
- более сложную форму области моделирования броуновского движения, например, круглую (как показано на фиг.3), кольцеобразную или несимметричную.
Для повышения скорости генерации случайных чисел можно, например, осуществлять считывание случайных чисел не только из первой строки, но также в каждом столбце и в каждой строке таблицы, то есть генерировать сразу 2n+1 случайных чисел.
Способ может применяться при построении программных, аппаратных и программно-аппаратных средств защиты информации от несанкционированного доступа, криптографической защиты информации и обеспечения целостности и доступности информации, а также для решения любых технических задач, требующих применения случайных чисел, высокой скорости генерации и хороших статистических свойств.
Реализация предлагаемого способа не вызывает затруднений, так как все блоки и узлы, входящие в устройство, реализующее способ, общеизвестны и широко описаны в технической литературе.
В качестве физического датчика случайных чисел может быть использована частота процессора ЭВМ, запоминающее устройство (таблица случайной замены) может быть реализовано на базе любого машиночитаемого носителя информации [10, 11], тактовый генератор (таймер) - на базе кварцевого генератора и делителя частоты [5, 9], вычислительное устройство и устройство чтения случайных чисел - в виде специализированных устройств на микроконтроллерах по принципам и методам, описанным в [5-9], взаимное соединение блоков может быть реализовано по стандартным схемам подключения устройств [12].
Источники информации
1. Осмоловский С.А. Способ генерации случайных чисел. Патент на изобретение №2246129 от 10.02.2005.
2. Шредер. М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. Ижевск: НИЦ "Регулярная и хаотическая динамика", 2001. - 528 с.
3. P.M.Кроновер. Фракталы и хаос в динамических системах. Основы теории. М.: Постмаркет, 2000. - 352 с.
4. Нечаев И.А. Конструкции на логических элементах цифровых микросхем. - М.: "Радио и связь", 1992. - 123 с.
5. Белов А.В. Создаем устройства на микроконтроллерах. - СПб.: Наука и техника, 2007. - 304 с.
6. Конструкторско-технологическое проектирование электронной аппаратуры. Учебник для вузов. Серия: Информатика в техническом университете. Под ред. Шахнова В.А. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2003. - 528 с.: ил.
7. Суворова Е., Шейнин Ю. Проектирование цифровых систем на VHDL. Серия "Учебное пособие". - СПб.: БХВ-Петербург, 2003. - 576 с.: ил.
8. Овчинников В.А. Алгоритмизация комбинаторно-оптимизационных задач при проектировании ЭВМ и систем. Серия: Информатика в техническом университете. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2001. - 288 с.: ил.
9. Новиков Ю.В. Основы цифровой схемотехники. Базовые элементы и схемы. Методы проектирования. - М.: Мир, 2001. - 379 с.
10. Левин В.И. Носители информации в цифровом веке / Под общ. ред. Д.Г.Красковского. - М.: КомпьютерПресс, 2000. - 256 с.: ил.
11. Гук М. Дисковая подсистема ПК. - СПб.: Питер, 2001. - 336 с.: ил. Пей Ан. Сопряжение ПК с внешними устройствами. - М.: ДМК Пресс, 2003. - 320 с. ил.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ генерации случайных чисел | 2020 |
|
RU2743326C1 |
| СПОСОБ ГЕНЕРАЦИИ СЛУЧАЙНЫХ ЧИСЕЛ | 2003 |
|
RU2246129C2 |
| СПОСОБ ГЕНЕРАЦИИ РАВНОМЕРНО РАСПРЕДЕЛЕННЫХ И НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ЧИСЕЛ | 2013 |
|
RU2583729C2 |
| СПОСОБ И УСТРОЙСТВО ГЕНЕРАЦИИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ СЛУЧАЙНЫХ ЧИСЕЛ | 2018 |
|
RU2716357C1 |
| УСТРОЙСТВО И СПОСОБ ВЫЧИСЛЕНИЯ ЗНАЧЕНИЙ МЯГКОГО РЕШЕНИЯ, ПОДАВАЕМЫХ НА ВХОД ДЕКОДЕРА КАНАЛА В СИСТЕМЕ ПЕРЕДАЧИ ДАННЫХ | 2002 |
|
RU2248678C2 |
| СПОСОБ ЗАЩИТЫ ИНФОРМАЦИИ | 2017 |
|
RU2648598C1 |
| Генератор случайного марковского процесса | 1989 |
|
SU1619262A1 |
| Генератор случайной последовательности | 2016 |
|
RU2635898C1 |
| УСТРОЙСТВО ОБРАБОТКИ ИНФОРМАЦИИ, СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И ПРОГРАММА | 2012 |
|
RU2595924C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ДИСКРЕТНЫХ ПОЛИНОМИАЛЬНЫХ ПРЕОБРАЗОВАНИЙ | 2012 |
|
RU2517694C1 |
Изобретение относится к криптографии и защите информации от несанкционированного доступа, может применяться для генерации случайных чисел. Техническим результатом является улучшение статистических свойств генерируемой последовательности за счет устранения периодичности. Способ заключается в следующем: заполняют таблицу случайной замены от физического датчика случайных чисел неповторяющимися значениями случайных чисел, используют значения случайных чисел таблицы как параметры броуновских частиц, имитируют движение броуновских частиц внутри области А путем периодического пересчета через промежуток времени параметров броуновских частиц в соответствии с законами движения броуновских частиц, сохраняют пересчитанные параметры в таблице случайной замены; выделяют область А', представляющую собой совокупность всех точек области А, в которых может находиться центр любой броуновской частицы; разбивают область А' на М равных по площади кусочков, выбирают ключевые кусочки аi; формируют значение i-го двоичного разряда случайного двоичного числа Z путем анализа наличия центров броуновских частиц в ключевом кусочке аi, при этом присваивают i-му двоичному разряду числа Z значение 1, если в ключевом кусочке аi находится центр хотя бы одной броуновской частицы, присваивают значение 0 в противном случае. 3 ил.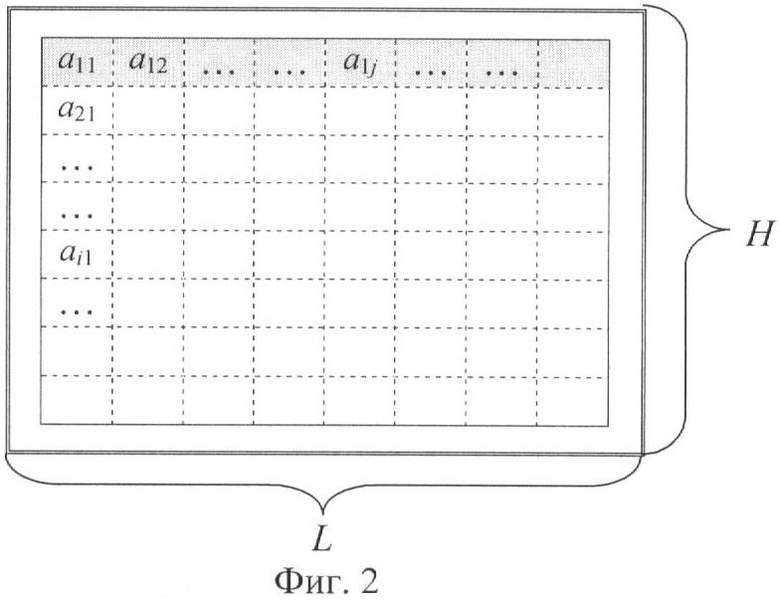
Способ генерации случайных чисел, заключающийся в начальном заполнении таблицы случайной замены, выполняемом от физического датчика случайных чисел неповторяющимися значениями случайных чисел, для чего сравнивают очередное значение случайного числа с ранее записанными значениями случайных чисел, отбрасывают новое значение при совпадении нового значения числа с любым из ранее записанных, записывают в очередную ячейку таблицы замены - при несовпадении, отличающийся тем, что значения случайных чисел skn, записанные в k-й строке n-го столбца таблицы случайной замены, используют как n-й параметр рn k-й броуновской частицы qk, где k=1,…, К, причем К - количество броуновских частиц, a n=3,…, N, причем N - количество параметров броуновских частиц, при этом параметры p1 и p2 используют как координаты в двумерном пространстве xk, уk, а параметр p3 - как угол вектора движения φk броуновской частицы qk, причем координаты хk, уk частицы qk такие, что qk располагается внутри области моделирования броуновского движения А, а угол вектора движения φk∈[0; 2π] рад; имитируют движение броуновских частиц qk внутри области А, путем периодического пересчета через промежуток времени Δt параметров рn броуновских частиц qk в соответствии с законами движения броуновских частиц в замкнутом пространстве с абсолютно упругими соударениями частиц между собой и со стенками области моделирования броуновского движения, с последующим сохранением пересчитанных параметров рn броуновских частиц qk в виде числа skn таблицы случайной замены; выделяют внутри области моделирования броуновского движения А область А', представляющей собой совокупность всех точек области А, в которых может находиться центр любой броуновской частицы; разбивают выделенную область А' на М равных по площади кусочков, причем М≥2, из которых выбирают ключевые кусочки аi, при этом i=1,…, I, где I - количество разрядов генерируемого случайного числа, причем 2≤I≤М; формируют значение i-го двоичного разряда очередного I-разрядного случайного двоичного числа Z путем анализа наличия центров броуновских частиц в ключевом кусочке аi выделенной области А', присваивают i-му двоичному разряду числа Z значение 1, если в ключевом кусочке аi находится центр хотя бы одной броуновской частицы, присваивают i-му двоичному разряду числа Z значение 0 в противном случае, возвращают сформированное I-разрядное случайное двоичное число Z.
| СПОСОБ ГЕНЕРАЦИИ СЛУЧАЙНЫХ ЧИСЕЛ | 2003 |
|
RU2246129C2 |
| Устройство для моделирования случайных процессов | 1984 |
|
SU1223227A1 |
| FR 2849938 А1, 16.07.2004 | |||
| JP 2004171549 А, 17.06.2004 | |||
| JP 2006155168 А, 15.06.2006. | |||
Авторы
Даты
2011-07-20—Публикация
2009-10-05—Подача