Область техники
[0001] Кронекер сказал: Бог создал натуральные числа; все остальное является делом рук человека. Как предполагают изобретатели, он имел в виду то, что вся математика основана на изобретенных Богом натуральных числах или рекуррентной формуле xk+1=xk+1 при x1=1; после чего труды, вдохновенные идеи и мысли известных людей позволили нам иметь рациональные числа, вещественные числа, комплексные числа, матрицы, геометрию, анализ и алгебру. В настоящее время изобретатели находятся на далеком расстоянии от уровня знания глубины и красоты математики того времени. Тем не менее, такая концепция, что вся математическая система построена на простейших рекуррентных формулах, обнадеживает нас. В настоящем документе мы представляем исследования по генерации случайных чисел на компьютере. В частности, мы показываем, что произвольная последовательность равномерно распределенных и независимых случайных чисел на компьютере может рассматриваться, как последовательность, генерируемая посредством мультипликативного конгруэнтного метода, и кладем этот факт в основу технологического способа генерации случайных чисел. Надеемся, что мы не будем бросать вызов Богам, но Боги благословят нас на блестящую перспективу, осуществимую руками человека.
[0002] Использование дистиллированной воды без примесей является необходимым для обеспечения устойчивых и правильных химических преобразований. Случайные числа с различной статистикой получают на компьютере при помощи высокоточных аналитических преобразований равномерно распределенных и независимых случайных чисел. Таким образом, генерация случайных чисел с высокоточной равномерностью и независимостью имеет важное значение для любого компьютерного моделирования, использующего различные типы случайных чисел. Наша задача состоит в представлении изобретений для способов генерации последовательностей случайных чисел на компьютере с радикально улучшенной точностью при своей статистике. Следует отметить, что теория вероятности или теория стохастических процессов неизменно основаны на предположении, что последовательности состоят из бесконечного количества элементов, и что обработанные числа имеют бесконечную степень точности вещественных чисел. Эти предположения вводят много упрощений, а также унификацию в форме предельных теорем или эргодических теорем. Напротив, компьютеры могут обрабатывать только последовательности конечной длины Т, какой бы большой не могла бы быть эта длина Т. А вещественные числа могут быть заданы только дискретно с наименьшей единицей точности. Конечность последовательностей и дискретность чисел обычно вызывает сложности. Несмотря на это, наше сознательное утверждение конечности и дискретности освобождает нас от различных метафизических проблем, таких как вопрос самой возможности генерации случайных чисел на компьютерах. Таким образом, мы здесь исходим из явного условия конечности обработанных чисел и последовательностей. Как будет вскоре объяснено, это позволяет нам сконцентрироваться на мультипликативной и конгруэнтной генерации равномерно распределенных и независимых случайных чисел, которая
содержит положительное целое число d, называемое модулем,
содержит положительное целое число z, взаимно простое с d и называемое множителем,
содержит положительное целое число n, взаимно простое с d и называемое начальным значением или начальным числом,
порождает последовательность {rk≡n zk| 0<rk<d, k=0,1,2,···} целых чисел рекуррентно при помощи отношений конгруэнтности
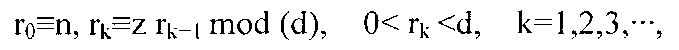
и дает последовательность {v1,v2,v3,…} случайных чисел в интервале (0,1) как
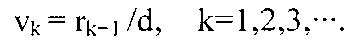
Отметим ступенчатое задание vk и rk-1, адаптированное здесь для дальнейшего удобства. Мультипликативный конгруэнтный генератор равномерно распределенных и независимых случайных чисел с модулем d, множителем z и начальным значением n будет символически обозначен, как (d, z, n). Если начальное число n не имеет отношения к аргументам, то это символическое обозначение будет сокращено до (d, z). Информация о случайных числах не сокращена до трех чисел (d, z, n); она получена как объект указаний, заданных посредством (d, z, n) и как огромное количество вычислительной работы для получения указанной последовательности. Для предотвращения путаницы и удобства обозначения образование степеней, таких как pi в степени jk, будет обозначено, как (pi)^jk.
Уровень техники
[0003] Начнем с общего технологического и математического описания проблемы. Требуется, чтобы генераторы случайных чисел на компьютере были воспроизводимыми, т.е. они должны давать одинаковую последовательность случайных чисел по запросу пользователя, например, когда пользователям надо отлаживать свои программы моделирования. Генераторы также должны быть переносимыми, т.е. они должны воспроизводить одинаковую последовательность случайных чисел на любых компьютерах и в любых вычислительных языках. А также моделирование обычно требует хранения в памяти компьютера слишком большого количества случайных чисел. Таким образом, случайные числа на компьютере могут быть сгенерированы только последовательно при помощи целочисленной арифметики, которая свободна от ошибок усечения и округления и дает одинаковые результаты на любых компьютерах или в любых вычислительных языках. Говоря более ясным языком, компьютеры должны производить последовательность {x1, x2,···, xT} целых чисел, ограниченную как 0≤xk<z для всех k при достаточно большом целом числе z, и выводить ассоциированную последовательность uk:=xk/z последовательно для k=1,2,… как равномерно распределенные и независимые случайные числа при помощи арифметики вещественных или рациональных чисел. Количество различных состояний на любом компьютере, доступных для определения следующего целочисленного результата, конечно. Следовательно, его начальное состояние постоянно повторяется, а длина последовательности случайных чисел, обозначенная Т, ограничена. Пусть последовательность {x1, x2,···, xT} будет произвольной конечной последовательностью целых чисел в пределах интервала 0≤xk<z. За исключением двух случаев, когда все {x1, x2,···,xT} равны нулю и все равны d-1, мы получаем простое условие, что эта последовательность соответствует периоду
периодической последовательности, возникающей в процессе деления несократимой дроби n/d на основание z при x=n/d, удовлетворяющему условию <x<1,
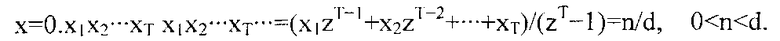
Поскольку делитель d является множителем zT-1, то d и z будут взаимно простыми. Процесс деления n на d никогда не заканчивается и выражается следующими уравнениями:
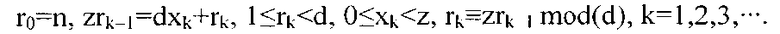
Основная особенность, которую следует отметить, состоит в том, что изменение одного числа в последовательности {x1, x2,···, xT}, скажем xj на хj′, изменит вид несократимой дроби n/d, а наглядная близость целочисленных последовательностей может обычно приводить к очень различным формам неделимых дробей, хотя процессы деления будут почти параллельны. Другая особенность состоит в том, что второе уравнение, деленное на dz, дает ключевую оценку,
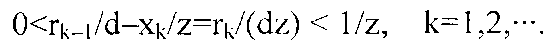
Эта оценка показывает очевидный факт: если при делении n на d остаток мал, то следующее частное будет также мало. Однако этот результат совсем не является очевидным. На практике целое число z больше, чем 230, a 1/z в качестве границы интервала пренебрежимо мало. Неравенство служит доказательством, что каждый член в любой последовательности {uk:=xk/z| k=1, 2,···,T}, которая должна давать равномерно распределенные случайные числа на компьютере, аппроксимируется, как vk-1/z<uk<vk в малых и равномерно распределенных границах погрешности 1/z≈2-30 соответствующей последовательности
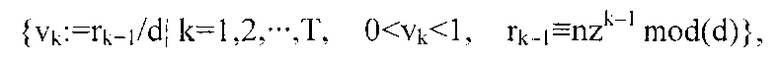
которая является именно мультипликативной конгруэнтной последовательностью случайных чисел, сгенерированной при помощи генератора (d, z, n). Следовательно, в качестве математического принципа нам нужно только сосредоточиться на обнаружении мультипликативного конгруэнтного генератора (d, z, n) случайных чисел с достаточно длинным периодом Т с хорошей равномерностью и независимостью. Этот ясный и твердый взгляд на проблему дополнительно подкреплен спектральными тестами, которые неотделимо связаны с мультипликативной конгруэнтной генерацией случайных чисел.
[0004] В известном уровне техники существовали два различных типа для пары чисел (d, z) для мультипликативного конгруэнтного генератора. Один тип образован при помощи большого нечетного простого модуля d=p с множителем z его первообразного корня и реализует период Т=φ(р)=р-1, где φ является фи-функцией Эйлера. Другой тип состоит из модуля d=2i при i≥4 и любого множителя z=5 mod(8) для периода Т=2i-2. Оба эти генератора реализуют большой период среди всех возможных выборов множителей для соответствующих модулей и, вероятно, принимают соответствующие спектральные тесты согласно очевидным математическим правилам, опуская получающуюся в результате большую вычислительную нагрузку. Настоящее изобретение является прямым потомком первого из них, пары нечетного простого модуля и его первообразного корня. Фишман и Мур (1986) предоставили монументальные спектральные тесты на простой модуль Мерсенна d=p=231-1 и показали общий и убедительный факт, что хороший генератор (d, z) может быть найден только при помощи тщательного тестирования всех первообразных корней без каких-либо пристрастий. Однако такой вывод выявил значительную сложность; количество вычислений в полных спектральных тестах увеличилось пропорционально dθ при показателе степени θ не большем, чем 3/2. Сам по себе тест должен быть выполнен на самом быстром современном компьютере. Требуется, чтобы компьютер был оборудован генератором случайных чисел для обеспечения наибольшего количества Т случайных чисел, которые могут быть использованы или вычислены в моделировании, скажем, месяца. Это число Т должно быть нижним пределом периода, который должен иметь генератор (d, z) случайных чисел, но выражение T≤d/2 является структурным ограничением мультипликативного конгруэнтного способа. Таким образом, компьютеры имеют предел вычислимости, пропорциональный d, но исчерпывающие спектральные тесты требуют общее количество вычислений, пропорциональное dθ, при θ≥3/2. В этом и состоит проблема невычислимости. Накадзава и Накадзава (2012а, b) совершили важный прорыв в отношении этих трудностей путем использования модулей, образованных при помощи произведения двух степеней нечетных простых чисел. Такие способы уменьшают время вычисления исчерпывающих спектральных тестов до O(dθ) при θ<1, в то же время сохраняя отношение периода Т к модулю d настолько большим, как в случае пары простого модуля и его первообразного корня.
Фишман и Мур (1986): Дж.С. Фишман и Л.Р. Мур, Полный анализ мультипликативных конгруэнтных генераторов случайных чисел с модулем 231-1. Журнал SIAM (Society for Industrial and Applied Mathematics, Общество промышленной и прикладной математики) научных и статистических вычислений, том 7, стр. 24-45.
Накадзава и Накадзава (2012а): Н. Накадзава и Н. Накадзава, Вычислительные процессы в спектральных тестах мультипликативных конгруэнтных генераторов для равномерно распределенных и независимых случайных чисел, реализованных посредством модулей, образованных двумя нечетными простыми числами. Название файла computable.pdf, загружаемого с http://www10.plala.or.jp/h-nkzw/ (26 октября 2012 г.).
Накадзава и Накадзава (2012b): Н. Накадзава и Н. Накадзава, Мультипликативные конгруэнтные генераторы с модулями, образованными посредством двух нечетных простых множителей, для равномерно распределенных и независимых случайных чисел I. Вычислительный анализ структур. Название файла revpopesql.pdf, загружаемого с http://www10.plala.or.jp/h-nkzw/ (15-17 сентября 2012 г., исправлен 31 октября 2012 г.).
Кратное раскрытие сущности изобретения
[0005] Следующие пункты (i1)-(i3) кратко излагают изобретения, которые будут представлены. Хотя они относятся к новым разработкам для соответствующей отдельной грани генерации равномерно распределенных и независимых случайных чисел, их объединение будет работать явно усиливая друг друга.
(i1) Новая расширенная разработка спектральных тестов в качестве усиленного фильтра для извлечения лучшей пары (d, z) нечетного модуля d и множителя z, являющегося взаимно простым с d, как мультипликативного конгруэнтного генератора для равномерно распределенных и независимых случайных чисел с достоверной статистической характеристикой.
(i2) Новая система разработок для мультипликативного конгруэнтного генератора (d, z), содержащего модуль d и множитель z, характеризующегося следующими условиями 2a)-2e);
2а) модуль d=d1d2 является произведением парных взаимно простых множителей d1 и d2, образованных при помощи двух различных нечетных простых чисел p1 и p2 как dk=pk^ik для k=1,2 при i1≥1 и i2≥1,
2b) нечетное простое число p1 имеет вид p1=2q+1, а нечетное простое число p2 имеет вид p2=4r+1, при этом q и r - другие нечетные простые числа.
2c) множитель z удовлетворяет либо отношению конгруэнтности z≡z1 mod(d1), либо отношению конгруэнтности z≡-z1 mod(d1) для первообразного корня z2 для d2,
2d) множитель z удовлетворяет отношению конгруэнтности z≡z2 mod(d2) для первообразного корня z2 для d2,
2e) все упомянутые нечетные простые числа p1, p2, q, r являются различными.
(i3) Другая новая система разработок для мультипликативного конгруэнтного генератора (d, z), содержащего модуль d и множитель z, характеризующегося следующими условиями 3а)-3е);
3а) модуль d=d1d2 является произведением парных взаимно простых множителей d1 и d2, образованных при помощи двух различных нечетных простых чисел p1 и p2 как dk=pk^ik для k=1,2 при i1>1 и i2≥1,
3b) нечетное простое число p1 имеет вид p1=2q1+1, а нечетное простое число p2 имеет вид p2=2q2+1, при этом q1 и q2 - другие нечетные простые числа,
3c) множитель z удовлетворяет либо отношению конгруэнтности z≡z1 mod(d1), либо отношению конгруэнтности z≡-z1 mod(d1) для первообразного корня z1 для d1,
3d) множитель z удовлетворяет либо отношению конгруэнтности z≡z2 mod(d2), либо отношению конгруэнтности z≡-z2 mod(d2) для первообразного корня z2 для d2,
3е) все упомянутые нечетные простые числа p1, р2, q1, q2 являются различными.
[0006] Использование упомянутого изобретения (i2) следует начинать с принятия достаточно больших множителей первообразных корней z1 для d1 и z2 для d2 в указанных пунктах 2c) и 2d). Рекомендуется отфильтровывать их в процессе подготовки при помощи расширенного спектрального теста по п.(i1). Затем, принимая выбранные ±z1 и z2 один за другим, нам следует использовать построение Сунь Цзы для множителя z при помощи системы отношений конгруэнтности в пунктах 2c) и 2d), чтобы позволить (d, z) подвергнуться (i1) как спектральному тесту второго уровня, и получить целевой превосходный генератор для использования на компьютерах. Аналогично, использование упомянутого изобретения (i3) следует начинать с принятия достаточно больших множителей первообразных корней z1 для d1 и z2 для d2 в указанных пунктах 3с) и 3d). Принимая выбранных кандидатов ±z1 и ±z2 один за другим, мы снова используем построение Сунь Цзы для множителя z при помощи системы отношений конгруэнтности в пунктах 3c) и 3d), чтобы позволить (d, z) подвергнуться (i1), как спектральному тесту второго уровня, и получить целевой превосходный генератор для использования на компьютерах.
Подробное описание изобретений
Подробное описание первого изобретения
[0007] Для того, чтобы исключить из настоящего описания двусмысленность толкования, последовательность {n, nz, nz2,···} от мультипликативного конгруэнтного генератора (d, z, n) сначала будет принята в качестве бесконечной последовательности без отношений эквивалентности по модулю d. Соответствующие случайные числа воспроизводятся как
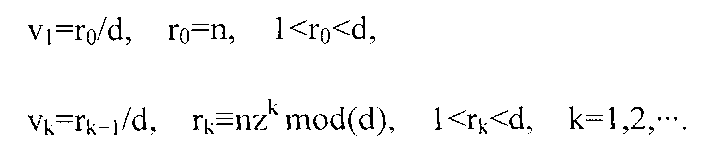
Начнем со спектрального теста второй степени, взяв последовательные наборы из двух чисел из сгенерированной последовательности. Зададим вектор Qk:=(nzk-1,nzk)=nzk-1(1,z). Пусть Qk′ обозначает любой целочисленный вектор с координатами, равными координатам вектора Qk по модулю d. Очевидно, что вектор Qk′ получен из вектора Qk посредством некоторых целочисленных кратных d смещений по координатным осям. Указанное d смещение по второй координатной оси осуществляется посредством сложения вектора e2:=(0, d), d смещение по первой координатной оси осуществляется посредством сложения e1′:=d(1,z)-z(0,d)=d(1,z)-ze2. Следовательно, каждый вектор Qk′ с координатами, равными Qk по модулю d является интегральной линейной комбинацией базисных векторов
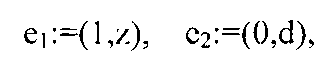
которые являются линейно независимыми в том смысле, что они дают отличный от нуля детерминант. Все векторы или точки с координатами, равными координатам вектора Qk, таким образом, находятся в решетке, образованной базисными векторами (или базисом) {е1,е2}. Мы говорим - узлы в решетке, поскольку они не могут занимать все узлы решетки. Обычно Qk′ не может быть любой из точек, чьи одна или обе координаты равны О по модулю d. Пусть Cd обозначает квадрат в евклидовой плоскости Е2, исходящий из начала координат с отрезком [0,d) в качестве сторон вдоль осей. В качестве удобного доказательства мы можем отметить, что вектора {е1,е2} образуют площадь d их детерминанта, тогда как квадрат Cd имеет площадь d2. Более убедительно, вектор решетки je1+ke2=j(1,z)+k(0,d)=(j,jz+kd) с целыми числами j,k имеет первый компонент j, который может принимать только d различных значений {0,1,···,d-1} в Cd; как только определено j, целое число к будет единственным таким образом, чтобы для второго компонента выражение jz+kd находилось в интервале [0,d). Таким образом, квадрат Cd имеет ровно d узлов решетки. Генератор (d, z, n) дает точки {Qk} в квадрате Cd, чей эквивалент по модулю d посажен на эти d узлов решетки. Степень заполнения этих опорных узлов решетки может быть максимально только (d-1)/d.
[0008] Аргументы могут быть распространены на последовательные наборы из L целых чисел при L=2,3,···, чтобы дать
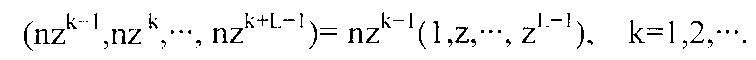
Рассмотренный в качестве вектора или точки в L-мерном евклидовом пространстве EL, этот вектор и все его d смещения по координатным осям очевидно находятся в L-мерной решетке, образованной базисными векторами
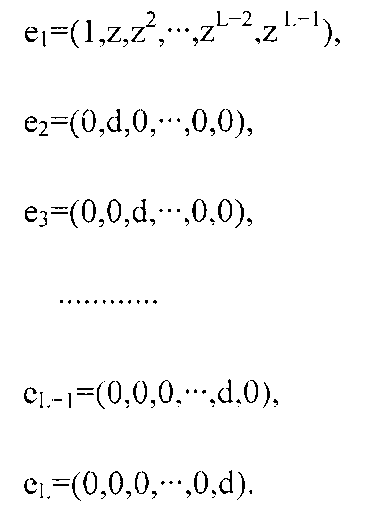
Примечательный факт состоит в том, что эта решетка снова имеет d узлов решетки в L-мерном гиперкубе Cd, исходящем из начала координат со сторонами длиной d вдоль осей. Это будет очевидно при помощи двух доказательств для случая количества измерений L=2, данного выше.
[0009] Указанное обстоятельство, что только d узлов решетки существуют в Cd независимо от количества измерений L, являются главной частью проблемы, возникающей при спектральных тестах. Ее понимание требует сначала представления об используемом периоде мультипликативных конгруэнтных последовательностей. Для простоты возьмем нечетный простой модуль d=p. Если множитель z является первообразным корнем для р, тогда генератор (p, z) дает циклическую последовательность {1,z,z2,···,zp-1≡1} по модулю р; последний член добавлен здесь для напоминания о небольшой теореме Ферма. Каждое из целых чисел {1,2,···,р-1≡-1} используется этой циклической последовательностью раз в период Т=φ(р)=р-1. В результате чего zT/2=z(p-1)/2≡-1 mod(p) удерживается в средней точке. Остаток последовательности равен {-1,-z,-z2,···} и фактически является повторением первой части, Для независимых случайных чисел используется только длина Т-Т/2 последовательности. Так как вычислительная нагрузка генерации случайных чисел с помощью генератора (d, z) является пропорциональной d, мы задаем вычислительную эффективность, или просто эффективность этого генератора (d, z) как τ:=T′/d≈1/2. Такой результат для пары из нечетного простого числа и множителя его первообразного корня обычно и справедливо предполагает, что τ≈1/2 является верхней границей для всех мультипликативных конгруэнтных генераторов. Подробные исследования показывают, что существует два типа (а) и (b) модулей, упомянутых ниже, которые реализуют эту самую большую эффективность τ≈1/2 посредством надлежащего выбора множителя z
(a) d=pi при нечетном простом числе р и показателе степени i≥1,
(b) d={(p1)^i1}×{(p2)^i2} при различных нечетных простых числах р1 и р2 и показателях i1,i2≥1,
где одно из простых чисел, скажем, p1, дает нечетное q1:=(p1-1)/2, а другое дает q2:=(p2-1)/2.
Подробное доказательство со спецификацией множителей можно увидеть в заявке на патент Китая, опубликованной в Журнале патентов на изобретения с номером публикации CN 1031356961 А; предмет заявки позже был отмечен в документе (2012b) Накадзава и Накадзава.
[0010] Предположим, что моделирование требует период Т≈257. Тогда генератору (d, z) нужен модуль d≈258 или больше. Различные наборы из двух чисел (zk,zk+1) из используемой мультипликативной конгруэнтной последовательности существуют не более чем d/2 и заполняют только до 1/2 узлов решетки в квадрате Cd со сторонами [0,d) в евклидовой плоскости E2. Таким образом, последовательные наборы из двух нормализованных независимых случайных чисел по большей мере могут быть 257 в единичном квадрате С1 в E2. Если стороны C1 разделены с шириной d-1/2≈2-29, маленькие квадраты или ячейки с площадью d-1 могут быть заняты с вероятностью ½ различными последовательными парами случайных чисел, появляющимися в одном используемом периоде. Спектральный тест второй степени нацелен на оценку геометрической конфигурации этих занятых ячеек посредством геометрии узлов решетки, в которых размещены упомянутые пары. Способ оценки будет упомянут кратко. Если геометрическая конфигурация решетки лучше, у нас будет меньше причин для отрицания статистического вывода, что случайные числа распределены независимо и равномерно. Таким образом, спектральные тесты с высокой точностью подходят к структурам мультипликативных конгруэнтных генераторов случайных чисел. Однако в это же время наука показывает, что этот успех незначителен. Возьмем случай последовательных наборов из L чисел Qk:=(zk-1,zk,···,zk+L-1) для L=2,3,···, образующих точки гиперкуба Cd со сторонами [0,d) в L-мерном евклидовом пространстве EL. Снова существует по большей части только d/2 различных точек, образованных в используемом периоде. Следовательно, наборы из L последовательных случайных чисел должны быть многозначительно наблюдаемы посредством деления единичного отрезка на ширину δ=d-1/L, которую оценивают как 1/512>δ>1/1024 в случае d=258 и L=6. Эта ширина небольшая, но грубая с точки зрения нормальной точности фиксированных вещественных чисел на компьютерах. Тем не менее, статистическое предположение, что последовательные наборы из L чисел из мультипликативной конгруэнтной последовательности выглядят равномерными и независимыми, будет менее сомнительным, если точки в этом грубом делении единичного гиперкуба в EL заняты более равномерно. Мы должны подчеркнуть, что производительность спектральных тестов снижается с увеличением степени L теста, заданной текущим числом L случайных чисел, взятых для теста, но, напротив, также что спектральные тесты более низкой степени должны рассматриваться как ключевые для статистической точности в проблемах случайных чисел.
[0011] На основе качественных данных спектральных тестов, обратимся теперь к их количественным аспектам. Начинаем снова с очевидного случая L=2. Двумерная решетка нашей задачи определена посредством (d, z) и образована базисными векторами е1, е2. Эта решетка имеет много линий решетки {гиперплоскости решетки L-1 измерения, для общего количества измерений L≥2), которые проходят через произвольные L=2 узлы решетки; на протяжении этих линий решетки находятся фактически бесконечно много узлов решетки. Среди большого количества расстояний между смежными параллельными линиями решетки пусть самое большое расстояние будет обозначено как λd(L)(z) при L=2. Если область, образованная базисными векторами e1 e2, прикреплена к d, тут вводят геометрические ограничения, которые обуславливают, что λd (2)(z) должна иметь нижнюю границу 




[0012] Углубимся дальше в смысл спектральных тестов. Пусть мы начнем снова с тестов второй степени. Как обсуждалось выше, тесты изучают, может ли отношение zk и zk+1 быть названо независимым. Мы также надеемся придти к выводу, что zk и zk+2 будут независимыми. Верно это, или нет, можно легко проанализировать, взяв генератор (d, z2) и протестировав его спектрально. Аналогично, мы хотим, чтобы генератор (d, z3), (d, z4),),··· имел хорошую оценку, как генератор независимых случайных величин. На фиг.2 мы разместили Списки 1A-1E, которые отображают пять превосходных генераторов первообразных корней, обнаруженных Фишманом и Муром (1986) для простого модуля Мерсенна d=p=231-1. Развитие компьютерных центральных процессоров, произошедшее за долгое время с тех пор, сделало спектральные тесты по этому модулю очень простыми. Строки, обозначенные а) в Списках 1A-1E показывают значения, найденные Фишманом и Муром. Следующая строка 1/а) изображает обратное значение этого значения, которое совпадает с соответствующим значением ρd (L)(z) в наших обозначениях. Строка b) изображает перерасчет ρd (L)(z) для 2≤L≤6, чтобы увидеть совпадение с 1/а). Оставшаяся строка, обозначенная с), изображает исполнение второй степени ρd (2)(zk) для 2≤k≤6 множителей z2, z3,···,z6. Обратившись к фиг.1A и 1B, мы признаем, что эти множители не являются хорошими с точки зрения независимости случайных чисел, сгенерированных посредством их степеней.
[0013] Указанное открытие почти тривиально следует из вычислений, но выводы являются тяжелыми и угнетающими: любой существующий мультипликативный конгруэнтный генератор (d, z) должен быть повторно исследован с своими оценками по (d, z2), (d, z3),···; а если характеристики не являются удовлетворительными, то они должны быть заменены на генераторы с более надежной статистикой. Мы разместили эту разработку спектральных тестов в качестве пункта 1 формулы изобретения для обеспечения его непосредственного и широкого применения. Подробное описание второго и третьего изобретений
[0014] С более общей точки зрения факты, перечисленные на фиг.2, раскрывают, что простой модуль Мерсенна d=p=231-1 может не иметь множителя первообразного корня с удовлетворительными характеристиками. Мы должны исследовать больше нечетных простых чисел, степеней нечетных простых чисел или произведений двух таких степеней нечетных простых чисел посредством спектральных тестов и найти хорошие мультипликативные конгруэнтные генераторы. Прежде всего, модуль d=p=231-1 слишком мал для современных компьютеров, и мы должны перейти, скажем, к d≈248 или большему. Таким образом, мы сталкиваемся с трудностями вычислимости, и единственным выходом является выбор модулей, образованных двумя нечетными простыми числами или степенями нечетных простых чисел. Мы дополнительно обнаружили, что более необходимо решать новые проблемы, возникающие с соответственными генераторами (d, z2), (d, z3),···. Мы должны сначала исследовать их периоды, запрашивая также, существует или нет -1 в генерируемых ими последовательностях. Затем, должны быть исполнены тесты по меньшей мере второй ступени для (d, z2), (d, z3),··· для того, чтобы найти требуемый диапазон (d, z) и, в конечном итоге, перейти к спектральным тестам от третьей до шестой степени для (d, z). Вычислительная нагрузка должна быть уменьшена любыми средствами. По милости натуральных чисел существует две новые разработки, которые особенно подходят для снижения некоторых частей этой нагрузки. Сконцентрируемся на их описании, воздерживаясь от общих или исчерпывающих изысканий.
[0015] Начнем с двух математических следствий. Пусть нечетное простое число р выражено как p=2q+1, а также предположим, что целое число q также является нечетным простым числом. Примеры р=7 при q=3 и р=23 при q=11 доказывают существование таких простых пар. В действительности, компьютерные эксперименты предполагают их многочисленное бесконечное наличие. Это поддерживает верность следующего.
(Следствие 1) Если нечетное простое число р≥7 имеет вид p=2q+1, при этом q является другим нечетным простым числом, тогда z=2 является первообразным корнем из р порядка φ(p)=p-1=2q или имеет порядок q, как первообразный корень из р, взятый с противоположным знаком.
(Доказательство) Возьмем группу целых чисел Zp≡{1,2,···,p-1=2q}, состоящую из 2q элементов, заданных посредством умножения по модулю р. Теорема Лагранжа доказывает, что порядок z=2 является делителем 2q. Предположение р≥7 подразумевает, что этот порядок не может быть равен 2. Следовательно, он является q или 2q, поскольку q - нечетное простое число. Если порядок z равен 2q, тогда z=2 является первообразным корнем из р. Если порядок z=2 равен q, тогда (-z)q=-zq=-1 mod(p), a -z является первообразным корнем из р. ■
[0016] Теперь рассмотрим нечетное простое число р по формуле р=4r+1, где r является другим нечетным простым числом. Примеры р=13 или 29, а компьютерные эксперименты легко убеждают нас, что такие нечетные простые числа существуют без ограничения.
(Следствие 2) Если нечетное простое число р>13 имеет вид р=4r+1, где r является другим нечетным простым числом, тогда z=2 является первообразным корнем из р.
(Доказательство) Прямые вычисления степени 2 для р=13 показывают, что 2 является первообразным корнем по модулю 13. Поэтому мы предполагаем, что р>29, г>7. Группа целых чисел, взаимно простых для р, состоит из ф(р)=4 r классов эквивалентности, а теорема Лагранжа доказывает, что порядок z=2 является множителем 4 r, который исчерпывается {1, 2, 4, r, 2 r, 4 r}. Предположение р>29 доказывает, что порядок z=2 не равен 1, 2, 4. Мы доказываем, что z2r=-l mod(p); это доказывает, что zr не эквивалентно 1 по модулю р, так что порядок z=2 будет 4 r и полным. Произведение
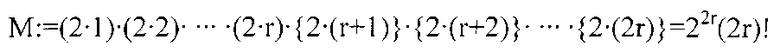
имеет другое выражение по модулю р:
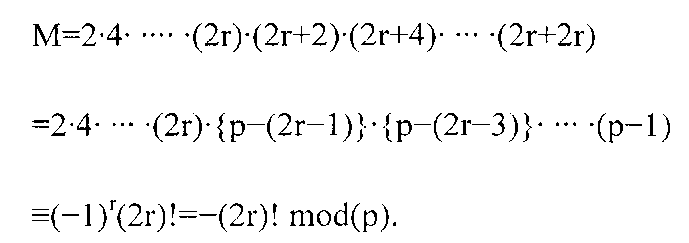
Отметим, что R является нечетным. Таким образом, мы имеем 22r(2r)!≡-(2r)! mod(p) или 22r=-1 mod(p), поскольку (2r)! является взаимно простым для нечетного простого числа р=4r+1. ■
Это доказательство было передано Хироши Накадзава при посредничестве Наойа Накадзава 17 апреля 2013 г.
[0017] Вычисления с учетом упомянутых следствий сразу предполагают следующее:
(Предположение 3) Если нечетное простое число р≥7 выражено как p=2q+1, где q является другим нечетным простым числом, тогда для любой интегральной экспоненты i≥1 множитель z=2 будет либо первообразным корнем из d=pi порядка φ(pi)=2qpi-1=2qd/p, либо взятым с противоположным знаком первообразным корнем из рi с полуполным порядком qpi-1=qd/p.(Конец предположения 3).
(Предположение 4) Если нечетное простое число p≥13 выражено как р=4r+1, где r является другим нечетным простым числом, тогда для любой интегральной экспоненты i≥1 множитель z=2 будет первообразным корнем из рi с полным порядком φ(рi)=4rpi-1=4rd/p.(Конец предположения 4).
Эти предположения являются верными в том случае, если только они могут быть показаны для случая i=2, но мы не можем придти к доказательству. Однако компьютеры доказывают, что они являются верными вплоть до to р<107=223,25; их легко можно предположить верными и, если нам нужны несколько модулей в виде рi, мы сначала легко можем позволить компьютеру подтвердить это предположение при z=2. Указанные следствия и предположения предполагают для разработки мультипликативных конгруэнтных генераторов только с нечетными простыми числами указанных типов. Они дают φ(рi) при небольших количествах простых множителей и значительно облегчают разработку генераторов (d, z). Помимо концептуальных и практических средств мы должны взять только степени 2 для множителей в сканировании первообразных корней или первообразных корней, взятых с противоположным знаком, они позволяют нам найти полезные и реализуемые структуры периодов, объясняемых ниже.
[0018] За счет второго и третьего изобретений будет целесообразно обобщить необходимые понятия. Все необходимые вычисления выполнены на стадии модулей, образованных посредством двух степеней простых чисел, и содержат двух основных игроков, пары первообразных корней для соответствующих степеней простых чисел, которые создают множители посредством системы отношений конгруэнтности. Наша задача состоит в том, чтобы вычислять периоды, реализуемые посредством упомянутых схем, а также отвечать на вопрос, возникает ли -1 или нет в сгенерированных последовательностях. Аргументы в значительной степени помогут нам посредством следующих следствий.
(Следствие 5) Пусть d1, d2 являются взаимно простыми целыми числами, а zk является множителем, взаимно простым с dk при k=1,2. Предположим, что генератор (dk, zk) имеет порядок или период Тк, а они синтезированы в генератор (d, z), заданный посредством
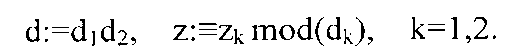
Циклическая последовательность, сгенерированная (d,z) и заданная теперь как G(z;d):≡{1, z, z2,···} mod(d), имеет порядок или период Т, как наименьшее общее кратное T:=LCM(T1,T2).
(Доказательство) По этому случаю мы ссылаемся на построение Сунь Цзы, относящееся к его теореме, которое дает решение z для указанной системы отношений конгруэнтности по модулю d. Поскольку d1 и d2 являются взаимно простыми при GCD(d1, d2)=1, алгоритм Евклида обеспечивает существование целых чисел А, В, удовлетворяющих условию Ad1+Bd2=1. Целые числа U1:=Bd2=1-Ad1 и U2:=Ad1=1-Bd2 определены посредством исключительно лишь d1 и d2 без какого-либо отношения к z1 и z2, и удовлетворяют условию Uj mod(dk)=δjk. Таким образом, решение z для указанной системы отношений конгруэнтности будет
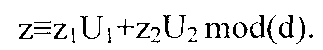
Любое другое решение z′ дает z-z′=0 mod(dk) при k=1,2,, так что z-z′ является кратным взаимно простым d1 и d2. Значит, z′=z mod(d) остается верным вследствие единственности модуля d. Прямые вычисления zj и соблюдение zj≡(zk)j mod(dk) для k=1,2 сразу доказывает

Увеличивая j до Т, мы имеем
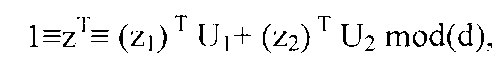
для которого (zk)T≡1 mod(dk) должно оставаться верным при k=1,2. Таким образом, порядок или период G(z;d) является наименьшим общим кратным Т1 и Т2. ■
Утверждение ниже будет очевидным.
(Следствие 6) Предположим, что генератор (d, z) или его циклическая последовательность G(z;d) имеет период или порядок Т. Генератор (d, zj) или циклическая последовательность G(zj;d) реализуют период T(j):=T/{GCD(j,T)} при любом показателе степени j=1,2,···. (Конец следствия 6)
Мы можем отметить несколько выводов, которые помогут нам в обсуждении того, появляется ли -1 или нет в циклической последовательности G(zj;d), заданной генератором (d, zj), в частности, когда z задано посредством z≡zk mod(dk) при k=1,2 и взаимно простых d1 и d2.
(Следствие 7) (А1) Если циклическая последовательность G(z;d) не содержит -1 mod(d), тогда циклические последовательности G(zj;d) при любых индексах j=1,2,··· свободны от -1 по модулю d.
(A2) Продолжим обозначение T(j) для порядка или периода циклической последовательности G(zj;d) при любых j=1, 2,···. Для того, чтобы G(zj;d) содержала -1 mod(d), T(j) обязательно является четным. Контрапозиция будет: Если является нечетным, то циклическая последовательность G(zj;d) не содержит -1 по модулю d.
(В) Если модуль d=d1d2 является произведением двух взаимно простых множителей d1 и d2, a z задано посредством z≡zk mod(dk) для k=1,2, тогда следующие утверждения (B1) и (B2) останутся верными относительно того, появится или нет -1 в циклической последовательности G(zj;d).
(B1) Если по меньшей мере одна из компонентных циклических последовательностей G(zk;dk) для k=1 или 2 свободна от -1 по модулю dk, тогда циклическая последовательность G(zj;d) для любого индекса j=1,2,··· свободна от -1 по модулю d.
(B2) В случае составного модуля d=d1d2 четный период T(j) при любых j=1, 2,··· для циклической последовательности G(zj;d) не всегда является достаточным для появления -1 по модулю d в последовательности G(zj;d). Необходимым и достаточным условием для появления -1 по модулю d в последовательности G(zj;d) является то, что T(j) является четным и циклические последовательности {G(z′;dk)|z′:≡(zk)j mod(dk), k=1,2} имеют -1 по модулю dk согласно Т(j)/2, т.е. для k=1 и 2 остается верным выражение (zk)^(T(j)/2)≡-1 mod(dk).
(Доказательство) (A1) Утверждение очевидно, поскольку циклическая последовательность или циклическая группа G(zj;d) при любых j=2,3,··· является подмножеством или подгруппой, содержащейся в большей уменьшенной группе класса вычетов G(z;d) целых чисел по модулю d.
(A2) Если циклическая последовательность G(zj;d) содержит -1≡d-1 mod(d) при 0<Т′<Т(j), тогда мы имеем
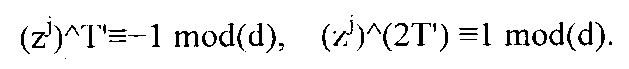
Таким образом, 0<2T′<2T(j) является кратным T(j), выражение 2T′=T(j) остается верным, а Т(j) обязательно является четным при T′=T(j)/2.
(B1) Если циклическая последовательность G(z;d) содержит -1≡d-1 mod(d),, тогда G(zk;dk)=G(z;d) mod(dk) содержит -1 mod(dk) для обоих k=1,2. Контрапозиция доказывает указанное утверждение.
(B2) Мы скоро увидим пример последовательности G(zj;d) с четным T(j), при этом в циклической последовательности не содержится -1. Докажем необходимую и достаточную часть. Необходимость четного T(j) установлено в (A2), а доказательство этого показывает, что (zj)^(T(j)/2)≡-1 mod(d). Следовательно, мы имеем уравнения
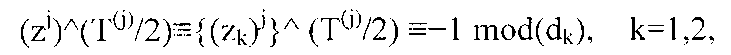
которые доказывают необходимую часть (А2). Напротив, предположим, что T(j) является четным, и что отношения конгруэнтности {(z1)j}^(Т(j)/2)≡-1 mod(d1) и {(z2)j}^(T(j)/2)≡-1 mod(d2) остаются верными. Построение Сунь Цзы доказывает (zj)^(T(j)/2)≡{(zk)j}^(Т(j)/2) mod(dk) для k=1,2, так что (zj)^(Т(j)/2) является по модулю d уникальным решением этой системы отношений конгруэнтности
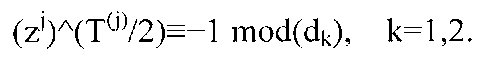
Заведомо (zj)^(T(j))/2)=-1 mod(d) является решением, и доказательство закончено. ■
[0019] Обратимся к описанию двух изобретений, которые участвуют в разработке мультипликативного конгруэнтного генератора (d, z). Первое будет позже размещено в качестве пункта 2 формулы изобретения и пояснено здесь. Пусть (d, z) будет мультипликативным конгруэнтным генератором, удовлетворяющим семи условиям (2a)-(2g), перечисленным ниже:
(2a) Модуль d является произведением двух взаимно простых множителей d=d1d2,, где d1 и d2 будут называться подмодулями,
(2b) подмодуль d1=(p1)^i1 является нечетным простым числом p1 в степени i1, причем целый показатель степени i1≥1, а нечетное простое число p1 выражено в виде p1=2q+1, где q является другим нечетным целым числом,
(2c) подмодуль d2=(p2)^i2 является нечетным простым числом p2 в степени i2, причем целый показатель степени i2≥1, а нечетное простое число p2 выражено в виде p2=4r+1, где r является другим нечетным целым числом,
(2d) все нечетные простые числа p1, p2, q, r являются различными,
(2e) множитель z задан посредством системы конгруэнтных уравнений
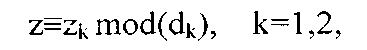
где z1 и z2 будут называться подмножителями,
(2f) подмножитель z1 является либо первообразным корнем, либо первообразным корнем, взятым с противоположным знаком, для подмодуля d1,
(2g) подмножитель z2 является первообразным корнем подмодуля d2.
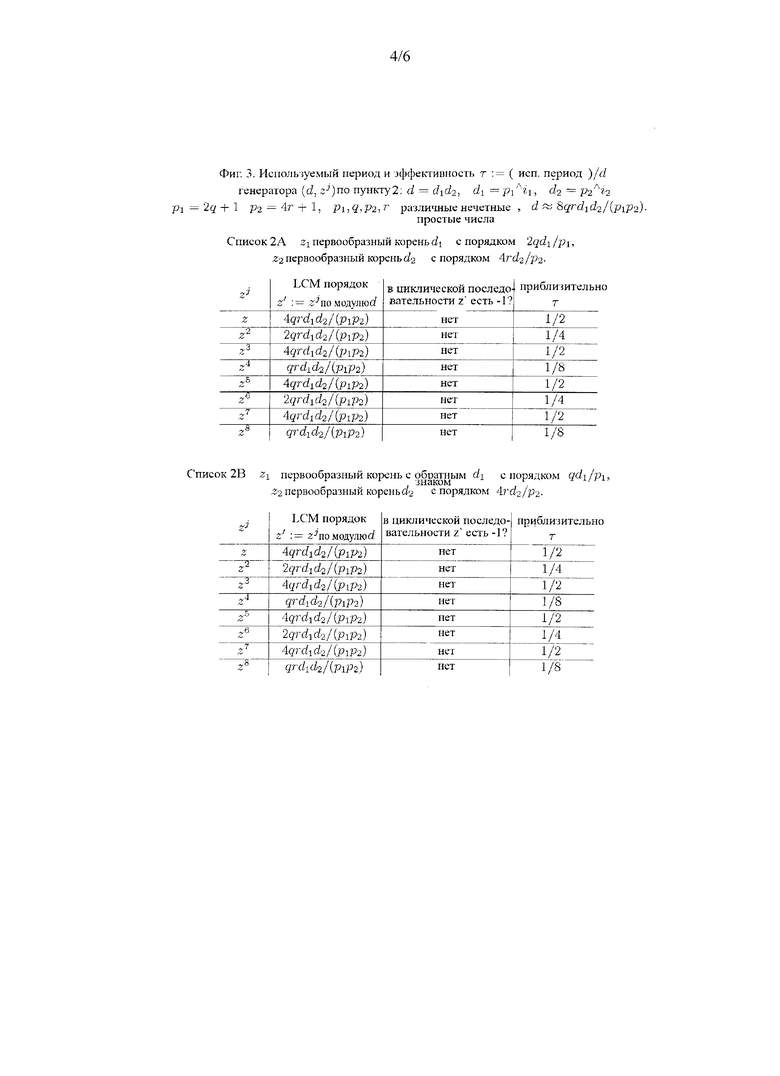
[0020] Характеристики этих разработок представлены в табличной форме на фиг.3 в виде Списка 2A и Списка 2B. Возьмем сначала разработку, которая использует в (2f) первообразный корень z1 подмодуля d1=(p1)^i1 для подмножителя по модулю d1. Мы начинаем работать с генератором (d1, z1), который будет называться подгенератором. По предположению z1 имеет наибольший порядок по модулю d1,

Аналогично, подгенератор (d2, z2) имеет z2 с наибольшим порядком по модулю d2,
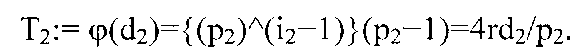
Генератор (d=d1d2,z) задан посредством системы отношений конгруэнтности, описанной в (1e), и в соответствии со (Следствием 5) синтезированный генератор (d, z) имеет порядок или период Т (d, z) наименьшего общего кратного
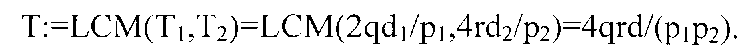
Порядок (d, zj) теперь может быть вычислен при помощи (Следствия 6) для любых j=1, 2, 3,···:
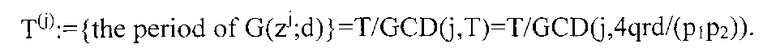
Эта формула дает три существенных факта благодаря вышеуказанным предположениям (2a)-(2d):
(2A1) Если j<min(q, r) является нечетным, тогда порядок Т(j)=Т.
(2A2) Если j<min(q, r) является четным, но не кратным 4, тогда Т(j)=Т/2.
(2A3) Если j<min(q, r) кратно 4, тогда Т(j)=Т/4.
Теперь мы должны обратиться к изучению вопроса, возникает ли -1 или нет в циклической последовательности G(zj;d), и найти пригодный период, который обозначим Тu (j), последовательности G(zj;d) для независимых случайных чисел. Мы должны пройти сквозь такую ситуацию, где подмножители z1, z2 являются первообразными корнями, и необходимо отследить соответствующую -1 в их циклических последовательностях. Таким образом мы прибегаем к (B2) и (A1) (Следствия 7) и показываем рассогласование вследствие G(z1;d1). Из T=4qrd/(p1p2) и T/2=T1×(целое число) мы имеем

Таким образом, в последовательности G(z;d)-1 не возникает, а (A1) (Следствия 7) обеспечивает отсутствие -1 в последовательностях G(zj;d) для любого показателя степени j<min(q, r). Все порядки или периоды циклических последовательностей в Таблице 2A являются пригодными: Тu(j)=T(j). Мы делаем вывод относительно эффективности τ:=(длина используемого периода)/d,
(2A1) для строк с нечетным] j: τ=T/d≈1/2,
(2A2) для строк с четным j, но не кратным 4: τ=(T/2)/d≈1/4,
(2A3) для строк с j, кратным 4: τ=(T/4)/d≈1/8.
Доказательство Списка 2A на фиг.3 закончено.
[0021] За счет Списка 2B на фиг.3, который изображает характеристики изобретения, образующего вторую половину пункта 2 формулы изобретения, мы сначала должны дать описание подмножителя, который является взятым с противоположным знаком первообразным корнем по модулю d1, как предложено разработкой (2f). Подмножитель по модулю d1 будет обозначен -z1, подразумевая, что z1 является первообразным корнем для d1. Первообразный корень z1 генерирует циклическую последовательность, состоящую их целых чисел, различных, по модулю d1.
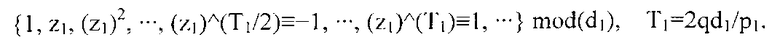
В частности, целые числа {z1, (z1)2,···,(z1)^(T1/2-1)} не эквивалентны ±1 по модулю d1. Следовательно, предположение, что нечетность T1/2=qd1/p1 доказывает, что (-z1)^(T1/2)≡1 mod(d1) впервые возникает в последовательности {-z1, (-z1)2,···}. Таким образом, порядок или период циклической последовательности G(-z1;d1) равен T1/2 и будет четным. Подмножитель -z1 не является первообразным корнем для d1. Однако, (Следствие 6) обеспечивает, что порядок или период последовательности G(z;d) равен
(порядок z по модулю d)=LCM(T1/2,T2)=LCM(qd1/p1,4rd2/p2)=4qrd/(p1p2).
Это заметно является идентичным со случаем подмножителя z1 первообразного корня, и все результирующие порядки zj для j<min(q, r) аналогично являются неизменными. И нечетный порядок для -z1 обуславливает, что циклическая последовательность G(-z1;d1) не содержит -1, а (A2) (Следствия 7) доказывает, что вся Таблица 2B относится к случаю Tu (j)=T(j). Здесь нет никаких изменений по сравнению со Списком 2A, и все элементы Списка 2 В соответствуют.
[0022] Отметив важность тестирования zj при j=2, 3,···, как множителей, мы обнаружили результаты, обобщенные в Списках 2A и 2B на фиг.3. Эффективность τ была обнаружена изменяющейся в диапазоне от 1/2 до 1/8, что может быть справедливо названо правильной флуктуацией, в частности, по сравнению со случаем модуля d=2i, который будет пояснен позже. Фактически, мы получим небольшую возможность использовать эти случайные числа вплоть до d/8. Однако, указанные изменения используемых периодов для z, z2,··· могут восприниматься едва заметными, хотя технологически это может стать естественной идеей для искусственного сокращения пригодных периодов до d/8 для предотвращения взаимозависимостей, опровергающих независимость. После всего, нам нужны трудные вычисления спектральных тестов для того, чтобы получить генератор (d, z) с надежной статистикой, и неизвестно, будут ли естественно плоские и красивые используемые периоды для z, z2,··· способствовать большим множителям для получения лучших характеристик. Хотя наша интуиция искушает нас, шепотом скажем, что более плоские или четные используемые периоды могли бы быть лучше. Следующее изобретение по пункту 3 формулы изобретения фактически обеспечивает плоскостность за счет уменьшения наибольшего значения используемых периодов. Предложенная разработка согласно этому изобретению определяется семью условиями (3a)-(3g), перечисленными ниже.
(3a) Модуль d является произведением двух взаимно простых множителей d=d1d2,, где d1 и d2 будут также называться подмодулями,
(3b) подмодуль d1=(p1)^i1 является нечетным простым числом p1 в степени i1 причем целый показатель степени i2≥1, а нечетное простое число p2 выражено в виде p2=2q2+1, где q2 является другим нечетным целым числом,
(3c) подмодуль d2=(p2)^i2 является нечетным простым числом p2 в степени i2, причем целый показатель степени i2≥1, а нечетное простое число p2 выражено в виде p2=2q2+1, где q2 является другим нечетным целым числом,
(3d) все нечетные простые числа p1, p2, q1, q2 являются различными,
(3e) множитель z задан посредством системы конгруэнтных уравнений,
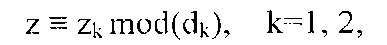
where z1 and z2 will be called submultipliers, где z1 и z2 будут называться подмножителями,
(3f) подмножитель z1 является либо первообразным корнем, либо первообразным корнем, взятым с противоположным знаком, для подмодуля d1,
(3g) подмножитель z2 является либо первообразным корнем, либо первообразным корнем, взятым с противоположным знаком, для подмодуля d2.
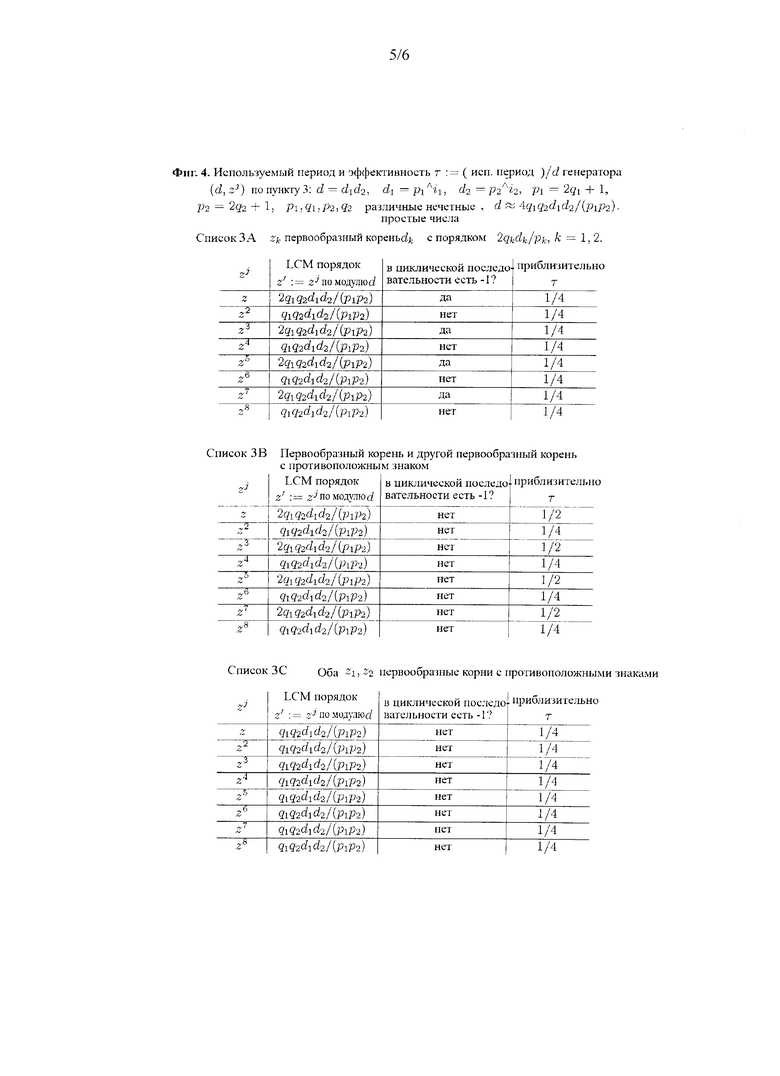
Результирующие характеристики генератора (d, z) обобщены на фиг.4 в виде Списков 3A-3C. Мы доказываем эти списки, показывая преимущество указанных разработок.
[0023] Возьмем сначала разработку, которая использует подмножители z1 и z2 первообразных корней. Подгенераторы (dk, zk) при k=1, 2 имеют четные порядки
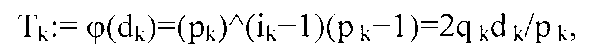
и реализуют (zk)^(Tk/2)≡-1 mod(dk) в середине. Также, (Следствие 5) доказывает порядок Т для G(z;d), как
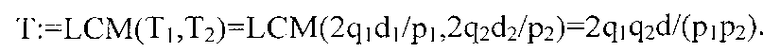
Порядок T(j) циклической последовательности G(zi;d) теперь разделен на две группы при помощи (Следствия 6):
(3A - нечетное) нечетное j<min(q1,q2):Т(j)=T=T1(T2/2)=(T1/2)T2=(четное),
(3A - четное) четное j<min(q1,q2):T(j)=T/2=q1q2d/(p1p2)=(нечетное).
Возьмем сначала четное j с нечетным Т(j). Посредством (A2) (Следствия 7) -1 отсутствует в G(zj;d), а равенство Tu (j)=T(j) является верным. Мы имеем
(эффективность т для каждого четного j)=T(j)/d≈1/4,
и четные j строки Списка 3A доказаны. Напротив, нечетное j требует вычислений {(zk)j}^(T(j)/2) mod(dk) при k=1,2. Поскольку в этом случае T(j)/2=T/2=(T1/2)(T2/2) является произведением нечетных целых чисел, мы имеем
{(zk)j}^(T/2)={[(zk)j]^(Tk/2)}^(нечетное целое число)
={(zk)^(Tk/2)}^{j×(нечетное целое число)}
≡(-1)^(нечетное целое число)≡-1 mod(dk).
Циклические последовательности G((zk)j;dk) c любыми нечетными j для k=1 и 2 таким образом являются созвучными. А (B2) (Следствия 7) доказывает (zj)^(Т/2)≡-1 mod(d). Используемый период последовательности G(zj;d) равен Tu (j)=T(j)/2=T/2. Эффективность τ=(T/2)/d≈l/4. Эти полные доказательства нечетных j строк и всего Списка 3A.
[0024] Рассмотрим теперь случай, когда один из подмножителей является первообразным корнем, взятым с противоположным знаком, результаты которого показаны в Списке 3B на фиг.4. Мы принимаем без потерь общее утверждение, что первый подмножитель является первообразным корнем, взятым с противоположным знаком, и обозначен как -z1, при этом z1 является первообразным корнем для d1, a z2 является первообразным корнем для d2. Циклическая последовательность G(-z1;d1) имеет порядок T1′:=T1/2=q1d1/p1, который является нечетным. Таким образом, (A2) (Следствия 7) утверждает, что свободно от -1 для любых j=1, 2,···. Все порядки G(zj;d) являются используемыми. Порядок последовательности G(z;d) будет
(порядок для z)=LCM(T1′, T2)=LCM(q1d1/р1,2q2d2/p2)=2q1q2d/(p1p2)=T.
Это совпадает с порядком Т предыдущего случая, где оба подмножителя являются первообразными корнями. Значит, все циклические последовательности G(zj;d) для целых показателей степеней j<min(q1,q2) имеют одинаковые порядки, как и раньше. Логические рассуждения доказывают, что порядки T(j) будут следующими:
(3B - нечетное) нечетное j<min(q1,q2):Т(j)=Т=Т1(Т2/2)=(T1/2)Т2,
(3B - четное) четное j<min(q1,q2):Т(j)=Т/2=(Т1/2)(T2/2).
Разница по сравнению с предыдущим случаем состоит в том, что независимо от того, является j четным или нечетным, все эти порядки являются используемыми в связи с отсутствием -1.
(нечетное j): τ=T/d≈1/2, (четное j): τ=(T/2)/d≈1/4,
которые все должны быть доказаны для Таблицы 3B.
[0025] Возьмем оставшийся случай, когда оба подмножителя являются превообразными корнями, взятыми с противоположными знаками, которые будут обозначены -z1 и -z2. Подгенераторы (d1, -z1) и (d2, -z2) имеют соответствующие порядки Т1′ и Т2′:
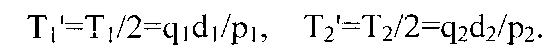
Период Т′ синтезированной последовательности G(z;d) задан посредством
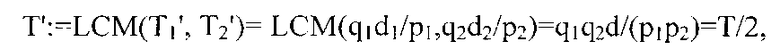
который является нечетным. Циклическая последовательность G(zj;d) при j<min(q1, q2) имеет один и тот же нечетный порядок T′/GCD(j,T′)=T′. Исходя из этого, или при помощи любого из (A1), (A2) или (B1) (Следствия 7) для всех рассматриваемых генераторах отсутствует -1 в их циклических последовательностях, а эффективность τ унифицирована до
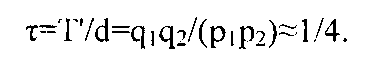
Это доказывает все из Списка 3C. ■
[0026] В последних нескольких параграфах мы должны более подробно описать вычислительные процедуры спектральных тестов. Позже мы также должны дать заключение по поводу случая модуля d=2i при i≥4, но до этого мультипликативный конгруэнтный генератор (d, z) предполагается содержащим произвольное нечетное целое d в качестве модуля и любое целое число, взаимно простое с d, в качестве множителя. Пусть L≥2 будет целым числом. Последовательный набор из L чисел из генератора (d, z) задан здесь в виде Qk:=(zk,zk+1,···,zk+L-1)=zk(1,z,···,zL-1) при k=0, 1,··· без эквивалентности по модулю d, и рассматривается в виде вектора в L-мерном евклидовом пространстве EL. Мы увидели, что его d смещения по координатным осям реализованы при помощи интегральных линейных комбинаций векторов

которые являются очевидно линейно независимыми относительно детерминанта dL-1. Интегральные линейные комбинации этих векторов задают решетку в пространстве EL при помощи базисных векторов {e1,e2,···,eL}. Задачей спектральных тестов степени 1 является вычисление наибольшего расстояния λd(L)(z) между смежными параллельными гиперплоскостями решетки размерности L-1, которая проходит сквозь 1 линейно независимых векторов решетки, и вычисления отношения ρd (L)(z):=λd (L)(z)/―,λd(L)>1 в качестве оценки спектрального теста степени L, где ―,λd (L) for L=2, 3,···, 6 является наименьшими возможными значениями λd (L)(z), реализованных при помощи геометрически идеальных форм решеток. Выражения, ―, λd (L) в табличной форме представлены, как Список 4 на фиг.5.
[0027] Наиболее абстрактная часть вычислений спектральных тестов обобщена в следующем утверждении:
(Теорема 8) Зададим векторы {f1, f2,···, fL}обратной или дуальной решетки, соответствующие базисным векторам {е1, е2,···, eL, как показано ниже:
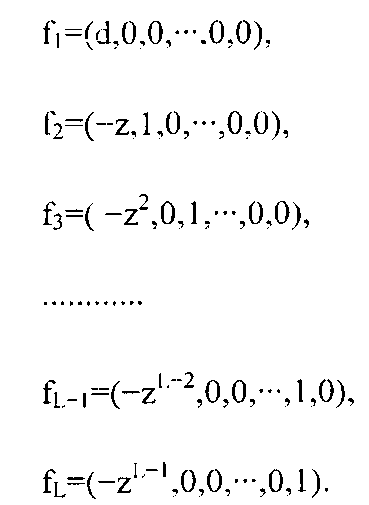
Векторы, образованные интегральными линейными комбинациями векторов {f1, f2,···,fL}, составляют дуальную решетку для генератора (d, z). Пусть amin (L)(z) означает наименьшую ненулевую длину вектора в L-мерной (d, z) обратной решетке. Тогда наибольшее расстояние λd (L)(z) между смежными параллельными гиперплоскостями исходной решетки выражается формулой λd (L)(z)=d/amin (L)(z). (Конец Теоремы 8)
Полное доказательство Теоремы 8 дано Накадзава и Накадзава (2012 с). Для того чтобы дать в этом документе доказательство в полном объеме, нужно слишком большое количество бумаги. Поэтому мы опускаем это описание, отсылая читателей к первоисточнику, и описываем здесь процедуры простейшего второго теста, необходимого для подачи пункта 1 формулы изобретения. Обратные базисные вектора со степенью 2 для генератора (d, z) будут
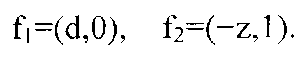
Общая перспектива, полезная также и для более высоких измерений L=3, 4,···, получена посредством рассматривания вектора с декартовыми целочисленными координатами f=(j1, j2) которые находятся в обратной решетке. Мы имеем следующее:
(Следствие 9) Необходимое и достаточное условие для того, чтобы целочисленный вектор f=G 1J2) находился в 2-мерной обратной решетке генератора (d,z), задано следующим:

(Доказательство) Для того, чтобы вектор f=(j1, j2) находился в указанной обратной решетке, обязательно должны существовать целые числа m1, m2 и давать f=m1f1+m2f2 или
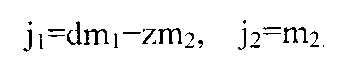
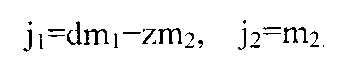 Следовательно, условие j1+zj2=dm1≡0 mod(d) является необходимым. Напротив, если это условие удовлетворяется, существует целое число k, которое дает j1+zj2=kd, или
Следовательно, условие j1+zj2=dm1≡0 mod(d) является необходимым. Напротив, если это условие удовлетворяется, существует целое число k, которое дает j1+zj2=kd, или
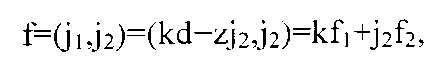
и f является вектором дуальной решетки. Таким образом, это условие является достаточным. ■
Одним из достоинств представления в системе декартовых координат f=(j1, j2) является то, что длина вектора f задана при помощи простой евклидовой нормы 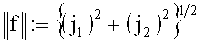
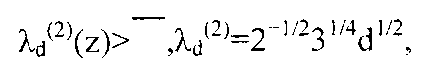
которые остаются верными по геометрическим причинам для любой пары (d, z) из нечетного модуля d и множителя z, взаимно простого с d, или для любой пары взаимно простых целых чисел d и z, говорит нам о существовании очень полезных границ,
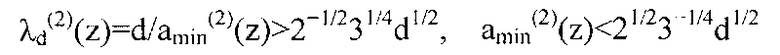
для длины 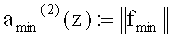
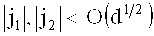
Накадзава и Накадзава (2012 с): Н. Накадзава и Н. Накадзава, Мультипликативные конгруэнтные генераторы с модулями, образованными посредством двух нечетных простых множителей для равномерно распределенных и независимых случайных чисел II. Структуры, относящиеся к спектральным тестам. Название файла popesq2.pdf, загружаемого с http://www10.plala.or.jp/h-nkzw/ (15 октября, 2012).
[0028] Мультипликативные конгруэнтные генераторы для равномерно распределенных и независимых случайных чисел имеют другую существенную разработку, которая принимает степень простого числа 2 в качестве модуля d=2i Простое условие z≡5 mod(8) обеспечивает, что множитель z должен дать наибольший возможный период T=2i-2=d/4. В другой эпохальной работе Фишмана (1990) выполнены спектральные тесты для модуля d=232, исчерпавшие все возможные множители z≡5 (8), а также исследована часть множителей для d=248; в последнем случае вычислительные сложности помешали ему выполнить исчерпывающие тесты. Накадзава и Накадзава (2008) показали, что эта проблема не может быть решена посредством использования составных модулей. Если степень числа 2 вводит модуль d в качестве множителя в произведение с нечетными простыми числами или степенями нечетных простых чисел, это неизбежно приносит взаимозависимость среди степеней подмножителей, а результирующие случайные числа не могут быть приняты независимыми; это является ужасным недостатком в том смысле, что он не может быть обнаружен посредством спектральных тестов. Иными словами, для мультипликативного конгруэнтного генератора модуль d=2i должен использоваться в единственном числе, а сильные затруднения в вычислениях для исчерпывающих спектральных тестов не дают возможность облегчить статусное положение, бывшее у Фишмана (1990). Отметим здесь другую проблему. Предположим, у нас есть генератор (d, z), где d=2i и z=5 mod(8). Мы увидели, что (d, zj) для j=2, 3,··· также должны быть хорошими генераторами случайных чисел, а трудности возникают с их порядками. Поскольку генератор (d=2i, z) имеет порядок Т=2i-2, генератор (d, zj) имеет
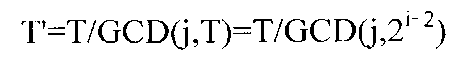
в качестве своего порядка. Если экспонента j указанного множителя достигает j=2m для m<i-2, возникает внезапное изменение Т′=Т/2m. Эта особенность будет непригодна для генераторов (d=2i, zj) с различными показателями степени j для реализации хорошей независимости случайных чисел. Конечно, это только мысленная догадка, сопоставленная с очень трудными вычислениями спектральных тестов, и, однако, действительные характеристики генераторов должны распознаваться при помощи числовых экспериментов.
Фишман (1990): Дж.С. Фишман, Мультипликативные конгруэнтные генераторы случайных чисел с модулями 2β: Исчерпывающий анализ для β=32 и частичный анализ для β=48. Математика вычислений, Том 54 (1990), стр. 331-344 Накадзава и Накадзава (2008): Н. Накадзава и Н. Накадзава, Разработки равномерно распределенных и независимых случайных чисел с большим периодом и высокой точностью - управление последовательной геометрией посредством произведения групповых структур и конфигураций решеток. Название файла 3978erv.pdf, загружаемого с http://www10.plala.or.jp/h-nkzw/ (9 марта - 8 июля, 2008).
Краткое описание чертежей
[0029] (Фиг.1A, 1B). Типичные распределения точек, образованные посредством последовательных наборов из двух случайных чисел, порожденных мультипликативным конгруэнтным генератором (d, z); показанные распределения соответствуют оценке ρ:=ρd (2)(z) приблизительно 1,05, 1,10,···; изображенные квадраты взяты немного большими, чем единичные квадраты, а генератор (d, z) может быть прочитан в подписи под изображениями.
[0030] (Фиг.2) Списки 1A-1E, изображающие характеристики пяти лучших множителей из работы Фишмана и Мура (1986); в строке а) находится значение, показанное в их работе, строка 1/а) изображает обратное значение для а) и совпадает с представленным ρd (L)(z),, в строке b) находится расчет ρd (L)(z) согласно настоящему изобретению, а оставшиеся строки показывают ρd (2)(zj) для j=2, 3,···, 6.
[0031] (Фиг.3) Списки 2A и 2B для генераторов (d, zj) для j=1, 2,···, показывающие порядок для zj, существование или отсутствие -1 в циклической последовательности из генератора (d, zj) и эффективность τ, где генератор (d, z) разработан в соответствии с положениями, указанными в пункте 2 формулы изобретения.
[0032] (Фиг.4) Списки 3A-3C для генераторов (d, zj) для j=1, 2,···, показывающие порядок для zj, существование или отсутствие -1 в циклической последовательности и эффективность τ, где генератор (d, z) разработан в соответствии с положениями, указанными в пункте 3 формулы изобретения.
[0033] (Фиг.5). Список 4, показывающий наименьшее значение ―,λd (L) для максимального расстояния λd (L)(z) смежных параллельных гиперплоскостей решетки в размерности L-1, реализованных при помощи геометрически идеальных форм решетки в L-мерном евклидовом пространстве, где объем единичной ячейки решетки един для dL-1.




Изобретение относится к области вычислительной техники и может быть использовано для генерации случайных чисел. Техническим результатом является повышение точности. Способ генерации равномерно распределенных и независимых случайных чисел с нечетным модулем d и множителем z, взаимно простым с d, начинает с произвольно заданного целого числа n, взаимно простого с d, и рекуррентно порождает последовательность целых чисел {r0, r1, r2, …} при помощи отношений конгруэнтности r0≡n mod(d), 0<r0<d, rk≡zrk-1 mod(d), 0<rk<d, k=1, 2, 3, …, и дает на выходе случайные числа {vk:=rk-1/d| k=1, 2, …}, при этом множитель z выбран таким образом, что удовлетворяет условию, что генератор (d,z′) при z′≡zj mod(d) для целого j по меньшей мере в диапазоне 1≤j≤6 проходит спектральный тест второй степени в пределах оценки 1,25, а именно, для любого целого j в диапазоне 1≤j≤6 генератор (d, z′) при z′≡zj mod(d) удовлетворяет условию, что вектор f дуальной решетки, заданный для (d, z′) посредством линейной комбинации f:=m1f1+m2f2 базисных векторов {f1, f2} дуальной решетки, f1:=(d,0), f2:=(-z′,1), с целочисленными коэффициентами {m1,m2} и длиной ||f||:={(dm1-z′m2)2+(m2)2}1/2>0, имеет наименьший ненулевой вектор fmin с длиной amin (2)(z′):=||fmin||>0, удовлетворяя условию ρd (2)(z′):=21/2d1/2/{31/4amin (2)(z′)}<l,25. 6 ил.
Способ использования мультипликативного конгруэнтного генератора (d, z) равномерно распределенных и независимых случайных чисел с нечетным модулем d и множителем z, взаимно простым с d, который начинает с произвольно заданного целого числа n, взаимно простого с d, и рекуррентно порождает последовательность целых чисел {r0, r1, r2, …} при помощи отношений конгруэнтности
r0≡n mod(d), 0<r0<d,
rk≡zrk-1 mod(d), 0<rk<d, k=1, 2, 3, …,
и дает на выходе случайные числа {vk:=rk-1/d| k=1, 2, …}, при этом множитель z выбран таким образом, что удовлетворяет условию, что генератор (d,z′) при z′≡zj mod(d) для целого j по меньшей мере в диапазоне 1≤j≤6 проходит спектральный тест второй степени в пределах оценки 1,25, а именно, для любого целого j в диапазоне 1≤j≤6 генератор (d, z′) при z′≡zj mod(d) удовлетворяет условию, что вектор f дуальной решетки, заданный для (d, z′) посредством линейной комбинации f:=m1f1+m2f2 базисных векторов {f1, f2} дуальной решетки,
f1:=(d,0), f2:=(-z′,1),
с целочисленными коэффициентами {m1,m2} и длиной
||f||:={(dm1-z′m2)2+(m2)2}1/2>0,
имеет наименьший ненулевой вектор fmin с длиной amin (2)(z′):=||fmin||>0, удовлетворяя условию
ρd (2)(z′):=21/2d1/2/{31/4amin (2)(z′)}<l,25.
| US 20120290632 A1, 15.11.2012 | |||
| US 8443021 B2, 14.05.2013 | |||
| US 5541996 A, 30.07.1996 | |||
| RU 2008131612 С, 10.02.2010. |
Авторы
Даты
2016-05-10—Публикация
2013-12-09—Подача