УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ДИСКРЕТНЫХ ПОЛИНОМИАЛЬНЫХ ПРЕОБРАЗОВАНИЙ Российский патент 2014 года по МПК G06F17/14 

Заявляемое изобретение относится к области цифровой обработки сигналов (ЦОС) различного назначения и может быть использовано при обработке видео- и аудиосигналов в реальном масштабе времени. Для решения задач ЦОС различного назначения применимы определенные подклассы дискретных полиномиальных преобразований (ДПП). Например, дискретных ортогональных (унитарных) преобразований - дискретного преобразования Фурье (ДПФ) и Хартли (ДПХ), как прямого, так и обратного [1, стр.21], а также цифровых фильтров с импульсной характеристикой конечной длительности (КИХ-фильтров) [2, стр.357].

Существенной проблемой при проектировании устройств для выполнения ДПП является выбор такой его структуры, при которой обеспечивается как высокое быстродействие, так и универсальность данного устройства применительно к реализации заданного подкласса ДПП. Одним из способов повышения быстродействия указанного устройства является реализация конвейерной обработки данных с сохранением промежуточных результатов. Для устройств вычислительной техники (ВТ), реализованных указанным способом, максимальное быстродействие определено как сумма максимального времени задержки функционирования одной из ступеней конвейера и максимального времени задержки одного из регистров, сохраняющих промежуточные результаты. Универсальность устройства для вычисления ДПП достигается за счет возможности варьирования элементов системы функций φ_ki(x_k), 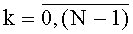$$k=\overline{\mathrm{0,}(N-1)}$$ , $$i=\overline{\mathrm{0,}(N-1)}$$ на конечном интервале длины N, N=2^c вида [1, стр.21]

$$y_i=\frac{1}{N}{\displaystyle \sum _{i=0}^{N-1}{\varphi }_{ki}(x_k)}.\text{ (1)}$$

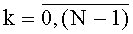
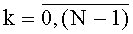
Согласно [2, стр.357], КИХ-фильтр (нерекурсивный цифровой фильтр) реализуем на основе (1) для системы функций φ_k(x_k)=a _k·х_k на конечном интервале длины N, N=2^c, где x_k - значение сигнала в k-й момент времени, $$k=\overline{\mathrm{0,}(N-1)}$$ , с - целые положительные значения. Согласно [3, стр.157], данная система функций (1) в совокупности с определенным коэффициентами a _k, $$k=\overline{\mathrm{0,}(N-1)}$$ , образует «фильтрующий» полином.

Известна реализация быстрого преобразования Хартли и Фурье при использовании конвейеризации процесса вычисления базовой операции («бабочки») алгоритма быстрого ДПФ и ДПХ [RU⁽¹¹⁾ 2190874⁽¹³⁾ , C2 G06F 17/14, 20.07.1999]. Недостатком данной реализации является ограничение по количеству выполняемых дискретных преобразований.

Известна реализация ДПФ на конечном интервале N=2^c при использовании процессоров, для которой обеспечивается максимальное быстродействие за счет оптимизации процесса извлечения коэффициентов ДПФ из памяти [RU⁽¹¹⁾ 2290687^(13), C1 G06F 17/14 (2006.01), 31.05.2005]. Недостатком данной реализации является ограничение по количеству выполняемых дискретных преобразований.

Известна реализация универсального цифрового фильтра с программируемой структурой, которая, помимо КИХ-фильтра, позволяет реализовать и авторегрессионный фильтр [RU⁽¹¹⁾ 2399152^(13), C2 H03H 17/04, H03H 17/06, H03H 21/00 (2006.01), 12.03.2008]. Недостатки данной реализации - ограничение по количеству выполняемых дискретных преобразований и низкое быстродействие.

Наиболее близким по технической сущности к заявляемому изобретению является устройство для формирования остатка по заданному модулю, содержащее Т блоков формирования частичных остатков с сохранением вычисленных результатов, два параллельных регистра, мультиплексор, компаратор и блок вычитания, причем t-й блок формирования частичных остатков, 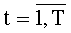$$t=\overline{\mathrm{1,}T}$$ , содержит комбинационный сумматор с (n-p) (p+1)-разрядными входами и (p+q)-разрядным выходом, где n-разрядность чисел, (p+1)-разрядность заданного модуля, q=]log₂(n-p)[ [RU⁽¹¹⁾ 2421781^(13), C1 G06F 7/72, H03M 7/18 (2006.01), 19.10.2009]. Данное устройство позволяет производить конвейерное вычисление значений остатков от деления по заданному модулю с сохранением промежуточных результатов (частичных остатков), следствием чего является существенное увеличение быстродействия данного устройства при обработке потока чисел. Недостаток данного устройства - ограничение по количеству выполняемых дискретных преобразований.

К причинам, препятствующим достижению технического результата при использовании известного устройства, относится ограничение по количеству выполняемых ими дискретных преобразований, что существенно ограничивает область его применения.

Технический результат заключается в расширении функциональных возможностей устройства для вычисления ДПП, структура которого может быть настроена для выполнения различных подклассов ДПП (например, Фурье, Уолша, Хаара, Хартли, косинусного и т.п.), а также для реализации КИХ-фильтров. 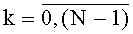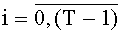Настройка производится путем задания системы функций на конечном интервале длины N и заключается в занесении всевозможных значений функций φ_ki(x_k) при заданных значениях x_k, $$k=\overline{\mathrm{0,}(N-1)}$$ , $$i=\overline{\mathrm{0,}(T-1)}$$ , в параллельные регистры значений разрядов функций каждого из блоков вычисления системы функций ДПП, а также в изменении количества блоков вычисления системы функций ДПП и блоков комбинационных сумматоров для N ƒ-разрядных двоичных чисел. Количество каждого из указанных блоков определено как Т - количество элементов образа заданного подкласса ДПП. В устройстве реализовано параллельное вычисление каждого из Т элементов указанных подклассов ДПП, причем в каждом из блоков вычисления системы функций ДПП и в каждом из комбинационных сумматоров для N ƒ-разрядных двоичных чисел производится конвейерное вычисление с сохранением промежуточных результатов.

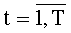
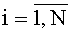
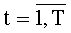
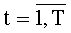
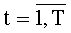
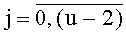
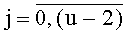
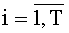
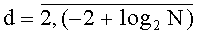
Технический результат достигается тем, что в устройство для вычисления дискретных полиномиальных преобразований, содержащее t-й комбинационный сумматор для N ƒ-разрядных двоичных чисел с одним выходом на (ƒ+log₂N) разрядов каждый, $$t=\overline{\mathrm{1,}T}$$ , введены система из n N-разрядных регистров сдвига с входом на n двоичных разрядов, с синхровходом и с N n-разрядными двоичными выходами, а также Т блоков вычисления системы функций ДПП с N n-разрядными двоичными входами, с Т входами значений разрядов функций ДПП на N·ƒ·2ⁿ двоичных разрядов каждый, с синхровходом, с входом инициализации и с N выходами на ƒ двоичных разрядов каждый, причем вход системы из n N-разрядных регистров сдвига является входом устройства на n двоичных разрядов, каждый из N выходов системы из n N-разрядных регистров сдвига соединен с N n-разрядными двоичными входами каждого из Т блоков вычисления системы функций ДПП, при этом N ƒ-разрядных выходов каждого из Т блоков вычисления системы функций ДПП соединены с N входами соответствующего ему комбинационного сумматора для N ƒ-разрядных двоичных чисел, (ƒ+log₂N)-разрядные выходы каждого из комбинационных сумматоров для N ƒ-разрядных двоичных чисел являются выходами устройства для вычисления ДПП, синхровход системы из n N-разрядных регистров сдвига, синхровход каждого из Т блоков вычисления системы функций ДПП и синхровход каждого из Т комбинационных сумматоров для N ƒ-разрядных двоичных чисел является синхровходом устройства для вычисления ДПП, каждый вход значений разрядов функций ДПП t-го блока вычисления системы функций ДПП соединен с t-м входом значений разрядов функций ДПП на N·ƒ·2ⁿ двоичных разрядов устройства для вычисления ДПП, $$t=\overline{\mathrm{1,}T}$$ , а вход инициализации каждого из Т блоков вычисления системы функций ДПП является входом инициализации устройства, система из n N-разрядных регистров сдвига содержит n N-разрядных регистров сдвига с последовательным входом, синхровходом и N двоичными выходами каждый, причем последовательный вход каждого N-разрядного регистра сдвига соединен с соответствующим двоичным разрядом n-разрядного входа устройства для вычисления ДПП, синхровход каждого из n N-разрядных регистров сдвига соединен с синхровходом устройства для вычисления ДПП, а i-е разряды N-разрядных регистров сдвига являются i-м выходом системы из n N-разрядных регистров сдвига на n двоичных разрядов каждый, $$i=\overline{\mathrm{1,}N}$$ , t-й блок вычисления системы функций ДПП, $$t=\overline{\mathrm{1,}T}$$ , содержит N·ƒ параллельных регистров значений разрядов функций разрядности 2ⁿ каждый с синхровходом, N·ƒ мультиплексоров «2ⁿ в 1», N параллельных ƒ-разрядных регистров с синхровходом, причем синхровход каждого из параллельных регистров значений разрядов функций соединен с входом инициализации устройства для вычисления ДПП, вход данных каждого из N·ƒ параллельных регистров значений разрядов функций соединен с соответствующими входами значений разрядов функций ДПП на N·ƒ·2ⁿ двоичных разрядов устройства для вычисления ДПП, а выходы данных каждого из N·ƒ параллельных регистров значений разрядов функций соединены с входами данных соответствующих им мультиплексоров «2ⁿ в 1», управляющие входы каждого из ƒ элементов i-й группы мультиплексоров «2ⁿ в 1» соединены с i-м входом n-разрядных двоичных чисел t-го блока вычисления системы функций ДПП, выходы данных i-й группы мультиплексоров «2ⁿ в 1» соединены с входом данных i-го параллельного ƒ-разрядного регистра, синхровход каждого из которых соединен с синхровходом устройства для вычисления ДПП, а выход данных каждого из которых является i-м выходом ƒ-разрядных двоичных чисел t-го блока вычисления системы функций ДПП, $$i=\overline{\mathrm{1,}N}$$ , $$t=\overline{\mathrm{1,}T}$$ , t-й комбинационный сумматор для N ƒ-разрядных двоичных чисел, $$t=\overline{\mathrm{1,}T}$$ , содержит (N-1) двухвходовых сумматора, из которых 2^u-2-j имеют разрядность (ƒ+j); $$j=\overline{\mathrm{0,}(u-2)}$$ , u=1+logN, а также (N-1) параллельных регистра с синхровходом, из которых 2^u-2-j имеют разрядность (ƒ+j+1), $$j=\overline{\mathrm{0,}(u-2)}$$ , u=1+logN, N входов на ƒ двоичных разрядов каждый, причем каждый из N входов на ƒ двоичных разрядов N/2 двухвходовых сумматоров соединен с N входами t-го блока вычисления системы функций ДПП разрядности ƒ, $$i=\overline{\mathrm{1,}T}$$ , выходы N/2 двухвходовых сумматоров соединены с входами N/2 (ƒ+1)-разрядных параллельных регистров, выходы которых, в свою очередь, соединены с входами N/4 двухвходовых сумматоров, выходы которых соединены с входами N/4 (ƒ+2)-разрядных параллельных регистров, выходы N/2^d (ƒ+d)-разрядных параллельных регистров соединены c входами N/2^d+1 двухвходовых сумматоров, выходы которых соединены с входами N/2^d-1 (ƒ+d+1)-разрядных параллельных регистров, $$d=\overline{\mathrm{2,}(-2+{\log }_{2}N)}$$ , выходы двух (ƒ-1+log₂N)-разрядных параллельных регистров соединены с входами двухвходового сумматора, выход которого соединен с входом параллельного регистра разрядности (ƒ+log₂N), выход которого является выходом t-го комбинационного сумматора для N ƒ-разрядных двоичных чисел, $$t=\overline{\mathrm{1,}T}$$ , синхровходы каждого из (N-1)-го параллельного регистра соединены с синхровходом устройства для вычисления ДПП.

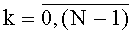
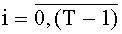
Каждый из Т блоков вычисления системы функций ДПП может быть настроен для реализации произвольной системы функций φ_ki(x_k) от заданных значений x_k, $$k=\overline{\mathrm{0,}(N-1)}$$ , $$i=\overline{\mathrm{0,}(T-1)}$$ , соответствующей указанному подклассу ДПП (см. выше). При этом для комплексной и для вещественной составляющей каждого элемента образа заданного подкласса ДПП применимы отдельные пары блоков вычисления системы функций ДПП и комбинационных сумматоров для N ƒ-разрядных двоичных чисел. Например, для реализации ДПФ на конечном интервале N требуется T=2N указанных блоков, для реализации ДПХ-Т=N пар указанных блоков, а для реализации КИХ-фильтра порядка N достаточно одной пары данных блоков, соответственно. Кроме того, внутри каждого из Т комбинационных сумматоров для N ƒ-разрядных двоичных чисел предусмотрена возможность сохранения промежуточных результатов, частичных сумм, в параллельных регистрах с синхровходом.

Схема устройства для вычисления дискретных полиномиальных преобразований представлена на фиг.1, а схемы системы из n N-разрядных регистров сдвига, t-го блока вычисления системы функций ДПП и t-го комбинационного сумматора для N ƒ-разрядных двоичных чисел, 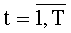$$t=\overline{\mathrm{1,}T}$$ , приведены на фиг.2, фиг.3 и фиг.4, соответственно.

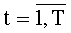
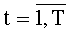
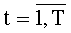
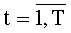
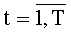
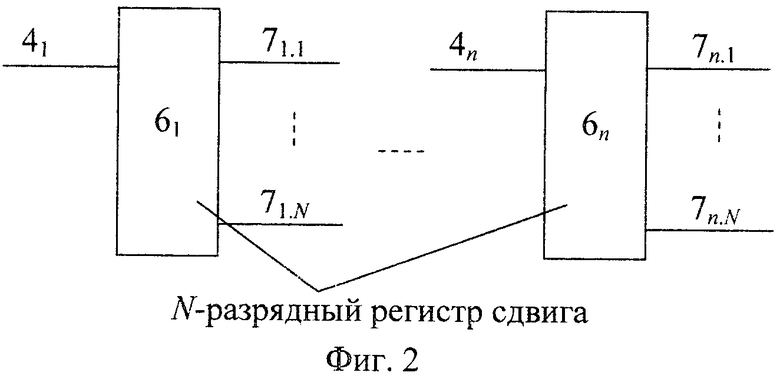
Устройство для вычисления ДПП, содержит Т комбинационных сумматоров 1₁, …, 1_T для N ƒ-разрядных двоичных чисел, систему 2 из n N-разрядных регистров сдвига, блоки 3_t вычисления системы функций ДПП, $$t=\overline{\mathrm{1,}T}$$ , причем каждая из данных функций представлена ƒ-разрядными двоичными числами, где Т - количество элементов образа заданного подкласса ДПП, представленных (ƒ+log₂N)-разрядными двоичными числами, N=2^c - длина интервала последовательности, над которой выполняется ДПП, ƒ=n+r, r - максимальное количество двоичных разрядов постоянных коэффициентов для заданного подкласса ДПП, n - количество двоичных разрядов входа устройства, причем вход системы 2 из n N-разрядных регистров сдвига, представленный n-разрядным двоичных значением x_k, является входом 4 устройства для вычисления ДПП, синхровход системы 2 из n N-разрядных регистров сдвига, а также каждого из блоков 3_t вычисления системы функций ДПП и каждого из комбинационных сумматоров 1_t для N ƒ-разрядных двоичных чисел, $$t=\overline{\mathrm{1,}T}$$ , является синхровходом устройства для вычисления ДПП (на фиг.1 не показаны), вход инициализации каждого из блоков 3_t вычисления системы функций ДПП, $$t=\overline{\mathrm{1,}T}$$ , является входом инициализации устройства для вычисления ДПП (на фиг.1 не показаны), вход значений разрядов функции ДПП соответствующего блока 3_t вычисления системы функций ДПП на N·ƒ·2ⁿ двоичных разрядов является t-м входом значений разрядов функции ДПП устройства для вычисления ДПП, $$t=\overline{\mathrm{1,}T}$$ (на фиг.1 не показаны), выход системы 2 из n N-разрядных регистров сдвига, представленный n·N-разрядным двоичным числом, соединен с входами каждого из блоков 3_t вычисления системы функций ДПП, $$t=\overline{\mathrm{1,}T}$$ , выход каждого из блоков 3_t вычисления системы функций ДПП, представленный ƒ-разрядным двоичным значением, соединен с входом соответствующего комбинационного сумматора 1_t для N ƒ-разрядных двоичных чисел, $$t=\overline{\mathrm{1,}T}$$ , а выход каждого комбинационного сумматора 1_t для N ƒ-разрядных двоичных чисел, определенный как (ƒ+log₂N)-разрядное двоичное число, является выходом 5_t устройства для вычисления ДПП, $$t=\overline{\mathrm{1,}T}$$ .

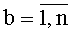
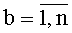
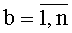
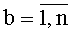
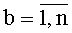
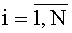
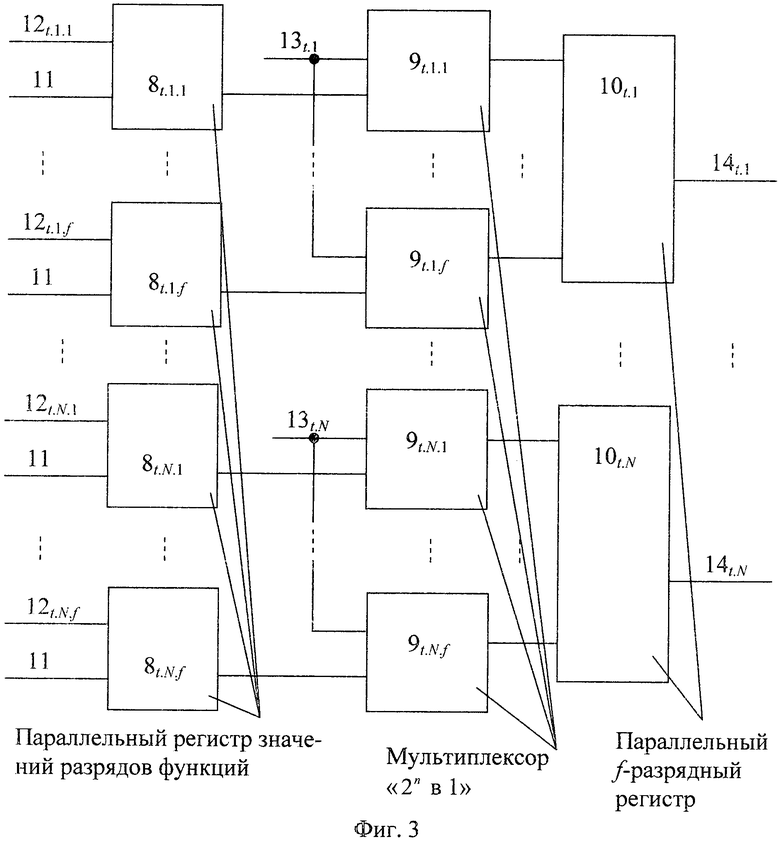
На фиг.2 представлена система 2 из n N-разрядных регистров сдвига, которая включает n N-разрядных регистров сдвига 6_b, $$b=\overline{\mathrm{1,}n}$$ , причем последовательные входы каждого из регистров сдвига 6_b, $$b=\overline{\mathrm{1,}n}$$ , соединены с соответствующим двоичным разрядом входа устройства 4 для вычисления ДПП - 4_b, $$b=\overline{\mathrm{1,}n}$$ , синхровходы каждого из N-разрядных регистров сдвига 6_b, $$b=\overline{\mathrm{1,}n}$$ , соединены с синхровходом устройства для вычисления ДПП (на фиг.2 не показаны), а выходы 7_b,i, каждого из N-разрядных регистров сдвига 6_b, $$b=\overline{\mathrm{1,}n}$$ , образуют i-й выход системы 2 из n N-разрядных регистров сдвига на n двоичных разрядов каждый, $$i=\overline{\mathrm{1,}N}$$ .

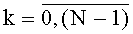
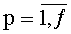
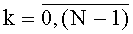
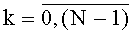
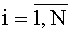
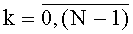
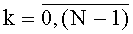
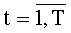
На фиг.3 представлен один из блоков 3_t вычисления системы функций ДПП вида φ_k(t-1)(x_k), $$k=\overline{\mathrm{0,}(N-1)}$$ , $$t=\overline{\mathrm{1,}T}$$ , который включает N·ƒ параллельных регистров 8_t.(k+1)p, $$p=\overline{\mathrm{1,}ƒ}$$ , значений p-го разряда функции φ_k(t-1)(x_k) разрядности 2ⁿ каждый, N·ƒ мультиплексоров 9_t.(k+1).p «2ⁿ в 1» и N параллельных ƒ-разрядных регистров 10_t.(k+1), причем синхровход каждого из параллельных регистров 8_t.(k+1).p значений разрядов функций, $$k=\overline{\mathrm{0,}(N-1)}$$ , $$p=\overline{\mathrm{1,}ƒ}$$ , соединен с входом инициализации 11 устройства для вычисления ДПП, каждый вход данных параллельного регистра 8_t(k+1)p значений разрядов функций ДПП φ_k(t-1)(x_k), $$k=\overline{\mathrm{0,}(N-1)}$$ , соединен с соответствующим входом 12_t.(k+1).p значений p-го разряда указанных функции на N·ƒ·2ⁿ двоичных разрядов, $$p=\overline{\mathrm{1,}ƒ}$$ , $$i=\overline{\mathrm{1,}N}$$ , выход каждого из параллельных регистров 8_t(k+1).p соединен с соответствующими входами данных мультиплексора 9_t.(k+1)p «2ⁿ в 1», тогда как управляющие входы каждого мультиплексора «2ⁿ в 1» из группы 9_t.(k+1).1 … 9_t.(k+1).ƒ, $$k=\overline{\mathrm{0,}(N-1)}$$ , соединены с n-разрядным входом 13_t.(k+1) значений x_k, разряды каждого из которых соединены с двоичными выходами 7_1.(k+1)…7_n.(k+1) системы 2 из n N-разрядных регистров сдвига (см. фиг.2), выходы мультиплексоров 9_t.(k+1).1…9_t.(k+1).ƒ «2ⁿ в 1» соединены с входами параллельных ƒ-разрядных регистров 10_t.(k+1), $$k=\overline{\mathrm{0,}(N-1)}$$ , синхровход каждого из которых соединен с синхровходом устройства для вычисления ДПП (на фиг.3 не указаны), а выходы параллельных ƒ-разрядных регистров 10_t.(k+1) являются ƒ-разрядными выходами 14_t.(k+1) блока 3_t вычисления системы функций ДПП, $$k=\overline{\mathrm{0,}(N-1)}$$ , $$t=\overline{\mathrm{1,}T}$$ , соответственно.

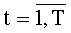
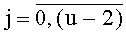
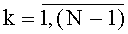
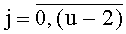
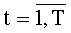
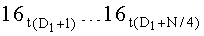
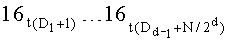
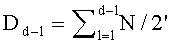
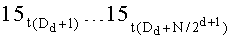
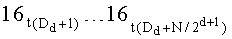
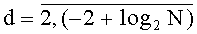
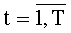
На фиг.4 изображен комбинационный сумматор 1_t, $$t=\overline{\mathrm{1,}T}$$ , для N ƒ-разрядных двоичных чисел, $$t=\overline{\mathrm{1,}T}$$ , который содержит (N-1) двухвходовых сумматора 15_t.1…15_t.(N-1), из которых 2^u-2-j имеют разрядность (ƒ+j), $$j=\overline{\mathrm{0,}(u-2)}$$ , u=1+logN, а также (N-1) параллельных регистра 16_t.1…16_t.(N-1) с синхровходом, $$k=\overline{\mathrm{1,}(N-1)}$$ , из которых 2^u-2-j имеют разрядность (ƒ+j+1), $$j=\overline{\mathrm{0,}(u-2)}$$ , u=1+logN, N входов на ƒ двоичных разрядов каждый, причем каждый из N входов на ƒ двоичных разрядов N/2 двухвходовых сумматоров 15_t.1…15_t.(N/2) соединен с N входами блока 3_t. вычисления системы функций ДПП разрядности ƒ, $$t=\overline{\mathrm{1,}T}$$ , выходы N/2 двухвходовых сумматоров 15_t.1…15_t.(N/2) соединены с входами N/2 (ƒ+1)-разрядных параллельных регистров 16_t.1…16_t.(N/2), выходы которых, в свою очередь, соединены с входами N/4 двухвходовых сумматоров $${15}_t{}_{(D_1+1)}\dots {15}_{t(D_1+N/4)}$$ , D₁=N/2, выходы которых соединены с входами N/4 (ƒ+2)-разрядных параллельных регистров $${16}_t{}_{(D_1+1)}\dots {16}_{t(D_1+N/4)}$$ , выходы N/2^d (ƒ+d)- разрядных параллельных регистров $${16}_t{}_{(D_1+1)}\dots {16}_{t(D_{d-}{}_1+N/2^d)}$$ , $$D_{d-1}={\displaystyle {\sum }_{l=1}^{d-1}N/2\text{'}}$$ , соединены с входами N/2^d+1 двухвходовых сумматоров $${15}_t{}_{(D_d+1)}\dots {15}_{t(D_d+N/2^{d+1})}$$ , выходы которых соединены с входами N/2^d+1 (ƒ+d+1)-разрядных параллельных регистров $${16}_t{}_{(D_d+1)}\dots {16}_{t(D_d+N/2^{d+1})}$$ , $$d=\overline{\mathrm{2,}(-2+{\log }_{2}N)}$$ , выходы двух (ƒ-1+log₂N)-разрядных параллельных регистров 16_t(N-3) 16_t(N-2) соединены с входами двухвходового сумматора 15_t.(N-1), выход которого соединен с входом параллельного регистра 16_t.(N-1) разрядности (ƒ+log₂N), выход которого является выходом 5_t t-го комбинационного сумматора для N ƒ-разрядных двоичных чисел, $$t=\overline{\mathrm{1,}T}$$ , синхровходы каждого из (N-1)-го параллельного регистра 16_t.1…16_t.(N-1) соединены с синхровходом устройства для вычисления ДПП (на фиг.4 не указаны).

Рассмотрим устройство для вычисления дискретных полиномиальных преобразований в работе.

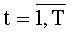
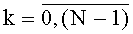
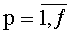
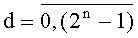
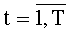
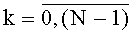
В предлагаемом устройстве на этапе инициализации в параллельные регистры 8_t.(k+1).p значений разрядов функции разрядности 2ⁿ по сигналу 11 инициализации параллельно заносятся соответствующие значения p-x двоичных разрядов значения функций φ_k(t-1)(x_k) системы (1), $$t=\overline{\mathrm{1,}T}$$ , $$k=\overline{\mathrm{0,}(N-1)}$$ , $$p=\overline{\mathrm{1,}ƒ}$$ . При этом значение в d-м разряде каждого из регистров 8_t.(k+1).p соответствует p-му разряду значения функции φ_k(t-1)(d), $$d=\overline{\mathrm{0,}(2^n-1)}$$ . Через период времени от момента прихода сигнала инициализации 11 устройства для вычисления ДПП до момента занесения информации в регистры 8_t.(k+1).p, $$t=\overline{\mathrm{1,}T}$$ , $$k=\overline{\mathrm{0,}(N-1)}$$ , $$p=\overline{\mathrm{1,}ƒ}$$ , устройство для вычисления ДПП готово к работе.

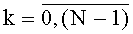
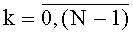
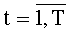
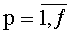
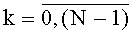
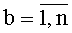
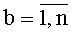
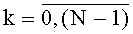
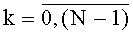
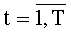
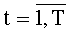
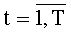
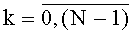
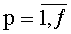
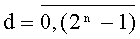
На этапе функционирования на каждом такте работы устройства для вычисления ДПП на вход 4 по синхросигналам, генерируемым через период времени Т_УТПП, поступают n-разрядные двоичные числа x_k, $$k=\overline{\mathrm{0,}(N-1)}$$ . На основании последовательности указанных чисел конечной длины N производится определенный подкласс дискретных полиномиальных преобразований. Генератор синхросигналов и синхровходы регистров 6₁, … 6_N, 8_t.(k+1).p, $$k=\overline{\mathrm{0,}(N-1)}$$ , $$t=\overline{\mathrm{1,}T}$$ , $$p=\overline{\mathrm{1,}ƒ}$$ , 10_t.1, … 10_t.N, 16_t.1, … 16_t.(N-1) на фиг.2, фиг.3 и фиг.4 не указаны. По синхросигналу b-й разряд каждого из значений x_k, $$k=\overline{\mathrm{0,}(N-1)}$$ , $$b=\overline{\mathrm{1,}n}$$ , сохраняется поразрядно в N-разрядном регистре сдвига 6_b, $$b=\overline{\mathrm{1,}n}$$ (см. фиг.2). В результате, через период времени N·Т_УТПП, когда в регистрах сдвига 6₁…6_N будет находиться последовательность {x_k}, $$k=\overline{\mathrm{0,}(N-1)}$$ длины N, элементы указанной последовательности параллельно поступают на входы 13_t.(k+1) блоков 3_t вычисления системы функций ДПП, φ_ki(x_k), $$k=\overline{\mathrm{0,}(N-1)}$$ , $$i=\overline{\mathrm{0,}(T-1)}$$ , $$t=\overline{\mathrm{1,}T}$$ , (см. фиг.3). В случае, если на вход 13_t.(k+1) блока 3_t вычисления системы функций ДПП, $$t=\overline{\mathrm{1,}T}$$ , являющийся также управляющим входом мультиплексора 9_t.(k+1).p «2ⁿ в 1», поступает значение d, представленное n-разрядным двоичным числом, то на выход мультиплексора 9_t.(k+1).p «2ⁿ в 1» поступает p-й разряд значения функции φ_k(t-1)(d), который был сохранен в d-м разряде параллельного регистра 8_t.(k+1).p значений разрядов функции на этапе инициализации, $$t=\overline{\mathrm{1,}T}$$ , $$k=\overline{\mathrm{0,}(N-1)}$$ , $$p=\overline{\mathrm{1,}ƒ}$$ , $$d=\overline{\mathrm{0,}(2^{{}_n}-1)}$$ .

Во время поступления следующего, (N·Т_УТПП+1)-го, синхросигнала значения с выходов каждого из мультиплексоров 9_t.(k+1).p «2ⁿ в 1» сохраняются в параллельных ƒ-разрядных регистрах 10_t.(k+1), $$k=\overline{\mathrm{0,}(N-1)}$$ , $$p=\overline{\mathrm{1,}ƒ}$$ , которые затем поступают на выходы 14_t.(k+1) каждого из блоков 3_t вычисления системы функций ДПП, $$t=\overline{\mathrm{1,}T}$$ (см. фиг.3). Значения на выходах 14_t.(k+1) являются также входами комбинационных сумматоров 1_t для N ƒ-разрядных двоичных чисел, $$t=\overline{\mathrm{1,}T}$$ , и поступают на сумматоры 15_t.1, …, 15_t.N/2 (см. фиг.4).

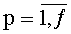
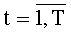
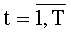
Во время поступления синхросигнала под номером (N·Т_УТПП+2) значения частичных сумм, снимаемых с выходов сумматоров 15_t.1, …, 15_t.N/2, сохраняются в параллельных регистрах 16_t.1, …, 16_t.N/2 разрядности (ƒ+1), соответственно, 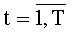$$t=\overline{\mathrm{1,}T}$$ , (см. фиг.4) и т.д.

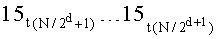
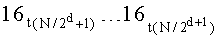
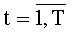
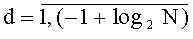
Во время поступления синхросигнала под номером (N·Т_УТПП+d+2) значения частичных сумм, снимаемых с выходов сумматоров $${15}_t{}_{(N/2^d+1)}\dots {15}_{t(N/2^{d+1})}$$ , сохраняются в параллельных регистрах $${16}_t{}_{(N/2^d+1)}\dots {16}_{t(N/2^{d+1})}$$ разрядности (ƒ+d+1), соответственно, $$t=\overline{\mathrm{1,}T}$$ , $$d=\overline{\mathrm{1,}(-1+{\log }_{{}^2}N)}$$ .

Во время поступления синхросигнала под номером (N·Т_УТПП+2+logN) значение, снимаемое с выхода сумматора 15_t.(N-1), сохраняется в параллельном регистре 16_t.(N-1) разрядности (ƒ+log₂N) и поступает на выход 5_t, который является одним из t выходов устройства для вычисления ДПП, 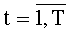$$t=\overline{\mathrm{1,}T}$$ .

В результате, за (N·Т_УТПП+2+logN) тактов работы устройства для вычисления ДПП возможно вычисление значений Т элементов образов для заданного подкласса дискретных полиномиальных преобразований. При этом минимальный интервал времени между поступлениями синхросигналов рассчитывается согласно формуле вида

Т_УТПП=max(T_MX, T(Σ))+T_R,

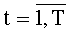
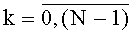
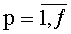
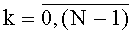
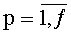
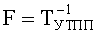
где T_MX, T(Σ) и T_R - оценки максимального времени задержки мультиплексоров 9_t.(k+1).p «2ⁿ в 1», двухвходового сумматора 15_t.(k+1) для $$t=\overline{\mathrm{1,}T}$$ , $$k=\overline{\mathrm{0,}(N-1)}$$ , $$p=\overline{\mathrm{1,}ƒ}$$ , а также максимального времени задержки функционирования регистров: N-разрядных регистров сдвига 6₁, …, 6_N, параллельных регистров 8_t(k+1).p значений разрядов функций, параллельных ƒ-разрядных регистров 10_t.(k+1) и параллельных регистров 16_t.(k+1), $$t=\overline{\mathrm{1,}T}$$ , $$k=\overline{\mathrm{0,}(N-1)}$$ , $$p=\overline{\mathrm{1,}ƒ}$$ , соответственно. Величина Т_УТПП позволяет определить верхнюю оценку частоты работы устройства для вычисления ДПП - $$F=T_{УТПП}^{-1}$$ .

При этом значения n-разрядных двоичных элементов обрабатываемых последовательностей, а также значения элементов образов заданного подкласса дискретных полиномиальных преобразований поступают на n-разрядный вход 4 и снимаются с Т(ƒ+log₂N)-разрядных выходов 5₁, …, 5_T устройства для вычисления ДПП, соответственно, по синхросигналам, поступающим через период времени не менее чем Т_УТПП.

Таким образом, предлагаемое устройство для вычисления ДПП по сравнению с прототипом позволяет производить вычисление широкого класса дискретных полиномиальных преобразований, задаваемых системой полиномиальных функций вида (1), при использовании конвейерной обработки данных с сохранением промежуточных результатов, что позволяет обеспечивать высокое быстродействие предлагаемого устройства.

Источники информации

1. Крот A.M. Дискретные модели динамических систем на основе полиномиальной алгебры. Минск: Навука i тэхника, 1990. 311 с.

2. Калабеков Б.А. Микропроцессоры и их применение в системах передачи и обработки сигналов: учебн. пособие для вузов. М.: Радио и связь, 1988. 312 с.

3. Блейхуд Р. Теория и практика кодов, контролирующих ошибки. Пер. с англ. под ред. Зигангирова К.Ш. М.: Мир, 1986. 576 с.

4. RU⁽¹¹⁾ 2190874^(13), C2 G06F 17/14, 20.07.1999.

5. RU⁽¹¹⁾ 2290687^(13), C1 G06F 17/14 (2006.01), 31.05.2005.

6. RU⁽¹¹⁾ 2399152^(13), C2 H03H 17/04, H03H 17/06, H03H 21/00 (2006.01), 12.03.2008.

7. RU⁽¹¹⁾ 2421781^(13), C1 G06F 7/72, H03M 7/18 (2006.01), 19.10.2009.

Изобретение относится к области цифровой обработки сигналов и может быть использовано при обработке видео- и аудиосигналов в реальном масштабе времени. Техническим результатом является обеспечение выполнения различных подклассов дискретных полиномиальных преобразований (ДПП) и для реализации КИХ-фильтров с использованием заданной системы функций на конечном интервале длины N=2^c. Устройство содержит систему из n N-разрядных регистров сдвига, Т блоков вычисления системы функций ДПП и Т блоков комбинационных сумматоров для N ƒ-разрядных двоичных чисел, где Т - количество элементов образа заданного подкласса ДПП, представленных (ƒ-1+log₂N)-разрядными двоичными числами, ƒ=n+r, n - количество двоичных разрядов входа устройства, r - максимальное количество двоичных разрядов постоянных коэффициентов для заданного подкласса ДПП. 4 ил.

Устройство для вычисления дискретных полиномиальных преобразований, содержащее T комбинационных сумматоров для N f-разрядных двоичных чисел с одним выходом на (f+log₂N) разрядов каждый, где T - количество элементов образа заданного подкласса дискретных полиномиальных преобразований (далее - ДПП), представленных (f+log₂N)-разрядными двоичными числами, N=2^c - длина интервала последовательности, над которой выполняется ДПП, c - целое положительное число, f=n+r, r - максимальное количество двоичных разрядов постоянных коэффициентов для заданного подкласса ДПП, n - количество двоичных разрядов входа устройства, отличающееся тем, что в него введены: система из n N-разрядных регистров сдвига с входом на n двоичных разрядов, с синхровходом и с N n-разрядными двоичными выходами, а также T блоков вычисления системы функций ДПП с N n-разрядными двоичными входами, с T входами значений разрядов функций ДПП на N·f·2ⁿ двоичных разрядов каждый, с синхровходом, с входом инициализации и с N выходами на f двоичных разрядов каждый, причем вход системы из n N-разрядных регистров сдвига является входом устройства на n двоичных разрядов, каждый из N выходов системы из n N-разрядных регистров сдвига соединен с N n-разрядными двоичными входами каждого из T блоков вычисления системы функций ДПП, при этом N f-разрядных выходов каждого из T блоков вычисления системы функций ДПП соединены с N входами соответствующего ему комбинационного сумматора для N f-разрядных двоичных чисел, (f+log₂N)-разрядные выходы каждого из комбинационных сумматоров для N f-разрядных двоичных чисел являются выходами устройства для вычисления ДПП, синхровход системы из n N-разрядных регистров сдвига, синхровход каждого из T блоков вычисления системы функций ДПП и синхровход каждого из T комбинационных сумматоров для N f-разрядных двоичных чисел является синхровходом устройства для вычисления ДПП, каждый вход значений разрядов функций ДПП t-то блока вычисления системы функций ДПП соединен с t-м входом значений разрядов функций ДПП на N·f·2ⁿ двоичных разрядов устройства для вычисления ДПП, 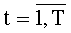, а вход инициализации каждого из Т блоков вычисления системы функций ДПП является входом инициализации устройства, система из n N-разрядных регистров сдвига содержит n N-разрядных регистров сдвига с последовательным входом, синхровходом и N двоичными выходами каждый, причем последовательный вход каждого N-разрядного регистра сдвига соединен с соответствующим двоичным разрядом n-разрядного входа устройства для вычисления ДПП, синхровход каждого из n N-разрядных регистров сдвига соединен с синхровходом устройства для вычисления ДПП, а i-e разряды N-разрядных регистров сдвига являются i-м выходом системы из n N-разрядных регистров сдвига на n двоичных разрядов каждый, , t-й блок вычисления системы функций ДПП, 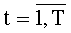, содержит N·f параллельных регистров значений разрядов функций разрядности 2ⁿ каждый с синхровходом, N·f мультиплексоров «2ⁿ в 1», N параллельных f-разрядных регистров с синхровходом, причем синхровход каждого из параллельных регистров значений разрядов функций соединен с входом инициализации устройства для вычисления ДПП, вход данных каждого из N·f параллельных регистров значений разрядов функций соединен с соответствующими входами значений разрядов функций ДПП на N·f·2ⁿ двоичных разрядов устройства для вычисления ДПП, а выходы данных каждого из N·f параллельных регистров значений разрядов функций соединены с входами данных соответствующих им мультиплексоров «2ⁿ в 1», управляющие входы каждого из f элементов i-й группы мультиплексоров «2ⁿ в 1» соединены с i-м входом n-разрядных двоичных чисел t-го блока вычисления системы функций ДПП, выходы данных i-й группы мультиплексоров «2ⁿ в 1» соединены с входом данных i-го параллельного f-разрядного регистра, синхровход каждого из которых соединен с синхровходом устройства для вычисления ДПП, а выход данных каждого из которых является i-м выходом f-разрядных двоичных чисел t-го блока вычисления системы функций ДПП, 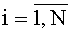, , t-й комбинационный сумматор для N f-разрядных двоичных чисел, 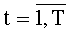, содержит (N-1) двухвходовых сумматора, из которых 2^u-2-j имеют разрядность (f+j), 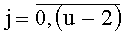, u=1+logN, а также (N-1) параллельных регистра с синхровходом, из которых 2^u-2-j имеют разрядность (f+j+1), 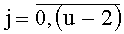, u=1+logN, N входов на f двоичных разрядов каждый, причем каждый из N входов на f двоичных разрядов N/2 двухвходовых сумматоров соединен с N выходами t-го блока вычисления системы функций ДПП разрядности f, , выходы N/2 двухвходовых сумматоров соединены с входами N/2 (f+1)-разрядных параллельных регистров, выходы которых, в свою очередь, соединены с входами N/4 двухвходовых сумматоров, выходы которых соединены с входами N/4 (f+2)-разрядных параллельных регистров, выходы N/2^d (f+d)-разрядных параллельных регистров соединены с входами N/2^d+1 двухвходовых сумматоров, выходы которых соединены с входами N/2^d+1 (f+d+1)-разрядных параллельных регистров, 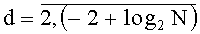, выходы двух (f-1+log₂N)-разрядных параллельных регистров соединен с входами двухвходового сумматора, выход которого соединен с входом параллельного регистра разрядности (f+log₂N), выход которого является выходом t-го комбинационного сумматора для N f-разрядных двоичных чисел, 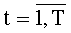, синхровходы каждого из (N-1)-го параллельного регистра соединены с синхровходом устройства для вычисления ДПП.