Область техники, к которой относится изобретение
Настоящее изобретение относится к арифметической схеме логарифмического отношения правдоподобия и арифметическому способу логарифмического отношения правдоподобия для вычисления и вывода логарифмического отношения правдоподобия (LLR) и устройству передачи, включающему в себя арифметическую схему логарифмического отношения правдоподобия.
Уровень техники
В последние годы, так как повысился спрос на коды с более высоким выигрышем от коррекции ошибок для применения в системах передачи данных, все в большей степени используются коды с более высоким выигрышем типа выполнения итеративного декодирования, использующего коды с мягким решением, такие как (сверточный) турбокод, код с низкой плотностью проверок на четность (LDPC) и турбокод произведения. Далее, так как количество передач данных увеличивается независимо от систем передачи, таких как систем беспроводной/проводной передачи данных, или систем хранения, таких как носители записи, также повысился спрос на системы передачи данных большей емкости.
Входные сигналы декодера, используемые для таких кодов с высоким выигрышем, представляют собой сигналы, называемые LLR. Первоначально, LLR квадратурной модуляции (квадратурной амплитудной модуляции: QAM), в которой точка сигнала является двумерной, вычисляется на основе квадрата расстояния между точками сигнала приема, выраженного в двух измерениях и всеми точками сигнала (16 частей, если 16-QAM). Так как является сложным вычисление квадрата расстояния, в основном использовался метод, при котором таблица, вычисленная и сгенерированная заранее программой, хранится в постоянном запоминающем устройстве (ROM) или в логической схеме (таблице истинности), соответствующей ROM, и LLR вычисляется с ссылкой на хранимую таблицу (см., например, непатентный документ 1).
Далее, в качестве устройства вычисления LLR посредством арифметической операции, патентный документ 1 описывает устройство, которое вычисляет логарифмическое отношение правдоподобия каждого бита в сигналах, модулированных М-арной QAM, для эффективной передачи в системе передачи данных, чтобы уменьшить время арифметического вычисления LLR.
Патентный документ 1: Выложенная публикация патента Японии № 2002-330188
Непатентный документ 1: «AHA Application Note Non-Square QAM Implementation for AHA 4540» AHA Inc.
Раскрытие изобретения
Проблемы, решаемые изобретением
В случае использования способа вычисления LLR, описанного в непатентном документе 1 в системе, требующей соответствующие LLR, справочная таблица, которая была вычислена и создана, заранее сохраняется в схеме, такой как ROM, и сигнал, включающий в себя координаты точек сигнала приема, вводится по адресу схемы, посредством чего выводится LLR.
Если способ ссылки на таблицу, как описано выше, применяется к системе, использующей квадратурную многоуровневую модуляцию (квадратурную амплитудную модуляцию: QAM), количество битов адреса ROM и количество битов вывода ROM становятся очень большими, что вызывает трудности при монтаже из-за размеров схемы и времени задержки.
Конкретно, сигнал координат сигнала приема 2ch, в котором демодулируется квадратурная модуляция, вводится в ROM, хранящий описанную выше таблицу, и ROM выводит LLR. В случае способа многоуровневой модуляции сигнал приема выражается посредством использования множества битов. В таком случае, так как LLR в отношении множества битов, выделенных одному символу, требуются для вывода одновременно, количество битов вывода ROM также большое.
Например, в случае 128-QAM, если одна часть мягкого решения квадратурного канала имеет 3 бита, одна точка сигнала приема выражается (4+3)×2=14 битами, в которые также включены 4 бита части жесткого решения. Если LLR для 1 бита включает в себя 5 битов, LLR для 7 битов, подлежащих передаче в одном символе, имеют в сумме 35 битов. Чтобы преобразовать точку сигнала приема данного случая в LLR, требуется подготовка ROM для 14-битового ввода и 35-битового вывода, и чтобы реализовать такое ROM, размер схемы становится очень большим. Далее, так как время задержки от ввода адреса до вывода данных большое, не может выполняться высокоскоростная операция.
Далее, в устройстве для выполнения арифметической операции, описанной в патентном документе 1, объем операции снижается посредством использования симметричного свойства в отображении Грея (соответствие между битами и символом). Поэтому это не может применяться к способу модуляции, в котором количество символов составляет нечетную степень двух, где исходные условия отображения Грея не удовлетворяются. Далее, так как окончательное LLR вычисляется посредством вычисления квадрата расстояния, все еще является большим объем арифметической операции для вычисления LLR.
Задачей настоящего изобретения является обеспечение арифметической схемы логарифмического отношения правдоподобия, устройства передачи и арифметического способа логарифмического отношения правдоподобия, способных вычислять логарифмическое отношение правдоподобия с высокой скоростью, в то же время уменьшая размер схемы и потребляемую мощность, независимо от способа модуляции и битовой точности LLR.
Средства для решения проблем
Арифметическая схема логарифмического отношения правдоподобия согласно настоящему изобретению представляет собой арифметическую схему логарифмического отношения правдоподобия для вычисления логарифмического отношения правдоподобия из информации о координатах точки сигнала приема для применения в системе передачи данных, использующей способ квадратурной амплитудной модуляции, отличающуюся тем, что область действия, в пределах которой значение логарифмического отношения правдоподобия изменяется в соответствии с положением точки сигнала приема, ограничивается интервалом между соседними точками сигнала, включающим в себя пороговое значение жесткого решения битов.
Устройство передачи согласно настоящему изобретению представляет собой устройство передачи, включающее в себя арифметическую схему логарифмического отношения правдоподобия для вычисления логарифмического отношения правдоподобия из информации о координатах точки сигнала приема для применения в системе передачи данных, использующей способ квадратурной амплитудной модуляции. Арифметическая схема логарифмического отношения правдоподобия отличается тем, что область действия, в пределах которой значение логарифмического отношения правдоподобия изменяется в соответствии с положением точки сигнала приема, ограничивается интервалом между соседними точками сигнала, включающим в себя пороговое значение жесткого решения битов.
Арифметический способ логарифмического отношения правдоподобия согласно настоящему изобретению представляет собой арифметический способ логарифмического отношения правдоподобия для вычисления логарифмического отношения правдоподобия из информации о координатах точки сигнала приема для применения в системе передачи данных, использующей способ квадратурной амплитудной модуляции. Способ отличается тем, что область действия, в пределах которой значение логарифмического отношения правдоподобия изменяется в соответствии с положением точки сигнала приема, ограничивается интервалом между соседними точками сигнала, включающим в себя пороговое значение жесткого решения битов.
Результаты изобретения
Согласно настоящему изобретению в системе передачи данных, использующей способ квадратурной амплитудной модуляции, вычисление логарифмического отношения правдоподобия, которое обычно выполняется в двух измерениях, разлагается на одно измерение, и объем арифметической операции может быть значительно уменьшен. Далее, так как вся или почти вся операция по вычислению логарифмического отношения правдоподобия может выполняться логическим арифметическим блоком, нет необходимости использовать большое ROM, и размер схемы и потребляемая мощность могут быть снижены, независимо от способа модуляции и точности в битах логарифмического отношения правдоподобия. Далее, так как может быть повышено быстродействие схемы, может быть реализована система передачи данных большой емкости. Следовательно, можно повысить скорость вычисления логарифмического отношения правдоподобия, в то же время, снижая размеры схемы.
Далее, с конфигурацией для выполнения квази-кодирования Грея, используя способ квадратурной амплитудной модуляции, в котором интенсивность побитовых ошибок становится минимальной, также можно выполнять вычисление LLR с более высокой скоростью, в то же время, уменьшая размеры схемы, даже в случае использования способа квадратурной амплитудной модуляции, имеющей точки сигнала нечетной степени двух.
Наилучший способ осуществления изобретения
Ниже описывается примерный вариант осуществления изобретения со ссылкой на чертежи.
В системе передачи данных, выполняющей модуляцию и демодуляцию, координаты точек сигнала приема, которые представляют собой выходной сигнал демодулятора, выражаются как комбинация ортогональных сигналов двух каналов. В битах (m+n) сигнала верхние (старшие) m биты указывают сигнал с жестким решением (биты, способные задавать модулированный символ), и нижние (младшие) n биты указывают сигнал с мягким решением (биты, указывающие промежуточное положение символа).
Как показано на фиг.1 и 13, арифметическая схема логарифмического отношения правдоподобия согласно примерному варианту осуществления изобретения включает в себя, в качестве базовой конфигурации, первые арифметические блоки (101А, 102А, 103А, 104С, 104D и 210), которые представляют собой арифметические схемы логарифмического отношения правдоподобия для вычисления логарифмического отношения правдоподобия сигнала приема, выраженного в двух измерениях и способного разлагаться на одномерные сигналы, причем схемы принимают один одномерный сигнал, который вводится в них, и выполняют логическую арифметическую операцию, используя информацию о координатах точек сигнала введенного одномерного сигнала, и вторые блоки (101В, 102В, 103В, 104D, 104Е и 201) вычисления, которые принимают введенный в них другой одномерный сигнал и выполняют логическую арифметическую операцию, используя информацию о координатах точки сигнала введенного одномерного сигнала, таким образом вычисляя логарифмическое отношение правдоподобия.
Первые блоки вычисления и вторые блоки вычисления ограничивают область действия, в которой значение логарифмического отношения правдоподобия изменяется в соответствии с положением точки сигнала приема, интервалом между соседними точками сигнала, включающим порог жесткого решения бита, и вычисляют окончательное логарифмическое отношение правдоподобия.
Согласно примерному варианту осуществления настоящего изобретения вычисление логарифмического отношения правдоподобия, выполняемое двухмерно, разлагается на одно измерение, и может быть значительно снижен объем вычислений. Далее, так как все или почти все вычисления логарифмического отношения правдоподобия могут конфигурироваться логическим арифметическим блоком, нет необходимости использовать большое ROM, и могут быть снижены размеры схемы и потребляемая мощность, независимо от способа модуляции и битовой точности логарифмического отношения правдоподобия. Далее, так как может быть повышено быстродействие схемы, может быть реализована система передачи данных большой емкости. По существу, логарифмическое отношение правдоподобия может вычисляться с большей скоростью, в то же время, уменьшая размеры схемы.
Далее, с конфигурацией для выполнения квази-кодирования Грея, так что интенсивность побитовых ошибок становится минимальной, можно сделать размеры схемы меньше и выполнять вычисление LLR с более высокой скоростью даже в случае использования способа квадратурной амплитудной модуляции, имеющего точки сигнала нечетной степени двух.
Первый примерный вариант осуществления
Ниже в качестве первого примерного варианта осуществления описывается арифметическая схема логарифмического отношения правдоподобия, которая является оптимальной для способа квадратурной амплитудной модуляции, имеющего точку сигнала нечетной степени двух. Фиг.1 представляет собой блок-схему, изображающую примерную конфигурацию арифметической схемы логарифмического отношения правдоподобия (арифметической схемы LLR) согласно первому примерному варианту осуществления изобретения. В настоящем варианте осуществления в качестве примера описывается арифметическая схема LLR 16-QAM. Далее, в примерном варианте осуществления предполагается, что количество битов жесткого решения 16-QAM равно 2. Хотя количество битов мягкого решения изменяется в зависимости от требуемых характеристик, количество битов мягкого решения предполагается равным 3 битам в примерном варианте осуществления. Далее, арифметическая схема LLR, показанная на фиг.1, предусматривается для устройства передачи системы беспроводной СВЧ передачи данных, использующей, например, QAM (способ квадратурной амплитудной модуляции).
Как показано на фиг.1, арифметическая схема LLR включает в себя схемы 101А и 101В обнаружения области, схемы 102А и 102В LLR, преобразователи 103А и 103В LLR и преобразователи 104А и 104В LLR.
Отметим, что, если схемы 101А и 101В обнаружения области указываются вместе, или указывается любая из них, они могут указываться просто как схема 101 обнаружения области. Аналогично, если схемы 102А и 102В LLR указываются вместе, или указывается любая из них, они могут указываться просто как схема 102 LLR. Аналогично, если преобразователи 103А и 103В LLR указываются вместе, или указывается любой из них, они могут указываться просто как преобразователь 103 LLR. Аналогично, если преобразователи 104А и 104В LLR указываются вместе, или указывается любой из них, они могут указываться просто как преобразователь 104 LLR.
В схему 101А обнаружения области вводится бит жесткого решения из числа битов, указывающих координаты по оси Р точки сигнала приема, и, основываясь на введенном бите жесткого решения, схема 101А обнаружения области обнаруживает и выводит область на фазовой плоскости, где присутствуют координаты по оси Р точки сигнала приема.
В схему 101В обнаружения области вводится бит жесткого решения из числа битов, указывающих координаты по оси Q точки сигнала приема, и, основываясь на введенном бите жесткого решения, схема 101В обнаружения области обнаруживает и выводит область на фазовой плоскости, где присутствуют координаты по оси Q точки сигнала приема.
В схему 102A LLR вводится бит мягкого решения из числа битов, указывающих координаты по оси Р точки сигнала приема, и, основываясь на введенном бите мягкого решения, схема 102А LLR вычисляет первичное логарифмическое отношение правдоподобия (LLR).
В схему 102В LLR вводится бит мягкого решения из числа битов, указывающих координаты по оси Q точки сигнала приема, и, основываясь на введенном бите мягкого решения, схема 102В LLR вычисляет первичное логарифмическое отношение правдоподобия (LLR).
В примерном варианте осуществления выходной сигнал схемы 102 LLR представляет собой значение первичного LLR, зависящее только от бита мягкого решения. В примерном варианте осуществления значение первичного LLR, выводимое из схемы 102 LLR, преобразуется с битом жесткого решения, посредством чего вычисляется значение окончательного LLR.
В преобразователи 103 и 104 LLR вводится выходной сигнал (первичное LLR) схемы 102 LLR, и, основываясь на выходном сигнале (результате обнаружения области) схемы 101 обнаружения области, преобразователи 103 и 104 LLR вычисляют окончательное LLR.
В примерном варианте осуществления выходной сигнал от схемы 102 LLR применяется с любым одним из четырех преобразований, включающих в себя (1) непосредственный вывод выходного сигнала от схемы 102 LLR, (2) инвертирование и вывод выходного сигнала от схемы 102 LLR, (3) замену выходного сигнала предварительно определенным максимальным значением LLR и его вывод, и (4) замену выходного сигнала предварительно определенным минимальным значением LLR и его вывод, согласно результату обнаружения схемы 101 обнаружения области. Затем сигнал выводится в качестве значения окончательного LLR.
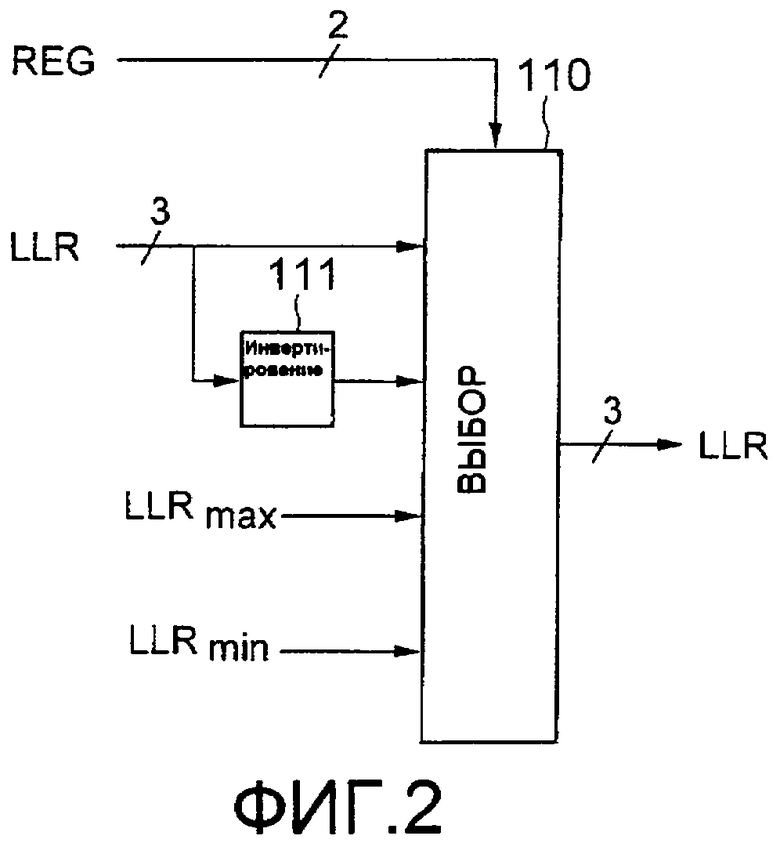
Фиг.2 представляет собой блок-схему, изображающую примерную схемную конфигурацию преобразователей 103 и 104 LLR. Как показано на фиг.2, каждый из преобразователей 103 и 104 LLR включает в себя схему 110 выбора и инвертор 111.
Инвертор 111 инвертирует бит выходного сигнала схемы 102 LLR и выводит его.
В схему 110 выбора вводятся выходной сигнал (первичное LLR) от схемы 102 LLR, выходной сигнал от схемы 102 LLR, который инвертирован инвертором 111, предварительно определенное максимальное значение LLR и предварительно определенное минимальное значение LLR. Далее, в соответствии с результатом обнаружения схемы 101 обнаружения области схема 110 выбора выбирает любой один из выходного сигнала от схемы 102 LLR, выходной сигнал, инвертированный инвертором 111, предварительно определенное максимальное значение LLR и предварительно определенное минимальное значение LLR и выводит его. Отметим, что предварительно определенное максимальное значение LLR и предварительно определенное минимальное значение LLR заранее сохраняются, например, в запоминающем устройстве, таком как память.
Схема 101 обнаружения области определяет исходя из положения точки сигнала приема, где присутствует точка сигнала приема из числа четырех областей, включающих в себя (1) область, в которой LLR изменяется с положительным наклоном, пересекая порог жесткого решения, (2) область, в которой LLR изменяется с отрицательным наклоном, пересекая порог жесткого решения, (3) область, в которой LLR не изменяется при максимальном значении без пересечения порога жесткого решения, и (4) область, в которой LLR не изменяется при минимальном значении без пересечения порога жесткого решения. Затем схема 101 обнаружения области выводит сигнал, соответствующий результату определения.
Отметим, что обработка, выполняемая схемой 101 обнаружения области, схемой 102 LLR, преобразователями 103 и 104 LLR, полностью идентична в случае обработки битов, указывающих координаты по оси Р, и в случае обработки битов, указывающих координаты по оси Q.
В примерном варианте осуществления в арифметическую схему LLR вводится сигнал приема, который выражается в двух измерениях и может быть разложен на одномерные сигналы (сигнал по оси Р и сигнал по оси Q). В арифметической схеме LLR одномерный сигнал (сигнал по оси Р), который получают посредством разложения сигнала приема, вводится в схему 101А обнаружения области, схему 102А LLR и преобразователи 103А и 104А LLR, которые конфигурируют первый арифметический блок для вычисления логарифмического отношения правдоподобия (LLR) посредством выполнения логической арифметической операции, используя информацию о координатах точки сигнала введенного одномерного сигнала. Далее, другой одномерный сигнал (сигнал по оси Q), который представляет собой одномерный сигнал, полученный посредством разложения сигналов приема, вводится в схему 101В обнаружения области, схему 102В LLR и преобразователи 103В и 104В LLR, которые конфигурируют второй арифметический блок для вычисления логарифмического отношения правдоподобия (LLR) посредством выполнения логической арифметической операции, используя информацию о координатах точки сигнала введенного одномерного сигнала. С этими конфигурациями арифметическая схема LLR выполняет всю или почти всю арифметическую операцию для вычисления логарифмического отношения правдоподобия посредством выполнения логической арифметической операции, используя информацию о точке сигнала приема.
Ниже описывается работа. Перед описыванием заданной операции арифметической схемы LLR, сначала будет описан способ вычисления логарифмического отношения правдоподобия (LLR).
LLR в способе многоуровневой квадратурной модуляции (QAM) вычисляется для каждого бита, назначенного символу модуляции. Например, в случае 16-QAM, используют 16 частей символа модуляции, и 4 бита выделяют каждому символу. По существу, в случае использования 16-QAM, LLR для 4 битов должны вычисляться из одного сигнала приема.
Определение LLR
Ниже изображается способ вычисления LLR. Сначала описывается способ вычисления LLR в случае двоичной фазовой модуляции (BPSK), которая представляет собой одномерную модуляцию. Если сигнал передачи представляет собой 2 значения, равных ±1, и это одномерная модуляция, LLR(λ) определяется следующим уравнением:
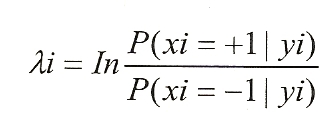
уравнение (1)
В уравнении (1) P(xi=b|yi) представляет собой апостериорную вероятность, где сигнал передачи, когда принимается сигнал приема yi, представляет собой b, и i представляет собой суффикс, указывающий время.
Далее, апостериорная вероятность P(xi=b|yi) в отношении теплового шума, в котором амплитуда становится нормальным распределением, выражается посредством использования уравнения (2), где мощность шума равна σ2.
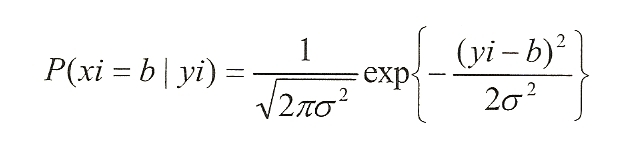
уравнение (2)
Поэтому, LLR(λ) вычисляется посредством назначения апостериорной вероятности, показанной в уравнении (2), в уравнение (1), как показано в уравнении (3):
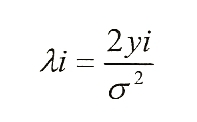
уравнение (3)
В уравнении (3), предположив, что σ2 представляет собой постоянное значение, и не учитывается коэффициент пропорциональности, включающий σ2, LLR(λi) становится самим сигналом приема (yi). Отметим, что, если алгоритм минимальной суммы используется в качестве алгоритма декодирования, установка σ2 равным постоянной величине никогда не будет оказывать влияние на характеристики декодирования. Далее, даже в случае использования алгоритма, иного, чем алгоритм минимальной суммы, так как возможность коррекции кода коррекции ошибки, которым является текущий объект, является высокой, только незначительное улучшение отношения сигнала к мощности шума выведет интенсивность побитовых ошибок вне измеряемого интервала. Следовательно, разумно понять, что σ2 является постоянной.
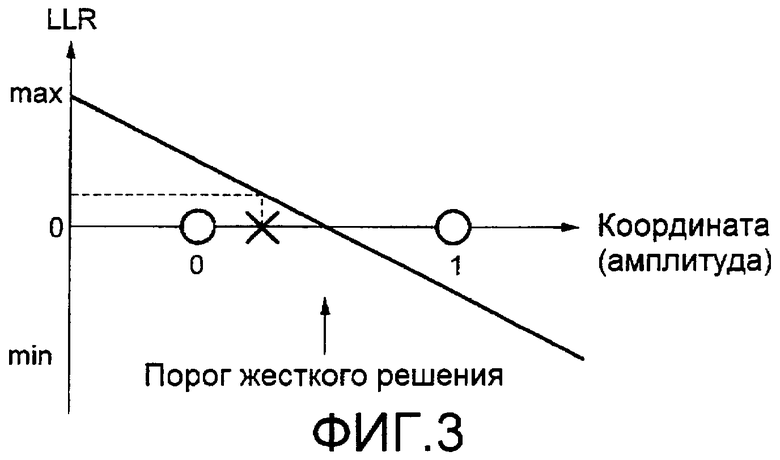
Фиг.3 изображает позиционное соотношение между LLR и точкой сигнала приема в BPSK. Предполагается, что LLR выражается числом дополнения до 2, как форма, подходящая для работы декодера в последнем каскаде арифметической схемы LLR. В данном случае, так как окончательный выходной результат демодулятора, если LLR после демодуляции равно 0 или более, бит приема определяется как 0, и, если LLR представляет собой отрицательное значение, бит приема определяется как 1. Другими словами, старший значащий бит (MSB) LLR становится результатом определения. Отметим, что оперирование LLR в качестве дополнения до 2 не является существенным. В случае рассмотрения LLR в качестве двоичной формы смещения, полярность будет противоположной.
Затем способ вычисления LLR в случае использования способа одномерной модуляции, описанный выше, расширяется на квадратурную модуляцию (QAM или способ двумерной модуляции). Даже в случае использования многоуровневой QAM, в которой множество битов соответствует одному символу, один бит выражается двумя значениями ±1. Если это 16-QAM, воздействие всех 16 частей точек сигнала будет вычисляться для 4 битов посредством использования уравнения (2), соответственно. Отметим, что yi в уравнении (2) выражается посредством использования квадратурных координат, и вычисление квадрата расстояния в показатели степени уравнения (2) выполняется двумерно.
Хотя вычисление LLR, описанное выше, не требует никакого ограничения для отображения, нельзя вычислить простую форму, как показано в уравнении (3). Поэтому очень трудно выполнить вычисление арифметической схемой, построенной в виде аппаратных средств. По существу, необходимо вычислять LLR для всех точек сигнала приема, заранее используя вычислитель, и сохранять в ROM в табличном виде.
Далее, так как является большим многоуровневое число модуляции, становится большим количество битов, указывающих точку сигнала приема, и количество битов, распределенных одному символу. Поэтому, чтобы выводить все LLR для каждого символа, причем координаты точек сигнала приема являются вводом, размер ROM для хранения LLR становится очень большим, который не может быть реализован практически.
В качестве примера схемы, использующей способ двумерной модуляции, документ «Product Specification AHA4541» (ниже в данном документе документ А) описывает, что AHA4541, которая представляет собой большую интегральную схему (БИС) для турбокода произведения, производимую компанией AHA Corp. США, может поддерживать до 256-QAM. Однако документ А не описывает способ вычисления LLR, используемый для БИС (AHA4541).
Далее, «AHA Application Note Non-Square QAM Implementation for aha4540» (непатентный документ 1), который представляет собой документ, описывающий AHA4541, которая представляет собой БИС для турбокода произведения, производимую компанией AHA Corp. США, описывает в разделе 4.1 программу для вычисления LLR. Однако непатентный документ 1 нигде не описывает рабочий способ, который может выполняться аппаратными средствами и схемной конфигурацией.
Далее, в качестве способа реализации вычисления LLR при помощи простой операции, имеется одна, которая описывается в выложенной публикации патента Японии № 2002-330188 «Method and Apparatus for Bit Log Likelihood Ratio Operation of QAM Signal» (патентный документ 1).
Уровень техники, описанный в патентном документе 1, строго вычисляет LLR, основываясь на формуле определения LLR посредством процессора цифровой обработки сигналов (DSP) (БИС обработки цифрового сигнала), и описывает способ упрощения вычисления LLR. С другой стороны, способ, описанный в патентном документе 1, может существенно снижать первоначально требуемое количество операций кодирования Грея отображения и использования симметричного свойства.
Однако отображение кодирования Грея не может быть реализовано в способе модуляции, имеющем количество точек сигнала, равных несчетной степени двух, подобно 128-QAM. В отношении этого аспекта патентный документ 1 указывает, что диапазон применения ограничивается случаем использования способа модуляции, который позволяет выполнять кодирование Грея (отображение Карно). По существу, даже в способе патентного документа 1, LLR вычисляется как разность квадрата расстояния между положением точки сигнала приема и точки сигнала, соответствующей «0», и точки сигнала, соответствующей «1», поэтому операция все еще является сложной.
По меньшей мере, не присутствует арифметическая схема LLR, которая может быть реализована аппаратными средствами, поддерживающими способ модуляции QAM, в котором количество символов представляет собой нечетную степень двух. Кроме того, не является хорошо известной арифметическая схема LLR, не требующая вычисления квадрата расстояния в способе модуляции QAM четной степени двух, имеющем такую же схемную конфигурацию способа с нечетной степенью двух.
В противоположность этому, примерный вариант осуществления может поддерживать способ модуляции QAM, в котором количество символов равно нечетной степени двух и реализует арифметическую схему LLR, которая может приводить к упрощенной схемной конфигурации даже для способа модуляции QAM, в котором количество символов равно четной степени двух.
Упрощение, когда количество символов равно четной степени двух
Ниже описывается упрощение схемной конфигурации арифметической схемы LLR, когда количество символов сигнала приема представляет собой четную степень двух. Чтобы реализовать операцию LLR, в которой количество символов равно четной степени двух, на схеме практического размера, необходимо использовать арифметическую схему, основанную не на табличном формате, но на предварительно определенном правиле. Ниже в данном документе описывается способ существенного упрощения операции LLR без снижения точности.
Сначала для упрощения операции предлагаются следующие два предположения.
Предположение (а): может иметь место ошибка битов, и область, которая является предметом операции LLR, ограничивается частью между двумя точками сигнала, соответствующими различным битам.
Предположение (b): реализуется отображение, так что даже двумерный сигнал может независимо вычисляться посредством каждого одномерного сигнала.
Ниже описывается значение этих двух предположений и их ограничения.
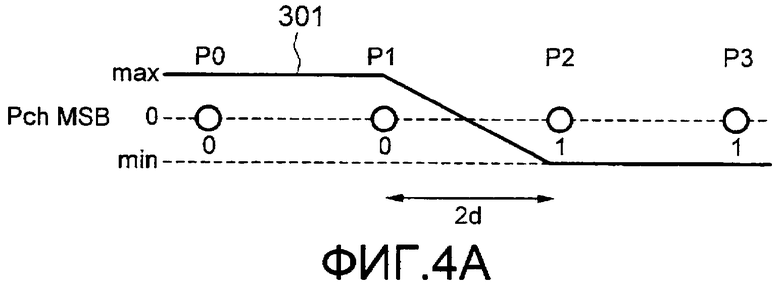
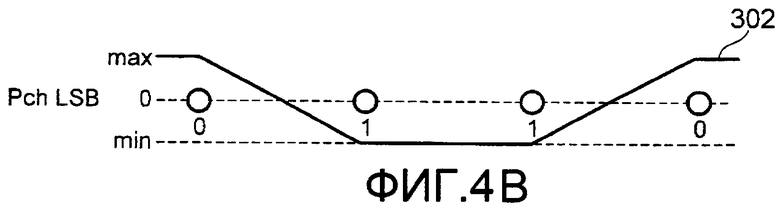
Предположение (а) означает, что расстояние между точками сигнала равно 2d, амплитуда шума равна 2d или меньше. Например, фиг.4 изображает пример позиционной зависимости между LLR и точкой сигнала приема в 16-QAM. Фиг.4А указывает примерную позиционную зависимость между LLR и точкой сигнала приема в случае MSB Pch, и фиг.4В указывает примерную позиционную зависимость между LLR и точкой сигнала приема в случае LSB Pch (младшего значащего бита).
Как показано на фиг.4А, в случае MSB Pch существует четыре точки сигнала P0-P3. Как показано на фиг.4А, в случае MSB Pch значение бита изменяется от 0 до 1 между точками сигнала Р1-Р2. В данном случае, если точка сигнала приема присутствует между Р1 и Р2, точкой сигнала передачи может быть Р1 или Р2, и, так как точка сигнала приема находится ближе к Р1, определяется, что возможность того, что точкой сигнала передачи является Р1, является высокой, и что точка сигнала передачи никогда не будет Р0 или Р3.
В примере, показанном на фиг.4А, вызывается ошибка бита, когда амплитуда шума превышает d. Если возможность ошибки бита составляет примерно 0,01 или меньше, возможность, что амплитуда шума в соответствии с нормальным распределением превышает 2d, составляет примерно 1×10-6. В случае, когда необходимо рассматривать влияние шума, имеющего амплитуду 2d или более, очень большое количество ошибок было вызвано между шумами с амплитудой от d до 2d, и нет выигрыша в коррекции ошибок. В этом случае, не обеспечивается улучшение интенсивности ошибок посредством операции коррекции ошибок.
Далее, даже вычисление, в котором рассматриваются влияния всех точек сигнала, выполняется на основе определения LLR, влияние точек сигнала, за исключением ближайших точек сигнала, очень малое, так что влияния не будут отражаться на значении LLR, которое квантуется до примерно 3-5 битов. Следовательно, предположение (а) не будет снижать точность операции коррекции ошибок.
Как описано выше, существует только часть между сигналами (часть, где значение бита изменяется от 0 до 1 или от 1 до 0 между двумя сигналами), соответствующая различным битам, в которых может вызываться ошибка бита, и требуется информация об определенности посредством LLR. Вне ее возможно, что значение LLR является фиксированным на максимальном значении или минимальном значении. Далее, существует только часть между сигналами, пересекающая порог принятия решения 0 и 1, где необходимо изменить значение LLR в соответствии с положением точки сигнала приема.
Ниже описывается предположение (b). Отображение, реализующее условия предположения (b), представляет собой отображение, выполняемое посредством кодирования Грея, которое, как правило, применяется для того, чтобы сделать оптимальной интенсивность побитовых ошибок, когда используется код коррекции ошибок, который представляет собой предмет примерного варианта осуществления. Например, документ А, описывающий AHA4541, которая представляет собой БИС для турбокода произведения, производимую компанией AHA Corp., также описывает отображение кодирования Грея.
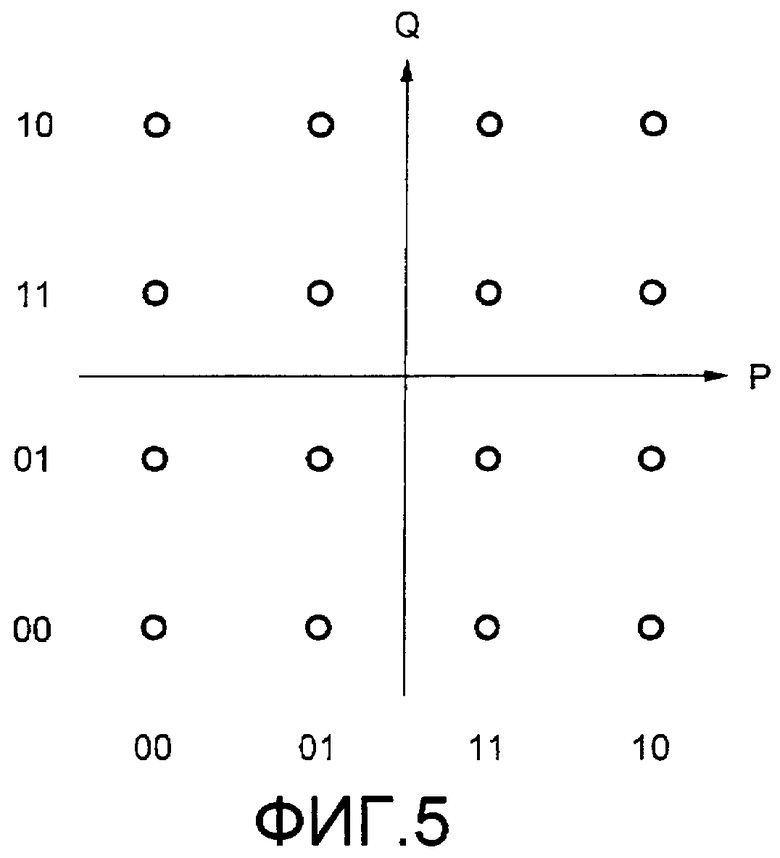
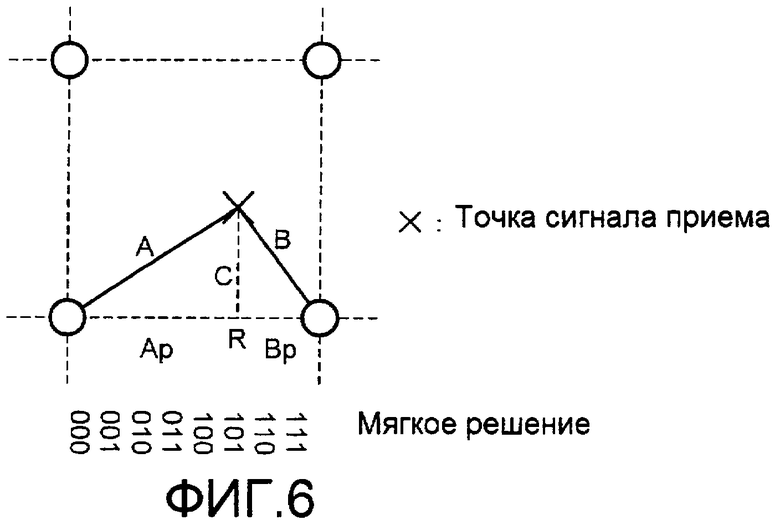
Фиг.5 изображает отображение кодирования Грея в 16-QAM. Если отображение выполняется кодированием Грея, бит Pch является общим в символах, выровненных вертикально (направление по оси Q). Следовательно, необходимо только заменить числитель в «exp» уравнения (2) со значениями степени двух расстояний (А, В) на символы, соответствующие битам 0 и 1, которые являются самыми ближайшими к точкам сигнала приема. В данном случае, хотя, как правило, имеется сдвиг С в направлении оси Q, так как сдвиг С является общим для обоих из двух расстояний, он ликвидируется при вводе в уравнение (1) LLR. Как показано на фиг.6, предполагая, что ортогональная проекция точки сигнала приема на горизонтальную линию, связывающую две точки сигнала, представляет собой точку R, и расстояния до точек 0 и 1 сигнала представляют собой Ap и Bp, соответственно, числитель в «exp» в уравнении (2), введенный в уравнение (1), показан как уравнение (4).
А2-В2=(Ар2+С2)-(Вр2+С2)=АР2-Вр2
уравнение (4)
Как показано в уравнении (4), LLR окончательно может вычисляться только из ортогональной проекции (т.е. одноканальное значение) точки сигнала приема. Конечно, то же самое относится и к Qch. Таким образом, даже если вычисление LLR представляет собой способ двумерной модуляции, если оно может быть разложено на два независимых одномерных сигнала, способ модуляции может рассматриваться одномерным. По существу, понятно, что LLR легко может быть вычислено из координат точки сигнала приема.
В случае многоуровневой QAM, распределения точек сигнала, в которые распределяются 0 и 1, отличаются уровнями битов (MSB, 2SB (значащий бит),… LSB). Поэтому хотя необходимо изменить схему вычисления из-за уровня битов, для которых должно вычисляться LLR, если оно рассматривается в пределах области, где изменяется значение LLR, уровень бита не имеет никакого отношения. По существу, общей является схема части, где LLR изменяется в соответствии с координатами точки сигнала приема. Другими словами, необходимо только изменить выходной сигнал общей схемы вычисления LLR в соответствии с уровнем бита.
Как описано выше, два предположения (а) и (b) обеспечивают эффект существенного упрощения процедур вычисления LLR без существенного оказания обратного влияния на арифметическую точность LLR и свободу при реализации устройств. Далее, так как нет необходимости рассматривать влияния точки сигнала, которая не является предметом обсуждения, относительная позиционная зависимость между точкой сигнала приема и точкой сигнала, и связь со значениями LLR не зависит от уровней битов (MSB, 2SB,… LSB).
Фиг.4 изображает состояние значений LLR в Pch 16-QAM. В MSB имеется наклон в одном месте (между Р1 и Р2). Далее, в LSB имеется два наклона (между Р0 и Р1, и между Р2 и Р3), и их полярности противоположны. Уровни наклона одинаковые в MSB и LSB. Аналогично в случае с Qch.
На фиг.4 LLR, соответствующее биту «0», устанавливается на максимальное значение, и LLR, соответствующее биту «1», устанавливается на минимальное значение. Это потому, что, когда часть бита мягкого решения, указывающего положение точки сигнала приема, рассматривается как выражение дополнения до 2, MSB совпадает со значение жесткого решения бита. Далее, причина рассматривания в качестве выражения дополнения до 2 имеет место потому, что это удобно при выполнении операции числового значения, основанной на LLR посредством декодера, поэтому это не является существенным. Далее, может быть установлена полярность LLR, в то же время, рассматривая совместимость с окружающей схемой.
Так как значения LLR в области, где LLR изменяется в соответствии с положением точки сигнала приема, становятся одинаковыми независимо от значений битов жесткого решения, LLR может вычисляться, ссылаясь только на бит мягкого решения. Поэтому, даже если количество битов мягкого решения равно, например, 5, имеется максимально 32 варианта LLR. Даже если эта часть создается с использованием ROM, размер схемы может быть очень маленьким. Далее, если допустимо, что положение между точками сигнала и LLR находится в пропорциональной зависимости, сигналом с мягким решением сигнала приема может быть непосредственно LLR, поэтому не требуется схема вычисления LLR. Т.е. схема 102 LLR, показанная на фиг.1, может быть создана посредством только использования соединения. В целом, этим способом могут быть получены достаточные характеристики. Если желательно изменить выигрыш LLR, необходимо только изменить наклон LLR посредством использования мультиплексора внутри декодера, который фактически обрабатывает LLR, или т.п.
Чтобы зафиксировать значение LLR в соответствии с положением точки сигнала приема и инвертировать LLR, выходной сигнал схемы 102 вычисления LLR, необходимо только ввести сигнал, сгенерированный посредством инвертирования выходного сигнала, и ввести фиксированные значения (минимальное значение и максимальное значение) в схему 110 выбора. Затем в соответствии с выходным результатом схемы обнаружения области схема 110 выбора выбирает и выводит любой один из входных сигналов.
Далее, так как Pch и Qch являются одинаковыми при отображении кодирования Грея, две одинаковые схемы могут применяться для каналов Pch и Qch соответственно.
С учетом вышесказанного, арифметическая схема LLR 16-QAM может быть сконфигурирована так, как показано на фиг.1 и 2.
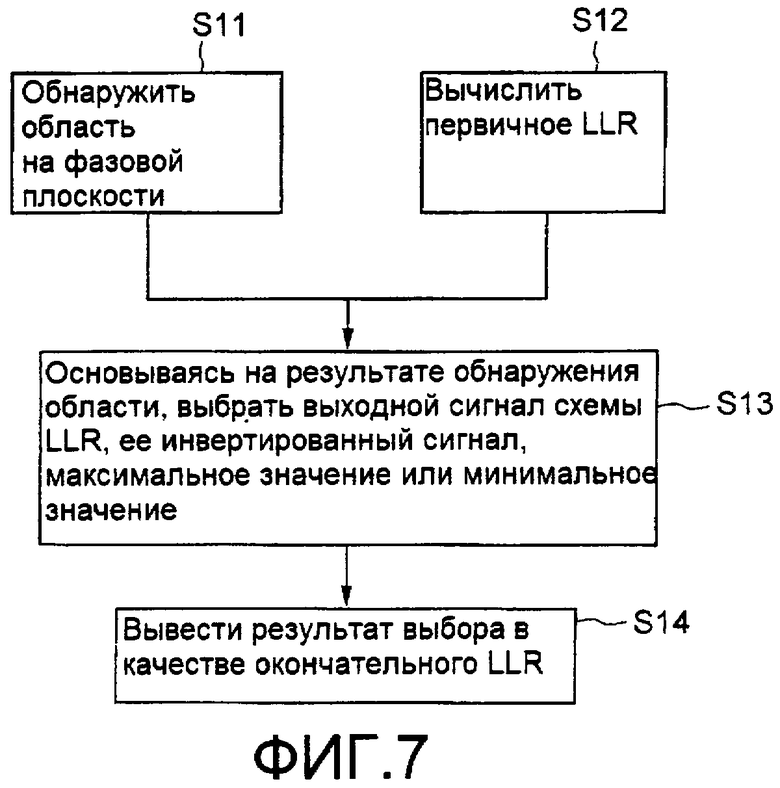
Ниже описывается конкретная операция арифметической схемы LLR. Фиг.7 представляет собой блок-схему последовательности операций, изображающую примерный процесс вычисления LLR посредством арифметической схемы LLR. Хотя ниже описывается случай вычисления LLR на стороне Pch, также является аналогичным случай вычисления LLR на стороне Qch. Это означает в нижеследующем описании, что вычисление LLR на стороне Qch может быть описано заменой схемы 101А обнаружения области на схему 101В обнаружения области, заменой схемы 102А LLR на схему 102В LLR, заменой преобразователей 103А и 104А LLR на преобразователи 103В и 104В LLR, и заменой оси Р на ось Q.
В процессе вычисления LLR сначала в схему 101А обнаружения области арифметической схемы LLR вводится бит жесткого решения из числа битов, указывающих координаты по оси Р точки сигнала приема. Затем, основываясь на введенном бите жесткого решения схема 101А обнаружения области обнаруживает область на фазовой плоскости, где присутствуют координаты по оси Р точки сигнала приема (этап S11). Затем схема 101А обнаружения области выводит результат обнаружения области на фазовой плоскости на преобразователи 103А и 104А LLR.
На этапе S11 схема 101А обнаружения области в частности обнаруживает, является ли область на фазовой плоскости, где присутствуют координаты по оси Р точки сигнала приема, (1) областью, в которой LLR изменяется с положительным наклоном, пересекая порог жесткого решения, (2) областью, где LLR изменяется с отрицательным наклоном, пересекая порог жесткого решения, (3) областью, где LLR не пересекает порог жесткого решения и не изменяется на максимальном значении, или (4) областью, где LLR не пересекает порог жесткого решения и не изменяется при минимальном значении, и затем схема 101А обнаружения области выводит результат.
Далее, в схему 102А LLR вводится бит мягкого решения из числа битов, указывающих координаты по оси Р точки сигнала приема. Затем, основываясь на введенном бите мягкого решения, схема 102А LLR вычисляет первичное LLR (этап S12). Затем схема 102А LLR выводит вычисленное первичное LLR на преобразователи 103А и 104А LLR.
В схемы 110 выбора преобразователей 103А и 104А LLR вводятся выходной сигнал (первичное LLR) схемы 102А LLR, выходной сигнал схемы 102А LLR, который инвертируется инвертором 111, предварительно определенное максимальное значение LLR и предварительно определенное минимальное значение LLR. Затем, основываясь на результате обнаружения схемы 101А обнаружения области, схема 110 выбора выбирает один из выходного сигнала схемы 102А LLR, выходного сигнала, инвертированного инвертором 111, предварительно определенного максимального значения LLR и предварительно определенного минимального значения LLR (этап S13). Затем схема 110 выбора выводит результат выбора этапа S13 в качестве окончательного LLR (этап S14).
В частности, если результат обнаружения схемы 101А обнаружения области представляет собой вышеупомянутый пункт (1), т.е. область, в которой LLR изменяется с положительным наклоном, пересекая порог жесткого решения, схема 110 выбора непосредственно выбирает и выводит выходной сигнал схемы 102 LLR. Если результат обнаружения схемы 101А обнаружения области представляет собой вышеупомянутый пункт (2), т.е. область, в которой LLR изменяется с отрицательным наклоном, пересекая порог жесткого решения, схема 110 выбора выбирает и выводит выходной сигнал схемы 102А LLR, который инвертируется инвертором 111. Если результат обнаружения схемы 101А обнаружения области представляет собой вышеупомянутый пункт (3), т.е. область, в которой LLR не пересекает порог жесткого решения и не изменяется при максимальном значении, схема 110 выбора выбирает и выводит предварительно определенное максимальное значение LLR. Если результат обнаружения схемы 101А обнаружения области представляет собой вышеупомянутый пункт (4), т.е. область, в которой LLR не пересекает порог жесткого решения и не изменяется при минимальном значении, схема 110 выбора выбирает и выводит предварительно определенное минимальное значение LLR.
При помощи вышеописанного процесса схема 110 выбора вычисляет сигнал с мягким решением, показанный одномерным между соседними точками сигнала по двум (0,1) порогам решения, непосредственно в качестве логарифмического отношения правдоподобия. Далее, схема 110 выбора вычисляет сигнал с мягким решением, показанный одномерным между соседними точками сигнала, не пересекающим два (0,1) порога решения, в качестве логарифмического отношения правдоподобия, в то же время, фиксируя на предварительно определенном максимальном значении или на предварительно определенном минимальном значении, в соответствии с положению точки сигнала на фазовой плоскости.
Ниже описываются различия между устройством, описанным в патентном документе 1, и арифметической схемой LLR, изображенной в примерном варианте осуществления. В патентном документе вычисление LLR выполняется посредством использования только вышеупомянутого предположения (b). Хотя является обычным для примерного варианта осуществления использование принципа, что отображение при помощи кодирования Грея может рассматриваться одномерным, так как предположение (а) не принимается во внимание, устройство в патентном документе 1 вычисляет LLR, используя уравнение (4). Поэтому объем операции для вычисления LLR не может быть существенно снижен. В примерном варианте осуществления объем операции снижается больше, чем у устройства, описанного в патентном документе 1, без значительного снижения характеристик из-за влияния предположения (а).
Вышеприведенный арифметический способ описывается ниже в качестве примера, используя случай с 16-QAM. Предполагается, что координаты сигнала приема выражены в виде натуральных кодов, в которых объединяются бит жесткого решения и младший бит мягкого решения (в Pch, левые края все раны «0», и правые края все равны «1»).
Сначала описывается LLR в отношении MSB жесткого решения Pch. MSB Pch формируется так, что 8 частей в правой половине точки сигнала равны 1, и 8 частей в левой половине равны 0 (ссылка на фиг.5). Поэтому частью, которая формирует порог решения значений MSB Pch, является ось Q.
Если точка сигнала приема присутствует слева от линии точки сигнала на непосредственно левой стороне оси Q, нет возможности, что сигнал передачи будет равен «1», поэтому LLR представляет собой максимальное значение. В противоположность этому, если точка сигнала приема присутствует справа от линии точки сигнала на непосредственно правой стороне оси Q, нет возможности, что сигнал передачи будет равен «0», поэтому LLR представляет собой минимальное значение. Так как ошибка может быть вызвана в MSB Pch только тогда, когда точка сигнала приема находится между точками сигнала на оси Q, необходимо значение LLR, соответствующее положению точки сигнала приема. Так как вероятность низкая (вероятности 0 и 1 близки), когда точка сигнала приема около оси Q, абсолютное значение LLR становится меньше. По мере того как точка сигнала приема удаляется от оси Q, вероятность того, что сигнал передачи будет равен «0» или «1», становится выше, поэтому абсолютное значение LLR становится больше.
Если битом мягкого решения является LLR, то это дополнение до 2, и оно является отрицательным значением, когда оно больше порога, тогда как оно является положительным значением, когда оно меньше порога. Этот MSB совпадает со значением жесткого решения бита. Фиг.6 изображает случай, когда биты мягкого решения равны 3 битам.
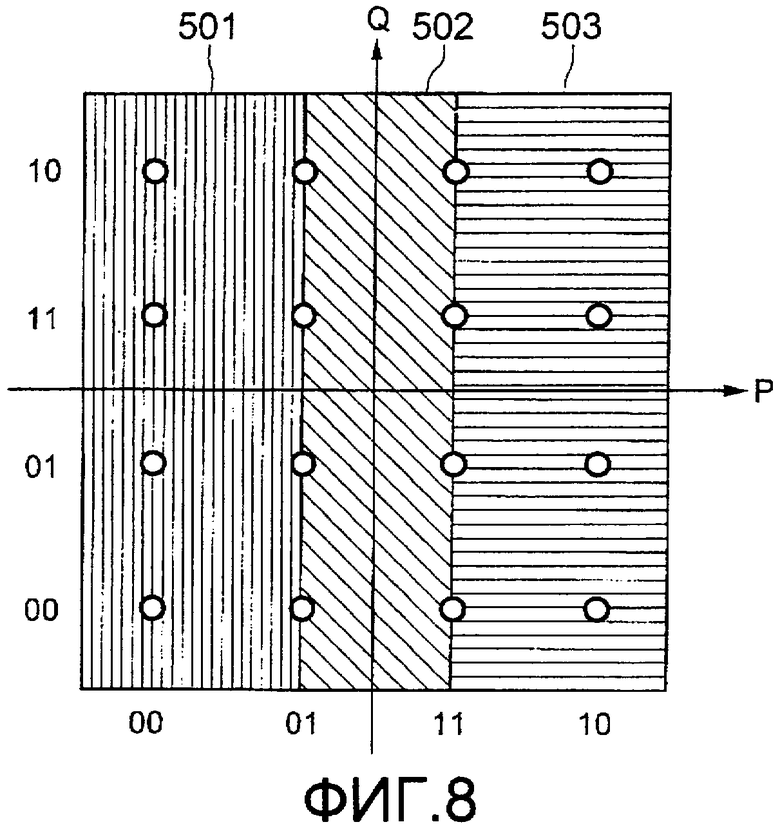
Фиг.8 иллюстрирует пример, изображающий секции области LLR относительно MSB Pch. Как показано на фиг.8, имеется три области в секциях области LLR для MSB Pch, включающие в себя слева направо область 501, где LLR равно максимальному значению, область 502, где LLR изменяется из положительного в отрицательное, и область 503, где LLR равно минимальному значению.
Далее, LLR относительно MSB Qch также определяется аналогичным образом, что и для MSB Pch.
Ниже описывается LLR в отношении 2SB (2-ого значащего бита в данном случае, также LSB) Pch. 2SB Pch включает в себя 0, 1, 1 и 0 от линии точки сигнала слева, и имеется две части, формирующие пороги решения. В этих двух положениях (между точками сигнала) LLR изменяется как в случае MSB. В данном случае, хотя биты находятся в порядке 0 и 1 в положениях порогов слева, что аналогично случаю с MSB, биты находятся в порядке 1 и 0 в положениях порогов справа, который является порядком, противоположным порядку MSB. Поэтому необходимо изменить полярность LLR в двух положениях порогов.
Так как не будет происходить ошибка между точками сигнала, где оба бита равны 1, LLR устанавливается на минимальное значение (отрицательное максимальное абсолютное значение). Далее, так как не вызывается ошибка вне двух линий по обеим сторонам фазовой плоскости, LLR устанавливается на максимальное значение (положительное максимальное абсолютное значение) (ссылка на фиг.4В).
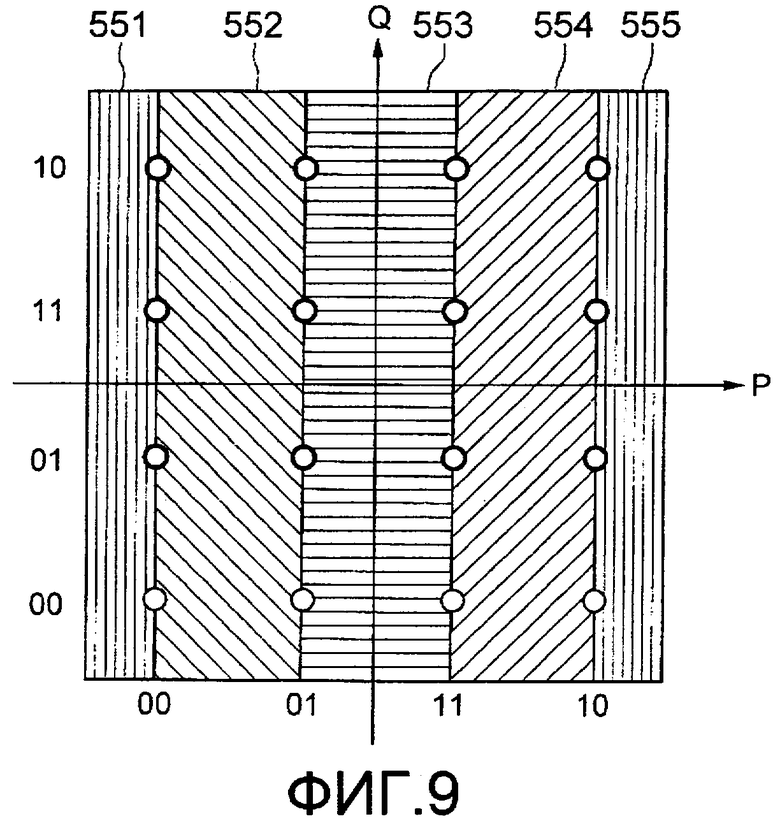
Фиг.9 иллюстрирует пример, изображающий секции области LLR относительно 2SB (LSB) Pch. Как показано на фиг.9, секции области LLR в отношении 2SB (LSB) Pch имеют 5 областей, включая слева область 551, где LLR имеет максимальное значение, область 552, где LLR изменяется с положительного на отрицательное, область 553, где LLR представляет собой минимальное значение, область 554, где LLR изменяется с отрицательного на положительное, и область 555, где LLR представляет собой максимальное значение.
LLR в отношении 2SB Qch устанавливается аналогично тому, как описано для 2SB Pch.
Далее, в случае применения в способе модуляции, в котором точки многоуровневого сигнала представляют собой четную степень двух (например, 64-QAM, 256-QAM и т.д.), необходимо только добавить 3SB или далее аналогичным образом.
В схемной конфигурации арифметической схемы LLR, показанной в примерном варианте осуществления, размер схемы не будет существенно меняться, даже если увеличивается многоуровневое число модуляции. Поэтому, когда многоуровневое число большое, скорость снижения размера схемы становится больше по сравнению со схемной конфигурацией для реализации схемы для операции LLR, использующей ROM. По существу, арифметическая схема LLR может быть реализована без необходимости большого ROM, независимо от способа модуляции. Следовательно, легко реализовать высокоскоростную операцию, по сравнению с относящейся схемной конфигурацией для арифметической операции LLR.
Как описано выше, согласно примерному варианту осуществления можно разложить вычисление LLR, которое первоначально выполняется двумерно, в одномерное и существенно уменьшить объем операции в системе передачи данных, использующей QAM. Далее, так как вся или почти вся арифметическая операция LLR может быть выполнена логическим арифметическим блоком, нет необходимости использовать большое ROM, и размер схемы и потребляемая мощность могут быть снижены независимо от способа модуляции и битовой точности LLR. Далее, может быть повышено быстродействие схемы, и, следовательно, может быть реализована система передачи данных с большой емкостью. Следовательно, можно реализовать вычисление LLR с более высокой скоростью, в то же время, уменьшая размер схемы.
Хотя элементы (101А, 101В, 102А, 102В, 103А, 103В, 104А, 104В), конфигурирующие арифметическую схему LLR, показанную на фиг.1 и 2, выполнены в виде аппаратных средств, также допустимо составить функции, выполняемые этими элементами в качестве программ, которые представляют собой программное обеспечение, и вызвать выполнение компьютером этих программ, тем самым, осуществляя процессы, выполняемые арифметической схемой LLR.
Второй примерный вариант осуществления
Ниже описывается второй примерный вариант осуществления настоящего изобретения со ссылкой на чертежи. Хотя первый примерный вариант осуществления описал случай, когда количество символов представляет собой четную степень двух, примерный вариант осуществления описывает случай, когда количество символов представляет собой нечетную степень двух. Перед тем как будет описана конкретная конфигурация и операция арифметической схемы LLR, сначала описывается способ вычисления LLR, когда количество символов представляет собой нечетную степень двух. Отображение кодирования Грея может быть реализовано только в случае использования способа квадратурной модуляции, в котором количество точек сигнала представляет собой четную степень двух. В случае использования способа модуляции, в котором количество точек сигнала представляет собой нечетную степень двух (например, 32-QAM, 128-QAM), кодирование Грея не может быть реализовано.
Однако можно создать отображение, в котором части, где разность битов (расстояние Хэмминга) между соседними точками сигнала равна 2 или более, составлены минимально возможными посредством использования принципа кодирования Грея. Ниже в данном документе это называется квази-кодирование Грея в примерном варианте осуществления.
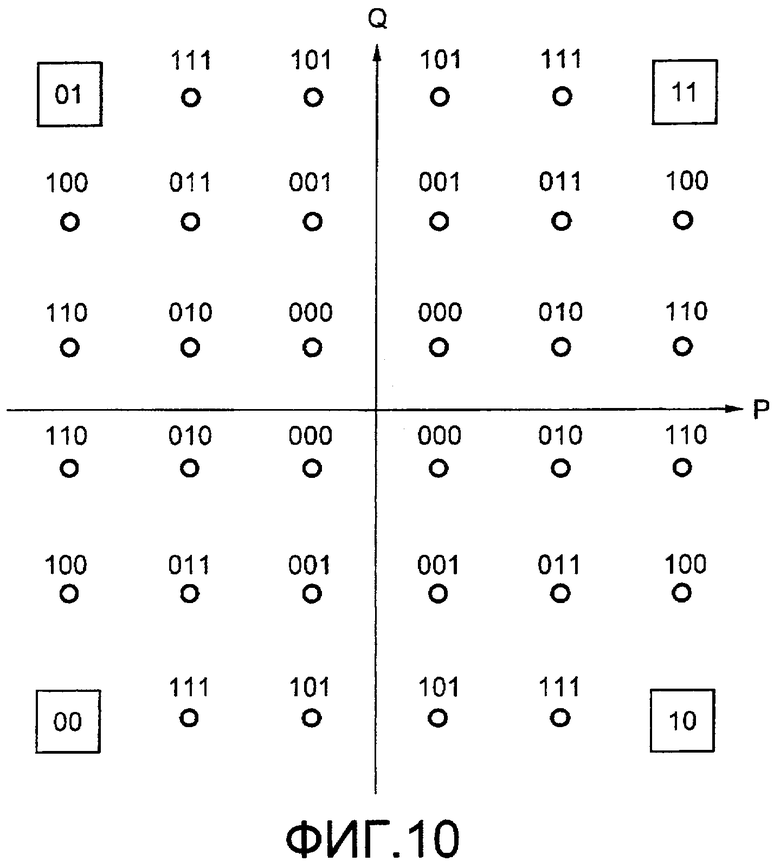
Фиг.10 представляет собой отображение, изображающее квази-кодирование Грея в случае использования 32-QAM. При квази-кодировании Грея MSB (старший бит) ортогональных двух каналов кодируется по Грею. Далее, LSB (самый младший бит) также может кодироваться по Грею в зависимости от многоуровневого числа. Следовательно, эти биты могут рассматриваться посредством разложения в одно измерение аналогично тому, как в способе модуляции, где количество точек сигнала представляет собой четную степень двух.
Хотя биты, которые без кодирования Грея, расположены двумерно, когда отображение определяется с использованием принципа кодирования Грея, количество пороговых значений решений 0, 1 может быть уменьшено, рассматривая их как одну и ту же группу битов. Фиг.10 изображает примерное отображение 32-QAM, вычисленное на основе этого принципа. На фиг.10 каждым из чисел, окруженных квадратом, является MSB. Далее, те, которые расположены около символа, представляют собой 3 бита, кроме MSB.
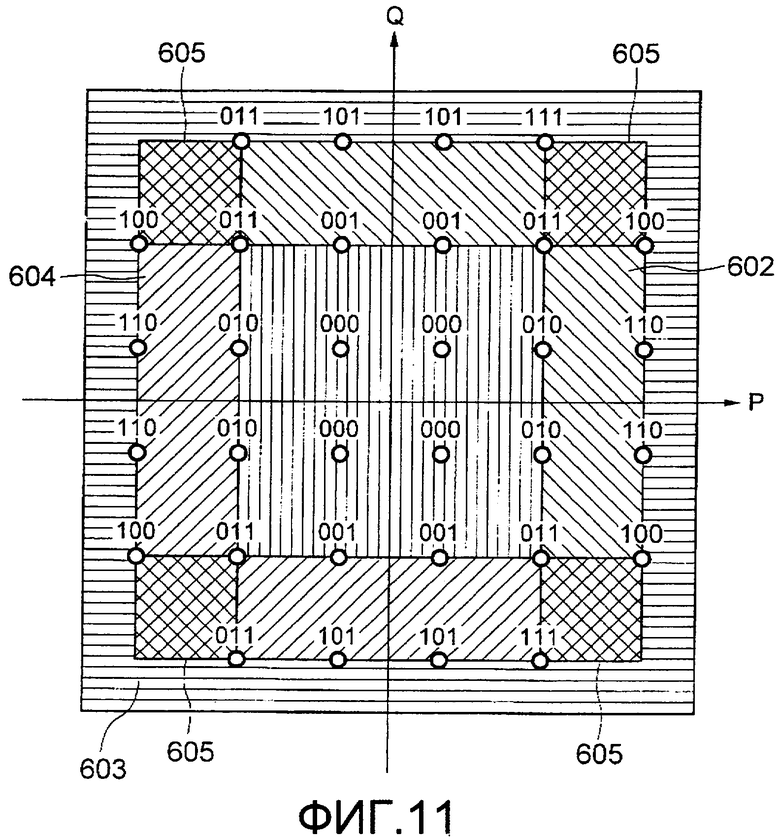
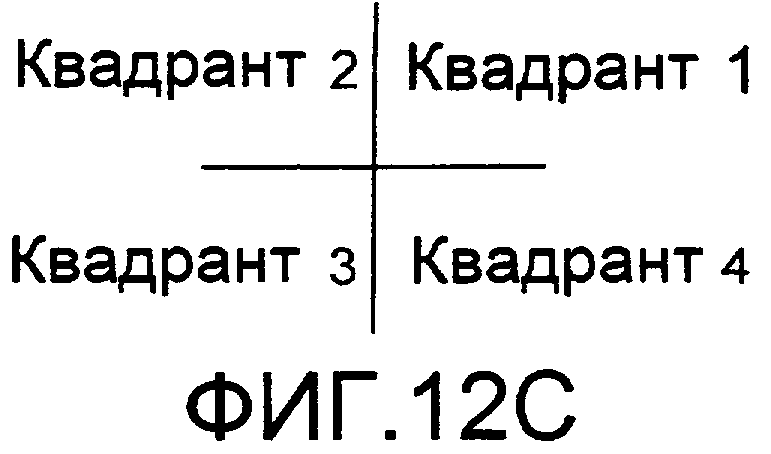
Фиг.11 иллюстрирует пример области LLR для 3SB (левый край 3 битов) 32-QAM. Как показано на фиг.11, 3SB в 32-QAM не разделено в одном направлении, чем отличается от случая, когда каждая область кодируется по Грею, но разделена в двух направлениях по оси Р и по оси Q. На фиг.11, в отношении части 605, где перекрываются области, разделенные по двум направлениям, необходимо вычислить LLR, в то же время, учитывая информацию двух направлений. Ниже в данном документе, такие области называются специальными областями. Как показано на фиг.11, в 3SB 32-QAM, четыре специальные области присутствуют на фазовой плоскости, каждая из которых размещается в каждом квадранте. Имеются некоторые типы специальных областей, в зависимости от зависимости с точками сигнала или битами, и способ обработки вычисления LLR отличается, соответствуя типу специальной области.
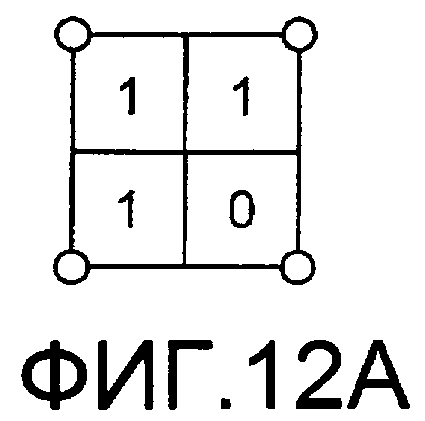
Фиг.12 иллюстрирует примеры специальных областей. На фиг.12 два типа специальных областей показаны в качестве примера. Фиг.12А изображает случай, когда точки сигнала присутствуют в четырех квадрантах специальной области, и три бита из числа четырех битов точки сигнала являются одинаковыми. Так как специальная область разделена на четыре области битом, который на один уровень ниже, чем бит жесткого решения, числа, которые такие же что числа квадрантов ортогональных координат, распределены четырем областям (см. фиг.12С).
Сначала будет рассмотрен случай, когда точка сигнала приема присутствует в квадранте 1. В квадранте 1 и квадранте 2 биты равны 1, т.е. одинаковые, и не будет вызываться ошибка. Однако так как биты отличаются в квадранте 1 и квадранте 4, т.е. 1 и 0, может быть вызвана ошибка, и значением мягкого решения в направлении оси Q становится LLR. В случае, когда точка сигнала приема присутствует в квадранте 2, так как бит такой же, что и бит квадранта 1 и квадранта 3, т.е. 1, не будет вызываться ошибка, поэтому LLR имеет минимальное значение. В случае, когда точка сигнала приема присутствует в квадранте 3, бит отличен от бита квадранта 4, т.е. 1 и 0, поэтому значением мягкого решения в направлении оси Р становится LLR.
Далее, в случае, когда точка сигнала приема присутствует в квадранте 4, так как биты равны 1 и 0 с квадрантами 1 и 3, два LLR будут получены из значений мягкого решения в направлении оси Р и в направлениях оси Q. Тогда LLR, имеющее меньшее абсолютное значение (имеющее более высокую вероятность ошибки) из двух LLR, выбирается в качестве LLR.
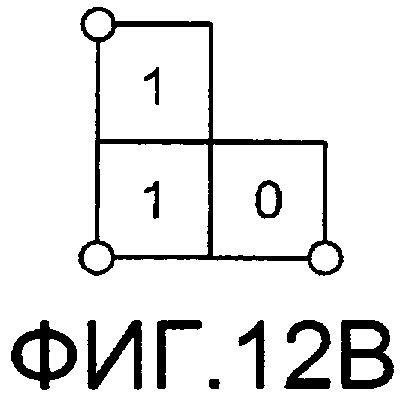
Фиг.12В изображает случай, когда точки сигнала присутствуют только в трех углах специальной области. Способ деления специальной области тот же самый, что и показанный на фиг.12А. Так как могут учитываться два направления, когда точка сигнала приема присутствует в квадранте 1, и когда точка сигнала присутствует в квадранте 3, выбирается LLR, имеющее меньшее абсолютное значение из двух LLR. Далее, так как нет влияния от отсутствующих точек сигнала, когда точка сигнала приема присутствует в квадранте 2, и когда точка сигнала приема присутствует в квадранте 4, LLR получается для одного направления, где присутствует точка сигнала.
Вкратце, даже в любой специальной области можно определить обработку сигнала в четырех или трех квадрантах внутри области согласно правилам, описанным ниже.
Правило 1: Если биты в двух направлениях (направление оси Р и направление оси Q) одинаковые, LLR равно максимальному значению или минимальному значению.
Правило 2: Если бит только в одном направлении (направлении оси Р или направлении оси Q) является другим, выбирается LLR в направлении, где бит является другим.
Правило 3: Если оба бита в двух направлениях (направление оси Р и направление оси Q) различны, в качестве LLR выбирается LLR, имеющее меньшее абсолютное значение из двух LLR.
Правило 4: Для направления без точки сигнала не будет вызываться ошибка бита.
Правило 5: Если точка сигнала приема присутствует в области без точки сигнала, выбирается LLR, имеющее меньшее абсолютное значение из числа LLR в направлении оси Р и в направлении оси Q.
Для 4SB и 5SB (LSB) LLR в специальной области может быть получено применением этого же принципа, хотя секции областей отличаются. По существу, LLR всех битов могут быть вычислены арифметической схемой вместе с MSB (двух каналов), где возможно кодирование Грея.
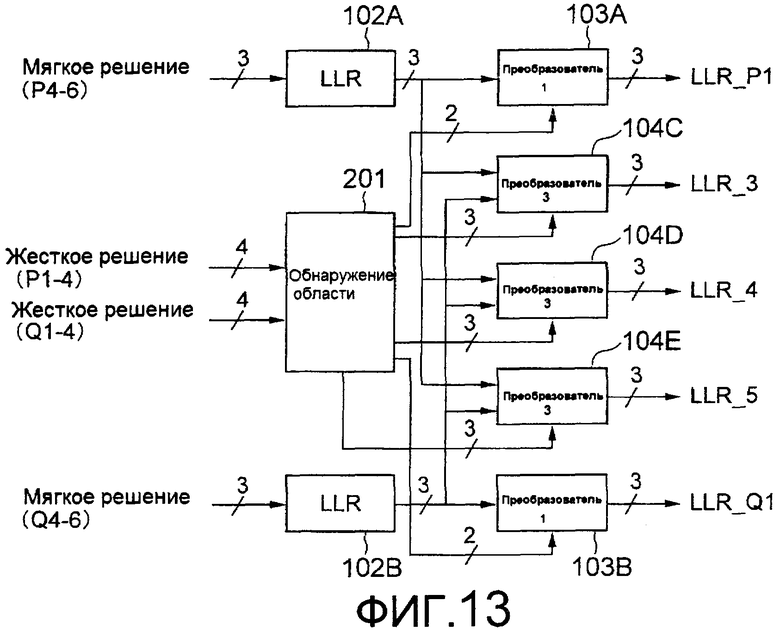
Как описано выше, так как специальная область присутствует в случае 32-QAM, так что необходимо выполнять принятие решения по области, используя младший бит бита жесткого решения, арифметическая схема LLR в случае использования 32-QAM может конфигурироваться так, как показано на фиг.13 и 14.
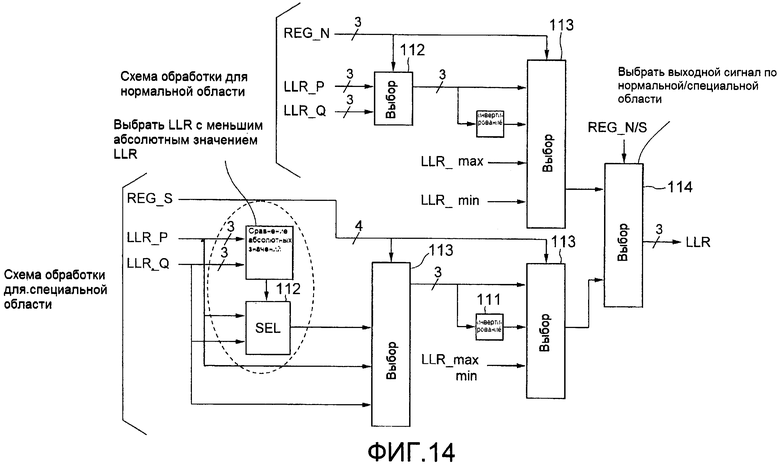
Фиг.13 представляет собой блок-схему, изображающую другую примерную конфигурацию арифметической схемы LLR, и фиг.14 представляет собой блок-схему, изображающую другую примерную конфигурацию преобразователей 104С, 104D и 104Е LLR. Как показано на фиг.14, в примерном варианте осуществления арифметическая схема LLR включает в себя схему обработки для нормальной области, которая вычисляет LLR для нормальной области, включающей в себя только биты, которые полностью кодируются по Грею из числа битов с квази-кодированием Грея, выводимых с кодера, и схему обработки для специальной области, которая вычисляет LLR для специальной области, включающей в себя биты, которые не кодируются полностью по Грею из числа битов с квази-кодированием Грея, выводимых с кодера.
Ниже в данном документе описывается операция арифметической схемы LLR, показанной на фиг.13 и 14. Сначала, как выражено кодами Грея в MSB (P/Q 2 бита), операция арифметической схемы LLR аналогична операции для 16-QAM.
Затем в случае 3-5SB (3 бита), когда должна выполняться обработка нормальной области, арифметическая схема LLR может (1) выводить максимальное значение (фиксированное значение) LLR, (2) выводить минимальное значение (фиксированное значение) LLR, (3) непосредственно выводить LLR, если наклон LLR является положительным, или (4) генерировать и выводить сигнал, в котором все биты LLR инвертируются, если наклон LLR является отрицательным. В данном случае, LLR включает в себя направление Р и направление Q. Основываясь на результате принятия решения по области (2 бита) схемы 201 обнаружения области, арифметическая схема LLR выбирает выходной сигнал любого одного из пунктов (1)-(4) выше.
В данном случае результат (REG_N) принятия решения по области указывает точность задания одной области, окруженной четырьмя соседними точками сигнала. Далее, LLR представляет собой информацию, указывающую только часть мягкого решения из числа битов, указывающих точку сигнала приема.
В случае выполнения обработки специальной области арифметическая схема LLR может (1) выводить максимальное значение (может быть положительным или отрицательным, полярность определяется битовой строкой (3-5SB)) абсолютного значения, (2) всегда выводить LLR в направлении Р, (3) всегда выводить LLR в направлении Q, или (4) выводить LLR, имеющее меньшее абсолютное значение (min (|P|, |Q|), из LLR в направлении Р и направлении Q, используя компаратор абсолютного значения LLR. В данном случае арифметическая схема LLR выбирает любой один из вышеупомянутых пунктов (1)-(4), основываясь на результате (REG_S) принятия решения о квадранте внутри специальной области посредством схемы 201 обнаружения области. Отметим, что выбранные сигналы представляют собой 4 бита, так как имеется четыре квадранта в каждой из четырех специальных областей. Далее, полярность может быть противоположной в выходных сигналах (2)-(4).
Так как специальные области являются разными в соответствующих битовых строках 3-5SB, выходной сигнал решения по области в отношении одной и той же точки сигнала приема является различным для каждой битовой строки. Далее, арифметическая схема LLR выбирает и выводит любой один из двух результатов (выходной сигнал схемы обработки в нормальной области и выходной сигнал схемы обработки в специальной области) в зависимости от разделяющего сигнала нормальной области и специальной области. В данном случае для выходного сигнала, не выбранного арифметической схемой LLR, может выводиться любой сигнал.
Схема принятия решения по области (схема 201 обнаружения области) включает в себя два типа схем, т.е. DET 1 для битовых строк в отображении Грея, и DET 2 для битовых строк, которые не находятся в отображении Грея. Далее, DET 2 выводит три типа сигналов, включая REG_N для нормальной области, REG_S для специальной области и REG_N для разделения нормальной области и специальной области.
Отметим, что конструкция схем, показанная в примерном варианте осуществления, является примером, и в фактической конструкции схемы существует множество путей реализации арифметических схем LLR, кроме арифметической схемы LLR, показанной в примерном варианте осуществления. В примерном варианте осуществления описываются нормальная область и специальная область, причем разделяются так, что легко понятна необходимая обработка сигнала.
В случае применения способа модуляции, в котором точками многоуровневого сигнала являются нечетная степень двух (например, 128-QAM, 512-QAM), необходимо только установить область LLR битовых строк, которые не могут кодироваться по Грею аналогично тому, как описано выше. В способе модуляции для 128-QAM или более (например, 512-QAM) LSB (2 бита) также могут кодироваться по Грею, которые могут быть реализованы со схемой, которая проще, чем для 32-QAM.
В схемной конфигурации арифметической схемы LLR, показанной в примерном варианте осуществления, размер схемы не меняется существенно, даже если становится больше многоуровневое число модуляции. Поэтому, когда увеличивается многоуровневое число, скорость уменьшения размера схемы становится больше по сравнению со схемной конфигурацией в случае реализации схемы для операции LLR, использующей ROM. Поэтому можно реализовать арифметическую схему LLR без потребности в большом ROM, независимо от способа модуляции. По существу, легко может быть реализована операция с более высокой скоростью по сравнению с относящейся схемной конфигурацией для операции LLR.
Хотя элементы (102А, 102В, 201, 103А, 103В, 104С, 104D, 104Е, 112, 113 и 114), конфигурирующие арифметическую схему LLR, показанную на фиг.13 и 14, построены в виде аппаратных средств, функции, выполняемые этими элементами, могут быть построены в виде программ, которые представляют собой программные средства, подлежащие исполнению компьютером, так что осуществляется обработка, выполняемая арифметической схемой LLR.
Как описано выше, согласно примерному варианту осуществления, даже если используется QAM, имеющая точку сигнала нечетной степени двух, можно выполнить вычисление LLR с более высокой скоростью, в то же время, снижая размер схемы посредством выполнения квази-кодирования Грея.
Отметим, что арифметическая схема LLR, показанная в каждом примерном варианте осуществления, может применяться для кодов коррекции ошибок для итеративного декодирования сигнала с мягким решением и декодера для этого. Примеры этих кодов, которые были известны, включают в себя (сверточный) турбокод, турбокод произведения (TPC) и код с низкой плотностью проверок на четность (LDPC).
Далее, при использовании арифметической схемы LLR, показанной в каждом примерном варианте осуществления, LLR может использоваться в качестве метрики входного сигнала корректора. По существу, арифметическая схема LLR, показанная в каждом примерном варианте осуществления, может использоваться в качестве арифметической схемы LLR входного сигнала корректора посредством оценки последовательности с максимальным правдоподобием, кроме декодера кода коррекции ошибок.
Далее, в каждом примерном варианте осуществления арифметическая схема LLR может включать в себя ROM, в которое вводится сигнал с мягким решением, показанный одномерным между соседними точками сигнала, имеющими два (0, 1) порога решения между ними, и который выводит вычисленное заранее логарифмическое отношение правдоподобия, или схему вывода логарифмического отношения правдоподобия, включающую в себя логическую схему, соответствующую ей. Далее, также допустимо, что схема вывода логарифмического отношения правдоподобия совместно используется всеми точками сигнала приема, и в соответствии с положением фазовой плоскости точек сигнала приема выходной результат LLR может выводиться посредством замены фиксированным значением.
Ниже описывается другой примерный вариант осуществления изобретения.
Арифметическая схема логарифмического отношения правдоподобия может устанавливать отношение соответствия между битом и символом, так что интенсивность побитовых ошибок становится минимальной. Далее, арифметическая схема логарифмического отношения правдоподобия может устанавливать отношение соответствия между битом и символом, когда способ модуляции имеет точки сигнала четной степени двух, находящиеся в отображении Грея. Далее, арифметическая схема логарифмического отношения правдоподобия может устанавливать отношение соответствия между битом и символом, когда способ модуляции имеет точки сигнала нечетной степени двух, находящиеся в квази-отображении Грея, где интенсивность побитовых ошибок становится минимальной. Далее, также допустимо, что арифметическая схема логарифмического отношения правдоподобия может выполнять всю или почти всю операцию для вычисления логарифмического отношения правдоподобия посредством логической операции, используя информацию о координатах точки сигнала приема.
Далее, арифметическая схема логарифмического отношения правдоподобия может выводить часть битов мягкого решения 1CH из числа информации о координатах точки сигнала приема, указанных в 2CH непосредственно или посредством их инвертирования, в качестве логарифмического отношения правдоподобия области, где изменяется логарифмическое отношение правдоподобия. Далее, арифметическая схема логарифмического отношения правдоподобия может выводить максимальное значение или минимальное значение логарифмического отношения правдоподобия в качестве логарифмического отношения правдоподобия области, где логарифмическое отношение правдоподобия не изменяется. Далее, если имеется область, которая не может быть определена, основываясь только на информации о бите жесткого решения ICH из числа информации о координатах точки сигнала приема, показанных в 2CH, также допустимо, что для области, где ошибка битов никогда не будет вызвана при условиях, описанных в пункте 1 формулы изобретения, арифметическая схема логарифмического отношения правдоподобия выводит максимальное значение или минимальное значение логарифмического отношения правдоподобия, и для области, где ошибка битов может быть вызвана, арифметическая схема логарифмического отношения правдоподобия выводит бит мягкого решения меньшего правдоподобия 2CH.
Далее, в арифметической схеме логарифмического отношения правдоподобия выбор логарифмического отношения правдоподобия может выполняться посредством использования результата решения по области, основываясь на информации о бите жесткого решения в 1CH информации о координатах сигнала приема, указанных в 2CH. Далее, в арифметической схеме логарифмического отношения правдоподобия выбор логарифмического отношения правдоподобия может выполняться посредством использования результата решения по области посредством ссылки на биты на один уровень ниже, чем жесткое решение, если имеется область, где решение по области не может быть выполнено, основываясь только на информации о бите жесткого решения в 1CH информации о координатах точки сигнала приема, указанных в 2CH. Далее, в арифметической схеме логарифмического отношения правдоподобия логарифмическим отношением правдоподобия может быть то, которое преобразуется из бита мягкого решения в другое значение.
Арифметическая схема логарифмического отношения правдоподобия (LLR) согласно примерному варианту осуществления не ссылается на предварительно определенную таблицу, но непосредственно вычисляет LLR из координат точки сигнала приема при помощи арифметической операции, используя фактическое время. В такой конфигурации, по сравнению со случаем конфигурирования схемы, используя ROM, размер схемы может быть очень маленьким, и также может быть реализована операция с высокой скоростью. Далее, арифметическая схема логарифмического отношения правдоподобия согласно настоящему изобретению разлагает координаты точки сигнала приема в двух измерениях на два одномерных сигнала и выполняет операцию LLR для каждого бита, распределенного символу. По существу, арифметическая схема логарифмического отношения правдоподобия также может быть реализована с использованием небольшой схемы с малой задержкой, такой как схема выбора, большой и малый компаратор или инвертор. Следовательно, схемная конфигурация упрощается посредством разложения координат точки сигнала приема, которые первоначально в двух измерениях, в два одномерных сигнала. Далее, способ модуляции, применимый к арифметической схеме логарифмического отношения правдоподобия согласно примерному варианту осуществления, не имеет ограничительных условий по количеству символов. Далее, так как само LLR упрощается в контексте не оказания влияния на характеристики декодирования с коррекцией ошибок, не требуется операция по вычислению квадрата расстояния.
Хотя настоящее изобретение было описано с ссылкой на примерные варианты осуществления, настоящее изобретение не ограничивается вышеописанными примерными вариантами осуществления. Конфигурация и подробности настоящего изобретения могут быть модифицированы различными путями в пределах объема настоящего изобретения, что может быть понятным для специалиста в данной области техники.
Настоящая заявка испрашивает приоритет, основываясь на заявке на патент Японии № 2006-266523, поданной 29 сентября 2006 г., все описание которой включено в данный документ.
Промышленная применимость
Настоящее изобретение применяется в системах передачи данных, использующих способ квадратурной многоуровневой модуляции (способ квадратурной амплитудной модуляции) и применимо к арифметической схеме LLR, которая вычисляет логарифмическое отношение правдоподобия, служащее в качестве входного сигнала декодера с коррекцией ошибок и корректора.
Краткое описание чертежей
Фиг.1 представляет собой блок-схему, изображающую примерную конфигурацию арифметической схемы логарифмического отношения правдоподобия (арифметическую схему LLR), согласно настоящему изобретению.
Фиг.2 представляет собой блок-схему, изображающую примерную схемную конфигурацию преобразователя LLR.
Фиг.3 представляет собой иллюстрацию, изображающую позиционную зависимость между LLR и точкой сигнала приема в BPSK.
Фиг.4 представляет собой иллюстрацию, изображающую пример позиционной зависимости между LLR и точкой сигнала приема в 16-QAM.
Фиг.5 представляет собой иллюстрацию, изображающую отображение кодирования Грея (отображение битов жесткого решения) 16-QAM.
Фиг.6 представляет собой иллюстрацию, изображающую пример, в котором битами мягкого решения являются 3 бита.
Фиг.7 представляет собой блок-схему последовательности операций, изображающую примерную обработку, в которой арифметическая схема LLR вычисляет LLR.
Фиг.8 представляет собой иллюстрацию, изображающую пример секций области LLR в отношении MSB Pch.
Фиг.9 представляет собой иллюстрацию, изображающую пример секций области LLR в отношении 2SB (LSB) Pch.
Фиг.10 представляет собой иллюстрацию, изображающую отображение квази-кодирования Грея, когда используется 32-QAM.
Фиг.11 представляет собой иллюстрацию, изображающую пример областей LLR для 3SB (левый край 3 битов) 32-QAM.
Фиг.12 представляет собой иллюстрацию, изображающую пример специальной области, присутствующей тогда, когда используется способ модуляции, в котором количеством символов является нечетная степень двух.
Фиг.13 представляет собой блок-схему, изображающую другую примерную конфигурацию арифметической схемы LLR.
Фиг.14 представляет собой блок-схему, изображающую другую примерную конфигурацию преобразователя LLR.
Описание позиций
101А, 101В - схема обнаружения области
102А, 102В - схема LLR
103А, 103В, 104А, 104В - преобразователь LLR
110 - схема выбора
111 - инвертор
Заявленное изобретение относится к арифметической схеме логарифмического отношения правдоподобия (LLR). Техническим результатом является вычисление логарифмического отношения правдоподобия, выполняемое с более высокой скоростью, в то же время, снижая размеры схемы и потребляемую мощность, независимо от многоуровневого числа способа модуляции. Для этого бит жесткого решения из битов, указывающих координату по оси Р точки сигнала приема, вводится в схему обнаружения области, и, основываясь на введенном бите жесткого решения, схема обнаружения области обнаруживает и выводит область на фазовой плоскости, где присутствует координата точки сигнала приема. Бит мягкого решения из битов, указывающих координату точки сигнала приема, вводится в схему LLR, и, основываясь на введенном бите мягкого решения, схема LLR вычисляет первичное LLR. Преобразователь LLR вычисляет окончательное LLR, основываясь на выходном сигнале (результате обнаружения области) от схемы обнаружения области. В такой конфигурации вычисляется логарифмическое отношение правдоподобия, в то же время, ограничивая область действия, в пределах которой значение логарифмического отношения правдоподобия изменяется в соответствии с положением точки сигнала приема, интервалом между соседними точками сигнала, включающим в себя порог жесткого решения бита. 2 н. и 20 з.п. ф-лы, 17 ил.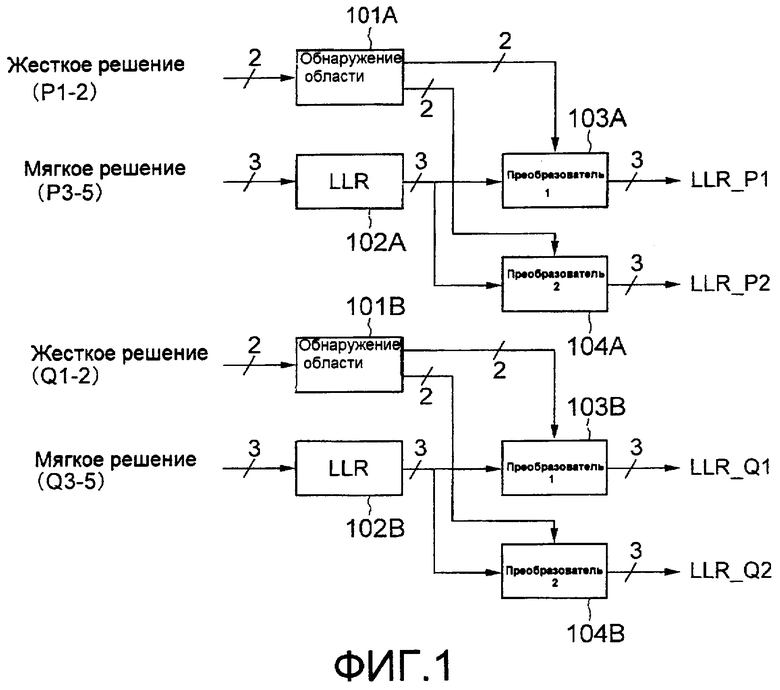
1. Арифметическая схема логарифмического отношения правдоподобия для вычисления логарифмического отношения правдоподобия из информации координаты точки сигнала приема для применения в системе связи, выполняющей модуляцию и демодуляцию, причем схема содержит:
схему обнаружения области для ввода бита жесткого решения из числа битов, указывающих координату точки сигнала приема, который выражается двумерно и способен разлагаться на два одномерных сигнала, и на основании введенного бита жесткого решения - вывода сигнала, идентифицирующего область, который ограничивает область, в которой значение логарифмического отношения правдоподобия изменяется, до интервала между соседними точками сигнала, включающего в себя порог жесткого решения упомянутого бита, который должен быть назначением логарифмического отношения правдоподобия; и
схему преобразования логарифмического отношения правдоподобия для ввода бита мягкого решения из числа битов, указывающих координату точки сигнала приема, который выражается двумерно и способен разлагаться на одномерные сигналы, на основании введенного бита мягкого решения, вычисления первичного логарифмического отношения правдоподобия согласно упомянутому сигналу, идентифицирующему область, выведенному посредством схемы обнаружения области, и преобразования первичного логарифмического отношения правдоподобия на основании бита жесткого решения так, чтобы вычислить окончательное логарифмическое отношения правдоподобия.
2. Арифметическая схема логарифмического отношения правдоподобия по п.1, в которой схема обнаружения области выводит сигнал, идентифицирующий область, посредством установления отношения соответствия между упомянутым битом и символом модуляции так, что интенсивность побитовых ошибок становится минимальной.
3. Арифметическая схема логарифмического отношения правдоподобия по п.2, в которой схема обнаружения области выводит сигнал, идентифицирующий область, посредством установления отношения соответствия между упомянутым битом и символом модуляции, когда способ модуляции имеет точки сигнала четной степени двух, в отображении Грея.
4. Арифметическая схема логарифмического отношения правдоподобия по п.2, в которой схема обнаружения области выводит сигнал, идентифицирующий область, посредством установления отношения соответствия между упомянутым битом и символом модуляции, когда способ модуляции имеет точки сигнала нечетной степени двух, в квазипреобразовании Грея, когда интенсивность побитовых ошибок становится минимальной.
5. Арифметическая схема логарифмического отношения правдоподобия по п.1, в которой схема преобразования логарифмического отношения правдоподобия выполняет все или почти все операции для вычисления логарифмического отношения правдоподобия посредством логической операции, используя информацию координат точек сигнала приема.
6. Арифметическая схема логарифмического отношения правдоподобия по п.1, в которой схема преобразования логарифмического отношения правдоподобия выводит часть битов мягкого решения одномерного сигнала из информации координат точек сигнала приема, указанных в двумерном сигнале, непосредственно или посредством их инвертирования, в качестве логарифмического отношения правдоподобия области, где логарифмическое отношение правдоподобия изменяется.
7. Арифметическая схема логарифмического отношения правдоподобия по п.2, в которой схема преобразования логарифмического отношения правдоподобия выводит максимальное значение или минимальное значение логарифмического отношения правдоподобия в качестве логарифмического отношения правдоподобия области, где логарифмическое отношение правдоподобия не изменяется.
8. Арифметическая схема логарифмического отношения правдоподобия по п.2, в которой схема преобразования логарифмического отношения правдоподобия выводит, если имеется область, которая не может быть определена на основании только информации бита жесткого решения одномерного сигнала из информации координат точек сигнала приема, показанных в двумерном сигнале, максимальное значение или минимальное значение логарифмического отношения правдоподобия для области, где битовая ошибка никогда не будет вызвана при условии, что область, в которой значение логарифмического отношения правдоподобия изменяется, ограничена на основании введенного бита жесткого решения до интервала между соседними точками сигнала, включающего в себя порог жесткого решения упомянутого бита, который должен быть назначением логарифмического отношения правдоподобия, и выводит бит мягкого решения более низкого правдоподобия для двумерного сигнала для области, где может быть вызвана битовая ошибка.
9. Арифметическая схема логарифмического отношения правдоподобия по п.5 или 6, в которой схема преобразования логарифмического отношения правдоподобия использует для выбора логарифмического отношения правдоподобия результат обнаружения области на основании информации бита жесткого решения в одномерном сигнале из информации координат точки сигнала приема, указанной в двумерном сигнале.
10. Арифметическая схема логарифмического отношения правдоподобия по п.7, в которой схема преобразования логарифмического отношения правдоподобия использует для выбора логарифмического отношения правдоподобия результат обнаружения области посредством обращения к битам на один уровень ниже, чем бит жесткого решения, если имеется область, где обнаружение области не может быть выполнено на основании только информации бита жесткого решения в одномерном сигнале из информации координат точки сигнала приема, указанных в двумерном сигнале.
11. Арифметическая схема логарифмического отношения правдоподобия по п.5 или 7, в которой схема преобразования логарифмического отношения правдоподобия выводит в качестве логарифмического отношения правдоподобия области, где логарифмическое отношение правдоподобия изменяется, бит мягкого решения, к которому добавлено преобразование.
12. Арифметический способ вычисления логарифмического отношения правдоподобия для вычисления логарифмического отношения правдоподобия из информации координаты точки сигнала приема для применения в системе связи, выполняющей модуляцию и демодуляцию, причем способ содержит этапы:
вводят в схему обнаружения области бит жесткого решения из числа битов, указывающих координату точки сигнала приема, который выражается двумерно и способен разлагаться на два одномерных сигнала, и на основании введенного бита жесткого решения выводят сигнал, идентифицирующий область, который ограничивает область, в которой значение логарифмического отношения правдоподобия изменяется, до интервала между соседними точками сигнала, включающего в себя порог жесткого решения упомянутого бита, который должен быть назначением логарифмического отношения правдоподобия; и
вводят в схему преобразования логарифмического отношения правдоподобия бит мягкого решения из числа битов, указывающих координату точки сигнала приема, который выражается двумерно и способен разлагаться на два одномерных сигнала, на основании введенного бита мягкого решения, вычисляют первичное логарифмическое отношения правдоподобия согласно упомянутому сигналу, идентифицирующему область, выведенному посредством схемы обнаружения области, и преобразуют первичное логарифмическое отношения правдоподобия на основании бита жесткого решения так, чтобы вычислить окончательное логарифмическое отношения правдоподобия.
13. Способ по п.12, в котором выводят сигнал, идентифицирующий область, посредством установления отношения соответствия между упомянутым битом и символом модуляции так, что интенсивность побитовых ошибок становится минимальной.
14. Способ по п.12, в котором выводят сигнал, идентифицирующий область, посредством установления отношения соответствия между упомянутым битом и символом модуляции, когда способ модуляции имеет точки сигнала четной степени двух, в отображении Грея.
15. Способ по п.13, в котором выводят сигнал, идентифицирующий область, посредством установления отношения соответствия между упомянутым битом и символом модуляции, когда способ модуляции имеет точки сигнала нечетной степени двух, в квазипреобразовании Грея, когда интенсивность побитовых ошибок становится минимальной.
16. Способ по п.12, в котором выполняют все или почти все операции для вычисления логарифмического отношения правдоподобия посредством логической операции, используя информацию координат точек сигнала приема.
17. Способ по п.13, в котором часть битов мягкого решения одномерного сигнала из информации координат точек сигнала приема, указанных в двумерном сигнале, выводят непосредственно или посредством их инвертирования в качестве логарифмического отношения правдоподобия области, где логарифмическое отношение правдоподобия изменяется.
18. Способ по п.13, в котором максимальное значение или минимальное значение логарифмического отношения правдоподобия выводят в качестве логарифмического отношения правдоподобия области, где логарифмическое отношение правдоподобия не изменяется.
19. Способ по п.13, в котором, если имеется область, которая не может быть определена на основании только информации бита жесткого решения одномерного сигнала из информации координат точек сигнала приема, показанных в двумерном сигнале, выводят максимальное значение или минимальное значение логарифмического отношения правдоподобия для области, где битовая ошибка никогда не будет вызвана при условии, что область, в которой значение логарифмического отношения правдоподобия изменяется, ограничена на основании введенного бита жесткого решения до интервала между соседними точками сигнала, включающего в себя порог жесткого решения упомянутого бита, который должен быть назначением логарифмического отношения правдоподобия, и выводят бит мягкого решения более низкого правдоподобия для двумерного сигнала для области, где может быть вызвана побитовая ошибка.
20. Способ по п.16 или 17, в котором для выбора логарифмического отношения правдоподобия используют результат обнаружения области на основании информации бита жесткого решения в одномерном сигнале из информации координат точки сигнала приема, указанной в двумерном сигнале.
21. Способ по п.18, в котором для выбора логарифмического отношения правдоподобия используют результат обнаружения области посредством обращения к битам на один уровень ниже, чем бит жесткого решения, если имеется область, где обнаружение области не может быть выполнено на основании только информации бита жесткого решения в одномерном сигнале из информации координат точки сигнала приема, указанной в двумерном сигнале.
22. Способ по п.16 или 17, в котором выводят в качестве логарифмического отношения правдоподобия области, где логарифмическое отношение правдоподобия изменяется, бит мягкого решения, к которому добавлено преобразование.
| СПОСОБ И УСТРОЙСТВО БЫСТРОГО ВЫЧИСЛЕНИЯ ДИСКРЕТНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ СИГНАЛА С ПРОИЗВОЛЬНЫМ ШАГОМ ДИСКРЕТИЗАЦИИ МАСШТАБНЫХ КОЭФФИЦИЕНТОВ | 2003 |
|
RU2246132C2 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Топчак-трактор для канатной вспашки | 1923 |
|
SU2002A1 |
Авторы
Даты
2011-11-20—Публикация
2007-09-28—Подача