Изобретение относится к радиоэлектронным системам и может быть использовано в различных областях техники, в частности при разработке и создании устройств распознавания при проектировании фрактальных радиосистем, основанных на фрактальных методах обработки информации.
Становление теории фракталов - яркий пример развития нового направления науки, в равной мере основанного как на достижениях в весьма абстрактных областях математики, так и на новом взгляде на давно известный эмпирический материал, который до создания адекватных теоретических моделей не поддавался научному описанию и интерпретации.
Новые геометрические и топологические представления фрактального анализа в будущем станут такой же непременной частью анализа сигналов и волн, какой стал Фурье-анализ (Новейшие методы обработки изображений. / Под ред. А.А.Потапова. - М.: ФИЗМАТЛИТ, 2008).
Известны также способы анализа структуры изображения, основанные на методах сегментации, которые подразделяют изображение на составляющие его области или объекты. Один из возможных методов сегментации основан на выделении контуров на изображении. Контуры в свою очередь - это такие кривые на изображении, вдоль которых происходит резкое изменение яркости (разрыв яркости) или ее производных по пространственным переменным. Во многих ситуациях именно контуры являются наиболее информативными составляющими изображения. Существуют три основные причины возникновения контуров на изображении:
- нарушения непрерывности ориентации поверхности;
- изменения отражательной способности поверхности;
- эффекты, связанные с освещением, такие как, например, тени.
Выделение контуров - ключевой начальный шаг в оптической локации. К этой задаче относится задача зависимого использования различных двумерных производных. Во многих случаях, это аналогично выделению участков, соответствующих характерным точкам производной, например таким, как ее максимумы или нули. В определенных случаях прежние алгоритмы, основанные на бинарных признаках, а именно на наличии или отсутствии контуров, полностью совпадают или аналогичны алгоритмам, в которых непосредственно используются непрерывные значения производных. С этой точки зрения задача, обычно называемая выделением контуров, состоит в выборе дифференциального оператора, пригодного для дальнейшей обработки изображений (Маар Д. Зрение. Информационный подход к изучению представления и обработки зрительных образов. - М.: Радио и связь, 1987).
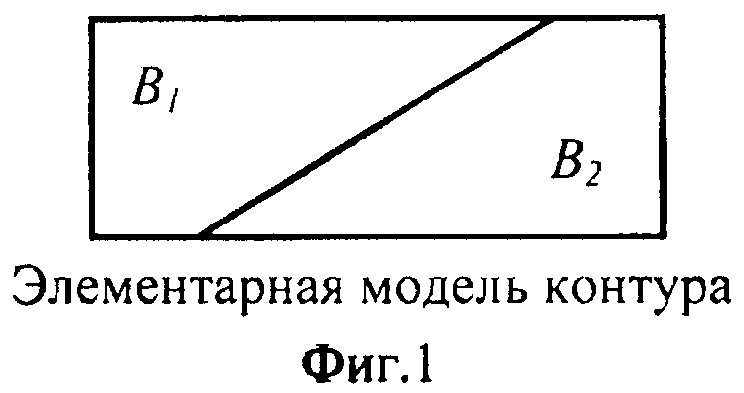
Простейшей моделью контура на изображении является прямая, разделяющая две области с постоянной яркостью В1 и В2, как изображено фиг.1. Для данной модели необходимо определить единичную ступенчатую функцию u(z) в виде
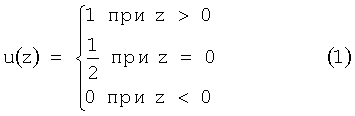
Данная функция является интегралом от одномерного единичного импульса

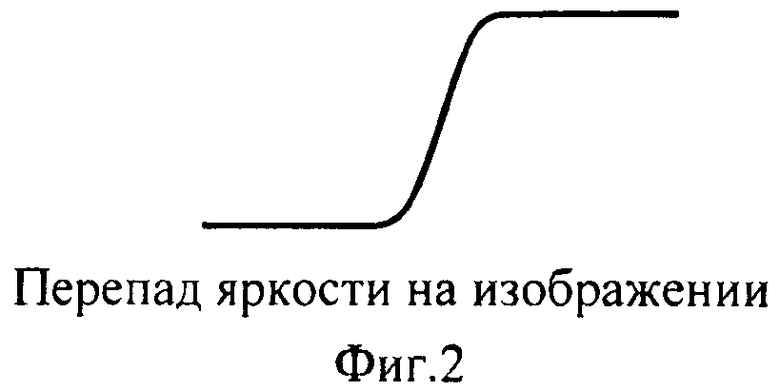
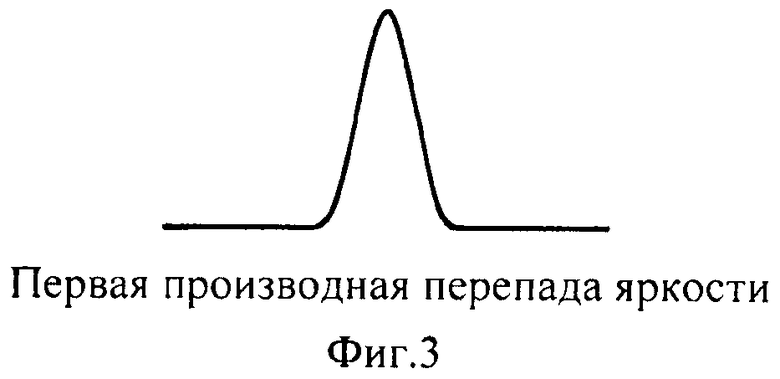
Резкое изменение яркости приводит к возникновению пика или впадины первой производной, что эквивалентно пересечению нулевого уровня со второй производной, как показано на фиг.2-4.
Таким образом, в результате вычисляется величина (первая, вторая производная, контрастность), которая может принимать широкий спектр значений. Однако результат выделения контура должен быть бинарным, т.е. точки, в которых идентифицирован контур, принимаются равными единице, а все остальные точки равны нулю. За применением операторов, использующих первую производную, должен следовать поиск экстремальных значений результата. Наиболее простой способ - это введение порога. Если значение оператора больше некоторого порогового значения, то данная точка является точкой контура, в противном случае считается, что в данной точке контур не обнаружен.
Следовательно, возникает трудность при разработке вычислительных схем для выделения контуров (контур пропущен или ложный контур).
Цель изобретения - классификация объектов по их изображениям с применением фрактальной размерности, которая представляет собой меру самоподобия сигнала, т.е. для ее вычисления требуется определить фрактальную сигнатуру S на нескольких масштабах.
Цель достигнута тем, что проводится преобразование масштаба изображения, расчет матриц разложения, измерение фрактальной сигнатуры изображения и расчет фрактальной размерности изображений для последующей классификации объектов.
Моделью для измерения фрактальной сигнатуры является двумерная сцена с рельефом, высотами которого являются значения яркостей элементов (пикселей) изображения. На фиг.5 изображен простейший треугольник Серпинского и его представление в виде рельефа.
Мерой S может служить площадь полученного рельефа. Вычисление площади будем производить методом триангуляции. При этом четыре соседних узла массива-изображения разбиваются на две тройки, а затем производится измерение площади треугольника «вперед» - Sf и треугольника «назад» - Sb. Общая площадь составит S1=Sf+Sb. Для вычисления площади всего изображения необходимо перебрать все четверки узлов.
Таким образом, получим значение фрактальной сигнатуры на одном масштабе. Для вычисления фрактальной размерности необходимы эти значения как минимум на двух масштабах. А для уверенного распознавания на нескольких (до 6-7).
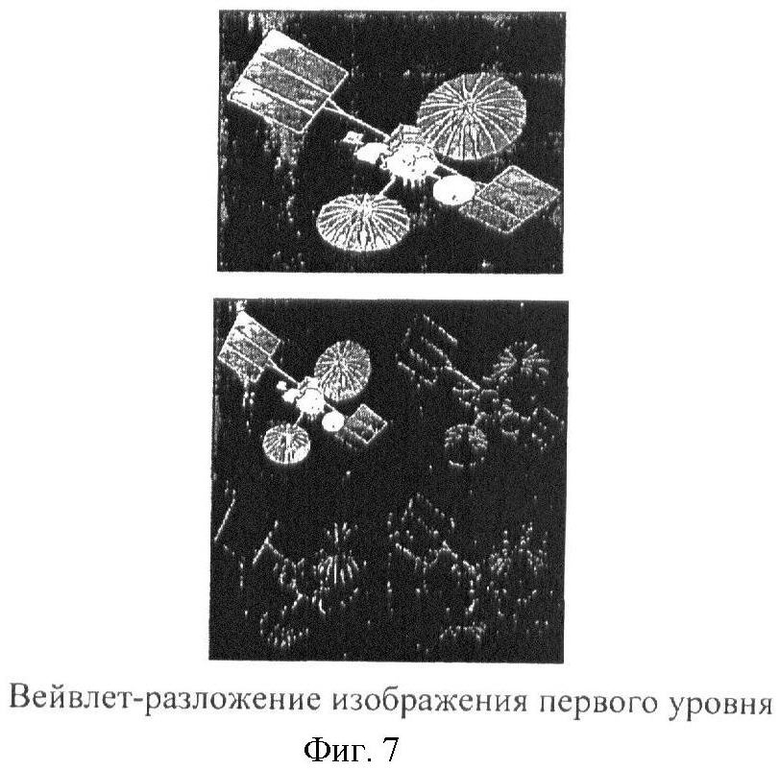
Несомненно, наиболее мощным инструментом для анализа изображений на различных масштабах является вейвлет-преобразование. Применяя это преобразование к изображению, получаем аппроксимирующее изображение-массив (А) более крупного масштаба и четыре детализирующих изображения-массива для горизонтальных, вертикальных и диагональных деталей (Н, V, D). Далее, это преобразование применяется итеративно к матрице А для каждого уровня изображения. Таким образом, получаем многоуровневое разложение изображения по масштабам, кратности 2. На фиг.6 изображена схема многоуровневого вейвлет-разложения, а на фиг.7 пример вейвлет-разложения первого уровня.
Таким образом, имеется изображение на масштабах, кратных 2. Фрактальная размерность вычисляется по следующей формуле (Новейшие методы обработки изображений. / Под ред. А.А.Потапова. - М.: ФИЗМАТЛИТ, 2008):
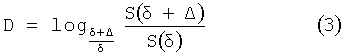
где S - фрактальная сигнатура;
δ - масштаб;
Δ - шаг дискретизации по масштабу;
Эта фрактальная размерность вычисляется для нескольких уровней вейвлет-разложения и строится график.
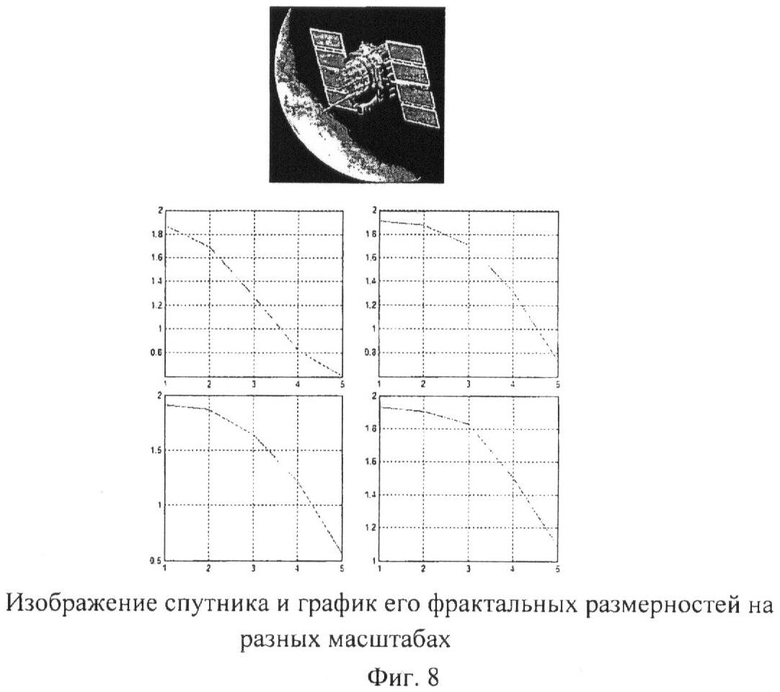
На фиг.8, в качестве примера, нами представлено изображение спутника и графики его фрактальных размерностей D на разных масштабах A, H, V, D соответственно. Как видно, изображение нефрактально (D отлично от 2).
В классическом подходе задача обнаружения объекта на фоне звездного неба является весьма нетривиальной. Применяются детекторы границ, различные корреляционные методы, однако, все эти методы подходят для частных случаев и требуют постоянной подстройки под новую задачу. Предлагаемый способ фрактально-вейвлетного распознавания решает такую задачу с легкостью. Дело в том, что звездное небо представляет собой фрактальную структуру, а спутник - творение человека, наоборот, не фрактален. Таким образом, если спутника нет на изображении, фрактальная размерность близка к двум. Как только на изображении появляется спутник - фрактальная размерность резко меняется. Также, помимо звездного неба, фрактальными структурами являются природные ландшафты, на фоне которых успешно могут быть распознаны различные объекты, созданные человеком.
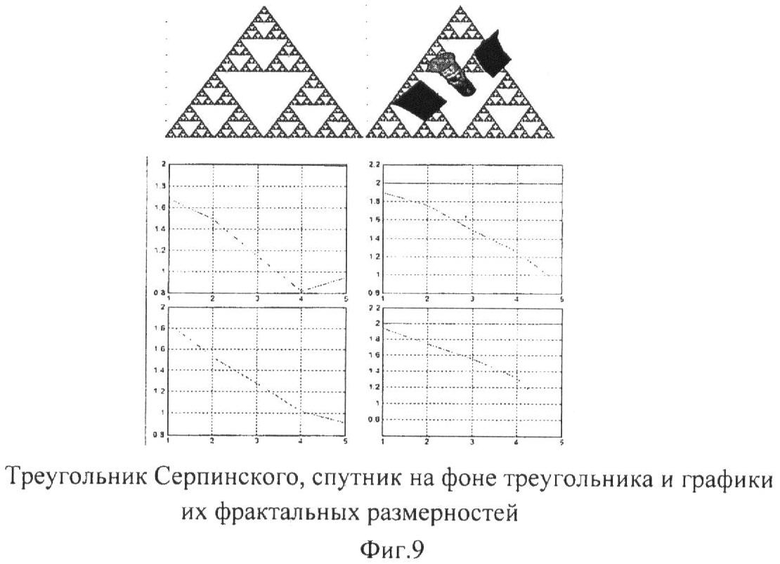
На фиг.9 изображен треугольник Серпинского и спутник на его фоне и графики их фрактальных размерностей. Треугольник Серпинского - один из примеров классических фрактальных изображений. Как видно из графиков, спектральная размерность изображения, на котором присутствует спутник, резко отличается. Таким образом, возможен анализ изображения с использованием фрактального детектора.
Для распознавания, в первую очередь, нужно учитывать фрактальные размерности для матрицы-изображения А, которая показывается на левом верхнем графике.
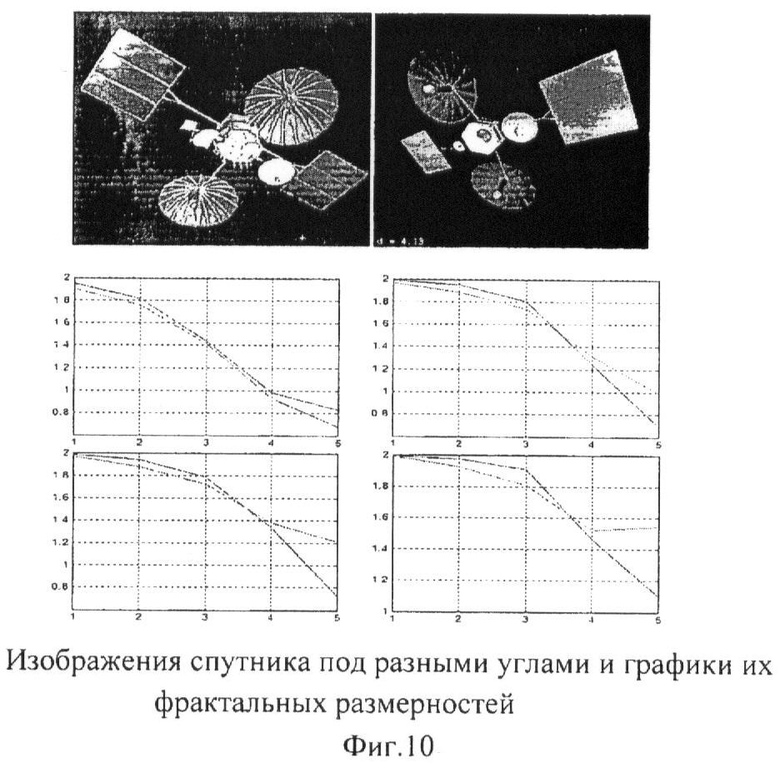
На фиг.10 приведены изображения спутника под разными углами и графики их фрактальных размерностей. Как видно из графиков, а в особенности из графика фрактальной размерности для А, фрактальные размерности изображений близки.
Теперь вычислим фрактальные размерности для изображений разных спутников.
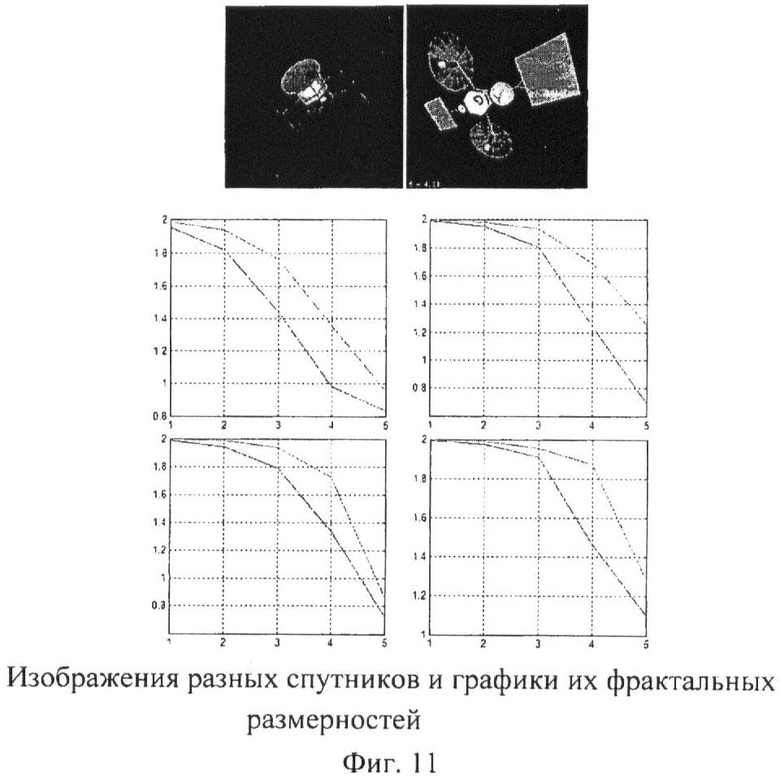
На фиг.11 приведены изображения разных спутников и графики их фрактальных размерностей. Как видно из графиков, а в особенности из графика фрактальной размерности для А, фрактальные размерности изображений рознятся. Таким образом, возможно, построить фрактальный классификатор, который не будет зависеть от поворота спутника на изображении.
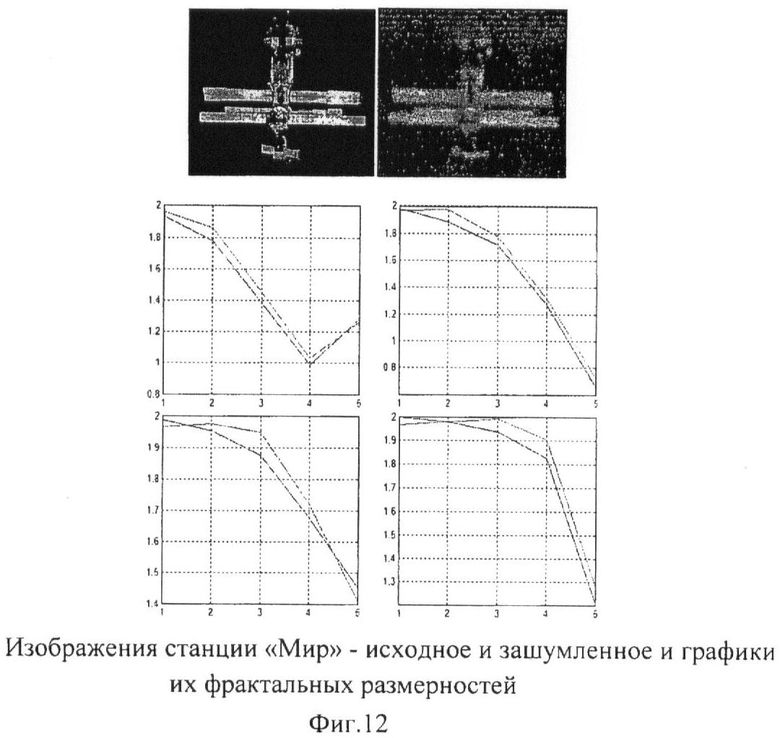
Была проведена проверка применения способа при воздействии шумов. На фиг.12 приведены изображения космической станции «Мир» - исходное и зашумленное Гауссовским размытием и шумом и графики их фрактальных размерностей. Как видно из графиков, а в особенности из графика фрактальной размерности для А, фрактальные размерности изображений близки. Следовательно, можно сделать вывод об устойчивости способа фрактально-вейвлетного распознавания к воздействию помех.
Источники информации
1. Новейшие методы обработки изображений. / Под ред. А.А.Потапова. - М.: ФИЗМАТЛИТ, 2008.
2. Вопросы перспективной радиолокации. Коллективная монография. / Под ред. А.В.Соколова. - М.: Радиотехника, 2003.
3. Маар Д. Зрение. Информационный подход к изучению представления и обработки зрительных образов. - М.: Радио и связь, 1987.
4. Зотов Р.В., Тормосин А.С. Шеванев Д.Н. Некоторые подходы к формированию эталонных признаков в системе распознавания космических объектов на основе фрактального анализа. - М: РАН сборник научных трудов «Избранные труды Российской школы по проблемам науки и технологий», 2010.
5. Зотов Р.В., Лучин А.А. Метод формирования диаграмм отражения от элементов конструкции КА. - М.: Сборник научно - методических материалов. В/ч 03425. 2001.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КАРТОГРАФИЧЕСКОГО ОТОБРАЖЕНИЯ ДВУХМЕРНЫХ РАСПРЕДЕЛЕНИЙ, ЗАДАННЫХ В ЦИФРОВОЙ ФОРМЕ | 2011 |
|
RU2484427C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ОБЪЕКТОВ НА ЦИФРОВЫХ ИЗОБРАЖЕНИЯХ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ МЕТОДОМ НЕЧЕТКОЙ ТРИАНГУЛЯЦИИ ДЕЛОНЕ | 2018 |
|
RU2729557C2 |
| СПОСОБ АВТОМАТИЧЕСКОЙ ИДЕНТИФИКАЦИИ ОБЪЕКТОВ НА ИЗОБРАЖЕНИЯХ | 2012 |
|
RU2514155C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЗАГРЯЗНЕНИЙ МОРСКОЙ ПОВЕРХНОСТИ | 2016 |
|
RU2632176C1 |
| СПОСОБ ПОЛУЧЕНИЯ ИЗОБРАЖЕНИЙ ВЫСОКОГО ПРОСТРАНСТВЕННОГО РАЗРЕШЕНИЯ ОПТИКО-ЭЛЕКТРОННЫМ СРЕДСТВОМ НАБЛЮДЕНИЯ ЗА УДАЛЕННЫМИ ОБЪЕКТАМИ | 2022 |
|
RU2806249C1 |
| СПОСОБ ВЫДЕЛЕНИЯ ПРОТЯЖЕННЫХ ЛИНЕЙНЫХ ОБЪЕКТОВ НА АЭРОКОСМИЧЕСКИХ ИЗОБРАЖЕНИЯХ | 2012 |
|
RU2523944C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ ОЧАГОВ ЗЕМЛЕТРЯСЕНИЙ | 2003 |
|
RU2242773C2 |
| СПОСОБ ПОМЕХОУСТОЙЧИВОГО ГРАДИЕНТНОГО ВЫДЕЛЕНИЯ КОНТУРОВ ОБЪЕКТОВ НА ЦИФРОВЫХ ПОЛУТОНОВЫХ ИЗОБРАЖЕНИЯХ | 2016 |
|
RU2648954C2 |
| Способ нахождения соответствия особых точек цифровых изображений | 2015 |
|
RU2614494C2 |
| Способ идентификации загрязнений морской поверхности | 2015 |
|
RU2664255C2 |


Изобретение относится к радиоэлектронным системам. Техническим результатом является расширение функциональных возможностей за счет классификации объектов по их изображениям с применением фрактальной размерности. Классификация объектов по их изображениям с применением фрактальной размерности представляет собой меру самоподобия сигнала, основанную на преобразовании масштаба изображения, расчете матриц разложения, измерения фрактальной сигнатуры изображения и расчете фрактальной размерности изображений для последующей классификации объекта. Применяя вейвлет-преобразование к изображению, получают аппроксимирующее изображение-массив (А) более крупного масштаба и четыре детализирующих изображения-массива для горизонтальных, вертикальных и диагональных деталей (H, V, D). Это преобразование применяется итеративно к матрице А для каждого уровня изображения и получают многоуровневое разложение изображения по масштабам, позволяющее проводить анализ и распознавание объекта вне зависимости от ракурса наблюдения и воздействия помех. 12 ил.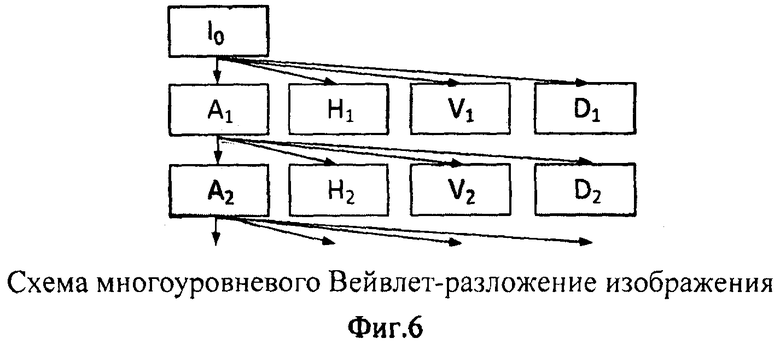
Способ распознавания объектов на основе фрактально-вейвлетного анализа, основанный на преобразовании масштаба изображения, расчете матриц разложения, измерения фрактальной сигнатуры изображения и расчете фрактальной размерности изображений для последующей классификации объекта, заключающийся в том, что
применяя вейвлет-преобразование к изображению получаем аппроксимирующее изображение-массив (А) более крупного масштаба и четыре детализирующих изображения-массива для горизонтальных, вертикальных и диагональных деталей (Н, V, D), далее это преобразование применяется итеративно к матрице А для каждого уровня изображения, таким образом, получаем многоуровневое разложение изображения по масштабам, кратности 2, позволяющее на основе фрактальной размерности проводить анализ и распознавание объекта вне зависимости от ракурса наблюдения и воздействия помех.
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| US 20040264774 A1, 30.12.2004 | |||
| СПОСОБ ВИЗУАЛЬНОГО ПРЕДСТАВЛЕНИЯ И АНАЛИЗА АНОМАЛЬНЫХ ЗНАЧЕНИЙ ИЗМЕРИТЕЛЬНЫХ ПАРАМЕТРОВ МНОГОМЕРНОГО ОБЪЕКТА ИЛИ ПРОЦЕССА | 2001 |
|
RU2237273C2 |
| СПОСОБ АНАЛИЗА СИГНАЛОВ О СОСТОЯНИИ ОБЪЕКТА | 2005 |
|
RU2301446C2 |
Авторы
Даты
2012-01-20—Публикация
2010-12-02—Подача