Изобретение относится к измерительной технике, в частности к аналого-цифровому преобразованию, а именно к кодовым шкалам преобразователей угловых перемещений в код.
В настоящее время и в перспективе одной из актуальных и технически сложных задач является цифровое измерение угловых перемещений подвижных органов многочисленных систем автоматического управления различными объектами. Эту функцию выполняют преобразователи угловых перемещений.
Развитие преобразователей угловых перемещений - поставщиков первичной информации в значительной степени обусловлено повсеместным использованием управляющих микроЭВМ и различных вычислительных устройств на основе микропроцессорных и других больших и сверхбольших интегральных схем.
В целом к преобразователям угловых перемещений, отличающимся большим разнообразием, предъявляется совокупность самых различных и, как правило, высоких технических требований.
Анализ литературных источников позволяет отметить у преобразователей с непосредственным преобразованием перемещения в код, основанных на считывании с использованием пространственного кодирования, следующие достоинства: возможность использования различных физических методов считывания информации, высокое быстродействие, для преобразователей углового перемещения высокая скорость вращения кодируемого вала от 100 до 150 об/мин, высокая разрешающая способность (до 20 двоичных разрядов), устойчивость к воздействию внешних дестабилизирующих факторов, возможность удовлетворения различным условиям применения, возможность функционального преобразования перемещения в код и др. Основным элементом таких преобразователей, определяющим их наиболее важные характеристики, является кодовая шкала (КШ).
Элементарный участок (квант) кодовой дорожки (КД) шкалы представляется, как правило, одним двоичным символом, где единичным символам соответствуют активные участки шкалы, а нулевым - пассивные.
Учитывая, что преобразователи угловых перемещений, построенные по методу считывания, могут быть реализованы на различных физических способах считывания информации, под активными и пассивными элементарными участками КД шкалы понимают соответственно токопроводящие и нетокопроводящие участки шкалы при контактном методе съема информации, прозрачные и непрозрачные участки шкалы при фотоэлектрическом методе съема информации, наличие металлической обкладки и изоляции на участках шкалы при емкостном методе съема информации, наличие и отсутствие магнитного материала на участках шкалы при электромагнитном методе съема информации и т.д.
В настоящее время существенный вклад в развитие преобразователей угловых перемещений вносит микроэлектроника, использование которой позволяет более полно решить проблему технологичности, обеспечив максимальное упрощение прецизионных механических узлов, основным из которых является КШ [1].
Известна рекурсивная кодовая шкала (РКШ) для преобразователей угловых перемещений, построенная на основе нелинейных двоичных последовательностей [2]. Достоинством РКШ можно считать возможность ее реализации с использованием большинства известных методов считывания информации. Недостатками такой шкалы является ее сложность и, как следствие, увеличенные габариты рекурсивной кодовой шкалы за счет использования четырех кодовых дорожек.
Наиболее близкой по техническому решению и выбранной авторами за прототип является рекурсивная кодовая шкала для преобразователей угловых перемещений, построенная на основе нелинейных двоичных последовательностей [3].
Рекурсивная кодовая шкала содержит первую информационную кодовую дорожку, выполненную в соответствии с символами нелинейной двоичной последовательности длиной N=2n, и считывающих элементов, размещенных вдоль первой информационной кодовой дорожки с угловым шагом, равным величине кванта информационной кодовой дорожки δ=360°/N, вторую информационную кодовую дорожку, выполненную в соответствии с символами N периодов нелинейной двоичной последовательности длиной М=2m, m считывающих элементов, размещенных вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), где δ2=360°/NM - величина кванта второй информационной кодовой дорожки, регулярную кодовую дорожку, выполненную в соответствии с символами {0,1, …, 0,1, …, 0,1} двоичной последовательности длиной 2NM, равномерно квантованной с периодом квантования δшк=360°/2NM, являющимся одновременно величиной кванта рекурсивной кодовой шкалы, считывающий элемент регулярной кодовой дорожки, смещенный относительно первого из n считывающих элементов на угловое расстояние k=2еδшк.+(δшк./2), е=0, 1, 2, 3, … и размещенный вдоль регулярной кодовой дорожки, mдоп.=m дополнительных считывающих элементов, смещенных относительно первого из m считывающих элементов на угловое расстояние km=(j+m)δ+δшк., j=0, 1, 2, … и размещенных вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), nдoп.=n дополнительных считывающих элементов, смещенных относительно последнего из n считывающих элементов на угловое расстояние kn=(iδ+δшк.), i=1, 2, 3, … и размещенных вдоль первой информационной кодовой дорожки с угловым шагом, равным δ, преобразователь кода на n входов и n выходов, выходы nдоп. считывающих элементов соединены со входами преобразователя кода, выходы которого, а также выходы n, m, mдоп. считывающих элементов и выход считывающего элемента регулярной кодовой дорожки предназначены для снятия информации об угловом положении рекурсивной кодовой шкалы.
Недостатком прототипа является то, что он не универсален при использовании. Информация с устройства-прототипа снимается в виде рекурсивного двоичного кода, тогда как большинство устройств систем управления и вычислительной техники, в составе которых предполагается использование рекурсивной кодовой шкалы, осуществляют обработку информации в обыкновенном двоичном коде. Другим недостатком прототипа является то, что он имеет увеличенное (по сравнению с фактической информационной емкостью рекурсивной кодовой шкалы) число внешних выходов, т.е. для получения (2n+1) разрядов рекурсивной кодовой шкалы, используются (4n+1) выходов.
В предлагаемом изобретении решается задача обеспечения универсальности применения рекурсивной кодовой шкалы в составе устройств систем управления и вычислительной техники, осуществляющих обработку информации в обыкновенном двоичном коде, а также упрощение рекурсивной кодовой шкалы в части уменьшения ее внешних выходов.
Для достижения технического результата рекурсивная кодовая шкала содержит первую информационную кодовую дорожку, выполненную в соответствии с символами нелинейной двоичной последовательности длиной N=2n, n считывающих элементов, размещенных вдоль первой информационной кодовой дорожки с угловым шагом, равным величине кванта первой информационной кодовой дорожки δ=360°/N, вторую информационную кодовую дорожку, выполненную в соответствии с символами N периодов нелинейной двоичной последовательности длиной М=2m, m считывающих элементов, размещенных вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), где δ2=360°/NM - величина кванта второй информационной кодовой дорожки, регулярную кодовую дорожку, выполненную в соответствии с символами {0,1, …, 0,1, …, 0,1} двоичной последовательности длиной 2NM, равномерно квантованной с периодом квантования δшк=360°/2NM, являющимся одновременно величиной кванта рекурсивной кодовой шкалы, считывающий элемент регулярной кодовой дорожки, смещенный относительно первого из n считывающих элементов на угловое расстояние k=2еδшк.+(δшк./2), е=0, 1, 2, 3, … и размещенный вдоль регулярной кодовой дорожки, nдoп.=n дополнительных считывающих элементов, смещенных относительно последнего из n считывающих элементов на угловое расстояние kn=(iδ+δшк.), i=1, 2, 3, … и размещенных вдоль первой информационной кодовой дорожки с угловым шагом, равным δ, mдoп.=m дополнительных считывающих элементов, смещенных относительно первого из m считывающих элементов на угловое расстояние km=(j+m)δ+δшк., j=0, 1, 2, … и размещенных вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), преобразователь кода на n входов и n выходов, выходы nдоп. считывающих элементов соединены со входами преобразователя кода, инвертор, n двухвходовых элементов И, m двухвходовых элементов И, nдоп. двухвходовых элементов И, mдоп. двухвходовых элементов И, n двухвходовых элементов ИЛИ, m двухвходовых элементов ИЛИ, первый и второй дешифраторы, выходы n считывающих элементов соединены соответственно с первыми входами n двухвходовых элементов И, вторые входы которых соединены с выходом считывающего элемента регулярной дорожки, выходы m считывающих элементов соединены соответственно с первыми входами m двухвходовых элементов И, вторые входы которых соединены с выходом считывающего элемента регулярной дорожки, выходы преобразователя кода соединены соответственно с первыми входами nдоп. двухвходовых элементов И, вторые входы которых соединены через инвертор с выходом считывающего элемента регулярной дорожки, выходы mдоп. считывающих элементов соединены соответственно с первыми входами mдоп. двухвходовых элементов И, вторые входы которых соединены через инвертор с выходом считывающего элемента регулярной дорожки, выходы n двухвходовых элементов И соединены соответственно с первыми входами n двухвходовых элементов ИЛИ, вторые входы которых соединены соответственно с выходами nдоп. двухвходовых элементов И, выходы m двухвходовых элементов И соединены соответственно с первыми входами m двухвходовых элементов ИЛИ, вторые входы которых соединены соответственно с выходами mдоп. двухвходовых элементов И, выходы n двухвходовых элементов ИЛИ соединены со входами первого дешифратора, выходы m двухвходовых элементов ИЛИ соединены со входами второго дешифратора, выходы первого и второго дешифраторов, а также выход считывающего элемента регулярной дорожки предназначены для снятия информации об угловом положении рекурсивной кодовой шкалы.
Новым в предлагаемом изобретении является снабжение рекурсивной кодовой шкалы блоком обработки рекурсивного двоичного кода и преобразования его в обыкновенный двоичный код, состоящим из инвертора, (n+m+nдоп.+mдоп.) двухвходовых элементов И, (n+m) двухвходовых элементов ИЛИ, первого и второго дешифраторов.
Совокупность существенных признаков в предлагаемом изобретении позволила обеспечить универсальность применения рекурсивной кодовой шкалы в составе устройств систем управления и вычислительной техники, осуществляющих обработку информации в обыкновенном двоичном коде, а также упростить рекурсивную кодовую шкалу в части уменьшения ее внешних выходов.
В результате можно сделать вывод о том, что
- предлагаемое техническое решение обладает изобретательским уровнем, т.к. оно явным образом не следует из уровня техники;
- изобретение является новым, так как из уровня техники по доступным источникам информации не выявлено аналогов с подобной совокупностью признаков;
- изобретение является промышленно применимым, так как может быть использовано во всех областях, где требуется высокоточное позиционное определение углового положения объекта с использованием преобразователей угловых перемещений на основе заявляемых рекурсивных кодовых шкал.
Предлагаемое изобретение поясняется чертежом, где показана линейная развертка семиразрядной рекурсивной кодовой шкалы, а также функциональная схема блока обработки рекурсивного двоичного кода и преобразования его в обыкновенный двоичный код.
Заявляемая рекурсивная кодовая шкала 1 содержит первую информационную кодовую дорожку 2, вторую информационную кодовую дорожку 3, регулярную кодовую дорожку 4, считывающие элементы 5, 6, 7 (n=3), считывающие элементы 8, 9, 10 (nдоп.=3), считывающие элементы 11, 12, 13 (m=3), считывающие элементы 14, 15, 16 (mдоп.=3), считывающий элемент 17 регулярной кодовой дорожки, а также блок обработки рекурсивного двоичного кода и преобразования его в обыкновенный двоичный код, включающий в себя инвертор 18 со входом 17 и выходом 44, преобразователь кода 19 на три входа 8-10 и три выхода 20-22, три двухвходовых элемента И 24, 26, 28 (n=3), три двухвходовых элемента И 30, 32, 34 (m=3), три двухвходовых элемента И 23, 25, 27 (nдоп.=3), три двухвходовых элемента И 29, 31, 33 (mдоп.=3), три двухвходовых элемента ИЛИ 35, 36, 37 (n=3), три двухвходовых элемента ИЛИ 38, 39, 40 (m=3), первый 41 и второй 42 дешифраторы, а также шину 43.
Для пояснения сути изобретения приведем некоторые теоретические предпосылки.
В [4] предложены КШ для преобразователей угловых перемещений, названные псевдослучайными кодовыми шкалами (ПСКШ), и строящиеся на основе использования теории псевдослучайных двоичных последовательностей максимальной длины (М - последовательностей). ПСКШ имеют всего одну информационную кодовую дорожку, выполненную в соответствии с символами М - последовательности a0a1…aL-1, и n считывающих элементов (СЭ), размещенных вдоль дорожки. Считывающие элементы дают возможность получить при полном обороте шкалы L=2n-1 различных n-разрядных кодовых комбинаций и обеспечивают разрешающую способность преобразователя угловых перемещений на основе ПСКШ δ=360°/L.
Как следует из метода построения ПСКШ, ее разрешающая способность определяется длиной М-последовательности L=2n-1. Очевидно, что при любой разрядности шкалы теряется одна (нулевая) кодовая комбинация. Однако при построении некоторых технических систем с использованием преобразователей угловых перемещений необходимо обеспечить разрешающую способность последних, равную 2n.
В [5] рассмотрены использованные в изобретении рекурсивные кодовые шкалы (РКШ), получившие название нелинейные кодовые шкалы (НКШ) и строящиеся на основе нелинейных двоичных последовательностей, которые обеспечивают разрешающую способность шкалы δ=360°/2n.
Нелинейная последовательность - это последовательность двоичных символов {aj} длиной N=2n, удовлетворяющих рекурсивному соотношению [6]
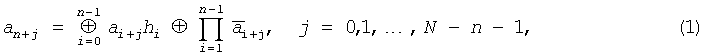
где знак ⊕ означает суммирование по модулю два, а индексы при символах последовательности берутся по модулю N. Начальные значения символов a0a1…an-1 последовательности выбираются произвольно.
В (1) hi - коэффициенты, зависящие от вида примитивного полинома степени n с коэффициентами поля Галуа GF(2) [7], т.е.
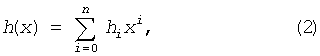
где h0=hn=1, а hi=0,1 при 0<i<n,
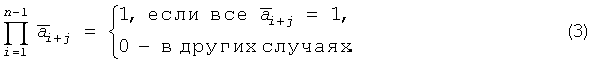
Первое слагаемое в (1) определяет правило образования линейной по отношению к оператору суммирования по модулю 2 М-последовательности. Второе слагаемое (3) в (1) указывает на операцию умножения значений n-1 кодовых символов. Это приводит к тому, что полученная последовательность символов становится нелинейной и в ней появляется комбинация, содержащая n последовательных нулей.
В табл.1 приведены полиномы h(x) до n=20 включительно, которые могут быть использованы для генерации соответствующих М-последовательностей [7].
Рассмотрим метод построения n-разрядной однодорожечной РКШ на основе нелинейной последовательности.
1. В зависимости от требуемой разрядности шкалы n из табл.1 выбирается полином h(x) степени n.
2. Используя рекурсивное соотношение (1), генерируется последовательность {aj}.
3. Элементарные участки (кванты) шкалы δ выполняются в соответствии с символами нелинейной последовательности {aj}, где символам 1 последовательности соответствуют активные, а символам 0 - пассивные участки информационной дорожки. Для определенности символы последовательности отображаются на информационной кодовой дорожке по ходу часовой стрелки в порядке a0a1…aN-1.
4. Осуществляется размещение на шкале n считывающих элементов с шагом, равным одному кванту, т.е. в соответствии с полиномом размещения
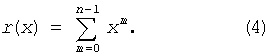
Единственность такого размещения объясняется нелинейными свойствами рассматриваемой последовательности.
Поясним построение информационных кодовых дорожек РКШ 1, приведенных на чертеже.
В примере первая информационная кодовая дорожка 2 РКШ 1 построена в соответствии с символами нелинейной последовательности {aj}=а0а1…a7=00010111 длиной N=2n=23=8, для получения которой использован примитивный полином h(x)=х3+x+1, а символы а3+j последовательности {aj} при начальных значениях a0=a1=a2=0 удовлетворяют рекурсивному соотношению 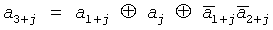 , j=0, 1, …, 4. Нелинейная последовательность должна быть нанесена на РКШ в виде активных (единицы последовательности) и пассивных (нули последовательности) участков (квантов) первой информационной кодовой дорожки 2, например, по ходу часовой стрелки, причем на первую информационную кодовую дорожку 2 РКШ 1 наносится только один период последовательности. Нелинейная последовательность с периодом N=2n определяет число квантов первой информационной кодовой дорожки 2 РКШ 1, которое в данном примере равно N=8. Отсюда величина кванта δ=360°/N=360°/8=45°. В примере размещение СЭ 5, 6 и 7 (n=3) вдоль первой информационной кодовой дорожки 2 определяется полиномом r(x)=1+x+х2 и осуществляется с шагом, равным величине одного кванта первой информационной кодовой дорожки δ по ходу часовой стрелки.
, j=0, 1, …, 4. Нелинейная последовательность должна быть нанесена на РКШ в виде активных (единицы последовательности) и пассивных (нули последовательности) участков (квантов) первой информационной кодовой дорожки 2, например, по ходу часовой стрелки, причем на первую информационную кодовую дорожку 2 РКШ 1 наносится только один период последовательности. Нелинейная последовательность с периодом N=2n определяет число квантов первой информационной кодовой дорожки 2 РКШ 1, которое в данном примере равно N=8. Отсюда величина кванта δ=360°/N=360°/8=45°. В примере размещение СЭ 5, 6 и 7 (n=3) вдоль первой информационной кодовой дорожки 2 определяется полиномом r(x)=1+x+х2 и осуществляется с шагом, равным величине одного кванта первой информационной кодовой дорожки δ по ходу часовой стрелки.
Фиксируя считывающими элементами 5, 6 и 7 последовательно кодовую комбинацию при перемещении РКШ 1 циклически на один элементарный участок (квант), например, против хода часовой стрелки, получаем восемь различных трехразрядных рекурсивных кодовых комбинаций: 000, 001, 010, 101, 011, 111, 110 и 100.
По такому принципу может быть построена однодорожечная рекурсивная кодовая шкала любой разрядности.
На чертеже вторая информационная кодовая дорожка 3 РКШ 1 построена в соответствии с символами нелинейной последовательности {aj}=а0а1…a7=00010111 длиной M=2m=23=8, для получения которой использован примитивный полином h(x)=х3+x+1, а символы а3+j последовательности {aj} при начальных значениях а0=а1=a2=0 удовлетворяют рекурсивному соотношению 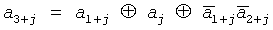 , j=0, 1, …, 4. Нелинейная последовательность должна быть нанесена на РКШ 1 в виде активных (единицы последовательности) и пассивных (нули последовательности) участков (квантов) второй информационной кодовой дорожки 3, например, по ходу часовой стрелки, причем на вторую информационную кодовую дорожку 3 РКШ 1 наносятся N=8 периодов последовательности. Восемь периодов нелинейной последовательности длиной M=23=8 определяют число квантов второй информационной кодовой дорожки 3 РКШ 1, которое в данном примере равно NM=64. Отсюда величина кванта второй информационной кодовой дорожки 3 δ2=360°/NM=360°/64=5,625°.
, j=0, 1, …, 4. Нелинейная последовательность должна быть нанесена на РКШ 1 в виде активных (единицы последовательности) и пассивных (нули последовательности) участков (квантов) второй информационной кодовой дорожки 3, например, по ходу часовой стрелки, причем на вторую информационную кодовую дорожку 3 РКШ 1 наносятся N=8 периодов последовательности. Восемь периодов нелинейной последовательности длиной M=23=8 определяют число квантов второй информационной кодовой дорожки 3 РКШ 1, которое в данном примере равно NM=64. Отсюда величина кванта второй информационной кодовой дорожки 3 δ2=360°/NM=360°/64=5,625°.
Таким образом, в примере размещение СЭ 11,12 и 13 (m=3) вдоль второй информационной кодовой дорожки 2 осуществляется с шагом, равным величине (δ+δ2)=45°+5,625°=50,625° по ходу часовой стрелки.
В нашем примере суммарная разрядность, обеспечиваемая первой информационной и второй информационной кодовыми дорожками при рассмотренном выше размещении СЭ, будет равна (n+m)=3+3=6.
Фиксируя считывающими элементами 5, 6, 7 и 11, 12, 13 последовательно кодовую комбинацию, при перемещении РКШ циклически на один элементарный участок (квант) второй информационной кодовой дорожки 3 δ2, например, против хода часовой стрелки, получаем 64 различных шестиразрядных кодовых комбинаций, которые соответствуют 64 угловым положениям шкалы. Эти кодовые комбинации приведены в табл.2.
В рассматриваемом примере для построения первой информационной кодовой дорожки 2 и второй информационной кодовой дорожки 3 использована одна и та же нелинейная двоичная последовательность, т.е. N=M=8. В общем случае допускается N≠M. Например, шестиразрядная рекурсивная кодовая шкала может быть построена еще двумя способами, где (n=4, m=2) и (n=2, m=4). С увеличением разрядности двухдорожечной рекурсивной кодовой шкалы число вариантов ее построения также возрастает. Данный подход дает дополнительные возможности для выбора наиболее технологичного варианта построения РКШ (и как следствие, преобразователя угловых перемещений на ее основе), что связано с возможностью многовариантного размещения на шкале считывающих элементов.
На чертеже nдоп.=3 считывающих элемента 8, 9 и 10 смещены относительно последнего 7 из n считывающих элементов на угловое расстояние kn=(iδ+δшк.)=δ+δшк.=45°+2,8125°=47,8125°, i=1 и размещены вдоль первой информационной кодовой дорожки с угловым шагом, равным величине кванта первой информационной кодовой дорожки δ=45°; mдоп.=3 считывающих элементов 14, 15 и 16 смещены относительно первого 11 из m считывающих элементов на угловое расстояние km=(j+m)δ+δшк.=mδ+δшк.=3×45°+2,8125°=137,8125°, j=0 и размещены вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2)=45°+2,8125°=47,8125°.
В предлагаемом изобретении на выходах считывающих элементов 5, 6 и 7 и дополнительных считывающих элементов 8, 9 и 10 формируются различные рекурсивные цифровые коды. В связи с этим требуется согласование отсчетов, т.е. приведение кодовой комбинации, считываемой с nдоп. считывающих элементов, к кодовой комбинации, получаемой с n считывающих элементов. Такое согласование отсчетов осуществляется посредством преобразователя кода 19, который может быть реализован, например, с использованием постоянного запоминающего устройства (ПЗУ) на три входа и три выхода.
Если принять за начальное положение РКШ 1 нулевую кодовую комбинацию, то входные 8, 9 и 10 и выходные 20, 21 и 22 сигналы преобразователя кода 19 должны выглядеть так, как показано в табл.3.
На чертеже регулярная кодовая дорожка 4 выполнена в соответствии с символами {0,1, …, 0,1, …, 01} двоичной последовательности длиной 2NM=2×8×8=128, равномерно квантованной с периодом квантования δшк.=360°/2NM=360°/128=2,8125°. Считывающий элемент 17 регулярной кодовой дорожки размещен вдоль регулярной кодовой дорожки относительно первого 5 из n=3 считывающих элементов 5, 6, 7 на угловом расстоянии k=2eδшк.+(δшк./2)=2×4×2,8125°+(2,8125°/2)=22,50°+1,40625°=23,90626°, e=4.
С целью упрощения рекурсивной кодовой шкалы в части уменьшения ее внешних выходов с (4n+1) до (2n+1) выходов, РКШ снабжена инвертором, (n+m+nдоп.+mдоп.) двухвходовыми элементами И, (n+m) двухвходовыми элементами ИЛИ.
С целью обеспечения универсальности применения рекурсивной кодовой шкалы в составе устройств систем управления и вычислительной техники, осуществляющих обработку информации в обыкновенном двоичном коде, РКШ снабжена первым и вторым дешифраторами.
Процесс считывания с РКШ 1 информации осуществляется следующим образом.
При произвольном положении РКШ 1 с первой информационной 2 и второй информационной 3 кодовых дорожек посредством считывающих элементов снимается соответствующий шестиразрядный рекурсивный цифровой код. Выходной сигнал со считывающего элемента 17 регулярной кодовой дорожки 4 формирует самый младший 7-й разряд РКШ, а также управляет режимом считывания кодовой комбинации с первой информационной 2 и второй информационной 3 кодовых дорожек.
При этом, если выходной сигнал со считывающего элемента 17 равен нулю, то рекурсивный цифровой код снимается с nдоп.=3 считывающих элементов 8, 9 и 10 и mдоп.=3 считывающих элементов 14, 15 и 16. Если же выходной сигнал со считывающего элемента 17 равен единице, то рекурсивный цифровой код снимается с n=3 считывающих элементов 5, 6 и 7 и m=3 считывающих элементов 11, 12 и 13. Для реализации рассмотренного алгоритма считывания информации с первой информационной 2 и второй информационной 3 кодовых дорожек используется схема, состоящая из инвертора 18, двухвходовых логических элементов И (23-34) и двухвходовых логических элементов ИЛИ (35-40). Логика работы схемы однозначно определяется чертежом.
Таким образом, с выходов считывающих элементов 5-7, 11-16, а также с выходов 20-22 преобразователя кода, схемой, состоящей из инвертора 18, двухвходовых логических элементов И (23-34) и двухвходовых логических элементов ИЛИ (35-40), будут сформированы шесть разрядов РКШ. Причем три старших разряда рекурсивного цифрового кода шкалы, получаемого со считывающих элементов 5-7 и выходов 20-22 преобразователя кода, снимаются с выходов трех двухвходовых логических элементов ИЛИ (35-37), а три младших разряда рекурсивного цифрового кода шкалы, получаемого со считывающих элементов 11-16, снимаются с выходов трех двухвходовых логических элементов ИЛИ (38-40).
Седьмой, самый младший разряд РКШ, формируется непосредственно считывающим элементом 17 регулярной кодовой дорожки 4. Соответствующие кодовые комбинации семиразрядной рекурсивной кодовой шкалы, приведенной на чертеже, представлены в табл.4.
Однако общеизвестно, что большинство устройств систем управления и вычислительной техники, в составе которых предполагается использование рекурсивной кодовой шкалы, осуществляют обработку информации в обыкновенном двоичном коде.
На чертеже, для преобразования рекурсивных кодовых комбинаций в обыкновенный двоичный код используются первый 41 и второй 42 дешифраторы, которые могут быть реализованы посредством ПЗУ на три входа и три выхода, причем на входы первого дешифратора 41 поступают сигналы с выходов двухвходовых логических элементов ИЛИ 35-37, а на входы второго дешифратора 42 поступают сигналы с выходов двухвходовых логических элементов ИЛИ 38-40.
Поскольку в рассматриваемом примере для построения кодовых масок первой информационной 2 и второй информационной 3 кодовых дорожек использована одна и та же нелинейная двоичная последовательность, оба дешифратора могут быть выполнены по одной схеме. Входные и выходные сигналы дешифраторов 41 и 42 должны выглядеть так, как показано в табл.5.
Следовательно, на выходе дешифраторов 41 и 42 будет сформирован шестиразрядный обыкновенный двоичный код, причем с выходов дешифратора 41 снимаются три старших, а с выходов дешифратора 42 - три его младших разряда. Как указывалось ранее, самый младший седьмой разряд РКШ снимается непосредственно со считывающего элемента 17 регулярной кодовой дорожки. Соответствующие выходные кодовые комбинации в обыкновенном двоичном коде семиразрядной рекурсивной кодовой шкалы, приведенной на чертеже, представлены в табл.6.
Таким образом, в предлагаемом изобретении решена задача обеспечения универсальности применения рекурсивной кодовой шкалы в составе устройств систем управления и вычислительной техники, осуществляющих обработку информации в обыкновенном двоичном коде, а также достигнуто упрощение рекурсивной кодовой шкалы в части уменьшения ее внешних выходов. С учетом современных достижений в области микроэлектроники весь блок обработки рекурсивного двоичного кода и преобразования его в обыкновенный двоичный код может быть легко реализован на одной программируемой логической интегральной схеме.
Литература
1. Домрачев В.Г., Мейко Б.С. Цифровые преобразователи угла: принципы построения, теория точности, методы контроля. - М.: Энергоатомиздат, 1984. - 328 с.
2. Заявка на изобретение RU 2010147699, приоритет 22.11.2010.
3. Заявка на изобретение RU 2011110234, приоритет 17.03.2011.
4. Ожиганов А.А. Псевдослучайные кодовые шкалы // Изв. Вузов. Приборостроение, 1987. Т.20. N.2. С.40-43.
5. Азов А.К, Ожиганов А.А., Тарасюк М.В. Рекурсивные кодовые шкалы // Издательство "Машиностроение" Информационные технологии, 1998, N6. С.39-43.
6. Агульник А.Р., Мусаелян С.С. Построение нелинейных двоичных последовательностей // Радиоэлектроника. 1983. N4. С.19-28.
7. Макуильямс Ф.Д., Слоан Н.Д. Псевдослучайные последовательности и таблицы // ТИИЭР. 1976. Т.64. N12. С.80-95.
| название | год | авторы | номер документа |
|---|---|---|---|
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2011 |
|
RU2446557C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2444126C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2434323C1 |
| КОДОВАЯ ШКАЛА | 2014 |
|
RU2560782C1 |
| Кодовая шкала | 2017 |
|
RU2653323C1 |
| Кодовая шкала | 2015 |
|
RU2612622C1 |
| КОДОВАЯ ШКАЛА | 2012 |
|
RU2497275C1 |
| ИНВЕРСНО-СОПРЯЖЕННАЯ КОДОВАЯ ШКАЛА | 2013 |
|
RU2553079C1 |
| КОДОВАЯ ШКАЛА | 2016 |
|
RU2658188C2 |
| КОДОВАЯ ШКАЛА | 2012 |
|
RU2490790C1 |
Изобретение относится к измерительной технике, в частности к аналого-цифровому преобразованию, а именно к кодовым шкалам преобразователей угла поворота вала в код. Техническим результатом является упрощение рекурсивной кодовой шкалы. Устройство содержит первую информационную кодовую дорожку длиной N=2n, n считывающих элементов, размещенных вдоль нее с угловым шагом δ=360°/N, вторую информационную кодовую дорожку длиной M=2m, m считывающих элементов, размещенных вдоль нее с угловым шагом (δ+δ2), где δ2=360°/NM, регулярную кодовую дорожку длиной 2NM, равномерно квантованной с периодом квантования δшк.=360°/2NM, считывающий элемент регулярной кодовой дорожки, смещенный относительно первого из n считывающих элементов на угловое расстояние k=2eδшк.+(δшк./2), n дополнительных считывающих элементов, смещенных относительно последнего из n считывающих элементов на угловое расстояние kn=(iδ+δшк.) и размещенных вдоль первой информационной кодовой дорожки с угловым шагом, равным δ, m дополнительных считывающих элементов, смещенных относительно первого из m считывающих элементов на угловое расстояние km=(j+m)δ+δшк., и размещенных вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), преобразователь кода, инвертор, элементы И, элементы ИЛИ, дешифраторы. 1 ил., 6 табл.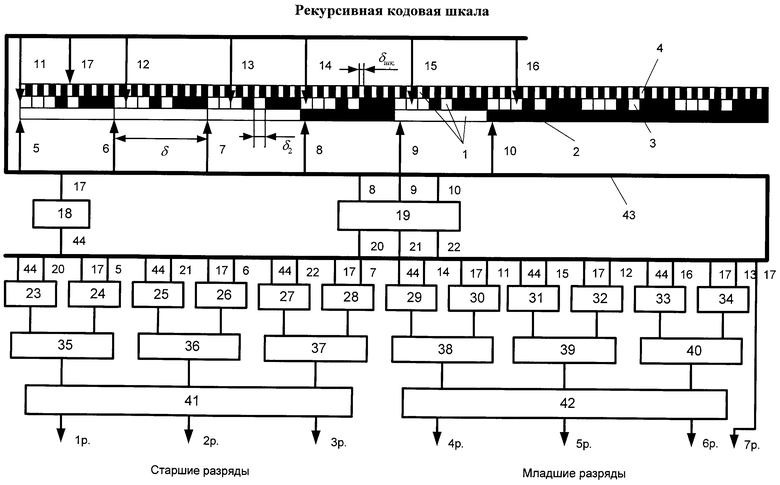
Рекурсивная кодовая шкала, содержащая первую информационную кодовую дорожку, выполненную в соответствии с символами нелинейной двоичной последовательности длиной N=2n, n считывающих элементов, размещенных вдоль первой информационной кодовой дорожки с угловым шагом, равным величине кванта первой информационной кодовой дорожки δ=360°/N, вторую информационную кодовую дорожку, выполненную в соответствии с символами N периодов нелинейной двоичной последовательности длиной M=2m, m считывающих элементов, размещенных вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), где δ2=360°/NM - величина кванта второй информационной кодовой дорожки, регулярную кодовую дорожку, выполненную в соответствии с символами {0,1, …, 0,1, …, 0,1} двоичной последовательности длиной 2NM, равномерно квантованной с периодом квантования δшк=360°/2NM, являющимся одновременно величиной кванта рекурсивной кодовой шкалы, считывающий элемент регулярной кодовой дорожки, смещенный относительно первого из n считывающих элементов на угловое расстояние k=2еδшк.+(δшк./2), е=0, 1, 2, 3,… и размещенный вдоль регулярной кодовой дорожки, nдоп.=n дополнительных считывающих элементов, смещенных относительно последнего из n считывающих элементов на угловое расстояние kn=(iδ+δшк.), i=1, 2, 3,… и размещенных вдоль первой информационной кодовой дорожки с угловым шагом, равным δ, mдоп.=m дополнительных считывающих элементов, смещенных относительно первого из m считывающих элементов на угловое расстояние km=(j+m)δ+δшк., j=0, 1, 2,… и размещенных вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), преобразователь кода на n входов и n выходов, выходы nдоп. считывающих элементов соединены со входами преобразователя кода, отличающаяся тем, что рекурсивная кодовая шкала снабжена инвертором, n двухвходовыми элементами И, m двухвходовыми элементами И, nдоп. двухвходовыми элементами И, mдоп. двухвходовыми элементами И, n двухвходовыми элементами ИЛИ, m двухвходовыми элементами ИЛИ, первым и вторым дешифраторами, выходы n считывающих элементов соединены соответственно с первыми входами n двухвходовых элементов И, вторые входы которых соединены с выходом считывающего элемента регулярной дорожки, выходы m считывающих элементов соединены соответственно с первыми входами m двухвходовых элементов И, вторые входы которых соединены с выходом считывающего элемента регулярной дорожки, выходы преобразователя кода соединены соответственно с первыми входами nдоп. двухвходовых элементов И, вторые входы которых соединены через инвертор с выходом считывающего элемента регулярной дорожки, выходы mдоп. считывающих элементов соединены соответственно с первыми входами mдоп. двухвходовых элементов И, вторые входы которых соединены через инвертор с выходом считывающего элемента регулярной дорожки, выходы n двухвходовых элементов И соединены соответственно с первыми входами n двухвходовых элементов ИЛИ, вторые входы которых соединены соответственно с выходами nдоп. двухвходовых элементов И, выходы m двухвходовых элементов И соединены соответственно с первыми входами m двухвходовых элементов ИЛИ, вторые входы которых соединены соответственно с выходами mдоп. двухвходовых элементов И, выходы n двухвходовых элементов ИЛИ соединены со входами первого дешифратора, выходы m двухвходовых элементов ИЛИ соединены со входами второго дешифратора, выходы первого и второго дешифраторов, а также выход считывающего элемента регулярной дорожки предназначены для снятия информации об угловом положении рекурсивной кодовой шкалы.
| Фрикционная передача вращения | 1948 |
|
SU79360A1 |
| Преобразователь угол-код | 1987 |
|
SU1534748A1 |
| Преобразователь перемещение-код | 1984 |
|
SU1166304A1 |
| Устройство для защиты электроустановки с магнитопроводом от витковых замыканий | 1976 |
|
SU678582A1 |
| Способ контроля частотных характеристик аппарата магнитной записи | 1980 |
|
SU911610A2 |
| DE 4123444 C1, 01.10.1992. | |||
Авторы
Даты
2012-05-10—Публикация
2011-04-29—Подача