Изобретение относится к измерительной технике, в частности к аналого-цифровому преобразованию, а именно к кодовым шкалам преобразователей угловых перемещений в код.
В настоящее время и в перспективе одной из актуальных и технически сложных задач является цифровое измерение угловых перемещений подвижных органов многочисленных систем автоматического управления различными объектами. Эту функцию выполняют преобразователи угловых перемещений.
Развитие преобразователей угловых перемещений - поставщиков первичной информации в значительной степени обусловлено повсеместным использованием управляющих микроЭВМ и различных вычислительных устройств на основе микропроцессорных и других больших и сверхбольших интегральных схем.
В целом к преобразователям угловых перемещений, отличающимся большим разнообразием, предъявляется совокупность самых различных и, как правило, высоких технических требований.
Анализ литературных источников позволяет отметить у преобразователей с непосредственным преобразованием перемещения в код, основанных на считывании с использованием пространственного кодирования, следующие достоинства: возможность использования различных физических методов считывания информации, высокое быстродействие, для преобразователей углового перемещения высокая скорость вращения кодируемого вала (100…150 об/мин), высокая разрешающая способность (до 20 дв. раз.), устойчивость к воздействию внешних дестабилизирующих факторов, возможность удовлетворения различным условиям применения, возможность функционального преобразования перемещения в код и др. Основным элементом таких преобразователей, определяющим их наиболее важные характеристики, является кодовая шкала (КШ).
Элементарный участок (квант) кодовой дорожки (КД) шкалы представляется, как правило, одним двоичным символом, где единичным символам соответствуют активные участки шкалы, а нулевым - пассивные.
Учитывая, что преобразователи угловых перемещений, построенные по методу считывания, могут быть реализованы на различных физических способах считывания информации, под активными и пассивными элементарными участками КД шкалы понимают соответственно токопроводящие и нетокопроводящие участки шкалы при контактном методе съема информации, прозрачные и непрозрачные участки шкалы при фотоэлектрическом методе съема информации, наличие металлической обкладки и изоляции на участках шкалы при емкостном методе съема информации, наличие и отсутствие магнитного материала на участках шкалы при электромагнитном методе съема информации и т.д.
Известны кодовые шкалы преобразователей угловых перемещений [1, 2], маска которых выполнена в обыкновенном двоичном коде или в коде Грея. В классическом варианте построения таких шкал число кодовых дорожек равно разрядности шкалы. Поэтому масса и габариты КШ в основном определяются диаметром шкалы и с увеличением разрядности также возрастают. При этом, как следствие, ухудшается технологичность таких шкал.
Наиболее близкой по техническому решению и выбранной авторами за прототип является рекурсивная кодовая шкала для преобразователей угловых перемещений, построенная на основе нелинейных двоичных последовательностей [3].
Рекурсивные кодовые шкалы на основе нелинейных двоичных последовательностей имеют всего одну информационную кодовую дорожку с расположенными вдоль нее n считывающими элементами с шагом, равным одному кванту шкалы, и обеспечивают разрешающую способность δ=360°/2n. Такие шкалы могут быть реализованы с использованием большинства известных методов считывания информации.
Недостатки прототипа
Низкая технологичность рекурсивной кодовой шкалы объясняется размещением вдоль кодовой дорожки шкалы считывающих элементов с шагом в один квант. Поскольку реальные считывающие элементы имеют конечные размеры, то при их размещении с шагом в один квант они вносят ограничения на габариты рекурсивной кодовой шкалы при заданной разрешающей способности.
В предлагаемом изобретении решается задача повышения технологичности рекурсивной кодовой шкалы на основе нелинейных двоичных последовательностей.
Для достижения технического результата рекурсивная кодовая шкала, содержащая информационную кодовую дорожку, выполненную в соответствии с символами нелинейной двоичной последовательности длиной N=2n, и n считывающих элементов, размещенных вдоль информационной кодовой дорожки с угловым шагом, равным величине кванта информационной кодовой дорожки δ=360°/N, снабжена второй информационной кодовой дорожкой, выполненной в соответствии с символами N периодов нелинейной двоичной последовательности длиной М=2m, и m считывающими элементами, размещенными вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), где δ2=360°/NM - величина кванта второй информационной кодовой дорожки и одновременно величина кванта рекурсивной кодовой шкалы, выходы n и m считывающих элементов в сумме определяют выходную разрядность рекурсивной кодовой шкалы.
Новым в предлагаемом изобретении является:
- совместное выполнение маски рекурсивной кодовой шкалы в виде двух кодовых дорожек: информационной кодовой дорожки, выполненной в соответствии с символами нелинейной двоичной последовательности длиной N=2n, второй информационной кодовой дорожки, выполненной в соответствии с символами N периодов нелинейной двоичной последовательности длиной М=2m, где единичным символам последовательностей соответствуют активные участки шкалы, а нулевым - пассивные;
- обеспечение разрешающей способности рекурсивной кодовой шкалы δ2=360°/NM, являющейся одновременно величиной кванта второй информационной кодовой дорожки;
- снабжение рекурсивной кодовой шкалы m считывающими элементами, размещенными вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2).
Совокупность существенных признаков в предлагаемом изобретении позволила:
- повысить технологичность рекурсивной кодовой шкалы за счет совместного соответствующего выполнения кодовой маски шкалы в виде двух информационных кодовых дорожек на основе нелинейных двоичных последовательностей, а также соответствующего размещения на них n и m считывающих элементов.
В результате этого можно сделать вывод о том, что предлагаемое изобретение позволяет получить технический результат.
Изобретение является новым, так как из уровня техники по доступным источникам информации не выявлено аналогов с подобной совокупностью признаков.
Изобретение является промышленно применимым, так как может быть использовано во всех областях, где требуется высокоточное позиционное определение углового положения объекта с использованием преобразователей угловых перемещений на основе заявляемых рекурсивных кодовых шкал.
Предлагаемое изобретение поясняется чертежом, где показана линейная развертка шестиразрядной рекурсивной кодовой шкалы.
Заявляемая рекурсивная кодовая шкала содержит информационную кодовую дорожку 1, вторую информационную кодовую дорожку 2, считывающие элементы 3, 4, 5 (n=3) и считывающие элементы 6, 7, 8 (m=3).
Для пояснения сути изобретения приведем некоторые теоретические предпосылки.
В [4] предложены КШ для преобразователей угловых перемещений, названные псевдослучайными кодовыми шкалами (ПСКШ) и строящиеся на основе использования теории псевдослучайных двоичных последовательностей максимальной длины (M-последовательностей). ПСКШ имеют всего одну информационную кодовую дорожку, выполненную в соответствии с символами M-последовательности a 0 a 1…a L-1, и n считывающих элементов (СЭ), размещенных вдоль дорожки. Считывающие элементы дают возможность получить при полном обороте шкалы L=2n-1 различных n-разрядных кодовых комбинаций и обеспечивают разрешающую способность преобразователя угловых перемещений на основе ПСКШ δ=360°/L.
Как следует из метода построения ПСКШ, ее разрешающая способность определяется длиной M-последовательности L=2n-1. Очевидно, что при любой разрядности шкалы теряется одна (нулевая) кодовая комбинация. Однако при построении некоторых технических систем с использованием преобразователей угловых перемещений необходимо обеспечить разрешающую способность последних, кратную 2n.
В [4] рассмотрены использованные в изобретении рекурсивные кодовые шкалы (РКШ), получившие название нелинейные кодовые шкалы (НКШ) и строящиеся на основе нелинейных двоичных последовательностей, которые обеспечивают разрешающую способность шкалы δ=360°/2n.
Нелинейная последовательность - это последовательность двоичных символов {a j} длиной N=2n, удовлетворяющих рекурсивному соотношению [5]
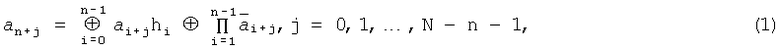
где знак ⊕ - означает суммирование по модулю два, а индексы при символах последовательности берутся по модулю N. Начальные значения символов a 0 a 1…a n-1 последовательности выбираются произвольно.
В (1) hi - коэффициенты, зависящие от вида примитивного полинома степени n с коэффициентами поля Галуа GF(2) [6], т.е.

где h0=hn=1, а hi=0,1 при 0<i<n,
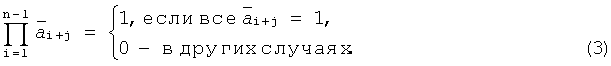
Первое слагаемое в (1) определяет правило образования линейной по отношению к оператору суммирования по модулю 2 M-последовательности. Второе слагаемое (3) в (1) указывает на операцию умножения значений n-1 кодовых символов. Это приводит к тому, что полученная последовательность символов становится нелинейной и в ней появляется комбинация, содержащая n последовательных нулей.
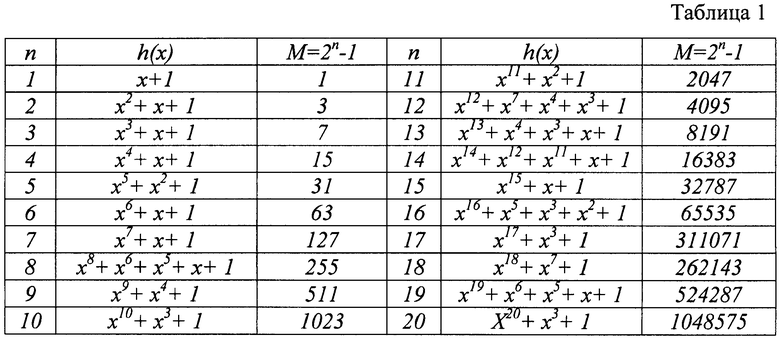
В табл.1 приведены полиномы h(x) до n=20 включительно, которые могут быть использованы для генерации соответствующих M-последовательностей [6].
Рассмотрим метод построения n-разрядной однодорожечной РКШ на основе нелинейной последовательности.
1. В зависимости от требуемой разрядности шкалы n из табл.1 выбирается полином h(x) степени n.
2. Используя рекурсивное соотношение (1), генерируется последовательность {a j}.
3. Элементарные участки (кванты) шкалы δ выполняются в соответствии с символами нелинейной последовательности {a j}, где символам 1 последовательности соответствуют активные, а символам 0 - пассивные участки информационной дорожки. Для определенности символы последовательности отображаются на информационной кодовой дорожке по ходу часовой стрелки в порядке a 0 a 1…a N-1.
4. Осуществляется размещение на шкале n считывающих элементов с шагом, равным одному кванту, т.е. в соответствии с полиномом размещения

Единственность такого размещения объясняется нелинейными свойствами рассматриваемой последовательности.
Поясним построение информационных кодовых дорожек РКШ, приведенных на чертеже.
В примере информационная кодовая дорожка 1 шкалы построена в соответствии с символами нелинейной последовательности {a
j}=a
0
a
1…a
7=0001011l длиной N=2n=23=8, для получения которой использован примитивный полином h(x)=х3+х+1, а символы а3+j последовательности {a
j} при начальных значениях a
0=a
1=a
2=0 удовлетворяют рекурсивному соотношению 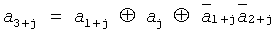 , j=0,1,…, 4. Нелинейная последовательность должна быть нанесена на шкалу в виде активных (единицы последовательности) и пассивных (нули последовательности) участков (квантов) информационной кодовой дорожки 1, например, по ходу часовой стрелки, причем на информационную кодовую дорожку 1 шкалы наносится только один период последовательности. Нелинейная последовательность с периодом N=2n определяет число квантов информационной кодовой дорожки 1 шкалы, которое в данном примере равно N=8. Отсюда величина кванта δ=360°/N=360°/δ=45°. В примере размещение СЭ 3, 4 и 5 (n=3) вдоль информационной кодовой дорожки 1 определяется полиномом r(x)=1+х+x2 и осуществляется с шагом, равным величине одного кванта информационной кодовой дорожки δ по ходу часовой стрелки.
, j=0,1,…, 4. Нелинейная последовательность должна быть нанесена на шкалу в виде активных (единицы последовательности) и пассивных (нули последовательности) участков (квантов) информационной кодовой дорожки 1, например, по ходу часовой стрелки, причем на информационную кодовую дорожку 1 шкалы наносится только один период последовательности. Нелинейная последовательность с периодом N=2n определяет число квантов информационной кодовой дорожки 1 шкалы, которое в данном примере равно N=8. Отсюда величина кванта δ=360°/N=360°/δ=45°. В примере размещение СЭ 3, 4 и 5 (n=3) вдоль информационной кодовой дорожки 1 определяется полиномом r(x)=1+х+x2 и осуществляется с шагом, равным величине одного кванта информационной кодовой дорожки δ по ходу часовой стрелки.
Фиксируя считывающими элементами 3, 4 и 5 последовательно кодовую комбинацию при перемещении РКШ циклически на один элементарный участок (квант), например, против хода часовой стрелки, получаем восемь различных трехразрядных кодовых комбинаций: 000, 001, 010, 101, 011, 111, 110 и 100.
По такому принципу теоретически может быть построена однодорожечная рекурсивная кодовая шкала любой разрядности.
Однако такой подход к построению однодорожечных рекурсивных кодовых шкал однозначно предполагает размещение считывающих элементов вдоль информационной дорожки шкалы с шагом в один квант. Поскольку реальные считывающие элементы имеют конечные размеры, то при таком их размещении они не позволят выполнить РКШ (а соответственно, и преобразователь угловых перемещений на ее основе) в заданных массогабаритных характеристиках при высокой (10 и выше) разрядности шкалы, что понижает технологичность ее изготовления.
С целью повышения технологичности рекурсивной кодовой шкалы в данном изобретении рекурсивную кодовую шкалу предлагается снабдить второй информационной кодовой дорожкой, выполненной в соответствии с символами N периодов нелинейной двоичной последовательности длиной М=2m, и m считывающими элементами, размещенными вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), где δ2=360°/NM - величина кванта второй информационной кодовой дорожки.
Повышение технологичности рекурсивной кодовой шкалы достигается за счет того, что:
- для построения информационной и второй информационной кодовых дорожек РКШ используются нелинейные двоичные последовательности малой длины. При этом суммарная разрядность двухдорожечной рекурсивной кодовой шкалы будет определяться как (n+m);
- использование для построения информационной кодовой дорожки шкалы нелинейной двоичной последовательности малой длины обеспечивает (за счет достаточного углового шага δ) технологичное размещение вдоль такой дорожки n СЭ;
- размещение m считывающих элементов вдоль второй информационной кодовой дорожки выполнено с угловым шагом (δ+δ2), где δ2=360°/NM - величина кванта второй информационной кодовой дорожки.
На чертеже вторая информационная кодовая дорожка 2 РКШ построена в соответствии с символами нелинейной последовательности {a
j}=a
0
a
1…a
7=00010111 длиной M=2m=23=8, для получения которой использован примитивный полином h(x)=х3+x+1, а символы а
3+j последовательности {a
j} при начальных значениях a
0=a
1=a
2=0 удовлетворяют рекурсивному соотношению 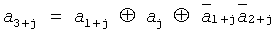 , j=0,1,…,4. Нелинейная последовательность должна быть нанесена на РКШ в виде активных (единицы последовательности) и пассивных (нули последовательности) участков (квантов) информационной кодовой дорожки 2, например, по ходу часовой стрелки, причем на информационную кодовую дорожку 2 РКШ наносятся N=8 периодов последовательности. Восемь периодов нелинейной последовательности длиной M=23=8 определяют число квантов второй информационной кодовой дорожки РКШ, которое в данном примере равно NM=64. Отсюда величина кванта второй информационной кодовой дорожки δ2=360°/NM=360°/64=5,625°.
, j=0,1,…,4. Нелинейная последовательность должна быть нанесена на РКШ в виде активных (единицы последовательности) и пассивных (нули последовательности) участков (квантов) информационной кодовой дорожки 2, например, по ходу часовой стрелки, причем на информационную кодовую дорожку 2 РКШ наносятся N=8 периодов последовательности. Восемь периодов нелинейной последовательности длиной M=23=8 определяют число квантов второй информационной кодовой дорожки РКШ, которое в данном примере равно NM=64. Отсюда величина кванта второй информационной кодовой дорожки δ2=360°/NM=360°/64=5,625°.
Таким образом, в примере размещение СЭ 6, 7 и 8 (m=3) вдоль второй информационной кодовой дорожки 2 осуществляется с шагом, равным величине (δ+δ2)=45°+5,625°=50,625° по ходу часовой стрелки.
В нашем примере суммарная разрядность, обеспечиваемая информационной и второй информационной кодовыми дорожками при рассмотренном выше размещении СЭ, будет равна (n+m)=3+3=6.
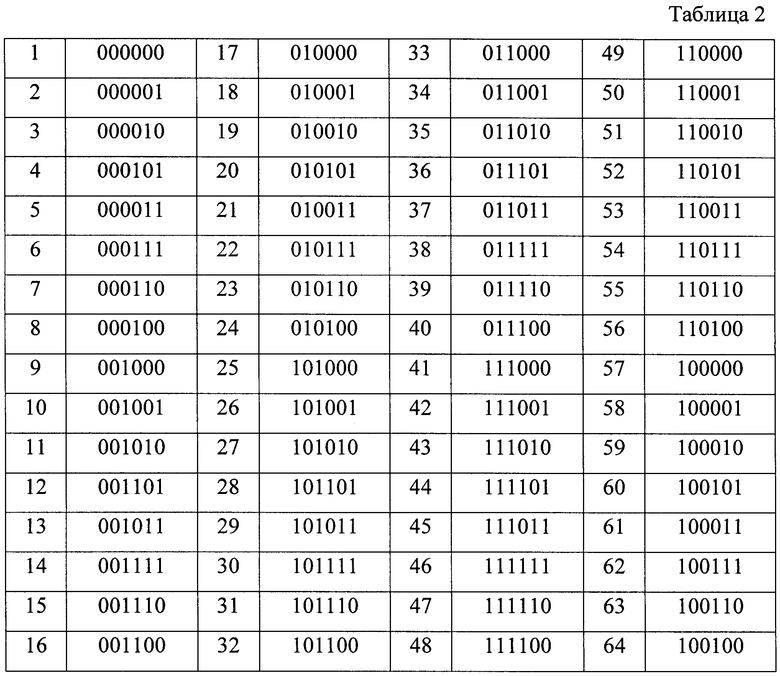
Фиксируя считывающими элементами 3, 4, 5 и 6, 7, 8 последовательно кодовую комбинацию, при перемещении РКШ циклически на один элементарный участок (квант) второй информационной кодовой дорожки δ2, например, против хода часовой стрелки, получаем 64 различных шестиразрядных кодовых комбинаций, которые соответствуют 64 угловым положениям шкалы. Эти кодовые комбинации приведены в табл.2.
В рассматриваемом примере для построения информационной 1 и второй информационной кодовых дорожек 2 использована одна и та же нелинейная двоичная последовательность, т.е. N=M=8. В общем случае допускается N≠M. Например, шестиразрядная рекурсивная кодовая шкала может быть построена еще двумя способами, где (n=4, m=2) и (n=2, m=4). С увеличением разрядности двухдорожечной рекурсивной кодовой шкалы число вариантов ее построения также возрастает. Данный подход дает дополнительные возможности для выбора наиболее технологичного варианта построения РКШ (и, как следствие, преобразователя угловых перемещений на ее основе), что связано с возможностью многовариантного размещения на шкале считывающих элементов.
Таким образом, предлагаемое изобретение позволяет повысить технологичность рекурсивных кодовых шкал, построенных на основе нелинейных двоичных последовательностей.
Литература
1. Фотоэлектрические преобразователи информации. / Л.Н.Преснухин, С.А.Майоров, И.В.Меськин, В.Ф.Шаньгин. Под ред. Л.Н.Преснухина. - М.: Машиностроение, 1974. - 375 с.
2. Домрачев В.Г., Мейко Б.С. Цифровые преобразователи угла: принципы построения, теория точности, методы контроля. - М.: Энергоатомиздат, 1984. - 328 с.
3. Азов А.К, Ожиганов А.А., Тарасюк М.В. Рекурсивные кодовые шкалы. //Издательство "Машиностроение" Информационные технологии, 1998, № 6. С.39-43.
4. Ожиганов А.А. Псевдослучайные кодовые шкалы. // Изв. Вузов. Приборостроение, 1987. Т.30. № 2. С.40-43.
5. Агульник А.Р., Мусаелян С.С. Построение нелинейных двоичных последовательностей. // Радиоэлектроника. 1983. № 4. С.19-28.
6. Макуильямс Ф.Д., Слоан Н.Д. Псевдослучайные последовательности и таблицы. //ТИИЭР. 1976. Т.64. № 12. С.80-95.
| название | год | авторы | номер документа |
|---|---|---|---|
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2010 |
|
RU2444126C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2011 |
|
RU2446557C1 |
| РЕКУРСИВНАЯ КОДОВАЯ ШКАЛА | 2011 |
|
RU2450437C1 |
| ИНВЕРСНО-СОПРЯЖЕННАЯ КОДОВАЯ ШКАЛА | 2013 |
|
RU2553079C1 |
| КОДОВАЯ ШКАЛА | 2016 |
|
RU2658188C2 |
| Псевдослучайная кодовая шкала | 2019 |
|
RU2709666C1 |
| Псевдослучайная кодовая шкала | 2017 |
|
RU2660609C1 |
| Псевдослучайная кодовая шкала | 2021 |
|
RU2761058C1 |
| Псевдослучайная кодовая шкала | 2022 |
|
RU2777832C1 |
| ПСЕВДОСЛУЧАЙНАЯ КОДОВАЯ ШКАЛА | 2012 |
|
RU2510572C1 |
Изобретение относится к измерительной технике, в частности к аналого-цифровому преобразованию, а именно к кодовым шкалам преобразователей угла поворота вала в код. Технический результат - повышение технологичности рекурсивной кодовой шкалы на основе нелинейных двоичных последовательностей. Рекурсивная кодовая шкала содержит информационную кодовую дорожку, выполненную в соответствии с символами нелинейной двоичной последовательности длиной N=2n, и n считывающих элементов, размещенных вдоль информационной кодовой дорожки с угловым шагом, равным величине кванта информационной кодовой дорожки δ=360°/N, вторую информационную кодовую дорожку, выполненную в соответствии с символами N периодов нелинейной двоичной последовательности длиной M=2m и m считывающих элементов, размещенных вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), где δ2=360°/NM - величина кванта второй информационной кодовой дорожки и одновременно величина кванта рекурсивной кодовой шкалы, выходы пит считывающих элементов в сумме определяют выходную разрядность рекурсивной кодовой шкалы. 1 ил., 2 табл.
Рекурсивная кодовая шкала, содержащая информационную кодовую дорожку, выполненную в соответствии с символами нелинейной двоичной последовательности длиной N=2n и n считывающих элементов, размещенных вдоль информационной кодовой дорожки с угловым шагом, равным величине кванта информационной кодовой дорожки δ=360°/N, отличающаяся тем, что рекурсивная кодовая шкала снабжена второй информационной кодовой дорожкой, выполненной в соответствии с символами N периодов нелинейной двоичной последовательности длиной M=2m, и m считывающими элементами, размещенными вдоль второй информационной кодовой дорожки с угловым шагом (δ+δ2), где δ2=360°/NM - величина кванта второй информационной кодовой дорожки и одновременно величина кванта рекурсивной кодовой шкалы, выходы n и m считывающих элементов в сумме определяют выходную разрядность рекурсивной кодовой шкалы.
| Фрикционная передача вращения | 1948 |
|
SU79360A1 |
| Преобразователь угол-код | 1987 |
|
SU1474843A1 |
| Преобразователь угол-код | 1987 |
|
SU1534748A1 |
| US 6445316 В1, 03.10.2002. | |||
Авторы
Даты
2011-11-20—Публикация
2010-08-16—Подача