Изобретение относится к области аэрокосмической техники, а именно к способам определения аэродинамических характеристик (AX) - зависимостей коэффициентов аэродинамических сил и моментов, действующих на воздушные суда (ВС), от определяющих параметров: числа М полета, углов атаки и скольжения, углов отклонения управляющих поверхностей и т.п. Изобретение может быть использовано при обработке материалов летных испытаний воздушных судов.
Получение достоверной модели аэродинамических характеристик воздушного судна во всем исследованном в летных испытаниях диапазоне изменения параметров полета и управления позволит:
- повысить эффективность летных испытаний;
- использовать полученные характеристики, соответствующие реальным аэродинамическим характеристикам данного типа воздушных судов, подтвержденные материалами летных испытаний, при создании тренажеров;
- сократить сроки летных испытаний и снизить затраты на их проведение.
Основные термины и определения
Силы и моменты, действующие на ВС в полете
В полете на ВС действуют следующие силы и моменты:
- сила тяжести (вес воздушного судна) G;
- проекции аэродинамической силы, обусловленной воздействием обтекающего потока воздуха: аэродинамическая продольная сила Х, аэродинамическая нормальная сила Y , аэродинамическая поперечная сила Z. Аэродинамические характеристики, т.е. зависимости коэффициентов аэродинамических сил и моментов от различных параметров (от значений угла атаки, угла скольжения, углов отклонения поверхностей управления и т.п.), получаемые в результате продувок в аэродинамических трубах и используемые для моделирования динамики ВС, могут быть представлены в различных системах координат, используемых для исследования динамики полета ВС: в связанной, в скоростной или в полусвязанной системах координат. В зависимости от используемой системы координат аэродинамические силы, моменты, а также коэффициенты сил и моментов записываются с соответствующими индексами. В связанной системе координат нормальная, продольная и поперечная силы (составляющие аэродинамической силы по осям OY, ОХ и OZ) обозначаются буквами Y, Х и Z. В скоростной системе координат подъемная сила (составляющая по оси OYa) обозначается Ya, сила лобового сопротивления (составляющая по оси ОХa) - Хa, боковая сила (составляющая по оси OZa) - Za. Соответствующие коэффициенты составляющих аэродинамической силы в связанной системе координат обозначаются Сy, Сx, Сz, а в скоростной системе координат - Сya, Сxa и Сza. В настоящей работе мы будем для краткости использовать представление аэродинамических характеристик в связанной системе координат. Выражения в других системах координат имеют аналогичный вид, отличающийся только использованием соответствующих индексов для обозначения системы координат (см. В.Г.Микеладзе, В.М.Титов. «Основные геометрические и аэродинамические характеристики самолетов и ракет». Справочник. Москва, «Машиностроение», 1990). Формулы для пересчета сил и моментов (и коэффициентов сил и моментов) из одной системы координат в другую приведены, например, в С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник». Москва, «Машиностроение», 1969; В.Г.Микеладзе, В.М.Титов. «Основные геометрические и аэродинамические характеристики самолетов и ракет». Справочник. Москва, «Машиностроение», 1990; М.И.Хейфец. «Обработка результатов испытаний. Алгоритмы, номограммы, таблицы». Москва, «Машиностроение», 1988. (Справочная библиотека авиационного инженера-испытателя);
- проекции вектора тяги на оси системы координат (Px, Рy и Рz);
- проекции аэродинамического момента Мx, Мy и Мz на соответствующие оси;
- проекции момента силы тяжести на соответствующие оси;
- проекции момента тяги на оси системы координат (Мрx, Мрy и Мрz).
Коэффициенты аэродинамических сил и моментов
Величины аэродинамических сил и моментов, действующих на ВС, зависят от величины скоростного напора набегающего потока воздуха, поэтому их представляют в виде произведений:
X=Cx·q·S
Y=Cy·q·S
Z=Cz·q·S

My=my·q·S·l
Mz=mz·q·S·ba,
где X, Y и Z - составляющие аэродинамической силы, Сx, Сy, Сz - коэффициенты аэродинамических сил в связанной системе координат, Мx, My и Мz - проекции аэродинамического момента на соответствующие оси, mx, my и mz - коэффициенты аэродинамических моментов, q - скоростной напор, S - площадь крыла, l - размах крыла, ba - средняя аэродинамическая хорда. В скоростной системе координат подъемная сила (составляющая по оси OYa) обозначается Ya, сила лобового сопротивления (составляющая по оси ОХa) - Хa, боковая сила (составляющая по оси OZa) - Za. В настоящей работе в основном мы будем для краткости использовать представление аэродинамических характеристик в связанной системе координат. Выражения в других системах координат имеют аналогичный вид, отличающийся только использованием соответствующих индексов для обозначения системы координат (см. В.Г.Микеладзе, В.М.Титов. «Основные геометрические и аэродинамические характеристики самолетов и ракет». Справочник. Москва, «Машиностроение», 1990). Формулы для пересчета сил и моментов (и коэффициентов сил и моментов) из одной системы координат в другую приведены, например, в С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник». Москва, «Машиностроение», 1969; В.Г.Микеладзе, В.М.Титов. «Основные геометрические и аэродинамические характеристики самолетов и ракет». Справочник. Москва, «Машиностроение», 1990; М.И.Хейфец. «Обработка результатов испытаний. Алгоритмы, номограммы, таблицы». Москва, «Машиностроение», 1988. (Справочная библиотека авиационного инженера-испытателя). Проекции вектора тяги на оси связанной системы координат обозначают Рx, Рy и Рz, а соответствующие коэффициенты проекций силы тяги - 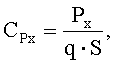
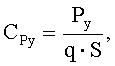
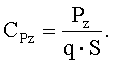
Математическая модель аэродинамических характеристик
Математическая модель аэродинамических характеристик (AX) - это алгоритм расчета коэффициентов аэродинамических сил и моментов, действующих на ВС в полете, и данные, которые используются при расчете. Другими словами, математическая модель АХ является совокупностью зависимостей коэффициентов аэродинамических сил и моментов от различных параметров, определяющих обтекание планера. Как правило, такие зависимости определяются в результате продувок моделей планера ВС в аэродинамических трубах (АДТ). При этом аэродинамические силы и моменты измеряют с помощью аэродинамических весов. Эксперименты в АДТ планируют таким образом, чтобы измерить аэродинамические силы и моменты, действующие на продуваемую модель планера ВС при различных заданных значениях числа М, различных заданных значениях параметров углов атаки и скольжения, а также при различных заданных положениях поверхностей управления и механизации крыла. В результате получают таблицы значений коэффициентов аэродинамических сил и моментов при заданных значениях параметров. Для получения значений в промежуточных точках используют тот или иной метод интерполяции (чаще всего - линейную интерполяцию).
Обычно для современных ВС выражения для вычисления коэффициентов аэродинамических сил и моментов представляют собой суммы некоторого количества слагаемых (составляющих), каждое из которых вычисляют с помощью интерполяции по соответствующим таблицам значений. Иногда результат интерполяции еще умножается на какой-либо параметр или коэффициент. Например, выражение для вычисления коэффициента аэродинамической нормальной силы в крейсерской конфигурации некоторого ВС может иметь вид:
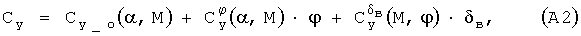
где α - угол атаки, М - число Маха, φ - угол отклонения стабилизатора, δв - угол отклонения руля высоты, Сy_о(α,M) - функция, описывающая зависимость коэффициента подъемной силы от угла атаки и числа Маха при нейтральных положениях стабилизатора и руля высоты, 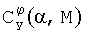 - функция, описывающая зависимость производной коэффициента подъемной силы по отклонению стабилизатора от угла атаки и числа Маха,
- функция, описывающая зависимость производной коэффициента подъемной силы по отклонению стабилизатора от угла атаки и числа Маха, 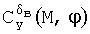 - функция, описывающая зависимость производной коэффициента подъемной силы по отклонению руля высоты от числа Маха и угла отклонения стабилизатора. Аналогичное выражение для другого ВС, у которого, например, отсутствует стабилизатор, может иметь и несколько другой вид, например, такой:
- функция, описывающая зависимость производной коэффициента подъемной силы по отклонению руля высоты от числа Маха и угла отклонения стабилизатора. Аналогичное выражение для другого ВС, у которого, например, отсутствует стабилизатор, может иметь и несколько другой вид, например, такой:
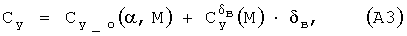
или такой:
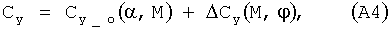
если руль высоты отсутствует, а зависимость коэффициента подъемной силы от числа Маха и угла отклонения стабилизатора ΔСy(М,φ) нелинейная. Значения функций Сy_о(α,М), 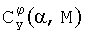 ,
, 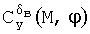 (и других функций, входящих в выражения для вычисления коэффициентов аэродинамических сил и моментов) для заданных значений угла атаки α, числа М полета, угла отклонения стабилизатора φ и т.п. часто задают с помощью таблиц значений и вычисляют посредством интерполяции. Возможны и другие способы задания и вычисления таких функций, например, с помощью полиномов или сплайн-функций.
(и других функций, входящих в выражения для вычисления коэффициентов аэродинамических сил и моментов) для заданных значений угла атаки α, числа М полета, угла отклонения стабилизатора φ и т.п. часто задают с помощью таблиц значений и вычисляют посредством интерполяции. Возможны и другие способы задания и вычисления таких функций, например, с помощью полиномов или сплайн-функций.
Аналогично, для вычисления других коэффициентов аэродинамических сил и моментов в результате продувок в АДТ получают выражения в виде сумм составляющих, каждую из составляющих вычисляют с помощью линейной интерполяции по соответствующей таблице (массиву данных) или каким-либо другим способом.
Во взлетно-посадочной конфигурации зависимость коэффициентов аэродинамических сил и моментов от числа М обычно не учитывается, однако в этой конфигурации необходимо учитывать зависимости всех коэффициентов от положения органов механизации крыла, от выпуска шасси, воздушных тормозов, влияние близости земли («экрана») и т.п.
Алгоритм вычисления (или способ определения) составляющих тяги силовой установки, краткое описание возможных способов определения составляющих тяги в условиях полета (с использованием результатов исследований на стендах, на летающих лабораториях, расчета высотно-скоростных характеристик (ВСХ) и т.д.).
Алгоритм, реализующий способ определения составляющих тяги силовой установки в условиях полета, вычисления составляющих тяги силовой установки в условиях полета на основе измерения того или иного набора параметров, характеризующих работу силовой установки (положение рычага управления двигателями (РУД), режим работы двигателей, частоты вращения роторов двигателей, отборы воздуха, отборы мощности, и т.п.). В простейшем случае - это алгоритм расчета составляющих тяги на основе ВСХ двигателей или какой-либо выборки из ВСХ, полученной специально для некоторой области параметров полета и режимов работы силовой установки. Подобную выборку можно рассчитать, например, с помощью математической (газодинамической) модели двигателя.
Это могут быть также алгоритмы расчета составляющих тяги силовой установки в случае достаточно подробного дополнительного (экспериментального, «нештатного») препарирования входного и выходного сечений двигателей или установки специальных датчиков для измерения усилий в узлах подвески двигателей. Это может быть также какой-либо алгоритм, реализующий комплексный метод определения составляющих тяги силовой установки, когда используется газодинамическая модель двигателя и некоторый набор штатных замеров. Известно, что для регулирования современных двигателей используют достаточно большое количество измеряемых в полете параметров (штатных замеров), многие из которых регистрируются в системе бортовых измерений и оказываются полезными для определения (вычисления) составляющих тяги силовой установки в условиях полета. Параметры математической модели силовой установки определяют в результате испытаний на стендах и уточняют в результате летных испытаний опытных экземпляров двигателей (обычно имеющих некоторое дополнительное экспериментальное препарирование, т.е. дополнительный набор измеряемых параметров, характеризующих работу двигателей).
В число задач летных испытаний ВС входят задачи определения летно-технических характеристик и задачи определения (или уточнения и проверки достоверности) математической модели аэродинамических характеристик ВС, полученной на основе продувок в АДТ (АХ), а также проверка соответствия тягово-расходных характеристик силовой установки, полученных на основе стендовых исследований и испытаний, материалам летных испытаний. В случае получения на основе летных испытаний достоверной уточненной модели динамики ВС (т.е. модели аэродинамических характеристик в совокупности с тягово-расходными характеристиками) значительная часть летно-технических характеристик может быть получена расчетным путем, что может значительно сократить сроки летных испытаний и расходы на их проведение. Кроме того, наличие достоверной модели динамики ВС необходимо для создания тренажеров, на которых будут проходить обучение пилоты ВС данного типа.
Известен способ определения некоторых параметров аэродинамических и тяговых характеристик, в котором используется идентификация (оценивание) по методу наименьших квадратов (далее - МНК) (см. Д.Худсон. «Статистика для физиков». Москва, издательство «Мир», 1970).
В известном способе в ходе эксперимента измеряют (или вычисляют на основе измерений некоторого набора параметров) некоторый изменяющийся параметр 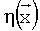 , который называется наблюдаемым параметром. При этом результаты измерений содержат случайную ошибку измерений
, который называется наблюдаемым параметром. При этом результаты измерений содержат случайную ошибку измерений 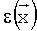 . Всего мы имеем n результатов измерений yi:
. Всего мы имеем n результатов измерений yi:
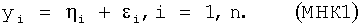
Параметр 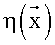 представляют в виде линейной комбинации некоторых m заданных функций
представляют в виде линейной комбинации некоторых m заданных функций 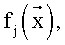 значения которых также могут быть определены в результате эксперимента, т.е. они измеряются или могут быть вычислены на основе некоторого набора измеренных параметров, который можно назвать вектором
значения которых также могут быть определены в результате эксперимента, т.е. они измеряются или могут быть вычислены на основе некоторого набора измеренных параметров, который можно назвать вектором 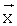 :
:
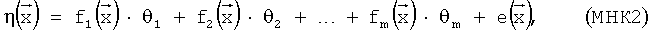
причем значения множителей θj неизвестны. Здесь 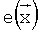 - ошибка (погрешность) представления
- ошибка (погрешность) представления 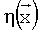 в виде разложения по
в виде разложения по 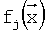 . Можно считать, что ошибка представления мала по сравнению с погрешностью измерения εi и в явном виде ее далее можно не упоминать. Значения m заданных функций для каждого i-го измерения уi параметра
. Можно считать, что ошибка представления мала по сравнению с погрешностью измерения εi и в явном виде ее далее можно не упоминать. Значения m заданных функций для каждого i-го измерения уi параметра 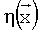 и соответствующего набора измеренных параметров, составляющих вектор
и соответствующего набора измеренных параметров, составляющих вектор 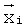 , составляют строку матрицы А, т.е.
, составляют строку матрицы А, т.е.
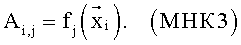
Более компактно записывают в матричном виде:
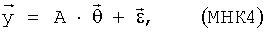
где 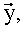
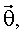
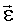 - вектора размерностей n, m и n соответственно, А - матрица размерности n·m. Матрицу А ранга m часто называют структурной, конструкционной или регрессионной матрицей. Задача состоит в получении оценок множителей θj, j=1, …, m на основе измерений параметров в процессе проведения эксперимента. Оценки получают с помощью метода наименьших квадратов (МНК). Минимизируется остаточная сумма квадратов
- вектора размерностей n, m и n соответственно, А - матрица размерности n·m. Матрицу А ранга m часто называют структурной, конструкционной или регрессионной матрицей. Задача состоит в получении оценок множителей θj, j=1, …, m на основе измерений параметров в процессе проведения эксперимента. Оценки получают с помощью метода наименьших квадратов (МНК). Минимизируется остаточная сумма квадратов 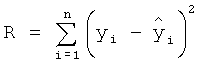 , где
, где 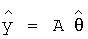 . Если ввести вектор остатков
. Если ввести вектор остатков 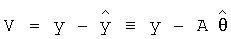 , то минимизация величины R, которая определена равенством (II.12), эквивалентна минимизации квадратичной формы R=V'V (штрих означает операцию транспонирования). В результате минимизации получаем оценку вектора множителей θ:
, то минимизация величины R, которая определена равенством (II.12), эквивалентна минимизации квадратичной формы R=V'V (штрих означает операцию транспонирования). В результате минимизации получаем оценку вектора множителей θ:
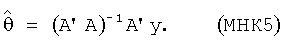
Если известна структурная матрица А и матрица, обратная (А'·А), существует, то оценку значений множителей 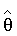 получают с помощью формулы (МНК5). Случай некоррелированных ошибок εi с одинаковыми дисперсиями чаще всего имеет место при проведении летных испытаний, однако, вообще говоря, МНК применим и для случая коррелированных погрешностей измерений с неодинаковыми дисперсиями. Будем считать, что ошибки ε подчиняются совместному распределению с нулевым математическим ожиданием, т.е. что
получают с помощью формулы (МНК5). Случай некоррелированных ошибок εi с одинаковыми дисперсиями чаще всего имеет место при проведении летных испытаний, однако, вообще говоря, МНК применим и для случая коррелированных погрешностей измерений с неодинаковыми дисперсиями. Будем считать, что ошибки ε подчиняются совместному распределению с нулевым математическим ожиданием, т.е. что
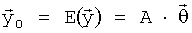 ,
,
где E(…) - операция получения математического ожидания, 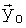 - математическое ожидание, и
- математическое ожидание, и 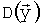 - ковариационная матрица ранга n
- ковариационная матрица ранга n

где 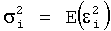 , и σiσjρi,j=E(εi·εj). Оценка вектора множителей
, и σiσjρi,j=E(εi·εj). Оценка вектора множителей 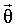 по МНК при наличии коррелированных ошибок измерений вычисляется по формуле:
по МНК при наличии коррелированных ошибок измерений вычисляется по формуле:
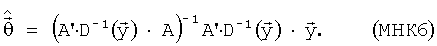
Определение коэффициентов аэродинамических сил и моментов в фактических условиях полета
В литературе описаны некоторые известные способы определения аэродинамических характеристик ВС с применением методов идентификации. Все рассматриваемые в этих работах способы основаны на том, что вначале определяют значения коэффициентов аэродинамических сил и моментов в фактических условиях полета (см., например, В.А.Касьянов, Е.П.Ударцев. «Определение характеристик воздушных судов методами идентификации». Москва, Машиностроение, 1988, стр.150-164; «Методы исследований на летающих моделях». Справочная библиотека авиационного инженера-испытателя. Летные испытания самолетов и вертолетов. /Под общей редакцией А.Д.Миронова. Москва, Машиностроение, 1988, с.41-52; «Методы определения характеристик устойчивости и управляемости самолета». Справочная библиотека авиационного инженера-испытателя. Летные испытания самолетов и вертолетов. /Под общей редакцией Ю.И.Снешко. Москва, Машиностроение, 1994, с.126-136).
При проведении летных испытаний воздушных судов измеряют параметры движения: высоту, скорость полета, температуру заторможенного потока наружного воздуха, углы атаки и скольжения, угловое положение относительно поверхности Земли, угловые скорости и ускорения, перегрузки. Угловые ускорения часто определяют (вычисляют) методами численного дифференцирования (см. К.К.Васильченко, В.А.Леонов, И.М.Пашковский, Б.К.Поплавский. «Летные испытания самолетов». Москва, «Машиностроение», 1996; И.М.Пашковский, В.А.Леонов, Б.К.Поплавский. «Летные испытания самолетов и обработка результатов испытаний». Москва, «Машиностроение», 1985). Измеряют параметры (суммарный остаток топлива, возможно - остатки топлива в баках, и т.п.), позволяющие определить массово-инерционные характеристики воздушного судна (массу, положение центра масс и моменты инерции). Также измеряют параметры, необходимые для определения положения поверхностей управления и составляющих тяги двигателей (частоты вращения роторов двигателей, положения рычагов управления двигателями и т.д.). На основании этих измерений вычисляют значения коэффициентов аэродинамических сил и моментов, действующих на ВС в фактических условиях полета.
В процессе предполетной подготовки определяют угол установки датчиков перегрузки Δαуст. Для этого ВС устанавливают в линию полета и регистрируют показания датчика продольной перегрузки 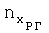 . Значение Δαуст вычисляют по формуле
. Значение Δαуст вычисляют по формуле 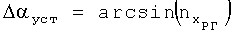 . В летных испытаниях измеряют углы отклонения поверхностей управления (углы отклонения стабилизаторов φСТ, рулей высоты δв, рулей направления δН, элеронов δЭ и т.д., в зависимости от конструкции типа ВС и рассматриваемой конфигурации (например, крейсерской, взлетно-посадочной)). Также в полете измеряют продольную
. В летных испытаниях измеряют углы отклонения поверхностей управления (углы отклонения стабилизаторов φСТ, рулей высоты δв, рулей направления δН, элеронов δЭ и т.д., в зависимости от конструкции типа ВС и рассматриваемой конфигурации (например, крейсерской, взлетно-посадочной)). Также в полете измеряют продольную 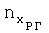 , нормальную
, нормальную 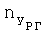 перегрузки в связанных осях и угол атаки α самолета. Далее с использованием зарегистрированных значений перегрузок
перегрузки в связанных осях и угол атаки α самолета. Далее с использованием зарегистрированных значений перегрузок 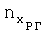 и
и 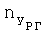 и полученного ранее значения угла установки датчиков перегрузки Δαуст вычисляют значения перегрузок nx (продольной) и ny (нормальной) в связанных осях:
и полученного ранее значения угла установки датчиков перегрузки Δαуст вычисляют значения перегрузок nx (продольной) и ny (нормальной) в связанных осях:
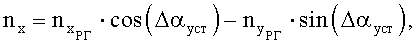
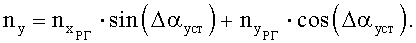
Если, как часто бывает, коэффициенты аэродинамических сил заданы в скоростной системе координат, то на основе измеренных значений перегрузок в связанной системе координат вычисляют по известным формулам (см. С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник». Москва, «Машиностроение», 1969; М.И.Хейфец. «Обработка результатов испытаний. Алгоритмы, номограммы, таблицы». Москва, «Машиностроение», 1988. (Справочная библиотека авиационного инженера-испытателя) значения перегрузок в скоростной системе координат:
nXa=nX·cos(α)·cos(β)-nY·sin(α)·cos(β)+nZ·sin(β)
nYa=nX·sin(α)+nY·cos(α)
nZa=-nX·cos(α)·sin(β)+nY·sin(α)·sin(β)+nZ·cos(β),
и далее вычисляют значения коэффициентов результирующих сил:
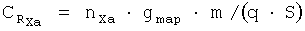
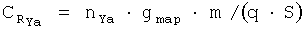
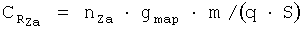 ,
,
предварительно вычислив по известным алгоритмам (см. B.C.Ведров, М.А.Тайц. «Летные испытания самолетов». Государственное издательство оборонной промышленности, Москва, 1951; М.Г.Котик, А.В.Павлов, И.М.Пашковский, Н.Г.Щитаев. «Летные испытания самолетов». Москва, «Машиностроение», 1968) число М полета и скоростной напор q на основе измеренных значений приборной высоты и приборной скорости, а также вычислив текущее значение массы самолета m на основе измерения остатка топлива (или интегрирования мгновенного расхода топлива). Здесь gmap - значение ускорения свободного падения в месте тарировки датчиков, если тарировка производится с помощью грузиков и/или установки датчиков под углом к вертикали.
Ниже приводятся алгоритмы вычисления коэффициентов аэродинамических сил и моментов в связанной системе координат. Коэффициенты моментов аэродинамических сил часто задаются именно в связанной системе координат, независимо от того, в какой системе координат заданы коэффициенты аэродинамических сил. Сначала на основе измерений высотно-скоростных параметров, перегрузок, углов, угловых скоростей и т.п. определяются коэффициенты результирующих сил и моментов:
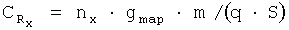
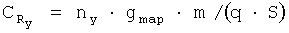
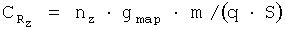
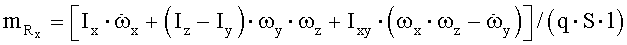

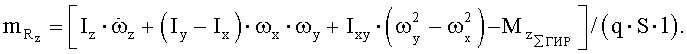
Здесь 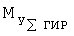 - суммарная проекция гироскопического момента роторов двигателей на связанную ось ОY,
- суммарная проекция гироскопического момента роторов двигателей на связанную ось ОY, 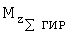 - суммарная проекция гироскопического момента роторов двигателей на связанную ось OZ. Проекция гироскопического момента одного ротора на связанную ось OY вычисляется по формуле
- суммарная проекция гироскопического момента роторов двигателей на связанную ось OZ. Проекция гироскопического момента одного ротора на связанную ось OY вычисляется по формуле  , где IP - момент инерции ротора, ωP - угловая скорость ротора, а проекция гироскопического момента одного ротора на связанную ось OZ - по формуле
, где IP - момент инерции ротора, ωP - угловая скорость ротора, а проекция гироскопического момента одного ротора на связанную ось OZ - по формуле 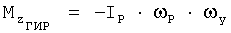 . Далее вычисляют значения коэффициентов аэродинамических сил и моментов, вычитая из значений коэффициентов результирующих сил и моментов соответствующие коэффициенты проекций тяги двигательной установки и моментов тяги двигательной установки на оси связанной системы координат:
. Далее вычисляют значения коэффициентов аэродинамических сил и моментов, вычитая из значений коэффициентов результирующих сил и моментов соответствующие коэффициенты проекций тяги двигательной установки и моментов тяги двигательной установки на оси связанной системы координат:
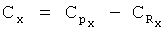 ,
,
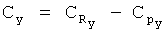 ,
,
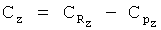 ,
,
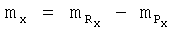 ,
,
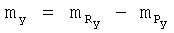 ,
,
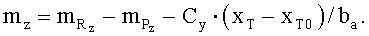
Здесь 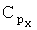 ,
, 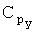 ,
, 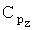 - коэффициенты проекций силы тяги двигательной установки на оси связанной системы координат,
- коэффициенты проекций силы тяги двигательной установки на оси связанной системы координат, 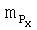 ,
, 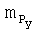 ,
, 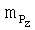 - коэффициенты проекций моментов тяги двигательной установки на оси связанной системы координат, Сy·(xT-xT0)/ba - поправка к значению коэффициента mz для учета смещения центра масс ВС, xT - текущее положение центра масс, хT0 - положение центра масс, для которого определены (заданы) «продувочные» значения mz (см. С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник». Москва, «Машиностроение», 1969, стр.273, раздел 5.3.10).
- коэффициенты проекций моментов тяги двигательной установки на оси связанной системы координат, Сy·(xT-xT0)/ba - поправка к значению коэффициента mz для учета смещения центра масс ВС, xT - текущее положение центра масс, хT0 - положение центра масс, для которого определены (заданы) «продувочные» значения mz (см. С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник». Москва, «Машиностроение», 1969, стр.273, раздел 5.3.10).
После того как получены наборы значений коэффициентов аэродинамических сил Сx, Сy, Cz, mz, mx, my и соответствующие наборы значений параметров полета, углы атаки и скольжения, число М, отклонения поверхностей управления в фактических условиях, переходят к определению зависимостей коэффициентов аэродинамических сил и моментов от параметров полета и отклонений поверхностей управления. Для этого применяют идентификацию по методу наименьших квадратов. Процедуру идентификации осуществляют для каждого коэффициента Сx, Сy, mz, Сz, mx, my по- отдельности.
В работе В.А. Касьянов, Е.П.Ударцев. «Определение характеристик воздушных судов методами идентификации». Москва, Машиностроение, 1988, стр.150-164 приведен пример идентификации зависимостей коэффициентов Сx, Сy, mz от угла атаки α и числа М полета (зависимости коэффициентов от угла отклонения руля высоты в данной работе не рассматривали).
При идентификации зависимости коэффициента Сy в качестве координат вектора измерений yi, i=1,n использовали вычисленные в различные моменты времени ti значения коэффициента подъемной силы Сy:
yi=Cy(ti).
В качестве координат вектора 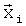 в указанной работе использовали полученные в различные моменты времени ti значения угла атаки αi и числа Мi полета. В качестве «заданных функций»
в указанной работе использовали полученные в различные моменты времени ti значения угла атаки αi и числа Мi полета. В качестве «заданных функций» 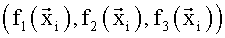 выбрали:
выбрали:
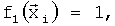
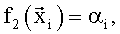
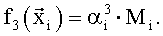
Далее вычислили по формуле (5) вектор оценок множителей 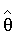 и значения координат вектора присвоили следующим параметрам:
и значения координат вектора присвоили следующим параметрам:
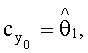
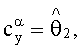
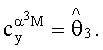
В результате получили зависимость коэффициента подъемной силы от угла атаки и числа М следующего вида:
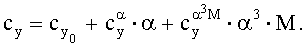
При идентификации зависимости коэффициента Сx в качестве координат вектора измерений yi, i=1,n использовали вычисленные в различные моменты времени ti значения коэффициента лобового сопротивления Сx:
yi=Cx(ti).
В качестве «заданных функций» 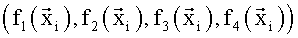 выбрали:
выбрали:
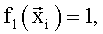
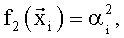
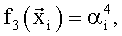
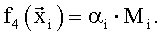
После вычисления по формуле (5) вектора оценок множителей 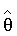 и значения координат вектора присвоили параметрам:
и значения координат вектора присвоили параметрам:
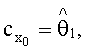

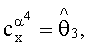

Полученная в результате зависимость имеет вид:
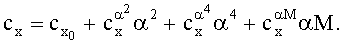
Для идентификации зависимости коэффициента mz в качестве координат вектора измерений yi, i=1,n использовали вычисленные в различные моменты времени ti значения коэффициента момента mz:
yi=mz(ti).
В качестве координат в вектор 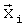 были добавлены параметры Сy и производная по времени коэффициента Сy. В качестве «заданных функций» выбрали:
были добавлены параметры Сy и производная по времени коэффициента Сy. В качестве «заданных функций» выбрали:
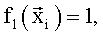
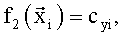
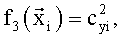


После вычисления по формуле (5) вектора оценок множителей 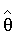 и значения координат вектора присвоили параметрам:
и значения координат вектора присвоили параметрам:
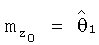 ,
, 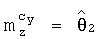 ,
, 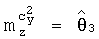 ,
, 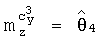 ,
, 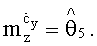
Полученная в результате зависимость имеет вид:

В работе «Методы исследований на летающих моделях». Справочная библиотека авиационного инженера-испытателя. Летные испытания самолетов и вертолетов./ Под общей редакцией А.Д.Миронова. Москва, Машиностроение, 1988, с.41-52 определяют (идентифицируют) зависимость коэффициента момента mz от коэффициента подъемной силы Сy, угла атаки α, отклонения руля высоты δ и угловой скорости ωz. В итоге получают выражение:

Наиболее близким аналогом изобретения является способ определения аэродинамических характеристик воздушных судов, включающий исследование модели воздушного судна в аэродинамической трубе и проведение летных испытаний, в процессе исследования модели воздушного судна в аэродинамической трубе измеряют параметры потока воздуха в аэродинамической трубе, угловое положение модели относительно потока воздуха, угловые отклонения поверхностей управления воздушным судном, аэродинамические силы и моменты, действующие на модель воздушного судна в различных конфигурациях, в результате обработки полученных данных получают продувочные зависимости составляющих коэффициентов аэродинамических сил и моментов, представленные в виде таблиц или совокупности коэффициентов сплайн-функций, а также в виде аналитических выражений и алгоритмов, включающих интерполяцию по табличным зависимостям или вычисление значений сплайн-функций, с помощью которых вычисляют суммарные значения коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в заданных условиях, при моделировании динамики и расчете летно-технических характеристик, при этом составляющие коэффициентов аэродинамических сил и моментов задают с помощью таблиц значений составляющих в узловых точках, а для получения значений в промежуточных точках используют тот или иной метод интерполяции, что позволяет учесть нелинейный характер зависимостей аэродинамических характеристик от различных параметров, при проведении летных испытаний воздушных судов в дискретные моменты времени измеряют и регистрируют параметры движения: высоту, скорость полета, температуру заторможенного потока наружного воздуха, углы атаки и скольжения, угловое положение относительно поверхности Земли, угловые скорости и ускорения, перегрузки, измеряют параметры, позволяющие определить массово-инерционные характеристики воздушного судна, кроме того, измеряют углы отклонения поверхностей управления и параметры, необходимые для определения составляющих тяги двигателей, на основании этих измерений вычисляют значения составляющих тяги двигателей и множество значений коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в фактических условиях полета в дискретные моменты времени, на основе полученного множества значений коэффициентов аэродинамических сил и моментов с применением методов идентификации, в том числе и по методу наименьших квадратов, с использованием заданных функций, с помощью которых строится структурная или конструкционная матрица, определяют зависимости этих коэффициентов от параметров полета и отклонений поверхностей управления для того, чтобы полученные в результате летных испытаний зависимости обеспечивали вычисление значений коэффициентов аэродинамических сил и моментов в заданных условиях полета при моделировании динамики и расчете летно-технических характеристик воздушного судна (Bruma J.H. Evaluation of a method to extract performance data from dynamic manoeuvers for a jet transport aircraft. ICAS proceedings, 1978, v.2, p.475-488). В указанном способе затрагивается и вопрос определения составляющих тяги в условиях полета и рассматривается идентификация зависимостей коэффициентов Сх, Сy и mz (т.е. аэродинамических характеристик продольного движения). Полученные зависимости имеют вид:
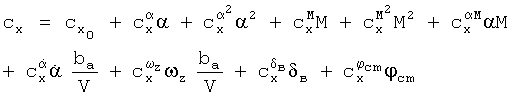
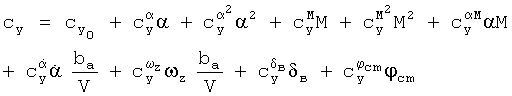
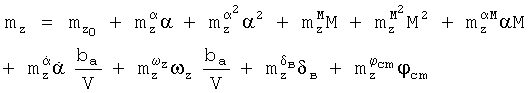
Здесь для зависимостей всех трех коэффициентов Сх, Сy и mz в качестве координат вектора 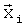 использованы полученные в различные моменты времени ti значения угла атаки α и производной от него, числа М, угловой скорости ωz, значения отклонений руля высоты δв и стабилизатора ϕст. В качестве заданных функций выбрали:
использованы полученные в различные моменты времени ti значения угла атаки α и производной от него, числа М, угловой скорости ωz, значения отклонений руля высоты δв и стабилизатора ϕст. В качестве заданных функций выбрали:
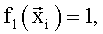
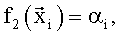
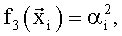
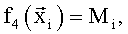
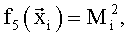
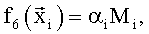
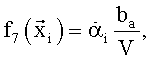
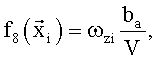
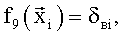
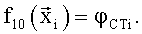
В качестве недостатка аналогов и прототипа можно отметить некоторую произвольность выбора заданных функций. Несмотря на то, что для фиксированного набора экспериментальных данных, полученных в летных испытаниях, на основе анализа остаточной суммы квадратов

можно выбрать оптимальный набор заданных функций, однако это не гарантирует что для другого набора испытательных режимов (набора экспериментальных данных) тот же набор заданных функций будет оптимальным. Можно также отметить слабое физическое обоснование таких, например, наборов заданных функций, которые приводят к выражениям 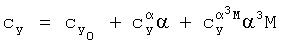 или
или
 (см. В.А.Касьянов, Е.П.Ударцев. «Определение характеристик воздушных судов методами идентификации». Москва, Машиностроение, 1988, стр.150-164).
(см. В.А.Касьянов, Е.П.Ударцев. «Определение характеристик воздушных судов методами идентификации». Москва, Машиностроение, 1988, стр.150-164).
Можно предположить, что подобные результаты в значительной степени объясняются особенностями тестовых режимов (маневров) и конкретных выборок зарегистрированных и обрабатываемых данных. Причем основную роль играют, скорее всего, размер и границы области значений зарегистрированных параметров полета, используемых для идентификации аэродинамических характеристик. Можно ожидать, что при изменении или расширении исследуемой области параметров полета могут измениться не только значения полученных коэффициентов, но и набор заданных функций.
Основной недостаток заключается в том, что при подобном способе выбора заданных функций не используется огромный объем знаний о структуре и параметрах аэродинамических характеристик, полученный в результате расчетов, исследований в АДТ и в результате предшествующего опыта разработки, создания и летных испытаний ВС.
Технический результат, на достижение которого направлено изобретение, заключается в повышении достоверности определения аэродинамических характеристик в летных испытаниях ВС и обеспечении технологичности их определения с применением идентификации по методу наименьших квадратов.
Указанный технический результат достигается тем, что в способе определения аэродинамических характеристик воздушных судов, включающем исследование модели воздушного судна в аэродинамической трубе и проведение летных испытаний, в процессе исследования модели воздушного судна в аэродинамической трубе измеряют параметры потока воздуха в аэродинамической трубе, угловое положение модели относительно потока воздуха, угловые отклонения поверхностей управления воздушным судном, аэродинамические силы и моменты, действующие на модель воздушного судна в различных конфигурациях, в результате обработки полученных данных получают продувочные зависимости составляющих коэффициентов аэродинамических сил и моментов, представленные в виде таблиц или совокупности коэффициентов сплайн-функций, а также в виде аналитических выражений и алгоритмов, включающих интерполяцию по табличным зависимостям или вычисление значений сплайн-функций, с помощью которых вычисляют суммарные значения коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в заданных условиях, при моделировании динамики и расчете летно-технических характеристик, при этом составляющие коэффициентов аэродинамических сил и моментов задают с помощью таблиц значений составляющих в узловых точках, а для получения значений в промежуточных точках используют тот или иной метод интерполяции, что позволяет учесть нелинейный характер зависимостей аэродинамических характеристик от различных параметров, при проведении летных испытаний воздушных судов в дискретные моменты времени измеряют и регистрируют параметры движения: высоту, скорость полета, температуру заторможенного потока наружного воздуха, углы атаки и скольжения, угловое положение относительно поверхности Земли, угловые скорости и ускорения, перегрузки, измеряют параметры, позволяющие определить массово-инерционные характеристики воздушного судна, кроме того, измеряют углы отклонения поверхностей управления и параметры, необходимые для определения составляющих тяги двигателей, на основании этих измерений вычисляют значения составляющих тяги двигателей и множество значений коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в фактических условиях полета в дискретные моменты времени, на основе полученного множества значений коэффициентов аэродинамических сил и моментов с применением методов идентификации, в том числе и по методу наименьших квадратов, с использованием заданных функций, с помощью которых строится структурная или конструкционная матрица, определяют зависимости этих коэффициентов от параметров полета и отклонений поверхностей управления для того, чтобы полученные в результате летных испытаний зависимости обеспечивали вычисление значений коэффициентов аэродинамических сил и моментов в заданных условиях полета при моделировании динамики и расчете летно-технических характеристик воздушного судна, в качестве наблюдаемых параметров принимаются суммарные значения коэффициентов аэродинамических сил и моментов, вычисленные на основе измерений параметров в полете, а в качестве заданных функций, с помощью которых строится структурная или конструкционная матрица при идентификации по методу наименьших квадратов, используют функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах, и единичную функцию, и определяют по методу наименьших квадратов масштабные множители для заданных функций, определяют основную область значений параметров полета, в которой выбранный набор заданных функций с учетом масштабных множителей обеспечивает удовлетворительную аппроксимацию множества полученных в летных испытаниях дискретных значений коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в фактических условиях полета, и далее, если основная область значений параметров полета не покрывает всю область значений параметров полета, исследованную в летных испытаниях, строят непрерывные расширения модели, полученной для основной области значений параметров полета значений параметров полета, используя в качестве наблюдаемых параметров разности между измеренными значениями коэффициентов аэродинамических сил и моментов и значениями соответствующих коэффициентов, вычисленных по модели с использованием масштабных множителей, полученных для основной области значений параметров полета, а в качестве заданных функций, с помощью которых строится структурная или конструкционная матрица, для построения непрерывных расширений используют функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах с кусочно-линейными множителями или произведениями кусочно-линейных множителей, обеспечивающими непрерывность расширений вне основной области значений параметров полета.
В качестве заданных функций для построения непрерывных расширений зависимостей аэродинамических характеристик вне основной области значений параметров полета могут быть использованы полиномиальные функции с кусочно-линейными множителями или произведениями кусочно-линейных множителей, обеспечивающими непрерывность расширений вне основной области значений параметров полета.
В качестве наблюдаемых параметров при определении коэффициентов сил лобового сопротивления используют значения коэффициента результирующей силы - аэродинамической силы сопротивления и силы тяги двигательной установки, а в качестве заданных функций, с помощью которых строится структурная или конструкционная матрица при идентификации по методу наименьших квадратов, могут быть использованы функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах, а также проекцию коэффициента тяги двигательной установки.
В качестве наблюдаемых параметров при определении коэффициентов сил и моментов могут быть приняты разности суммарных значений коэффициентов аэродинамических сил или моментов, полученных на основе измерений в полете перегрузок и производных угловых скоростей, и соответствующих суммарных значений коэффициентов аэродинамических сил или моментов, вычисленных для тех же фактических условий полета и измеренных положений поверхностей управления на основе модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах - «продувочные» значения коэффициентов.
В качестве наблюдаемых параметров при определении коэффициента тангенциальной силы или силы лобового сопротивления могут быть приняты значения коэффициента результирующей силы, а в качестве заданных функций, с помощью которых строится структурная или конструкционная матрица при идентификации по методу наименьших квадратов, используют функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах, а также проекции коэффициента тяги двигательной установки.
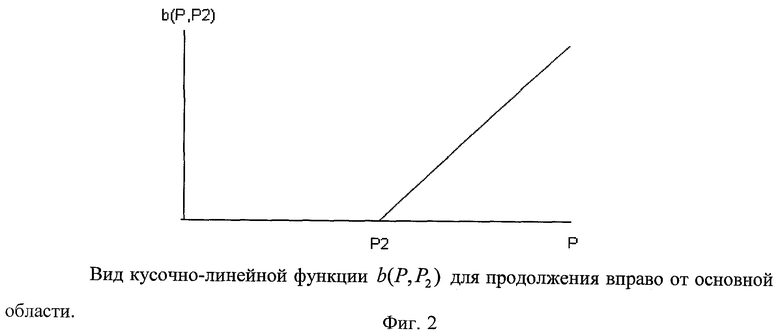
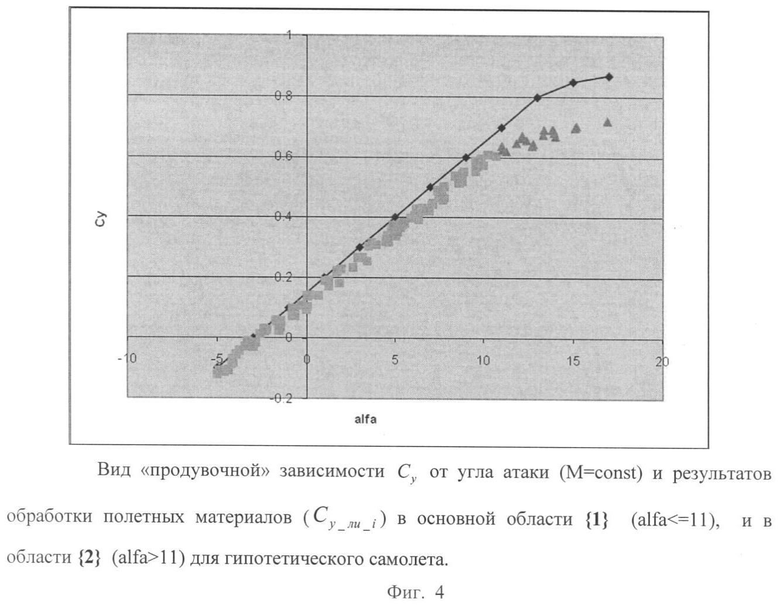
Изобретение поясняется графическими материалами, где на фиг.1 изображен пример расположения областей {k}, k=1, …, 4 для непрерывного расширения зависимостей 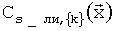 по двум параметрам (углу атаки α и числу М); на фиг.2 - вид кусочно-линейной функции b(Р,Р2) для продолжения вправо от основной области; на фиг.3 - вид кусочно-линейной функции b_(Р,Р1) для построения непрерывного продолжения влево от основной области; на фиг.4 - вид «продувочной» зависимости Сy от угла атаки (M=const) и результатов обработки полетных материалов (Сy_ли_i) в основной области {1} (alfa<=11), и в области {2} (alfa>11) для гипотетического самолета.
по двум параметрам (углу атаки α и числу М); на фиг.2 - вид кусочно-линейной функции b(Р,Р2) для продолжения вправо от основной области; на фиг.3 - вид кусочно-линейной функции b_(Р,Р1) для построения непрерывного продолжения влево от основной области; на фиг.4 - вид «продувочной» зависимости Сy от угла атаки (M=const) и результатов обработки полетных материалов (Сy_ли_i) в основной области {1} (alfa<=11), и в области {2} (alfa>11) для гипотетического самолета.
Заявляемый способ определения аэродинамических характеристик воздушных судов (ВС) по результатам летных испытаний с использованием моделей аэродинамических характеристик, полученных в результате предварительных исследований в аэродинамических трубах (АДТ), а также с использованием характеристик двигательной (силовой) установки (ДУ), полученных при проведении стендовых и летных испытаний, заключается в следующем.
До начала летных испытаний ВС проводят исследования моделей ВС в АДТ. При этом измеряют параметры потока воздуха в АДТ (скорость, температуру, давления, влажность и т.п.), угловое положение модели относительно потока воздуха (угол атаки, угол скольжения), угловые отклонения поверхностей управления ВС, аэродинамические силы и моменты, действующие на модель ВС в различных конфигурациях (крейсерской, взлетно-посадочной, с убранным или выпущенным шасси и т.п.). В результате обработки полученных данных получают «теоретические» или «продувочные» зависимости коэффициентов аэродинамических сил и моментов, которые, как ожидается, будут действовать на ВС в полете, от высотно-скоростных параметров (числа М, иногда - от высоты Н (или числа Рейнольдса)) от углов атаки и скольжения, от положений поверхностей управления и от конфигурации. Такие зависимости представляют в виде таблиц, графиков для иллюстрации, а также в виде аналитических выражений и алгоритмов (алгоритмы часто включают в себя интерполяцию по табличным зависимостям), с помощью которых можно вычислить значения коэффициентов аэродинамических сил и моментов, действующих на ВС в заданных условиях. Такие зависимости (алгоритмы, аналитические выражения, графики и таблицы) называют моделью аэродинамических характеристик и используют при моделировании динамики ВС для расчета летно-технических характеристик, а также при создании пилотажных стендов и тренажеров.
Также до начала летных испытаний ВС проводят исследования ДУ на стендах, в АДТ, а также на летающих лабораториях. При этом измеряют параметры потока воздуха на входе в ДУ, на выходе из ДУ, положения органов управления ДУ, параметры работы ДУ (частоты вращения роторов, расход топлива, температуры отдельных узлов или температуры потока газов в определенных точках или сечениях и т.п.). Кроме того, измеряют усилия в узлах крепления ДУ. В результате обработки полученных данных получают «теоретические» или «стендовые» зависимости тяговых и расходных характеристик ДУ от высотно-скоростных параметров (числа М, иногда - от высоты Н (или числа Рейнольдса), температуры воздуха и т.п.), положения органов управления ДУ, параметров работы ДУ (частоты вращения роторов и т.п.). Такие зависимости, представленные в виде таблиц, графиков, аналитических выражений и алгоритмов, с помощью которых можно вычислить значения тяги (или составляющих тяги) ДУ в заданных условиях, называют высотно-скоростными характеристиками (ВСХ) ДУ. Их также используют при моделировании динамики ВС, для расчета летно-технических характеристик, а также при создании пилотажных стендов и тренажеров.
При проведении летных испытаний ВС измеряют параметры движения: высоту, скорость полета, температуру заторможенного потока наружного воздуха, углы атаки и скольжения, угловое положение относительно поверхности Земли, угловые скорости и ускорения, перегрузки. Угловые ускорения часто определяют (вычисляют) методами численного дифференцирования. Измеряют параметры (суммарный остаток топлива, возможно - остатки топлива в баках, и т.п.), позволяющие определить массово-инерционные характеристики воздушного судна (массу, положение центра масс и моменты инерции). Также измеряют параметры, необходимые для определения положения поверхностей управления и составляющих тяги двигателей (частоты вращения роторов двигателей, положения рычагов управления двигателями, и т.д.). На основании этих измерений вычисляют значения коэффициентов аэродинамических сил и моментов, действующих на ВС в фактических условиях полета. Измеряют параметры, необходимые для определения проекций тяги двигательной установки и моментов тяги на оси связанной системы координат (частоту вращения роторов двигателей, положение рычагов управления двигателями, мгновенные расходы топлива, и т.п.).
В процессе предполетной подготовки определяют угол установки датчиков перегрузки Δαуст. Для этого ВС устанавливают в линию полета и регистрируют показания датчика продольной перегрузки 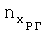 . Значение Δαуст вычисляют по формуле
. Значение Δαуст вычисляют по формуле 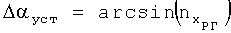 . В летных испытаниях измеряют углы отклонения поверхностей управления (углы отклонения стабилизаторов φСТ, рулей высоты δв, рулей направления δн, элеронов δэ и т.д., в зависимости от конструкции типа ВС и рассматриваемой конфигурации (например, крейсерской, взлетно-посадочной)). Также в полете измеряют продольную
. В летных испытаниях измеряют углы отклонения поверхностей управления (углы отклонения стабилизаторов φСТ, рулей высоты δв, рулей направления δн, элеронов δэ и т.д., в зависимости от конструкции типа ВС и рассматриваемой конфигурации (например, крейсерской, взлетно-посадочной)). Также в полете измеряют продольную 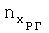 , нормальную
, нормальную 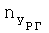 перегрузки в связанных осях и угол атаки α самолета. Далее с использованием зарегистрированных значений перегрузок
перегрузки в связанных осях и угол атаки α самолета. Далее с использованием зарегистрированных значений перегрузок 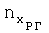 и
и 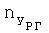 и полученного ранее значения угла установки датчиков перегрузки Δαуст вычисляют значения перегрузок nx (продольной) и ny (нормальной) в связанных осях:
и полученного ранее значения угла установки датчиков перегрузки Δαуст вычисляют значения перегрузок nx (продольной) и ny (нормальной) в связанных осях:
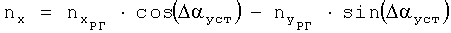 ,
,
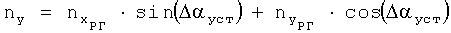 .
.
Если, как часто бывает, коэффициенты аэродинамических сил заданы в скоростной системе координат, то на основе измеренных значений перегрузок в связанной системе координат вычисляют по известным формулам (см. С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник». Москва, «Машиностроение», 1969; М.И.Хейфец. «Обработка результатов испытаний. Алгоритмы, номограммы, таблицы». Москва, «Машиностроение», 1988. (Справочная библиотека авиационного инженера-испытателя)) значения перегрузок в скоростной системе координат:
nXa=nX·cos(α)·cos(β)-nY·sin(α)·cos(β)+nZ·sin(β)
nYa=nX·sin(α)+nY·cos(α)
nZa=-nX·cos(α)·sin(β)+nY·sin(α)·sin(β)+nZ·cos(β),
и далее вычисляют значения коэффициентов результирующих сил:
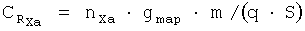
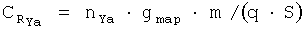
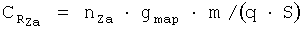 ,
,
предварительно вычислив по известным алгоритмам (см. B.C.Ведров, М.А.Тайц. «Летные испытания самолетов». Государственное издательство оборонной промышленности, Москва, 1951; М.Г.Котик, А.В.Павлов, И.М.Пашковский, Н.Г.Щитаев. «Летные испытания самолетов». Москва, «Машиностроение», 1968) число М полета и скоростной напор q на основе измеренных значений приборной высоты и приборной скорости, а также вычислив текущее значение массы самолета m на основе измерения остатка топлива (или интегрирования мгновенного расхода топлива). На основе измерений необходимых параметров в соответствии с применяемым способом определения тяги в полете вычисляют значение коэффициента тяги Ср. Затем, пользуясь соотношениями
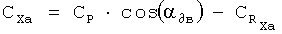
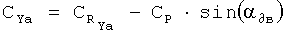
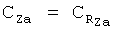
(здесь α∂в - угол между вектором тяги двигательной установки и вектором скорости ЛА, может несколько отличаться от угла атаки самолета) вычисляют значения коэффициентов аэродинамических сил в скоростной системе координат.
Ниже приведены алгоритмы вычисления коэффициентов аэродинамических сил и моментов в связанной системе координат. Коэффициенты моментов аэродинамических сил часто задаются именно в связанной системе координат, независимо от того, в какой системе координат заданы коэффициенты аэродинамических сил. Сначала на основе измерений высотно-скоростных параметров, перегрузок, углов, угловых скоростей и т.п. определяются коэффициенты результирующих сил и моментов:
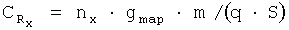
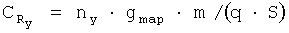
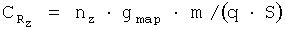

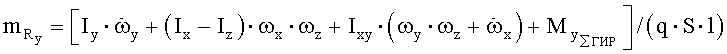
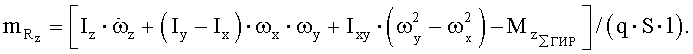
Здесь 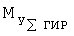 - суммарная проекция гироскопического момента роторов двигателей на связанную ось Y,
- суммарная проекция гироскопического момента роторов двигателей на связанную ось Y, 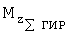 - суммарная проекция гироскопического момента роторов двигателей на связанную ось OZ. Проекция гироскопического момента одного ротора на связанную ось OY вычисляется по формуле
- суммарная проекция гироскопического момента роторов двигателей на связанную ось OZ. Проекция гироскопического момента одного ротора на связанную ось OY вычисляется по формуле 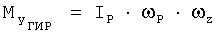 , где IP - момент инерции ротора, ωP - угловая скорость ротора, а проекция гироскопического момента одного ротора на связанную ось OZ - по формуле
, где IP - момент инерции ротора, ωP - угловая скорость ротора, а проекция гироскопического момента одного ротора на связанную ось OZ - по формуле 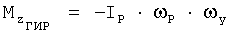 . Далее вычисляют значения коэффициентов аэродинамических сил и моментов, вычитая из значений коэффициентов результирующих сил и моментов соответствующие значения коэффициентов проекций тяги двигательной установки и моментов тяги двигательной установки на оси связанной системы координат:
. Далее вычисляют значения коэффициентов аэродинамических сил и моментов, вычитая из значений коэффициентов результирующих сил и моментов соответствующие значения коэффициентов проекций тяги двигательной установки и моментов тяги двигательной установки на оси связанной системы координат:
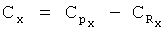 ,
,
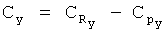 ,
,
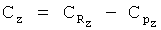 ,
,
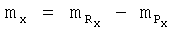 ,
,
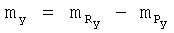 ,
,
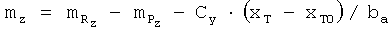 .
.
Здесь 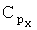 ,
, 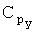 ,
, 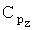 - коэффициенты проекций силы тяги двигательной установки на оси связанной системы координат,
- коэффициенты проекций силы тяги двигательной установки на оси связанной системы координат, 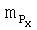 ,
, 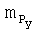 ,
, 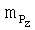 - коэффициенты проекций моментов тяги двигательной установки на оси связанной системы координат, Сy·(xT-xT0)/ba - поправка к значению коэффициента mz для учета смещения центра масс ВС, xT - текущее положение центра масс, xT0 - положение центра масс, для которого определены (заданы) «продувочные» значения mz (см. С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник», Москва. «Машиностроение», 1969, стр.273, раздел 5.3.10).
- коэффициенты проекций моментов тяги двигательной установки на оси связанной системы координат, Сy·(xT-xT0)/ba - поправка к значению коэффициента mz для учета смещения центра масс ВС, xT - текущее положение центра масс, xT0 - положение центра масс, для которого определены (заданы) «продувочные» значения mz (см. С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник», Москва. «Машиностроение», 1969, стр.273, раздел 5.3.10).
После того как получены наборы значений коэффициентов аэродинамических сил Сx, Сy, mz, Сz, mx, my и соответствующие наборы значений параметров полета, углы атаки и скольжения, число М, отклонения поверхностей управления в фактических условиях, переходят к определению зависимостей коэффициентов аэродинамических сил и моментов от параметров полета и отклонений поверхностей управления. Для этого применяют идентификацию по методу наименьших квадратов. Процедуру идентификации осуществляют для каждого коэффициента Сx, Сy, mz, Сz, mx, my по отдельности. Кроме того, следует отметить, что, как правило, по материалам различных типов испытательных маневров определяют различные группы множителей при соответствующих заданных функциях, в зависимости от того, какие функции изменяются в соответствующих случаях.
В случае необходимости, когда продувочные значения коэффициентов аэродинамических сил или моментов заданы в скоростной или полусвязанной системе координат, а значения коэффициентов сил и моментов получены в результате обработки измерений в летных испытаниях для связанной системы координат, пересчитывают в соответствующую (скоростную или полусвязанную) систему координат. Формулы для пересчета приведены в С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник». Москва, «Машиностроение», 1969, стр.242, таблица 5.6а - С.А.Горбатенко, Э.М.Макашов, Ю.Ф.Полушкин, Л.В.Шефтель. «Механика полета (общие сведения, уравнения движения) инженерный справочник». Москва, «Машиностроение», 1969.
Формулы пересчета значений коэффициентов сил и моментов из связанной системы координат в скоростную систему координат:
CXa=CX·cos(α)·cos(β)+CY·sin(α)·cos(β)-CZ·sin(β),
CYa=CY·cos(α)+CX·sin(α),
CZa=CX·cos(α)·sin(β)+CY·sin(α)·sin(β)+CZ·cos(β),
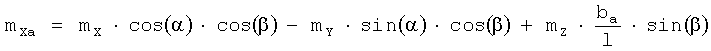 ,
,
mYa-mX·sin(α)+mY·cos(α),
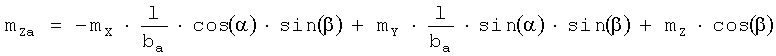 .
.
Следует отметить, что часто коэффициенты аэродинамических сил задаются в скоростной системе координат, коэффициенты моментов - в связанной системе координат. Возможны и случаи, когда одни из коэффициентов сил представлены в скоростной системе координат, а другие - в связанной.
Формулы пересчета значений коэффициентов сил и моментов из связанной системы координат в полусвязанную систему координат:
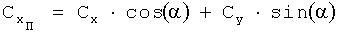 ,
,
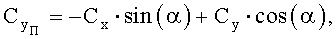
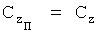 ,
,
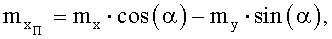
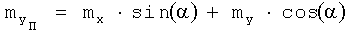 ,
,
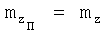 .
.
Значения угла атаки α и угла скольжения β, необходимые для пересчета значений коэффициентов сил и моментов из одной системы координат в другую, получают на основе измерений в полете.
Для тех же условий полета, углов атаки и скольжения, углов отклонения поверхностей управления, в которых получены экспериментальные значения коэффициентов аэродинамических сил и моментов, можно вычислить на основе модели АХ, полученной в результате предварительных исследований в АДТ, расчетные значения коэффициентов аэродинамических сил и моментов. Если имеет место совпадение расчетных и экспериментальных значений коэффициентов (в пределах погрешностей измерений), то можно говорить о том, что расчетная (продувочная) модель АХ соответствует результатам летных испытаний. Однако на практике такое совпадение маловероятно, и приходится каким-то образом корректировать теоретическую (продувочную) модель АХ для приведения ее в соответствие (для согласования) с результатами летных испытаний.
Особенность предлагаемого способа определения модели аэродинамических и тяговых характеристик от аналогов и прототипа заключается в способе выбора заданных функций, т.е. функций, с помощью которых строится структурная или конструкционная матрица при идентификации методом наименьших квадратов. В предлагаемом способе в качестве заданных функций используют те функции, которые являются составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, получаемой на основе продувок в аэродинамических трубах и, дополнительно, единичную функцию (функцию, имеющую постоянное значение, равное единице). Как правило, такие функции (составляющие коэффициентов аэродинамических сил и моментов) задают с помощью таблиц значений составляющих в узловых точках, а для получения значений в промежуточных точках используют тот или иной метод (процедура или функция) интерполяции. Такое представление позволяет учесть нелинейный характер аэродинамических характеристик. Непосредственная идентификация (определение значений) всей совокупности табличных значений практически невозможна ввиду большой размерности таблиц (большого количества узловых значений аргументов и функций). Предлагаемый способ позволит определить множители при составляющих коэффициентов аэродинамических сил и моментов.
Например, для крейсерской конфигурации некоторого ВС выражение для вычисления коэффициента подъемной силы, полученное в результате продувок в АДТ (или модель коэффициента аэродинамической подъемной силы), имеет вид:
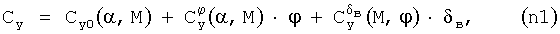
где каждую из составляющих вычисляют с помощью линейной интерполяции по соответствующей таблице (массиву данных). В этом случае можно в качестве заданных функций использовать составляющие Cy0(α,M), 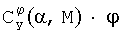 и
и 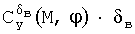 . Линейное (по этим заданным функциям) выражение для определения экспериментальной зависимости коэффициента подъемной силы от соответствующих параметров будет иметь вид:
. Линейное (по этим заданным функциям) выражение для определения экспериментальной зависимости коэффициента подъемной силы от соответствующих параметров будет иметь вид:
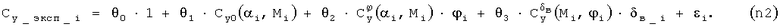
При идентификации множители θ0, θ1, θ2 и θ3 определяют по методу наименьших квадратов.
Вычислительных трудностей в этом случае не ожидается, т.к. размерность обращаемой матрицы невелика. Даже достаточно подробные модели коэффициентов аэродинамических сил и моментов содержат, как правило, меньше десятка составляющих.
В некоторых случаях может оказаться, что ввод дополнительной единичной заданной функции будет излишним, когда модель какого-либо коэффициента уже содержит свободный член или некое его подобие (например, функцию, почти постоянную в исследуемой области). Тогда включение дополнительной единичной заданной функции может приводить к вырожденности или плохой обусловленности матрицы А'А. В этом случае можно будет принять θ0=0 и определять с помощью метода наименьших квадратов (МНК) только множители θ1, …, θm.
Для того чтобы описать способ определения АХ в общем виде, будем использовать обозначение Сs для любого из коэффициентов аэродинамических сил и моментов (СX, СY, mZ, СZ, mZ, mY). Итак, если «продувочная модель» какого-либо коэффициента Сs имеет вид
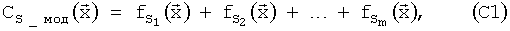
где  - вектор параметров, от которых зависит значение коэффициента СS, то для применения МНК для построения структурной (конструкционной, регрессионной) матрицы А в качестве заданных функций можно использовать функции
- вектор параметров, от которых зависит значение коэффициента СS, то для применения МНК для построения структурной (конструкционной, регрессионной) матрицы А в качестве заданных функций можно использовать функции 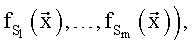 дополнив в случае необходимости этот набор единичной функцией (напомним, что
дополнив в случае необходимости этот набор единичной функцией (напомним, что 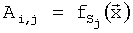 ). Линейное по этим заданным функциям выражение для определения экспериментальной зависимости коэффициента СS от соответствующих параметров по материалам летных испытаний будет иметь вид:
). Линейное по этим заданным функциям выражение для определения экспериментальной зависимости коэффициента СS от соответствующих параметров по материалам летных испытаний будет иметь вид:
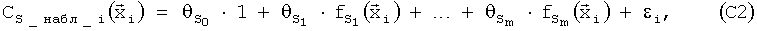
где 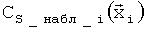 - наблюдаемый параметр, т.е. значение соответствующего коэффициента аэродинамической силы или момента, вычисленное на основе измеренных в полете параметров. Следует отметить, что в некоторых случаях слагаемое
- наблюдаемый параметр, т.е. значение соответствующего коэффициента аэродинамической силы или момента, вычисленное на основе измеренных в полете параметров. Следует отметить, что в некоторых случаях слагаемое 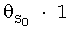 может отсутствовать, т.е. значение множителя
может отсутствовать, т.е. значение множителя 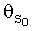 может быть тождественно равно нулю. Такие случаи имеют место тогда, когда с введением слагаемого
может быть тождественно равно нулю. Такие случаи имеют место тогда, когда с введением слагаемого 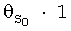 матрица А'А (или A'·D-1(y)·A) становится плохо обусловленной или вырожденной. Множители θ1, …, θm и, возможно, θ0 (точнее, вектор оценок множителей
матрица А'А (или A'·D-1(y)·A) становится плохо обусловленной или вырожденной. Множители θ1, …, θm и, возможно, θ0 (точнее, вектор оценок множителей 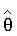 ) определяют по методу наименьших квадратов
) определяют по методу наименьших квадратов 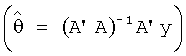 или, в случае неодинаковых дисперсий ошибок
или, в случае неодинаковых дисперсий ошибок 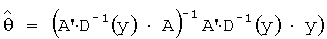 , и в результате получают зависимость
, и в результате получают зависимость
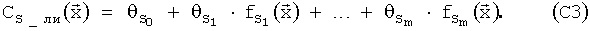
В случае близости множителей θ1, …, θm к единице, а θ0 - к нулю можно сделать вывод о соответствии продувочной модели материалам летных испытаний. В любом случае полученная зависимость (С3) является уточненной по материалам зависимостью (моделью, согласованной с материалами летных испытаний) соответствующего коэффициента аэродинамической силы или момента от параметров полета и положений поверхностей управления.
Дополнительной характеристикой (признаком) «соответствия» расчетной (продувочной) модели материалам летных испытаний является величина суммы квадратов невязок 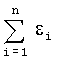 . Важно обратить внимание на поведение суммы квадратов невязок в зависимости от параметров полета и положения поверхностей управления (значений вектора
. Важно обратить внимание на поведение суммы квадратов невязок в зависимости от параметров полета и положения поверхностей управления (значений вектора 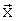 ). Опыт показывает, что в полной области исследованных в летных испытаниях значений вектора
). Опыт показывает, что в полной области исследованных в летных испытаниях значений вектора 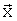 практически всегда имеется область, в которой аэродинамические характеристики, определяемые по данным летных испытаний, близки к продувочной модели АХ, во всяком случае, удовлетворительного их совпадения в этой области можно добиться с помощью небольших смещений и изменений наклонов кривых. Именно это и обеспечивается с помощью множителей
практически всегда имеется область, в которой аэродинамические характеристики, определяемые по данным летных испытаний, близки к продувочной модели АХ, во всяком случае, удовлетворительного их совпадения в этой области можно добиться с помощью небольших смещений и изменений наклонов кривых. Именно это и обеспечивается с помощью множителей 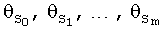 , определенных по методу наименьших квадратов. Назовем эту область основной областью, и в дальнейшем будем ее обозначать {1}, и к множителям, определенным для этой основной области, добавим индекс {1}. Итак, в основной области {1} с помощью МНК вычисляют оценки множителей
, определенных по методу наименьших квадратов. Назовем эту область основной областью, и в дальнейшем будем ее обозначать {1}, и к множителям, определенным для этой основной области, добавим индекс {1}. Итак, в основной области {1} с помощью МНК вычисляют оценки множителей 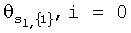 , m для получения зависимости
, m для получения зависимости
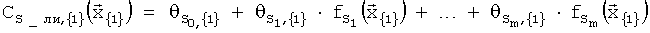 ,
,
которые обеспечивают удовлетворительное совпадение значений коэффициентов аэродинамических сил и моментов, вычисленных по формуле (С3) для полетных значений вектора параметров 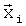 , не выходящих за пределы области {1} (для чего и используем обозначение
, не выходящих за пределы области {1} (для чего и используем обозначение 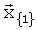 ) и значений коэффициентов аэродинамических сил и моментов
) и значений коэффициентов аэродинамических сил и моментов  , полученных на основе измерений в полете перегрузок, угловых скоростей и прочих необходимых параметров. Обычно это так называемая «линейная область», т.е. область линейной зависимости коэффициента подъемной силы от угла атаки. Иногда эта область бывает шире линейной области и даже может совпадать со всей допустимой областью режимов полета. Однако в некоторых случаях, например, когда в летных испытаниях обнаруживается, что срывы потока на крыле начинаются при меньших значениях угла атаки, чем в АДТ, такая область может оказаться меньше линейной области, определенной в результате продувок.
, полученных на основе измерений в полете перегрузок, угловых скоростей и прочих необходимых параметров. Обычно это так называемая «линейная область», т.е. область линейной зависимости коэффициента подъемной силы от угла атаки. Иногда эта область бывает шире линейной области и даже может совпадать со всей допустимой областью режимов полета. Однако в некоторых случаях, например, когда в летных испытаниях обнаруживается, что срывы потока на крыле начинаются при меньших значениях угла атаки, чем в АДТ, такая область может оказаться меньше линейной области, определенной в результате продувок.
Другая особенность предлагаемого способа определения модели аэродинамических и тяговых характеристик от аналогов и прототипа состоит в способе построения непрерывных расширений характеристик, полученных для основной области, за границы основной области, до границ области, исследованной в летных испытаниях. Постепенно расширяя границы, определяют основную область, т.е. находят границы области, в которой зависимость вида (С3) достаточно хорошо совпадает с результатами обработки полетных материалов, причем при дальнейшем расширении этой области зависимость вида (С3) не обеспечивает удовлетворительного совпадения с результатами обработки полетных материалов во всей расширенной области. Построить (сконструировать, получить) зависимость для непрерывного продолжения зависимости вида (С3), удовлетворительно совпадающей с результатами обработки полетных материалов в расширенной области, можно следующим образом. Может появиться необходимость строить непрерывные расширения не только по одному параметру, но и по двум или более. В любом случае процедура непрерывного расширения будет начинаться с расширения по одному параметру, чаще всего по углу атаки. Пусть значение угла атаки на правой границе основной области {1} равно α2 (см. фиг.1).
Тогда выражение для получения непрерывного продолжения зависимости 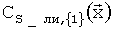 вправо в область {2} будет иметь следующий вид:
вправо в область {2} будет иметь следующий вид:
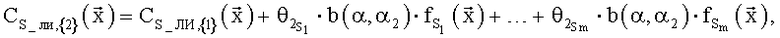
где b(α,α2) - кусочно-линейная функция (b(Р,Р2)=0 при Р<Р2 и b(Р,Р2)=Р-Р2 при Р≥Р2).
Для применения МНК в качестве наблюдаемого параметра yi,{2} будем вычислять разности
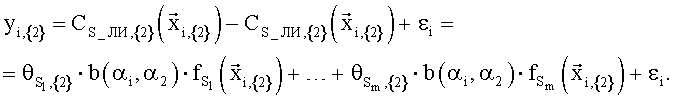
В случае необходимости получения непрерывного продолжения зависимости 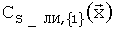 в область {3} выражение для продолжения зависимости будет иметь следующий вид:
в область {3} выражение для продолжения зависимости будет иметь следующий вид:
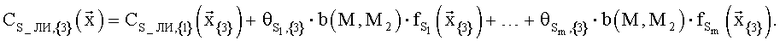
и, аналогично, для применения МНК в качестве наблюдаемого параметра yi,{3} будем вычислять разности
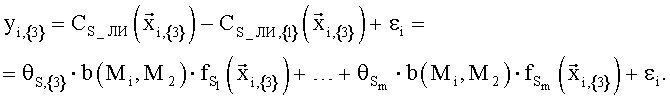
После определения множителей 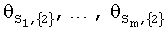 для области {2} и
для области {2} и 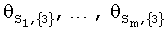 для области {3} можно построить непрерывное продолжение для области {4} (см. фиг.1) по двум параметрам (по углу атаки α и числу М). Для этого представим выражение для коэффициента CS в области {4} в следующем виде:
для области {3} можно построить непрерывное продолжение для области {4} (см. фиг.1) по двум параметрам (по углу атаки α и числу М). Для этого представим выражение для коэффициента CS в области {4} в следующем виде:
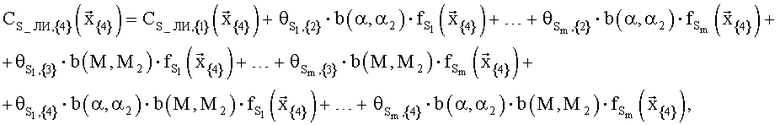
а для применения МНК в качестве наблюдаемого параметра yi,{4} будем вычислять
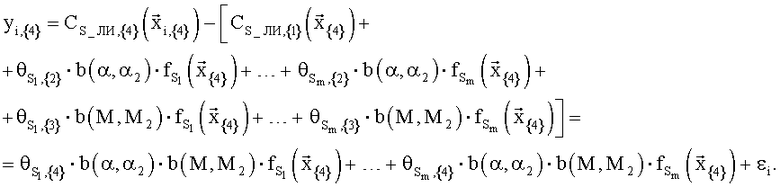
Легко видеть, что такой способ построения обеспечивает непрерывность продолжений из области {1} в области {2} и {3}, а затем и в область {4}.
В том случае, если возникнет необходимость построения непрерывных продолжений по трем или большему количеству параметров, придется продвигаться последовательно. Сначала построить все продолжения по одному параметру в соседние прилегающие области, затем - продолжения по двум параметрам в соседние угловые области, затем снова все возможные продолжения по одному и двум параметрам, но уже с учетом других переменных. Далее появляется возможность строить угловое непрерывное продолжение по трем переменным. При этом в выражении для коэффициента CS в угловой трехмерной области появятся произведения вида 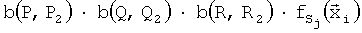 и т.д. для большего количества параметров, по которым требуется непрерывное продолжение.
и т.д. для большего количества параметров, по которым требуется непрерывное продолжение.
В случае необходимости получения непрерывного продолжения зависимости влево можно использовать функцию b_(Р,Р1) (см. фиг.3), b_(Р,Р1)=0 при Р>Р1 и b_(P,P1)=-(P-P1) при Р≤Р1.
Возможно, «реальная модель» окажется близкой к «продувочной» и будет достаточно одного диапазона. В этом случае не будет необходимости построения непрерывных продолжений (расширения области).
В итоге получают зависимости коэффициентов аэродинамических сил и моментов от параметров полета и т.п. Для основной («линейной») области значения коэффициентов аэродинамических сил и моментов можно вычислить с помощью выражений (n3). Для следующей области (α2<α<=α3) значения коэффициента подъемной силы можно вычислить с помощью выражений (n4) и так далее.
Для иллюстрации предлагаемого способа на фиг.4 приведен пример «продувочной» зависимости коэффициента подъемной силы от угла атаки и пример результатов обработки полетных материалов для гипотетического самолета. На графике ромбами обозначен пример «продувочной» зависимости Сy от угла атаки для некоторого значения числа М, а квадратами - пример измеренных (полученных в результате обработки полетных материалов) значений Сy_ли_i в основной области {1} (alfa<=11). В этом случае множитель θ0 (смещение графиков вблизи нулевых значений Сy) имеет значение ~ -0.0028, а множитель θ1 ~ 0.93. Треугольниками обозначены значения Сy_ли_i, полученные в области {2}.
Следует отметить, что предлагаемый способ может применяться не только к «полной» совокупности испытательных режимов (маневров) одновременно, но также и к определенным подмножествам полной совокупности. В таких случаях следует выделять и соответствующие подмножества m1 заданных функций (m1<m) таким образом, чтобы полученная конструкционная (структурная матрица) из m1 столбцов имела ранг m1 и существовала бы матрица, обратная к матрице (А'·А) или к матрице (A'·D-1(y)·А).
Очевидным преимуществом предлагаемого способа является то, что он позволяет использовать огромный объем информации о структуре и параметрах моделей аэродинамических и тяговых характеристик, полученный на основе расчетов и продувок в аэродинамических трубах, а также всю информацию, накопленную в результате опыта построения и использования моделей аэродинамических и тяговых характеристик других ВС, в том числе аналогичных. Кроме того, очевидна «технологичность» предлагаемого подхода, позволяющего последовательно, по мере расширения диапазона в процессе проведения летных испытаний ВС, уточнять модели аэродинамических характеристик с использованием измеренных и зарегистрированных в полете значений параметров и расширять область, в которой модель аэродинамических характеристик уточнена по материалам летных испытаний.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ НЕЛИНЕЙНЫХ АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЛЕТАТЕЛЬНОГО АППАРАТА ПО РЕЗУЛЬТАТАМ ЛЁТНЫХ ИССЛЕДОВАНИЙ | 2014 |
|
RU2560244C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АЭРОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ C И С НА ОСНОВЕ ОПРЕДЕЛЕНИЯ СУММАРНОЙ ТЯГИ ДВИГАТЕЛЬНОЙ УСТАНОВКИ ПО РЕЗУЛЬТАТАМ ЛЕТНЫХ ИСПЫТАНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2012 |
|
RU2503941C1 |
| СИСТЕМА УПРАВЛЯЕМЫХ АВИАЦИОННЫХ СРЕДСТВ ПОРАЖЕНИЙ ДЛЯ ФУНКЦИОНАЛЬНО-МОДЕЛИРУЮЩЕГО КОМПЛЕКСА | 2005 |
|
RU2298835C1 |
| Способ и система управления продольным движением при разбеге по взлётно-посадочной полосе и наборе высоты беспилотного летательного аппарата со специально расположенными передними и задними крыльями | 2018 |
|
RU2695897C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АЭРОДИНАМИЧЕСКОГО УГЛА ЛЕТАТЕЛЬНОГО АППАРАТА | 2007 |
|
RU2341775C1 |
| БОРТОВАЯ ИНТЕГРИРОВАННАЯ СИСТЕМА ИНФОРМАЦИОННОЙ ПОДДЕРЖКИ ЭКИПАЖА И КОГНИТИВНЫЙ ФОРМАТ ПРЕДСТАВЛЕНИЯ ПОЛЕТНОЙ ИНФОРМАЦИИ НА ЭТАПЕ "ВЗЛЕТ" МНОГОДВИГАТЕЛЬНОГО ВОЗДУШНОГО СУДНА | 2013 |
|
RU2550887C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЛЕТАТЕЛЬНОГО АППАРАТА ПО РЕЗУЛЬТАТАМ ЛЕТНОГО ЭКСПЕРИМЕНТА | 2022 |
|
RU2790358C1 |
| Способ определения углов атаки и скольжения беспилотного летательного аппарата | 2022 |
|
RU2792261C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЯГИ ПРИ ИЗМЕНЕНИИ РЕЖИМА РАБОТЫ ДВИГАТЕЛЕЙ САМОЛЕТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2601367C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЛЕТАТЕЛЬНОГО АППАРАТА ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ | 2009 |
|
RU2419775C1 |

Изобретение относится к области экспериментальной аэродинамики, а именно к способам определения аэродинамических характеристик воздушных судов. Способ включает исследование модели воздушного судна (ВС) в аэродинамической трубе и проведение летных испытаний. В качестве наблюдаемых параметров принимаются суммарные значения коэффициентов аэродинамических сил и моментов, вычисленные на основе измерений параметров в полете, а в качестве заданных функций, с помощью которых строится структурная или конструкционная матрица при идентификации по методу наименьших квадратов, используют функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах, и единичную функцию. По методу наименьших квадратов определяют масштабные множители для заданных функций, определяют основную область значений параметров полета, в которой выбранный набор заданных функций с учетом масштабных множителей обеспечивает удовлетворительную аппроксимацию множества полученных в летных испытаниях дискретных значений коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в фактических условиях полета. Технический результат заключается в повышении достоверности определения аэродинамических характеристик в летных испытаниях ВС и обеспечении технологичности их определения с применением идентификации по методу наименьших квадратов. 4 з.п. ф-лы, 4 ил.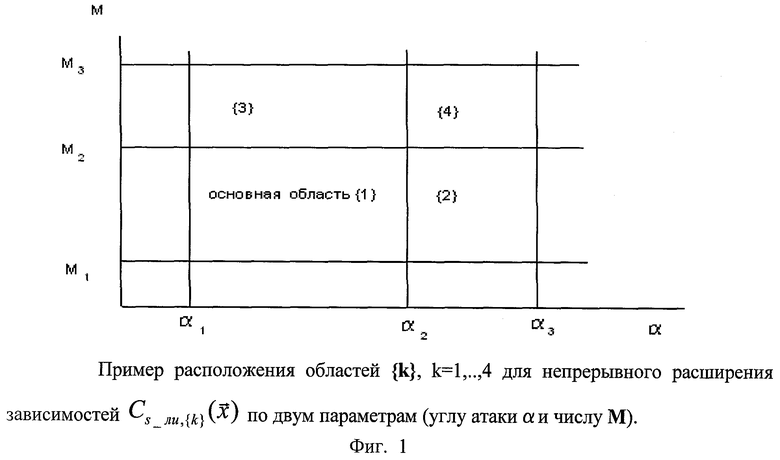
1. Способ определения аэродинамических характеристик воздушных судов, включающий исследование модели воздушного судна в аэродинамической трубе и проведение летных испытаний, в процессе исследования модели воздушного судна в аэродинамической трубе измеряют параметры потока воздуха в аэродинамической трубе, угловое положение модели относительно потока воздуха, угловые отклонения поверхностей управления воздушным судном, аэродинамические силы и моменты, действующие на модель воздушного судна в различных конфигурациях, в результате обработки полученных данных получают продувочные зависимости составляющих коэффициентов аэродинамических сил и моментов, представленные в виде таблиц или совокупности коэффициентов сплайн-функций, а также в виде аналитических выражений и алгоритмов, включающих интерполяцию по табличным зависимостям или вычисление значений сплайн-функций, с помощью которых вычисляют суммарные значения коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в заданных условиях, при моделировании динамики и расчете летно-технических характеристик, при этом составляющие коэффициентов аэродинамических сил и моментов задают с помощью таблиц значений составляющих в узловых точках, а для получения значений в промежуточных точках используют тот или иной метод интерполяции, что позволяет учесть нелинейный характер зависимостей аэродинамических характеристик от различных параметров, при проведении летных испытаний воздушных судов в дискретные моменты времени измеряют и регистрируют параметры движения: высоту, скорость полета, температуру заторможенного потока наружного воздуха, углы атаки и скольжения, угловое положение относительно поверхности Земли, угловые скорости и ускорения, перегрузки, измеряют параметры, позволяющие определить массово-инерционные характеристики воздушного судна, кроме того, измеряют углы отклонения поверхностей управления и параметры необходимые для определения составляющих тяги двигателей, на основании этих измерений вычисляют значения составляющих тяги двигателей и множество значений коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в фактических условиях полета в дискретные моменты времени, на основе полученного множества значений коэффициентов аэродинамических сил и моментов с применением методов идентификации, в том числе и по методу наименьших квадратов, с использованием заданных функций, с помощью которых строится структурная или конструкционная матрица, определяют зависимости этих коэффициентов от параметров полета и отклонений поверхностей управления для того, чтобы полученные в результате летных испытаний зависимости обеспечивали вычисление значений коэффициентов аэродинамических сил и моментов в заданных условиях полета при моделировании динамики и расчете летно-технических характеристик воздушного судна, отличающийся тем, что в качестве наблюдаемых параметров принимаются суммарные значения коэффициентов аэродинамических сил и моментов, вычисленные на основе измерений параметров в полете, а в качестве заданных функций, с помощью которых строится структурная или конструкционная матрица при идентификации по методу наименьших квадратов, используют функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах, и единичную функцию, и определяют по методу наименьших квадратов масштабные множители для заданных функций, определяют основную область значений параметров полета, в которой выбранный набор заданных функций с учетом масштабных множителей обеспечивает удовлетворительную аппроксимацию множества полученных в летных испытаниях дискретных значений коэффициентов аэродинамических сил и моментов, действующих на воздушное судно в фактических условиях полета, и далее, если основная область значений параметров полета не покрывает всю область значений параметров полета, исследованную в летных испытаниях, строят непрерывные расширения модели, полученной для основной области значений параметров полета значений параметров полета, используя в качестве наблюдаемых параметров разности между измеренными значениями коэффициентов аэродинамических сил и моментов и значениями соответствующих коэффициентов, вычисленных по модели с использованием масштабных множителей, полученных для основной области значений параметров полета, а качестве заданных функций, с помощью которых строится структурная или конструкционная матрица, для построения непрерывных расширений используют функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах с кусочно-линейными множителями, или произведениями кусочно-линейных множителей, обеспечивающими непрерывность расширений вне основной области значений параметров полета.
2. Способ по п.1, отличающийся тем, что в качестве заданных функций для построения непрерывных расширений зависимостей аэродинамических характеристик вне основной области значений параметров полета используют полиномиальные функции с кусочно-линейными множителями, или произведениями кусочно-линейных множителей, обеспечивающими непрерывность расширений вне основной области значений параметров полета.
3. Способ по п.1, отличающийся тем, что в качестве наблюдаемых параметров при определении коэффициентов сил лобового сопротивления используют значения коэффициента результирующей силы - аэродинамической силы сопротивления и силы тяги двигательной установки, а в качестве заданных функций, с помощью которых строится структурная или конструкционная матрица при идентификации по методу наименьших квадратов, используют функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах, а также проекцию коэффициента тяги двигательной установки.
4. Способ по п.1, отличающийся тем, что в качестве наблюдаемых параметров при определении коэффициентов сил и моментов принимают разности суммарных значений коэффициентов аэродинамических сил или моментов, полученных на основе измерений в полете перегрузок и производных угловых скоростей, и соответствующих суммарных значений коэффициентов аэродинамических сил или моментов, вычисленных для тех же фактических условий полета и измеренных положений поверхностей управления на основе модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах - «продувочные» значения коэффициентов.
5. Способ по п.1, отличающийся тем, что в качестве наблюдаемых параметров при определении коэффициента тангенциальной силы или силы лобового сопротивления принимают значения коэффициента результирующей силы, а в качестве заданных функций, с помощью которых строится структурная или конструкционная матрица при идентификации по методу наименьших квадратов, используют функции, являющиеся составляющими коэффициентов аэродинамических сил и моментов в модели аэродинамических характеристик, полученной на основе продувок в аэродинамических трубах, а также проекции коэффициента тяги двигательной установки.
| Bruma J.H | |||
| Evaluation of a method to extract performance data from dynamic manoeuvers for a jet transport aircraft | |||
| ICAS proceedings, 1978, v.2, p.475-488 | |||
| Методы исследований на летающих моделях | |||
| Справочная библиотека авиационного инженера-испытателя | |||
| Летные испытания самолетов и вертолетов./ Под общей ред | |||
| А.Д.Миронова | |||
| - М.: Машиностроение, |
Авторы
Даты
2012-09-10—Публикация
2011-03-28—Подача