Изобретение относится к технике определения параметров движения и к области оценки и измерения углового положения летательного аппарата (ЛА) и может быть использовано для восстановления углов атаки и скольжения летательного аппарата при отсутствии таковых. Предлагается способ для определения углов атаки и скольжения при отсутствии датчиков аэродинамических углов с идентификацией скорости ветра, используя спутниковую навигационную систему, путем параметрической идентификации. Изобретение направлено на повышение точности определения угловых параметров бортовыми средствами измерения.
Углы атаки и скольжения, или аэродинамические углы, являются важнейшими параметрами, характеризующими движение летательного аппарата. Аэродинамические углы во многом определяют характеристики устойчивости, управляемости и маневренности, допустимый диапазон режимов полета. Между тем на беспилотных летательных аппаратах (БПЛА) датчики углов атаки и скольжения часто не устанавливаются в силу ограничений по габаритам и массе. Поэтому актуальной является задача нахождения оценок этих углов по измерительной информации от других бортовых систем. Бортовая навигационная система обеспечивает измерение трех проекций скорости БПЛА, а также углов ориентации (углы крена, тангажа, рыскания). На основе соотношений между земной, связанной и скоростной системами координат, можно получить искомые оценки двух аэродинамических углов: атаки и скольжения. Этот очевидный результат, однако, имеет силу только для спокойной атмосферы, то есть при отсутствии ветра. В общем случае влияние ветра может создавать существенные погрешности.
В предлагаемом способе для учета влияния ветра предлагается применить параметрическую идентификацию трех проекций скорости ветра, а вместо отсутствующих датчиков углов атаки и скольжения использовать информацию об аэродинамических коэффициентах подъемной и боковой сил. При этом точные значения аэродинамических коэффициентов не являются обязательными, соответствующая неопределенность также преодолевается путем идентификации.
Известно устройство определения погрешностей измерения углов атаки и скольжения, описанное в патенте РФ №2579551, МПК G01P 21/00, опубл.: 10.04.2016, бюл. №10, где, используя инерциальную навигационную систему (ИНС) и спутниковую навигационную систему (СНС), определяют модель искомого объекта и наблюдение сигналов датчиков углов. В итоге используют функционал максимума правдоподобия. Для минимизации функционала предлагается использовать одну из модификаций классического метода Ньютона. Определение и компенсацию погрешности измерения воздушной скорости осуществляют при выполнении летательным аппаратом маневра типа «змейка» или при установившемся развороте с изменением курса на 60-90 градусов.
Недостатком вышеуказанного способа является невозможность восстановления углов атаки и скольжения при отсутствии датчика угла атаки (ДУА) и датчика угла скольжения (ДУС).
Цель данного изобретения - получить возможность восстановления величин углов атаки и скольжения при отсутствии предназначенных для этого измерительных приборов.
Поставленная цель достигается за счет того, что согласно заявленному способу определения углов атаки и скольжения беспилотного летательного аппарата измеряют земную скорость при помощи спутниковой навигационной системы, используя значения углов пространственной ориентации летательного аппарата переводят ее в систему координат, связанную с летательным аппаратом, на основании полученных данных определяют значение воздушной скорости, дополнительно идентифицируют три проекции скорости ветра в связанной системе координат, используют данные об аэродинамических коэффициентах подъемной и боковой сил. Находят оценки углов атаки и скольжения, полученные через аэродинамические коэффициенты подъемной и боковой сил, тягу двигателей, а также через перегрузки, измеряемые бортовыми датчиками в связанной системе координат. Получают два вида оценок углов атаки и скольжения - на основе значений аэродинамических коэффициентов, - зависящую от ветра, и на основе измерений навигационной системы, в которых движение воздуха не учитывается, определяют модель объекта, модель измерений и вектор оцениваемых параметров и путем параметрической идентификации восстанавливают углы атаки и скольжения.
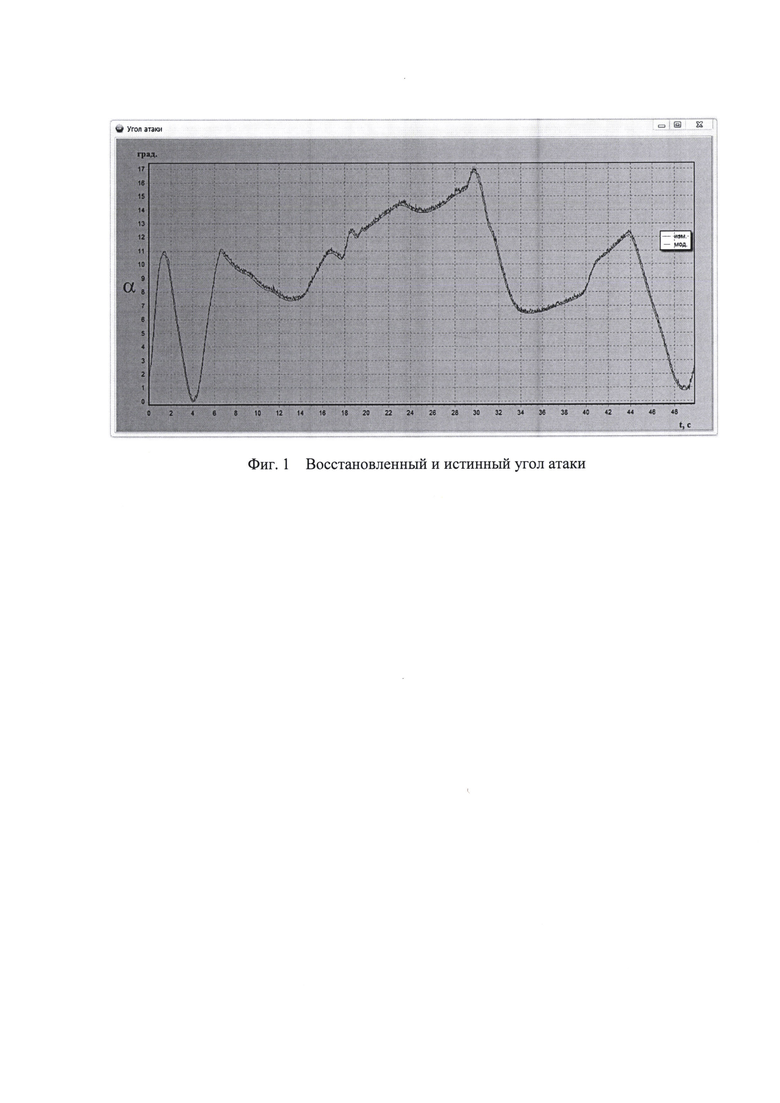
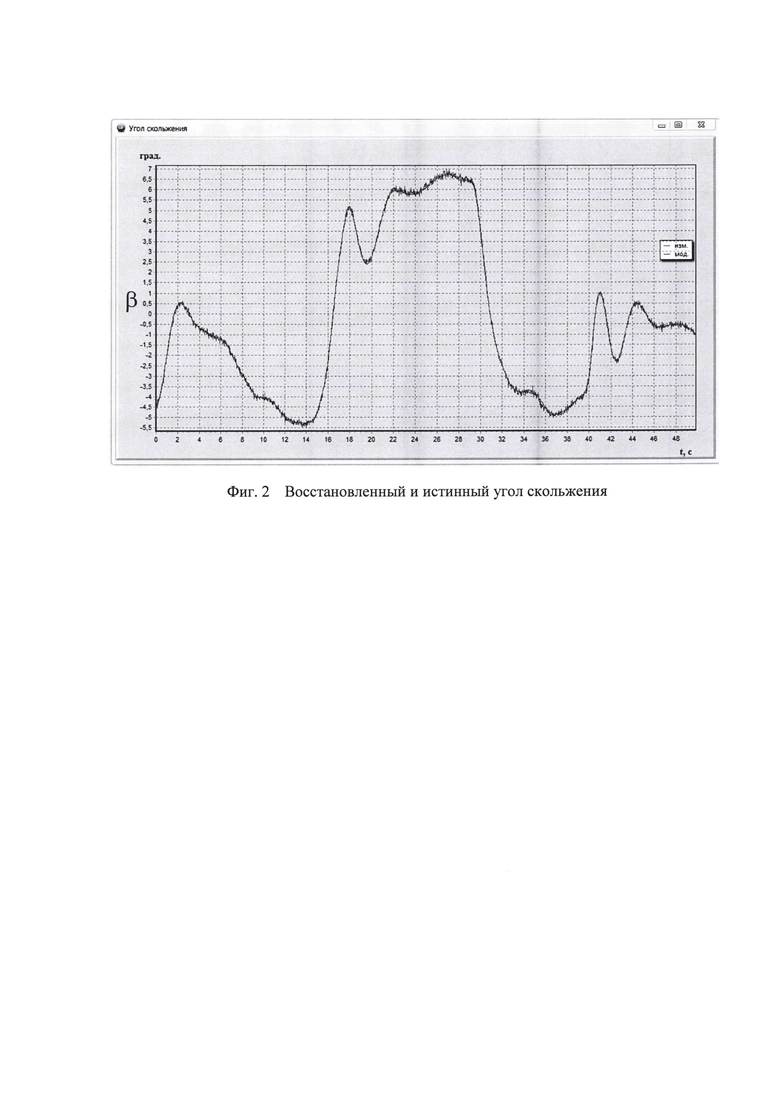
Результаты исследований работоспособности предложенного изобретения представлены на графиках. На фиг. 1 - представлен восстановленный и истинный углы атаки. На фиг. 2 - восстановленный и истинный углы скольжения.
Описание изобретения
Используют измерения трех проекций скорости БЛА и углов ориентации, а также барометрическую высоту полета (она необходима для определения плотности воздуха при расчете скоростного напора) и воздушную скорость.
Для коэффициентов подъемной и боковой сил имеет место линейная модель:

где Ya, Za - подъемная и боковая силы; α, β - углы атаки и скольжения; 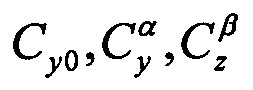 - аэродинамические коэффициенты;
- аэродинамические коэффициенты; 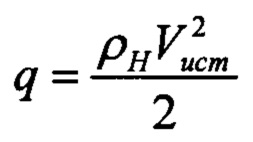 - скоростной напор; ρН - плотность воздуха на высоте полета Н, определяемая по стандартной атмосфере; Vист - истинная воздушная скорость, измеряемая на борту; S - эквивалентная площадь крыла.
- скоростной напор; ρН - плотность воздуха на высоте полета Н, определяемая по стандартной атмосфере; Vист - истинная воздушная скорость, измеряемая на борту; S - эквивалентная площадь крыла.
Алгоритм решения
Определяют модель объекта. Уравнения проекций воздушной скорости в земной нормальной системе координат имеют вид:
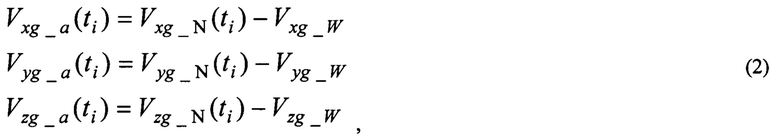
где 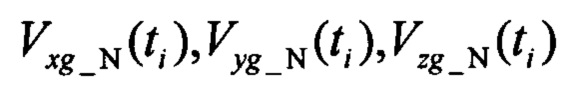 - измерения трех составляющих скорости ЛА в земной системе координат, выполняемые СНС;
- измерения трех составляющих скорости ЛА в земной системе координат, выполняемые СНС; 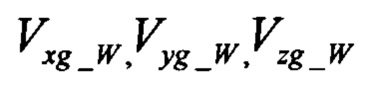 - неизвестные проекции скорости ветра, подлежащие определению при выполнении идентификации.
- неизвестные проекции скорости ветра, подлежащие определению при выполнении идентификации.
Проекции воздушной скорости в связанной системе координат получают, используя приведенное ниже выражение:

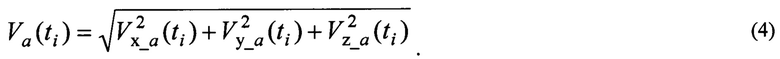
Получают первый вариант уравнений для углов атаки и скольжения:

где 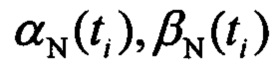 - оценки углов атаки и скольжения по данным навигационной системы.
- оценки углов атаки и скольжения по данным навигационной системы.
Следует отметить, что формулы (2.23) - (2.26) позволяют найти оценки углов атаки и скольжения только при отсутствии ветра, то есть при условии:
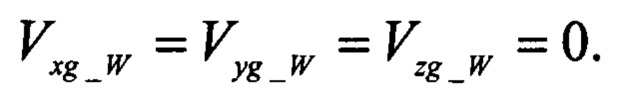
Для идентификации трех проекций скорости ветра используют данные об аэродинамических коэффициентах подъемной и боковой сил. Поскольку аэродинамические силы обычно рассматривают в скоростной системе координат, проекции перегрузок в скоростной системе определяют, используя матрицу перехода от связанной системы координат к скоростной системе координат:
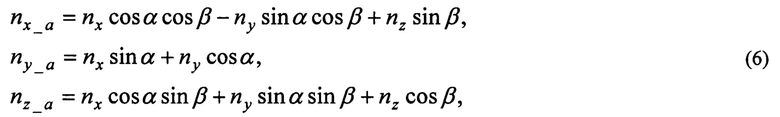
где nх, nу, nz - перегрузки в связанной системе координат, измеряемые бортовыми датчиками перегрузок.
Нормальная и боковая перегрузка выражаются через аэродинамические силы и тягу двигателя следующим образом:
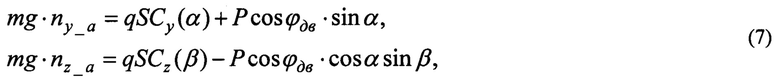
где Р - сила тяги двигателя, относительно которой принимают допущение, что она направлена вдоль оси двигателя; ϕдв - угол установки двигателя на ЛА, то есть угол между осью двигателя и осью Ох связанной системы координат.
Линейная аппроксимация аэродинамических сил правомерна при малых углах атаки и скольжения, поэтому принимают: cos α ≈ 1, sin β ≈ β.
Тогда:

Из (8) находят углы атаки и скольжения. Для краткости принимают ϕдв=0, то есть cosϕдв=1, и вводят индекс АДХ, указывающий на зависимость от аэродинамических характеристик:

Выражение (9) дает оценки углов атаки и скольжения, полученные через аэродинамические коэффициенты подъемной и боковой сил, тягу двигателей, а также через перегрузки, измеряемые бортовыми датчиками в связанной системе координат (6). Итак, получены два вида оценок углов атаки и скольжения - на основе значений аэродинамических коэффициентов (9), зависящих от ветра, и на основе измерений навигационной системы (5), в которых движение воздуха не учитывается.
Приводят полученные результаты к виду, позволяющему применить параметрическую идентификацию. Для этого определяют модель объекта, модель измерений и вектор оцениваемых параметров.
Варианты решения
Рассматривают следующие варианты в зависимости от полноты и достоверности исходных данных.
Случай точных априорных данных
Предполагают, что аэродинамические коэффициенты и сила тяги известны точно, а воздушная скорость измеряется без погрешностей. Тогда в качестве модели объекта принимают выражения (1) - (5). Они основаны на измерениях трех проекций скорости 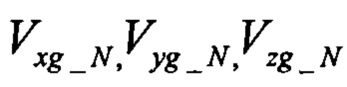 в земной системе, выполняемых СНС, включают три неизвестных параметра - проекции скорости ветра
в земной системе, выполняемых СНС, включают три неизвестных параметра - проекции скорости ветра 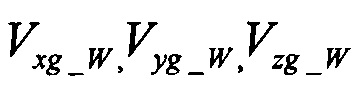 и позволяют найти оценку Va (4) воздушной скорости и оценки (5) углов атаки и скольжения.
и позволяют найти оценку Va (4) воздушной скорости и оценки (5) углов атаки и скольжения.
Модель наблюдений включает формулы (6) - (9), основана на бортовых измерениях перегрузок nx, nу, nz в связанной системе и позволяет получить оценки (9) углов атаки и скольжения. Она включает также барометрические измерения воздушной скорости Vбар.
Вводят вектор оценок измерений по аэродинамическим характеристикам следующим образом:

Тогда модель измерений примет вид:

где 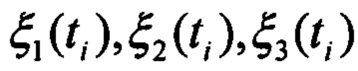 - случайные погрешности измерений, которые считают нормальными, независимыми случайными величинами с нулевыми математическими ожиданиями и постоянными дисперсиями.
- случайные погрешности измерений, которые считают нормальными, независимыми случайными величинами с нулевыми математическими ожиданиями и постоянными дисперсиями.
В (11) αN(ti), βN(ti) рассчитывают по формуле (3), а оценку скорости Va(ti) - по формуле (4). Вектор неизвестных параметров, подлежащих идентификации, включает три проекции скорости ветра:
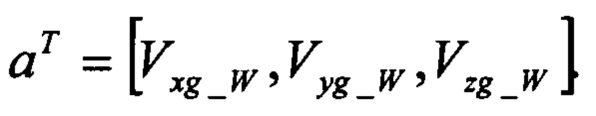
Случай с учетом неопределенности априорных данных
Модель (11) является идеализированной, поскольку барометрические измерения скорости обычно имеют систематическую постоянную погрешность CV. Кроме того, аэродинамические коэффициенты и сила тяги двигателей также известны с погрешностями. Для учета этого фактора вводят аддитивные и мультипликативные погрешности в каналах измерений углов атаки и скольжения. Модель измерений представляют в более полном виде:

где Kα, Kβ - коэффициенты мультипликативных погрешностей в каналах углов атаки и скольжения; Cα, Cβ, CV - аддитивные постоянные погрешности в каналах углов атаки, скольжения и воздушной скорости.
Сравнивая (12) и (9), получают соотношения между коэффициентами погрешностей и аэродинамическими коэффициентами. Если значения аэродинамических коэффициентов и силы тяги, используемые в (9), равны истинным значениям (погрешности отсутствуют), то коэффициенты мультипликативных погрешностей Kα=Kβ=1, а аддитивная погрешность Сα=0. Тогда отклонение коэффициента Kα от 1 характеризует относительную погрешность множителя множителя 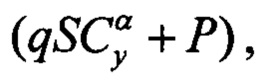 отклонение Kβ от 1 - относительную погрешность множителя
отклонение Kβ от 1 - относительную погрешность множителя 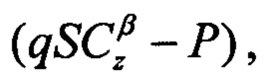 а погрешность qSCy0 определяет величину ΔСа.
а погрешность qSCy0 определяет величину ΔСа.
При использовании модели измерений (12) вектор идентифицируемых параметров представляют в следующем виде:
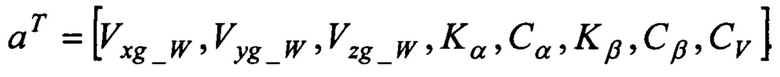
При выполнении расчетов по формулам (6) в качестве априорных значений для углов атаки и скольжения используют оценки (5), вычисленные при условии нулевой скорости ветра. После выполнения идентификации в качестве оценок углов атаки и скольжения также выбирают оценки (5), которые теперь будут учитывать и оценки трех проекций скорости ветра. При наличии подробного банка аэродинамических характеристик, формулу (9) записывают в виде:
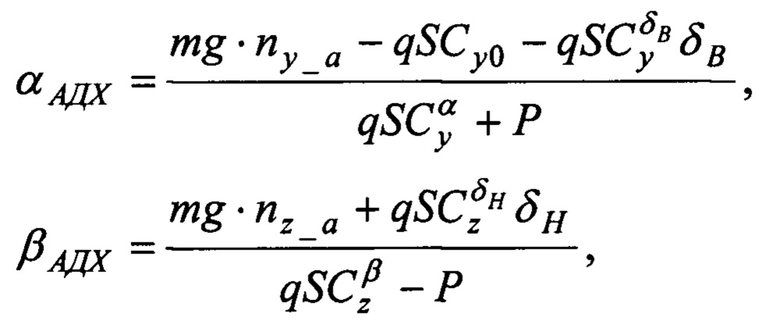
где δB, δН - отклонения руля высоты и руля направления; 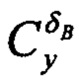 - коэффициент подъемной силы руля высоты;
- коэффициент подъемной силы руля высоты; 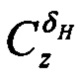 - коэффициент боковой силы руля направления.
- коэффициент боковой силы руля направления.
Представленные выше модели объекта и наблюдений можно представить в следующей общей векторной форме
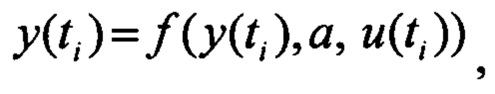
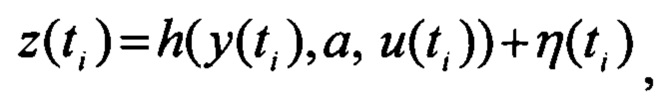
где y(t), u(t) - векторы выходных и входных сигналов размерности n и m соответственно, z(ti) - вектор измерений размерности r, а - вектор неизвестных параметров, подлежащий идентификации, z(fi) - шум измерений, представляющий собой векторную нормальную случайную последовательность типа белого шума с нулевым математическим ожиданием и известной дисперсионной матрицей R(ti).
Предполагается, что u(t) есть известная функция времени. Начальные условия y(t0) или предполагаются известными, или включаются в вектор оцениваемых параметров.
Шумы измерений представляют собой нормальные и независимые случайные векторные величины. Поэтому их совместная плотность распределения вероятностей равна произведению плотностей для каждого момента 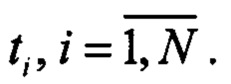
Известно, что максимум функции правдоподобия при указанных допущениях о свойствах шумов приводит к несмещенным и эффективным оценкам. Функционал максимума правдоподобия имеет следующий вид:
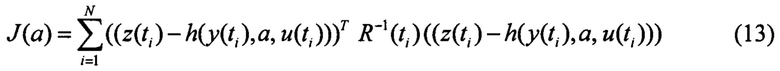
Несложно заметить, что (13) представляет собой функционал метода наименьших квадратов с матрицей весовых коэффициентов 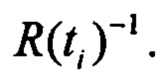 Таким образом, при указанных выше допущениях о свойствах шумов функционал максимума правдоподобия совпадает с взвешенным функционалом метода наименьших квадратов.
Таким образом, при указанных выше допущениях о свойствах шумов функционал максимума правдоподобия совпадает с взвешенным функционалом метода наименьших квадратов.
Для минимизации (13) предлагается использовать одну из модификаций классического метода Ньютона
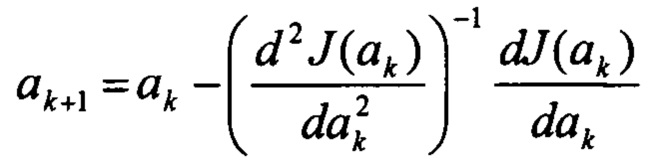
где:
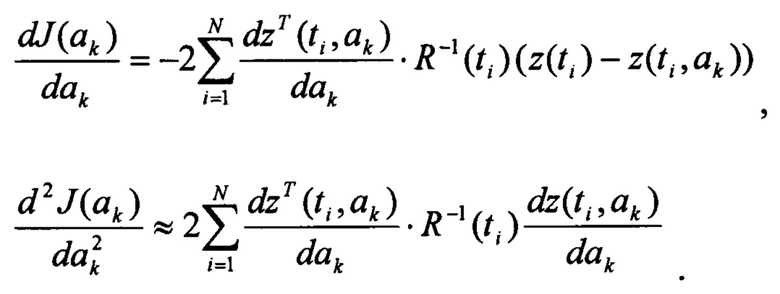
Производные оценок прогноза измерений определяются численно для моментов времени 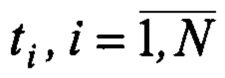 по формулам:
по формулам:
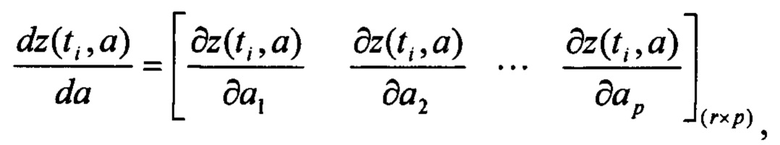
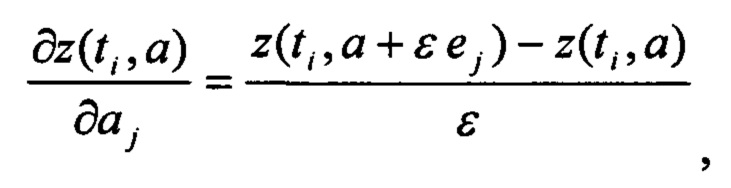
где ej - вектор размерности р, все элементы которого равны нулю за исключением j-го элемента, который равен 1; ε - малое число, обычно задаваемое на уровне 0,001…0,1% от номинального значения параметров.
Оценки 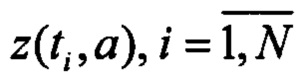 определяются численным решением уравнений объекта и измерений при η(ti)=0. Идентификации заканчивается по условию
определяются численным решением уравнений объекта и измерений при η(ti)=0. Идентификации заканчивается по условию 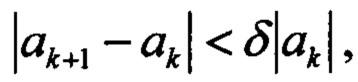 где δ=0,005. При обработке в реальном масштабе времени целесообразно жестко задать число шагов, например, пять, чтобы зафиксировать число итераций.
где δ=0,005. При обработке в реальном масштабе времени целесообразно жестко задать число шагов, например, пять, чтобы зафиксировать число итераций.
Исследование метода восстановления углов атаки и скольжения по данным стендового моделирования
Для исследования характеристик предложенного алгоритма обрабатывались 9 участков полета, выполненных на пилотажно-навигационном стенде. Постоянный ветер моделировался продольной, поперечной и вертикальной проекциями скорости 5, 7 и 2 м/сек, соответственно.
Преимущество моделируемых данных при оценке точности алгоритма состоит в том, что нам известны истинные значения углов атаки и скольжения, которые в алгоритме не используются. Исследованиями установлено, что с.к.о. рассогласований между истинными, то есть вычисленными при моделировании, и восстановленными значениями аэродинамических углов не превышают 0,269 градуса по углу атаки и 0,106 градуса по углу скольжения. Эта точность является высокой и соответствует уровню точности существующих датчиков, то есть метод оценивания углов обеспечивает точности, сопоставимые с прямыми измерениями. Из результатов исследований также следует, что отношение с.к.о. невязки и с.к.о. сигнала не превысило 7% в канале угла атаки и 4% в канале угла скольжения.
На фиг. 1 и фиг. 2 представлены истинные (полученные при моделировании на пилотажно-навигационном стенде) и измеренные углы атаки и скольжения, соответственно. Как видим, степень соответствия весьма высокая. На остальных участках результаты восстановления аналогичны.
Технический результат
Предложен Способ восстановления аэродинамических углов при отсутствии соответствующих датчиков, использующий измерения трех проекций скорости полета, определяемых навигационной системой, а также значения углов ориентации.
Представлены результаты проверки предложенного метода по данным стендового моделирования, которые показывают, что предложенный способ оценивания углов атаки и скольжения обеспечивает точности, сопоставимые с прямыми измерениями.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ УГЛОВ АТАКИ И СКОЛЬЖЕНИЯ | 2014 |
|
RU2579551C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ ИЗМЕРЕНИЯ ВОЗДУШНОЙ СКОРОСТИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2579550C1 |
| СПОСОБ КОНЕЧНОГО ПРИВЕДЕНИЯ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА В ПРОДОЛЬНОЙ ПЛОСКОСТИ НА ОСНОВЕ КВАЗИОПТИМАЛЬНОГО ЗАКОНА НАВЕДЕНИЯ | 2020 |
|
RU2737840C2 |
| Комплексный способ навигации летательных аппаратов | 2016 |
|
RU2646957C1 |
| СПОСОБ ГРАДУИРОВКИ ДАТЧИКА АЭРОДИНАМИЧЕСКОГО УГЛА ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2277698C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АЭРОДИНАМИЧЕСКОГО УГЛА ЛЕТАТЕЛЬНОГО АППАРАТА | 2007 |
|
RU2341775C1 |
| СИСТЕМА И СПОСОБ ОЦЕНКИ ВОЗДУШНОЙ СКОРОСТИ ЛЕТАТЕЛЬНОГО АППАРАТА НА ОСНОВАНИИ МОДЕЛИ НАКОПЛЕНИЯ ДАННЫХ О ПОГОДЕ. | 2018 |
|
RU2755843C2 |
| СПОСОБ И УСТРОЙСТВО ВЫЧИСЛЕНИЯ ТЕКУЩЕГО ЗНАЧЕНИЯ УГЛОВ АТАКИ И СКОЛЬЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА | 2016 |
|
RU2663315C2 |
| СПОСОБ УПРАВЛЕНИЯ АВИАЦИОННОЙ БУКСИРОВОЧНОЙ ТРОСОВОЙ СИСТЕМОЙ | 2009 |
|
RU2395430C1 |
| Малогабаритный навигационный комплекс | 2016 |
|
RU2644632C1 |
Изобретение относится к технике определения параметров движения и к области оценки и измерения углового положения летательного аппарата (ЛА) и может быть использовано для восстановления углов атаки и скольжения летательного аппарата при отсутствии таковых. Согласно способу используют земную скорость, измеряемую посредством спутниковой навигационной системы, а также значения углов пространственной ориентации летательного аппарата от навигационной системы. Определяют значение воздушной скорости и идентифицируют три проекции скорости ветра. Находят оценки углов атаки и скольжения, полученные через аэродинамические коэффициенты подъемной и боковой сил, тягу двигателей, а также через перегрузки, измеряемые бортовыми датчиками в связанной системе координат. Таким образом, получают два вида оценок углов атаки и скольжения - на основе значений аэродинамических коэффициентов, зависящие от ветра, и на основе измерений навигационной системы, в которых движение воздуха не учитывается. Определяют модель объекта, модель измерений и вектор оцениваемых параметров. Путем параметрической идентификации восстанавливают углы атаки и скольжения. Технический результат заключается в возможности восстановления величин углов атаки и скольжения при отсутствии предназначенных для этого измерительных приборов. 2 ил.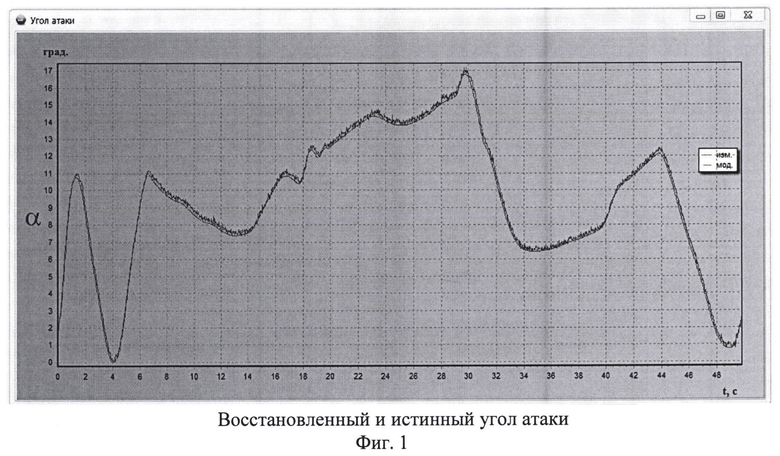
Способ определения углов атаки и скольжения беспилотного летательного аппарата, согласно которому измеряют земную скорость при помощи спутниковой навигационной системы, используют значения углов пространственной ориентации летательного аппарата, переводят их в систему координат, связанную с летательным аппаратом, на основании полученных данных определяют значение воздушной скорости, отличающийся тем, что дополнительно идентифицируют три проекции скорости ветра в связанной системе координат, используют аэродинамические коэффициенты подъемной и боковой сил, находят оценки углов атаки и скольжения, полученные через аэродинамические коэффициенты подъемной и боковой сил, тягу двигателей, а также через перегрузки, измеряемые бортовыми датчиками в связанной системе координат, получают два вида оценок углов атаки и скольжения на основе значений аэродинамических коэффициентов, зависящие от ветра, и на основе измерений навигационной системы, в которых движение воздуха не учитывается, определяют модель объекта, модель измерений и вектор оцениваемых параметров, путем параметрической идентификации восстанавливают углы атаки и скольжения.
| УСТРОЙСТВО ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ УГЛОВ АТАКИ И СКОЛЬЖЕНИЯ | 2014 |
|
RU2579551C1 |
| Контрольный микроманометр колокольного типа | 1952 |
|
SU99181A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВ ПРОСТРАНСТВЕННОЙ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2589495C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЗДУШНЫХ ПАРАМЕТРОВ В ЛЕТНЫХ ИСПЫТАНИЯХ ЛЕТАТЕЛЬНОГО АППАРАТА НА БОЛЬШИХ УГЛАХ АТАКИ | 2009 |
|
RU2396569C1 |
| US 8718840 B2 06.05.2014. | |||
Авторы
Даты
2023-03-21—Публикация
2022-02-03—Подача