Анализ существующего состояния вопроса
В этом разделе рассматриваются наиболее близкие технические решения (аналоги), нацеленные на защиту информации с помощью криптографических и стеганографических способов.
Способы криптографической защиты информации
Изобретение относится к области телекоммуникаций и предназначено для защиты секретной информации от несанкционированного прочтения.
Известен способ шифрования информации, при реализации которого открытый текст делят на несколько блоков данных, последовательно нумеруют полученные блоки данных, шифруют порядковые номера всех блоков данных, результат шифрования суммируют с помощью логической операции Исключающее ИЛИ с соответствующим блоком открытого текста и над полученной суммой выполняют операцию блочного шифрования [18].
Перечисленные в формуле изобретения операции математически описываются так:
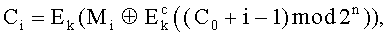
где Ci - i-й зашифрованный блок; Ek - операция блочного шифрования на ключе k; Mi - i-й блок открытого текста; ⊕ - логическая операция Исключающее ИЛИ (XOR); 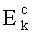 - операция шифрования счетчика; С0 - вектор инициализации (псевдослучайная величина); i - порядковый номер блока; n - размер блока.
- операция шифрования счетчика; С0 - вектор инициализации (псевдослучайная величина); i - порядковый номер блока; n - размер блока.
При помощи операции 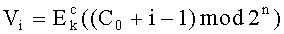 формируется псевдослучайный вектор Vi (гамма), величина которого зависит от порядкового номера блока i. Вектор Vi перед шифрованием с помощью операции Ek прибавляется к открытому тексту Mi. Таким образом, результат шифрования будет зависеть не только от открытого текста, алгоритмов шифрования, ключей, но и порядкового номера шифруемого блока.
формируется псевдослучайный вектор Vi (гамма), величина которого зависит от порядкового номера блока i. Вектор Vi перед шифрованием с помощью операции Ek прибавляется к открытому тексту Mi. Таким образом, результат шифрования будет зависеть не только от открытого текста, алгоритмов шифрования, ключей, но и порядкового номера шифруемого блока.
Расшифровывается криптограмма с помощью соотношения:
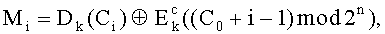
где Dk операция дешифрования, обратная операции шифрования Ek.
Изобретение [18] нацелено на создание способа работы с зашифрованной базой данных в реальном масштабе времени. Такой подход позволяет работать индивидуально с каждым блоком данных (осуществлять запись и считывание отдельных блоков независимо друг от друга). При формировании запроса расшифровывается только один блок данных, необходимый для работы, а все остальные блоки данных остаются в памяти ЭВМ зашифрованными.
В патенте [18] решена задача, позволяющая работать с отдельными блоками независимо от остальных блоков базы данных.
В заявляемом техническом решении требуется решение другой задачи: выполнить шифрующее преобразование таким образом, чтобы содержимое каждого зашифрованного блока зависело от содержимого всех имеющихся в криптограмме блоков.
Наиболее близким по сущности к заявляемому изобретению является американский стандарт шифрования DES [17]. Алгоритм DES обрабатывает информацию блоками по 64 бит с использованием ключа длиной 56 бит.
В процессе шифрования с помощью DES выполняются следующие преобразования открытого текста и шифруемых данных.
1. В 64-битном блоке двоичных данных осуществляется начальная перестановка битов в соответствии с таблицей, определяющей порядок перестановок разрядов.
2. Полученный после перестановок битов блок делится на два субблока по 32 бита (субблоки А и В). Над субблоками производится 16 раундов шифрующих преобразований:
Ai=Bi-1;
Bi=Ai-1⊕f(Bi-1, Ki),
где i - номер текущего раунда шифрования; ⊕ - логическая операция Исключающее ИЛИ (XOR, суммирование по модулю два без переноса, неравнозначность); Ki - ключ i-го раунда.
Приведенные выражения математически описывают сеть Фейстеля, которая успешно используется во многих широко известных шифрах (см. фиг.1).
Шифрующее преобразование f(Bi-1,Ki) включает в себя несколько операций:
- расширяющую перестановку, в результате которой 32-разрядный субблок превращается в 48-разрядный блок Pi;
- суммирование (операция XOR) полученного блока с 48-битным ключом данного раунда Pi⊕Ki;
- полученный результат разбивается на 8 частей по 6 бит; каждая 6-битная часть подвергается шифрованию методом замен на 4-битное число в соответствии с фиксированными таблицами замен; в результате формируется 32-битный блок.
3. Полученные в результате 16 раундов шифрования субблоки А16 и В16 объединяются в 64-битный блок, в котором выполняется финальная перестановка бит (разрядов) в соответствии с фиксированной таблицей.
Заметим, что в заявляемом техническом решении в качестве первой шифрующей функции могут использоваться любые алгоритмы, в том числе действующий американский стандарт AES [19], отечественный стандарт [6], шифры RC6, Twofish, IDEA, KASUMI [1] и другие.
Наибольший интерес в контексте заявляемого технического решения представляют собой режимы работы стандарта DES.
Шифр DES имеет четыре режима формирования криптограммы, которые существенно расширяют возможности этого шифра.
1. Электронная кодовая книга ЕСВ (Electronics Code Book).
2. Сцепление блоков шифра СВС (Cipher Block Chaining).
3. Обратная связь по шифртексту СFВ (Chiper Feed Back).
4. Обратная связь по выходу OFB (Output Feed Back).
Режим электронной книги ЕСВ используется для шифрования открытого текста отдельными (не связанными между собой) блоками. Этот режим предназначен для шифрования текста, который не содержит одинаковых фрагментов, например ключей шифрования. При шифровании одинаковых блоков открытого текста блоки криптограммы будут идентичными. Очевидно, что это дает зацепку для криптоаналитиков.
В режиме СВС к зашифрованному блоку прибавляется (по правилу Исключающее ИЛИ) предыдущий зашифрованный блок. В этом случае удается уменьшить вероятность появления одинаковых блоков криптограммы. В этом режиме работы шифра расшифрование части криптограммы возможно, если есть в наличии два соседних блока криптограммы.
Режим CFB используется для формирования псевдослучайной гаммы, которая накладывается с помощью операции Исключающее ИЛИ на открытый текст. Причем при генерировании гаммы используется уже сформированная криптограмма. Отсюда становится понятным название этого режима: Обратная связь по шифртексту, то есть обратная связь используется для формирования гаммы.
В режиме OFB гамма формируется без участия шифртекста и поэтому гамма может быть сформирована заранее (про запас). В одной из разновидностей этого режима при формировании гаммы используется режим Счетчика. Здесь после инициализации одного из регистров шифратора его содержимое просто инкрементируется перед очередным формированием фрагмента гаммы. Таким образом, состав гаммы зависит от порядкового номера раунда (то есть от содержимого счетчика).
Многие идеи, используемые в стандарте DES, принадлежат Хорсту Фейстелю [14], [21].
Способы стеганографического сокрытия информации
Сформированные в процессе второго шифрования блоки должны быть скрытно размещены в стеганографических контейнерах.
Для сокрытия зашифрованной информации могут быть использованы контейнеры различного типа и разнообразные алгоритмы. Большое число алгоритмов сокрытия информации описано в отечественных источниках [4, 7-10]. Значительно большее число идей описано в зарубежных источниках.
Наибольшую популярность получил метод замены наименьшего значащего бита (LSB). Суть этого метода заключается в том, что незначительные изменения цифрового сигнала не обнаруживаются органами чувств человека. Поэтому, заменяя последний бит, можно передавать информацию с помощью графических файлов формата BMP, звуковых файлов формата WAV и т.п.
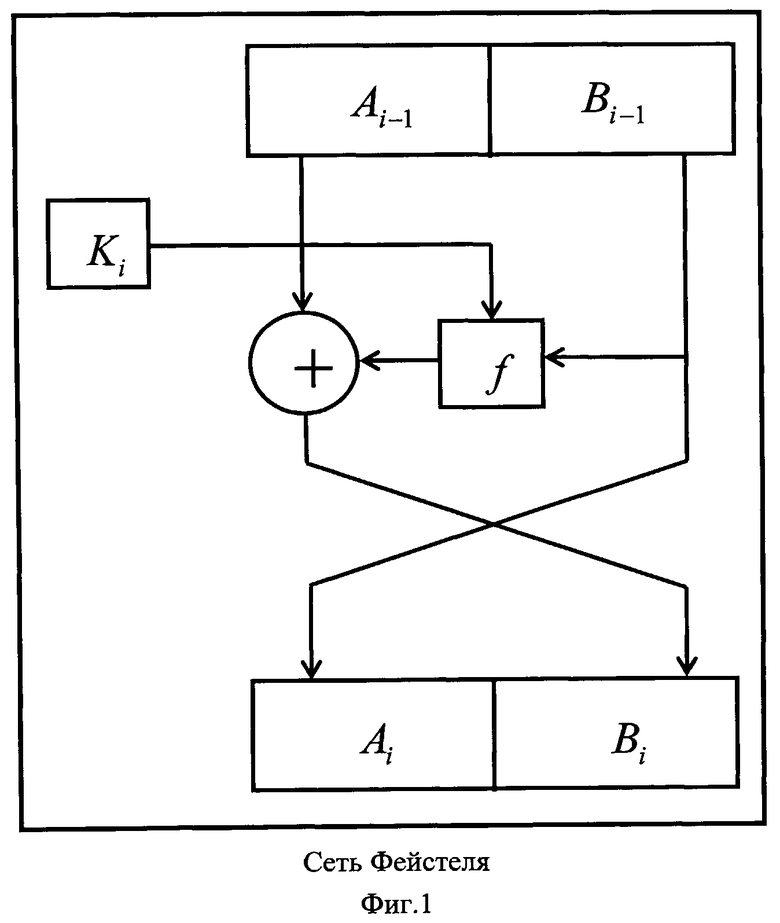
Внедрение скрываемой информации осуществляют с помощью секретного ключа, затрудняющего несанкционированное извлечение информации. Например, в WAV-файле внедрение ведут не подряд, а через определенное число отсчетов. На фиг.2 показана процедура аналого-цифрового преобразования звукового сигнала. Внедрение секретной информации может вестись, скажем, только в четные отсчеты. Отсчеты могут вычисляться по определенной секретной формуле [9].
В качестве контейнеров могут быть выбраны (использованы) звуковые файлы формата MIDI [12]. Сокрытие информации в них осуществляют за счет незначительного изменения громкости или длительности звучания нот. Такие музыкальные произведения нередко размещают на HTML-страницах.
Известны методы сокрытия информации в текстовых документах путем изменения числа пробелов между словами [9]. Причем эти и другие алгоритмы можно использовать и для скрытой передачи информации в субтитрах видеофильма [11].
Скрытно передать информацию можно путем принудительной вариации длины TCP/IP пакета [13].
Информацию можно незаметно разместить на HTML-странице [4]. Запись скрываемой информации осуществляют с помощью непечатаемых символов (пробел и табуляция).
Скрытно внедрить информацию можно даже в криптограмму.
Способ, предложенный Густавусом Симмонсом (Gustavus Simmons), устанавливает скрытый канал связи на основе криптограмм, внедряя в них дополнительную информацию. Предложенные им методы базируются на изменении способа выбора переменных, используемых в ключе. Рассмотрим метод внедрения в схему цифровой подписи Эль-Гамаля [20]. Генерация ключа выполняется так же, как и в основной схеме подписи Эль-Гамаля.
Сначала выбирается простое число p и два случайных числа g и r, меньших p. Затем вычисляется:
K=grmodp
Открытым ключом служат K, g и p. Закрытым (секретным) ключом является r. Помимо передающей стороны значение r известно и на приемной стороне, это число используется не только для подписи безобидного сообщения, но и в качестве ключа для отправки и чтения скрытого сообщения.
Для отправки скрытого сообщения M в составе безобидного сообщения числа М', M и p должны быть взаимно простыми, кроме того, взаимно простыми должны быть значения M и p-1. Передающая сторона вычисляет:
X=gMmodp
И решается следующее уравнение для Y (с помощью расширенного алгоритма Евклида):
M'=rX+MYmod(p-1)
Как и в базовой схеме Эль-Гамаля, подписью является пара чисел: Х и Y. Третья сторона (криптоаналитик, злоумышленник) может проверить подпись Эль-Гамаля, убедившись, что:
KXXY≡gM'(modp)
Приемная сторона может восстановить скрытое сообщение. Сначала убеждается, что:
(gr)XXY≡gM'(modp)
Если это так, приемная сторона считает сообщение подлинным (не подделанной третьей стороной). Затем для восстановления M вычисляется:
M=(Y-1(M'-rX))mod(p-1)
Пример
Пусть p=11, а g=2. Закрытый ключ r выбирается равным 8. Это означает, что открытым ключом, который третья сторона может использовать для проверки подписи, будет:
grmodp=28mod11=3
Чтобы отправить скрытое сообщение М=9, используя безобидное сообщение М'=5. Передающая сторона проверяет, что 9 и 11, а также 5 и 11 попарно взаимно простые числа. Также убеждается, что взаимно простые числа 9 и 11-1=10. Это и в самом деле так, поэтому вычисляется:
X=gMmodp=29mod11=6
Затем решается следующее уравнение для Y:
5=8·6+9·Ymod10
Y=3, поэтому подписью служит пара чисел 6 и 3 (X и Y). Приемная сторона убеждается, что:
(gr)XXY≡gM'(modp)
(28)663≡25(mod11)
Эти равенства справедливы, поэтому приемная сторона может раскрыть скрытое сообщение, вычисляя:
M=(Y-1(M'-rX))mod(p-1)=3-1(5-8·6)mod(11-1)=7(7)mod10=49mod10=9
Достоинством рассмотренного способа внедрения информации в криптограмму является то, что скрытая информация защищена ключом.
Недостатки способа [20].
Данный способ не позволяет разбивать подпись на блоки.
На передаваемые сообщения накладывается ряд ограничений. Это связанно с тем, что необходимо учитывать взаимную простоту скрытно передаваемого сообщения с другими значениями схемы цифровой подписи. Поэтому не в каждое сообщение можно внедрить необходимую информацию. Кроме того, ключ зависит от внедряемой информации.
Естественно, что большое число технических решений по внедрению скрытой информации в различные контейнеры, защищено патентами.
В патенте [15] описан способ скрытой передачи информации в графическом файле. Способ предотвращает искажение (уничтожение) скрытой информации в результате преобразования изображения (обрезка, вращение, корректировка контрастности, яркости, цветности и т.п.). Устойчивость к искажениям достигается тем, что для внедрения находят точки экстремума (сигнатурные точки) и их используют для передачи скрытой информации. Сигнатурные точки не могут быть найдены или удалены без первоначальных знаний об их местоположении.
Определение точек экстремумов осуществляется так называемым методом «Определения разности средних» [15]. При этом определяют разность между средним значением пикселей в малой окрестности и средним значением пикселей в большой окрестности исследуемого участка изображения. Если разность велика по сравнению с разностью для соседних участков изображения (пикселя), то в этом месте имеется локальный максимум или минимум.
Количество локальных экстремумов на изображении может казаться большим и для внедрения информации авторы [15] рекомендуют отобрать часть точек вручную или по случайному закону.
Один бит скрываемых данных внедряется в одну сигнатурную точку изображения, изменяя значения пикселей, окружающих точку. Изображение изменяется путем малой (2…10%) положительной или отрицательной корректировки значения пикселя в определенной сигнатурной точке для представления бинарным нулем или единицей.
Предложенный способ внедрения рекомендован для подписи изображения с целью обозначения авторских прав. Для извлечения внедренной информации на приеме используются оригинальное изображение и контейнер с внедренной информацией.
Способ может быть использован для формирования «водяных знаков». Однако для передачи скрытой текстовой информации он не приемлем из-за имеющихся недостатков. Первый недостаток заключается в малой пропускной способности скрытого канала из-за использования небольшого числа сигнатурных точек. Второй недостаток заключается в отсутствии секретного ключа, который однозначно определяет местоположение внедренных битов в графическом файле. По этой причине целесообразно использовать способы внедрения информации в графические файлы, которые определяют место начала внедрения, порядок внедрения и место окончания внедрения [9].
Сокрытие (внедрение) информации можно осуществить в различные контейнеры, например в звуковые файлы формата MIDI.
Стандартный MIDI-файл не является звуковым файлом с оцифрованным звуком (как, скажем, МР3). MIDI-файл скорее похож на партитуру, которая определяет, какой инструмент должен играть и каковы параметры воспроизводимых звуков. Музыкальная информация кодируется путем формирования управляющих сигналов.
В способе [16] внедрение скрываемой информации осуществляется путем изменения числа тиков (тактов) между двумя соседними событиями. Причем эти события умышленно выбираются такими, чтобы они не влияли на воспроизведение музыки. Недостатком описанного способа внедрения является отсутствие ключа, который затрудняет извлечение информации криптоаналитиками.
Технические результатом заявляемого технического решения является повышение криптостойкости передаваемой информации.
Сущность заявляемого способа скрытой передачи зашифрованной информации по множеству каналов связи состоит в том, что осуществляют обмен между корреспондентами секретными ключами, разбивают открытый текст на блоки, шифруют эти блоки с помощью шифра со сцеплением блоков 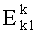 на ключе k1, состоящим из элементов е1е2е3…en, в результате чего получают криптограмму С1, состоящую из m блоков, полученные m сцепленных блоков первой криптограммы C1 повторно шифруют шифром
на ключе k1, состоящим из элементов е1е2е3…en, в результате чего получают криптограмму С1, состоящую из m блоков, полученные m сцепленных блоков первой криптограммы C1 повторно шифруют шифром 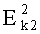 на ключе k2, в результате второго шифрования получают вторую криптограмму С2, состоящую из r блоков, в каждый блок второй криптограммы С2, при шифровании помещают несколько блоков первой криптограммы С1, скрытно нумеруют все блоки второй криптограммы С2, в n блоков второй криптограммы С2 скрытно помещают n элементов ключа k1, r блоков второй криптограммы С2 стеганографически скрывают в r контейнерах различного типа с использованием ключа k3, который определяет тип контейнера и секретные параметры алгоритмов внедрения, r контейнеров пересылают по нескольким каналам связи в соответствии со схемой организации и расписанием связи, которые определяет ключ k4, на приемной стороне извлекают информацию из стеганографических контейнеров с помощью ключа k3, осуществляют дешифрацию второй криптограммы С2 с помощью ключа k2, в результате дешифрации получают первую криптограмму С1, при дешифрации из n блоков второй криптограммы С2 извлекают n элементов ключа k1 и их порядковые номера, составляют из элементов e1e2e3…en ключ k1, который используют для дешифрации первой криптограммы С1.
на ключе k2, в результате второго шифрования получают вторую криптограмму С2, состоящую из r блоков, в каждый блок второй криптограммы С2, при шифровании помещают несколько блоков первой криптограммы С1, скрытно нумеруют все блоки второй криптограммы С2, в n блоков второй криптограммы С2 скрытно помещают n элементов ключа k1, r блоков второй криптограммы С2 стеганографически скрывают в r контейнерах различного типа с использованием ключа k3, который определяет тип контейнера и секретные параметры алгоритмов внедрения, r контейнеров пересылают по нескольким каналам связи в соответствии со схемой организации и расписанием связи, которые определяет ключ k4, на приемной стороне извлекают информацию из стеганографических контейнеров с помощью ключа k3, осуществляют дешифрацию второй криптограммы С2 с помощью ключа k2, в результате дешифрации получают первую криптограмму С1, при дешифрации из n блоков второй криптограммы С2 извлекают n элементов ключа k1 и их порядковые номера, составляют из элементов e1e2e3…en ключ k1, который используют для дешифрации первой криптограммы С1.
Заявляемый способ может иметь несколько модификаций.
В качестве шифра со сцеплением 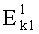 используют шифр, в котором осуществляется сцепление всех блоков первой криптограммы в следующей последовательности:
используют шифр, в котором осуществляется сцепление всех блоков первой криптограммы в следующей последовательности: 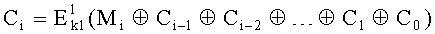 , указанное шифрующее преобразование выполняют повторно, причем при повторном шифровании блоки криптограммы, полученные после первого шифрования, зеркально переставляют местами, где С0 - вектор инициализации (псевдослучайный вектор); Ci - очередной блок криптограммы; k1 - ключ шифрования; Mi - очередной блок открытого текста;
, указанное шифрующее преобразование выполняют повторно, причем при повторном шифровании блоки криптограммы, полученные после первого шифрования, зеркально переставляют местами, где С0 - вектор инициализации (псевдослучайный вектор); Ci - очередной блок криптограммы; k1 - ключ шифрования; Mi - очередной блок открытого текста; 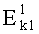 - шифрующее преобразование на ключе k1; ⊕ - логическая операция Исключающее ИЛИ.
- шифрующее преобразование на ключе k1; ⊕ - логическая операция Исключающее ИЛИ.
В качестве шифра 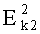 для формирования второй криптограммы С2 используют адаптивный многоалфавитный шифр с интегральным преобразованием, при реализации которого составляют секретную таблицу многоалфавитной замены, выбирают секретную подынтегральную функцию f(x), секретную информацию в виде ключа k2 предварительно передают на приемную сторону, в процессе шифрования на передающей стороне каждый символ открытого текста заменяют вещественным числом I из таблицы многоалфавитной замены, генерируют случайное число a таким образом, чтобы обеспечить равномерность гистограммы, которая описывает распределение чисел в формируемой второй криптограмме С2, вычисляют второе число b с учетом используемой подынтегральной функции f(x), выбранных I и а по формуле b=φ(a, I), которая определяется видом подынтегральной функции, осуществляют сокрытие номера блока криптограммы и одного элемента ключа k1 путем кодирования двоичной информации за счет изменения положения пределов интегрирования в гистограмме, сформированные числа a и b передают на приемную сторону, на приемной стороне принятые числа a и b используют для вычисления интеграла
для формирования второй криптограммы С2 используют адаптивный многоалфавитный шифр с интегральным преобразованием, при реализации которого составляют секретную таблицу многоалфавитной замены, выбирают секретную подынтегральную функцию f(x), секретную информацию в виде ключа k2 предварительно передают на приемную сторону, в процессе шифрования на передающей стороне каждый символ открытого текста заменяют вещественным числом I из таблицы многоалфавитной замены, генерируют случайное число a таким образом, чтобы обеспечить равномерность гистограммы, которая описывает распределение чисел в формируемой второй криптограмме С2, вычисляют второе число b с учетом используемой подынтегральной функции f(x), выбранных I и а по формуле b=φ(a, I), которая определяется видом подынтегральной функции, осуществляют сокрытие номера блока криптограммы и одного элемента ключа k1 путем кодирования двоичной информации за счет изменения положения пределов интегрирования в гистограмме, сформированные числа a и b передают на приемную сторону, на приемной стороне принятые числа a и b используют для вычисления интеграла 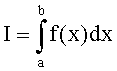 , с помощью рассчитанного числа I по таблице многоалфавитной замены определяют символ открытого текста, анализируют последовательность размещения чисел а и b в гистограмме и извлекают скрытую информацию.
, с помощью рассчитанного числа I по таблице многоалфавитной замены определяют символ открытого текста, анализируют последовательность размещения чисел а и b в гистограмме и извлекают скрытую информацию.
При организации связи между корреспондентами используют S=Sc+Sm доступных каналов связи, причем в текущем сеансе связи с помощью ключа k4 выделяют не все, а только часть доступных каналов связи Sc, по всем доступным каналам связи S=Sc+Sm непрерывно передают камуфлирующие сигналы, а передачу сигналов, несущих полезную информацию, осуществляют в псевдослучайные моменты времени.
Передающая и приемная стороны предварительно обмениваются ключами K(k2, k3, k4), которые определяют секретные параметры второго шифра Е2, тип контейнеров и параметры алгоритмов внедрения информации в стего контейнеры, схему организации связи и расписание передачи информации, а ключ k1 генерируют на лету только на передающей стороне в момент формирования блоков первой криптограммы С1 и на приемную сторону предварительно не передают, а скрытно размещают элементы ключа k1 в нескольких блоках второй криптограммы С2.
Шифрование блоков первой криптограммы С1 на передающей стороне ведут на ключе k1, для определения которого многократно вычисляют хэш-функцию от элементов e1e2e3…en, на приемной стороне с помощью элементов e1e2e3…en многократно вычисляют хэш-функцию, значение которой используют в качестве ключа k1 для расшифрования первой криптограммы С1.
Осуществление изобретения
При описании реализации изобретения использована такая структура описания: изложена основная идея, дано подробное описание операций, выполняемых на передающей и приемной сторонах, а детали реализации приведены в Приложениях 1 и 2.
Основная идея
Способ защиты информации сводится к каскадному шифрованию данных с помощью двух шифров: блочного шифра со сцеплением данных и адаптивного многоалфавитного шифра с интегральным преобразованием. Термин «сцепление блоков» используется в американском стандарте DES (режим СВС - Cipher Block Chaining) [17]. Полученные в результате шифрования блоки скрываются в стего контейнерах, которые передаются на приемную сторону по множеству каналов связи в псевдослучайном порядке и в псевдослучайные моменты времени.
Передающая и приемная стороны предварительно обмениваются ключами K(k2, k3, k4), а ключ k1 формируют только на передающей стороне и на приемную сторону предварительно не передают. Ключ k1 скрытно передается в нескольких блоках криптограммы.
Рассмотрим принципы обработки информации с помощью заявляемого способа на передающей и принимающей сторонах.
Передающая сторона
На передающей стороне открытый текст M шифруют с помощью ключа k1. Ключ k1 состоит из множества элементов e1e2e3…en. В результате шифрования формируют криптограмму 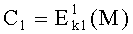 . При шифровании используют некоторый блочный шифр (например, DES) со сцеплением E1 с ключом k1. В результате зашифрования формируется m сцепленных (связанных между собой) блоков.
. При шифровании используют некоторый блочный шифр (например, DES) со сцеплением E1 с ключом k1. В результате зашифрования формируется m сцепленных (связанных между собой) блоков.
Ключ k1 на приемной стороне априори неизвестен, его заранее не передают. Корреспонденты предварительно не обмениваются элементами этого ключа. Ключ k1 сеансовый и он меняется непрерывно, не повторяясь ни в одном сеансе связи. Ключ не хранят, а генерируют (аппаратно или программно) в момент шифрования сообщения, то есть создают в момент формирования криптограммы С1 (на лету).
Описание одной из множества возможных реализаций шифра E1 приведено в Приложении 1. Текст программы умышленно сделан упрощенным, подробным и прозрачным. Это позволяет рассмотреть все детали преобразований.
Криптограмму С1 повторно шифруют с помощью второго шифра Е2, используя второй ключ k2: 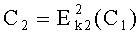 . Реализация одной из возможных реализаций алгоритма Е2 описана в Приложении 2.
. Реализация одной из возможных реализаций алгоритма Е2 описана в Приложении 2.
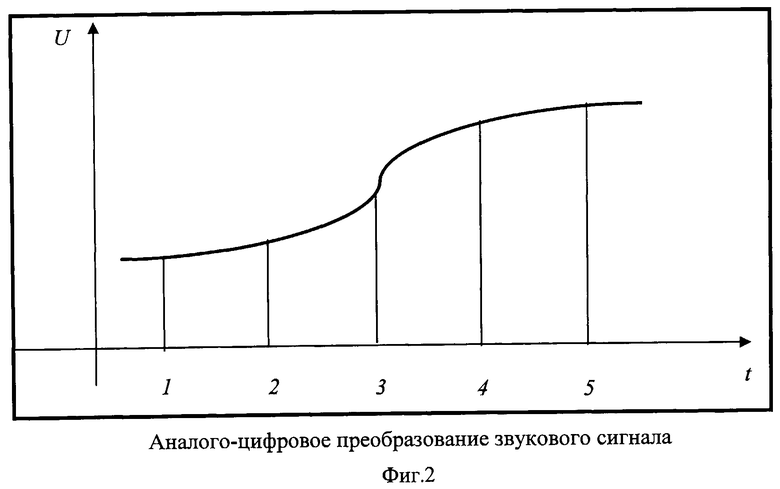
Ключ k2 известен как на передающей, так и на приемной стороне. В процессе формирования криптограммы С2 она разбивается на r блоков. Заметим, что это совсем другие блоки по сравнению с блоками, сформированными в процессе первого шифрования Е1. Размеры (объем, вместительность, длина) блоков второй криптограммы С2 больше размеров блоков первой криптограммы С1. Во время второго шифрования несколько блоков первой криптограммы попадают в один блок второй криптограммы. Число блоков первой криптограммы, уместившихся в одном блоке второй криптограммы, не является целым числом, то есть числа m и r не кратны друг другу (см. фиг.3). По этой причине некоторые блоки криптограммы С1 могут размещаться в разных блоках криптограммы С2.
Итак, в результате второго шифрования получают r блоков криптограммы С2, причем число блоков во второй криптограмме r≥n. Другими словами: число раздельно передаваемых блоков r криптограммы С2 формируют не меньше числа элементов (составных частей, символов), из которых состоит ключ k1. Блоки криптограммы С2 в процессе шифрования последовательно нумеруют. В результате второго шифрования на ключе k2 формируется криптограмма С2, состоящая из r блоков.
Комментарии к фиг.3.
Блоки b11, b12, …,b1m криптограммы С1 размещаются в блоках b21, b22, …,b2r криптограммы С2. Причем в блоке b21 размещаются блоки b11, b12 и часть блока b13. В блоке b21 скрытно указывается порядковый номер этого блока. В данном случае это число 1. В блоке b2r размещаются блоки bm-1, bm и скрытно указывается число r, которое определяет порядковый номер этого блока. Элементы ключа k1 e1e2e3…en скрытно размещаются в блоках криптограммы C2: b21, b22, …,b2n (n≤r). При этом порядковые номера элементов ключа k1 и порядковые номера блоков криптограммы С2 совпадают.
Таким образом, в блоках криптограммы С2 размещаются блоки криптограммы С1, порядковые номера блоков С2 и элементы ключа k1. Заметим, что скрытые порядковые номера содержатся во всех блоках криптограммы С2, а элементы ключа k1 - только в части блоков криптограммы С2.
В процессе второго шифрования с использованием ключа k2 элементы e1e2e3…en первого ключа k1 внедряют (скрывают) в n блоках криптограммы С2, причем скрытые номера блоков криптограммы С2 совпадают с порядковыми номерами элементов e1e2e3…en первого ключа k1. Другими словами: первый элемент e1 ключа k1 скрывают в первом блоке криптограммы С2, элемент е2 скрывают во втором блоке криптограммы С2, элемент еi ключа k1 скрывают в i-м блоке криптограммы С2, а элемент n ключа k1 скрывают в n-м блоке криптограммы С2. За счет этого по известному номеру блока криптограммы С2 на приеме можно определить положение элемента ei в ключе k1.
Общими словами предыдущий абзац можно сформулировать так. Сокрытие элементов ключа k1 ведут таким образом, чтобы по порядковому номеру блока криптограммы b2i на приеме можно было определить положение элемента ei в ключе k1.
Далее каждый блок криптограммы С2 скрывают в отдельном контейнере. В качестве контейнеров используют файлы различного формата (текстовые, графические, звуковые, видео, HTML-страницы, субтитры, коды программ и т.д.). В результате такого стеганографического сокрытия получают r стего контейнеров, в которых внедрены (скрыты) r блоков криптограммы С2. Внедрение блоков криптограммы С2 в стего контейнеры производят на ключе k3, который определяет типы используемых контейнеров (текстовый, графический, звуковой…) и особенности (параметры) каждого из r алгоритмов стеганографического внедрения.
Число и вид используемых каналов связи определяет секретный ключ k4, который известен как на передающей, так и на приемной стороне.
Стего контейнеры в хаотичном (псевдослучайном) порядке отправляют (передают) на приемную сторону по Sc (нескольким) каналам связи и в псевдослучайные моменты времени. Во время такой передачи фактически происходит дополнительная перестановка блоков криптограммы С2 (по крайней мере, во времени). При этом передача информационных блоков по каналам связи перемежается передачей маскирующих (камуфлирующих, дезинформирующих) блоков информации. Передача ведется в соответствии с ключом k4.
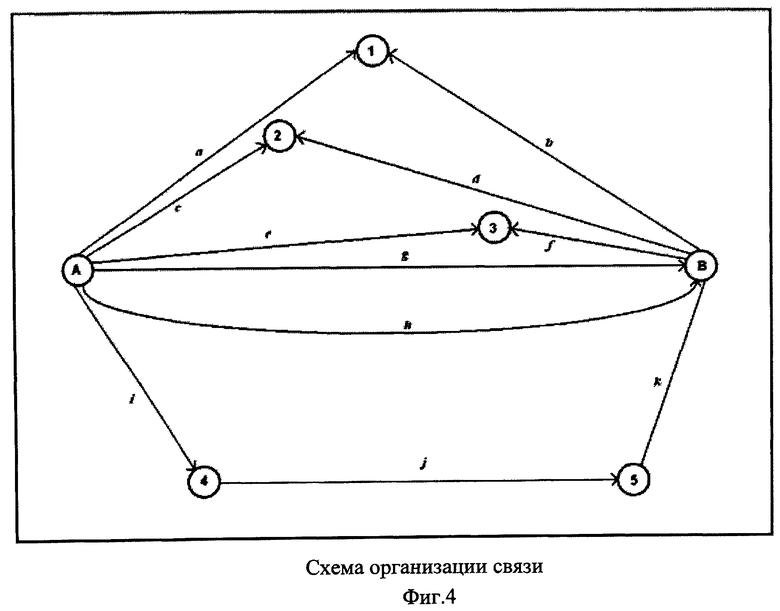
Схема связи между корреспондентами А и В показана на фиг.4.
Комментарии к фиг.4.
В сети имеется передающая сторона А и принимающая сторона В. В их распоряжении имеется S=Sc+Sm каналов связи. В текущем сеансе связи используются не все доступные каналы S, а только их часть Sc. Остальные каналы Sm имитируют активность (передают шум, дезинформацию). Камуфлирующие сообщения должны передаваться не только по каналам Sm, но и по каналам Sc.
Корреспондент А может передавать блоки криптограммы С2 (точнее контейнеры стеганограммы) по телекоммуникационным каналам различного вида. Например, каналы g и h позволяют вести прямую (непосредственную) связь корреспондентов между собой. Такие каналы можно создать с помощью радиостанций или проложенных напрямую линий связи (проводных, кабельных, оптоволоконных, радиорелейных).
Для связи могут быть использованы локальные и глобальные сети. Так по каналу a абонент А может отправить электронное письмо на почтовый сервер 1. Абонент B по каналу b имеет возможность скачать это письмо. Для маскировки электронные письма могут передаваться с пересылкой (форвардингом). Письмо с почтового сервера 4 будет автоматически переправлено на почтовый сервер 5, к которому имеется доступ у абонента В.
Каналы c и d позволяют обмениваться информацией, например, через файл-сервер или сервер мессенджеров (типа ICQ). Каналы g и f могут передавать сообщения с помощью чата, установленного на сервере 3.
Очевидно, что приведенный граф не описывает всех возможных вариантов организации связи (например, передачу информации по проводной телефонной линии или с помощью беспроводной мобильной телефонной сети, Wi-Fi и т.д.).
Таким образом, обмен информацией между корреспондентами ведется по множеству телекоммуникационных каналов S, из которых в соответствии с ключом k4 в данном сеансе используется только Sc каналов. Передача информации между корреспондентами ведется по расписанию, которое определяется ключом k4.
Рассматриваемый способ усложняет процедуру перехвата сообщений. Так криптоаналитикам приходится учитывать, что на 232 миллионах сайтах в определенный момент времени могут быть размещены мультимедиа контейнеры со стеганографическими вложениями. Специализированные программы сканируют ранее неучтенные домены в Интернете со скоростью 2500 страниц в час. Таким образом, использование для передачи информации нескольких Web-страниц снижает вероятность перехвата сообщения.
Приемная сторона
На приемной стороне из каждого принятого стего контейнера извлекается один блок криптограммы С2. При извлечении криптограммы из стего контейнера используется ключ k3. Блоки криптограммы С2 независимо друг от друга (по отдельности) расшифровывают с помощью ключа k2: 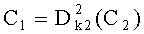 . Алгоритм расшифрования D2 является обратным по отношению к алгоритму шифрования Е2.
. Алгоритм расшифрования D2 является обратным по отношению к алгоритму шифрования Е2.
В процессе расшифрования r блоков криптограммы С2 восстанавливают m блоков криптограммы С1, извлекают элементы ключа k1, определяют номера блоков криптограммы С2, а значит, и порядок (последовательность) размещения n элементов е1е2е3…en в ключе k1. При этом порядковые номера блоков криптограммы С2 определяют порядок размещения блоков криптограммы C1.
После приема и извлечения всех блоков криптограммы С1, определения порядковых номеров блоков, размещения блоков по своим местам и восстановления принятого ключа k1 осуществляют расшифрование криптограммы С1 и извлечение открытого текста: 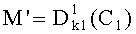 .
.
Детальное описание алгоритмов зашифрования и расшифрования E 1 и D 1
В качестве алгоритма формирования первой криптограммы Е1 можно использовать большое число различных блочных шифров, различающихся между собой криптостойкостью, скоростью шифрования, устойчивостью к атакам разного вида, наличием слабых ключей и т.п. [1].
Однако самым ценным свойством блочного алгоритма в данном случае является невозможность (точнее, вычислительная сложность) дешифрации криптограммы при отсутствии хотя бы одного блока криптограммы С1. Эта устойчивость к расшифрованию должна сохраняться даже при известном (скомпрометированном) ключе k1, на котором производилось зашифрование криптограммы.
Алгоритм DES
В качестве алгоритма 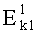 может быть использован блочный шифр со сцеплением блоков, описанный в прежнем американском стандарте DES [17]. Это позволяет при отсутствии одного блока криптограммы С1 на приемной стороне предотвратить дешифрацию сцепленного с ним блока криптограммы (вычислительно сложно дешифрировать еще один блок криптограммы).
может быть использован блочный шифр со сцеплением блоков, описанный в прежнем американском стандарте DES [17]. Это позволяет при отсутствии одного блока криптограммы С1 на приемной стороне предотвратить дешифрацию сцепленного с ним блока криптограммы (вычислительно сложно дешифрировать еще один блок криптограммы).
Алгоритм сцепления блоков в режиме СВС описывается выражением:
Ci=Ek(Mi⊕Ci-1).
Перед шифрованием каждого блока выполняется его побитное сложение по правилу Исключающее ИЛИ с результатом шифрования предыдущего блока.
При шифровании первого блока криптограммы используется вектор инициализации С0:
C1=Ek(M1⊕C0).
Такой алгоритм не решает поставленной задачи, так как отсутствие нескольких блоков затрудняет дешифрацию только соседних блоков, а не всей криптограммы в целом.
В дальнейшем будут рассмотрены алгоритмы (режимы шифрования), которые условно названы HALF и FULL.
Алгоритм HALF
Частично устранить этот недостаток позволяет следующий алгоритм, в котором идет сцепление всех ранее сформированных блоков:
Ci=Ek(Mi⊕C0⊕C1⊕…⊕Ci-2⊕Ci-1),
причем первый блок шифруется в соответствии с выражением:
C1=Ek(M1⊕C0).
Здесь С0 - вектор инициализации (псевдослучайный вектор).
Этот алгоритм может предотвратить дешифрацию всей криптограммы, если отсутствует первый блок криптограммы. Если же потерян (не перехвачен криптоаналитиками) блок из середины криптограммы, то невозможна дешифрация всех блоков, сформированных позднее потерянного блока (правые блоки, с большими индексами). Дешифрация блоков, сформированных раньше потерянного блока (левые блоки, с меньшими индексами), происходит стандартно и без искажений. При потере первого блока криптограммы невозможна дешифрация всех блоков. При потере последнего блока невозможна дешифрация только потерянного (не перехваченного) блока. Детальное описание этого алгоритма приведено в Приложении 1 (программа составлена в математической системе Mathcad).
Полностью исключить возможность дешифрации криптограммы С1 при отсутствии хотя бы одного блока криптограммы позволяет следующий алгоритм.
Алгоритм FULL
Основная идея работы этого алгоритма состоит в следующем.
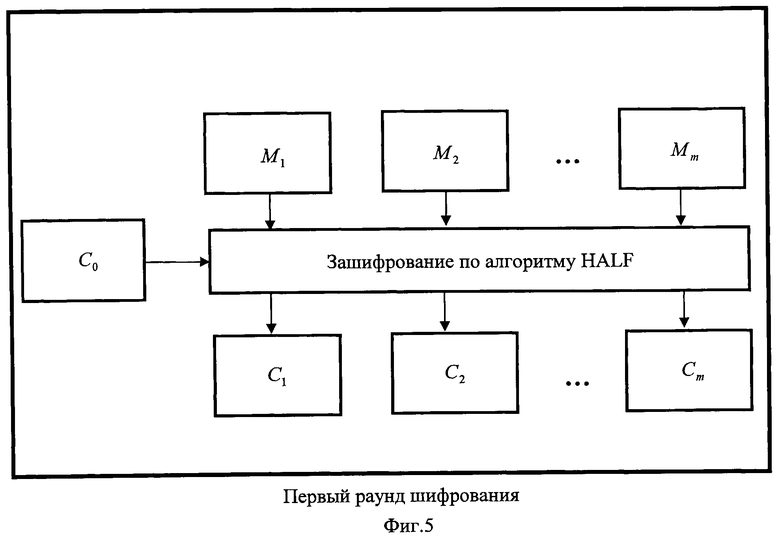
Первый раунд шифрования осуществляется в соответствии с алгоритмом HALF. Полученные блоки криптограммы зеркально меняются местами (первый - последний, второй - предпоследний т.д.).
P1=Cm, P2=Cm-1, …,Pm-1=C2, Pm=C1.
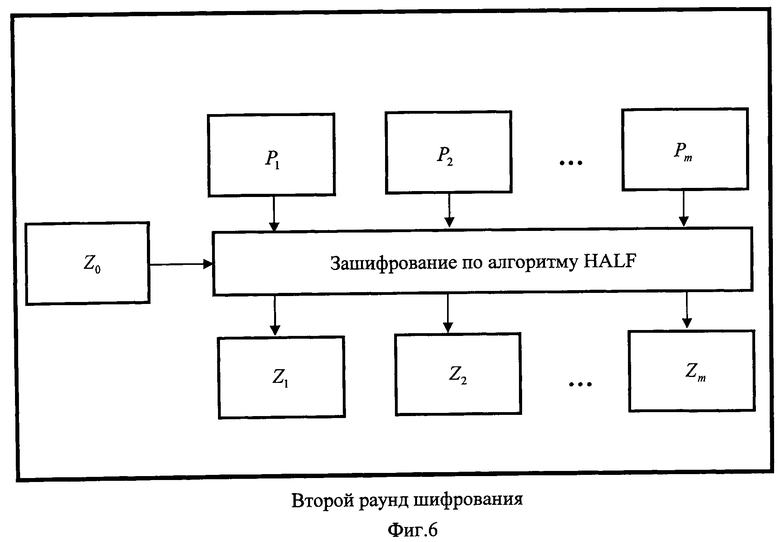
Следующие рисунки (фиг.5 и фиг.6) иллюстрируют эти два раунда шифрования.
Новая последовательность блоков повторно шифруется по алгоритму HALF (второй раунд).
Zi=Ek(Pi⊕Z0⊕Z1⊕…⊕Zi-2⊕Zi-1).
Как видно из приведенных формул, и в первом и во втором раундах шифрования указана одна и та же шифрующая операция Ek.
Здесь нужно принять к сведению следующие соображения. В качестве шифрующего преобразования Ek может быть использован любой известный (подходящий) алгоритм шифрования (шифр) [1]. С помощью этого шифра зашифрование может выполняться дважды: в первом и втором раунде.
Однако возможны варианты в реализации шифрующего преобразования первого и второго раундов. В каждом раунде можно использовать разные алгоритмы шифрования. Например, в простейшем случае в первом раунде можно осуществить только перестановку столбцов в матрице (блоке), а во втором - циклический сдвиг строк.
Достоинства заявляемого способа
Заявляемый способ защиты передаваемой информации создает несколько уровней защиты передаваемой информации.
Для взлома шифра криптоаналитику (противнику, злоумышленнику) необходимо перехватить не менее r стего контейнеров (блоков криптограммы С2), которые скрытно переносят ключ k1. Процесс перехвата стего контейнеров осложняется тем, что передача ведется по множеству неопределенных для криптоаналитика (злоумышленника) каналов связи и в псевдослучайные моменты времени. Каналы связи могут быть самыми разнообразными: кабельными, проводными, спутниковыми, радио и радиорелейными. Передача информационных блоков перемежается передачей маскирующих (дезинформирующих) блоков. Перехват злоумышленником нескольких зашифрованных блоков (не всех блоков) и их взлом не позволяет дешифровать криптограмму С1, так как ключ k1 меняется в каждом сеансе, а отсутствие хотя бы одного блока криптограммы С1 практически предотвращает дешифрацию криптограммы криптоаналитиками. В сильной степени дешифрацию криптограммы С1 осложняет использование сцепления всех блоков криптограммы. Тем самым передаваемый открытый текст становится элементом секретного ключа.
Таким образом, для криптоанализа потребуется не только решение задач криптоанализа и стеганоанализа, но и непрерывный мониторинг большого числа каналов связи. При этом схема организации связи и расписание пересылки контейнеров остаются неизвестными для противника. Очевидно, что этому препятствуют ограничения на технические ресурсы противника (наличие телекоммуникационных средств перехвата сообщений, быстродействующих ЭВМ и памяти большого объема).
Блоки криптограммы (точнее - стего контейнеры) могут передаваться по сетям сотовой мобильной связи (с помощью MMS), по проводным телефонным сетям, по беспроводным локальным сетям Wi-Fi и Bluetooth, по локальным, глобальным кабельным и спутниковым сетям. Контейнеры, содержащие криптограмму, можно пересылать в чатах (Web-чаты, IRC…), в мессенджерах (ICQ, QIP, MSN…), скрытно размещаться на Web-страницах, в Skype, в блогах, микроблогах (Twitter, Juick, Jaiku…), в видеохостинге (YouTube, RuTube, Яндекс-видео), в системах комментирования (дневники, социальные сети, гостевые книги), передаваться по электронной почте, храниться на заранее оговоренных (выбранных) файл-серверах, через файлообменные сети (BitTorrent, eDonkey2000, Direct Connect) и сервисы (Rapideshare, iFolder, Depositefiles) и т.д.
Помимо традиционных задач криптоанализа и стеганоанализа криптоаналитикам придется решать сложно выполнимую задачу непрерывного контроля (мониторинга) множества разнообразных каналов связи, выполнять (осуществлять) фильтрацию (разделение) информационных и маскирующих сообщений (блоков). Криптоаналитикам нужно собирать и хранить информацию со множества сайтов, серверов, вести мониторинг разнообразного графика в Глобальной сети, вести радиоперехват и хранение телефонных сообщений, электронной почты и обычной почты. Задача криптоанализа становится многомерной и вычислительно сложно выполнимой. При этом можно выбрать такие параметры системы защиты информации, что техническая реализация криптоанализа становится невозможной (ограничение памяти ЭВМ, недостаточные средства мониторинга, быстродействие ЭВМ).
Рассмотренный способ позволяет повысить надежность (помехоустойчивость) передачи секретной информации за счет дублирования передачи информации по разным каналам связи и в разные моменты времени, что бывает важно в условиях действия радиопомех или сбоев в работе Сети. При этом пронумерованные блоки на приеме дают возможность найти отсутствующий блок и не использовать повторно принятый.
Многие особенности рассматриваемого способа усложняют и без того вычислительно сложную задачу криптоанализа.
Например, отсутствие у криптоаналитика хотя бы одного стего контейнера (блока) не позволит восстановить ключ k1, а значит, и дешифровать криптограмму С1. Ключ k1 не может быть похищен (перехвачен, атакован) до начала сеанса связи на передающей стороне, так как он не формируется заранее. Он создается аппаратно или программно в процессе шифрования (на лету). Значение этого ключа неизвестно даже сотрудникам, обслуживающим засекречивающую аппаратуру.
Заявляемый способ повышает криптостойкость за счет высокой вычислительной сложности восстановления ключа k1 в случае отсутствия хотя бы одного элемента ключа. Для реализации этой идеи в одном из вариантов предлагаемого способа на передающей стороне в качестве ключа используют хэш-функцию от значений элементов k1=h(e1e2…en). Злоумышленник при отсутствии одного элемента ключа будет вынужден находить ключ не силовым подбором отсутствующего элемента, а производить многократное вычисление хэш-функции. Это существенно удлиняет процедуру подбора отсутствующего элемента.
Библиографический список
1. Панасенко С.П. Алгоритмы шифрования. Специальный справочник. - СПб.: БХВ-Петербург, 2009. - 576 с.
2. Алексеев А.П. Математические методы формирования многоалфавитных шифров замены // Инфокоммуникационные технологии, том 7, №2, 2009. Стр. 21-25.
3. Алексеев А.П., Блатов И.А., Макаров М.И., Похлебаев В.А. Многоалфавитный адаптивный шифр, основанный на интегральных преобразованиях // Инфокоммуникационные технологии, том 8, №1, 2010. Стр.70-75.
4. Алексеев А.П., Орлов В.В. Стеганографические и криптографические методы защиты информации: учебное пособие. - Самара: ИУНЛ ПГУТИ, 2010. - 330 с.
5. Алексеев А.П., Камышенков Г.Е. Использование ЭВМ для математических расчетов. - Самара: Парус, 1998 г. - 190 с.
6. ГОСТ 28147-89. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования. - М.: Госстандарт СССР, 1989.
7. Аграновский А.В., Девянин П.Н., Хади Р.А., Черемушкин А.В. Основы компьютерной стеганографии. - М.: Радио и связь. - 152 с.
8. Грибунин В.Г., Оков И.Н., Туринцев И.В. Цифровая стеганография. - М.: СОЛОН-Пресс, 2002. - 272 с.
9. Конахович Г.Ф., Пузыренко А.Ю. Компьютерная стеганография. Теория и практика. - К.: «МК-Пресс», 2006. - 288 с.
10. Алексеев А.П. Информатика 2007. Учебное пособие с грифом УМО. - М.: СОЛОН-ПРЕСС, 2007. - 608 с.
11. Макаров М.И., Батаев А.Ф., Алексеев А.П. Стеганографические методы вложения информации в субтитры мультимедиа-контейнеров формата ASF, AVI и MATROSKA // Инфокоммуникационные технологии, том 8, №2, 2010. Стр.32-36.
12. Алексеев А.П. Сокрытие информации в midi-файлах. Тезисы докладов Шестой Международной НТК «Проблемы техники и технологий телекоммуникаций» ПТиТТ-2008. Казань 25…27 ноября 2008 г., с.444…445.
13. Орлов В.В., Алексеев А.П. Активная стеганография в сетях TCP/IP // Инфокоммуникационные технологии, том 7, №2, 2009. Стр.73-79.
14. United States Patent US 3798359, Horst Feistel. Block Cipher Cryptographic System, Mar.19, 1974.
15. United States Patent US 6317505, Robert D. Powell, Mark J. Nitzberg. Image Marking with Error Correction. Nov.13, 2001.
16. United States Patent US 6798885. Jerry W. Malcolm. Method and apparatur for Encoding security Information in a MIDI Data stream. Sep. 28, 2004.
17. Data Encryption Standard (DES). Federal Information Processing Standards (FIPS). Publication 46-3. 25.10.1999. - 22 P.
18. United States Patent US 7319751. Alexey Kirichenko. Data Encryption. Jan. 15, 2008.
19. US National Institute of Standards. Specification for the Advanced Encryption Standard (AES). Draft Federal Information Processing Standards, Feb. 28, 2001. Based on: J. Daemen and V. Rijmen, "AES Proposal: Rijndael." 20 Sep. 3, 1999.
20. G.J.Simmons, "The Subliminal Channel and Digital Signatures, " Advances in Cryptology: Proceedings of EUROCRYPT 84, Springer-Verlag, 1985, pp.364-378
21. United States Patent US 3798360, Horst Feistel. Step Code Ciphering System. Jun. 30, 1971.






Приложение 2
Адаптивный многоалфавитный шифр с интегральным преобразованием и сокрытием номеров блоков и элементов ключа
В шифрах многоалфавитной замены каждому символу открытого текста ставится в соответствие не один, а несколько символов алфавита замены [4]. Для создания криптостойких шифров может быть использован различный математический аппарат, например интегральное исчисление [2].
Для увеличения криптостойкости шифра можно с помощью многоалфавитной замены и интегральных преобразований обеспечить равномерное распределение числовых данных криптограммы, разбить криптограмму на блоки в общем случае различной длины, скрытно пронумеровать блоки (вложить в каждый блок дополнительную информацию) и передать их по разным каналам связи.
Основная идея построения рассматриваемого шифра заключается в формировании криптограммы в виде равномерной смеси вещественных чисел.
Равномерность распределения вещественных чисел в криптограмме достигается (и контролируется) тем, что в процессе шифрования ведется анализ получающегося распределения чисел шифрограммы. С этой целью непрерывно строится гистограмма распределения чисел в криптограмме. При этом очередные элементы шифровки формируются таким образом, чтобы они попали в те места распределения, где наблюдаются минимумы. Возможность изменения (варьирования) положения очередного элемента криптограммы на числовой оси имеется благодаря тому, что при шифровании используются многоалфавитная замена и интегральное преобразование [3].
Алгоритм шифрования таков, что осуществляется постоянный анализ выходного распределения и выполняется такая коррекция (адаптация) шифра, при которой обеспечивается приближение формируемых чисел криптограммы к равномерному закону распределения.
Многоалфавитное шифрование предполагает, что каждый символ открытого текста многократно встречается в таблице замен на различных участках числовой оси. В таблице 1 приведен фрагмент некоторой упрощенной таблицы многоалфавитной замены (ТМЗ). При этом считается, что буква «е» встречается в открытом тексте чаще других, а буква «д» - реже других. По этой причине для буквы «е» выделено 6 интервалов многоалфавитной замены, а для буквы «д» - только 2.
Рассмотрим, как осуществляется шифрование с помощью таблицы многоалфавитной замены. Предположим, что нужно зашифровать фразу «где абба». Шифровку можно создать бесконечным числом способов. При этом каждую букву допустимо заменять любым вещественным числом из указанных интервалов. Приведем две криптограммы для указанной фразы:
15,33-9,101-22,99-18,06-14,57-2,331-5,064
7,105-1,102-12,98-8,473-10,16-14,91-23,26
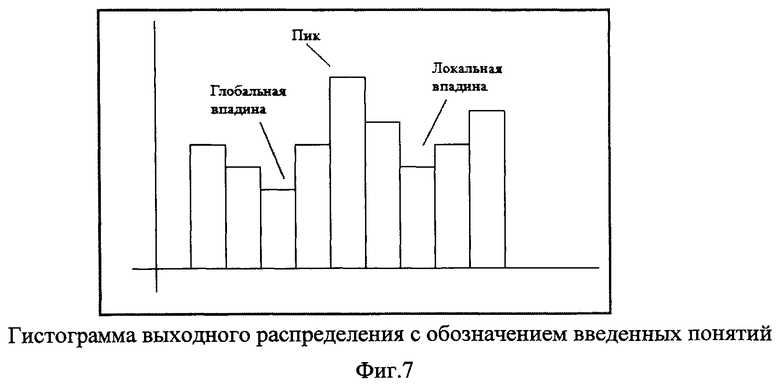
В предлагаемом шифре после многоалфавитной замены осуществляется интегральное преобразование каждого полученного числа. Это дает возможность один из пределов интегрирования выбирать по случайному закону [3]. При этом нужно находить очередной предел интегрирования таким образом, чтобы формируемое число криптограммы попало в зону наибольшего провала (в зону глобальной впадины) на гистограмме.
Для шифрования адаптивным (подстраиваемым) шифром необходимо постоянно решать такую задачу: по найденному числу в выходном распределении (находящегося в зоне глобальной впадины) выбирать такое значение предела интегрирования, которое обязательно попадет в заданный интервал гистограммы. Фиг.7 схематично иллюстрирует эту идею. После зашифрования очередного символа гистограмма достраивается (пополняется). На гистограмме выделяются максимальное значение (пик), минимальное значение (глобальная впадина) и провалы (локальные впадины). Формирование криптограммы ведется таким образом, чтобы с максимально возможной степенью выровнять имеющееся выходное распределение (чисел в криптограмме).
Предположим, что наибольший провал на гистограмме наблюдается в интервале чисел формируемой криптограммы [ci,ci+1]. Пусть при этом для интегрального преобразования используется некоторая подынтегральная функция f(x):
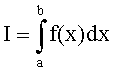
Для того чтобы уменьшить глубину глобальной впадины на гистограмме, генерируется случайное число a из интервала [ci,ci+1]. По таблице многоалфавитной замены определяется значение интеграла I, которое соответствует шифруемому символу. По известному значению нижнего предела интегрирования а и величине интеграла I, находят значение верхнего предела интегрирования b:
b=φ(a, I)
Полученные числа а и b передают в линию в составе блоков криптограммы С2. Эти числа являются элементами криптограммы (шифровкой). Заметим, что пределы интегрирования можно формировать и в обратном порядке: сначала выбрать b, а потом вычислить а.
В таблице 2 приведены соотношения между интегралом и пределами интегрирования для некоторых подынтегральных функций. Напомним, что вид интегрального преобразования противнику неизвестен, а корреспонденты предварительно определяют подынтегральную функцию с помощью ключа k2.
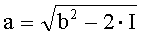
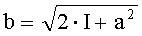
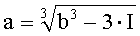
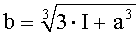
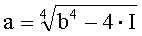
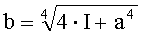
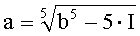
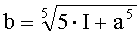
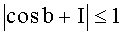
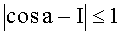
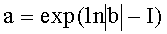
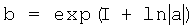
На приемной стороне известны вид использованного интегрального преобразования (подынтегральная функция) и конфигурация таблицы многоалфавитной замены. Эти два элемента определяются секретным ключом k2. Поэтому процесс расшифрования криптограммы для законного пользователя не вызывает затруднений. Он сводится к вычислению определенного интеграла по известным значениям нижнего и верхнего пределов интегрирования и определению принятого символа по таблице многоалфавитной замены.
Таким образом, сформированная величина a обязательно попадет в зону наибольшего провала (глобального минимума) гистограммы, а верхний предел интегрирования b случайно окажется в одной из зон гистограммы.
Величину b в процессе шифрования также можно попытаться приблизить к одной из локальных впадин на гистограмме (эта величина даже может попасть в зону глобальной впадины). Для этого нужно произвести расчеты верхнего предела интегрирования b при имеющемся значении нижнего предела интегрирования a, поочередно выбирая допустимые значения интеграла I из таблицы многоалфавитной замены. При расчете верхнего предела интегрирования b желательно не допустить попадание этого числа в зону пика (максимума) гистограммы. Все другие результаты расчетов (варианты выбора предела интегрирования) являются приемлемыми.
Число интервалов k на гистограмме, предназначенной для контроля выходного распределения чисел в криптограмме С2, можно примерно оценить по формуле Стержесса [5]:
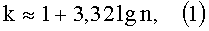
здесь n - число элементов (вещественных чисел) в криптограмме.
Таблица 3 показывает зависимость числа интервалов в гистограмме k от длины (числа символов) зашифрованного текста n.
С учетом того, что при шифровании каждый символ открытого текста s заменяется двумя вещественными числами (n=2·s), то при длине открытого текста (сообщения) s=500 символов число интервалов k на гистограмме оценивается числом 10,96 (его следует округлить до числа 11).
Таблица многоалфавитной замены служит на передающей стороне для замены символа открытого текста на некоторое вещественное число. Это число эквивалентно значению определенного интеграла, для которого определяются значения верхнего и нижнего пределов интегрирования. На приемной стороне таблица многоалфавитной замены используется для определения значения принятого символа по величине определенного интеграла, вычисленного с помощью полученных значений верхнего и нижнего пределов интегрирования. Таблица многоалфавитной замены является элементом секретного ключа k2.
Рассмотрим порядок формирования таблицы многоалфавитной замены.
1. Вначале нужно определить типичную длину текстовых сообщений, которые будут подвергаться шифрованию. Пусть Smax=50000 символов. Тогда число вещественных чисел, из которых будет состоять криптограмма, n=100000.
2. По формуле (1) следует оценить число необходимых интервалов на гистограмме. Для выбранного значения Smax число интервалов k=17,6 (после округления k=18).
3. Определить общее число интервалов (ячеек) в таблице многоалфавитной замены t, которое должно быть на один - два порядка больше числа k. Кроме того, число интервалов в ТМЗ должно быть минимум в 5 раз больше числа символов в алфавите открытого текста. Таким образом, число интервалов в таблице многоалфавитной замены лежит в пределах 180…1800. Примем t=1000.
4. Найти сумму нормированных частот символов открытого текста
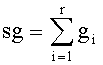
Здесь r - число символов в алфавите открытого текста (r=256 при использовании всех символов таблицы СР-1251, а при использовании только русских строчных или заглавных букв r=33); gi - нормированная частота.
Нормированные частоты появления символов в открытом тексте gi получают путем деления абсолютных частот на наименьшее значение абсолютной частоты.
5. Вычислить число интервалов замен для каждого i-го символа алфавита открытого текста:
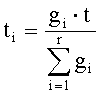
Для примера вычислим число интервалов замен для букв «а» и «б»:
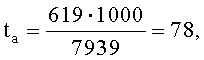
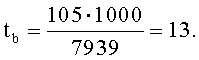
6. Задать диапазон (ширину) гистограммы и ее положение на числовой оси. Это означает, что задаются значения amin и bmax (это для случаев, когда определенный интеграл принимает только положительные значения). Задать ширину и положение на числовой оси таблицы многоалфавитной замены, то есть определить значения Imin и Imax. Перечисленные величины связаны между собой и соотношения между ними зависят от вида подынтегральной функции:
Imax=φ(a min, bmax), a Imin≈0
Например, для подынтегральной функции f(x)=х4 правая граница для таблицы многоалфавитной замены вычисляется по формуле:
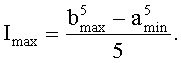
Вычислить ширину одного интервала замен:
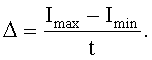
Пусть ∆=0,1.
7. Составить таблицу многоалфавитной замены, в которой ширина каждого интервала замен равна ∆, а общее число интервалов замен равно t. Все интервалы замен образуют непрерывный интервал чисел шириной ∆·t. Для рассматриваемого случая ∆·t=0,1·1000=100. Каждому интервалу замен ставят в соответствие один из символов алфавита открытого текста. При этом число интервалов замен для буквы «а» равно ta, для буквы «б» равно tб и т.д. Интервалы замен для каждого символа располагаются на числовой оси в случайном порядке.
Конфигурация таблицы многоалфавитной замены является одним из элементов секретного ключа. Вторым элементом ключа является вид подынтегральной функции. Заметим, что криптоанализ рассматриваемого шифра усложняется еще за счет того, что выбираемое из ТМЗ число и один из пределов интегрирования выбираются по случайному закону.
Рассмотрим пример шифрования с помощью адаптивного многоалфавитного шифра.
Предположим, что в текущий момент времени необходимо зашифровать букву «в». В качестве первого ключевого элемента используется таблица 1. Вторым элементом секретного ключа является вид подынтегральной функции. Пусть
f(x)=х4.
Предположим, что на гистограмме, сформированной на предыдущих шагах шифрования, наблюдается глобальная впадина в диапазоне чисел [6…10).
Для зашифрования буквы «в» по случайному закону из таблицы 1 выбирается один из четырех интервалов замен. Допустим, что выбран интервал 3, то есть (17…18]. Из этого интервала генерируется случайное число, например, I=17,58.
Для заполнения провала на гистограмме генерируется случайное число а из интервала [6…10). Пусть а=8,02. С учетом формулы Ньютона-Лейбница для выбранной подынтегральной функции получаем:
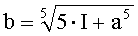
Расчет верхнего предела интегрирования дает значение: b=8,024. Таким образом, оба числа а и b попали в зону глобальной впадины. «Рассеяние» (отличие, отклонение) пределов интегрирования в рассмотренном случае небольшое.
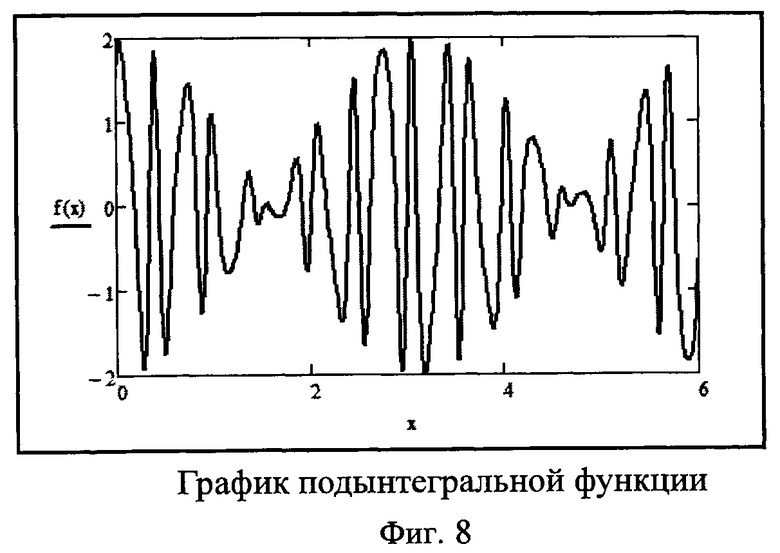
В качестве подынтегральной функции желательно выбрать функцию, у которой с изменением аргумента существенно меняются амплитуда и частота колебаний. График подобной функции приведен на фиг.8.
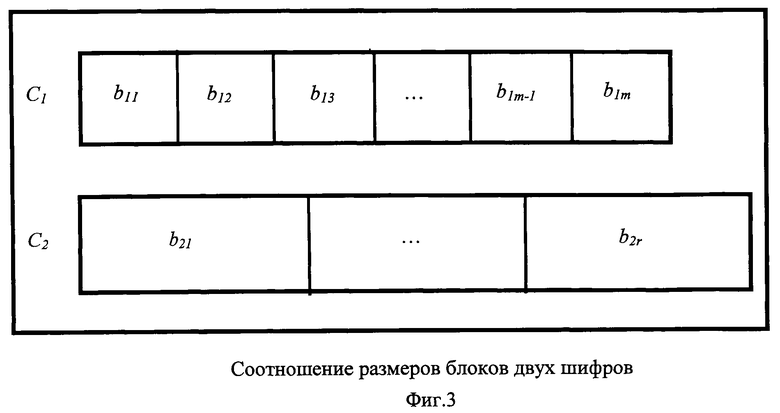
При выборе вида подынтегральной функции f(х) и нахождении первообразной F(x) можно воспользоваться следующими соображениями. Представим подынтегральную функцию в виде:
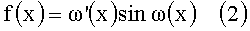
Тогда с учетом известного соотношения
F'(x)=f(x)
для подынтегральной функции (2) получим:
F(x)=-cos ω(x).
В качестве ω(х) можно использовать большой класс функций, например
ω(x)=Ax+C sin Bx.
Тогда
f(x)=(A+BC cos Bx) sin(Ax+C sin Bx).
В этом случае первообразная определяется выражением
F(x)=-cos(Ax+C sin Bx).
Понятно, что первообразная должна быть использована при вычислении нижнего и верхнего пределов интегрирования, которые являются элементами шифра.
Коэффициенты А, В и С можно использовать в качестве элементов ключа рассмотренного шифра.
Пространственно-временное распыление информации
Каждый блок криптограммы на передаче получает порядковый номер, с помощью которого сообщение на приеме восстанавливается в исходную последовательность блоков, независимо от порядка и времени поступления блоков криптограммы в каналы связи на передаче. В данном шифре скрываемой информацией будут порядковый номер блока криптограммы С2 и один элемент ключа k1.
Для сокрытия одного элемента ключа k1 потребуется 8 бит. Для сокрытия номера блока криптограммы можно отвести 16…32 бита. Значит, скрытно нужно передать в одном блоке криптограммы С2 24…40 бит информации.
Внедрение информации в криптограмму
Номер каждого блока криптограммы и элемент ключа k1 представляют в двоичной системе счисления [10]. При сокрытии считывается внедряемый бит двоичного числа и если он равен 1, то при шифровании выбирается столбец, ближайший к началу гистограммы (если допустимо, то используется крайний левый столбец).
Под выражением «выбирается столбец» следует понимать следующее. В процессе шифрования нужно сформировать два числа: а и b, которые являются нижним и верхним пределами определенного интеграла. Введенный для краткости изложения термин «выбор столбца» означает выбор такого числа, который попадает в интервал чисел, занимаемый данным столбцом.
Если внедряемый бит равен 0, то выбирается столбец гистограммы (точнее - интервал) с максимальным удалением от начала числовой оси (крайний правый столбец). Если отсутствует выбор среди столбцов (то есть остается единственный допустимый интервал гистограммы), то внедрение двоичных чисел переносится на следующие шаги алгоритма (см. фиг.9). На приемной стороне после расшифрования переданного сообщения по полученным нижним и верхним пределам интегрирования и вычисленным значениям интеграла производится поэтапное восстановление (реконструкция) гистограммы. При этом на приеме необходимо восстановить последовательность заполнения гистограммы, реализованную на передающей стороне.
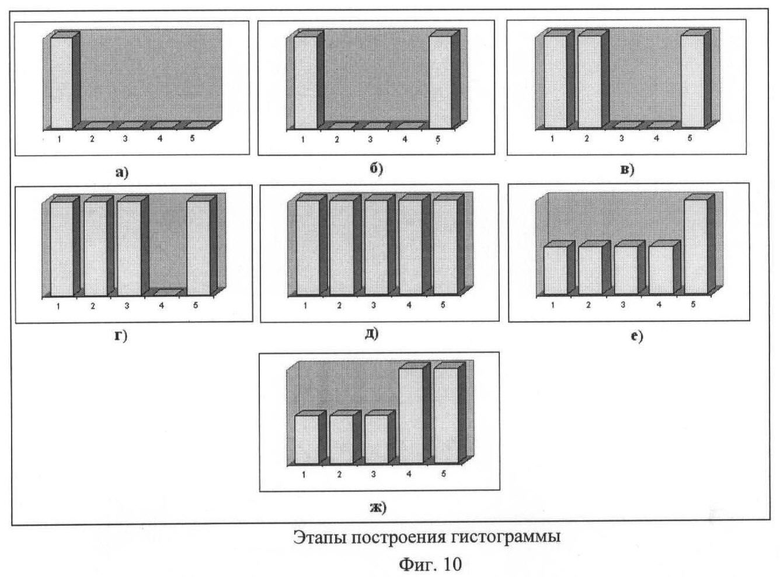
Рассмотрим пример, в котором таблица многоалфавитной замены составлена так, что при заданной подынтегральной функции, например х4, выбор предела интегрирования мог осуществляться из всех интервалов гистограммы. Допустим, что число интервалов (столбцов гистограммы) пять. Пусть очередному блоку криптограммы требуется присвоить порядковый десятичный номер 44 (двоичное число 101100). Заметим, что внедрение элемента ключа k1 осуществляется аналогично внедрению порядкового номера.
В первоначальном состоянии гистограммы (в момент начала шифрования) все интервалы гистограммы пустые (столбцов еще нет). Так как первый бит (старший бит числа) скрываемого номера блока равен 1, то выбирается предел интегрирования из интервала первого столбца гистограммы (крайний левый столбец, фиг.10а).
Далее производится предварительный расчет второго предела интегрирования для всех возможных значений интеграла для данного шифруемого символа (буквы). В данном примере ТМЗ составлена так, что предел интегрирования может попасть в любой интервал гистограммы. На данном этапе идет выбор между интервалами (столбцами) 2, 3, 4 и 5. Так как второй бит скрываемого числа равен 0, то выбирается число (предел интегрирования) из пятого интервала (крайний правый столбец, фиг.10б).
Рассмотрим процесс шифрования второго символа криптограммы С1. Интервал выбирается среди столбцов с номерами 2, 3 и 4. Так как нужно скрыть бит со значением 1 (третий бит), то выбирается столбец 2 (крайний левый среди незаполненных столбцов гистограммы, фиг.10в). Для значения второго предела интегрирования выбирается интервал чисел, покрываемых столбцами 3 и 4. При сокрытии четвертого бита скрываемого числа, который равен 1, выбирается третий диапазон (крайний левый среди минимально заполненных столбцов гистограммы, фиг.10г).
Следующий этап - выбор интервала для первого предела интегрирования третьей буквы. В этой ситуации выбора нет, так как есть только один допустимый интервал - четвертый, откуда и выбирается очередной предел интегрирования. В подобных случаях (когда нет выбора между двумя допустимыми столбцами) скрыть очередной бит числа невозможно. В такой ситуации сокрытие информации не происходит, а идет штатное формирование криптограммы (фиг.10д).
Затем выбирается второй предел интегрирования для третьей буквы. Сейчас интервалов с минимальным заполнением пять - 1, 2, 3, 4 и 5. Теперь требуется скрыть пятый бит двоичного числа (номера блока), равный 0. Выбирается крайний правый столбец - пятый (фиг.10е). Далее выбирается первый предел интегрирования для четвертой буквы из интервалов с номерами 1, 2, 3 и 4. Так как требуется скрыть бит, равный 0, то выбирается четвертый интервал (крайний правый допустимый, фиг.10ж).
Разбиение криптограммы на отдельные блоки
Разбиение криптограммы С2 на блоки происходит в тех местах алгоритма (в те моменты времени), когда при шифровании все столбцы гистограммы имеют одинаковую высоту.
Таким образом, каждый блок криптограммы С2 на приеме можно расшифровывать отдельно, задав все начальные значения гистограммы нулевыми. Это приведет к верному расшифрованию каждого блока криптограммы и правильному извлечению скрытого номера блока и одного элемента ключа k1.
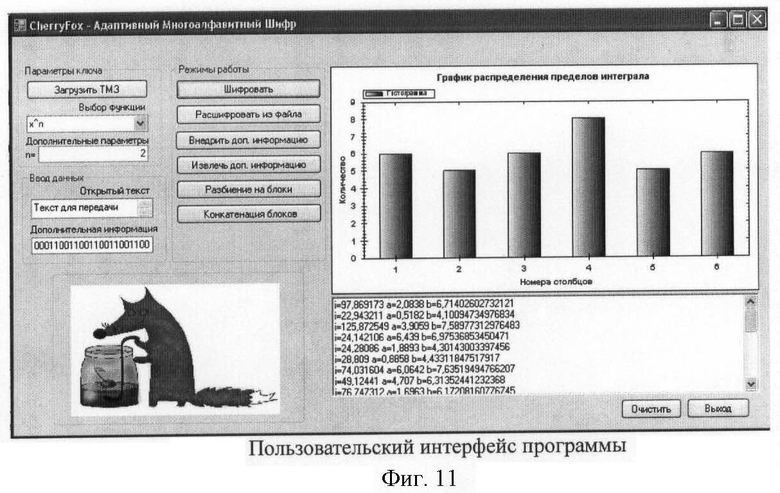
На следующем рисунке (фиг.11) представлен пользовательский интерфейс программы, которая реализует адаптивный многоалфавитный шифр со скрытием дополнительной информации в блоках криптограммы.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СТЕГАНОГРАФИЧЕСКОГО СОКРЫТИЯ ИНФОРМАЦИИ | 2008 |
|
RU2374770C1 |
| СПОСОБ ШИФРОВАНИЯ АДАПТИВНЫМ МЕТОДОМ МНОГОАЛФАВИТНОЙ ЗАМЕНЫ | 2010 |
|
RU2469484C2 |
| СПОСОБ ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ ЗАЩИТЫ ИНФОРМАЦИИ | 2019 |
|
RU2703972C1 |
| СПОСОБ И СИСТЕМА СКРЫТОГО ПОМЕХОУСТОЙЧИВОГО ОПОВЕЩЕНИЯ | 2017 |
|
RU2665251C1 |
| СПОСОБ СКРЫТОЙ ЗАЩИЩЕННОЙ ПЕРЕДАЧИ ТЕЛЕМЕТРИЧЕСКИХ ДАННЫХ В РОБОТОТЕХНИЧЕСКИХ КОМПЛЕКСАХ | 2020 |
|
RU2765811C1 |
| Способ безопасного кодирования информации для ее передачи по открытым каналам связи методами стеганографии | 2016 |
|
RU2649753C2 |
| СПОСОБ СТЕГАНОГРАФИЧЕСКОГО ВНЕДРЕНИЯ ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ В СЕМПЛЫ ЦИФРОВЫХ ЗВУКОВЫХ СИГНАЛОВ | 2016 |
|
RU2618379C1 |
| СПОСОБ ЗАЩИТЫ ИНФОРМАЦИИ | 2017 |
|
RU2648598C1 |
| СПОСОБ ПОТОКОВОЙ СТЕГАНОГРАФИЧЕСКОЙ ПЕРЕДАЧИ ДВОИЧНЫХ ДАННЫХ | 2010 |
|
RU2448420C1 |
| СПОСОБ ШИФРОВАНИЯ СООБЩЕНИЯ М, ПРЕДСТАВЛЕННОГО В ВИДЕ МНОГОРАЗРЯДНОГО ДВОИЧНОГО ЧИСЛА | 2011 |
|
RU2459276C1 |
Изобретение относится к области телекоммуникаций, а именно к способу скрытой передачи зашифрованной информации по множеству каналов связи. Техническим результатом является повышение криптостойкости передаваемой информации. Технический результат достигается тем, что в способе осуществляют обмен между корреспондентами секретными ключами, разбивают открытый текст на блоки, шифруют их с помощью шифра со сцеплением блоков 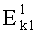 на ключе k1, состоящим из элементов e1e2e3…en, в результате чего получают первую криптограмму C1, состоящую из m блоков, которые повторно шифруют шифром
на ключе k1, состоящим из элементов e1e2e3…en, в результате чего получают первую криптограмму C1, состоящую из m блоков, которые повторно шифруют шифром 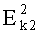 на ключе k2, в результате чего получают вторую криптограмму С2, состоящую из r блоков, в каждый блок С2 при шифровании помещают несколько блоков C1, скрытно нумеруют все блоки С2, в n блоков C2 скрытно помещают n элементов k1, r блоков С2 стеганографически скрывают в r контейнерах различного типа с использованием ключа k3, который определяет тип контейнера и секретные параметры алгоритмов внедрения, r контейнеров пересылают по нескольким каналам связи в соответствии со схемой организации и расписанием связи, которые определяет ключ k4. 5 з.п. ф-лы, 11 ил., 3 табл., 2 пр.
на ключе k2, в результате чего получают вторую криптограмму С2, состоящую из r блоков, в каждый блок С2 при шифровании помещают несколько блоков C1, скрытно нумеруют все блоки С2, в n блоков C2 скрытно помещают n элементов k1, r блоков С2 стеганографически скрывают в r контейнерах различного типа с использованием ключа k3, который определяет тип контейнера и секретные параметры алгоритмов внедрения, r контейнеров пересылают по нескольким каналам связи в соответствии со схемой организации и расписанием связи, которые определяет ключ k4. 5 з.п. ф-лы, 11 ил., 3 табл., 2 пр.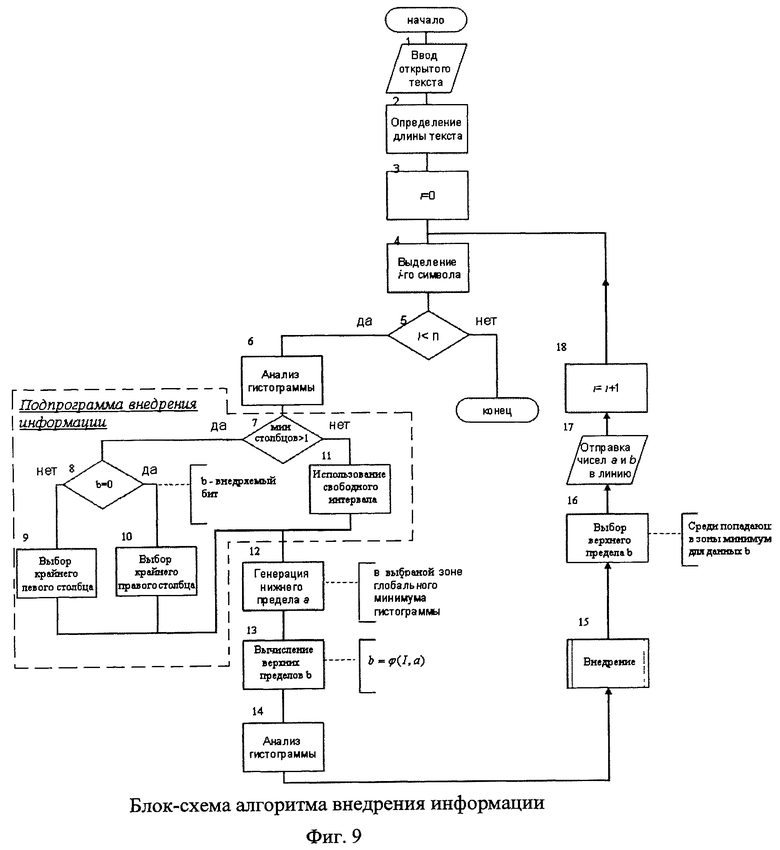
1. Способ скрытой передачи зашифрованной информации по множеству каналов связи, заключающийся в том, что корреспонденты обмениваются секретными ключами, разбивают открытый текст на блоки, шифруют эти блоки с помощью шифра со сцеплением блоков 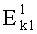 на ключе k1, состоящим из элементов e1e2e3…en, в результате чего получают криптограмму C1, состоящую из m блоков, отличающийся тем, что полученные m сцепленных блоков первой криптограммы C1 повторно шифруют шифром
на ключе k1, состоящим из элементов e1e2e3…en, в результате чего получают криптограмму C1, состоящую из m блоков, отличающийся тем, что полученные m сцепленных блоков первой криптограммы C1 повторно шифруют шифром 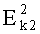 на ключе k2, в результате второго шифрования получают вторую криптограмму C2, состоящую из r блоков, в каждый блок второй криптограммы С2 при шифровании помещают несколько блоков первой криптограммы C1, скрытно нумеруют все блоки второй криптограммы С2, в n блоков второй криптограммы C2 скрытно помещают n элементов ключа k1, r блоков второй криптограммы C2 стеганографически скрывают в r контейнерах различного типа с использованием ключа k3, который определяет тип контейнера и секретные параметры алгоритмов внедрения, r контейнеров пересылают по нескольким каналам связи в соответствии со схемой организации и расписанием связи, которые определяет ключ k4, на приемной стороне извлекают информацию из стеганографических контейнеров с помощью ключа k3, осуществляют дешифрацию второй криптограммы C2 с помощью ключа k2, в результате дешифрации получают первую криптограмму C1, при дешифрации из n блоков второй криптограммы С2 извлекают n элементов ключа k1 и их порядковые номера, составляют из элементов e1e2e3-en ключ k1, который используют для дешифрации первой криптограммы C1.
на ключе k2, в результате второго шифрования получают вторую криптограмму C2, состоящую из r блоков, в каждый блок второй криптограммы С2 при шифровании помещают несколько блоков первой криптограммы C1, скрытно нумеруют все блоки второй криптограммы С2, в n блоков второй криптограммы C2 скрытно помещают n элементов ключа k1, r блоков второй криптограммы C2 стеганографически скрывают в r контейнерах различного типа с использованием ключа k3, который определяет тип контейнера и секретные параметры алгоритмов внедрения, r контейнеров пересылают по нескольким каналам связи в соответствии со схемой организации и расписанием связи, которые определяет ключ k4, на приемной стороне извлекают информацию из стеганографических контейнеров с помощью ключа k3, осуществляют дешифрацию второй криптограммы C2 с помощью ключа k2, в результате дешифрации получают первую криптограмму C1, при дешифрации из n блоков второй криптограммы С2 извлекают n элементов ключа k1 и их порядковые номера, составляют из элементов e1e2e3-en ключ k1, который используют для дешифрации первой криптограммы C1.
2. Способ по п.1, отличающийся тем, что в качестве шифра со сцеплением 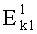 используют шифр, в котором осуществляется сцепление всех блоков первой криптограммы в следующей последовательности:
используют шифр, в котором осуществляется сцепление всех блоков первой криптограммы в следующей последовательности: 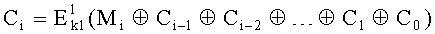 , указанное шифрующее преобразование выполняют повторно, причем при повторном шифровании блоки криптограммы, полученные после первого шифрования, зеркально переставляют местами, где С0 - вектор инициализации (псевдослучайный вектор); Ci - очередной блок криптограммы; k1 - ключ шифрования; Mi - очередной блок открытого текста;
, указанное шифрующее преобразование выполняют повторно, причем при повторном шифровании блоки криптограммы, полученные после первого шифрования, зеркально переставляют местами, где С0 - вектор инициализации (псевдослучайный вектор); Ci - очередной блок криптограммы; k1 - ключ шифрования; Mi - очередной блок открытого текста; 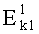 - шифрующее преобразование на ключе k1; ⊕ - логическая операция Исключающее ИЛИ.
- шифрующее преобразование на ключе k1; ⊕ - логическая операция Исключающее ИЛИ.
3. Способ по п.1, отличающийся тем, что в качестве шифра 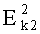 для формирования второй криптограммы С2 используют адаптивный многоалфавитный шифр с интегральным преобразованием, при реализации которого составляют секретную таблицу многоалфавитной замены, выбирают секретную подынтегральную функцию f(x), секретную информацию в виде ключа k2 предварительно передают на приемную сторону, в процессе шифрования на передающей стороне каждый символ открытого текста заменяют вещественным числом I из таблицы многоалфавитной замены, генерируют случайное число а таким образом, чтобы обеспечить равномерность гистограммы, которая описывает распределение чисел в формируемой второй криптограмме С2, вычисляют второе число b с учетом используемой подынтегральной функции f(x), выбранных I и а по формуле b=φ(а,I), которая определяется видом подынтегральной функции, осуществляют сокрытие номера блока криптограммы и одного элемента ключа k1 путем кодирования двоичной информации за счет изменения положения пределов интегрирования в гистограмме, сформированные числа а и b передают на приемную сторону, на приемной стороне принятые числа а и b используют для вычисления интеграла
для формирования второй криптограммы С2 используют адаптивный многоалфавитный шифр с интегральным преобразованием, при реализации которого составляют секретную таблицу многоалфавитной замены, выбирают секретную подынтегральную функцию f(x), секретную информацию в виде ключа k2 предварительно передают на приемную сторону, в процессе шифрования на передающей стороне каждый символ открытого текста заменяют вещественным числом I из таблицы многоалфавитной замены, генерируют случайное число а таким образом, чтобы обеспечить равномерность гистограммы, которая описывает распределение чисел в формируемой второй криптограмме С2, вычисляют второе число b с учетом используемой подынтегральной функции f(x), выбранных I и а по формуле b=φ(а,I), которая определяется видом подынтегральной функции, осуществляют сокрытие номера блока криптограммы и одного элемента ключа k1 путем кодирования двоичной информации за счет изменения положения пределов интегрирования в гистограмме, сформированные числа а и b передают на приемную сторону, на приемной стороне принятые числа а и b используют для вычисления интеграла 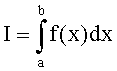 , с помощью рассчитанного числа I по таблице многоалфавитной замены определяют символ открытого текста, анализируют последовательность размещения чисел а и b в гистограмме и извлекают скрытую информацию.
, с помощью рассчитанного числа I по таблице многоалфавитной замены определяют символ открытого текста, анализируют последовательность размещения чисел а и b в гистограмме и извлекают скрытую информацию.
4. Способ по п.1, отличающийся тем, что при организации связи между корреспондентами используют S=Sc+Sm доступных каналов связи, причем в текущем сеансе связи с помощью ключа k4 выделяют не все, а только часть доступных каналов связи Sc, по всем доступным каналам связи S=Sc+Sm непрерывно передают камуфлирующие сигналы, а передачу сигналов, несущих полезную информацию, осуществляют в псевдослучайные моменты времени.
5. Способ по п.1, отличающийся тем, что передающая и приемная стороны предварительно обмениваются ключами К(k2, k3, k4), которые определяют секретные параметры второго шифра Е2, тип контейнеров и параметры алгоритмов внедрения информации в стего контейнеры, схему организации связи и расписание передачи информации, а ключ k1 генерируют на лету только на передающей стороне в момент формирования блоков первой криптограммы C1 и на приемную сторону предварительно не передают, а скрытно размещают элементы ключа k1 в нескольких блоках второй криптограммы C2.
6. Способ по п.1, отличающийся тем, что шифрование блоков первой криптограммы C1 на передающей стороне ведут на ключе k1, для определения которого многократно вычисляют хэш-функцию от элементов e1e2e3…en, на приемной стороне с помощью элементов e1e2e3-en многократно вычисляют хэш-функцию, значение которой используют в качестве ключа k1 для расшифрования первой криптограммы C1.
| СПОСОБ СТЕГАНОГРАФИЧЕСКОГО СОКРЫТИЯ ИНФОРМАЦИИ | 2008 |
|
RU2374770C1 |
| Устройство для обвалования карт намыва гидротехнических сооружений | 1954 |
|
SU101299A1 |
| RU 2008127313 A, 20.01.2010 | |||
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| US 5297208 A, 22.03.1994. | |||
Авторы
Даты
2012-09-27—Публикация
2011-07-08—Подача