ОБЛАСТЬ ИЗОБРЕТЕНИЯ
Настоящее изобретение, в общем, относится к алгоритмам шифрования с открытым ключом, а более определенно к сжатым представлениям RSA модулей (Rivest-Shamir-Adleman).
Область техники, к которой относится изобретение
Этот раздел предназначен для ознакомления читателя с различными аспектами уровня техники, которые имеют отношение к различным аспектам настоящего изобретения, которые описаны и/или приведены в формуле изобретения ниже. Предполагается, что данное описание будет полезно, так как оно дает читателю основополагающую информацию, способствующую лучшему пониманию различных аспектов настоящего изобретения. Соответственно, должно быть понятно, что эти аспекты следует воспринимать в упомянутом смысле, а не как признание предшествующего уровня техники.
Пусть N=pq - это произведение двух больших простых чисел. Обозначим через e и d открытый и секретный показатели, удовлетворяющие ed=1 (mod λ(N)), при этом gcd(e,λ(N))=1, где λ - это функция Кармикаэля (Carmichael). Так как N=pq, получаем, что λ(N)=lcm(p-1,q-1). Для данного x<N открытая операция (например, шифрование сообщения или проверка подписи) состоит в возведении числа x в степень e по модулю N, то есть в вычислении y=x e mod N. Тогда, имея y, соответствующая секретная операция (расшифровка зашифрованного текста или генерация подписи) состоит в вычислении y d mod N. Из определения e и d, очевидно, получаем, что y d ≡x(mod N). Эта секретная операция может быть осуществлена с высокой скоростью посредством китайских остатков (режим CRT - Chinese Remainder Theorem). Производятся независимые вычисления по модулю p и q, которые затем объединяются. В данном случае, секретными параметрами являются {p,q, d p , d q , i q }, где d p =d mod(p-1), d q =d mod(q-1), а iq=q -1 mod p. После этого мы получаем y d mod N как CRT(x p, x q )=x q +q [i q (x p -x q )mod p], где x p =y dp mod p и x q =y dq mod q.
Подводя итог, (двухфакторный) RSA модуль N=pq является произведением двух больших простых чисел p и q, удовлетворяющих gcd(λ(N),e)=1. Если n представляет собой размер числа N в битах, то для некоторого 1<n0<n p должно лежать в интервале 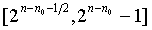 , а q - в интервале
, а q - в интервале 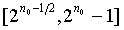 , так что 2
n-1
<N=pq<2
n. Из соображений безопасности, как правило, предпочитают использовать так называемые сбалансированные модули, что означает, что n=2n
0.
, так что 2
n-1
<N=pq<2
n. Из соображений безопасности, как правило, предпочитают использовать так называемые сбалансированные модули, что означает, что n=2n
0.
Типичный диапазон RSA модуля находится в пределах от 1024 до 4096 битов. Для традиционных приложений обычно требуются модули по меньшей мере 2048 битов. Однако программы и/или устройства, выполняющие RSA приложения, могут быть созданы лишь для поддержки 1024-битных модулей. Идея заключается в сжатии модулей для того, чтобы они помешались в более короткие буферы или полосы пропускания: вместо того, чтобы хранить/передавать полные RSA модули, используют их сжатое представление без потерь. Это заодно решает проблему совместимости между различными версиями программ и/или устройств. Самостоятельный интерес имеет и использование такого сжатия для улучшения эффективности: экономия памяти и/или полосы пропускания.
Arjen K. Lenstra (Generating RSA moduli with a predetermined portion. Advances in Cryptology -ASIACRYPT '98, volume 1514 of Lecture Notes in Computer Science, pages 1-10. Springer, 1998) предложил способ генерации, но этот способ не годится для устройств с ограниченными ресурсами, типа пластиковых карт c микросхемами (смарткарты), так как второе простое число q создается с приращениями, что может привести к недопустимо большому времени выполнения.
Настоящее изобретение преодолевает проблемы, возникавшие у предшествующего уровня техники, путем использования генерации сжатых RSA модулей с помощью генерации двух простых чисел в предопределенном интервале. В результате выгодным может быть использование эффективных алгоритмов генерации простых чисел, такие как алгоритмы, предложенные Marc Joye, Pascal Paillier и Serge Vaudenay (Efficient generation of prime numbers. Cryptographic Hardware and Embedded Systems -CHES 2000, volume 1965 of Lecture Notes in Computer Science, pages 340-354. Springer, 2000) и усовершенствованные Marc Joye и Pascal Paillier (Fast generation of prime numbers on portable devices: An update. Cryptographic Hardware and Embedded Systems -CHES 2006, volume 4249 of Lecture Notes in Computer Science, pages 160-173, Springer, 2006). В частности, они хорошо приспособлены для использования в ситуациях, где необходима генерация 2048 битного RSA модуля N (то есть n=2048) с фиксированным открытым показателем e=216 +1, так как для хранения или представления N требуется (намного) меньше чем 2048 бит.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
В первом аспекте изобретение направлено на способ генерации множителей RSA модуля N с предопределенной частью N h. RSA модуль содержит, по меньшей мере, два множителя. Сначала генерируется первое простое число p, получается число N h , которое формирует часть модуля N, генерируется второе простое число q, а на выходе получаем, по меньшей мере, сжатое представление модуля N без потерь, причем сжатое представление без потерь позволяет однозначно восстановить модуль N. Второе простое число q генерируется в некотором интервале, зависящем от p и N h, таким образом, что pq представляет собой RSA модуль, который «совместно использует» N h.
В первом предпочтительном варианте воплощения эта предопределенная часть N
h возглавляет RSA модуль. Преимуществом является то, что RSA модуль - это n-битный модуль, и предопределенная часть N
h содержит k бит, а первое простое число p генерируется в интервале 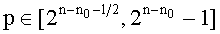 так, чтобы gcd(p-1,e)=1; второе простое число q генерируется в интервале
так, чтобы gcd(p-1,e)=1; второе простое число q генерируется в интервале 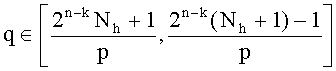 так, чтобы gcd(q-1,e)=1; а N=N
h||N
1, где N
1
=(pq)mod 2
n-k.
так, чтобы gcd(q-1,e)=1; а N=N
h||N
1, где N
1
=(pq)mod 2
n-k.
Во втором предпочтительном варианте воплощения эта предопределенная часть N
h завершает RSA модуль. Преимуществом является то, что первое простое число p генерируется в интервале 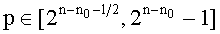 так, чтобы gcd(p-1,e)=1; второе простое число q генерируется вычислением q=C+q'2
k
, где
так, чтобы gcd(p-1,e)=1; второе простое число q генерируется вычислением q=C+q'2
k
, где 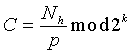 , а q' генерируется в интервале
, а q' генерируется в интервале 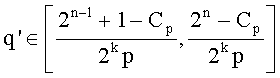 так, чтобы gcd(q-1,e)=1, определяется
так, чтобы gcd(q-1,e)=1, определяется 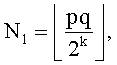 и на выходе получаем Ñ={N
1
, s
0
[k,n]}.
и на выходе получаем Ñ={N
1
, s
0
[k,n]}.
В третьем предпочтительном варианте воплощения модуль N h получается посредством зашифровывания, по меньшей мере, части первого простого числа p.
Во втором аспекте изобретение посвящено устройству для генерации множителей RSA модуля N с предопределенной частью N h, где RSA модуль состоит, по меньшей мере, из двух множителей. Данное устройство включает в себя процессор для генерации первого простого числа p, получения значения N h, которое формирует часть модуля N, и генерации второго простого числа q в интервале, зависящем от p и N h, таким образом, чтобы pq представлял собой RSA модуль, который (совместно) использует N h. Кроме того, это устройство также содержит интерфейс для вывода, по меньшей мере, сжатого представления модуля N без потерь, что позволяет осуществить однозначное восстановление модуля N.
В первом предпочтительном варианте воплощения это устройство является пластиковой картой с микросхемой (смарткартой).
Термин «совместно использует» интерпретируется как имеющее одинаковое значение в той части, которая совместно используется. Например, десятичные представления чисел 1234567890abcdef и 123456789abcdef0 совместно используют (содержат как часть) число 123456789 в начале этих чисел.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Различные признаки и преимущества данного изобретения и предпочтительных вариантов воплощения будут теперь описаны со ссылками на сопроводительные чертежи, которые приведены только для иллюстрации, но не ограничивают объем настоящего изобретения, среди которых на фиг.1 показано устройство для генерации RSA модулей, согласно предпочтительному варианту воплощения данного изобретения.
ПОДРОБНОЕ ОПИСАНИЕ ПРЕДПОЧТИТЕЛЬНЫХ ВАРИАНТОВ ВОПЛОЩЕНИЙ
Общая идея
Общая идея изобретения состоит в фиксации большой части RSA модуля N (например, вплоть до его передней половины предпочтительного варианта воплощения), в результате чего простые числа, образующие N, могут быть произвольным образом взяты из некоторого интервала (а не перебираются с некоторым шагом, как это предлагалось ранее). Эта большая часть RSA модуля либо вычисляется генератором (открытого) псевдослучайного числа из короткого случайного начального числа или же совместно используется среди пользователей.
Это приводит к более быстрой (и более легкой для осуществления) технике сжатия RSA модулей. Более того, совместно произведенные таким образом RSA модули неотличимы от обычных RSA модулей (то есть нет различий в распределении выходных данных). И, наконец, они совместимы с самой современной техникой генерации простых чисел (и это не приводит к дополнительным расходам).
Предпочтительный вариант воплощения
Пусть 1<k≤n 0. RSA модуль N размера n-бит, являющийся произведением двух больших простых чисел, может быть сгенерирован следующим образом.
1. Используя генератор псевдослучайных чисел, производится k-битное целое число N h, исходя из случайного начального числа s0:
 .
.
Отметим, что применение операции ИЛИ c числом 2 k-1 обеспечивает то, что старшим битом числа N h является 1.
Специалист в данной области техники должен оценить и то, что, естественно, также возможен и выбор значения N h.
2. Генерируется случайное простое число  такое, что gcd(p-1,e)=1.
такое, что gcd(p-1,e)=1.
3. Генерируется случайное простое число q:
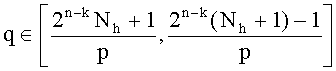
такое, что gcd(q-1,e)=1. Если такое простое число q найти не удалось, процесс повторяется.
4. Определяется N 1 =(pq)mod 2 n-k , и на выходе получаем Ñ={N 1 ,s 0 ,[k,n]}.
Имея данное представление Ñ, теперь легко открыто восстановить соответствующий n-битный RSA модуль N, а именно N= N
h
||N
l, где N
h представляет собой k-битное целое число, получаемое как 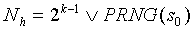 .
.
Следует заметить, что если 2n-k <p, то диапазон, из которого выбирается число q, может оказаться пустым. Именно поэтому число k должно быть равно, самое большее, n 0 . Следовательно, в самом лучшем случае, данный способ сжимает n-битные RSA модули вплоть до n0 бит. Самый плохой случай - это сбалансированные RSA модули (то есть n=2n 0), позволяющие получить (в самом лучшем случае) только коэффициент сжатия 1:2.
Первый альтернативный вариант воплощения
В этом альтернативном варианте фиксируются хвостовые биты модуля N.
1. Производится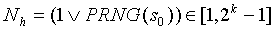 из начального числа s
0. Естественно, число Nh также может быть просто выбрано.
из начального числа s
0. Естественно, число Nh также может быть просто выбрано.
2. Генерируется первое простое число  и gcd(p-1,e)=1.
и gcd(p-1,e)=1.
3. Пусть 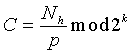 генерирует второе простое число q
генерирует второе простое число q
q=C+q'2
k, где 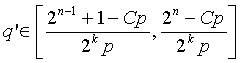 , и gcd(q-1,e)=1, если есть такое число q.
, и gcd(q-1,e)=1, если есть такое число q.
4. Определяют 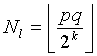 и выдают Ñ={N
l
,s
0
,[k,n]}.
и выдают Ñ={N
l
,s
0
,[k,n]}.
Важным является то, что не нужно включать старший бит числа N 1 в Ñ, так как он гарантированно равен 1.
Более того, можно также фиксировать несколько начальных битов и несколько битов в хвостовой части модуля N.
Второй альтернативный вариант воплощения
Предлагаемые способы могут быть адаптированы для адаптации RSA модулей, состоящих не только из двух, но и из большего числа множителей, например, 3-факторные RSA модули (с тремя простыми множителями) или RSA модули вида N=p r q. Для дальнейшего описания этого полезно обратиться к статье Tsuyoshi Takagi (Fast RSA-type cryptosystem modulo p k q. Advances in Cryptology -CRYPTO'98, volume 1462 of Lecture Notes in Computer Science, pages 318-326. Springer, 1998).
Третий альтернативный вариант воплощения
Предлагаемые нами способы применимы также и в случае, когда общая часть RSA модуля N, скажем Nh, совместно используется среди пользователей или является общей для всех пользователей для данного приложения. В этом случае нет необходимости пересылать случайное начальное число s 0 (также как и значения k и n).
Устройство
На Фиг.1 показано устройство для генерации RSA модулей в представленном варианте воплощения изобретения. Устройство 100 для генерации содержит, по меньшей мере, один процессор 110, по меньшей мере, одну память 120, средства 130 коммуникации, которые могут содержать отдельные блоки ввода и вывода, и, вероятно, пользовательский интерфейс 140. Обрабатывающее средство выполнено с возможностью осуществления любого из способов, описанных выше.
Депонирование ключей
Важным является и то, что данное изобретение с успехом может применяться для целей депонирования ключей. В случае RSA модулей N=pq знание примерно половины бит у числа p (или q) позволяет восстановить секретный ключ, например, путем использования техники сокращения базиса решетки (lattice reduction). Следовательно, если около половины (или больше) бит числа p зашифрованы с использованием секретного ключа K и вложены в представление открытого RSA модуля N, тогда «авторитетный специалист», знающий K, может восстановить число p по числу N и, таким образом, вычислить соответствующий секретный RSA ключ. Зашифрованные биты числа p могут содержаться в предопределенной заранее части RSA модуля.
Еще более важным является то, что способ настоящего изобретения особенно выгоден для использования в смарткартах и других устройствах с ограниченными ресурсами, так как этот способ использует относительно мало ресурсов.
Каждый из признаков, раскрытых в данном описании изобретения, а также (если это приемлемо) в формуле изобретения и чертежах может быть представлен как по отдельности, так и в подходящей комбинации. При необходимости признаки могут быть реализованы как в оборудовании, так и в программном обеспечении или в их комбинации.
При этом всюду ссылка на "один конкретный вариант воплощения" или на "вариант воплощения" означает, что тот или иной признак, структура или характеристика, описанная в связи с этим вариантом воплощения, может быть включена, по меньшей мере, в одну из реализаций данного изобретения. Любые появления фразы "в варианте воплощения" в различных местах данного текста не обязательно все ссылаются на один и тот же вариант воплощения, также как отдельные или альтернативные варианты воплощений не обязательно взаимно исключают другие варианты воплощения.
Ссылочные позиции, приведенные в формуле изобретения, предназначены лишь для иллюстрации и не накладывают какого-либо ограничения на объем формулы изобретения.
Изобретение относится к защите информации, а именно к алгоритмам шифрования с открытым ключом. Техническим результатом является повышение быстродействия. Технический результат достигается тем, что в способе генерации множителей RSA модуля N с заранее определенной частью Nh и заранее неопределенной частью N1 RSA модуль содержит, по меньшей мере, два множителя, при этом способ содержит этапы, на которых: генерируют первое простое число p в интервале 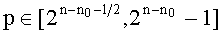 таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p; получают значение Nh, которое образует часть N; генерируют второе простое число q в интервале
таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p; получают значение Nh, которое образует часть N; генерируют второе простое число q в интервале 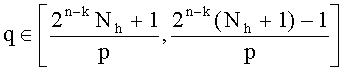 таким образом, что gcd(q-1,e)=1 и N=Nh || N1, где N1=(pq)mod 2n-k; и выдают по меньшей мере сжатое без потерь представление N, что позволяет однозначно восстановить N; при этом q случайным образом генерируется в заранее определенном интервале, зависящем от p и Nh так, чтобы pq было RSA модулем, частью которого является Nh, которое содержит k бит и возглавляет RSA модуль, который является n-битным модулем. 4 н. и 2 з.п. ф-лы, 1 ил.
таким образом, что gcd(q-1,e)=1 и N=Nh || N1, где N1=(pq)mod 2n-k; и выдают по меньшей мере сжатое без потерь представление N, что позволяет однозначно восстановить N; при этом q случайным образом генерируется в заранее определенном интервале, зависящем от p и Nh так, чтобы pq было RSA модулем, частью которого является Nh, которое содержит k бит и возглавляет RSA модуль, который является n-битным модулем. 4 н. и 2 з.п. ф-лы, 1 ил.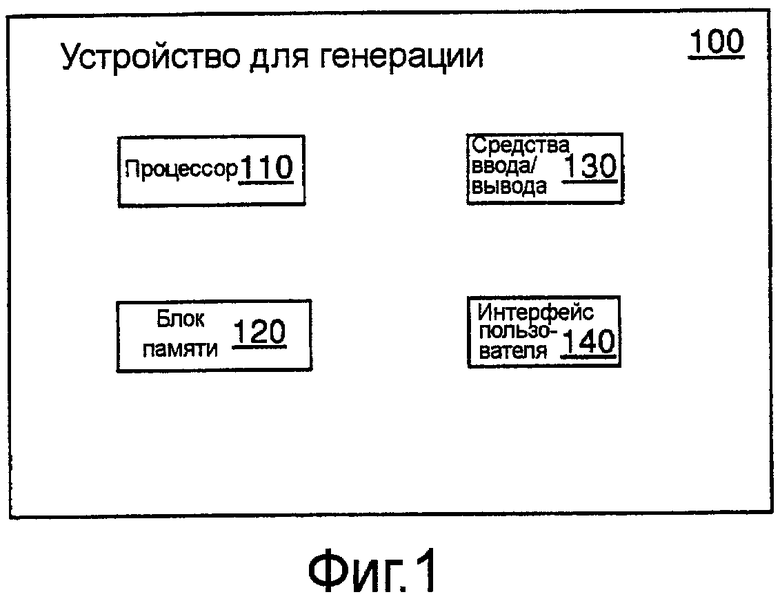
1. Способ генерации множителей RSA модуля N с заранее определенной частью Nl и заранее неопределенной частью N1, причем RSA модуль содержит, по меньшей мере, два множителя, при этом способ содержит этапы, на которых:
генерируют первое простое число p;
получают значение Nh, которое образует часть модуля N;
генерируют второе простое число q; и
выдают по меньшей мере сжатое без потерь представление RSA модуля N, что позволяет однозначно восстановить RSA модуль N;
при этом второе простое число q случайным образом генерируется в заранее определенном интервале, зависящем от р и Nh так, чтобы произведение pq было RSA модулем, частью которого является Nh; причем заранее определенная часть Nh возглавляет RSA модуль; причем способ, отличающийся тем, что RSA модуль является n-битным модулем, а заранее определенная часть Nh содержит k бит, и первое простое число p генерируется в интервале 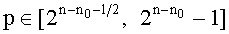 таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p;
таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p;
второе простое число q генерируется в интервале 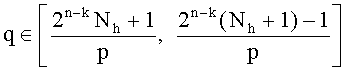 таким образом, что gcd(q-1,e)=1; и N=Nh || Nl, где Nl=(pq)mod 2n-k.
таким образом, что gcd(q-1,e)=1; и N=Nh || Nl, где Nl=(pq)mod 2n-k.
2. Способ генерации множителей RSA модуля N с заранее определенной частью Nh и заранее неопределенной частью N1, причем RSA модуль содержит, по меньшей мере, два множителя, при этом способ содержит этапы, на которых:
генерируют первое простое число p в интервале 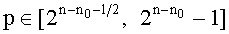 таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p;
таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p;
получают значение Nh, которое образует часть модуля N;
генерируют второе простое число q посредством вычисления q=C+q'2k, где 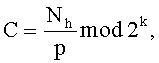 а q' генерируется в интервале
а q' генерируется в интервале 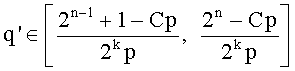 так, чтобы gcd(q-1,e)=1; определяют заранее неопределенную часть Nl как
так, чтобы gcd(q-1,e)=1; определяют заранее неопределенную часть Nl как 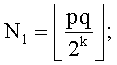 и
и
выдают по меньшей мере сжатое без потерь представление Ñ RSA модуля N, что позволяет однозначно восстановить RSA модуль N, где Ñ={Nl,s0,[k,n]}; причем второе простое число q случайным образом генерируется в заранее определенном интервале, зависящем от р и Nh так, чтобы произведение pq было RSA модулем, частью которого является Nh; и причем заранее определенная часть Nh завершает RSA модуль.
3. Способ по п.1 или 2, в котором Nh получают шифрованием, по меньшей мере, части первого простого числа р.
4. Устройство для генерации множителей RSA модуля N с заранее определенной частью Nh и заранее неопределенной частью Nl, причем RSA модуль содержит, по меньшей мере, два множителя, при этом упомянутое устройство содержит: процессор (110) сконфигурированный с возможностью:
генерировать первое простое число p;
получать значение Nh, которое образует часть модуля N; и
случайным образом генерировать второе простое число q в заранее определенном интервале, зависящем от р и Nh так, чтобы число pq было RSA модулем, частью которого является Nh; и интерфейс, сконфигурированный с возможностью выводить, по меньшей мере, сжатое без потерь представление RSA модуля N, что делает возможным однозначное восстановление RSA модуля N; причем заранее определенная часть Nh возглавляет RSA модуль; причем RSA модуль является n-битным модулем, а заранее определенная часть Nh содержит k бит, и первое простое число p генерируется в интервале 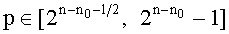 таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p; второе простое число q генерируется в интервале
таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p; второе простое число q генерируется в интервале  таким образом, что gcd(q-1,e)=1; и N=Nh || Nl, где Nl=(pq)mod 2n-k.
таким образом, что gcd(q-1,e)=1; и N=Nh || Nl, где Nl=(pq)mod 2n-k.
5. Устройство для генерации множителей RSA модуля N с заранее определенной частью Nh и заранее неопределенной частью Nl, причем RSA модуль содержит, по меньшей мере, два множителя, при этом упомянутое устройство содержит: процессор (110), сконфигурированный с возможностью:
генерировать первое простое число p в интервале 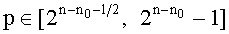 таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p;
таким образом, что gcd(p-1,e)=1, где е является открытым показателем и (n-n0) является битовой длиной p;
получать значение Nh, которое образует часть RSA модуля N; и
генерировать второе простое число q посредством вычисления q=C+q'2k, где  a q' генерируется в интервале
a q' генерируется в интервале  так, чтобы gcd(q-1,e)=1; определять заранее неопределенную часть Nl как
так, чтобы gcd(q-1,e)=1; определять заранее неопределенную часть Nl как 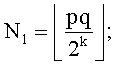 и интерфейс, сконфигурированный с возможностью:
и интерфейс, сконфигурированный с возможностью:
выдавать по меньшей мере сжатое без потерь представление Ñ RSA модуля N, что позволяет однозначно восстановить RSA модуль N, где Ñ={Nl, s0, [k,n]}; причем второе простое число q случайным образом генерируется в заранее определенном интервале, зависящем от p и Nh так, чтобы произведение pq было RSA модулем, частью которого является Nh; и причем заранее определенная часть Nh завершает RSA модуль.
6. Устройство по п.4 или 5, в котором устройство является смарткартой.
| Топчак-трактор для канатной вспашки | 1923 |
|
SU2002A1 |
| EP 1251654 A2, 23.10.2002 | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| КРИПТОГРАФИЧЕСКИЙ СПОСОБ И ЧИП-КАРТА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2276465C2 |
| US 6330332 B1, 11.12.2001 | |||
| СПОСОБ ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2005 |
|
RU2280896C1 |
| Arjen K | |||
| Lenstra, "Generating RSA moduli with a Predetermined Portion", Lecture notes in computer science, Springer Verlag, Berlin, 01.10.1998, найдено в Интернете 23.01.2012 по адресу: "http://infoscience.epfl.ch/record/149484/files/EPFL-CONF-149484.pdf". | |||
Авторы
Даты
2012-12-27—Публикация
2008-02-19—Подача