Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области информационной безопасности телекоммуникационных систем, в частности, может быть использовано в криптографических системах, обеспечивающих конфиденциальность сообщений, передаваемых по открытым каналам связи.
Известен способ шифрования путем формирования секретного ключа, генерации ключевого потока в виде последовательности битов, зависящих от секретного ключа, и сложения текущих битов ключевого потока с текущими битами передаваемого сообщения [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. С-Петербург: Лань, 2000. - 218 с.; см. с. 88-89]. Недостатком этого способа шифрования является необходимость синхронизации ключевого потока и потока данных.
Также известен способ шифрования, включающий генерацию 56-битового секретного ключа, формирование сообщения М в виде 64-битовой строки, генерацию криптограммы, представляющей собой 64-битовую строку в зависимости от секретного ключа [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. С-Петербург: Лань, 2000. - 218 с.; см. с. 68-73]. При этом генерация криптограммы осуществляется путем разбиения сообщения М на две 32-битовые строки и поочередное преобразование 32-битовых строк в зависимости от секретного ключа. Недостатком этого способа является малый размер секретного ключа, что не обеспечивает криптостойкости, соответствующей современным требованиям.
Также известен способ шифрования сообщения М, представленного в виде битовой строки, описанный в патенте США №4424414 [Hellman М.Е., Pohlig S.C. Exponentiation Cryptographic Apparatus and Method // U.S. Patent № 4,424,414. Jan. 3, 1984] и в книге [Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. - М.: Издательство ТРИУМФ, 2002. - 815 с.; см. с. 577-578]. Данный способ включает следующие действия:
1. Генерируют простое многоразрядное двоичное число (МДЧ) p.
2. Генерируют секретный ключ в виде двух МДЧ e и d, удовлетворяющих условию ed≡1 mod p-1.
3. Формируют криптограмму в виде МДЧ C по формуле C=Me mod p.
4. Восстанавливают сообщение M из криптограммы C по формуле M=Cd mod p.
Наиболее близким по своей технической сущности к заявленному способу шифрования сообщения, представленного в виде МДЧ М, является известный способ шифрования (способ-прототип), включающий генерацию секретного ключа в виде двух больших простых МДЧ p и q, генерацию открытого ключа в виде МДЧ n, формирование криптограммы в виде МДЧ C по формуле C=M2 mod n [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - С-Петербург. Петербург-БХВ, 2010. - 304 с.; см. с. 78] и восстановление сообщения M из криптограммы C путем вычисления квадратных корней из криптограммы по модулю n, а именно по формуле 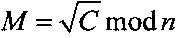 , из которой вычисляются четыре различных корня, одним из которых является сообщение M. Недостатком этого способа шифрования является то, что после расшифрования криптограммы требуется выполнить процедуру распознавания исходного сообщения среди четырех восстановленных сообщений, кроме того, для исходных сообщений не содержащих избыточности перед их зашифрованием, требуется ввести в них избыточную информацию или переслать избыточную информацию как дополнительное к криптограмме сообщение.
, из которой вычисляются четыре различных корня, одним из которых является сообщение M. Недостатком этого способа шифрования является то, что после расшифрования криптограммы требуется выполнить процедуру распознавания исходного сообщения среди четырех восстановленных сообщений, кроме того, для исходных сообщений не содержащих избыточности перед их зашифрованием, требуется ввести в них избыточную информацию или переслать избыточную информацию как дополнительное к криптограмме сообщение.
Задачей заявленного нового технического решения является разработка способа шифрования, в котором устраняется необходимость выполнения процедуры распознавания исходного сообщения после выполненной процедуры расшифрования криптограммы.
Техническим результатом нового способа шифрования сообщения М, представленного в виде МДЧ, является упрощение процедуры извлечения сообщения из криптограммы.
Указанный технический результат достигается тем, что в способе шифрования сообщения, представленного в виде многоразрядного двоичного числа М, заключающемся в том, что генерируют секретный ключ (р, q) в виде двух простых МДЧ р и q, генерируют открытый ключ в зависимости от секретного ключа, формируют криптограмму C в зависимости от сообщения, представленного в виде МДЧ М, и открытого ключа и восстанавливают сообщение М из криптограммы C по секретному ключу (p, q).
Новым является то, что генерируют открытый ключ в виде пары МДЧ (n, N), где n=pq, и N-МДЧ, удовлетворяющее соотношениям 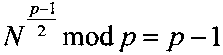 и
и 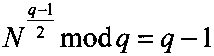 , и формируют криптограмму C в виде тройки (А, В, D) МДЧ A, B и D путем генерации вспомогательного МДЧ R<n и вычисления тройки (А, В, D) в зависимости от сообщения М, открытого ключа (n, N) и МДЧ R, а восстанавливают сообщение М путем вычисления корней уравнений x3+Ax2+Bx+D=0 mod р, x3+Ax2+Bx+D=0 mod q и x3+Ax2+Bx+D=0 mod n с неизвестным x и формирования сообщения М по корню последнего из указанных уравнений.
, и формируют криптограмму C в виде тройки (А, В, D) МДЧ A, B и D путем генерации вспомогательного МДЧ R<n и вычисления тройки (А, В, D) в зависимости от сообщения М, открытого ключа (n, N) и МДЧ R, а восстанавливают сообщение М путем вычисления корней уравнений x3+Ax2+Bx+D=0 mod р, x3+Ax2+Bx+D=0 mod q и x3+Ax2+Bx+D=0 mod n с неизвестным x и формирования сообщения М по корню последнего из указанных уравнений.
Генерация вспомогательного МДЧ R<n, имеющего разрядность, примерно равную разрядности МДЧ n, устраняет возможность нахождения решений уравнения x3+Ax2+Bx+D=0 mod n без знания разложения МДЧ n на простые множители р и q для сообщений М, представленных в виде МДЧ любого размера, включая короткие сообщения, например, размером от 1 до 500 бит.
Новым также является и то, что формируют криптограмму C в виде тройки (А, В, D) МДЧ A, B и D путем генерации вспомогательного МДЧ R<n и дополнительного МДЧ U=R2/4-N mod n и вычисления МДЧ А, В и D по формулам A=R-М mod n, В=U-MR mod n и D=-MU mod n.
Использование МДЧ N, для которого выполняются условия 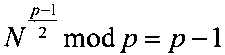 и
и 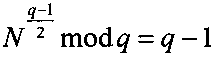 , и МДЧ U=R2/4-N mod n обеспечивает снижение вычислительной сложности процедуры восстановления сообщения М из криптограммы за счет того, что эти условия обеспечивают наличие единственного решения для каждого из следующих трех уравнений x3+Ax2+Bx+D=0 mod р, x3+Ax2+Bx+D=0 mod q и x3+Ax2+Bx+D=0 mod n.
, и МДЧ U=R2/4-N mod n обеспечивает снижение вычислительной сложности процедуры восстановления сообщения М из криптограммы за счет того, что эти условия обеспечивают наличие единственного решения для каждого из следующих трех уравнений x3+Ax2+Bx+D=0 mod р, x3+Ax2+Bx+D=0 mod q и x3+Ax2+Bx+D=0 mod n.
Новым является и то, что формируют криптограмму C в виде тройки (А, В, D) МДЧ A, B и D путем генерации первого дополнительного МДЧ T<n, генерации вспомогательного МДЧ R=(T-N)mod n и генерации второго дополнительного МДЧ U=(R2/4-N)mod n и вычисления МДЧ А, В и D по формулам А=(Т-N-М)mod n, В=(U-MR)mod n и D=-MU mod n.
Использование операции генерации дополнительного МДЧ T<n дополнительно к операциям генерации вспомогательного МДЧ R<n по формуле R=T-N mod n и формирования МДЧ А, В и D по формулам A=Т-N-М mod n, В=U-MR mod n и D=-MU mod n позволяет при выборе в качестве МДЧ Т дополнительного сообщения осуществить совместное шифрование двух сообщений, которые восстанавливаются из криптограммы C=(A, B, D) путем вычисления корня уравнения x3+Ax2+Bx+D=0 mod n с неизвестным x. При этом указанные формулы, по которым формируются коэффициенты последнего уравнения, задают равенство корня сообщению М, а дополнительное сообщение восстанавливается по формуле T=A+N+M mod n.
Изобретательский замысел заявленного нового технического решения состоит в том, что генерируют секретный ключ (р, q) в виде двух простых многоразрядных двоичных чисел p и q, генерируют открытый ключ в виде пары МДЧ (n, N), где МДЧ N является квадратичным невычетом по модулю n, т.е. таким МДЧ, которое непредставимо в виде квадрата некоторого числа и уравнение вида x2=N mod n не имеет решений. Для этого вычисляют n=pq, а затем путем выбора произвольных чисел находят такое число N, для которого выполняются следующие два равенства
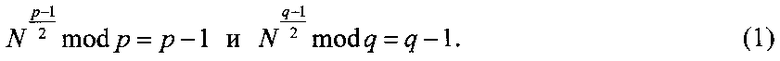
Обеспечение однозначности процедуры расшифрования, состоящей в решении кубичного уравнения x3+Ax2+Bx+D=0 mod n, состоит в формировании криптограммы C в виде тройки МДЧ (А, В, D), которые задают кубичное выражение x3+Ax2+Bx+D, которое представимо в виде произведения многочлена первой степени х-М, где М - шифруемое сообщение (M<n), и многочлена второй степени x2+Rx+U, такого, что уравнение x2+Rx+U mod n не имеет решений. При этом генерируют вспомогательное МДЧ R<n, такое, что дискриминант (R2/4-U)mod n многочлена x2+Rx+U имеет значение, равное квадратичному невычету N. Шифрование сообщения М выполняется с использованием открытого ключа (n, N) следующим образом:
1. Генерируют вспомогательное МДЧ R<n.
2. Вычисляют МДЧ U=R2/4-N mod n.
2. Формируют криптограмму в виде трех МДЧ (А, В, D), используя следующие формулы
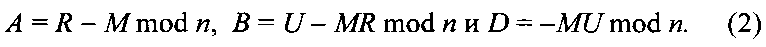
Восстанавливают сообщение М из криптограммы С по секретному ключу (р, q) путем решения уравнений
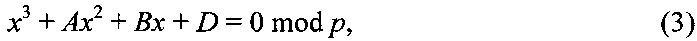
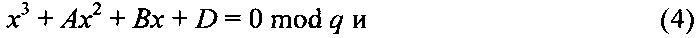
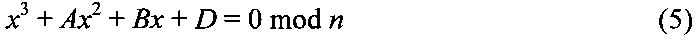
относительно неизвестного МДЧ x. Легко видеть, что в силу условий (2) уравнения (3), (4) и (5) представимы в следующем виде
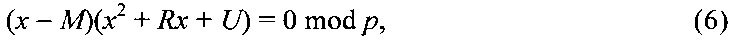
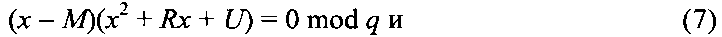
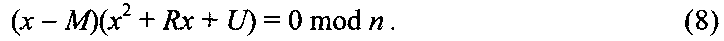
Условия (1) означают, что МДЧ N является квадратичным невычетом по модулям р и q, следовательно, уравнения x2+Rx+U=0 mod p и x2+Rx+U=0 mod q не имеют решений, поэтому каждое из уравнений (3), (4) и (5) имеет только одно решение. Восстановление из сообщения М из криптограммы C=(А, В, D) осуществляется следующим образом. Используя секретный ключ в виде пары простых чисел р, q, находят корень xp=Mp уравнения (3) и корень xq=Mq уравнения (4), по которым вычисляют корень xn=Mn=M уравнения (5) по формуле
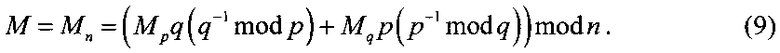
Основной вклад в трудоемкость процедуры расшифрования вносит процесс решения уравнений (3) и (4). Рассмотрим, каким образом можно выполнить решение кубичного уравнения в конечном поле, например уравнения (3). По аналогии со способом решения кубичных уравнений в поле действительных чисел (см. с. 234-238 в книге [Курош А.Г. Курс высшей алгебры. М.: Наука, 1971. - 431 с.]) путем замены переменной по формуле х=z-А/3 mod p перейдем к решению следующего уравнения, свободного от квадрата неизвестного,

где 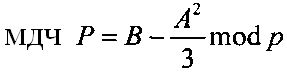 и
и 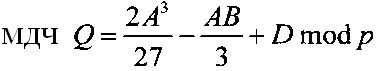 . Поскольку заведомо известно, что существует решение уравнения (10), то вывод формулы для корней кубичного уравнения, приведенный в [7] (см. с. 234-238 в книге [Курош А.Г. Курс высшей алгебры. М. Наука, 1971. - 431 с.]) может быть применен и в рассматриваемом случае. Такой подход дает следующую формулу для корней (10)
. Поскольку заведомо известно, что существует решение уравнения (10), то вывод формулы для корней кубичного уравнения, приведенный в [7] (см. с. 234-238 в книге [Курош А.Г. Курс высшей алгебры. М. Наука, 1971. - 431 с.]) может быть применен и в рассматриваемом случае. Такой подход дает следующую формулу для корней (10)

где
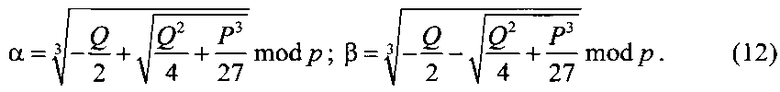
При этом при наличии нескольких значений кубичного корня в формулах (12) следует выбирать такие пары, которые удовлетворяют соотношению

Поскольку при открытом шифровании используются случайные значения, т.е. этот процесс является вероятностным, то под квадратным корнем в выражениях (12) может оказаться как МДЧ, которое является квадратичным вычетом, так и МДЧ, которое является квадратичным невычетом. В первом случае значение квадратного корня существует и может быть легко вычислено (см., например, с. 25-28 в книге [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - СПб. Петербург-БХВ, 2010. - 304 с.]). При этом, если выбрать в качестве секретного ключа пару простых МДЧ р и q, таких, что число 3 не делит ни одно из МДЧ р-1 и q-1, то существует единственный кубичный корень из любого МДЧ, поэтому существует единственный корень для каждого из уравнений (6), (7) и (8), а значит и для каждого из уравнений (3), (4) и (5). Этот корень вычисляется непосредственно по формулам (11), (12) и (9) соответственно.
Во втором случае для нахождения решения уравнения (10) требуется перейти в поле GF(p2) и выполнить вычисления по формулам (11) и (12) и взять в качестве искомых значений те, которые лежат в поле GF(p), вложенном в поле GF(p2). В качестве поля GF(p2) удобно выбрать поле двоичных векторов (см. с. 158-159 в книге [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - СПб. Петербург-БХВ, 2010. - 304 с.]), заданных над полем GF(p) при определении операций сложения и умножения векторов V=(a, b)∈GF(p2) и U=(c, d)∈GF(p2) по формулам
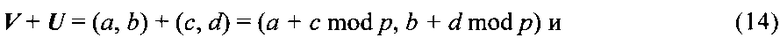
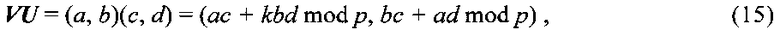
где k∈GF(p) - некоторый заданный квадратичный невычет.
Вместо уравнения (10) будем рассматривать уравнение над конечным полем двоичных векторов вида

где двухмерный вектор 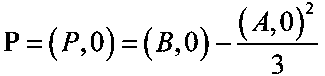 и двухмерный вектор
и двухмерный вектор 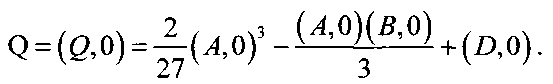
Поскольку заведомо известно, что существует решение уравнения (10), то существуют и решения уравнения (16), и имеем следующую формулу для корней (16):

где
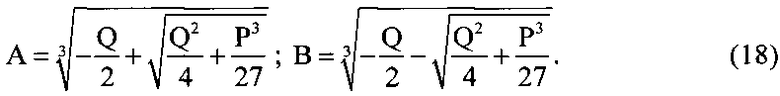
При этом при наличии нескольких значений кубичного корня в формулах (18) следует выбирать такие пары, которые удовлетворяют соотношению

Использование соотношения (19) позволяет уменьшить трудоемкость вычисления корня xp=Mp уравнения (3). Аналогично вычисляется корень xq=Mq уравнения (4). По значениям Mp и Mq вычисляется корень xn=Mn уравнения (5), который равен исходному сообщению Mn=М.
Проведенный анализ уровня техники позволил установить, что в известных источниках информации аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного изобретения условию патентоспособности «новизна». Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
Корректность заявленного способа шифрования сообщения М, представленного в виде МДЧ, обеспечивается тем, что корень уравнения (5) удовлетворяет также уравнениям (3) и (4), поскольку модули р и q делят модуль n, т.е. выполняется следующая система линейных сравнений с неизвестным значением Mn:
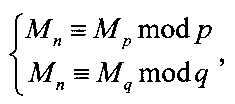
Где значения Mp и Mq вычисляются, используя секретный ключ, представляющий собой пару простых МДЧ p и q. В соответствии с китайской теоремой об остатках [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - С-Петербург. Петербург-БХВ, 2010. - 304 с.; см. с. 15-16] решением этой системы сравнений являются МДЧ, вычисляемое по формуле (9).
Рассмотрим частные примеры реализации заявленного способа шифрования сообщения М, представленного в виде МДЧ.
Пример 1
Данный пример иллюстрирует реализацию заявленного способа по пп. 1 и 2 формулы изобретения. В данном частном варианте реализации способа выполняются следующие действия:
1. Генерируют секретный ключ (р, q) в виде двух простых 512-разрядных двоичных чисел p и q.
2. Генерируют открытый ключ в виде МДЧ n=pq и МДЧ N, для которого выполняются следующие равенства 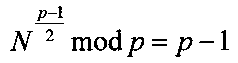 и
и 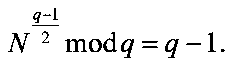
3. Формируют криптограмму C в виде тройки МДЧ (А, В, D) в зависимости от сообщения M и открытого ключа n путем выполнения следующих действий:
3.1. Генерируют вспомогательное МДЧ R<n, например, путем генерации случайного МДЧ.
3.2. Формируют дополнительное МДЧ U=(R2/4-N)mod n.
3.3. Генерируют МДЧ А по формуле А=(R-М)mod n.
3.4. Генерируют МДЧ В по формуле B=(U-MR)mod n.
3.5. Генерируют вспомогательное МДЧ D по формуле D=-MU mod n.
4. Восстанавливают сообщение М из криптограммы С по секретному ключу (р, q) путем выполнения следующих действий:
4.1. Вычисляют корень уравнения x3+Ax2+Bx+D=0 mod р в виде МДЧ Mp.
4.2. Вычисляют корень уравнения x3+Ax2+Bx+D=0 mod q в виде МДЧ Mq.
4.3. Используя формулу (9) по значениям Mp и Mq, вычисляют корень уравнения x3+Ax2+Bx+D=0 mod n в виде МДЧ Mn и формируют сообщение M=Mn.
Пример 2
Данный пример иллюстрирует реализацию заявленного способа по п. 3 формулы изобретения для одновременного шифрования двух независимых сообщений, представленных в виде МДЧ M<n и МДЧ T<n. В данном частном варианте реализации способа выполняются следующие действия:
1. Генерируют секретный ключ (р, q) в виде двух простых 768-разрядных двоичных чисел p и q.
2. Генерируют открытый ключ в виде пары МДЧ (n, N), для чего выполняют следующие действия:
2.1. Формируют МДЧ n по формуле n=pq.
2.2. Формируют МДЧ N путем выбора произвольных 10-разрядных двоичных чисел и отбора в качестве N такого 10-разрядного двоичного числа, для которого выполняются следующие равенства 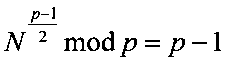 и
и 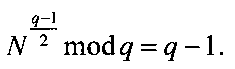
3. Формируют криптограмму C в виде тройки МДЧ (А, В, D) в зависимости от сообщения М и открытого ключа n путем выполнения следующих действий:
3.1. Формируют первое дополнительное МДЧ T<n путем формирования дополнительного сообщения, представленного в виде МДЧ Т.
3.2. Генерируют вспомогательное МДЧ R=(T-N)mod n.
3.3. Генерируют второе дополнительное МДЧ U=(R2/4-N)mod n.
3.4. Генерируют МДЧ А по формуле A=(T-N-М)mod n.
3.5. Генерируют МДЧ В по формуле B=(U-MR)mod n.
3.6. Генерируют вспомогательное МДЧ D по формуле и D=-MU mod n.
4. Восстанавливают сообщение M из криптограммы C по секретному ключу (р, q) путем выполнения следующих действий:
4.1. Вычисляют корень уравнения x3+Ax2+Bx+D=0 mod р в виде МДЧ Mp.
4.2. Вычисляют корень уравнения x3+Ax2+Bx+D=0 mod q в виде МДЧ Mq.
4.3. Используя формулу (9), по значениям Mp и Mq вычисляют корень уравнения x3+Ax2+Bx+D=0 mod n в виде МДЧ Mn и формируют сообщение M=Mn.
5. Восстанавливают дополнительное сообщение, представленное в виде МДЧ Т по формуле T=(А+N+М)mod n.
Корректное восстановление дополнительного сообщения, представленного в виде МДЧ T<n, обеспечивается тем, что МДЧ R связано с МДЧ А, являющегося первым элементом криптограммы (А, В, D), соотношением A=R-М mod n. Поэтому при генерации МДЧ R по формуле R=T-N mod n имеет место соотношение A=Т-N-М mod n, т.е. T=A+N+M mod n.
Таким образом, приведенные математические выкладки и конкретные примеры реализации показывают, что заявленный способ шифрования сообщения М, представленного в виде МДЧ, технически реализуем и позволяет достичь сформулированного технического результата.
Заявляемый способ шифрования сообщения, представленного в виде МДЧ, может быть применен для разработки средств защиты информации, передаваемой по открытым телекоммуникационным каналам, от несанкционированного доступа.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ШИФРОВАНИЯ СООБЩЕНИЯ, ПРЕДСТАВЛЕННОГО В ВИДЕ МНОГОРАЗРЯДНОГО ДВОИЧНОГО ЧИСЛА | 2014 |
|
RU2542926C1 |
| СПОСОБ ШИФРОВАНИЯ СООБЩЕНИЯ М, ПРЕДСТАВЛЕННОГО В ВИДЕ МНОГОРАЗРЯДНОГО ДВОИЧНОГО ЧИСЛА | 2011 |
|
RU2485600C2 |
| СПОСОБ ШИФРОВАНИЯ СООБЩЕНИЯ М, ПРЕДСТАВЛЕННОГО В ВИДЕ МНОГОРАЗРЯДНОГО ДВОИЧНОГО ЧИСЛА | 2011 |
|
RU2459276C1 |
| СПОСОБ ШИФРОВАНИЯ | 2009 |
|
RU2411666C1 |
| СПОСОБ ШИФРОВАНИЯ СООБЩЕНИЯ, ПРЕДСТАВЛЕННОГО В ВИДЕ БИТОВОЙ СТРОКИ | 2013 |
|
RU2558621C2 |
| СПОСОБ ШИФРОВАНИЯ N-БИТОВОГО БЛОКА ДАННЫХ М | 2013 |
|
RU2518950C9 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2401513C2 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2382505C1 |
| СПОСОБ ГЕНЕРАЦИИ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2006 |
|
RU2325768C1 |
| СПОСОБ ФОРМИРОВАНИЯ ОБЩЕГО СЕКРЕТНОГО КЛЮЧА ДВУХ УДАЛЕННЫХ АБОНЕНТОВ | 2009 |
|
RU2420892C1 |
Изобретение относится к области электросвязи, а именно к области криптографии. Технический результат - упрощение процедуры извлечения сообщения из криптограммы. Способ шифрования включает следующую последовательность действий: генерируют секретный ключ в виде двух простых многоразрядных двоичных чисел (МДЧ) р и q, генерируют открытый ключ в виде пары МДЧ (n, N), где n=pq и N-МДЧ, удовлетворяющее соотношениям 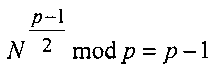 и
и 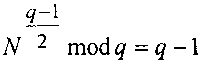 , формируют криптограмму C в виде тройки (А, В, D) МДЧ А, В и D путем генерации вспомогательного МДЧ R<n вычисления тройки (А, В, D) в зависимости от сообщения М, открытого ключа (n, N) и МДЧ R и восстанавливают сообщение M путем вычисления корней уравнений x3+Ax2+Bx+D=0 mod р, x3+Ax2+Bx+D=0 mod q и x3+Ax2+Bx+D=0 mod n с неизвестным x и формирования сообщения М по корню последнего из указанных уравнений. В частном случае формируют криптограмму C путем генерации первого дополнительного МДЧ T<n, генерации вспомогательного МДЧ R=(Т-N) mod n, генерации второго дополнительного МДЧ U=(R2/4-N)mod n и вычисления МДЧ А, В и D по формулам A=(T-N-M)mod n, B=(U-MR) mod n и D=-MU mod n. 2 з.п. ф-лы.
, формируют криптограмму C в виде тройки (А, В, D) МДЧ А, В и D путем генерации вспомогательного МДЧ R<n вычисления тройки (А, В, D) в зависимости от сообщения М, открытого ключа (n, N) и МДЧ R и восстанавливают сообщение M путем вычисления корней уравнений x3+Ax2+Bx+D=0 mod р, x3+Ax2+Bx+D=0 mod q и x3+Ax2+Bx+D=0 mod n с неизвестным x и формирования сообщения М по корню последнего из указанных уравнений. В частном случае формируют криптограмму C путем генерации первого дополнительного МДЧ T<n, генерации вспомогательного МДЧ R=(Т-N) mod n, генерации второго дополнительного МДЧ U=(R2/4-N)mod n и вычисления МДЧ А, В и D по формулам A=(T-N-M)mod n, B=(U-MR) mod n и D=-MU mod n. 2 з.п. ф-лы.
1. Способ шифрования сообщения, представленного в виде многоразрядного двоичного числа, заключающийся в том, что генерируют секретный ключ (р, q) в виде двух простых многоразрядных двоичных чисел р и q, генерируют открытый ключ в зависимости от секретного ключа, формируют криптограмму С в зависимости от сообщения, представленного в виде многоразрядного двоичного числа М, и открытого ключа и восстанавливают сообщение М из криптограммы С по секретному ключу (p, q), отличающийся тем, что генерируют открытый ключ в виде пары многоразрядных двоичных чисел (n, N), где n=pq и N - многоразрядное двоичное число, удовлетворяющее соотношениям 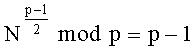
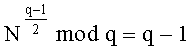
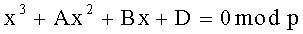
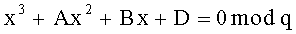
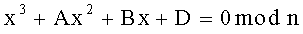
2. Способ по п. 1, отличающийся тем, что формируют криптограмму C в виде тройки (А, В, D) многоразрядных двоичных чисел A, B и D путем генерации вспомогательного многоразрядного двоичного числа R<n и дополнительного многоразрядного двоичного числа 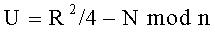
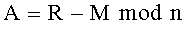
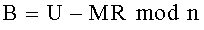
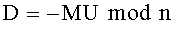
3. Способ по п. 1, отличающийся тем, что формируют криптограмму С в виде тройки (А, В, D) многоразрядных двоичных чисел A, B и D путем генерации первого дополнительного многоразрядного двоичного числа T<n, генерации вспомогательного многоразрядного двоичного числа 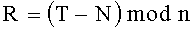
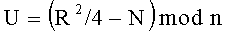
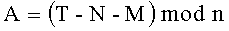
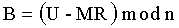
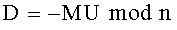
Авторы
Даты
2016-04-10—Публикация
2015-05-20—Подача