Изобретение относится к вычислительной технике и может быть использовано для построения средств автоматики, функциональных узлов систем управления и др.
Известны мажоритарные модули (см., например, патент РФ 2300137, кл. G06F 7/38, 2007 г.), которые реализуют мажоритарную функцию n аргументов - входных двоичных сигналов либо дизъюнкцию (конъюнкцию) тех же n аргументов, где n≠1 есть любое нечетное натуральное число.
К причине, препятствующей достижению указанного ниже технического результата при использовании известных мажоритарных модулей, относятся большие аппаратурные затраты, обусловленные тем, что известные мажоритарные модули содержат mN-1 логических элементов, где m=0,5(n+1),
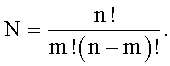
Наиболее близким устройством того же назначения к заявленному изобретению по совокупности признаков является принятый за прототип мажоритарный модуль (патент РФ 2242044, кл. G06F 7/38, 2004 г.), который содержит трехвходовые мажоритарные элементы и реализует мажоритарную функцию n аргументов - входных двоичных сигналов либо дизъюнкцию (конъюнкцию) тех же n аргументов, где n≠1 есть любое нечетное натуральное число.
К причине, препятствующей достижению указанного ниже технического результата при использовании прототипа, относятся большие аппаратурные затраты, обусловленные тем, что прототип содержит mN-1 мажоритарных элементов, где m=0,5(n+1),
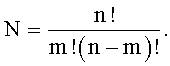
Техническим результатом изобретения является уменьшение аппаратурных затрат при сохранении функциональных возможностей прототипа.
Указанный технический результат при осуществлении изобретения достигается тем, что в мажоритарном модуле, содержащем группы мажоритарных элементов, имеющих по три входа, в каждой из которых выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, особенность заключается в том, что i-я 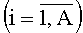 , j-я
, j-я 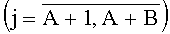 и (A+B+1)-я группы содержат соответственно m-2, m-1 и А+В мажоритарных элементов, а выход (m-2)-го мажоритарного элемента первой и выходы (m-2)-х мажоритарных элементов второй, …, A-й групп подключены соответственно к второму входу первого и третьим входам первого, …, (A-1)-го мажоритарных элементов (А+В+1)-й группы, в которой третий вход j-го и выход (А+В)-го мажоритарных элементов соединены соответственно с выходом (m-1)-го мажоритарного элемента j-й группы и выходом мажоритарного модуля, подключенного первым и вторым настроечными входами соответственно к объединенным первому входу A-го мажоритарного элемента (А+В+1)-й группы, первым входам всех мажоритарных элементов i-й, j-й групп и объединенным первым входам всех кроме A-го мажоритарных элементов (А+В+1)-й группы, при этом
и (A+B+1)-я группы содержат соответственно m-2, m-1 и А+В мажоритарных элементов, а выход (m-2)-го мажоритарного элемента первой и выходы (m-2)-х мажоритарных элементов второй, …, A-й групп подключены соответственно к второму входу первого и третьим входам первого, …, (A-1)-го мажоритарных элементов (А+В+1)-й группы, в которой третий вход j-го и выход (А+В)-го мажоритарных элементов соединены соответственно с выходом (m-1)-го мажоритарного элемента j-й группы и выходом мажоритарного модуля, подключенного первым и вторым настроечными входами соответственно к объединенным первому входу A-го мажоритарного элемента (А+В+1)-й группы, первым входам всех мажоритарных элементов i-й, j-й групп и объединенным первым входам всех кроме A-го мажоритарных элементов (А+В+1)-й группы, при этом
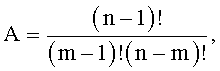
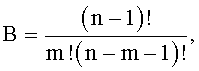
m=0,5(n+1), n≠1 есть любое нечетное натуральное число.
На чертеже представлена схема предлагаемого мажоритарного модуля.
Мажоритарный модуль содержит имеющие по три входа мажоритарные элементы (111, …, 1(A+B+1)(A+B)), где
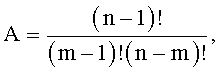
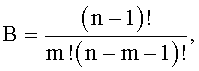 m=0,5(n+1), n≠1 есть любое нечетное натуральное число. Все мажоритарные элементы сгруппированы так, что i-я
m=0,5(n+1), n≠1 есть любое нечетное натуральное число. Все мажоритарные элементы сгруппированы так, что i-я 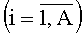 , j-я
, j-я 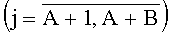 и (A+B+1)-я группы содержат соответственно мажоритарные элементы 1i1, …, 1i(m-2), 1j1, …, 1j(m-1) и 1(A+B+1)1, …, 1(A+B+1)(A+B), причем в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, выход элемента 11(m-2) и выходы элементов 12(m-2), …, 1A(1m-2) подключены соответственно к второму входу элемента 1(A+B+1)1 и третьим входам элементов 1(A+B+1)1, …, 1{A+B+1)(A-1), а третий вход элемента 1(A+B+1)j и выход элемента 1(А+B+1)(A+B) соединены соответственно с выходом элемента 1j(m-1) и выходом мажоритарного модуля, подключенного первым и вторым настроечными входами соответственно к объединенным первым входам элементов 1(A+B+1)A, 1i1, …, 1i(m-2), 1j1, …, 1j(m-1) и объединенным первым входам элементов 1(A+B+1)1, …, 1(A+B+1)(A-1), 1(A+B+1)j.
и (A+B+1)-я группы содержат соответственно мажоритарные элементы 1i1, …, 1i(m-2), 1j1, …, 1j(m-1) и 1(A+B+1)1, …, 1(A+B+1)(A+B), причем в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, выход элемента 11(m-2) и выходы элементов 12(m-2), …, 1A(1m-2) подключены соответственно к второму входу элемента 1(A+B+1)1 и третьим входам элементов 1(A+B+1)1, …, 1{A+B+1)(A-1), а третий вход элемента 1(A+B+1)j и выход элемента 1(А+B+1)(A+B) соединены соответственно с выходом элемента 1j(m-1) и выходом мажоритарного модуля, подключенного первым и вторым настроечными входами соответственно к объединенным первым входам элементов 1(A+B+1)A, 1i1, …, 1i(m-2), 1j1, …, 1j(m-1) и объединенным первым входам элементов 1(A+B+1)1, …, 1(A+B+1)(A-1), 1(A+B+1)j.
Работа предлагаемого мажоритарного модуля осуществляется следующим образом. На его первом, втором настроечных входах фиксируются соответственно необходимые двоичные сигналы f1, f2. На второй вход элемента 1j1 и третьи входы элементов 1j1, …, 1j(m-1) 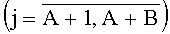 подаются соответственно входные двоичные сигналы xji и xj2, …, xjm (xj1, …, xjm∈{х1, …, xn-1}, m=0,5(n+1), 1≤j1<…<jm≤n-1, n≠1 есть любое нечетное натуральное число) так, чтобы наборы
подаются соответственно входные двоичные сигналы xji и xj2, …, xjm (xj1, …, xjm∈{х1, …, xn-1}, m=0,5(n+1), 1≤j1<…<jm≤n-1, n≠1 есть любое нечетное натуральное число) так, чтобы наборы
x(A+1)1, …, x(A+1)m-x(A+B)1, …, x(A+B)m были неповторяющимися
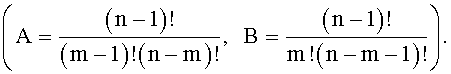
На третий вход элемента 1(A+B+1)A подается входной двоичный сигнал xn. На второй вход элемента 1i1 и третьи входы элементов 1i1, …, 1i(m-2) 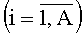 подаются соответственно входные двоичные сигналы xi1 и xi2, …, xi(m-1) (xi1, …, xi(m-1)∈{x1, …, xn-1}, 1≤i1<…<i(m-1)≤n-1, n - нечетное натуральное число, удовлетворяющее условию n>3) так, чтобы наборы x11, …, x1(m-1)-xA1, …, xA(m-1) были неповторяющимися. Если n=3, то m=2, A=2, B=1 и неповторяющиеся входные двоичные сигналы x11, x21∈{x1, x2} подаются соответственно на второй, третий входы элемента 141. Сигнал на выходе мажоритарного элемента равен 1 (0) только тогда, когда на двух или на всех входах этого элемента действуют сигналы, равные 1 (0). Следовательно, если на первом входе мажоритарного элемента присутствует 1 (0), то этот элемент будет выполнять операцию ИЛИ (И) над сигналами, действующими на его втором и третьем входах. Таким образом, операция, воспроизводимая предлагаемым модулем, определяется выражением
подаются соответственно входные двоичные сигналы xi1 и xi2, …, xi(m-1) (xi1, …, xi(m-1)∈{x1, …, xn-1}, 1≤i1<…<i(m-1)≤n-1, n - нечетное натуральное число, удовлетворяющее условию n>3) так, чтобы наборы x11, …, x1(m-1)-xA1, …, xA(m-1) были неповторяющимися. Если n=3, то m=2, A=2, B=1 и неповторяющиеся входные двоичные сигналы x11, x21∈{x1, x2} подаются соответственно на второй, третий входы элемента 141. Сигнал на выходе мажоритарного элемента равен 1 (0) только тогда, когда на двух или на всех входах этого элемента действуют сигналы, равные 1 (0). Следовательно, если на первом входе мажоритарного элемента присутствует 1 (0), то этот элемент будет выполнять операцию ИЛИ (И) над сигналами, действующими на его втором и третьем входах. Таким образом, операция, воспроизводимая предлагаемым модулем, определяется выражением
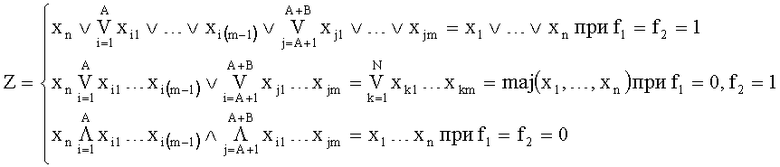
где ∨ и ·, ∧ есть символы операций ИЛИ и И;
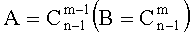 есть число сочетаний из n-1 по m-1 (по m);
есть число сочетаний из n-1 по m-1 (по m);
xk1, …, xkm∈{x1, …, xn}, 1≤k1<…<km≤n;
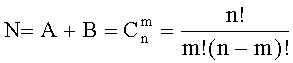 есть количество неповторяющихся конъюнкций xk1…xkm, определяемое как число сочетаний из n по m.
есть количество неповторяющихся конъюнкций xk1…xkm, определяемое как число сочетаний из n по m.
Равенство 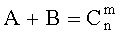 получено на основе известного свойства сочетаний (см. рекуррентное соотношение на стр.30 в книге Сачков В.Н. Комбинаторные методы дискретной математики. - М.: Наука, 1977 г.).
получено на основе известного свойства сочетаний (см. рекуррентное соотношение на стр.30 в книге Сачков В.Н. Комбинаторные методы дискретной математики. - М.: Наука, 1977 г.).
Вышеизложенные сведения позволяют сделать вывод, что предлагаемый мажоритарный модуль реализует мажоритарную функцию n аргументов - входных двоичных сигналов либо дизъюнкцию (конъюнкцию) тех же n аргументов, где n≠1 есть любое нечетное натуральное число, и содержит mN-A мажоритарных элементов, что на A-1 элементов меньше, чем в аппаратурном составе прототипа.
| название | год | авторы | номер документа |
|---|---|---|---|
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2013 |
|
RU2533079C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2018 |
|
RU2700555C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2006 |
|
RU2300137C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2005 |
|
RU2287897C1 |
| ЛОГИЧЕСКИЙ ПРОЦЕССОР | 2005 |
|
RU2294008C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2003 |
|
RU2242044C1 |
| УСТРОЙСТВО ДЛЯ МАЖОРИТАРНОГО ВЫБОРА СИГНАЛОВ | 2016 |
|
RU2628890C1 |
| ЛОГИЧЕСКИЙ ПРОЦЕССОР | 2003 |
|
RU2251142C2 |
| РАНГОВЫЙ ФИЛЬТР | 2015 |
|
RU2580805C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2023 |
|
RU2803610C1 |
Изобретение относится к области вычислительной техники и может быть использовано в системах цифровой вычислительной техники как средство предварительной обработки информации для реализации мажоритарной функции либо дизъюнкции, либо конъюнкции входных двоичных сигналов. Техническим результатом является уменьшение аппаратурных затрат. Устройство содержит m(А+В)-А мажоритарных элементов (111,…,1(А+В+1)(А+B)), при этом
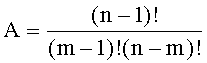
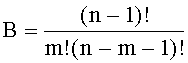
m=0,5(n+1). 1 ил.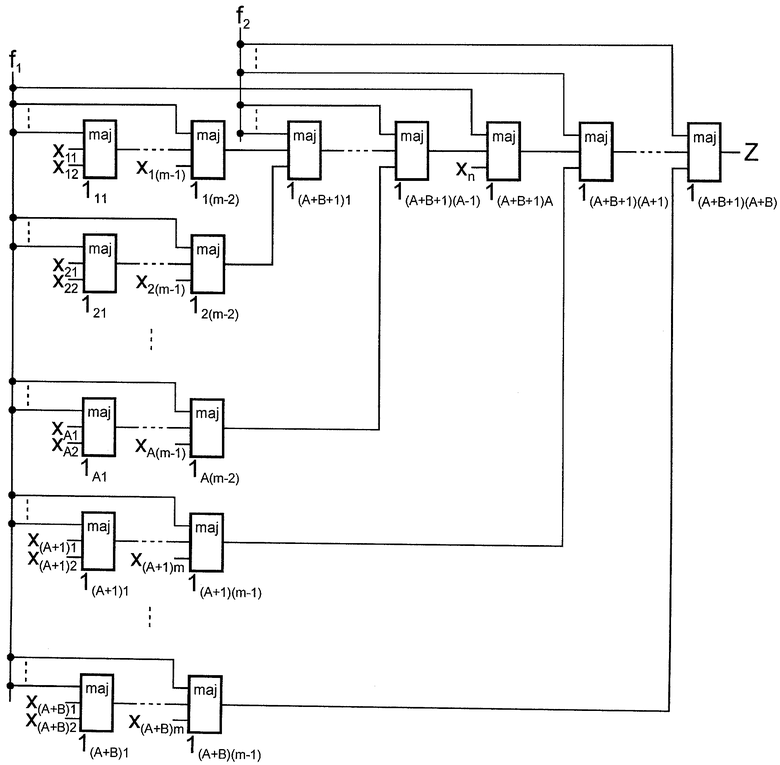
Мажоритарный модуль, содержащий группы мажоритарных элементов, имеющих по три входа, в каждой из которых выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, отличающийся тем, что i-я 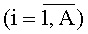 , j-я
, j-я 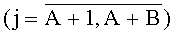 и (А+В+1)-я группы содержат соответственно m-2, m-1 и А+В мажоритарных элементов, а выход (m-2)-го мажоритарного элемента первой и выходы (m-2)-х мажоритарных элементов второй, ..., А-й групп подключены соответственно к второму входу первого и третьим входам первого, …, (A-1)-гo мажоритарных элементов (А+В+1)-й группы, в которой третий вход j-го и выход (А+В)-го мажоритарных элементов соединены соответственно с выходом (m-1)-гo мажоритарного элемента j-й группы и выходом мажоритарного модуля, подключенного первым и вторым настроечными входами соответственно к объединенным первому входу А-го мажоритарного элемента (А+В+1)-й группы, первым входам всех мажоритарных элементов i-й, j-й групп и объединенным первым входам всех кроме А-го мажоритарных элементов (А+В+1)-й группы, при этом
и (А+В+1)-я группы содержат соответственно m-2, m-1 и А+В мажоритарных элементов, а выход (m-2)-го мажоритарного элемента первой и выходы (m-2)-х мажоритарных элементов второй, ..., А-й групп подключены соответственно к второму входу первого и третьим входам первого, …, (A-1)-гo мажоритарных элементов (А+В+1)-й группы, в которой третий вход j-го и выход (А+В)-го мажоритарных элементов соединены соответственно с выходом (m-1)-гo мажоритарного элемента j-й группы и выходом мажоритарного модуля, подключенного первым и вторым настроечными входами соответственно к объединенным первому входу А-го мажоритарного элемента (А+В+1)-й группы, первым входам всех мажоритарных элементов i-й, j-й групп и объединенным первым входам всех кроме А-го мажоритарных элементов (А+В+1)-й группы, при этом 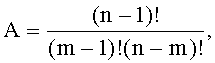
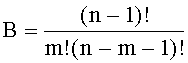 , m=0,5(n+1), n≠1 есть любое нечетное натуральное число.
, m=0,5(n+1), n≠1 есть любое нечетное натуральное число.
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2003 |
|
RU2242044C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2006 |
|
RU2300137C1 |
| JP 63171023 A, 14.07.1988 | |||
| JP 62176217 A, 03.08.1987 | |||
| JP 2005258911 A, 22.09.2005. | |||
Авторы
Даты
2013-01-27—Публикация
2012-02-08—Подача