Изобретение относится к вычислительной технике и может быть использовано для построения средств автоматики, функциональных узлов систем управления и др.
Известны мажоритарные модули (см., например, рис. 18.2а на стр.315 в книге Каяцкас А.А. Основы радиоэлектроники. М.: Высш. шк., 1988.), которые реализуют мажоритарную функцию maj(x1,x2,x3)=x1x2∨x1x3∨x2x3 трех аргументов - входных двоичных сигналов x1,x2,x3∈{0,1}.
К причине, препятствующей достижению указанного ниже технического результата при использовании известных мажоритарных модулей, относятся ограниченные функциональные возможности, обусловленные тем, что не допускается обработка любого нечетного количества входных сигналов.
Наиболее близким устройством того же назначения к заявленному изобретению по совокупности признаков является, принятый за прототип, мажоритарный модуль (патент РФ 2242044, кл. G 06 F 7/38, 2004 г.), который содержит мажоритарные элементы и реализует мажоритарную функцию n аргументов (входных двоичных сигналов), где n≠1 есть любое нечетное натуральное число.
К причине, препятствующей достижению указанного ниже технического результата при использовании прототипа, относятся ограниченные функциональные возможности, обусловленные тем, что не выполняется реализация субмажоритарной или супрамажоритарной функции тех же n аргументов. Отметим, что субмажоритарная (супрамажоритарная) функция n аргументов - это функция, которая равна 1, когда не менее m-1 (m+1) ее аргументов равны 1, где m=0,5(n+1).
Техническим результатом изобретения является расширение функциональных возможностей за счет обеспечения реализации субмажоритарной, мажоритарной или супрамажоритарной функции n аргументов (входных двоичных сигналов), где n≠1 есть любое нечетное натуральное число.
Указанный технический результат при осуществлении изобретения достигается тем, что в мажоритарном модуле, содержащем мажоритарные элементы, которые имеют по три входа и сгруппированы в N+1 групп так, что i-я (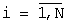 ) и (N+1)-я группы содержат соответственно m-1 и N-1 мажоритарных элементов, в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, а выход (m-1)-го мажоритарного элемента первой и выходы (m-1)-х мажоритарных элементов второй,...,N-й групп подключены соответственно к второму входу первого и третьим входам первого,..., (N-1)-го мажоритарных элементов (N+1)-й группы, в которой выход (N-1)-го мажоритарного элемента является выходом мажоритарного модуля, подключенного вторым настроечным входом к первым входам всех мажоритарных элементов (N+1)-й группы, при этом
) и (N+1)-я группы содержат соответственно m-1 и N-1 мажоритарных элементов, в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, а выход (m-1)-го мажоритарного элемента первой и выходы (m-1)-х мажоритарных элементов второй,...,N-й групп подключены соответственно к второму входу первого и третьим входам первого,..., (N-1)-го мажоритарных элементов (N+1)-й группы, в которой выход (N-1)-го мажоритарного элемента является выходом мажоритарного модуля, подключенного вторым настроечным входом к первым входам всех мажоритарных элементов (N+1)-й группы, при этом 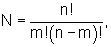
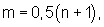 n≠1 есть любое нечетное натуральное число, особенность заключается в том, что первые входы первых мажоритарных элементов первой,...,N-й групп объединены и образуют первый настроечный вход мажоритарного модуля, третий настроечный вход которого образован объединенными первыми входами остальных мажоритарных элементов первой,...,N-й групп.
n≠1 есть любое нечетное натуральное число, особенность заключается в том, что первые входы первых мажоритарных элементов первой,...,N-й групп объединены и образуют первый настроечный вход мажоритарного модуля, третий настроечный вход которого образован объединенными первыми входами остальных мажоритарных элементов первой,...,N-й групп.
На чертеже представлена схема предлагаемого мажоритарного модуля.
Мажоритарный модуль содержит мажоритарные элементы 111,...,1(N+1)(N-1), где 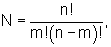
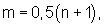 n≠1 есть любое нечетное натуральное число. Все мажоритарные элементы сгруппированы в N+1 групп так, что i-я (
n≠1 есть любое нечетное натуральное число. Все мажоритарные элементы сгруппированы в N+1 групп так, что i-я (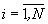 ) и (N+1)-я группы содержат соответственно элементы 1i1,...,1i(m-1) и 1(N+1)1,...,1(N+1)(N-1), в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, а выход элемента 11(m-1) и выходы элементов 12(m-1),...,1N(m-1) подключены соответственно к второму входу элемента 1(N+1)1 и третьим входам элементов 1(N+1)1,...,1(N+1)(N-1), выход элемента 1(N+1)(N-1) является выходом мажоритарного модуля, первый, второй и третий настроечные входы которого образованы соответственно объединенными первыми входами элементов 111,...,1N1, объединенными первыми входами элементов 1(N+1)1,...,1(N+1)(N-1) и объединенными первыми входами элементов 1i2,...,1i(m-1) (
) и (N+1)-я группы содержат соответственно элементы 1i1,...,1i(m-1) и 1(N+1)1,...,1(N+1)(N-1), в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, а выход элемента 11(m-1) и выходы элементов 12(m-1),...,1N(m-1) подключены соответственно к второму входу элемента 1(N+1)1 и третьим входам элементов 1(N+1)1,...,1(N+1)(N-1), выход элемента 1(N+1)(N-1) является выходом мажоритарного модуля, первый, второй и третий настроечные входы которого образованы соответственно объединенными первыми входами элементов 111,...,1N1, объединенными первыми входами элементов 1(N+1)1,...,1(N+1)(N-1) и объединенными первыми входами элементов 1i2,...,1i(m-1) (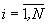 ).
).
Работа предлагаемого мажоритарного модуля осуществляется следующим образом. На его первом, втором и третьем настроечных входах фиксируются соответственно необходимые двоичные сигналы f1, f2 и f3; на второй вход элемента 1i1, третьи входы элементов 1i1,...,1i(m-1) (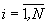 ) подается соответственно неповторяющийся набор хi1,...,xim,
) подается соответственно неповторяющийся набор хi1,...,xim, 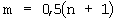 , n≠1 - любое нечетное натуральное число), образованный m неповторяющимися сигналами из входного кортежа двоичных сигналов x1,...,xn. Неповторяющиеся наборы x11,...,x1m-xN1,...,xNm формируются так, чтобы наборы х12,...,х1m-хN2,...,хNm тоже были неповторяющимися. Примеры упомянутых наборов при n=5 приведены в таблице.
, n≠1 - любое нечетное натуральное число), образованный m неповторяющимися сигналами из входного кортежа двоичных сигналов x1,...,xn. Неповторяющиеся наборы x11,...,x1m-xN1,...,xNm формируются так, чтобы наборы х12,...,х1m-хN2,...,хNm тоже были неповторяющимися. Примеры упомянутых наборов при n=5 приведены в таблице.
Сигнал на выходе мажоритарного элемента равен 1 (0) только тогда, когда на двух или на всех входах этого элемента действуют сигналы, равные 1 (0). Следовательно, если на первом входе мажоритарного элемента присутствует 1 (0), то этот элемент будет выполнять операцию ИЛИ (И) над сигналами, действующими на его втором и третьем входах. Таким образом, операция, воспроизводимая предлагаемым модулем, определяется выражением
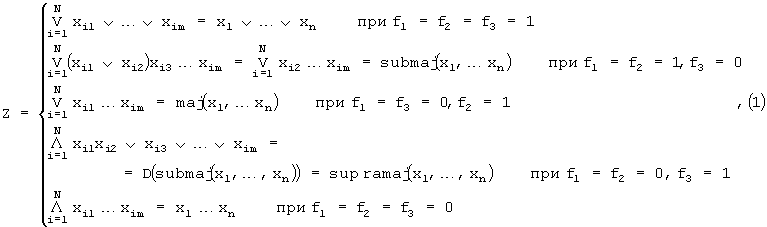 где D(·) есть оператор двойственного преобразования, а символами ∨ и · либо ∧ обозначены соответственно операции ИЛИ и И. В качестве примера запишем (с учетом представленной выше таблицы) соотношения, к которым сводятся при n=5 формулы, приведенные на второй и четвертой строках правой части выражения (1):
где D(·) есть оператор двойственного преобразования, а символами ∨ и · либо ∧ обозначены соответственно операции ИЛИ и И. В качестве примера запишем (с учетом представленной выше таблицы) соотношения, к которым сводятся при n=5 формулы, приведенные на второй и четвертой строках правой части выражения (1):
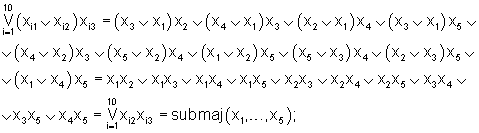
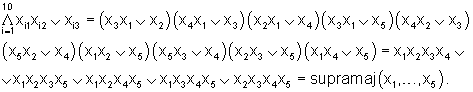
Вышеизложенные сведения позволяют сделать вывод, что предлагаемый мажоритарный модуль обладает более широкими по сравнению с прототипом функциональными возможностями, так как обеспечивает реализацию субмажоритарной, мажоритарной или супрамажоритарной функции n аргументов (входных двоичных сигналов), где n≠1 есть любое нечетное натуральное число. Следует отметить, что предлагаемый мажоритарный модуль, так же как и прототип, может выполнять операцию ИЛИ либо И над n входными двоичными сигналами.
| название | год | авторы | номер документа |
|---|---|---|---|
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2012 |
|
RU2473954C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2003 |
|
RU2242044C1 |
| ЛОГИЧЕСКИЙ ПРОЦЕССОР | 2005 |
|
RU2294008C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2006 |
|
RU2300137C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2013 |
|
RU2533079C1 |
| ЛОГИЧЕСКИЙ ПРОЦЕССОР | 2003 |
|
RU2251142C2 |
| ЛОГИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ | 2011 |
|
RU2440601C1 |
| ЛОГИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ | 2005 |
|
RU2294007C1 |
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2018 |
|
RU2700555C1 |
| РЕЛЯТОРНЫЙ СЕЛЕКТОР | 2005 |
|
RU2294594C1 |
Изобретение относится к вычислительной технике и может быть использовано для построения средств автоматики, функциональных узлов систем управления. Техническим результатом является расширение функциональных возможностей устройства за счет обеспечения реализации субмажоритарной и супрамажоритарной функций. Устройство содержит мажоритарные элементы, сгруппированные в (N+1) группу так, что i-я (i=1, N) и (N+1)-я группы содержат соответственно m-1 и N-1 мажоритарных элементов, где 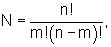 m=0,5(n+1), n≠1 - любое нечетное натуральное число. 1 табл., 1 ил.
m=0,5(n+1), n≠1 - любое нечетное натуральное число. 1 табл., 1 ил.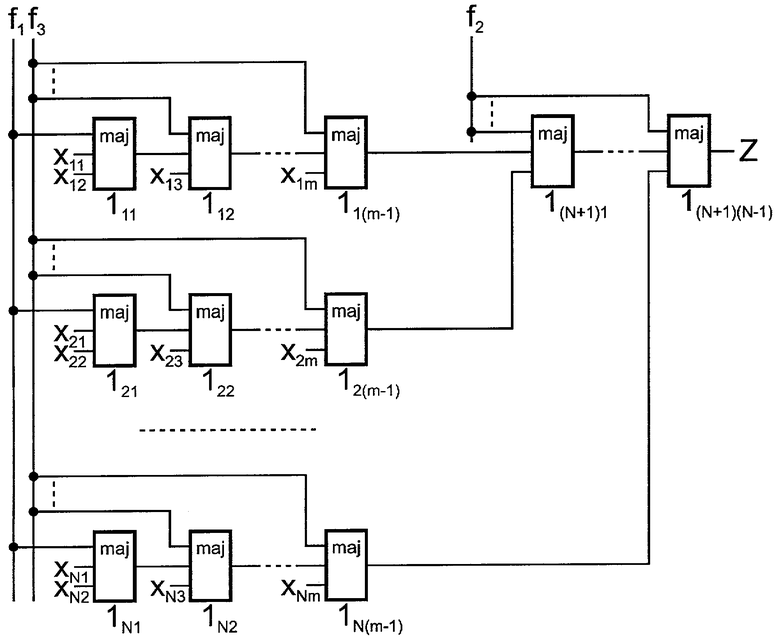
Мажоритарный модуль, содержащий мажоритарные элементы, которые имеют по три входа и сгруппированы в N+1 групп так, что i-я (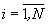 ) и (N+1)-я группы содержат соответственно m-1 и N-1 мажоритарных элементов, в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, а выход (m-1)-го мажоритарного элемента первой и выходы (m-1)-х мажоритарных элементов второй,..., N-й групп подключены соответственно к второму входу первого и третьим входам первого,..., (N-1)-го мажоритарных элементов (N+1)-й группы, в которой выход (N-1)-го мажоритарного элемента является выходом мажоритарного модуля, подключенного первым и вторым настроечными входами соответственно к объединенным первым входам первых мажоритарных элементов первой,..., N-й групп и объединенным первым входам всех мажоритарных элементов (N+1)-й группы, при этом
) и (N+1)-я группы содержат соответственно m-1 и N-1 мажоритарных элементов, в каждой группе выход предыдущего мажоритарного элемента соединен с вторым входом последующего мажоритарного элемента, а выход (m-1)-го мажоритарного элемента первой и выходы (m-1)-х мажоритарных элементов второй,..., N-й групп подключены соответственно к второму входу первого и третьим входам первого,..., (N-1)-го мажоритарных элементов (N+1)-й группы, в которой выход (N-1)-го мажоритарного элемента является выходом мажоритарного модуля, подключенного первым и вторым настроечными входами соответственно к объединенным первым входам первых мажоритарных элементов первой,..., N-й групп и объединенным первым входам всех мажоритарных элементов (N+1)-й группы, при этом 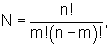 m=0,5(n+1), n≠1 есть любое нечетное натуральное число, отличающийся тем, что третий настроечный вход мажоритарного модуля образован объединенными первыми входами остальных мажоритарных элементов первой,...,N-й групп, при этом мажоритарный модуль реализует следующие операции:
m=0,5(n+1), n≠1 есть любое нечетное натуральное число, отличающийся тем, что третий настроечный вход мажоритарного модуля образован объединенными первыми входами остальных мажоритарных элементов первой,...,N-й групп, при этом мажоритарный модуль реализует следующие операции:
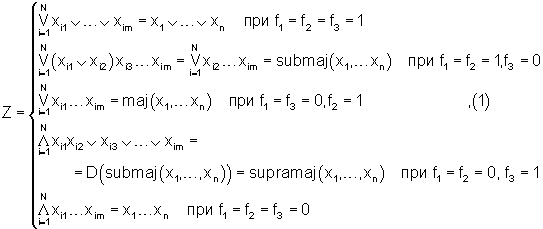
| МАЖОРИТАРНЫЙ МОДУЛЬ | 2003 |
|
RU2242044C1 |
| АНАЛОГОВЫЙ ПРОЦЕССОР | 2000 |
|
RU2177643C1 |
| SU 1547668 А1, 10.05.1996 | |||
| JP 62175016, 31.07.1987. | |||
Авторы
Даты
2006-11-20—Публикация
2005-05-11—Подача