Область техники
Настоящее изобретение относится к усовершенствованным методикам для обработки данных измерения потенциального поля при аэросъемке, например при гравиметрических съемках, и к способам, устройству и коду компьютерной программы для таких методик.
Уровень техники
Настоящее описание относится к аэросъемкам и, более конкретно, к гравиметрическим съемкам. Однако описываемые методики не ограничиваются этими примерами съемки и могут быть применены к другим съемкам потенциального поля, включая, но без ограничений, съемку магнитного поля, например магнитотеллурические съемки, электромагнитные съемки и т.п.
Съемка потенциального поля выполняется посредством измерения данных потенциального поля, которые, для гравиметрической съемки, могут содержать одни или несколько гравиметрических данных (измерение гравитационного поля) или данные гравитационного градиентометра (измерение градиента гравитационного поля), данные векторного магнитометра, достоверные данные магнитного градиентометра и другие типы данных, хорошо известных специалистам в данной области техники. Общая цель геофизической съемки потенциального поля заключается в том, чтобы найти характерные признаки, потенциально указывающие на ценные минеральные отложения.
Традиционно аэросъемки потенциального поля, например гравиметрические съемки, проводятся по координатной сетке. Сетка задается ортогональными рядами параллельных линий (траектории полета) на двумерной поверхности, которая огибает земную поверхность. Однако огибаемая поверхность ограничивается разрешенным для летательного аппарата приближением к Земле и максимальной скоростью подъема/спуска летательного аппарата. Некоторые улучшенные методики для аэросъемок потенциального поля, которые облегчают сбор данных на малом расстоянии от Земли, описаны в находящейся на рассмотрении PCT Патентной заявке авторов "Обработка данных гравиметрической съемки", PCT/GB2006/050211, тем самым полностью включенной в данное описание посредством ссылки.
После того как данные потенциального поля собраны, но до интерпретации данных, обычно применяется коррекция рельефа местности, компенсирующая поверхностные вариации высоты. Поверхностный профиль может быть получен в форме цифровых данных повышения рельефа местности или определен из (D) GPS ((Дифференциальная) Глобальная Система Позиционирования) и/или из бортовых методик, например LIDAR (Лазерная Система Обнаружения, Отображения и Определения расстояния) и SAR (радар с синтезированной апертурой). Ускорение летательного аппарата, ориентация, угловая скорость и данные углового ускорения могут также быть использованы для коррекции выходных данных аппаратуры измерения потенциального поля. Авторы описывают некоторые улучшенные методики для коррекции рельефа местности при геофизических съемках в своей, находящейся на рассмотрении Патентной заявке Соединенного Королевства "Системы коррекции рельефа местности", №0601482.3, поданной 25 января 2006 г. и также полностью включенной в данное описание посредством ссылки.
Однако несмотря на улучшенные методики авторы ранее отмечали, что низкочастотный шум, или дрейф, в бортовых измерениях при съемке остается проблемой. (Хотя термин дрейф иногда относится к случайному монотонному изменению, в настоящем описании он используется для обозначения любого вида коррелированного шума с характерной частотой, намного меньшей частоты основных, представляющих интерес сигналов.)
Термин "нивелировка" используется в данной области техники как общий термин, относящийся к обычным методикам приведения данных в соответствие. Эти методики включают в себя удаление низкочастотного дрейфа, согласование низкочастотного вклада соседних линий и отнесение данных к плоскости фиксированной высоты. Например, точки пересечения стандартной координатной съемки могут быть использованы для перекрестной нивелировки, когда данные по линиям съемки корректируются для минимизации различий в этих точках.
Имеется, однако, потребность в улучшенной обработке данных и, в частности, в улучшенной обработке шума.
Сущность изобретения
Таким образом, в соответствии с первым объектом изобретения предоставляется способ обработки измеренных данных потенциального поля из аэро- или морской съемки потенциального поля для определения массива картографических параметров поля для картографирования поля, содержащий: введение упомянутых измеренных данных потенциального поля, причем упомянутые измеренные данные потенциального поля содержат множество измерений, определяющих данные потенциального поля, каждое с соответственным положением измерения и временем измерения; и определение упомянутого массива картографических параметров поля, используя модель, содержащую комбинацию пространственной части, отображающей пространственную вариацию упомянутого потенциального поля, и временной части, отображающей временной шум в упомянутых измеренных данных потенциального поля, причем упомянутое определение содержит подгонку упомянутых измеренных данных потенциального поля к обеим упомянутым, пространственной и временной, частям упомянутой модели.
В некоторых предпочтительных вариантах осуществления пространственные и временные части модели содержат пространственные и временные члены модельного уравнения, которые определены совместно для определения картографических параметров поля. Предпочтительно модель имеет линейный вид; это упрощает инверсию. В частности, модель может иметь вид
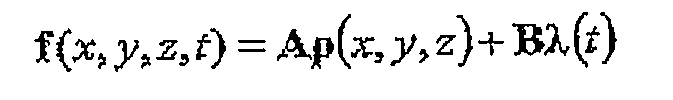 ,
,
где ρ и λ - векторы пространственного и временного модельных параметров соответственно, A и B - матрицы, и f содержит вектор прямого расчета измерений, оцениваемый из модели.
Предпочтительно модель имеет достаточно высокую временную разрешающую способность для интервалов между измерениями, меньшую ожидаемого времени корреляции прибора или измерительного шума. Таким образом, предпочтительно, чтобы время между узловыми точками выбиралось в зависимости от измеренного, или ожидаемого, характеристического или корреляционного времени шума в упомянутых измеренных данных; это может быть получено из спецификации изготовителя измерительного прибора.
В некоторых предпочтительных вариантах осуществления пространственная часть модели удовлетворяет уравнению Лапласа. Предпочтительно пространственная часть модели содержит модель эквивалентного источника.
Предпочтительно временная часть модели содержит линию, определенную дискретными точками по времени (узловые точки). В вариантах осуществления линия содержит наборы кусочно-линейных разделов, соединяющих эти узловые точки; в других вариантах осуществления могут быть использованы интерполяционные функции высших порядков. Предпочтительно узловые точки находятся в интервалах времени, по меньшей мере, 60, 120, 180, 240, 300, 360 или 420 секунд. Предпочтительно модель шума отображает измеряемый дрейф (который не должен быть монотонным).
Предпочтительно определение картографических параметров поля содержит решение системы совместных уравнений. Поскольку уравнения могут быть некорректными, предпочтительно используется регуляризация, но предпочтительно пространственные и временные части модели регуляризуются раздельно, для облегчения различия между дрейфом и истинными пространственными вариациями. Таким образом, в некоторых предпочтительных вариантах осуществления градиентная регуляризация используется для пространственной части модели, и регуляризация другого типа, например регуляризация Тихонова, используется для временной части модели. Это помогает, например, различать истинную пространственную вариацию и аппаратурный дрейф, который может быть, например, в различных пространственных направлениях в смежных линиях съемки, осуществляемой в противоположных направлениях. Будет ясно, что в вариантах осуществления методик описываются картографические параметры поля, определяемые посредством подгонки к модели с использованием данных из измерений потенциального поля от множества различных линий съемки одновременно (в том смысле, что подгонка измеренных данных к модели определяет глобальную подгонку для множества линий съемки, в вариантах осуществления для всех обрабатываемых измерительных данных).
Таким образом, в вариантах осуществления подгонка содержит совместно подгоняемые данные измерений потенциального поля от множества различных линий съемки для (аэро-) съемки потенциального поля, простирающейся по длинам линий. Эти линии съемки могут быть по существу параллельными или по существу не быть параллельными, например, по существу ортогональными. В вариантах осуществления линии съемки содержат больше чем две, и предпочтительно по существу все полетные линии при съемке, иначе говоря, в предпочтительных вариантах осуществления по существу все данные, собранные от съемки, предоставляются для модели, которая моделирует и пространственную, и временную вариацию для полной съемки. (В этом последнем случае съемка предпочтительно содержит множество полетных линий, располагаемых так, чтобы охватить снимаемую область, которая может иметь любую разумную физическую протяженность.)
Измеренные данные потенциального поля предпочтительно содержат гравитационные данные, например гравиметрические данные (измерение гравитационного поля), и/или гравитационные градиентометрические данные (измерение градиента гравитационного поля) и могут включать в себя множественные компоненты. Например, измеренные данные потенциального поля могут содержать компоненту Gzz гравитационного градиента. Таким образом, в вариантах осуществления картографированное поле содержит гравитационное поле, хотя это может быть отображено посредством данных гравитационного градиента. Вместе с тем, в других вариантах осуществления измеренные данные потенциального поля могут содержать векторные магнитометрические данные, истинные магнитные градиентометрические данные или другие данные потенциального поля (например, скалярные гравиметрические данные).
Картографические параметры поля предпочтительно содержат параметры или коэффициенты, которые позволяют характеризовать потенциальное поле и, в частности, которые могут быть использованы для создания подобных данных потенциального поля из прямого расчета в вариантах осуществления.
Таким образом, в вариантах осуществления значения параметра определяют потенциальное поле, например гравитационное поле или поле гравитационного градиента, которое отображает наилучшее приближение к измеренным данным потенциального поля. Это наилучшее приближение предпочтительно минимизирует остаток, который зависит от разности между прямым расчетом потенциального поля из модели и измеренными данными потенциального поля, например среднеквадратичную ошибку, значение модуля разности или некоторый другой остаток.
В вариантах осуществления картографические параметры поля извлекаются из пространственной части модели и могут содержать значения для эквивалентных массовых элементов источника или, в общем случае, эквивалентные элементы источника с соответственной силой источника, когда картографические параметры поля могут содержать эти силы источников.
В вариантах осуществления способ дополнительно содержит определение карты, используя массив картографических параметров поля, и она может отображать или данные потенциального поля, или данные, извлеченные из данных потенциального поля, например, после дополнительной обработки. Такая карта может отображать или двумерные, или трехмерные данные, и в вариантах осуществления карта конструируется посредством выполнения прямого расчета для определения потенциального поля, например, на поверхности, из массива картографических параметров поля. Картографические параметры поля могут быть использованы в прямом расчете, например, чтобы позволить определение и картографирование потенциального поля, например гравитационного поля, или поля гравитационного градиента, или соответственного скалярного потенциала.
Специалисту в данной области техники должно быть ясно, что в общем случае при измерении данных потенциального поля фактически измеряется гравитация и/или градиент гравитации (хотя другие величины, полученные из пространственных производных потенциального поля, могут быть измерены дополнительно или альтернативно).
В некоторых предпочтительных вариантах осуществления способ, который использует эквивалентное отображение источника, значения поверхностной массы (или плотность) для множества поверхностных массовых элементов, предпочтительно на плоской поверхности (но необязательно, поскольку поверхность может быть выбрана так, чтобы приблизить поверхность земли в области съемки), используется в прямом расчете для картографирования одной или нескольких компонент поля на ровной картографической плоскости или некоторой другой удобной поверхности.
В другом соответствующем объекте изобретения обеспечивается способ эквивалентного источника для обработки измеренных данных потенциального поля для определения полевых картографических данных, в которых упомянутые измеренные данные потенциального поля моделируются как комбинация пространственного сигнала и компоненты временного шума, причем способ содержит определение общего наилучшего приближения упомянутых измеренных данных потенциального поля к упомянутой моделируемой комбинации.
Изобретение дополнительно обеспечивает управляющий процессором код для осуществления вышеописанных способов, в частности, на носителе информации, например на диске, CD или DVD-ROM, запрограммированной памяти, такой как постоянное запоминающее устройство (Встроенное программное обеспечение), или на таком носителе информации, как, например, оптический носитель или носитель электрического сигнала. Код (и/или данные) для осуществления вариантов осуществления изобретения может содержать источник, объектный или исполняемый код в обычном языке программирования (интерпретируемый или компилированный), например C, или ассемблерный код, код для установки или управления ASIC (специализированная интегральная схема) или FPGA (полевая программируемая вентильная матрица) или код для языка описания аппаратных средств, например Verilog (Товарный знак) или VHDL (язык описания сверхвысокоскоростной интегральной схемы). Специалисту в данной области техники должно быть ясно, что такой код и/или данные могут быть распределены между множеством связанных компонентов в коммуникации друг с другом, например распределены по сети.
Изобретение дополнительно обеспечивает систему обработки данных, сконфигурированную для осуществления вариантов осуществления вышеописанных способов.
Таким образом, в дополнительном объекте изобретения обеспечена система обработки данных для обработки измеренных данных потенциального поля из съемки потенциального поля для определения массива картографических параметров поля при картографировании поля, причем система содержит: устройство сохранения данных для упомянутых измеренных данных потенциального поля, причем упомянутые измеренные данные потенциального поля содержат данные, определяющие множество измерений потенциального поля, каждое с соответственным положением измерения и временем измерения; и устройство хранения программ, хранящее управляющий процессором код; и процессор, связанный с упомянутым устройством хранения данных и с упомянутым устройством хранения программы для загрузки и осуществления упомянутого управляющего кода, причем упомянутый код содержит код, чтобы управлять процессором для: ввода упомянутых измеренных данных потенциального поля; и определения упомянутого массива картографических параметров поля с использованием модели, содержащей комбинацию пространственной части, отображающей пространственную вариацию упомянутого потенциального поля, и временной части, отображающей временной шум в упомянутых измеренных данных потенциального поля, причем упомянутый код для определения упомянутого массива картографических параметров поля сконфигурирован для подгонки упомянутых измеренных данных потенциального поля к обеим упомянутым, пространственной и временной, частям упомянутой модели.
Изобретение дополнительно обеспечивает носитель, переносящий структуру данных, причем структура данных содержит данные, определяющие значения, по меньшей мере, A и ρ, причем A и ρ определяются так, что для массива измерений потенциального поля m(x, y, z, t) значение L(f, m) минимизируется, где L(f, m) отображает меру различия между f и m, где
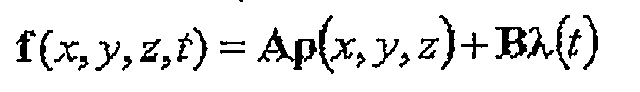 ,
,
где ρ и λ - векторы пространственного и временного модельных параметров соответственно, A и B - матрицы, и причем упомянутые данные, переносимые упомянутой структурой данных, сопоставляются с упомянутым массивом упомянутых измерений m(x, y, z, t) или включают их в себя.
Изобретение дополнительно обеспечивает носитель, переносящий структуру данных, определяющую карту, полученную из данных, определяющих значения, по меньшей мере, A и ρ, причем A и ρ определяются так, что для массива измерений потенциального поля m(x, y, z, t) значение L(f, m) минимизируется, где L(f, m) отображает меру различия между f и m, где
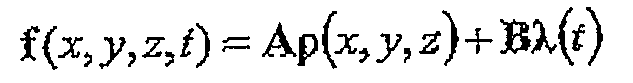 ,
,
где ρ и λ - векторы пространственного и временного модельных параметров соответственно, A и B - матрицы, и причем упомянутые данные, переносимые упомянутой структурой данных, сопоставляются с упомянутым массивом упомянутых измерений m(x, y, z, t) или включают их в себя.
Изобретение дополнительно обеспечивает носитель информации, такой как описан выше для переноса массива картографических параметров поля, определенных посредством предварительно описанного способа.
Краткое описание чертежей
Эти и другие объекты изобретения описываются ниже только в качестве примера в связи с сопровождающими чертежами, на которых:
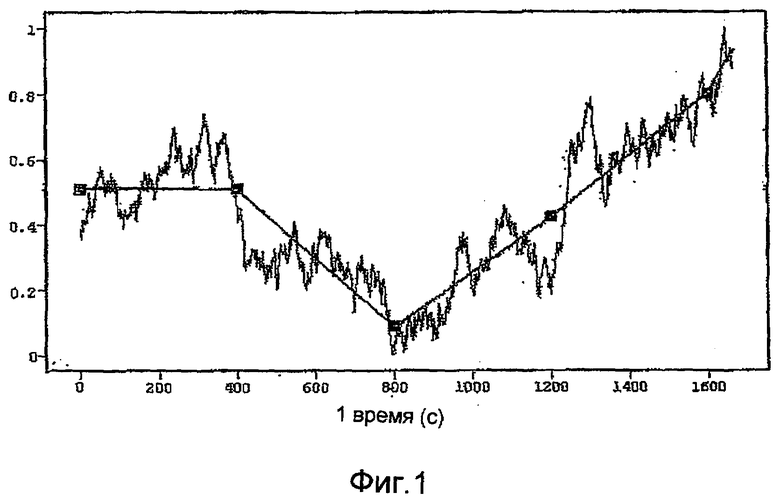
на фиг.1 изображен пример временной интерполяционной функции для совместной модели эквивалентного источника и временного дрейфа в соответствии с вариантом осуществления изобретения;
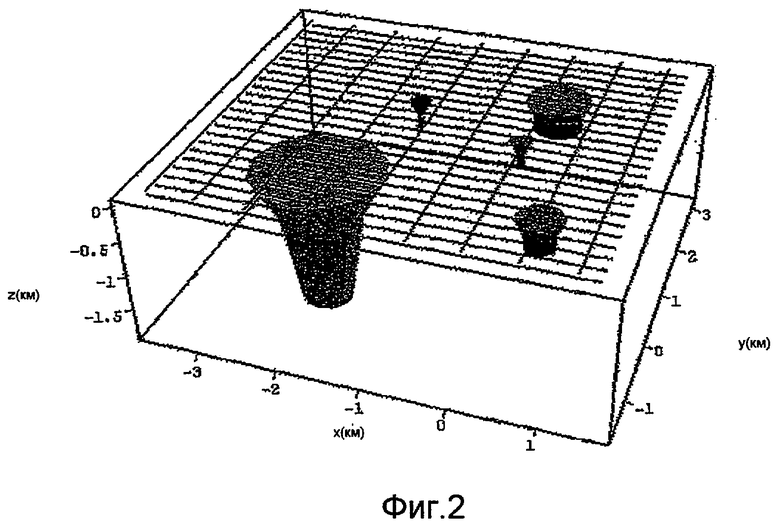
на фиг.2 изображена синтетическая модель и моделируемая картина полета;
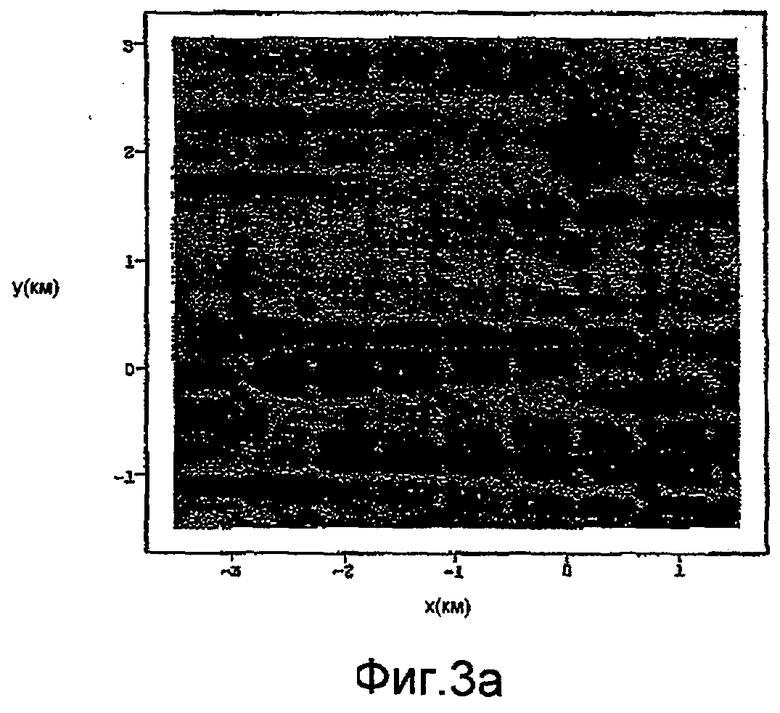
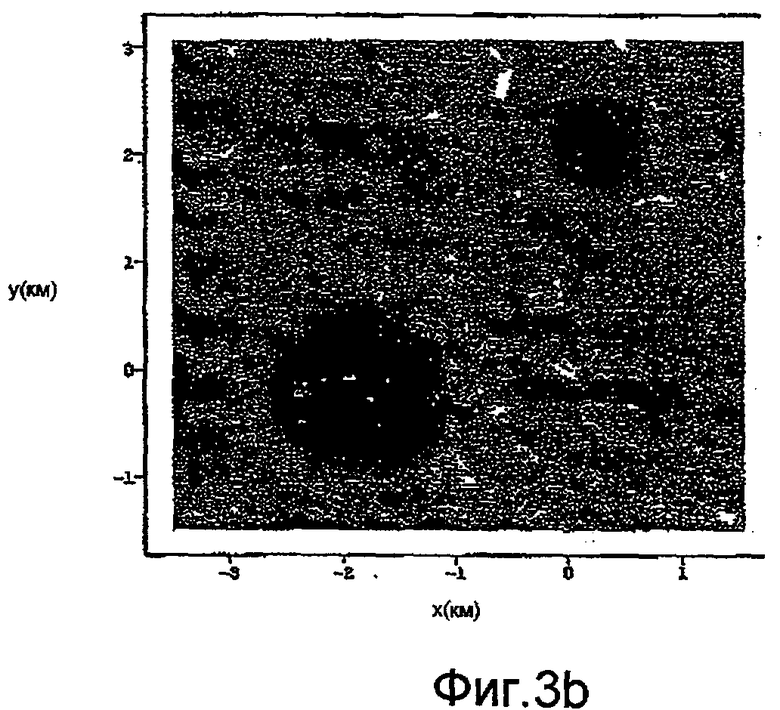
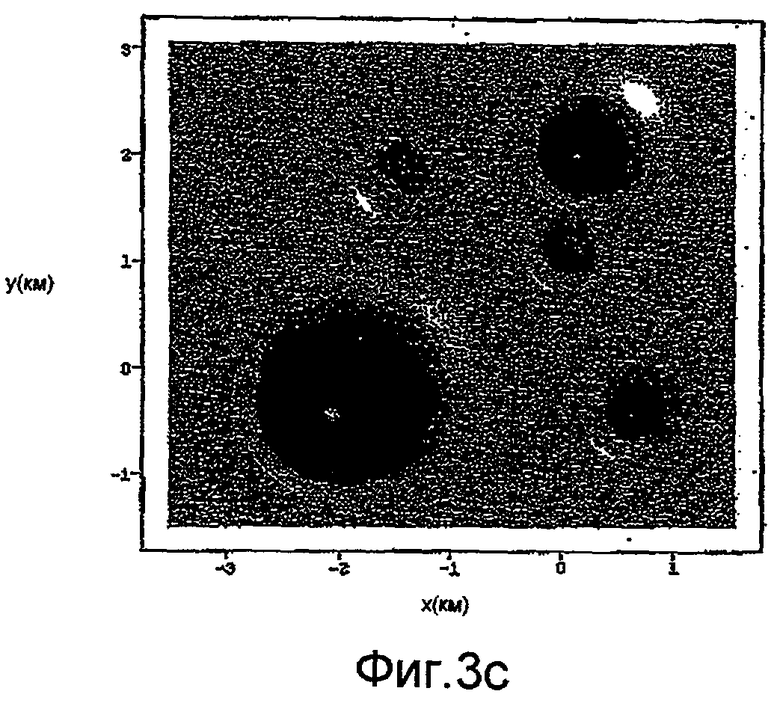
на фиг.3a-3c изображено сравнение предсказанной Gzz от инверсий эквивалентного источника с использованием синтетических измерений: a) без моделирования дрейфа (только пространственный эквивалентный источник), b) с одновременным моделированием дрейфа (дополненная модель) в соответствии с вариантом осуществления изобретения, и c) без синтетического измерения шума, добавленного к модели (истинный сигнал - нет шума);
на фиг.4 изображен летательный аппарат с данными аэросъемки и пример системы обработки данных, сконфигурированной для осуществления варианта осуществления способа в соответствии с изобретением; и
на фиг.5 изображена блок-схема последовательности операций в процедуре для обработки измеренных данных потенциального поля для осуществления варианта осуществления способа в соответствии с изобретением.
Подробное описание предпочтительных вариантов осуществления
Ниже описываются методики, которые в вариантах осуществления используют совместное моделирование эквивалентного источника и временного дрейфа для измеренных данных потенциального поля.
Там, где речь идет о поле, в частности о гравитационном поле, оно не ограничивается векторным полем, но включает в себя скалярное поле и тензорное поле, потенциальное поле и любые производные, получаемые из потенциальной поля.
Данные потенциального поля включают в себя, но без ограничений, гравиметрические данные, гравитационные градиентометрические данные, векторные магнитометрические данные и истинные магнитные градиентометрические данные. Элементы и представления потенциального поля могут быть получены из скалярной величины.
Для гравитации соответственным потенциалом является гравитационный скалярный потенциал Ф(r), определяемый как
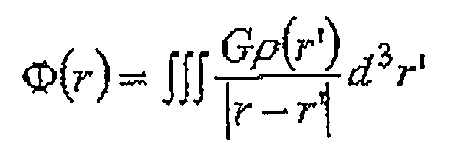 ,
,
где r, ρ(r'), G - соответственно положение измерения гравитационного поля, массовая плотность в местоположении r' и гравитационная постоянная. Гравитационное ускорение, которое является мерой гравитационного поля, является пространственной производной скалярного потенциала. Ускорение силы тяжести - это вектор, который задает его направление. Он представляется тремя компонентами относительно любой выбранной Декартовой системы координат:
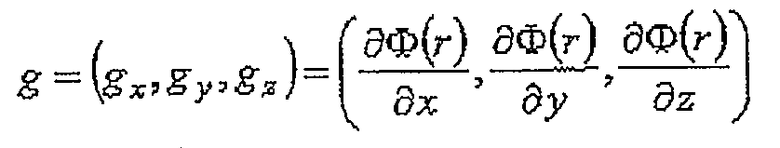 .
.
Каждая из этих трех компонент изменяется в каждом из трех направлений, и девять величин, таким образом, формируют тензор гравитационного градиента:
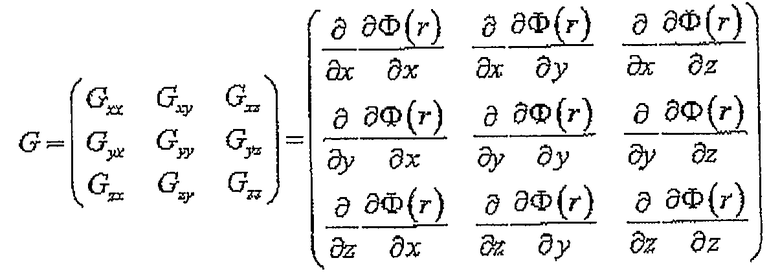 .
.
Фундаментальные уравнения и соотношения для потенциальных полей следуют из анализа свойств скалярной потенциальной функции, ее производных, ее преобразований Фурье и других математических величин.
Из одной из теорем Грина следует, что в случае если известны любые пространственные производные скалярного потенциала (включая и сам скалярный потенциал) по замкнутой поверхности, то значение пространственной производной известно во всех точках в пределах объема, ограниченного этой поверхностью. Следствием этого является то, что как только эта величина известна во всех точках, дифференцированием и интегрированием могут быть получены все другие производные скалярного потенциала, включая и сам скалярный потенциал. Таким образом, скалярный потенциал и все его производные фактически известны во всех точках в пределах объема, если известна только одна из его производных по поверхности, заключающей этот объем. Это означает, что полное измерение любой компоненты любой из производных скалярного потенциала позволяет вычисление любой другой компоненты любой производной скалярного потенциала. Из этого также следует, что не имеет значения, по меньшей мере, в теории, какая величина измеряется, в этом случае просто выбирается тот аппарат, который измеряет желаемую величину с наибольшим отношением сигнал-шум.
Дифференцирование вышеуказанного гравитационного скалярного потенциала с необходимостью дает:
 ,
,
что независимо от областей переходит в уравнение Лапласа - важное фундаментальное соотношение в теории гравитации:
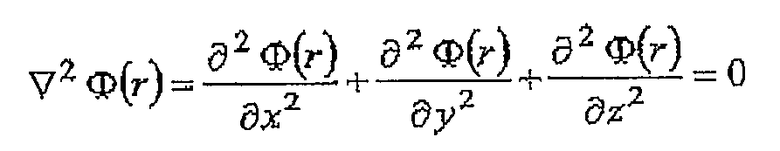 .
.
Гармонические функции удовлетворяют уравнению Лапласа, и они имеют много свойств, которые могут быть использованы при анализе данных, собранных во время съемок потенциального поля.
Данные могут быть проанализированы и обработаны с использованием ряда методик, которые работают с данными, собранными во время съемки как отправная точка, но которые затем изменяют и данные, и/или их формат так, что все значения, соотнесенные с измеренными величинами, появляются на правильной 2D сетке, которая находится на горизонтальной, с фиксированной высотой аналитической плоскости (нивелировка и гриддинг).
При гриддинге, вообще говоря, снимаемая область разделяется на прямоугольные ячейки, стороны которых предпочтительно выравниваются с основными направлениями полета для съемки, и затем фактические данные измерения заменяются данными (данные с координатной привязкой), которые являются "эквивалентными" измеренным данным, но которые теперь являются отмеченными значениями в точках в середине каждой ячейки. Размер каждой ячейки может быть выбран исходя из среднего разделения линий полета в двух ортогональных направлениях. Как только данные помещены в этот координатный формат, их намного проще математически обработать. Данные могут быть обработаны как набор чисел, например, посредством статистических или других способов, предоставляя наилучшую оценку потенциального поля на горизонтальной аналитической плоскости.
Авторы предварительно описали улучшенный способ эквивалентного источника (см. PCT/GB2006/050211, включенный в данном случае посредством ссылки).
Способы эквивалентного источника
Для понимания вариантов осуществления изобретения полезно описать некоторые аспекты способов моделирования эквивалентного источника.
Известно, что гравитационное поле вне тела может быть смоделировано как происходящее от вещества, расположенного целиком в бесконечно тонком слое у поверхности тела и который в точности повторяет форму поверхности тела. Такой слой определяет двумерный эквивалентный источник - то есть источник гравитации, который производит по существу (теоретически точно) те же самые гравитационные признаки, как и собственно тело. Имеется много вариантов определения эквивалентных источников: они могут быть такими, как указано выше, или они могут быть строго горизонтальными, они могут быть полностью или частично выше или ниже поверхности земли; они могут быть двух- или трехмерными. Однако они имеют то общее свойство, что обычно образуют по существу то же самое гравитационное поле, что и образуемое снимаемым участком земли. Для дальнейших сведений можно сослаться на книгу R.J.Blakely, "Potential Theory in Gravity and Magnetic Applications", Cambridge University Press, 1995.
При съемке можно измерить Gzz как функцию положения, rmeasure, используя гравитационный градиентометр и работу с ним без необходимости в создании других элементов тензора гравитационного градиента. Это может быть использовано для создания отображения основного массового распределения. Вышеупомянутая теорема Грина показывает, что основное массовое распределение может быть получено, в принципе, из Gzz, хотя в вариантах осуществления методик описывается более поздняя теорема Грина, не требуемая для использования явно.
В примере способа эквивалентного источника поверхность зоны съемки разбивается на маленькие части, обычно со стороной порядка 50 м, которые можно считать пластинками или массовыми элементами. Разрешающая способность модели может быть выбрана для грубого соответствия разрешающей способности измерений. Легко непосредственно рассчитать гравитацию каждой пластинки (см., например, R.J.Blakely, "Potential Theory in Gravity and Magnetic Applications", Cambridge University Press, 1995), масса которой корректируется до тех пор, пока не будет получена наилучшая полная подгонка к измеренным данным. Это массовое определение может использовать стандартную процедуру подгонки по методу наименьших квадратов. Подгонка может быть получена посредством согласования данных в истинных положениях измерения с гравитационным полем, созданным посредством предложенного эквивалентного источника в идентичных истинных положениях измерения. Этот процесс математически строг и не требует введения каких-либо искусственных корректировок с данными, чтобы они соответствовали горизонтальной прямоугольной съемке.
Как только подгонка получена, модель считается первичным массивом данных. Весь последующий анализ для определения геологической структуры может (но необязательно) затем заключаться в сравнении и минимизации разности между гравитационным полем, которое любая данная геологическая структура может создать, и гравитационным полем эквивалентного источника. Одно существенное преимущество этой методики заключается в том, что наилучшая подгонка возникает из массового распределения, хотя и синтетического, и поэтому решение для наилучшей подгонки автоматически удовлетворит уравнению Лапласа. Это представляет собой усовершенствование способа, который дает численную наилучшую подгонку, но который не накладывает дополнительное ограничение удовлетворения данных уравнению Лапласа, то есть она может проистекать из реального массового распределения.
Способ эквивалентного источника не использует поверхность, соответствующую топографии, он может использовать источники, которые покрывают любую поверхность, которая может быть постоянной по высоте или нет, выше или ниже истинной поверхности земли, которая может разрезать истинную поверхность земли или нет и т.д. Дополнительно, способ эквивалентного источника не использует поверхность, но может использовать трехмерную модель. Аналогично, пластинки могут иметь любой размер или форму в двух или трех измерениях (или даже могут быть точечными), и они даже не должны соответствовать по размерам или форме; действительно, это способствует эффективности анализа, если их размеры и геометрия могут варьироваться в зависимости от того, как быстро топография и/или геология могут варьироваться в каждой области.
Эквивалентный источник, следующий топографии или даже основной геологии, насколько он может быть разумно обозначен, вероятно, произведет меньшее варьирование массы отдельных пластинок, но окончательный результат, в принципе, не будет существенно затронут никаким разумным выбором. Таким образом, например, если подозревается наличие конкретного геологического слоя или, например, геологической аномалии, например кимберлитовой трубки, эквивалентный источник может быть определен с учетом этого. Аналогично, больше источников может быть добавлено в области, где имеется более детальное или быстрое изменение геологической структуры. Таким образом, в некоторых отношениях выбор форм эквивалентных источников может быть задуман как подобный дискретизации технического изделия при анализе методом конечных элементов.
Отчасти математическая сложность процесса определяется числом используемых источников и тем, сколько этих источников используется в анализе в каждом положении при съемке. Преимущество методики заключается в том, что для некоторых компонентов гравитации или гравитационного градиента возможно использование непосредственных источников в области измерительной точки, что может существенно снизить сложность анализа. Пороговое расстояние составляет обычно несколько километров, например в пределах от 1 до 10 километров, хотя это зависит до некоторой степени от географии (например, может быть необходимо продлить расстояние для охвата большой близлежащей горы). Например, элемент источника на одной стороне области съемки вряд ли внесет значительный вклад в измеряемое поле на другой стороне области съемки, и где влияние элемента источника намного меньше ожидаемого или фактического шума, такие вклады могут игнорироваться (устанавливаться на нуль). Это полезно, поскольку такая матрица может содержать, например, 100 К на 500 К матричных элементов, и трудности обработки значительно снижаются, если они по большей части нули.
Ниже определяется уравнение, в которое вклады элементов источника в измеренный сигнал зависят от матричных значений влияния источника, и где (как это обычно бывает на практике) влияние многих источников может игнорироваться, эта матрица становится разреженной матрицей, позволяя более эффективную численную обработку.
Как только эквивалентный источник создан, то оказывается возможным предсказать любую производную скалярного гравитационного потенциала на поверхности посредством непосредственного прямого расчета. Этот процесс полезен и для анализа, и для перспективы визуализации. Таким образом, как только массив массовых элементов найден, прямой расчет (то есть суммирование влияния массовых элементов) позволяет получить другие компоненты скалярного потенциала и посредством дифференцирования другие компоненты G. Полученные значения G могут сравниваться с геологической моделью (обозначаемой как "интерпретация") для определения основной геологической структуры.
Более подробно, учитывая массы (или плотности) каждого элемента источника, прямой расчет используется для предсказания того, какое значение получится для измеренной величины, то есть значение компоненты вектора гравитации или тензора гравитационного градиента в каждой точке измерения. В общем случае это будет суммированием в показанной ниже форме. Здесь мы используем gg как обозначение для измеренной величины, которая, как отмечено выше, является величиной Gzz в некоторых предпочтительных вариантах осуществления.
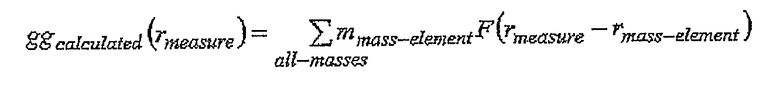 .
.
В вышеприведенном уравнении функция F называется функцией Грина (Blakely, там же, с.185, включенная посредством ссылки), и rmass-element определяет местоположение массового элемента (например, центр гравитации или некоторую другую определенную точку).
Функции F представляют собой стандартные функции, хорошо известные специалистам в данной области техники (и их применения не ограничиваются гравиметрическими съемками). Это, по существу, влияние источника (массового элемента) единичной массы или плотности и определенной формы, имеющихся в определенной (измерительной) точке. Источником может быть точечный источник, сфера или эллипсоид, но в практических применениях методики источник чаще бывает призмой, которая может быть неправильной. Множество учебников перечисляют функции Грина для простых форм; функции для более сложных геометрий источника могут быть найдены в литературе. Кроме того, влияние источника накладывается так, что если сложная форма может быть дискретизирована на множество более простых форм, то функции Грина для дискретных форм могут быть просуммированы. Это в принципе позволяет определить числовые значения функции Грина для любой произвольной формы, хотя обычно практически предпочтительны относительно простые формы. В качестве примера функция Грина F для прямоугольной призмы определена там же, в книге Blakely, с.187, и в данном случае она включена посредством ссылки; при этом имеется 8 членов, каждый из которых соответствует вершине призмы.
Способ инверсии эквивалентного источника может объединить множественные измерения распределения потенциального поля (наблюдаемые величины потенциального поля фактически являются пространственными производными) в единственную модель. Способ включает в себя нахождение параметров модели источника (например, плотности или геометрии) таким образом, что рассчитанные из модели данные подгоняются к данному массиву измерений. Модель инвертированного эквивалентного источника может затем восстановить сигнал при измерениях и в определенных пределах может быть использована для повторного проектирования данных для различающихся местоположений. В целом, число регулируемых модельных параметров меньше числа независимых измерений, и, таким образом, в соответствии с законом больших чисел сигналы, повторно рассчитанные из модели, будут иметь большие отношения сигнал-шум, чем при исходных измерениях.
Конструкция эквивалентного источника больше, чем измерение методики усреднения, поскольку она отображает удобный и реальный способ составления массива пространственных базисных функций, которые поддерживают функциональный вид основного измерительного сигнала. Базисные функции могут позволить объединение различного типа измерений потенциального поля, например; гравитационные измерения и измерения тензора гравитационного градиента могут все быть инвертированы к единственной модели. Базисные функции могут также способствовать большей устойчивости инвертированной модели относительно некоторых ложных вариаций в измерениях, поскольку если они не проявляются как истинные вариации потенциального поля, то они не поддерживаются функциональной формой модели. Модель эквивалентного источника может дополнительно сосредоточить свое функциональное пространство посредством исключения решений, которые известны как физически недопустимые. Например, модель эквивалентного источника, помещенная вблизи или ниже уровня земли, естественно отфильтрует нефизические высокочастотные вариации в измерениях (хотя модель может, в принципе, быть помещена где угодно). Такие вариации в другом случае могут создавать большие ошибки в менее ограниченной модели.
Увеличение отношения числа измерений к числу степеней свободы модели улучшает точность инверсии, делая получающуюся модель эквивалентного источника менее чувствительной к измерительному шуму и помехам. Однако во многих случаях из-за практических трудностей, связанных со сбором полной выборки вариаций потенциального поля, это отношение часто становится малым, и инверсия эквивалентного источника может стать затруднительной.
Низкочастотный шум (дрейф) в измерениях аэросъемки ухудшает процесс инверсии, поскольку эти явления могут походить на истинный сигнал (хотя термин дрейф обычно относится к случайному монотонному изменению, в этом описании он используется для отображения любого вида скоррелированного шума с характерной частотой, намного меньшей частоты доминирующих и представляющих интерес сигналов). Такое изменение может, поэтому, легко быть учтено моделью эквивалентного источника, особенно в местах, где оно не определено. Следствия из последовательных прямых расчетов эквивалентного источника затем демонстрируют ложные признаки, коррелирующие с картиной измерения. В дополнение к этому когерентные компоненты шума не усредняются в процессе инверсии и поэтому приводят к худшей оценке модельного параметра.
Ниже описывается дополнение к методике эквивалентного источника, при которой вводится отдельная модель для компенсации коррелированного временного шума. Посредством использования отдельной модели, работающей одновременно с моделью эквивалентного источника, можно сделать оценку параметра источника менее восприимчивой к этому типу шума при измерениях. После инверсии дополненная модель может раздельно предсказать желаемое пространственное распределение потенциального поля и длинноволновый временной шум, сопровождающий измерения.
Совместное моделирование эквивалентного источника и временного дрейфа
Измеряемая величина m при геофизической съемке, соответствующая местоположению (x, y, z) и моменту времени t, может быть разбита на ряд членов
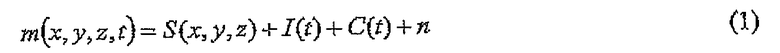 ,
,
где S(x, y, z) отображает сигнал, I(t) - источник помехи, C(t) - коррелированный шум, и n - чисто случайный шум. Главная цель обработки после съемки заключается в определении с наилучшей точностью истинного сигнала S(x, y, z). Источники помехи I(t) корректируемы подходящими измерениями основных возмущений и соответствующих передаточных функций с ошибкой. В теории после этих исправлений единственные остающиеся нежелательные члены - коррелированный шум C(t) и белый шум n. Белый шум фундаментален, и его влияние может быть только снижено посредством закона больших чисел при множественных измерениях. Большая часть мощности коррелированного шума может, однако, быть смоделирована интерполяционной функцией с временным периодом, который подобен или короче характерного временного периода шума.
На фиг.1 показана простая временная интерполяционная функция, образованная сшиванием между собой кусочно-линейных участков с одинаковыми интервалами. Более конкретно, на фиг.1 показан экспоненциально коррелированный шум с характерным временем в 500 секунд, смоделированный кусочно-линейным интерполятором, соединяющим узловые точки (квадраты) каждые 400 секунд.
Интерполятор непрерывен в определенных пределах, но имеет разрывные производные в узловых точках. Модель полностью определена посредством значений в узловых точках и поэтому делает число степеней свободы равным числу узловых точек. В этом случае узловые значения становятся модельными подгоночными параметрами при оптимизации (см. ниже). Если используются более сложные интерполяционные функции, например полиномы высокого порядка или сплайны, то число степеней свободы может быть большим. Как видно из фиг.1, длинноволновые компоненты коррелированного шума могут быть вполне смоделированы посредством основного интерполятора с временным периодом, несколько меньшим, чем таковой для шума. Описываемая одновременная модель эквивалентного источника и временного дрейфа позволяет модели дрейфа низкого порядка поглотить большую часть временного коррелированного шума в пределах массива измерений, оставляя модель эквивалентного источника только для установления соответствия с пространственно коррелированным сигналом. Остающаяся несмоделированная часть измерений (остаточная подгонка) является тогда в значительной степени белым шумом, показывая, что статистические данные инверсии совместимы с хорошей оценкой модельного параметра.
В случае модели линейной инверсии дополненная модель может быть записана как
 ,
,
где f - модельный вектор прямого расчета измерений, ρ - вектор модельных параметров эквивалентного источника (например, плотность или дискретные модули-источники массы), A - матрица, которая связывает отклики элементов источника с местоположениями измерения, λ - вектор параметров модели дрейфа (например, узловые значения в кусочно-линейной модели), и B - матрица, которая связывает интерполяцию модели дрейфа с моментами измерений. В таком виде при данном массиве измерений m(x, y, z, t), модельные параметры ρ и λ могут быть определены посредством любой стандартной методики оптимизации, которая минимизирует остаток при подгонке
 ,
,
где L отображает меру остатка; норма L2, например, выполняет оптимизацию по методу наименьших квадратов. Минимизация квадратичной ошибки, норма L2, имеет преимущество из-за простого вычисления, и имеется много коммерчески доступных компонентов математических пакетов/библиотек для осуществления подгонки по методу наименьших квадратов. Другой вариант заключается в использовании модуля вместо этого (норма L1). Это может привести к возможному пропуску выбросов точек данных, что делает оптимизацию более трудоемкой; и в этом случае подходящие математические компоненты пакетов/библиотек коммерчески доступны, но вычислительные затраты могут оказаться слишком большими (поскольку требуется более сложный математический аппарат).
После полной инверсии член эквивалентного источника используется изолированно или для оценки исходного сигнала, лежащего в основе измерений,
 ,
,
или для предсказания различных величин в возможных различных местоположениях. Аналогично, второй член в (2) может быть использован изолированно для оценки дрейфа при измерениях

Модель уравнения (2) может быть дополнена для совместного моделирования сигналов от множественных источников данных измеряемого потенциального поля. В этом случае общая модель эквивалентного источника может быть использована для различных источников данных измеряемого потенциального поля, но предпочтительно члены отдельного шума (дрейфа) включены в модель для каждого отличающегося источника измеряемых данных. Различные источники измеряемых данных потенциального поля могут быть, например, различными устройствами измерения различных компонент G (Gxx, Gyy, Gzz, Gxy, Gxz, Gyz - таким образом, возможны шесть различных устройств этого типа) и/или различными устройствами измерения g (gx, gy, gz - таким образом, возможны три устройства этого типа). Например, одна или несколько компонент данных гравитационного и гравитационного градиентного потенциального поля могут быть совместно измерены таким образом с множественными измерительными устройствами (хотя они могут быть объединены в единственном измерительном приборе). Подгоночная минимизация может быть выполнена так же, как отмечено выше (и рассмотрено дополнительно ниже), хотя и с большим числом определяемых параметров дрейфа.
На этом этапе полезно более подробно определить матрицы A и B и векторы ρ и λ. Продолжая рассматривать пространственную часть модели, начальный этап заключается обычно в построении модели, которая следует за ландшафтом в области съемки. Модель дискретизируется на ряд конечных элементов, каждый из которых определяет массовый элемент, плотность которого определяется посредством обратного решения. Матричный элемент Aij отображает модельный, непосредственно рассчитанный сигнал, дающий вклад от массового элемента j в положении i измерения, когда единичная плотность приписывается массовому элементу. Тип используемого прямого расчета соответствует типу сигнала измерения, например; если имеется n измерений и m были предприняты в том же самом положении, но n измерений являются измерениями гравитационного градиента Gzz, и m измерений являются измерениями гравитационного градиента Gxx, то соответствующие прямые расчеты от массового элемента j, An,j и Am,j будут соответствовать Gzz и Gxx соответственно.
Вектор ρ определяет массив фактических плотностей массовых элементов, определяющих модель, и после оптимизации содержит часть решения эквивалентного источника. Таким образом, вектор ρ фактически предоставляет массив параметров, отображающих поле. Как упомянуто выше, произведение Аρ служит для предсказания фактического сигнала при измерениях.
Для облегчения оптимизации (2) аппроксимации могут быть введены при построении матрицы A. Это может принять вид усечения, когда пренебрежимо малые матричные элементы заменяются нулями), или усреднения, когда влияния нескольких отдельных элементов объединяются в единственный элемент, отображающий среднее влияние. Оба вышеупомянутых приближения становятся справедливыми, когда расстояние между точкой измерения и исходным элементом становится большим по сравнению с размером источника. При использовании таких приближений пространственная матрица A становится разреженной, позволяя более эффективные численные матричные вычисления.
Элементы матрицы В определяют уравнения, которые связывают предсказанный дрейф в измерениях с параметрами λ модели дрейфа. Для случая кусочно-линейной интерполяционной функции (относящейся к фиг.1), если i-тое измерение было выполнено в момент времени ti, что попадает между узловыми параметрами λj и λj+1 дрейфа, определяемыми в (узловая точка) моменты времени Tj и Tj+1, то линейное интерполяционное предсказание для дрейфа в измерениях задается посредством
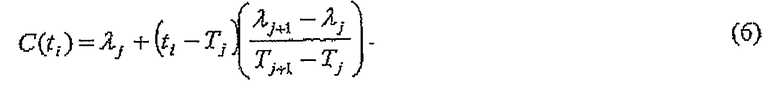
Выраженное в соответствии с матричным уравнением (2) вышеприведенное уравнение определяет матричные элементы Bi,j и Bi,j+1 следующим образом:
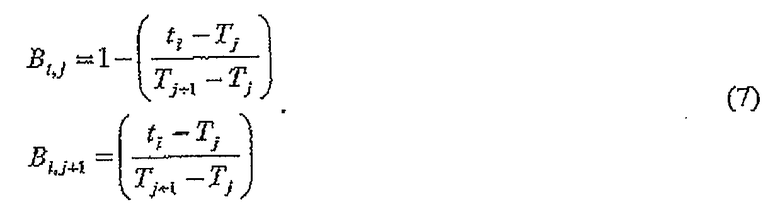
Времена Tj узловых параметров дрейфа определяют разрешающую способность модели дрейфа. Когда имеется разрыв в массиве данных измерений, например, в конце линии съемки, или когда регистрация данных приостанавливается по каким-либо причинам, предпочтительно перезапустить модель дрейфа посредством форсирования параметра дрейфа в тот момент времени, в который измерения возобновляются.
В случае множественных типов измерения в той же самой съемке (например, когда имеются несколько приборных каналов вывода) удобно разделить матричное уравнение (2) так, чтобы каждый тип измерения занимал блок строк в матрицах A и B. Таким образом, первая группа параметров дрейфа в λ отображает моделируемый дрейф для первого типа измерений, второй массив отображает второй тип измерений и так далее. Важно отметить, что хотя каждый тип измерений имеет свою собственную модель дрейфа, есть только одна модель эквивалентного источника.
Если спектр остатка (f-m) не достаточно белый во временной области, то это указывает, что разрешающая способность модели дрейфа может быть неадекватной, и выигрышным может оказаться более короткий временной период или интерполятор более высокого порядка. Аналогично, если остаток представлен в пространственной области, это может указывать, что модель эквивалентного источника слишком ограничена. Если при этом остаток все же демонстрирует заметную корреляцию, то возможна более фундаментальная проблема, например чрезмерная помеха при измерениях или плохо спроектированная модель эквивалентного источника, например.
Поскольку природа сигнала и дрейфа различна, один коррелирован в пространственной области, а другой коррелирован во временной области, разделение этих величин на два члена в правой части (2) представляется естественным при оптимизации. Чтобы проиллюстрировать это, рассмотрим две смежные линии из аэросъемки. Хотя дрейф сильно коррелирован вдоль отдельных линий, при рассмотрении в пространственной области нет никакой корреляции между линиями - смежные линии могли быть получены с интервалом в недели, или даже с различными приборами. При оптимизации (3), поскольку вариация этого типа хорошо не аппроксимируется моделью эквивалентного источника, она может корректно описываться членом модели дрейфа. И наоборот, истинный сигнал обычно появляется вне диапазона модели дрейфа и поэтому предпочтительно описывается членом модели эквивалентного источника.
Вместе с тем, имеется много ситуаций, особенно в неопределенном случае, когда трудно различить низкочастотный шум прибора и истинный длинноволновый сигнал. Если случается, что дрейфы вдоль смежных линий имеют ту же самую общую тенденцию, шум может казаться пространственно коррелированным и во время инверсии может войти и исказить член эквивалентного источника. И наоборот, большая длина волны геологического сигнала может легко возникнуть как дрейф во времени, поэтому обнаружение себя относится к неправильному члену в (2). Результатом является потеря интенсивности сигнала в предсказаниях (4) эквивалентного источника, связанных с нежелательными шумовыми тенденциями.
Для добавления уровня управления по этой проблеме можно ввести отдельную регуляризацию для двух частей расширенной модели (2). Градиентная регуляризация предпочтительна для распределения плотности ρ эквивалентного источника, поскольку, при том что геометрия модели походит на нечто физически правдоподобное, реальные распределения плотности стремятся иметь гладкие вариации. Предпочтительно выбирать более гладкие решения для плотности, которые поэтому стремятся улучшать целостность инверсии. Для параметров модели дрейфа, λ, стандартная регуляризация Тихонова является предпочтительным выбором. При регуляризации выражение (3) принимает вид
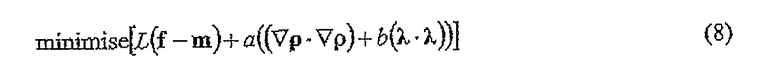 ,
,
где a - коэффициент полной регуляризации, и b - коэффициент, управляющий относительной регуляризацией между двумя моделями (практически, члены регуляризации нормированы модельными матрицами). Увеличение b делает модель эквивалентного источника более значимой посредством приписывания неоднозначной вариации в измерениях, предпочтительно вариации плотности, а не дрейфа. Нет никакого определенного способа получить правильные значения для коэффициентов регуляризации, но анализ с "L - кривой" и другие эмпирические способы могут дать направление определения лучшего регуляризационного компромисса между подгонкой к измерениям и поведением решения. В конечном счете, для определения наилучших значений для a и b требуется последовательность тестов параметров.
Таким образом, вообще говоря, в некоторых предпочтительных вариантах осуществления вводится регуляризация, которая в пространственной части модели призвана отыскать самое гладкое распределение, подгоняемое к измерениям (предполагаемые большие изменения в подземной плотности предпочтительно учитываются, где это возможно, посредством конструкции начальной модели элемента источника). В широком смысле значение a определяет, до какой степени следует добиваться гладкого решения с моделью, и практически этот параметр может варьироваться в соответствии с ожидаемой основной геологией и для достижения того, что окажется хорошим результатом. Кроме того, выбор большого значения для b отменяет выделение членов модели дрейфа (поскольку меньшие члены модели дрейфа необходимы затем для полной минимизации уравнения (8)).
Вместе с тем, наиболее эффективный путь разрешения неоднозначности между дрейфом и сигналом заключается в гарантии того, что имеется достаточно измерений при съемке, которые близки в пространстве, но хорошо разделены во времени. Рассмотрим, например, точки в массиве данных съемки, где две линии (часто перпендикулярные) пересекаются. В этих местоположениях сигнал S(x, y, z) является общим для двух измерений на каждой линии. (Пару измерений можно считать правильной точкой пересечения, если их разделение достаточно мало по сравнению с шириной корреляции сигнала, соизмеримого с высотой съемки.) Различие между измерениями, выполненными в моменты времени t1 и t2, должно, поэтому, быть обусловленным коррелированным шумом, I(t2)-I(t1) плюс некоторый случайный шум. В матричной конструкции (2) эти пары точек приводят к дублированным строкам в члене эквивалентного источника, но независимо для строк в члене модели дрейфа. Поэтому они вместе предоставляют уравнения, которые только по существу влияют на решение для дрейфа, и поэтому могут разрешить неоднозначность между длинноволновым сигналом и дрейфом. Посредством учета пространственной вариации сигнала одновременное решение модели эквивалентного источника и модели дрейфа является более точным, чем пересечение по нивелировке, поскольку модель дрейфа по существу выводится из измерений в съемке во множественных положениях на различных линиях съемки, потенциально всех измерений, а не только тех, что для точек пересечения.
Для демонстрации характеристик объединенных модели эквивалентного источника и модели дрейфа представлен синтетический пример. Синтетическая модель содержит выбор 5 кимберлитовых трубок с различными размерами, снятыми посредством бортового гравитационного градиентометра в соответствии с регулярной картиной аэросъемки, как показано на фиг.2, которая иллюстрирует синтетическую модель и моделируемую картину полета.
При моделировании компонента гравитационного градиента, Gzz, была непосредственно рассчитана для местоположения картины съемки для отображения сигнала, измеренного гравитационным градиентометром. Экспоненциально коррелированный временной шум был затем добавлен к синтетическому сигналу для отображения дрейфа и другого низкочастотного шума, который присутствовал бы в реальной измерительной системе. Моделируемые измерения были использованы для инвертирования модели эквивалентного источника, во-первых, без и затем с добавлением модели дрейфа. В обоих случаях инвертированная модель была использована для прямого вычисления Gzz для массива координатных точек, имеющих ту же самую высоту, как и в исходной съемке. На фиг.3 показано сравнение предсказанной величины Gzz из инверсий эквивалентного источника, используя синтетические измерения: a) без, b) с одновременным моделированием дрейфа, c) совершенный ответ, достигнутый без синтетического измерительного шума, добавленного в модель.
В вышеприведенном примере для иллюстрации текущего способа никакие дополнительные процедуры обработки данных для снижения шума не выполнялись, хотя на практике обычные методики снижения шума, например фильтрация/ограничение, могут (и часто предпочтительно должны) также быть использованы. Результаты, получаемые от расширенной модели эквивалентного источника (b), ясно показывают уровень надежности и защищенности относительно коррелированного шума в измерениях. Без этого расширения результаты (a) демонстрируют значительные артефакты, коррелированные с картиной съемки, и почти полную маскировку истинного сигнала.
Таким образом, дополнение способа инверсии эквивалентного источника моделью временного дрейфа и последующее решение для обеих моделей одновременно предоставляет способ надежной обработки массивов данных потенциального поля, которые содержат значительный низкочастотный шум. Хотя уровень низкочастотного шума может быть снижен обычными процедурами нивелировки, эти способы не работают, например, когда съемка имеет недостаточно пересекающихся точек. Преимущество связи модели дрейфа с моделью эквивалентного источника заключается в том, что поведение дрейфа может быть выведено из большего числа или по существу из всех измерений при съемке.
На фиг.4 показан пример летательного аппарата 10 для проведения съемки потенциального поля для получения данных для обработки в соответствии с описанным выше способом. Летательный аппарат 10 содержит инерциальную платформу 12, на которой установлен гравитационный градиентометр 14 (и/или векторный магнитометр), который предоставляет данные съемки потенциального поля на систему 16 сбора данных. Инерциальная платформа 12 оснащена модулем 18 инерциального измерения (IMU), который также предоставляет данные на систему 16 сбора данных, обычно содержащие данные положения в пространстве (например, данные по углу тангажа, крену и отклонению от курса), данные об угловой скорости и угловом ускорении и данные ускорения летательного аппарата. Летательный аппарат также оборудован дифференциальной системой 20 GPS и системой 22 LIDAR или подобной для предоставления данных относительно высоты летательного аппарата над основным рельефом местности. Данные положения и времени предпочтительно получаются от (D) GPS, произвольно в комбинации с IMU для точности.
Летательный аппарат 10 может также быть оборудован другой аппаратурой 24, например магнитометром, TDEM (Временная Электромагнитная Система) системой и/или гиперспектральной отображающей системой, также питающими систему сбора данных. Система 16 сбора данных также имеет ввод от общей аппаратуры 26 летательного аппарата, которая может содержать, например, высотомер, данные воздушной скорости и/или скорости относительно земли и т.п. Система 16 сбора данных может предоставлять некоторую начальную предварительную обработку данных, например, для коррекции данных LIDARa для движения летательного аппарата и/или для объединения данных от IMU 18 и DGPS 20. Система 16 сбора данных может быть снабжена линией 16a связи и/или энергонезависимым устройством 16b памяти для обеспечения возможности сохранять собранные данные потенциального поля и данные о положении для последующей обработки. Сетевой интерфейс (не показан) также может быть предоставлен.
Обработка данных для создания картографических данных для съемки потенциального поля в общем случае (но необязательно) выполняется автономно, иногда в другой стране, где данные съемки были собраны. Видно, что система 50 обработки данных содержит процессор 52, соединенный с устройством 54 сохранения кода и данных, и систему 56 ввода/вывода (например, содержащую интерфейсы для сети, и/или носителей данных, и/или другой связи) с пользовательским интерфейсом 58, например, содержащим клавиатуру и/или мышь. Код и/или данные, сохраняемые в устройстве 54 памяти, могут быть предоставлены на сменном носителе 60 данных. При работе данные включают в себя данные, собранные из съемки потенциального поля, и код содержит код для обработки этих данных для создания картографических данных в вариантах осуществления в соответствии с процедурой, показанной на фиг.5, описанной ниже.
На фиг.5 показан пример процедуры, осуществляемой процессором данных, который в вариантах осуществления может содержать универсальную компьютерную систему для обработки данных от полетной съемки в соответствии с предварительно описанными методиками. Таким образом, на этапе S200 процедура вводит измеренные данные потенциального поля, например, от гравитационного градиентометра и соответственные 3D данные положения. При необходимости на этапе S200a может быть применена некоторая предварительная обработка, например, для удаления аномалий и/или для снижения (или увеличения) или выбора обрабатываемых данных.
На этапе S202 процедура заполняет матрицы A и В, как описано выше, и затем создает разреженное матричное уравнение, относящееся к измеренным данным потенциального поля, например Gzz, измеренному 3D положению и временным данным, пространственным картографическим параметрам (ρ) поля и параметрам временного дрейфа (λ). Модель эквивалентного источника снятого рельефа местности (S202a) может быть специально построенной, или может быть использована стандартная регулярная сетка. Процедура затем решает матричное уравнение (S206) для определения массива картографических параметров поля, более конкретно массива сил элементов эквивалентных источников, и они могут предоставить выходные данные от процедуры как картографические данные. Альтернативно, карта может быть непосредственно рассчитана как часть процедуры (S208) посредством выполнения прямого расчета с использованием этих параметров. Например, могут быть созданы двумерная карта типа той, что показана на фиг.3, или трехмерная карта (более точная геологическая модель) типа той, что показана на фиг.2.
Без сомнения много других эффективных альтернатив будут очевидны для специалистов в данной области техники. Например, описанная методика может быть осуществлена в Фурье представлении, например, вдоль линий, описанных в рассматриваемой авторской заявке PCT там же (PCT/GB2006/050211, включенной посредством ссылки).
Хотя здесь описана методика, использующая предпочтительный пример аэросъемки потенциального поля, варианты осуществления могут также использоваться для морских съемок потенциального поля, выполняемых на судне, и, в общем случае, для съемок потенциального поля, выполняемых на других подвижных платформах или транспортных средствах.
Методики не ограничиваются обработкой гравитационных данных, но могут также использоваться, например, при обработке данных магнитного поля. Измеренные данные потенциального поля могут, таким образом, быть получены, посредством измерения магнитного поля, и/или вектора плотности потока, и/или его величины, например, используя измерение, выполненное с магнитным градиентометром. Элементы эквивалентного источника могут тогда иметь, например, плотность поверхностного тока или напряженность поля.
Следует понимать, что изобретение не ограничивается описанными вариантами осуществления и охватывает модификации, очевидные специалистам в данной области техники, находящиеся в пределах существа и объема притязаний приложенных формул.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМЫ ВНЕСЕНИЯ ПОПРАВОК НА РЕЛЬЕФ МЕСТНОСТИ | 2008 |
|
RU2468394C2 |
| ОБРАБОТКА ДАННЫХ ГРАВИМЕТРИЧЕСКОЙ РАЗВЕДКИ | 2006 |
|
RU2431873C2 |
| СИСТЕМЫ ПОПРАВКИ НА РЕЛЬЕФ МЕСТНОСТИ | 2007 |
|
RU2442193C2 |
| Способ контроля точности площадной гравиметрической съемки | 2021 |
|
RU2781761C1 |
| СПОСОБ ПРОСТРАНСТВЕННО ПАРАМЕТРИЗОВАННОЙ ОЦЕНКИ ВЕКТОРОВ ДВИЖЕНИЯ | 2024 |
|
RU2839709C1 |
| Автоматизированная система сбора и распространения цифровой картографической информации водных путей | 2024 |
|
RU2833209C1 |
| СПОСОБ ПРОСТРАНСТВЕННОЙ ПОЛЯРИЗАЦИОННО-ЧУВСТВИТЕЛЬНОЙ ЛОКАЛИЗАЦИИ МНОГОЛУЧЕВЫХ РАДИОСИГНАЛОВ | 2008 |
|
RU2385467C1 |
| СПОСОБ ПОЛЯРИЗАЦИОННО-НЕЗАВИСИМОГО ПЕЛЕНГОВАНИЯ МНОГОЛУЧЕВЫХ РАДИОСИГНАЛОВ | 2010 |
|
RU2431862C1 |
| СПОСОБ ПЕЛЕНГОВАНИЯ С ПОВЫШЕННОЙ РАЗРЕШАЮЩЕЙ СПОСОБНОСТЬЮ | 2004 |
|
RU2285938C2 |
| СПОСОБ МОРСКОЙ МАГНИТНОЙ СЪЕМКИ | 2008 |
|
RU2390803C2 |

Изобретение относится к усовершенствованию методики обработки данных измерения потенциального поля при аэросъемке и может быть использовано при обработке данных гравиметрической съемки. Согласно изобретению способ обработки измеренных данных потенциального поля при авиационной или морской съемках потенциального поля включает определение массива полевых картографических параметров для картирования поля и введение в процессор измеренных данных потенциального поля. Измеренные данные потенциального поля содержат данные, определяющие множество измерений потенциального поля, каждое с соответственным положением измерения и временем измерения. Массив полевых картографических параметров определяют с использованием модели, содержащей комбинацию пространственной части, отображающей пространственную вариацию упомянутого потенциального поля, и временной части, отображающей временной шум в упомянутых измеренных данных потенциального поля, причем упомянутое определение включает подгонку измеренных данных потенциального поля как к пространственной, так и к временной частям упомянутой модели. Благодаря этому обеспечивается решение проблемы низкочастотного шума (дрейфа) при бортовой съемке потенциального поля. 8 н. и 19 з.п. ф-лы, 5 ил.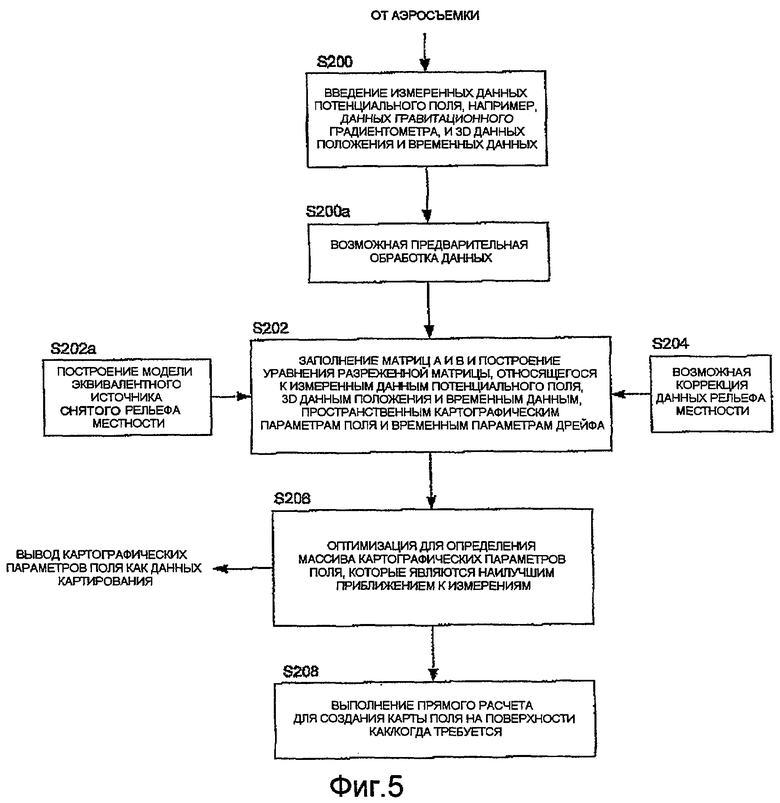
1. Реализуемый с помощью компьютера способ обработки измеренных данных потенциального поля, полученных из аэро- или морской съемки потенциального поля для определения массива картографических параметров поля для модели для картографирования поля, причем способ содержит:
введение в процессор измеренных данных потенциального поля из аэро- или морской съемки потенциального поля, причем упомянутые измеренные данные потенциального поля содержат данные, определяющие множество измерений потенциального поля, каждое с соответственным положением измерения и временем измерения; и
определение с помощью процессора упомянутого массива картографических параметров поля посредством подгонки указанной модели к упомянутым измеренным данным потенциального поля, причем модель содержит комбинацию пространственной части, отображающей пространственную вариацию упомянутого потенциального поля, и временной части, отображающей временной шум в упомянутых измеренных данных потенциального поля.
2. Способ по п.1, в котором упомянутые пространственная и временная части упомянутой модели содержат пространственные и временные члены модельного уравнения, и причем упомянутое определение содержит совместно определяемые оценки упомянутых пространственных и временных членов для определения упомянутых картографических параметров поля.
3. Способ по п.1, в котором упомянутая модель имеет вид:

где ρ и λ - векторы пространственного и временного модельных параметров, соответственно, A и B - матрицы, и f содержит вектор прямого расчета измерений, оцениваемых из модели.
4. Способ по п.1, в котором упомянутая пространственная часть упомянутой модели содержит модель эквивалентного источника.
5. Способ по п.1, в котором упомянутая временная часть упомянутой модели содержит интерполяционную функцию для интерполяции между узловыми точками во временных интервалах, больших, чем 60 с.
6. Способ по п.1, в котором упомянутая временная часть упомянутой модели содержит кусочно-линейную модель.
7. Способ по п.1, в котором упомянутый шум содержит измеряемый дрейф.
8. Способ по п.1, в котором упомянутое определение содержит минимизацию меры различия между упомянутыми измеренными данными потенциального поля и данными, предсказанными посредством упомянутого массива картографических параметров поля для определения упомянутого массива картографических параметров поля.
9. Способ по п.1, в котором упомянутое определение содержит регуляризацию упомянутой пространственной части и упомянутой временной части упомянутой модели.
10. Способ по п.1, в котором упомянутое определение содержит регуляризацию упомянутой пространственной части упомянутой модели с первой регуляризацией и регуляризацию упомянутой временной части упомянутой модели со второй, отличающейся регуляризацией.
11. Способ по п.9, содержащий использование градиентной регуляризации для упомянутой пространственной части упомянутой модели.
12. Способ по п.9, содержащий использование регуляризации Тихонова для упомянутой временной части упомянутой модели.
13. Способ по п.1, в котором упомянутая подгонка содержит совместную подгонку данных из измерений потенциального поля от множества различных линий съемки упомянутой съемки потенциального поля.
14. Способ по п.1, в котором упомянутые измеренные данные потенциального поля содержат одни или несколько гравиметрических данных и гравитационных градиентометрических данных.
15. Способ по п.1, в котором упомянутые картографические параметры поля содержат значения для элементов магнитного эквивалентного источника.
16. Способ по п.1, в котором упомянутые картографические параметры поля содержат значения для элементов эквивалентного источника массы.
17. Способ по п.1, в котором упомянутые измеренные данные потенциального поля содержат данные от множества источников измерения потенциального поля, причем упомянутая пространственная часть упомянутой модели является общей для упомянутого множества источников измерения, и причем отдельная упомянутая временная часть упомянутой модели предоставлена для каждого упомянутого источника измерения потенциального поля.
18. Способ по п.1, дополнительно содержащий определение карты с использованием упомянутых картографических параметров поля.
19. Носитель, переносящий управляющий процессором код для осуществления при его запуске способа по любому из предшествующих пунктов.
20. Система обработки данных для обработки измеренных данных потенциального поля по съемке потенциального поля для определения массива картографических параметров поля для картографирования поля, причем система содержит:
память данных для упомянутых измеренных данных потенциального поля, причем упомянутые измеренные данные потенциального поля содержат данные, определяющие множество измерений потенциального поля, каждое с соответственным положением измерения и временем измерения; и
память программы, хранящую управляющий процессором код; и
процессор, связанный с упомянутой памятью данных и с упомянутой памятью программы для загрузки и осуществления упомянутого управляющего кода, причем упомянутый код содержит код, чтобы управлять процессором для: ввода упомянутых измеренных данных потенциального поля; и
определения упомянутого массива картографических параметров поля, используя модель, содержащую комбинацию пространственной части, отображающей пространственную вариацию упомянутого потенциального поля, и временной части, отображающей временной шум в упомянутых измеренных данных потенциального поля, причем упомянутый код для определения упомянутого массива картографических параметров поля сконфигурирован для подгонки упомянутых измеренных данных потенциального поля и к упомянутым пространственным частям, и к упомянутым временным частям упомянутой модели.
21. Реализуемый с помощью компьютера способ эквивалентного источника обработки измеренных данных потенциального поля для определения картографических данных поля для модели, в которой потенциальное поле смоделировано как комбинация пространственного сигнала и компонента временного шума, причем способ содержит
измерение данных потенциального поля с помощью аэро- или морской съемки потенциального поля;
определение с помощью процессора совместного наилучшего приближения упомянутых измеренных данных потенциального поля к упомянутой моделируемой комбинации пространственного сигнала и компонента временного шума, для определения картографических данных поля для модели.
22. Способ по п.21, дополнительно содержащий включение одной или обеих пространственной регуляризации и временной регуляризации в упомянутой моделируемой комбинации упомянутого пространственного сигнала и упомянутого временного шума.
23. Способ по п.21, в котором упомянутые измеренные данные потенциального поля содержат гравитационные данные.
24. Носитель, переносящий управляющий процессором код, который при его запуске осуществляет способ по пп.21, 22 или 23.
25. Система обработки данных, включающая в себя носитель по п.24.
26. Носитель, переносящий массив картографических параметров поля, определяемых посредством способа по любому из пп.1-17.
27. Носитель, переносящий картографические данные, определенные посредством способа по любому из пп.21-23.
| J.M.Torta and al | |||
| "A model of the secular change of the geomagnetic field for Antarctica", In press on Tectonophysics | |||
| ЩИТОВОЙ ДЛЯ ВОДОЕМОВ ЗАТВОР | 1922 |
|
SU2000A1 |
| US 7113868 A, 26.09.2006 | |||
| US 5661649 A, 26.08.1997 | |||
| DE 102004005676 A1, 25.08.2005 | |||
| ГЕОФИЗИЧЕСКАЯ СИСТЕМА СБОРА И ОБРАБОТКИ ИНФОРМАЦИИ | 1994 |
|
RU2091820C1 |
| RU 2004124952 A, 27.10.2005 | |||
| СПОСОБ ОБРАБОТКИ РЕЗУЛЬТАТОВ ГРАВИМЕТРИЧЕСКОЙСЪЕМКИ | 0 |
|
SU186155A1 |
Авторы
Даты
2013-06-27—Публикация
2008-01-30—Подача