Данное изобретение относится к усовершенствованным методам обработки данных измерений потенциального поля, полученных при авиационной разведке, например гравиметрической разведке, и к усовершенствованным методам сбора данных, которые обеспечиваются за счет усовершенствованных методов обработки данных.
Традиционно, авиационная разведка потенциального поля, например гравиметрическая разведка, проводится по схеме сетки. Сетка задается ортогональными наборами параллельных линий (маршруты полета) на двухмерной поверхности, которая огибает нижележащий рельеф. Огибающая поверхность удовлетворяет ограничению минимальной высоты (т.е. минимальной высотой над землей, на которой разрешено летать самолету) и ограничению по максимальной скорости подъема/спуска самолета, обычно около трех процентов. Этот подход годится для плоского рельефа, но для холмистого или гористого рельефа, поверхность, на которой летит самолет, может варьироваться в пределах двух-трех километров от, скажем, дна нижележащей долины до вершины гористого района/ района разведки, поэтому необходим другой подход.
Полезно иметь возможность собирать данные потенциального поля, в частности гравиметрические данные, вблизи земли, т.е. на низкой высоте. При гравиметрической разведке близлежащая масса обеспечивает данные высокой и низкой (пространственной) частоты, тогда как влияние более глубоколежащей массы наблюдается в основном только на низких частотах. При поиске нижележащих аномалий промежуточная масса имеет преобладающее влияние, и для обеспечения точного представления глубинных особенностей желательно иметь хорошее представление поверхностных особенностей, чтобы иметь возможность вычитать, в частности, высокие частоты (которые преобладают в энергетическом спектре). Например, сигнал с длиной волны λ ослабевает с высотой z по закону exp(-kz), где k=2π/λ, откуда можно оценить, что составляющая сигнала с длиной волны 200 метров от массы на глубине 100 метров ослабевает приблизительно в 20 раз от своего первоначального значения на поверхности земли (и дополнительно ослабевает в геометрической прогрессии с ростом высоты), тогда как можно видеть, что более длинные длины волны ослабевают значительно медленнее. В общем случае размер и позиция разведки выбираются согласно шкале длины волны, соответствующей сигнатуре, предполагаемой в соответствии с размером и глубиной цели.
Из вышеприведенного рассмотрения следует, что в общем случае желательно иметь возможность осуществлять авиационную разведку на низкой высоте, но на практике ограничения самолета и схема полетов, привязанная к сетке, может накладывать значительные ограничения. Схема полетов, привязанная к сетке, необходима, поскольку традиционные методы обработки данных гравиметрической разведки опираются на предположение постоянной высоты. В широком смысле предположение состоит в том, что для глубинного источника высота самолета приблизительно постоянна, и отклонение от этого предположения рассматривается лишь как небольшая коррекция. Кроме того, традиционные методы обработки данных гравиметрической разведки опираются на регулярно размещенные элементы данных, обычно в количестве степени двойки, что позволяет применять (быстрое) преобразование Фурье, тем самым задавая требование для ортогональных наборов параллельных маршрутов полета. Необходимо, чтобы маршруты полета располагались на общей поверхности, поскольку существующие методы предполагают, например, что если два маршрута пересекаются, то они пересекаются на одной и той же высоте. Дополнительная проблема с существующими маршрутами полета возникает, когда область разведки не является в точности прямоугольной, например вследствие локального рельефа. В этом случае, чтобы иметь возможность применять традиционные методы, элементы данных "забиваются", например, путем интерполяции или экстраполяции для генерации регулярного набора элементов данных в прямоугольной области. Затем длины волны (или, в частности, волновые числа), используемые для Фурье-анализа, определяются по максимальным размерам x и y (длине и ширине) забитой прямоугольной области.
Ввиду вышеизложенных недостатков традиционных методов требуются усовершенствованные методы обработки данных разведки потенциального поля и схемы разведывательных полетов.
Согласно первому аспекту настоящего изобретения предусмотрен способ обработки данных измерений потенциального поля, полученных при разведке потенциального поля земли для определения картографических данных для картографирования поля, способ содержит этапы, на которых вводят данные измерений потенциального поля, причем данные измерений потенциального поля содержат данные, задающие совокупность измерений потенциального поля и соответствующих позиций, причем каждая позиция задает позицию измерения потенциального поля в трехмерном пространстве; определяют совокупность соотношений между измерениями потенциального поля и позициями, причем каждое соотношение соотносит измерение потенциального поля с функцией соответствующей позиции в трехмерном пространстве, умноженной на параметр картографирования поля; и определяют, по существу, самосогласованный набор параметров картографирования поля для совокупности соотношений для определения, таким образом, картографических данных.
Данные потенциального поля могут содержать гравиметрические данные (данные измерения гравитационного поля), данные гравитационного градиентометра (данные измерения градиента магнитного поля), данные векторного магнитометра, данные истинного магнитного градиентометра или аналогичные данные. Параметры картографирования поля (коэффициенты или параметры, позволяющие описывать потенциальное поле) можно использовать для генерации аналогичных данных потенциального поля и, согласно вариантам осуществления, в общем случае параметры определяются выбором значений параметров, которые задают данные потенциального поля, например гравитационного поля или градиента гравитационного поля, которые наиболее точно аппроксимируют данные измерений потенциального поля. Это может быть, например, минимизация среднеквадратической ошибки или другая аналогичная оптимизация.
Согласно вариантам осуществления соотношения содержат систему уравнений, которую можно представить, например, матрицей, и определение содержит решение этих уравнений. Предпочтительно уравнения являются избыточно ограниченными, и решение содержит решение посредством процедуры понижения шума, например оптимизации методом наименьших квадратов. Предпочтительно соотношения таковы, что они имеют вид поля реального (гравитационного) потенциала, благодаря чему шум, который обычно не имеет такого вида, в итоге отфильтровывается в процедуре оптимизации. Таким образом, предпочтительно функция (трехмерной) позиции удовлетворяет уравнению Лапласа. В ряде репрезентативных примеров способа может быть порядка 10K параметров и 100K позиций.
Картографические данные могут просто содержать набор параметров картографирования поля (коэффициенты или параметры потенциального поля), поскольку эти данные можно использовать для генерации диапазона данных потенциального поля (например, данных гравитационного поля или градиента гравитационного поля) в зависимости от нужной высоты, зоны покрытия и/или картографируемой поверхности. Однако способ может дополнительно содержать определение нужного поля, обычно на поверхности, из набора параметров картографирования поля для генерации карты, т.е. осуществление прямого вычисления данных потенциального поля из набора параметров картографирования поля. Согласно объяснению, приведенному ниже, варианты осуществления способа предусматривают генерацию того же типа данных потенциального поля, которые измеряются, по меньшей мере, неявно, при определении параметров картографирования поля посредством процедуры, целью которой является минимизация или иная оптимизация различий между вычисленными и измеренными значениями. То, что это работает независимо от того, содержат ли данные потенциального поля, скажем, гравиметрические данные или данные гравитационного градиентометра, можно видеть, применяя одну из теорем Грина. Кроме того, зная один тип данных потенциального поля, например гравитационное поле или градиент гравитационного поля, можно определить другой путем интегрирования/дифференцирования, а также скалярный потенциал.
В одном варианте осуществления способа применяется представление эквивалентного источника данных потенциального поля. В этом варианте осуществления находят значения поверхностной плотности (или массы) для совокупности массивных элементов поверхности, которые совместно создают гравитационное (или другое) поле, которое наилучшим образом аппроксимирует измеренное гравитационное (или другое) поле. Поверхность в общем случае, но не обязательно, является плоской, и ее, например, можно выбирать для аппроксимации поверхности земли в районе разведки. Найдя значения для этих массивных элементов, можно применять простое прямое вычисление для прогнозирования скалярного потенциала, или гравитационного поля, или градиента гравитационного поля, например для генерации любой нужной карты района разведки. Обычно прямое вычисление производится для определения одной или нескольких составляющих поля на плоскости плоского картографирования.
В общих чертах, согласно вариантам осуществления этого способа квадрат разности между измеренным полем и полем, определенным из масс эквивалентного источника (измеряется/вычисляется гравитационное поле или градиент гравитационного поля), является функцией ошибок по массе. Таким образом, беря частную производную этой функции по, отдельно, массе каждого элемента поверхности, составляем систему уравнений, в которой переменными являются только массы всех массивных элементов поверхности (при условии, что позиция измерения в отношении массивного элемента поверхности, r-r′, известна). Эту систему уравнений удобно представить в виде матрицы и решать относительно значений массивных элементов поверхности. Поскольку количество измерений обычно много больше количества уравнений в системе (т.е. количества массивных элементов), например, по меньшей мере, в пять или десять раз больше, система уравнений является избыточно ограниченной. Это полезно, поскольку значения массивных элементов поверхности ни в коем случае не будут соответствовать шуму; вместо процедуры оптимизации для определения значений массивных элементов поверхности используется, например, аппроксимация методом наименьших квадратов, что позволяет понизить шум. Кроме того, благодаря использованию физической модели гравитационного поля, уравнения подчиняются уравнению Лапласа, что позволяет аппроксимировать гравитационное поле, а не шум.
Во втором варианте осуществления способа применяется метод модифицированных базисных функций Фурье. Согласно этому методу для представления данных измерений используется двухмерное разложение в ряд Фурье, но благодаря умножению на высотно-зависимый коэффициент (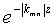 ) каждой двухмерной составляющей (
) каждой двухмерной составляющей (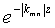 ), это представление все же является наиболее общим и подчиняется уравнению Лапласа (при дифференцировании множителей высотно-зависимого коэффициента и сокращении двухмерных составляющих). Разложение можно обрезать в той или иной точке, в зависимости от нужной точности представления, например, определяемой количеством переменных, сделанных зависимыми. Можно применять другие разложения, например по сферическим гармоникам, которые полезны для более обширных областей, в частности, когда кривизной земли нельзя пренебречь.
), это представление все же является наиболее общим и подчиняется уравнению Лапласа (при дифференцировании множителей высотно-зависимого коэффициента и сокращении двухмерных составляющих). Разложение можно обрезать в той или иной точке, в зависимости от нужной точности представления, например, определяемой количеством переменных, сделанных зависимыми. Можно применять другие разложения, например по сферическим гармоникам, которые полезны для более обширных областей, в частности, когда кривизной земли нельзя пренебречь.
В общем случае коэффициенты разложения определяются следующим образом. В позиции r измеренное потенциальное поле (гравитационное поле или градиент гравитационного поля) известно, и для конкретной пары значений k
m и k
n значение 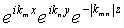 также известно. Таким образом, при разложении в ряд Фурье (например, согласно приведенному ниже уравнению (3)) каждый элемент данных можно в итоге рассматривать по отдельности, и, как и в первом варианте осуществления, описанном выше, формируется система уравнений, которую можно решить относительно коэффициентов разложения в ряд Фурье. Эти коэффициенты затем можно использовать для определения (путем прямого вычисления) гравитационного поля или градиента гравитационного поля на любой двухмерной поверхности, которую нужно картографировать. Очевидно, что в этом (и предыдущем) варианте осуществления данные можно выбирать произвольным образом, поскольку элементы данных фактически не связаны между собой - все, что необходимо, это набор измерений и соответствующих (x, y, z) позиций, чтобы иметь возможность определения гравитационного поля или градиента гравитационного поля на любом другом наборе точек, в частности на поверхности или плоскости, то есть карте. Кроме того, отсюда следует, что, с использованием традиционных методов, нет необходимости забивать данные измерений для построения прямоугольника. В принципе, элементы данных можно рассматривать как участок произвольной формы двухмерной области максимальных размеров, определяемых максимальными длинами волны для разложения в ряд Фурье в направлениях x и y (хотя, как можно видеть, данные измерений не обязаны лежать на двухмерной поверхности). Отсюда следует, что значения k
m и k
n можно выбирать независимо от размеров области разведки (здесь k - волновое число, т.е. 2π/λ, тогда как при традиционной разведке максимальная длина волны должна соответствовать длине или ширине прямоугольной области разведки).
также известно. Таким образом, при разложении в ряд Фурье (например, согласно приведенному ниже уравнению (3)) каждый элемент данных можно в итоге рассматривать по отдельности, и, как и в первом варианте осуществления, описанном выше, формируется система уравнений, которую можно решить относительно коэффициентов разложения в ряд Фурье. Эти коэффициенты затем можно использовать для определения (путем прямого вычисления) гравитационного поля или градиента гравитационного поля на любой двухмерной поверхности, которую нужно картографировать. Очевидно, что в этом (и предыдущем) варианте осуществления данные можно выбирать произвольным образом, поскольку элементы данных фактически не связаны между собой - все, что необходимо, это набор измерений и соответствующих (x, y, z) позиций, чтобы иметь возможность определения гравитационного поля или градиента гравитационного поля на любом другом наборе точек, в частности на поверхности или плоскости, то есть карте. Кроме того, отсюда следует, что, с использованием традиционных методов, нет необходимости забивать данные измерений для построения прямоугольника. В принципе, элементы данных можно рассматривать как участок произвольной формы двухмерной области максимальных размеров, определяемых максимальными длинами волны для разложения в ряд Фурье в направлениях x и y (хотя, как можно видеть, данные измерений не обязаны лежать на двухмерной поверхности). Отсюда следует, что значения k
m и k
n можно выбирать независимо от размеров области разведки (здесь k - волновое число, т.е. 2π/λ, тогда как при традиционной разведке максимальная длина волны должна соответствовать длине или ширине прямоугольной области разведки).
Согласно другому аспекту изобретения предусмотрена система обработки данных для обработки данных измерений потенциального поля, полученных при разведке потенциального поля земли, для определения картографических данных для картографирования поля, система содержит устройство хранения данных для хранения данных измерений потенциального поля, причем данные измерений потенциального поля содержат данные, задающие совокупность измерений потенциального поля и соответствующих позиций, причем каждая позиция задает позицию измерения потенциального поля в трехмерном пространстве; устройство хранения программ для хранения кода управления процессором; и процессор, подключенный к устройству хранения данных и устройству хранения программ, для загрузки и выполнения кода управления, причем код содержит код, предписывающий процессору вводить данные измерений потенциального поля; определять совокупность соотношений между измерениями потенциального поля и позициями, причем каждое соотношение соотносит измерение потенциального поля с функцией соответствующей позиции в трехмерном пространстве, умноженной на параметр картографирования поля; и определять, по существу, самосогласованный набор параметров картографирования поля для совокупности соотношений для определения, таким образом, картографических данных.
Согласно дополнительному аспекту изобретения предусмотрен способ обработки данных измерений, полученных в авиационной гравиметрической разведке для обеспечения данных для карты гравитационного поля, причем данные измерений содержат совокупность измерений гравитационного потенциального поля, с каждым из которых связана позиция измерения в трехмерном пространстве, способ содержит этапы, на которых используют данные измерений для оценки коэффициентов, на которые умножается функция трехмерной позиции в гармоническом разложении, для определения, таким образом, представления гравитационного поля в районе разведки для карты гравитационного поля.
Изобретение дополнительно предусматривает способ обработки данных измерений, полученных в авиационной гравиметрической разведке для обеспечения данных для карты гравитационного поля, причем данные измерений содержат совокупность измерений гравитационного потенциального поля, с каждым из которых связана позиция измерения в трехмерном пространстве, способ содержит этапы, на которых используют данные измерений для оценки совокупности массивных элементов, каждый из которых умножается на функцию трехмерной позиции в представлении эквивалентного источника гравитационного поля, для обеспечения, таким образом, данных для карты гравитационного поля.
Изобретение дополнительно предусматривает способ картографирования гравитационного поля, способ содержит этапы, на которых вводят данные измерений, полученные в авиационной гравиметрической разведке, причем данные измерений содержат совокупность измерений гравитационного потенциального поля, с каждым из которых связана позиция измерения в трехмерном пространстве; определяют совокупность соотношений между измерениями потенциального поля и позициями, причем каждое соотношение соотносит измерение потенциального поля с функцией соответствующей позиции в трехмерном пространстве, умноженной на параметр картографирования поля; и картографируют гравитационное поле, определяя, по существу, самосогласованный набор параметров картографирования поля для совокупности соотношений.
Варианты осуществления вышеописанных способов дополнительно содержат разведку поля для получения данных измерений потенциального поля путем облета набора маршрутов, которые не обязаны быть параллельными или образовывать схему прямоугольной сетки.
Как упомянуто выше, варианты осуществления вышеописанного способа можно применять, при желании, к фактически произвольно выбранным данным. Хотя произвольная выборка может оказаться неудобной с практической точки зрения, тем не менее очевидно, что, поскольку описанные здесь способы, в общем случае, не ограничены, маршруты авиационной разведки можно выбирать так, чтобы получить лучшие начальные данные, в частности, за счет возможно более низкого полета, ограниченного только общими соображениями безопасности и возможностями самолета. Таким образом, например, в широком смысле традиционный набор маршрутов можно дополнять полетами вдоль линий долин и/или модифицировать, например, искривляя один или несколько маршрутов полета для повторения горного рельефа.
Хотя маршруты не обязаны пересекаться на, по существу, одинаковой высоте ("перекрещивание"), тем не менее перекрещивания полезны для понижения шума и низкочастотного дрейфа, поскольку они обеспечивают два сильно коррелирующих измерения аналогичных участков. Однако в отличие от традиционных методов разведки маршруты не обязаны пересекаться на одной и той же высоте. Кроме того, возможны различные схемы пересечения, например, в долине два кусочно-линейных или змеевидных маршрута могут извиваться в противоположных направлениях для обеспечения последовательности перекрещиваний вдоль маршрутов.
Поэтому согласно дополнительному аспекту изобретения предусмотрен способ проведения авиационной разведки потенциального поля, способ содержит этапы, на которых ведут самолет по набору маршрутов и измеряют данные потенциального поля в точках на маршрутах, в котором набор маршрутов имеет одну или несколько из следующих особенностей: два маршрута пересекаются на высотах, отличающихся, по меньшей мере, на 50 метров; в районе разведки маршруты в одном и том же общем направлении не параллельны более чем на 5 градусов; маршруты включают в себя криволинейные маршруты; маршруты из набора маршрутов, вместе взятые, по существу, не лежат на поверхности; маршруты из набора маршрутов, вместе взятые, задают поверхность, в котором, по меньшей мере, один из маршрутов задает одно из двух ортогональных направлений на поверхности, так что скорости изменения высоты с расстоянием в разных ортогональных направлениях поверхности отличаются более чем на 5 процентов.
Согласно вариантам осуществления вышеописанных способов два маршрута пересекаются на высотах, отличающихся более чем на 50, 100, 150 или 200 метров. Маршруты могут быть прямолинейными, кусочно-линейными или искривленными и в общем случае соседние маршруты полета могут отклоняться от параллельности более чем на два градуса, три градуса, пять градусов, десять градусов или более. Как отмечено выше, маршруты, вместе взятые, не обязаны, по существу, лежать на поверхности, в частности, по причине отсутствия ограничения "по существу, постоянной высоты". Однако один удобный метод построения набора маршрутов для такой авиационной разведки предусматривает обеспечение традиционной разведки с ее последующей модификацией в сторону приближения к земле, в частности, на низинных участках, где желательно лучшее покрытие.
Типичный способ обеспечения традиционной разведки предусматривает построение двухмерной поверхности, огибающей рельеф, на котором должна производиться разведка. В высоких точках нижележащего рельефа высота поверхности обычно определяется минимально разрешенной высотой полета самолета (для безопасности), и затем высота поверхности уменьшается вследствие присущих самолету ограничений на скорость подъема/спуска, обычно порядка двух-трех процентов. Поскольку маршруты ограничиваются прямоугольной сеткой, эти ограничения применяются в двух ортогональных направлениях. В отличие от вариантов осуществления вышеописанного способа такое ограничение нужно применять только в одном направлении (в одном измерении, а не в двух). В итоге для определения маршрутов полета можно применять одномерную огибающую. Таким образом, согласно вариантам осуществления описанного здесь способа набор маршрутов, вместе взятых, задает поверхность, на которой лежит маршрут, задающий один или два ортогональных направления, причем в другом направлении поверхности разрешено иметь скорость изменения высоты с расстоянием, превышающую разрешенную скорость подъема/спуска самолета, например, более чем на три процента, пять процентов, десять процентов, двадцать процентов или более.
Изобретение также предусматривает носитель данных, переносящий навигационные данные самолета для такого набора маршрутов авиационной разведки потенциального поля.
Изобретение дополнительно предусматривает код управления процессором для реализации вышеописанных способов, в частности, на носителе данных, например диске, CD- или DVD-ROM, в программируемой памяти, например постоянной памяти (программно-аппаратное обеспечение), или на носителе данных, например носителе оптического или электрического сигнала. Код (и/или данные) для реализации вариантов осуществления изобретения может содержать исходный, объектный или исполнимый код, на традиционном языке программирования (интерпретируемом или компилируемом), например C, или код ассемблера, код для настройки и управления ASIC (специализированной интегральной схемой) или FPGA (вентильной матрицей, программируемой пользователем), или код на языке описания аппаратных средств, например Verilog (торговая марка) или VHDL (языке описания аппаратных средств для высокоскоростных интегральных схем). Специалисту очевидно, что такой/ие код и/или данные могут распределяться между рядом компонентов, осуществляющих связь друг с другом.
Ниже изложены дополнительные аспекты изобретения.
Способ проведения разведки потенциального поля с воздуха, для чего самолет снабжен комплектом оборудования для геофизических измерений, включающим в себя один или несколько приборов для измерения потенциального поля, например векторный гравиметр, гравитационный градиентометр, магнитометр, магнитный градиентометр или другие приборы, и согласно которому самолет облетает нерегулярный набор разъединенных, не находящихся на одном уровне, непрямолинейных маршрутов полета, которые покрывают район разведки, предпочтительно с наименьшим возможным расстоянием между поверхностью и самолетом для каждой линии полета и с приблизительно однородным покрытием района разведки (такие линии согласуются с безопасной эксплуатацией самолета). Предпочтительно, согласно этому способу, величина потенциального поля земли, представляющего интерес, определяется с использованием алгоритмов, которые работают с данными измерений, полученными с помощью прибора для измерения потенциального поля, собранными вдоль линий разведки как есть, без необходимости выравнивать данные, приводить данные к общей горизонтальной плоскости или привязывать данные к сетке, причем такие данные включают в себя измерение самой величины потенциального поля и (мгновенную) позицию и, в необязательном порядке, высоту прибора(ов) для измерения потенциального поля.
Способ проведения разведки потенциального поля с воздуха, описанный выше, но в котором схема полета немного изменена с целью достижения приемлемого количества "перекрещиваний" на единицу площади, причем в данном случае "перекрещивание" представляет собой точку, где линии полета самолета с разными курсовыми направлениями номинально пересекаются в одной и той же точке в пространстве.
Способ проведения разведки потенциального поля с воздуха, описанный выше, где некоторые линии из набора, по существу, параллельных, но не обязательно прямых линий, сознательно сделаны извивающимися для увеличения количества перекрещиваний с другими линиями в этом наборе, которые проходятся параллельно.
Способ проведения разведки потенциального поля с воздуха, описанный выше, где все линии проходятся с целью обеспечения максимального (возможного) количества перекрещиваний по всему району разведки (с учетом ограничения, например, на суммарную/ое длину/время полета). Ни одна из линий разведки не обязана быть параллельной какой-либо другой линии разведки, также ни одна из линий не обязана быть прямой, и в общем случае многие линии не будут пересекать весь район разведки от края до края.
Способ проведения разведки потенциального поля с воздуха, описанный выше, но в котором самолет осуществляет разведку по более традиционной схеме, например по схеме разведки с двухмерной огибающей или постоянной высотой или какой-либо другой схеме, которая запутывает линии полета и связывает их с тем, чтобы они пересекались в каждом перекрещивании. (Например, навигационные данные могут задавать точное пересечение, хотя на практике пилот достигает этого лишь с точностью, например, 10 м или 20 м.)
Способ проведения разведки потенциального поля с воздуха, описанный выше, в котором данные "выравниваются" до обработки. Выравнивание здесь является общим термином, который охватывает методы, включающие в себя один или несколько из: понижения шума, удаления низкочастотного дрейфа, согласования низкочастотного спектра соседних линий, соотнесения данных с плоскостью фиксированной высоты и пр. Данные также можно привязывать к сетке до обработки.
Способ проведения разведки потенциального поля с воздуха, описанный выше, где первая стадия анализа содержит удаление или регулировку данных, которые никоим образом не могут быть обусловлены никакими геологическими структурами, являющимися предметом исследования или геоморфологии (рельефом), в районе разведки. Влияние рельефа также можно использовать для корректировки данных на любой стадии обработки до расчета гравитационного потенциала земли.
Способ проведения разведки потенциального поля с воздуха, описанный выше, где создается точная DEM (цифровая модель рельефа) с использованием лидара (лазерного радара) совместно с IMU (инерциальным измерительным блоком), а также с DGPS (дифференциальной системой глобального позиционирования) для корректировки данных лидара для плоского движения. Данные DEM и DGPS также можно использовать для корректировки данных измерений потенциального поля с учетом рельефа. Аналогично данные ускорения, высоты, ориентации, угловой скорости и углового ускорения самолета также можно использовать для корректировки выходных данных аппаратуры для измерения потенциального поля. Любой бортовой или дистанционный датчик можно использовать для обеспечения информации положения и движения для самолета и/или аппаратуры для измерения потенциального поля.
Поэтому предпочтительно оборудовать самолет различными дополнительными стандартными авиационными приборами геофизической разведки, например аппаратурой для GPS, DGPS, альтиметра, измерения высоты, измерения давления, гиперспектрального сканера, системы электромагнитных измерений (EM), системы измерения переходных электромагнитных процессов (TDEM), векторного магнитометра, акселерометра, гравиметра и других устройств, включая другие устройства измерения потенциального поля.
Способ проведения разведки потенциального поля с воздуха, описанный выше, в котором выходные сигналы аппаратуры на самолете разведки корректируются с использованием аппаратуры на стационарной или подвижной базовой станции, например, согласно наилучшей практике в данное время. Такое оборудование может включать в себя аппаратуру GPS и магнитную аппаратуру и высококачественные наземные гравиметры.
Способ проведения разведки потенциального поля с воздуха, описанный выше, в котором данные, собранные согласно любому из вышеописанных способов, объединяются с любыми данными наземной или спутниковой разведки для улучшения анализа, причем такие данные включают в себя данные рельефа, спектральные, магнитные или другие данные.
Эти и другие аспекты изобретения будут дополнительно описаны исключительно в порядке примера, со ссылкой на прилагаемые чертежи, на которых:
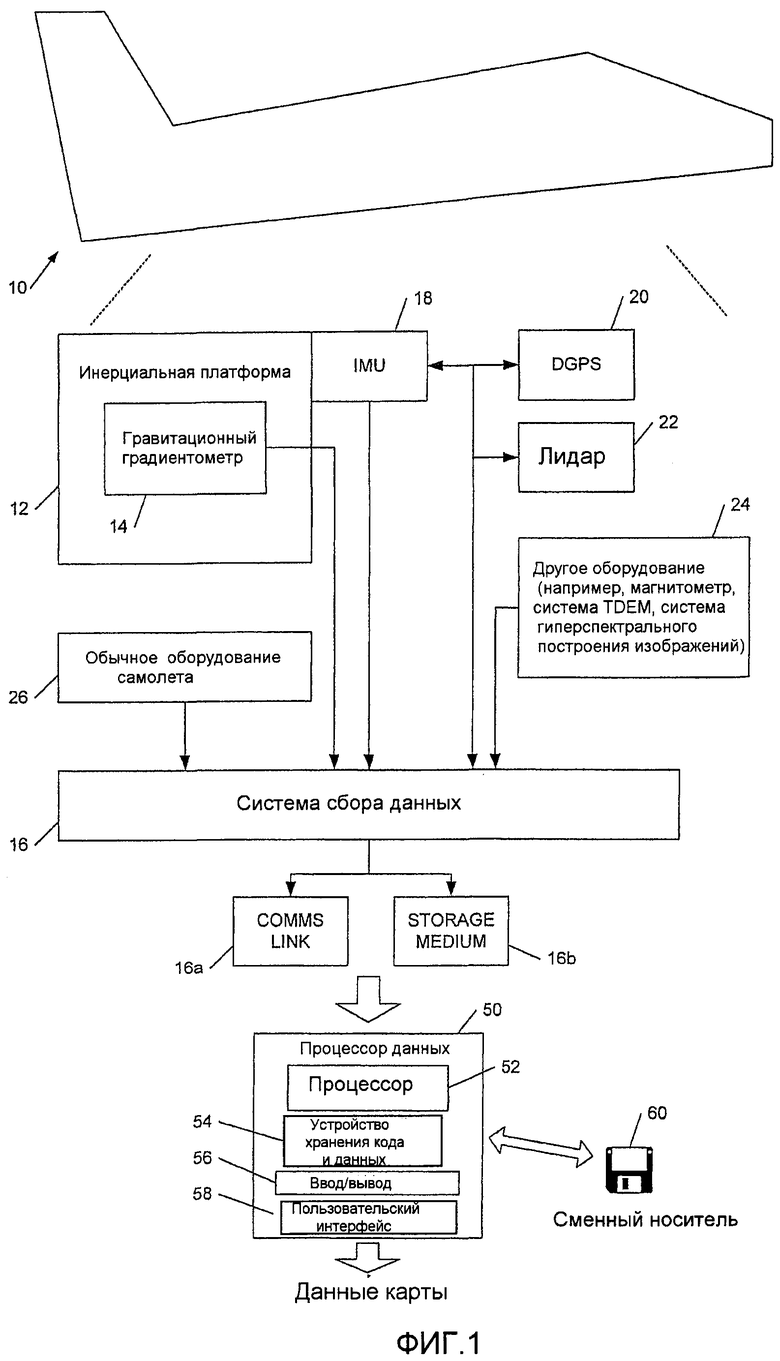
Фиг. 1 - самолет с данными авиационной разведки и пример системы обработки данных, приспособленной для реализации варианта осуществления способа, отвечающего изобретению;
Фиг. 2 - логическая блок-схема процедуры обработки данных измерений потенциального поля для реализации варианта осуществления способа, отвечающего изобретению;
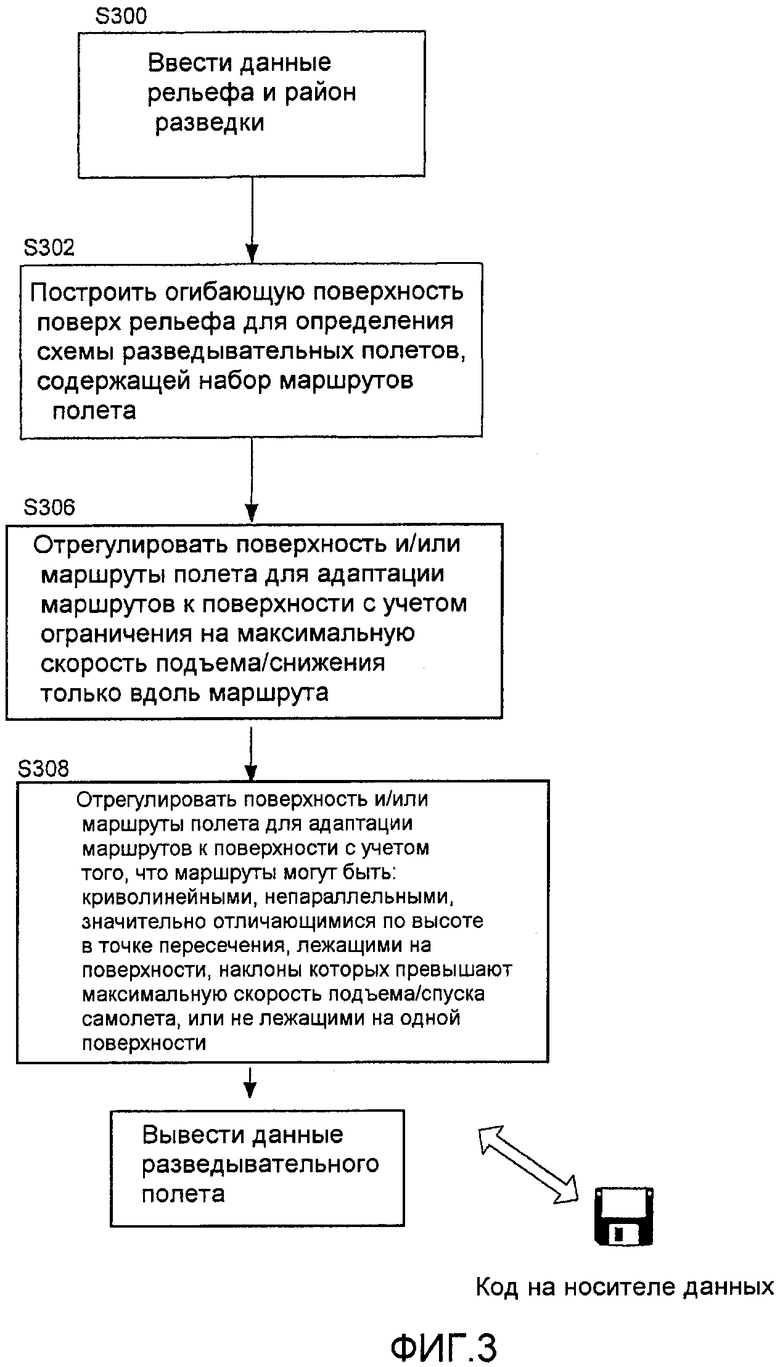
Фиг. 3 - логическая блок-схема процедуры генерации данных маршрутов полета для осуществления авиационной разведки потенциального поля согласно варианту осуществления способа, отвечающего изобретению; и
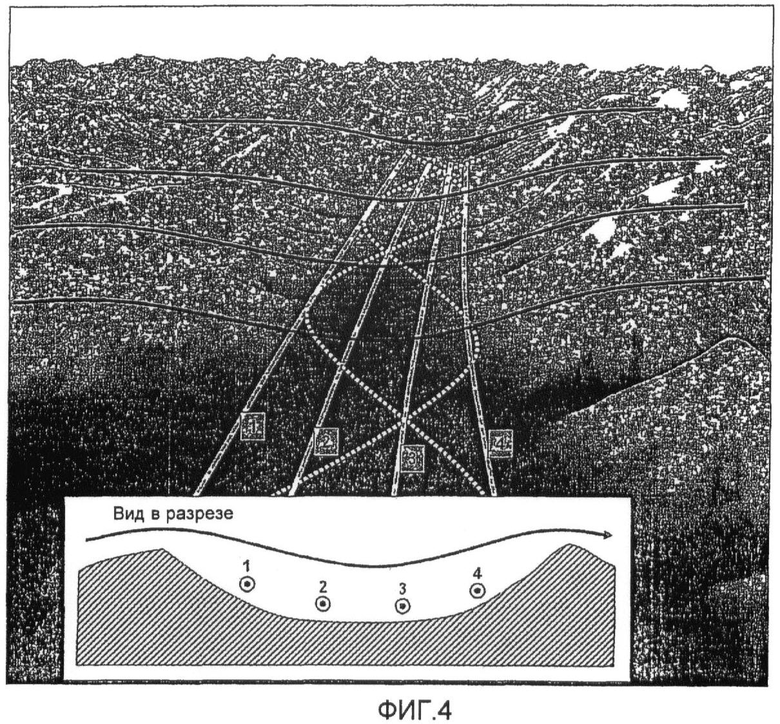
Фиг. 4 - иллюстративный набор маршрутов полета для авиационной разведки потенциального поля, данные которых можно обрабатывать согласно вариантам осуществления изобретения.
Теоретическое обоснование
Сначала обратимся к теоретическим основам, которые позволяют лучше понять изобретение.
Данные потенциального поля включают в себя, но без ограничения, гравиметрические данные, данные гравитационного градиентометра, данные векторного магнитометра и данные истинного магнитного градиентометра. Такие данные можно математически описать рядом соотношений, которые определяют характер изменения величин в зависимости от пространственных координат с учетом различных типов измерения. Элементы и представления потенциального поля можно вывести из скалярной величины.
Для гравитационного поля соответствующий потенциал представляет собой скалярный потенциал гравитационного поля, Φ(r), определяемый как
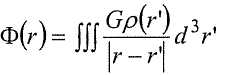
где r, ρ(r′), G - соответственно позиция измерения гравитационного поля, массовая плотность в положении r′ и гравитационная постоянная. Напряженность гравитационного поля, выражающая действие гравитационного поля, равна пространственной производной скалярного потенциала. Напряженность гравитационного поля - это вектор, поскольку имеет направление, которое всем известно - сила тяжести действует вниз. Ее можно представить тремя составляющими относительно любой выбранной декартовой системы координат:
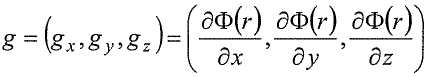
Каждая из этих трех составляющих изменяется в каждом из этих трех направлений, вследствие чего градиент гравитационного поля представляет собой тензор, имеющий девять составляющих:
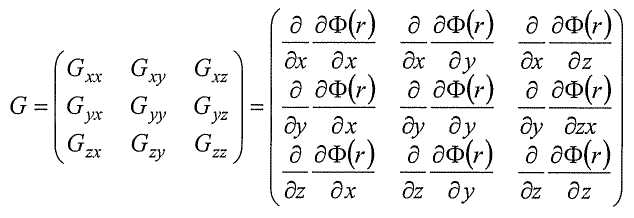
Математическая теория потенциальных полей и фундаментальные уравнения и соотношения вытекают из анализа свойств скалярной потенциальной функции, ее производных, ее преобразований Фурье и других математических величин.
Согласно одной из теорем Грина если на замкнутой поверхности известна любая из пространственных производных скалярного потенциала (включая сам скалярный потенциал), то значение этой пространственной производной известно во всех точках объема, ограниченного этой поверхностью. Отсюда следует, что если эта величина известна во всех точках, то путем дифференцирования и интегрирования можно получить все остальные производные скалярного потенциала, включая сам скалярный потенциал, и все его производные фактически известны во всех точках объема, когда лишь одна из производных известна на поверхности, охватывающей этот объем. Это говорит о том, что полное измерение любой составляющей любой производной скалярного потенциала позволяет вычислить любую другую составляющую любой производной скалярного потенциала. Отсюда следует, что, по меньшей мере, теоретически не имеет значения, какую величину измерять, и выбор аппаратуры определяется исключительно тем, какой прибор измеряет нужную величину с наибольшим отношением сигнал/шум.
Дифференцирование вышеописанного скалярного потенциала гравитационного поля (после решения некоторых вопросов, связанных с 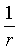 , когда r→0) в конце концов дает:
, когда r→0) в конце концов дает:

которое в областях, свободных от материи, сводится к уравнению Лапласа, важному фундаментальному соотношению в теории гравитации:

Гармонические функции удовлетворяют уравнению Лапласа и многие из их свойств можно использовать в анализе данных, собранных в ходе разведки потенциального поля.
Данные можно анализировать и обрабатывать с использованием различных методов, которые работают с данными, собранными при разведке, в качестве начальной точки, но которые затем изменяют данные и/или их формат таким образом, что все значения, связанные с измеренными величинами, оказываются на регулярной двухмерной сетке, расположенной на горизонтальной плоскости анализа фиксированной высоты, используемые процессы называются "выравниванием" и "привязкой к сетке".
Привязка к сетке - это геофизический метод численной обработки, основной принцип которой состоит в:
- разбиении района разведки на прямоугольные ячейки, стороны которых обычно выровнены с основными направлениями прохождения разведки,
- замене фактических данных измерений данными, которые полностью "эквивалентны" данным измерений, но которые являются назначенными значениями в точках посередине каждой ячейки.
Такие данные называются данными, "привязанными к сетке". Существует много способов убедиться, что данные, "задуманные" как представляющие данные измерений, действительно "эквивалентны" данным измерений. Также существует много способов выбора размеров каждой ячейки, но все они связаны с усредненным разбиением линий, проведенных в двух ортогональных направлениях. Когда линии разведки проведены не регулярно, как описано здесь, идею привязки к сетке, хотя и не обязательно, но все же можно использовать, но при этом существует гораздо больше возможностей выбора размера и ориентации ячеек.
Когда данные имеют этот формат, их значительно удобнее подвергать математическим преобразованиям. Никакие данные, участвующие в этих процессах, не обязаны удовлетворять уравнению Лапласа. Данные рассматриваются как набор чисел, и к числам применяются статистические и другие методы для получения наилучшей оценки потенциального поля на горизонтальной плоскости анализа.
Данные можно свести к двухмерному ряду Фурье таким образом, чтобы в дополнение к требованию, чтобы данные находились на фиксированной высоте, действовало требование, чтобы каждая линия данных имела 2n элементов данных, чтобы можно было применять метод быстрого преобразования Фурье и чтобы сбор данных осуществлялся в ортогональных направлениях.
Общий вид представления в виде двухмерного ряда Фурье для градиента гравитационного поля можно представить в виде суммы двухмерных пространственных синусоидальных волн в виде:
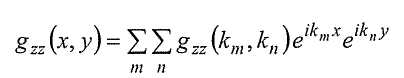
где волновые числа k m, k n связаны с размером области разведки, L x, L y в направлениях x, y соответственно:

Это разложение пригодно только при постоянной высоте. Однако мы позже опишем зависимость коэффициентов g zz(k m,k n) от волнового числа и высоты, которые совместно задают двухмерное преобразование Фурье градиента гравитационного поля.
Подробное описание предпочтительных вариантов осуществления
Данные не требуется обрабатывать согласно описанному выше, если используются свойства гравитационного или магнитного потенциальных полей. Нижеприведенное описание посвящено гравитационному полю, но его легко распространить на магнитные поля.
Прежде всего, выскажем несколько утверждений, касающихся гравитационного поля.
1. Гравитационное поле вне тела можно моделировать во всех отношениях, как если бы оно порождалось материей, целиком расположенной в бесконечно тонком слое на поверхности тела, который в точности повторяет очертания поверхности тела. Такой слой задает эквивалентный источник, т.е. источник гравитации, который создает, по существу, (теоретически в точности) такую же гравитационную сигнатуру, как само тело. Существует много способов задания эквивалентных источников, они могут быть подобны вышеописанным или могут быть строго горизонтальными, они могут полностью или частично находиться над или под поверхностью земли или располагаться иным образом, но все они имеют одно и то же свойство, а именно они генерируют такое же гравитационное поле, как земля. Дополнительную информацию можно найти в книге R.J. Blakely, "Potential Theory in Gravity and Magnetic Applications", Cambridge University Press, 1995.
2. Гравитационное поле вне тела также можно уникальным образом записать в виде последовательности модифицированных двухмерных базисных функций Фурье, которая пригодна для всех позиций вне тела. Эта функция является явно выраженной гармонической функцией и воспроизведена ниже. Ее форма является самой общей и может представлять любое возможное распределение массы в теле.
Согласно предпочтительным вариантам осуществления мы измеряет G zz как функцию позиции r measure с использованием гравитационного градиентометра и работаем с ней без необходимости генерировать другие элементы тензора градиента гравитационного поля. Это можно использовать для генерации представления нижележащего распределения массы. Здесь мы опишем два метода, которые можно применять, а именно метод эквивалентного источника и метод модифицированных базисных функций Фурье. Из вышеупомянутой теоремы Грина следует, что нижележащее распределение массы можно вывести, в принципе, из G zz, хотя в описанных здесь методах теорема Грина не используется в явном виде.
Метод эквивалентного источника
В этом варианте осуществления поверхность района разведки разбивается на малые участки со стороной обычно порядка 50 м - они называются пластинки (далее массивные элементы). Нетрудно непосредственно вычислить гравитационное поле каждой пластинки Blakely (там же), масса которой регулируется до тех пор, пока не будет получено наилучшее общее совпадение с данными измерений. Это определение массы производится посредством стандартной процедуры аппроксимации методом наименьших квадратов. Аппроксимация осуществляется путем сопоставления данных в истинной позиции измерения с гравитационным полем, генерируемым предложенным эквивалентным источником в тех же самых истинных позициях измерения. Этот процесс математически строг и не предполагает никаких искусственных регулировок данных для их согласования с горизонтальной прямоугольной областью разведки.
После получения такой аппроксимации она рассматривается как первичный набор данных. В ходе всего последующего анализа для определения геологической структуры осуществляется сравнение и минимизация различий между гравитационным полем, которое генерировала бы любая данная геологическая структура, с полем, генерируемым эквивалентным источником. Одно реальное преимущество метода в том, что наилучшая аппроксимация исходит из распределения массы, хотя и искусственного, и потому решение наилучшей аппроксимации автоматически будет удовлетворять уравнению Лапласа. В этом состоит отличие от вышеописанного традиционного метода, который создает численную наилучшую аппроксимацию, но не налагает дополнительное ограничение, что данные должны удовлетворять уравнению Лапласа, т.е. что она должна исходить из реального распределения массы.
Метод эквивалентного источника не обязан использовать поверхность, согласованную с топографией, он может использовать источники, которые покрывают любую поверхность, которая может находиться на постоянной высоте, выше или ниже истинной поверхности земли, может пересекать истинную поверхность земли и т.д. Выбор поверхности, соответствующей топографии, скорее всего, приведет к меньшему варьированию массы отдельных пластинок, но общий результат, в принципе, не будет сильно отличаться для любого разумного выбора поверхности.
Аналогично, пластинки могут быть любого размера и любой формы, они даже не обязаны быть одного размера - действительно, анализ будет эффективнее, если допустить изменение их размера и геометрии в зависимости от того, насколько быстро изменяется топография на каждом участке. Математическая сложность процесса определяется исключительно количеством используемых пластинок и тем, сколько из этих пластинок используется при анализе в каждой позиции в области разведки. Одно преимущество этого метода в том, что для некоторых составляющих гравитационного поля или градиента гравитационного поля можно использовать только пластинки на участке элемента данных, и это значительно снижает сложность анализа. Ясно, что этот анализ осуществляется в пространстве.
После генерации эквивалентного источника можно прогнозировать любую производную скалярного потенциала гравитационного поля на любой поверхности путем прямого вычисления. Этот процесс полезен как с точки зрения анализа, так и с точки зрения визуализации.
В частности, с учетом массы каждого элемента поверхности прямое вычисление используется для прогнозирования значения, которое получила бы измеренная величина в каждой точке измерения, если бы эта величина была составляющей вектора гравитационного поля или тензора градиента гравитационного поля. В общем случае оно получается суммированием показанной ниже формы. Здесь мы используем gg для обозначения измеренной величины, которая, как указано выше, является G zz в некоторых предпочтительных вариантах осуществления.
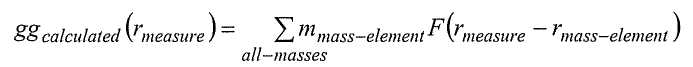
В вышеприведенном Уравнении F обозначает функцию Грина (Blakely, там же, на стр. 185, включена посредством ссылки) и r mass-element задает положение массивного элемента (например, его центра тяжести или какой-либо другой заданной точки). Функция F является стандартной и известна специалистам в данной области техники (и может быть выведена для любой геометрии массивных элементов). Например, функция Грина F для прямоугольной призмы задана в Blakely, там же, на стр. 187, включена посредством ссылки; она имеет 8 членов, каждый из которых соответствует вершине призмы.
В связи с этим соотношением важно указать, что функция "F" известна, а масса каждого элемента - нет. Вычисленное значение в общем случае не будет совпадать с измеренным значением, и согласно одному подходу мы составляем следующую сумму:
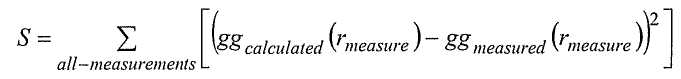
Величина S в итоге задает суммарную квадратическую ошибку S (шум и ошибки моделирования), и, минимизируя ее, можно найти наилучшую аппроксимацию gg calculated. Это можно делать посредством стандартных процедур, например с использованием Matlab (RTM).
Обобщая вышеприведенное доказательство, для величины S неизвестными являются только фактические массы всех массивных элементов и, конечно, шум измерения, связанный с измерением в каждой точке. Наилучшая аппроксимация, т.е. наилучшая оценка значений этих массивных элементов, получается, если потребовать, чтобы S было минимальным в отношении вариаций массы каждого элемента. После получения правильных коэффициентов величина S является просто суммой квадратов шумовых членов, связанных с каждым измерением, и это минимальное значение, которое может принимать S. Дифференцируя S по массе каждого массивного элемента, т.е. первая производная S по m mass-element должна быть равна нулю для каждого массивного элемента. В результате получается система уравнений, в которой переменными являются только массы всех массивных элементов поверхности и где количество уравнения равно количеству массивных элементов, участвующих в процедуре аппроксимации. Эту систему уравнений удобно представить в виде матрицы и решать относительно значений массивных элементов поверхности. Поскольку количество измерений обычно много больше количества уравнений в системе (т.е. количества массивных элементов), например, по меньшей мере, в пять или десять раз больше, система уравнений является избыточно ограниченной. Это полезно, поскольку значения массивных элементов поверхности ни в коем случае не будут соответствовать шуму; вместо процедуры оптимизации для определения значений массивных элементов поверхности используется, например, аппроксимация методом наименьших квадратов, что позволяет понизить шум. Кроме того, благодаря использованию физической модели гравитационного поля (реальных массивных элементов) уравнения подчиняются уравнению Лапласа, что позволяет аппроксимировать гравитационное поле, а не шум.
На практике массивными элементами, удаленными более чем на заданное расстояние, можно фактически пренебречь, например, взвешивая массивные элементы согласно расстоянию и задавая вес, равный нулю, за пределами порогового расстояния. Это пороговое расстояние обычно составляет несколько километров, например в пределах от 1 до 10 километров, хотя оно зависит в некоторой степени от географии (например, может потребоваться увеличить расстояние для охвата находящейся неподалеку большой горы). Результатом взвешивания массивных элементов для пренебрежения теми из них, которые располагаются дальше порогового расстояния, является то, что матрица, представляющая различие между вычисленными и измеренными значениями, оказывается разреженной матрицей. Это полезно, поскольку такая матрица может содержать, например, от 100K до 500K элементов данных, и затраты на обработку значительно снижаются, если большинство ее элементов будут равны нулю.
Специалисту ясно, что заданная выше величина S является всего лишь одним вариантом подгонки расчетных данных к данным измерений, и существует много других вариантов. Когда плоскость для эквивалентной поверхности для массивных элементов задана, независимыми параметрами являются массы массивных элементов (поскольку функция расстояния известна); специалисту ясно, что существует много численных методов, которые можно применять для аппроксимации этих независимых параметров, включая, например, итерационный числовой поиск. Один метод, оказавшийся полезным на практике, состоит в использовании разновидности Уравнения 2, в которой вместо квадратичной функции используется модуль.
После нахождения массивных элементов прямое вычисление (т.е. суммирование вкладов массивных элементов) позволяет найти другие составляющие скалярного потенциала и, путем дифференцирования, другие составляющие G. Полученные значения G можно сравнивать с геологической моделью (именуемой здесь "интерпретацией") для определения нижележащей геологической структуры.
Метод модифицированных базисных функций Фурье
Во втором варианте осуществления способа применяется метод модифицированных базисных функций Фурье. Согласно этому методу для представления данных измерений используется двухмерное разложение в ряд Фурье, но каждый двухмерный коэффициент A
mn каждой составляющей (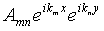 ) двухмерного преобразования Фурье гравитационного поля переписан в виде произведения коэффициента, не зависящего от позиции (C
mn) и высотно-зависимого коэффициента (
) двухмерного преобразования Фурье гравитационного поля переписан в виде произведения коэффициента, не зависящего от позиции (C
mn) и высотно-зависимого коэффициента ( ). Т.е.
). Т.е. 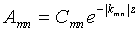 . В явном виде можно записать гравитационное поле любого распределения массы в форме
. В явном виде можно записать гравитационное поле любого распределения массы в форме
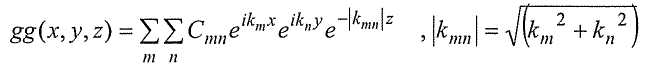
На языке преобразований Фурье A mn - это двухмерное преобразование Фурье гравитационного поля. Это представление является самым общим, и каждая составляющая разложения, представляющего гравитационное поле в явном виде, подчиняется уравнению Лапласа (при дифференцировании множителей высотно-зависимого коэффициента и сокращении двухмерных составляющих). Таким образом, выявлена высотная зависимость каждого коэффициента Фурье, а также ясно, что представление гравитационного поля, обеспечиваемое знанием коэффициентов C mn, позволяет полностью определить гравитационное поле в любой точке пространства, где нет массы. Разложение, предусмотренное этим модифицированным рядом Фурье, можно обрезать в той или иной точке, в зависимости от нужной точности представления.
В позиции r измеренное потенциальное поле (гравитационное поле или градиент гравитационного поля) известно, и для конкретной пары значений k
m и k
n, известных как волновые числа, значение каждой базисной функции модифицированного ряда Фурье 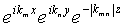 также известно. Каждое волновое число выражает гармоническое пространственное изменение базисной функции Фурье, например, каждый коэффициент с данным волновым числом k
m
=2π/λm будет периодически изменяться в пространстве с периодом λm. Дополнительное свойство метода Фурье состоит в том, что для каждого из независимых направлений каждое волновое число будет целым кратным минимального волнового числа, которое соответствует длине волны, в общем случае эквивалентной размеру области разведки.
также известно. Каждое волновое число выражает гармоническое пространственное изменение базисной функции Фурье, например, каждый коэффициент с данным волновым числом k
m
=2π/λm будет периодически изменяться в пространстве с периодом λm. Дополнительное свойство метода Фурье состоит в том, что для каждого из независимых направлений каждое волновое число будет целым кратным минимального волнового числа, которое соответствует длине волны, в общем случае эквивалентной размеру области разведки.
Можно применять другие разложения, например по сферическим гармоникам, которые полезны для более обширных областей, в частности, когда кривизной земли нельзя пренебречь.
В общем случае коэффициенты разложения определяются практически так же, как описано выше для метода эквивалентного источника. Выбрав максимальную длину волны, представляющую интерес, для каждого направления и ориентацию и начало отсчета системы координат для измерения, можно определить значение базисных функций в каждой точке пространства. После этого та же самая функция квадратов разностей S вычисляется для измеренной величины, и наилучшие значения коэффициентов C mn определяются путем минимизации такой функции по отношению к вариациям C mn. Таким образом, как и в первом варианте осуществления, описанном выше, формируется система уравнений, которую можно решить относительно коэффициентов разложения в ряд Фурье. Эти коэффициенты затем можно использовать для определения (путем прямого вычисления) гравитационного поля или градиента гравитационного поля на любой двухмерной поверхности, которую нужно картографировать. Будет показано, что в этом (и предыдущем) варианте осуществления данные можно выбирать произвольным образом, поскольку элементы данных фактически не связаны между собой - все, что необходимо, это набор измерений и соответствующих (x, y, z) позиций, чтобы иметь возможность определения гравитационного поля или градиента гравитационного поля на любом другом наборе точек или действительно на плоскости, то есть карте. Кроме того, отсюда следует, что нет необходимости забивать данные измерений для построения прямоугольника. В принципе, элементы данных можно рассматривать как участок произвольной формы двухмерной области максимальных размеров, определяемых максимальными длинами волны для разложения в ряд Фурье в направлениях x и y (хотя, как можно видеть, данные измерений не обязаны лежать на двухмерной поверхности). Отсюда следует, что значения km и k n можно выбирать независимо от размеров области разведки (здесь k - волновое число, т.е. 2π/λ, тогда как при традиционной разведке максимальная длина волны должна соответствовать длине или ширине прямоугольной области разведки).
В частности, идея за пределами курса рядов Фурье состоит в решении задачи, выраженной Уравнением (1), в области Фурье, а не в пространственной области. Далее мы будем предполагать, что g zz - это измеренная величина (также обозначаемая выше как G zz).
Гравитационное поле любого тела или распределения массы можно выразить в самом общем виде:
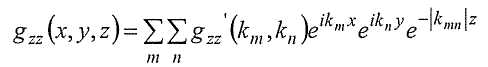
где
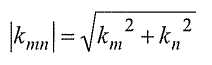
В Уравнении (3) коэффициенты g zz '(k m,k n) формально не зависят от высоты и волнового числа, они зависят только от исследуемой геологии. Обратите внимание на формальную схожесть Уравнения (3) с общим видом представления в виде двухмерного ряда Фурье, приведенным выше. Выражения идентичны, что нам и нужно, только если
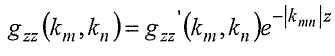
Наблюдается сильная зависимость от высоты и волнового числа стандартных преобразований Фурье, т.е. коэффициентов g zz′(k m,k n). Вот почему нецелесообразно с практической точки зрения осуществлять стандартное преобразование Фурье данных, собранных при разведке с переменной высотой. Также понятно, почему невозможно пересчитывать "вверх" данные от точки к точке; пересчет вверх работает только, если известен точный частотный состав величины. Также можно видеть, что каждая составляющая разложения Уравнения (3) имеет отдельную высотную зависимость.
Однако описанный здесь метод модифицированных базисных функций Фурье не пытается осуществлять преобразование Фурье само по себе - это, как описано выше, не математический подход.
Данный процесс предусматривает, что все элементы данных обрабатываются аналогично и что величине 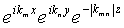 можно присвоить значение, которое является точным, когда позиция измерения известна. Дело в том, что мы выбираем значения k, как описано ниже, и r(x,y,z) известно. По существу, выбираются максимальное и минимальное значения для k
x и k
y, например, путем построения вокруг (или немного внутри) района разведки воображаемого прямоугольника, который приблизительно представляет район разведки, и размеры прямоугольника задают максимальную длину волны (значения k). Минимальные значения можно выбирать, например, в зависимости от приближенной средней высоты разведки, например кратного средней высоты разведки между 0.5 и 3. Дело в том, что масштаб длин вариаций зависит от высоты разведки, и, в общем случае, минимальное значение выбирается для представления вариаций, которые ожидаются или наблюдаются на средней высоте разведки, превышающие пороговую значимость, с учетом вычислительной мощности. Для иллюстрации идеи вышеупомянутый член exp(-kz), где z= высота разведки, уменьшен приблизительно в e-6 раз для длин волны, равных высоте разведки.
можно присвоить значение, которое является точным, когда позиция измерения известна. Дело в том, что мы выбираем значения k, как описано ниже, и r(x,y,z) известно. По существу, выбираются максимальное и минимальное значения для k
x и k
y, например, путем построения вокруг (или немного внутри) района разведки воображаемого прямоугольника, который приблизительно представляет район разведки, и размеры прямоугольника задают максимальную длину волны (значения k). Минимальные значения можно выбирать, например, в зависимости от приближенной средней высоты разведки, например кратного средней высоты разведки между 0.5 и 3. Дело в том, что масштаб длин вариаций зависит от высоты разведки, и, в общем случае, минимальное значение выбирается для представления вариаций, которые ожидаются или наблюдаются на средней высоте разведки, превышающие пороговую значимость, с учетом вычислительной мощности. Для иллюстрации идеи вышеупомянутый член exp(-kz), где z= высота разведки, уменьшен приблизительно в e-6 раз для длин волны, равных высоте разведки.
Тогда мы имеем систему уравнений, базирующихся на Уравнении (3) в количестве, равном количеству используемых элементов данных, благодаря чему измеренные значения градиента гравитационного поля, включающие в себя шум, и величина 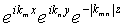 известны в каждой точке измерения данных. После этого неизвестными являются коэффициенты g
zz′(k
m,k
n), и процесс аппроксимации однозначно становится только процессом получения наилучших оценок коэффициентов.
известны в каждой точке измерения данных. После этого неизвестными являются коэффициенты g
zz′(k
m,k
n), и процесс аппроксимации однозначно становится только процессом получения наилучших оценок коэффициентов.
Согласно Уравнению (3) это дает вычисленные g zz, и по аналогии с Уравнением (1) можно вывести вариант Уравнения (2). Это обеспечивает систему уравнений в количестве, равном количеству неизвестных, которые в этом случае являются значениями коэффициентов g′zz. Это делается таким же образом, как в методе эквивалентного источника, т.е. коэффициенты определяются посредством процедуры аппроксимации методом наименьших квадратов. Важный момент состоит в том, что в этом виде коэффициенты g zz′(k m,k n) не имеют явной зависимости от высоты и волнового числа.
Этот метод имеет аналогичное преимущество перед распределением эквивалентных источников в том, что решение является гармоническим, поскольку каждый член в разложении Уравнения (3) явно является гармоническим. Аппаратурный шум не является гармоническим, поэтому этот метод, даже сам по себе, имеет возможность существенно устранять шум в процессе.
Этот метод, как и метод эквивалентного источника, не нуждается в привязке данных к регулярной сетке. Одно неожиданное дополнительное преимущество метода состоит в том, что он в отличие от самого по себе метода рядов Фурье не ограничен длинами волны, которые можно использовать для анализа. Это неявный результат, зависящий от пригодности метода модифицированных рядов Фурье, в самом общем выражении, к любой области, могущей представлять интерес. Процесс предусматривает выбор максимальных длин волны, представляющих интерес, в двух ортогональных направлениях плоскости разведки, что приводит к максимальной длине волны, представляющей интерес, в каждом направлении, λx max, λy max. Эта длина волны отражает минимальное волновое число в каждом направлении, определенное как
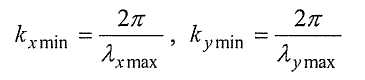
Все волновые числа в разложении Уравнения (3) являются их целыми кратными. Таким образом:
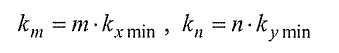
Дополнительное преимущество состоит в том, что этот метод не обязан иметь степень 2 в качестве количества элементов данных для использования в анализе каждой линии, что необходимо согласно методу быстрого преобразования Фурье. Это избавляет от необходимости набивать данные для достижения такой ситуации.
В отличие от метода эквивалентного источника, где анализ осуществляется в пространственной области, анализ рядов Фурье осуществляется в частотной области. Под частотой мы понимаем пространственную частоту, которая указывает, сколько периодов данная составляющая имеет на протяжении единичной меры расстояния, и это выражается вышеописанными волновыми числами - чем больше волновое число, тем больше количество периодов на единицу расстояния и тем короче расстояние повторения. Предложенный метод не работает в явном виде в любой области, он лишь позволяет составить систему уравнений, из которой можно вычислить наилучшие оценки неизвестных.
Методы Фурье в практическом применении обычно требуют измерения в прямоугольной области, и минимальные волновые числа представляют наибольшие длины волны, которые можно использовать для представления данных - наибольшие длины волны явно выражают размер области разведки в каждом направлении. Когда область разведки не удовлетворяет этому критерию, данные обычно формируются в процессе, именуемом набивкой, таким образом, чтобы преобразованный набор данных соответствовал ему.
Метод модифицированных базисных функций Фурье имеет много преимуществ по сравнению с традиционным Фурье-анализом. Например:
1. Вовсе не обязательно осуществлять преобразования Фурье - мы знаем, что будет стандартный формат, и коэффициенты в разложении Уравнения (3) нужно определять посредством процесса наилучшей аппроксимации, а не путем вычисления преобразований Фурье в явном виде.
2. Волновые числа, подлежащие использованию, не обязаны быть целыми кратными размера или формы области разведки. Дело в том, что нам известна форма преобразования Фурье, и мы определяем коэффициенты посредством вышеописанного процесса наилучшей аппроксимации.
Возможно, наиболее впечатляющий результат состоит в том, что данные разведки можно собирать на непостоянной высоте. Традиционно используемые двухмерные преобразования Фурье нужно осуществлять на постоянной высоте, и преобразования Фурье, включенные в Уравнение (3), сильно зависят от высоты. Эта функциональная зависимость в явном виде выражена в Уравнении (3), и коэффициенты g zz′(k m,k n) уже не зависят от высоты.
Обзор
Варианты осуществления описанных здесь методов позволяют в полной мере использовать фактические данные измерений, и оба являются математически строгими; они не повреждают данные за счет привязки их к регулярной сетке постоянной высоты, генерируемые решения являются гармоническими, и данные не обязаны иметь степень двойки в качестве количества элементов данных в двух ортогональных направлениях.
В общем случае процесс предусматривает использование всех данных из каждого элемента данных и пытается генерировать эквивалентное поверхностное распределение массы или набор коэффициентов модифицированного ряда Фурье с наилучшей аппроксимацией данных в области разведки.
В этом состоит принципиальное отличие от метода обработки, в котором предполагается, что данные собираются с фиксированной высоты, даже если это не соответствует действительности, и новые данные генерируются из данных измерений с единственной целью генерации данных на регулярной двухмерной сетке. Этот набор данных "привязанный к сетке" присваивает значения данным измерений, которые не измерены и назначены позициям, где самолет не собирал данные, хотя это неправильно.
Ошибки, возникающие в таком процессе, с большой степенью вероятности приобретают значительные размеры, если в данной ситуации аппроксимация фиксированной высоты слаба. Они также велики, если пилот пытается лететь как можно ближе к земле для максимизации сигнала от малых особенностей, расположенных сравнительно близко к поверхности земли - эти особенности обуславливают возникновение коротковолновых составляющих в разложении в модифицированный ряд Фурье. Наконец, ошибки не столь велики при наличии большого аппаратурного шума, поскольку ошибки, связанные с экстраполяцией меньше, чем ошибки, связанные с прибором.
На Фиг. 1 показан пример самолета 10 для проведения разведки потенциального поля для получения данных для обработки в соответствии с вышеописанным методом. Самолет 10 содержит инерциальную платформу 12, на которой установлен гравитационный градиентометр 14, который выдает данные разведки потенциального поля на систему 16 сбора данных. Инерциальная платформа 14 жестко связана с инерциальным измерительным блоком (IMU) 18, который также выдает на систему 16 сбора данных данные, обычно содержащие данные ориентации (например, данные тангажа, крена и рыскания), данные угловой скорости и углового ускорения и данные ускорения самолета. Самолет также оборудован дифференциальной системой GPS 20 и системой LIDAR 22 или аналогичной системой для обеспечения данных о высоте самолета над нижележащей местностью. Самолет 10 также может быть оборудован другой аппаратурой 24, например магнитометром, системой TDEM и/или гиперспектральной системой построения изображения, которые опять же подают свои сигналы на систему сбора данных. Система 16 сбора данных также принимает сигналы от обычной аппаратуры 26 самолета, которые могут содержать, например, данные альтиметра, скорости относительно воздуха и/или земли и пр. Система 16 сбора данных может обеспечивать некоторую начальную предварительную обработку данных, например, для корректировки данных лидара для движения самолета и/или для объединения данных из IMU 18 и DGPS 20. Система 16 сбора данных может быть снабжена линией связи 16a и/или энергонезависимым хранилищем 16b для обеспечения хранения собранных данных потенциального поля и позиции для дальнейшей обработки. Также может быть предусмотрен сетевой интерфейс (не показан).
Обработка данных для генерации картографических данных для разведки потенциального поля обычно (но не обязательно) осуществляется в автономном режиме, иногда не в той стране, где были собраны данные разведки. Показанная система 50 обработки данных содержит процессор 52, подключенный к устройству 54 хранения данных и кодов, системе ввода/вывода 56 (например, содержащей интерфейсы для сети и/или носителей информации и/или других средств связи), и к пользовательскому интерфейсу 58, например, содержащему клавиатуру и/или мышь. Код и/или данные, хранящиеся в памяти 54, могут передаваться на сменный носитель информации 60. В ходе работы данные включают в себя данные, собранные в ходе разведки потенциального поля, и код содержит код для обработки этих данных для генерации картографических данных, например, в соответствии с процедурой, показанной на Фиг. 2, описанной ниже.
На Фиг. 2 показана иллюстративная процедура, реализуемая на процессоре данных, который может, согласно вариантам осуществления, содержать компьютерную систему общего назначения для обработки данных авиационной разведки в соответствии с вышеописанными методами. Таким образом, на этапе S200 процедура вводит данные измерений потенциального поля, например гравитационного градиентометра, и соответствующие данные трехмерной позиции. В необязательном порядке на этапе S200a может применяться некоторая предварительная обработка, например, для удаления аномалий и/или для снижения (или повышения) или выбора данных, подлежащих обработке.
На этапе S202 процедура строит избыточно ограниченную систему уравнений, связывающую данные потенциального поля, данные трехмерной позиции и набор параметров картографирования поля. В частности, процедура строит систему уравнений, которые соотносят измерение потенциального поля с функцией соответствующей трехмерной позиции (s(r - r′)), умноженной на параметр картографирования поля. Предпочтительно процедура использует представление потенциального поля, в частности функцию позиции, которое подчиняется уравнению Лапласа, например, посредством вышеописанного эквивалентного источника или модифицированной базисной функции Фурье. В необязательном порядке на этом этапе (S204) могут быть включены данные поправки на рельеф. Процедура решает эту систему уравнений (S206), например, традиционным методом наименьших квадратов для определения, по существу, самосогласованного набора параметров картографирования поля. Они фактически задают карту разведанного потенциального поля и поэтому составляют один предпочтительный выходной сигнал процедуры. Затем (S208) можно осуществлять прямое вычисление с использованием этих параметров для генерации нужной карты потенциального поля на поверхности, например поверхности, аппроксимирующей участок земли, где и когда это требуется.
Для традиционной авиационной гравиметрической разведки не требовалось летать очень близко к земле, поскольку приборы были относительно нечувствительными и дополнительно были настроены на восприятие только больших длин волны. Разведку проводили на более или менее постоянной высоте или на высоте, на которой разумно было бы предполагать, что данные приходят с постоянной высоты.
Однако для любой разведки с использованием новых, высокочувствительных, систем гравитационного градиентометра, которые также способны разрешать гораздо более короткие волны, желательно летать как можно ближе к земле для максимизации сигнала, в частности, содержащегося в коротковолновых составляющих. Маловероятно, чтоб такие типы разведки адекватно удовлетворяли критерию постоянной высоты, но все современные методы анализа основаны на том, что это так и есть.
Однако можно использовать метод эквивалентного источника или модифицированного преобразования Фурье для обработки данных и объединять его с принципиально новым методом полета для разведки потенциального поля.
В самом общем виде метод предусматривает облет полностью разрозненного набора линий разведки, сбор данных из линий и с использованием данных и абсолютной позиции их сбора получение параметров наилучшей аппроксимации к массам пластинок эквивалентного источника или к составляющим модифицированного преобразования Фурье.
Линии разведки не обязаны быть прямыми, не обязаны быть горизонтальными, не обязаны проходить в ортогональных направлениях, линии в приблизительно ортогональных направлениях не обязаны пересекаться. В идеале маршруты полета должны по возможности точно следовать рельефу без каких-либо других ограничений. Конечно, возможен любой другой метод полета, занимающий промежуточное положение между этим методом разведывательного полета и методами, предусматривающими пересекающиеся под прямым углом маршруты полета на постоянной высоте, и любая разведка может включать в себя элементы любого метода полета. Мощь и математическая точность аналитических методов делает эти полетные процедуры возможными.
Очевидно, что данные, собранные с использованием этого метода полета, можно дополнительно обрабатывать до и после использования любого из вышеописанных процессов. Можно использовать любые существующие методы понижения шума или объединения данных. Топографические эффекты можно в значительной степени устранять с использованием высококачественных DEM, в действительности можно использовать любые процессы, связанные с более традиционной обработкой данных.
Самолет может представлять собой любой самолет для геофизической разведки, способный летать на малых высотах. На практике, на самолет будет загружено столько оборудования, сколько он сможет нести, исходя из требований безопасности и разумного времени полета. Выбранное оборудование будет измерять сигналы, связанные с геологией, и сигналы, связанные с плоским движением. Последние используются, в частности, для гравиметрической разведки, для корректировки измерений, произведенных аппаратурой, выбранной для измерения геологических свойств.
На Фиг. 3 показана логическая блок-схема процедуры для генерации данных авиационной разведки, задающих схему полета для разведки потенциального поля, результаты которой можно обрабатывать с использованием вышеописанных методов.
На этапе S300 процедура вводит данные рельефа и, например, через пользовательский интерфейс данные, задающие нужный район разведки. Затем на этапе S302 процедура строит огибающую поверхность поверх выбранного участка рельефа для определения схемы разведывательного полета, содержащей набор маршрутов полета. Построение огибающей поверхности может подлежать ограничению на максимальный наклон в любом направлении на поверхности и первоначально маршруты полета могут следовать регулярной схеме. Затем, однако, на этапе S306 процедура регулирует поверхность и/или маршруты полета для адаптации маршрутов к поверхности. Здесь вступает в силу ограничение на максимальную скорость подъема/спуска (определенную на основании характеристик самолета), но его нужно применять только вдоль маршрута. Таким образом, в других направлениях, например, ортогональных к маршруту, наклон поверхности может превышать значение, заданное этим ограничением. Дополнительно или альтернативно, на этапе S308 процедура регулирует поверхность и/или маршруты полета для более точной адаптации маршрутов к поверхности нижележащего рельефа. Для этого необходимо допустить, чтобы маршруты могли быть криволинейными, непараллельными, значительно отличающимися по высоте в точке пересечения (например, более чем на 50 метров, 100 метров или 200 метров), лежащими на поверхности, наклоны которых превышают максимальную скорость подъема/спуска самолета, или не лежащими на одной поверхности. После проведения такой адаптации процедура выводит данные авиационной разведки (S310), задающие определенный набор маршрутов полета. Эти данные пилот может затем использовать для пилотирования самолета в соответствии с определенной схемой разведки.
Очевидно, что в отличие от традиционных систем привязки к сетке, такие методы позволяют задавать маршруты полета вдоль долин, вблизи дна долины, где другие методы будут ограничены минимальным приближением самолета к земле в такой ситуации, вследствие сочетания схемы, привязанной к сетке, и максимальной скорости подъема/спуска самолета. Также очевидно, что в общем случае можно задавать набор маршрутов, следующих рельефу, поскольку описанные здесь методы позволяют обрабатывать данные такой авиационной разведки. Преимущество состоит в том, что данные, полученные такими методами, значительно более точны благодаря значительной скорости спада амплитуды возмущений потенциального поля с высотой над поверхностью земли.
На Фиг. 4 показан пример маршрута авиационной разведки, данные из которого можно обрабатывать вышеописанными методами. На фигуре показаны примеры типов маршрутов, по которым эти методы позволяют летать.
На плоских участках все стратегии полета сходятся, но на холмистых или действительно гористых участках предложенный метод проявляет значительные преимущества. На таких участках каждая часть района разведки анализируется относительно независимо, и вырабатывается стратегия полетов над таким участком.
В таких ситуациях район разведки анализируется на предмет его топографии, и вырабатывается стратегия авиационной разведки на основании геологических целей, представляющих интерес, и того, как можно облететь район, чтобы наилучшим образом идентифицировать эти геологические цели. Если, как в обычном случае, необходимо лететь как можно ближе к земле во всех точках разведки, то линии разведки станут разрозненными с относительно малой связностью. Самолет может только подниматься и снижаться с данной скоростью, и необходим соответствующий клиренс, чтобы безопасно проходить над гребнями гор. Линии полета, идущие "вниз" или "вверх" по долинам, не будут пересекаться с линиями, "пересекающими" долины, или будут пересекаться с гораздо меньшим количеством перекрещиваний. Перекрещивания обычно считаются важными для избавления от низкочастотного шума (часто называемого дрейфом), и это еще одно соображение, которое нужно принимать во внимание при проектировании разведки.
Оборудование, желательное для стандартной разведки, включает в себя гравитационный градиентометр; гравиметр; инерциальный измерительный блок (IMU); GPS; лидар; магнитный градиентометр; магнитометр; альтиметр; радиолокационный высотомер; барометр; спектрометр; гиперспектральный построитель изображений; EM; TDEM; навигационное ПО; оборудование сбора данных.
Когда выработана стратегия полета, производится фактическая разведка и сбор данных. При анализе используются реальные данные из системы измерения потенциального поля, эти данные корректируются на любые известные артефакты, связанные с измерениями (например, наклон самолета, ускорения самолета, артефакты давления и т.д.), и затем данные анализируются вышеописанным способом. Полет осуществляется на малых высотах ввиду сильной высотной зависимости измеренного сигнала, в частности сигналов, имеющих малые длины волны, т.е. большие волновые числа.
Несомненно, специалист может предложить много других эффективных альтернатив. Следует понимать, что изобретение не ограничивается описанными вариантами осуществления и охватывает модификации, очевидные для специалистов в данной области, в рамках сущности и объема прилагаемой формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ С ИСПОЛЬЗОВАНИЕМ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА (БПЛА) | 2018 |
|
RU2697474C1 |
| ОБРАБОТКА ДАННЫХ ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ | 2008 |
|
RU2486549C2 |
| СИСТЕМЫ ПОПРАВКИ НА РЕЛЬЕФ МЕСТНОСТИ | 2007 |
|
RU2442193C2 |
| АЭРОГРАВИМЕТРИЧЕСКИЙ КОМПЛЕКС | 1996 |
|
RU2090911C1 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ ИЗМЕРЕНИЯ ГРАВИТАЦИИ | 1995 |
|
RU2144686C1 |
| СПОСОБ МНОГОКОМПОНЕНТНОГО ГРАВИМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ ГЕОЛОГИЧЕСКОЙ СРЕДЫ | 2007 |
|
RU2364895C1 |
| ДАТЧИК ГРАВИТАЦИИ И ЕГО ПРИМЕНЕНИЕ ДЛЯ РАЗВЕДКИ УГЛЕВОДОРОДОВ | 2013 |
|
RU2608632C2 |
| БЕСПИЛОТНЫЙ МОБИЛЬНЫЙ КОМПЛЕКС | 2011 |
|
RU2583851C2 |
| СИСТЕМЫ ВНЕСЕНИЯ ПОПРАВОК НА РЕЛЬЕФ МЕСТНОСТИ | 2008 |
|
RU2468394C2 |
| СПОСОБ ИМИТАЦИИ РАДИОСИГНАЛА, ОТРАЖЕННОГО ОТ ПРОСТРАНСТВЕННО РАСПРЕДЕЛЕННОЙ ДИНАМИЧЕСКОЙ РАДИОФИЗИЧЕСКОЙ СЦЕНЫ, В РЕАЛЬНОМ ВРЕМЕНИ | 2008 |
|
RU2386143C2 |
Данное изобретение относится к усовершенствованным методам обработки данных измерений потенциального поля, полученных при авиационной разведке, например гравиметрической разведке, и к усовершенствованным методам сбора данных, которые обеспечиваются за счет усовершенствованных методов обработки данных. Здесь описан способ обработки данных измерений потенциального поля, полученных при разведке потенциального поля земли для определения картографических данных для картографирования поля, способ содержит этапы, на которых вводят данные измерений потенциального поля, причем данные измерений потенциального поля содержат данные, задающие совокупность измерений потенциального поля и соответствующих позиций, причем каждая позиция задает позицию измерения потенциального поля в трехмерном пространстве; определяют совокупность соотношений между измерениями потенциального поля и позициями, причем каждое соотношение соотносит измерение потенциального поля с функцией соответствующей позиции в трехмерном пространстве, умноженной на параметр картографирования поля; и определяют, по существу, самосогласованный набор параметров картографирования поля для совокупности соотношений для определения, таким образом, картографических данных. 12 н. и 17 з.п. ф-лы, 4 ил.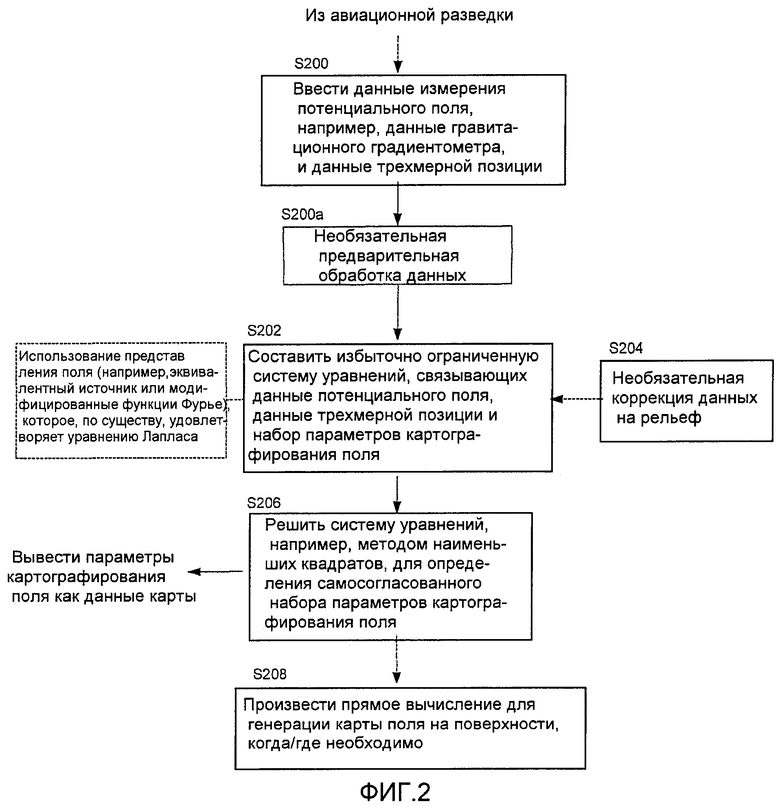
1. Способ проведения разведки потенциального поля земли для определения картографических данных для картографирования поля содержит этапы, на которых
выполняют авиационную гравиметрическую разведку потенциального поля земли в трех измерениях и получают данные измерений потенциального поля;
вводят данные измерений потенциального поля, причем данные измерений потенциального поля содержат данные, задающие совокупность измерений потенциального поля и соответствующих позиций, причем каждая позиция задает позицию измерения потенциального поля в трехмерном пространстве,
определяют совокупность соотношений связывающих измерение потенциального поля с функцией соответствующей позиции в трехмерном пространстве, умноженной на параметр картографирования поля, и
определяют, по существу, самосогласованный набор параметров картографирования поля для совокупности соотношений для определения, таким образом, картографических данных.
2. Способ по п.1, в котором картографические данные содержат набор параметров картографирования поля.
3. Способ по п.1, в котором картографические данные содержат данные, картографирующие поле на поверхности, способ дополнительно содержит этап, на котором определяют поле на поверхности из набора параметров картографирования поля.
4. Способ по п.1, 2 или 3, в котором соотношения содержат совместные уравнения, и в котором на этапе определения параметра картографирования поля решают совместные уравнения.
5. Способ по п.4, в котором количество измерений совокупности потенциального поля больше количества совместных уравнений, и в котором на этапе решения используют процедуру понижения шума.
6. Способ по п.1, 2 или 3, в котором соотношения задают посредством разреженной матрицы и в котором на этапе определения параметров картографирования поля применяют численный метод.
7. Способ по п.1, в котором функция соответствующей позиции, по существу, удовлетворяет уравнению Лапласа.
8. Способ по п.1, в котором поле представляют совокупностью массивных элементов, каждая из которых имеет соответствующую массу и соответствующее положение, в котором каждый параметр картографирования поля содержит положение массы, и в котором функция соответствующего положения представляет собой функцию разности между положением измерения потенциального поля и положением массивного элемента.
9. Способ по п.1, в котором поле представляют гармоническим разложением, имеющим совокупность коэффициентов разложения, и в котором каждый параметр картографирования поля содержит коэффициент разложения.
10. Способ по п.9, в котором коэффициенты в представлении, по существу, не зависят от высоты над землей.
11. Способ по п.1, в котором данные измерений потенциального поля содержат одно или несколько из гравиметрических данных и данных гравитационного градиентометра, и в котором поле представляет гравитационное поле.
12. Носитель, переносящий код управления процессором для реализации способа по п.1.
13. Система обработки данных для обработки данных измерений потенциального поля, полученных при разведке потенциального поля земли для определения картографических данных для картографирования поля, содержит
устройство хранения данных для хранения данных измерений потенциального поля, причем данные измерений потенциального поля содержат данные, задающие совокупность измерений потенциального поля и соответствующих позиций, причем каждая позиция задает позицию измерения потенциального поля в трехмерном пространстве,
устройство хранения программ для хранения кода управления процессором и
процессор, подключенный к устройству хранения данных и устройству хранения программ, для загрузки и выполнения кода управления, причем код содержит код, предписывающий процессору
вводить данные измерений потенциального поля,
определять совокупность соотношений между измерениями потенциального поля и позициями, причем каждое соотношение соотносит измерение потенциального поля с функцией соответствующей позиции в трехмерном пространстве, умноженной на параметр картографирования поля, и
определять, по существу, самосогласованный набор параметров картографирования поля для совокупности соотношений для определения, таким образом, картографических данных.
14. Способ проведения авиационной гравиметрической разведки для обеспечения данных для карты гравитационного поля, в котором выполняют авиационную гравиметрическую разведку потенциального поля земли в трех измерениях и получают данные измерений потенциального поля;
причем данные измерений содержат совокупность измерений гравитационного потенциального поля, с каждым из которых связана позиция измерения в трехмерном пространстве, используют данные измерений для оценки коэффициентов, на которые умножается функция трехмерной позиции в гармоническом разложении для определения, таким образом, представления гравитационного поля в районе разведки для карты гравитационного поля.
15. Способ по п.14, в котором гармоническое разложение содержит разложение в ряд Фурье, и в котором функция трехмерной позиции содержит функцию, имеющую вид, эквивалентный 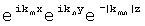 , где x, y и z задают позицию в трехмерном пространстве, km и kn положительны, и
, где x, y и z задают позицию в трехмерном пространстве, km и kn положительны, и 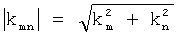 .
.
16. Способ по п.14 или 15, в котором коэффициенты формально не зависят от высоты.
17. Способ проведения авиационной гравиметрической разведки для обеспечения данных для карты гравитационного поля, в котором выполняют авиационную гравиметрическую разведку потенциального поля земли в трех измерениях и получают данные измерений потенциального поля;
причем данные измерений содержат совокупность измерений гравитационного потенциального поля, с каждым из которых связана позиция измерения в трехмерном пространстве,
используют эквивалентного источника представление гравитационного поля, содержащего совокупности массивных элементов, имеющих соответствующую массу и соответствующее положение,
определяют вычисленное значение потенциального поля в каждой позиции измерения;
умножают функцию разности между измеренной позицией и положением массивного элемента на соответствующую массу и
используют данные измерения для оценки масс и совокупности массивных элементов для карты гравитационного поля.
18. Способ картографирования гравитационного поля содержит этапы, на которых
вводят данные измерений, полученные в авиационной гравиметрической разведке, проведенной в трехмерном пространстве, причем данные измерений содержат совокупность измерений гравитационного потенциального поля, с каждым из которых связана позиция измерения в трехмерном пространстве,
определяют совокупность соотношений между измерениями потенциального поля и позициями, причем каждое соотношение соотносит измерение потенциального поля с функцией соответствующей позиции в трехмерном пространстве, умноженной на параметр картографирования поля, и
картографируют гравитационное поле, определяя, по существу, самосогласованный набор параметров картографирования поля для совокупности соотношений.
19. Способ по п.1, дополнительно содержащий этап, на котором разведывают поле с использованием самолета для сбора данных измерений для определения совокупности соотношений, и в котором на этапе разведки облетают набор маршрутов, имеющих одну или несколько из следующих особенностей:
два маршрута пересекаются на высотах, отличающихся, по меньшей мере, на 50 м,
в районе разведки маршруты в одном и том же общем направлении не параллельны более, чем на 5°,
маршруты включают в себя криволинейные маршруты,
маршруты из набора маршрутов, вместе взятые, по существу, не лежат на поверхности,
высоты с расстоянием в разных ортогональных направлениях поверхности отличаются более чем на 5%.
20. Способ по п.14, дополнительно содержащий этап, на котором разведывают поле с использованием самолета для сбора данных измерений для определения совокупности соотношений, и в котором на этапе разведки облетают набор маршрутов, имеющих одну или несколько из следующих особенностей:
два маршрута пересекаются на высотах, отличающихся, по меньшей мере, на 50 м,
в районе разведки маршруты в одном и том же общем направлении не параллельны более, чем на 5°,
маршруты включают в себя криволинейные маршруты,
маршруты из набора маршрутов, вместе взятые, по существу, не лежат на поверхности,
маршруты из набора маршрутов, вместе взятые, задают поверхность, в котором, по меньшей мере, один из маршрутов задает одно из двух ортогональных направления на поверхности, так что скорости изменения высоты с расстоянием в разных ортогональных направлениях поверхности отличаются более чем на 5%.
21. Способ по п.17, дополнительно содержащий этап, на котором разведывают поле с использованием самолета для сбора данных измерений для определения совокупности соотношений, и в котором на этапе разведки облетают набор маршрутов, имеющих одну или несколько из следующих особенностей:
два маршрута пересекаются на высотах, отличающихся, по меньшей мере, на 50 м,
в районе разведки маршруты в одном и том же общем направлении не параллельны более, чем на 5°,
маршруты включают в себя криволинейные маршруты,
маршруты из набора маршрутов, вместе взятые, по существу, не лежат на поверхности,
маршруты из набора маршрутов, вместе взятые, задают поверхность, в котором, по меньшей мере, один из маршрутов задает одно из двух ортогональных направления на поверхности, так что скорости изменения высоты с расстоянием в разных ортогональных направлениях поверхности отличаются более чем на 5%.
22. Способ по п.18, дополнительно содержащий этап, на котором разведывают поле с использованием самолета для сбора данных измерений для определения совокупности соотношений, и в котором на этапе разведки облетают набор маршрутов, имеющих одну или несколько из следующих особенностей:
два маршрута пересекаются на высотах, отличающихся, по меньшей мере, на 50 м,
в районе разведки маршруты в одном и том же общем направлении не параллельны более, чем на 5°,
маршруты включают в себя криволинейные маршруты,
маршруты из набора маршрутов, вместе взятые, по существу, не лежат на поверхности,
маршруты из набора маршрутов, вместе взятые, задают поверхность, в котором, по меньшей мере, один из маршрутов задает одно из двух ортогональных направления на поверхности, так что скорости изменения высоты с расстоянием в разных ортогональных направлениях поверхности отличаются более чем на 5%.
23. Носитель, переносящий код управления процессором для реализации способа по любому из пп.14, 15 и 17-20.
24. Способ проведения авиационной разведки потенциального поля содержит этапы, на которых ведут самолет по набору маршрутов и измеряют данные потенциального поля в точках на маршрутах, в котором набор маршрутов имеет одну или несколько из следующих особенностей:
два маршрута пересекаются на высотах, отличающихся, по меньшей мере, на 50 м,
в районе разведки маршруты в одном и том же общем направлении не параллельны более чем на 5°,
маршруты включают в себя криволинейные маршруты,
маршруты из набора маршрутов, вместе взятые, по существу, не лежат на поверхности,
маршруты из набора маршрутов, вместе взятые, задают поверхность, в котором, по меньшей мере, один из маршрутов задает одно из двух ортогональных направления на поверхности, так что скорости изменения высоты с расстоянием в разных ортогональных направлениях поверхности отличаются более чем на 5%.
25. Носитель данных, переносящий навигационные данные, задающие набор маршрутов авиационной разведки потенциального поля по п.24.
26. Способ генерации данных авиационной разведки содержит этапы, на которых
определяют схему разведывательных полетов путем наложения поверхности на рельеф, подлежащий разведке, в соответствии с условием максимальной скорости подъема/спуска самолета, и
генерируют данные авиационной разведки для совокупности маршрутов, по существу, на поверхности, и
в котором способ дополнительно содержит этап, на котором регулируют поверхность и/или один или несколько маршрутов для снижения высоты одного или нескольких маршрутов, таким образом, чтобы в, по меньшей мере, одном направлении на поверхности, ортогональном маршруту, условие максимальной скорости подъема/спуска было превышено.
27. Способ генерации данных авиационной разведки по п.26, в котором данные авиационной разведки задают способ проведения авиационной разведки потенциального поля содержит этапы, на которых ведут самолет по набору маршрутов и измеряют данные потенциального поля в точках на маршрутах, в котором набор маршрутов имеет одну или несколько из следующих особенностей:
два маршрута пересекаются на высотах, отличающихся, по меньшей мере, на 50 м,
в районе разведки маршруты в одном и том же общем направлении не параллельны более чем на 5°,
маршруты включают в себя криволинейные маршруты,
маршруты из набора маршрутов, вместе взятые, по существу, не лежат на поверхности,
маршруты из набора маршрутов, вместе взятые, задают поверхность, в котором, по меньшей мере, один из маршрутов задает одно из двух ортогональных направления на поверхности, так что скорости изменения высоты с расстоянием в разных ортогональных направлениях поверхности отличаются более чем на 5%.
28. Носитель, переносящий код управления процессором для реализации способа по п.26 или 27.
29. Носитель данных, переносящий данные авиационной разведки по п.26 или 27.
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЗАЛЕЖЕЙ УГЛЕВОДОРОДОВ | 1987 |
|
SU1484122A3 |
| US 5673191 A, 30.09.1997 | |||
| СПОСОБ ДИФФЕРЕНЦИАЛЬНОЙ ЗАЩИТЫ ЭЛЕКТРОУСТАНОВКИ | 2004 |
|
RU2261510C1 |
| US 5602731 A, 11.02.1997 | |||
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
Авторы
Даты
2011-10-20—Публикация
2006-07-17—Подача