Изобретение относится к области связи, в частности к радиотехническим беспроводным коммуникационным системам, а более конкретно к способам приема сигнала в системе передачи, использующей технологию многоантенной приемопередачи.
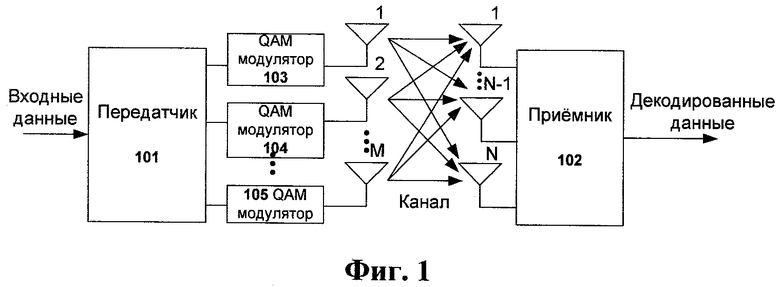
Системы многоантенной приемо-передачи, далее упоминаемые как MIMO (Multiple-In/Multiple-Out), являются сравнительно новым направлением развития технологии в области беспроводных систем связи. Такие системы используют множество передающих и приемных антенн для параллельной передачи сигнала по нескольким пространственно разнесенным каналам в одном и том же диапазоне спектра и демонстрируют высокую спектральную эффективность (см. Фиг.1).
MIMO система в частотной области обычно описывается матричным уравнением:

где Y-N-мерный вектор комплексных значений принятого сигнала, Х - М-мерный вектор переданного комплексного сигнала, з - вектор отсчетов комплексного шума размерностью N×1 с нулевым средним и дисперсией 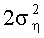
Каждая компонента xi вектора Х может принимать одно из 2К комплексных значений в зависимости от применяемой схемы модуляции. Таким образом, каждая компонента содержит информацию о К переданных бит, т.е. имеем: 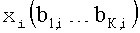
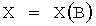
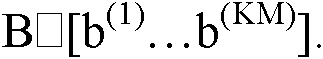
Согласно алгоритму максимального правдоподобия (МП) функция правдоподобия вектора Х вычисляется как:
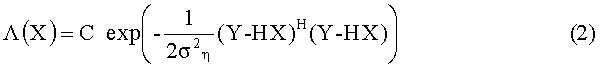
Таким образом, алгоритм МП позволяет определить отношение правдоподобия для каждого бита следующим образом:

Суммирование в (3) осуществляется по всем возможным значениям В, число которых может быть весьма высоким. Таким образом, сложность алгоритма МП может быть чрезмерно большой для высокого ранга матрицы Н и модуляции с большим алфавитом. Требуется учесть все возможные варианты значений Х, что сложно реализовать в случае большого количества антенн и многопозиционной модуляции (модуляции с большим алфавитом). Так для 4-х передающих антенн (4 параллельных информационных потока) и модуляции QAM-16 в приемнике необходимо проанализировать 65536 возможных варианта векторах.
Существует ряд способов добиться рабочих характеристик, близких к характеристикам алгоритма МП, и в то же время сохранить сложность реализации на приемлемом для практических систем уровне. Одним из таких способов является традиционный алгоритм K-best, который относится к квазиоптимальным алгоритмам и позволяет достичь приемлемого компромисса между сложностью реализации и рабочими характеристиками.
Из уровня техники известны различные подходы к решению проблем, возникающих при практической реализации телекоммуникационных систем, основанных на технологии многоантенной приемопередачи. В частности, в источнике [1] предложен способ MIMO детектирования, основанный на QR разложении матрицы канала Н

и применении поиска символов-кандидатов «в ширину». Данный подход также использован в [2], и в дальнейшем упоминается как традиционный алгоритм K-best.
Указанный алгоритм является вариантом сферического декодера с поиском «в ширину», для которого функция правдоподобия определяется для ограниченного числа (К) кандидатов, лежащих в окрестности точки с максимальным значением функции правдоподобия 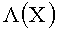
QR разложение (4) необходимо для эффективной реализации указанных процедур поиска. Здесь R - верхняя треугольная матрица, а Q - унитарная матрица. С помощью QR разложения матрица канала преобразуется к верхней треугольной форме, а элементы шумового вектора, в свою очередь, остаются некоррелированными. Исходные варианты всех указанных методов поиска, а также их модификации используют в качестве основного компонента модуль QR разложения.
Умножение обеих частей (1) на QH не меняет статистическое распределение шумовой компоненты в векторе принятого сигнала. Таким образом, при помощи QR разложения (1) преобразуется к следующей форме:
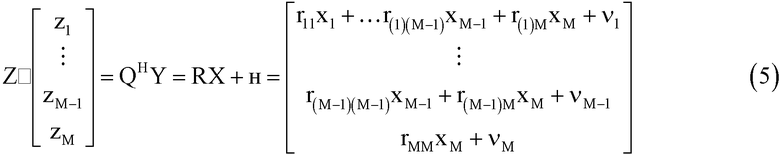
где н=QHз - вектор, состоящий из некоррелированных шумовых компонент (т.к. матрица Q - унитарная).
Аналогично (2), функция правдоподобия для (5) запишется в следующем виде:
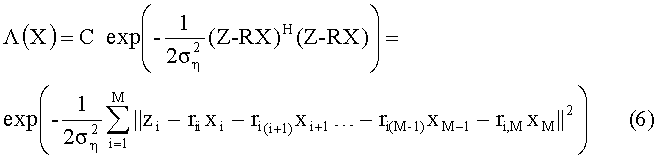
Благодаря верхней треугольной форме матрицы R вычисление показателя экспоненты для функции правдоподобия может осуществляться послойно, начиная с нижних слоев в восходящем порядке в соответствии с (7):
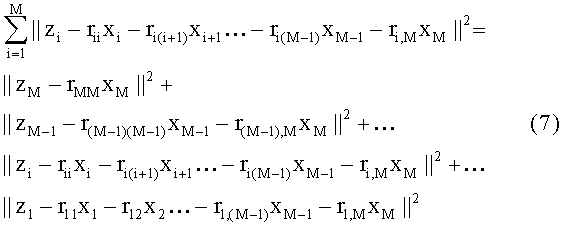
Поиск символов-кандидатов, лежащих в окрестности точки максимального правдоподобия, происходит пошагово, начиная с М-го слоя. Так как первое слагаемое в правой части (7) зависит только от xM, можно легко определить метрики для всех возможных значений xM:

В рассматриваемом примере в качестве метрики ветви используется квадрат Евклидова расстояния. Ветвь - структура, объединяющая символы-кандидаты в нескольких последовательно расположенных слоях, берущая начало на слое М и проходящая только через один символ-кандидат в каждом из последующих просмотренных слоев - см. Фиг.2 (виды 2.1 и 2.2).
При проведении «поиска в ширину» на основе критерия минимума метрики (8) можно определить К лучших кандидатов 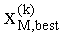
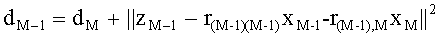
где второе слагаемое - часть метрики, полученная на М-1-ом слое, а первое слагаемое - составляющая метрики ветви, полученная на М-ом слое (8). Таким образом, на каждом шаге осуществляется накопление метрики ветви. В каждом слое сохраняются К лучших ветвей с минимальными накопленными метриками.
Для того, чтобы поиск начался со слоя с максимальной энергией (наиболее надежного слоя), перед началом поиска производится процедура сортировки столбцов матрицы канала Н и соответствующей перестановке элементов вектора X. В этом случае минимизируется влияние ошибки при выборе выживших символов-кандидатов на начальных шагах алгоритма (ошибка на раннем этапе поиска приводит к существенному отклонению К лучших выживших ветвей на финальном этапе от окрестности решения МП). Указанная сортировка может быть осуществлена в порядке возрастания норм столбцов матрицы Н и соответствующей перестановке элементов в векторе X. Кроме того, существует ряд альтернативных способов (например, [6]). Применение сортировки столбцов канальной матрицы позволяет приблизить рабочие характеристики традиционного алгоритма К-лучших к рабочим характеристикам алгоритма МП, сохраняя при этом количество кандидатов на существенно более низком уровне в сравнении с алгоритмом МП.
После окончания процедуры поиска на основе набора выживших ветвей (К лучших ветвей) принимается решение о значении переданного вектора Х (жесткое или мягкое). Для принятия жесткого решения элементы вектора Х принимаются равными символам-кандидатам ветви с наименьшей накопленной метрикой. В случае мягкого решения рассчитываются отношения логарифма правдоподобия согласно (3), причем в качестве Х(В) рассматриваются только К выживших ветвей.
При проведении «поиска в глубину», который является альтернативным способом нахождения наилучшей комбинации символов-кандидатов (см. Фиг.2, вид 2.2), выполняются следующие операции: начиная со слоя М, детектор последовательно просматривает слой за слоем, накапливая метрику ветви в соответствии с (7) и сравнивая ее с порогом δ, определяющим радиус гиперсферы, внутри которой осуществляется отбор К лучших ветвей. Ветвь продлевается каждый раз, когда детектор находит символ-кандидат в i-м слое, удовлетворяющий условию нахождения всей ветви внутри указанной гиперсферы, при этом на следующем шаге детектор осуществляет поиск продолжения данной ветви в слое i-1. Если метрика ветви на i-м слое превышает порог δ, данная ветвь отбрасывается (окончательно или временно), равно как и все ее продолжения, берущие начало в i-м слое. В этом случае детектор начинает проверку других ветвей.
Все указанное выше относительно сортировки столбцов и детектирования символа при «поиске в ширину» применимо также и при «поиске в глубину».
Согласно представленному выше подходу каждый i-й детектируемый слой зависит только от предшествующих ему i+1..M слоев и не зависит от последующих 1..i-1. Таким образом, очевидно, что при ошибочных решениях на ранних этапах (выбраны кандидаты, не находящиеся в окрестности решения МП), среди выживших ветвей не будет решения МП и К лучших ветвей окажутся вдалеке от области МП решения. Данная проблема отчасти решается за счет применения поиска с возвратом и изменением списка выживших ветвей на предыдущих слоях. Такой метод, равно как и традиционный сферический декодер, обладает непостоянной сложностью и переменной задержкой, что делает затруднительным их практическую реализацию. При этом очевидно, что описанные алгоритмы K-best с «поиском в ширину» [1] и «поиском в глубину» [4], равно как и их модификации [2, 3, 5, 6], основанные на QR разложении, не могут рассматриваться как единственно возможные способы поиска наилучших символов-кандидатов. Для целей заявляемого изобретения в качестве прототипа выбрано решение, описанное в [1].
Задачей заявленного изобретения является создание усовершенствованного способа MIMO детектирования с меньшей сложностью и лучшими рабочими характеристиками, чем наилучшие имеющиеся аналоги. Иными словами, требуется новый более эффективный и простой в реализации квазиоптимальный способ MIMO детектирования, позволяющий с более высокой надежностью осуществлять выбор кандидатов из окрестности МП решения.
Технический результат достигается за счет применения усовершенствованного способа детектирования сигнала в системах связи с MIMO (Multiple-In/Multiple-Out), каналом, который включает в себя выполнение следующих операций:
- принимают сигналы, модулированные переданными QAM (Quadrature Amplitude Modulation) символами через несколько приемных антенн;
- осуществляют частотное преобразование принятых сигналов на нулевую несущую частоту;
- формируют отсчеты принятых и преобразованных сигналов путем квантования и дискретизации, которые рассматриваются как выходные отсчеты MIMO канала, и описываются формулой Y=НХ+η, где Y - N-мерный вектор выходных отсчетов MIMO канала, Х - М-мерный вектор входных отсчетов MIMO канала, η - N-мерный вектор отсчетов шума, Н - канальная матрица MIMO канала размера N×M, при этом полагают, что частота дискретизации равна частоте следования QAM символов, поэтому вектор входных отсчетов MIMO канала Х является также вектором переданных QAM символов;
- по полученным выходным отсчетам MIMO канала оценивают канальную матрицу MIMO канала Н, дисперсию шума 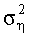
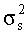
- детектируют QAM символы на основе выходных отсчетов MIMO канала и восстанавливают оригинальные данные, содержащиеся в детектированных QAM символах, посредством оценки апостериорной вероятности переданных бит, выполняя следующие шаги:
- осуществляют упорядочивание QAM символов по критерию максимума энергии сигнала от передающей антенны;
- формируют верхне-треугольную матрицу для поиска наиболее вероятных переданных символов;
- осуществляют послойный поиск К наилучших кандидатов на основе сформированной верхне-треугольной матрицы, начиная с нижнего слоя и заканчивая верхним слоем;
- производят оценку вероятности принятых символов на основе евклидовых метрик, вычисленных для К наилучших кандидатов;
при этом заявляемый способ отличается от прототипа тем, что:
- формируют MMSE (Minimum Mean Square Error) оценку принятого вектора QAM символов и вычисляют матрицу ковариации;
- формируют верхне-треугольную матрицу 
- начиная с нижнего слоя, формируют список из К наилучших (наиболее вероятных) векторов символов-кандидатов согласно критерию минимальности модифицированного евклидового расстояния;
- модифицированное евклидовое расстояние для слоя k определяется как суммарное расстояние, рассчитанное для всех предшествующих слоев, плюс расстояние до символа-кандидата текущего слоя согласно выражению:
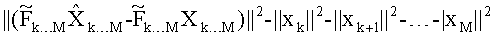
где 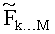
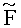
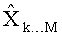
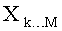
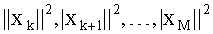
- после обработки всех слоев оценивают вероятность переданных символов (либо бит) на основе модифицированных Евклидовых расстояний для списка из К наилучших векторов символов-кандидатов.
Таким образом, в заявляемом изобретении предложен способ послойного поиска, основанный на оценке вектора переданного сигнала по критерию минимума среднего квадрата ошибки (MMSE - minimum mean square error). Предложенный способ обладает лучшими рабочими характеристиками и схожей или меньшей сложностью реализации, нежели прототип [1].
Далее существо заявляемого изобретения поясняется в деталях с привлечением графических материалов.
Фиг.1 - Приемопередающая MIMO система с М передающими, N приемными антеннами и параллельной приемопередачей множества слоев данных.
Входные данные обрабатываются в передатчике 101, модулируются в QAM модуляторах 103-105 и передаются М антеннами через канал. Переданный сигнал претерпевает искажения в канале (искажения могут быть вызваны многолучевым распространением, аддитивным шумом и т.п.), принимается на N приемных антенн и обрабатывается в приемнике 102. Приемник 102 включает в себя модули синхронизации, оценки канала, MIMO детектирования, декодирования и другие блоки, необходимые для получения декодированных данных на приемном конце.
Фиг.2 (вид 2.1) - Схема «поиска в ширину» для 2-х лучших ветвей (К=2) и модуляции QPSK (Qaudrature Phase Shift Keying).
Поиск начинается со слоя 4, где находятся два лучших символа-кандидата с минимальной метрикой (8), от которых процедура поиска переходит к слою 3 (два лучших символа-кандидата при модуляции QPSK порождают восемь проверяемых ветвей). На слое 3 определяются два лучших символа-кандидата, которые наряду с лучшими символами-кандидатами со слоя 4 образуют выжившие ветви с минимальными накопленными метриками (7). Лучшие символы-кандидаты слоя 3 используются в качестве отправных точек для продолжения поиска на слое 2 и т.д. Таким образом, после выбора двух лучших символов-кандидатов на слое 1 формируются две выживших ветви, включающих в себя символы-кандидаты из всех четырех слоев, на основе которых принимается мягкое или жесткое решение о значении переданного вектора. Описанная процедура предполагает анализ K*L ветвей на каждом слое (L - размер алфавита выбранной схемы модуляции). Существуют несколько способов, позволяющих сократить количество анализируемых ветвей - [1], [2], [3]. Подходы, аналогичные предложенным в [1], [2], [3], могут быть использованы при реализации способа MIMO детектирования, заявленного в настоящем изобретении.
Фиг.2 (вид 2.2) - Схема «поиска в глубину» для одной лучшей ветви (К=1) и модуляции QPSK (Qaudrature Phase Shift Keying).
На первом этапе определяется лучший символ-кандидат с минимальной метрикой (8) на слое 4 - символ 2. Начиная с этого символа, поиск продолжается в слое 3, где в первую очередь просматривается символ 3 (очередность проверки символов на принадлежность к выжившей ветви определяется на основе процедуры предварительной сортировки символов в каждом слое для каждой просматриваемой ветви, например - см. [1], [2], [3]). В приведенном примере символ 3 принимается как лучший символ-кандидат (соответствующая накопленная метрика ветви (7) меньше порогового значения δ) и поиск продолжается в слое 2, где в порядке очередности, установленном предварительной сортировкой, просматриваются все возможные символы-кандидаты и ни один из них не позволяет продолжить текущую ветвь так, чтобы ее накопленная метрика оказалась меньше порогового значения δ. Как следствие, все ветви, начинающиеся с символа 2 в слое 4 и содержащие символ 3 в слое 3, исключаются из дальнейшего поиска (исключенные ветви). Поиск возобновляется со слоя 4 (лучший символ-кандидат для слоя 4 уже найден) и продолжается в слое 3, для которого лучшим символом-кандидатом принимается символ 2 (символ 2 следует за символом 3 в предварительно отсортированном списке для слоя 3 и ветви, берущей начало с символа 2 в слое 4), т.к. накопленная метрика ветви для него меньше порогового значения δ. Поиск продолжается в слое 2 и слое 1, в каждом из которых накопленная метрика, соответствующая просматриваемому в первую очередь символу 1, не превышает порогового значения δ. Таким образом, находится выжившая ветвь, которая используется для вынесения мягкого или жесткого решения о значении переданного вектора.
Фиг.3 - Зависимость вероятности блоковой ошибки от ОСШ для MIMO-OFDM 8х8 системы (N=8, М=8, система совместима со стандартом LTE Rel.10).
В качестве декодера, исправляющего ошибки, использован 4-х итеративный Max-Log-MAP Турбо декодер. Модуляция - QAM-16, скорость кодирования - ¾, канал - ЕРА-5 [7]. Кривые 1 и 2 соответствуют прототипу [1] с количеством выживших ветвей-кандидатов К=40 и К=1000 соответственно. Линия 3 соответствует заявляемому способу с количеством выживший ветвей-кандидатов К=40. Представленная иллюстрация демонстрирует преимущество заявляемого изобретения в сравнении с прототипом [1].
Фиг.4 - Блок-схема, поясняющая заявляемое изобретение.
Принятый входной сигнал Y 302 направляют в модуль 301 оценки канала, который формирует оценку канальной матрицы Н, а также оценку дисперсии шумовой компоненты 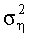
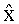
В заявляемом способе MIMO детектирования треугольная матрица формируется на основе MMSE решения следующим образом.
На первом этапе переставляют столбцы канальной матрицы в порядке возрастания их нормы для получения оптимального расположения слоев в процессе MIMO детектирования. Этот процесс называют также сортировкой слоев. В результате сортировки получают вектор MMSE решения 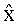
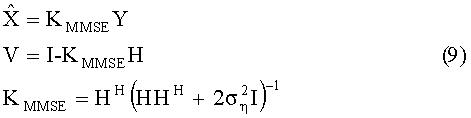
где 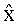
Полагаем, что искомый вектор имеет Гауссовское распределение с математическим ожиданием X и ковариационной матрицей V.
Введем дополнительные обозначения:
ρM - нижний диагональный элемент матрицы V,
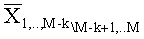
V(M-k) - ковариационная матрица, характеризующая условное распределение вероятности слоев 1..M-k при заданных нижних слоях М-k+1..M, размерность матрицы (M-k)x(M-k),
ρ(M-k) - нижний диагональный элемент матрицы V(M-k).
Введем также представление ковариационной матрицы V в виде совокупности четырех компонентов:

где V1…M-1 - исходная матрица без последней строки и столбца, V(1…M-1),M - последний столбец без нижнего элемента, 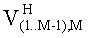
Формирование треугольной матрицы описывается следующей последовательностью шагов для слоев с М-го по 1-й.
- Шаг 1. Для слоя М математическое ожидание и дисперсия совпадают с MMSE оценкой, т.е.:

- Шаг 2. Для слоев 1…М-1 определяем параметры условного распределения вероятности, зависящие от решения на слое М. Математическое ожидание для слоев 1…М-1 определяется выражением:
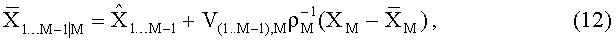
где XM - один из возможных символов созвездия на слое М, определяемого типом модуляции. Ковариационная матрица задается выражением:
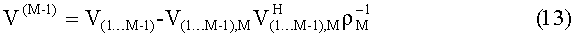
Для слоя М-1 можно задать маргинальное распределение вероятности, зависящее от символа на слое М, причем математическое ожидание 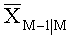
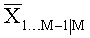
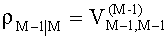
- Шаг 3. Для слоев 1…М-2:
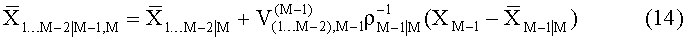
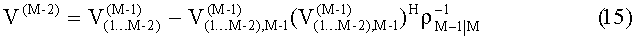
Соответственно маргинальные дисперсия ρM-2|M-1,M и математическое ожидание 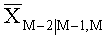
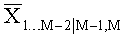
………
………
- Шаг М. Для слоя 1:
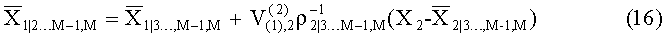
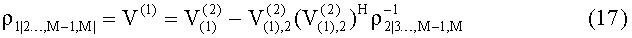
Из приведенных выражений следует, что математическое ожидание и дисперсия условного распределения вероятности слоя k зависят только от элементов матрицы ковариации MMSE решения V, от значений символов созвездия Xk+1,k+2,…,M (т.е. символов-кандидатов на слоях k+1…М) и элементов вектора MMSE решения 
Вероятность передачи всего вектора Х=(х1,х2,…,xM-1,xM)T равна произведению вероятностей:
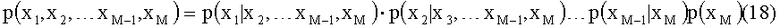
Каждый из сомножителей в (18) есть Гауссовская экспонента, определяемая выражениями (11)-(17), и, следовательно, вероятность для полного вектора можно описать выражением:
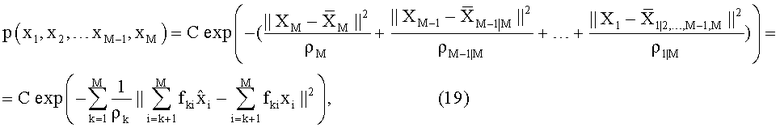
где 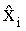
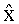
Назовем такой способ формирования треугольной матрицы “процедурой послойной оценки маргинальных вероятностей”.
Выражение (19) можно переписать в виде:
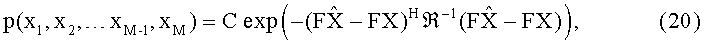
где F - верхне-треугольная матрица, ℜ - диагональная матрица со значениями ρk на диагонали.
Зададим верхне-треугольную матрицу 
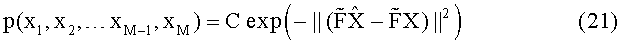
Нетрудно видеть, что вероятность неполного вектора (только для слоев k,…,М) может быть определена аналогичным выражением
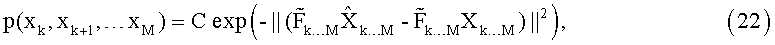
где 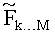
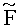
Отсюда очевидно, что процесс поиска кандидатов может производиться послойно аналогично K-best, причем кандидаты на слое k выбираются из условия минимизации метрики 
Вероятности (21) и (22) получены на основе MMSE решения, которое дает смещенную оценку вектора 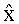

где Λ(Y|xk,xk+1,…xM) - истинная функция правдоподобия, основанная на измерениях (т.е. без априорной информации о принимаемых символах), PPr(xk,xk+1,…,xM) - априорная информация о символах.
MMSE решение подразумевает Гауссовскую аппроксимацию искомого сигнала с нулевым математическим ожиданием и единичной дисперсией. Таким образом:
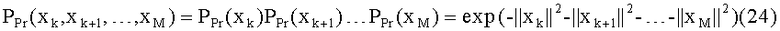
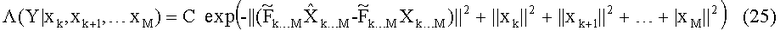
Для нахождения наилучшего кандидата на слое k мы ищем символ созвездия, дающий минимальную метрику:
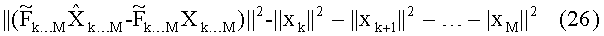
Будем называть метрику (26) “модифицированным Евклидовым расстоянием”. После обработки всех слоев истинная функция правдоподобия для полного вектора переданных символов определяется выражением:
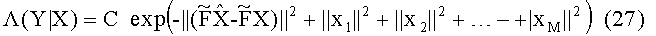
В качестве примера приведем расчет элементов треугольной матрицы F для MIMO системы 3х3.
Пусть MMSE решение дает исходную матрицу ковариации

Для слоя 3:

Для слоя 2:
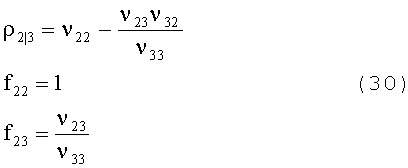
Для слоя 1:
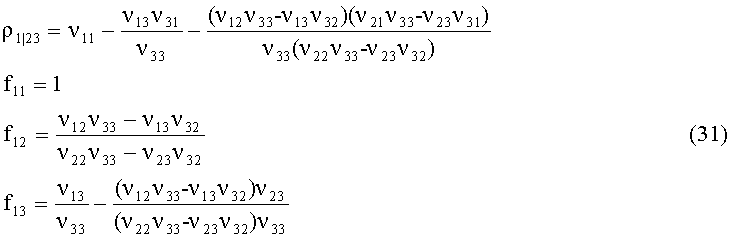
Существуют решения, позволяющие существенно упростить процедуру поиска наилучших кандидатов на слое. В [3] в процедуре К-best, основанной на QR декомпозиции, определяют кандидатов, имеющих наилучшие метрики в соответствии с иерархией, основанной на решении для текущего слоя. Для слоя k в соответствии с выражением (7) вычисляют «мягкий» символ
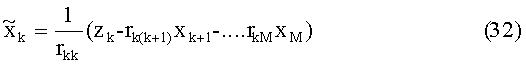
При этом метрики кандидатов на слое проверяют в соответствии с порядком, задаваемым значением 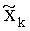
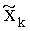
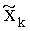
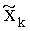
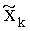
Однако в нашем случае это не так, поскольку, как следует из (25), метрика определяется также энергией символа-кандидата 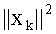
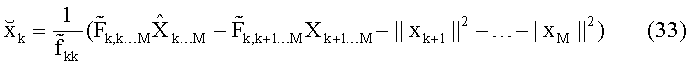
где 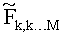
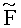

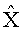
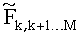
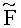
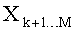
Затем осуществляют поиск наилучших кандидатов в соответствии с иерархией, задаваемой округленным значением 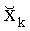
Как видно из (33), мы пренебрегаем энергией символа при определении иерархии символов-кандидатов на текущем слое, что, безусловно, может приводить к некоторой деградации в работе алгоритма. Однако, как показывает моделирование, эта деградация не превышает нескольких десятых децибела. Заметим также, что приближенное значение (33) используется только для установления иерархии символов-кандидатов (т.е. при установлении порядка, в котором исследуются наилучшие метрики). В то же время при подсчете самих метрик по-прежнему используется точное выражение (26), учитывающее энергию символа на текущем слое.
В приведенном выше примере был рассмотрен вариант послойного поиска, который принято также называть «поиск в ширину» (“Breadth-first search”). Тем не менее предложенный подход может быть применен и к альтернативному методу поиска наилучших кандидатов, называемому «поиском в глубину» (“Depth-first search”). При данном методе метрика (26) на слое k сравнивается с пороговым значением, и в случае, если значение метрики меньше порога, поиск с данным набором кандидатов продолжают для слоя k-1. В противном случае данную ветвь поиска прекращают, возобновляя поиск со слоя k+1.
Также заметим, что верхне-треугольная матрица 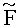
Предварительная сортировка столбцов матрицы Н задает порядок слоев, в котором осуществляют поиск символов-кандидатов. Существуют также иные методы сортировки, дающие близкие результаты. Например, можно сортировать слои в соответствии с модулями диагональных элементов матрицы ковариации MMSE решения V. При этом поиск по слоям осуществляют в порядке возрастания модулей соответствующих элементов.
Заявляемый способ обладает низкой вычислительной сложностью и, таким образом, может быть реализован в базовых станциях, фемто- и пико- сотах, а также в пользовательских терминалах и других элементах приемопередающих систем и сетей, использующих технологию многоантенной приемопередачи MIMO.
Источники информации
[1] - Scalable VLSI architecture for K-best Breadth-First Decoding, Patent No.: US 7889807 B2, Feb. 15, 2011.
[2] - Adaptive selection of survival symbol replica candidates based on Maximum reliability in QRM-MLD for OFCDM MIMO multiplexing. K.Higuchi et al. / IEEE Communication Society Globecom 2004. Pp.2480-2486.
[3] - MIMO multiplexing Communication system and a signal separation method. Patent No.: US 7864897 B2, Jan. 4, 2011.
[4] - Spherical decoder for wireless communications. Patent No.: 7822150 B2, Oct. 26, 2010.
[5] - Apparatus and method for detecting signals in multi-input multi-output system. Patent Application No.: US 2007/0291882 Al, Dec. 20, 2007.
[6] - Near ML Decoding method based on metric-first search and branch length threshold. Patent Application No.: US 2010/0157785 A1, Jun. 24, 2010.
[7] - 3GPP TR 36.803v1.1.0 (2008-04). 3rd Generation Partnership Project; Technical Specification Group Radio Access Network; Evolved Universal Terrestrial Radio Access (E-UTRA); User Equipment (UE) radio transmission and reception; (Release 8).
| название | год | авторы | номер документа |
|---|---|---|---|
| УСОВЕРШЕНСТВОВАННЫЙ СПОСОБ ДЕКОДИРОВАНИЯ В СИСТЕМЕ МНОГОАНТЕННОЙ ПРИЕМОПЕРЕДАЧИ И УСТРОЙСТВО ДЛЯ РЕАЛИЗАЦИИ СПОСОБА | 2009 |
|
RU2426255C2 |
| СПОСОБ ИТЕРАТИВНОГО ДЕТЕКТИРОВАНИЯ И ДЕКОДИРОВАНИЯ СИГНАЛА В СИСТЕМАХ СВЯЗИ С MIMO КАНАЛОМ | 2012 |
|
RU2523190C1 |
| СФЕРИЧЕСКОЕ ОБНАРУЖЕНИЕ И ВЫБОР СКОРОСТИ ДЛЯ ПЕРЕДАЧИ MIMO | 2007 |
|
RU2423012C2 |
| СПОСОБ ДЕТЕКТИРОВАНИЯ СИГНАЛА В СИСТЕМАХ СВЯЗИ С MIMO КАНАЛОМ | 2010 |
|
RU2444846C1 |
| СИСТЕМА МОБИЛЬНОЙ СВЯЗИ, ПРИЕМНОЕ УСТРОЙСТВО И СПОСОБ ПЕРЕДАЧИ СИГНАЛА | 2009 |
|
RU2481712C2 |
| ДЕТЕКТИРОВАНИЕ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ МЕТОДА СФЕРИЧЕСКОГО ДЕКОДИРОВАНИЯ | 2005 |
|
RU2352064C2 |
| СПОСОБ ПРИЕМА СИГНАЛА В СИСТЕМЕ СВЯЗИ С НЕСКОЛЬКИМИ КАНАЛАМИ ПЕРЕДАЧИ И ПРИЕМА | 2006 |
|
RU2303330C1 |
| ДЕТЕКТИРОВАНИЕ И ДЕКОДИРОВАНИЕ С УМЕНЬШЕННОЙ СЛОЖНОСТЬЮ ДЛЯ ПРИЕМНИКА В СИСТЕМЕ СВЯЗИ | 2006 |
|
RU2414062C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ МАТРИЦЫ ПРЕДВАРИТЕЛЬНОГО КОДИРОВАНИЯ, СООТВЕТСТВУЮЩЕЙ КАНАЛУ БЕСПРОВОДНОЙ СЕТИ, И СПОСОБ АППРОКСИМАЦИИ ПРОПУСКНОЙ СПОСОБНОСТИ БЕСПРОВОДНОГО КАНАЛА В БЕСПРОВОДНОЙ СЕТИ | 2010 |
|
RU2510920C2 |
| УСТРОЙСТВО И СПОСОБ УПРАВЛЕНИЯ СХЕМОЙ ПЕРЕДАЧИ СОГЛАСНО СОСТОЯНИЮ КАНАЛА В СИСТЕМЕ СВЯЗИ | 2004 |
|
RU2323525C2 |

Изобретение относится к области связи, в частности к радиотехническим беспроводным коммуникационным системам. Технический результат состоит в повышении точности приема информации. Для этого в системах связи с MIMO формируют оценку принятого вектора QAM символов и вычисляют матрицу ковариации; формируют верхнетреугольную матрицу 
1. Способ детектирования сигнала в системах связи с MIMO (Multiple-In/Multiple-Out) каналом, включающий в себя выполнение следующих операций:
принимают сигналы, модулированные переданными QAM (Quadrature Amplitude Modulation) символами через несколько приемных антенн;
осуществляют частотное преобразование принятых сигналов на нулевую несущую частоту;
формируют отсчеты принятых и преобразованных сигналов путем квантования и дискретизации, которые рассматриваются как выходные отсчеты MIMO канала, и описываются формулой Y=HX+η, где Y - N-мерный вектор выходных отсчетов MIMO канала; Х - М-мерный вектор входных отсчетов MIMO канала; η - N-мерный вектор отсчетов шума; Н -канальная матрица MIMO канала размера N×M, при этом полагают, что частота дискретизации равна частоте следования QAM символов, поэтому вектор входных отсчетов MIMO канала Х является также вектором переданных QAM символов,
по полученным выходным отсчетам MIMO канала оценивают канальную матрицу MIMO канала Н, дисперсию шума 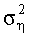
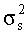
детектируют QAM символы на основе выходных отсчетов MIMO канала и восстанавливают оригинальные данные, содержащиеся в детектированных QAM символах, путем оценки апостериорной вероятности переданных бит, выполняя следующие шаги:
осуществляют упорядочивание QAM символов по критерию максимума энергии сигнала от передающей антенны;
формируют верхне-треугольную матрицу для поиска наиболее вероятных переданных символов;
осуществляют послойный поиск К наилучших кандидатов на основе сформированной верхне-треугольной матрицы, начиная с нижнего слоя и заканчивая верхним слоем;
производят оценку вероятности принятых символов на основе Евклидовых метрик, вычисленных для К наилучших кандидатов;
отличающийся тем, что
формируют MMSE (минимум среднего квадрата ошибки) оценку принятого вектора QAM символов и вычисляют матрицу ковариации;
формируют верхне-треугольную матрицу F на основе матрицы ковариации MMSE оценок с помощью процедуры послойной оценки маргинальных вероятностей;
начиная с нижнего слоя, формируют список из К наилучших векторов символов-кандидатов согласно критерию минимальности модифицированного Евклидового расстояния;
модифицированное Евклидовое расстояние для слоя k определяется как суммарное расстояние, рассчитанное для всех предшествующих слоев, плюс расстояние до символа-кандидата текущего слоя согласно выражению:

где 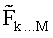
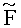
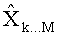
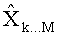
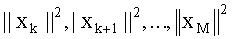
после обработки всех слоев оценивают вероятность переданных символов на основе модифицированных Евклидовых расстояний для списка из К наилучших векторов символов-кандидатов.
2. Способ по п.1, отличающийся тем, что при формировании списка из К наилучших векторов символов-кандидатов на слое k осуществляют поиск наилучших кандидатов на основе заранее сформированного иерархического списка, определяемого значением "мягкого" символа

где 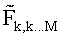
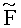
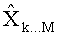
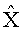
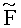
3. Способ по п.1, отличающийся тем, что поиск кандидатов осуществляется вглубь по слоям, начиная с последнего, таким образом, что сначала выбирают наиболее вероятный символ-кандидат на последнем слое, затем находят наиболее вероятный символ кандидат на следующем слое при условии передачи выбранного символа-кандидата на первом слое и так далее, при этом, если на каком-либо слое модифицированное Евклидовое расстояние для цепочки символов-кандидатов оказывается больше порогового значения, данную ветвь поиска обрывают и возобновляют поиск, начиная с предыдущего слоя, если при поиске достигают первого слоя и при этом модифицированное Евклидовое расстояние для такой полной цепочки символов-кандидатов оказывается меньше порогового значения, такой вектор-кандидат считается выжившим, и поиск новой цепочки возобновляется с предшествующего слоя, поиск осуществляется до тех пор, пока не будут исследованы все возможные ветви поиска, причем выжившие векторы-кандидаты участвуют в формировании оценок вероятности переданных символов.
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| СПОСОБ ПЛАНИРОВАНИЯ СКОРОСТИ ПЕРЕДАЧИ ПО ПРЯМОМУ КАНАЛУ И ПЛАНИРОВЩИК, РАБОТАЮЩИЙ ПО ЭТОМУ СПОСОБУ | 2002 |
|
RU2297731C2 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
Авторы
Даты
2013-07-27—Публикация
2012-01-10—Подача