АДАПТИВНЫЙ ДЕКОДЕР ПРОИЗВЕДЕНИЯ КОДОВ РАЗМЕРНОСТИ 3D Российский патент 2013 года по МПК H04L1/20 

Изобретение относится к технике связи и может использоваться при проектировании новых и модернизации существующих систем передачи дискретной информации.

Известны устройства восстановления стираний и исправления ошибок, использующие индексы достоверности символов или мягкие решения (МР) для повышения достоверности приема информации (см. Р.Морелос-Сарагоса. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М., Техносфера, с.103, …, 105; а также У.Питерсон. Коды исправляющие ошибки / У.Питерсон, Э.Уэлдон; пер. с англ; под редакцией Р.Л.Добрушина, С.Н.Самойленко. - М.: Мир, 1976; 594 с.; а также Д.Форни. Каскадные коды / Д.Форни. - М.: Мир, 1970. - 207 с.).

Кроме того, известны методы использования гиперкодов (см. Hunt A., «Hyper -Codes: High-Performance Low-Complexity Error-Correcting Codes», Master's Thesis, Carleton University, Ottawa, Canada, defended March 25, 1998; а также Hunt A., Crozier S., Falconer D., «Hyper-Codes: High-performance Low-Complexity Error-Correcting Codes», 19-th Biennial Symposium on Communications, Ontario, Canada, pp.263-267, May 31-June 3, 1998) а также устройства по патентам РФ на изобретения №2166235; 2209519; 2209520; 2256294; 2344556).

Наиболее близким устройством такого же назначения является декодер с исправлением стираний (см. патент РФ на изобретения №2344556), содержащий блок приема, один выход которого через анализатор сигналов подключен к накопителю, а другой подключен к входу накопителя кодовой комбинации, выход которого подключен к первому входу блока исправления стираний, отличающийся тем, что введены коммутатор проверок, блок определения кластера, блок коррекции кластера, блок прямых координат, блок инвариантных координат и блок сравнения, выход которого подключен ко второму входу блока исправления стираний, при этом первый вход коммутатора проверок подключен к выходу накопителя, второй вход коммутатора проверок подключен к выходу накопителя кодовых комбинации, а выход подключен к одному из входов блока определения кластера, а также к входу блока прямых координат, один выход которого через блок инвариантных координат подключен к третьему входу блока сравнения, второй вход которого подключен к выходу блока прямых координат, при этом первый выход блока определения кластера подключен к входу блока коррекции кластера, выход которого подключен к другому входу блока определения кластера, второй выход которого подключен к первому входу блока сравнения.

К недостаткам работы аналогов, в том числе и прототипа, следует отнести невозможность использования режимов работы с адаптацией, по параметру вводимой в код избыточности, сложность реализации процедуры синхронизации кодера и декодера по выбранному порождающему полиному при изменении избыточности и необходимости ситуативной трансформации программно-аппаратных средств, реализующих заданный ко дек.

Кроме того, итеративные преобразования, выполняемые в блоке коррекции кластера аналога, требуют большого числа итераций для исправления ошибочного символа кластера из-за необходимости вычисления апостериорных оценок без учета знака корректируемых символов и непродуктивного первого шага итераций, когда апостериорные оценки считаются равными нулю.

Технический результат состоит в повышении достоверности и скорости передачи информации. Для достижения технического результата в адаптивный декодер произведения кодов размерности 3D, содержащий блок приема (1), первый выход которого через накопитель кодовой комбинации (3) подключен к одному входу блока совмещения данных (4), другой вход которого через один выход накопителя мягких решений (2) подключен к второму выходу блока приема (1), предлагается ввести дополнительно накопитель параметров ID (5), матричный накопитель (6), блок параметров 2D (7), накопитель параметров 2D (8), блок итеративных преобразований 2D (9), блок распределения данных (10), блок запросов (11), накопитель параметров столбцов (12), матричный накопитель 3D (13), накопитель параметров строк (14), блок итеративных преобразований 3D (15) и накопитель информации (16), при этом выход блока совмещения данных (4) подключен к входу накопителя параметров ID (5), один выход которого подключен к входу матричного накопителя (6), первый выход которого через последовательно соединенные блок параметров 2D (7) и накопитель параметров 2D (8) подключен к третьему входу блока итеративных преобразований 2D (9), тогда как его второй и первый входы подключены соответственно к другому выходу матричного накопителя (6) и к другому выходу накопителя параметров 1D (5), а выход блока итеративных преобразований 2D (9) подключен к входу блока распределения данных (10), при этом первый выход этого блока соединен с другим входом накопителя информации (16), тогда как второй выход блока распределения данных (10) соединен с одним входом матричного накопителя 3D (13), а третий выход блока распределения данных подключен к входу накопителя параметров столбцов (12), при этом четвертый выход блока распределения данных (10) подключен к другому входу блока запросов (11), выход которого подключен к каналу обратной связи, а другой выход накопителя параметров столбцов (12) подключен к другому входу матричного накопителя 3D (13), второй выход которого через накопитель параметров строк (14) подключен к третьему входу блока итеративных преобразований 3D (15), при этом второй и первый входы этого блока подключены соответственно к одному выходу матричного накопителя 3D (13) и к одному выходу накопителя параметров столбцов (12), а выход блока итеративных преобразований 3D (15) подключен к одному входу накопителя информации (16), а один вход блока запросов (11) подключен к другому выходу накопителя мягких решений (2).

Работу адаптивного декодера рассмотрим на примере обработки матриц размерности 4×4, которые формируются передатчиком в результате проверки четности трехбитовых последовательностей.

Пусть передатчик сформировал последовательность вида:

Матрица 2D №1 Матрица 2D №2 Матрица 2D №3 Матрица 2D №4 $$\begin{array}{cccc}1& 1& 1& 1\\ 0& 1& 1& 0\\ 1& 0& 1& 0\\ 0& 0& 1& 1\end{array}$$ $$\begin{array}{cccc}1& 0& 0& 1\\ 0& 0& 0& 0\\ 0& 1& 1& 0\\ 0& 1& 1& 1\end{array}$$ $$\begin{array}{cccc}1& 1& 0& 0\\ 0& 0& 1& 1\\ 0& 1& 0& 1\\ 1& 0& 1& 0\end{array}$$ $$\begin{array}{cccc}1& 0& 1& 0\\ 0& 1& 0& 1\\ 1& 0& 0& 1\\ 0& 1& 1& 0\end{array}$$

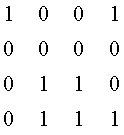
Первые три матрицы представляют собой произведения кодов размерности 2D (проверка четности по строкам и по столбцам), четвертая матрица является проверкой четности одноименных элементов первых трех матриц и в совокупности с ними определяет произведение кодов размерности 3D. После передачи первых трех матриц по каналу с помехами каждый бит двоичной последовательности фиксируется блоком приема в виде двух последовательностей. (Матрица №4 передается только в случае поступления на передатчик от приемника запроса). Первая последовательность представляется множеством жестких решений в виде логических нулей или единиц, а вторая последовательность представляется множеством мягких решений, номера которых синхронны номерам последовательности жестких решений.

Жесткие решения с первого выхода блока приема 1 передаются в накопитель кодовой комбинации 3 и объединяются с мягкими решениями в блоке совмещения данных. Мягкие решения на основе параметров принятого сигнала, получаемых в блоке 1, формируются в виде целочисленных значений и накапливаются в накопителе мягких решений 2, а затем через один выход блока 2 передаются на другой вход блока 4. Блок 2 выполняет функции анализа состояния канала связи. В этом блоке задается число символов порога, преодоление которого приводит к отказу от декодирования кодовой комбинации. Подобные символы должны иметь низкие градации мягких решений. Если в блоке 2 достигнут установленный порог, то другому выходу этого блока передается сигнал на один вход блока запросов 11, что является предупредительной сигнализацией о неудовлетворительном состоянии канала связи. В блоке 4 информационные единицы заменяются на знак (+), а нули заменяются на знак (-), и принятая последовательность матриц размерности 2D принимает вид:

Матрица 2D №1 Матрица 2D №2 Матрица 2D №3 $$\begin{array}{cccc}+5& -\widehat{1}& +7& +7\\ -7& +6& +7& -7\\ +6& +\widehat{3}& +4& +\widehat{2}\\ -7& -7& +6& +7\end{array}$$ $$\begin{array}{cccc}+6& -3& -2& +2\\ +\widehat{2}& +\widehat{3}& -3& +\widehat{2}\\ +\widehat{1}& +3& -\widehat{3}& -3\\ +\widehat{2}& -\widehat{2}& +1& +5\end{array}$$ $$\begin{array}{cccc}+5& -\widehat{2}& -4& -5\\ -6& -6& +7& +7\\ -7& -\widehat{3}& -4& +6\\ +7& -7& +7& -7\end{array}$$

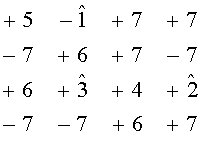
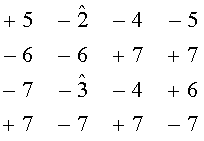
В приведенных матрицах символом 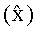$$(\widehat{x})$$ отмечены биты, жесткие решения для которых из-за влияния помех в канале связи оказались искаженными. Совмещение данных в блоке 4 происходит по строкам матриц. После обработки все элементы каждой строки данных из блока 4 поступают в накопитель параметров 1D (блок 5), где производится оценка выполнения условия четности принятой последовательности, среднее значение мягких решений и степень их отклонения от этого среднего значения.

При выполнении четности в анализируемой строке матрицы ей присваивается индекс: sign=(+), в противном случае: sign=(-). Среднее значение оценивается по формуле $$M(\lambda )=(1/n){\displaystyle {\sum }_{i=1}^n\left|{\lambda }_i\right|}$$ , где λ_i - мягкие решения символов строки (столбца), а степень отклонения от М(λ) как $$\sigma (\lambda )=(1/n-1){\displaystyle {\sum }_{i=1}^n(\left|M(\lambda )\right|-\left|{\lambda }_i\right|}{)}^2$$ . Например, в ходе работы блока 5 для первой строки матрицы 2D №1 будут сформированы следующие данные:

$$\begin{array}{cccc}+5& -\widehat{1}& +7& +7\end{array}$$ -M(λ)=-5; σ(λ_i)=8.

Подобные данные формируются для каждой строки всех матриц 2D. При этом оперативные данные, относящиеся к символам обработанной строки матрицы 2D, передаются последовательно строка за строкой в матричный накопитель 6. При образовании в накопителе 6 всех столбцов данных для них формируются в блоке параметров 2D (блок 7) данные, аналогичные данным для строк: sign, М(λ), σ(λ), которые синтезируются для каждого столбца в накопителе параметров 2D (блок 8). После выполнения всех действий над строками и столбцами матрицы 2D ее данные передаются в блок итеративных преобразований 2D (блок 9), освобождая, таким образом, блоки 6, 7 и 8 для обработки последующей группы данных. Следовательно, перед выполнением первого шага итерации в блоке 9 будет зафиксирована матрица вида:

$$\begin{array}{cccccc}+5& -\widehat{1}& +7& -7& -5& 8\\ -7& +6& +7& -7& +\mathrm{6,75}& \mathrm{0,25}\\ +6& +\widehat{3}& +4& +\widehat{2}& +\mathrm{3,75}& \mathrm{2,92}\\ -7& -7& +6& +7& +\mathrm{6,75}& \mathrm{0,25}\\ +\mathrm{6,25}& +\mathrm{4,25}& +6& -\mathrm{5,75}& 0& 0\\ \mathrm{0,92}& \mathrm{7,58}& \mathrm{2,0}& \mathrm{6,25}& 0& 0\end{array}$$

Блок итеративных преобразований 2D на первом шаге осуществляет выбор строк (столбцов), для которых не выполняется условие четности. Критерием эффективности в процедуре выбора является аналитическое выражение вида:

$$Q\left\{S;M(\lambda );\sigma (\lambda )\right\}\Rightarrow \underset{S\to -\lambda }{sign(M(\lambda ))};\left|\underset{\max }{M(\lambda )}\right|;\underset{\min }{\sigma (\lambda )}$$

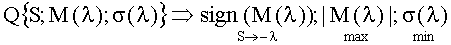
В соответствии с этим критерием в полученной матрице выделяется четвертый столбец. Коррекция в столбце (строке) осуществляется по правилу:

$$L({\lambda }_i)+L({\lambda }_p)={(-1)}^{1-f}\times \left[L({\lambda }_1)\right]\times sign\left[L({\lambda }_p)\right]\times \min (\left|L({\lambda }_i)\right|,\left|L({\lambda }_p)\right|)$$ ,

где sign[•] возвращает значение своего аргумента; L(λ_i) - мягкое решение для символа, участвующего в формировании проверки на четность; Δ(λ_р) - мягкое решение для проверочного символа; f - число сворачиваемых положительных мягких решений только среди информационных разрядов. В выбранной строке (столбце) блок 9 осуществляет отбор наиболее надежных символов, после чего выполняет итеративные преобразования в строке (столбце). Для приведенной матрицы и выбранного четвертого столбца получим: 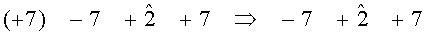$$\begin{array}{cccccccc}(+7)& -7& +\widehat{2}& +7& \Rightarrow & -7& +\widehat{2}& +7\end{array}$$ , в скобках показан символ, исключаемый из процедуры восстановления.

Для полученного соотношения f=1, поскольку из процедуры итеративных преобразований удален наиболее надежный символ (+7). Следовательно:

[+2-7]+7=-5 - новая апостериорная оценка для (-7);

[-7+2]+7=-5 - новая апостериорная оценка для $$(+\widehat{2})$$ .

Результаты коррекции для строки: $$+7(-7-5)(+\widehat{2}-5)+7=+7-13-3+7$$

Значения индексов по абсолютной величине больше 7 в блоке заменяются на значение 7 для сохранения разрядной сетки представления индексов МР.

Ошибка на третьей позиции исправлена. Матрица принимает вид:

$$\begin{array}{cccccc}+5& -\widehat{1}& +7& +7& -5& 8\\ -7& +6& +7& -7& +\mathrm{6,75}& \mathrm{0,25}\\ +6& +\widehat{3}& +4& -3& -\mathrm{4,00}& \mathrm{2,00}\\ -7& -7& +6& +7& +\mathrm{6,75}& \mathrm{0,25}\\ +\mathrm{6,25}& +\mathrm{4,25}& +6& \mathrm{6,00}& 0& 0\\ \mathrm{0,92}& \mathrm{7,58}& \mathrm{2,0}& \mathrm{4,00}& 0& 0\end{array}$$

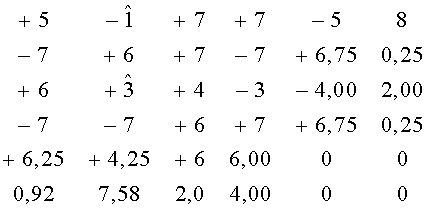
Поскольку у первой строки в этой матрице значение М(λ_i) имеет отрицательный знак и М(λ_i) для нее наибольшее среди выявленных отрицательных. Для коррекции декодер выбирает первую строку: 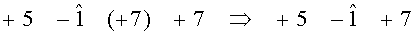$$\begin{array}{cccccccc}+5& -\widehat{1}& (+7)& +7& \Rightarrow & +5& -\widehat{1}& +7\end{array}$$ и f=1.

Далее в соответствии с итеративным преобразованием:

[-1+5]+7=+4 - корректирующая оценка для (+5);

[+5-1]+7=+4 - корректирующая оценка для $$(-\widehat{1})$$ .

Результаты коррекции для строки:(+5+4)(-1+4)+7+7=+9+3+7+7.

В блоке значения индексов по абсолютной величине больше 7 заменяются на значение 7 для сохранения разрядной сетки представления индексов МР.

Ошибка в третьей строке исправлена. Матрица принимает вид:

$$\begin{array}{cccccc}+5& +3& +7& +7& \mathrm{5,50}& \mathrm{3,67}\\ -7& +6& +7& -7& +\mathrm{6,75}& \mathrm{0,25}\\ +6& +\widehat{3}& +4& -3& -\mathrm{4,00}& \mathrm{2,00}\\ -7& -7& +6& +7& +\mathrm{6,75}& \mathrm{0,25}\\ +\mathrm{6,25}& -\mathrm{4,75}& +\mathrm{6,00}& \mathrm{6,00}& 0& 0\\ \mathrm{0,92}& \mathrm{4,25}& \mathrm{2,00}& \mathrm{4,00}& 0& 0\end{array}$$

В соответствии с критерием эффективности для коррекции ошибки во втором столбце или третьей строке необходимо выбрать строку (столбец) с наибольшим критерием М(λ). Таковым является второй столбец, у которого среднее значение выше и наибольший λ_p. Следовательно, для коррекций выделяется последовательность $$\begin{array}{cccccccc}(+3)& +6& +\widehat{3}& -7& \Rightarrow & +6& +\widehat{3}& -7\end{array}$$ , при этом f=1. Символ (+3) вычеркнут, поскольку он был подвергнут коррекции на предыдущем шаге, поэтому его достоверность не вызывает сомнений, кроме того, он по абсолютной величине равен другому корректируемому символу с индексом 3.

При одинаковых знаках корректируемых символов процесс итеративных преобразований затягивается и становится неэффективным. Для сокращения числа итераций последовательность $$\begin{array}{ccc}+6& +\widehat{3}& -7\end{array}$$ циклически сдвигается на шаг влево. Полученная последовательность $$\begin{array}{ccc}+\widehat{3}& -7& +6\end{array}$$ обрабатывается обычным образом.

$$\lfloor -7+\widehat{3}\rfloor +6=-4$$ - новая апостериорная оценка для $$(+\widehat{3})$$ ;

$$\lfloor +\widehat{3}-7\rfloor +6=-4$$ - новая апостериорная оценка для (-7).

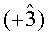
После коррекции последовательность $$\begin{array}{ccc}+\widehat{3}& -7& +6\end{array}$$ преобразуется к виду $$\begin{array}{ccc}-1& -14& +6\end{array}$$ . Второй шаг итерации дает:

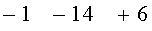
[-14-1]+6=-6 - новая апостериорная оценка для (-1);

[-1-14]+6=-6 - новая апостериорная оценка для (-14).

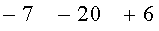
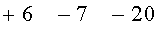
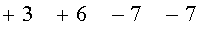
Получаем последовательность $$\begin{array}{ccc}-7& -20& +6\end{array}$$ и после циклического сдвига вправо $$\begin{array}{ccc}+6& -7& -20\end{array}$$ или окончательно $$\begin{array}{cccc}+3& +6& -7& -7\end{array}$$ .

$$\begin{array}{cccccc}+5& +3& +7& +7& +\mathrm{5,50}& \mathrm{3,67}\\ -7& +6& +7& -7& +\mathrm{6,75}& \mathrm{0,25}\\ +6& -7& +4& -3& +\mathrm{5,00}& \mathrm{3,33}\\ -7& -7& +6& +7& \mathrm{6,75}& \mathrm{0,25}\\ +\mathrm{6,25}& +\mathrm{5,75}& +\mathrm{6,00}& +\mathrm{6,00}& 0& 0\\ \mathrm{0,92}& \mathrm{3,58}& \mathrm{2,00}& \mathrm{4,00}& 0& 0\end{array}$$

Данные этой матрицы через блок распределения данных 10 направляются в блоки 12 и 13. В блок 12 - накопитель параметров столбцов через третий выход блока распределения данных направляются параметры столбцов. Например:

1 столбец 2 столбец 3 столбец 4 столбец +6,25 +5,75 +6,00 +6,00 0,92 3,58 2,00 4,00

В матричный накопитель 3D (блок 13) через второй выход блока 10 поступают данные об информационных символах откорректированной матрицы. Например:

$$\begin{array}{cccc}+5& +3& +7& +7\\ -7& +6& +7& -7\\ +6& -7& +4& -3\\ -7& -7& +6& +7\end{array}$$

Для формирования произведения коэффициентов размерности 3D матричный накопитель 3D распределяет полученные данные по столбцам новых матриц. Например:

Матрица 3D №1 Матрица 3D №2 Матрица 3D №3 Матрица 3D №4 $$\begin{array}{cccc}+5& \dots & \dots & \dots \\ -7& \dots & \dots & \dots \\ +6& \dots & \dots & \dots \\ -7& \dots & \dots & \dots \\ +\mathrm{6,25}& \dots & \dots & \dots \\ \mathrm{0,92}& \dots & \dots & \dots \end{array}$$ $$\begin{array}{cccc}+3& \dots & \dots & \dots \\ +6& \dots & \dots & \dots \\ -7& \dots & \dots & \dots \\ -7& \dots & \dots & \dots \\ +\mathrm{5,75}& \dots & \dots & \dots \\ 3.58& \dots & \dots & \dots \end{array}$$ $$\begin{array}{cccc}+7& \dots & \dots & \dots \\ +7& \dots & \dots & \dots \\ +4& \dots & \dots & \dots \\ +6& \dots & \dots & \dots \\ +\mathrm{6,00}& \dots & \dots & \dots \\ \mathrm{2,00}& \dots & \dots & \dots \end{array}$$ $$\begin{array}{cccc}+7& \dots & \dots & \dots \\ -7& \dots & \dots & \dots \\ -3& \dots & \dots & \dots \\ +7& \dots & \dots & \dots \\ +\mathrm{6,00}& \dots & \dots & \dots \\ \mathrm{4,00}& \dots & \dots & \dots \end{array}$$

В этот момент накопитель мягких решений 2 обрабатывает данные матрицы 2D №2 и фиксирует большое количество мягких решений с низким индексом. Накопитель мягких решений 2 через другой выход и через один вход блока запросов 11 выдает команду на организацию запроса к передатчику и передаче дополнительной избыточности, поэтому данные матрицы 2D №2 через матричный накопитель 6 и блок итеративных преобразований 9 без выполнения итеративных преобразований с выхода блока 9 направляются на вход блока распределения данных 10, при этом каждый столбец этой матрицы сопровождается значениями signM(λ), M(λ) и σ(λ). Например:

Матрица 3D №1 Матрица 3D №2 Матрица 3D №3 Матрица 3D №4 $$\begin{array}{cccc}+7& +6& \dots & \dots \\ -7& +\widehat{2}& \dots & \dots \\ +6& +\widehat{1}& \dots & \dots \\ -7& +\widehat{2}& \dots & \dots \\ +\mathrm{6,75}& +\mathrm{2,75}& \dots & \dots \\ \mathrm{0,25}& \mathrm{0,25}& \dots & \dots \end{array}$$ $$\begin{array}{cccc}+3& -3& \dots & \dots \\ +6& +\widehat{3}& \dots & \dots \\ -7& +3& \dots & \dots \\ -7& -\widehat{2}& \dots & \dots \\ +\mathrm{5,75}& \mathrm{2,75}& \dots & \dots \\ \mathrm{3,58}& \mathrm{0,25}& \dots & \dots \end{array}$$ $$\begin{array}{cccc}+7& -2& \dots & \dots \\ +7& -3& \dots & \dots \\ +4& -\widehat{3}& \dots & \dots \\ +6& +1& \dots & \dots \\ +\mathrm{6,00}& -\mathrm{2,25}& \dots & \dots \\ \mathrm{2,00}& \mathrm{0,92}& \dots & \dots \end{array}$$ $$\begin{array}{cccc}+7& +2& \dots & \dots \\ -7& +\widehat{2}& \dots & \dots \\ -3& -3& \dots & \dots \\ +7& +5& \dots & \dots \\ +\mathrm{6,00}& -\mathrm{3,00}& \dots & \dots \\ \mathrm{4,00}& \mathrm{2,00}& \dots & \dots \end{array}$$

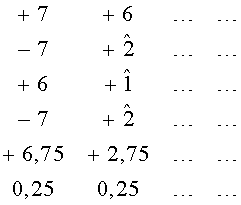
Матрица 2D №3 преобразуется в результате итеративных преобразований к виду. Исходная матрица:

$$\begin{array}{cccccc}+5& -\widehat{2}& -4& -5& -\mathrm{4,00}& \mathrm{2,00}\\ -6& -6& +7& +7& +\mathrm{6,50}& \mathrm{0,30}\\ -7& -\widehat{3}& -4& +6& -\mathrm{5,00}& \mathrm{3,30}\\ +7& -7& +7& -7& +\mathrm{7,00}& 0\\ +\mathrm{6,25}& +\mathrm{4,50}& +\mathrm{5,50}& +\mathrm{6,25}& 0& 0\\ \mathrm{0,92}& \mathrm{5,67}& \mathrm{3,00}& \mathrm{0,92}& 0& 0\end{array}$$

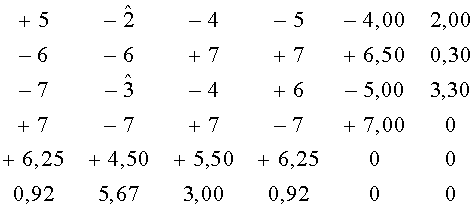
В соответствии с алгоритмом декодирования выбирается для последующей коррекции третья строка, имеющая большое значение параметра М(λ_i).

Следовательно, $$\begin{array}{cccccccc}(-7)& -\widehat{3}& -4& +6& \Rightarrow & -\widehat{3}& -4& +6\end{array}$$ и f=0, поскольку удаленное мягкое решение имеет отрицательный знак. Последовательность $$\begin{array}{ccc}-\widehat{3}& -4& +6\end{array}$$ циклически сдвигается на шаг вправо. Полученная последовательность $$\begin{array}{ccc}+6& -\widehat{3}& -4\end{array}$$ обрабатывается обычным образом. Тогда:

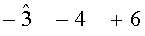
[-3+6]-4=+3 - новая апостериорная оценка для (+6);

[+6-3]-4=+3 - новая апостериорная оценка для $$(-\widehat{3})$$ .

После коррекции последовательность 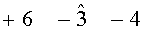$$\begin{array}{ccc}+6& -\widehat{3}& -4\end{array}$$ преобразуется к виду $$\begin{array}{ccc}+9& \widehat{0}& -4\end{array}$$ . Второй шаг итерации дает:

[0+9]-4=+4 - новая апостериорная оценка для (+9);

[9+0]-4=+4- новая апостериорная оценка для $$(\widehat{0})$$ .

Получаем последовательность $$\begin{array}{ccc}+13& +4& -4\end{array}$$ и после циклического сдвига влево $$\begin{array}{ccc}4& -4& 13\end{array}$$ или окончательно $$\begin{array}{cccc}-7& +4& -4& 7\end{array}$$ . Матрица принимает вид:

$$\begin{array}{cccccc}+5& -\widehat{2}& -4& -5& -\mathrm{4,00}& \mathrm{2,00}\\ -6& -6& +7& +7& +\mathrm{6,50}& \mathrm{0,33}\\ -7& +4& -4& +7& +\mathrm{5,50}& \mathrm{3,00}\\ +7& -7& +7& -7& +\mathrm{7,00}& 0\\ +\mathrm{6,25}& -\mathrm{4,75}& +\mathrm{5,50}& +\mathrm{6,50}& 0& 0\\ \mathrm{0,92}& \mathrm{4,92}& \mathrm{3,00}& \mathrm{1,00}& 0& 0\end{array}$$

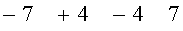
В соответствии с частным алгоритмом выбирается второй столбец, тогда - $$\begin{array}{cccccccc}-\widehat{2}& (-6)& +4& -7& \Rightarrow & -\widehat{2}& +4& -7\end{array}$$ и f=0, поскольку удаляется отрицательный символ.

Далее в соответствии с итеративным преобразованием:

[+4-2]-7=+2 - корректирующая оценка для $$(-\widehat{2})$$ ;

[-2+4]-7=+2 - корректирующая оценка для (+4).

После коррекции последовательность $$\begin{array}{ccc}-\widehat{2}& +4& -7\end{array}$$ преобразуется к виду $$\begin{array}{ccc}\widehat{0}& +6& -7\end{array}$$ . Второй шаг итерации дает:

[+6+0]-7=+6 - корректирующая оценка для 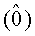$$(\widehat{0})$$ ;

[0+6]-7=+6 - корректирующая оценка для (+6).

Получаем последовательность $$\begin{array}{ccc}+6& +12& -7\end{array}$$ или окончательно $$\begin{array}{cccc}+6& -6& +7& -7\end{array}$$ . Матрица принимает вид:

$$\begin{array}{cccccc}+5& +6& -4& -5& +\mathrm{5,00}& \mathrm{0,67}\\ -6& -6& +7& +7& +\mathrm{6,50}& \mathrm{0,33}\\ -7& +7& -4& +7& +\mathrm{6,25}& \mathrm{2,25}\\ +7& -7& +7& -7& +\mathrm{7,00}& 0\\ +\mathrm{6,25}& +\mathrm{6,50}& +\mathrm{5,50}& +\mathrm{6,50}& 0& 0\\ \mathrm{0,92}& \mathrm{0,33}& \mathrm{3,00}& \mathrm{1,00}& 0& 0\end{array}$$

Таким образом, в матричном накопителе 3D (блок 13) к моменту приема запрашиваемого блока образуется последовательность символов:

Матрица 3D №1 Матрица 3D №2 $$\begin{array}{cccc}+7& +6& +5& \dots \\ -7& +\widehat{2}& -6& \dots \\ +6& +\widehat{1}& -7& \dots \\ -7& +\widehat{2}& +7& \dots \\ +\mathrm{6,75}& +\mathrm{2,75}& +\mathrm{6,25}& \dots \\ \mathrm{0,25}& \mathrm{4,91}& \mathrm{0,92}& \dots \end{array}$$ $$\begin{array}{cccc}+3& -3& +6& \dots \\ +6& +\widehat{3}& -6& \dots \\ -7& +3& +7& \dots \\ -7& -\widehat{2}& -7& \dots \\ +\mathrm{5,75}& +\mathrm{2,75}& +\mathrm{5,50}& \dots \\ \mathrm{3,58}& \mathrm{0,25}& \mathrm{0,333}& \dots \end{array}$$ Матрица 3D №3 Матрица 3D №4 $$\begin{array}{cccc}+7& -2& -4& \dots \\ +7& -3& +7& \dots \\ +4& -\widehat{3}& -4& \dots \\ +6& +1& +7& \dots \\ +\mathrm{6,00}& -\mathrm{2,50}& +\mathrm{5,50}& \dots \\ \mathrm{2,00}& \mathrm{0,33}& \mathrm{3,00}& \dots \end{array}$$ $$\begin{array}{cccc}+7& +2& -5& \dots \\ -7& -\widehat{2}& +7& \dots \\ -3& -3& +7& \dots \\ +7& +5& -7& \dots \\ +\mathrm{6,00}& -\mathrm{3,00}& +\mathrm{6,50}& \dots \\ \mathrm{4,00}& \mathrm{2,00}& \mathrm{1,00}& \dots \end{array}$$

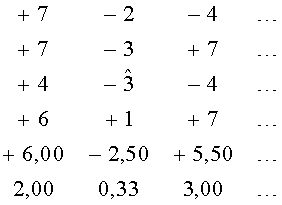
По отмеченным в приведенных матрицах ошибкам заметно, что декодирование на уровне размерности 3D играет роль своеобразного перемежителя и восстановление символов не вызывает трудностей при условии качественной передачи символов дополнительной избыточности. Пусть матрица 2D №4 принята в виде:

$$\begin{array}{cccccc}+7& -5& +7& -7& +\mathrm{6,50}& \mathrm{1,00}\\ -5& +6& -6& +6& +\mathrm{5,75}& \mathrm{0,25}\\ +6& -7& -7& -7& +\mathrm{6,75}& \mathrm{0,25}\\ -7& +6& +7& -7& +\mathrm{6,75}& \mathrm{0,25}\\ +\mathrm{6,25}& +\mathrm{6,00}& +\mathrm{6,75}& +\mathrm{6,75}& 0& 0\\ \mathrm{0,92}& \mathrm{0,67}& \mathrm{0,25}& \mathrm{0,25}& 0& 0\end{array}$$

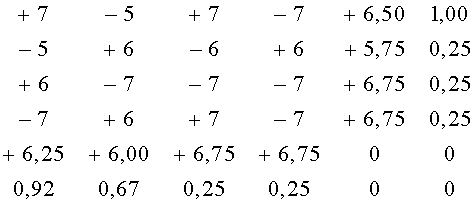
После поступления этой матрицы в блок 13 в накопителе параметров строк (14) формируются данные по строкам, относящиеся к математическому ожиданию и дисперсии. На основании этих данных в блоке итеративных преобразований 3D (15) осуществляется параллельная обработка матриц 3D. Это становится возможным из-за отсутствия между матрицами взаимоувязанных отношений. Таким образом, в блок 15 поступают матрицы:

Матрица 3D №1 Матрица 3D №2 $$\begin{array}{cccccc}+5& +6& +5& +7& +\mathrm{5,75}& \mathrm{0,92}\\ -7& +\widehat{2}& -6& -5& -\mathrm{5,00}& \mathrm{4,67}\\ +6& +\widehat{1}& -7& +6& -\mathrm{5,00}& \mathrm{7,33}\\ -7& +\widehat{2}& +7& -7& +\mathrm{5,75}& \mathrm{6,25}\\ +\mathrm{6,25}& +\mathrm{2,75}& +\mathrm{6,25}& +\mathrm{6,25}& 0& 0\\ \mathrm{0,92}& \mathrm{4,92}& \mathrm{0,92}& \mathrm{0,92}& 0& 0\end{array}$$ $$\begin{array}{cccccc}+3& -3& +6& -5& +\mathrm{4,25}& \mathrm{2,25}\\ +6& +\widehat{3}& -6& +6& -\mathrm{5,25}& \mathrm{2,25}\\ -7& +3& +7& -7& +\mathrm{6,00}& \mathrm{4,00}\\ -7& -\widehat{2}& -7& +6& -\mathrm{5,50}& \mathrm{5,67}\\ +\mathrm{5,75}& +\mathrm{2,75}& +\mathrm{6,50}& +\mathrm{6,00}& 0& 0\\ \mathrm{3,58}& \mathrm{0,25}& \mathrm{0,33}& \mathrm{0,67}& 0& 0\end{array}$$

Матрица 3D №3 Матрица 3D №4 $$\begin{array}{cccccc}+7& -2& -4& +7& +\mathrm{5,00}& \mathrm{6,00}\\ +7& -3& +7& -6& +\mathrm{5,75}& \mathrm{3,58}\\ +4& -\widehat{3}& -4& -7& -\mathrm{4,50}& \mathrm{3,00}\\ +6& +1& +7& +7& +\mathrm{5,25}& \mathrm{8,25}\\ +\mathrm{6,00}& -\mathrm{,25}& +\mathrm{5,50}& +\mathrm{6,75}& 0& 0\\ \mathrm{2,0}& \mathrm{0,92}& \mathrm{3,00}& \mathrm{0,25}& 0& 0\end{array}$$ $$\begin{array}{cccccc}+7& +2& -5& -7& +\mathrm{5,25}& \mathrm{5,58}\\ -7& +\widehat{2}& +7& +6& -\mathrm{5,50}& \mathrm{5,67}\\ -3& -3& +7& -7& +\mathrm{5,00}& \mathrm{5,33}\\ +7& +5& -7& -7& +\mathrm{6,50}& \mathrm{1,00}\\ +\mathrm{6,00}& -\mathrm{3,00}& +\mathrm{6,50}& -\mathrm{6,75}& 0& 0\\ \mathrm{4,00}& \mathrm{2,00}& \mathrm{1,00}& \mathrm{0,25}& 0& 0\end{array}$$

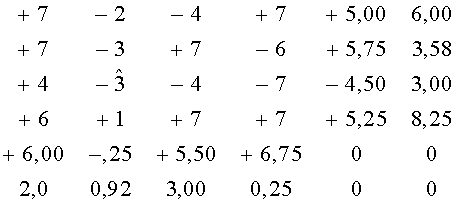
Таким образом, предложенный декодер позволяет реализовать принцип параметрической адаптации по параметру введенной в код избыточности, выполнить процедуру декорреляции ошибок без применения перемежителей и деперемежителей. Применение итеративной процедуры восстановления символов дополнено вычисляемым параметром средней оценки мягких решений на длине кодового вектора и оценкой разброса мягких решений, что повышает качество работы декодера.

Изобретение относится к технике связи и может использоваться при проектировании новых и модернизации существующих систем передачи дискретной информации. Технический результат - повышение достоверности и скорости передачи информации. Для достижения технического результата используется система произведения трех кодов с проверкой на четность, которые в совокупности образуют трехмерный массив данных. При этом проверочные соотношения, относящиеся к контролю четности по третьему измерению, запрашиваются декодером только в случае высокого уровня мешающих факторов, индикатором которого являются мягкие решения относительно принятых символов с малыми показателями достоверности. Предложенная схема декодера в ходе обработки данных по третьему измерению осуществляет декорреляцию возможных ошибок без использования в схеме кодер - декодер специальных перемежителей или деперемежителей. Обработка принятых данных по каждому измерению осуществляется с использованием итеративных преобразований мягких решений на основе среднего значения подобных решений и показателя разброса оценок на длине каждого кодового вектора. 1 ил.

Адаптивный декодер произведения кодов размерности 3D, содержащий блок приема, первый выход которого через накопитель кодовой комбинации подключен к одному входу блока совмещения данных, другой вход которого через один выход накопителя мягких решений подключен к второму выходу блока приема, отличающийся тем, что дополнительно введены накопитель параметров 1D, матричный накопитель, блок параметров 2D, накопитель параметров 2D, блок итеративных преобразований 2D, блок распределения данных, блок запросов, накопитель параметров столбцов, матричный накопитель 3D, накопитель параметров строк, блок итеративных преобразований 3D и накопитель информации, при этом выход блока совмещения данных подключен к входу накопителя параметров 1D, один выход которого подключен к входу матричного накопителя, первый выход которого через последовательно соединенные блок параметров 2D и накопитель параметров 2D подключен к третьему входу блока итеративных преобразований 2D, тогда как его второй и первый входы подключены соответственно к другому выходу матричного накопителя и к другому выходу накопителя параметров 1D, a выход блока итеративных преобразований 2D подключен к входу блока распределения данных, при этом первый выход этого блока соединен с другим входом накопителя информации, тогда как второй выход блока распределения данных соединен с одним входом матричного накопителя 3D, а третий выход блока распределения данных подключен к входу накопителя параметров столбцов, при этом четвертый выход блока распределения данных подключен к другому входу блока запросов, выход которого подключен к каналу обратной связи, а другой выход накопителя параметров столбцов подключен к другому входу матричного накопителя 3D, второй выход которого через накопитель параметров строк подключен к третьему входу блока итеративных преобразований 3D, при этом второй и первый входы этого блока подключены соответственно к одному выходу матричного накопителя 3D и к одному выходу накопителя параметров столбцов, а выход блока итеративных преобразований 3D подключен к одному входу накопителя информации, а один вход блока запросов подключен к другому выходу накопителя мягких решений.