3159
Изобретение относится к вычислительной технике и технике связи и может быть использовано в системах пе- редачи дискретной информации с применением двоичной относительной фазовой модуляции (ОФМ).
Цель изобретения - повышение достоверности декодирования кода, принятого из канала с ОФМо
На чертеже приведена функциональная схема декодера.
Декодер циклического кода содержит . первый буферный накопитель 1, первый
Используя введенное в 2. понятие фиктивного кода, который для одинаковых ошибок в канале связи образует те же синдромы при передаче по схеме с абсолютной модуляцией, какие Порождает реальный код при передаче в ОФМ, можно полностью использовать исправляющую способность реального кода.
и второй блоки 2, 3 формирования синдро--. который имеет длину и число информа.. -/г- I -J
ма,первый и второй блоки 4, 5 вычисления локаторов ошибок, первый и второй блоки 6,7 вычисления поправок,первый - четвертый сумматоры 8-11 по модулю два, .Элемент 12 задержки,второй и третий бу- - ферный накопители 1 3,14 ,первый - четвертый элементы ИЛИ ,15-18 , первый - третий триггеры 19-21, первый и второй элементы И 22j 23о На чертеже обозначены
ционных символов на 1 меньше, чем со- ответствуюи ие числа для фиктивного кода, Иначе говоря,возможность исправ ления ошибок, вызванных сбоями фазы и, одновременно, сохранение исправляющей способности кода для обычных ошибок при передаче сигнала ОФМ можно реализовать, если один и тот же код использовать для исправления ошибок в двух режимах: в режиме фиктивного кода и в обычном режиме. Эта возможность имеет место для таких кодов,которым соответствуют фиктивные коды, являю1циеся циклическими кодами.
информационный вход 24, вход 25 обнуления , информационный выход 26 и выход 27 ошибки.
Буферные накопители 1, 13, 14 представляют собой регистры сдвига
Элемент 12 обеспечивает задержку сигнала на один такт, т.е. является разрядом такого же регистра сдвига.
Блоки 2, 3 формирования синдрома выполнены на основе схем формирования остатка отделения в поле Галуа и мет- ричного умножения в соответствии с выбранными кодами.
Клоки 4, 5 вычисления локаторов ошибок могут быть выполнены, как в прототипе .
Блоки 6, 7 вычисления поправок реализуются так- же, как в 4, причем на их вторых выходах формируются сигналы, свидетельствующие о наличии неисправимой ошибки I
Работа всех указанных блоков тактируется с распределителя импульсов (не показан),
В основе работы декодера лежит следующее
25
30
35
40
45
ционных символов на 1 меньше, чем со- ответствуюи ие числа для фиктивного кода, Иначе говоря,возможность исправления ошибок, вызванных сбоями фазы и, одновременно, сохранение исправляющей способности кода для обычных ошибок при передаче сигнала ОФМ можно реализовать, если один и тот же код использовать для исправления ошибок в двух режимах: в режиме фиктивного кода и в обычном режиме. Эта возможность имеет место для таких кодов,которым соответствуют фиктивные коды, являю1циеся циклическими кодами.
Для рассматриваемых двоичных кодов L2j показано, что циклическому (п, К() - коду длиной п. 1 (здесь m - целое число) с минимальным весом dm, порождающий многочлен которого g,(x) не содержит множителя х+1, соответствует реальньш (п. К)-код, п п (р - 1, К Кф - 1 с минимальным весом d do,. При этом реальным кодом является специальным образом укороченный 1щклический код с порождающим многочленом g(x)g(j,(x)(x+1 ) у (п+1 ,К) - кода полной длины с порождающим много-- членом g(x), который ниже будем называть дополнительным кодом, удален крайний проверочньп символ, а не информационные символы, как у обычных укороченных циклических кодов.
Декодер функционирует следующим образом.
I
Перед приемом каждого нового кодоОтносительная фазовая модуляция по- вого слова сигналом со входа 25 триг- лучила широкое распространение для геры 19-21 обнуляются. Синдром, вычис
зи вызовет также искажение (j+1)-ro бита с Поэтому исправляющая способность обычного декодера, подключенного на выходе демодулятора, понижается примерно в два раза.
Используя введенное в 2. понятие фиктивного кода, который для одинаковых ошибок в канале связи образует те же синдромы при передаче по схеме с абсолютной модуляцией, какие Порождает реальный код при передаче в ОФМ, можно полностью использовать исправляющую способность реального кода.
который имеет длину и число информаJ
-
5
0
5
0
5
ционных символов на 1 меньше, чем со- ответствуюи ие числа для фиктивного кода, Иначе говоря,возможность исправления ошибок, вызванных сбоями фазы и, одновременно, сохранение исправляющей способности кода для обычных ошибок при передаче сигнала ОФМ можно реализовать, если один и тот же код использовать для исправления ошибок в двух режимах: в режиме фиктивного кода и в обычном режиме. Эта возможность имеет место для таких кодов,которым соответствуют фиктивные коды, являю1циеся циклическими кодами.
Для рассматриваемых двоичных кодов L2j показано, что циклическому (п, К() - коду длиной п. 1 (здесь m - целое число) с минимальным весом dm, порождающий многочлен которого g,(x) не содержит множителя х+1, соответствует реальньш (п. К)-код, п п (р - 1, К Кф - 1 с минимальным весом d do,. При этом реальным кодом является специальным образом укороченный 1щклический код с порождающим многочленом g(x)g(j,(x)(x+1 ) у (п+1 ,К) - кода полной длины с порождающим много-- членом g(x), который ниже будем называть дополнительным кодом, удален крайний проверочньп символ, а не информационные символы, как у обычных укороченных циклических кодов.
Декодер функционирует следующим образом.
I
Перед приемом каждого нового кодо








Изобретение относится к вычислительной технике и технике связи. Его использование в системах передачи дискретной информации с применением двоичной относительной фазовой модуляции (ОФМ) позволяет повысить достоверность декодирования кода, принятого из канала с ОФМ. Декодер содержит буферный накопитель 1, блок 2 формирования синдрома, блок 4 вычисления локаторов ошибок, блок 6 вычисления поправок и сумматор 8 по модулю два. Благодаря введению блока 3 формирования синдрома, блока 5 вычисления локаторов ошибок, блока 7 вычисления поправок, сумматоров 9-11 по модулю два, элемента 12 задержки, буферных накопителей 13, 14, элементов ИЛИ 15-18, триггеров 19-21 и элементов И 22, 23 в декодере исправляются ошибки от сбоя фазы при сохранении исправляющей способности кода к комбинации независимых ошибок. 1 ил.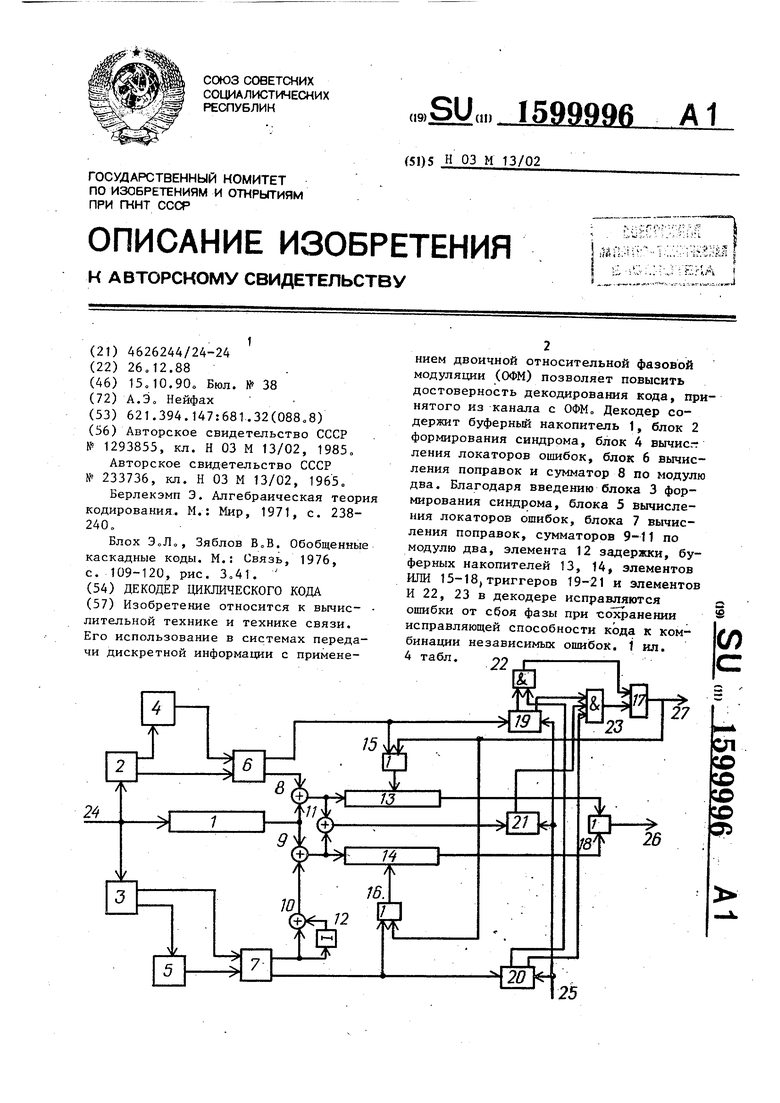
передачи дискретной информации по каналу связи. Однако применение корректирующих кодов в системах передачи дискретной информации затруднено эф- фектом преобразования одиночных ошибок в двойные смежные, поскольку при ОФМ искажение j-ro бита в канале св-яляемый различным образом в формирователях синдрома 2,3 (соответственно для реального и фиктивного кодов) при поступлении из канала связи на вход 24 кодового слова, используется в блоках 4,6, как синдром реального кода, а в блоках 5,7, как синдром фиктивного
5, 159
кода. Поправка, вычисляемая блоком 6, прибавляется в сумматоре 8 к информации, задержанной буферным накопителем 1, непосредственно, а поправка, определенная блоком 7, прибавляется к информации в сумматоре 10 дважды, поскольку при ОФМ искажение j-ro символа в канале связи вызовет инвертирование j-ro и (j+1)-ro символов для j 1-(п-1).
Если число ошибок в кодовом слове не превышает половины исправляющей способности кода, то они могут быть
исправлены обеими половинами декодера (2,4,6 и 3,5,7)о В накопители
13и 14 поступит при этом одинаковая информация, которая через элемент ИЛ 18 подается на выход 26. Данный вариант в случае появления ошибок наиболее вероятен, поскольку .ошибки большей кратности обычно происходят реже а вероятность сбоя фазы значительно меньше вероятности обычной ошибки символа.
Если число ошибок будет также невелико, но в канале появится одиночная ошибка, вызванная сбоем фазы, то блоки 3,5,7, оперирующие с фиктивным кодом, не смогут ее исправить и с большой вероятностью на выходе блока 7 будет сформирован сигнал Ошибка, которьш через элемент ИЛИ 16 произведет сброс третьего накопителя 14. Происходящий при этом переброс триггера 20 не приведен к формированию сигнала Ошибка элементами 22, 23 и 17, если не будет переброшен триггер 19, Блоки 4 и 6 произведут в сумматоре 8 исправление ошибок вместе с ошибкой фазы и исправленная информация из накопителя 13 поступит на выход 26 к потребителю.
Если число ошибок кодового слова превысит половину исправляющей спо-. собности кода, но не превзойдет последнюю, то блоки 4 и 6 не смогут исправить последовательность ошибок и сформированный с большой вероятностью сигнал Ошибка на выходе блока 6 произведет сброс накопителя 13, а исправленная информация с накопителя
14поступит на выход 26. Одновременный сброс накопителей
13 и 14 и формирование сигнала Ошиб- ка н а выходе элемента ИЛИ 17 прои- зойдет в декодере в двух случаях: если сигнал Ошибка возникает в обоих блоках 6 и 7 - через элемент И 22, и при появлении сигнала несовпадения
0
5
0
0
5
5
0
5
исправленной информации, выделяв сумматором 11. Это позволяет снизь, вероятность необнаруженной ошибки в информации в случае появления неисправляемой комбинации ошибок.
Рассмотрим особенности функционирования блоков 2-7 декодеров реального и фиктивного кодов при использовании итеративной процедуры декодирования Берлекэмпа, разработанного первоначально для обычного циклического кода полной длины. Реакльный код не является таким Кодом, поскольку он получается укорочением дополнительного циклического кода полной длины. Поэтому для декодирования реального кода можно использовать процедуру декодирования дополнительного кода, у которого крайний проверочный символ будем считать стертым 31.
Алгоритм декодирования реального (п. К)-кода, основанный на алгоритме декодирования дополненного (п+1,К)- кода, у которого крайний стертый проверочный символ будем считать первым .по счету, удобно представить в следующем виде.
Алгоритм I
1 о Вычислить взвешенные степенные симметрические функции S , S, ) S.i
n-t-f от локаторов искажений S: х..
1 2
Многочлен локаторов с тираний . 2, Определить многочлен Т(2)
I . d-1 . d 1 +L
I Решение ключевого уравнения
(1 + Z:T z ). A(z) 5 (z)linod . 3; К о,л 1, С 1,D(0) О, О - исходные данные. Определить Л коэффициент при
d-
в многочлене ( )9 (z) . kc2
T,z (i + SLs.z i-A.
B(0) 4.
,
5
n
(к) (к) о
true, то - пер.8. иначе -Jiep..
-i-«fK -{ l
-1 в(.к;,с . .
to. к. К+1 Пер.4.
Вьпшсление и исправление ошибок
ошибка о Пер.6.
16,
п + 1 Да - пер о 20. Нет- ю матрице, то сложение последней и предпоследней строк матрицы 1 для удаления правой 1 в предпоследней строке приведет также к проверочной матрице дополненного кода, удаление правого столбца и нижней строки которой приведен к матрице реального кода 101110
Исправление ошибки, (z) 1 Нет - пер.13. Ошибки исправлены. Неисправляемая комбинация оши15
20
25
(
17
18 19 20
бок.
При этом раздел алгоритма 1 Решение ключевого уравнения (блоки 3- 10 алгоритма) реализуется в блоке 4 декодера, а раздел Вычисление и исправление ошибок (блоки 11-20) алгоритма - в блоке 6 декодера.
Рассмотрим особенности выполнения блока 2, в котором реализуется блок 1 алгоритма 1. Для декодирования обычных циклических кодов по процедуре Берлекэмпа степенные симметрические. функции S вычисляются следующим образом.
1 с Производится вычисление остатка от деления принятого кодового слова R(x) на минимальный многочлен М(б/- ) элемента расширенного поля Галуа(Х,
Для рассматриваемого реального- кода, не являющегося циклическим, эта процедура требует модификации, которую только для удобства изложения рассмотрим на примере простейшего реального (6,3)-кода, для которого 45 сб - корень неприводимого многочлена.. Одновременно, только для этого примера порождающий многочлен фиктивного (7,4) - кода g(b(x) хЗ + х + К
30
35
40
(f)V
Проверочная матрица дополненного (7,3) - кода имеет вид
н г 5l
Лоп L 1 1 1 1 1 1 1 J
50
Р
111001(2)
10001 1 Матрица (2) отличается от вьщелен- ной подматрицы матрицы (1) только инверсией нижней строки, поскольку нижняя
строка единиц матрицы (1) является проверкой на четность. Для того, чтобы получить необходимые для декодирования степенные симметрические функции S, в виде линейных комбинаций столбцов выделенной подматрицы матрицы (1), нужно в процедуре вычисления функций S, просто повторить вьшепри- веденные операции с матрицей и получится процедура вычисления степенных симметрических функций S в следующем виде. Процедура 2,.
Проиллюстрируем применение алгоритма 1 и процедуры 2 в полном объеме на примере реального (30, 15) - кода, которому соответствуют фиктивньй (31, 16)-код, имеющий минимальньй вес d с d
(1)
К подматрице, матрицы (1) размерности 6x3, отмеченной пунктиром, следует привести проверочную матрицу реального кода с целью применения блоков 3-20 алгоритма 1 декодирования. Поскольку линейная операция над строками проверочной матрицы линейного i кода приводит также к проверочной
0
5
5
0
5
0
0
5
Р
111001(2)
10001 1 Матрица (2) отличается от вьщелен- ной подматрицы матрицы (1) только инверсией нижней строки, поскольку нижняя
строка единиц матрицы (1) является проверкой на четность. Для того, чтобы получить необходимые для декодирования степенные симметрические функции S, в виде линейных комбинаций столбцов выделенной подматрицы матрицы (1), нужно в процедуре вычисления функций S, просто повторить вьшепри- веденные операции с матрицей и получится процедура вычисления степенных симметрических функций S в следующем виде. Процедура 2,.
Проиллюстрируем применение алгоритма 1 и процедуры 2 в полном объеме на примере реального (30, 15) - кода, которому соответствуют фиктивньй (31, 16)-код, имеющий минимальньй вес d с d
мин
мин 8
7 и дополненный (30,15)-код с проверочной матрицей
Чо7
..c.. V oi V V VV V VVV «iVV o6b
« V oi o6 oi VV Voi V otVW( oi V«ei20 8,«,, 1 o//«ot.6 ai V 6t VVoi oCo6 oi oi ui2V V VV Oi . o °cd oi V V V VV6/« « b
Ot2V ei V 5oi VV ot V ct o6 Ci V cC«Ci2ot2V25oi2.,r,, j
ot ot V iV oi si VV V fliV c V e (i Vee V V V e VVV oi oi2 o( M oi ot ji SiV (ot « oi «o . V W |
Гз)
1 1 4 « 4 1
где (для этого примера) cxl - корень в табл. 1 показаны матрицы умножения для 6-го этапа процедуры 2 вычис- ления степенных сумм S( - Sg.
Благодаря такому выполнению по п.1 алгоритма 1 проверочная матрица реального кода для целен декодирования получается в виде отмеченной пункти-, ром части матрицы (3), т.е. без столбца и строки, состоящих их единиц,
В табл. 2 представлены результаты этапов вьтолнения процедуры 2 вычисле-- ния функций S при искажений в принимаемом кодовом слове 5-го символа
минимального многочлена М(оО х +х2+1. Кодирование следует производить путем приписывания к передаваемой информационной части слова п-К+1 16 15 нулей, деления на порождающий многочлен реального кода gp(x) х + + х + х + х + 1, отбрасывания младшего проверочного разряда (степени х°) и вывода оставшихся 20 п-К 15 символов в качестве проверочной части кодового слова. Многочлен gp(x) (x+1)-g((x), где ,(x) - порождающий многочлен фиктивного кода ga,(x) М((/).М(огЪ-М(о ), в котором М (о) х + х + х + 1, М (сх) х X + х + X +1. Отметим, что элементы 2-ой, 4-ой и 6-ой строк матрицы (3) являются четньши степенями соответственно элементов 30 1-ой и 3-ей строк, не нужны для определения кода данного примера и включены в матрицу (3) лишь для удобства пояснения процесса декодирования.
Степенные симметрические функции SJ, определяемые в п. 1 алгоритма 1, представляют собой сумму элементов j-й строки матрицы (3), соответствующих искаженным при приеме символам кодового слова
Для нахождения степенных функций применим процедуру 2, в пунктах 1-5 которой для S,, Sg, 84 будет использоваться г (о(.) - остаток от деления на М({у:) X + X + 1, для S 5 и S - г () - остаток от деления на М(.) и для 85 - соответственно г (&) .
В процедуре матричного умножения по п. 6 матрица, используемая для получения S., оказывается единичной, поэтому S просто совпадает с пяти- битом (для данного примера), полученным в п. 5. Однако, вычисление г. S& требует более сложной схемы. Схемы связи для этих матриц умножения
35
рождающий многочлен фиктивного кода,, 4
/э ,5ч25 справа (степени х , поскольку в принимаемом кодовом слове правый бит соответствует нулевой степени многочлена) .
В табл. 3 приведены результаты этапов решения ключевого уравнения для реального кода по алгоритму 1 при искажении в принимаемом блоке первого и второго символов справа (х+1).
В результате решения ключевого уравнения алгоритм 1 в данном примере переходит к п., 11 с - (z) 1-f-od z + + (1+oiz)(). Дальнейшее выполнение алгоритма J приводит к исправлению двух ошибок при следующей последовательности операций с указанием их результатов в угловых скобках 12 j 13 7(0/-) О ; (z) . 17; 18; 13
-AJV- ) Jt 0 ; 14 15; 13 (Ы ) 16(z) 1 ; 17,- 18;
--
Дпя рассмотрения принципов работы блоков 3,5,7 при декодировании фиктивного кода вернемся к простейшему при- меру реального (6, 3)-кода, для которого желательный (в целях удобства декодирования) вид матрицы фиктивного (7, 4)-кода будет матрица (1) без нижней строки единиц. Если воспользоваться формулами преобразования провероч40
45
- - - i- --- «IP---1- л жд.л Лл ч
полу чаются из правых пяти столбцов ° матрицы фиктивного кода в проверасширенной матрицы Нддр(З), в которойРочную матрицу реального кода
столбцами показаны двоичные (пятираз-j 4 j j- J
рядные) эквиваленты элементов oi .а - ° + Ь () (5)
Гз)
-
11
1599996
где a , b - соответственно i-e столб- ЦЫ проверочной матрицы реального и фиктивного кодов (при этом,имеем также соотношение для матрицы фиктивного кода
Zb о
(6)
где ,0 J - нулевой вектор) и если матрица фиктивного кода представлена в каноническом виде, т.е. правая подматрица размерности (п-К)(п-К) представляют собой единичную матрицу „.(,, то в правой ча сти матрицы реального кода получим после преобразования (5) подматрицу вида
1
О
1
М
Например, из верхней части матрицы (1) получим проверочную матрицу реального кода .
С
Поскольку линейное преобразование над строками проверочной матрицы линейного кода приводит также к проверочной матрице, то в матрице (7) можно заменить вторую строку суммой первой и второй строк, а затем третью строку - суммой трех строк. В результате получим проверочную матрицу в каноническом виде
(8)
С другой стороны, i-й столбец мат,- ритды (8) Тможно получить с помощью следующей процедуры:
-(X + х2 + 1).(х+1)х + х2.+ X + 1.
3с Удаление младшего символа остатка.
Для того, чтобы получить необходи- мые Для декодирования в фиктивном коде степенные симметрические функции S, в виде линейных комбинаций столбцов верхней подматрицы матрицы (1), нужно
12
в процедуре вычисления функций повторить приведенные операции для получения матрицы (8) и получится процедура вычисления степенных симметричных функций
в следующем виде
Процедура 3
m-l
Z.
.1
j
(9)
последовательно, с ростом i, где га - степень минимального,многочлена M(ot ). 5 Преобразование результата процедурой матричного умножения аналогично процедуре 2.
Вычисленные с помощью процедуры 3 симметрические функции могут быть использованы для обьмной итеративной процедуры декодирования, в частности, может быть использован .приведенный выше алгоритм 1, в котором операция 12 заменена следующей: 12., алгоритм 1 со скорректированной операцией 12 назовем Алгоритм 1а.
Проиллюстрируем применение процедуры 3 и алгоритма 1 Q в полном объеме на примере реального (30, 15)-кода, которому соответствует фиктивный (31,16)-код, имеющий проверочную матрицу (3) с удаленной нижней строкой II.
единиц
Пусть на блок 3 поступает нулевое кодовое слово с искаженным пятым-и шестым символами справа (двучлен х) . В табл. 4 представлены результаты чЭтапов выполнения процедуры 3 вычисления функций S:.
Отметим, что на этапе 2 процедуры 3 вычисляются остатки от деления на
многочлен (x+1) M(oi) х +
+ строк.
X + 1 для 1-ой, 2-ой и 4-ой (х+1)-М( X +
X
+ X + 1 для 3-ой и 6-ой строк и (х+1) М(« ) для j:-oй строки матрицы (3).
Вычисленные значения образуют в матрице (3) шестой столбец справа, который -породит единичный импульс исправления с декодирующего выхода блока 7, но на выходе сумматора 10 из-за задержки в элементе 12 будут сформированы сигналы для исправления двух соседних символов,
Отметим также, что процедура 3 может быть упрощена за счет совмещения операций 4 и 5, поскольку преобразование синдрома по формуле (8) может быть выполнено методом матричного умножения на матрицу преобразований
0 I 1О О О О
11 000
oi 11100
с 111 1 О
1 |11 1 1 1
(10)
1 3 г
X X X X
Согласно математическому определению матрицы последовательное вьтол- нение двух матричных преобразований можно заменить одним преобразованием в соответствии с матрицей - произведнием двух частиц.
В качестве примера для оценки эф- фективности изобретения рассмотрим двоичный (63, 33)-код, порождающий многочлен которого не содержит умножителя х+1 (элемент показателя О не является корнем многочлена) и минимальный вес которого d, 11. Такой ход может быть фиктивным (п 63), а реальный (62, 32)-код, у которого пф 62, также имеет d, 11 и может исправлять до t (d -1) ошибок.
По фиктивному коду декодер (блоками 3,5,7) исправляет до 5 ошибок битов, но без сбоя фазы. По реальному коду декодер (блоками 2,4,6) может исправлять не более двух ошибок символов, поскольку каждое искажение ошибочного символа в канале дает в результате сдвоенную ошибку в приемнике ОФМ. Однако, декодер по реальному коду может в кодовом слове длиной 62 бита исправлять одну ошибку фазы и до двух ошибок символов или 2 ошибки фазы и одну ошибку символа (пренебрежем появлением большего числа сбоев фазы в слове, чем лишь занизим исправляющую способность декоде- ра)о
Пусть в канале вероятность искажения символа Р, J а вероятность сбоя фазы на данном символе Р фаз 10, причем искажения символов и сбоев фазы распределены случайно и независимо друг от друга. Рассмотрим сначала возможности декодера аналога
21, исправляющего ошибки только в фиктивном коде при условии отсутствия сбоев фазы в кодовом слове
Обозначим через
Hjeвероятность
невозможности декодирования слова, пораженного ошибками символов, при условии отсутствия сбоев фазы в канале, под этим будем понимать как отказ от декодирования, так и ошибочное декодирование. Через Рф, обозначим ве-м роятность сбоев фазы в слове. Ввиду независимости искажений символов и сбоев фазы вероятность невозможности декодирования в 2j будет
где ,j 1-(1-P«f,
1 - ()(1-P«,), (11)
(12),
n
.Р
Для вычисления Р...,. удобно воспрль- (Я
зоваться формулой
п Чср« с
)( т )) (. ) «. T - r+i+f f-
в которой достаточную точность расчета можно получить при использовании первых четырех слагаемых по знакам суммы, t 5о
Дпя данного примера Р. 0,00618, а Р - 0,826 10 ; из значительного превьшхения над , что исправляющая способность кода недоиспользуется за счет невозможности исправления в прототипе сбоев фазы. Поскольку P,pj PHJC , подстановка этих значений в (11) даст РИД- 0,00618.
Для предложенногоiдекодера с п целью учета рассмотренных выше возможностей блоков 2,4,6 из рассчитан0
5
0
ной величины Pt,,j следует рычесть поп+С МР п-р
2 П
равку формула для которой получается в виде
(7)Pin( -Р,с.) - (1-PjU ppL(1-P.cM
п-Р V (pj . LMCM. icM
Чр-гт
(1-P,c«) (14)
Расчет по формуле (14) даст АР( 0,616-10-2, а разность Рно-ЛР(рс 0,00002 показывает, что верхняя оценка вероятности ошибочного декодирования предложенного декодера по-. лучается для параметров.данного при-. 5 мера на 2,5 порядка ниже, чем для аналога 2.
Теперь предположим, что в декодере циклического кода прототипа 4 реализован рассматриваемый (63,33)-код
Боуза-Чоудхури. Код может гарантиро- ваино исправлять t 2 пары ошибок, но исправлять 3 пары ошибок в общем случае не может.
Подставляя в формулу (13) значения п 63 и t 2 вместо соответственно Пд, и t,, получим для прототипа при использовании первых двух слагаемых под знаком.суммы величину HIJC 0,00385, которая заведомо меньше результата использования всех слагаемых формулы (13), но значительно больше оцененной выше величины Р„- предложенного декодера.
Формула изобретения
Декодер циклического кода, содеращий первый буферный накопитель, вход ко.торого объединен с входом пер- 20 вого блока формирования синдрома и является информационным входом декодера, первый и второй выходы первого блока формирования синдрома подключены соответственно к первому входу 25 первого блока вычисления поправок и к входу первого блока вычисления локаторов ошибок, выход которого соединен с вторым входом первого блока вычисления поправок, первый выход ко- зо торого и выход первого буферного накопителя подключены к первому и второму входам первого сумматора по модулю два, отличающийся тем, что, с целью повьш ения достоверности декодирования кода, принятого из канала с относительной фазовой модуляцией, в декодер введены второй и третий буферные накопители, второй - четвертый сумматоры по модулю два, элемент задержки, первый - третий триггеры, первый - четвертый элементы ИЛИ, первый и второй элементы И, второй блок вычисления локаторов ошибок второй блок вычисления поправок и второй блок формирования синдрома, вход которого подключен к информацион.- ному входу декодера, а первьй и вто- пой выходы соединены соответственно
35
40
45
5 о
5
0
5
16
с первым входом второго,блока вычисления поправок и входом второго блока вычисления локаторов ошибок, выход которого подключен к второму входу второго блока вычисления поправок, первьй выход которого непосредственно и через элемент задержки соединен с первым и вторым входами третьего сумматора по модулю два, выход которого соединен с первым входом BTO-I рого сумматора по модулю два, второй вход которого подключен к выходу первого буферного накопителя, вторые выходы первого и второго блоков вычисления поправок подключены к установочным входам одноименных триггеров и первым входам одноименных элементов ИЛИ, выходы которых соединены с входами обнуления соответственно второго и третьего буферных накопителей, выходы которых подключены к первому и второму входам четвертого элемента ИЛИ, выход которого является информационным выходом декодера, входы обнуления первого - третьего триггеров объединены и являются входом обнуления декодера, первые выходы первого и второго триггеров подключены к первому и второму входам первого элемента И, выход которого соединен с первым входом третьего элемента ИЛИ, выходы первого и второго сумматоров по модулю два подключены к информа-- ционным входам соответственно второго и третьего буферных накопителей и соответственно к первому и второму входам четвертого сумматора по модулю два, выход которого соединен с установочным входом третьего триггера, выход которого и вторые выходы первого и второго триггеров подключены к первому - третьему входам второго элемента И, выход -которого соединен с вторым входом третьего элемента ИЛИ, выход которого подключен к вторым входам первого и второго элементов ИЛИ и является выходом ошибки декодера.
Та б лица 1
, 1 О О О О/|0 О t О О
о 1 О О ОИз строки 1 1 О О ОИз строки 2
.мо.о , о с ;,77. 1 ° о 0
00010(для S,)pi|OlOOO(для S)
1|iJ0001IMOOOI
Результат матриц-о( , , , v v i « «о
него перемножения о/ +1 о; ( - «. « Jj« °
, - .J
19
1599996
Этапы
Результаты этапов декодирования
A+1+z; S,-« ; S Ы ; S (у ; S. ы ; s. о
Многочлен T(z) 1 + Cx z+ z4oi r.Vo z 6( z Уравнение: (1+o;-°z+c 2ez +oi z -t-o z) (z) (z) | mod z
Циклы решения ключевого уравнения (К 0,1,...)
А ( А, )
о(
30
5 (()
6 (уход)Пер.к-п.7
8(D, В, (К+1)) Нет
9(D, В, (К+1)) 1; 1;0i
Пер. к п. 7 Пер. к п. 7 Пер. ко. 11
Нет
Нет
1; 0;
0( +
2 ; 1;
Остаток от деления
на многочлен хЧх%х +1 х + х +х +1 +1 +1 +1 (x+1)-M((v:J) Удаление компонента с х Преобразование
синдрома00101 х + 1
Матричное умно- +х +1
+1 х -+х +1 +1 +1
Х+Х+Х+1 X +1X +Х Х +1. +1
жение
(у: 41 u( + el ° (| c/Vtx; (у ( o( + (. -(
iO
Таблица
Т
0(
15
Р
cxL
lVz+oi z И-о(%
Нет
Нет
2 ; 1;
т а б л и ц а
iO
| Устройство декодирования с исправлением ошибок | 1985 |
|
SU1293855A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Алгебраическая теория кодирования | |||
| М.: Мир, 1971, с | |||
| Ручная тележка для грузов, превращаемая в сани | 1920 |
|
SU238A1 |
| Блох ЭоЛо, Зяблов ВоВ | |||
| Обобщенные каскадные коды | |||
| М.: Связь, 1976, с | |||
| Шкив для канатной передачи | 1920 |
|
SU109A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1990-10-15—Публикация
1988-12-26—Подача