Изобретение относится к антенной техники, а именно к способам размещения элементов на разреженной фазированной антенной решетке (ФАР).
Традиционным способом размещения элементов в ФАР является способ, обеспечивающий плотное заполнение всех узлов эквидистантной антенной решетки (Фельд Я.Н., Бененсон Л.С. Основы теории антенн. М.: Дрофа, 2007).
Недостатками такого способа являются высокая стоимость, проблемы теплоотвода, взаимного электромагнитного влияния элементов, невозможность обеспечения высоких требований к быстродействию вычислительных схем управления элементами.
В качестве альтернативы в настоящее время разрабатывают способы построения разреженных ФАР путем размещения элементов на регулярной сетке узлов, обеспечивающие сохранение основных свойств ФАР по разрешающей способности и уровню боковых лепестков, но с пониженной плотностью заполнения.
Известны способы размещения элементов по спирали (US 6433754, кл. H01Q 21/00, опубл. 13.08.2002; RU №2349997, опубл. 20.03.2009).
Недостатками таких способов является размещение элементов вне узлов регулярной сетки, что затрудняет построение системы управления лучом, особенно если применять временное фазирование (Л.Г.Содин. Некоторые проблемы теории фазированных антенных решеток, актуальные для радиоастрономии. Радиофизика и радиоастрономия. 2005, т.10, специальный выпуск, с.128-142).
Прототипом настоящего изобретения является размещение элементов на разреженной регулярной сетке узлов фазированной антенной решетке по методу двумерных разностных множеств (Л.Е.Копилович, Л.Г.Содин. Синтез двухмерных неэквидистантных антенных решеток на основе теории разностных множеств. Радиотехника и Электроника. 1994 г., вып.3, стр.380 - 389). Свойства этого метода были также рассмотрены в более поздних публикациях (Л.Г.Содин. Некоторые проблемы теории фазированных антенных решеток, актуальные для радиоастрономии. Радиофизика и радиоастрономия. 2005, т.10, специальный выпуск, с.128-142; Leeper D.C., Isophoric Arrays-Massive Thinned Phased Arrays with Well-Controlled Side-lobes, IEEE Trans. Antennas Propag., 1999, Vol.47, N.12, p.p.1825-1835).
Разностные множества, взятые из комбинаторики, являются частным случаем более общего понятия "блок-схема", представляющая собой систему подмножеств конечного множества, удовлетворяющие некоторому условию, связанному с частотой появления пар элементов множества в подмножествах системы.
Применительно к задаче построения ФАР содержанием разностных множеств являются номера узлов эквидистантной сетки, в которых должно располагаться заданное количество элементов ФАР. Выполнением указанного выше условия является заданная частота появления разностей значений узлов, принадлежащих тому же исходному конечному множеству, между несовпадающими номерами узлов которого, взятых по модулю, равному числу узлов в сетке. Нижний уровень функции автокорреляции распределения элементов на сетке узлов, состоящего из нулей и единиц, равен заданной частоте появления пар в разностных множествах, которая также определяет контролируемый уровень боковых лепестков диаграммы направленности ФАР, построенной методом разностных множеств (метод РМ).
К недостаткам такого способа размещения элементов относятся: малое, не более двух, число независимых лучей, которые могут быть сформированы из элементов решетки (Leeper D.C., Isophoric Arrays-Massive Thinned Phased Arrays with Well-Controlled Side-lobes, IEEE Trans. Antennas Propag., 1999, Vol.47, N.12, p.p.1825-1835); ограничения на варианты размещения элементов методом РМ при размерах решетки менее 50 на 50, на которой могут размещаться элементы таким способом (Л.Г.Содин. Некоторые проблемы теории фазированных антенных решеток, актуальные для радиоастрономии. Радиофизика и радиоастрономия. 2005, т.10, специальный выпуск, C.128-142); ограничение снизу на плотность заполнения решетки (Л.Е.Копилович, Л.Г.Содин. Синтез двухмерных неэквидистантных антенных решеток на основе теории разностных множеств. Радиотехника и Электроника. 1994 г., вып.3, стр.380-389); жесткая связь между задаваемым уровнем боковых лепестков и числом размещаемых элементов.
Техническим результатом настоящего изобретения является повышение эксплуатационных возможностей решетки путем размещения элементов, обеспечивающего построение подрешеток с диаграммами направленности, формируемых по регулируемому числу совпадающих элементов от полного совпадения до совпадения только в двух узлах.
Для достижения технического результата предлагается способ размещения элементов на разреженной фазированной антенной решетке, при котором на регулярной сетке узлов элементы размещают по методу двумерных разностных множеств, отличающийся тем, что фазированную антенную решетку формируют из набора подрешеток, каждая из которых состоит из φ(m)-1 элементов, где числовой модуль m принимает значения pα, 2pα, α - число натурального ряда, р - простое число, φ(m) - функция Эйлера, максимальное количество подрешеток равно φ(φ(m)), то есть числу первообразных (ПО) корней числа m, а каждый из φ(m)-1 элементов подрешетки размещают в узлах сетки по одному на каждом столбце и не более чем по одному на каждой строке так, что для j-го элемента номер строки k определяют по заданному номеру столбца j по правилу
k=(gl)jmodm
где gl - l-й первообразный корень числа m, l принимает значения от 1 до значения, равного числу первообразных корней модуля m, φ(φ(m)), номер столбца j изменяется от 1 до φ(m)-1, номер строки k изменяется в диапазоне от 1 до m, принимая все значения за исключением кратных m;
Простые числа р принимают значения 3, 5, 7, 11, 13, 17, 19, 23, …, так что при α=1 число m может принимать значения 3, 5, 7, 11, 13, 17, 19, 23, …, а также 10, 14, 22, …, и при α≥1: 25, 27, 49, …
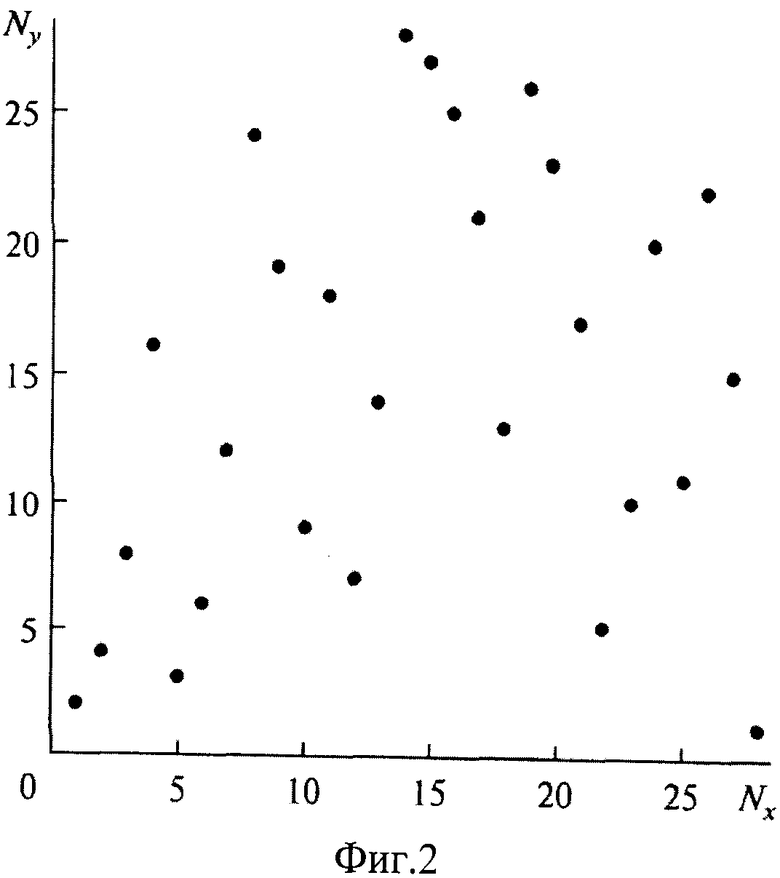
Например, для m=р=29 число элементов в одной подрешетке равно числу вычетов числа 29, т.е. 28, число ПО корней равно φ(29-1)=12, а список ПО корней дается списком: {2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27}. При ПО корне gl=2 координаты узлов, в которых располагают элементы подрешетки, даются списком:
{{1,2}, {2,4}, {3,8}, {4,16}, {5,3}, {6,6}, {7,12}, {8,24}, {9,19}, {10,9}, {11,18}, {12,7}, {13,14}, {14,28}, {15,27}, {16,25}, {17,21}, {18,13}, {19,26}, {20,23}, {21,17}, {22,5}, {23,10}, {24,20}, {25,11}, {26,22}, {27,15}, {28,1}}, где на первой позиции стоит номер столбца, на второй - номер строки.
При ПО корне gl=27 координаты узлов, в которых располагают элементы подрешетки, даются списком:
{{1,27}, {2,4}, {3,21}, {4,16}, {5,26}, {6,6}, {7,17}, {8,24}, {9,10}, {10,9}, {11,11}, {12,7}, {13,15}, {14,28}, {15,2}, {16,25}, {17,8}, {18,13}, {19,3}, {20,23}, {21,12}, {22,5}, {23,19}, {24,20}, {25,18}, {26,22}, {27,14}, {28,1}}.
Из сопоставления обоих списков нетрудно видеть, что координаты половины элементов обоих подрешеток совпадают.
Путем выбора иных ПО корней возможно снижение числа узлов, в которых совпадают элементы, принадлежащие разным подрешеткам. Так, при р=29 для ПО корня 14 координаты узлов решетки даются списком:
{{1,14}, {2,22}, {3,18}, {4,20}, {5,19}, {6,5}, {7,12}, {8,23}, {9,3}, {10,13}, {11,8}, {12,25}, {13,2}, {14,28}, {15,15}, {16,7}, {17,11}, {18,9}, {19,10}, {20,24}, {21,17}, {22,6}, {23,26}, {24,16}, {25,21}, {26,4}, {27,27}, {28,1}},
из сопоставления которого с предыдущими видно, что число совпадающих узлов равно 4, что приводит к резкому снижению статистической зависимости диаграмм направленности (ДН) разных подрешеток.
Таким образом, предлагаемый способ размещения элементов на разреженной регулярной сетке узлов основан на использовании алгебраических кодов, ставящих номер элемента в однозначное соответствие номеру столбца и номеру строки, на которых размещается данный элемент. В соответствии со свойствами числовых модулей при использовании в качестве основания для кодов значения первообразных корней выбранного числового модуля обеспечивается отсутствие повторений номеров строки при изменении номеров столбцов.
Сущность изобретения иллюстрируется на чертежах, где:
на Фиг.1 представлен чертеж расположения плоской регулярной сетки узлов с расстояниями, равными по каждой из осей, но отличающимися друг от друга;
на Фиг.2 представлено расположение 28-ми элементов при gl=2 согласно приведенному списку;
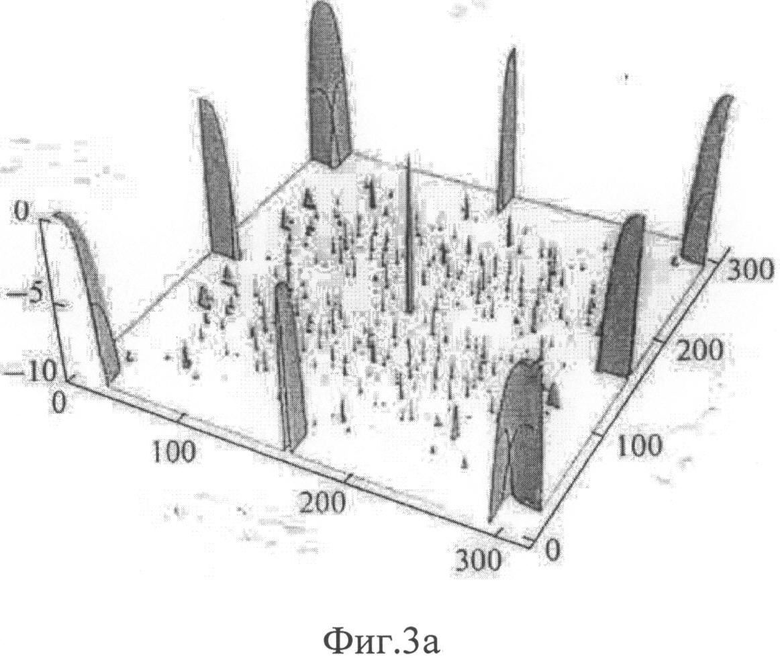
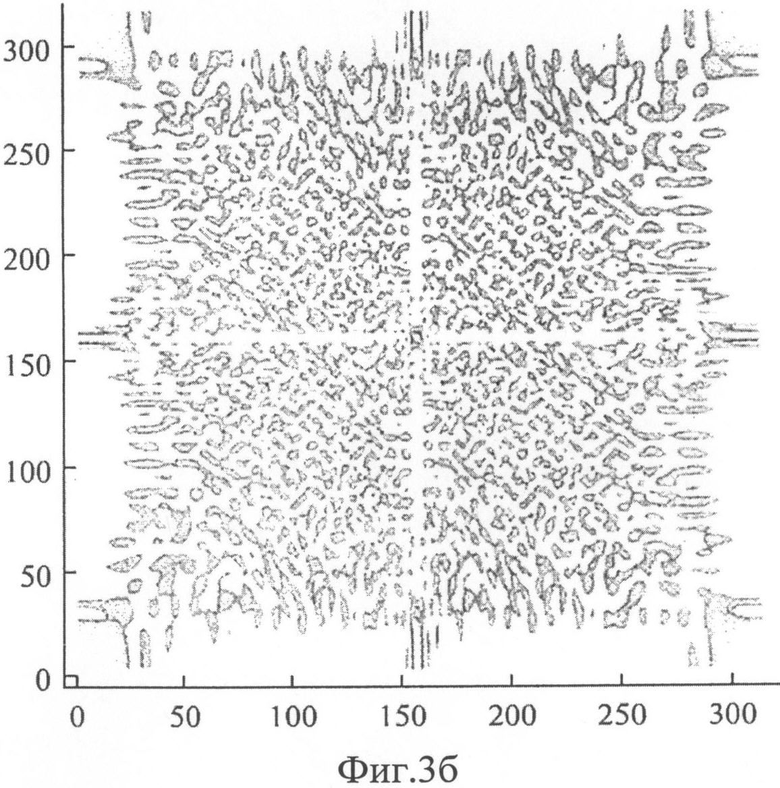
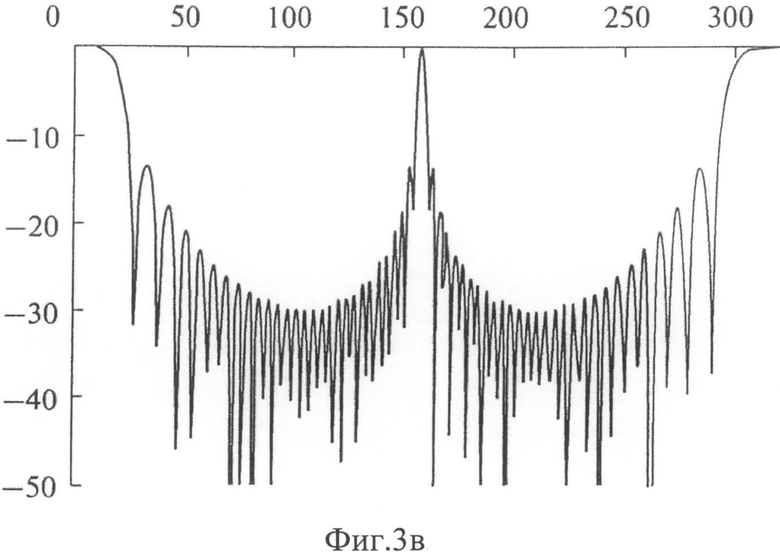
на фигурах 3-4 представлены графическое отображение диаграмм направленности (ДН) подрешетки, построенной на 28-ми элементах, представленных на Фиг.2, при расстоянии между узлами dx=dy=λ/2;
на Фиг.3а. ДН, в децибелах, в зависимости от углов биконической системы координат δx, δy, в интервалах (0, π) относительно нормали к решетке с дискретом 0.01 рад, по осям - номера дискретов, вид сбоку, луч по нормали к решетке,
на Фиг.3б ДН, вид сверху, сечение по уровню - 15 дБ;
на Фиг.3в ДН, одномерное сечение по осям;
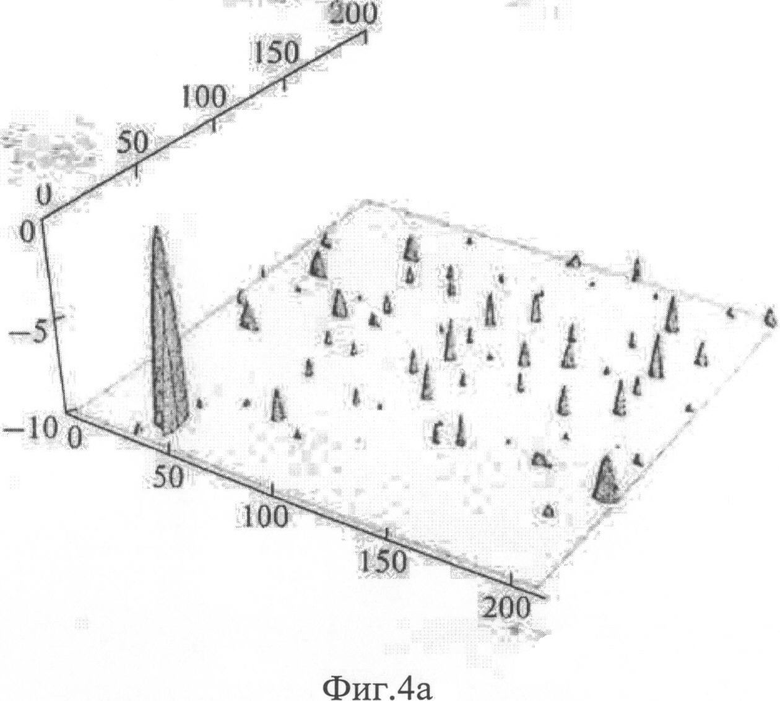
на Фиг.4а ДН, в децибелах, в зависимости от углов биконической системы координат δx, δy, в интервалах (π/3, 2π/3) относительно нормали к решетке с дискретом 0.01 рад, вид сбоку, луч со смещением: (2π/9, 5π/18) относительно нормали;
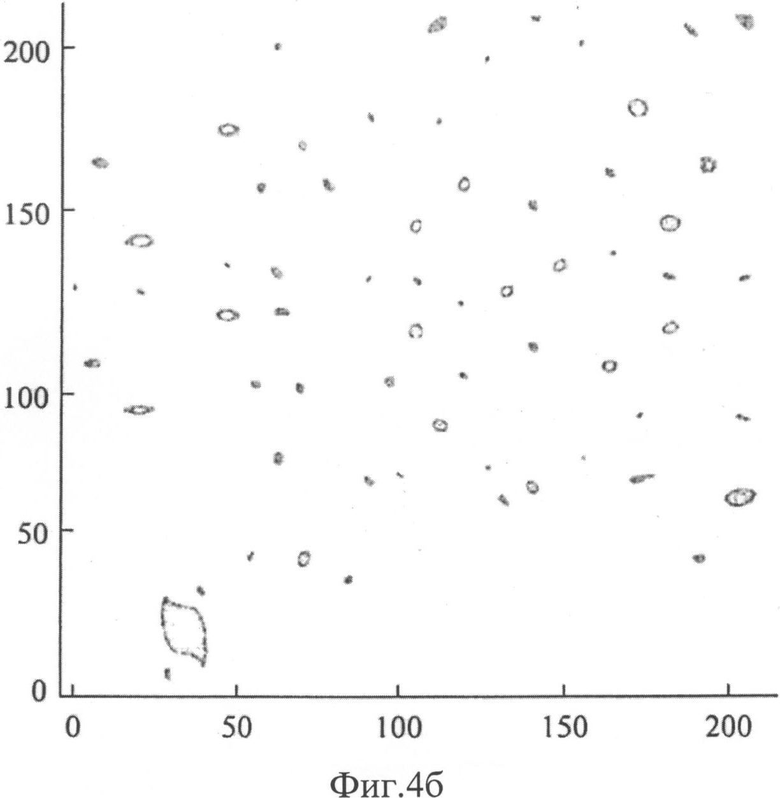
на Фиг.4б ДН, вид сверху, сечение по уровню - 15 дБ,
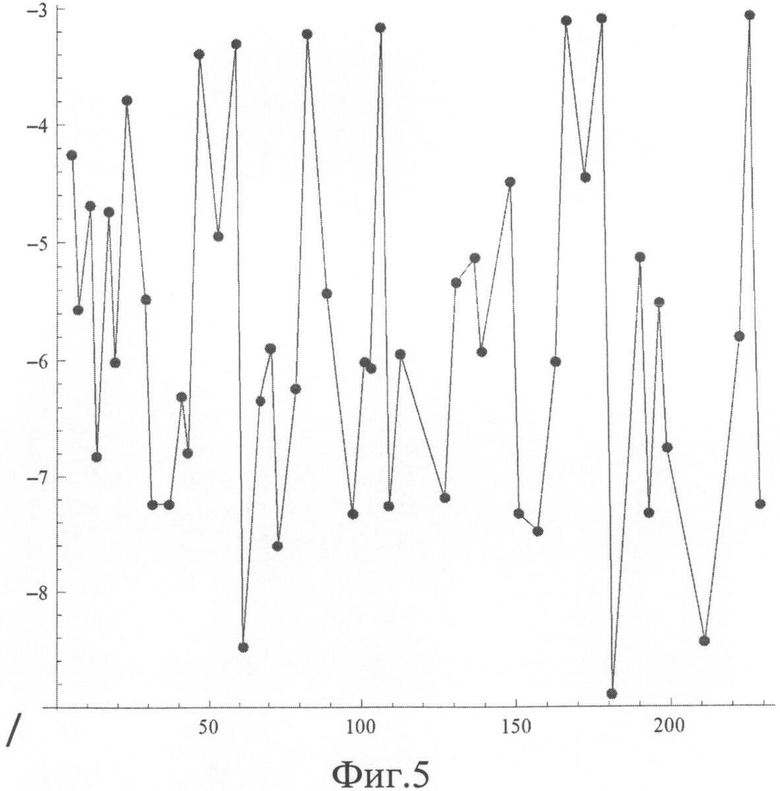
на Фиг.5 Зависимость коэффициента заполнения узлов от простого модуля в диапазоне от 5 до 229,
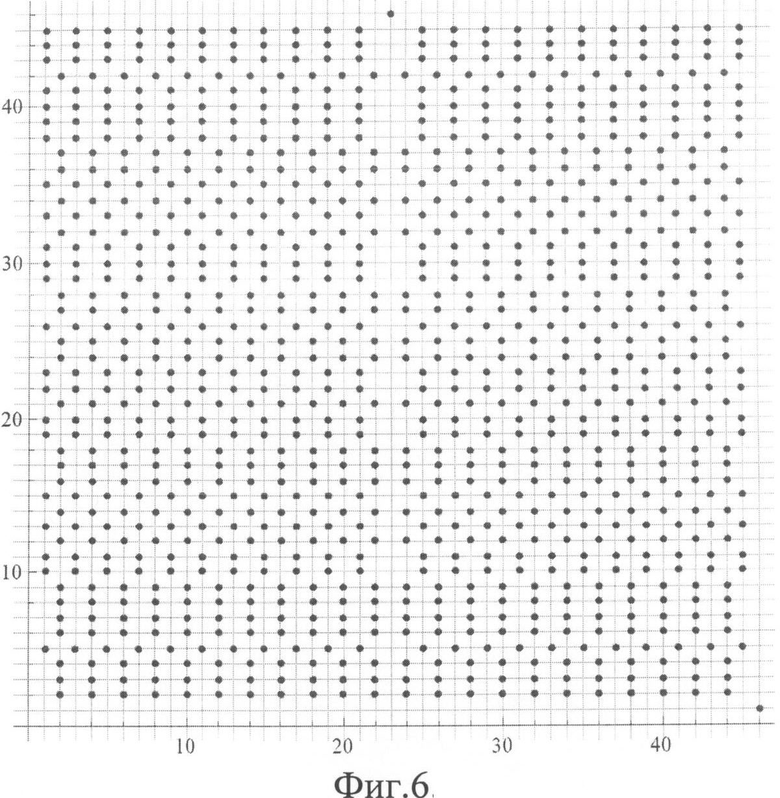
на Фиг.6 Расположение элементов на сетке узлов для для р=47, всего 22 ФАР-К(1);
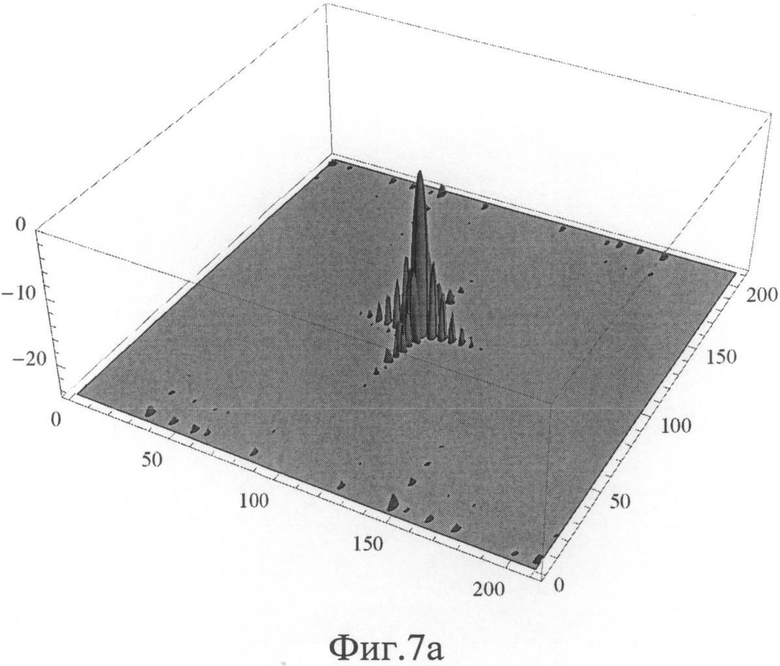
на Фиг.7а ДН для ФАР, заполненной 22-мя ФАР-К(1), при р=47 в интервалах [π/3, 2π/3), по осям - номера дискрета, цена дискрета: 0.01 рад, луч не смещен, вид сбоку,
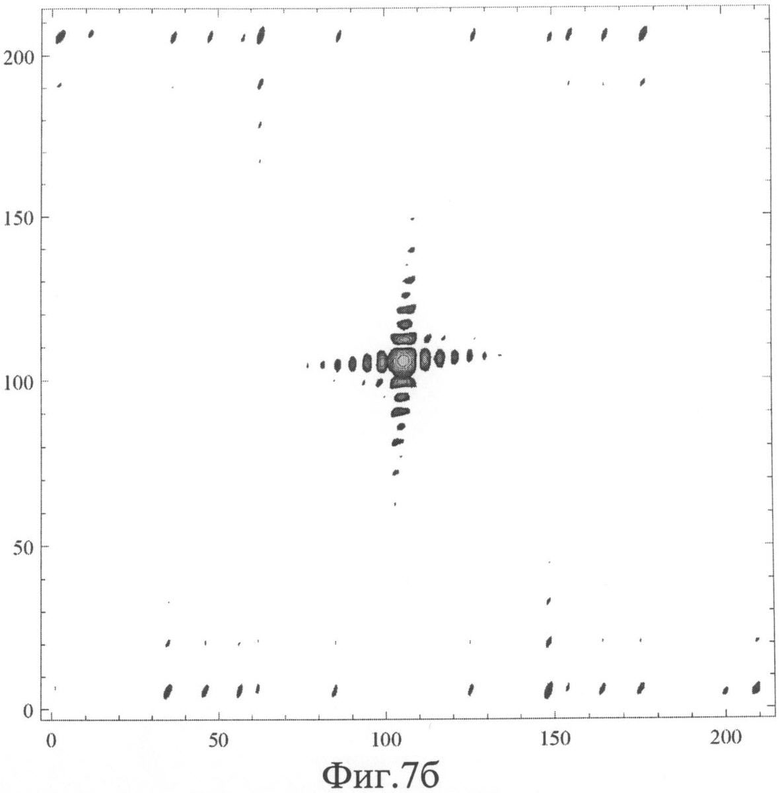
на Фиг.7б ДН, вид сверху, сечение по уровню - 25 дБ,
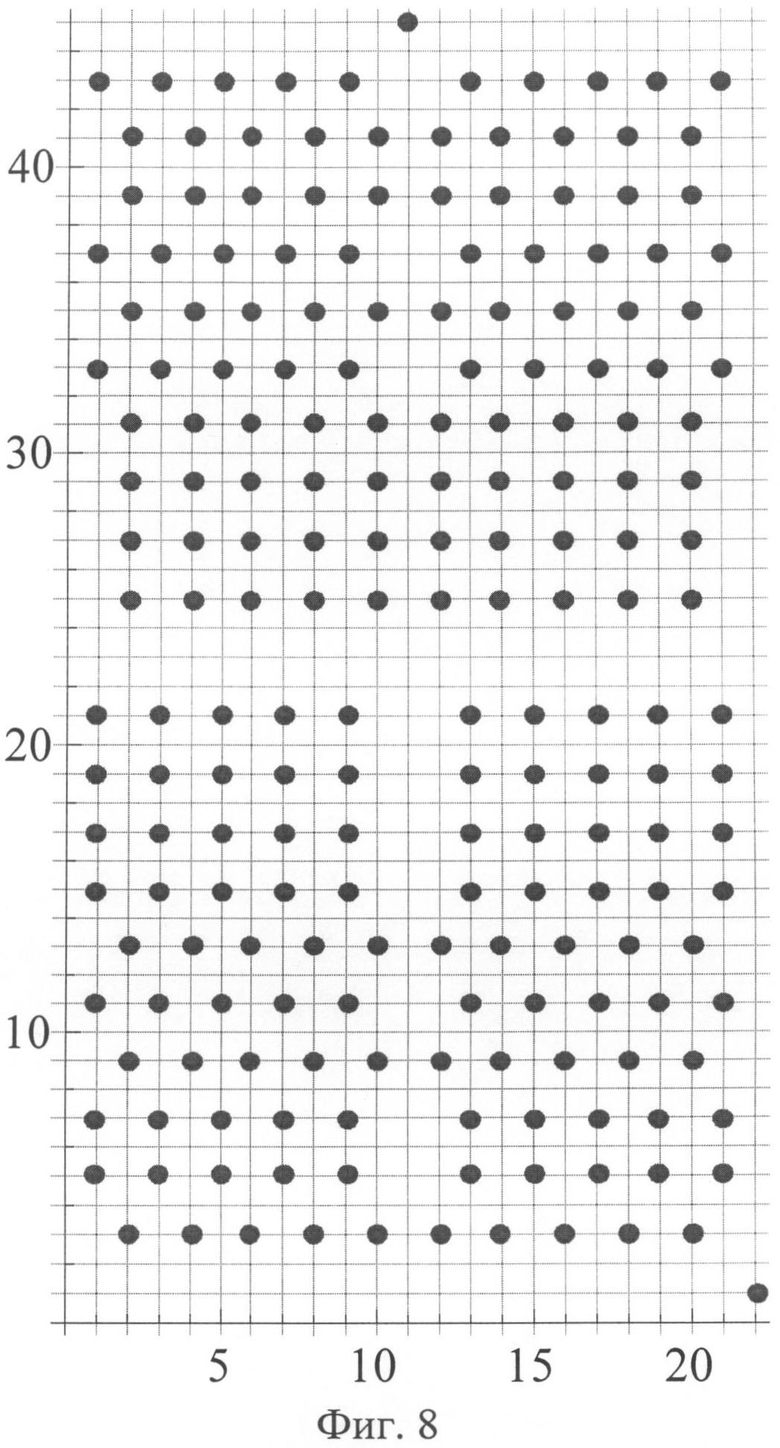
на Фиг.8 Расположение элементов на сетке узлов для р=23*46;
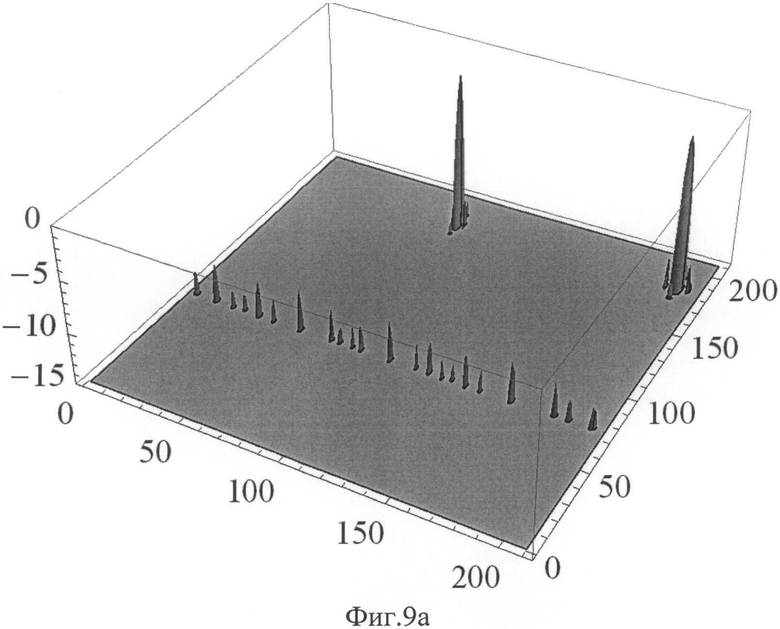
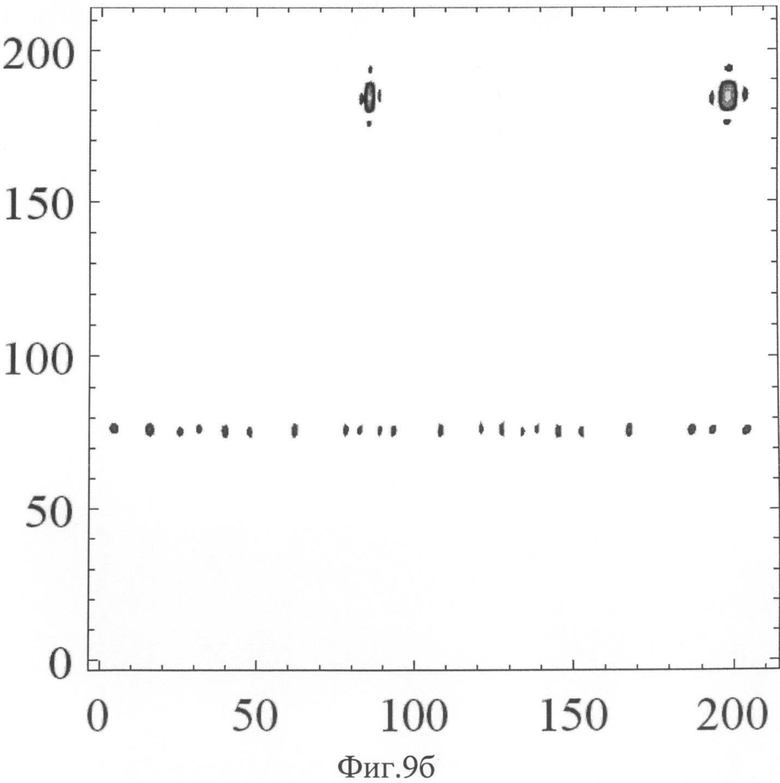
на Фиг.9а ДН для ФАР, заполненной 22-мя ФАР, при р=23*46 в интервалах (π/3, 2π/3), луч смещен на (π/4, 8π/27), вид сбоку, по осям - номер дискрета, цена дискрета: 0.01 рад,
на Фиг.9б ДН, вид сверху, сечение по уровню - 15 дБ,
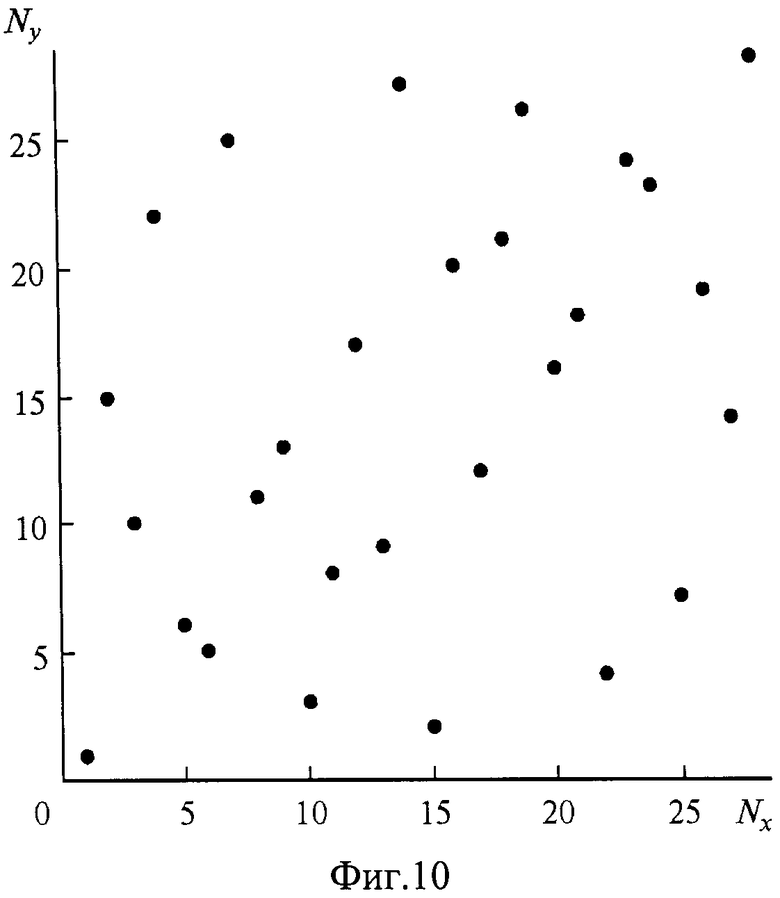
на Фиг.10 Расположение элементов на сетке узлов для р=29 при кодировании обеих координат.
Для упрощения расчетов и графического отображения ДН приведены без учета известного ограничения на сумму квадратов косинусов углов δx, δy.
Установлено, что построенные таким способом решетки имеют ДН с шириной по углам биконической системы координат, определяемой размерами апертуры, и уровнем боковых лепестков (УБЛ), близким к ФАР с эквидистантным заполнением при совпадающем числе элементов. Значения уровня первого бокового лепестка и статистические характеристики при различных модулях р приведены в табл.1
В зависимости от значения m стороны сетки узлов имеют соотношение от квадрата до прямоугольника с различным пропорциями. Так, для m=p сетка узлов является квадратом с соотношением сторон (p-1)×(p-1); для m=1p - прямоугольником с соотношением сторон (p-1)×(2р-1), т.е. практически 1:2; для составного модуля m=pα - прямоугольником с соотношением сторон: (pα-1-(p-1)-1)×(pα-1).
Например, для составного модуля p=2*29=58 при ПО корне, равном 3, координаты узлов даются списком:
{{1,3}, {2,9}, {3,27}, {4,23}, {5,11}, {6,33}, {7,41}, {8,7}, {9,21}, {10,5}, {11,15},
{12,45}, {13,19}, {14,57}, {15,55}, {16,49}, {17,31}, {18,35}, {19,47}, {20,25},
{21,17}, {22,51}, {23,37}, {24,53}, {25,43}, {26,13}, {27,39}, {28,1},
где номера столбцов изменяют свои значения от 1 до 28, а координаты строк - от 1 до 58 за исключением кратных 58.
Для составного модуля р=72=49 при ПО корне, равном 3, координаты узлов даются списком:
{{1,3}, {2,9}, {3,27}, {4,32}, {5,47}, {6,43}, {7,31}, {8,44}, {9,34}, {10,4}, {11,12},
{12,36}, {13,10}, {14,30}, {15,41}, {16,25}, {17,26}, {18,29}, {19,38}, {20,16},
{21,48}, {22,46}, {23,40}, {24,22}, {25,17}, {26,2}, {27,6}, {28,18}, {29,5}, {30,15},
{31,45}, {32,37}, {33,13}, {34,39}, {35,19}, {36,8}, {37,24}, {38,23}, {39,20},
{40,11}, {41,33}, {42,1},
где номера столбцов изменяют свои значения от 1 до 42, а координаты строк - от 1 до 49, за исключением кратных 49.
Для j-го элемента номер строки k рассчитывают по заданному номеру столбца j по правилу:
k=(gl)modp,
где простое число р принимает значения 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, 359, 383, 467, 479, 503, 563, 587, 719, 839, 863, 887, 983, j - последовательно изменяется от 1 до р-1, а k изменяется в пределах от 1 до р-1, gl - один из ПО корней простого числа р, число которых, для перечисленных значений р, равно (р-3)/2.
Установлено, что коэффициент заполнения сетки узлов для выбранных значений р равен (p-3)/(2(p-1)) и стремится к 0.5.
На Фиг.5 показана зависимость в децибелах коэффициента заполнения узлов от простого модуля в диапазоне от 5 до 229, которая иллюстрирует указанные свойства перечисленных значений р.
Количество подрешеток равно числу ПО корней и равно величине (р-3)/2. Элементы разных подрешеток совпадают только в двух узлах с координатами: ((p-3)/2), p-1); (p-1,1).
Такое малое число совпадающих элементов предопределяет независимость ДН подрешеток, построенных по разным ПО корням перечисленных числовых модулей. Влияние единичных элементов незначительно и их можно отбросить при формировании ДН.
На Фиг.6 показано расположение элементов на сетке узлов для для р=47, составляющих 22 подрешетки с 46-ю элементами каждая, узлы с совпадающими элементами видны на рисунке, так как они выступают за границы общего контура расположения элементов.
На Фиг.7а, 7б показаны соответствующие ДН для всей ФАР, состоящей из 22-х подрешеток, в интервалах изменения по углам δx, δy, равного (π/3, 2π/3), по осям отложены номера дискрета, цена дискрета: 0.01 рад, луч не смещен; Фиг.7а: вид сбоку; Фиг.7б. вид сверху, сечение по уровню - 25дБ.
На Фиг.8 показано расположение элементов на сетке узлов для m=2*23;
На Фиг.9а показана соответствующая ДН для ФАР, составленная из 11-и ФАР, при m=2*23 в интервалах (π/3, 2π/3), луч смещен на (π/4, 8π/27), вид сбоку, по осям - номер дискрета, цена дискрета: 0.01 рад, и на Фиг.9б, вид сверху, сечение по уровню - 15 дБ.
При смещенном луче появляется два дифракционных пика, характерных для решетки с соотношением сторон 1:2. Ложный пик может быть убран алгоритмически путем совместной обработки ДН, построенной на всей решетке, и ДН, построенной также на половине решетки, имеющей одиночный дифракционный пик.
Эти рисунки иллюстрируют возможность построения решеток описанным способом с диаграммами направленности, обладающими нужными свойствами.
Размещение элементов на регулярной сетке узлов ФАР осуществляют так, что j-й элемент размещают в столбце с номером kx и строке с номером ky, определяемым по правилам:
kx=(gl)jmodm
ky=(gn)jmodm
где gl, gn - l-й и n-й первообразные корни числа m, l, n принимают значения от 1 до значения, равного числу первообразных корней модуля m: φ(φ(m)), номер столбца kx изменяется от 1 до φ(m)-1, номер строки ky изменяется в диапазоне от 1 до (φ{m)-1.
В этом случае номер элемента не совпадает с номером столбца, а является «синхронизирующим» параметром при расчете координат элементов.
В качестве иллюстрации приведено расположение элементов с координатами, кодированными по паре ПО корней модуля 29: (2,15). Координаты даются списком:
{{2,15}, {422}, {8,11}, {16,20}, {3,10}, {6,5}, {12,17}, {24,23}, {19,26}, {9,13}, {18,21}, {7,25},
{14,27}, {28,28}, {27,14}, {25,7}, {21,18}, {13,9}, {26,19}, {23,24}, {17,12}, {5,6}, {10,3}, {20,16},
{11,8}, {22,4}, {15,2}, {1,1}}.
На Фиг.10 показано расположение элементов по этому списку. К совпадающему расположению приводит кодирование также по другим парам ПО корней: (14,27), (3,18), (26,11), (8,10), (21,19).
По сравнению с прототипом предлагаемый в настоящем изобретении способ размещения элементов в разреженной фазированной антенной решетке, иллюстрированный на чертежах, позволяет:
- формировать на регулярной сетке узлов ФАР, состоящую из набора подрешеток с диаграммами направленности, формируемыми по различным элементам, совпадающими на регулируемое число элементов, от полного их совпадения до совпадения только двух элементов, что обеспечивает статистическую независимость ДН и возможность их автономного управления;
- заполнять сетки узлов с малым шагом: 1/(р-1), от высокоразреженной, с плотностью заполнения 1/(р-1) до заполненной практически наполовину;
- обеспечивать максимальное разрешение по углам при заданном числе элементов;
Эти технические результаты обеспечивают расширение эксплуатационных свойств ФАР путем гибкого использования потенциала ФАР за счет комбинирования ДН различных подрешеток: их сложения, умножения или самостоятельного использования, что актуально при наблюдении объектов в большом динамическом диапазоне по дальности, для сопровождения многих объектов или составления карты помех.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ СКОРОСТИ ДВИЖЕНИЯ ТРАНСПОРТНОГО СРЕДСТВА | 1997 |
|
RU2126164C1 |
| ФАЗИРОВАННАЯ АНТЕННАЯ РЕШЕТКА ОТРАЖАТЕЛЬНОГО ТИПА | 1991 |
|
RU2048699C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПРОВАЛОВ В НАПРАВЛЕНИЯХ ИСТОЧНИКОВ ПОМЕХ В ДИАГРАММАХ НАПРАВЛЕННОСТИ ПЛОСКИХ ФАЗИРОВАННЫХ АНТЕННЫХ РЕШЕТОК С НЕПРЯМОУГОЛЬНОЙ ГРАНИЦЕЙ РАСКРЫВА | 2013 |
|
RU2559763C2 |
| Устройство управления ферритовыми фазовращателями модульной фазированной антенной решетки | 2018 |
|
RU2698957C1 |
| ФАЗОВЫЙ СПОСОБ ФОРМИРОВАНИЯ ПРОВАЛОВ В ДИАГРАММЕ НАПРАВЛЕННОСТИ ПЛОСКОЙ ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКИ | 2011 |
|
RU2579610C2 |
| Вычислитель положения луча фазированной антенной решетки | 1982 |
|
SU1841199A1 |
| Вычислитель положения луча фазированной антенной решетки | 1982 |
|
SU1841222A1 |
| СПОСОБ ФАЗОВОГО ФОРМИРОВАНИЯ НУЛЕЙ В ДИАГРАММЕ НАПРАВЛЕННОСТИ ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКИ | 2008 |
|
RU2373620C1 |
| СПОСОБ КАЛИБРОВКИ ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКИ В БЛИЖНЕЙ ЗОНЕ | 2024 |
|
RU2832105C1 |
| ФАЗИРОВАННАЯ АНТЕННАЯ РЕШЕТКА С УПРАВЛЯЕМОЙ ШИРИНОЙ ДИАГРАММЫ НАПРАВЛЕННОСТИ | 2012 |
|
RU2507647C1 |
Изобретение относится к области антенной техники. Технический результат - повышение эксплуатационных возможностей решетки. Способ размещения элементов на разреженной фазированной антенной решетке, при котором на регулярной сетке узлов элементы размещают по методу двумерных разностных множеств, отличается тем, что фазированную антенную решетку формируют из набора подрешеток, каждая из которых состоит из φ(m)-1 элементов, где числовой модуль m принимает значения pα, 2рα, α - число натурального ряда, p - простое число, φ(m) - функция Эйлера, и максимальное количество подрешеток равно φ(φ(m)) - числу первообразных корней числа m, при этом каждый из φ(m)-1 элементов данной подрешетки размещают в узлах сетки по одному на каждом столбце и не более чем по одному, на каждой строке так, что для j-го элемента номер строки k определяют по заданному номеру столбца j по правилу: k=(gl)jmodm, где gl - l-й первообразный корень числа m, l принимает значения от 1 до значения, равного числу первообразных корней модуля m: φ(φ(m)), номер столбца j изменяется от 1 до φ(m)-1, номер строки k изменяется в диапазоне от 1 до m, принимая все значения за исключением кратных m. 2 з.п. ф-лы, 1 табл., 10 ил.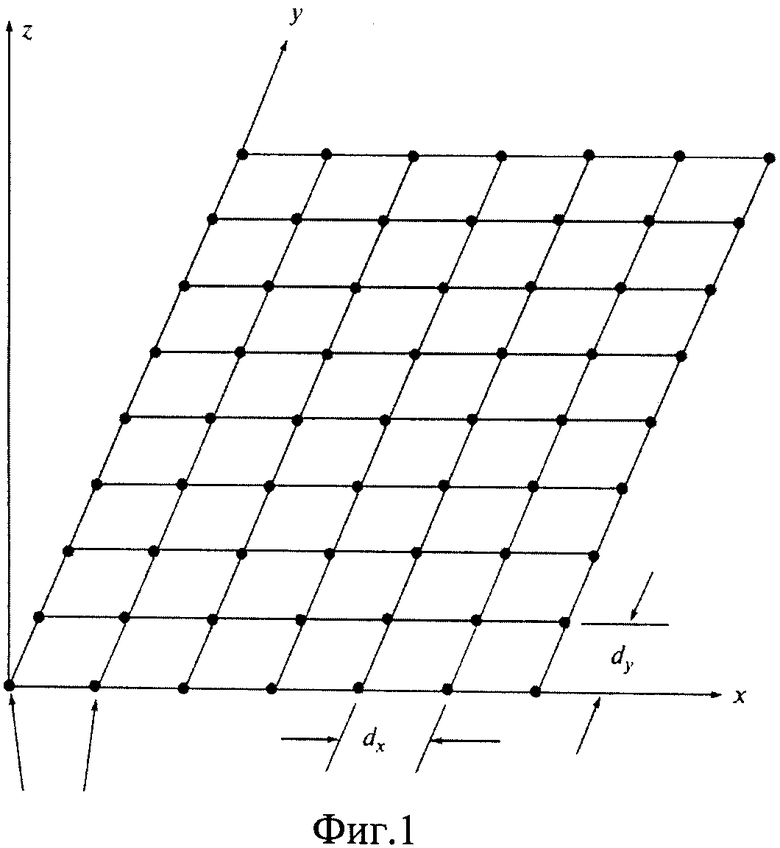
1. Способ размещения элементов на разреженной фазированной антенной решетке, при котором на регулярной сетке узлов элементы размещают по методу двумерных разностных множеств, отличающийся тем, что фазированную антенную решетку формируют из набора подрешеток, каждая из которых состоит из φ(m)-1 элементов, где числовой модуль m принимает значения pα, 2рα, α - число натурального ряда, p - простое число, φ(m) - функция Эйлера, и максимальное количество подрешеток равно φ(φ(m)) - числу первообразных корней числа m, при этом каждый из φ(m)-1 элементов данной подрешетки размещают в узлах сетки по одному на каждом столбце и не более чем по одному, на каждой строке так, что для j-го элемента номер строки k определяют по заданному номеру столбца j по правилу:
k=(gl)jmodm
где gl - l-й первообразный корень числа m, l принимает значения от 1 до значения, равного числу первообразных корней модуля m: φ(φ(m)), номер столбца j изменяется от 1 до φ(m)-1, номер строки k изменяется в диапазоне от 1 до m, принимая все значения за исключением кратных m.
2. Способ по п.1, по которому для j-го элемента номер строки k рассчитывают по заданному номеру столбца j по правилу:
k=(gl)jmodp,
где простое число р принимает значения 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, 359, 383, 467, 479, 503, 563, 587, 719, 839, 863, 887, 983, j - последовательно изменяется от 1 до р-1, а k изменяется в пределах от 1 до р-1, gl - один из первообразных корней простого числа p, число которых для перечисленных значений p равно величине (р-3)/2.
3. Способ по п.1, при котором для j-го элемента, где j изменяется от 1 до р-1, номер столбца kx рассчитывают по правилу:
kx=(gl)jmodp,
а номер строки ky рассчитывают по правилу:
ky=(gn)jmodp,
где номера строк и столбцов изменяются в пределах от 1 до р-1, gl, gn - различные первообразные корни числа p, l, n - номера несовпадающих первообразных корней, изменяющихся от 1 до φ(р-1), так что общее количество подрешеток достигает значения φ(p-1)(φ(p-1)-1)/2.
| Разреженная неэквидистантная фазированная антенная решетка | 1986 |
|
SU1377942A1 |
| RU 2004125811 A, 10.02.2006 | |||
| СПОСОБ РАЗМЕЩЕНИЯ ЭЛЕМЕНТОВ В ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКЕ (ФАР) | 2008 |
|
RU2349997C1 |
| CN 102280714 A, 14.12.2011 | |||
| US 4071848 A, 31.01.1978 | |||
| US 6433754 B1, 13.08.2002. | |||
Авторы
Даты
2013-12-20—Публикация
2012-06-19—Подача