Изобретение относится к области медицинского приборостроения.
Известны диагностическое устройство [1] и диагностический комплекс [2] для измерения медико-биологических характеристик кожи и слизистых оболочек in vivo включающий посылку оптического излучения на тестируемую ткань и регистрацию отраженного тканью излучения, которые определяют соответственно степень насыщения кислородом гемоглобина артериальной крови, частоту пульса и состояние кровотока в системе микроциркуляции. При этом коэффициент рассеяния ткани не определяется, а значит результат измерения вышеуказанных параметров подвержен существенному влиянию рассеивающих свойств ткани.
Известны также способы определения оптических и биофизических параметров биологических тканей по отраженному излучению с использованием интегрирующей сферы [3, 4] и оптоволоконного устройства, содержащего два соосных волновода, расположенных на фиксированном расстоянии друг от друга, для посылки и регистрации излучения [5]. В обоих случаях обратная задача по интерпретации спектральных коэффициентов диффузного отражения (КДО) ткани осуществляется путем минимизации разницы между экспериментальными и рассчитанными в рамках модели биоткани спектрами КДО. В [3, 4] предполагается измерение таких параметров кожи, как толщина эпидермиса, концентрация меланина и степень оксигенации гемоглобина. В [5] определяются коэффициент поглощения и транспортный коэффициент рассеяния слизистых оболочек полости рта, пищевода, желудка и легких, концентрации в них кровеносных сосудов и насыщение крови кислородом. К недостаткам данных способов следует отнести узкую область корректности используемых методов расчета характеристик переноса излучения, неоднозначность решения обратной задачи, вследствие невозможности разделения вкладов рассеяния и поглощения ткани в измеряемый спектр, и необходимость использования большого объема априорной информации об исследуемой среде (в частности, для корректной оценки поглощающих свойств ткани необходимо располагать информацией об ее рассеивающих свойствах, и наоборот).
Известны способы и устройства для определения оптических параметров однородной [6, 7] биоткани с использованием измерений рассеянного тканью света на нескольких расстояниях L от точки освещения. Способы позволяют определять коэффициент поглощения k и транспортный коэффициент µs рассеяния ткани. В [6] это достигается путем сопоставления расчетных и экспериментальных пространственных профилей диффузного отражения. Для расчета пространственного профиля КДО - R(L) используется уравнение полиномиальной множественной регрессии между R(L) и оптическими параметрами среды - k и µs, установленное на основе измерений R(L) для множества калибровочных образцов с известными оптическими параметрами. Данный способ требует строгое совпадения показателей преломления и индикатрис рассеяния реальных тканей и калибровочных образцов, что редко достигается в действительности. Кроме того, способ может давать неадекватные или не соответствующие реальности результаты, если значения параметров k и µs выйдут за пределы области, охватываемой калибровочными образцами. В способе [7] для восстановления параметров k и µs из измерений R(L) используется специально обученная нейронная сеть. Обучающий массив данных получен на основе расчета R(L) методом Монте-Карло для множества комбинаций значений k и µs. При этом в расчетах не учитываются вариации показателя преломления среды и фактора анизотропии рассеяния, что приводит к неудовлетворительным результатам использования данного метода для расстояний L<2 мм. В способах [6, 7] не учитывается многослойное строение ткани, поэтому их использование для кожи и других тканей, состоящих из нескольких слоев с принципиально отличающимся биохимическим составом и оптическими свойствами, не является корректным. Кроме того, данные способы предполагают, что КДО измеряются в спектральной области малых поглощений хромофоров ткани (меланин, билирубин, гемоглобин, оксигемоглобин и т.п.) - λ=660-1000 нм. Это обуславливает высокую чувствительность коэффициентов поглощения, определяемых на основе данных способов, к погрешностям измерения диффузного рассеяния и делает необходимым использования больших расстояний между точками освещения и регистрации, что, в свою очередь, приводит к невысокому уровню сигнала на фоне шумов измерительного устройства и большой вероятности искажения результатов измерений неоднородностью объема ткани, с которым взаимодействует излучение.
Наиболее близким к заявляемому изобретению является способ определения концентрации гемоглобина, основанный на измерении диффузного отражения ткани на двух изобестических длинах волн окси- и деоксигемоглобина, включающий посылку излучения на образец ткани, измерение диффузного отражения от ткани, вычисление отношения интенсивностей диффузного отражения на двух изобестических длинах волн с использованием измеренного диффузного отражения и определение концентрации гемоглобина в ткани посредством подстановки вычисленного отношения в предопределенное аналитическое выражение, соответствующее используемым изобестическим длинам волн [8]. К недостаткам данного способа следует отнести влияние вариаций рассеивающих свойств ткани и ее многослойного строения на точность измерений гемоглобина, а также невозможность определения комплекса других важных биофизических и оптических параметров ткани. Кроме того, при использовании данного способа для кожи, результаты измерения гемоглобина будут существенно искажены влиянием пигментации кожи.
Предлагаемое изобретение направлено на решение задачи расширения функциональных возможностей за счет одновременного определения комплекса как оптических, так и биофизических параметров биологической ткани в режиме реального времени, повышение точности измерения данных параметров за счет учета их общей вариативности, а также за счет исключения калибровочных измерений для нормированного r(Z, λ) спектрально-пространственного профиля коэффициента диффузного отражения ткани и использования априорной информации.
Для решения данной задачи посылку излучения на ткань в одну или несколько точек осуществляют на длинах волн λ из диапазона 350-1600 нм, измеряют диффузное отражение P(L, λ) на длинах волн посылаемого излучения для каждой из точек освещения, где L - расстояние между точками освещения и регистрации диффузного отражения на поверхности ткани, определяют абсолютный R(L, λ) или нормированный r(L, λ) спектрально-пространственный профиль коэффициента диффузного отражения ткани, как R(L, λ)=P(L, λ)/(P0 (λ)A(L,λ)) или r(L, λ)=P(L, λ)/P(L0, λ), где Р0(λ) - мощность излучения, посылаемого на ткань; A(L, λ) - аппаратурная константа, определяемая экспериментально с использованием эталонного отражателя, или рассчитываемая по известным геометрическим параметрам и спектральным характеристикам измерительного устройства; L0 - одно из расстояний между точками освещения и регистрации диффузного отражения; а оптические и биофизические параметры (X) определяют на основе аналитических выражений, представляющих собой множественные регрессии между X и R(L, λ) или между X и r(L, λ), которые получают путем измерения или расчета методом Монте-Карло коэффициентов диффузного отражения для множества образцов биоткани или моделирующих ее фантомов с известными оптическими и биофизическими параметрами, накопления ансамбля реализации оптических и биофизических параметров биоткани и соответствующих им спектрально-пространственных профилей R(L, λ), r(L, λ) для возможных диапазонов вариаций оптических и биофизических параметров ткани.
В качестве биоткани в предлагаемом изобретении используют кожу, молочную железу, слизистую оболочку полости рта, пищевода, органов желудочно-кишечного тракта и легких как in vivo, так и in vitro. Определяют такие оптические параметры ткани как коэффициент поглощения, транспортный коэффициент рассеяния, фактор анизотропии рассеяния, и такие биофизические параметры как объемная концентрация меланина, интегральное содержание меланина в эпидермисе, концентрация общего гемоглобина, насыщение гемоглобина кислородом, концентрация билирубина, средний диаметр и объемная концентрация капилляров с кровью, концентрация и размер эффективных рассеивателей ткани, содержание воды в ткани.
Коэффициенты диффузного отражения определяют или на характеристических длинах волн спектров поглощения и рассеяния компонентов исследуемой ткани, или же во всем диапазоне посылаемого излучения с последующей интерполяцией или экстраполяцией полученных коэффициентов R(L, λ) и r(L, λ) к длинам волн, соответствующим аналитическим выражениям, на основе которых осуществляется переход от R(L, λ) и r(L, λ) к определяемым параметрам ткани.
Предопределенные аналитические выражения между профилями R(L, λ), r(L, λ) и определяемыми оптическими и биофизическими параметрами ткани в виде множественных регрессий устанавливают путем измерения или расчета методом Монте-Карло коэффициентов диффузного отражения для множества образцов биоткани или моделирующих ее фантомов с известными оптическими и биофизическими параметрами, накопления ансамбля реализации оптических и биофизических параметров биоткани и соответствующих им спектрально-пространственных профилей R (L, λ), r(L, λ) и использования регрессионного или других математических методов анализа полученного ансамбля реализации.
Оптические и биофизические параметры ткани можно также определять на основе множественных регрессий между X и линейно-независимыми компонентами профиля R(L, λ) или r(L, λ), определяемыми как проекции профиля R(L, λ) или r(L, λ) на пространство из собственных векторов его ковариационной матрицы.
Свойства, появляющиеся у заявляемого технического решения, следующие:
1) повышение точности определения оптических и биофизических параметры ткани за счет учета их общей вариативности, исключения использования априорной информации, устранения калибровочных измерений для нормированного r(L, λ) спектрально-пространственного профиля коэффициента диффузного отражения ткани
2) расширение функциональных возможностей за счет одновременного определения комплекса оптических и биофизических параметров ткани в режиме реального времени, что не достигается с использованием известных способов.
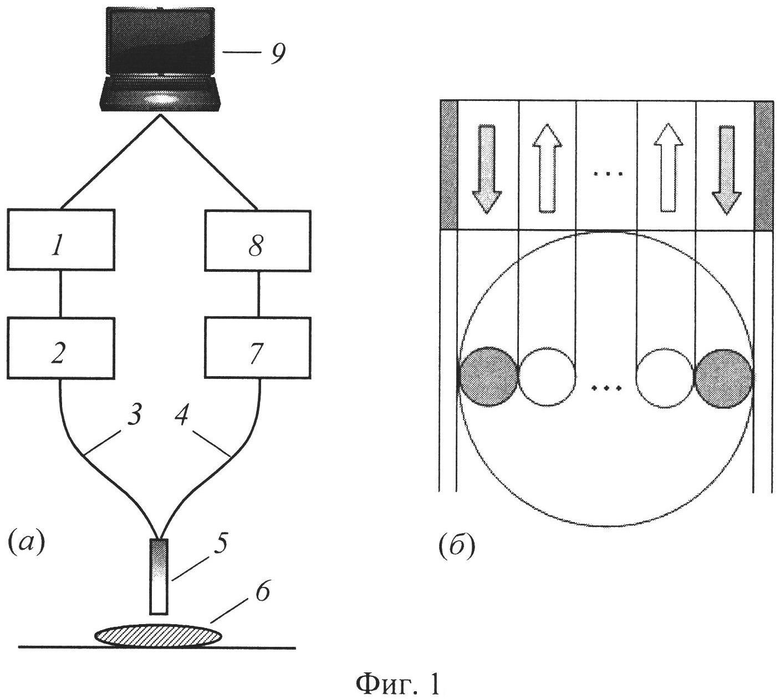
Сущность данного изобретения поясняется с помощью фиг.1-8. На фиг.1, а изображена блок-схема устройства, реализующая предлагаемый способ, включающая блок светового излучения (1), оптоволоконный зонд (5), оснащенный освещающими (3) и принимающими (4) волокнами, монохроматор (2) или спектрометр (7), устройство регистрации (8) и устройство обработки измерительной информации (9). В качестве альтернативы оптоволоконному зонду 5 для посылки света на образец биоткани 6 и сбора отраженного ей потока может использоваться светопередающая оптика. Устройство регистрации 8 может быть выполнено как прибор с зарядовой связью (ПЗС). Вместо ПЗС могут использоваться фотоумножитель (ФЭУ) или фотодиоды. Блоком светового излучения 1 может служить лампа белого света (ксеноновая, аргоновая или криптоновая) или светодиоды (СД). Альтернативой монохроматору 2 является набор сменных фильтров. Оптоволоконный зонд 5 может включать эластичную трубку, содержащую множество оптических волокон (т.е., по крайней мере, одно освещающее и не менее двух принимающих), позволяя тем самым регистрировать спектрально-пространственный профиль сигналов диффузного отражения относительно освещающих волокон. Зонд 5 может быть также оснащен твердым наконечником, в котором множество волокон расставляются в различные геометрические конфигурации «освещение-регистрация».
Свет от источника излучения 1, пропущенный через монохроматор 2, поступает в оптоволоконный зонд 5, в котором по одному или нескольким освещающим волокнам 3 попадает на биоткань 6. Принимающие волокна 4 в оптоволоконном зонде 5 собирают диффузно отраженный свет и передают его на спектрометр 7. Сигналы диффузного отражения от различных принимающих волокон пространственно разделяются при помощи ПЗС 8, позволяя, таким образом, одновременно измерять спектры диффузного отражения для различных расстояний между каналами освещения и приема излучения.
На фиг.1, б представлен один из возможных вариантов расположения каналов возбуждения и регистрации сигналов диффузного отражения. Оптическое излучение подается в каналы возбуждения, расположенные на различных расстояниях L от точек регистрации сигналов отражения (в данном варианте по двум каналам). Сравнение профилей рассеянного излучения от каналов возбуждения позволяет оценить степень неоднородности освещаемого объема и тем самым выбрать оптимальный для проведения измерений участок объекта. Диффузное отражение измеряют или во всем спектральном диапазоне посылаемого на ткань излучения с некоторым спектральным разрешением, или же, на характеристических длинах волн спектров поглощения и рассеяния компонентов исследуемой биоткани с последующей интерполяцией или экстраполяцией к длинам волн, соответствующим используемым аналитическим выражениям для перехода к определяемым параметрам биоткани. Для получения пространственных значений коэффициентов отражения диффузное отражение измеряют не менее чем на двух расстояниях от точек освещения. После измерения спектра отражения ткани, полученные данные поступают на блок обработки 9, позволяющий получать абсолютные R(L, λ) или нормированные r(L, λ) спектрально-пространственные профили КДО ткани, а также вычисляющий значения оптических и биофизических параметров ткани (X) на основе множественных регрессий между X и спектрально-пространственными профилями КДО ткани или их линейно-независимыми компонентами.
Регистрируемые сигналы P(L, λ) зависят от спектрально-пространственного профиля КДО ткани - R(L, λ), а также от аппаратурной константы A(L, λ) и спектральной мощности источника света P0(λ):
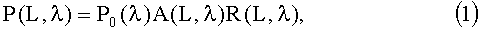
где A(L, λ)=G(L)τ(λ)S(λ), L - расстояние между освещающим и принимающим волокнами, G(L) - числовая апертура оптических волокон, S(λ) - спектральная чувствительности приемника, τ(λ) - функция пропускания оптической системы. Профили R(L, λ) определяются путем сопоставления соответствующих им сигналов P(L, λ) с сигналами Pstd(L, λ), соответствующими эталонному диффузному отражателю:
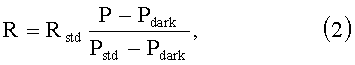
где Rstd - КДО эталонного диффузного отражателя; Pdark - мощность сигнала в отсутствии освещения, соответствующая темновому току.
Для устранения необходимости проведения калибровочных измерений параметры ткани следует определять по нормированному профилю ее КДО R(L, λ)/R(L0, λ), который можно получить в виде отношения сигналов диффузного отражения для пространственно разнесенных каналов регистрации, как r(L, λ)=P(L, λ)/P(L0, λ), где L0 - расстояние между освещающим и одним из светопринимающих волокон. Профили r(L, λ) не зависят от спектральных характеристик компонент измерительного устройства, а определяются только разностью оптических путей световых потоков для двух пространственно разнесенных каналов регистрации.
Для получения множественных регрессий, на основе которых определяются параметры ткани X, используется ансамбль реализации X и профилей R(L, λ), получаемый путем моделирования процесса переноса излучения в исследуемой ткани при широкой вариации ее параметров и расчета R(L, λ), r(L, λ) методом Монте-Карло [9] с учетом конструктивных параметров измерительного устройства (геометрической конфигурации волокон и их числовых апертур). Таким образом, аналитические выражения, связывающие X с профилями КДО ткани, получают путем многократных решений прямой задачи методом Монте-Карло (расчета КДО ткани) при различных комбинациях параметров оптической модели ткани и последующего статистического анализа полученных данных.
Ниже, возможности и достоинства предлагаемого способа демонстрируются на примере кожной ткани и слизистых оболочек полых органов (полости рта, пищевода, желудочно-кишечного тракта и легких).
Оптическая модель слизистой оболочки. Известно, что основными параметрами, характеризующими распространение оптического излучения в рассеивающей среде, являются коэффициенты поглощения k, рассеяния β и индикатриса рассеяния или ее средний косинус g. Причем, в оптике биологических тканей, как очень мутных сред, для описания световых полей достаточно знать не сами величины β и g, а их комбинацию - транспортный коэффициент рассеяния µs=β(1-g).
Спектр коэффициента поглощения слизистой оболочки k(λ) моделируется в виде линейной комбинации спектров поглощения ее хромофоров. В видимой области основными поглощающими хромофорами биоткани являются оксигемоглобин и деоксигемоглобин. В связи с этим, выражение для коэффициента поглощения имеет вид:
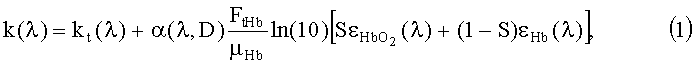
где kt(λ)=A·exp[-B[λ-λ0)] - коэффициент поглощения обескровленной ткани, λ0=632 нм, A (мм-1) и B (нм-1) - параметры, характеризующие спектральную зависимость kt; FtHb (г/л) - концентрация общего гемоглобина в биологической ткани; µHb=64.5 мг/моль - молярная масса гемоглобина; 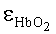 и εHb - молярные коэффициенты поглощения соответственно оксигемоглобина и деоксигемоглобина [10]; S - насыщение гемоглобина кислородом; α - поправочный коэффициент, учитывающий эффект локализованного поглощения света кровеносными сосудами [11]. Суть введения коэффициента α состоит в учете того, что кровь не равномерно распределена в объеме ткани, а локализована в капиллярах. Для хаотически распределенных капилляров с диаметром D коэффициент α определяется на основе следующего выражения [11]:
и εHb - молярные коэффициенты поглощения соответственно оксигемоглобина и деоксигемоглобина [10]; S - насыщение гемоглобина кислородом; α - поправочный коэффициент, учитывающий эффект локализованного поглощения света кровеносными сосудами [11]. Суть введения коэффициента α состоит в учете того, что кровь не равномерно распределена в объеме ткани, а локализована в капиллярах. Для хаотически распределенных капилляров с диаметром D коэффициент α определяется на основе следующего выражения [11]:
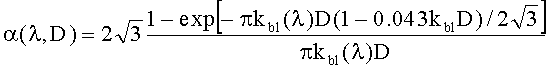
где 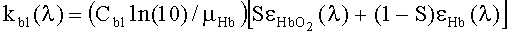 - коэффициент поглощения крови, CHb=150 г/литр - концентрация гемоглобина в крови.
- коэффициент поглощения крови, CHb=150 г/литр - концентрация гемоглобина в крови.
Транспортный коэффициент рассеяния биологических тканей в видимой области спектра с хорошей точностью аппроксимируется степенной зависимостью:
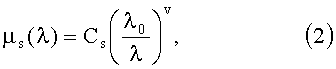
где λ0=632 нм; Cs и ν - структурные параметры ткани, характеризующие объемное содержание и размер ее «эффективных» рассеивателей. Для описания процесса рассеяния излучения используется однопараметрическая функция Хеньи-Гринштейна [9] с фактором анизотропии рассеяния g.
Таким образом, оптическая модель слизистой оболочки определяется параметрами g, A, B, C, ν, FtHb, D, S. Кроме того, для учета отражения падающего света от поверхности ткани, а также многократных переотражений вызванного им диффузного излучения между внутренними слоями и поверхностью ткани необходимо располагать информацией о ее показателе преломления nt. В табл.1 приведены диапазоны вариаций модельных параметров, выбранные путем критического анализа результатов различных авторов [5, 12-22] для нормальных и опухолевых тканей организма (слизистых оболочек полости рта, пищевода, органов желудочно-кишечного тракта и легких).
Вариации модельных параметров будем осуществлять независимо друг от друга, но при этом будем контролировать, чтобы при каждой их комбинации значения оптических параметров ткани, получаемые по формулам (1) и (2), не выходили из диапазонов, наблюдаемых в эксперименте. Исходя их вышеуказанных литературных данных, выбраны следующие ограничения: 1) β'(700 нм)≥0.2 мм-1; 2) k(632 нм)=0.02-0.5 мм-1; 3) ktis(450 нм)≤0.35 мм-1; 4) Λ'(632 нм)=0.5-0.98, где Λ'=β'/(k+β') - транспортное альбедо однократного рассеяния ткани.
Оптико-статистическая модель кожи. Верхний слой кожи - эпидермис с толщиной Lepi, нижний - дерма, которая в оптическом плане считается бесконечно толстой. Показатель преломления слоев кожи nskin относительно воздуха считается одинаковым, поэтому френелевское отражение излучения имеет место только на границе раздела кожи с внешней средой.
Полагаем, что основой кожи является слабопоглощающая, обескровленная ткань. Зависимость ее коэффициента поглощения kt [см-1] от длины волны λ [нм] аппроксимируется следующим выражением:
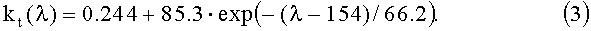
В качестве индикатрисы рассеяния "эффективных" рассеивателей ткани (основными из которых являются упакованные в жгуты коллагеновые и эластиновые волокна дермы, а также кератиноциты и меланоциты эпидермиса) используем функцию Хеньи-Гринштейна, спектральная зависимость фактора анизотропии (среднего косинуса) которой может быть описана эмпирическим соотношением:
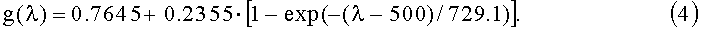
Спектр транспортного коэффициента рассеяния µs(λ) кожи в видимой и ближней ИК-областях спектра рассчитывается как суперпозиция спектров µs(λ), соответствующих рассеивателям Ми и Рэлея с размерами d≥λ и d<<λ соответственно:
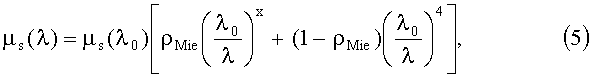
где λ0=400 нм; ρMie - доля рассеяния Ми; x - параметр спектральной зависимости редуцированного коэффициента рассеяния Ми, зависящий от размера рассеивателей и их показателя преломления.
Коэффициенты поглощения слоев кожи определяются по известным правилам сложения оптических величин как сумма коэффициентов поглощения отдельных компонент с весами, равными их объемным концентрациям. Спектр коэффициента поглощения эпидермиса рассчитывается в соответствии с объемными концентрациями меланина fmel и воды wepi в его составе:
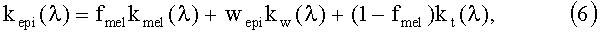
где kmel и kw - коэффициенты поглощения меланина и воды.
Коэффициент поглощения дермы зависит от содержания в ней капилляров с кровью fblood, воды wderm и билирубина Gbil:
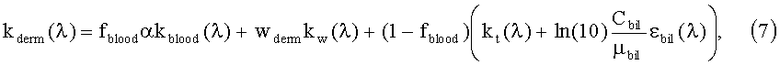
где εbil - молярный коэффициент поглощения билирубина в см-1/(моль/л); µbil=585 г/моль - молярная масса билирубина; kblood - коэффициент поглощения крови; α - корректирующий фактор, учитывающий эффект локализованного поглощения света кровеносными сосудами.
Коэффициент поглощения крови kblood в зависимости от длины волны излучения может быть представлен в виде суммы коэффициентов поглощения гемоглобина (окисленного и не окисленного) и билирубина:
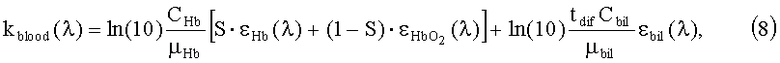
где CHb [г/л] - концентрации общего гемоглобина в крови; µHb=64500 г/моль - молярная масса гемоглобина; 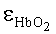 и εHb - молярные коэффициенты поглощения оки- и деоксигемоглобина в см-1 моль/литр); S - насыщение крови кислородом (доля окисленного гемоглобина в общем гемоглобине); tdif=5 - отношение концентраций билирубина в крови и в окружающей ткани (полагается фиксированным).
и εHb - молярные коэффициенты поглощения оки- и деоксигемоглобина в см-1 моль/литр); S - насыщение крови кислородом (доля окисленного гемоглобина в общем гемоглобине); tdif=5 - отношение концентраций билирубина в крови и в окружающей ткани (полагается фиксированным).
Таким образом, оптическая модель кожи определяется следующими параметрами: показатель преломления цельной кожи - nskin, параметры спектральной зависимости редуцированного коэффициента рассеяния - µs(λ0), ρMie и x; толщина эпидермиса Lepi; объемные концентрации меланина и воды в эпидермисе -fmel и wepi; объемные концентрации капилляров с кровью, воды и билирубина в дерме - fblood, wderm и Cbil; средний диаметр капилляров - D; концентрация общего гемоглобина в крови - CtHb; насыщение крови кислородом - S. Диапазоны вариаций модельных параметров, выбранные путем критического анализа результатов различных авторов, приведены в табл.2.
Схема моделируемого эксперимента. Будем полагать, что излучение инжектируются в среду посредством передающего волновода с диаметром сердцевины 0.2 мм. Рассеянное тканью в заднее полупространство излучение попадает в принимающие волноводы, расположенные на расстояниях L=0.23, 0.46, 0.69, 0.92, 1.15 мм от центра передающего волновода (диаметр сердцевины всех волноводов 0.2 мм). Для кожи канал регистрации с L=1.15 мм не рассматривается из-за низкого уровня сигнала при λ≤500 нм на фоне шума за счет сильного поглощения меланином и билирубином.
Расчет R(L, λ) осуществляется по следующей схеме. Случайным образом выбираются значения модельных параметров из диапазонов, указанных в табл.1 и 2. Для каждой реализации параметров производится расчет k(λ) и µs(λ) по формулам (1)-(8) на 26 длинах волн (λ=450, 460, 470, 480, 495, 506, 514, 522, 530, 540, 548, 560, 564, 568, 574, 580, 586, 594, 600, 610, 620, 630, 640, 660, 676, 700 нм) для слизистой оболочки и на 30 длинах волн (λ=452, 460, 470, 480, 495, 506, 514, 522, 530, 540, 548, 560, 564, 568, 574, 580, 586, 594, 600, 610, 620, 630, 640, 660, 676, 700, 720, 740, 760, 780, 800 нм) для кожи. Указанные λ характеризуют основные особенности спектральных кривых поглощения хромофоров ткани в видимой области спектра. В соответствии с рассчитанными спектральными значениями оптических параметров, а также фактора анизотропии рассеяния и показателя преломления ткани методом Монте-Карло моделируется профиль R(L, λ). Фантом ткани представляет собой цилиндр с радиусом 10 мм и высотой 5 мм. Такие размеры выбираются с тем расчетом, чтобы, с одной стороны, устранить эффект границ, а с другой - уменьшить время счета. В расчете принимается, что излучение вводится в среду в направлении нормали к ее поверхности и равномерно распределено по площади сечения освещающего световода. Числовые апертуры всех волокон условно приняты равными 1.0 (разумеется, что при решении задачи интерпретации реальных оптоволоконных измерений расчет профилей R(L, λ) должен осуществляться в строгом соответствии со значениями апертур волокон и угловым распределением инжектируемого в среду излучения). Количество фотонов, вводимых в среду, зависит от транспортного альбедо однократного рассеяния среды - Λ=µs/k и варьируется от 6·106 при Λ≤0.5 до 2·105 при Λ≥10. Данная процедура повторяется для 2·103 реализации R(L, λ), что, как будет видно ниже, является достаточным для получения статистически-значимых результатов.
Следует отметить, что при использовании в качестве источников излучения светодиодов, расчет диффузного отражения в соответствующих им спектральных интервалах Δλ должен осуществляться с учетом реальной формы линии излучения P0(λ) и спектральной чувствительности приемника S(λ). Для того, чтобы избежать трудоемких вычислений монохроматического КДО и его последующего интегрирования в интервале Δλ с учетом аппаратурных функций, можно моделировать длину волны каждого фотона как случайное число, равномерно распределенное на интервале интегрирования и по значениям счетчиков вылетающих из среды фотонов получать оценку значений искомого интеграла как:
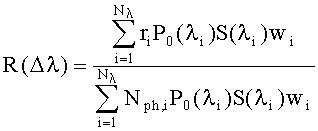
где Nλ - число подинтервалов на которые разбивается интервал интегрирования Δλ; Nph,i - общее число фотонов с длиной волны из i-го подинтервала, пропущенных через среду (начальный "вес" каждого фотона равен единице); ri - суммарный "вес" фотонов с длиной волны из i-го подинтервала, вылетевших из среды; wi - квадратурные коэффициенты, зависящие от используемого метода численного интегрирования.
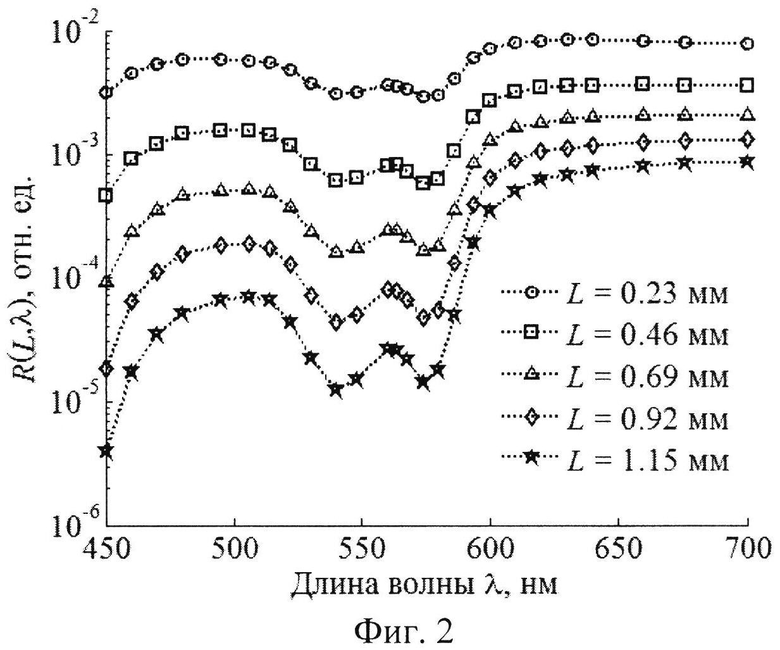
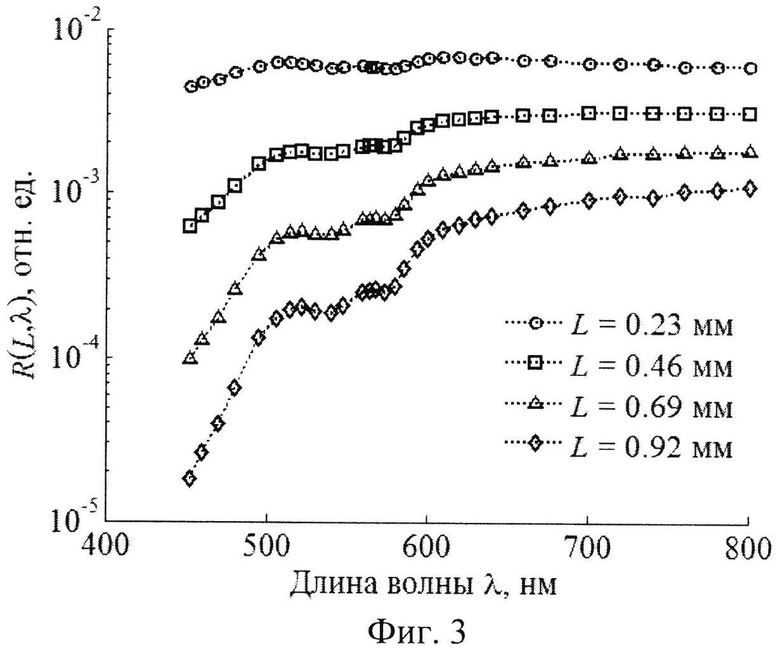
Решение обратной задачи. На фиг.2 изображен пример смоделированных спектральных зависимостей КДО слизистой оболочки на пяти различных расстояниях от точки освещения, образующих в совокупности спектрально-пространственный профиль R(L, λ). На фиг.3 изображен аналогичный профиль для кожи. Обратная задача состоит в восстановлении модельных параметров из профилей R(L, λ), Совокупность значений R(L, λ), определяемых в моделируемом эксперименте, удобно представлять в виде вектора измерений r из NλNL компонент, где Nλ и NL - количество спектральных и пространственных каналов регистрации КДО ткани соответственно (для кожи Nλ=30, NL=4; для слизистой оболочки Nλ=26, NL=5). Для удобства работы с числами одного порядка будем использовать логарифмическое представление измерений, т.е. компонентами r будут lnR(L, λ).
С помощью метода главных компонент [23, 24] вектор r разлагается по системе ортогональных векторов, причем оптимальной аппроксимацией r является разложение по собственным векторам его ковариационной матрицы
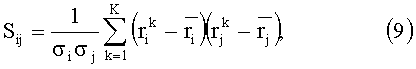
где 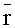 и σ - среднее значение и дисперсия r, рассчитанные по набору векторов rk, K - число векторов в наборе (количество реализации параметров вышерассмотренной модели кожи); 1≤i, j≤Nmes. Искомое разложение любой реализации r имеет вид:
и σ - среднее значение и дисперсия r, рассчитанные по набору векторов rk, K - число векторов в наборе (количество реализации параметров вышерассмотренной модели кожи); 1≤i, j≤Nmes. Искомое разложение любой реализации r имеет вид:

где V - матрица размером Nmes×NPC, столбцами которой являются собственные векторы vn матрицы S; NPC - число главных компонент; ξ - вектор из коэффициентов разложения ξn (линейно-независимых компонент), которые находятся по формуле
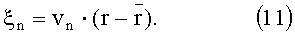
В связи с быстрой сходимостью рассматриваемого разложения на первые ортогональные функции (собственные векторы) приходится большая часть изменчивости компонент вектора r. Таким образом, метод главных компонент позволяет значительно уменьшить размерность исходных данных и выделить из них несколько линейно-независимых компонент, содержащих в себе столько же информации, сколько ее было в исходных данных. Очевидно, что при малом количестве измеряемой информации, когда суммарное количество спектральных и пространственных каналов регистрации не превышает количества линейно-независимых компонент в профилях R(L, λ), определять искомые параметры ткани можно напрямую из измеряемых значений R(L, λ) без извлечения из них линейно-независимых компонент, например при помощи полиномиальных регрессий
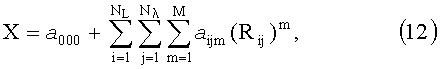
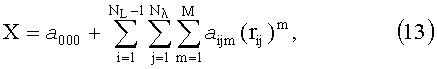
где Rij=R(Li, λj) или Rij=lnR(Li, λj); rij=r(Li, λj) или rij=lnr(Li, λj); Nλ и NL - соответственно количество длин волн и расстояний от точки освещения, на которых осуществляются измерения диффузного отражения, a ijm - коэффициенты регрессий, численные значения которых определяются методом наименьших квадратов; M - степень полинома; X - оптический или биофизический параметр (или его логарифм).
При большом количестве оптических измерений Nmes восстанавливать параметры ткани предпочтительно не из самих КДО, измеряемых непосредственно в эксперименте, а из коэффициентов их разложения по ортогональным функциям, например, по собственным векторам ковариационной матрицы (9). При этом для определения количественных значений оптических биофизических параметров биоткани удобно использовать полиномиальные регрессии
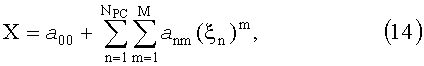
где a nm - коэффициенты регрессий; M≥1 - степень полинома; X - оптический или биофизический параметр (или его логарифм); ξn - линейно-независимые компоненты спектрально-пространственных профилей R(L, λ), r(L, λ) или их логарифмов, NPC - количество главных компонент (собственных векторов vn), используемых для определения параметра X (NPC=1, …, NLNλ). Использование в (14) логарифмического представления измерений и искомых параметров позволяет оперировать с числами одного порядка и устраняет возможность получения отрицательных значений определяемых параметров.
Степень полиномов M в (14) выбирается, исходя из среднеквадратичной погрешности аппроксимации статистической связи между ξn и X. Как правило, для аппроксимации достаточно использовать М=3. Оптимальное количество главных компонент NPC в (14) для каждого из модельных параметров X определяется путем замкнутого численного эксперимента, заключающегося в следующем. Первоначально по формуле (11) определяются линейно-независимые компоненты всех реализации профилей R(L, λ) и устанавливаются регрессии между первыми NPC компонентами ξn и параметром X. Далее перебираются все реализации модельных параметров и для каждой реализации осуществляется расчет X с использованием (11), (14) при наложении на R(L, λ) случайных отклонений в пределах δR (моделирующих погрешности измерения КДО). Полученное в результате значение X* сравнивается со значением X, соответствующем рассматриваемой реализации, и рассчитывается погрешность восстановления X. После перебора всех реализации вычисляется средняя погрешность восстановления X. Оптимальное значение NPC соответствует минимуму этой погрешности.
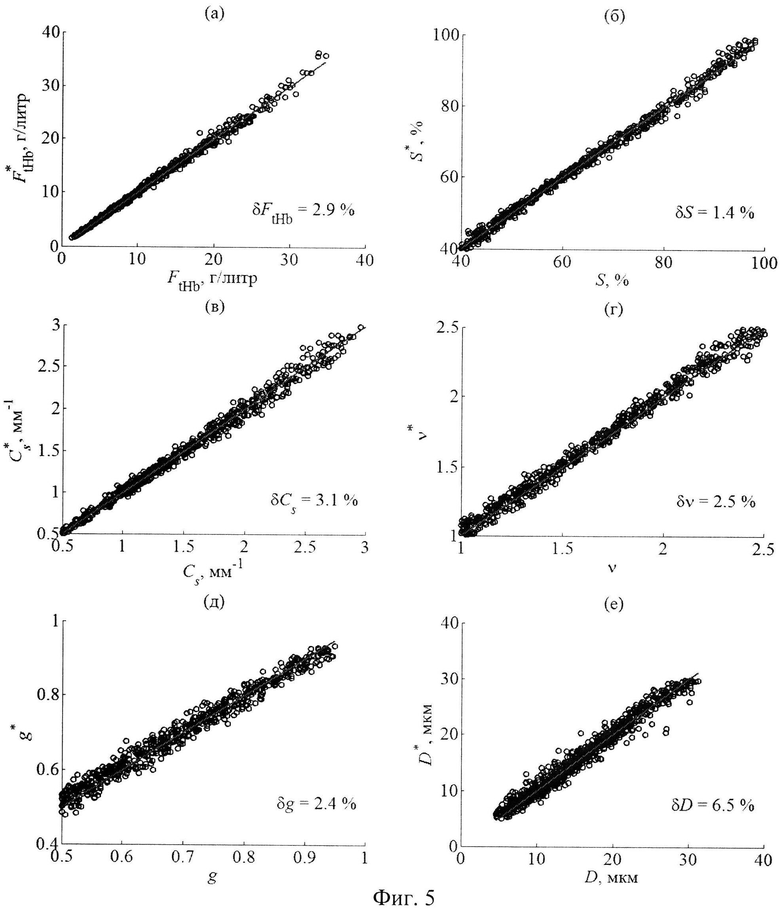
На фиг.4 приведены результаты вышеописанного численного эксперимента для следующих параметров слизистой оболочки: FtHb - концентрация общего гемоглобина в ткани; S - насыщение гемоглобина кислородом; Cs и ν - параметры спектральной зависимости редуцированного коэффициента рассеяния ткани, характеризующие объемную концентрацию и размер «эффективных» рассеивателей ткани соответственно. Зависимости средних по ансамблю погрешностей восстановления модельных параметров от количества главных компонент получены при наложении на R(L, λ) случайных отклонений в пределах 1% (окружности), 5% (квадраты) и 10% (треугольники). Видно, что при малых погрешностях оптических измерений (δR=1%) погрешности восстановления модельных параметров - δX уменьшаются с увеличением NPC. При δR=5-10% для восстановления рассматриваемых параметров оптимально использовать от 9 до 12 главных компонент. На фиг.5 приведены результаты сопоставления значений параметров FtHb S, Cs и ν, восстановленных из смоделированных профилей R(L, λ) при NPC=12, со значениями этих же параметров, соответствующих модельным реализациям R(L, λ). На рисунках также указаны средние погрешности восстановления параметров. Поскольку восстановление искомых параметров осуществлялось без наложения на профили R(L, λ) случайных отклонений, то разброс точек на диаграммах относительно прямой X=X* характеризует чувствительность результатов восстановления параметра X к вариациям всех других модельных параметров.
На фиг.6 представлены результаты восстановления биофизических параметров кожи. Вышеописанный численный эксперимент проводился для наиболее важных диагностических параметров: концентрация общего гемоглобина в дерме FtHb=fbloodCtHb (г/л); насыщение гемоглобина кислородом S; концентрация билирубина в крови Cbil (мг/л); интегральное содержание меланина в эпидермисе ODepi=fmelLepi (мкм); параметры Cs и ν спектральной зависимости редуцированного коэффициента рассеяния кожи µs(λ)=Cs·(632/λ)ν в диапазоне 600-700 нм, характеризующие структурные свойства ткани (объемную концентрацию и размер «эффективных» рассеивателей). Параметр ODepi восстанавливался из абсолютных значений R(L, λ). Для восстановления параметров FtHb, S, Cbil, Cs и ν использовались нормированные профили КДО - r(L, λ), где L0=0.23 мм. Невозможность восстановления параметра ODepi из профилей r(L, λ) связана с тем, что профили r(L, λ) практически не зависят от меланиновой пигментации кожи, поскольку оптические пути, проходимых светом в тонком верхнем слое кожи (эпидермисе), для рядом расположенных принимающих волокон примерно одинаковы и поэтому слабо влияют на отношение соответствующих им сигналов P(L, λ) и P(L0, λ). Следует отметить, что использование для решения обратной задачи профилей r(L, λ) позволяет устранить влияние аппаратурных констант и мощности посылаемого излучения на точность восстановления искомых параметров, а значит устройство, реализующее измерения r(L, λ) не нуждается в калибровке. Погрешность восстановления параметра S зависит от концентрации капилляров с кровью fblood и резко возрастает с ее уменьшением. В связи с этим коэффициенты регрессии (3) для данного параметра получены на основе реализации r(L, λ), соответствующих значениям fblood более 1%. При получении регрессий для параметра Cbil, напротив, использовались реализации r(L, λ) для которых fblood<3%, поскольку более высокие значения fblood не характерны для нормальной кожи.
Знание параметров FtHb, S, Cbil, ODepi, C и ν имеет большое значение для решения широкого круга задач диагностики и терапии различных заболеваний. Так, имеется ряд данных о различии параметров ODepi, FtHb, Cs и ν в нормальных и опухолевых тканях, поэтому информация о них может использоваться для поиска и диагностики злокачественных новообразований (например, меланомы). Параметр FtHb также может использоваться для обнаружения внутреннего кровоизлияния и для непрерывного мониторинга уровня гемоглобина в крови при хирургических операциях и переливаниях крови. Параметр Cbil имеет огромное значение при мониторинге желтухи у новорожденных.
Определение концентрации гемоглобина. Для сравнения с прототипом рассмотрим также возможности предлагаемого способа по отношению к гемоглобину. Вышерассмотренная обратная задача решалась для большого количества спектральных и пространственных каналов регистрации КДО. Это с одной стороны позволяет повысить устойчивость решения обратной задачи, с другой - увеличивает время измерения, требует использования дорогостоящего спектрометрического оборудования и сложной оптики блока регистрации рассеянного излучения. Кроме того, для проведения абсолютных измерений R(L, λ) необходимо знание аппаратурных констант и мощности посылаемого на ткань излучения, т.е. устройство, реализующее данные измерения, требует калибровки. С точки зрения экономичности и простоты реализации наибольший интерес представляет метод определения параметров ткани, основанный на измерении ее КДО в небольшом количестве спектральных участков, соответствующих излучению нескольких светодиодов. Устранить необходимость калибровки таких измерений можно, если определять параметры ткани из разности логарифмов сигналов диффузного отражения P(L, λ) для двух пространственно разнесенных каналов регистрации, которая, при равенстве апертур принимающих волокон, определяется только разностью оптических путей соответствующих световых потоков.
В связи со сказанным выше рассмотрим возможность определения концентрации общего гемоглобина FtHb по измерениям отношения сигналов r(λ)=P(L2, λ)/P(L1, λ) в небольшом количестве спектральных участков. Следует отметить, что именно локальное увеличение содержания гемоглобина в месте образования опухоли является наиболее существенным признаком патологических процессов [5, 21], поэтому разработка простого и эксплуатационно-надежного способа неинвазивного определения концентрации гемоглобина в биологических тканях является чрезвычайно актуальной задачей.
Минимальное количество спектральных участков, необходимое для восстановления FtHb, можно определить на основе замкнутых численных экспериментов. Компонентами вектора измерений r являются спектральные значения r(λ), поэтому количество линейно-независимых компонент r соответствует количеству независимых длин волн оптического зондирования Nλ. Анализ зависимости погрешности восстановления FtHb от Nλ проводился для отношения сигналов, соответствующего наибольшему пути между принимающими световодами в вышерассмотренной схеме оптических измерений, т.е. L1=0.23 мм и L2=1.15 мм. Результаты такого анализа показывают, что при погрешности измерения r(λ), равной 5-10%, для определения FtHb достаточно четырех длин волн оптического зондирования. Таким образом, задача планирования измерений FtHb сводится к выбору четырех оптимальных спектральных участков. Такой выбор осуществлялся путем компьютерного перебора всех возможных комбинаций из исходного набора λ (26 значений) и оценивания соответствующих им погрешностей восстановления FtHb.
Очевидно, что интерпретация измерений r(λ) в четырех спектральных участках невозможна с использованием строгих математических методов решения обратных задач, поскольку количество измерений меньше количества модельных параметров. Однако предлагаемый способ позволяет решать обратную задачу и при малом количестве оптических измерений. В данном случае в качестве оператора решения обратной задачи (оператора преобразования r(λ) в FtHb) использовались полиномиальные регрессии следующего вида:
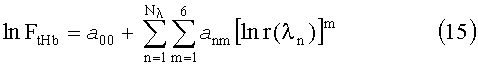
Оптимальный набор λn в уравнении (15) определяется точностью восстановления FtHb и устойчивостью данного уравнения к случайным отклонениям δr соответствующих спектральных значений r(λn). Влияние δr на результат восстановления FtHb оценивается на модельном ансамбле реализации FtHb и r(λn) путем проведения замкнутого численного эксперимента в котором для всех реализации r(λn) осуществляется расчет FtHb с использованием (15) при наложении на r(λn) случайных отклонений в пределах δr=5%. После перебора всех реализации вычисляется средняя по ансамблю погрешность восстановления FtHb, которая и служит критерием выбора оптимальной комбинации λn. Для рассматриваемого набора из 26 длин волн такой комбинацией является λ1=480 нм; λ2=574 нм; λ3=586 нм; λ4=630 нм. Соответствующая ей погрешность восстановления FtHb составляет 9.2 и 10.8% при δr=1 и 5% соответственно. Коэффициенты регрессии (15), соответствующие выбранным длинам волн, приведены в табл.3.
Определение оптических параметров. Известно, что оптические параметры (ОП) биологических тканей (коэффициент поглощения k, транспортный коэффициент рассеяния µs и фактор анизотропии рассеяния g) несут обширную информацию об их структуре и биохимическом составе. Помимо этого, знание ОП тканей необходимо для оценки глубины проникновения в них излучения, определяющей выбор дозы облучения при фототерапии различных заболеваний. В связи с этим рассмотрим более детально способ определения ОП биологических тканей по измерениям их КДО на нескольких расстояниях L от точки освещения. Исходя из точности и оперативности определения ОП, несомненный практический интерес представляет возможность получения значений ОП на основе аналитического преобразования измеряемых пространственных профилей КДО - R(L). Оператор такого преобразования (оператор решения обратной задачи) может быть получен на основе смоделированного ансамбля реализаций k(λ), µs(λ), g(λ) и R(L, λ). Учитывая, что процедура восстановления ОП из измерений R(L) может выполняться безотносительно к длине волны зондирующего излучения, сформируем на основе смоделированных спектральных значений k(λ), µs(λ), g(λ) и R(L, λ) один общий ансамбль, соответствующий диапазонам вариаций ОП, характерным для большинства биологических тканей в видимой области спектра: 0.01≤k≤5 мм-1, 0.45≤µs≤6 мм-1, 0.5≤g≤0.95 мм-1. При этом из ансамбля исключены те реализации, для которых отношение КДО для наиболее близкого и наиболее удаленного каналов регистрации превышает 4 порядка, поскольку динамический диапазон соответствующих им сигналов выходит за пределы линейности применяемых приемников излучения.
Количество линейно-независимых компонент в измерениях R(L) (Z=0.23, 0.46, 0.69, 0.92, 1.15 мм) можно определить путем анализа собственных чисел матрицы ковариаций R(L). Каждое из собственных чисел li (i=1, …, 5) этой матрицы определяет относительный вклад соответствующего ему собственного вектора в вариации R(L). Доля, вносимая первыми n собственными векторами в суммарную дисперсию R(L) определяется как 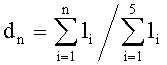 [23, 24]. В нашем случае на три первых собственных вектора, соответствующих наибольшим собственным числам матрицы ковариаций R(L), приходится 99.99% суммарной дисперсии R(L). Этот факт является вполне понятным, если принять во внимание, что вариации профилей R(L) обусловлены влиянием трех основных ОП - k, µs и g. Таким образом, для определения ОП ткани в принципе можно ограничиться измерениями ее КДО на трех расстояниях от точки освещения. Однако мы все же будем использовать для восстановления ОП профили R(L), соответствующие пяти вышеуказанным значениям L, что позволяет повысить устойчивость решения обратной задачи и, тем самым, снизить требования к точности измерений R(L). При этом для решения обратной задачи выбраны операторы вида
[23, 24]. В нашем случае на три первых собственных вектора, соответствующих наибольшим собственным числам матрицы ковариаций R(L), приходится 99.99% суммарной дисперсии R(L). Этот факт является вполне понятным, если принять во внимание, что вариации профилей R(L) обусловлены влиянием трех основных ОП - k, µs и g. Таким образом, для определения ОП ткани в принципе можно ограничиться измерениями ее КДО на трех расстояниях от точки освещения. Однако мы все же будем использовать для восстановления ОП профили R(L), соответствующие пяти вышеуказанным значениям L, что позволяет повысить устойчивость решения обратной задачи и, тем самым, снизить требования к точности измерений R(L). При этом для решения обратной задачи выбраны операторы вида
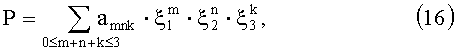
где P - один из ОП (k, µs или g); ξ1, ξ2, ξ3 - линейно-независимые компоненты профилей R(L), для расчета которых используется формула (11), в которой r - вектор измерений с компонентами, равными R(Ln) (n=1, …, 5), a vn - собственные векторы его ковариационной матрицы; a mnk - коэффициенты, численные значения которых рассчитываются методом наименьших квадратов на основе ансамбля реализации ξn и P.
Результаты замкнутых численных экспериментов по восстановлению ОП с использованием формул (11), (16) позволяют сделать следующие выводы. Для восстановления параметра g погрешность измерения R(L) должна быть ~ 1-3%. Так, при δR=1% информативность профилей R(L) относительно данного параметра (как отношение априорной неопределенности g к апостериорной) составляет примерно 5.6, но уже при δR=7% апостериорная неопределенность параметра g практически равна априорной. Эти результаты не вызывают особого удивления, поскольку хорошо известно, что световые поля в сильно рассеивающих средах (к которым относятся биологические ткани) определяются не величинами их коэффициента рассеяния β и фактора анизотропии рассеяния g по отдельности, а произведением µs=β(1-g). Для более точного восстановления параметра g необходимы измерения R(L) для расстояний L от точки освещения, на которых преобладает однократное или малократное рассеяние. Следует отметить, что слабое проявление индикатрисы рассеяния в рассматриваемых профилях R(L), оправдывает правомерность используемого при моделировании предположения об отсутствии спектральной зависимости у параметра g.
Средняя по ансамблю реализации модельных параметров погрешность восстановления µs составляет 2.9 и 4.6% при δR=1 и 5% соответственно. Коэффициент поглощения k при тех же значениях δR восстанавливается с погрешностями 8.2 и 9.3%, причем наибольшие погрешности соответствуют спектральной области малых поглощений биологических тканей λ>600 нм. Последнее обстоятельство объясняется малыми оптическими путями между каналами возбуждения и регистрации (L≤1.15 мм), на которых изменение интенсивности зондирующего излучения за счет поглощения хромофорами ткани находится в пределах погрешности измерений и, кроме того, маскируется значительно более сильным влиянием рассеяния. Повысить точность восстановления параметра k можно путем использования дополнительных каналов регистрации, расположенных на расстояниях L≥1.15 мм от канала возбуждения. При этом максимальное значение L не должно превышать диаметр инструментального канала эндоскопа, типичные значения которого составляют 2-3 мм. В связи с этим рассмотрим, как изменится точность восстановления параметров k, µs, и g с использованием дополнительных каналов регистрации с L=1.38, 1.61, 1.84, 2.07 мм. Для этого разобьем ансамбль реализации параметров k, µs, g и R(L) на две части, соответствующие спектральным областям сильного (λ<600 нм) и слабого (λ≥600 нм) поглощения. Полагаем, что для восстановления k и µs в области слабого поглощения доступны все каналы регистрации, а для области сильного поглощения только каналы с L≤1.15 мм (поскольку регистрировать оптические сигналы с более удаленных участков ткани сложно из-за их низкого уровня на фоне «шума»). При этом для восстановления ОП в обоих случаях будем использовать формулы (11), (16). Собственные векторы vn ковариационной матрицы вектора измерений и коэффициенты a mnk для спектральных областей сильного и слабого поглощения ткани, входящие в формулы (11), (16) приведены в табл.4 и 5.
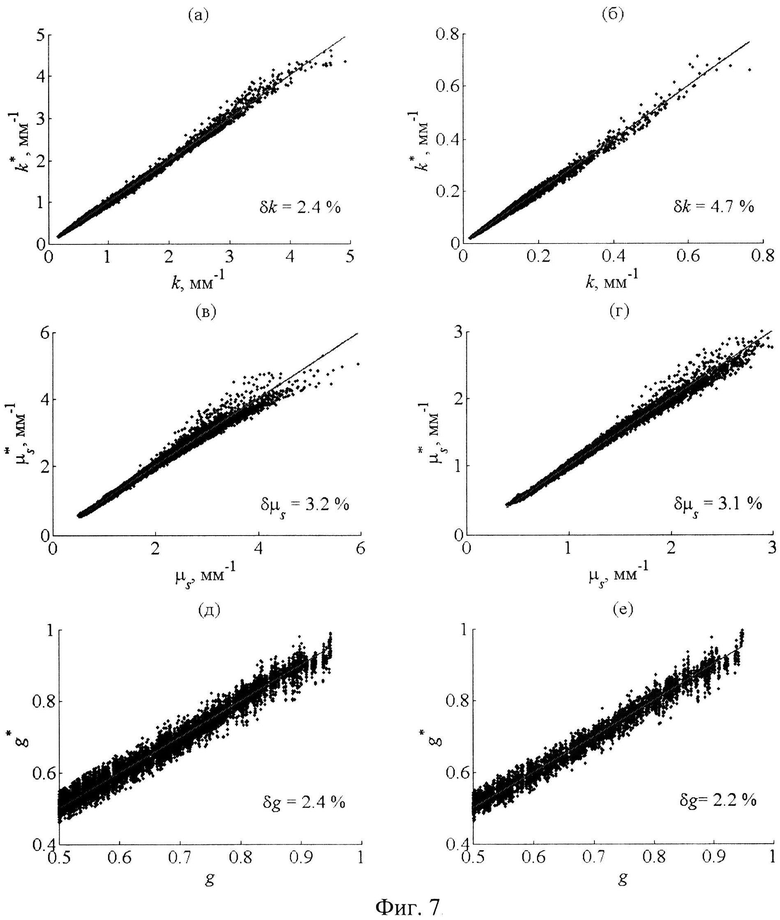
О точности восстановления параметров k, µs и g в условиях их общей вариативности можно судить по представленным на фиг.7 диаграммам, которые иллюстрируют результаты восстановления ОП слизистой оболочки для спектральных областей сильного (а, в, д) и слабого (б, г, е) поглощений. Данные диаграммы получены в предположении, что профили R(L) измеряются с погрешностью, равной 1%. В табл.6 даны средние погрешности восстановления ОП при наложении на значения R(Ln) (n=1, …, 9) случайных отклонений δR в пределах 5 и 10%. Видно, что погрешности восстановления µs практически не отличаются от аналогичных погрешностей, соответствующих всей видимой области спектра. Погрешность же восстановления параметра k уменьшается более чем два раза. Результаты восстановления g по-прежнему являются сильно чувствительными к погрешностям измерений R(L), однако при δR=1-3% данный параметр можно восстанавливать с удовлетворительной точностью.
Разработанный способ определения оптических и биофизических параметров биотканей и устройство для его реализации могут использоваться для поиска и диагностики злокачественных новообразований кожи (например, меланомы), а также в ходе проведения эндоспопических исследований слизистой оболочки полости рта, пищевода, органов желудочно-кишечного тракта и легких. Способ может также применяться для контроля газового состава крови в реанимации, токсикологии, при интенсивной терапии, для определения влияния на газовый состав гемоглобина факторов внешней среды (экологической обстановки, радиационного воздействия), для обнаружения внутреннего кровоизлияния, для непрерывного мониторинга уровня гемоглобина в крови при хирургических операциях и переливаниях крови, мониторинга желтухи у новорожденных, для определения состояния сосудистой системы и оценки жизнеспособности ткани при обморожениях и ожогах, а также в дерматологии и косметологии (диагностика и терапия таких изменений кожи как отек, красная волчанка, витилиго, солнечные лентинго и др.).
Разработанный способ позволяет в режиме реального времени осуществлять совместную интерпретацию спектральных и пространственных измерений диффузного отражения биотканей, что позволяет повысить точность определения как оптических, так и биофизических параметров ткани по сравнению со случаями раздельной интерпретации спектральной или пространственной составляющих информации. Повышается точность измерения данных параметров и за счет учета вариаций структурных и биохимических параметров биоткани, исключения использования априорной информации и устранения калибровочных измерений для нормированного r(L, λ) спектрально-пространственного профиля коэффициента диффузного отражения ткани
Литература.
1. Патент РФ №2234853, A61B 5/05, G01N 33/72; 27.08.2004.
2. Патент РФ №2337608, A61B 5/05, G01N 21/47; 10.11.2007.
3. Yudovsky, D. Rapid and accurate estimation of blood saturation, melanin content, and epidermis thickness from spectral diffuse reflectance / D. Yudovsky, L. Pilon // Appl. Opt. - 2010. - V.49, №10. - P.1707-1719.
4. Иванов, А.П. Спектры отражения света как средство диагностики структурных и биофизических параметров кожи / А.П. Иванов, В.В. Барун // Оптика и спектр. - 2008. - Т.104, №2. - С.344-351.
5. Bargo, P.R. In vivo determination of optical properties of normal and tumor tissue with white light reflectance and an empirical light transport model during endoscopy / P.R. Bargo [et. al.] // J. Biomed. Opt. - 2005. - Vol.10, №3. - P.034018-1-15.
6. Dam, J.S. Fiber-optic probe for noninvasive real-time determination of tissue optical properties at multiple wavelengths / J.S. Dam, C.B. Pedersen, T. Dalgaard, P.E. Fabricius, P. Aruna, S. Andersson-Engels // Appl. Opt. - 2001. - Vol.40 №7. P.1155-1164.
7. Kienle, A. Spatially resolved absolute diffuse reflectance measurements for noninvasive determination of the optical scattering and absorption coefficients of biological tissue / Kienle, L. Lilge, M.S. Patterson, R. Hibst, R. Steiner, B.C. Wilson // Appl. Opt. - 1996. - Vol.35, №15. P.2304-2314.
8. Междунар. заявка WO 2011068998/А2, G01N 33/49, G01N 33/72, G01N 21/47, A61B 5/1455; 09.06.2011.
9. Wang, L. MCML - Monte Carlo modeling of photon transport in multi-layered tissues / L. Wang, S.L. Jacques, L. Zheng // Computers Methods and Programs in Biomedicine. - 1995. - №47. - P.131-146.
10. Prahl, S.A. Optical absorption of hemoglobin [Электронный ресурс] / S.A. Prahl, - Режим доступа: http://omlc.ogi.edu/spectra/hemoglobin/index.html, свободный. - Название с экрана.
11. Барун, В.В. Оценка вклада локализованного поглощения света кровеносными сосудами в оптические свойства биологической ткани / В.В. Барун, А.П. Иванов // Оптика и спектр. - 2004. Vol.96, №6. P.1019-1024.
12. Saidi, I. Transcutaneous Optical Measurement of Hyperbilirubinemia in Neonates / I. Saidi // PhD thesis [Electronic resource]. - Rice University, - 1992. - Mode of access: http://scholarship.rice.edu/handle/1911/19082. - Date of access: 10.10.2011.
13. Jacques, S.L. Origins of tissue optical properties in the UVA, visible, and NIR regions / S.L. Jacques // Advances in Optical Imaging and Photon Migration. - 1996. - Vol.2. - P.364-369.
14. Jacques, S.L. Developing an optical fiber reflectance spectrometer to monitor bilirubinemia in neonates / S.L. Jacques, I. Saidi, A. Ladner, D. Oelberg // SPIE Proceedings. - 1997. - Vol.2975, №115. P.115-124.
15. Mourant, J.R. Mechanisms of light scattering from biological cells relevant to noninvasive optical-tissue diagnostics / J.R. Mourant [et. al.] // Appl. Opt. - 1998. - Vol.37, №16. - P.3586-3593.
16. Zonios, G. Diffuse Reflectance Spectroscopy of Human Adenomatous Colon Polyps In Vivo / G. Zonios [et. al.] // Appl. Opt. - 1999. - Vol.38, №31. - P.6628-6637.
17. Ghosh, N. Measurement of optical transport properties of normal and malignant human breast tissue / N. Ghosh [et. al.] // Appl. Opt. - 2001. - Vol.40, №1. - P.176-184.
18. Wei, H.J. Determination of optical properties of normal and adenomatous human colon tissues in vitro using integrating sphere techniques / H.J. Wei [et. al.] // World J. Gastroenterol. - 2005. - Vol.11, №16. - P.2413-2419.
24. Hidovic-Rowea, D. Modelling and va lidation of spectral reflectance for the colon / D. Hidovic-Rowea, E. Claridge // Phys. Med. Biol. - 2005. Vol.50. - P.1071-1093.
19. Salomatina E. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range / E. Salomatina [et. al.] // J. Biomed. Opt. - 2006. - Vol.11, №6. - P.064026-1-9.
20. Bashkatov, A.N. Optical properties of human stomach mucosa in the spectral range from 400 to 2000 nm: Prognosis for gastroenterology / A.N. Bashkatov [et. al.] // Medical Laser Application. - 2007. - Vol.22. - P.95-104.
21. Claridge, E. Quantifying mucosal blood volume fraction from multispectral images of the colon / E. Claridge, D. Hidovic-Rowe, P. Taniere, T. Ismail. // SPIE proceedings, 6511: Medical Imaging 2007: Physiology, Function, and Structure from Medical Images, (2007) 6511 ОС. DOI: 10.1117/12.709559.
22. Гираев, К.М. Спектры поглощения и рассеяния света тканями желудка при патологии / К.М. Гираев, Н.А. Ашурбеков, М.А. Лахина // Журн. прикл. спектр. - 2011. - Т.78, №1. - C.104-113.
23. Зуев, В.Е. Статистические модели температуры и газовых компонент земной атмосферы / В.Е. Зуев, B.C. Комаров. - Ленинград: Гидрометеоиздат., 1986. - С.47-50.
24. Veselovskii, I. Information content of multiwavelength lidar data with respect to microphysical particle properties derived from eigenvalue analysis /I. Veselovskii [et. al.] // Appl. Opt. - 2005. - Vol.44, №25. - P.5292-5303.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ ГЕМОГЛОБИНА В БИОЛОГИЧЕСКИХ ТКАНЯХ | 2012 |
|
RU2501522C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИЙ ХРОМОФОРОВ БИОЛОГИЧЕСКОЙ ТКАНИ | 2012 |
|
RU2506567C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ ГЕМОГЛОБИНА И СТЕПЕНИ ОКСИГЕНАЦИИ КРОВИ В СЛИЗИСТЫХ ОБОЛОЧКАХ | 2013 |
|
RU2528087C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ БИЛИРУБИНА | 2012 |
|
RU2511747C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЛУБИНЫ ПРОНИКНОВЕНИЯ СВЕТА В КОЖУ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2521838C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИЙ ПРОИЗВОДНЫХ ГЕМОГЛОБИНА В БИОЛОГИЧЕСКИХ ТКАНЯХ | 2013 |
|
RU2517155C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-БИОЛОГИЧЕСКИХ ПАРАМЕТРОВ КОЖИ И КОНЦЕНТРАЦИЙ ПРОИЗВОДНЫХ ГЕМОГЛОБИНА В КРОВИ | 2013 |
|
RU2545814C1 |
| СПОСОБ ФОТОДИНАМИЧЕСКОЙ ТЕРАПИИ ОНКОЛОГИЧЕСКИХ ЗАБОЛЕВАНИЙ | 2013 |
|
RU2539367C1 |
| СПОСОБ ФОТОДИНАМИЧЕСКОЙ ТЕРАПИИ ОНКОЛОГИЧЕСКИХ ЗАБОЛЕВАНИЙ | 2010 |
|
RU2438733C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОДЕРЖАНИЯ ПРОИЗВОДНЫХ ГЕМОГЛОБИНА В КРОВИ | 2013 |
|
RU2536217C1 |


Изобретение относится к области медицинского приборостроения и применяется для определения оптических и биофизических параметров биоткани. Сущность способа: посылку излучения на ткань в одну или несколько точек осуществляют на длинах волн λ из диапазона 350-1600 нм, измеряют диффузное отражение P(L, λ) на длинах волн посылаемого излучения для каждой из точек освещения, определяют абсолютный R(L, λ) или нормированный r(L, λ) спектрально-пространственный профиль коэффициента диффузного отражения ткани, а оптические и биофизические параметры (X) определяют на основе аналитических выражений, представляющих собой множественные регрессии между Х и R(L, λ) или между Х и r(L, λ), которые получают путем измерения или расчета методом Монте-Карло R(L, λ), r(L, λ) для множества образцов биоткани или моделирующих ее фантомов с известными оптическими и биофизическими параметрами, накопления ансамбля реализации оптических и биофизических параметров биоткани и соответствующих им спектрально-пространственных профилей R(L, λ), r(L, λ) для возможных диапазонов вариаций оптических и биофизических параметров ткани. Использование способа позволяет расширить функциональные возможности за счет одновременного определения комплекса как оптических, так и биофизических параметров биологической ткани в режиме реального времени, обеспечивает повышение точности измерения данных параметров за счет учета их общей вариативности, а также за счет исключения калибровочных измерений и использования априорной информации. 4 з.п. ф-лы, 6 табл., 7 ил.
1. Способ определения оптических и биофизических параметров биоткани путем посылки излучения на ткань, измерения диффузного отражения от ткани, в том числе посредством системы мультиспектральной визуализации, и определения параметров ткани на основе аналитических выражений, связывающих диффузное отражение с определяемыми параметрами, отличающийся тем, что посылку излучения на ткань в одну или несколько точек осуществляют на длинах волн λ из диапазона 350-1600 нм, измеряют диффузное отражение P(L, λ) на длинах волн посылаемого излучения для каждой из точек освещения, где L - расстояние между точками освещения и регистрации диффузного отражения на поверхности ткани, определяют абсолютный R(L, λ) или нормированный r(L, λ) спектрально-пространственный профиль коэффициента диффузного отражения ткани, как R(L, λ)=P(L, λ)/(P0(λ)A(L, λ)) или r(L, λ)=R(L, λ)/R(L0, λ), где P0(λ) - мощность излучения, посылаемого на ткань; A(L, λ) - аппаратурная константа, определяемая экспериментально с использованием эталонного отражателя или рассчитываемая по известным геометрическим параметрам и спектральным характеристикам измерительного устройства; L0 - одно из расстояний между точками освещения и регистрации диффузного отражения; а оптические и биофизические параметры (X) определяют на основе аналитических выражений, представляющих собой множественные регрессии между X и R(L, λ) или между X и r(L, λ), которые получают путем измерения или расчета методом Монте-Карло R(L, λ), r(L, λ) для множества образцов биоткани или моделирующих ее фантомов с известными оптическими и биофизическими параметрами, накопления ансамбля реализаций оптических и биофизических параметров биоткани и соответствующих им спектрально-пространственных профилей R(R(L, λ), r(L, λ)) для возможных диапазонов вариаций оптических и биофизических параметров ткани.
2. Способ по п.1, отличающийся тем, что в качестве биоткани используют кожу, молочную железу, слизистую оболочку полости рта, пищевода, органов желудочно-кишечного тракта и легких как in vivo, так и in vitro.
3. Способ по п.1, отличающийся тем, что определяют такие оптические параметры ткани как коэффициент поглощения, транспортный коэффициент рассеяния, фактор анизотропии рассеяния, и такие биофизические параметры как объемная концентрация меланина, интегральное содержание меланина в эпидермисе, концентрация общего гемоглобина, насыщение гемоглобина кислородом, концентрация билирубина, средний диаметр и объемная концентрация капилляров с кровью, концентрация и размер эффективных рассеивателей ткани, содержание воды в ткани.
4. Способ по п.1, отличающийся тем, что коэффициенты диффузного отражения определяют или на характеристических длинах волн спектров поглощения и рассеяния компонентов исследуемой ткани, или же во всем диапазоне посылаемого излучения с последующей интерполяцией или экстраполяцией полученных коэффициентов R(L, λ) и r(L, λ) к длинам волн, соответствующим аналитическим выражениям, на основе которых осуществляется переход R(L, λ) и r(L, λ) к определяемым параметрам ткани.
5. Способ по п.1, отличающийся тем, что оптические и биофизические параметры определяют на основе множественных регрессий между X и линейно-независимыми компонентами профиля R(L, λ) или r(L, λ), определяемыми как проекции профиля R(L, λ) или r(L, λ) на пространство из собственных векторов его ковариационной матрицы.
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТОЯНИЯ БИОЛОГИЧЕСКОЙ ТКАНИ И ДИАГНОСТИЧЕСКАЯ СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2002 |
|
RU2234242C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-БИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК КОЖИ | 2003 |
|
RU2251963C2 |
| Сетевой переключатель | 1925 |
|
SU4208A1 |
| ЛЫСЕНКО С.А | |||
| и др | |||
| Топка с несколькими решетками для твердого топлива | 1918 |
|
SU8A1 |
| Печь для сжигания твердых и жидких нечистот | 1920 |
|
SU17A1 |
| Сборник статей - Минск, 2011 - с.172-175 | |||
| ПУШКАРЕВА А.Е. | |||
Авторы
Даты
2014-03-27—Публикация
2012-04-24—Подача