Область техники
Способ преобразования и обработки цифрового изображения на основе многоцентричной развертки (МЦР) относится к области обработки изображений. Способ предназначен для преобразования строчного (растрового) представления изображения в самоподобные квадраты согласно отображениям типа кривой заполняющей плоскость (КЗП).
Применение МЦР позволяет в несколько раз поднять эффективность реализации процедур по существующим классам системы обработки изображений (СОИ), а именно: анализ, преобразование, синтез, передача.
Эффективность задается тройкой параметров:
- быстродействие,
- простота аппаратной реализации,
- повышение степени релевантности (т.е. по информационной ценности для наблюдателя) на начальном уровне представления изображения.
Последний компонент тройки ориентирован на выделения семантических зон интересов в изображении без предварительных обработок.
Быстродействие достигается за счет увеличения размера окрестности исследуемой точки изображения (пиксела) по площади сходимости.
Простота аппаратной реализации достигается декларированием процедуры отображения плоскости в отрезок. Условия повышения уровня релевантности заложены в пирамидальном представлении цифрового изображения в памяти процессора деревом с основанием 9, листья которого размещены на разных уровнях, то есть применяется неравномерное дерево.
Аналоги и их недостатки
В работах [1, 2] показаны и исследованы более 10 существующие КЗП разверток и их приложений для СОИ. Известные КЗП Пеано, Гильберта, Мура, Серпинского и др. Эти КЗП, являясь самоподобными (это преимущество), обладают общим недостатком, а именно сходимостью к точке интереса, которая заявлена как 4p, где p - мера сходимости как вложенность квадратов. Кроме того, в этих КЗП отсутствует режим развертки от центра изображения (наиболее информативного) и низкая сходимость как на этапе отображения изображения из двухмерного в одномерное, так и на этапе адресации к памяти процессора для СОИ.
Прототипы
Наиболее широко применяемой является КЗП Гильберта. Это базис для всех на сегодня существующих КЗП - в силу наличия предельного индекса окрестности (Jp=4.6) ее элемента [1. стр.10]. Такая КЗП, в отличие от других, проработана вплоть до ее аппаратной реализации [2. стр.233]. Достоинство КЗП Гильберта в форме согласованности с двоичным форматом организации памяти для работы вычислителя, то есть 4p или вычислитель работает с блоками типа байт, слово и так далее. КЗП Гильберта - четная КЗП. Недостаток четных КЗП указан выше в предыдущем разделе. Кроме того, эталонная ячейка этой КЗП (2×2) не позволяет строить геометрические примитивы, то есть создавать семантические базисы, например, в виде отрезка прямой.
Уровень техники
Изобретение относится к области обработки изображений. Его применение - преобразование строчной развертки изображения в самоподобные квадраты, со стороной размером 3p, где p - степень сходимости, p=0…10.
В специальных приложениях допускается, например, при 100-кратном увеличении исходного изображения (задача построения баннера), применяется p<0. Такой принцип обеспечивает независимую центровку квадрата с наличием прямого доступа к его краю. Отображение этих квадратов в памяти процессора выполняется по правилам кривой заполняющей плоскость (КЗП), или отрезками длиной 9p, а наличие центра обеспечивает параллельный доступ к этим отрезкам. Отсюда и название - многоцентричная развертка.
При этом центр изображения (монохромного, полутонового, цветного) задан в памяти первым номером первого отрезка. Предлагаемая развертка элементов (пикселов) изображения позволяет (за счет организации памяти и сверх параллельного доступа) в десятки раз увеличить скорость обработки изображения по всем его классам процедур.
Раскрытие изобретения
Изобретение относится к области обработки изображений и создано для
преобразования изображения из растра в квадрат, с помощью самоподобных отображений от центра квадрата - многоцентричная развертка по правилам Кривой Заполняющей Плоскость (КЗП).
Технический результат изобретения в следующем:
- повышение степени сжатия изображения без потерь;
- повышение скорости сжатия и обработки цифрового изображения в преобразованном сжатом виде по всем классам процедур (анализ, преобразование, синтез, передача), что достигается, в том числе, посредством организации независимого (сверхпараллельного) доступа процедур обработки изображения к памяти вычислителя;
- возможность эффективной работы с оцифрованными сигналами любого частотного диапазона и полученных любым типом сенсоров, например оптических, ультразвуковых, рентгеновских, радиоволновых, магниторезонансных, инфракрасных, или их комбинаций, др., задающих многозональный спектр.
Заявленный способ отличается тем, что выполняют управляемую перестановку пикселов из строчной развертки в квадратную, сторона которого равна 3p, где p - степень приближения области реального изображения к зоне точки интереса заказчика или это управляемый уровень сходимости для точки 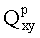
Способ преобразования и обработки изображения на основе многоцентричной развертки (МЦР), построенной по правилам кривой заполняющей плоскость (КЗП), с установкой начала и направления рекурсии, определяют тем, что начальную ячейку МЦР (начало рекурсии) задают как дискретный квадрат, состоящий из девяти клеток (3×3=9), имеющий свой центр и свои четыре грани (стороны); развертка начальной ячейки МЦР (направление рекурсии) стартует от центра к краю квадрата и далее с обходом остальных ячеек по кругу (таким образом, возможны 16 путей обхода из учета 8 граничных клеток и двух вариантов обхода - по и против часовой стрелки).
Приоритетным, в т.ч. для сканирования и визуализации изображений, является путь с обходом влево от центра и далее по кругу по часовой стрелке (фиг.1).
Такую конструкция представляет собой фасет pFas, где p - шаг рекурсии, при р=1 имеем описанную выше начальную ячейку (3×3=9).
Для формирования направления рекурсии будем различать четыре типа обхода (фиг.2) необходимые для описания 2Fas:
- описанный ранее обход w1 как начальный (1Fas1);
- обход w2 как зеркальный от 1Fas1 в левую сторону (1Fas2),
- обход w3 как зеркальный от 1Fas2 в верхнюю сторону (1Fas3),
- обход w4 как зеркальный от 1Fas3 в правую сторону.
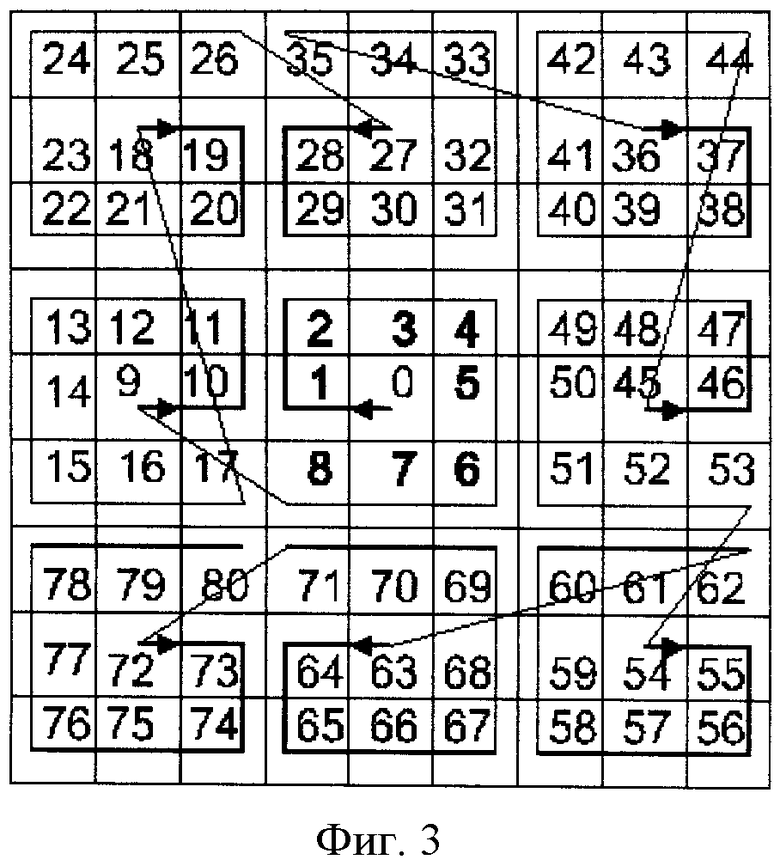
Для получения рекурсий МЦР выполняют 2Fas (фиг.3) (р=2, со стороной 9 клеток, 9×9=81), где исходной служит начальная 1Fas, которая (на основе выше указанных вращений w), выполняема в последовательности с начальным движением в квадрат влево от 1Fas и далее по часовой вокруг 1Fas: w1 w2 w3 w4 w3 w2 w3 w4 w3. Собственно это и порождает направление рекурсий.
Каждая последующая рекурсия pFas (p>2) строится на основе 1Fas и 2Fas. Пример для 3Fas дан на фиг.4.
Включение рекурсии МЦР на основе 1Fas и 2Fas (р>2) позволяет плоскость представить в координатах вращения (w), носителем которых является pFas, причем точкой этой плоскости, далее 
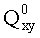
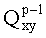
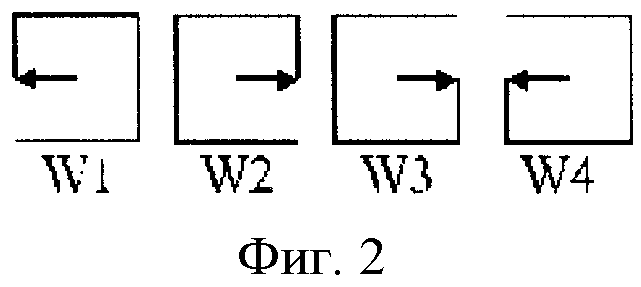
Таким образом МЦР создает многокоординатное пространство точки Q:
- две координаты декартового измерения (x,y координаты),
- координата измерения вращения (w),
- координата измерения вложенности точки в дерево Q,
- координата измерения размера граней фасета pFas,
- координата измерения вложений обрабатываемой точки из Оp-1 в Qp,
- координата измерения номера хранения 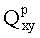
Причем эти координаты измерений свободно комбинируют в зависимости от поставленных задач.
Общим для координат является отображение декартовой плоскости в память при взаимно однозначном отображении точки 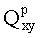
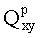
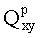
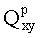
Важным преимуществом представляемого способа является то, что в изображении, представленном МЦР, выделение площади сегмента изображения по заданному критерию релевантности (т.е. по информационной ценности для наблюдателя) в плоскости изображения (для выделения линий прямых, областей постоянной яркости или цветности, хаотичных скоплений пикселей и др.), выполняют в форме управляемых вложений pFas по параметру p=1…10 в точку зоны интереса релеванта, с точностью p, с помощью представления точки интереса в изображении на основании таблиц преобразования, получаемых, как описано выше (1Fas или 2Fas или pFas). И все это не требует применения уравнений местонахождения точки на физическом уровне представления изображения через его габариты.
Следующим преимуществом представляемого способа является то, что в изображении, представленном в памяти в форме МЦР, т.е. представленном в форме графа типа «лес», с учетом ранее представленных процедур вложенности, выполняют выделение графа типа «дерево» из «леса», при том, что "дерево" есть pFas (где p=1…10, в зависимости от содержимого изображения).
Тем самым выполняют прямой доступ (в т.ч. несколькими процессорами независимо) к точке интереса или группам точек интереса изображения по схеме 9p; где каждый процессор отрабатывает свое «дерево» из вышеуказанного «леса», при этом доступ выполняется минимальной шириной захвата пикселей 91 или в зависимости от параметра p=1…10. При этом процессоры однородны, и их количество зависит от габарита входного изображения.
В представляемом способе эффективно определяют восьмисвязную окрестность любой точки зоны интереса на изображении путем использования таблиц преобразований (без средств маскирования): эта восьмисвязная окрестность определяется, для 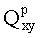
Представляемый способ, по умолчанию, также выполняет сжатие изображения без потерь. Путь (трек) развертки задан от его (квадрата) центра по правилам кривых заполняющих плоскость (КЗП); при p=1 (форма КЗП) изображение, независимо от своих габаритов (w, h), сегментируется на 9 квадратов, каждый из которых сегментируется снова на 9 квадратов или p=2 (направление КЗП). Остальные КЗП (p>2) строятся рекурсивно на длине p=0…10. При p=10 габарит изображения или w, h равны по 59049 пикселов. Формально, многоцентричная развертка (МЦР) выполняет взаимно однозначное отображение xi, yj в rj, где пара xi, yj - декартовые координаты пиксела или Pxy, rj - номер из натурального ряда чисел отрезком 1…59049×59049.
Представим алгоритм преобразования растра в МЦР.
Исходные данные:
1. Исходный BMP-файл шириной w и высотой h пикселей (w - длина по x, h -длина по y); w,h>=243;
2. Таблицы развертки TN (N от 1 до 4), TN=(tn0, tn1, …tnj, …tn59048), где tnj=(xnj,ynj) - декартова координата точки;
3. Таблица вращений R=(r0,…) - определяет номер N используемой таблицы развертки для каждой обрабатываемой области 243×243 точки. Элемент таблицы (rt) задается как rt=(y1jmod2)+(x1jmod2)+1, где mod - операция взятия целочисленного остатка от деления.
Этапы алгоритма:
Шаг 1. Определяется минимальное целое p, такое что H=3p<=max(w,h) (исходный растр изображения вложим в квадрат со стороной H);
Шаг 2. Определяются смещения левого верхнего угла исходного растра относительно левого верхнего угла растра со стороной H:
смещение по оси абсцисс xoffset=(H-w)/2,
смещение по оси ординат yoffset=(H-h)/2,
здесь и далее «/» означает операцию целочисленного деления;
Шаг 3. Последовательно выполняются выбор и представление одномерной формой H2/59049 областей размером 243×243 точки, каждой из которых присваивается последовательный номер t от 0 до Н2/59049-1.
Алгоритм выполнения итерации следующий:
Шаг 3.1. По таблице R определяется текущая таблица развертки Tr=rt;
Шаг 3.2. Определяются смещения верхнего левого угла текущей области (xoffset2, yoffset2) относительно верхнего левого угла растра со стороной Н:
xoffset2=x1t*243;
yoffset2=y1t*243;
Шаг 3.3. Определяется область покрытия исходным растром текущей области 243×243 точки (если w,h<>Н, то граница исходного растра может не совпадать с границей области 243×243 точки) как прямоугольный фрагмент, лежащий по ширине - от xStart до xEnd, по высоте - от yStart до yEnd. А также определяются промежуточные переменные xFileOffset, yFileOffset, используемые для вычисления смещения позиции файлового указателя (курсора), относительно начала файла, по которому будет позиционироваться «окно» доступа к области файла.
Шаг 3.3.1. Если xoffset2>=xoffset, то: xStart=0; xFileOffset=xoffset2-xoffset; иначе: xStart=xoffset-xoffset2; xFileOffset=0;
Шаг 3.3.2. Если yoffset2>=yoffse, то: yStart=0; yFileOffset=yoffset2-yoffset; иначе: yStart=yoffset-yoffset2; yFileOffset=0;
Шаг 3.3.3. Если xFileOffset+243<=w, то: xEnd=242; иначе: xEnd=w -xoffset2;
Шаг 3.3.4. Если yFileOffset+243<=h, то yEnd=242; иначе: yEnd=h-yoffset2;
Шаг 3.4. Определяется позиция M (смещение относительно начала файла до байта) и размер S (число последовательных байтов файла) «окна», по которому осуществляется доступ к области файла на данной итерации с использованием механизма «отображения файлов в память» (File Mapping). При этом учитывается «перевернутое» хранения растра изображения в bmp-файле, для чего вводится вспомогательная переменная yFileOffset2:
Шаг 3.4.1. yFileOffset=h-yFileOffset-243;
Шаг 3.4.2. Если yFileOffset<0, то yFileOffset2=-yFileOffset-1; yFileOffset=0;
иначе: yFileOffset2=0;
Шаг 3.4.3. М=54+(3*xFileOffset)+(L*yFileOffset), где 54 - фрейм bmp-файла;
L - число байтов на одну горизонтальную строку исходного растра,
определяется следующим образом:
если (h*3)mod4=0, то L=h*3, иначе: L=h*3+4-((h*3)mod3);
Шаг 3.4.4. S=243*L;
Шаг 3.5. Строится функция F, выполняющая частичное отображение байтового массива P в три матрицы субпикселей MR, MG, MB (красная, зеленая и синяя компонента соответственно) размером 243×243 точки каждая. Здесь P - одномерный байтовый массив длины S, представляющий собой «окно» доступа к последовательной области файла, полученное в пункте 3.4. Функция F описывается следующим образом:
Шаг 3.5.1. r(x,y)=p((x-xStart)*3+(242-y-yFileOffset2)*L), где r(x,y) - элемент матрицы MR с заданными индексами x, y; p(Z) - элемент массива p с индексом, заданным выражением Z;
Шаг 3.5.2. g(x,y)=p((x-xStart)*3+(242-y-yFileOffset2)*L+1), где g(x,y) - элемент матрицы MG с заданными индексами x, y;
Шаг 3.5.3. b(x,y)=p((x-xStart)*3+(242-y-yFileOffset2)*L+2), где b(x,y) - элемент матрицы MB с заданными индексами x, y.
Далее, полученная в пункте 3.5 область размером 243×243 точек обрабатывается по таблице развертки, рассчитанной в пункте 3.1.
Особенностью реализации механизма отображения последовательной области файла в память (параметры которого рассчитываются в пункте 3.4), характерного для ОС Windows, является то, что позиция М и размер S «окна» должны быть кратны 64 килобайтам. В этом случае вводится поправочный коэффициент А=М mod 65036. Тогда параметры MW, SW, PW «окна», с учетом особенностей Windows, будут скорректированы следующим образом:
MW=M-A; SW=S+A; PW:pW(Z)=p(Z+А).
Краткое описание чертежей
На Фиг.1 показана начальная ячейка МЦР, названная 1Fas, которая представляет собой дискретный квадрат, состоящий из девяти клеток (3×3=9), имеющий свой центр и свои четыре грани (стороны); развертка МЦР начальной ячейки стартует от центра с обходом влево от центра и далее по кругу по часовой стрелке.
На Фиг.2 показаны четыре типа обхода квадрата, состоящего из девяти клеток (3×3=9): обход w1, описанный как начальный (1Fas1); обход w2 - как зеркальный от 1Fas1 в левую сторону (1Fas2), обход w3 - как зеркальный от 1Fas2 в верхнюю сторону (1Fas3), обход w4 - как зеркальный от 1Fas3 в правую сторону; эти типы обхода необходимы для получения направления рекурсии МЦР для 2Fas.
На Фиг.3 показано направление рекурсии МЦР для 2Fas (p=2, со стороной 9 клеток, 9×9=81), где исходной служит начальная 1Fas, на основе выше указанных вращений w в последовательности с движением в квадрат влево от 1Fas и далее по часовой вокруг 1Fas: w1 w2 w3 w4 w3 w2 w3 w4 w3.
На Фиг.4 показана рекурсия МЦР для 3Fas (p=3, со стороной 27 клеток).
Промышленная применимость
МЦР обеспечивает прямой доступ к блокам изображения, лежащим в оперативной памяти, в зависимости от их информационной ценности (релевантности).
МЦР позволяет упорядочить содержимое изображения по его релевантам.
МЦР минимизирует число обращений к внешней памяти, хранящей сотни миллионов изображений.
МЦР в состоянии формировать в изображении семантические единицы, состоящие из сотен и выше пикселов, отражающих смысловой запрос, пусть через сканер пользователя.
МЦР обемпечивает повышение степени сжатия изображения без потерь и повышение скорости обработки цифрового изображения в преобразованном сжатом виде по всем классам процедур (анализ, преобразование, синтез, передача).
Возможна эффективная работы с оцифрованными сигналами любого частотного диапазона и полученных любым типом сенсоров, например оптических, ультразвуковых, рентгеновских, радиоволновых, магниторезонансных, инфракрасных или их комбинаций, др., задающих многозональный спектр.
Способ имеет аппаратную и программно-аппаратную реализации.
Источники информации
1. Н.Д. Горский, С.Н. Мысько, В.П. Сухаричев. Сравнительное исследование некоторых характеристик двумерных разверток. Препринт ЛНИВЦ АН СССР, №44, Л., 1982.
2. Генри Уоррен, мл. Алгоритмические трюки для программистов. "Вильямс", Москва, 2004.
3. Александров В.В., Горский Н.Д., Поляков А.О. Рекурсивные алгоритмы представления и обработки данных. - В кн.: Алгоритмы и системы автоматизации исследований и проектирования. - М.: Наука, 1980.
4. Александров В.В., Горский Н.Д. Структуризация иерархических систем. - В кн.: Алгоритмические модели в автоматизации исследований. - М.: Наука, 1980.
5. Р.М. Кроновер. Фракталы и хаос в динамических системах. Основы теории. - М.: Постмаркет, 2000.
6. Федер Е. Фракталы. - М.: Мир, 1991.
7. Орловский В.А. Передача факсимильных изображений. - М.: Связь, 1980.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АЛФАВИТНОГО ПРЕДСТАВЛЕНИЯ ИЗОБРАЖЕНИЯ | 2012 |
|
RU2519445C2 |
| СПОСОБ ПОСТРОЕНИЯ И ОБРАБОТКИ ИЗОБРАЖЕНИЙ И СИСТЕМА ЕГО РЕАЛИЗУЮЩАЯ | 2019 |
|
RU2728949C1 |
| Способ построения трехмерной модели местности вдоль полотна железнодорожного пути | 2020 |
|
RU2726256C1 |
| ФОТОГРАММЕТРИЧЕСКОЕ РАБОЧЕЕ МЕСТО | 2004 |
|
RU2277262C1 |
| МЕТОД ОПРЕДЕЛЕНИЯ ЗОНЫ ДВИЖЕНИЯ И САМОСТОЯТЕЛЬНОГО ОБЪЕЗДА ПРЕПЯТСТВИЙ ДЛЯ БЕСПИЛОТНОГО ТРАНСПОРТНОГО ОБОРУДОВАНИЯ В ПОДЗЕМНЫХ ЗАМКНУТЫХ ПРОСТРАНСТВАХ | 2022 |
|
RU2803671C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ПОВЕРХНОСТНЫХ ДЕФЕКТОВ ЦИЛИНДРИЧЕСКИХ ОБЪЕКТОВ | 2006 |
|
RU2323492C2 |
| СПОСОБ РАСЧЕТА ДВИЖЕНИЯ С КОРРЕКЦИЕЙ ОККЛЮЗИЙ | 2012 |
|
RU2517727C2 |
| УСТРОЙСТВО И СПОСОБ ВНЕШНЕГО ПРЕДСКАЗАНИЯ | 2019 |
|
RU2785725C2 |
| СИСТЕМА И СПОСОБ ФОРМИРОВАНИЯ И ВОСПРОИЗВЕДЕНИЯ ТРЕХМЕРНОГО ВИДЕОИЗОБРАЖЕНИЯ | 2009 |
|
RU2421933C2 |
| СПОСОБ ОБНАРУЖЕНИЯ И АВТОСОПРОВОЖДЕНИЯ ОБЪЕКТОВ ЦЕЛЕУКАЗАНИЯ ОПТИКО-ЭЛЕКТРОННОЙ СИСТЕМОЙ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2020 |
|
RU2748763C1 |

Изобретение относится к средствам обработки цифровых изображений. Техническим результатом является повышение степени сжатия изображения без потерь. В способе начальную ячейку многоцентричной развертки (МЦР) представляют дискретным квадратом из девяти клеток, развертку начальной ячейки выполняют от центра к краю квадрата и далее с обходом остальных ячеек по кругу, приоритетным является путь с направлением обхода влево от центра квадрата и далее по часовой стрелке, формируемая конструкция является фасетом (pFas), где p - шаг рекурсии, при p=1 имеют описанную выше начальную ячейку; для построения дальнейших направлений рекурсий различают четыре типа обхода: обход w1 как начальный (1Fas1), обход w2 как зеркальный от 1Fas1 в левую сторону (1Fas2), обход w3 как зеркальный от 1Fas2 в верхнюю сторону (1Fas3), обход w4 как зеркальный от 1Fas3 в правую сторону, выполняют обход в последовательности с начальным движением в квадрат влево от 1Fas и далее по часовой стрелке вокруг 1Fas. 4 ил.
Способ преобразования и обработки цифрового изображения на основе многоцентричной развертки, построенной по правилам кривой заполняющей плоскость (КЗП), отличающийся тем, что начальную ячейку многоцентричной развертки (МЦР) представляют дискретным квадратом, состоящим из девяти клеток (3×3=9), имеющим свой центр и свои четыре грани (стороны); развертку начальной ячейки МЦР выполняют от центра к краю квадрата и далее с обходом остальных ячеек по кругу; приоритетным является путь с направлением обхода влево от центра квадрата и далее по часовой стрелке; формируемая конструкция является фасетом (pFas), где p - шаг рекурсии, при p=1 имеют описанную выше начальную ячейку (3×3=9); для построения дальнейших направлений рекурсий различают четыре типа обхода: описанный выше обход w1 как начальный (1Fas1), обход w2 как зеркальный от 1Fas1 в левую сторону (1Fas2), обход w3 как зеркальный от 1Fas2 в верхнюю сторону (1Fas3), обход w4 как зеркальный от 1Fas3 в правую сторону; для получения направления рекурсий МЦР применяют 2Fas (p=2, со стороной в 9 клеток, 9×9=81), где центром задают 1Fas; на основе вышеуказанных вращений w выполняют обход в последовательности с начальным движением в квадрат влево от 1Fas и далее по часовой стрелке вокруг 1Fas: w1 w2 w3 w4 w3 w2 w3 w4 w3; далее запускают рекурсию МЦР на основе 1Fas и 2Fas (p>2), представляя плоскость в координатах вращения (w), носителем которых является pFas, а точкой этой плоскости, 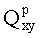



| УСТРОЙСТВО ДЛЯ ПОЛУЧЕНИЯ ИЗОБРАЖЕНИЯ РАЗВЕРТКИ ПОВЕРХНОСТИ ОБЪЕКТОВ, БЛИЗКИХ К ЦИЛИНДРУ ИЛИ К ПЛОСКОСТИ | 2002 |
|
RU2212651C1 |
| УСТРОЙСТВО ДЛЯ ВВОДА ПОЛУТОНОВЫХ ИЗОБРАЖЕНИЙ В ЭВМ | 1991 |
|
RU2009542C1 |
| RU 2008102962 A, 10.08.2009 | |||
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| WO 2008143168 A1, 27.11.2008 | |||
Авторы
Даты
2014-05-27—Публикация
2012-08-09—Подача