Изобретение относится к области контрольно-измерительной техники и может быть использовано для определения параметров диффузии кислорода в твердых поликристаллических телах в материаловедении и физике твердого тела.
Наиболее близким, принятым за прототип является способ определения диффузионных констант в поликристаллических материалах (Патент РФ №2169914, МПК 7 G 07 N 13/00, опубликован 27.06.2001, Бюллетень №18).
Согласно способу, у образца удаляют тонкие поверхностные слои до достижения величины энергии активации электрической проводимости Еа в приповерхностном слое образца значения 0.19-0.20 эВ, после чего образец нагревают, выдерживают в нагретом состоянии, охлаждают, измеряют в образце глубинное распределение энергии активации электрической проводимости Еа(х), определяют коэффициенты диффузии аппроксимацией распределения выражением, связывающим величину энергии активации электрической проводимости с концентрацией продиффундировавших ионов, задаваемой, в свою очередь, в виде решения уравнения Фика с соответствующими граничными условиями, указанную последовательность действий повторяют для различных температур нагрева образца, строят график температурной зависимости коэффициентов диффузии, определяют диффузионные константы по результатам аппроксимации данной зависимости законом Аррениуса.
Недостатком способа является его высокая трудоемкость и низкая точность определения диффузионных констант.
Задачей изобретения является снижение трудоемкости способа и повышение точности определения диффузионных констант.
Решение данной задачи предлагается осуществлять способом определения диффузионных констант в поликристаллических материалах, заключающемся в том, что так же как в прототипе у образца удаляют тонкие поверхностные слои до достижения величины энергии активации электрической проводимости в приповерхностном слое образца значения 0.19-0.20 эВ, после чего образец нагревают, выдерживают в нагретом состоянии, охлаждают, определяют в образце глубинное распределение энергии активации электрической проводимости, определяют коэффициенты диффузии аппроксимацией распределения выражением, связывающим величину энергии активации электрической проводимости с концентрацией продиффундировавших ионов, задаваемой, в свою очередь, в виде решения уравнения Фика с соответствующими граничными условиями. Указанную последовательность действий повторяют для различных температур нагрева образца, строят график температурной зависимости коэффициентов диффузии, определяют диффузионные константы по результатам аппроксимации данной зависимости законом Аррениуса. В отличие от прототипа после каждого охлаждения образца на его поверхности формируют косой шлиф под углом от 5 до 6 градусов, а глубинное распределение энергии активации электрической проводимости в образце определяют путем проведения измерений энергий активации электрической проводимости в различных участках поверхности косого шлифа.
Значительное уменьшение трудоемкости предлагаемого способа и увеличение точности определения диффузионных констант достигается за счет измерения энергий активации электрической проводимости в различных участках косого шлифа. Выбор значений угла косого шлифа 5-6 градусов сделан исходя из следующих соображений. Во время выдержки в нагретом состоянии профиль глубинного распределения энергии активации электрической проводимости в приповерхностном слое феррита формируется на глубину не более 0.5 мм, следовательно, расстояние по глубине образца от исходной поверхности до крайней точки на поверхности косого шлифа, в которой будет проводиться измерение энергии активации электрической проводимости, должно быть не менее 0.5 мм. Как правило, в образцах поликристаллических материалов область наибольшей однородности свойств в центральной части образца имеет размеры не более 5-6 мм. Для того чтобы косой шлиф в данной области образца имел максимальную глубину 0.5 мм, его угол по отношению к исходной поверхности должен быть равным от 5 до 6 градусов. Уменьшение данного угла ниже 5 градусов приведет к увеличению протяженности поверхности косого клина более 6 мм, что отрицательно скажется на точности измерения глубинного распределения энергии активации электрической проводимости, а следовательно, на точности определения диффузионных констант. А увеличение угла более чем 6 градусов приведет к уменьшению разрешения по глубине при измерении глубинного распределения энергии активации электрической проводимости, что также отрицательно скажется на точности измерения глубинного распределения энергии активации электрической проводимости и соответственно на точности определения диффузионных констант.
На фиг.1 изображено устройство для формирования косого шлифа на поверхности образцов.
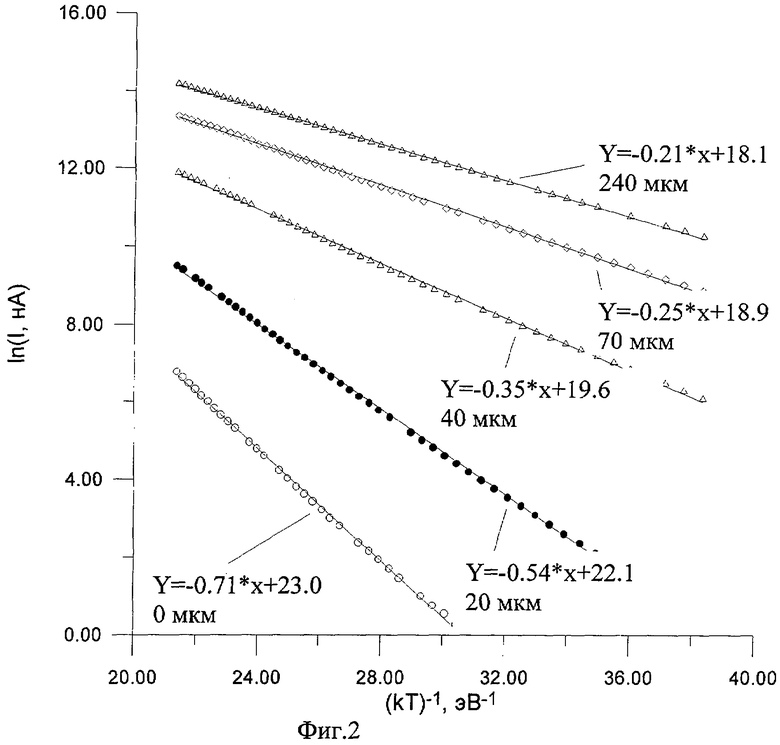
На фиг.2 представлены температурные зависимости тока поверхностной проводимости для образца после проведения теплового отжига на воздухе при температуре 700°С в течение 4 часов, измеренные в различных участках косого шлифа. Зависимости построены в аррениусовских координатах. Значки обозначают экспериментальные измерения, прямые линии - аппроксимацию экспериментальных зависимостей линейной. Под каждой кривой записано ее уравнение, полученное по результатам аппроксимации, и расстояние от исходной поверхности образца.
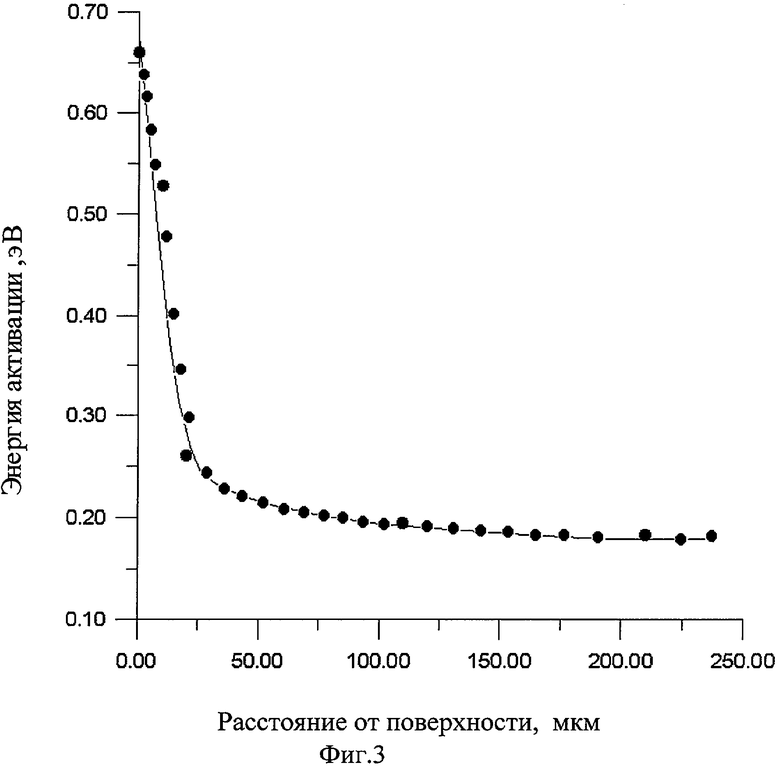
На фиг.3 представлено глубинное распределение величины Еа(х) в образце после проведения теплового отжига на воздухе при температуре 700°С в течение 4 часов. Значки - эксперимент, линия - аппроксимация аналитическим выражением.
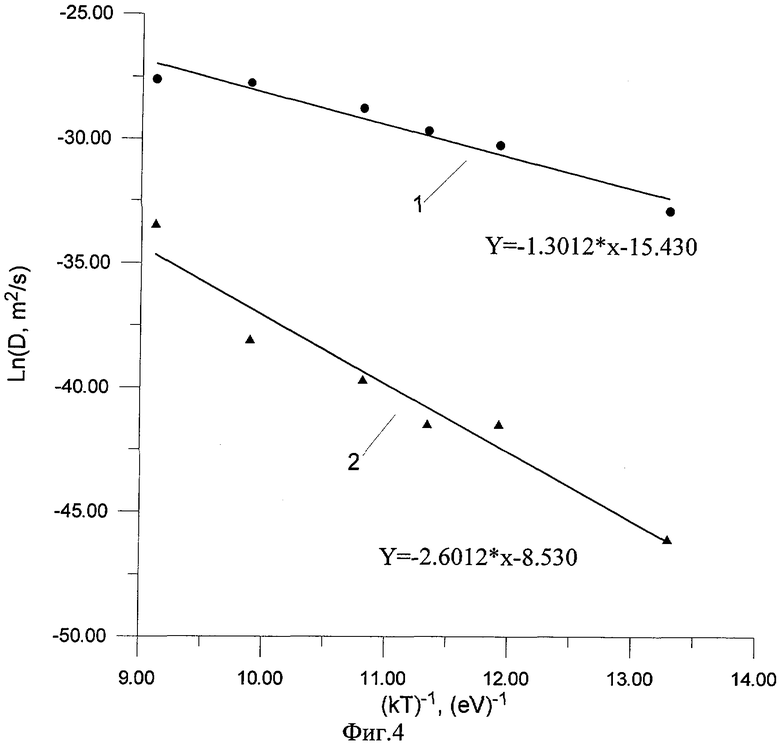
На фиг.4 представлены температурные зависимости коэффициентов зернограничной (кривая 1) и объемной (кривая 2) диффузии, построенные в аррениусовских координатах. Значки - эксперимент, линии - аппроксимации линейной зависимостью. Под каждой кривой записано ее уравнение, определенное по результатам аппроксимации.
В таблице 1 представлены значения диффузионных констант, определенные для литий-титанового феррита по предлагаемому способу и по способу-прототипу.
Предложенный способ осуществляется следующим образом. Образцы представляли собой Li-Ti-феррит марки 3СЧ-18. Пресс-порошок синтезировался керамическим методом из механической смеси состава (в вес. %): Li2СО3-11.2%, MnO-2.7%, TiO2-18.65%, ZnO-7.6%, Fe2O3-59.81%. Образцы формовались односторонним прессованием с помощью пресса ПГПр в виде таблеток диаметром 18 мм и толщиной 3 мм. Спекание образцов осуществлялось в электропечи СУОЛ - 0.4.4/12-М2 на воздухе при T=1100°С в течение 4 ч. Температура образцов при спекании контролировалась при помощи термопары платина - 90% платины, 10% родия. Термо-ЭДС термопары измерялась с помощью вольтметра В7-38. Охлаждение образцов до комнатной температуры осуществлялось на воздухе в печи при ее естественном охлаждении. После охлаждения с каждого образца с торцевых поверхностей удалялся тонкий поверхностный слой толщиной 290-300 мкм, что обеспечивало снятие поверхностного слоя, формируемого во время спекания, с неравномерным содержанием кислорода по глубине. Удаление тонких слоев производилось путем механической шлифовки с использованием абразивного корундового микропорошка со средним размером частиц 5 мкм. Для обеспечения плоскопараллельности торцевых плоскостей образца образец при шлифовке помещался в стальную обойму с внешним диаметром 60 мм. После удаления поверхностного слоя производилось измерение величины Еа(х) на поверхности образца способом обработки результатов температурных измерений токов поверхностной проводимости, который будет описан подробно ниже. Если величина Еа(х) составляла 0.19-0.20 эВ, образец использовался для проведения теплового отжига на воздухе. Если величина Еа(х) превышала значение 0.20 эВ, образец выбраковывался.
Приготовленные таким образцом образцы использовались для определения температурной зависимости коэффициентов диффузии в исследуемом материале. Тепловой отжиг образцов производился при фиксированных значениях температуры соответственно 600, 700,750, 800, 900, 1000°С на воздухе в электропечи СУОЛ - 0.4.4/12-М2. При всех значениях температуры теплового отжига на воздухе время выдержки составляло 4 часа. Температура теплового отжига контролировалась при помощи термопары платина - 90% платины, 10% родия. Термо-ЭДС термопары измерялась с помощью вольтметра В7-38. Охлаждение образцов до комнатной температуры осуществлялось на воздухе в печи при ее естественном охлаждении.
После проведения теплового отжига и охлаждения на поверхности образцов путем шлифовки поверхности формировался косой шлиф под углом 5, 5.5 и 6 градусов. Соответственно для каждого значения угла косого шлифа в образце проводилось измерение глубинного распределения энергии активации электрической проводимости. Формирование косого шлифа осуществлялось механической шлифовкой поверхности образца, размещенного в специальное устройство фиг.1, конструкция которого позволяла задавать и контролировать угол косого шлифа. Устройство представляет собой пуансон, пресс-шайба 1 которого на торце имеет косой шлиф под заданным углом по отношению к торцовой плоскости матрицы пуансона 2. Изменение угла косого шлифа проводилось заменой пресс-шайбы на другую с фиксированным углом косого шлифа на торце. Перед шлифовкой образец 3 приклеивался к торцу пресс-шайбы 1 на пицеин. Шлифовка проводилась абразивным корундовым микропорошком со средним размером зерен 5 мкм. Толщина удаляемого слоя х определялась путем измерения толщины образца до и после шлифовки в начальном и конечном участке косого шлифа с использованием индикатора И4 часового типа (ГОСТ 577-68). После шлифовки образец промывался в спирте-ректификате и подвергался сушке на воздухе при атмосферных условиях в течение 5 минут.
Коэффициенты зернограничной и объемной диффузии в образцах, подвергнутых тепловому отжигу на воздухе, определялись независимо от температуры теплового отжига следующим образом.
В образце, подвергнутом тепловому отжигу на воздухе, производилось измерение глубинного распределения величины Еа(х) путем определения величины Еа(х) на различных участках косого шлифа, соответствующих определенной глубине образца.
Величина Еа(х) при заданном значении х определялась по результатам температурных измерений токов поверхностной проводимости между двумя нихромовыми зондами, приложенных к поверхности косого шлифа образца.
Температурные измерения токов поверхностной проводимости производились при помещении образца в нагревательный элемент, представляющий собой керамический проволочный резистор марки ПЭВР-50 номиналом 39 Ом, нагревание которого осуществлялось путем пропускания переменного тока. Температура нагревательного элемента регулировалась величиной подаваемого напряжения, которая изменялась в пределах 0-70 В. Напряжение подавалось от автотрансформатора ЛАТР. Температура образца во время нагрева измерялась при помощи термопары хромель-алюмель. Термо-ЭДС термопары измерялась вольтметром В7-38. Напряжение на измерительные зонды подавалось от источника питания постоянного тока Б5-31. Величина напряжения была равной 3 В. Ток поверхностной проводимости между зондами измерялся при помощи универсального вольтметра В7-21А.
При достижении температуры образца заданного фиксированного значения и последующей стабилизации ее при данном значении проводились измерения электропроводности в различных участках косого шлифа. При этом перемещение измерительных зондов относительно поверхности косого шлифа осуществлялось при помощи микрометрической подачи, которая обеспечивала разрешение по глубине образца не хуже 2 мкм.
Для примера ниже приводятся результаты построения глубинного распределения величины Еa(х) и определения по результатам его аппроксимации коэффициентов диффузии при температуре теплового отжига на воздухе 700°С. Угол косого шлифа был равен 5 градусам. Измерения Еа(х) были произведены для значений х=0-230 мкм с шагом 10 мкм следующим образом. При заданном значении х величина Еа(х) определялась по углу наклона кривой температурной зависимости тока поверхностной проводимости, построенной в координатах Ln(I)-1/kT, где k -постоянная Больцмана; Т - температура образца. В общем случае температурная зависимость подчиняется закону Аррениуса I=I0·exp(-Ea/kT), где I0 - не зависящая от температуры постоянная. В указанных координатах она имеет линейный вид. На фиг.2 показаны экспериментальные зависимости тока поверхностной проводимости при различных значениях х, построенные в аррениусовских координатах (оси у соответствует величина LnI, а оси х - величина 1/kT), и их аппроксимации линейной зависимостью. Под каждой кривой записано ее уравнение и расстояние от исходной поверхности. В уравнении кривой коэффициент перед х численно равен значению Еа(х) на данном расстоянии от исходной поверхности образца.
Далее по результатам измерений значений Еа(х) при разных значениях х строился график глубинного распределения величины Еa(х) в исследуемом образце, который представлен на фиг.3. Экспериментальные значения на графике представлены в виде значков.
Следующий этап - это определение коэффициентов зернограничной и объемной диффузии в образце при данной температуре теплового отжига на воздухе. Коэффициенты зернограничной D1(T) и объемной D2(T) диффузии определялись аппроксимацией экспериментально измеренного глубинного распределения величины Еа(х) выражением, устанавливающим аналитическую связь между величиной Еа(х) и N0(x) (УДК 541.12.012.4 Применение электрических измерений для анализа диффузионных процессов в поликристаллических ферритах (Суржиков А.П., Притулов А.М., Гынгазов С.А., Лысенко Е.Н., Никифоренко И.В.; Том. Политехн. Ун-т. - Томск, 1998. - 20 с. Библиогр.: 10 назв. - Рус. - Деп. в ВИНИТИ. 27.07.98, №2392-В98.):
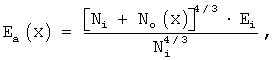
где Ei значение Еа(х) на глубине, где оно не зависит от х (обычно эта величина находится в области значений 0.19-0.20 эВ);
Ni - исходная избыточная концентрация ионов кислорода в межзеренной прослойке.
Концентрация ионов кислорода, продиффундировавших на глубину х, при аппроксимации глубинного распределения величины Еа(х) задавалась в виде решения Уиппли (Whipple R.T.F. // Phil. Mag. - 1954. - V.45 - Р.1225-1236.):
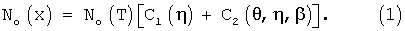
В этом уравнении

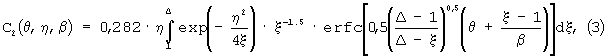
где θ, η и β - безразмерные переменные, которые соответствуют y, х и t, а Δ- безразмерный параметр;
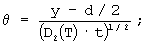
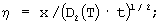
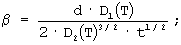
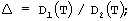
D1(T) и D2(T) - коэффициенты диффузии соответственно в межзеренной прослойке и зерне;
NO(T) - концентрация кислорода в атмосфере при температуре теплового отжига;
Т - температура теплового отжига;
t - время теплового отжига;
d - толщина межзеренной прослойки;
у - расстояние от центра межзеренной границы в глубь зерна.
В качестве подгоночных параметров были использованы величины D1/(T), D2(T), d и Ni. Результат аппроксимации представлен на фиг.3 в виде сплошной линии. Аппроксимация осуществлялась на персональном компьютере типа IBM в математическом редакторе MathCAD PLUS 7.0 PRO с помощью стандартной встроенной программы genfit. Таким образом, для температуры теплового отжига на воздухе 700°С получены следующие значения подгоночных параметров: D1(T)=1.5·10-13 м2/с, D2(T)=1.8·10-18 м2/с, d=6·10-7 м и Ni=8.5·109 м-3.
Подобно описанному выше были построены графики глубинных распределений величины Еa(х) и определены коэффициенты D1(t) и D2(T) для температур теплового отжига на воздухе 600, 750, 800, 900, 1000°С. Результаты определения коэффициентов D1(T) и D2(T) для всех температур теплового отжига на воздухе представлены в виде графика на фиг.4, построенного в аррениусовских координатах (оси у соответствует величина LnD(T), а оси х - величина 1/kT).
Определение диффузионных констант в выражениях для коэффициентов зернограничной и объемной диффузии в исследуемых образцах с использованием данного графика проводилось следующим образом. Температурная зависимость коэффициента диффузии обычно подчиняется закону Аррениуса:
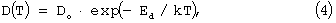
где Do - не зависящая от температуры постоянная;
Ed - энергия активации диффузии;
k - постоянная Больцмана;
Т - температура теплового отжига.
Величины Do и Ed называют вместе диффузионными константами.
Диффузионные константы определены аппроксимацией экспериментальных кривых линейной зависимостью (кривые 1 и 2 на фиг.4). Уравнение прямой, определенной по результатам аппроксимации, записано под соответствующей кривой на фиг.4. Угол наклона прямой линии (коэффициент перед х) дает значения Ed, равные 1.30 эВ и 2.60 эВ для D1(t) и D2(T) соответственно, а точка пересечения с осью у (второй член в уравнении прямой) - значения LnD0, равные - 15.430 и - 8.530 для D1(T) и D2(T) соответственно. По результатам аппроксимации экспериментальных зависимостей D1(T) и D2(T) выражения для коэффициентов зернограничной D1(T) и объемной D2(T) диффузии запишутся в следующем виде:
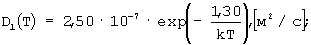
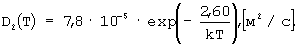
Таким образом, в результате произведенных экспериментальных измерений и численных аппроксимаций определены значения диффузионных констант в выражениях для коэффициентов зернограничной и объемной диффузии в исследуемых образцах Li-Ti ферритов.
Аналогичным образом были определены диффузионные параметры в данных образцах для угла косого шлифа 5.5 и 6 градусов. Результаты представлены в таблице 1.
Как видно из таблицы 1, значения предэкспоненциальных множителей и энергий активации диффузии, то есть диффузионных констант, для зернограничной и объемной диффузии, полученные по предлагаемому способу для разных значений угла косого клина, мало отличаются друг от друга и заметно отличаются от соответствующих величин, определенных по способу-прототипу, что можно объяснить только повышением точности определения диффузионных параметров. Последнее достигается за счет увеличения точности измерения глубинных профилей в образцах вследствие применения косого шлифа. При этом по той же причине удалось на порядок сократить временные затраты на проведение полного цикла измерений.
Таким образом, предлагаемый способ позволяет в 5-10 раз уменьшить время, необходимое для определения диффузионных констант, и существенно повысить точность определения диффузионных констант.
Способ определения диффузионных констант в поликристаллических телах.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИФФУЗИОННЫХ КОНСТАНТ В ПОЛИКРИСТАЛЛИЧЕСКИХ ТЕЛАХ | 1999 |
|
RU2169914C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИФФУЗИОННЫХ КОНСТАНТ В ПОЛИКРИСТАЛЛИЧЕСКИХ МАТЕРИАЛАХ | 2005 |
|
RU2289118C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИФФУЗИОННЫХ КОНСТАНТ В ПОЛИКРИСТАЛЛИЧЕСКИХ МАТЕРИАЛАХ | 2007 |
|
RU2338180C1 |
| СПОСОБ ПОСЛОЙНОГО АНАЛИЗА ТОНКИХ ПЛЕНОК | 2002 |
|
RU2229116C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ДИФФУЗИИ В ПОРОШКОВЫХ МАТЕРИАЛАХ И СПОСОБ ОПРЕДЕЛЕНИЯ ТОЛЩИНЫ И ПОКАЗАТЕЛЯ ЦЕЛОСТНОСТИ ПОКРЫТИЯ НА ЧАСТИЦАХ ПОРОШКОВЫХ МАТЕРИАЛОВ | 2012 |
|
RU2522757C1 |
| Способ определения диффузионных констант в кристаллических телах с примесной неоднородностью | 1987 |
|
SU1548709A1 |
| Способ определения коэффициента диффузии в полупроводниках | 1982 |
|
SU1053189A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ДИФФУЗИИ ПРИМЕСНЫХ АТОМОВ В ПОЛУПРОВОДНИКЕ | 2009 |
|
RU2408952C1 |
| Способ определения коэффициента диффузии | 1981 |
|
SU1117491A1 |
| СПОСОБ ФОРМИРОВАНИЯ УЛЬТРАМЕЛКОЗЕРНИСТОЙ СТРУКТУРЫ В ЦВЕТНЫХ СПЛАВАХ НА ОСНОВЕ МЕДИ И АЛЮМИНИЯ (ВАРИАНТЫ) | 2013 |
|
RU2551041C2 |
Изобретение относится к области контрольно-измерительной техники и может быть использовано для определения параметров диффузии кислорода в твердых поликристаллических телах в материаловедении и физике твердого тела. Технический результат изобретения: снижение трудоемкости и повышение точности определения диффузионных констант в поликристаллических материалах. Сущность: способ включает удаление у образца тонких поверхностных слоев до достижения величины энергии активации электрической проводимости в приповерхностном слое образца значения 0.19-0.20 эВ, после чего образец нагревают, выдерживают в нагретом состоянии, охлаждают, на его поверхности формируют косой шлиф под углом от 5 до 6 градусов. Затем определяют глубинное распределение энергии активации электрической проводимости в образце путем определения энергий активации электрической проводимости в различных участках поверхности косого шлифа. Коэффициенты диффузии определяют аппроксимацией распределения выражением, связывающим величину энергии активации электрической проводимости с концентрацией продиффундировавших ионов, задаваемой, в свою очередь, в виде решения уравнения Фика с соответствующими граничными условиями, указанную последовательность действий повторяют для различных температур нагрева образца, строят график температурной зависимости коэффициентов диффузии, определяют диффузионные константы по результатам аппроксимации данной зависимости законом Аррениуса. 1 табл., 4 ил.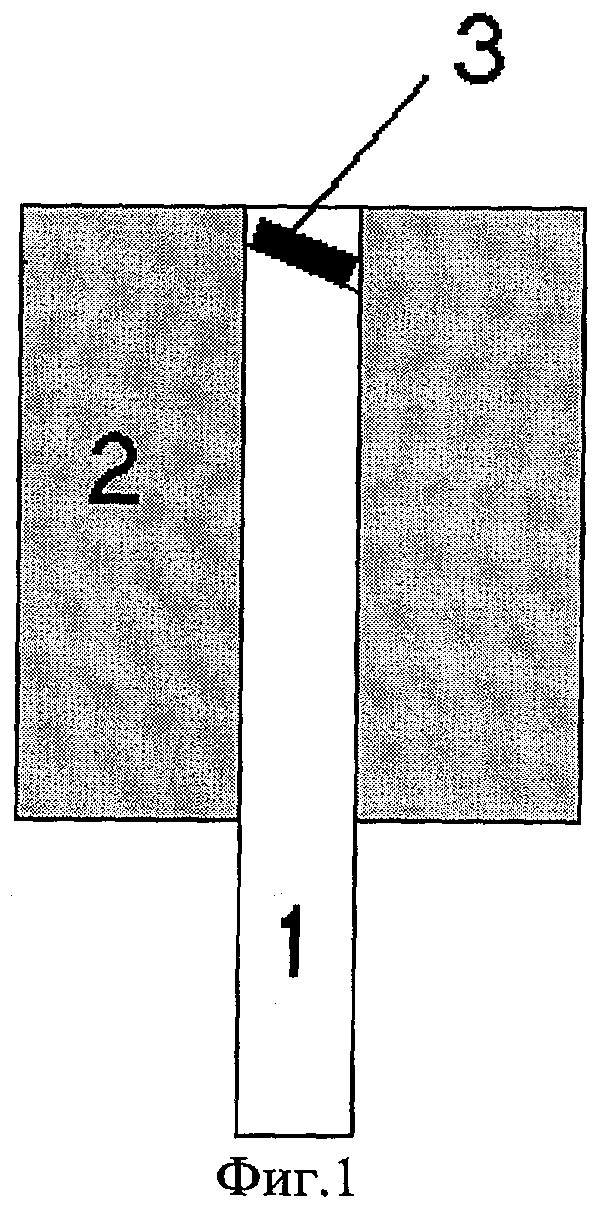
Способ определения диффузионных констант в поликристаллических материалах, в частности ферритах, заключающийся в том, что у образца удаляют тонкие поверхностные слои до достижения величины энергии активации электрической проводимости в приповерхностном слое образца значения 0.19-0.20 эВ, после чего образец нагревают, выдерживают в нагретом состоянии, охлаждают, определяют в образце глубинное распределение энергии активации электрической проводимости, определяют коэффициенты диффузии аппроксимацией распределения выражением, связывающим величину энергии активации электрической проводимости с концентрацией продиффундировавших ионов, задаваемой, в свою очередь, в виде решения уравнения Фика с соответствующими граничными условиями, указанную последовательность действии повторяют для различных температур нагрева образца, строят график температурной зависимости коэффициентов диффузии, определяют диффузионные константы по результатам аппроксимации данной зависимости законом Аррениуса, отличающийся тем, что после каждого охлаждения образца на его поверхности формируют косой шлиф под углом от 5 до 6 градусов, а глубинное распределение энергии активации электрической проводимости в образце определяют путем проведения измерений энергий активации электрической проводимости в различных участках поверхности косого шлифа.
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИФФУЗИОННЫХ КОНСТАНТ В ПОЛИКРИСТАЛЛИЧЕСКИХ ТЕЛАХ | 1999 |
|
RU2169914C2 |
| Способ определения коэффициента объемной диффузии примеси в порошковом материале | 1987 |
|
SU1492240A1 |
| Способ определения диффузионных констант в кристаллических телах с примесной неоднородностью | 1987 |
|
SU1548709A1 |
| US 5627329, 06.05.1997 | |||
| JP 2004085528, 18.03.2004 | |||
| JP 63172941, 16.07.1988 | |||
| JP 61226637, 08.10.1986. | |||
Авторы
Даты
2005-09-20—Публикация
2004-04-13—Подача