Изобретение относится к измерительной технике и может быть использовано для измерения углов взаимной ориентации установочных площадок под приборы научной аппаратуры летательных аппаратов, а также в машиностроении, станкостроении.
Известен способ контроля [1], включающий: установку на контролируемые площадки измерительных устройств, каждое из которых содержит два измерительных преобразователя, измеряющие углы отклонения от горизонта по двум взаимно перпендикулярным направлениям, измерение углов наклона каждой из площадок относительно горизонта, вычисление углов взаимной ориентации. Недостатком способа является то, что при больших углах азимутального рассогласования и при колебаниях основания возникают динамическая погрешность, снижающая точность измерений, и невозможность данным способом определить угол азимутального рассогласования между площадками.
Кроме способа, предложенного в [1], известны способы контроля трех пространственных угловых координат [2], основанные на применении оптико-электронных измерительных устройств. Недостатки этого метода: мал диапазон измеряемых углов ±20 уг.мин и большое рабочее расстояние 3÷6 м, что затрудняет контроль площадок, расположенных в труднодоступных местах объекта.
Наиболее близким по технической сущности к предлагаемому решению является способ измерения, описанный в патенте [1].
Задачей создания изобретения является разработка способа, при использовании которого достигается технический результат, заключающийся в повышении точности измерения углового рассогласования и расширении функциональных возможностей способа, а именно возможность дополнительного измерения угла азимутального рассогласования.
Указанный технический результат достигается признаками, указанными в формуле изобретения, общими с прототипом, такими как способ контроля взаимного пространственного положения установочных площадок, заключающийся в горизонтировании изделия, установке на контролируемые площадки измерительных устройств, каждое из которых содержит два измерительных преобразователя, измеряющие углы отклонения от горизонта по двум взаимно перпендикулярным направлениям, измерении углов наклона каждой из площадок относительно горизонта, вычисление углов взаимной ориентации, и отличительными существенными признаками, такими как оси чувствительности измерительных преобразователей ориентируют вдоль базовых осей площадок, затем разворачивают ось чувствительности преобразователя установленного на первой площадке на угол, равный номинальному значению угла азимутального рассогласования между осями ОХ1 и ОХ2, который берется из чертежа изделия; одновременно измеряют углы контролируемых площадок относительно горизонтальных осей, затем разворачивают оси чувствительности преобразователя на угол 90° в азимутальной плоскости, одновременно измеряют углы контролируемых площадок относительно горизонтальных осей, затем разворачивают оси чувствительности преобразователя на угол минус 90° в азимутальной плоскости, далее отклоняют изделие относительно горизонтальной оси на угол, одновременно измеряют углы отклонения контролируемых площадок от горизонта, разворачивают оси чувствительности преобразователя на угол 90°, одновременно измеряют углы отклонения контролируемых площадок от горизонта, затем вычисляют углы рассогласования контролируемых площадок относительно горизонтальных осей, а угол азимутального рассогласования определяют из соотношений:
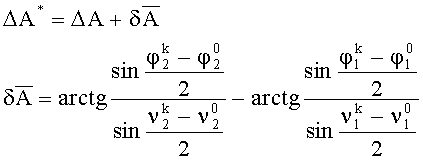
ΔА* - угол азимутального рассогласования;
ΔА - угол азимутального рассогласования, взятый из чертежа изделия;
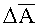
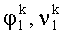
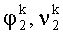
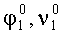
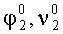
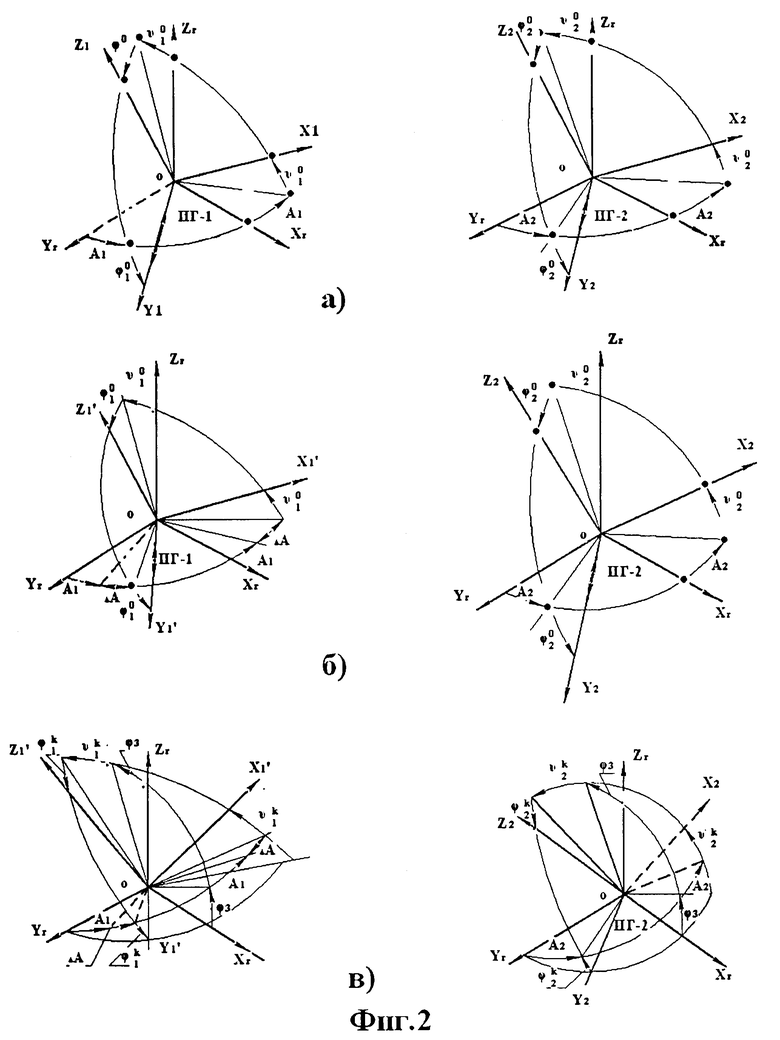
Сущность предлагаемого технического решения поясняется чертежами, где на фиг.1 показана последовательность операций способа, а на фиг.2 - расположение систем координат преобразователей и площадок при выполнении операций.
Установочные площадки развернуты относительно друг друга в азимуте на угол ΔА, на фиг.1 система координат X1OY1Z1 связана с площадкой 1, система координат X2OY2Z2 связана с площадкой 2. Первую измерительную головку (ИГ-1) устанавливают на площадку 1 так, чтобы ось чувствительности измерителя наклона ориентировалась вдоль оси ОХ1, вторую измерительную головку устанавливают так, чтобы ось чувствительности была ориентирована вдоль оси ОХ2.
В качестве измерителя наклона могут быть использованы прецизионные акселерометры, например, струнный акселерометр или акселерометр по авторскому свидетельству СССР[3].
Затем платформу с измерителем наклона головки ИГ-1 разворачивают в азимуте на угол, равный номинальному углу азимутального рассогласования между осями ОХ1 и ОХ2, значение номинального угла рассогласования берут из чертежа изделия, далее измеряют углы наклона осей чувствительности ИГ-1 и ИГ-1 от горизонта 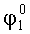
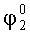
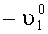
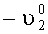
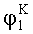
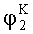
Поворачивают платформы с измерителями наклона на угол +90°, в азимутальной плоскости измеряют углы отклонения осей чувствительности ИГ-1 и ИГ-2: 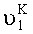
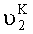
Для обоснования предлагаемого способа измерения рассмотрим расположение систем координат, связанных с изделием XГOYГZГ, установочными площадками X1OY1Z1 и X2OY2Z2, которое представлено на фиг.2. На фиг.2а система координат XГOYГZГ связана с изделием, причем оси ОХГ и OYГ расположены в плоскости горизонта, а ось OZГ направлена по вертикали. Угол А1 определяет поворот системы координат X1OY1Z1, связанный с контролируемой площадкой 1 в азимуте, угол 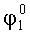
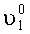
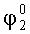
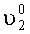
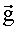
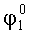
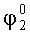
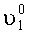
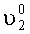
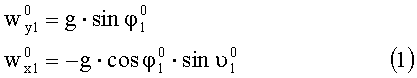
А для ИГ-2 значения измеряемых ускорений запишутся в виде:
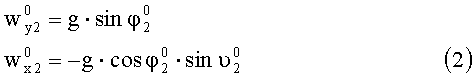
На фиг.2в представлено расположение осей систем координат X1OY1Z1 и X2OY2Z2 относительно системы XГOYГZГ при развороте изделия относительно оси ОХГ на угол φ3. Проекции ускорения силы тяжести, измеряемые в этом случае измерителями наклона головок ИГ-1 и ИГ-1, запишутся в виде:
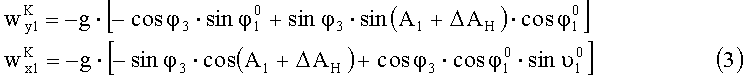
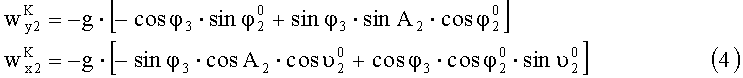
Считая угол φ3 малым, запишем выражения (3) и (4) в виде:
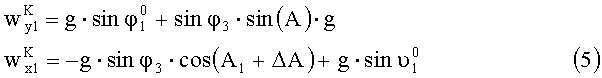
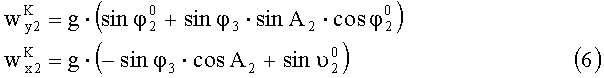
С другой стороны, ускорения 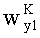
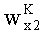
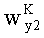
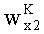
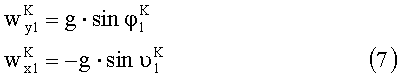
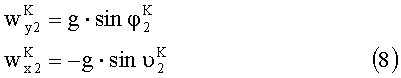
С учетом (7) и (8) выражения (5) и (6) могут быть записаны в виде:
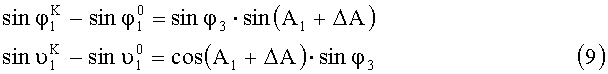
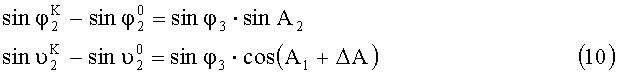
Из выражений (9) и (10) определим:
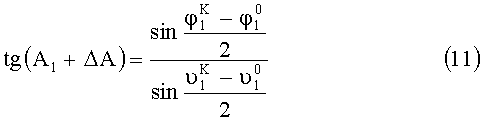
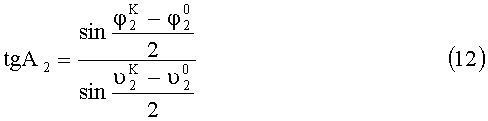
Углы отклонения от горизонта найдем из выражений (1), (2), (7), (8):



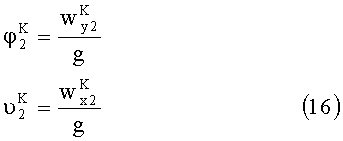
В реальных условиях контроля изделие может совершать низкочастотные колебания, обусловленные колебаниями основания, которые приводят к динамической погрешности измерения углового рассогласования. Пусть вдоль оси OYГ действует ускорение:
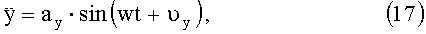
а вдоль оси ОХГ действует ускорение:
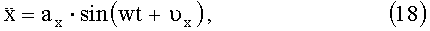
где ау и ах - амплитуды действующих ускорений,
ω - частота колебаний,
υу, υх - начальные фазы,
t - время.
Оценим динамическую ошибку измерения углов отклонения контролируемой площадки 1 от горизонта.
Проекции измеряемого ускорения запишутся в виде:
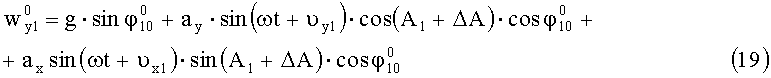
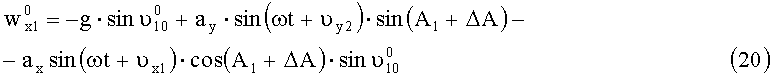
Измеряемое значение углов:

Представим:

С учетом (21) и (22) представим выражение (19) в виде:
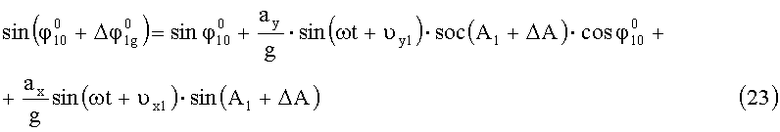
Откуда: динамическая ошибка измерения угла 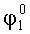
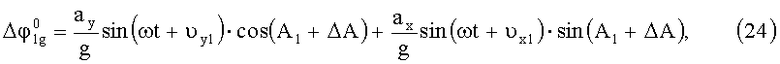
а динамическая ошибка измерения угла 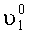
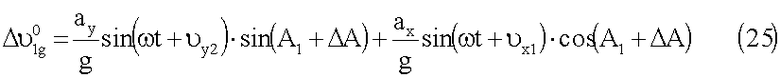
Для второй контролируемой площадки:
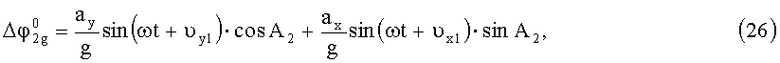
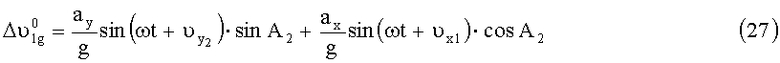
Динамическую погрешность измерения угла азимутального рассогласования определим, записав проекции ускорений, действующих на оси ОХ1, OY1 с учетом (17) и (18) при φ3≠0:
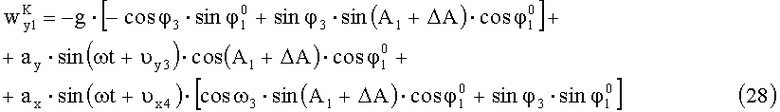
Для малых углов 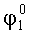
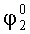
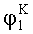
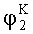
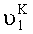
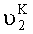
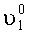
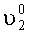
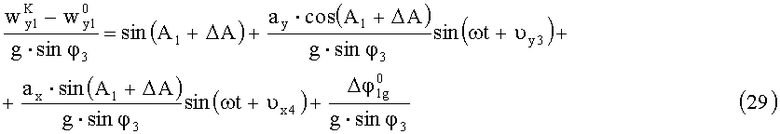
Так как:

где δAg1 - динамическая погрешность измерения азимутального угла
площадки 1, то с учетом (30 и (24) погрешность определения азимутального угла с учетом малости δAg1, для первой площадки запишется в виде:
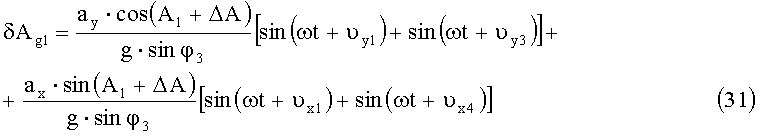
Динамическая погрешность определения азимутального угла для второй площадки:
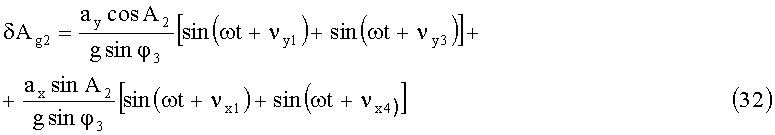
Определим погрешность измерения разности горизонтальных углов с учетом (24)÷(26):
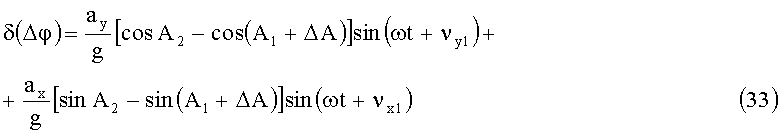
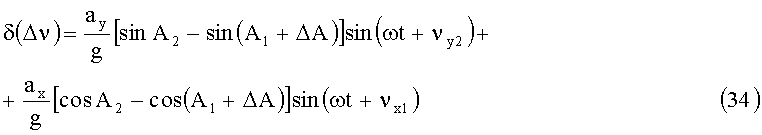
Максимальные значения величин (33) и (34):
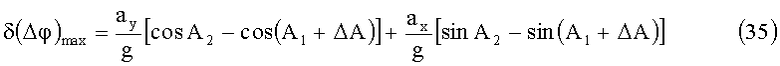
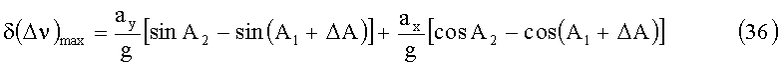
Для разности азимутальных углов динамическая погрешность с учетом (31) и (32) выразится в виде:
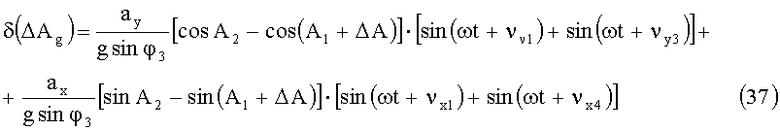
Оценим величину динамических погрешностей при отсутствии операции разворота измерительного преобразователя в азимутальной плоскости на угол ΔА. Тогда в выражениях (35) - (37) ΔА=0. Допустим, что:
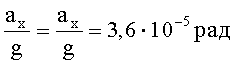
A1=0
A2=45°
Тогда согласно (35) и (36) с учетом ΔА=0 получим:
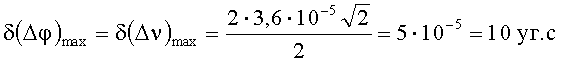
Максимальное значение погрешности разности азимутальных углов с учетом (32) запишем в виде:
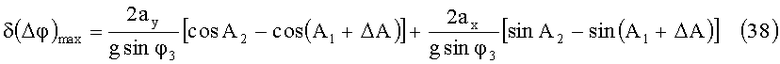
Угол наклона изделия имеет порядок 5°. Тогда:
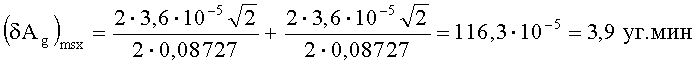
При развороте платформы ИГ-1 с измерителем наклона на угол ΔA в азимутальной плоскости, значение угла А2 можно представить в виде:
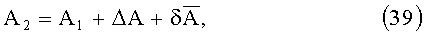
где ΔА - угол равный номинальному значению угла азимутального рассогласования между осями ОХ1 и ОХ2 площадок 1 и 2 (взят из чертежа изделия).
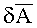
Тогда с учетом малости 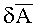
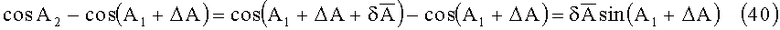
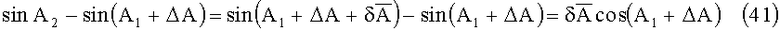
Тогда с учетом (40) и (41) выражения (35) и (36) можно представить в виде:
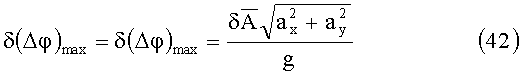
Выражение (37) с учетом (40) и (41) запишется в виде:
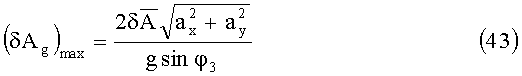
Оценим динамическую погрешность с учетом того, что 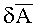
Тогда:
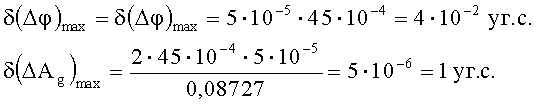
Следовательно, предлагаемый способ позволяет снизить динамическую составляющую погрешности измерения углов отклонения от горизонта в 200 раз, а динамическую погрешность измерения угла азимутального рассогласования в 230 раз. Угол азимутального рассогласования согласно предлагаемому способу определяем следующим образом:
С учетом формул (11) и (12) находим угол 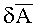
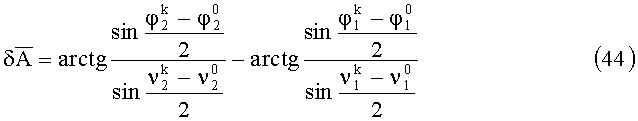
Затем определяем угол азимутального рассогласования между площадками по формуле:

где ΔA - угол, равный номинальному углу рассогласования, взятому из чертежа и измеренному датчиком угла (например, оптико-электронного типа ВЕ-198).
В результате выполнения технологических операций предлагаемого способа получить величины (13) - (16), (44) и (45), которые позволяют определить углы рассогласования между осями системы координат 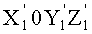
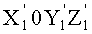
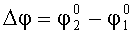
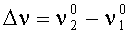
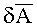
Направляющие косинусы системы координат X20Y2Z2 в системе 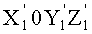

Перейдем от системы координат 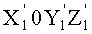
Изображенной на фиг.2б и системе координат X10Y1Z1 изображенной на фиг.2а, матрица перехода будет иметь вид:

Тогда:
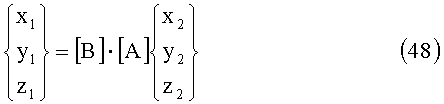
Элементы матрицы М определяются соотношениями (46). Тогда направляющие косинусы системы координат второй площадки в системе координат первой площадки запишутся в виде:
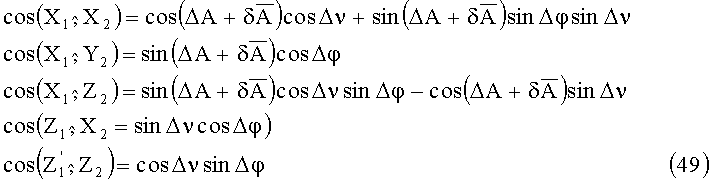

Величины, входящие в соотношения (49), определены выше.
Следовательно, предлагаемый способ контроля позволяет снизить динамическую погрешность измерения углов, обусловленную низкочастотными колебаниями основания в 200 раз, и полностью определить угловую ориентацию второй установочной площадки относительно первой, тогда как известный метод контроля позволяет лишь определить угловое рассогласование установочных площадок относительно горизонтальных осей.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Преобразователь перемещений и наклона. Заявка Великобритании №2092754, приоритет 10.02.81, опубл. 18.08.82, МКИ G01В 7/30. НКИ С1.
2. Высокоточные угловые измерения (под редакцией Ю.Г. Якушенкова). М.: ″Машиностроение″. 1987.
3. Авторское свидетельство СССР №517787, МКИ G01С 9/02.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ПРОСТРАНСТВЕННЫХ УГЛОВЫХ ОТКЛОНЕНИЙ | 2012 |
|
RU2495374C1 |
| СПОСОБ НАВЕДЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ НА НАЗЕМНЫЕ ОБЪЕКТЫ | 2012 |
|
RU2525650C2 |
| СПОСОБ ПРИВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА К НАЗЕМНОМУ ОБЪЕКТУ | 2012 |
|
RU2521890C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАПРАВЛЕНИЯ НА ГИДРОАКУСТИЧЕСКИЙ МАЯК-ОТВЕТЧИК В УСЛОВИЯХ МНОГОЛУЧЕВОГО РАСПРОСТРАНЕНИЯ НАВИГАЦИОННОГО СИГНАЛА | 2012 |
|
RU2515179C1 |
| СПОСОБ ОПЕРАТИВНОГО ПРОГНОЗА ЗЕМЛЕТРЯСЕНИЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2507546C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА | 2012 |
|
RU2510618C2 |
| СПОСОБ ПЕРСОНАЛЬНОЙ АВТОНОМНОЙ НАВИГАЦИИ | 2013 |
|
RU2523753C1 |
| СПОСОБ РАСПОЗНАВАНИЯ ТРЕХМЕРНОЙ ФОРМЫ ОБЪЕКТОВ | 2012 |
|
RU2491503C1 |
| СПОСОБ ЗАХОДА НА ПОСАДКУ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА В АВАРИЙНЫХ УСЛОВИЯХ | 2019 |
|
RU2725640C1 |
| СПОСОБ ОЦЕНКИ ОШИБОК И КОНТРОЛЯ ДАТЧИКОВ ПЕРВИЧНОЙ ИНФОРМАЦИИ В СОСТАВЕ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ В НАЗЕМНЫХ УСЛОВИЯХ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2537513C2 |
Способ контроля взаимного пространственного положения установочных площадок заключается в горизонтировании изделия, установке на контролируемые площадки измерительных устройств, каждое из которых содержит два измерительных преобразователя, измеряющие углы отклонения от горизонта по двум взаимно перпендикулярным направлениям, измерении углов наклона каждой из площадок относительно горизонта, вычисление углов взаимной ориентации. Оси чувствительности измерительных преобразователей ориентируют вдоль базовых осей площадок, затем разворачивают ось чувствительности преобразователя, установленного на первой площадке на угол, равный номинальному значению угла азимутального рассогласования между осями ОХ1 и ОХ2, который берется из чертежа изделия. Одновременно измеряют углы контролируемых площадок относительно горизонтальных осей, затем разворачивают оси чувствительности преобразователя на угол 90° в азимутальной плоскости. Одновременно измеряют углы контролируемых площадок относительно горизонтальных осей, затем разворачивают оси чувствительности преобразователя на угол минус 90° в азимутальной плоскости, далее отклоняют изделие относительно горизонтальной оси на угол φ3, одновременно измеряют углы отклонения контролируемых площадок от горизонта, разворачивают оси чувствительности преобразователя на угол 90°, одновременно измеряют углы отклонения контролируемых площадок от горизонта, затем вычисляют углы рассогласования контролируемых площадок относительно горизонтальных осей, а угол азимутального рассогласования определяют из соотношений:
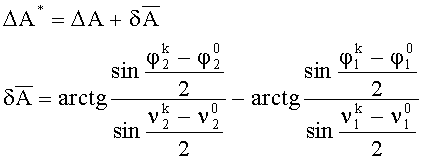
где
ΔА* - угол азимутального рассогласования;
ΔА - угол азимутального рассогласования, взятый из чертежа изделия;
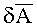
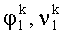 - углы отклонения первой контролируемой площадки относительно горизонта при наклоне изделия;
- углы отклонения первой контролируемой площадки относительно горизонта при наклоне изделия;
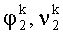 - углы отклонения второй контролируемой площадки относительно горизонта при наклоне изделия;
- углы отклонения второй контролируемой площадки относительно горизонта при наклоне изделия;
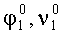 - углы отклонения первой контролируемой площадки относительно горизонта при горизонтальном положении осей изделия;
- углы отклонения первой контролируемой площадки относительно горизонта при горизонтальном положении осей изделия;
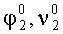 - углы отклонения второй контролируемой площадки относительно горизонта при горизонтальном положении осей изделия. 2 ил.
- углы отклонения второй контролируемой площадки относительно горизонта при горизонтальном положении осей изделия. 2 ил.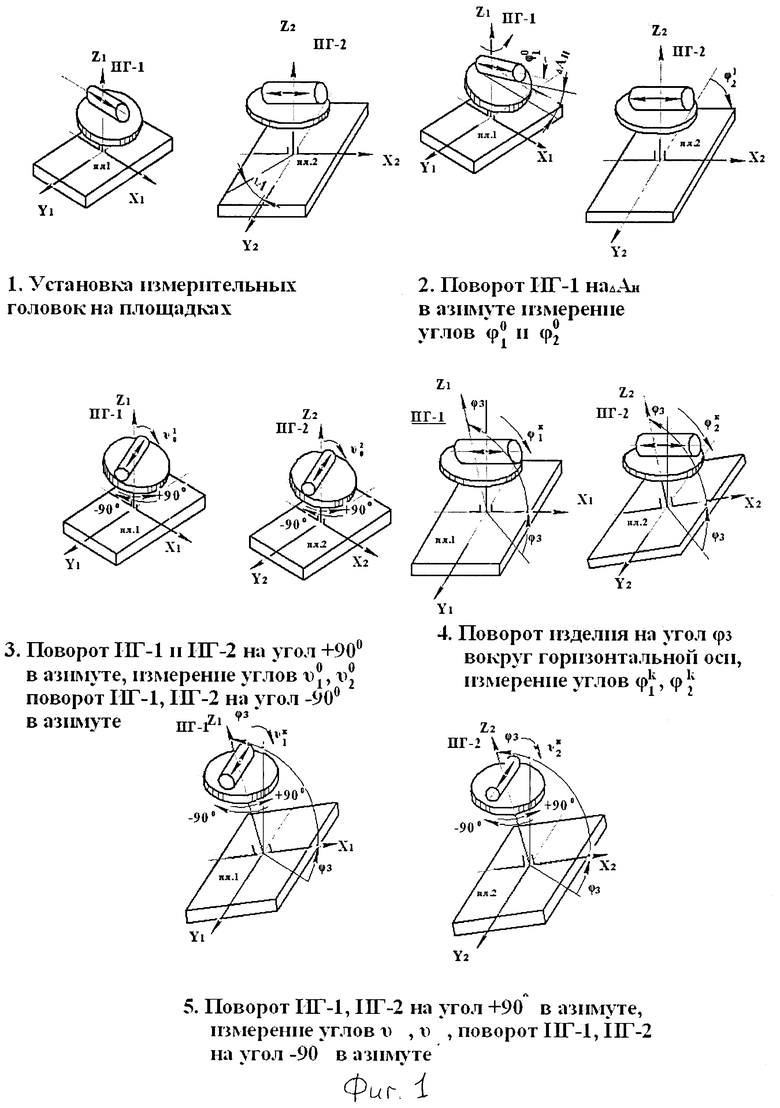
Способ контроля взаимного пространственного положения установочных площадок, заключающийся в горизонтировании изделия, установке на контролируемые площадки измерительных устройств, каждое из которых содержит два измерительных преобразователя, измеряющие углы отклонения от горизонта по двум взаимно перпендикулярным направлениям, измерении углов наклона каждой из площадок относительно горизонта, вычисление углов взаимной ориентации, отличающейся тем, что оси чувствительности измерительных преобразователей ориентируют вдоль базовых осей площадок, затем разворачивают ось чувствительности преобразователя, установленного на первой площадке на угол, равный номинальному значению угла азимутального рассогласования между осями ОХ1 и ОХ2, который берется из чертежа изделия, одновременно измеряют углы контролируемых площадок относительно горизонтальных осей, затем разворачивают оси чувствительности преобразователя на угол 90° в азимутальной плоскости, одновременно измеряют углы контролируемых площадок относительно горизонтальных осей, затем разворачивают оси чувствительности преобразователя на угол минус 90° в азимутальной плоскости, далее отклоняют изделие относительно горизонтальной оси на угол φ3, одновременно измеряют углы отклонения контролируемых площадок от горизонта, разворачивают оси чувствительности преобразователя на угол 90°, одновременно измеряют углы отклонения контролируемых площадок от горизонта, затем вычисляют углы рассогласования контролируемых площадок относительно горизонтальных осей, а угол азимутального рассогласования определяют из соотношений:
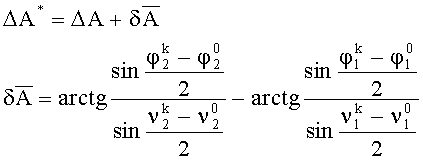 , где:
, где:
ΔА* - угол азимутального рассогласования;
ΔА - номинальный угол азимутального рассогласования, взятый из чертежа изделия;
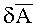 - угол азимутального рассогласования определенный в результате измерений;
- угол азимутального рассогласования определенный в результате измерений;
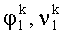 - углы отклонения первой контролируемой площадки относительно горизонта при наклоне изделия;
- углы отклонения первой контролируемой площадки относительно горизонта при наклоне изделия;
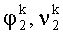 - углы отклонения второй контролируемой площадки относительно горизонта при наклоне изделия;
- углы отклонения второй контролируемой площадки относительно горизонта при наклоне изделия;
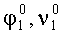 - углы отклонения первой контролируемой площадки относительно горизонта при горизонтальном положении осей изделия;
- углы отклонения первой контролируемой площадки относительно горизонта при горизонтальном положении осей изделия;
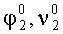 - углы отклонения второй контролируемой площадки относительно горизонта при горизонтальном положении осей изделия.
- углы отклонения второй контролируемой площадки относительно горизонта при горизонтальном положении осей изделия.
| УСТРОЙСТВО ДЛЯ ВВОДА ЖИДКОГО ПРОДУКТА В СУБЛИМАТОР | 1992 |
|
RU2092754C1 |
| Высокоточные угловые измерения (под редакцией Ю.Г.Якушенкова) | |||
| М | |||
| "Машиностроение" | |||
| Кузнечная нефтяная печь с форсункой | 1917 |
|
SU1987A1 |
| Наклономер | 1974 |
|
SU517787A1 |
| US 4378693 А1, 05.04.1983 | |||
Авторы
Даты
2014-07-20—Публикация
2013-01-15—Подача