Изобретение относится к способам расчета упругих свойств горных пород: продольного импеданса (Ip), поперечного импеданса (Is) и плотности (ρ) по сейсмическим данным.
Для этой цели разработан метод пластовой адаптивной инверсии сейсмических данных, который реализован в варианте пластовой акустической инверсии для суммированных сейсмических данных и пластовой синхронной инверсии для несуммированных сейсмических данных.
В XX веке для обеспечения прироста запасов углеводородов (УВ) основная ставка делалась на поиск крупных месторождений, содержащих мощные (десятки и даже сотни метров) пласты-коллекторы, являющиеся резервуарами для залежей нефти и газа. В настоящее время обнаружение месторождений УВ такого типа становится весьма редким явлением. Основной прирост запасов осуществляется за счет средних и мелких месторождений, содержащих маломощные коллекторы, толщина которых составляет обычно единицы и первые десятки (до 20) метров.
Прогнозирование свойств коллекторов по данным сейсморазведки выполняется способами динамической интерпретации (ДИ), основным элементом которой является сейсмическая инверсия, осуществляющая оптимизационный подбор модели среды. На сегодняшний день практически во всех имеющихся отечественных и зарубежных системах используются способы инверсии, основанные на тонкослоистых моделях среды. В этих моделях временная мощность пластов постоянна и равна шагу дискретизации, что соответствует толщинам слоев порядка 3-4 м. Поскольку вследствие регуляризации получаемые такими способами кривые импедансов и плотностей являются сглаженными, уместно назвать эти способы термином «непрерывная инверсия». Теоретические исследования и практические примеры опробования показали, что непрерывная инверсия дает надежные оценки акустических свойств достаточно мощных (15-20 м) однородных коллекторов, тогда как тонкие пласты-коллекторы мощностью до 10 м либо не отображаются на результатах инверсии, либо их акустические свойства оцениваются с недопустимо большими погрешностями (до 30-40%).
Для обработки 2D сейсмических данных нами разработана система динамической интерпретации OTRI (в русской аббревиатуре ОТДИ), в состав которой входит оригинальная процедура акустической инверсии, основанная на применении пластовой модели среды («пластовая инверсия»). Эта технология позволяет оценивать акустические свойства пластов с высокой точностью (единицы процентов). Как показали наши исследования в случае различия акустических свойств коллекторов и вмещающих пород, применение пластовой инверсии позволяет оценивать эффективные мощности коллекторов, начиная с Нэф=2-3 м. Данная точность достаточна для построения детальных геологических моделей, используемых не только на этапе разведки, но и на этапе эксплуатации месторождений, например при дизайне гидроразрыва пласта.
Однако на данный момент не разработаны алгоритмы и методика применения данной технологии для 3D сейсмических данных. Не разработана упругая пластовая инверсия, позволяющая оценивать литологический состав пород коллекторов и характер насыщения.
Выявление коллекторов и изучение распределения их емкостных свойств по площади, что необходимо для разведки и рациональной эксплуатации месторождений, осуществляется в результате применения динамической интерпретации (ДИ) сейсморазведки в комплексе с геофизическим исследованием скважин (ГИС). Основным элементом динамической интерпретации сейсморазведки является сейсмическая инверсия, осуществляющая трансформацию сейсмических волновых полей в детальные модели среды, описывающие распределение в пространстве акустических параметров: скоростей Vp и Vs продольных и поперечных волн, а также плотностей ρ. Совокупная интерпретация полученных по данным сейсморазведки прогнозных акустических параметров и имеющихся данных ГИС позволяет прогнозировать литологию пород, емкостные свойства коллекторов и характер их насыщения (газ или жидкость).
В практике интерпретации данных сейсморазведки используются разнообразные способы одномерной (акустической) и двумерной (упругой) сейсмических инверсий. Одномерная сейсмическая инверсия обрабатывает трассы суммарных сейсмических разрезов с целью получения акустических импедансов Ip=ρ*Vp и используется для оценки емкостных свойств коллекторов. Двумерная инверсия обрабатывает исходные сейсмограммы (до суммирования) продольных волн, получает все три акустических параметра и используется для прогнозирования литологического состава пород и характера насыщения коллекторов.
Все программы сейсмической инверсии, содержащиеся в широко применяемых зарубежных интерпретационных системах, основаны на тонкослоистых моделях среды, в которых минимальные мощности пластов составляют 3-4 м. Казалось бы, что именно такие программы являются наиболее эффективными для прогнозирования свойств маломощных коллекторов, имеющих подобные толщины. Однако вследствие неминуемого ограничения частотного диапазона сейсморазведки, ее реальная разрешающая способность (обычно 10-15 м) не позволяет надежно оценивать параметры отдельных пластов, слагающих используемые тонкослоистые модели [Veeken P., Da Silva. M., 2004]. Теоретические исследования и многочисленные практические эксперименты показали, что эти программы инверсии позволяют с высокой точностью (единицы процентов) определять параметры однородной группы тонких слоев, объединяющихся в более мощные пласты (от 15-20 м и более) [Buland A., Omre H., 2003, Bosch et al., 2010]. То есть такие способы инверсии дают хорошие результаты при прогнозировании свойств достаточно мощных коллекторов, но не пригодны для исследования коллекторов, мощность которых не превышает 10-15 м. На полученных практических результатах видно, что ошибки оценки акустических свойств отдельных тонких пластов с резко отличными акустическими свойствами, мощность которых не превышает 5-10 м, могут достигать 30% и более.
Выход из казалось бы неразрешимой ситуации с исследованием маломощных коллекторов состоит в использовании при выполнении сейсмической инверсии пластовых моделей среды, в которых минимальная мощность пластов соответствует реальной разрешающей способности сейсморазведки в конкретных сейсмогеологических условиях. При этом имеется возможность оценить с высокой точностью акустические параметры пластов, мощность которых составляет 15-20 м. Это оказывается достаточным для того, чтобы выявить наличие в таких пластах маломощных коллекторов (от 2-3 м), отличающихся по акустическим свойствам от вмещающих пород, а также количественно оценить их эффективные толщины Нэф, а в некоторых ситуациях - их линейные емкости Е=Нэф*Кп (Кп - коэффициент пористости).
Нами разработана оригинальная отечественная система одномерной инверсии ОТДИ, основанная на использовании пластовой модели среды [Кондратьев И.К. и др., 2005, Рыжков В.И. и др., 2008]. Эта система при практическом применении с использованием 2D сейсморазведки на десятках месторождений, расположенных в России и за рубежом (Казахстан, Узбекистан, Китай, Алжир), показала высокую эффективность прогнозирования маломощных коллекторов, в том числе и в сложных сейсмогеологических условиях Восточной Сибири, а также в подсолевых отложениях Прикаспия [Кондратьев И.К. и др., 2010].
Однако на сегодня существует только одномерная пластовая инверсия, применяемая для обработки данных 2D сейсморазведки. Именно из-за этого она не находит широкого применения, и нефтяные компании вынуждены использовать импортные программные продукты. Необходимо развить подход, реализующий пластовую инверсию, на вариант двумерной инверсии и сделать пластовую инверсию пригодной для обработки данных 3D сейсморазведки. Необходимо также опробовать новые варианты пластовой инверсии в основных нефтегазоносных провинциях России и разработать методические рекомендации по ее использованию для эффективного прогнозирования маломощных коллекторов.
Известен «СПОСОБ ПОИСКА, РАЗВЕДКИ, ИССЛЕДОВАНИЯ, ОЦЕНКИ И ПРОГНОЗИРОВАНИЯ РАЗРАБОТКИ ЗАЛЕЖИ И МЕСТОРОЖДЕНИЯ ПОЛЕЗНЫХ ИСКОПАЕМЫХ» (RU 2001120889, опубл. 2004, Миколаевский Э.Ю.).
Способ представляет собой поиск статистических связей и установления корреляционных зависимостей множества разнородных параметров, полученных разными геофизическими методами. Данный подход оправдан на этапе поиска достаточно крупных объектов, которые находят отражения в большом количестве параметров. Для сложноустроенных пластов-коллекторов малой мощности результат статистической обработки множества параметров непредсказуем и слабо поддается контролю.
Предлагаемый нами метод предназначен для изучения пластов малой мощности и основывается на модели физики пласта (rock physics).
Известна «АВТОМАТИЗИРОВАННАЯ СИСТЕМА ПОИСКА, РАЗВЕДКИ, ИССЛЕДОВАНИЯ, ОЦЕНКИ И ПРОЕКТИРОВАНИЯ РАЗРАБОТКИ ЗАЛЕЖИ И МЕСТОРОЖДЕНИЙ ПОЛЕЗНЫХ ИСКОПАЕМЫХ» (RU 22831U, Миколаевский Э.Ю.).
Данная система предназначена для реализации способа поиска и разведки, описанного в заявке RU 2001120889. Автоматическая обработка большого количества разнородных параметров требует мощного логического блока, который является центральным звеном данной системы. Устойчивые статистические связи разнородных параметров характерны только для массивных однородных пластов. Сложноустроенные коллекторы малой мощности не находят отклик в большинстве геофизических полей, регистрируемых на поверхности, и имеют сложные корреляционные связи геофизического параметр-петрофизического свойства.
Предлагаемый нами метод направлен на повышение разрешающей способности сейсморазведки при измерении конкретного петрофизического свойства - акустического импеданса в тонких пластах.
Известен патент CN 2577296 «UNDERGROUND MULTI-FREQUENCY ACOUSTIC COMBINED DETECTOR», HOU CHUNHUI [CN]; CHU ZEHAN [CN]; LI JIANHAO [CN].
В данном решении для измерения акустических свойств пластов предлагается многоканальный многочастотный зонд. Данный прибор позволяет изучать свойства пласта-коллектора с высоким разрешением (десятки сантиметров), но на расстоянии не более 1 м от ствола скважины.
Наш метод позволяет изучать акустические свойства пласта с меньшим разрешением (первые единицы метров), но на существенном удалении от скважины (десятки километров), что необходимо при неоднородном строении пласта.
Известен патент EP 0889331 «METHODE POUR MODELISER EN 3D L'IMPEDANCE D'UN MILIEU HETEROGENE», Grizon, Laurent, Leger Michel, Richard Vincent и др.
В решении описан метод оптимизации априорно заданной трехмерной модели импедансов, полученной в результате сейсмической интерпретации и интерполяции данных ГИС имеющихся скважин.
Недостатки предложенного подхода: жесткое влияние априорной модели на конечный результат, что приводит к сглаживанию аномалий в межскважинном пространстве, уточнение импедансов в непрерывном режиме (с шагом дискретности Δt) с последующей полосовой фильтрацией результатов по оси t, что приводит к пропуску аномалий, вызываемых маломощными (единицы метров) продуктивными пластами.
Преимущество нашего подхода: гибкое задание априорной информации в виде диапазонов изменения импедансов реперов и межреперного пространства, что особенно эффективно при малом числе имеющихся скважин, использование при оптимизации пластовой модели среды существенно повышает точность определения акустических параметров пластов, что позволяет выявить присутствие в них тонких продуктивных пластов мощностью в единицы метров, отличающихся по акустическим свойствам от вмещающих пород.
Известен «СПОСОБ ДЛЯ ОБНАРУЖЕНИЯ ПОТЕНЦИАЛЬНОГО ВОДНОГО ПОТОКА С МАЛОЙ ГЛУБИНОЙ ЗАЛЕГАНИЯ» (RU 2319983, за авт. Надир Дуттаб, Субхашис Маллик).
Данный способ является ближайшим аналогом и имеет ту же физическую основу, что и предлагаемый нами способ - это высокоточное прогнозирование акустических свойств по сейсмическим данным. Авторы предлагают использовать его для прогноза неглубокозалегающих рыхлых песчаных тел, несущих опасность при бурении.
Мы применяем данный подход для изучения маломощных коллекторов на большой глубине.
Известна международная заявка WO 2010/092084 «FINITE ELEMENT MODELLING OF BOREHOLE SEISMIC RESPONSES IN LAYERED ANISOTROPIC FORMATIONS AND ITS USE FOR ELASTIC INVERSION», JORGENSEN Ole.
Данное решение также является ближайшим аналогом и посвящено решению прямой задачи (моделирование волнового поля при известных свойствах среды) в слоистых анизотропных средах.
Наша работа посвящена способу решения обратной задачи (прогноз неизвестных свойств среды на основе зарегистрированного волнового поля).
Цель изобретения - создание технологических основ, обеспечивающих возможность надежного изучения емкостных параметров и литологического состава маломощных (от 1-2 м) пластов-коллекторов по данным сейсморазведки.
Для достижения поставленной цели необходимо решить следующие задачи:
a) разработка алгоритмов и методики пластовой акустической инверсии данных 3D сейсморазведки;
b) разработка алгоритмов и методики пластовой синхронной инверсии данных 3D сейсморазведки;
c) разработка методических рекомендаций оптимального комплексирования акустической и синхронной пластовой инверсии.
Технический результат: обеспечивается повышение точности оценки упругих свойств горных пород, повышение эффективности прогнозирования коллекторов в сложных сейсмогеологических условиях. Кроме того, способ реализуем при исследовании слабоизученных районов с небольшим количеством (первые единицы) имеющихся скважин.
Указанный технический результат достигается за счет того, что способ определения упругих свойств горных пород на основе пластовой адаптивной инверсии сейсмических данных, характеризующийся применением пластовых моделей среды, в которых минимальные временные мощности τmin пластов соответствуют реальной разрешающей способности сейсморазведки и геологии осадконакопления и вычисляются согласно формуле:
τmin(мс)=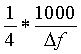
Благодаря тому что способ основан на применении пластовых моделей среды, в которых минимальные временные мощности τmin пластов соответствуют реальной разрешающей способности сейсморазведки и геологии осадконакопления, эмпирическая формула, связывающая τmin с качеством исходных сейсмических материалов (отношение сигнал/помеха, реальная полоса частот сейсмических сигналов), применение пластовой сейсмической инверсии обеспечивают максимальную точность оценки упругих свойств горных пород. Другие способы сейсмической инверсии основаны на применении эквидистантных моделей среды с постоянной мощностью пластов, равной интервалу дискретности Δt сейсмической записи. Реализуемое в пластовой инверсии согласование детальности получаемых сейсмоакустических разрезов с качеством исходных материалов и границ геологических пластов позволяет эффективно использовать метод для прогнозирования коллекторов в сложных сейсмогеологических условиях.
Особенностью нового способа адаптивной пластовой инверсии является гибкий учет априорной информации об упругих свойствах изучаемых геологических разрезов. При этом задаются диапазоны изменения упругих свойств в отдельных хорошо выраженных (реперных) пластах. В каждом регионе существуют присутствующие повсеместно реперные пласты (слои глин и карбонатов) с выдержанными физическими свойствами. Поэтому способ адаптивной пластовой инверсии имеет преимущества перед традиционными способами при исследовании слабоизученных районов с небольшим количеством (первые единицы) имеющихся скважин.
Осуществление изобретения
Перечень исходных данных, требуемых для реализации способа:
τmin - минимальная временная мощность пластов получаемых моделей, соответствующая реальной разрешающей способности сейсморазведки;

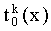
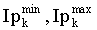

ΔIpmax,ΔIsmax - максимальное значение изменения импедансов на одну итерацию.
Для задания τmin используют эмпирическую формулу, характеризующую оптимальное значение этой величины по критерию точности аппроксимации «истинной» детальной модели соответствующей трассой полученного сейсмоакустического разреза:
τmin(мс)=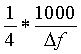
В этой формуле Δf - рабочая полоса частот, в которой, после всех примененных процедур обработки, уровень сигналов превышает уровень.
Исходной моделью 
Главным вопросом в задании линий 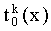
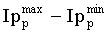
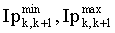
Алгоритм пластовой акустической инверсии
Постановка задачи пластовой акустической инверсии
Введем следующие обозначения:
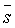
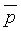
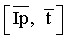

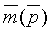
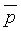
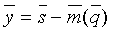
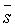

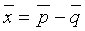

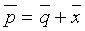
Целью акустической инверсии является преобразование сейсмического временного разреза s(t, х) в детальную пластовую модель акустических импедансов Iр(t, х), называемую сейсмоакустическим разрезом. Основой нашего алгоритма является обобщенная линейная инверсия, которая модифицирована нами для введения априорной информации о диапазонах изменения акустических параметров слоев. Ниже приводится описание математической основы модифицированного алгоритма обобщенной линейной инверсии (МОЛИ).
Базовые уравнения обобщенной линейной инверсии
Реальную трассу 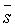
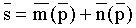
где 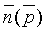
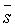
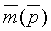
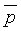
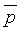

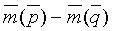
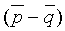
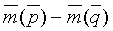
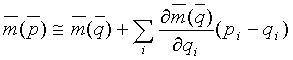
Уравнение (2) можно представить в матричной форме:

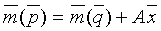
или:
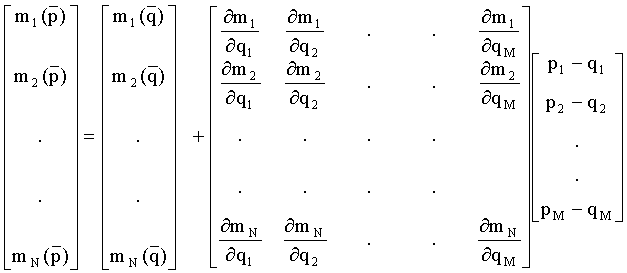
Далее под 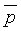
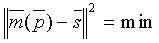
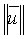
(

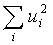
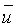
Второе условие оптимальности - определенные ограничения на отклонение компонент 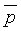

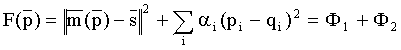
Подставляя 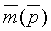
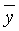
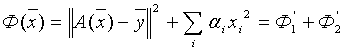
Минимизируя Ф(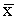
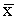
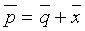
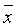
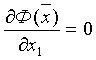
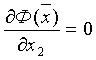
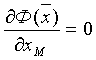
которая в матричной форме имеет вид:
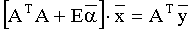
где 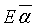
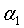
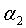
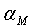
Расчет демпфирующих множителей 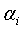
Основной особенностью модифицированного алгоритма инверсии является способ задания демпфирующих множителей 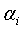
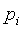
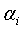
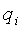
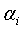
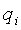
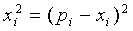
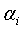
А. Оба слагаемых в функционалах (6), (7) должны быть примерно одинаковы по величине.
В. Величины 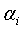
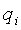
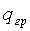
Предварительно заметим, что в (6) и (7) Ф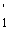
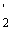
Для того чтобы определить 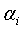
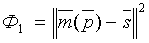
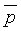
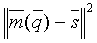
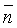
С1=0,25; С2=0,5; С3=0,7. (9)
Тогда величину Ф1 можно оценить формулой:
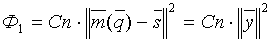
В предыдущем разделе говорилось о том, что оптимизация выполняется на каждом шаге итерации последовательно: вначале по вектору 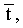
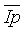
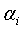
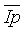
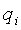
Вначале рассмотрим частный случай, когда значения 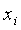
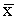
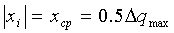
В данном случае Δqmax=ΔIpmax - максимальное изменение 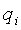
Тогда, согласно условию А, требуя равенство Ф1 и Ф2 в формуле (7) и учитывая (10), получим одинаковые значения 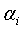
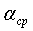
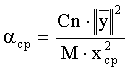
где М - число слоев в модели.
Теперь перейдем к общему случаю, задавая 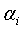
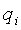
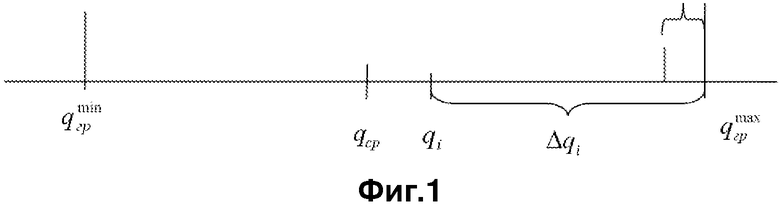
На Фиг.1:
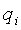
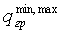
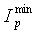
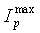
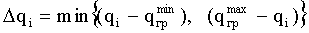
δ - минимальное допускаемое расстояние между 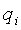
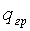

δ=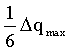
где 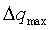
Теперь, для выполнения условия В, зададим 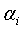
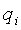
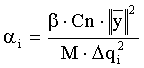
В выражении (15) β находится путем тестирования при обработке конкретных реальных материалов по отдельным профилям, исходя из условия обеспечения устойчивости результата при внесении вариаций в исходную модель 
Посмотрим на отдельных примерах, как меняется 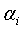
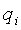
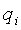
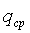
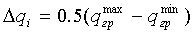
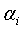
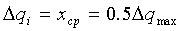
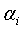
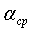
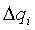
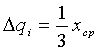
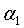
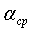
Рассмотрим теперь способ определения демпфирующих множителей 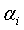
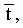
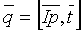
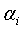
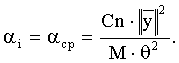
В этом выражении θ представляет собой ожидаемый средний сдвиг границ модели при оптимизации, зависит от детальности модели, определяемой величиной τmin. Опытным путем для величины θ найдено следующее выражение
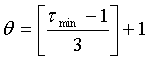
где [] означает целую часть.
Рассчитанные в результате решения уравнения (8) величины Δti (компоненты вектора 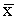
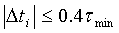
после чего они добавляются в значения ti исходной модели 


Редактирование вектора 
Учитывая итерационность оптимизированного процесса, полученные после некоторого шага оптимизации векторы 

Редактирование вектора 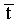

Компоненты вектора 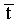
а) для реперных пластов с заданными временами tk (k=1, 2, …, K) допускается объединение только с подстилающими пластами;
б) при объединении пластов скорость нового пласта рассчитывается как средневзвешенная скоростей компонент с весами, равными временной мощности τi объединяемых пластов.
Редактирование вектора 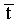
- проверяется выполнение условия τi>Δt, если нет, то два (или более) соседних пластов объединяются до выполнения этого условия;
- границы всех пластов выставляются на ближайшие точки шкалы дискретности;
- пласты с временной мощностью τi<τmin объединяются с одним из двух соседних пластов, у которого Ip ближе к Ipi (в отношении реперных пластов смотри а)).
Редактирование вектора 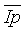

Выполняется проверка: если 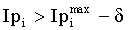
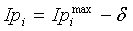
а где 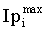
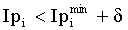
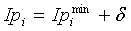
Редактирование вектора 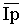
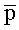
Окончательную модель 
если 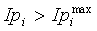
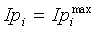
если 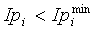
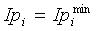
Алгоритм пластовой синхронной инверсии
Алгоритм синхронной инверсии является некоторым обобщением алгоритма акустической инверсии с увеличением размерности исходных данных (сейсмические трассы) и параметров модели. В частности теперь вектор 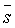
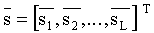
где компоненты 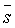


=[q1, q2, …, qM, qM+1, qM+2, …, q2M, q2M+1, q2M+2, …, q3M]. (20)
Вопрос о структуре вектора 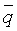
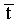

По аналогии с акустической инверсией, далее нам требуется рассчитать модельную сейсмограмму 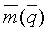
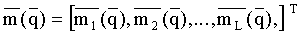
трассы которой m(t, ξ1), m(t, ξ2), …, m(t, ξL), рассчитываются для тех же удалений ξ, что и в соответствующих трассах реальной сейсмограммы 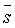
Для расчета 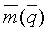
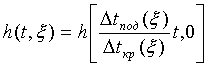
Учитывая сложность и времяемкость вычислительного процесса синхронной инверсии, мощность исследуемой пачки слоев ΔНобщ ограничивают сравнительно небольшим интервалом, включающим основные продуктивные пласты. При этом ΔНобщ обычно на порядок меньше глубины Н до кровли пачки. В этой ситуации можно пренебречь преломлением лучей внутри пачки и считать, что угол падения θ одинаков для всех плоскопараллельных границ пластов, слагающих исследуемую пачку. При этом реальное двойное время пробега волн в i-ом пласте выражается формулой:
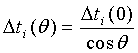
где Δti(0) - временная мощность пласта в модели Ip(t), выбираемой из сейсмоакустического разреза. Как сказано в разделе 1.1, в исходную сейсмограмму 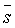
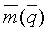
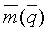
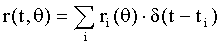
где ri(θ) - коэффициент отражения от кровли i-го пласта при падении луча под углом θ,
ti - время прихода отражения от кровли i-го пласта в модели Ip(t),
δ(t) - единичный импульс.
При обычных для практики небольших углах наклона β отражающих границ (до 10°) угол θ определяется по формуле
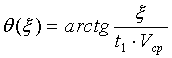
где Vср - средняя скорость до кровли пачки, определяется в процессе предшествующих структурных построений.
Коэффициент отражения Ri(θ) описывается формулой
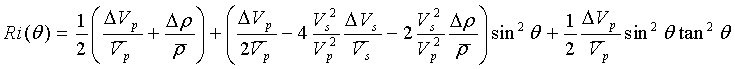
где 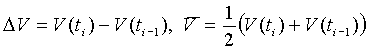
После этих промежуточных вычислений, трассы m(t, ξ) - компоненты вектора 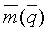
m(t, ξ)=h(t, ξ) * r[t, θ(ξ)]. (27)
Введем обозначения:
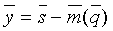

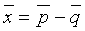

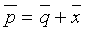
Применяя в случае синхронной инверсии тот же метод обобщенной линейной инверсии, как и для акустической инверсии, корректирующий вектор 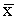
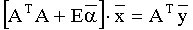
В данном случае матрица А представляется в виде:

В этом выражении 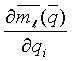
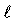
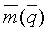

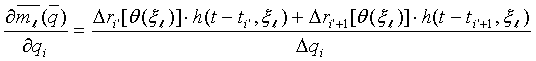
где i' - номер слоя (i'=1, 2, …, M), соответствующего параметру qi - см. (20),
Δri', Δri'+1 - изменения коэффициентов отражения от кровли и подошвы слоя i' при замене qi на qi+Δqi,
ti', ti'+1 - положение на оси t кровли и подошвы слоя i' в модели Ip(t), полученной в результате акустической инверсии.
Для составления уравнения (28), так же, как и в случае акустической инверсии, нужно задать демпфирующие множители 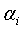
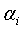
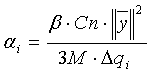
где 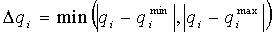
Изобретение относится к области геофизики и может быть использовано для определения упругих свойств горных пород по сейсмическим данным. Заявлен способ определения упругих свойств горных пород на основе пластовой адаптивной инверсии сейсмических данных, характеризующийся применением пластовых моделей среды, в которых минимальные временные мощности τmin пластов соответствуют реальной разрешающей способности сейсморазведки и геологии осадконакопления и вычисляются согласно формуле:
τmin(мс)=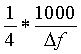
Способ определения упругих свойств горных пород на основе пластовой адаптивной инверсии сейсмических данных, характеризующийся применением пластовых моделей среды, в которых минимальные временные мощности τmin пластов соответствуют реальной разрешающей способности сейсморазведки и геологии осадконакопления и вычисляются согласно формуле:
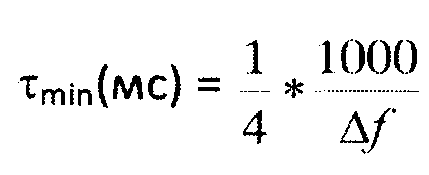 ,
,
где
Δf - рабочая полоса частот;
причем в качестве исходной модели используют откорректированную геоакустическую модель импедансов соответствующей скважины, либо трассу импедансов полученного ранее сейсмоакустического разреза по секущему профилю; а при построении рабочей модели преобразуют сейсмический временной разрез в детальную пластовую модель акустических импедансов (сейсмоакустический разрез), по которой свидетельствуют о диапазонах изменения акустических параметров слоев.
| SU 1235338 А1, 15.11.1993 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЛУБИННО-СКОРОСТНЫХ ПАРАМЕТРОВ СРЕДЫ И ПОСТРОЕНИЯ ЕЕ ИЗОБРАЖЕНИЯ ПО СЕЙСМИЧЕСКИМ ДАННЫМ - СИСТЕМА PRIME | 1998 |
|
RU2126984C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ ЗОН РАЗВИТИЯ ВТОРИЧНЫХ КОЛЛЕКТОРОВ В ФУНДАМЕНТЕ | 1994 |
|
RU2085975C1 |
| Машина для удаления камней из почвы | 1922 |
|
SU231A1 |
| CN 102230973 A, 02.11.2011 | |||
| Способ растворения силикатов | 1980 |
|
SU891562A1 |
Авторы
Даты
2014-08-27—Публикация
2012-08-29—Подача