Область техники, к которой относится изобретение
Настоящее изобретение относится к способу кодирования, способу декодирования, кодеру и декодеру с использованием сверточных кодов разреженного контроля по четности (LDPC-CC), поддерживающим множество скоростей кодирования.
Уровень техники
В последние годы внимание привлечено к коду разреженного контроля по четности (LDPC) в качестве кода коррекции ошибок, который предоставляет высокую способность к коррекции ошибок с осуществимым размером схем. Вследствие своей высокой способности к коррекции ошибок и простоты реализации, LDPC-код приспособлен в схеме кодирования с коррекцией ошибок для систем высокоскоростной беспроводной LAN по стандарту IEEE802.11n, систем цифровой широковещательной передачи и т.д.
LDPC-код является кодом коррекции ошибок, заданным посредством матрицы H разреженного контроля по четности. Кроме того, LDPC-код является блочным кодом, имеющим длину блока, идентичную числу столбцов N контрольной матрицы H (см. непатентный документ 1, непатентный документ 2, непатентный документ 3). Например, случайный LDPC-код, QC-LDPC-код (QC: квазициклический) предлагаются.
Тем не менее, характеристика многих современных систем связи заключается в том, что информация передачи совместно передается в расчете на пакет или кадр переменной длины, как в случае Ethernet (зарегистрированная торговая марка). Проблема с применением LDPC-кода, который является блочным кодом, к системе этого вида, например, заключается в том, как заставить кодовый LDPC-блок фиксированной длины соответствовать Ethernet-кадру (зарегистрированная торговая марка) переменной длины. IEEE802.11n применяет обработку дополнения или обработку прореживания к последовательности информации передачи и тем самым регулирует длину последовательности информации передачи и длину блока LDPC-кода. Тем не менее, трудно не допускать изменения скорости кодирования или передачи избыточной последовательности через дополнение или прореживание.
Проводятся исследования для LDPC-CC (сверточных кодов разреженного контроля по четности), допускающих выполнение кодирования или декодирования информационной последовательности произвольной длины для LDPC-кода (в дальнейшем в этом документе, он представлен посредством "LDPC-BC: блочный код разреженного контроля по четности") такого блочного кода (например, см. непатентный документ 8 и непатентный документ 9).
LDPC-CC является сверточным кодом, заданным посредством матрицы разреженного контроля по четности. Например, матрица HT[0, n] контроля по четности LDPC-CC со скоростью кодирования R=1/2 (=b/c) показывается на фиг. 1. Здесь, элемент h1 (m)(t) HT[0, n] принимает 0 или 1.
Все элементы, отличные от h1 (m)(t), равны 0. M представляет емкость запоминающего устройства LDPC-CC, и n представляет длину кодового LDPC-CC-слова. Как показано на фиг. 1, характеристика матрицы LDPC-CC-контроля заключается в том, что она является матрицей в форме параллелограмма, в которой 1 размещается только в диагональных элементах матрицы, а соседние элементы и левый нижний и правый верхний элементы матрицы являются нулями.
LDPC-CC-кодер, заданный посредством матрицы HT[0, n] контроля по четности, когда h1 (0)(t)=1 и h2 (0)(t)=1, здесь представляется посредством фиг. 2. Как показано на фиг. 2, LDPC-CC-кодер формируется с помощью 2*(M+1) сдвиговых регистров с длиной c в битах и сумматора по модулю 2 (оператора "исключающее ИЛИ"). Таким образом, признак LDPC-CC-кодера заключается в том, что он может быть реализован с помощью очень простой схемы по сравнению со схемой, которая выполняет умножение порождающей матрицы, или LDPC-BC-кодера, который выполняет вычисление на основе способа обратной (прямой) подстановки.
Кроме того, поскольку кодер на фиг. 2 является кодером на основе сверточного кода, необязательно разделять информационную последовательность на блоки фиксированной длины при кодировании, и информационная последовательность любой длины может быть кодирована.
Патентный документ 1 описывает способ формирования LDPC-CC на основе полинома контроля по четности. В частности, патентный документ 1 описывает способ формирования LDPC-CC с использованием полиномов контроля по четности с изменяющимся во времени периодом 2, изменяющимся во времени периодом 3, изменяющимся во времени периодом 4 и изменяющимся во времени периодом кратным 3.
Список библиографических ссылок
Патентные документы
PTL 1.
Выложенная Патентная заявка (Япония) номер 2009-246926
Непатентные документы
NPL 1
R. G. Gallager, "Low-density parity check codes", IRE Trans. Inform. Theory, IT-8, стр. 21-28, 1962 год.
NPL 2
D. J. C. Mackay, "Good error-correcting codes based on very sparse matrices", IEEE Trans. Inform. Theory, том 45, № 2, стр. 399-431, март 1999 года.
NPL 3
M. P. C. Fossorier, "Quasi-cyclic low-density parity-check codes from circulant permutation matrices", IEEE Trans. Inform. Theory, том 50, № 8, стр. 1788-1793, ноябрь 2001 года.
NPL 4
M. P. C. Fossorier, M. Mihaljevic and H. Imai, "Reduced complexity iterative decoding of low density parity check codes based on belief propagation", IEEE Trans. Commun., том 47, № 5, стр. 673-680, май 1999 года.
NPL 5
J. Chen, A. Dholakia, E. Eleftheriou, M. P. C. Fossorier and X.-Yu Hu, "Reduced-complexity decoding of LDPC codes", IEEE Trans. Commun., том 53, № 8, стр. 1288-1299, август 2005 года.
NPL 6
J. Zhang and M. P. C. Fossorier, "Shuffled iterative decoding", IEEE Trans. Commun., том 53, № 2, стр. 209-213, февраль 2005 года.
NPL 7
Стандарт IEEE для локальных вычислительных сетей и общегородских вычислительных сетей, IEEE P802.16e/D12, октябрь 2005 года.
NPL 8
A. J. Feltstrom and K. S. Zigangirov, "Time-varying periodic convolutional codes with low-density parity-check matrix", IEEE Trans. Inform. Theory, том 45, № 6, стр. 2181-2191, сентябрь 1999 года.
NPL 9
R. M. Tanner, D. Sridhara, A. Sridharan, T. E. Fuja and D. J. Costello Jr., "LDPC block and convolutional codes based on circulant matrices", IEEE Trans. Inform. Theory, том 50, № 12, стр. 2966-2984, декабрь 2004 года.
NPL 10
H. H. Ma and J. K. Wolf, "On tail biting convolutional codes", IEEE Trans. Commun., том com-34, № 2, стр. 104-111, февраль 1986 года.
NPL 11
C. Weib, C. Bettstetter and S. Riedel, "Code construction and decoding of parallel concatenated tail-biting codes", IEEE Trans. Inform. Theory, том 47, № 1, стр. 366-386, январь 2001 года.
NPL 12
M. B. S. Tavares, K. S. Zigangirov and G. P. Fettweis, "Tail-biting LDPC convolutional codes", Proc. of IEEE ISIT 2007, стр. 2341-2345, июнь 2007 года.
NPL 13
G. Muller and D. Burshtein, "Bounds on the maximum likelihood decoding error probability of low-density parity check codes", IEEE Trans. Inf. Theory, том 47, № 7, стр. 2696-2710, ноябрь 2001 года.
NPL 14
R. G. Gallager, "a simple derivation of the coding theorem and some applications", IEEE Trans. Inf. Theory, том IT-11, № 1, стр. 3-18, январь 1965 года.
NPL 15
A. J. Viterbi, "Error bounds for convolutional codes and the asymptotically optimum decoding algorithm", IEEE Trans. Inf. Theory, том IT-13, № 2, стр. 260-269, апрель 1967 года.
NPL 16
A. J. Viterbi and J. K. Omura, "Principles of digital communication and coding", McGraw-Hill, Нью-Йорк, 1979 год.
Сущность изобретения
Техническая задача
Тем не менее, хотя патентный документ 1 описывает подробности способа формирования LDPC-CC с изменяющимися во времени периодами 2, 3 и 4 и изменяющимся во времени периодом кратным 3, изменяющиеся во времени периоды ограничены.
Следовательно, задача настоящего изобретения заключается в том, чтобы предоставить способ кодирования, способ декодирования, кодер и декодер изменяющегося во времени LDPC-CC, имеющего высокую способность к коррекции ошибок.
Решение задачи
Одним аспектом способа кодирования настоящего изобретения является способ кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, причем способ содержит прием информационной последовательности в качестве входных данных и кодирование информационной последовательности с использованием уравнения 116 в качестве g-го (g=0, 1,..., q-1) полинома контроля по четности, который удовлетворяет 0.
Одним аспектом способа кодирования настоящего изобретения является способ кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, причем способ содержит прием информационной последовательности в качестве входных данных и кодирование информационной последовательности с использованием полинома контроля по четности, который удовлетворяет:
"a#0,k,1%q=a#1,k,1%q=a#2,k,1%q=a#3,k,1%q=... =a#g,k,1%q=... =a#q-2,k,1%q=a#q-1,k,1%q=vp=k (vp=k: фиксированное значение)",
"b#0,1%q=b#1,1%q=b#2,1%q=b#3,1%q=... =b#g,1%q=... =b#q-2,1%q=b#q-1,1%q=w (w: фиксированное значение)",
"a#0,k,2%q=a#1,k,2%q=a#2,k,2%q=a#3,k,2%q=... =a#g,k,2%q=... =a#q-2,k,2%q=a#q-1,k,2%q=yp=k (yp=k: фиксированное значение)",
"b#0,2%q=b#1,2%q=b#2,2%q=b#3,2%q=... =b#g,2%q=... =b#q-2,2%q=b#q-1,2%q=z (z: фиксированное значение)", и
"a#0,k,3%q=a#1,k,3%q=a#2,k,3%q=a#3,k,3%q=... =a#g,k,3%q=... =a#q-2,k,3%q=a#q-1,k,3%q=sp=k (sp=k: фиксированное значение)"
g-го (g=0, 1,..., q-1) полинома контроля по четности, который удовлетворяет 0, представленного посредством уравнения 117 для k=1, 2,..., n-1.
Одним аспектом кодера настоящего изобретения является кодер, который выполняет сверточное кодирование на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, включающий в себя модуль формирования, который принимает информационный бит Xr[i] (r=1, 2,..., n-1) в момент времени i в качестве входных данных, обозначает уравнение, эквивалентное g-му(g=0, 1,..., q-1) полиному контроля по четности, который удовлетворяет 0, представленному посредством уравнения 116, в качестве уравнения 118 и формирует бит P[i] четности в момент времени i с использованием уравнения с подстановкой k вместо g в уравнении 118, когда i%q=k, и модуль вывода, который выводит бит P[i] четности.
Одним аспектом способа декодирования настоящего изобретения является способ декодирования, соответствующий вышеописанному способу кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q (простое число, превышающее 3) с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), для декодирования кодированной информационной последовательности, кодированной с использованием уравнения 116, в качестве g-го (g=0, 1,..., q-1) полинома контроля по четности, который удовлетворяет 0, причем способ содержит прием кодированной информационной последовательности в качестве входных данных и декодирование кодированной информационной последовательности с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 116, которое является g-ым полиномом контроля по четности, который удовлетворяет 0.
Одним аспектом декодера настоящего изобретения является декодер, соответствующий вышеописанному способу кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q (простое число, превышающее 3) с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), который выполняет декодирование кодированной информационной последовательности, кодированной с использованием уравнения 116, в качестве g-го (g=0, 1,..., q-1) полинома контроля по четности, который удовлетворяет 0, включающий в себя модуль декодирования, который принимает кодированную информационную последовательность в качестве ввода и декодирует кодированную информационную последовательность с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 116, которое является g-ым полиномом контроля по четности, который удовлетворяет 0.
Преимущества изобретения
Настоящее изобретение может достигать высокой способности к коррекции ошибок и тем самым может обеспечивать высокое качество данных.
Краткое описание чертежей
Фиг. 1 показывает матрицу LDPC-CC-контроля;
Фиг. 2 показывает конфигурацию LDPC-CC-кодера;
Фиг. 3 показывает пример матрицы LDPC-CC-контроля с изменяющимся во времени периодом m;
Фиг. 4A показывает полиномы контроля по четности LDPC-CC с изменяющимся во времени периодом 3 и конфигурацию матрицы H контроля по четности этого LDPC-CC;
Фиг. 4B показывает взаимосвязь элементов на основе доверительного распространения, связанных с X(D) "контрольных уравнений #1-3" на фиг. 4A;
Фиг. 4C показывает взаимосвязь элементов на основе доверительного распространения, связанных с X(D) "контрольных уравнений #1-6";
Фиг. 5 показывает матрицу контроля по четности сверточного кода (7, 5);
Фиг. 6 показывает пример конфигурации матрицы H LDPC-CC-контроля со скоростью кодирования 2/3 и изменяющимся во времени периодом 2;
Фиг. 7 показывает пример конфигурации матрицы LDPC-CC-контроля со скоростью кодирования 2/3 и изменяющимся во времени периодом m;
Фиг. 8 показывает пример конфигурации матрицы LDPC-CC-контроля со скоростью кодирования (n-1)/n и изменяющимся во времени периодом m;
Фиг. 9 показывает пример конфигурации модуля LDPC-CC-кодирования;
Фиг. 10 является блок-схемой, показывающей пример матрицы контроля по четности;
Фиг. 11 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом 6;
Фиг. 12 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом 6;
Фиг. 13 показывает пример конфигурации матрицы LDPC-CC-контроля со скоростью кодирования (n-1)/n и изменяющимся во времени периодом 6;
Фиг. 14 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом 7;
Фиг. 15A показывает пример схемы кодера со скоростью кодирования 1/2;
Фиг. 15B показывает пример схемы кодера со скоростью кодирования 1/2;
Фиг. 15C показывает пример схемы кодера со скоростью кодирования 1/2;
Фиг. 16 показывает способ завершения нулем;
Фиг. 17 показывает пример контрольной матрицы, когда завершение нулем выполняется;
Фиг. 18A показывает пример контрольной матрицы, когда дополнение битами концевой части выполняется;
Фиг. 18B показывает пример контрольной матрицы, когда дополнение битами концевой части выполняется;
Фиг. 19 показывает общее представление системы связи;
Фиг. 20 является концептуальной схемой системы связи с использованием кодирования с коррекцией со стиранием ошибок с использованием LDPC-кода;
Фиг. 21 является схемой общей конфигурации системы связи;
Фиг. 22 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;
Фиг. 23 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;
Фиг. 24 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;
Фиг. 25 показывает пример конфигурации кодера с коррекцией со стиранием ошибок;
Фиг. 26 является схемой общей конфигурации системы связи;
Фиг. 27 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;
Фиг. 28 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;
Фиг. 29 показывает пример конфигурации модуля кодирования с коррекцией со стиранием ошибок, поддерживающего множество скоростей кодирования;
Фиг. 30 показывает общее представление кодирования посредством кодера;
Фиг. 31 показывает пример конфигурации модуля кодирования с коррекцией со стиранием ошибок, поддерживающего множество скоростей кодирования;
Фиг. 32 показывает пример конфигурации модуля кодирования с коррекцией со стиранием ошибок, поддерживающего множество скоростей кодирования;
Фиг. 33 показывает пример конфигурации декодера, поддерживающего множество скоростей кодирования;
Фиг. 34 показывает пример конфигурации матрицы контроля по четности, используемой посредством декодера, поддерживающего множество скоростей кодирования;
Фиг. 35 показывает пример конфигурации пакета, когда кодирование с коррекцией со стиранием ошибок выполняется, и когда кодирование с коррекцией со стиранием ошибок не выполняется;
Фиг. 36 показывает взаимосвязь между контрольными узлами, соответствующими полиномам контроля по четности #α и #β, и переменным узлом;
Фиг. 37 показывает субматрицу, сформированную посредством извлечения только частей, связанных с X1(D) матрицы H контроля по четности;
Фиг. 38 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом 7;
Фиг. 39 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом h изменяющегося во времени периода 6;
Фиг. 40 показывает BER-характеристику регулярных TV11-LDPC-CC #1, #2 и #3 в таблице 9;
Фиг. 41 показывает матрицу контроля по четности, соответствующую g-му(g=0, 1,..., h-1) полиному контроля по четности (83) со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h;
Фиг. 42 показывает пример шаблона переупорядочения, когда пакеты информации и пакеты четности конфигурируются независимо;
Фиг. 43 показывает пример шаблона переупорядочения, когда пакеты информации и пакеты четности конфигурируются без различения между ними;
Фиг. 44 показывает подробности способа кодирования (способа кодирования на уровне пакета) на уровне выше физического уровня;
Фиг. 45 показывает подробности другого способа кодирования (способа кодирования на уровне пакета) на уровне выше физического уровня;
Фиг. 46 показывает пример конфигурации группы четности и субпакетов четности;
Фиг. 47 показывает способ укорачивания (способ #1-2);
Фиг. 48 показывает правило вставки в способе укорачивания (способе #1-2);
Фиг. 49 показывает взаимосвязь между позициями, в которых известная информация вставляется, и способностью к коррекции ошибок;
Фиг. 50 показывает соответствие между полиномом контроля по четности и моментами времени;
Фиг. 51 показывает способ укорачивания (способ #2-2);
Фиг. 52 показывает способ укорачивания (способ #2-4);
Фиг. 53 является блок-схемой, показывающей пример связанной с кодированием части, когда переменная скорость кодирования приспосабливается на физическом уровне;
Фиг. 54 является блок-схемой, показывающей другой пример связанной с кодированием части, когда переменная скорость кодирования приспосабливается на физическом уровне;
Фиг. 55 является блок-схемой, показывающей пример конфигурации модуля декодирования с коррекцией ошибок на физическом уровне;
Фиг. 56 показывает способ коррекции со стиранием ошибок (способ #3-1);
Фиг. 57 показывает способ коррекции со стиранием ошибок (способ #3-3);
Фиг. 58 показывает "завершение информационным нулем" LDPC-CC со скоростью кодирования (n-1)/n;
Фиг. 59 показывает способ кодирования согласно варианту 12 осуществления;
Фиг. 60 является схемой, схематично показывающей полином контроля по четности LDPC-CC со скоростями кодирования 1/2 и 2/3, который дает возможность совместного использования схемы между кодером и декодером;
Фиг. 61 является блок-схемой, показывающей пример основных компонентов кодера согласно варианту 13 осуществления;
Фиг. 62 показывает внутреннюю конфигурацию первого модуля вычисления информации;
Фиг. 63 показывает внутреннюю конфигурацию модуля вычисления четности;
Фиг. 64 показывает другой пример конфигурации кодера согласно варианту 13 осуществления;
Фиг. 65 является блок-схемой, показывающей пример основных компонентов декодера согласно варианту 13 осуществления;
Фиг. 66 иллюстрирует операции модуля задания логарифмического отношения правдоподобия в случае скорости кодирования 1/2;
Фиг. 67 иллюстрирует операции модуля задания логарифмического отношения правдоподобия в случае скорости кодирования 2/3;
Фиг. 68 показывает пример конфигурации устройства связи, содержащего кодер согласно варианту 13 осуществления;
Фиг. 69 показывает пример формата передачи; и
Фиг. 70 показывает пример конфигурации устройства связи, содержащего кодер согласно варианту 13 осуществления.
Подробное описание вариантов осуществления
Далее подробно описаны варианты осуществления настоящего изобретения со ссылкой на прилагаемые чертежи.
До описания конкретных конфигураций и операций вариантов осуществления, LDPC-CC на основе полиномов контроля по четности, описанный в патентном документе 1, сначала описывается.
LDPC-CC на основе полинома контроля по четности
Во-первых, описывается LDPC-CC с изменяющимся во времени периодом 4. Случай, в котором скорость кодирования составляет 1/2, описывается ниже в качестве примера.
Рассмотрим уравнения 1-1-1-4 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 4. В это время, X(D) является полиномиальным представлением данных (информации), и P(D) является полиномиальным представлением четности. Здесь, в уравнениях 1-1-1-4, допускаются полиномы контроля по четности, в которых существует четыре элемента в X(D) и P(D), соответственно, при этом причина заключается в том, что четыре элемента требуются с точки зрения достижения хорошего качества приема.
[1]
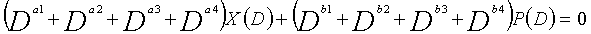 ... (уравнение 1-1)
... (уравнение 1-1)
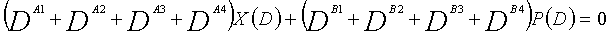 ... (уравнение 1-2)
... (уравнение 1-2)
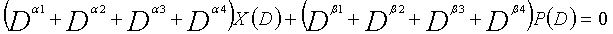 ... (уравнение 1-3)
... (уравнение 1-3)
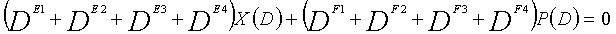 ... (уравнение 1-4)
... (уравнение 1-4)
В уравнении 1-1, предполагается, что a1, a2, a3 и a4 являются целыми числами (где a1≠a2≠a3≠a4 и a1-a4 взаимно отличаются). Использование системы обозначений "X≠Y≠... ≠Z" предполагается, чтобы выражать тот факт, что X, Y,..., Z взаимно отличаются. Кроме того, предполагается, что b1, b2, b3 и b4 являются целыми числами (где b1≠b2≠b3≠b4). Полином контроля по четности уравнения 1-1 называется "контрольным уравнением #1", и субматрица на основе полинома контроля по четности уравнения 1-1 обозначается как первая субматрица H1.
В уравнении 1-2, предполагается, что A1, A2, A3 и A4 являются целыми числами (где A1≠A2≠A3≠A4). Кроме того, предполагается, что B1, B2, B3 и B4 являются целыми числами (где B1≠B2≠B3≠B4). Полином контроля по четности уравнения 1-2 называется "контрольным уравнением #2", и субматрица на основе полинома контроля по четности уравнения 1-2 обозначается как вторая субматрица H2.
В уравнении 1-3, предполагается, что α1, α2, α3 и α4 являются целыми числами (где α1≠α2≠α3≠α4). Кроме того, предполагается, что β1, β2, β3 и β4 являются целыми числами (где β1≠β2≠β3≠β4). Полином контроля по четности уравнения 1-3 называется "контрольным уравнением #3", и субматрица на основе полинома контроля по четности уравнения 1-3 обозначается как третья субматрица H3.
В уравнении 1-4, предполагается, что E1, E2, E3 и E4 являются целыми числами (где E1≠E2≠E3≠E4). Кроме того, предполагается, что F1, F2, F3 и F4 являются целыми числами (где F1≠F2≠F3≠F4). Полином контроля по четности уравнения 1-4 называется "контрольным уравнением #4", и субматрица на основе полинома контроля по четности уравнения 1-4 обозначается как четвертая субматрица H4.
Затем, рассмотрим LDPC-CC с изменяющимся во времени периодом 4, который формирует контрольную матрицу, как показано на фиг. 3, из первой субматрицы H1, второй субматрицы H2, третьей субматрицы H3 и четвертой субматрицы H4.
В это время, если k обозначается как остаток после деления значений комбинаций порядков X(D) и P(D), (a1, a2, a3, a4), (b1, b2, b3, b4), (A1, A2, A3, A4), (B1, B2, B3, B4), (α1, α2, α3, α4), (β1, β2, β3, β4), (E1, E2, E3, E4) и (F1, F2, F3, F4), в уравнениях 1-1-1-4 на 4, предусматривается по одному каждому из остатков 0, 1, 2 и 3, которые должны быть включены в наборы из четырех коэффициентов, представленные так, как показано выше (например, (a1, a2, a3, a4)), и является справедливым для всех вышеуказанных наборов из четырех коэффициентов.
Например, если порядки (a1, a2, a3, a4) X(D) "контрольного уравнения #1" задаются как (a1, a2, a3, a4)=(8, 7, 6, 5), остатки k после деления порядков (a1, a2, a3, a4) на 4 - это (0, 3, 2, 1), и по одному каждому из 0, 1, 2 и 3 включаются в набор из четырех коэффициентов в качестве остатков k. Аналогично, если порядки (b1, b2, b3, b4) P(D) "контрольного уравнения #1" задаются как (b1, b2, b3, b4)=(4, 3, 2, 1), остатки k после деления порядков (b1, b2, b3, b4) на 4 - это (0, 3, 2, 1), и по одному каждому из 0, 1, 2 и 3 включаются в набор из четырех коэффициентов в качестве остатков k. Предполагается, что вышеуказанное условие по "остатку" также справедливо для наборов из четырех коэффициентов X(D) и P(D) других уравнений контроля по четности ("контрольного уравнения #2", "контрольного уравнения #3" и "контрольного уравнения #4").
Посредством этого весовой коэффициент столбца матрицы H контроля по четности, сконфигурированной из уравнений 1-1-1-4, становится 4 для всех столбцов, что предоставляет возможность формирования регулярного LDPC-кода. Здесь, регулярный LDPC-код является LDPC-кодом, который задается посредством матрицы контроля по четности, для которой весовой коэффициент каждого столбца является в равной степени фиксированным, и отличается посредством того факта, что его характеристики являются стабильными, и минимальный уровень ошибки практически никогда не возникает. В частности, поскольку характеристики являются хорошими, когда весовой коэффициент столбца равняется 4, LDPC-CC, предлагающий хорошие характеристики приема, может достигаться посредством формирования LDPC-CC так, как описано выше.
Таблица 1 показывает пример LDPC-CC (LDPC-CC #1-3) с изменяющимся во времени периодом 4 и скоростью кодирования 1/2, для которого справедливо вышеуказанное условие по "остатку". В таблице 1, LDPC-CC с изменяющимся во времени периодом 4 задаются посредством четырех полиномов контроля по четности: "контрольного полинома #1", "контрольного полинома #2", "контрольного полинома #3", и "контрольного полинома #4".
Контрольный полином #2: (D287+D213+D130+1)X(D)+(D545+D542+D103+1)P(D)=0
Контрольный полином #3: (D557+D495+D326+1)X(D)+(D561+D502+D351+1)P(D)=0
Контрольный полином #4: (D426+D329+D99+1)X(D)+(D321+D55+D42+1)P(D)=0
Контрольный полином #2: (D518+D473+D203+1)X(D)+(D598+D499+D145+1)P(D)=0
Контрольный полином #3:
Контрольный полином #4: (D483+D385+D94+1)X(D)+(D426+D415+D413+1)P(D)=0
Контрольный полином #2: (D583+D545+D506+1)X(D)+(D325+D71+D66+1)P(D)=0
Контрольный полином #3: (D430+D425+D407+1)X(D)+(D582+D47+D45+1)P(D)=0
Контрольный полином #4: (D434+D353+D127+1)X(D)+(D345+D207+D38+1)P(D)=0
Случай для скорости кодирования 1/2 описан выше в качестве примера, но даже когда скорость кодирования составляет (n-1)/n, если вышеуказанное условие по "остатку" также справедливо для наборов из четырех коэффициентов информации X1(D), X2(D),..., Xn-1(D), соответственно, код является по-прежнему регулярным LDPC-кодом, и хорошее качество приема может достигаться.
В случае изменяющегося во времени периода 2, также подтверждено, что код с хорошими характеристиками может находиться, если вышеуказанное условие по "остатку" применяется. LDPC-CC с изменяющимся во времени периодом 2 с хорошими характеристиками описывается ниже. Случай, в котором скорость кодирования составляет 1/2, описывается ниже в качестве примера.
Рассмотрим уравнения 2-1 и 2-2 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 2. В это время, X(D) является полиномиальным представлением данных (информации), и P(D) является полиномиальным представлением четности. Здесь, в уравнениях 2-1 и 2-2, допускаются полиномы контроля по четности, в которых существует четыре элемента в X(D) и P(D), соответственно, при этом причина заключается в том, что четыре элемента требуются с точки зрения достижения хорошего качества приема.
[2]
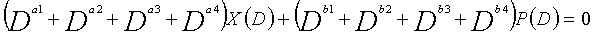 ... (уравнение 2-1)
... (уравнение 2-1)
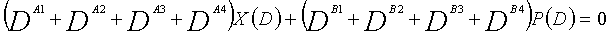 ... (уравнение 2-2)
... (уравнение 2-2)
В уравнении 2-1, предполагается, что a1, a2, a3 и a4 являются целыми числами (где a1≠a2≠a3≠a4). Кроме того, предполагается, что b1, b2, b3 и b4 являются целыми числами (где b1≠b2≠b3≠b4). Полином контроля по четности уравнения 2-1 называется "контрольным уравнением #1", и субматрица на основе полинома контроля по четности уравнения 2-1 обозначается как первая субматрица H1.
В уравнении 2-2, предполагается, что A1, A2, A3 и A4 являются целыми числами (где A1≠A2≠A3≠A4). Кроме того, предполагается, что B1, B2, B3 и B4 являются целыми числами (где B1≠B2≠B3≠B4). Полином контроля по четности уравнения 2-2 называется "контрольным уравнением #2", и субматрица на основе полинома контроля по четности уравнения 2-2 обозначается как вторая субматрица H2.
Затем, рассмотрим LDPC-CC с изменяющимся во времени периодом 2, сформированный из первой субматрицы H1 и второй субматрицы H2.
В это время, если k обозначается как остаток после деления значений комбинаций порядков X(D) и P(D), (a1, a2, a3, a4), (b1, b2, b3, b4), (A1, A2, A3, A4), (B1, B2, B3, B4), в уравнениях 2-1 и 2-2 на 4, предусматривается по одному каждому из остатков 0, 1, 2 и 3, которые должны быть включены в наборы из четырех коэффициентов, представленные так, как показано выше (например, (a1, a2, a3, a4)), и является справедливым для всех вышеуказанных наборов из четырех коэффициентов.
Например, если порядки (a1, a2, a3, a4) X(D) "контрольного уравнения #1" задаются как (a1, a2, a3, a4)=(8, 7, 6, 5), остатки k после деления порядков (a1, a2, a3, a4) на 4 - это (0, 3, 2, 1), и по одному каждому из 0, 1, 2 и 3 включаются в набор из четырех коэффициентов в качестве остатков k. Аналогично, если порядки (b1, b2, b3, b4) P(D) "контрольного уравнения #1" задаются как (b1, b2, b3, b4)=(4, 3, 2, 1), остатки k после деления порядков (b1, b2, b3, b4) на 4 - это (0, 3, 2, 1), и по одному каждому из 0, 1, 2 и 3 включаются в набор из четырех коэффициентов в качестве остатков k. Предполагается, что вышеуказанное условие по "остатку" также справедливо для наборов из четырех коэффициентов X(D) и P(D) "контрольного уравнения #2".
Посредством этого весовой коэффициент столбца матрицы H контроля по четности, сконфигурированной из уравнений 2-1 и 2-2, становится 4 для всех столбцов, что предоставляет возможность формирования регулярного LDPC-кода. Здесь, регулярный LDPC-код является LDPC-кодом, который задается посредством матрицы контроля по четности, для которой весовой коэффициент каждого столбца является в равной степени фиксированным, и отличается посредством того факта, что его характеристики являются стабильными, и минимальный уровень ошибки практически никогда не возникает. В частности, поскольку характеристики являются хорошими, когда весовой коэффициент столбца равняется 8, LDPC-CC, предоставляющий возможность дополнительного улучшения характеристик приема, может достигаться посредством формирования LDPC-CC так, как описано выше.
Таблица 2 показывает примеры LDPC-CC (LDPC-CC #1 и #2) с изменяющимся во времени периодом 2 и скоростью кодирования 1/2, для которых справедливо вышеуказанное условие по "остатку". В таблице 2, LDPC-CC с изменяющимся во времени периодом 2 задаются посредством двух полиномов контроля по четности: "контрольного полинома #1" и "контрольного полинома #2".
Контрольный полином #2: (D443+D433+D54+1)X(D)+(D559+D557+D546+1)P(D)=0
Контрольный полином #2: (D275+D226+D213+1)X(D)+(D298+D147+D45+1)P(D)=0
Выше описан случай, в котором (LDPC-CC с изменяющимся во времени периодом 2), скорость кодирования составляет 1/2 в качестве примера, но даже когда скорость кодирования составляет (n-1)/n, если вышеуказанное условие по "остатку" справедливо для наборов из четырех коэффициентов в информации X1(D), X2(D),..., Xn-1(D), соответственно, код является по-прежнему регулярным LDPC-кодом, и хорошее качество приема может достигаться.
В случае изменяющегося во времени периода 3, также подтверждено, что код с хорошими характеристиками может находиться, если следующее условие по "остатку" применяется. LDPC-CC с изменяющимся во времени периодом 3 с хорошими характеристиками описывается ниже. Случай, в котором скорость кодирования составляет 1/2, описывается ниже в качестве примера.
Рассмотрим уравнения 3-1-3-3 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 3. В это время, X(D) является полиномиальным представлением данных (информации), и P(D) является полиномиальным представлением четности. Здесь, в уравнениях 3-1-3-3, полиномы контроля по четности допускаются так, что существует три элемента в X(D) и P(D), соответственно.
[3]
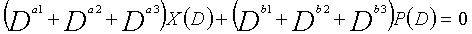 ... (уравнение 3-1)
... (уравнение 3-1)
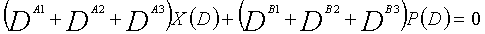 ... (уравнение 3-2)
... (уравнение 3-2)
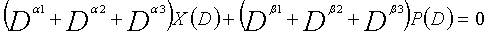 ... (уравнение 3-3)
... (уравнение 3-3)
В уравнении 3-1, предполагается, что a1, a2 и a3 являются целыми числами (где a1≠a2≠a3). Кроме того, предполагается, что b1, b2 и b3 являются целыми числами (где b1≠b2≠b3). Полином контроля по четности уравнения 3-1 называется "контрольным уравнением #1", и субматрица на основе полинома контроля по четности уравнения 3-1 обозначается как первая субматрица H1.
В уравнении 3-2, предполагается, что A1, A2 и A3 являются целыми числами (где A1≠A2≠A3). Кроме того, предполагается, что B1, B2 и B3 являются целыми числами (где B1≠B2≠B3). Полином контроля по четности уравнения 3-2 называется "контрольным уравнением #2", и субматрица на основе полинома контроля по четности уравнения 3-2 обозначается как вторая субматрица H2.
В уравнении 3-3, предполагается, что α1, α2 и α3 являются целыми числами (где α1≠α2≠α3). Кроме того, предполагается, что β1, β2 и β3 являются целыми числами (где β1≠β2≠β3). Полином контроля по четности уравнения 3-3 называется "контрольным уравнением #3", и субматрица на основе полинома контроля по четности уравнения 3-3 обозначается как третья субматрица H3.
Затем, рассмотрим LDPC-CC с изменяющимся во времени периодом 3, сформированный из первой субматрицы H1, второй субматрицы H2 и третьей субматрицы H3.
В это время, если k обозначается как остаток после деления значений комбинаций порядков X(D) и P(D), (a1, a2, a3), (b1, b2, b3), (A1, A2, A3), (B1, B2, B3), (α1, α2, α3) и (β1, β2, β3), в уравнениях 3-1-3-3 на 3, предусматривается по одному каждому из остатков 0, 1 и 2, которые должны быть включены в наборы из трех коэффициентов, представленные так, как показано выше (например, (a1, a2, a3)), и является справедливым для всех вышеуказанных наборов из трех коэффициентов.
Например, если порядки (a1, a2, a3) X(D) "контрольного уравнения #1" задаются как (a1, a2, a3)=(6, 5, 4), остатки k после деления порядков (a1, a2, a3) на 3 - это (0, 2, 1), и по одному каждому из 0, 1, 2 включаются в набор из трех коэффициентов в качестве остатков k. Аналогично, если порядки (b1, b2, b3) P(D) "контрольного уравнения #1" задаются как (b1, b2, b3)=(3, 2, 1), остатки k после деления порядков (b1, b2, b3) на 3 - это (0, 2, 1), и по одному каждому из 0, 1, 2 включаются в набор из трех коэффициентов в качестве остатков k. Предполагается, что вышеуказанное условие по "остатку" также справедливо для наборов из трех коэффициентов X(D) и P(D) "контрольного уравнения #2" и "контрольного уравнения #3".
Посредством формирования LDPC-CC так, как описано выше, можно формировать регулярный LDPC-CC-код, в котором весовой коэффициент строки равен во всех строках, и весовой коэффициент столбца равен во всех столбцах, без каких-либо исключений. Здесь, "исключения" означают часть в начале матрицы контроля по четности и часть в конце матрицы контроля по четности, в которых весовые коэффициенты строк и весовые коэффициенты столбцов не являются идентичными весовым коэффициентам строк и весовым коэффициентам столбцов другой части. Кроме того, когда BP-декодирование выполняется, доверие в "контрольном уравнении #2" и доверие в "контрольном уравнении #3" распространяются точно на "контрольное уравнение #1", доверие в "контрольном уравнении #1" и доверие в "контрольном уравнении #3" распространяются точно на "контрольное уравнение #2", а доверие в "контрольном уравнении #1" и доверие в "контрольном уравнении #2" распространяются точно на "контрольное уравнение #3". Следовательно, LDPC-CC с лучшим качеством приема может достигаться. Это обусловлено тем, что при рассмотрении в единицах столбцов, позиции, в которых "1" присутствует, размещаются так, чтобы точно распространять доверие, как описано выше.
Вышеуказанное доверительное распространение описывается ниже с использованием прилагаемых чертежей. Фиг. 4A показывает полиномы контроля по четности LDPC-CC с изменяющимся во времени периодом 3 и конфигурацию матрицы H контроля по четности этого LDPC-CC.
"Контрольное уравнение #1" иллюстрирует случай, в котором (a1, a2, a3)=(2, 1, 0) и (b1, b2, b3)=(2, 1, 0) в полиноме контроля по четности уравнения 3-1, и остатки после деления коэффициентов на 3 следующие: (a1%3, a2%3, a3%3)=(2, 1, 0) и (b1%3, b2%3, b3%3)=(2, 1, 0), где "Z%3" представляет остаток после деления Z на 3.
"Контрольное уравнение #2" иллюстрирует случай, в котором (A1, A2, A3)=(5, 1, 0) и (B1, B2, B3)=(5, 1, 0) в полиноме контроля по четности уравнения 3-2, и остатки после деления коэффициентов на 3 следующие: (A1%3, A2%3, A3%3)=(2, 1, 0) и (B1%3, B2%3, B3%3)=(2, 1, 0)
"Контрольное уравнение #3" иллюстрирует случай, в котором (α1, α2, α3)=(4, 2, 0) и (β1, β2, β3)=(4, 2, 0) в полиноме контроля по четности уравнения 3-3, и остатки после деления коэффициентов на 3 следующие: (α1%3, α2%3, α3%3)=(1, 2, 0) и (β1%3, β2%3, β3%3)=(1, 2, 0).
Следовательно, пример LDPC-CC с изменяющимся во времени периодом 3, показанного на фиг. 4A, удовлетворяет вышеуказанному условию по "остатку", т.е. такому условию, что
(a1%3, a2%3, a3%3),
(b1%3, b2%3, b3%3),
(A1%3, A2%3, A3%3),
(B1%3, B2%3, B3%3),
(α1%3, α2%3, α3%3), и
(β1%3, β2%3, β3%3) являются любыми из следующего: (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) и (2, 1, 0).
Снова возвращаясь к фиг. 4A, далее поясняется доверительное распространение. Посредством вычисления по столбцам для столбца 6506 при BP-декодировании, для "1" области 6201 "контрольного уравнения #1", доверие распространяется из "1" области 6504 "контрольного уравнения #2" и из "1" области 6505 "контрольного уравнения #3". Как описано выше, "1" области 6201 "контрольного уравнения #1" является коэффициентом, для которого остаток после деления на 3 равняется 0 (a3%3=0 (a3=0) или b3%3=0 (b3=0)). Кроме того, "1" области 6504 "контрольного уравнения #2" является коэффициентом, для которого остаток после деления на 3 равняется 1 (A2%3=1 (A2=1) или B2%3=1 (B2=1)). Кроме того, "1" области 6505 "контрольного уравнения #3" является коэффициентом, для которого остаток после деления на 3 равняется 2 (α2%3=2 (α2=2) или β2%3=2 (β2=2)).
Таким образом, для "1" области 6201, для которого остаток равняется 0 в коэффициентах "контрольного уравнения #1" в вычислении по столбцам для столбца 6506 при BP-декодировании, доверие распространяется из "1" области 6504, для которого остаток равняется 1 в коэффициентах "контрольного уравнения #2", и из "1" области 6505, для которого остаток равняется 2 в коэффициентах "контрольного уравнения #3".
Аналогично, для "1" области 6202, для которого остаток равняется 1 в коэффициентах "контрольного уравнения #1" в вычислении по столбцам для столбца 6509 при BP-декодировании, доверие распространяется из "1" области 6507, для которого остаток равняется 2 в коэффициентах "контрольного уравнения #2", и из "1" области 6508, для которого остаток равняется 0 в коэффициентах "контрольного уравнения #3".
Аналогично, для "1" области 6203, для которого остаток равняется 2 в коэффициентах "контрольного уравнения #1" в вычислении по столбцам для столбца 6512 при BP-декодировании, доверие распространяется из "1" области 6510, для которого остаток равняется 0 в коэффициентах "контрольного уравнения #2", и из "1" области 6511, для которого остаток равняется 1 в коэффициентах "контрольного уравнения #3".
Дополнительное пояснение доверительного распространения приводится далее с использованием фиг. 4B. Фиг. 4B показывает взаимосвязь элементов на основе доверительного распространения, связанных с X(D) "контрольных уравнений #1-3" на фиг. 4A. "Контрольные уравнения #1-3" на фиг. 4A иллюстрируют случаи, в которых (a1, a2, a3)=(2, 1, 0), (A1, A2, A3)=(5, 1, 0) и (α1, α2, α3)=(4, 2, 0), в элементах, связанных с X(D) уравнений 3-1-3-3.
На фиг. 4B, элементы (a3, A3, α3) в квадратах указывают коэффициенты, для которых остаток после деления на 3 равняется 0, элементы (a2, A2, α2) в кругах указывают коэффициенты, для которых остаток после деления на 3 равняется 1, и элементы (a1, A1, α1) в ромбовидных прямоугольниках указывают коэффициенты, для которых остаток после деления на 3 равняется 2.
Как можно видеть из фиг. 4B, для a1 "контрольного уравнения #1", доверие распространяется из A3 "контрольного уравнения #2" и из α1 "контрольного уравнения #3", для которых остатки после деления на 3 отличаются; для a2 "контрольного уравнения #1", доверие распространяется из A1 "контрольного уравнения #2" и из α3 "контрольного уравнения #3", для которых остатки после деления на 3 отличаются; и, для a3 "контрольного уравнения #1", доверие распространяется из A2 "контрольного уравнения #2" и из α2 "контрольного уравнения #3", для которых остатки после деления на 3 отличаются. Хотя фиг. 4B показывает взаимосвязь элементов на основе доверительного распространения, связанных с X(D) "контрольных уравнений #1-3", это применимо и к элементам, связанным с P(D).
Таким образом, для "контрольного уравнения #1", доверие распространяется из коэффициентов, для которых остатки после деления на 3 равны 0, 1 и 2, среди коэффициентов "контрольного уравнения #2". Другими словами, для "контрольного уравнения #1", доверие распространяется из коэффициентов, для которых остатки после деления на 3 отличаются, среди коэффициентов "контрольного уравнения #2". Следовательно, доверия с низкой корреляцией распространяются на "контрольное уравнение #1".
Аналогично, для "контрольного уравнения #2", доверие распространяется из коэффициентов, для которых остатки после деления на 3 равны 0, 1 и 2, среди коэффициентов "контрольного уравнения #1". Другими словами, для "контрольного уравнения #2", доверие распространяется из коэффициентов, для которых остатки после деления на 3 отличаются, среди коэффициентов "контрольного уравнения #1". Кроме того, для "контрольного уравнения #2", доверие распространяется из коэффициентов, для которых остатки после деления на 3 равны 0, 1 и 2, среди коэффициентов "контрольного уравнения #3". Другими словами, для "контрольного уравнения #2", доверие распространяется из коэффициентов, для которых остатки после деления на 3 отличаются, среди коэффициентов "контрольного уравнения #3".
Аналогично, для "контрольного уравнения #3", доверие распространяется из коэффициентов, для которых остатки после деления на 3 равны 0, 1 и 2, среди коэффициентов "контрольного уравнения #1". Другими словами, для "контрольного уравнения #3", доверие распространяется из коэффициентов, для которых остатки после деления на 3 отличаются, среди коэффициентов "контрольного уравнения #1". Кроме того, для "контрольного уравнения #3", доверие распространяется из коэффициентов, для которых остатки после деления на 3 равны 0, 1 и 2, среди коэффициентов "контрольного уравнения #2". Другими словами, для "контрольного уравнения #3", доверие распространяется из коэффициентов, для которых остатки после деления на 3 отличаются, среди коэффициентов "контрольного уравнения #2".
Посредством обеспечения порядков полиномов контроля по четности уравнений 3-1-3-3, чтобы удовлетворять вышеуказанному условию по "остатку" таким образом, доверие обязательно распространяется во всех вычислениях по столбцам, так что можно выполнять доверительное распространение эффективно во всех контрольных уравнениях и дополнительно увеличивать способность к коррекции ошибок.
Случай, в котором скорость кодирования составляет 1/2, описан выше для LDPC-CC с изменяющимся во времени периодом 3, но скорость кодирования не ограничивается 1/2. Регулярный LDPC-код также формируется, и хорошее качество приема может достигаться, когда скорость кодирования составляет (n-1)/n (где n является целым числом, равным или превышающим 2), если вышеуказанное условие по "остатку" справедливо для наборов из трех коэффициентов в информации X1(D), X2(D),..., Xn-1(D).
Случай, в котором скорость кодирования составляет (n-1)/n (где n является целым числом, равным или превышающим 2), описывается ниже.
Рассмотрим уравнения 4-1-4-3 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 3. В это время, X1(D), X2(D),..., Xn-1(D) являются полиномиальными представлениями данных (информации) X1, X2,..., Xn-1, а P(D) является полиномиальным представлением четности. Здесь, в уравнениях 4-1-4-3, полиномы контроля по четности допускаются так, что существует три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), соответственно.
[4]
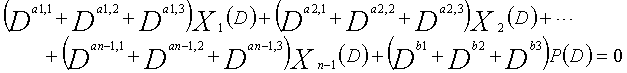 ... (уравнение 4-1)
... (уравнение 4-1)
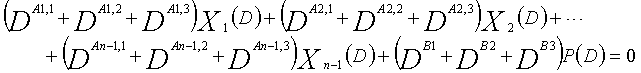 ... (уравнение 4-2)
... (уравнение 4-2)
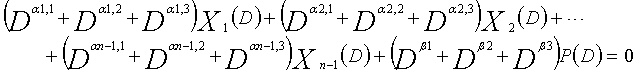 ... (уравнение 4-3)
... (уравнение 4-3)
В уравнении 4-1, предполагается, что ai,1, ai,2 и ai,3 (где i=1, 2,..., n-1) являются целыми числами (где ai,1≠ai,2≠ai,3). Кроме того, предполагается, что b1, b2 и b3 являются целыми числами (где b1≠b2≠b3). Полином контроля по четности уравнения 4-1 называется "контрольным уравнением #1", и субматрица на основе полинома контроля по четности уравнения 4-1 обозначается как первая субматрица H1.
В уравнении 4-2, предполагается, что Ai,1, Ai,2 и Ai,3 (где i=1, 2,..., n-1) являются целыми числами (где Ai,1≠Ai,2≠Ai,3). Кроме того, предполагается, что B1, B2 и B3 являются целыми числами (где B1≠B2≠B3). Полином контроля по четности уравнения 4-2 называется "контрольным уравнением #2", и субматрица на основе полинома контроля по четности уравнения 4-2 обозначается как вторая субматрица H2.
В уравнении 4-3, предполагается, что αi,1, αi,2 и αi,3 (где i=1, 2,..., n-1) являются целыми числами (где αi,1≠αi,2≠αi,3). Кроме того, предполагается, что β1, β2 и β3 являются целыми числами (где β1≠β2≠≠β3). Полином контроля по четности уравнения 4-3 называется "контрольным уравнением #3", и субматрица на основе полинома контроля по четности уравнения 4-3 обозначается как третья субматрица H3.
Затем, LDPC-CC с изменяющимся во времени периодом 3, сформированный из первой субматрицы H1, второй субматрицы H2 и третьей субматрицы H3, рассматривается.
В это время, если k обозначается как остаток после деления значений комбинаций порядков X1(D), X2(D),..., Xn-1(D) и P(D),
(a1,1, a1,2, a1,3),
(a2,1, a2,2, a2,3),...,
(an-1,1, an-1,2, an-1,3),
(b1, b2, b3),
(A1,1, A1,2, A1,3),
(A2,1, A2,2, A2,3),...,
(An-1,1, An-1,2, An-1,3),
(B1, B2, B3),
(α1,1, α1,2, α1,3),
(α2,1, α2,2, α2,3),...,
(αn-1,1, αn-1,2, αn-1,3),
(β1, β2, β3),
в уравнениях 4-1-4-3 на 3, предусматривается по одному каждому из остатков 0, 1 и 2, которые должны быть включены в наборы из трех коэффициентов, представленные так, как показано выше (например, (a1,1, a1,2, a1,3)), и является справедливым для всех вышеуказанных наборов из трех коэффициентов.
Другими словами, предусматривается, что
(a1,1%3, a1,2%3, a1,3%3),
(a2,1%3, a2,2%3, a2,3%3),...,
(an-1,1%3, an-1,2%3, an-1,3%3),
(b1%3, b2%3, b3%3),
(A1,1%3, A1,2%3, A1,3%3),
(A2,1%3, A2,2%3, A2,3%3),...,
(An-1,1%3, An-1,2%3, An-1,3%3),
(B1%3, B2%3, B3%3),
(α1,1%3, α1,2%3, α1,3%3),
(α2,1%3, α2,2%3, α2,3%3),...,
(αn-1,1%3, αn-1,2%3, αn-1,3%3), и
(β1%3, β2%3, β3%3)
являются любыми из следующего: (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) и (2, 1, 0).
Формирование LDPC-CC, таким образом, предоставляет возможность формирования регулярного LDPC-CC-кода. Кроме того, когда BP-декодирование выполняется, доверие в "контрольном уравнении #2" и доверие в "контрольном уравнении #3" распространяются точно на "контрольное уравнение #1", доверие в "контрольном уравнении #1" и доверие в "контрольном уравнении #3" распространяются точно на "контрольное уравнение #2", а доверие в "контрольном уравнении #1" и доверие в "контрольном уравнении #2" распространяются точно на "контрольное уравнение #3". Следовательно, LDPC-CC с лучшим качеством приема может достигаться аналогичным образом, как в случае скорости кодирования 1/2.
Таблица 3 показывает примеры LDPC-CC (LDPC-CC #1, #2, #3, #4, #5 и #6) с изменяющимся во времени периодом 3 и скоростью кодирования 1/2, для которых вышеуказанное связанное с "остатком" условие справедливо. В таблице 3, LDPC-CC с изменяющимся во времени периодом 3 задаются посредством трех полиномов контроля по четности: "контрольного (полиномиального) уравнения #1", "контрольного (полиномиального) уравнения #2" и "контрольного (полиномиального) уравнения #3".
Контрольный полином #2: (D538+D380+ 1)X(D)+(D449+D1+1)P(D)=0
Контрольный полином #3: (D583+D170+ 1)X(D)+(D364+D242+1)P(D)=0
Контрольный полином #2: D215+D106+1)X(D)+(D566+D142+1)P(D)=0
Контрольный полином #3: (D590+D559+1)X(D)+(D127+D110+1)P(D)=0
Контрольный полином #2: (D103+D47+1)X(D)+(D85+D83+1)P(D)=0
Контрольный полином #3: (D148+D89+1)X(D)+(D146+D49+1)P(D)=0
Контрольный полином #2: (D529+D32+1)X(D)+(D238+D188+1)P(D)=0
Контрольный полином #3: (D592+D572+1)X(D)+(D578+D568+1)P(D)=0
Контрольный полином #2: (D875+D796+1)X(D)+(D962+D871+1)P(D)=0
Контрольный полином #3: (D605+D547+1)X(D)+(D950+D439+1)P(D)=0
Контрольный полином #2: (D457+D197+1)X(D)+(D491+D22+1)P(D)=0
Контрольный полином #3: (D485+D70+1)X(D)+(D236+D181+1)P(D)=0
Кроме того, таблица 4 показывает примеры LDPC-CC с изменяющимся во времени периодом 3 и скоростью кодирования 1/2, 2/3, 3/4 и 5/6, а таблица 5 показывает примеры LDPC-CC с изменяющимся во времени периодом 3 и скоростью кодирования 1/2, 2/3, 3/4 и 4/5.
Контрольный полином #2: (D457+D197+1)X1(D)+(D491+D22+1)P(D)=0
Контрольный полином #3: (D485+D70+1)X1(D)+(D236+D181+1)P(D)=0
(D373+D56+1)X1(D)+(D86+D4+1)X2(D)+(D406+D218+1)P(D)=0
Контрольный полином #2:
(D457+D197+1)X1(D)+(D368+D295+1)X2(D)+(D491+D22+1)P(D)=0
Контрольный полином #3:
(D485+D70+1)X1(D)+(D475+D398+1)X2(D)+(D236+D181+1)P(D)=0
(D373+D56+1)X1(D)+(D86+D4+1)X2(D)+(D388+D134+1)X3(D)+(D406+D218+1)P(D)=0
Контрольный полином #2:
(D457+D197+1)X1(D)+(D368+D295+1)X2(D)+(D155+D136+1)X3(D)+(D491+D22+1)P(D)=0
Контрольный полином #3:
(D485+D70+1)X1(D)+(D475+D398+1)X2(D)+(D493+D77+1)X3(D)+(D236+D181+1)P(D)=0
(D373+D56+1)X1(D)+(D86+D4+1)X2(D)+(D388+D134+1)X3(D)+(D250+D197+1)X4(D)+(D295+D113+1)X5(D)+(D406+D218+1)P(D)=0
Контрольный полином #2:
(D457+D197+1)X1(D)+(D368+D295+1)X2(D)+(D155+D136+1)X3(D)+(D220+D146+1)X4(D)+(D311+D115+1)X5(D)+(D491+D22+1)P(D)=0
Контрольный полином #3:
(D485+D70+1)X1(D)+(D475+D398+1)X2(D)+(D493+D77+1)X3(D)+(D490+D239+1)X4(D)+(D394+D278+1)X5(D)+(D236+D181+1)P(D)=0
Контрольный полином #2: (D370+D317+1)X1(D)+(D95+D22+1)P(D)=0
Контрольный полином #3: (D346+D86+1)X1(D)+(D88+D26+1)P(D)=0
(D268+D164+1)X1(D)+(D385+D242+1)X2(D)+(D92+D7+1)P(D)=0
Контрольный полином #2:
(D370+D317+1)X1(D)+(D125+D103+1)X2(D)+(D95+D22+1)P(D)=0
Контрольный полином #3:
(D346+D86+1)X1(D)+(D319+D290+1)X2(D)+(D88+D26+1)P(D)=0
(D268+D164+1)X1(D)+(D385+D242+1)X2(D)+(D343+D284+1)X3(D)+(D92+D7+1)P(D)=0
Контрольный полином #2:
(D370+D317+1)X1(D)+(D125+D103+1)X2(D)+(D259+D14+1)X3(D)+(D95+D22+1)P(D)=0
Контрольный полином #3:
(D346+D86+1)X1(D)+(D319+D290+1)X2(D)+(D145+D11+1)X3(D)+(D88+D26+1)P(D)=0
(D268+D164+1)X1(D)+(D385+D242+1)X2(D)+(D343+D284+1)X3(D)+(D310+D113+1)X4(D)+(D92+D7+1)P(D)=0
(D370+D317+1)X1(D)+(D125+D103+1)X2(D)+(D259+D14+1)X3(D)+(D394+D188+1)X4(D)+(D95+D22+1)P(D)=0
Контрольный полином #3:
(D346+D86+1)X1(D)+(D319+D290+1)X2(D)+(D145+D11+1)X3(D)+(D239+D67+1)X4(D)+(D88+D26+1)P(D)=0
Подтверждено, что, как в случае изменяющегося во времени периода 3, код с хорошими характеристиками может находиться, если условие по "остатку" ниже применяется к LDPC-CC, имеющему изменяющийся во времени период кратный 3 (например, 6, 9, 12,...,). LDPC-CC с кратным изменяющегося во времени периода 3 с хорошими характеристиками описывается ниже. Случай LDPC-CC со скоростью кодирования 1/2 и изменяющимся во времени периодом 6 описывается ниже в качестве примера.
Рассмотрим уравнения 5-1-5-6 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 6.
[5]
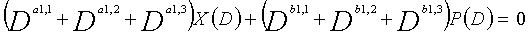 ... (уравнение 5-1)
... (уравнение 5-1)
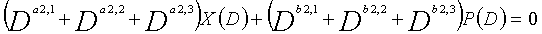 ... (уравнение 5-2)
... (уравнение 5-2)
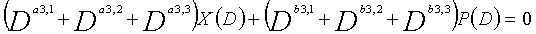 ... (уравнение 5-3)
... (уравнение 5-3)
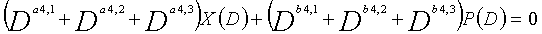 ... (уравнение 5-4)
... (уравнение 5-4)
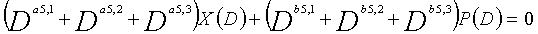 ... (уравнение 5-5)
... (уравнение 5-5)
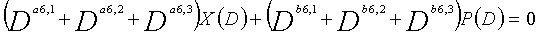 ... (уравнение 5-6)
... (уравнение 5-6)
В это время, X(D) является полиномиальным представлением данных (информации), и P(D) является полиномиальным представлением четности.
Для LDPC-CC с изменяющимся во времени периодом 6, если i%6=k (где k=0, 1, 2, 3, 4, 5) допускается для четности Pi и информации Xi в момент времени i, полином контроля по четности уравнения 5-(k+1) является справедливым. Например, если i=1,i%6=1 (k=1), уравнение 6 справедливо.
[6]
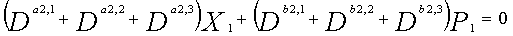 ... (уравнение 6)
... (уравнение 6)
Здесь, в уравнениях 5-1-5-6, полиномы контроля по четности допускаются так, что существует три элемента в X(D) и P(D), соответственно.
В уравнении 5-1, предполагается, что a1,1, a1,2, a1,3 являются целыми числами (где a1,1≠a1,2≠a1,3). Кроме того, предполагается, что b1,1, b1,2 и b1,3 являются целыми числами (где b1,1≠b1,2≠b1,3). Полином контроля по четности уравнения 5-1 называется "контрольным уравнением #1", и субматрица на основе полинома контроля по четности уравнения 5-1 обозначается как первая субматрица H1.
В уравнении 5-2, предполагается, что a2,1, a2,2 и a2,3 являются целыми числами (где a2,1≠a2,2≠a2,3). Кроме того, предполагается, что b2,1, b2,2 и b2,3 являются целыми числами (где b2,1≠b2,2≠b2,3). Полином контроля по четности уравнения 5-2 называется "контрольным уравнением #2", и субматрица на основе полинома контроля по четности уравнения 5-2 обозначается как вторая субматрица H2.
В уравнении 5-3, предполагается, что a3,1, a3,2 и a3,3 являются целыми числами (где a3,1≠a3,2≠a3,3). Кроме того, предполагается, что b3,1, b3,2 и b3,3 являются целыми числами (где b3,1≠b3,2≠b3,3). Полином контроля по четности уравнения 5-3 называется "контрольным уравнением #3", и субматрица на основе полинома контроля по четности уравнения 5-3 обозначается как третья субматрица H3.
В уравнении 5-4, предполагается, что a4,1, a4,2 и a4,3 являются целыми числами (где a4,1≠a4,2≠a4,3). Кроме того, предполагается, что b4,1, b4,2 и b4,3 являются целыми числами (где b4,1≠b4,2≠b4,3). Полином контроля по четности уравнения 5-4 называется "контрольным уравнением #4", и субматрица на основе полинома контроля по четности уравнения 5-4 обозначается как четвертая субматрица H4.
В уравнении 5-5, предполагается, что a5,1, a5,2 и a5,3 являются целыми числами (где a5,1≠a5,2≠a5,3). Кроме того, предполагается, что b5,1, b5,2 и b5,3 являются целыми числами (где b5,1≠b5,2≠b5,3). Полином контроля по четности уравнения 5-5 называется "контрольным уравнением #5", и субматрица на основе полинома контроля по четности уравнения 5-5 обозначается как пятая субматрица H5.
В уравнении 5-6, предполагается, что a6,1, a6,2 и a6,3 являются целыми числами (где a6,1≠a6,2≠a6,3). Кроме того, предполагается, что b6,1, b6,2 и b6,3 являются целыми числами (где b6,1≠b6,2≠b6,3). Полином контроля по четности уравнения 5-6 называется "контрольным уравнением #6", и субматрица на основе полинома контроля по четности уравнения 5-6 обозначается как шестая субматрица H6.
Затем, рассматривается LDPC-CC с изменяющимся во времени периодом 6, который формируется из первой субматрицы H1, второй субматрицы H2, третьей субматрицы H3, четвертой субматрицы H4, пятой субматрицы H5 и шестой субматрицы H6.
В это время, если k обозначается как остаток после деления значений комбинаций порядков X(D) и P(D),
(a1,1, a1,2, a1,3),
(b1,1, b1,2, b1,3),
(a2,1, a2,2, a2,3),
(b2,1, b2,2, b2,3),
(a3,1, a3,2, a3,3),
(b3,1, b3,2, b3,3),
(a4,1, a4,2, a4,3),
(b4,1, b4,2, b4,3),
(a5,1, a5,2, a5,3),
(b5,1, b5,2, b5,3),
(a6,1, a6,2, a6,3),
(b6,1, b6,2, b6,3), в уравнениях 5-1-5-6 на 3, предусматривается по одному каждому из остатков 0, 1 и 2, которые должны быть включены в наборы из трех коэффициентов, представленные так, как показано выше (например, (a1,1, a1,2, a1,3)), и является справедливым для всех вышеуказанных наборов из трех коэффициентов. Другими словами, предусматривается, что
(a1,1%3, a1,2%3, a1,3%3),
(b1,1%3, b1,2%3, b1,3%3),
(a2,1%3, a2,2%3, a2,3%3),
(b2,1%3, b2,2%3, b2,3%3),
(a3,1%3, a3,2%3, a3,3%3),
(b3,1%3, b3,2%3, b3,3%3),
(a4,1%3, a4,2%3, a4,3%3),
(b4,1%3, b4,2%3, b4,3%3),
(a5,1%3, a5,2%3, a5,3%3),
(b5,1%3, b5,2%3, b5,3%3),
(a6,1%3, a6,2%3, a6,3%3), и
(b6,1%3, b6,2%3, b6,3%3)
являются любыми из следующего: (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) и (2, 1, 0).
Посредством формирования LDPC-CC таким образом, если ребро присутствует, когда граф Таннера отрисовывается для "контрольного уравнения #1", доверие в "контрольном уравнении #2 или контрольном уравнении #5" и доверие в "контрольном уравнении #3 или контрольном уравнении #6" распространяются точно.
Кроме того, если ребро присутствует, когда граф Таннера отрисовывается для "контрольного уравнения #2", доверие в "контрольном уравнении #1 или контрольном уравнении #4" и доверие в "контрольном уравнении #3 или контрольном уравнении #6" распространяются точно.
Если ребро присутствует, когда граф Таннера отрисовывается для "контрольного уравнения #3", доверие в "контрольном уравнении #1 или контрольном уравнении #4" и доверие в "контрольном уравнении #2 или контрольном уравнении #5" распространяются точно. Если ребро присутствует, когда граф Таннера отрисовывается для "контрольного уравнения #6", доверие в "контрольном уравнении #1 или контрольном уравнении #4" и доверие в "контрольном уравнении #2 или контрольном уравнении #5" распространяются точно.
Если ребро присутствует, когда граф Таннера отрисовывается для "контрольного уравнения #6", доверие в "контрольном уравнении #1 или контрольном уравнении #4" и доверие в "контрольном уравнении #3 или контрольном уравнении #5" распространяются точно. Если ребро присутствует, когда граф Таннера отрисовывается для "контрольного уравнения #6", доверие в "контрольном уравнении #1 или контрольном уравнении #4" и доверие в "контрольном уравнении #2 или контрольном уравнении #5" распространяются точно.
Следовательно, LDPC-CC с изменяющимся во времени периодом 6 может поддерживать лучшую способность к коррекции ошибок аналогичным образом тому, когда изменяющийся во времени период равняется 3.
В этом отношении, доверительное распространение описывается с использованием фиг. 4C. Фиг. 4C показывает взаимосвязь элементов на основе доверительного распространения, связанных с X(D) "контрольных уравнений #1-6". На фиг. 4C, квадрат указывает коэффициент, для которого остаток после деления на 3 на оси y (где x=1, 2, 3, 4, 5, 6 и y=1, 2, 3) равен 0.
Круг указывает коэффициент, для которого остаток после деления на 3 на оси y (где x=1, 2, 3, 4, 5, 6 и y=1, 2, 3) равняется 1. Ромбовидный прямоугольник указывает коэффициент, для которого остаток после деления на 3 на оси y (где x=1, 2, 3, 4, 5, 6 и y=1, 2, 3) равняется 2.
Как можно видеть из фиг. 4C, если ребро присутствует, когда граф Таннера отрисовывается для a1,1 "контрольного уравнения #1", доверие распространяется из "контрольного уравнения #2 или #5" и "контрольного уравнения #3 или #6", для которых остатки после деления на 3 отличаются. Аналогично, если ребро присутствует, когда граф Таннера отрисовывается для a1,2 "контрольного уравнения #1", доверие распространяется из "контрольного уравнения #2 или #5" и "контрольного уравнения #3 или #6", для которых остатки после деления на 3 отличаются.
Аналогично, если ребро присутствует, когда граф Таннера отрисовывается для a1,3 "контрольного уравнения #1", доверие распространяется из "контрольного уравнения #2 или #5" и "контрольного уравнения #3 или #6", для которых остатки после деления на 3 отличаются. Хотя фиг. 4C показывает взаимосвязь элементов на основе доверительного распространения, связанных с X(D) "контрольных уравнений #1-6", это применимо и к элементам, связанным с P(D).
Таким образом, доверие распространяется на каждый узел на графе Таннера "контрольного уравнения #1" из узлов коэффициентов, отличных от "контрольного уравнения #1". Следовательно, доверия с низкой корреляцией распространяются на "контрольное уравнение #1", предоставляя возможность ожидания повышения способности к коррекции ошибок.
На фиг. 4C, фокус обращен на "контрольное уравнение #1", но граф Таннера может быть отрисован похожим способом для "контрольного уравнения #2-6", и доверие распространяется на каждый узел на графе Таннера "контрольного уравнения #K" из узлов коэффициентов, отличных от "контрольного уравнения #K". Следовательно, доверия с низкой корреляцией распространяются на "контрольное уравнение #K" (где K=2, 3, 4, 5, 6), предоставляя возможность ожидания повышения способности к коррекции ошибок.
Посредством обеспечения порядков полиномов контроля по четности уравнений 5-1-5-6, чтобы удовлетворять вышеуказанному условию по "остатку" таким образом, доверие может распространяться эффективно во всех контрольных уравнениях, и возможность дополнительно повышать способность к коррекции ошибок увеличивается.
Случай, в котором скорость кодирования составляет 1/2, описан выше для LDPC-CC с изменяющимся во времени периодом 6, но скорость кодирования не ограничивается 1/2. Возможность достижения хорошего качества приема может быть увеличена, когда скорость кодирования составляет (n-1)/n (где n является целым числом, равным или превышающим 2), если вышеуказанное условие по "остатку" справедливо для наборов из трех коэффициентов в информации X1(D), X2(D),..., Xn-1(D).
Случай, в котором скорость кодирования составляет (n-1)/n (где n является целым числом, равным или превышающим 2), описывается ниже.
Рассмотрим уравнения 7-1-7-6 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 6.
[7]
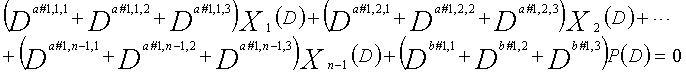 (уравнение 7-1)
(уравнение 7-1)
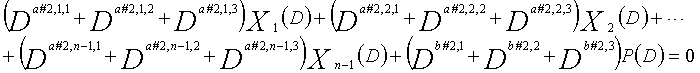 ... (уравнение 7-2)
... (уравнение 7-2)
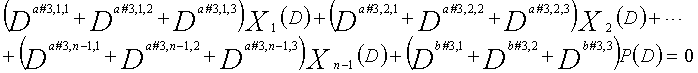 ... (уравнение 7-3)
... (уравнение 7-3)
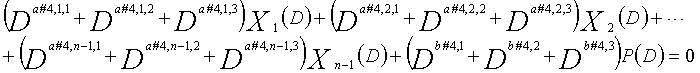 ... (уравнение 7-4)
... (уравнение 7-4)
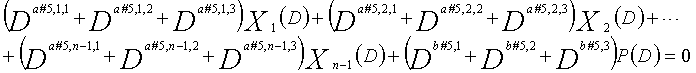 ... (уравнение 7-5)
... (уравнение 7-5)
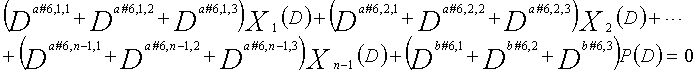 ... (уравнение 7-6)
... (уравнение 7-6)
В это время, X1(D), X2(D),..., Xn-1(D) являются полиномиальными представлениями данных (информации) X1, X2,..., Xn-1, а P(D) является полиномиальным представлением четности. Здесь, в уравнениях 7-1-7-6, полиномы контроля по четности допускаются так, что существует три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), соответственно. Как в случае вышеуказанной скорости кодирования 1/2 и в случае изменяющегося во времени периода 3, возможность достигать более высокой способности к коррекции ошибок увеличивается, если условие ниже (условие #1) удовлетворяется в LDPC-CC с изменяющимся во времени периодом 6 и скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), представленном посредством полиномов контроля по четности уравнений 7-1-7-6.
В LDPC-CC с изменяющимся во времени периодом 6 и скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, Xi,2,..., Xi,n-1, соответственно. Если i%6=k (где k=0, 1, 2, 3, 4, 5) допускается в это время, полином контроля по четности уравнения 7-(k+1) является справедливым. Например, если i=8, i%6=2 (k=2), уравнение 8 справедливо.
[8]
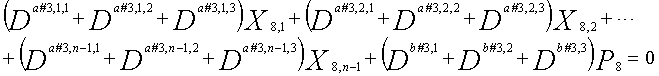 ... (уравнение 8)
... (уравнение 8)
Условие #1
В уравнениях 7-1-7-6, комбинации порядков X1(D), X2(D),..., Xn-1(D) и P(D) удовлетворяют следующему условию:
(a#1,1,1%3, a#1,1,2%3, a#1,1,3%3),
(a#1,2,1%3, a#1,2,2%3, a#1,2,3%3),...,
(a#1,k,1%3, a#1,k,2%3, a#1,k,3%3),...,
(a#1,n-1,1%3, a#1,n-1,2%3, a#1,n-1,3%3), и
(b#1,1%3, b#1,2%3, b#1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где k=1, 2, 3,..., n-1);
(a#2,1,1%3, a#2,1,2%3, a#2,1,3%3),
(a#1,2,1%3, a#1,2,2%3, a#1,2,3%3),...,
(a#2,k,1%3, a#2,k,2%3, a#2,k,3%3),...,
(a#2,n-1,1%3, a#2,n-1,2%3, a#2,n-1,3%3), и
(b#2,1%3, b#2,2%3, b#2,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где k=1, 2, 3,..., n-1);
(a#3,1,1%3, a#3,1,2%3, a#3,1,3%3),
(a#3,2,1%3, a#3,2,2%3, a#3,2,3%3),...,
(a#3,k,1%3, a#3,k,2%3, a#3,k,3%3),...,
(a#3,n-1,1%3, a#3,n-1,2%3, a#3,n-1,3%3), и
(b#3,1%3, b#3,2%3, b#3,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где k=1, 2, 3,..., n-1);
(a#4,1,1%3, a#4,1,2%3, a#4,1,3%3),
(a#4,2,1%3, a#4,2,2%3, a#4,2,3%3),...,
(a#4,k,1%3, a#4,k,2%3, a#4,k,3%3),...,
(a#4,n-1,1%3, a#4,n-1,2%3, a#4,n-1,3%3), и
(b#4,1%3, b#4,2%3, b#4,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где k=1, 2, 3,..., n-1);
(a#5,1,1%3, a#5,1,2%3, a#5,1,3%3),
(a#5,2,1%3, a#5,2,2%3, a#5,2,3%3),...,
(a#5,k,1%3, a#5,k,2%3, a#5,k,3%3),...,
(a#5,n-1,1%3, a#5,n-1,2%3, a#5,n-1,3%3), и
(b#5,1%3, b#5,2%3, b#5,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где k=1, 2, 3,..., n-1); и
(a#6,1,1%3, a#6,1,2%3, a#6,1,3%3),
(a#6,2,1%3, a#6,2,2%3, a#6,2,3%3),...,
(a#6,k,1%3, a#6,k,2%3, a#6,k,3%3),...,
(a#6,n-1,1%3, a#6,n-1,2%3, a#6,n-1,3%3), и
(b#6,1%3, b#6,2%3, b#6,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где k=1, 2, 3,..., n-1).
В вышеприведенном описании, код, имеющий высокую способность к коррекции ошибок, описан для LDPC-CC с изменяющимся во времени периодом 6, но код, имеющий высокую способность к коррекции ошибок, также может быть сформирован, когда LDPC-CC с изменяющимся во времени периодом 3g (где g=1, 2, 3, 4,...,) (т.е. LDPC-CC, имеющий изменяющийся во времени период кратный 3) создается аналогично способу разработки для LDPC-CC с изменяющимся во времени периодом 3 или 6. Способ конфигурирования для этого кода описывается подробно ниже.
Рассмотрим уравнения 9-1-9-3g в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 3g (где g=1, 2, 3, 4,...,) и скорость кодирования (n-1)/n (где n является целым числом, равным или превышающим 2).
[9]
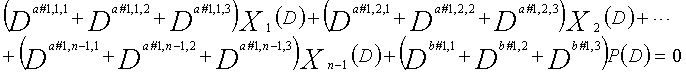 ... (уравнение 9-1)
... (уравнение 9-1)
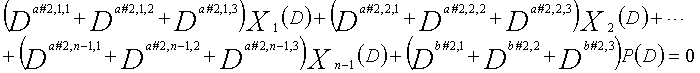 ... (уравнение 9-2)
... (уравнение 9-2)
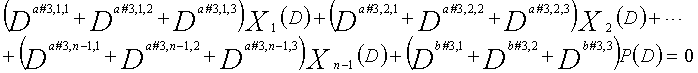 ... (уравнение 9-3)
... (уравнение 9-3)
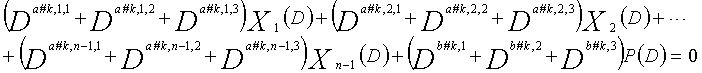 ... (уравнение 9-k)
... (уравнение 9-k)
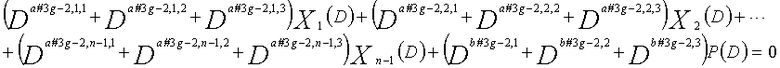 ... (уравнение 9-(3g-2))
... (уравнение 9-(3g-2))
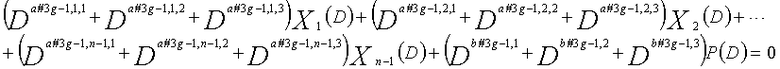 ... (уравнение 9-(3g-1))
... (уравнение 9-(3g-1))
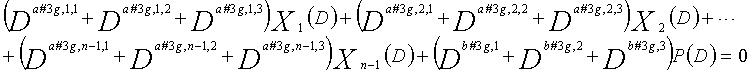 ... (уравнение 9-3g)
... (уравнение 9-3g)
В это время, X1(D), X2(D),..., Xn-1(D) являются полиномиальными представлениями данных (информации) X1, X2,..., Xn-1, а P(D) является полиномиальным представлением четности. Здесь, в уравнениях 9-1-9-3g, полиномы контроля по четности допускаются так, что существует три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), соответственно.
Как в случае LDPC-CC с изменяющимся во времени периодом 3 и LDPC-CC с изменяющимся во времени периодом 6, возможность достигать более высокой способности к коррекции ошибок увеличивается, если условие ниже (условие #2) удовлетворяется в LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), представленном посредством полиномов контроля по четности уравнений 9-1-9-3g.
В LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, Xi,2,..., Xi,n-1, соответственно.
Если i%3g=k (где k=0, 1, 2,..., 3g-1) допускается в это время, полином контроля по четности уравнения 9-(k+1) является справедливым. Например, если i=2, i%3g=2 (k=2), уравнение 10 справедливо.
[10]
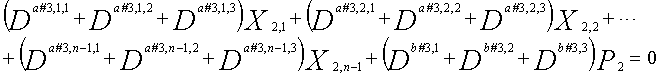 ... (уравнение 10)
... (уравнение 10)
В уравнениях 9-1-9-3g, предполагается, что a#k,p,1, a#k,p,2 и a#k,p,3 являются целыми числами (где a#k,p,1≠a#k,p,2≠a#k,p,3) (где k=1, 2, 3,..., 3g и p=1, 2, 3,..., n-1). Кроме того, предполагается, что b#k,1, b#k,2 и b#k,3 являются целыми числами (где b#k,1≠b#k,2≠b#k,3). Полином контроля по четности уравнения 9-k (где k=1, 2, 3,..., 3g) называется "контрольным уравнением #k", и субматрица на основе полинома контроля по четности уравнения 9-k обозначается как k-ая субматрица Hk. Затем, рассматривается LDPC-CC с изменяющимся во времени периодом 3g, который формируется из первой субматрицы H1, второй субматрицы H2, третьей субматрицы H3,..., и 3g-ой субматрицы H3g.
Условие #2
В уравнениях 9-1-9-3g, комбинации порядков X1(D), X2(D),..., Xn-1(D) и P(D) удовлетворяют следующему условию:
(a#1,1,1%3, a#1,1,2%3, a#1,1,3%3),
(a#1,2,1%3, a#1,2,2%3, a#1,2,3%3),...,
(a#1,p,1%3, a#1,p,2%3, a#1,p,3%3),...,
(a#1,n-1,1%3, a#1,n-1,2%3, a#1,n-1,3%3), и
(b#1,1%3, b#1,2%3, b#1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1);
(a#2,1,1%3, a#2,1,2%3, a#2,1,3%3),
(a#2,2,1%3, a#2,2,2%3, a#2,2,3%3),...,
(a#2,p,1%3, a#2,p,2%3, a#2,p,3%3),...,
(a#2,n-1,1%3, a#2,n-1,2%3, a#2,n-1,3%3), и
(b#2,1%3, b#2,2%3, b#2,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1), или (2, 1, 0) (где p=1, 2, 3,..., n-1);
(a#3,1,1%3, a#3,1,2%3, a#3,1,3%3),
(a#3,2,1%3, a#3,2,2%3, a#3,2,3%3),...,
(a#3,p,1%3, a#3,p,2%3, a#3,p,3%3),...,
(a#3,n-1,1%3, a#3,n-1,2%3, a#3,n-1,3%3), и
(b#3,1%3, b#3,2%3, b#3,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1);
(a#k,1,1%3, a#k,1,2%3, a#k,1,3%3),
(a#k,2,1%3, a#k,2,2%3, a#k,2,3%3),...,
(a#k,p,1%3, a#k,p,2%3, a#k,p,3%3),...,
(a#k,n-1,1%3, a#k,n-1,2%3, a#k,n-1,3%3), и
(b#k,1%3, b#k,2%3, b#k,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1) (где k=1, 2, 3,..., 3g);
(a#3g-2,1,1%3, a#3g-2,1,2%3, a#3g-2,1,3%3),
(a#3g-2,2,1%3, a#3g-2,2,2%3, a#3g-2,2,3%3),...,
(a#3g-2,p,1%3, a#3g-2,p,2%3, a#3g-2,p,3%3),...,
(a#3g-2,n-1,1%3, a#3g-2,n-1,2%3, a#3g-2,n-1,3%3), и
(b#3g-2,1%3, b#3g-2,2%3, b#3g-2,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1);
(a#3g-1,1,1%3, a#3g-1,1,2%3, a#3g-1,1,3%3),
(a#3g-1,2,1%3, a#3g-1,2,2%3, a#3g-1,2,3%3),...,
(a#3g-1,p,1%3, a#3g-1,p,2%3, a#3g-1,p,3%3),...,
(a#3g-1,n-1,1%3, a#3g-1,n-1,2%3, a#3g-1,n-1,3%3), и
(b#3g-1,1%3, b#3g-1,2%3, b#3g-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1); и
(a#3g,1,1%3, a#3g,1,2%3, a#3g,1,3%3),
(a#3g,2,1%3, a#3g,2,2%3, a#3g,2,3%3),...,
(a#3g,p,1%3, a#3g,p,2%3, a#3g,p,3%3),...,
(a#3g,n-1,1%3, a#3g,n-1,2%3, a#3g,n-1,3%3), и
(b#3g,1%3, b#3g,2%3, b#3g,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1).
С учетом простоты выполнения кодирования, желательно, чтобы один "0" присутствовал в трех элементах (b#k,1%3, b#k,2%3, b#k,3%3) (где k=1, 2,..., 3g) в уравнениях 9-1-9-3g. Это обусловлено таким признаком, что если D0=1 справедливо, и b#k,1, b#k,2 и b#k,3 являются целыми числами, равными или превышающими 0 в это время, четность P может находиться последовательно.
Кроме того, чтобы предоставлять релевантность между битами четности и битами данных с идентичным моментом времени и упрощать поиск кода, имеющего высокую корректирующую способность, желательно, чтобы:
- один "0" присутствовал в трех элементах (a#k,1,1%3, a#k,1,2%3, a#k,1,3%3);
- один "0" присутствовал в трех элементах (a#k,2,1%3, a#k,2,2%3, a#k,2,3%3);
- один "0" присутствовал в трех элементах (a#k,p,1%3, a#k,p,2%3, a#k,p,3%3);
- один "0" присутствовал в трех элементах (a#k,n-1,1%3, a#k,n-1,2%3, a#k,n-1,3%3), (где k=1, 2,..., 3g).
Затем, LDPC-CC с изменяющимся во времени периодом 3g (где g=2, 3, 4, 5,...,), который учитывает простоту кодирования, рассматривается. В это время, если скорость кодирования составляет (n-1)/n (где n является целым числом, равным или превышающим 2), полиномы контроля по четности LDPC-CC могут представляться так, как показано ниже.
[11]
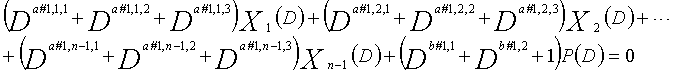 ... (уравнение 11-1)
... (уравнение 11-1)
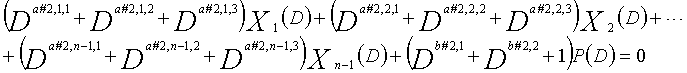 ... (уравнение 11-2)
... (уравнение 11-2)
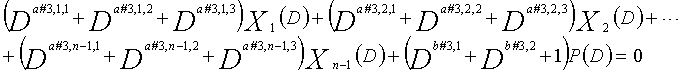 ... (уравнение 11-3)
... (уравнение 11-3)
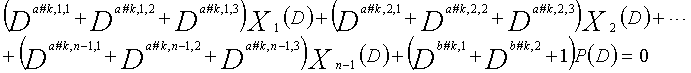 ... (уравнение 11-k)
... (уравнение 11-k)
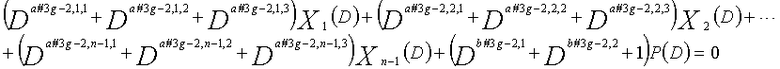 ... (уравнение 11-(3g-2))
... (уравнение 11-(3g-2))
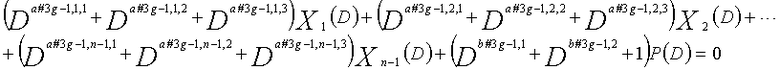 ... (уравнение 11-(3g-1))
... (уравнение 11-(3g-1))
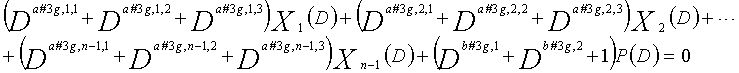 ... (уравнение 11-3g)
... (уравнение 11-3g)
В это время, X1(D), X2(D),..., Xn-1(D) являются полиномиальными представлениями данных (информации) X1, X2,..., Xn-1, а P(D) является полиномиальным представлением четности. Здесь, в уравнениях 11-1-11-3g, полиномы контроля по четности допускаются так, что существует три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), соответственно. В LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, Xi,2,..., Xi,n-1, соответственно. Если i%3g=k (где k=0, 1, 2,..., 3g-1) допускается в это время, полином контроля по четности уравнения 11-(k+1) является справедливым. Например, если i=2, i%3=2 (k=2), уравнение 12 справедливо.
[12]
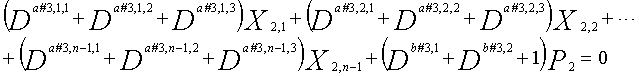 ... (уравнение 12)
... (уравнение 12)
Если условие #3 и условие #4 удовлетворяются в это время, возможность создавать код, имеющий более высокую способность к коррекции ошибок, увеличивается.
Условие #3
В уравнениях 11-1-11-3g, комбинации порядков X1(D), X2(D),..., Xn-1(D) и P(D) удовлетворяют следующему условию:
(a#1,1,1%3, a#1,1,2%3, a#1,1,3%3),
(a#1,2,1%3, a#1,2,2%3, a#1,2,3%3),...,
(a#1,p,1%3, a#1,p,2%3, a#1,p,3%3),..., и
(a#1,n-1,1%3, a#1,n-1,2%3, a#1,n-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1);
(a#2,1,1%3, a#2,1,2%3, a#2,1,3%3),
(a#2,2,1%3, a#2,2,2%3, a#2,2,3%3),...,
(a#2,p,1%3, a#2,p,2%3, a#2,p,3%3),..., и
(a#2,n-1,1%3, a#2,n-1,2%3, a#2,n-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1);
(a#3,1,1%3, a#3,1,2%3, a#3,1,3%3),
(a#3,2,1%3, a#3,2,2%3, a#3,2,3%3),...,
(a#3,p,1%3, a#3,p,2%3, a#3,p,3%3),..., и
(a#3,n-1,1%3, a#3,n-1,2%3, a#3,n-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1);
(a#k,1,1%3, a#k,1,2%3, a#k,1,3%3),
(a#k,2,1%3, a#k,2,2%3, a#k,2,3%3),...,
(a#k,p,1%3, a#k,p,2%3, a#k,p,3%3),..., и
(a#k,n-1,1%3, a#k,n-1,2%3, a#k,n-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1 и k=1, 2, 3,..., 3g);
(a#3g-2,1,1%3, a#3g-2,1,2%3, a#3g-2,1,3%3),
(a#3g-2,2,1%3, a#3g-2,2,2%3, a#3g-2,2,3%3),...,
(a#3g-2,p,1%3, a#3g-2,p,2%3, a#3g-2,p,3%3),..., и
(a#3g-2,n-1,1%3, a#3g-2,n-1,2%3, a#3g-2,n-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1);
(a#3g-1,1,1%3, a#3g-1,1,2%3, a#3g-1,1,3%3),
(a#3g-1,2,1%3, a#3g-1,2,2%3, a#3g-1,2,3%3),...,
(a#3g-1,p,1%3, a#3g-1,p,2%3, a#3g-1,p,3%3),..., и
(a#3g-1,n-1,1%3, a#3g-1,n-1,2%3, a#3g-1,n-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1); и
(a#3g,1,1%3, a#3g,1,2%3, a#3g,1,3%3),
(a#3g,2,1%3, a#3g,2,2%3, a#3g,2,3%3),...,
(a#3g,p,1%3, a#3g,p,2%3, a#3g,p,3%3),..., и
(a#3g,n-1,1%3, a#3g,n-1,2%3, a#3g,n-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где p=1, 2, 3,..., n-1).
Помимо этого, в уравнениях 11-1-11-3g, комбинации порядков P(D) удовлетворяют следующему условию:
(b#1,1%3, b#1,2%3),
(b#2,1%3, b#2,2%3),
(b#3,1%3, b#3,2%3),...,
(b#k,1%3, b#k,2%3),...,
(b#3g-2,1%3, b#3g-2,2%3),
(b#3g-1,1%3, b#3g-1,2%3), и
(b#3g,1%3, b#3g,2%3) являются либо (1, 2), либо (2, 1) (где k=1, 2, 3,..., 3g).
Условие #3 имеет взаимосвязь относительно уравнений 11-1-11-3g, аналогичную той, которую условие #2 имеет относительно уравнений 9-1-9-3g. Если условие ниже (условие #4) добавляется для уравнений 11-1-11-3g в дополнение к условию #3, возможность создавать LDPC-CC, имеющий более высокую способность к коррекции ошибок, увеличивается.
Условие #4
Порядки P(D) уравнений 11-1-11-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в значениях порядков 6g
(b#1,1%3g, b#1,2%3g),
(b#2,1%3g, b#2,2%3g),
(b#3,1%3g, b#3,2%3g),...,
(b#k,1%3g, b#k,2%3g),...,
(b#3g-2,1%3g, b#3g-2,2%3g),
(b#3g-1,1%3g, b#3g-1,2%3g),
(b#3g,1%3g, b#3g,2%3g) (в этом случае, два порядка формируют пару, и, следовательно, число порядков, формирующих пары 3g пары, составляет 6g).
Возможность достижения хорошей способности к коррекции ошибок является высокой, если существует также случайность, в то время как закономерность поддерживается для позиций, в которых единицы присутствуют в матрице контроля по четности. Для LDPC-CC, имеющего изменяющийся во времени период 3g (где g=2, 3, 4, 5,...,) и скорость кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), который имеет полиномы контроля по четности уравнений 11-1-11-3g, если создается код, в котором условие #4 применяется в дополнение к условию #3, можно предоставлять случайность при поддержании закономерности для позиций, в которых единицы присутствуют в матрице контроля по четности, и, следовательно, возможность достижения хорошей способности к коррекции ошибок увеличивается.
Затем, рассматривается LDPC-CC с изменяющимся во времени периодом 3g (где g=2, 3, 4, 5,...,), который предоставляет возможность простого выполнения кодирования и обеспечивает релевантность для битов четности и битов данных с идентичным моментом времени. В это время, если скорость кодирования составляет (n-1)/n (где n является целым числом, равным или превышающим 2), полиномы контроля по четности LDPC-CC могут представляться так, как показано ниже.
[13]
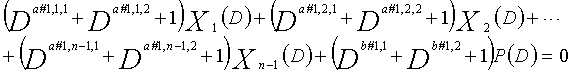 ... (уравнение 13-1)
... (уравнение 13-1)
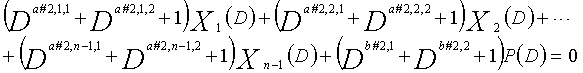 ... (уравнение 13-2)
... (уравнение 13-2)
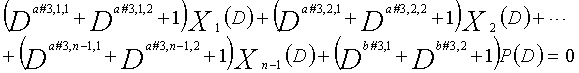 ... (уравнение 13-3)
... (уравнение 13-3)
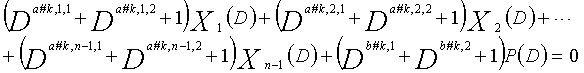 ... (уравнение 13-k)
... (уравнение 13-k)
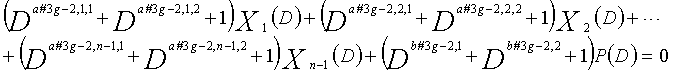 ... (уравнение 13-(3g-2))
... (уравнение 13-(3g-2))
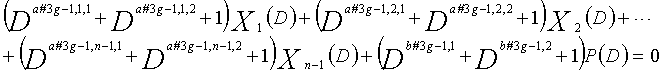 ... (уравнение 13-(3g-1))
... (уравнение 13-(3g-1))
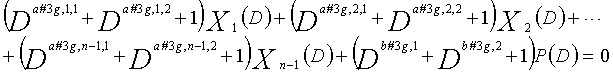 ... (уравнение 13-3g)
... (уравнение 13-3g)
В это время, X1(D), X2(D),..., Xn-1(D) являются полиномиальными представлениями данных (информации) X1, X2,..., Xn-1, а P(D) является полиномиальным представлением четности. В уравнениях 13-1-13-3g, полиномы контроля по четности допускаются так, что существует три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), соответственно, и элемент D0 присутствует в X1(D), X2(D),..., Xn-1(D) и P(D) (где k=1, 2, 3,..., 3g).
В LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, Xi,2,..., Xi,n-1, соответственно. Если i%3g=k (где k=0, 1, 2,..., 3g-1) допускается в это время, полином контроля по четности уравнения 13-(k+1) является справедливым. Например, если i=2, i%3g=2 (k=2), уравнение 14 справедливо.
[14]
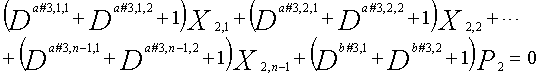 ... (уравнение 14)
... (уравнение 14)
Если следующие условие #5 и условие #6 удовлетворяются в это время, возможность создавать код, имеющий более высокую способность к коррекции ошибок, увеличивается
Условие #5
В уравнениях 13-1-13-3g, комбинации порядков X1(D), X2(D),..., Xn-1(D) и P(D) удовлетворяют следующему условию:
(a#1,1,1%3, a#1,1,2%3),
(a#1,2,1%3, a#1,2,2%3),...,
(a#1,p,1%3, a#1,p,2%3),..., и
(a#1,n-1,1%3, a#1,n-1,2%3) являются любыми из (1, 2), (2, 1) (p=1, 2, 3,..., n-1);
(a#2,1,1%3, a#2,1,2%3),
(a#2,2,1%3, a#2,2,2%3),...,
(a#2,p,1%3, a#2,p,2%3),..., и
(a#2,n-1,1%3, a#2,n-1,2%3) являются либо (1, 2), либо (2, 1) (где p=1, 2, 3,..., n-1);
(a#3,1,1%3, a#3,1,2%3),
(a#3,2,1%3, a#3,2,2%3),...,
(a#3,p,1%3, a#3,p,2%3),..., и
(a#3,n-1,1%3, a#3,n-1,2%3) являются либо (1, 2), либо (2, 1) (где p=1, 2, 3,..., n-1);
(a#k,1,1%3, a#k,1,2%3),
(a#k,2,1%3, a#k,2,2%3),...,
(a#k,p,1%3, a#k,p,2%3),..., и
(a#k,n-1,1%3, a#k,n-1,2%3) являются либо (1, 2), либо (2, 1) (где p=1, 2, 3,..., n-1) (где k=1, 2, 3,..., 3g)
(a#3g-2,1,1%3, a#3g-2,1,2%3),
(a#3g-2,2,1%3, a#3g-2,2,2%3),...,
(a#3g-2,p,1%3, a#3g-2,p,2%3),..., и
(a#3g-2,n-1,1%3, a#3g-2,n-1,2%3) являются либо (1, 2), либо (2, 1) (где p=1, 2, 3,..., n-1);
(a#3g-1,1,1%3, a#3g-1,1,2%3),
(a#3g-1,2,1%3, a#3g-1,2,2%3),...,
(a#3g-1,p,1%3, a#3g-1,p,2%3),..., и
(a#3g-1,n-1,1%3, a#3g-1,n-1,2%3) являются либо (1, 2), либо (2, 1) (где p=1, 2, 3,..., n-1); и
(a#3g,1,1%3, a#3g,1,2%3),
(a#3g,2,1%3, a#3g,2,2%3),...,
(a#3g,p,1%3, a#3g,p,2%3),..., и
(a#3g,n-1,1%3, a#3g,n-1,2%3) являются либо (1, 2), либо (2, 1) (где p=1, 2, 3,..., n-1).
Помимо этого, в уравнениях 13-1-13-3g, комбинации порядков P(D) удовлетворяют следующему условию:
(b#1,1%3, b#1,2%3),
(b#2,1%3, b#2,2%3),
(b#3,1%3, b#3,2%3),...,
(b#k,1%3, b#k,2%3),...,
(b#3g-2,1%3, b#3g-2,2%3),
(b#3g-1,1%3, b#3g-1,2%3), и
(b#3g,1%3, b#3g,2%3) являются либо (1, 2), либо (2, 1) (где k=1, 2, 3,..., 3g).
Условие #5 имеет взаимосвязь относительно уравнений 13-1-13-3g, аналогичную той, которую условие #2 имеет относительно уравнений 9-1-9-3g. Если условие ниже (условие #6) добавляется для уравнений 13-1-13-3g в дополнение к условию #5, возможность создавать код, имеющий высокую способность к коррекции ошибок, увеличивается.
Условие #6
Порядки X1(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,1,1%3g, a#1,1,2%3g),
(a#2,1,1%3g, a#2,1,2%3g),...,
(a#p,1,1%3g, a#p,1,2%3g),..., и
(a#3g,1,1%3g, a#3g,1,2%3g) (где p=1, 2, 3,..., 3g);
Порядки X2(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,2,1%3g, a#1,2,2%3g),
(a#2,2,1%3g, a#2,2,2%3g),...,
(a#p,2,1%3g, a#p,2,2%3g),..., и
(a#3g,2,1%3g, a#3g,2,2%3g) (где p=1, 2, 3,..., 3g);
Порядки X3(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,3,1%3g, a#1,3,2%3g),
(a#2,3,1%3g, a#2,3,2%3g),...,
(a#p,3,1%3g, a#p,3,2%3g),..., и
(a#3g,3,1%3g, a#3g,3,2%3g) (где p=1, 2, 3,..., 3g);
Порядки Xk(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,k,1%3g, a#1,k,2%3g),
(a#2,k,1%3g, a#2,k,2%3g),...,
(a#p,k,1%3g, a#p,k,2%3g),..., и
(a#3g,k,1%3g, a#3g,k,2%3g) (где p=1, 2, 3,..., 3g и k=1, 2, 3,..., n-1);
Порядки Xn-1(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,n-1,1%3g, a#1,n-1,2%3g),
(a#2,n-1,1%3g, a#2,n-1,2%3g),...,
(a#p,n-1,1%3g, a#p,n-1,2%3g),..., и
(a#3g,n-1,1%3g, a#3g,n-1,2%3g) (где p=1, 2, 3,..., 3g); и
Порядки P(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(b#1,1%3g, b#1,2%3g),
(b#2,1%3g, b#2,2%3g),
(b#3,1%3g, b#3,2%3g),...,
(b#k,1%3g, b#k,2%3g),...,
(b#3g-2,1%3g, b#3g-2,2%3g),
(b#3g-1,1%3g, b#3g-1,2%3g), и
(b#3g,1%3g, b#3g,2%3g) (где k=1, 2, 3,..., n-1).
Возможность достижения хорошей способности к коррекции ошибок является высокой, если существует также случайность, в то время как закономерность поддерживается для позиций, в которых единицы присутствуют в матрице контроля по четности. Для LDPC-CC, имеющего изменяющийся во времени период 3g (где g=2, 3, 4, 5,...,) и скорость кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), который имеет полиномы контроля по четности уравнений 13-1-13-3g, если создается код, в котором условие #6 применяется в дополнение к условию #5, можно предоставлять случайность при поддержании закономерности для позиций, в которых единицы присутствуют в матрице контроля по четности, и, следовательно, возможность достижения хорошей способности к коррекции ошибок увеличивается.
Возможность создавать LDPC-CC, имеющий более высокую способность к коррекции ошибок, также увеличивается, если код создается с использованием условия #6' вместо условия #6, т.е. с использованием условия #6' в дополнение к условию #5.
Условие #6'
Порядки X1(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,1,1%3g, a#1,1,2%3g),
(a#2,1,1%3g, a#2,1,2%3g),...,
(a#p,1,1%3g, a#p,1,2%3g),..., и
(a#3g,1,1%3g, a#3g,1,2%3g) (где p=1, 2, 3,..., 3g);
Порядки X2(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,2,1%3g, a#1,2,2%3g),
(a#2,2,1%3g, a#2,2,2%3g),...,
(a#p,2,1%3g, a#p,2,2%3g),..., и
(a#3g,2,1%3g, a#3g,2,2%3g) (где p=1, 2, 3,..., 3g);
Порядки X3(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,3,1%3g, a#1,3,2%3g),
(a#2,3,1%3g, a#2,3,2%3g),...,
(a#p,3,1%3g, a#p,3,2%3g),..., и
(a#3g,3,1%3g, a#3g,3,2%3g) (где p=1, 2, 3,..., 3g);
Порядки Xk(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,k,1%3g, a#1,k,2%3g),
(a#2,k,1%3g, a#2,k,2%3g),...,
(a#p,k,1%3g, a#p,k,2%3g),...,
(a#3g,k,1%3g, a#3g,k,2%3g) (где p=1, 2, 3,..., 3g и k=1, 2, 3,..., n-1);
Порядки Xn-1(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,n-1,1%3g, a#1,n-1,2%3g),
(a#2,n-1,1%3g, a#2,n-1,2%3g),...,
(a#p,n-1,1%3g, a#p,n-1,2%3g),...,
(a#3g,n-1,1%3g, a#3g,n-1,2%3g) (где p=1, 2, 3,..., 3g); или
Порядки P(D) уравнений 13-1-13-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(b#1,1%3g, b#1,2%3g),
(b#2,1%3g, b#2,2%3g),
(b#3,1%3g, b#3,2%3g),...,
(b#k,1%3g, b#k,2%3g),...,
(b#3g-2,1%3g, b#3g-2,2%3g),
(b#3g-1,1%3g, b#3g-1,2%3g),
(b#3g,1%3g, b#3g,2%3g) (где k=1, 2, 3,..., 3g).
Вышеприведенное описание относится к LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2). Ниже, условия описываются для порядков LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования 1/2 (n=2).
Рассмотрим уравнения 15-1-15-3g в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 3g (где g=1, 2, 3, 4,...,) и скорость кодирования 1/2 (n=2).
[15]
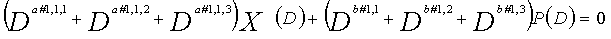 ... (уравнение 15-1)
... (уравнение 15-1)
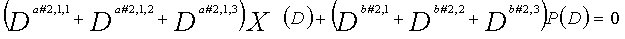 ... (уравнение 15-2)
... (уравнение 15-2)
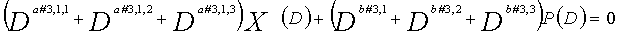 ... (уравнение 15-3)
... (уравнение 15-3)
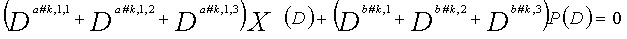 ... (уравнение 15-k)
... (уравнение 15-k)
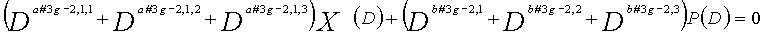 ... (уравнение 15-(3g-2))
... (уравнение 15-(3g-2))
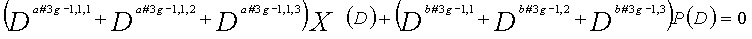 ... (уравнение 15-(3g-1))
... (уравнение 15-(3g-1))
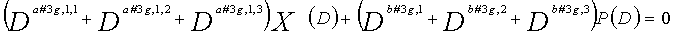 ... (уравнение 15-3g)
... (уравнение 15-3g)
В это время, X(D) является полиномиальным представлением данных (информации) X, а P(D) является полиномиальным представлением четности. Здесь, в уравнениях 15-1-15-3g, полиномы контроля по четности допускаются так, что существует три элемента в X(D) и P(D), соответственно.
При размышлении аналогичным образом, как в случае LDPC-CC с изменяющимся во времени периодом 3 и LDPC-CC с изменяющимся во времени периодом 6, увеличивается возможность достигать более высокой способности к коррекции ошибок, если условие ниже (условие #2-1) удовлетворяется в LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования 1/2 (n=2) представленном посредством полиномов контроля по четности уравнений 15-1-15-3g.
В LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования 1/2 (n=2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, соответственно.
Если i%3g=k (где k=0, 1, 2,..., 3g-1) допускается в это время, полином контроля по четности уравнения 15-(k+1) является справедливым. Например, если i=2, i%3g=2 (k=2), уравнение 16 справедливо.
[16]
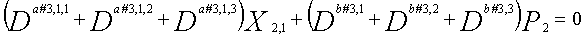 ... (уравнение 16)
... (уравнение 16)
В уравнениях 15-1-15-3g, предполагается, что a#k,1,1, a#k,1,2 и a#k,1,3 являются целыми числами (где a#k,1,1≠a#k,1,2≠a#k,1,3) (где k=1, 2, 3,..., 3g). Кроме того, предполагается, что b#k,1, b#k,2 и b#k,3 являются целыми числами (где b#k,1≠b#k,2≠b#k,3). Полином контроля по четности уравнения 15-k (k=1, 2, 3,..., 3g) называется "контрольным уравнением #k", и субматрица на основе полинома контроля по четности уравнения 15-k обозначается как k-ая субматрица Hk. Затем, рассмотрим LDPC-CC с изменяющимся во времени периодом 3g, сформированный из первой субматрицы H1, второй субматрицы H2, третьей субматрицы H3,..., 3g-ой субматрицы H3g.
Условие #2-1
В уравнениях 15-1-15-3g, комбинации порядков X(D) и P(D) удовлетворяют следующему условию:
(a#1,1,1%3, a#1,1,2%3, a#1,1,3%3), и
(b#1,1%3, b#1,2%3, b#1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0);
(a#2,1,1%3, a#2,1,2%3, a#2,1,3%3), и
(b#2,1%3, b#2,2%3, b#2,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0);
(a#3,1,1%3, a#3,1,2%3, a#3,1,3%3), и
(b#3,1%3, b#3,2%3, b#3,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0);
(a#k,1,1%3, a#k,1,2%3, a#k,1,3%3), и
(b#k,1%3, b#k,2%3, b#k,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где k=1, 2, 3,..., 3g);
(a#3g-2,1,1%3, a#3g-2,1,2%3, a#3g-2,1,3%3), и
(b#3g-2,1%3, b#3g-2,2%3, b#3g-2,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0);
(a#3g-1,1,1%3, a#3g-1,1,2%3, a#3g-1,1,3%3), и
(b#3g-1,1%3, b#3g-1,2%3, b#3g-1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0); и
(a#3g,1,1%3, a#3g,1,2%3, a#3g,1,3%3), и
(b#3g,1%3, b#3g,2%3, b#3g,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0).
С учетом простоты выполнения кодирования, желательно, чтобы один "0" присутствовал в трех элементах (b#k,1%3, b#k,2%3, b#k,3%3) (где k=1, 2,..., 3g) в уравнениях 15-1-15-3g. Это обусловлено таким признаком, что если D0=1 справедливо, и b#k,1, b#k,2 и b#k,3 являются целыми числами, равными или превышающими 0 в это время, четность P может находиться последовательно.
Кроме того, чтобы предоставлять релевантность между битами четности и битами данных с идентичным моментом времени и упрощать поиск кода, имеющего высокую корректирующую способность, желательно, чтобы один "0" присутствовал в трех элементах (a#k,1,1%3, a#k,1,2%3, a#k,1,3%3) (где k=1, 2,..., 3g).
Затем, LDPC-CC с изменяющимся во времени периодом 3g (где g=2, 3, 4, 5,...,), который учитывает простоту кодирования, рассматривается. В это время, если скорость кодирования составляет 1/2 (n=2), полиномы контроля по четности LDPC-CC могут представляться так, как показано ниже.
[17]
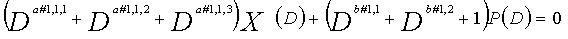 ... (уравнение 17-1)
... (уравнение 17-1)
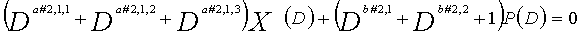 ... (уравнение 17-2)
... (уравнение 17-2)
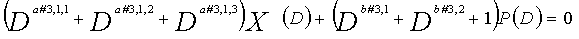 ... (уравнение 17-3)
... (уравнение 17-3)
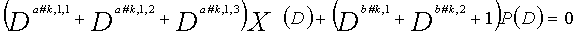 ... (уравнение 17-k)
... (уравнение 17-k)
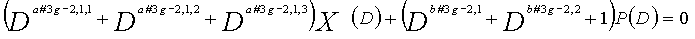 ... (уравнение 17-(3g-2))
... (уравнение 17-(3g-2))
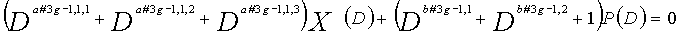 ... (уравнение 17-(3g-1))
... (уравнение 17-(3g-1))
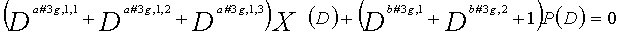 ... (уравнение 17-3g)
... (уравнение 17-3g)
В это время, X(D) является полиномиальным представлением данных (информации) X, а P(D) является полиномиальным представлением четности. Здесь, в уравнениях 17-1-17-3g, полиномы контроля по четности допускаются так, что существует три элемента в X(D) и P(D), соответственно. В LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования 1/2 (n=2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, соответственно. Если i%3g=k (где k=0, 1, 2,..., 3g-1) допускается в это время, полином контроля по четности уравнения 17-(k+1) является справедливым. Например, если i=2, i%3g=2 (k=2), уравнение 18 справедливо.
[18]
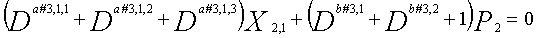 ... (уравнение 18)
... (уравнение 18)
Если условие #3-1 и условие #4-1 удовлетворяется в это время, возможность создавать код, имеющий более высокую способность к коррекции ошибок, увеличивается.
Условие #3-1
В уравнениях 17-1-17-3g, комбинации порядков X(D) удовлетворяют следующему условию:
(a#1,1,1%3, a#1,1,2%3, a#1,1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0);
(a#2,1,1%3, a#2,1,2%3, a#2,1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0);
(a#3,1,1%3, a#3,1,2%3, a#3,1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0);
(a#k,1,1%3, a#k,1,2%3, a#k,1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0) (где k=1, 2, 3,..., 3g);
(a#3g-2,1,1%3, a#3g-2,1,2%3, a#3g-2,1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0);
(a#3g-1,1,1%3, a#3g-1,1,2%3, a#3g-1,1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0); и
(a#3g,1,1%3, a#3g,1,2%3, a#3g,1,3%3) являются любыми из (0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1) или (2, 1, 0).
Помимо этого, в уравнениях 17-1-17-3g, комбинации порядков P(D) удовлетворяют следующему условию:
(b#1,1%3, b#1,2%3),
(b#2,1%3, b#2,2%3),
(b#3,1%3, b#3,2%3),...,
(b#k,1%3, b#k,2%3),...,
(b#3g-2,1%3, b#3g-2,2%3),
(b#3g-1,1%3, b#3g-1,2%3), и
(b#3g,1%3, b#3g,2%3) являются либо (1, 2), либо (2, 1) (k=1, 2, 3,..., 3g).
Условие #3-1 имеет взаимосвязь относительно уравнений 17-1-17-3g, аналогичную той, которую условие #2-1 имеет относительно уравнений 15-1-15-3g. Если условие ниже (условие #4-1) добавляется для уравнений 17-1-17-3g в дополнение к условию #3-1, возможность создавать LDPC-CC, имеющий более высокую способность к коррекции ошибок, увеличивается.
Условие #4-1
Порядки P(D) уравнений 17-1-17-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(b#1,1%3g, b#1,2%3g),
(b#2,1%3g, b#2,2%3g),
(b#3,1%3g, b#3,2%3g),...,
(b#k,1%3g, b#k,2%3g),...,
(b#3g-2,1%3g, b#3g-2,2%3g),
(b#3g-1,1%3g, b#3g-1,2%3g) и (b#3g,1%3g, b#3g,2%3g).
Возможность достижения хорошей способности к коррекции ошибок является высокой, если существует также случайность, в то время как закономерность поддерживается для позиций, в которых единицы присутствуют в матрице контроля по четности. Для LDPC-CC, имеющего изменяющийся во времени период 3g (где g=2, 3, 4, 5,...,) и скорость кодирования 1/2 (n=2), который имеет полиномы контроля по четности уравнений 17-1-17-3g, если создается код, в котором условие #4-1 применяется в дополнение к условию #3-1, можно предоставлять случайность при поддержании закономерности для позиций, в которых единицы присутствуют в матрице контроля по четности, и, следовательно, возможность достижения лучшей способности к коррекции ошибок увеличивается.
Затем, рассматривается LDPC-CC с изменяющимся во времени периодом 3g (где g=2, 3, 4, 5,...,), который предоставляет возможность простого выполнения кодирования и обеспечивает релевантность для битов четности и битов данных с идентичным моментом времени. В это время, если скорость кодирования составляет 1/2 (n=2), полиномы контроля по четности LDPC-CC могут представляться так, как показано ниже.
[19]
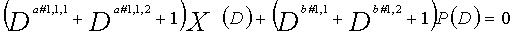 ... (уравнение 19-1)
... (уравнение 19-1)
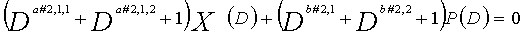 ... (уравнение 19-2)
... (уравнение 19-2)
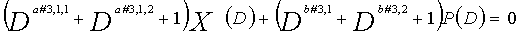 ... (уравнение 19-3)
... (уравнение 19-3)
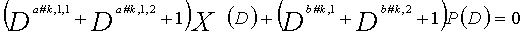 ... (уравнение 19-k)
... (уравнение 19-k)
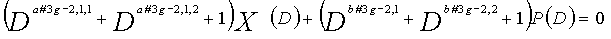 ... (уравнение 19-(3g-2))
... (уравнение 19-(3g-2))
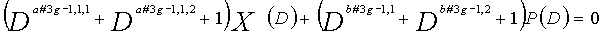 ... (уравнение 19-(3g-1))
... (уравнение 19-(3g-1))
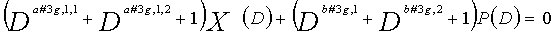 ... (уравнение 19-3g)
... (уравнение 19-3g)
В это время, X(D) является полиномиальным представлением данных (информации) X, а P(D) является полиномиальным представлением четности.
В уравнениях 19-1-19-3g, полиномы контроля по четности допускаются так, что существует три элемента в X(D) и P(D), соответственно, и элемент D0 присутствует в X(D) и P(D) (где k=1, 2, 3,..., 3g).
В LDPC-CC с изменяющимся во времени периодом 3g и скоростью кодирования 1/2 (n=2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, соответственно. Если i%3g=k (где k=0, 1, 2,..., 3g-1) допускается в это время, полином контроля по четности уравнения 19-(k+1) является справедливым. Например, если i=2, i%3g=2 (k=2), уравнение 20 справедливо.
[20]
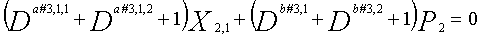 ... (уравнение 20)
... (уравнение 20)
Если следующие условие #5-1 и условие #6-1 удовлетворяются в это время, возможность создавать код, имеющий более высокую способность к коррекции ошибок, увеличивается.
Условие #5-1
В уравнениях 19-1-19-3g, комбинации порядков X(D) удовлетворяют следующему условию:
(a#1,1,1%3, a#1,1,2%3) являются (1, 2) или (2, 1);
(a#2,1,1%3, a#2,1,2%3) являются (1, 2) или (2, 1);
(a#3,1,1%3, a#3,1,2%3) являются (1, 2) или (2, 1);
(a#k,1,1%3, a#k,1,2%3) являются (1, 2) или (2, 1) (где k=1, 2, 3,..., 3g);
(a#3g-2,1,1%3, a#3g-2,1,2%3) являются (1, 2) или (2, 1),
(a#3g-1,1,1%3, a#3g-1,1,2%3) являются (1, 2) или (2, 1); и
(a#3g,1,1%3, a#3g,1,2%3) являются (1, 2) или (2, 1).
Помимо этого, в уравнениях 19-1-19-3g, комбинации порядков P(D) удовлетворяют следующему условию:
(b#1,1%3, b#1,2%3),
(b#2,1%3, b#2,2%3),
(b#3,1%3, b#3,2%3),...,
(b#k,1%3, b#k,2%3),...,
(b#3g-2,1%3, b#3g-2,2%3),
(b#3g-1,1%3, b#3g-1,2%3), и
(b#3g,1%3, b#3g,2%3) являются либо (1, 2), либо (2, 1) (где k=1, 2, 3,..., 3g).
Условие #5-1 имеет взаимосвязь относительно уравнений 19-1-19-3g, аналогичную той, которую условие #2-1 имеет относительно уравнений 15-1-15-3g. Если условие ниже (условие #6-1) добавляется для уравнений 19-1-19-3g в дополнение к условию #5-1, возможность создавать LDPC-CC, имеющий более высокую способность к коррекции ошибок, увеличивается.
Условие #6-1
Порядки X(D) уравнений 19-1-19-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,1,1%3g, a#1,1,2%3g),
(a#2,1,1%3g, a#2,1,2%3g),...,
(a#p,1,1%3g, a#p,1,2%3g),...,
(a#3g,1,1%3g, a#3g,1,2%3g) (где p=1, 2, 3,..., 3g); и
Порядки P(D) уравнений 19-1-19-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(b#1,1%3g, b#1,2%3g),
(b#2,1%3g, b#2,2%3g),
(b#3,1%3g, b#3,2%3g),...,
(b#k,1%3g, b#k,2%3g),...,
(b#3g-2,1%3g, b#3g-2,2%3g),
(b#3g-1,1%3g, b#3g-1,2%3g) и (b#3g,1%3g, b#3g,2%3g) (где k=1, 2, 3,..., 3g).
Возможность достижения хорошей способности к коррекции ошибок является высокой, если существует также случайность, в то время как закономерность поддерживается для позиций, в которых единицы присутствуют в матрице контроля по четности. Для LDPC-CC, имеющего изменяющийся во времени период 3g (где g=2, 3, 4, 5,...,) и скорость кодирования 1/2, который имеет полиномы контроля по четности уравнений 19-1-19-3g, если создается код, в котором условие #6-1 применяется в дополнение к условию #5-1, можно предоставлять случайность при поддержании закономерности для позиций, в которых единицы присутствуют в матрице контроля по четности, так что возможность достижения лучшей способности к коррекции ошибок увеличивается.
Возможность создавать код, имеющий более высокую способность к коррекции ошибок, также увеличивается, если код создается с использованием условия #6'-1 вместо условия #6-1, т.е. с использованием условия #6'-1 в дополнение к условию #5-1.
Условие #6'-1
Порядки X(D) уравнений 19-1-19-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(a#1,1,1%3g, a#1,1,2%3g),
(a#2,1,1%3g, a#2,1,2%3g),...,
(a#p,1,1%3g, a#p,1,2%3g),..., и (a#3g,1,1%3g, a#3g,1,2%3g) (где p=1, 2, 3,..., 3g); или
Порядки P(D) уравнений 19-1-19-3g удовлетворяют следующему условию: все значения, отличные от кратных 3 (т.е. 0, 3, 6,..., 3g-3) из целых чисел от 0 до 3g-1 (0, 1, 2, 3, 4,..., 3g-2, 3g-1), присутствуют в следующих значениях 6g
(b#1,1%3g, b#1,2%3g),
(b#2,1%3g, b#2,2%3g),
(b#3,1%3g, b#3,2%3g),...,
(b#k,1%3g, b#k,2%3g),...,
(b#3g-2,1%3g, b#3g-2,2%3g),
(b#3g-1,1%3g, b#3g-1,2%3g) и (b#3g,1%3g, b#3g,2%3g) (где k=1, 2, 3, ..., 3g).
Примеры LDPC-CC со скоростью кодирования 1/2 и изменяющимся во времени периодом 6, имеющего хорошую способность к коррекции ошибок, показаны в таблице 6.
Контрольный полином #2: (D596+D553+ 1)X(D)+(D586+D461+1)P(D)=0
Контрольный полином #3: (D550+D143+ 1)X(D)+(D470+D448+1)P(D)=0
Контрольный полином #4: (D470+D223+1)X(D)+(D256+D41+1)P(D)=0
Контрольный полином #5: (D89+D40+1)X(D)+(D316+D71+1)P(D)=0
Контрольный полином #6: (D320+D190+1)X(D)+(D575+D136+1)P(D)=0
Контрольный полином #2: (D547+D287+1)X(D)+(D467+D1+1)P(D)=0
Контрольный полином #3: (D289+D62+1)X(D)+(D503+D502+1)P(D)=0
Контрольный полином #4: (D401+D55+1)X(D)+(D443+D106+1)P(D)=0
Контрольный полином #6: (D136+D59+1)X(D)+(D599+D559+1)P(D)=0
Контрольный полином #2: (D595+D143+1)X(D)+(D598+D95+1)P(D)=0
Контрольный полином #3: (D97+D11+1)X(D)+(D592+D491+1)P(D)=0
Контрольный полином #4: (D50+D10+1)X(D)+(D368+D112+1)P(D)=0
Контрольный полином #5: (D286+D221+1)X(D)+(D517+D359+1)P(D)=0
Контрольный полином #6: (D407+D322+1)X(D)+(D283+D257+1)P(D)=0
LDPC-CC с изменяющимся во времени периодом g с хорошими характеристиками описан выше. Кроме того, для LDPC-CC, можно предоставлять кодированные данные (кодовое слово) посредством умножения вектора информации n на порождающую матрицу G. Т.е. кодированные данные (кодовое слово) c могут быть представлены посредством c=n*G. Здесь, порождающая матрица G находится на основе матрицы H контроля по четности, разработанной заранее. Более конкретно, порождающая матрица G означает матрицу, удовлетворяющую G*HT=0.
Например, сверточный код со скоростью кодирования 1/2 и с порождающим полиномом G=[1 G1(D)/G0(D)] рассматривается в качестве примера. В это время, G1 представляет полином с прямой связью, а G0 представляет полином с обратной связью. Если полиномиальным представлением информационной последовательности (данных) является X(D), а полиномиальным представлением последовательности четности является P(D), полином контроля по четности представляется так, как показано в уравнении 21 ниже.
[21]
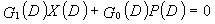 ... (уравнение 21),
... (уравнение 21),
где D является оператором задержки.
Фиг. 5 показывает информацию, связанную со сверточным кодом (7, 5). Порождающий полином сверточного кода (7, 5) представляется как G=[1 (D2+1)/(D2+D+1)]. Следовательно, полином контроля по четности является таким, как показано в уравнении 22 ниже.
[22]
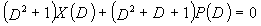 ... (уравнение 22)
... (уравнение 22)
Здесь, данные в момент времени i представляются посредством Xi и бита четности посредством Pi, и последовательность Wi передачи представляется как Wi=(Xi, Pi). Затем вектор w передачи представляется как w=(X1, P1, X2, P2,..., Xi, Pi,...,)T. Таким образом, из уравнения 22, матрица H контроля по четности может представляться так, как показано на фиг. 5. В это время, реляционное уравнение в уравнении 23 ниже справедливо.
[23]
H w=0... (уравнение 23)
Следовательно, с помощью матрицы H контроля по четности, сторона декодирования может выполнять декодирование с использованием декодирования по алгоритму доверительного распространения (BP), декодирование по алгоритму минимальной суммы, аналогичное BP-декодированию, BP-декодирование со смещением, нормализованное BP-декодирование, перемешанное BP-декодирование или тому подобное доверительное распространение, как показано в непатентном документе 4, непатентном документе 5 и непатентном документе 6.
Независимый от времени/изменяющийся во времени LDPC-CC (скорость кодирования (n-1)/n) (n: натуральное число) на основе сверточного кода
Краткое описание независимых от времени/изменяющихся во времени LDPC-CC на основе сверточного кода приводится ниже.
Рассматривается полином контроля по четности, представленный так, как показано в уравнении 24, с полиномиальными представлениями скорости кодирования R=(n-1)/n в качестве информации X1, X2,..., Xn-1 в качестве X1(D), X2(D),..., Xn-1(D) и полиномиальным представлением четности P в качестве P(D).
[24]
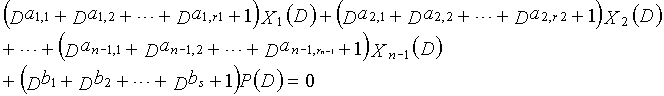 ... (уравнение 24)
... (уравнение 24)
В уравнении 24, в это время, ap,p (где p=1, 2,..., n-1 и q=1, 2,..., rp), например, является натуральным числом и удовлетворяет условию ap,1≠ap,2≠...≠ap,rp. Кроме того, bq (где q=1, 2,..., s) является натуральным числом и удовлетворяет условию b1≠b2≠...≠bs. Код, заданный посредством матрицы контроля по четности на основе полинома контроля по четности уравнения 24 в это время, называется независимым от времени LDPC-CC здесь.
Здесь, m различных полиномов контроля по четности на основе уравнения 24 предоставляются (где m является целым числом, равным или превышающим 2). Эти полиномы контроля по четности представляются так, как показано ниже.
[25]
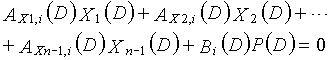 ... (уравнение 25)
... (уравнение 25)
Здесь, i=0, 1,..., m-1.
Затем информация X1, X2,..., Xn-1 в момент времени j представляется как X1,j, X2,j,..., Xn-1,j, четность P в момент времени j представляется как Pj и uj=(X1,j, X2,j,..., Xn-1,j, Pj)T.
В это время, информация X1,j, X2,j,..., Xn-1,j и четность Pj в момент времени j удовлетворяют полиному контроля по четности уравнения 26.
[26]
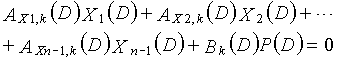 (k=j mod m)... (уравнение 26)
(k=j mod m)... (уравнение 26)
Здесь, "j mod m" является остатком после деления j на m.
Код, заданный посредством матрицы контроля по четности на основе полинома контроля по четности уравнения 26, называется изменяющимся во времени LDPC-CC здесь. В это время, независимый от времени LDPC-CC, заданный посредством полинома контроля по четности уравнения 24, и изменяющийся во времени LDPC-CC, заданный посредством полинома контроля по четности уравнения 26, имеют характеристику предоставления возможности простого последовательного нахождения битов четности посредством регистра и исключающего ИЛИ.
Например, конфигурация матрицы H LDPC-CC-контроля с изменяющимся во времени периодом 2 и скоростью кодирования 2/3 на основе уравнений 24-26 показывается на фиг. 6. Два различных контрольных полинома с изменяющимся во времени периодом 2 на основе уравнения 26 разрабатываются как "контрольное уравнение #1" и "контрольное уравнение #2". На фиг. 6, (Ha, 111) является частью, соответствующей "контрольному уравнению #1", и (Hc, 111) является частью, соответствующей "контрольному уравнению #2". Ниже, (Ha, 111) и (Hc, 111) задаются как субматрицы.
Таким образом, матрица H LDPC-CC-контроля с изменяющимся во времени периодом 2 этого предложения может быть задана посредством первой субматрицы, представляющей полином контроля по четности "контрольного уравнения #1", и посредством второй субматрицы, представляющей полином контроля по четности "контрольного уравнения #2". В частности, в матрице H контроля по четности, первая субматрица и вторая субматрица размещаются попеременно в направлении строк. Когда скорость кодирования составляет 2/3, используется конфигурация, в которой субматрица сдвигается на три столбца вправо между i-ой строкой и (i+1)-ой строкой, как показано на фиг. 6.
В случае изменяющегося во времени LDPC-CC с изменяющимся во времени периодом 2, i-ая субматрица строки и (i+1)-вая субматрица строки являются различными субматрицами. Другими словами, субматрица (Ha, 11) либо субматрица (Hc, 11) является первой субматрицей, а другая является второй субматрицей. Если вектор u передачи представляется как u=(X1,0, X2,0, P0, X1,1, X2,1, P1,..., X1,k, X2,k, Pk,...,)T, взаимосвязь Hu=0 является справедливой (см. уравнение 23).
Затем, LDPC-CC, имеющий изменяющийся во времени период m, рассматривается в случае скорости кодирования 2/3. Аналогичным образом тому, когда изменяющийся во времени период равняется 2, полиномы контроля по четности m, представленные посредством уравнения 24, предоставляются. Затем "контрольное уравнение #1", представленное посредством уравнения 24, предоставляется. "Контрольное уравнение #2-m", представленное посредством уравнения 24, предоставляется похожим способом. Данные X и четность P момента времени mi+1 представляются посредством Xmi+1 и Pmi+1, соответственно, данные X и четность P момента времени mi+2 представляются посредством Xmi+2 и Pmi+2, соответственно,..., и данные X и четность P момента времени mi+m представляются посредством Xmi+m и Pmi+m, соответственно (где i является целым числом).
Рассмотрим LDPC-CC, для которого четность Pmi+1 момента времени mi+1 находится с использованием "контрольного уравнения #1", четность Pmi+2 момента времени mi+2 находится с использованием "контрольного уравнения #2",..., и четность Pmi+m момента времени mi+m находится с использованием "контрольного уравнения #m". LDPC-CC-код этого вида предоставляет следующие преимущества:
- кодер может конфигурироваться просто, и биты четности могут находиться последовательно;
- уменьшение числа битов завершения и повышение качества приема прореживания при завершении может ожидаться.
Фиг. 7 показывает конфигурацию вышеуказанной матрицы LDPC-CC-контроля со скоростью кодирования 2/3 и изменяющимся во времени периодом m. На фиг. 7, (H1, 111) является частью, соответствующей "контрольному уравнению #1", (H2, 111) является частью, соответствующей "контрольному уравнению #2",..., и (Hm, 111) является частью, соответствующей "контрольному уравнению #m". Ниже, (H1, 111) задается как первая субматрица, (H2, 111) задается как вторая субматрица,..., и (Hm, 111) задается как m-ая субматрица.
Таким образом, матрица H LDPC-CC-контроля с изменяющимся во времени периодом m этого предложения может быть задана посредством первой субматрицы, представляющей полином контроля по четности "контрольного уравнения #1", второй субматрицы, представляющей полином контроля по четности "контрольного уравнения #2",..., и m-ой субматрицы, представляющей полином контроля по четности "контрольного уравнения #m". В частности, в матрице H контроля по четности, первая- m-ая субматрица периодически размещаются в направлении строк (см. фиг. 7). Когда скорость кодирования составляет 2/3, используется конфигурация, в которой субматрица сдвигается на три столбца вправо между i-ой строкой и (i+1)-ой строкой (см. фиг. 7).
Если вектор u передачи представляется как u=(X1,0, X2,0, P0, X1,1, X2,1, P1,..., X1,k, X2,k, Pk,...,)T, взаимосвязь Hu=0 является справедливой (см. уравнение 23).
В вышеприведенном описании, случай скорости кодирования 2/3 описан в качестве примера независимого от времени/изменяющегося во времени LDPC-CC на основе сверточного кода со скоростью кодирования (n-1)/n, но контрольная матрица независимого от времени/изменяющегося во времени LDPC-CC на основе сверточного кода со скоростью кодирования (n-1)/n может быть создана при размышлении аналогичным образом.
Другими словами, в случае скорости кодирования 2/3, на фиг. 7, (H1, 111) является частью (первой субматрицей), соответствующей "контрольному уравнению #1", (H2, 111) является частью (второй субматрицей), соответствующей "контрольному уравнению #2",..., и (Hm, 111) является частью (m-ой субматрицей), соответствующей "контрольному уравнению #m", в то время как, в случае скорости кодирования (n-1)/n, ситуация является такой, как показано на фиг. 8. Другими словами, часть (первая субматрица), соответствующая "контрольному уравнению #1", представляется посредством (H1, 11,..., 1), а часть (k-ая субматрица), соответствующая "контрольному уравнению #k" (где k=2, 3,..., m), представляется посредством (Hk,11,..., 1). В это время, число единиц части, отличной от Hk k-ой субматрицы, составляет n. В контрольной матрице H используется конфигурация, в которой субматрица сдвигается на n столбцов вправо между i-ой строкой и (i+1)-ой строкой (см. фиг. 8).
Если вектор u передачи представляется как u=(X1,0, X2,0,..., Xn-1,0, P0, X1,1, X2,1,..., Xn-1,1, P1,..., X1,k, X2,k,..., Xn-1,k, Pk,...,)T, взаимосвязь Hu=0 является справедливой (см. уравнение 23),
Фиг. 9 показывает пример конфигурации LDPC-CC-кодера, когда скорость кодирования составляет R=1/2. Как показано на фиг. 9, LDPC-CC-кодер 100 содержит, главным образом, модуль 110 вычисления данных, модуль 120 вычисления четности, модуль 130 управления весовыми коэффициентами и сумматор 140 по модулю 2 (компьютер на основе "исключающее ИЛИ").
Модуль 110 вычисления данных содержит сдвиговые регистры 111-1-111-M и умножители 112-0-112-M весовых коэффициентов.
Модуль 120 вычисления четности содержит сдвиговые регистры 121-1-121-M и умножителям 122-0-122-M весовых коэффициентов.
Сдвиговые регистры 111-1-111-M и 121-1-121-M являются регистрами, сохраняющими v1,t-i и v2,t-i (где i=0,..., M), соответственно, и в то время, когда следующий ввод выполняется, отправляют сохраненное значение в смежный сдвиговый регистр справа и сохраняют новое значение, отправляемое из смежного сдвигового регистра слева. Начальное состояние всех сдвиговых регистров - это нуль.
Умножители 112-0-112-M и 122-0-122-M весовых коэффициентов переключают значения h1 (m) и h2 (m) на 0 или 1 в соответствии с управляющим сигналом, выведенным из модуля 130 управления весовыми коэффициентами.
На основе матрицы контроля по четности, сохраненной внутренне, модуль 130 управления весовыми коэффициентами выводит значения h1 (m) и h2 (m) в это время и предоставляет их в умножители 112-0-112-M и 122-0-122-M весовых коэффициентов.
Сумматор 2140 по модулю суммирует все результаты вычисления по модулю 2 для выводов умножителей 112-0-112-M и 122-0-122-M весовых коэффициентов и вычисляет v2,t.
Посредством использования этого вида конфигурации LDPC-CC-кодер 100 может выполнять LDPC-CC-кодирование в соответствии с матрицей контроля по четности.
Если компоновка строк матрицы контроля по четности, сохраненная посредством модуля 130 управления весовыми коэффициентами, отличается построчно, LDPC-CC-кодер 100 является изменяющимся во времени сверточным кодером. Кроме того, в случае LDPC-CC со скоростью кодирования (q-1)/q должна использоваться конфигурация, в которой предоставляются (q-1) модулей 110 вычисления данных, и сумматор 2140 по модулю выполняет суммирование по модулю 2 (вычисление "исключающее ИЛИ") выводов умножителей весовых коэффициентов.
Первый вариант осуществления
Настоящий вариант осуществления описывает способ конфигурирования кода LDPC-CC на основе полинома контроля по четности с изменяющимся во времени периодом, превышающим 3, имеющего превосходную способность к коррекции ошибок.
Изменяющийся во времени период 6
Во-первых, описывается LDPC-CC с изменяющимся во времени периодом 6 в качестве примера.
Рассмотрим уравнения 27-0-27-5 в качестве полиномов контроля по четности (которые удовлетворяют 0) LDPC-CC со скоростью кодирования (n-1)/n (n является целым числом, равным или превышающим 2) и изменяющимся во времени периодом 6.
[27]
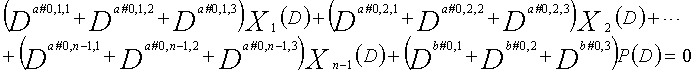 ... (уравнение 27-0)
... (уравнение 27-0)
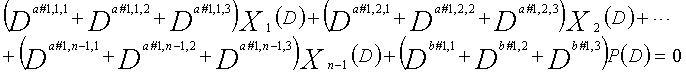 ... (уравнение 27-1)
... (уравнение 27-1)
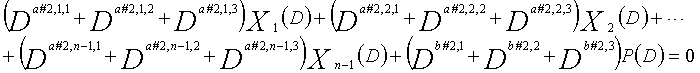 ... (уравнение 27-2)
... (уравнение 27-2)
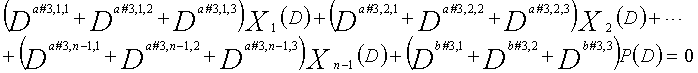 ... (уравнение 27-3)
... (уравнение 27-3)
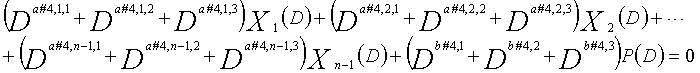 ... (уравнение 27-4)
... (уравнение 27-4)
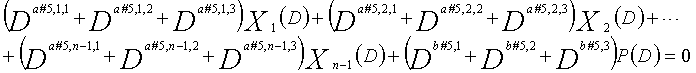 ... (уравнение 27-5)
... (уравнение 27-5)
В это время, X1(D), X2(D),..., Xn-1(D) являются полиномиальными представлениями данных (информации) X1, X2,..., Xn-1, и P(D) является полиномиальным представлением четности. В уравнениях 27-0-27-5, когда, например, скорость кодирования составляет 1/2, только элементы X1(D) и P(D) присутствуют, а элементы X2(D),..., Xn-1(D) не присутствуют. Аналогично, когда скорость кодирования составляет 2/3, только элементы X1(D), X2(D) и P(D) присутствуют, а элементы X3(D),..., Xn-1(D) не присутствуют. Другие скорости кодирования также могут рассматриваться аналогичным образом.
Здесь, уравнения 27-0-27-5 допускаются как имеющие такие полиномы контроля по четности, что три элемента присутствуют в каждом из X1(D), X2(D),..., Xn-1(D) и P(D).
Кроме того, в уравнениях 27-0-27-5, предполагается, что следующее справедливо для X1(D), X2(D),..., Xn-1(D) и P(D).
В уравнении 27-q предполагается, что a#q,p,1, a#q,p,2 и a#q,p,3 являются натуральными числами, и a#q,p,1≠a#q,p,2, a#q,p,1≠a#q,p,3 и a#q,p,2≠a#q,p,3 справедливо. Кроме того, предполагается, что b#q,1, b#q,2 и b#q,3 являются натуральными числами, и b#q,1≠b#q,2, b#q,1≠b#q,3 и b#q,1≠b#q,3 справедливо (q=0, 1, 2, 3, 4, 5; p=1, 2,..., n-1).
Полином контроля по четности уравнения 27-q называется "контрольным уравнением #q", и субматрица на основе полинома контроля по четности уравнения 27-q называется q-ой субматрицей Hq. Затем, рассмотрим LDPC-CC с изменяющимся во времени периодом 6, сформированный из 0-ой субматрицы H0, первой субматрицы H1, второй субматрицы H2, третьей субматрицы H3, четвертой субматрицы H4 и пятой субматрицы H5.
В LDPC-CC с изменяющимся во времени периодом 6 и скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, Xi,2,..., Xi,n-1, соответственно.
Если i%6=k (где k=0, 1, 2, 3, 4, 5) допускается в это время, полином контроля по четности уравнения 27-(k) является справедливым. Например, если i=8, i%6=2 (k=2), уравнение 28 справедливо.
[28]
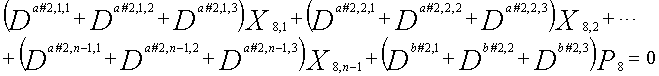 ... (уравнение 28)
... (уравнение 28)
Кроме того, когда субматрица (вектор) уравнения 27-g допускается как Hg, матрица контроля по четности может быть создана с использованием способа, описанного в "LDPC-CC на основе полинома контроля по четности".
Предполагается, что a#q,1,3=0 и b#q,3=0 (q=0, 1, 2, 3, 4, 5), с тем чтобы упрощать взаимосвязь между битами четности и информационными битами в уравнениях 27-0-27-5 и последовательно находить биты четности. Следовательно, полиномы контроля по четности (которые удовлетворяют 0) уравнений 27-0-27-5 представляются так, как показано в уравнениях 29-0-29-5.
[29]
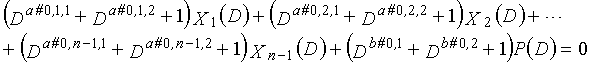 ... (уравнение 29-0)
... (уравнение 29-0)
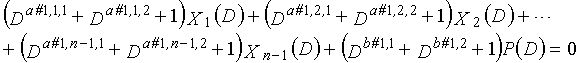 ... (уравнение 29-1)
... (уравнение 29-1)
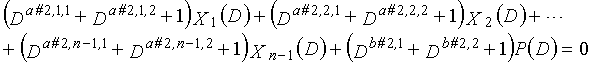 ... (уравнение 29-2)
... (уравнение 29-2)
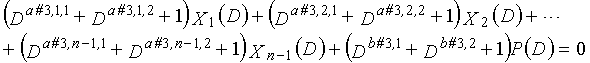 ... (уравнение 29-3)
... (уравнение 29-3)
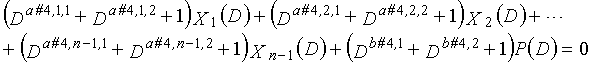 ... (уравнение 29-4)
... (уравнение 29-4)
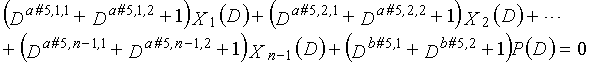 ... (уравнение 29-5)
... (уравнение 29-5)
Кроме того, предполагается, что 0-вая субматрица H0, первая субматрица H1, вторая субматрица H2, третья субматрица H3, четвертая субматрица H4 и пятая субматрица H5 представляются так, как показано в уравнениях 30-0-30-5.
[30]
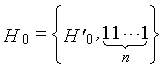 ... (уравнение 30-0)
... (уравнение 30-0)
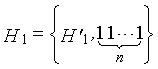 ... (уравнение 30-1)
... (уравнение 30-1)
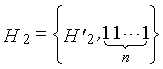 ... (уравнение 30-2)
... (уравнение 30-2)
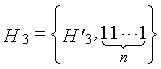 ... (уравнение 30-3)
... (уравнение 30-3)
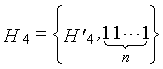 ... (уравнение 30-4)
... (уравнение 30-4)
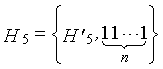 ... (уравнение 30-5)
... (уравнение 30-5)
В уравнениях 30-0-30-5, n непрерывных единиц соответствуют элементам X1(D), X2(D),..., Xn-1(D) и P(D) в каждом из уравнений 29-0-29-5.
В это время, матрица H контроля по четности может представляться так, как показано на фиг. 10. Как показано на фиг. 10, используется конфигурация, в которой субматрица сдвигается на n столбцов вправо между i-ой строкой и (i+1)-ой строкой в матрице H контроля по четности (см. фиг. 10). При условии вектора u передачи как u=(X1,0, X2,0,..., Xn-1,0, P0, X1,1, X2,1,..., Xn-1,1, P1,..., X1,k, X2,k,..., Xn-1,k, Pk,...,)T, Hu=0 справедливо.
Здесь, предлагаются условия для полиномов контроля по четности в уравнениях 29-0-29-5, при которых может достигаться высокая способность к коррекции ошибок.
Условие #1-1 и условие #1-2 ниже являются важными для элементов, связанных с X1(D), X2(D),..., Xn-1(D). В следующих условиях, "%" означает "по модулю", и, например, "α%6" представляет остаток после деления α на 6.
Условие #1-1
"a#0,1,1%6=a#1,1,1%6=a#2,1,1%6=a#3,1,1%6=a#4,1,1%6=a#5,1,1%6=vp=1 (vp=1: фиксированное значение)"
"a#0,2,1%6=a#1,2,1%6=a#2,2,1%6=a#3,2,1%6=a#4,2,1%6=a#5,2,1%6=vp=2 (vp=2: фиксированное значение)"
"a#0,3,1%6=a#1,3,1%6=a#2,3,1%6=a#3,3,1%6=a#4,3,1%6=a#5,3,1%6=vp=3 (vp=3: фиксированное значение)"
"a#0,4,1%6=a#1,4,1%6=a#2,4,1%6=a#3,4,1%6=a#4,4,1%6=a#5,4,1%6=vp=4 (vp=4: фиксированное значение)"
"a#0,k,1%6=a#1,k,1%6=a#2,k,1%6=a#3,k,1%6=a#4,k,1%6=a#5,k,1%6=vp=k (vp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,1%6=a#1,n-2,1%6=a#2,n-2,1%6=a#3,n-2,1%6=a#4,n-2,1%6=a#5,n-2,1%6=vp=n-2 (vp=n-2: фиксированное значение)"
"a#0,n-1,1%6=a#1,n-1,1%6=a#2,n-1,1%6=a#3,n-1,1%6=a#4,n-1,1%6=a#5,n-1,1%6=vp=n-1 (vp=n-1: фиксированное значение)"
и:
"b#0,1%6=b#1,1%6=b#2,1%6=b#3,1%6=b#4,1%6=b#5,1%6=w (w: фиксированное значение)"
Условие #1-2
"a#0,1,2%6=a#1,1,2%6=a#2,1,2%6=a#3,1,2%6=a#4,1,2%6=a#5,1,2%6=yp=1 (yp=1: фиксированное значение)"
"a#0,2,2%6=a#1,2,2%6=a#2,2,2%6=a#3,2,2%6=a#4,2,2%6=a#5,2,2%6=yp=2 (yp=2: фиксированное значение)"
"a#0,3,2%6=a#1,3,2%6=a#2,3,2%6=a#3,3,2%6=a#4,3,2%6=a#5,3,2%6=yp=3 (yp=3: фиксированное значение)"
"a#0,4,2%6=a#1,4,2%6=a#2,4,2%6=a#3,4,2%6=a#4,4,2%6=a#5,4,2%6=yp=4 (yp=4: фиксированное значение)"
"a#0,k,2%6=a#1,k,2%6=a#2,k,2%6=a#3,k,2%6=a#4,k,2%6=a#5,k,2%6=yp=k (yp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,2%6=a#1,n-2,2%6=a#2,n-2,2%6=a#3,n-2,2%6=a#4,n-2,2%6=a#5,n-2,2%6=yp=n-2 (yp=n-2: фиксированное значение)"
"a#0,n-1,2%6=a#1,n-1,2%6=a#2,n-1,2%6=a#3,n-1,2%6=a#4,n-1,2%6=a#5,n-1,2%6=yp=n-1 (yp=n-1: фиксированное значение)", и
"b#0,2%6=b#1,2%6=b#2,2%6=b#3,2%6=b#4,2%6=b#5,2%6=z (z: фиксированное значение)"
Посредством обозначения условия #1-1 и условия #1-2 как ограничивающих условий, LDPC-CC, который удовлетворяет ограничивающим условиям, становится регулярным LDPC-кодом и тем самым может достигать высокой способности к коррекции ошибок.
Далее описываются другие важные ограничивающие условия.
Условие #2-1
В условии #1-1, vp=1, vp=2, vp=3, vp=4,..., vp=k,..., vp=n-2, vp=n-1 и w задаются равными "1", "4" и "5". Т.е. vp=k (k=1, 2,..., n-1) и w задаются равными "1" и "являются натуральными числами, отличными от делителей изменяющегося во времени периода 6".
Условие #2-2
В условии #1-2, yp=1, yp=2, yp=3, yp=4,..., yp=k,..., yp=n-2, yp=n-1 и z задаются равными "1", "4" и "5". Т.е. yp=k (k=1, 2,..., n-1) и z задаются равными "1" и "являются натуральными числами, отличными от делителей изменяющегося во времени периода 6".
Посредством добавления ограничивающих условий (условия #2-1 и условия #2-2) или ограничивающих условий (условия #2-1 или условия #2-2), можно безусловно предоставлять эффект увеличения изменяющегося во времени периода по сравнению со случаем, в котором изменяющийся во времени период является небольшим, к примеру, изменяющийся во времени период в 2 или 3. Это подробно описывается с использованием прилагаемых чертежей.
Для простоты пояснения рассматривается случай, в котором X1(D) в полиномах контроля по четности 29-0-29-5 LDPC-CC с изменяющимся во времени периодом 6 и скоростью кодирования (n-1)/n на основе полиномов контроля по четности имеет два элемента. В это время, полиномы контроля по четности представляются так, как показано в уравнениях 31-0-31-5.
[31]
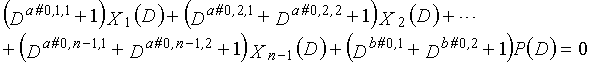 ... (уравнение 31-0)
... (уравнение 31-0)
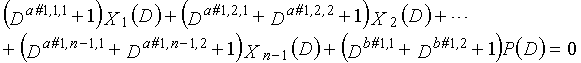 ... (уравнение 31-1)
... (уравнение 31-1)
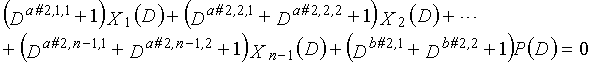 ... (уравнение 31-2)
... (уравнение 31-2)
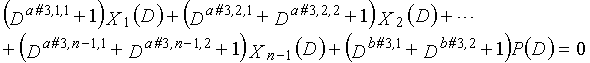 ... (уравнение 31-3)
... (уравнение 31-3)
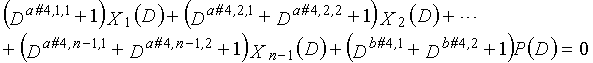 ... (уравнение 31-4)
... (уравнение 31-4)
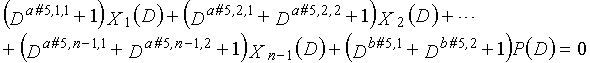 ... (уравнение 31-5)
... (уравнение 31-5)
Здесь, рассматривается случай, в котором vp=k (k=1, 2,..., n-1) и w задаются равными "3". "3" является делителем изменяющегося во времени периода 6.
Фиг. 11 показывает дерево контрольных узлов и переменных узлов, когда фокус обращен только на информацию X1, когда предполагается, что vp=1 и w задаются равными "3" и (a#0,1,1%6=a#1,1,1%6=a#2,1,1%6=a#3,1,1%6=a#4,1,1%6=a#5,1,1%6=3).
Полином контроля по четности уравнения 31-q называется "контрольным уравнением #q". На фиг. 11, дерево отрисовывается из "контрольного уравнения #0". На фиг. 11, символы "○" (один круг) и "◎" (двойной круг) представляют переменные узлы, а символ "□" (квадрат) представляет контрольный узел. Символ "○" (один круг) представляет переменный узел, связанный с X1(D), а символ "◎" (двойной круг) представляет переменный узел, связанный с Da#q,1,1X1(D). Кроме того, символ "□" (квадрат), описанный как #Y (Y=0, 1, 2, 3, 4, 5), означает контрольный узел, соответствующий полиному контроля по четности уравнения 31-Y.
На фиг. 11, значения, которые не удовлетворяют условию #2-1, т.е. vp=1, vp=2, vp=3, vp=4,..., vp=k,..., vp=n-2, vp=n-1 (k=1, 2,..., n-1) и w, задаются равными делителю, отличному от 1, из делителей изменяющегося во времени периода 6 (w=3).
В это время, как показано на фиг. 11, #Y имеет только ограниченные значения, к примеру, 0 или 3 в контрольных узлах. Т.е. даже если изменяющийся во времени период увеличивается, доверие распространяется только из конкретного полинома контроля по четности, что означает то, что эффект увеличения изменяющегося во времени периода не достигается.
Другими словами, условие для того, чтобы #Y имело только ограниченные значения, состоит в том, чтобы "задавать vp=1, vp=2, vp=3, vp=4,..., vp=k,..., vp=n-2, vp=n-1 (k=1, 2,..., n-1) и w для делителя, отличного от 1, из делителей изменяющегося во времени периода 6".
В отличие от этого, фиг. 12 показывает дерево, когда vp=k (k=1, 2,..., n-1) и w задаются равными "1" в полиноме контроля по четности. Когда vp=k (k=1, 2,..., n-1) и w задаются равными "1", условие (условие #2-1) удовлетворяется.
Как показано на фиг. 12, когда условие (условие #2-1) удовлетворяется, #Y принимает все значения от 0 до 5 в контрольных узлах. Т.е. когда условие (условие #2-1) удовлетворяется, доверие распространяется посредством всех полиномов контроля по четности, соответствующих значениям #Y. Как результат, даже когда изменяющийся во времени период увеличивается, доверие распространяется из широкого диапазона, и эффект увеличения изменяющегося во времени периода может достигаться. Т.е. очевидно, что условие #2-1 является важным условием для того, чтобы достигать эффекта увеличения изменяющегося во времени периода. Аналогично, условие #2-2 становится важным условием для того, чтобы достигать эффекта увеличения изменяющегося во времени периода.
Изменяющийся во времени период 7
Когда вышеприведенное описание учитывается, то, что изменяющийся во времени период является простым числом, является важным условием для того, чтобы достигать эффекта увеличения изменяющегося во времени периода. Это подробнее описывается ниже.
Во-первых, рассмотрим уравнения 32-0-32-6 в качестве полиномов контроля по четности (которые удовлетворяют 0) LDPC-CC со скоростью кодирования (n-1)/n (n является целым числом, равным или превышающим 2) и изменяющимся во времени периодом 7.
[32]
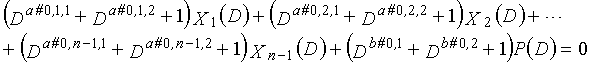 ... (уравнение 32-0)
... (уравнение 32-0)
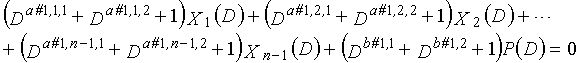 ... (уравнение 32-1)
... (уравнение 32-1)
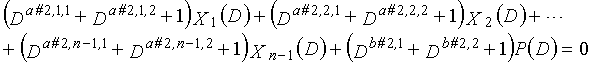 ... (уравнение 32-2)
... (уравнение 32-2)
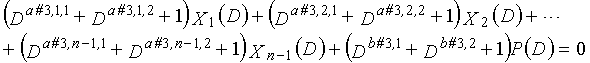 ... (уравнение 32-3)
... (уравнение 32-3)
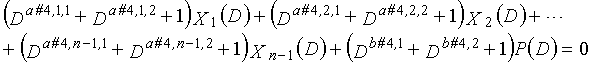 ... (уравнение 32-4)
... (уравнение 32-4)
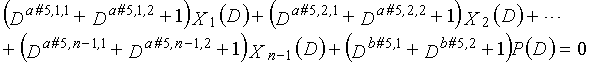 ... (уравнение 32-5)
... (уравнение 32-5)
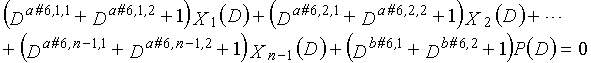 ... (уравнение 32-6)
... (уравнение 32-6)
В уравнении 32-q, предполагается, что, a#q,p,1 и a#q,p,2 являются натуральными числами, равными или превышающими 1, и a#q,p,1≠a#q,p,2 справедливо. Кроме того, предполагается, что b#q,1 и b#q,2 являются натуральными числами, равными или превышающими 1, и b#q,1≠b#q,2 справедливо (q=0, 1, 2, 3, 4, 5, 6; p=1, 2,..., n-1).
В LDPC-CC с изменяющимся во времени периодом 7 и скоростью кодирования (n-1)/n (n является целым числом, равным или превышающим 2), бит четности и информационные биты в момент времени i представляются посредством Pi и Xi,1, Xi,2,..., Xi,n-1, соответственно. В это время, если i%7=k (k=0, 1, 2, 3, 4, 5, 6), полином контроля по четности уравнения 32-(k) является справедливым.
Например, если i=8, i%7=1 (k=1), уравнение 33 справедливо.
[33]
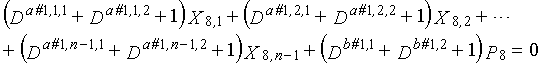 ... (уравнение 33)
... (уравнение 33)
Кроме того, когда субматрица (вектор) уравнения 32-g допускается как Hg, матрица контроля по четности может быть создана с использованием способа, описанного в "LDPC-CC на основе полинома контроля по четности". Здесь, 0-вая субматрица, первая субматрица, вторая субматрица, третья субматрица, четвертая субматрица, пятая субматрица и шестая субматрица представляются так, как показано в уравнениях 34-0-34-6.
[34]
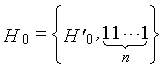 ... (уравнение 34-0)
... (уравнение 34-0)
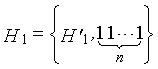 ... (уравнение 34-1)
... (уравнение 34-1)
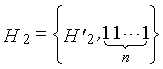 ... (уравнение 34-2)
... (уравнение 34-2)
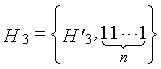 ... (уравнение 34-3)
... (уравнение 34-3)
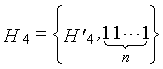 ... (уравнение 34-4)
... (уравнение 34-4)
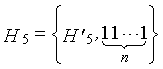 ... (уравнение 34-5)
... (уравнение 34-5)
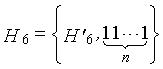 ... (уравнение 34-6)
... (уравнение 34-6)
В уравнениях 34-0-34-6, n непрерывных единиц соответствуют элементам X1(D), X2(D),..., Xn-1(D) и P(D) в каждом из уравнений 32-0-32-6.
В это время, матрица H контроля по четности может представляться так, как показано на фиг. 13. Как показано на фиг. 13, используется конфигурация, в которой субматрица сдвигается на n столбцов вправо между i-ой строкой и (i+1)-ой строкой в матрице H контроля по четности (см. фиг. 13). Когда вектор u передачи допускается равным u=(X1,0, X2,0,..., Xn-1,0, P0, X1,1, X2,1,..., Xn-1,1, P1,..., X1,k, X2,k,..., Xn-1,k, Pk,...,)T, Hu=0 является справедливой.
Здесь, условие для достижения посредством полиномов контроля по четности в уравнении 32-0-32-6 высокой способности к коррекции ошибок заключается в следующем, как в случае изменяющегося во времени периода 6. В следующих условиях, "%" означает "по модулю", и, например, "α%7" представляет остаток после деления α на 7.
Условие #1-1'
"a#0,1,1%7=a#1,1,1%7=a#2,1,1%7=a#3,1,1%7=a#4,1,1%7=a#5,1,1%7=a#6,1,1%7=vp=1 (vp=1: фиксированное значение)"
"a#0,2,1%7=a#1,2,1%7=a#2,2,1%7=a#3,2,1%7=a#4,2,1%7=a#5,2,1%7=a#6,2,1%7=vp=2 (vp=2: фиксированное значение)"
"a#0,2,1%7=a#1,2,1%7=a#2,2,1%7=a#3,2,1%7=a#4,2,1%7=a#5,2,1%7=a#6,2,1%7=vp=2 (vp=2: фиксированное значение)"
"a#0,3,1%7=a#1,3,1%7=a#2,3,1%7=a#3,3,1%7=a#4,3,1%7=a#5,3,1%7=a#6,3,1%7=vp=3 (vp=3: фиксированное значение")
"a#0,4,1%7=a#1,4,1%7=a#2,4,1%7=a#3,4,1%7=a#4,4,1%7=a#5,4,1%7=a#6,4,1%7=vp=4 (vp=4:фиксированное значение)"
"a#0,k,1%7=a#1,k,1%7=a#2,k,1%7=a#3,k,1%7=a#4,k,1%7=a#5,k,1%7=a#6,k,1%7=vp=k (vp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,1%7=a#1,n-2,1%7=a#2,n-2,1%7=a#3,n-2,1%7=a#4,n-2,1%7=a#5,n-2,1%7=a#6,n-2,1%7=vp=n-2 (vp=n-2: фиксированное значение)"
"a#0,n-1,1%7=a#1,n-1,1%7=a#2,n-1,1%7=a#3,n-1,1%7=a#4,n-1,1%7=a#5,n-1,1%7=a#6,n-1,1%7=vp=n-1 (vp=n-1: фиксированное значение)", и
"b#0,1%7=b#1,1%7=b#2,1%7=b#3,1%7=b#4,1%7=b#5,1%7=b#6,1%7=w (w: фиксированное значение)"
Условие #1-2'
"a#0,1,2%7=a#1,1,2%7=a#2,1,2%7=a#3,1,2%7=a#4,1,2%7=a#5,1,2%7=a#6,1,2%7=yp=1 (yp=1: фиксированное значение)"
"a#0,2,2%6=a#1,2,2%6=a#2,2,2%6=a#3,2,2%6=a#4,2,2%6=a#5,2,2%6=yp=2 (yp=2: фиксированное значение)"
"a#0,3,2%7=a#1,3,2%7=a#2,3,2%7=a#3,3,2%7=a#4,3,2%7=a#5,3,2%7=a#6,3,2%7=yp=3 (yp=3: фиксированное значение)"
"a#0,4,2%7=a#1,4,2%7=a#2,4,2%7=a#3,4,2%7=a#4,4,2%7=a#5,4,2%7=a#6,4,2%7=yp=4 (yp=4: фиксированное значение)"
"a#0,k,2%7=a#1,k,2%7=a#2,k,2%7=a#3,k,2%7=a#4,k,2%7=a#5,k,2%7=a#6,k,2%7=yp=k (yp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,2%7=a#1,n-2,2%7=a#2,n-2,2%7=a#3,n-2,2%7=a#4,n-2,2%7=a#5,n-2,2%7=a#6,n-2,2%7=yp=n-2 (yp=n-2: фиксированное значение)"
"a#0,n-1,2%7=a#1,n-1,2%7=a#2,n-1,2%7=a#3,n-1,2%7=a#4,n-1,2%7=a#5,n-1,2%7=a#6,n-1,2%7=yp=n-1 (yp=n-1: фиксированное значение)", и
"b#0,2%7=b#1,2%7=b#2,2%7=b#3,2%7=b#4,2%7=b#5,2%7=b#6,2%7=z (z: фиксированное значение)"
Посредством обозначения условия #1-1' и условия #1-2' как ограничивающих условий, LDPC-CC, который удовлетворяет ограничивающим условиям, становится регулярным LDPC-кодом и тем самым может достигать высокой способности к коррекции ошибок.
В случае изменяющегося во времени периода 6, достижение высокой способности к коррекции ошибок дополнительно требует условия #2-1 и условия #2-2 либо условия #2-1 или условия #2-2. В отличие от этого, когда изменяющийся во времени период является простым числом, как в случае изменяющегося во времени периода 7, условие, соответствующее условию #2-1 и условию #2-2 либо условию #2-1 или условию #2-2, требуемым в случае изменяющегося во времени периода 6, является необязательным.
Другими словами, в условии #1-1', значения vp=1, vp=2, vp=3, vp=4,..., vp=k,..., vp=n-2, vp=n-1 (k=1, 2,..., n-1) и w могут быть одним из значений "0, 1, 2, 3, 4, 5 и 6".
Кроме того, в условии #1-2', значения yp=1, yp=2, yp=3, yp=4,..., yp=k,..., yp=n-2, yp=n-1 (k=1, 2,..., n-1) и z могут быть одним из значений "0, 1, 2, 3, 4, 5 и 6".
Причина описывается ниже.
Для простоты пояснения рассматривается случай, в котором X1(D) в полиномах контроля по четности 32-0-32-6 LDPC-CC с изменяющимся во времени периодом 7 и скоростью кодирования (n-1)/n на основе полиномов контроля по четности имеет два элемента. В этом случае, полиномы контроля по четности представляются так, как показано в уравнениях 35-0-35-6.
[35]
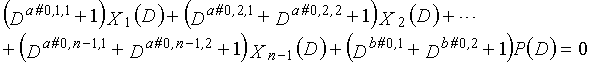 ... (уравнение 35-0)
... (уравнение 35-0)
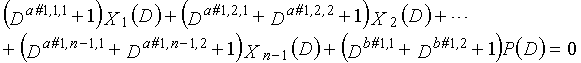 ... (уравнение 35-1)
... (уравнение 35-1)
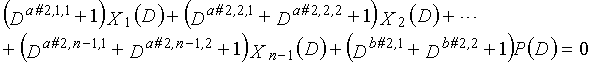 ... (уравнение 35-2)
... (уравнение 35-2)
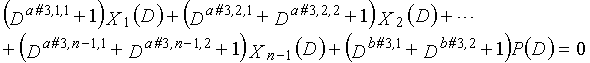 ... (уравнение 35-3)
... (уравнение 35-3)
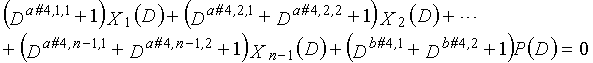 ... (уравнение 35-4)
... (уравнение 35-4)
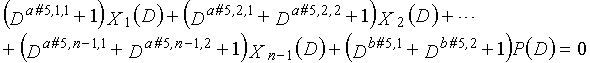 ... (уравнение 35-5)
... (уравнение 35-5)
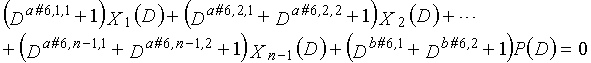 ... (уравнение 35-6)
... (уравнение 35-6)
Здесь, рассматривается случай, в котором vp=k (k=1, 2,..., n-1) и w задаются равными "2".
Фиг. 14 показывает дерево контрольных узлов и переменных узлов, когда фокус обращен только на информацию X1, когда vp=1 и w задаются равными "2" и a#0,1,1%7=a#1,1,1%7=a#2,1,1%7=a#3,1,1%7=a#4,1,1%7=a#5,1,1%7=a#6,1,1%7=2.
Полином контроля по четности уравнения 35-q называется "контрольным уравнением #q". На фиг. 14, дерево отрисовывается из "контрольного уравнения #0". На фиг. 14, символы "○" (один круг) и "◎" (двойной круг) представляют переменные узлы, а символ "□" (квадрат) представляет контрольный узел. Символ "○" (один круг) представляет переменный узел, связанный с X1(D), а символ "◎" (двойной круг) представляет переменный узел, связанный с Da#q,1,1X1(D). Кроме того, символ "□" (квадрат), описанный как #Y (Y=0, 1, 2, 3, 4, 5, 6), означает контрольный узел, соответствующий полиному контроля по четности уравнения 35-Y.
В случае изменяющегося во времени периода 6, например, как показано на фиг. 11, могут быть случаи, в которых #Y имеет только ограниченное значение, и контрольные узлы соединяются только с ограниченными полиномами контроля по четности. В отличие от этого, когда изменяющийся во времени период составляет 7 (простое число), к примеру, изменяющийся во времени период 7, как показано на фиг. 14, #Y имеют все значения от 0 до 6, и контрольные узлы соединяются со всеми полиномами контроля по четности. Таким образом, доверие распространяется посредством всех полиномов контроля по четности, соответствующих значениям #Y. Как результат, даже когда изменяющийся во времени период увеличивается, доверие распространяется из широкого диапазона, и можно достигать эффекта увеличения изменяющегося во времени периода. Хотя фиг. 14 показывает дерево, когда a#q,1,1%7 (q=0, 1, 2, 3, 4, 5, 6) задается равным "2", контрольные узлы могут соединяться со всеми применимыми полиномами контроля по четности, если a#q,1,1%7 задается равным какому-либо значению, отличному от "0".
Таким образом, очевидно, что если изменяющийся во времени период задается равным простому числу, таким образом, ограничивающие условия, связанные с настройками параметров для достижения высокой способности к коррекции ошибок, существенно смягчаются по сравнению со случаем, в котором изменяющийся во времени период не является простым числом. Когда ограничивающие условия смягчаются, добавление другого ограничивающего условия предоставляет возможность достижения более высокой способности к коррекции ошибок. Такой способ конфигурирования кода подробно описывается ниже.
Изменяющийся во времени период q (q является простым числом, превышающим 3): (уравнение 36)
Во-первых, рассматривается случай, в котором g-ый (g=0, 1,..., q-1) полином контроля по четности со скоростью кодирования (n-1)/n и изменяющимся во времени периодом q (q является простым числом, превышающим 3) представляется так, как показано в уравнении 36.
[36]
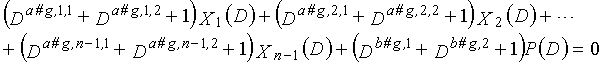 ... (уравнение 36)
... (уравнение 36)
В уравнении 36, также предполагается, что a#g,p,1 и a#g,p,2 являются натуральными числами, равными или превышающими 1, и a#g,p,1≠a#g,p,2 справедливо. Кроме того, также предполагается, что b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 справедливо (g=0, 1, 2,..., q-2, q-1; p=1, 2,..., n-1).
Аналогично вышеприведенному описанию, условие #3-1 и условие #3-2, описанные ниже, являются одним из важных требований для достижения посредством LDPC-CC высокой способности к коррекции ошибок. В следующих условиях, "%" означает "по модулю", и, например, "α%q" представляет остаток после деления α на q.
Условие #3-1
"a#0,1,1%q=a#1,1,1%q=a#2,1,1%q=a#3,1,1%q=... =a#g,1,1%q=... =a#q-2,1,1%q=a#q-1,1,1%q=vp=1 (vp=1: фиксированное значение)"
"a#0,2,1%q=a#1,2,1%q=a#2,2,1%q=a#3,2,1%q=... =a#g,2,1%q=... =a#q-2,2,1%q=a#q-1,2,1%q=vp=2 (vp=2: фиксированное значение)"
"a#0,3,1%q=a#1,3,1%q=a#2,3,1%q=a#3,3,1%q=... =a#g,3,1%q=... =a#q-2,3,1%q=a#q-1,3,1%q=vp=3 (vp=3: фиксированное значение)"
"a#0,4,1%q=a#1,4,1%q=a#2,4,1%q=a#3,4,1%q=... =a#g,4,1%q=... =a#q-2,4,1%q=a#q-1,4,1%q=vp=4 (vp=4: фиксированное значение)"
"a#0,k,1%q=a#1,k,1%q=a#2,k,1%q=a#3,k,1%q=... =a#g,k,1%q=... =a#q-2,k,1%q=a#q-1,k,1%q=vp=k (vp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,1%q=a#1,n-2,1%q=a#2,n-2,1%q=a#3,n-2,1%q=... =a#g,n-2,1%q=... =a#q-2,n-2,1%q=a#q-1,n-2,1%q=vp=n-2 (vp=n-2: фиксированное значение)"
"a#0,n-1,1%q=a#1,n-1,1%q=a#2,n-1,1%q=a#3,n-1,1%q=... =a#g,n-1,1%q=... =a#q-2,n-1,1%q=a#q-1,n-1,1%q=vp=n-1 (vp=n-1: фиксированное значение)", и
"b#0,1%q=b#1,1%q=b#2,1%q=b#3,1%q=... =b#g,1%q=... =b#q-2,1%q=b#q-1,1%q=w (w: фиксированное значение)"
Условие #3-2
"a#0,1,2%q=a#1,1,2%q=a#2,1,2%q=a#3,1,2%q=... =a#g,1,2%q=... =a#q-2,1,2%q=a#q-1,1,2%q=yp=1 (yp=1: фиксированное значение)"
"a#0,2,2%q=a#1,2,2%q=a#2,2,2%q=a#3,2,2%q=... =a#g,2,2%q=... =a#q-2,2,2%q=a#q-1,2,2%q=yp=2 (yp=2: фиксированное значение)"
"a#0,3,2%q=a#1,3,2%q=a#2,3,2%q=a#3,3,2%q=... =a#g,3,2%q=... =a#q-2,3,2%q=a#q-1,3,2%q=yp=3 (yp=3: фиксированное значение)"
"a#0,4,2%q=a#1,4,2%q=a#2,4,2%q=a#3,4,2%q=... =a#g,4,2%q=... =a#q-2,4,2%q=a#q-1,4,2%q=yp=4 (yp=4: фиксированное значение)"
"a#0,k,2%q=a#1,k,2%q=a#2,k,2%q=a#3,k,2%q=... =a#g,k,2%q=... =a#q-2,k,2%q=a#q-1,k,2%q=yp=k (yp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,2%q=a#1,n-2,2%q=a#2,n-2,2%q=a#3,n-2,2%q=... =a#g,n-2,2%q=... =a#q-2,n-2,2%q=a#q-1,n-2,2%q=yp=n-2 (yp=n-2: фиксированное значение)"
"a#0,n-1,2%q=a#1,n-1,2%q=a#2,n-1,2%q=a#3,n-1,2%q=... =a#g,n-1,2%q=... =a#q-2,n-1,2%q=a#q-1,n-1,2%q=yp=n-1 (yp=n-1: фиксированное значение)", и
"b#0,2%q=b#1,2%q=b#2,2%q=b#3,2%q=... =b#g,2%q=... =b#q-2,2%q=b#q-1,2%q=z (z: фиксированное значение)"
Помимо этого, когда условие #4-1 или условие #4-2 справедливо для набора (vp=1, yp=1), (vp=2, yp=2), (vp=3, yp=3),..., (vp=k, yp=k),..., (vp=n-2, yp=n-2), (vp=n-1, yp=n-1) и (w, z), высокая способность к коррекции ошибок может достигаться. Здесь, k=1, 2,..., n-1.
Условие #4-1
Рассмотрим (vp=i, yp=i) и (vp=j, yp=j), где предполагается, что i=1, 2,..., n-1,j=1, 2,..., n-1 и i≠j. В это время, i и j (i≠j) присутствуют, если (vp=i, yp=i)≠(vp=j, yp=j) и (vp=i, yp=i)≠(yp=j, vp=j) справедливо.
Условие #4-2
Рассмотрим (vp=i, yp=i) и (w, z), где предполагается, что i=1, 2,..., n-1. В это время, i присутствует, если (vp=i, yp=i)≠(w, z) и (vp=i, yp=i)≠(z, w) справедливо.
Таблица 7 показывает полиномы контроля по четности LDPC-CC с изменяющимся во времени периодом 7 и скоростями кодирования 1/2 и 2/3.
Контрольный полином #1: (D577+D426+1)X1(D)+(D477+D488+1)P(D)=0
Контрольный полином #2: (D500+D370+1)X1(D)+(D407+D502+1)P(D)=0
Контрольный полином #3: (D563+D230+1)X1(D)+(D197+D411+1)P(D)=0
Контрольный полином #4: (D542+D76+1)X1(D)+(D1+D33+1)P(D)=0
Контрольный полином #5: (D535+D517+1)X1(D)+(D344+D75+1)P(D)=0
Контрольный полином #6: (D570+D538+1)X1(D)+(D512+D572+1)P(D)=0
(D575+D81+1)X1(D)+(D597+D402+1)X2(D)+(D558+D118+1)P(D)=0
Контрольный полином #1:
(D526+D186+1)X1(D)+(D576+D157+1)X2(D)+(D586+D174+1)P(D)=0
Контрольный полином #2:
(D533+D410+1)X1(D)+(D534+D535+1)X2(D)+(D411+D272+1)P(D)=0
Контрольный полином #3:
(D554+D473+1)X1(D)+(D590+D38+1)X2(D)+(D243+D230+1)P(D)=0
Контрольный полином #4:
(D582+D137+1)X1(D)+(D527+D570+1)X2(D)+(D474+D55+1)P(D)=0
Контрольный полином #5:
(D547+D375+1)X1(D)+(D590+D402+1)X2(D)+(D117+D363+1)P(D)=0
(D533+D592+1)X1(D)+(D590+D150+1)X2(D)+(D523+D580+1)P(D)=0
В таблице 7, для кода со скоростью кодирования 1/2,
"a#0,1,1%7=a#1,1,1%7=a#2,1,1%7=a#3,1,1%7=a#4,1,1%7=a#5,1,1%7=a#6,1,1%7=vp=1=3"
"b#0,1%7=b#1,1%7=b#2,1%7=b#3,1%7=b#4,1%7=b#5,1%7=b#6,1%7=w=1"
"a#0,1,2%7=a#1,1,2%7=a#2,1,2%7=a#3,1,2%7=a#4,1,2%7=a#5,1,2%7=a#6,1,2%7=yp=1=6"
"b#0,2%7=b#1,2%7=b#2,2%7=b#3,2%7=b#4,2%7=b#5,2%7=b#6,2%7=z=5" поддерживаются.
В это время, поскольку (vp=1, yp=1)=(3, 6), (w, z)=(1, 5), условие #4-2 справедливо.
Аналогично, в таблице 7, для кода со скоростью кодирования 2/3,
"a#0,1,1%7=a#1,1,1%7=a#2,1,1%7=a#3,1,1%7=a#4,1,1%7=a#5,1,1%7=a#6,1,1%7=vp=1=1"
"a#0,2,1%7=a#1,2,1%7=a#2,2,1%7=a#3,2,1%7=a#4,2,1%7=a#5,2,1%7=a#6,2,1%7=vp=2=2"
"b#0,1%7=b#1,1%7=b#2,1%7=b#3,1%7=b#4,1%7=b#5,1%7=b#6,1%7=w=5"
"a#0,1,2%7=a#1,1,2%7=a#2,1,2%7=a#3,1,2%7=a#4,1,2%7=a#5,1,2%7=a#6,1,2%7=yp=1=4"
"a#0,2,2%7=a#1,2,2%7=a#2,2,2%7=a#3,2,2%7=a#4,2,2%7=a#5,2,2%7=a#6,2,2%7=yp=2=3"
"b#0,2%7=b#1,2%7=b#2,2%7=b#3,2%7=b#4,2%7=b#5,2%7=b#6,2%7=z=6" поддерживается.
В это время, поскольку (vp=1, yp=1)=(1, 4), (vp=2, yp=2)=(2, 3) и (w, z)=(5, 6), условие #4-1 и условие #4-2 справедливо.
Кроме того, таблица 8 показывает полиномы контроля по четности LDPC-CC со скоростью кодирования 4/5, когда изменяющийся во времени период равняется 11, в качестве примера.
(D200+D9+1)X1(D)+(D234+D204+1)X2(D)+(D158+D63+1)X3(D)+(D181+D73+1)X4(D)+(D232+D98+1)P(D)=0
Контрольный полином #1:
(D200+D240+1)X1(D)+(D223+D83+1)X2(D)+(D235+D52+1)X3(D)+(D159+D128+1)X4(D)+(D166+D230+1)P(D)=0
Контрольный полином #2:
(D211+D75+1)X1(D)+(D234+D171+1)X2(D)+(D235+D96+1)X3(D)+(D159+D128+1)X4(D)+(D1+D43+1)P(D)=0
Контрольный полином #3:
(D145+D97+1)X1(D)+(D223+D61+1)X2(D)+(D235+D206+1)X3(D)+(D203+D73+1)X4(D)+(D78+D175+1)P(D)=0
Контрольный полином #4:
(D145+D119+1)X1(D)+(D212+D160+1)X2(D)+(D202+D30+1)X3(D)+(D214+D194+1)X4(D)+(D210+D230+1)P(D)=0
Контрольный полином #5:
(D167+D174+1)X1(D)+(D223+D94+1)X2(D)+(D235+D8+1)X3(D)+(D225+D95+1)X4(D)+(D56+D10+1)P(D)=0
Контрольный полином #6:
(D222+D185+1)X1(D)+(D234+D193+1)X2(D)+(D202+D74+1)X3(D)+(D236+D205+1)X4(D)+(D122+D153+1)P(D)=0
(D178+D64+1)X1(D)+(D201+D160+1)X2(D)+(D224+D206+1)X3(D)+(D159+D7+1)X4(D)+(D45+D142+1)P(D)=0
Контрольный полином #8:
(D189+D9+1)X1(D)+(D179+D182+1)X2(D)+(D235+D118+1)X3(D)+(D236+D106+1)X4(D)+(D78+D131+1)P(D)=0
Контрольный полином #9:
(D200+D163+1)X1(D)+(D223+D61+1)X2(D)+(D235+D8+1)X3(D)+(D148+D238+1)X4(D)+(D177+D131+1)P(D)=0
Контрольный полином #10:
(D222+D218+1)X1(D)+(D190+D226+1)X2(D)+(D213+D195+1)X3(D)+(D214+D172+1)X4(D)+(D1+D43+1)P(D)=0
Посредством задания более серьезными ограничивающих условий
(условие #4-1, условие #4-2), более вероятно иметь возможность формировать LDPC-CC с изменяющимся во времени периодом q (q является простым числом, равным или превышающим 3) с более высокой способностью к коррекции ошибок. Условие состоит в том, что условие #5-1 и условие #5-2 либо условие #5-1 или условие #5-2 должны быть справедливыми.
Условие #5-1
Рассмотрим (vp=i, yp=i) и (vp=j, yp=j), где предполагается, что i=1, 2,..., n-1,j=1, 2,..., n-1 и i≠j. В это время, (vp=i, yp=i)≠(vp=j, yp=j) и (vp=i, yp=i)≠(yp=j, vp=j) справедливо для всех i и j (i≠j).
Условие #5-2
Рассмотрим (vp=i, yp=i) и (w, z), где предполагается, что i=1, 2,..., n-1. В это время, (vp=i, yp=i)≠(w, z) и (vp=i, yp=i)≠(z, w) справедливо для всех i.
Кроме того, когда vp=i≠yp=i (i=1, 2,..., n-1), и w≠z справедливо, можно подавлять возникновение коротких контуров на графе Таннера.
Помимо этого, когда 2n<q, если (vp=i, yp=i) и (z, w) являются различными значениями, более вероятно иметь возможность формировать LDPC-CC с изменяющимся во времени периодом q (q является простым числом, превышающим 3) с более высокой способностью к коррекции ошибок.
Кроме того, когда 2n≥q, если (vp=i, yp=i) и (z, w) задаются так, что все значения 0, 1, 2,..., q-1 присутствуют, более вероятно иметь возможность формировать LDPC-CC с изменяющимся во времени периодом q (q является простым числом, превышающим 3) с более высокой способностью к коррекции ошибок.
В вышеприведенном описании, уравнение 36, имеющее три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), обработано в качестве g-го полинома контроля по четности LDPC-CC с изменяющимся во времени периодом q (q является простым числом, превышающим 3). В уравнении 36, также вероятно иметь возможность достигать высокой способности к коррекции ошибок, когда число элементов любого из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 1 или 2. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 1 или 2. В случае изменяющегося во времени периода q существуют q полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 1 или 2 для всех q полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 1 или 2 для всех q полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 1 или 2 для любого числа (равного или меньшего q-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., Xn-1(D) и P(D). В этом случае, удовлетворение вышеописанному условию составляет важное условие в достижении высокой способности к коррекции ошибок. Тем не менее, условие, связанное с удаленными элементами, является необязательным.
Даже когда число элементов любого из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 4 или более, также вероятно иметь возможность достигать высокой способности к коррекции ошибок. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 4 или более. В случае изменяющегося во времени периода q существуют q полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 4 или более для всех q полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 4 или более для всех q полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 4 или более для любого числа (равного или меньшего q-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., Xn-1(D) и P(D). В это время, вышеописанное условие исключается для добавленных элементов.
Между прочим, уравнение 36 является g-ым полиномом контроля по четности LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом q (q является простым числом, превышающим 3). В этом уравнении, в случае, например, скорости кодирования 1/2, g-ый полином контроля по четности представляется так, как показано в уравнении 37-1. Кроме того, в случае скорости кодирования 2/3, g-ый полином контроля по четности представляется так, как показано в уравнении 37-2. Кроме того, в случае скорости кодирования 3/4, g-ый полином контроля по четности представляется так, как показано в уравнении 37-3. Кроме того, в случае скорости кодирования 4/5, g-ый полином контроля по четности представляется так, как показано в уравнении 37-4. Кроме того, в случае скорости кодирования 5/6, g-ый полином контроля по четности представляется так, как показано в уравнении 37-5.
[37]
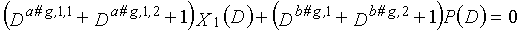 ... (уравнение 37-1)
... (уравнение 37-1)
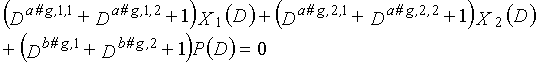 ... (уравнение 37-2)
... (уравнение 37-2)
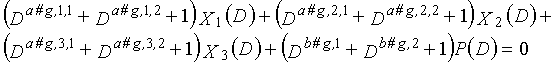 ... (уравнение 37-3)
... (уравнение 37-3)
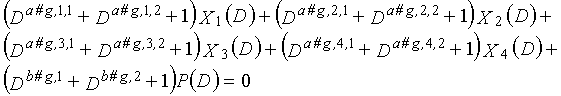 ... (уравнение 37-4)
... (уравнение 37-4)
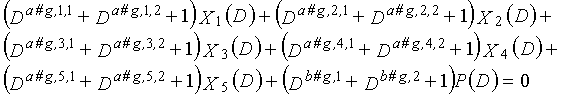 ... (уравнение 37-5)
... (уравнение 37-5)
Изменяющийся во времени период q (q является простым числом, превышающим 3): уравнение 38
Затем, рассматривается случай, в котором g-ый (g=0, 1,..., q-1) полином контроля по четности со скоростью кодирования (n-1)/n и изменяющимся во времени периодом q (q является простым числом, превышающим 3) представляется так, как показано в уравнении 38.
[38]
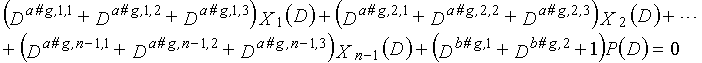 ... (уравнение 38)
... (уравнение 38)
В уравнении 38, предполагается, что a#g,p,1, a#g,p,2 и a#g,p,3 являются натуральными числами, равными или превышающими 1, и a#g,p,1≠a#g,p,2, a#g,p,1≠a#g,p,3 и a#g,p,2≠a#g,p,3 справедливо. Кроме того, предполагается, что b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 справедливо (g=0, 1, 2,..., q-2, q-1; p=1, 2,..., n-1).
Аналогично вышеприведенному описанию, условие #6-1, условие #6-2 и условие #6-3, описанные ниже, являются одним из важных требований для достижения посредством LDPC-CC высокой способности к коррекции ошибок. В следующих условиях, "%" означает "по модулю", и, например, "α%q" представляет остаток после деления α на q.
Условие #6-1
"a#0,1,1%q=a#1,1,1%q=a#2,1,1%q=a#3,1,1%q=... =a#g,1,1%q=... =a#q-2,1,1%q=a#q-1,1,1%q=vp=1 (vp=1: фиксированное значение)"
"a#0,2,1%q=a#1,2,1%q=a#2,2,1%q=a#3,2,1%q=... =a#g,2,1%q=... =a#q-2,2,1%q=a#q-1,2,1%q=vp=2 (vp=2: фиксированное значение)"
"a#0,3,1%q=a#1,3,1%q=a#2,3,1%q=a#3,3,1%q=... =a#g,3,1%q=... =a#q-2,3,1%q=a#q-1,3,1%q=vp=3 (vp=3: фиксированное значение)"
"a#0,4,1%q=a#1,4,1%q=a#2,4,1%q=a#3,4,1%q=... =a#g,4,1%q=... =a#q-2,4,1%q=a#q-1,4,1%q=vp=4 (vp=4: фиксированное значение)"
"a#0,k,1%q=a#1,k,1%q=a#2,k,1%q=a#3,k,1%q=... =a#g,k,1%q=... =a#q-2,k,1%q=a#q-1,k,1%q=vp=k (vp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,1%q=a#1,n-2,1%q=a#2,n-2,1%q=a#3,n-2,1%q=... =a#g,n-2,1%q=... =a#q-2,n-2,1%q=a#q-1,n-2,1%q=vp=n-2 (vp=n-2: фиксированное значение)"
"a#0,n-1,1%q=a#1,n-1,1%q=a#2,n-1,1%q=a#3,n-1,1%q=... =a#g,n-1,1%q=... =a#q-2,n-1,1%q=a#q-1,n-1,1%q=vp=n-1 (vp=n-1: фиксированное значение)", и
"b#0,1%q=b#1,1%q=b#2,1%q=b#3,1%q=... =b#g,1%q=... =b#q-2,1%q=b#q-1,1%q=w (w: фиксированное значение)"
Условие #6-2
"a#0,1,2%q=a#1,1,2%q=a#2,1,2%q=a#3,1,2%q=... =a#g,1,2%q=... =a#q-2,1,2%q=a#q-1,1,2%q=yp=1 (yp=1: фиксированное значение)"
"a#0,2,2%q=a#1,2,2%q=a#2,2,2%q=a#3,2,2%q=... =a#g,2,2%q=... =a#q-2,2,2%q=a#q-1,2,2%q=yp=2 (yp=2: фиксированное значение)"
"a#0,3,2%q=a#1,3,2%q=a#2,3,2%q=a#3,3,2%q=... =a#g,3,2%q=... =a#q-2,3,2%q=a#q-1,3,2%q=yp=3 (yp=3: фиксированное значение)"
"a#0,4,2%q=a#1,4,2%q=a#2,4,2%q=a#3,4,2%q=... =a#g,4,2%q=... =a#q-2,4,2%q=a#q-1,4,2%q=yp=4 (yp=4: фиксированное значение)"
"a#0,k,2%q=a#1,k,2%q=a#2,k,2%q=a#3,k,2%q=... =a#g,k,2%q=... =a#q-2,k,2%q=a#q-1,k,2%q=yp=k (yp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,2%q=a#1,n-2,2%q=a#2,n-2,2%q=a#3,n-2,2%q=... =a#g,n-2,2%q=... =a#q-2,n-2,2%q=a#q-1,n-2,2%q=yp=n-2 (yp=n-2: фиксированное значение)"
"a#0,n-1,2%q=a#1,n-1,2%q=a#2,n-1,2%q=a#3,n-1,2%q=... =a#g,n-1,2%q=... =a#q-2,n-1,2%q=a#q-1,n-1,2%q=yp=n-1 (yp=n-1: фиксированное значение)", и
"b#0,2%q=b#1,2%q=b#2,2%q=b#3,2%q=... =b#g,2%q=... =b#q-2,2%q=b#q-1,2%q=z (z: фиксированное значение)"
Условие #6-3
"a#0,1,3%q=a#1,1,3%q=a#2,1,3%q=a#3,1,3%q=... =a#g,1,3%q=... =a#q-2,1,3%q=a#q-1,1,3%q=sp=1 (sp=1: фиксированное значение)"
"a#0,2,3%q=a#1,2,3%q=a#2,2,3%q=a#3,2,3%q=... =a#g,2,3%q=... =a#q-2,2,3%q=a#q-1,2,3%q=sp=2 (sp=2: фиксированное значение)"
"a#0,3,3%q=a#1,3,3%q=a#2,3,3%q=a#3,3,3%q=... =a#g,3,3%q=... =a#q-2,3,3%q=a#q-1,3,3%q=sp=3 (sp=3: фиксированное значение)"
"a#0,4,3%q=a#1,4,3%q=a#2,4,3%q=a#3,4,3%q=... =a#g,4,3%q=... =a#q-2,4,3%q=a#q-1,4,3%q=sp=4 (sp=4: фиксированное значение)"
"a#0,k,3%q=a#1,k,3%q=a#2,k,3%q=a#3,k,3%q=... =a#g,k,3%q=... =a#q-2,k,3%q=a#q-1,k,3%q=sp=k (sp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)
"a#0,n-2,3%q=a#1,n-2,3%q=a#2,n-2,3%q=a#3,n-2,3%q=... =a#g,n-2,3%q=... =a#q-2,n-2,3%q=a#q-1,n-2,3%q=sp=n-2 (sp=n-2: фиксированное значение)"
"a#0,n-1,3%q=a#1,n-1,3%q=a#2,n-1,3%q=a#3,n-1,3%q=... =a#g,n-1,3%q=... =a#q-2,n-1,3%q=a#q-1,n-1,3%q=sp=n-1 (sp=n-1: фиксированное значение)"
Помимо этого, рассмотрим набор (vp=1, yp=1, sp=1), (vp=2, yp=2, sp=2), (vp=3, yp=3, sp=3),..., (vp=k, yp=k, sp=k),..., (vp=n-2, yp=n-2, sp=n-2), (vp=n-1, yp=n-1,sp=n-1) и (w, z, 0). Здесь, предполагается, что k=1, 2,..., n-1. Когда условие #7-1 или условие #7-2 справедливо, высокая способность к коррекции ошибок может достигаться.
Условие #7-1
Рассмотрим (vp=i, yp=i, sp=i) и (vp=j, yp=j, sp=j), где i=1, 2,..., n-1,j=1, 2,..., n-1 и i≠j. В это время, предполагается, что набор из vp=i, yp=i и sp=i, размещаемых в порядке убывания, - это (αp=i, βp=i, γp=i), где αp=i≥βp=i и βp=i≥γp=i. Кроме того, предполагается, что набор из vp=j, yp=j и sp=j, размещаемых в порядке убывания, - это (αp=j, βp=j, γp=j), где αp=j≥βp=j и βp=j≥γp=j. В это время, предусмотрены i и j (i≠j), для которых (αp=i, βp=i, γp=i)≠(αp=j, βp=j, γp=j) справедливо.
Условие #7-2
Рассмотрим (vp=i, yp=i, sp=i) и (w, z, 0), где предполагается, что i=1, 2,..., n-1. В это время, предполагается, что набор из vp=i, yp=i и sp=i, размещаемых в порядке убывания, - это (αp=i, βp=i, γp=i), где предполагается, что αp=i≥βp=i и βp=i≥γp=i. Кроме того, предполагается, что набор из w, z и 0, размещаемых в порядке убывания, - это (αp=i, βp=i, 0), где предполагается, что αp=i≥βp=i. В это время, существуют i, для которых (vp=i, yp=i, sp=i)≠(w, z, 0) справедливо.
Посредством задания более серьезными ограничивающих условий
(условие #7-1, условие #7-2), более вероятно иметь возможность формировать LDPC-CC с изменяющимся во времени периодом q (q является простым числом, равным или превышающим 3) с более высокой способностью к коррекции ошибок. Условие состоит в том, что условие #8-1 и условие #8-2 либо условие #8-1 или условие #8-2 должны быть справедливыми.
Условие #8-1
Рассмотрим (vp=i, yp=i, sp=i) и (vp=j, yp=j, sp=j), где предполагается, что i=1, 2,..., n-1,j=1, 2,..., n-1 и i≠j. В это время, предполагается, что набор из vp=i, yp=i и sp=i, размещаемых в порядке убывания, - это (αp=i, βp=i, γp=i), где предполагается, что αp=i≥βp=i и βp=i≥γp=i. Кроме того, предполагается, что набор из vp=j, yp=j и sp=j, размещаемых в порядке убывания, - это (αp=j, βp=j, γp=j), где предполагается, что αp=j≥βp=j и βp=j≥γp=j. В это время, (αp=i, βp=i, γp=i)≠(αp=j, βp=j, γp=j) справедливо для всех i и j (i≠j).
Условие #8-2
Рассмотрим (vp=i, yp=i, sp=i) и (w, z, 0), где предполагается, что i=1, 2,..., n-1. В это время, предполагается, что набор из vp=i, yp=i и sp=i, размещаемых в порядке убывания, - это (αp=i, βp=i, γp=i), где предполагается, что αp=i≥βp=i и βp=i≥γp=i. Кроме того, предполагается, что набор из w, z и 0, размещаемых в порядке убывания, - это (αp=i, βp=i, 0), где предполагается, что αp=i≥βp=i. В это время, (vp=i, yp=i, sp=i)≠(w, z, 0) справедливо для всех i.
Кроме того, когда vp=i≠yp=i, vp=i≠syp=i, yp=i≠sp=i (i=1, 2,..., n-1) и w≠z справедливо, можно подавлять возникновение коротких контуров на графе Таннера.
В вышеприведенном описании, уравнение 38, имеющее три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), обработано в качестве g-го полинома контроля по четности LDPC-CC с изменяющимся во времени периодом q (q является простым числом, превышающим 3). В уравнении 38, также вероятно иметь возможность достигать высокой способности к коррекции ошибок, когда число элементов любого из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 1 или 2. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 1 или 2. В случае изменяющегося во времени периода q существуют q полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 1 или 2 для всех q полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 1 или 2 для всех q полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 1 или 2 для любого числа (равного или меньшего q-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., Xn-1(D) и P(D). В этом случае, удовлетворение вышеописанному условию составляет важное условие в достижении высокой способности к коррекции ошибок. Тем не менее, условие, связанное с удаленными элементами, является необязательным.
Кроме того, высокая способность к коррекции ошибок также может с большой вероятностью достигаться даже когда число элементов любого из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 4 или более. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 4 или более. В случае изменяющегося во времени периода q существуют q полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 4 или более для всех q полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 4 или более для всех q полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 4 или более для любого числа (равного или меньшего q-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., Xn-1(D) и P(D). В это время, вышеописанное условие исключается для добавленных элементов.
Изменяющийся во времени период h (h является целым числом, отличным от простых чисел, превышающим 3): уравнение 39
Затем рассматривается способ конфигурирования кода, когда изменяющийся во времени период h является целым числом, отличным от простых чисел, превышающим 3.
Во-первых, рассматривается случай, в котором g-ый (g=0, 1,..., h-1) полином контроля по четности со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h (h является целым числом, отличным от простых чисел, превышающим 3) представляется так, как показано в уравнении 39.
[39]
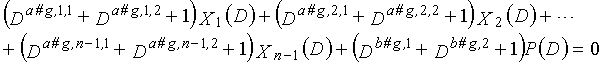 ... (уравнение 39)
... (уравнение 39)
В уравнении 39, предполагается, что a#g,p,1 и a#g,p,2 являются натуральными числами, равными или превышающими 1, и a#g,p,1≠a#g,p,2 справедливо. Кроме того, предполагается, что b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 справедливо (g=0, 1, 2,..., q-2, q-1; p=1, 2,..., n-1).
Аналогично вышеприведенному описанию, условие #9-1 и условие #9-2, описанные ниже, являются одним из важных требований для достижения посредством LDPC-CC высокой способности к коррекции ошибок. В следующих условиях, "%" означает "по модулю", и, например, "α%h" представляет остаток после деления α на h.
Условие #9-1
"a#0,1,1%h=a#1,1,1%h=a#2,1,1%h=a#3,1,1%h=... =a#g,1,1%h=... =a#h-2,1,1%h=a#h-1,1,1%h=vp=1 (vp=1: фиксированное значение)"
"a#0,2,1%h=a#1,2,1%h=a#2,2,1%h=a#3,2,1%h=... =a#g,2,1%h=... =a#h-2,2,1%h=a#h-1,2,1%h=vp=2 (vp=2: фиксированное значение)"
"a#0,3,1%h=a#1,3,1%h=a#2,3,1%h=a#3,3,1%h=... =a#g,3,1%h=... =a#h-2,3,1%h=a#h-1,3,1%h=vp=3 (vp=3: фиксированное значение)"
"a#0,4,1%h=a#1,4,1%h=a#2,4,1%h=a#3,4,1%h=... =a#g,4,1%h=... =a#h-2,4,1%h=a#h-1,4,1%h=vp=4 (vp=4: фиксированное значение)"
"a#0,k,1%h=a#1,k,1%h=a#2,k,1%h=a#3,k,1%h=... =a#g,k,1%h=... =a#h-2,k,1%h=a#h-1,k,1%h=vp=k (vp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,1%h=a#1,n-2,1%h=a#2,n-2,1%h=a#3,n-2,1%h=... =a#g,n-2,1%h=... =a#h-2,n-2,1%h=a#h-1,n-2,1%h=vp=n-2 (vp=n-2: фиксированное значение)"
"a#0,n-1,1%h=a#1,n-1,1%h=a#2,n-1,1%h=a#3,n-1,1%h=... =a#g,n-1,1%h=... =a#h-2,n-1,1%h=a#h-1,n-1,1%h=vp=n-1 (vp=n-1: фиксированное значение)", и
"b#0,1%h=b#1,1%h=b#2,1%h=b#3,1%h=... =b#g,1%h=... =b#h-2,1%h=b#h-1,1%h=w (w: фиксированное значение)"
Условие #9-2
"a#0,1,2%h=a#1,1,2%h=a#2,1,2%h=a#3,1,2%h=... =a#g,1,2%h=... =a#h-2,1,2%h=a#h-1,1,2%h=yp=1 (yp=1: фиксированное значение)"
"a#0,2,2%h=a#1,2,2%h=a#2,2,2%h=a#3,2,2%h=... =a#g,2,2%h=... =a#h-2,2,2%h=a#h-1,2,2%h=yp=2 (yp=2: фиксированное значение)"
"a#0,3,2%h=a#1,3,2%h=a#2,3,2%h=a#3,3,2%h=... =a#g,3,2%h=... =a#h-2,3,2%h=a#h-1,3,2%h=yp=3 (yp=3: фиксированное значение)"
"a#0,4,2%h=a#1,4,2%h=a#2,4,2%h=a#3,4,2%h=... =a#g,4,2%h=... =a#h-2,4,2%h=a#h-1,4,2%h=yp=4 (yp=4: фиксированное значение)"
"a#0,k,2%h=a#1,k,2%h=a#2,k,2%h=a#3,k,2%h=... =a#g,k,2%h=... =a#h-2,k,2%h=a#h-1,k,2%h=yp=k (yp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)
"a#0,n-2,2%h=a#1,n-2,2%h=a#2,n-2,2%h=a#3,n-2,2%h=... =a#g,n-2,2%h=... =a#h-2,n-2,2%h=a#h-1,n-2,2%h=yp=n-2 (yp=n-2: фиксированное значение)"
"a#0,n-1,2%h=a#1,n-1,2%h=a#2,n-1,2%h=a#3,n-1,2%h=... =a#g,n-1,2%h=... =a#h-2,n-1,2%h=a#h-1,n-1,2%h=yp=n-1 (yp=n-1: фиксированное значение)", и
"b#0,2%h=b#1,2%h=b#2,2%h=b#3,2%h=... =b#g,2%h=... =b#h-2,2%h=b#h-1,2%h=z (z: фиксированное значение)"
Помимо этого, как описано выше, высокая способность к коррекции ошибок может достигаться посредством добавления условия #10-1 или условия #10-2.
Условие #10-1
В условии #9-1, vp=1, vp=2, vp=3, vp=4,..., vp=k,..., vp=n-2, vp=n-1 (k=1, 2,..., n-1) и w задаются равными "1" и "являются натуральными числами, отличными от делителей изменяющегося во времени периода h".
Условие #10-2
В условии #9-2, yp=1, yp=2, yp=3, yp=4,..., yp=k,..., yp=n-2, yp=n-1 (k=1, 2,..., n-1) и z задаются равными "1" и "являются натуральными числами, отличными от делителей изменяющегося во времени периода h".
Затем, рассмотрим набор (vp=1, yp=1), (vp=2, yp=2), (vp=3, yp=3),..., (vp=k, yp=k),..., (vp=n-2, yp=n-2), (vp=n-1, yp=n-1) и (w, z). Здесь, предполагается, что k=1, 2,..., n-1. Если условие #11-1 или условие #11-2 справедливо, более высокая способность к коррекции ошибок может достигаться.
Условие #11-1
Рассмотрим (vp=i, yp=i) и (vp=j, yp=j), где предполагается, что i=1, 2,..., n-1,j=1, 2,..., n-1 и i≠j. В это время, предусмотрены i и j (i≠j), для которых (vp=i, yp=i)≠(vp=j, yp=j) и (vp=i, yp=i)≠(yp=j, vp=j) справедливо.
Условие #11-2
Рассмотрим (vp=i, yp=i) и (w, z), где предполагается, что i=1, 2,..., n-1. В это время, существуют i, для которых (vp=i, yp=i)≠(w, z) и (vp=i, yp=i)≠(z, w) справедливо.
Кроме того, посредством задания более серьезными ограничивающих условий (условия #11-1, условия #11-2), более вероятно иметь возможность формировать LDPC-CC с изменяющимся во времени периодом h (h является целым числом, отличным от простых чисел, превышающим 3) с более высокой способностью к коррекции ошибок. Условие состоит в том, что условие #12-1 и условие #12-2 либо условие #12-1 или условие #12-2 должны быть справедливыми.
Условие #12-1
Рассмотрим (vp=i, yp=i) и (vp=j, yp=j), где предполагается, что i=1, 2,..., n-1,j=1, 2,..., n-1 и i≠j. В это время, (vp=i, yp=i)≠(vp=j, yp=j) и (vp=i, yp=i)≠(yp=j, vp=j) справедливо для всех i и j (i≠j).
Условие #12-2
Рассмотрим (vp=i, yp=i) и (w, z), где предполагается, что i=1, 2,..., n-1. В это время, (vp=i, yp=i)≠(w, z) и (vp=i, yp=i)≠(z, w) справедливо для всех i.
Кроме того, когда p=i≠yp=i (i=1, 2,..., n-1) и w≠z справедливо, можно подавлять возникновение коротких контуров на графе Таннера.
В вышеприведенном описании, уравнение 39, имеющее три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), обработано в качестве g-го полинома контроля по четности LDPC-CC с изменяющимся во времени периодом h (h является целым числом, отличным от простых чисел, превышающим 3). В уравнении 39, также вероятно иметь возможность достигать высокой способности к коррекции ошибок, когда число элементов любого из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 1 или 2. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 1 или 2. В случае изменяющегося во времени периода h существуют h полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 1 или 2 для всех h полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 1 или 2 для всех h полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 1 или 2 для любого числа (равного или меньшего h-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., Xn-1(D) и P(D). В этом случае, удовлетворение вышеописанному условию составляет важное условие в достижении высокой способности к коррекции ошибок. Тем не менее, условие, связанное с удаленными элементами, является необязательным.
Кроме того, даже когда число элементов любого из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 4 или более, также вероятно иметь возможность достигать высокой способности к коррекции ошибок. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 4 или более. В случае изменяющегося во времени периода h существуют h полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 4 или более для всех h полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 4 или более для всех h полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 4 или более для любого числа (равного или меньшего h-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., Xn-1(D) и P(D). В это время, вышеописанное условие исключается для добавленных элементов.
Между прочим, уравнение 39 является g-ым полиномом контроля по четности LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h (h является целым числом, отличным от простых чисел, превышающим 3). В этом уравнении, в случае, например, скорости кодирования 1/2, g-ый полином контроля по четности представляется так, как показано в уравнении 40-1. Кроме того, в случае скорости кодирования 2/3, g-ый полином контроля по четности представляется так, как показано в уравнении 40-2. Кроме того, в случае скорости кодирования 3/4, g-ый полином контроля по четности представляется так, как показано в уравнении 40-3. Кроме того, в случае скорости кодирования 4/5, g-ый полином контроля по четности представляется так, как показано в уравнении 40-4. Кроме того, в случае скорости кодирования 5/6, g-ый полином контроля по четности представляется так, как показано в уравнении 40-5.
[40]
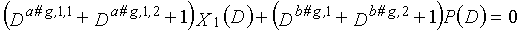 ... (уравнение 40-1)
... (уравнение 40-1)
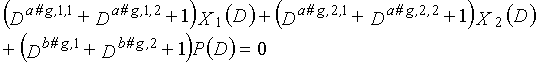 ... (уравнение 40-2)
... (уравнение 40-2)
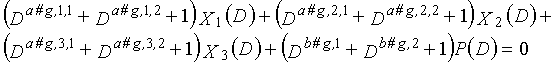 ... (уравнение 40-3)
... (уравнение 40-3)
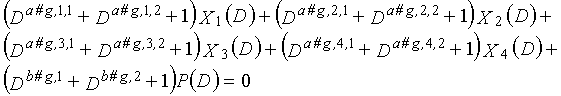 ... (уравнение 40-4)
... (уравнение 40-4)
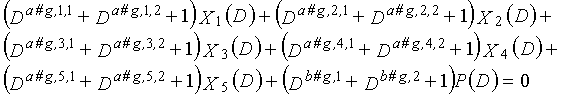 ... (уравнение 40-5)
... (уравнение 40-5)
Изменяющийся во времени период h (h является целым числом, отличным от простых чисел, превышающим 3): уравнение 41
Затем, рассматривается случай, в котором g-ый (g=0, 1,..., h-1) полином контроля по четности (который удовлетворяет 0) с изменяющимся во времени периодом h (h является целым числом, отличным от простых чисел, превышающим 3) представляется так, как показано в уравнении 41.
[41]
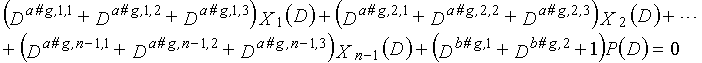 ... (уравнение 41)
... (уравнение 41)
В уравнении 41, предполагается, что a#g,p,1, a#g,p,2 и a#g,p,3 являются натуральными числами, равными или превышающими 1, и a#g,p,1≠a#g,p,2, a#g,p,1≠a#g,p,3 и a#g,p,2≠a#g,p,3 справедливо. Кроме того, предполагается, что b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 справедливо (g=0, 1, 2,..., q-2, q-1; p=1, 2,..., n-1).
Как в случае вышеприведенного описания, условие #13-1, условие #13-2 и условие #13-3, описанные ниже, являются одним из важных требований для достижения посредством LDPC-CC высокой способности к коррекции ошибок. В следующих условиях, "%" означает "по модулю", и, например, "α%h" представляет остаток после деления α на q.
Условие #13-1
"a#0,1,1%h=a#1,1,1%h=a#2,1,1%h=a#3,1,1%h=... =a#g,1,1%h=... =a#h-2,1,1%h=a#h-1,1,1%h=vp=1 (vp=1: фиксированное значение)"
"a#0,2,1%h=a#1,2,1%h=a#2,2,1%h=a#3,2,1%h=... =a#g,2,1%h=... =a#h-2,2,1%h=a#h-1,2,1%h=vp=2 (vp=2: фиксированное значение)"
"a#0,3,1%h=a#1,3,1%h=a#2,3,1%h=a#3,3,1%h=... =a#g,3,1%h=... =a#h-2,3,1%h=a#h-1,3,1%h=vp=3 (vp=3: фиксированное значение)"
"a#0,4,1%h=a#1,4,1%h=a#2,4,1%h=a#3,4,1%h=... =a#g,4,1%h=... =a#h-2,4,1%h=a#h-1,4,1%h=vp=4 (vp=4: фиксированное значение)"
"a#0,k,1%h=a#1,k,1%h=a#2,k,1%h=a#3,k,1%h=... =a#g,k,1%h=... =a#h-2,k,1%h=a#h-1,k,1%h=vp=k (vp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)
"a#0,n-2,1%h=a#1,n-2,1%h=a#2,n-2,1%h=a#3,n-2,1%h=... =a#g,n-2,1%h=... =a#h-2,n-2,1%h=a#h-1,n-2,1%h=vp=n-2 (vp=n-2: фиксированное значение)"
"a#0,n-1,1%h=a#1,n-1,1%h=a#2,n-1,1%h=a#3,n-1,1%h=... =a#g,n-1,1%h=... =a#h-2,n-1,1%h=a#h-1,n-1,1%h=vp=n-1 (vp=n-1: фиксированное значение)", и
"b#0,1%h=b#1,1%h=b#2,1%h=b#3,1%h=... =b#g,1%h=... =b#h-2,1%h=b#h-1,1%h=w (w: фиксированное значение)"
Условие #13-2
"a#0,1,2%h=a#1,1,2%h=a#2,1,2%h=a#3,1,2%h=... =a#g,1,2%h=... =a#h-2,1,2%h=a#h-1,1,2%h=yp=1 (yp=1: фиксированное значение)"
"a#0,2,2%h=a#1,2,2%h=a#2,2,2%h=a#3,2,2%h=... =a#g,2,2%h=... =a#h-2,2,2%h=a#h-1,2,2%h=yp=2 (yp=2: фиксированное значение)"
"a#0,3,2%h=a#1,3,2%h=a#2,3,2%h=a#3,3,2%h=... =a#g,3,2%h=... =a#h-2,3,2%h=a#h-1,3,2%h=yp=3 (yp=3: фиксированное значение)"
"a#0,4,2%h=a#1,4,2%h=a#2,4,2%h=a#3,4,2%h=... =a#g,4,2%h=... =a#h-2,4,2%h=a#h-1,4,2%h=yp=4 (yp=4: фиксированное значение)"
"a#0,k,2%h=a#1,k,2%h=a#2,k,2%h=a#3,k,2%h=... =a#g,k,2%h=... =a#h-2,k,2%h=a#h-1,k,2%h=yp=k (yp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)
"a#0,n-2,2%h=a#1,n-2,2%h=a#2,n-2,2%h=a#3,n-2,2%h=... =a#g,n-2,2%h=... =a#h-2,n-2,2%h=a#h-1,n-2,2%h=yp=n-2 (yp=n-2: фиксированное значение)"
"a#0,n-1,2%h=a#1,n-1,2%h=a#2,n-1,2%h=a#3,n-1,2%h=... =a#g,n-1,2%h=... =a#h-2,n-1,2%h=a#h-1,n-1,2%h=yp=n-1 (yp=n-1: фиксированное значение)", и
"b#0,2%h=b#1,2%h=b#2,2%h=b#3,2%h=... =b#g,2%h=... =b#h-2,2%h=b#h-1,2%h=z (z: фиксированное значение)"
Условие #13-3
"a#0,1,3%h=a#1,1,3%h=a#2,1,3%h=a#3,1,3%h=... =a#g,1,3%h=... =a#h-2,1,3%h=a#h-1,1,3%h=sp=1 (sp=1: фиксированное значение)"
"a#0,2,3%h=a#1,2,3%h=a#2,2,3%h=a#3,2,3%h=... =a#g,2,3%h=... =a#h-2,2,3%h=a#h-1,2,3%h=sp=2 (sp=2: фиксированное значение)"
"a#0,3,3%h=a#1,3,3%h=a#2,3,3%h=a#3,3,3%h=... =a#g,3,3%h=... =a#h-2,3,3%h=a#h-1,3,3%h=sp=3 (sp=3: фиксированное значение)"
"a#0,4,3%h=a#1,4,3%h=a#2,4,3%h=a#3,4,3%h=... =a#g,4,3%h=... =a#h-2,4,3%h=a#h-1,4,3%h=sp=4 (sp=4: фиксированное значение)"
"a#0,k,3%h=a#1,k,3%h=a#2,k,3%h=a#3,k,3%h=... =a#g,k,3%h=... =a#h-2,k,3%h=a#h-1,k,3%h=sp=k (sp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)
"a#0, n-2,3%h=a#1, n-2,3%h=a#2, n-2,3%h=a#3, n-2,3%h=... =a#g, n-2,3%h=... =a#h-2, n-2,3%h=a#h-1, n-2,3%h=sp=n-2 (sp=n-2: фиксированное значение)"
"a#0, n-1,3%h=a#1, n-1,3%h=a#2, n-1,3%h=a#3, n-1,3%h=... =a#g, n-1,3%h=... =a#h-2, n-1,3%h=a#h-1, n-1,3%h=sp=n-1 (sp=n-1: фиксированное значение)"
Помимо этого, рассмотрим набор (vp=1, yp=1, sp=1), (vp=2, yp=2, sp=2), (vp=3, yp=3, sp=3),..., (vp=k, yp=k, sp=k),..., (vp=n-2, yp=n-2, sp=n-2), (vp=n-1, yp=n-1,sp=n-1) и (w, z, 0). Здесь, предполагается, что k=1, 2,..., n-1. Когда условие #14-1 или условие #14-2 справедливо, высокая способность к коррекции ошибок может достигаться.
Условие #14-1
Рассмотрим (vp=i, yp=i, sp=i) и (vp=j, yp=j, sp=j), где i=1, 2,..., n-1,j=1, 2,..., n-1 и i≠j. В это время, предполагается, что набор из vp=i, yp=i, sp=i, размещаемых в порядке убывания, - это (αp=i, βp=i, γp=i), где αp=i≥βp=i, βp=i≥γp=i. Кроме того, предполагается, что набор из vp=j, yp=j, sp=j, размещаемых в порядке убывания, - это (αp=j, βp=j, γp=j), где αp=j≥βp=j, βp=j≥γp=j. В это время, предусмотрены i и j (i≠j), для которых (αp=i, βp=i, γp=i)≠(αp=j, βp=j, γp=j) справедливо.
Условие #14-2
Рассмотрим (vp=i, yp=i, sp=i) и (w, z, 0), где предполагается, что i=1, 2,..., n-1. В это время, предполагается, что набор из vp=i, yp=i, sp=i, размещаемых в порядке убывания, - это (αp=i, βp=i, γp=i), где предполагается, что αp=i≥βp=i и βp=i≥γp=i. Кроме того, предполагается, что набор из w, z и 0, размещаемых в порядке убывания, - это (αp=i, βp=i, 0), где предполагается, что αp=i≥βp=i. В это время, существуют i, для которых (vp=i, yp=i, sp=i)≠(w, z, 0) справедливо.
Кроме того, посредством задания более серьезными ограничивающих условий (условия #14-1, условия #14-2), более вероятно иметь возможность формировать LDPC-CC с изменяющимся во времени периодом h (h является целым числом, отличным от простых чисел, равным или превышающим 3) с более высокой способностью к коррекции ошибок. Условие состоит в том, что условие #15-1 и условие #15-2 либо условие #15-1 или условие #15-2 должны быть справедливыми.
Условие #15-1
Рассмотрим (vp=i, yp=i, sp=i) и (vp=j, yp=j, sp=j), где предполагается, что i=1, 2,..., n-1,j=1, 2,..., n-1 и i≠j. В это время, предполагается, что набор из vp=i, yp=i, sp=i, размещаемых в порядке убывания, - это (αp=i, βp=i, γp=i), где предполагается, что αp=i≥βp=i и βp=i≥γp=i. Кроме того, предполагается, что набор из vp=j, yp=j, sp=j, размещаемых в порядке убывания, - это (αp=j, βp=j, γp=j), где αp=j≥βp=j и βp=j≥γp=j. В это время, (αp=i, βp=i, γp=i)≠(αp=j, βp=j, γp=j) справедливо для всех i и j (i≠j).
Условие #15-2
Рассмотрим (vp=i, yp=i, sp=i) и (w, z, 0), где предполагается, что i=1, 2,..., n-1. В это время, предполагается, что набор из vp=i, yp=i, sp=i, размещаемых в порядке убывания, - это (αp=i, βp=i, γp=i), где предполагается, что αp=i≥βp=i и βp=i≥γp=i. Кроме того, предполагается, что набор из w, z и 0, размещаемых в порядке убывания, - это (αp=i, βp=i, 0), где предполагается, что αp=i≥βp=i. В это время, (vp=i, yp=i, sp=i)≠(w, z, 0) справедливо для всех i.
Кроме того, когда vp=i≠yp=i, vp=i≠sp=i, yp=i≠sp=i (i=1, 2,..., n-1) и w≠z справедливо, можно подавлять возникновение коротких контуров на графе Таннера.
В вышеприведенном описании, уравнение 41, имеющее три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), обработано в качестве g-го полинома контроля по четности LDPC-CC с изменяющимся во времени периодом h (h является целым числом, отличным от простых чисел, превышающим 3). В уравнении 41, также вероятно иметь возможность достигать высокой способности к коррекции ошибок, когда число элементов любого из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 1 или 2. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 1 или 2. В случае изменяющегося во времени периода h существуют h полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 1 или 2 для всех h полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 1 или 2 для всех h полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 1 или 2 для любого числа (равного или меньшего h-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., Xn-1(D) и P(D). В этом случае, удовлетворение вышеописанному условию составляет важное условие в достижении высокой способности к коррекции ошибок. Тем не менее, условие, связанное с удаленными элементами, является необязательным.
Кроме того, вероятно иметь возможность достигать высокой способности к коррекции ошибок также тогда, когда число элементов любого из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 4 или более. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 4 или более. В случае изменяющегося во времени периода h существуют h полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 4 или более для всех h полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 4 или более для всех h полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 4 или более для любого числа (равного или меньшего h-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., Xn-1(D) и P(D). В это время, вышеописанное условие исключается для добавленных элементов.
Как описано выше, настоящий вариант осуществления описывает LDPC-CC на основе полиномов контроля по четности с изменяющимся во времени периодом, превышающим 3, а более конкретно, способ конфигурирования кода LDPC-CC на основе полиномов контроля по четности с изменяющимся во времени периодом со значением простого числа, превышающего 3. Как описано в настоящем варианте осуществления, можно достигать более высокой способности к коррекции ошибок посредством формирования полиномов контроля по четности и выполнения кодирования LDPC-CC на основе полиномов контроля по четности.
Второй вариант осуществления
Настоящий вариант осуществления подробно описывает способ LDPC-CC-кодирования и конфигурацию кодера на основе полиномов контроля по четности, описанных в варианте 1 осуществления.
Во-первых, рассмотрим LDPC-CC со скоростью кодирования 1/2 и изменяющимся во времени периодом 3 в качестве примера. Полиномы контроля по четности с изменяющимся во времени периодом 3 предоставляются ниже.
[42]
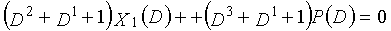 ... (уравнение 42-0)
... (уравнение 42-0)
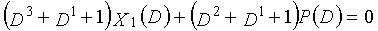 ... (уравнение 42-1)
... (уравнение 42-1)
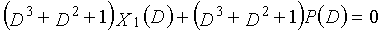 ... (уравнение 42-2)
... (уравнение 42-2)
В это время, P(D) получается, как показано в уравнениях ниже.
[43]
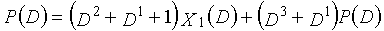 ... (уравнение 43-0)
... (уравнение 43-0)
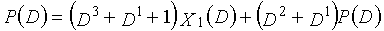 ... (уравнение 43-1)
... (уравнение 43-1)
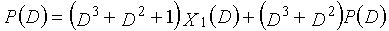 ... (уравнение 43-2)
... (уравнение 43-2)
Уравнения 43-0-43-2 затем представляются следующим образом:
[44]
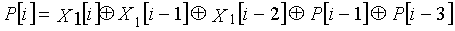 ... (уравнение 44-0)
... (уравнение 44-0)
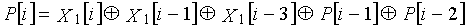 ... (уравнение 44-1)
... (уравнение 44-1)
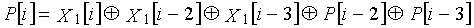 ... (уравнение 44-2),
... (уравнение 44-2),
где символ " " представляет исключающее ИЛИ.
" представляет исключающее ИЛИ.
В это время, фиг. 15A показывает схему, соответствующую уравнению 44-0, фиг. 15B показывает схему, соответствующую уравнению 44-1, и фиг. 15C показывает схему, соответствующую уравнению 44-2.
В момент времени i=3k, бит четности в момент времени i получается через схему, показанную на фиг. 15A, соответствующую уравнению 43-0, т.е. уравнение 44-0. В момент времени i=3k+1, бит четности в момент времени i получается через схему, показанную на фиг. 15B, соответствующую уравнению 43-1, т.е. уравнение 44-1. В момент времени i=3k+2, бит четности в момент времени i получается через схему, показанную на фиг. 15C, соответствующую уравнению 43-2, т.е. уравнение 44-2. Следовательно, кодер может приспосабливать конфигурацию, аналогичную конфигурации по фиг. 9.
Кодирование может быть выполнено также, когда изменяющийся во времени период отличается от 3, и скорость кодирования равняется (n-1)/n, аналогично тому, как описано выше. Например, g-ый (g=0, 1,..., q-1) полином контроля по четности LDPC-CC с изменяющимся во времени периодом q и скоростью кодирования (n-1)/n представляется так, как показано в уравнении 36, и, следовательно, P(D) представляется следующим образом, где q не ограничивается простым числом.
[45]
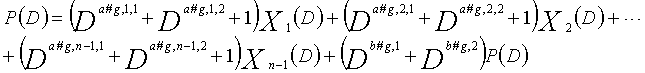 ... (уравнение 45)
... (уравнение 45)
При выражении аналогичным образом уравнениям 44-0-44-2, уравнение 45 представляется следующим образом:
[46]
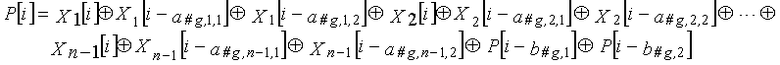 ... (уравнение 46),
... (уравнение 46),
где символ " " представляет исключающее ИЛИ.
" представляет исключающее ИЛИ.
Здесь, Xr[i] (r=1, 2,..., n-1) представляет информационный бит в момент времени i, а P[i] представляет бит четности в момент времени i.
Следовательно, когда i%q=k в момент времени i, бит четности в момент времени i в уравнении 45 и уравнении 46 может достигаться с использованием уравнения, получающегося в результате подстановки k вместо g в уравнении 45 и уравнении 46.
Поскольку LDPC-CC согласно изобретению настоящей заявки является видом сверточного кода, обеспечение доверия при декодировании информационных битов требует завершения или дополнения битами концевой части. Настоящий вариант осуществления должен рассматривать случай, в котором завершение выполняется (в дальнейшем "завершение информационным нулем" или просто "завершение нулем").
Фиг. 16 является схемой, иллюстрирующей "завершение информационным нулем" в LDPC-CC со скоростью кодирования (n-1)/n. Предполагается, что информационные биты X1, X2,..., Xn-1 и бит P четности в момент времени i (i=0, 1, 2, 3,..., s) представляются посредством X1,i, X2,i,..., Xn-1,i и бит Pi четности, соответственно. Как показано на фиг. 16, Xn-1,s допускается как конечный бит информации, которую следует передавать.
Если кодер выполняет кодирование только до момента времени s, и передающее устройство на стороне кодирования выполняет передачу только вплоть до Ps в приемное устройство на стороне декодирования, качество приема информационных битов декодера значительно ухудшается. Чтобы разрешать эту проблему, кодирование выполняется при условии, что информационные биты от конечного информационного бита Xn-1,s и далее (в дальнейшем "виртуальные информационные биты") равны "0", и бит (1603) четности формируется.
Более конкретно, как показано на фиг. 16, кодер выполняет кодирование при условии, что X1,k, X2,k,..., Xn-1,k (k=t1, t2,..., tm) составляет "0", и получает Pt1, Pt2,..., Ptm. После передачи X1,s, X2,s,..., Xn-1,s и Ps в момент времени s, передающее устройство на стороне кодирования передает Pt1, Pt2,..., Ptm. Декодер выполняет декодирование с использованием преимущества знания того, что виртуальные информационные биты являются нулями с момента времени s и далее.
При завершении, к примеру, "завершении информационным нулем", например, LDPC-CC-кодер 100 на фиг. 9 выполняет кодирование при условии, что начальное состояние регистра составляет "0". В качестве другой интерпретации, когда кодирование выполняется с момента времени i=0, если, например, z меньше 0 в уравнении 46, кодирование выполняется при условии, что X1[z], X2[z],..., Xn-1[z] и P[z] равны "0".
При условии, что субматрица (вектор) в уравнении 36 является Hg, g-ая субматрица может представляться как уравнение ниже.
[47]
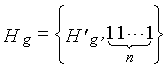 ... (уравнение 47)
... (уравнение 47)
Здесь, n непрерывных единиц соответствуют элементам X1(D), X2(D),..., Xn-1(D) и P(D) в уравнении 36.
Следовательно, когда завершение используется, матрица LDPC-CC-контроля со скоростью кодирования (n-1)/n и изменяющимся во времени периодом q, представленная посредством уравнения 36, представляется так, как показано на фиг. 17. Фиг. 17 имеет конфигурацию, аналогичную конфигурации по фиг. 5. Вариант 3 осуществления, который описывается ниже, описывает подробную конфигурацию дополнения битами концевой части контрольной матрицы.
Как показано на фиг. 17, используется конфигурация, в которой субматрица сдвигается на n столбцов вправо между i-ой строкой и (i+1)-ой строкой в матрице H контроля по четности (см. фиг. 17). Тем не менее, элемент слева от первого столбца (H'1 в примере по фиг. 17) не отражается в контрольной матрице (см. фиг. 5 и фиг. 17). Когда вектор u передачи допускается как u=(X1,0, X2,0,..., Xn-1,0, P0, X1,1, X2,1,..., Xn-1,1, P1,..., X1,k, X2,k,..., Xn-1,k, Pk,...,)T, Hu=0 является справедливой.
Как описано выше, кодер принимает информационные биты Xr[i] (r=1, 2,..., n-1) в момент времени i в качестве ввода, формирует бит P[i] четности в момент времени i с использованием уравнения 46, выводит бит [i] четности и тем самым может выполнять кодирование LDPC-CC, описанного в варианте 1 осуществления.
Третий вариант осуществления
Настоящий вариант осуществления, в частности, описывает способ конфигурирования кода для достижения более высокой способности к коррекции ошибок, когда простое дополнение битами концевой части, описанное в непатентных документах 10 и 11, выполняется для LDPC-CC на основе полиномов контроля по четности, описанных в варианте 1 осуществления.
В варианте 1 осуществления описан случай, в котором g-ый (g=0, 1,..., q-1) полином контроля по четности LDPC-CC с изменяющимся во времени периодом q (q является простым числом, превышающим 3) и скоростью кодирования (n-1)/n представляется так, как показано в уравнении 36. Число элементов каждого из X1(D), X2(D),..., Xn-1(D) и P(D) в уравнении 36 составляет 3, и в этом случае, вариант 1 осуществления имеет конкретно описанный способ конфигурирования кода (ограничивающее условие) для достижения высокой способности к коррекции ошибок. Кроме того, вариант 1 осуществления указывает то, что даже когда число элементов одного из X1(D), X2(D),..., Xn-1(D) и P(D) равняется 1 или 2, высокая способность к коррекции ошибок может с большой вероятностью достигаться.
Здесь, когда элемент P(D) допускается равным 1, код является сверточным кодом с прямой связью (LDPC-CC), и, следовательно, дополнение битами концевой части может выполняться просто на основе непатентных документов 10 и 11. Настоящий вариант осуществления описывает этот аспект более конкретно.
Когда элемент P(D) g-го (g=0, 1,..., q-1) полинома контроля по четности (36) LDPC-CC с изменяющимся во времени периодом q и скоростью кодирования (n-1)/n равняется 1, g-ый полином контроля по четности представляется так, как показано в уравнении 48.
[48]
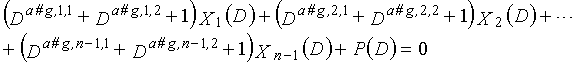 ... (уравнение 48)
... (уравнение 48)
Согласно настоящему варианту осуществления, изменяющийся во времени период q не ограничивается простым числом, равным или превышающим 3. Тем не менее, предполагается, что ограничивающее условие, описанное в варианте 1 осуществления, должно наблюдаться. Тем не менее, предполагается, что условие, связанное с удаленными элементами P(D), должно исключаться.
Из уравнения 48, P(D) представляется так, как показано ниже.
[49]
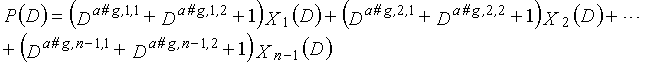 ... (уравнение 49)
... (уравнение 49)
При представлении аналогичным образом уравнениям 44-0-44-2, уравнение 49 представляется следующим образом:
[50]
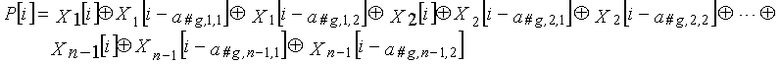 ... (уравнение 50),
... (уравнение 50),
где "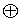 " представляет исключающее ИЛИ.
" представляет исключающее ИЛИ.
Следовательно, когда i%q=k в момент времени i, бит четности в момент времени i может достигаться в уравнении 49 и уравнении 50 с использованием уравнения, получающегося в результате подстановки k вместо g в уравнении 49 и уравнении 50. Тем не менее, подробности операции при выполнении дополнения битами концевой части описываются ниже.
Затем подробно описывается конфигурация и размер блока контрольной матрицы при выполнении дополнения битами концевой части для LDPC-CC с изменяющимся во времени периодом q и скоростью кодирования (n-1)/n, заданного в уравнении 49.
Непатентный документ 12 описывает общее уравнение матрицы контроля по четности при выполнении дополнения битами концевой части для изменяющегося во времени LDPC-CC. Уравнение 51 является матрицей контроля по четности при выполнении дополнения битами концевой части, описанного в непатентном документе 12.
[51]
 ... (уравнение 51)
... (уравнение 51)
В уравнении 51, H представляет матрицу контроля по четности, и HT представляет синдромный формирователь. Кроме того, HT i(t) (i=0, 1,..., Ms) представляет субматрицу c*(c-b), и Ms представляет емкость запоминающего устройства.
Тем не менее, непатентный документ 12 не показывает конкретный код матрицы контроля по четности, и при этом он не описывает способа конфигурирования кода (ограничивающее условие) для достижения высокой способности к коррекции ошибок.
В дальнейшем в этом документе подробно описывается способ конфигурирования кода (ограничивающее условие) для достижения высокой способности к коррекции ошибок при выполнении дополнения битами концевой части для LDPC-CC с изменяющимся во времени периодом q и скоростью кодирования (n-1)/n, заданного в уравнении 49.
Чтобы достигать высокой способности к коррекции ошибок в LDPC-CC с изменяющимся во времени периодом q и скоростью кодирования (n-1)/n, заданном в уравнении 49, следующее условие становится важным в матрице H контроля по четности, считающейся необходимой при декодировании.
Условие #16
- Число строк матрицы контроля по четности является кратным q.
- Следовательно, число столбцов матрицы контроля по четности является кратным n*q. Т.е. (например) логарифмическое отношение правдоподобия, требуемое при декодировании, соответствует битам кратного n*q.
Тем не менее, полином контроля по четности LDPC-CC с изменяющимся во времени периодом q и скоростью кодирования (n-1)/n, требуемый в вышеуказанном условии #16, не ограничивается уравнением 48, а может быть полиномом контроля по четности, таким как уравнение 36 или уравнение 38. Кроме того, число элементов каждого из X1(D), X2(D),..., Xn-1(D) и P(D) в уравнении 38 равняется 3, но число элементов не ограничивается 3. Кроме того, изменяющийся во времени период q может быть любым значением, равным или превышающим 2.
Здесь, условие #16 поясняется.
Когда информационные биты X1, X2,..., Xn-1 и бит P четности в момент времени i представляются посредством X1,i, X2,i,..., Xn-1,i и Pi, соответственно, дополнение битами концевой части выполняется как i=1, 2, 3,..., q,..., q*(N-1)+1, q*(N-1)+2, q*(N-1)+3,..., q*N, чтобы удовлетворять условию #16.
В это время, последовательность u передачи становится u=(X1,1, X2,1,..., Xn-1,1, P0, X1,2, X2,2,..., Xn-1,2, P2,..., X1,k, X2,k,..., Xn-1,k, Pk,..., X1,q*N, X2,q*N,..., Xn-1,q*N, Pq*N)T, и Hu=0 является справедливой. Конфигурация матрицы контроля по четности в это время описывается с использованием фиг. 18A и фиг. 18B.
При условии, что субматрица (вектор) уравнения 48 является Hg, g-ая субматрица может представляться так, как показано в уравнении ниже.
[52]
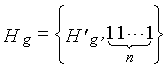 ... (уравнение 52)
... (уравнение 52)
Здесь, n непрерывных единиц соответствуют элементам X1(D), X2(D),..., Xn-1(D) и P(D) в уравнении 48.
Из матрицы контроля по четности, соответствующей последовательности u передачи, заданной выше, фиг. 18A показывает матрицу контроля по четности рядом с моментом времени q*N-1 (1803) и моментом времени q*N (1804). Как показано на фиг. 18A, используется конфигурация, в которой субматрица сдвигается на n столбцов вправо между i-ой строкой и (i+1)-ой строкой в матрице H контроля по четности (см. фиг. 18A).
На фиг. 18A, строка 1801 показывает (q*N)-ную строку (последнюю строку) матрицы контроля по четности. Когда условие #16 удовлетворяется, строка 1801 соответствует (q-1)-вому полиному контроля по четности. Кроме того, строка 1802 показывает (q*N-1)-вую строку матрицы контроля по четности. Когда условие #16 удовлетворяется, строка 1802 соответствует (q-2)-рому полиному контроля по четности.
Кроме того, группа 1804 столбцов представляет группу столбцов, соответствующую моменту времени q*N. В группе 1804 столбцов последовательность передачи размещается в порядке X1,q*N, X2,q*N,..., Xn-1,q*N и Pq*N. Группа 1803 столбцов представляет группу столбцов, соответствующую моменту времени q*N-1. В группе 1803 столбцов последовательность передачи размещается в порядке X1,q*N-1, X2,q*N-1,..., Xn-1,q*N-1 и Pq*N-1.
Затем, порядок последовательности передачи изменяется на u=(..., X1,q*N-1, X2,q*N-1,..., Xn-1,q*N-1, Pq*N-1, X1,q*N, X2,q*N,..., Xn-1,q*N, Pq*N, X1,0, X2,1,..., Xn-1,1, P1, X1,2, X2,2,..., Xn-1,2, P2,...,)T. Из матрицы контроля по четности, соответствующей последовательности u передачи, фиг. 18B показывает матрицу контроля по четности рядом с моментом времени q*N-1 (1803), моментом времени q*N (1804), моментом времени 1 (1807) и моментом времени 2 (1808).
Как показано на фиг. 18B, используется конфигурация, в которой субматрица сдвигается на n столбцов вправо между i-ой строкой и (i+1)-ой строкой в матрице H контроля по четности. Кроме того, как показано на фиг. 18A, когда матрица контроля по четности рядом с моментом времени q*N-1 (1803) и моментом времени q*N (1804), столбец 1805 является столбцом, соответствующим (q*N*n)-вому столбцу, а столбец 1806 является столбцом, соответствующим первому столбцу.
Группа 1803 столбцов представляет группу столбцов, соответствующую моменту времени q*N-1, и группа 1803 столбцов размещается в порядке X1,q*N-1, X2,q*N-1,..., Xn-1,q*N-1 и Pq*N-1. Группа 1804 столбцов представляет группу столбцов, соответствующую моменту времени q*N, и группа 1804 столбцов размещается в порядке X1,q*N, X2,q*N,..., Xn-1,q*N и Pq*N. Группа 1807 столбцов представляет группу столбцов, соответствующую моменту времени 1, и группа 1807 столбцов размещается в порядке X1,1, X2,1,..., Xn-1,1 и P1. Группа 1808 столбцов представляет группу столбцов, соответствующую моменту времени 2, и группа 1808 столбцов размещается в порядке X1,2, X2,2,..., Xn-1,2 и P2.
Когда матрица контроля по четности рядом с моментом времени q*N-1 (1803) или моментом времени q*N (1804) представляется так, как показано на фиг. 18A, строка 1811 является строкой, соответствующей (q*N)-ной строке, и строка 1812 является строкой, соответствующей первой строке.
В это время, часть матрицы контроля по четности, показанной на фиг. 18B, т.е. часть слева от границы столбца 1813 и ниже границы строки 1814 составляет характерную часть, когда дополнение битами концевой части выполняется. Очевидно, что эта характерная часть имеет конфигурацию, аналогичную конфигурации уравнения 51.
Когда матрица контроля по четности удовлетворяет условию #16, если матрица контроля по четности представляется так, как показано на фиг. 18A, матрица контроля по четности начинается со строки, соответствующей 0-вому полиному контроля по четности, который удовлетворяет 0, и завершается в строке, соответствующей (q-1)-вому полиному контроля по четности, который удовлетворяет 0. Это является важным в достижении более высокой способности к коррекции ошибок.
Изменяющийся во времени LDPC-CC, описанный в варианте 1 осуществления, является таким кодом, что число коротких циклов (циклов длины) на графе Таннера сокращается. Вариант 1 осуществления показывает условие для того, чтобы формировать такой код, при котором число коротких циклов на графе Таннера сокращается. Здесь, когда дополнение битами концевой части выполняется, важно, чтобы число строк матрицы контроля по четности было кратным q (условие #16), чтобы сокращать число коротких циклов на графе Таннера. В этом случае, если число строк матрицы контроля по четности является кратным q, все полиномы контроля по четности с изменяющимся во времени периодом q используются. Таким образом, как описано в варианте осуществления 1, посредством приспособления кода, в котором число коротких циклов на графе Таннера сокращается для полинома контроля по четности, можно сокращать число коротких циклов на графе Таннера также при выполнении дополнения битами концевой части. Таким образом, условие #16 является важным требованием для сокращения числа коротких циклов на графе Таннера также при выполнении дополнения битами концевой части.
Тем не менее, система связи может требовать некоторой изобретательности, чтобы удовлетворять условию #16 для длины блока (или длины информации), требуемой в системе связи при выполнении дополнения битами концевой части. Это описывается посредством рассмотрения примера.
Фиг. 19 является принципиальной схемой системы связи. Система связи на фиг. 19 имеет передающее устройство 1910 на стороне кодирования и приемное устройство 1920 на стороне декодирования.
Кодер 1911 принимает информацию в качестве ввода, выполняет кодирование и формирует и выводит последовательность передачи. Модуль 1912 модуляции принимает последовательности передачи в качестве ввода, выполняет предварительно определенную обработку, такую как преобразование, квадратурная модуляция, преобразование частоты и усиление, и выводит передаваемый сигнал. Передаваемый сигнал поступает в приемный модуль 1921 приемного устройства 1920 через среду связи (радиосреду, линию электросети, световую среду и т.п.).
Приемный модуль 1921 принимает принимаемый сигнал в качестве ввода, выполняет обработку, такую как усиление, преобразование частоты, квадратурная демодуляция, оценка канала и обратное преобразование, и выводит сигнал в полосе модулирующих частот и сигнал оценки канала.
Модуль 1922 формирования логарифмических отношений правдоподобия принимает сигнал в полосе модулирующих частот и сигнал оценки канала в качестве ввода, формирует логарифмическое отношение правдоподобия в единицах битов и выводит сигнал логарифмического отношения правдоподобия.
Декодер 1923 принимает сигнал логарифмического отношения правдоподобия в качестве ввода, выполняет итеративное декодирование с использованием BP-декодирования, в частности, здесь и выводит последовательность передачи для оценки и/или последовательность информации для оценки.
Например, рассмотрим LDPC-CC со скоростью кодирования 1/2 и изменяющимся во времени периодом 11. При условии, что дополнение битами концевой части выполняется в это время, заданная длина информации обозначается 16384. Информационные биты обозначаются X1,1, X1,2, X1,3,..., X1,16384. Если биты четности определяются без какой-либо изобретательности, P1, P2, P3,..., P16384 определяются.
Тем не менее, даже когда матрица контроля по четности создается для последовательности u передачи=(X1,1, P1, X1,2, P2, ..., X1,16384, P16384), условие #16 не удовлетворяется. Следовательно, X1,16385, X1,16386, X1,16387, X1,16388 и X1,16389 могут добавляться в качестве последовательности передачи, так что кодер 1911 определяет P16385, P16386, P16387, P16388 и P16389.
В это время, кодер, 1911 задает, например, X1,16385=0, X1,16386=0, X1,16387=0, X1,16388=0 и X1,16389=0, выполняет кодирование и определяет P16385, P16386, P16387, P16388 и P16389. Тем не менее, если условие, что X1,16385=0, X1,16386=0, X1,16387=0, X1,16388=0 и X1,16389=0 заданы, совместно используется между кодером 1911 и декодером 1923, X1,16385, X1,16386, X1,16387, X1,16388 и X1,16389 не должны быть переданы.
Следовательно, кодер 1911 принимает информационную последовательность=(X1,1, X1,2, X1,3,..., X1,16384, X1,16385, X1,16386, X1,16387, X1,16388, X1,16389)=(X1,1, X1,2, X1,3,..., X1,16384, 0, 0, 0, 0, 0) в качестве ввода и получает последовательность (X1,1, P1, X1,2, P2,..., X1,16384, P16384, X1,16385, P16385, X1,16386, P16386, X1,16387, P16387, X1,16388, P16388, X1,16389, P16389)=(X1,1, P1, X1,2, P2,..., X1,16384, P16384, 0, P16385, 0, P16386, 0, P16387, 0, P16388, 0, P16389).
Передающее устройство 1910 затем удаляет нули, известные между кодером 1911 и декодером 1923, и передает (X1,1, P1, X1,2, P2,..., X1,16384, P16384, P16385, P16386, P16387, P16388, P16389) в качестве последовательности передачи.
Приемное устройство 1920 получает, например, логарифмические отношения правдоподобия для каждой последовательности передачи в качестве LLR(X1,1), LLR(P1), LLR(X1,2), LLR(P2),..., LLR(X1,16384), LLR(P16384), LLR(P16385), LLR(P16386), LLR(P16387), LLR(P16388) и LLR(P16389).
Приемное устройство 1920 затем формирует логарифмические отношения правдоподобия LLR(X1,16385)=LLR(0), LLR(X1,16386)=LLR(0), LLR(X1,16387)=LLR(0), LLR(X1,16388)=LLR(0) и LLR(X1,16389)=LLR(0) для значений X1,16385, X1,16386, X1,16387, X1,16388 и X1,16389 в нуль, не передаваемых из передающего устройства 1910. Приемное устройство 1920 получает LLR(X1,1), LLR(P1), LLR(X1,2), LLR(P2),..., LLR(X1,16384), LLR(P16384), LLR(X1,16385)=LLR(0), LLR(P16385), LLR(X1,16386)=LLR(0), LLR(P16386), LLR(X1,16387)=LLR(0), LLR(P16387), LLR(X1,16388)=LLR(0), LLR(P16388) и LLR(X1,16389)=LLR(0), LLR(P16389) и тем самым выполняет декодирование с использованием этих логарифмических отношений правдоподобия и матрицы контроля по четности 16389*32778 LDPC-CC со скоростью кодирования 1/2 и изменяющимся во времени периодом 11 и тем самым получает последовательность передачи для оценки и/или последовательность информации для оценки. В качестве способа декодирования, доверительное распространение, к примеру, декодирование по алгоритму BP (доверительного распространения), декодирование по алгоритму минимальной суммы, которое является аппроксимацией BP-декодирования, BP-декодирование со смещением, нормализованное BP-декодирование, перемешанное BP-декодирование может быть использовано, как показано в непатентном документе 4, непатентном документе 5 и непатентном документе 6.
Как очевидно из этого примера, когда дополнение битами концевой части выполняется в LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом q, приемное устройство 1920 выполняет декодирование с использованием такой матрицы контроля по четности, которая удовлетворяет условию #16. Следовательно, это означает то, что декодер 1923 имеет матрицу контроля по четности в (строк)*(столбцов)=(q*M)*(q*n*M) в качестве матрицы контроля по четности (M является натуральным числом).
В кодере 1911, соответствующему этому, число информационных битов, необходимых для кодирования, составляет q*(n-1)*M. С использованием этих информационных битов q*M битов четности получаются.
В это время, если число информационных битов, введенное в кодер 1911, меньше q*(n-1)*M биты (например, нули (также могут быть единицы)), известные между передающим и приемным устройствами (кодером 1911 и декодером 1923), вставляются так, что число информационных битов составляет q*(n-1)*M в кодере 1911. Кодер 1911 затем получает q*M битов четности. В это время, передающее устройство 1910 передает информационные биты за исключением вставленных известных битов и полученных битов четности. Здесь, известные биты могут передаваться, и q*(n-1)*M информационных битов и q*M битов четности могут всегда передаваться, что, тем не менее, должно приводить к снижению скорости передачи на величину, соответствующую передаваемым известным битам.
Затем, описывается способ кодирования в LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом q, заданном посредством полинома контроля по четности уравнения 48, когда дополнение битами концевой части выполняется. LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом q, заданный посредством полинома контроля по четности уравнения 48, является видом сверточного кода с прямой связью. Следовательно, дополнение битами концевой части, описанное в непатентном документе 10 и непатентном документе 11, может быть выполнено. В дальнейшем в этом документе приводится краткое описание процедуры для способа кодирования при выполнении дополнения битами концевой части, описанного в непатентном документе 10 и непатентном документе 11.
Процедура является такой, как показано ниже.
Процедура 1
Например, когда кодер 1911 приспосабливает конфигурацию, аналогичную конфигурации на фиг. 9, начальное значение каждого регистра (ссылки с номерами опускаются) допускается равным "0". Т.е. в уравнении 50 при условии, что g=k, когда (i-1)%q=k в момент времени i (i=1, 2,...,), бит четности в момент времени i определяется. Когда z в X1[z], X2[z],..., Xn-1[z] и P[z] в уравнении 50 меньше 1, кодирование выполняется при условии, что эти значения являются нулями. Кодер 1911 затем определяет вплоть до последнего бита четности. Состояние каждого регистра кодера 1911 в это время сохраняется.
Процедура 2
В процедуре 1 кодирование выполняется снова, чтобы определять биты четности от момента времени i=1 из состояния каждого регистра, сохраненного в кодере 1911 (поэтому, значения, полученные в процедуре 1, используются, когда z в X1[z], X2[z],..., Xn-1[z] и P[z] в уравнении 50 меньше 1).
Бит четности и информационные биты, полученные в это время, составляют кодированную последовательность, когда дополнение битами концевой части выполняется.
Настоящий вариант осуществления описывает LDPC-CC с изменяющимся во времени периодом q и скоростью кодирования (n-1)/n, заданный посредством уравнения 48, в качестве примера. В уравнении 48, число элементов X1(D), X2(D),..., и Xn-1(D) равняется 3. Тем не менее, число элементов не ограничивается 3, но высокая способность к коррекции ошибок также может с большой вероятностью достигаться, даже когда число элементов одного из X1(D), X2(D),..., и Xn-1(D) в уравнении 48 равняется 1 или 2. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 1 или 2. В случае изменяющегося во времени периода q существуют q полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 1 или 2 для всех q полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 1 или 2 для всех q полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 1 или 2 для любого числа (равного или меньшего q-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо также и к X2(D),..., и Xn-1(D). В этом случае, удовлетворение условию, описанному в варианте 1 осуществления, составляет важное условие в достижении высокой способности к коррекции ошибок. Тем не менее, условие, связанное с удаленными элементами, является необязательным.
Кроме того, даже когда число элементов одного из X1(D), X2(D),..., и Xn-1(D) равняется 4 или более, высокая способность к коррекции ошибок может с большой вероятностью достигаться. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 4 или более. В случае изменяющегося во времени периода q существуют q полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 4 или более для всех q полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 4 или более для всех q полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 4 или более для любого числа (равного или меньшего q-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо также и к X2(D),..., и Xn-1(D). В это время, вышеописанное условие исключается для добавленных элементов.
Кроме того, дополнение битами концевой части согласно настоящему варианту осуществления также может быть выполнено для кода, для которого g-ый (g=0, 1,..., q-1) полином контроля по четности LDPC-CC с изменяющимся во времени периодом q и скоростью кодирования (n-1)/n представляется так, как показано в уравнении 53.
[53]
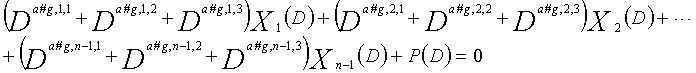 ... (уравнение 53)
... (уравнение 53)
Тем не менее, предполагается, что ограничивающее условие, описанное в варианте 1 осуществления, наблюдается. Тем не менее, условие, связанное с удаленными элементами в P(D), должно исключаться.
Из уравнения 53, P(D) представляется так, как показано ниже.
[54]
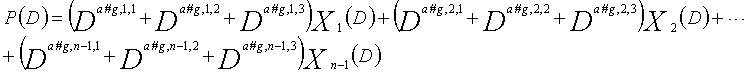 ... (уравнение 54)
... (уравнение 54)
При представлении аналогичным образом уравнениям 44-0-44-2, уравнение 54 представляется так, как показано ниже.
[55]
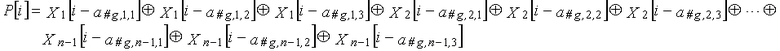 ... (уравнение 55),
... (уравнение 55),
где символ " " представляет исключающее ИЛИ.
" представляет исключающее ИЛИ.
Высокая способность к коррекции ошибок может с большой вероятностью достигаться даже когда число элементов одного из X1(D), X2(D),..., и Xn-1(D) в уравнении 53 равняется 1 или 2. Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 1 или 2. В случае изменяющегося во времени периода q существуют q полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 1 или 2 для всех q полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 1 или 2 для всех q полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 1 или 2 для любого числа (равного или меньшего q-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо также и к X2(D),..., и Xn-1(D). В этом случае, удовлетворение условию, описанному в варианте 1 осуществления, составляет важное условие в достижении высокой способности к коррекции ошибок. Тем не менее, условие, связанное с удаленными элементами, является необязательным.
Кроме того, высокая способность к коррекции ошибок также может с большой вероятностью достигаться даже когда число элементов одного из X1(D), X2(D),..., и Xn-1(D) равняется 4 или более, Например, следующий способ доступен в качестве способа задания числа элементов X1(D) равным 4 или более. В случае изменяющегося во времени периода q существуют q полиномов контроля по четности, которые удовлетворяют 0, и число элементов X1(D) задается равным 4 или более для всех q полиномов контроля по четности, которые удовлетворяют 0. Альтернативно, вместо задания числа элементов X1(D) равным 4 или более для всех q полиномов контроля по четности, которые удовлетворяют 0, число элементов X1(D) может задаваться равным 4 или более для любого числа (равного или меньшего q-1) полиномов контроля по четности, которые удовлетворяют 0. Это применимо и к X2(D),..., и Xn-1(D). В это время, вышеописанное условие исключается для добавленных элементов. Кроме того, кодированная последовательность, когда дополнение битами концевой части выполняется, может достигаться с использованием вышеописанной процедуры также для LDPC-CC, заданного в уравнении 53.
Как описано выше, кодер 1911 и декодер 1923 используют матрицу контроля по четности LDPC-CC, описанного в варианте 1 осуществления, число строк которой является кратным изменяющегося во времени периода q, и тем самым могут достигать высокой способности к коррекции ошибок, даже когда простое дополнение битами концевой части выполняется.
Четвертый вариант осуществления
Настоящий вариант осуществления описывает изменяющийся во времени LDPC-CC со скоростью кодирования R=(n-1)/n снова на основе полинома контроля по четности. Информационные биты X1, X2,..., и Xn-1 и бит P четности в момент времени j представляются посредством X1,j, X2,j,..., Xn-1,j и Pj, соответственно. Вектор uj в момент времени j представляется посредством uj=(X1,j, X2,j,..., Xn-1,j, Pj). Кроме того, кодированная последовательность представляется посредством u=(u0, u1,..., uj,...,)T. При условии, что D является оператором задержки, полином информационных битов X1, X2,..., Xn-1 представляется посредством X1(D), X2(D),..., Xn-1(D), и полином бита P четности представляется посредством P(D). В это время, рассмотрим полином контроля по четности, который удовлетворяет 0, представленный так, как показано в уравнении 56.
[56]
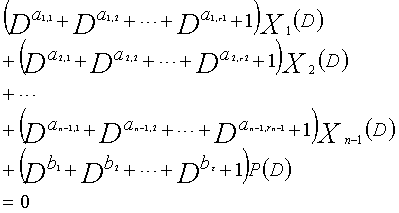 ... (уравнение 56)
... (уравнение 56)
В уравнении 56, предполагается, что ap,q (p=1, 2,..., n-1; q=1, 2,..., rp) и bs (s=1, 2,..., ε) являются натуральными числами. Кроме того, ap,y≠ap,z удовлетворяется для ∀(y, z) y, z=1, 2,..., rp, y≠z. Кроме того, by≠bz удовлетворяется для ∀(y, z) при y, z=1, 2,..., ε, y≠z. Здесь, ∀ является квантором всеобщности.
Чтобы создавать LDPC-CC со скоростью кодирования R=(n-1)/n и изменяющимся во времени периодом m, полином контроля по четности на основе уравнения 56 предоставляется. В это время, i-ый (i=0, 1,..., m-1) полином контроля по четности представляется так, как показано в уравнении 57.
[57]
 ... (уравнение 57)
... (уравнение 57)
В уравнении 57, максимальные порядки D AXδ,i(D) (δ=1, 2,..., n-1) и Bi(D) представляются посредством ΓXδ,i и ΓP,i, соответственно. Максимальное значение ΓXδ,i и ΓP,i допускается равным Γi. Максимальное значение Γi (i=0, 1,..., m-1) допускается равным Γ. Когда кодированная последовательность u учитывается с использованием Γ, вектор hi, соответствующий i-ой матрице контроля по четности, представляется так, как показано в уравнении 58.
[58]
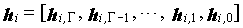 ... (уравнение 58)
... (уравнение 58)
В уравнении 58, hi,v (v=0, 1,..., Γ) является вектором 1*n и представляется так, как показано в уравнении 59.
[59]
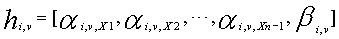 ... (уравнение 59)
... (уравнение 59)
Это обусловлено тем, что полином контроля по четности уравнения 57 имеет αi,v,XwDvXw(D) и βi,vDvP(D) (w=1, 2,..., n-1 и αi,v,Xw, βi,v ∈ [0, 1]). В это время, полином контроля по четности, который удовлетворяет 0 в уравнении 57, имеет D0X1(D), D0X2(D),..., D0Xn-1(D) и D0P(D) и, следовательно, удовлетворяет уравнению 60.
[60]
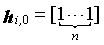 ... (уравнение 60)
... (уравнение 60)
В уравнении 60, Λ(k)=Λ(k+m) удовлетворяется для ∀k, где Λ(k) соответствует hi на k-ой строке матрицы контроля по четности.
С использованием уравнения 58, уравнения 59 и уравнения 60, матрица LDPC-CC-контроля на основе полинома контроля по четности со скоростью кодирования R=(n-1)/n и изменяющимся во времени периодом m представляется так, как показано в уравнении 61.
[61]
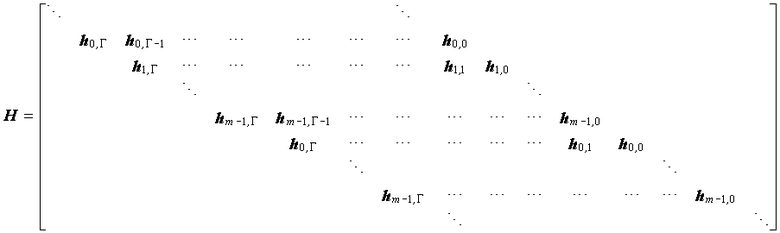 ... (уравнение 61)
... (уравнение 61)
Пятый вариант осуществления
Настоящий вариант осуществления описывает случай, в котором изменяющийся во времени LDPC-CC, описанный в варианте 1 осуществления, применяется к схеме коррекции со стиранием ошибок. Тем не менее, изменяющийся во времени период LDPC-CC также может быть изменяющимся во времени периодом 2, 3 или 4.
Например, фиг. 20 показывает концептуальную схему системы связи с использованием кодирования с коррекцией со стиранием ошибок с использованием LDPC-кода. На фиг. 20, устройство связи на стороне кодирования выполняет LDPC-кодирование для пакетов 1-4 информации, которые следует передавать, и формирует пакеты a и b четности. Процессор верхнего уровня выводит кодированный пакет, который является пакетом четности, добавленным к пакету информации, на нижний уровень (физический уровень (PHY) в примере по фиг. 20), и процессор физического уровня нижнего уровня преобразует кодированный пакет в пакет, который может быть передан через канал связи, и выводит кодированный пакет в канал связи. Фиг. 20 показывает пример случая, в котором канал связи является каналом беспроводной связи.
В устройстве связи на стороне декодирования, процессор физического уровня на нижнем уровне выполняет обработку приема. В это время предполагается, что битовая ошибка возникает на нижнем уровне. Может иметь место то, что вследствие этой битовой ошибки пакет, включающий в себя соответствующий бит, не может быть декодирован корректно на верхнем уровне, пакет может быть потерян. Пример на фиг. 20 показывает случай, когда пакет 3 информации потерян. Процессор верхнего уровня применяет обработку LDPC-декодирования к принимаемому столбцу пакета и тем самым декодирует потерянный пакет 3 информации. Для LDPC-декодирования и т.п. используется декодирование суммы-произведения, которое выполняет декодирование с использованием способа доверительного распространения (BP) или гауссова стирания.
Фиг. 21 является схемой общей конфигурации вышеописанной системы связи. На фиг. 21, система связи включает в себя устройство 2110 связи на стороне кодирования, канал 2120 связи и устройство 2130 связи на стороне декодирования.
Устройство 2110 связи на стороне кодирования включает в себя связанный с кодированием с коррекцией со стиранием ошибок процессор 2112, модуль 2113 кодирования с коррекцией ошибок и передающее устройство 2114.
Устройство 2130 связи на стороне декодирования включает в себя приемное устройство 2131, модуль 2132 декодирования с коррекцией ошибок и связанный с декодированием с коррекцией со стиранием ошибок процессор 2133.
Канал 2120 связи представляет канал, через который передается сигнал, передаваемый из передающего устройства 2114 устройства 2110 связи на стороне кодирования, до тех пор, пока он не принимается посредством приемного устройства 2131 устройства 2130 связи на стороне декодирования. В качестве канала 2120 связи, может быть использован Ethernet (зарегистрированная торговая марка), линия электросети, металлический кабель, оптоволокно, беспроводная линия, световая линия (видимый свет, инфракрасное излучение и т.п.) или комбинация вышеозначенного.
Модуль 2113 кодирования с коррекцией ошибок вводит код коррекции ошибок на физическом уровне помимо кода коррекции со стиранием ошибок, чтобы корректировать ошибки, сформированные в канале 2120 связи. Следовательно, модуль 2132 декодирования с коррекцией ошибок декодирует код коррекции ошибок на физическом уровне. Следовательно, уровень, к которому применяется кодирование/декодирование с коррекцией со стиранием ошибок, отличается от уровня (т.е. физического уровня), к которому применяется кодирование с коррекцией ошибок, и декодирование по алгоритму мягких решений выполняется при декодировании с коррекцией ошибок на физическом уровне, в то время как операция восстановления потерянных битов выполняется при декодировании с коррекцией со стиранием ошибок.
Фиг. 22 показывает внутреннюю конфигурацию связанного с кодированием с коррекцией со стиранием ошибок процессора 2112. Способ кодирования с коррекцией со стиранием ошибок посредством связанного с кодированием с коррекцией со стиранием ошибок процессора 2112 описывается с использованием фиг. 22.
Модуль 2211 формирования пакетов принимает информацию 2241 в качестве ввода, формирует пакет 2243 информации и выводит пакет 2243 информации в модуль 2215 переупорядочения. В дальнейшем в этом документе описывается случай в качестве примера, в котором пакет 2243 информации формируется с помощью пакетов информации #1-n.
Модуль 2215 переупорядочения принимает пакет 2243 информации (здесь, пакеты информации #1-n) в качестве ввода, переупорядочивает информацию и выводит переупорядоченную информацию 2245.
Кодер 2216 с коррекцией со стиранием ошибок (модуль формирования пакетов четности) принимает переупорядоченную информацию 2245 в качестве ввода, выполняет кодирование, например, LDPC-CC (сверточного кода разреженного контроля по четности) для информации 2245 и формирует четность. Кодер 2216 с коррекцией со стиранием ошибок (модуль формирования пакетов четности) извлекает только сформированную часть четности, формирует и выводит пакет 2247 четности (посредством сохранения и переупорядочения четности) из извлеченной части четности. В это время, когда пакеты четности #1-m формируются для пакетов информации #1-n, пакет 2247 четности формируется с помощью пакетов четности #1-m.
Модуль 2217 добавления кода с обнаружением ошибок принимает пакет 2243 информации (пакеты информации #1-n) и пакет 2247 четности (пакеты четности #1-m) в качестве ввода. Модуль 2217 добавления кода с обнаружением ошибок добавляет код с обнаружением ошибок, например, CRC к пакету 2243 информации (пакетам информации #1-n) и пакету 2247 четности (пакетам четности #1-m). Модуль 2217 добавления кода с обнаружением ошибок выводит пакет информации и пакет 2249 четности с добавленным CRC. Следовательно, пакет информации и пакет 2249 четности с добавленным CRC формируются с помощью пакетов информации #1-n и пакетов четности #1-m с добавленным CRC.
Кроме того, фиг. 23 показывает другую внутреннюю конфигурацию связанного с кодированием с коррекцией со стиранием ошибок процессора 2112. Связанный с кодированием с коррекцией со стиранием ошибок процессор 2312, показанный на фиг. 23, выполняет способ кодирования с коррекцией со стиранием ошибок, отличающийся от способа связанного с кодированием с коррекцией со стиранием ошибок процессора 2112, показанного на фиг. 22. Модуль 2314 кодирования с коррекцией со стиранием ошибок конфигурирует пакеты #1-#n+m с допущением информационных битов и битов четности в качестве данных без различения между пакетами информации и пакетами четности. Тем не менее, при конфигурировании пакетов, модуль 2314 кодирования с коррекцией со стиранием ошибок временно сохраняет информацию и четность во внутреннем запоминающем устройстве (не показано), затем выполняет переупорядочение и конфигурирует пакеты. Модуль 2317 добавления кода с обнаружением ошибок затем добавляет код с обнаружением ошибок, например, CRC к этим пакетам и выводит пакеты #1-#n+m с добавленным CRC.
Фиг. 24 показывает внутреннюю конфигурацию связанного с декодированием с коррекцией со стиранием ошибок процессора 2433. Способ декодирования с коррекцией со стиранием ошибок посредством связанного с декодированием с коррекцией со стиранием ошибок процессора 2433 описывается с использованием фиг. 24.
Модуль 2435 обнаружения ошибок принимает пакет 2451 после декодирования кода коррекции ошибок на физическом уровне в качестве ввода и выполняет обнаружение ошибок с использованием, например, CRC. В это время, пакет 2451 после декодирования кода коррекции ошибок на физическом уровне формируется с помощью декодированных информационных пакетов #1-n и декодированных пакетов четности #1-m. Когда имеются потерянные пакеты в декодированных информационных пакетах и декодированных пакетах четности в результате обнаружения ошибок, как показано, например, на фиг. 24, модуль 2435 обнаружения ошибок назначает номера пакетов пакетам информации и пакетам четности, в которых потери пакетов не возникают, и выводит эти пакеты в качестве пакета 2453.
Декодер 2436 с коррекцией со стиранием ошибок принимает пакет 2453 (пакеты информации (с номерами пакетов), в котором потери пакетов не возникают, и пакеты четности (с номерами пакетов)) в качестве ввода. Декодер 2436 с коррекцией со стиранием ошибок выполняет (переупорядочение и затем) декодирование на основе кода коррекции со стиранием ошибок для пакета 2453 и декодирует пакет 2455 информации (пакеты информации #1-n). Когда кодирование выполняется посредством связанного с кодированием с коррекцией со стиранием ошибок процессора 2312, показанного на фиг. 23, пакеты без различения между пакетами информации и пакетами четности вводятся в декодер 2436 с коррекцией со стиранием ошибок, и декодирование с коррекцией со стиранием ошибок выполняется.
Когда совместимость между повышением эффективности передачи и повышением способности к коррекции со стиранием ошибок рассматривается, желательно иметь возможность изменять скорость кодирования с помощью кода коррекции со стиранием ошибок согласно качеству связи. Фиг. 25 показывает пример конфигурации кодера 2560 с коррекцией со стиранием ошибок, который может изменять скорость кодирования кода коррекции со стиранием ошибок согласно качеству связи.
Первый кодер 2561 с коррекцией со стиранием ошибок является кодером для кода коррекции со стиранием ошибок скорости кодирования 1/2. Кроме того, второй кодер 2562 с коррекцией со стиранием ошибок является кодером для кода коррекции со стиранием ошибок скорости кодирования 2/3. Кроме того, третий кодер 2563 с коррекцией со стиранием ошибок является кодером для кода коррекции со стиранием ошибок скорости кодирования 3/4.
Первый кодер 2561 с коррекцией со стиранием ошибок принимает информацию 2571 и управляющий сигнал 2572 в качестве ввода, выполняет кодирование, когда управляющий сигнал 2572 обозначает скорость кодирования 1/2, и выводит данные 2573 после кодирования с коррекцией со стиранием ошибок в модуль 2564 выбора. Аналогично, второй кодер 2562 с коррекцией со стиранием ошибок принимает информацию 2571 и управляющий сигнал 2572 в качестве ввода, выполняет кодирование, когда управляющий сигнал 2572 обозначает скорость кодирования 2/3, и выводит данные 2574 после кодирования с коррекцией со стиранием ошибок в модуль 2564 выбора. Аналогично, третий кодер 2563 с коррекцией со стиранием ошибок принимает информацию 2571 и управляющий сигнал 2572 в качестве ввода, выполняет кодирование, когда управляющий сигнал 2572 обозначает скорость кодирования 3/4, и выводит данные 2575 после кодирования с коррекцией со стиранием ошибок в модуль 2564 выбора.
Модуль 2564 выбора принимает данные 2573, 2574 и 2575 после кодирования с коррекцией со стиранием ошибок и управляющий сигнал 2572 в качестве ввода и выводит данные 2576 после кодирования с коррекцией со стиранием ошибок, соответствующего скорости кодирования, обозначенной посредством управляющего сигнала 2572.
Посредством изменения скорости кодирования кода коррекции со стиранием ошибок согласно ситуации связи и задания надлежащей скорости кодирования таким образом, можно реализовывать совместимость между повышением качества приема обменивающейся данными стороны и повышением скорости передачи данных (информации).
В это время, кодер должен реализовывать множество скоростей кодирования при небольшом размере схем и достигать высокой способности к коррекции со стиранием ошибок одновременно. В дальнейшем в этом документе подробно описывается способ кодирования (кодер) и способ декодирования для реализации этой совместимости.
Способ кодирования/декодирования, который описывается в дальнейшем, использует LDPC-CC, описанный в вариантах 1-3 осуществления, в качестве кода для коррекции со стиранием ошибок. Если фокус обращен на способность к коррекции со стиранием ошибок в это время, когда, например, LDPC-CC со скоростью кодирования, превышающей 3/4, используется, высокая способность к коррекции со стиранием ошибок может достигаться. С другой стороны, когда LDPC-CC с более низкой скоростью кодирования, чем 2/3, используется, имеется проблема в том, что трудно достигать высокой способности к коррекции со стиранием ошибок. В дальнейшем в этом документе описывается способ кодирования, который может разрешать эту проблему и реализовывать множество скоростей кодирования при небольшом размере схем.
Фиг. 26 является схемой общей конфигурации системы связи. На фиг. 26, система связи включает в себя устройство 2600 связи на стороне кодирования, канал 2607 связи и устройство 2608 связи на стороне декодирования.
Канал 2607 связи представляет тракт, через который передается сигнал, передаваемый из передающего устройства 2605 устройства 2600 связи на стороне кодирования, до тех пор, пока он не принимается посредством приемного устройства 2609 устройства 2608 связи на стороне декодирования.
Приемное устройство 2613 принимает принимаемый сигнал 2612 в качестве ввода и получает информацию (информацию обратной связи) 2615, возвращенную из устройства 2608 связи, и принятые данные 2614.
Связанный с кодированием с коррекцией со стиранием ошибок процессор 2603 принимает информацию 2601, управляющий сигнал 2602 и информацию 2615, возвращенную из устройства 2608 связи, в качестве ввода. Связанный с кодированием с коррекцией со стиранием ошибок процессор 2603 определяет скорость кодирования кода коррекции со стиранием ошибок на основе управляющего сигнала 2602 или информации 2615 обратной связи из устройства 2608 связи, выполняет кодирование и выводит пакет после кодирования с коррекцией со стиранием ошибок.
Модуль 2604 кодирования с коррекцией ошибок принимает пакеты после кодирования с коррекцией со стиранием ошибок, управляющий сигнал 2602 и информацию 2615 обратной связи из устройства 2608 связи в качестве ввода. Модуль 2604 кодирования с коррекцией ошибок определяет скорость кодирования кода коррекции ошибок на физическом уровне на основе управляющего сигнала 2602 или информации 2615 обратной связи из устройства 2608 связи, выполняет кодирование с коррекцией ошибок на физическом уровне и выводит кодированные данные.
Передающее устройство 2605 принимает кодированные данные в качестве ввода, выполняет обработку, такую как квадратурная модуляция, преобразование частоты и усиление, и выводит передаваемый сигнал. Здесь, предполагается, что передаваемый сигнал включает в себя символы, к примеру, символы для передачи управляющей информации, известные символы в дополнение к данным. Кроме того, предполагается, что передаваемый сигнал включает в себя управляющую информацию, к примеру, информацию по скорости кодирования кода коррекции ошибок на физическом уровне и скорости кодирования кода коррекции со стиранием ошибок.
Приемное устройство 2609 принимает принимаемый сигнал в качестве ввода, применяет обработку, такую как усиление, преобразование частоты, квадратурная демодуляция, выводит принимаемое логарифмическое отношение правдоподобия, оценивает окружение канала связи, такое как окружение распространения, интенсивность электрического поля приема из известных символов, включенных в передаваемый сигнал, и выводит сигнал оценки. Кроме того, приемное устройство 2609 демодулирует символы для управляющей информации, включенной в принимаемый сигнал, тем самым получает информацию по скорости кодирования кода коррекции ошибок и скорости кодирования кода коррекции со стиранием ошибок на физическом уровне, заданных посредством передающего устройства 2605, и выводит информацию в качестве управляющего сигнала.
Модуль 2610 декодирования с коррекцией ошибок принимает принимаемое логарифмическое отношение правдоподобия и управляющий сигнал в качестве ввода и выполняет надлежащее декодирование с коррекцией ошибок на физическом уровне с использованием скорости кодирования кода коррекции ошибок на физическом уровне, включенной в управляющий сигнал. Модуль 2610 декодирования с коррекцией ошибок выводит декодированные данные и выводит информацию о том, выполнена успешно или нет коррекция ошибок на физическом уровне (информацию успешности/ошибки коррекции ошибок (например, ACK/NACK)).
Связанный с декодированием с коррекцией со стиранием ошибок процессор 2611 принимает декодированные данные и управляющий сигнал в качестве ввода и выполняет декодирование с коррекцией со стиранием ошибок с использованием скорости кодирования кода коррекции со стиранием ошибок, включенной в управляющий сигнал. Связанный с декодированием с коррекцией со стиранием ошибок процессор 2611 затем выводит декодированные данные коррекции со стиранием ошибок и выводит информацию о том, выполнена успешно или нет коррекция ошибок при коррекции со стиранием ошибок (информацию успешности/ошибки коррекции со стиранием ошибок (например, ACK/NACK)).
Передающее устройство 2617 принимает информацию для оценки (RSSI: индикатор интенсивности принимаемого сигнала, или CSI: информацию состояния канала), которая является оценкой окружения канала связи, такой как окружение распространения, интенсивность электрического поля приема, информация успешности/ошибки коррекции ошибок на физическом уровне и информация обратной связи на основе информации успешности/ошибки коррекции со стиранием ошибок при коррекции со стиранием ошибок, и передаваемые данные в качестве ввода. Передающее устройство 2617 применяет обработку, такую как кодирование, преобразование, квадратурная модуляция, преобразование частоты, усиление, и выводит передаваемый сигнал 2618. Передаваемый сигнал 2618 передается в устройство 2600 связи.
Способ изменения скорости кодирования кода коррекции со стиранием ошибок в связанном с кодированием с коррекцией со стиранием ошибок процессоре 2603 описывается с использованием фиг. 27. На фиг. 27, частям, работающим аналогично частям на фиг. 22, назначаются идентичные ссылки с номерами. Фиг. 27 отличается от фиг. 22 тем, что управляющий сигнал 2602 и информация 2615 обратной связи вводятся в модуль 2211 формирования пакетов и кодер 2216 с коррекцией со стиранием ошибок (модуль формирования пакетов четности). Связанный с кодированием с коррекцией со стиранием ошибок процессор 2603 изменяет размер пакета и скорость кодирования кода коррекции со стиранием ошибок на основе управляющего сигнала 2602 и информации 2615 обратной связи.
Кроме того, фиг. 28 показывает другую внутреннюю конфигурацию связанного с кодированием с коррекцией со стиранием ошибок процессора 2603. Связанный с кодированием с коррекцией со стиранием ошибок процессор 2603, показанный на фиг. 28, изменяет скорость кодирования кода коррекции со стиранием ошибок с использованием способа, отличающегося от способа связанного с кодированием с коррекцией со стиранием ошибок процессора 2603, показанного на фиг. 27. На фиг. 28, частям, работающим аналогично частям на фиг. 23, назначаются идентичные ссылки с номерами. Фиг. 28 отличается от фиг. 23 тем, что управляющий сигнал 2602 и информация 2615 обратной связи вводятся в кодер 2316 с коррекцией со стиранием ошибок и модуль 2317 добавления кода с обнаружением ошибок. Связанный с кодированием с коррекцией со стиранием ошибок процессор 2603 затем изменяет размер пакета и скорость кодирования кода коррекции со стиранием ошибок на основе управляющего сигнала 2602 и информации 2615 обратной связи.
Фиг. 29 показывает пример конфигурации модуля кодирования согласно настоящему варианту осуществления. Кодер 2900 на фиг. 29 является модулем LDPC-CC-кодирования, поддерживающим множество скоростей кодирования. В дальнейшем в этом документе, описывается случай, в котором кодер 2900, показанный на фиг. 29, поддерживает скорость кодирования 4/5 и скорость кодирования 16/25.
Модуль 2902 переупорядочения принимает информацию X в качестве ввода и сохраняет информационные биты X. Когда четыре информационных бита X сохраняются, модуль 2902 переупорядочения переупорядочивает информационные биты X и выводит информационные биты X1, X2, X3 и X4 параллельно в четырех линиях информации. Тем не менее, эта конфигурация является просто примером. Операции модуля 2902 переупорядочения описываются ниже.
LDPC-CC-кодер 2907 поддерживает скорость кодирования 4/5. LDPC-CC-кодер 2907 принимает информационные биты X1, X2, X3 и X4 и управляющий сигнал 2916 в качестве ввода. LDPC-CC-кодер 2907 выполняет LDPC-CC-кодирование, показанное в вариантах 1-3 осуществления, и выводит бит (P1) 2908 четности. Когда управляющий сигнал 2916 указывает скорость кодирования 4/5, информация X1, X2, X3 и X4 и четность (P1) становятся выводами кодера 2900.
Модуль 2902 переупорядочения принимает информационные биты X1, X2, X3, X4, бит P1 четности и управляющий сигнал 2916 в качестве ввода. Когда управляющий сигнал 2916 указывает скорость кодирования 4/5, модуль 2909 переупорядочения не работает. С другой стороны, когда управляющий сигнал 2916 указывает скорость кодирования 16/25, модуль 2909 переупорядочения сохраняет информационные биты X1, X2, X3 и X4 и бит P1 четности. Модуль переупорядочения 2909 затем переупорядочивает сохраненные информационные биты X1, X2, X3 и X4 и бит P1 четности, выводит переупорядоченные данные #1 (2910), переупорядоченные данные #2 (2911), переупорядоченные данные #3 (2912) и переупорядоченные данные #4 (2913). Способ переупорядочения в модуле 2909 переупорядочения описывается ниже.
Аналогично LDPC-CC-кодеру 2907, LDPC-CC-кодер 2914 поддерживает скорость кодирования 4/5. LDPC-CC-кодер 2914 принимает переупорядоченные данные #1 (2910), переупорядоченные данные #2 (2911), переупорядоченные данные #3 (2912), переупорядоченные данные #4 (2913) и управляющий сигнал 2916 в качестве ввода. Когда управляющий сигнал 2916 указывает скорость кодирования 16/25, LDPC-CC-кодер 2914 выполняет кодирование и выводит бит (P2) 2915 четности. Когда управляющий сигнал 2916 указывает скорость кодирования 4/5, переупорядоченные данные #1 (2910), переупорядоченные данные #2 (2911), переупорядоченные данные #3 (2912), переупорядоченные данные #4 (2913) и бит (P2) (2915) четности становятся выводами кодера 2900.
Фиг. 30 показывает общее представление способа кодирования посредством кодера 2900. Модуль 2902 переупорядочения принимает информационный бит X(4N) в качестве ввода из информационного бита X(1), и модуль 2902 переупорядочения переупорядочивает информационные биты X. Модуль 2902 переупорядочения затем выводит переупорядоченные информационные биты в четырех параллельных линиях. Следовательно, модуль 2902 переупорядочения сначала выводит [X1(1), X2(1), X3(1), X4(1)] и затем выводит [X1(2), X2(2), X3(2), X4(2)]. Модуль 2902 переупорядочения в завершение выводит [X1(N), X2(N), X3(N), X4(N)].
LDPC-CC-кодер 2907 со скоростью кодирования 4/5 кодирует [X1(1), X2(1), X3(1), X4(1)] и выводит бит P1(1) четности. LDPC-CC-кодер 2907 аналогично выполняет кодирование, формирует и выводит биты P1(2), P1(3),..., P1(N) четности после этого.
Модуль 2909 переупорядочения принимает [X1(1), X2(1), X3(1), X4(1), P1(1)], [X1(2), X2(2), X3(2), X4(2), P1(2)],..., [X1(N), X2(N), X3(N), X4(N), P1(N)] в качестве ввода. Модуль 2909 переупорядочения выполняет переупорядочение, включающее в себя биты четности в дополнение к информационным битам.
Например, в примере, показанном на фиг. 30, модуль 2909 переупорядочения выводит переупорядоченные [X1(50), X2(31), X3(7), P1(40)],..., [X2(39), X4(67), P1(4), X1(20)],..., [P2(65), X4(21), P1(16), X2(87)].
LDPC-CC-кодер 2914 со скоростью кодирования 4/5 выполняет кодирование для [X1(50), X2(31), X3(7), P1(40)], как показано посредством кадра 3000 на фиг. 30, и формирует бит P2(1) четности. LDPC-CC-кодер 2914 аналогично формирует и выводит биты P2(1), P2(2),..., P2(m) после этого.
Когда управляющий сигнал 2916 указывает скорость кодирования 4/5, кодер 2900 формирует пакеты с использованием [X1(1), X2(1), X3(1), X4(1), P1(1)], [X1(2), X2(2), X3(2), X4(2), P1(2)],..., [X1(N), X2(N), X3(N), X4(N), P1(N)].
Кроме того, когда управляющий сигнал 2916 указывает скорость кодирования 16/25, кодер 2900 формирует пакеты с использованием [X1(50), X2(31), X3(7), P1(40), P2(1)], [X2(39), X4(67), P1(4), X1(20), P2(2)],..., [P2(65), X4(21), P1(16), X2(87), P2(m)].
Как описано выше, согласно настоящему варианту осуществления, кодер 2900 приспосабливает конфигурацию соединения LDPC-CC-кодеров 2907 и 2914 со скоростью кодирования в 4/5 и размещения модулей 2902 переупорядочения и 2909 перед LDPC-CC-кодерами 2907 и 2914, соответственно. Кодер 2900 затем изменяет данные, которые должны быть выведены, согласно обозначенной скорости кодирования. Таким образом, можно поддерживать множество скоростей кодирования при небольшом размере схем и достигать эффекта достижения высокой способности к коррекции со стиранием ошибок на каждой скорости кодирования.
Фиг. 29 описывает конфигурацию кодера 2900, в котором соединяются два LDPC-CC-кодера 2907 и 2914 со скоростью кодирования 4/5, но конфигурация не ограничивается этим. Например, как показано на фиг. 31, кодер 2900 также может иметь конфигурацию, в которой LDPC-CC-кодеры 3102 и 2914 с различными скоростями кодирования соединяются. На фиг. 31, частям, работающим аналогично частям на фиг. 29, назначаются идентичные ссылки с номерами.
Модуль 3101 переупорядочения принимает информацию X битов в качестве ввода и сохраняет информационные биты X. Когда пять информационных битов X сохраняются, модуль 3101 переупорядочения переупорядочивает информационные биты X и выводит информационные биты X1, X2, X3, X4 и X5 в пяти параллельных линиях.
LDPC-CC-кодер 3103 поддерживает скорость кодирования 5/6. LDPC-CC-кодер 3103 принимает информационные биты X1, X2, X3, X4, X5 и управляющий сигнал 2916 в качестве ввода, выполняет кодирование для информационных битов X1, X2, X3, X4 и X5 и выводит бит (P1) 2908 четности. Когда управляющий сигнал 2916 указывает скорость кодирования 5/6, информационные биты X1, X2, X3, X4, X5 и бит (P1) 2908 четности становятся выводами кодера 2900.
Модуль 3104 переупорядочения принимает информационные биты X1, X2, X3, X4, X5, бит (P1) 2908 четности и управляющий сигнал 2916 в качестве ввода. Когда управляющий сигнал 2916 указывает скорость кодирования 2/3, модуль 3104 переупорядочения сохраняет информационные биты X1, X2, X3, X4, X5 и бит (P1) 2908 четности. Модуль 3104 переупорядочения переупорядочивает сохраненные информационные биты X1, X2, X3, X4, X5 и бит (P1) 2908 четности и выводит переупорядоченные данные в четырех параллельных линиях. В это время, четыре линии включают в себя информационные биты X1, X2, X3, X4, X5 и бит (P1) четности.
LDPC-CC-кодер 2914 поддерживает скорость кодирования 4/5. LDPC-CC-кодер 2914 принимает четыре линии данных и управляющий сигнал 2916 в качестве ввода. Когда управляющий сигнал 2916 указывает скорость кодирования 2/3, LDPC-CC-кодер 2914 выполняет кодирование для четырех линий данных и выводит бит (P2) четности. Следовательно, LDPC-CC-кодер 2914 выполняет кодирование с использованием информационных битов X1, X2, X3, X4, X5 и бита P1 четности.
Кодер 2900 может задавать скорость кодирования равной любому значению. Кроме того, когда кодеры с идентичной скоростью кодирования соединяются, они могут быть кодерами идентичного кода или кодерами различных кодов.
Кроме того, хотя фиг. 29 и фиг. 31 показывают примеры конфигураций кодера 2900, поддерживающего две скорости кодирования, кодер 2900 может поддерживать три или более скоростей кодирования. Фиг. 32 показывает пример конфигурации кодера 3200, поддерживающего три или более скоростей кодирования.
Модуль 3202 переупорядочения принимает информационные биты X в качестве ввода и сохраняет информационный бит sX. Модуль 3202 переупорядочения переупорядочивает сохраненные информационные биты X и выводит переупорядоченные информационные биты X в качестве первых данных 3203, которые должны быть кодированы посредством следующего LDPC-CC-кодера 3204.
LDPC-CC-кодер 3204 поддерживает скорость кодирования (n-1)/n. LDPC-CC-кодер 3204 принимает первые данные 3203 и управляющий сигнал 2916 в качестве ввода, выполняет кодирование для первых данных 3203 и управляющего сигнала 2916 и выводит бит (P1) 3205 четности. Когда управляющий сигнал 2916 указывает скорость кодирования (n-1)/n, первые данные 3203 и бит (P1) 3205 четности становятся выводами кодера 3200.
Модуль 3206 переупорядочения принимает первые данные 3203, бит (P1) 3205 четности и управляющий сигнал 2916 в качестве ввода. Когда управляющий сигнал 2916 указывает скорость кодирования {(n-1)(m-1)/(nm)} или меньше, модуль 3206 переупорядочения сохраняет первые данные 3203 и битовую четность (P1) 3205. Модуль 3206 переупорядочения переупорядочивает сохраненные первые данные 3203 и бит (P1) 3205 четности и выводит переупорядоченные первые данные 3203 и бит (P1) 3205 четности в качестве вторых данных 3207, которые должны быть кодированы посредством следующего LDPC-CC-кодера 3208.
LDPC-CC-кодер 3208 поддерживает скорость кодирования (m-1)/m. LDPC-CC-кодер 3208 принимает вторые данные 3207 и управляющий сигнал 2916 в качестве ввода. Когда управляющий сигнал 2916 указывает скорость кодирования {(n-1)(m-1)/(nm)} или меньше, LDPC-CC-кодер 3208 выполняет кодирование для вторых данных 3207 и выводит четность (P2) 3209. Когда управляющий сигнал 2916 указывает скорость кодирования {(n-1)(m-1)/(nm)}, вторые данные 3207 и бит (P2) 3209 четности становится выводом кодера 3200.
Модуль 3210 переупорядочения принимает вторые данные 3207, бит (P2) 3209 четности и управляющий сигнал 2916 в качестве ввода. Когда управляющий сигнал 2916 указывает скорость кодирования {(n-1)(m-1)(s-1)}/(nms) или меньше, модуль 3210 переупорядочения сохраняет вторые данные 3209 и бит (P2) 3207 четности. Модуль 3210 переупорядочения переупорядочивает сохраненные вторые данные 3209 и бит (P2) 3207 четности и выводит переупорядоченные вторые данные 3209 и четность (P2) 3207 в качестве третьих данных 3211, которые должны быть кодированы посредством следующего LDPC-CC-кодера 3212.
LDPC-CC-кодер 3212 поддерживает скорость кодирования (s-1)/s. LDPC-CC-кодер 3212 принимает третьи данные 3211 и управляющий сигнал 2916 в качестве ввода. Когда управляющий сигнал 2916 указывает скорость кодирования {(n-1)(m-1)(s-1)}/(nms) или меньше, LDPC-CC-кодер 3212 выполняет кодирование для третьих данных 3211 и выводит бит (P3) 3213 четности. Когда управляющий сигнал 2916 указывает скорость кодирования {(n-1)(m-1)(s-1)}/(nms), третьи данные 3211 и бит (P3) 3213 четности становятся выводами кодера 3200.
Посредством дополнительного соединения нескольких LDPC-CC-кодеров, можно реализовывать больше скоростей кодирования. Это позволяет реализовывать множество скоростей кодирования при небольшом размере схем и достигать эффекта возможности достигать высокой способности к коррекции со стиранием ошибок на каждой скорости кодирования.
На фиг. 29, фиг. 31 и фиг. 32, переупорядочение (переупорядочение на начальной стадии) информационных битов X не всегда необходимо. Кроме того, хотя модуль переупорядочения описан как имеющий конфигурацию, в которой переупорядоченные информационные биты X выводятся параллельно, модуль переупорядочения не ограничивается этой конфигурацией, и переупорядоченные информационные биты X также могут быть последовательно выведены.
Фиг. 33 показывает пример конфигурации декодера 3310, соответствующего кодеру 3200 на фиг. 32.
Когда последовательность ui передачи в момент времени i допускается как ui=(X1,i, X2,i,..., Xn-1,i, P1,i, P2,i, P3,i,...,), последовательность u передачи представляется как u=(u0, u1,..., ui,...,)T.
На фиг. 34, матрица 3300 представляет матрицу H контроля по четности, используемую посредством декодера 3310. Кроме того, матрица 3301 представляет субматрицу, соответствующую LDPC-CC-кодеру 3204, матрица 3302 представляет субматрицу, соответствующую LDPC-CC-кодеру 3208, и матрица 3303 представляет субматрицу, соответствующую LDPC-CC-кодеру 3212. Субматрицы в матрице H контроля по четности продолжаются аналогично далее. Декодер 3310 выполнен с возможностью иметь матрицу контроля по четности с наименьшей скоростью кодирования.
В декодере 3310, показанном на фиг. 33, BP-декодер 3313 является BP-декодером на основе матрицы контроля по четности с наименьшей скоростью кодирования из поддерживаемых скоростей кодирования. BP-декодер 3313 принимает потерянные данные 3311 и управляющий сигнал 3312 в качестве ввода. Здесь, потерянные данные 3311 состоят из битов, которые уже определены как равные "0" или "1", и биты, которые еще не определены как равные "0" или "1". BP-декодер 3313 выполняет BP-декодирование на основе скорости кодирования, обозначенной посредством управляющего сигнала 3312, и тем самым выполняет коррекцию со стиранием ошибок и выводит данные 3314 после коррекции со стиранием ошибок.
В дальнейшем в этом документе описываются операции декодера 3310.
Например, когда скорость кодирования составляет (n-1)/n, данные, соответствующие P2, P3,..., не присутствуют в потерянных данных 3311. Тем не менее, в этом случае BP-декодер 3313 выполняет операцию декодирования с допущением данных, соответствующих P2, P3,..., равными "0" и тем самым может реализовывать коррекцию со стиранием ошибок.
Аналогично, когда скорость кодирования составляет {(n-1)(m-1)}/(nm), данные, соответствующие P2, P3,..., не присутствуют в потерянных данных 3311. Тем не менее, в этом случае, BP-декодер 3313 выполняет операцию декодирования с допущением данных, соответствующих P3,..., равными "0" и тем самым может реализовывать коррекцию со стиранием ошибок. BP-декодер 3313 может работать аналогично для других скоростей кодирования.
Таким образом, декодер 3310 имеет матрицу контроля по четности с наименьшей скоростью кодирования из поддерживаемых скоростей кодирования и поддерживает BP-декодирование на множестве скоростей кодирования с использованием этой матрицы контроля по четности. Это позволяет поддерживать множество скоростей кодирования при небольшом размере схем и достигать эффекта достижения высокой способности к коррекции со стиранием ошибок на каждой скорости кодирования.
В дальнейшем в этом документе описывается случай, в котором кодирование с коррекцией со стиранием ошибок фактически выполняется с использованием LDPC-CC. Поскольку LDPC-CC является видом сверточного кода, LDPC-CC требует завершения или дополнения битами концевой части, чтобы достигать высокой способности к коррекции со стиранием ошибок.
Ниже в качестве примера изучается случай, в котором завершение нулем, описанное в варианте 2 осуществления, используется. В частности, описывается способ вставки последовательности завершения.
Предполагается, что число информационных битов равно 16384, а число битов, составляющих один пакет, равно 512. Здесь рассматривается случай, в котором кодирование выполняется с использованием LDPC-CC со скоростью кодирования 4/5. В это время, если информационные биты кодируются на скорости кодирования 4/5 без выполнения завершения, поскольку число информационных битов равно 16384, число битов четности равно 4096 (16384/4). Следовательно, когда один пакет формируется с помощью 512 битов (при этом 512 битов не включают в себя биты, отличные от информации, к примеру, код с обнаружением ошибок), 40 пакетов формируются.
Тем не менее, если кодирование выполняется без выполнения завершения таким образом, способность к коррекции со стиранием ошибок значительно снижается. Чтобы разрешать эту проблему, последовательность завершения должна вставляться.
Таким образом, способ вставки последовательности завершения предложен ниже с учетом числа битов, составляющих пакет.
Более конкретно, предложенный способ вставляет последовательность завершения таким образом, что сумма числа информационных битов (не включающих в себя последовательность завершения), числа битов четности и числа битов последовательности завершения становится целым кратным числа битов, составляющих пакет. Тем не менее, биты, составляющие пакет, не включают в себя управляющую информацию, к примеру, код с обнаружением ошибок, и число битов, составляющих пакет, означает число битов данных, связанных с кодированием с коррекцией со стиранием ошибок.
Следовательно, в вышеприведенном примере, последовательность завершения 512*h битов (h является натуральным числом) добавляется. Посредством выполнения этого, можно предоставлять эффект вставки последовательности завершения и тем самым достигать высокой способности к коррекции со стиранием ошибок и эффективно конфигурировать пакет.
Как описано выше, LDPC-CC со скоростью кодирования (n-1)/n используется, и когда число информационных битов составляет (n-1)*c битов, c битов четности получаются. Затем рассматривается взаимосвязь между числом битов завершения d нулем и числом битов, составляющим один пакет z. Тем не менее, число битов, составляющих пакет z, не включает в себя управляющую информацию, к примеру, код с обнаружением ошибок, и число битов, составляющих пакет z, означает число битов данных, связанных с кодированием с коррекцией со стиранием ошибок.
В это время, если число битов завершения d нулем определяется таким образом, что уравнение 62 справедливо, можно предоставлять эффект вставки последовательности завершения, достигать высокой способности к коррекции со стиранием ошибок и эффективно конфигурировать пакет.
[62]
(n-1)*c+c+d=nc+d=Az... (уравнение 62),
где A является целым числом.
Тем не менее, (n-1)*c информационных битов могут включать в себя дополненные фиктивные данные (не исходные информационные биты, а известные биты (например, "0"), добавленные к информационным битам, чтобы упрощать кодирование). Дополнение описывается ниже.
Когда кодирование с коррекцией со стиранием ошибок выполняется, предусмотрен модуль (2215) переупорядочения, как очевидно из фиг. 22. Модуль переупорядочения, в общем, конструируется с использованием RAM. По этой причине, модулю 2215 переупорядочения трудно реализовывать аппаратные средства, которые поддерживают переупорядочение всех размеров информационных битов (размера информации). Следовательно, инструктирование модулю переупорядочения поддерживать несколько типов размера информации является важным при подавлении увеличения размера аппаратных средств.
Можно легко поддерживать как вышеуказанный случай, в котором кодирование с коррекцией со стиранием ошибок выполняется, так и случай, в котором кодирование с коррекцией со стиранием ошибок не выполняется. Фиг. 35 показывает конфигурации пакетов в этих случаях.
Когда кодирование с коррекцией со стиранием ошибок не выполняется, только пакеты информации передаются.
Когда кодирование с коррекцией со стиранием ошибок выполняется, рассмотрим случай, в котором пакеты передаются с использованием одного из следующих способов:
1. Пакеты формируются и передаются посредством различения между пакетами информации и пакетами четности.
2. Пакеты формируются и передаются без различения между пакетами информации и пакетами четности.
В этом случае, чтобы подавлять увеличение аппаратного размера схем, желательно корректировать число битов, составляющих пакет z, независимо от того, выполняется или нет кодирование с коррекцией со стиранием ошибок.
Следовательно, когда число информационных битов, используемых для кодирования с коррекцией со стиранием ошибок, допускается равным I, уравнение 63 должно быть справедливым. Тем не менее, в зависимости от числа информационных битов, дополнение должно быть выполнено.
[63]
I=α*z... (уравнение 63)
Здесь, α допускается равным целому числу. Кроме того, z является числом битов, составляющим пакет, биты, составляющие пакет, не включают в себя управляющую информацию, к примеру, код с обнаружением ошибок, и число битов, составляющих пакет z, означает число битов данных, связанных с кодированием с коррекцией со стиранием ошибок.
В вышеописанном случае, число битов информации, требуемой для кодирования с коррекцией со стиранием ошибок, составляет α*z. Тем не менее, информация всех α*z битов не всегда фактически доступна для кодирования с коррекцией со стиранием ошибок, а только информация меньше α*z битов может быть доступной. В этом случае, способ вставки фиктивных данных используется, так что число битов становится α*z. Следовательно, когда число битов информации для кодирования с коррекцией со стиранием ошибок меньше α*z, известные данные (например, "0") вставляются, так что число битов становится α*z. Кодирование с коррекцией со стиранием ошибок выполняется для информации α*z битов, сформированных таким образом.
Биты четности получаются посредством выполнения кодирования с коррекцией со стиранием ошибок. Затем предполагается, что завершение нулем выполняется для того, чтобы достигать высокой способности к коррекции со стиранием ошибок. В это время, при условии, что число битов четности, полученных через кодирование с коррекцией со стиранием ошибок, составляет C, и число битов завершения нулем составляет D, пакеты эффективно конфигурируются, когда уравнение 64 справедливо.
[64]
C+D=βz... (уравнение 64)
Здесь, β допускается равным целому числу. Кроме того, z является числом битов, составляющим пакет, биты, составляющие пакет, не включают в себя управляющую информацию, к примеру, код с обнаружением ошибок, и число битов, составляющих пакет z, означает число битов данных, связанных с кодированием с коррекцией со стиранием ошибок.
Здесь, биты, составляющие пакет z, зачастую конфигурируются в единицах байтов. Следовательно, когда скорость кодирования LDPC-CC составляет (n-1)/n, если уравнение 65 справедливо, можно не допускать такой ситуации, что дополняющие биты всегда требуются, когда кодирование с коррекцией со стиранием ошибок выполняется.
[65]
(n-1)=2k... (уравнение 65),
где K является целым числом, равным или превышающим 0.
Следовательно, когда кодер с коррекцией со стиранием ошибок, который реализует множество скоростей кодирования, конфигурируется, если скорости кодирования, которые должны поддерживаться, допускаются равными R=(n0-1)/n0, (n1-1)/n1, (n2-1)/n2,..., (ni-1)/ni,..., (nv-1)/nv (i=0, 1, 2,..., v-1, v; v является целым числом, равным или превышающим 1), и уравнение 66 справедливо, можно не допускать такой ситуации, что дополняющие биты всегда требуются, когда кодирование с коррекцией со стиранием ошибок выполняется.
[66]
(ni-1)=2k... (уравнение 64),
где K является целым числом, равным или превышающим 0.
Когда условие, соответствующее этому условию, рассматривается, например, относительно скорости кодирования кодера с коррекцией со стиранием ошибок на фиг. 32, если предполагается, что уравнения 67-1-67-3 являются справедливыми, можно не допускать такой ситуации, что дополняющие биты всегда необходимы, когда кодирование с коррекцией со стиранием ошибок выполняется.
[67]
(n-1)=2k1... (уравнение 67-1)
(n-1)(m-1)=2k2... (уравнение 67-2)
(n-1)(m-1)(s-1)=2k3... (уравнение 67-3),
где k1, k2 и k3 являются целыми числами, равными или превышающими 0.
Хотя случай для LDPC-CC описан выше, то же самое может аналогично рассматриваться в отношении QC-LDPC-кода, LDPC-кода (блочного LDPC-кода), к примеру, случайного LDPC-кода, как показано в непатентном документе 1, непатентном документе 2, непатентном документе 3 и непатентном документе 7. Например, рассмотрим кодер с коррекцией со стиранием ошибок, который использует блочный LDPC-код в качестве кода коррекции со стиранием ошибок и поддерживает множество скоростей кодирования R=b0/a0, b1/a1, b2/a2,..., bi/ai,..., bv-1/av-1, bv/av (i=0, 1, 2,..., v-1,v; v является целым числом, равным или превышающим 1; ai является целым числом, равным или превышающим 1, bi является целым числом, равным или превышающим 1, ai≥bi). В это время, если уравнение 68 справедливо, можно не допускать такой ситуации, что дополняющие биты всегда требуются, когда кодирование с коррекцией со стиранием ошибок выполняется.
[68]
bi=2ki... (уравнение 68),
где ki является целым числом, равным или превышающим 0.
Кроме того, относительно взаимосвязи между числом информационных битов, числом битов четности и числом битов, составляющим пакет, рассматривается случай, в котором блочный LDPC-код используется в качестве кода коррекции со стиранием ошибок. В это время, при условии, что число информационных битов, используемых для кодирования с коррекцией со стиранием ошибок, составляет I, уравнение 69 может быть справедливым. Тем не менее, в зависимости от числа информационных битов, дополнение должно быть выполнено.
[69]
I=α*z... (уравнение 69)
Здесь, α допускается равным целому числу. Оно также является числом битов, составляющих пакет, и биты, составляющие пакет, не включают в себя управляющую информацию, к примеру, код с обнаружением ошибок, и число битов, составляющих пакет z, означает число битов данных, связанных с кодированием с коррекцией со стиранием ошибок.
В вышеописанном случае, число битов информации, необходимой для того, чтобы выполнять кодирование с коррекцией со стиранием ошибок, составляет α*z. Тем не менее, вся информация α*z битов не всегда фактически доступна для кодирования с коррекцией со стиранием ошибок, а только информация битов меньше α*z битов может быть доступной. В этом случае, способ вставки фиктивных данных используется, так что число битов становится α*z. Следовательно, когда число битов информации для кодирования с коррекцией со стиранием ошибок меньше α*z, известные данные (например, "0") вставляются, так что число битов становится α*z. Кодирование с коррекцией со стиранием ошибок выполняется для информации α*z битов, сформированных таким образом.
Биты четности получаются посредством выполнения кодирования с коррекцией со стиранием ошибок. В это время, при условии, что число битов четности, полученных через кодирование с коррекцией со стиранием ошибок, составляет C, пакеты эффективно конфигурируются, когда уравнение 70 справедливо.
[70]
C=βz... (уравнение 70),
где β допускается равным целому числу.
Поскольку длина блока определяется, когда дополнение битами концевой части выполняется, этот случай может обрабатываться аналогичным образом тому, когда блочный LDPC-код применяется к коду коррекции со стиранием ошибок.
Шестой вариант осуществления
Настоящий вариант осуществления описывает важные элементы, связанные с "LDPC-CC на основе полинома контроля по четности с изменяющимся во времени периодом, превышающим 3", описанным в варианте 1 осуществления.
1: LDPC-CC
LDPC-CC является кодом, заданным посредством матрицы разреженного контроля по четности, как в случае LDPC-BC, может быть задан посредством изменяющейся во времени матрицы контроля по четности по четности бесконечной длины, но может фактически рассматриваться с периодически изменяющейся во времени матрицей контроля по четности.
При условии, что матрица контроля по четности - это H, и синдромный формирователь - это HT, HT LDPC-CC со скоростью кодирования R=d/c (d<c) может представляться так, как показано в уравнении 71.
[71]
 ... (уравнение 71)
... (уравнение 71)
В уравнении 71, HT i(t) (i=0, 1,..., ms) является периодической субматрицей c*(c-d), и если период допускается равным Ts, HT i(t)=HT i(t+Ts) справедливо для ∀i и ∀t. Кроме того, Ms является емкостью запоминающего устройства.
LDPC-CC, заданный посредством уравнения 71, является изменяющимся во времени сверточным кодом, и этот код называется "изменяющимся во времени LDPC-CC". Что касается декодирования, BP-декодирование выполняется с использованием матрицы H контроля по четности. Когда вектор u кодированной последовательности допускается, следующее выражение отношения справедливо.
[72]
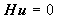 ... (уравнение 72)
... (уравнение 72)
Информационная последовательность получается посредством выполнения BP-декодирования с использованием выражения отношения в уравнении 72.
2: LDPC-CC на основе полинома контроля по четности
Рассмотрим систематический сверточный код со скоростью кодирования R=1/2 порождающей матрицы G=[1 G1(D)/G0(D)]. В это время, G1 представляет полином с прямой связью, и G0 представляет полином с обратной связью.
При условии, что полиномиальным представлением информационной последовательности является X(D), а полиномиальным представлением последовательности четности является P(D), полином контроля по четности, который удовлетворяет 0, может представляться так, как показано ниже.
[73]
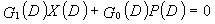 ... (уравнение 73)
... (уравнение 73)
Здесь, полином контроля по четности предоставляется в качестве уравнения 74, который удовлетворяет уравнению 73.
[74]
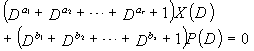 ... (уравнение 74)
... (уравнение 74)
В уравнении 74, ap и bq являются целыми числами, равными или превышающими 1 (p=1, 2,..., r; q=1, 2,..., s), элементы D0 присутствуют в X(D) и P(D). Код, заданный посредством матрицы контроля по четности на основе полинома контроля по четности, который удовлетворяет 0 в уравнении 74, становится независимым от времени LDPC-CC.
M (m является целым числом, равным или превышающим 2) различных полиномов контроля по четности на основе уравнения 74 предоставляются. Полином контроля по четности, который удовлетворяет 0, представляется так, как показано ниже.
[75]
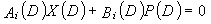 ... (уравнение 75)
... (уравнение 75)
В это время, i=0, 1,..., m-1.
Данные и четность в момент времени j представляются посредством Xj и Pj в качестве uj=(Xj, Pj). Затем предполагается, что полином контроля по четности, который удовлетворяет 0 в уравнении 76, является справедливым.
[76]
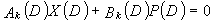 (k=j mod m)... (уравнение 76)
(k=j mod m)... (уравнение 76)
Четность Pj в момент времени j затем может быть определена из уравнения 76. Код, заданный посредством матрицы контроля по четности, сформированной на основе полинома контроля по четности, который удовлетворяет 0 в уравнении 76, становится LDPC-CC с изменяющимся во времени периодом m (TV-m-LDPC-CC: изменяющийся во времени LDPC-CC с периодом времени m).
В это время, существуют элементы D0 в P(D) независимого от времени LDPC-CC, заданного в уравнении 74, и TV-m-LDPC-CC, заданного в уравнении 76, где bj является целым числом, равным или превышающим 1. Следовательно, существует такая характеристика, что четность может легко находиться последовательно посредством регистра и исключающего ИЛИ.
Модуль декодирования создает матрицу H контроля по четности из уравнения 74 с использованием независимого от времени LDPC-CC и создает матрицу H контроля по четности из уравнения 76 с использованием TV-m-LDPC-CC. Модуль декодирования выполняет BP-декодирование для кодированной последовательности u=(u0, u1,..., uj,...,)T с использованием уравнения 72 и получает информационную последовательность.
Затем, рассмотрим независимый от времени LDPC-CC и TV-m-LDPC-CC со скоростью кодирования (n-1)/n. Предполагается, что информационная последовательность X1, X2,..., Xn-1 и четность P в момент времени j представляются посредством X2,j,..., Xn-1,j и Pj, соответственно, и uj=(X1,j, X2,j,..., Xn-1,j, Pj). Когда предполагается, что полиномиальное представление информационной последовательности X1, X2,..., Xn-1 является X1(D), X2(D),..., Xn-1(D), полином контроля по четности, который удовлетворяет 0, представляется так, как показано ниже.
[77]
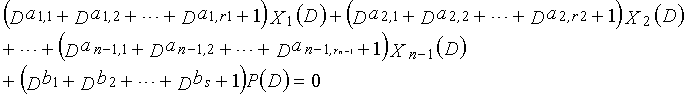 ... (уравнение 77)
... (уравнение 77)
В уравнении 77, ap,i является целым числом, равным или превышающим 1 (p=1, 2,..., n-1; i=1, 2,..., rp), и удовлетворяет ap,y≠ap,z (∀(y, z) | y, z=1, 2,..., rp, y≠z) и b≠bz (∀(y, z) | y, z=1, 2,..., ε, y≠z).
M (m является целым числом, равным или превышающим 2) различных полиномов контроля по четности на основе уравнения 77 предоставляются. Полином контроля по четности, который удовлетворяет 0, представляется так, как показано ниже.
[78]
 ... (уравнение 78),
... (уравнение 78),
где i=0, 1,..., m-1.
Затем предполагается, что уравнение 79 справедливо для X1,j, X2,j,..., Xn-1,j и Pj информации X1, X2,..., Xn-1 и четности P в момент времени j.
[79]
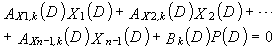 (k=j mod m)... (уравнение 79)
(k=j mod m)... (уравнение 79)
В это время, коды на основе уравнения 77 и уравнения 79 становятся независимым от времени LDPC-CC и TV-m-LDPC-CC со скоростью кодирования (n-1)/n.
3: Регулярный TV-m-LDPC-CC
Во-первых, описывается регулярный TV-m-LDPC-CC, обрабатываемый в данном исследовании.
Известно, что когда длина кодового ограничения является практически идентичной, TV3-LDPC-CC может получать лучшую способность к коррекции ошибок, чем LDPC-CC (TV2-LDPC-CC) с изменяющимся во времени периодом 2. Также известно, что хорошая способность к коррекции ошибок может достигаться посредством использования регулярного LDPC-кода для TV3-LDPC-CC. Данное исследование направлено на то, чтобы создавать обычный LDPC-CC с изменяющимся во времени периодом m (m>3).
Q-ый полином контроля по четности TV-m-LDPC-CC со скоростью кодирования (n-1)/n, который удовлетворяет 0, предоставляется, как показано ниже (q=0, 1,..., m-1).
[80]
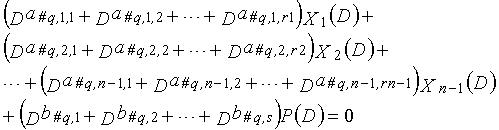 ... (уравнение 80)
... (уравнение 80)
В уравнении 80, a#q,p,i является целым числом, равным или превышающим 0 (p=1, 2,..., n-1; i=1, 2,..., rp), и удовлетворяет a#q,p,y≠a#q,p,z (∀(y, z)|y, z=1, 2,..., rp, y≠z) и b#q,y≠b#q,z (∀(y, z)|y, z=1, 2,..., ε, y≠z).
Следующие признаки затем предоставляются.
Признак 1
Существует взаимосвязь, как показано ниже, между элементом Da#α,p,iXp(D) полинома контроля по четности #α, элементом Da#β,p,jXp(D) полинома контроля по четности #β (α, β=0, 1,..., m-1; p=1, 2,..., n-1; i, j=1, 2,..., rp) и между элементом Db#α,iP(D) полинома контроля по четности #α и элементом Db#β,jP(D) полинома контроля по четности #β (α, β=0, 1,..., m-1 (β≥α); i, j=1, 2,..., rp).
1. Когда β=α:
Когда {a#α,p,i mod m=a#β,p,j mod m}∩{ij} справедливо, присутствует переменный узел $1, который формирует ребра как контрольного узла, соответствующего полиному контроля по четности #α, так и контрольного узла, соответствующего полиному контроля по четности #β, как показано на фиг. 36. Когда {b#α,i mod m=b#β,j mod m}∩{ij} справедливо, присутствует переменный узел $1, который формирует ребра как контрольного узла, соответствующего полиному контроля по четности #α, так и контрольного узла, соответствующего полиному контроля по четности #β, как показано на фиг. 36.
2. Когда β≠α:
Предполагается, что β-α=L.
1) Когда a#α,p,i mod m<a#β,p,j mod m
Когда (a#β,p,j mod m)-(a#α,p,i mod m)=L, присутствует переменный узел $1, который формирует ребра как контрольного узла, соответствующего полиному контроля по четности #α, так и контрольного узла, соответствующего полиному контроля по четности #β, как показано на фиг. 36.
2) Когда a#α,p,i mod m>a#β,p,j mod m
Когда (a#β,p,j mod m)-(a#α,p,i mod m)=L+m, присутствует переменный узел $1, который формирует ребра как контрольного узла, соответствующего полиному контроля по четности #α, так и контрольного узла, соответствующего полиному контроля по четности #β, как показано на фиг. 36.
3) Когда b#α,i mod m<b#β,j mod m
Когда (b#β,j mod m)-(b#α,i mod m)=L, присутствует переменный узел $1, который формирует ребра как контрольного узла, соответствующего полиному контроля по четности #α, так и контрольного узла, соответствующего полиному контроля по четности #β, как показано на фиг. 36.
4) Когда b#α,i mod m>b#β,j mod m
Когда (b#β,j mod m)-(b#α,i mod m)=L+m, присутствует переменный узел $1, который формирует ребра как контрольного узла, соответствующего полиному контроля по четности #α, так и контрольного узла, соответствующего полиному контроля по четности #β, как показано на фиг. 36.
Теорема 1 является справедливой для длины цикла 6 (CL6: длина цикла 6) TV-m-LDPC-CC.
Теорема 1: Следующие два условия предоставляются для полинома контроля по четности, который удовлетворяет 0 в TV-m-LDPC-CC:
Существует p и q, которые удовлетворяют C#1.1: a#q,p,i mod m=a#q,p,j mod m=a#q,p,k mod m, где i≠j, i≠k и j≠k. Существует q, который удовлетворяет C#1.2: b#q,i mod m=b#q,j mod m=b#q,k mod m, где i≠j, i≠k и j≠k. Существует, по меньшей мере, одна CL6, когда C#1.1 или C#1.2 удовлетворяются.
Доказательство:
Если можно доказать, что, по меньшей мере, одна CL6 присутствует, когда a#0,1,i mod m=a#0,1,j mod m=a#0,1,k mod m, когда p=1 и q=0, можно доказать, что, по меньшей мере, одна CL6 присутствует также для X2(D),..., Xn-1(D), P(D), посредством подстановки X2(D),..., Xn-1(D), P(D) для X1(D), если C#1.1 и C#1.2 справедливо, когда q=0
Кроме того, когда q=0, если вышеприведенное описание может быть доказано, можно доказать, что "по меньшей мере, одна CL6 присутствует также тогда, когда "q=1,..., m-1, если C#1.1 и C#1.2 справедливо" аналогично этому.
Следовательно, когда p=1, q=0, если a#0,1,i mod m=a#0,1,j mod m=a#0,1,k mod m справедливо, можно доказать, что, по меньшей мере, одна CL6 присутствует.
В X1(D), когда q=0 допускается для полинома контроля по четности, который удовлетворяет 0 в TV-m-LDPC-CC в уравнении 80, если два или меньше элементов присутствует, никогда не удовлетворяют C#1.1.
В X1(D), когда q=0 допускается для полинома контроля по четности, который удовлетворяет 0 в TV-m-LDPC-CC в уравнении 80, если три элемента присутствуют, и a#q,p,i mod m=a#q,p,j mod m=a#q,p,k mod m удовлетворяется, полином контроля по четности, который удовлетворяет 0 при q=0, может представляться так, как показано в уравнении 81.
[81]
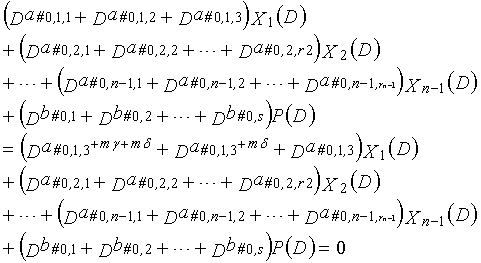 ... (уравнение 81)
... (уравнение 81)
Здесь, даже когда a#0,1,1>a#0,1,2>a#0,1,3 допускается, общность не теряется, и γ и δ становятся натуральными числами. В это время, в уравнении 81, когда q=0, фокус обращен на элемент, связанный с X1(D), т.е. (Da#0,1,3+mγ+mδ+Da#0,1,3+mδ+Da#0,1,3) X1(D). В это время, субматрица, сформированная посредством извлечения только части, связанной с X1(D) в матрице H контроля по четности, представляется так, как показано на фиг. 37. На фиг. 37, h1,X1, h2,X1,..., hm-1,X1 являются векторами, сформированными посредством извлечения только частей, связанных с X1(D), когда q=1, 2,..., m-1 в полиноме контроля по четности, который удовлетворяет 0 в уравнении 81, соответственно.
В это время, взаимосвязь, как показано на фиг. 37, является справедливой, поскольку (1) признака 1 справедливо. Следовательно, CL6, сформированная с "1", показанным посредством символа "△", как показано на фиг. 37, всегда формируется только в субматрице, сформированной посредством извлечения только части, связанной с X1(D) матрицы контроля по четности в уравнении 81 независимо от значений γ и δ.
Когда четыре или более связанных с X1(D) элемента присутствуют, три элемента выбираются из числа четырех или более элементов, и если a#0,1,i mod m=a#0,1,j mod m=a#0,1,k mod m справедливо в выбранных трех элементах, CL6 формируется так, как показано на фиг. 37.
Как показано выше, когда q=0, если a#0,1,i mod m=a#0,1,j mod m=a#0,1,k mod m справедливо относительно X1(D), CL6 присутствует.
Кроме того, посредством подстановки также X1(D) для X2(D),..., Xn-1(D), P(D), по меньшей мере, одна CL6 возникает, когда C#1.1 или C#1.2 справедливо.
Кроме того, аналогично этому, также для q=1,..., m-1, по меньшей мере, одна CL6 присутствует, когда C#1.1 или C#1.2 удовлетворяются.
Следовательно, в полиноме контроля по четности, который удовлетворяет 0 в уравнении 80, когда C#1.1 или C#1.2 справедливо, по меньшей мере, одна CL6 формируется.
□ (конец доказательства)
Q-ый полином контроля по четности, который удовлетворяет 0 в TV-m-LDPC-CC со скоростью кодирования (n-1)/n, который описывается в дальнейшем в этом документе, предоставляется ниже на основе уравнения 74 (q=0,..., m-1):
[82]
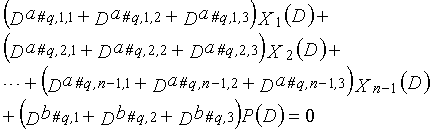 ... (уравнение 82)
... (уравнение 82)
Здесь, в уравнении 82, предполагается, что существует три элемента в X1(D), X2(D),..., Xn-1(D) и P(D), соответственно.
Согласно теореме 1, чтобы подавлять возникновение CL6, необходимо удовлетворять a#q,p,1 mod m≠a#q,p,2 mod m ∩ a#q,p,1 mod m≠a#q,p,3 mod m ∩ a#q,p,2 mod m≠a#q,p,3 mod m в Xq(D) уравнения 82. Аналогично, необходимо удовлетворять b#q,1 mod m≠b#q,2 mod m ∩ b#q,1 mod m≠b#q,3 mod m ∩ b#q,2 mod m≠b#q,3 mod m в P(D). ∩ представляет пересечение.
Затем, согласно признаку 1, следующее условие рассматривается в качестве примера условия регулярного LDPC-кода.
C#2: для ∀q, (a#q,p,1 mod m, a#q,p,2 mod m, a#q,p,3 mod m)=(Np,1, Np,2, Np,3) ∩ (b#q,1 mod m, b#q,2 mod m, b#q,3 mod m)=(M1, M2, M3) справедливо. Тем не менее, {a#q,p,1 mod m≠a#q,p,2 mod m} ∩ {a#q,p,1 mod m≠a#q,p,3 mod m ∩ a#q,p,2 mod m≠a#q,p,3 mod m} и {b#q,1 mod m≠b#q,2 mod m ∩ b#q,1 mod m≠b#q,3 mod m} ∩ {b#q,2 mod m≠b#q,3 mod m} удовлетворяется. Здесь, символ "∀" ∀q является квантором всеобщности, и ∀q означает все q.
Следующее пояснение обсуждает регулярный TV-m-LDPC-CC, который удовлетворяет условию C#2.
Разработка кода регулярного TV-m-LDPC-CC
Непатентный документ 13 показывает частоту ошибок декодирования, когда равномерно случайный регулярный LDPC-код подвергается декодированию по способу максимального правдоподобия в двоичном входном и выходном симметричном канале, и показывает, что доверительная функция Галлэджера (см. непатентный документ 14) может достигаться посредством равномерно случайного регулярного LDPC-кода. Тем не менее, когда BP-декодирование выполняется, непонятно, может или нет доверительная функция Галлэджера достигаться посредством равномерно случайного регулярного LDPC-кода.
Между прочим, LDPC-CC принадлежит сверточному коду. Непатентный документ 15 и непатентный документ 16 описывают доверительную функцию сверточного кода и описывают, что доверие зависит от длины кодового ограничения. Поскольку LDPC-CC является сверточным кодом, он имеет структуру, конкретную для сверточного кода в матрице контроля по четности, но когда изменяющийся во времени период увеличивается, позиции, в которых "1" существуют s матрицы контроля по четности, аппроксимируются к равномерной случайности. Тем не менее, поскольку LDPC-CC является сверточным кодом, матрица контроля по четности имеет структуру, конкретную для сверточного кода, и позиции, в которых "1" существуют s, зависят от длины кодового ограничения.
Из этих результатов логический вывод (логический вывод #1) по разработке кода предоставляется в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2.
Логический вывод #1:
Когда BP-декодирование используется, если изменяющийся во времени период m TV-m-LDPC-CC увеличивается в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, равномерная случайность аппроксимируется для позиций, в которых единицы существуют в матрице контроля по четности, и код с высокой способностью к коррекции ошибок получается.
Способ реализации логического вывода #1 поясняется ниже.
Признак регулярного TV-m-LDPC-CC
Описывается признак, который является справедливым при отрисовке дерева относительно уравнения 82, которое является q-ым полиномом контроля по четности, который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2 скорости кодирования (n-1)/n, которое должно обсуждаться в настоящем пояснении.
Признак 2
В регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда изменяющийся во времени период m является простым числом, рассмотрим случай, в котором C#3.1 справедливо с фокусом на одном из X1(D),..., Xn-1(D).
C#3.1: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, a#q,p,i mod m≠a#q,p,j mod m справедливо в Xp(D) для ∀q (q=0,..., m-1), где i≠j.
В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Da#q,p,iXp(D) и Da#q,p,jXp(D), которые удовлетворяют C#3.1.
В это время, согласно признаку 1, существуют контрольные узлы, соответствующие всем #0-m-1 полиномам контроля по четности для ∀q в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82.
Аналогично, когда изменяющийся во времени период m является простым числом в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассмотрим случай, в котором C#3.2 справедливо с фокусом на элементе P(D).
C#3.2: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, b#q,i mod m≠b#q,j mod m справедливо в P(D) для ∀q, где i≠j.
В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Db#q,iP(D) и Db#q,jP(D), которые удовлетворяют C#3.2.
В это время, согласно признаку 1, существуют контрольные узлы, соответствующие всем #0-m-1 полиномам контроля по четности для ∀q в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82.
Пример: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, предполагается, что изменяющийся во времени период m=7 (простое число) и (b#q,1, b#q,2)=(2, 0) справедливо для ∀q. Следовательно, C#3.2 удовлетворяется.
Когда дерево отрисовывается исключительно для переменных узлов, соответствующих Db#q,1P(D) и Db#q,2P(D), дерево, начальная точка которого является контрольным узлом, соответствующим #0-вому полиному контроля по четности, который удовлетворяет 0 в уравнении 82, представляется так, как показано на фиг. 38. Как очевидно из фиг. 38, изменяющийся во времени период m=7 удовлетворяет признаку 2.
Признак 3
В регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда изменяющийся во времени период m не является простым числом, рассмотрим случай, в котором C#4.1 справедливо с фокусом на одном из X1(D),..., Xn-1(D).
C#4.1: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда a#q,p,i mod m≥a#q,p,j mod m в Xp(D) для ∀q, |a#q,p,i mod m-a#q,p,j mod m| является делителем, отличным от 1, для m, где i≠j.
В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Da#q,p,iXp(D) и Da#q,p,jXp(D), которые удовлетворяют C#4.1. В это время, согласно признаку 1, в дереве, начальная точка которого соответствует q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82, отсутствуют контрольные узлы, соответствующие всем #0-m-1 контрольным полиномам четности для ∀q.
Аналогично, в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассмотрим случай, в котором C#4.2 справедливо, когда изменяющийся во времени период m не является простым числом, с фокусом на элементе P(D).
C#4.2: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда b#q,i mod m≥b#q,j mod m в P(D) для ∀q, |b#q,i mod m-b#q,j mod m| является делителем, отличным от 1, для m, где i≠j.
В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Db#q,iP(D) и Db#q,jP(D), которые удовлетворяют C#4.2. В это время, согласно признаку 1, в дереве, начальная точка которого является контрольным узлом, соответствует q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82, нет всех контрольных узлов, соответствующих #0-m-1 полиномам контроля по четности для ∀q.
Пример: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, предполагается, что изменяющийся во времени период m=6 (не простое число) и (b#q,1, b#q,2)=(3, 0) справедливо для ∀q. Следовательно, C#4.2 удовлетворяется.
Когда дерево отрисовывается исключительно для переменных узлов Db#q,1P(D) и Db#q,2P(D), дерево, начальная точка которого является контрольным узлом, соответствующим #0-вому полиному контроля по четности, который удовлетворяет 0 в уравнении 82, представляется так, как показано на фиг. 39. Как очевидно из фиг. 39, изменяющийся во времени период m=6 удовлетворяет признаку 3.
Затем, в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, описывается признак, который, в частности, относится к тому, когда изменяющийся во времени период m является четным числом.
Признак 4
В регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда изменяющийся во времени период m является четным числом, рассмотрим случай, в котором C#5.1 справедливо с фокусом на одном из X1(D),..., Xn-1(D).
C#5.1: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда a#q,p,i mod m≥a#q,p,j mod m в Xp(D) для ∀q, |a#q,p,i mod m-a#q,p,j mod m| является четным числом, где i≠j.
В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Da#q,p,iXp(D) и Da#q,p,jXp(D), которые удовлетворяют C#5.1. В это время, согласно признаку 1, когда q является нечетным числом, существуют только контрольные узлы, соответствующие полиномам контроля по четности с нечетным номером в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82. С другой стороны, когда q является четным числом, существуют только контрольные узлы, соответствующие полиномам контроля по четности с четным номером в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82.
Аналогично, в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда изменяющийся во времени период m является четным числом, рассмотрим случай, в котором C#5.2 справедливо с фокусом на элементе P(D).
C#5.2: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда b#q,i mod m≥b#q,j mod m в P(D) для ∀q, |b#q,i mod m-b#q,j mod m| является четным числом, где i≠j.
В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Db#q,iP(D) и Db#q,jP(D), которые удовлетворяют C#5.2. В это время, согласно признаку 1, когда q является нечетным числом, только контрольные узлы, соответствующие полиномам контроля по четности с нечетным номером, присутствуют в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82. С другой стороны, когда q является четным числом, только контрольные узлы, соответствующие полиномам контроля по четности с четным номером, присутствуют в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82.
Способ разработки регулярного TV-m-LDPC-CC
Политика разработки рассматривается для предоставления высокой способности к коррекции ошибок в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2. Здесь рассматривается случай C#6.1, C#6.2 и т.п.
C#6.1: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Da#q,p,iXp(D) и Da#q,p,jXp(D) (где i≠j). В это время, все контрольные узлы, соответствующие #0-m-1 полиномам контроля по четности для ∀q, не присутствуют в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82.
C#6.2: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Db#q,iP(D) и Db#q,jP(D) (где i≠j). В это время, все контрольные узлы, соответствующие #0-m-1 полиномам контроля по четности для ∀q, не присутствуют в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82.
В таких случаях, как C#6.1 и C#6.2, поскольку "все контрольные узлы, соответствующие #0-m-1 полиномам контроля по четности для ∀q, не присутствуют", эффект в логическом выводе #1, когда изменяющийся во времени период увеличивается, не получается. Следовательно, с учетом вышеприведенного описания, следующая политика разработки предоставляется, чтобы обеспечивать высокую способность к коррекции ошибок.
Политика разработки: В регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, условие C#7.1 предоставлено с фокусом на одном из X1(D),..., Xn-1(D).
C#7.1: Рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Da#q,p,iXp(D) и Da#q,p,jXp(D) в полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2 (где i≠j). В это время, контрольные узлы, соответствующие всем #0-m-1 полиномам контроля по четности, присутствуют в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82 для ∀q.
Аналогично, в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, условие C#7.2 предоставлено с фокусом на элементе P(D).
C#7.2: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, рассматривается случай, в котором дерево отрисовывается исключительно для переменных узлов, соответствующих Db#q,iP(D) и Db#q,jP(D) (где i≠j). В это время, контрольные узлы, соответствующие всем #0-m-1 полиномам контроля по четности, присутствуют в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82 для ∀q.
В настоящей политике разработки предполагается, что C#7.1 справедливо для ∀(i, j) и также справедливо для ∀p, а C#7.2 справедливо для ∀(i, j).
Логический вывод #1 затем удовлетворяется.
Далее описывается теорема, связанная с политикой разработки.
Теорема 2: Удовлетворение политике разработки требует удовлетворения a#q,p,i mod m≠a#q,p,j mod m и b#q,i mod m≠b#q,j mod m, где i≠j.
Доказательство: Когда дерево отрисовывается исключительно для переменных узлов, соответствующих Da#q,p,iXp(D) и Da#q,p,jXp(D) в уравнении 82 для полинома контроля по четности, который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, если теорема 2 удовлетворяется, контрольные узлы, соответствующие всем #0-m-1 полиномам контроля по четности, присутствуют в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82. Это справедливо для всех p. Аналогично, когда дерево отрисовывается исключительно для переменных узлов, соответствующих Db#q,iP(D) и Db#q,jP(D) в уравнении 82 для полинома контроля по четности, который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, если теорема 2 удовлетворяется, контрольные узлы, соответствующие всем #0-m-1 полиномам контроля по четности, присутствуют в дереве, начальная точка которого является контрольным узлом, соответствующим q-муполиному контроля по четности, который удовлетворяет 0 в уравнении 82. Следовательно, теорема 2 доказана.
□ (конец доказательства)
Теорема 3: В регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда изменяющийся во времени период m является четным числом, отсутствует код, который удовлетворяет политике разработки.
Доказательство: В полиноме контроля по четности (82), который удовлетворяет 0 в регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, когда p=1, если можно доказать, что политика разработки не удовлетворяется, это означает то, что теорема 3 доказана. Следовательно, доказательство продолжается при условии, что p=1.
В регулярном TV-m-LDPC-CC, который удовлетворяет условию C#2, (Np,1, Np,2, Np,3)=("o", "o", "o") U ("o", "o", "e") U ("o", "e", "e") U ("e", "e", "e") может представлять все случаи. Тем не менее, "o" представляет нечетное число, а "e" представляет четное число. Следовательно, (Np,1, Np,2, Np,3)=("o", "o", "o") U ("o", "o", "e") U ("o", "e", "e") U ("e", "e", "e") показывает, что C#7.1 не удовлетворяется. U представляет объединение.
Когда (Np,1, Np,2, Np,3)=("o", "o", "o"), C#5.1 удовлетворяется, так что i, j=1, 2, 3 (i≠j) удовлетворяется в C#5.1, нет разницы, каким может быть значение набора (i, j).
Когда (Np,1, Np,2, Np,3)=("o", "o", "e"), C#5.1 удовлетворяется, когда (i, j)=(1, 2) в C#5.1.
Когда (Np,1, Np,2, Np,3)=("o", "e", "e"), C#5.1 удовлетворяется, когда (i, j)=(2, 3) в C#5.1.
Когда (Np,1, Np,2, Np,3)=("e", "e", "e"), C#5.1 удовлетворяется, так что i, j=1, 2, 3 (i≠j) удовлетворяется в C#5.1, нет разницы, каким может быть значение набора (i, j).
Следовательно, когда (Np,1, Np,2, Np,3)=("o", "o", "o") U ("o", "o", "e") U ("o", "e", "e") U ("e", "e", "e"), всегда существуют наборы (i, j), которые удовлетворяют C#5.1. Таким образом, теорема 3 доказана согласно признаку 4.
□ (конец доказательства)
Следовательно, чтобы удовлетворять политике разработки, изменяющийся во времени период m должен быть нечетным числом. Кроме того, чтобы удовлетворять политике разработки, следующие условия являются эффективными согласно признаку 2 и признаку 3.
- изменяющийся во времени период m является простым числом.
- изменяющийся во времени период m является нечетным числом, и число делителей m является небольшим.
В частности, когда условие, что "изменяющийся во времени период m является нечетным числом и числом делителей m, является небольшим", учитывается, следующие случаи могут рассматриваться в качестве примеров условий, при которых коды высокой способности к коррекции ошибок с большой вероятностью достигаются:
(1) Изменяющийся во времени период допускается равным α*β, где α и β являются нечетными числами, отличными от 1, и являются простыми числами.
(2) Изменяющийся во времени период допускается равным αn, где α является нечетным числом, отличным от 1, и является простым числом, и n является целым числом, равным или превышающим 2.
(3) Изменяющийся во времени период допускается равным α*β*γ, где α, β и γ являются нечетными числами, отличными от 1, и являются простыми числами.
Тем не менее, когда z mod m (z является целым числом, равным или превышающим 0) вычисляется, существуют значения m, которые могут быть приняты, и, следовательно, число принимаемых значений, когда z mod m вычисляется, увеличивается по мере того, как m увеличивается. Следовательно, когда m увеличивается, проще удовлетворять вышеописанной политике разработки. Тем не менее, когда изменяющийся во времени период m допускается равным четному числу, это не означает то, что код, имеющий высокую способность к коррекции ошибок, не может быть получен.
4: Пример поиска кода и оценки характеристик
Пример поиска кода:
Таблица 9 показывает примеры LDPC-CC (#1 и #2 в таблице 9) на основе полиномов контроля по четности с изменяющимися во времени периодами 2 и 3, поясненных выше. Помимо этого, таблица 9 также показывает пример регулярного TV11-LDPC-CC (#3 в таблице 9) с изменяющимся во времени периодом 11, который удовлетворяет вышеуказанной политике разработки. Тем не менее, предполагается, что скорость кодирования, заданная для поиска кода, составляет R=2/3, а максимальная длина Kmax кодового ограничения составляет 600.
Пример LDPC-CC на основе полинома контроля по четности со скоростью кодирования R=2/3
(AX1,1(D),AX2,1(D),B1(D))=(D558+D215+D124+1, D591+D154+D7+1, D594+D425+D137+1)
(AX1,1(D),AX2,1(D),B1(D))=(D413+D175+1, D455+D178+1, D514+D452+1)
(AX1,2(D),AX2,2(D),B2(D))=(D523+D164+1, D568+D140+1, D257+D208+1)
(AX1,1(D),AX2,1(D),B1(D))=(D585+D392+1, D597+D523+1, D254+D49+1)
(AX1,2(D),AX2,2(D),B2(D))=(D541+D469+1, D520+D17+1, D408+D115+1)
(AX1,3(D),AX2,3(D),B3(D))=(D563+D282+1, D531+D281+1, D544+D474+1)
(AX1,4(D),AX2,4(D),B4(D))=(D579+D541+1, D575+D292+1, D335+D155+1)
(AX1,5(D),AX2,5(D),B5(D))=(D596+D271+1, D575+D523+1, D529+D302+1)
(AX1,6(D),AX2,6(D),B6(D))=(D552+D62+1, D545+D531+1, D595+D566+1)
(AX1,7(D),AX2,7(D),B7(D))=(D596+D557+1, D520+D193+1, D148+D144+1)
(AX1,8(D),AX2,8(D),B8(D))=(D596+D524+1, D575+D358+1, D357+D298+1)
(AX1,9(D),AX2,9(D),B9(D))=(D552+D150+1, D564+D39+1, D463+D60+1)
Оценка BER-характеристики:
Фиг. 40 показывает взаимосвязь BER (BER-характеристики) относительно Eb/No (отношения энергии в расчете на бит к спектральной плотности шума) TV2-LDPC-CC (#1 в таблице 9), регулярного TV3-LDPC-CC (#2 в таблице 9) и регулярного TV11-LDPC-CC (#3 в таблице 9) со скоростью кодирования R=2/3 в окружении AWGN (с аддитивным белым гауссовым шумом). Тем не менее, при моделировании предполагается, что схемой модуляции является BPSK (двухпозиционная фазовая манипуляция), BP-декодирование на основе нормализованного BP (1/v=0,75) используется в качестве способа декодирования, и число итераций I=50. Здесь, v является коэффициентом нормализации.
Как показано на фиг. 40, когда Eb/No=2,0 или более, очевидно, что BER-характеристика регулярного TV11-LDPC-CC лучше BER-характеристик TV2-LDPC-CC и TV3-LDPC-CC.
Из вышеприведенного, можно подтверждать, что TV-m-LDPC-CC с большим изменяющимся во времени периодом на основе вышеуказанной политики разработки имеет лучшую способность к коррекции ошибок, чем способность к коррекции ошибок TV2-LDPC-CC и TV3-LDPC-CC, и подтверждать эффективность политики разработки, поясненной выше.
Седьмой вариант осуществления
Настоящий вариант осуществления описывает способ переупорядочения процессора кодирования с коррекцией со стиранием ошибок на уровне пакета, когда LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h (h является целым числом, равным или превышающим 4), описанный в варианте 1 осуществления, применяется к схеме коррекции со стиранием ошибок. Конфигурация процессора кодирования с коррекцией со стиранием ошибок согласно настоящему варианту осуществления является общей с конфигурацией процессора кодирования с коррекцией со стиранием ошибок, показанного на фиг. 22 или фиг. 23 и т.п., и, следовательно, описывается с использованием фиг. 22 или фиг. 23.
Вышеуказанный фиг. 8 показывает пример матрицы контроля по четности, когда LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом m, описанный в варианте 1 осуществления, используется. G-ый (g=0, 1,..., h-1) полином контроля по четности со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h представляется так, как показано в уравнении 83.
[83]
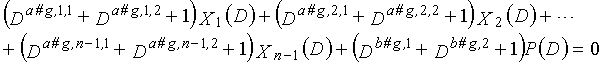 ... (уравнение 83)
... (уравнение 83)
В уравнении 83, a#g,p,1 и a#g,p,2 являются натуральными числами, равными или превышающими 1, и a#g,p,1≠a#g,p,2 поддерживается. Кроме того, b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 (g=0, 1, 2,..., h-2, h-1; p=1, 2,..., n-1) поддерживается.
Ссылаясь на матрицу контроля по четности, показанную на фиг. 8, матрица контроля по четности, соответствующая g-му(g=0, 1,..., h-1) полиному контроля по четности (83) со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h, представляется так, как показано на фиг. 41. В это время, информация X1, X2,..., Xn-1 и четность P в момент времени k представляются посредством X1,k, X2,k,..., Xn-1,k и Pk, соответственно.
На фиг. 41, часть с назначенной ссылкой с номером 5501 является частью строки матрицы контроля по четности и является вектором, соответствующим 0-вому полиному контроля по четности, который удовлетворяет 0 в уравнении 83. Аналогично, часть с назначенной ссылкой с номером 5502 является частью строки матрицы контроля по четности и является вектором, соответствующим первому полиному контроля по четности, который удовлетворяет 0 в уравнении 83.
"11111" с назначенной ссылкой с номером 5503 соответствует элементам X1(D), X2(D), X3(D), X4(D) и P(D) 0-вого полинома контроля по четности, который удовлетворяет 0 в уравнении 83. При сравнении с X1,k, X2,k,..., Xn-1,k и Pk в момент времени k, "1" ссылки с номером 5510 соответствует X1,k, "1" ссылки с номером 5511 соответствует X2,k, "1" ссылки с номером 5512 соответствует X3,k, "1" ссылки с номером 5513 соответствует X4,k, и "1" ссылки с номером 5514 соответствует Pk (см. уравнение 60).
Аналогично, "11111" с назначенной ссылкой с номером 5504 соответствует элементам X1(D), X2(D), X3(D), X4(D) и P(D) первого полинома контроля по четности, который удовлетворяет 0 в уравнении 83. При сравнении с X1,k+1, X2,k+1,..., Xn-1,k+1 и Pk+1 в момент времени k+1, "1" ссылки с номером 5515 соответствует X1,k+1, "1" ссылки с номером 5516 соответствует X2,k+1, "1" ссылки с номером 5517 соответствует X3,k+1, "1" ссылки с номером 5518 соответствует X4,k+1, и "1" ссылки с номером 5519 соответствует Pk+1 (см. уравнение 60).
Затем, описывается способ переупорядочения информационных битов пакета информации, когда пакеты информации и пакеты четности конфигурируются отдельно (см. фиг. 22), с использованием фиг. 42.
Фиг. 42 показывает пример шаблона переупорядочения, когда пакеты информации и пакеты четности конфигурируются отдельно.
Шаблон $1 показывает пример шаблона с низкой способностью к коррекции со стиранием ошибок, и шаблон $2 показывает пример шаблона с высокой способностью к коррекции со стиранием ошибок. На фиг. 42, #Z указывает данные Z-го пакета.
В шаблоне $1, X1,k и X4,k из X1,k, X2,k, X3,k и X4,k в момент времени k являются данными идентичного пакета (пакета #1). Аналогично, X3,k+1 и X4,k+1 в момент времени k+1 также являются данными идентичного пакета (пакета #2). В это время, когда, например, пакет #1 потерян (потери), трудно восстанавливать потерянные биты (X1,k и X4,k) через вычисление по строкам при BP-декодировании. Аналогично, когда пакет #2 потерян (потери), трудно восстанавливать потерянные биты (X3,k+1 и X4,k+1) через вычисление по строкам при BP-декодировании. Из аспектов, описанных выше, шаблон $1 может упоминаться в качестве примера шаблона с низкой способностью к коррекции со стиранием ошибок.
С другой стороны, в шаблоне $2, относительно X1,k, X2,k, X3,k и X4,k предполагается, что X1,k, X2,k, X3,k и X4,k состоят из данных с различными номерами пакетов во все моменты времени k. В это время, поскольку более вероятно иметь возможность восстанавливать потерянные биты через выч0исление по строкам при BP-декодировании, шаблон $2 может упоминаться в качестве примера шаблона с высокой способностью к коррекции со стиранием ошибок.
Таким образом, когда пакеты информации и пакеты четности конфигурируются отдельно (см. фиг. 22), модуль 2215 переупорядочения может приспосабливать шаблон $2, описанный выше, в качестве шаблона переупорядочения. Т.е. модуль 2215 переупорядочения принимает пакет 2243 информации (пакеты информации #1-n) в качестве ввода и может переупорядочивать последовательность информации так, что данные с различными номерами пакетов назначаются X1,k, X2,k, X3,k и X4,k во все моменты времени k.
Затем, описывается способ переупорядочения информационных битов в пакете информации, когда пакеты информации и пакеты четности конфигурируются без различения (см. фиг. 23), с использованием фиг. 43.
Фиг. 43 показывает пример шаблона переупорядочения, когда пакеты информации и пакеты четности конфигурируются без различения.
В шаблоне $1, X1,k и Pk из X1,k, X2,k, X3,k, X4,k и Pk в момент времени k состоят из данных идентичного пакета. Аналогично, X3,k+1 и X4,k+1 в момент времени k+1 также состоят из данных идентичного пакета, и X2,k+2, и Pk+2 в момент времени k+2 также состоят из данных идентичного пакета.
В это время, когда, например, пакет #1 потерян, трудно восстанавливать потерянные биты (X1,k и Pk) через вычисление по строкам при BP-декодировании. Аналогично, когда пакет #2 потерян, невозможно восстанавливать потерянные биты (X3,k+1 и X4,k+1) через вычисление по строкам при BP-декодировании, а когда пакет #5 потерян, трудно восстанавливать потерянные биты (X2,k+2 и Pk+2) через вычисление по строкам при BP-декодировании. Из аспекта, описанного выше, шаблон $1 может упоминаться в качестве примера шаблона с низкой способностью к коррекции со стиранием ошибок.
С другой стороны, в шаблоне $2, относительно X1,k, X2,k, X3,k, X4,k и Pk предполагается, что X1,k, X2,k, X3,k, X4,k и Pk состоят из данных с различными номерами пакетов во все моменты времени k. В это время, поскольку более вероятно иметь возможность восстанавливать потерянные биты через вычисление по строкам при BP-декодировании, шаблон $2 может упоминаться в качестве примера шаблона с высокой способностью к коррекции со стиранием ошибок.
Таким образом, когда пакеты информации и пакеты четности конфигурируются без различения (см. фиг. 23), модуль 2314 кодирования с коррекцией со стиранием ошибок может приспосабливать шаблон $2, описанный выше, в качестве шаблона переупорядочения. Т.е. модуль 2314 кодирования с коррекцией со стиранием ошибок может переупорядочивать информацию и четность так, что информация X1,k, X2,k, X3,k, X4,k и четность Pk назначаются пакетам с различными номерами пакетов во все моменты времени k.
Как описано выше, настоящий вариант осуществления предлагает конкретную конфигурацию для повышения способности к коррекции со стиранием ошибок в качестве способа переупорядочения в модуле кодирования с коррекцией со стиранием ошибок на уровне пакета, когда LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h (h является целым числом, равным или превышающим 4), описанный в варианте 1 осуществления, применяется к схеме коррекции со стиранием ошибок. Тем не менее, изменяющийся во времени период h не ограничивается целым числом, равным или превышающим 4, но даже когда изменяющийся во времени период равняется 2 или 3, способность к коррекции со стиранием ошибок может быть повышена посредством выполнения аналогичного переупорядочения.
Восьмой вариант осуществления
Настоящий вариант осуществления подробно описывает способ кодирования (способ кодирования на уровне пакета) на уровне выше физического уровня.
Фиг. 44 показывает пример способа кодирования на уровне выше физического уровня. На фиг. 44, предполагается, что скорость кодирования кода коррекции ошибок составляет 2/3, и размер данных за исключением избыточной информации, к примеру, управляющей информации и кода с обнаружением ошибок в одном пакете составляет 512 битов.
На фиг. 44, кодер, который выполняет кодирование на уровне выше физического уровня (кодирование на уровне пакета), выполняет кодирование для пакетов информации #1-8 после переупорядочения и получает биты четности. Кодер затем пакетирует биты четности, полученные в единице в 512 битов, чтобы конфигурировать один пакет четности. Здесь, поскольку скорость кодирования, поддерживаемая посредством кодера, составляет 2/3, четыре пакета четности, т.е. пакеты четности #1-4 формируются. Таким образом, пакеты информации, описанные в других вариантах осуществления, соответствуют пакетам информации #1-8 на фиг. 44, и пакеты четности соответствуют пакетам четности #1-4 на фиг. 44.
Один простой способ задания размера пакета четности является способом, который задает идентичный размер для пакета четности и пакета информации. Тем не менее, эти размеры не должны быть идентичными.
Фиг. 45 показывает пример способа кодирования на уровне выше физического уровня, отличающийся от фиг. 44. На фиг. 45, пакеты информации #1-512 являются исходными пакетами информации, и размер данных одного пакета за исключением избыточной информации, к примеру, управляющей информации, кода с обнаружением ошибок допускается равным 512 битов. Кодер затем разделяет пакет информации #k (k=1, 2,..., 511, 512) на 8 частей и формирует субпакеты информации #k-1, #k-2,..., и #k-8.
Кодер затем применяет кодирование к субпакетам информации #1-n, #2-n, #3-n,..., #511-n, #512-n (n=1, 2, 3, 4, 5, 6, 7, 8) и формирует группу четности #n. Кодер затем разделяет группу четности #n на m частей, как показано на фиг. 46, и формирует суб-(пакеты) четности #n-1, #n-2,..., и #n-m.
Таким образом, пакеты информации, описанные в варианте 5 осуществления, соответствуют пакетам информации #1-512 на фиг. 45, и пакеты четности являются суб-(пакетами) четности #n-1, #n-2,..., и #n-m (n=1, 2, 3, 4, 5, 6, 7, 8) на фиг. 37. В это время, один пакет информации имеет 512 битов, в то время как один пакет четности не должен всегда иметь 512 битов. Т.е. один пакет информации и один пакет четности не должны всегда иметь идентичный размер.
Кодер может рассматривать сам субпакет информации, полученный посредством деления пакета информации, в качестве одного пакета информации.
В качестве другого способа, вариант 5 осуществления также может быть реализован посредством рассмотрения пакетов информации, описанных в варианте 5 осуществления, как субпакетов информации #k-1, #k-2,..., и #k-8 (k=1, 2,..., 511, 512), описанных в настоящем варианте осуществления. В частности, вариант 5 осуществления описывает способ вставки последовательности завершения и способ конфигурирования пакета. Здесь, вариант 5 осуществления также может быть реализован посредством рассмотрения "субпакетов информации" и "субпакетов четности" в настоящем варианте осуществления как "субпакетов информации" и "пакетов четности", описанных в варианте 5 осуществления. Тем не менее, вариант осуществления может быть реализован проще, если число битов, составляющих субпакет информации, является идентичным числу битов, составляющих субпакет четности.
В варианте 5 осуществления данные, отличные от информации (например, кода с обнаружением ошибок), добавляются к пакету информации. Кроме того, в варианте 5 осуществления, данные, отличные от битов четности, добавляются к пакету четности. Тем не менее, условия, связанные с завершением, показанные в уравнениях 62-70, становятся важными условиями при применении к случаю, не включающему в себя данные, отличные от информационных битов и битов четности, и случаю, связанному с числом информационных битов пакета информации, и случаю, связанному с числом битов четности пакета четности.
Девятый вариант осуществления
Вариант 1 осуществления описывает LDPC-CC, имеющий хорошие характеристики. Настоящий вариант осуществления описывает способ укорачивания, который задает скорость кодирования переменной, когда LDPC-CC, описанный в варианте 1 осуществления, применяется к физическому уровню. "Укорачивание" означает формирование кода со второй скоростью кодирования из кода первой скорости кодирования (первая скорость кодирования>вторая скорость кодирования).
В дальнейшем в этом документе описывается способ укорачивания для формирования LDPC-CC со скоростью кодирования 1/3 из LDPC-CC с изменяющимся во времени периодом h (h является целым числом, равным или превышающим 4) и скоростью кодирования 1/2, описанного в варианте 1 осуществления, в качестве примера.
Рассматривается случай, в котором g-ый (g=0, 1,..., h-1) полином контроля по четности со скоростью кодирования 1/2 и изменяющимся во времени периодом h представляется так, как показано в уравнении 84.
[84]
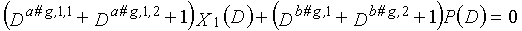 ... (уравнение 84)
... (уравнение 84)
В уравнении 84 допускается, что a#g,1,1 и a#g,1,2 являются натуральными числами, равными или превышающими 1, и a#g,1,1≠a#g,1,2 справедливо. Кроме того, предполагается, что b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 справедливо (g=0, 1, 2,..., h-2, h-1).
Уравнение 84 допускается как удовлетворяющее условию #17 ниже.
Условие #17
"a#0,1,1%h=a#1,1,1%h=a#2,1,1%h=a#3,1,1%h=... =a#g,1,1%h=... =a#h-2,1,1%h=a#h-1,1,1%h=vp=1 (vp=1: фиксированное значение)"
"b#0,1%h=b#1,1%h=b#2,1%h=b#3,1%h=... =b#g,1%h=... =b#h-2,1%h=b#h-1,1%h=w (w: фиксированное значение)"
"a#0,1,2%h=a#1,1,2%h=a#2,1,2%h=a#3,1,2%h=... =a#g,1,2%h=... =a#h-2,1,2%h=a#h-1,1,2%h=yp=1 (yp=1: фиксированное значение)"
"b#0,2%h=b#1,2%h=b#2,2%h=b#3,2%h=... =b#g,2%h=... =b#h-2,2%h=b#h-1,2%h=z (z: фиксированное значение)"
Когда матрица контроля по четности создается, как в случае варианта 4 осуществления, если предполагается, что информацией и четностью во время i является Xi и Pi, соответственно, кодовое слово w представляется посредством w=(X0, P0, X1, P1,..., Xi, Pi,...,)T.
В это время, способ укорачивания настоящего варианта осуществления использует следующие способы.
Способ #1-1'
Способ #1-1 вставляет известную информацию (например, 0) в информацию X на регулярной основе (правило вставки способа #1-1). Например, известная информация вставляется в hk (=h*k) битов из информационных 2hk (=2*h*k) битов (этап вставки), и кодирование выполняется для информации 2hk битов, включающей в себя известную информацию, с использованием LDPC-CC со скоростью кодирования 1/2. Четность в 2hk битов формируется (этап кодирования) таким образом. В это время, известная информация hk битов из информации 2hk битов обозначается как биты, которые не следует передавать (этап передачи). Скорость кодирования 1/3 может быть реализована таким образом.
Известная информация не ограничивается 0, а может иметь 1 или предварительно определенное значение, отличное от 1, и может сообщаться в устройство связи обменивающейся данными стороны или определяться в качестве технических требований.
В дальнейшем в этом документе, главным образом, описываются отличия от правила вставки способа #1-1.
Способ #1-2'
В отличие от способа #1-1, как показано на фиг. 47, способ #1-2 допускает 2*h*2k битов, сформированных с информацией и четностью в качестве одного периода, и вставляет известную информацию в идентичной позиции в каждый период (правило вставки способа #1-2).
Правило вставки для известной информации (правило вставки способа #1-2) описывается с фокусом на отличиях от способа #1-1 с использованием фиг. 48 в качестве примера.
Фиг. 48 показывает пример, в котором, когда изменяющийся во времени период равняется 4, 16 битов, сформированных с информацией и четностью, обозначаются как один период. В это время, способ #1-2 вставляет известную информацию (например, 0 (или 1, или предварительно определенное значение)) в X0, X2, X4 и X5 в первый один период.
Кроме того, способ #1-2 вставляет известную информацию (например, 0 (или 1, или предварительно определенное значение)) в X8, X10, X12 и X13 в следующий один период,..., и вставляет известную информацию в X8i, X8i+2,X8i+4 и X8i+5 в i-ый один период. С i-го одного периода и далее, способ #1-2 вставляет известную информацию в идентичных позициях в каждый период.
Затем, аналогично способу #1-1, способ #1-2 вставляет известную информацию, например, в hk битов из информационных 2hk битов и выполняет кодирование для информации 2hk битов, включающей в себя известную информацию, с использованием LDPC-CC со скоростью кодирования 1/2. Таким образом, четность 2hk битов формируется. В это время, когда известная информация hk битов допускается как биты, которые не следует передавать, скорость кодирования 1/3 может быть реализована.
В дальнейшем в этом документе описывается взаимосвязь между позициями, в которых известная информация вставляется, и способностью к коррекции ошибок с использованием фиг. 49 в качестве примера.
Фиг. 49 показывает соответствие между частью контрольной матрицы H и кодовым словом w (X0, P0, X1, P1, X2, P2,..., X9, P9). В строке 4001 на фиг. 49, элементы "1" размещаются в столбцах, соответствующих X2 и X4. Кроме того, в строке 4002 на фиг. 49, элементы "1" размещаются в столбцах, соответствующих X2 и X9. Следовательно, когда известная информация вставляется в X2, X4 и X9, вся информация, соответствующая столбцам, элементы которых равняются "1" в строке 4001 и строке 4002, известна. Следовательно, поскольку неизвестные значения являются только четностью в строке 4001 и строке 4002, логарифмическое отношение правдоподобия с высоким доверием может быть обновлено через вычисление по строкам при BP-декодировании.
Т.е. при реализации более низкой скорости кодирования, чем исходная скорость кодирования посредством вставки известной информации, важно, с точки зрения достижения высокой способности к коррекции ошибок, увеличивать число строк, все из которых соответствуют известной информации, или строк, значительное число которых соответствуют известной информации (например, все биты, за исключением одного бита, соответствуют известной информации) информации из четности и информации в каждой строке контрольной матрицы, т.е. полинома контроля по четности.
В случае изменяющегося во времени LDPC-CC существует закономерность в шаблоне матрицы H контроля по четности, в которой размещаются элементы "1". Следовательно, посредством вставки известной информации на регулярной основе в каждый период на основе матрицы H контроля по четности, можно увеличивать число строк, неизвестные значения которых соответствуют только четности, или строк с меньшим числом неизвестных информационных битов, когда четность и информация являются неизвестными. Как результат, можно предоставлять LDPC-CC со скоростью кодирования 1/3, предоставляющего хорошие характеристики.
Согласно следующему способу #1-3, можно реализовывать LDPC-CC, имеющий высокую способность к коррекции ошибок, скорость кодирования 1/3 и изменяющийся во времени период h (h является целым числом, равным или превышающим 4), из LDPC-CC, имеющего хорошие характеристики, скорость кодирования 1/2 и изменяющийся во времени период h, описанного в варианте 1 осуществления.
Способ #1-3'
Способ #1-3 вставляет известную информацию (например, 0) в h*k Xj из 2*h*k битов информации X2hi, X2hi+1, X2hi+2,..., X2hi+2h-1,..., X2h(i+k-1), X2h(i+k-1)+1, X2h(i+k-1)+2,..., X2h(i+k-1)+2h-1 в течение периода 2*h*2k битов, сформированных с информацией и четностью (поскольку четность включается).
Здесь, j принимает значение одного из 2hi-2h(i+k-1)+2h-1, и присутствует h*k различных значений. Кроме того, известная информация может составлять 1 или предварительно определенное значение.
В это время, когда известная информация вставляется в h*k Xj, предполагается, что из остатков после деления h*k различных j на h, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)", составляет 1 или меньше. (Для vp=1 yp=1 см. условие #7-1 и условие #7-2). По меньшей мере, один такой γ присутствует.
Таким образом, посредством предоставления условия для позиций, в которых известная информация вставляется, можно увеличивать число строк, в которых вся информация является известной информацией, или строк с множеством фрагментов известной информации (например, все биты, за исключением одного бита, соответствуют известной информации), в максимально возможной степени в каждой строке матрицы H контроля по четности, т.е. полинома контроля по четности.
LDPC-CC с изменяющимся во времени периодом h, описанный выше, удовлетворяет условию #17. В это время, поскольку g-ый (g=0, 1,..., h-1) полином контроля по четности представляется так, как показано в уравнении 84, субматрица (вектор), соответствующая полиному контроля по четности уравнения 84 в матрице контроля по четности, представляется так, как показано на фиг. 50.
На фиг. 50, "1" ссылки с номером 4101 соответствует Da#g,1,1X1(D). Кроме того, "1" ссылки с номером 4102 соответствует Da#g,1,2X1(D). Кроме того, "1" ссылки с номером 4103 соответствует X1(D). Кроме того, "1" ссылки с номером 4104 соответствует P(D).
В это время, когда "1" ссылки с номером 4103 представляется посредством Xj при условии, что его момент времени равен j, "1" ссылки с номером 4101 представляется посредством Xj-a#g,1,1, и "1" ссылки с номером 4102 представляется посредством Xj-a#g,1,2.
Следовательно, когда j рассматривается как опорная позиция, "1" ссылки с номером 4101 находится в позиции, соответствующей кратному vp=1, и "1" ссылки с номером 4102 находится в позиции, соответствующей кратному yp=1. Кроме того, это не зависит от g.
Когда это учитывается, можно сделать следующие выводы. Т.е. способ #1-3 является одним из важных требований для того, чтобы "увеличивать число строк, вся информация которых является известной информацией, или строк с множеством фрагментов известной информации (например, известной информации, за исключением одного бита) в максимально возможной степени в каждой строке матрицы H контроля по четности, т.е. в полиноме контроля по четности посредством предоставления условий для позиций, в которых вставляется известная информация".
В качестве примера, предполагается, что изменяющийся во времени период h=4 и vp=1=1, yp=1=2. На фиг. 48, рассматривается случай, в котором при условии, что 4*2*2*1 битов (т.е. k=1) составляют один период, известная информация (например, 0 (или 1, или предварительно определенное значение)) вставляется в X8i, X8i+2, X8i+4, X8i+5 из информации и четности X8i, P8i, X8i+1, P8i+1, X8i+2, P8i+2, X8i+3, P8i+3, X8i+4, P8i+4, X8i+5, P8i+5, X8i+6, P8i+6, X8i+7, P8i+7.
В этом случае, в качестве j Xj, в которые вставляется известная информация, существует четыре различных значения 8i, 8i+2, 8i+4 и 8i+5. В это время, остаток после деления 8i на 4 равняется 0, остаток после деления 8i+2 на 4 равняется 2, остаток после деления 8i+4 на 4 равняется 0, и остаток после деления 8i+5 на 4 равняется 1. Следовательно, число остатков, которые становятся 0, равняется 2, число остатков, которые становятся vp=1=1, равняется 1, число остатков, которые становятся yp=1=2, равняется 1, и правило вставки вышеуказанного способа #1-3] удовлетворяется (где γ=0). Следовательно, пример, показанный на фиг. 48, может упоминаться в качестве примера, который удовлетворяет правилу вставки вышеуказанного способа #1-3.
В качестве более жестких условий способа #1-3 следующий способ #1-3' может предоставляться.
Способ #1-3'
Способ #1-3' вставляет известную информацию (например, 0) в h*k Xj 2*h*k битов информации X2hi, X2hi+1, X2hi+2,..., X2hi+2h-1,..., X2h(i+k-1), X2h(i+k-1)+1, X2h(i+k-1)+2,..., X2h(i+k-1)+2h-1 в течение периода 2*h*2k битов, сформированных с информацией и четностью (поскольку четность включается). Тем не менее, j принимает значение одного из 2hi-2h(i+k-1)+2h-1, и существует h*k различных значений. Кроме того, известная информация может составлять 1 или предварительно определенное значение.
В это время, когда известная информация вставляется в h*k Xj, предполагается, что из остатков после деления h*k различных j на h, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)", составляет 1 или меньше. (Для vp=1, yp=1, см. условие #7-1 и условие #7-2). По меньшей мере, один такой γ присутствует.
Для γ, который не удовлетворяет вышеприведенному описанию, "число остатков, которые становятся (0+γ) mod h", "число остатков, которые становятся (vp=1+γ) mod h" и "числом остатков, которые становятся (yp=1+γ) mod h" становится 0.
Кроме того, чтобы эффективнее реализовывать способ #1-3, одно из следующих трех условий может удовлетворяться в LDPC-CC на основе вышеуказанного полинома контроля по четности с помощью условия #17 изменяющегося во времени периода h (правило вставки способа #1-3'). Тем не менее, предполагается, что vp=1<yp=1 в условии #17.
- yp=1-vp=1=vp=1-0, т.е. yp=1=2*vp=1
- vp=1-0=h-yp=1, т.е. vp=1=h-yp=1
- h-yp=1=yp=1-vp=1, т.е. h=2*yp=1-vp=1
Когда это условие добавляется, посредством предоставления условия для позиций, в которых известная информация вставляется, можно увеличивать число строк, вся информация которых является известной информацией, или строк с множеством фрагментов известной информации (например, все биты, за исключением одного бита, соответствуют известной информации), в максимально возможной степени в каждой строке матрицы H контроля по четности, т.е. полинома контроля по четности. Это обусловлено тем, что LDPC-CC имеет конкретную конфигурацию матрицы контроля по четности.
Затем, описывается способ укорачивания, который реализует более низкую скорость кодирования, чем скорость кодирования (n-1)/n, из LDPC-CC с изменяющимся во времени периодом h (h является целым числом, равным или превышающим 4) и скоростью кодирования (n-1)/n (n является целым числом, равным или превышающим 2), описанного в варианте 1 осуществления.
Рассматривается случай, в котором g-ый (g=0, 1,..., h-1) полином контроля по четности со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h представляется так, как показано в уравнении 85.
[85]
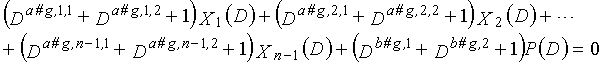 ... (уравнение 85)
... (уравнение 85)
В уравнении 85, предполагается, что a#g,p,1 и a#g,p,2 являются натуральными числами, равными или превышающими 1, и a#g,p,1≠a#g,p,2 справедливо. Кроме того, предполагается, что b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 справедливо (g=0, 1, 2,..., q-2, q-1; p=1, 2,..., n-1).
В уравнении 85, предполагается, что следующие условие #18-1 и условие #18-2 удовлетворяются.
Условие #18-1
"a#0,1,1%h=a#1,1,1%h=a#2,1,1%h=a#3,1,1%h=... =a#g,1,1%h=... =a#h-2,1,1%h=a#h-1,1,1%h=vp=1 (vp=1: фиксированное значение)"
"a#0,2,1%h=a#1,2,1%h=a#2,2,1%h=a#3,2,1%h=... =a#g,2,1%h=... =a#h-2,2,1%h=a#h-1,2,1%h=vp=2 (vp=2: фиксированное значение)"
"a#0,3,1%h=a#1,3,1%h=a#2,3,1%h=a#3,3,1%h=... =a#g,3,1%h=... =a#h-2,3,1%h=a#h-1,3,1%h=vp=3 (vp=3: фиксированное значение)"
"a#0,4,1%h=a#1,4,1%h=a#2,4,1%h=a#3,4,1%h=... =a#g,4,1%h=... =a#h-2,4,1%h=a#h-1,4,1%h=vp=4 (vp=4: фиксированное значение)"
"a#0,k,1%h=a#1,k,1%h=a#2,k,1%h=a#3,k,1%h=... =a#g,k,1%h=... =a#h-2,k,1%h=a#h-1,k,1%h=vp=k (vp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,1%h=a#1,n-2,1%h=a#2,n-2,1%h=a#3,n-2,1%h=... =a#g,n-2,1%h=... =a#h-2,n-2,1%h=a#h-1,n-2,1%h=vp=n-2 (vp=n-2: фиксированное значение)"
"a#0,n-1,1%h=a#1,n-1,1%h=a#2,n-1,1%h=a#3,n-1,1%h=... =a#g,n-1,1%h=... =a#h-2,n-1,1%h=a#h-1,n-1,1%h=vp=n-1 (vp=n-1: фиксированное значение)"
"b#0,1%h=b#1,1%h=b#2,1%h=b#3,1%h=... =b#g,1%h=... =b#h-2,1%h=b#h-1,1%h=w (w: фиксированное значение)"
Условие #18-2
"a#0,1,2%h=a#1,1,2%h=a#2,1,2%h=a#3,1,2%h=... =a#g,1,2%h=... =a#h-2,1,2%h=a#h-1,1,2%h=yp=1 (yp=1: фиксированное значение)"
"a#0,2,2%h=a#1,2,2%h=a#2,2,2%h=a#3,2,2%h=... =a#g,2,2%h=... =a#h-2,2,2%h=a#h-1,2,2%h=yp=2 (yp=2: фиксированное значение)"
"a#0,3,2%h=a#1,3,2%h=a#2,3,2%h=a#3,3,2%h=... =a#g,3,2%h=... =a#h-2,3,2%h=a#h-1,3,2%h=yp=3 (yp=3: фиксированное значение)"
"a#0,4,2%h=a#1,4,2%h=a#2,4,2%h=a#3,4,2%h=... =a#g,4,2%h=... =a#h-2,4,2%h=a#h-1,4,2%h=yp=4 (yp=4: фиксированное значение)"
"a#0,k,2%h=a#1,k,2%h=a#2,k,2%h=a#3,k,2%h=... =a#g,k,2%h=... =a#h-2,k,2%h=a#h-1,k,2%h=yp=k (yp=k: фиксированное значение) (поэтому, k=1, 2,..., n-1)"
"a#0,n-2,2%h=a#1,n-2,2%h=a#2,n-2,2%h=a#3,n-2,2%h=... =a#g,n-2,2%h=... =a#h-2,n-2,2%h=a#h-1,n-2,2%h=yp=n-2 (yp=n-2: фиксированное значение)"
"a#0,n-1,2%h=a#1,n-1,2%h=a#2,n-1,2%h=a#3,n-1,2%h=... =a#g,n-1,2%h=... =a#h-2,n-1,2%h=a#h-1,n-1,2%h=yp=n-1 (yp=n-1: фиксированное значение)", и
"b#0,2%h=b#1,2%h=b#2,2%h=b#3,2%h=... =b#g,2%h=... =b#h-2,2%h=b#h-1,2%h=z (z: фиксированное значение)"
Способы укорачивания для реализации с более низкой скоростью кодирования, чем скорость кодирования (n-1)/n с высокой способностью к коррекции ошибок, с использованием вышеуказанного LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h являются такими, как показано ниже.
Способ #2-1
Способ #2-1 вставляет известную информацию (например, 0 (или 1, или предварительно определенное значение)) в информацию X на регулярной основе (правило вставки способа #2-1).
Способ #2-2
В отличие от способа #2-1, способ #2-2 использует h*n*k битов, сформированных с информацией и четностью в качестве одного периода, как показано на фиг. 51, и вставки известной информации в идентичных позициях в каждый период (правило вставки способа #2-2). "Вставка известной информации в идентичных позициях в каждый период" выполняется так, как описано в вышеуказанном способе #1-2 с использованием фиг. 48.
Способ #2-3
Способ #2-3 выбирает Z битов из h*(n-1)*k битов информации X1,hi, X2,hi,..., Xn-1,hi,..., X1,h(i+k-1)+h-1, X2,h(i+k-1)+h-1,..., Xn-1,h(i+k-1)+h-1 в течение периода h*n*k битов, сформированных с информацией и четностью, и вставляет известную информацию (например, 0 (или 1, или предварительно определенное значение)) выбранных Z битов (правило вставки способа #2-3).
В это время, способ #2-3 вычисляет остатки после деления всех j на h в информации X1,j (где j принимает значение одного из hi-h(i+k-1)+h-1), в которые вставляется известная информация.
Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше. По меньшей мере, один такой γ присутствует.
Аналогично, способ #2-3 вычисляет остатки после деления всех j на h в информации X2,j (где j принимает значение одного из hi-h(i+k-1)+h-1), в которые вставляется известная информация. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=2+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=2+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=2+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=2+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше. По меньшей мере, один такой γ присутствует.
Способ #2-3 может быть описан похожим способом также тогда, когда информация Xf,j (f=1, 2, 3,..., n-1) допускается. Способ #2-3 вычисляет остатки после деления всех j на h в Xf,j (где j принимает значение одного из hi-h(i+k-1)+h-1), в которые вставляется известная информация. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше. По меньшей мере, один такой γ присутствует.
Таким образом, посредством предоставления условия в позициях, в которых известная информация вставляется, можно формировать больше "строк, неизвестные значения которых являются битами четности и информационными битами" в матрице H контроля по четности, аналогично способу #1-3. Таким образом, можно реализовывать более низкую скорость кодирования, чем скорость кодирования (n-1)/n с высокой способностью к коррекции ошибок, с использованием вышеописанного LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h, имеющего хорошие характеристики.
В способе #2-3 описан случай, в котором число фрагментов известной вставленной информации является идентичным в каждый период, но число фрагментов известной вставленной информации может отличаться между периодами. Например, как показано на фиг. 52, также можно предусматривать N0 фрагментов информации, которые должны обозначаться как известная информация в первый период, N1 фрагментов информации, которые должны обозначаться как известная информация в следующий период, и Ni фрагментов информации, которые должны обозначаться как известная информация в i-ый период.
Таким образом, когда число фрагментов известной вставленной информации отличается между периодами, понятие "периода" является незначащим. Когда правило вставки способа #2-3 представляется без использования понятия "периода", правило вставки представляется так, как показано в способе #2-4.
Способ #2-4
Z битов выбираются из битовой последовательности информации X1,0, X2,0,..., Xn-1,0,..., X1,v, X2,v,..., Xn-1,v в последовательности данных, сформированной с информацией и четностью, и известная информация (например, 0 (или 1, или предварительно определенное значение)) вставляется в выбранные Z битов (правило вставки способа #2-4).
В это время, способ #2-4 вычисляет остатки после деления всех j на h в X1,j (где j принимает значение одного из 0-v), в которые вставляется известная информация. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше. По меньшей мере, один такой γ присутствует.
Аналогично, способ #2-4 вычисляет остатки после деления всех j на h в X2,j (где j принимает значение одного из 0-v), в которые вставляется известная информация. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=2+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=2+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=2+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=2+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше. По меньшей мере, один такой γ присутствует.
Т.е. способ #2-4 вычисляет остатки после деления всех j на h в Xf,j (где j принимает значение одного из 0-v), в которые вставляется известная информация. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше (f=1, 2, 3,..., n-1). По меньшей мере, один такой γ присутствует.
Таким образом, посредством предоставления условия для позиций, в которых известная информация вставляется, можно формировать больше "строк, неизвестные значения которых являются битами четности и информационными битами" в матрице H контроля по четности, аналогично способу #2-3, даже когда число битов известной вставленной информации отличается между периодами. Таким образом, можно реализовывать более низкую скорость кодирования, чем скорость кодирования (n-1)/n с высокой способностью к коррекции ошибок, с использованием вышеописанного LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h, имеющего хорошие характеристики.
Кроме того, чтобы эффективнее реализовывать способ #2-3 и способ #2-4, одно из следующих трех условий может удовлетворяться в вышеуказанном LDPC-CC на основе полинома контроля по четности условия #18-1 и условия #18-2 изменяющегося во времени периода h. Тем не менее, предполагается, что vp=s<yp=s (s=1, 2,..., n-1) в условии #18-1 и условии #18-2.
- yp=s-vp=s=vp=s-0, т.е. yp=s=2*vp=s
- vp=s-0=h-yp=s, т.е. vp=s=h-yp=s
- h-yp=s=yp=s-vp=s, т.е. h=2*yp=s-vp=s
Когда это условие добавляется, посредством предоставления условия для позиций, в которых известная информация вставляется, можно увеличивать число строк, вся информация которых является известной информацией, или строк с множеством фрагментов известной информации (например, все биты, за исключением одного бита, соответствуют известной информации), в максимально возможной степени в каждой строке матрицы H контроля по четности, т.е. полинома контроля по четности. Это обусловлено тем, что LDPC-CC имеет конкретную конфигурацию матрицы контроля по четности.
Как описано выше, устройство связи вставляет информацию, известную обменивающейся данными стороне, выполняет кодирование на скорости кодирования 1/2 для информации, включающей в себя известную информацию, и формирует биты четности. Устройство связи затем не передает известную информацию, а передает информацию, отличную от известной информации, и полученные биты четности и тем самым реализует скорость кодирования 1/3.
Фиг. 53 является блок-схемой, показывающей пример конфигурации частей, связанных с кодированием (модуля 44100 кодирования с коррекцией ошибок и передающего устройства 44200), когда переменная скорость кодирования используется на физическом уровне.
Модуль 4403 вставки известной информации принимает информацию 4401 и управляющий сигнал 4402 в качестве ввода и вставляет известную информацию согласно информации по скорости кодирования, включенной в управляющий сигнал 4402. Более конкретно, когда скорость кодирования, включенная в управляющий сигнал 4402, меньше скорости кодирования, поддерживаемой посредством кодера 4405, и укорачивание должно быть выполнено, известная информация вставляется согласно вышеуказанному способу укорачивания, и информация 4404 после вставки известной информации выводится. С другой стороны, когда скорость кодирования, включенная в управляющий сигнал 4402, равна скорости кодирования, поддерживаемой посредством кодера 4405, и укорачивание должно быть выполнено, известная информация не вставляется, и информация 4401 выводится в качестве информации 4404 как есть.
Кодер 4405 принимает информацию 4404 и управляющий сигнал 4402 в качестве ввода, выполняет кодирование для информации 4404, формирует четность 4406 и выводит четность 4406.
Модуль 4407 удаления известной информации принимает информацию 4404 и управляющий сигнал 4402 в качестве ввода, удаляет, когда известная информация вставляется в модуль 4403 вставки известной информации, известную информацию из информации 4404 на основе информации по скорости кодирования, включенной в управляющий сигнал 4402, и выводит информацию 4408 после удаления. С другой стороны, когда известная информация не вставляется, модуль 4403 вставки известной информации выводит информацию 4404 в качестве информации 4408 как есть.
Модуль 4409 модуляции принимает четность 4406, информацию 4408 и управляющий сигнал 4402 в качестве ввода, модулирует четность 4406 и информацию 4408 на основе информации схемы модуляции, включенной в управляющий сигнал 4402, и формирует и выводит сигнал 4410 в полосе модулирующих частот.
Фиг. 54 является блок-схемой, показывающей другой пример конфигурации частей, связанных с кодированием (модуля 44100 кодирования с коррекцией ошибок и передающего устройства 44200), когда переменная скорость кодирования используется на физическом уровне, отличающаяся от скорости кодирования на фиг. 53. Как показано на фиг. 54, посредством приспособления такой конфигурации, что информация 4401, введенная в модуль 4403 вставки известной информации, вводится в модуль 4409 модуляции, переменная скорость кодирования может быть использована, как в случае по фиг. 53, даже когда модуль 4407 удаления известной информации на фиг. 53 опускается.
Фиг. 55 является блок-схемой, показывающей пример конфигурации модуля 46100 декодирования с коррекцией ошибок на физическом уровне. Модуль 4603 вставки логарифмического отношения правдоподобия для известной информации принимает сигнал 4601 логарифмического отношения правдоподобия принимаемых данных и управляющий сигнал 4602 в качестве ввода. На основе информации скорости кодирования, включенной в управляющий сигнал 4602, если логарифмическое отношение правдоподобия известной информации должно вставляться, модуль 4603 вставки логарифмического отношения правдоподобия вставляет логарифмическое отношение правдоподобия известной информации, имеющей высокое доверие, в сигнал 4601 логарифмического отношения правдоподобия. Модуль 4603 вставки логарифмического отношения правдоподобия выводит сигнал 4604 логарифмического отношения правдоподобия после вставки логарифмического отношения правдоподобия известной информации. Информация скорости кодирования, включенная в управляющий сигнал 4602, передается, например, из обменивающейся данными стороны.
Модуль 4605 декодирования принимает управляющий сигнал 4602 и сигнал 4604 логарифмического отношения правдоподобия после вставки логарифмического отношения правдоподобия известной информации в качестве ввода, выполняет декодирование на основе информации способа кодирования, к примеру, скорости кодирования, включенной в управляющий сигнал 4602, декодирует принимаемые данные и выводит декодированные данные 4606.
Модуль 4607 удаления известной информации принимает управляющий сигнал 4602 и декодированные данные 4606 в качестве ввода, удаляет, когда известная информация вставляется, известную информацию на основе информации способа кодирования, к примеру, скорости кодирования, включенной в управляющий сигнал 4602, и выводит информацию 4608 после удаления известной информации.
Выше описан способ укорачивания, который реализует более низкую скорость кодирования, чем скорость кодирования кода, из LDPC-CC с изменяющимся во времени периодом h, описанного в варианте 1 осуществления. Когда LDPC-CC с изменяющимся во времени периодом h используется на уровне пакета, описанном в варианте 1 осуществления, использование способа укорачивания согласно настоящему варианту осуществления позволяет повышать эффективность передачи и способность к коррекции со стиранием ошибок одновременно. Даже когда скорость кодирования изменяется на физическом уровне, хорошая способность к коррекции ошибок может достигаться.
В случае сверточного кода, к примеру, LDPC-CC, последовательность завершения может добавляться при завершении последовательности информации передачи, чтобы выполнять обработку завершения (завершение). В это время, модуль кодирования 4405 принимает известную информацию (например, все нули) в качестве ввода, и последовательность завершения формируется только с помощью последовательности четности, полученной посредством кодирования известной информации. Таким образом, последовательность завершения может включать в себя части, которые не следуют известному правилу вставки информации, описанному в изобретении настоящей заявки. Кроме того, может быть часть, соответствующая правилу вставки, и часть, в которой известная информация не вставляется, также в частях, отличных от завершения, чтобы повышать скорость передачи. Обработка завершения (завершение) описывается в варианте 11 осуществления.
Десятый вариант осуществления
Настоящий вариант осуществления описывает способ коррекции со стиранием ошибок, который реализует более низкую скорость кодирования, чем скорость кодирования (n-1)/n с высокой способностью к коррекции ошибок, с использованием LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h (h является целым числом, равным или превышающим 4), описанного в варианте 1 осуществления. Тем не менее, описание LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h (h является целым числом, равным или превышающим 4) допускается равным идентичным описанию в варианте 9 осуществления.
Способ #3-1
Как показано на фиг. 56, способ #3-1 допускает h*n*k битов (k является натуральным числом), сформированных с информацией и четностью в качестве периода, и вставляет известную информацию, включенную в известный пакет информации в идентичной позиции, в каждый период (правило вставки способа #3-1). Вставка известной информации, включенной в известный пакет информации в идентичной позиции, в каждый период описана в способе #2-2 варианта 9 осуществления и т.п.
Способ #3-2
Способ #3-2 выбирает Z битов из h*(n-1)*k битов информации X1,hi, X2,hi,..., Xn-1,hi,..., X1,h(i+k-1)+h-1, X2,h(i+k-1)+h-1,..., Xn-1,h(i+k-1)+h-1 в период h*n*k битов, сформированных с информацией и четностью, и вставляет данные известного пакета информации (например, 0 (или 1, или предварительно определенное значение)) в выбранные Z битов (правило вставки способа #3-2).
В это время, способ #3-2 вычисляет остатки после деления всех j на h в X1,j (где j принимает значение одного из hi-h(i+k-1)+h-1), в который вставляются данные известного пакета информации. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше. По меньшей мере, один такой γ присутствует.
Т.е. способ #3-2 вычисляет остатки после деления всех j на h в Xf,j (где j принимает значение одного из hi-h(i+k-1)+h-1), в который вставляются данные известного пакета информации. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше (f=1, 2, 3,..., n-1). По меньшей мере, один такой γ присутствует.
Таким образом, посредством предоставления условия в позициях, в которых известная информация вставляется, можно формировать больше "строк, неизвестные значения которых являются битами четности и меньшим числом информационных битов" в матрице H контроля по четности. Таким образом, можно реализовывать систему, допускающую изменение скорости кодирования кода коррекции со стиранием ошибок с высокой способностью к коррекции со стиранием ошибок и низким размером схем с использованием вышеописанного LDPC-CC со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h.
Способ коррекции со стиранием ошибок с использованием переменной скорости кодирования кода коррекции со стиранием ошибок описан выше как способ коррекции со стиранием ошибок на верхнем уровне.
Относительно конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора и связанного с декодированием с коррекцией со стиранием ошибок процессора с использованием переменной скорости кодирования кода коррекции со стиранием ошибок на верхнем уровне, скорость кодирования кода коррекции со стиранием ошибок может быть изменена посредством вставки известного пакета информации перед связанным с кодированием с коррекцией со стиранием ошибок процессором 2112 на фиг. 21.
Таким образом, скорость кодирования задается переменной, например, согласно ситуации связи, и тем самым можно увеличивать скорость кодирования, когда ситуация связи является хорошей, и повышать эффективность передачи. Кроме того, когда скорость кодирования снижается, можно повышать способность к коррекции со стиранием ошибок посредством вставки известной информации, включенной в известный пакет информации согласно контрольной матрице, как в случае способа #3-2.
В способе #3-2 описан случай, в котором число фрагментов данных известного вставленного пакета информации является идентичным для различных периодов, но число вставленных фрагментов данных может отличаться между периодами. Например, как показано на фиг. 57, можно предположить, что N0 фрагментов информации обозначаются как данные известного пакета информации в первый период, N1 фрагментов информации обозначаются как данные известного пакета информации в следующий период, и Ni фрагментов информации обозначаются как данные известного пакета информации в i-ый период.
Когда число фрагментов данных известного вставленного пакета информации отличается между периодами таким образом, понятие "периода" является незначащим. Когда правило вставки способа #3-2 представляется без использования понятия "периода", правило вставки является таким, как показано в способе #3-3.
Способ #3-3
Z битов выбираются из битовой последовательности информации X1,0, X2,0,..., Xn-1,0,..., X1,v, X2,v,..., Xn-1,v в последовательности данных, сформированной с информацией и четностью, и известная информация (например, 0 (или 1, или предварительно определенное значение)) вставляется в выбранные Z битов (правило вставки способа #3-3).
В это время, способ #3-3 вычисляет остатки после деления всех j на h в X1,j (где j принимает значение одного из 0-v), в которые вставляется известная информация. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше. По меньшей мере, один такой γ присутствует.
Т.е. способ #3-3 вычисляет остатки после деления всех j на h в Xf,j (где j принимает значение одного из 0-v), в которые вставляется известная информация. Затем, предполагается, что: разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше (f=1, 2, 3,..., n-1). По меньшей мере, один такой γ присутствует.
Выше описана система с использованием переменной скорости кодирования кода коррекции со стиранием ошибок, которая использует способ реализации с более низкой скоростью кодирования, чем скорость кодирования кода, из LDPC-CC с изменяющимся во времени периодом h, описанного в варианте 1 осуществления. С использованием переменного способа скорости кодирования настоящего варианта осуществления, можно повышать эффективность передачи и способность к коррекции со стиранием ошибок одновременно и достигать хорошей способности к коррекции со стиранием ошибок, когда скорость кодирования изменяется во время коррекции со стиранием ошибок.
Одиннадцатый вариант осуществления
Когда LDPC-CC, связанный с настоящим изобретением, используется, завершение или дополнение битами концевой части необходимы для того, чтобы обеспечивать доверие при декодировании информационных битов. Таким образом, настоящий вариант осуществления подробно описывает способ, когда завершение (называемое "завершением информационным нулем" или называемое просто "завершением нулем") выполняется.
Фиг. 58 является схемой, иллюстрирующей "завершение информационным нулем" LDPC-CC со скоростью кодирования (n-1)/n. Информационные биты X1, X2,..., Xn-1 и бит P четности в момент времени i (i=0, 1, 2, 3,..., s) допускаются как X1,i, X2,i,..., Xn-1,i и бит Pi четности, соответственно. Как показано на фиг. 58, Xn-1,s допускается как конечный бит (4901) информации, которую следует передавать. Тем не менее, чтобы поддерживать качество приема в декодере, также необходимо кодировать информацию с момента времени s и далее во время кодирования.
По этой причине, когда кодер выполняет кодирование только до момента времени s, и передающее устройство на стороне кодирования выполняет передачу в приемное устройство на стороне декодирования только до Ps, качество приема информационных битов в декодере не ухудшается значительно. Чтобы разрешать эту проблему, кодирование выполняется при условии, что информационные биты (в дальнейшем "виртуальные информационные биты") от конечного информационного бита Xn-1,s и далее равны "0", и бит четности (4903) формируется.
Более конкретно, как показано на фиг. 58, кодер выполняет кодирование при условии, что X1,k, X2,k,..., Xn-1,k (k=t1, t2,..., tm) составляет "0", и получает Pt1, Pt2,..., Ptm. Передающее устройство на стороне кодирования передает X1,s, X2,s,..., Xn-1,s, Ps в момент времени s и затем передает Pt1, Pt2,..., Ptm. С момента времени s и далее, декодер выполняет декодирование с использованием преимущества знания того, что виртуальные информационные биты являются нулями. Выше описан случай, в котором виртуальные информационные биты "0" в качестве примера, но настоящее изобретение не ограничено этим и может быть аналогично реализовано при условии, что виртуальные информационные биты являются данными, известными для передающих/приемных устройств.
Само собой разумеется, что все варианты осуществления настоящего изобретения также могут быть реализованы, даже когда завершение выполняется.
Двенадцатый вариант осуществления
Настоящий вариант осуществления описывает пример конкретного способа формирования LDPC-CC на основе полиномов контроля по четности, описанных в варианте 1 осуществления и варианте 6 осуществления.
Вариант 6 осуществления описывает, что следующие условия являются эффективными, поскольку изменяющийся во времени период LDPC-CC, описанный в варианте 1 осуществления:
- изменяющийся во времени период является простым числом.
- изменяющийся во времени период является нечетным числом, и число делителей является небольшим относительно значения изменяющегося во времени периода.
Здесь, рассматривается случай, в котором изменяющийся во времени период увеличивается, и код формируется. В это время, код формируется с использованием случайного числа, с помощью которого ограничивающее условие предоставляется, но когда изменяющийся во времени период увеличивается, число параметров, которые должны задаваться с использованием случайного числа, увеличивается, приводя к такой проблеме, что трудно искать код, имеющий высокую способность к коррекции ошибок. Чтобы разрешать эту проблему, настоящий вариант осуществления описывает способ формирования другого кода с использованием LDPC-CC на основе полиномов контроля по четности, описанных в варианте 1 осуществления и варианте 6 осуществления.
Способ разработки LDPC-CC на основе полинома контроля по четности со скоростью кодирования 1/2 и изменяющимся во времени периодом 15 описывается в качестве примера.
Рассмотрим уравнения 86-0-86-14 в качестве полиномов контроля по четности (которые удовлетворяют 0) LDPC-CC со скоростью кодирования (n-1)/n (n является целым числом, равным или превышающим 2) и изменяющимся во времени периодом 15.
[86]
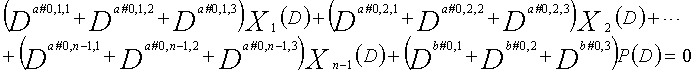 ... (уравнение 86-0)
... (уравнение 86-0)
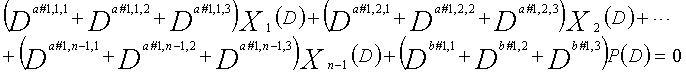 ... (уравнение 86-1)
... (уравнение 86-1)
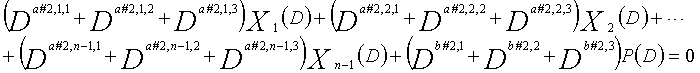 ... (уравнение 86-2)
... (уравнение 86-2)
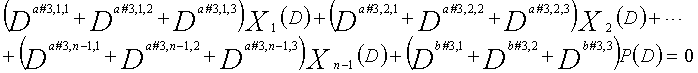 ... (уравнение 86-3)
... (уравнение 86-3)
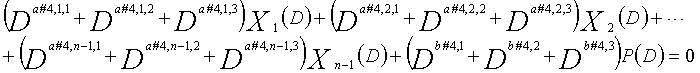 ... (уравнение 86-4)
... (уравнение 86-4)
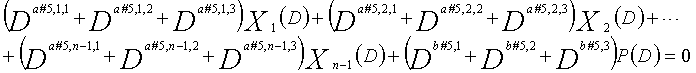 ... (уравнение 86-5)
... (уравнение 86-5)
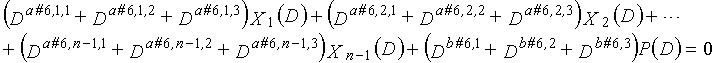 ... (уравнение 86-6)
... (уравнение 86-6)
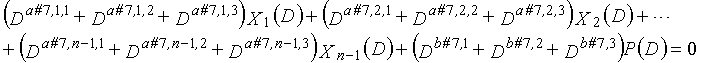 ... (уравнение 86-7)
... (уравнение 86-7)
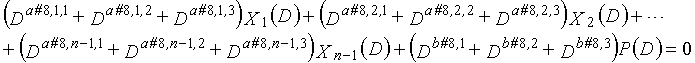 ... (уравнение 86-8)
... (уравнение 86-8)
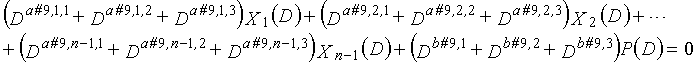 ... (уравнение 86-9)
... (уравнение 86-9)
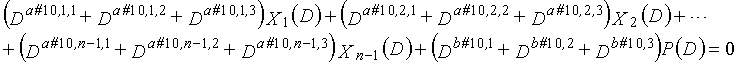 ... (уравнение 86-10)
... (уравнение 86-10)
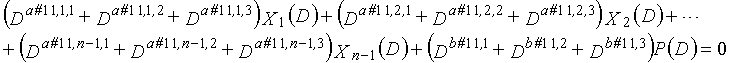 ... (уравнение 86-11)
... (уравнение 86-11)
 ... (уравнение 86-12)
... (уравнение 86-12)
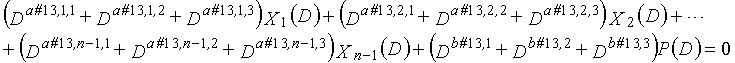 ... (уравнение 86-13)
... (уравнение 86-13)
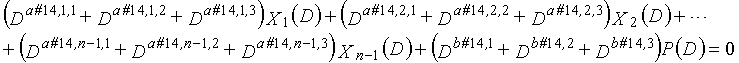 ... (уравнение 86-14)
... (уравнение 86-14)
В это время, X1(D), X2(D),..., Xn-1(D) являются полиномиальными представлениями данных (информации) X1, X2,..., Xn-1, и P(D) является полиномиальным представлением четности. В уравнениях 86-0 86-14, когда, например, скорость кодирования составляет 1/2, существуют только элементы X1(D) и P(D), а элементы X2(D),..., Xn-1(D) отсутствуют. Аналогично, когда скорость кодирования составляет 2/3, существуют только элементы X1(D), X2(D) и P(D), а элементы X3(D),..., Xn-1(D) отсутствуют. Другие скорости кодирования также могут рассматриваться аналогично. Здесь, уравнения 86-0-86-14 допускаются в качестве таких полиномов контроля по четности, что существует три элемента в каждом из X1(D), X2(D),..., Xn-1(D) и P(D).
Кроме того, предполагается, что следующее справедливо для X1(D), X2(D),..., Xn-1(D) и P(D) в уравнениях 86-0-86-14.
В уравнении 86-q предполагается, что a#q,p,1, a#q,p,2 и a#q,p,3 являются натуральными числами, и a#q,p,1≠a#q,p,2, a#q,p,1≠a#q,p,3 и a#q,p,2≠a#q,p,3 справедливо. Кроме того, предполагается, что b#q,1, b#q,2 и b#q,3 являются натуральными числами, и b#q,1≠b#q,2, b#q,1≠b#q,3 и b#q,1≠b#q,3 справедливо (q=0, 1, 2,..., 13, 14; p=1, 2,..., n-1).
Полином контроля по четности уравнения 86-q называется "контрольным уравнением #q", и субматрица на основе полинома контроля по четности уравнения 86-q называется q-ой субматрицей Hq. Рассматривается LDPC-CC с изменяющимся во времени периодом 15, сформированный из 0-ой субматрицы H0, первой субматрицы H1, второй субматрицы H2,..., 13-ой субматрицы H13 и 14-ой субматрицы H14. Таким образом, способ конфигурирования кода, способ формирования матрицы контроля по четности, способ кодирования и способ декодирования являются аналогичными способам, описанным в варианте 1 осуществления и варианте 6 осуществления.
Как описано выше, случай для скорости кодирования 1/2 описывается, и, следовательно, далее существуют только элементы X1(D) и P(D).
В варианте 1 осуществления и варианте 6 осуществления, при условии, что изменяющийся во времени период равняется 15, как изменяющийся во времени период коэффициента X1(D), так и изменяющийся во времени период коэффициента P(D) равняются 15. В отличие от этого, настоящий вариант осуществления предлагает способ конфигурирования кода LDPC-CC с изменяющимся во времени периодом 15 посредством задания изменяющегося во времени периода коэффициентов X1(D) равным 3 и изменяющегося во времени периода коэффициентов P(D) равным 5 в качестве примера. Т.е. настоящий вариант осуществления конфигурирует код, в котором изменяющийся во времени период LDPC-CC составляет LCM(α, β), посредством задания изменяющегося во времени периода коэффициентов X1(D) равным α, а изменяющегося во времени периода коэффициентов P(D) равным β (α≠β), где LCM(X, Y) допускается как наименьшее общее кратное X и Y.
Чтобы достигать высокой способности к коррекции ошибок, следующие условия предоставляются для коэффициента X1(D), как в случаях варианта 1 осуществления и варианта 6 осуществления. В следующих условиях, "%" означает "по модулю", и, например, "α%15" представляет остаток после деления α на 15.
Условие #19-1
"a#0,1,1%15=a#1,1,1%15=a#2,1,1%15=... =a#k,1,1%15=... =a#14,1,1%15=vp=1 (vp=1: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
"a#0,1,2%15=a#1,1,2%15=a#2,1,2%15=... =a#k,1,2%15=... =a#14,1,2%15=yp=1 (yp=1: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
"a#0,1,3%15=a#1,1,3%15=a#2,1,3%15=... =a#k,1,3%15=... =a#14,1,3%15=zp=1 (zp=1: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
Кроме того, поскольку изменяющийся во времени период коэффициента X1(D) равняется 3, следующее условие справедливо.
Условие #19-2
Когда i%3=j%3 (i, j=0, 1,..., 13, 14; i≠j) справедливо, следующие три уравнения являются справедливыми.
[87]
a#i,1,1=a#j,1,1... (уравнение 87-1)
a#i,1,2=a#j,1,2... (уравнение 87-2)
a#i,1,3=a#j,1,3... (уравнение 87-3)
Аналогично, следующие условия предоставляются для коэффициента P(D).
Условие #20-1
"b#0,1%15=b#1,1%15=b#2,1%15=... =b#k,1%15=... =b#14,1%15=d (d: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
"b#0,2%15=b#1,2%15=b#2,2%15=... =b#k,2%15=... =b#14,2%15=e (e: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
"b#0,3%15=b#1,3%15=b#2,3%15=... =b#k,3%15=... =b#14,3%15=f (f: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
Кроме того, поскольку изменяющийся во времени период коэффициента P(D) равняется 5, следующие условия являются справедливыми.
Условие #20-2
Когда i%5=j%5 (i, j=0, 1,..., 13, 14; i≠j) справедливо, следующие три уравнения являются справедливыми.
[88]
b#i,1=b#j,1... (уравнение 88-1)
b#i,2=b#j,2... (уравнение 88-2)
b#i,3=b#j,3... (уравнение 88-3)
Предоставление вышеописанных условий позволяет сокращать число параметров, заданных с использованием случайных чисел, при увеличении изменяющегося во времени периода и достигать эффекта упрощения поиска кода. Условие #19-1 и условие #20-1 не всегда являются необходимыми условиями. Т.е. только условие #19-2 и условие #20-2 могут предоставляться в качестве условий. Кроме того, условия (условие #19-1' и условие #20-1') также могут предоставляться вместо условия #19-1 и условия #20-1.
Условие #19-1'
"a#0,1,1%3=a#1,1,1%3=a#2,1,1%3=... =a#k,1,1%3=... =a#14,1,1%3=vp=1 (vp=1: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
"a#0,1,2%3=a#1,1,2%3=a#2,1,2%3=... =a#k,1,2%3=... =a#14,1,2%3=yp=1 (yp=1: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
"a#0,1,3%3=a#1,1,3%3=a#2,1,3%3=... =a#k,1,3%3=... =a#14,1,3%3=zp=1 (zp=1: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
Условие #20-1'
"b#0,1%5=b#1,1%5=b#2,1%5=... =b#k,1%5=... =b#14,1%5=d (d: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
"b#0,2%5=b#1,2%5=b#2,2%5=... =b#k,2%5=... =b#14,2%5=e (e: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
"b#0,3%5=b#1,3%5=b#2,3%5=... =b#k,3%5=... =b#14,3%5=f (f: фиксированное значение) (поэтому k=0, 1, 2,..., 14)"
С использованием вышеприведенного примера в качестве ссылки и при условии, что изменяющийся во времени период коэффициента X1(D) составляет α, а изменяющийся во времени период коэффициента P(D) составляет β, описывается способ конфигурирования кода LDPC-CC с изменяющимся во времени периодом LCM(α, β), где изменяющийся во времени период LCM(α, β)=s.
I-ый (i=0, 1, 2,..., s-2, s-1) полином контроля по четности, который удовлетворяет 0 в LDPC-CC на основе полинома контроля по четности с изменяющимся во времени периодом s и скоростью кодирования 1/2, представляется так, как показано в уравнении ниже.
[89]
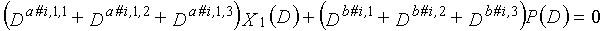 ... (уравнение 89-1)
... (уравнение 89-1)
С использованием вышеприведенного описания в качестве ссылки, следующее условие становится важным в способе конфигурирования кода настоящего варианта осуществления.
Следующее условие предоставляется для коэффициента X1(D).
Условие #21-1
"a#0,1,1%s=a#1,1,1%s=a#2,1,1%s=... =a#k,1,1%s=... =a#s-1,1,1%s=vp=1 (vp=1: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
"a#0,1,2%s=a#1,1,2%s=a#2,1,2%s=... =a#k,1,2%s=... =a#s-1,1,2%s=yp=1 (yp=1: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
"a#0,1,3%s=a#1,1,3%s=a#2,1,3%s=... =a#k,1,3%s=... =a#s-1,1,3%s=zp=1 (zp=1: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
Кроме того, поскольку изменяющийся во времени период коэффициента X1(D) составляет α, следующее условие справедливо.
Условие #21-2
Когда i%α=j%α (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующие три уравнения являются справедливыми.
[90]
a#i,1,1=a#j,1,1... (уравнение 90-1)
a#i,1,2=a#j,1,2... (уравнение 90-2)
a#i,1,3=a#j,1,3... (уравнение 90-3)
Аналогично, следующее условие предоставляется для коэффициента P(D).
Условие #22-1
"b#0,1%s=b#1,1%s=b#2,1%s=... =b#k,1%s=... =b#s-1,1%s=d (d: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
"b#0,2%s=b#1,2%s=b#2,2%s=... =b#k,2%s=... =b#s-1,2%s=e (e: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
"b#0,3%s=b#1,3%s=b#2,3%s=... =b#k,3%s=... =b#s-1,3%s=f (f: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
Кроме того, поскольку изменяющийся во времени период коэффициента P(D) составляет β, следующее условие справедливо.
Условие #22-2
Когда i%β=j%β (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующие три уравнения являются справедливыми.
[91]
b#i,1=b#j,1... (уравнение 91-1)
b#i,2=b#j,2... (уравнение 91-2)
b#i,3=b#j,3... (уравнение 91-3)
Посредством предоставления следующих условий, можно сокращать число параметров, заданных с использованием случайных чисел, при увеличении изменяющегося во времени периода и предоставлять эффект упрощения поиска кода. Условие #21-1 и условие #22-1 не всегда являются необходимыми условиями. Т.е. только условие #21-2 и условие #22-2 могут предоставляться в качестве условий. Кроме того, вместо условия #21-1 и условия #22-1, условия (условие #21-1' и условие #22-1') также могут предоставляться.
Условие #21-1'
"a#0,1,1%α=a#1,1,1%α=a#2,1,1%α=... =a#k,1,1%α=... =a#s-1,1,1%α=vp=1 (vp=1: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
"a#0,1,2%α=a#1,1,2%α=a#2,1,2%α=... =a#k,1,2%α=... =a#s-1,1,2%α=yp=1 (yp=1: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
"a#0,1,3%α=a#1,1,3%α=a#2,1,3%α=... =a#k,1,3%α=... =a#s-1,1,3%α=zp=1 (zp=1: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
Условие #22-1
"b#0,1%β=b#1,1%β=b#2,1%β=... =b#k,1%β=... =b#s-1,1%β=d (d: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
"b#0,2%β=b#1,2%β=b#2,2%β=... =b#k,2%β=... =b#s-1,2%β=e (e: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
"b#0,3%β=b#1,3%β=b#2,3%β=... =b#k,3%β=... =b#s-1,3%β=f (f: фиксированное значение) (поэтому k=0, 1, 2,..., s-1)"
I-ый (i=0, 1, 2,..., s-2, s-1) полином контроля по четности, который удовлетворяет 0 в LDPC-CC на основе полинома контроля по четности с изменяющимся во времени периодом s и скоростью кодирования 1/2, представлен так, как показано в уравнении 89-i, но при фактическом использовании полином контроля по четности, который удовлетворяет 0, представляется посредством следующего уравнения.
[92]
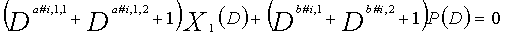 ... (уравнение 92-1)
... (уравнение 92-1)
Кроме того, рассмотрим обобщение полинома контроля по четности. I-ый (i=0, 1, 2,..., s-2, s-1) полином контроля по четности, который удовлетворяет 0, представляется так, как показано в уравнении ниже.
[93]
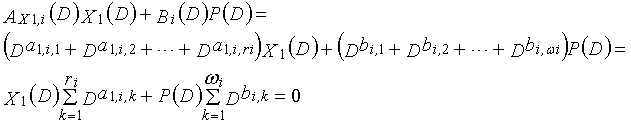 ... (уравнение 93-1)
... (уравнение 93-1)
Т.е. рассматривается случай, в котором число элементов X1(D) и P(D) в качестве полинома контроля по четности не ограничивается тремя, как показано в уравнении 93-i. С использованием вышеприведенного описания в качестве ссылки, следующее условие становится важным в способе конфигурирования кода настоящего варианта осуществления.
Условие #23
Когда i%α=j%α (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующее уравнение справедливо.
[94]
AX1,i(D)=AX1,j(D)... (уравнение 94)
Условие #24
Когда i%β=j%β (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующее уравнение справедливо:
[95]
Bi(D)=Bj(D)... (уравнение 95)
Предоставление вышеописанных условий позволяет сокращать число параметров, заданных с использованием случайных чисел, при увеличении изменяющегося во времени периода и достигать эффекта упрощения поиска кода. В это время, чтобы эффективно увеличивать изменяющийся во времени период, α и β могут быть "простыми числами друг для друга" (взаимно-простыми). Описание "α и β являются взаимно-простыми" означает то, что α и β имеют взаимосвязь отсутствия общего делителя, отличного от 1 (и -1).
В это время, изменяющийся во времени период может быть представлен посредством α*β. Тем не менее, даже когда нет такой взаимосвязи, что α и β являются взаимно-простыми, высокая способность к коррекции ошибок может с большой вероятностью достигаться. Кроме того, на основе описания варианта 6 осуществления, α и β могут быть нечетными числами. Тем не менее, даже когда α и β не являются нечетными числами, высокая способность к коррекции ошибок может с большой вероятностью достигаться.
Затем, относительно LDPC-CC на основе полинома контроля по четности с изменяющимся во времени периодом s и скоростью кодирования (n-1)/n, описывается способ конфигурирования кода LDPC-CC, в котором изменяющийся во времени период коэффициента X1(D) составляет α1, изменяющийся во времени период коэффициента X2(D) составляет α2,..., изменяющийся во времени период коэффициента Xk(D) составляет αk (k=1, 2,..., n-2,n-1),..., изменяющийся во времени период коэффициента Xn-1(D) составляет αn-1, а изменяющийся во времени период коэффициента P(D) составляет β. В это время, изменяющийся во времени период s=LCM(α1, α2,..., αn-2, αn-1, β). Т.е. изменяющийся во времени период s является наименьшим общим кратным α1, α2,..., αn-2, αn-1, β.
I-ый (i=0, 1, 2,..., s-2, s-1) полином контроля по четности, который удовлетворяет 0 в LDPC-CC на основе полинома контроля по четности с изменяющимся во времени периодом s и скоростью кодирования (n-1)/n, является полиномом контроля по четности, который удовлетворяет 0, представленным так, как показано в уравнении ниже.
[96]
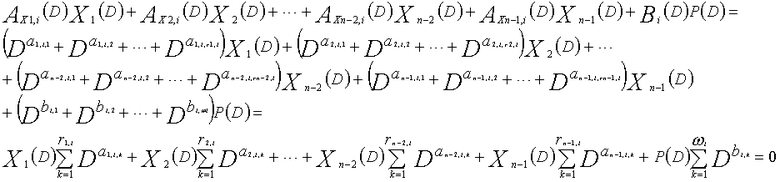 … (уравнение 96-1),
… (уравнение 96-1),
где X1(D), X2(D),..., Xn-1(D) являются полиномиальными представлениями информационных последовательностей X1, X2,..., Xn-1 (n является целым числом, равным или превышающим 2), P(D) является полиномиальным представлением последовательности четности.
Т.е. рассматривается случай, в котором число элементов X1(D), X2(D),..., Xn-2(D), Xn-1(D) и P(D) не ограничивается тремя. С использованием вышеприведенного описания в качестве ссылки, следующее условие становится важным в способе конфигурирования кода согласно настоящему варианту осуществления.
Условие #25
Когда i%αk=j%αk (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующее уравнение справедливо.
[97]
AXk,i(D)=AXk,j(D)... (уравнение 97),
где, k=1, 2,..., n-2,n-1.
Условие #26
Когда i%β=j%β (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующее уравнение справедливо.
[98]
Bi(D)=Bj(D)... (уравнение 98)
Т.е. способ кодирования согласно настоящему варианту осуществления является способом кодирования сверточного кода разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом s, включает в себя этап предоставления i-го (i=0, 1,..., s-2, s-1) полинома контроля по четности, представленного посредством уравнения 96-i, и этап обнаружения кодового LDPC-CC-слова посредством линейного вычисления 0-вого-(s-1)-вого полиномов контроля по четности и входных данных, и предполагается, что изменяющийся во времени период коэффициента AXk,i Xk(D) составляет αk (αk является целым числом, превышающим 1) (k=1, 2,..., n-2,n-1), изменяющийся во времени период коэффициента BXk,i P(D) составляет β (β является целым числом, превышающим 1), изменяющийся во времени период s является наименьшим общим кратным α1, α2,..., αn-2, αn-1 и β, уравнение 97 справедливо, когда i%αk=j%αk (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, и уравнение 98 справедливо, когда i%β=j%β (i, j=0, 1,..., s-2, s-1; i≠j) справедливо (см. фиг. 59).
Предоставление вышеописанных условий позволяет сокращать число параметров, заданных с использованием случайных чисел, при увеличении изменяющегося во времени периода и достигать эффекта упрощения поиска кода.
В это время, чтобы эффективно увеличивать изменяющийся во времени период, если α1, α2,..., αn-2, αn-1 и β являются "взаимно-простыми", изменяющийся во времени период может быть увеличен. В это время, изменяющийся во времени период может быть представлен посредством α1*α2*...*αn-2*αn-1*β.
Тем не менее, даже если нет такой взаимосвязи как взаимно-простых, высокая способность к коррекции ошибок может с большой вероятностью достигаться. На основе описания варианта 6 осуществления, α1, α2,..., αn-2, αn-1 и β могут быть нечетными числами. Тем не менее, даже когда они не являются нечетными числами, высокая способность к коррекции ошибок может с большой вероятностью достигаться.
Тринадцатый вариант осуществления
Относительно LDPC-CC, описанного в варианте 12 осуществления, настоящий вариант осуществления предлагает LDPC-CC, который позволяет конфигурировать кодер/декодер при небольшом размере схем.
Во-первых, описывается способ конфигурирования кода со скоростью кодирования 1/2, 2/3, имеющий вышеуказанные признаки.
Как описано в варианте осуществления 12, i-ый (i=0, 1, 2,..., s-2, s-1) полином контроля по четности, который удовлетворяет 0 в LDPC-CC на основе полинома контроля по четности, в котором изменяющийся во времени период X1(D) составляет α1, изменяющийся во времени период P(D) составляет β, изменяющийся во времени период s составляет LCM(α1, β) и скорость кодирования 1/2, представляется так, как показано в уравнении ниже.
[99]
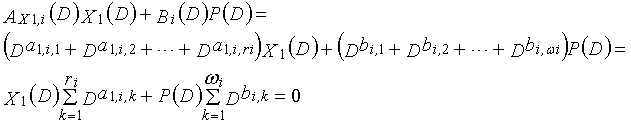 ...(уравнение 99-1)
...(уравнение 99-1)
С использованием варианта 12 осуществления в качестве ссылки, справедливо следующее условие.
Условие #26-1
Когда i%α1=j%α1 (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующее уравнение справедливо.
[100]
AX1,i(D)=AX1,j(D)... (уравнение 100)
Условие #27
Когда i%β=j%β (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующее уравнение справедливо.
[101]
Bi(D)=Bj(D)... (уравнение 101)
Здесь, рассмотрим LDPC-CC со скоростью кодирования 1/2 и LDPC-CC со скоростью кодирования 2/3, которые дают возможность совместного использования схем между кодером и декодером. I-ый (i=0, 1, 2,..., z-2, z-1) полином контроля по четности, который удовлетворяет 0 на основе полинома контроля по четности со скоростью кодирования 2/3 и изменяющимся во времени периодом z, представляется так, как показано в уравнении ниже.
[102]
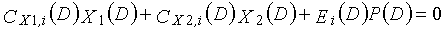 ... (уравнение 102-1)
... (уравнение 102-1)
В это время, условия LDPC-CC на основе полинома контроля по четности со скоростью кодирования 1/2 и LDPC-CC со скоростью кодирования 2/3, которые дают возможность совместного использования схем между кодером и декодером на основе уравнения 99-i, описываются ниже.
Условие #28
В полиноме контроля по четности, который удовлетворяет 0 в уравнении 102-i, когда изменяющийся во времени период X1(D) составляет α1, и i%α1=j%α1 (i=0, 1,..., s-2, s-1,j=0, 1,..., z-2, z-1;) справедливо, следующее уравнение справедливо.
[103]
AX1,i(D)=CX1,j(D)... (уравнение 103)
Условие #29
В полиноме контроля по четности, который удовлетворяет 0 в уравнении 102-i, когда изменяющийся во времени период P(D) составляет β, и i%β=j%β (i=0, 1,..., s-2, s-1,j=0, 1,..., z-2, z-1) справедливо, следующее уравнение справедливо.
[104]
Bi(D)=Ej(D)... (уравнение 104)
В полиноме контроля по четности, который удовлетворяет 0 в уравнении 102-i, поскольку изменяющийся во времени период X2(D) может допускаться как α2, следующее условие справедливо.
Условие #30
[105]
CX2,i(D)=CX2,j(D)... (уравнение 105)
В это время, α2 может быть α1, или β, α2 может быть натуральным числом, которое является взаимно-простым с α1 и β. Тем не менее, α2 имеет характеристику предоставления возможности эффективного увеличения изменяющего во времени периода при условии, что, он является натуральным числом, взаимно-простым с α1 и β. На основе описания варианта 6 осуществления, α1, α2 и β предпочтительно являются нечетными числами. Тем не менее, даже когда α1, α2 и β не являются нечетными числами, высокая способность к коррекции ошибок может с большой вероятностью достигаться.
Изменяющийся во времени период z составляет LCM(α1, α2, β), т.е. наименьшее общее кратное α1, α2 и β.
Фиг. 60 схематично показывает полином контроля по четности LDPC-CC со скоростью кодирования 1/2, 2/3, который дает возможность совместного использования схем между кодером и декодером.
LDPC-CC со скоростью кодирования 1/2 и LDPC-CC со скоростью кодирования 2/3, которые дают возможность совместного использования схем между кодером и декодером, описаны выше. В дальнейшем в этом документе, с дополнительным обобщением, описывается способ конфигурирования кода для LDPC-CC со скоростью кодирования (n-1)/n и LDPC-CC со скоростью кодирования (m-1)/m (n<m), которые дают возможность совместного использования схем между кодером и декодером.
I-ый (i=0, 1, 2,..., s-2, s-1) полином контроля по четности, который удовлетворяет 0 в LDPC-CC на основе полинома контроля по четности (n-1)/n, в котором изменяющийся во времени период X1(D) составляет α1, изменяющийся во времени период X2(D) составляет α2,..., изменяющийся во времени период Xn-1(D) составляет αn-1, изменяющийся во времени период P(D) составляет β, изменяющийся во времени период s составляет LCM(α1, α2,..., αn-1, β), т.е. наименьшее общее кратное α1, α2,..., αn-1, β представляется так, как показано в уравнении ниже.
[106]
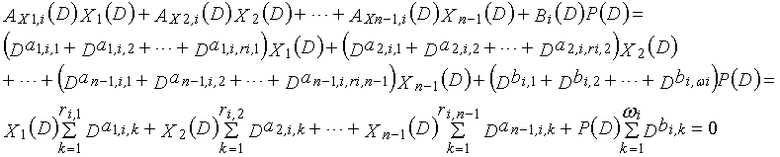 …(уравнение 106-1)
…(уравнение 106-1)
С использованием варианта 12 осуществления в качестве ссылки, справедливо следующее условие:
Условие #31
Когда i%αk=j%αk (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующее уравнение справедливо.
[107]
AXk,i(D)=AXk,j(D)... (уравнение 107),
где, k=1, 2,..., n-1.
Условие #32
Когда i%β=j%β (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, следующее уравнение справедливо.
[108]
Bi(D)=Bj(D)... (уравнение 108)
Здесь, рассмотрим LDPC-CC со скоростью кодирования (n-1)/n и LDPC-CC со скоростью кодирования (m-1)/m, которые дают возможность совместного использования схем между кодером и декодером. I-ый (i=0, 1, 2,..., z-2, z-1) полином контроля по четности, который удовлетворяет 0 на основе полинома контроля по четности со скоростью кодирования (m-1)/m и изменяющийся во времени период z, представляется так, как показано в уравнении ниже.
[109]
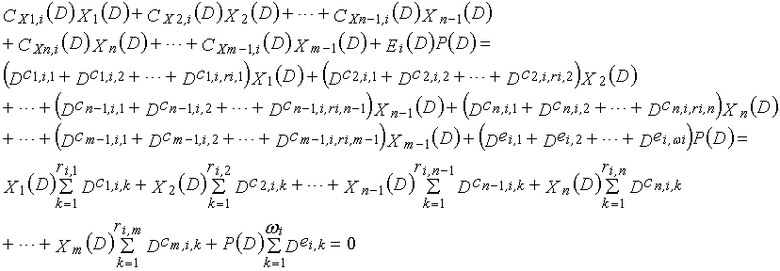
...(уравнение 109-1)
В это время, условия LDPC-CC на основе полинома контроля по четности со скоростью кодирования (n-1)/n, представленные посредством уравнения 106-i, и LDPC-CC со скоростью кодирования (m-1)/m, которые дают возможность совместного использования схем между кодером и декодером, описываются ниже.
Условие #33
В полиноме контроля по четности, который удовлетворяет 0 в уравнении 109-i, когда изменяющийся во времени период Xk(D) составляет αk (k=1, 2,..., n-1) и i%αk=j%αk (i=0, 1,..., s-2, s-1; j=0, 1,..., z-2, z-1) справедливо, следующее уравнение справедливо.
[110]
AXk,i(D)=CXk,j(D)... (уравнение 110)
Условие #34
В полиноме контроля по четности, который удовлетворяет 0 в уравнении 109-i, когда изменяющийся во времени период P(D) составляет β, и i%β=j%β (i=0, 1,..., s-2, s-1; j=0, 1,..., z-2, z-1) справедливо, следующее уравнение справедливо.
[111]
Bi(D)=Ej(D)... (уравнение 111)
В полиноме контроля по четности, который удовлетворяет 0 в уравнении 109-i, поскольку изменяющийся во времени период Xh(D) может задаваться равным αh (h=n, n+1,..., m-1), следующее условие справедливо.
Условие #35
Когда i%αh=j%αh(i, j=0, 1,..., z-2, z-1; i≠j) справедливо, следующее уравнение справедливо.
[112]
CXh,i(D)=CXh,j(D)... (уравнение 112)
В это время, αh может быть натуральным числом. Если все α1, α2,..., αn-1, αn,..., αm-1 и β являются натуральными числами, взаимно-простыми друг с другом, существует характеристика предоставления возможности эффективного увеличения изменяющегося во времени периода. Кроме того, на основе описания варианта 6 осуществления, α1, α2,..., αn-1, αn,..., αm-1 и β предпочтительно являются нечетными числами. Тем не менее, даже когда они не являются нечетными числами, высокая способность к коррекции ошибок может с большой вероятностью достигаться.
Изменяющийся во времени период z составляет LCM(α1, α2,..., αn-1, αn,..., αm-1, β), т.е. наименьшее общее кратное α1, α2,..., αn-1, αn,..., αm-1, β.
Затем, описывается конкретный способ конфигурирования кодера/декодера для вышеуказанного LDPC-CC, поддерживающего множество скоростей кодирования, который позволяет конфигурировать кодер/декодер при небольшом размере схем.
Во-первых, в кодере/декодере согласно настоящему изобретению, наибольшая скорость кодирования из скоростей кодирования, предназначенных для совместно использования схем, допускается равной (q-1)/q. Когда, например, скорости кодирования, поддерживаемые посредством передающего/приемного устройства, допускаются равными 1/2, 2/3, 3/4 и 5/6, предполагается, что коды скоростей кодирования 1/2, 2/3 и 3/4 дают возможность совместного использования схем между кодером и декодером, и скорость кодирования 5/6 не предназначена для совместного использования схем между кодером и декодером. В это время, вышеуказанная наибольшая скорость кодирования (q-1)/q составляет 3/4. В дальнейшем в этом документе описывается кодер для создания LDPC-CC с изменяющимся во времени периодом z (z натуральное число), который может поддерживать множество скоростей кодирования (r-1)/r (r является целым числом, равным или превышающим 2 и равным или меньшим q).
Фиг. 61 является блок-схемой, показывающей пример основных компонентов кодера согласно настоящему варианту осуществления. Кодер 5800, показанный на фиг. 61, является кодером, поддерживающим скорости кодирования 1/2, 2/3 и 3/4. Кодер 5800, показанный на фиг. 61, главным образом, содержит модуль 5801 формирования информации, первый модуль 5802-1 вычисления информации, второй модуль 5802-2 вычисления информации, третий модуль 5802-3 вычисления информации, модуль 5803 вычисления четности, модуль 5804 суммирования, модуль 5805 задания скорости кодирования и модуль 5806 управления весовыми коэффициентами.
Модуль 5801 формирования информации задает информацию X1,k, информацию X2,k и информацию X3,k в момент времени k согласно скорости кодирования, обозначенной посредством модуля 5805 задания скорости кодирования. Когда, например, модуль 5805 задания скорости кодирования задает скорость кодирования в 1/2, модуль 5801 формирования информации задает входные информационные данные Sj в информации X1,k в момент времени k и задает 0 в информации X2,k в момент времени k и информации X3,k в момент времени k.
Кроме того, когда скорость кодирования составляет 2/3, модуль 5801 формирования информации задает входные информационные данные Sj в информации X1,k в момент времени k, задает входные информационные данные Sj+1 в информации X2,k в момент времени k и задает 0 в информации X3,k в момент времени k.
Кроме того, когда скорость кодирования составляет 3/4, модуль 5801 формирования информации задает входные информационные данные Sj в информации X1,k в момент времени k, задает входные информационные данные Sj+1 в информации X2,k в момент времени k и задает входные информационные данные Sj+2 в информации X3,k в момент времени k.
Таким образом, модуль 5801 формирования информации задает входные информационные данные в информации X1,k, информации X2,k и информации X3,k в момент времени k согласно скорости кодирования, заданной посредством модуля 5805 задания скорости кодирования, выводит заданную информацию X1,k в первый модуль 5802-1 вычисления информации, выводит заданную информацию X2,k во второй модуль 5802-2 вычисления информации и выводит заданную информацию X3,k в третий модуль 5802-3 вычисления информации.
Первый модуль 5802-1 вычисления информации вычисляет X1(D) согласно AX1,i(D) уравнения 106-i (также соответствует уравнению 109-i, поскольку уравнение 110 справедливо). Аналогично, второй модуль 5802-2 вычисления информации вычисляет X2(D) согласно AX2,i(D) уравнения 106-2 (также соответствует уравнению 109-i, поскольку уравнение 110 справедливо). Аналогично, третий модуль вычисления информации 580-3 вычисляет X3(D) согласно CX3,i(D) уравнения 109-i.
В это время, как описано выше, поскольку уравнение 109-i удовлетворяет условию #33 и условию #34, даже когда скорость кодирования изменяется, необходимо не изменять ни конфигурацию первого модуля 5802-1 вычисления информации, ни конфигурацию второго модуля 5802-2 вычисления информации.
Следовательно, когда множество скоростей кодирования поддерживается, посредством использования конфигурации кодера с наибольшей скоростью кодирования в качестве ссылки из скоростей кодирования для совместного использования схем кодера, другие скорости кодирования могут поддерживаться посредством вышеуказанной операции. Т.е. вышеуказанный LDPC-CC имеет преимущество возможности совместно использовать первый модуль 5802-1 вычисления информации и второй модуль 5802-2 вычисления информации, которые являются основными частями кодера, независимо от скорости кодирования.
Фиг. 62 показывает конфигурацию в первом модуле 5802-1 вычисления информации. Первый модуль 5802-1 вычисления информации на фиг. 62 содержит сдвиговые регистры 5901-1-5901-M, умножители 5902-0-5902-M весовых коэффициентов и сумматор 5903.
Сдвиговые регистры 5901-1-5901-M являются регистрами, которые сохраняют X1,i-t (t=0,..., M-1), соответственно, отправляют сохраненное значение, когда следующий ввод выполняется в сдвиговый регистр справа, и сохраняют значение, выведенное из сдвигового регистра слева.
Умножители 5902-0-5902-M весовых коэффициентов переключают значение h1 (t) на 0 или 1 согласно управляющему сигналу, выведенному из модуля 5904 управления весовыми коэффициентами.
Сумматор 5903 выполняет операцию "исключающее ИЛИ" для выводов умножителей 5902-0-5902-M весовых коэффициентов, вычисляет результат Y1,k вычисления и выводит вычисленный Y1,k в сумматор 5804 на фиг. 61.
Кроме того, конфигурации во втором модуле 5802-2 вычисления информации и третьем модуле 5802-3 вычисления информации являются идентичными первому модулю 5802-1 вычисления информации, и, следовательно, их пояснение пропускается. Второй модуль 5802-2 вычисления информации вычисляет результат Y2,k вычисления, как в случае первого модуля 5802-1 вычисления информации и выводит вычисленный Y2,k в сумматор 5804 на фиг. 61. Третий модуль 5802-3 вычисления информации вычисляет результат Y3,k вычисления, как в случае первого модуля 5802-1 вычисления информации, и выводит вычисленный Y3,k в сумматор 5804 на фиг. 61.
Модуль 5803 вычисления четности на фиг. 61 вычисляет P(D) согласно Bi(D) уравнения 106-i (который также соответствует уравнению 109-i, поскольку уравнение (111) справедливо).
Фиг. 63 показывает конфигурацию в модуле 5803 вычисления четности на фиг. 61. Модуль 5803 вычисления четности на фиг. 63 содержит сдвиговые регистры 6001-1-6001-M, умножители 6002-0-6002-M весовых коэффициентов и сумматор 6003.
Сдвиговые регистры 6001-1-6001-M являются регистрами, которые сохраняют Pi-t (t=0,..., M-1), соответственно, отправляют сохраненное значение, когда следующий ввод вводится в сдвиговый регистр справа, и сохраняют значение, выведенное из сдвигового регистра слева.
Умножители 6002-0-6002-M весовых коэффициентов переключают значение h2 (t) на 0 или 1 согласно управляющему сигналу, выведенному из модуля 6004 управления весовыми коэффициентами.
Сумматор 6003 выполняет операцию "исключающее ИЛИ" для выводов умножителей 6002-0-6002-M весовых коэффициентов, вычисляет результат Zk вычисления и выводит вычисленный Zk в сумматор 5804 на фиг. 61.
Снова возвращаясь к фиг. 61, сумматор 5804 выполняет операцию "исключающее ИЛИ" для результатов Y1,k, Y2,k, Y3,k и Zk вычисления, выведенных из первого модуля 5802-1 вычисления информации, второго модуля 5802-2 вычисления информации, третьего модуля 5802-3 вычисления информации, и модуль 5803 вычисления четности получает четность P во время k и выводит четность Pk. Сумматор 5804 также выводит четность Pk во время k в модуль 5803 вычисления четности.
Модуль 5805 задания скорости кодирования задает скорость кодирования кодера 5800 и выводит информацию скорости кодирования в модуль 5801 формирования информации.
Модуль 5806 управления весовыми коэффициентами выводит значение h1 (m) во время k на основе полинома контроля по четности, который удовлетворяет 0 в уравнении 106-i и уравнении 109-i, сохраненного в модуле 5806 управления весовыми коэффициентами, в первый модуль 5802-1 вычисления информации, второй модуль 5802-2 вычисления информации, третий модуль 5802-3 вычисления информации и модуль 5803 вычисления четности. Кроме того, модуль 5806 управления весовыми коэффициентами выводит значение h2 (m) во время в 6002-0-6002-M на основе полинома контроля по четности, который удовлетворяет 0, соответствующего уравнению 106-i и уравнению 109-i, сохраненного в модуле 5806 управления весовыми коэффициентами.
Кроме того, фиг. 64 показывает другую конфигурацию кодера согласно настоящему варианту осуществления. В кодере по фиг. 64, компонентам, идентичным компонентам в кодере по фиг. 61, назначаются идентичные ссылки с номерами.
Кодер 5800 на фиг. 64 отличается от кодера 5800 на фиг. 61 тем, что модуль 5805 задания скорости кодирования выводит информацию скоростей кодирования в первый модуль 5802-1 вычисления информации, второй модуль 5802-2 вычисления информации, третий модуль 5802-3 вычисления информации и модуль 5803 вычисления четности.
Когда скорость кодирования составляет 1/2, второй модуль 5802-2 вычисления информации не выполняет обработку вычисления и выводит 0 в сумматор 5804 в качестве результата Y2,k вычисления. С другой стороны, когда скорость кодирования составляет 1/2 или 2/3, третий модуль 5802-3 вычисления информации не выполняет обработку вычисления и выводит 0 в сумматор 5804 в качестве результата Y3,k вычисления.
В кодере 5800 на фиг. 61, модуль 5801 формирования информации задает информацию X2,i и информацию X3,i в момент времени i равной 0 согласно скорости кодирования, тогда как в кодере 5800 на фиг. 64, второй модуль 5802-2 вычисления информации и третий модуль 5802-3 вычисления информации прекращают обработку вычисления согласно скорости кодирования, выводят 0 в качестве результатов Y2,k и Y3,k вычисления, и, следовательно, полученные результаты вычисления являются идентичными результатам в кодере 5800 на фиг. 61.
Таким образом, в кодере 5800 по фиг. 64, второй модуль 5802-2 вычисления информации и третий модуль 5802-3 вычисления информации прекращают обработку вычисления согласно скорости кодирования, так что можно уменьшать обработку вычисления по сравнению с кодером 5800 по фиг. 61.
Как показано в конкретном примере выше, относительно кодов LDPC-CC со скоростью кодирования (n-1)/n, описанного с использованием уравнения 106-i и уравнения 109-i, и LDPC-CC со скоростью кодирования (m-1)/m (n<m), которые дают возможность совместного использования схем между кодером и декодером, можно совместно использовать схемы кодера посредством предоставления кодера LDPC-CC с большой скоростью кодирования (m-1)/m, задания вывода вычисления, связанного с Xk(D) (где k=n, n+1,..., m-1), равным 0, когда скорость кодирования составляет (n-1)/n, и вычисления четности, когда скорость кодирования составляет (n-1)/n.
Затем, подробнее описывается способ совместного использования схем декодера LDPC-CC, описанного в настоящем варианте осуществления.
Фиг. 65 является блок-схемой, показывающей основные компоненты декодера согласно настоящему варианту осуществления. Здесь, декодер 6100, показанный на фиг. 65, означает декодер, который может поддерживать скорости кодирования 1/2, 2/3 и 3/4. Декодер 6100 по фиг. 65, главным образом, содержит модуль 6101 задания логарифмического отношения правдоподобия и модуль 6102 вычисления при матричной обработке.
Модуль 6101 задания логарифмического отношения правдоподобия принимает в качестве ввода логарифмическое отношение правдоподобия приема и скорость кодирования, вычисленную в модуле вычисления логарифмического отношения правдоподобия (не показан), и вставляет известное логарифмическое отношение правдоподобия в логарифмическое отношение правдоподобия приема согласно скорости кодирования.
Когда, например, скорость кодирования составляет 1/2, это соответствует кодеру 5800, передающему нули, аналогично X2,k и X3,k, и, следовательно, модуль 6101 задания логарифмического отношения правдоподобия вставляет фиксированное логарифмическое отношение правдоподобия, соответствующее известным битам "0", в качестве логарифмических отношений X2,k правдоподобия и X3,k и выводит логарифмические отношения правдоподобия, вставленные в модуль 6102 вычисления при матричной обработке. Это поясняется ниже с использованием фиг. 66.
Как показано на фиг. 66, когда скорость кодирования составляет 1/2, модуль 6101 задания логарифмического отношения правдоподобия принимает в качестве ввода принимаемые логарифмические отношения LLRX1,k и LLRPk правдоподобия, соответствующие X1,k и Pk в момент времени k. Модуль 6101 задания логарифмического отношения правдоподобия затем вставляет принятые логарифмические отношения LLRX2,k и LLR3,k правдоподобия, соответствующие X2,k и X3,k. На фиг. 66, принимаемые логарифмические отношения правдоподобия, окруженные посредством пунктирных линий, представляют принятые логарифмические отношения LLRX2,k и LLR3,k правдоподобия, вставленные посредством модуля 6101 задания логарифмического отношения правдоподобия. Модуль 6101 задания логарифмического отношения правдоподобия вставляет логарифмическое отношение правдоподобия с фиксированными значениями в качестве принимаемых логарифмических отношений LLRX2,k и LLR3,k правдоподобия.
Кроме того, когда скорость кодирования составляет 2/3, это соответствует кодеру 5800, передающему "0", аналогично X3,k, и, следовательно, модуль 6101 задания логарифмического отношения правдоподобия вставляет фиксированное логарифмическое отношение правдоподобия, соответствующее известному биту "0", в качестве логарифмического отношения X3,k правдоподобия и выводит вставленное логарифмическое отношение правдоподобия в модуль 6102 вычисления при матричной обработке. Это поясняется с использованием фиг. 67.
Как показано на фиг. 67, когда скорость кодирования составляет 2/3, модуль 6101 задания логарифмического отношения правдоподобия принимает в качестве ввода принимаемые логарифмические отношения LLRX1,k, LLRX2,k и LLRPk правдоподобия, соответствующие X1,k, X2,k и Pk. Таким образом, модуль 6101 задания логарифмического отношения правдоподобия вставляет принятое логарифмическое отношение LLR3,k правдоподобия, соответствующее X3,k. На фиг. 67, принимаемые логарифмические отношения правдоподобия, окруженные посредством пунктирных линий, представляют принимаемое логарифмическое отношение LLR3,k правдоподобия, вставленное посредством модуля 6101 задания логарифмического отношения правдоподобия. Модуль 6101 задания логарифмического отношения правдоподобия вставляет логарифмическое отношение правдоподобия с фиксированным значением в качестве принимаемого логарифмического отношения LLR3,k правдоподобия.
Модуль 6102 вычисления при матричной обработке на фиг. 65 содержит модуль 6103 хранения, модуль 6104 вычисления при обработке по строкам и модуль 6105 вычисления при обработке по столбцам.
Модуль 6103 хранения сохраняет логарифмическое отношение правдоподобия, внешнее значение αmn, полученное посредством обработки по строкам, и априорное значение βmn, полученное посредством обработки по столбцам.
Модуль 6104 вычисления при обработке по строкам хранит шаблон весовых коэффициентов в направлении строк матрицы H LDPC-CC-контроля с максимальной скоростью кодирования 3/4 из скоростей кодирования, поддерживаемых посредством кодера 5800. Модуль 6104 вычисления при обработке по строкам считывает необходимое априорное значение βmn из модуля 6103 хранения согласно этому шаблону весовых коэффициентов в направлении строк и выполняет вычисление при обработке по строкам.
В вычислении при обработке по строкам, модуль 6104 вычисления при обработке по строкам декодирует один код контроля по четности с использованием априорного значения βmn и находит внешнее значение αmn.
Обработка m-ой строки поясняется.
Здесь, двоичная матрица M*N H={Hmn} допускается как контрольная матрица LDPC-кода, который должен быть декодирован. Внешнее значение αmn обновляется с использованием следующего уравнения обновления для всех наборов (m, n), которые удовлетворяют Hmn=1.
[113]
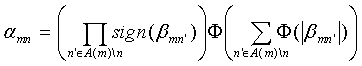 ... (уравнение 113),
... (уравнение 113),
где Φ(x) называется f-функцией Галлэджера и задается посредством следующего уравнения.
[114]
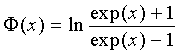 ... (уравнение 114)
... (уравнение 114)
Модуль 6105 вычисления при обработке по столбцам хранит шаблон весовых коэффициентов в направлении столбцов матрицы H LDPC-CC-контроля с максимальной скоростью кодирования 3/4 из скоростей кодирования, поддерживаемых посредством кодера 5800. Модуль 6105 вычисления при обработке по столбцам считывает необходимое внешнее значение αmn из модуля 321 хранения согласно этому шаблону весовых коэффициентов в направлении столбцов и находит априорное значение βmn.
В вычислении при обработке по столбцам, модуль 6105 вычисления при обработке по столбцам выполняет итеративное декодирование с использованием входного логарифмического отношения λn правдоподобия и внешнего значения αmn и находит априорное значение βmn.
Обработка m-го столбца поясняется.
βmn обновляется с использованием следующего уравнения обновления для всех наборов (m, n), которые удовлетворяют Hmn=1. Тем не менее, начальное вычисление выполняется при условии, что αmn=0.
[115]
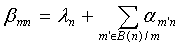 ... (уравнение 115)
... (уравнение 115)
Декодер 6100 получает апостериорное логарифмическое отношение правдоподобия посредством повторения вышеуказанной обработки по строкам и обработки по столбцам предварительно определенное число раз.
Как описано выше, настоящий вариант осуществления допускает, что наибольшая скорость кодирования из скоростей кодирования, которые могут поддерживаться, составляет (m-1)/m, и когда модуль 5805 задания скорости кодирования задает скорость кодирования равной (n-1)/n, модуль 5801 формирования информации задает информацию (информацию Xn,k-Xm-1,k) равной 0.
Когда, например, поддерживаемые скорости кодирования составляют 1/2, 2/3 и 3/4 (m=4), первый модуль 5802-1 вычисления информации принимает информацию X1,k в момент времени k в качестве ввода и вычисляет элемент X1(D). Кроме того, второй модуль 5802-2 вычисления информации принимает информацию X2,k в момент времени k в качестве ввода и вычисляет элемент X2(D). Кроме того, третий модуль 5802-3 вычисления информации принимает информацию X3,k в момент времени k в качестве ввода и вычисляет элемент X3(D).
Кроме того, модуль 5803 вычисления четности принимает четность Pk-1 в момент времени k-1 в качестве ввода и вычисляет элемент P(D). Кроме того, сумматор 5804 получает исключающее ИЛИ результатов вычисления первого модуля 5802-1 вычисления информации, второго модуля 5802-2 вычисления информации и третьего модуля 5802-3 вычисления информации и результат вычисления модуля 5803 вычисления четности в качестве четности Pk во время k.
При этой конфигурации, после создания LDPC-CC, поддерживающего различные скорости кодирования, можно совместно использовать конфигурации модулей вычисления информации согласно вышеприведенному пояснению, так что можно предоставлять LDPC-CC-кодер и декодер, которые могут поддерживать множество скоростей кодирования при небольшой вычислительной сложности.
Посредством добавления модуля 6101 задания логарифмического отношения правдоподобия к конфигурации декодера, соответствующей максимальной скорости кодирования из числа скоростей кодирования, поддерживающих совместное использование схем кодера/декодера, можно выполнять декодирование, поддерживающее множество скоростей кодирования. Модуль 6101 задания логарифмического отношения правдоподобия задает логарифмические отношения правдоподобия, соответствующие информации (информации Xn,k-Xm-1,k) в момент времени k, равными предварительно определенным значениям согласно скорости кодирования.
Хотя выше описан случай, в котором максимальная скорость кодирования, поддерживаемая посредством кодера 5800, составляет 3/4, максимальная поддерживаемая скорость кодирования не ограничивается этим, и скорость кодирования в (m-1)/m (m является целым числом, равным или превышающим 5) также может поддерживаться (естественно, максимальная скорость кодирования также может составлять 2/3). В этом случае, кодер 5800 может быть выполнен с возможностью включать в себя первый-(m-1)-вый модули вычисления информации, и сумматор 5804 может быть выполнен с возможностью получать исключающее ИЛИ результатов вычисления первого-(m-1)-вого модулей вычисления информации и результата вычисления модуля 5803 вычисления четности в качестве четности Pk во время k.
Кроме того, когда все скорости кодирования, поддерживаемые посредством передающего/приемного устройства (кодера/декодера), являются кодами на основе вышеуказанного способа, предоставление кодера/декодера с наибольшей скоростью кодирования из поддерживаемых скоростей кодирования позволяет поддерживать кодирование и декодирование на множестве скоростей кодирования, и эффект уменьшения объема вычислений в это время является очень большим.
Кроме того, хотя декодирование суммы-произведения описано выше в качестве примера схемы декодирования, способ декодирования не ограничивается этим, и настоящее изобретение может быть аналогично реализовано посредством использования способа декодирования (BP-декодирования) с использованием алгоритма передачи сообщений, такого как декодирование по алгоритму минимальной суммы, нормализованное декодирование по алгоритму BP (доверительного распространения), перемешанное BP-декодирование, BP-декодирование со смещением, описанные в непатентных документах 4-6.
Затем, поясняется случай, в котором настоящее изобретение применяется к устройству связи, которое адаптивным образом переключает скорость кодирования согласно состоянию связи. Кроме того, поясняется примерный случай, в котором настоящее изобретение применяется к устройству радиосвязи, настоящее изобретение не ограничено этим, но является в равной степени применимым к устройству PLC (связи по линиям электросети), устройству связи в диапазоне видимого света или устройству оптической связи.
Фиг. 68 показывает конфигурацию устройства 6200 связи, которое адаптивным образом переключает скорость кодирования. Модуль 6203 определения скорости кодирования устройства 6200 связи на фиг. 68 принимает в качестве ввода принимаемый сигнал, передаваемый из устройства связи обменивающейся данными стороны (например, информацию обратной связи, передаваемую из обменивающейся данными стороны), и выполняет обработку приема принимаемого сигнала. Дополнительно, модуль 6203 определения скорости кодирования обнаруживает информацию состояния связи с устройством связи обменивающейся данными стороны, к примеру, частоту ошибок по битам, частоту ошибок по пакетам, частоту ошибок по кадрам и интенсивность поля приема (например, из информации обратной связи) и определяет скорость кодирования и схему модуляции из информации состояния связи с устройством связи обменивающейся данными стороны.
Дополнительно, модуль 6203 определения скорости кодирования выводит определенную скорость кодирования и схему модуляции в кодер 6201 и модуль 6202 модуляции в качестве управляющего сигнала. Тем не менее, скорость кодирования не должна всегда определяться на основе информации обратной связи из обменивающейся данными стороны.
С использованием, например, формата передачи, показанного на фиг. 69, модуль 6203 определения скорости кодирования включает информацию скорости кодирования в символы управляющей информации и сообщает скорость кодирования, используемую в кодере 6201, в устройство связи обменивающейся данными стороны. Здесь, как не показано на фиг. 69, обменивающаяся данными сторона включает в себя, например, известные сигналы (к примеру, преамбулу, пилотный символ и опорный символ), которые необходимы при демодуляции или оценке канала.
Таким образом, модуль 6203 определения скорости кодирования принимает сигнал модуляции, передаваемый из устройства 6300 связи (см. фиг. 70) обменивающейся данными стороны, и посредством определения скорости кодирования передаваемого сигнала модуляции на основе состояния связи переключает скорость кодирования адаптивным образом. Кодер 6201 выполняет LDPC-CC-кодирование на вышеуказанных этапах на основе скорости кодирования, обозначенной посредством управляющего сигнала. Модуль 6202 модуляции модулирует кодированную последовательность с использованием схемы модуляции, обозначенной посредством управляющего сигнала.
Фиг. 70 показывает пример конфигурации устройства связи обменивающейся данными стороны, которая обменивается данными с устройством 6200 связи. Модуль 6304 формирования управляющей информации устройства 6300 связи на фиг. 70 извлекает управляющую информацию из символа управляющей информации, включенного в сигнал в полосе модулирующих частот. Символ управляющей информации включает в себя информацию скорости кодирования. Модуль 6304 формирования управляющей информации выводит извлеченную информацию скорости кодирования в модуль 6302 формирования логарифмических отношений правдоподобия и декодер 6303 в качестве управляющего сигнала.
Приемный модуль 6301 обнаруживает сигнал в полосе модулирующих частот посредством применения обработки, такой как преобразование частоты и квадратурная демодуляция, к принимаемому сигналу для сигнала модуляции, передаваемого из устройства 6200 связи, и выводит сигнал в полосе модулирующих частот в модуль 6302 формирования логарифмических отношений правдоподобия. Кроме того, с использованием известных сигналов, включенных в сигнал в полосе модулирующих частот, приемный модуль 6301 оценивает изменение в канале для канала (например, радиоканала) между устройством 6200 связи и устройством 6300 связи и выводит оцененный сигнал оценки канала в модуль 6302 формирования логарифмических отношений правдоподобия.
Кроме того, с использованием известных сигналов, включенных в сигнал в полосе модулирующих частот, приемный модуль 6301 оценивает изменение в канале для канала (например, радиоканала) между устройством 6200 связи и устройством 6300 связи и формирует и выводит информацию обратной связи (к примеру, само изменение канала, которое означает, например, информацию состояния канала) для определения состояния канала. Эта информация обратной связи передается в обменивающуюся данными сторону (т.е. устройство 6200 связи) через передающее устройство (не показано) в качестве части управляющей информации. Модуль 6302 формирования логарифмических отношений правдоподобия вычисляет логарифмическое отношение правдоподобия каждой последовательности передачи с использованием сигнала в полосе модулирующих частот и выводит результирующие логарифмические отношения правдоподобия в декодер 6303.
Как описано выше, согласно скорости кодирования (s-1)/s, обозначенный посредством управляющего сигнала, декодер 6303 задает логарифмические отношения правдоподобия для информации (информации Xs,k-Xm-1,k) в момент времени k равными предварительно определенным значениям и выполняет BP-декодирование с использованием матрицы LDPC-CC-контроля на основе максимальной скорости кодирования из скоростей кодирования, чтобы совместно использовать схемы декодера 6303.
Таким образом, скорости кодирования устройства 6200 связи и устройства 6300 связи обменивающейся данными стороны, к которой применяется настоящее изобретение, адаптивным образом изменяются согласно состоянию связи.
Здесь, способ изменения скорости кодирования не ограничивается вышеуказанным, и устройство 6300 связи обменивающейся данными стороны может включать в себя модуль 6203 определения скорости кодирования и обозначать требуемую скорость кодирования. Кроме того, устройство 6300 связи может оценивать изменение канала из сигнала модуляции, передаваемого из устройства 6200 связи, и определять скорость кодирования. В этом случае, вышеуказанная информация обратной связи не необходима.
Одним аспектом способа кодирования настоящего изобретения является способ кодирования, который выполняет сверточное кодирование на основе разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, причем способ содержит прием последовательности информации в качестве ввода и кодирование информационной последовательности с использованием уравнения 116 в качестве g-го (g=0, 1,..., q-1) полинома контроля по четности, который удовлетворяет 0.
[116]
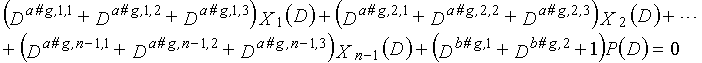 ... (уравнение 116)
... (уравнение 116)
В уравнении 116, "%" означает "по модулю", и коэффициент удовлетворяет следующему относительно k=1, 2,..., n-1:
"a#0,k,1%q=a#1,k,1%q=a#2,k,1%q=a#3,k,1%q=... =a#g,k,1%q=... =a#q-2,k,1%q=a#q-1,k,1%q=vp=k (vp=k: фиксированное значение)"
"b#0,1%q=b#1,1%q=b#2,1%q=b#3,1%q=... =b#g,1%q=... =b#q-2,1%q=b#q-1,1%q=w (w: фиксированное значение)"
"a#0,k,2%q=a#1,k,2%q=a#2,k,2%q=a#3,k,2%q=... =a#g,k,2%q=... =a#q-2,k,2%q=a#q-1,k,2%q=yp=k (yp=k: фиксированное значение)"
"b#0,2%q=b#1,2%q=b#2,2%q=b#3,2%q=... =b#g,2%q=... =b#q-2,2%q=b#q-1,2%q=z (z: фиксированное значение)"
"a#0,k,3%q=a#1,k,3%q=a#2,k,3%q=a#3,k,3%q=... =a#g,k,3%q=... =a#q-2,k,3%q=a#q-1,k,3%q=sp=k (sp=k: фиксированное значение)"
В уравнении 116, a#g,k,1, a#g,k,2, a#g,k,3 являются натуральными числами, равными или превышающими 1, и a#g,k,1≠a#g,k,2, a#g,k,1≠a#g,k,3, a#g,k,2≠a#g,k,3 поддерживается. Кроме того, b#g,1, b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 поддерживается.
Кроме того, в уравнении 116, vp=k, yp=k являются натуральными числами, равными или превышающими 1.
Одним аспектом способа кодирования настоящего изобретения является способ кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, причем способ содержит прием последовательности информации в качестве ввода и кодирование информационной последовательности с использованием полинома контроля по четности, который удовлетворяет:
"a#0,k,1%q=a#1,k,1%q=a#2,k,1%q=a#3,k,1%q=... =a#g,k,1%q=... =a#q-2,k,1%q=a#q-1,k,1%q=vp=k (vp=k: фиксированное значение)",
"b#0,1%q=b#1,1%q=b#2,1%q=b#3,1%q=... =b#g,1%q=... =b#q-2,1%q=b#q-1,1%q=w (w: фиксированное значение)",
"a#0,k,2%q=a#1,k,2%q=a#2,k,2%q=a#3,k,2%q=... =a#g,k,2%q=... =a#q-2,k,2%q=a#q-1,k,2%q=yp=k (yp=k: фиксированное значение)",
"b#0,2%q=b#1,2%q=b#2,2%q=b#3,2%q=... =b#g,2%q=... =b#q-2,2%q=b#q-1,2%q=z (z: фиксированное значение)", и
"a#0,k,3%q=a#1,k,3%q=a#2,k,3%q=a#3,k,3%q=... =a#g,k,3%q=... =a#q-2,k,3%q=a#q-1,k,3%q=sp=k (sp=k: фиксированное значение)"
g-го (g=0, 1,..., q-1) полинома контроля по четности, который удовлетворяет 0, представленного посредством уравнения 117 для k=1, 2,..., n-1.
[117]
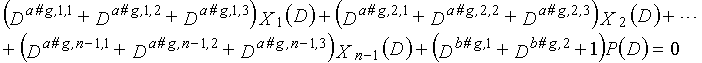 ... (уравнение 117)
... (уравнение 117)
Одним аспектом кодера настоящего изобретения является кодер, который выполняет сверточное кодирование на основе разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, включающий в себя модуль формирования, который принимает информационный бит Xr[i] (r=1, 2,..., n-1) в момент времени i в качестве ввода, обозначает уравнение, эквивалентное g-му(g=0, 1,..., q-1) полиному контроля по четности, который удовлетворяет 0, представленному посредством уравнения 116, в качестве уравнения 118 и формирует бит P[i] четности в момент времени i с использованием уравнения с подстановкой k вместо g в уравнении 118, когда i%q=k, и модуль вывода, который выводит бит P[i] четности.
[118]
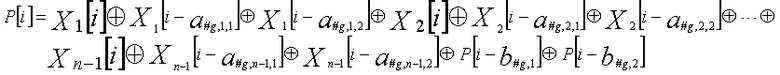 ... (уравнение 118)
... (уравнение 118)
Одним аспектом способа декодирования настоящего изобретения является способ декодирования, соответствующий вышеописанному способу кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом q (простое число, превышающее 3) с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), для декодирования кодированной информационной последовательности, кодированной с использованием уравнения 116, в качестве g-го (g=0, 1,..., q-1) полинома контроля по четности, который удовлетворяет 0, причем способ содержит прием кодированной информационной последовательности в качестве ввода и декодирование кодированной информационной последовательности с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 116, которое является g-ым полиномом контроля по четности, который удовлетворяет 0.
Одним аспектом декодера настоящего изобретения является декодер, соответствующий вышеописанному способу кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом q (простое число, превышающее 3) с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), который выполняет декодирование кодированной информационной последовательности, кодированной с использованием уравнения 116, в качестве g-го (g=0, 1,..., q-1) полинома контроля по четности, который удовлетворяет 0, включающий в себя модуль декодирования, который принимает кодированную информационную последовательность в качестве ввода и декодирует кодированную информационную последовательность с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 116, которое является g-ым полиномом контроля по четности, который удовлетворяет 0.
Одним аспектом способа кодирования настоящего изобретения является способ кодирования для сверточного кода разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом s, включающий в себя этап предоставления i-го (i=0, 1,..., s-2, s-1) полинома контроля по четности, представленного посредством уравнения 98-i, и этап обнаружения кодового LDPC-CC-слова посредством линейного вычисления между 0-вым-(s-1)-вым полиномами контроля по четности и входными данными, при этом изменяющийся во времени период коэффициента AXk,i Xk(D) составляет αk (αk является целым числом, превышающим 1) (k=1, 2,..., n-2,n-1), изменяющийся во времени период коэффициента BXk,i P(D) составляет β (β является целым числом, превышающим 1), изменяющийся во времени период s является наименьшим общим кратным α1, α2,..., αn-2, αn-1 и β, уравнение 97 справедливо, когда i%αk=j%αk (i, j=0, 1,..., s-2, s-1; i≠j) справедливо, и уравнение 98 справедливо, когда i%β=j%β (i, j=0, 1,..., s-2, s-1; i≠j) справедливо.
Одним аспектом способа кодирования настоящего изобретения является вышеописанный способ кодирования, в котором изменяющиеся во времени периоды α1, α2,..., αn-1 и β являются взаимно-простыми друг с другом.
Одним аспектом кодера настоящего изобретения является кодер для сверточного кода разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности), включающий в себя модуль вычисления четности, который вычисляет последовательность четности с использованием вышеописанного способа кодирования.
Одним аспектом способа декодирования настоящего изобретения является способ декодирования для декодирования кодированной информационной последовательности, кодированной с использованием уравнения 98-i, в качестве i-го (i=0, 1,..., s-1) полинома контроля по четности, который удовлетворяет 0 в вышеописанном способе кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом s, причем способ содержит прием кодированной информационной последовательности в качестве ввода и декодирование кодированной информационной последовательности с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 98-i, которое является i-ым полиномом контроля по четности, который удовлетворяет 0.
Одним аспектом декодера настоящего изобретения является декодер, который декодирует сверточный код разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с использованием доверительного распространения (BP), включающий в себя модуль вычисления при обработке по строкам, который выполняет вычисление при обработке по строкам с использованием контрольной матрицы, соответствующей полиному контроля по четности, используемому в вышеописанном кодере, модуль вычисления при обработке по столбцам, который выполняет вычисление при обработке по столбцам с использованием контрольной матрицы, и модуль определения, который оценивает кодовое слово с использованием результатов вычисления в модуле вычисления при обработке по строкам и модуле вычисления при обработке по столбцам.
Одним аспектом способа кодирования настоящего изобретения является способ кодирования для формирования сверточного кода разреженного контроля по четности со скоростью кодирования 1/3 и изменяющимся во времени периодом h из сверточного кода разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности), заданного на основе g-го (g=0, 1,..., h-1) полинома контроля по четности со скоростью кодирования 1/2 и изменяющимся во времени периодом h, представленного посредством уравнения 119, причем способ включает в себя этап выбора Z-битовой информации Xj из битовой последовательности информации в последовательности данных, сформированной с информационными битами и битами четности, которые являются кодированными выводами с использованием сверточного кода разреженного контроля по четности со скоростью кодирования 1/2, и изменяющимся во времени периодом h (момент времени j является моментом времени, включенным в момент времени j1-j2, и j1 и j2 являются четными числами или нечетными числами, и Z=(j2-j1)/2), этап вставки известной информации в выбранную Z-битовую информацию Xj и этап получения бита четности из информации, включающей в себя известную информацию, при этом на этапе выбора Z-битовая информация Xj выбирается на основе каждого числа из h типов остатков, полученных посредством деления всех j, включенных в j1-j2, на h.
[119]
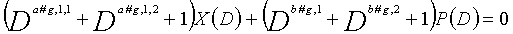 ... (уравнение 119)
... (уравнение 119)
В уравнении 119, X(D) является полиномиальным представлением информации X, и P(D) является полиномиальным представлением четности. Кроме того, a#g,1,1 и a#g,1,2 являются натуральными числами, равными или превышающими 1, a#g,1,1≠a#g,1,2 поддерживается. Кроме того, b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, b#g,1≠b#g,2 поддерживается (g=0, 1, 2,..., h-2, h-1).
В уравнении 119, следующее условие #17 удовлетворяется. Здесь, "c%d"i является остатком после деления c на d.
Условие #17
"a#0,1,1%h=a#1,1,1%h=a#2,1,1%h=a#3,1,1%h=... =a#g,1,1%h=... =a#h-2,1,1%h=a#h-1,1,1%h=vp=1 (vp=1: фиксированное значение)"
"b#0,1%h=b#1,1%h=b#2,1%h=b#3,1%h=... =b#g,1%h=... =b#h-2,1%h=b#h-1,1%h=w (w: фиксированное значение)"
"a#0,1,2%h=a#1,1,2%h=a#2,1,2%h=a#3,1,2%h=... =a#g,1,2%h=... =a#h-2,1,2%h=a#h-1,1,2%h=yp=1 (yp=1: фиксированное значение)"
"b#0,2%h=b#1,2%h=b#2,2%h=b#3,2%h=... =b#g,2%h=... =b#h-2,2%h=b#h-1,2%h=z (z: фиксированное значение)"
В одном аспекте способа кодирования настоящего изобретения момент времени j1 является моментом времени 2hi, момент времени j2 является моментом времени 2h(i+k-1)+2h-1, Z битов являются hk битов, и на этапе выбора Z-битовая информация Xj выбирается из 2*h*k битов информации X2hi, X2hi+1, X2hi+2,..., X2hi+2h-1,..., X2h(i+k-1), X2h(i+k-1)+1, X2h(i+k-1)+2,..., X2h(i+k-1)+2h-1 так, что из остатков после деления всех моментов времени j, включенных в момент времени j1-j2, на h, по меньшей мере, один γ присутствует, который удовлетворяет условию, при котором разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=1+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=1+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше.
В одном аспекте способа кодирования настоящего изобретения, для γ, который не удовлетворяет условию, "число остатков, которые становятся (0+γ) mod h", "число остатков, которые становятся (vp=1+γ) mod h" и "число остатков, которые становятся (yp=1+γ) mod h", равны 0.
Одним аспектом способа декодирования настоящего изобретения является способ декодирования для декодирования кодированной информационной последовательности, кодированной с использованием уравнения 119 в качестве g-го (i=0, 1,..., h-1) полинома контроля по четности, который удовлетворяет 0 в способе кодирования по п. 1, для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом h, причем способ содержит прием кодированной информационной последовательности в качестве ввода и декодирование кодированной информационной последовательности с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 119, которое является g-ым полиномом контроля по четности, который удовлетворяет 0.
Одним аспектом кодера настоящего изобретения является кодер, который создает сверточный код разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) из сверточного кода и включает в себя модуль вычисления, который вычисляет четность с использованием вышеописанного способа кодирования.
Одним аспектом декодера настоящего изобретения является декодер, который декодирует сверточный код разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с использованием доверительного распространения (BP), включающий в себя модуль вычисления при обработке по строкам, который выполняет вычисление при обработке по строкам с использованием контрольной матрицы, соответствующей полиному контроля по четности, используемому в вышеописанном кодере, модуль вычисления при обработке по столбцам, который выполняет вычисление при обработке по столбцам с использованием контрольной матрицы, и модуль определения, который оценивает кодовое слово с использованием результатов вычисления в модуле вычисления при обработке по строкам и модуле вычисления при обработке по столбцам.
Одним аспектом способа кодирования настоящего изобретения является способ кодирования для формирования сверточного кода разреженного контроля по четности с более низкой скоростью кодирования, чем скорость кодирования (n-1)/n, и изменяющимся во времени период h из сверточного кода разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности), заданного на основе g-го (g=0, 1,..., h-1) полинома контроля по четности со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h, представленного посредством уравнения 120-g, причем способ включает в себя этап выбора Z-битовой информации Xf,j (f=1, 2, 3,..., n-1, j является временем) из битовой последовательности информации в последовательности данных, сформированной с информационными битами и битами четности, которые являются кодированными выводами с использованием сверточного кода разреженного контроля по четности со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h, этап вставки известной информации в выбранную информацию Xf,j и этап получения бита четности из информации, включающей в себя известную информацию, при этом на этапе выбора информация Xf,j выбирается на основе остатка после деления всех времен j на h и числа времен j, в которые остаток вычисляется.
[120]
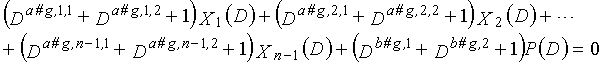 ... (уравнение 120-g)
... (уравнение 120-g)
В уравнении 120-g, Xp(D) является полиномиальным представлением информации X, и P(D) является полиномиальным представлением четности (p=1, 2,..., n-1). Кроме того, a#g,p,1 и a#g,p,2 являются натуральными числами, равными или превышающими 1, и a#g,p,1≠a#g,p,2 поддерживается. Кроме того, b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 поддерживается (g=0, 1, 2,..., h-2, h-1; p=1, 2,..., n-1).
Кроме того, в уравнении 120-g, следующие условие #18-1 и условие #18-2 удовлетворяются. Здесь, "c%d" представляет "остаток после деления c на d".
Условие #18-1
"a#0,k,1%h=a#1,k,1%h=a#2,k,1%h=a#3,k,1%h=... =a#g,k,1%h=... =a#h-2,k,1%h=a#h-1,k,1%h=vp=k (vp=k: фиксированное значение) (, k=1, 2,..., n-1)", и
"b#0,1%h=b#1,1%h=b#2,1%h=b#3,1%h=... =b#g,1%h=... =b#h-2,1%h=b#h-1,1%h=w (w: фиксированное значение)"
Условие #18-2
"a#0,k,2%h=a#1,k,2%h=a#2,k,2%h=a#3,k,2%h=... =a#g,k,2%h=... =a#h-2,k,2%h=a#h-1,k,2%h=yp=k (yp=k: фиксированное значение) (, k=1, 2,..., n-1)", и
"b#0,2%h=b#1,2%h=b#2,2%h=b#3,2%h=... =b#g,2%h=... =b#h-2,2%h=b#h-1,2%h=z (z: фиксированное значение)"
Одним аспектом способа кодирования настоящего изобретения является вышеописанный способ кодирования, в котором время j является временем, которое принимает значение одного из hi-h(i+k-1)+h-1, и на этапе выбора, Z-битовая информация Xf,j выбирается из h*(n-1)*k битов информации X1,hi, X2,hi,..., Xn-1,hi,..., X1,h(i+k-1)+h-1, X2,h(i+k-1)+h-1,..., Xn-1,h(i+k-1)+h-1, и эта информация Xf,j выбирается так, что из остатков после деления Z-битовой информации Xf,j на h для всех времен j, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше (f=1, 2, 3,..., n-1), и, по меньшей мере, один такой γ присутствует.
В одном аспекте способом кодирования настоящего изобретения является вышеописанный способ кодирования, в котором время j принимает значение одного из 0-v, и на этапе выбора, Z-битовая информация Xf,j выбирается из битовой последовательности информации X1,0, X2,0,..., Xn-1,0,..., X1,v, X2,v,..., Xn-1,v, и эта информация Xf,j выбирается так, что из остатков после деления Z-битовой информации Xf,j на h для всех времен j, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, разность между "числом остатков, которые становятся (0+γ) mod h (где число остатков является ненулевым)" и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше, и разность между "числом остатков, которые становятся (vp=f+γ) mod h (где число остатков является ненулевым)", и "числом остатков, которые становятся (yp=f+γ) mod h (где число остатков является ненулевым)" равняется 1 или меньше (f=1, 2, 3,..., n-1), и, по меньшей мере, один такой γ присутствует.
Одним аспектом способа декодирования настоящего изобретения является способ декодирования для декодирования кодированной информационной последовательности, кодированной с использованием уравнения 120-g в качестве g-го (i=0, 1,..., h-1) полинома контроля по четности, который удовлетворяет 0 в вышеописанном способе кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с изменяющимся во времени периодом h, причем способ содержит прием кодированной информационной последовательности в качестве ввода и декодирование кодированной информационной последовательности с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 120-g, которое является g-ым полиномом контроля по четности, который удовлетворяет 0.
Одним аспектом кодера настоящего изобретения является кодер, который создает сверточный код разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) из сверточного кода, включающий в себя модуль вычисления, который вычисляет четность с использованием вышеописанного способа кодирования.
Одним аспектом декодера настоящего изобретения является декодер, который декодирует сверточный код разреженного контроля по четности (LDPC-CC: сверточный код разреженного контроля по четности) с использованием доверительного распространения (BP), включающий в себя модуль вычисления при обработке по строкам, который выполняет вычисление при обработке по строкам с использованием контрольной матрицы, соответствующей полиному контроля по четности, используемому в вышеописанном кодере, модуль вычисления при обработке по столбцам, который выполняет вычисление при обработке по столбцам с использованием контрольной матрицы, и модуль определения, который оценивает кодовое слово с использованием результатов вычисления в модуле вычисления при обработке по строкам и модуле вычисления при обработке по столбцам.
Настоящее изобретение не ограничено вышеописанными вариантами осуществления и может быть реализовано с различными изменениями. Например, хотя вышеописанные варианты осуществления, главным образом, описывают случай, в котором настоящее изобретение применяется к случаю, в котором кодер реализуется, настоящее изобретение не ограничено этим, а также является применимым к случаю, в котором устройство связи реализуется. Настоящее изобретение также может быть сконфигурировано посредством LSI (большой интегральной схемы).
Также можно реализовывать способ кодирования и способ декодирования в качестве программного обеспечения. Например, можно предусматривать программу, которая выполняет вышеописанный способ кодирования и способ связи, которая должна быть сохранена в ROM (постоянном запоминающем устройстве) заранее, и эта программа должна выполняться посредством CPU (центрального процессора).
Кроме того, программа, которая выполняет вышеописанный способ кодирования, может быть сохранена на машиночитаемом носителе хранения данных, программа, сохраненная на носителе хранения данных, может записываться в RAM (оперативное запоминающее устройство) компьютера, и компьютер может работать согласно программе.
Само собой разумеется, что настоящее изобретение не ограничено радиосвязью и также применимо при связи по линиям электросети (PLC), связи в диапазоне видимого света и оптической связи.
Настоящее описание изобретения описывает "изменяющийся во времени период", и он является периодом, в течение которого формируется изменяющийся во времени LDPC-CC.
Раскрытия сущности заявки на патент (Япония) номер 2009-260503, поданной 13 ноября 2009 года, заявки на патент (Япония) номер 2010-157991, поданной 12 июля 2010 года, заявки на патент (Япония) номер 2010-172577, поданной 30 июля 2010 года, и заявки на патент (Япония) номер 2010-231807, поданной 14 октября 2010 года, в том числе подробные описания, чертежи и рефераты, полностью содержатся в данном документе по ссылке.
Промышленная применимость
Способ кодирования и кодер и т.п. согласно настоящему изобретению имеют высокую способность к коррекции ошибок и тем самым могут обеспечивать высокое качество приема данных.
Список номеров ссылок
100, 2907, 2914, 3204, 3103, 3208, 3212 - LDPC-CC-кодер
110 - модуль вычисления данных
120 - модуль вычисления четности
130 - умножители весовых коэффициентов
140 - сумматор по модулю 2 (оператор "исключающее ИЛИ")
111-1-111-M, 121-1-121-M, 221-1-221-M, 231-1-231-M - сдвиговый регистр
112-0-112-M, 122-0-122-M, 222-0-222-M, 232-0-232-M - умножитель весовых коэффициентов
1910, 2114, 2617, 2605 - передающее устройство
1911, 2900, 3200 - кодер
1192 - модуль модуляции
1920, 2131, 2609, 2613 - приемное устройство
1921 - приемный модуль
1922 - модуль формирования логарифмических отношений правдоподобия
1923, 3310 - декодер
2110, 2130, 2600, 2608 - устройство связи
2112, 2312, 2603 - связанный с кодированием с коррекцией со стиранием ошибок процессор
2113, 2604 - модуль кодирования с коррекцией ошибок
2120, 2607 - канал связи
2132, 2610 - модуль декодирования с коррекцией ошибок
2133, 2433, 2611 - связанный с декодированием с коррекцией со стиранием ошибок процессор
2211 - модуль формирования пакетов
2215, 2902, 2909, 3101, 3104, 3202, 3206, 3210 - модуль переупорядочения
2216 - кодер с коррекцией со стиранием ошибок (модуль формирования пакетов четности)
2217, 2317 - модуль добавления кода с обнаружением ошибок
2314 - модуль кодирования с коррекцией со стиранием ошибок
2316, 2560 - кодер с коррекцией со стиранием ошибок
2435 - модуль обнаружения ошибок
2436 - декодер с коррекцией со стиранием ошибок
2561 - первый кодер с коррекцией со стиранием ошибок
2562 - второй кодер с коррекцией со стиранием ошибок
2563 - третий кодер с коррекцией со стиранием ошибок
2564 - модуль выбора
3313 - BP-декодер
4403 - модуль вставки известной информации
4405 - кодер
4407 - модуль удаления известной информации
4409 - модуль модуляции
4603 - модуль вставки логарифмического отношения правдоподобия
4605 - модуль декодирования
4607 - модуль удаления известной информации
44100 - модуль кодирования с коррекцией ошибок
44200 - передающее устройство
46100 - модуль декодирования с коррекцией ошибок
5800 - кодер
5801 - модуль формирования информации
5802-1 - первый модуль вычисления информации
5802-2 - второй модуль вычисления информации
5802-3 - третий модуль вычисления информации
5803 - модуль вычисления четности
5804, 5903, 6003 - сумматор
5805 - модуль задания скорости кодирования
5806, 5904, 6004 - модуль управления весовыми коэффициентами
5901-1-5901-M, 6001-1-6001-M - сдвиговый регистр
5902-0-5902-M, 6002-0-6002-M - умножитель весовых коэффициентов
6100 - декодер
6101 - модуль задания логарифмического отношения правдоподобия
6102 - модуль вычисления при матричной обработке
6103 - модуль хранения
6104 - модуль вычисления при обработке по строкам
6105 - модуль вычисления при обработке по столбцам
6200, 6300 - устройство связи
6201 - кодер
6202 - модуль модуляции
6203 - модуль определения скорости кодирования
6301 - приемный модуль
6302 - модуль формирования логарифмических отношений правдоподобия
6303 - декодер
6304 - модуль формирования управляющей информации
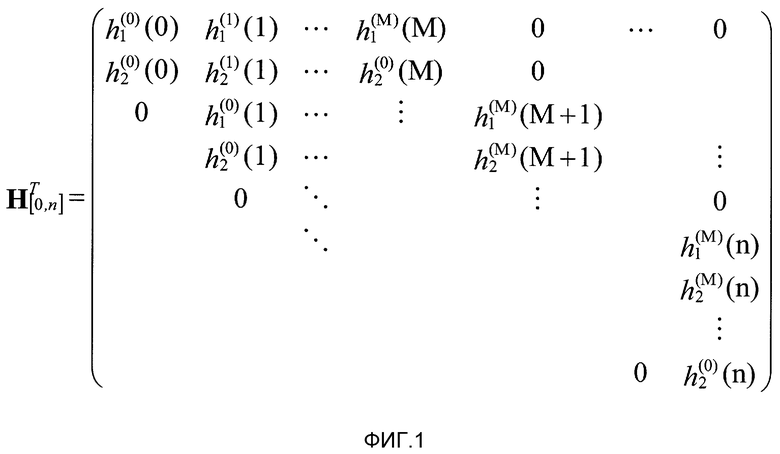
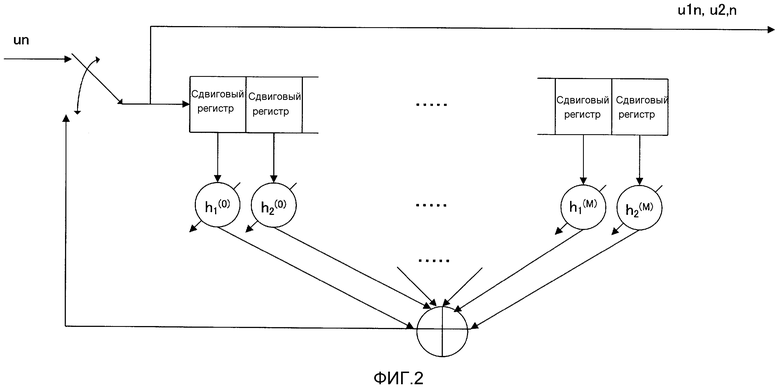

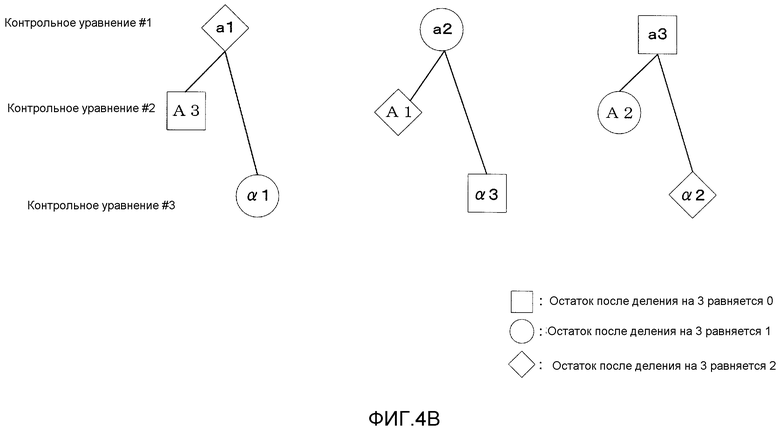
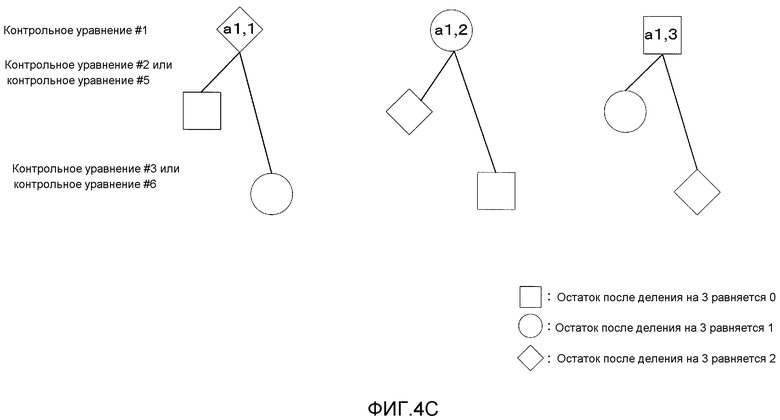

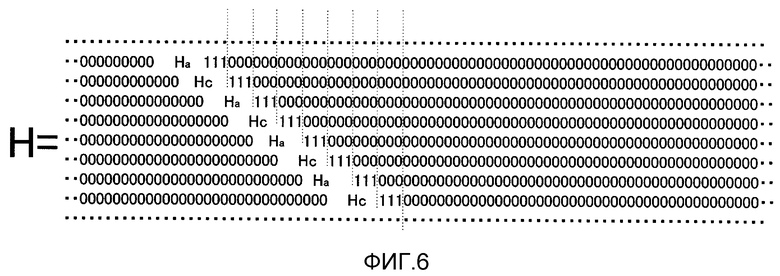

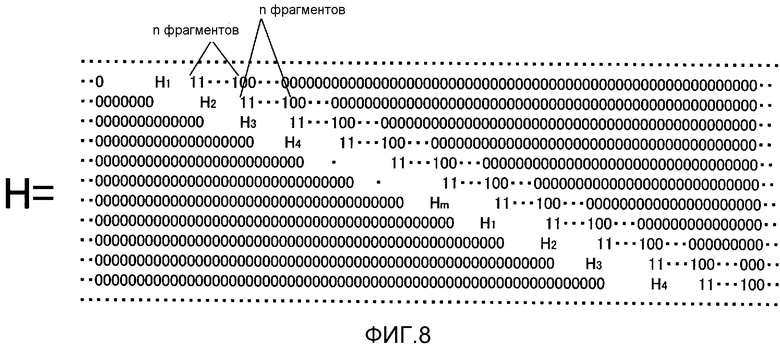
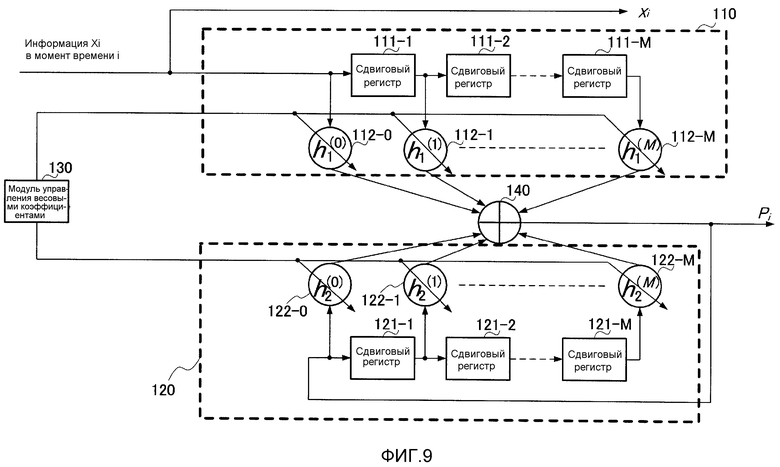
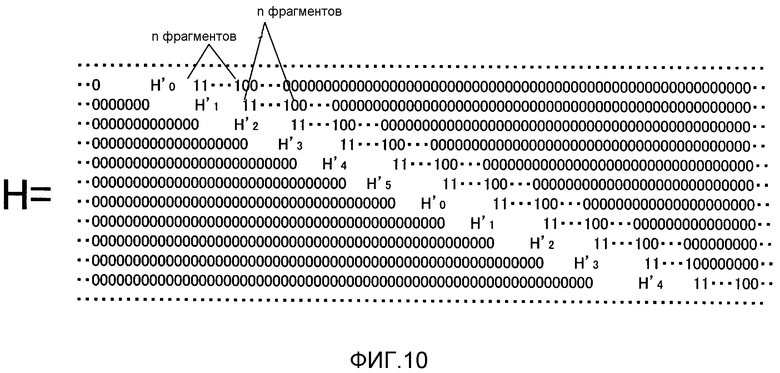
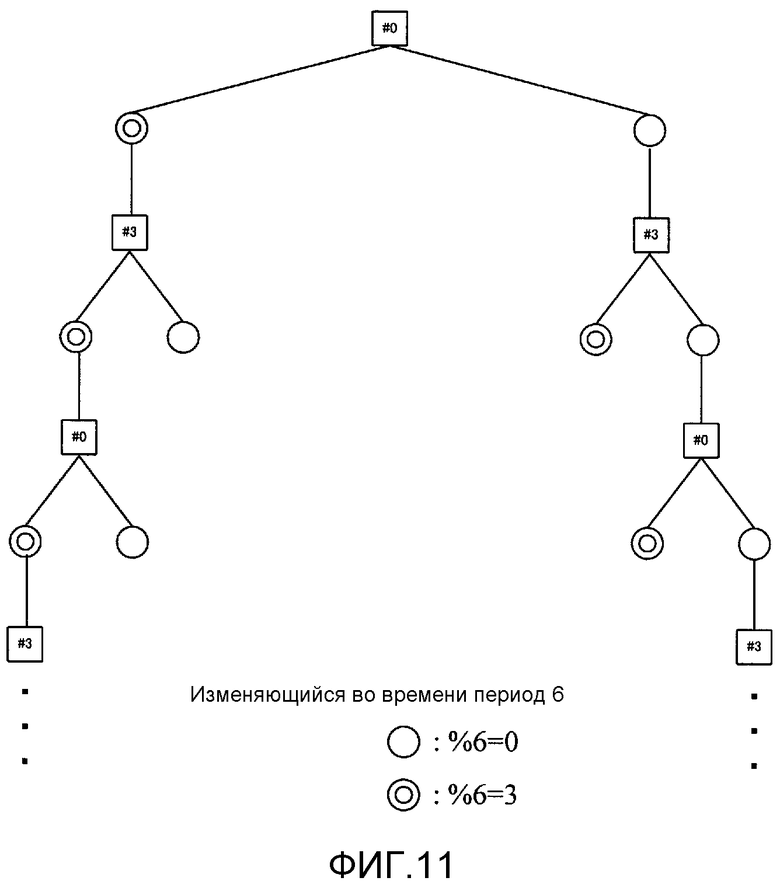
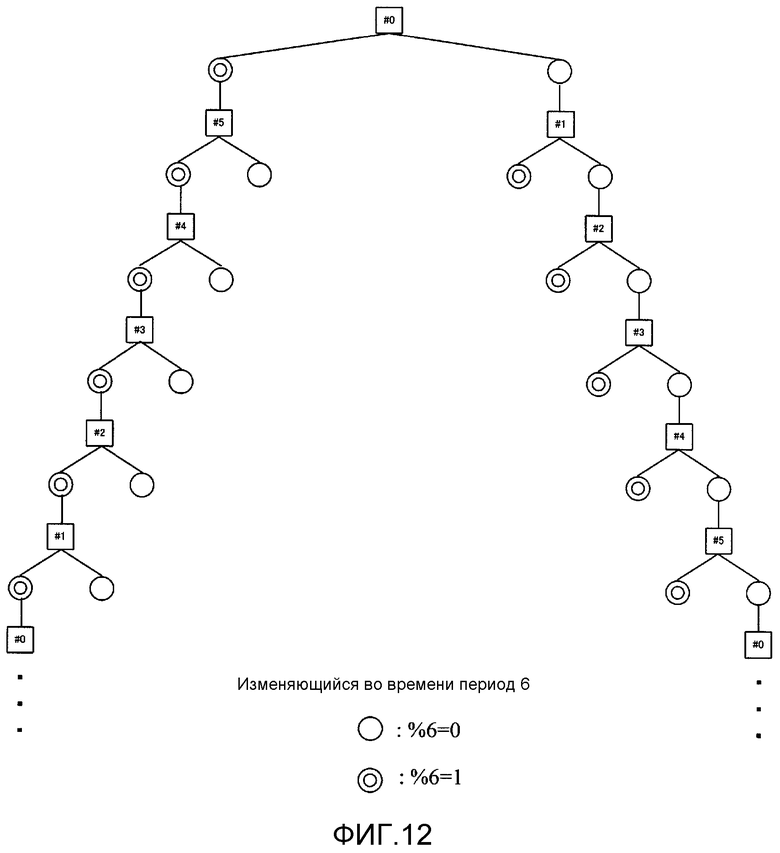
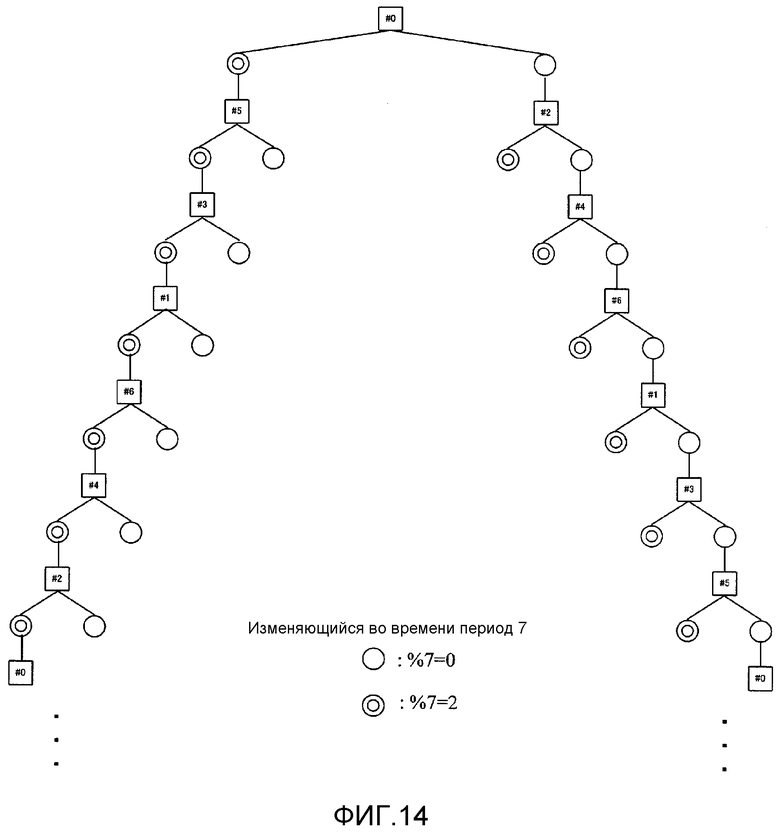
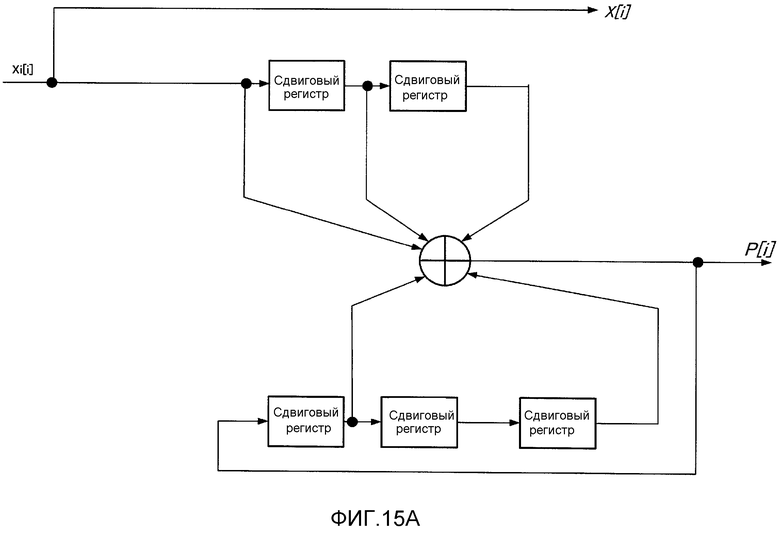
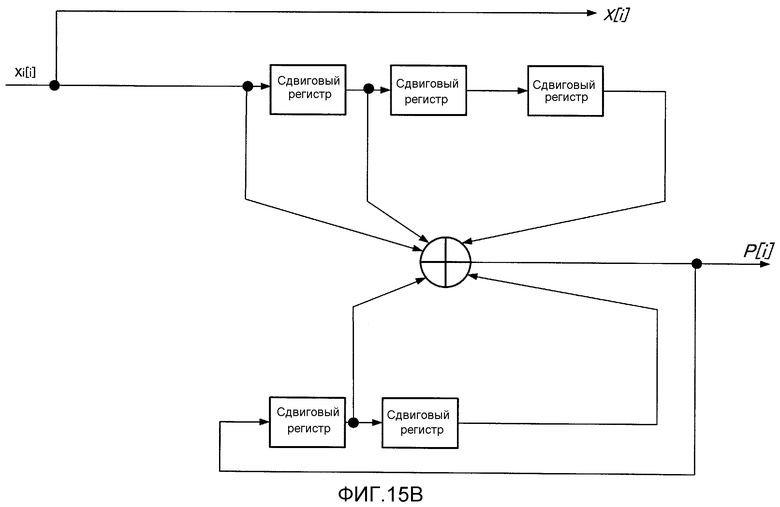
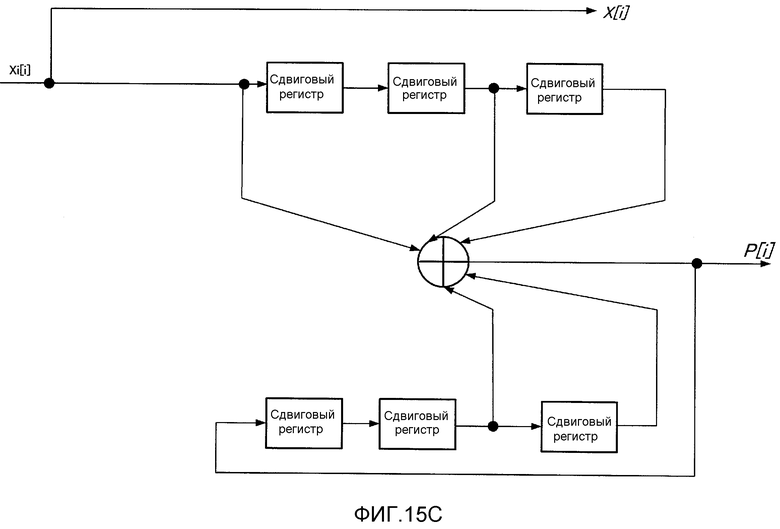
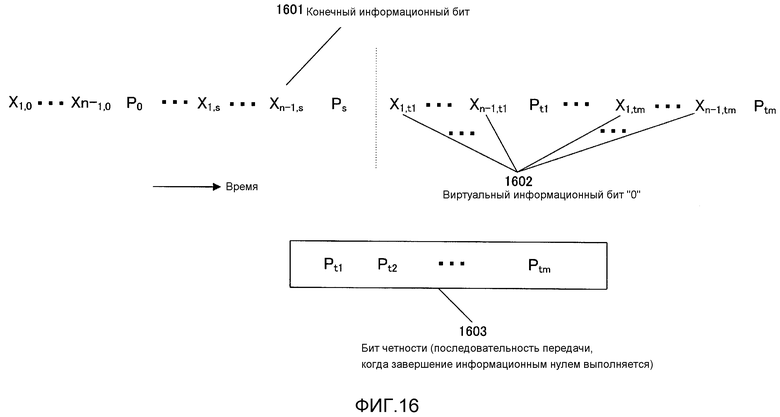
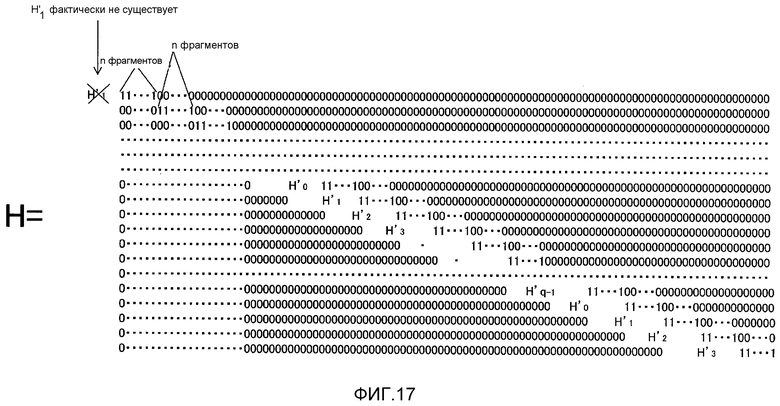
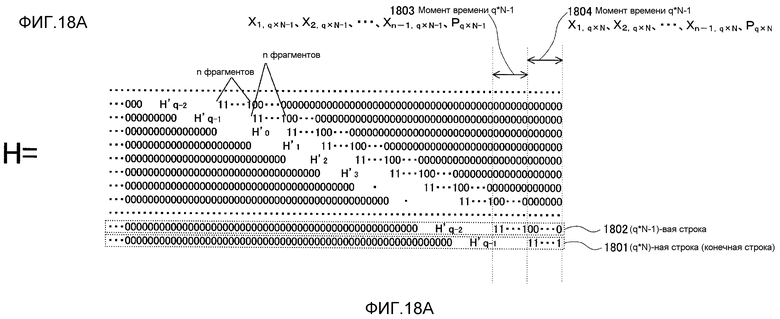
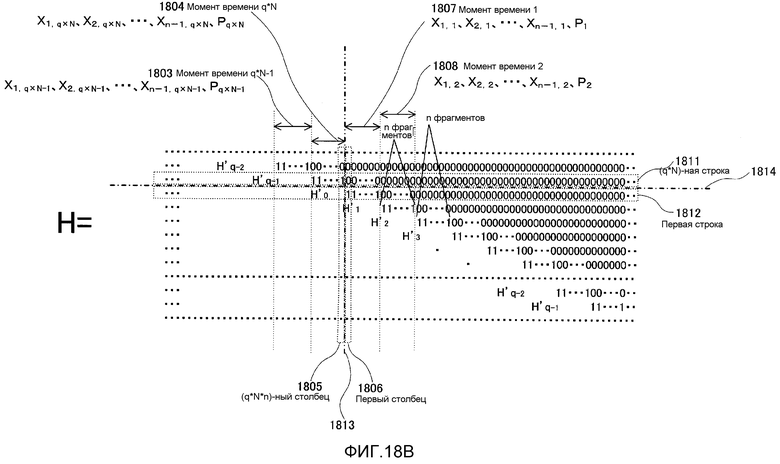
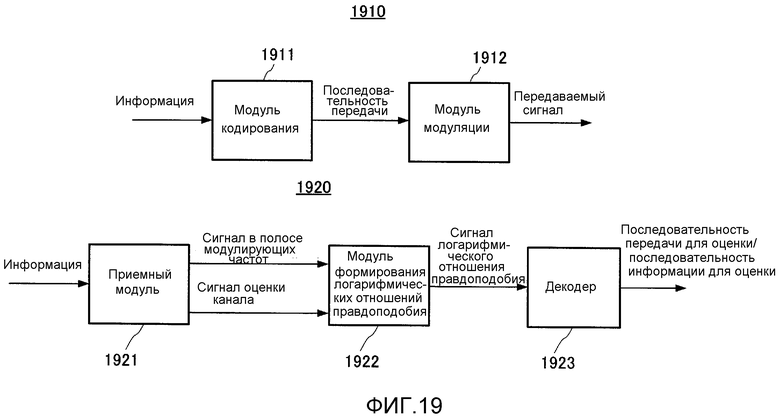
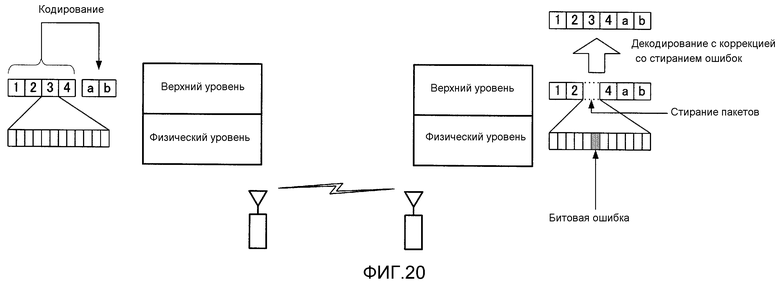
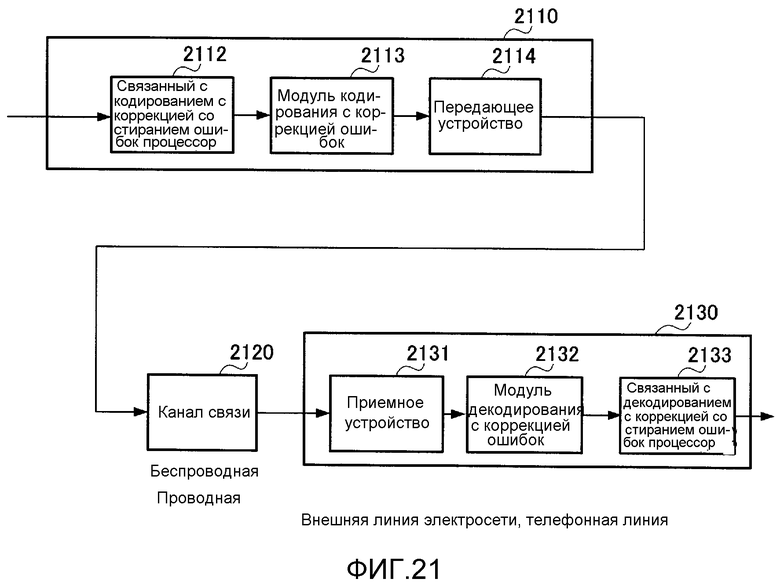
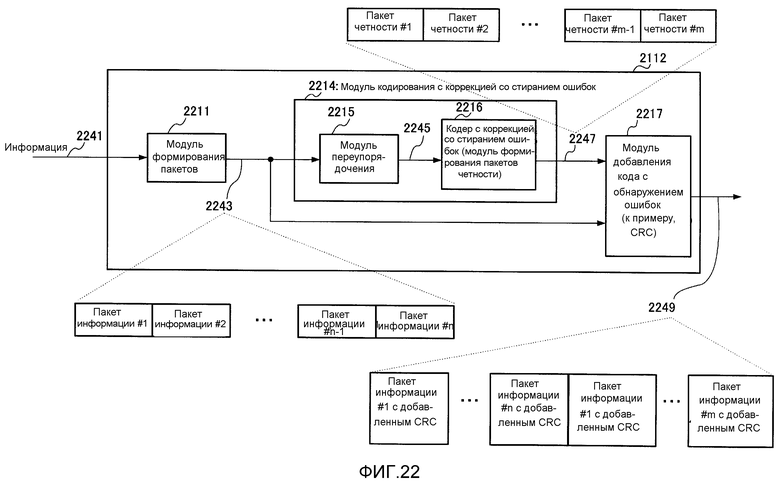
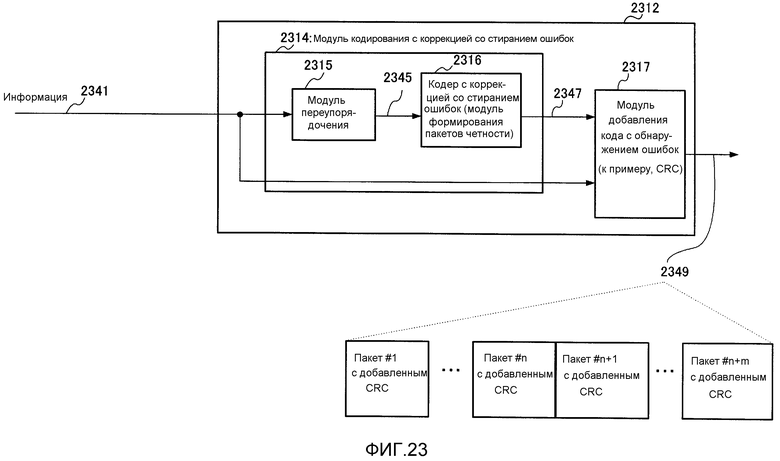
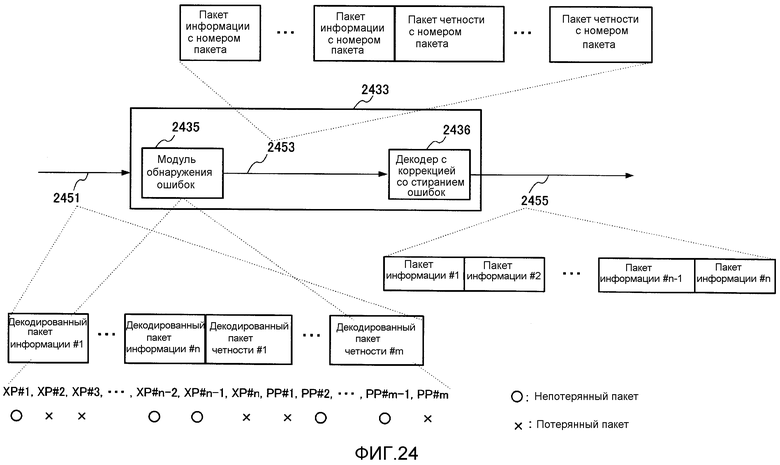
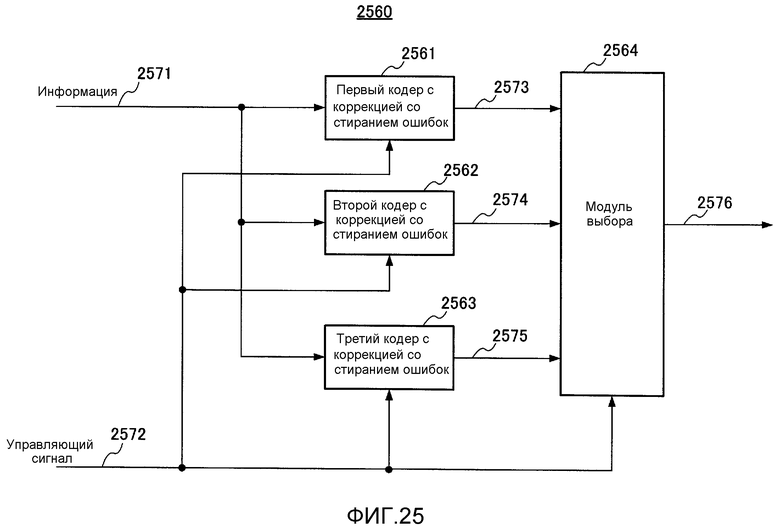
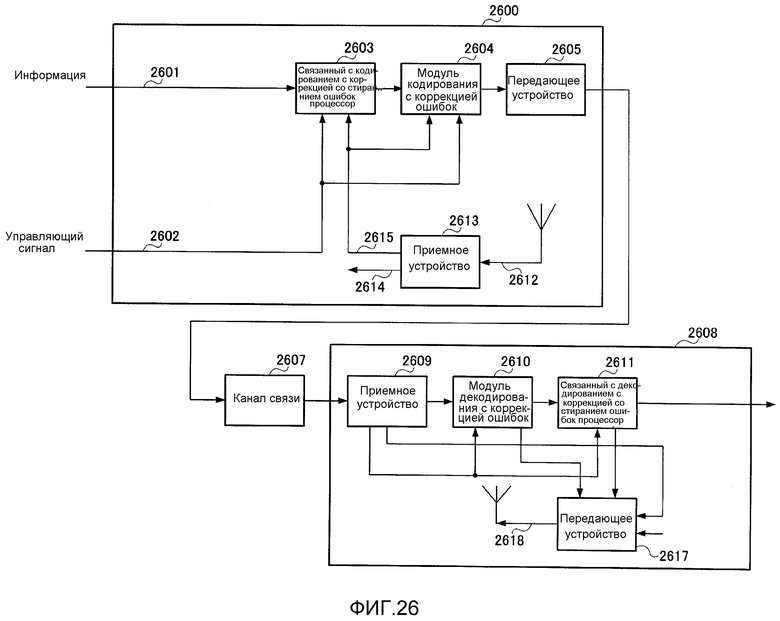
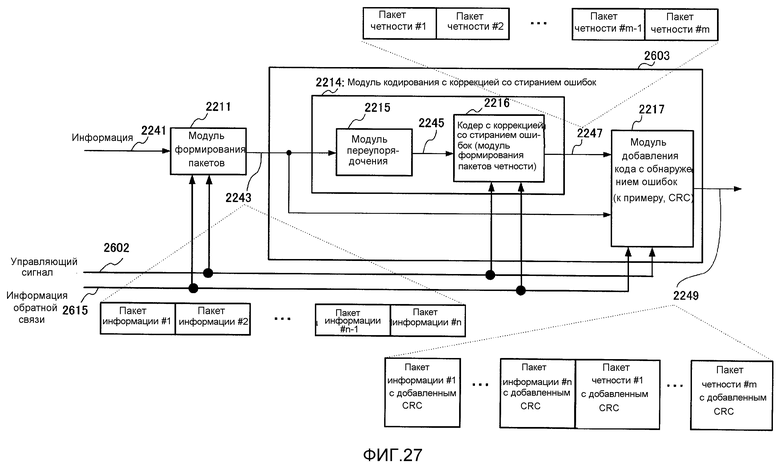
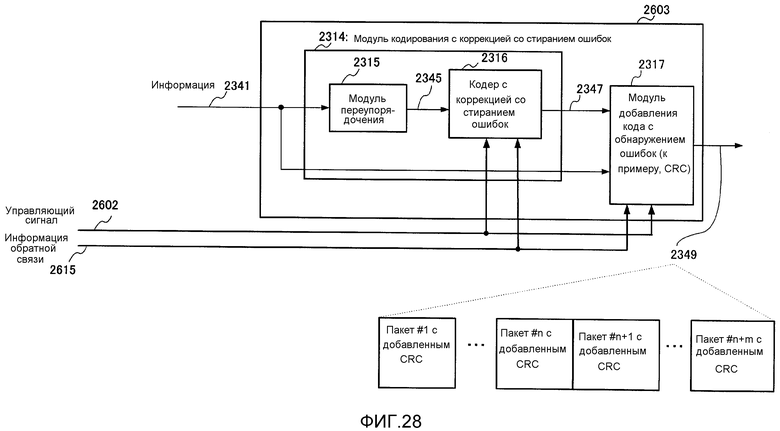
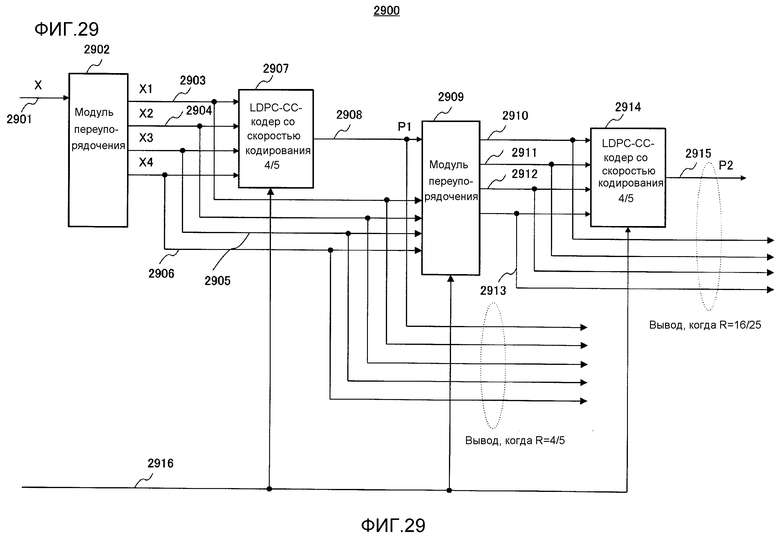
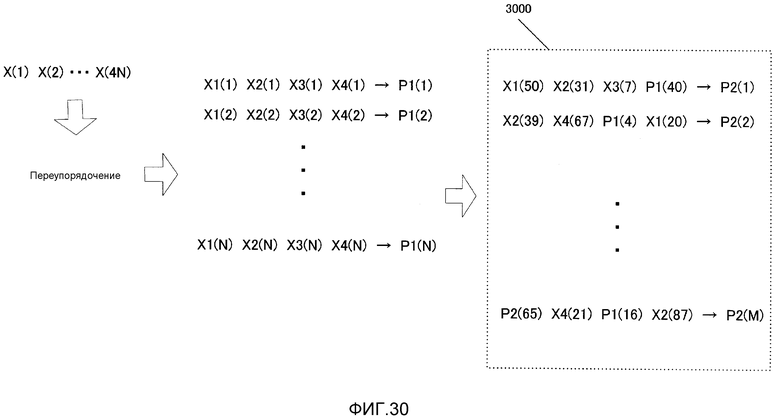
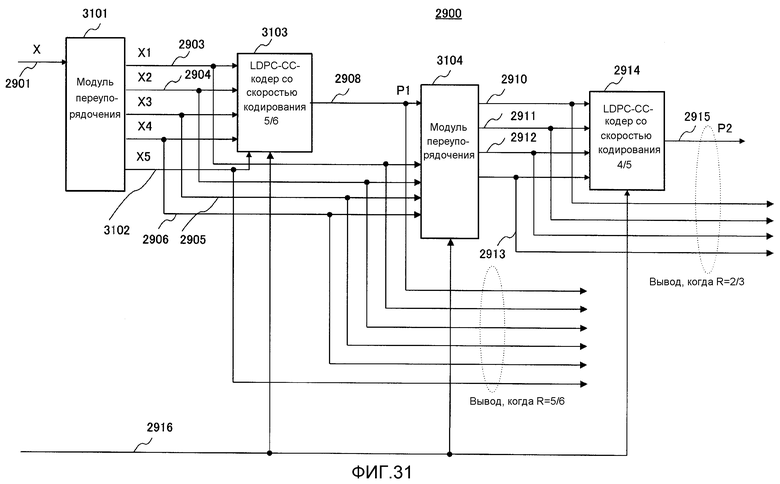
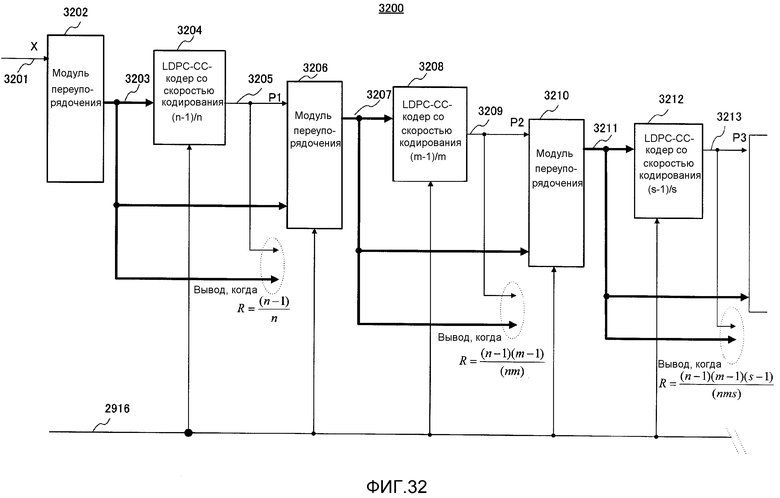
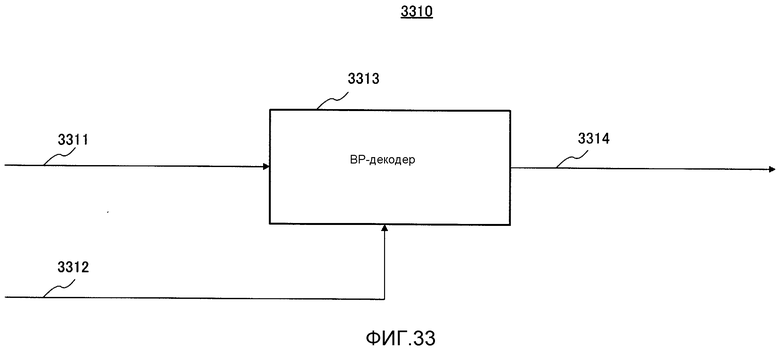
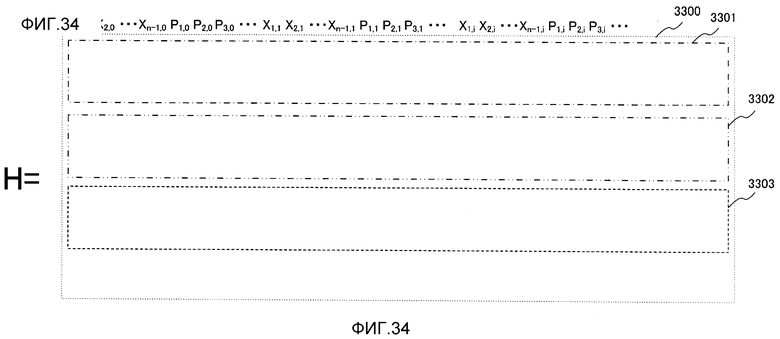
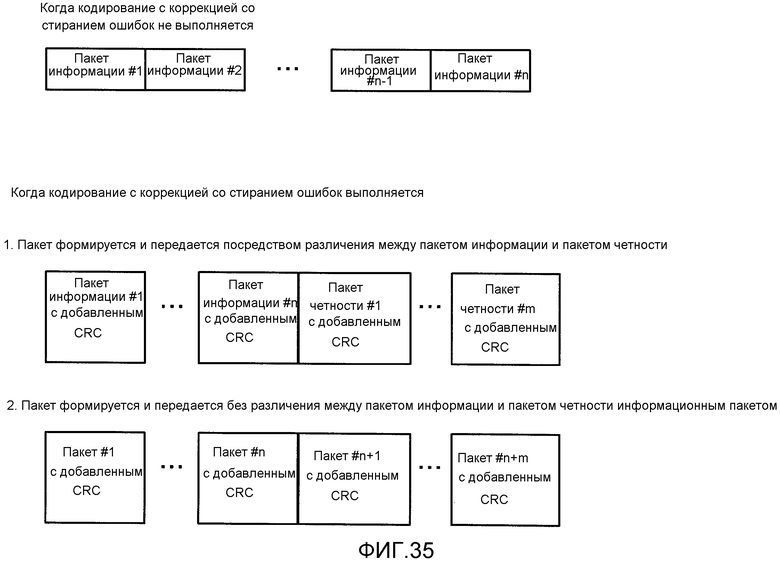
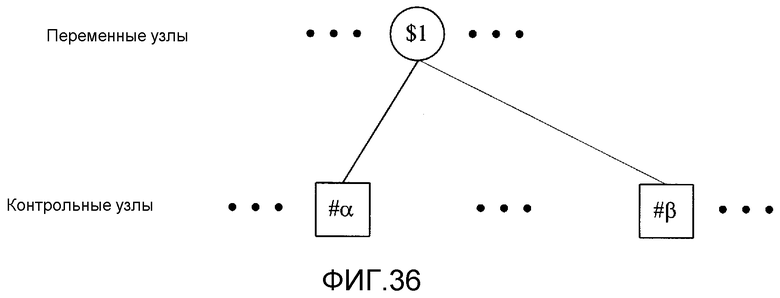
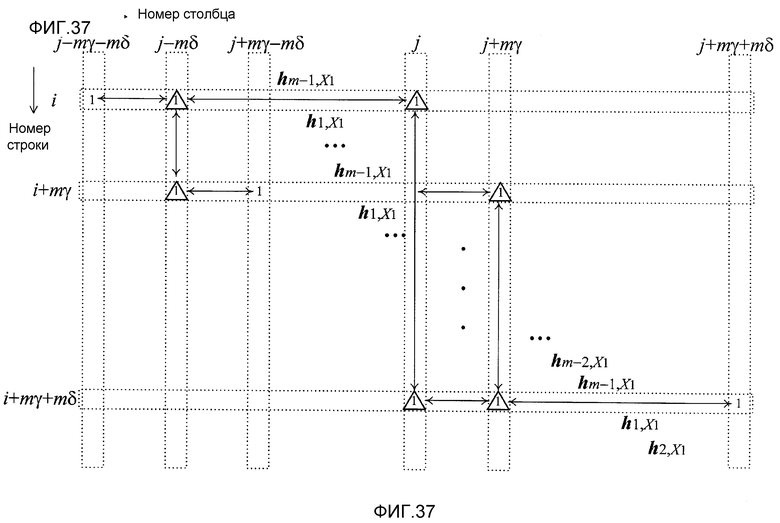
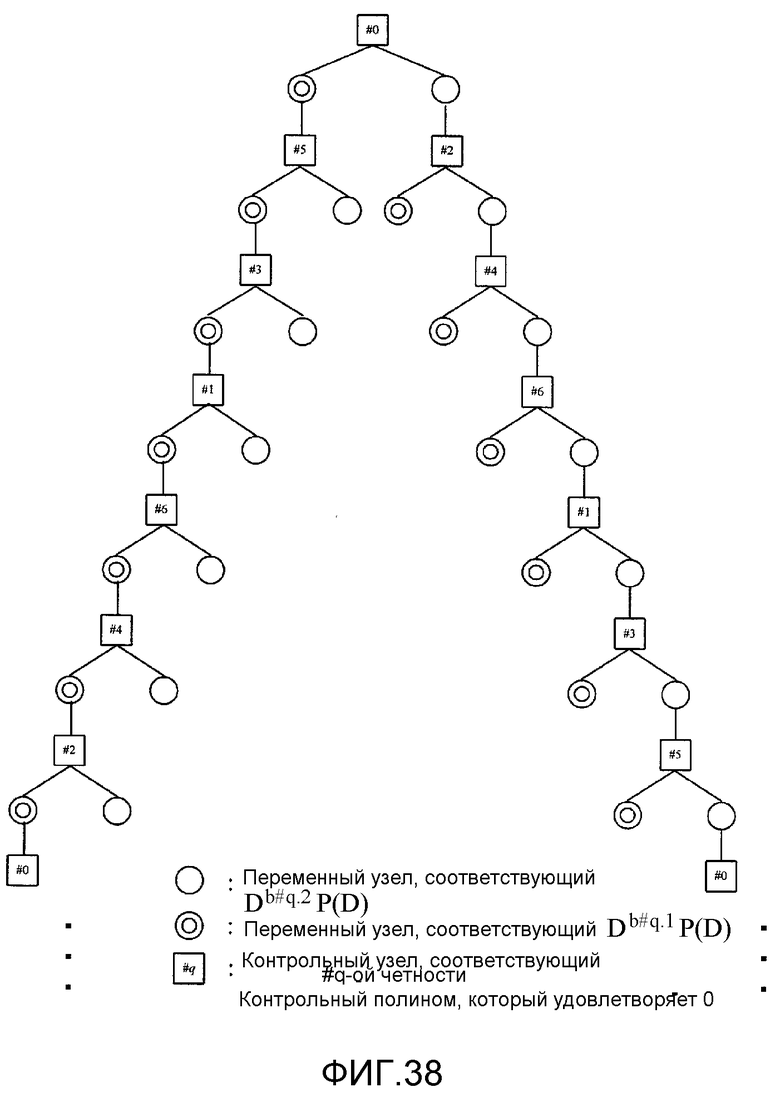
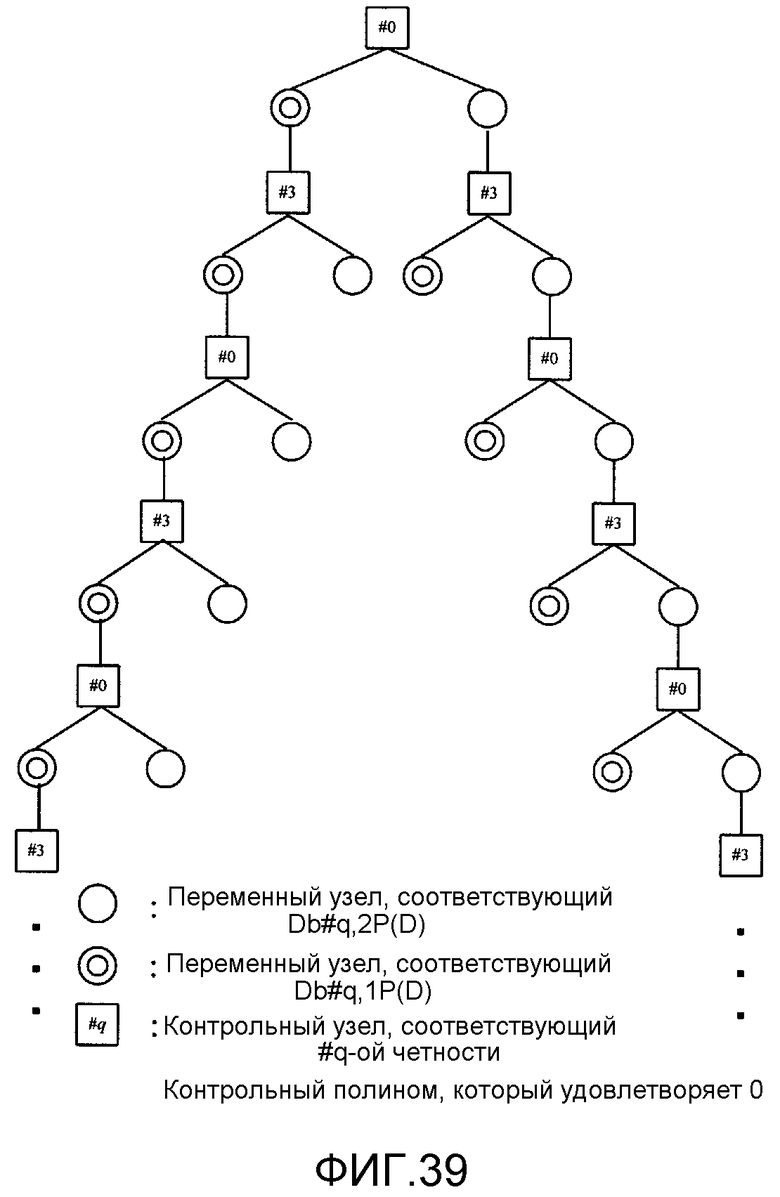
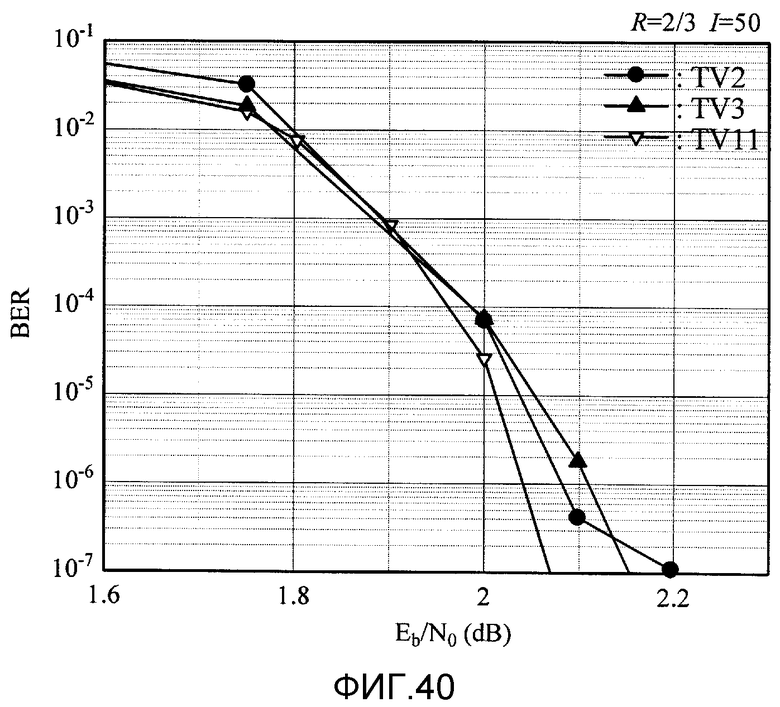
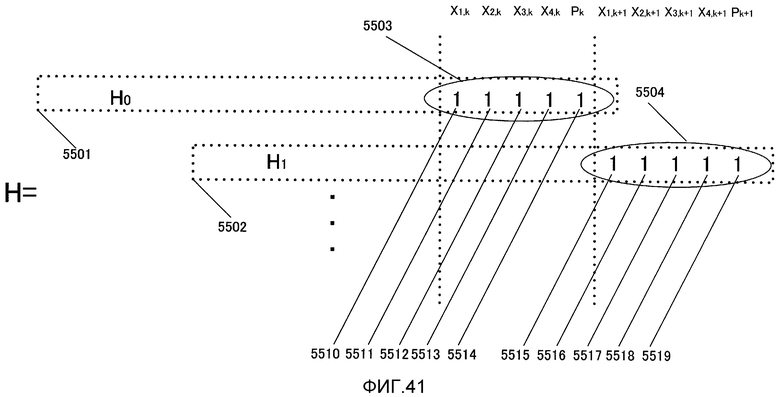
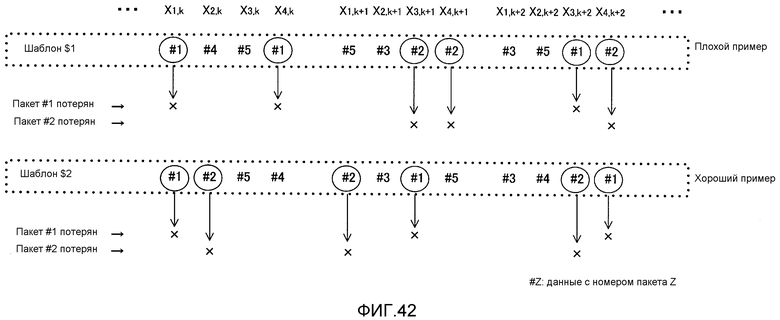
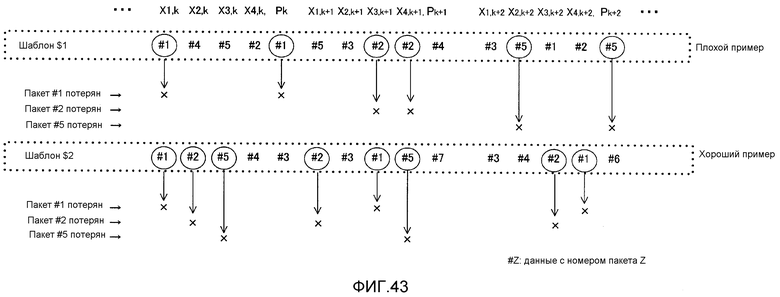
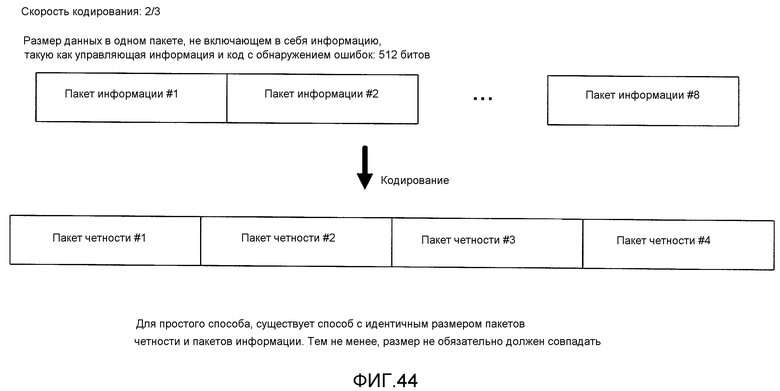
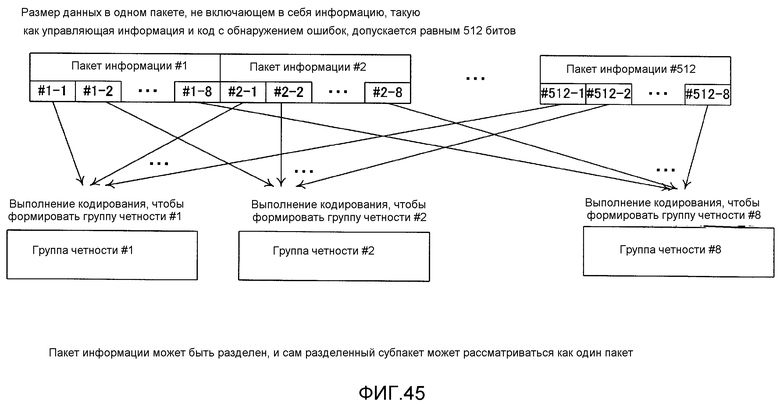
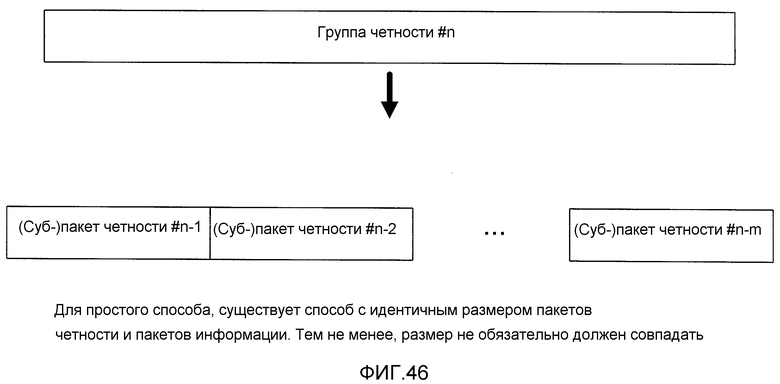
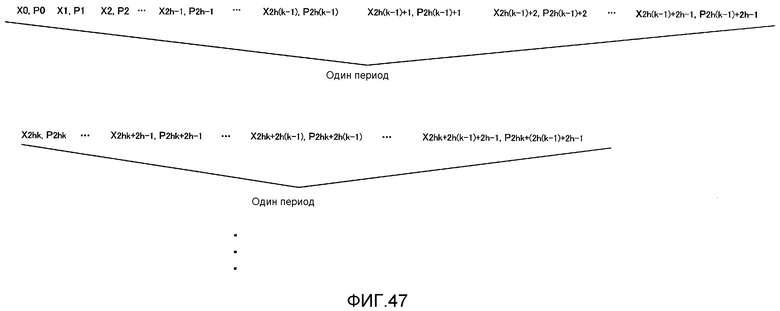
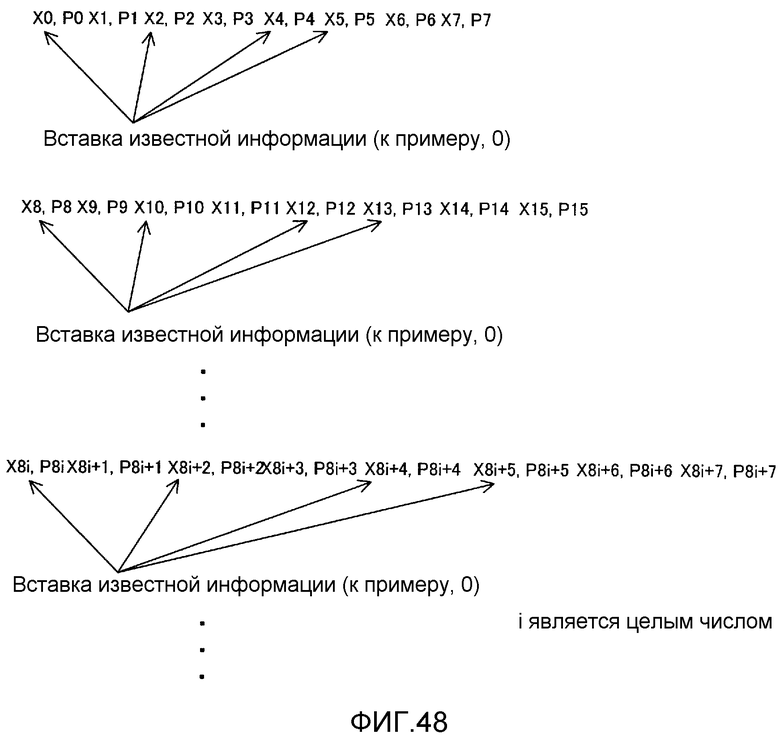
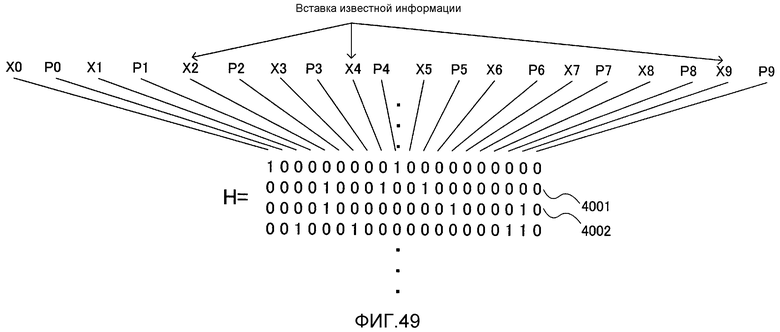
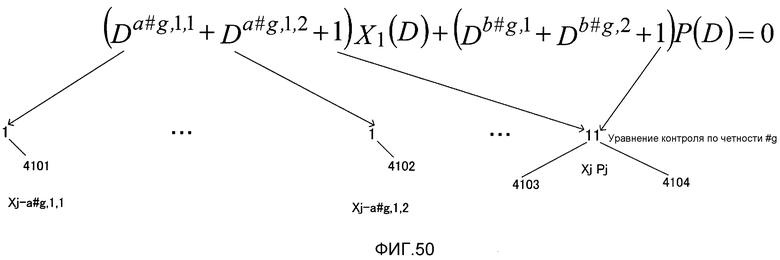
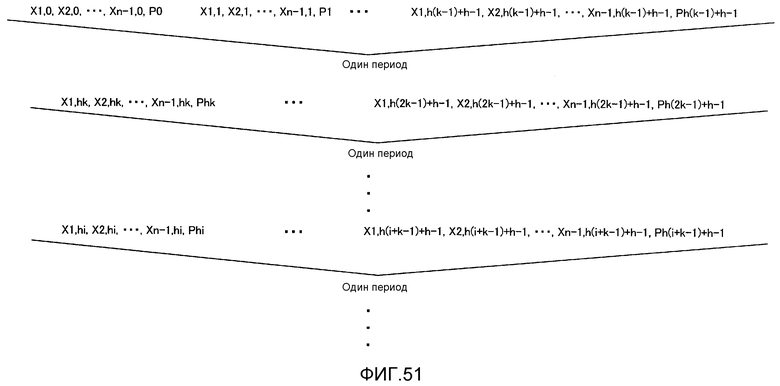
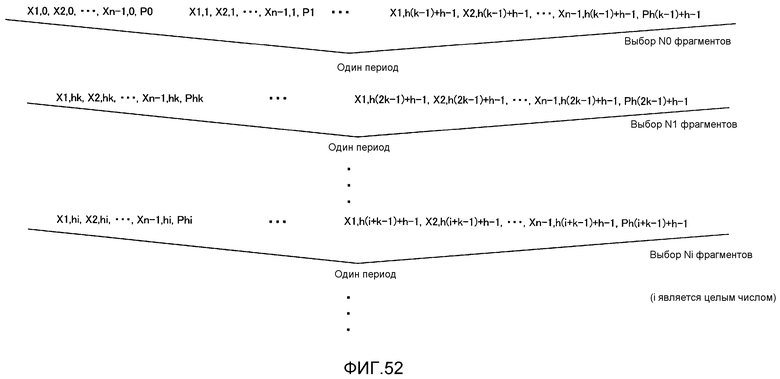
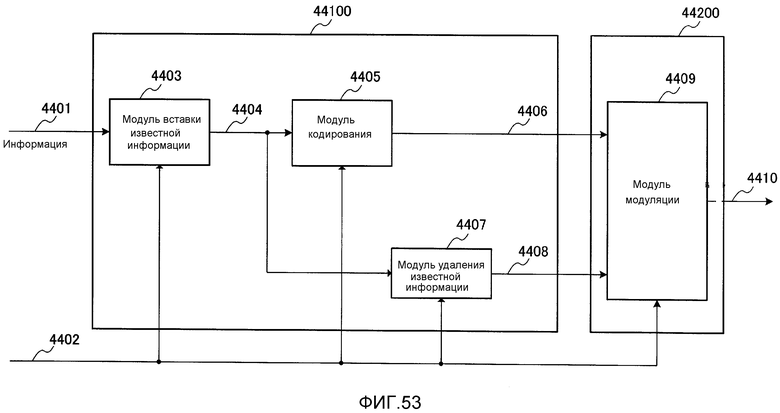
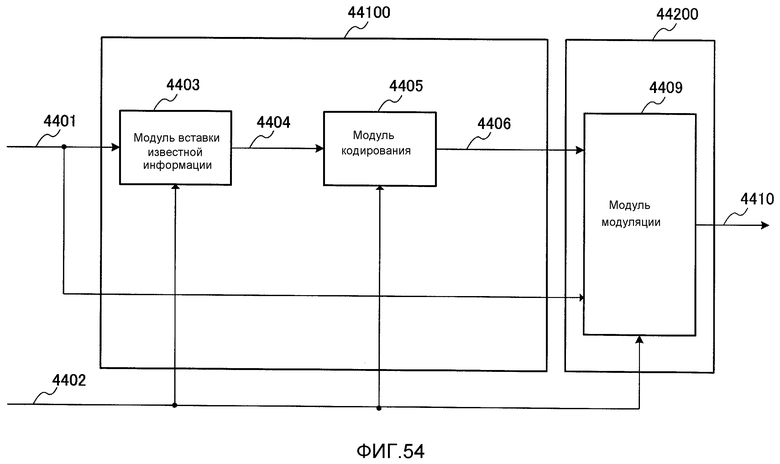
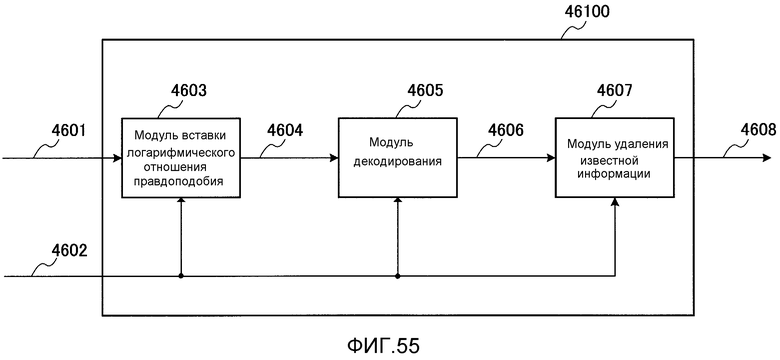
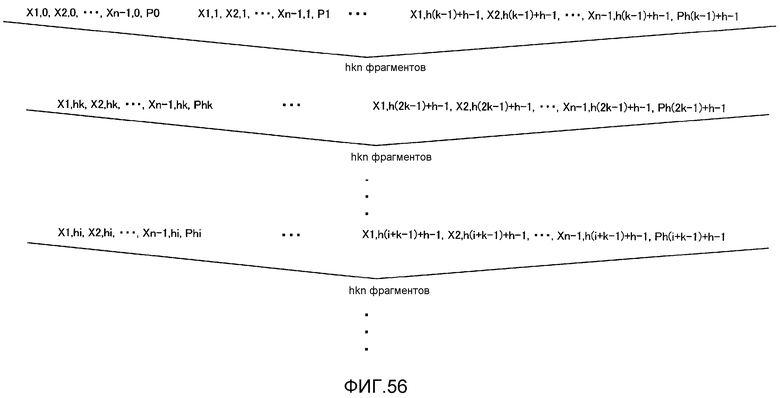
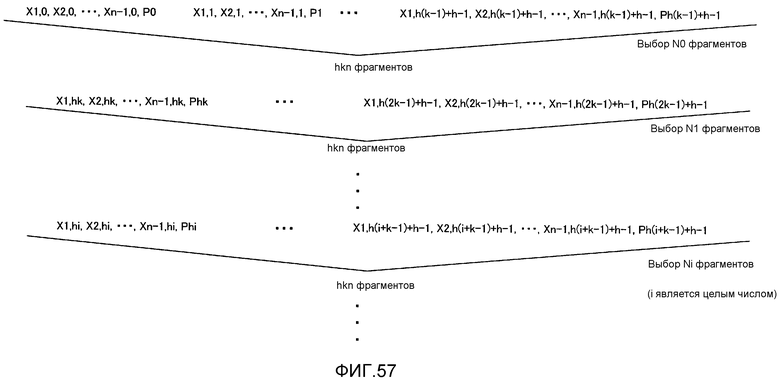
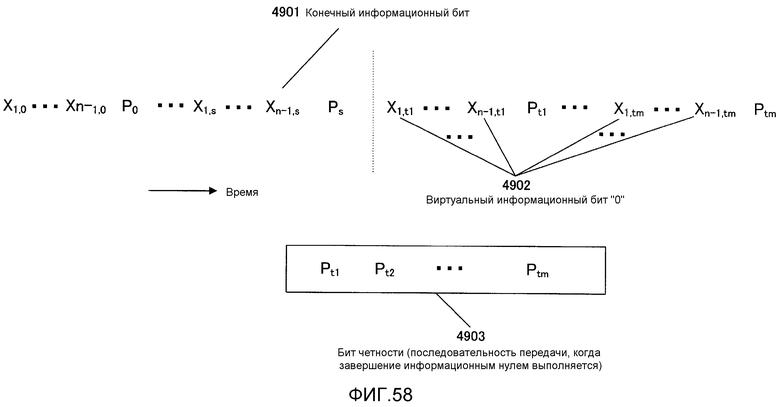

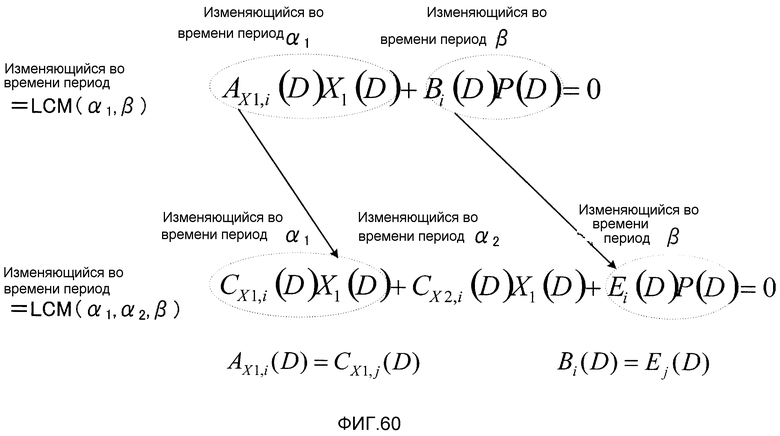
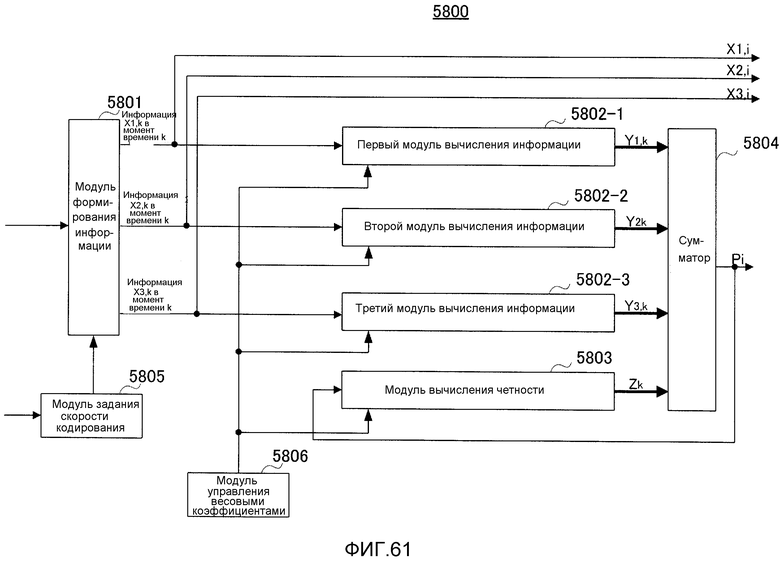
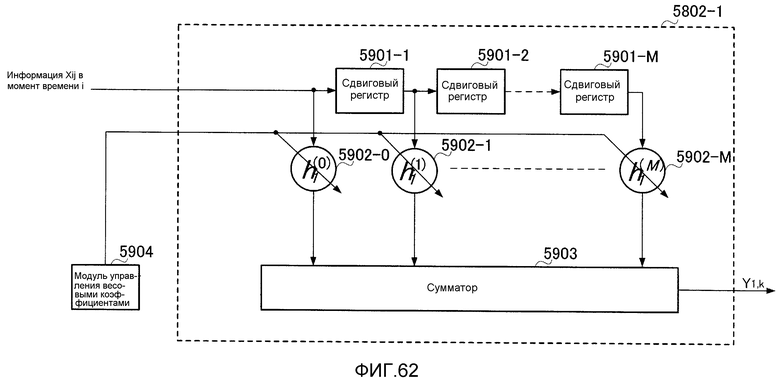
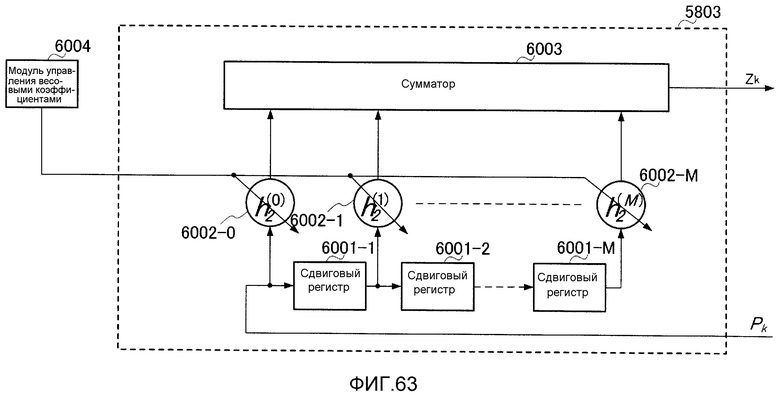
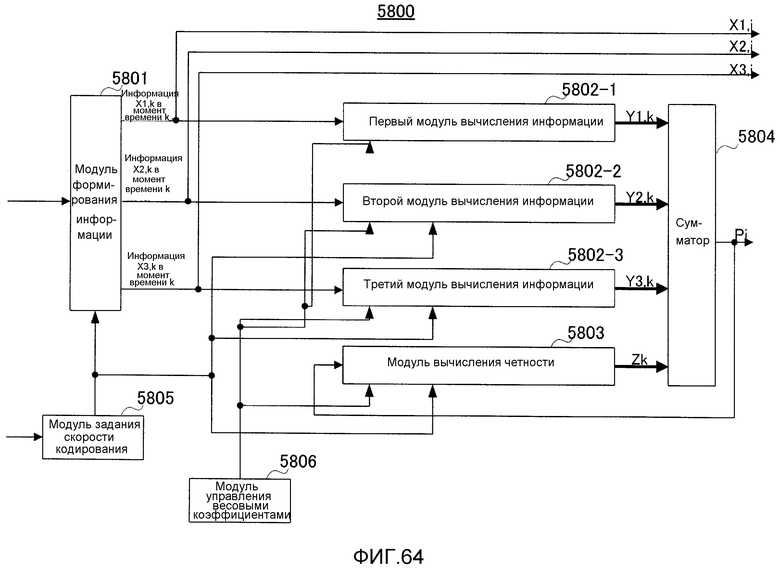
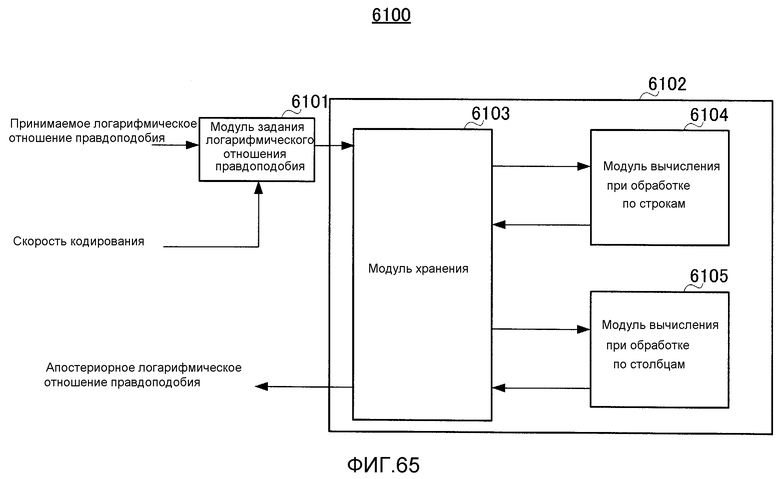
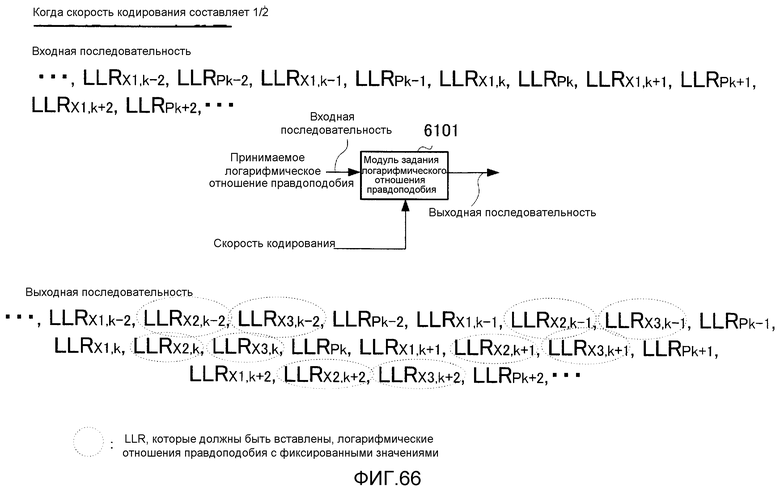
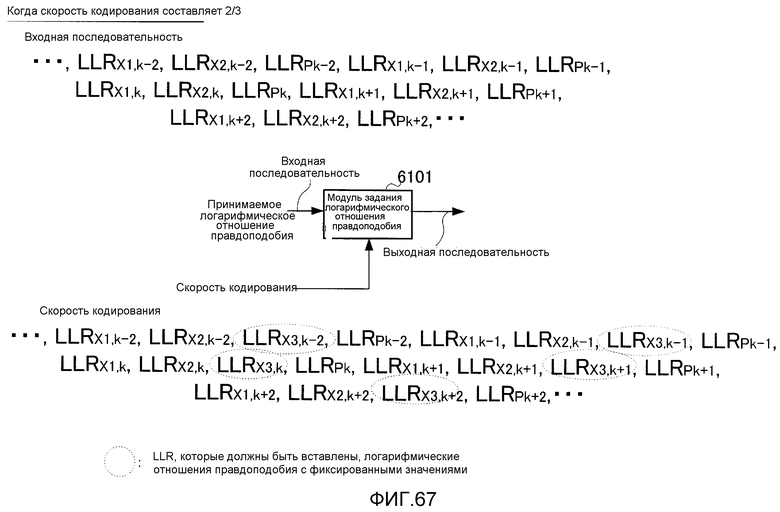
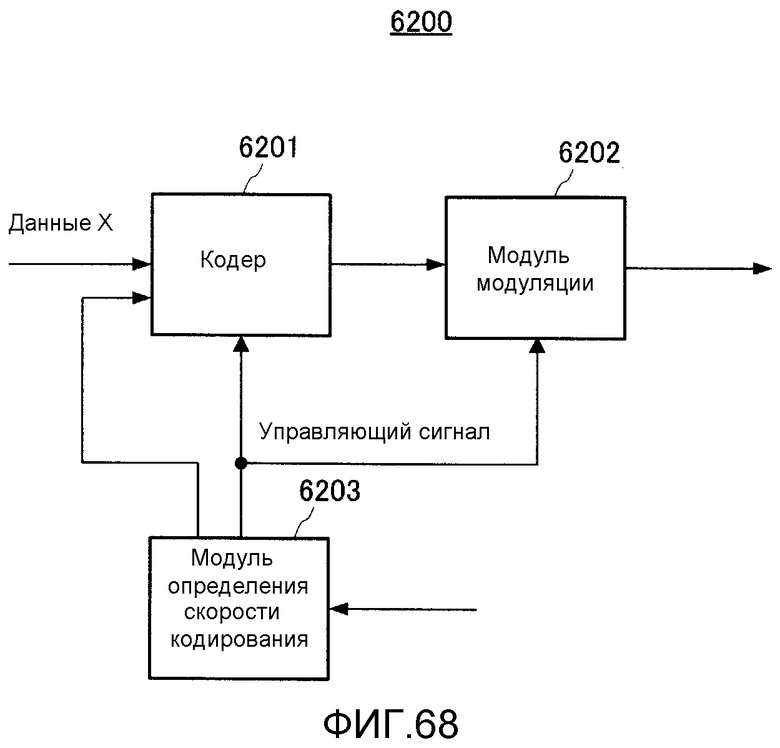
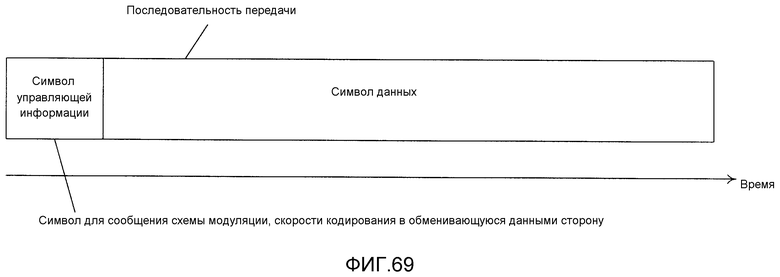
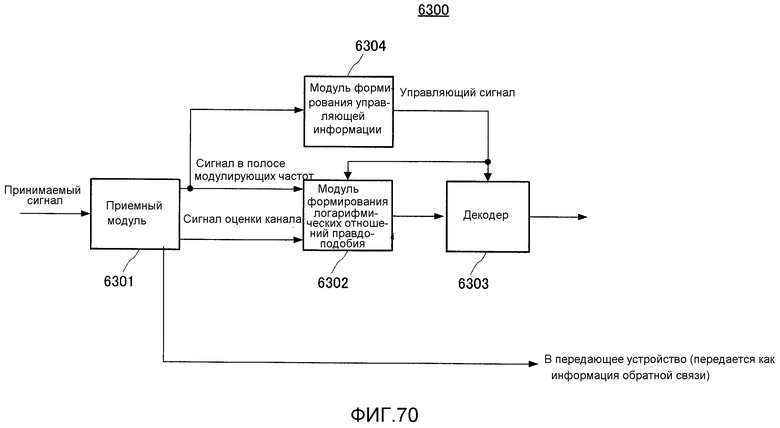
Изобретение относится к вычислительной технике. Технический результат заключается в обеспечении повышенной способности к коррекции ошибок. Способ кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), в котором используют простое число, превышающее 3, в качестве изменяющегося во времени периода q; принимают информационную последовательность в качестве входных данных; и кодируют информационную последовательность с использованием уравнения в качестве g-го (g=0, 1,..., q-1) полинома контроля по четности, чтобы удовлетворять 0: 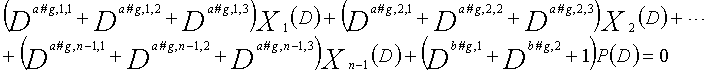 . 5 н. и 10 з.п. ф-лы, 75 ил., 9 табл.
. 5 н. и 10 з.п. ф-лы, 75 ил., 9 табл.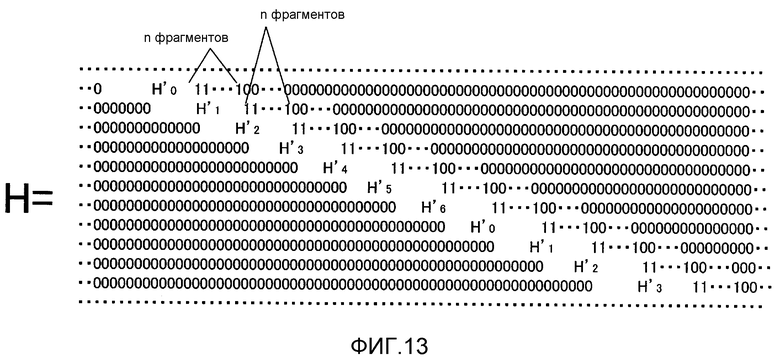
1. Способ кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), при этом способ содержит этапы, на которых:
используют простое число, превышающее 3, в качестве изменяющегося во времени периода q;
принимают информационную последовательность в качестве входных данных; и
кодируют информационную последовательность с использованием уравнения 1 в качестве g-го (g=0, 1,..., q-1) полинома контроля по четности, чтобы удовлетворять 0:
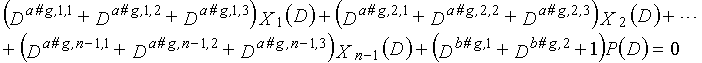 ... (уравнение 1),
... (уравнение 1),
где в уравнении 1:
"%" представляет по модулю, и каждый коэффициент удовлетворяет следующему относительно k=1, 2, … , n-1:
a#0,k,1%q=a#1,k,1%q=a#2,k,1%q=a#3,k,1%q= … =a#g,k,1%q= … =a#q-2,k,1%q=a#q-1,k,1%q=vp=k (vp=k: фиксированное значение);
b#0,1%q=b#1,1%q=b#2,1%q=b#3,1%q= … =b#g,1%q= … =b#q-2,1%q=b#q-1,1%q=w (w: фиксированное значение);
a#0,k,2%q=a#1,k,2%q=a#2,k,2%q=a#3,k,2%q= … =a#g,k,2%q= … =a#q-2,k,2%q=a#q-1,k,2%q=yp=k (yp=k: фиксированное значение);
b#0,2%q=b#1,2%q=b#2,2%q=b#3,2%q= … =b#g,2%q= … =b#q-2,2%q=b#q-1,2%q=z (z: фиксированное значение); и
a#0,k,3%q=a#1,k,3%q=a#2,k,3%q=a#3,k,3%q= … =a#g,k,3%q= … =a#q-2,k,3%q=a#q-1,k,3%q=sp=k (sp=k: фиксированное значение);
a#g,k,1, a#g,k,2 и a#g,k,3 являются натуральными числами, равными или превышающими 1, и a#g,k,1≠a#g,k,2, a#g,k,1≠a#g,k,3 и a#g,k,2≠a#g,k,3 справедливо;
b#g,1 и b#g,2 являются натуральными числами, равными или превышающими 1, и b#g,1≠b#g,2 справедливо; и
vp=k и yp=k являются натуральными числами, равными или превышающими 1.
2. Способ кодирования по п. 1, в котором a#g,k,3=0.
3. Способ по п. 1, в котором:
i и j (i≠j) присутствуют, если уравнение 2-1 и уравнение 2-2 справедливо, или
i присутствует, если уравнение 2-3 и уравнение 2-4 справедливо,
(vp=i, yp=i)≠(vp=j, yp=j)... (уравнение 2-1)
(vp=i, yp=i)≠(yp=j, vp=j)... (уравнение 2-2)
(vp=i, yp=i)≠(w, z)... (уравнение 2-3)
(vp=i, yp=i)≠(z, w)... (уравнение 2-4),
где i=1, 2, …, n-1,j=1, 2, …, n-1 и i≠j справедливо.
4. Способ кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), при этом способ содержит этапы, на которых:
используют простое число, превышающее 3, в качестве изменяющегося во времени периода q;
принимают информационную последовательность в качестве входных данных; и
кодируют информационную последовательность с использованием g-го (g=0, 1, …, q-1) полинома контроля по четности, чтобы удовлетворять 0, представленного посредством уравнения 3:
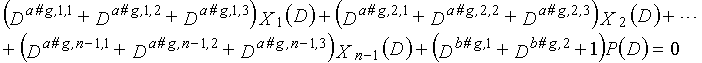 ... (уравнение 3),
... (уравнение 3),
где g-й полином контроля по четности удовлетворяет следующему относительно k=1, 2, …, n-1:
a#0,k,1%q=a#1,k,1%q=a#2,k,1%q=a#3,k,1%q= … =a#g,k,1%q= … =a#q-2,k,1%q=a#q-1,k,1%q=vp=k (vp=k: фиксированное значение);
b#0,1%q=b#1,1%q=b#2,1%q=b#3,1%q= … =b#g,1%q= … =b#q-2,1%q=b#q-1,1%q=w (w: фиксированное значение);
a#0,k,2%q=a#1,k,2%q=a#2,k,2%q=a#3,k,2%q= … =a#g,k,2%q= … =a#q-2,k,2%q=a#q-1,k,2%q=yp=k (yp=k: фиксированное значение),
b#0,2%q=b#1,2%q=b#2,2%q=b#3,2%q= … =b#g,2%q= … =b#q-2,2%q=b#q-1,2%q=z (z: фиксированное значение); и
a#0,k,3%q=a#1,k,3%q=a#2,k,3%q=a#3,k,3%q= … =a#g,k,3%q= … =a#q-2,k,3%q=a#q-1,k,3%q=sp=k (sp=k: фиксированное значение).
5. Способ кодирования по п. 4, в котором a#g,k,3=0.
6. Способ по п. 4, в котором:
i и j (i≠j) присутствуют, если уравнение 4-1 и уравнение 4-2 справедливо; или
i присутствует, если уравнение 4-3 и уравнение 4-4 справедливо,
(vp=i, yp=i)≠(vp=j, yp=j)... (уравнение 4-1)
(vp=i, yp=i)≠(yp=j, vp=j)... (уравнение 4-2)
(vp=i, yp=i)≠(w, z)... (уравнение 4-3)
(vp=i, yp=i)≠(z, w)... (уравнение 4-4),
где i=1, 2, …, n-1, j=1, 2, …, n-1 и i≠j справедливо.
7. Кодер для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2) с использованием простого числа, превышающего 3, в качестве изменяющегося во времени периода q, причем кодер содержит:
модуль формирования, который принимает информационный бит Xr[i] (r=1, 2, …, n-1) в момент времени i в качестве входных данных, обозначает уравнение, эквивалентное g-му(g=0, 1, …, q-1) полиному контроля по четности, чтобы удовлетворять 0, представленному посредством уравнения 1, в качестве уравнения 5 и формирует бит P[i] четности в момент времени i с использованием уравнения с подстановкой k вместо g в уравнении 5 когда i%q=k; и
модуль вывода, который выводит, бит P[i] четности:
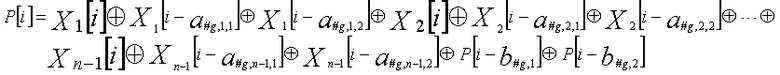 … (уравнение 5),
… (уравнение 5),
где  представляет исключающее ИЛИ, и g=0, 1, …, q-1.
представляет исключающее ИЛИ, и g=0, 1, …, q-1.
8. Кодер по п. 7, в котором a#g,k,3=0.
9. Кодер по п. 7, в котором:
i и j (i≠j) присутствуют, если уравнение 2-1 и уравнение 2-2 справедливо, или
i присутствует, если уравнение 2-3 и уравнение 2-4 справедливо.
10. Способ декодирования, соответствующий способу кодирования по п. 1 для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q (простое число, превышающее 3) с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем способ декодирования содержит декодирование кодированной информации последовательности, кодированной с использованием уравнения 1, в качестве g-го (g=0, 1, …, q-1) полинома контроля по четности, чтобы удовлетворять 0, и содержит этапы, на которых:
принимают кодированную информационную последовательность в качестве входных данных; и
декодируют кодированную информационную последовательность с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 1, которое является g-м полиномом контроля по четности, чтобы удовлетворять 0.
11. Способ декодирования по п. 10, в котором a#g,k,3=0.
12. Способ декодирования по п. 10, в котором:
i и j (i≠j) присутствуют, если уравнение 1-1 и уравнение 1-2 справедливо; или
i присутствует, если уравнение 1-3 и уравнение 1-4 справедливо.
13. Декодер, соответствующий способу кодирования по п. 1 для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q (простое число, превышающее 3) с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем декодер декодирует кодированную информационную последовательность, кодированную с использованием уравнения 1, в качестве g-го (g=0, 1, …, q-1) полинома контроля по четности, чтобы удовлетворять 0, и содержит:
модуль декодирования, который принимает кодированную информационную последовательность в качестве входных данных и декодирует кодированную информационную последовательность с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 1, которое является g-м полиномом контроля по четности, чтобы удовлетворять 0.
14. Декодер по п. 13, в котором a#g,k,3=0.
15. Декодер по п. 13, в котором:
i и j (i≠j) присутствуют, если уравнение 1-1 и уравнение 1-2 справедливо; или
i присутствует, если уравнение 1-3 и уравнение 1-4 справедливо.
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| A | |||
| E | |||
| PUSANE et al | |||
| Implementation Aspects of LDPC Convolutional Codes | |||
| IEEE Transactions on Communications, vol | |||
| Приспособление для разматывания лент с семенами при укладке их в почву | 1922 |
|
SU56A1 |
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| УСТРОЙСТВА ДЛЯ ПРИЕМА РЕЧИ, ПЕРЕДАННОЙ ПО РАДИОТЕЛЕФОНУ | 1924 |
|
SU1060A1 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ СВЕРТОЧНОГО КОДИРОВАНИЯ В ЦИФРОВОЙ СИСТЕМЕ | 1999 |
|
RU2214677C2 |
| ПЕРЕМЕЖИТЕЛЬ ТУРБОКОДА, ИСПОЛЬЗУЮЩИЙ ЛИНЕЙНЫЕ КОНГРУЭНТНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ | 1999 |
|
RU2235424C2 |
Авторы
Даты
2014-11-10—Публикация
2010-11-12—Подача