Область техники, к которой относится изобретение
Настоящее изобретение относится, в общем, к способу кодирования данных и, в частности, к способу кодирования кода разреженного контроля четности (LDPC).
Уровень техники
В общем, система связи кодирует передаваемые данные перед передачей, чтобы повысить стабильность передачи, и предотвращает избыточные повторные передачи, чтобы повысить эффективность передачи. Для кодирования передаваемых данных система мобильной связи использует сверточное кодирование, турбокодирование и квазидополняемое турбокодирование (QCTC). Использование вышеперечисленных схем кодирования направлено на повышение стабильности передачи данных и эффективности передачи.
В последнее время системы беспроводной связи эволюционируют в усовершенствованные системы беспроводной связи, допускающие передачу данных на очень высокой скорости. Усовершенствованная система беспроводной связи должна передавать данные на более высокой скорости. Следовательно, существует потребность в усовершенствованной схеме кодирования, допускающей получение более высокой эффективности, чем эффективность текущих вышеперечисленных схем кодирования.
Кодирование с разреженным контролем четности (LDPC) предусмотрено в качестве новой схемы кодирования для удовлетворения указанной потребности. Подробное описание кода разреженного контроля четности приведено в данном документе далее. Код разреженного контроля четности впервые был предложен Галлагером в начале 60-ых гг. и пересмотрен Маккеем в конце 90 -х гг. Код разреженного контроля четности, проанализированный Маккеем, основан на алгоритме суммы-произведения. Благодаря использованию декодирования распространения убежденности код разреженного контроля четности начал привлекать всеобщее внимание как код, позволяющий демонстрировать отличную производительность, аппроксимируя ограничение по пропускной способности Шэннона.
В дальнейшем Ричардсон и Чанг предложили методику эволюции плотности для отслеживания вариации согласно итерации в распределении вероятностей сообщений, генерируемых и обновляемых в ходе декодирования, на графе множителей, составляющем код разреженного контроля четности. Для методики эволюции плотности и бесконечных итераций на графе множителей без циклов Ричардсон и Чанг изобрели параметр канала (или порог), допускающий схождение вероятности ошибки к 0. Т.е. Ричардсон и Чанг предложили распределение степеней, допускающее максимизацию параметров каналов переменных узлов и контрольных узлов на графе множителей. Помимо этого, Ричардсон и Чанг теоретически показали, что этот случай может быть применен даже к коду LDPC конечной длины, в котором предусмотрены циклы.
Помимо этого, Ричардсон и Чанг показали, что теоретическая пропускная способность канала нерегулярного кода LDPC может аппроксимировать ограничение по пропускной способности Шэннона до всего лишь 0,0045 дБ с помощью методики эволюции плотности. В частности, компания Flarion Co., ведущий разработчик структуры и аппаратных средств кода LDPC, предложила многоконтурный векторный код LDPC, допускающий реализацию параллельного декодера, имеющего частоту ошибок по кадрам меньше, чем частота ошибок для турбокода, даже для кода LDPC с короткой длиной.
Код LDPC рассматривается как серьезная альтернатива турбокоду в системах мобильной связи следующего поколения. Это обусловлено параллельной структурой и небольшой сложностью кода LDPC для реализации декодера, а также низким минимальным уровнем ошибок и хорошей частотой ошибок по кадрам касательно производительности. Поэтому ожидается, что дальнейшие научные исследования предоставят коды LDPC, имеющие лучшие характеристики.
Тем не менее, в реализации текущий код LDPC более сложен, чем турбокод, при процессе декодирования и требует структуры оптимизированного кода, допускающего предоставление более высокой производительности, чем турбокод, при небольшом размере кадра. Хотя проводились активные исследования, чтобы разрешить эту проблему, не было предложено схем, допускающих кодирование оптимизированного кода LDPC.
Раскрытие изобретения
Таким образом, цель настоящего изобретения - предоставить способ кодирования LDPC с простым процессом кодирования.
Еще одна цель изобретения - предоставить способ кодирования LDPC, имеющий более высокую производительность при небольшом размере кадра.
Чтобы достичь вышеуказанных и других целей, предусмотрен способ генерирования кода разреженного контроля четности, состоящего из матрицы информационной части и матрицы части четности. Способ содержит этапы изменения матрицы информационной части на структуру кода массива и выделения последовательности степеней каждому из столбцов подматрицы; расширения матрицы части четности таким образом, чтобы значение смещения между диагональными линиями имело заранее определенное значение в обобщенной двухдиагональной матрице, которая является матрицей части четности; повышения обобщенной двухдиагональной матрицы; определения значения смещения для циклического сдвига столбцов в каждой подматрице повышенной обобщенной двухдиагональной матрицы; и выполнения процесса кодирования для определения символа четности, соответствующего столбцу матрицы части четности.
Предпочтительно, последовательность степеней состоит из D={15, 15, 15, 5, 5, 5, 4, 3, 3, 3, 3, 3, 3, 3, 3}, а значения смещения между диагональными линиями являются взаимно простыми относительно числа столбцов в обобщенной двухдиагональной матрице.
Предпочтительно, разность между суммой значений смещения для циклического сдвига строк подматрицы на диагональной линии в обобщенной двухдиагональной матрице, которая является матрицей части четности, и суммой значений смещения для циклического сдвига строк подматрицы на диагональной линии смещения не равна 0.
Предпочтительно, процесс кодирования содержит процесс (a) определения символа четности первой строки в подматрице с индексом 0 столбца подматрицы на диагональной линии матрицы части четности; (b) задания индекса строки в подматрице символа четности, идентичного определенному символу четности в индексе столбца в подматрице на диагональной линии смещения, имеющей такой же индекс столбца подматрицы, что и индекс столбца подматрицы заданного символа четности; (c) определения символа четности, имеющего такой же индекс строки в заданной подматрице в подматрице на диагональной линии, имеющей такой же индекс строки подматрицы, что и индекс строки подматрицы на диагональной линии смещения; и (d) многократного выполнения этапов (b) и (c) до тех пор, пока создание матрицы четности не будет завершено.
Предпочтительно, на этапе (a) символ четности определяется суммой информационных символов матрицы информационной части, существующих в той же строке, что и индекс строки в подматрице, символы четности которой определяются.
Краткое описание чертежей
Вышеуказанные и другие цели, признаки и преимущества настоящего изобретения станут более понятными из последующего подробного описания, рассматриваемого вместе с прилагаемыми чертежами, из которых:
Фиг.1 - это схема, иллюстрирующая матрицу контроля четности для общего кода массива (p, r);
Фиг.2 - это схема, иллюстрирующая пример матрицы Hd в случае, когда максимальное число единиц, существующих в конкретном столбце, задано как dv, число этих столбцов подматрицы задано как nv, а число единиц, существующих в оставшихся столбцах подматрицы, всегда равно 3;
Фиг.3 - это схема, иллюстрирующая структуру графа множителей нерегулярного повторяющегося кода накопления;
Фиг.4 - это схема, иллюстрирующая матрицу кода разреженного контроля четности, имеющего нерегулярный повторяющийся код накопления;
Фиг 5 - это схема, иллюстрирующая матрицу четности, в которой значение смещения T двухдиагональной матрицы повышено до конкретного значения;
Фиг.6 - это схема, иллюстрирующая процесс последовательного вычисления значений p0, pr-f, pr-2f,... в процессе кодирования Фиг. 5;
Фиг.7 - это схема, иллюстрирующая пример информационной части Hd матрицы контроля четности, сгенерированной в способе, описанном в разделе A, при котором максимальная степень переменного узла составляет 15;
Фиг.8 - это схема, иллюстрирующая матрицу 12х12, полученную посредством повышения базовой матрицы 4х4 в способе замены каждого элемента в матрице 4х4 на единичную матрицу 3х3 или нулевую матрицу 3х3;
Фиг.9 - это схема, иллюстрирующая матрицу Hp четности, составленную посредством повышения матрицы на подматрицу циклической перестановки pхp;
Фиг.10 - это блок-схема последовательности операций, иллюстрирующая способ генерирования матрицы части четности согласно предпочтительному варианту осуществления настоящего изобретения;
Фиг.11 - это схема, иллюстрирующая матрицу четности обобщенной двухдиагональной матрицы, повышенной для r=15, f=7 и p=89;
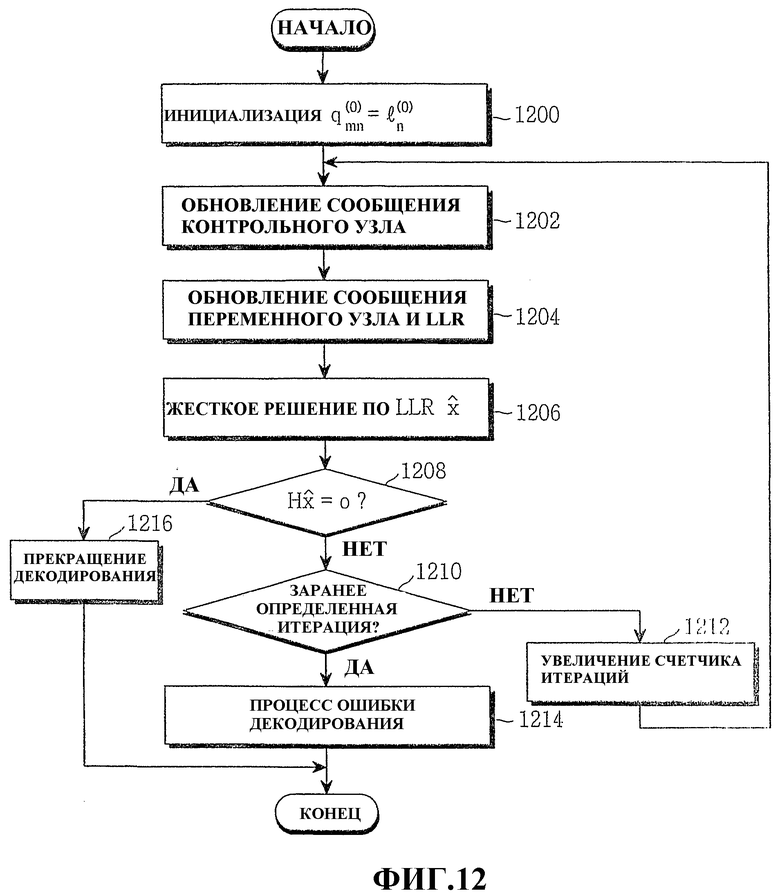
Фиг.12 - это блок-схема последовательности операций, иллюстрирующая итеративный процесс декодирования распространения убежденности для исследования эффективности настоящего изобретения;
Фиг.13A - это схема, иллюстрирующая пример матрицы информационной части Hd для n=870 и p=29;
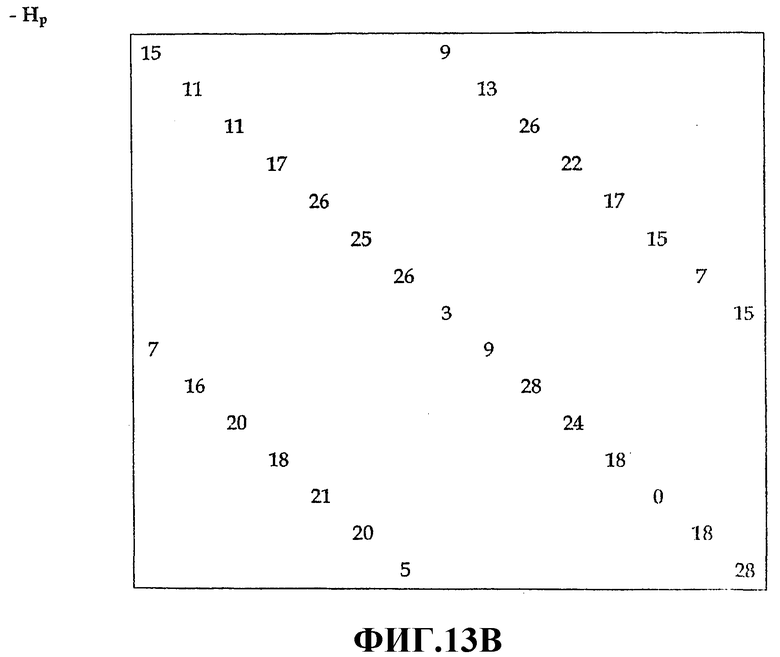
Фиг.13B - это схема, иллюстрирующая пример матрицы части Hp четности для n=870 и p=29;
Фиг.13C - это график моделирования результатов, иллюстрирующий сравнение кода разреженного контроля четности и турбокода;
Фиг.14A - это схема, иллюстрирующая пример матрицы информационной части Hd для n=1590 и p=53;
Фиг.14B - это схема, иллюстрирующая пример матрицы части Hp четности для n=1590 и p=53;
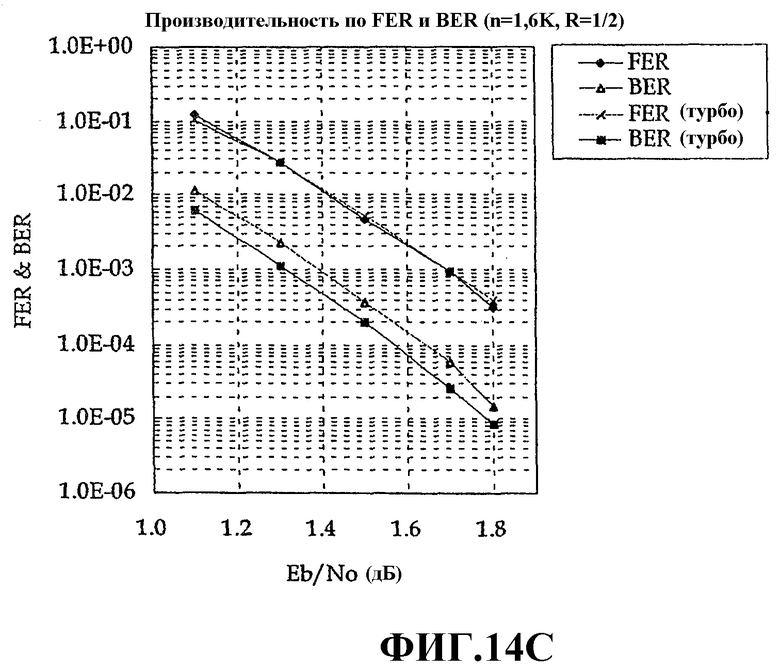
Фиг.14C - это график моделирования результатов, иллюстрирующий сравнение кода разреженного контроля четности и турбокода;
Фиг.15A - это схема, иллюстрирующая пример матрицы информационной части Hd для n=3090 и p=103;
Фиг.15B - это схема, иллюстрирующая пример матрицы части Hp четности для n=3090 и p=103;
Фиг.15C - это график моделирования результатов, иллюстрирующий сравнение кода разреженного контроля четности и турбокода;
Фиг.16A - это схема, иллюстрирующая пример матрицы информационной части Hd для n=7710 и p=257;
Фиг.16B - это схема, иллюстрирующая пример матрицы части Hp четности для n=7710 и p=257;
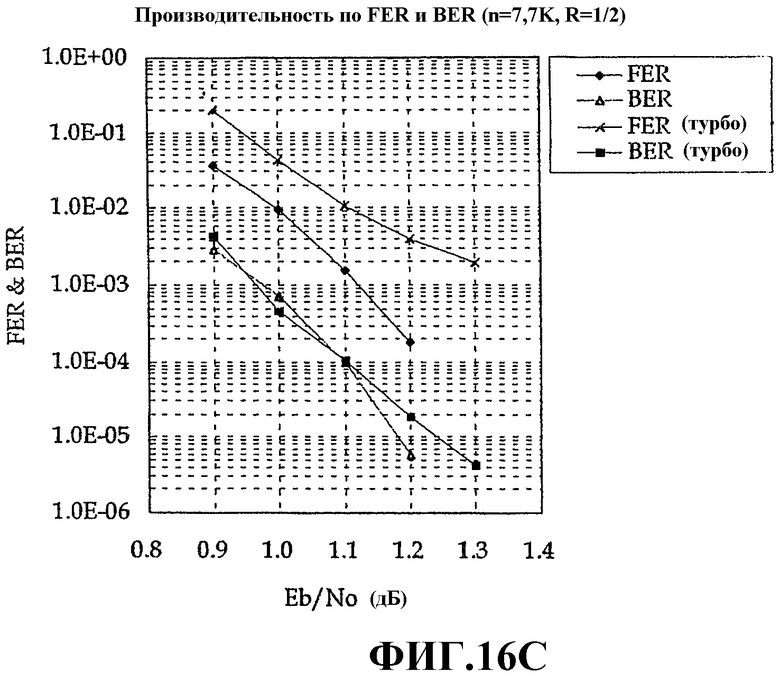
Фиг.16C - это график моделирования результатов, иллюстрирующий сравнение кода разреженного контроля четности и турбокода; и
Фиг.16D - это график моделирования результатов для кода разреженного контроля четности согласно вариации в числе итераций.
Осуществление изобретения
Далее подробно описан предпочтительный вариант осуществления настоящего изобретения со ссылками на прилагаемые чертежи. На чертежах одинаковые или подобные элементы обозначаются одними и теми же ссылками с номерами, даже если они изображены на различных чертежах. В последующем описании подробное описание известных функций и конфигураций, содержащихся в данном документе, опущено в целях краткости.
В последующем описании настоящее изобретение предлагает новый код LDPC, позволяющий демонстрировать простое кодирование и хорошую производительность. С этой целью настоящее изобретение задает новую матрицу контроля четности. Т.е. настоящее изобретение предлагает новый код LDPC, который использует новую матрицу контроля четности. Помимо этого, настоящее изобретение демонстрирует, что новый код LDPC может быть просто закодирован посредством линейного вычисления, и предлагает его способ кодирования. В заключение, настоящее изобретение демонстрирует, что вследствие декодирования распространения убежденности новый код LDPC имеет более оптимальную производительность декодирования, чем производительность турбокода, используемого в стандарте CDMA2000 1хEV-DV.
Для удобства описание настоящего изобретения сделано в отношении производительности и реализации кода LDPC с кодовой скоростью 1/2. Тем не менее, кодовая скорость может быть повышена в рамках области применения настоящего изобретения.
1. Структура матрицы контроля четности
В этом разделе настоящее изобретение задает новую матрицу контроля четности, сгенерированную посредством наращивания и применения структур матрицы контроля четности, которые задают код массива и нерегулярный повторяющийся код накопления (IRA-код). Также приводится описание способа генерирования матрицы, имеющей больший размер, одновременно сохраняя характеристики базовой матрицы, сгенерированной таким способом.
A. Структура кода массива
В общем, матрица контроля четности для кода массива (p,r) задается, как на Фиг.1. Фиг.1 - это схема, иллюстрирующая матрицу контроля четности для общего кода массива (p,r). Далее приводится описание матрицы контроля четности для общего кода массива (p,r) со ссылкой на Фиг.1.
На Фиг.1 p означает простое число, а σjозначает матрицу циклической перестановки pхp, получаемую посредством циклического сдвига соответствующих строк единичной матрицы pхp I, которая является квадратной матрицей, имеющей размер p, на j. Строка и столбец, каждый составленный из набора σj, называются строкой подматрицы и столбцом подматрицы соответственно. Столбец и строка матрицы контроля четности, задающей код массива, равномерно имеют p единиц и r единиц соответственно. Когда p достаточно большое, соотношение единиц в матрицы уменьшается, приводя к структуре кода разреженного контроля четности. Этот код массива не имеет циклической структуры с длиной 4. Т.е. если элементы, принадлежащие 4 частичным матрицам σia, σib, σja и σjb (ij), формирующим квадрат или цикл-4, в матрице контроля четности имеют структуру цикл-4, следующее отношение должно удовлетворяться:
ia - ib =ja -jb(i-j) = (a-b) (mod p) (1)
В уравнении (1) должно удовлетворяться, что a=b. Тем не менее, поскольку a и b, существующие в различных строках, всегда имеют различные значения, уравнение (1) не может быть удовлетворено. Поэтому вышеописанный код массива, имеющий матрицу контроля четности, имеет структуру не цикл-4.
Настоящее изобретение генерирует новую структуру матрицы посредством модификации структуры матрицы контроля четности вышеописанного кода массива. Далее приводится описание процесса генерирования новой матричной структуры, которая должна быть использована в настоящем изобретении. Цель модификации состоит в том, чтобы получить нерегулярную структуру, в которой распределение единиц, существующих в каждом столбце матрицы, который должен быть сгенерирован, является нерегулярным, на основе структуры кода массива, не имеющего структуру цикл-4. Этот процесс должен быть выполнен таким образом, чтобы распределение единиц, существующих в каждой строке, было относительно однородным, т.е. всего существует два типа. Далее приводится описание способа генерирования новой матричной структуры, используемой в настоящем изобретении.
(1) j-тый столбец подматрицы матрицы контроля четности, формирующей код массива, составлен из подматриц, представленных как:

(2) В зависимости от заранее определенного распределения степеней последовательность степеней каждого столбца подматрицы задается как:
D = [d0 d1... ds-1] (3)
В уравнении (3) dj означает степень столбца, соответствующего j-тому столбцу подматрицы, а s означает общее число столбцов подматрицы. Помимо этого, s задается таким образом, чтобы быть идентичным общему числу dv единиц, существующих в конкретном столбце.
(3) В зависимости от степени последовательности D, заданной в (2), j-тый столбец подматрицы модифицируется как:

tj = tj-1 + dj-1(mod s) (4)
В уравнении (4) tj означает номер строки подматрицы, с которой начинается ненулевая подматрица в j-том столбце Hj подматрицы.
(4) Матрица Hd, которая должна быть сгенерирована, задается уравнением (5), в котором столбцы подматрицы заменены на векторы-столбцы:

Когда конкретный столбец подматрицы матрицы задается согласно вышеописанному процессу, конкретный столбец, существующий в каждом столбце подматрицы, всегда имеет ровно столько единиц, сколько составляет значение степени, назначенной соответствующему столбцу подматрицы. Матрица, составленная из столбцов подматрицы, минимизирует перекрытие подматриц между матрицами. Поэтому число единиц, существующих в конкретной строке всей матрицы, также минимизируется. Т.е. можно легко понять, что число единиц в одной строке во всей матрице всегда будет равно 2 или 1. Поскольку сгенерированная матрица Hd имеет структуру, полученную посредством удаления некоторых подматриц из структуры кода массива, она всегда имеет структуру не цикл-4, как у кода массива.
Фиг.2 - это схема, иллюстрирующая пример матрицы Hd в случае, когда максимальное число единиц, существующих в конкретном столбце, задано как dv, число этих столбцов подматрицы задано как nv, а число единиц, существующих в оставшихся столбцах подматрицы, всегда равно 3.
В настоящем изобретении матрица Hd 220 информационной части матрицы H контроля четности, заданная на основе структуры кода массива, описанной в связи с Фиг.2, используется в качестве подматрицы матрицы H контроля четности кода разреженного контроля четности, который должен быть задан в настоящем изобретении. Далее приводится описание нерегулярного повторяющегося кода накопления (IRA-кода) для генерирования подматрицы, формирующей часть четности матрицы H контроля четности.
B. Обобщенная двухдиагональная матрица
Известно, что нерегулярный повторяющийся код накопления (IRA-код) имеет простую структуру кодера и имеет относительно высокую производительность посредством декодера обмена сообщениями. Этот нерегулярный повторяющийся код накопления может быть рассмотрен как один тип режима разреженного контроля четности.
Фиг.3 - это схема, иллюстрирующая структуру графа множителей нерегулярного повторяющегося кода накопления. Далее приводится описание структуры графа множителей нерегулярного повторяющегося кода накопления со ссылкой на Фиг. Граф множителей нерегулярного повторяющегося кода накопления Фиг.3 - это систематическая версия, в которой все узлы четности, соответствующие символам четности кодового слова, за исключением только одного узла четности, имеют степень 2. Т.е. каждый из узлов четности 301, 302, 303,..., 304, 305, 306 и 307 имеет 2 ребра, подсоединенные к нему. Такая структура узлов четности является выгодной в том, что генерирование символов четности на основе данных информационных символов достигается просто линейным вычислением. Помимо этого, как можно понять из Фиг.3, информационные узлы нерегулярного повторяющегося кода накопления могут иметь различные распределения степеней. Значения информационных узлов связаны с контрольными узлами посредством случайной перестановки 320.
Структура матрицы нерегулярного повторяющегося кода накопления, имеющего граф множителей Фиг.3, может быть проиллюстрирована на Фиг.4. Фиг.4 - это схема, иллюстрирующая матрицу кода разреженного контроля четности, имеющего нерегулярный повторяющийся код накопления.
В матрице кода разреженного контроля четности, проиллюстрированной на Фиг.4, диагональные линии в части четности представляют 1, а смещение f (401) между диагональными линиями имеет значение 1 в общем нерегулярном повторяющемся коде накопления. Поэтому подматрица, соответствующая части четности матрицы контроля четности, задающей нерегулярный повторяющийся код накопления, имеет структуру двухдиагональной матрицы. Число единиц, существующих в каждом столбце информационной части в матрице контроля четности, имеет нерегулярное распределение. Это распределение задается блоком случайных перестановок Фиг.4.
Настоящее изобретение рассматривает только часть четности нерегулярного повторяющегося кода накопления. Поэтому настоящее изобретение обобщает только часть четности и предлагает новый тип матрицы.
В случае общего нерегулярного повторяющегося кода накопления Фиг.4 смещение f между диагональными линиями имеет значение 1 (f=1). В настоящем изобретении, если значение смещения f повышено таким образом, что оно имеет конкретное значение, двухдиагональная матрица части четности может быть обобщена так, как проиллюстрировано на Фиг.5. На Фиг.5 первая диагональная линия 501 формирует диагональную линию от позиции в первом столбце и первой строке до позиции в последнем столбце и последней строке матрицы. Первая частичная диагональная линия 502a второй диагональной линии имеет значение 0 в столбце первой позиции, смещенном на значение смещения, и имеет значение 1 в оставшихся позициях до своей последней точки. Вторая частичная диагональная линия 502b второй диагональной линии формирует диагональную линию со значением 1 из первого столбца в следующей строке.
При этом фиг 5 - это схема, иллюстрирующая матрицу четности, в которой значение смещения двухдиагональной матрицы повышено до конкретного значения. Хотя значение смещения изменено, как проиллюстрировано на Фиг.5, всегда существует столбец, имеющий только одну 1. Следует отметить, что если число единиц, существующих в каждом столбце, равно 2, ранг двухдиагональной матрицы становится меньше, чем число строк в матрице. Поэтому первая строка второй диагональной линии должна иметь 0, а не 1, как проиллюстрировано на Фиг.5. В случае матрицы rхr, т.е. квадратной матрицы с размером r матрицы, проиллюстрированной на Фиг.5, если значение f смещения двухдиагональной матрицы и размер r матрицы не имеют общего множителя, можно сгенерировать все из r символов четности посредством простого выполнения сложения над набором данных информационных символов r раз. Чтобы доказать это, рассматриваются следующие теоремы.
Теорема 1: В абелевой группе AGr={0, 1, 2,..., r-1} все элементы генерируются посредством выполнения сложения над конкретным элементом f, который является взаимно-простым для r и не равен 0, меньше r раз. Чтобы доказать это, если все элементы в AGr не могут быть сгенерированы посредством выполнения сложения над конкретным элементом f, который является взаимно-простым для r и не равен 0, меньше r, то существует k меньше r, которое удовлетворяет условию уравнения (6).
kf = 0 (mod r) (6)
Тем не менее, уравнение (6) противоречит допущению, что f является взаимно-простым для r. Т.е. минимальное значение k, удовлетворяющее уравнению (6), всегда должно быть r. Поэтому все элементы в AGr могут быть сгенерированы посредством выполнения сложения над элементом f r раз.
Двухдиагональная матрица, проиллюстрированная на Фиг.5, - это матрица, соответствующая части четности матрицы контроля четности. Поэтому в отношении i-того столбца в матрице Фиг.5 можно всегда получить информацию, показанную в уравнении (7), из i-того столбца в матрице, соответствующей оставшейся информационной части матрицы контроля четности.
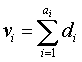 (7)
(7)
В уравнении (7) di означает i-тый информационный символ, а ai означает число единиц, существующих в i-том столбце матрицы, соответствующем информационной части матрицы контроля четности. Помимо этого, ∑ означает сложение в GF(2). GF(2) ссылается на поле Галуа по 2 и означает конечное поле, заданное в модуле 2. Термин "конечное поле" означает набор, в котором число элементов конечно и элементы закрыты для сложения и умножения по модулю 2, существует нейтральный элемент и обратный элемент для сложения, существует нейтральный элемент для умножения и обратный элемент для ненулевого элемента, и закон перестановки, сочетательный закон и распределительный закон удовлетворяются для сложения и умножения. Поэтому GF(2) означает набор {0, 1}, удовлетворяющий этому свойству. В результате первый символ четности, который может быть получен уравнением контроля четности, соответствующим первому столбцу в матрице Фиг.5, задается как:
p0 = v0(8)
В структуре матрицы Фиг.5 отношение между индексом столбца и индексом строки для конкретных единиц, существующих в диагональной линии и диагональной линии смещения, задается как:
y1 = x1, y2 = x2 - f (9)
Если две формулы, показанные в уравнении (9), используются, pr-f может быть рассчитан с помощью p0 в соответствии с уравнением (10):
pr-f = p0 + vr-f (10)
Помимо этого, поскольку матрица контроля четности имеет структуру двухдиагональной матрицы, проиллюстрированной на Фиг.5, уравнение (10) может быть модифицировано в:
pr-if = pr-(i-1)f + vr-if, i = 1, ..., r-1 (11)
Таким образом, конкретный символ pr-if четности может быть получен посредством уравнения (11), и на основе теоремы 1, если r является взаимно-простым для f, по мере того, как i увеличивается, значение (r-if) (модуль r) имеет значение 1 для r-1 только один раз. Следовательно, если r является взаимно-простым для f, значения всех символов четности могут быть рассчитаны посредством вышеописанного процесса. Поэтому в вышеописанном способе матрица контроля четности, имеющая часть четности, проиллюстрированную на Фиг.5, всегда может проходить простое кодирование посредством линейного вычисления. Фиг.6 - это схема, иллюстрирующая процесс последовательного вычисления значений p0, pr-f, pr-2f,... в процессе кодирования.
Ссылаясь на Фиг.6, выполнена связь из значения позиции нулевого столбца и нулевой строки со значением положения нулевого столбца и (r-f)-той строки, представленного ссылкой с номером 601. Следует заметить, что значение позиции нулевого столбца и (r-f)-той строки связано со значением положения (r-f)-того столбца и (r-f)-той строки, представленного ссылкой с номером 602. Таким образом, единицы размещены только в первой диагональной линии 610, первой частичной линии 620a второй диагональной линии и второй частичной линии 620b второй диагональной линии. Поскольку только одно значение в 1 существует в первом столбце диагональных линий, функция второго порядка вычисляется посредством непрерывного поиска значения 1 вышеописанным способом. В результате все значения могут быть найдены.
Вышеописанная структура обобщенной двухдиагональной матрицы используется в качестве подматрицы Hp части четности в матрице H контроля четности кода разреженного контроля четности, который должен быть задан в настоящем изобретении. Далее приводится описание способа генерирования матрицы контроля четности кода разреженного контроля четности, который должен быть задан в настоящем изобретении.
C. Структура матрицы контроля четности
В этом разделе приводится описание способа генерирования новой матрицы H контроля четности согласно настоящему изобретению с помощью структуры обобщенной двухдиагональной матрицы, описанной в разделе B, а также описание ее структуры. Матрица контроля четности, описанная ниже, задает матрицу Hd, заданную на основе структуры кода массива, описанной в разделе A, как информационную часть матрицы H контроля четности. Дополнительно, описанная ниже матрица контроля четности задает нормализованную двухдиагональную матрицу Hp, описанную в разделе B, как часть четности матрицы H информационной части. Поэтому матрица H контроля четности, задающая код разреженного контроля четности, которая должна быть разработана в настоящем изобретении, имеет структуру, представленную как:
H=[Hd | Hp] (12)
где Hd - подматрица контроля четности для информационной части
Hp - подматрица контроля четности для части четности
В уравнении (12) соответствующие столбцы подматрицы в матрице Hd информационной части матрицы проверки четности задаются посредством последовательности степеней D на основе заранее заданного распределения степеней, а единичная матрица σij, составляющая каждый столбец подматрицы, является матрицей циклической перестановки, получаемой посредством смещения столбцов единичной матрицы pхp с размером p на ij, которое является произведением индекса i столбца подматрицы и индекса j строки подматрицы. При этом p всегда является простым числом. Помимо этого, Hp повышает единицы и нули, существующие в матрице, в матрицу pхp и нулевую матрицу, соответственно, чтобы сопоставить ее структуру со структурой Hd.
Далее приводится описание процессов генерирования кода разреженного контроля четности согласно варианту осуществления настоящего изобретения.
(I) Распределение степеней и структура Hd
Ричардсон и другие показали, что когда достигается декодирование обмена сообщениями в графе множителей, задающем код разреженного контроля четности, можно отслеживать варьирование посредством процесса обновления сообщений переменных и контрольных узлов и процесса итеративной обработки по алгоритму суммы-произведения за счет варьирования вероятностного распределения. Дополнительно, Ричардсон и другие показали, что существует порог параметра канала, допускающий определение того, сходится ли к нулю средняя вероятность ошибки кода разреженного контроля четности, заданного с помощью графа множителей, имеющего распределение степеней посредством этой методики эволюции плотности. Помимо этого, Ричардсон и другие показали, что для параметра канала ниже порога параметра канала, когда бесконечная итерация допускается в процессе декодирования, вероятность ошибки по битам всегда может сходиться к нулю. Поэтому такая методика эволюции плотности может быть использована в качестве средства проектирования, допускающего оптимизацию распределения степеней кода разреженного контроля четности, допускающего повышение порога для конкретного канального окружения. Таким образом, было проведено множество научных исследований, чтобы рассчитать распределение степеней, оптимизированное для кода разреженного контроля четности и порога в это время.
Настоящее изобретение аппроксимирует заранее определенное оптимизированное распределение степеней переменных узлов к распределению степеней переменных узлов матрицы H контроля четности, которая должна быть задана в настоящем изобретении. В этом случае переменные узлы со степенью 2 все назначены соответствующим столбцам в части Hp четности матрицы H, а переменные узлы со степенью больше 2 назначены соответствующим столбцам в информационной части Hd матрицы H. Помимо этого, из структуры кода массива, описанной в разделе A, и структуры подматриц обобщенной двухдиагональной матрицы, описанной в разделе B, степень контрольного узла матрицы H контроля четности всегда имеет только один или два минимизированных типа относительно числа всех данных единиц.
Далее определяется последовательность степеней для задания информационной части Hd матрицы контроля четности, которая должна быть задана в настоящем изобретении. Если максимальная степень переменного узла в графе множителей, задающем код разреженного контроля четности, задается как dv, распределение соответствующих ребер, существующих в переменном узле, может быть выражено с помощью полинома, представляемого как:

В уравнении (13) Xi означает соотношение ребер, существующих в переменном узле, со степенью i. Отношение cj ребер, существующих в переменном узле, со степенью j в графе множителей для данного X(x) может быть выражено как:

Рассматривая реализацию в уравнении (14), структура матрицы контроля четности описывается для максимальной степени переменного узла = 15. Известно, что когда значение максимальной степени переменного узла в графе множителей, задающем код разреженного контроля четности, равно 15, оптимальное распределение степеней для кодовой скорости 1/2 в канальном окружении с аддитивным белым гауссовым шумом с двоичным входом (Bi-AWGN) задается, как показано в уравнении (15), посредством методики эволюции плотности.
λ2 = 0,23802, λ3= 0,20997, λ4= 0,03492, λ5 = 0,12015, (15)
λ7 = 0,01587,λ14= 0,00480,λ15= 0,37627
В канале с аддитивным белым гауссовым шумом (AWGN) для обеспечения возможность вероятности ошибок переменных узлов сводиться к нулю, максимальная дисперсия шума параметра канала, σ* равна 0,9622, и это равно 0,3348 дБ в показателях Eb/No. Т.е. код разреженного контроля четности, заданный посредством графа коэффициентов, имеющего вышеуказанное распределение степеней, показывает производительность, аппроксимирующую ограничение по пропускной способности Шэннона на 0,3348 дБ посредством декодирования распространения убежденности, для которого предполагается бесконечный размер блока и бесконечная итерация. В графе коэффициентов, имеющем вышеуказанное распределение степеней, соотношения переменных узлов, имеющих соответствующие степени, задается как:
c2=0,47709, c3=0,28058, c4=0,034997, c5=0,096332 (16)
c7=0,0090386, c14=0,001374, c15=0,100560
В матрице контроля четности, которая должна быть задана в настоящем изобретении, переменные узлы со степенью 2 всегда должны быть назначены части Hp четности, и только другие переменные узлы, за исключением переменных узлов со степенью 2, всегда должны быть назначены информационной части Hd. Помимо этого, все столбцы в каждом столбце подматрицы информационной части Hd имеют одинаковый вес столбца. Поэтому соотношения переменных узлов, имеющих соответствующие степени в графе коэффициентов матрицы H контроля четности, аппроксимируются, как показано уравнением (17)
c2=1/2=0,5, c3=8/30=0,26667, c4=1/30=0,03333, c5=3/30= 0,1, (17)
c7=c14=0, c15=3/30=0,1
При использовании соотношений переменных узлов, показанных в уравнении (17), полином распределения степеней X(x) является вычисляемым приростом, и порог в AWGN кода разреженного контроля четности, заданного соответствующим распределением степеней, вычисляется в соответствии с уравнением (18):
σ* = 0,9352 (Eb/No)* = 0,5819 dB (18)
Значение, определенное уравнением (18), - это значение, соответствующее коду разреженного контроля четности с кодовой скоростью 1/2. Это значение извлекается с помощью методики эволюции плотности на основе значения гауссовой аппроксимации в качестве методики анализа, и если оцененная вероятность ошибки по битам меньше 10-6, соответствующее значение вычисляется с учетом того, что ошибки нет. Последовательность степеней, назначаемых каждому столбцу подматрицы информационной части Hd с помощью вычисленного значения, может быть задана как:
D = {15, 15, 15, 5, 5, 5, 4, 3, 3, 3, 3, 3, 3, 3, 3} (19)
В настоящем изобретении информационная часть Hd матрицы H контроля четности в разделе A, где описана структура кода массива, может быть задана на основе структуры кода массива согласно последовательности степеней, заданной уравнением (18).
Фиг.7 - это схема, иллюстрирующая пример информационной части Hd матрицы контроля четности, сгенерированной в способе, описанном в разделе A, в котором максимальная степень переменного узла равна 15. В структуре матрицы, проиллюстрированной на Фиг.7, столбцы и строки представляют столбцы подматрицы и строки подматрицы соответственно. Цифры, обозначающие столбцы и строки, представляют циклический сдвиг столбцов подматрицы и строк подматрицы. Каждая из цифр составлена из подматрицы pхp, в которой p=89. Поэтому матрицы информационной части Hd, сгенерированная в вышеуказанном способе, становится матрицей (dv·p) х (dv·p).
(II) Повышение и структура Hp
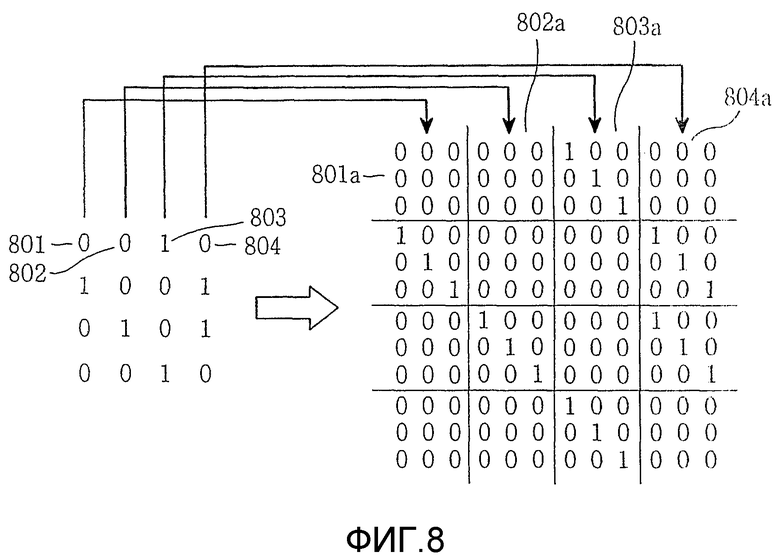
В общем, повышение матрицы относится к способу повышения размера базовой матрицы посредством замены подматрицы для матрицы, имеющей 0 и 1 в конкретной позиции. Это описывается со ссылкой на Фиг.8 Фиг.8 - это схема, иллюстрирующая матрицу 12х12, полученную посредством повышения базовой матрицы 4х4 в способе замены каждого элемента в матрице 4х4 на единичную матрицу 3х3 или нулевую матрицу 3х3.
Как проиллюстрировано на Фиг.8, повышение матрицы формирует квадратную матрицу, имеющую число элементов, равных 0, кратное целевому размеру повышения для элементов 0. Описывается только первая строка. Элементы соответствующих столбцов, размещенных в первой строке, становятся равными {0, 0, 1, 0}, и ссылки с номерами 801, 802, 803 и 804 назначены им соответственно. Из всех элементов три элемента 801, 802 и 804, имеющие значение 0, повышаются до матриц 801a, 802a и 804a 3х3 соответственно. Элемент 803, имеющий значение 1 в первой строке, повышается до единичной матрицы 803a 3х3. Такое же повышение матрицы также применяется к элементам в других строках.
Как описано выше, повышение матрицы, в общем, относится к способу увеличения размера матрицы посредством вставки подматрицы kхk в позицию каждого элемента, составленного из 0 и 1. В общем, матрица циклической перестановки, полученная посредством циклического сдвига каждого столбца единичной матрицы, используется в качестве вставленной матрицы kхk.
Часть Hp четности матрицы H контроля четности, которая должна быть задана в настоящем изобретении, - это обобщенная двухдиагональная матрица, описанная в разделе B. Помимо этого, при условии, что Hd, сгенерированная в способе, описанном в (I) раздела C, составлена из подматриц pхp, Hp также создается посредством повышения обобщенной двухдиагональной матрицы rхr с помощью подматрицы pхp.
Фиг.9 - это схема, иллюстрирующая матрицу Hp четности, составленную посредством повышения матрицы на подматрицу циклической перестановки pхp. Далее приводится описание повышения матрицы четности со ссылкой на Фиг.9. Матрица, повышенная посредством подматрицы циклической перестановки, удаляет 1, существующие в первой строке 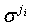 , для линейного временного кодирования кода разреженного контроля четности и линейной независимости между соответствующими строками. Часть Hp четности, созданная способом Фиг.9, становится матрицей (rp)х(rp), и в каждой подматрице
, для линейного временного кодирования кода разреженного контроля четности и линейной независимости между соответствующими строками. Часть Hp четности, созданная способом Фиг.9, становится матрицей (rp)х(rp), и в каждой подматрице 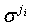 ji означает значение смещения для циклического сдвига столбцов, назначенного каждой подматрице. Далее приводится описание способа предоставления возможности кодирования посредством линейного вычисления.
ji означает значение смещения для циклического сдвига столбцов, назначенного каждой подматрице. Далее приводится описание способа предоставления возможности кодирования посредством линейного вычисления.
Следует заметить, что когда описание, выполненное в разделе "B. Обобщенная двухдиагональная матрица", применяется к части Hp четности, повышенной в способе Фиг.9, каждый столбец подматрицы части Hp четности выбирается только один раз посредством r вычислений, где r является взаимно-простым для f. В этом процессе одного выбора можно выполнить операцию вычисления символа четности, соответствующего конкретному столбцу в столбце подматрицы. Поэтому, чтобы вычислить символы четности, соответствующие всем столбцам в конкретной подматрице 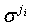 pхp, вычисление символов четности, соответствующих p столбцам, должно быть выполнено только один раз в течение rp вычислений. Далее приводится описание условия для значения смещения подматрицы для удовлетворения вышеупомянутому условию.
pхp, вычисление символов четности, соответствующих p столбцам, должно быть выполнено только один раз в течение rp вычислений. Далее приводится описание условия для значения смещения подматрицы для удовлетворения вышеупомянутому условию.
В структуре матрицы части Hp четности, проиллюстрированной на Фиг.9, отношение между индексом y(1) i строки и индексом x(1) i столбца в подматрице с индексом строки подматрицы = i на диагональной линии задается как:
y(2) i = x(2) i - j2i (mod p) (20)
Отношение между индексом y(2) i строки и индексом x(2) i столбца в подматрице с индексом строки подматрицы = i на диагональной линии смещения задается как:
y(2) i = x(2) i - j2i+1 (mod p) (21)
На основе уравнения (20) и уравнения (21) значение символа Pj0четности может быть получено из первой строки в подматрицах  и
и  с индексом строки подматрицы 0 в соответствии с уравнением (22)
с индексом строки подматрицы 0 в соответствии с уравнением (22)

В уравнении (22) ν0 означает значение частичной контрольной суммы, полученное из первой строки информационной части Hd в матрице контроля четности. Для индекса столбца = j0 индекс строки в подматрице диагональной линии смещения, совместно использующей один и тот же столбец, может быть выражен как:
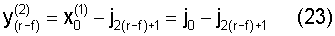
Индекс столбца в подматрице диагональной линии, совместно использующей один и тот же индекс строки, может быть выражен как:
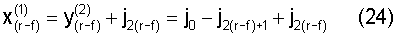
Если r и f уравнения (23) и уравнения (24) являются взаимно-простыми относительно друг друга, все подматрицы в части Hp четности могут быть выбраны только один раз, хотя этот процесс повторяется r раз. Поэтому индекс строки в подматрице, полученный снова посредством повторения вышеупомянутого процесса r раз, может быть выражен как:

В уравнении (25), если повышение выполняется со всеми другими индексами столбцов подматрицы, дисперсия x в индексах столбцов, обновленных для подматрицы 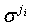 , существующей в диагональной линии, посредством r вычислений, определяется как:
, существующей в диагональной линии, посредством r вычислений, определяется как:

Теорема 2: Все ненулевые элементы в конечном поле Fp = {0, 1, 2,..., p-1}, заданном посредством конкретного простого числа p, всегда могут быть сгенерированы только один раз посредством выполнения над ними меньше, чем p сложений. Если существует k, меньше чем p, удовлетворяющее уравнению (27) для конкретного ненулевого элемента a в конечном поле Fp, чтобы доказать это, допущение о том, что p является простым числом, не выполняется. Поэтому минимальное значение k, удовлетворяющее уравнению (27), это всегда p:

Поэтому все ненулевые элементы a в конечном поле Fр могут быть сгенерированы посредством выполнения их сложения меньше p раз. Из теоремы 2, если дисперсия индекса столбца конкретной подматрицы 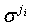 , обновленной посредством r линейных вычислений, не равна 0, когда j линейных вычислений повторяются всего p раз, символы четности для индексов столбцов p могут быть сгенерированы. Таким образом, все символы четности rp могут быть сгенерированы. Т.е. условие уравнения (28) удовлетворяется:
, обновленной посредством r линейных вычислений, не равна 0, когда j линейных вычислений повторяются всего p раз, символы четности для индексов столбцов p могут быть сгенерированы. Таким образом, все символы четности rp могут быть сгенерированы. Т.е. условие уравнения (28) удовлетворяется:

Можно обобщить символы четности, соответствующие всем столбцам в подматрице, посредством повторения r вычислений уравнения (28) p раз. Помимо этого, символы четности, соответствующие конкретному столбцу в каждой из подматриц (r-1), существующих на диагональной линии, могут быть сгенерированы поочередно в ходе r вычислений. Поэтому следует отметить, что символы четности, имеющие rp различных индексов столбцов, могут быть сгенерированы только один раз посредством rp линейных вычислений.
Процесс генерирования матрицы части Hp четности в вышеописанном способе описан со ссылкой на Фиг.10. Фиг.10 - это блок-схема последовательности операций, иллюстрирующая способ генерирования матрицы части четности согласно предпочтительному варианту осуществления настоящего изобретения.
На этапе 1000 индексу n вычисления символов четности присваивается значение 0, чтобы сгенерировать матрицу части четности. После этого на этапе 1002 сумма ν0 информационных символов рассчитывается согласно структуре матрицы информационной части Hd для первого столбца в подматрице с индексом столбца подматрицы = 0, а символу Pioчетности для первой строки в соответствующий подматрице присваивается значение ν0. На этапе 1004 индексу x(1) 0 столбца для символа четности, существующего в подматрице с индексом столбца подматрицы = 0 на диагональной линии части Hp четности, задается начальное значение j0.
После определения символа Pioчетности для первой строки посредством вычисления суммы ν0 информационных символов согласно структуре матрицы информационной части Hd и инициализации индекса столбца процедура переходит к этапу 1006. На этапе 1006 для конкретного индекса x(1) i столбца индекс y(2) i+(r-f) строки в подматрице, существующей на диагональной линии смещения, совместно использующей один и тот же столбец, вычисляется как:
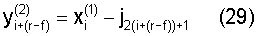
Далее на этапе 1008 индекс x(1) i+(r-f) столбца в подматрице, существующей на диагональной линии, имеющий тот же индекс строки, что и индекс y(2) i+(r-f) строки на диагональной линии смещения, рассчитывается как:

На этапе вычисляется сумма ν(2) i+(r-f) информационных символов, существующих в строке с индексом y(2) i+(r-f) строки в подматрице с индексом i+(r-f) строки подматрицы.
Затем на этапе 1012 символ  четности, соответствующий индексу
четности, соответствующий индексу  строки, рассчитывается с помощью уравнения (31):
строки, рассчитывается с помощью уравнения (31):
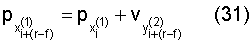
Далее на этапе 1014 n увеличивается на 1. На этапе 1016 индекс строки подматрицы обновляется, как показано ниже:
i = i + (r - 2f) (32)
На этапе 1018 определяется, равно ли n rp. Т.е. на этапе 1018 определяется, завершено ли кодирование. Если на этапе 1018 определено, что n равно rp, процедура заканчивается, определяя, что кодирование завершено. Тем не менее, если на этапе 1018 определено, что n не равно rp, процедура возвращается к этапу 1006 и повторяет последующие этапы, чтобы непрерывно выполнять кодирование.
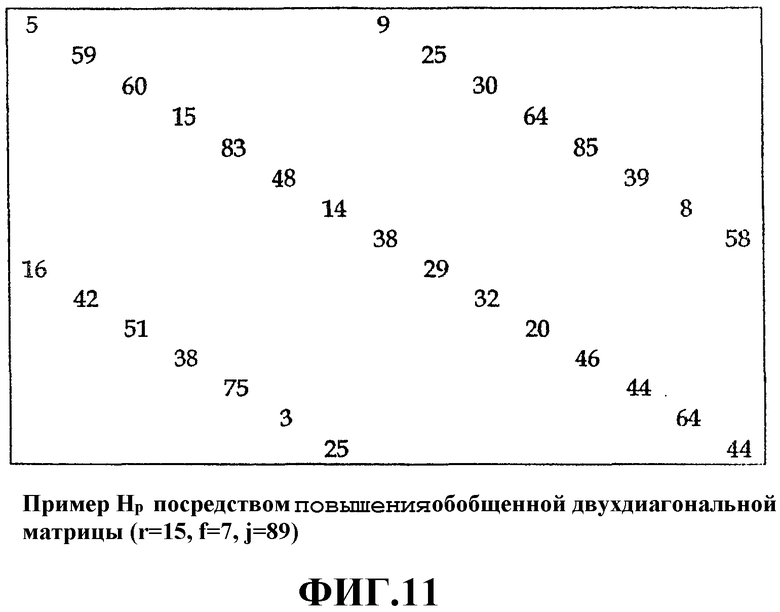
В вышеописанном процессе следует отметить, что все вычисления индексов - индекса строки подматрицы и индекса строки - означают вычисление по модулю p, и вычисления с нижними и верхними индексами в процессе вычисления индексов также означают вычисление по модулю p. Добавление в процесс вычисления символов четности или информационных символов - это вычисление по модулю 2. Пример Hp, сгенерированной так, чтобы удовлетворять этому условию, проиллюстрирован на Фиг.11. Значения цифр, проиллюстрированных на Фиг.11, означают значения смещения подматриц.
(III) Общая структура H
Матрица H контроля четности для кода разреженного контроля четности, которая должна быть задана в настоящем изобретении, задается посредством деления матрицы на информационную часть Hd и часть четности Hp и их конкатенации для систематического кодирования. Генерирование информационной части Hd и части Hp четности выполняется в способе, описанном в разделе (I) и разделе (II), и сгенерированная информационная часть Hd и часть Hp четности становится матрицей (dv·p)х(dv·p) и матрицей (rp)х(rp), соответственно. При этом dv означает максимальную степень переменного узла, существующую в нерегулярном коде разреженного контроля четности, p означает размерность подматрицы, а r означает размерность базовой матрицы, заданной до повышения части Hp четности. Поэтому r должно быть равно dv для конкатенации.
Легко можно понять, что в информационной части Hd и части Hp четности матрицы отсутствует цикл длины 4. Кроме того, можно легко понять, что если диагональному смещению f части Hp четности присвоено значение, аппроксимирующее r/2, отсутствует цикл длины 4 между столбцом подматрицы информационной части Hd, где вес столбца меньше r/2, и частью Hp четности. Тем не менее, в случае столбцов, имеющих максимальную степень переменного узла в качестве веса информационной части Hd, возможен случай, при котором существуют столбцы части Hp четности и цикл длины 4. Если значение смещения подматрицы части Hp четности выполнено надлежащим образом, можно исключить цикл длины 4 из используемых во всей матрице H контроля четности посредством простого удаления.
2. Производительность кода LDPC
До сих пор приводилось описание структуры матрицы контроля четности для задания нерегулярного кода разреженного контроля четности со скоростью 1/2, который может легко подвергаться систематическому кодированию посредством линейных вычислений. Матрица контроля четности, заданная в главе 1, делится на информационную часть и часть четности, чтобы сгенерировать символы четности кодового слова согласно предоставленным информационным символам. Матрица информационной части создается таким образом, чтобы вес каждого столбца в структуре матрице, основанной на структуре кода массива, имел степень, аппроксимирующую оптимальное нерегулярное распределение степеней переменного узла, а матрицы части четности создается посредством повышения обобщенной двухдиагональной структуры матрицы с помощью подматрицы, имеющей случайное смещение. При этом переменный узел со степенью 2 всегда назначается столбцам части четности.
Далее приводится описание производительности кода разреженного контроля четности, созданного посредством матрицы контроля четности, заданной в описании выше. Для этого сначала приводится описание алгоритма декодирования и экспериментального окружения для оценки производительности кода разреженного контроля четности.
A. Итеративное декодирование распространения убежденности
Код разреженного контроля четности, заданный посредством матрицы контроля четности MxN, может быть выражен посредством графа множителей, состоящего из M контрольных узлов и N переменных узлов. Обобщая процесс обновления сообщений в контрольном узле со степенью dc и переменном узле со степенью dv в логарифмической области, обновление сообщений в контрольном узле может быть выражено как уравнение (33), обновление сообщений в переменном узле может быть выражено как уравнение (34), а коэффициент логарифмического правдоподобия (LLR) может быть выражен как уравнение (35):
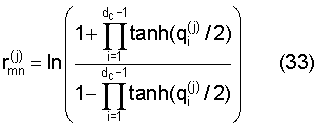
где r(j) mn - это сообщение от контрольного узла m переменному узлу n на j-ой итерации, а q(j) i - это перекомпонованное сообщение, случайное для контрольного узла m с q0 (j) = qmn (j) на j-ой итерации.
В уравнении (33) r(j) mn - это значение, полученное в j-ом итеративном процессе декодирования в полуитеративном процессе декодирования, и оно означает сообщение, доставленное из контрольного узла m в переменный узел n. Помимо этого, q(j) i означает сообщение, доставленное из переменного узла i в контрольный узел m в j-ом итеративном процессе декодирования. При этом i означает значение, полученное посредством перекомпоновки переменных узлов, соединенных с контрольным узлом m, от 0 до dc-1. Поэтому для i=0 это означает переменный узел n.

где q(j) mn - это сообщение от переменного узла n контрольному узлу m на j-ой итерации, а q(0) mn - это первоначальное сообщение от времени доступности канала. ri (j) - это перекомпонованное сообщение, случайное для переменного узла n с r0 (j) =rmn (j) на j-ой итерации.
В уравнении (34) q(j+1) mn - это значение, полученное в j-ом итеративном процессе декодирования, и оно означает сообщение, доставленное из переменного узла n контрольному узлу m. При этом r(j) i означает сообщение, доставленное из контрольного узла i переменному узлу n в j-ом итеративном процессе декодирования, а i означает значение, полученное посредством перекомпоновки контрольных узлов, соединенных с переменным узлом n, от 0 до dv-2. Поэтому для i=0 это означает контрольный узел m.

где ln (j) - это вывод LLR закодированного символа n на j-ой итерации, а ln (0) - это первоначальный вывод LLR от времени доступности канала.
В уравнении (35)  означает значение LLR, заданное для переменного узла n в j-ом итеративном процессе декодирования.
означает значение LLR, заданное для переменного узла n в j-ом итеративном процессе декодирования.
Далее приводится описание итеративного процесса декодирования распространения убежденности с помощью процессов уравнений (33)-(35). Фиг.12 - это блок-схема последовательности операций, иллюстрирующая итеративный процесс декодирования распространения убежденности с помощью уравнений (33)-(35).
Фиг.12 иллюстрирует процесс декодирования принятого сообщения в приемном устройстве. Поэтому первоначальное сообщение переменного узла n для принятого сообщения задается как время доступности канала n-ного символа принятого кодового слова, и это может быть выражено как:
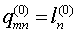
В уравнении (36) 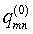 означает начальное значение первоначально определенного сообщения переменного узла, а
означает начальное значение первоначально определенного сообщения переменного узла, а 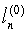 означает начальное значение LLR для первоначального заданного переменного узла. На этапе 1200 первоначальное сообщение задается как время доступности канала n-ного символа принятого кодового слова, как показано в уравнении (36). Кроме того, счетчик итераций сброшен до нуля. Поэтому на этапе 1202 сообщение контрольного узла обновляется в способе, заданном уравнением (33). На этапе 1204 переменный узел и коэффициент логарифмического правдоподобия обновляются. Сообщение переменного узла обновляется в способе уравнения (34), коэффициент логарифмического правдоподобия обновляется в способе уравнения (35).
означает начальное значение LLR для первоначального заданного переменного узла. На этапе 1200 первоначальное сообщение задается как время доступности канала n-ного символа принятого кодового слова, как показано в уравнении (36). Кроме того, счетчик итераций сброшен до нуля. Поэтому на этапе 1202 сообщение контрольного узла обновляется в способе, заданном уравнением (33). На этапе 1204 переменный узел и коэффициент логарифмического правдоподобия обновляются. Сообщение переменного узла обновляется в способе уравнения (34), коэффициент логарифмического правдоподобия обновляется в способе уравнения (35).
После того, как контрольный узел, переменный узел и коэффициент логарифмического правдоподобия обновлены в вышеописанном процессе, значение обновленного коэффициента правдоподобия проходит жесткий процесс принятия решений на этапе 1206. После этого на этапе 1208 выполняется контроль четности для принятого сообщения на основе жестко полученного решения. Если результат контроля четности имеет значение 0, означающее, что декодирование было успешно выполнено, декодирование заканчивается на этапе 1216. Тем не менее, если результат контроля четности не имеет значения 0, на этапе 1210 определяется, достигла ли итерация заранее определенного числа итераций. Если на этапе 1210 определено, что итерация достигла заранее определенного числа итераций, выполняется процесс ошибки декодирования на этапе 1214, определяя, что хотя декодирование выполнено дополнительно, существует очень маленькая вероятность того, что декодирование проведено успешно. Тем не менее, если на этапе 1210 определено, что итерация не достигла заранее определенного числа итераций, счетчик итераций увеличивается на 1 на этапе 1212, и процедура возвращается к этапу 1202.
B. Моделирующее окружение
Экспериментальное окружение для оценки производительности кода разреженного контроля четности, созданного посредством матрицы контроля четности, заданной в настоящем изобретении, проиллюстрировано в таблице 1.
- Смещение (f) в Hp = 7
- Размер кадра = 435 (p=29), 795 (p=53), 1545 (p=103), 3855 (p=257)
- Бинарная противофазная передача сигналов по каналу AWGN
- Итеративное декодирование распространения убежденности
- Моделирование с плавающей запятой
- Максимальное число итераций = 160
- Прекращение по контролю четности на каждой итерации
- Оценка частоты ошибок по кадрам (FER) и частоты ошибок по информационным битам (BER)
Для удобства настоящее изобретение ограничивает кодовую скорость кода разреженного контроля четности до 1/2. Тем не менее, структура матрицы контроля четности кода разреженного контроля четности для поддержки различных кодовых скоростей может быть описана как способ повышения схемы, предложенной в настоящем изобретении, согласно кодовой скорости. Максимальной степени переменного узла присваивается значение 15 на графе множителей кода разреженного контроля четности посредством матрицы контроля четности, заданной в настоящем изобретении, чтобы достичь отличной производительности и предотвратить увеличение числа аппаратных средств в реализации. Смещению f в матрице части Hp четности присвоено значение 7, чтобы просто удалить цикл длины 4 из матрицы контроля четности способом, описанным в (III) раздела C. Размеру кадра кода разреженного контроля четности, моделируемому в настоящем изобретении, присваивается значение, аналогичное размеру пакета кодера (EP), заданному в стандарте cdma2000 1xEV-DV, так чтобы производительность кода разреженного контроля четности сравнивалась с производительностью турбодекодера, используемого в настоящее время в стандарте cdma2000 1xEV-DV. В процессе декодирования турбокода для сравнения производительности используется алгоритм log-MAP, а максимальное число итераций ограничено 8.
Максимальное число итераций итеративного декодера распространения убежденности для кода разреженного контроля четности равно 160, учитывая тот факт, что скорость сходимости кода разреженного контроля четности относительно низка в общей методике эволюции плотности. Для экспериментов с декодером выполнено моделирование с плавающей запятой, выражающее внешнюю информацию и информацию LLR в вещественных значениях. В процессе обновления контрольного узла, чтобы не допустить переполнения функции (p(x) = -log(tanh(|x|/2), значение p(x) ограничено 20 для x при |x| <10-8. Декодер для кода разреженного контроля четности выполняет контроль четности на каждой итерации и принимает результат проверки четности в качестве критерия прекращения, так чтобы не было обнаружено ошибок в процессе контроля четности. Тем не менее, когда ошибка происходит фактически, декодер классифицирует дефектный кадр как кадр, имеющий нераспознанную ошибку. В завершение, частота ошибок по кадрам и частота ошибок по битам используются в качестве показателей для оценки производительности кода разреженного контроля четности, разработанного в настоящем изобретении. Ошибка по кадрам/битам учитывается только в том случае, когда ошибка возникает в информационных символах. Далее приводится описание производительности кода разреженного контроля четности, моделируемого в вышеописанном моделирующем окружении.
C. Результаты моделирования
Фиг.13A - это схема, иллюстрирующая пример матрицы информационной части Hd для n=870 и p=29, Фиг.13B - это схема, иллюстрирующая пример матрицы части Hp четности для n=870 и p=29, а Фиг.13C - это график моделирования результатов, иллюстрирующий сравнение кода разреженного контроля четности и турбокода.
Матрица информационной части и матрица части четности, проиллюстрированные на Фиг.13A и 13B, составлены в вышеописанном способе согласно настоящему изобретению и фактически две матрицы конкатенируются перед кодированием. Далее приводится описание условий для случая, когда производительность, проиллюстрированная на Фиг.13C, доступна. Для сравнения производительности двух способов кодирования производительность для случая, когда размер пакета кодера (EP) стандарта cdma2000 1xEV-DV равен 408 и кодовая скорость равна 1/2, показана одновременно. Как проиллюстрировано на Фиг.13C, следует понимать, что для небольшого размера блока производительность турбокода, используемого в стандарте cdma2000 1xEV-DV, немного больше производительности кода разреженного контроля четности, предлагаемого в настоящем изобретении, в показателях частоты ошибок по кадрам (FER) и частоты ошибок по битам (BER). Это показывает, что структура матрицы контроля четности, задающая код разреженного контроля четности, заданный в настоящем изобретении, не является оптимизированной структурой в показателях производительности декодирования кодового слова с небольшим размером.
Т.е. следует отметить, что когда размер кодированного блока кода разреженного контроля четности небольшой, чтобы код разреженного контроля четности демонстрировал более оптимальную производительность по сравнению с существующим известным турбокодом, операция оптимизации матрицы должна быть выполнена дополнительно. Тем не менее, показано, что код разреженного контроля четности превосходит турбокод в показателях производительности кодового слова с большим размером блока.
Таблица 2 иллюстрирует среднее число итераций по каждому Eb/No для n=870. Согласно таблице 2, хотя максимум 160 итераций выполняется с данным кодом разреженного контроля четности, фактический результат декодирования показывает, что можно получить достаточную производительность только с помощью меньше 10 итераций, учитывая высокий SNR за 20 итераций.
Фиг.14A - это схема, иллюстрирующая пример матрицы информационной части Hd для n=1590 и p=53, Фиг.14B - это схема, иллюстрирующая пример матрицы части Hp четности для n=1590 и p=53, а Фиг.14C - это график моделирования результатов, иллюстрирующий сравнение кода разреженного контроля четности и турбокода.
Матрица информационной части и матрица части четности, проиллюстрированные на Фиг.14A и 14B, составлены в вышеописанном способе согласно настоящему изобретению и фактически две матрицы конкатенируются перед кодированием.
Далее приводится описание условий для случая, когда производительность, проиллюстрированная на Фиг.14C, доступна. Для сравнения производительности двух способов кодирования производительность для случая, когда размер пакета кодера (EP) стандарта cdma2000 1xEV-DV равен 792 и кодовая скорость равна 1/2, показана одновременно. Следует отметить на Фиг.14C, что по мере того, как размер блока кода разреженного контроля четности растет, код разреженного контроля четности становится практически аналогичен существующему турбокоду по частоте ошибок по кадрам. Тем не менее, код разреженного контроля четности по-прежнему хуже существующего турбокода по частоте ошибок по битам. Это обусловлено тем, что турбокод ниже, чем код разреженного контроля четности, в показателе отношения ошибок по битам, имеющихся в дефектном кадре турбокода. Т.е. турбокод ниже, чем код разреженного контроля четности по BER/FER для одного Eb/No. В данном случае это означает, что турбокод ниже, чем код разреженного контроля четности, по среднему числу ошибок по битам, имеющихся в дефектном кадре. Тем не менее, в фактической системе беспроводной связи, использующей гибридный запрос на автоматическую повторную передачу (ARQ), поскольку более предпочтительно, чтобы производительность FER была выше, чем производительность BER, из Фиг.14C можно сделать вывод, что для n=1590 код разреженного контроля четности согласно настоящему изобретению равен по производительности турбокоду, используемому в стандарте cdma2000 1xEV-DV.
Таблица 3 иллюстрирует среднее число итераций по каждому Eb/No для n=1590. По мере того, как размер блока растет, среднее число итераций становится немного больше, чем значение в таблице 2. Тем не менее, следует понимать, что при достаточно высоком SNR достаточно высокая производительность может быть получена за меньше чем 20 итераций.
Фиг.15A - это схема, иллюстрирующая пример матрицы информационной части Hd для n=3090 и p=103, Фиг.15B - это схема, иллюстрирующая пример матрицы части Hp четности для n=3090 и p=103, а Фиг.15C - это график моделирования результатов, иллюстрирующий сравнение кода разреженного контроля четности и турбокода.
Матрица информационной части и матрица части четности, проиллюстрированные на Фиг.15A и 15B, составлены в вышеописанном способе согласно настоящему изобретению и фактически две матрицы конкатенируются перед кодированием.
Далее приводится описание условий для случая, когда производительность, проиллюстрированная на Фиг.15C, доступна. Для сравнения производительности двух способов кодирования производительность для случая, когда размер пакета кодера стандарта cdma2000 1xEV-DV равен 1560 и кодовая скорость равна 1/2, показана одновременно. Следует отметить на Фиг.15C, что по мере того, как размер блока кода разреженного контроля четности растет, код разреженного контроля четности превосходит существующий турбокод с аналогичным размером по частоте ошибок по кадрам. Хотя код разреженного контроля четности по-прежнему хуже существующего турбокода по частоте ошибок по битам, как проиллюстрировано на Фиг.14C, разница между ними значительно уменьшена, близко аппроксимируя производительность турбокода.
Таблица 4 иллюстрирует среднее число итераций по каждому Eb/No для n=3090. По мере того, как размер блока растет, среднее число итераций становится немного больше, чем значение в таблице 2. Тем не менее, следует понимать, что при достаточно высоком SNR достаточно высокая производительность может быть получена за меньше чем 20 итераций.
Фиг.16A - это схема, иллюстрирующая пример матрицы информационной части Hd для n=7710 и p=257, Фиг.16B - это схема, иллюстрирующая пример матрицы части Hp четности для n=7710 и p=257, Фиг.16C - это график моделирования результатов, иллюстрирующий сравнение кода разреженного контроля четности и турбокода, а Фиг.16D - это график моделирования результатов для кода разреженного контроля четности согласно дисперсии в числе итераций.
Матрица информационной части и матрица части четности, проиллюстрированные на Фиг.16A и 16B, составлены в вышеописанном способе согласно настоящему изобретению и фактически две матрицы конкатенируются перед кодированием.
Далее приводится описание условий для случая, когда производительность, проиллюстрированная на Фиг.16C, доступна. Для сравнения производительности двух способов кодирования производительность для случая, когда размер пакета кодера стандарта cdma2000 1xEV-DV равен 3864 и кодовая скорость равна 1/2, показана одновременно. Следует отметить на Фиг.16C, что когда размер блока кода разреженного контроля четности становится очень большим, код разреженного контроля четности значительно превосходит существующий турбокод с аналогичным размером по производительности. В частности, следует понимать, что в случае турбокода с длиной кадра 3864, используемого в стандарте cdma2000 1xEV-DV, и частота ошибок по кадрам, и частота ошибок по битам имеют минимальный уровень ошибок при высоком SNR. Тем не менее, отмечено, что в случае кода разреженного контроля четности, заданного в настоящем изобретении, этот минимальный уровень ошибок не возникает. Эта производительность очень выгодна для системы связи, использующей H-ARQ. Следовательно, можно отметить, что код разреженного контроля четности, заданный в настоящем изобретении, значительно превосходит по производительности турбокод, используемый в существующем стандарте. Таблица 5 иллюстрирует среднее число итераций по каждому Eb/No для n=7710.
В таблице 5 по мере того, как размер блока кода разреженного контроля четности растет, среднее число итераций увеличивается с высокой скоростью по сравнению со значениями таблицы 4. Т.е. код разреженного контроля четности, поддерживающий максимальный размер кадра, аналогичный размеру, заданному в стандарте cdma2000 1xEV-DV, требует 20 или более итеративных декодирований даже при высоком SNR. Поэтому, чтобы показать оптимальную производительность с минимальной задержкой, необходимо изучать производительность декодера LDPC согласно числу итераций.
Фиг.16C - это схема, иллюстрирующая доступную производительность FER/BER кода разреженного контроля четности, имеющего структуры, показанные на Фиг.16A и 16B, в которых максимальное число итераций ограничено 40, 80, 120 и 160. В отличие от этого, если максимальное число итераций ограничено 40, 80 и 120, возникает небольшое ухудшение производительности. Тем не менее, за исключением случая, когда максимальное число итераций ограничено 40, ухудшение производительности незначительное. Поэтому, хотя максимальное число итераций ограничено около 80, проблема ухудшения производительности не существенна. В частности, когда размер блока меньше этого, ухудшение производительности, вызываемое ограничением максимального числа итераций до 80, дополнительно уменьшается, так что становится игнорируемым. Поэтому код разреженного контроля четности, предлагаемый в настоящем изобретении, может получать достаточную производительность при декодировании, если максимальному числу итераций присвоено значение примерно 80 при допущении, что максимальный размер блока составляет 7710.
3. Заключение
Настоящее изобретение задает код разреженного контроля четности, допускающий обеспечение эффективного кодирования и получение отличной производительности декодирования только для кодовой скорости = 1/2. С этой целью настоящее изобретение разделяет матрицу контроля четности, задающую код разреженного контроля четности, на две части и задает часть, соответствующую информации по кодовому слову в матрице контроля четности, использующей структуру кода массива, вес столбца которой больше 2. Помимо этого, настоящее изобретение задает часть, соответствующую четности кодового слова в матрице контроля четности, в качестве обобщенной двухдиагональной матрицы, веса столбцов которой все равны 2. Матрица контроля четности, заданная таким образом, генерирует нерегулярный код разреженного контроля четности, максимальная степень переменного узла которого dv=15, в котором порог безошибочности составляет 0,9352 в канале AWGN, посредством методики эволюции плотности, основанной на гауссовой аппроксимации. Это показывает производительность, аппроксимирующую пропускную способность канала Шэннона до 0,5819 дБ для кода со скоростью 1/2.
На основе того факта, что доступно линейное кодирование, после того, как матрица четности разработана в случайной схеме без рассмотрения возможности фактического линейного кодирования, отличный код разреженного контроля четности, аппроксимирующий порог Шэннона до 0,5819 дБ или ближе, может быть сгенерирован. В этом случае процесс кодирования становится усложненным, затрудняя фактическую реализацию. Поскольку обеспечение линейного кодирования выступает в качестве одного ограничивающего условия для матрицы контроля четности, задающей код разреженного контроля четности, матрица контроля четности должна иметь произвольную структуру. Поэтому возможность демонстрации отличной производительности ниже, чем возможность матрицы контроля четности, произвольно заданной без учета линейного кодирования. Таким образом, применение настоящего изобретения демонстрирует относительно хорошую производительность с учетом линейного кодирования. Т.е. настоящее изобретение показывает относительно хорошую производительность несмотря на ограничение матрицы контроля четности вследствие линейного кодирования.
Чтобы продемонстрировать отличную производительность декодирования, размер кодового слова увеличивается и максимальная степень переменного узла увеличивается соответственно при задании распределения степеней матрицы контроля четности, делая возможным создание кода разреженного контроля четности, имеющего производительность, аппроксимирующую ограничение по пропускной способности Шэннона. Тем не менее, в этом случае, поскольку увеличение максимальной степени переменного узла увеличивает сложность декодера при декодировании, оно не может вносить вклад в фактическую реализацию. Поэтому то, что такая сложность декодера допустима, означает, что максимальная степень переменного узла задается в реализации.
Код разреженного контроля четности посредством матрицы контроля четности, заданной в настоящем изобретении, имеет обобщенную двухдиагональную матрицу, в которой часть четности кодового слова в матрице контроля четности повышена посредством циклической перестановки единичной матрицы pxp. Поэтому он может быть просто закодирован посредством простых линейных вычислений. Помимо этого, когда производительность декодирования посредством итеративного распространения убежденности сравнивалась с производительностью декодирования турбокода, используемого в стандарте cdma2000 1xEV-DV, было доказано посредством моделирования, что более низкая частота ошибок по кадрам может быть получена для аналогичного размера кадра. В частности, по сравнению с турбокодом код разреженного контроля четности согласно настоящему изобретению имеет более низкую частоту ошибок по кадрам, и когда он используется вместе с методикой Hybrid-ARQ, он выступает в качестве точки преимущества. Поэтому код разреженного контроля четности, заданный в настоящем изобретении, может быть просто закодирован посредством простых линейных вычислений. Кроме того, в реализации декодера процессы контрольных узлов и процессоры переменных узлов реализованы параллельно в строках и столбцах соответствующих подматриц, тем самым предоставляя возможность быстрого декодирования.
В коде разреженного контроля четности, заданном в настоящем изобретении, можно просто проверить, что отсутствует цикл длины 4 в графе множителей, задающем код разреженного контроля четности, согласно характеристике компоновки подматриц, составляющих матрицу контроля четности.
Как описано выше, применение настоящего изобретения может обеспечивать производительность, аналогичную или превосходящую производительность турбо-декодера, и, в частности, может генерировать код разреженного контроля четности, допускающий уменьшение частоты ошибок по кадрам. Помимо этого, код разреженного контроля четности согласно настоящему изобретению может уменьшать сложность декодирования.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО И СПОСОБ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ БЛОЧНОГО КОДА РАЗРЕЖЕННОГО КОНТРОЛЯ ЧЕТНОСТИ | 2005 |
|
RU2348103C2 |
| КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ LDPC ПАКЕТОВ ПЕРЕМЕННЫХ РАЗМЕРОВ | 2008 |
|
RU2443053C2 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И УСТРОЙСТВО СВЯЗИ | 2017 |
|
RU2740154C1 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ КОДИРОВАНИЯ/ДЕКОДИРОВАНИЯ КОДА РАЗРЕЖЕННОГО КОНТРОЛЯ ЧЕТНОСТИ С ПЕРЕМЕННОЙ ДЛИНОЙ БЛОКА | 2005 |
|
RU2341894C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ | 2005 |
|
RU2370886C2 |
| АППАРАТУРА, СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И АППАРАТУРА СВЯЗИ | 2018 |
|
RU2758968C2 |
| УСТРОЙСТВО И СПОСОБ ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ БЛОЧНЫХ КОДОВ С НИЗКОЙ ПЛОТНОСТЬЮ КОНТРОЛЯ ПО ЧЕТНОСТИ С ПЕРЕМЕННОЙ СКОРОСТЬЮ КОДИРОВАНИЯ | 2005 |
|
RU2354045C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПРОСТРАНСТВЕННО-ВРЕМЕННОГО КОДИРОВАНИЯ В СИСТЕМЕ БЕСПРОВОДНОЙ СВЯЗИ С ИСПОЛЬЗОВАНИЕМ КОДОВ ПРОВЕРКИ НА ЧЕТНОСТЬ С НИЗКОЙ ПЛОТНОСТЬЮ, ПОДДЕРЖИВАЮЩИХ ПОДНЯТИЕ | 2004 |
|
RU2327287C2 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И УСТРОЙСТВО СВЯЗИ | 2017 |
|
RU2740151C1 |
| УСТРОЙСТВО И СПОСОБ КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ БЛОЧНОГО КОДА ПРОВЕРКИ НА ЧЕТНОСТЬ С НИЗКОЙ ПЛОТНОСТЬЮ С ПЕРЕМЕННОЙ ДЛИНОЙ БЛОКА | 2005 |
|
RU2369008C2 |


















Изобретение относится к способу кодирования данных. Технический результат заключается в повышении эффективности кодирования. Устройство и способ кодирования кодов разреженного контроля четности (LDPC). Способ генерирования кода разреженного контроля четности, формируемого из матрицы информационной части и матрицы части четности, содержит этапы преобразования матрицы информационной части в структуру кода массива и назначения последовательности степеней каждому столбцу подматрицы; расширения двухдиагональной матрицы, соответствующей матрице части четности, таким образом, чтобы значение смещения между диагоналями имело случайное значение; повышения нормализованной двухдиагональной матрицы; определения значения смещения для циклического сдвига столбцов в каждой подматрице повышенной нормализованной двухдиагональной матрицы; и определения символа четности, соответствующего столбцу в матрице контроля четности. 8 з.п. ф-лы, 25 ил., 5 табл.
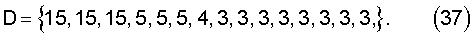
(a) определяют символ четности первой строки в подматрице с индексом 0 столбца подматрицы на диагональной линии матрицы части четности;
(b) задают индекс строки в подматрице символа четности, идентичного определенному символу четности в индексе столбца в подматрице в подматрице на диагональной линии смещения, имеющей такой же индекс столбца подматрицы, что и индекс столбца подматрицы заданного символа четности;
(c) определяют символ четности, имеющий такой же индекс строки в заданной подматрице в подматрице на диагональной линии, имеющей такой же индекс строки подматрицы, что и индекс строки подматрицы на диагональной линии смещения; и
(d) многократно выполняют этапы (b) и (с) до тех пор, пока создание матрицы четности не будет завершено.

где  означает индекс строки в подматрице с индексом i столбца подматрицы на диагональной линии смещения, х(l) i означает индекс столбца в подматрице с индексом i столбца, существующем на диагональной линии, а j2(i+(r-j))+l означает значения смешения для циклического сдвига столбцов подматрицы с индексом i столбца подматрицы на диагональной линии смещения.
означает индекс строки в подматрице с индексом i столбца подматрицы на диагональной линии смещения, х(l) i означает индекс столбца в подматрице с индексом i столбца, существующем на диагональной линии, а j2(i+(r-j))+l означает значения смешения для циклического сдвига столбцов подматрицы с индексом i столбца подматрицы на диагональной линии смещения.

где 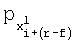 означает символ четности, соответствующий x(l) i+(r-f),
означает символ четности, соответствующий x(l) i+(r-f),  означает символ четности, соответствующий индексу столбца х(l) i, a
означает символ четности, соответствующий индексу столбца х(l) i, a 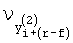 означает сумму информационных символов, существующих в строке с индексом
означает сумму информационных символов, существующих в строке с индексом  строки в подматрице с индексом i+(r-f) столбца подматрицы.
строки в подматрице с индексом i+(r-f) столбца подматрицы.
| СИСТЕМА ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 1991 |
|
RU2007042C1 |
| US 2002042899 A1, 11.04.2002 | |||
| US 2003152158 A1, 14.08.2003 | |||
| US 2003079171 A1, 24.04.2003. | |||
Авторы
Даты
2007-10-20—Публикация
2004-10-14—Подача