Уровень техники изобретения
Область техники, к которой относится изобретение
Настоящее изобретение относится к устройству и способу кодирования и декодирования блочных кодов LDPC (разреженного контроля четности).
Описание предшествующего уровня техники
В связи наиболее существенной проблемой является эффективная и надежная передача данных по каналу. Мобильная мультимедийная система связи следующего поколения, которая исследуется в настоящее время, требует системы связи с высокой скоростью передачи, допускающей обработку и передачу различной информации, например, изображения или данных радиовещания, помимо предыдущей, ориентированной на голос услуги. Следовательно, необходимо повышать эффективность системы с помощью использования схемы кодирования канала, подходящей для системы.
Передача данных неизбежно страдает от ошибок из-за шума, помех и замирания в соответствии с условиями канала, таким образом вызывая потерю большого количества информации. Для того, чтобы уменьшить потерю информации, в настоящее время используются различные схемы контроля ошибок, которые основаны частично на характеристиках канала для улучшения тем самым надежности мобильной системы связи. Самая элементарная схема исправления ошибок использует коды исправления ошибок.
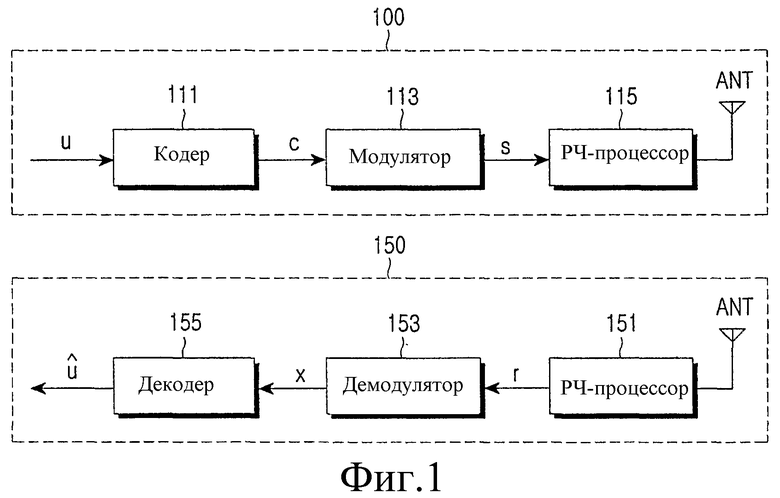
Фиг.1 - это схема, иллюстрирующая приемопередатчик в традиционной системе мобильной связи. Ссылаясь на фиг.1, в передатчике сообщение 'u' передачи кодируется посредством кодера 101 с помощью предопределенной схемы кодирования перед передачей по каналу. Закодированный символ 'c', кодируемый посредством кодера 101, модулируется посредством модулятора 103, используя предопределенную схему модуляции, и модулированный сигнал 's' передается приемнику по каналу 105.
В приемнике принятый сигнал 'r' является искаженным сигналом, в котором сигнал 's', переданный передатчиком, смешивается с несколькими шумами соответственно условиям канала. Принятый сигнал 'r' демодулируется посредством демодулятора 107 с помощью схемы демодуляции, соответствующей схеме модуляции, используемой в модуляторе 103 передатчика, и демодулированный сигнал 'x' декодируется посредством декодера 109 с помощью схемы декодирования, соответствующей схеме кодирования, используемой в кодере 101 передатчика. Сигнал, декодируемый посредством декодера 109, обозначается посредством û.
Соответственно, существует необходимость высокоэффективных кодера и декодера канала для возможности приемнику восстанавливать сигнал 'u', переданный посредством передатчика без ошибки. В частности, когда канал 105 является беспроводным каналом, ошибки, вызванные каналом, должны рассматриваться более серьезно. Декодер 109 приемника может оценивать сообщение передачи на основе данных, принятых по каналу 105.
В связи со стремительным развитием системы мобильной связи существует потребность в технологии, допускающей возможность передачи данных в беспроводной сети, имеющих большую емкость, приближающуюся к таковой в беспроводной сети. Так как существует потребность в быстродействующей высокопроизводительной системе связи, допускающей обработку и передачу мультимедийных данных, например, изображения и данных радиовещания помимо ориентированной на голос службы, то необходимо увеличивать эффективность передачи в системе с помощью использования подходящей схемы кодирования канала для улучшения производительности системы. Тем не менее, система мобильной связи неизбежно страдает от ошибок, которые обычно происходят из-за шума, помех и замирания соответственно условиям канала во время передачи данных. Как описано выше, возникновение ошибок вызывает потерю информационных данных.
Для того, чтобы уменьшить потерю информационных данных из-за возникновения ошибок, возможно улучшать надежность мобильной системы связи посредством использования методик контроля ошибок. Методика, использующая коды исправления ошибок, является наиболее распространенной используемой методикой контроля ошибок. В настоящий момент будет сделано описание турбокодов и кодов LDPC (разреженного контроля четности), которые являются обычными кодами исправления ошибок.
Хорошо известно, что турбокод превосходит в повышении производительности сверточный код, традиционно используемый для исправления ошибок во время высокоскоростной передачи данных. Турбокод является выгодным в том, что он может эффективно исправлять ошибку, вызванную шумами, сформированными в канале передачи, таким образом повышая надежность передачи данных.
Код LDPC может быть декодирован с использованием итеративного алгоритма декодирования на основе алгоритма суммы-произведения в графе множителей. Так как декодер использует для кода LDPC итеративный алгоритм декодирования, основанный на алгоритме суммы-произведения, то он менее сложен по отношению к декодеру для турбокода. Кроме того, декодер для кода LDPC легко реализовать с помощью декодера параллельной обработки, по сравнению с декодером для турбокода.
Теорема Шэннона о кодировании канала показывает, что надежная связь возможна только при скорости передачи данных, не превышающей пропускную способность канала связи. Тем не менее, теорема Шэннона о кодировании канала не предложила подробного способа кодирования и декодирования для канала для поддержания скорости передачи данных до предела пропускной способности канала связи. Хотя случайный код, имеющий очень большой размер блока, показывает производительность, приближающуюся к пределу пропускной способности канала связи по теореме Шэннона о кодировании канала, фактически невозможно реализовать способ декодирования с максимумом апостериорной вероятности (MAP) или максимально правдоподобный (ML) из-за его сложной вычислительной нагрузки.
Турбокод был предложен Берроу, Главо и Титимаджшима в 1993 г. и имеет более высокую производительность, приближающуюся к пределу пропускной способности канала связи согласно теореме Шэннона о кодировании канала. Предложение турбокода инициировало активное исследование по итеративному декодированию и графическому представлению кодов, и коды LDPC, предложенные Галлагером в 1962 г., вновь находятся в центре внимания исследований. Циклы существуют в графе множителей турбокода и кода LDPC, и хорошо известно, что итеративное декодирование в графе множителей кода LDPC, где существуют циклы, является условно оптимальным. Также экспериментально доказано, что код LDPC имеет прекрасную производительность по итеративному декодированию. Известно, что код LDPC имеет самую высокую производительность, которую когда-либо показывает производительность, имеющая разность лишь около 0,04 [дБ] при пределе пропускной способности канала связи по теореме Шэннона о кодировании канала при частоте появления ошибочных битов (BER) 10-5, используя размер блока 107. Кроме того, хотя код LDPC, определенный в поле Галуа (GF) c q>2, т.е. GF(q), увеличивает сложность в своем декодировании, он является превосходящим по своей производительности двоичный код. Тем не менее, не предусмотрено удовлетворительное теоретическое описание успешного декодирования посредством итеративного алгоритма декодирования для кода LDPC, определенного в GF(q).
Код LDPC, предложенный Галлагером, определяется посредством матрицы контроля четности, в которой основные элементы имеют значение 0 и второстепенные элементы, т.е. элементы, не имеющие значение 0, имеют значение 1. Например, код LDPC (N, j, k) является линейным блочным кодом, имеющим длину блока N, и определяется матрицей разреженного контроля четности, в которой каждый столбец имеет j элементов, имеющих значение 1, каждый ряд имеет k элементов, имеющих значение 1, и все элементы за исключением элементов, имеющих значение 1, имеют значение 0.
Код LDPC, в котором вес каждого столбца в матрице контроля четности фиксируется на 'j' и вес каждой строки в матрице контроля четности фиксируется на 'k', как изложено выше, называется "регулярным кодом LDPC". В этом документе "вес" относится к количеству элементов, имеющих ненулевое значение среди элементов, включенных в порождающую матрицу и матрицу контроля четности. В отличие от обычного кода LDPC, код LDPC, в котором вес каждого столбца в матрице контроля четности и вес каждой строки в матрице контроля четности не являются зафиксированными, называется "нерегулярным кодом LDPC". Общеизвестно, что нерегулярный код LDPC является более высоким по производительности по отношению к регулярному коду LDPC. Тем не менее, в случае нерегулярного кода LDPC, так как вес каждого столбца и вес каждой строки в матрице контроля четности не зафиксированы, т.е. нерегулярны, то вес каждого столбца в матрице контроля четности и вес каждой строки в матрице контроля четности должны быть должным образом установлены для того, чтобы гарантировать отличную производительность.
Фиг.2 - это схема, иллюстрирующая матрицу контроля четности общего кода LDPC (8, 2, 4). Ссылаясь на фиг.2, матрица H контроля четности кода LDPC (8, 2, 4) имеет 8 столбцов и 4 строки, в которой вес каждого столбца зафиксирован на 2 и вес каждой строки зафиксирован на 4. Так как вес каждого столбца и вес каждой строки в матрице контроля четности являются регулярными, код LDPC (8, 2, 4), проиллюстрированный на фиг.2, становится регулярным кодом LDPC.
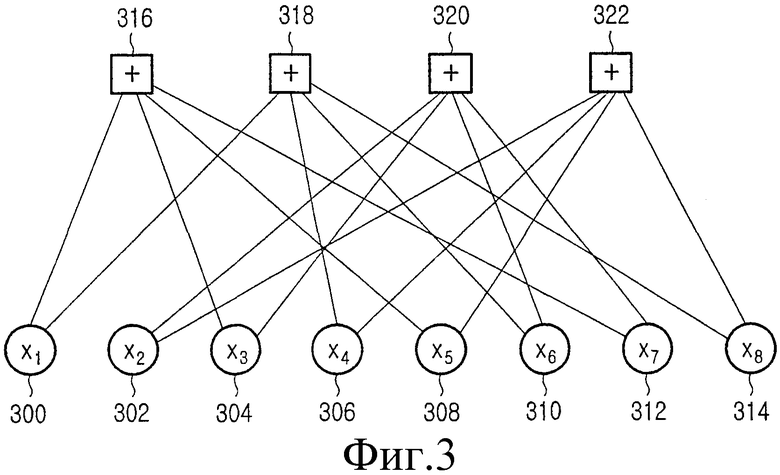
Фиг.3 является схемой, иллюстрирующей граф множителей кода LDPC (8, 2, 4) на фиг.2. Ссылаясь на фиг.3, граф множителей кода LDPC (8, 2, 4) включает в себя 8 переменных узлов x1 300, x2 302, x3 304, x4 306, x5 308, x6 310, x7 312 и x8 314 и 4 контрольных узла 316, 318, 320 и 322. Когда элемент, имеющий значение 1, т.е. ненулевое значение существует в точке, где i-тая строка и j-тый столбец матрицы контроля четности кода LDPC (8, 2, 4) пересекаются друг с другом, создается ветвь между переменным узлом xi и контрольным j-тым узлом.
Так как матрица контроля четности кода LDPC имеет очень небольшой вес, то возможно выполнять декодирование посредством итеративного декодирования, даже в блочном коде, имеющем относительно большой размер, который показывает производительность, приближающуюся к пределу пропускной способности канала связи по теореме Шэннона о кодировании канала, например, турбокода, в то время, как размер блока блочного кода постоянно увеличивается. Мак Кей и Нил доказали, что итеративный процесс декодирования кода LDPC, используя схему диаграммы потока, приближается к итеративному процессу декодирования турбокода по производительности.
Для того, чтобы сформировать высокопроизводительный код LDPC, должны выполняться следующие условия.
(1) Циклы в графе множителей кода LDPC должны быть приняты во внимание.
Термин "цикл" относится к петле, образованной гранями, соединяющими переменные узлы с контрольными узлами в графе множителей кода LDPC, и длина цикла определяется как число граней, составляющих петлю. Цикл петли означает, что число граней, соединяющих переменные узлы с контрольными узлами, составляющих петлю в графе множителей кода LDPC, является большим. В противоположность этому, короткий цикл означает, что число граней, соединяющих переменные узлы с контрольными узлами, составляющих петлю в графе множителей кода LDPC, является небольшим.
Как только циклы в графе множителей кода LDPC становятся длиннее, относительный уровень производительности кода LDPC возрастает. Т.е. когда длинные циклы формируются в графе множителей кода LDPC, становится возможным предотвращать ухудшение производительности, например, минимальный уровень ошибки, происходящей, когда слишком много циклов с небольшой длиной существуют в графе множителей кода LDPC.
(2) Эффективное кодирование кода LDPC должно быть принято во внимание
Код LDPC сложно подвергнуть кодированию в реальном масштабе времени, по сравнению со сверточным кодом или турбокодом из-за высокой сложности его кодирования. Для того, чтобы уменьшить сложность кодирования кода LDPC, предложен код RA (повторного накопления). Тем не менее, код RA также имеет предел в уменьшении сложности кодирования кода LDPC. Следовательно, эффективное кодирование кода LDPC должно быть принято во внимание.
(3) Распределение степеней в графе множителей кода LDPC должно быть принято во внимание.
В целом нерегулярный код LDPC превосходит в производительности регулярный код LDPC, так как граф множителей нерегулярного кода LDPC имеет различные степени. Термин "степень" относится к числу граней, соединенных с переменными узлами и контрольными узлами в графе множителей кода LDPC. Дополнительно, фраза "распределение степеней" в графе множителей кода LDPC относится к соотношению числа узлов, имеющих конкретную степень к общему числу узлов. Кроме того, Ричардсоном доказано, что код LDPC, имеющий конкретное распределение степеней, является превосходящим по производительности.
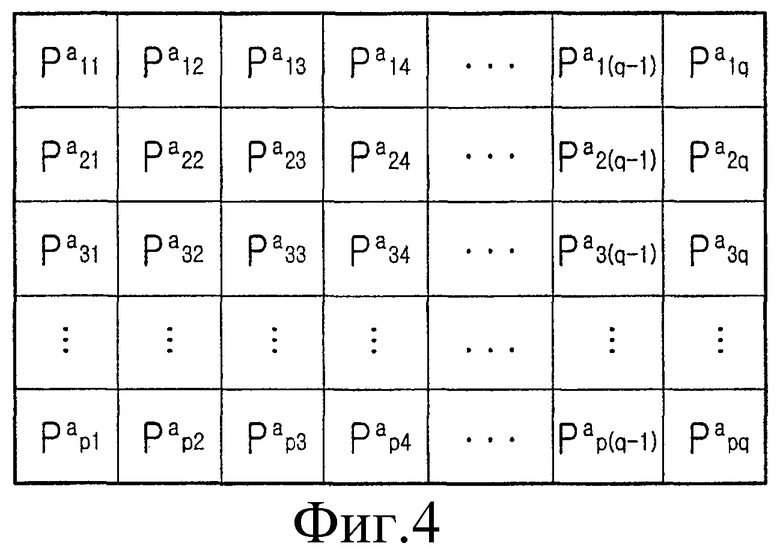
Фиг.4 - это схема, иллюстрирующая матрицу контроля четности для общего блочного кода LDPC. Тем не менее, до того, как будет дано описание фиг.4, следует заметить, что блочный код LDPC является новым кодом LDPC, что эффективное кодирование и эффективное хранение и повышение производительности матрицы контроля четности были приняты во внимание и блочный код LDPC является кодом LPDC, расширенным посредством обобщения структуры регулярного кода LDPC.
Ссылаясь на фиг.4, матрица контроля четности блочного кода LDPC разделена на множество частных блоков, и матрица перестановок сопоставлена с каждым из частных блоков. На фиг.4 'P' представляет матрицу перестановок, имеющую размер NsxNs и верхний индекс (или показатель степени)apq матрицы P перестановок является либо 0pqs-l, либо apq=. Кроме того, 'p' указывает, что соответствующая матрица перестановок располагается в p-той строке частных блоков матрицы контроля четности, и 'q' указывает, что соответствующая матрица перестановок располагается в q-том столбце частных блоков матрицы контроля четности. То есть 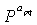 представляет матрицу перестановок, расположенную в частном блоке, где p-тая строка и q-тый столбец матрицы контроля четности, содержащей множество частных блоков, пересекают друг друга. Более конкретно, 'p' и 'q' представляют собой число строк и число столбцов частных блоков, сопоставленных, соответственно, информационной части в матрице контроля четности.
представляет матрицу перестановок, расположенную в частном блоке, где p-тая строка и q-тый столбец матрицы контроля четности, содержащей множество частных блоков, пересекают друг друга. Более конкретно, 'p' и 'q' представляют собой число строк и число столбцов частных блоков, сопоставленных, соответственно, информационной части в матрице контроля четности.
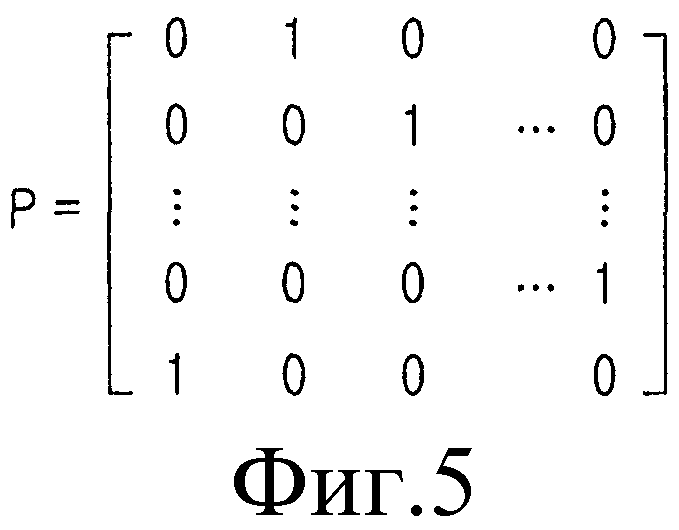
Фиг.5 является схемой, иллюстрирующей матрицу P перестановок по фиг.4. Как проиллюстрировано на фиг.5, матрица перестановок P является квадратной матрицей, имеющей размер NsxNs и каждый из столбцов Ns, включенный в матрицу P перестановок, имеет вес 1 и каждая из строк Ns, включенная в матрицу P перестановок, также имеет вес 1. В этом документе, хотя размер матрицы P перестановок и выражен как NsxNs, он будет также выражаться и как Ns, так как матрица P перестановок является квадратной матрицей.
На фиг.4 матрица P перестановок с верхним индексом apq=0, т.е. матрица перестановок P° представляет собой единичную матрицу INsxNs и матрица P перестановок с верхним индексом apq=, т.е. матрица Р перестановок представляет собой нулевую матрицу. В данном документе INsxNs представляет собой единичную матрицу размером NsxNs.
В полной матрице контроля четности блочного кода LDPC, проиллюстрированного на фиг.4, так как общее количество строк - Nsxp и общее количество столбцов - Nsxq (для p), когда полная матрица контроля четности кода LDPC имеет полный ранг, скорость кода может быть выражена уравнением (1) независимо от размера частных блоков.

Если apq для всех p и q, то матрицы перестановок, соответствующие частным блокам, не являются нулевыми матрицами и частные блоки составляют регулярный код LDPC, в котором значение веса каждого столбца и значение веса каждой строки в каждой из матриц перестановок, соответствующих частным блокам, являются p и q соответственно. В данном документе каждая из матриц перестановок, соответствующих частным блокам, будет указываться как "частная матрица".
Так как зависимые строки (p-1) существуют в матрице контроля четности, скорость кодирования выше, чем скорость кодирования, вычисленная посредством уравнения (1). В блочном коде LDPC, если положение веса первой строки каждой из частных матриц, включенных в полную матрицу контроля четности, определено, то положения весов остающихся строк (Ns-1) может быть определено. Следовательно, требуемый размер памяти сводится к 1/NS, по сравнению с тем, когда веса нерегулярно выбираются для хранения информации во всей матрице контроля четности.
Как описано выше, термин "цикл" относится к петле, образованной гранями, соединяющими переменные узлы с контрольными узлами в графе множителей кода LDPC, и длина цикла определяется как число граней, составляющих петлю. Длинный цикл означает, что число граней, соединяющих переменные узлы с контрольными узлами, составляющих петлю в графе множителей кода LDPC, является большим. Когда циклы в графе множителей кода LDPC становятся длиннее, относительный уровень производительности кода LDPC возрастает. В противоположность, когда циклы в графе множителей кода LDPC становятся короче, возможность исправления ошибок кода LDPC возрастает, так как происходит ухудшение производительности, например, минимального уровня ошибки. То есть, когда существует много циклов небольшой длины в графе множителей кода LDPC, информация на конкретном узле, принадлежащая циклу небольшой длины, начиная от него, возвращается после небольшого числа итераций. Когда число итераций возрастает, информация возвращается к соответствующему узлу чаще, так, что информацию нельзя правильно обновить, тем самым ухудшая возможность исправления ошибок кода LDPC.
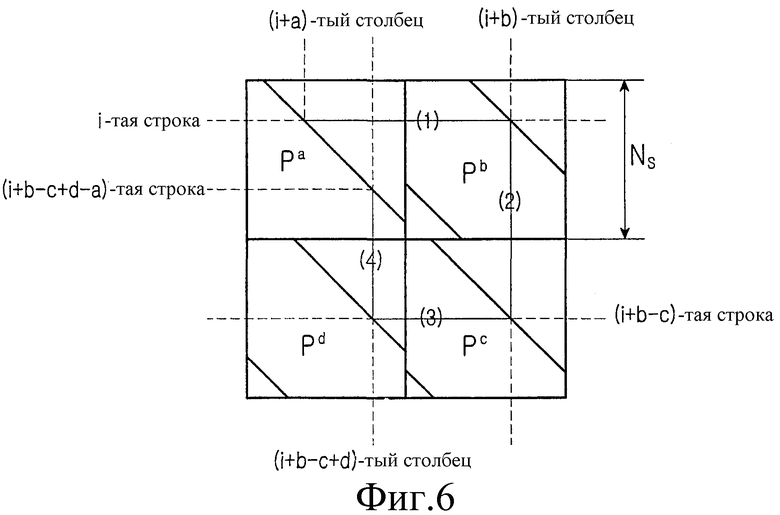
Фиг.6 является схемой, иллюстрирующей структуру цикла блочного кода LDPC, матрица контроля четности которого включает в себя 4 частных матрицы. Тем не менее, до того, как дано описание фиг. 6, следует заметить, что блочный код LDPC является новым кодом LDPC, что эффективное кодирование и эффективное хранение и повышение производительности матрицы контроля четности были приняты во внимание. Блочный код LDPC является также кодом LDPC, расширенным посредством обобщения структуры регулярного кода LDPC.
Матрица контроля четности блочного кода LDPC, проиллюстрированная на фиг.6, включает в себя 4 частных блока. Диагональная линия представляет собой положение, где располагаются элементы, имеющие значение 1 и части, отличные от частей на диагонали, представляют собой положения, в которых расположены элементы, имеющие значение 0. Кроме того, 'P' представляет собой ту же самую матрицу перестановок, что и матрица перестановок, описанная в связи с фиг.5.
Для того, чтобы проанализировать структуру цикла блочного кода LDPC, проиллюстрированного на фиг.6, элемент, имеющий значение 1, расположенный в i-той строке частной матрицы Pa, определяется как опорный элемент и элемент, имеющий значение 1, расположенный в i-той строке, будет указываться как "отметка-0". В данном документе "частная матрица" будет относится к матрице, соответствующей частному блоку. Отметка 0 расположена в (i+a)-томстолбце частной матрицы Pa.
Элемент, имеющий значение 1 в частной матрице Pb, расположенный в той же строке, что и нулевая отметка, будет указываться как "отметка-1". По той же причине, что и отметка-0, отметка-1 располагается в (i+b)-том столбце частной матрицы Pb.
Элемент, имеющий значение 1 в частной матрице Pc, расположенный в том же столбце, что и отметка-1, будет указываться как "отметка-2". Так как частная матрица Pc является матрицей, полученной посредством сдвига соответствующих столбцов единичной матрицы I вправо относительно модуля Ns на c, отметка-2 располагается в (i+b-c)-той строке частной матрицы Pc.
Кроме того, элемент, имеющий значение 1 в частной матрице Pb, расположенный в той же строке, что и отметка-2, будет упоминаться как "отметка-3". Отметка-3 располагается в (i+b-c+d)-томстолбце частной матрицы Pd.
Элемент, имеющий значение 1 в частной матрице Pa, расположенный в том же столбце, что и отметка-3, будет указываться как "отметка-4". Отметка-4 располагается в (i+b-c+d-a)-тойстроке частной матрицы Pa.
В структуре цикла кода LDPC, проиллюстрированного на фиг.6, если существует цикл длины 4, то отметка-0 и отметка-4 располагаются в том же самом положении. То есть отношение между отметкой-0 и отметкой-4 определяется посредством уравнения (2)
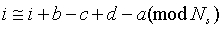 или
или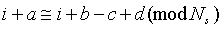
Уравнение (2) может быть перезаписано, как показано в уравнении (3).
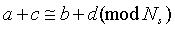
Когда зависимость уравнения (3) выполняется, то формируется цикл диной 4. В общем, когда отметка-0 и отметка-4p сначала идентичны друг другу, то задана зависимость 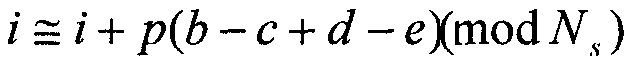 и зависимость, показанная в уравнении (4), выполняется.
и зависимость, показанная в уравнении (4), выполняется.
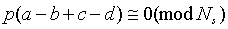
То есть, если положительное целое число, имеющее минимальное значение среди положительных целых чисел, удовлетворяющих уравнению (4) для заданных a, b, c и d, определяется как 'p', то цикл с длиной 4p становится циклом, имеющим минимальную длину в структуре цикла блочного кода LDPC, проиллюстрированного на фиг.6.
Соответственно, как описано выше, для (a-b+c-d)0, если выполняется gcd(Ns, a-b+c-d)=l, тогда p = Ns. Следовательно, цикл длиной 4NS становится циклом с минимальной длиной.
Ниже в данном документе будет использоваться методика Ричардсона-Урбанке, как методика кодирования для блочного кода LDPC. Так как методика Ричардсона-Урбанке используется как методика кодирования, то сложность кодирования может быть минимизирована, поскольку вид матрицы контроля четности становится аналогичным виду полной нижней треугольной матрицы.
Фиг.7 является схемой, иллюстрирующей матрицу контроля четности, имеющей форму, аналогичную той, которую имеет полная нижняя треугольная матрица. Тем не менее, матрица контроля четности, проиллюстрированная на фиг.7, имеет отличную четную часть, чем матрица контроля четности, имеющая форму полной нижней треугольной матрицы.
Ссылаясь на фиг.7, верхний индекс (или показатель степени) apq матрицы P перестановок части информации является либо 0pqs-1, либо apq=. Матрица P перестановок с верхним индексом apq=0, т.е. матрица перестановок P° информационной части представляет собой единичную матрицу INsxNs и матрица P перестановок с верхним индексом apq=, т.е. матрица Р перестановок представляет собой нулевую матрицу. Кроме того, 'p' представляет собой число строк частных блоков, сопоставленных информационной части в матрице контроля четности, и 'q' представляет собой число столбцов частных блоков, сопоставленных информационной части. К тому же, верхние индексы ap, x и y матриц P перестановок, сопоставленных четной части, представляют собой степени матрицы P перестановок. Тем не менее, для удобства различные верхние индексы ap, x и y используются для различия четной части от информационной части. То есть на фиг.7 c 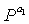 по
по 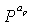 являются также матрицами перестановок и верхние индексы с a1по ap последовательно индексируются по отношению к частным матрицам, расположенным в диагональной части четной части.
являются также матрицами перестановок и верхние индексы с a1по ap последовательно индексируются по отношению к частным матрицам, расположенным в диагональной части четной части.
Кроме того, Px и Py являются также матрицами перестановок и для удобства они индексируются по-разному, чтобы отличать четную часть от информационной части. Если размер блока блочного кода LDPC, имеющего матрицу контроля четности, изображенную на фиг.7, предполагается в размере N, то сложность кодирования блочного кода LDPC линейно возрастает относительно размера блока N(O(N)).
Самой большой проблемой кода LDPC, имеющего матрицу контроля четности по фиг.7, является то, что если размер частного блока определяется как Ns, то формируются Ns контрольных узлов, степень которых всегда 1 в графе множителей блочного кода LDPC. Контрольные узлы со степенью 1 не могут влиять на повышение производительности на основе итеративного декодирования. Следовательно, стандартный нерегулярный код LDPC, основанный на методике Ричардсона-Урбанке, не включает в себя контрольный узел со степенью 1.
Соответственно, матрица контроля четности по фиг.7 будет предполагаться в качестве основной матрицы контроля четности для того, чтобы рассчитать матрицу контроля четности так, что она делает возможным эффективное кодирование, в то же время не включая в себя контрольный узел со степенью 1.
В матрице контроля четности по фиг.7, включающей в себя частные матрицы, выбор частной матрицы является очень важным фактором для повышения производительности блочного кода LDPC, так, что поиск подходящего критерия выбора для частной матрицы также становится очень важным фактором.
Для того, чтобы облегчить способ расчета матрицы контроля четности блочного кода LDPC и способ кодирования блочного кода LDPC, предполагается, что матрица контроля четности, проиллюстрированная на фиг.7, составлена с помощью 6 частных матриц, как проиллюстрировано на фиг.8.
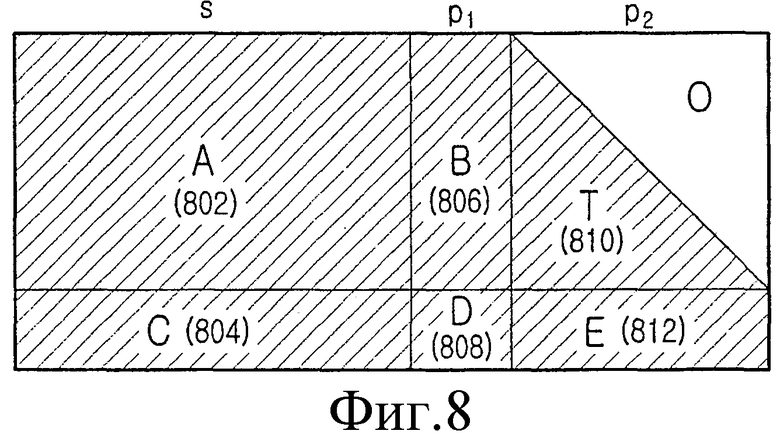
Фиг.8 является схемой, иллюстрирующей матрицу контроля четности по фиг.7, которая разделена на 6 частных блоков. Ссылаясь на фиг.8, матрица контроля четности блочного кода LDPC, проиллюстрированная на фиг.7, разделяется на информационную часть 's', первую четную часть p1 и вторую четную часть p2. Информационная часть 's' представляет часть матрицы контроля четности, сопоставленной с действительным информационным словом во время процесса кодирования блочного кода LDPC, подобно информационной части, описанной в связи с фиг.7, и для удобства информационная часть 's' представляется посредством различных символов ссылки. Первая четная часть p1 и вторая четная часть p2 представляют часть матрицы контроля четности, сопоставленной с фактической четностью во время процесса кодирования блочного кода LDPC, подобно четной части, описанной в связи с фиг.7, и четная часть разделяется на две части.
Частные матрицы A и C соответствуют частным блокам A (802) и C (804) информационной части 's', частные матрицы B и D соответствуют частным блокам B (806) и D (808) первой четной части p1, и частные матрицы T и E соответствуют частным блокам T (810) и E (812) второй четной части p2. Хотя матрица контроля четности разделяется на 7 частных блоков на фиг.8, следует заметить, что так как '0' не является отдельным частным блоком и частная матрица T, соответствующая частному боку T (810) имеет полную нижнюю треугольную форму, область, где располагаются нулевые матрицы на основе диагонального деления, представлена посредством '0'. Процесс упрощения способа кодирования, используя частные матрицы информационной части 's', первую четную часть p1 и вторую четную часть p2, будет описан позже со ссылкой на фиг.10.
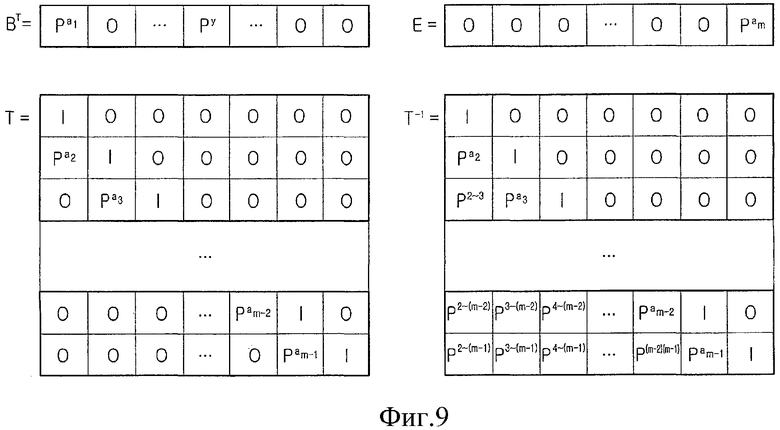
Фиг.9 является схемой, иллюстрирующей транспонированную матрицу частной матрицы B, проиллюстрированной на фиг.8, частной матрицы E, частной матрицы T и обратной матрицы частной матрицы T в матрице контроля четности, проиллюстрированной на фиг.7. Ссылаясь на фиг.9, частная матрица BT представляет собой транспонированную матрицу частной матрицы B и частная матрица T-1 представляет обратную матрицу частной матрицы T. P(k1˜k2) представляет  .
.
Матрицы перестановок, проиллюстрированные на фиг.9, например, 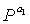 могут являться единичными матрицами. Как описано выше, если показатель степени матрицы перестановок, т.е. a1 является 0, то матрица
могут являться единичными матрицами. Как описано выше, если показатель степени матрицы перестановок, т.е. a1 является 0, то матрица 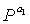 перестановок будет являться единичной матрицей. К тому же, если показатель степени матрицы перестановок, т.е. a1 увеличивается на заранее определенную величину, то матрица перестановок циклически сдвигается на заранее определенную величину, из условия, что матрица
перестановок будет являться единичной матрицей. К тому же, если показатель степени матрицы перестановок, т.е. a1 увеличивается на заранее определенную величину, то матрица перестановок циклически сдвигается на заранее определенную величину, из условия, что матрица 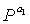 будет являться единичной матрицей.
будет являться единичной матрицей.
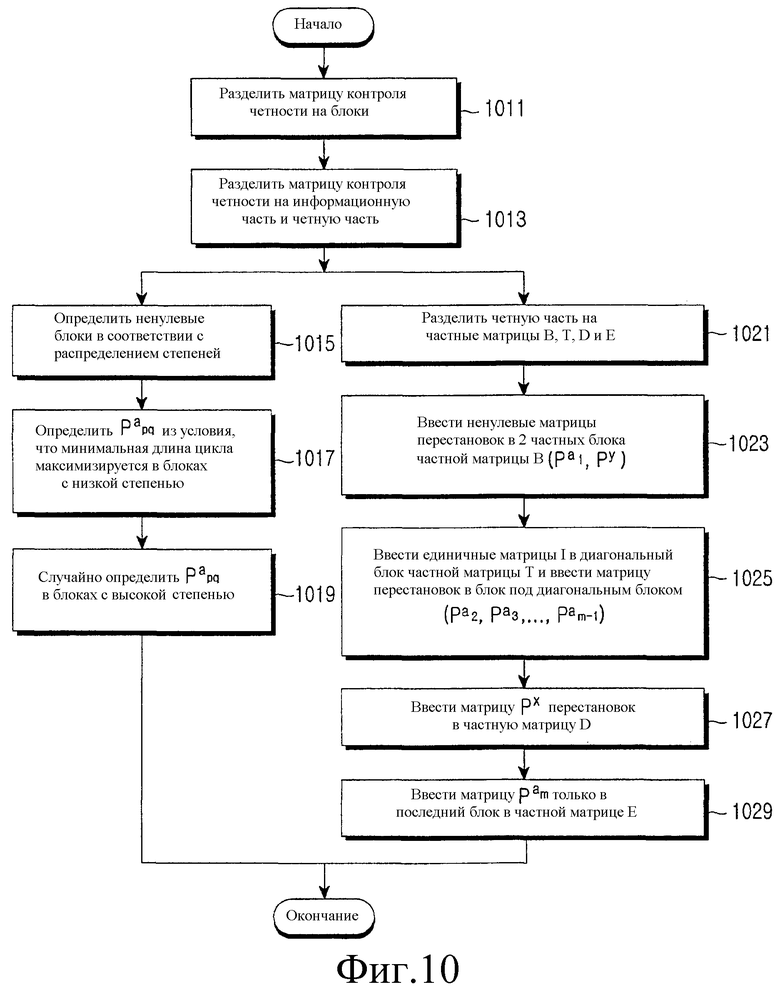
Фиг.10 - это блок-схема последовательности операций способа, иллюстрирующая алгоритм для формирования матрицы контроля четности общего блочного кода LDPC. Тем не менее, до того, как дается описание фиг.10, следует заметить, что для формирования блочного кода LDPC размер кодового слова и скорость кодирования блочного кода LDPC, которые необходимо сформировать, должны быть определены и размер матрицы контроля четности должен определяться согласно определенному размеру кодового слова и скорости кодирования. Если размер кодового слова блочного кода LDPC представляется посредством N и скорость кодирования представляется посредством R, то размер матрицы контроля четности обращается в N(1-R)xN.
Фактически алгоритм для формирования матрицы контроля четности блочного кода LDPC, проиллюстрированного на фиг.10, выполняется только один раз, так как матрица контроля четности первоначально формируется, подходящей для ситуации в системе связи, и после этого используется сформированная матрица контроля четности.
Ссылаясь на фиг.10 на этапе 1011, контроллер разделяет матрицу контроля четности с размером N(1-R)xN на сумму блоков pxq, включающих в себя p блоков по горизонтальной оси и q блоков по вертикальной оси. Так как каждый из блоков имеет размер NsxNs, то матрица контроля четности включает в себя Nsxp строк и Nsxq столбцов. На этапе 1013 контроллер классифицирует блоки pxq, разделенные матрицей контроля четности на информационную часть 's', первую четную часть p1 и вторую четную часть p2.
На этапе 1015 контроллер разделяет информационную часть 's' на ненулевые блоки или ненулевые матрицы и нулевые блоки или нулевые матрицы согласно распределению степеней для гарантирования достаточной производительности блочного кода LDPC. Так как распределение степеней для гарантирования достаточной производительности блочного кода LDPC описано выше, то подробное описание этого будет здесь пропущено.
На этапе 1017 контроллер определяет матрицы 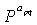 перестановок из условия, что минимальная длина блочного цикла должна быть максимизирована, как описано выше в частях ненулевой матрицы в блоках, имеющих низкую степень среди блоков, определенных согласно распределению степеней для гарантирования достаточной производительности блочного кода LDPC. Матрицы
перестановок из условия, что минимальная длина блочного цикла должна быть максимизирована, как описано выше в частях ненулевой матрицы в блоках, имеющих низкую степень среди блоков, определенных согласно распределению степеней для гарантирования достаточной производительности блочного кода LDPC. Матрицы 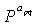 перестановок должны определяться, принимая во внимание блочные циклы информационной части 's', первую четную часть p1 и вторую четную часть p2.
перестановок должны определяться, принимая во внимание блочные циклы информационной части 's', первую четную часть p1 и вторую четную часть p2.
На этапе 1019 контроллер случайно определяет матрицы 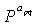 перестановок в частях ненулевой матрицы в блоках, имеющих высокую степень среди блоков, определенных согласно распределению степеней, для гарантирования хорошей производительности блочного кода LDPC и затем заканчивает алгоритм. Даже когда матрицы
перестановок в частях ненулевой матрицы в блоках, имеющих высокую степень среди блоков, определенных согласно распределению степеней, для гарантирования хорошей производительности блочного кода LDPC и затем заканчивает алгоритм. Даже когда матрицы 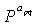 перестановок определяются для использования в частях ненулевой матрицы в блоках, имеющих высокую степень, матрицы
перестановок определяются для использования в частях ненулевой матрицы в блоках, имеющих высокую степень, матрицы 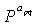 перестановок должны определяться из условия, что минимальная длина блочного цикла максимизируется. Матрицы
перестановок должны определяться из условия, что минимальная длина блочного цикла максимизируется. Матрицы 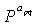 перестановок определяются, принимая во внимание блочные циклы информационной части 's', первую четную часть p1 и вторую четную часть p2. Пример матриц
перестановок определяются, принимая во внимание блочные циклы информационной части 's', первую четную часть p1 и вторую четную часть p2. Пример матриц 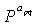 перестановок, расположенных в информационной части 's' матрицы контроля четности, проиллюстрирован на фиг.9.
перестановок, расположенных в информационной части 's' матрицы контроля четности, проиллюстрирован на фиг.9.
На этапе 1021 контроллер разделяет первую часть p1 и вторую четную часть p2 на 4 частных матрицы B, T, D и E. На этапе 1023 контроллер вводит ненулевые матрицы Py и 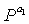 перестановок в 2 частных блока среди частных блоков, включенных в частную матрицу B. Структура для ввода ненулевых матриц Py и
перестановок в 2 частных блока среди частных блоков, включенных в частную матрицу B. Структура для ввода ненулевых матриц Py и 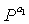 перестановок в 2 частных блока среди частных блоков, составляющих частную матрицу B, описана выше со ссылкой на фиг.9.
перестановок в 2 частных блока среди частных блоков, составляющих частную матрицу B, описана выше со ссылкой на фиг.9.
На этапе 1025 контроллер вводит единичные матрицы I в диагональные частные блоки частной матрицы T и вводит конкретные матрицы перестановок 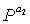 ,
, 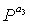 ,...,
,...,  в частные блоки (i, i+1)th под диагональные элементы частной матрицы T. Структура для ввода единичных матриц I в диагональные частные блоки частной матрицы T и ввода конкретных матриц перестановок
в частные блоки (i, i+1)th под диагональные элементы частной матрицы T. Структура для ввода единичных матриц I в диагональные частные блоки частной матрицы T и ввода конкретных матриц перестановок 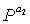 ,
, 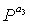 ,...,
,..., 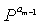 в частные (i, i+1)-тые блоки под диагональные элементы частной матрицы T описана выше со ссылкой на фиг.9.
в частные (i, i+1)-тые блоки под диагональные элементы частной матрицы T описана выше со ссылкой на фиг.9.
На этапе 1027 контроллер вводит матрицу Px перестановок в частную матрицу D. На этапе 1029 контроллер вводит матрицу 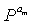 перестановок только в последний частный блок в частной матрице E и затем заканчивает алгоритм. Структура для ввода 2 матриц
перестановок только в последний частный блок в частной матрице E и затем заканчивает алгоритм. Структура для ввода 2 матриц 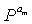 перестановок только в последний частный блок среди частных блоков, составляющих частную матрицу E, описана выше со ссылкой на фиг.9.
перестановок только в последний частный блок среди частных блоков, составляющих частную матрицу E, описана выше со ссылкой на фиг.9.
Как описано выше, известно, что код LDPC вместе с турбокодом обладает серьезным увеличением производительности во время передачи данных на высокой скорости и эффективно исправляет ошибки, вызванные шумами, сформированными в канале передачи, посредством этого увеличивая надежность передачи данных. Тем не менее, код LDPC является невыгодным в терминах скорости кодирования. То есть, так как код LDPC имеет относительно высокую скорость кодирования, то он имеет ограничение в терминах скорости кодирования. Среди кодов LDPC, доступных в настоящее время, основные коды LDPC имеют скорость кодирования 1/2 и только неосновные коды LDPC имеют скорость кодирования 1/3. Ограничение в скорости кодирования оказывает неизбежное влияние на высокоскоростную высокопроизводительную передачу данных.
Хотя распределение степеней, представляющих оптимальные характеристики, может быть вычислено, используя схему эволюции плотности, чтобы реализовать относительно низкую скорость кодирования для кода LDPC, является сложным реализовать код LDPC, имеющий распределение степеней, показывающих оптимальные характеристики из-за различных ограничений, таких как, структура цикла в графе множителей и аппаратная реализация.
Сущность изобретения
Целью настоящего изобретения, следовательно, является предоставление устройства и способа для кодирования и декодирования блочных кодов LDPC (разреженного контроля четности).
Другим аспектом настоящего изобретения является предоставление устройства и способа для кодирования и декодирования блочных кодов LDPC с минимизированной сложностью кодирования в системе мобильной связи.
В соответствии с одним аспектом настоящего изобретения предусматривается способ для кодирования блочного кода LDPC. Способ содержит этапы приема вектора информационного слова и кодирование вектора информационного слова в блочный код LDPC в соответствии с предопределенной порождающей матрицей.
В соответствии с другим аспектом настоящего изобретения предусматривается устройство для кодирования блочного кода LDPC. Устройство содержит кодер для кодирования вектора информационного слова в блочном коде LDPC в соответствии с предопределенной порождающей матрицей; модулятор для модулирования блочного кода LDPC в символе модуляции, используя предопределенную схему модуляции; и передатчик для передачи символа модуляции.
В соответствии с другим дополнительным аспектом настоящего изобретения предусматривается способ декодирования блочного кода LDPC. Способ содержит этапы: прием сигнала; декодирование принятого сигнала, используя матрицу контроля четности, предопределенную в соответствии с длиной блочного кода LDPC, который необходимо декодировать; и обнаружение блочного кода LDPC из декодированного принятого сигнала.
В соответствии с еще одним аспектом настоящего изобретения предусматривается устройство для декодирования блочного кода LDPC. Устройство содержит приемник для приема сигнала; и декодер для декодирования принятого сигнала, используя матрицу контроля четности, предопределенную в соответствии с длиной блочного кода LDPC, который необходимо декодировать; и обнаружение блочного кода LDPC из декодированного принятого сигнала.
Краткое описание чертежей
Вышеуказанная и другие цели, признаки и преимущества настоящего изобретения станут более понятными из последующего подробного описания, рассматриваемого вместе с прилагаемыми чертежами, из которых:
Фиг.1 - это схема, иллюстрирующая приемопередатчик в традиционной системе мобильной связи;
Фиг.2 - это схема, иллюстрирующая матрицу контроля четности для стандартного кода LDPC (8, 2, 4);
Фиг.3 является схемой, иллюстрирующей граф множителей кода LDPC (8, 2, 4), проиллюстрированного на фиг.2;
Фиг.4 - это схема, иллюстрирующая матрицу контроля четности стандартного блочного кода LDPC;
Фиг.5 является схемой, иллюстрирующей матрицу P перестановок, проиллюстрированной на фиг.4;
Фиг.6 является схемой, иллюстрирующей структуру цикла блочного кода LDPC, матрица контроля четности которого включает в себя 4 частных матрицы;
Фиг.7 является схемой, иллюстрирующей матрицу контроля четности, имеющей форму, аналогичную той, которую имеет полная нижняя треугольная матрица;
Фиг.8 является схемой, иллюстрирующей матрицу контроля четности на фиг.7, которая разделена на 6 частных блоков;
Фиг.9 является схемой, иллюстрирующей транспонированную матрицу частной матрицы B, проиллюстрированной на фиг.8, частной матрицы E, частной матрицы T и обратной матрицы частной матрицы T;
Фиг.10 - это блок-схема последовательности операций способа, иллюстрирующая алгоритм формирования матрицы контроля четности стандартного блочного кода LDPC;
Фиг.11 является схемой, иллюстрирующей транспонированную матрицу BT частной матрицы B, частную матрицу D и частную матрицу T среди 6 частных матриц, отделенных от матрицы контроля четности нерегулярного блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения;
Фиг.12 является схемой, иллюстрирующей матрицу F, используемую для формирования матрицы H' в соответствии с вариантом осуществления настоящего изобретения;
Фиг.13 является схемой, иллюстрирующей матрицу контроля четности нерегулярного блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения;
Фиг.14 является схемой, иллюстрирующей порождающую матрицу нерегулярного блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения;
Фиг.15 является схемой, иллюстрирующей процесс кодирования нерегулярного блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения;
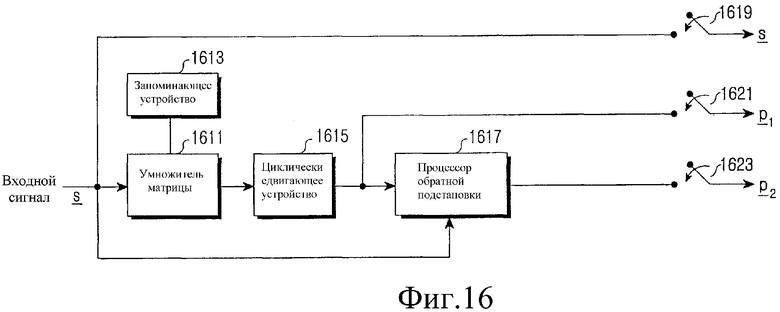
Фиг.16 является схемой, иллюстрирующей внутреннюю структуру устройства кодирования нерегулярного блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения; и
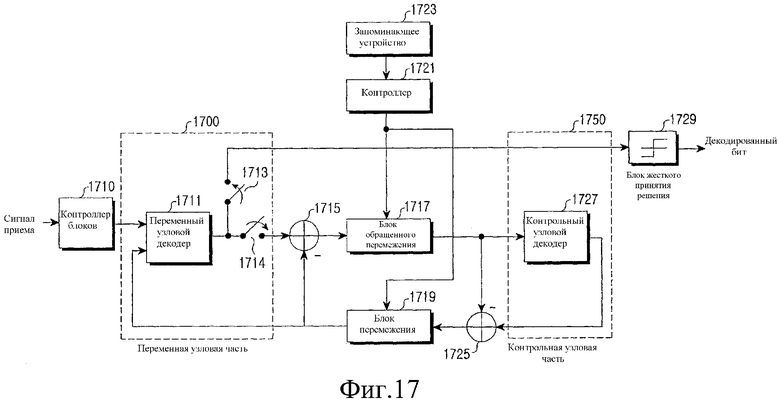
Фиг.17 является схемой, иллюстрирующей внутреннюю структуру устройства декодирования нерегулярного блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения.
Подробное описание предпочтительного варианта осуществления
Предпочтительные варианты осуществления настоящего изобретения далее подробно описаны в данном документе ниже со ссылкой на прилагаемые чертежи. В последующем описании подробное описание известных функций и конфигураций, включенных в материалы настоящей заявки, опущено для краткости.
Настоящее изобретение представляет устройство и способ кодирования и декодирования блочных кодов LDPC, обеспечивающих высокую производительность. То есть настоящее изобретение представляет устройство и способ кодирования и декодирования блочных кодов LDPC, в которых длина минимального цикла в графе множителей максимизируется, сложность кодирования минимизируется и распределение степеней в графе множителей имеет самое лучшее распределение степеней в единицу. Хотя в данном документе не проиллюстрировано отдельно, устройство для кодирования и декодирования блочных кодов LDPC в соответствии с настоящим изобретением может применяться к приемопередатчику, описанному со ссылкой на фиг.1.
Фиг.11 является схемой, иллюстрирующей транспонированную матрицу BT частной матрицы B, частную матрицу D и частную матрицу T из числа 6 частных матриц, отделенных от матрицы контроля четности блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения.
До того, как дается описание фиг.11, следует заметить, что матрица контроля четности имеет структуру частных блоков, описанную в разделе предыдущего уровня техники со ссылкой на фиг.8. То есть матрица контроля четности блочного кода LDPC разделяется на частные блоки для информационной части 's', первой четной части pl и второй четной части p2. Информационная часть 's' представляет часть матрицы контроля четности, сопоставленной с фактическим информационным словом во время процесса кодирования блочного кода LDPC. Первая четная часть p1 и вторая четная часть p2 представляют части матрицы контроля четности, сопоставленные с фактической четностью во время процесса кодирования блочного кода LDPC.
Как проиллюстрировано на фиг.8, информационная часть 's' разделяется на частный блок A и частный блок C, первая четная часть p1 разделятся на частный блок B и частный блок D, вторая четная часть p2 разделяется на частный блок T и частный блок E. Частные матрицы A и C соответствуют частным блокам A и C, частные матрицы B и D соответствуют частным блокам B и D, частные матрицы T и E соответствуют частным блокам T и E.
Ссылаясь на фиг.11, частная матрица B включает в себя две единичные матрицы 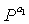 перестановок и нулевые матрицы. Матрица P перестановок является квадратной матрицей с размером NsxNs, в которой вес каждой строки Ns равен 1 и вес каждого столбца равен также 1. Хотя размер матрицы P перестановок выражается как NsxNs, размер матрицы P перестановок, которая является квадратной матрицей, будет выражаться как Ns для удобства.
перестановок и нулевые матрицы. Матрица P перестановок является квадратной матрицей с размером NsxNs, в которой вес каждой строки Ns равен 1 и вес каждого столбца равен также 1. Хотя размер матрицы P перестановок выражается как NsxNs, размер матрицы P перестановок, которая является квадратной матрицей, будет выражаться как Ns для удобства.
В вышеприведенном описании, данном со ссылкой на фиг.9, частная матрица B включает в себя матрицы 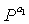 и Px перестановок и нулевые матрицы. В случае стандартного блочного кода LDPC, чтобы удовлетворять равенству ET-1B + D = I, матрицы
и Px перестановок и нулевые матрицы. В случае стандартного блочного кода LDPC, чтобы удовлетворять равенству ET-1B + D = I, матрицы 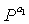 и Px перестановок, отличные от нулевых матриц частной матрицы B, должны быть зафиксированы в положении, как проиллюстрировано на фиг.9, и матрицы
и Px перестановок, отличные от нулевых матриц частной матрицы B, должны быть зафиксированы в положении, как проиллюстрировано на фиг.9, и матрицы 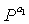 и Px перестановок являются отличными друг от друга. Тем не менее, в настоящем изобретении две матрицы
и Px перестановок являются отличными друг от друга. Тем не менее, в настоящем изобретении две матрицы 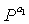 перестановок, отличные от нулевых матриц частной матрицы B, не должны быть зафиксированы в положении, и две матрицы перестановок
перестановок, отличные от нулевых матриц частной матрицы B, не должны быть зафиксированы в положении, и две матрицы перестановок 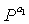 обладают переменным положением и равны друг другу. Частная матрица T имеет единичные матрицы I в двухдиагональной структуре и нулевые матрицы. Частная матрица D включает в себя частную матрицу Px.
обладают переменным положением и равны друг другу. Частная матрица T имеет единичные матрицы I в двухдиагональной структуре и нулевые матрицы. Частная матрица D включает в себя частную матрицу Px.
На фиг.11 верхние индексы aiи x матрицы P перестановок представляют степени матрицы P перестановок.
Хотя две матрицы 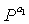 перестановок сопоставляются с транспонированной матрицей BT частной матрицы B и матрица Px перестановок сопоставляется с частной матрицей D на фиг.11 в качестве примера, тот же самый результат может быть достигнут, если матрицы
перестановок сопоставляются с транспонированной матрицей BT частной матрицы B и матрица Px перестановок сопоставляется с частной матрицей D на фиг.11 в качестве примера, тот же самый результат может быть достигнут, если матрицы 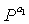 перестановок сопоставляются только с двумя матрицами перестановок среди всего трех матриц перестановок, будучи сопоставленными с транспонированной матрицей BT частной матрицы B и частной матрицей D. То есть, хотя матрица
перестановок сопоставляются только с двумя матрицами перестановок среди всего трех матриц перестановок, будучи сопоставленными с транспонированной матрицей BT частной матрицы B и частной матрицей D. То есть, хотя матрица 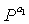 перестановок сопоставляется с любой из двух матриц перестановок, существующих в транспонированной матрице BT частной матрицы B, и матрица
перестановок сопоставляется с любой из двух матриц перестановок, существующих в транспонированной матрице BT частной матрицы B, и матрица 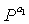 перестановок сопоставляется с матрицей перестановок, существующей в частной матрице D, то может быть достигнут тот же самый результат.
перестановок сопоставляется с матрицей перестановок, существующей в частной матрице D, то может быть достигнут тот же самый результат.
Альтернативно, тот же самый эффект может быть достигнут, даже если матрицы 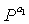 перестановок сопоставляются с двумя из двух матриц перестановок, существующих в транспонированной матрице BT частной матрицы B и матрице перестановок, существующей в частной матрице D.
перестановок сопоставляются с двумя из двух матриц перестановок, существующих в транспонированной матрице BT частной матрицы B и матрице перестановок, существующей в частной матрице D.
Кроме того, на фиг.11 матрица 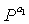 перестановок может быть единичной матрицей, так как если степень матрицы перестановок равна a1=0, то матрица
перестановок может быть единичной матрицей, так как если степень матрицы перестановок равна a1=0, то матрица 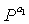 перестановок становится единичной матрицей, как описано выше. К тому же, показатель a1 матрицы перестановок увеличивается на предопределенную величину, матрица перестановок циклически сдвигается на предопределенную величину, так, что матрица
перестановок становится единичной матрицей, как описано выше. К тому же, показатель a1 матрицы перестановок увеличивается на предопределенную величину, матрица перестановок циклически сдвигается на предопределенную величину, так, что матрица 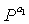 перестановок будет являться единичной матрицей.
перестановок будет являться единичной матрицей.
В случае стандартного блочного кода LDPC нетронутая матрица контроля четности, используемая в декодере, используется как порождающая матрица для кодера. Тем не менее, в случае блочного кода LDPC, предложенного в настоящем изобретении, матрица контроля четности, используемая в декодере, модифицируется до использования ее в качестве порождающей матрицы для кодера, таким образом минимизируя сложность кодирования блочного кода LDPC.
Матрица контроля четности, представленная посредством H, может выражаться, как показано в уравнении (5).
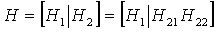
В уравнении (5) H1 обозначает матрицу, сопоставленную с информационным словом, т.е. матрицу, сопоставленную с информационной частью 's' в матрице H контроля четности, и H2 обозначает матрицу, сопоставленную с четностью, т.е. матрицу, сопоставленную с первой четной частью p1 и второй четной частью p2 в матрице H контроля четности. То есть H1 представляет матрицу, включающую в себя частную матрицу A и частную матрицу C, и H2 представляет матрицу, включающую частную матрицу B, частную матрицу T, частную матрицу D и частную матрицу E. Тем не менее, так как схема кодирования, предложенная в настоящем изобретении, не основывается на методике Ричардсона-Урбанке, то предложенная схема кодирования не требует разделения матрицы контроля четности блочного кода LDPC на шесть частных матриц, как в методике Ричардсона-Урбанке. Вместо этого предложенная схема разделяет матрицу контроля четности на матрицу H1, сопоставленную с информационной частью, и матрицы H21 и H22, сопоставленные с первой четной частью и второй четной частью.
Порождающая матрица, предусмотренная модификацией матрицы H контроля четности, используемой в кодере, представляется посредством H', и порождающая матрица H' может выражаться уравнением (6), используя новую матрицу F.
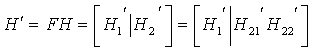
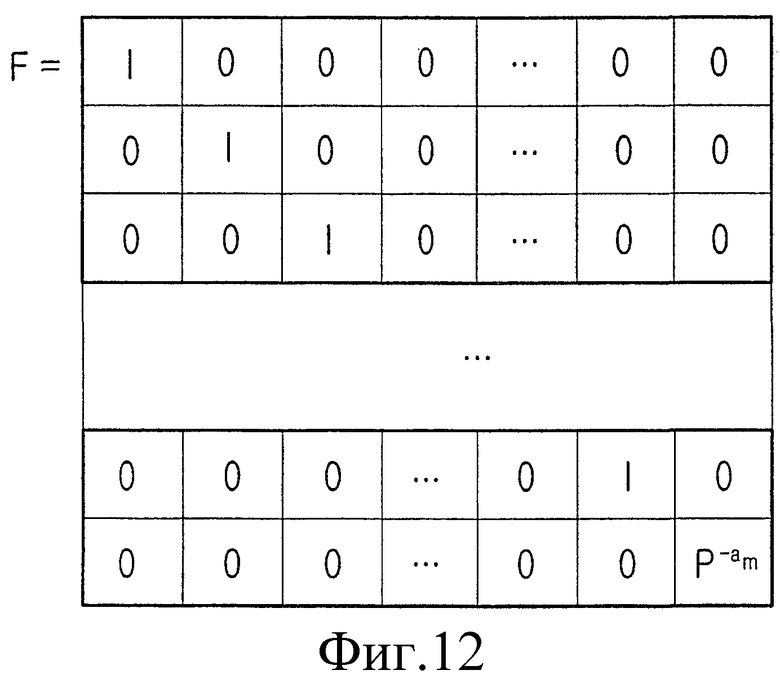
В уравнении (6) F обозначает матрицу с размером (N-K)x(N-K), N обозначает размер блока или длину кодового слова кода и K обозначает длину информационного слова. Матрица F проиллюстрирована на фиг.12 и будет описана позже. Аналогично матрице H контроля четности, описанной со ссылкой на уравнение (5), порождающая матрица H' делится на H1', сопоставленную с информационным словом, и H2', сопоставленную с четностью, и H2' делится на H21', сопоставленную с первой четностью, и H22', сопоставленную со второй четностью.
В порождающей матрице H', показанной в уравнении (6), степени всех ненулевых матриц перестановок, соответствующие последнему увеличению блока на am посредством действия по модулю Ns, H22', сопоставленная со второй четностью, имеет единичные матрицы в двухдиагональной структуре на каждый блок, и все остающиеся матрицы, за исключением единичных матриц, включают в себя нулевые матрицы.
Сейчас будет сделано описание процесса кодирования блочного кода LDPC, используя порождающую матрицу H'.
Вектор c кодового слова блочного кода LDPC может разделяться на вектор s информационного слова, первый вектор 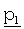 четности и второй вектор
четности и второй вектор  четности. Как описано выше, первый вектор
четности. Как описано выше, первый вектор 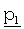 четности сопоставляется с частными блоками B и D и второй вектор
четности сопоставляется с частными блоками B и D и второй вектор 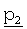 четности сопоставляется с частными блоками T и E.
четности сопоставляется с частными блоками T и E.
Кодирование первого вектора 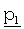 четности достигается применением уравнения (7) и уравнения (8), приведенными ниже. Так как HcT = H'cT = 0, то зависимость уравнения (7) выполняется
четности достигается применением уравнения (7) и уравнения (8), приведенными ниже. Так как HcT = H'cT = 0, то зависимость уравнения (7) выполняется
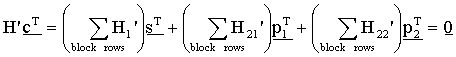
В уравнении (7)  обозначает матрицу NsxK, предусмотренную суммированием строк блоков по всем строкам в каждом блоке в H'. Когда вычисление матрицы, основанное на суммировании по каждому блоку, применяется к матрице контроля четности, описанной со ссылкой на фиг.4, результирующая матрица становится матрицей NsxqN, и каждая матрица NsxNs становится матрицей, заданной суммированием всех матриц перестановок, соответствующих каждому столбцу блока. Например, первая матрица NsxNs имеет значение
обозначает матрицу NsxK, предусмотренную суммированием строк блоков по всем строкам в каждом блоке в H'. Когда вычисление матрицы, основанное на суммировании по каждому блоку, применяется к матрице контроля четности, описанной со ссылкой на фиг.4, результирующая матрица становится матрицей NsxqN, и каждая матрица NsxNs становится матрицей, заданной суммированием всех матриц перестановок, соответствующих каждому столбцу блока. Например, первая матрица NsxNs имеет значение 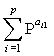 на фиг.4.
на фиг.4.
Аналогично  ,
,  обозначает матрицу NsxNs, обеспеченную суммированием всех строк каждого блока в H21'. Подобным образом
обозначает матрицу NsxNs, обеспеченную суммированием всех строк каждого блока в H21'. Подобным образом  обозначает матрицу Nsx(N-K-Ns), обеспеченную суммированием всех строк каждого блока в H22'.
обозначает матрицу Nsx(N-K-Ns), обеспеченную суммированием всех строк каждого блока в H22'.
Выражение "суммирование строк в матрице в каждом блоке" относится к суммированию строк в частных блоках, включенных в соответствующую матрицу таким способом, что 1-тые строки в частных блоках складываются исключительно друг с другом. Что касается расчета  в уравнении (7), так как H22' имеет двухдиагональную структуру аналогично частной матрице T, проиллюстрированной на фиг.11, матрица, полученная суммированием строк каждого блока, становится нулевой матрицей Nsx(N-K-Ns), в которой все элементы равны 0. Так как
в уравнении (7), так как H22' имеет двухдиагональную структуру аналогично частной матрице T, проиллюстрированной на фиг.11, матрица, полученная суммированием строк каждого блока, становится нулевой матрицей Nsx(N-K-Ns), в которой все элементы равны 0. Так как  становится нулевой матрицей Nsx(N-K-Ns), то элемент
становится нулевой матрицей Nsx(N-K-Ns), то элемент 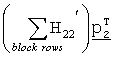 удаляется из уравнения (7), следовательно, матрица H21' может выражаться в уравнении (8) в соответствии со свойством частной матрицы B, описанной со ссылкой на фиг.11
удаляется из уравнения (7), следовательно, матрица H21' может выражаться в уравнении (8) в соответствии со свойством частной матрицы B, описанной со ссылкой на фиг.11
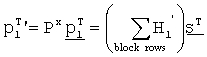
В уравнении (8) 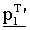 является вектором, полученным циклическим сдвигом
является вектором, полученным циклическим сдвигом 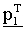 на x, и
на x, и 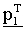 представляет транспонированный вектор первого вектора
представляет транспонированный вектор первого вектора 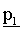 четности.
четности.
Второй вектор p2 четности может быть легко вычислен обратной подстановкой, так как H22' имеет двухдиагональную структуру. Так как блочный код LDPC, отличный от кода RA, имеет блочную структуру, он может выполнять обратную подстановку в каждом блоке, увеличивая скорость вычисления второго вектора 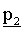 четности.
четности.
Более конкретно, если предполагается, что код RA имеет вектор p=(p1, p2,..., pN-K) четности, то P2 может вычисляться после того, как определяется p1. Подобным образом p3 может вычисляться после того, как определяется p2. Следовательно, биты (N-K) четности могут вычисляться последовательно.
Тем не менее, в процессе кодирования блочного кода LDPC, как предложено в настоящем изобретении, так как частный блок, сопоставленный с четностью порождающей матрицы H', имеет двухдиагональную структуру, то p1 по pNs могут вычисляться одновременно, и следующие Ns бит могут быть вычислены одновременно, используя Ns бит с P1 по pNs, вычисленных на предыдущем этапе. Следовательно, процесс кодирования блочного кода LDPC, предложенный в настоящем изобретении, в Ns раз быстрее, чем процесс кодирования кода RA.
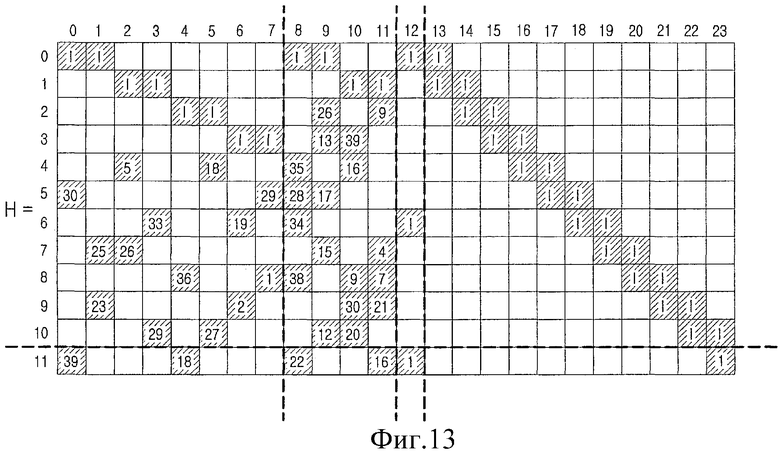
Фиг.13 является схемой, иллюстрирующей матрицу контроля четности блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения. Матрица контроля четности, проиллюстрированная на фиг.13, представляет матрицу контроля четности блочного кода LDPC со скоростью кодирования 1/2 и включает 12 x 24 блоков.
На фиг.13 цифры, записанные в блоках, представляют степени матриц перестановок, расположенных в соответствующих блоках, и 'I' представляет единичные матрицы, расположенные в соответствующих блоках. Величина степени матрицы перестановки для матрицы контроля четности блочного кода LDPC с размером блока Ns может быть вычислена выполнением действия по модулю Ns над каждым показателем степени матриц перестановок, расположенных в соответствующих блоках. Если показатель соответствующего блока выше, чем размер Ns соответствующего блока, то это означает, что нужно выполнить действие по модулю Ns.
В общем, показатель должен быть меньше, чем Ns. Тем не менее, когда та же самая матрица контроля четности в общем используется и для большого, и для малого размера блоков, то значение показателя, большее, чем Ns, включается в матрицу случайно. В этом случае многие матрицы контроля четности необходимы в соответствии со скоростью кодирования и размерами блоков, увеличивая требуемую емкость памяти. Если величина, достигнутая выполнением действия по модулю Ns над показателем степени матрицы перестановок, равна 0, то матрица перестановок, расположенная в соответствующем блоке, становится единичной матрицей.
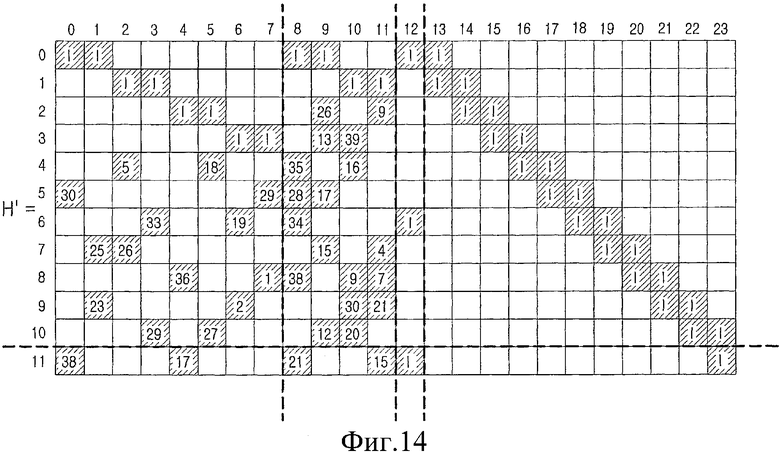
Фиг.14 является схемой, иллюстрирующей порождающую матрицу блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения. Тем не менее, до того, как задано описание фиг.14, следует заметить, что порождающая матрица H' является матрицей, сформированной умножением матрицы H контроля четности на матрицу F, как описано выше. Матрица F будет описана со ссылкой на Фиг.12.
Фиг.12 является схемой, иллюстрирующей матрицу F, используемую для формирования матрицы H' в соответствии с вариантом осуществления настоящего изобретения. Ссылаясь на фиг.12, в матрице F единичные матрицы I располагаются вдоль линии диагонали и матрица 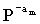 перестановок располагается в последнем элементе линии диагонали. Матрица
перестановок располагается в последнем элементе линии диагонали. Матрица  перестановок является матрицей перестановок, имеющей отрицательный показатель степени для матрицы
перестановок является матрицей перестановок, имеющей отрицательный показатель степени для матрицы 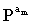 перестановок, расположенной в последней части матрицы E перестановок матрицы контроля четности. На фиг.12 предполагается, что am=1.
перестановок, расположенной в последней части матрицы E перестановок матрицы контроля четности. На фиг.12 предполагается, что am=1.
Ссылаясь на фиг.14, порождающая матрица H' формируется умножением матрицы H контроля четности на матрицу F, как описано выше. Тем не менее, так как матрица  перестановок, расположенная в последней части матрицы F, является P-1, как описано выше, то порождающая матрица H' сравнивается с матрицей H контроля четности, и только матрицы, расположенные в последней строке блока порождающей матрицы H', имеют значения степеней меньше на 1 по сравнению со степенями матрицы H перестановок.
перестановок, расположенная в последней части матрицы F, является P-1, как описано выше, то порождающая матрица H' сравнивается с матрицей H контроля четности, и только матрицы, расположенные в последней строке блока порождающей матрицы H', имеют значения степеней меньше на 1 по сравнению со степенями матрицы H перестановок.
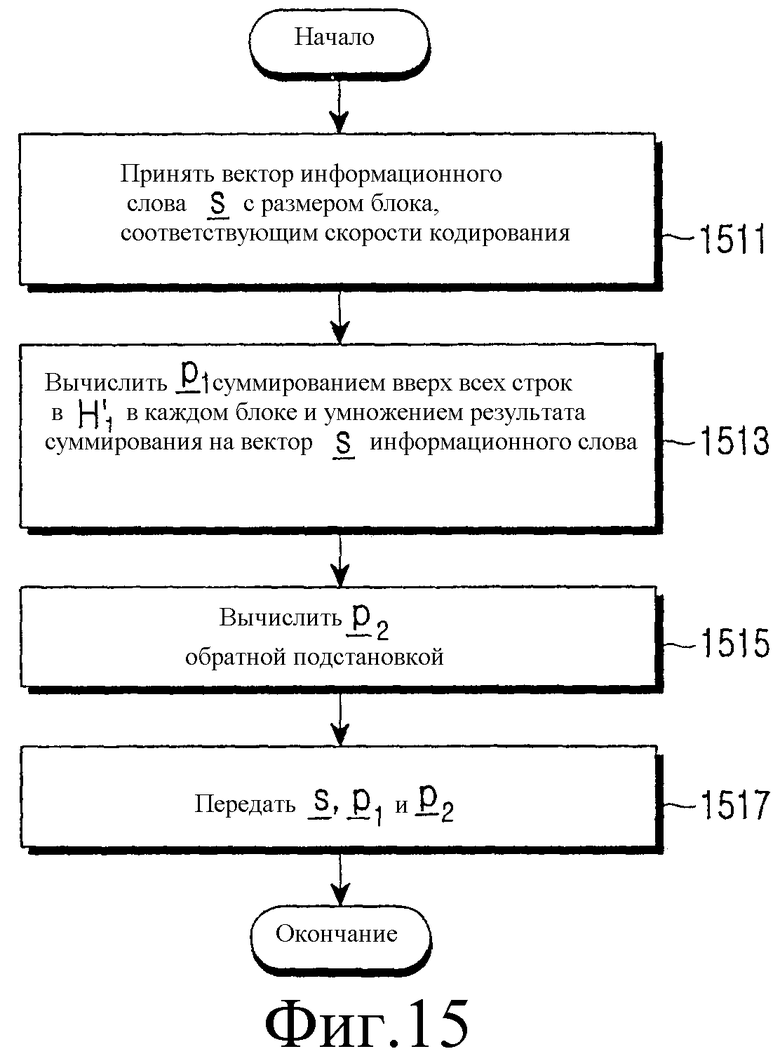
Фиг.15 является блок-схемой операций способа, иллюстрирующей процесс кодирования блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения. Ссылаясь на фиг.15 на этапе 1511, контроллер принимает вектор s информационного слова для кодирования в блочный код LDPC. В данном документе предполагается, что вектор s информационного слова имеет размер, соответствующий скорости кодирования для кодирования в блочный код LDPC, и размер вектора s информационного слова равен k.
На этапе 1513 контроллер вычисляет первый вектор 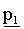 четности, используя матрицу, сформированную суммированием всех строк в H1' порождающей матрицы H' в каждом блоке, и транспонированный вектор принятого вектора s информационного слова. Матрица, сформированная суммированием всех строк в H1' порождающей матрицы H' имеет размер NsxK, и первый вектор
четности, используя матрицу, сформированную суммированием всех строк в H1' порождающей матрицы H' в каждом блоке, и транспонированный вектор принятого вектора s информационного слова. Матрица, сформированная суммированием всех строк в H1' порождающей матрицы H' имеет размер NsxK, и первый вектор 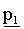 четности вычисляется, используя уравнение (8).
четности вычисляется, используя уравнение (8).
На этапе 1515, контроллер вычисляет второй вектор  четности обратной подстановкой, используя вектор s информационного слова и первый вектор
четности обратной подстановкой, используя вектор s информационного слова и первый вектор 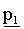 четности. На этапе 1517 контроллер формирует вектор c кодового слова, используя вектор s информационного слова, первый вектор
четности. На этапе 1517 контроллер формирует вектор c кодового слова, используя вектор s информационного слова, первый вектор 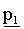 четности и второй вектор
четности и второй вектор  четности, и передает сформированный вектор c кодового слова.
четности, и передает сформированный вектор c кодового слова.
Фиг.16 является блок-схемой, иллюстрирующей внутреннюю структуру устройства кодирования блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения. Ссылаясь на фиг.16, устройство для кодирования блочного кода LDPC включает в себя умножитель 1611 матрицы, запоминающее устройство 1613, циклическое сдвигающее устройство 1615, процессор 1617 обратной подстановки и переключатели 1619, 1621 и 1623.
Входной сигнал, т.е. вектор s информационного слова длиной k, который необходимо кодировать в блочный код LDPC, используется переключателем 1619, матричным умножителем 1611 и процессором 1617 обратной подстановки. Матричный умножитель 1611 умножает вектор s информационного слова на матрицу NsxK, сформированную суммированием всех строк в H1' порождающей матрицы H', сохраненных в запоминающем устройстве 1613 на каждый блок, и выводит результат на циклическое сдвигающее устройство 1615. Вывод сигнала от матричного умножителя 1611 является вектором 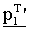 , полученным циклическим сдвигом транспонированного вектора
, полученным циклическим сдвигом транспонированного вектора 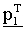 первого вектора
первого вектора 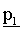 четности на x.
четности на x.
Циклическое сдвигающее устройство 1615 вычисляет транспонированный вектор 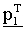 первого вектора
первого вектора 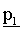 четности обратным циклическим сдвигом сигнала, выводимого от матричного умножителя 1611 на x, вычисляет первый вектор
четности обратным циклическим сдвигом сигнала, выводимого от матричного умножителя 1611 на x, вычисляет первый вектор 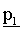 четности, используя транспонированный вектор
четности, используя транспонированный вектор 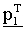 первого вектора
первого вектора 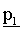 четности, и выводит результат на процессор 1617 обратной подстановки и переключатель 1621. Процессор 1617 обратной подстановки вычисляет второй вектор
четности, и выводит результат на процессор 1617 обратной подстановки и переключатель 1621. Процессор 1617 обратной подстановки вычисляет второй вектор 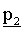 четности обратной заменой, используя вектор s информационного слова и первый вектор
четности обратной заменой, используя вектор s информационного слова и первый вектор 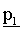 четности, выведенный из циклического сдвигающего устройства 1615, и выводит результат на переключатель 1623.
четности, выведенный из циклического сдвигающего устройства 1615, и выводит результат на переключатель 1623.
Каждый из переключателей 1619, 1621 и 1623 включается только в свой интервал времени передачи, чтобы передать свой ассоциативно связанный сигнал. То есть переключатель 1619 включается во время передачи вектора s информационного слова, переключатель 1621 включается во время передачи первого вектора P1 четной части и переключатель 1623 включается во время передачи второго вектора P2 четной части.
Все коды серии LDPC могут декодироваться в графе множителей, используя алгоритм частного произведения (sub-product). Схема декодирования кода LDPC может быть примерно разделена на схему двунаправленной передачи и схему передачи потока. Когда операция декодирования выполняется, используя схему двунаправленной передачи, каждый контрольный узел имеет узловой процессор, таким образом, увеличивая сложность декодирования пропорционально числу контрольных узлов. Тем не менее, так как все контрольные узлы одновременно обновляются, то скорость декодирования резко возрастает.
Отличная от этого, схема передачи потока имеет единственный узловой процессор и узловой процессор обновляет информацию, проходя через все узлы в графе множителей. Следовательно, схема передачи потока ниже по сложности декодирования, но увеличение в размере матрицы контроля четности, т.е. увеличение количества узлов вызывает снижение в скорости декодирования. Тем не менее, матрица контроля четности формируется на каждый блок аналогично блочному коду LDPC, предложенному в настоящем изобретении, затем количество узловых процессоров, равное количеству блоков, составляющих матрицу контроля четности, используется во время декодирования. В этом случае возможно реализовать декодер, который менее сложен в декодировании, чем схема двунаправленной передачи, и с более высокой скоростью декодирования, чем схема передачи потока.
Фиг.17 является блок-схемой, иллюстрирующей внутреннюю структуру устройства декодирования для блочного кода LDPC в соответствии с вариантом осуществления настоящего изобретения. Ссылаясь на фиг.17, устройство декодирования для блочного кода LDPC включает в себя контроллер 1710 блоков, переменную узловую часть 1700, сумматор 1715, обращенный перемежитель 1717, перемежитель 1719, контроллер 1721, запоминающее устройство 1723, сумматор 1725, контрольную узловую часть 1750 и блок 1729 жесткого выбора решения. Переменная узловая часть 1700 включает в себя переменный узловой декодер 1711 и переключатели 1713 и 1714, и контрольная узловая часть включает в себя контрольный узловой декодер 1727.
Сигнал, принятый по радиоканалу, является входным для контроллера 1710 блоков. Контроллер 1710 блоков определяет размер блоков принятого сигнала. Если существует часть информационного слова, прокалываемая в устройстве кодирования, соответствующем устройству декодирования, то контроллер 1710 блоков вставляет '0' в проколотую часть информационного слова, чтобы регулировать размер полного блока, и выводит результирующий сигнал на переменный узловой декодер 1711. Переменный узловой декодер 1711 вычисляет значения вероятности вывода сигнала контроллера 1710 блоков, обновляет вычисленные значения вероятности и выводит обновленные значения вероятности на переключатели 1713 и 1714. Переменный узловой декодер 1711 соединяет переменные узлы в соответствии с матрицей контроля четности, предварительно заданной в устройстве декодирования для блочного кода LDPC, и выполняет операцию обновления над столькими входными и выходными значениями, как и число единиц, соединенных с переменными узлами. Число единиц, соединенных с переменными узлами, равно весу каждого из столбцов, составляющих матрицу контроля четности. Внутреннее функционирование переменного узлового декодера 1711 отличается в соответствии с весом каждого из столбцов, составляющих матрицу контроля четности. За исключением ситуации, когда включен переключатель 1713, переключатель 1714 включается для вывода выходного сигнала переменного узлового декодера 1711 к сумматору 1715.
Сумматор 1715 принимает выход сигнала от переменного узлового декодера 1711 и выводит сигнал перемежителя 1719 в предыдущем итеративном процессе декодирования, вычитает выходной сигнал перемежителя 1719 в предыдущем итеративном процессе декодирования из выходного сигнала переменного узлового декодера 1711 и выводит итог вычитания на обращенный перемежитель 1717. Если процесс декодирования является первоначальным процессом декодирования, следует полагать, что выходной сигнал перемежителя 1719 равен 0.
Обращенный перемежитель 1717 устраняет перемежение выходного сигнала от сумматора 1715 согласно предопределенной схеме перемежения и выводит сигнал с устраненным перемежением на сумматор 1725 и контрольный узловой декодер 1727. Обращенный перемежитель 1717 имеет внутреннее устрйство, соответствующее матрице контроля четности, так как выходное значение для входного значения перемежителя 1719, соответствующего обращенному перемежителю 1717, является различным в соответствии с положением элементов, имеющих значение 1 в матрице контроля четности.
Сумматор 1725 принимает выходной сигнал контрольного узлового декодера 1711 в предыдущем итеративном процессе декодирования и выходной сигнал обращенного перемежителя 1717, вычитает выходной сигнал обращенного перемежителя 1717 из выходного сигнала контрольного узлового декодера 1727 в предыдущем процессе итеративного декодирования и выводит итог вычитания на перемежитель 1719. Контрольный узловой декодер 1727 соединяет контрольные узлы в соответствии с матрицей контроля четности, предварительно заданной в устройстве декодирования для блочного кода LDPC, и выполняет операцию обновления над столькими входными и выходными значениями, сколько число единиц, соединенных с контрольными узлами. Число единиц, соединенных с контрольными узлами, равно весу каждой строки, включенной в матрицу контроля четности. Следовательно, внутренняя работа контрольного узлового декодера 1727 отличается в соответствии с весом каждой строки, составляющей матрицу контроля четности.
Перемежитель 1719 под управлением контроллера 1721 перемежает выходной сигнал от сумматора 1725 в соответствии с предопределенной схемой перемежения и выводит перемеженный сигнал на сумматор 1715 и переменный узловой декодер 1711. Контроллер 1721 считывает информацию, относящуюся к перемежению, сохраненную в запоминающем устройстве 1723, и управляет схемой перемежения перемежителя 1719 согласно считываемой информации. Аналогично, если процесс декодирования является первоначальным процессом декодирования, то следует принять во внимание, что выходной сигнал обращенного перемежителя 1717 равен 0.
Итеративно выполняя вышеупомянутые процессы, устройство декодирования выполняет надежное безошибочное декодирование.
После того, как итеративное декодирование выполняется предопределенное число раз, переключатель 1714 выключает соединение между переменным узловым декодером 1711 и сумматором 1715, и переключатели 1713 включают соединение между переменным узловым декодером 1711 и блоком 1729 принятия жесткого решения, чтобы обеспечить выход сигнала от переменного узлового декодера 1711 на блок 1729 жесткого принятия решения. Блок 1729 выбора жесткого решения применяет жесткое решение над выходным сигналом из переменного узлового декодера 1711 и выводит итог жесткого решения, и выходная величина блока 1729 выбора жесткого решения становится окончательно декодированной величиной.
Как может быть принято во внимание из вышеуказанного описания, настоящее изобретение предлагает блочный код LDPC, минимальная длина цикла которого максимизируется в системе мобильной связи, таким образом максимизируя возможность исправления ошибок. Следовательно, устройство декодирования может правильно декодировать принятые данные, используя блочный код LDPC, обеспечивая надежное декодирование.
Кроме того, настоящее изобретение формирует эффективную порождающую матрицу, используя матрицу контроля четности, таким образом, минимизируя сложность кодирования блочного кода LDPC.
То есть настоящее изобретение предлагает обеспечить таким образом блочному коду LDPC высокую производительность путем использования итеративного декодирования в графе множителей.
Кроме того, настоящее изобретение создает матрицу контроля четности блочного кода LDPC, блок за блоком, таким образом делая возможным реализацию декодера с минимальной сложностью декодирования, усовершенствованной в плане скорости декодирования. В особенности, настоящее изобретение минимизирует сложность кодирования, используя простое перемножение матриц и поблочную обратную подстановку.
Несмотря на то, что настоящее изобретение показано и описано со ссылкой на его конкретные варианты осуществления, специалистам в данной области техники следует понимать, что различные изменения по форме и содержанию могут быть сделаны без отступления от духа и объема настоящего изобретения, как задано прилагаемой формулой изобретения.


Изобретение относится к устройству и способу кодирования блочного кода разреженного контроля четности (LDPC). Сущность изобретения состоит в том, что при приеме вектора информационного слова кодер кодирует вектор информационного слова в блочный код LDPC в соответствии с предопределенной порождающей матрицей. Модулятор модулирует блочный код LDPC в символ модуляции, используя предопределенную схему модуляции. Передатчик передает символ модуляции. Технический результат - обеспечение надежности декодирования при минимизации сложности кодирования блочного кода LDPC. 4 н. и 7 з.п. ф-лы, 17 ил.
причем блочный код LDPC включает в себя вектор информационного слова, первый вектор четности и второй вектор четности, и порождающая матрица включает в себя первую матрицу, сопоставленную с вектором информационного слова, вторую матрицу, сопоставленную с первым вектором четности, и третью матрицу, сопоставленную со вторым вектором четности; первая матрица формируется умножением четвертой матрицы, сопоставленной с вектором информационного слова матрицы контроля четности, соответствующей длине, которую необходимо использовать, когда формируют вектор информационного слова в блочном коде LDPC, на предопределенную пятую матрицу, вторая матрица формируется умножением шестой матрицы, сопоставленной с первым вектором четности матрицы контроля четности, на пятую матрицу, и третья матрица формируется умножением седьмой матрицы, сопоставленной со вторым вектором четности матрицы контроля четности, на пятую матрицу; причем этап кодирования вектора информационного слова в блочном коде LDPC в соответствии с предопределенной порождающей матрицей содержит этапы, на которых формируют первый вектор четности из условия, что вектор, сформированный умножением матрицы, сформированной суммированием всех строк четвертой матрицы в каждом блоке, на транспонированный вектор вектора информационного слова, становится вектором, сформированным циклическим сдвигом транспонированного вектора первого вектора четности на предопределенную величину; формируют второй вектор четности, используя обратную подстановку; и формируют блочный код LDPC соединением первого вектора четности и второго вектора четности в вектор информационного слова.
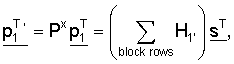
где s обозначает вектор информационного слова,  обозначает первый вектор четности, sT обозначает транспонированный вектор вектора информационного слова,
обозначает первый вектор четности, sT обозначает транспонированный вектор вектора информационного слова, 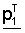 обозначает транспонированный вектор первого вектора четности, Рx обозначает матрицу, сформированную циклическим сдвигом матрицы перестановок с размером NsxNs на х, р1 T' обозначает вектор, сформированный циклическим сдвигом
обозначает транспонированный вектор первого вектора четности, Рx обозначает матрицу, сформированную циклическим сдвигом матрицы перестановок с размером NsxNs на х, р1 T' обозначает вектор, сформированный циклическим сдвигом 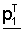 на х, и
на х, и 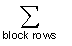 обозначает действие суммирования всех строк соответствующей матрицы в каждом блоке, H1' обозначает матрицу, сопоставленную с вектором информационного слова, в которую включена порождающая матрица, х обозначает показатель степени матрицы перестановок.
обозначает действие суммирования всех строк соответствующей матрицы в каждом блоке, H1' обозначает матрицу, сопоставленную с вектором информационного слова, в которую включена порождающая матрица, х обозначает показатель степени матрицы перестановок.
декодирования принятого сигнала, используя матрицу контроля четности; и
выделения блочного кода LDPC из декодированного принятого сигнала,
причем этапы декодирования принятого сигнала, используя матрицу контроля четности, и выделения блочного кода LDPC из декодированного принятого сигнала содержат этапы, на которых определяют схему устранения перемежения и схему перемежения в соответствии с матрицей контроля четности; обнаруживают значения вероятности принятого сигнала; формируют выходной сигнал переменного узлового декодера посредством вычисления значения вероятности сигнала, выводимого из принятого сигнала и сигнала предыдущей обработки декодирования; формируют первый сигнал вычитанием сигнала, сформированного в предшествующем процессе декодирования, из значений вероятности выходного сигнала переменного узлового декодера; устраняют перемежение первого сигнала, используя упомянутую схему устранения перемежения; обнаруживают значения вероятности из сигнала с устраненным перемежением; формируют выходной сигнал контрольного узлового декодера из сигнала с устраненным перемежением; формируют второй сигнал вычитанием сигнала с устраненным перемежением из значений вероятности выходного сигнала контрольного узлового декодера; перемежают второй сигнал, используя схему перемежения; и определяют блочный код LDPC итеративным декодированием сигнала с перемежением.
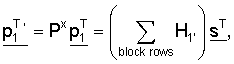
где s обозначает вектор информационного слова, 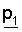 обозначает первый вектор четности, sT обозначает транспонированный вектор вектора информационного слова,
обозначает первый вектор четности, sT обозначает транспонированный вектор вектора информационного слова,  обозначает транспонированный вектор первого вектора четности, Рх обозначает матрицу, сформированную циклическим сдвигом матрицы перестановок с размером NsxNs на х, р1 T обозначает вектор, сформированный циклическим сдвигом
обозначает транспонированный вектор первого вектора четности, Рх обозначает матрицу, сформированную циклическим сдвигом матрицы перестановок с размером NsxNs на х, р1 T обозначает вектор, сформированный циклическим сдвигом 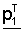 на х, и
на х, и 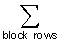 обозначает действие суммирования всех строк соответствующей матрицы в каждом блоке.
обозначает действие суммирования всех строк соответствующей матрицы в каждом блоке.
| US 2003037298 А, 20.02.2003 | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| US 2003014718 А, 16.01.2003 | |||
| Устройство для декодирования информации с исправлением ошибок | 1985 |
|
SU1505451A3 |
| RU 2001118276 А, 27.06.2003. | |||
Авторы
Даты
2009-02-27—Публикация
2005-08-10—Подача