Область техники, к которой относится изобретение
Настоящее изобретение в целом относится к кодированию и декодированию данных, а в частности к способу и устройству для кодирования данных, использующему коды с контролем четности низкой плотности (LDPC).
Уровень техники изобретения
Как описано в патентной заявке США с порядковым номером № 10/839995, которая включена в материалы настоящего документа посредством ссылки, код с контролем четности низкой плотности является кодом линейных блоков, заданным проверочной матрицей H. В общем случае, LDPС-код определен на поле Галуа GF(q), q≥2. Если q=2, код является бинарным кодом. Все коды линейных блоков могут быть описаны как произведение k-битного информационного вектора s1×k на кодогенерирующую матрицу Gk×n для порождения n-битовой кодовой комбинации
x1×n, где кодовая скорость равна r=k/n. Кодовая комбинация x передается через канал с помехами, и принятый вектор y сигнала передается на декодер для оценки вектора s1xk сигнала.
При заданном n-мерном пространстве строки G охватывают k-мерное подпространство C кодовых комбинаций, а строки проверочной матрицы Hm×n охватывают m-мерное дуальное пространство C⊥, где m=n-k. Поскольку x=sG и GHT=0, следует, что xHT=0 для всех кодовых комбинаций в подпространстве С, где “T” (или "T") обозначает транспонирование матрицы. При обсуждении LDPС-кодов, в общем, написано, что
Hx т =0 т ,(1)
где 0 - вектор-строка из нулей, и кодовая комбинация
x=[s р]=[s 0 , s 1 ,...,s k-1 ,p 0 ,p 1 ,...,p m-1], где p 0 ,...,p m-1 являются контрольными битами; а s 0 ,…,s k-1 являются систематическими битами, равными информационным битам в информационном векторе.
Для LDPС-кода плотность ненулевых позиций в H низкая, т.е. существует только маленькая доля 1 в H, позволяющая лучшую эффективность корректировки ошибок и более простое декодирование, чем использование плотного H. Проверочная матрица может быть также описана двудольным графом. Двудольный граф является не только графическим описанием кода, но также моделью декодера. В двудольном графе бит кодовой комбинации (следовательно, каждой колонки H) представлен переменной вершиной слева, и каждое проверочное уравнение (следовательно, каждая строка H) представлено проверочной вершиной справа. Каждая переменная вершина соответствует колонке H, и каждая проверочная вершина соответствует строке H, здесь “переменная вершина” и “колонка” H упоминаются взаимозаменяемо, как и “проверочная вершина” и “строка” H. Переменные вершины являются присоединенными только к проверочным вершинам, и проверочные вершины являются присоединенными только к переменным вершинам. Для кода с n битами кодовой комбинации и m битами четности переменная вершина v i присоединена к проверочной вершине с посредством ребра, если бит i кодовой комбинации участвует в проверочном уравнении j, i = 0,1...,n-1, j = 0,1,...,m-l.
Другими словами, переменная вершина i присоединена к проверочной вершине j, если позиция h ji проверочной матрицы H равна 1. Отображающее уравнение (1), переменная вершина представляет допустимую кодовую комбинацию, если все проверочные вершины имеют равную четность.
Ниже показан пример для иллюстрирования отношения между проверочной матрицей, проверочными уравнениями и двудольным графом. Пусть n=12, код Ѕ скорости будет определен посредством

с левой частью, соответствующей k (=6) информационным битам s, и с правой частью, соответствующей m (=6) битам p четности. Применяя (1), H в (2) определяет 6 проверочных уравнений следующим образом:
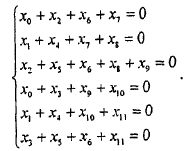
H также имеет соответствующий двудольный граф, показанный на фиг.1.
Как обсуждалось выше, получатель получает загрязненную версию y переданной кодовой комбинации x. Для декодирования у и определения исходной информационной последовательности s применяется итеративный декодирующий алгоритм на основе двудольного графа, такой как распространение доверия. Гибкая информация в формате логарифмического отношения правдоподобия (LLRs) битов кодовой комбинации передается между набором переменных вершин и набором проверочных вершин. Итерация останавливается, когда все проверочные уравнения удовлетворены или достигается максимально допущенный предел итераций.
Структурированная модель LDPС-кода начинается с маленькой m b ×n b базовой матрицы Hb, создает z копий Hb, и соединяет z копий для построения большой m×n матрицы H, где m = m b ×z, n = n b ×z. Используя матричное представление, для построения H из Hb каждая 1 в Hb заменена z×z подматрицей перестановок, и каждый 0 в Hb заменен z×z подматрицей, состоящей из нулей. Эта процедура по существу отображает каждое ребро Hb в ребро вектора длины z в H, каждую переменную вершину Hb в переменную вершину вектора длины z в H, и каждую проверочную вершину Hb в проверочную вершину вектора длины z в H. Преимуществами векторизации маленькой матрицы Hb для построения большой матрицы H являются:
1. Посредством использования различных значений z коды скорости k b /n b , где k b =n b -m b , могут быть разработаны для многих различных информационных последовательностей размеров k = z×k b из одной базовой матрицы Hb.
2. Требования к памяти значительно уменьшены. Со структурированной моделью LDPС только базовая матрица Hb и перестановка для ее 1 нуждается в сохранении, что требует существенно меньше памяти, поскольку Hb типично много меньше, чем H, и перестановка может быть очень простой.
3. Кодирование и декодирование могут выполняться на группе битов, а не над одиночными битами. Например, группа из z сообщений может быть извлечена из памяти, подвергнута перестановке и передана между векторной переменной вершиной и векторной проверочной вершиной.
Хотя философия структурированной модели LDPC значительно уменьшает сложность осуществления, не существует методики для конструирования базовой матрицы и определения матриц перестановок для заданной целевой H размера, которая имеет результатом LDPC-код, который имеет хорошую эффективность корректировки ошибок и может быть эффективно кодирован и декодирован. Поэтому существует потребность в способе и устройстве для конструирования структурированной H и способе и устройстве для кодирования и декодирования данных, использующих структурированную матрицу H.
Краткое описание чертежей
Фиг.1 иллюстрирует двудольный граф матрицы H (12, 6).
Фиг.2 иллюстрирует отношения между базовой матрицей Нb, модельной матрицей
Нbm и конечной расширенной матрицей H.
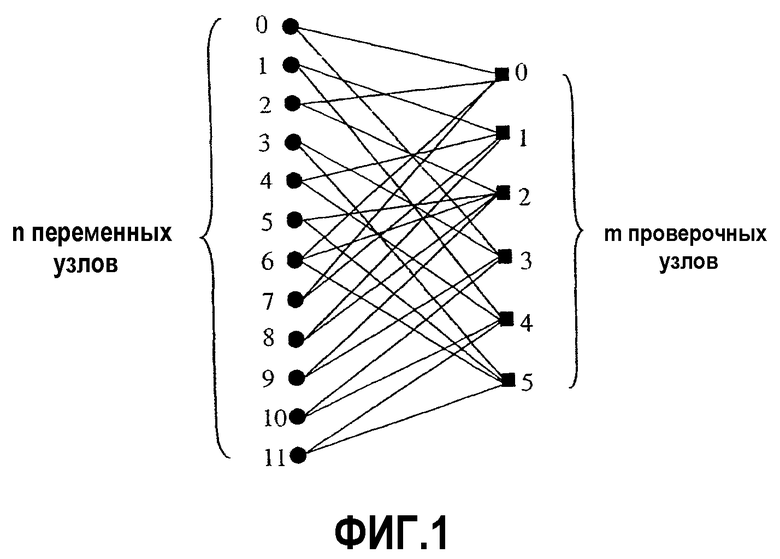
Фиг.3 - блок-схема кодировщика.
Фиг.4 - блок-схема декодировщика.
Фиг.5 - схема последовательности операций кодировщика на фиг.3.
Фиг.6 - схема последовательности операций декодировщика на фиг.4.
Описание чертежей
Чтобы направить усилия на вышеупомянутые потребности, предлагается структурированная проверочная матрица H, где H является расширением базовой матрицы Нb и где Нb содержит секцию Нb1 и секцию Нb2, и где Нb2 содержит первую часть, содержащую колонку hb, имеющую нечетный вес больше 2, и вторую часть, содержащую матричные элементы для строки i, столбца j, равные 1 для i=j, 1 для i=j+1 и 0 в других местах. Расширение базовой матрицы Нb использует идентичные подматрицы для 1 в каждой колонке второй части Н'b2, и расширение использует парные подматрицы для четного количества единиц в hb.
Настоящее изобретение осуществляет способ для управления передатчиком, который генерирует биты p=(p 0,...,p m-1) контроля четности на основе текущего набора s=(s 0 ,...,s k-1) символов. Способ содержит шаги приема текущего набора s=(s 0 ,...,s k-1) символов и использования матрицы H для определения битов контроля четности. Биты контроля четности передаются наряду с текущим набором символов. Матрица Н является расширением базовой матрицы Нb, где Нb содержит секцию Нb1 и секцию Нb2 и где Нb2 содержит первую часть, содержащую колонку hb, имеющую нечетный вес больше 2, и вторую часть Н'b2, содержащую матричные элементы для строки i, столбца j, равные 1 для i=j, 1 для i=j+1 и 0 в других местах. Расширение базовой матрицы Нb использует идентичные подматрицы для единиц в каждой колонке второй части Н'b2, и в котором расширение использует парные подматрицы для четного количества единиц в hb.
Настоящее изобретение дополнительно осуществляет способ для управления приемником, который оценивает текущий набор s=(s 0 ,..., s k-1) символов. Способ содержит шаги приема принятого вектора у=(у 0 ... у n-1 ) сигнала и использования матрицы H для оценки текущего набора s=(s0,..., sk-1) символов. Матрица Н является расширением базовой матрицы Нb, где Нb содержит секцию Нb1 и секцию Нb2, с Нb2, содержащей первую часть, содержащую колонку hb, имеющую нечетный вес больше 2, и вторую часть Н'b2, содержащую матричные элементы для строки i, столбца j, равные 1 для i=j, 1 для i=j+1 и 0 в других местах. Расширение базовой матрицы Нb использует идентичные подматрицы для единиц в каждой колонке второй части Н'b2, и где расширение использует парные подматрицы для четного количества единиц в hb.
Настоящее изобретение дополнительно осуществляет устройство, содержащее средства хранения для хранения матрицы H, микропроцессор, использующий матрицу H для определения битов контроля четности, где H является расширением базовой матрицы Нb и Нb содержит секцию Нb1 и секцию Нb2, с Нb2, содержащей первую часть, содержащую колонку hb, имеющую нечетный вес больше 2, и вторую часть Н'b2, содержащую матричные элементы для строки i, столбца j, равные 1 для i=j, 1 для i=j+1 и 0 в других местах. Расширение базовой матрицы Нb использует идентичные подматрицы для единиц в каждой колонке второй части Н'b2, и где расширение использует парные подматрицы для четного количества единиц в hb.
Настоящее изобретение осуществляет устройство, содержащее средства хранения для хранения матрицы H, приемник для приема вектора y=(у 0... у n-1 ) сигнала и микропроцессор, использующий матрицу H для определения текущего набора s=(s 0 ,...,
s k-1) символов. Матрица Н является расширением базовой матрицы Нb, с Нb, содержащей секцию Нb1 и секцию Нb2, и где Нb2 содержит первую часть, содержащую колонку hb, имеющую нечетный вес больше 2. Нb2 содержит вторую часть Н'b2, имеющую матричные элементы для строки i, столбца j, равные 1 для i=j, 1 для i=j+1 и 0 в других местах. Две идентичные подматрицы используются для расширения единиц в каждой колонке Н'b2, и парные подматрицы используются для расширения четного количества единиц в hb.
Обращаясь к чертежам, на которых аналогичные числа обозначают аналогичные компоненты, фиг.3 - блок-схема кодировщика 300 в соответствии с первым вариантом осуществления настоящего изобретения. Как показано, кодировщик 300 содержит микропроцессор 301 и таблицу 303 поиска. В первом варианте осуществления настоящего изобретения микропроцессор 301 содержит цифровой процессор сигналов (DSP), таких как, но не ограниченных, DSP MSC8300 и DSP56300. Дополнительно, таблица 303 поиска служит в качестве средства хранения для хранения матрицы и содержит постоянную память; тем не менее, рядовой специалист в данной области техники будет отдавать себе отчет, что другие виды памяти (например, память с произвольной выборкой, магнитная запоминающая память и т.д.) могут быть также использованы. Во втором варианте осуществления функциональность микропроцессора 301 и таблицы 303 поиска может быть включена в специализированную интегральную схему (ASIC) или программируемую вентильную матрицу (FPGA). В частности, таблица 303 поиска может быть реализована в виде памяти, соответствующей наличию или отсутствию путей сигнала в схеме.
Как обсуждалось выше, закодированные данные обычно выводятся как множество битов контроля четности в дополнение к систематическим битам, где вместе биты контроля четности и систематические биты формируют кодовую комбинацию x. В первом варианте осуществления настоящего изобретения проверочная матрица H хранится в таблице 303 поиска и выбирается микропроцессором 301 для решения уравнения (1). В частности, микропроцессор 301 определяет соответствующие значения для битов p=(p 0 ,..., p m-1) контроля четности на основе текущего набора символов и s=(s 0 ,..., s k-1) проверочной матрицы H.
Биты контроля четности и набор символов затем переправляются передатчику и передаются на приемник.
Фиг.4 - блок-схема декодера 400 согласно одному варианту осуществления настоящего изобретения. Как показано, кодировщик 400 содержит микропроцессор 401 и таблицу 403 поиска. В первом варианте осуществления настоящего изобретения микропроцессор 401 представляет собой цифровой процессор сигналов (DSP), например, DSP MSC8300 и DSP56300, но не ограничиваясь ими. Дополнительно, таблица 403 поиска действует как средство хранения для хранения матрицы H и содержит постоянную память. Тем не менее, рядовой специалист в данной области техники будет отдавать себе отчет, что другие виды памяти (например, память с произвольной выборкой, магнитная запоминающая память и т.д.) могут быть также использованы. Во втором варианте осуществления функциональность микропроцессора 401 и таблицы 403 поиска может быть включена в специализированную интегральную схему (ASIC) или программируемую вентильную матрицу (FPGA). В частности, таблица 403 поиска может быть реализована в виде памяти, соответствующей наличию или отсутствию путей сигнала в схеме.
Принятый вектор y=(y 0 ,..., y n-1) сигнала (принятый посредством приемника) соответствует кодовой комбинации x, переданной через канал с шумом, где закодированные данные x, как обсуждалось выше, являются вектором кодовой комбинации. В первом варианте осуществления настоящего изобретения проверочная матрица H хранится в таблице 403 поиска и выбирается микропроцессором 401 для декодирования y и оценки текущего набора s символов (т.е. текущего набора (s 0 ,..., s k-1) символов). В частности, микропроцессор 401 оценивает текущий набор (s 0 ,..., s k-1) символов, основанный на принятом векторе y=(y 0 ,..., y n-1) сигнала и проверочной матрице H.
Как хорошо известно в данной области техники, существует много способов того, как декодер 400 может использовать матрицу H контроля четности в микропроцессоре 401 для декодирования. Одним таким способом является выполнение векторно-матричного перемножения с H для определения вероятной карты ошибок. Другим подобным способом является использование H для построения двудольного графа, где вершины графа соответствуют 1 в H, и итеративно обработать y на двудольном графе.
Для структурированного LDPС подматрица z×z может быть матрицей перестановок, суммой матриц перестановок или любым типом бинарных матриц. Так как матрица перестановок P имеет единственную 1 в каждой строке и единственную 1 в каждой колонке, распределение веса расширенной матрицы H будет таким же, как у базовой матрицы Нb, если используется подматрица перестановок.
Поэтому распределение веса Нb выбрано настолько близко к требуемому конечному распределению веса, насколько возможно. Последующее описание иллюстрирует случай, где позиции Нb заменены матрицами перестановок, хотя и другие матрицы могут быть использованы. Если подматрица перестановок Рz×z векторного ребра имеет 1 в позиции (строка, колонка) (p(i), i), то i-е ребро в векторном ребре переставлено в p(i) позицию до того, как векторное ребро присоединено к векторной проверочной вершине. Другими словами, эта перестановка делает i-ю переменную вершину в связанной переменной векторной вершине соединенной с p(i)-й проверочной вершиной в связанной проверочной векторной вершине.
Перестановки, включающие H, могут быть очень простыми, без риска ухудшения производительности, такими как простые циклические сдвиги и/или инверсии битов. Например, может быть использован простой циклический сдвиг вправо. С этим ограничивающим условием каждая матрица H может быть представлена m b ×n b модельной матрицей Нbm, которая может быть получена посредством
- замены каждого 0 в Hb -1 для обозначения z×z нулевой подматрицы и
- замены каждой h ij=1 в Нb циклическим сдвигом размера p(i,j), где p(i,j) неотрицательно.
Так как циклический сдвиг влево (x mod z) раз эквивалентен циклическому правому сдвигу ((z-х) mod z) раз, достаточно обсудить циклический сдвиг вправо и упоминать его как циклический сдвиг для краткости. Как предварительно обсуждалось, существует отображение один к одному между H и Нbm. Следовательно, Нbm является кратким представлением H, если z задано. Относительно обозначений, модельная матрица выделена от базовой матрицы нижним индексом 'bm', а расширенная матрица выделена посредством удаления нижнего индекса 'bm'. Отношения между тремя матрицами продемонстрированы на фиг.2. Используя структуру, код имеет эффективность корректировки ошибок, сходную эффективности случайной H размера m×n, в то время как кодирование и декодирование выполняются на основе, намного меньшей Hbm.
Например, матрица уравнения (2) может быть использована в качестве базовой матрицы Нb для построения модельной матрицы Нbm следующим образом:
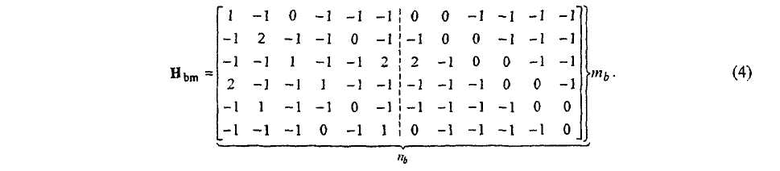
Когда z=3, Hbm преобразуется в (m b ×z)×(n b ×z) матрицу H посредством замены каждой -1 подматрицей 3×3 из нулей и каждой i подматрицей Pi, i=0,1,2, где

Отметим, что P0 является единичной матрицей, и строки Рi , i>0 являются колонками
P0, циклически сдвинутыми вправо i раз.
Пусть задан вектор q=[q 0 ,q 1 ,q 2], qP0=[q 0 ,q 1 ,q 2 ], qP1=[q 2 ,q 0 ,q 1], qP 2 =[q 1 ,q 2 ,q 0]. Другими словами, qPi имеет результатом циклический сдвиг вправо вектора q. С другой стороны, Pi q T имеет результатом циклический сдвиг вверх q T или эквивалентно циклический левый сдвиг q. Сходные правила применяются, когда используется z×z матрица Q:QPi, имеет результатом циклический сдвиг вправо колонок Q, PiQ имеет результатом циклический верхний сдвиг строк Q.
Базовая матрица H
Для LDPС-кода без векторизации матрица H с модифицированной ступенчатой структурой для части четности H приводит к эффективному кодированию без риска ухудшения производительности. Вообще, при условии, что
x=[s p]=[s 0 , s 1 ,...,s k-1 ,p 0 ,p 1 ,...p m-1] m на n, матрица H может быть разделена на две подматрицы,

где H2 имеет модифицированную ступенчатую структуру и H1 может быть любой бинарной матрицей размера m на k. Эта одинаковая структура может быть использована для построения базовой матрицы Hb в структурированной модели LDPC. Сходным образом, используя модифицированную структуру, Hb может быть разделена на две секции, где Нb1 соответствует систематическим битам s, Hb2 соответствует битам контроля четности p:
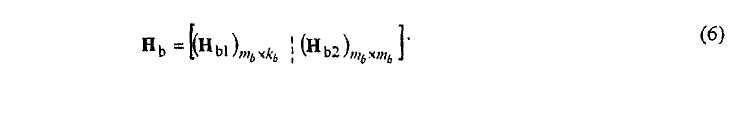
Секция Hb2 может быть дополнительно разделена на две секции, где вектор hb имеет нечетный вес w h , а H'b2 имеет ступенчатую структуру:

Секция Нb1 может быть построена случайным образом. Предпочтительно, вся матрица Hb имеет распределение веса, настолько близкое к требуемому распределению веса, насколько возможно.
Величины сдвигов
Для преобразования базовой матрицы Нb в модельную m b ×n b матрицу Нbm (которая расширяется до H), требуется определить циклический сдвиг величины p(i,j) для каждой 1 в Нb. Величины сдвигов могут быть сперва заданы для H2. После того как величины сдвигов для H2 определены, размеры сдвигов секции H1 могут быть определены для достижения суммарной хорошей эффективности H. Часть H1 базовой матрицы и величины сдвигов части H1 базовой матрицы (секции Hbm1) могут быть определены многими различными способами. Например, могут быть выбраны и приняты случайные значения для величин сдвигов, если величины сдвигов не вызывают существенного ухудшения производительности. Ухудшение производительности может иметь результатом включение избыточных количеств коротких циклов комбинаций с низким весом. Также могут быть использованы другие методики, имеющиеся в области техники LDPC.
Величины p(i,j) циклических сдвигов для заданного целевого H размера могут быть заданы для предоставления возможности эффективной кодировки без риска для эффективности декодирования. Для облегчения кодировки сдвиги могут быть определены такие, что все, кроме одной матрицы сдвига, соответствующей 1 в hb, сокращаются, когда складываются вместе, и все векторные строки H'b2 сокращаются, когда суммируются. Это транслируется в определение величин сдвигов hb в пары, кроме одной позиции, и определение одинаковых величин сдвигов обоим 1 в каждой колонке H'b2. Например, если hb = [1 0 0 1 0 0 1]T, допустимо иметь hbm = [3 -1 -1 3 -1 -1 4]T как соответствующую колонку в модельной матрице, так как величина сдвига 3 определена в парах. Поскольку всем из ненулевых позиций (обе 1) в каждой колонке H'b2 определены одинаковые величины сдвигов, любой выбор величины сдвига эквивалентен величине сдвига 0 (т.е. единичные подматрицы) плюс перестановка битов внутри векторной колонки. Таким образом, все величины сдвигов H'b2 могут быть определены как 0 для удобства, т.е. каждая 1 в H'b2 заменяется единичной подматрицей z×z во время расширения до H.
Вследствие существования циклов величины сдвигов hbm могут быть тщательно назначены. Могут быть применены правила, чтобы избежать коротких циклов кодовых последовательностей с низким весом. Одним свойством, которое может быть использовано для того, чтобы избежать циклов, является:
если в базовой матрице Hb 2c ребер из цикла длиной 2c, тогда в расширенной матрице H соответствующие 2c векторных ребер из z циклов длины 2c тогда и только тогда, если

где z является коэффициентом расширения, p(i) величиной циклического сдвига ребра i в модельной матрице Hbm, и ребра 0, 1, 2,..., 2c-1 (в этом порядке) формируют цикл в Hb.
Вследствие структуры Hb2 существуют циклы между hb и H'b2. Соответственно, любые две идентичные величины сдвига в hbm будут иметь результатом замену цикла z раз в расширенной матрице H согласно вышеописанному свойству. Тем не менее, если два сдвига расположены на большом расстоянии друг от друга, то циклы имеют большую длину и имеют небольшой результат при итеративном декодировании. Следовательно, в предпочтительном варианте осуществления, когда hb базовой матрицы имеет три 1, для максимизации длины цикла, две 1, которым заданы равные величины сдвига, могут быть расположены вверху и внизу hbm (настолько далеко друг от друга, насколько возможно), в то же время оставляя одну 1 в центре hb с непарной величиной сдвига. Например, hbm = [3 -1 3 -1 -1 -1 4]T будет иметь результатом z циклов длины 6 между h и H2', в то время как hbm = [3 -1 4 -1 -1 -1 3]T будут иметь результатом z циклов длины 14 между h и H2', где h и H'2 расширены из hb и H'b2 . Таким образом, секция Hb2 отображена на модельную матрицу

где k b = n b - m b, существует w h (нечетный, w h >=3) неотрицательных позиций в hbm, и позиции -1 в H'bm2 оставлены пустыми для краткости. Все значения p(i,k b ) появляются четное количество раз в hbm, кроме одного, которое может быть отображено в любую ненулевую подматрицу. Поэтому все сдвиги w h могут быть заданы одинаковыми значениями (например, 0), так как w h нечетное. Для Н'bm2 p(i,j) = p(i+1,j), j=k b +1,k b +2, …, nb-1, i=j-k b -1.
В предпочтительном варианте осуществления, при условии, что wh=3, один пример имеет hbm = [0 -1...-1 ph -1... -1...0]т, ph mod z≠0 и p(i,j) = p(i+l,j) = 0, j=kb+1,kb+2,..., nb-1, i=j-kb-1 в части H'bm2.
Хотя вышеприведенное обсуждение сфокусировано на использование подматриц, которые являются циклическими сдвигами единичной матрицы, вообще, могут быть использованы другие подматрицы (и быть представлены эквивалентом к базовой модельной матрице). Для облегчения кодировки ограничивающие условия в таком случае:
1. В каждой колонке H'bm2 две ненулевые подматрицы идентичны;
2. w h (нечетное, w h>=3) ненулевых подматриц hbm парны (т.е. одна подматрица идентична другой подматрице), кроме одной подматрицы, которая может быть любой ненулевой матрицей.
Кодирование
Кодирование является процессом определения последовательности четности p заданной информационной последовательности s. Для кодирования структурированного LDPС-кода, вместо одного бита, каждая операция выполняется над группой z битов. В качестве альтернативы векторные операции не должны быть использованы, и уравнения ниже реализованы в эквивалентной скалярной форме. Для кодировки s разделяется на k b =n b -m b групп из z битов. Пусть это сгруппированное s будет обозначено u,
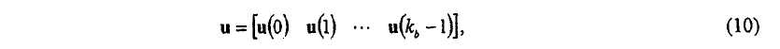
где каждый элемент u является вектором колонки, как показано ниже
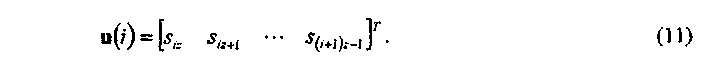
Используя модельную матрицу Hbm, равноценная последовательность p определена в группах z. Пусть сгруппированное p будет обозначено v,

где каждый элемент v является вектором колонки, как показано ниже
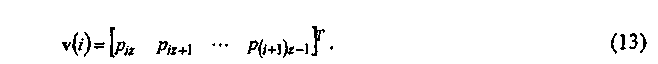
Кодировка продолжается за два шага: (a) инициализации, которая определяет v(0), и (b) рекурсии, которая определяет v(i+l) из v(i), 0≤i≤m b -2.
Выражение для v(0) может быть выведено суммированием строк уравнения (1) для получения

где x является индексом строки hbm, где позиция неотрицательна и используется нечетное количество раз. В предпочтительном варианте осуществления верхняя и нижняя позиции hbm парны, соответственно 1≤x≤m b -2.
Уравнение (14) решается для v(0) умножением обеих сторон на P-1 p(x,kb) . Для особого случая, рассматриваемого здесь, где р(х,k b ) представляет циклический сдвиг,
P-1 p(x,kb)=Pz-p(x,kb). Другими словами, v(0) получается посредством
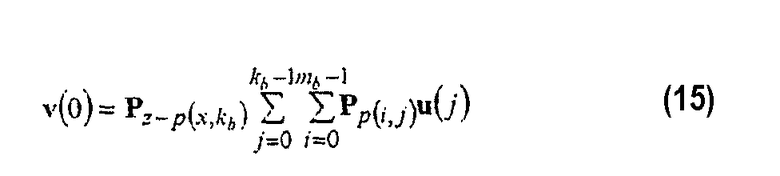
Вообще, рекурсии, выраженные в уравнениях (16) и (17), могут быть выведены, принимая во внимание H'bm,
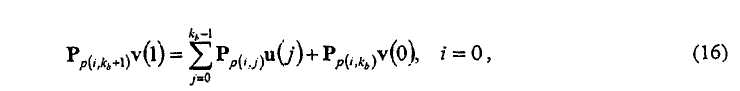
и
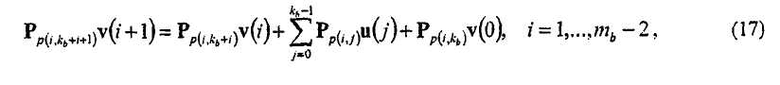
где

Соответственно, все биты четности, не в v(0), определяются посредством итеративного вычисления уравнений (16) и (17) для 0≤i≤ m b -2.
В предпочтительном варианте осуществления, где величины сдвигов 1 в Н'b2 все являются нулевыми, уравнения (16) и (17) могут быть упрощены до уравнений (19) и (20),

и
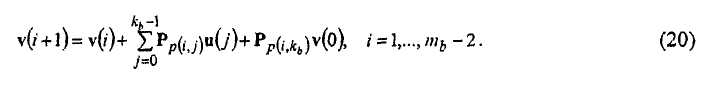
Соответственно, как в общем случае, все биты четности, не в v(0), определяются посредством итеративного вычисления уравнений (19) и (20) для 0≤i≤m b -2.
Уравнения (14), (19) и (20) описывают алгоритм кодировки. Эти уравнения также имеют непосредственную интерпретацию в терминах стандартных цифровых логических архитектур. Первое, поскольку неотрицательные элементы p(i,j) Hbm представляют циклические сдвиги величин вектора, все произведения вида Рр(i,j)u(j) могут быть реализованы посредством многорегистровой циклической схемы сдвига размера z. Нулевая величина циклического сдвига может не требовать быть циклически сдвигаемой. Так как многорегистровая схема циклического сдвига, которая реализует все возможные циклические сдвиги, должна предоставлять связи от каждого входного бита ко всем выходным битам, скорость, с которой она может функционировать, зависит от z. Для заданного z сложность может быть уменьшена, а скорость увеличена посредством разрешения только правильного поднабора из всех возможных циклических сдвигов. Например, Hbm может быть сконструирована только с четными величинами циклических сдвигов. Суммирования в уравнениях (14), (19) и (20) представляют векторные XOR (исключающее ИЛИ) операции, которые закрываются (т.е. не обновляются), когда p(i,j)= -1.
Для реализации суммирований в уравнениях (14), (19) и (20) позиции p(i,j) Hbm,
0≤i≤k b , 0≤j≤m b-l могут храниться в постоянной памяти (ROM) длины log2z+1 битов. Сгруппированная информационная последовательность может храниться в памяти размера z, которая может быть считана в последовательном порядке. Когда каждый вектор информации u(j) считывается, соответствующая позиция из Нbm ROM может быть считана, и она инструктирует многорегистровую схему циклического сдвига о необходимом циклическом сдвиге. После циклического сдвига регистр, содержащий частичное суммирование, обновляется. Для выражения (14), после завершения каждого внутреннего суммирования, результат может быть использован для обновления другого регистра, содержащего внешнее суммирование. Когда внешнее суммирование завершено, оно может быть циклически сдвинуто на z-р(х,k b ).
При условии, что циклическое смещение может быть реализовано в одном периоде тактовых импульсов, кодирование может быть завершено за приблизительно (k b +1)m b тактовых импульсов. Это число может быть уменьшено ценой m b -1 экстра z-широких регистров вычислением и хранением сумм уравнений (19) и (20), используя результаты, которые становятся доступны, когда уравнение (14) вычислено.
Расширение матрицы
Процедура расширения кода может быть применена к структурированному коду для достижения кода с более низкой кодовой скоростью. Постепенно код с более низкой кодовой скоростью может быть использован в последующих передачах процедуры (IR) инкрементальной избыточности. Конкретно, если модельная матрица первой передачи

тогда модельная матрица второй передачи может использовать

и т.д., где для каждой передачи i подматрица Hbm2 (i) имеет формат в (9) и имеет размер m (i) b ×m (i) b . Первая передача может отправлять n (1) b=k b+m (1) b групп битов, [u(0),u(1),...,u(k b-1),v (1)(0),v (l)(1),...,v(1)(mb (l)-1)], каждая группа имеет размер z. Декодирование после первой передачи выполняется с использованием сигналов [u(0),u(1),...,u(k b-1),v (1)(0),v (1)(1),...,v(l)(mb (1)-1)] и (21). Вторая передача может отправлять другие mb (2) групп битов размера z, [v (2)(0),v (2)(1),...,v (2)(m b (2)-1)],
где m 2 = m b (2) z, и биты первой передачи и второй передачи вместе [u(0), u(1),...,u(k b -1),v (1) (m b (1) -1),v (2) (0),v (2) (1),...,v (2) (m b (2) -1)] являются кодовой комбинацией, соответствующей (22).
Поэтому декодирование после второй передачи выполняется на основе (22) и комбинированного принятого сигнала от первой передачи и второй передачи. Эта процедура может быть повторена для дальнейших передач. Декодирование после второй передачи основано на коде скорости k b /n b (2) = k b /(n b (1) + m b (2) ), которая ниже, чем у первой передачи. Эта процедура может быть повторена для дальнейших передач с каждой дополнительной передачей, способствующей более сильному, низкоскоростному коду.
Фиг.5 - схема последовательности операций кодировщика 300 и, в частности, микропроцессорa 301. Поток начинается на шаге 501, где текущий набор символов (s 0 ,...,s k-1) принимается микропроцессором 301. На шаге 503 значения битов контроля четности определяются на основе текущего набора символов и H. В частности, биты контроля четности (p 0 ,..., p m-1) определяются, как описано выше, с H, являющейся расширением базовой матрицы Нb. Как обсуждалось, Нb содержит секцию Нb1 и секцию Нb2, и где Нb2 содержит первую часть, содержащую колонку hb, имеющую нечетный вес больше 2, и вторую часть, содержащую матричные элементы для строки i, столбца j, равные 1 для i=j, 1 для i=j+1 и 0 в других местах. В дополнение, расширение базовой матрицы Нb (для создания Н) использует единичные подматрицы для единиц в каждой колонке второй части Н'b2, и где расширение использует парные подматрицы для четного количества 1 в hb. На шаге 505 текущий набор символов и биты контроля четности передаются через передачу в эфир.
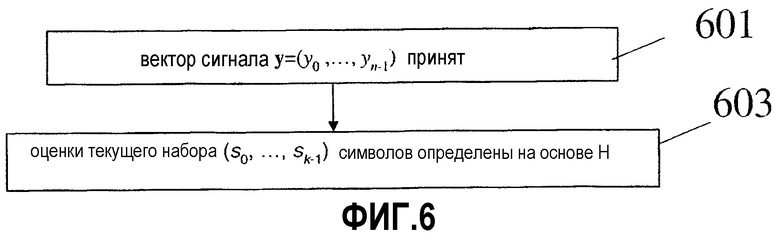
Фиг.6 - схема последовательности операций кодировщика 400 и, в частности, микропроцессора 401. Поток логики начинается на шаге 601, где принятый вектор сигнала y=(y 0,..., y n-1) принимается. На шаге 603 оценки текущего набора символов s (т.е. текущего набора символов (s0,..., s k-1 )) определяются на основе H. Как обсуждалось, H является расширением базовой матрицы Нb, и где Нb содержит секцию Нb1 и секцию Нb2, и где Нb2 содержит первую часть, содержащую столбец hb, имеющий нечетный вес больше 2, и вторую часть, содержащую матричные элементы для строки i, столбца j, равные 1 для i=j, 1 для i=j+1 и 0 в других местах.
Несмотря на то что изобретение было подробно показано и описано со ссылкой на определенный предпочтительный вариант осуществления, специалистами в данной области техники будет понятно, что в нем могут быть сделаны различные изменения по форме и содержанию, не выходя из сущности и объема изобретения. Например, в то время как изобретение было показано с упорядочиванием по s i и p i в рамках определенного x, рядовой специалист в данной области техники будет отдавать себе отчет, что может возникать другое упорядочивание битов в рамках x, так как биты кодовой комбинации могут быть собраны в любом порядке при условии, что колонки H переупорядочены соответствующим способом. Дополнительно, в то время как приведенное выше описание было показано и описано со ссылкой на двоичные коды (т.е. коды, определенные на поле Галуа GF(2)), рядовой специалист в данной области техники будет отдавать себе отчет, что точно так же может быть использовано произвольное GF. Хотя примеры, данные выше, показаны в одном формате, возможны другие форматы, которые позволяют сходные процедуры кодировки и модификации кода. Например, строки H могут быть переставлены без затрагивания значений битов контроля четности. В другом примере может быть использована модифицированная ступенчатая структура для поднабора битов контроля четности. В еще одном примере могут быть выполнены дополнительные шаги во время расширения базовой матрицы до расширенной матрицы. Матрица H может быть также использована в любом типе декодировщика, который основан на проверочной матрице. Подразумевается, что такие изменения учитываются в объеме последующей формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ | 2005 |
|
RU2365034C2 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И УСТРОЙСТВО СВЯЗИ | 2017 |
|
RU2740151C1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И УСТРОЙСТВО СВЯЗИ | 2017 |
|
RU2740154C1 |
| АППАРАТУРА, СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И АППАРАТУРА СВЯЗИ | 2018 |
|
RU2758968C2 |
| СПОСОБЫ И СИСТЕМЫ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ LDPC КОДОВ | 2016 |
|
RU2716044C1 |
| СПОСОБЫ СОГЛАСОВАНИЯ СКОРОСТИ ДЛЯ LDPC-КОДОВ | 2017 |
|
RU2730434C1 |
| Способ и устройство обработки информации и устройство связи | 2017 |
|
RU2667772C1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ, ПРИСПОСОБЛЕНИЕ И УСТРОЙСТВО СВЯЗИ | 2018 |
|
RU2769096C2 |
| КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ LDPC ПАКЕТОВ ПЕРЕМЕННЫХ РАЗМЕРОВ | 2008 |
|
RU2443053C2 |
| ВЫСОКОСКОРОСТНЫЕ ДЛИННЫЕ LDPC КОДЫ | 2017 |
|
RU2733826C1 |


Изобретение относится к кодированию и декодированию данных, использующему коды с контролем четности низкой плотности (LDPC). Технический результат - повышение точности кодирования и декодирования данных. Предложена структурированная проверочная матрица H, где H является расширением базовой матрицы Hb и где Hb содержит первую часть, содержащую колонку hb, имеющую нечетный вес больше чем 2, и вторую часть, содержащую матричные элементы для строки i, колонки j, равные 1 для i=j, 1 для i=j+1 и 0 в других местах. Расширение базовой матрицы Hb использует идентичные подматрицы для 1 в каждой колонке второй части H'b2, и расширение использует парные подматрицы для четного количества 1 в hb. 3 н. и 7 з.п. ф-лы, 6 ил.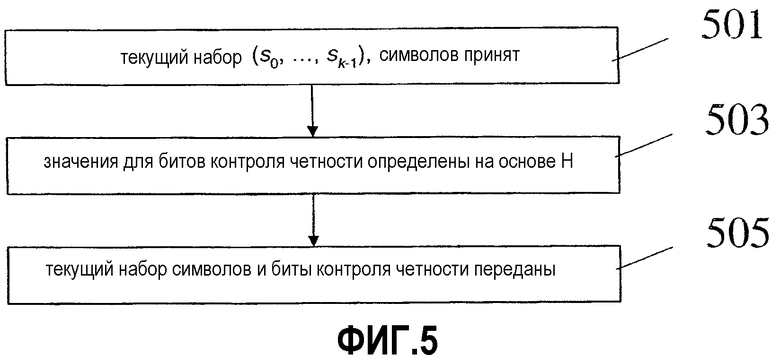
1. Способ управления передатчиком, который генерирует биты контроля четности p=(p0, …, pm-1) на основании текущего набора символов s=(s0, …, sk-1), причем способ содержит этапы, на которых
принимают упомянутый текущий набор символов s=(s0, …, sk-1);
используют матрицу Н для определения битов контроля четности; и
передают биты контроля четности наряду с текущим набором символов;
где Н является расширением базовой матрицы Hb, причем Hb содержит секцию Hb1 и секцию Hb2, причем Hb2 содержит первую часть, имеющую колонку hb, имеющую нечетный вес больше 2, и вторую часть H'b2, содержащую матричные элементы для строки i, столбца j, равные
1 для i=j,
1 для i=j+1,
0 в других местах;
где упомянутое расширение базовой матрицы Hb использует идентичные подматрицы для единиц в каждой колонке второй части Н'b2, и где упомянутое расширение использует парные подматрицы для четного количества единиц в hb.
2. Способ по п.1, в котором Hb расширена заменой каждой позиции Hb подматрицей размера z×z для порождения H.
3. Способ по п.1, в котором Hb расширена заменой каждого нулевого элемента Hb нулевой подматрицей размера z×z для порождения H.
4. Способ по п.1, в котором Hb расширена заменой каждого ненулевого элемента Hb ненулевой подматрицей для порождения H.
5. Способ по п.1, в котором Hb расширена заменой каждого ненулевого элемента Hb ненулевой подматрицей перестановок для порождения H.
6. Способ по п.1, в котором
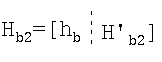
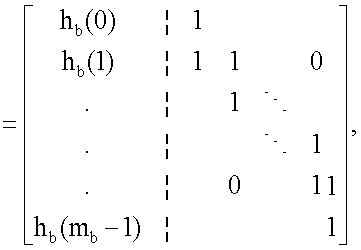
где вектор hb имеет нечетный вес wh>=3.
7. Устройство для кодирования данных, содержащее
средство хранения для хранения матрицы H;
микропроцессор, использующий матрицу H для определения битов контроля четности; и
передатчик для передачи битов контроля четности;
где Н является расширением базовой матрицы Hb, причем Hb содержит секцию Hb1 и секцию Hb2, причем Hb2 содержит первую часть, имеющую колонку hb, имеющую нечетный вес больше 2, и вторую часть Н'b2, содержащую матричные элементы для строки i, столбца j, равные
1 для i=j,
1 для i=j+1,
0 в других местах; и
где две идентичные подматрицы используются для расширения единиц в каждой колонке Н'b2, и парные подматрицы используются для расширения четного количества 1 в hb.
8. Устройство по п.7, в котором
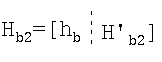

где вектор hb имеет нечетный вес wh>=3.
9. Устройство для кодирования данных, содержащее
средство хранения для хранения матрицы H;
приемник для приема вектора y=(y0, …, yn-1) сигнала; и
микропроцессор, использующий матрицу H для определения текущего набора (s0, …, sk-1) символов, где H является расширением базовой матрицы Hb, причем Hb содержит секцию Hb1 и секцию Hb2, причем Hb2 содержит первую часть, содержащую колонку hb, имеющую нечетный вес больше 2, и вторую часть H'b2, содержащую матричные элементы для строки i, колонки j, равные
1 для i=j,
1 для i=j+1,
0 в других местах; и
где две идентичные подматрицы используются для расширения 1 в каждой колонке H'b2, и парные подматрицы используются для расширения четного количества единиц в hb.
10. Устройство по п.9, в котором
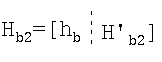
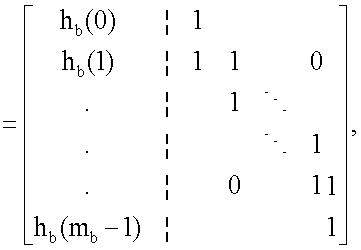
где вектор hb имеет нечетный вес wh>=3.
| US 5140596 A, 18.08.1992 | |||
| УСТРОЙСТВО И СПОСОБ ВСТАВКИ ЗАРАНЕЕ ИЗВЕСТНЫХ БИТОВ НА ВХОДНОМ КАСКАДЕ КАНАЛЬНОГО КОДЕРА | 1999 |
|
RU2190296C2 |
| ПАРАЛЛЕЛЬНЫЙ КАСКАДНЫЙ СВЕРТОЧНЫЙ КОД С КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ БИТОВ И ДЕКОДЕР ДЛЯ ТАКОГО КОДА | 1997 |
|
RU2187196C2 |
| US 6578171 B1, 10.10.2003 | |||
| Подмости | 1979 |
|
SU806839A1 |
Авторы
Даты
2009-10-20—Публикация
2005-08-03—Подача