РОДСТВЕННЫЕ ЗАЯВКИ
Настоящая заявка испрашивает приоритет предварительной заявки на патент США №61/476012, поданной 15 апреля 2011 г., содержание которой полностью включено в настоящее описание посредством ссылки.
ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Изобретение относится к способу восстановления и улучшения сигнала и, в частности, к способу адаптивного уменьшения шума во входном объекте.
ПРЕДПОСЫЛКИ СОЗДАНИЯ ИЗОБРЕТЕНИЯ
Оптимальное извлечение данных, содержащихся в сигнале, требует устранения дефектов, таких как шум, и приборных ограничений. Ключевой областью, в которой проводится поиск оптимизированного извлечения и восстановления данных, является область улучшения изображений. Несмотря на то что приборы могут быть выполнены практически свободными от шумов, остаются сигнатуры приборов, связанные с конечным пространственным, спектральным или временным разрешением. На данном этапе восстановление изображений требуется для удаления сигнатур приборов. Процессы улучшения изображения и источники шума и другие факторы, способные отрицательно влиять на извлечение данных, охватывают широкий диапазон, включающий астрономические наблюдения и исследование планет, где источники могут быть слабыми и атмосферные помехи создают шум и искажение, наблюдение в военных целях и с целью обеспечения безопасности, где свет может быть тусклым и быстрое перемещение целей приводит к слабой контрастности и размытию, работа с медицинскими изображениями, которой часто свойственно отсутствие четкости, и видеоизображения, где ограничения, связанные с передачей и приборами, и потребность в отклике в режиме реального времени может отрицательно влиять на резкость и детализированность изображения.
Цифровая обработка изображений была разработана для предоставления высококачественного надежного восстановления размытых и зашумленных данных, собранных разнообразными датчиками. Данная область существует, поскольку невозможно построить приборы для работы с изображениями, создающие изображения с постоянной четкостью, не искаженные шумом при измерении. Тем не менее, возможно математически восстановить базовое изображение из неидеальных данных, полученных с помощью реальных приборов, так что информацию, имеющуюся в наличии, но скрытую в данных, можно извлечь с меньшим количеством размытия и шума. Многие подобные способы используют процесс, в котором создают прогнозирующую модель и сравнивают ее с данными для оценки точности соответствия модели данным.
В этом письменном описании термин "данные" относится к любой измеренной величине, из которого вычисляют неизвестное "изображение" с помощью процесса восстановления изображений. Термин изображение обозначает как вычисленное решение, так и истинное базовое изображение, служащее основанием для наблюдаемых данных. Обсуждение обычно уточняет применяемый контекст; в случаях возможной двусмысленности термин "модель изображения" используется для обозначения рассчитанного решения. Следует отметить, что данные и изображение не обязательно должны быть подобными и даже могут иметь различную размерность, например, целью томографических восстановлений является определение трехмерного изображения на основе проецированных двухмерных данных. Термином, альтернативным изображению, является "объект", передающий идею, заключающуюся в том, что модель может быть более общей, чем изображение. В дальнейшем эти два термина используются в качестве синонимов.
Специалисты по статистике долгое время стремились ограничить параметры, используемые для аппроксимации данных с целью улучшения интерпретации и точность прогноза аппроксимации. Стандартные техники представляют собой выбор подмножества, в котором обнаружено, что некоторые параметры не являются значимыми и они исключены из аппроксимации (например, Miller 2002), и гребневую регрессию, в которой величины параметров ограничивают путем добавления терма регуляризации к оценочной функции, используемой в аппроксимации (например, Tikhonov 1963). Tibshirani (1996) объединил два способа в технике, известной как метод лассо Тибширани (Least Absolute Shrinkage and Selection (LASSO)).
Необходимость ограничения некоторого количества параметров в аппроксимации является обязательной для недоопределенных или слабо определенных задач, в которых количество параметров больше или сравнимо с количеством точек данных. Как было отмечено создателями статистических способа наименьших квадратов (Gauss 1809) и способа максимального правдоподобия (Fisher 1912, 1922), эти способы действительны лишь в асимптотическом пределе, в котором количество точек данных значительно превышает количество аппроксимированных параметров. Вне асимптотического предела шум аппроксимируют как сигнал, и аппроксимация теряет свою интерпретирующую и прогнозирующую силу.
Puetter и др. (2005) рассмотрели многочисленные алгоритмы восстановления, применяемые в настоящее время, включая итеративные способы восстановления изображений, которые итеративно аппроксимируют модели изображения относительно данных. Многие итеративные схемы известного уровня техники, разработанные таким образом, чтобы сходиться к решению максимального правдоподобия, сходятся медленно, даже при их раннем прекращении во избежание переаппроксимации. Более быстрое схождение можно достичь путем использования матрицы Гессе частных производных второго порядка оценочной функции относительно переменной (Hesse 1876). К сожалению, даже при использовании данного подхода матрица Гессе является слишком большой для вычисления при работе над крупномасштабными задачами, часто встречающимися в восстановлении изображений, например, когда изображение содержит большое количество пикселей со значительным излучением. В подобных случаях количество элементов матрицы может исчисляться триллионами. Матрицы подобного размера попросту не могут быть обработаны современными компьютерами или даже сохранены в памяти.
Желание ограничить количество параметров в недоопределенных или слабо определенных задачах - разреженность, как это называется в настоящее время - основано на более абстрактной идее минимальной сложности (Solomonoff 1964; Kolmogorov 1965; Chaitin 1966), которая восходит к средневековой работе Уильяма Оккама, поддерживающего принцип экономии постулатов. Проще говоря, при равных прочих условиях, простое объяснение лучше более сложного объяснения.
Нахождение решения разреженности, например, путем добавления терма регуляризации нормы l0 к оценочной функции, является N-P сложной задачей, в которой вычислительные затраты увеличиваются быстрее любого полинома в определенном количестве параметров. Это привело к замене нормы l0 нормой l1 (Chen, Donoho & Saunders 1999), так что оптимизация аппроксимации относительно параметров стала решаемой выпуклой задачей. Candes, Romberg & Tao (2004) сделали шаг вперед и продемонстрировали, как случайным образом уменьшить количество данных, требуемых для аппроксимации при условии несвязанности, технику, известную как "compressed sensing" (сжатое распознавание). Donoho (2006) продемонстрировал, что при подобном условии несвязанности среди базисных функций, используемых в параметризации, решение минимальной нормы l1 также является наиболее разреженным решением.
Недостатки способов нормы l1 имеют две стороны. Во-первых, многие интересующие задачи попросту не отвечают условию несвязанности и не подходят для способов нормы l1. Во-вторых, даже если они отвечают условию несвязанности, крупномасштабные задачи требуют чрезмерных вычислительных затрат. Таким образом, хотя они являются выпуклыми задачами и решаемы в принципе, их невозможно применить на практике к современным задачам с миллионами или более параметров, при этом данная проблема также затрагивает традиционные статистические способы. Donoho и др. (2006) описывают, как более эффективно применить случайный характер к подобным крупномасштабным задачам, не используя норму l1.
Способ pixon является эффективной техникой для получения минимально сложных решений данных, основанных на пикселях - включая крупномасштабные задачи - без необходимости в строгой разреженности и без условия несвязанности, требуемых способами, использующими норму l1 (см., например, Pina & Puetter 1993; Puetter & Yahil 1999; Puetter, Gosnell & Yahil 2005, и патенты США №5912993, 6353688, 6490374, 6895125, 6993204, 7863574, 7928727, 8014580, 8026846, 8058601, 8058625, 8086011, 8090179, 8094898, 8103487, содержания которых включены в настоящее описание посредством ссылки). Следовательно, способ pixon применим для крупномасштабных недоопределенных или слабо определенных обратных задач, таких как восстановление изображений или спектральный анализ. Минимальную сложность достигают путем адаптивного сглаживания в местоположении каждого пикселя с помощью наиболее широкого ядра из библиотеки ядер, так что сглаживание с помощью данного ядра и всех более узких ядер предоставляет достаточную аппроксимацию отпечатка данных рассматриваемого пикселя. Карта, уточняющая, какое ядро необходимо использовать в каждом пикселе, называется картой pixon.
В своей современной форме восстановление pixon состоит из трех этапов. На первом этапе оно восстанавливает "псевдоизображение" без каких-либо ограничений pixon. На втором этапе данное псевдоизображение используют для определения карты pixon. На третьем этапе получают готовое изображение путем неполного восстановления, управляемого картой pixon. Второй и третий этапы могут повторяться несколько раз, но на практике в этом обычно нет необходимости, при условии что на первом этапе было получено приемлемое псевдоизображение. См. Puetter & Yahil (1999), Puetter и др. (2005) и патенты США №5912993, 6353688, 6490374, 6895125, 6993204, 7863574, 7928727, 8014580, 8058601, 8058625, 8086011, 8090179, 8094898 и 8103487 для более полных описаний способа pixon и его применения.
На фиг.2 изображена типовая система 200 формирования изображений с детектором 210 изображений и блоком 220 восстановления pixon. Восстановление основано на способе pixon, использующем карту P pixon, взаимодействующую с алгоритмом 230 восстановления pixon. Способ pixon относится к способу, сглаживающему каждую точку в пространстве объекта (далее "точка объекта") путем присваивания формы или объема каждой точке объекта в качестве основы для сглаживания pixon. Пространство объекта представляет собой пространство, в котором определен результат восстановления изображений и который соответствует области, изображение которой было получено с использованием системы 200 формирования изображений. (Следует отметить, что "пространство изображения" является термином, синонимичным термину "пространство объекта" и два термина в дальнейшем используются взаимозаменяемо.) Соответствующее пространство данных предоставлено точками данных, измеренными детектором 210 изображений.
Способ pixon предоставляет высококачественное восстановление объекта I изображения в пространстве объекта из измеренного набора d данных в пространстве данных. В качестве пространственно адаптивного способа восстановления, способ pixon применяет обусловленную данными операцию сглаживания к каждой точке объекта. Таким образом, способ pixon использует принцип минимальной сложности при присваивании каждой точке объекта функции ядра pixon, которая является основой операции сглаживания. Внутри блока 220 восстановления pixon карта pixon P определяет, какая из функций ядра pixon присвоена каждой из точек объекта.
В системе 200 формирования изображений детектор 210 изображений обнаруживает и связывает измеренный набор d данных с блоком 220 восстановления pixon. Блок 220 восстановления pixon использует специальным образом адаптированные алгоритмы 230 восстановления pixon для восстановления полученного набора d данных в объект I изображения. Таким образом, алгоритм 230 восстановления pixon использует матрицу H системы для описания свойств системы 200 формирования изображений и для расчета итеративно улучшенного объекта изображения путем регулировки модели данных, которая является основой для объекта I изображения. Объект I изображения, например, отображают на устройстве 240 отображения, используя известные техники визуализации.
Для каждой точки объекта карта P pixon предоставляет функцию ядра pixon, определенную на основании способа минимальной сложности. Данная функция ядра pixon используется в операции сглаживания pixon, применяемой в пространстве объекта.
Способ pixon также может позволить сжатое распознавание в форме сверхвысокого разрешения, используя неотрицательность изображения и минимальную сложность для восстановления изображения с более мелкими пикселями, чем те пиксели, для которых получены данные. Это не является нарушением теоремы отсчетов за авторством Найквиста (1928) и Шеннона (1949) из-за дополнительных условий неотрицательности и минимальной сложности (например, Puetter и др., 2005). Пространственные частоты за дифракционным пределом, усеченные в данных, подобным образом могут быть восстановлены в изображении.
На фиг.3 изображена примерная последовательность процесса согласно способу pixon. Сглаживание pixon применяют последовательно к стандартному алгоритму восстановления.
Используя стандартный алгоритм восстановления, входное изображение аппроксимируют к измеренному набору d данных (этап 300). В соответствии с вышеописанным использованием оператора К ядра pixon, итоговое вычисление изображения называется псевдоизображением. Карту P pixon определяют, используя псевдоизображение и измеренный набор d данных (этап 310). Псевдоизображение также является исходным объектом для операции сглаживания pixon (этап 320). В ходе операции сглаживания pixon (этап 320) выполняют сглаживание каждой точки объекта псевдоизображения посредством функции ядра pixon. (В некоторых вариантах существующих способов pixon карта pixon также может быть обновлена в каждой итерации путем вычисления из обновленного изображения.)
Итеративные способы восстановления изображений итеративно аппроксимируют модели изображения к измеренным данным и таким образом минимизируют воздействие шума на конечное изображение. Результат алгоритма восстановления представляет собой аппроксимированное изображение, которое аппроксимировано к измеренному набору d данных согласно правилам алгоритма.
В способе pixon аппроксимированное изображение может быть использовано в качестве входного объекта для сглаживания pixon, для восстановления pixon и для определения карты pixon.
Способ pixon включает в себя поиск наиболее широкой из возможных функций ядра pixon в каждой точке в пространстве объекта, которые вместе поддерживают достаточную аппроксимацию объекта к измеренному набору d данных. В частности, карта pixon присваивает каждой точке объекта определенную функцию ядра pixon.
Этап, на котором вначале вычисляют псевдоизображение, из которого затем может быть определена карта pixon, может обладать недостатками. Этот процесс требует больше вычислений и связан с риском внесения искажений в псевдоизображение, способных исказить карту pixon и, следовательно, окончательное восстановление изображений. Кроме этого, определение карты pixon работает хуже, если преобразование из пространства объекта в пространство данных является нелокальным (Bhatnagar & Cornwell 2004). Например, в интерферометрии и получении изображений с помощью магнитного резонанса, данные представляют собой преобразования Фурье изображения (плюс шум), при этом каждая волна Фурье (базисная функция изображения) распространяется по всему изображению. Другим примером является частично нелокальное преобразование в томографии. Данные представляют собой двухмерные проекции трехмерного изображения (плюс шум), преобразование, являющееся локальным в направлении, перпендикулярном направлению проекции, но нелокальным вдоль направления проекции.
В свете вышеизложенного, существует потребность в улучшенном способе определения карты pixon в пределах способа pixon.
КРАТКОЕ ИЗЛОЖЕНИЕ СУЩНОСТИ ИЗОБРЕТЕНИЯ
Согласно изобретению, описанному здесь, вышеупомянутых трудностей способа pixon, состоящего из трех этапов, можно избежать путем вычисления и обновления карты pixon в ходе итерации. Улучшенный подход определяет карту pixon из переменной, используемой для обновления изображения в итерации, т.е. "обновляющей переменной", и сглаживает данную обновляющую переменную в ходе итерации. Обновленное изображение обычно также дополнительно сглаживают в конце итерации, используя карту pixon, определенную в ходе итерации. В отличие от этого способа, существующие способы pixon определяют карту pixon из изображения после его обновления и переходят к сглаживанию изображения, используя эту карту pixon.
Согласно настоящему изобретению обновляющая переменная зависит от способа восстановления, но обычно представляет собой градиент оценочной функции или мультипликативный коэффициент обновления (например, Puetter и др. 2005). Эту обновляющую переменную сглаживают с помощью ядер pixon, и ядро, выбранное в каждой координате изображения, является наиболее широким ядром, для которого соотношение между квадратом изменения обновляющей переменной в результате сглаживания и дисперсией обновляющей переменной меньше предопределенного порогового значения для данного ядра и всех более узких ядер. Обычно то же ядро впоследствии также используют для сглаживания обновленного изображения в той координате перед переходом к следующей итерации. Дополнительное улучшение позволяет использовать "интерполированные ядра".
В одном аспекте изобретения способ восстановления модели объекта из набора данных, полученных из физического процесса, где набор данных содержит шум, включает в себя этапы, на которых: получают набор данных, определенных в пространстве данных; создают модель объекта в пространстве объекта, где модель объекта содержит множество точек объекта; разрабатывают преобразование модели объекта из пространства объекта в пространство данных, результатом которого является модель данных, где преобразование соответствует физическому процессу, посредством которого получен набор данных; выбирают оценочную функцию для определения аппроксимации модели данных к набору данных; определяют обновляющую переменную модели объекта в пространстве объекта на основании оценочной функции; выполняют сглаживание обновляющей переменной для определения сглаженной обновляющей переменной следующим образом: выполняют свертывание обновляющей переменной с помощью каждого из множества ядер pixon; и выбирают для каждой точки входного объекта ядро pixon, обладающее наибольшим размером и соответствующее предопределенным минимальным критериям; генерируют карту pixon путем присваивания индексов в каждой точке входного объекта, соответствующих выбранному ядру pixon; и генерируют выходную информацию, содержащую модель объекта с существенно сниженным шумом на основании индексов в пределах карты pixon. В одном варианте осуществления оценочную функцию определяют, используя способ сопряженных градиентов, и обновляющая переменная представляет собой неградиент.
В другом аспекте изобретения постоянный машиночитаемый носитель, содержащий предварительно записанное программное обеспечение, содержит команды для восстановления модели объекта из набора данных, полученных из физического процесса, где набор данных содержит шум, и команды включают в себя следующее: получают набор данных, определенных в пространстве данных; создают модель объекта в пространстве объекта, где модель объекта содержит множество точек объекта; разрабатывают преобразование модели объекта из пространства объекта в пространство данных, результатом которого является модель данных, где преобразование соответствует физическому процессу, посредством которого получен набор данных; выбирают оценочную функцию для определения аппроксимации модели данных к набору данных; определяют обновляющую переменную модели объекта в пространстве объекта на основании оценочной функции; выполняют сглаживание обновляющей переменной для определения сглаженной обновляющей переменной следующим образом: выполняют свертывание обновляющей переменной с помощью каждого из множества ядер pixon; и выбирают для каждой точки входного объекта ядро pixon, обладающее наибольшим размером и соответствующее предопределенным минимальным критериям; генерируют карту pixon путем присваивания индексов в каждой точке входного объекта, соответствующих выбранному ядру pixon. В примерном варианте осуществления оценочную функцию определяют, используя способ сопряженных градиентов, и обновляющая переменная представляет собой неградиент.
КРАТКОЕ ОПИСАНИЕ ГРАФИЧЕСКИХ МАТЕРИАЛОВ
На фиг.1 изображена блок-схема общей вычислительной среды, в которой настоящее изобретение может быть реализовано на практике.
На фиг.2 изображено общее представление системы формирования изображений известного уровня техники, основанной на способе pixon.
На фиг.3 изображена технологическая схема, демонстрирующая пример восстановления изображений, используя подход известного уровня техники для восстановления pixon.
На фиг.4 изображена технологическая схема, демонстрирующая пример восстановления изображений, используя способ pixon согласно настоящему изобретению.
На фиг.5 изображена технологическая схема, демонстрирующая пример альтернативного процесса восстановления изображений, используя способ pixon.
На фиг.6 показано не содержащее шум, нормальное, протонной плотности (PD) SBD "истинное" изображение мозга.
На фиг.7 изображен логарифм (основание 10) абсолютной величины преобразования Фурье изображения по фиг.6 в пространство данных.
На фиг.8 показано изображение по фиг.6 со случайным (белым) гауссовым шумом, добавленным к изображению со стандартным отклонением, равным 3% самого яркого вокселя изображения.
На фиг.9 изображен логарифм (основание 10) абсолютной величины преобразования Фурье изображения по фиг.8 в пространство данных.
На фиг.10 изображены те же данные, что и на фиг.9, с усеченными высокими частотами, соответствующие частотному покрытию, ограниченному третьей частью доступных частот. Данные на фиг.10 содержат входную информацию для восстановлений изображения, изображенных на фиг.11-14.
На фиг.11 изображено простое обратное преобразование Фурье данных по фиг.10, раскрывающее два типа искажений: коррелированный (не белый) шум и реверберацию на острых краях.
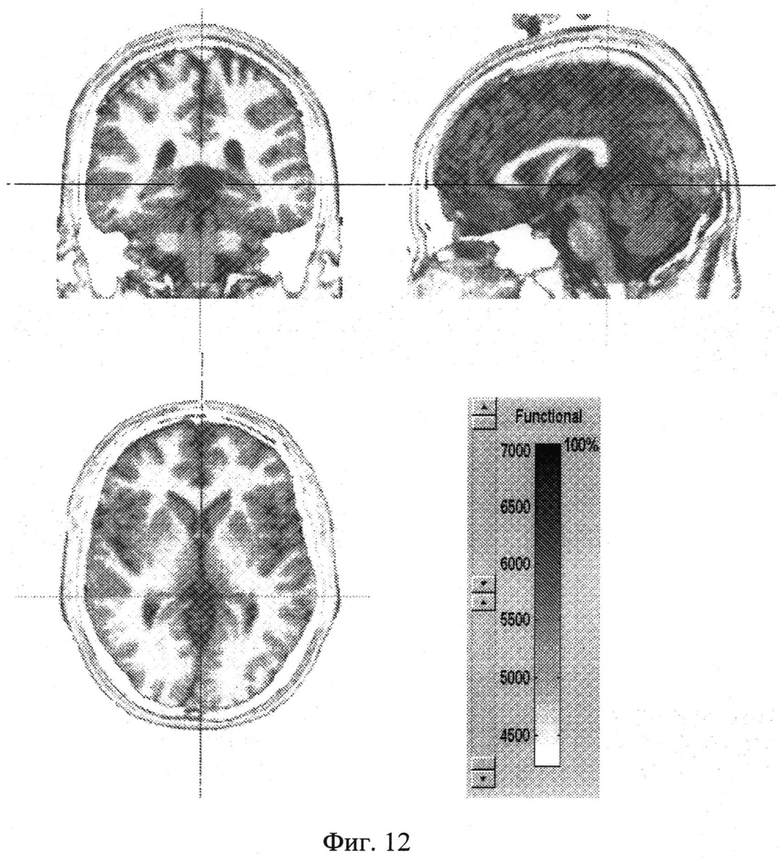
На фиг.12 изображен результат восстановления pixon данных по фиг.10 с коэффициентом pixon, равным 0,3.
На фиг.13 изображен результат восстановления pixon данных по фиг.10 с коэффициентом pixon, равным 0,5.
На фиг.14 изображен результат восстановлений pixon данных по фиг.10 с коэффициентом pixon, равным 1,0.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
Перед описанием аспектов настоящего изобретения может быть полезно предоставить краткое описание подходящей системы вычислительной среды 100 (фиг.1), на которой может быть реализовано изобретение. Система вычислительной среды 100 является лишь одним примером подходящей вычислительной среды и не предназначена для введения какого-либо ограничения объема применения или функциональности изобретения. Также не следует интерпретировать вычислительную среду 100 как обладающую какой-либо зависимостью или требованием относительно любого компонента или комбинации компонентов, изображенных в примере рабочей среды 100.
Изобретение может работать со многими другими универсальными или специализированными системами вычислительной среды или конфигурациями. Примеры хорошо известных вычислительных систем, сред и/или конфигураций, которые могут подходить для использования с изобретением, включают в себя, но не ограничиваются следующим: персональные компьютеры, серверные компьютеры, карманные или портативные устройства, многопроцессорные системы, системы на основе микропроцессоров, телевизионные абонентские приставки, программируемая бытовая электроника, сетевые ПК, мини-компьютеры, большие универсальные ЭВМ, телефонные системы, распределенные вычислительные среды, включающие в себя любые из вышеописанных систем или устройств, и т.п.
Изобретение может быть описано в общем контексте команд, выполняемых компьютером, таких как программные модули, выполняемые компьютером. В общем, программные модули включают в себя подпрограммы, программы, объекты, компоненты, структуры данных и т.д., выполняющие определенные задачи или реализующие определенные абстрактные типы данных. Специалисты в данной области могут реализовать описание и/или фигуры, приведенные здесь, в виде команд, выполняемых компьютером, которые могут быть воплощены в любой форме машиночитаемых носителей, описанных ниже.
Изобретение также может быть реализовано на практике в распределенных вычислительных средах, где задачи выполняются устройствами дистанционной обработки данных, соединенными посредством коммуникационной сети. В распределенной вычислительной среде программные модули могут находиться как на локальном, так и на удаленном компьютерном носителе данных, включая запоминающие устройства.
Со ссылкой на фиг.1, примерная система для реализации изобретения включает в себя универсальное вычислительное устройство в форме компьютера 110. Компоненты компьютера 110 могут включать в себя, но не ограничиваться следующими: процессор 120, системную память 130 и системную шину 121, соединяющую различные компоненты системы, в том числе системную память с процессором 120. Системная шина 121 может представлять собой любой из нескольких типов структур шины, включая шину памяти или контроллер памяти, периферийную шину и локальную шину, использующие любой вариант архитектуры шины. В качестве примера, но не ограничения, подобные архитектуры включают в себя шину стандартной промышленной архитектуры (ISA), шину микроканальной архитектуры (МСА), шину расширенной ISA (EISA), локальную шину ассоциации по стандартам в области видеоэлектроники (VESA) и шину соединения периферийных компонентов (PCI), также известную как шина расширения.
Компьютер 110 обычно содержит различные машиночитаемые носители. Машиночитаемые носители могут представлять собой любые имеющиеся в наличии носители, к которым может получить доступ компьютер 110, и включают в себя энергозависимые и энергонезависимые носители, съемные и несъемные носители. В качестве примера, но не ограничения, машиночитаемые носители могут содержать компьютерные запоминающие устройства и коммуникационные носители. Компьютерные запоминающие устройства включают в себя энергозависимые и энергонезависимые носители, съемные и несъемные носители, реализованные в любом способе или технологии для хранения информации, такой как машиночитаемые команды, структуры данных, программные модули или другие данные. Компьютерные запоминающие устройства включают в себя, но не ограничиваются следующими: ОЗУ, ПЗУ, ЭСППЗУ, флеш-память или другую технологию запоминающих устройств, CD-ROM, универсальные цифровые диски (DVD) или другой оптический дисковый накопитель, магнитные кассеты, магнитную ленту, магнитный дисковый накопитель или другие магнитные устройства хранения данных или любой другой носитель, который можно использовать для хранения желаемой информации и к которому может получить доступ компьютер 110. Коммуникационные носители обычно включают в себя машиночитаемые команды, структуры данных, программные модули или другие данные в модулированном сигнале данных, таком как несущая волна или другой транспортный механизм, и включают в себя любой носитель для доставки информации. Термин "модулированный сигнал данных" означает сигнал, в котором одна или несколько его характеристик задана или изменена таким образом, чтобы кодировать информацию в сигнале. В качестве примера, но не ограничения, коммуникационные носители включают в себя проводные носители, такие как проводную сеть или прямое проводное соединение, и беспроводные носители, такие как акустические, РЧ, инфракрасные и другие беспроводные носители. Сочетания любых из вышеописанных носителей также должны быть включены в объем термина "машиночитаемые носители".
Системная память 130 включает в себя компьютерные запоминающие устройства в форме энергозависимых и/или энергонезависимых запоминающих устройств, таких как постоянное запоминающее устройство (ПЗУ) 131 и оперативное запоминающее устройство (ОЗУ) 132. Базовая система 133 ввода/вывода (BIOS), содержащая базовые подпрограммы, помогающие передавать информацию между элементами внутри компьютера 110, например, при запуске компьютера, обычно хранится в ПЗУ 131. ОЗУ 132 обычно содержит данные и/или программные модули, непосредственно доступные процессору 120 или обрабатываемые процессором в настоящий момент. В качестве примера, но не ограничения, на фиг.1 изображена операционная система 134, прикладные программы 135, другие программные модули 136 и программные данные 137.
Компьютер 110 также может содержать другие съемные/несъемные энергозависимые/энергонезависимые компьютерные запоминающие устройства. Лишь в качестве примера, на фиг.1 изображен жесткий диск 141, считывающий или записывающий данные на несъемный энергонезависимый магнитный носитель, привод 151 для магнитных дисков, считывающий или записывающий данные на съемный энергонезависимый магнитный диск 152, и привод 155 для оптических дисков, считывающий или записывающий данные на съемный энергонезависимый оптический диск 156, такой как CD-ROM или другие оптические носители. Другие съемные/несъемные энергозависимые/энергонезависимые компьютерные запоминающие устройства, которые могут быть использованы в примерной рабочей среде, включают в себя, но не ограничиваются следующими: кассеты с магнитной лентой, карты флеш-памяти, универсальные цифровые диски, лента с цифровой видеозаписью, твердотельное ОЗУ, твердотельное ПЗУ и т.п. Жесткий диск 141 обычно соединен с системной шиной 121 посредством интерфейса несъемного запоминающего устройства, такого как интерфейс 140, и привод 151 для магнитных дисков и привод 155 для оптических дисков обычно соединены с системной шиной 121 посредством интерфейса съемного запоминающего устройства, такого как интерфейс 150.
Приводы и их соответствующие компьютерные запоминающие устройства, описанные выше и изображенные на фиг.1, обеспечивают хранение машиночитаемых команд, структур данных, программных модулей и других данных для компьютера 110. На фиг.1, например, изображено, что жесткий диск 141 хранит операционную систему 144, прикладные программы 145, другие программные модули 146 и программные данные 147. Следует отметить, что эти компоненты могут быть такими же, что и операционная система 134, прикладные программы 135, другие программные модули 136 и программные данные 137, или отличаться от них. В данном случае операционной системе 144, прикладным программам 145, другим программным модулям 146 и программным данным 147 присвоены другие номера для того, чтобы показать, что они как минимум представляют собой разные копии.
Пользователь может вводить команды и информацию в компьютер 110 посредством устройств ввода, таких как клавиатура 162, микрофон 163 (который также представляет собой ввод, предоставленный посредством телефона) и координатно-указательное устройство 161, такое как мышь, трекбол или сенсорная панель. Другие устройства ввода (не изображены) могут включать в себя джойстик, игровой контроллер, спутниковую антенну, сканер или т.п. Эти и другие устройства ввода часто соединены с процессором 120 посредством интерфейса 160 пользовательского ввода, соединенного с системной шиной, но могут быть присоединены посредством других структур интерфейса и шины, таких как параллельный порт, игровой порт или универсальная последовательная шина (USB). Монитор 191 или другой тип устройства отображения также соединен с системной шиной 121 посредством интерфейса, такого как видеоинтерфейс 190. Помимо монитора, компьютеры также могут содержать другие периферийные устройства вывода, такие как динамики 197 и принтер 196, которые могут быть присоединены посредством выходного периферийного интерфейса 195.
Компьютер 110 может работать в сетевой среде, используя логические соединения с одним или несколькими удаленными компьютерами, такими как удаленный компьютер 180. Удаленный компьютер 180 может представлять собой персональный компьютер, карманное устройство, сервер, роутер, сетевой ПК, одноранговое устройство или другой узел общей сети и обычно содержит многие элементы или все элементы, описанные выше в отношении компьютера ПО. Логические соединения, описанные на фиг.1, включают в себя локальную сеть (LAN) 171 и глобальную сеть (WAN) 173, но также могут включать в себя другие сети. Подобные сетевые среды распространены в офисах, корпоративных компьютерных сетях, интрасетях и в сети Интернет.
При использовании в сетевой среде LAN, компьютер 110 соединен с LAN 171 посредством сетевого интерфейса или адаптера 170. При использовании в сетевой среде WAN, компьютер 110 обычно содержит модем 172 или другие средства установки соединения по сети WAN 173, такой как Интернет. Модем 172, который может быть внутренним или внешним, может быть присоединен к системной шине 121 посредством интерфейса 160 пользовательского ввода или другого подходящего механизма. В сетевой среде, программные модули, изображенные относительно компьютера 110 или его частей, могут быть сохранены в удаленном запоминающем устройстве. В качестве примера, но не ограничения, на фиг.1 изображены удаленные прикладные программы 185, постоянно хранящиеся на удаленном компьютере 180. Следует понимать, что изображенные сетевые соединения являются примерными и могут быть использованы другие средства установки связи между компьютерами.
В данной заявке термин "pixon" используется для обозначения того, что термин, способ, объект и т.д. относится к способу pixon, т.е. к использованию определенных форм точек объекта при сглаживании объекта изображения, как описано в патентах США №5912993, 6895125 и других родственных патентах. Например, присвоенные формы определены функциями ядра pixon и карта P pixon хранит информацию о том, какая/какие из функций ядра pixon присвоена/присвоены каждой точке объекта.
Аппроксимация к данным является решением зашумленной обратной задачи. Данные выражены моделью

где d представляет собой массив, содержащий измеренные данные, I представляет собой массив, содержащий параметры аппроксимации, H представляет собой функцию преобразования из пространства параметров в пространство данных и ε
Для многих применений преобразование H является линейным, и уравнение (1) может быть записано в виде

где d и I рассматривают как векторы и H как матрицу, известную как системная матрица. Следующее описание ограничено линейным случаем уравнения (2), но оно может быть обобщено к нелинейным задачам путем линеаризации, т.е. рассматривания ограниченной области изображения, в которой H(I) является приблизительно линейным.
Следует отметить, что в реальности d и I могут быть многомерными и даже не должны обладать одинаковой размерностью (например, в томографии). Однако многомерные пиксели всегда могут быть расположены в виде длинных векторов и можно представить H в виде матрицы. Модель данных

представляет собой сигнальную часть данных, не содержащую шум. Она также является ожидаемой величиной данных

поскольку ожидаемая величина шума, без потери универсальности, может быть идентичным образом задана равной нулю для всех точек данных

Ковариационная матрица шума, в общем, не равна нулю и может быть функцией положения (координаты пикселя) и/или величины модели данных

Обычно, точки данных являются независимыми, поэтому V представляет собой диагональную матрицу, но также могут присутствовать коррелированные данные, в этом случае V имеет недиагональные, не равные нулю элементы.
Восстановление изображений представляет собой обратную задачу решения уравнения (2) - или, в более общем смысле, уравнения (1) - для изображения I, заданных данных d, системной матрицы H и статистической модели шума ε. Эту задачу решают путем оптимизации оценочной функции данных, учитывая модель данных

Выбор оценочной функции зависит от статистик шума. Обычно в качестве оценочной функции выбирают логарифмическую функцию правдоподобия (LLF), относящуюся к максимальному правдоподобию (например, Puetter и др., 2005).
Для гауссова шума LLF сводят к χ2

где суммирование по i проводят в отношении пикселей данных, где суммирование по α проводят в отношении пикселей изображения, σi является среднеквадратичным гауссовым отклонением шума в пикселе i. Гауссова LLF имеет преимущество, заключающееся в ее квадратичности в изображении I, так что ее градиент относительно I является линейным в I.
Для пуассоновского шума LLF является более сложной нелинейной функцией

которую можно решить нелинейной оптимизацией (например, Press и др., 2007) или использованием суррогатной функции (Lange, Hunter & Yang 1999). Mighell (1999) предложил использовать вместо этого квадратичную аппроксимацию к пуассоновской LLF, результатом чего является неискаженная модель данных, даже в пределе с малыми единицами счета
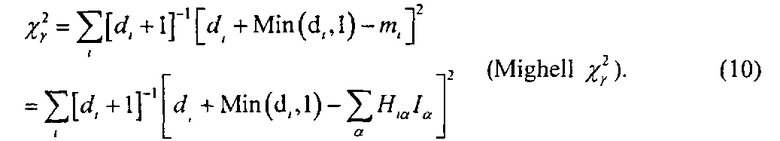
Существует множество способов оптимизации оценочной функции, но немногие подходят для крупномасштабных задач, поскольку системная матрица H и ее транспонированная матрица HT становятся слишком большими для вычисления и хранения - даже используя техники разреженных матриц - и могут быть применены лишь как операторы. Это оставляет по сути два способа: способы максимизации ожидания (ЕМ) (Richardson 1972; Lucy 1974; Dempster, Laird & Rubin 1977; Shepp & Vardi 1982) или способы сопряженных градиентов (CG) (Fox, Huskey & Wilkinson 1948; Hestenes & Stiefel 1952; Press и др., 2007). Минимизация ожидания упорядоченных подмножеств (OSEM) является ускоренным вариантом EM, использующим лишь подмножество данных в каждой итерации (Hudson & Larkin 1994). Ту же процедуру можно также применить к CG.
Способ CG осуществляют путем поиска последовательных минимальных нисходящих градиентов оценочной функции. Точнее, он использует направления сопряженных градиентов, представляющие собой линейные комбинации градиентов (например, Press и др., 2007). Полезная концепция заключается в неградиенте, определенном как половина отрицательного градиента оценочной функции относительно изображения. Для гауссовой оценочной функции, уравнение (8), неградиент представляет собой

в векторно-матричной системе обозначений уравнение (11) может быть записано в виде

где

являются остатками и дисперсия шума представляет собой

где Diag(σ2) обозначает диагональную матрицу, чьи диагональные элементы представляют собой σ2, квадраты среднеквадратичных отклонений.
Для пуассоновского шума неградиент 

Неградиент Mighell Poisson также линеен в изображении I и может быть записан в компактной векторно-матричной системе обозначений уравнения (12), где остатки представляют собой

и дисперсия шума представляет собой

CG способ можно значительно ускорить путем добавления предобусловливателя (например, Golub & Van Loan 1996; Saad 2003), меняя градиент оценочной функции на

где линейное уравнение

можно легко решить. Итоговый способ известен как предусловленный способ сопряженных градиентов (PCG).
Ограничения часто можно решить с помощью способа проецирования на выпуклые множества (Biemond, Lagendijk & Mersereau 1990). Например, неотрицательность, I≥0, может быть принудительно введена после каждой итерации путем простого усечения отрицательных компонентов изображения до нуля и продолжения, как будто усечения не происходило (Puetter и др. 2005). Также полезно после каждой итерации устанавливать нулевое значение любого отрицательного компонента сопряженного градиента в пикселях с нулевой величиной изображения в этой итерации. Это предотвращает участие этих пикселей в минимизации лишь для того, чтобы их итоговые отрицательные величины изображения были усечены до нуля в конце минимизации.
В изобретении, описанном здесь, карту pixon определяют из обновляющей переменной и не из изображения после его обновления и обновляющую переменную сглаживают в соответствии с этой картой pixon. Это устраняет потребность в вычислении начального псевдоизображения, поскольку карту pixon обновляют и обновляющую переменную сглаживают в каждой итерации.
Для CG способа в качестве обновляющей переменной выбирают неградиент, уравнение (12). (Предусловленный неградиент, уравнение (18), решают аналогичным образом.) Неградиент сглаживают с помощью ядер в библиотеке ядер pixon, и ядро, выбранное в каждой координате изображения, является наиболее широким ядром, для которого соотношение между квадратом изменения неградиента в результате сглаживания и дисперсией неградиента меньше предопределенного порогового значения для данного ядра и всех более узких ядер.
В частности, выбирают библиотеку функций ядра, определенных в пространстве объекта

Нулевые и первые моменты функций ядра устанавливают следующими:


и вторые моменты размещают в порядке возрастания

где интегралы аппроксимированы, на практике, путем суммирования по пикселям. Вторые моменты обычно разработаны таким образом, чтобы образовывать повышающиеся геометрические последовательности для оптимального определения характеристик многомасштабных структур изображения. Следует отметить, что размерность важна в уравнениях (21)-(23); следовательно, индексы α пикселей одномерного изображения, используемые ранее, заменяют векторными индексами τ и x.
Последовательность изменений ΔG(j) сглаженного неградиента затем получают путем свертывания неградиента поочередно с каждым из ядер и вычитания первоначального неградиента

В этом случае карта pixon представляет собой изображение индексов, так что в каждом пикселе выбранный индекс является наибольшим из индексов, для которых квадрат изменения сглаженного неградиента меньше или равен множителю p2 неградиента

где p представляет собой коэффициент pixon, описанный ниже. Сглаженный неградиент получают путем добавления к неградиенту в каждом пикселе изображения изменения сглаженного неградиента, соответствующего индексу его пикселя

Как хорошо видно из уравнения (25), коэффициент pixon p, изменяемый пользователем, регулирует силу сглаживания pixon. Большая величина p может позволить большей величине j удовлетворять уравнению (25) в любом пикселе x, тем самым повышая величину M(x). Результатом является более сильное сглаживание неградиента, уравнение (26). В отличие от этого, меньшая величина p может ограничить j меньшей величиной, тем самым уменьшая M(x) и уменьшая сглаживание. В результате пользователь может регулировать p для выбора оптимального соотношения между шумом и сглаживанием. Большая величина p лучше подавляет шум за счет некоторой потери разрешения, в то время как меньшая величина р лучше сохраняет разрешение за счет более высокого уровня шума.
На фиг.4 изображена примерная технологическая схема улучшенного способа определения карты pixon в процессе восстановления изображений. На этапе 400, восстановление изображений начинают путем оптимизации оценочной функции данных d, учитывая модель данных уравнения (7). В примерном варианте осуществления использован способ сопряженных градиентов (CG). На этапе 402 CG способ используют для определения неградиента, который будет использован в качестве обновляющей переменной (UV). На этапе 404 выполняют свертывание неградиента с каждым ядром из библиотеки 406 ядер pixon для сглаживания UV. Ядро, выбранное в каждой координате изображения, является наиболее широким ядром, для которого соотношение между квадратом изменения обновляющей переменной в результате сглаживания и дисперсией обновляющей переменной меньше предопределенного порогового значения для данного ядра и всех более узких ядер. Формируют карту pixon 410, используя изображение индексов выбранных ядер. Обычно то же ядро впоследствии также используют для сглаживания обновленного изображения 408 в той координате перед переходом к следующей итерации. Согласно существующему способу pixon, итеративно улучшенное изображение является основой для выходного изображения I, которое может быть отображено на устройстве отображения и/или сохранено в запоминающем устройстве.
Как было отмечено ранее, пример применения восстановления изображений не предназначен для ограничения, и улучшенный способ применим к любому процессу восстановления сигнала, использующему способ pixon. Возможно обобщить функции ядра до нелокальных, выполняющих более сложное сглаживание. Например, в изображении многоквартирного здания, содержащего много идентичных окон, возможно сгладить все окна в изображении вместе взятые, используя одно независимое ядро. Как вариант, данные могут вообще не иметь геометрического значения, например цены акций, в данном случае пикселизацию заменяют какой-либо схемой индексации для акций. Интеграл свертки, уравнение (24), в подобных системах заменяют более общим отношением

Обычно выгодно сохранять условие нормализации, подобное уравнению (21)

но уравнения (22)-(23) больше не имеют смысла и должны быть заменены условиями, определенными для задач. Что касается способа pixon, важно, что функции ядра сохраняют порядок предпочтений, так что уравнения (25)-(26) сохраняют свое значение.
Дополнительное улучшение заключается в создании непрерывной карты pixon с "дробными индексами" и "промежуточными ядрами" путем интерполяции между пробными неградиентами. Это дополнительно сглаживает неградиенты и/или позволяет использовать меньше функций ядра. Промежуточный индекс pixon определен как M(x)+δ(x), где M(x) является целочисленным индексом pixon, определенным уравнением (25), и δ(x) является прибавляемой величиной, линейно интерполирующей


и уравнение (26) заменяют уравнением
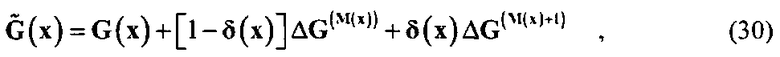
соответствующим использованию интерполированных ядер

Итеративный CG способ проходит, как обычно (например, Press и др., 2007), при этом сглаженный неградиент заменяет первоначальный, несглаженный неградиент.
Также полезно сглаживать непрерывную карту pixon, M(x)+δ(x), с помощью самой себя, используя интерполированные ядра согласно уравнению (31). Рациональное обоснование этого заключается в том, что карта pixon должна быть сглажена в каждой координате изображения в масштабе ширины ядра pixon, соответствующего индексу pixon в этой координате. Таким образом, сглаживание карты pixon с помощью самой себя не должно привносить в изображение значительное дополнительное сглаживание, но может сглаживать искажения, которые были введены в процесс вычисления карты pixon.
Обновленное изображение обычно дополнительно сглаживают после итерации с помощью интерполированных ядер, уравнение (31). Тем не менее, дополнительное сглаживание может привести к некоторой осцилляции решения с итерацией, так как ядра, верно сглаживающие неградиент, склонны к чрезмерному сглаживанию полного изображения. Простым способом подавления осцилляции является сглаживание изображения со средней величиной ядра, определенной в текущей и предыдущей итерациях. (Для первой итерации "предыдущее" ядро представляет собой дельта-функцию.)
На фиг.5 изображена примерная технологическая схема улучшенного способа определения карты pixon в процессе восстановления изображений с использованием интерполированных ядер. На этапе 500 восстановление изображений начинают путем оптимизации оценочной функции данных d, учитывая модель данных уравнения (7). В примерном варианте осуществления использован способ сопряженных градиентов (CG). На этапе 502 CG способ используют для определения неградиента, который будет использован в качестве обновляющей переменной (UV). На этапе 504 выполняют свертывание неградиента с каждым ядром из библиотеки 506 ядер pixon для сглаживания UV. Ядро, выбранное в каждой координате изображения, является наиболее широким ядром, для которого соотношение между квадратом изменения обновляющей переменной и дисперсией обновляющей переменной меньше предопределенного порогового значения для данного ядра и всех более узких ядер. Формируют карту pixon 510, используя изображение индексов выбранных ядер. После завершения свертки с ядрами из библиотеки ядер pixon, интерполированные ядра могут быть сгенерированы на этапе 508 для дополнительного сглаживания переменных UV, используемых для создания карты pixon. То же интерполированное ядро может быть использовано для сглаживания обновленного изображения 512 в той координате перед переходом к следующей итерации. Согласно существующему способу pixon, итеративно улучшенное изображение является основой для выходного изображения I, которое может быть отображено на устройстве отображения и/или сохранено в запоминающем устройстве.
Дисперсию неградиента, важную для определения карты pixon, нужно вычислять с осторожностью, так как транспонированная системная матрица, HT, уравнение (12), создает корреляции среди пикселей изображения, даже если данные статистически независимы. В некоторых случаях, например когда HT представляет собой преобразование Фурье, дисперсию неградиента можно вычислить аналитически. В других способах, удобный способ Монте Карло для вычисления дисперсии для крупномасштабных задач заключается в делении данных на несколько неперекрывающихся подмножеств данных и в вычислении неградиента G из уравнения (12) для каждого подмножества, заменяя остаток r случайно реализацией шума ε.

где верхний индекс s указывает на подмножество.
Поскольку ожидаемая величина шума равна нулю в каждом пикселе, уравнение (5), ожидаемая величина каждого градиента подмножества также равна нулю

Следовательно, в пределе большого количества подмножеств дисперсия неградиента может быть аппроксимирована как сумма квадратов градиентов подмножества

Относительная погрешность оценки дисперсии, полученной способом Монте Карло, равна

где S является количеством подмножеств.
Следует отметить, что для гауссова шума дисперсия неградиента зависит лишь от среднеквадратичного отклонения шума, σ, и не от данных или изображения. Следовательно, она не изменяется с итерацией и должна быть вычислена лишь один раз в начале восстановления изображений.
То же самое не всегда справедливо для пуассоновского неградиента по Mighell 

Поэтому, хотя дисперсия аппроксимации остатков в уравнении (36) действительно зависит от данных, она не зависит от изображения. Следовательно, она также не изменяется с итерацией и может быть вычислена лишь один раз в начале восстановления изображений.
Аналогичный способ pixon также может быть применен к ЕМ восстановлениям. Тем не менее, в данном случае задача заключается в том, что дисперсия мультипликативных коэффициентов обновления (Richardson 1972; Lucy 1974; Shepp & Vardi 1982) изменяется с итерацией и должна быть повторно вычислена в каждой итерации. Это значительно увеличивает вычислительные затраты, в дополнение к хорошо известному более медленному восстановлению разрешения согласно ЕМ способу, требующему значительно больше итераций для той же степени восстановления разрешения. В совокупности эти факторы выступают в пользу использования CG способа, а не EM способа.
Далее приведены примеры применений новаторского способа для восстановления входного сигнала, используя способ pixon. Эти примеры приведены лишь для наглядности и не предназначены для ограничения.
Примеры
Пример 1: Апертурный синтез
Апертурный синтез является типом интерферометрии, смешивающим сигналы из системы телескопов для создания изображений, обладающих одинаковым угловым разрешением, в качестве инструмента, охватывающего всю систему. При каждом разделении и ориентировании диаграмма лепестков интерферометра производит выходную информацию, представляющую собой один компонент преобразования Фурье пространственного распределения яркости наблюдаемого объекта. Изображение (или "карту") источника создают из этих измерений. Апертурный синтез возможен, только если амплитуда и фаза входящего сигнала измерены каждым телескопом. Для радиочастот это возможно посредством электроники, в то время как для оптических источников света электромагнитное поле не может быть измерено напрямую и коррелировано в программном обеспечении, но должно быть передано чувствительной оптикой и оптически интерферировано.
Для создания высококачественного изображения необходимо большое количество различных разделений между разными телескопами (проецированное разделение между любыми двумя телескопами, видимое из источника космического радиоизлучения, называется базой) - требуется как можно больше разных баз для получения качественного изображения. Количество баз (nb) для системы, состоящей из n телескопов, рассчитывают уравнением nb=(n2-n)/2. Например, в астрономических радиотелескопах очень большая система (VLA) содержит 27 телескопов, одновременно предоставляющих 351 независимых баз, в то время как большая атакамская миллиметровая/субмиллиметровая система (ALMA), в настоящее время находящаяся в процессе постройки, после завершения будет содержать 66 телескопов, предоставляющих 2145 независимых баз. Большинство интерферометров с апертурным синтезом используют вращение Земли для увеличения числа ориентации баз, включенных в наблюдение. Сбор данных в разное время предоставляет измерения с различными разделениями и углами телескопов без потребности в приобретении дополнительных телескопов или в ручном перемещении телескопов, поскольку вращение Земли перемещает телескопы на новые базы. Дополнительную гибкость предоставляют путем разрешения перемещать отдельные телескопы в различные конфигурации, что предоставляет системе мощное изменяемое "приближение".
Другие применения апертурного синтеза включают в себя интерферометрический радиолокатор с синтезированной апертурой (IfSAR или InSAR), радиолокатор с синтезированной апертурой (SAR) и радиолокатор с обратной синтезированной апертурой (ISAR), гидролокатор с синтезированной апертурой, формирование луча и магнитометрию с синтезированной апертурой.
Изначально считалось необходимым выполнять измерения по существу на каждом отрезке и в каждой ориентации базы до определенного максимума: подобное преобразование Фурье с полной выборкой формально содержит информацию, точно эквивалентную изображению из обычного телескопа с диаметром апертуры, равным максимальной базе, отсюда и название "апертурный синтез". Было быстро обнаружено, что во многих случаях полезные изображения могут быть созданы с относительно разреженной и неравномерной системой баз с помощью способов нелинейного восстановления изображений.
Способ pixon представляет собой мощный способ нелинейного восстановления изображений, но его использование осложнялось нелокальной природой преобразования Фурье (Bhatnagar & Cornwell 2004). Новый способ определения карты pixon согласно настоящему изобретению может преодолеть это затруднение.
Пример 2: Магнитно-резонансная томография
Магнитно-резонансная томография (МРТ) представляет собой технику получения медицинских изображений, применяемую в радиологии для детальной визуализации внутренних структур. МРТ использует свойство ядерного магнитного резонанса чтобы создавать изображение ядер атомов внутри тела. Аппарат МРТ использует мощное магнитное поле для выравнивания намагниченности некоторых ядер атомов в теле и высокочастотные поля для систематического изменения выравнивания этой намагниченности. Это заставляет ядра создавать вращающееся магнитное поле, которое может быть обнаружено сканером - и данную информацию записывают для создания изображения просканированной области тела. Градиенты магнитного поля заставляют ядра в разных точках вращаться с разными скоростями. Путем использования градиентов в разных направлениях двухмерные изображения или трехмерные объемные изображения могут быть получены в любой произвольной ориентации. МРТ используют для создания изображения каждой части тела и особенно полезно для тканей с большим количеством ядер водорода и небольшим плотностным контрастом, таких как мозг, мышцы, соединительная ткань и большинство опухолей.
Большая часть тела состоит из молекул воды. Каждая молекула воды содержит два ядра или протона водорода. Когда человек находится в мощном магнитном поле сканера, направление среднего магнитного момента многих протонов выравнивается относительно направления поля. Радиочастотный передатчик включают на короткий период времени, и он создает изменяющееся электромагнитное поле. Это электромагнитное поле имеет необходимую частоту, известную как резонансная частота, для своего поглощения и изменения спина протонов в магнитном поле. После выключения электромагнитного поля спины протонов возвращаются в термодинамическое равновесие и объемная намагниченность повторно выравнивается относительно статического магнитного поля. В ходе данного возвращения в исходное состояние генерируется радиочастотный сигнал, который можно измерить приемными катушками. Протоны в разных тканях возвращаются в свое состояние равновесия с разными скоростями возврата. Разные переменные тканей, включая спиновую плотность, T1 и T2 время возврата в исходное состояние, и потоковые и спектральные сдвиги могут быть использованы для построения изображений. Путем изменения настроек сканера данный эффект используют для создания контраста между различными типами тканей тела или между другими свойствами, как в функциональной МРТ (ФМРТ) и диффузионной МРТ.
Информация о происхождении сигнала в трехмерном пространстве может быть получена путем применения дополнительных магнитных полей при сканировании. Эти поля, сгенерированные электрическими токами, проходящими через градиентные катушки, изменяют силу магнитного поля в зависимости от положения внутри магнита. Поскольку это также приводит к прогнозируемой зависимости частоты выпущенного радиосигнала от его происхождения, распределение протонов в теле можно математическим способом восстановить из сигнала, обычно путем использования обратного преобразования Фурье.
Большим ограничением МРТ является длительность сканирования, что приводит к повышенному дискомфорту пациента и низкой скорости обработки информации пациентов. МРТ сканирование можно ускорить одним из двух способов или их комбинацией. Длительность сканирования на каждой радиочастоте можно сократить, и/или можно сократить количество сканированных радиочастот. Первое приводит к увеличению шума, в то время как второе приводит к неполному покрытию частот, требуя техники, подобной апертурному синтезу. Нелинейное восстановление изображений pixon может помочь уменьшить шум и компенсировать утраченные данные Фурье, как изображено ниже.
К сожалению, не существует "наземных контрольных данных" или золотого стандарта для анализа данных МРТ, полученных на живых организмах. Таким образом, База данных моделирования мозга (SBD) была создана в Университете Макгилла (база данных является общедоступной во всемирной сети по адресу bic.mni.mcgill.ca/brainweb; Kwan, Evans & Pike 1999). SBD содержит набор реалистичных объемов данных МРТ, созданных моделью МРТ. Эти данные могут использоваться сообществом специалистов по нейровизулиализации для оценки производительности различных способов оценки изображений в условиях с известной истинной информацией.
В настоящее время SBD содержит моделированные данные МРТ мозга, основанные на двух анатомических моделях: нормальной модели и модели рассеянного склероза (MS). Для обеих моделей были смоделированы полные трехмерные объемы данных, используя три последовательности (T1-, T2- и взвешенной протонной плотности- (PD-)) и различные величины толщины срезов, уровней шума и уровней неравномерности интенсивности. Эти данные доступны для просмотра в трех прямоугольных видах (поперечном, сагиттальном и фронтальном), а также доступны для загрузки. Дополнительные подробности о создании SBD доступны из общественных источников.
На фиг.6 показано не содержащее шум, нормальное, протонной плотности (PD) SBD "истинное" изображение мозга, и на фиг.7 изображен логарифм (основание 10) абсолютной величины его преобразования в пространство данных. На обеих фигурах верхние панели демонстрируют коронарный срез (левая панель) и сагиттальный срез (правая панель). На нижней панели показан поперечный срез. Преобразование из пространства объекта в пространство данных состояло из двухмерных преобразований Фурье, по одному поперечному срезу за раз, и отображение циклически смещалось в поперечном направлении, для того чтобы отображать нулевую частоту в его центре. На фиг.8 показано изображение по фиг.6 со случайным (белым) гауссовым шумом, добавленным к изображению со стандартным отклонением, равным 3% самого яркого вокселя изображения. На фиг.9 изображено преобразование Фурье по фиг.8 в пространство данных. Видно, что шум преобладает над данными на высоких частотах (поперечные границы отображений данных). На фиг.10 изображены те же данные, что и на фиг.9, с усеченными высокими частотами, соответствующие частотному покрытию, ограниченному третьей частью доступных частот. Данные на фиг.10 содержат входную информацию для восстановлений изображения.
На фиг.11 изображено простое обратное преобразование Фурье данных, демонстрирующих два типа искажений. Во-первых, на всем изображении ясно виден шум; он больше не представляет собой некоррелированный белый шум из-за отсечки частоты данных. Во-вторых, видна реверберация рядом с острыми краями, вызванная явлением, впервые описанным Гиббсом (1898, 1899). Неотрицательные наименьшие квадраты (NNLS), аппроксимированные к данным (не изображены), по существу идентичны прямому обратному преобразованию Фурье. Различия между этими изображениями видны лишь на экстракорпоральном фоне, не представляющем интереса, и в любом случае являются очень малыми. Более значительные улучшения изображения видны на фиг.12-14, на которых изображен результат восстановлений pixon с коэффициентами pixon, равными 0,3, 0,5 и 1,0, соответственно. Все восстановления значительно уменьшают шум и реверберацию по Гиббсу, но не на одинаковую величину. Как описано выше в контексте уравнений (25)-(26), существует оптимальное соотношение между шумом и сглаживанием, регулируемое пользователем с помощью коэффициента pixon p. Большая величина p лучше подавляет шум за счет некоторой потери разрешения, в то время как меньшая величина p лучше сохраняет разрешение за счет более высокого уровня шума. Данное оптимальное соотношение видно на фиг.12-14, на которых изображено усиление сглаживания по мере увеличения p, с небольшой результирующей потерей разрешения.
Пример 3: Компьютерная томография
Компьютерная томография (КТ) предоставляет способ диагностики и измерения для медицины и испытательной техники, с помощью которого можно обследовать внутренние структуры пациента или испытываемого объекта без необходимости в процессе выполнения хирургических операций на пациенте или в повреждении испытываемого объекта. В данном случае с разных углов записываются несколько проекций обследуемого объекта, из которых возможно вычислить трехмерное описание объекта.
Томографические изображения создают путем конвертации наблюдаемых проекций (данных) в изображение. Например, в рентгеновской КТ визуализации рентгеновские лучи направляют на объект и лучи ослабляются на разную величину из-за различных структур, находящихся внутри объекта. На другой стороне объекта ослабленные лучи измеряют детекторами. Подобные проекции создаются под многими различными углами вокруг объекта. Эти измерения не только содержат шум, но кроме этого, относительный уровень шума зависит от величины ослабления. Проекции сквозь плотные материалы, такие как кость и особенно металл, обладают меньшим отношением "сигнал-шум", чем проекции сквозь мышечную ткань, воду или другие менее плотные материалы. Работа с большими и изменяющимися в пространстве флуктуациями количества обнаруженных фотонов часто требует техники статистического сглаживания для улучшения изображения.
В подходах статистического восстановления изображений проблема заключается в нахождении изображений, которые наилучшим образом подходят к измерениям согласно (возможно нелинейной) физической модели и статистической модели. Правильное статистическое моделирование может привести к менее зашумленным изображениям, тем самым позволяя уменьшить дозу рентгеновского излучения для пациента.
Пример 4: Эмиссионная томография
Эмиссионная томография представляет собой технику медицинской радиоизотопной визуализации, создающей трехмерное изображение функциональных процессов в теле, используя томографические техники, подобные использующимся в КТ. Отличие заключается в том, что гамма-активный или позитронно-активный радиоизотоп (называемый радионуклидом) вводят в кровоток пациента. Гамма-активные радионуклиды излучают единственный фотон, и способ визуализации известен под названием однофотонная эмиссионная компьютерная томография (ОФЭКТ или иногда ОФЭТ). В отличие от этого способа, излученные позитроны взаимно уничтожаются с электронами в теле и образуют два фотона, движущихся в противоположных направлениях, обнаруживаемых одновременно; этот способ визуализации известен под названием "позитронно-эмиссионная томография" (ПЭТ).
Большую часть времени маркерный радиоизотоп, представляющий интерес только благодаря своим радиоактивным свойствам, присоединен к определенному лиганду для создания радиолиганда, представляющего интерес благодаря своей способности связывания с определенными типами тканей. Данное соединение позволяет осуществлять комбинирование лиганда и радиоизотопа (радиофармацевтического средства) и связывать полученную комбинацию с интересующей областью тела, что затем (благодаря прямому или непрямому гамма-излечению изотопа) позволяет визуализировать концентрацию лиганда.
Радионуклидные сканирования все чаще считывают вместе со сканированиями КТ или МРТ, при этом данная комбинация предоставляет как анатомическую, так и метаболическую информацию (т.е. информацию о структуре и о биохимических процессах). Поскольку радионуклидная визуализация наиболее полезна в сочетании с анатомической визуализацией, современные радионуклидные сканеры в настоящее время содержат встроенные высококлассные сканеры с несколькими рядами детекторов КТ или, в недавнее время, МРТ. Поскольку два сканирования могут быть выполнены непосредственно друг за другом или даже одновременно, в ходе одного сеанса, при этом пациент не меняет свое положение между двумя типами сканирования, два комплекта изображений регистрируются с большей точностью, так что области, содержащие аномалии на изображениях, полученных посредством радионуклидной визуализации, можно с большей точностью коррелировать с анатомией на изображениях КТ или МРТ. Это очень полезно при демонстрации увеличенных изображений движущихся органов или структур с более высокой анатомической вариацией, которая более распространена вне мозга.
Технику, подобную восстановлению компьютерной томографии (КТ), обычно используют для создания трехмерного изображения, хотя набор данных, собранных при радиоизотопной визуализации, содержит намного меньше протонов, чем КТ, поэтому техники восстановления являются более сложными. Обработка pixon затем может быть использована для улучшения качества изображения и/или снижения дозы, вводимой пациенту.
Пример 5: Спектральный анализ
Анализатор спектра измеряет амплитуду входящего сигнала в сравнении с частотой в пределах полного частотного диапазона инструмента. Основное применение заключается в измерении мощности спектра известных и неизвестных сигналов. Входящий сигнал, измеряемый анализатором спектра, является электрическим, однако спектральные составы других сигналов, таких как волны акустического давления и оптические волны, могут быть рассмотрены путем использования соответствующего преобразователя. Путем анализа спектров электрических сигналов, преобладающей частоты, мощности, искажения, гармонических колебаний, ширины полосы пропускания и других спектральных компонентов сигнала можно рассмотреть другие спектральные компоненты сигнала, которые сложнее обнаружить в формах волны временной области. Эти параметры полезны при определении характеристик электронных приборов, таких как беспроводные передатчики.
Типы анализатора спектра обусловлены способами, используемыми для получения спектра сигнала. Такими типами являются перестраиваемые анализаторы спектра с преобразованием развертки и анализаторы на основе быстрого преобразования Фурье (FFT). Перестраиваемый анализатор спектра с преобразованием развертки использует супергетеродинный приемник для понижающего преобразования части спектра входящего сигнала (используя генератор, управляемый напряжением, и преобразователь частоты) для центровки частоты полосового фильтра. С помощью супергетеродинной архитектуры генератор, управляемый напряжением, перестраивают по диапазону частот, что позволяет рассматривать весь диапазон частот инструмента. Анализатор спектра FFT вычисляет быстрое преобразование Фурье, тем самым преобразовывая входящий сигнал в компоненты его частотного спектра. Некоторые анализаторы спектра, такие как анализаторы спектра в режиме реального времени, используют гибридную технику, где входящий сигнал сначала преобразуют с понижением до более низкой частоты, используя супергетеродинные техники, и затем анализируют, используя техники FFT.
Это является одномерным примером, в котором спектр ("изображение") соотнесен с входными данными с помощью нелокального преобразования Фурье. Способ pixon может быть применен к подобным данным аналогичным способом, как и другие приведенные примеры преобразований Фурье.
Источники информации
1. Bhatnagar S, Cornwell TJ. 2004. Astron. Astrophys. 426:747-754.
2. Biemond J, Lagendijk RL, Mersereau RM. 1990. Proc. IEEE 78:856-883.
3. Candes EJ, Romberg J, Tao T. 2004, IEEE Tans. Info. Thry. 52:489-509.
4. Chaitin GJ. 1966. J. Assoc. Comput. Mach. 13:547-569.
5. Chen S, Donoho D, Saunders MA. 1999. SIAM J. Sci. Сотр. 20:33-61.
6. Dempster AP, Laird NM, Rubin DB. 1977. J. R. Stat. Soc. В 39:1-38.
7. Donoho DL 2006, Com. Pure Appl. Math. 59:797-829.
8. Donoho DL, Tsaig Y, Drori I, Starck JL. 2006. "Sparse Solution of Underdetermined Linear Equations by Stagewise Orthogonal Matching Pursuit", Stanford Technical Report.
9. Fisher RA 1912. Messenger Math. 41:155cl60.
10. Fisher RA 1922. Phil. Trans. Roy. Soc. A 222:309-368.
11. FoxL, Huskey HD, Wilkinson JH. 1948. Quart. J. Mech. Appl. Math. 1:149-173.
12. Gauss CF 1809. Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium, English translation, 1963. Theory of Motion of the Heavenly Bodies (New York: Dover).
13. Gibbs JW. 1898. Nature 59:200.
14. Gibbs JW. 1899. Nature 59:606.
15. Golub GH, Van Loan CF. 1996. Matrix Computations, 3е изд. (Baltimore: Johns Hopkins University Press).
16. Hesse LO. 1876. Vorlesungen über Analytische Geometrie des Raumes, Insbesondere über Oberflächen Zweiter Ordnung, (Leipzig: Teubrier).
17. Hestenes MR, Stiefel E. 1952. J. Res. Nat. Bur. Standards, 49:409-436.
18. Hudson HM, Larkin RS. 1994. IEEE Trans. Med. Imag. 13:601-609.
19. Kolmogorov AN. 1965. Problems Inf. Transm. 1:4-7.
20. Kwan RKS Evans AC Pike GB 1999. IEEE Trans. Med. Imag. 18:1085-97.
21. Lange K, Hunter DR, Yang I. 2000. J. Comp. Graph. Statist. 9:1-59.
22. Lucy LB. 1974. Astron. J. 79:745-54.
23. Mighell KJ. 1999. Astrophys. J. 518:380-393.
24. Miller, A 2002, Subset Selection in Regression, 2е изд. (Boca Raton: Chapman & Hall/CRC).
25. Nyquist H 1928. Trans. AIEE 47:617-644.
26. Piña RK, Puetter RC. 1993. Publ. Astron. Soc. Рас.105:630-637.
27. Press WH, Teukolsky SA, Vetterling WT & Flannery BP. 2007. Numerical Recipes, 3е изд., (Cambridge: Cambridge University Press).
28. Puetter RC, Gosnell TR & Yahil A 2005. Annu. Rev. Astron. Astrophys. 43:139-194.
29. Puetter RC, Yahil A. 1999. Astron. Soc. Рас. Conf. Ser. 172:307-316.
30. Richardson W. 1972. J. Opt. Soc. Am. 62:55-59.
31. Saad Y.2003. Iterative Methods for Sparse Linear Systems, 2е изд. (Philadelphia: SIAM).
32. Shannon CE. 1949. Proc. Institu. Radio Engineers. 37:10-21.
33. Shepp LA, Vardi Y. 1982. IEEE Trans. Med. Imaging 1:113-22.
34. Solomonoff RJ. 1964. Inf. Control 7:1-22.
35. Tibshirani R 1996. J. R. Statist. Soc. В 58:267-288.
36. Tikhonov AN. 1963. Soviet Math. 4:1035-1038.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОРРЕКТИРОВКИ ОШИБКИ ИЗМЕРЕНИЯ ГЛУБИНЫ TOF-КАМЕРЫ | 2021 |
|
RU2770153C1 |
| СПОСОБ И УСТРОЙСТВО СУБПИКСЕЛЬНОГО УТОЧНЕНИЯ ВЕКТОРОВ ДВИЖЕНИЯ | 2022 |
|
RU2803233C1 |
| СИСТЕМА ОБРАБОТКИ ИЗОБРАЖЕНИЙ И СПОСОБ УСТРАНЕНИЯ РАСТРОВОЙ СТРУКТУРЫ ИЗОБРАЖЕНИЯ ЧЕРЕЗ РАЗРЕЖЕННОЕ ПРЕДСТАВЛЕНИЕ СКАНИРОВАННЫХ ПЕЧАТНЫХ КОПИЙ | 2014 |
|
RU2595635C2 |
| АВТОМАТИЗИРОВАННОЕ ОПРЕДЕЛЕНИЕ И ОБРЕЗКА НЕОДНОЗНАЧНОГО КОНТУРА ДОКУМЕНТА НА ИЗОБРАЖЕНИИ | 2017 |
|
RU2680765C1 |
| СПОСОБ ОБРАБОТКИ ИЗОБРАЖЕНИЙ, УСТРОЙСТВО ОБРАБОТКИ ИЗОБРАЖЕНИЙ И НОСИТЕЛЬ ДАННЫХ | 2018 |
|
RU2709437C1 |
| СПОСОБ РЕНТГЕНОВСКОЙ ТОМОГРАФИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2505800C2 |
| ОБНАРУЖЕНИЕ ТЕКСТОВЫХ ПОЛЕЙ С ИСПОЛЬЗОВАНИЕМ НЕЙРОННЫХ СЕТЕЙ | 2018 |
|
RU2699687C1 |
| АВТОМАТИЗИРОВАННЫЕ СПОСОБЫ И СИСТЕМЫ ВЫЯВЛЕНИЯ НА ИЗОБРАЖЕНИЯХ, СОДЕРЖАЩИХ ДОКУМЕНТЫ, ФРАГМЕНТОВ ИЗОБРАЖЕНИЙ ДЛЯ ОБЛЕГЧЕНИЯ ИЗВЛЕЧЕНИЯ ИНФОРМАЦИИ ИЗ ВЫЯВЛЕННЫХ СОДЕРЖАЩИХ ДОКУМЕНТЫ ФРАГМЕНТОВ ИЗОБРАЖЕНИЙ | 2016 |
|
RU2647670C1 |
| РЕКОНСТРУКЦИЯ ВРЕМЯПРОЛЕТНОЙ ПОЗИТРОННО-ЭМИССИОННОЙ ТОМОГРАФИИ С ПОМОЩЬЮ СОДЕРЖАНИЯ ИЗОБРАЖЕНИЯ, ФОРМИРУЕМОГО ПОЭТАПНО НА ОСНОВЕ ВРЕМЯПРОЛЕТНОЙ ИНФОРМАЦИИ | 2010 |
|
RU2527211C2 |
| СПОСОБ И СИСТЕМА ЭФФЕКТИВНОЙ ПОДГОТОВКИ СОДЕРЖАЩИХ ТЕКСТ ИЗОБРАЖЕНИЙ К ОПТИЧЕСКОМУ РАСПОЗНАВАНИЮ СИМВОЛОВ | 2016 |
|
RU2636097C1 |












Изобретение относится к средствам восстановлении объекта наблюдения на изображении. Техническим результатом является обеспечение уменьшения шума объекта на восстановленном изображении. Способ содержит создание модели объекта в пространстве, преобразование модели объекта из пространства объекта в пространство данных с получением модели данных, выбор оценочной функции для определения аппроксимации модели данных, определение обновляющей переменной модели объекта, сглаживание обновляющей переменной ее свертыванием с помощью каждого ядра pixon, выбор для каждой точки входного объекта ядра pixon, обладающего наибольшим размером и соответствующего предопределенному минимальному критерию, генерирование карты pixon присваиванием индексов в каждой точке объекта, соответствующих выбранному ядру pixon, генерирование выходной модели объекта на основании индексов в пределах карты pixon. 2 н. и 19 з.п. ф-лы, 14 ил.
1. Способ восстановления модели объекта из набора данных, содержащего шум, при этом способ включает:
получение в процессоре набора данных, определенных в пространстве данных, при этом процессор обеспечивает:
создание модели объекта в пространстве объекта, при этом модель объекта содержит множество точек объекта;
разработку преобразования модели объекта из пространства объекта в пространство данных, результатом которого является модель данных, при этом преобразование соответствует физическому процессу, посредством которого получают набор данных;
выбор оценочной функции для определения аппроксимации модели данных к набору данных;
определение обновляющей переменной модели объекта в пространстве объекта на основании оценочной функции;
сглаживание обновляющей переменной для определения сглаженной обновляющей переменной посредством:
свертывания обновляющей переменной с помощью каждого из множества ядер pixon; и
выбора для каждой точки входного объекта ядра pixon, обладающего наибольшим размером и соответствующего предопределенному минимальному критерию;
генерирование карты pixon путем присваивания индексов в каждой точке объекта, соответствующих выбранному ядру pixon; и
генерирование выходной информации, содержащей модель объекта с существенно сниженным шумом, на основании индексов в пределах карты pixon.
2. Способ по п.1, в котором процессор дополнительно обеспечивает сглаживание модели объекта путем свертывания модели объекта в каждой точке объекта с выбранным ядром pixon согласно карте pixon.
3. Способ по п.1, отличающийся тем, что оценочную функцию определяют, используя способ сопряженных градиентов.
4. Способ по п.3, отличающийся тем, что обновляющая переменная представляет собой неградиент.
5. Способ по п.3, в котором процессор дополнительно обеспечивает добавление предобусловливателя.
6. Способ по п.1, в котором процессор дополнительно обеспечивает:
итеративное сглаживание обновляющей переменной и обновление карты pixon и модели объекта на основании сглаженной обновляющей переменной до тех пор, пока оценочная функция не будет оптимизирована.
7. Способ по п.1, в котором процессор дополнительно обеспечивает, после этапа свертывания обновляющей переменной, вычитание обновляющей переменной для определения изменения обновляющей переменной.
8. Способ по п.7, отличающийся тем, что предопределенный минимальный критерий основан на соотношении между квадратом изменения обновляющей переменной и дисперсией обновляющей переменной.
9. Способ по п.1, отличающийся тем, что набор данных содержит интерферометрические данные, сгенерированные в сочетании с процессом анализа, выбранного из группы, состоящей из апертурного синтеза, интерферометрического радиолокатора с синтезированной апертурой (IfSAR или InSAR), радиолокатора с синтезированной апертурой (SAR) и радиолокатора с обратной синтезированной апертурой (ISAR), гидролокатора с синтезированной апертурой, формирования луча и магнитометрии с синтезированной апертурой.
10. Способ по п.1, отличающийся тем, что набор данных содержит данные магнитно-резонансной томографии.
11. Способ по п.1, отличающийся тем, что набор данных содержит вычисленные данные или данные эмиссионной томографии.
12. Способ по п.1, отличающийся тем, что набор данных содержит данные спектрального анализа.
13. Способ по п.1, отличающийся тем, что набор данных содержит множество входящих сигналов от различных инструментов и модель объекта со сниженным шумом содержит единственный выходной сигнал, соответствующий смеси входных сигналов.
14. Постоянный машиночитаемый носитель, содержащий предварительно записанное программное обеспечение, при этом программное обеспечение включает в себя команды для восстановления входного сигнала из набора данных, содержащего шум, при этом команды включают:
получение набора данных, определенных в пространстве данных;
создание модели объекта в пространстве объекта, при этом модель объекта содержит множество точек объекта;
разработку преобразования модели объекта из пространства объекта в пространство данных, результатом которого является модель данных, при этом преобразование соответствует физическому процессу, посредством которого получен набор данных;
выбор оценочной функции для определения аппроксимации модели данных к набору данных;
определение обновляющей переменной модели объекта в пространстве объекта на основании оценочной функции;
сглаживание обновляющей переменной для определения сглаженной обновляющей переменной посредством:
свертывания обновляющей переменной с помощью каждого из множества ядер pixon; и
выбора для каждой точки входного объекта ядра pixon, обладающего наибольшим размером и соответствующего предопределенному минимальному критерию; и
генерирование карты pixon путем присваивания индексов в каждой точке входного объекта, соответствующих выбранному ядру pixon.
15. Постоянный машиночитаемый носитель по п.14, дополнительно включающий сглаживание набора данных путем свертывания модели объекта в каждой точке с выбранным ядром pixon согласно карте pixon.
16. Постоянный машиночитаемый носитель по п.14, отличающийся тем, что оценочная функция определена с использованием способа сопряженных градиентов.
17. Постоянный машиночитаемый носитель по п.16, отличающийся тем, что обновляющая переменная представляет собой неградиент.
18. Постоянный машиночитаемый носитель по п.17, дополнительно содержащий добавление предобусловливателя.
19. Постоянный машиночитаемый носитель по п.14, дополнительно включающий:
итеративное сглаживание обновляющей переменной и обновление карты pixon и модели объекта на основании итеративно сглаженной обновляющей переменной до тех пор, пока оценочная функция не будет оптимизирована.
20. Постоянный машиночитаемый носитель по п.19, дополнительно включающий, после этапа свертывания обновляющей переменной, вычитание обновляющей переменной для определения изменения обновляющей переменной.
21. Постоянный машиночитаемый носитель по п.20, отличающийся тем, что предопределенный минимальный критерий основан на соотношении между квадратом изменения обновляющей переменной и дисперсией обновляющей переменной.
| US 6993204 B1, 31.01.2006 | |||
| US 20100119166 A1, 13.05.2010 | |||
| US 20100054564 A1, 04.03.2010 | |||
| US 20080270465 A1, 30.10.2008 | |||
| RU 2009139403 A, 27.05.2011 |
Авторы
Даты
2014-11-10—Публикация
2012-04-16—Подача