СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКИХ ПАРАМЕТРОВ ВОДЫ Российский патент 2015 года по МПК G01N13/02 

Изобретение относится к физике контактного взаимодействия жидкокристаллической материальной среды - воды в условиях гравитационного воздействия.

Известен способ определения гравитационного давления в массиве связной материальной среды, заключающийся в том, что от дневной поверхности устанавливают глубину h замера давления, на глубине h определяют тангенциальное напряжение τ=ρ·g·h=γ·h, МПа, где γ=ρg, кг/см³ - удельный вес материальной среды, ρ - плотность среды, кг/м³, g - ускорение свободного падения, м/с², удельное структурное сцепление с_стр, МПа, и угол φ_стр внутреннего трения среды, отличающийся тем, что нормальное гравитационное (бытовое) давление на глубине h массива связной материальной среды определяют по зависимости p_б=(γ·h-с_стр)ctgφ_стр, МПа, связную материальную среду на глубине h<с_стр/γ принимают находящейся в растянутом по вертикали напряженном состоянии и уравновешенной газовым атмосферным давлением планеты [1].

Чистую воду принято считать с позиций классической механики бессвязной средой, не обладающей внутренним трением и сцеплением (с=0, φ=0) при положительных температурах окружающей среды (T>0°C) и нормальном давлении (p_атм.ср=1,033 кг/см³=0,1014 МПа). Однако вода в чистом виде обладает поверхностным натяжением верхнего слоя (пленки) σ_пл.

Известен способ определения поверхностного натяжения поверхностного слоя (пленки) воды по зависимости σ_пл=P/l, которое определяют по силе P, приложенной к метрической единице прямолинейного участка границы поверхности воды по направлению касательной к жидкой поверхности при ее равновесии, причем при различных температурах T°C величину поверхностного натяжения σ_пл пленки воды определяют опытным путем [2].

Поверхностное натяжение воды обусловлено ее связностью, то есть вода должна характеризоваться физическими параметрами, присущими всем материальным средам - углом φ_в внутреннего трения и удельным сцеплением с_в. На сегодняшний день опытным путем определяют только ее коэффициент α поверхностного натяжения при заданной температуре. Так, при Т=0°C - справочный оптимальный коэффициент α=σ_пл=75,6·10^-3Н/м [2].

Технический результат по способу определения удельного сцепления и угла φ_в внутреннего трения воды, заключающийся в том, что определяют температуру T°C воды при нормальном атмосферном давлении p_атм.ср=1,033 кг/см², удельный вес воды принимают γ_в=981 кг/м³, устанавливают толщину h поверхностного слоя пленки воды, отличающийся тем, что толщину растянутого поверхностного слоя пленки воды определяют по зависимости 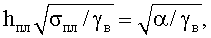$$h_{пл}\sqrt{{\sigma }_{пл}/{\gamma }_{в}}=\sqrt{\alpha /{\gamma }_{в}},$$ где σ_пл, кг/см, - величина поверхностного натяжения верхнего слоя пленки воды при температуре T°C и атмосферном давлении p_атм.ср=1,033 кг/см² окружающей среды, удельное сцепление воды при температуре T°C рассчитывают по зависимости и принимают равным c_в=τ=γ_в·h_пл=274,642·10^-6 кг/см²=27,446 Па при h_пл=27,978·10^-4 м; а угол φ_в внутреннего трения воды по глубине H водоема определяют из зависимости tgφ_в=1-[c_в/(γ_в·H)] и для жидкокристаллической структуры воды коэффициент внутреннего трения принимают f=tg44,7°=0,99≈1 с глубины H=28 см.

Пример 1. При гравитационном давлении в материальной среде p_б=(γ_в·h-c_в)ctgφ_в=0 на водной глади образуется пленка толщиной p_б=0, при (γ_в·h-c_в=0), h=c_в/γ_в, где c_в - удельное сцепление поверхностной пленки воды толщиной h и воды в целом, то есть c_в=τ-p·tgφ=τ_в=γ_в·h=ρ_вgh, то есть удельное сцепление воды определяется тангенциальным (касательным) напряжением натяжения ее поверхностной пленки c_в=τ_в. Толщину пленки воды, находящейся в состоянии поверхностного натяжения, уравновешенного атмосферным давлением, определяют по зависимости 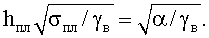$$h_{пл}\sqrt{{\sigma }_{пл}/{\gamma }_{в}}=\sqrt{\alpha /{\gamma }_{в}}.$$ При γ_в=981 кг/м³ и α=σ_пл=0,00739 кг/м величина h_пл=274,642·10^-4 м, а удельное сцепление воды c_в=τ_в=γ_вh_пл=274,642·10^-6 кг/см²=27,446 Па (таблица 1, фиг.1).

Таблица 1 Физические характеристики воды по глубине H, при γ_в=981 кг/см³ Глубина воды H, см Угол внутреннего терния, φ° Коэффициент внутреннего терния, f=tgφ Удельное сцепление с_в, Па 0,2796 0 0 0 0,3068 5 0,875 27,446 0,33989 10 0,1763 0,38243 15 0,2680 0,44017 20 0,3640 0,52457 25 0,4663 0,6239 30 0,5774 0,93385 35 0,7002 1,74 40 0,8391 2,1418 41 0,8693 2,811 42 0,9004 8,1594 44 0,9657 80,343 44,9 0,9965 100 44,92 0,9972 802,17 44,99 0,9965 8020,4 44,999 1 80203 44,9999 1 8,0202 км 44,99999 1

Коэффициент поверхностного натяжения водной глади (при заданной температуре) α=с_пл=τ_вh_пл=с_вh=γ_вh²=(981 кг/м³)·(27,978·10^-4 м)²=76,79·10^-4 кг/м=75,33·10^-3 Н/м. При T=0°C справочный опытный коэффициент поверхностного натяжения воды равен α=75,6·10^-3 Н/м [2].

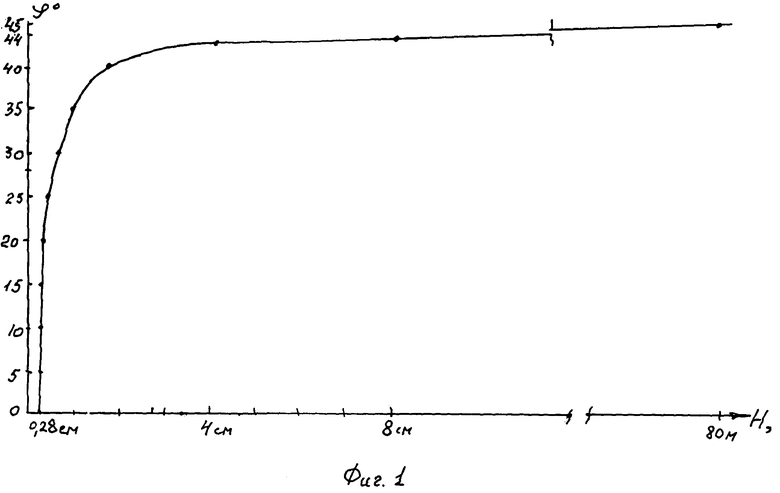
Пример 2. Гравитационное (бытовое) давление воды по глубине H водоема составляет величину p_б=(γ_в·H-с_в)ctgφ_в. При удельном сцеплении воды с_в=274,642·10^-6 кг/см² на заданной глубине H водоема угол внутреннего трения будет равен φ_в=arctg[(γ_в·H-с_в)/p_б], то есть tgφ_в=(γ_в·H-с_в)p_б=1-с_в/(γ_в·H), так как гравитационное давление воды равно ее гидростатическому давлению p_б=γ_в·H. При γ_в=981 кг/м³ и с_в=274,642·10^-6 кг/см² вода становится под давлением собственного веса структурированной жидкокристаллической с углом внутреннего трения φ=44,99999°=45° и коэффициентом внутреннего трения f=tgφ_в=1 с глубины H=с_в/[γ_в(1-tg44,99999°)]=274,642·10^-6/[981·10^-6(1-tgφ)}=802027,3 см=8,02 км, например, в Марианской впадине. Практически с глубины H=1 м величина φ_в=44,92°≈45° (таблица 1, фиг.1).

Впервые определены физические параметры угол φ_в внутреннего трения и удельное сцепление с_в воды по глубине водоема, ранее считавшиеся отсутствующими. Угол внутреннего трения воды растет с глубиной и становится равным φ=45° (практически с глубины H=1 м), это объясняет равенство нормального и тангенциального давления на глубине воды

τ_в=p_вtgφ_в+с_в=p_вtg45°+с_в=p_в+с_в=[(γ_вH-с_в)/tgφ_в]+с_в=γ_вH-с_в+с_в=γ_вH

или p_в=τ_в=γ_в·H, то есть нормальное давление становится всесторонним, что подтверждается экспериментально.

Источники информации

1. Заявка на патент №2013135028/(052474)

«Способ определения гравитационного давления в массиве связной материальной среды» от «25» июля 2013 г.

2. Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике / Изд-е 5, перераб. и доп. - «Наука», 1972. - с.84.

Изобретение относится к области физики материального взаимодействия, конкретно к способу определения физических характеристик φ_в - угла внутреннего трения и удельного сцепления - с_в воды с жидкокристаллической структурой. По зависимости $$h_{пл}=\sqrt{{\sigma }_{пл}/{\gamma }_{в}}=\sqrt{\alpha /{\gamma }_{в}}$$ , где σ_пл - величина поверхностного натяжения верхнего слоя пленки воды при температуре T°C и нормальном атмосферном давлении p_атм.ср=1,033 кг/см² окружающей среды, α - опытный справочный коэффициент, определяют толщину поверхностной пленки воды, удельное сцепление воды определяют как с_в=τ=γ_в·h_пл=27,446 Па при h_пл=27,978·10^-4 м, а угол φ_в внутреннего трения воды определяют из зависимости tgφ_в=1-[с_в/(γ_в·H)] на заданной глубине H. Техническим результатом является создание способа определения физических характеристик угла внутреннего трения и удельного сцепления воды с жидкокристаллической структурой. 1 табл., 1 ил.

Способ определения удельного сцепления и угла φ_в внутреннего трения воды, заключающийся в том, что определяют температуру T°C воды при нормальном атмосферном давлении p_атм.ср=1,033 кг/см², удельный вес воды принимают γ_в=981 кг/м³, устанавливают толщину h поверхностного слоя пленки воды, отличающийся тем, что толщину растянутого поверхностного слоя пленки воды определяют по зависимости $$h_{пл}\sqrt{{\sigma }_{пл}/{\gamma }_{в}}=\sqrt{\alpha /{\gamma }_{в}},$$ где σ_пл, кг/см - величина поверхностного натяжения верхнего слоя пленки воды при температуре T°C и атмосферном давлении p_атм.ср=1,033 кг/см² окружающей среды, удельное сцепление воды при температуре T°C рассчитывают по зависимости и принимают равным c_в=τ=γ_в·h_пл=274,642·10^-6 кг/см²=27,446 Па при h_пл=27,978·10^-4 м; а угол φ_в внутреннего трения воды по глубине H водоема определяют из зависимости tgφ_в=1-[c_в/(γ_в·H)] и для жидкокристаллической структуры воды коэффициент внутреннего трения принимают f=tg44,7°=0,99≈1 с глубины Н=28 см.