Изобретение относится к физике контактного взаимодействия частиц связной материальной среды в массиве полупространства в условиях гравитационного воздействия.
Известен способ определения природного гравитационного (бытового) давления в массиве жидкой и газовой бессвязной материальной среды, заключающийся в том, что определяют глубину h замера давления от поверхности полупространства с плотностью ρ и удельным весом γ=ρ·g, где g - ускорение свободного падения материального тела в условиях гравитации, а гравитационное природное давление определяют по расчетной зависимости pб=γ·h [1].
Природное давление pб=γ·h для бессвязных материальных сред (газ, вода) при отсутствии сил трения является всесторонним под их поверхностью в условиях полупространства и нормально действующим на погружаемые в них поверхности объектов. Величина тангенциального напряжения τ и нормального давления pб на заданной глубине равны друг другу τ=pб=γh.
Известен способ определения гравитационного давления несвязной материальной среды, заключающийся в том, что определяют глубину h замера давления от поверхности полупространства с плотностью ρ и удельным весом γ=ρ·g, где g - ускорение свободного падения материального тела в условиях гравитации, принимают угол внутреннего трения идеально чистой материальной среды φ=45° при коэффициенте внутреннего трения f=tgφ=1, а удельное сцепление с≈0, рассчитывают по закону Кулона тангенциальное напряжение как τ=p·tgφ+c=p, а гравитационное давление определяют, как и тангенциальное pб=τ=γ·h [2].
Технический результат по способу определения гравитационного давления в массиве связной материальной среды, заключающемуся в том, что устанавливают от поверхности массива глубину h замера давления, на глубине h определяют тангенциальное напряжение по зависимости τ=ρ·g·h=γ·h, МПа, где ρ - плотность, кг/м3, γ - удельный вес материальной среды с учетом взвешивающей силы воды, кг/м3, g - ускорение свободного падения тела в условиях гравитации, м/с2, удельное структурное сцепление cстр, МПа, и угол φстр внутреннего трения среды, достигается тем, что нормальное гравитационное давление на глубине h массива связной материальной среды определяют расчетным путем по зависимости pб=(τ-cстр)ctgφстр=(γ·h-cстр)ctgφстр, МПа, а связную материальную среду на глубине h<cстр/γ принимают находящейся в растянутом по вертикали напряженном состоянии и уравновешенной атмосферным давлением.
Величина нормального гравитационного давления pб на глубине h от поверхности структурно-устойчивого связного материального полупространства поясняется графически на фиг. 1 через зависимость Кулона τ=pб·tgφ+cстр для предельно нагруженной грунтовой среды.
Предлагаемый способ определения гравитационного давления в необводненном массиве связной материальной среды реализуется следующим образом.
В процессе инженерных изысканий массива среды определяют глубину h (см) его исследования, с которой отбирают образцы с ненарушенной структурой. В лаборатории по образцам среды определяют ее удельный вес γ=ρ·g (кг/см3), где ρ (кг/см3) - плотность среды, g (м/с2) - ускорение свободного падения тела, и производят расчет тангенциального напряжения на глубине h (см) исследуемого массива по зависимости τ=ρ·g·h=γ·h, пригодной для связной и несвязной материальной среды. По результатам лабораторных испытаний образцов среды в сдвиговых приборах или в стабилометрах строят график зависимости τ=p·tgφстр+cстр (кг/см2) Кулона-Мора предельного состояния материальной среды и устанавливают значения ее прочностных параметров - угла φстр внутреннего трения и cстр (кт/см2) удельного сцепления при не менее трех ступенях возрастающего сжимающего давления ρ (кг/см2) (фиг. 1). По графику τ=p·tgφстр+cстр определяют значение p=pб=(τ-cстр)ctgφстр=(γ·h-cстр)ctgφстр (кг/см2), соответствующее гравитационному давлению в массиве среды на глубине исследования h.
На глубине h<cстр/γ поверхность земной коры находится в состоянии растяжения и
удерживается от отделения в космическое пространство давлением атмосферы. На глубине h=cстр/γ природное (бытовое) давление в грунтовом массиве отсутствует.
Гравитационное давление проявляется на глубине h>cстр/γ от земной поверхности.
Пример 1. Археологические раскопки сохранившихся исторических ценностей в связной грунтовой среде с удельным сцеплением cстр=0,02 МПа; удельным весом γстр=0,0019 кг/см2 следует производить с глубины h=cстр/γстр=1,05 м. Если захоронения произведены на глубине h<1,05 м, то с годами на дневную поверхность грунтовой среды могут быть вытеснены надгробные кресты, что отмечено сегодня «как чудо» верующими людьми и до сих пор не объяснено учеными.
Пример 2. Вода в чистом виде обладает поверхностным натяжением верхнего слоя - пленки σпл=P/l, определяемым силой P, приложенной к метрической единице прямолинейного участка границы поверхности воды по направлению касательной к поверхности жидкости при ее равновесии. При температуре Τ=20°C поверхностное натяжение σпл=0,0725 дж/м2 = 0,0725 Н/м ≈ 0,00739 кг/м. При ускорении свободного падения g=9,81 м/с2 и плотности чистой воды ρ=1000 кг/м3 удельный вес воды составляет γ=981 кг/м3. Удельное сцепление поверхностной пленки воды толщиной hпл и воды в целом равно cв=ρв·g·hпл=γв·hпл=τв=σпл/ hпл, где τв - тангенциальное (касательное) напряжение. Толщина пленки воды, находящейся в состоянии поверхностного растяжения, 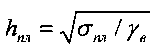 . При σпл=0,00739 кг/м, γв=981 кг/м3 получаем hпл=27,978·10-4 м, а удельное сцепление воды cв=τв=γв·hпл=274,642·10-6 кг/см2=27,446 Па.
. При σпл=0,00739 кг/м, γв=981 кг/м3 получаем hпл=27,978·10-4 м, а удельное сцепление воды cв=τв=γв·hпл=274,642·10-6 кг/см2=27,446 Па.
Коэффициент поверхностного натяжения водной глади при заданной температуре равен α=σпл=τв·hпл=cвhпл=γвh2 пл=981 кг/м3 (27,978·10-4 м)2=76,79·10-4 кг/м =75,33·10-3 Н/м. При Т=0°C опытный коэффициент поверхностного натяжения воды равен α=σпл =75,6·10-3 Н/м [4].
Источники информации
1. Ландсберг Г.А. Элементарный учебник физики / Механика. Теплота. Молекулярная физика. - T.1, издание 8. - М.: «Наука». - С.122, 323-327.
2. Цытович Н.А. Механика грунтов / Краткий курс: Изд-е 3, доп. - М.: «Наука», 1979. - С.46-47.
3. Ландсберг Г.А. Элементарный учебник физики / Механика. Теплота. Молекулярная физика. - T.1, издание 8. - М.: «Наука». - С.509-513.
4. Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике / Изд-е 5, перераб. и доп. - «Наука», 1972. - С.84.
Изобретение относится к области физики материального взаимодействия, конкретно к способу определения гравитационного (бытового) давления в массиве связной материальной среды. Величину гравитационного давления определяют по зависимости pб=(γ·h-cстр)ctgφстр, где γ - удельный вес материальной среды, h - глубина определения давления в массиве среды, cстр - структурное удельное сцепление среды, φстр - угол внутреннего трения структурированной среды в естественном залегании. Технический результат - повышение точности определения величины бытового давления. 1 ил.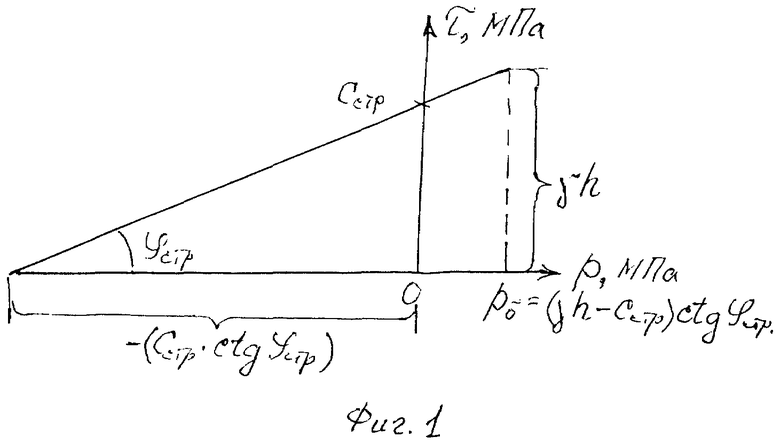
Способ определения гравитационного давления в массиве связной материальной среды, заключающийся в том, что устанавливают от поверхности массива среды глубину h замера давления, на глубине h определяют тангенциальное напряжение τ=ρ·g·h=γ·h, МПа, где удельный вес γ=ρ·g, кг/м3, самой среды, где ρ - плотность среды, кг/м3, g - ускорение свободного падения, м/с2, удельное структурное сцепление cстр, МПа, и угол φстр внутреннего трения среды, отличающийся тем, что нормальное гравитационное давление на глубине h массива связной материальной среды определяют расчетным путем по зависимости pб=(γ·h-cстр)ctgφстр, МПа, а связную материальную среду на глубине h<сстр/γ принимают находящейся в растянутом по вертикали напряженном состоянии и уравновешенной атмосферным давлением.
| Механика грунтов//Цытович Н.А.//М.: "Наука", 1979 | |||
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОГО МЕСТОРОЖДЕНИЯ НА ЗАКЛЮЧИТЕЛЬНОЙ СТАДИИ С ПОМОЩЬЮ УСТАНОВЛЕНИЯ ФОРСИРОВАННОГО РЕЖИМА ОТБОРА | 1996 |
|
RU2120543C1 |
| Справочник по элементарной физике//Кошкин Н.И | |||
| и др.//М.: "Наука", 1972 | |||
| Элементарный учебник физики | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
2015-04-10—Публикация
2013-07-25—Подача