Предлагаемое изобретение относится к теплофизическим измерениям и может быть использовано для определения комплекса теплофизических параметров изотропных материалов методом активного теплового неразрушающего контроля, заключающегося в измерении пространственного распределения теплофизических параметров (ТФП) с применением теплового воздействия от инфракрасного источника нагрева на поверхность изотропного материала и дистанционным измерением тепловизионным приемником радиационной температуры во всех точках пространственной сетки исследуемого изотропного материала в процессе нагрева-остывания.
Известен способ определения теплофизических параметров (температуропроводности), заключающийся в том, что исследуемый образец нагревают точечным источником тепла постоянной мощности, измеряют температуру поверхности образца датчиком температуры при взаимном относительном перемещении по прямой линии образца и датчика, жестко связанного с источником тепла, измеряют амплитудное значение импульсного сигнала датчика, определяют скорость перемещения источника тепла и зависимости координат точки визирования датчика от времени (авторское свидетельство СССР №1695203, МПК: G01N 25/18 (2006.01), 30.11.1991).
Недостатком этого способа является значительная методическая погрешность измерения теплофизических параметров, связанная с использованием в математической модели упрощенных тепловых моделей рассматриваемых физических процессов.
Известен наиболее близкий к данному техническому решению способ идентификации скрытых подповерхностных объектов в грунте (патент РФ №2395074 С2, МПК: G01N 25/18 (2006.01), 20.07.2010), заключающийся в том, что осуществляют тепловое воздействие от инфракрасного источника нагрева на поверхность грунта, измеряют радиационную температуру на поверхности грунта, рассчитывают математическую модель прямой задачи теплопроводности на основе метода конечных разностей, при этом производят измерение радиационной температуры во всех точках пространственной сетки зондируемой (исследуемой) поверхности при нагреве грунта в течение 90 с и последующем остывании в течение 90 с и применяют для восстановления температурного поля по глубине прогрева одномерную промежуточную сеточную функцию источника нагрева на поверхности грунта.
Недостатком данного способа является низкая точность измерения теплофизических параметров (температуропроводности и теплопроводности), ограниченная площадь исследуемой поверхности грунта, определяемая растром изображения тепловизионного приемника, а также большие вычислительные затраты (длительное время вычисления искомых значений теплофизических параметров), связанные с применением в используемых математических моделях разностных аппроксимаций, построенных на основе явных схем.
Задачей предлагаемого изобретения является уменьшение методической погрешности определения теплофизических параметров на основе применения эталонного изотропного материала, увеличение площади исследуемой поверхности изотропного материала, а также сокращение времени вычисления искомых значений теплофизических параметров.
Техническим результатом изобретения является повышение точности определения теплофизических параметров изотропных материалов и сокращение времени вычисления искомых значений теплофизических параметров за счет использования неявных разностных схем.
Технический результат достигается тем, что в способе определения комплекса теплофизических параметров изотропных материалов, включающем тепловое воздействие от инфракрасного источника нагрева по всей поверхности исследуемого изотропного материала, измерение тепловизионным приемником радиационной температуры во всех точках пространственной сетки поверхности исследуемого изотропного материала и расчет математической модели прямой задачи теплопроводности на основе метода конечных разностей, размещают инфракрасный источник нагрева перед тепловизионным приемником на заданном расстоянии друг от друга и от поверхности эталонного/исследуемого изотропного материала так, чтобы отраженное от поверхности изотропного материала тепловое излучение от инфракрасного источника нагрева не попадало в объектив тепловизионного приемника, тепловизионный приемник размещают стационарно над поверхностью эталонного/исследуемого материала на высоте, определяемой наименьшей измеряемой точкой, осуществляют непрерывный равномерный нагрев поверхности эталонного/исследуемого изотропного материала от перемещаемого инфракрасного источника нагрева, при этом с началом перемещения радиационную температуру измеряют на поверхности эталонного изотропного материала с известными теплофизическими параметрами - температуропроводности и теплопроводности - в одной точке пространственной сетки поверхности эталонного изотропного материала, попадаемой в объектив тепловизионного приемника, после чего радиационную температуру измеряют на поверхности исследуемого изотропного материала во всех точках пространственной сетки поверхности исследуемого изотропного материала в процессе остывания, применяют разностную модель с использованием неявных схем:
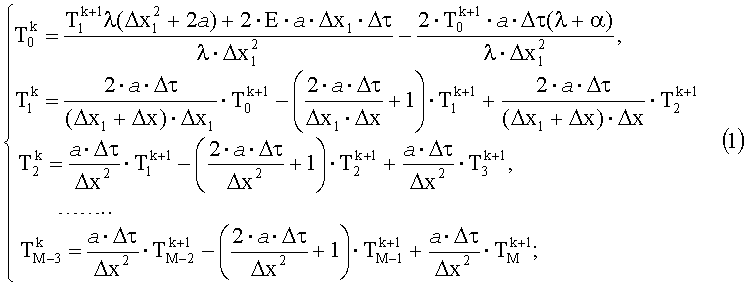
на основании численного решения данной системы уравнений получают дискретную функцию зависимости температуры на поверхности исследуемого изотропного материала от времени: 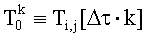
решают оптимизационную параметрическую задачу для поверхности эталонного изотропного материала в наименьшей измеряемой точке:
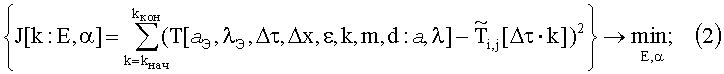
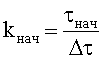
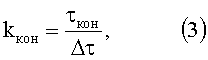
находят из минимума невязки численные оценки 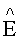
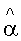
решают оптимизационную параметрическую задачу для исследуемого изотропного материала в каждой точке пространственного разрешения в соответствии с растром изображения:
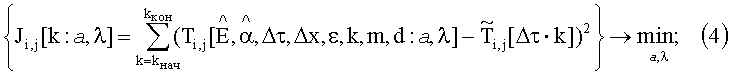
определяют из минимума невязки искомые оцененные значения теплофизических параметров исследуемого изотропного материала 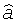
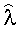
a - температуропроводность исследуемого изотропного материала;
λ - теплопроводность исследуемого изотропного материала;
a Э - температуропроводность эталонного изотропного материала;
λЭ - теплопроводность эталонного изотропного материала;
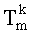
ε - коэффициент излучения;
k - номер отсчета для сеточной функции по времени, где 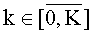
m - номер отсчета для сеточной функции по пространству, где 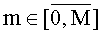
Δτ - шаг сетки по времени;
Δx, Δx1 - шаг сетки по расстоянию;
E - плотность теплового потока от инфракрасного источника нагрева, отнесенная к единице площади пространственной сетки;
α - коэффициент теплоотдачи, отнесенный к единице площади поперечного сечения пространственной сетки;
Ji,j - функционал невязки;
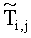
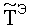
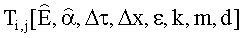
i, j - номера отсчетов пространственной сетки на поверхности исследуемого изотропного материала, где 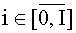
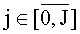
I×J - растр изображения;
d - заданное расстояние между инфракрасным источником нагрева и тепловизионным приемником;
kнач и kкон - начальные и конечные номера отсчетов, соответствующие времени начала и окончания наблюдения;
τнач и τкон - момент времени начала и окончания наблюдения;
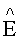
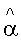
Сущность изобретения заключается в следующем.
Поверхность исследуемого/эталонного изотропного материала нагревают в течение заданного времени тепловым потоком постоянной мощности от инфракрасного источника нагрева, движущегося прямолинейно с постоянной скоростью. С помощью средств инфракрасной термографии измеряют радиационные температуры на поверхности исследуемого/эталонного изотропного материала в заданном интервале времени. Данный физический процесс в одномерном пространстве можно описать математической моделью нелинейной задачи теплопроводности (1) с учетом теплообмена исследуемого изотропного материала с окружающей средой:
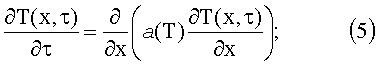
T(x, 0)=0, T(±∞, τ)→0,
граничные условия на поверхности исследуемого/эталонного изотропного материала:
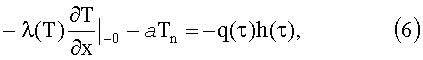
где Tn - температура поверхности исследуемого изотропного материала и фона, h(τ) - ступенчатая функция, q(τ) - тепловой поток, а - коэффициент температуропроводности, λ(T) - нелинейная функция теплопроводности. Нелинейную задачу теплопроводности (5) при граничных условиях (6) решают методом конечных разностей. Система уравнений, аппроксимирующая неоднородное дифференциальное уравнение (5) и граничные условия (6), на основе использования неявных разностных схем будет иметь вид (1). Граничные условия аппроксимируют на основании выражения:
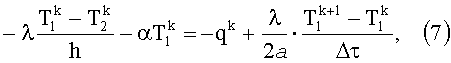
где λ - коэффициент теплопроводности, α - коэффициент теплоотдачи, a - коэффициент температуропроводности, h - ступенчатая функция, k - номер отсчета для сеточной функции по времени, T - значение радиационной температуры исследуемого изотропного материала и фона. При этом E и α отнесены к единице площади поперечного сечения пространственной сетки и выражены в Вт/м2 и Дж/(м2·К) соответственно.
Сущность изобретения поясняется чертежами.
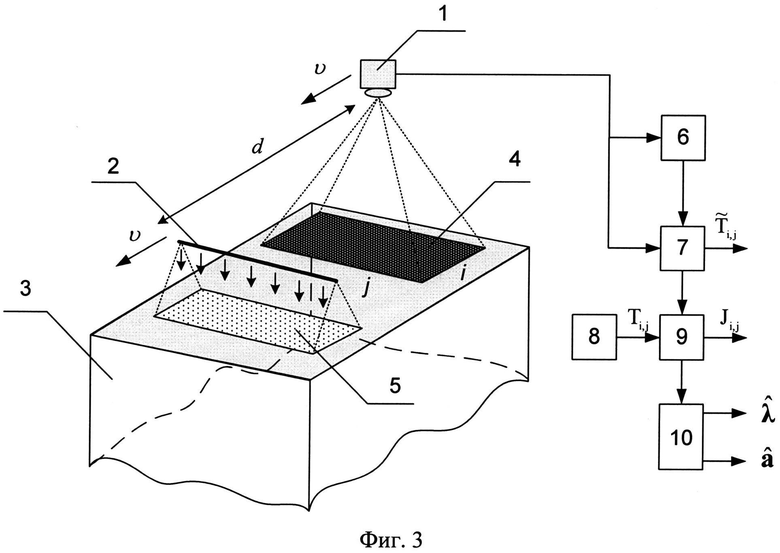
На фиг.1 представлен вариант размещения инфракрасного источника нагрева перед тепловизионным приемником, которые располагают на заданном расстоянии друг от друга так, чтобы отраженное от поверхности исследуемого/эталонного изотропного материала тепловое излучение от инфракрасного источника нагрева не попадало в объектив тепловизионного приемника, и на высоте, определяемой наименьшей измеряемой точкой, от поверхности эталонного изотропного материала, где:
1 - тепловизионный приемник (ТПВП);
2 - инфракрасный источник нагрева (ИКИН);
3 - исследуемый/эталонный изотропный материал;
υ - скорость прямолинейного перемещения ИКИН и ТПВП;
S1 - площадь поверхности исследуемого/эталонного изотропного материала, попадаемая в объектив тепловизионного приемника;
S2 - площадь нагрева поверхности исследуемого/эталонного изотропного материала;
D1 - ширина S1;
D2 - ширина S2;
d - заданное расстояние между ИКИН и ТПВП;
B - наименьшая измеряемая точка, расположенная неподвижно в системе координат изотропного материала в центре площади S1.
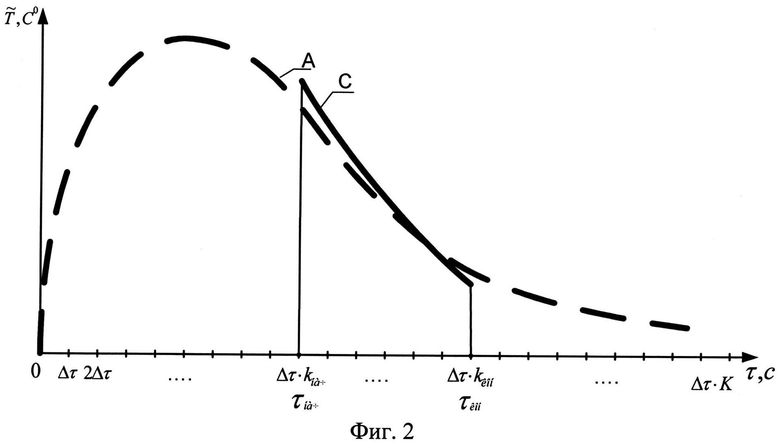
На фиг.2 приведены графики огибающих дискретных значений разности между радиационной температурой исследуемого/эталонного изотропного материала и температурой окружающей среды в координатах T-τ, где кривая А - график, построенный на основе математической модели; кривая С - экспериментальный график, полученный с помощью средств инфракрасной термографии на интервале времени [τнач, τкон] в точке В:
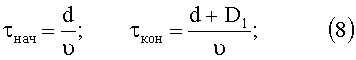
где: τнач - время начала наблюдения; τкон - время окончания наблюдения.
На фиг.3 представлена схема устройства, реализующая предлагаемый способ определения комплекса теплофизических параметров изотропных материалов, где:
1 - тепловизионный приемник;
2 - инфракрасный источник нагрева;
3 - исследуемый/эталонный изотропный материал;
4 - площадь поверхности исследуемого/эталонного материала, попадаемая в объектив тепловизионного приемника (S1);
5 - площадь нагрева поверхности исследуемого/эталонного изотропного материала (S2);
6 - запоминающее устройство;
7 - вычислительное устройство;
8 - блок формирования математической модели нагрева-остывания поверхности исследуемого/эталонного изотропного материала;
9 - блок вычислителя квадратичного отклонения;
10 - блок решения двухпараметрической оптимизационной задачи.
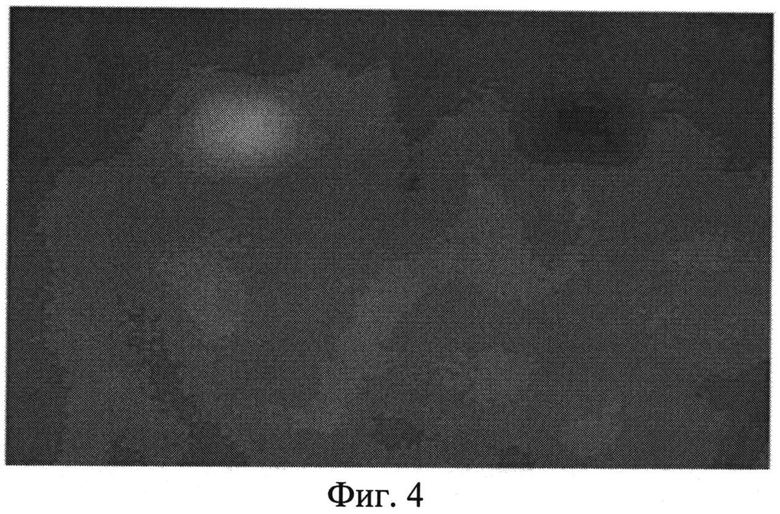
На фиг.4 представлено инфракрасное изображение поверхности исследуемого материала в момент времени 100 с после начала испытания с длительностью теплового воздействия 60 с.
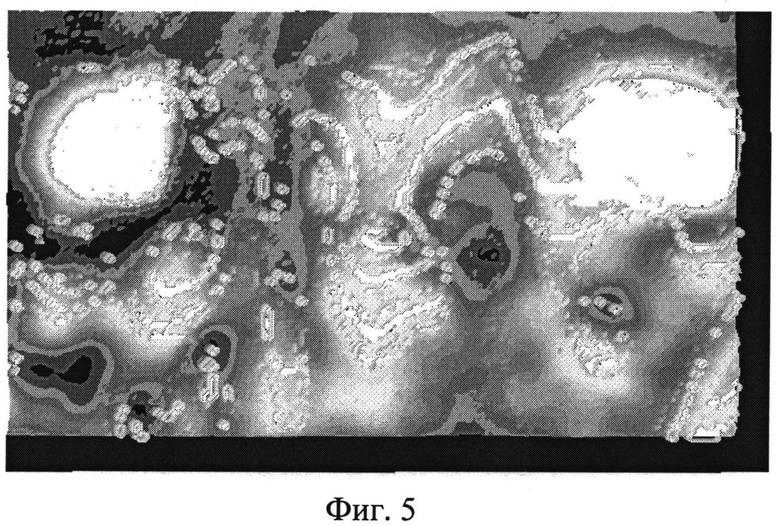
На фиг.5 представлена тепловая томограмма скрытых подповерхностных объектов по пространственному распределению невязки.
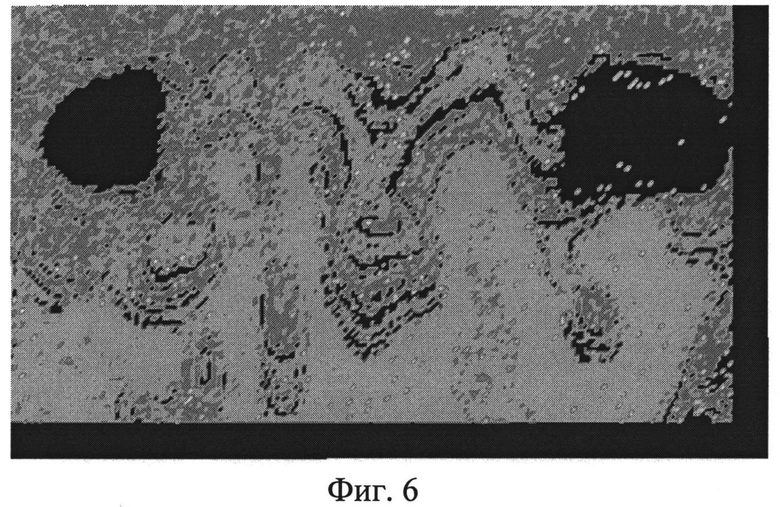
На фиг.6 представлена тепловая томограмма значений теплопроводности.
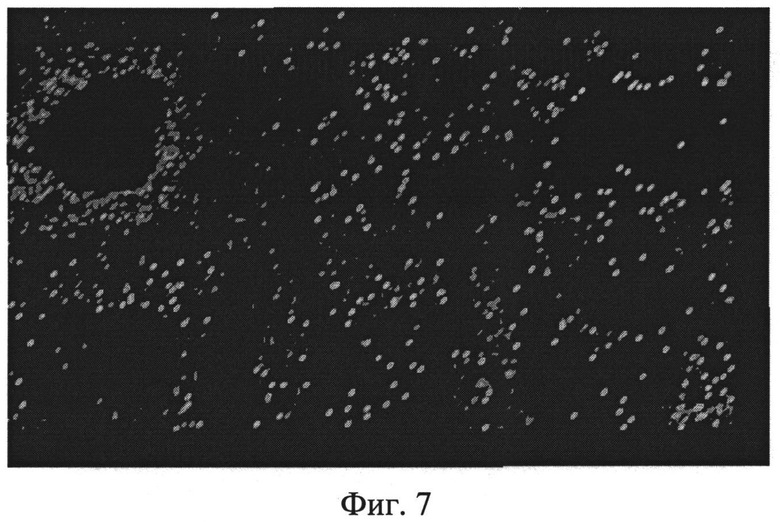
На фиг.7 представлена тепловая томограмма значений температуропроводности.
Устройство (фиг.3) содержит исследуемый/эталонный изотропный материал 3, который подвергают тепловому воздействию поверхность 5 площадью S2 от инфракрасного источника нагрева 2, движущегося прямолинейно с постоянной скоростью υ, обеспечивая непрерывный равномерный нагрев поверхности исследуемого/эталонного материала, после чего тепловизионным приемником 1 регистрируют значения радиационных температур на поверхности 4 площадью S1 в момент остывания во всех точках пространственной сетки в соответствии с растром изображения (I×J). Далее информация с тепловизионного приемника 1 поступает на запоминающее устройство 6 и на вычислительное устройство 7, где производится расчет разности между радиационной температурой поверхности исследуемого/эталонного материала и температурой окружающей среды. Блок 9 выполняет функцию вычисления квадратичного отклонения значений параметров математической модели, формируемых в блоке математической модели 8 от значений параметров, измеренных тепловизионным приемником 1. Блок 10 осуществляет решение двухпараметрической оптимизационной задачи с выводом матриц пространственного распределения оцененных значений теплофизических параметров 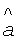
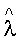
Способ определения комплекса теплофизических параметров осуществляют в 2 этапа.
Первый этап заключается в оценке неизвестных параметров математической модели на основе использования эталонного изотропного материала 3, для чего инфракрасный источник нагрева 2, расположенный перед тепловизионным приемником 1 на расстоянии d таком, чтобы отраженное от поверхности эталонного изотропного материала 3 тепловое излучение от инфракрасного источника нагрева 2 не попадало в объектив тепловизионного приемника 1, прямолинейно перемещают вместе с тепловизионным приемником 1 (либо тепловизионный приемник 1 размещают стационарно над поверхностью эталонного материала 3 на высоте, определяемой наименьшей измеряемой точкой) с постоянной скоростью над эталонной поверхностью изотропного материала. При этом инфракрасный источник нагрева 2 производит непрерывный равномерный нагрев поверхности эталонного изотропного материала 3, а с помощью тепловизионного приемника 1 измеряют радиационную температуру в одной из наименьшей измеряемой точке в центре площади поверхности эталонного материала 3, попадаемой в объектив тепловизионного приемника 1 (точка В на фиг.1).
Наблюдение радиационных температур, измеренных тепловизионным приемником в одной наименьшей измеряемой точке, производят на интервале времени [τнач, τкон] (фиг.2).
Используя данные радиационных температур, измеренных в одной наименьшей измеряемой точке пространства разрешения эталонного материала, решают оптимизационную задачу (2), в результате чего получают оцененные значения параметров математической модели 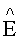
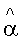
Второй этап заключается в оценке теплофизических параметров в каждой точке пространства разрешения исследуемого изотропного материала 3. Для этого инфракрасный источник нагрева 2, расположенный перед тепловизионным приемником 1, прямолинейно перемещают вместе с тепловизионным приемником 1 (либо тепловизионный приемник размещают стационарно над поверхностью исследуемого материала на высоте, определяемой наименьшей измеряемой точкой) с постоянной скоростью над поверхностью исследуемого изотропного материала 3. Инфракрасный источник нагрева 2 производит непрерывный равномерный нагрев поверхности исследуемого изотропного материала 3. При этом графики радиационных температур получают в каждой точке пространственного разрешения (фиг.2).
Решают оптимизационную параметрическую задачу (4) для исследуемого изотропного материала в каждой точке пространства разрешения, в результате чего получают пространственное распределение оцененных значений теплофизических параметров исследуемого изотропного материала:
температуропроводности
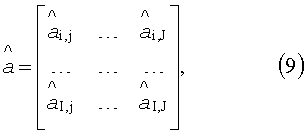
теплопроводности
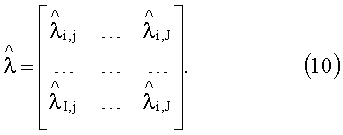
Пример реализации способа.
При помощи вышеописанного устройства предложенный способ был апробирован для определения комплекса теплофизических параметров ряда изотропных материалов с известной теплопроводностью и температуропроводностью, заранее определенных стандартизированными методами. В качестве эталонного материала использовали кварцевый песок с теплопроводностью 0.9 Вт·м-1·К-1, температуропроводностью 9·10-7 м2·с-1. Исследованию подвергался кварцевый песок с размещенными в нем на глубине 10 мм двумя инородными объектами: алюминиевый брусок размером 3×3×1 см с теплопроводностью 237 Вт·м-1·К-1, температуропроводностью 8.418·10-5 м2·с-1 и полиспен размером 3×3×1 см с теплопроводностью 0.028 Вт·м-1·К-1, температуропроводностью 1·10-7 м2·с-1. Инфракрасное (ИК) изображение поверхности исследуемого материала в момент времени 100 с после начала испытания с длительностью теплового воздействия 60 с представлено на фиг.4. В результате решения двухпараметрической оптимизационной задачи (4) с коэффициентами теплоотдачи α=10 Дж·м-2·К-1, релаксации нагрева β1=0.001, релаксации остывания β2=10, плотности теплового потока Е=2700 Вт·м-2, шага дискретизации по времени t=1c, шага дискретизации по поверхности h=0.003, шага дискретизации по пространству h1=0,00001, λ=0.9 Вт·м-1·К-1, температуропроводности a=9·10-7 м2·с-1 и количества шагов дискретизации по времени m=150 получают матрицы распределения оцененных значений теплофизических параметров поверхности исследуемого изотропного материала 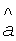
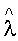

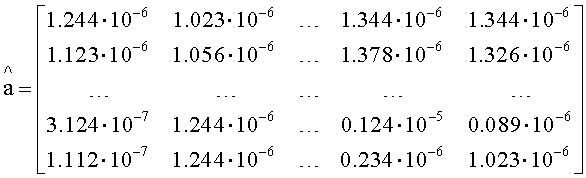
и тепловую томограмму скрытых подповерхностных объектов по пространственному распределению невязки (фиг.5), значений теплопроводности (фиг.6) и температуропроводности (фиг.7).
Погрешность измерения теплофизических параметров предложенным способом меньше, чем у рассмотренного способа-прототипа, так как погрешность аппроксимации неоднородного дифференциального уравнения с использованием явных схем, применяемых в способе-прототипе, имеет погрешность первого порядка O(x), а для неявных схем, применяемых в предлагаемом способе, погрешность аппроксимации неоднородных дифференциальных уравнений имеет погрешность второго порядка O(x2) (см. Самарский А.А. Введение в численные методы - М.: Наука. Главная редакция физико-математической литературы, 1982. - 271 с.).
Применяемые неявные схемы требуют для решения неоднородных дифференциальных уравнений на один порядок меньше шагов вычисления по времени и соответственно вычислительных операций по сравнению с явными схемами.
Площадь поверхности исследуемого изотропного материала увеличивается в соответствии с перемещением и зависит от времени движения средств инфракрасной термографии.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОЦЕНКИ РАЗЛИЧИЯ ТЕПЛОФИЗИЧЕСКИХ ПАРАМЕТРОВ ВИДИМОЙ ПОВЕРХНОСТИ ИЗОТРОПНОГО ОБЪЕКТА С УЧЕТОМ ФОНА | 2013 |
|
RU2544894C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ПАРАМЕТРОВ ИЗОТРОПНЫХ МАТЕРИАЛОВ | 2013 |
|
RU2544890C1 |
| СПОСОБ ДИСТАНЦИОННОЙ ОЦЕНКИ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ПАРАМЕТРОВ МАТЕРИАЛОВ | 2022 |
|
RU2801295C1 |
| СПОСОБ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ПАРАМЕТРОВ ЗЕМНОЙ ПОВЕРХНОСТИ | 2019 |
|
RU2707387C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ МАТЕРИАЛОВ | 2008 |
|
RU2374631C2 |
| Способ дистанционного определения пространственного распределения теплофизических параметров поверхности земли | 2016 |
|
RU2659461C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ МАТЕРИАЛОВ ДЛЯ ОБНАРУЖЕНИЯ СКРЫТЫХ ОБЪЕКТОВ (МИН) В ГРУНТЕ | 2007 |
|
RU2357235C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ СКРЫТЫХ ОБЪЕКТОВ В ГРУНТЕ | 2008 |
|
RU2395074C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРОПРОВОДНОСТИ ОПТИЧЕСКИ ПРОЗРАЧНЫХ МАТЕРИАЛОВ | 2019 |
|
RU2725695C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ ТВЕРДЫХ МАТЕРИАЛОВ | 2005 |
|
RU2303777C2 |
Изобретение относится к теплофизическим измерениям и может быть использовано для определения комплекса теплофизических параметров изотропных материалов. Способ определения комплекса теплофизических параметров изотропных материалов включает тепловое воздействие от инфракрасного источника нагрева по всей поверхности исследуемого изотропного материала. Измерение тепловизионным приемником радиационной температуры производят во всех точках пространственной сетки поверхности исследуемого изотропного материала. Осуществляют непрерывный равномерный нагрев поверхности эталонного/исследуемого изотропного материала от перемещаемого инфракрасного источника нагрева. При этом с началом перемещения радиационную температуру измеряют на поверхности эталонного изотропного материала с известными теплофизическими параметрами в одной точке пространственной сетки поверхности эталонного изотропного материала, попадаемой в объектив тепловизионного приемника. После чего радиационную температуру измеряют на поверхности исследуемого изотропного материала во всех точках пространственной сетки поверхности исследуемого изотропного материала в процессе остывания. Применяют разностную модель с использованием неявных схем. Решают оптимизационную параметрическую задачу для исследуемого изотропного материала в каждой точке пространственного разрешения в соответствии с растром изображения. Определяют из минимума невязки искомые оцененные значения теплофизических параметров исследуемого изотропного материала. Технический результат - повышение точности получаемых данных. 7 ил.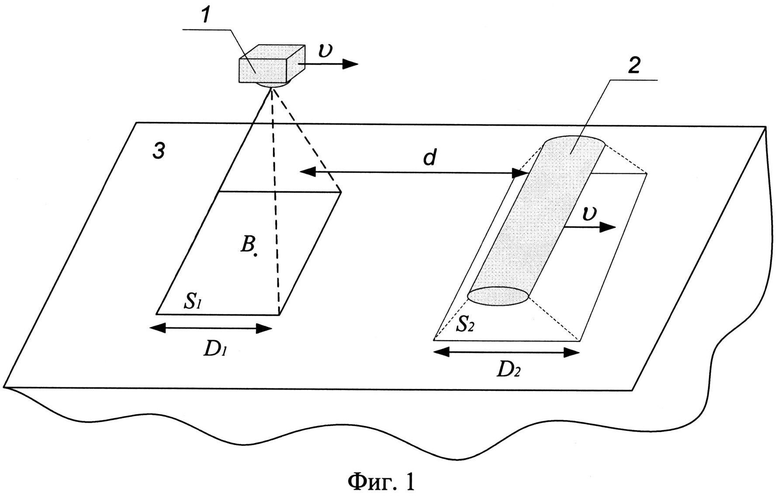
Способ определения комплекса теплофизических параметров изотропных материалов, включающий тепловое воздействие от инфракрасного источника нагрева по всей поверхности исследуемого изотропного материала, измерение тепловизионным приемником радиационной температуры во всех точках пространственной сетки поверхности исследуемого изотропного материала в процессе нагрева-остывания и расчет математической модели прямой задачи теплопроводности на основе метода конечных разностей, отличающийся тем, что размещают инфракрасный источник нагрева перед тепловизионным приемником на заданном расстоянии друг от друга и от поверхности эталонного/исследуемого изотропного материала так, чтобы отраженное от поверхности изотропного материала тепловое излучение от инфракрасного источника нагрева не попадало в объектив тепловизионного приемника, тепловизионный приемник размещают стационарно над поверхностью эталонного/исследуемого материала на высоте, определяемой наименьшей измеряемой точкой, осуществляют непрерывный равномерный нагрев поверхности эталонного/исследуемого изотропного материала от перемещаемого инфракрасного источника нагрева, при этом с началом перемещения радиационную температуру измеряют на поверхности эталонного изотропного материала с известными теплофизическими параметрами - температуропроводности и теплопроводности - в одной точке пространственной сетки поверхности эталонного изотропного материала, попадаемой в объектив тепловизионного приемника, после чего радиационную температуру измеряют на поверхности исследуемого изотропного материала во всех точках пространственной сетки поверхности исследуемого изотропного материала в процессе остывания, применяют разностную модель с использованием неявных схем:
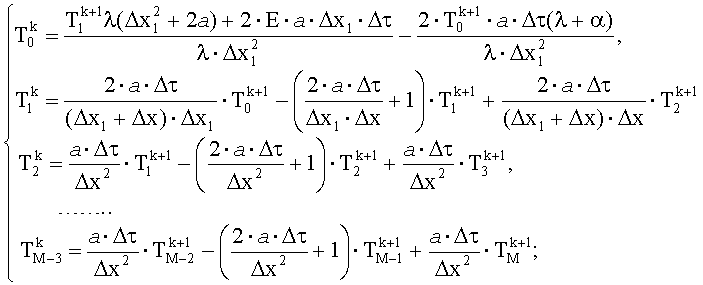
на основании численного решения данной системы уравнений получают дискретную функцию зависимости температуры на поверхности исследуемого изотропного материала от времени: 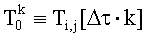
решают оптимизационную параметрическую задачу для поверхности эталонного изотропного материала в наименьшей измеряемой точке:
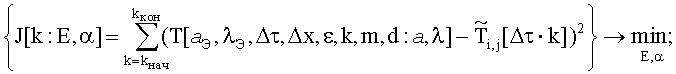
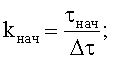
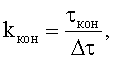
находят из минимума невязки численные оценки 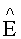
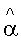
решают оптимизационную параметрическую задачу для исследуемого изотропного материала в каждой точке пространственного разрешения в соответствии с растром изображения:
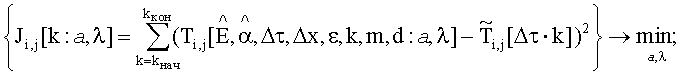
определяют из минимума невязки искомые оцененные значения теплофизических параметров исследуемого изотропного материала 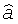
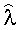
a - температуропроводность исследуемого изотропного материала;
λ - теплопроводность исследуемого изотропного материала;
a
Э - температуропроводность эталонного изотропного материала;
λЭ - теплопроводность эталонного изотропного материала;
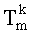
ε - коэффициент излучения;
k - номер отсчета для сеточной функции по времени, где 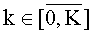
m - номер отсчета для сеточной функции по пространству, где 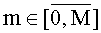
Δτ - шаг сетки по времени;
Δx, Δx1 - шаг сетки по расстоянию;
E - плотность теплового потока от инфракрасного источника нагрева, отнесенная к единице площади пространственной сетки;
α - коэффициент теплоотдачи, отнесенный к единице площади поперечного сечения пространственной сетки;
Ji,j - функционал невязки;
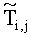
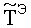
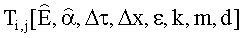
i, j - номера отсчетов пространственной сетки на поверхности исследуемого изотропного материала, где 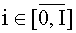
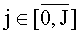
I×J - растр изображения;
d - заданное расстояние между инфракрасным источником нагрева и тепловизионным приемником;
kнач и kкон - начальные и конечные номера отсчетов, соответствующие времени начала и окончания наблюдения;
τнач и τкон - момент времени начала и окончания наблюдения;
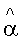
| СПОСОБ ИДЕНТИФИКАЦИИ СКРЫТЫХ ОБЪЕКТОВ В ГРУНТЕ | 2008 |
|
RU2395074C2 |
| Способ определения температуропроводности материалов | 1989 |
|
SU1695203A1 |
| Способ определения теплофизических свойств плоских твердых тел | 1982 |
|
SU1040391A1 |
| СПОСОБ БЕСКОНТАКТНОГО КОНТРОЛЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 1999 |
|
RU2168168C2 |
| Способ определения теплофизических свойств материалов | 1982 |
|
SU1100549A2 |
Авторы
Даты
2015-03-20—Публикация
2013-08-23—Подача