ПЕРЕКРЕСТНЫЕ ССЫЛКИ
Данная заявка частично продолжает патентную заявку США №12/604773, поданную 23 октября 2009 года (заявители M.Amin Shokrollahi и др.) под заголовком "Method and Apparatus Employing FEC Codes with Permanent Inactivation of Symbols for Encoding and Decoding Processes" и кроме того испрашивает приоритет следующих предварительных заявок (заявители M. Amin Shokrollahi и др.) под названием "Method and Apparatus Employing FEC Codes with Permanent Inactivation of Symbols for Encoding and Decoding Processes": предварительной патентной заявки США №61/353910, поданной 11 июня 2010 года; предварительной патентной заявки США №61/257146, поданной 2 ноября 20009 года; и предварительной патентной заявки США №61/235285, поданной 19 августа 2009 года. Каждая из вышеупомянутых предварительных и не предварительных заявок включена сюда по ссылке для всех целей.
Следующие ссылочные материалы целиком включены сюда посредством ссылки для всех целей:
1) Патент США №6307487, выданный Michael G. Luby под заголовком "Information Additive Code Generator and Decoder for Communication Systems" (далее "Luby I");
2) Патент США №6320520, выданный Michael G. Luby под заголовком "Information Additive Group Code Generator and Decoder for Communication Systems" (далее "Luby II");
3) Патент США №7068729, выданный M. Amin Shokrollahi под заголовком "Multi-Stage Code Generator and Decoder for Communication Systems" (далее "Shokrollahi I");
4) Патент США №6856263, выданный M. Amin Shokrollahi под заголовком "Systems and Processes for Decoding a Chain Reaction Code Through Inactivation" (далее "Shokrollahi II");
5) Патент США №6909383, выданный M. Amin Shokrollahi под заголовком "Systematic Encoding and Decoding of Chain Reaction Codes" (далее "Shokrollahi III");
6) Патентная публикация США №2006/0280254 заявителей Michael G. Luby и M. Amin Shokrollahi под заголовком "In-Place Transformations with Applications to Encoding and Decoding Various Classes of Codes" (далее "Luby III");
7) Патентная публикация США №2007/0195894 заявителей M. Amin Shokrollahi под заголовком "Multiple-Field Based Code Generator and Decoder for Communications Systems" (далее "Shokrollahi IV").
ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Настоящее изобретение относится к кодированию и декодированию данных в системах связи и, в частности, к системам связи, в которых данные кодируются и декодируются эффективным образом с учетом ошибок и пробелов в переданных данных.
УРОВЕНЬ ТЕХНИКИ
В литературе широко обсуждаются способы передачи файлов по каналу вязи между отправителем и получателем. Получатель, как правило, желает получить точную копию данных, переданных по каналу отправителем с некоторым уровнем достоверности. Поскольку канал не обеспечивает абсолютную верность передачи информации (что относится практически ко всем физически реализуемым системам), одной из проблемой является то, как поступать с данными, потерянными или искаженными при передаче. Часто легче иметь дело с потерянными данными (уничтоженные данные), чем с искаженными данными (ошибки), поскольку получатель не всегда может сказать, когда искаженные данные являются данными, принятыми с ошибкой. Для коррекции уничтоженных данных и/или ошибок разработано множество кодов с исправлением ошибок. Как правило, конкретный код, подлежащий использованию, выбирают на основе некоторой информации о неточностях передачи данных по данному каналу, и характере передаваемых данных. Например, если известно, что в данном канале имеются длительные периоды неточной передачи, для такого случая возможно наиболее подходящим окажется код коррекции пакета ошибок. Если ожидаются только короткие и не частые периоды передачи с ошибками, то наилучшим вариантом может быть простой код с контролем по четности.
Используемый здесь термин «исходные данные» относится к данным, доступным для одного или нескольких отправителей, для получения которых используется приемник, выполняющий их восстановление из переданной последовательности с или без ошибок и/или уничтоженных данных и т.д. Используемый здесь термин «кодированные данные» относится к пересылаемым данным, которые можно использовать для восстановления или получения исходных данных. В простом случае кодированные данные представляют собой копию исходных данных, но в том случае, если принятые кодированные данные отличаются (из-за ошибок и/или уничтоженных данных) от переданных кодированных данных, то в этом простом случае исходные данные невозможно восстановить полностью в отсутствии дополнительной информации об исходных данных. Передача может осуществляться в пространстве или времени. В более сложном случае кодированные данные создают на основе исходных данных при помощи преобразования и передают их получателям от одного или нескольких отправителей. Говорят, что кодирование является «систематическим», если обнаруживается, что исходные данные представляют собой часть кодированных данных. В простом примере систематического кодирования для формирования кодированных данных в конец исходных данных добавляется избыточная информация об исходных данных.
Также используемый здесь термин «входные данные» относится к данным, присутствующим на входе устройства-кодера с прямым исправлением ошибок (FEC) или модуля, компоненты, шага и т.д. кодера FEC («кодер FEC»), а термин «выходные данные» относится к данным, присутствующим на выходе кодера FEC. Соответственно предполагается присутствие выходных данных на входе декодера FEC, и предполагается, что декодер FEC выдает входные данные или их эквивалент на основе выходных данных, которые он обработал. В некоторых случаях входные данные представляют собой или включают в себя исходные данные, а в некоторых случаях выходные данные представляют собой или включают в себя кодированные данные. В других случаях устройство отправителя (или программный код отправителя) может содержать больше одного кодера FEC, то есть, исходные данные преобразуются в кодированные данные в цепочке, состоящей из множества кодеров FEC. Аналогичным образом, в приемнике может быть более одного декодера FEC, используемого для создания исходных данных из принятых кодированных данных.
Данные можно представить как состоящие из множества символов. Кодер представляет собой компьютерную систему, устройство, электронную схему или т.п., которая создает кодированные символы или выходные символы из последовательности исходных символов или входных символов, а декодер представляет собой дополняющую часть, которая восстанавливает последовательность исходных символов или входных символов из принятых или восстановленных кодированных символов или выходных символов. Кодер и декодер разделены во времени и/или пространстве каналом, причем любые принятые кодированные символы не могут точно совпадать с соответствующими переданными кодированными символами, и не могут приниматься точно в той последовательности, в которой они были переданы. «Размер» символа может измеряться в битах, независимо от того, оказался ли в действительности данный символ в битовом потоке, где символ имеет размер M бит, когда символ выбирается из алфавита, содержащего 2М символов. Здесь во многих примерах символы измеряются в байтах, и коды могут быть в области, состоящей из 256 возможных вариантов (здесь это 256 возможных 8-битовых шаблонов), но следует понимать, что можно использовать и другие, единицы измерения данных, широко известно много способов измерения данных.
В Luby I описано использование кодов, таких как коды с цепной реакцией, обеспечивающих эффективное исправление ошибок с точки зрения использования вычислительной мощности, памяти и полосы пропускания. Одно из свойств кодированных символов, создаваемых кодером с цепной реакцией, состоит в том, что приемник способен восстановить первоначальный файл, как только принято достаточное количество кодированных символов. В частности, для восстановления К первоначальных символов с высокой вероятностью приемнику необходимо иметь приблизительно К+А кодированных символов.
«Абсолютная величина служебных данных» для данной ситуации представлена значением А, в то время как «относительную величину служебных данных» можно вычислить как отношение А/К. Абсолютная величина служебных данных при приеме является показателем того, сколько дополнительных данных необходимо принять сверх теоретически минимального количества данных, причем этот показатель может зависеть от надежности декодера и может изменяться в функции числа К исходных символов. Аналогичным образом, относительная величина служебных данных при приеме (А/К) является показателем того, сколько дополнительных данных необходимо принять сверх теоретически минимального количества данных по отношению к объему восстанавливаемых исходных данных, причем этот показатель также может зависеть от надежности декодера и может изменяться в функции числа К исходных символов.
Коды с цепной реакцией весьма полезны для осуществления связи по сети с пакетной коммуникацией. Однако иногда они могут быть достаточно интенсивными в плане вычислений. Декодер может декодировать чаще или легче, если исходные символы закодированы с использованием статического кодера до использования динамического кодера, который осуществляет кодирование с использованием кода с цепной реакцией или другого кода без фиксированной скорости. Указанные декодеры описаны, например, в Shokrollahi I. В показанных здесь примерах исходные символы являются входными символами для статического кодера, создающего выходные символы, которые, в свою очередь, являются входными символами для динамического кодера, создающего выходные символы, являющиеся кодированными символами, где динамический кодер является кодером без фиксированной скорости, способный создавать выходные символы в количестве, которое не является фиксированной нормой по отношению к количеству входных символов. Статический кодер может включать в себя более одного кодера с фиксированной скоростью. Например, статический кодер можете включать в себя кодер Хэмминга, кодер с контролем по четности с низкой плотностью («LDPC»), кодер с контролем по четности с высокой плотностью («HDPC») или т.п.
Коды с цепной реакцией обладают свойством, состоящим в том, что некоторые символы восстанавливаются в декодере из принятых символов, причем эти символы могут быть использованы для восстановления дополнительных символов, которые, в свою очередь, можно использовать для восстановления еще нескольких символов. Предпочтительно, чтобы цепная реакция нахождения символов в декодере могла продолжаться до восстановления всех необходимых символов, прежде чем будет использован буфер принятых символов. Преимущественно вычислительная сложность выполнения процессов кодирования и декодирования с цепной реакцией не велика.
Процесс восстановления в декодере может включать в себя: определение того, какие символы были приняты; создание матрицы, которая преобразует первоначальные входные символы в указанные принятые кодированные символы; обращение матрицы и выполнение умножения обращенной матрицы на вектор принятых кодированных символов. В типовой системе реализация указанных операций методом прямого перебора может потребовать чрезмерного объема вычислений и памяти. Конечно, для конкретного набора принятых кодированных символов восстановление всех первоначальных входных символов окажется невозможным, но даже в том случае, когда это возможно, для получения результата могут потребоваться очень большие вычислительные ресурсы.
В Shokrollahi II описан подход, называемый «инактивация» (inactivation), согласно которому декодирование выполняется в два шага. На первом шаге декодер подытоживает, какие имеются принятые кодированные символы, возможный вид матрицы и определяет, по меньшей мере, приблизительно последовательность шагов декодирования, которые позволят завершить обработку цепной реакции с данными принятыми кодированными символами. На втором шаге декодер выполняет декодирование на основе цепной реакции в соответствии с определенной последовательностью шагов декодирования. Это может быть реализовано эффективным образом с точки зрения использования памяти (то есть, таким образом, который потребует меньший объем памяти для операции, чем менее эффективный с точки зрения использования памяти процесс).
При использовании подхода на основе инактивации первый шаг декодирования включает в себя манипулирование упомянутой матрицей или ее эквивалентом для определения некоторого количества входных символов, которые можно найти, и, когда определение остановилось, обозначение одного из входных символов как «инактивированный символ», и продолжение процесса определения в предположении, что инактивированный символ действительно найден; а затем в конце - нахождение инактивированных символов с использованием гауссова исключения или какого-либо другого метода для обращения матрицы, значительно меньшей, чем первоначальная матрица декодирования. При использовании указанного определения последовательность цепной реакции может быть реализована на принятых кодированных символах для получения восстановленных входных символов, которые могут представлять собой либо все первоначальные входные символы либо подходящий набор первоначальных входных символов.
Для некоторых приложений, которые накладывают жесткие ограничения на декодер, например, когда декодер входит в состав маломощного устройства с ограниченной памятью и вычислительной мощностью, или, например, когда имеют место жесткие ограничения на допустимые абсолютные или относительные величины служебных данных при приеме, можно указать улучшенные способы в отношении вышеописанного подхода на основе инактивации.
Также могут оказаться полезными способы разбиения файла или большого блока данных на несколько исходных блоков, сколько возможно в зависимости от ограничения на минимальный размер субсимвола, и затем в зависимости от этого разбиения на несколько субблоков, сколько возможно в зависимости от ограничений на максимальный размер субблока.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Согласно одному варианту осуществления кодера в соответствии с аспектами настоящего изобретения предложен кодер у отправителя, в отправителе или для отправителя, передающий упорядоченный набор исходных символов от одного или нескольких отправителей на один или несколько приемников по каналу связи, где кодер создает данные, подлежащие пересылке, которые включают в себя множество кодированных символов, созданных из исходных символов. На первом шаге из исходных символов создают промежуточные символы с использованием способа, являющегося обратимым, то есть, также имеется обратный способ для создания исходных символов из промежуточных символов. На другом шаге промежуточные символы разбивают на первый набор промежуточных символов и второй набор промежуточных символов, где имеется, по меньшей мере, один промежуточный символ в первом наборе промежуточных символов и имеется, по меньшей мере, один промежуточный символ во втором наборе промежуточных символов, и по меньшей мере из одного промежуточного символа из каждого из двух упомянутых наборов создают по меньшей мере один кодированный символ. В некоторых версиях имеется более двух наборов.
В некоторых вариантах осуществления создают значения для первого набора и второго набора временных символов, где значения первого набора временных символов зависят от значений первого набора промежуточных символов, а значения для второго набора временных символов зависят от значений второго набора промежуточных символов. Из первого набора и второго набора временных символов создают значения для кодированных символов.
В некоторых версиях количество кодированных символов, которые могут быть созданы, не зависит от количества исходных символов.
Также обеспечены варианты осуществления декодера. Согласно одному варианту осуществления декодера в соответствии с аспектами настоящего изобретения декодер у приемника, в приемнике или для приемника принимает кодированные символы, созданные из промежуточных символов, где промежуточные символы создают из исходных символов с использованием способа, являющегося обратимым, то есть, также имеется обратный способ для создания исходных символов из промежуточных символов, и где, по меньшей мере, один из промежуточных символов назначают постоянно инактивированным символом, и где имеется, по меньшей мере, еще один из промежуточных символов, которого нет среди постоянно инактивированных символов. Декодер декодирует набор промежуточных символов из принятых кодированных символов и учитывает, по меньшей мере, один постоянно инактивированный символ, а затем создает исходные символы из декодированного набора промежуточных символов, используя обратный способ.
При декодировании шаги декодирования планируют, отменяя планирование постоянно инактивированных символов. Постоянно инактивированные символы можно найти, используя новые или традиционные способы, и затем использовать их при нахождении других промежуточных символов. Одним из подходов к нахождению постоянных инактивированных символов (и других инактиваций на ходу, если они используются) является применение гауссова исключения для нахождения инактивированных символов. Некоторые из оставшихся промежуточных символов восстанавливают на основе значений восстановленных постоянно инактивированных символов и принятых кодированных символов.
В некоторых версиях данного способа декодирования постоянно инактивированные символы содержат второй набор промежуточных символов из вариантов осуществления кодирования. В некоторых версиях данного способа декодирования постоянно инактивированные символы содержат поднабор промежуточных символов, где соответствующий способ кодирования не является многоступенчатым кодом на основе цепной реакции. Указанные способы кодирования могут включать в себя один или несколько кодов Торнадо, код Рида-Соломона, код на основе цепной реакции (его примеры описаны в Luby I) или т.п. для поднабора промежуточных символов.
Промежуточные символы используют для кодирования и декодирования, причем для требуемого набора рабочих характеристик, например, декодируемость, указывают способ создания промежуточных символов из исходных символов и соответствующий обратный способ. В некоторых вариантах осуществления промежуточные символы содержат исходные символы. В некоторых вариантах осуществления промежуточные символы содержат исходные символы наряду с избыточными символами, которые создают из исходных символов, где избыточные символы могут представлять собой символы, полученные на основе цепной реакции, символы LDPC, символы HDPC или избыточные символы других типов. Альтернативно, промежуточные символы могут быть основаны на предписанных соотношениях между символами, например, соотношения между промежуточными символами и исходными символами, и дополнительные соотношения LDPC И HDPC между промежуточными символами, где способ декодирования используют для создания промежуточных символов из исходных символов на основе упомянутых предписанных соотношений.
Упомянутые способы и системы можно реализовать с помощью электронных схем или обрабатывающего устройства, которое выполняет программные команды и имеет соответствующий программный код с командами для реализации кодирования и/или декодирования.
Настоящее изобретение обеспечивает множество преимуществ. Например, в одном конкретном варианте осуществления сокращаются вычислительные затраты на кодирование данных для их передачи по каналу. В другом конкретном варианте осуществления сокращаются вычислительные затраты на декодирование указанных данных. Еще в одном конкретном варианте осуществления существенно сокращаются абсолютные и относительные величины служебных данных при приеме. В зависимости от варианта осуществления может быть достигнуто одно или несколько из указанных преимуществ. Эти и другие преимущества более подробно раскрыты в последующем описании.
Дополнительное понимание раскрытых здесь сущности и преимуществ изобретения можно получить, обратившись к представленным ниже разделам описания и прилагаемым чертежам.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Фиг. 1 - блок-схема системы связи, где наряду с другими признаками и элементами используется многоступенчатое кодирование, включающее в себя постоянную инактивацию;
фиг. 2 - таблица переменных, массивов и т.п., используемых здесь в различных других чертежах;
фиг. 3 - блок-схема конкретного варианта осуществления кодера, показанного на фиг. 1;
фиг. 4 - блок-схема, более подробно показывающая динамический кодер по фиг. 3;
фиг. 5 - блок-схема, иллюстрирующая процесс кодирования с постоянной инактивацией (PI);
фиг. 6 - блок-схема, иллюстрирующая процесс динамического кодирования;
фиг. 7 - блок-схема операции вычисления веса для вычисления символов;
фиг. 8 - таблица, которая может храниться в памяти и использоваться для определения степени символа на основе искомого значения;
фиг. 9 - матрица, используемая в процессе кодирования или декодирования;
фиг. 10 - уравнение, представляющее части матрицы, показанной на фиг. 9, для конкретного минимального полинома;
фиг. 11 - блок-схема, иллюстрирующая процесс установки массива для использования при кодировании или декодировании;
фиг. 12 - матричное представление набора уравнений, решаемых декодером для восстановления массива С(), представляющее восстановленные исходные символы из массива D(), представляющее принятые кодированные символы с использованием субматрицы SE, представляющей R статических символов или уравнений, известных декодеру;
фиг. 13 - матрица, являющаяся результатом перестановки строк/столбцов матрицы по фиг. 12 с использованием инактивации OTF;
фиг. 14 - блок-схема, описывающая процесс создания матрицы по фиг. 12;
фиг. 15 - матричное представление набора уравнений, решаемых декодером, для восстановления массива С(), представляющее восстановленные исходные символы из массива D(), представляющее принятые кодированные символы, с использованием субматрицы SE, и субматрицы, соответствующей постоянно инактивированным символам;
фиг. 16 - блок-схема, иллюстрирующая процесс создания субматрицы LT, которую можно использовать в матрице по фиг. 12 или матрице по фиг. 15;
фиг. 17 - блок-схема, иллюстрирующая процесс создания субматрицы PI, которую можно использовать в матрице по фиг. 15;
фиг. 18 - блок-схема генератора матрицы;
фиг. 19 - блок-схема, иллюстрирующая процесс создания субматрицы SE;
фиг. 20 - блок-схема, иллюстрирующая процесс создания субматрицы PI;
фиг. 21 - блок-схема, иллюстрирующая процесс нахождения восстановленных символов в декодере;
фиг. 22 показывает матричное представление после перестановок набора уравнений, решаемых декодером для восстановления массива C(), представляющее восстановленные исходные символы из массива D(), который представляет принятые кодированные символы;
фиг. 23 показывает матричное представление набора уравнений, решаемых декодером, и соответствующее матрице, показанной на фиг. 26;
фиг. 24 показывает матричное представление, используемое как часть процесса декодирования;
фиг. 25 показывает матричное представление, используемое как другая часть процесса декодирования;
фиг. 26 показывает матричное представление набора уравнений, решаемых декодером после частного решения;
фиг. 27 - блок-схема, иллюстрирующая другой процесс нахождения восстановленных символов в декодере;
фиг. 28 показывает матричное представление набора уравнений, решаемых декодером;
фиг. 29 показывает матричное представление набора уравнений, решаемых декодером;
фиг. 30 - примерная система кодирования, которая может быть реализована в виде аппаратных модулей, программных модулей или частей программного кода, хранящегося в хранилище программ и выполняемого процессором, возможно в виде не разделенного совместного кодового блока, как показано на этом чертеже;
фиг. 31 - примерная система кодирования, которая может быть реализована в виде аппаратных модулей, программных модулей или частей программного кода, хранящегося в хранилище программ и выполняемого процессором, возможно в виде не разделенного коллективного кодового блока, как показано на этой фигуре.
Приложение А представляет собой спецификацию кода для конкретного варианта осуществления системы «кодер/декодер», схемы исправления ошибок и приложений для надежной доставки объектов данных, иногда с использованными деталями настоящего изобретения, которое также включает в себя описание того, каким образом может использоваться систематический кодер/декодер при транспортировке доставляемых объектов. Следует понимать, что конкретные варианты осуществления, описанные в Приложении А, не являются ограничивающими примерами изобретения и что в некоторых аспектах изобретения могут быть использованы идеи, изложенные в приложении А, в то время как в других аспектах - нет. Также следует понимать, что ограничительные положения в Приложении А могут накладывать ограничения в отношении требований к конкретным вариантам осуществления, и указанные ограничительные положения могут иметь, а могут и не иметь отношения к заявленному изобретению, и, следовательно, язык формулы изобретения не обязательно должен быть ограничен указанными ограничительными положениями.
ПОДРОБНОЕ ОПИСАНИЕ КОНКРЕТНЫХ ВАРИАНТОВ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
Заимствованные детали для реализации частей кодеров и декодеров раскрыты в ссылочных материалах Luby I, Luby II, Shokrollahi I, Shokrollahi II, Shokrollahi III, Luby III и Shokrollahi IV, и для краткости целиком здесь не повторяются. Все содержание этих материалов включено сюда по ссылке для всех целей, причем следует понимать, что эти реализации не являются обязательными для настоящего изобретения, то есть, можно также использовать множество других вариаций, модификаций или альтернатив, если не указано иное.
При описанном здесь многоступенчатом кодировании исходные данные кодируются на множестве ступеней. Как правило, но не всегда, на первой ступени в исходные данные вводится заранее определенная величина избыточности. Затем на второй ступени используют код с цепной реакцией или т.п. для создания кодированных символов из первоначальных исходных данных и избыточных символов, вычисляемых на первой ступени кодирования. В одном конкретном варианте осуществления принятые данные декодируют сначала, используя процесс декодирования с цепной реакцией. Если этот процесс оказывается безуспешным в плане полного восстановления первоначальных данных, то можно применить вторую ступенью декодирования.
Некоторые из раскрытых здесь вариантов осуществления могут быть применены ко многим другим типам кодов, например, к кодам, описанным в Internet Engineering Task Force (IETF) (специальная комиссия интернет разработок) Request for Comments (RFC) (запрос на комментарии) 5170 (далее «коды IETF LDPC») и к кодам, описанным в патентах США №№6073250, 6081909 и 6163870 (далее «коды Торнадо»), что приводит к повышению надежности и/или улучшению рабочих характеристик компьютера и/или памяти для указанных типов кодов.
Одно из преимуществ ряда раскрытых здесь вариантов осуществления заключается в том, что для создания кодированных символов требуется меньше арифметических операций, по сравнению со случаем использования только кодирования с цепной реакцией. Другое преимущество некоторых конкретных вариантов осуществления, включающих в себя первую ступень кодирования и вторую ступень кодирования, состоит в том, что первая ступень кодирования и вторая ступень кодирования могут выполняться в разное время и/или разными устройствами, что позволяет распределить вычислительную нагрузку и минимизировать общую вычислительную нагрузку, а также требования к объему памяти и шаблону доступа. В вариантах осуществления многоступенчатого кодирования избыточные символы создают из входного файла на первой ступени кодирования. В этих вариантах осуществления на второй ступени кодирования, кодированные символы создают из комбинации входного файла и избыточных символов. В некоторых из этих вариантов осуществления кодированные символы могут создаваться, когда это необходимо. В тех вариантах осуществления, в которых вторая ступень содержит кодирование с цепной реакцией, каждый кодированный символ может быть создан независимо от того, каким образом создаются другие кодированные символы. После создания этих кодированных символов их можно поместить в пакеты и передать адресату, причем каждый пакет содержит один или несколько кодированных символов. Вместо или наряду с этим можно использовать технологии непакетированной передачи.
Используемый здесь термин «файл» относится к любым данным, которые хранятся в одном или нескольких источниках и должны быть доставлены как блок одному или нескольким адресатам. Таким образом, примерами доставляемых «файлов» являются документ, изображение и файл из запоминающего устройства сервера или компьютера. Файлы могут иметь известный размер (например, изображение размером один мегабайт, хранящиеся на жестком диске) или могут иметь неизвестный размер (например, файл, полученный с выхода источника потоковой передачи). В любом случае файл представляет собой последовательность исходных символов, где каждый исходный символ имеет позицию в файле и свое значение. Термин «файл» также может использоваться для обращения к короткой части источника потоковой передачи, то есть, поток данных может быть разделен на односекундные интервалы, и тогда «файлом» может считаться блок исходных данных в пределах каждого указанного односекундного интервала. В другом примере блоки данных от источника потокового видео могут быть дополнительно разбиты на множество частей на основе приоритетов данных, определенных, например, видеосистемой, которая может воспроизводить видеопоток, и тогда «файлом» может считаться каждая часть каждого блока. Таким образом, термин «файл» используется широко, и не предполагает наличие значительных ограничений.
Используемые здесь исходные символы представляют данные, подлежащие передаче или пересылке, а кодированные символы представляют собой данные, созданные на основе исходных символов, которые пересылают по сети связи или хранят, причем обеспечивается возможность надежного приема и/или восстановления исходных символов. Промежуточные символы представляют символы, используемые или создаваемые на промежуточной ступени процессов кодирования или декодирования, причем, как правило, имеется способ создания промежуточных символов из исходных символов и соответствующий обратный способ для создания исходных символов из промежуточных символов. Входные символы представляют данные, которые вводятся в один или нескольких шагов во время процесса кодирования или декодирования, а выходные символы представляют данные, которые выводятся из одного или нескольких шагов во время процесса кодирования или декодирования.
Во многих вариантах осуществления указанные различные типы или метки символов могут быть одинаковыми или могут содержать, по меньшей мере, частично, другие типы символов, причем в некоторых примерах упомянутые термины используют как взаимозаменяемые. В качестве одного примера предположим, что файлом, подлежащим передаче, является текстовый файл, состоящий из 1000 знаков, каждый из которых считается исходным символом. Если эти 1000 исходных символов подать в кодер в том виде как они есть, который, в свою очередь, выдает кодированные символы для передачи, исходные символы также будут входными символами. Однако в вариантах осуществления, где на первом шаге 1000 исходных символов преобразуются в 1000 (или больше, или меньше) промежуточных символов, а промежуточные символы на втором шаге подаются в кодер для создания кодированных символов, на первом шаге исходные символы являются входными символами, а промежуточные символы являются выходными символами, а на втором шаге промежуточные символы являются входными символами, а кодированные символы являются выходными символами, в то время как все исходные символы являются входными символами для указанного двухступенчатого кодера, и все кодированные символы являются выходными символами этого двухступенчатого кодера. Если в данном примере кодер является систематическим кодером, то тогда кодированные символы могут содержать исходные символы вместе с символами для восстановления, созданными из промежуточных символов, в то время как промежуточные символы отличаются как от исходных символов, так и от кодированных символов. Если в этом примере кодер не является систематическим кодером, то тогда промежуточные символы могут содержать исходные символы вместе с избыточными символами, созданными из исходных символов, с использованием на первом шаге, например, кодера LDPC и/или HDPC, в то время как кодированные символы отличаются как от исходных символов, так и от промежуточных символов.
В других примерах имеется несколько символов, причем каждый символ представляет более одного знака. В любом случае, когда в передатчике используется преобразование исходных символов в промежуточные, приемник может использовать соответствующее обратное преобразование промежуточных символов в исходные.
Передача представляет собой процесс передачи данных от одного или нескольких отправителей одному или нескольким получателям через канал с целью доставки файла. Иногда отправитель также называется кодером. Если отправитель соединен с некоторым количеством получателей по идеальному каналу, принятые данные могут быть точной копией исходного файла, поскольку все данные будут правильно приняты. Здесь предполагается, что канал не является идеальным, что характерно для абсолютного большинства реальных каналов. Из множества несовершенств каналов интерес представляют два несовершенства: уничтожение данных и неполнота данных (которую можно трактовать как особый случай уничтожения данных). Уничтожение данных возникает, когда данные в канале теряются или выпадают. Неполнота данных возникает, когда получатель не начинает прием данных, пока не прошла некоторая часть данных, получатель прекращает прием данных до окончания передачи, получатель принимает решение о приеме только части переданных данных и/или получатель периодически прекращает и начинает вновь прием данных. В качестве примера возникновения неполноты данных, движущийся спутниковый отправитель данных, который может передавать данные, представляющие исходный файл, начинает передачу, до того как получатель вошел в область. Как только получатель оказывается в области, можно принимать данные, пока спутник не выйдет из области, и тогда получатель может перенаправить свою спутниковую антенну (в то время, когда он не принимает данные) для начала приема данных о том же входном файле, передаваемом другим спутником, который вошел в область. Из данного описания должно быть понятно, что неполнота данных является особым случаем уничтожения данных, поскольку получатель может рассматривать неполноту данных (причем получатель имеет аналогичные проблемы), как если бы он находился в области все время, но в канале были потеряны все данные вплоть до момента, когда получатель начал прием данных. Так же, как хорошо известно, разработчикам систем связи, обнаруживаемые ошибки можно считать эквивалентными уничтожению данных в результате простого сбрасывания всех блоков данных или символов данных, которые содержат обнаруживаемые ошибки.
В некоторых системах связи получатель принимает данные, созданные множеством отправителей или одним отправителем, с использованием множества соединений. Например, для ускорения загрузки получатель может одновременно соединиться с более чем одним отправителем для передачи данных, относящихся к одному и тому же файлу. В другом примере при групповой передаче может передаваться множество потоков данных групповой передачи, чтобы дать возможность получателям подсоединиться к одному или нескольким из указанных потоков для согласования скорости агрегатной передачи с полосой частот канала, соединяющего их с отправителем. Во всех указанных случаях вопрос заключается в обеспечении независимого использования всех переданных данных получателем, то есть, множество исходных данных не является избыточным между указанными потоками даже в том случае, когда скорости передачи сильно различаются для разных потоков, и когда имеются произвольные шаблоны потерь.
В общем случае канал связи представляет собой канал для передачи данных, соединяющий отправителя и получателя. Канал связи может быть каналом, работающим в режиме реального времени, когда канал перемещает данные от отправителя получателю по ходу получения данных, либо канал связи может представлять собой канал с памятью, который хранит некоторую часть либо все данные в его доставке от отправителя к получателю. Примером последнего является дисковое запоминающее устройство или иное запоминающее устройство. В этом примере программа или устройство, создающее данные, может рассматриваться как отправитель, передающий данные в запоминающее устройство. Приемник представляет собой программу или устройство, которое считывает данные из запоминающего устройства. Механизмы, которые использует отправитель для подачи данных в запоминающее устройство, само запоминающее устройство и механизмы, которые использует получатель для получения данных из запоминающего устройства, все вместе образуют упомянутый канал. Если имеется вероятность того, что эти механизмы или запоминающее устройство могут потерять данные, то тогда это можно трактовать как уничтожение данных в канале связи.
Когда отправитель и получатель разделены каналом связи, в котором возможно уничтожение символов, предпочтительно не передавать точную копию входного файла, а вместо этого передавать данные, созданные из входного файла, что способствует восстановлению уничтоженных данных. Кодер представляет собой схему, устройство, модуль или кодовый сегмент, который обрабатывает эту задачу. Один из путей просмотра функционирования кодера состоит в том, что кодер создает кодированные символы из исходных символов, где последовательность значений исходных символов представляет входной файл. Таким образом, каждый исходный символ имеет позицию во входном файле и свое значение. Декодер представляет собой схему, устройство, модуль или кодовый сегмент, который восстанавливает исходные символы из кодированных символов, принятых получателем. При многоступенчатом кодировании кодер и декодер иногда дополнительно разделяют на субмодули, каждый из которых выполняет разные задачи.
В вариантах осуществления систем многоступенчатого кодирования кодер и декодер могут быть дополнительно разделены на субмодули, каждый из которых выполняет свою задачу. Например, в некоторых вариантах осуществления кодер содержит то, что здесь называется статическим кодером и динамическим кодером. Используемый здесь термин «статический кодер» представляет кодер, который создает несколько избыточных символов из набора исходных символов, где количество избыточных символов определяют перед кодированием. При использовании статического кодирования в системе многоступенчатого кодирования комбинацию исходных символов и избыточных символов, созданных из исходных символов с использованием статического кодера, часто называют промежуточными символами. Примеры возможных статических кодирующих кодов включают в себя коды Рида-Соломона, коды Торнадо, коды Хэмминга, коды LDPC, такие как коды IETF LDPC и т.д. Термин «статический декодер» используется здесь для названия декодера, который может декодировать данные, закодированные статическим кодером.
Используемый здесь термин «динамический кодер» представляет собой кодер, создающий кодированные символы из набора входных символов, где количество возможных кодированных символов не зависит от количества входных символов, и где количество создаваемых кодированных символов не обязательно должно быть фиксированным. Часто в многоступенчатом коде входные символы являются промежуточными символами, созданными с использованием статического кода, причем эти кодированные символы создаются из промежуточных символов с использованием динамического кодера. Одним из примеров динамического кодера является кодер с цепной реакцией, например, кодеры, раскрытые в Luby I и Luby II. Термин «динамический декодер» используется здесь для названия декодера, который декодирует данные, закодированные динамическим кодером.
В некоторых вариантах осуществления при кодировании с применением многоступенчатого кода и систематического кода используется процесс декодирования, применяемый для исходных символов, с целью получения значений промежуточных символов на основе соотношений, определенных статическим кодером между промежуточными символами, и соотношений, определенных динамическим кодером между промежуточными символами и исходными символами, после чего используется динамический кодер для создания дополнительных кодированных символов, или символов для восстановления, из промежуточных символов. Аналогичным образом, соответствующий декодер реализует процесс декодирования, для приема кодированных символов и выполнения их декодирования из них значений промежуточных символов, на основе соотношений, определенных статическим кодером, между промежуточными символами, и определенных динамическим кодером, между промежуточными символами и принятыми кодированными символами, и после чего используют динамический кодер для создания пропущенных исходных символов из промежуточных символов.
Варианты осуществления многоступенчатого кодирования не обязательно сводятся к какому-либо конкретному типу символа. Как правило, значения символов выбирают из алфавита, состоящего из 2М символов, где М - положительное целое число. В указанных случаях исходный символ можно представить в виде последовательности из М бит данных входного файла. Значение М часто определяют на основе, например, использований приложения, канала связи и/или размера кодированных символов. Вдобавок, размер кодированного символа часто определяют на основе конкретного приложения, канала и/или размера исходных символов. В некоторых случаях процесс кодирования можно упростить, если значения кодированных символов и значения исходных символов имели одинаковый размер (то есть, их можно представить одинаковым количеством бит или выбрать из одного и того же алфавита). Если речь идет о таком случае, то размер исходного символа ограничен, когда ограничен размер кодированного символа. Например, возможно требуется поместить кодированные символы в пакеты ограниченного размера. Если необходимо передать некоторые данные о ключе, связанном с кодированными символами, чтобы восстановить этот ключ в приемнике, то предпочтительно, чтобы кодированный символ имел небольшой размер, достаточный, чтобы подходить для одного пакета значения кодированного символа и данных о ключе.
Например, если входной файл имеет объем в несколько мегабайт, то входной файл можно разбить на тысячи, десятки тысяч или сотни тысяч исходных символов, причем каждый исходный символ кодирует тысячи, сотни или всего несколько байт. В другом примере для канала Интернет на основе пакетов может подойти пакет с полезной нагрузкой 1024 байта (один байт равен 8 бит). В данном примере, если предположить, что каждый пакет содержит один кодированный символ и 8 байт вспомогательной информации, то подходящим окажется размер кодированного символа, равный 8128 бит ((1024-8)*8). Таким образом, размер исходного символа можно определить как M=(1024-8)*8, или 8128 бит. В другом примере в некоторых спутниковых системах используется стандарт пакетов MPEG, где полезная нагрузка каждого пакета составляет 188 байт. В этом примере, если предположить, что каждый пакет содержит один кодированный символ и 4 байта вспомогательной информации, то подходящим окажется размер кодированного символа, равный 1472 бита ((188-4)*8). Таким образом, размер исходного символа можно определить как M=(188-4)*8, или 1472 бита. В системе связи общего назначения, где используется многоступенчатое кодирование, параметрами, специфичными для конкретного приложения, такими как размер исходного символа (то есть, М - количество бит, кодируемых на один исходный символ), могут быть переменные, установленные данным приложением.
Каждый кодированный символ имеет значение. В одном предпочтительном варианте осуществления, рассматриваемом ниже, каждый кодированный символ также связан с идентификатором, называемым «ключом». Предпочтительно, чтобы получатель мог легко определить ключ каждого кодированного символа, чтобы получатель мог отличить один кодированный символ от других кодированных символов. Предпочтительно, чтобы ключ кодированного символа отличался от ключей всех других кодированных символов. Имеется множество различных способов присваивания ключей, обсуждаемых специалистами в данной области техники. Например, в Luby I описываются различные виды присваивания ключей, которые можно использовать в вариантах осуществления настоящего изобретения. В других предпочтительных вариантах осуществления, например, в описанном в Приложении А, ключ для кодированного символа называется «идентификатор кодированного символа» или «кодирующий идентификатор символа», или сокращенно «ESI».
Многоступенчатое кодирование особенно полезно, когда ожидается уничтожение данных при передаче или когда получатель начинает и заканчивает прием не именно тогда, когда передача начинается и заканчивается. Последнее состояние называется здесь «неполнота данных». Что касается событий уничтожения данных, то многоступенчатое кодирование использует многие преимущества кодирования с цепной реакцией, раскрытые в Luby I. В частности, символы, закодированные в многоступенчатом режиме, представляют собой информационную добавку, так что для восстановления входного файла с требуемой степенью точности можно использовать любое подходящее количество пакетов. Указанные состояния не оказывают неблагоприятное воздействие на процесс связи при использовании многоступенчатого кодирования, поскольку кодированные символы, созданные с использованием многоступенчатого кодирования, представляют собой информационную добавку. Например, если потеряна сотня пакетов из-за всплеска шумов, вызвавшего уничтожение данных, можно получить дополнительную сотню пакетов после этого всплеска для замены потерянных пакетов. Если потеряны тысячи пакетов из-за того, что приемник не настроился на передатчик, когда передача началась, приемник может получить эти тысячи пакетов на любом другом интервале передачи или даже от другого передатчика. При многоступенчатом кодировании приемник не ограничен в получении любого конкретного набора пакетов, так что он может принять некоторые пакеты от одного передатчика, переключиться на другой передатчик, потерять некоторые пакеты, пропустить начало или конец данной передачи и все же восстановить входной файл. Способность присоединяться и прекращать передачу без координации работы приемника и передатчика помогает упростить процесс связи.
В некоторых вариантах осуществления передача файла с использованием многоступенчатого кодирования может включать в себя создание, формирование или извлечение исходных символов из входного файла, вычисление избыточных символов, кодирование исходных и избыточных символов с получением одного или нескольких кодированных символов, где каждый кодированный символ создают на основе его ключа независимо от всех других кодированных символов, и передачу кодированных символов по каналу одному или нескольким получателям. Вдобавок, в некоторых вариантах осуществления прием (и восстановление) копии входного файла с использованием многоступенчатого кодирования может включать в себя прием некоторого набора или поднабора кодированных символов из одного из множества потоков данных и декодирование исходных символов исходя из значений и ключей принятых кодированных символов.
СИСТЕМАТИЧЕСКИЕ КОДЫ И НЕСИСТЕМАТИЧЕСКИЕ КОДЫ
Систематический код представляет собой код, где исходные символы находятся среди кодированных символов, которые могут передаваться. В этом случае кодированные символы состоят из исходных символов и избыточных символов, также называемых символами для восстановления, которые создаются из исходных символов. Систематический код по различным причинам является более предпочтительным, чем несистематический код, для многих приложений. Например, в приложении для доставки файлов полезно иметь возможность начинать передачу данных в последовательном порядке, когда данные используются для создания данных для восстановления, причем процесс создания данных для восстановления может занимать некоторое время. В другом примере во многих приложениях предпочтение отдается посылке первоначальных исходных данных в последовательном порядке в не модифицированном виде в один канал и посылке данных для восстановления в другой канал. Одной из типовых причин этого является поддержка обычных приемников, которые не используют декодирование с FEC, обеспечивая в то же время лучшее восприятие для усовершенствованных приемников, которые используют декодирование FEC, причем обычные приемники работают, только с каналом исходных данных, а усовершенствованные приемники объединяют как канал исходных данных, так и канал данных для восстановления.
В этих и родственных приложениях иногда может возникнуть ситуация, когда шаблон потерь и доля потерь среди принятых приемником исходных символов достаточно отличаются от того, что наблюдается среди принятых символов для восстановления. Например, когда исходные символы посылаются перед символами для восстановления, то из-за всплесков потерь в канале доля и шаблон потерь среди исходных символов могут достаточно отличаться от соответствующей доли или шаблона потерь среди символов для восстановления, и шаблон потерь среди символов восстановления может быть далек от возможной типового шаблона, по сравнению со случаем, когда потери были случайными с равномерным распределением. В другом примере, когда исходные данные посылают по одному каналу, а данные для восстановления по другому каналу, возможно наличие достаточно разных условий в отношении потерь в этих двух каналах. Следовательно, желательно иметь систематический код с FEC, который хорошо работает в условиях наличия потерь различных типов.
Хотя приведенные здесь примеры относятся к систематическим кодам (где выходные или кодированные символы включают в себя исходные или входные символы), либо к несистематическим кодам, изложенные здесь основные принципы следует считать применимыми к обоим типам кодов, если не указано иное. В Shokrollahi III раскрыты способы преобразования несистематического кода с цепной реакцией в систематический код, таким образом, при котором свойства помехозащищенности несистематического кода поддерживаются систематическим кодом, построенным вышеуказанным способом.
В частности, сконструированный систематический код, использующий способы, раскрытые в Shokrollahi III, обладает свойством, состоящим в наличии небольшого отличия в отношении восстанавливаемости посредством декодера между потерянными исходными символами и потерянными символами для восстановления, то есть, вероятность восстановления при декодировании по существу одинакова для данной величины общих потерь, практически не зависящей от доли потерь в исходных символах по сравнению с долей потерь в символах для восстановления. Кроме того, шаблон потерь среди кодированных символов незначительно влияет на вероятность восстановления при декодировании. По сравнению со структурами других систематических кодов, таких как структуры, описанные для кодов Торнадо или кодов IETF LDPC, имеет место множество случаев значительного различия в отношении восстанавливаемости, обеспечиваемой декодером, между потерянными исходными символами и потерянными символами для восстановления, то есть, вероятность восстановления при декодировании может значительно изменяться для данной величины общих потерь в зависимости от доли потерь среди исходных символов по сравнению с долей потерь среди символов для восстановления. Кроме того, шаблон потерь среди кодированных символов может сильно повлиять на вероятность восстановления при декодировании. Коды Торнадо и коды IETF LDPC имеют достаточно хорошие восстановительные свойства, если потери кодированных символов распределены равномерно среди всех кодированных символов, но восстановительные свойства ухудшаются, если модель потерь отклоняется от потерь с равномерным распределением. Таким образом, в этом смысле варианты осуществления изобретения, раскрытые в Shokrollahi III, имеют преимущество над другими структурами систематических кодов.
Что касается кода с FEC, обладающего свойством, состоящим в наличии значительного влияния декодера на восстанавливаемость в зависимости от доли потерянных исходных символов и потерянных символов для восстановления и в зависимости от шаблонов потерь, то один подход, преодолевающий указанную особенность при его применении, заключается в посылке кодированных символов в случайном порядке с равномерным распределением, то есть, комбинация исходных символов и символов для восстановления посылается в случайном порядке с равномерным распределением, в результате чего исходные символы оказываются случайным образом рассеянными между символами для восстановления. Посылка кодированных символов в случайном порядке дает преимущество, состоящее в том, что независимо от модели потерь в канале, независимо от того, имеют ли потери пульсирующий вид или являются равномерно распределенными случайными, или являются потерями какого-либо иного типа), потери кодированных символов все-таки остаются случайными. Однако, как было отмечено выше, такой подход для некоторых приложений нежелателен, например, для приложений, где требуется последовательная посылка исходных символов перед символами для восстановления, или когда исходные символы посылают по каналу, отличному от канала для символов для восстановления.
В указанных случаях необходимо иметь структуры систематических кодов, где шаблон потерь среди кодированных символов несильно влияет на восстановительные свойства декодера, некоторые примеры которых приведены в этом описании.
Используемые здесь термины «случайный» и «псевдослучайный» часто являются эквивалентными и/или взаимозаменяемыми и могут зависеть от контекста. Например, случайные потери могут относиться к символам, потерянным в канале, что может действительно являться случайным событием, в то время как случайный выбор соседних символов в действительности может представлять собой повторяемый псевдослучайный выбор согласно не случайному процессу, но при этом имеют место одинаковые или подобные свойства или поведение, как в случае с действительно случайным выбором. Если в явном виде (или из контекста) не указано иное, какой-либо объект характеризуется как случайный, что не означает исключение его псевдослучайного характера.
В одном подходе к построению указанного систематического кодера с FEC исходные символы поступают в кодер, который включает в себя множество субблоков или субпроцессов, один из которых действует как декодер, создающий промежуточные символы, которые являются входными символами для другого субблока или субпроцесса. Затем промежуточные символы подаются в другой субблок или субпроцесс, который кодирует промежуточные символы с получением кодированных символов, так что кодированные символы включают в себя исходные символы (наряду с дополнительными, избыточными символами), созданными в ходе одного согласованного процесса, что обеспечивает помехоустойчивость и другие преимущества над систематическим кодером, в котором используется один процесс (например, копирование) с целью получения исходных символов для набора кодированных символов и другой процесс для получения избыточных символов для набора кодированных символов.
Выходное кодирование может быть реализовано кодером с цепной реакцией, статическим кодером или другими вариантами. В Приложении А описывается вариант осуществления с использованием систематического кода. После ознакомления с настоящим описанием специалисты в данной области техники без труда смогут расширить основные идеи, раскрытые в Shokrollahi III, на систематические коды, такие как коды Торнадо и коды IETF LDPC, для получения новых версий этих кодов, которые также являются систематическими кодами, но имеют улучшенные восстановительные свойства. В частности, новые версии этих кодов, полученные с применением общего способа, описанного ниже, усовершенствованы в том плане, что доля потерь среди исходных символов по сравнению с долей потерь среди символов для восстановления незначительно влияет на вероятность восстановления при декодировании, и кроме того, на вероятность восстановления при декодировании шаблон потерь также влияет незначительно. Таким образом, эти коды можно эффективно использовать в вышеописанных приложениях, где требуется использование систематических кодов с FEC с восстановительными свойствами, на которые несильно влияют различные уровни потерь среди исходных символов и символов для восстановления, или различные шаблоны потерь.
В общем случае этот новый способ кодирования может быть применен при кодировании с использованием систематических кодов с FEC, несистематических кодов с FEC, кодов с FEC и фиксированной скоростью и кодов с FEC и цепной реакцией, что дает общий способ кодирования для новых усовершенствованных систематических кодов FEC. Также может найти применение соответствующий новый способ декодирования.
ПРИМЕР ДЕКОДЕРА В КОДЕРЕ
Далее описывается пример декодера в кодере.
Пусть способ Е кодирования представляет собой способ кодирования, используемый кодером (в передатчике или где-то еще) для (несистематического или систематического) кода Е с FEC с фиксированной скоростью, который генерирует N кодированных символов из К исходных символов, где N по меньшей мере равно К. Аналогичным образом пусть способ Е декодирования представляет собой соответствующий способ декодирования для кода Е с FEC, используемый декодером в приемнике или где-то еще.
Предположим, что код Е с FEC имеет свойство, состоящее в том, что случайный набор К из N кодированных символов достаточен для восстановления K первоначальных исходных символов с подходящей вероятностью с использованием способа Е декодирования, где подходящая вероятность может, например, составлять 1/2. Подходящая вероятность может представлять собой некоторое требование, установленное особенностью использования кода или особенностями данного приложения, и может иметь значение, отличное от 1/2. Следует понимать, что построение конкретного кода не обязательно привязано к конкретной вероятности восстановления, но указанные приложения и системы могут быть спроектированы для удовлетворения конкретного уровня помехоустойчивости. В некоторых случаях вероятность восстановления может возрастать благодаря рассмотрению большего, чем K символов с последующим определением с использованием процесса декодирования набора из K символов из числа этих рассмотренных символов, что позволяет обеспечить успешное декодирование.
Положим, что для кода Е с FEC идентификатор ESI (идентификатор кодированного символа) связан с каждым кодированным символом и что ESI идентифицирует данный кодированный символ. Без потери общности идентификаторы ESI обозначены здесь номерами 0, 1, 2,..., N-1.
В одном варианте осуществления способа F систематического кодирования для систематического кода F с FEC, созданного с использованием способов для кода E c FEC, входными параметрами являются K и N. Исходные символы для кода F с FEC будут иметь идентификаторы ESI 0,..., K-1, а символы для восстановления для кода F с FEC будут иметь следующие ESI: K,..., N-1. Способ F систематического кодирования для кода F c FEC создает N кодированных символов из K исходных символов C(0),...,C(K-1) с использованием способа E кодирования и способа E декодирования для кода E с FEC, реализуемых аппаратными и/или программными средствами следующим образом:
(1) выполняют рандомизированную перестановку N идентификаторов ESI, связанных с кодом E с FEC, для получения переставленного набора идентификаторов ESI X(0),..., X(N-1), для кода E с FEC, где этот переставленный набор идентификаторов ESI организован таким образом, что К исходных символов кода E с FEC можно декодировать из первых K кодированных символов кода E с FEC в соответствии с порядком перестановки идентификаторов ESI X(0),..., X(K-1);
(2) для каждого i=0,..., N-1, индекс i идентификатора ESI кода F с FEC связывают с идентификатором X(i) кода Е с FEC;
(3) для каждого i=0,..., K-1, устанавливают значение кодированного символа кода E с FEC с идентификатором X(i) равным значению исходного символа C(i);
(4) применяют способ Е декодирования к исходным символам C(0),..., C(K-1) с соответствующими идентификаторами X(0),..., X(K-1) кода E с FEC для создания декодированных символов E(0),..., E(K-1); и
(5) применяют способ Е кодирования к декодированным символам E(0),..., E(K-1) для создания кодированных символов D(0),..., D(N-1) кода E c FEC со связанными идентификаторами 0, 1,..., N-1 кода с FEC;
(6) кодированными символами для способа F кодирования с идентификаторами 0, 1,...,N-1 будут D(X(0)),..., D(X(I)), D(X(N-1)).
Заметим, что выходом способа F кодирования являются N кодированных символов, у которых первые K символов являются исходными символами C(0),..., C(K-1) со связанными идентификаторами ESI 0, 1,..., K-1. Таким образом, способ F кодирования обеспечивает систематического кодирование исходных данных.
Один из вариантов осуществления способа F декодирования, соответствующий только что описанному способу F кодирования, описан ниже, где K и N - входные параметры для этого способа, которые используются в нем повсеместно. Этот способ F декодирования восстанавливает K исходных символов C(0),..., C(K-1) из K принятых кодированных символов D(0),..., D(K-1) со связанными идентификаторами ESI Y(0),..., Y(K-1) кода F с FEC. Принятые символы не обязательно будут точно совпадать с посланными символами. Описываемый способ, выполняемый аппаратными и/или программными средствами, состоит из следующих шагов:
(1) выполнение рандомизированной перестановки N идентификаторов, связанных с кодом E с FEC, для получения переставленного набора идентификаторов ESI X(0),..., X(N-1) кода Е с FEC, где этот переставленный набор идентификаторов ESI организован таким образом, что может быть декодировано K исходных символов кода E с FEC из первых K кодированных символов кода E c FEC в соответствии с порядком перестановки идентификаторов ESI X(0),..., X(K-1);
(2) применение способа E декодирования к кодированным символам D(0),..., D(K-1) со связанными идентификаторами ESI X(Y(0)),..., X(Y(K-1)) кода E с FEC для создания декодированных символов E(0),..., E(K-1);
(3) создание с использованием способа Е кодирования кодированных символов C(0),..., C(K-1) с идентификаторами ESI X(0),...,X(K-1) кода Е с FEC из E(0),...,E(K-1);
(4) декодированными исходными символами кода F с FEC с идентификаторами ESI 0, K-1 будут C(0),..., C(K-1).
Способы и устройство, функционирующее так, как было описано выше, обладают рядом требуемых свойств. Рассмотрим, например, код Е с FEC, который является систематическим кодом и обладает свойством, обеспечивающим возможность декодирования с высокой вероятностью случайного набора из К принятых кодированных символов, но он также обладает свойством, состоящим в том, что при приеме К кодированных символов и при условии, что доля исходных символов среди принятых кодированных символов существенно отличается от К/N, невозможно декодирование с высокой вероятностью. Для этого случая в данном варианте осуществления описан новый код F с FEC, в котором используются способы кодирования и декодирования кода Е с FEC, и новый код F с FEC обладает требуемым свойством, состоящим в том, что обеспечивается декодирование с высокой вероятностью на основе набора из К принятых кодированных символов независимо от доли принятых кодированных символов, являющихся исходными символами.
Вышеописанный вариант осуществления имеет множество версий. Например, на шаге (1) способа F кодирования рандомизированная перестановка идентификаторов ESI может быть псевдослучайной либо может быть основана на некотором другом способе, который предоставляет хороший выбор идентификаторов ESI, но это выполняется, ни случайным, ни псевдослучайным образом. В случае, когда код Е с FEC является систематическим кодом, предпочтительно, чтобы часть первых К идентификаторов ESI в перестановке, выбранной на шаге (1) из числа систематических идентификаторов ESI, была пропорциональна скорости кода Е с FEC, то есть, пропорциональна К/N. Предпочтительно, чтобы случайный выбор идентификаторов ESI, выполняемый на шаге (1) согласно новому способу F кодирования, можно было представить сжатым количеством данных, например, путем использования начального числа для хорошо известного или общепринятого псевдослучайного генератора вместе с общепринятым способом выбора идентификаторов ESI на основе этого начального числа и режима работы псевдослучайного генератора, так что новый способ F декодирования может на шаге (1) выполнить точно такую же перестановку идентификаторов ESI на основе того же начального числа и псевдослучайного генератора, а также способов создания идентификаторов ESI. В общем случае предпочтительно, чтобы процесс, используемый в новом способе F кодирования на шаге (1) создавал последовательности идентификаторов ESI, и процесс, используемый в новом способе F декодирования на шаге (1) создавал последовательности идентификаторов ESI, оба создают одинаковые последовательности идентификаторов ESI, чтобы обеспечить, что новый способ F декодирования должен быть обратным по отношению к новому способу F кодирования.
Также имеются другие варианты, в которых, например, идентификаторы ESI в явном виде не используются, а вместо этого используется уникальный идентификатор кодированного символа, задаваемый его позицией относительно других символов или другим образом.
В предшествующем описании первоначальные идентификаторы ESI кода Е с FEC повторного преобразуются кодом F с FEC, так что упорядоченному набору исходных символов присваиваются идентификаторы ESI 0,..., K-1 в последовательном порядке, а символам для восстановления присваивают идентификаторы ESI K,..., N-1. Возможны другие варианты, например, повторное преобразование идентификаторов ESI может иметь место у отправителя сразу после того, как способом F кодирования созданы кодированные символы, но до их передачи, а обратное повторное преобразование идентификаторов ESI может иметь место в приемнике при приеме кодированных символов, но перед их обработкой с целью восстановления первоначальных исходных символов способом F декодирования.
В качестве другого варианта на шаге (1) нового способа F кодирования перестановка может быть выбрана путем первого выбора К+А идентификаторов ESI кода Е с FEC, где А является значением, которое выбирают для обеспечения декодируемости с высокой вероятностью, а затем во время имитации процесса декодирования определяют, какие К идентификаторов из числа К+А идентификаторов ESI действительно будут использованы при декодировании, и выбранная перестановка может обеспечить выбор К идентификаторов ESI, действительно используемых во время декодирования, из начального набора, состоящего из К+А идентификаторов ESI, являющихся первыми К идентификаторами ESI данной перестановки. Аналогичные варианты применяются для нового способа F декодирования.
В качестве другого варианта способа F кодирования начальное число, используемое для создания случайной перестановки, предварительно вычисляется для значения К для обеспечения возможности декодирования первых К кодированных символов кода Е с FEC, связанного с перестановкой идентификаторов ESI, выполненной на шаге (1), и тогда это начальное число будет всегда использоваться для К на шаге (1) способа F кодирования и соответствующего способа F декодирования для создания перестановки на шаге (1). Способы для выбора указанного начального числа включают в себя рандомизированный выбор начальных чисел до тех пор, пока не будет найдено одно начальное число, обеспечивающее декодируемость на шаге (1), а затем осуществляется выбор этого начального числа. В качестве альтернативы, начальное число может создаваться динамически с этими свойствами с помощью способа F кодирования, после чего это начальное число может быть сообщено в в способ F декодирования.
В другой версии способа F кодирования на шаге (1) может быть выбрана частичная перестановка, то есть, на шаге (1) нового способа F кодирования должны быть созданы не все идентификаторы ESI, и нет необходимости создания всех кодированных символов, если они не нужны на шагах (5) и (6), например, поскольку они соответствуют исходным символам, являющимся частью кодированных символов, либо поскольку необходимо создать меньше, чем N кодированных символов. В других версиях нет необходимости повторного вычисления всех кодированных символов на шагах (3) и (4) нового способа F декодирования, так как некоторые из принятых кодированных символов могут соответствовать некоторым восстанавливаемым исходным символам. Аналогичным образом, на шаге (2) нового способа F декодирования нет необходимости декодировать все К символов E(0),..., E(K-1), например, если некоторые символы, декодированные на шаге (2), не нужны в последующих шагах для создания кодированных символов.
Вышеописанные способы и варианты осуществления имеют множество приложений. Например, способ F кодирования и способ F декодирования и их варианты можно применить к кодам Торнадо и кодам IETF LDPC, чтобы обеспечить улучшение объема служебных данных при приеме и вероятности неудач при декодировании. В общем случае эти новые способы применимы к любому коду с FEC с фиксированной скоростью. Версии этих новых способов можно также применить к кодам с FEC, которые не имеют фиксированную скорость, то есть, к кодам FEC, таким как коды, с цепной реакцией, где количество кодированных символов, которое можно создать, не зависит от количества исходных символов.
В Shokrollahi III раскрыты аналогичные принципы создания способов систематического кодирования и декодирования для кодов с цепной реакцией. В некоторых вариантах осуществления способы Е кодирования и декодирования, используемые для этих кодов, изложены в Luby I, Luby II, Shokrollahi I, Shokrollahi II, Luby III, Shokrollahi IV. Для описания систематических кодеров часто достаточно описать способ Е кодирования и способ Е декодирования и использовать вышеописанные общие принципы, известные из этих ссылочных материалов, для преобразования этих способов в способы F систематического кодирования и способы F систематического декодирования. Таким образом, специалистам в данной области техники после ознакомления с этим описанием и процитированными ссылочными материалами должно быть очевидно, каким образом реализовать основные идеи, лежащие в основе способов Е кодирования и способов Е декодирования и применить их к способам F систематического кодирования и способам F систематического декодирования, или т.п.
ИНАКТИВАЦИЯ
Декодирование с инактивацией, раскрытое в Shokrollahi II, является общим способом, который можно применить в сочетании с принципом распространения надежности при вычислении набора неизвестных переменных из набора известных значений линейных уравнений, и, в частности, его выгодно использовать при реализации способов эффективного кодирования и декодирования, основанных на системах линейных уравнений. Чтобы различить декодирование с инактивацией, описанное в Shokrollahi II, и декодирование с постоянной инактивацией, описанное ниже, используют инактивацию «на ходу» (обозначаемую сокращенно инактивация OTF) для обращения к способам и основным принципам, изложенным в Shokrollahi II, в то время как «постоянную инактивацию» используют при обращении к изложенным здесь способам и основным принципам, где инактивации выбирают заранее.
Одним из основных положений декодирования с распространением надежности является то, что при любой возможности во время процесса декодирования декодер должен использовать (возможно, приведенное) уравнение, зависящее от одной оставшейся неизвестной переменной, для нахождения этой переменной, причем это уравнение, таким образом, связано с указанной переменной, а затем декодер должен сократить оставшиеся неиспользованные уравнения путем исключения зависимости этих уравнений от вычисленной переменной. Указанный процесс простого декодирования на основе распространения надежности был использован, например, в некоторых вариантах осуществления кодов Торнадо, кодов с цепной реакцией, как это описано в Luby I, Luby II, Shokrollahi I, Shokrollahi II, Luby III, Shokrollahi IV, и кодов IETF LDPC.
Выполнение декодирования с инактивацией OTF состоит из множества фаз. На первой фазе способа декодирования с инактивацией OTF, всякий раз, когда процесс декодирования с распространением надежности не может продолжаться из-за отсутствия остаточного уравнения, зависящего только от одной оставшейся неизвестной переменной, декодер будет выполнять инактивацию OTF одной или нескольких неизвестных переменных и посчитает их «найденными» согласно процессу распространения надежности и «исключенными» из оставшихся уравнений (даже в случае, когда они в действительности отсутствуют), что дает возможность продолжать процесс декодирования с распространением надежности. Затем находят переменные, инактивированные на ходу во время первой фазы, например, с использованием гауссова исключения или более эффективных вычислительных методов, например, на второй фазе, а затем на третьей фазе значения этих инактивированных на ходу переменных используют для окончательного нахождения переменной, связанной с упомянутыми уравнениями во время первой фазы декодирования.
Декодирование с инактивацией OTF, более подробно раскрытое в Shokrollahi II, можно применить к кодам многих других типов кроме кодов с цепной реакцией. Например, такое декодирование можно применить к общему классу кодов LDPC и LDGM, в частности, к кодам IETF LDPC и кодам Торнадо, что повышает надежность (уменьшает вероятность сбоя при декодировании) и/или улучшает рабочие характеристики CPU и/или памяти (увеличивает скорость кодирования и/или декодирования и/или уменьшает требования к объему памяти и/или шаблону доступа) для этих типов кодов.
Некоторые из версий вариантов осуществления кода с цепной реакцией в сочетании с декодированием с инактивацией OTF описаны в Shokrollahi IV. Другие версии описаны в настоящем приложении.
ОБЗОР СИСТЕМЫ
На фиг. 1 представлена блок-схема системы 100 связи, в которой используется многоступенчатое кодирование. Эта система аналогична системе, показанной в Shokrollahi I, но в данном случае кодер 115 учитывает, какие промежуточные символы назначены «постоянно инактивированными» и обращается с этими промежуточным символами не так, как с промежуточными символами, не являющимися постоянно инактивированными во время процесса динамического кодирования. Аналогичным образом, декодер 155 при декодировании учитывает постоянно инактивированные промежуточные символы.
Как показано на фиг. 1, в кодер 115 вводятся K исходных символов (C(0),..., C(K-1)), и, если декодирование символов, ставших доступными декодеру 155, оказалось успешным, то декодер 115 может осуществить вывод копии этих K исходных символов. В некоторых вариантах осуществления поток разбивается на блоки из K символов, а в некоторых вариантах осуществления файл из некоторого количества символов, превышающее K, делится на символьные блоки размером K и передается в таком виде. В некоторых вариантах осуществления, где предпочтительно, чтобы размер блока K′>K, к K исходным символам могут быть добавлены K′-K дополняющих символов. Эти дополняющие символы могут иметь значение 0 или любое другое фиксированное значение, известное как кодеру 115, так и декодеру 155 (или, в противном случае, может быть определено в декодере 155). Следует понимать, что кодер 115 может содержать множество кодеров, модулей или т.п., и что это же относится к декодеру 155.
Как показано на фиг. 1, кодер 115 также принимает последовательность динамических ключей от генератора 120 динамических ключей и последовательность статических ключей от генератора 130 статических ключей, каждый из которых может возбуждаться генератором 135 случайных чисел. Выход генератора 120 динамических ключей может представлять собой просто кардинальную числовую последовательность, но это не является обязательным. Функционирование этих генераторов ключей может быть таким, как показано в Shokrollahi I.
Следует понимать, что различные функциональные блоки, показанные на приведенных фигурах, могут быть реализованы в виде аппаратных средств со специальными входами, обеспеченными в виде входных сигналов, либо они могут быть реализованы процессором, выполняющим команды, которые хранятся в памяти команд и выполняются в необходимом порядке для реализации соответствующей функции. В некоторых случаях специализированные аппаратные средства используют для выполнения указанных функций и/или исполнения программного кода. Программный код и процессор не всегда показаны, но специалисты в данной области техники, ознакомившись с этим описанием, поймут, как реализовать указанные детали.
Кодер 115 также принимает входные сигналы от блока 125 назначения инактивации и другие параметры, введенные в систему 100 по линиям, описанным здесь в разных местах. Выходы блока 125 назначения инактивации могут включать в себя значение P, представляющее количество промежуточных символов, назначенных в качестве «постоянно инактивированных» в целях декодирования («список PI» указывает, какое количество P промежуточных символов входит в этот список). Как здесь поясняется, промежуточные символы, используемые для процессов кодирования - это K исходных символов в некоторых вариантах осуществления, но в других вариантах осуществления имеет место тип обработки, преобразования, кодирования, декодирования и т.д., который обеспечивает создание промежуточных символов из K исходных символов сразу после их копирования.
Входные параметры могут включать в себя: случайные начальные числа, используемые генераторами ключей и/или в процессах кодирования, выполняемых кодером (более подробно описаны ниже); количество создаваемых кодированных символов; количество создаваемых символов LDPC; количество создаваемых символов HDPC; количество создаваемых промежуточных символов; количество создаваемых избыточных символов и т.д. и/или некоторые из этих значений вычисляют исходя из других значений, доступных кодеру 115. Например, количество создаваемых символов LDPC можно полностью вычислить по фиксированной формуле, зная значение K.
Кодер 115, используя входные сигналы, создает последовательность кодированных символов (B(I0), B(I1), B(I2),) и подает их в передающий модуль 140, который также получает значения (I0, I1, I2,) динамических ключей от генератора 120 динамических ключей, но возможно это окажется не обязательным, если имеется другой способ пересылки указанной информации. Передающий модуль 140 пересылает данные о том, что задано каналу 145, возможно традиционным образом, который нет необходимости более подробно здесь описывать. Приемный модуль 150 принимает кодированные символы и значения динамических ключей (когда это необходимо). Канал 145 может представлять пространственный канал (для передачи из одного места в другое место, где выполняется прием), либо временной канал (для записи на носитель, например, с целью воспроизведения в более позднее время). В канале 145 могут произойти потери некоторых кодированных символов. Следовательно, кодированные символы B(Ia), B(Ib), которые декодер 115 получает от приемного модуля 150, могут не совпасть с кодированными символами, которые послали передающие модули. Это указывается разными нижними индексами.
Предпочтительно, чтобы декодер 155 мог восстановить ключи, используемые для принятых символов (которые могут отличаться друг от друга) с использованием восстановителя 160 динамических ключей, генератора 163 случайных чисел и генератора 165 статических ключей и принимать в качестве входных данных различные параметры декодирования. Некоторые из этих входных данных могут быть жестко закодированными (то есть, введены во время изготовления устройства), а другие могут представлять собой изменяемые входные данные.
На фиг. 2 представлена таблица переменных, массивов и т.д. с кратким описанием обозначений, чаще всего используемых в других фигурах и во всем этом описании. Если не указано иное, то K обозначает количество исходных символов для кодера, R обозначает количество избыточных символов, создаваемых статическим кодером, а L представляет количество «промежуточных символов», то есть, комбинацию исходных и избыточных символов, причем L=K+R.
Как поясняется ниже, в некоторых вариантах осуществления статического кодера создается два типа избыточных символов. В одном конкретном варианте осуществления, используемом здесь во многих примерах, первый набор содержит символы LDPC, а второй набор содержит символы HDPC. Без потери общности, во многих приведенных здесь примерах S представляет количество символов LDPC, а H - количество символов HDPC. Возможно наличие более двух типов избыточных символов, так как не требуется, чтобы R=S+H. Символы LDPC и символы HDPC имеют разные распределения степени, и специалисты в данной области техники, ознакомившись с этим описанием, без труда поймут, каким образом использовать избыточные символы, не являющиеся символами LDPC или HDPC, но, где избыточные символы содержат два (или более) набора символов, где каждый набор имеет распределение степени, отличное от распределений степени других наборов. Как известно, распределение степени набора избыточных символов относится к распределению степени, где степень избыточного символа относится к количеству исходных символов, от которых зависит избыточный символ.
P обозначает количество постоянно инактивных (неактивных) символов среди промежуточных символов. Постоянно инактивные символы - это те символы, которые назначены для конкретной обработки, а именно, должны быть «установлены отдельно» или «инактивированы» в сети с распространением надежности, чтобы обеспечить продолжение распространение надежности (а затем возвратиться к решению после нахождения инактивированных символов), где постоянно инактивированные символы отличаются от других инактивированных символов тем, что постоянно инактивированные символы предназначены в кодере для указанной обработки.
N обозначает количество принятых символов, которые декодер 155 пытается декодировать, а А - это количество символов, относящихся к «служебным данным», то есть, количество принятых кодированных символов сверх K. Следовательно, A=N-K.
K, R, S, H, P, N и A являются целыми числами, как правило, большими или равными единице, но в конкретных вариантах осуществления некоторые из них могут быть равны единице или нулю (например, R=0 в том случае, когда нет избыточных символов, а P=0 относится к случаю, описанному в Shokrollahi II, когда имеется только инактивация OTF).
Вектор исходных символов обозначен как (C(0),..., C(K-1)), а вектор избыточных символов обозначен как (C(K),..., C(L-1)). Следовательно, (C(0),..., C(L-1)) обозначает вектор промежуточных символов в систематическом случае. Промежуточные символы в количестве P назначены в качестве «постоянно инактивных». «Список PI» указывает, какие из промежуточных символов являются постоянно инактивными. Во многих вариантах осуществления список PI просто указывает на P последних промежуточных символов, то есть, C(L-P),..., C(L-1), но это не обязательно. Этот случай рассмотрен лишь для упрощения остальных частей данного описания.
Промежуточные символы, которые не входят в список PI, называются здесь «промежуточными символами LT». В данном примере промежуточными символами LT будут C(0),..., C(L-P-1). D(0),..., D(N-1) обозначают принятые кодированные символы.
Следует заметить, что при описании массива значений в виде "N(0),..., N(x)" или т.п., не следует полагать, что для этого потребуется, по меньшей мере, три значения, так как предполагается включение сюда случая, когда имеется только одно или два значения.
Способ кодирования с использованием постоянной инактивации
На фиг. 3 представлена блок-схема одного конкретного варианта осуществления кодера 115, показанного на фиг. 1. Исходные символы, как здесь показано, хранят во входном буфере 205 и подают в статический кодер 210 и динамический кодер 220, которые также принимают входные сигналы ключей и другие входные сигналы. Статический кодер 210 может включать в себя внутреннее хранилище 215 (память, буфер, виртуальная память, запоминающее устройство на регистрах и т.д.) для хранения внутренних значений и программных команд. Аналогичным образом динамический кодер 220 может включать в себя внутреннее хранилище 225 (память, буфер, виртуальная память, запоминающее устройство на регистрах и т.д.) для хранения внутренних значений и программных команд.
В некоторых вариантах осуществления вычислитель 230 избыточности определяет количество R избыточных символов, которые надо создать. В некоторых вариантах осуществления статический кодер 210 создает два отличающихся набора избыточных символов в одном конкретном варианте осуществления, причем первый набор представляет первые S избыточных символов, то есть, символы C(K),..., C(K+S-1), причем они являются символами LDPC, в то время как второй набор представляет собой следующие H избыточных символов, то есть, C(L-H),..., C(L-1), при этом они являются символами HDPC. Если список PI содержит P последних избыточных символов, то тогда в списке PI могут быть все H избыточных символов (если P≥H), либо все P избыточных символов могут быть символами HDPC (если P<H).
Операции, приводящие к созданию этих двух наборов символов, могут несколько отличаться друг от друга. Например, в некоторых описанных ниже вариантах осуществления операции для создания избыточных символов LDPC являются двоичным операциями, а операции для создания символов HDPC не являются двоичными.
Далее со ссылками на фиг. 4 объясняется функционирование динамического кодера 220. Согласно одному варианту осуществления динамический кодер 220 содержит два кодера: кодер PI 240 и кодер LT 250. В некоторых вариантах осуществления кодер LT 250 является кодером с цепной реакцией, а кодер PI 240 является кодером с цепной реакцией конкретного типа. В других вариантах осуществления эти два кодера могут быть весьма схожими, либо кодер PI 240 не является кодером с цепной реакцией. Независимо от того, как определены эти кодеры, они создают символы, причем кодер LT 250 создает символы из промежуточных символов LT C(0),..., C(L-P-1), которые назначены в качестве не постоянно инактивных, в то время как кодер PI 240 создает символы из постоянно инактивных промежуточных символов C(L-P),..., C(L-1). Эти два созданных символа поступают на вход объединителя 260, который создает финальный кодированный символ 270.
В некоторых вариантах осуществления настоящего изобретения некоторые из постоянно инактивированных символов могут участвовать в процессе кодирования LT, а некоторые символы, которые не являются постоянно инактивированными символами, могут участвовать в процессе кодирования PI. Другими словами, список PI и набор символов, содержащих промежуточные символы LT, не обязательно будет разъединены.
В предпочтительных вариантах осуществления символы, подаваемые на объединитель 260, могут иметь одинаковую длину, а функция, выполняемая объединителем 260, представляет собой логическую операцию «исключающее ИЛИ» с этими символами для создания кодированного символа 270. Однако это не является обязательным для работы данного изобретения. Могут быть представлены сумматоры других типов, способные привести к аналогичным результатам.
В других вариантах осуществления промежуточные символы разделяют на более чем два набора, например, один набор символов LT и несколько (более одного) наборов символов PI, каждый с его связанным кодером 240. Конечно, каждый связанный кодер можно реализовать в виде общего вычислительного элемента или аппаратного элемента, который работает по различным командам согласно процессу кодирования, действуя всякий раз как разный кодер для разных наборов.
Пример реализации процесса 241 кодирования PI, который может выполняться кодером PI 240, показан на фиг. 5. Используя ключ I_a, соответствующий кодированному символу, подлежащему созданию, кодер на шаге 261 определяет положительный вес WP и список ALP, содержащий целые WP в диапазоне между L-P и L-1 включительно. На шаге 263, если список ALP=(t(0),..., t(WP-l)), то тогда значение символа Х устанавливается как X=C(t(O)) ⊕ C(t(l)) ⊕ ... ⊕ C(t(WP-l)), где ⊕ обозначает операцию «исключающее ИЛИ».
В некоторых вариантах осуществления вес WP имеет некоторое фиксированное значение, например, 3, 4 или какое-либо иное фиксированное число. В других вариантах осуществления вес WP может принадлежать небольшому набору указанных возможных чисел, например, вес WP выбирают равным 2 или 3. Как показано в качестве примера в варианте осуществления Приложения А, вес WP зависит от веса символа, созданного в процессе 251 кодирования LT, поскольку он может выполняться кодером LT 250. Если вес, созданный кодером LT 250 равен 2, то значение WP выбирают из двух значений (2 или 3) в зависимости от ключа I_a, где доли времени, когда WP равен 2 или 3, приблизительно одинаковы; если вес, созданный кодером LT 250, больше 3, то тогда WP выбирают равным 2.
На фиг. 6 показан пример процесса 251 кодирования LT согласно одному из вариантов осуществления настоящего изобретения с использованием основных принципов, раскрытых в Luby I и Shokrollahi I. На шаге 267 используют ключ I_a для создания веса WL и списка AL соответственно. На шаге 269, если список ALP=(j(0),..., j(WL-1), то тогда значение символа X устанавливают как X=C(j(0)) ⊕ C(j(1)) ⊕ ... ⊕ C(j(WL-1)).
На фиг. 7 показана операция вычисления веса WL. Как здесь показано, на шаге 272 создают число v, которое связано с кодированным символом, подлежащим созданию, и которое можно вычислить на основе ключа I_a для этого кодированного символа. Это может быть индекс, представительная метка и т.д. кодированного символа или отличное число, до тех пор, пока кодеры и декодеры могут быть согласованными. В данном примере v находится в диапазоне от 0 до 220, но в других примерах возможны другие диапазоны (например, от 0 до 232). Операция создания v может выполняться в явном виде с использованием рандомизированных таблиц, но точный процесс создания этих случайных чисел может изменяться.
Предположим, что кодер имеет доступ к таблице М, пример которой приведен на фиг. 8. Таблица М, называемая таблицей «поиска распределения степени», содержит два столбца и множество строк. В левом столбце представлены возможные значения веса WL, а в правом столбце - целые числа от 0 до 220 включительно. Для любого значения v имеется только одна клетка в столбце M[d] таблицы поиска распределения степени, где выполняется неравенство M[d-1]<v≤M[d]. Для этой одной клетки имеется соответствующее значение в столбце d, и кодер использует его в качестве веса WL для кодированного символа. Например, когда кодированный символ имеет значение v=900,000, вес для этого кодированного символа составит WL=7.
Статический кодер 210 имеет доступ к элементам SE(k,j), где k=0, R-1, а j=0, L-1. Эти элементы могут принадлежать любому конечному полю, для которого имеется операция * между элементами α поля и символами X, такая, что α*X есть символ, а α*(X⊕Y)=α*X ⊕ α*Y, где ⊕ обозначает операцию «исключающее ИЛИ». Указанные поля и операции подробно раскрыты в Shokrollahi IV. Операция статического кодера 210 может быть описана в виде вычисления для данной последовательности исходных символов C(0),..., C(K-1) последовательности избыточных символов C(K),..., C(L-1), удовлетворяющих соотношению, показанному в уравнении 1, где Z(O),..., Z(R-1)- значения, известные кодеру и декодеру (например, 0).

В уравнении 1 все элементы SE(k,j) могут быть двоичными, либо некоторые из них могут принадлежать полю GF(2), в то время как другие могут принадлежать другим полям. В качестве примера на фиг. 9 дана соответствующая матрица для варианта осуществления в Приложении А. Она содержит две субматрицы: одну с S строками и одну с H строками. Верхняя субматрица содержит две части: субматрицу, содержащую P последних столбцов, где каждая строка имеет две последовательных единицы (где позиции рассчитываются по модулю P). Первые W=L-P столбцов этой матрицы содержат циркулянтные матрицы, за которыми следует матрица тождественности S×S. Циркулянтные матрицы содержат B столбцов, причем каждая (возможно кроме последней) имеет S строк. Количество этих циркулянтных матриц равно ceil(B/S), где операция ceil - операция деления с округлению в большую сторону. Каждый столбец в этих циркулянтных матрицах имеет ровно 3 единицы. Первый столбец k-й циркулянтной матрицы имеет единицы на позициях 0, (k+1) mod (остаток от целочисленного деления) S и (2k+l) mod S. Другие столбцы представляют собой циклические сдвиги первого столбца. Нижележащие H строк на фиг. 9 содержат матрицу Q с элементами в GF(256), за которыми следует матрица тождественности H×H.
Если α обозначает элемент из GF(256) с минимальными полиномом x8+x4+x3+x2+l, то тогда матрица Q равна матрице, заданной на фиг. 10. Здесь Δl,,..., ΔK+S-1 являются столбцами с весом 2, для которых позиции 2 ненулевых элементов определяются псевдослучайным образом согласно процедуре, изложенной в разделе 5.3.3.3 Приложения А. Для обоснованных выборов значений S, P и H (например, единиц, предложенных в Приложении А) матрица на фиг. 10 обеспечивает отличные восстановительные свойства соответствующего кода. Вышеописанная процедура представлена в виде примера на фиг. 11. На шаге 276 выполняется инициализация матрицы SE в 0. На шаге 278 процесс обеспечивается входной переменной S, равной количеству символов LDPC, а значения SE(i,j) устанавливают равными 1 для пар (i,j), так, что i=j mod S, или i=(l+floor(j/S))+j mod S,, где floor - операция деления с округлением в меньшую сторону, или i=2*(l+floor(j/S))+j mod S. Этот шаг отвечает за циркулянтные матрицы на фиг. 9.
На шаге 280 позиции, соответствующие матрице IS тождественности на фиг. 9 устанавливают равными единице. На шаге 282 позиции, соответствующие части PI матрицы на фиг. 9 устанавливают равными 1. Эти позиции имеют вид (i,l) и (i,t), где 1=i mod P, а t=(i+l) mod P. На шаге 284 устанавливают позиции, соответствующие матрице Q на фиг. 9. Соответственно, матрица Q обеспечена в качестве дополнительных входных данных для этого шага. На шаге 286 позиции, соответствующие матрице IH тождественности в матрице по фиг. 9, устанавливают в единицу.
Возможны другие значения для матрицы SE, что зависит от конкретного приложения и требований, диктуемых кодом в целом. Независимо от того, как выбрана матрица в уравнении 1, задача статического кодера 210 может быть выполнена множеством различных путей. Например, в качестве процесса для восстановления неизвестных значений C(K),..., C(L-1) можно использовать гауссово исключение, как станет очевидным специалистам в данной области техники после ознакомления с этим описанием.
ДЕКОДИРОВАНИЕ И ПОСТОЯННАЯ ИНАКТИВАЦИЯ
Проблему декодирования можно сформулировать следующим образом: декодер 155 имеет N кодированных символов B(Ia), B(Ib),..., с соответствующими ключами Ia, Ib. Полный набор этих кодированных символов или его поднабор может быть получен декодером, в то время как другие кодированные символы могут быть предоставлены декодеру другими способами. Целью декодера является восстановление исходных символов C(0),..., C(K-1). Для упрощения представления обозначим принятые кодированные символы как D(0),..., D(N-1).
Множество операций декодирования можно вкратце описать, используя язык матриц и операций над указанными матрицами, в частности, в терминах решения систем уравнений с помощью указанных матриц. В последующем описании уравнения могут соответствовать принятым кодированным символам, а переменные могут соответствовать исходным символам или комбинированному набору исходных и избыточных символов, созданных из исходных символов, которые часто называют промежуточными символами, причем они должны вычисляться на основе принятых кодированных символов. В описании, обеспеченном в виде Приложения А, кодированные символы могут называться «кодирующими символами» (причем имеются и другие варианты), но специалистам в данной области техники после ознакомления с полным описанием и Приложением А станет понятно, к чему относятся указанные термины. Также следует понимать, что матрицы, операции и решения уравнений могут быть реализованы в виде компьютерных команд, соответствующих математическим операциям, и на самом деле нецелесообразно выполнять указанные операции без компьютера, процессора, аппаратных средств или какого-либо электронного элемента.
Постоянную инактивацию используют для определения в декодере набора переменных для инактивации, которые называются постоянно инактивированными символами или переменными до инициирования первой фазы процесса декодирования. Описанные ниже способы декодирования с постоянной инактивацией можно применить либо к существующим кодам, либо можно разработать специальные коды для более эффективного функционирования в сочетании с декодированием с постоянной инактивацией. Способы декодирования с постоянной инактивацией можно применить для решения любой системы линейных уравнений и, в частности, можно применить к кодам с цепной реакцией, кодам IETF LDPC и кодам Торнадо.
Декодирование с постоянной инактивацией является общим способом, который можно применять в сочетании с декодированием с распространением надежности и/или декодированием с инактивацией OTF при вычислении набора неизвестных переменных исходя из набора известных значений линейных уравнений, и, в частности, это выгодно при реализации эффективных способов кодирования и декодирования, основанных на системах линейных уравнений. На первой фазе на основе структуры известного способа кодирования или на основе принятых уравнений декларируется набор неизвестных переменных, подлежащих постоянной инактивации, и эти постоянно инактивированные переменные удаляют из линейных уравнений и рассматривают их как «найденные» на второй фазе процесса декодирования (за исключением того, что при сокращении линейных уравнений на второй фазе аналогичные сокращения выполняются по постоянно инактивированным переменным).
На второй фазе к неизвестным переменным, не являющимся постоянно инактивированными, применяется либо декодирование с распространением надежности с использованием вышеописанного способа декодирования с распространением надежности, либо к неизвестным переменным, не являющимся постоянно инактивированными, применяется декодирование с инактивацией OTF по аналогии с тем, как это было описано для первой фазы способа декодирования с инактивацией OTF, что обеспечивает создание набора сокращенных кодированных символов или уравнений. Сокращенные кодированные символы или уравнения, полученные в результате второй фазы, обладают свойством, состоящим в том, что исключена их зависимость от не активированных переменных или символов, и таким образом, сокращенные кодированные символы или уравнения зависят только от инактивированных переменных или символов. Заметим, что также можно сохранить первоначальные кодированные символы или уравнения, так что в некоторых реализациях могут быть доступны как первоначальные кодированные символы, так и сокращенные кодированные символы.
На третьей фазе находят постоянно инактивированные переменные вместе с дополнительными инактивированными на ходу переменными, созданными на второй фазе, с использованием декодирования с инактивацией OTF для использования сокращенных кодированных символов или уравнений, например, с использованием гауссова исключения, или для решения, более эффективного, чем гауссово исключение, используют специальную структуру соотношений (если она существует) между постоянно инактивированными переменными и указанными линейными уравнениями.
На четвертой фазе значения найденных инактивированных переменных, либо инактивированных на ходу переменных, либо постоянно инактивированных переменных, используют в сочетании с первоначальными кодированными символами или уравнениями (повторно полученные первоначальные кодированные символы или уравнения) для нахождения переменных, которые не были инактивированы.
Одним из преимуществ способов декодирования с постоянной инактивацией состоит в том, что количество w инактиваций OTF, отличных от постоянных инактиваций, может в общем случае быть невелико или равно нулю и может сильно зависеть от того, какие кодированные символы были приняты. Это дает возможность обеспечить слабую зависимость сложности декодирования от того, какие кодированные символы были приняты, обеспечить более надежное декодирование и иметь более предсказуемые доступы, требующие меньше памяти, которые можно более эффективно планировать. Поскольку на второй фазе имеется лишь небольшое количество инактиваций OTF и поскольку инактивации OTF на второй фазе обычно определяют только во время процесса декодирования, что может сделать шаблон операций с символами в некотором отношении непредсказуемым, шаблоны доступа к памяти во время декодирования являются более предсказуемыми, что позволяет в целом обеспечить более предсказуемые и эффективные процессы декодирования.
Имеется множество вариантов вышеизложенного. Например, упомянутые фазы могут выполняться не в указанной последовательности, перемежаясь друг с другом. В другом примере инактивированные символы, в свою очередь, могут быть найдены на третьей фазе с использованием либо декодирования с инактивацией OTF, либо декодирования с постоянной инактивацией на множестве дополнительных фаз. Еще в одном примере декодирование с постоянной инактивацией можно применить к системе линейных уравнений и переменных, которые можно использовать для кодов с исправлением ошибок или кодов с восстановлением уничтоженных данных, либо для других приложений, в которых возможно решение с использованием систем линейных уравнений. В другом примере эти способы можно применить как к систематическим кодам, так и к несистематическим кодам. Еще в одном примере эти способы можно также применить в ходе процесса кодирования, например, при кодировании с использование способов, раскрытых в Shokrollahi III, для создания систематических кодов из несистематических кодов.
В некоторых случаях можно разработать процесс кодирования, при котором способы декодирования с постоянной инактивацией будут особенно эффективны. Например, известно что декодирование с распространением надежности выгодно с точки зрения эффективности вычислений, если только его можно применить, но также, известно, что оно не может обеспечить высоконадежное декодирование само по себе. При использовании декодирования с распространением надежности в рамках декодирования с инактивацией OTF обработка шагов распространения надежности может быть весьма эффективной, но шаги инактивации OTF, выполняемые внутри шагов распространения надежности, могут замедлить процесс декодирования, и чем больше указанных шагов инактивации OTF, тем медленнее будет процесс декодирования.
В типовых вариантах осуществления декодирования с инактивацией OTF при попытке нахождения K+R неизвестных переменных с использованием N+R значений линейных уравнений количество шагов инактивации OTF, как правило, очень велико при N=K, то есть, при попытке нахождения переменных, используя нулевой объем служебных данных. С другой стороны, когда N превышает K, как правило, сложность декодирования с инактивацией OTF уменьшается из-за уменьшения шагов инактивации OTF, когда N достаточно велик, так что в некоторых случаях шаги инактивации OTF отсутствуют, и декодирование с инактивацией также эффективно или почти также эффективно в отношении вычислений как декодирование с распространением надежности. В других вариантах осуществления декодирования с инактивацией OTF количествоинактиваций OTF может оставаться большим даже в том случае, когда N значительно больше K.
В одном предпочтительном варианте осуществления декодирования с постоянной инактивацией количество P постоянно инактивированных переменных и структуру линейных уравнений формируют так, что при нахождении L-P переменных, не являющихся постоянно инактивированными, с использованием декодирования с инактивацией OTF исходя из K+R значений линейных уравнений, количество шагов инактивации OTF во время декодирования с инактивацией OTF мало, а в некоторых случаях равно нулю, и, следовательно, шаг декодирования с инактивацией OTF почти также эффективен в отношении вычислений как распространение надежности.
В предпочтительных вариантах осуществления структура линейных уравнений разрабатывают так, чтобы фаза декодирования с инактивацией OTF была по эффективности близкой к декодированию с распространением надежности. В указанных предпочтительных вариантах осуществления соотношения между постоянно инактивированным переменными и линейными уравнениями таковы, что фаза нахождения инактивированных переменных, состоящих из постоянно инактивированных переменных вместе с инактивированными OTF переменными из фазы декодирования с инактивацией OTF, может выполняться эффективным образом. Кроме того, в предпочтительных вариантах осуществления структура постоянно инактивированных символов такова, что фаза завершения нахождения не инактивированных переменных из найденных инактивированных переменных является вычислительно эффективной.
ДЕКОДИРОВАНИЕ КОДОВ С ЦЕПНОЙ РЕАКЦИЕЙ И ПОСТОЯННОЙ ИНАКТИВАЦИЕЙ
Фиг. 12 иллюстрирует матричное представление набора переменных, которые необходимо найти, декодером с использованием N принятых кодированных символов или уравнений и R известных статических символов или уравнений. Задача декодера состоит в решении системы линейных уравнений, заданных на этой фигуре. Как правило, символы/уравнения представлены значениями, хранящимися в памяти или запоминающем устройстве, доступном декодеру, а матричные операции, описанные ниже, реализуются с помощью команд, исполняемых декодером.
Матрица, показанная на фиг. 12, содержит L=K+R столбцов и N+R строк. Субматрица LT представляет соотношения между N кодированными символами и L-P символами из L промежуточных символов, определенных в процессе кодирования LT 251. Субматрица PI представляет соотношения между N кодированными символами и P символами из L промежуточных символов, определенных в процессе 241 кодирования PI. Матрица SE в уравнении 1 представляет соотношения между промежуточными символами, определенными статическим кодером 210. Декодер может определить эти соотношения на основе ключей для принятых кодовых символов и из структуры кода.
Система линейных уравнений по фиг. 12 решается путем перестановок строк/столбцов вышеописанной матрицы с использованием инактивации OTF, изложенной в Shokrollahi II, для преобразования их в форму, показанную на фиг. 13. Она содержит треугольную матрицу LO 310 более низкого порядка, причем количество столбцов, образующих матрицу 320 (называемую OTFI), соответствует инактивациям OTF, матрица 330 PI соответствует набору постоянно инактивных промежуточных символов или их поднабору, а матрица EL 340 соответствует кодированным или статическим символам, не используемым в процессе триангуляции, приводящем к матрице LO.
На фиг. 14 представлена блок-схема, описывающая элементы, которые могут выполнить процесс, приводящий к созданию матрицы на фиг. 12. Блок-схема содержит генератор 347 матрицы LT, генератор 349 матрицы PI и генератор 350 статической матрицы. После приема ключей Ia, Ib,..., генератор матрицы LT создает матрицу LT по фиг. 12, в то время как генератор 349 матрицы PI создает матицу PI по фиг. 12. Конкатенация этих двух матриц поступает в генератор 350 статической матрицы, который может в качестве дополнительных полезных данных принять статические ключи S_0, S_l.... Задача генератора статической матрицы заключается в создании матрицы SE, а его выход представляет собой полную матрицу, заданную на фиг. 12.
Операции генератора 347 матрицы LT и генератора 349 матрицы PI тесно связаны с операциями кодера LT 250 и кодера PI 240 на фиг. 15 соответственно. Операция генератора 350 статической матрицы представляет собой повторное создание матрицы SE из уравнения 1, используемой для статического кодирования.
Далее со ссылками на операции, которые они могут выполнить, подробно описывается генератор 347 матрицы LT, генератор 349 матрицы PI и генератор статической матрицы.
На фиг. 16 представлена блок-схема, иллюстрирующая один вариант 500 осуществления способа, используемого генератором 347 матрицы LT. На шаге 505 генератор 347 матрицы LT инициализирует матрицу LT формата N×(L-P), устанавливая все нули. Затем на шаге 510 используют ключи Ia, Ib...., для создания весов WL(0),..., WL(N-1) и списков AL(0),..., AL(N-1) соответственно. Каждый из этих списков AL(i) содержит WL(i) целых чисел (j(0),..., j(WL(i)-l)) в диапазоне 0, L-P-1. На шаге 515 эти целые числа используют для установки в 1 элементов LT(i,j(0)),..., LT(i,j(WL(i)-l)). Как было объяснено выше, матрица LT вносит вклад в систему уравнений для неизвестных (C(0),..., C(L-1)) в через принятые символы (D(0),..., D(N-1)).
Как очевидно специалистам в данной области техники, описанная здесь операция, выполняемая генератором матрицы LT, аналогична операции, выполняемой в процессе 251 кодирования LT по фиг. 6.
На фиг. 17 представлена блок-схема, иллюстрирующая один вариант 600 осуществления способа, используемого генератором 349 матрицы PI. На шаге 610 генератор 349 матрицы PI инициализирует матрицу PI формата N×P, устанавливая все нули. Далее на шаге 615 используют ключи Ia, Ib..., для создания весов WP(0),..., WP(N-1) и списков ALP(0),..., ALP(N-1) соответственно. Каждый из списков ALP(i) содержит WP(i) целых чисел (j(0),..., j(WP(i)-l)) в диапазоне 0, P-1. На шаге 620 эти целые числа используют для установки в 1 элементов PI(i,j(0)),..., PI(i,j(WP(i)-1)). Операция, выполняемая генератором матрицы PI, аналогична операции, выполняемой в процессе 241 кодирования PI на фиг. 5.
Как было объяснено выше, матрицы LT и PI вносят вклад в систему уравнений с неизвестными (C(0),..., C(L-1)) через принятые символы (D(0),..., D(N-1)). Причина этого заключается в следующем: как только кодер LT выберет вес WL(i) и связанный список AL(i)=(j(0),..., j(WL(i)-l)), а кодер PI выберет вес WP(i) и связанный список ALP(i)=(t(0),..., t(WP(i)-l)), получают соответствующий кодированный символ D(i), как показано ниже. Эти уравнения, аккумулированные для всех значений i между 0 и N-1, приводят к требуемой системе уравнений, представленных в уравнении 2.
D(i)=C(j(0)) ⊕ ... ⊕C(j(WL(i)-l)) ⊕ C(t(0))⊕ ... ⊕ C(t(WP(i)-l)) (Уравнение 2)
Веса WL можно вычислить, используя процедуру, аналогичную процедуре, заданной на фиг. 7. Ознакомившись с этим описанием, специалисты в данной области техники поймут, каким образом можно расширить этот подход на случай, когда имеется более двух кодеров, каждый из которых работает с разным распределением степени.
На фиг. 18 представлена несколько другая блок-схема матричного генератора. Она содержит генератор 710 матрицы LT, генератор 715 статической матрицы и генератор 720 матрицы PI. После приема ключей Ia, Ib,..., генератор 710 матрицы LT создает матрицу LT, показанную на фиг. 15, в то время как генератор 715 статической матрицы создает матрицу SE, показанную на фиг. 15, и может принять дополнительные статические ключи S_0, S_l,..., в качестве дополнительных входных данных. Конкатенация этих двух матриц подается в генератор 720 матрицы PI, который создает матрицу PI. Операция, выполняемая генератором 710 матрицы LT, может точно совпадать с операцией, выполняемой генератором 347 матрицы LT, подробно показанным на фиг. 16. Операция, выполняемая генератором 715 статической матрицы, может отличаться от операции, выполняемой генератором 350 статической матрицы на фиг. 14. В частности, на фиг. 19 детально представлен примерный вариант осуществления указанной операции.
На шаге 725 выполняется инициализация матрицы SE с установкой в 0. На шаге 730 процесс обработки обеспечивается входной переменной S, равной количеству символов LDPC, а значения SE(i,j) устанавливают в 1 для пар (i, j), когда i=j mod S, i=(l+floor(j/S))+j mod S, или i=2*(l+floor(j/S))+j mod S. На шаге 735 устанавливают в единицу позиции, соответствующие матрице IS тождественности на фиг. 9. На шаге 740 в качестве дополнительных входных данных для этого шага обеспечивают позиции, соответствующие матрице T. Эта матрица может иметь элементы на множестве конечных полей и может отличаться у разных приложений. Выбор может быть сделан на основе требований, предъявляемых кодом.
На фиг. 20 представлена упрощенная блок-схема, иллюстрирующая один вариант осуществления способа, используемого генератором 720 матрицы PI. На шаге 745 генератор 349 матрицы PI инициализирует матрицу PI формата (N+R)×P, устанавливая все нули. Далее на шаге 750 используют ключи I_a, I_b,..., для создания весов WP(0),..., WP(N-1) и списков ALP(0),..., ALP(N-1) соответственно. Каждый из этих списков ALP(i) содержит WP(i) целых чисел (J(0),..., j(WP(i)-l)) в диапазоне 0, P-1. На шаге 755 эти целые числа используют для установки в 1 элементов PI(i,j(0)),..., PI(i,j(WP(i)-l)). Операция, выполняемая генератором матрицы PI на фиг. 20 аналогична операции, выполняемой генератором матрицы PI по фиг. 17, за исключением того, что этот матричный генератор создает матрицу с большим на R числом строк, которая тесно связана с матрицей на фиг. 15.
Система уравнений на фиг. 12 или фиг. 15, как правило, является разреженной, то есть, количество ненулевых элементов в матрицах, как правило, много меньше половины возможных элементов. В указанном случае эти матрицы не обязательно хранить непосредственно, а можно хранить индикацию, которая помогает повторно создать каждый отдельный элемент в этих матрицах. Например, для каждой строки в матрицах LT или PI в процессе обработки, возможно понадобится сохранить вес и список соседей, как это вычисляется на фиг. 5-6. Также возможны и другие способы, причем многие из них были здесь раскрыты либо их описание включено сюда по ссылке.
После того, как матричный генератор создал систему уравнений в виде, заданном на фиг. 12 или фиг. 15, задачей декодера будет решение этой системы для неизвестных значений C(0),..., C(L-1). Для достижения этой цели может быть использовано несколько различных способов, включая, но не только гауссово исключение или любой из способов, описанных в Luby I, Luby II, Shokrollahi I, II, III, IV, или V.
Возможный способ решения системы уравнений на фиг. 12 или фиг. 15 раскрывается со ссылками на фиг. 21-26. Блок-схема функционирования декодера согласно некоторым вариантам осуществления настоящего изобретения определена на фиг. 21. На шаге 1305 создают матрицу декодирования с использованием некоторых из описанных ранее способов. На шаге 1310 выполняется перекомпоновка этой матрицы с использованием перестановок строк и столбцов. Как было упомянуто выше, указанную матрицу можно получить из любой из матриц на фиг. 12 или фиг. 15 путем применения перестановок строк и столбцов. Для достижения этого можно использовать декодирование с цепной реакцией в сочетании с декодированием (Shokrollahi II) с инактивацией на ходу. Таким образом, имеет место перестановки pi, выполняемые на наборе {0, 1,..., L-1} и операции tau, выполняемые на наборе {0, 1,..., N+R-1}, так чтобы удовлетворялось уравнение на фиг. 22.
Здесь w обозначает количество строк и столбцов в матрице LO на фиг. 13, то есть, количество промежуточных символов, которые не являются ни постоянно инактивированными, ни инактивированными на ходу. На шаге 1315 матрицу LO по фиг. 13 используют для обнуления всех элементов матрицы LO, лежащих ниже диагонали. При выполнении этого для набора символов в правой части уравнения на фиг. 23 необходимы те же самые операции, с тем, чтобы получить новую правую часть системы уравнений с помощью операций «исключающее ИЛИ» над некоторыми из D(tau(i)).
Как показано на фиг. 24, после этой операции матрица 810 превращается в матрицу тождественности, матрица EL в области 840 останется неизменной, а матрицы OTFI и PI преобразуются в OTFI-2 в области 820 и PI-2 в области 830, поскольку для процесса декодирования необходима операция «исключающее ИЛИ» для строк этих матриц в соответствии с операциями, которые были необходимы для приведения матрицы LO к матрице тождественности.
Следующим шагом процесса декодирования может быть шаг 1320, на котором исключают остаток матрицы ниже LO для получения матрицы в форме, показанной на фиг. 25. Если обозначить переставленные и сокращенные значения первоначальных символов D(0),..., D(N R-1) после этого шага как E(0),..., E(N+R-1), обозначить количество строк в матрице EL_2 как u и обозначить как g количество столбцов в матрице EL_2, то структура матрицы на фиг. 25 приведет к меньшей системе из u линейных уравнений для значений C(pi(L-g)),..., C(pi(L-l)) согласно уравнению 3.
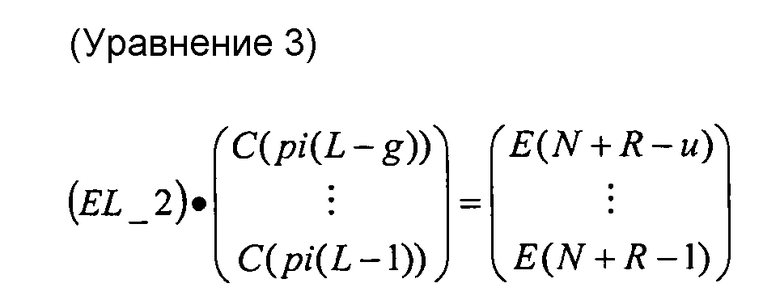
Процесс декодирования, например, процесс, описанный на фиг. 21, позволяет решить систему уравнений на шаге 1330 множеством различных способов, например, используя процесс гауссова исключения, комбинацию кодирования с цепной реакцией и гауссово исключения, либо с использованием другого приложения декодирования с инактивацией или другими средствами. Гауссово исключение можно модифицировать так, чтобы отделить вычисления в поле GF(2) от вычислений в более крупных полях, например, GF(256), если матрица EL имеет элементы, принадлежащие множеству полей, как было изложено в качесвте примера в Shokrollahi IV.
Если система уравнений в Уравнении 3 не может быть решена с использованием процессов, реализуемых декодером, то тогда декодер может на шаге 1335 предпринять соответствующие контрмеры. Указанные контрмеры могут включать в себя установку флага ошибки и прекращение процесса, либо могут включать в себя запрос дополнительных кодированных символов, либо возможна остановка процесса обработки и возврат к приложению с использованием списка промежуточных символов или исходных символов, которые декодер имел до сих пор для восстановления. Если систему уравнений можно решить, то тогда декодер может восстановить значения инактивированных промежуточных символов C(pi(L-g)),..., C(pi(L-l)). В некоторых вариантах также возможно восстановление на шаге 1330 некоторых других промежуточных символов кроме инактивированных промежуточных символов.
После восстановления значений этих символов декодер переходит к шагу 1340, который включает обратную замену. Восстановление значений C(pi(L-g)),..., C(pi(L-l)) приводит к системе уравнений того типа, который показан на фиг. 26. Эта система решается легче, чем обычная система. Например, для получения решения декодер может использовать процесс, показанный на фиг. 23. Процесс получения первого вектора в правой части по фиг. 23 можно назвать обратной заменой, так как он представляет собой процесс замены значений известных символов в указанной системе уравнений. Специалистам в данной области техники при ознакомлении с данным описанием станет очевидным, что системы, заданные на фиг. 23 и 26, являются математически эквивалентными.
На фиг. 23 декодер получает неизвестные значения C(pi(0)),..., C(pi(L-g-l)), реализуя процесс, в котором элементы в матрице с правой стороны умножаются на элементы, уже найденные для вектора C(pi(L-g)),..., C(pi(L-l)) с использованием правил матричного умножения, и выполняя операцию «исключающее ИЛИ» с E(0),..., E(L-g-l). Процесс выполнения операции «исключающее ИЛИ» полученных элементов с E(0),..., E(L-g-l) и восстановления, таким образом, значений C(pi(0)),..., C(pi(L-g-l)) содержит шаг 1345, выполняемый декодером на фиг. 21.
Будучи полезным в некоторых приложениях, этот способ может привести к большим вычислительным издержкам в некоторых предпочтительных вариантах осуществления, поскольку матрица в правой части на фиг. 23, как правило, не разрежена, и, следовательно, для получения одного из элементов C(pi(j)) должно выполняться количество операций «исключающее ИЛИ», пропорциональное величине g. В некоторых вариантах осуществления это количество может быть большим, например, поскольку было выбрано большое количество P постоянных инактиваций для начала процесса, и g, по меньшей мере, может быть таким же большим, как P. Это может наложить серьезные ограничения на значение P (количество постоянно инактивированных символов), а, если использовать меньшее значение P, то это можете привести к увеличению количества инактивированных на ходу промежуточных символов.
На фиг. 27 описан модифицированный процесс декодирования, который может быть более эффективным с точки зрения вычислений, чем процесс, описанный на фиг. 21. Шаги с 1405 по 1435 этого процесса могут совпадать с соответствующими шагами процесса на фиг. 14. Необязательно этот процесс может поддерживать копию первоначальной матрицы на фиг. 12 или фиг. 15, либо релевантные части этой матрицы, а также первоначальные символы D(0),..., D(N+R-1) в дополнительной ячейке памяти для использования их в будущем. Это не является обязательным для работы указанного процесса, но это может дать дополнительные преимущества в отношении скорости, если приложение имеет остаточные ресурсы памяти для поддержания упомянутых копий. В качестве альтернативы, данный процесс может поддерживать только копию первоначальных символов D(0),..., D(N+R-1), но не матрицу, и повторно создавать матрицу, когда это необходимо. На шаге 1440 либо используется сохраненная копия матрицы, либо процесс возвращается к шагу 1415 для получения первоначальной системы уравнений по фиг. 22 или только верхней части этой системы, заданной на фиг. 28. На этом этапе матрица 1510, заданная на фиг. 29, является разреженной, а значения C(pi(w)),..., C(pi(L-1)) являются известными, где w=L-g.
Как известно, правую часть уравнения на фиг. 29 можно вычислить, используя эффективный с точки зрения минимизации объема вычислений процесс, включающий в себя небольшое количество операций «исключающее ИЛИ» с символами, то есть, равное количеству ненулевых элементов в матрице OTFI плюс количество ненулевых элементов в матрице PI. Этот шаг процесса обозначен на фиг. 27 ссылочной позицией 1445. После завершения этого шага вычисляют правую сторону уравнения на фиг. 29, и необходимо решить систему уравнений, в которой неизвестными являются значения C(pi(0)),..., C(pi(w-l)). Система может быть решена на шаге 1450 с использованием декодирования с цепной реакцией, поскольку в правой части меньшая треугольная матрица LO является разреженной, то есть, количество операций «исключающее ИЛИ» над символами для решения этой системы уравнений равно количеству ненулевых элементов в матрице LO, причем это количество, как правило, намного меньше w*w, возможного максимального количества ненулевых элементов.
ВЫБОР КОЛИЧЕСТВА ПОСТОЯННЫХ ИНАКТИВАЦИЙ
Выбор количества постоянных инактиваций может повлиять на все рабочие характеристики, так что этот выбор может быть очень важен. С одной стороны, это количество необходимо выбрать как можно большим: если это количество велико, то можно будет сократить количество инактиваций OTF до минимума, а иногда даже до нуля. Причина этого заключается в том, что комбинация матриц LT и SE на фиг. 15 (или их соответствующие варианты на фиг. 23) представляет собой матрицу эффективного декодирования для кода с цепной реакцией и с большим объемом служебных данных. Это обстоятельство делает количество инактиваций OTF очень малым. В некоторых вариантах осуществления управлять инактивациями OTF может быть трудно, так как сокращение их количества может дать преимущество с точки зрения скорости и/или требуемой памяти.
С другой стороны, увеличение количества постоянных инактиваций может отрицательно сказаться на времени обработки: например, шаг 1330 в процессе декодирования по фиг. 21 и соответствующий шаг 1430 в процессе на фиг. 27 требуют решения системы уравнений, которая имеет, по меньшей мере, P строк и столбцов. Одним из путей решения является идентификация обратимой субматрицы матрицы EL-2 на фиг. 25, обращение этой матрицы и использование обращенной матрицы для получения значений промежуточных символов C(pi(L-g-l)),..., C(pi(L-l)). Поскольку матрица EL-2 во многих вариантах осуществления может оказаться не разреженной, для получения значений промежуточных символов может потребоваться порядка g×g операций «исключающее ИЛИ» с символами. Поскольку g, по меньшей мере, равно P, количество операций «исключающее ИЛИ» с символами может составить, по меньшей мере, P×P, так что, если необходимо поддерживать количество операций «исключающее ИЛИ» с символами линейным по K, хорошим выбором будет установка количества P пропорциональным корню квадратному из K. В конкретном варианте осуществления Приложения А величину P выбирают равной порядка 2,5*sqrt(K), и придерживаются этого выбора. Это хороший выбор для P, так как при таком подходе к выбору P количество инактиваций OTF, как правило, очень мало, и оно изменяется от значения, близкого к P, до очень близкого к нулю или равного нулю значения.
Другой величиной, представляющей интерес, является среднее количество I инактивированных промежуточных символов-соседей, имеющихся у кодированного символа или статического символа. Для выполнения шага 1445 процесса декодирования на фиг. 27 может потребоваться в среднем до I операций «исключающее ИЛИ» символов для не восстановленных промежуточных символов. Если I велико, то количество операций «исключающее ИЛИ» может оказаться слишком большим для памяти и вычислительных ресурсов процессов, реализующих декодирование или процесса кодирования. С другой стороны, если I слишком мало, то тогда матрица EL-2 на фиг. 25 возможно не будет иметь полный ранг, и декодируемость может оказаться под угрозой.
Более подробный анализ показывает, что важным аспектом постоянной инактивации является необходимость получения матрицы PI по фиг. 15 таким образом, чтобы ее столбцы были линейно независимы друг от друга, то есть, матрица была бы матрицей полного ранга, насколько этого возможно. Специалистам в данной области техники известно, что если PI является случайной двоичной матрицей, то может быть достигнут полный ранг в рамках возможных ограничений. С другой стороны, матрица PI может иметь в среднем в каждом столбце долю единиц, обратно пропорциональную квадратному корню из K, и гарантировать такие же ранговые свойства, как свойства чисто случайной матрицы. По этой причине в конкретном варианте осуществления Приложения А величину I выбирают равной 2 или 3, причем выбор P пропорционально квадратному корню из K означает, что количество единиц в каждом столбце матрицы PI в среднем обратно пропорционально квадратному корню из K.
Имеется много вариантов этих способов, с которыми специалисты в данной области техники смогут познакомиться, прочитав это описание. Например, операция «исключающее ИЛИ» может быть заменена другими операторами, например, линейными операторами над большими конечными полями, либо операторы могут представлять собой комбинацию различных операторов, например, некоторые линейные операторы над большими конечными полями для некоторых операций и другие линейные операторы над меньшими конечными полями для других операций.
КОНКРЕТНЫЙ ПРИМЕР СО ССЫЛКАМИ НА ПРИЛОЖЕНИЕ А
Как было подробно описано выше, без постоянных инактиваций (то есть, заранее определенных решений, в которых кодированные символы не являются частью матричного манипулирования, составляющего часть процесса определения последовательности для декодирования с цепной реакцией), количество инактиваций OTF может быть вполне случайной величиной, что порождает потенциальные проблемы с точки зрения расхода памяти. Когда количество исходных символов очень велико, и объем служебных данных очень мал, вероятность ошибки может оказаться неприемлемо близкой к 1.
Из-за высокой вероятности ошибки при небольшом объеме служебных данных ожидаются серьезные затруднения в поиске хорошей систематической информации, когда количество исходных символов велико. Здесь понятие систематической информации относится к информации, необходимой для кодера и декодера, чтобы иметь возможность построить систематический код в том смысле, о котором говорится в Shokrollahi III. Кроме того, при каждом получении систематической информации следует ожидать, что функциональные возможности кода будут очень далеки от его усредненных функциональных возможностей, поскольку «усредненный код» окажется неработоспособным при нулевом объеме служебных данных.
Некоторые из параметров, необходимых для построения кода с цепной реакцией и постоянной инактивацией, могут включать в себя распределение Ω, используемое для кодера LT 250 по фиг. 4, параметры для кодера PI 240, определение количества постоянно инактивированных символов, определение количества избыточных статических символов и их структуру, причем конкретные случайные числа могут генерироваться и совместно использоваться кодером 115 и декодером 155 на фиг. 1.
КОДЕРЫ И ДЕКОДЕРЫ, ИСПОЛЬЗУЮЩИЕ RQ КОД
Предпочтительный вариант осуществления кода, называемый далее «RQ код», который использует описанные здесь способы, подробно описан в разделе 5 Приложения А. В остальной части Приложения А описан один способ применения RQ кода для надежной доставки объектов по широковещательным сетям или сетям групповой передачи.
RQ код использует ранее описанные и ниже описанные способы для реализации систематического кода, что означает, что все исходные символы находятся среди кодированных символов, которые могут быть созданы, и поэтому кодированные символы можно рассматривать как комбинацию первоначальных исходных символов и символов для восстановления, созданных кодером.
Хотя некоторые из ранее описанных кодов обладают хорошими характеристиками, имеется ряд усовершенствований, которые могли бы расширить их практическое применение. Два важных потенциальных улучшения - это увеличение крутизны кривой «объем служебных данных - вероятность неудачи» и увеличение количества поддерживаемых исходных символов на один исходный блок. Объем служебных данных представляет собой разность между количеством принятых кодированных символов и количеством исходных символов в исходном блоке, например, объем служебных данных, равный 2, означает, что принято K+2 кодированных символов для декодирования исходного блока с K исходными символами. Вероятность неудачи при данном объеме служебных данных - это вероятность того, что декодер не в состоянии полностью восстановить ресурсный блок, когда количество принятых кодированных символов соответствует указанному объему служебных данных. Кривая «объем служебных данных - вероятность сбоя» представляет собой график, показывающий, как уменьшается вероятность неудачи при возрастании объема служебных данных, начиная с нулевого объема служебных данных. Кривая «объем служебных данных - вероятность неудачи» улучшается, если вероятность неудачи декодера быстро или круто спадает, как функция объема служебных данных.
Случайный двоичный код имеет кривую «объем служебных данных - вероятность неудачи», где вероятность неудачи уменьшается фактически вдвое с каждым дополнительным символом служебных данных, при неосуществимой вычислительной сложности, но предмет настоящего обсуждения ограничен кривой «объем служебных данных - вероятность неудачи», но не вычислительной сложностью. В некоторых приложениях достаточно иметь указанную кривую «объем служебных данных - вероятность неудачи», но для некоторых других приложений предпочтительно иметь более крутую кривую «объем служебных данных - вероятность неудачи». Например, в потоковом приложении диапазон значений количества исходных символов в исходном блоке может быть широк, например, K=40, K=200, K=1000, K=10000. Для обеспечения хорошего потокового представления, возможно, потребуется иметь низкие значения вероятности неудачи, например, 10-5 или 10-6. Поскольку ширина полосы пропускания часто является главной характеристикой для потоковых приложений, процент символов для восстановления, посылаемых как некоторая часть исходных символов, должен быть минимизирован. Предположим, например, что сеть, по которой посылается поток, должна быть защищена от потерь (не более 10% пакетных потерь) при использовании исходных блоков с K=200, и требуемой вероятности неудачи не более, чем 10-6. Для случайного двоичного кода требуется объем служебных данных, равный, по меньшей мере, 20, для достижения вероятности неудачи, равной 10-6, то есть, приемнику для декодирования с указанной вероятностью неудачи необходимо 220 кодированных символов. Для удовлетворения указанных требований необходимо послать всего 245 кодированных символов для каждого исходного блока, поскольку ceil(220/(l-0,1))=245. Таким образом, символы для восстановления добавляют еще 22,5% к требованиям к полосе пропускания для потока.
RQ код, описанный здесь и в разделе 5 Приложения А, обеспечивает вероятность неудачи, меньшую 10-2, 10-4, и 10-6 для объема служебных данных 0, 1, и 2 соответственно для значений K=K′ для всех поддерживаемых значений K′, а также для значений K=1 и K=K′+l для всех, кроме последнего поддерживаемого значения K. Для множества различных вероятностей потерь были сделаны тесты, например, для вероятностей потерь 10%, 20%, 50%, 70%, 90% и 95%.
Для вышеописанного примера использования RQ кода объем служебных данных равный 2 достаточен для достижения вероятности неудачи равной 10-6 и, следовательно, для удовлетворения упомянутых требований для каждого исходного блока необходимо послать всего 225 кодированных символов, поскольку ceil(202/(l-0,1))=225. В этом случае символы для восстановления добавляют еще 12,5% в требования к полосе частот для потока, то есть, на 10% меньшие издержки для полосы частот, чем это требуется для случайного двоичного кода. Таким образом, улучшенная кривая «объем служебных данных - вероятность неудачи» RQ кода имеет ряд очень позитивных практических следствий.
Имеются приложения, где желательна поддержка большого количества исходных символов на исходный блок. Например, в приложении для широковещательной мобильной передачи файлов полезно с точки зрения эффективности сети кодировать файл в виде единого исходного блока или, в частном случае, разбить файл на несколько исходных блоков, насколько это возможно. Предположим, например, что необходима широковещательная передача файла, содержащего 50 миллионов байт, и что доступный размер каждого пакета для пересылки кодированного символа составляет одну тысячу байт. Для кодирования данного файла в виде единого исходного блока потребуется поддерживать значение K=50000. (заметим, что имеются вышеописанные способы разбиения на субблоки, которые позволяют выполнять декодирование с использованием существенно меньшего объема памяти).
Имеется несколько причин, по которым возможно ограничение количества исходных символов, поддерживаемых для кода. Одна типовая причина заключается в том, что при возрастании K вычислительная сложность становится неприемлемой, например, для кодов Рида-Соломона, но это не относится к кодам, таким как коды с цепной реакцией. Другая причина может состоять в том, что вероятность неудачи при нулевом объеме служебных данных увеличивается почти до 1 с ростом K, что затрудняет нахождение систематических индексов, обеспечивающих построение хорошего систематического кода. Вероятность неудачи при нулевом объеме служебных данных может затруднить получение хорошей структуры кода, поскольку по существу это вероятность того, что при случайном выборе систематического индекса, результирующая структура систематического кода имеет свойство, состоящее в том, что первые K кодированных символов позволяют декодировать K исходных символов.
Поскольку кривая «объем служебных данных - вероятность неудачи» для исполнения RQ кода круто падает для всех значений K, можно легко найти хорошие систематические индексы, а значит, поддерживать гораздо большие значения K. RQ код, описанный в разделе 5 Приложения А, поддерживает значения K вплоть до 56403, а также поддерживает общее количество кодированных символов вплоть до 16777216 на один исходный блок. Эти пределы поддерживаемых значений для RQ кода были установлены из практических соображений на основе очевидных прикладных требований, а не из-за ограничений проекта RQ кода. В других вариантах осуществления, сверх показанных в Приложении А, могут использоваться другие значения.
RQ код ограничивает количество разных размеров исходного блока, поддерживаемых следующим образом. Если задан исходный блок с K исходными символами, подлежащими кодированию или декодированию, то значение K′ выбирают на основе таблицы, показанной в разделе 5.6 Приложения А. В первом столбце этой Таблицы перечислены возможные значения для K′. Выбранное значение K′ является минимальным из множества возможных значений, так что K≤K′. K исходных символов C′(0),..., C′(K-1) заполняются K′-K символами C′(K),..., C′(K′-1), имеющими значения, установленные в нуль, для создания исходного блока, содержащего K′ исходных символов C′(0),..., C′(K′-l), после чего выполняется кодирование и декодирование этого заполненного исходного блока.
Вышеописанный подход имеет преимущество, заключающееся в сокращении количества систематических индексов, которое необходимо поддерживать, то есть, только несколько сот вместо десятков тысяч. Отсутствуют недостатки с точки зрения зависимости «объем служебных данных - вероятность неудачи» для K, так как эта зависимость совпадает с кривой «объем служебных данных - вероятность неудачи» для выбранного K′. При данном значении K декодер может вычислить значение K′ и установить в нуль значения C′(K),..., C′(K′-l), и, следовательно, декодер должен декодировать только остальные K из K′ исходных символов исходного блока. Единственными потенциальными недостатками являются: возможная необходимость иметь несколько больше ресурсов памяти или вычислительных ресурсов для кодирования и декодирования с использованием несколько большего количества исходных символов. Однако интервал между последовательными значениями K′ приблизительно составляет 1% для больших значений K′, и поэтому этот потенциальный недостаток незначителен.
Из-за заполнения исходного блока от K до K′ идентификатор для кодированных символов C′(0),..., C′(I), в RQ коде называется внутренним символьным идентификатором (сокращенно ISI), где C′(0),..., C(K′-1) - исходные символы, а C′(K′), C′(K′+1),..., - символы для восстановления.
Во внешних приложениях, где применяется кодер и декодер, используют идентификатор кодированных символов, называемый также идентификатором кодирующих символов (сокращенно ESI), находящийся в диапазоне значений от 0 до K-1, для идентификации первоначальных исходных символов C′(0),..., C′(K-1), причем этот идентификатор использует продолжение индексов K, K+l,..., для идентификации символов для восстановления C′(K′), C′(K′+1),.... Таким образом, символ C′(X) для восстановления, идентифицированный с помощью ISI X в RQ коде, идентифицируется внешним образом с помощью ESI X-(K′-K). Более подробно это описано в разделе 5.3.1 Приложения А.
Кодирование и декодирование для RQ кодов определяется двумя типами соотношений: ограничительные соотношения между промежуточными символами и соотношения LT-PI между промежуточными символами и кодированными символами. Ограничительные соотношения соответствуют соотношениям между промежуточным символами, определенными матрицей SE, как показано, например, на фиг. 12 или фиг. 15. Соотношения LT-PI соответствуют соотношениям между промежуточными символами и кодированными символами, определенными матрицей LT и матрицей PI, как показано в качестве примера на фиг. 12 или фиг. 15.
Кодирование происходит путем определения значений промежуточных символов на основе: (1) значений исходных символов; (2) соотношений LT-PI между исходными символами и промежуточными символами; и (3) ограничительных соотношений между промежуточными символами. Значения символов для восстановления можно создать из промежуточных символов на основе соотношений LT-PI между промежуточными символами и символами для восстановления.
Аналогичным образом декодирование происходит путем определения значений промежуточных символов на основе: (1) принятых значений кодированных символов; (2) соотношений LT-PI между принятыми кодированными символами и промежуточными символами; и (3) ограничительных соотношений между промежуточными символами. Значения пропущенных исходных символов можно получить из промежуточных символов на основе соотношений LT-PI между промежуточными символами и пропущенными исходными символами. Таким образом, кодирование и декодирование фактически являются симметричными процедурами.
ПРИМЕРНЫЕ АППАРАТНЫЕ КОМПОНЕНТЫ
На фиг. 30-31 показаны блок-схемы аппаратных средств, которые можно использовать для реализации вышеописанных способов. Каждый элемент может представлять собой аппаратное средство, программный код или команды, выполняемые процессором общего назначения или специализированным процессором, либо их комбинацией.
На фиг. 30 показана примерная система 1000 кодирования, которую можно реализовать в виде аппаратных модулей, программных модулей или частей программного кода, хранящихся в запоминающем устройстве 1002 программ и выполняемых процессором 1004, возможно в виде общего блока кода, как показано на этой фигуре. Система 1000 кодирования принимает сигнал, несущий исходные символы и информацию о параметрах, и выводит сигнал, несущий эту информацию.
Интерфейс 1006 ввода хранит поступающие исходные символы в буфере 1008 исходных символов. Генератор 1010, преобразующий исходные символы в промежуточные, создает промежуточные символы из исходных символов. В некоторых вариантах осуществления это может быть средство транзитной пересылки, а в других вариантах осуществления (например, «систематический» вариант осуществления) это может быть декодерный модуль.
Генератор 1012 избыточных символов создает избыточные символы из исходных символов. Он может быть реализован в виде кодера с цепной реакцией, кодера LDPC, кодера HDPC или т.п. Блок 1014 инактивации получает исходные символы, промежуточные символы и/или избыточные символы, как возможный случай, и хранит некоторые из них (постоянно инактивированные символы) в буфере PI 1018, и подает их в выходной кодер 1016. Этот процесс может быть только логическим, а не физическим.
Оператор 1020, например, оператор «исключающее ИЛИ», работает с одними несколькими кодированными символами из выходного кодера 1016 (в некоторых вариантах осуществления с одним символом) и одним или несколькими символами PI из буфера PI 1018 (в некоторых вариантах осуществления с одним символом), а результат этой операции подается в интерфейс 1030 передачи, который выводит полученный сигнал из системы 1000.
На фиг. 31 показана примерная система 1100 декодирования, которую можно реализовать в виде аппаратных модулей, программных модулей или частей программного кода, хранящихся в запоминающем устройстве 1102 программ и выполняемых процессором 1104, возможно в виде неразделенного общего блока кода, как показано на этой фигуре. Некоторые процессы могут быть реализованы только логически, а не физически.
Система 1100 декодирования получает входной сигнал и возможно другую информацию и выводит исходные данные, если она способна на это. Входной сигнал подается в приемный интерфейс 1106, который хранит принятые символы в буфере 1108. В матричный генератор 1110 подаются идентификаторы ESI принятых символов, а генератор создает описанные здесь матрицы в зависимости от принятых конкретных символов и хранит результаты в памяти 1112 матриц.
Планировщик 1114 может считывать элементы матрицы из памяти 1112 матриц и создает план, хранимый в памяти 1016 планирования. Планировщик 1114 может также создать сигнал «сделано» и переслать матрицу PI в блок 1118 для нахождения параметров PI по завершении. Блок 1118 для нахождения параметров PI подает найденные значения символов PI в блок 1120 для нахождения, который также использовал упомянутый план, для декодирования промежуточных символов на основе принятых символов, плана и символов PI.
Промежуточные символы подаются в генератор 1122, преобразующий промежуточные символы в исходные, который может представлять собой кодер или средство транзитной пересылки. Выход генератора 1122, преобразующего промежуточные символы в исходные, подается на выходной интерфейс 1124, который выводит исходные данные или сообщает о наличии исходных данных для вывода.
ДРУГИЕ СООБРАЖЕНИЯ
В некоторых ситуациях может понадобится обеспечить улучшенную декодируемость. В приведенных в данном описании примерах, когда кодированные символы имели соседей LT и соседей PI, символы LDPC имели только соседей LT или соседей PI, которых не было среди символов HDPC. В некоторых случаях декодируемость улучшается, если LDPC символы также имеют соседей PI, которые включают в себя символы HDPC. При наличии соседей из числа всех символов PI, включая символы HDPC, ценность декодирования символов LDPC может быть ближе к ценности кодированных символов. Как пояснялось в этом описании, символы зависят от символов LT (которые можно легко кодировать и декодировать) и также зависят от символов PI, включая символы HDPC (которые могут обеспечить высоконадежное декодирование), так что могут иметь место оба преимущества.
В одном примере каждый символ LDPC имеет двух соседей PI, то есть, значение символа LDPC зависит от значений двух символов PI.
В некоторых ситуациях декодируемость можно также улучшить, если сократить число появлений дублированных кодированных символов, где два кодированных символа являются дубликатами, если они имеют точно такой же полный набор соседей, где полный набор соседей для кодированного символа состоит из набора соседей LT и набор соседей PI. Кодированные символы-дубликаты с одинаковым общим набором соседей несут одинаковую информацию о промежуточном исходном блоке, из которого они были созданы, и поэтому нет выгоды при декодировании на основе принятых более одного кодированных символов-дубликатов, по сравнению с декодированием на основе одного принятого символа из числа кодированных символов-дубликатов, то есть, прием более одного символа-дубликата увеличивает служебные данные при приеме, и для декодирования полезен только один из кодированных символов-дубликатов.
Предпочтительно, чтобы каждый принятый кодированный символ не являлся дубликатом любого другого принятого кодированного символа, поскольку это означает, что каждый принятый кодированный символ может быть полезным для декодирования. Таким образом, предпочтительно сокращать количество указанных дублирований или уменьшить вероятность появления дубликатов.
Один из подходов состоит в ограничении количества соседей LT, которое может иметь каждый кодированный символ. Например, если имеется W возможных соседей, то максимальное количество соседей может быть ограничено величиной W-2. Это уменьшает вероятность того, что полные наборы соседей в некоторых случаях будут продублированы, поскольку набор соседей, содержащий все W возможных соседей, не будет разрешен. Если ограничение представляет собой Deg[v]=min(d, W-2), где min возвращает минимум из двух чисел, оператор Deg[] обозначает степень, имеется W*(W-l)/2 различных наборов соседей степени W-2. Таким образом, можно уменьшить вероятность создания полных дублированных наборов соседей для кодированных символов. Вместо указанного ограничения можно использовать другие ограничения, например, min(d, W-Wg) для некоторого Wg, отличного от Wg=2, или какое-либо другое ограничение.
Другой способ, который можно использовать автономно или в сочетании с вышеописанным способом сокращения дублирования состоит в выборе более одного соседа PI для каждого кодированного символа, что уменьшает вероятность наличия дублированных соседей PI для кодированных символов, и таким образом уменьшает вероятность создания полных наборов соседей-дубликатов для кодированных символов. Соседи PI могут создаваться теми же способами, какими создаются соседи LT, например, путем создания в начале a(d1, a1, b1), как показано в Приложении А, радел 5.3.5.4 в соответствии с фрагментом кода, приведенным ниже:
если (d<4), тогда {dl=2+Rand [y, 3 , 2]}, в противном случае {dl=2};
al=1+Rand [y, 4 , Pl-1];
bl=Rand [y, 5 , Pl];
Заметим, что в этом примере имеется нетривиальное случайное распределение степени, определенное на нескольких соседях PI d1 и что это распределение зависит от выбранного количества d соседей LT, а количество соседей PI скорее всего будет больше, когда количество соседей LT меньше. Это обеспечивает свойство, характеризующееся тем, что полная степень кодированного символа такова, что уменьшается вероятность создания дублированных кодированных символов, а значит, их приема.
Значение кодированного символа можно создать, используя соседей, определенных как (dl, al, bl) как показано в Приложении А, раздел 5.3.5.3, и с помощью следующего фрагмента кода: когда (bl>=P) выполнить {bl=(bl+al) % P1};
result = result Λ C [W+bl];
Для j=1, dl-1 выполнить
bl=(bl+al) % Pl;
когда (bl>=P) выполнить {bl=(bl+al) % P1};
result = result Λ C [W+bl];
Выдача результата;
Для поддержки указанных характеристик декодируемости или отдельно для обеспечения декодируемости можно использовать разный систематический индекс J(K′) для значений K′, например, индекс показанный в Таблице 8 раздела 5.6 в Приложении А.
Далее показан пример процесса, который можно выполнить в передающей и/или приемной системе для создания систематического индекса J(K′). Для каждого K′ в списке возможных K′ один процесс, который можно выполнить, как правило, с помощью должным образом запрограммированной схемы или процессора, состоит в проверке нескольких индексов на возможность их применения. Например, схема/процессор может проверить для J=1..., 1000 [или некоторого другого ограничения], удовлетворяются ли следующие критерии в отношении возможного систематического индекса J:
(а) Возможно ли декодирование с нулевым объемом служебных данных из K′ исходных символов?
Если да, то запись нескольких инактиваций на ходу
(b) Имеется ли среди первых K′/0,06 возможных кодированных символов (с идентификаторами 0,..., K′/0,06) полные наборы дублированных соседей? [вместо этого можно использовать другие пороговые значения]
(с) Ниже ли вероятность неудачи декодирования, чем 0,007 [или какого-либо другого порогового значения], при декодировании с использованием первых K′ принятых кодированных символов в рамках 10000 прогонов [или какой-либо другой тест], когда вероятность потери каждого кодированного символа составляет 0,93 [или какое-либо другое пороговое значение] на каждом прогоне независимо от других кодированных символов?
Затем схема/процессор выбирает из числа возможных систематических индексов J индекс, который удовлетворяет вышеописанным критериям (a) (b) и (c), выбирая систематический индекс, который зафиксировал среднее количество инактиваций на ходу, на шаге (а).
Заметим, что имеется множество вариаций для выбранных выше критериев. Например, в некоторых случаях, возможно, окажется предпочтительней выбрать систематический индекс, который удовлетворяет критериям (а) (b) и (с) и дает минимальное количество неудач декодирования на шаге (с) в рамках заданного количества прогонов. В другом примере при выборе систематического индекса может быть рассмотрена комбинация количества инактиваций на ходу и вероятности неудачи декодирования. Еще в одном примере возможно наличие множества систематических индексов для каждого значения K′, и тогда один из них выбирают случайным образом в конкретных приложениях.
Систематические индексы для значений K′, перечисленные в Таблице 8 в разделе 5.6 Приложения А, представляют собой один потенциальный список систематических индексов для кода, описанного в Приложении А.
ВЕРСИИ ПРОЦЕССА РАЗБИЕНИЯ НА СУББЛОКИ
Известно разбиение на субблоки, то есть, физическое или логическое разбиение блоков на более мелкие блоки для дальнейшей обработки, для различных целей. Например, это используется в документе IETF RFC 5053. Также это известно из Патента США №7072971. Одной из главных целей использования способа разбиения на субблоки является возможность защиты большого блока данных как единого целого с помощью кода с FEC с одновременным использованием в приемнике объема памяти, гораздо меньшего, чем размер блока данных, для восстановления блока данных с использованием декодера с FEC.
Один из способов выбора количества субблоков, описанный в документе IETF RFC 5053, обеспечивает хорошее разбиение на исходные блоки и разбиение на субблоки для множества подходящих настроек параметров, но в некоторых обстоятельствах это может привести к решению, которое возможно будет не точно удовлетворять ограничению на верхнюю границу размера WS субблока (хотя даже в этих случаях получают решения, где размер субблока незначительно превышает заданное ограничение WS на размер субблока). В другом примере в draft-luby-rmt-bb-fec-raptorg-object-00 (где максимальное количество исходных символов в исходном блоке гораздо больше, чем в IETF RFC 5053) в разделе 4.2 обеспечено предписание для вычисления T, Z и N, где T- размер символа, Z- количество исходных блоков, на которое разбивают файл (или блок данных) и N- количество субблоков. Также P′ представляет собой размер полезной пакетной нагрузки для символов, F- размер файла в байтах, K′max - максимальное количество поддерживаемых исходных символов (например, 56404), Al- коэффициент выравнивания, определяющий, какие символы или субсимволы должны быть по размеру кратными Al байт, чтобы обеспечить более эффективное декодирование, например, предпочтительно, чтобы Al=4 для современного CPU, и WS- требуемая верхняя граница размера субблока в байтах.
Заметим, что на стороне отправителя или альтернативного сервера возможно отклонение параметров T, Z, и N на основе значений F, Al, и P′. Приемнику необходимо знать только значения F, Al, T, Z, и N, чтобы определить структуру субблока и исходного блока для файла или блока данных в принятых пакетах, относящихся к данному файлу или блоку данных. Приемник может определить P′ по размеру принятых пакетов. Заметим, что посланные и принятые пакеты, как правило, также содержат другую информацию, идентифицирующую содержание пакета, например, ID полезной нагрузки FEC, который как правило, имеет размер 4 байта и содержит номер исходного блока (SBN), а также идентификатор кодированного символа (ESI) для первого символа, пересылаемого в данном пакете.
Предыдущий способ, описанный в разделе 4.2. документа draft-luby-rmt-bb-fec-raptorg-object-00 для вычисления T, Z, N, предназначен для установки следующих значений этих параметров:
• T=P′
• Kt=ceil(F/T)
• Z=ceil(Kt/K′_max)
• N =min{ceil(ceil(Kt/Z)*T/WS), T/Al}
В этих вычислениях ceil() - функция, которая выдает минимальное целое число, большее или равное введенному значению, а floor() - функция, которая выдает максимальное целое число, меньшее или равное введенному значению. Также min() - функция, которая выводит минимальное из введенных значений.
Одной из проблем, связанной с некоторыми настройками параметров путем получения исходных блоков и разбиения их на субблоки, является то, что, если T/Al меньше ceil(ceil(Kt/Z)*T/WS), то тогда может быть не соблюдена верхняя граница размера W субблока.
Вторая потенциальная проблема состоит в том, что это позволяет обеспечить размер субсимволов до минимального Al, как правило, установленного равным 4 байта, что может оказаться слишком малой величиной для эффективного практического применения. Как правило, чем меньше размер субсимвола, тем больше объем служебных данных обработки, при декодировании или кодировании субблоков. Кроме того, особенно в приемнике меньший размер субсимвола означает, что для демультиплексирования и декодирования потребуется больше субблоков, а это может привести к повышенному расходу ресурсов приемника, таких как тактовые циклы CPU и доступы к памяти. С другой стороны, меньший доступный размер субсимвола означает, что исходный блок можно разбить на большее количество субблоков, для которых соблюдается заданная верхняя граница WS размера субблока. Таким образом, использование субсимволов меньшего размера позволяет поддерживать исходный блок большего размера, и, следовательно, защита FEC, обеспечиваемая через этот исходный блок, дает лучшую защиту и более высокую эффективность сети. На практике во многих случаях предпочтительно обеспечить, по меньшей мере, заданный минимальный размер субсимволов, что открывает возможность обеспечить более хороший баланс между требованиями обработки и требованиями к памяти в приемнике и эффективному использованию сетевых ресурсов.
Ниже приведен пример параметров, полученных с использованием предыдущего способа, описанного в разделе 4.2 draft- luby-rmt-bb-fec-raptorg-object-00 для вычисления T, Z, N:
Входные данные:
F=56,404 Кбайт
P′=1 Кбайт =1,024 байта
WS=128 Кбайт
Al=4
K_max =56,404
Вычисления:
T=1 Кбайт
Kt=56,404
Z=1
N=256 (из-за второго входа в функцию min)
В этом примере будет один исходный блок, содержащий 256 субблоков, где каждый субблок содержит примерно 220 Кбайт (больше, чем WS), причем, по меньшей мере, некоторые субблоки имеют размер субсимвола, равный 4 байта (очень мал). Третья проблема заключается в том, что решение AL-FEC может не поддерживать все возможные значения количества исходных символов, то есть, может поддерживаться только выбранный список из K′ значений, где K′- поддерживаемое количество исходных символов в исходном блоке, и тогда, если действительное количество исходных символов К, требуемое в исходном блоке, не содержится в K′ значениях, то К подтягивают до ближайшего значения K′, а это означает, что размер используемого исходного блока может быть несколько большим значения K, вычисленного выше.
Далее описываются новые способы разбиения на субблоки, которые представляют собой улучшенные версии предыдущих способов, описанных выше. Для примера модуль для разбиения на субблоки может получать в качестве входных данных, подлежащих разбиению, значение F, а также значения WS, Al, SS и P′, где значение этих переменных более подробно описано ниже.
WS представляет предложенное ограничение на максимальный размер субблока, возможно в байтах, который можно декодировать с использованием рабочей памяти приемника. Al представляет параметр выравнивания памяти. Поскольку память приемника может работать более эффективно, если символы и субсимволы в памяти выровнены вдоль ее границ, возможно окажется полезным отслеживать величину Al и хранить значения, кратные Al байт. Например, как правило, Al=4, поскольку многие устройства памяти осуществляют естественную адресацию данных в памяти в границах четырех байт. Также возможны другие значения Al, например, Al=2 или Al=8. Как правило, Al можно установить как наименьшее общее кратное для выравнивания памяти по всему множеству возможных приемников. Например, если приемники поддерживают 2-байтовое выравнивание памяти, а другие приемники поддерживают 4-байтвое выравнивание памяти, то тогда рекомендуется, чтобы Al=4.
Параметр SS определяют на основе предпочтительной нижней границы размера субсимвола, так чтобы нижняя граница размера субсимвола была равна SS* Al байт. Возможно, будет предпочтительно иметь размер субсимвола, кратный Al, поскольку операции декодирования, как правило, выполняются с субсимволами.
Далее подробно объясняется способ разбиения данных F на Z исходных блоков, а затем разбиение этих Z исходных блоков на N субблоков. В этом описании P′ относится к переменной, хранящейся в памяти (или предполагаемой) и представляющей доступные байты в пакетах для символов, предназначенных для посылки, причем предполагается, что P′ кратно Al. T- это переменная, представляющая размер символов, которые должны быть размещены в посылаемых пакетах. Другие переменные можно вывести из текста.
Новый способ разбиения на субблоки для определения T, Z и N
• T=P′
• Kt=ceil(F/T);
• N_max = floor(T/(SS*Al));
• Для всех n=1, N_max
◦ KL(n)- максимальное значение K′, поддерживаемое в качестве возможного количества исходных символов в исходном блоке, которое удовлетворяет неравенству
▪ K′≤WS/(Al*(ceil(T/(Al*n))));
• Z=ceil(Kt/KL(N_max));
• N= минимальное n, так что ceil(Kt/Z)≤KL(n);
После определения этих параметров можно определить размер каждого из Z исходных блоков и размеры субсимволов из N субблоков каждого исходного блока, как это описано в документе IETF RFC 5053, то есть, Kt=ceil(F/T), (KL, KS, ZL, ZS)=Partition[Kt, Z], и (TL, TS, NL, NS)=Partition[T/Al, N].
Kt представляет количество исходных символов в файле. В модуле субблоков Kt исходных символов разбиваются на Z исходных блоков: ZL исходных блоков с KL исходными символами каждый и ZS исходных блоков с KS исходными символами каждый. Затем KL округляют до KL′, где KL′- минимальное поддерживаемое количество исходных символов, то есть, по меньшей мере KL (и дополнительные KL′-KL заполненных нулями символов добавляют в исходный блок в целях кодирования и декодирования, но эти дополнительные символы, как правило, не посылаются или не принимаются), и аналогичным образом KS округляют до KS′, где KS′- минимальное поддерживаемое количество исходных символов, то есть, по меньшей мере, KS (и дополнительные KS′-KS заполненных нулями символов добавляют в исходный блок в целях кодирования и декодирования, но эти дополнительные символы, как правило, не посылаются, или не принимаются).
Эти вычисления (выполняемые модулем субблоков, другим программным модулем или аппаратными средствами) обеспечивают, насколько это возможно, равные значения количества исходных символов в исходных блоках, согласно ограничению, состоящему в том, что их общее количество равняется количеству Kt исходных символов в файле. Эти вычисления также обеспечивают, насколько это возможно, равенство размеров субсимволов для субблоков, согласно ограничению, состоящему в том, что они должны быть кратны Al и их размеры равняются размеру символа.
Затем вычисляют параметры субсимволов TL, TS, NL и NS, где имеется NL субблоков с большим размером TL* Al субсимволов, и имеется NS субблоков с меньшим размером TS* Al субсимволов. Функция Partition[I, J] реализуется программными или аппаратными средствами и определяется как функция, выход которой представляет собой последовательность четырех целых чисел (IL, IS, JL, JS), где IL=ceil(I/J), IS=floor(I/J), JL=I IS*J, и JS=J-JL.
Некоторые из свойств этих новых способов заслуживают внимания. Модуль субблоков может определить нижнюю границу, получаемую на основе используемого минимального размера субсимвола. Из приведенных выше уравнений следует, что TS=floor(T/(Al*N)), где TS*Al- используемый минимальный размер символа, поскольку TS≤TL. Заметим, что минимальный субсимвол используют, когда N=N_max. Если X/(fioor(Y))≥X/Y для положительных X и Y, то TS по меньшей мере равно floor(T/(Al*floor(T/(SS*Al)))), что, в свою очередь, по меньшей мере равно floor(SS)=SS. Из-за этого минимальный размер субсимвола, создаваемого описанным здесь способом разбиения, составит, по меньшей мере, TS*Al=SS*Al, если это необходимо.
Модуль субблоков моет определить верхнюю границу, полученную из максимального размера субблока. Используемый максимальный размер субблока составляет TL*A1* KL′, где KL′- минимальное значение K′ в вышеуказанной таблице, то есть, по меньшей мере, KL=ceil(Kt/Z). Заметим, что согласно определению N выполняется неравенство KL′≤KL(N), и TL=ceil(T/(Al*N)). Поскольку KL(N)≤WS/(Al*(ceil(T/(Al*N)))), то WS≥KL(N)*Al*ceil(T/(Al*N))≥ KL′*A1*TL.
Переменная N_max может представлять максимальное количество субсимволов, на которое может быть разбит исходный символ размера Т. Установка N_max равным floor(T/(SS*Al)) гарантирует то, что минимальный размер субсимвола будет, по меньшей мере, равен SS*A1. KL(n) представляет максимальное количество исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиты каждый на n субсимволов, что гарантирует, что размер каждого из субблоков исходного блока не будет превышать WS.
Количество Z исходных блоков можно выбрать как можно меньшим в соответствии с ограничением, состоящим в том, что количество исходных символов в каждом исходном блоке составляет не более KL(N_max), что гарантирует возможность разбиения каждого исходного символа на субсимволы с размером, по меньшей мере, равным SS*A1, и гарантирует, что размер результирующих субблоков не превысит WS. Модуль субблоков определяет, исходя из величины Z, количество исходных блоков и количество символов в каждом из Z исходных блоков.
Заметим, что, если используется значение Z, меньшее, чем создаваемое при использовании этого способа разбиения, то тогда либо получится субблок одного из исходных блоков с размером, превышающим WS, либо субблок одного из исходных блоков с размером субсимвола, меньшим, чем SS*A1. Также в соответствии с этими двумя ограничениями минимальный из исходных блоков, созданный в результате использования этого способа разбиения, будет максимальным, насколько это возможно, то есть, нет другого способа разбиения файла или блока данных на исходные блоки, который соблюдает оба ограничения, так что минимальный исходный блок будет больше минимального исходного блока, созданного с использованием этого способа разбиения. Таким образом, значение Z, созданное с помощью этого способа разбиения, в этом смысле является оптимальным.
Количестве N субблоков, на которое разбивают исходный блок, можно выбрать минимально возможным в соответствии с ограничением, состоящим в том, что для каждого субблока размер субсимволов субблока, кратный количеству исходных символов в исходном блоке, не превышает WS.
Заметим, что при использовании значения N, меньшего, чем значение, создаваемое этим способом разбиения исходя из значения Z, получится, по меньшей мере, один субблок, чей размер будет превышать WS. Также минимальный размер субсимвола, который получается при использовании этого способа измерения исходя из заданного значения Z, является максимально возможным с учетом ограничения, состоящего в том, что максимальный размер субблока не должен превышать WS, то есть, нет другого способа создания субблоков исходных блоков, определяемых значением Z, который соблюдает ограничение на максимальный субблок, так что минимальный размер субсимвола будет больше минимального размера субсимвола, создаваемого с помощью этого способа разбиения. Таким образом, значение N, созданное в результате использования этого способа разбиения, в этом смысле является оптимальным.
В последующих примерах предполагается, что поддерживаются все возможные значения K′, представляющие количество исходных символов в исходном блоке.
ПРИМЕР 1
Входные данные:
SS=5
Al=4 байта
(Минимальный размер субсимвола =20 байт)
WS=128 Кбайт=131,072 байт
P′=1,240 байт
F=6 Мбайт=6,291,456 байт
Вычисления:
T=1,240 байт
Kt=5,074
N_max=62
KL(N_max)=6,553
Z=1
KL=ceil(Kt/Z)=5,074
N=52(KL(N)=5,461)
TL=6, больший субсимвол =24 байта
TS=5, меньший субсимвол =20 байт
TL*AL*KL=121,776
Пример 2
Входные данные:
SS=8
Al=4 байта
(Минимальный размер субсимвола =32 байта)
WS=128 Кбайт =131,072 байта
P′ = 1 Кбайт =1,024 байта
F=56404 Кбайт =57,757,696 байта
Вычисления:
T=1,024 байта
Kt=56,404
N_max=32
KL(N_max)=4,096
Z=14
KL=ceil(Kt/Z)=4,029
N=32 (KL(N)=4,096)
TL=8, больший субсимвол =32 байта
TS=8, меньший субсимвол =32 байта
TL*AL*KL=128,928
Имеется множество вариантов вышеописанных способов. Например, для некоторого кода с FEC желательно иметь, по меньшей мере, минимальное количество исходных символов в исходном блоке для минимизации объема служебных данных при приеме исходных блоков в коде с FEC. Поскольку для действительно малых размеров файла или размеров F блоков данных размер исходного символа может оказаться слишком маленьким, возможно, также иметь максимальное количество исходных символов, на которое разбивается пакет. Например, в документе IETF RFC 5053 требуемое минимальное количество исходных символов в исходном блоке составляет Kmin=1024, а максимальное количество исходных символов, на которое разбит пакет, составляет Gmax=10.
Ниже описывается другая версия нового вышеописанного способа разбиения на субблоки, в которой учитываются только что описанные дополнительные параметры Kmin и Gmax, где G- количество символов для исходного блока, переносимых в каждом пакете, которое может обрабатываться модулем разбиения на субблоки или модулем более общего назначения, либо программными или аппаратными средствами в кодере, декодере, передатчике и/или приемнике.
В этой версии каждый пакет несет идентификатор ESI первого символа в пакете, и тогда каждый последующий символ в пакете имеет в неявном виде ESI, который на единицу больше, чем предшествующий символ в пакете.
Новый способ разбиения на блоки для определения G, T, Z и N
• G=min(ceil(P′*Kmin/F), floor(P′/(SS*Al)), Gmax);
• T=floor(P′/(Al*G))*Al;
• Kt=ceil(F/T);
• N_max=floor(T/(SS*Al));
• Для всех n=1, N_max
◦ KL(n)- максимальное значение K′, поддерживаемое в качестве возможного количества исходных символов в исходном блоке, которое удовлетворяет неравенству
▪K′≤WS/(Al*(ceil(T/(Al*n))));
• Z=ceil(Kt/KL(N_max));
• N= минимальное n, обеспечивающее выполнение ceil(Kt/Z)≤KL(n);
Между прочим, заметим, что вычисление G гарантирует, что размер символа будет, по меньшей мере, равен SS*A1, то есть, размер символа будет, по меньшей мере, минимальным размером субсимвола. Заметим также, что SS*A1 должно, по меньшей мере, быть равно P′, чтобы гарантировать, чтобы размер символа мог быть по меньшей мере равен SS*Al (причем, если это не так, то G будет стремиться к нулю).
Пример 3
Входные данные:
SS=5
Al=4 байта
(Минимальный размер субсимвола =20 байт)
WS=256 Кбайт =262,144 байт
P′=1,240 байт
F=500 Кбайт =512,000 байт
Kmin=1,024
Gmax=10
Вычисления:
G=3
T=412
Kt=1,243
N_max=20
KL(N_max)=10,992
Z=1
KL=ceil(Kt/Z)=1,243
N=2(KL(N)=1,260)
TL=52, больший субсимвол =208 байт
TS = 51, меньший субсимвол =204 байт
TL*AL*KL=258,544
Как было описано, эти новые способы вводят ограничение на минимальный размер субсимвола, используемый для любого субблока. В этом описании предложены новые способы для разбиения на субблоки, которые соблюдают это дополнительное ограничение, при одновременном жестком соблюдении ограничения на максимальный размер субблока. Эти способы создают решения, касающиеся разбиения на исходные блоки и субблоки, которые удовлетворяют целям разбиения файла или блока данных на несколько исходных блоков, возможно с ограничением на минимальный размер субсимвола, а затем в соответствии с разбиением на как можно меньшее количество субблоков в соответствии с ограничением на минимальный размер субблока.
ВАРИАНТЫ
В некоторых приложениях допускается отсутствие возможности декодирования всех исходных символов или наличие возможности декодирования всех исходных символов, но с относительно низкой вероятностью. В таких приложениях приемник может прекратить попытку декодировать все исходные символы после приема K+A кодированных символов. Либо приемник может прекратить прием кодированных символов после приема менее K+A кодированных символов. В некоторых приложениях приемник может принимать только K или менее кодированных символов. Таким образом, следует понимать, что в некоторых вариантах осуществления настоящего изобретения требуемая точность не обязательно должна обеспечивать полное восстановление всех исходных символов.
Кроме того, в некоторых приложениях, где допустимо неполное восстановление, данные могут кодироваться так, что не все исходные символы будут восстановлены, или так, что полное восстановление символов потребует приема гораздо большего количества кодированных символов, чем количество исходных символов. Такое кодирование в общем случае требует меньших вычислительных затрат, и, следовательно, его можно применить для уменьшения вычислительных затрат при кодировании.
Должно быть понятно, что различные функциональные блоки на вышеописанных фигурах могут быть реализованы комбинацией аппаратных и/или программных средств и что в конкретных реализациях некоторые или все функциональные возможности некоторых блоков могут быть объединены. Аналогичным образом, также следует понимать, что сформулированные здесь различные способы могут быть реализованы комбинацией аппаратных и/или программных средств.
Приведенное выше описание носит иллюстративный характер и не является ограничением. Специалистам в данной области техники после ознакомления с этим описанием станут очевидными множество вариантов осуществления данного изобретения. Следовательно, объем изобретения должен определяться не со ссылкой на приведенное выше описание, а со ссылкой на приложенную формулу изобретения, равно как и на весь спектр эквивалентов.
Приложение А
Надежная групповая пересылка
Проект документа Интернет
Предполагаемый статус: сопровождение стандартов
Дата окончания действия: 12 февраля 2011 года
Авторы:
M. Luby
Qualcomm Incorporated
M. Watson
Qualcomm Incorporated
T. Stockhammer
Nomor Research
L. Minder
Qualcomm Incorporated
Август 11, 2010
Схема RaptorQ с непосредственным исправлением ошибок для доставки объектов
draft-ietf-rmt-bb-fec-raptorq-04
Реферат
В этом документе описывается полностью детализированная схема с FEC, соответствующая ID 6 кодирования с FEC (подлежащая утверждению (tbc)), для кода с непосредственным исправлением ошибок RaptorQ и ее приложение для надежной доставки объектов данных.
Коды RaptorQ представляют собой новое семейство кодов, которые обеспечивают повышенную гибкость, поддерживают большие размеры исходных блоков и более высокую эффективность кодирования, чем коды Raptor в документе RPC5053. Код RaptorQ также является фонтанным кодом, то есть, кодер может создать «на ходу» столько кодирующих символов, сколько это необходимо, из исходных символов исходного блока данных. Декодер способен восстановить исходный блок из любого набора кодирующих символов, количество которых в большинстве случаев равно количеству исходных символов, а в редких случаях чуть больше количества исходных символов.
Описанный здесь код RaptorQ является систематическим кодом, а это значит, что все исходные символы содержатся среди кодирующих символов, которые могут быть созданы.
Статус этого изложения
Данный проект документа Интернет предложен в полном соответствии с положениями документов BCP 78 и BCP 79.
Проекты документов Интернет являются рабочими документами Рабочей группы инженеров Интернет (IETF). Заметим, что распределять рабочие документы в виде проектов документов Интернет могут также и другие группы. Список текущих проектов документов Интернет находится по адресу http://datatracker.ietf.org/drafts/current/.
Проекты документов Интернет действительны в течение максимум шести месяцев и могут быть обновлены, заменены или выведены из употребления другими документами в любое время. Нельзя использовать проекты документов Интернет в качестве ссылочного материала или для их цитирования, кроме как в ходе их разработки. Срок действия этого проекта документа Интернет истекает 12 февраля 2011 года.
Замечание по поводу авторских прав
Copyright (С) 2010 IETF TRUST и лица, указанные как авторы документа. Все права зарезервированы.
Этот документ подпадает под действие BCP 78 и юридических положений IETF Trust, относящихся к документам IETF (http://trustee.ietf.org/license-info), действующим, начиная с даты публикации этого документа. Пожалуйста, тщательно изучите эти документы, поскольку в них описаны Ваши права и ограничения в соответствии с этим документом. Извлеченные из этого документа кодовые компоненты должны включать в себя упрощенный текст лицензии BSD, описанный в разделе 4.е Trust Legal Provisions, причем они предоставляются без гарантии, как это описано в упрощенной лицензии BSD.
Проект документа Интернет Схема с FEC RaptorQ Август 2010
Оглавление
1. Введение.
2. Требования к терминологии
3. Форматы и коды
3.1. Идентификаторы (ID) полезной нагрузки FEC
3.2. Информация для передачи объектов FEC
3.2.1. Обязательная
3.2.2. Общая
3.2.3. Специальная.
4. Процедуры
4.1. Введение
4.2. Требования Протокола доставки контента
4.3. Примерный алгоритм получения параметров
4.4. Доставка объектов
4.4.1. Построение исходного блока
4.4.2. Построение кодирующего пакета
5. Спецификация кода RaptorQ с FEC
5.1. Определения, символы и аббревиатуры
5.1.1. Определения
5.1.2. Символы
5.1.3. Аббревиатуры
5.2. Обзор
5.3. Систематический кодер RaptorQ
5.3.1. Введение
5.3.2. Обзор кодирования
5.3.3. Первый шаг кодирования: Создание промежуточных символов
5.3.4. Второй шаг кодирования: Кодирование
5.3.5. Генераторы
5.4. Примерный декодер с FEC
5.4.1. Общие положения
5.4.2. Декодирование расширенного исходного блока
5.5. Случайные числа
5.5.1. Таблица V0
5.5.2. Таблица Vl
5.5.3. Таблица V2
5.5.4. Таблица V3
5.6. Систематические индексы и другие параметры
5.7. Операции с октетами, символами и матрицами
5.7.1. Общие положения
5.7.2. Арифметические операции с октетами
5.7.3. Таблица OCT_EXP
5.7.4. Таблица OCT_LOG
5.7.5. Операции с символами
5.7.6. Операции с матрицами
5.8. Требования к совместимому декодеру
6. Соображения по поводу безопасности
7. Соображения по поводу IANA
8. Благодарности
9. Ссылки
9.1. Нормативные ссылки
9.2. Информативные ссылки
Адреса авторов
1. Введение
Этот документ задает схему FEC для кода RaptorQ с непосредственным исправлением ошибок для приложений доставки объектов. Концепция схемы FEC определена в RFC5052 [RFC5052], и данный документ следует предписанному там формату и использует терминологию указанного документа. Описанный здесь код RaptorQ относится к следующему поколению кода Raptor, описанному в документе RFC5053 [RFC5053]. Код RaptorQ обеспечивает высокую надежность, повышенную эффективность кодирования и поддерживает большие размеры исходных блоков, чем код Raptor в RFC5053 [RFC5053]. Эти усовершенствования упрощают использование кода RaptorQ в Протоколе доставки контента объекта по сравнению с RFC5053 [RFC5053].
Схема FEC RaptorQ является полностью детализированной схемой FEC, соответствующей ID 6 (tbc) кодирования с FEC.
Примечание редактора: окончательный ID кодирования с FEC еще должен быть определен, но в качестве временного значения в этом проекте документа Интернет используют значение ′6 (tbc)′, ожидая последующее использование идентификаторов кодирования с FEC в процессе регистрации администрацией IANA («Администрация адресного пространства Интернет»).
RaptorQ является фонтанным кодом, то есть, кодер может на ходу создавать столько кодирующих символов, сколько это необходимо, из исходных символов блока. Декодер способен восстановить исходный блок из любого набора кодирующих символов, лишь слегка превышающего количество исходных символов.
Описанный в этом документе код является систематическим кодом, то есть, первоначальные исходные символы могут посылаться, будучи не модифицированными, от отправителя на приемник вместе с несколькими символами для восстановления. Дополнительные предпосылки использования кодов с непосредственным исправлением ошибок при надежной групповой передаче изложены в документе [RFC3453].
2. Требования к терминологии
Ключевые слова «должен», «не должен», «требуемый», «обязан», «не обязан», «следует», «не следует», «рекомендован», «может» и «не обязательный» в этом документе должны интерпретироваться так, как это описано в документе [RFC2119].
3. Форматы и коды
3.1. Идентификаторы (ID) полезной нагрузки FEC
ID полезной нагрузки FEC должен представлять собой 4-октетное поле, определенное следующим образом:

Таблица 1. Формат ID полезной нагрузки FEC
Номер исходного блока (SBN), (8 бит, целое число без знака) не отрицательный целочисленный идентификатор для исходного блока, указывающий, какие кодирующие символы в пакете к нему относятся.
ID кодирующего символа (ESI), (24 бита, целое число без знака) не отрицательный целочисленный идентификатор для кодирующих символов в данном пакете.
Интерпретация номера исходного блока и идентификатора кодирующего символа определена в разделе 4.
3.2. Информация для передачи объектов FEC
3.2.1. Обязательная
Значение ID кодирования с FEC должно быть равно 6, как это присвоено администрацией IANA (смотри раздел 7).
3.2.2. Общая
Общими информационными элементами для передачи объектов FEC, используемыми в этой схеме FEC, являются:
Длина пересылки (F), (40 бит, целое число без знака) не отрицательное целое число, не превышающее 946270874880. Этот элемент представляет длину пересылки объекта в октетах.
Размер символа (Т), (16 бит, целое число без знака) положительное целое число, меньшее 2ΛΛ16. Этот элемент представляет размер символа в октетах.
Формат закодированной общей информации для пересылки объектов FEC показан в Таблице 2.

Таблица 2. Кодированная общая информация для передачи объектов FEC для схемы RaptorQ с FEC.
Примечание 1: Предельное значение 946270874880 длины пересылки является следствием ограничения размера символа величиной 216-1, ограничения на количество символов в исходном блоке величиной 56403 и ограничения на количество исходных блоков величиной 28.
3.2.3. Специальная
Для данной схемы FEC в специальном информационном элементе для передачи объектов FEC переносятся следующие параметры:
количество исходных блоков (Z) (12 бит, целое число без знака);
количество субблоков (N) (12 бит, целое число без знака);
параметр выравнивания символов (Al) (8 бит, целое число без знака).
Все эти параметры являются положительными целыми числами. Закодированная специализированная информация для передачи объектов представляет собой 4-октетное поле, состоящее из параметров Z, N и Al, как показано в Таблице 3.

Таблица 3. Закодированная специальная информация для передачи объектов FEC
Эта закодированная информация для передачи объектов FEC представляет собой 12-октетное поле, состоящее из конкатенации закодированной общей информации для передачи объектов FEC и закодированной специализированной информации для передачи объектов FEC.
Эти три параметра определяют разбиение исходного блока, как это описано в разделе 4.4.1.2.
4. Процедуры
4.1. Введение
Для любых используемых в этом разделе не определенных символов или функций, в частности, функций "ceil" и "floor" обратитесь к разделу 5.1.
4.2. Требования Протокола доставки контента
В этом разделе описывается информационный обмен между схемой RaptorQ с FEC и любым Протоколом доставки контента (CDP), который предусматривает использование схемы RaptorQ с FEC для доставки объектов.
Для схемы кодера RaptorQ и схемы декодера RaptorQ для доставки объектов требуется следующая информация из протокола CDP:
длина пересылки объекта F в октетах;
параметр выравнивания символов -Al;
размер T символа в октетах, который должен быть кратен Al;
количество исходных блоков -Z;
количество субблоков в каждом исходном блоке -N.
Для схемы кодера RaptorQ для доставки объекта дополнительно требуется:
объект, подлежащий кодированию, F октетов.
Схема кодера RaptorQ задает CDP вместе со следующей информацией для каждого пакета, подлежащего пересылке:
номер исходного блока (SBN);
ID кодирующего символа (ESI);
кодирующий символ (символы).
CDP должен передать эту информацию на приемник.
4.3. Примерный алгоритм получения параметров
В этом разделе даны рекомендации для получения трех параметров транспортировки: T, Z и N. Эта рекомендация основана на следующих входных параметрах:
◦ F- длина пересылки объекта в октетах;
◦ WS- блок максимального размера, который можно декодировать в рабочей памяти в октетах;
◦ P′- максимальный размер полезной нагрузки в октетах, который, как предполагается, кратен Al;
◦ Al- параметр выравнивания символов, в октетах;
◦ SS= параметр, где требуемая нижняя граница размера субсимвола составляет SS*A1;
◦ K′_max- максимальное количество исходных символов на один исходный блок.
Примечание: В разделе 5.1.2 число K′_max определено равным 56403.
На основе вышеуказанных входных данных параметры T, Z и N транспортировки вычисляют следующим образом:
Пусть,
◦ T=P′
◦ Kt=ceil (F/T)
◦ N_max=floor (T/ (SS*A1))
◦ Для всех n=l, N_max
◦ KL (n)- максимальное K′ значение в таблице 2 в разделе 5.6, так чтобы
◦ K′<=WS/ (Al* (ceil (T/(Al*n))
◦ Z=ceil (Kt/KL(N_max))
◦ N- минимум n=l, N_max, так чтобы ceil (Kt/Z)<=KL (n)
Рекомендуется, чтобы каждый пакет содержал, ровно один символ. Однако приемники обязаны поддерживать прием пакетов, которые содержат множество символов.
Значение Kt это общее количество символов, необходимых для представления исходных данных объекта.
Вышеуказанный алгоритм и алгоритм, определенный в разделе 4.4.1.2, обеспечивают кратность размеров субсимволов параметру Al выравнивания символов. Это полезно, поскольку операции суммирования, используемые при кодировании и декодировании, обычно выполняются несколько октетов за раз, например, 4 октета за раз на 32-разрядносм процессоре. Таким образом, кодирование и декодирование могут выполняться быстрее, если размеры субсимволов кратны указанному количеству октетов.
Рекомендуется устанавливать значение входного параметра Al, равным 4.
Параметр WS можно использовать для создания кодированных данных, которые могут быть эффективно декодированы при использовании ограниченной рабочей памяти в декодере. Заметим, что действительное требование к максимальному объему памяти декодера для данного значения WS зависит от конкретной реализации, но возможно реализовать декодирование с использованием рабочей памяти, лишь слегка превышающей WS.
4.4. Доставка объектов
4.4.1. Построение исходного блока
4.4.1.1. Общие положения
Чтобы применить кодер RaptorQ к исходному объекту, этот объект должен быть разбит на Z>=1 блоков, известных как исходные блоки. Кодер RaptorQ применяется независимо от каждого исходного блока. Каждый исходный блок идентифицируется уникальным номером исходного блока (SBN), где первый исходный блок имеет SBN, равный нулю, второй имеет SBN, равный единице, и т.д. Каждый исходный блок делят на несколько (K) исходных символов с размером T октетов. Каждый исходный символ идентифицируется уникальным идентификатором кодирующего символа (ESI), где первый исходный символ исходного блока имеет ESI, равный нулю, второй имеет ESI, равный единице, и т.д.
Каждый исходный блок с K исходными символами разделяют на N>=1 субблоков, которые достаточно малы для декодирования в рабочей памяти. Каждый субблок разделяют на K субсимволов с размером T′.
Заметим, что значение K не обязательно должно быть одинаковым для каждого исходного блока объекта, а значение T′ не обязательно быть одинаковым для каждого субблока исходного блока. Однако, размер T символа одинаков для всех исходных блоков объекта, а количество K символов одинаково для каждого субблока исходного блока. Точное разбиение объекта на исходные блоки и субблоки описано ниже в разделе 4.4.1.2.
4.4.1.2. Разбиение исходных блоков и субблоков
Построение исходных блоков и субблоков определяется на основе пяти входных параметров F, Al, T, Z и N и функции Partition[]. Эти пять входных параметров определяются следующим образом:
◦ F- длина пересылки объекта, в октетах;
◦ Al- параметр выравнивания символов, в октетах;
◦ T- размер символа в октетах, который должен быть кратен Al
◦ Z- количество исходных блоков;
◦ N- количество субблоков в каждом исходном блоке.
Эти параметры должны быть установлены так, чтобы ceil (ceil (F/T)/Z) <=K′_max. Рекомендации для получения этих параметров даны в разделе 4.3.
Функция Partition[] берет пару положительных целых чисел (I, J) в качестве входных данных и получает в результате четыре не отрицательных целых числа (IL, IS, JL, JS) в качестве выходных данных. В частности, значение Partition [I, J] представляет собой последовательность (IL, IS, JL, JS), где IL=ceil(I/J), IS=floor(I/J), JL=I-IS*J и JS=J-JL. Функция Partition[] получает параметры для разбиения блока с размером I на J блоков приблизительно равного размера. В частности, - JL блоков длиной IL и JS блоков длиной IS.
Исходный объект должен разбиваться на исходные блоки и субблоки следующим образом:
Пусть
◦ Kt=ceil (F/T),
◦ (KL, KS, ZL, ZS)= Partition [Kt, Z],
◦ (TL, TS, NL, NS)= Partition [T/Al, N].
Затем объект должен быть разбит на Z=ZL+ZS сопряженных исходных блоков, где первые ZL исходных блоков содержат каждый KL*T октетов, то есть, KL исходных символов из T октетов каждый, а остальные ZS исходных боков содержат каждый KS*T октетов, то есть, KS исходных символов из T октетов каждый.
Если Kt*T>F, то для осуществления кодирования последний символ последнего исходного блока должен быть заполнен в конце Kt*T-F нулевыми октетами.
Далее каждый исходный блок с K исходными символами должен быть разделен на N=NL+NS сопряженных субблоков, где первые NL субблоков состоят каждый из K сопряженных субсимволов с размером в TL*A1 октетов, а остальные NS субблоков состоят каждый из K сопряженных субсимволов с размером TS*A1 октетов. Параметр Al выравнивания символов обеспечивает кратность субсимволов Al октетам.
Наконец, m-ый символ исходного блока состоит из конкатенации m-ых субсимволов из каждого из N субблоков. Заметим, что это подразумевает, что при N>1 символ не является сопряженной частью объекта.
4.4.2. Построение кодирующего пакета
Каждый кодирующий пакет содержит следующую информацию:
номер исходного блока (SBN);
ID кодирующего символа (ESI);
кодирующий символ (символы).
Каждый исходный блок кодируют независимо от других. Исходные блоки нумеруют последовательно, начиная с нуля.
Значения ID кодирующего символа от 0 до K-1 идентифицируют исходные символы исходного блока в последовательном порядке, где K- количество исходных символов в исходном блоке. K идентификаторов кодирующих символов идентифицируют далее символы для восстановления, созданные из исходных символов с использованием кодера RaptorQ.
Каждый кодирующий пакет состоит либо целиком из исходных символов (исходный пакет), либо целиком из символов для восстановления (пакет для восстановления). Один пакет может содержать любое количество символов из одного и того же исходного блока. В том случае, когда последний исходный символ в исходном пакете включает в себя заполняющие октеты, добавленные для осуществления кодирования с FEC, такой октет не обязательно включается в данный пакет. В противном случае, должны быть включены только целые символы.
ID кодирующего символа (X), переносимый в каждом исходном пакете, является ID кодирующего символа для первого исходного символа, переносимого в данном пакете. Последующие исходные символы в пакете имеют идентификаторы кодирующего символа от Х+1 до X+G-l в последовательном порядке, где G- количество символов в пакете.
Аналогичным образом, ID кодирующего символа (X), помещенный в пакет для восстановления, является ID кодирующего символа первого символа для восстановления в пакете для восстановления, а последующие символы для восстановления в этом пакете имеют ID кодирующих символов от X+l до X+G-l в последовательном порядке, где G- количество символов в пакете.
Заметим, что приемник не обязательно должен иметь информацию об общем количестве пакетов для восстановления.
5. Спецификация кода RaptorQ с FEC
5.1. Определения, символы и аббревиатуры
В этом разделе в целях спецификации кода RaptorQ с FEC используются следующие определения, символы и аббревиатуры.
5.1.1. Определения
◦ Исходный блок - блок из K исходных символов, которые рассматриваются вместе в целях кодирования и декодирования RaptorQ.
◦ Расширенный исходный блок - блок из K′ исходных символов, где K′>=K, построенный из исходного блока и нуля или более заполняющих символов.
◦ Символ - блок данных. Размер символа в октетах известен как символьный размер. Символьный размер всегда является положительным целым числом.
◦ Исходный символ - минимальный блок данных, используемый в процессе кодирования. Все исходные символы в исходном блоке имеют одинаковый размер.
◦ Заполняющий символ - символ, у которого все биты нулевые; он добавляется к исходному блоку для формирования расширенного исходного блока.
◦ Кодирующий символ - символ, который может быть послан в качестве части процесса кодирования исходного блока. Кодирующие символы исходного блока состоят из исходных символов исходного блока и символов для восстановления, создаваемых из исходного блока. Символы для восстановления, созданные из исходного блока, имеют тот же размер, что и исходные символы данного исходного блока.
◦ Символы для восстановления - кодирующие символы исходного блока, не являющиеся исходными символами. Символы для восстановления создают на основе исходных символов исходного блока.
◦ Промежуточные символы - символы, создаваемые из исходных символов с использованием процесса обратного кодирования. Затем создают символы для восстановления непосредственно из промежуточных символов. Кодирующие символы не включают в себя промежуточные символы, то есть, промежуточные символы не посылаются в качестве части процесса кодирования исходного блока. Промежуточные символы разбивают на LT символов и PI символов.
◦ LT символов - поднабор промежуточных символов, которые могут быть LT соседями кодирующего символа.
◦ PI символов - поднабор промежуточных символов, которые могут быть PI соседями кодирующего символа.
◦ Систематический код - код, в котором все исходные символы включены как часть кодирующих символов исходного блока. Описанный здесь код RaptorQ является систематическим кодом.
◦ ID кодирующего символа (ESI) - информация, которая уникальным образом идентифицирует каждый кодирующий символ, связанный с исходным блоком, в целях его посылки и приема.
◦ Внутренний ID символа (ISI) - информация, которая уникальным образом идентифицирует каждый символ, связанный с расширенным исходным блоком, в целях кодирования и декодирования.
◦ Арифметические операции с октетами, символами и матрицами - операции, используемые для создания кодирующих символов из исходных символов и наоборот. Смотри раздел 5.7.
5.1.2. Символы
i, j, u, v, h, d, a, b, dl, al, b1, v, m, x, y представляют значения или переменные того или иного типа в зависимости от контекста.
X обозначает не отрицательное целочисленное значение, которое равно либо значению ISI, либо значению ESI в зависимости от контекста.
ceil (x) обозначает минимальное целое число, большее или равное x, где x имеет действительное значение.
floor (x) обозначает максимальное целое число, меньшее или равное x, где x имеет действительное значение.
min(x,y) обозначает минимальное значение из значений x и y и в общем случае - минимальное значение из всех значений аргумента.
max(x,y) - обозначает максимальное значение из значений x и y и в общем случае - максимально значение из всех значений аргумента.
i% j обозначает остаток от деления i на j.
i+j обозначает сумму i и j. Если i и j- октеты (соответственно символы), это означает арифметическую операцию с октетами (соответственно с символами), как определено в разделе 5.7. Если i и j целые числа - это означает обычное целочисленное суммирование.
i*j означает произведение i на j. Ели i и j октеты, это обозначает арифметическую операцию с октетами, как определено в разделе 5.7. Если i- октет, а j- символ, это означает умножение символа на октет, что также определено в разделе 5.7. Наконец, если i и j- целые числа, то i*j означает обычное целочисленное произведение.
а ˆˆ b означает операцию возведения в степень b. Если a- октет, и b- не отрицательное целое число, это означает, что a*a*...*a (b членов), где ′*′- произведение октетов, как определено в разделе 5.7.
u ˆ v означает для битовых цепочек u и v равной длины двоичную операцию «исключающее ИЛИ» с u и v.
Transpose [A] означает транспонированную матрицу матрицы А. В этой спецификации все матрицы имеют элементы, являющиеся октетами.
A-ˆˆ1 обозначает обращенную матрицу матрицы А. В этой спецификации все матрицы в качестве элементов имеют октеты, из чего следует, что операции с элементами матрицы должны выполняться, как это установлено в разделе 5.7., а Aˆˆ-1 является обратной матрицей матрицы А согласно октетной арифметике.
K обозначает количество символов в одном исходном блоке.
K′ обозначает суммарное количество исходных и заполняющих символов в расширенном исходном блоке. В большей части этой спецификации заполняющие символы рассматриваются как дополнительные исходные символы.
K′_max обозначает максимальное количество исходных символов, которое может находиться в одном исходном блоке. Это число установлено равным 56403.
L обозначает количество промежуточных символов для одного расширенного исходного блока.
S обозначает количество символов LDPC для одного расширенного исходного блока. Оно составляет LT символов. Для каждого значения K′, показанного в Таблице 8 в разделе 5.6., соответствующее значение S является простым числом.
H обозначает количество символов HDPC для одного расширенного исходного блока, это число составляет PI символов.
B обозначает количество промежуточных символов, а именно, LT символов, включая символы LDPC.
W обозначает количество промежуточных символов, а именно, LT символов. Для каждого значения K′ в Таблице 8, показанной в разделе 5.6., соответствующее значение W является простым числом.
P обозначает количество промежуточных символов, а именно, PI символов. Все они содержат символы HDPC.
P1 обозначает минимальное простое число, больше или равное P.
U обозначает количество промежуточных символов, не являющихся символами HDPC, а именно, PI символов.
С обозначает массив промежуточных символов C[0], C[1], C [2],.C[L -1].
C′ обозначает массив символов расширенного исходного блока, где C′[0], C′[1], C′[2],..., C′[K-1] - исходные символы исходного блока, а C′[K], C′[K+l],..., C′[K′ -1] - заполняющие символы.
VO, Vl, V2 , V3 обозначают четыре массива 32-разрядных целых чисел без знака V0[0], V0[1],...,V0 [255]; Vl[0], V1[1], ...,V1 [255]; V2[0],...,V2 [1], V2 [255]; и V3 [0],..., V3 [1] ,V3 [255] как показано в разделе 5.5.
Rand[y, i, m] обозначает генератор псевдослучайных чисел.
Deg [v] обозначает генератор степени.
Enc [K′, C, (d, a, b, d1, a1, b1)] обозначает генератор кодирующих символов.
Tuple [K′, X] обозначает функцию генератора кортежа.
T обозначает символьный размер в октетах.
J(K′) обозначает систематический индекс, связанный с K′.
G обозначает любую матрицу генератора.
I_S обозначает матрицу тождественности S×S
5.1.3. Аббревиатуры
ESI- ID кодирующего символа
HDPC- контроль по четности с высокой плотностью
ISI- внутренний ID символа
LDPC- контроль по четности с низкой плотностью
LT- преобразование Luby
PI- постоянно инактивный
SBN- номер исходного блока
SBL- длина исходного блока (в символах).
5.2. Обзор
Этот раздел определяет систематический код RaptorQ с FEC.
Символы являются фундаментальными блоками данных в процессе кодирования и декодирования. Для каждого исходного блока все символы имеют одинаковый размер, называемый символьным размером T. Элементарные операции, выполняемые с символами, как при кодировании, так и при декодировании, являются арифметическими операциями, определенными в разделе 5.7.
Базовый кодер описан в разделе 5.3. Этот кодер сначала получает блок промежуточных символов из исходных символов исходного блока. Этот промежуточный блок имеет свойство, состоящее в возможности создания из него как исходных символов, так и символов для восстановления с использованием, одинакового процесса обработки. Кодер создает символы для восстановления из промежуточного блока, используя эффективный процесс, где каждый указанный символ для восстановления представляет собой результат операции «исключающее ИЛИ» с небольшим количеством промежуточных символов из упомянутого блока. Исходные символы также могут быть воспроизведены из промежуточных символов с использованием того же самого процесса. Кодирующие символы представляют собой комбинацию исходных символов и символов для восстановления.
Один пример декодера описан в разделе 5.4. Процесс создания исходных символов и символов для восстановления из промежуточного блока разработан так, что промежуточный блок можно восстановить из любого достаточно большого набора кодирующих символов независимо от соотношения исходных символов и символов для восстановления в этом наборе. После восстановления промежуточного блока могут быть восстановлены пропущенные символы исходного блока с использованием процесса кодирования.
Требования к совместимому декодеру RaptorQ сформулированы в разделе 5.8. Для удовлетворения этих требований можно использовать ряд алгоритмов декодирования. Эффективный алгоритм декодирования для удовлетворения указанных требований изложен в разделе 5.4.
Построение промежуточных символов и символов для восстановления частично основано на использовании генератора псевдослучайных чисел, описанного в разделе 5.3. Работа этого генератора основана на фиксированном наборе из 1024 случайных чисел, которые должны быть доступны как отправителю, так и приемнику. Эти числа представлены в разделе 5.5. В операциях кодирования и декодирования для RaptorQ используются операции с октетами. В разделе 5.7. описано, как выполнять эти операции.
Наконец, построение промежуточных символов из исходных символов диктуется использованием «систематических индексов», значения которых приведены в разделе 5.6. для конкретных размеров расширенного исходного блока в диапазоне от 6 до K′_max =56403 исходных символа. Таким образом, код RaptorQ поддерживает исходные блоки в диапазоне от 1 до 56403 исходных символов.
5.3. Систематический кодер RaptorQ
5.3.1. Введение
Для данного исходного блока, состоящего из K исходных символов, для кодирования и декодирования исходный бок дополняется K′- K дополнительными заполняющими символами, где K′ имеет весьма малое значение, равное по меньшей мере K, в Таблице 8 систематических индексов в разделе 5.6. Причина дополнения исходного блока множеством K′ состоит в необходимости дать возможность ускорить кодирование и декодирование и минимизировать объем табличной информации, которую необходимо хранить в кодере и декодере.
При передаче и приеме данных значение K используют для определения количества исходных символов в исходном блоке, и поэтому K должно быть известно отправителю и приемнику. В этом случае отправитель и приемник могут вычислить K′ из K, после чего K′- K заполняющих символов могут быть автоматически добавлены к исходному блоку без какой-либо дополнительной передачи. Отправитель и приемник используют ID кодирующего символа (ESI) для идентификации кодирующих символов исходного блока, где кодирующие символы исходного блока состоят из исходных символов и символов восстановления, связанных с исходным блоком. Для исходного блока с K исходными символами идентификаторы ESI для исходных символов представляют собой 0,1,2,...,K-1, причем идентификаторы ESI для символов для восстановления представляют собой K, K+l,..., K+2,.... Использование ESI для идентификации кодирующих символов при транспортировке обеспечивает непрерывную последовательность значений ESI между исходными символами и символами для восстановления.
Для кодирования и декодирования, данных значение K′, полученное из K, используют в качестве количества исходных символов расширенного исходного блока, после чего выполняют операции кодирования и декодирования, где K′ исходных символов состоят из K первоначальных исходных символов и K′-K дополнительных заполняющих символов. Внутренний идентификатор символа (ISI) используется кодером и декодером для идентификации символов, связанных с расширенным исходным блоком, то есть, для создания кодирующих символов и для декодирования. Для исходного блока с K первоначальными исходными символами идентификаторы ISI для первоначальных исходных символов представляют собой 0,1,2,..., K-1, идентификаторы ISI для K′-K заполняющих символов представляют собой K, K+l, K+2,..., K′-l, а идентификаторы ISI для символов для восстановления представляют собой K′, K′+l, K′+2.... Использование идентификаторов ISI для кодирования и декодирования позволяет обрабатывать заполняющие символы расширенного исходного блока таким же образом, как другие исходные символы расширенного исходного блока, причем для данного количества K′ исходных символов в расширенном исходном блоке независимо от K создается сходным образом заданный префикс из символов для восстановления.
Соотношение между идентификаторами ESI и ISI просты: идентификаторы ESI и идентификаторы ISI для K первоначальных исходных символов одинаковые, K′-K заполняющих символов имеют ISI, но не имеют соответствующий ESI (поскольку они являются символами, которые и не посылаются, и не принимаются), ISI символа для восстановления представляет собой просто ESI символа для восстановления плюс K′-K. Трансляция между идентификаторами ESI, используемых для идентификации посланных и принятых кодирующих символов и соответствующими идентификаторами ISI, используемыми для кодирования и декодирования, и правильное заполнение расширенного исходного блока заполняющими символами, используемыми для кодирования и декодирования, лежит на функции заполнения в кодере/декодере RaptorQ.
5.3.2. Обзор кодирования
Систематический кодер RaptorQ используют для создания некоторого количества символов для восстановления из исходного блока, состоящего из K исходных символов, которые размещены в расширенном исходном блоке C′. В таблице 4 представлены основные положения о кодировании. Первый шаг кодирования состоит в построении расширенного исходного блока путем добавления нулевых заполняющих символов или заполняющих символов с ненулевым значением, так чтобы общее количество символов K′ представляло собой одно из значений, перечисленных в разделе 5.6. Каждый заполняющий символ состоит из T октетов, где значение каждого октета равно нулю. K′ должно выбираться как минимальное значение K′ из Таблицы в разделе 5.6., причем K′ больше или равно K.
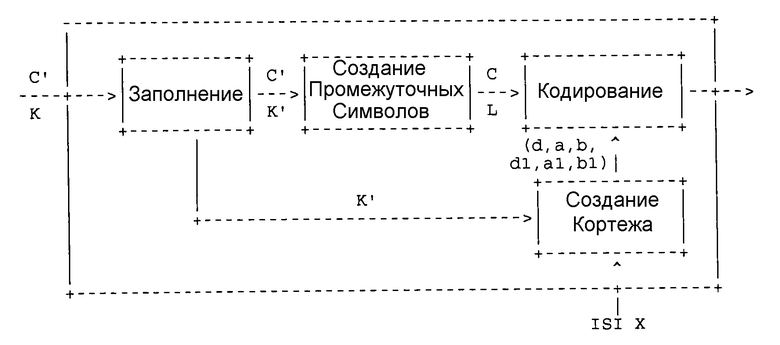
Таблица 4. Обзор кодирования
Пусть, C′[0],..., C′[K-1] обозначает K исходных символов.
Пусть, C′[K],..., C′[K′-1] обозначает K′-K заполняющих символов, каждый из которых имеет значение нуль бит. Далее C′[0],...,C′[K′-1] представляют символы расширенного исходного блока, после чего выполняется кодирование и декодирование.
В оставшейся части данного описания эти заполняющие символы рассматриваются как дополнительные исходные символы, причем они так и называются. Однако эти заполняющие символы не являются частью кодирующих символов, то есть, они не посылаются как часть символов при кодировании. В приемнике значение K′ может быть вычислено на основе K, после чего приемник может добавить K′-K заполняющих символов в конец исходного блока, состоящего из K′ исходных символов, и восстановить оставшиеся K исходных символов исходного блока из принятых кодирующих символов.
Второй шаг кодирования состоит в создании набора из промежуточных символов (L>K′) из K′ исходных символов. На этом шаге создают K′ исходных кортежей (d[0], a[0], b[0], d1 [0], a1[0], b1 [0]),..., (d[K′-1], a[K′-1], b[K′-1], d1[K′-1], a1[K′-1], b1 [K′ -1]) с использованием генератора Tuple[], как описано в разделе 5.3.5.4. K′ исходных кортежей ISI K′ и идентификаторы ISI, связанные с K′ исходными символами, используют для определения L промежуточных символов C[0],..., C[L -1] из исходных символов с использованием процесса обратного декодирования. Этот процесс может быть реализован с помощью процесса декодирования RaptorQ.
В L промежуточных символах должны поддерживаться определенные «соотношения для предварительного кодирования». Эти соотношения описаны в разделе 5.3.3.3. В разделе 5.3.3.4 описано, каким образом из исходных символов создают промежуточные символы.
После создания промежуточных символов могут быть созданы символы для восстановления. Для символа для восстановления с ISI (X>K′) с использованием генератора Tuple [], описанного в разделе 5.3.5.4., может быть создан кортеж из не отрицательных целых чисел (d, a, b, d1 , a1, b1). Затем кортеж (d, a, b, dl, a1, b1) и ISI X используют для создания соответствующего символа для восстановления из промежуточных символов с применением генератора Enc[], описанного в разделе 5.3.5.3. Тогда соответствующий ESI для этого символа для восстановления будет представлять собой X-(K′-K). Заметим, что исходные символы расширенного исходного блока можно также создать с использованием одного и того же процесса, то есть, для любого X<K′ символ, создаваемый с использованием этого процесса, имеет такое же значение, как C′[X].
5.3.3. Первый шаг кодирования: создание промежуточных символов
5.3.3.1. Общие сведения
Этот шаг кодирования является шагом предварительного кодирования для создания L промежуточных символов C[0],..., C[L -1] из исходных символов C′[0],...,C′[K′ -1], где L>K′ определено в разделе 5.3.3.3. Промежуточные символы определены уникальным образом двумя наборами ограничений:
1. Промежуточные символы связаны с исходными символами набором кортежей исходных символов и идентификаторами ISI исходных символов. Создание кортежей исходных символов определено в разделе 5.3.3.2 с использованием генератора Tuple [], описанного в разделе 5.3.5.4.
2. В самих промежуточных символах поддерживается ряд соотношений для предварительного кодирования. Они определены в разделе 5.3.3.3.
Далее в разделе 5.3.3.4. определено создание L промежуточных символов.
5.3.3.2. Кортежи исходных символов. Каждый из K′ исходных символов связан с кортежем исходных символов (d [X], a [X], b [X], dl [X], al [X], bl [X]) для 0<=X<K′. Кортежи исходных символов определены с использованием генератора кортежей, определенного в разделе 5.3.5.4. следующим образом:
Для каждого X, 0<=X<K′
(d[X], a [X], b[X], d1 [X], a1 [X] , b1 [X])=Tuple [K, X].
5.3.3.3. Соотношения для предварительного кодирования
Соотношения для предварительного кодирования среди L промежуточных символов определены требованием, заключающимся в том, что набор из S+H линейных комбинаций промежуточных символов оценен нулем. Имеется S символов LDPC и H символов HDPC, и, следовательно, L=K′+S+H. Другая часть из L промежуточных символов разделена на два набора: один набор из W символов LT и другой набор из P символов PI; и, таким образом, это относится к случаю, когда L=W+P. P символов PI обрабатывают не так, как обрабатывают W символов LT в процессе кодирования. P символов PI состоят из H символов HDPC вместе с набором U=P-H других K′ промежуточных символов. W символов LT состоят из S символов LDPC вместе с W-S другими K′ промежуточными символами. Значения этих параметров определяют из K′, как описано ниже, где H (K′), S (K′), и W (K′) определяют из Таблицы 8 в разделе 5.6.
Пусть
◦ S=S(K′)
◦ H=H(K′)
◦ W=W(K′)
◦ L=K′+S+H
◦ P=L-W
◦ Pl обозначает минимальное простое число, большее или равное P
◦ U=P-H
◦ B=W-S
◦ C[0],...,C[B -1] обозначают промежуточные символы, которые являются символами LT, но не символами LDPC.
◦ C[B],...,C[B+S-1] обозначают S символов LDPC, которые также являются символами LT
◦ C[W],..., C[W+U-1] обозначают промежуточные символы, которые являются символами PI, но не являются символами HDPC.
◦ C[L-H],..., C[L-1] обозначают H символов HDPC, которые также являются символами PI.
Первый набор соотношений для предварительного кодирования, называемый соотношениями LDPC, описан ниже, причем он требует, чтобы в конце этого процесса в наборе символов D[0],..., D[S-1] были все нули:
Инициализация символов D[0]=C [B], D[S-1]=C[B+S-1].
Для i=0, B-1 выполнить
٭ a=1+floor (i/S)
٭ b=i% S
٭ D [b]=D[b]+C[i]
٭ b=(b+a) % S
٭ D[b]=D[b]+C[i]
٭ b=(b+a) % S
٭ D [b]=D[b]+C[i]
٭ Для i=0, S-1 выполнить
٭ a=i% P
٭ b=(i+1) % P
٭ D[i]=D[i]+C [W+a]+C [W+b]
Напоминаем, что добавление символов должно выполняться так, как это определено в разделе 5.7.
Заметим, что определенные в вышеописанном алгоритме соотношения LDPC являются линейными, то есть, существует матрица G_LDPC, 1 размером S x B и матрица G_LDPC,2 размером S×P, так что
G_LDPC, 1 * Transpose [(C [0],..., C[B-1])]+G_LDPC,2 *
Transpose (C [W],..., C[W+P-1]) + Transpose [(C [B],..., C[B+S-1])]=0
(Матрица G_LDPC,1 определяется первым циклом в вышеописанном алгоритме, а матрицу G_LDPC,2 можно получить из второго цикла).
Второй набор соотношений между промежуточными символами C[0],..., C[L-1] представляет собой соотношения HDPC, которые определяются следующим образом:
Пусть
◦ alpha обозначает октет, представленный целым числом 2 как это определено в разделе 5.7.
◦ MT обозначает матрицу октетов H×(K′+S), где для j=0,..., K′+S-2 элемент MT[i,j]- октет, представленный целым числом 1; если i= Rand [j+1, 6,H] или i=(Rand [j+1, 6 ,H]+Rand[j+1,7,H-1]+1)% H и MT[i,j] - нулевой элемент для всех других значений i, и для j=K′+S-l, MT[i,j]=alphaΛΛi для i=0,..., H-l.
◦ GAMMA обозначает матрицу октетов (K′+S)×(K′+S), где
GAMMA [i, j]=
alpha ˆˆ (i-j) для i>=j ,
0 в противном случае.
Далее соотношение между первыми K′+S промежуточным символами C[0],..., C[K′+S-1] и H символами HDPC C [K′ +S],..., C[K′+S+H-1] задается как:
Transpose [C [K′+S],...,C[K′+S+H-1]]+MT*GAMMA *
Transpose [C[0],..., C[K′+S-1]]=0,
где ′ * ′ представляет стандартное матричное умножение с использованием умножения октетов для определения умножения матрицы октетов и матрицы символов (в частности, вектора столбцов символов), а ′+′ обозначает суммирование октетных векторов.
5.3.3.4. Промежуточные символы
5.3.3.4.1. Определение
Для заданных K′ исходных символов C′[0], C[1],...,C′[K′-1]: L промежуточных символов C[0], C[1],..., C[L-1] представляют собой уникальным образом определенные символьные значения, удовлетворяющие следующим условиям:
1. K′ исходных символов C′[0], C′[1],..., C′[K′-1] удовлетворяют K′ ограничениям
C [X]=Enc [K′, (C [0],..., C [L-1] ), (d[X], a[X], b [X], dl [X], al [X], bl[X])], для всех X, где 0<=X<K′,
где (d[X], a [X], b [X], dl [X], al [X], bl [X])= Tuple [K′, X]; Tuple [] определен в разделе 5.3.5.4, а Enc [] описан в разделе 5.3.5.3.
2. L промежуточных символов C[0], C[1],..., C[L-1] удовлетворяют соотношениям для предварительного кодирования, определенным в разделе 5.3.3.3.
5.3.3.4.2. Примерный способ вычисления промежуточных символов
В этом разделе описывается возможный способ вычисления L промежуточных символов C[0], C[1],..., C[L-1], удовлетворяющих ограничениям в разделе 5.3.3.4.1.
L промежуточных символов можно вычислить следующим образом:
Пусть
◦ С обозначает вектор столбцов из L промежуточных символов C[0], C[1],..., C[L-1].
◦ D обозначает вектор столбцов, состоящий из S+H нулевых символов, за которыми следуют K′ исходных символов C [0],..., C[1], C [K′ -1].
Далее вышеуказанные ограничения определяют матрицу A октетов размером L×L, так что:
A*C=D.
Матрица A может быть построена следующим образом:
Пусть:
G_LDPC,1 и G_LDPC,2 представляют собой матрицы S×B и S×P, определенные в разделе 5.3.3.3.
G_HDPC представляет собой матрицу H x (K′ +S), так что
G_HDPC * Transpose (C [0],..., C [K′+S -1])= Transpose (C [K′+S]..., C[L-1]),
то есть, G_HDPC = MT*GAMMA
I_S представляет собой матрицу тождественности S×S
I_H представляет собой матрицу тождественности H×H
G_ENC представляет матрицу K′×L, так что
G_ENC * Transpose [(C[0],..., C[L-1])]=
Transpose [(C′[0],C′[l],..., C′[K′-l])],
то есть, G_ENC[i,j]=1, если и только если C[j] включен в символы, которые суммируют для создания Enc[K′, (C[O],...,
C[L-1] ), (d[i], a[i], b[i], dl [i], al [i], bl [i])] и
G_ENC[i,j]=0 в противном случае.
Далее:
Первые S строк матрицы A равны G_LDPC,1|I_S|G_LDPC,2.
Следующие H строк матрицы A равны G_HDPC|I_H.
Остальные K′ строк матрицы A равны G_ENC.
Матрица A показана ниже в Таблице 5:
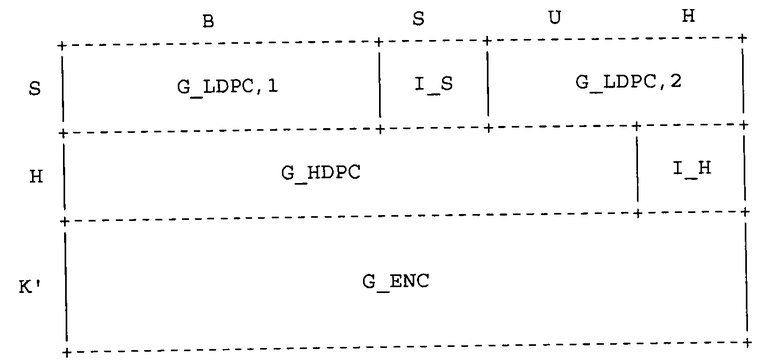
Таблица 5. Матрица А
Затем вычисляют промежуточные символы как:
C=(Aˆˆ-1)*D
Исходные кортежи создают таким образом, чтобы для любого K′ матрица А имела полный ранг и, следовательно, была обратимой. Это вычисление можно реализовать путем использования процесса декодирования RaptorQ для K′ исходных символов C′[0],..., C′[1], C′[K′-1] с целью создания L промежуточных символов C[0],..., C[1], C[L-1].
Для эффективного создания промежуточных символов из исходных символов рекомендуется использовать вариант реализации эффективного декодера, например, декодера, описанного в разделе 5.4.
5.3.4. Второй шаг кодирования: кодирование
На втором шаге кодирования создается символ для восстановления с ISI X (X>=K′) с применением генератора Enc [K′, (C[0], C[1],..., C[L-1]), (d, a, b, dl, al, bl) ], определенного в разделе 5.3.5.3., для L промежуточных символов C[0], C[1],..., C[L-1] с использованием кортежа (d, a, b, dl, al, bl)=Tuple [K′ ,X].
5.3.5. Генераторы
5.3.5.1. Генератор случайных чисел
Генератор Rand[y, i, m] случайных числе определен следующим образом: y не отрицательное целое число, i не отрицательное целое число, меньшее 256, и m положительное целое число, причем создаваемое значение является целым числом между 0 и m-1. Пусть VO, Vl, V2 и V3 - массивы, обеспеченные в разделе 5.5.
Пусть
◦ x0=(y+i) mod 2ˆˆ8
◦ xl=(floor(y/2ˆˆ8)+i)mod 2ˆˆ8
◦ x2=(floor(y/2ˆˆ16)+i)mod 2ˆˆ8
◦ x3=(floor(y/2ˆˆ24)+i)mod 2ˆˆ8
Далее
Rand [y, i, m]=(V0 [x0] ˆ Vl [xl] ˆ V2[x2] ˆ V3 [x3]) % m
5.3.5.2. Генератор степени
Генератор Deg[v] степени определяется следующим образом: где v не отрицательное целое число, меньшее 2ˆˆ20=1048576. При заданном v находят индекс d в Таблице 6, так чтобы выполнялось неравенство f [d-1]<=v<f [d], и устанавливают Deg [v]=min(d, W-2). Напоминаем, что W получают из K′, как это описано в разделе 5.3.3.3.
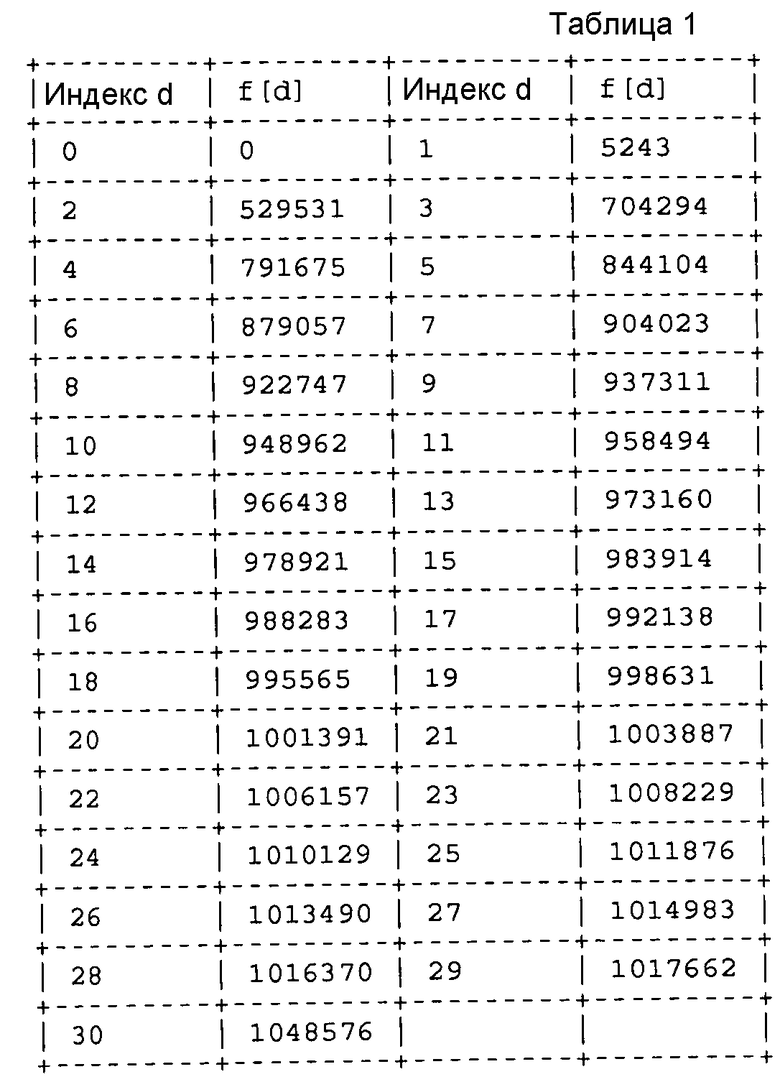
Таблица 6: Определяет распределение степени для кодирующих символов
5.3.5.3. Генератор кодирующих символов
Генератор кодирующих символов Enc[K′, (C[0], C[1],..., C[L-1]), (d, a, b, dl, al, b1)] получает следующие входные данные:
K′ количество исходных символов для расширенного исходного блока.
Пусть L, W, B, S, P и Pl получают из K′, как это описано в разделе 5.3.3.3.
(C[0], C[1],..., C[L-1]) массив из L промежуточных символов (субсимволы), созданных, как это описано в разделе 5.3.3.4.
٭ (d, a, b, dl , al, b1) исходный кортеж, определенный из ISI X с использованием генератора кортежа, определенного в разделе 5.3.5.4., где
٭d- положительное целое число, обозначающее степень LT кодирующего символа
٭a- положительное целое число между 1 и W-1 включительно
٭b- не отрицательное целое число между 0 и W-1 включительно
٭d1- положительное целое число, имеющее значение 2 или 3 включительно, обозначающее степень PI кодирующего символа
٭a1- положительное целое число между 1 и P1-1 включительно
٭b1- не отрицательное целое число между 0 и P1-1 включительно.
Генератор кодирующих символов создает один кодирующий символ в качестве выходных данных (называемых результатом) согласно следующему алгоритму:
◦ result=C [b]
◦ Для j=1, d-1 выполнить
◦ b=(b+a) % W
◦ result = result+C [b]
◦ пока (b1>=P) выполнить b1=(b1+al) % P1
◦ result = result+C[W+b1]
◦ Для j=1,..., d1-1 выполнить
٭ b1=(b1+a1) % P1
٭ пока (b1>=P) выполнить b1=(b1+a1) % P1
٭ result = result+C [W+b1]
◦ Возвращение результата
5.3.5.4. Генератор кортежей
Генератор кортежей Tuple [K′,X] получает следующие входные данные:
◦ K′ количество исходных символов в расширенном исходном блоке
◦ X-An ISI.
Пусть
◦ L определяется из K′, как описано в разделе 5.3.3.3.
◦ J=J(K′) систематический индекс, связанный с K′, как это определено в Таблице 2 в разделе 5.6.
Выходом генератора кортежей является кортеж (d, a, b, d1, a1, b1) определенный следующим образом:
◦ A=53591+J*997
◦ если (A% 2=0) {A=A+1}
◦ B=10267*(J+1)
◦ y=(B+X*A) % 2ΛΛ32
◦ v=Rand[y, 0, 2ΛΛ20]
◦ d=Deg [v]
◦ a=1+Rand[y, 1, W-1]
◦ b=Rand[y, 2, W]
◦ Если (d<4) {d1=2+Rand [X, 3, 2]}, в противном случае {d1=2}
◦ a1=1+Rand[X, 4, P1-1]
◦ b1=Rand [X, 5, P1]
5.4. Примерный декодер с FEC
5.4.1. Общие положения
В этом разделе описывается эффективный алгоритм декодирования для кода RaptorQ, предложенного в этой спецификации. Заметим, что каждый принятый кодирующий символ представляет собой известную линейную комбинацию промежуточных символов. Так, каждый принятый кодирующий символ обеспечивает линейное уравнение, связывающее промежуточные символы, которое, вместе с известными линейными соотношениями для предварительного кодирования между промежуточными символами, приводит к системе линейных уравнений. Таким образом, любой алгоритм для решения систем линейных уравнений может обеспечить успешное декодирование промежуточных символов, а значит, и исходных символов. Однако, выбранный алгоритм оказывает большое влияние на вычислительную эффективность декодирования.
5.4.2. Декодирование расширенного исходного блока
5.4.2.1. Общие положения
Предполагается, что декодер имеет информацию о структуре исходного блока, подлежащего декодированию, включая символьный размер T и количество K символов в исходном блоке, а также количество K′ исходных символов в расширенном исходном блоке.
Из описания алгоритмов в разделе 5.3. следует, что декодер RaptorQ может вычислить общее количество L=K′+S+H промежуточных символов и определить, каким образом они были созданы из расширенного исходного блока, подлежащего декодированию. В этом описании предполагается, что принятые кодирующие символы для расширенного исходного блока, подлежащего декодированию, поступают в упомянутый декодер. Кроме того, предполагается, что для каждого указанного кодирующего символа в декодер поступает количество и набор промежуточных символов, чья сумма равна кодирующему символу. В случае исходных символов, включающих в себя заполняющие символы, кортежи исходных символов, описанные в разделе 5.3.3.2, указывают количество и набор промежуточных символов, которые суммируются, образуя каждый исходный символ.
Пусть N>=K′ - количество принятых кодирующих символов, подлежащих использованию для декодирования, включая заполняющие символы для расширенного исходного блока, и пусть M=S+H+N. Тогда с использованием обозначений в разделе 5.3.3.4.2. получим, что A*C=D.
Декодирование расширенного исходного блока эквивалентно декодированию C исходя из известных матриц A и D. Очевидно, что матрицу C можно декодировать, если и только если ранг матрицы A равен L. После декодирования матриц C можно получить пропущенные исходные символы путем использования кортежей исходных символов для определения количества и набора промежуточных символов, которые необходимо просуммировать для получения каждого пропущенного исходного символа.
Первый шаг декодирования матрицы С состоит в формировании плана декодирования. На этом шаге выполняется преобразование матрицы А с использованием гауссова исключения (с использованием операций со строками и переупорядочивания строк и столбцов), и после отбрасывания M-L строк, в L с помощью матрицы тождественности L. План декодирования состоит из последовательности операций со строками и переупорядочивания строк и столбцов в ходе процесса гауссова исключения, причем этот план зависит, только от матрицы A и не зависит от матрицы D. Декодирование матрицы C из матрицы D может выполняться одновременно с формированием плана декодирования, либо декодирование может выполняться после, на основе указанного плана декодирования.
Соответствие между планом декодирования и декодированием матрицы C состоит в следующем. Пусть изначально с [0]=0, c [1]=1,..., c [L-1]=L-1 и d[0]=0, d[l]=1,..., d[M-1]=M-1.
Каждый раз, когда в плане декодирования к строке i′ добавляется множество (beta) строки i матрицы A, в процессе декодирования к символу D[d[i′]] добавляется символ beta*D[d[i]].
Каждый раз, когда строка i матрицы A умножается на beta (в октетах), в процессе декодирования символ D[d[i]] также умножается на beta. Каждый раз, когда строка i заменяется строкой i′ в плане декодирования, в процессе декодирования значение d[i] заменяется значением d[i′].
Каждый раз, когда столбец j заменяется столбцом j′ в плане декодирования, в процессе декодирования значение c[j] заменяется значением c [j′].
Из этого соответствия, очевидно, вытекает, что общее количество операций с символами при декодировании расширенного исходного блока равно количеству операций со строками (не связанных с заменой) при гауссовом исключении. Поскольку матрица A после гауссова исключения и отбрасывания последних M-L строк представляет собой матрицу тождественности L×L, очевидно, что в конце процесса успешного декодирования L символов D[d[0]], D [d[1]],..., D [d[L-1]] будут представлять собой значения L символов C[c[0]],..., C[C[1]], C[C[L-1]].
Порядок, в котором выполняется гауссово исключение для формирования плана декодирования, не зависит от того, является ли декодирование успешным. Однако скорость декодирования сильно зависит от порядка выполнения гауссова исключения. (Кроме того, крайне важным является поддержка разреженного представления матрицы A, хотя это здесь не описано). Оставшаяся часть этого раздела посвящена описанию возможного относительно эффективного порядка выполнения гауссова исключения.
5.4.2.2. Первая фаза
На первой фазе гауссова исключения матрица A концептуально разбивается на субматрицы, и дополнительно создается матрица X. Эта матрица имеет столько же строк и столбцов, что и матрица A, и она будет представлять нижнюю треугольную матрицу на всей первой фазе. В начале этой фазы матрица A копируется, образуя матрицу X.
Размеры субматрицы параметризируются не отрицательными целыми числами i и u, которые инициализируются в 0 и P, количество символов PI соответственно. Субматрицами матрицы A являются:
1. Субматрица I, определенная пересечением первых i строк и первых i столбцов. В конце каждого шага на этой фазе это будет матрица тождественности.
2. Субматрица, определенная пересечением первых i строк и всех столбцов, кроме первых i столбцов и последних u столбцов. Все элементы этой субматрицы равны нулю.
3. Субматрица, определенная пересечением первых i столбцов и всех строк, кроме первых i строк. Все элементы этой субматрицы равны нулю.
4. Субматрица U, определенная пересечением всех строк и последних u столбцов.
5. Субматрица V, сформированная пересечением всех столбцов, кроме первых i столбцов и последних u столбцов, и всех строк, кроме первых i строк.
В Таблице 7 показаны субматрицы матрицы A. В начале первой фазы V=A. На каждом шаге выбирают строку из матрицы A.
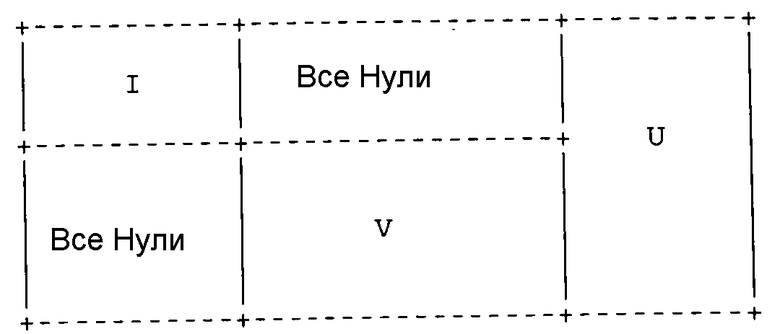
Таблица 7. Субматрицы матрицы A на первой фазе
При определении того, какую выбрать строку из матрицы A, используют следующий граф, определенный структурой субматрицы V. Узлами в этом графе являются столбцы, которые пересекают субматрицу V, а дугами графа, которые соединяют два столбца (узла) в местах двух узлов, являются строки, которые имеют ровно 2 ненулевых элемента в субматрице V и не являются строками HDPC. Компонентой в этом графе является максимальный набор узлов (столбцов) и дуг (строк), так что имеется путь между каждой парой узлов/дуг в этом графе. Размер компоненты это количество узлов (столбцов) в данной компоненте.
На первой фазе имеет место не более L шагов. Эта фаза успешно заканчивается, когда i+u=L, то есть, когда субматрица V и все нулевые субматрицы выше субматрицы V исчезли, а матрица A состоит из субматрицы I, всех нулевых субматриц ниже субматрицы I и субматрицы U. Эта фаза заканчивается безрезультатно при неудаче декодирования, если на каком-либо шаге до исчезновения субматрицы V отсутствует ненулевая строка в субматрице V для выбора на этом шаге. На каждом шаге строку из матрицы A выбирают следующим образом:
Если все элементы субматрицы V являются нулевыми, то ни одна строка не выбирается, и декодирование терпит неудачу.
Пусть r является минимальным целым числом, таким, что по меньшей одна строка матрицы A имеет ровно r единиц в субматрице V.
Если r=2, то тогда выбирают строку, имеющую ровно r единиц в субматрице V с минимальной исходной степенью среди всех указанных строк за исключением того, что строки HDPC выбирать не следует, пока не будут обработаны все строки, не относящиеся к HDPC.
Если r=2, то тогда выбирают любую строку, имеющую ровно 2 единицы в субматрице V, которая является частью компоненты с максимальным размером в вышеописанном графе, определяемом субматрицей V.
После выбора строки на этом шаге первая строка матрицы A которая пересекает субматрицу V, заменяется выбранной строкой, так что выбранная строка оказывается первой строкой, которая пересекает субматрицу V. Столбцы матрицы A из числа столбцов пересекающих субматрицу V, переупорядочивают так, что в первом столбце субматрицы V появляется единица из r единиц в выбранной строке, и так, что в последних столбцах субматрицы V появляются остальные r-1 единиц. Аналогичные операции со строками и столбцами выполняются также для матрицы X. Затем ко всем другим строкам матрицы A, лежащим ниже выбранной строки, которые имеют ненулевой элемент в первом столбце матрицы V, добавляется подходящий множитель выбранной строки. В частности, если строка ниже выбранной строки имеет в первом столбце субматрицы V элемент beta, и выбранная строка имеет в первом столбце субматрицы V элемент alpha, то тогда к этой строке добавляют beta/alpha, умножаемый на выбранную строку, чтобы оставить нулевое значение в первом столбце субматрицы V. В конце, увеличивают i на 1, а u увеличивают на r-1, на чем этот шаг завершается.
Заметим, что эффективность обработки можно повысить, если операции со строками, определенные выше, реально не выполнять, пока сама затронутая строка не будет выбрана в процессе декодирования. Это позволяет избежать выполнение операций для строк, которые, в конечном счете, не используются в процессе декодирования, и, в частности, избежать обработку тех строк, для которых beta =1, пока этого действительно не потребуется. Кроме того, операции со строками, необходимые для строк HDPC, могут выполняться для всех указанных строк в рамках одного процесса путем использования алгоритма, описанного в разделе 5.3.3.3.
5.4.2.3. Вторая фаза
В этот момент отброшены все элементы матрицы X вне первых i строк и i столбцов, так что X имеет вид нижней треугольной матрицы. Последние i строк и столбцов матрицы X отброшены, так что матрица X имеет теперь i строк и i столбцов. Субматрица U дополнительно разбита на первые i строк, U_upper, и остальные M-i строк, U_lower. На второй фазе на строках U_lower выполняется гауссово исключение, чтобы либо определить, что ее ранг меньше u (неудача декодирования), либо преобразовать ее в матрицу, где первые u строк являются матрицей тождественности (успешное выполнение второй фазы). Обозначим эту матрицу тождественности u х u как I_u. M-L строк матрицы A, которые пересекают U_lower I_u, отбрасывают. После этого матрица A имеет L строк и L столбцов.
5.4.2.4. Третья фаза
После второй фазы только часть матрицы A, которую необходимо обнулить для окончания преобразования матрицы A в матрицу тождественности L x L, окажется субматрицей U_upper. Количество строк i субматрицы U_upper обычно гораздо больше количества u столбцов субматрицы U_upper. Кроме того, в этот момент матрица U_upper, как правило, является плотной, то есть, количество ненулевых элементов этой матрицы велико. Чтобы привести эту матрицу к разреженному виду, необходимо выполнить в обратном порядке последовательность операций, выполняемых для получения матрицы U_lower. С этой целью матрицу X умножают на субматрицу из матрицы A, состоящую из первых i строк матрицы A. После этой операции субматрица из матрицы A, состоящая из пересечения первых i строк и столбцов, будет равна X, в то время как матрица U_upper преобразуется к разреженному виду.
5.4.2.5. Четвертая фаза
Для каждой из первых i строк субматрицы U_upper выполняется следующее: если строка имеет ненулевой элемент на позиции j, и если значение этого ненулевого элемента равно b, то тогда к этой строке добавляется b раз строка j из I_u. После этого шага субматрица матрицы A, состоящая из пересечения первых i строк и столбцов, будет равна X, субматрица U_upper будет состоять из нулей, субматрица, состоящая из пересечения последних u строк и первых i столбцов, будет состоять из нулей, а субматрица, состоящая из последних u строк и столбцов, будет представлять собой матрицу I_u.
5.4.2.6. Пятая фаза
Для j от 1 до i выполняются следующие операции:
1. Если A[j, j] - не единица, то тогда деление строки j матрицы A на A[j , j ].
2. Для l от 1 до j-1, если A[j,l] не равен нулю, то тогда добавление A[j,l], умноженного на строку l матрицы A, к строке j матрицы A.
После этой фазы матрица A представляет собой матрицу тождественности L×L, и успешно формируется полный план декодирования. Затем может выполняться соответствующее декодирование, состоящее в суммировании известных кодирующих символов, для восстановления промежуточных символов на основе плана декодирования. Кортежи, связанные со всеми исходными символами, вычисляют согласно разделу 5.3.3.2. Кортежи для принятых исходных символов используют при декодировании. Кортежи для пропущенных исходных символов используют для определения того, какие промежуточные символы следует суммировать для восстановления пропущенных исходных символов.
5.5. Случайные числа
Ниже представлены четыре массива, VO, Vl, V2 и V3, используемые в разделе 5.3.5.1. В каждом из этих четырех массивов имеется 256 записей. Индексация в каждом массиве начинается с 0, а записи являются 32-разрядными целыми числами без знака.
5.5.1. Таблица V0




5.5.3. Таблица V2


5.5.4. Таблица V3


5.6. Систематические индексы и другие параметры
В Таблице 8, представленной ниже, заданы поддерживаемые значения K′. Эта таблица также задает для каждого поддерживаемого значения K′ систематический индекс J (K′), количество H(K′) символов HDPC, количество S(K′) символов LDPC и количество W(K′) символов LT. Для каждого значения K′ соответствующие значения S(K′) и W(K′) являются простыми числами.
Систематический индекс J(K′) предназначен для того, чтобы набор кортежей исходных символов (d[0], a[0], b[01, d1 [0] , a1 [0], b1 [0]),..., (d[K′-1l], a[K′-1], b[K′-1], dl[K′-1], a1[K′-1], b1[K′-1]) обеспечивал уникальное определение L промежуточных символов, то есть, матрица A в Таблице 7 имела бы полный ранг и, следовательно, была обратимой.
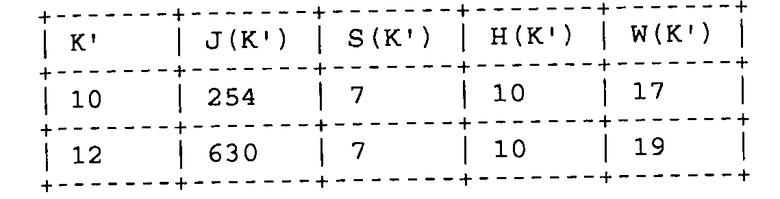
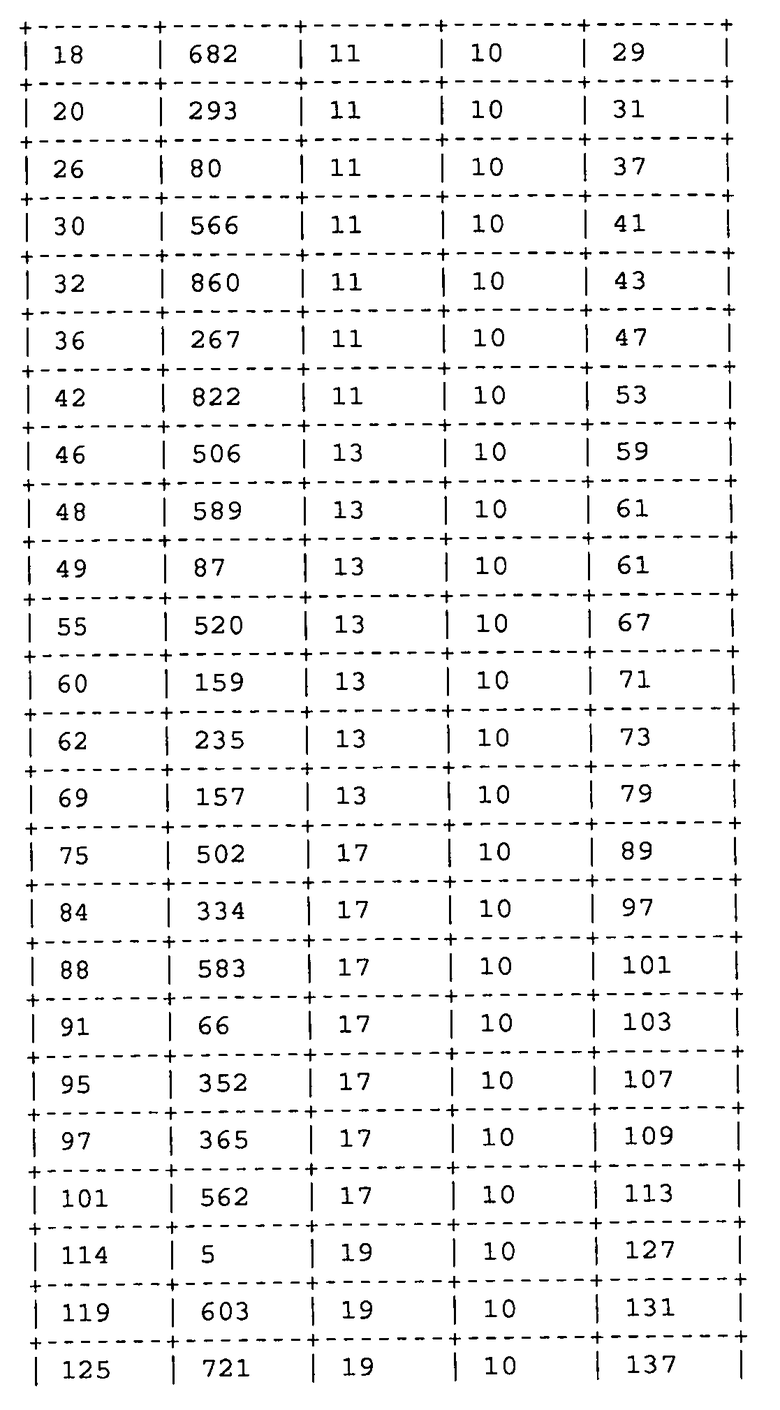
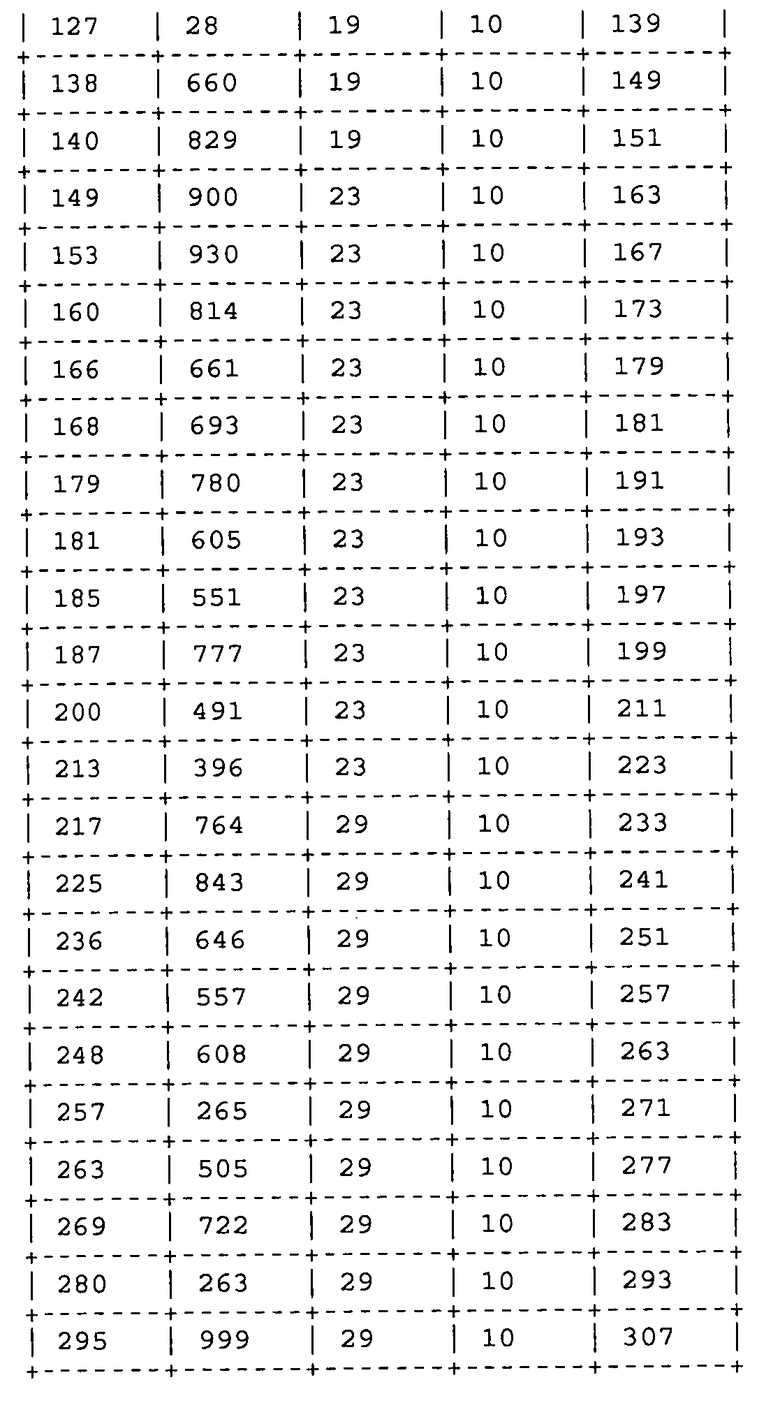
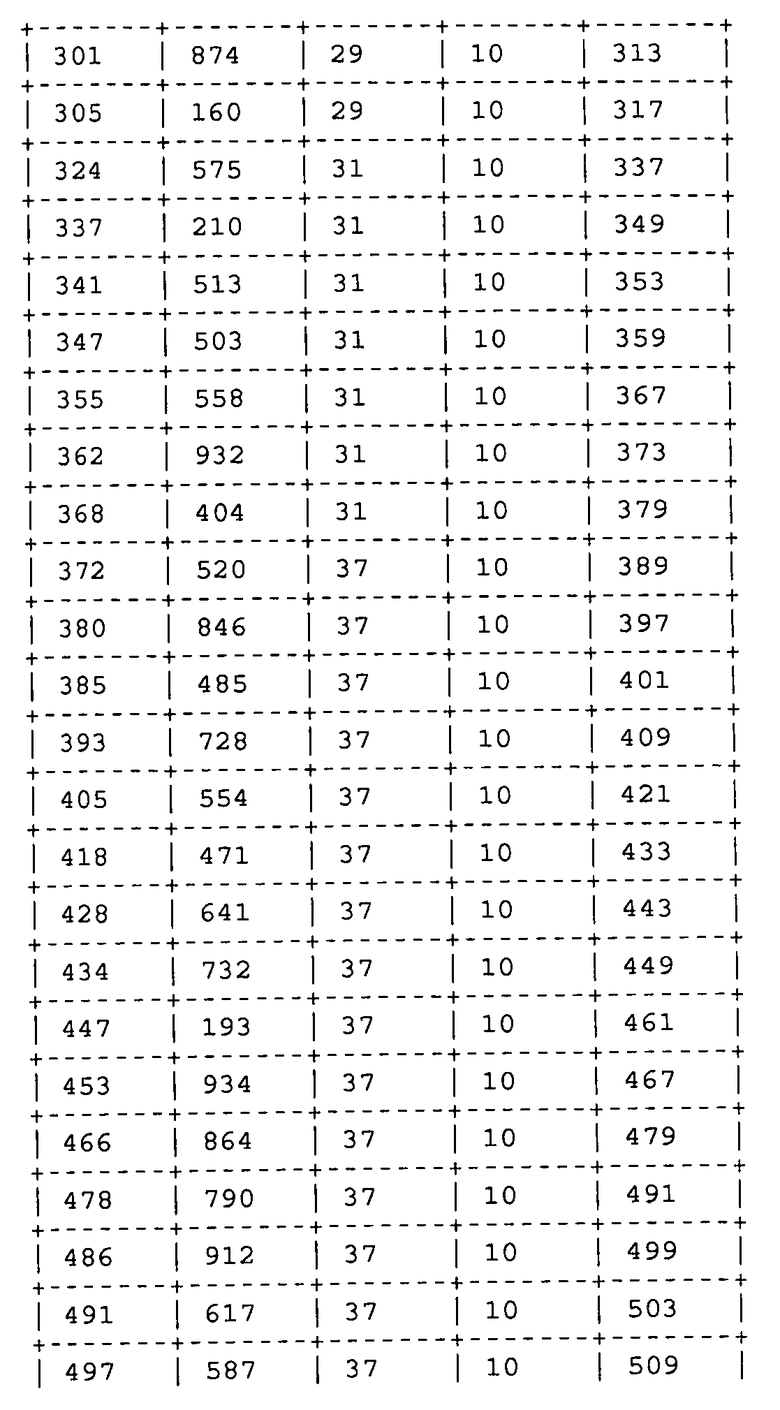
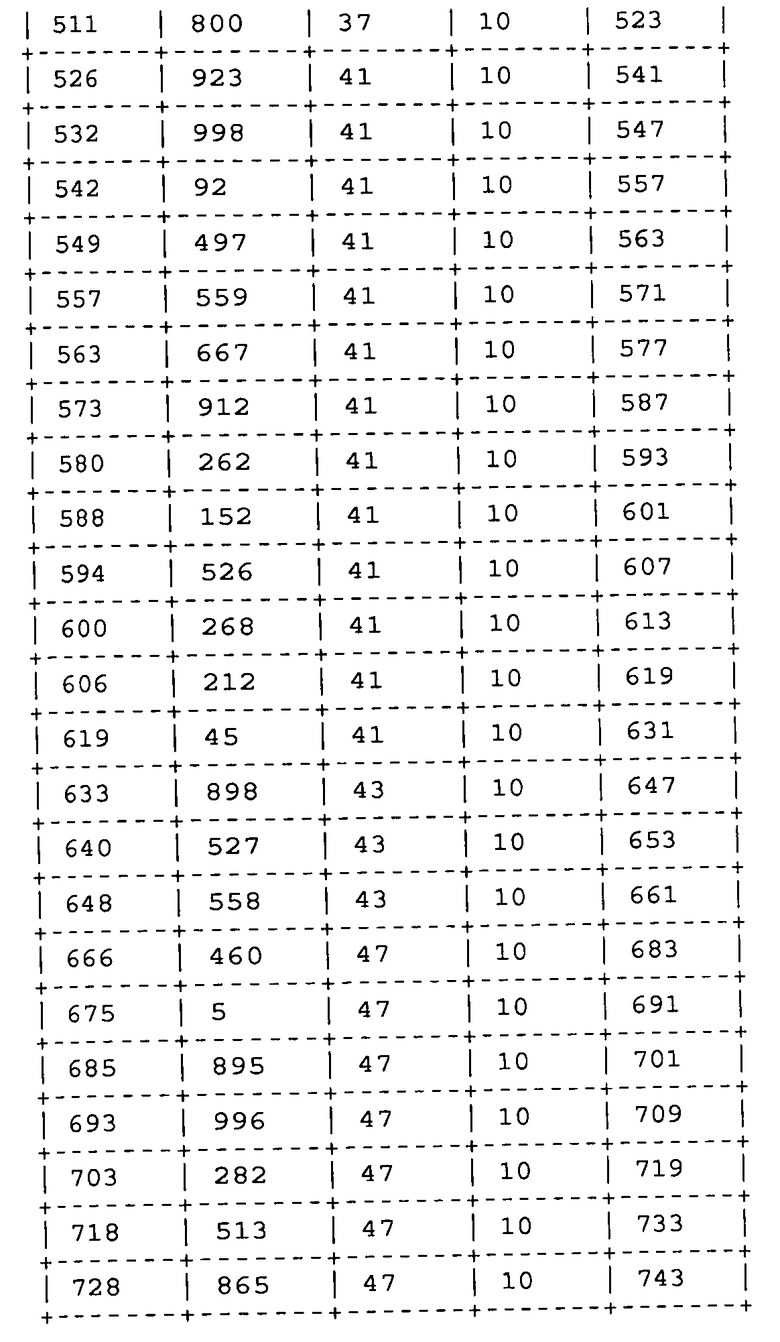
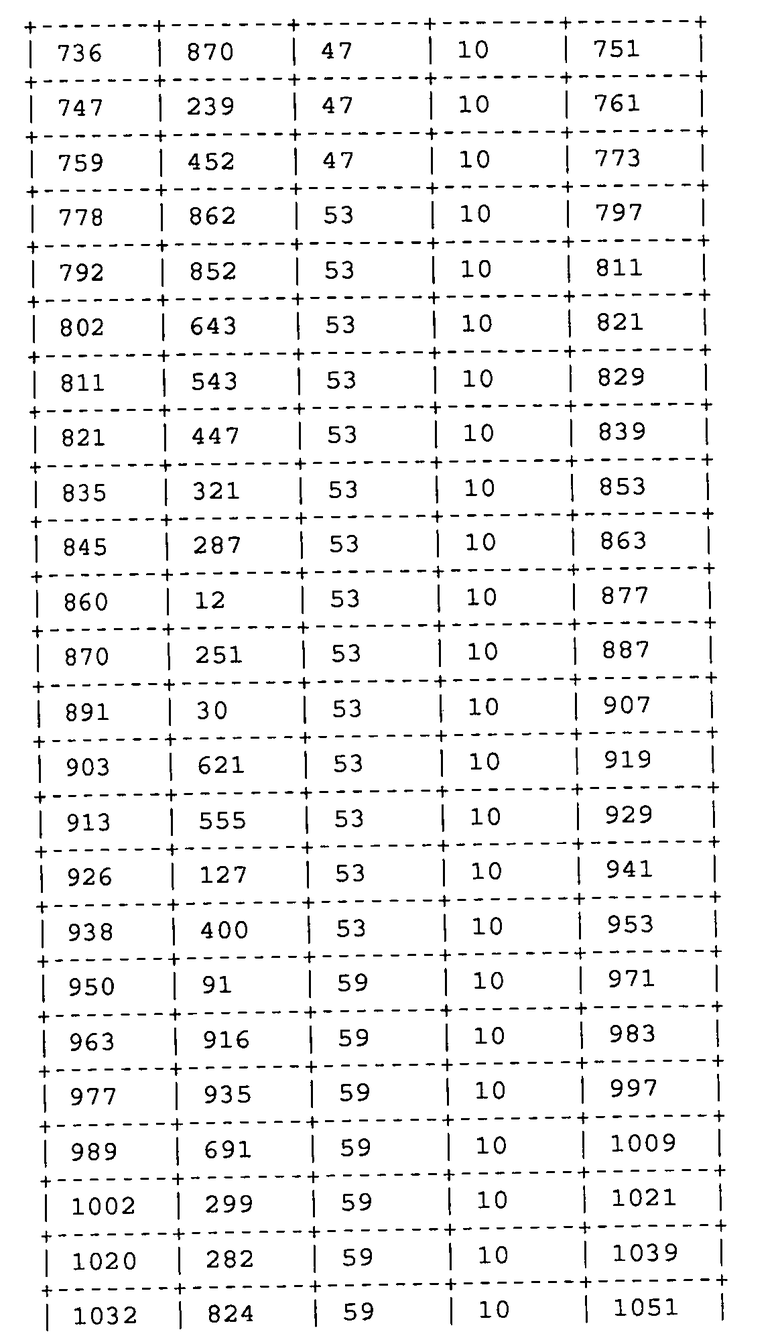

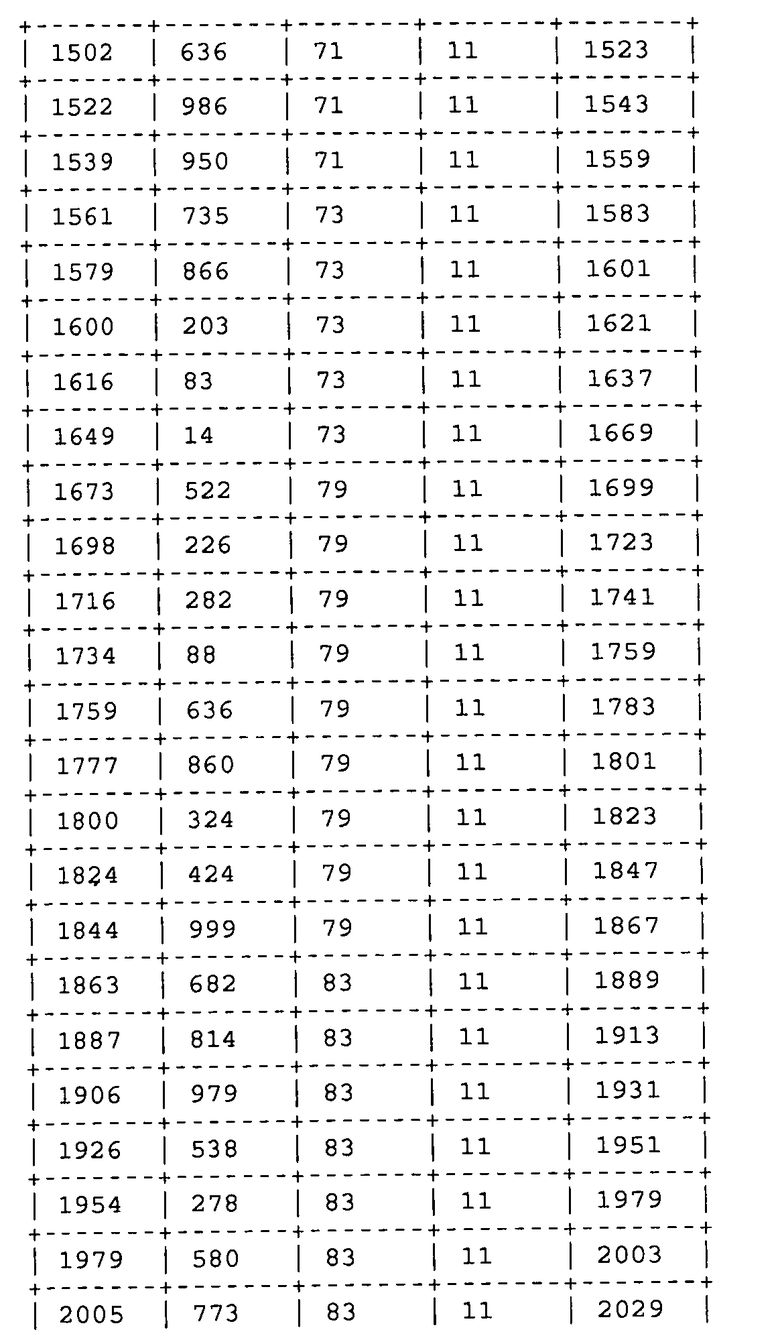
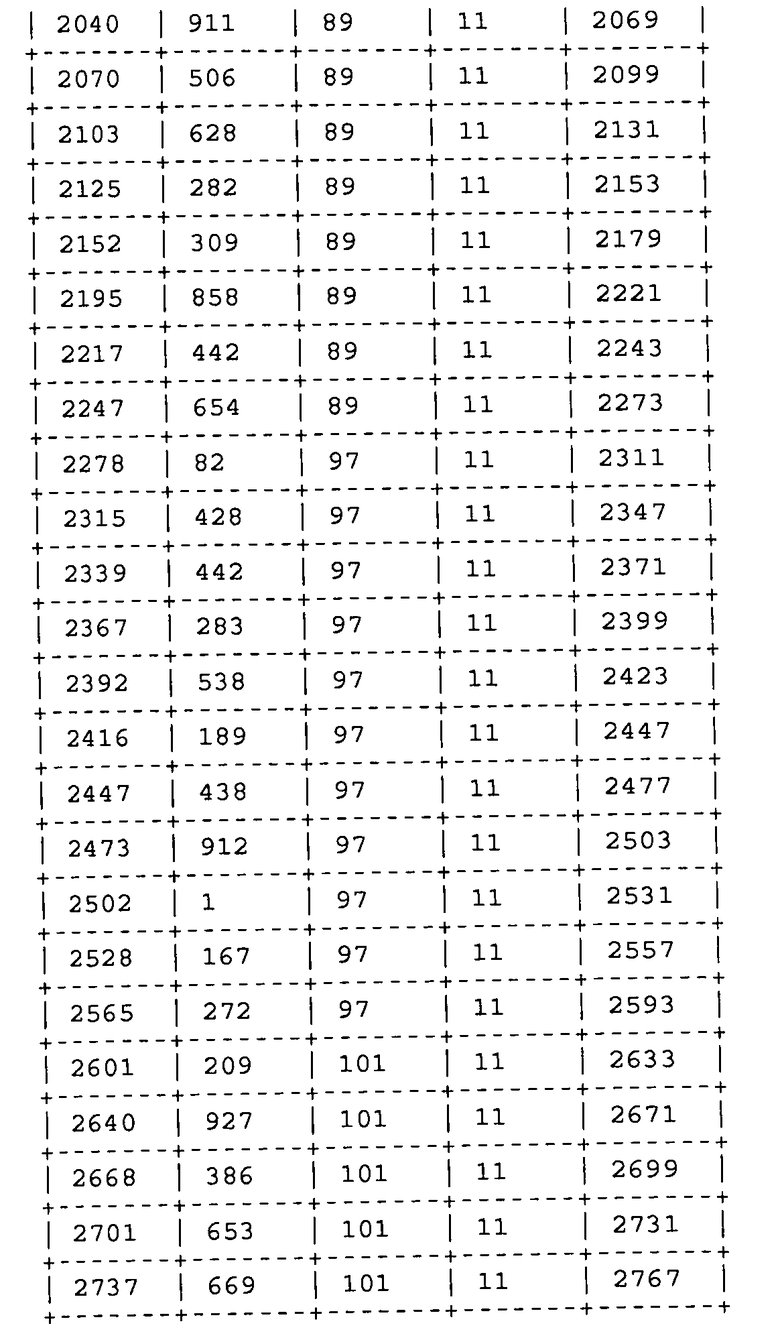
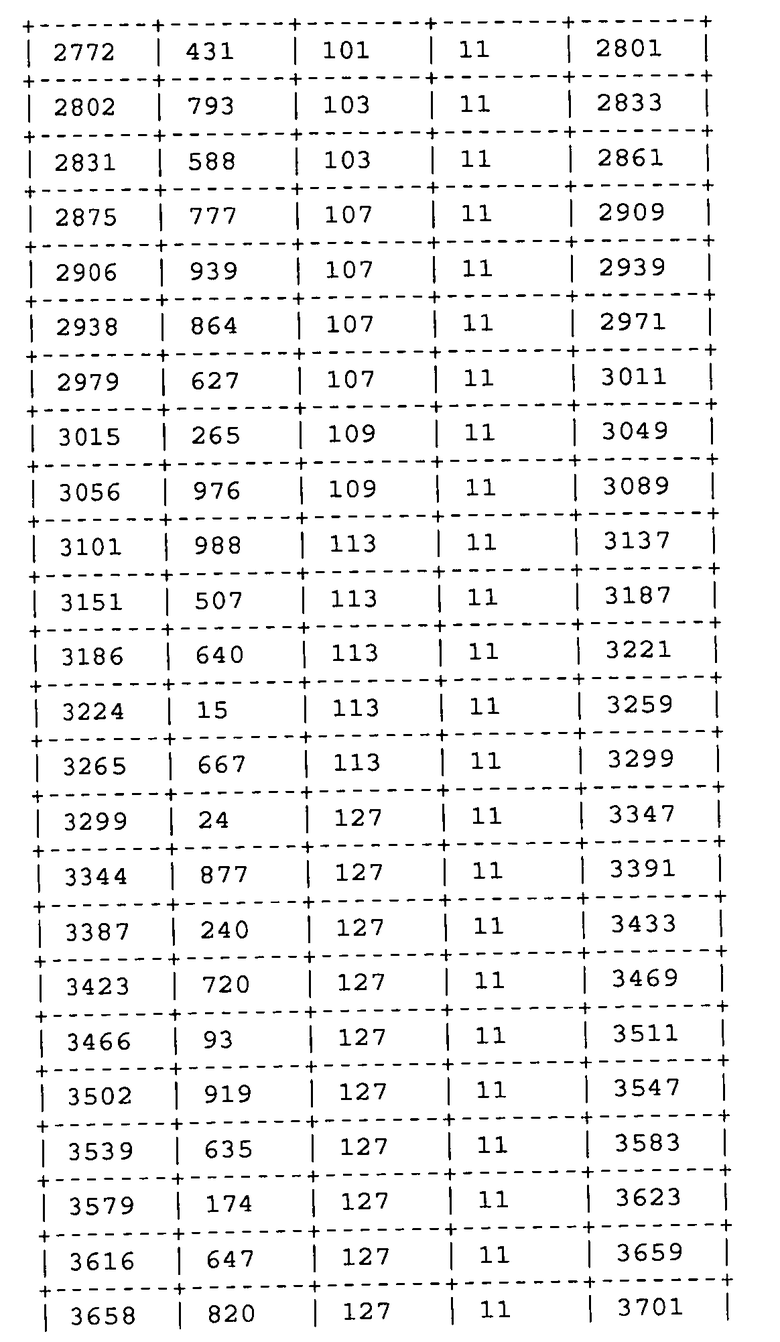
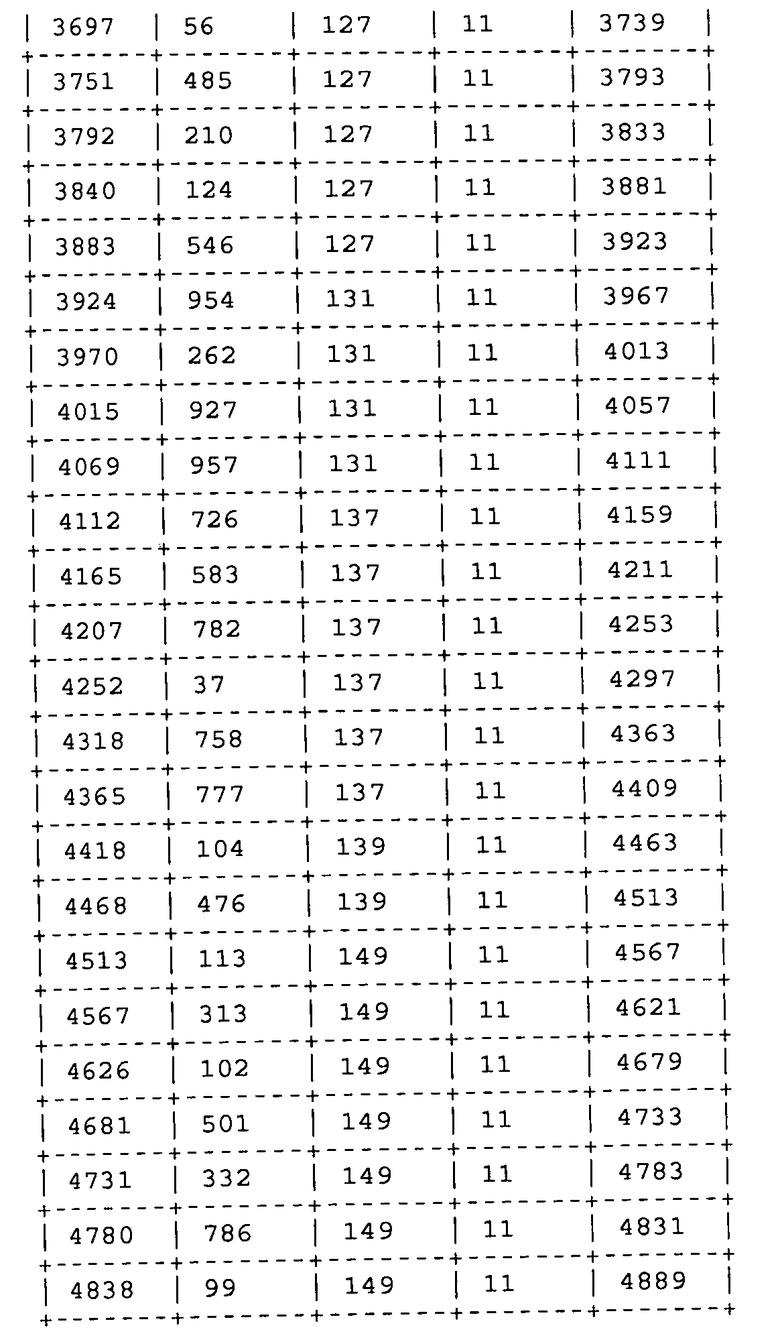
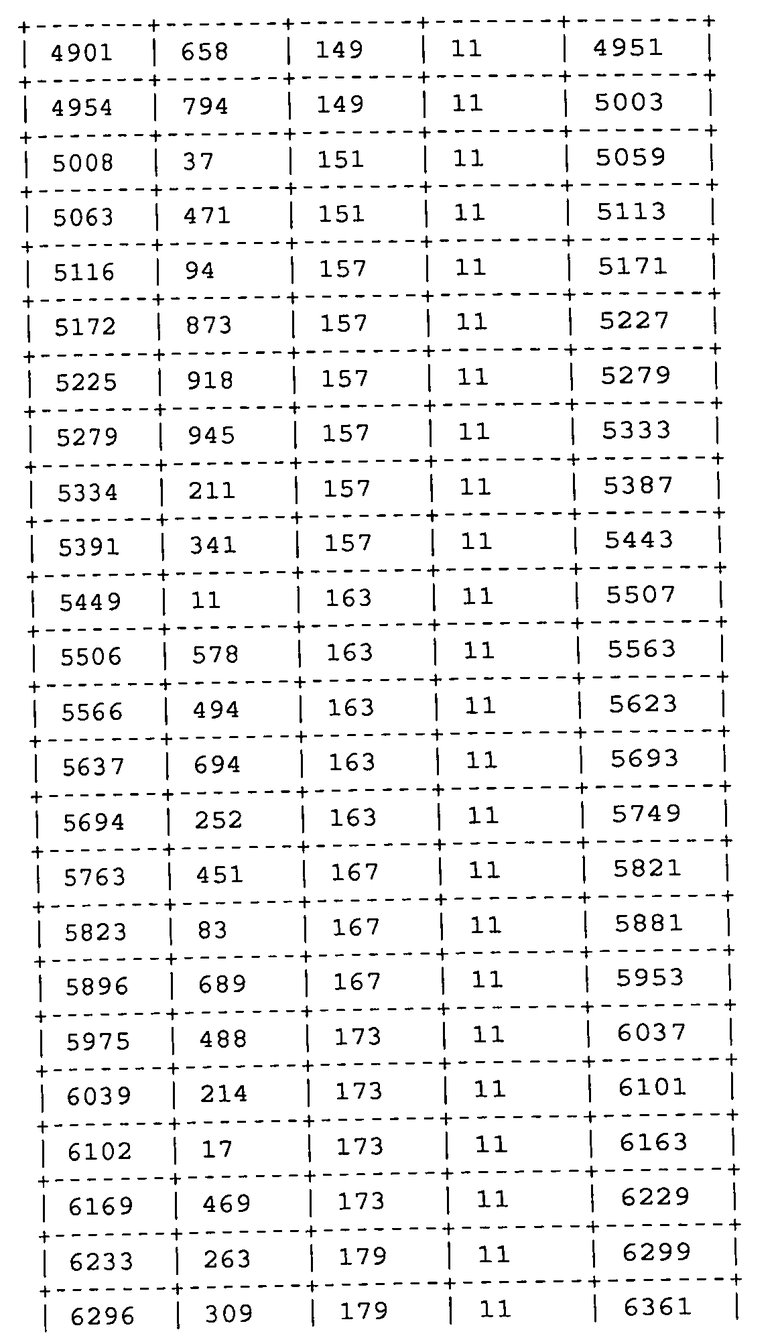
Таблица 8. Систематические индексы и другие параметры
5.7. Операции с октетами, символами и матрицами
5.7.1. Общие положения
В оставшейся части этого раздела описываются арифметические операции, которые используют для создания кодирующих символов из исходных символов и для создания исходных символов из кодирующих символов. Математически октеты можно рассматривать как элементы конечного поля, то есть, конечного поля GF(256) с 256 элементами, для которого определены операции суммирования и умножения и элементы тождественности и операции, обратные вышеуказанным операциям. Матричные операции и символьные операции определены на основе арифметических операций с октетами. Это позволяет полностью реализовать указанные арифметические операции без необходимости понимания базовых математических основ конечных полей.
5.7.2. Арифметические операции с октетами
Октеты преобразуют в неотрицательные целые числа в диапазоне от 0 до 255 обычным путем: один октет данных из одного символа, B [7] ,B [6] ,B [5] ,B [4] ,B [3] ,B [2] ,B [1] ,B [0], где B[7] - бит высшего порядка, а B[0] - бит низшего порядка, преобразуют в целое число i=B[7]*128+B[6]*64+B[5]*32+B[4]*16+B[3]*8+B[2]*4+B[l]*2+B[0].
Суммирование двух октетов u и v, определено как операция «исключающее ИЛИ», то есть,
u+v=u ˆ v.
Вычитание определено аналогичным образом, так что
u-v=u ˆ v.
Нулевой элемент (аддитивная тождественность) является октетом, представленным целочисленным 0. Аддитивной инверсией u является просто u, то есть
u+u=0.
Умножение двух октетов определяется с помощью двух таблиц OCT_EXP и OCT_LOG, которые приведены в разделе 5.7.3 и разделе 5.7.4 соответственно. Таблица OCT_LOG преобразует октеты (отличные от нулевого элемента) в не отрицательные целые числа, а таблица OCT_EXP преобразует не отрицательные целые числа в октеты. Для двух октетов u и v определено, что
u*v=
0, если либо u, либо v равно 0,
OCT_EXP [OCT_LOG [u] + OCT_LOG [v]], в противном случае.
Заметим, что знак ′+′ с правой стороны в вышеуказанном выражении является обычным целочисленным сложением, поскольку его аргументы являются обыкновенными целым числами.
Деление u/v двух октетов u и v, где v=0, определяется следующим образом:
u/v=
0, если u=0,
0CT_EXP [0CT_L0G [u]-0CT_L0G [v] + 255], в противном случае.
Единичный элемент (мультипликативная тождественность) является октетом, представленным целым числом 1. Для октета u, не являющегося нулевым элементом, то есть, мультипликативная инверсия u будет представлять собой
OCT_EXP[255 - OCT_LOG [u]].
Октет, обозначенный как alpha - это октет, представленный целом числом 2. Если i является не отрицательным целым числом, причем 0<=i<256, имеем
alphaˆˆi=OCT_EXP[i].
5.7.3. Таблица OCT_EXP
Таблица OCT_EXP содержит 510 октетов. Индексация начинается с 0 и продолжается до 509, причем записи являются октетами со следующим предположительным целочисленным представлением:


5.7.4. Таблица OCT_LOG
Таблица OCT_LOG содержит 255 не отрицательных целых числа. Эта таблица индексирована октетами, представленными в виде целых чисел. Октет, соответствующий нулевому элементу, который представлен целым числом 0, включен в качестве индекса, и индексация начинается с 1 и продолжается до 255, причем записи выглядят следующим образом

5.7.5. Операции с символами
Операции с символами имеют в этой спецификации такую же семантику, что и операции с векторами октетов длиной T. Таким образом, если U и V являются двумя символами, сформированными октетами u[0],..., u [T-1] и v[0],..., v[T-1] соответственно, то сумма символов U + V определяется как покомпонентная сумма октетов, то есть, равна символу D сформированному октетами d[0],..., d [T-1], так что
d[i]=u[i]+v[i], 0<=i<T.
Кроме того, если beta является октетом, то произведение beta*U определяется как символ D, полученный путем умножения каждого октета из U на beta, то есть,
d[i]=beta*u[i], 0<=i<T.
5.7.6. Операции с матрицами
Все матрицы в этой спецификации имеют элементы, являющиеся октетами, и, следовательно, матричные операции и определения заданы в терминах базовой октетной арифметики, например, операции с матрицей, матричным рангом и обращением матрицы.
5.8. Требования к совместимому декодеру
Если совместимый декодер RaptorQ принимает достаточный с математической точки зрения набор кодирующих символов, созданных в соответствии со спецификацией кодера в разделе 5.3. для восстановления исходного блока, то тогда указанный декодер должен восстановить весь исходный блок. Совместимый декодер RaptorQ должен иметь следующие восстановительные свойства для исходных блоков с K′ исходными символами для всех значений K′ в Таблице 8 раздела 5.6.
1. Если декодер принимает K′ кодирующих символов, созданных согласно спецификации кодера в разделе 5.3., с соответствующими идентификаторами ESI, выбранными независимо и равномерно случайным образом из диапазона возможных идентификаторов ESI, то тогда в среднем неудача при восстановлении декодером всего исходного блока составит не более одного раза на 100.
2. Если декодер принимает K′+1 кодирующих символов, созданных согласно спецификации кодера в разделе 5.3., с соответствующими идентификаторами ESI, выбранными независимо и равномерно случайным образом из диапазона возможных идентификаторов ESI, то тогда в среднем неудача при восстановлении декодером всего исходного блока составит не более одного раза на 1000.
3. Если декодер принимает K′+2 кодирующих символов, созданных согласно спецификации кодера в разделе 5.3., с соответствующими идентификаторами ESI, выбранными независимо и равномерно случайным образом из диапазона возможных идентификаторов ESI, то тогда в среднем неудача при восстановлении декодером всего исходного блока составит не более одного раза на 1000000.
Заметим, что примерный декодер с FEC, определенный в разделе 5.4., удовлетворяет обоим требованиям, а именно:
1) он может восстановить исходный блок, при условии, что он примет достаточный с математической точки зрения набор кодирующих символов, созданных в соответствии со спецификацией кодера в разделе 5.3.;
2) он обладает обязательными восстановительными свойствами, описанными выше.
6. Соображения по поводу безопасности
Процесс доставки данных, может быть, подвергнут воздействиям, вызывающим неудачу в обслуживании пользователей, со стороны хакеров, которые посылают искаженные пакеты, воспринимаемые приемниками как легитимные. Это особенно касается групповой пересылки, поскольку искаженный пакет может быть введен в сеанс связи близко с корнем дерева групповой передачи, и в этом случае этот искаженный пакет поступит на множество приемников. Это особенно опасно, когда используют код, описанный в этом документе, поскольку использование даже одного искаженного пакета, содержащего данные кодирования, может привести к тому, что декодирование объекта будет полностью искажено, и результат декодирования нельзя будет использовать. Следовательно, рекомендуется перед отправкой объектов в приложение выполнить применительно к декодированным объектам аутентификацию источника и проверку их целостности. Например, перед передачей может быть добавлен хэш SHA-1 [SHA1] объекта, причем хэш SHA-1 вычисляют и проверяют после того, как объект декодирован, но перед тем, как он будет доставлен в приложение. Следует обеспечить аутентификацию источниках, например, путем включения цифровой подписи, проверяемой приемником, которую вычисляют вдобавок к значению хэша. Также для обнаружения и отбрасывания искаженных пакетов после их поступления рекомендуется использовать протокол аутентификации пакетов, такой как TESLA [RFC4082]. Этот способ можно также использовать для обеспечения аутентификации источника. Кроме того, рекомендуется обеспечить возможность проверки переадресации в обратном направлении во всех сетевых маршрутизаторах и переключателях на пути от отправителя к приемникам для ограничения возможности успешного внедрения искаженного пакета в тракт данных дерева групповой передачи со стороны подозрительного агента.
Другая проблема, связанная с безопасностью, заключается в том, что приемники могут получить некоторую информацию, касающуюся FEC, вне полосы пропускания в описании связи, и, если описание сеанса связи подделано или искажено, приемники не станут использовать правильный протокол для декодирования контента из принятых пакетов. Во избежание этих проблем рекомендуется предпринять меры для предотвращения получения приемниками некорректных описаний сеансов, например, путем использования аутентификации источника для гарантирования того, что приемники будут принимать только легитимные описания сеансов от авторизованных отправителей.
7. Соображения по поводу IANA
Значения идентификаторов кодирования с FEC и идентификаторов экземпляров FEC регистрируются в агентстве IANA. Основополагающие положения IANA для их применения к этому документу смотри в [RFC5052]. Этот документ присваивает «коду RaptorQ» полностью специализированный идентификатор кодирования с FEC: ID 6 (tbc) согласно ietf: rmt: fec: кодирующее имя-пространство для «кода RaptorQ».
8. Благодарности
Выражаем признательность Ranganathan (Ranga) Krishnan. Ranga Krishnan очень поддержал нас при решении вопросов, связанных с реализацией конкретных деталей и систематических индексов. Вдобавок, Habeeb Mohiuddin Mohammed и Antonios Pitarokoilis, которые работают в технологическом университете Мюнхена, и Alan Shinsato создали два независимых варианта реализации кодера/декодера RaptorQ, которые помогли понять и решить проблемы, связанные с этой спецификацией.
9. Ссылки
9.1. Нормативные ссылки
[FC2119] - Bradner, S., "Key words for use in RFCs to Indicate Requirement Levels", BCP 14, RFC 2119, March 1997.
[RFC4082] - Perrig, A., Song, D., Canetti, R., Tygar, J., and B. Briscoe, "Timed Efficient Stream Loss-Tolerant Authentication (TESLA): Multicast Source Authentication Transform Introduction", RFC 4082, June 2005.
[SHA1] - "Secure Hash Standard", Federal Information Processing Standards Publication (FIPS PUB) 180-1, April 2005.
[RFC5052] - Watson, M., Luby, M., and L. Vicisano, "Forward Error Correction (FEC) Building Block", RFC 5052, August 2007.
9.2. Информативные ссылки
[RFC3453] - Luby, M., Vicisano, L., Gemmell, J., Rizzo, L., Handley,M., and J. Crowcroft, "The Use of Forward Error Correction (FEC) in Reliable Multicast", RFC 3453, December 2002.
[RFC5053] - Luby, M., Shokrollahi, A., Watson, M., and T. Stockhammer, "Raptor Forward Error Correction Scheme for Object Delivery", RFC 5053, October 2007.
Адреса авторов
Michael Luby
Qualcomm Incorporated
3165 Kifer Road
Santa Clara, CA 95051
U.S.A.
Email: luby@qualcomm.com
Amin Shokrollahi
EPFL
Laboratoire d′ algorithmique
EPFL
Station 14
Batiment BC
Lausanne 1015
Switzerland
Email: amin.shokrollahi@epf1.ch
Mark Watson
Qualcomm Incorporated
3165 Kifer Road
Santa Clara, CA 95051
U.S.A.
Email: watson@qualcomm.com
Thomas Stockhammer
Nomor Research
Brecherspitzstrasse 8
Munich 81541
Germany
Email: stockhammer@nomor.de
Lorenz Minder
Qualcomm Incorporated
3165 Kifer Road
Santa Clara, CA 95051
U.S.A.
Email: lminder@qualcomm.com

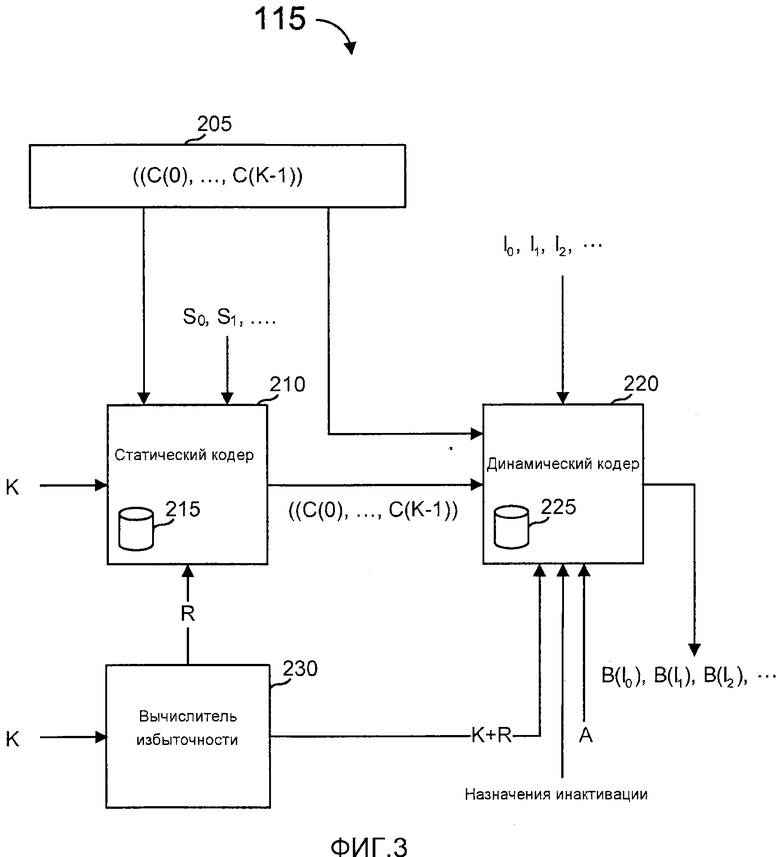
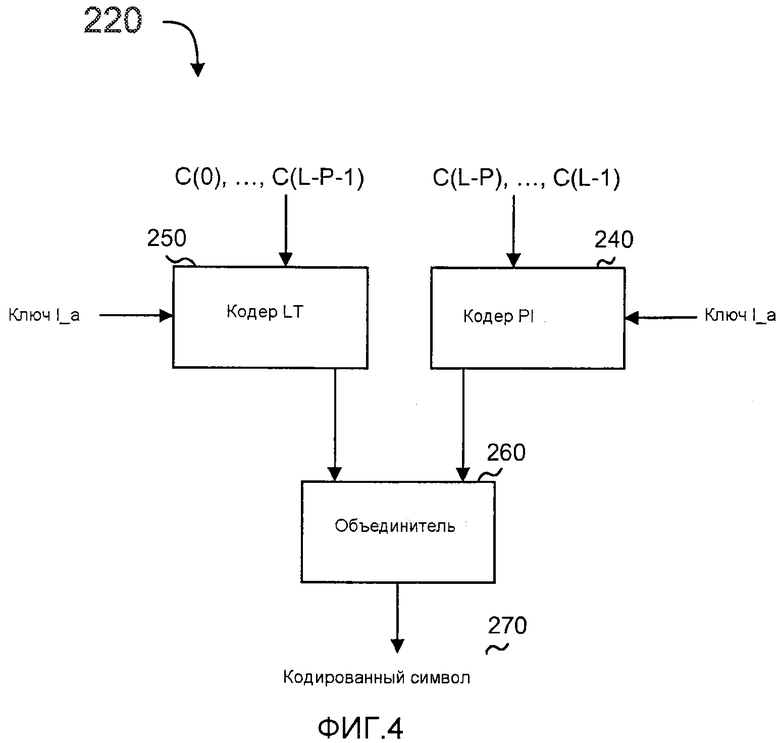
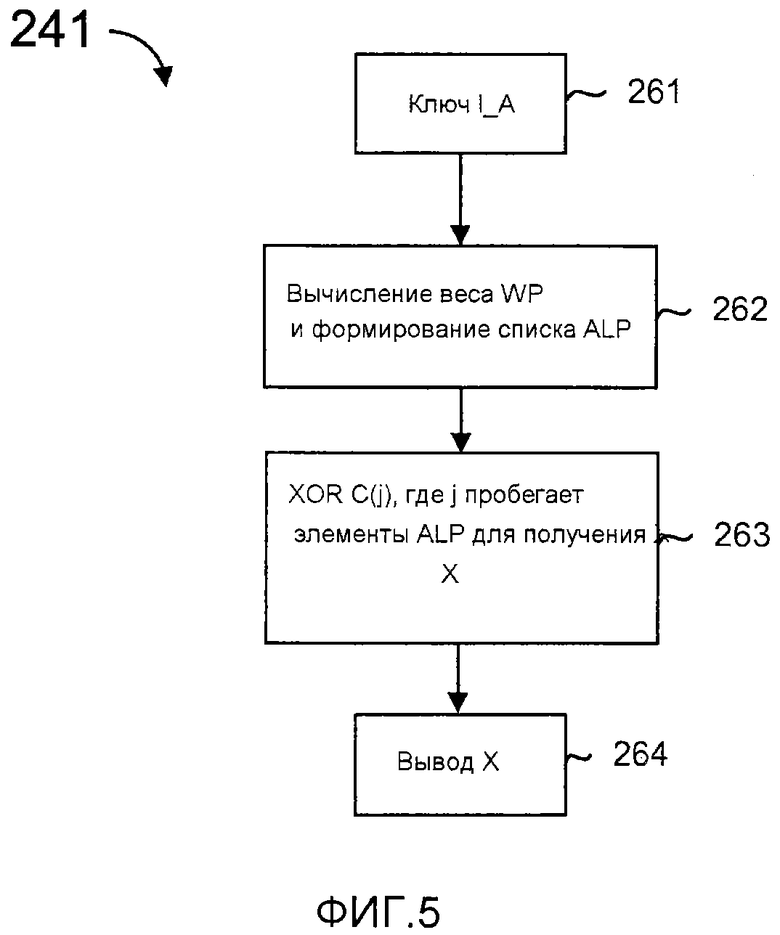
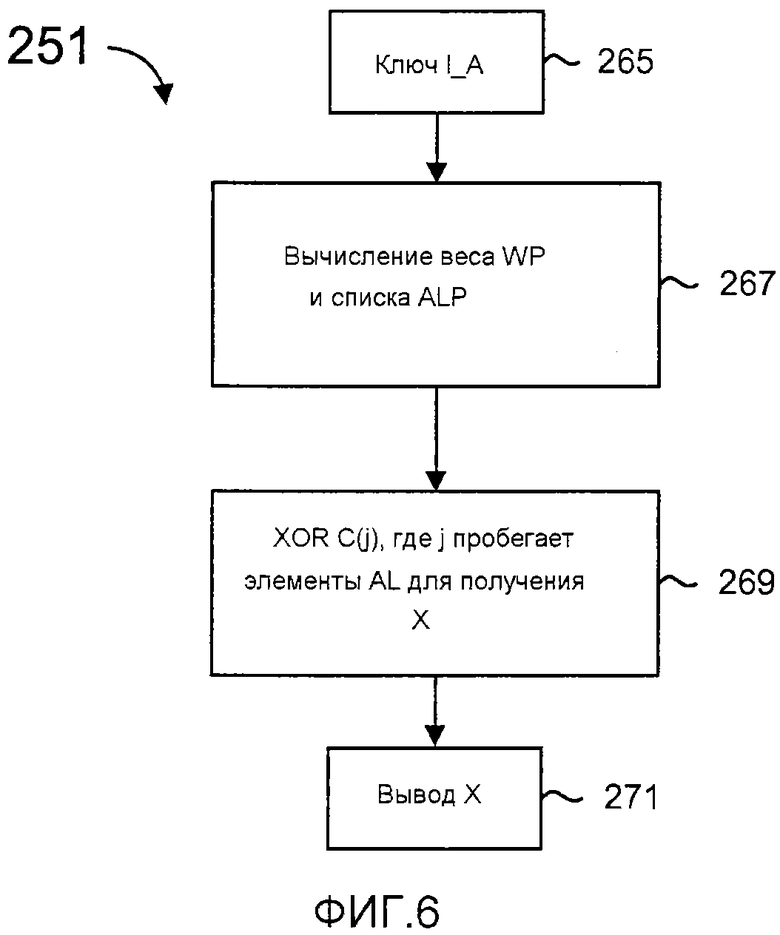
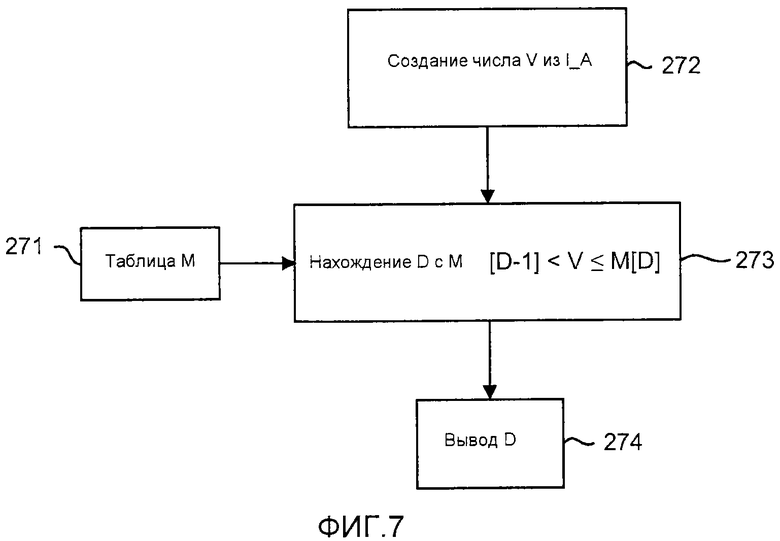
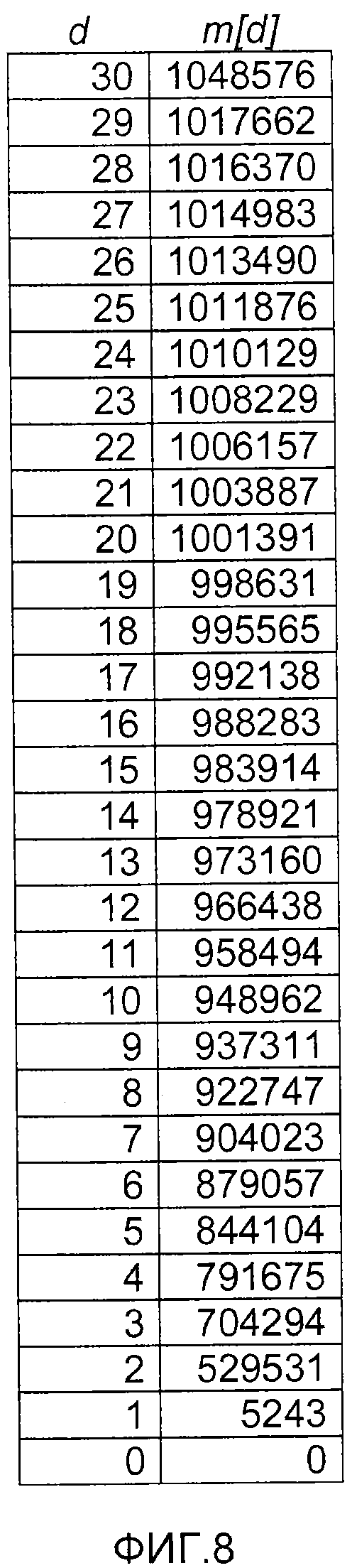
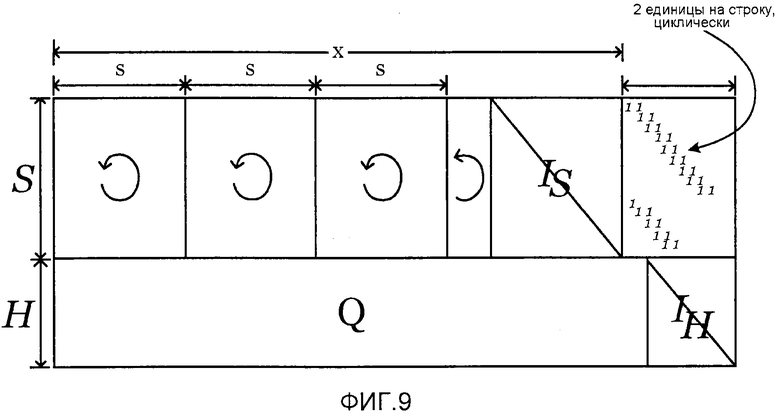
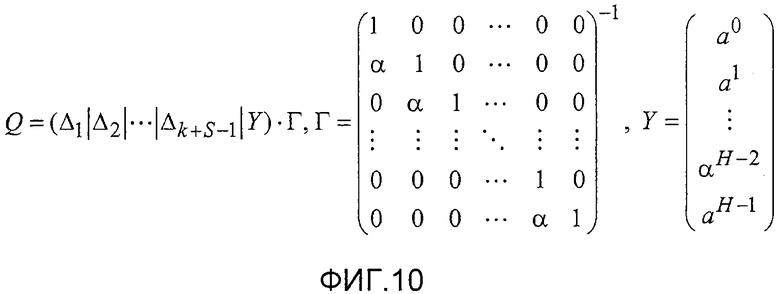
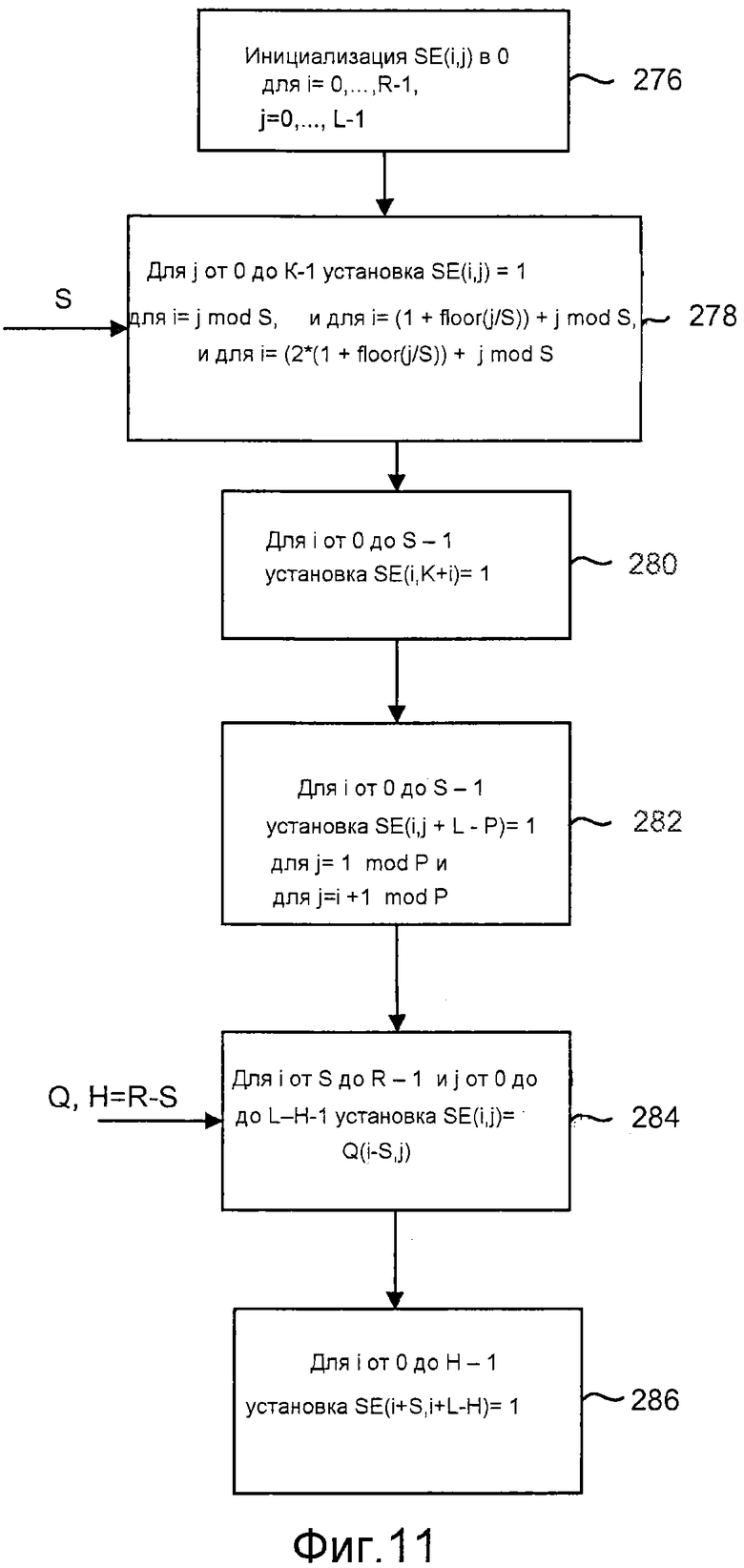
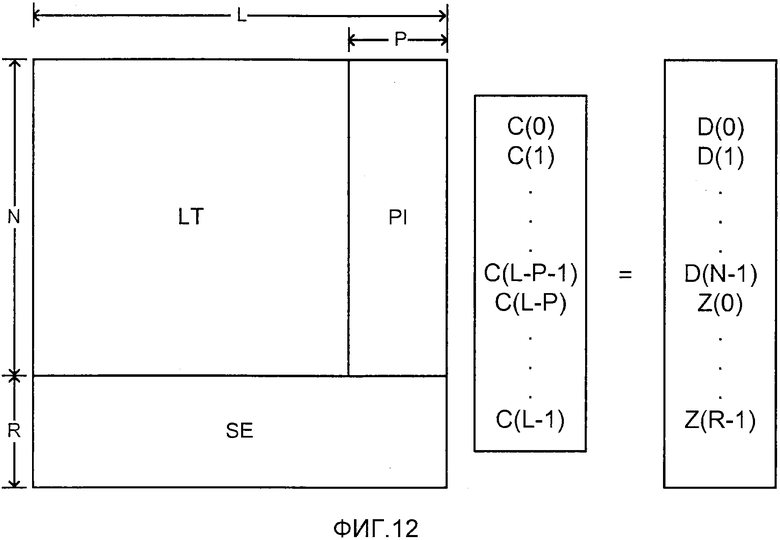
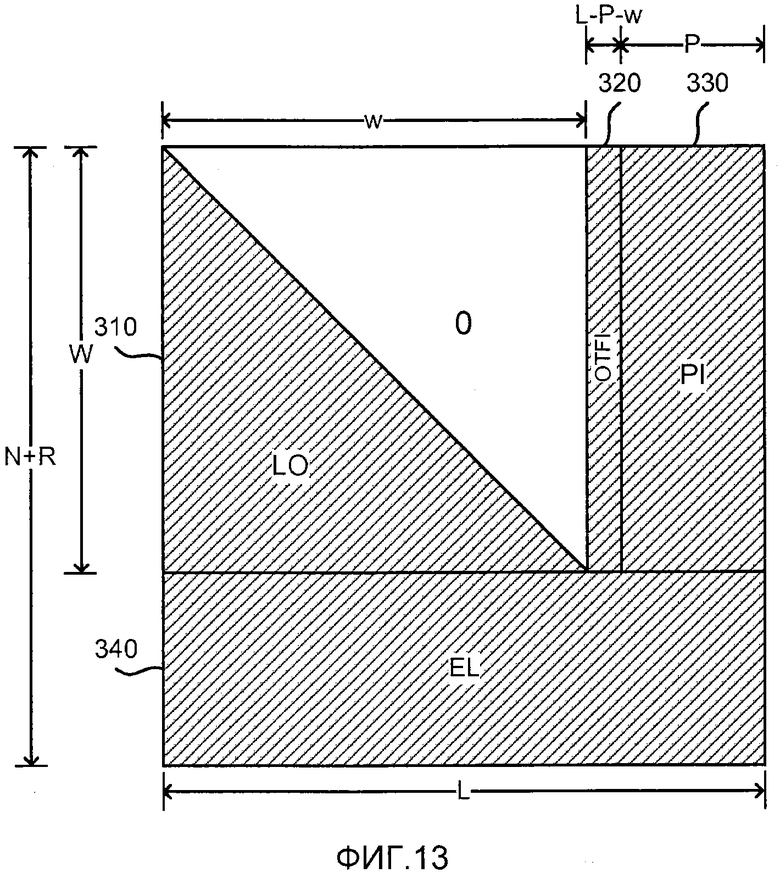
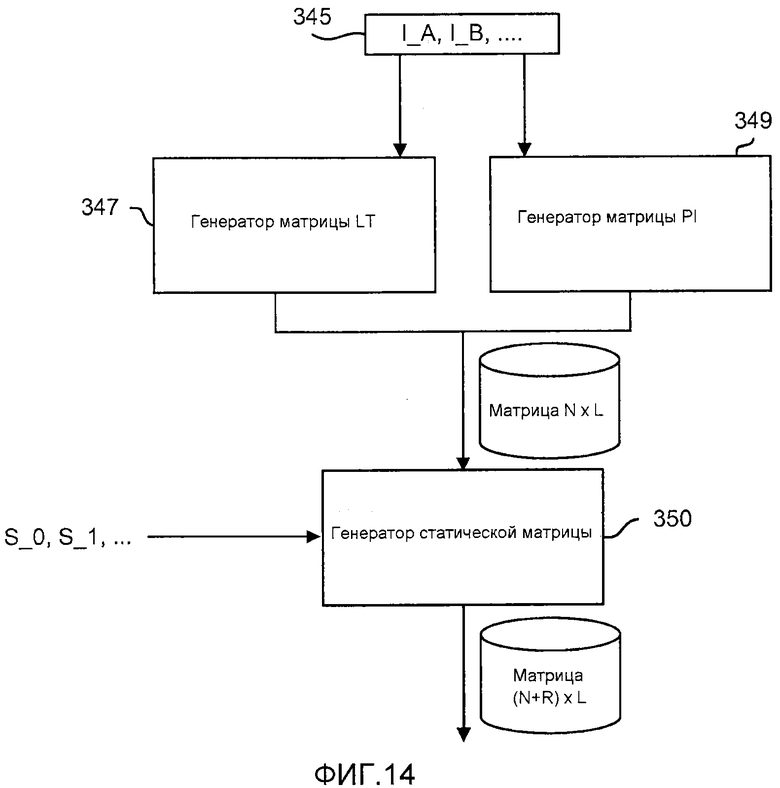
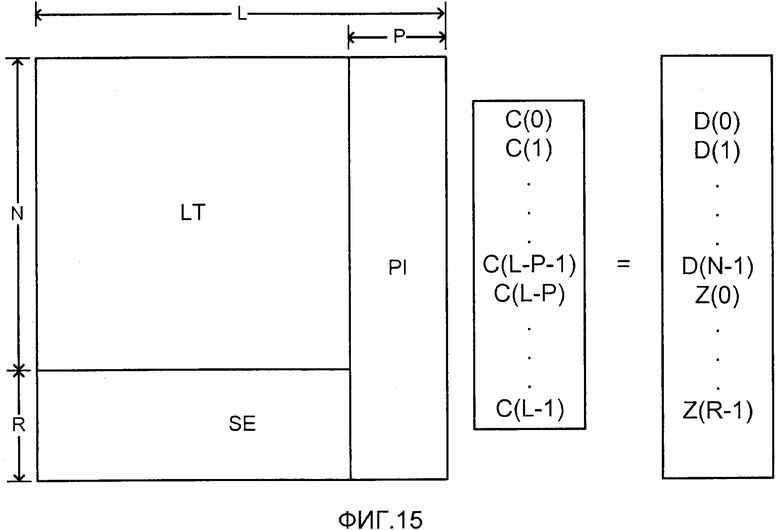
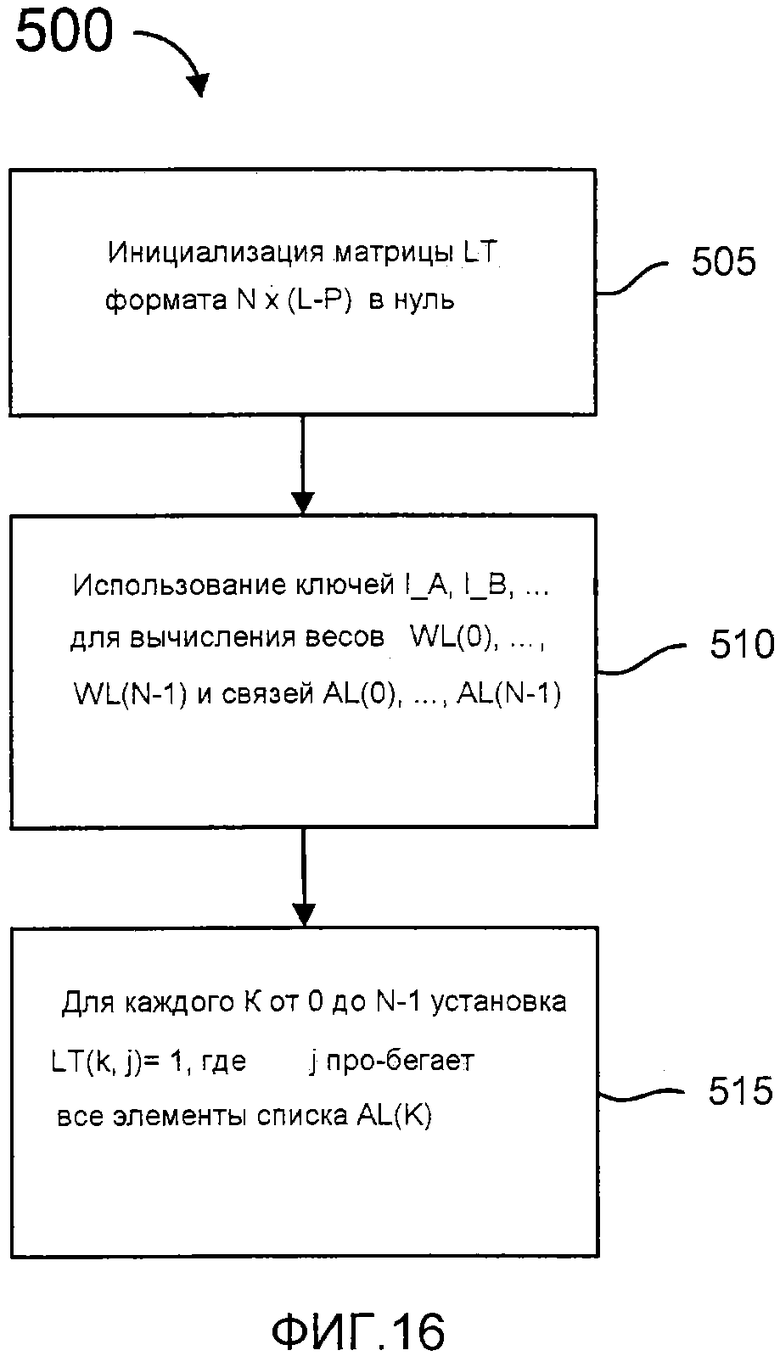
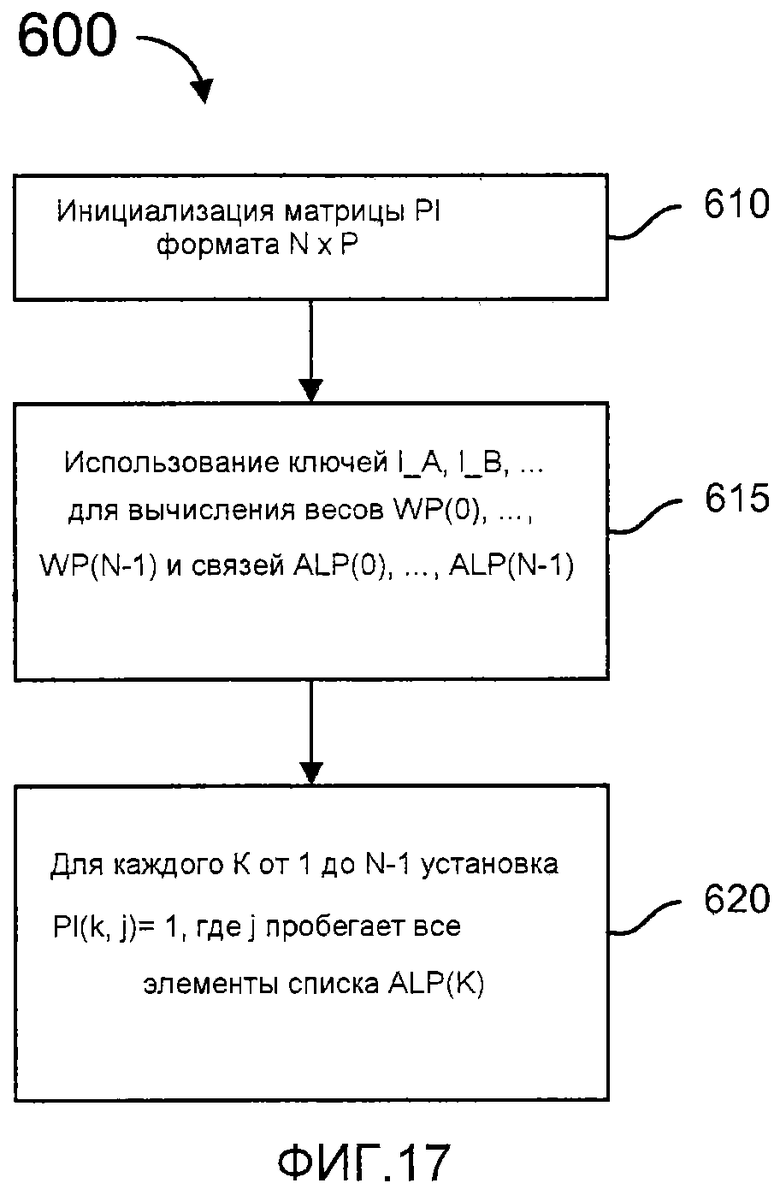
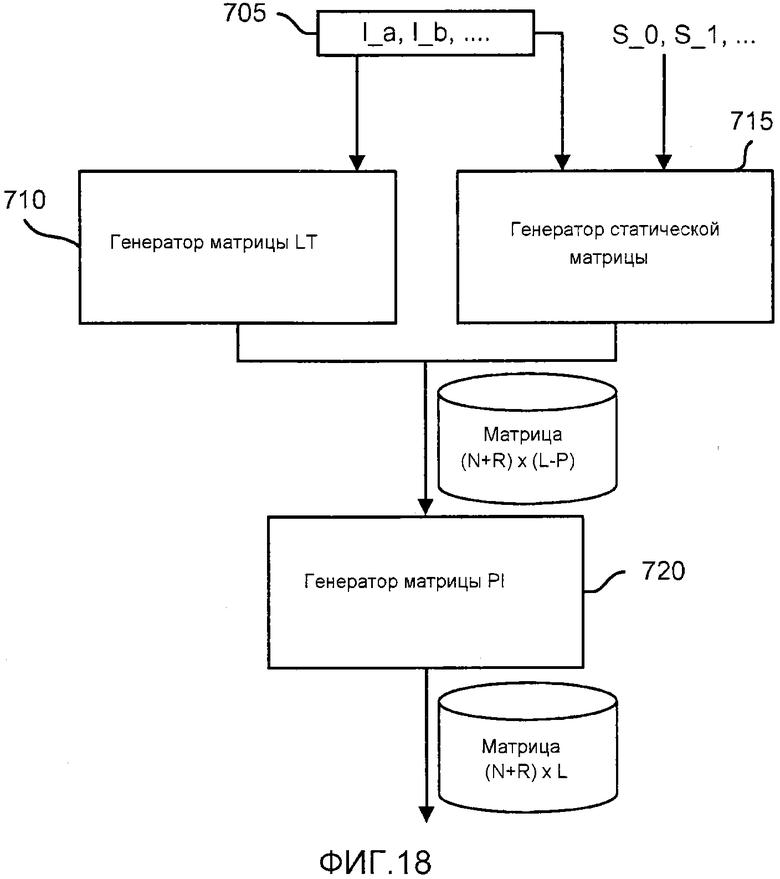
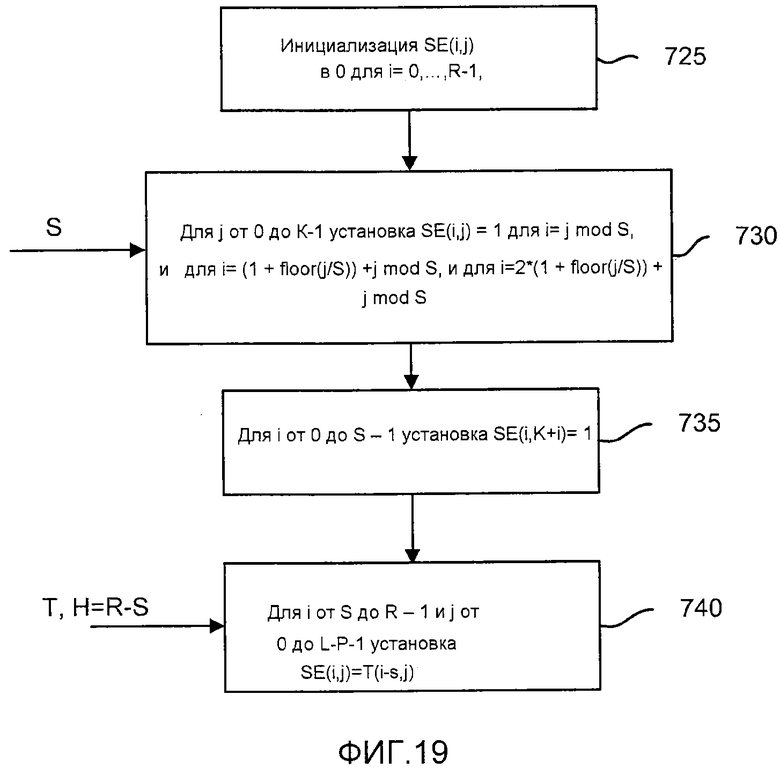
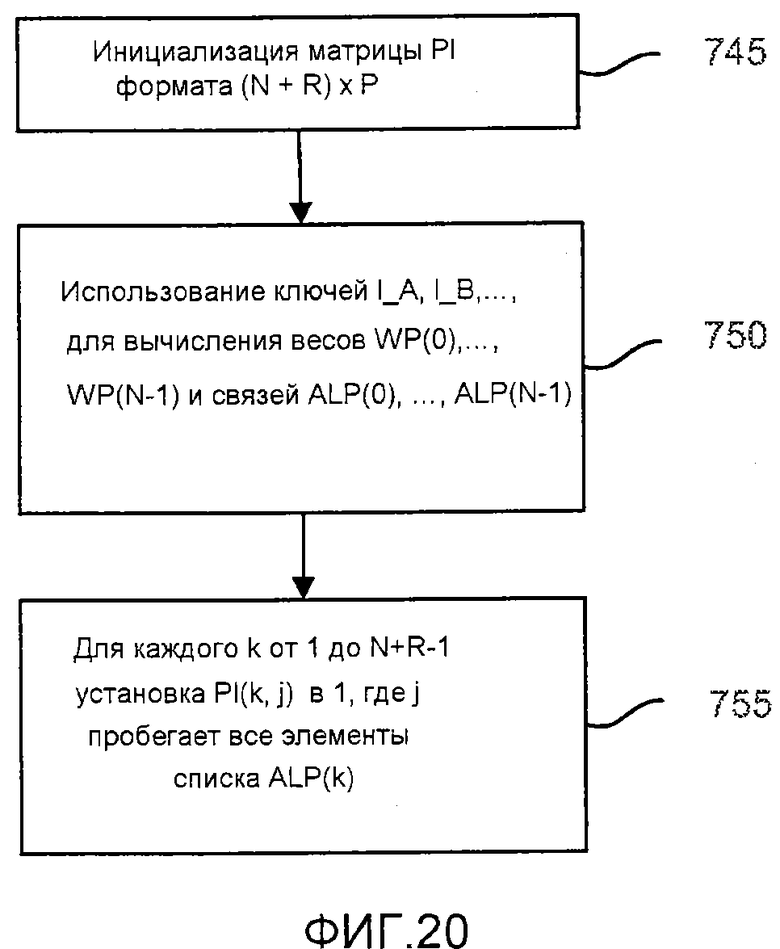
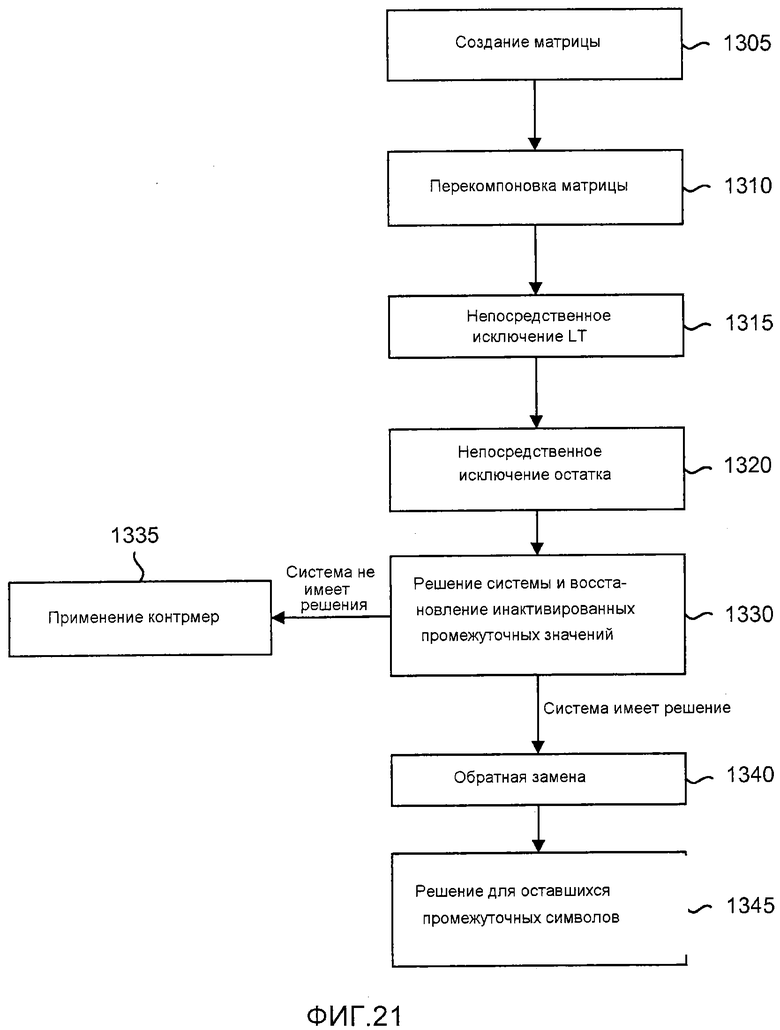
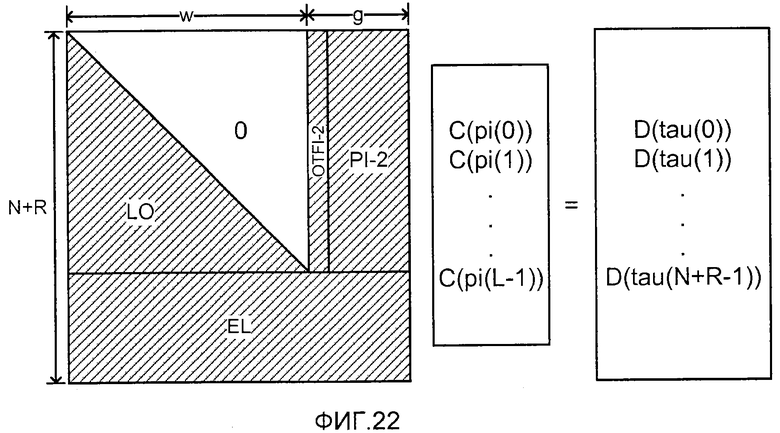
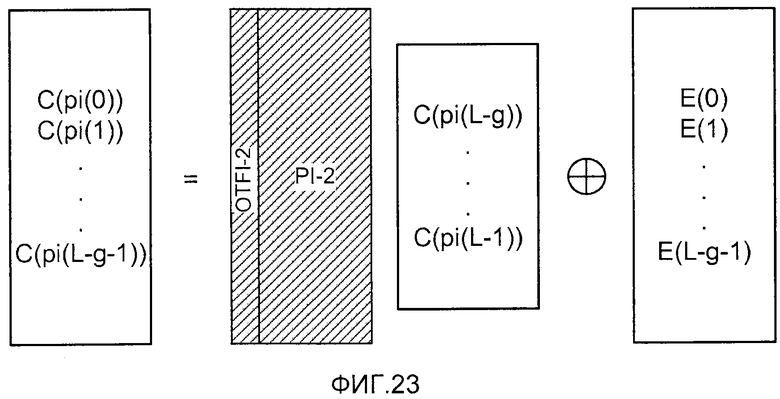
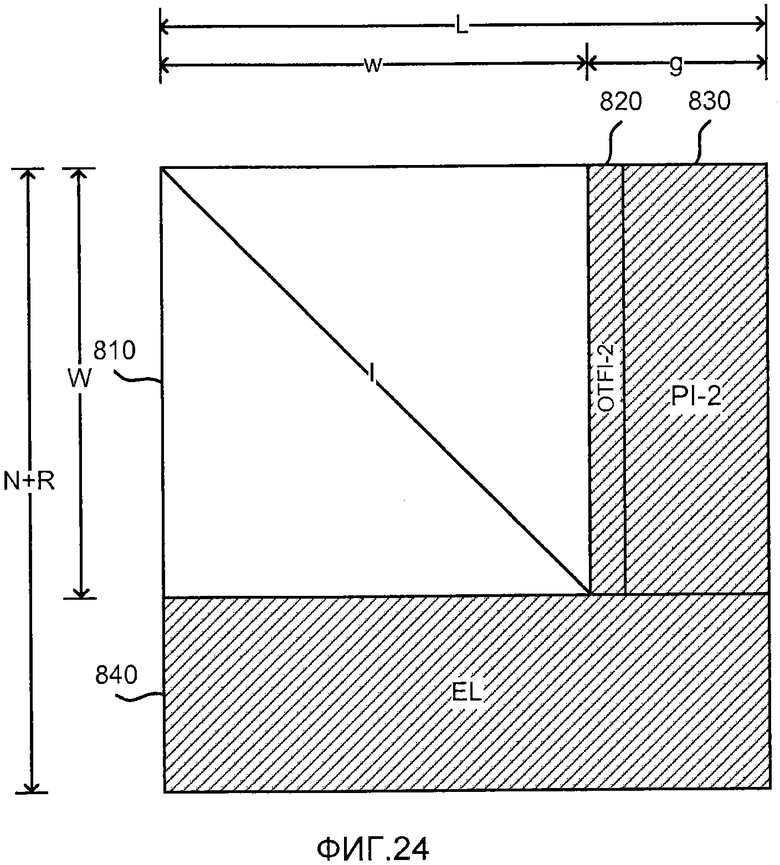
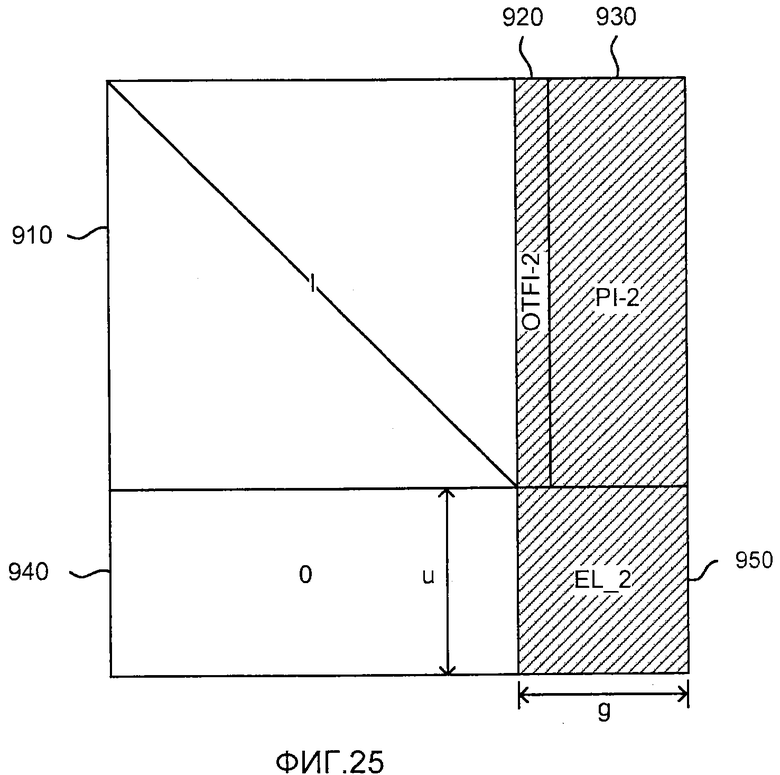
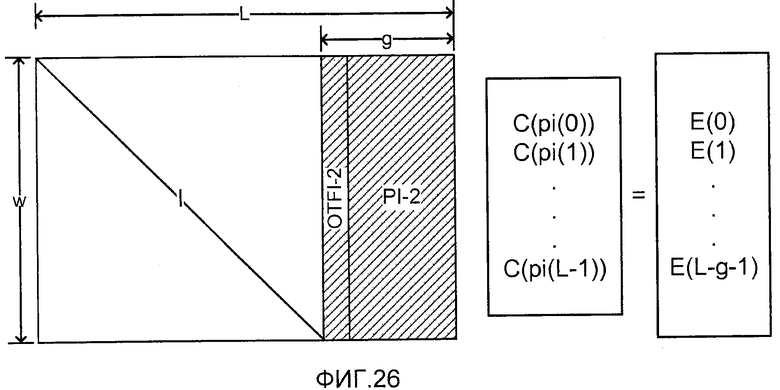
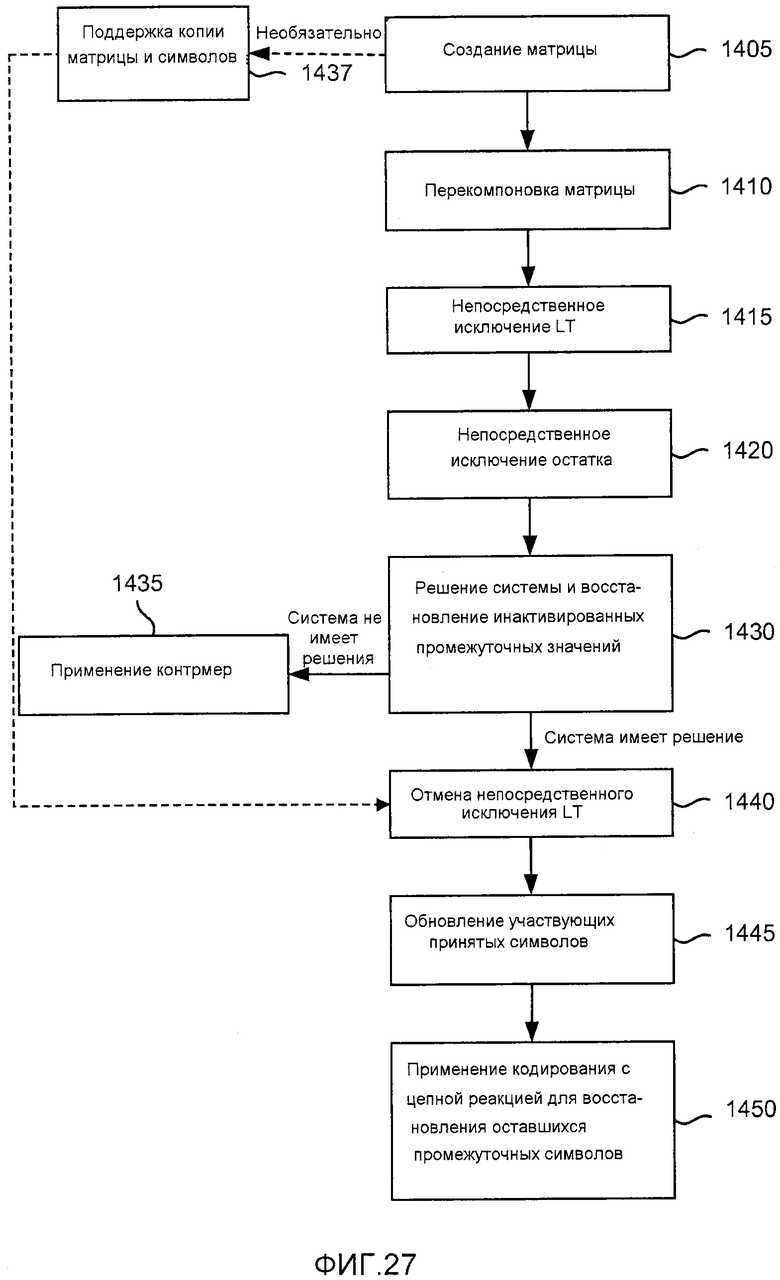
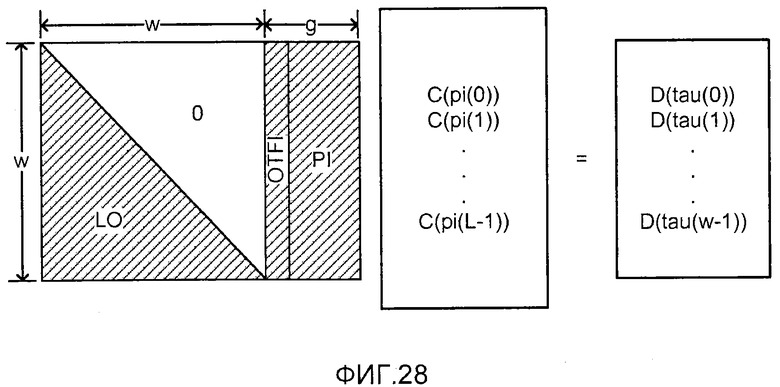
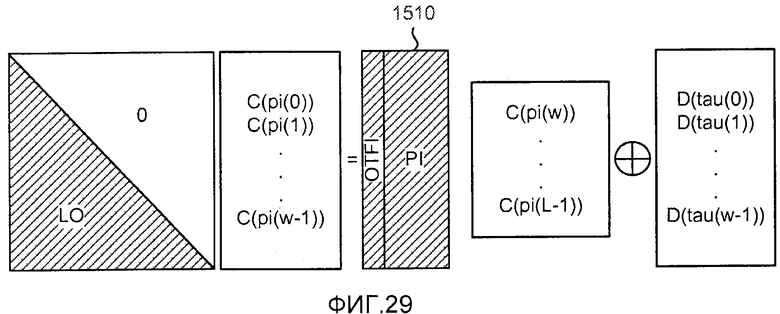
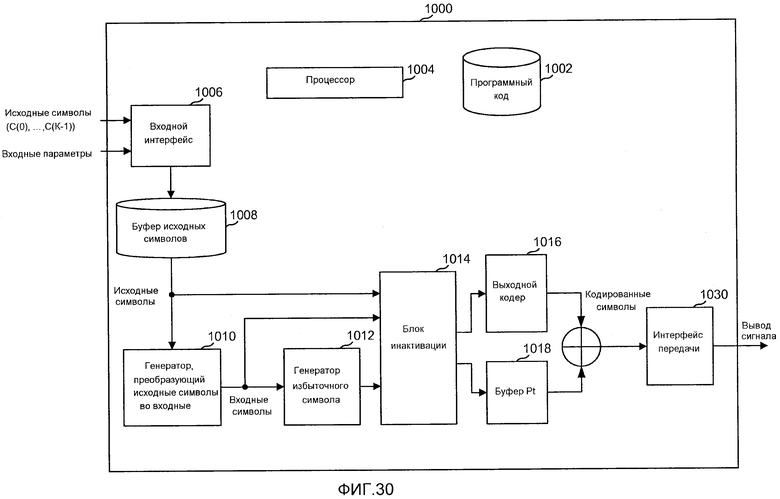
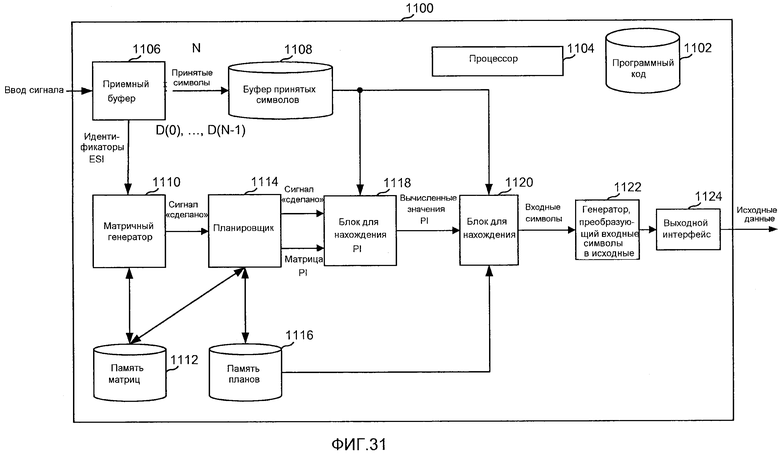
Изобретение относится к вычислительной технике. Технический результат заключается в повышении эффективности кодирования и декодирования с учетом ошибок и пробелов в переданных данных. Способ обслуживания файла с использованием сервера, соединенного с сетью данных, который содержит разбиение входного файла на целое количество блоков, причем каждый блок включает в себя по меньшей мере один субблок и причем каждый субблок включает в себя по меньшей мере один исходный символ; определение значения WS, представляющего максимальный размер субблока, на основе ограничения памяти; определение значения SS, где SS*AL представляет нижнюю границу для размера субсимвола в единицах предпочтительного размера AL блока памяти; определение того, какие блоки из целочисленного количества блоков следует организовать в множество субблоков, и для каждого такого блока организацию блока в множество субблоков, имеющих размер, определенный доступным пространством P', в пакетах для кодированных символов, подлежащих посылке, и размера Т символа, который необходимо использовать в каждом посылаемом пакете так, чтобы обеспечить количество исходных символов для исходных блоков равным в пределах порогового значения, причем количество исходных символов в целом равно количеству Kt исходных символов в файле; создание кодированных символов из блоков; вывод созданных кодированных символов. 6 н. и 14 з.п. ф-лы, 31 ил., 8 табл.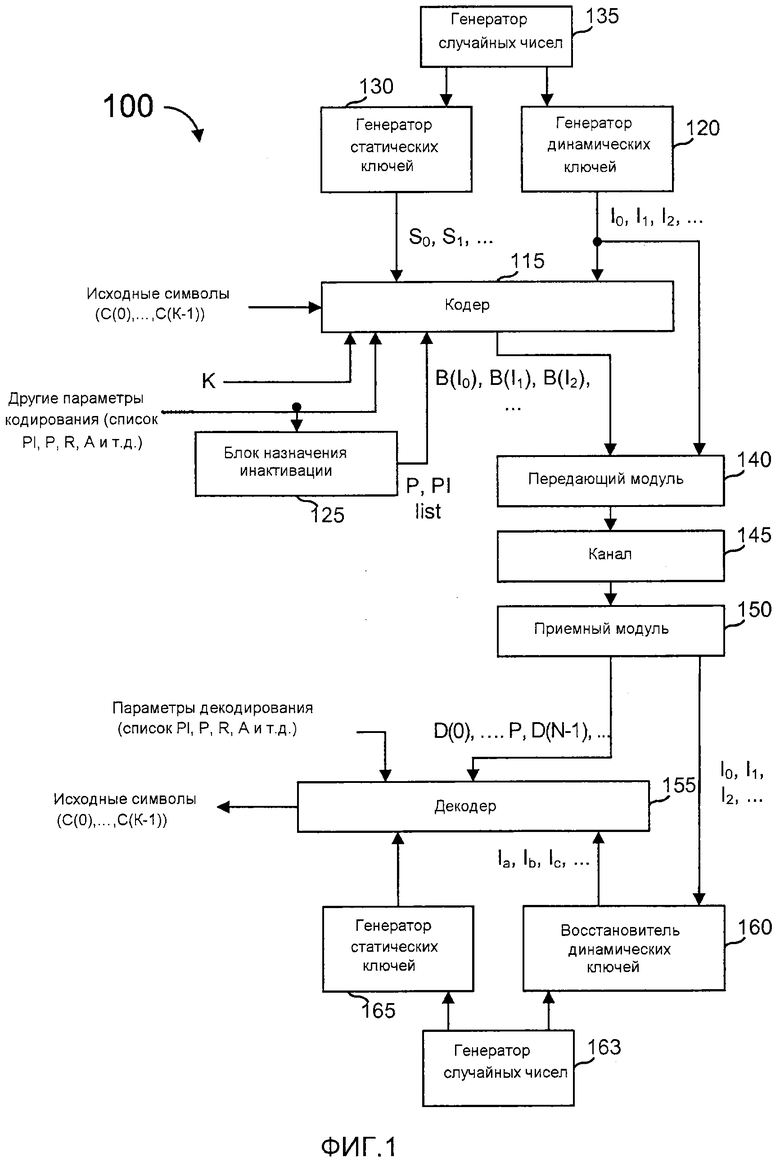
1. Способ обслуживания файла с использованием сервера, соединенного с сетью данных, причем обслуживание включает в себя организацию данных файла в один или более блоков, создание одного или более кодированных символов для блока на основе данных этого блока, и причем по меньшей мере один блок физически или логически организуют в множество субблоков, и по меньшей мере один кодированный символ физически или логически организуют во множество субсимволов, причем способ содержит:
разбиение входного файла на целое количество блоков, причем каждый блок включает в себя по меньшей мере один субблок и причем каждый субблок включает в себя по меньшей мере один исходный символ;
определение значения WS, представляющего максимальный размер субблока, на основе ограничения памяти;
определение значения SS, где SS*AL представляет нижнюю границу для размера субсимвола в единицах предпочтительного размера AL блока памяти;
определение того, какие блоки из целочисленного количества блоков следует организовать в множество субблоков, и для каждого такого блока организацию блока в множество субблоков, имеющих размер, определенный доступным пространством P', в пакетах для кодированных символов, подлежащих посылке, и размера Т символа, который необходимо использовать в каждом посылаемом пакете, таким путем, чтобы обеспечить, что количество исходных символов для исходных блоков было равным в пределах порогового значения, причем это количество исходных символов в целом равно количеству Kt исходных символов в файле, и чтобы обеспечить, что размер субсимвола каждого субблока составляет по меньшей мере SS*AL, и обеспечить, что размер каждого субблока составляет не более WS;
создание кодированных символов из блоков, причем субсимволы создают из субблоков, так что каждый кодированный символ зависит от данных из одного блока;
вывод созданных кодированных символов.
2. Способ по п. 1, в котором организация блока во множество субблоков дополнительно содержит определение Т, Z и N, причем
Z является количеством исходных блоков, на которое разбит упомянутый файл,
N является количеством субблоков, на которое разбиты исходные блоки.
3. Способ по п. 2, в котором Т определяют, используя Р'.
4. Способ по п. 3, в котором Т определяют, используя Р', Kmin и Gmax, причем
Kmin является минимальным количеством исходных символов в исходном блоке, и
Gmax является максимальным количеством исходных символов, на которое разбит пакет.
5. Способ по п. 2, в котором Z определяют, используя Kt и KL(N_max), причем
KL(N_max) является наибольшим количеством исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиваются на N_max субсимволов каждый, чтобы обеспечить, что размер каждого субблока равен не более WS, и
N_max является наибольшим количеством субсимволов, на которое исходный символ размера Т может быть разбит.
6. Способ по п. 2, в котором N определяют, используя Kt и KL(n), причем
KL(n) является наибольшим количеством исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиваются на n субсимволов каждый, чтобы обеспечить, что размер каждого субблока равен не более WS.
7. Способ восстановления блоков данных файла в приемнике с использованием клиента, подсоединенного к сети данных, причем блок включает в себя группу из одного или более субблоков, причем способ содержит:
прием множества кодированных символов, созданных из упомянутых блоков, причем каждый кодированный символ включает в себя множество субсимволов, созданных из по меньшей мере одного субблока, с использованием общего набора операций;
определение значения WS, представляющего максимальный размер субблока на основе ограничения памяти;
определение значения SS, где SS*AL представляет нижнюю границу для размера субсимвола в единицах предпочтительного размера AL блока памяти;
определение, какие блоки из целочисленного количества блоков организованы в множество субблоков, и для каждого такого блока организацию этого блока в множество субблоков, имеющих размер, определенный первым параметром, установленным отправителем и представляющим доступное пространство P', в пакетах, и вторым параметром, представляющим размер Т символа, использованный в каждом пакете, при этом упомянутые параметры таковы, что количество исходных символов для исходных блоков является равным в пределах порогового значения и это количество исходных символов в целом равно количеству Kt исходных блоков в файле;
декодирование блоков из принятых кодированных символов, причем субблоки декодируют из субсимволов и субблоки образуют блоки, причем размер субсимвола каждого субблока составляет по меньшей мере SS*AL, а размер каждого субблока составляет не более WS; и
вывод декодированных блоков.
8. Способ по п. 7, в котором организация блока во множество субблоков дополнительно содержит определение Т, Z и N, причем
Z является количеством исходных блоков, на которое разбит упомянутый файл,
N является количеством субблоков, на которое разбиты исходные блоки.
9. Способ по п. 8, в котором Т определяют, используя Р'.
10. Способ по п. 9, в котором Т определяют, используя Р', Kmin и Gmax, причем
Kmin является минимальным количеством исходных символов в исходном блоке, и
Gmax является максимальным количеством исходных символов, на которое разбит пакет.
11. Способ по п. 8, в котором Z определяют, используя Kt и KL(N_max), причем
KL(N_max) является наибольшим количеством исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиваются на N_max субсимволов каждый, чтобы обеспечить, что размер каждого субблока равен не более WS, и
N_max является наибольшим количеством субсимволов, на которое исходный символ размера Т может быть разбит.
12. Способ по п. 8, в котором N определяют, используя Kt и KL(n), причем
KL(n) является наибольшим количеством исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиваются на n субсимволов каждый, чтобы обеспечить, что размер каждого субблока равен не более WS.
13. Система для обслуживания файла, причем обслуживание включает в себя организацию данных файла в один или более блоков, создание одного или более кодированных символов для блока на основе данных этого блока, и причем по меньшей мере один блок физически или логически организован во множество субблоков, и по меньшей мере один кодированный символ физически или логически организован во множество субсимволов, причем система содержит:
кодер для разбиения входного файла на целое количество блоков, причем каждый блок включает в себя по меньшей мере один субблок и причем каждый субблок включает в себя по меньшей мере один исходный символ; определения значения WS, представляющего максимальный размер субблока, на основе ограничения памяти; определения значения SS, где SS*AL представляет нижнюю границу для размера субсимвола в единицах предпочтительного размера AL блока памяти; определения того, какие блоки из целочисленного количества блоков следует организовать в множество субблоков, и для каждого такого блока организации блока во множество субблоков, имеющих размер, определенный доступным пространством P', в пакетах для кодированных символов, подлежащих посылке, и размера Т символа, который необходимо использовать в каждом посылаемом пакете, таким путем, чтобы обеспечить, что количество исходных символов для исходных блоков было равным в пределах порогового значения, причем это количество исходных символов в целом равно количеству Kt исходных символов в файле, и чтобы обеспечить, что размер субсимвола каждого субблока составляет по меньшей мере SS*AL, и обеспечить, что размер каждого субблока составляет не более WS; создания кодированных символов из блоков, причем субсимволы созданы из субблоков, так что каждый кодированный символ зависит от данных из одного блока; и
модуль передачи для вывода созданных кодированных символов в сеть передачи данных.
14. Система по п. 13, в которой кодер выполнен с возможностью организации блока во множество субблоков посредством определения Т, Z и N, причем
Z является количеством исходных блоков, на которое разбит упомянутый файл,
N является количеством субблоков, на которое разбиты исходные блоки,
Z и N определяют, используя Kt и KL(n), причем
KL(n) является наибольшим количеством исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиваются на n субсимволов каждый, чтобы обеспечить, что размер каждого субблока составляет не более WS.
15. Система для восстановления блоков данных файла в приемнике, причем блок включает в себя группу из одного или более субблоков, причем система содержит:
приемник для приема множества кодированных символов, созданных из упомянутых блоков, причем каждый кодированный символ включает в себя множество субсимволов, созданных из по меньшей мере одного субблока, с использованием общего набора операций;
декодер для определения значения WS, представляющего максимальный размер субблока на основе ограничения памяти; определения значения SS, где SS*AL представляет нижнюю границу для размера субсимвола в единицах предпочтительного размера AL блока памяти; определения, какие из блоков организованы во множество субблоков, и для каждого такого блока организации этого блока в множество субблоков, имеющих размер, определенный первым параметром, установленным отправителем и представляющим доступное пространство P', в пакетах, и вторым параметром, представляющим размер Т символа, использованный в каждом пакете, при этом упомянутые параметры таковы, что количество исходных символов для исходных блоков является равным в пределах порогового значения и это количество исходных символов в целом равно количеству Kt исходных блоков в файле; и декодирования блоков из принятых кодированных символов, причем субблоки декодированы из субсимволов и субблоки образуют блоки, причем размер субсимвола каждого субблока составляет по меньшей мере SS*AL, а размер каждого субблока составляет не более WS; и
вывод для вывода декодированных блоков.
16. Система по п. 15, в которой декодер выполнен с возможностью организации блока во множество субблоков посредством определения Т, Z и N, причем
Z является количеством исходных блоков, на которое разбит упомянутый файл,
N является количеством субблоков, на которое разбиты исходные блоки,
Z и N определены, используя Kt и KL(n), причем
KL(n) является наибольшим количеством исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиты на n субсимволов каждый, чтобы обеспечить, что размер каждого субблока составляет не более WS.
17. Считываемый компьютером носитель, хранящий выполняемые процессором инструкции для обслуживания файла, причем обслуживание включает в себя организацию данных файла в один или более блоков, создание одного или более кодированных символов для блока на основе данных этого блока, и причем по меньшей мере один блок физически или логически организован в множество субблоков, и по меньшей мере один кодированный символ физически или логически организован во множество субсимволов, причем выполняемые процессором инструкции выполнены с возможностью вынуждать процессор:
разбивать входной файл на целое количество блоков, причем каждый блок включает в себя по меньшей мере один субблок и причем каждый субблок включает в себя по меньшей мере один исходный символ;
определять значение WS, представляющее максимальный размер субблока, на основе ограничения памяти;
определять значение SS, где SS*AL представляет нижнюю границу для размера субсимвола в единицах предпочтительного размера AL,блока памяти;
определять, какие блоки из целочисленного количества блоков следует организовать во множество субблоков, и для каждого такого блока организовывать блок во множество субблоков, имеющих размер, определенный доступным пространством P', в пакетах для кодированных символов, подлежащих посылке, и размер Т символа, который необходимо использовать в каждом посылаемом пакете, таким путем, чтобы обеспечить, что количество исходных символов для исходных блоков было равным в пределах порогового значения, причем это количество исходных символов в целом равно количеству Kt исходных символов в файле, и чтобы обеспечить, что размер субсимвола каждого субблока составляет по меньшей мере SS*AL, и обеспечить, что размер каждого субблока составляет не более WS;
создавать кодированные символы из блоков, причем субсимволы создаются из субблоков, так что каждый кодированный символ зависит от данных из одного блока;
выводить созданные кодированные символы для вывода в сеть передачи данных.
18. Носитель по п. 17, в котором выполняемые процессором инструкции выполнены с возможностью вынуждать процессор организовывать блок во множество субблоков и дополнительно вынуждать процессор определять Т, Z и N, причем
Z является количеством исходных блоков, на которое разбит упомянутый файл,
N является количеством субблоков, на которое разбиты исходные блоки,
Z и N определены, используя Kt и KL(n), причем
KL(n) является наибольшим количеством исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиты на n субсимволов каждый, чтобы обеспечить, что размер каждого субблока составляет не более WS.
19. Считываемый компьютером носитель, хранящий выполняемые процессором инструкции для восстановления блоков данных файла, причем блок включает в себя группу из одного или более субблоков, причем выполняемые процессором инструкции вынуждают процессор:
обращаться ко множеству кодированных символов, созданных из упомянутых блоков, причем каждый кодированный символ включает в себя множество субсимволов, созданных из по меньшей мере одного субблока, с использованием общего набора операций;
определять значение WS, представляющее максимальный размер субблока на основе ограничения памяти;
определять значение SS, где SS*AL представляет нижнюю границу для размера субсимвола в единицах предпочтительного размера AL блока памяти;
определять, какие из блоков организованы во множество субблоков, и для каждого такого блока организовывать этот блок в множество субблоков, имеющих размер, определенный первым параметром, установленным отправителем и представляющим доступное пространство P', в пакетах, и вторым параметром, представляющим размер Т символа, использованный в каждом пакете, при этом упомянутые параметры таковы, что количество исходных символов для исходных блоков является равным в пределах порогового значения и это количество исходных символов в целом равно количеству Kt исходных блоков в файле; и
декодировать блоки из принятых кодированных символов, причем субблоки декодируются из субсимволов и субблоки образуют блоки, причем размер субсимвола каждого субблока составляет по меньшей мере SS*AL, а размер каждого субблока составляет не более WS; и
выдавать декодированные блоки для вывода.
20. Носитель по п. 19, в котором выполняемые процессором инструкции выполнены с возможностью вынуждать процессор организовывать блок во множество субблоков и дополнительно вынуждать процессор определять Т, Z и N, причем
Z является количеством исходных блоков, на которое разбит упомянутый файл,
N является количеством субблоков, на которое разбиты исходные блоки,
Z и N определены, используя Kt и KL(n), причем
KL(n) является наибольшим количеством исходных символов в исходном блоке, которое может поддерживаться, когда символы исходного блока разбиты на n субсимволов каждый, чтобы обеспечить, что размер каждого субблока составляет не более WS.
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| Дорожная спиртовая кухня | 1918 |
|
SU98A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПЕРЕДАЧИ ИНФОРМАЦИИ ПО СЕТИ ЭНЕРГОСНАБЖЕНИЯ | 1998 |
|
RU2154343C2 |
Авторы
Даты
2015-06-27—Публикация
2010-08-19—Подача