Заявленное изобретение относится к области высокопроизводительных многопроцессорных вычислительных систем. Изобретение может быть применено для организации системных сетей многопроцессорных систем с большим числом процессорных узлов (абонентов), в которых требуется быстрая параллельная передача информации между абонентами с минимальным числом промежуточных скачков (запоминаний в буферах) (Arimili B., Arimili R., Chung V., et al. The PERCS High-Performance Interconnect // 18th IEEE Symposium on High Performance Interconnects. 2009. P. 75 - 82. Alverson R., Roweth D. and Kaplan L. The Gemini System Interconnect // 18th IEEE Symposium on High Performance Interconnects. 2009. P. 83 - 87).
В таких сетях процессорные узлы (связка многоядерных процессоров) используются в тесной связке с многопортовыми связными узлами. Множество портов в них требуется для возможно большего распараллеливания системной сети, объединяющей связные узлы. Топология связей узлов сети, соответствующая полному графу, обеспечивает неблокируемость и самомаршрутизируемость при прокладывании маршрутов. Это свойство позволяет иметь бесконфликтное расписание на произвольной перестановке пакетов между вершинами графа, которое составляется в каждой вершине независимо от других вершин.
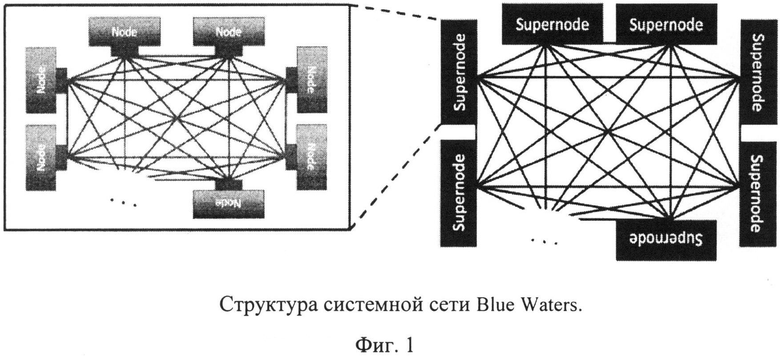
Известна системная сеть суперкомпьютера, который разрабатывался IBM для проекта Blue Waters (Arimili B., Arimili R., Chung V., et al. The PERCS High-Performance Interconnect // 18th IEEE Symposium on High Performance Interconnects. 2009. P. 75 - 82. Hruska J. After Years of Work IBM, NCSA Cancel «BlueWaters» Supercomputer // Aug. 2011. URL: http://hothardware.com/News/After-Years-of-Work-IBM-NCSA-Cancel-Blue-Waters-Supercomputer/). Системная сеть имеет топологию двухуровневого полного графа (фиг. 1). Каждый узел связи (node) имеет 47 межузловых каналов трех видов с разной пропускной способностью. Суперузел (supernode) образуется из 32 узлов связи, которые связаны в нем по схеме полного графа. Суперузлы связаны также по схеме полного графа. Каждый суперузел имеет 512 каналов. В максимальной конфигурации суперкомпьютера каждый такой канал используется для связи с другим суперузлом по схеме полного графа. В этом случае он содержит 513 суперузлов. Передача пакета между любыми двумя узлами занимает не более трёх смен каналов с промежуточной буферизацией пакетов (скачков).
Недостатками данной системной сети являются неоптимальное использование портов узла связи для создания связей внутри суперузлов и между суперузлами, а также отсутствие резервных трехскачковых путей, что приводит к ухудшению отказоустойчивости системной сети.
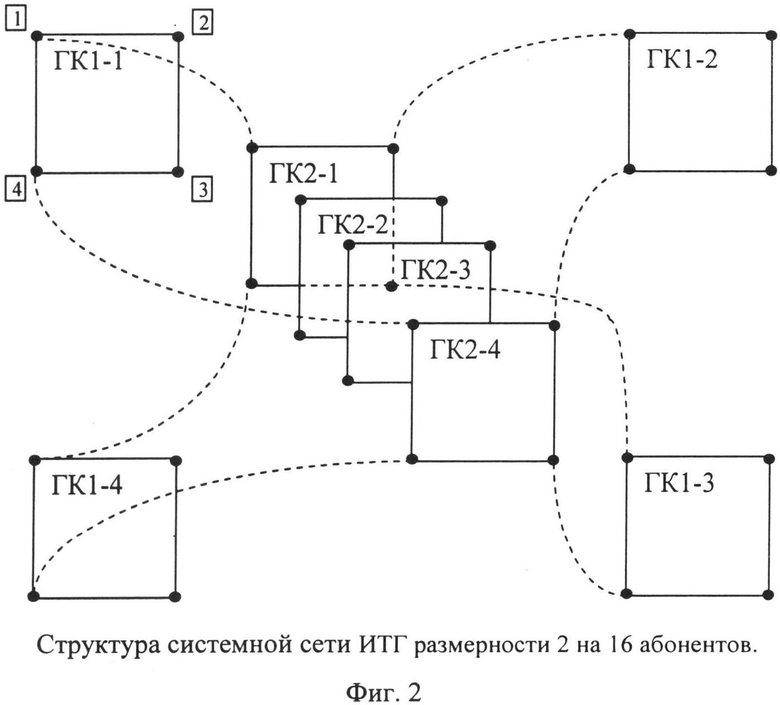
Другим примером иерархической сети такого класса является Иерархический толстый гиперкуб, базирующийся на подсетях с топологией гиперкуба (US 5669008 A, 16.09.1997, Hierarchical fat hypercube architecture for parallel processing systems. United States Patent Patent Number 5,669,008. Issued September 16, 1997). Эта сеть выбрана в качестве прототипа. Она строилась для удовлетворения требованиям масштабируемости, высокой пропускной способности, малого диаметра и высокой бисекционной пропускной способности, отражающей параллельность сети. Величина бисекции B определяется как минимальное число каналов «точка-точка» между множествами, разделенных пополам, абонентов.
В иерархическом толстом гиперкубе (ИТГ) абоненты подсоединяются к коммутаторам, расположенным в узлах подсетей первого уровня, а те соединяются через подсети второго уровня. Подсети первого уровня, так же как и второго, имеют топологию гиперкуба (группа гиперкубов второго уровня называется авторами метакубом). Пример толстого иерархического гиперкуба с базовыми гиперкубами размерности 2 на 16 абонентов представлен на фиг. 2. На Фиг. 2 гиперкубы первого уровня называются ГК1-1, ГК1-2, ГК1-3 и ГК1-4, а метакуб состоит из гиперкубов ГК2-1, ГК2-2, ГК2-3 и ГК2-4. При этом ГК2-1 связывает первые узлы гиперкубов первого уровня, ГК2-2 - вторые узлы гиперкубов первого уровня и т.д. На Фиг. 2 для наглядности показаны связи только для ГК2-1 и ГК2-4. Соединения ГК2-2, ГК2-3 с гиперкубами нижнего уровня аналогичны.
Недостатками ИТГ являются высокая схемная и проводная сложность из-за наличия большого числа коммутаторов в метакубе, сравнительно большой диаметр из-за использования обычных гиперкубов и наличие конфликтов при параллельной передаче в гиперкубах.
Задачей изобретения является упрощение сетей с большим числом процессорных узлов (абонентов), в которых требуется быстрая параллельная передача информации между абонентами, уменьшение числа скачков в них и уменьшение числа конфликтов при параллельной передаче.
При осуществлении изобретения может быть получен следующий технический результат:
1. По сравнению с иерархически толстым коммутатором - это, во-первых, уменьшение сложности и, во-вторых, уменьшение диаметра, уменьшение числа конфликтов, увеличение бисекционной пропускной способности и, как следствие, уменьшение задержeк передачи данных по сети.
2. По сравнению с сетями, использующими полнографовые связи - это увеличение числа узлов (примерно в квадрат раз), а также повышение отказоустойчивости при сохранении числа проводов и диаметра; или уменьшение числа проводов (примерно в корень квадратный раз) при сохранении числа узлов и диаметра, или многократное увеличение пропускной способности и отказоустойчивости системной сети при сохранении числа узлов.
Технический результат достигается тем, что системная сеть с топологией расширенного n-мерного R-ичного обобщенного гиперкуба, n ≥ 2, R ≥ 3, имеет вид n-мерного R-ичного расширенного обобщенного гиперкуба из R n узлов, при этом в каждом узле расположен абонент и полный коммутатор (n+1)×(n+1), а для связи узлов каждого из n×R n-1 ребер обобщённого гиперкуба имеется расширенный самомаршрутизируемый неблокируемый коммутатор R×R, состоящий из коммутаторов m×m, m ≥ 2, каждый из R портов которого соединен одним каналом с коммутатором (n+1)×(n+1) каждого из R узлов ребра, причём оставшийся порт каждого из коммутаторов подсоединен к абоненту своего узла.
На фиг.1 представлена Структура системной сети Blue Waters.
На фиг.2 представлена Структура системной сети Иерархического толстого гиперкуба, ИТГ, размерности 2 на 16 абонентов.
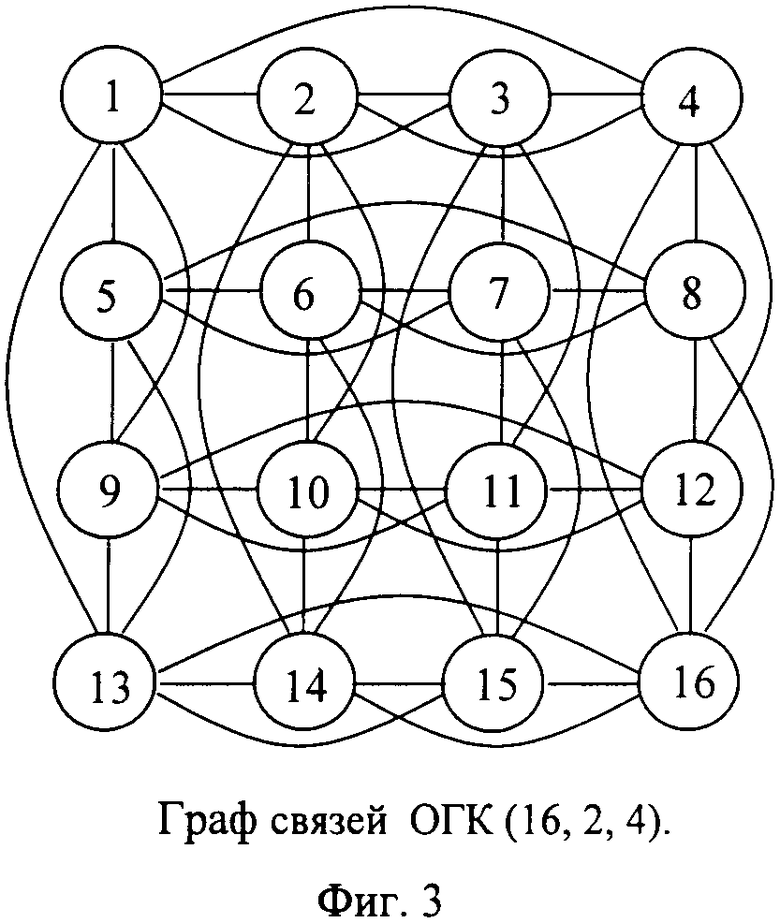
На фиг.3 изображён граф обобщённого гиперкуба, ОГК, с числом вершин 16, размерности 2, арности 4.
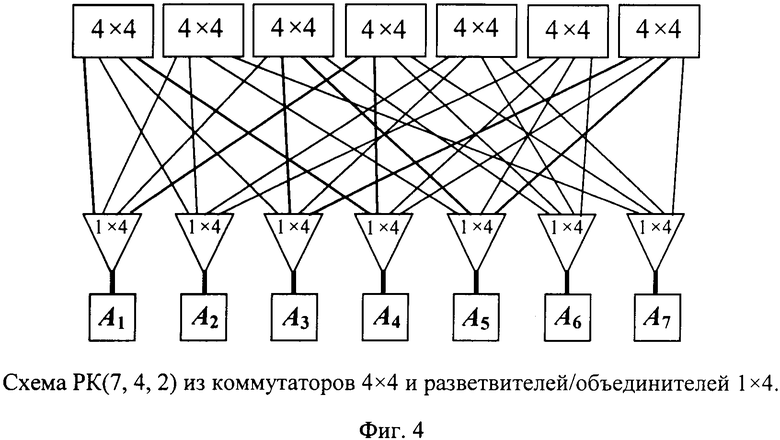
На фиг.4 представлен Расширенный коммутатор РК(7,4,2) из коммутаторов 4×4 и разветвителей/объединителей 1×4.
На фиг. 5 представлена Сеть с топологией обобщенного расширенного гиперкуба РОГК(49, 2, 7, 4, 2).
Предлагаемая системная сеть имеет топологию, основанную на расширении топологии обобщённого гиперкуба (ОГК), названной расширенным обобщённым гиперкубом (РОГК). Для аппаратной реализации связей между абонентами используются неблокируемые самомаршрутизируемые расширенные коммутаторы (РК), полученные согласно «Способу построения неблокируемого самомаршрутизируемого расширенного коммутатора (патент (19)RU(11) 2 435 295(13) C2)», предложенному авторами ранее.
Обобщенный гиперкуб, ОГК(V, d, s), обычно задается как d-мерный s-ичный гиперкуб, который имеет V=s d узлов степени d(s-1) каждый, размещенных в строках по s узлов, задающих «ребра» d-мерного куба. «Ребра» здесь понимаются не в графовом, а в геометрическом смысле. Наоборот, в графовом смысле «ребро» есть полный граф, т.е. все s узлов одного геометрического «ребра» связаны s(s-1) графовыми ребрами. Пример такого обобщённого гиперкуба ОГК(16, 2, 4) представлен на фиг.3. Содержательно ОГК можно представить как результат тиражирования двоичного гиперкуба во всех измерениях в s-1 экземплярах со «склейкой» смежных рёбер и с сохранением полноты связей в каждом геометрическом ребре.
Рассмотрим сеть с топологией РОГК, использующую РК, полученный выше названным Способом (патент (19)RU(11) 2 435 295(13) C2), использующим базовую таблицу соединений для использования дуплексных каналов (с топологией неполной уравновешенной блок-схемы). По этой таблице может быть построен РК(N, m, σ), являющийся «идеальной» сетью, которая имеет возможность использования прямых каналов (без промежуточной буферизации пакетов) для бесконфликтной реализации произвольной перестановки пакетов данных между узлами. Пример расширенного коммутатора РК(7, 4, 2) из коммутаторов 4×4 и разветвителей/объединителей 1×4 приведён на фиг.4. По построению распределенный полный коммутатор РК(N, m, σ) является неблокируемым самомаршрутизируемым коммутатором N×N, как и исходный коммутатор m×m. Это означает, что произвольная перестановка пакетов данных между абонентами может осуществляться в нем бесконфликтно по прямым (без промежуточной буферизации пакетов) каналам.
С формальной точки зрения диаметр РК(N, m, σ) равен 2 (D=2). Однако диаметр можно выражать и в числе скачков (передач по прямым каналам без промежуточной буферизации пакетов). Такой диаметр равен 1 (D=1).
Фактически РК(N, m, σ) реализует минимальные квазиполные графы связей между входными портами N, осуществляемые через коммутаторы m×m, с числом независимых связей, равным σ.
Расширение обобщенного гиперкуба можно осуществить за счет замены топологии связей в каждом геометрическом ребре с топологии полного графа на топологию квазиполного графа с помощью РК.
Рассмотрим устройство системной сети с топологией расширенного n-мерного R -ичного обобщенного гиперкуба. В нём Q=R n абонентов расположены в узлах ОГК(Q, n, R). На фиг. 5 показан пример сети, имеющей в основе граф ОГК с параметрами Q=49, n=2, R=7. В каждом узле также находится полный коммутатор (n+1)×(n+1), одним портом связанный с абонентом, а оставшиеся порты (число их равно размерности гиперкуба) используются для организации связей следующим образом. Для объединения узлов в каждом геометрическом ребре ОГК используем РК(R, m, σ) (в примере R=7, m=4, σ=2), где R=m(m-1)/σ+1. Всего таких рёбер n×R, по R рёбер в каждой размерности гиперкуба. В результате получим сеть с Q=R n узлами, в котором узлы каждого геометрического ребра связаны прямыми каналами через свой коммутатор R×R, как показано на фиг.5. Абоненты узлов разных рядов связываются через полные коммутаторы (n+1)×(n+1), расположенные в каждом узле гиперкуба. Топологию такой сети будем называть расширенным обобщенным n-мерным R-ичным гиперкубом и обозначать её РОГК(Q, n, R, m, σ). На фиг.5 для примера показана сеть с топологией РОГК(49, 2, 7, 4, 2).
Подчеркнём, что предложенная сеть может иметь в рёбрах σ>1 параллельных каналов, что позволяет повышать пропускную способность, либо отказоустойчивость сети, а произвольная перестановка пакетов данных между абонентами может осуществляться в ребре бесконфликтно по прямым (без промежуточной буферизации пакетов) каналам.
Оценим преимущества предложенной сети перед прототипом. Рассчитаем параметры 2-уровнего толстого гиперкуба, построенного посредством коммутаторов m×m. Учитывая один процессор и одну связь с метакубом, из них можно построить гиперкуб с числом узлов (абонентов) K=2m-2. Каждый узел метакуба содержит K коммутаторов, из которых можно построить метакуб с M=2m-1=2K узлами. В результате толстый гиперкуб содержит Q=KM=2K 2 абонентов, имеет схемную сложность S=Km 2 MKm 2=QKm 4=4K 3 m 4≈11,2Q 3/2 m 4 и проводную сложность W=KmWKm/4=K 3 m 2≈2,8 Q 3/2 m 2 .
Диаметр толстого гиперкуба D=m-2+m-1+m-2=3m-5, бисекционная пропускная способность B=G/2.
Пусть m=8, тогда K=64, M=128 и Q=8·1024, S=4·643·642=4·645=4·8·512·8·512·64=
=64·10242·64=4·10243, W=128·10242 , B=4·1024, D=19.
Для сравнения рассчитаем параметры нашего 2-мерного расширенного обобщенного гиперкуба, построенного из тех же коммутаторов m×m. Будем использовать схему расширенного обобщённого гиперкуба РОГК(Q, 2, R, m, 1), использующего расширенные коммутаторы РК(R, m, 1) с таблицами построения, рассчитанными на использование симплексных каналов. Тогда в каждом измерении содержится R=m 2 узлов, общее число узлов и абонентов - Q=R 2=m 4, схемная сложность S=Q(2m 2+2m)=2(m 6+m 5)=2(Q 3/2+Q 5/4) и проводная сложность W=Q2m=2Q 5/4. Диаметр D=4 или D=2, если считать расширенный коммутатор РК(R, m, 1) 1-скачковым. Бисекционная пропускная способность B=m 2 m 3/4=Q 5/4/4.
Пусть m=8, тогда K=64 и Q=642 =4·1024, S=2·(64·64·64+8·64·64)=2·72·64·64=142·8·512= =564·1024, W=8·1024·8=64·1024, B=85/4=2·642 =8·1024 и D=4.
При вдвое меньшем числе абонентов предлагаемая сеть с топологией РОГК имеет вдвое большую бисекционную пропускную способность, во много раз меньший диаметр и на много порядков меньшую сложность. Для того чтобы уравнять число узлов достаточно взять в РОГК m=10 (на четверть больше). При этом все остальные сравнения останутся справедливыми.
Покажем, что предложенное решение лучше по сравнению с вариантом сети, когда связи в рёбрах обобщённого гиперкуба реализуют полный граф.
Табл. 1 показывает, что сеть РОГК(Q, 3, R, m, σ) по сравнению с ОГК(V, 3, s) может иметь во много раз большее число узлов и/или в σ раз большую пропускную способность каждого геометрического ребра
Таблица 1. Фактор Q/V при m=s-1.
В табл. 2 показывается степень узла s (равная числу дуг узла) по каждому измерению в ОГК(V, d, s), имеющего такое же число узлов, как и РОГК(Q, n, R, m, σ), V=Q. Табл. 2 показывает, что РОГК(Q, n, R, m, σ) по сравнению с ОГК(V, d, s) может иметь во много раз меньшее число портов в каждом узле и/или в несколько раз большую пропускную способность каждого геометрического ребра.
Таблица 2. Значение s при V=Q (s=N) .
Рассмотрим работу сети с топологией РОГК на примере алгоритма зеркального отображения матрицы в сети РОГК(49, 2, 7, 4, 2), представленной на фиг. 5. В результате выполнения этого алгоритма 1-й элемент матрицы меняется местами с 49-м, 2-й элемент - с 48-м, 3-й элемент - с 47-м и т.д. Перед выполнением алгоритма элементы строк исходной матрицы размерности 7×7 находятся в абонентах соответствующих горизонтальных рёбер РОГК. На первом шаге алгоритма производится зеркальное отображение элементов матрицы во всех абонентах вертикальных рядов одновременно, на втором шаге производится зеркальное отображение элементов матрицы во всех абонентах горизонтальных рядов одновременно. В этом алгоритме на каждом шаге в расширенных коммутаторах РК(7, 4, 2) осуществляется перестановка 7 элементов за один такт параллельно и бесконфликтно. В случае выполнения более сложных операций в сети с топологией РОГК (в частности, с промежуточной буферизацией данных) произвольной размерности и арности (РОГК(Q, n, R, m, σ)) могут быть использованы известные алгоритмы параллельных вычислений и маршрутизации (Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем. Н.Новгород, ННГУ. 2003).
Предлагаемая организация сети обладает следующими преимуществами:
- обеспечивает уменьшение сложности, задержек передачи данных по сети, а также увеличение пропускной способности,
- позволяет в зависимости от области применения увеличивать либо количество узлов, либо вводить избыточные связи при экономном расходовании аппаратуры и проводов для связей,
- приводит к уменьшению числа конфликтов при параллельной передаче данных в сети за счёт применения неблокируемых самомаршрутизируемых расширенных коммутаторов.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ организации системной сети в виде отказоустойчивого неблокируемого трехмерного разреженного р-ичного гиперкуба | 2019 |
|
RU2720553C1 |
| СПОСОБ ПОСТРОЕНИЯ НЕБЛОКИРУЕМОГО САМОМАРШРУТИЗИРУЕМОГО РАСШИРЕННОГО КОММУТАТОРА | 2009 |
|
RU2435295C2 |
| Способ организации системной сети в виде неблокируемого самомаршрутизируемого трехмерного р-ичного мультикольца | 2018 |
|
RU2703351C1 |
| Способ построения коммутируемых управляющих сетей с топологией квазиполного орграфа | 2023 |
|
RU2815332C1 |
| ОБОБЩЕННЫЕ НЕБЛОКИРУЕМЫЕ ДВУХКАСКАДНЫЕ СЕТИ КЛОЗА | 2014 |
|
RU2580100C2 |
| Способ организации оптимальных отказоустойчивых многомерных торов на основе малопортовых маршрутизаторов и разветвителей дуплексных каналов | 2020 |
|
RU2753147C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ ПОИСКА ПОДВИЖНЫХ АБОНЕНТОВ НА СЕТЯХ СВЯЗИ | 2013 |
|
RU2514144C1 |
| МНОГОКАСКАДНЫЙ ОПТОЭЛЕКТРОННЫЙ КОММУТАТОР | 1993 |
|
RU2088960C1 |
| СИСТЕМА И СПОСОБ СВЯЗИ | 1997 |
|
RU2222869C2 |
| СПОСОБ НЕБЛОКИРУЕМОЙ МАРШРУТИЗАЦИИ | 2011 |
|
RU2472293C1 |
Изобретение относится к области высокопроизводительных многопроцессорных вычислительных систем. Техническим результатом является обеспечение надежных высокоэффективных сетей с большим числом процессорных узлов. Системная сеть с топологией расширенного n-мерного R-ичного обобщенного гиперкуба, n≥2, R≥3, характеризуется тем, что сеть имеет вид n-мерного R-ичного расширенного обобщенного гиперкуба из Rn узлов, при этом в каждом узле расположен абонент и полный коммутатор (n+1)×(n+1), а для связи узлов каждого из n×Rn-1 ребер обобщенного гиперкуба имеется расширенный самомаршрутизируемый неблокируемый коммутатор R×R, состоящий из коммутаторов m×m, m≥2, каждый из R портов которого соединен одним каналом с коммутатором (n+1)×(n+1) каждого из R узлов ребра, причем оставшийся порт каждого из коммутаторов подсоединен к абоненту своего узла. 5 ил., 2 табл.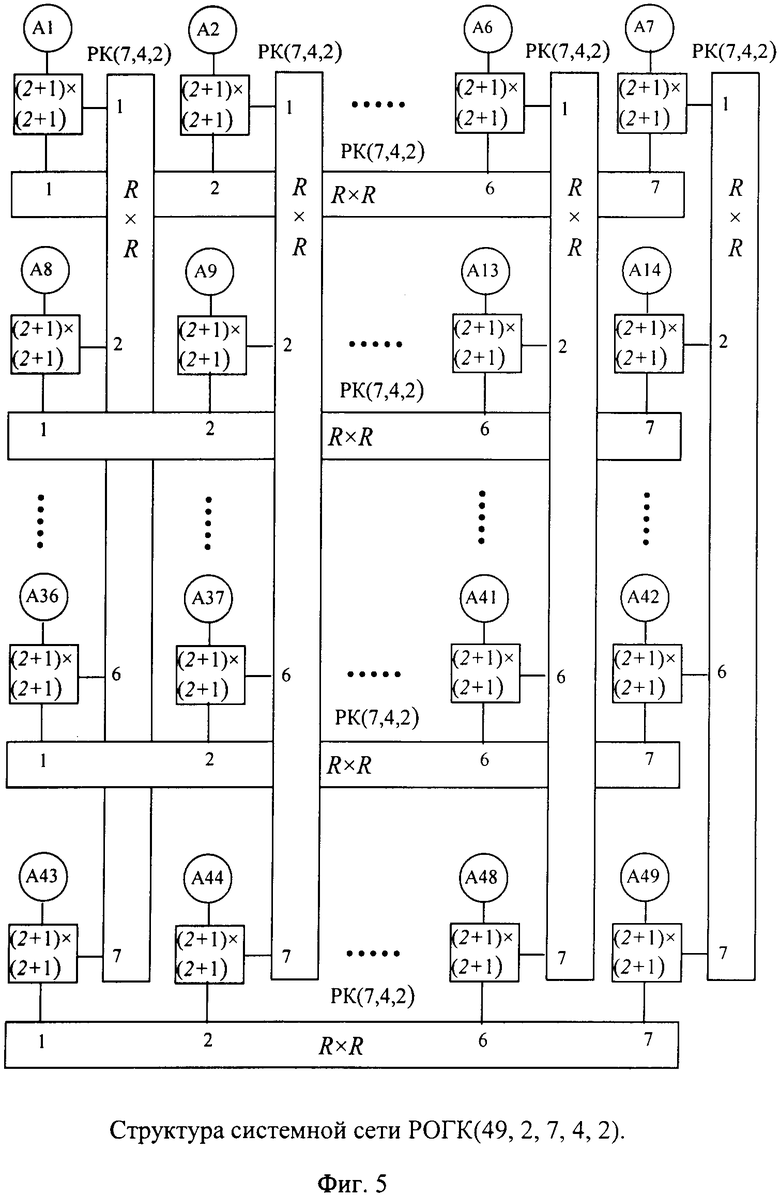
Системная сеть с топологией расширенного n-мерного R-ичного обобщенного гиперкуба, n≥2, R≥3, отличающаяся тем, что сеть имеет вид n-мерного R-ичного расширенного обобщенного гиперкуба из Rn узлов, при этом в каждом узле расположен абонент и полный коммутатор (n+1)×(n+1), а для связи узлов каждого из n×Rn-1 ребер обобщенного гиперкуба имеется расширенный самомаршрутизируемый неблокируемый коммутатор R×R, состоящий из коммутаторов m×m, m≥2, каждый из R портов которого соединен одним каналом с коммутатором (n+1)×(n+1) каждого из R узлов ребра, причем оставшийся порт каждого из коммутаторов подсоединен к абоненту своего узла.
| US 5669008 A, 16.09.1997 | |||
| US 5170482 A1, 08.12.1992 | |||
| Экономайзер | 0 |
|
SU94A1 |
| US 6230252 B1, 08.05.2001 | |||
| СПОСОБ ПОСТРОЕНИЯ НЕБЛОКИРУЕМОГО САМОМАРШРУТИЗИРУЕМОГО РАСШИРЕННОГО КОММУТАТОРА | 2009 |
|
RU2435295C2 |
Авторы
Даты
2015-07-10—Публикация
2013-03-21—Подача