Изобретение относится к области вычислительной техники.
Сети Клоза широко применяется для построения параллельных МВС (Scott S., Abts D., Kim J. and Dally W. The black widow high-radix Clos network // Proc. 33rd Intern. Symp. Сотр. Arch. (ISCA'2006). 2006. URL: http://www.scc. acad.bg/ncsa/articles/librarv/Switches%20and%20Networks/High_Radix_Clos_Stanford.pdf).
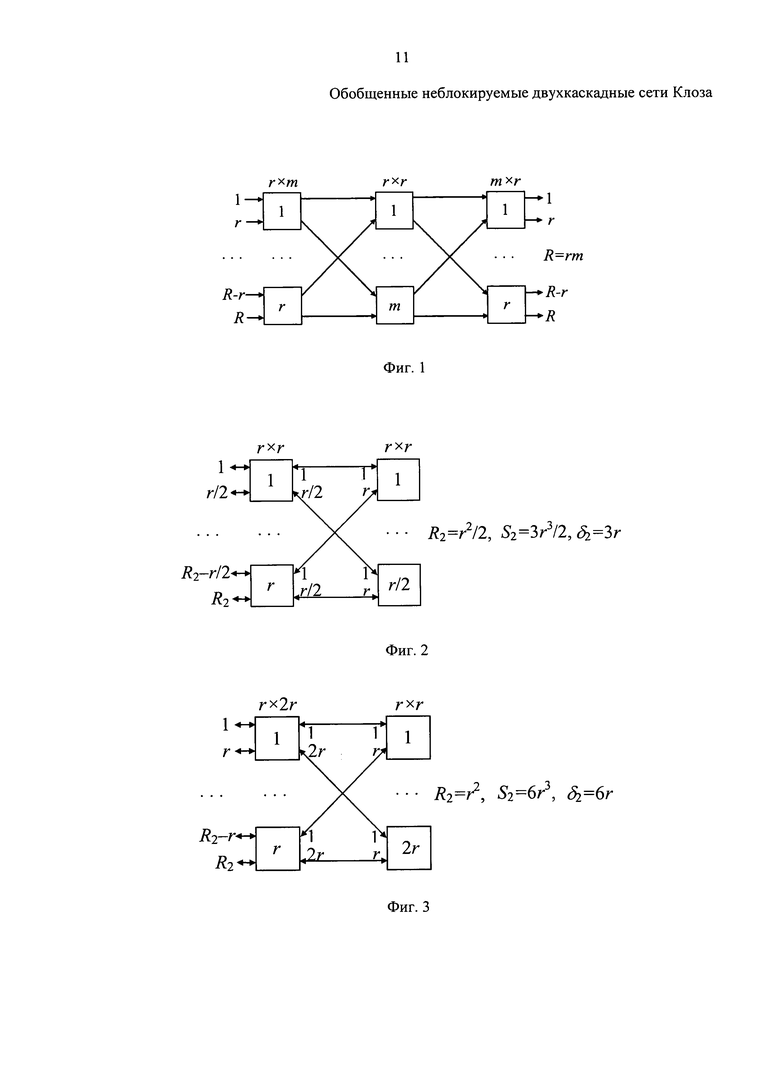
На фиг. 1 показана базовая сеть Клоза (Pipenger N. On rearrangeable and non-blocking switching networks. J. Comput. Syst. Sci. 1978. V.17. p. 307-311) на R портов, в которой используются однонаправленные коммутаторы с симплексными портами. Она имеет три каскада полных коммутаторов r×m, m×r (1-й и 3-й каскады) и r×r (2-й каскад - хребет), полностью задается параметрами m, n, r (R=mr) и является перестраиваемой при m=r и неблокируемой при m≥2r-1.
Перестраиваемая сеть Клоза имеет отдельное бесконфликтное расписание для любой перестановки данных между входными и выходными портами, которое в общем случае неизвестно, и требуется выполнения отдельной процедуры для его построения, а неблокируемая сеть допускает возможность прокладки нового бесконфликтного пути между любой парой свободных портов, не изменяя имеющихся путей (Pipenger N. On rearrangeable and non-blocking switching networks. J. Comput. Syst. Sci. 1978. V.17. p. 307-311).
При m=2r неблокируемая сеть Клоза содержит R3=r2 портов и состоит из коммутаторов разного состава - r×2r и 2r×r в 1-м и 3-м каскаде и r×r в хребте.
Неблокируемая сеть Клоза выбрана в качестве прототипа.
Неблокируемая сеть Клоза также может иметь сложенный вид (фиг. 2), в котором одноименные коммутаторы 1-го и 3-го каскадов выполняются в виде одного каскада из коммутаторов r×2r с 3r дуплексными портами, а в качестве коммутаторов центрального каскада (хребта) используются коммутаторов r×r с r дуплексными портами. Очевидно, что базовую сеть Клоза (фиг. 1) можно получить «разложением» сложенной, отображая 1-ый каскад зеркально в 3-ий относительно хребтового каскада и использованием в полученной структуре однонаправленных коммутаторов с симплексными портами.
Перестраиваемая сеть также может быть представлена в сложенном виде.
Ранее авторами были предложены обобщенные сети Клоза, в которых межкаскадные связи имеют топологию квазиполного графа (Подлазов B.C., Соколов В.В. Обобщенные сети Клоза // АиТ. 2009, №10, с. 158-170). В данном изобретении предлагаются обобщенные неблокируемые двухкаскадные сети Клоза нового вида (далее сокращенно OHCK2), которые, при прочих равных условиях по сравнению с прототипом, имеют меньшие задержки и большее число абонентов, а по критерию сложность/быстродействие эти сети оказываются достаточно близкими.
Техническим результатом изобретения является вдвое большее число абонентов, чем в обычных неблокируемых сетях Клоза, и вчетверо большее число абонентов, чем в перестраиваемых сетях Клоза, при использовании одинаковых коммутаторов в хребтовых каскадах, причем задержки передачи данных в предложенной сети уменьшаются.
Технический результат достигается тем, что первый каскад в сетях ОНСК2 состоит из N коммутаторов r×2r с 3r дуплексными портами, причем r портов всех коммутаторов первого каскада образуют R=N×r внешних портов OHCK2, а внутренние 2r портов соединены со 2-м каскадом (хребтом), который состоит из 2N коммутаторов r×r с r дуплексными портами, причем первые r портов из 2r внутренних портов коммутаторов 1-го каскада соединены с r портами первых N коммутаторов хребта, а вторые r портов из 2r внутренних портов коммутаторов 1-го каскада соединены с r портами вторых N коммутаторов хребта в соответствии с одной и той же таблицей соединения, удовлетворяющей условию N=2(r-1)+1, причем таблица соединений имеет N строк и r столбцов, в ячейке ij которой указан номер коммутатора 1-го каскада, который соединен с i-м коммутатором хребта через j-е порты каждого из них, как это показано, например для N=7 и r=4.
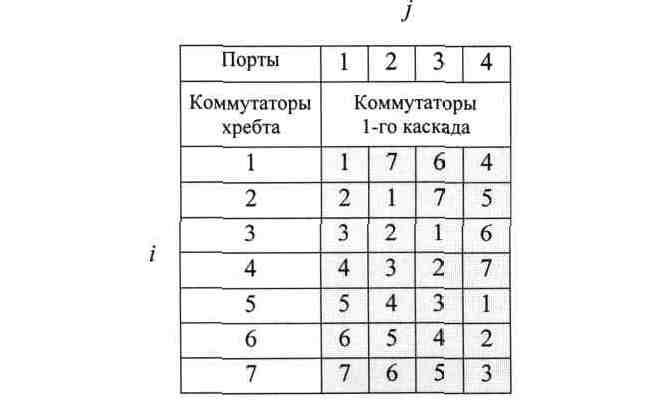
Сокращенный вариант сети OHCK2 с R=N×r/2 внешними портами содержит во 2-ом каскаде (хребте) только первые N коммутаторов r×r с r портами, а 1-ый каскад состоит из уменьшенных вдвое коммутаторов r/2×r.
В симплексном варианте сети OHCK2, с симплексными R входными и R выходными портами, порты коммутаторов есть симплексные порты, причем внешние порты 1-го каскада есть входные порты ОНСК2, внутренние порты 1-го каскада есть выходные порты, соединенные в соответствии с таблицей соединения по п. 1 или 2. с входными портами хребтовых коммутаторов r×r, которые содержат также r выходных портов, соединенных с внутренними входными портами 3-его каскада, являющимися зеркальным отображением 1-го, а именно, таблица соединения 3-го каскада с хребтом такая же, как и 1-го с хребтом, при этом количество выходных портов 3-го каскада равно R и эти порты являются выходными симплексными портами ОНСК2.
Следующие иллюстрации объясняют изобретение.
На фиг. 1 представлена базовая трехкаскадная сеть Клоза.
На фиг. 2 - сложенная двухкаскадная перестраиваемая сеть Клоза СПСК2(R2, r).
На фиг. 3 - сложенная двухкаскадная неблокируемая сеть Клоза CHCK2(R2, r).
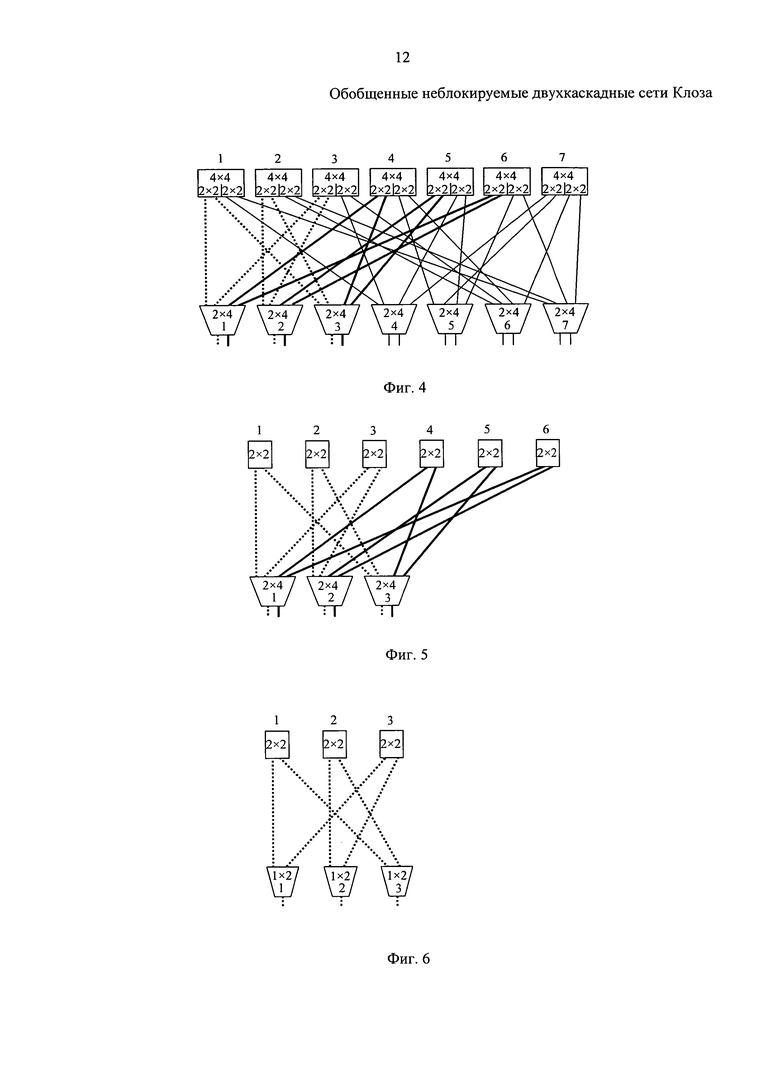
На фиг. 4 - обобщенная одинарная неблокируемая сеть Клоза ООСК2(14, 4, 2).
На фиг. 5 - обобщенная двойная неблокируемая сеть Клоза ОДСК2(6, 2, 2).
На фиг. 6 - обобщенная одинарная сеть Клоза ООСК2(3, 2, 1).
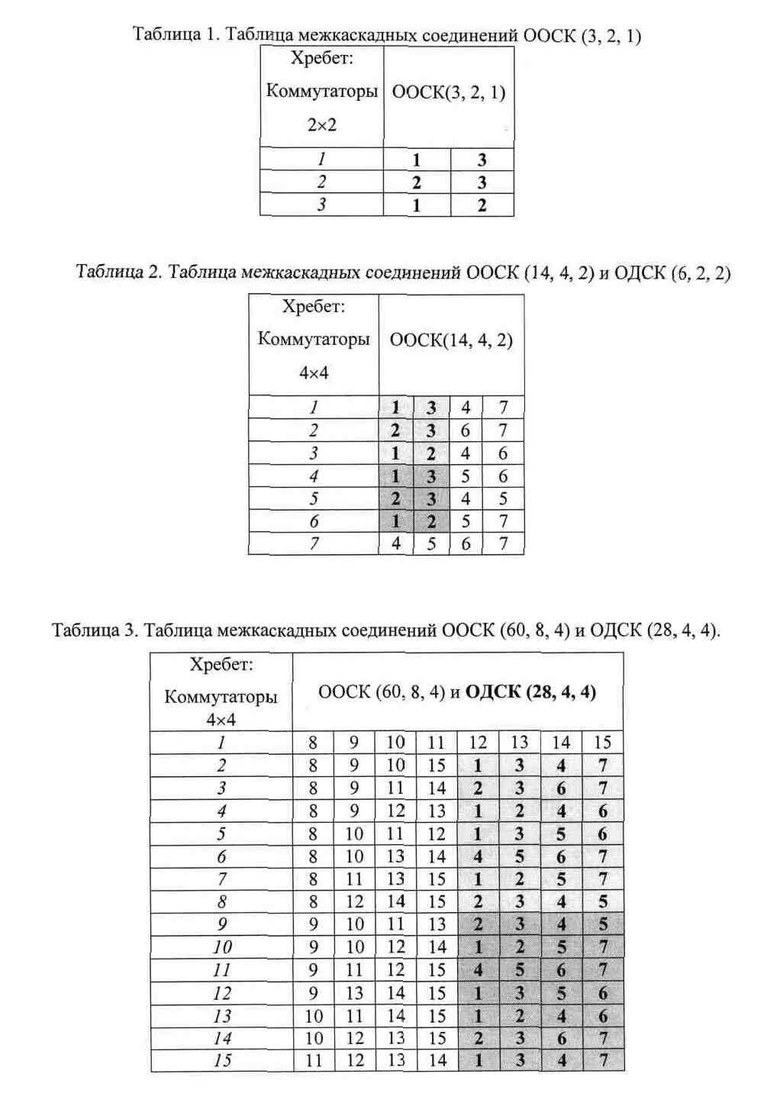
В Табл.1. Таблица межкаскадного соединения для ООСК2(14, 4, 2).
В Табл.2. Таблица межкаскадного соединения для OOCK2(14, 4, 2) и ОДСК2(6, 2, 2).
В Табл.3. Таблица межкаскадного соединения для ООСК2(60, 8, 4) и ОДСК2(14, 4, 4).
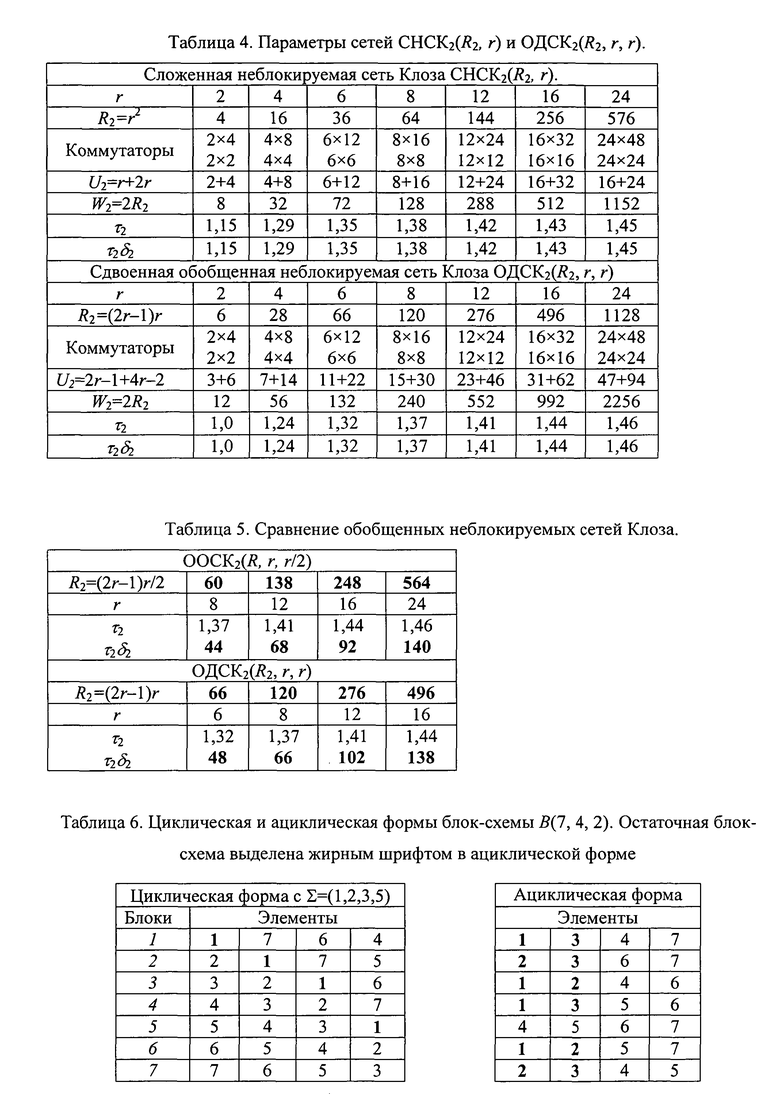
В Табл.4. Параметры сетей CHCK2(R2, r) и ОДСК2(R2, r, r).
В Табл.5. Сравнение обобщенных неблокируемых сетей Клоза ООСК2(R2, r, r/2) и ОДСК2(R2, r, r).
Опишем структуру и характеристики новых подвидов обобщенной неблокируемой двухкаскадной сети Клоза, ОНСК2: обобщенной сдвоенной двухкаскадной сложенной сети Клоза, ОДСК2, и обобщенной одинарной сложенной двухкаскадной сети Клоза, ООСК2, заявляемых соответственно в первом и втором пункте Формулы. Оба вида ОНСК2 могут быть представлены и в «разложенном» симплексном виде, который заявляется в третьем пункте Формулы. Все эти сети являются неблокируемыми, и буква Н в аббревиатуре опущена для облегчения чтения.
Одинарная сложенная ООСК2(R2, r, r/2) имеет в первом каскаде N дуплексных коммутаторов r/2×r и во втором каскаде N дуплексных r×r хребтовых коммутаторов. Таким образом, сеть имеет R2 дуплексных входов, равное N×r/2. При этом число прямых каналов, которыми любые два коммутатора 1-го каскада могут быть соединены через разные коммутаторы 2-го каскада, должно быть равно r/2. Пример ООСК2(14, 4, 2) для r=4 представлен на фиг. 4.
Структура ООСК2(R2, r, r/2) обеспечивается Таблицей межкаскадных связей определенного вида:
- таблица соединений имеет N строк и r столбцов, в ячейке ij которой указан номер коммутатора 1-го каскада, который соединен с i-ым коммутатором хребта через j-ые порты каждого из них, как это показано, например, в Таблицах 1-3 межкаскадного соединения для ООСК2(3, 2, 1), ОOСK2(14, 4, 2) и ООСК2(60, 8, 4),
- параметры Таблицы должны удовлетворять соотношению N=r(r-1)/σ+1, где σ - число прямых каналов, которыми любые два коммутатора 1-го каскада могут быть соединены через разные коммутаторы 2-го каскада, значение σ должно быть равно r/2, то есть в разных строках таблицы должны встречаться пары номеров коммутаторов 1-го каскада r/2 раз. Так, в Таблице ООСК2(3, 2, 1) (табл.1) эти пары встречаются 1 раз, в Таблице ООСК2(14, 4, 2) (табл.2) - по 2 раза, и в Таблице ООСК2(60, 8, 4) (табл.3) - по 4 раза.
ООСК2(R2, r, r/2) является неблокируемой по прямым каналам сетью, поскольку число коммутаторов N удовлетворяет неблокируемости Клоза m≥2r-1, а именно: N≥2r-1 (Бенеш В.Е. Математические основы теории телефонных сообщений М.: Связь, 1968. С.83-150).
Обобщенную сдвоенную двухкаскадную сеть Клоза, ОДСК2 можно представить как композицию двух одинарных. Пример ОДСК2(6, 2, 2) как результат композиции двух ООСК2(3, 2, 1) представлен на фиг. 5. Видно, что композиция двух одинарных сетей ООСК2(3, 2, 1) (одна сеть изображена на фиг. 6) происходит путем слияния одноименных коммутаторов 1-го каскада (в результате чего получаются коммутаторы с удвоенными входами и выходами) и удвоения N коммутаторов хребтового каскада, причем все межкаскадные соединения одинарных сетей сохраняются. Одинарная сеть может быть «урезанным» вариантом сдвоенной, полученная путем удаления вторых N хребтовых коммутаторов, их связей с 1-ым каскадом и соответствующим уменьшением числа выходов и входов 1-го каскада в 2 раза. Именно так это зафиксировано во п. 2 Формулы изобретения.
Сдвоенная сеть обозначается ОДСК2(R2, r, r), где R2 - число дуплексных входов сети, r - число входов каждого из N хребтовых коммутаторов и число входов каждого из N коммутаторов 1-го каскада.
Таблица межкаскадных соединений сдвоенной сети может быть получена как остаточная путем сокращения таблицы соединения одинарной сети большей размерности.
Поясним на примере. В Таблице OOCK2(14, 4, 2), представленной в табл.2 (соответствующая ей структура на фиг. 4), где N=7, удаляем 7-ый хребтовый коммутатор, далее все коммутаторы 1-го каскада, с ним связанные (коммутаторы 4-7), и далее все связи, идущие от удаляемых коммутаторов на хребтовые с соответствующим уменьшением числа входов хребтовых коммутаторов. Остается выделенная часть Таблицы ООСК2(14, 4, 2), соответствующая Таблице ОДСК2(6, 2, 2), структура которой представлена на фиг. 5. Поэтому сети ОДСК2 называем также и остаточными обобщенными сетями Клоза.
Математической моделью, описывающей обобщенные сети Клоза, в которых межкаскадные связи имеют топологию квазиполного графа, являются неполные уравновешенные блок-схемы, в частности, симметричные блок-схемы, исследуемые в комбинаторике (Холл М. Комбинаторика // Главы 10-12. М.: Мир. 1970. 424 с.).
Симметричная блок-схема B(N, r, σ) состоит из элементов, составляющих одну долю графа, и блоков, составляющих другую долю графа. Число элементов и блоков одинаково и равно N. Параметр r задает число блоков, в которые входит каждый элемент, и число элементов, входящих в каждый блок. Параметр σ<r задает число блоков, в которые входит каждая пара элементов. Параметры симметричной блок-схемы B(N, r, σ) связаны соотношением N=r(r-1)/σ+1.
Таким образом, симметричная блок-схема описывает квазиполный граф, состоящий из двух долей по N узлов (Каравай М.Ф., Пархоменко П.П., Подлазов B.C. Комбинаторные методы построения двудольных однородных минимальных квазиполных графов (симметричных блок-схем) // АиТ. 2009. №2. с. 153-170), и отождествление коммутаторов 1-го и 2-го каскада соответственно с элементами и блоками неполных уравновешенных блок-схем дает возможность технического использования результатов исследований в комбинаторике.
Рассмотрим характеристики предложенных неблокируемых обобщенных сетей Клоза в сравнении с известными.
Сложность коммутатора r×r для оценок равна r2, а сложность коммутатора r×2r равна 4r2.
Для сложенной двухкаскадной перестраиваемой сети Клоза СПСК2(R2, r) число входов сети R2=r2/2, сложность сети S2=3r3/2, удельная (на одного абонента) сложность δ2 составляет δ2=S2/R2=3r.
Для сложенной двухкаскадной неблокируемой сети Клоза CHCK2(R2, r) эти зависимости представляются таким образом: R2=r2, S2=6r3 и δ2=6r. Удельная сложность неблокируемой сети в 2 раза больше, чем у перестраиваемой.
Рассмотрим характеристики ООСК2(R2, r, r/2). Она содержит R2=Nr/2=r2-r/2 дуплексных портов абонентов. Ее сложность составляет S2=4(r-1/2)r2, а удельная сложность - δ2=4r, т.е. в 4/3 раза больше чем, у перестраиваемой сети Клоза СПСК2(R2, r), и в 3/2 раза меньше, чем у неблокируемой сети Клоза СНСК2(R2, r).
Для ОДСК2(R2, r, r) эти зависимости таковы: R2=(2r-1)r, S2=6(2r-1)r2, δ2=6r. Результаты сравнения ОДСК2(R2, r, r) и СНСК2(R2, r) с учетом имитационного моделирования представлены в Табл.4. Характеристики сетей Клоза получались посредством имитационного моделирования для перестановочного графика, при котором пакет каждого источника входит в состав произвольной перестановки, т.е. он может передаваться одному и только одному приемнику. В Табл.4 использованы результаты моделирования, в котором применялась самомаршрутизация по номеру прямого канала, а именно: i-й источник в качестве выходного канала в некотором каскадном коммутаторе использовал i-й прямой канал из данного коммутатора. Заметим, что номер прямого канала в общем случае не совпадает с номером выходного канала, через который он реализуется, но последний определяется однозначно по номерам входного и выходного каскадных коммутаторов и номерам источника и приемника в этих коммутаторах {Подлазов B.C., Каравай М.Ф. Системные сети с прямыми каналами для многопроцессорных вычислительных систем - идеальные системные сети // Palmarium Academic Publishing. 2012. 168 с. URL: http://www.ipu.ru/sites/default/files/publications/18125/3747-18125.pdf)
Были рассмотрены и другие способы маршрутизации, отличающиеся логикой выбора маршрута, но характер соотношений при этом сохранялся.
В Таблице переменная U2 задает число коммутаторов, переменная W2 - число кабелей, а τ - средняя задержка пакетов в сети.
Заметим, что сеть ОДСК2(R2, r, r) имеет одинаковый схемный базис со сложенной неблокируемой сетью СНСК2(R2, r), и удельные сложности у них одинаковые. Поэтому их легко сравнивать (Табл.4). Видно, что сеть ОДСК2(R2, r, r) имеет в (2-1/r) раз больше абонентов за счет использования большего числа проводов и хребтовых коммутаторов. При этом задержки τ2 в сети ОДСK2(R2, r, r) практически одинаковы с задержками τ2, в сложенной неблокируемой сетью (Табл.4), а при сравнимом числе абонентов они даже меньше. Поэтому по критерию min(τδ) при примерно равном числе абонентов сеть ОДСК2(R2, r, r) вдвое превосходит сеть СНСК2(R2, r) и более чем вдвое сеть СПСК2(R2, r).
Сети OOCK2(R2, r, r/2) трудно сравнивать с ОДСК2(R2, r, r), т.к. они имеют разный схемный базис. Однако при примерно равном числе абонентов с учетом разных значений r они имеют и примерно одинаковые значения τ2 и τ2δ2 (Табл.5). По критерию min(τ2δ2) обобщенная одинарная неблокируемая сеть OOCK2(R2, r, r/2) на 30% лучше неблокируемой сети СНСК2(R2, r).
Построение Таблиц межкаскадных связей для OOCK2 и ОДСК2 сводится к построению таблиц симметричных блок-схем B(N, r, σ) и несимметричных блок-схем, являющихся остаточными к B(N, r, σ), соответственно. Симметричная блок-схема определятся с точностью до состава блоков, т.е. набором элементов в каждом блоке. Поэтому изменение номеров блоков, номеров элементов во всех блоках и порядка элементов в блоках не меняет блок-схему и являются ее тождественными преобразованиями. При этом внешний вид квазиполных графов, соответствующих блок-схемам, полученных тождественными преобразованиями меняется, а сами графы остаются изоморфными.
Симметричная блок-схема явно задается таблицей, состоящей из N строк и r+1 столбцов. Первый столбец таблицы содержит номера блоков, занумерованных от 1 до N. Элементы также нумеруются с 1 до N. В ячейках i-й строки остальных столбцов содержатся номера элементов, входящих в i-й блок.
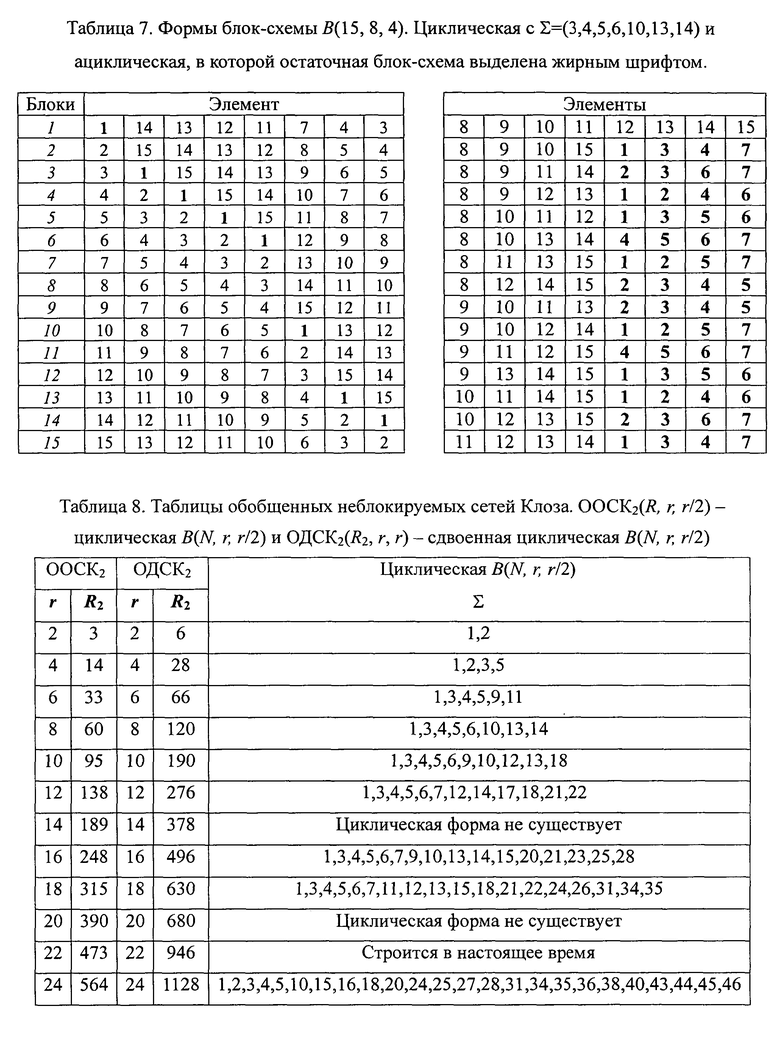
Симметричная блок-схема имеет две формы канонического представления - циклическую и ациклическую, примеры которых для блок-схемы B(7, 4, 2) приведены в Табл.6. Ациклическая форма является более общей - некоторые блок-схемы могут существовать в ациклической форме, но не могут быть представлены в циклической. Любая циклическая блок-схема может быть тождественными преобразованиями превращена в ациклическую, но не наоборот.
Циклическая блок-схема имеет форму представления, в которой столбцы таблицы содержат сдвинутые по строкам циклические последовательности номеров элементов 1, 2, …, N. Будем характеризовать такую блок-схему набором номеров блоков (строк), в которые входит 1-й элемент. Обозначим этот набор как ∑. Циклическая блок-схема существует не для любого набора ∑ - его еще надо найти. Построение циклической блок-схемы сводится к нахождению набора ∑, и она однозначно задается этим набором, как это показано в Табл.6.
В силу эквивалентности циклической и ациклической форм блок-схем для практических нужд удобно использовать циклическую форму. Сеть OOCK2(R, r, r/2) имеет Таблицу в виде блок-схемы B(N, r, r/2), а сеть ОДСК2(R2, r, r) - в виде удвоенной блок-схемы B(N, r, r/2), как это было, например, показано выше для ООСК (3, 2, 1) и ОДСК (6, 2, 2). В табл.8 приводятся одно из возможных значений ∑ для этих сетей при разных r.
Таким образом, с помощью этого изобретения, используя одинаковые коммутаторы в хребтовых каскадах, можно при меньших задержках передачи обеспечить вдвое большее число коммутируемых абонентов, чем в обычных неблокируемых сетях Клоза, и вчетверо большее число абонентов, чем в перестраиваемых сетях Клоза.
Изобретение относится к области вычислительной техники и может быть использовано для построения параллельных вычислительных систем. Техническим результатом является уменьшение задержки передачи данных и повышение числа коммутируемых абонентов сети. Устройство состоит из двух каскадов, первый из которых состоит из N коммутаторов r×2r с 3r дуплексными портами, а второй каскад состоит из 2N коммутаторов r×r с r дуплексными портами, причем r портов всех коммутаторов первого каскада образуют R=N×r внешних портов устройства, первые r портов из 2r внутренних портов коммутаторов 1-го каскада соединены с r портами первых N коммутаторов 2-го каскада, а вторые r портов из 2r внутренних портов коммутаторов 1-го каскада соединены с r портами вторых N коммутаторов хребта в соответствии с одной и той же таблицей соединения, удовлетворяющей условию N=2(r-1)+1. Таблица межкаскадных соединений имеет N строк и r столбцов, в ячейке ij которой указан номер коммутатора 1-го каскада, который соединен с i-м коммутатором хребта через j-е порты каждого из них. 2 з.п. ф-лы, 6 ил., 8 табл.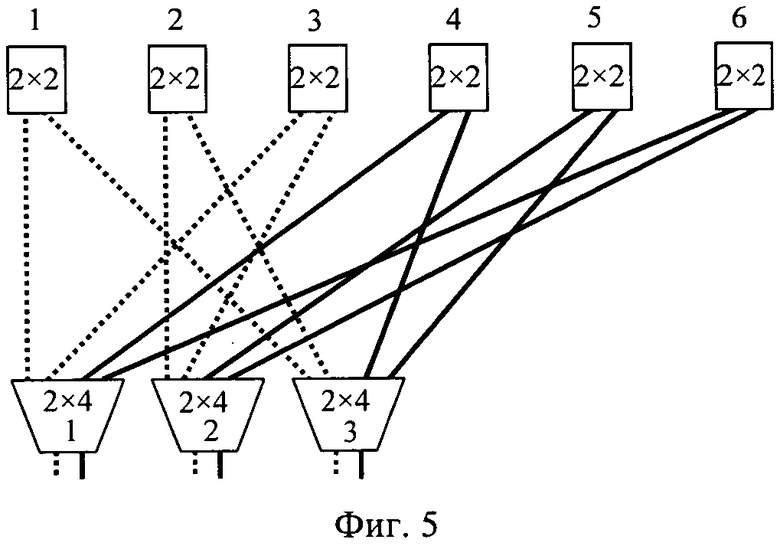
1. Обобщенная неблокируемая сложенная двухкаскадная сеть Клоза, ОНСК2, с R дуплексными портами характеризуется тем, что первый каскад состоит из N коммутаторов r×2r с 3r дуплексными портами, причем r портов всех коммутаторов первого каскада образуют R=N×r внешних портов ОНСК2, а внутренние 2r портов соединены со 2-м каскадом (хребтом), который состоит из 2N коммутаторов r×r с r дуплексными портами, причем первые r портов из 2r внутренних портов коммутаторов 1-го каскада соединены с r портами первых N коммутаторов хребта, а вторые r портов из 2r внутренних портов коммутаторов 1-го каскада соединены с r портами вторых N коммутаторов хребта в соответствии с одной и той же таблицей соединения, удовлетворяющей условию N=2(r-1)+1, причем таблица соединений имеет N строк и r столбцов, в ячейке ij которой указан номер коммутатора 1-го каскада, который соединен с i-м коммутатором хребта через j-е порты каждого из них.
2. Сеть по п. 1 характеризуется тем, что является сокращенным вариантом ОНСК2 с R=N×r/2 внешними портами, при этом 2-й каскад (хребет) содержит только первые N коммутаторов r×r c r портами, а 1-й состоит из уменьшенных вдвое коммутаторов r/2×r.
3. Сеть по п. 1 или 2 характеризуется тем, что является симплексным вариантом ОНСК2 с симплексными R входными и R выходными портами, порты коммутаторов сети есть симплексные порты, причем внешние порты 1-го каскада есть входные порты ОНСК2, внутренние порты 1-го каскада есть выходные порты, соединенные с входными портами хребтовых коммутаторов r×r, которые содержат также r выходных портов, соединенных с внутренними входными портами 3-го каскада, являющимся зеркальным отображением 1-го, а именно, таблица соединения 3-го каскада с хребтом такая же, как и 1-го с хребтом, при этом количество выходных портов 3-го каскада равно R и эти порты являются выходными симплексными портами ОНСК2.
| СПОСОБ ПОСТРОЕНИЯ НЕБЛОКИРУЕМОГО САМОМАРШРУТИЗИРУЕМОГО РАСШИРЕННОГО КОММУТАТОРА | 2009 |
|
RU2435295C2 |
| ГЛОБАЛЬНОЕ БЕСКОНФЛИКТНОЕ СОЕДИНЕНИЕ | 1997 |
|
RU2198481C2 |
| ОДНОРОДНАЯ СЕТЬ КОММУТАЦИИ С ТОПОЛОГИЕЙ МНОГОЗВЕННОГО ТОРА | 1990 |
|
RU2013878C1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| WO 2010147858 A1, 23.12.2010 | |||
| WO 2013160786 A1, 31.10.2013. | |||
Авторы
Даты
2016-04-10—Публикация
2014-05-16—Подача