Изобретение относится к области вычислительной техники, а именно к построению коммутируемых управляющих сетей. Коммутируемые управляющие сети (КУС) в настоящее время широко применяются в промышленности, авионике, робототехнике и других отраслях народного хозяйства. По сравнению с шинными управляющими сетями КУС за счет структурного параллелизма могут иметь более высокое быстродействие, возможность использования оборудования с более низкоскоростным интерфейсом и более высокой помехозащищенностью, отличаются более высокой масштабируемостью.
Особенностью управляющих сетей является разделение абонентов сети по назначению на активные и пассивные устройства (АУ и ПУ). Активные устройства (обычно меньшая часть абонентов) обмениваются сообщениями между собой и пассивными устройствами, а обмен сообщений между пассивными устройствами отсутствует.
В работе "Каравай М.Ф., Михайлов A.M. Design of local heterogeneous system control networks of a new generation with the preservation of the optimality of the main topological functionals of the network // Proceedings of the 5th International Scientific Conference on Information, Control, and Communication Technologies (ICCT-2021). Astrakhan: IOP Publishing, 2021. Vol.2091. C. https://iopscience.iop.org/issue/1742-6596/2091/1" впервые предложено строить КУС как сети с топологией квазиполных графов (сети ТКГ). Исходно эти сети состоят из N=m(m-1)/σ+1 m-портовых АУ, связанных дуплексными каналами через N коммутаторов m×m. Они являются неблокируемыми самомаршрутизируемыми сетями на произвольных перестановках пакетов между всеми АУ, и имеют σ разных каналов между любыми двумя АУ. В таких сетях N имеет максимально возможное значение N при заданных значениях m и σ. Соединения между коммутаторами и АУ задаются таблицами инцидентности симметричных блок-схем (block-designs) B(N, m, σ), изучаемых в комбинаторике ("Каравай М.Ф., П.П. Пархоменко П.П., Подлазов B.C. Комбинаторные методы построения двудольных однородных минимальных квазиполных графов (симметричных блок-схем) // АиТ. 2009 №2 С.153-170").
Назначая среди N устройств сети ТКГ α устройств активными, а π=N-α устройств пассивными, сокращая затем ненужные для обмена между ПУ связи и коммутаторы, получают коммутируемую управляющую сеть КУС(α; π, κ) с топологией квазиполных графов, где α, π, κ - число АУ, ПУ и коммутаторов.
В такой КУС все АУ сохраняют бесконфликтные соединения на произвольных перестановках пакетов между ними, каждый АУ имеет соединение с любым ПУ и все АУ имеют бесконфликтные соединения с ПУ.
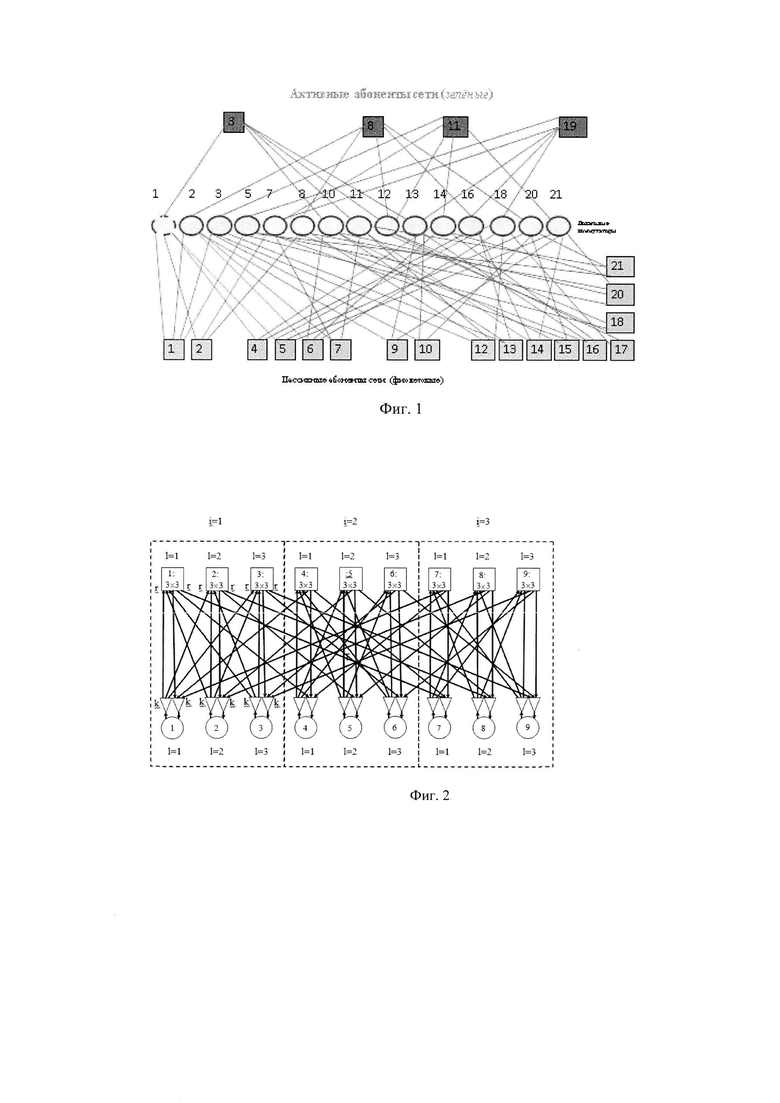
Пример структуры сети КУС(4, 17, 15) с ТКГ, построенной на основе таблицы инцидентности симметричной блок-схемы B(21, 5, 1) приведен на фиг. 1.
Описанный способ выбран в качестве прототипа.
Главный недостаток этого способа, заключается в том, что построенные КУС характеризуются слабой масштабируемостью, осуществляемой только за счет увеличения степени m, и довольно высокой сложностью за счет большого числа коммутаторов κ.
Технической задачей изобретения является разработка такого способа построения сети, который позволит получить КУС меньшей сложности и большей масштабируемости по сравнению с прототипом.
Техническим результатом способа является уменьшение коммутационной и канальной сложностей КУС с топологией квазиполных графов и возможность масштабирования сети без наращивания количества и размерности образующих ее коммутаторов.
Технический результат достигается тем, что способ построения неблокируемой коммутируемой управляющей сети с топологией квазиполного орграфа, КУС(m, N-m, 2m-1) состоит из m активных абонентов, которые имеют полные связи между собой и с пассивными абонентами, N-m пассивных абонентов, которые имеют связи только с активными абонентами (причем количество всех абонентов N=m2), и 2m-1 коммутаторов m×m, характеризующийся тем, что КУС(m, N-m, 2m-1) редуцируют из коммутируемой сети с топологией квазиполного орграфа, состоящей из N=m2 абонентов, N коммутаторов m×m и N пар демультиплексоров 1×m и мультиплексоров m×1 следующим образом (при этом абоненты, коммутаторы, демультиплексоры и мультиплексоры пронумерованы от 1 до N):
связи от N-m коммутаторов с номерами от m+1 до N к абонентам с номерами от m+1 до N и одноименные этим абонентам демультиплексоры и мультиплексоры удаляют, эти коммутаторы с номерами от m+1 до N объединяют в порядке возрастания номеров по m коммутаторов в m-1 группу коммутаторов и заменяют каждую из этих групп на соответствующий эквивалентный коммутатор m×m;
при этом в коммутируемой сети с топологией квазиполного орграфа коммутаторы и одноименные им абоненты, мультиплексоры и демультиплексоры разбивают на m равных групп, группы, а также абоненты, мультиплексоры и демультиплексоры в них нумеруют от 1 до m, причем i (1≤i≤m) задает номер группы, l (1≤l≤m) задает номер коммутатора, демультиплексора и мультиплексора в соответствующих группах, а r (1≤r≤m) задает номер порта коммутатора и k (1≤k≤m) - номер порта мультиплексора или демультиплексора;
для всех портов демультиплексоров, мультиплексоров и коммутаторов k-й выходной порт l-го демультиплексора i-й группы соединяют с l-м входным портом k-го коммутатора той же i-й группы, r-й выходной порт l-го коммутатора i-й группы соединяют с i-м входным портом l-го мультиплексора r-й группы;
выходы абонентов подсоединяют к входам одноименных демультиплексоров, выходы мультиплексоров подсоединяют к входам одноименных абонентов.
Следующие иллюстрации объясняют изобретение.
На фиг. 1 приведена Структура КУС(4, 17, 15) с ТКГ.
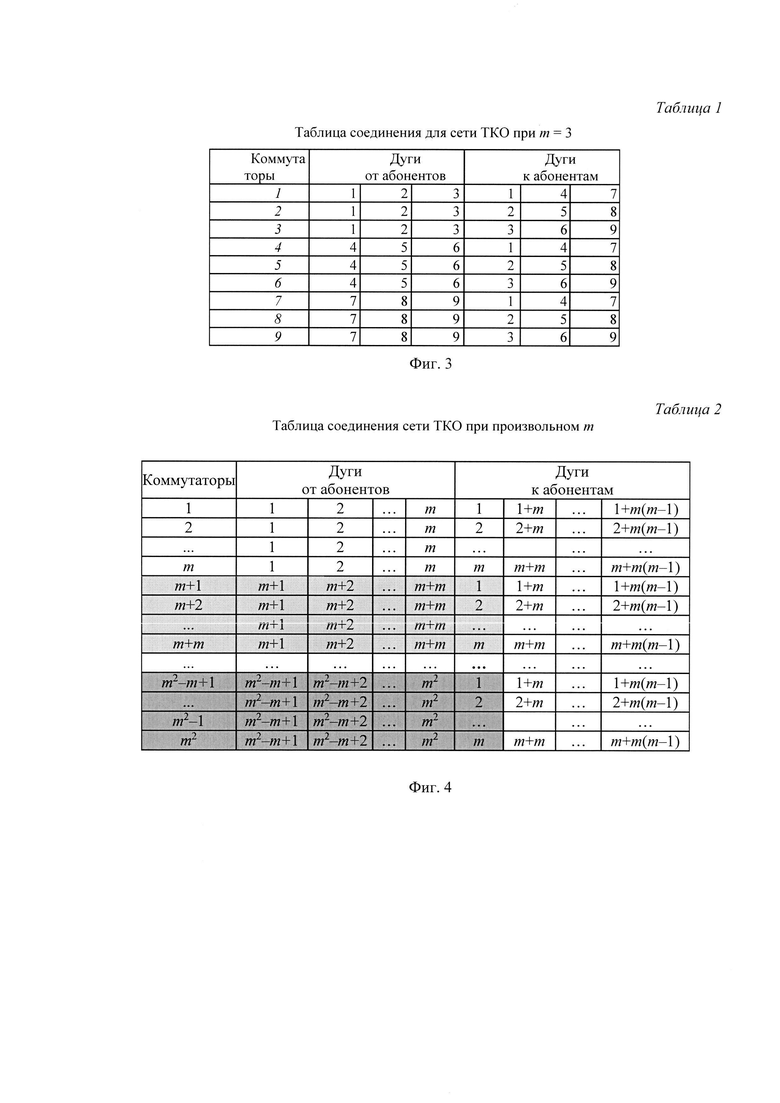
На фиг. 2 приведена Системная сеть с ТКО при m=3.
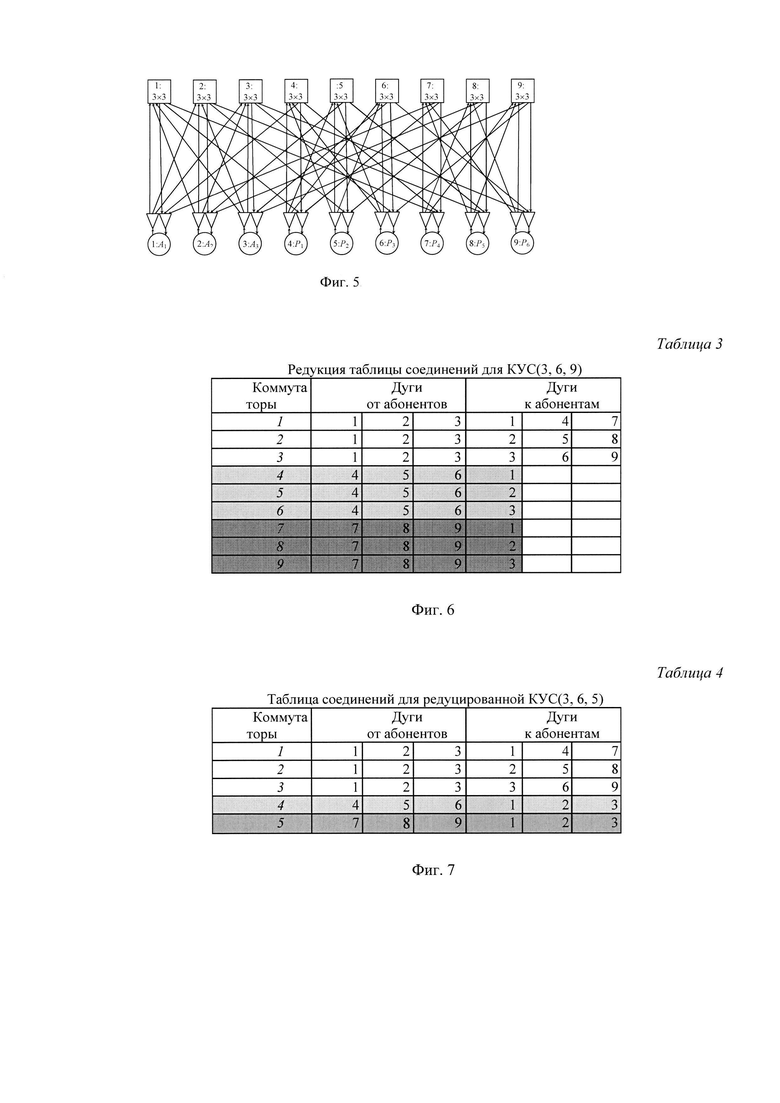
На фиг. 3 приведена Таблица 1 соединения для сети ТКО при m=3.
На фиг. 4 приведена Таблица 2 соединения для сети ТКО при произвольном m.
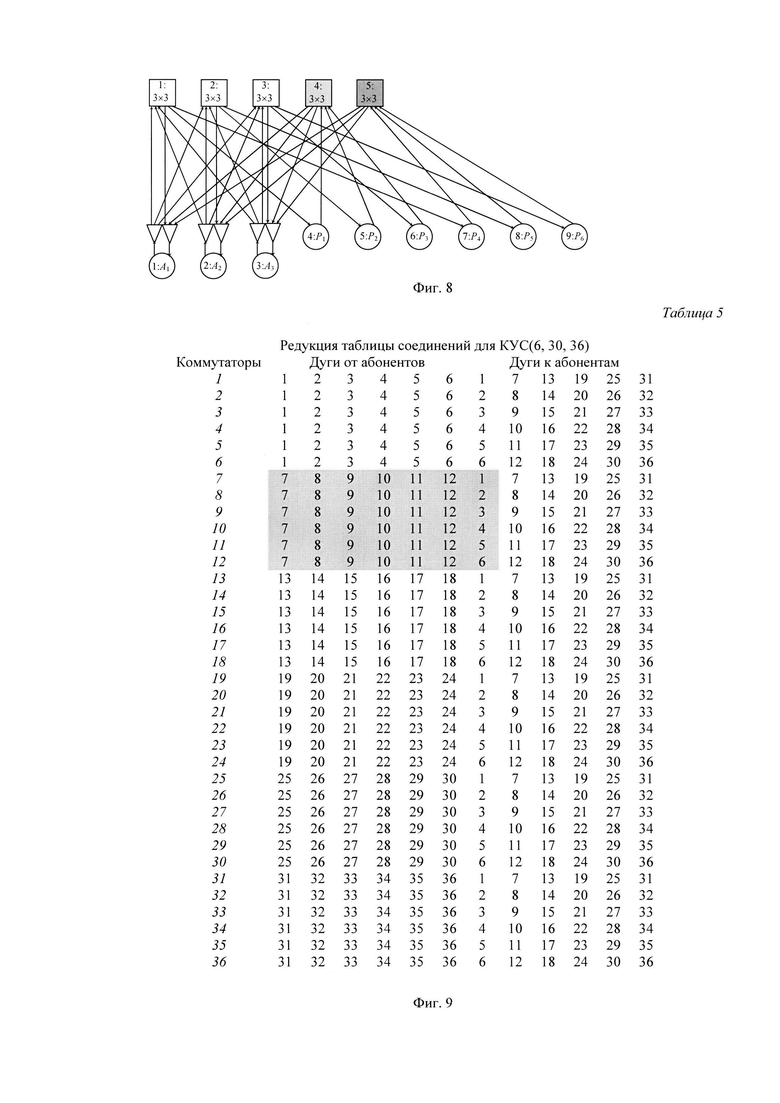
На фиг. 5 приведена Системная сеть КУС(3, 6, 9) с ТКО.
На фиг. 6 приведена Таблица 3 редукции таблицы соединений для КУС(3, 6, 9).
На фиг. 7 приведена Таблица 4 соединений для редуцированной КУС(3, 6, 5).
На фиг. 8 приведена Системная сеть редуцированной КУС(3, 6, 5).
На фиг. 9 приведена Таблица 5 редукции таблицы соединений для КУС(6, 30, 36).
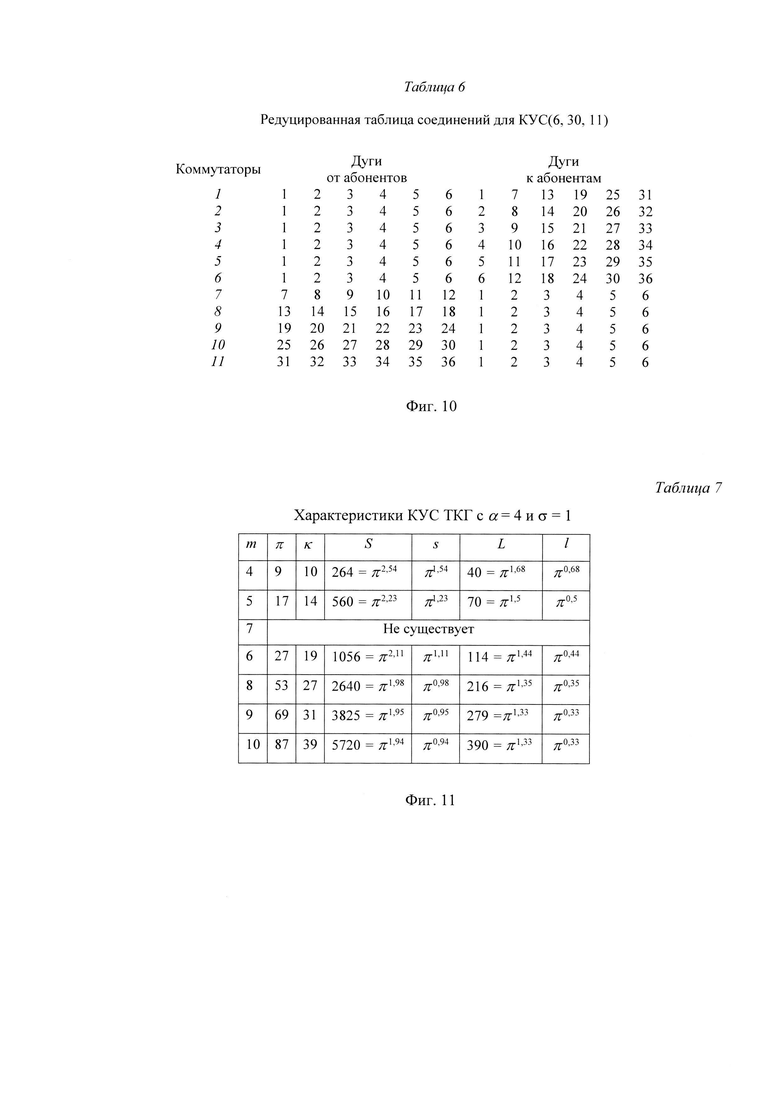
На фиг. 10 приведена Таблица 6 соединений для редуцированной КУС(6, 30, 36).
На фиг. 11 приведена Таблица 7 характеристик КУС ТКГ с α=4 и σ=1.
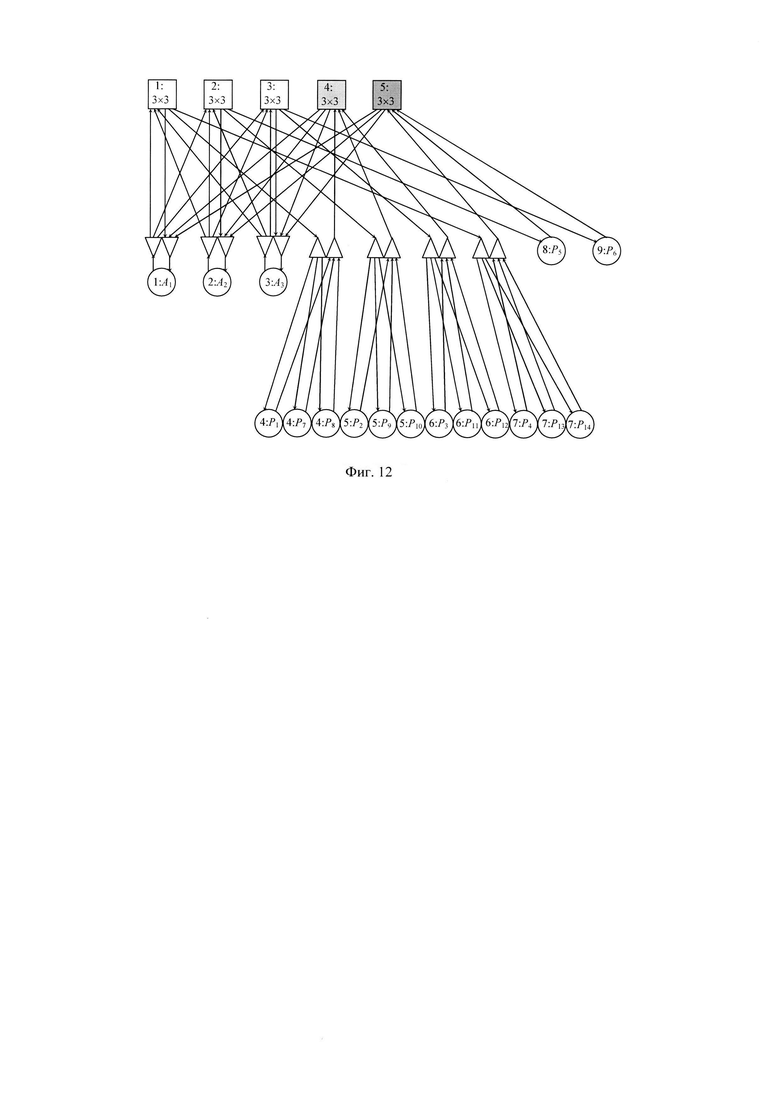
На фиг. 12 приведена Системная сеть с частичным 1-ярусным масштабированием КУС(3, 6, 5) в КУС(3, 14, 5).
Опишем способ построения коммутируемых управляющих сетей с топологией квазиполного орграфа.
В монографии "Каравай М.Ф., П.П. Подлазов B.C. Системные сети с прямыми каналами для параллельных вычислительных систем - комбинаторный подход. Глава 5. // https://www.ipu.ru/sites/default/files/publications/l8125/15058-18125.pdf были предложены теоретические основания построения системных сетей на базе квазиполных орграфов. Их преимущество - бесконфликтность на произвольных перестановках пакетов, самомаршрутизируемость, удобство масштабирования.
Такая системная сеть с топологией квазиполного орграфа (сеть ТКО) может быть представлена как двудольный квазиполный орграф с N=m2 коммутаторами m×m и N=m2 абонентами соответственно в верхней и нижней доле, фиг. 2. При этом связь между каждой парой абонентов осуществляется через один коммутатор, а множество m входных и m выходных портов каждого абонента создается посредством их подсоединения через мультиплексоры m×1 и демультиплексоры 1×m соответственно.
В сетях с топологией квазиполного орграфа связи между абонентами во встречных направлениях проходят по симплексным каналам по разным маршрутам.
Соединения в нем задаются разными таблицами инцидентности для дуг от абонентов к коммутаторам и дуг от коммутаторов к абонентам. На фиг. 3 приведена табл.1 соединения для сети ТКО с m=3, а на фиг. 4 для произвольного m. В таблицах по горизонтали указываются номера коммутаторов, по вертикали номера портов коммутаторов, на пересечении в левой части таблицы указывается номер абонента, с которого поступают данные на соответствующий порт соответствующего коммутатора, а в правой указывается номер абонента, на который передаются данные с соответствующего коммутатора.
Топология соединения может быть задана и не табличным способом следующим образом.
Разобьем коммутаторы и одноименные им абоненты, мультиплексоры и демультиплексоры на m равных групп (на фиг. 2 группы обведены штриховой линией), группы, а также абоненты, мультиплексоры и демультиплексоры в них пронумеруем от 1 до m, при этом i (1≤i≤m) задает номер группы, l (1≤l≤m) задает номер коммутатора, демультиплексора и мультиплексора в соответствующих группах, а r (1≤r≤m) задает номер порта коммутатора и k (1≤k≤m) - номер порта мультиплексора или демультиплексора. Для всех портов демультиплексоров, мультиплексоров и коммутаторов соединим k-й выходной порт l-го демультиплексора i-й группы с l-м входным портом l-го коммутатора той же i-й группы; соединим r-й выходной порт l-го коммутатора i-й группы с i-м входным портом l-го мультиплексора r-й группы.
Возможен и такой способ задания топологии сети ТКО:
k-й выход порта демультиплексора абонента с номером А=r+(i-1)m подсоединяют к r-му входу порта коммутатора с номером С=k+(i-1)m, где А и С (1≤А≤N, 1≤С≤N) задают номера абонентов и коммутаторов, r (1≤r≤m) задает номер порта коммутатора, k (1≤k≤m) - номер порта демультиплексора, а i (1≤i≤m) - номер группы, в которой расположены соответствующие коммутаторы, абоненты и демультиплексоры;
r-й выход порта коммутатора с номером С=l+(i-1)m подсоединяют к k-му входному порту мультиплексора абонента с номером А=l+(r-1)m, где l (1≤l≤m) задает номер коммутатора и мультиплексора в соответствующих группах, а номер входного порта мультиплексора k=i, где 1≤k≤m, i (1≤i≤m) - номер группы, в которой расположен коммутатор с номером С=l+(i-1)m.
На основе квазиполного орграфа можно построить коммутируемую управляющую сеть КУС(m, N-m, N) с двумя множествами абонентов - активных устройств Aj (1≤j≤m) и пассивных устройств Pj (m<j≤N), которая представлена на фиг. 5 для m=3. В схеме КУС(3, 6, 9) абоненты имеют двойную нумерацию - по таблице соединений (Таблица 1) и как АУ и ПУ.
В такой КУС все АУ имеют бесконфликтные соединения на произвольных перестановках пакетов между ними, каждый АУ имеет соединение с любым ПУ и все АУ имеют бесконфликтные соединения с ПУ.
Учитывая, что в КУС обмен сообщений между пассивными устройствами отсутствует, связи между ПУ в таблице соединений можно устранить без ущерба для других маршрутов. Таким образом, КУС(m, N-m, N) редуцируем в КУС(m, N-m, 2m-1). Покажем этот способ на примере таблицы соединений КУС(3, 6, 9) на фиг. 3.
Выделим в таблице 1 соединения от ПУ к коммутаторам с номерами больше 3 (или m для табл.2 с произвольным m) и удалим их (таблица 3 на фиг. 6). Тогда в редуцированной таблице соединений образуются группы строк по m коммутаторов с входами от одинаковых наборов ПУ и с выходами к одному АУ, имеющего разные номера для разных строк в группе. Эти группы выделены разной заливкой. Каждую такую группу строк можно заменить на одну строку с одним коммутатором и с входами от ПУ в группе и с выходами ко всем АУ. При этом образуется табл.4 на фиг. 7, которая задает таблицу соединений уже для КУС(3, 6, 5) с минимальным числом коммутаторов равным 5 (2m-1 для таблицы 2). На фиг. 8 представлена схема КУС(3, 6, 5), которая имеет вид минимального квазиполного орграфа.
Такую редукцию можно провести для любой КУС с ТКО. Например, для КУС(6, 30, 36), задаваемой табл.5 на фиг. 9, в которой заливкой выделена одна группа строк с одинаковым набором номеров ПУ. В результате описанного выше редуцирования образуется табл.6, которая является таблицей соединений для КУС(6, 30, 11) с минимальным числом коммутаторов.
Для такой КУС(m, N-m, 2m-1) заголовки пакетов от АУ должны содержать номера выходных портов демультиплексоров и коммутаторов в маршрутах к соответствующим ПУ, а заголовки от ПУ - номера выходных портов коммутаторов в маршрутах к соответствующим АУ.
Покажем, что оценки коммутационной и канальной сложности полученных сетей ниже, чем в прототипе.
Напомним, что множество портов каждого АУ создаются посредством их подсоединения через встречные демультиплексоры 1×m и мультиплексоры 1×m сложности m каждый. Тогда коммутационная сложность КУС(α; π, κ) с ТКГ задается как S=κm2+2mN=πγ, где γ=logπS, а канальная сложность - как L=mN=πλ, где λ=logπL, и по ним рассчитываются удельные сложности s=S/π=πγ-1 и l=L/π=πλ-1. В табл. 7 приводятся характеристики КУС(4, N-4, κ) при разных m.
В предлагаемой КУС(m, N-m, 2m-1) с ТКО все каналы являются полудуплексными. Поэтому канальная сложность сети в дуплексных каналах задается как L=m2+N-m=2m2-m. Коммутационная сложность этой сети задается как S=m(m2+2m)+(m-1)m2=2m3+m2. В частности, при m=4 для КУС(4, 12, 7) имеем L=28=π1,34, l=π2,0 и S=144=π2,0, s=π1,0. Это существенно меньше, чем в КУС(4, 9, 10) с топологией квазиполного графа (табл. 7) при меньшем числе ПУ в последней.
Полученную сеть КУС(m, π, κ) можно легко масштабировать, а именно преобразовать в сеть КУС(m, πr, κ) с πr=πmr, увеличивая число ПУ в mr раз. Для этого надо добавить r ярусов демультиплексоров и мультиплексоров. Масштабирование можно представить как итерационный процесс, начиная с первого яруса, следующим образом. Во входной и выходной каналы каждого ПУ вставляют соответственно демультиплексор 1×m и мультиплексор m×1, дополнительные свободные m-1 выходов демультиплексора и m-1 входов мультиплексора подсоединяют одноименными парами соответственно к парам входов-выходов m-1 дополнительных ПУ, таким образом увеличивая число ПУ в m раз. На фиг. 12 приведен пример частичного 1-ярусного масштабирования сети КУС(3, 6, 5).
При максимальном 1-ярусном масштабировании сеть КУС(3, 6, 5) преобразуется в КУС(3, 14, 5).
Важно подчеркнуть, что в масштабированной сети КУС(m, πr, κ) каждое АУ имеет двустороннюю связь с каждым из ПУ.
При 1-ярусном масштабирования канальная сложность КУС(m, π1, κ) задается как L1=L+πm=m2+N-m+(N-m)m=Nm+N-m=m3+m2-m, а коммутационная сложность - как S1=S+2mπ=2m3+m2+2(N-m)m=4m3-m2. В частности, при m=4 для КУС(4, 48, 7) имеем L1=76=π1,12, l1=π0,12, S1=240=π1,42, s1=π0,42, что существенно меньше, чем в КУС(4, 53, 27) с топологией квазиполного графа (табл. 7) при близком числе ПУ.
Для масштабированной КУС(m, πr, κ) заголовки пакетов от АУ должны дополнительно содержать номера выходных портов демультиплексоров в каждом добавленном ярусе.
В изобретении описан способ построения коммутационных управляющих сетей с топологией квазиполных орграфов, обеспечивающий бесконфликтные соединения на произвольных перестановках пакетов между АУ, а также между АУ и ПУ.
Показано, что они имеют существенно меньшую коммутационную сложность и существенно лучшую масштабируемость, чем ранее предложенные сети с топологией квазиполных графов. Например, коммутационная и канальная сложности построенной предлагаемым способом КУС(4, 12, 7), состоящей из 4-х АУ, 12- и ПУ и 7 коммутаторов тхт соответственно в 1,83 и 1,43 раза меньше по сравнению с аналогичной КУС(4, 9, 10) с топологией квазиполных графов, состоящей из 4-х АУ, 9-и ПУ и 10-и коммутаторов m×m с меньшим числом ПУ. А при масштабировании КУС(4, 12, 7) предлагаемым способом до КУС(4, 48, 7) увеличением количества ПУ в 4 раза ее коммутационная и канальная сложности соответственно в 10 и 2,7 раз меньше по сравнению с аналогичной КУС(4, 53, 27) с топологией квазиполного графа при близком числе ПУ.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ организации системной сети в виде отказоустойчивого неблокируемого трехмерного разреженного р-ичного гиперкуба | 2019 |
|
RU2720553C1 |
| СПОСОБ ПОСТРОЕНИЯ НЕБЛОКИРУЕМОГО САМОМАРШРУТИЗИРУЕМОГО РАСШИРЕННОГО КОММУТАТОРА | 2009 |
|
RU2435295C2 |
| Способ организации оптимальных отказоустойчивых многомерных торов на основе малопортовых маршрутизаторов и разветвителей дуплексных каналов | 2020 |
|
RU2753147C1 |
| ОБОБЩЕННЫЕ НЕБЛОКИРУЕМЫЕ ДВУХКАСКАДНЫЕ СЕТИ КЛОЗА | 2014 |
|
RU2580100C2 |
| СЕТЬ С ТОПОЛОГИЕЙ РАСШИРЕННОГО ОБОБЩЕННОГО ГИПЕРКУБА | 2013 |
|
RU2556458C2 |
| Световодная система кабельного телевидения | 1988 |
|
SU1727211A1 |
| ОДНОСТОРОННЯЯ КОММУТАЦИОННАЯ МАТРИЦА | 2009 |
|
RU2424560C1 |
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ЗАДАЧ НА ГРАФАХ | 1996 |
|
RU2100838C1 |
| МНОГОКАНАЛЬНЫЙ ОПТИЧЕСКИЙ МУЛЬТИПЛЕКСОР ВВОДА-ВЫВОДА | 2012 |
|
RU2502194C1 |
| СЕТЬ ДЛЯ МАРШРУТИЗАЦИИ СООБЩЕНИЙ | 1996 |
|
RU2115162C1 |
Изобретение относится к способу построения неблокируемой коммутируемой управляющей сети (КУС) с топологией квазиполного орграфа. Технический результат заключается в построении КУС на основе топологии квазиполных орграфов с меньшей сложностью и увеличенной масштабируемостью. В способе КУС (m, N-m, 2m-1), состоящую из m активных абонентов, которые имеют полные связи между собой и с пассивными абонентами, N-m пассивных абонентов, которые имеют связи только с активными абонентами (причем количество всех абонентов N=m2), и 2m-1 коммутаторов m×m, редуцируют из коммутируемой сети с топологией квазиполного орграфа, состоящей из N=m2 абонентов, N коммутаторов m×m и N пар демультиплексоров 1×m и мультиплексоров m×1 следующим образом (при этом абоненты, коммутаторы, демультиплексоры и мультиплексоры пронумерованы от 1 до N): связи от N-m коммутаторов с номерами от m+1 до N к абонентам с номерами от m+1 до N и одноименные этим абонентам демультиплексоры и мультиплексоры удаляют, эти коммутаторы с номерами от m+1 до N объединяют в порядке возрастания номеров по m коммутаторов в m-1 группу коммутаторов и заменяют каждую из этих групп на соответствующий эквивалентный коммутатор m×m; при этом в коммутируемой сети с топологией квазиполного орграфа коммутаторы и одноименные им абоненты, мультиплексоры и демультиплексоры разбивают на m равных групп, группы, а также абоненты, мультиплексоры и демультиплексоры в них нумеруют от 1 до m, причем i (1≤i≤m) задает номер группы, l (1≤l≤m) задает номер коммутатора, демультиплексора и мультиплексора в соответствующих группах, а r (1≤r≤m) задает номер порта коммутатора и k (1≤k≤m) - номер порта мультиплексора или демультиплексора; для всех портов демультиплексоров, мультиплексоров и коммутаторов k-й выходной порт l-го демультиплексора i-й группы соединяют с l-м входным портом k-го коммутатора той же i-й группы, r-й выходной порт l-го коммутатора i-й группы соединяют с i-м входным портом l-го мультиплексора r-й группы; выходы абонентов подсоединяют к входам одноименных демультиплексоров, выходы мультиплексоров подсоединяют к входам одноименных абонентов. 12 ил.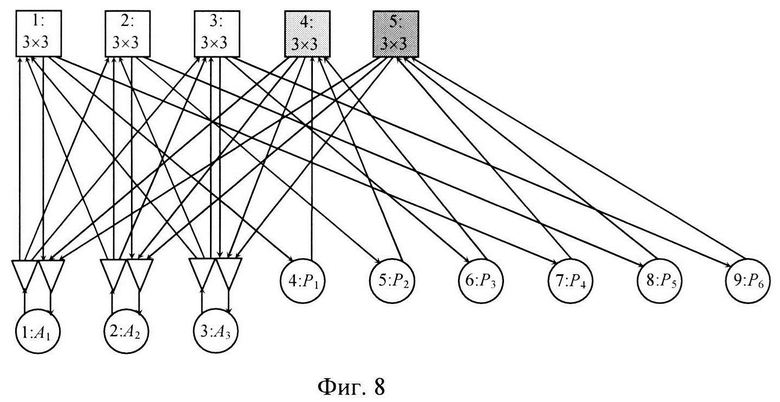
Способ построения неблокируемой коммутируемой управляющей сети с топологией квазиполного орграфа, КУС (m, N-m, 2m-1), состоящей из m активных абонентов, которые имеют полные связи между собой и с пассивными абонентами, N-m пассивных абонентов, которые имеют связи только с активными абонентами (причем количество всех абонентов N=m2), и 2m-1 коммутаторов m×m, характеризующийся тем, что КУС (m, N-m, 2m-1) редуцируют из коммутируемой сети с топологией квазиполного орграфа, состоящей из N=m2 абонентов, N коммутаторов m×m и N пар демультиплексоров 1×m и мультиплексоров m×1 следующим образом (при этом абоненты, коммутаторы, демультиплексоры и мультиплексоры пронумерованы от 1 до N):
связи от N-m коммутаторов с номерами от m+1 до N к абонентам с номерами от m+1 до N и одноименные этим абонентам демультиплексоры и мультиплексоры удаляют, эти коммутаторы с номерами от m+1 до N объединяют в порядке возрастания номеров по m коммутаторов в m-1 группу коммутаторов и заменяют каждую из этих групп на соответствующий эквивалентный коммутатор m×m;
при этом в коммутируемой сети с топологией квазиполного орграфа коммутаторы и одноименные им абоненты, мультиплексоры и демультиплексоры разбивают на m равных групп, группы, а также абоненты, мультиплексоры и демультиплексоры в них нумеруют от 1 до m, причем i (1≤i≤m) задает номер группы, l (1≤l≤m) задает номер коммутатора, демультиплексора и мультиплексора в соответствующих группах, а r (1≤r≤m) задает номер порта коммутатора и k (1≤k≤m) - номер порта мультиплексора или демультиплексора;
для всех портов демультиплексоров, мультиплексоров и коммутаторов k-й выходной порт l-го демультиплексора i-й группы соединяют с l-м входным портом k-го коммутатора той же i-й группы, r-й выходной порт l-го коммутатора i-й группы соединяют с i-м входным портом l-го мультиплексора r-й группы;
выходы абонентов подсоединяют к входам одноименных демультиплексоров, выходы мультиплексоров подсоединяют к входам одноименных абонентов.
| Способ организации системной сети в виде отказоустойчивого неблокируемого трехмерного разреженного р-ичного гиперкуба | 2019 |
|
RU2720553C1 |
| Способ организации оптимальных отказоустойчивых многомерных торов на основе малопортовых маршрутизаторов и разветвителей дуплексных каналов | 2020 |
|
RU2753147C1 |
| ОБОБЩЕННЫЕ НЕБЛОКИРУЕМЫЕ ДВУХКАСКАДНЫЕ СЕТИ КЛОЗА | 2014 |
|
RU2580100C2 |
| СЕТЬ С ТОПОЛОГИЕЙ РАСШИРЕННОГО ОБОБЩЕННОГО ГИПЕРКУБА | 2013 |
|
RU2556458C2 |
| US 7561584 B1, 14.07.2009 | |||
| Колосоуборка | 1923 |
|
SU2009A1 |
| DE 4002455 A1, 01.08.1991. | |||
Авторы
Даты
2024-03-13—Публикация
2023-02-14—Подача