Изобретение относится к построению отказоустойчивых неблокируемых самомаршрутизируемых системных сетей для многопроцессорных систем с сотнями абонентов-процессоров.
Отказоустойчивость в предлагаемой сети обеспечивается наличием нескольких разных прямых каналов между любыми процессорами. Неблокируемость на произвольной перестановке пакетов означает возможность параллельной их передачи от источников к приемникам по прямым каналам (без их буферизации в промежуточных узлах), что повышает быстродействие системы. Самомаршрутизация предполагает возможность прокладки путей локально по узлам без взаимодействия последних между собой.
В изобретении предложен способ организации отказоустойчивой неблокируемой самомаршрутизируемой системной сети в виде 3-мерного р-ичного разреженного гиперкуба на базе сетей с топологией p-ичного квазиполного графа, обеспечивающих канальную отказоустойчивость. В дальнейшем для простоты изложения полученную сеть будем называть и сокращенно «Отказоустойчивый неблокируемый трехмерный разреженный р-ичный гиперкуб».
Построенный неблокируемый разреженный гиперкуб может иметь несколько сотен абонентов (процессорных ядер) при двух-трех разных прямых каналах между ними. Наличие нескольких каналов не только обеспечивает отказоустойчивость данного гиперкуба, но и открывает возможность дальнейшего повышения его быстродействия за счет их параллельного использования.
Обобщенный r-мерный p-ичный гиперкуб («Bhuyan L.N. and Agrawal D.P. Generalized Hypercube and Hyperbus Structures for a Computer Network // IEEE Trans, on Computers. - 1984. - Vol. C - 33. No 4. - P. 323-333») со степенью узлов m=rp и числом узлов N=pr используется как системная сеть в некоторых современных многопроцессорных вычислительных системах («Alverson R., Froese Е., Kaplan L., and Roweth D. Cray® XC™ Series Network. - URL: https://www.cray.com/sites/default/files/resources/CrayXCNetwork.pdf (дата обращения 12.10.2018)». Однако эти сети не являются неблокируемыми.
Введенные в работе «Каравай М.Ф., Подлазов В.С. Распределенный полный коммутатор как «идеальная» системная сеть для многопроцессорных вычислительных систем // Управление большими системами. - 2011. - Вып. 34. - С. 92-116» сети обладают свойством неблокируемости. Эти сети имеют топологию квазиполных графа или орграфа и обладают квадратичной зависимостью числа узлов от их степени (сетевые узлы в этих сетях образованы объединением в одном узле процессора с одноименным коммутатором). Самомаршрутизация в этих сетях является статической, при которой маршрут из любого источника в любой приемник для произвольной перестановки пакетов данных между узлами однозначно определяется номерами узлов и поэтому любой источник самостоятельно прокладывает весь бесконфликтный путь к приемнику для произвольной перестановки пакетов данных между узлами. Главный недостаток этих сетей - малое число узлов в них. Топологию квазиполного орграфа имели сети в виде 2-мерного обобщенного гиперкуба и 2-мерного полного мультикольца, а топологию квазиполного графа имели сети, названные плоскими.
В работе «Подлазов B.C. Бесконфликтная самомаршрутизация для трехмерного обобщенного гиперкуба // Проблемы управления. - 2018. - №3. - С. 26-32.» на базе 2-мерного гиперкуба был построен неблокируемый 3-мерный p-ичный гиперкуб, для которого был предложен алгоритм динамической локальной самомаршрутизации. Он позволяет параллельно прокладывать бесконфликтные пути при произвольной перестановке пакетов данных между узлами на основе только локальной информации в промежуточных узлах без взаимодействия между ними. Эта сеть в виде неблокируемого 3-мерного p-ичного гиперкуба, предложенная в данной работе выбрана в качестве прототипа.
Главный недостаток сети, описанной в прототипе, заключается в том, что, будучи неблокируемой и самомаршрутизируемой, она не имеет канальной отказоустойчивости.
Технической задачей изобретения является разработка такого способа организации 3-мерной сети, который бы обеспечивал наряду со свойствами неблокируемости и самомаршрутизизации, также и заданную канальную отказоустойчивость в виде нескольких (σ) разных прямых путей передачи пакетов между процессорами.
Техническим результатом изобретения является возможность достижения (σ-1)-кратной канальной отказоустойчивости системной сети.
Технический результат достигается тем, что предложен новый способ организации системной сети в виде отказоустойчивого неблокируемого самомаршрутизируемого трехмерного p-ичного разреженного гиперкуба, характеризующегося тем, что R=Np узлов сети, пронумерованных от 0 до Np-1 (0, 1, 2, …, Np-1) располагают по N узлов в порядке их нумерации на гранях XYk (1≤k≤р) 3-х мерного p-ичного обобщенного гиперкуба,
причем каждая группа разбивается на р групп gi (1≤i≤p) с х узлами в первой группе (i=1) и по у узлов в остальных группах (i=2, 3, …, р) при соблюдении условия x+y(p-1)=N, после чего каждая группа gi располагается на пересечении грани XYk с гранью XZj (1≤j≤р), номер которой вычисляется по формуле j=modp(i+k-1),
при этом каждый узел сети включает процессор и коммутатор, связанные дуплексной линией, для связи с другими узлами сети в процессоре организуют группы OIXY, OIXZ по (р-1) дуплексных портов и группу SYZ из (р-1) симплексных выходов, а в коммутаторе организуют группы OIXY, OIXZ, MYZ, DYZ, CYZ, IXZ по (p-1) дуплексных портов и группу SYZ из (р-1) симплексных входов входных портов,
при этом (р-1) дуплексных портов OIXY каждого из N коммутаторов граней XYk соединяют по одному (р-1) дуплексными линиями с (р-1) портами разных (р-1) процессоров той же грани, и аналогично (р-1) дуплексных портов OIXZ каждого из N коммутаторов граней XZj соединяют по одному (р-1) дуплексными линиями с (p-1) портами разных (р-1) процессоров той же грани в соответствии со схемой соединений N коммутаторов и N процессоров, полученной из неполной симметричной блок-схемы заменой блоков на коммутаторы, элементов на процессоры, инцидентность блоков, и элементов на соединения коммутаторов и процессоров и имеющей вид таблицы из N строк и р+1 столбцов, каждая строка которой содержит номер одного коммутатора и номера р подсоединенных к нему процессоров, и согласно которой к каждому коммутатору подсоединено р различных процессоров, а каждый процессор подсоединен к р разным коммутаторам, и каждая пара процессоров подсоединена к σ разным коммутаторам так, что N=p(p-1)/σ+1, и σ задает число разных путей между любыми двумя процессорами через разные коммутаторы,
или в соответствии со схемой соединений N* коммутаторов и N* процессоров, полученной аналогично из расширенной блок-схемой в виде таблицы N* строк и р+1 столбцов, и согласно которой к каждому коммутатору подсоединено р различных процессоров, а каждый процессор подсоединен к р разным коммутатора, а каждая пара процессоров подсоединена к σ или к σ+1 разным коммутаторам так, что N*<p(p-1)/σ+1, и σ или σ+1 задают число разных путей между любыми двумя процессорами через разные коммутаторы;
(р-1) портов одноименных групп MYZ, DYZ, CYZ коммутаторов, расположенных на р разных гранях XZj (1≤j≤р) в узлах, имеющих равные по модулю N номера, то есть na≡nb (mod N) и na, nb ∈ [0, Np-1], соединяют группами по (р-1) дуплексных линий, то есть каждая пара коммутаторов в одноименной группе связана дуплексной линией;
(р-1) дуплексных портов коммутаторов группы IXZ соединяют дуплексными линиями параллельно линиям между узлами, которые соединены линиями OIXZ,
а (р-1) симплексных выходов коммутаторов группы SYZ соединяют с симплексными входами процессоров параллельно линиям между узлами, которые соединены линиями группы MYZ;
при этом внутри каждого коммутатора для маршрутизации организуют полнокоммутаторные связи от входов OXY к выходам IXY, IXZ, MYZ, DYZ (OXY и IXY - входы и выходы дуплексных портов OIXY, IXZ - выходы дуплексных портов OIXZ), от входов MYZ к выходам IXZ, от входов DYZ к выходам CYZ, от входов CYZ к выходам IXZ, от входов IXZ к выходам SYZ,
причем порты и идентичные им линии в названных группах пронумерованы от 1 до р-1 (1, 2, …, р-1) (номер 0 указывает на внутриузловую связь в группах OXY, OXZ или на отсутствие связи в группе MYZ) и задаются при маршрутизации в группе OXY числами m1 (0≤m1≤р-1), в группах IXZ и IXZ числами m3 (0≤m3≤р-1), в группе MYZ числами m2 (0≤m2≤р-1), в группе DYZ числами m*2 (0≤m*2≤р-1), в группах CYZ и SYZ числами m*3 (0≤m*3≤р-1), (числа m2, m*2, m*3=j-i, если (j-i)≥0, и m2, m*2, m*3=p+j-i, если (j-i)<0), i и j - номера граней XZ, на которых расположен узел-источник и узел-приемник),
а установление прямых путей при маршрутизации осуществляют методом червоточины посредством коммутаторов узлов независимо друг от друга с учетом параметров маршрутов, заданных числами m1, m2, m3, m*2=m1, m*3=⏐m2-m*2⏐ в заголовках пилотных пакетов, полученных коммутаторами, и наличия конфликтов на линиях групп MYZ и CYZ следующим образом:
параметры кратчайшего маршрута m1, m2, m3 в заголовке пилотного пакета, сформированном процессором, при отсутствии конфликтов задают три этапа прокладки прямого пути пакетом, а именно, от узла-источника по линии OXY(m1) в следующий узел сети (при m1=0 путь прокладывается в коммутатор исходного узла), коммутатор которого устанавливает путь по линии MYZ(m2) в следующий узел сети (при m2=0 второй этап отсутствует), коммутатор которого устанавливает путь по линии IXZ(m3) в узел-приемник (при m3=0 узел-приемник находится в том же узле, что и коммутатор),
если коммутатор обнаруживает конфликт при передаче пилотного пакета на линию MYZ(m2), то прокладывает путь на линию DYZ(m*2),
если коммутатор получает пилотный пакет по линии DYZ(m*2) и не обнаруживает конфликт на линии CYZ(m*3), то прокладывает путь на эту линию, или при обнаружении конфликта прокладывает путь на линию IXZ(m3),
если коммутатор получает пилотный пакет по линии CYZ(m*3), то прокладывает путь на линию IXZ(m3), а если коммутатор получает пилотный пакет по линии IXZ(m3), то прокладывает путь на линию SYZ(m*3).
Техническая сущность и принцип действия предложенной сети поясняются чертежами.
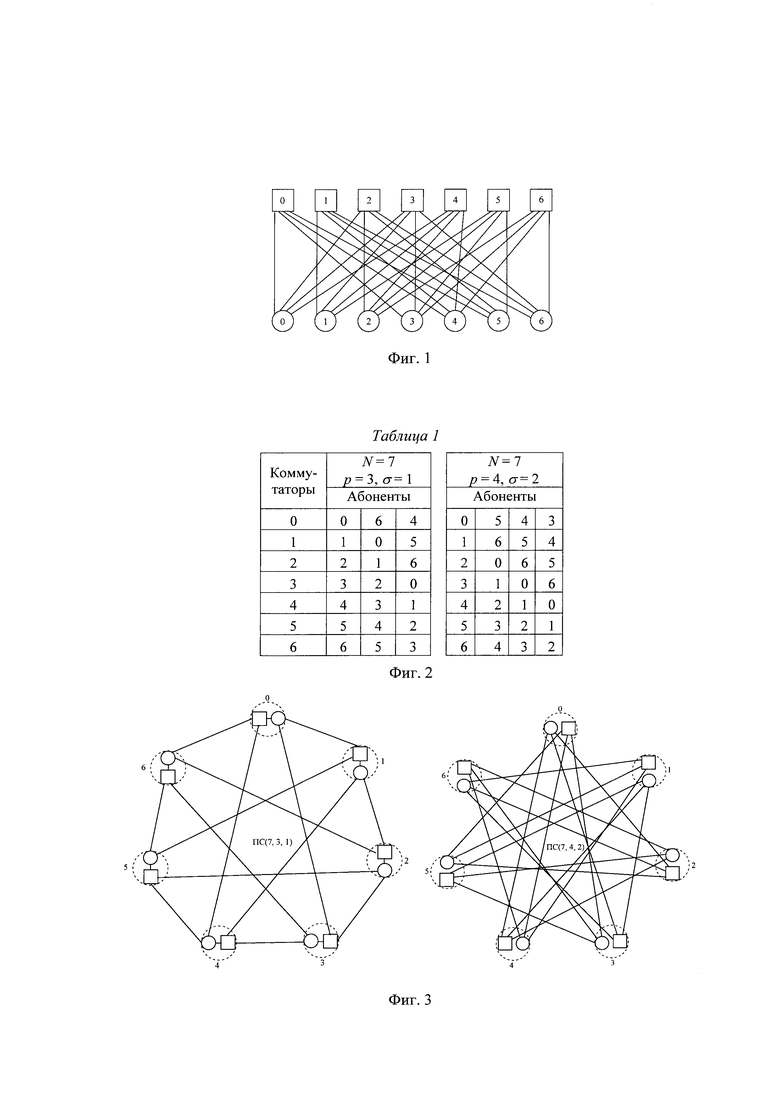
На фиг. 1 приведен квазиполный граф c N=7, p=4 и σ=2 (квадраты - коммутаторы).
На фиг. 2 приведена Таблица 1 со схемами соединений для двух квазиполных графов с N=7, р=4, σ=1 и N=7, p=4, σ=2
На фиг. 3 представлены неблокируемые плоские сети ПС(7, 3, 1) и ПС(7, 4, 2).
На фиг. 4 приведена Таблица 2 параметров блок-схем BD(N, р, σ) при малых значениях р и σ.
На фиг. 5 приведена Таблица 3 параметров блок-схем BD(N, p, σ) и 1-расширенных блок-схем BD(N*, р, σ|σ+1) при малых значениях р и σ.
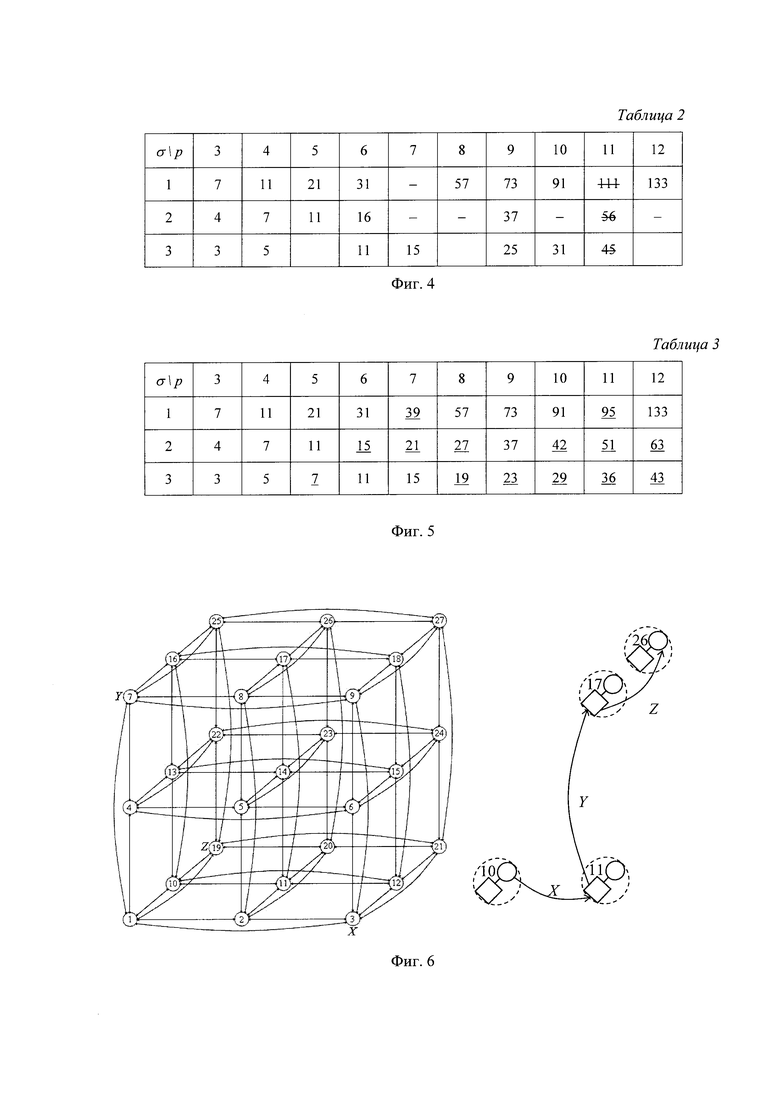
На фиг. 6 приведены 3-х мерный неблокируемый гиперкуб и пример неблокируемого маршрута в нем из узла 10 в узел 26.
На фиг. 7 приведен разреженный троичный гиперкуб из плоских сетей на плоскостях XYi и XZj.
На фиг. 8 и фиг. 9 приведены Таблицы 4 и 5 размещения плоских сетей ПС(7, 3, 1) и ПС(7, 3, 2) по плоскостям XY и XZ разреженного гиперкуба.
На фиг. 10 и фиг. 11 приведены соответственно Таблицы 6 и 7 размещения по группам для плоских сетей, изоморфных ПС(N, р, 2) и ПС(N р, 3).
На фиг. 12 приведена структура коммутатора узла разреженного гиперкуба на пересечении плоскостей XY и XZ.
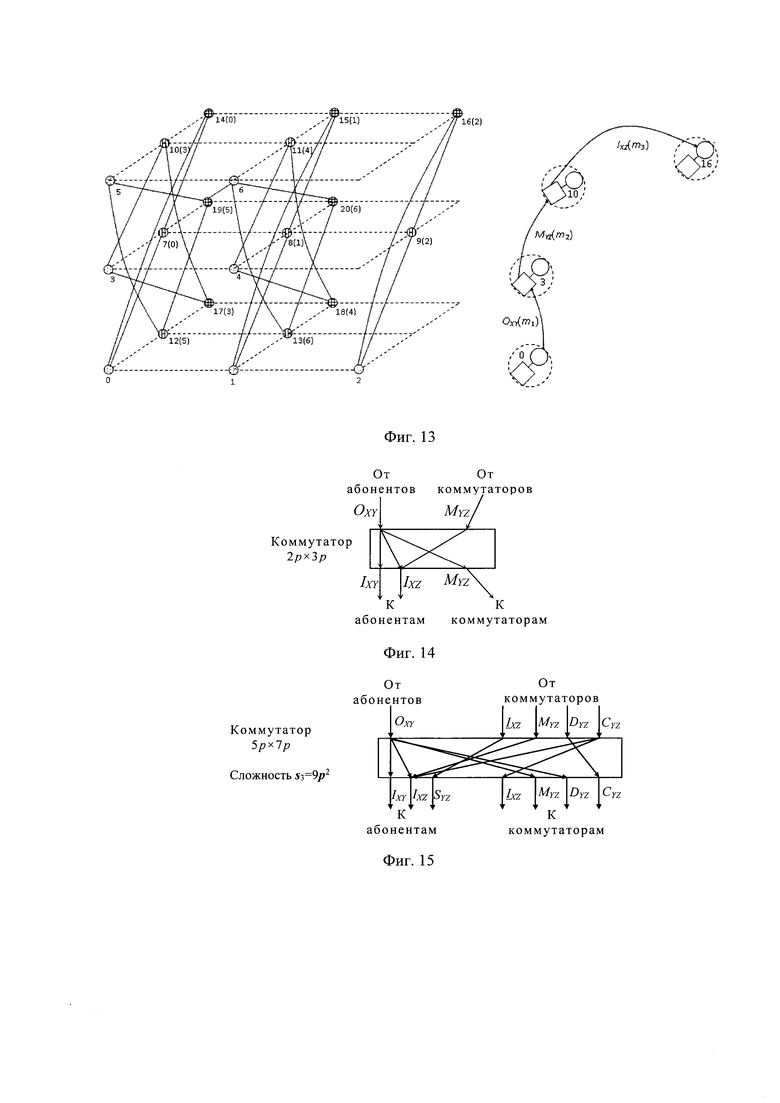
На фиг. 13 приведены структура троичного разреженного гиперкуба с секущими ребрами MYZ и пример 3-х этапного маршрута в нем.
На фиг. 14 и на фиг. 15 приведены соответственно структура коммутаторов узлов в разреженном отказоустойчивом гиперкубе и структура коммутаторов узлов в разреженном отказоустойчивом неблокируемом гиперкубе.
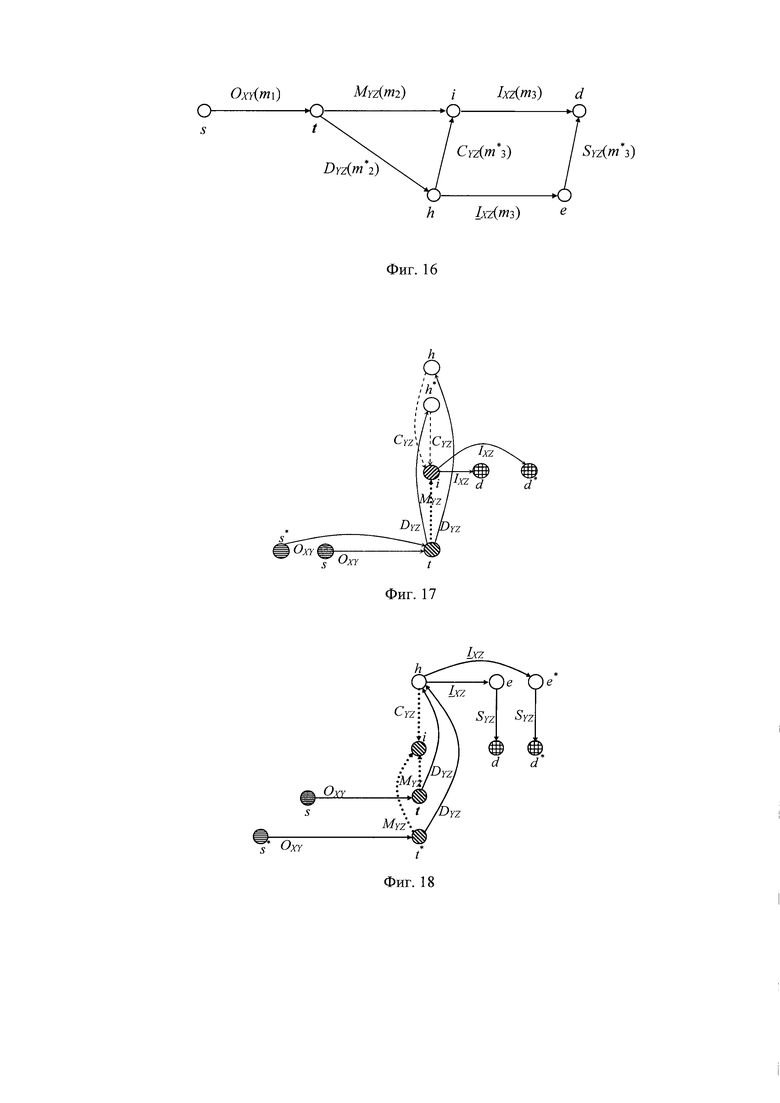
На фиг. 16 приведен граф прокладывания пути в разреженном отказоустойчивом неблокируемом гиперкубе.
На фиг. 17 и на фиг. 18 приведены соответственно иллюстрации конфликтов первого и второго типа и их разрешения.
На фиг. 19 приведена Таблица 8 с числом узлов R(p, σ) в 3-мерных разреженных гиперкубах.
Опишем способ организации предложенной системной сети.
Рассмотрим сначала сети, которые будем использовать для построения из них 3-х мерных разреженных р-ичных гиперкубов. В главе 2.3 работы «Каравай М.Ф., Подлазов B.C. Распределенный полный коммутатор как «идеальная» системная сеть для многопроцессорных вычислительных систем // Управление большими системами. - 2011. - Вып. 34. - С. 92-116» предложены сети, схемы соединения которых представляют собою особый двудольный граф, одну долю которого составляют коммутаторы, а другую - процессоры. Число вершин в каждой доле N, а степень всех вершин в каждой доле одинакова и равна р. Значение р выбирается минимальным, при котором любые два узла в одной доле связаны а путями длины два через разные узлы в другой доле. Каждый такой путь проходит через один коммутатор, и разные пути проходят через разные коммутаторы. Двудольный однородный граф с описанными свойствами мы называем минимальным квазиполным графом («Каравай М.Ф., Пархоменко П.П., Подлазов B.C. Комбинаторные методы построения двудольных однородных минимальных квазиполных графов (симметричных блок-схем) // АиТ. - 2009. - №2. - С. 153-170»). Пример такого графа приведен на фиг. 1 для р=4, N=7 и σ=2. Нетрудно видеть, что каждая пара абонентов связана двумя путями через разные коммутаторы. Здесь возникает вопрос о существовании, нахождении минимальных квазиполных графов и об их параметрах.
Оказывается, что он уже давно решен в комбинаторике. Такие графы описываются на языке неполных уравновешенных блок-схем, в частности, симметричных блок-схем («Холл М. Комбинаторика // Главы 10-12. Мир. М. 1970. 424 С.»). Симметричная блок-схема BD(N, р, σ) задает размещение N элементов по N блокам, при котором каждый блок содержит по р различных элементов, каждый элемент содержится в р разных блоках, а каждая пара элементов содержится в p разных блоках и соблюдается равенство N=р(р-1)/σ+1. Заменяя блоки на коммутаторы, элементы на процессоры, инцидентность блоков и элементов на соединения коммутаторов и процессоров, мы получаем минимальный квазиполный граф. Схемы соединений, полученные таким образом из симметричных блок-схем, совпадают со схемами соединения квазиполных графов и представлены в табл. 1 на фиг. 2. Таблица 1 со схемами соединений для двух квазиполных графов с N=7, р=4, σ=1 и N=7, р=4, σ=2. В каждой строке первая ячейка задает номер коммутатора, а остальные ячейки - номера процессоров, связанных с данным коммутатором ребром в виде дуплексного канала (двух встречных симплексных каналов).
Если объединить одноименные коммутатор с процессором квазиполного графа в одном сетевом узле, то мы получим плоскую сеть ПС(N, р, σ). Она является неблокируемой сетью с бесконфликтной статической самомаршрутизацией и обладает (σ-1)-канальной отказоустойчивостью при σ>1. На фиг. 3 представлены неблокируемые сети ПС(7, 3, 1) и ПС(7, 4, 2).
Самомаршрутизация в HC(N, р, σ). осуществляется по схеме соединений (табл. 1) с использованием номеров узлов абонента-источника и абонента-приемника. В таблице находятся номера коммутаторов, связанных дуплексными каналами с абонентами-приемниками. Среди этих коммутаторов находятся тот, который связан таким же каналом с абонентом-источником. По свойствам квазиполных графов таких коммутаторов σ.
Однако симметричные блок-схемы BD(N, р, σ) существуют и, тем более, построены не для всех значений параметров р и σ. В табл. 2 на фиг. 4 приводится значения N для блок-схем при малых значениях этих параметров. Пустые клетки отмечают блок-схемы, которые не существуют по определению. Прочерки в клетках отмечают блок-схемы, которые не могут существовать по теории, а перечеркнутые значения отмечают блок-схемы, которые еще не построены.
Необходимость построения отказоустойчивых сетей ПС(N, р, σ) требует некоторого эффективного заполнения пустых клеток в табл. 2. Для этого в работе «Каравай М.Ф., Подлазов B.C. Расширенные блок-схемы для идеальных системных сетей // Проблемы управления. - 2012. - №4. - С. 45-51.» были предложены и построены 1-расширенные блок-схемы BD(N*, p, σ|σ+1), задающие таблицы соединений для 1-расширенных плоских сетей ПС(N*,p, σ|σ+1), в которых малая часть абонентов связаны σ+1 разными путями, а остальные - точно σ разными путями. Значения N и N* числа узлов в вышеупомянутых блок-схемах приводится в табл. 3 на фиг. 5, где последние выделяются подчеркиванием.
Теперь покажем, как из этих отказоустойчивых неблокируемых самомаршрутизируемых плоских сетей строить 3-х мерный разреженный гиперкуб. Напомним, что в неблокируемом 3-мерном p-ичном гиперкубе, предложенном в прототипе, между двумя вершинами можно проложить неблокируемый прямой путь. Однако этот путь единственный и не имеет резервных путей. На фиг. 6 показан 3-х мерный гиперкуб и пример такого неблокируемый маршрута в нем из узла 10 в узел 26. Начальным этапом маршрута является симплексный канал на грани XY2 параллельно оси X от процессора узла 10 до коммутатора узла 11, вторым этапом - симплексный канал на грани XY2 параллельно оси Y от коммутатора узла 11 до коммутатора узла 17 и заключительным этапом - симплексный канал на грани XZ3 параллельно оси Z от коммутатора узла 17 до процессора узла 26, сокращенно 10→11→17→26.
В предложенном способе организации отказоустойчивой неблокируемой сети в виде самомаршрутизируемого разреженного 3-х мерного p-ичного гиперкуба можно выделить следующие фрагменты:
- размещение отказоустойчивых плоских сетей на гранях XY и XZ 3-х мерного гиперкуба таким образом, чтобы идентичные локальные номера узлов плоских сетей граней XY и XZ совпадали на пересечении граней, объединение идентичных коммутаторов в узлах,
- введение дополнительных линий между коммутаторами граней XZ с идентичными локальными номерами узлов для обеспечения полносвязности узлов разреженного гиперкуба,
- введение дополнительных линий в разреженный отказоустойчивый 3-х мерный гиперкуб для обеспечения неблокируемости полученной сети.
Продемонстрируем предлагаемый способ на примере построения 3-х мерного гиперкуба из плоских сетей ПС(7, 3, 1) без нарушения общности.
Пусть строим сеть с R=Np узлами. Пронумеруем их от 0 до Np-1 (0, 1, 2, …, Np-1) и расположим их по N узлов в порядке возрастания на вертикальных гранях XYk (1≤k≤р) 3-х мерного p-ичного обобщенного гиперкуба. Так на фиг. 7 приведен разреженный троичный гиперкуб с размещенными на плоскостях XYi и XZj плоскими сетями (связи в плоских сетях не показаны, но они такие как на фиг. 3).
В полученном разреженном гиперкубе кроме общей нумерации узлов введем значения этих номеров по mod N. Полученные номера, означают нумерацию узлов в пределах каждой грани и приведены на фиг. 7 в скобках. Заметим, что на всех гранях XY и XZ мы в результате получили по N узлов, пронумерованных от 0 до N. Эту нумерацию в отличие от общей назовем локальной.
Видно, что узлы с 0-го по 6-ой расположены на вертикальной грани XY1, узлы с 7-го по 13-ый на грани XY2, узлы с 14-го по 20-ый на грани XY3. При этом каждую серию из N узлов распределим по горизонтальным граням XZj (1≤j≤р) определенным образом. Так, на фиг. 7 видно, что узлы грани XY1 распределены по горизонтальным граням следующим образом: узлы 0, 1, 2 на грани XZ1, узлы 3, 4 на грани XZ2, узлы 5, 6 на грани XZ3, а каждая следующая серия из N узлов распределена по горизонтальным граням аналогично предыдущей, но с циклическим сдвигом на одну горизонтальную грань вверх. В общем виде способ разбиения по горизонтальным граням формулируется так: каждая серия N узлов разбивается на р групп gi (1≤i≤р) с х узлами в первой группе (i=1) и по у узлов в остальных группах (i=2, 3, …, p) при соблюдении условия х+у(р-1)=N, после чего каждая группа gi располагается на пересечении грани XYk с гранью XZj (1≤j≤р), номер которой вычисляется по формуле j=modp(i+k-1). Такое разбиение на группы gi (1≤i≤р), задаваемое парой (х, у) назовем d разбиением.
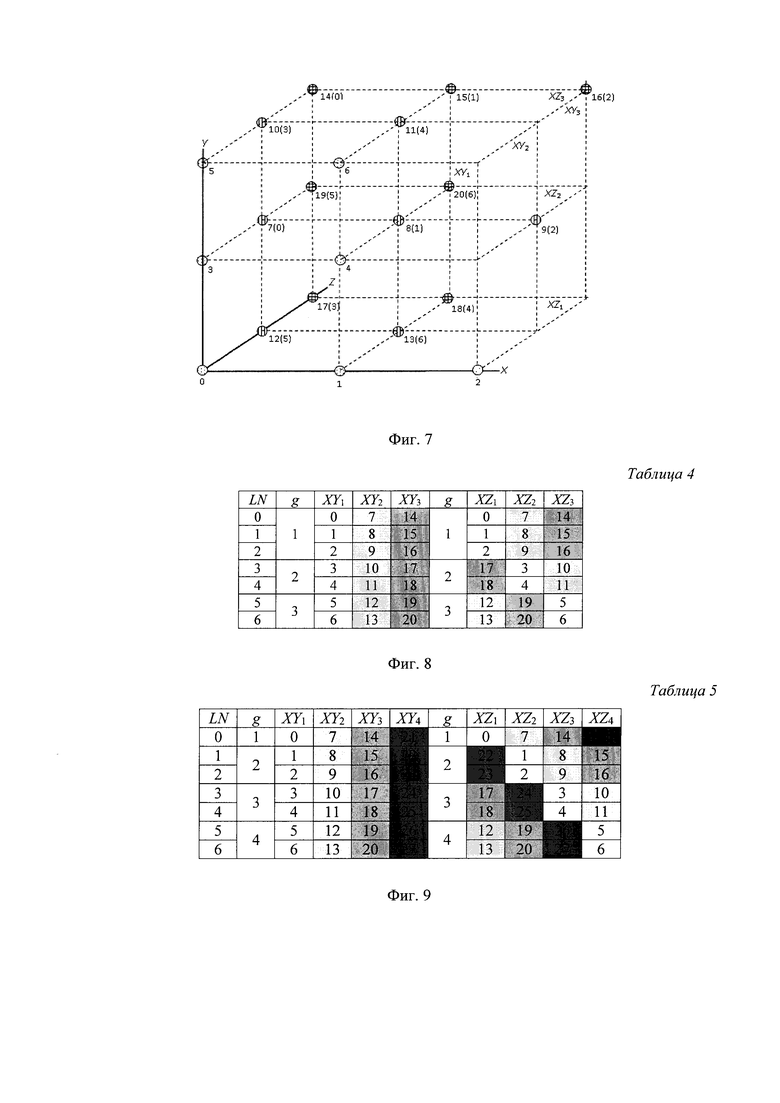
Пример такого размещения узлов ПС(7, 3, 1) по плоскостям XY и XZ в привязке к локальным номерам (LN), задаваемого d разбиением (3, 2) представлено в Таблице 4 на фиг. 8 (в общем случае d разбиение задается парой (р, р-1)). Пример аналогичного размещения для ПС(7, 4, 2), задаваемого d разбиением (1, 2) представлено в Таблице 5 на фиг. 9.
Разбиение d по группам для остальных сетей ПС(N, р, 2) представлено в таблице 6 на фиг. 10, а для сетей ПС(N, p, 3) в таблице 7 на фиг. 11.
Мы получили разреженный гиперкуб, у которого идентичные локальные номера N узлов сетей разных граней совпадают. Напомним, что в разреженном гиперкубе на фиг. 7 использована плоская сеть ПС(7, 3, 1), в общем случае узлы на каждой грани являются узлами плоской сети ПС(N, р, σ) (или расширенной плоской сети ПС(N*, р, σ|σ+1)) с σ|σ+1 разными путями.
Каждый коммутатор плоской сети на гранях XY также принадлежит некоторой плоской сети на гранях XZ. Эти коммутаторы обеспечивают пути между абонентами-источниками и абонентами-приемниками на этих гранях. Названные пути состоят из двух дуг - выходная дуга Oxy на грани XY от абонента-источника к коммутатору и либо входная дуга IXY от коммутатора к абоненту-приемнику на той же грани XY, либо входная дуга IXZ к абоненту-приемнику на гранях XZ (12).
Однако построенный разреженный отказоустойчивый гиперкуб не является полносвязным, т.к. в нем нет путей между частью абонентов, которые находятся в разных вертикальных и горизонтальных плоскостях, например, между абонентами 0 и 11 или 0 и 16 на фиг. 7.
Для обеспечения полносвязности дополнительно проложим ребра между узлами плоскостей XY и XZ, которые имеют одинаковый локальный номер как это сделано на фиг. 13. Такие ребра мы назовем секущими MYZ, т.к. они пересекают плоскости XY и XZ. Также они образуют полный граф между узлами с одинаковыми локальными номерами, то есть номерами na≡nb (mod N), где na, nb ∈ [0, Np-1],
При этом дуплексные каналы, соответствующие секущим ребрам, прокладываются только между коммутаторами узлов.
Теперь любой кратчайший путь, который не покрывается плоскими сетями XY и XZ, можно представить как трехэтапный, состоящий из линий групп OXY, MYZ и IXZ. Пусть узел абонента-источника находится на грани XYi,, а узел абонента-приемника - на грани XZj. Первая линия OXY находится на грани XYi и проходит от абонента-источника в коммутатор первого промежуточного узла, находящегося на грани XYi и грани XZk. Второе ребро MYZ проходит от грани XZk к грани XZj - от коммутатора первого промежуточного узла к коммутатору второго промежуточного узла. Третья линия IXZ находится на грани XZj и проходит от коммутатора второго промежуточного узла к абоненту-приемнику.
Рассмотрим пример маршрута в разреженном гиперкубе, построенном на базе ПС(7, 3, 1) (табл. 1 и рис. 2). Пусть узлы абонента-источника и абонента-приемника имеют номера 0 и 16(2). Они лежат на разных гранях - XY1 и XZ3 соответственно. Трехдуговой путь, пример которого приведен на фиг. 13 справа, содержит линию от процессора в узле 0 к коммутатору в узле 3 в плоской сети ПС(7, 3, 1) грани XY1, далее линию секущего ребра между коммутаторами в узлах 3 и 10(3) и линию от коммутатора в узле 10(3) к приемнику в узле 16(2) плоской сети ПС(7, 3, 1) грани XZ3. Сокращенно этот маршрут запишем в виде цепочки узлов 0→3→10(3)→16(2) или цепочки линий 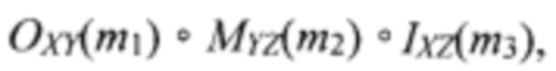 где значки в скобках указывают номера портов коммутаторов узлов 0, 3 и 10, к которым подсоединены одноименные линии. Для плоских сетей с σ>1 и выше в гиперкубе аналогично будут проложены резервные параллельные пути с использованием резервных путей содержащихся в исходных плоских сетях.
где значки в скобках указывают номера портов коммутаторов узлов 0, 3 и 10, к которым подсоединены одноименные линии. Для плоских сетей с σ>1 и выше в гиперкубе аналогично будут проложены резервные параллельные пути с использованием резервных путей содержащихся в исходных плоских сетях.
Для поддержания возможности построения таких 3-х этапных маршрутов в коммутатор кроме выше описанных связей, отображенных на фиг. 12, вводятся дополнительные связи с линии Oxy от абонентов на линию MYZ к коммутаторам и с линии MYZ от коммутаторов на линию IXZ к абонентам, что отображено на фиг. 14.
Таким образом, построена отказоустойчивая сеть в виде 3-мерного полносвязного разреженного гиперкуба. Однако в такой сети могут возникать конфликты при произвольной перестановке пакетов данных между узлами. Для обеспечения неблокируемости в гиперкуб введены дополнительные группы DYZ, CYZ, MYZ, SYZ, IXZ no p-1 линий и соответствующие дополнительные порты и линии коммутации в структуру коммутатора, что отображено на фиг. 15. Линии групп DYZ, CYZ, в гиперкубе проложены между коммутаторами параллельно MYZ, линии групп SYZ проложены между теми же узлами, что и MYZ, но от коммутаторов к абонентам. Линии групп IXZ проложены между теми же узлами, что и линии IXZ, но между коммутаторами узлов. Покажем, что эти дополнения обеспечивают требуемую неблокируемость.
На фиг. 16 приведен граф маршрутов в полученной сети, демонстрирующий работу коммутаторов узлов при прокладывании неблокируемых 3-х этапных путей с учетом возможных конфликтов методом червоточины. Для прокладки прямого пути из узла s в узел d пилотный пакет должен содержать пять чисел m1, m2, m3, и m*2, m*3, где m*2=m1, а m*3=⏐m2-m*2⏐. Числа указывают номера портов коммутаторов и совпадающие с ними номера линий в группах, которые будут использованы коммутаторами при самомаршрутизации, и вычисляются каждым источником заранее. На фиг. 16 можно проследить прокладывание 3-х вариантов путей: 1) в отсутствии конфликтов, 2) в случае конфликта первого рода на линии MYZ(m2), 3) в случае конфликта первого рода на линии MYZ(m2) и второго рода на линии CYZ(m*3).
В первом случае коммутаторы прокладывают путь, заданный тремя числами m1, m2, m3, который запишем в виде последовательности узлов и линий соответственно s→t→i→d и 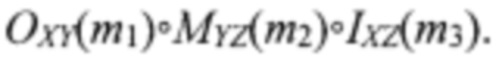 Во втором случае прокладывается обходной путь с использованием линий DYZ(m*2) и CYZ(m*3), а именно, s→t→h→i→d и
Во втором случае прокладывается обходной путь с использованием линий DYZ(m*2) и CYZ(m*3), а именно, s→t→h→i→d и 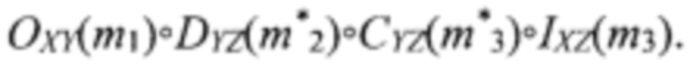 В третьем случае прокладывается обходной путь с использованием линий DYZ(m*2), IXZ(m3) и SYZ(m*3), а именно, s→t→h→e→d и
В третьем случае прокладывается обходной путь с использованием линий DYZ(m*2), IXZ(m3) и SYZ(m*3), а именно, s→t→h→e→d и 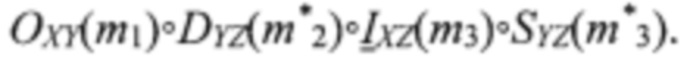
Рассмотрим подробнее причины возникновения конфликтов и способы их преодоления.
Будем задавать линии OXY, MYZ и IXZ номерами портов m1, m2 и m3 (0≤m1, m2, m3≤р-1), из которых они выходят. Для линий MYZ эти порты нумеруются в порядке возрастания длин линий, задаваемых следующим образом. Пусть линия MYZ проходит из плоскости XZi в плоскость XZj, тогда ее длина L(i, j)=j-i, если (j-i)≥0, и L(i, j)=p+j-i, если (j-i)<0. Порты групп линий DYZ, CYZ и SYZ нумеруются одинаково с MYZ, а линий OXY и IXZ единым образом для всех портов, из которых они выходят. Линии IXZ(m3) нумеруются аналогично линиям IXZ(m3).
Ситуация, при которой на одну вторую линию MYZ претендуют несколько путей, считается конфликтом первого типа. Такой конфликт имеет место, если на прохождение через узел t претендует несколько путей (фиг. 17) из разных узлов-источников s и s*. Здесь и далее для краткости мы обозначаем только два таких узла, которых на самом деле может быть любое количество от 2 до р-1. На фиг. 17 конфликтная линия обозначена жирным точечным пунктиром.
Разрешение конфликта осуществляется следующим образом: по заведомо разным линиям DYZ, определяемым для каждого пилотного пакета своим параметром m*2=m1, из узла t прокладываются пути в разные обходные узлы h и h* (фиг. 17) и осуществляется возврат из них в узел i по встречным линиям CYZ. Если на линиях CYZ нет конфликтов, то проложенные пути являются бесконфликтными. Они останутся бесконфликтными и на последних линиях IXZ от коммутатора узла i к приемникам в узлах d и d*. Линии DYZ являются заведомо разными, так как выходят из тех же по номерам портов, что и линии OXY из узлов s и s* в узел t. Разные и возвратные линии CYZ. Пусть конфликтная линия MYZ из узла t в узел i выходит из порта с номером m2, а линия DYZ - из порта с номером m*2. Тогда в качестве возвратной линии из узла h в узел i выбирается линия CYZ с номером m*3=⏐m2-m*2⏐. Такая линия всегда найдется, т.к. линии CYZ образуют полный граф.
Однако и на линиях CYZ могут возникать конфликты второго типа. Каждый из них происходит в том случае, если на проход через узел i на втором этапе претендует несколько путей из разных узлов t и t* после первого этапа (фиг. 18) и после возникновения конфликта первого типа.
Конфликт второго типа разрешается следующим образом (фиг. 18). Из промежуточного узла h пути прокладывается в обходные узлы е и е* по тем линиям IXZ, которые имеют одинаковые номера m3 с линиями IXZ из узла i соответственно к приемникам узлов d и d*. Все эти линии IXZ различны, т.к. они завершают прямые пути из узла i. Поэтому различны и линии IXZ, а пути прокладываются в разные обходные узлы е и е*, из которых они завершаются бесконфликтно по разным линиям SYZ, но проложенным от коммутаторов к абонентам. Это наглядно отображено и на фиг. 16.
В качестве иллюстрации, объясняющей работу полученной сети, приведем Алгоритм динамической самомаршрутизации, по которому прокладывается прямой путь методом червоточины (wormhole routing).
1. Если m1=0, то путь прокладывается по локальной линии в узле абонента-источника к коммутатору. Переход к п. 3.
Если m1>0, то путь прокладывается от абонента-источника по линии ОХУ(m1). Переход к п. 2.
2. Если m2=0 и m3=0, то путь прокладывается по локальной линии в узле абонента-приемника от коммутатора к абоненту. Конец алгоритма.
3. Если m2=0 и m3≠0, то путь прокладывается по линии IXZ(m3) к абоненту-приемнику. Конец алгоритма.
Если m2≠0 и m3=0, то путь прокладывается по линии MYZ(m2) к коммутатору узла абонента-приемника и по локальной линии к абоненту-приемнику. Конец алгоритма.
Если m2>0, то проверяется наличие конфликта на линии MYZ(m2). Если конфликта нет, то путь прокладывается по этой линии MYZ(m2). Переход к п. 4.
Если m2>0 и имеет место конфликт, то путь прокладывается по линии DYZ(m*2). Переход к п. 5.
4. Путь прокладывается по линии IXZ(m3) к абоненту-приемнику. Конец алгоритма.
5. Проверяется конфликтность пути по линии CYZ(m*3).
Если конфликта нет, то путь прокладывается по линии CYZ(m*3). Переход к п. 4.
Если же конфликт имеет место, то переход к п. 6.
6. Путь прокладывается по линии IXZ(m3). Переход к п. 7.
7. Путь прокладывается по линии SYZ(m*3). Конец алгоритма.
Отметим, что прокладка прямых путей по приведенному алгоритму может содержать до четырех этапов. Однако передача всех пакетов данных по прямым путям осуществляется за один скачок. Последнее свойство позволяет утверждать, что полученная сеть практически (по задержкам передачи) имеет единичный диаметр.
Предложена новая сеть в виде трехмерного неблокируемого отказоустойчивого гиперкуба на базе плоских сетей с топологией квазиполного графа. Данный гиперкуб назван разреженным p-ичным гиперкубом, т.к. он содержит меньше узлов, чем неблокируемый 3-мерный p-ичный гиперкуб, используемый в прототипе, но позволяет разменивать число узлов на число разных каналов между ними, что обеспечивает его канальную отказоустойчивость. Передача данных в предложенной сети осуществляется по прямым каналам между абонентами, что обеспечивает его наибольшее быстродействие. Внутриузловой коммутатор в полученной сети имеет в 9/8 больше большее число портов, чем в неблокируемом гиперкубе или мультикольце.
Построенная сеть может иметь несколько сотен абонентов (процессорных ядер) при двух-трех разных прямых каналов между ними. Наличие нескольких каналов не только обеспечивает отказоустойчивость данной сети, но и открывает возможность дальнейшего повышения ее быстродействия за счет их параллельного использования.
Областью применимости данного разреженного гиперкуба является системная сеть в многоядерном однокристальном процессоре-ускорителе.
На фиг. 18 в табл. 8 приведено число узлов R(р, σ) в построенных 3-мерных разреженных гиперкубах, определяющих топологию сетей, полученных предложенным способом. В ней подчеркнутые значения относятся к гиперкубам, поостренным на 1-расширенных плоских сетях HC(N*, р, σ|σ+1), в которых N*<N. Остальные значения задаются формулой R(p, σ)=N(p, σ)р, т.е. R(p, 1)=р3-р2+р, R(p, 2)=р3/2-р2/2+р и R(p, 3)=р3/3-р2/3+р.
| название | год | авторы | номер документа |
|---|---|---|---|
| СЕТЬ С ТОПОЛОГИЕЙ РАСШИРЕННОГО ОБОБЩЕННОГО ГИПЕРКУБА | 2013 |
|
RU2556458C2 |
| Способ организации системной сети в виде неблокируемого самомаршрутизируемого трехмерного р-ичного мультикольца | 2018 |
|
RU2703351C1 |
| Способ построения коммутируемых управляющих сетей с топологией квазиполного орграфа | 2023 |
|
RU2815332C1 |
| СПОСОБ ПОСТРОЕНИЯ НЕБЛОКИРУЕМОГО САМОМАРШРУТИЗИРУЕМОГО РАСШИРЕННОГО КОММУТАТОРА | 2009 |
|
RU2435295C2 |
| Способ организации оптимальных отказоустойчивых многомерных торов на основе малопортовых маршрутизаторов и разветвителей дуплексных каналов | 2020 |
|
RU2753147C1 |
| ОБОБЩЕННЫЕ НЕБЛОКИРУЕМЫЕ ДВУХКАСКАДНЫЕ СЕТИ КЛОЗА | 2014 |
|
RU2580100C2 |
| МУЛЬТИСЕРВИСНЫЙ ТЕЛЕКОММУНИКАЦИОННЫЙ КОМПЛЕКС | 2023 |
|
RU2833335C1 |
| МАСШТАБИРУЕМЫЕ ОПТИЧЕСКИЕ КОММУТАТОРЫ И МОДУЛИ КОММУТАЦИИ | 2012 |
|
RU2608300C2 |
| СИСТЕМНАЯ СЕТЬ ПЕРЕДАЧИ СООБЩЕНИЙ МНОГОМЕРНОГО ТОРА С ХОРДОВЫМИ СВЯЗЯМИ | 2015 |
|
RU2586835C1 |
| МОБИЛЬНЫЙ МНОГОФУНКЦИОНАЛЬНЫЙ УЗЕЛ СВЯЗИ | 2017 |
|
RU2645742C1 |

Изобретение относится к способу организации системной сети в виде отказоустойчивого неблокируемого трехмерного разреженного p-ичного гиперкуба для многопроцессорных систем с сотнями абонентов-процессоров. Техническим результатом изобретения является повышение отказоустойчивости системной сети, за счет наличия разных прямых каналов между любыми процессорами. В способе, при построении сети используется топология трехмерного р-ичного разреженного гиперкуба, представляющего собою оригинально организованную трехмерную композицию плоских сетей. Причем, способ включает определенным образом организованное расположение плоских сетей на гранях гиперкуба с последующим объединением коммутаторов этих сетей в узлах гиперкуба, которое совместно с дополнительно введенными между узлами сети каналами обеспечивает заявленные свойства изобретения. 19 ил.
Способ построения системной сети в виде отказоустойчивого неблокируемого трехмерного разреженного гиперкуба, характеризующийся тем, что R=Np узлов сети, пронумерованных от 0 до Np-1 (0, 1, 2, …, Np-1), располагают по N узлов в порядке их нумерации на гранях XYk (1≤k≤р) трехмерного р-ичного обобщенного гиперкуба, причем каждая группа разбивается на р групп gi (1≤i≤р) с х узлами в первой группе (i=1) и по у узлов в остальных группах (i=2, 3, …, р) при соблюдении условия x+y(p-1)=N, после чего каждая группа gi располагается на пересечении грани XYk с гранью XZj (1≤j≤р), номер которой вычисляется по формуле j=modp(i+k-1), при этом каждый узел сети включает процессор и коммутатор, связанные дуплексной линией, для связи с другими узлами сети в процессоре организуют группы OIXY, OIXZ по (р-1) дуплексных портов и группу SYZ из (р-1) симплексных выходов, а в коммутаторе организуют группы OIXY, OIXZ, MYZ, DYZ, CYZ, IXZ по (p-1) дуплексных портов и группу SYZ из (р-1) симплексных входов входных портов, при этом (р-1) дуплексных портов OIXY каждого из N коммутаторов граней XYk соединяют по одному дуплексными линиями с (р-1) портами разных (р-1) процессоров той же грани, и аналогично (р-1) дуплексных портов OIXZ каждого из N коммутаторов граней XZj соединяют по одному (р-1) дуплексными линиями с (р-1) портами разных (р-1) процессоров той же грани в соответствии со схемой соединений N коммутаторов и N процессоров, полученной из неполной симметричной блок-схемы заменой блоков на коммутаторы, элементов на процессоры, инцидентность блоков и элементов на соединения коммутаторов и процессоров и имеющей вид таблицы из N строк и р+1 столбцов, каждая строка которой содержит номер одного коммутатора и номера р подсоединенных к нему процессоров, и согласно которой к каждому коммутатору подсоединено р различных процессоров, а каждый процессор подсоединен к р разным коммутаторам, и каждая пара процессоров подсоединена к σ разным коммутаторам так, что N=p(p-1)/σ+1, и σ задает число разных путей между любыми двумя процессорами через разные коммутаторы, или в соответствии со схемой соединений N* коммутаторов и N* процессоров, полученной аналогично из расширенной блок-схемы в виде таблицы N* строк и р+1 столбцов, и согласно которой к каждому коммутатору подсоединено р различных процессоров, а каждый процессор подсоединен к р разным коммутаторам, а каждая пара процессоров подсоединена к σ или к σ+1 разным коммутаторам так, что N*<р(р-1)/σ+1, и стили σ+1 задают число разных путей между любыми двумя процессорами через разные коммутаторы; портов одноименных групп MYZ, DYZ, CYZ коммутаторов, расположенных на р разных гранях XZj (1≤j≤р) в узлах, имеющих равные по модулю N номера, то есть na≡nb (mod N) и na, nb ∈ [0, Np-1], соединяют группами по (р-1) дуплексных линий, то есть каждая пара коммутаторов в одноименной группе связана дуплексной линией; (р-1) дуплексных портов коммутаторов группы IXZ соединяют дуплексными линиями параллельно линиям между узлами, которые соединены линиями OIXZ, а (р-1) симплексных выходов коммутаторов группы SYZ соединяют с симплексными входами процессоров параллельно линиям между узлами, которые соединены линиями группы MYZ; при этом внутри каждого коммутатора для маршрутизации организуют полнокоммутаторные связи от входов Oxy к выходам IXY, IXZ, MYZ, DYZ (OXY и IXY - входы и выходы дуплексных портов OIXY, IXZ - выходы дуплексных портов OIXZ), от входов MYZ к выходам IXZ, от входов DYZ к выходам CYZ, от входов CYZ к выходам IXZ, от входов IXZ к выходам SYZ, причем порты и идентичные им линии в названных группах пронумерованы от 1 до р-1 (1, 2, …, р-1) (номер 0 указывает на внутриузловую связь в группах OXY, OXZ или на отсутствие связи в группе MYZ) и задаются при маршрутизации в группе OXY числами m1 (0≤m1≤р-1), в группах IXZ и IXZ числами m3 (0≤m3≤р-1), в группе MYZ числами m2 (0≤m2≤р-1), в группе DYZ числами m*2 (0≤m*2≤р-1), в группах CYZ и SYZ числами m*3 (0≤m*3≤р-1), (числа m2, m*2, m*3=j-i, если (j-i)≥0, и m2, m*2, m*3=p+j-i, если (j-i)<0), i и j - номера граней XZ, на которых расположен узел-источник и узел-приемник), а установление прямых путей при маршрутизации осуществляют методом червоточины посредством коммутаторов узлов независимо друг от друга с учетом параметров маршрутов, заданных числами m1, m2, m3, m*2=m1, m*3=⏐m2-m*2⏐ в заголовках пилотных пакетов, полученных коммутаторами, и наличия конфликтов на линиях групп MYZ и CYZ следующим образом: параметры кратчайшего маршрута m1, m2, m3 в заголовке пилотного пакета, сформированном процессором, при отсутствии конфликтов задают три этапа прокладки прямого пути пакетом, а именно, от узла-источника по линии OXY(m1) в следующий узел сети (при m1=0 путь прокладывается в коммутатор исходного узла), коммутатор которого устанавливает путь по линии MYZ(m2) в следующий узел сети (при m2=0 второй этап отсутствует), коммутатор которого устанавливает путь по линии IXZ(m3) в узел-приемник (при m3=0 узел-приемник находится в том же узле, что и коммутатор), если коммутатор обнаруживает конфликт при передаче пилотного пакета на линию MYZ(m2), то прокладывает путь на линию DYZ(m*2), если коммутатор получает пилотный пакет по линии DYZ(m*2) и не обнаруживает конфликт на линии CYZ(m*3), то прокладывает путь на эту линию, или при обнаружении конфликта прокладывает путь на линию IXZ(m3), если коммутатор получает пилотный пакет по линии CYZ(m*3), то прокладывает путь на линию IXZ(m3), а если коммутатор получает пилотный пакет по линии IXZ(m3), то прокладывает путь на линию SYZ(m*3).
| СПОСОБ ФУНКЦИОНИРОВАНИЯ ОПЕРАЦИОННОЙ СИСТЕМЫ ВЫЧИСЛИТЕЛЬНОГО УСТРОЙСТВА ПРОГРАММНО-АППАРАТНОГО КОМПЛЕКСА | 2016 |
|
RU2626350C1 |
| ОТКАЗОУСТОЙЧИВАЯ СВЯЗЬ В МАРШРУТИЗОВАННЫХ СЕТЯХ | 2006 |
|
RU2420897C2 |
| СЕТЬ С ТОПОЛОГИЕЙ РАСШИРЕННОГО ОБОБЩЕННОГО ГИПЕРКУБА | 2013 |
|
RU2556458C2 |
| US 5717943 A1, 10.02.1998 | |||
| US 5963746 A1, 05.10.1999 | |||
| М | |||
| Ф | |||
| Каравай, В | |||
| С | |||
| Подлазов, "Метод инвариантного расширения системных сетей многопроцессорных вычислительных систем | |||
| Идеальная системная сеть", Автомат | |||
| и телемех., 2010. | |||
Авторы
Даты
2020-05-12—Публикация
2019-10-18—Подача