Изобретение относится к космонавтике, в частности к области управления космическими аппаратами (КА) баллистического типа тягой двигательной установки при спуске с орбиты искусственного спутника Земли (ИСЗ) на заданные полигоны малых размеров, обеспечивающем высокий уровень точности и быстродействия при снижении потребных энергетических затрат.
Спуск КА с орбиты ИСЗ в заданную область поверхности Земли является завершающим этапом большинства космических экспедиций. От его успешной реализации во многом зависит выполнение программ полета КА.
Наиболее важными критериями осуществления спуска КА являются оперативность его выполнения, энергетическая оптимальность проведения ракетодинамических маневров, точность посадки аппарата на заданные полигоны.
Необходимость разработки и осуществления оперативных способов спуска связана с возможными возникновениями нештатных ситуаций на борту космического аппарата, что обуславливает жесткие требования к реализации срочной посадки КА. Это особенно важно при выполнении пилотируемых программ полета.
Обеспечение энергетической оптимальности реализации спуска связано с требованиями при проектировании космических миссий по увеличению доли полезной нагрузки в общем весовом балансе КА, в том числе за счет минимизации потребных энергетических затрат на проведение спуска аппарата с орбиты ИСЗ.
Выполнение точной посадки КА на поверхность Земли во многом обеспечивает возможность осуществления спуска на полигоны малых размеров.
Одним из наиболее распространенных типов спускаемых КА являются аппараты баллистического типа. Такие аппараты наиболее просты в изготовлении и не предусматривают создание систем управления аэродинамическими силами на этапе движения в атмосфере. При этом обеспечение оперативности, энергетической оптимальности и точности посадки таких КА на поверхность Земли требует разработки рациональных способов управления ракетодинамическими силами при сходе спускаемых аппаратов с обриты ИСЗ.
Известен ряд способов управления КА баллистического типа при спуске с орбиты ИСЗ на поверхность Земли.
При осуществлении схода аппарата со спутниковых орбит и спуска на поверхность Земли широко известен способ управления, состоящий в подаче импульса характеристической скорости в плоскости движения КА, описанный в работе - Иванов Н.М., Мартынов А.И. «Управление движением космического аппарата в атмосфере Марса». М.: «Наука», 1977, - [1], стр. 393-397. Универсальность данного способа заключается в том, что выбором двух управляющих параметров - величины импульса и угла между направлением его подачи и вектором скорости - обеспечивается вход КА в атмосферу с заданными значениями скорости и угла наклона вектора скорости к местному горизонту. Реализация таких значений фактически определяет дальность полета КА в атмосфере и при соответствующем выборе времени подачи импульса схода с орбиты может обеспечить удовлетворительную точность посадки КА в продольном направлении.
Вместе с тем, данный способ имеет существенные недостатки, ограничивающие его применение для обеспечения посадки КА на полигоны малых размеров. Во-первых, его реализация, как правило, сопровождается большими отклонениями от заданной точки посадки в боковом направлении, которые определяются удалением точки посадки от трассы полета КА на витке спуска и не могут быть скорректированы при осуществлении данного способа. Возможность снижения отклонений в боковом направлении связана с ожиданием спускового витка с наименьшим боковым смещением от полигона посадки за счет поворота Земли. Однако при этом значительно снижается оперативность осуществления спуска. Другой недостаток заключается в том, что выбранные значения величины и угла наклона импульса характеристической скорости для обеспечения заданных условий входа КА в атмосферу, как правило, являются не рациональными с точки зрения минимизации потребных энергетических затрат. В частности, подача импульса характеристической скорости под углом к вектору скорости КА, отличающемуся от 180°, сопровождается дополнительным расходом топлива.
Известен способ управления, предусматривающий подачу импульса характеристической скорости в направлении, противоположном вектору скорости КА, описанный в работе - «Навигационное обеспечение полета орбитального комплекса «Салют-6» - «Союз» - «Прогресс», под редакцией Петрова Б.Н., Бажинова И.К. М.: «Наука», 1985, - [2], стр. 280-284. Этот способ управления КА позволяет уменьшить потребные энергетические затраты по сравнению со способом [1]. В результате гашения скорости аппарат переводится на траекторию схода с орбиты, входит в атмосферу и осуществляет посадку на поверхность Земли. Обеспечение спуска в заданный район посадки достигается соответствующим выбором момента подачи импульса характеристической скорости. Данный способ неоднократно реализован в процессе выполнения программ полета транспортных пилотируемых и грузовых космических кораблей.
Основным недостатком данного способа является отсутствие возможности осуществления бокового маневра КА после выбора витка полета, на котором проводятся динамические операции спуска аппарата с орбиты. В связи с этим, при реализации такого способа практически невозможно осуществить посадку в малую область поверхности Земли. В результате возникает потребность в использовании посадочных полигонов крупных размеров. Во-вторых, осуществление такой программы проведения ракетодинамического маневра также не является энергетически оптимальной. Как правило, существует возможность снижения величины подаваемого импульса характеристической скорости и достижения того же района посадки за счет более раннего выполнения ракетодинамического маневра.
Известен способ управления КА при спуске с орбиты ИСЗ, предусматривающий предварительное проведение так называемой «коррекции прохождения», описанный в работе [2], стр. 273-274. Его суть заключается в предварительной подаче импульса характеристической скорости для коррекции периода обращения КА вокруг Земли и соответственно долготы межвиткового расстояния трассы полета. Соответствующим выбором величины и направления корректирующего импульса обеспечивается прохождение трассы полета КА над полигоном посадки, а путем определения момента схода КА с орбиты достигается высокая точность посадки аппарата в заданную малую область поверхности Земли.
При этом основным недостатком данного способа является низкая оперативность проведения операций по спуску КА. Так, для минимизации величины импульса схода для коррекции периода движения КА необходима подача этого импульса за несколько витков до схода аппарата с орбиты, что является неприемлемым в случаях необходимости реализации срочного спуска.
Другим недостатком данного способа является то, что его реализация сопровождается перерасходом топлива, связанного с необходимостью проведения, как импульса характеристической скорости для коррекции периода движения КА на орбите, так и импульса для схода КА с орбиты.
Наиболее близким по совокупности признаков к заявленному способу является способ управления КА, описанный в источнике информации - Иванов В.М., Соколов Н.Л. «Оптимальное управление космическим аппаратом за счет изменения вектора тяги двигательной установки при проведении межорбитальных маневров». Космонавтика и ракетостроение, изд. ЦНИИмаш, №2(75), 2014 - [3], стр. 80-88. Он заключается в подаче импульса характеристической скорости для перевода КА с орбиты ИСЗ на траекторию снижения при обеспечении как требуемых значений скорости и траекторного угла, так и боковой дальности при входе аппарата в атмосферу. При этом импульс имеет пространственную ориентацию. После расчета бокового смещения точки посадки космического аппарата относительно плоскости его движения Lбок определяются величина и ориентация импульса характеристической скорости, подаваемого при движении КА по орбите ИСЗ. Путем управления вектором тяги двигательной установки осуществляется изменение скорости и плоскости движения КА и обеспечивается его перевод с орбиты ИСЗ на траекторию спуска. Причем варьированием величины проекции импульса скорости на плоскость движения КА обеспечивается как снижение скорости КА, так и необходимая крутизна траектории спуска, а варьированием величины проекции импульса скорости на плоскость, перпендикулярную к направлению полета КА достигается требуемая боковая дальность КА. Применение этого способа позволяет, при достаточно высоком уровне оперативности, обеспечить возможность управления движением КА как в продольном, так и в боковом направлениях. Это позволит уменьшить отклонение точки посадки КА от заданной точки по сравнению с возможными отклонениями при реализации способов-аналогов [1-2]. Указанный способ [3] является наиболее близким аналогом к заявленному способу как по совокупности существенных признаков, так и по достигаемому результату и поэтому выбран в качестве прототипа.
Вместе с тем, рассматриваемый способ-прототип имеет ряд недостатков. Во-первых, при его реализации существует резерв в максимизации бокового маневра КА, а, следовательно, и в повышении быстродействия осуществления посадки на поверхность Земли. Указанные критерии могут быть достигнуты за счет выбора рациональных программ управления вектором тяги двигательной установки при подаче импульса для схода аппарата с орбиты ИСЗ, в первую очередь путем перераспределения общего запаса импульса характеристической скорости в сторону увеличения его боковой составляющей. Так, представляется эффективным сокращение продольной составляющей импульса скорости. Этого можно достигнуть как за счет подачи импульса скорости в направлении строго под углом 180° к вектору скорости КА (максимальная эффективность гашения скорости), так и за счет снижения абсолютной величины подаваемого импульса. К тому же способ-прототип не предусматривает определения и обоснования минимального абсолютного значения продольной составляющей подаваемого импульса. Возможное сокращение продольной составляющей импульса при существующем запасе топлива дает возможность увеличения боковой составляющей импульса и тем самым увеличения бокового маневра КА при спуске на поверхность Земли. Это в ряде случаев позволяет осуществить спуск КА в заданном районе посадки на текущем витке, а не откладывать реализацию проведения импульса на следующие витки, что позволит существенно повысить оперативность спуска КА.
Кроме того, способ-прототип предусматривает подачу только одного импульса характеристической скорости, обеспечивающего как заданные значения скорости и траекторного угла при входе КА в атмосферу, так и изменение плоскости движения аппарата для достижения необходимой боковой дальности спуска. Вместе с тем, представляется энергетически рациональным проведение двух импульсов характеристической скорости, обеспечивающих последовательное управление КА в продольной и боковой плоскостях. В этом случае уменьшение скорости КА за счет проведения первого тормозящего импульса является благоприятным фактором для снижения потребных энергозатрат при изменении плоскости движения КА, т.к. коррекцию плоскости движения КА энергетически рационально осуществлять при меньших скоростях полета КА.
Также недостатком способа-прототипа является то, что при его реализации не используются конечные аналитические формулы для расчета управляющих параметров КА (величины и углов ориентации импульсов характеристической скорости в пространстве и момента их подачи). Применение таких формул позволило бы в зависимости от существующих полетных условий (параметры орбиты КА, координаты полигона посадки, энергетические характеристики двигательных установок) оперативно определять рациональные управляющие параметры непосредственно на борту КА и реализовать выбранную программу управления. Тогда как определение таких программ наземными средствами с последующей их выдачей на борт в виде программно-командной информации существенно снижает оперативность выполнения операций по сходу КА с орбиты ИСЗ.
Сущность предлагаемого изобретения заключается в следующем. Осуществляется последовательная подача двух импульсов характеристической скорости: сначала в плоскости движения КА против вектора его скорости для обеспечения схода аппарата с орбиты, а затем в направлении, перпендикулярном к плоскости полета, - для управления боковой дальностью. Прежде всего, в обеспечение энергетической оптимальности применения данного способа определяется минимально необходимое значение подаваемого тормозного импульса схода КА с орбиты ИСЗ ΔVпрmin, которое фактически определяется максимально возможной абсолютной величиной траекторного угла входа КА в атмосферу 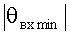
При известных значениях hπmax определяется минимально возможное абсолютное значение угла наклона вектора скорости к местному горизонту при входе космического аппарата в атмосферу 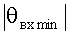
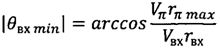 ,
,
где
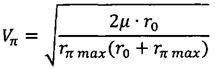 ;
; 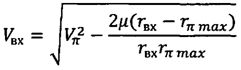 ;
;
Vπ - скорость космического аппарата в перигее оскулирующей орбиты, сформированной после завершения работы двигательной установки;
Vвх - скорость космического аппарата при входе в атмосферу;
rπmax=R+hπmax - максимально возможный радиус-вектор перигея оскулирующей орбиты, при котором обеспечивается захват космического аппарата атмосферой и его снижение на поверхность Земли;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу;
hπmax - максимально возможная высота перигея оскулирующей орбиты, при которой обеспечивается захват космического аппарата атмосферой и его снижение на поверхность Земли;
hатм=100 км - высота условной границы атмосферы;
R - средний радиус Земли;
µ - произведение гравитационной постоянной на массу Земли.
Обеспечение минимально допустимого значения 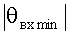
В зависимости от углов 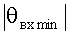
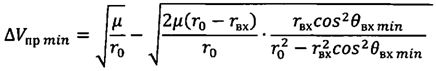 ,
,
где µ произведение гравитационной постоянной на массу Земли;
гвх=R+hатм - радиус-вектор КА при его входе в атмосферу;
hатм=100 км - высота условной границы атмосферы.
После определения минимального значения ΔVпрmin и зная величину суммарного располагаемого запаса импульса характеристической скорости ΔVΣ найдем максимальное значение второго импульса характеристической скорости для управления боковым маневром ΔVбок max=ΔVΣ-ΔVпрmin. Подача импульса характеристической скорости, ориентированного под углом 90° к плоскости орбиты, обеспечивает максимальный боковой маневр КА при его спуске с орбиты (такой режим подачи второго импульса не влияет на изменение скорости КА и, следовательно, на дальность полета аппарата). Это в значительной мере обеспечивает высокий уровень оперативности осуществления спуска КА в заданный район посадки, т.к. низкие маневренные возможности аппарата приводят к необходимости ожидания благоприятных спусковых витков за счет соответствующего поворота Земли, что сопровождается существенным снижением оперативности выполнения операций спуска. Учитывая импульсный характер двух включений двигательной установки, реализуемых непосредственно одно за другим, следует отметить, что продолжительность их проведения чрезвычайно мала и не влияет на общую дальность полета КА и момент схода аппарата с орбиты ИСЗ.
С целью обеспечения требуемой точности посадки КА с учетом известных параметров r0, 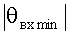
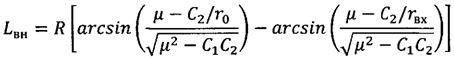 ,
,
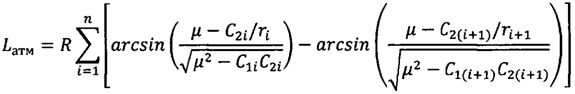 ,
,
где
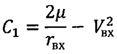 ;
; 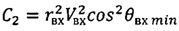 ;
;
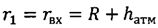 ;
; 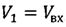 ;
; 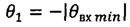 ;
;
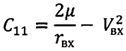 ;
; 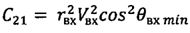 ;
;
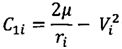 ;
; 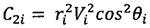 ;
;
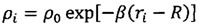 ;
; 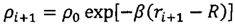 ;
;
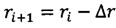 ;
; 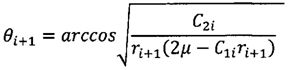 ;
;
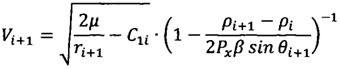 ;
;
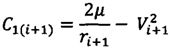 ;
; 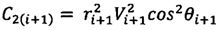 ;
;
R - средний радиус Земли;
µ - произведение гравитационной постоянной на массу Земли;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвн=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу;
Vвх - скорость космического аппарата при входе в атмосферу;
θвх min - минимальное абсолютное значение угла наклона вектора скорости к местному горизонту, при котором обеспечиваются гарантированный захват космического аппарата атмосферой и его посадка на поверхность Земли;
hатм=100 км - высота условной границы атмосферы;
ri - радиус-вектор КА на i-м интервале расчета координат;
ri+1 - радиус-вектор КА на (i+1)-м интервале расчета координат;
Vi - скорость КА на i-м интервале расчета координат;
Vi+1 - скорость КА на (i+1)-м интервале расчета координат;
θi - траекторный угол на i-м интервале расчета координат;
θi+1 - траекторный угол на (i+1)-м интервале расчета координат;
ρi - плотность атмосферы на i-м интервале расчета координат;
ρi+1 - плотность атмосферы на (i+1)-м интервале расчета координат, i=1, 2, 3…n;
Δr - интервал изменения радиус-вектора, при котором осуществляется расчет новых координат;
ρ0 - плотность атмосферы на поверхности Земли;
β - логарифмический коэффициент изменения плотности атмосферы от высоты;
Pх - приведенная нагрузка на лобовую поверхность КА.
Также сущность способа управления космическим аппаратом при его спуске с орбиты искусственного спутника Земли изобретения заключается в определении бокового смещения точки посадки космического аппарата относительно плоскости его движения Lбок, величины и ориентации импульса характеристической скорости, подаваемого при движении космического аппарата на орбите искусственного спутника Земли, управлении вектором тяги двигательной установки для изменения скорости и плоскости движения космического аппарата и перевода его с орбиты искусственного спутника Земли на траекторию спуска, при этом определяют минимально возможное абсолютное значение угла наклона вектора скорости к местному горизонту при входе космического аппарата в атмосферу 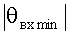
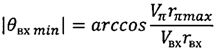 ,
,
где
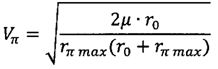 ;
; 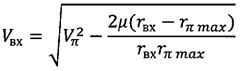 ;
;
Vπ - скорость космического аппарата в перигее оскулирующей орбиты, сформированной после завершения работы двигательной установки;
Vвх - скорость космического аппарата при входе в атмосферу;
rπmax=R+hπmax - максимально возможный радиус-вектор перигея оскулирующей орбиты, при котором обеспечиваются захват космического аппарата атмосферой и его снижение на поверхность Земли;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу Земли;
hπmax - максимально возможная высота перигея оскулирующей орбиты, при которой обеспечивается захват космического аппарата атмосферой и его снижение на поверхность Земли;
hатм=100 км - высота условной границы атмосферы;
R - средний радиус Земли;
µ - произведение гравитационной постоянной на массу Земли,
с использованием безытерационных аналитических формул определяют широту φсх и долготу λсх подспутниковой точки космического аппарата при включении двигательной установки, а также продольную дальность полета космического аппарата L от момента завершения работы двигательной установки до посадки на поверхность Земли:
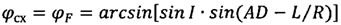 ,
,
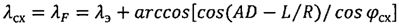 ,
,
L=Lвн+Lатм,
где
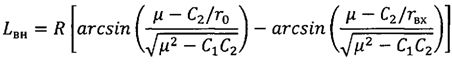 ;
;
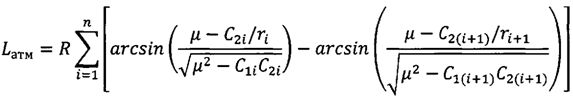 ;
;
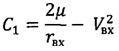 ;
; 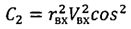 ;
;
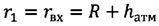 ;
; 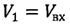 ;
; 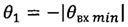 ;
;
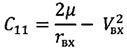 ;
; 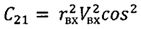 ;
;
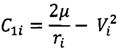 ;
; 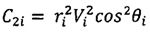 ;
;
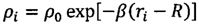 ;
; 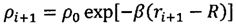 ;
;
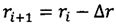 ;
; 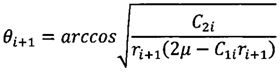 ;
;
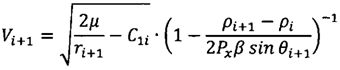 ;
;
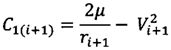 ;
; 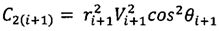 ;
;
I - наклонение орбиты;
AD - дуга, лежащая в плоскости орбиты движения космического аппарата (см. фиг.2), соединяющая точку пересечения экватора (точка А) с точкой D, образованной при пересечении плоскости орбиты движения космического аппарата и плоскости, перпендикулярной к ней и содержащей точку посадки В;
L - дальность полета космического аппарата от его схода с орбиты до посадки на поверхность Земли;
Lвн - дальность полета космического аппарата на внеатмосферном участке;
Lатм - дальность полета космического аппарата в атмосфере;
R - средний радиус Земли;
µ - произведение гравитационной постоянной на массу Земли;
λэ - долгота пересечения плоскости движения космического аппарата с плоскостью экватора;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу;
Vвх - скорость космического аппарата при входе в атмосферу;
θвх min - минимальное абсолютное значение угла наклона вектора скорости к местному горизонту, при котором обеспечиваются гарантированный захват космического аппарата атмосферой и его посадка на поверхность Земли;
hатм=100 км - высота условной границы атмосферы;
ri - радиус-вектор космического аппарата на i-м интервале расчета координат;
ri+1 - радиус-вектор космического аппарата на (i+1)-м интервале расчета координат;
Vi - скорость космического аппарата на i-м интервале расчета координат;
Vi+1 - скорость космического аппарата на (i+1)-м интервале расчета координат;
θi - траекторный угол на i-м интервале расчета координат;
θi+1 - траекторный угол на (i+1)-м интервале расчета координат;
ρi - плотность атмосферы на i-м интервале расчета координат;
ρi+1 - плотность атмосферы на (i+1)-м интервале расчета координат;
i=1, 2, 3…n;
Δr - интервал изменения радиус-вектора, при котором осуществляется расчет новых координат;
ρ0 - плотность атмосферы на поверхности Земли;
β - логарифмический коэффициент изменения плотности атмосферы от высоты;
Рх - приведенная нагрузка на лобовую поверхность космического аппарата, осуществляют подачу первого импульса характеристической скорости ΔVпрmin в направлении, противоположном вектору скорости космического аппарата, величина которого рассчитывается в соответствии с зависимостью:
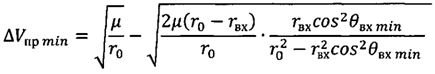 ,
,
где µ - произведение гравитационной постоянной на массу Земли;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу;
hатм=100 км - высота условной границы атмосферы;
θвх min - минимальное абсолютное значение угла наклона вектора скорости к местному горизонту, при котором обеспечиваются гарантированный захват космического аппарата атмосферой и его посадка на поверхность Земли,
по окончании отработки первого импульса осуществляют подачу второго импульса характеристической скорости под углом 90° к вектору скорости космического аппарата по часовой стрелке, если точка посадки расположена справа от плоскости движения космического аппарата и против часовой стрелки, если точка посадки расположена слева от этой плоскости, при этом величины второго импульса характеристической скорости ΔVбок и угла разворота вектора скорости космического аппарата в горизонтальной плоскости α (на который необходимо развернуть вектор скорости КА в горизонтальной плоскости путем приложения второго импульса характеристической скорости, чтобы плоскость движения спускаемого аппарата проходила через заданную точку посадки) вычисляются по формулам
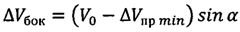 ,
,
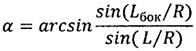 ,
,
где V0 - скорость движения космического аппарата по орбите искусственного спутника Земли до подачи импульсов характеристической скорости;
ΔVпр min - первый подаваемый импульс характеристической скорости;
L - дальность полета космического аппарата от его схода с орбиты до посадки на поверхность Земли;
Lбок - боковое смещение точки посадки космического аппарата относительно плоскости его движения;
R - средний радиус Земли,
после отработки второго импульса характеристической скорости осуществляют неуправляемое движение космического аппарата до посадки на поверхность Земли.
Анализ результатов, полученных с помощью зависимостей для определения дальности Lатм, показал, что при значении Δr=10 км погрешности вычислений дальности Lатм не превышают 1-2%. При этом продолжительность вычислений значений Lвн и Lатм не превышает 15-20 секунд.
Заявленный способ управления космическим аппаратом при его спуске с орбиты искусственного спутника Земли поясняется следующими чертежами.
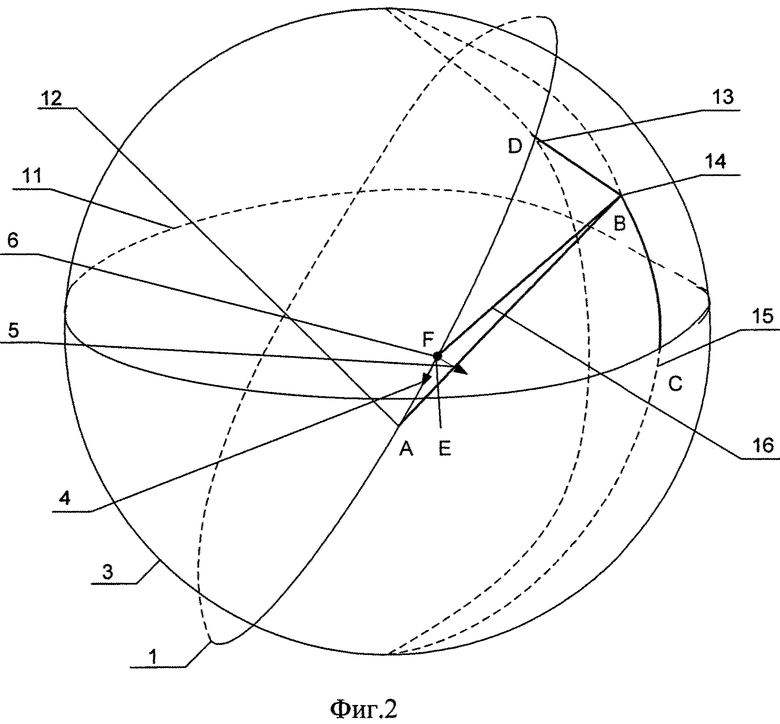
На фиг. 1 приведена схема, характеризующая этапы полета КА в плоскости его движения после приложения двух импульсов характеристической скорости.
На фиг. 2 представлена схема, характеризующая этапы полета КА относительно земного шара.
На фиг. 1, 2 приняты следующие обозначения:
1 - орбита ИСЗ, на которой происходит полет КА,
2 - условная граница атмосферы,
3 - поверхность Земли,
4 - подача импульса характеристической скорости ΔVпрmin, направленного против вектора скорости КА для его схода с орбиты ИСЗ,
5 - подача импульса характеристической скорости ΔVбок, направленного под углом 90° к вектору скорости КА в горизонтальной плоскости полета для изменения плоскости движения,
6 - сход КА с орбиты,
7 - оскулирующая орбита КА после приложения импульсов характеристической скорости,
8 - вход КА в атмосферу с траекторным углом θвх min,
9 - точка посадки КА на поверхность Земли,
10 - перигей оскулирующей орбиты КА с высотой hπmax,
11 - экватор,
12 - пересечение трассы полета КА с плоскостью экватора (точка А),
13 - пересечение плоскости орбиты с перпендикулярной к ней плоскостью, проходящей через точку посадки (точка D),
14 - точка посадки КА (точка В),
15 - пересечение плоскости экватора с полярной плоскостью, проходящей через точку посадки (точка С),
16 - трасса спуска КА на поверхность Земли.
С учетом вычисленного значения продольной дальности полета КА от момента схода с орбиты до посадки на поверхность Земли определяются координаты подспутниковой точки КА, на которой осуществляется сход аппарата с орбиты. Прежде всего рассмотрим сферический треугольник ABC, (см. фиг. 2), образованный тремя плоскостями большого круга: плоскостью, соединяющей точку на экваторе, через которую проходит трасса полета (точка А с известными географическими координатами) с точкой посадки КА (точка В с известными географическими координатами); полярной плоскостью, проходящей через точку посадки В; плоскостью экватора.
В связи с тем, что географические координаты точек А, В и С известны (точка С имеет нулевую широту и ту же долготу, что и точка посадки В) дуги АВ, ВС и АС могут быть вычислены в соответствии с известной формулой сферической тригонометрии, имеющей следующую структуру:
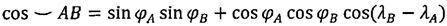 .
.
С использованием теоремы синусов определим угол ВАС:
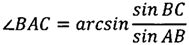 .
.
Далее рассмотрим сферический треугольник ADB - см. фиг. 2. Здесь AD - дуга, лежащая в плоскости движения КА, DB - дуга, лежащая в плоскости, перпендикулярной к плоскости движения КА, проходящей через точку посадки В, АВ - дуга, входящая в ранее рассмотренный сферический треугольник ABC.
Угол BAD можно определить как разность между наклонением орбиты I (или угол CAD) и ранее вычисленным углом ВАС:
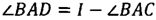 .
.
С использованием теоремы синусов определим дугу DB, т.е. угловое расстояние между плоскостью движения КА и точкой посадки:
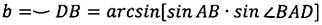 .
.
Дуга AD определяется по формуле
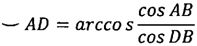 .
.
По вычисленным значениям продольной дальности L=Lвн-Lатм (дуга FD или дуга FB) и дуги DB определим угол α, на который необходимо развернуть вектор скорости КА в горизонтальной плоскости путем приложения второго импульса характеристической скорости, чтобы плоскость движения спускаемого аппарата проходила через заданную точку посадки:
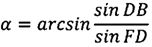 .
.
Для разворота вектора скорости в горизонтальной плоскости на угол α необходимо подать импульс характеристической скорости, определяемую по формуле
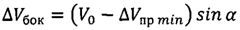 .
.
Из анализа данной формулы следует, что корректировать плоскость движения КА необходимо после предварительного гашения скорости аппарата: величина ΔVбок в этом случае будет меньше, чем при реализации одного пространственного импульса характеристической скорости.
Далее с использованием формул сферической тригонометрии определим координаты схода КА с орбиты φсх и λсх:
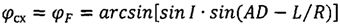 ,
,
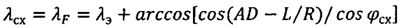 .
.
Использование разработанных, достаточно простых аналитических зависимостей позволяет в течение 20-30 секунд рассчитать параметры и условия подачи импульса схода КА с орбиты ИСЗ. Такие операции могут быть успешно реализованы на борту КА.
Таким образом, предложенный способ управления обладает рядом преимуществ по сравнению с рассмотренными аналогами и прототипом. Реализация данного способа обеспечивает минимизацию потребного импульса характеристической скорости при сходе КА с орбиты ИСЗ за счет рационального перераспределения общего запаса характеристической скорости между подаваемыми первым и вторым импульсами; обеспечивает повышенную оперативность полета за счет увеличения маневренных возможностей аппарата, а также за счет использования быстродействующих аналитических расчетных формул; обеспечивает высокую точность посадки в заданную область поверхности Земли за счет точного выбора координат схода КА с орбиты ИСЗ и реализации рациональной программы управления вектором тяги двигательной установки, учитывающей особенности динамики полета аппарата, как на внеатмосферном, так и на атмосферном участках.
Технический результат изобретения заключается в снижении потребных энергетических затрат и повышении оперативности управления КА ракетодинамическими силами при проведении маневра схода с орбиты ИСЗ, а также в повышении точности посадки аппарата на полигоны малых размеров. При этом применяются рациональные действия изменения вектора тяги двигательной установки, используются безытерационные быстродействующие аналитические алгоритмы расчета управляющих параметров. Это позволяет для широкого диапазона изменения высот орбиты, параметров КА и двигательной установки, граничных условий полета обеспечить посадку спускаемого аппарата в заданную малую область поверхности Земли.
Указанный технический результат достигается за счет автономного оперативного определения бортовыми средствами аппарата координат включения двигательной установки, величины и ориентации импульсов характеристической скорости КА, а именно: за счет того, что в известном способе управления космическим аппаратом при его спуске с орбиты искусственного спутника Земли, выбранном прототипом для заявленного способа и заключающимся в определении бокового смещения точки посадки космического аппарата относительно плоскости его движения Lбок, величины и ориентации импульса характеристической скорости, подаваемого при движении космического аппарата на орбите искусственного спутника Земли, управлении вектором тяги двигательной установки для изменения скорости и плоскости движения космического аппарата и перевода его с орбиты искусственного спутника Земли на траекторию спуска, дополнительно определяют минимально возможное абсолютное значение угла наклона вектора скорости к местному горизонту при входе космического аппарата в атмосферу 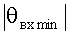
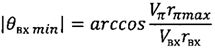 ,
,
где
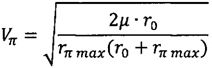 ;
; 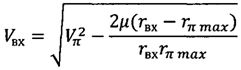 ;
;
Vπ - скорость космического аппарата в перигее оскулирующей орбиты, сформированной после завершения работы двигательной установки;
Vвх - скорость космического аппарата при входе в атмосферу;
rπmax=R+hπmax - максимально возможный радиус-вектор перигея оскулирующей орбиты, при котором обеспечиваются захват космического аппарата атмосферой и его снижение на поверхность Земли;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу Земли;
hπmax - максимально возможная высота перигея оскулирующей орбиты, при которой обеспечиваются захват космического аппарата атмосферой и его снижение на поверхность Земли;
hатм=100 км - высота условной границы атмосферы;
R - средний радиус Земли;
µ - произведение гравитационной постоянной на массу Земли,
с использованием безытерационных аналитических формул определяют широту φсх и долготу λсх подспутниковой точки космического аппарата при включении двигательной установки, а также продольную дальность полета космического аппарата L от момента завершения работы двигательной установки до посадки на поверхность Земли:
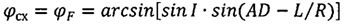 ,
,
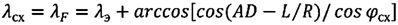 ,
,
L=Lвн+Lатм,
где
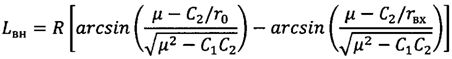 ;
;
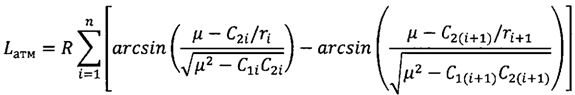 ;
;
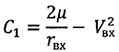 ;
; 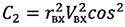 ;
;
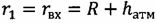 ;
; 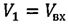 ;
; 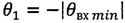 ;
;
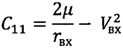 ;
; 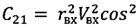 ;
;
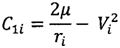 ;
; 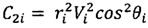 ;
;
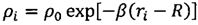 ;
; 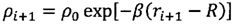 ;
;
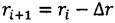 ;
; 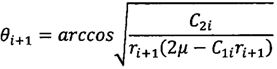 ;
;
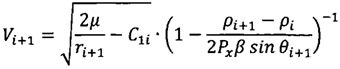 ;
;
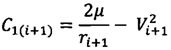 ;
; 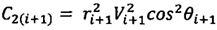 ;
;
I - наклонение орбиты;
AD - дуга, лежащая в плоскости орбиты движения космического аппарата, соединяющая точку пересечения экватора (точка А) с точкой D, образованной при пересечении плоскости орбиты движения космического аппарата и плоскости, перпендикулярной к ней и содержащей точку посадки В;
L - дальность полета космического аппарата от его схода с орбиты до посадки на поверхность Земли;
Lвн - дальность полета космического аппарата на внеатмосферном участке;
Lатм - дальность полета космического аппарата в атмосфере;
R - средний радиус Земли;
µ - произведение гравитационной постоянной на массу Земли;
λэ - долгота пересечения плоскости движения космического аппарата с плоскостью экватора;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу;
Vвх - скорость космического аппарата при входе в атмосферу;
θвх min - минимальное абсолютное значение угла наклона вектора скорости к местному горизонту, при котором обеспечиваются гарантированный захват космического аппарата атмосферой и его посадка на поверхность Земли;
hатм=100 км - высота условной границы атмосферы;
ri - радиус-вектор космического аппарата на i-м интервале расчета координат;
ri+1 - радиус-вектор космического аппарата на (i+1)-м интервале расчета координат;
Vi - скорость космического аппарата на i-м интервале расчета координат;
Vi+1 - скорость космического аппарата на (i+1)-м интервале расчета координат;
θi - траекторный угол на i-м интервале расчета координат;
θi+1 - траекторный угол на (i+1)-м интервале расчета координат;
ρi - плотность атмосферы на i-м интервале расчета координат;
ρi+1 - плотность атмосферы на (i+1)-м интервале расчета координат;
i=1, 2, 3…n;
Δr - интервал изменения радиус-вектора, при котором осуществляется расчет новых координат;
ρ0 - плотность атмосферы на поверхности Земли;
β - логарифмический коэффициент изменения плотности атмосферы от высоты;
Pх - приведенная нагрузка на лобовую поверхность космического аппарата, осуществляют подачу первого импульса характеристической скорости ΔVпрmin в направлении, противоположном вектору скорости космического аппарата, величина которого рассчитывается в соответствии с зависимостью:
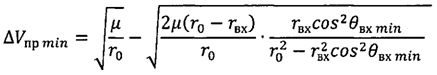 ,
,
где µ - произведение гравитационной постоянной на массу Земли;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу;
hатм=100 км - высота условной границы атмосферы;
θвх min - минимальное абсолютное значение угла наклона вектора скорости к местному горизонту, при котором обеспечиваются гарантированный захват космического аппарата атмосферой и его посадка на поверхность Земли,
по окончании отработки первого импульса осуществляют подачу второго импульса характеристической скорости под углом 90° к вектору скорости космического аппарата по часовой стрелке, если точка посадки расположена справа от плоскости движения космического аппарата, и против часовой стрелки, если точка посадки расположена слева от этой плоскости, при этом величины второго импульса характеристической скорости ΔVбок и угла разворота вектора скорости космического аппарата в горизонтальной плоскости α (на который необходимо развернуть вектор скорости КА в горизонтальной плоскости путем приложения второго импульса характеристической скорости, чтобы плоскость движения спускаемого аппарата проходила через заданную точку посадки) вычисляются по формулам
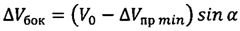 ,
,
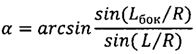 ,
,
где V0 - скорость движения космического аппарата по орбите искусственного спутника Земли до подачи импульсов характеристической скорости;
ΔVпр min - первый подаваемый импульс характеристической скорости;
L - дальность полета космического аппарата от его схода с орбиты до посадки на поверхность Земли;
Lбок - боковое смещение точки посадки космического аппарата относительно плоскости его движения;
R - средний радиус Земли,
после отработки второго импульса характеристической скорости осуществляют неуправляемое движение космического аппарата до посадки на поверхность Земли.
Покажем возможность осуществления изобретения, т.е. возможность его промышленного применения.
Как подробно указывалось выше, спуск КА с орбиты ИСЗ в заданную область поверхности Земли является завершающим этапом большинства космических экспедиций. От его успешной реализации во многом зависит выполнение программ полета КА. Таким образом, решаемая задача весьма актуальна.
Что касается технических средств, обеспечивающих управление вектором тяги двигательной установки для изменения скорости и плоскости движения космического аппарата и перевода его с орбиты искусственного спутника Земли на траекторию спуска и обеспечивающих определение параметров движения КА, то они известны - см., например, [1]-[3] или книгу Ю.Г. Сихарулидзе «Баллистика летательных аппаратов». М.: «Наука», 1982 - [4], стр. 158-204 и при необходимости приведенную в ней многочисленную библиографию.
В Приложении к материалам заявки помещен вывод используемых математических зависимостей для расчета траекторного угла входа КА в атмосферу 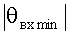
Приложение
Вывод используемых математических зависимостей для расчета траекторного угла входа космического аппарата (КА) в атмосферу 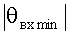
1. Вывод зависимостей для расчета 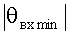
После подачи импульсов характеристической скорости формируется оскулирующая орбита с максимально возможным радиус-вектором перигея rπmax, при которой КА гарантированно не вылетает из атмосферы после прохождения ее верхних слоев.
Для апогея и перигея сформированной оскулирующей орбиты запишем кеплеровские интегралы энергии и площадей [1]:
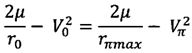 ,
,
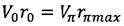 ,
,
где V0 - скорость движения КА после приложения импульсов характеристической скорости;
r0 - радиус-вектор КА после приложения импульсов характеристической скорости;
Vπ - скорость движения КА в перигее оскулирующей орбиты;
rπmax - максимально возможное значение радиус-вектора КА в перигее оскулирующей орбиты.
В приведенных уравнениях две переменные V0 и Vπ не известны, а переменные r0 и rπmax заданы в соответствии с исходными условиями.
Совместно решая уравнения двумя неизвестными, получим
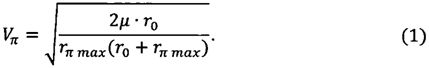
Далее составим кеплеровские интегралы энергии и площадей для моментов входа КА в атмосферу и перигея оскулирующей орбиты:
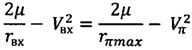 ,
,
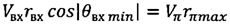 ,
,
гГде Vвх - скорость входа КА в атмосферу;
rвх - радиус-вектор входа КА в атмосферу;
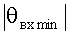
Vπ - скорость движения КА в перигее оскулирующей орбиты;
rπmax - максимально возможное значение радиус-вектора КА в перигее оскулирующей орбиты;
µ - произведение гравитационного параметра на массу Земли.
Решая приведенные уравнения, получим
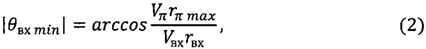
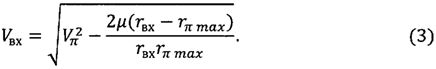
Таким образом, с помощью уравнений (1)-(3) рассчитывается минимальное абсолютное значение траекторного угла входа в атмосферу, при котором КА гарантированно не вылетает из атмосферы после прохождения ее верхних слоев 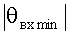
2. Вывод зависимостей для расчета дальности полета L КА.
Движение КА на внеатмосферном участке описывается известными дифференциальными уравнениями [2]:
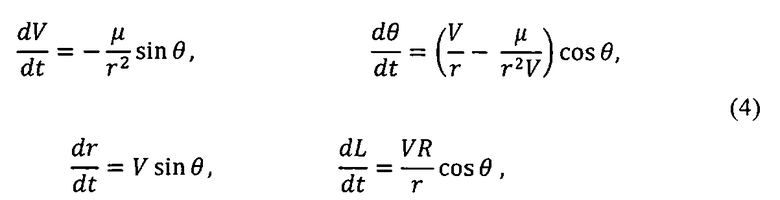
где V - скорость полета КА;
θ - угол наклона вектора скорости КА к местному горизонту;
r - радиус-вектор КА;
L - продольная дальность полета КА;
t - время полета КА;
µ - произведение гравитационного параметра на массу Земли;
R - средний радиус Земли.
Перейдем по формуле 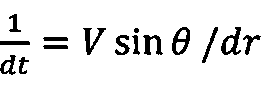 к новой независимой переменной r.
к новой независимой переменной r.
После замены переменной и интегрирования первого уравнения системы (4) получим следующую зависимость:

С ее учетом преобразуем второе и третье уравнения системы (4) к виду
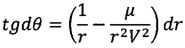 .
.
Из этого уравнения определим зависимость траекторного угла θ от радиуса-вектора r:
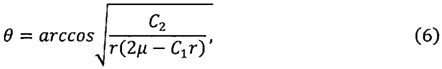
где С2=r2V2cos2θ.
Для получения зависимости продольной дальности L от величины r используем дифференциальное уравнение: dL/dr=R·ctgθ(r)/r.
После его интегрирования с учетом уравнений (5), (6) имеем
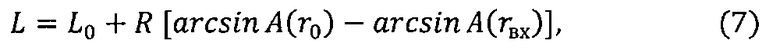
где
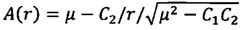 .
.
Это уравнение может быть преобразовано к виду
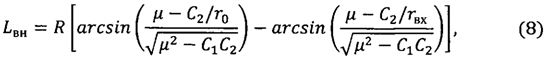
где
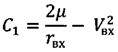 ,
, 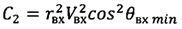 .
.
Таким образом, продольная дальность полета КА от его схода с орбиты ИСЗ до входа в атмосферу рассчитывается в соответствии с формулами (5)-(8).
Дальность полета КА баллистического типа в атмосфере может быть вычислена с помощью численного интегрирования системы уравнений (4) для заданных условий входа в атмосферу. Однако, с целью сокращения расчетного времени предлагаются формулы для ускоренного расчета. Отметим, что при пассивном полете в атмосфере система уравнений движения КА баллистического типа отличается от дифференциальных уравнений кеплеровского движения наличием в уравнении для скорости первого слагаемого, характеризующего действия аэродинамических сил - ρV2/2Px (Рх - приведенная нагрузка на лобовую поверхность КА). Суть разработки формул состоит в том, что в качестве опорного рассматривается аналитическое решение кеплеровских уравнений (6), (8).
По этим уравнениям для любого значения высот hi от hвх=100 км до h=0 вычисляются текущие величины скорости Vi, траекторного угла θi и дальности атмосферного участка Lатм i.
Поскольку из всех координат полета КА только скорость в явном виде зависит от аэродинамических сил (на остальные координаты аэродинамические силы оказывают опосредованное влияние), будем проводить расчет траекторий по формулам (6), (8) для интервалов изменения аргумента h, где аэродинамические силы принимаются постоянными, предварительно пересчитывая в начале каждого интервала значения скорости полета и соответствующих постоянных С1 и С2.
Итак, расчет дальности полета КА на атмосферном участке будет проводиться по следующим рекуррентным соотношениям:
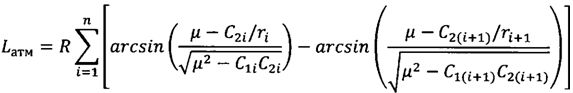 ,
,
где
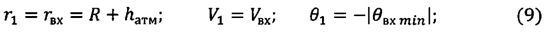
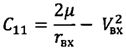 ;
; 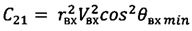 ;
;
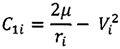 ;
; 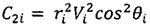 .
.
Зависимость для скорости полета с учетом влияния аэродинамических сил запишем в виде
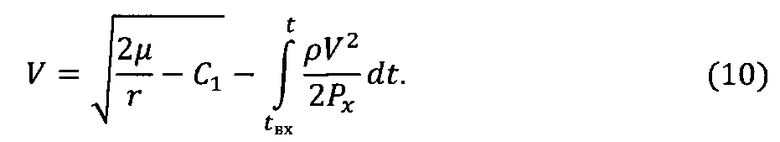
Используя допущение об экспоненциальном характере изменения плотности атмосферы от высоты
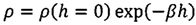 .
.
третье уравнение системы (4) преобразуем следующим образом:
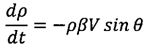 .
.
После замены переменной 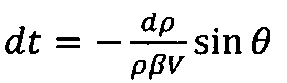 и упомянутого введения интервалов кусочного постоянства, формула (10) примет вид
и упомянутого введения интервалов кусочного постоянства, формула (10) примет вид
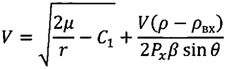 .
.
Решая это уравнение относительно переменной V, запишем окончательную зависимость для расчета полета КА баллистического типа в атмосфере
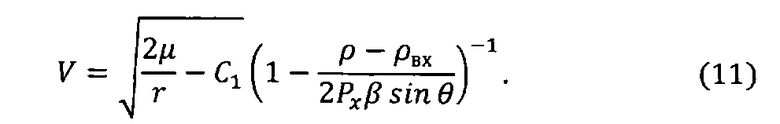
Далее, с использованием следующих рекуррентных соотношений поэтапно рассчитываются параметры движения КА для заданного интервала изменения высоты полета Δh (или радиуса-вектора КА Δr):
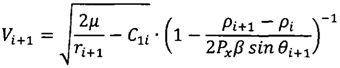 ,
,
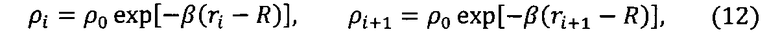
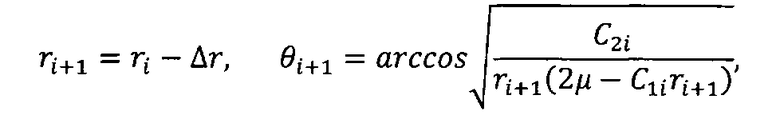
где ρ0 - плотность атмосферы на поверхности Земли;
β - логарифмический коэффициент изменения плотности атмосферы от высоты;
Pх - приведенная нагрузка на лобовую поверхность космического аппарата;
µ - произведение гравитационного параметра на массу Земли;
R - средний радиус Земли.
Остановимся на выборе интервала изменения аргумента Δh (или Δr), на котором сохраняется допущение о кусочном постоянстве аэродинамических сил. При выборе величины Δh следует исходить из требований к допустимым погрешностям вычислений и быстродействию расчетов. Проведенный анализ численных результатов показал, что для широкого диапазона варьируемых параметров при значении Δh=10 км погрешности вычисления дальности баллистического спуска δL не превышают ~1%. Продолжительность вычислений по сравнению с методами численного интегрирования при этом сокращаются более чем на порядок.
Таким образом, с помощью формул (8)-(12) определяются дальности полета КА на внеатмосферном Lвн и атмосферном Lатм участках полета от схода аппарата с орбиты ИСЗ до посадки в заданную область поверхности Земли.
3. Вывод зависимостей для расчета географических координат схода КА с орбиты ИСЗ φсх и λсх.
Из рассмотрения данных, приведенных на фиг. 2, выведем зависимости для расчета широты и долготы подспутниковой точки КА при его сходе с орбиты искусственного спутника Земли (ИСЗ). Представленные выводы основывались на использовании теории сферической тригонометрии [3].
Рассмотрим сферический треугольник AFE на фиг. 2, где Е - точка на экваторе с долготой, равной долготе точки F. Дуга AF определяется как разность между дугами AD и FD:
AF=AD-FD.
При этом дуга AD определяется из теоремы косинусов для сферического треугольника ABD
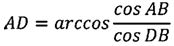 .
.
Дуга FD определяется как разность между дугой AD и угловой продольной дальностью полета КА при спуске с орбиты ИСЗ:
FD=AD-L/R.
Зная величину дуги AF и учитывая, что угол FAE является заданным наклонением орбиты КА i, согласно теореме синусов для сферического треугольника FAE запишем соотношение
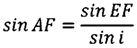 .
.
Из этого соотношения определим дугу EF, что и является широтой подспутниковой точки КА при его сходе с орбиты ИСЗ:
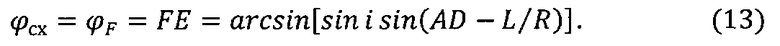
Далее на основе теоремы косинусов для треугольника FAE запишем соотношение:
cosAF=cosFE cosAE.
Учитывая, что значения дуг AF и FE известны, определим дугу АЕ, т.е. разницу между долготами схода КА с орбиты ИСЗ λсх и известным значением долготы экватора λэ:
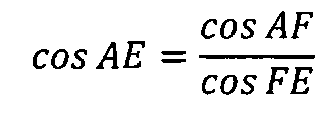 или
или 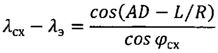 .
.
Окончательная зависимость для определения долготы подспутниковой точки КА при его сходе с орбиты ИСЗ λсх записывается следующим образом:
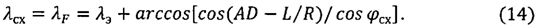
Таким образом, с использованием формул (13), (14) определяются географические координаты схода КА с орбиты ИСЗ.
Литература
1. Эльясберг П.Е. Введение в теорию полета искусственных спутников Земли. М.: Наука. 1961.
2. Авдуевский B.C., Антонов Б.М., Анфимов Н.А. и др. Основы теории полета космических аппаратов. М.: Машиностроение. 1972.
3. Степанов Н.Н. Сферическая тригонометрия. М. - Л.: ОГИЗ, 1948.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ СХОДОМ КОСМИЧЕСКОГО АППАРАТА С ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ | 2013 |
|
RU2559430C2 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА ПРИ ПОСАДКЕ В ЗАДАННУЮ ОБЛАСТЬ ПОВЕРХНОСТИ ПЛАНЕТЫ | 2014 |
|
RU2590775C2 |
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ ЦЕНТРА МАСС КОСМИЧЕСКОГО АППАРАТА | 2011 |
|
RU2487823C1 |
| СПОСОБ ГРУППОВОГО ОРБИТАЛЬНОГО ДВИЖЕНИЯ ИСКУССТВЕННЫХ СПУТНИКОВ | 2014 |
|
RU2569236C1 |
| Возвращаемый с околоземной орбиты научно-исследовательский космический аппарат | 2015 |
|
RU2634608C2 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА НА АКТИВНОМ УЧАСТКЕ ЕГО ВЫВЕДЕНИЯ НА ОРБИТУ ИСКУССТВЕННОГО СПУТНИКА ПЛАНЕТЫ | 2015 |
|
RU2596004C2 |
| КОСМИЧЕСКИЙ АППАРАТ ДЛЯ СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ И СПОСОБ СПУСКА КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТЫ | 1994 |
|
RU2083448C1 |
| КОСМИЧЕСКИЙ АППАРАТ ДЛЯ СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ И СПОСОБ ЕГО СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ (ВАРИАНТЫ) | 2001 |
|
RU2213682C2 |
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ С ИСПОЛЬЗОВАНИЕМ АЭРОДИНАМИЧЕСКОГО КАЧЕСТВА ПРИ СПУСКЕ В АТМОСФЕРЕ | 2014 |
|
RU2552770C1 |
| СПОСОБ ПРЕДСТАВЛЕНИЯ СВЕТОВЫХ ИЗОБРАЖЕНИЙ НА НЕБЕСНОЙ СФЕРЕ | 1992 |
|
RU2047911C1 |
Изобретение относится к космонавтике, в частности к области управления космическими аппаратами (КА). Бортовыми средствами аппарата определяются координаты включения двигательной установки, величины и ориентации импульсов характеристической скорости КА. При этом отрабатывается рациональное управление вектором тяги двигательной установки. Способ заключается в последовательной подаче двух импульсов характеристической скорости. Первый импульс подается в плоскости движения КА против вектора его скорости для обеспечения схода аппарата с орбиты. Второй импульс подается в направлении, перпендикулярном к плоскости полета, для управления боковой дальностью. Техническим результатом изобретения является снижение потребных энергетических затрат, повышение оперативности управления, повышение точности посадки аппарата на полигоны малых размеров. 2 ил.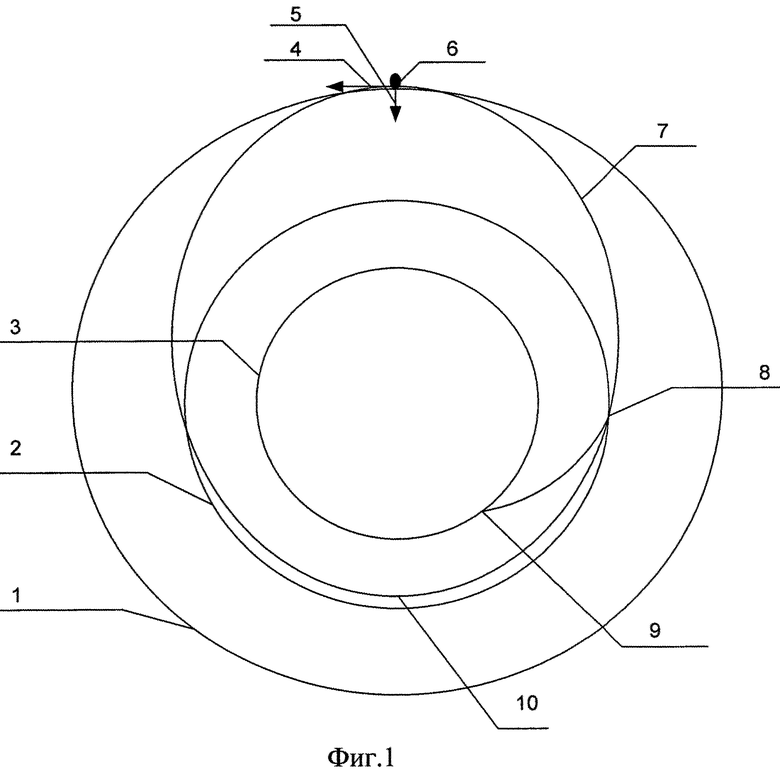
Способ управления космическим аппаратом при его спуске с орбиты искусственного спутника Земли, заключающийся в определении бокового смещения точки посадки космического аппарата относительно плоскости его движения Lбок, величины и ориентации импульса характеристической скорости, подаваемого при движении космического аппарата на орбите искусственного спутника Земли, управлении вектором тяги двигательной установки для изменения скорости и плоскости движения космического аппарата и перевода его с орбиты искусственного спутника Земли на траекторию спуска, отличающийся тем, что определяют минимально возможное абсолютное значение угла наклона вектора скорости к местному горизонту при входе космического аппарата в атмосферу |θвх min| в соответствии с зависимостью
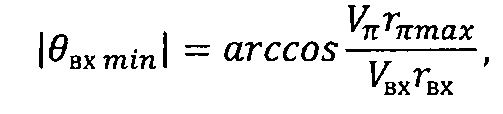
где
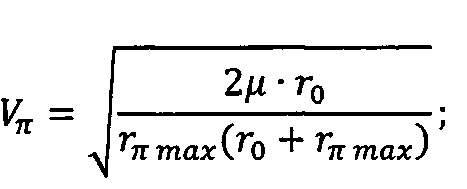
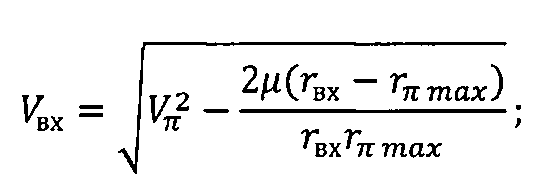
Vπ - скорость космического аппарата в перигее оскулирующей орбиты, сформированной после завершения работы двигательной установки;
Vвх - скорость космического аппарата при входе в атмосферу;
rπ max=R+hπ max - максимально возможный радиус-вектор перигея оскулирующей орбиты, при котором обеспечиваются захват космического аппарата атмосферой и его снижение на поверхность Земли;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу Земли;
hπ max - максимально возможная высота перигея оскулирующей орбиты, при которой обеспечиваются захват космического аппарата атмосферой и его снижение на поверхность Земли;
hатм=100 км - высота условной границы атмосферы;
R - средний радиус Земли;
µ - произведение гравитационной постоянной на массу Земли,
с использованием безытерационных аналитических формул определяют широту φсх и долготу λсх подспутниковой точки космического аппарата при включении двигательной установки, а также продольную дальность полета космического аппарата L от момента завершения работы двигательной установки до посадки на поверхность Земли:
φсх=φF=arcsin[sinI·sin(AD-L/R)],
λсх=λF=λэ+arccos[cos(AD-L/R)/cosφcx],
L=Lвн+Lатм,
где
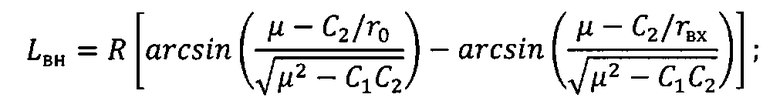
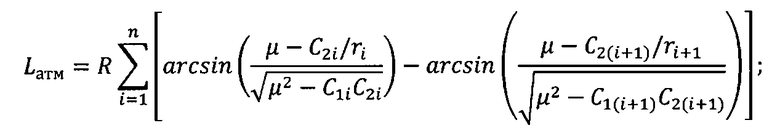
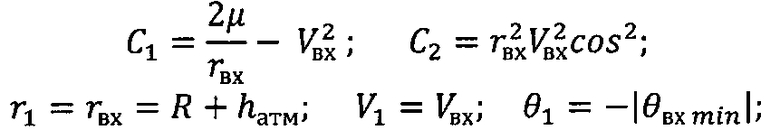
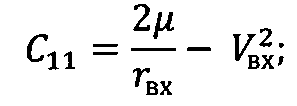
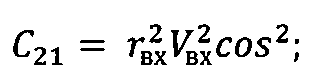
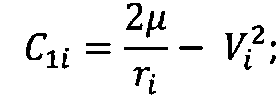
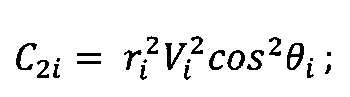
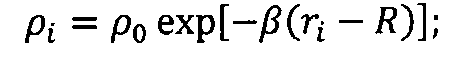
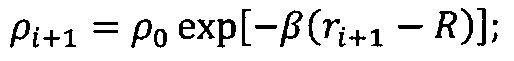
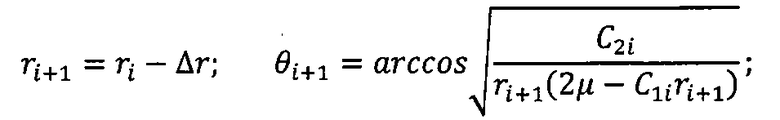
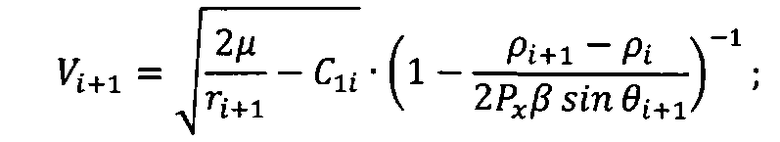
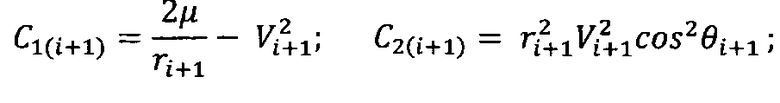
I - наклонение орбиты;
AD - дуга, лежащая в плоскости орбиты движения космического аппарата, соединяющая точку пересечения экватора с точкой, образованной при пересечении плоскости орбиты движения космического аппарата и плоскости, перпендикулярной к ней и содержащей точку посадки;
L - дальность полета космического аппарата от его схода с орбиты до посадки на поверхность Земли;
Lвн - дальность полета космического аппарата на внеатмосферном участке;
Lатм - дальность полета космического аппарата в атмосфере;
R - средний радиус Земли;
µ - произведение гравитационной постоянной на массу Земли;
λэ - долгота пересечения плоскости движения космического аппарата с плоскостью экватора;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу;
Vвх - скорость космического аппарата при входе в атмосферу;
θвх min - минимальное абсолютное значение угла наклона вектора скорости к местному горизонту, при котором обеспечивается гарантированный захват космического аппарата атмосферой и его посадка на поверхность Земли;
hатм=100 км - высота условной границы атмосферы;
ri - радиус-вектор космического аппарата на i-м интервале расчета координат;
ri+1 - радиус-вектор космического аппарата на (i+1)-м интервале расчета координат;
Vi - скорость космического аппарата на i-м интервале расчета координат;
Vi+1 - скорость космического аппарата на (i+1)-м интервале расчета координат;
θi - траекторный угол на i-м интервале расчета координат;
θi+1 - траекторный угол на (i+1)-м интервале расчета координат;
ρi - плотность атмосферы на i-м интервале расчета координат;
ρi+1 - плотность атмосферы на (i+1)-м интервале расчета координат; i=1, 2, 3…n;
Δr - интервал изменения радиуса-вектора, при котором осуществляется расчет новых координат;
ρ0 - плотность атмосферы на поверхности Земли;
β - логарифмический коэффициент изменения плотности атмосферы от высоты;
Рх - приведенная нагрузка на лобовую поверхность космического аппарата, осуществляют подачу первого импульса характеристической скорости ΔVпр min в направлении, противоположном вектору скорости космического аппарата, величина которого рассчитывается в соответствии с зависимостью
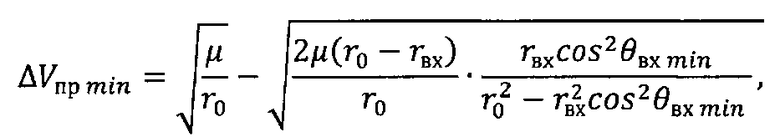
где µ - произведение гравитационной постоянной на массу Земли;
r0 - радиус-вектор космического аппарата после завершения работы двигательной установки;
rвх=R+hатм - радиус-вектор космического аппарата при его входе в атмосферу;
hатм=100 км - высота условной границы атмосферы;
θвх min - минимальное абсолютное значение угла наклона вектора скорости к местному горизонту, при котором обеспечиваются гарантированный захват космического аппарата атмосферой и его посадка на поверхность Земли,
по окончании отработки первого импульса осуществляют подачу второго импульса характеристической скорости под углом 90° к вектору скорости космического аппарата по часовой стрелке, если точка посадки расположена справа от плоскости движения космического аппарата, и против часовой стрелки, если точка посадки расположена слева от этой плоскости, при этом величины второго импульса характеристической скорости ΔVбок и угла разворота вектора скорости космического аппарата в горизонтальной плоскости α вычисляются по формулам
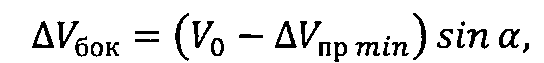
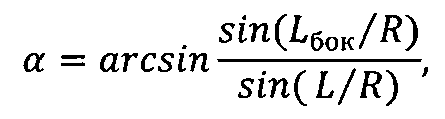
где V0 - скорость движения космического аппарата по орбите искусственного спутника Земли до подачи импульсов характеристической скорости;
ΔVпр min - первый подаваемый импульс характеристической скорости;
L - дальность полета космического аппарата от его схода с орбиты до посадки на поверхность Земли;
Lбок - боковое смещение точки посадки космического аппарата относительно плоскости его движения;
R - средний радиус Земли,
после отработки второго импульса характеристической скорости осуществляют неуправляемое движение космического аппарата до посадки на поверхность Земли.
| Иванов В.М., Соколов Н.Л., "Оптимальное управление космическим аппаратом за счет изменения вектора тяги двигательной установки при проведении межорбитальных маневров" | |||
| Космонавтика и ракетостроение, изд | |||
| ЦНИИмаш, N2(75), 2014, стр | |||
| Капельная масленка с постоянным уровнем масла | 0 |
|
SU80A1 |
| СПОСОБ УПРАВЛЕНИЯ СПУСКОМ КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТ | 2012 |
|
RU2493059C1 |
| RU 2002105088 A, 27.10.2003 | |||
| US 6398166 B1, 04.06.2002 | |||
Авторы
Даты
2015-08-27—Публикация
2014-04-30—Подача