Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области информационной безопасности телекоммуникационных систем и, в частности, может быть использовано в криптографических системах, обеспечивающих конфиденциальность сообщений, передаваемых по открытым каналам связи в виде двоичного цифрового электромагнитного сигнала.
Известен способ шифрования путем формирования секретного ключа, генерации ключевого потока в виде последовательности битов в двоичном цифровом электромагнитном сигнале, который вырабатывается в зависимости от секретного ключа, и сложения текущих битов ключевого потока с текущими битами передаваемого сообщения [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. С-Петербург, Лань, 2000. - 218 с; см. с. 88-89]. Недостатком этого способа шифрования является необходимость синхронизации ключевого потока и потока данных.
Также известен способ шифрования, включающий генерацию 56-битового секретного ключа, формирование сообщения М в виде 64-битовой строки, генерацию криптограммы, представляющей собой 64-битовую строку, в зависимости от секретного ключа [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. С-Петербург, Лань, 2000. - 218 с; см. с. 68-73]. При этом генерация криптограммы осуществляется путем разбиения сообщения M на две 32-битовые строки и поочередное преобразование 32-битовых строк в зависимости от секретного ключа. Недостатком этого способа является малый размер секретного ключа, что не обеспечивает криптостойкости, соответствующей современным требованиям.
Также известен способ шифрования, включающий формирование модуля в виде битовой строки, задающей трудно разложимое на простые множители многоразрядное двоичное число (МДЧ) n, генерацию секретного ключа в виде двух больших простых чисел p и q, генерацию открытого ключа в виде пары МДЧ (n, e), генерацию секретного ключа в виде МДЧ d, формирование сообщения в виде элемента М группы Г, групповой операцией которой является операция умножения чисел по модулю МДЧ n и элементами которой являются битовые строки, заданные в виде МДЧ, и генерацию криптограммы в виде элемента С группы Г путем возведения сообщения М в степень e по модулю n [Смарт Н. Мир программирования. Криптография. М., ТЕХНОСФЕРА, 2005. - 525 с; см. с. 192-193]. Модуль n задает множество МДЧ {1,2,3,…,n-1}, включающее подмножество взаимно простых с n чисел, которое образует конечную группу Г с групповой операцией, являющейся операцией умножения по модулю n. Восстановление сообщения из криптограммы С осуществляется путем возведения криптограммы С в степень d по модулю n. Недостатком этого способа шифрования является то, что данный способ шифрования не обладает свойством коммутативности, требуемой для решения ряда практических задач по защите информации. Этот недостаток связан с тем, что различные пользователи используют различные значения модуля n.
Наиболее близким по своей технической сущности к заявленному является известный способ шифрования сообщения, представленного в виде битовой строки M, описанный в патенте США №4424414 [Hellman М.Е., Pohlig S.C. Exponentiation Cryptographic Apparatus and Method // U.S. Patent # 4,424,414. Jan. 3, 1984]. Ближайший способ-аналог (прототип) включает следующие действия:
1. Формируют модуль в виде битовой строки, представляющей простое МДЧ p, разрядность которого составляет не менее 1024 бит. Модуль p задает операцию умножения по модулю p в качестве групповой операции * в конечной мультипликативной группе Г порядка Ω=p-1, включающей в качестве своих элементов множество битовых строк, заданных в виде МДЧ 1,2,…,p-1.
2. Генерируют секретный ключ в виде двух МДЧ e и d, удовлетворяющих условию ed=1 mod Ω, где Ω=p-1
3. Генерируют криптограмму в виде элемента С конечной мультипликативной группы Г путем преобразования сообщения М как элемента группы Г в зависимости от секретного ключа по формуле С=Me, где степень e обозначает то, что над битовой строкой М, как над элементом группы Г, выполняется (e-1)-кратная групповая операция, т.е. (е-1)-кратное умножение по модулю p:С=М*М*…*М(e множителей M).
4. Восстанавливают сообщение М из криптограммы С путем преобразования криптограммы как элемента группы Г по формуле М=Cd=С*С*…*С, в которой присутствуют d множителей С.
Недостатком ближайшего аналога является то, что по известному сообщению и известной криптограмме можно сравнительно легко вычислить некоторые биты секретного ключа.
Задачей заявленного нового технического решения является разработка способа шифрования, обеспечивающего увеличение стойкости за счет устранения указанного недостатка.
Техническим результатом нового способа шифрования сообщения, представленного в виде битовой строки, является повышение уровня защищенности информации, шифруемой с его применением.
Указанный технический результат достигается тем, что в способе шифрования сообщения, представленного в виде битовой строки, заключающемся в том, что формируют модуль в виде битовой строки, генерируют секретный ключ в виде двух МДЧ e и d, удовлетворяющих условию ed=1 mod Ω, где Ω - МДЧ, зависящее от модуля, генерируют криптограмму в виде элемента С конечной мультипликативной группы Г, групповой операцией которой является умножение по модулю, путем преобразования сообщения M, представленного в виде битовой строки, как элемента конечной мультипликативной группы Г в зависимости от секретного ключа по формуле C=Me и восстанавливают сообщение путем преобразования криптограммы C как элемента конечной мультипликативной группы Г по формуле M=Cd, при этом формируют модуль в виде битовой строки, представляющей неприводимый двоичный многочлен степени s, где s - МДЧ, такое, что МДЧ 2s-1 является простым, генерируют секретный ключ в виде двух МДЧ e и d, удовлетворяющих условию ed=1 mod Ω, где Ω=2s-1, и преобразуют сообщение M и криптограмму С как элементы конечной мультипликативной группы Г, групповой операцией которой является операция умножения двоичных многочленов по модулю неприводимого двоичного многочлена степени s и которая включает в себя двоичные многочлены, степень которых меньше МДЧ s.
Новым также является то, что МДЧ s равно одному из следующих трех МДЧ 10011111111, 100010011011 и 100011101001.
Использование указанных трех значений МДЧ s позволяет зашифровывать сообщения M, представляющие собой битовые строками длиной, равной 1279, 2203, и 2281 бит, соответственно, обеспечивая стойкость шифрования, примерно равную или превосходящую значение 280 групповых операций группы Г.
Новым также является и то, что МДЧ s равно одному из следующих трех МДЧ 110010010001, 1000010011101 и 1000101000111.
Использование этих трех значений МДЧ s позволяет зашифровывать сообщения M, представляющие собой битовые строки длиной, равной 3217, 4253 и 4423 бит, соответственно, обеспечивая стойкость шифрования, примерно равную или превосходящую значение 2128 групповых операций группы Г.
Новым является и то, что МДЧ s равно одному из следующих трех МДЧ 10010111011001, 10011011010101 и 10101111001101.
Использование последних трех значений МДЧ s позволяет зашифровывать сообщения М, представляющие собой битовые строки длиной, равной 9689, 9941 и 11213 бит, соответственно, обеспечивая стойкость шифрования, примерно равную или превосходящую значение 2160 групповых операций группы Г.
Также новым является то, что МДЧ s равно или превосходит МДЧ 100110111100001.
Использование значений МДЧ s≥100110111100001 позволяет зашифровывать сообщения М, представляющие собой битовые строками длиной, равной 19937 бит и более, обеспечивая повышение стойкости шифрования.
Изобретательский замысел заявленного нового технического решения состоит в применении конечных мультипликативных групп, обладающих простым значением порядка Ω, благодаря чему все элементы группы, отличные от единичного элемента группы, имеют порядок, равный простому значению Ω, что устраняет возможность относительно простого вычисления некоторых битов секретного ключа по известным значениям исходного сообщения и криптограммы, полученной путем зашифрования этого сообщения. Благодаря указанной новой совокупности существенных признаков достигнут сформулированный изобретательский замысел.
Корректность заявленного способа шифрования сообщения M, представленного в виде битовой строки, обеспечивается теоремой Лагранжа, согласно которой возведение любого элемента M конечной группы Г в степень, равную порядку Ω группы Г дает единичный элемент Е∈Г, т.е. МΩ=E, и тем, что два МДЧ e и d, составляющих секретный ключ, удовлетворяют условию ed=1 mod Ω. Поскольку в силу последнего условия при некотором натуральном значении z имеет место равенство ed=zΩ+1, расшифрование криптограммы С=Me путем возведения ее в степень d приводит к получению исходного сообщения:
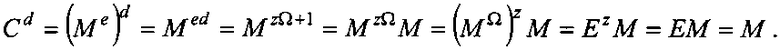
Рассмотрим частные примеры реализации заявленного способа шифрования сообщения М, представленного в виде битовой строки.
Пример 1
Данный пример иллюстрирует реализацию заявленного способа по п. 2 формулы изобретения. В данном частном варианте реализации способа выполняются следующие действия при выполнении процедуры шифрования сообщения M:
1. Формируют модуль в виде битовой строки 1000…010…01, задающей неприводимый двоичный многочлен η1(x)=x1279+x216+1, степень которого равна s=127910=100111111112 (правый нижний индекс обозначает систему счисления, в которой записано МДЧ: 10 - десятичная система счисления; 2 - двоичная система счисления). Модуль η1(x) задает операцию умножения двоичных многочленов по модулю η1(x) как групповую операцию * в мультипликативной конечной группе Г, элементами которой являются двоичные многочлены (за исключением нулевого многочлена, который представляется в виде битовой строки, которая включает в себя только нулевые биты), степени которых меньше МДЧ s=127910 и которые представлены в виде 1279-битовых строк, т.е. в виде последовательности своих коэффициентов при степенях переменной от 0 до 127810. Порядок Ω группы Г равен числу всех возможных многочленов, входящих в группу Г, т.е. Ω=2s-1=21279-1. При этом МДЧ 21279-1 является простым числом Мерсенна, т.е. порядок группы Г является простым МДЧ. (Список степеней s, для которых числа Мерсенна являются простыми, приведен, например, на сайте http://ru.wikipedia.org/wiki/Числа_Mepceннa).
2. Генерируют секретный ключ в виде двух МДЧ e и d, удовлетворяющих условию ed=1 mod Ω, где Ω=21279-1, для чего генерируют случайное МДЧ e:
e=858512411109702838170162833954081446489268604461673221400633, после чего вычисляют МДЧ d=е-1 mod Ω:
d=5180600497481846489443488242826579801456595112338223826123508199246493213273323717184385343692598623017564596545531486026131367875985989440035532853875698752563425744434928380923513920231069238020017806997971521939216689854098883365935565456074528813605742870939861629088708100733538407516373586938380040176608839702911069566865217403691936193763626063758637835591166407197594538015080.
3. Генерируют криптограмму С путем преобразования сообщения М, представленного в виде битовой строки, как элемента конечной мультипликативной группы Г в зависимости от секретного ключа по формуле С=Me, т.е. путем возведения битовой строки M, как двоичного многочлена, в степень e по формуле:
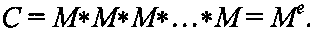
Операцию возведения в большую степень выполняют, используя алгоритм быстрого возведения в степень, описанный, например, в книге [Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. - С-Петербург. Петербург-БХВ, 2010. - 304 с; см. с. 55-57].
4. Восстанавливают сообщение M из криптограммы C путем преобразования криптограммы С как элемента конечной мультипликативной группы Г по формуле:
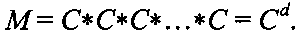
Пример 2
Данный пример иллюстрирует реализацию заявленного способа по п. 3 формулы изобретения. Выполняются следующие действия при выполнении процедуры шифрования сообщения М:
1. Формируют модуль в виде битовой строки 1000…010…01, задающей неприводимый двоичный многочлен η2(x)=x3217+x67+1, степень которого рана s=321710=1100100100012. Модуль η2(x) задает операцию умножения двоичных многочленов по модулю η2(x) как групповую операцию * в мультипликативной конечной группе Г, элементами которой являются двоичные многочлены, степени которых меньше МДЧ s=321710 и которые представлены в виде 3217-битовых строк, т.е. в виде последовательности своих коэффициентов при степенях переменной от 0 до 321610. Порядок Ω группы Г равен простому МДЧ Ω=2s-1=23217-1 (простое число Мерсенна).
2. Генерируют секретный ключ в виде двух МДЧ e и d, удовлетворяющих условию ed=1 mod Ω, где МДЧ Ω=23217-1, для чего генерируют случайное МДЧ e, после чего вычисляют МДЧ d=e-1 mod Ω.
3. Генерируют криптограмму в виде элемента С конечной мультипликативной группы Г, групповой операцией которой является умножение двоичных многочленов по модулю η2(x), путем преобразования сообщения М, представленного в виде битовой строки, как элемента конечной мультипликативной группы Г в зависимости от секретного ключа по формуле С=Me, т.е. путем возведения битовой строки М, как двоичного многочлена, в степень e по формуле:
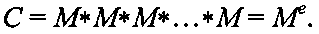
4. Восстанавливают сообщение М из криптограммы С путем преобразования криптограммы С как элемента конечной мультипликативной группы Г по формуле M=Cd, т.е. по формуле:
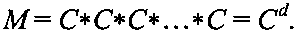
Пример 3
Данный пример иллюстрирует реализацию заявленного способа по п. 4 формулы изобретения. При выполнении процедуры шифрования сообщения М выполняются действия, описываемые шагами 1-4 в примерах 1 и 2, за исключением того, что на первом шаге формируют модуль в виде битовой строки, представляющей неприводимый двоичный многочлен η3(x)=x9689+x84+1, степень которого равна s=968910=100101110110012. Элементами группы Г являются 9689-битовые строки, представляющие ненулевые двоичные многочлены, степени которых меньше МДЧ s=968910, записанные в виде последовательности своих коэффициентов. Групповой операцией * группы Г является операция умножения двоичных многочленов по модулю многочлена η3(x). Порядок группы Г равен простому числу Мерсенна Ω=23217-1.
Пример 4
Данный пример иллюстрирует реализацию заявленного способа по п. 5 формулы изобретения. При выполнении процедуры шифрования сообщения М выполняются действия, описываемые шагами 1-4 в примерах 1 и 2, за исключением того, что на первом шаге формируют модуль в виде битовой строки, представляющей неприводимый двоичный многочлен η4(x)=x19937+x881+1, степень которого равна s=1993710=1001101111000012. Элементами группы Г являются 19937-битовые строки, представляющие ненулевые двоичные многочлены, степени которых меньше МДЧ s=1993710, записанные в виде последовательности своих коэффициентов. Групповой операцией * группы Г является операция умножения двоичных многочленов по модулю многочлена η3(x). Порядок Ω группы Г равен простому числу Мерсенна 219937-1, т.е. Ω=219937-1.
Повышение стойкости шифрования достигается за счет того, что в заявленном способе шифрования сообщения М, представленного в виде битовой строки, все возможные битовые строки, отличные от двух битовых строк - битовой строки, содержащей только нулевые биты, и битовой строки, содержащей только один единичный бит, занимающий крайнее левое положение, и все остальные нулевые биты являются элементами группы Г, имеющими порядок, равный порядку группы, т.е. равными простому МДЧ Ω. При шифровании указанных двух битовых строк они не изменяются, поэтому никакие биты секретного ключа не могут быть вычислены в таких двух случаях. При шифровании всех остальных битовых строк при атаке на основе известной криптограммы С и известного исходного сообщения атакующий для определения каких-либо битов ключа должен решать задачу дискретного логарифмирования, заданную по уравнению С=Me, в котором основание М имеет большой простой порядок, поэтому для вычисления значения e применение алгоритма больших и малых шагов, описанного, например, в книге [Молдовян Н.А. Практикум по криптосистемам с открытым ключом. - С-Петербург. Петербург-БХВ, 2007. - 298 с; см. с. 55-57], имеет высокую вычислительную сложность для всех возможных значений М.
Таким образом, приведенные математические выкладки и конкретные примеры реализации показывают, что заявляемый способ шифрования сообщения М, представленного в виде битовой строки, технически реализуем и позволяет достичь сформулированного технического результата.
Заявляемый способ шифрования сообщения М, представленного в виде битовой строки, может быть применен для разработки средств защиты информации, передаваемой по открытым телекоммуникационным каналам, от несанкционированного доступа.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ШИФРОВАНИЯ БЛОКА ДАННЫХ, ПРЕДСТАВЛЕННОГО В ВИДЕ БИТОВОЙ СТРОКИ | 2014 |
|
RU2542929C1 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2401513C2 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2380838C1 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2382505C1 |
| СПОСОБ ШИФРОВАНИЯ | 2009 |
|
RU2411666C1 |
| СПОСОБ ГЕНЕРАЦИИ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2392736C1 |
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2008 |
|
RU2380830C1 |
| СПОСОБ ФОРМИРОВАНИЯ ОБЩЕГО СЕКРЕТНОГО КЛЮЧА ДВУХ УДАЛЕННЫХ АБОНЕНТОВ | 2009 |
|
RU2420892C1 |
| Постквантовый способ формирования и проверки подлинности электронной цифровой подписи, заверяющей электронный документ | 2022 |
|
RU2809528C2 |
| СПОСОБ ШИФРОВАНИЯ СООБЩЕНИЯ, ПРЕДСТАВЛЕННОГО В ВИДЕ МНОГОРАЗРЯДНОГО ДВОИЧНОГО ЧИСЛА | 2014 |
|
RU2542926C1 |
Изобретение относится к области электросвязи и вычислительной техники. Технический результат заключается в повышении безопасности передачи данных. В способе формируют модуль в виде битовой строки, представляющей неприводимый двоичный многочлен степени s, где s - многоразрядное двоичное число, такое, что многоразрядное двоичное число 2s-1 является простым, генерируют секретный ключ в виде двух многоразрядных двоичных чисел e и d, удовлетворяющих условию ed=1 mod Ω, где Ω=2s-1, и преобразуют сообщение М и криптограмму С как элементы конечной мультипликативной группы Г, групповой операцией которой является операция умножения двоичных многочленов по модулю неприводимого двоичного многочлена степени s и которая включает в себя двоичные многочлены, степень которых меньше многоразрядного двоичного числа s. 4 з.п. ф-лы, 4 пр.
1. Способ шифрования сообщения, представленного в виде битовой строки, заключающийся в том, что формируют модуль в виде битовой строки, генерируют секретный ключ в виде двух многоразрядных двоичных чисел e и d, удовлетворяющих условию ed=1 mod Ω, где Ω - многоразрядное двоичное число, зависящее от модуля, генерируют криптограмму в виде элемента С конечной мультипликативной группы Г, групповой операцией которой является умножение по модулю, путем преобразования сообщения М, представленного в виде битовой строки, как элемента конечной мультипликативной группы Г в зависимости от секретного ключа по формуле С=Me и восстанавливают сообщение путем преобразования криптограммы С как элемента конечной мультипликативной группы Г по формуле М=Cd, отличающийся тем, что формируют модуль в виде битовой строки, представляющей неприводимый двоичный многочлен степени s, где s - многоразрядное двоичное число, такое, что многоразрядное двоичное число 2s-1 является простым, генерируют секретный ключ в виде двух многоразрядных двоичных чисел e и d, удовлетворяющих условию ed=1 mod Ω, где Ω=2s-1, и преобразуют сообщение М и криптограмму С как элементы конечной мультипликативной группы Г, групповой операцией которой является операция умножения двоичных многочленов по модулю неприводимого двоичного многочлена степени s и которая включает в себя двоичные многочлены, степень которых меньше многоразрядного двоичного числа s.
2. Способ по п. 1, отличающийся тем, что многоразрядное двоичное число s равно одному из следующих трех многоразрядных двоичных чисел 10011111111, 100010011011 и 100011101001.
3. Способ по п. 1, отличающийся тем, что многоразрядное двоичное число s равно одному из следующих трех многоразрядных двоичных чисел 110010010001, 1000010011101 и 1000101000111.
4. Способ по п. 1, отличающийся тем, что многоразрядное двоичное число s равно одному из следующих трех многоразрядных двоичных чисел 10010111011001, 10011011010101 и 10101111001101.
5. Способ по п. 1, отличающийся тем, что многоразрядное двоичное число s равно или превосходит многоразрядное двоичное число 100110111100001.
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПЕРЕДАЧИ ДАННЫХ СОДЕРЖИМОГО И УСТРОЙСТВО ЗАПИСИ И/ИЛИ ВОСПРОИЗВЕДЕНИЯ | 2001 |
|
RU2305904C2 |
| СПОСОБ ХРАНЕНИЯ И ИСПОЛЬЗОВАНИЯ КРИПТОГРАФИЧЕСКОГО КЛЮЧА | 2008 |
|
RU2417410C2 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2000 |
|
RU2183051C2 |
| Машина для разделения сыпучих материалов и размещения их в приемники | 0 |
|
SU82A1 |
Авторы
Даты
2015-08-10—Публикация
2013-06-11—Подача