По настоящей заявке испрашивается приоритет в соответствии с 35 U.S.C. §119 (e) на основании предшествующей заявки на патент США №13/546,053, поданной 11 июля 2012 г., и предварительной заявки на патент США №61/618,265, поданной 30 марта 2012 г., которые включены в настоящее описание путем ссылки в полном объеме.
Уровень техники
Настоящее изобретение относится к способам и системам для прогнозирования свойств потока текучих сред через пористые среды, такие как пористая порода и, в частности, относится к таким способам и системам для выбора из цифрового представления гетерогенной пористой среды наиболее репрезентативного подобразца, чтобы использовать его для прогнозирования свойств, таких как пористость, проницаемость и/или похожих характеристик.
Цифровые представления пористых сред, таких как порода, кость, почва и другие материалы, могут быть произведены с помощью изображений сканирования рентгеновской компьютерной томографии, сканирующей электронной микроскопии, конфокальной микроскопии и другими способами. Такие цифровые представления полезны для характеризации пористых сред с применением компьютерного моделирования (Knackstedt, M.A., et al., "Digital Core Laboratory: Properties of Reservoir Core Derived from 3D Images", Society of Petroleum Engineers, 2004; and Vermeulen, J.P., "New Developments in FESEM Technology", Carl Zeiss nano-technology Systems Division, http://www.zeiss.com/C1256E4600307C70/EmbedTitelIntern/NewDevelopmentinFESEMTechnology/$FileNew_Development_FESEM_Technology.pdf).
Важной проблемой в цифровом моделировании характеристик пористых сред является размер образца. Многие образцы, представляющие практический интерес, такие как пористая порода, являются неоднородными, и для получения усредненных свойств для больших объемов пористых сред потребовалась бы оцифровка очень больших образцов. Многие из характеристик породы, такие как абсолютная проницаемость, требуют значительных вычислительных ресурсов для моделирования, и в результате объемы образца часто являются намного меньшими, чем интересующий объем для репрезентативной характеризации. Подобразца могут быть выбраны визуально обученным геологом, но этот подход является субъективным, и его результаты сильно различаются. Кроме того, деловые и технические решения, такие как инвестиции в скважины, планы перфорации скважин, оценки извлекаемых ресурсов и другие подобные решения, принимаемые на основании цифрового моделирования характеристик породы, часто влекут большие затраты. В результате существует потребность в устранении субъективности, погрешности и вариаций в характеристиках таких пористых сред.
Один из подходов к идентификации соответствующих подобразцов заключается в идентификации репрезентативного элементарного объема (REV). REV является наименьшим объемом, для которого может быть выполнено конкретное измерение, которое даст значение, репрезентативное для всего объема. Объемы, меньшие REV, демонстрируют вариацию в конкретном измерении, что делает образцы, меньшие REV, не подходящими для моделирования. Способ вычисления REV с использованием объемной пористости в качестве измерения описывается в литературе Bear (Bear, J., Dynamics of Fluids in Porous Media; General Publishing Company Ltd., Canada, 1972, p. 19-21). Множество способов, которые обозначаются как REV, в конечном счете не являются действительно «элементарными». То есть многие применяемые способы позволяют найти подобъемы большего объема, которые являются репрезентативными для большего объема, но способ может не выдавать наименьший возможный или элементарный объем.
Razavi и соавт. описывают общий подход к REV (Razavi, et al., "Representative Elementary Volume Analysis of Sands Using X-Ray Computed Tomography", Geotechnical Testing Journal, Vol. 30, No. 3, Paper ID GTJ100164, 2006). Блок-схема способа, описанного Razavi и соавт., показана на Фиг. 1. В способе, показанном Razavi и соавт., выбирается точка приблизительно в центре образца, и затем анализируется сферический объем подобразца вокруг этой центральной точки. Свойства образца вычисляются для сферического подобразца. Радиус подобразца увеличивается, и свойства вычисляются повторно. Радиус подобразца увеличивается пошагово, пока не будет достигнут REV. У этого способа имеется множество недостатков. Он может не давать подходящего результата в определенных неоднородных образцах. Хотя он и может выдать приемлемый RV, он может не выдать REV. Как было указано выше, завершение проводимых вычислений на цифровых представлениях образцов породы может потребовать значительного количества машинного времени, поэтому определение наименьшего REV в образце имеет большое значение.
В патенте США №6,516,080 (Nur) раскрыт способ выбора REV из репрезентативной области. На Фиг. 2 этого документа показано, как квадратная область, центрированная на одной из сторон образца, увеличивается в размере до тех пор, пока не будет найдена репрезентативная область. Длина стороны квадрата репрезентативной области затем выбирается в качестве длины сторон куба, центрированного в трехмерном образце. Этот способ зависит от того, является ли образец однородным и изотропным. Это не является типичным для многих реальных образцов и пород.
Заявка на патент США №2011/0004447 (Hurley и соавт.) относится к способу характеризации трехмерных пористых сред с применением по меньшей мере одного измерительного инструмента, который получает два или более множеств переданных результатов измерений на двух или более глубинах в образце. В этом способе репрезентативный элементарный объем (REV) пористости оценивается посредством (1) случайного выбора множества неперекрывающихся блоков однородного размера из измеренного или смоделированного образца, (2) построения графика пористости отдельного блока в зависимости от объема соответствующего блока и (3) определение отклонения пористости, измеренного для каждого образца для заданного объема блока. Пористость является средней пористостью по выбранному образцу. Когда отклонение измеренной пористости опускается ниже выбранной пороговой величины, соответствующий объем является REV пористости исследуемой породы. В этом способе Hurley и соавт. объем не растет, начиная с точки, и поэтому будет покрывать больше возможных подобъемов, что фактически уменьшит размер образца. Способ имеет недостатки, заключающиеся в том, что он был разработан для использования множества подобразцов с тем, чтобы можно было получить статистически значимое отклонение и, возможно, причем потребуется использовать большой образец для того, чтобы получить требуемую сходимость; эти две потребности не всегда могут быть удовлетворены, что может привести к выбору всего исходного образца в качестве RV. Изобретатели настоящего изобретения показали, что это происходит в случае образца, подвергнутого лазерной сканирующей конфокальной микроскопии (LSCM). Способ Hurley и соавт. также, возможно, не сможет идентифицировать наименьший возможный REV в образце.
Интересным и мощным подходом для характеризации микроструктуры пористых сред является стохастический анализ теории локальной пористости Hilfer (1992). Этот способ формулируется зависимым от масштаба образом и дает хорошую оценку интегрального масштаба длины для REV. Однако способ локальный пористости не дает результатов относительно анизотропности пористого пространства. Усовершенствование данного способа было выполнено Liu и соавт. (2009 и 2010); причем оценивалось локальное распределение анизотропии зависимым от масштаба образом. Это усовершенствование потребовало применения способа Ketcham (2005), в котором анизотропия является функцией зависящего от направления изменения характера пористых структур.
Множество оценок свойств пористых сред, таких как порода, выполняются с применением закона Дарси. Закон Дарси является феноменологически выведенным уравнением, которое аппроксимирует поток текучей среды через пористую среду. Закон был сформулирован Генри Дарси на основании результатов экспериментов, которые он провел для потока воды через песчаный слой. Закон Дарси по существу является выражением закона сохранения импульса. Закон Дарси, поскольку он часто применяется для потока через пористые среды, такие как образцы породы, может применяться для выполнения оценки объемного потока с помощью уравнения 1, которая имеет параметры потока Дарси в соответствии с проиллюстрированным на фиг. 24:

где
Q = объемная скорость потока в пределах одной фазы образца за единицу времени,
k = абсолютная проницаемость пористой среды,
A = площадь сечения для потока,
µ - динамическая вязкость,
Pb, Pa = давление на входе и выходе из объема,
L = длина образца.
Формально, для выведения закона Дарси для определения проницаемости, например, из первого принципа, должна быть подтверждена некоторая гипотеза. В частности, как показано в работе Whitaker, S., Transport in Porous Media 1, 1986, pp. 3-25, способ выведения закона Дарси из уравнений Навье-Стокса (то есть уравнений для импульса) состоит в том, чтобы применить разложение Гари:
 ,
,
которое по существу является разложением шкал:  является усредненной величиной (в этом случае давление), которая, как предполагается, «правильно ведет себя» по усредненному интегральной шкале (которая может быть шкалой длины образца, такой как поперечная или продольная размерность). Другими словами, эти усредненные функции, как предполагается, достаточно описывают величины, которые они представляют. Например, сигнал давления, который быстро изменяется по шкале длины сопоставимому с усредненной шкалой длины, не может представлять давление по этой длине. Величина
является усредненной величиной (в этом случае давление), которая, как предполагается, «правильно ведет себя» по усредненному интегральной шкале (которая может быть шкалой длины образца, такой как поперечная или продольная размерность). Другими словами, эти усредненные функции, как предполагается, достаточно описывают величины, которые они представляют. Например, сигнал давления, который быстро изменяется по шкале длины сопоставимому с усредненной шкалой длины, не может представлять давление по этой длине. Величина  является флуктуирующей частью давления, причем она является вариацией функции. Гипотеза состоит в том, что усредненные величины не изменяются на малых шкалах, где флуктуирующая часть может иметь только небольшое изменение. Для того чтобы вывести закон Дарси вместе с разложением Гари, к уравнениям Навье-Стокса также должна быть применена операция усреднения (например, метод усреднения по объему). Однако в этом случае получают среднее градиентов полей, в то время как требуется градиент усредненных величин (как показано в законе Дарси). Можно легко доказать, что эти два оператора (градиент и усреднение) заменяются, когда применяются к функциям, которые не изменяются быстро по усредненным шкалам длины. В частности, если пористость является однородной, закон Дарси может быть записан в более общем виде как формула 2:
является флуктуирующей частью давления, причем она является вариацией функции. Гипотеза состоит в том, что усредненные величины не изменяются на малых шкалах, где флуктуирующая часть может иметь только небольшое изменение. Для того чтобы вывести закон Дарси вместе с разложением Гари, к уравнениям Навье-Стокса также должна быть применена операция усреднения (например, метод усреднения по объему). Однако в этом случае получают среднее градиентов полей, в то время как требуется градиент усредненных величин (как показано в законе Дарси). Можно легко доказать, что эти два оператора (градиент и усреднение) заменяются, когда применяются к функциям, которые не изменяются быстро по усредненным шкалам длины. В частности, если пористость является однородной, закон Дарси может быть записан в более общем виде как формула 2:
 ,
,
где
q (x)-= усредненная по объему плотность потока в позиции x,
k = абсолютная проницаемость пористой среды в позиции x,
µ = динамическая вязкость,
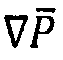 = Градиент внутреннего (в порах) среднего давления в позиции x.
= Градиент внутреннего (в порах) среднего давления в позиции x.
При использовании данной формулы рассматривается шкала, в которой усредненные значения изменяются в зависимости от позиции, и флуктуирующая часть отсутствует. Эта формула может применяться для моделирования потока в резервуаре.
Когда REV выбирается с помощью любого из средств, описанных выше, имеется возможность того, что может существовать вариация пористости в пределах REV, и это делает предположения о потоке Дарси некорректными и предрасположенными к ошибке. Кроме того, градиент давления может быстро изменяться вдоль направления потока, что делает невозможным определение проницаемости, связанной с конкретной частью образца. Это особенно верно для образцов, обладающих высокой неоднородностью, таких как образцы, которые могут быть обнаружены в реальных горных породах.
Изобретатели настоящего изобретения поняли, что существует потребность в более эффективном способе оценки репрезентативного элементарного объема (REV) в образце пористых сред, включая гетерогенные образцы. Кроме того, анализ должен учитывать направленное изменение строения пор в зависимости от направления, чтобы учесть анизотропию пористых сред и, в случае рассмотрения направленного свойства такого, как поток, учесть направление потока.
Раскрытие изобретения
Признак настоящего изобретения заключается в создании эффективного способа оценки репрезентативного элементарного объема (REV) в образце пористых сред, таких как порода, в котором выбранный подобъем является лучшим приближением элементарного объема по сравнению с существующими способами.
Дополнительный признак настоящего изобретения состоит в создании эффективного способа определения REV в образце пористых сред, таких как порода, в котором REV выбирается в отношении ожидаемого направления потока текучей среды через пористые среды.
Дополнительный признак настоящего изобретения состоит в создании эффективного способа количественного определения того, насколько хорошим (или насколько плохим) является цифровое представление породы и насколько точным будет описание потока текучей среды с помощью закона Дарси.
Дополнительный признак настоящего изобретения состоит в создании способа определения надежного критерия для понимания, когда тенденция проницаемости-пористости нарушается вследствие недостаточного размера подобразца.
Дополнительный признак настоящего изобретения состоит в создании способа анализа пористой структуры зависящим от масштаба образом, включая информацию о направлении изменения неоднородностей.
Чтобы достичь этих и других преимуществ, и в соответствии с задачами настоящего изобретения, как реализовано и в широком смысле описано в настоящем описании, настоящее изобретение относится, в одной своей части, к способу идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, который содержит этапы, на которых a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу; b) выводят среднее значение <P1> свойства первой целевой функции P1 для всего сегментированного объема; c) вычисляют среднеквадратическое отклонение σvol относительно среднего значения <P1> свойства для всего сегментированного объема; d) определяют множество подобъемов в объеме; e) вычисляют среднеквадратическое отклонение σi значения свойства P первой целевой функции P1 относительно среднего значения <P1> свойства для каждого из упомянутых подобъемов; f) находят все репрезентативные подобъемы-кандидаты, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σvol; g) выбирают и сохраняют репрезентативный подобъем из кандидатов; и h) используют репрезентативный подобъем для выведения по меньшей мере одного интересующего значения свойства.
Настоящее изобретение также относится к способу идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, который включает в себя этапы, на которых a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу; b) ориентируют выбранную ось декартовой системы координат сегментированного объема к определенному направлению потока; c) выводят значения как одной или более функций, по меньшей мере первой целевой функции P1 для всего сегментированного объема посредством анализа цифровых срезов, ортогональных определенному направлению потока; d) определяют множества подобъемов в объеме; e) вычисляют значения для одной или более функций, по меньшей мере первой целевой функции P1 для каждого из упомянутых подобъемов, соответствующих определенному направлению потока; f) находят все репрезентативные подобъемы-кандидаты, для которых функция (-и) идентифицирует(-ют) соответствие между значениями для объема и подобъема; g) выбирают репрезентативный объема из кандидатов; h) сохраняют репрезентативный подобъем; и i) используют репрезентативный подобъем для моделирования или выведения по меньшей мере одного интересующего значения свойства.
Настоящее изобретение также относится к способу получения эффективной оценки репрезентативного элементарного объема по большему цифровому 3-D изображению пористого образца, который содержит этапы, на которых a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу; b) выводят значения как по меньшей мере одной функции по меньшей мере первой целевой функции P1 для всего сегментированного объема; c) определяют множество подобъемов в объеме, причем на этом этапе определяют исходный размер для подобъема, заполняют весь объем подобъемами определенного исходного размера, итерируют размеры для последующих подобъемов и заполняют весь объем подобъемами такого размера и повторяют этот этап до тех пор, пока не будет выполнено условие прерывания; d) вычисляют значения как по меньшей мере одной функции по меньшей мере для первой целевой функции для каждого из упомянутых подобъемов; e) находят все репрезентативные -подобъемы-кандидаты для достаточно удовлетворяющих друг другу значений объема и подобъема; f) выбирают и сохраняют репрезентативный подобъем из кандидатов; и g) используют репрезентативный подобъем для проведения моделирования или выведения по меньшей мере одного интересующего значения свойства.
Настоящее изобретение также относится к способу получения эффективной оценки репрезентативного элементарного объема по большему цифровому 3-D изображению пористого образца, который содержит этапы, на которых a) получают сегментированный объем, характеризующего пространство пор и по меньшей мере одну твердую фазу; b) ориентируют выбранную ось декартовой системы координат сегментированного объема к определенному направлению потока; c), выводят среднее значение <P1> свойства первой целевой функции P1 для всего сегментированного объема с применением анализа множества цифровых срезов объема образца, взятых ортогонально к определенному направлению потока; d) вычисляют среднеквадратическое отклонение относительно среднего значения <P1> свойства для всего сегментированного объема; e) определяют множество подобъемов в пределах объема, причем на этом этапе определяют исходный размер для подобъема, заполняют весь объем подобъемами определенного исходного размера, итерируют размеры для дальнейших подобъемов от больших к меньшим и заполняют весь объем подобъемами такого размера и повторяют этот этап до тех пор, пока не будет выполнено условие прерывания; f) вычисляют среднеквадратическое отклонение σi свойства P относительно среднего значения <P1> свойства для каждого из упомянутых подобъемов, в отношении определенного направления потока; g) находят все репрезентативные -подобъемы-кандидаты, для которых σi удовлетворительно соответствует σvol; h) выбирают наименьший кандидат и его сохраняют в качестве репрезентативного элементарного объема; и i) используют репрезентативный элементарный объем для выведения по меньшей мере одного интересующего значения свойства.
Настоящее изобретение также относится к способу идентификации цифрового объема репрезентативного подобразца, соответствующего образцу пористых сред, который содержит этапы, на которых 1) загружают сегментированное трехмерное изображение пористой среды в компьютерную систему, причем сегментированное трехмерное изображение содержит вокселы, каждому из которых присваивается значение по шкале полутонов; 2) выбирают направление потока, которое определяется как направление Z; 3) определяют размеры объемов запроса, причем i) объем запроса является подобразцом исходного сегментированного трехмерного изображения с размерами Xi, Yi и Zi, причем размеры всего образца составляют Xs, Ys, Zs, ii) определяют максимальное число объемов запроса, imax, iii) устанавливают размеры в вокселах для каждого объема запроса (Xi, Yi, Zi), причем Xi, Yi и Zi определяют для значений i от 1 до imax, и iv) начальное значение i устанавливается равным 1; 4) вычисляют выбранные свойства Ps(0,0,0) через Ps (0,0, Zs) для каждого среза объема запроса; 5) вычисляют σs (0,0,0); 6) устанавливают максимальные координаты для того, чтобы объем запроса размера Xi, Yi, Zi занимал в пределах всего образца размера Xs, Ys, Zs, причем amax=Xs-Xi+1, bmax=Ys-Yi+1, cmax=Zs-Zi+1; 7) устанавливают координаты положения текущего объема запроса на a=b=c=0; 8) вычисляют выбранные свойства Pi(a, b, c) через Pi (a, b, c+Zi) для срезов текущего объема запроса, причем выбранные свойства содержат пористость, отношение площади поверхности к объему, похожие свойства или произвольную их комбинацию, 9) вычисляют σi (a, b, c), причем при необходимости значения Pi, которые используются для вычисления значения σi, фильтруются, причем при необходимости устанавливают среднее значение для Pi; 10) перемещают положение объема запроса на 1 воксел в направлении X, a=a+1; 11) повторяют этапы 8)-10) и сохраняют все величины Pi и σi, пока значение X-координаты текущего объема запроса, a, не будет равно максимальному значению, которое может занимать текущий объем запроса, amax; 12) устанавливают координату X текущего объема запроса равной нулю, a = 0, и увеличивают координату Y текущего положения объема на один воксел, b=b+1; 13) повторяют этапы 8) - 12), и сохраняют все величины Pi и σi, пока значение Y-координаты текущего объема запроса, b, не будет равно максимальному значению, которое может занимать текущий объем запроса, bmax; 14) устанавливают координату X текущего объема запроса равной нулю, a=0, устанавливают координату Y текущего объема запроса равной нулю, b=0, и увеличивают координату Z текущего положения объема на один воксел, c=c+1; 15) повторяют этапы 8)-14), и сохраняют всех величин Pi и σi, пока значение Z-координаты текущего объема запроса, c, не будет равно максимальному значению, которое может занимать текущий объем запроса, cmax; 16) увеличивают размер текущего объема запроса, причем на этом этапе i) выбирают следующее множество объемов запроса, посредством увеличения указателя до следующего объема запроса, i=i+1 и ii) устанавливают текущий размер запроса на Xi, Yi, Zi; 17) повторяют этапы 6)-16), пока все объемы запроса не будут выбраны, и все величины Pi и σi не будут вычислены и сохранены; 18) выбирают одно или более выбранных свойств для сопоставления 19) вычисляют λi для каждого объема запроса; 20) выбирают объем запроса с наименьшим значением λi, причем выбранный объем запроса является размером и положением REV; и 21) вычисляют свойства пористой среды.
Также предусмотрены компьютеризированные системы, машиночитаемые носители и программы для выполнения способов.
Следует понимать, что приведенное выше общее описание и приведенное ниже подробное описание являются примерными и поясняющими и предназначены только для обеспечения дальнейшего объяснения настоящего изобретения.
Сопровождающие чертежи, которые входят в состав и являются частью настоящей заявки, иллюстрируют некоторые из вариантов осуществления настоящего изобретения и вместе с описанием служат для объяснения принципов настоящего изобретения. Чертежи не обязательно изображены в масштабе. Аналогичные ссылочные позиции на чертежах относятся к аналогичным элементам на различных видах.
Краткое описание чертежей
Фиг. 1 - блок-схема, иллюстрирующая практику из уровня техники для идентификации REV с применением программы М-REV.
Фиг. 2 иллюстрирует другую схему взятия образцов из уровня техники для идентификации REV с выбором REV из репрезентативной области.
Фиг. 3 иллюстрирует другую схему взятия образцов из уровня техники для идентификации REV с применением способа пористости REV.
Фиг. 4 - график измеренного свойства в зависимости от объема образца, иллюстрирующий предшествующее определение REV.
Фиг. 5A и 5B иллюстрируют выбор подобразца со связностью полостей пор, смоделированной с помощью системы потока текучих сред, состоящей из труб, имеющих большие трубопроводы, соединенные через малые ограничивающие трубопроводы, в соответствии с примером из настоящей заявки.
Фиг. 6 иллюстрирует блок-схему способа оценки REV, основанного на статистической квалификации подобъемов в соответствии с примером из настоящей заявки.
Фиг. 7 иллюстрирует репрезентативной объем и объем запроса, которые включают в себя определение терминов, относящихся к образцу и объему запроса, в соответствии с примером из настоящей заявки.
Фиг. 8A и 8B иллюстрируют выбор подобъема в смоделированной системе потока текучей среды, имеющей явные характеристики направления потока текучей среды в соответствии с примером из настоящей заявки, причем фиг. 8A является видом сверху трубопроводов потока текучей среды, и фиг. 8B является сечением трубопроводов потока текучей среды, выполненное вдоль линии 8B-8B фиг. 8A.
Фиг. 9 иллюстрирует цифровой срез объема запроса в соответствии с примером из настоящей заявки.
Фиг. 10 - блок-схема, иллюстрирующая способ оценки REV, дополнительно включающий в себя ориентирование сетки в соответствии с потоком, тестирование пригодности подобъема относительно множества свойств, и систематического перемещения через подобъемы в соответствии с примером из настоящей заявки.
Фиг. 11A и 11B иллюстрируют выбор подобъема в более сложной смоделированной системе потока текучей среды в соответствии с примером из настоящей заявки, в котором декартова система координат перестраивается на фиг. 11A, и фиг. 11B является сечением, полученным на линии 11B-11B на фиг. 11A.
Фиг. 12 иллюстрирует сегментированный объем, представляющий образец естественной породы, имеющий по существу гетерогенные признаки в соответствии с примером из настоящей заявки.
Фиг. 13 иллюстрирует сегментированный объем, представляющий образец естественной породы, имеющий менее разнородную структуру, чем образец, проиллюстрированный на фиг. 12, в соответствии с примером из настоящей заявки.
Фиг. 14 - подробная блок-схема, описывающая один из вариантов осуществления в соответствии с примером из настоящей заявки.
Фиг. 15A и 15B иллюстрируют распределения среднеквадратическое отклонение для отношения поверхности/объема и пористости, соответственно, для системы потока текучей среды, смоделированной на фиг. 11A и 11B, причем размер объема запроса соответствует элементарной ячейке, которая соответствует периодичности в пределах всего образца в соответствии с примером из настоящей заявки.
Фиг. 16A-16E иллюстрируют среднеквадратическое отклонение пористости в системе потока текучей среды для различных размеров объема запроса в системе потока текучей среды, смоделированной на фиг. 11A-11B, в соответствии с примером из настоящей заявки.
Фиг. 17A-17E иллюстрируют среднеквадратическое отклонение отношения поверхности к объему для пространства пор в системе потока текучей среды для различных размеров объема запроса в системе потока текучей среды, смоделированной на фиг. 11A-11B в соответствии с примером из настоящей заявки.
Фиг. 18A-18B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 18A) и отношения поверхности к объему (фиг. 18B) для образца породы фиг. 13 для объема запроса 450×450×450, в соответствии с примером из настоящей заявки.
Фиг. 19A-19B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 19A) и отношения поверхности к объему (фиг. 19B) для образца породы фиг. 13 для объема запроса 300×300×300, в соответствии с примером из настоящей заявки.
Фиг. 20A-20B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 20A) и отношения поверхности к объему (фиг. 20B) для образца породы с фиг. 13 для объема запроса 200×200×200, в соответствии с примером из настоящей заявки.
Фиг. 21A-21B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 21A) и отношения поверхности к объему (фиг. 21B) для образца породы с фиг. 12 для объема запроса 450×450×450, в соответствии с примером из настоящей заявки.
Фиг. 22A-22B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 22A) и отношения поверхности к объему (фиг. 22B) для образца породы с фиг. 12 для объема запроса 300×300×300, в соответствии с примером из настоящей заявки.
Фиг. 23A-23B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 23A) и отношения поверхности к объему (фиг. 23B) для образца породы с фиг. 12 для объема запроса 200×200×200, в соответствии с примером из настоящей заявки.
Фиг. 24 - схематическая иллюстрация потока Дарси.
Фиг. 25 иллюстрирует три тенденции пористости-проницаемости на графике абсолютной проницаемости (мД) в зависимости от пористости (как дробную величину между 0 и 1,0) для образца породы Фонтенбло для размерности подобразца 95×95×95 (серые треугольники), 190×190×190 (серые круги) и 285×285×285 (серые кресты), и который содержит значение пористости-проницаемости для исходного размера образца 500×500×500 для линии тенденции (сплошная серая линия "UL", которая включает в себя точку данных в виде полого ромба), и черные символы являются оптимальными выборами, сделанными при использовании в качестве целевых значений и функции поверхности/объема и пористости в соответствии с примером из настоящей заявки. Эти две линии являются нижними и верхними пределами, соответственно, которые получены из экспериментов, сделанных для этих породах.
Фиг. 26 иллюстрирует тенденции корреляции пористости/проницаемости (poro-perm) на графике абсолютной проницаемости (мД) в зависимости от пористости для образца неуплотненного песчаника для размерностей подобразца 300×300×300 (серые кресты), 200×200×200 (серые круги) и 100×100×100 (серые треугольники), в соответствии с примером из настоящей заявки. Два набора данных, то есть «1_100» и «1_200», и также «2_100» и «2_200», представлены для двух различных образцов (образцов 1 и 2). Два образца очень похожи.
Фиг. 27 иллюстрирует кривые тенденции пористости-проницаемости на графике абсолютной проницаемости (мД) в зависимости от пористости для образца Фонтенбло более низкой пористости, чем образец с фиг. 25, который содержит тенденции пористости-проницаемости для размерности подобразца 190×190×190 (серые треугольники), 285×285×285 (серые круги) и 380×380×380 (серые кресты), и который включает значение пористости-проницаемости для исходного размера образца 500×500×500 для линии тенденции UL (сплошная серая линия, которая пересекает символ в виде полого ромба, и черные символы представляют оптимальный выбор, сделанный при использовании в качестве целевых значений и функции поверхности/объема, и пористости, в соответствии с примером из настоящей заявки. Кривая «нижнего лабораторного значения» является нижним пределом из экспериментов, сделанных для этих пород.
Фиг. 28A-28H иллюстрируют среднее значение отношения (A) распределения среднеквадратическое отклонение для пористости (фиг. 28A), отношения поверхности к объему (фиг. 28B), дисперсию (V) того же самого распределения для пористости (фиг. 28C), дисперсию отношения поверхности к объему (фиг. 28D), асимметрию для пористости (фиг. 28E), дисперсию асимметрии (фиг. 28F), эксцесс для пористости (фиг. 28G) и дисперсию эксцесса (фиг. 28H) - все в зависимости от размерности (размера) подобъема образца для двух различных пород Фонтенбло, рассматриваемых на фиг. 25 и фиг. 27 соответственно в соответствии с примером из настоящей заявки. Порода Фонтенбло, рассматриваемая на фиг. 25, представлена на фиг. 28A-28H кривыми, которые определены черными кругами, и порода, рассматриваемая на фиг. 27, представлена кривыми, определенными на фиг. 28A-28H серыми кругами. На фиг. 28A-28H графики пронумерованы в соответствии с номерами, приведенными во вставленных легендах и на фиг. 25 и 27.
Фиг. 29A-29H иллюстрируют среднюю величину отношения (A) распределения среднеквадратическое отклонение для пористости (фиг. 29A), отношения поверхности к объему (фиг. 29B), дисперсию (V) того же самого распределения для пористости (фиг. 29C), дисперсию отношения поверхности к объему (фиг. 29D), асимметрию для пористости (фиг. 29E), дисперсию асимметрии (фиг. 29F), эксцесс для пористости (фиг. 29G) и дисперсию эксцесса (фиг. 29H) - все в зависимости от размерности (размера) подобъема образца, для двух различных карбонатных пород, соответственно, причем один образец показан серыми кругами, и другой образец показан черными кругами на этих графиках, в соответствии с примером из настоящей заявки. На фиг. 29A-29H графики пронумерованы в соответствии с номерами, приведенными во вставленных легендах и на фиг. 29I и 29J.
Фиг. 29I-29J иллюстрируют тенденции пористости-проницаемости для двух различных карбонатных пород, рассматриваемых на фиг. 29A-29H, в соответствии с примером из настоящей заявки. Фиг. 29I содержит тенденции пористости-проницаемости для образца, идентифицированного серыми кругами на фиг. 29A-29H для размерностей подобразца 95×95×95, 190×190×190 и 285×285×285, и который включает в себя значение пористости-проницаемости для исходного измерения (размера) образца 500×500×500 для линии тенденции D1 (сплошная серая линия, символ полого ромба), и черные символы представляют оптимальный выбор, сделанный при использовании в качестве целевых значений и функции поверхности/объема, и пористости. Фиг. 29J содержит тенденции пористости-проницаемости для образца, идентифицированного черными кругами на фиг. 29A-29H для размерностей подобразца 190×190×190, 285×285×285 и 380×380×380, и который включает значение пористости-проницаемости для объема исходного образца 500×500×500 для линии тенденции D2 (сплошная серая линия, символ полого ромба), и черные символы являются оптимальным выбором, сделанным при использовании в качестве целевых значений и функции поверхности/объема, и пористости.
Фиг. 30A-30I иллюстрируют среднее значение отношения (A) распределения среднеквадратическое отклонение для пористости (фиг. 30A), отношения поверхности к объему (Фиг. 30B), дисперсию (V) того же самого распределения для пористости (фиг. 30C), дисперсию отношения поверхности к объему (фиг. 30D), асимметрию для пористости (фиг. 30E), дисперсию асимметрии (фиг. 30F), эксцесс для пористости (фиг. 30G) и дисперсию эксцесса (фиг. 30H) - все в зависимости от размерности (размера) подобъема образца для двух различных относительно однородных пород, соответственно, с одним образцом, показанным серыми кругами, и другим образцом, показанным черными кругами на этих графиках, в соответствии с примером из настоящей заявки. На фиг. 30A-30I, графики пронумерованы в соответствии с номерами, приведенными в условных обозначениях во вставленных легендах. Как и на предыдущих чертежах, на этих чертежах показаны графики для двух различных однородных образцов породы.
Фиг. 31A-31I иллюстрируют среднюю величину отношения (A) распределения среднеквадратическое отклонение для пористости (фиг. 31A), отношения поверхности к объему (фиг. 31B), дисперсию (V) того же самого распределения для пористости (фиг. 31C), дисперсию отношения поверхности к объему (фиг. 31D), асимметрию для пористости (фиг. 31E), дисперсию асимметрии (фиг. 31F), эксцесс для пористости (фиг. 31G) и дисперсию эксцесса (фиг. 31H) - все в зависимости от размерности (размера) подобъема образца для двух дополнительных пород, соответственно, с одним образцом, показанным серыми кругами, и другим образцом, показанным черными кругами на этих графиках, в соответствии с примером из настоящей заявки. На фиг. 31A-31I графики пронумерованы в соответствии с номерами, приведенными в условных обозначениях во вставленных легендах и на фиг. 31I и 31J. Породы, используемые в качестве образцов, являлись песчаниками (Фонтенбло).
Фиг. 31I-31J иллюстрируют тенденции пористости-проницаемости для двух различных пород, рассматриваемых на фиг. 31A-31I, в соответствии с примером из настоящей заявки. Фиг. 31I включает в себя тенденции пористости-проницаемости для образца, идентифицированного серыми кругами на фиг. 31A-31I для размерностей подобразца 190×190×190, 285×285×285 и 380×380×380 и который включает в себя значение пористости-проницаемости для исходного размера измерения образца 500×500×500 для линии тенденции D3 (сплошная серая линия, символ полого ромба), и черные символы являются оптимальным выбором, сделанным при использовании в качестве целевых значений и функции поверхности/объема, и пористости. Фиг. 31J включает в себя тенденции пористости-проницаемости для образца, идентифицированного черными кругами на фиг. 31A-31I, для размерностей подобразца 95×95×95, 190×190×190 и 285×285×285 и который включает значение пористости-проницаемости для объема исходного образца 500×500×500 для линии тенденции D4 (сплошная серая линия, символ полого ромба), и черные символы являются оптимальным выбором, сделанным при использовании в качестве целевых значений и функции поверхности/объема и пористости.
Фиг. 32A-32B, 33A-33B и 34A-34B иллюстрируют распределение среднеквадратическое отклонения для целевых функций пористости (фиг. 32A, 33A, 34A) и отношения поверхности к объему (фиг. 32B, 33B, 34B) для проанализированного образца породы песчаника с исходным размером 550×550×550, причем распределение среднеквадратическое отклонение было получено для подобразца 200×200×200, и причем разрешение сегментации составляло 10X для фиг. 32A-32B, 20X для фиг. 33A-33B и 40X для фиг. 34A-34B соответственно в соответствии с примером из настоящей заявки.
Фиг. 35A-35B и 36A-36B иллюстрируют среднеквадратическое отклонение для целевых функций пористости (фиг. 35A, 36A) и отношения поверхности к объему (фиг. 35B, 36B) для проанализированного образца породы песчаника с исходным размером 550×550×550, причем распределение среднеквадратического отклонения было получено для подобразца 200×200×200, и причем разрешение сегментации составляло 4X для фиг. 35A-35B и 10X для фиг. 36A-36B соответственно в соответствии с примером из настоящей заявки.
На фиг. 37 показана система, которая интегрирует анализ визуализации трехмерного (3-D) сканирования пористой среды со способом, применяемым к 3-D цифровому представлению пористой среды, в соответствии с примером из настоящей заявки.
Осуществление изобретения
Настоящее изобретение относится, в частности, к эффективному способу оценки репрезентативного элементарного объема (REV) в образце пористых сред, таких как порода, причем выбранный подобъем является более хорошим приближением элементарного объема, чем обеспечиваемый посредством существующих способов.
Настоящее изобретение также в частности относится к способу характеризации пористого образца, такого как пористая порода, посредством использования подобразца, которая обладает такими же или очень близкими выбранными характеристиками и изменением выбранных характеристик в направлении ожидаемого потока текучей среды через образец. Если образцы являются слишком большими, это может негативно сказаться на памяти компьютера, и для завершения расчетов может потребоваться завышенное машинное время. Поэтому настоящее изобретение частично относится к способу выбора REV в качестве подобразца таким образом, чтобы он являлся репрезентативным для образца в целом, в результате чего время вычисления может быть уменьшено, и на память компьютера не оказывается негативного воздействия. REV имеет объем образца и конкретное положение в исходном образце. REV может быть, например, физическим размером и положением в исходном образце, или REV может быть цифровым размером и положением подобразца в представлении исходного образца. Данный способ выдает подобразец в положении в образце, который наилучшим образом соответствует интересующим характеристикам пористой среды, таким как пористость и абсолютная проницаемость большего образца.
Способ по настоящему изобретению может быть выполнен на цифровом представлении образца пористой среды. Цифровое представление образца пористой среды может быть получено посредством создания исходного рентгеновского изображения компьютерной томографии для образца и последующей сегментации цифрового представления, с тем, чтобы идентифицировать каждый воксел как зерно или пору. Затем основное направление потока в образце может быть выбрано посредством выбора впускной поверхности, к которой будет приложено давление для последующих измерений с помощью анализа кернов (RCAL) и специального анализа кернов (SCAL). Такие свойства, как пористость, отношение поверхности к объему пространства пор (которое также обозначается как поверхность/объем в настоящем описании и вычисляется как отношение длины (2d) или площади (3d) границы между порой и твердым пространством и площадью (2d) или (3d) объемом пространства пор) и другие свойства образца или их сочетания вычисляются для каждого среза подобразца, ортогонального к направлению потока, так что для подобразца получают свойство, которое зависит только от координаты направления потока. Для такой функции свойств f(z) среднеквадратическое отклонение (число), относительно среднего значения fV для всего образца может быть вычислено по формуле:
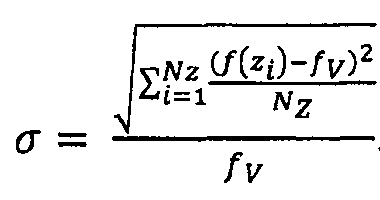
Если σ в предыдущей формуле является небольшим, то функция f образца отклоняется на небольшую величину относительно той же самой функции, оцененной в большом исходном домене (fV), поэтому это хорошее представление этой функции вдоль основного направления потока (так как ее вариации в этом направлении небольшие). В идеальном случае (то есть для бесконечно большой среды), значение σ стремится к нулю. Исходные размерности подобразца выбираются близкими к размеру исходного образца. Среднеквадратическое отклонение относительно среднего значения fV всего образца вычисляется для положения i подобразца. Следует отметить, что в этой процедуре «информация», содержащаяся в функции f, используется полностью: для каждого подобразца статистическая информация извлекается вдоль направления потока. В некоторых предыдущих патентах только усредненный объем использовался для каждого подобразца. Подобразец затем перемещается внутри исходного образца во все возможные положения x_i, и среднеквадратическое отклонение вычисляется для каждого положения. Это дает распределение T среднеквадратических отклонений S_i для выбранного свойства, описываемого f. Частота по всем подобразцам определяет распределение частотности. Дисперсия распределения (его среднеквадратическое отклонение) задается как V, среднее значение как A, и мода как М в описаниях здесь и ниже.
Размерности подобразца уменьшаются, например, на один или более вокселов по каждой стороне, или только в некотором направлении, и выбранные свойства вычисляются для всех возможных положений подобразца. Этот процесс повторяется, пока все возможные размеры подобразца не будут оценены или пока не будет выполнен некоторое условие прерывания.
REV выбирается посредством использования моды М или среднего значения A и дисперсии V распределения T среднеквадратических отклонений. Мода или среднее значение и дисперсия T являются хорошими показателями характеристик большего образца. Если мода распределения T близка к среднеквадратическому отклонению σ большего объема образца, и дисперсия распределения T является малой величиной, то большое количество подобразцов имеет то же самую вариацию выбранного свойства, что и исходный большой объем (например, гетерогенность, в случае, когда выбранное свойство является пористостью), таким образом, шкала длины подобъема является достаточно большим, чтобы представлять весь исходный объем. В случае, когда среднеквадратическое отклонение выбранного свойства исходного большого объема является малой величиной, и дисперсия V распределения также является малой величиной, могут быть сделаны два утверждения: 1) исходный размер всего объема является достаточно большим относительно вариации (например, неоднородности) в направлении потока, описанном функцией f. Эта шкала является суммарной шкалой относительно выбранного свойства для исходного объема, и 2) гетерогенность в направлении потока также является малой величиной для большинства подобъемов, таким образом, эти образцы являются хорошими кандидатами для представления большего объема. Если выбранные свойства являются, например, пористостью и отношением поверхности к объему, то ожидается, что подобразец, имеющая вариацию, соответствующую дисперсии исходного объема, будет обладать абсолютной проницаемостью, близкой к абсолютной проницаемости исходного объема. В предельном случае, когда среднеквадратическое отклонение выбранного свойства исходного объема равняется нулю и дисперсия распределения T также равна нулю, это означает, что исходный большой объем формируется посредством периодического копирования подобъема в направлении потока: в этом случае подобъем является элементарным объемом конкретной величины, описываемой f. Лучшее положение подобразца, REV, является положением, в котором среднеквадратическое отклонение одного, двух или более выбранных свойства настолько близко насколько это возможно соответствует среднеквадратическому отклонению для всего исходного образца. Если среднеквадратическое отклонение выбранного свойства подобразца меньше, чем отклонение для исходного образца, то подобразец имеет меньше вариаций, чем исходный образец, и это означает, что в нем отсутствуют некоторые неоднородности, которые имеет исходный образец, и он сделан лучше искусственным образом. Если среднеквадратическое отклонение больше, чем среднеквадратическое отклонение для исходного образца, то подобразец имеет большую неоднородность, чем исходный образец, и подобразец должна быть отклонена. В результате способ по настоящему изобретению может идентифицировать самую репрезентативный подобразец с размером, близким к элементарному, и он также может определить, является ли неоднородность исходного образца слишком большой, чтобы позволить использовать репрезентативную подобразец, поскольку в этом случае закон Дарси не может быть применен.
Как обсуждалось выше в описании уровня техники, фиг. 1-3 иллюстрируют предшествующие попытки идентификации REV для применения в представлении пористых материалов, таких как образцы породы, в цифровом моделировании и анализе. Фиг. 1 иллюстрирует блок-схему 300 для исследования концентрических сферических объемов подобразца с увеличивающимися диаметрами. Фиг. 2 иллюстрирует концентрические квадраты 302a, 302b и 302c, имеющие увеличивающиеся границы и преобразованные в трехмерные кубы с целью выбора подходящего REV. Фиг. 3 иллюстрирует смоделированный объем 310 с различными имеющими равномерный размер множествами подобъемов, здесь 312a, 312b и 312c, случайным образом (но без наложения) расположенных в объеме 310. Подобъемы показаны как имеющие геометрическую форму кубов или кубоидов. Объем 310 и подобъемы 312a, 312b, и 312c имеют соответствующие размеры, показанные на фиг. 3. Например, объем 310 имеет размерности 600×600×150, и подобъем 312a имеет размерности 150×150×150. Параметры, такие как пористость и/или проницаемость, выбираются и вычисляются для каждой подобразца, и вычисляется дисперсия или расхождение. Выбираются пределы дисперсии, и пригодность REV определяется соответствием такому пределу, например, плюс или минус (±) 5% относительно среднего значения величины.
Предшествующие попытки не обеспечили эффективного способа аппроксимирования наименьшего REV и не обрабатывали должным образом неоднородную природу естественных пород или других пористых образцов. Кроме того, предшествующие попытки не давали представление о пригодности REV для применения закона Дарси.
Фиг. 6 - блок-схема процесса по настоящему изобретению для лучшего решения проблемы гетерогенной природы реальных образцов. 3-D цифровое изображение образца получают как сегментированный объем 110, из которого выводятся одно или более значений свойств "P" и усредняются по всему объему, чтобы сформировать среднее значение свойства для всего объема, например, обозначаемого как <PVOL> или <P>, как показано на чертеже, такое, как показано на этапе 112. Как будет обсуждаться ниже в настоящем описании, пористость и площадь поверхности/объем являются удобными целевыми функциями или свойствами для применения в квалификации REV, хотя изобретение не ограничивается ими. Среднеквадратическое отклонение σVOL для выбранных свойств также вычисляется для всего объема на этапе 114 («σ»). Множество подобъемов определяется на этапе 116 и на этапе 118 перемещается через весь объем с вычислением среднеквадратическое отклонение σi для каждой целевой функции в каждом подобъеме. Выходные данные этапа 118 сравниваются с условиями прерывания 120, и если условия прерывания не выполняется, размер подобъемов корректируется на этапе 122 и этап 116 определения подобъемов, этап 118 перемещения через подобъемы и вычисления среднеквадратическое отклонение σ для каждой целевой функции, и этап 120 сравнения с условием прерывания многократно повторяются, пока условие прерывания 120 не будет выполнено. Условие прерывания может быть, например, заданным размером для подобъема, причем корректировка размера подобъема включает последовательное и прогрессивное уменьшение или увеличение подобъема. Конкретное подходящее условие прерывания описывается ниже в настоящем описании в иллюстрации реального применения. Когда условие прерывания 120 выполняется, способ переходит к этапу 124 поиска наименьшего пригодного подобъема REV. Пригодность проверяется, например, посредством сравнения среднеквадратическое отклонение подобразца σ со среднеквадратическим отклонением для полного объема σVOL относительно их согласованности. REV сохраняется и используется на этапе 126 для получения значений интересующих свойств, которые выводятся на этапе 128. Практическое применение этого аспекта настоящего изобретения предусматривает выбор наиболее репрезентативного REV, то есть такого, который соответствует гетерогенной природе всего объема образца, а также средним значениям свойств для одного или более свойств критериев выбора.
Фиг. 4 - график, схематично иллюстрирующий общее определение репрезентативного элементарного объема или REV. Измеренное свойство изображается на графике в зависимости от величины объема образца. Флуктуации измеряемого свойства, отслеживаемые кривой 320, уменьшаются с размером объема образца, пока не уменьшатся до точки, в которой значение для свойства в подобразце может быть принято как репрезентативное для всего объема. На данной иллюстрации это выполняется для области за пределами размера объема образца 322. REV является наименьшим размером образца, для которого это выполняется.
В то время как определение REV, проиллюстрированное на фиг. 4, является полезной идеализированной моделью, с которой можно начинать, она лучше всего подходит для случая, когда образец является однородным и изотропным. Часто это не так. Рассмотрим, например, ситуацию, смоделированную на фиг. 5A и 5B. В этом примере объем 130, который выделен на чертежах как кубический объем, имеет трубу 131, проходящую через него. Труба является пространством пор и имеет множество диаметров от большого трубопровода 134 до сужающегося малого трубопровода 132. Элементарная ячейка, содержащая типовую структуру в отношении поверхности/объема (не относительно пористости), в этом случае является сегментом трубы 131, который включает переход от большого трубопровода 134 к малому трубопроводу 132. Поверхность/объем всего образца объема 130 имеет в этом случае такое же значение, что и поверхность/объем для элементарной ячейки подобъема 136. Фактически, целый объем получают посредством целого числа повторений элементарной ячейки, повторяемой в направлении потока. Если, как на фиг. 5A, объем 136 запроса, используемый в анализе REV, является в точности объемом элементарной ячейки, и целевая функция является поверхностью/объем, то обеспечивается оптимальный выбор. Таким образом, среднеквадратическое отклонение σi для подобъема 136, которое точно соответствует среднеквадратическому отклонению σVOL поверхности/объема для всего объема 130 вдоль направления потока, является таким же, как объем элементарной ячейки.
Если элементарный объем меньше элементарной ячейки, см. подобъем 138 на фиг. 5B, то окончательным результатом будет объем, который обрезает участок трубы 131, с тем чтобы он соответствовал среднеквадратическому отклонению поверхности/объема для целого объема настолько близко, насколько это возможно.
Попытки предшествующего уровня техники по обнаружению REV, ограниченные случайным или концентрическим поиском вокруг выбранной точки, не подходят для обнаружения или идентификации такой элементарной ячейки. Таким образом, другим признаком практического применения настоящего изобретения является систематическое взятие части из образца, которое последовательно и с приращением продвигается через весь объем образца, причем подобъемы имеют переменные объемы с приращением. Этот аспект вводится в обсуждении фиг. 10 ниже, и ему способствует использование декартовой системы координат 140 для установки объема 142 образца с координатами a, b, c и установки размера (Xs, Ys, Zs), а также передвижение объема 144 запроса с циклически изменяющимся размером (Xi, Yi, Zi) через него, как показано на фиг. 7.
Вернемся к фиг. 5B; в лучшем случае подобъем 138 минимизирует разность между среднеквадратическим отклонением σi его собственного отношения поверхности/объема и среднеквадратическим отклонением поверхности/объема всего объема σVOL. Следует отметить, что для этого примера не имеет никакого смысла определять подобъем 138, который соответствует среднеквадратическому отклонению для пористости для целого образца. Другим признаком, приносящим пользу при практическом применении настоящего изобретения, является использование множества целевых функций или свойств для идентификации намного более надежного REV, полезного в широком диапазоне моделирований и выведений свойств. Например, ограничения, относящиеся к удовлетворению и пористости, и отношению поверхности/объема, посредством поиска соответствия или оптимизированной комбинации позволят получить более полезный REV. Это обсуждается в приведенном ниже в настоящем описании обсуждении фиг. 10.
Фиг. 5A и 5B вводят другой вопрос, важность направления потока и определение REV относительно фиксированного направления потока. Это иллюстрируется более подробно на фиг. 8A и 8B. Как показано на фиг. 8A, набор параллельных трубопроводов 152 проходят поперек объема образца 150. Фиг. 8B - сечение фиг. 8A, сделанное вдоль линии 8B-8B на фиг. 8А. Подобразец 154 - идентифицированный REV, имеющий в качестве целевых функций и среднеквадратическое отклонение пористости, и поверхность/объем. Важные свойства, включая свойства транспортировки текучей среды, достаточно часто являются анизотропными в пористых материалах, таких как образцы естественных пород. Таким образом, свойства обладают направлением. Выравнивание декартовой системы координат для того, чтобы принять это во внимание, способствует поиску истинного REV. Возвратимся к фиг. 7; выравнивание направления потока, например, с осью Z, облегчит решение. Визуальный осмотр сегментированного объема может быть достаточным для того, чтобы выровнять систему координат, посредством распознавания структуры среди трещин или трубопроводов, обеспечивающих связность пространства пор, или она может быть предложена на основании асимметрии поры. В другом случае, анизотропная природа свойств может быть определена посредством выведения предварительных оценок значений для образца или подобразцов. Также направление потока может быть зафиксировано в качестве ограничения относительно положения керна в резервуаре. В проиллюстрированных примерах направление потока является фиксированным, однако следует понимать, что может быть полезно реализовать изобретение для комбинации различных направлений потока.
Фиг. 9 иллюстрирует применение декартовой системы 160 координат, выровненной по направлению потока (стрелка 162) и проходящей через цифровые срезы 164 объема 166 запроса, взятые ортогонально к направлению потока. Объем 166 запроса и цифровой срез 164 состоят из отдельных вокселов 168. Последовательная обработка цифровых срезов, взятых ортогонально к направлению потока, способствуют не только вычислению среднеквадратического отклонения σ для объема запроса, но также применима для вычисления среднего значения для целевой(-ых) функции(-й) или свойства(-в) <P1>, <Pn> и среднеквадратического(-ых) отклонения(-й) σ1, σn для всего образца, таких как описываются в связи с обсуждением этапов 112 и 114 на фиг. 6.
Обработка для выбора REV с выравниванием по направлению потока является другим признаком, приносящим пользу при практическом применении настоящего изобретения, вводимое и иллюстрируемое на фиг. 10 ниже.
Фиг. 10 - блок-схема 170, функционально иллюстрирующая вариант осуществления настоящего изобретения, включающий признаки, введенные выше, и который будет подробнее обсуждаться ниже. Этап 172 получения сегментированного объема начинается с 3-D изображения по шкале полутонов образца природной породы или другого пористого материала, сделанного посредством рентгеновской компьютерной томографии (КТ), сканирующего электронного микроскопа с фокусированным ионным пучком, магнитно-резонансной визуализации, синхротронной визуализации или другого процесса микротомографиии или микрорентгенологии и т.п. Примеры соответствующих сканирующих устройств КТ для получения изображений, которые могут быть использованы в способах по настоящему изобретению, включают в себя, например, 3-D томографические просвечивающие микроскопы, такие как MicroXCT-200 и Ultra XRM-L200 CT, которые производятся компанией Xradia, Inc. (Плезентон, Калифорния, США). Изображение по шкале полутонов может, например, подвергаться фильтрации или другой предварительной обработке до сегментации на множество фаз, представляющих поровые пространства и одну или более твердых фаз, таких как зерна и возможно одну или более матричных фаз. Исходная сегментация может, например, включать в себя этапы последующей обработки для обеспечения улучшенного представления физического образца, изображение которого было исходно получено.
Однако, как обсуждалось выше, многие моделирования и выведения, с помощью которых можно наилучшим образом понять свойства и поведение образца, требуют больших вычислительных затрат и большого объема памяти и не являются ни эффективными, ни подходящими для проведения на всем образце. Таким образом, оценка наименьшего REV принесет большую пользу.
Как показано на фиг. 10, сегментированный объем, полученный на этапе 172, ориентируется в декартовой системе координат, выровненной с направлением потока, этап 174. Удобно выровнять ось Z с направлением потока, очевидным из визуального осмотра пространства пор в сегментированном объеме, представляющем образец.
Последовательные вертикальные срезы, взятые ортогонально к направлению потока, могут использоваться для получения средних значений <P1>, <Pn> на этапе 176 и среднеквадратических отклонений σ1, σn на этапе 178 для множества целевых функций или свойств, от P1 до Pn. В этом отношении делается ссылка на обсуждение фиг. 9. Предпочтительно, целевые функции не являются сложными для вычисления и также выбираются с тем, чтобы обеспечить многообразие входных данных, позволяющее получить надежную оценку REV, полезную для широкого диапазона моделирований и выведений свойств для приложений, представляющих большую сложность в вычислительном отношении и по требованиям к памяти. Пористость (φ) и отношение поверхности к объему пространства пор являются хорошими кандидатами. При использовании в настоящем описании пористость (φ) вычисляется просто как число вокселов, выделенных пространству пор в цифровом срезе, деленное на общее количество вокселов в срезе, и это дает основную целевую функцию. Вычисление площади поверхности для поверхности раздела между поровым пространством и твердый и матричной фазой(-ами) и деление этого значения на общую площадь в пространстве пор в цифровом срезе обеспечивают вторую полезную цифровую функцию. Для многих приложений эти два свойства соответствуют требуемым условиям для соответствующих целевых функций, хотя применяющим настоящее раскрытие и специалистам в данной области техники следует понимать, что другие свойства могут быть взяты в качестве замены и/или могут быть добавлены. Для каждого свойства значения для цифровых срезов усредняются, чтобы установить функцию целевого свойства, которая зависит только от направления потока, и оценить величины для полного объема образца. Другая возможность заключается в применении фильтра к целевой функции таким образом, чтобы изменить ее в конкретном положении вдоль фиксированного направления потока. Например, большая пористость, чем пористость исходной породы, может требоваться для подобразца на входе или выходе.
Размер подобразцов или подобъемов определяется на этапе 180. Подобъемы определенного размера затем распространяются по всему объему, завершая этап определения подобъема. Процесс может начинаться с очень маленького размера и увеличивать его шаг за шагом, см. базовое определение REV, проиллюстрированное на фиг. 4, или процесс может начинаться с большого размера и продвигаться в направлении меньших подобразцов. После определения непрерывной сетки подобъемов на этапе 182 происходит систематическое перемещение через подобразец и вычисление и сохранение среднеквадратического отклонения σ1, σn для каждой из выбранных целевых функций. На этапе 184 определяется, выполняется ли условие прерывания, и определяется, следует ли квалифицировать и выбрать REV из имеющихся подобразцов или вместо этого увеличить множество кандидатов. Условие прерывания может быть простым, таким как достижение предварительно выбранного размера, или может, например, быть основано на анализе одной или более дисперсий (V) или средних значений (A), вычисленных для последнего множества подобразцов в отношении предыдущего множества подобразцов. Если условие прерывания не выполняется, то пул подобразцов - кандидатов увеличивается посредством выполнения цикла итераций с изменением размера подобъемов в сторону возрастания на этапе 186 до возвращения к этапу 180 и посредством определения непрерывной сетки подобъемов, имеющих требуемый размер, по всему образцу. Стандартные отклонения снова вычисляются и сохраняются, и снова проверяется выполнение условия 184 прерывания. Когда условие прерывания выполняется, выбор REV продолжается посредством, сначала, идентификации всех подобъемов, для которых среднеквадратическое(-ие) отклонение(-я) подобъема удовлетворительно соответствует(-ют) значениям для объема образца, как показано этапе 186. В случае множественных целевых функций, например, пористости и отношения поверхности к объему пространства пор, может получиться так, что никакой образец не обеспечивает необходимого соответствия. В этом случае может потребоваться объединить эти две функции и применить процедуру минимизации, чтобы выбрать подобразца, которые соответствуют всем функциям настолько близко, насколько это возможно. Наименьшая подобразец из этого множества соответствующих подобразцов обнаруживается на этапе 188 и используется для моделирования или получения значений интересующих свойств, например, тех, которые требуют большей памяти и/или имеют большие вычислительные требования, на этапе 190.
Фиг. 11A и 11B иллюстрируют более сложную модель потока текучей среды для объема 192 образца. В данном случае объем, который будет анализироваться, получают посредством периодического копирования во всех направлениях элементарной ячейки 194. См. фиг. 5A и 5B. Элементарную ячейку получают посредством перехода от большого 196 к малому 198 значению, которые расположены со сдвигом в поперечном направлении потока. В этом случае декартова система 200 координат перестраивается для ее ориентации с направлением потока, и каждая плоскость X-Y в пределах элементарной ячейки, ортогональной к направлению потока, имеет одно и то же значение пористости и отношение поверхности к объему пространства пор, таким образом, среднеквадратическое отклонение этих величин в направлении потока является нулем (отсутствие вариаций). Образец в целом имеет такое же значение пористости и поверхности/объема элементарной ячейки, поскольку он формируется посредством копирования целого числа элементарных ячеек.
Как показано в примере на фиг. 5A и 5B, если объем запроса имеет одинаковую размерность элементарной ячейки, то вследствие периодичности весь возможный объем этой размерности в пределах всего образца будет иметь то же самое значение пористости и поверхности/объема с нулевым среднеквадратическим отклонением. В этом случае, смоделированном на фиг. 11A и 11B (фактически являющихся другими представлениями той же самой системы, проиллюстрированной на фиг. 8A и 8B, обсуждаемых выше), распределение среднеквадратического отклонения поверхности/объема или пористости будет равно нулю с дисперсией, которая также равна нулю. См., например, фиг. 15A и 15B, иллюстрирующие кривые одинакового среднеквадратического отклонения для пористости и для отношения поверхности к объему пространства пор соответственно.
Когда размерность объема запроса начинает изменяться относительно элементарной ячейки, распределения среднеквадратическое отклонение показывают, что конкретный размер больше не является периодическим во всей области: распределение с большей дисперсией является случаем, когда объем запроса меньше, чем элементарная ячейка. В этом случае, ожидается большая вариация, поскольку в направлении потока вариация пористости или поверхности/объема будут больше. Фиг. 16A-16E иллюстрируют распределение среднеквадратического отклонения пористости для различных размеров объема запроса. Элементарная ячейка, проиллюстрированная на фиг. 11B, имеет размерность 80×80×40. Фиг. 16A показывает объем запроса 20×20×10. Фиг. 16B показывает объем запроса 40×40×20, и фиг. 16C-E показывают размеры запроса 79×79×39, 81×81×41 и 120×120×60, соответственно. Фиг. 17A-E показывают распределение поверхности/объема для размеров объема запроса, соответствующих фиг. 16A-16E соответственно.
Из приведенных выше примеров должно быть понятно, что когда мода распределения близка к нулю и его дисперсия также является малой величиной, объем запроса является квазипериодической структурой во всем образце, в отношении конкретной целевой функции (или пористость, или отношение поверхность/объем).
Дополнительно полезным является применение такого же анализа к реальной породе, см. фиг. 12 и 13. На фиг. 12 образец имеет мало неоднородностей, в отличие от фиг. 13, которая иллюстрирует образец с большими неоднородностями. Размер образца для обеих пород составляет 500×500×500. Для каждого из этих пород получают три распределения для двух различных целевых функций, пористости и отношения поверхности/объема пространства пор, на основании объемов запроса изменяющегося размера. Распределения для менее гетерогенной породы, показанной на фиг. 12, приведены на фиг. 18A-18B, 19A-19B и 20A-20B, представляющих пары целевых функций для объемов с размером 450×450×450, 300×300×300 и 200×200×200, соответственно. На графиках фиг. 18A-18B, 19A-19B и 20A-20B представлены пары целевых функций, пористость показана на фиг. 18A, 19A, и 20A, и отношение поверхности/объема пространства пор показаны на фиг. 18B, 19B и 20B. Те же самые размеры образца и представление применяются для более гетерогенной породы, проиллюстрированной на фиг. 12, на фиг. 21A-21B, 22A-22B, и 23A и 23B. Каждый график является среднеквадратическим отклонением конкретного свойства всего образца <PVOL> как точку и распределение среднеквадратическое отклонение σi для подобразца запроса.
Соответственно, ясно, что, поскольку размерность подобъема уменьшается, дисперсия распределения увеличивается и его мода начинает сдвигаться в диапазон более высоких значений. Это означает, что вариации целевой функции в подобразце меньшего размера вдоль направления потока ожидаются, статистически, большими, чем в исходном объеме. Для обеих пород распределение имеет моду, очень близкую к величине среднеквадратического отклонения исходной породы, если размер подпороды очень близок к размерности исходной породы, или неоднородность целевой функции в направлении потока является малой величиной для выбранной размерности подпороды. Этот последний случай имеет место для менее гетерогенной породы (например, фиг. 12). В случае породы на фиг. 13, можно заметить, что распределение имеет очень большую дисперсию, и мода очень далека от величины исходной целой породы уже для размера 300×300×300.
Фиг. 14 - блок-схема, иллюстрирующую вариант осуществления настоящего изобретения. Следующие определения используются в отношении данного подробного описания этого варианта осуществления изобретения.
1) Направление потока перпендикулярно плоскости X-Y.
2) Xs = ширина образца в вокселах.
3) Ys = высота образца в вокселах.
4) Zs = глубина образца в вокселах.
5) Выбранными свойствами могут быть Φ, Sv, ect.
6) i = указатель на i-й объем запроса.
7) imax = количество объемов запроса.
8) Xi = ширина объема запроса i в вокселах.
9) Yi = высота объема запроса i в вокселах.
10) Zi = глубина объема запроса i в вокселах.
11) Xmin, Ymin, Zmin = минимальное измерение объема запроса.
12) Xmax, Ymax, Zmax = максимальное измерение объема запроса.
13) a, b, c = координаты объема запроса. Координаты a, b, c являются координатами X, Y и Z, соответственно, верхнего левого угла объема запроса, как изображено на Фиг. 6.
14) Ps (a, b, c) = выбранное свойство среза всего образца в местоположении a, b, c.
15) σs = среднеквадратическое отклонение множества выбранных свойств от Ps(a, b, c) до Ps(a, b, c+Zi).
16) Pi (a, b, c) = выбранное свойство среза объема запроса i в местоположении a, b, c.
17) σi = среднеквадратическое отклонение множества выбранных свойств от Pi(a, b, c) до Pi (a, b, c+Zi) относительно всего образца.
18) λi=|(σj)-( σs)|/|(µs-σs)|, где µ = среднее значение всех σj, то есть среднее распределения (A); σs является или среднеквадратическим отклонением всего образца, или является минимальным значением распределения в случае, когда этот минимум больше, чем значение исходного образца. Индекс i для λ относится к конкретной целевой функции, например пористости. Если присутствует множество целевых функций, то может рассматриваться суперпозиция (или комбинация) λi, где i - индекс целевой функции.
Этот иллюстративный пример настоящего изобретения может применять многие из функций, обсуждаемых выше, в комбинации, например, может включать в себя следующие этапы, причем номера, помещенные в круглых скобках, являются ссылками на соответствующие блоки блок-схемы процесса, идентифицированные на фиг. 14:
1) сегментированное трехмерное изображение пористой среды, такой как пористая порода, может быть загружено в компьютерную систему с целью обработки изображений и вычисления свойств породы (10);
i) сегментированное трехмерное изображение может быть сегментировано с применением любого способа сегментации, который применяется специалистами в данной области техники. Один или более способов сегментации, приведенных в патентах США №№8,170,799; 8,155,377; 8,085,974; 8,081,802 и 8,081,796, могут быть применены в данном случае, и эти патенты включены в настоящее описание путем ссылки в полном объеме. Сегментированные трехмерные изображения могут содержать вокселы, каждому из которых может быть присвоено значение по шкале полутонов, причем каждое значение является относительной плотностью воксела;
ii) Сегментированное трехмерное изображение может быть получено из необработанного изображения с рентгеновского сканера компьютерной томографии, которое затем сегментируется с помощью соответствующей программы с целью классификации воксела как зерна, поры или другого значения;
2) сегментированное трехмерное изображение затем будет применяться в моделировании для оценки потока текучих сред через пористую среду. Выбирается направление потока, и оно определяется как направление Z (11);
3) определяются размеры объемов запроса. Подробности данной номенклатуры показаны на фиг. 6;
i) объем запроса является подмножеством исходного сегментированного трехмерного изображения с размерностями Xi, Yi и Zi. Размерности всего образца составляют Xs, Ys, Zs (12);
ii) определяется максимальное число объемов запроса, imax;
iii) устанавливаются размерности в вокселах для каждого объема запроса (Xi, Yi, Zi). Xi, Yi и Zi определяются для величин i от 1 до imax (12);
iv. начальное значение i устанавливается равным 1 (12);
4) вычисляют выбранные свойства от Ps (0,0,0) до Ps (0,0, Zs) для каждого среза объема запроса (13). На Фиг. 7 заштрихованная область является срезом 5×5×5 объема запроса. Координаты углов сечения равны (0,0,0), (0,5,0), (5,5,0) и (5,0,0). В этом примере имеется 5 срезов, передвигающихся от Z=0 до Z=5. Координаты углов последнего среза равны (0,0,5), (0,5,0), (5,0,5) и (5,5,5);
5) вычисляют σs(0,0,0) (14);
6) устанавливают максимальные координаты, которые объем запроса размера Xi, Yi, Zi может занимать в пределах всего образца размером Xs, Ys, Zs (15);
i) amax=Xs-Xi+1;
ii) bmax=Ys-Yi+1;
iii) cmax=Zs-Zi+1;
7) устанавливают координаты положения текущего объема запроса равными a=b=c=0 (16);
8) вычисляют выбранные свойства от Pi (a, b, c) до Pi (a, b, c+Zi) для срезов текущего объема запроса (17);
i) Выбранные свойства содержат пористость, отношение площади поверхности к объему, аналогичные свойства, или произвольную комбинацию вышеуказанного;
9) вычисляют σi (a, b, c) (18);
i. при необходимости усредненные величины Ps, которые используются для вычисления значения σi, могут быть отфильтрованы (19);
ii. при необходимости может быть установлено среднее значение для Pi (20);
10) перемещают положения объема запроса на 1 воксел в направлении X, a=a+1 (21);
11) повторяют этапы 8)-10) данного способа, сохраняют все значения Pi и σi до тех пор, пока значение координаты X текущего объема запроса, a, не будет равно максимальному значению, которое может занимать текущий объем запроса, amax (22);
12) координату X текущего объема запроса устанавливают равной нулю, a=0, и координата Y положения текущего объема увеличивается на один воксел, b=b+1 (23);
13) повторяют этапы 8)-12) данного способа, сохранение всех значений Pi и σi до тех пор, пока значение координаты Y текущего объема запроса, b, не будет равно максимальному значению, которое может занимать текущий объем запроса, bmax (24);
14) координата X текущего объема запроса устанавливается равной нулю, a=0, координата Y текущего объема запроса устанавливается равной нулю, b=0, и координата Z положения текущего объема увеличивается на один воксел, c=c+1 (25);
15) повторяют этапы 8)-14) данного способа, сохраняют все значения Pi и σi до тех пор, пока значение координаты Z текущего объема запроса, c, не будет равно максимальному значению, которое может занимать текущий объем запроса, cmax (26);
16) увеличивают (или уменьшают) размер текущего объема запроса (27);
i) выбирают следующее множество объемов запроса путем увеличения указателя до следующего объема запроса, i=i+1;
ii) Текущий размер запроса устанавливается на Xi, Yi, Zi;
17) повторяют этапы 6)-16), пока все объемы запроса не были выбраны и все величины Pi, и σi не будут вычислены и сохранены (28);
18) выбирают одно или более выбранных свойств для сопоставления (29);
19) вычисляют λi для каждого объема запроса (30);
20) выбирают объем запроса с наименьшим значением λi. Он является размером и положением REV (31);
21) вычисляют требуемых свойств пористой среды;
i. требуемые свойства могут содержать стандартный анализ кернов (RCAL) и специальный анализ кернов (SCAL). Анализ RCAL включает в себя, но не ограничивается пористостью (связанной, закрытой, суммарной), содержанием керогена, абсолютной проницаемостью по множеству осей (x, y, z). Анализ SCAL включает в себя, но не ограничивается относительной проницаемостью (двухфазной относительной проницаемостью: замещение вода-масло, газ-масло или вода-газ), капиллярным давлением (значения капиллярного давления при каждом насыщении для первичного дренажа, впитывание и вторичные циклы дренажа), гранулометрическим составом, электрическими свойствами (коэффициентом сопротивления пласта, индексом удельного сопротивления, a, m, n), упругими свойствами (Vp.Vs, E, K, G, коэффициентом Пуассона) и аналогичными анализами.
Обратимся к фиг. 24; еще одним признаком настоящего изобретения является анализ пригодности REV для применения закона Дарси. Как отмечено выше, закон Дарси в его часто применяемой форме для потока через пористые среды, такие как порода, показан в формуле 1. Проницаемость часто получают посредством применения закона Дарси через уравнения Навье-Стокса (уравнение для импульса), включающее использование разложения Гари (см. формула 2). Однако, как обсуждалось выше, этот способ основывается на средней величине (в этом случае, давлении), которая, как предполагается, «правильно работает» по интегральной шкале усреднения. К сожалению, сигнал давления, который быстро изменяется по шкале длины в сравнении с усредненной шкалой длины, не может представить давление по этой длине для данных приложений таким образом, чтобы обеспечить надежные результаты. Когда REV выбирается в соответствии с приведенным выше, остается возможность, что в подобразце могут присутствовать вариации пористости, делая предположения о потоке Дарси неверными или приводящими к ошибке. Кроме того, градиент давления может быстро изменяться вдоль направления потока, что делает невозможным определение проницаемости, связанной с конкретным подобразцом. Это особенно верно для имеющих высокую гетерогенность образцов, которые могут встречаться в природных породах.
Таким образом, еще одним признаком настоящего изобретения является эффективный способ количественного определения того, насколько хорошее (или насколько плохое) является цифровое представление пород, и насколько точным будет описание потока текучей среды с помощью закона Дарси, то есть для прогнозирования надежным и эффективным образом тенденции корреляции пористости/проницаемости ("poro-perm"), поскольку цифровая подобразец стала слишком малой. Фиг. 25 описывает данную проблему и иллюстрирует тенденции пористости-проницаемости на сводном графике зависимости логарифма проницаемости от пористости.
В данном случае исходная порода является образцом хорошо задокументированной породы Фонтенбло, и исходный цифровой образец имеет размерности 500×500×500. Значение пористости-проницаемости, выведенное для всего цифрового образца, показано большим полым ромбом, и оно находится точно на «верхней лабораторной» опытной тенденции, показанной для пород Фонтенбло (сплошная серая линия "UL"). "LL" является нижним пределом. Это доказывает, что исходный размер является достаточно большим, чтобы иметь корректное соотношение пористости-проницаемости, что подтверждает, что он является RV (типичный объем). Может быть полезным узнать, можно ли проследить тенденцию пористости-проницаемости, подразделяющую исходную целую породу на меньшие образцы. Меньшие образцы будут корректно соответствовать тенденции пористости-проницаемости, показанной полым ромбом, если они будут достаточно большими, чтобы считаться RV. Вопрос заключается в точке, в которой единственный подобразец становится меньшей, чем REV, другими словами, когда подобразец больше не является типичным объемом. Символы серых крестов и серых кружков являются тенденциями пористости-проницаемости, полученными для подобразцов с размерностями 285×285×285 и 190×190×190, соответственно. При данных размерностях удовлетворяется «верхняя лабораторная» опытная тенденция. Однако данная тенденции не выполняется для размерностей около 100×100×100, что иллюстрируется тенденцией (серые треугольники) для размерности 95×95×95. Следует отметить, что оптимальная величина (черный треугольник), ограниченная этим размером подобразца по существу отделяется от опытной «верхней лабораторной» тенденции. Сравните оптимальные величины пористости-проницаемости, показанные для подобразцов с размерами 190×190×190 и 285×285×285 соответственно, которые показаны символами черного круга и креста соответственно.
Фиг. 26 является примером для другого типа породы, который является неуплотненным песчаником, и который показывает изучение точек данных, показанных серыми крестами, серыми кругами и серыми треугольниками для размерностей подобразца, составляющих 300×300×300, 200×200×200 и 100×100×100 соответственно, и демонстрирует, что элементарный объем для этой породы, очевидно, меньше либо равен 100×100×100.
Результаты для образца Фонтенбло с более низкой пористостью, чем образец с фиг. 25, иллюстрируются на фиг. 27. Значение пористости-проницаемости (полый ромб) для объема исходного образца 500×500×500 находится сверху «верхней лабораторной» экспериментальной кривой (верхняя сплошная серая линия "UL"), поэтому размер является типичным размером. "LL" является нижним пределом. В этом случае корреляция пористости-проницаемости не выполняется для размера, составляющего почти 300×300×300, со ссылкой, сделанной в этом отношении на значения, показанные серыми кругами для объемов образца 285×285×285, и по сравнению с тенденциями, показанными серыми треугольниками и серыми крестами для размеров образцов 190×190×190 и 380×380×380, соответственно.
Таким образом, сводные графики пористости - проницаемости фиг. 25-27 иллюстрируют совсем разное поведение. Очевидно, что было бы полезно иметь возможность точного и эффективного прогнозирования этого поведения.
Фиг. 28A-28H иллюстрируют среднее значение (A) распределения среднеквадратическое отклонение для пористости (фиг. 28A) и для отношения поверхности/объема (фиг. 28B), дисперсию (V) того же самого распределения для пористости (фиг. 28C), и дисперсию отношения поверхности/объема (фиг. 28D) в зависимости от размерности (размера) подобразца для двух пород Фонтенбло, рассматриваемых на фиг. 25 и 27, соответственно. Также оцениваются асимметрия и эксцесс, и результаты показаны на фиг. 28E-28H. На фиг. 25, 26 и 27 символы черного ромба, круга и креста представляют оптимальный выбор, сделанный посредством инструмента, имеющего в качестве целевых функций и поверхность/объем, и пористость. На фиг. 28A-28H заданные черными кругами линии приведены для образца с большей пористостью с фиг. 25 и заданные серыми кругами линии приведены для образца с меньшей пористостью с фиг. 27. Следующее становится очевидным из этих тенденций данных: оба средних значения распределения уменьшаются при увеличении размерности подпороды. Для конкретного размера скорость изменения среднего с размерностями подпороды становится малой величиной. Это происходит для размера 190 (для породы с высокой пористостью, черная линия) и размера 380 (для породы с низкой пористостью, серая линии). Дисперсия распределения также уменьшается, и достигает очень малой величины для той же самой размерности подпороды. Моменты более высокого порядка показывают симметрию распределения, и когда размер подобразца является достаточно большим, распределение становится близким к нормальному.
Вспомним смысл среднего значения и среднеквадратическое отклонение (или дисперсии) распределения; среднее, которое совпадает с модой в случае, когда распределение является нормальным, задает «положение» распределения относительно «нуля», и дисперсия учитывает разброс относительно среднего значения. Фиг. 11A-11B и 15A-15B демонстрируют, например, что распределение, имеющее центр в нуле и нулевую дисперсию, означает совершенную периодичность выбранного подобъема. Таким образом, среднее значение и дисперсия являются мерой «периодичности» для целевой функции (пористости или поверхности/объема) подобъема в пределах всей породы.
Когда размерность подпороды снижается, замедляясь относительно исходного размера (в пределе, уменьшаясь на 1 воксел за единицу времени), с распределением происходят различные события: во-первых, дисперсия начинает увеличиваться; во-вторых, когда размер уменьшается до значения, меньшего чем конкретная пороговая величина, среднее значение распределения начинает изменяться, и распределение становится несимметричным (оно увеличивается, что означает большее изменение целевой функции в направлении потока) относительно значения целевой функции, оцененной для всей исходной породы. В основном, распределение сдвигается направо от исходного положения (см. предыдущие графики, на которые делается ссылка для двух различных пород).
Очевидно, что для размерности подпороды, который приводит к сдвигу среднего значения, корреляция пористости-проницаемости нарушается. Это понятно, поскольку, когда среднее значение является большим и дисперсия также является большой, имеется высокая вероятность выбора подобразца с большой вариацией пористости и поверхности/объема относительно исходного значения этой вариации. Следует отметить, что когда среднее значение является таким же, как и в исходном целом образце, имеется большая вероятность выбора подобразца с той же самой вариацией пористости и поверхности/объема, но это не подразумевает то же самое значение пористости или поверхности/объема (то есть проницаемости). Другими словами, все еще может иметь место тенденция пористости-проницаемости. Чтобы дополнительно продемонстрировать данные признаки, случаи для карбонатов и песчаников приведены ниже.
Например, в качестве дальнейшей демонстрации фиг. 29A-29H иллюстрируют применение способов по настоящему изобретению для двух различных образцов карбонатов. Для обоих этих карбонатов видно, что результаты аналогичны, как и для предыдущей породы. Таким образом, когда среднее значение пористости и среднеквадратического отклонения прекращают уменьшаться (или уменьшаются с низкой скоростью) для конкретного размера, дисперсия также малая величина, и можно ожидать хорошей тенденции пористости-проницаемости. На фиг. 29A-29H заданные черными кругами линии приведены для образца карбоната с большей пористостью, и заданные серыми кругами линии приведены для образца карбоната с меньшей пористостью. Два образца карбонатов различаются по пористости и особенно по проницаемости. Образец с более низкой пористостью имеет проницаемость ниже 100 мД, и образец с более высокой пористостью имеет проницаемость, составляющую несколько сотен мД. На фиг. 29I, символы серого треугольника, серого круга и серого креста относятся к тенденции пористости-проницаемости для размерностей подобразцов, составляющих 95×95×95, 190×190×190 и 285×285×285 соответственно, в отношении тенденций пористости-проницаемости для образца, идентифицированного серыми кругами на фиг. 29A-29H. На фиг. 29J символы серого треугольника, серого круга и серого креста относятся к тенденциям пористости-проницаемости, представленным для размерностей подобразцов, составляющих 190×190×190, 285×285×285 и 380×380×380 соответственно, в отношении тенденций пористости-проницаемости для образца, идентифицированного черными кругами на фиг. 29A-29H. Следует отметить, что на каждом графике фиг. 29I и 29J символы черного треугольника, круга и креста представляют оптимальный выбор, сделанный посредством инструмента, имеющего в качестве целевых функций и поверхность/объем, и пористость.
Фиг. 30A-30H иллюстрируют другие применения настоящего изобретения, а именно, случаи, в которых порода является относительно однородной и может обеспечить хорошие тенденции пористости-проницаемости, начиная с размера подобразца, составляющего 100×100×100. Две различных относительно однородных породы использовались в данном исследовании. На фиг. 30A-30H заданная черными кругами линия представлена для образца с большей пористостью, и заданная серыми кругами линия представлена для образца с меньшей пористостью. Пористость-проницаемость для фиг. 30A-30H показана на фиг. 26.
На фиг. 31A-31H представлены дополнительные примеры, в которых исследуются две породы, где нарушение тенденции пористости-проницаемости происходит при размерностях, составляющих 100×100×100 и почти 200×200×200. На фиг. 31A-31H заданная черными кругами линия представлена для образца с большей пористостью, и заданная серыми кругами линия представлена для образца с меньшей пористостью. Образцы являлись песчаниками. На фиг. 31I символы серого треугольника (соответствующие внешнему обведенному графику), серый круг (соответствующие внутреннему обведенному графику) и серого креста относятся к тенденциям пористости-проницаемости для размерностей подобразца, составляющих 190×190×190, 285×285×285 и 380×380×380, соответственно, относящихся к тенденциям пористости-проницаемости для образца, идентифицированного серыми кругами на фиг. 31A-31H. На фиг. 31J символы серого треугольника (соответствующие самому большому обведенному графику), серого круга (соответствующие обведенному графику промежуточного размера) и серого креста (соответствующие самому маленькому обведенному графику) относятся к тенденциям пористости-проницаемости для размерностей подобразца, составляющих 95×95×95, 190×190×190 и 285×285×285 соответственно и относящихся к тенденциям пористости-проницаемости для образца, идентифицированного черными кругами на фиг. 31A-31H. На каждом из графиков фиг. 31I и 31J символы черного треугольника, круга и креста представляют оптимальный выбор, сделанный посредством инструмента, имеющего в качестве целевых функций и поверхность/объем, и пористость.
Другой способ применения настоящего изобретения состоит в оценке того, какое разрешение и поле обзора являются наиболее подходящими для породы. Фактически, размер подобразца может быть фиксирован, например, вплоть до 400×400×400, и причем будет изменяться разрешение и поле обзора при сканировании. Как правило, используемое число точек фиксируется сканером, и эти точки могут быть выделены в объеме другого размера. Это дает различное разрешение для сканирования породы: для меньшего поля обзора разрешение будет больше, чем для большего поля обзора. Одна из проблем заключается в том, чтобы понять, какое поле обзора (то есть разрешение) является подходящим для породы. Распределение среднеквадратическое отклонение целевых функций может использоваться для решения этой проблемы, причем размерность подобразца будет фиксированным для всего поля обзора. Например, на фиг. 32A-32B, 33A-33B, и 34A-34B, анализируется песчаник с исходным размером 550×550×550. Распределение среднеквадратическое отклонение (пористость - справа, поверхность/объем - слева) получают для подобразца размером 200×200×200. Для фиг. 32A-32B, фиг. 33A-33B и фиг. 34A-34B изменяется разрешение сегментации, причем сегментированный образец имеет разрешение 10X, 20X, и 40X, соответственно, которое может означать, что один воксел имеет размер 2, 1 и 0,5 микрона, соответственно. Из фиг. 33A-33B очевидно, что разрешение 20X имеет распределение с очень большой дисперсией и средним значением, которое намного больше, чем среднее значение для разрешения 10X, как показано на фиг. 32A-32B. Для того чтобы работать с разрешением 20X, при сегментации должно использоваться большее поле обзора. Разрешение 10X является приемлемым для этого примера.
В следующем примере, который иллюстрируется на фиг. 35A-35B и 36A-36B, анализируется другой песчаник, и распределение среднеквадратического отклонения (пористость - справа, поверхность/объем - слева) получают для подобразца размером 200×200×200, как и раньше. В этом случае разрешение 4X, которое показано на фиг. 35A-35B, является более подходящим, чем разрешение 10X, которое показано на фиг. 36A-36B, относительно разрешения в предыдущем примере, в котором разрешение 10X дает слишком большое среднее значение и дисперсию.
Обратимся к фиг. 37; показана система 100, которая может быть настроена для выполнения настоящих способов. Как показано в этом примере, трехмерные (3-D) изображения образцов пористой среды, полученные из источника 101, формируются сканером 102. Выходные 3-D изображения 103 сканера могут быть перенесены на компьютер 104, имеющий программные инструкции для выполнения анализа 3-D изображения и анализа упомянутых данных и проведения моделирования с целью формирования выходных результатов моделирования образца, которые могут быть переданы одному или более устройствам 105, таким как дисплей, принтер, запоминающее устройство или комбинации вышеуказанного. Компьютерные программы, используемые для анализа 3-D изображений и вычислений CFD и имитационного моделирования, могут быть сохранены как программный продукт, по меньшей мере на одном машиночитаемом носителе (например, на жестком диске, устройстве флэш-памяти, компакт-диске, магнитной ленте/диске или других носителях информации), объединенный с по меньшей мере одним процессором 104A (например, ЦП), который выполнен с возможностью выполнения программ, или могут быть сохранены на внешнем машиночитаемом носителе (не показан), который доступен процессору компьютера. Компьютер 104 может включать в себя по меньшей мере один блок 104C памяти для хранения программ, входных данных и выходных данных и других результатов программы или комбинаций вышеуказанного. Для показа выходных данных устройство 105 может быть, например, монитором, CRT или другими средствами визуального отображения (не показаны). Компьютер 104 может включать в себя один или более системных компьютеров, которые могут быть реализованы как единственный персональный компьютер или как сеть компьютеров. Однако специалистам в данной области техники будет понятно, что реализации различных методик, описанных в настоящем описании, могут применяться на практике во множестве конфигураций компьютерных систем, включая серверы гипертекстового протокола передачи данных (HTTP), карманные устройства, многопроцессорные системы, основанные на микропроцессорах или программируемая бытовая электроника, сетевые ПК, миникомпьютеры, центральные компьютеры и т.п. Модули системы 100, включающие в себя сканер 102, компьютер 104 и выходной дисплей, принтер и/или устройство/носитель 105 данных, могут быть соединены друг с другом для взаимодействия (например, передачи данных, и т.д.), через любое проводное соединение, радиочастотное соединение, телекоммуникации, интернет-соединение или другие средства связи.
Настоящее изобретение включает в себя следующие аспекты/варианты осуществления/признаки в любом порядке и/или в любом сочетании:
1. Настоящее изобретение относится к способу идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, содержащему этапы, на которых:
a) получают сегментированный объем, характеризующего пространство пор и по меньшей мере одну твердую фазу;
b) выводят среднее значение <P1> свойства первой целевой функции P1 для всего сегментированного объема;
c) вычисляют среднеквадратическое отклонение σVOL относительно среднего значения <P1> свойства для всего сегментированного объема;
d) определяют множество подобъемов в пределах объема;
e) вычисляют среднеквадратическое отклонение σi значения свойства P первой целевой функции P1 относительно среднего значения <P1> свойства для каждого из упомянутых подобъемов;
f) находят все кандидаты в репрезентативные подобъемы, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL;
g) выбирают и сохраняют репрезентативный подобъем из кандидатов; и
h) используют репрезентативный подобъем для выведения по меньшей мере одного интересующего значения свойства.
2. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, этап, в котором определяют множество подобъемов в объеме, дополнительно содержит этапы, на которых:
определяют исходный размер для подобъема;
заполняют весь объем подобъемами определенного исходного размера; и
итерируют размеры для последующих подобъемов и заполняют весь объем подобъемами такого размера, и повторяют этот шаг до тех пор, пока не будет выполнено условие прерывания.
3. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, в котором итерируют размеры от большего к меньшему значению с малым приращением.
4. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, этап, в котором выбирают и сохраняют репрезентативный объем, дополнительно содержит этап, в котором находят наименьший репрезентативный цифровой объем.
5. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, в котором условие прерывания содержит заданный размер для подобъема.
6. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, дополнительно содержит этапы, на которых:
ориентируют выбранную ось декартовой системы координат сегментированного объема с определенным направлением потока; и
причем:
этап, на котором выводят среднее значения <P1> свойства первой целевой функции P1 для всего сегментированного объема, содержит анализ множества цифровых срезов объем образца, взятых ортогонально к определенному направлению потока; и
этап, на котором вычисляют среднеквадратическое отклонение σi свойства P первой целевой функции P1 относительно среднего значения <P1> свойства для каждого из упомянутых подобъемов, происходит относительно определенного направления потока.
7. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, дополнительно содержит этапы, на которых:
выводят среднее значение <P2> свойства второй целевой функции P2 для всего сегментированного объема;
вычисляют среднеквадратическое отклонение σVOL относительно среднего значения <P2> свойства для всего сегментированного объема;
определяют множество подобъемов в объеме;
вычисляют среднеквадратическое отклонение σi значения свойства P второй целевой функции P2 относительно среднего значения <P2> свойства для каждого из упомянутых подобъемов;
находят все репрезентативные подобъемы, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL для сочетания первой целевой функции P1 и второй целевой функции P2.
8. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, в котором первая целевая функция P1 является пористостью и вторая целевая функция P2 является отношением площади поверхности к объему пространств пор.
9. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, дополнительно содержит этап квалификации подобъема - кандидата до его выбора, на котором определяют его пригодность для использования в выведении свойств транспортировки текучих сред с помощью закона Дарси, причем на упомянутом этапе:
строят распределение среднеквадратического отклонения целевых функций;
оценивают среднее значение или при необходимости любую другую характеристику первого порядка для распределения среднеквадратическое отклонение целевой функции, и дисперсию, эксцесс или асимметрию распределения;
оценивают тенденцию момента первого или более высокого порядка в отношении размера подобъема; и
останавливают уменьшение размера подобъема в случае, когда момент первого порядка изменяется по меньшей мере на 0,1 относительно его величины для распределения, основанного на большем подобъеме и/или когда моменты более высокого порядка превышают конкретную пороговую величину 0,1 для дисперсии.
10. Настоящее изобретение также относится к способу идентификации репрезентативного для подобразца цифрового объема, соответствующего образцу пористых сред, содержащему этапы, на которых:
a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу;
b) ориентируют выбранную ось декартовой системы координат сегментированного объема с определенным направлением потока;
c) выводят значений как одной или более функций, по меньшей мере первой целевой функции P1 для всего сегментированного объема посредством анализа цифровых срезов, ортогональных определенному направлению потока;
d) определяют множество подобъемов в пределах объема;
e) вычисляют значения для одной или более функций, по меньшей мере, первой целевой функции P1 для каждого из упомянутых подобъемов, соответствующих определенному направлению потока;
f) находят все репрезентативные подобъемы-кандидаты, для которых функция (-и) идентифицирует(-ют) соответствие между величинами значениями объема и подобъема;
g) выбирают репрезентативный объем из кандидатов;
h) сохраняют репрезентативный подобъем; и
i) используют репрезентативный подобъем для моделирования или выведения по меньшей мере одного интересующего значения свойства.
11. Настоящее изобретение также относится к способу получения эффективной оценки репрезентативного элементарного объема по большему цифровому 3-D изображению пористого образца, содержащего этапы, на которых:
a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу;
b) выводят значения как по меньшей мере одна функция для по меньшей мере первой целевой функции P1 для всего сегментированного объема;
c) определяют множество подобъемов в объеме, причем на этом этапе:
определяют исходный размер для подобъема,
заполняют весь объем подобъемами определенного исходного размера,
итерируют размеры для последующих подобъемов и заполняют всего объема подобъемами такого размера, и повторяют этот этап до тех пор, пока не будет выполнено условие прерывания;
d) вычисляют значения как по меньшей мере одна функция для по меньшей мере первой целевой функции для каждого из упомянутых подобъемов;
e) находят все репрезентативные подобъемы - кандидаты для достаточно удовлетворяющих друг другу значений объема и подобъема;
f) выбирают и сохраняют репрезентативный подобъем из кандидатов; и
g) используют репрезентативный подобъем для моделирования или выведения по меньшей мере одного интересующего значения свойства.
12. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, дополнительно содержащий квалификацию подобъема - кандидата до его выбора, на котором определяют его пригодность для использования в выведении свойств транспортировки текучих сред с помощью закона Дарси, причем на упомянутом этапе:
строят распределение среднеквадратическое отклонение целевых функций;
оценивают среднее значение или при необходимости любую другую характеристику первого порядка для распределения среднеквадратическое отклонение целевой функции и дисперсию, эксцесс или асимметрию распределения;
оценивают тенденцию момента первого или более высокого порядка относительно размера подобъема; и
останавливают уменьшение размер подобъема в случае, когда момент первого порядка изменяется по меньшей мере на 0,1 относительно его величины для распределения, основанного на большем подобъеме и/или когда моменты более высокого порядка превышают конкретную пороговую величину 0,1 для дисперсии.
13. Настоящее изобретение также относится к способу получения эффективной оценки репрезентативного элементарного объема по большему 3-D цифровому изображению пористого образца, содержащему этапы, на которых:
a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу;
b) ориентируют выбранную ось декартовой системы координат сегментированного объема к определенному направлению потока;
c) выводят среднее значение <P1> свойства первой целевой функции P1 для всего сегментированного объема с применением анализа множества цифровых срезов объема образца, взятых ортогонально к определенному направлению потока;
d) вычисляют среднеквадратическое отклонение относительно среднего значения <P1> свойства для всего сегментированного объема;
e) определяют множество подобъемов в объеме, причем на этом этапе:
определяют исходный размер для подобъема;
заполняют весь объем подобъемами определенного исходного размера,
итерируют размеры для последующих подобъемов от большего к меньшему значению и заполняют весь объем подобъемами такого размера и повторяют этот этап до тех пор, пока не будет выполнено условие прерывания;
f) вычисляют среднеквадратическое отклонение σi свойства P относительно среднего значения <P1> свойства для каждого из упомянутых подобъемов в отношении определенного направления потока;
g) находят все репрезентативные подобъемы - кандидаты, для которых σi удовлетворительно соответствует σvol;
h) выбирают наименьший кандидат и его сохраняют в качестве репрезентативного элементарного объема; и
i) используют репрезентативный элементарный объем для выведения по меньшей мере одного интересующего значения свойства.
14. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, дополнительно содержащий этапы, на которых:
получают среднее значение <P2> свойства второй целевой функции P2 для всего сегментированного объема;
вычисляют среднеквадратическое отклонение относительно среднего значения <P2> свойства для всего сегментированного объема;
определяют множество подобъемов в объеме;
вычисляют среднеквадратическое отклонение σi второй целевой функции P2 относительно среднего значения <P2> свойства для каждого из упомянутых подобъемов;
находят все репрезентативные подобъемы, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL для комбинации первой целевой функции P1 и второй целевой функции P2.
15. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, в котором первая целевая функция P1 является пористостью, и вторая целевая функция P2 является отношением площади поверхности к объему пространств пор.
16. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, дополнительно содержит этап квалификации подобъема - кандидата до его выбора, содержащий определение его пригодности для использования в выведении свойств транспортировки текучих сред с помощью закона Дарси, причем на упомянутом этапе:
строят распределение среднеквадратического отклонения целевых функций;
оценивают среднее значение или при необходимости любую другую характеристику первого порядка для распределения среднеквадратического отклонения целевой функции, и дисперсию, эксцесс или асимметрию распределения;
оценивают тенденцию момента первого или более высокого порядка относительно размера подобъема; и
останавливают уменьшение размера подобъема в случае, когда момент первого порядка изменяется по меньшей мере на 0,1 (или по меньшей мере на 0,5, 1, 2, 5, или произвольную величину) относительно его величины для распределения, основанного на большем подобъеме и/или когда моменты более высокого порядка превышают конкретную пороговую величину 0,1 (или другую величину) для дисперсии.
17. Способ идентификации цифрового объема репрезентативного подобразца, соответствующего образцу пористых сред, который содержит этапы, на которых
1) загружают сегментированное трехмерное изображение пористой среды в компьютерную систему, причем сегментированное трехмерное изображение содержит вокселы, каждому из которых присваивается значение по шкале полутонов;
2) выбирают направление потока, которое определяется как направление Z;
3) определяют размеры объемов запроса, причем
i) объем запроса является подобъемом исходного сегментированного трехмерного изображения с размерами Xi, Yi и Zi, причем размеры всего образца составляют Xs, Ys, Zs,
ii) задают максимальное число объемов запроса, imax,
iii) устанавливаются размеры в вокселах для каждого объема запроса (Xi, Yi, Zi), причем Xi, Yi и Zi определяются для значений i от 1 до imax, и
iv) начальное значение i устанавливают равным 1;
4) вычисляют выбранные свойства Ps(0,0,0) через Ps (0,0, Zs) для каждого среза объема запроса;
5) вычисляют σs (0,0,0);
6) устанавливают максимальные координаты такие, что объем запроса размера Xi, Yi, Zi занимает весь образец размера Xs, Ys, Zs, причем
i) amax=Xs-Xi+1,
ii) bmax=Ys-Yi+1,
iii) cmax=Zs-Zi+1;
7) устанавливают координаты положения текущего объема запроса на a=b=c=0;
8) вычисляют выбранные свойства Pi(a, b, c) через Pi (a, b, c+Zi) для срезов текущего объема запроса, причем выбранные свойства содержат пористость, отношение площади поверхности к объему, аналогичные свойства или произвольное их сочетание,
9) вычисляют σi (a, b, c), i) причем значения Pi, которые используются для вычисления значения σi, при необходимости фильтруются, ii)причем при необходимости устанавливается среднее значение для Pi;
10) перемещают положения объема запроса на 1 воксел в направлении X, a=a+1;
11) повторяют этапы 8)-10) и сохраняют все величины Pi и σi, пока значение X-координаты текущего объема запроса, a, не будет равно максимальному значению, которое может занимать текущий объем запроса, amax;
12) устанавливают координаты X текущего объема запроса равной нулю, a=0, и увеличивают координаты Y текущего положения объема на один воксел, b=b+1;
13) повторяют этапов 8)-12), и сохраняют все величины Pi и σi, пока значение Y-координаты текущего объема запроса, b, не будет равно максимальному значению, которое может занимать текущий объем запроса, bmax;
14) устанавливают координату X текущего объема запроса равной нулю, a=0, устанавливают координату Y текущего объема запроса равной нулю, b=0, и увеличивают координату Z текущего положения объема на один воксел, c=c+1;
15) повторяют этапы 8)-14), и сохраняют все величины Pi и σi, пока значение X-координаты текущего объема запроса, c, не будет равно максимальному значению, которое может занимать текущий объем запроса, cmax;
16) увеличивают размер текущего объема запроса, причем на этом этапе
i) выбирают следующее множество объемов запроса, посредством увеличения указателя до следующего объема запроса, i=i+1 и
ii) устанавливают текущий размер запроса на Xi, Yi, Zi;
17) повторяют этапы 6)-16), пока все объемы запроса не будут выбраны и все величины Pi и σi не будут вычислены и сохранены;
18) выбирают одно или более выбранных свойств для сопоставления
19) вычисляют λi для каждого объема запроса;
20) выбирают объем запроса с наименьшим значением λi, причем выбранный объем запроса является размером и положением REV; и
21) вычисляют свойства пористой среды.
18. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, в котором сегментированное трехмерное изображение получают как изображение образца, полученное сканирования образца с помощью сканера рентгеновской компьютерной томографии, и сегментируют изображение с помощью программы, чтобы классифицировать вокселы как зерно, пору и при необходимости как другие фазы.
19. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, в котором свойства содержат свойства стандартного анализа кернов (RCAL) и специального анализа кернов (SCAL), или обоих анализов.
20. Способ по любому из предшествующих или последующих вариантов осуществления/признаков/аспектов, в котором свойствами анализа RCAL являются пористость, содержание керогена, абсолютную проницаемость по множеству осей, и свойствами SCAL являются относительная проницаемость, капиллярное давление, гранулометрический состав, электрические свойства, упругие свойства и любые их сочетания.
21. Система для идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, содержащая:
a) сканер, выполненный с возможностью формирования трехмерного цифрового изображения пористой среды,
b) компьютер, содержащий по меньшей мере один процессор, выполненный с возможностью исполнения компьютерной программы, выполненной с возможностью получения сегментированного объема, характеризующего пространство пор и по меньшей мере одну твердую фазу,
c) компьютер (такой же или отличающийся от b)), содержащий по меньшей мере один процессор, выполненный с возможностью исполнения компьютерной программы, выполненной с возможностью произведения вычислений, причем упомянутые вычисления содержат этапы, на которых i) выводят среднее значение <P1> свойства первой целевой функции P1 для всего сегментированного объема, ii) вычисляют среднеквадратическое отклонение σVOL относительно среднего значения <P1> свойства для всего сегментированного объема, iii) определяют множество подобъемов в объеме, iv), вычисляют среднеквадратическое отклонение σi значения свойства P первой целевой функции P1 относительно среднего значения <P1> свойства для каждого из упомянутых подобъемов, v) находят все репрезентативные объемы - кандидаты, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL, vi) выбирают и сохраняют репрезентативный подобъем из кандидатов и vii) используют репрезентативный подобъем для выведения по меньшей мере одного интересующего значения свойства, и
d) по меньшей мере одно устройство для отображения, печати или сохранения результатов вычислений.
22. Компьютерный программный продукт на машиночитаемом носителе (например, постоянном), такой, что при выполнении на процессоре в компьютеризированном устройстве обеспечивает способ выполнения вычислений по одному или более упомянутым этапам предшествующего способа и системы.
Настоящее изобретение может включать в себя любое сочетание этих различных признаков или вариантов осуществления, приведенных выше и/или ниже, в соответствии с упомянутым в предложениях и/или абзацах. Любое сочетание раскрытых в настоящем описании признаков считается частью настоящего изобретения, и не предполагает какого-либо ограничения относительно объединяемых признаков.
Другие признаки, аспекты, и преимущества будут очевидны из предшествующего описания и прилагаемой формулы. Кроме того, не все признаки, аспекты или преимущества должны присутствовать в каждом варианте осуществления изобретения, и они могут появляться индивидуально, в различных сочетаниях, или в сочетании с другими признаками, аспектами или преимуществами без отступления от объема заявляемого изобретения.
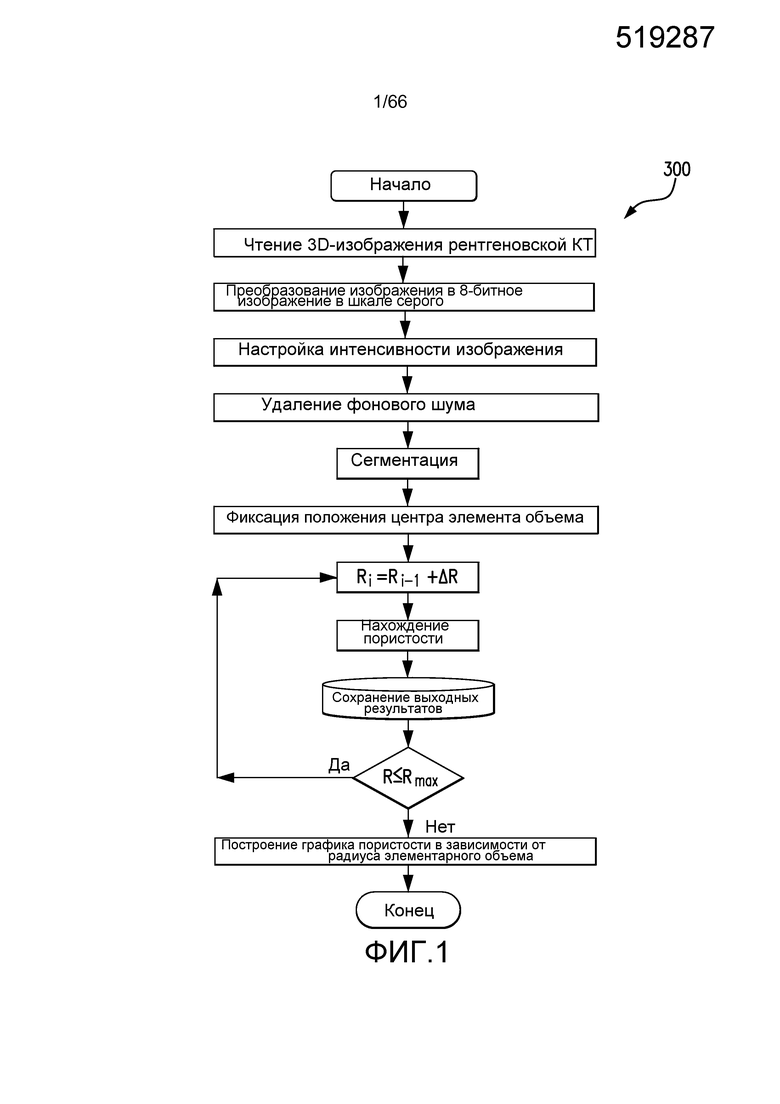
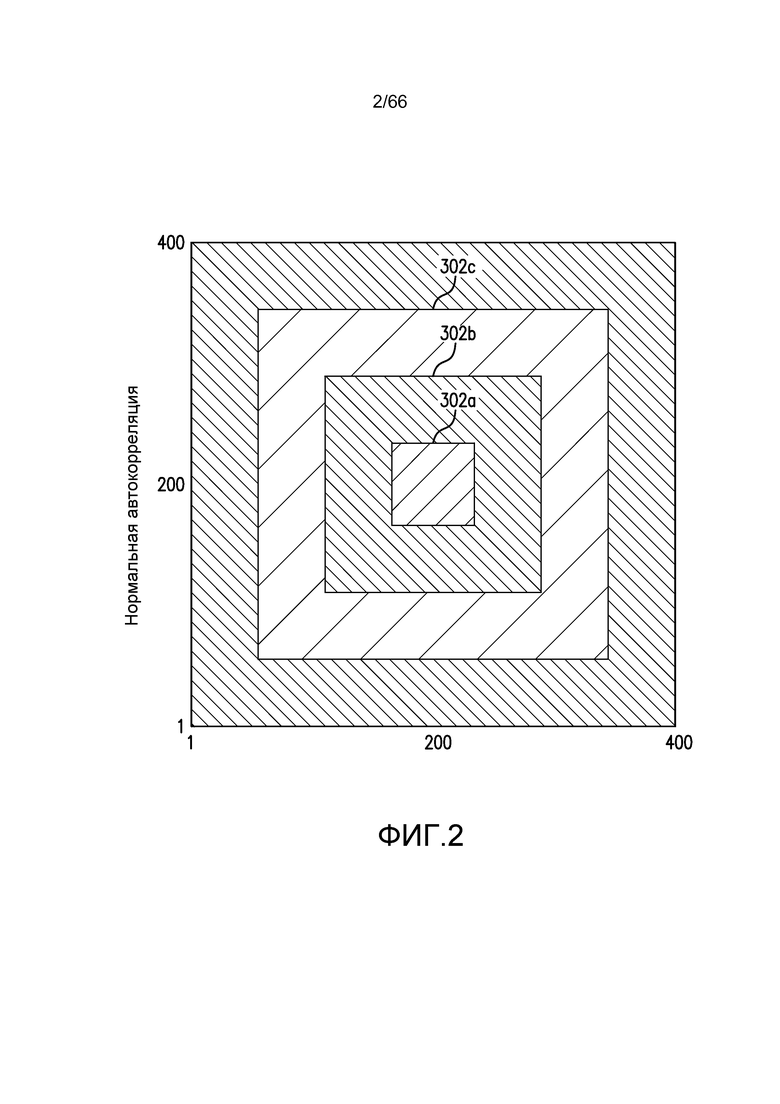


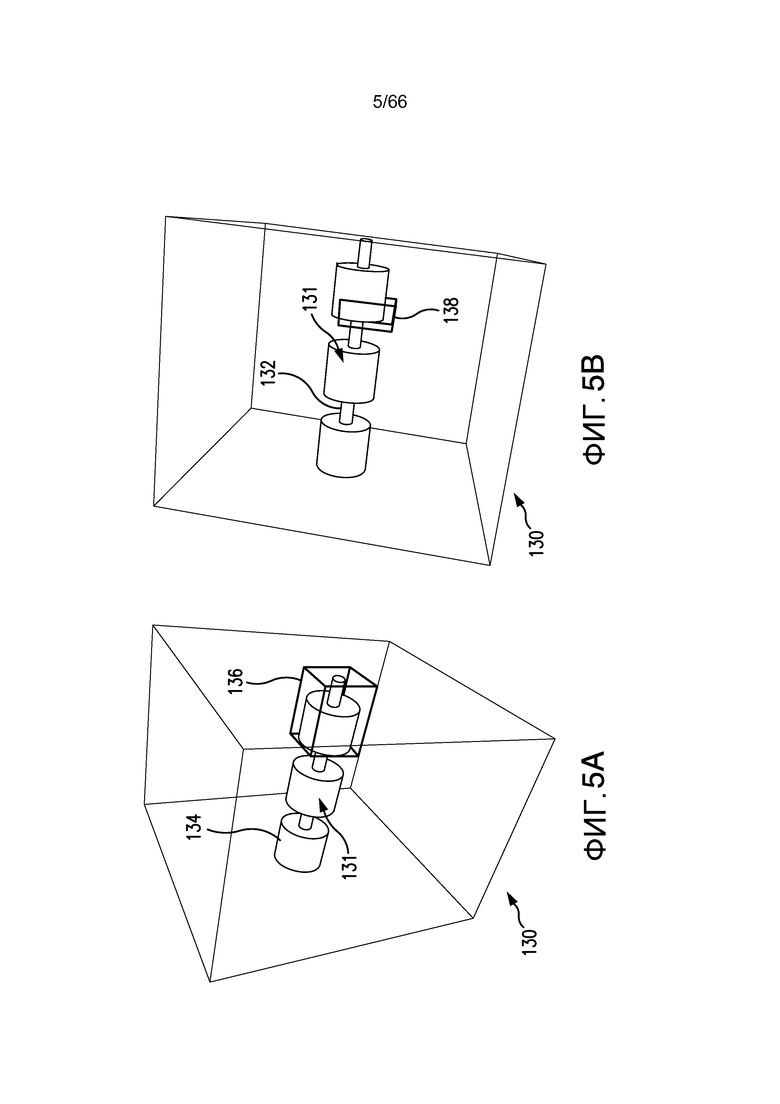
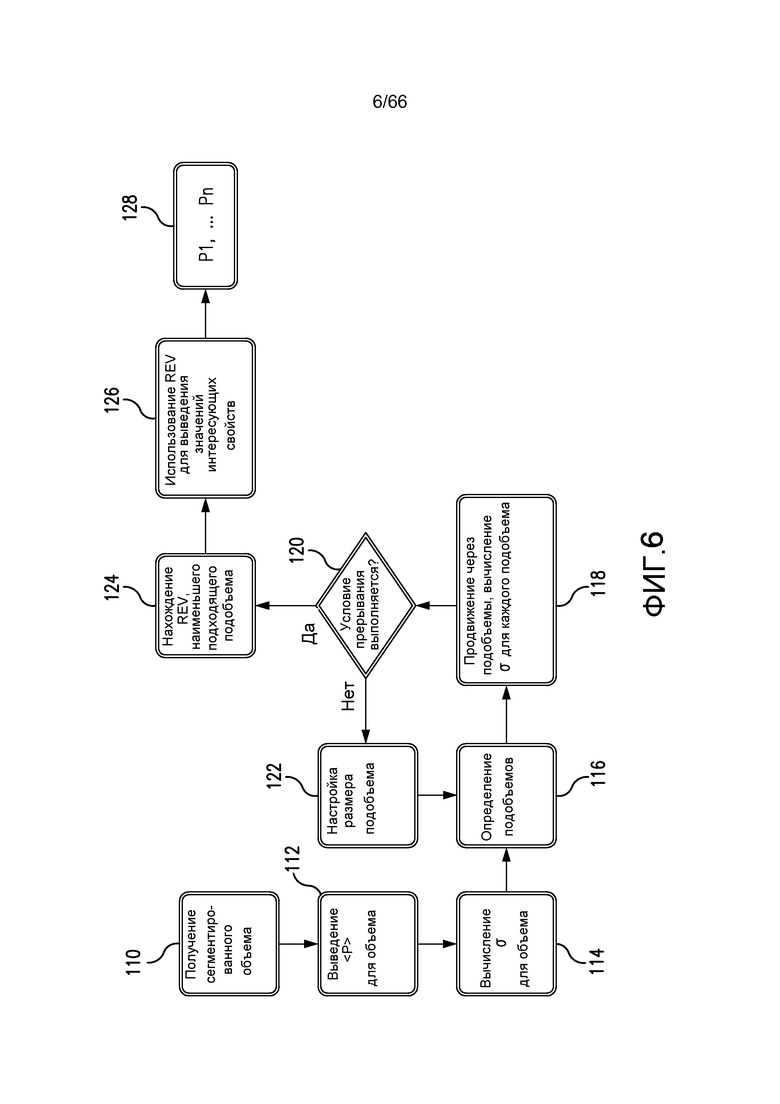

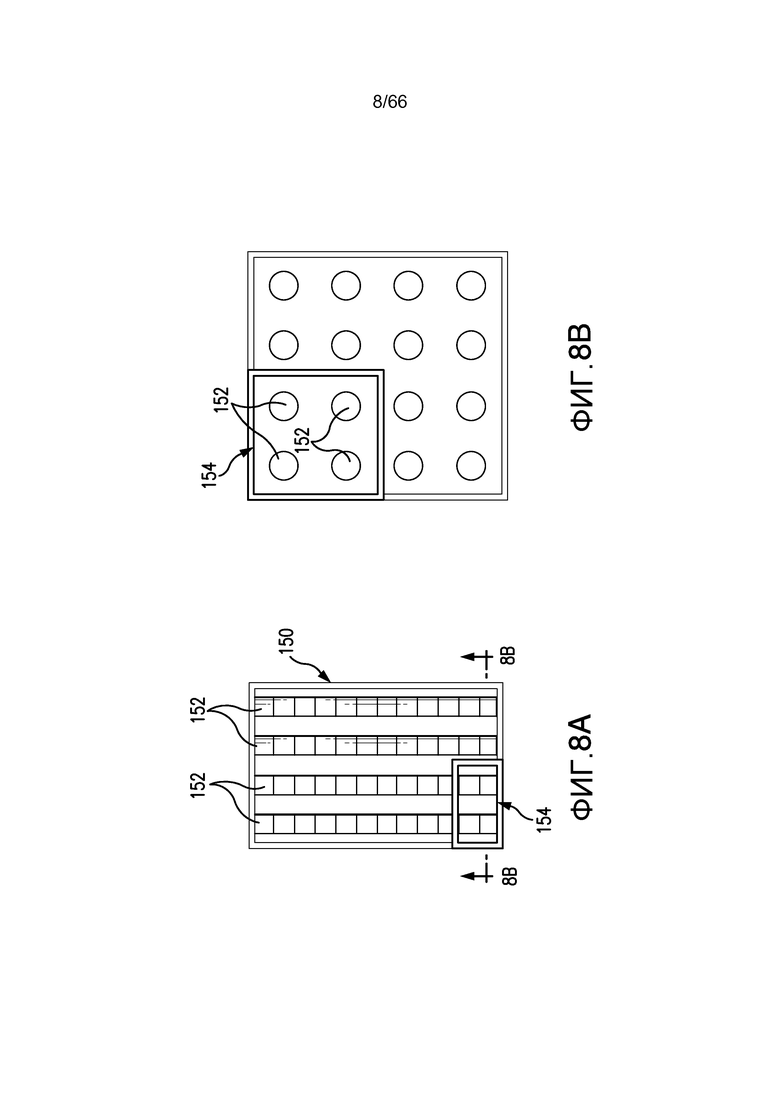

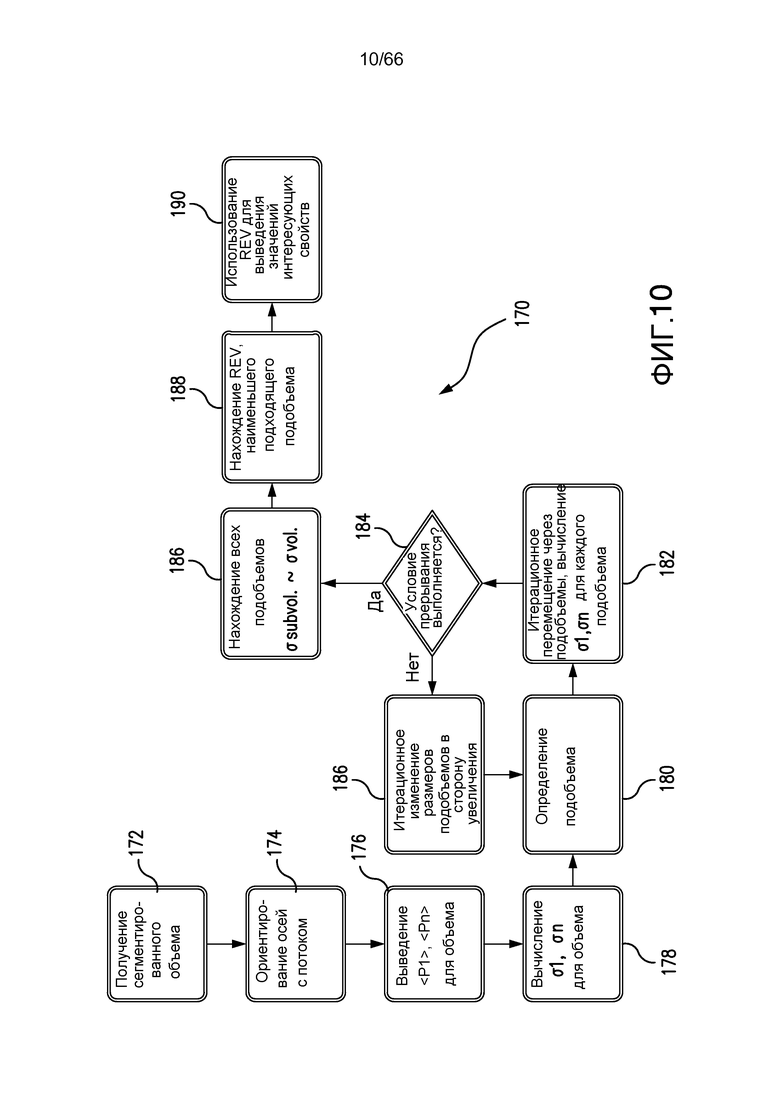
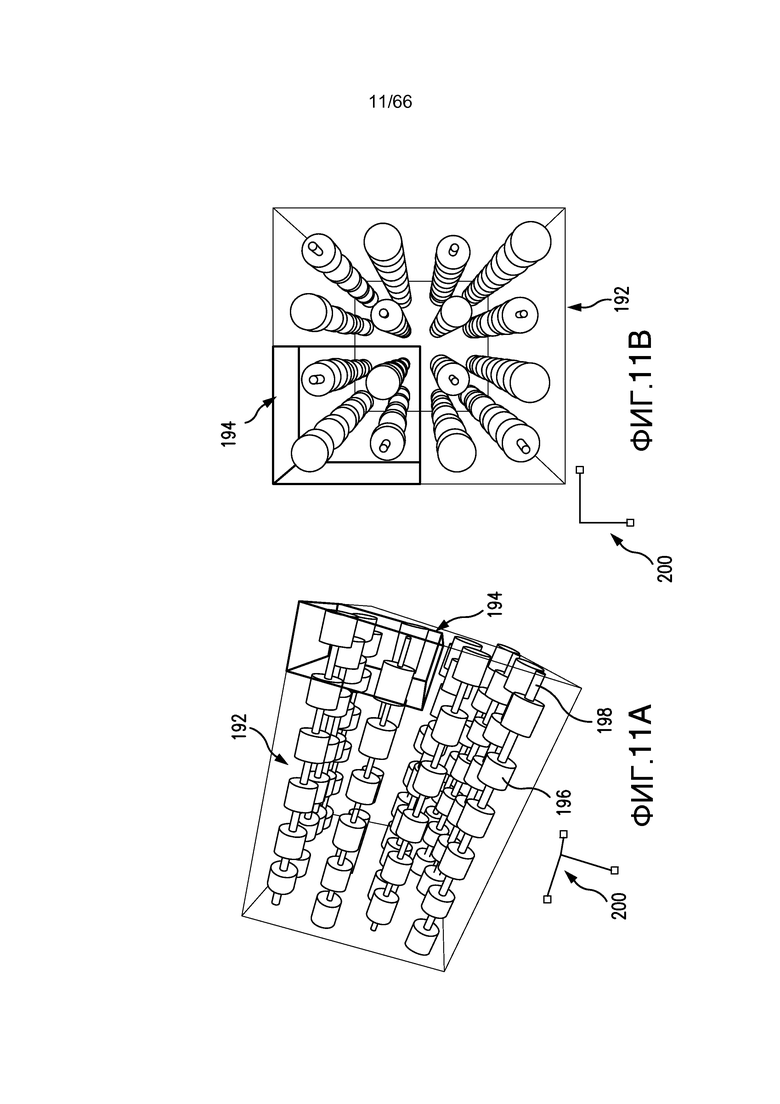

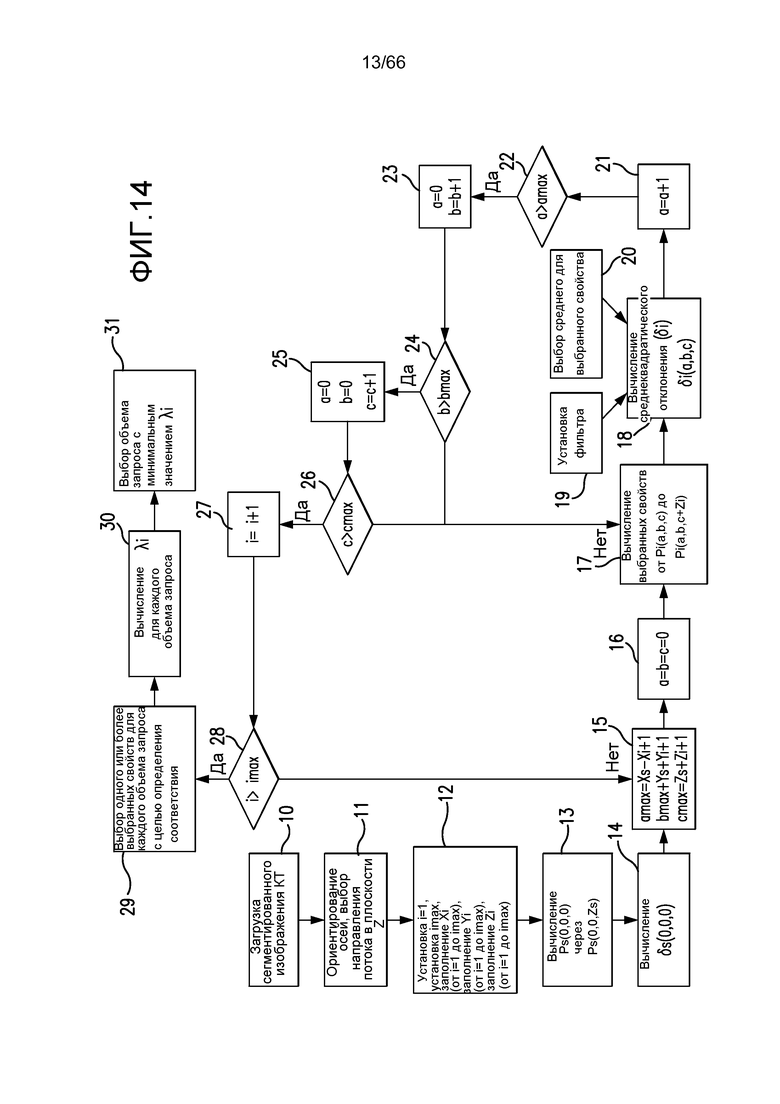



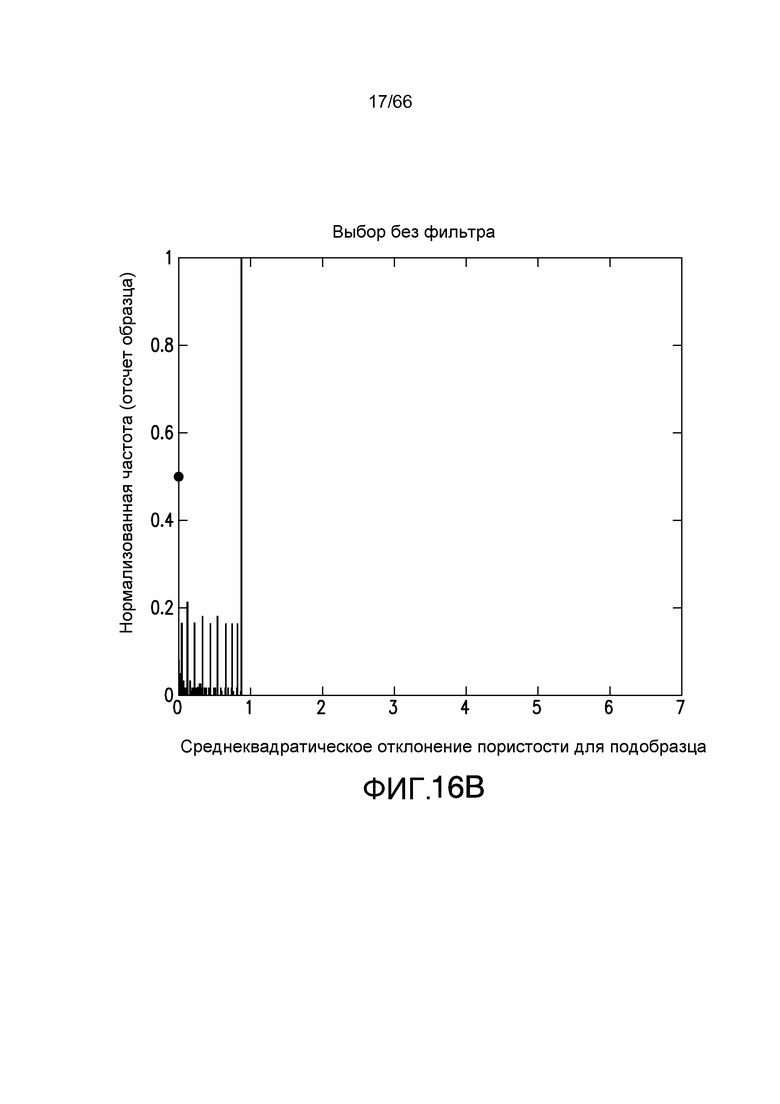
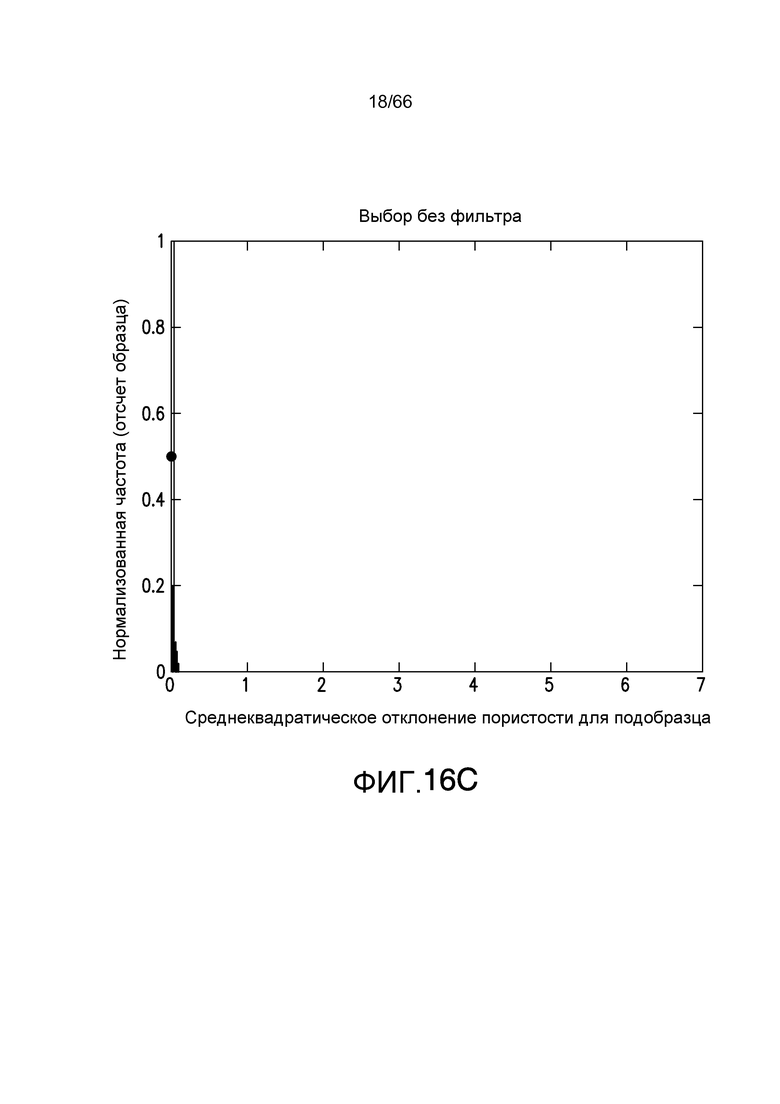
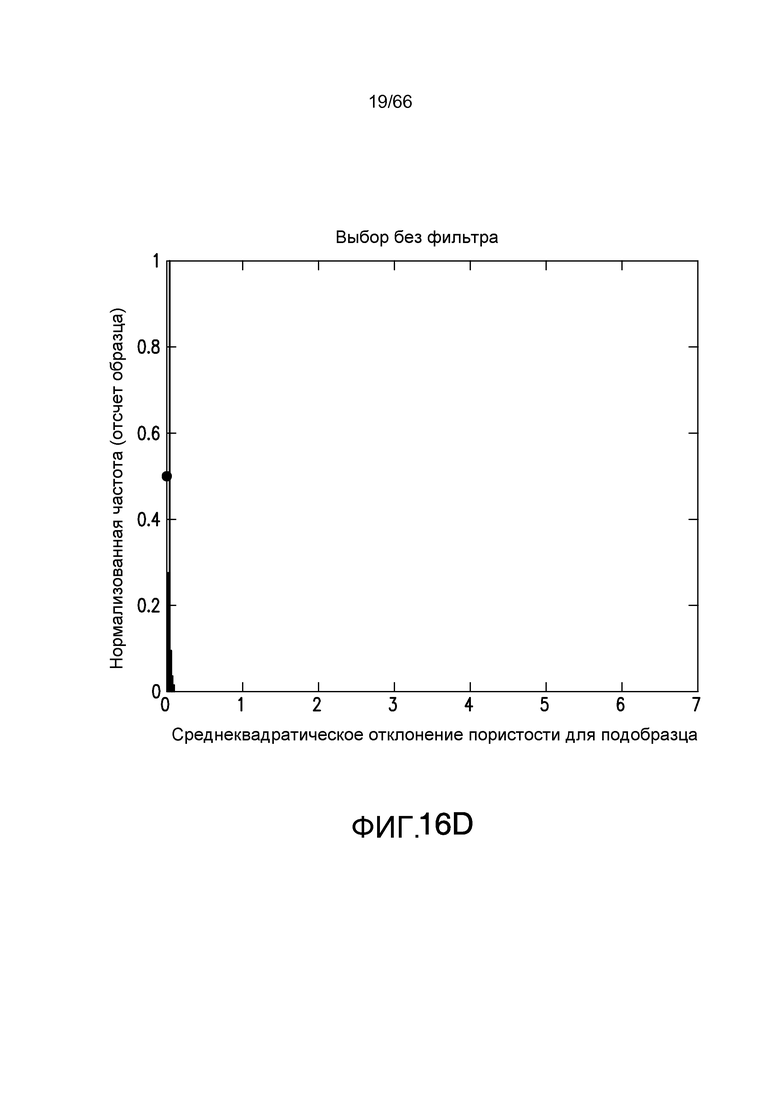



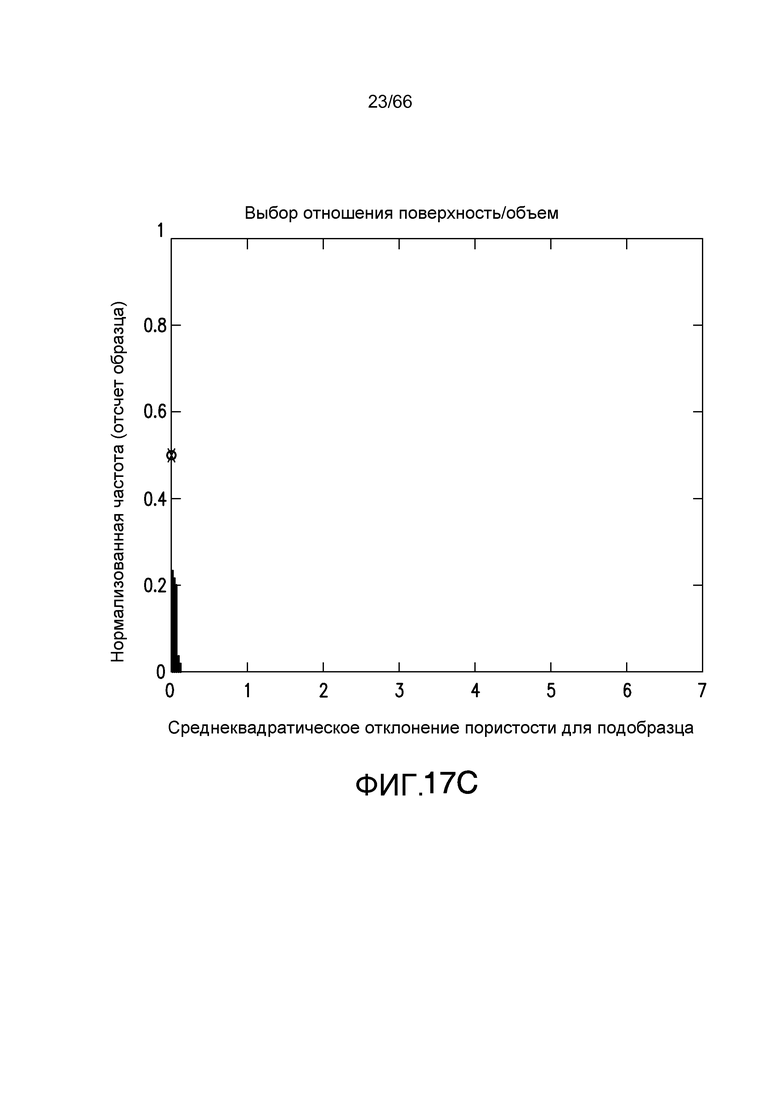
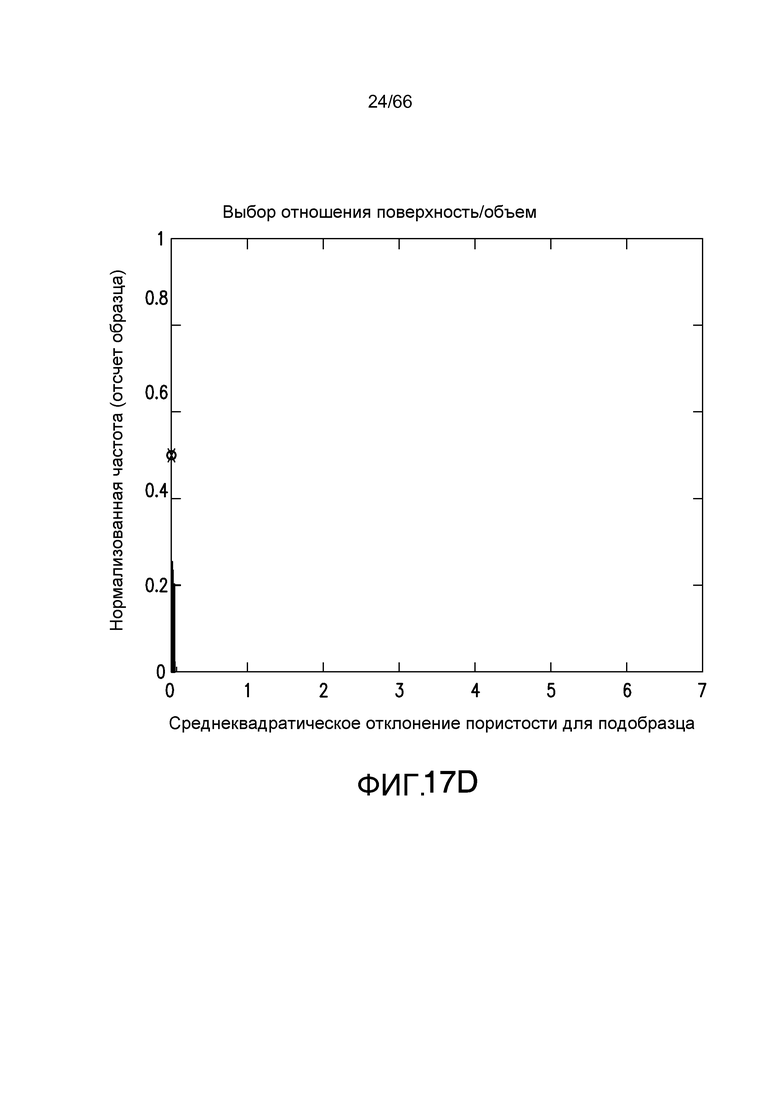
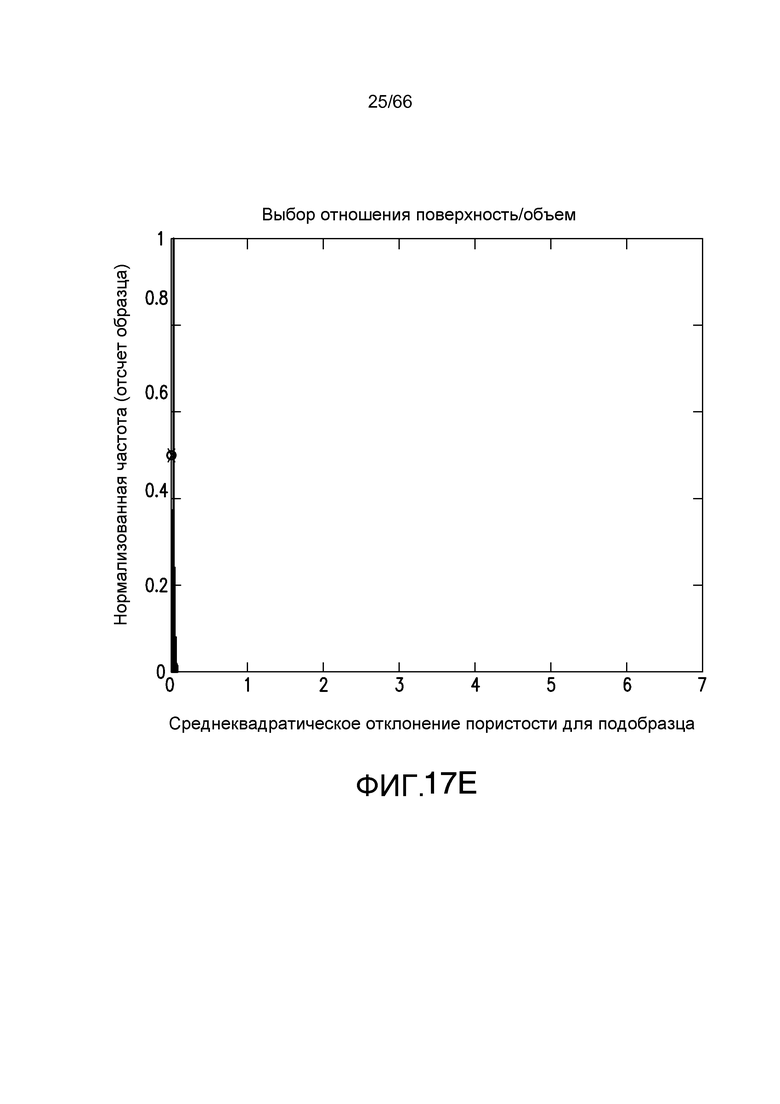
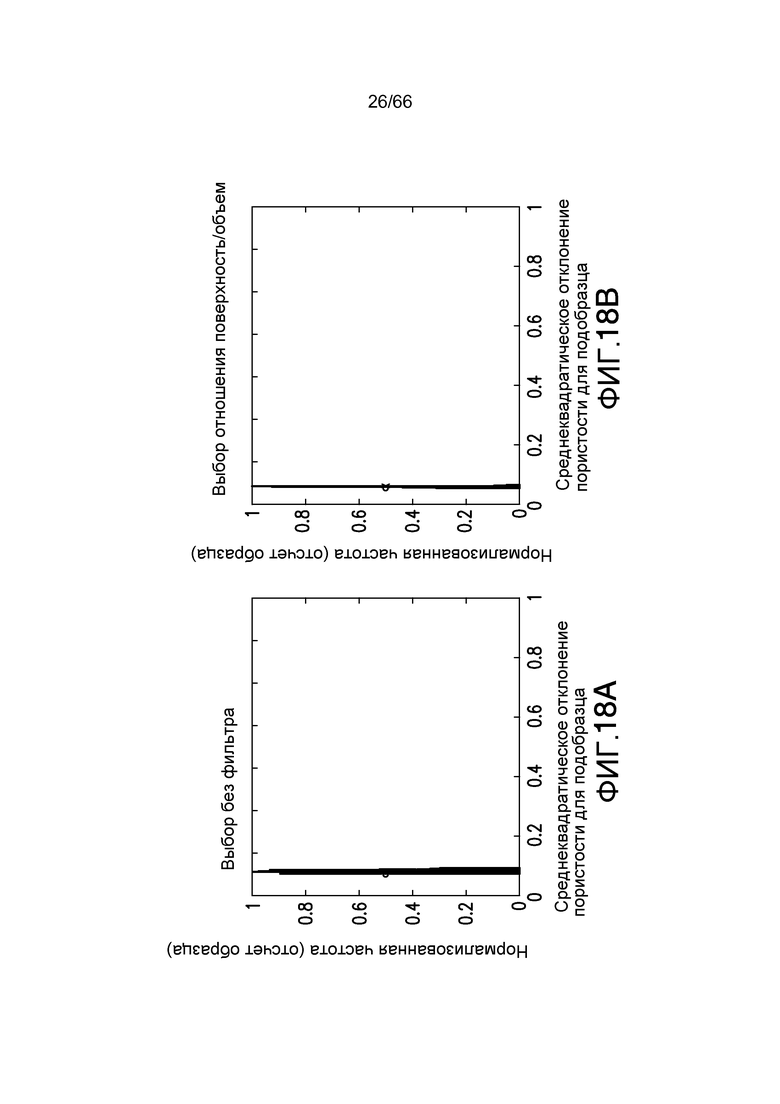
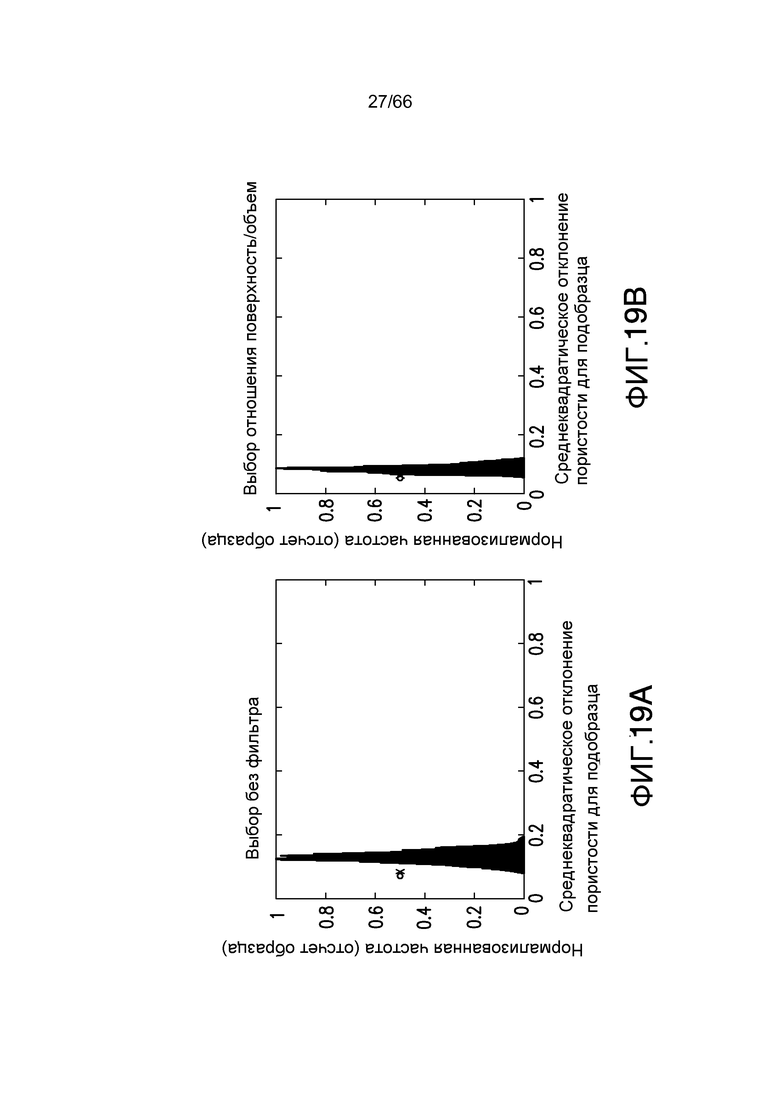
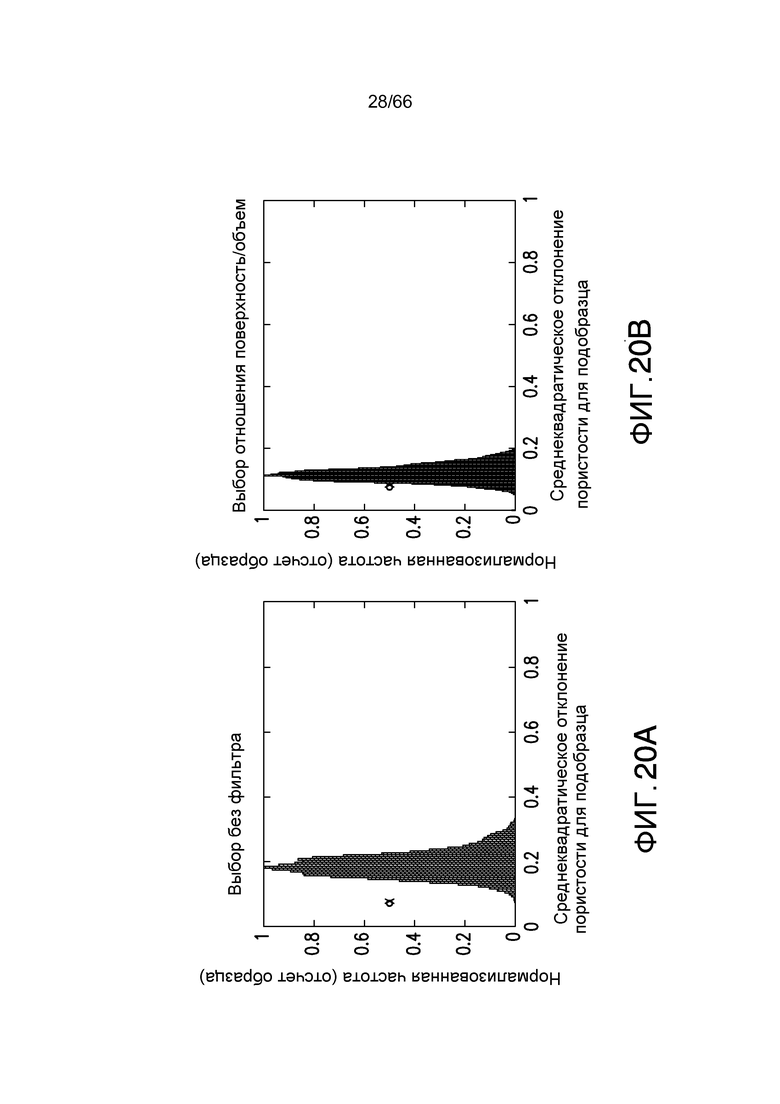


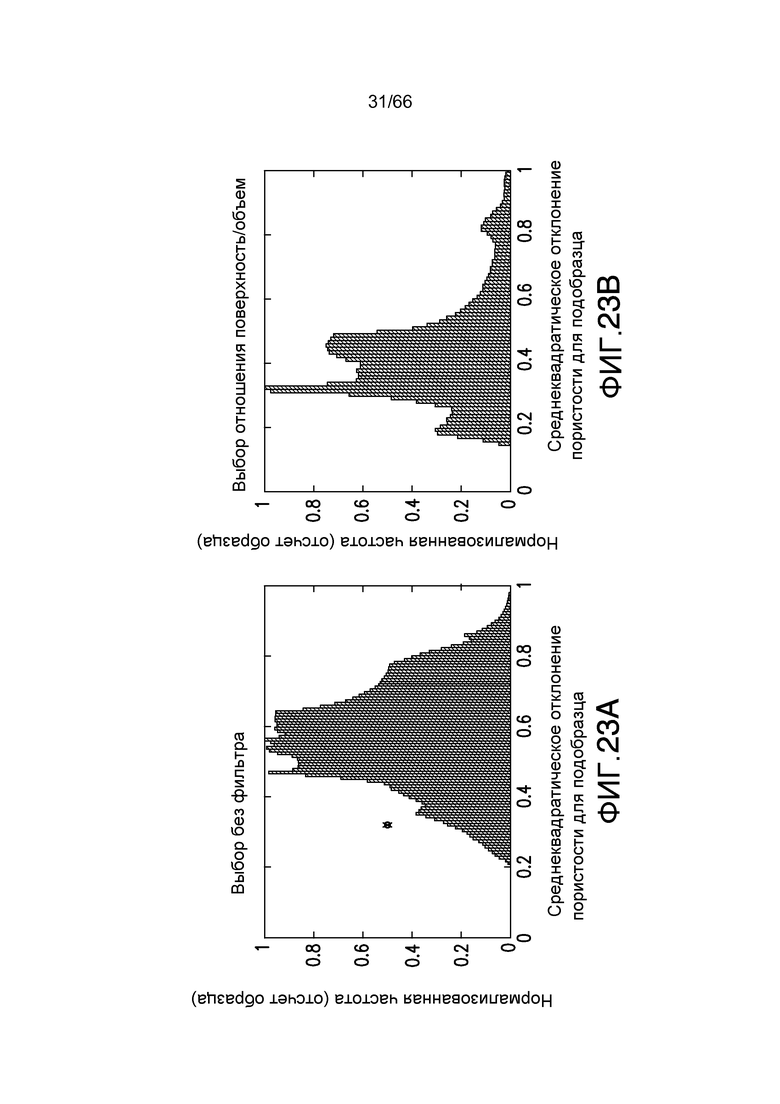
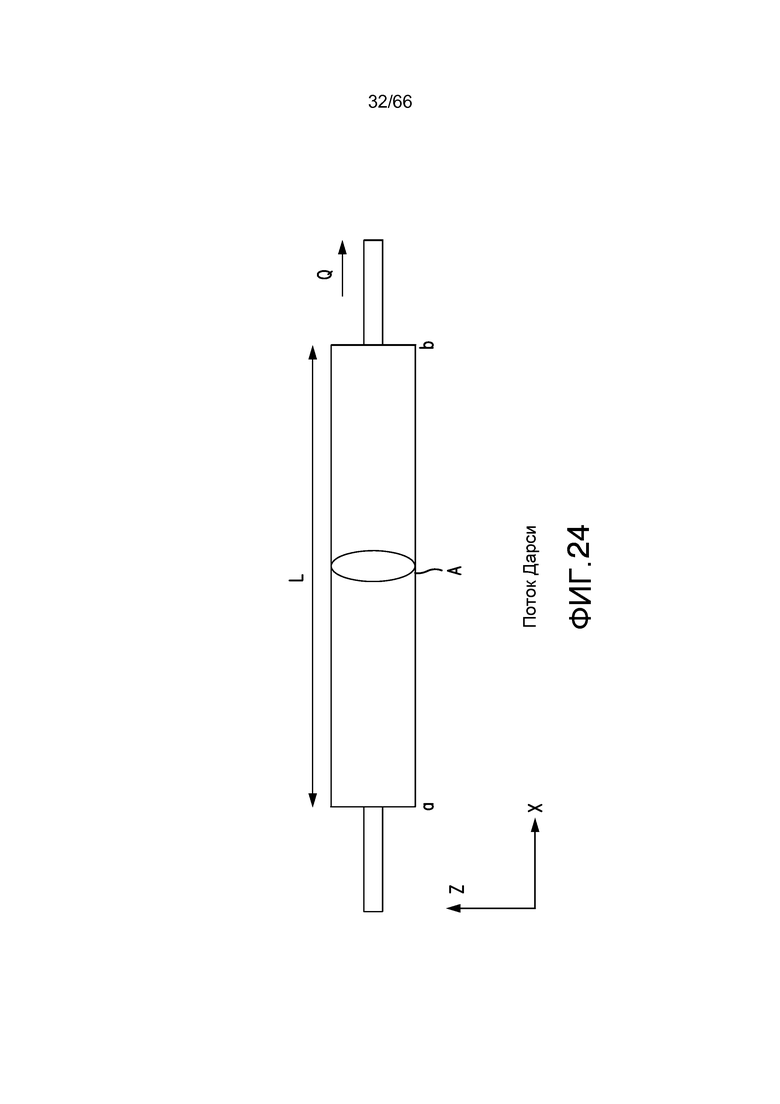

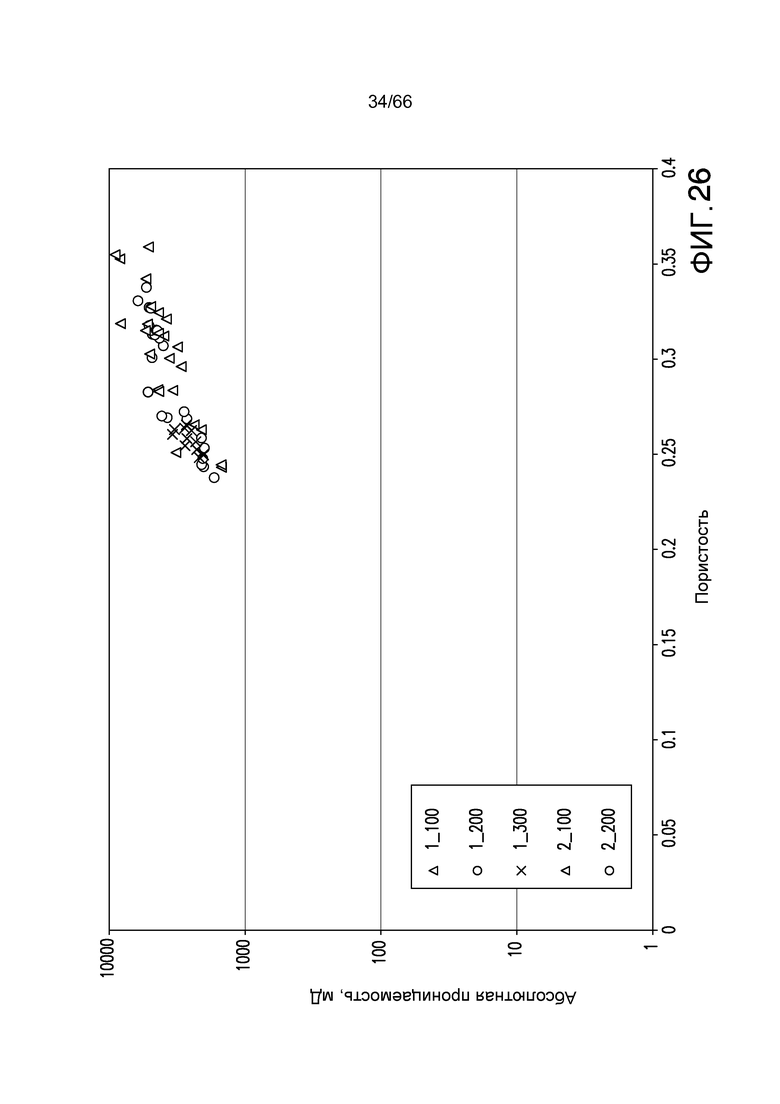



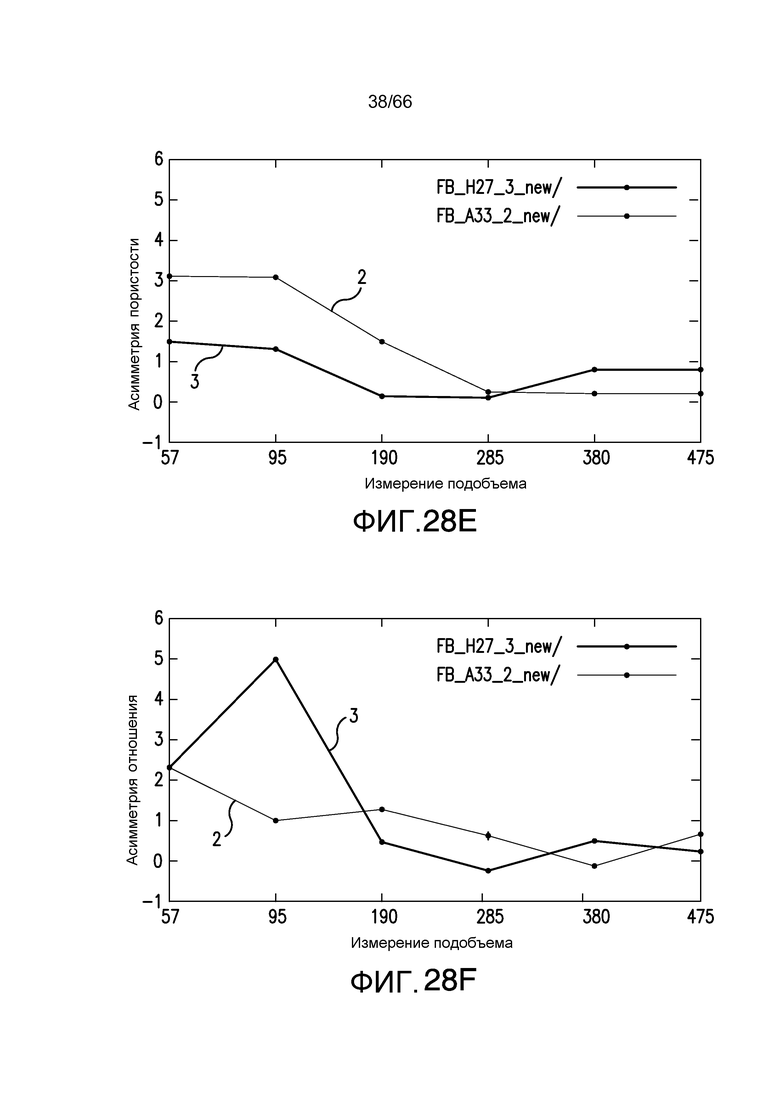

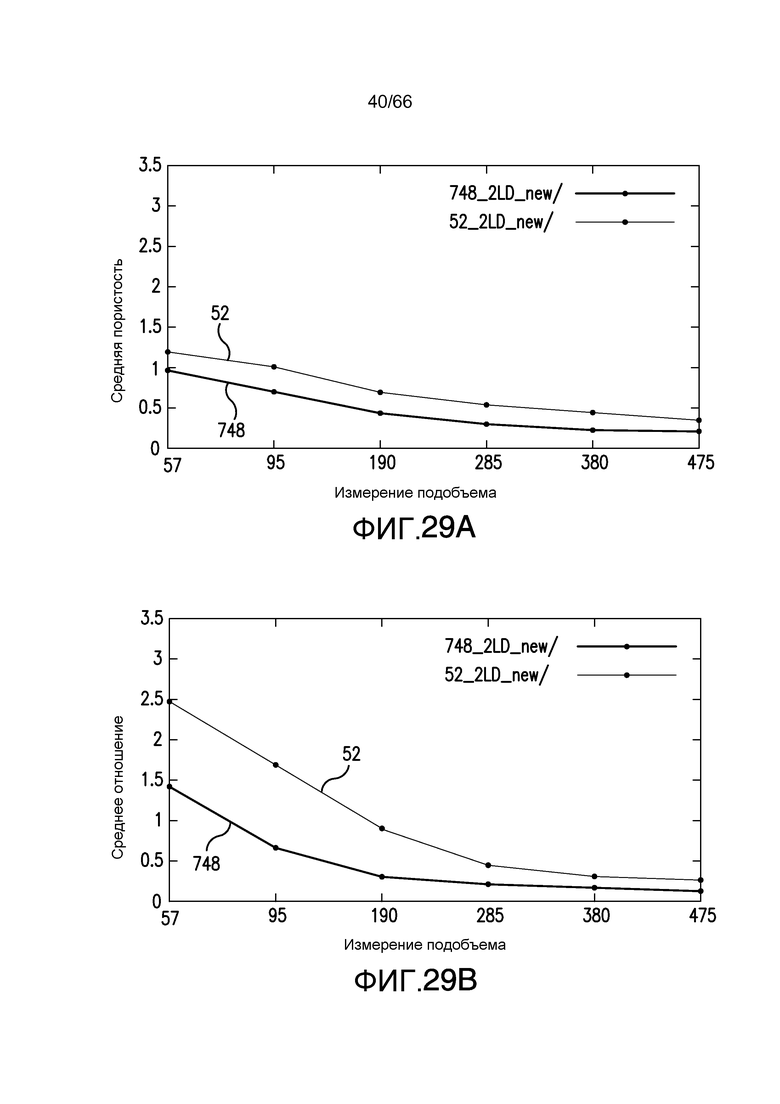

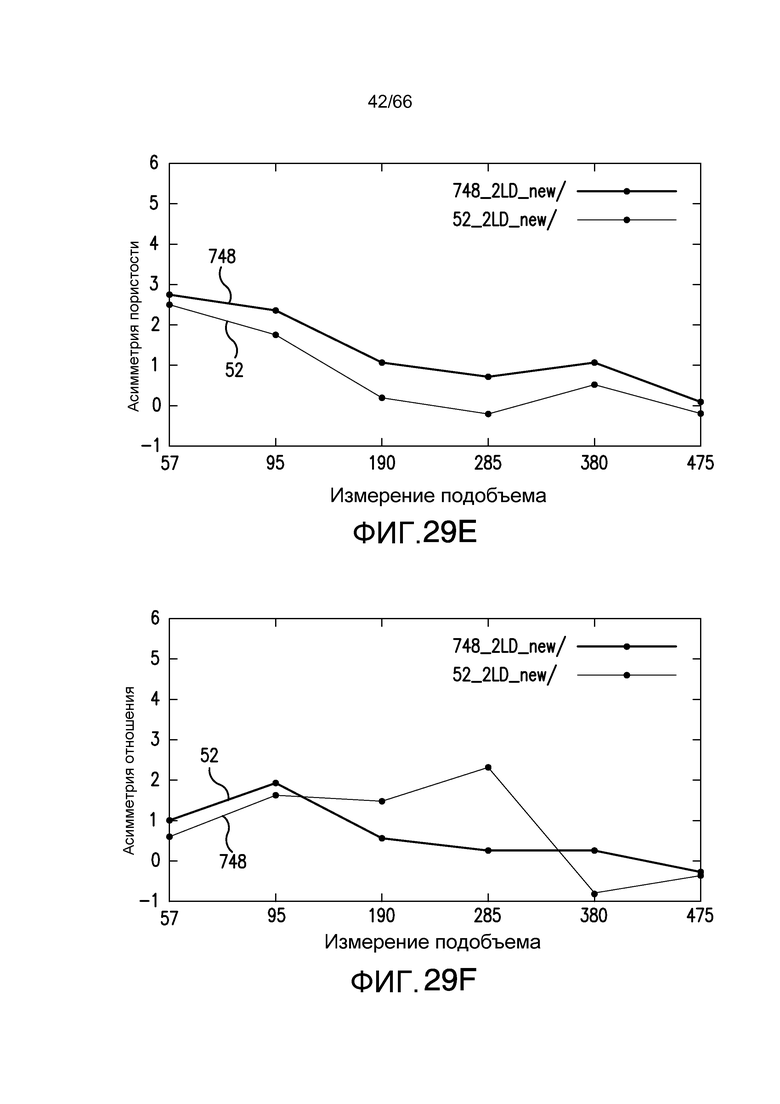










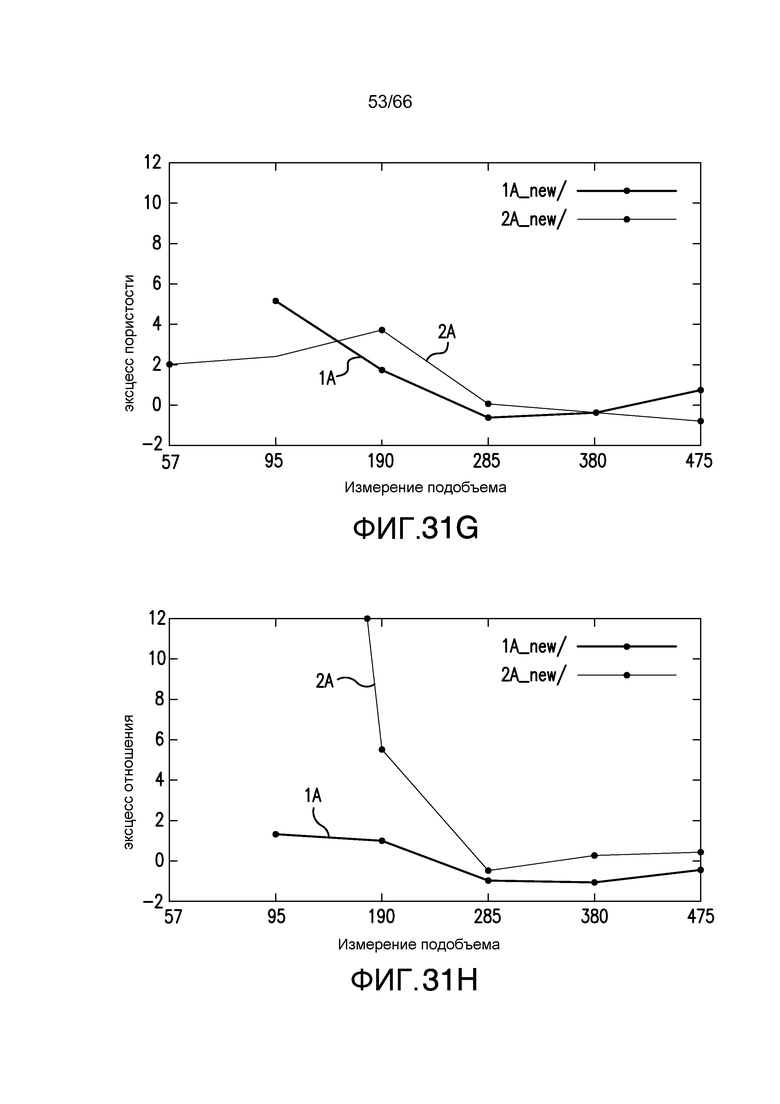

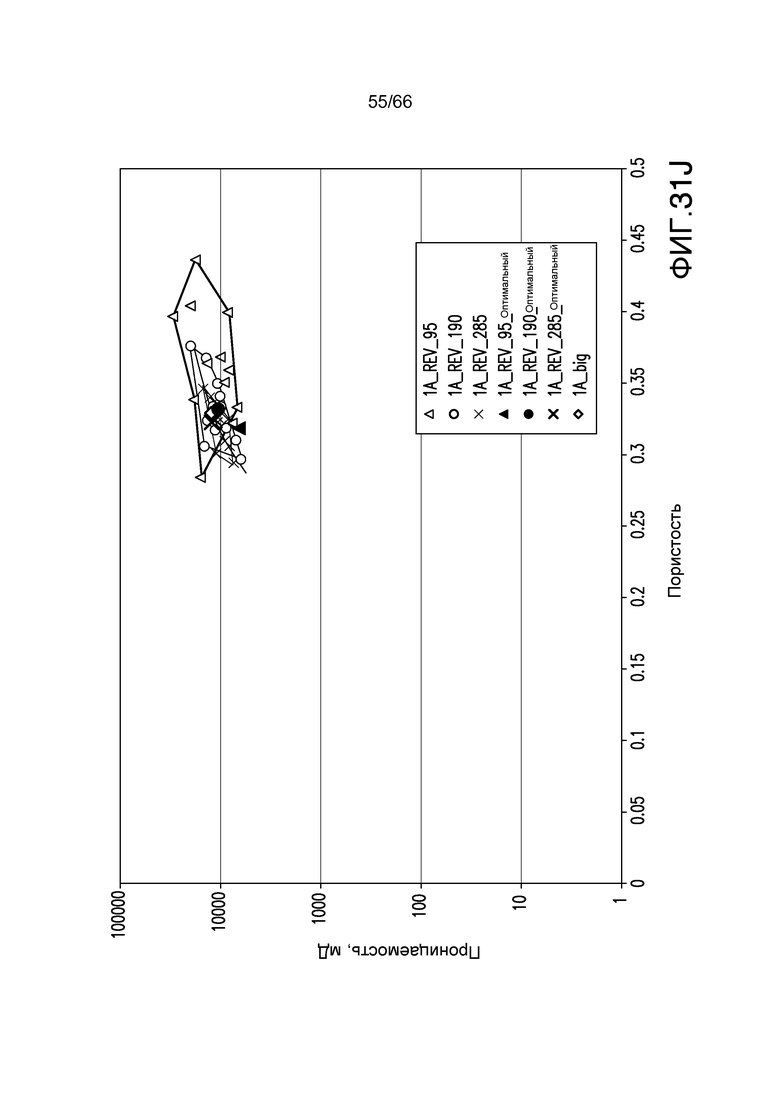


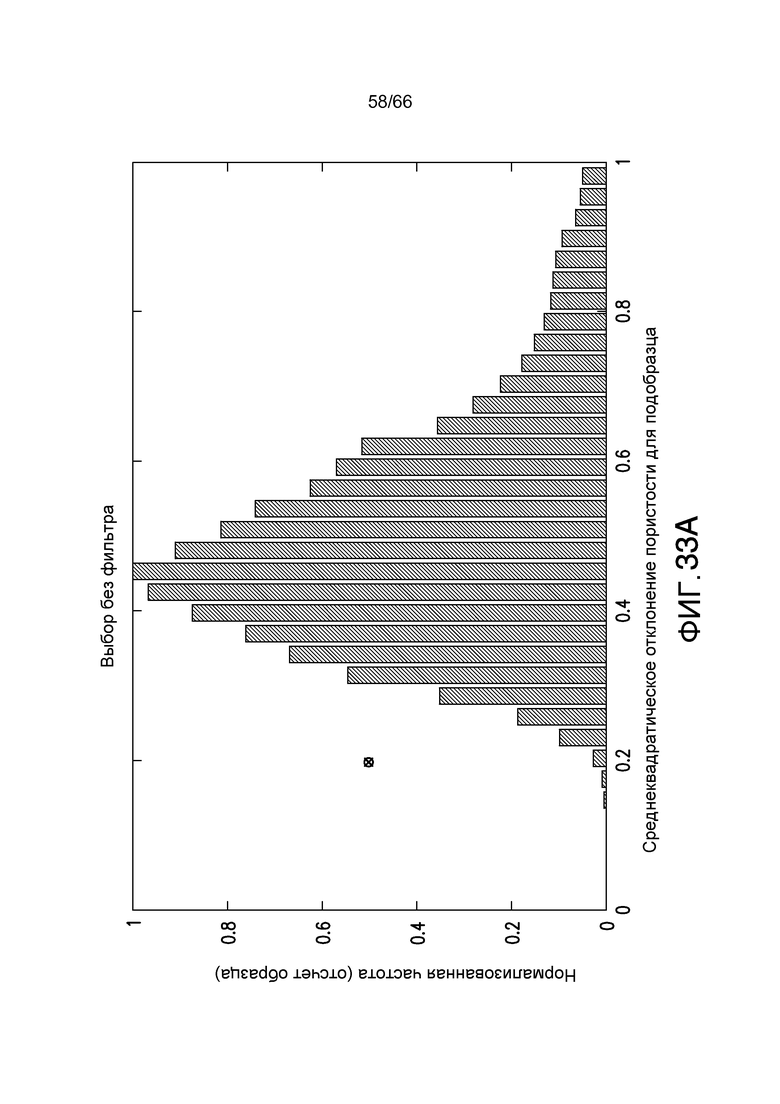






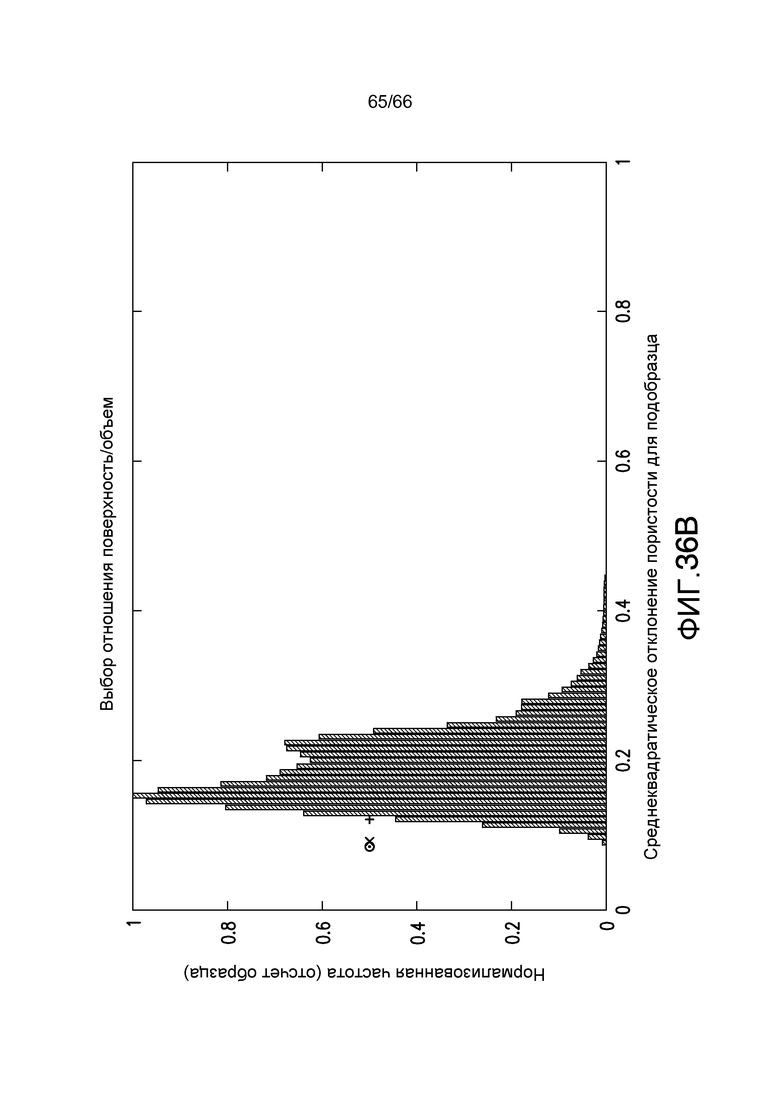

Использование: для идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред. Сущность изобретения заключается в том, что получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу; выводят среднее значение <Р1> свойства первой целевой функции Р1 для всего сегментированного объема; вычисляют среднеквадратическое отклонение σVOL относительно среднего значения <Р1> свойства для всего сегментированного объема; определяют множество подобъемов в объеме; вычисляют среднеквадратическое отклонение σi значения Р свойства первой целевой функции Р1 относительно среднего значения <Р1> свойства для каждого из упомянутых подобъемов; находят все репрезентативные подобъемы-кандидаты, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL; выбирают и сохраняют репрезентативный подобъем из кандидатов; и используют репрезентативный подобъем для получения по меньшей мере одного интересующего значения свойства. Технический результат: обеспечение возможности повышения достоверности оценки репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред. 6 н. и 15 з.п. ф-лы, 92 ил.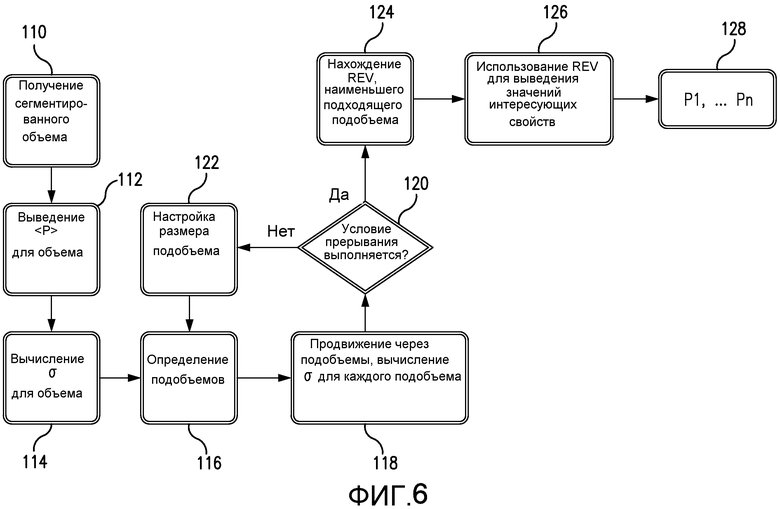
1. Способ идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, содержащий этапы, на которых:
a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу;
b) выводят среднее значение <Р1> свойства первой целевой функции Р1 для всего сегментированного объема;
c) вычисляют среднеквадратическое отклонение σVOL относительно среднего значения <Р1> свойства для всего сегментированного объема;
d) определяют множество подобъемов в объеме;
e) вычисляют среднеквадратическое отклонение σi значения Р свойства первой целевой функции Р1 относительно среднего значения <Р1> свойства для каждого из упомянутых подобъемов;
f) находят все репрезентативные подобъемы-кандидаты, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL;
g) выбирают и сохраняют репрезентативный подобъем из кандидатов; и
h) используют репрезентативный подобъем для получения по меньшей мере одного интересующего значения свойства.
2. Способ по п. 1, в котором этап, в котором определяют множество подобъемов в пределах объема, дополнительно содержит этапы, на которых:
определяют исходный размер для подобъема;
заполняют весь объем подобъемами определенного исходного размера; и
итерируют размеры для последующих подобъемов и заполняют весь объем подобъемами такого размера, и повторяют этот этап до тех пор, пока не будет выполнено условие прерывания.
3. Способ по п. 2, в котором итерируют размеры от большего к меньшему с малым приращением.
4. Способ по п. 3, в котором этап, на котором выбирают и сохраняют репрезентативный объем, дополнительно содержит этап, на котором находят наименьший репрезентативный цифровой объем.
5. Способ по п. 4, в котором условие прерывания содержит заданный размер для подобъема.
6. Способ по п. 2, дополнительно содержащий этапы, на которых:
ориентируют выбранную ось декартовой системы координат сегментированного объема с определенным направлением потока; и причем
этап, на котором выводят среднее значение <Р1> свойства первой целевой функции Р1 для всего сегментированного объема, содержит этап, на котором анализируют множество цифровых срезов объема образца, взятых ортогонально к определенному направлению потока; и
этап, на котором вычисляют среднеквадратическое отклонение σi свойства Р первой целевой функции Р1 относительно среднего значения <Р1> свойства для каждого из упомянутых подобъемов, выполняется относительно определенного направления потока.
7. Способ по п. 6, дополнительно содержащий этапы, на которых:
выводят среднее значение <Р2> свойства второй целевой функции Р2 для всего сегментированного объема;
вычисляют среднеквадратическое отклонение σVOL относительно среднего значения <Р2> свойства для всего сегментированного объема;
определяют множество подобъемов в объеме;
вычисляют среднеквадратическое отклонение σi значения свойства Р второй целевой функции Р2 относительно среднего значения <Р2> свойства для каждого из упомянутых подобъемов;
находят все репрезентативные подобъемы, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL для сочетания первой целевой функции Р1 и второй целевой функции Р2.
8. Способ по п. 7, в котором первая целевая функция Р1 представляет собой пористость и вторая целевая функция Р2 представляет собой отношение площади поверхности к объему пространств пор.
9. Способ по п. 8, дополнительно содержащий этап, на котором квалифицируют подобъем-кандидат до его выбора, содержащий этап, на котором определяют его пригодность для использования при выведении свойств транспортировки текучих сред с помощью закона Дарси, причем на упомянутом этапе:
строят распределение среднеквадратического отклонения целевых функций;
оценивают среднее значение или при необходимости любую другую характеристику первого порядка для распределения среднеквадратического отклонения целевой функции и дисперсию, эксцесс или асимметрию распределения;
оценивают тенденцию момента первого или более высокого порядка относительно размера подобъема; и
останавливают уменьшение размера подобъема в случае, когда момент первого порядка изменяется по меньшей мере на 0,1 относительно его величины для распределения, основанного на большем подобъеме, и/или когда моменты более высокого порядка превышают конкретную пороговую величину 0,1 для дисперсии.
10. Способ идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, содержащий этапы, на которых:
a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу;
b) ориентируют выбранную ось декартовой системы координат сегментированного объема с определенным направлением потока;
c) выводят значения как одну или более функций по меньшей мере первой целевой функции Р1 для всего сегментированного объема посредством анализа цифровых срезов, ортогональных определенному направлению потока;
d) определяют множество подобъемов в пределах объема;
e) вычисляют значения для одной или более функций по меньшей мере первой целевой функции Р1 для каждого из упомянутых подобъемов, соответствующих определенному направлению потока;
f) находят все репрезентативные подобъемы-кандидаты, для которых функция(-и) идентифицирует(-ют) соответствие между величинами значений объема и подобъема;
g) выбирают репрезентативный объем из кандидатов;
h) сохраняют репрезентативный подобъем; и
i) используют репрезентативный подобъем для моделирования или выведения по меньшей мере одного интересующего значения свойства.
11. Способ получения эффективной оценки репрезентативного элементарного объема по большему цифровому 3-D изображению пористого образца, содержащий этапы, на которых:
a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу;
b) выводят значения как по меньшей мере одну функцию для по меньшей мере первой целевой функции Р1 для всего сегментированного объема;
c) определяют множество подобъемов в пределах объема, причем данный этап содержит этапы, на которых:
определяют исходный размер для подобъема,
заполняют весь объем подобъемами определенного исходного размера,
итерируют размеры для последующих подобъемов и заполняют весь объем подобъемами такого размера, и повторяют этот этап до тех пор, пока не будет выполнено условие прерывания;
d) вычисляют значения как по меньшей мере одну функцию для по меньшей мере первой целевой функции для каждого из упомянутых подобъемов;
е) находят все репрезентативные подобъемы-кандидаты для достаточно удовлетворяющих друг другу значений объема и подобъема;
f) выбирают и сохраняют репрезентативный подобъем из кандидатов; и
g) используют репрезентативный подобъем для проведения симуляции или выведения по меньшей мере одного интересующего значения свойства.
12. Способ по п. 11, дополнительно содержащий этап, на котором квалифицируют подобъем-кандидат до его выбора, содержащий этап, на котором определяют его соответствие для использования в выведении свойств транспортировки текучих сред с помощью закона Дарси, причем на упомянутом этапе:
строят распределение среднеквадратического отклонения целевых функций;
оценивают среднее значение или при необходимости любую другую характеристику первого порядка для распределения среднеквадратического отклонения целевой функции и дисперсию, эксцесс или асимметрию распределения;
оценивают тенденцию момента первого или более высокого порядка относительно размера подобъема; и
останавливают уменьшение размера подобъема в случае, когда момент первого порядка изменится по меньшей мере на 0,1 относительно его величины для распределения, основанного на большем подобъеме, и/или когда моменты более высокого порядка превышают конкретную пороговую величину 0,1 для дисперсии.
13. Способ получения эффективной оценки репрезентативного элементарного объема из большего 3-D цифрового изображения пористого образца, содержащий этапы, на которых:
a) получают сегментированный объем, характеризующий пространство пор и по меньшей мере одну твердую фазу;
b) ориентируют выбранную ось декартовой системы координат сегментированного объема к определенному направлению потока;
c) выводят среднее значение <Р1> свойства первой целевой функции Р1 для всего сегментированного объема с применением анализа множества цифровых срезов объема образца, взятых ортогонально к определенному направлению потока;
d) вычисляют среднеквадратическое отклонение относительно среднего значения <Р1> свойства для всего сегментированного объема;
e) определяют множество подобъемов в пределах объема, причем на упомянутом этапе:
определяют исходный размер для подобъема;
заполняют весь объем подобъемами определенного исходного размера,
итерируют размеры для дополнительных подобъемов от большего к меньшему и заполняют весь объем подобъемами такого размера, и
повторяют этот этап до тех пор, пока не будет выполнено условие прерывания;
f) вычисляют среднеквадратическое отклонение σi свойства Р относительно среднего значения <Р1> свойства для каждого из упомянутых подобъемов в отношении определенного направления потока;
д) находят все репрезентативные подобъемы-кандидаты, для которых σi удовлетворительно соответствует σVOL;
h) выбирают наименьший кандидат и сохраняют его в качестве репрезентативного элементарного объема; и
i) используют репрезентативный элементарный объем для выведения по меньшей мере одного интересующего значения свойства.
14. Способ по п. 13, дополнительно содержащий этапы, на которых:
выводят среднее значение <Р2> свойства второй целевой функции Р2 для всего сегментированного объема;
вычисляют среднеквадратическое отклонение относительно среднего значения <Р2> свойства для всего сегментированного объема;
определяют множество подобъемов в объеме;
вычисляют среднеквадратическое отклонение σi второй целевой функции Р2 относительно среднего значения <Р2> свойства для каждого из упомянутых подобъемов;
находят все репрезентативные подобъемы, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL для комбинации первой целевой функции Р1 и второй целевой функции Р2.
15. Способ по п. 14, в котором первая целевая функция Р1 представляет собой пористость и вторая целевая функция Р2 представляет собой отношение площади поверхности к объему пространств пор.
16. Способ по п. 15, дополнительно содержащий этап, на котором квалифицируют подобъем-кандидат до его выбора, содержащий этап, на котором определяют его соответствие для использования в выведении свойств транспортировки текучих сред с помощью закона Дарси, причем на упомянутом этапе:
строят распределение среднеквадратического отклонения целевых функций;
оценивают среднее значение или при необходимости любую другую характеристику первого порядка для распределения среднеквадратического отклонения целевой функции и дисперсию, эксцесс или асимметрию распределения;
оценивают тенденцию момента первого или более высокого порядка относительно размера подобъема; и
останавливают уменьшение размера подобъема в случае, когда момент первого порядка изменяется по меньшей мере на 0,1 относительно его величины для распределения, основанного на большем подобъеме, и/или когда моменты более высокого порядка превышают конкретную пороговую величину 0,1 для дисперсии.
17. Способ идентификации репрезентативного цифрового объема репрезентативного подобразца соответствующего образцу пористых сред, содержащий этапы, на которых
1) загружают сегментированное трехмерное изображение пористой среды в компьютерную систему,
причем сегментированное трехмерное изображение содержит вокселы, каждому из которых присвоено значение по шкале полутонов;
2) выбирают направление потока, которое определяется как направление Z;
3) определяют размеры объемов запроса, причем
i) объем запроса представляет собой подобразец исходного сегментированного трехмерного изображения с размерами Xi, Yi и Zi, причем размеры всего образца составляют Xs, Ys, Zs,
ii) определяют максимальное число объемов запроса, imax,
iii) устанавливают размеры в вокселах для каждого объема запроса (Xi, Yi, Zi), причем Xi, Yi и Zi определяют для значений i от 1 до imax, и
iv) начальное значение i устанавливают равным 1;
4) вычисляют выбранные свойства Ps(0, 0, 0) через Ps(0, 0, Zs) для каждого среза объема запроса;
5) вычисляют σs (0, 0, 0);
6) устанавливают максимальные координаты таким образом, что объем запроса размера Xi, Yi, Zi занимает весь образец размера Xs, Ys, Zs, причем
i) amax = Xs-Xi+1,
ii) bmax = Ys-Yi+1,
iii) cmax = Zs-Zi+1;
7) устанавливают координаты положения текущего объема запроса на а=b=с=0;
8) вычисляют выбранные свойства Pi(а, b, с) через Pi (а, b, c+Zi) для сечений текущего объема запроса,
i) причем выбранные свойства содержат пористость, отношение площади поверхности к объему, подобные свойства или произвольное их сочетание,
9) вычисляют σi (а, b, с),
i) причем значения Pi, которые используют для вычисления значения σi, при необходимости фильтруют,
ii) причем при необходимости устанавливают среднее значение для Pi;
10) перемещают положения объема запроса на 1 воксел в направлении X, а=а+1;
11) повторяют этапы 8)-10) и сохраняют все величины Pi и σi, пока значение Х-координаты текущего объема запроса, а, не будет равно максимальному значению, которое может занимать текущий объем запроса, amax;
12) устанавливают координату X текущего объема запроса равной нулю, а=0, и увеличивают координаты Y текущего положение объема на один воксел, b=b+1;
13) повторяют этапы 8)-12), и сохраняют все величины Pi и σi, пока значение Y-координаты текущего объема запроса, b, не будет равно максимальному значению, которое может занимать текущий объем запроса, bmax;
14) устанавливают координату X текущего объема запроса равной нулю, а=0, устанавливают координату Y текущего объема запроса равной нулю, b=0, и увеличивают координаты Z текущего положения объема на один воксел, с=с+1;
15) повторяют этапы 8)-14), и сохраняют все величины Pi и σi, пока значение Z-координаты текущего объема запроса, с, не будет равно максимальному значению, которое может занимать текущий объем запроса, cmax;
16) увеличивают размер текущего объема запроса, причем на упомянутом этапе
i) выбирают следующее множество объемов запроса посредством увеличения указателя до следующего объема запроса, i=i+1, и
ii) устанавливают текущий размер запроса на Xi, Yi, Zi;
17) повторяют этапы 6)-16), пока все объемы запроса не будут выбраны и все величины Pi и σi не будут вычислены и сохранены;
18) выбирают одно или более выбранных свойств для сопоставления;
19) вычисляют λi для каждого объема запроса;
20) выбирают объем запроса с наименьшим значением λi, причем выбранный объем запроса является размером и положением REV; и
21) вычисляют свойства пористой среды.
18. Способ по п. 17, в котором сегментированное трехмерное изображение получают как изображение образца, полученное посредством сканирования образца сканером рентгеновской компьютерной томографии, и сегментируют изображение посредством программы, чтобы классифицировать вокселы как зерно, пору и при необходимости как другие фазы.
19. Способ по п. 17, в котором свойства содержат свойства стандартного анализа кернов (RCAL) и специального анализа кернов (SCAL) или обоих анализов.
20. Способ по п. 19, в котором свойствами анализа RCAL являются пористость, содержание керогена, абсолютная проницаемость по множеству осей, и свойствами SCAL являются относительная проницаемость, капиллярное давление, гранулометрический состав, электрические свойства, упругие свойства и любые их сочетания.
21. Система для идентификации репрезентативного цифрового объема подобразца, соответствующего образцу пористых сред, содержащая:
a) сканер, выполненный с возможностью формирования трехмерного цифрового изображения пористой среды,
b) компьютер, содержащий по меньшей мере один процессор, выполненный с возможностью исполнения компьютерной программы, выполненной с возможностью получения сегментированного объема, характеризующего пространство пор и по меньшей мере одну твердую фазу,
c) компьютер (тот же или отличный от b)), содержащий по меньшей мере один процессор, выполненный с возможностью выполнения компьютерной программы, выполненной с возможностью выполнения вычислений, причем упомянутые вычисления содержат этапы, на которых i) выводят среднее значение <Р1> свойства первой целевой функции Р1 для всего сегментированного объема, ii) вычисляют среднеквадратическое отклонение σVOL относительно среднего значения <Р1> свойства для всего сегментированного объема, iii) определяют множество подобъемов в объеме, iv) вычисляют среднеквадратическое отклонение σi значения свойства Р первой целевой функции Р1 относительно среднего значения <Р1> свойства для каждого из упомянутых подобъемов, v) находят все репрезентативные подобъемы-кандидаты, для которых среднеквадратическое отклонение σi удовлетворительно соответствует σVOL, vi) выбирают и сохраняют репрезентативный подобъем из кандидатов и vii) используют репрезентативный подобъем для выведения по меньшей мере одного интересующего значения свойства, и
d) по меньшей мере, одно устройство для отображения, печати или сохранения результатов вычислений.
| US 2011004447A1, 06.01.2011 | |||
| ПЕРЕДАЮЩЕЕ УСТРОЙСТВО, ПРИЕМНОЕ УСТРОЙСТВО, СИСТЕМА МОБИЛЬНОЙ СВЯЗИ И СПОСОБ УПРАВЛЕНИЯ ПЕРЕДАЧЕЙ | 2006 |
|
RU2414072C2 |
| US 8068579B1, 29.11.2011 | |||
| US 20100135536A1, 03.06.2010 | |||
| СПОСОБ ГЕНЕРИРОВАНИЯ ЧИСЛЕННЫХ ПСЕВДОКЕРНОВ С ИСПОЛЬЗОВАНИЕМ ИЗОБРАЖЕНИЙ СКВАЖИНЫ, ЦИФРОВЫХ ОБРАЗОВ ПОРОДЫ И МНОГОТОЧЕЧНОЙ СТАТИСТИКИ | 2009 |
|
RU2444031C2 |
Авторы
Даты
2016-06-10—Публикация
2013-02-04—Подача