Область техники, к которой относится изобретение
Настоящая технология относится к устройству обработки информации, способу обработки информации, программе и носителю информации.
Уровень техники
С бурным развитием технологий обработки информации и технологий связи, документы быстро преобразовывали в цифровую форму независимо от того, являются ли документы общего доступа или частными. С оцифровкой таких документов, многие люди и компании стали проявлять большой интерес к управлению безопасностью электронных документов. Меры противодействия взлому, такому как перехват сообщений или подделка электронных документов, активно исследовались в различных областях в ответ на увеличение к этому интереса. Что касается перехвата сообщений электронных документов, безопасность обеспечивается, например, путем шифрования электронных документов. Кроме того, что касается подделки электронных документов, безопасность обеспечивается, например, с помощью цифровых подписей. Однако когда шифрование или цифровая подпись, которую будут использовать, не имеет высокой устойчивости к взлому, достаточная безопасность не обеспечивается.
Цифровая подпись используется для точного определения автора электронного документа. Соответственно, только автор электронного документа должен иметь возможность генерирования цифровой подписи. Если злоумышленная третья сторона способна сгенерировать ту же самую цифровую подпись, то эта третья сторона может выдавать себя за автора электронного документа. То есть электронный документ подделывается злоумышленной третьей стороной. В отношении безопасности цифровой подписи высказывались различные мнения с целью предотвращения такой подделки. В качестве схем цифровой подписи, которые в настоящее широко используются, известны, например, схема подписи RSA и схема подписи DSA.
Схема подписи RSA принимает в расчет "трудности разложения на простые множители большого составного числа (здесь и далее по тексту задача разложения на простые множители)" в качестве основы безопасности. К тому же, схема подписи DSA принимает в расчет "трудности решения задачи дискретного логарифма" в качестве основы безопасности. Эти основы базируются на тех алгоритмах, которые не имеют эффективного решения задачи разложения на простые множители и задачи дискретного логарифма с использованием классического компьютера. То есть трудности, упомянутые выше, предполагают трудности вычисления на классическом компьютере. Однако считается, что решения задачи разложения на простые множители и задачи дискретного логарифма можно эффективным образом получить путем проведения вычислений с использованием квантового компьютера.
Аналогично схеме подписи RSA и схеме подписи DSA большинство схем цифровой подписи и схем аутентификации ключа общего доступа, которые используются в настоящее время, также принимают в расчет трудности задачи разложения на простые множители или задачи дискретного логарифма в качестве основы безопасности. Таким образом, если квантовый компьютер будет применяться на практике, нельзя будет обеспечить безопасность таких схем цифровой подписи и схем аутентификации ключа общего доступа. Соответственно, желательно, чтобы реализация новых схем цифровой подписи и схем аутентификации ключа общего доступа принимала в расчет в качестве основы безопасности задачу, которая отличалась бы от задач, таких как задача разложения на простые множители и задача решения дискретного логарифма, которые можно легко решить с помощью квантового компьютера. В качестве задачи, которую нелегко решить с помощью квантового компьютера, существует задача, которая относится, например, к многомерному полиному.
Например, в качестве схем цифровой подписи, которые принимают задачу многомерного полинома в качестве основы безопасности, известны схемы, основанные на криптографии Мацумото-Имаи (Matsumoto-Imai (MI)), криптографии, использующие уравнения скрытого поля (HFE), схемы подписи "масло-уксус" (OV) и криптографии, использующие способ ручного преобразования (ТТМ). Например, схема цифровой подписи на основе HFE раскрыта в следующей непатентной литературе 1 и 2.
Перечень цитируемой литературы
Непатентная литература
Непатентная литература 1: Jacques Patarin, «Asymmetric Cryptography with a Hidden Monomial», CRYPTO 1996, pp.45-60
Непатентная литература 2: Patarin, J., Courtois, N., and Goubin, L., «QUARTZ, 128-Bit Long Digital Signatures, In Naccache, D., Ed. Topics in Cryptology» - CT-RSA 2001 (San Francisco, CA, USA, April 2001), vol.2020 of Lecture Notes in Computer Science, Springer-Verlag., pp.282-297.
Раскрытие изобретения
Техническая задача
Как описано выше, задача многомерного полинома показана на примере задачи, которая называется как NP-трудная задача, которую трудно решить даже в том случае, когда используется квантовый компьютер. Обычно схема аутентификации ключа общего доступа, которая имеет задачу многомерного полинома, типичным примером которой служит HFE или тому подобное, использует многостепенную многомерную систему уравнений со специальной функцией-ловушкой. Например, выполнены многостепенная многомерная система уравнений F(x1, …, xn)=y, зависящих от х1, …, xn, и линейные преобразования А и В, и линейные преобразования А и В управляются секретным образом. В этом случае многостепенная многомерная система уравнений F и линейные преобразования А и В представляют собой функции-ловушки.
Объект, который знает функции-ловушки F, А и В, может решить уравнение B(F(A(x1, …, xn)))=у′, зависящее от x1, …, xn. С другой стороны, уравнение B(F(A(x1, …, xn)))=у′, зависящее от х1, …, xn, не может решить объект, который не знает функции-ловушки F, А и В. Используя этот механизм, можно реализовать схему аутентификации ключа общего доступа и схему цифровой подписи, которые имели трудности решения многостепенной многомерной системы уравнений в качестве основы безопасности.
Как упомянуто выше, для того чтобы реализовать схему аутентификации ключа общего доступа или схему цифровой подписи, необходимо подготовить специальную многостепенную многомерную систему уравнений, удовлетворяющую условию B(F(A(x1, …, xn)))=y. Кроме того, во время генерирования подписи, необходимо решить многостепенную многомерную систему уравнений F. По этой причине, имеющаяся многостепенная многомерная система уравнений F была ограничена относительно легко решаемыми уравнениями. То есть в ранее используемых схемах применялась только многостепенная многомерная система уравнений B(F(A(x1, …, xn)))=y объединенного вида из трех функций (функций-ловушек) В, F и А, которые можно относительно легко решить, и, таким образом, трудно обеспечить достаточную безопасность.
Настоящая технология разработана с учетом вышеупомянутых обстоятельств и предназначена для выполнения нового и усовершенствованного устройства обработки информации, нового и усовершенствованного способа обработки информации, новой и усовершенствованной программы и нового и усовершенствованного носителя записи с возможностью осуществления схемы аутентификации ключа общего доступа и схемы цифровой подписи, которые являются эффективными и имеют высокую безопасность, с использованием многостепенной многомерной системы уравнений, для которой не известно эффективное средство решения (функция-ловушка).
Решение задачи
Согласно варианту осуществления настоящей технологии выполнено устройство обработки информации содержащее блок генерирования сообщения для генерирования сообщения на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, который является элементом из набора Kn, блок подачи сообщения, который подает сообщение верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s)), блок генерирования промежуточной информации для генерирования третьей информации на основании первой информации, произвольно выбранной с помощью верифицирующей стороны, и второй информации, полученной во время генерирования сообщения, блок предоставления промежуточной информации для предоставления третьей информации верифицирующей стороне, и блок подачи отклика для предоставления верифицирующей стороне информации отклика, соответствующей образцу верифицирующей стороны, который верифицирующая сторона выбирает из k (где k≥2) образцов верифицирующей стороны. Вектор s представляет собой секретный ключ. Пара многостепенных многомерных полиномов F и векторы y представляют собой ключи общего доступа. Сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верифицирующей стороны, соответствующего информации отклика на основании ключей общего доступа, первой информации, третьей информации и информации отклика. Пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, х2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), был сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
Согласно варианту осуществления настоящей технологии, выполнено устройство обработки информации, включающее в себя блок хранения информации для хранения пары многостепенных многомерных полиномов F=(f1, …, fm) и векторов y=(y1, …, ym)=(f1(s), …, fm(s)), блок получения сообщения для получения сообщения, сгенерированного на основании пары многостепенных многомерных полиномов F и вектора s, который представляет собой элемент из набора Kn, блок предоставления информации для предоставления произвольно выбранной первой информации доказывающей стороне, которая выдает сообщение, блок получения промежуточной информации для получения третью информации, сгенерированной доказывающей стороной на основании первой информации и второй информации, полученной во время генерирования сообщения, блок предоставления информации об образце для предоставления доказывающей стороне информации относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации, блок получения отклика для получения информации отклика, соответствующей выбранному образцу верификации, от доказывающей стороны, и блок верификации для верификации того, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика. Вектор s представляет собой секретный ключ. Пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи. Сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика. Пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), был сконфигурирован как член, пропорциональный (x1l)q(z) (где 1≤i≤n, q(z)=qz и 1≤z≤k).
Согласно варианту осуществления настоящей технологии, выполнен способ обработки информации, содержащий этапы, на которых генерируют сообщение на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, который представляет собой элемент из набора Kn, подают сообщение на верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s)), генерируют третью информации на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения, предоставляют третью информацию верифицирующей стороне и предоставляет верифицирующей стороне информацию отклика, соответствующую образцу верификации, который выбирает верифицирующая сторона из k (где k≥2) образцов верификации. Вектор s представляет собой секретный ключ. Пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи. Сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика. Пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), был сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz и 1≤z≤k).
Согласно варианту осуществления настоящей технологии, выполнен способ обработки информации, включающий в себя этапы, на которых, с помощью устройства обработки информации, которое хранит пару многостепенных многомерных полиномов F=(f1, …, fm) и векторы y=(y1, …, ym)=(f1(s), …, fm(s)), получают сообщение, сгенерированное на основании пары многостепенных многомерных полиномов F и вектора s, который представляет собой элемент из набора Kn, предоставляют произвольно выбранную первую информацию доказывающей стороне, которая выдает сообщение, получают третью информацию, сгенерированную доказывающей стороной, на основании первой информации и второй информации, полученной во время генерирования сообщения, предоставляют доказывающей стороне информацию относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации, и получают информацию отклика, соответствующую выбранному образцу верификации, от доказывающей стороны, верифицируют то, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика. Вектор s представляет собой секретный ключ. Пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи. Сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика. Пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), был сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz и 1≤z≤k).
Согласно варианту осуществления настоящей технологии, выполнена программа, вызывающая выполнение компьютером функции генерирования сообщения, выполненной с возможностью генерирования сообщения на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, который представляет собой элемент из набора Kn, функции подачи сообщения, выполненной с возможностью подачи сообщения на верифицирующую сторону, хранящую пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s)), функции генерирования промежуточной информации, выполненной с возможностью генерирования третьей информации на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения, функцию предоставления промежуточной информации с возможностью предоставления третьей информации верифицирующей стороне и функцию подачи отклика с возможностью предоставления верифицирующей стороне информации отклика, соответствующей образцу верификации, который выбирает верифицирующая сторона из k (где k≥2) образцов верификации. Вектор s представляет собой секретный ключ. Пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи. Сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика. Пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), был сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz и 1≤z≤k).
Согласно варианту осуществления настоящей технологии, выполнена программа, вызывающая выполнение компьютером функции хранения информации, выполненной с возможностью хранения пары многостепенных многомерных полиномов F=(f1, fm) и векторов y=(y1, …, ym)=(f1(s), …, fm(s)), функцию получения сообщения, выполненной с возможностью получения сообщения, выработанного на основании пары многостепенных многомерных полиномов F и вектора s, который представляет собой элемент из набора Kn, функции предоставления информации, выполненной с возможностью предоставления произвольно выбранной первой информации доказывающей стороне, которая выдает сообщение, функции получения промежуточной информации, выполненной с возможностью получения третьей информации, сгенерированной доказывающей стороной, на основании первой информации и второй информации, полученной во время генерирования сообщения, функции предоставления информации об образце, выполненной с возможностью предоставления доказывающей стороне информации относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации, функции получения отклика, выполненной с возможностью получения информации отклика, соответствующей выбранному образцу верификации, от доказывающей стороны, и функции верификации, выполненной с возможностью верификации того, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика. Вектор s представляет собой секретный ключ. Пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи. Сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика. Пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, x2), определенный как G(x1, x2)=F(x1+х2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1,2), был сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz и 1≤z≤k).
Согласно варианту осуществления настоящей технологии, выполнен машиночитаемый носитель информации, хранящий программу, причем программа вызывает выполнение компьютером функции генерирования сообщения, выполненной с возможностью генерирования сообщения на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, который представляет собой элемент из набора Kn, функции подачи сообщения, выполненной с возможностью подачи сообщения на верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s)), функции генерирования промежуточной информации, выполненной с возможностью генерирования третьей информации на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения, функции предоставления промежуточной информации, выполненной с возможностью предоставления третьей информации верифицирующей стороне и функции подачи отклика с возможностью предоставления верифицирующей стороне информации отклика, соответствующей образцу верификации, который выбирает верифицирующая сторона из k (где k≥2) образцов верификации. Вектор s представляет собой секретный ключ. Пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи. Сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика. Пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), был сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz и 1≤z≤k).
Согласно варианту осуществления настоящей технологии, выполнен машиночитаемый носитель информации, хранящий программу, причем программа вызывает выполнение компьютером функции хранения информации, выполненной с возможностью хранения пары многостепенных многомерных полиномов F=(f1, …, fm) и векторов y=(y1, …, ym)=(f1(s), …, fm(s)), функции получения сообщения, выполненной с возможностью получения сообщения, сгенерированного на основании пары многостепенных многомерных полиномов F и вектора s, который представляет собой элемент из набора Kn, функции предоставления информации, выполненной с возможностью предоставления произвольно выбранной первой информации доказывающей стороне, которая выдает сообщение, функции получения промежуточной информации, выполненной с возможностью получения третьей информации, сгенерированной доказывающей стороной, на основании первой информации и второй информации, полученной во время генерирования сообщения, функцию предоставления информации об образце с возможностью предоставления доказывающей стороне информации относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации, функции получения отклика, выполненной с возможностью получения информации отклика, соответствующей выбранному образцу верификации, от доказывающей стороны и функции верификации, выполненной с возможностью верификации того, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика. Вектор s представляет собой секретный ключ. Пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи. Сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика. Пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам х1=(x1l, …, x1n) (где l=1, 2), был сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz и 1≤z≤k).
Полезные эффекты изобретения
Согласно настоящей технологии, описанной выше, можно осуществить схему аутентификации открытого ключа и схему цифровой подписи, которые являются эффективными и имеют высокую безопасность, с использованием многостепенной многомерной системы уравнений, для которой не известно средство эффективного решения (функция-ловушка).
Краткое описание чертежей
Фиг.1 - пояснительная схема для описания структуры алгоритма, которая относится к схеме аутентификации открытого ключа.
Фиг.2 - пояснительная схема для описания структуры алгоритма, которая относится к схеме цифровой подписи.
Фиг.3 - пояснительная схема для описания структуры алгоритма, которая относится к n-проходной схеме аутентификации открытого ключа.
Фиг.4 - пояснительная схема для описания примера конкретной структуры алгоритма, который относится к 3-проходной схеме аутентификации открытого ключа.
Фиг.5 - пояснительная схема для описания эффективного алгоритма, который относится к 3-проходной схеме аутентификации открытого ключа.
Фиг.6 - пояснительная схема для описания распараллеливания эффективных алгоритмов, которые относятся к 3-проходной схеме аутентификации открытого ключа.
Фиг.7 - пояснительная схема для описания примера алгоритма схемы аутентификации открытого ключа (схема #1) с использованием 3-проходной многостепенной многомерный полином.
Фиг.8 - пояснительная схема для описания примера распараллеленного алгоритма схемы аутентификации открытого ключа (схема #1) с использованием 3-проходной многостепенной многомерный полином.
Фиг.9 - пояснительная схема для описания примера конкретной структуры алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа.
Фиг.10 - пояснительная схема для описания примера эффективного алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа.
Фиг.11 - пояснительная схема для описания распараллеливания эффективного алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа.
Фиг.12 - пояснительная схема для описания примера алгоритма схемы аутентификации открытого ключа (схема #1) с использованием 5-проходного многостепенного многомерного полинома.
Фиг.13 - пояснительная схема для описания примера распараллеленного алгоритма схемы аутентификации открытого ключа (схема #1) с использованием 5-проходного многостепенного многомерного полинома.
Фиг.14 - пояснительная схема для описания примера алгоритма схемы аутентификации открытого ключа (схема #2) с использованием 5-проходного многостепенного многомерного полинома.
Фиг.15 - пояснительная схема для описания примера распараллеленного алгоритма схемы аутентификации открытого ключа (схема #2) с использованием 5-проходного многостепенного многомерного полинома.
Фиг.16 - пояснительная схема для описания примера " эффективного распараллеленного алгоритма схемы аутентификации открытого ключа (схема #2) с использованием 5-проходного многостепенного многомерного полинома.
Фиг.17 - пояснительная схема для описания примера дополнительного эффективного распараллеленного алгоритма схемы аутентификации открытого ключа (схема #2) с использованием 5-проходного многостепенного многомерного полинома.
Фиг.18 - пояснительная схема для описания способа модификации эффективного алгоритма, который относится к 3-проходной схеме аутентификации открытого ключа, в алгоритм схемы цифровой подписи.
Фиг.19 - пояснительная схема для описания способа модификации дополнительного эффективного алгоритма, который относится к 3-проходной схеме аутентификации открытого ключа, в алгоритм схемы цифровой подписи.
Фиг.20 - пояснительная схема для описания способа модификации эффективного алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа, в алгоритм схемы цифровой подписи.
Фиг.21 - пояснительная схема для описания способа модификации дополнительного эффективного алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа, в алгоритм схемы цифровой подписи.
Фиг.22 - пояснительная схема для описания параллельно-последовательной структуры эффективного алгоритма, который относится к 3-проходной схеме аутентификации открытого ключа.
Фиг.23 - пояснительная схема для описания последовательно-параллельной структуры эффективного алгоритма, который относится к 3-проходной схеме аутентификации открытого ключа.
Фиг.24 - пояснительная схема для описания параллельно-последовательной структуры (параллельно-последовательной структуры #1) эффективного алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа.
Фиг.25 - пояснительная схема для описания параллельно-последовательной структуры (параллельно-последовательной структуры #2) эффективного алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа.
Фиг.26 - пояснительная схема для описания последовательно-параллельной структуры (последовательно-параллельной структуры #1) эффективного алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа.
Фиг.27 - пояснительная схема для описания последовательно-параллельной структуры (последовательно-параллельной структуры #2) эффективного алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа.
Фиг.28 - пояснительная схема для описания примера конфигурации аппаратных средств устройства обработки информации с возможностью выполнения алгоритма согласно каждому варианту осуществления настоящей технологии.
Фиг.29 - пояснительная схема для описания весьма подходящего способа установки параметра, который используется в схеме аутентификации открытого ключа, согласно первому и второму вариантам осуществления настоящей технологии и преимущественным эффектам.
Осуществление изобретения
Ниже, со ссылкой на прилагаемые чертежи, будут подробно описаны предпочтительные варианты осуществления настоящего изобретения. Следует отметить, что, в этом описании и на чертежах, элементы, которые имеют, по существу, одинаковую функцию и структуру, обозначены одинаковыми ссылочными позициями, и их повторное объяснение будет опущено.
Последовательность описания
Здесь будет кратко описана последовательность операций вариантов осуществления настоящей технологии, которые будут представлены ниже. Сначала, со ссылкой на фиг.1, будет описана структура алгоритма схемы аутентификации открытого ключа. Затем, со ссылкой на фиг.2, будет описана структура алгоритма схемы цифровой подписи. Затем, со ссылкой на фиг.3, будет описана n-проходная схема аутентификации открытого ключа.
Далее, со ссылкой на фиг.4-8, будет описан пример структуры алгоритма, который относится к 3-проходной схеме аутентификации открытого ключа. Затем, со ссылкой на фиг.5-17, будет описан пример структуры алгоритма, который относится к 5-проходной схеме аутентификации открытого ключа. Далее, со ссылкой на фиг.18-21, будет описан способ модификации эффективных алгоритмов, который относится к 3-проходной и 5-проходной схемам аутентификации открытого ключа, в алгоритмах схемы цифровой подписи.
Далее, со ссылкой на фиг.22-27, будет описана параллельно-последовательная структура и последовательно-параллельная структура эффективных алгоритмов, которые относятся к 3-проходной и 5-проходной схемам аутентификации открытого ключа. Далее, со ссылкой на фиг.28, будет описан пример конфигурации аппаратных средств устройства обработки информации с возможностью реализации каждого алгоритм согласно первому и второму вариантам осуществления настоящей технологии. В конце будет кратко изложена техническая сущность настоящих вариантов осуществления и операционных преимущественных эффектов, полученных из технической сущности.
Содержание
1. Введение
1.1. Алгоритм схемы аутентификации открытого ключа
1.2. Алгоритмы для схемы цифровой подписи
1.3. N-проходная схема аутентификации открытого ключа
2. Структуры алгоритмов, которые относятся к 3-проходной схеме аутентификации открытого ключа
2.1. Пример конкретной структуры алгоритма
2.2. Эффективный алгоритм, основанный на квадратичном многомерном полиноме
2.2.1. Основная структура
2.2.2. Распараллеленный алгоритм
2.3. Эффективный алгоритм, основанный на многостепенном многомерном полиноме (схема #1)
2.3.1. Основная структура
2.3.2. Распараллеленный алгоритм
3. Структура алгоритма, которая относится к 5-проходной схеме аутентификации открытого ключа
3.1. Пример конкретной структуры алгоритма
3.2: Эффективный алгоритм, основанный на квадратичном многомерном полиноме
3.2.1. Основная структура
3.2.2. Распараллеленный алгоритм
3.3. Эффективный алгоритм, основанный на многостепенном многомерном полиноме (первый вариант осуществления)
3.3.1. Основная структура
3.3.2. Распараллеленный алгоритм
3.4. Эффективный алгоритм, основанный на многостепенном многомерном полиноме (второй вариант осуществления)
3.4.1. Основная структура
3.4.2. Распараллеленный алгоритм (пример 1 структуры)
3.4.3. Распараллеленный алгоритм (пример 2 структуры: высокая эффективность)
3.4.4. Распараллеленный алгоритм (пример 2 структуры: более высокая эффективность)
4. Модификация схемы цифровой подписи
4.1. Модификация 3-проходной схемы аутентификации открытого ключа в схему цифровой подписи
4.1.1. Алгоритм цифровой подписи (пример 1 структуры)
4.1.2. Алгоритм цифровой подписи (пример 2 структуры: высокая эффективность)
4.2. Модификация 5-проходной схемы аутентификации открытого ключа в схему цифровой подписи
4.2.1. Алгоритм цифровой подписи (пример 1 структуры)
4.2.2. Алгоритм цифровой подписи (пример 2 структуры: высокая эффективность)
5. Алгоритм гибридного типа
5.1. Алгоритм гибридного типа, который относится к 3-проходной схеме аутентификации открытого ключа
5.1.1. Параллельно-последовательный алгоритм
5.1.2. Последовательно-параллельный алгоритм
5.2. Алгоритм гибридного типа, который относится к 5-проходной схеме аутентификации открытого ключа
5.2.1. Параллельно-последовательный алгоритм (пример #1 структуры)
5.2.2. Параллельно-последовательный алгоритм (пример #2 структуры)
5.2.3. Последовательно-параллельный алгоритм (пример #1 структуры)
5.2.4. Последовательно-параллельный алгоритм (пример #2 структуры)
6. Приложение
6.1. Способ установки параметра системы
6.2. Способ реагирования на нерегулярный вызов
6.2.1. Способ реагирования доказывающей стороной
6.2.2. Способ реагирования верифицирующей стороной
7. Пример конфигурации аппаратных средств
8. Заключение
1. Введение
Представленные здесь варианты осуществления относятся к схеме аутентификации открытого ключа и схеме цифровой подписи, в основе безопасности которых лежат трудности многостепенных многомерных систем уравнений. Однако варианты осуществления, представленные здесь, отличаются от методов уровня техники, таких как схемы цифровой подписи HFE, и относятся к схеме аутентификации открытого ключа и схеме цифровой подписи, которые используют многостепенные многомерные системы уравнений, у которых отсутствует средство эффективного решения (функции-ловушки). Сначала будут кратко описаны алгоритмы для схемы аутентификации открытого ключа, алгоритмы для схемы цифровой подписи и n-проходная схема аутентификации открытого ключа.
1.1. Алгоритм схемы аутентификации открытого ключа
Сначала, со ссылкой на фиг.1, будет представлен обзор алгоритма схемы аутентификации открытого ключа. На фиг.1 изображена пояснительная схема для описания структуры алгоритма схемы аутентификации открытого ключа.
Аутентификация открытого ключа используется в случае, когда лицо (доказывающая сторона) убеждает другое лицо (верифицирующую сторону), что оно само представляет собой доказывающую сторону, используя открытый ключ pk и секретный ключ sk. Например, открытый ключ pkA доказывающей стороны А становится известен верифицирующей стороне В. С другой стороны, секретный ключ skA доказывающей стороны А управляется секретным образом доказывающей стороной А. Согласно схеме аутентификации открытого ключа, лицо, которое знает секретный ключ skA, соответствующий открытому ключу pkA, рассматривается непосредственно как доказывающая сторона А.
Чтобы доказывающей стороне А доказать верифицирующей стороне В, что она является сама доказывающей стороной А с использованием установку аутентификации открытого ключа, доказывающая сторона А посредством интерактивного протокола предоставляет доказательство верифицирующей стороне В, показывающее, что она знает секретный ключ skA, соответствующий открытому ключу pkA. Доказательство, показывающее, что доказывающая сторона А знает секретный ключ skA, затем предоставляется верифицирующей стороне В, и в том случае, когда верифицирующая сторона В сможет подтвердить это доказательство, доказывается достоверность доказывающей стороны А (тот факт, что доказывающая сторона А представляет саму себя).
Однако для обеспечения безопасности установка аутентификации открытого ключа требует выполнения следующих условий.
Первое условие состоит в том, чтобы "уменьшить по возможности вероятность устанавливаемой фальсификации во время выполнения интерактивного протокола с помощью фальсификатора, не имеющего секретный ключ sk". То, что это первое условие удовлетворено, называется "корректностью". Другими словами, корректность означает, что "фальсификации не устанавливается во время выполнения интерактивного протокола фальсификатором, не имеющим секретного ключа sk, с не пренебрежимо малой вероятностью". Второе условие состоит в том, что "даже в случае, если интерактивный протокол выполняется, информация относительно секретного ключа skA доказывающей стороны А совершенно не передается верифицирующей стороне В". То, что это второе условие удовлетворено, называется "нулевым знанием".
Выполнение аутентификации открытого ключа безопасным образом включает в себя использование интерактивного протокола, проявляющего как корректность, так и нулевое знание. Если бы процесс аутентификации проводился бы гипотетически с использованием интерактивного протокола, не имеющего корректности и нулевого знания, то был бы определенный шанс ложной верификации и определенный шанс разглашения информации о секретном ключе, и, таким образом, достоверность доказывающей стороны не будет доказана даже в случае, если сам процесс завершится успешно. Следовательно, вопрос относительно того, как обеспечить корректность и нулевое знание протокола сеанса связи, является важным.
Модель
В модели схемы аутентификации открытого ключа представлено два объекта, а именно доказывающая сторона и верифицирующая сторона, как показано на фиг.1. Доказывающая сторона генерирует пару из открытого ключа pk и секретного ключа sk, уникальную для доказывающей стороны с использованием алгоритма Gen генерирования ключей. Затем доказывающая сторона выполняет интерактивный протокол с верифицирующей стороной с использованием пары из секретного ключа sk и открытого ключа pk, сгенерированной с использованием алгоритма Gen генерирования ключей. В это же время доказывающая сторона выполняет интерактивный протокол с помощью алгоритма Р доказывающей стороны. Как описано выше, во время интерактивного протокола, доказывающая сторона доказывает верифицирующей стороне, с помощью алгоритма Р доказывающей стороны, что она обладает секретным ключом sk.
С другой стороны, верифицирующая сторона выполняет интерактивный протокол с помощью алгоритма V верифицирующей стороны и верифицирует то, обладает или нет доказывающая сторона секретным ключом, соответствующим открытому ключу, который опубликовала доказывающая сторона. То есть верифицирующая сторона представляет собой объект, который верифицирует то, обладает или нет доказывающая сторона секретным ключом, соответствующим открытому ключу. Как описано, модель схемы аутентификации открытого ключа сконфигурирована из двух объектов, а именно доказывающей стороны и верифицирующей стороны, и из трех алгоритмов, а именно алгоритма Gen генерирования ключей, алгоритма Р доказывающей стороны и алгоритма V верифицирующей стороны.
Дополнительно, выражения "доказывающая сторона" и "верифицирующая сторона" используются в последующем описании, но эти выражения строго означают объекты. Поэтому субъект, который выполняет алгоритм Gen генерирования ключей и алгоритм Р доказывающей стороны, представляет собой устройство обработки информации, соответствующее объекту "доказывающей стороны". Аналогично, субъект, который выполняет алгоритм V верифицирующей стороны, представляет собой устройство обработки информации. Конфигурация аппаратных средств этих устройств обработки информации представляет собой конфигурацию, которая показана, например, на фиг.28. То есть алгоритм Gen генерирования ключей, алгоритм Р доказывающей стороны и алгоритм V верифицирующей стороны выполняются с помощью ЦПУ 902 на основании программы, записанной в ПЗУ 904, ОЗУ 906, запоминающем устройстве 920, съемном носителе 928 записи или т.п.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей используется доказывающей стороной. Алгоритм Gen генерирования ключей представляет собой алгоритм генерирования пары открытых ключей pk и секретного ключа sk, уникального для доказывающей стороны. Открытый ключ pk, сгенерированный с помощью алгоритма Gen генерирования ключей публикуется. Более того, опубликованный открытый ключ pk используется верифицирующей стороной. С другой стороны, секретный ключ sk, сгенерированный с помощью алгоритма Gen генерирования ключей, управляется секретным образом доказывающей стороной. Секретный ключ sk, который управляется секретным образом доказывающей стороной, используется, чтобы доказать верифицирующей стороне обладание секретным ключом sk, соответствующим открытому ключу pk, доказывающей стороной. Формально алгоритм Gen генерирования ключей представлен в виде формулы (1) ниже в качестве алгоритма, который получает параметр безопасности 1λ, (λ - целое число, которое больше или равно 0) в виде входных данных и выводит секретный ключ sk и открытый ключ pk.
[Формула 1]
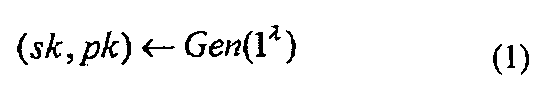
Алгоритм Р доказывающей стороны
Алгоритм Р доказывающей стороны используется доказывающей стороной. Алгоритм Р доказывающей стороны представляет собой алгоритм для предоставления доказательства верифицирующей стороне, что доказывающая сторона обладает секретным ключом sk, соответствующим открытому ключу pk. Другими словами, алгоритм Р доказывающей стороны представляет собой алгоритм, который получает открытый ключ pk и секретный ключ sk в виде входных данных и выполняет интерактивный протокол.
Алгоритм V верифицирующей стороны
Алгоритм V верифицирующей стороны используется верифицирующей стороной. Алгоритм V верифицирующей стороны представляет собой алгоритм, который верифицирует то, обладает или нет доказывающая сторона секретным ключом sk, соответствующим открытому ключу pk во время протокола сеанса связи. Алгоритм V верифицирующей стороны представляет собой алгоритм, который принимает открытый ключ pk в виде входных данных и выводит 0 или 1 (1 бит) согласно результатам выполнения протокола сеанса связи. На данном этапе, верифицирующая сторона принимает решение относительно того, что доказывающая сторона является недействительной в том случае, когда алгоритм V верифицирующей стороны выводит 0 и принимает решение относительно того, что доказывающая сторона является действительной в том случае, когда алгоритм V верифицирующей стороны выводит 1. Формально, алгоритм V верифицирующей стороны выражается в виде следующей формулы (2).
[Формула 2]

Как указано выше, реализация значимой аутентификации открытого ключа включает в себя наличие интерактивного протокола, удовлетворяющего двум условиям, таким как корректность и нулевое знание. Однако доказательство того, что доказывающая сторона обладает секретным ключом sk, включает в себя выполнение доказывающей стороной процедуры, которая зависит от секретного ключа sk, и после уведомления верифицирующей стороны относительно результата, побуждают верифицирующую сторону выполнять верификацию на основании содержания уведомления. Процедура, зависящая от секретного ключа sk, выполняется для того, чтобы обеспечить корректность. В то же самое время, отсутствие информации относительно секретного ключа sk должно быть обнаружено на верифицирующей стороне. По этой причине, вышеупомянутые алгоритм Gen генерирования ключа, алгоритм Р доказывающей стороны и алгоритм V верифицирующей стороны разрабатывают искусственно для того, чтобы удовлетворить этим требованиям.
Таким образом, выше кратко изложены алгоритмы, которые выполняются в схеме аутентификации открытого ключа.
1.2. Алгоритмы для схемы цифровой подписи
Далее, со ссылкой на фиг.2, будут кратко изложены алгоритмы для схемы цифровой подписи. На фиг.2 изображена пояснительная схема суммирования алгоритмов для схемы цифровой подписи.
В отличие бумажных документов, в данном случае невозможно физически подписать или поставить печать на оцифрованные данные. По этой причине, доказательство создателя цифровых данных включает в себя электронную установку, создающую эффекты, аналогичные физическому подписанию или постановке печати на бумажный документ. Эта установка представляет собой цифровые подписи. Цифровая подпись относится к установке, которая связывает исходные данные с данными подписи, известными только создателю данных, предоставляет данные подписи получателю и верифицирует, что данные подписи находятся на стороне получателя.
Модель
Как показано на фиг.2, два идентификационных номера подписывающей стороны, и верифицирующая сторона существуют в модели схемы цифровой подписи. В добавление к этому, модель схемы цифровой подписи состоит из трех алгоритмов: алгоритм Gen генерирования ключей, алгоритм Sig генерирования подписи и алгоритм Ver верификации подписи.
Подписывающая сторона использует алгоритм Gen генерирования ключей для генерирования парных ключа sk подписи и ключа pk верификации, которые являются уникальными для подписывающей стороны. Подписывающая сторона также использует алгоритм Sig генерирования подписи для генерирования цифровой подписи q, чтобы прикрепить ее к сообщению М. Другими словами, Подписывающая сторона представляет собой лицо, которое прикрепляет цифровую подпись к сообщению М. Между тем, верифицирующая сторона использует алгоритм Ver верификации подписи для верификации цифровой подписи, прикрепленной к сообщению М. Другими словами, верифицирующая сторона представляет собой объект, который верифицирует цифровую подпись q для того, чтобы подтвердить то, является ли создатель сообщения М подписывающей стороной.
Следует отметить, что хотя термины "подписывающая сторона" и "верифицирующая сторона" используются в дальнейшем описании, эти термины, в конечном счете, означают объекты. Следовательно, агент, который выполняет алгоритм Gen генерирования ключа и алгоритм Sig генерирования подписи, представляет собой устройство обработки информации, соответствующее "объекту подписывающей стороны". Аналогичным образом, агент, который выполняет алгоритм Ver верификации подписи, представляет собой устройство обработки информации. Конфигурация аппаратных средств этого устройства обработки информации является такой, как, например, показано на фиг.28. Другими словами, алгоритм Gen генерирования ключей, алгоритм Sig генерирования подписи и алгоритм Ver верификации подписи выполняются с помощью устройства, такого как ЦПУ 902 на основе программы, записанной на устройстве, таком как ПЗУ 904, ОЗУ 906, запоминающее устройство 920 или съемный носитель 928 записи.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей используется подписывающей стороной. Алгоритм Gen генерирования ключей представляет собой алгоритм, который генерирует парные ключ sk подписи и ключ pk верификации, которые являются уникальным для подписывающей стороны. Ключ pk верификации, сгенерированный с помощью алгоритма Gen генерирования ключей становится общедоступным. Между тем, подписывающая сторона сохраняет ключ sk подписи, сгенерированный с помощью алгоритма Gen генерирования ключей, секретным. Ключ sk подписи используется затем для генерирования цифровой подписи q, чтобы прикрепить ее к сообщению М. Например, алгоритм Gen генерирования ключей принимает параметр безопасности 1р (где р - целое число, которое больше или равно 0) в виде входных данных и выводит ключ sk подписи и ключ pk верификации. В этом случае алгоритм Gen генерирования ключей можно формально выразить в виде следующей формулы (3).
[Формула 3]
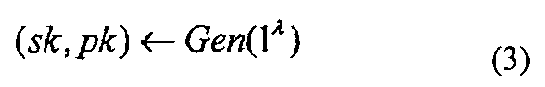
Алгоритм Sig генерирования подписи
Алгоритм Sig генерирования подписи используется подписывающей стороной. Алгоритм Sig генерирования подписи представляет собой алгоритм, который генерирует цифровую подпись q, чтобы прикрепить ее к сообщению М. Алгоритм Sig генерирования подписи представляет собой алгоритм, который принимает ключ sk подписи и сообщение М в виде входных данных и выводит цифровую подпись q. Алгоритм Sig генерирования подписи можно формально выразить в виде следующей формулы (4).
[Формула 4]
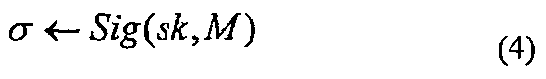
Алгоритм Ver верификации подписи
Алгоритм Ver верификации подписи используется верифицирующей стороной. Алгоритм Ver верификации подписи представляет собой алгоритм, который верифицирует то, является ли цифровая подпись q действительной цифровой подписью для сообщения М. Алгоритм Ver верификации подписи представляет собой алгоритм, который принимает ключ pk верификации подписывающей стороны, сообщение М и цифровую подпись q в виде входных данных и выводит 0 или 1 (1 бит). Алгоритм Ver верификации подписи можно выразить формально в виде следующей формулы (5). На данном этапе, верифицирующая сторона принимает решение относительно того, что цифровая подпись q является недействительной в том случае, когда алгоритм Ver верификации подписи выводит 0 (случай, где ключ pk верификации отклоняет сообщение М и цифровую подпись q), и принимает решение относительно того, что цифровая подпись q является действительной в том случае, когда алгоритм Ver верификации подписи выводит 1 (случай, где ключ pk верификации принимает сообщение М и цифровую подпись q).
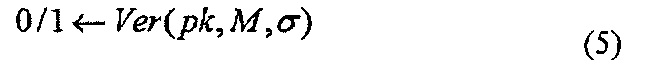
Таким образом, выше кратко изложены алгоритмы в схеме цифровой подписи.
1.3. N-проходная схема аутентификации открытого ключа
Далее будет описана n-проходная схема аутентификации открытого ключа со ссылкой на фиг.3. На фиг.3 изображена пояснительная схема, иллюстрирующая n-проходную схему аутентификации открытого ключа.
Как указано выше, схема аутентификации открытого ключа представляет собой схему аутентификации, которая доказывает верифицирующей стороне то, что доказывающая сторона обладает секретным ключом sk, соответствующим открытому ключу pk, во время интерактивного протокола. В добавление к этому, интерактивный протокол должен удовлетворять двум условиям, таким как корректность и нулевое знание. По этой причине, во время интерактивного протокола как доказывающая сторона, так и верифицирующая сторона обмениваются информацией n раз при выполнении соответствующих процессов, как показано на фиг.3.
В случае n-проходной схемы аутентификации открытого ключа, доказывающая сторона выполняет процесс с использованием алгоритма Р доказывающей стороны (операция #1) и передает информацию Т1 верифицирующей стороне. Затем верифицирующая сторона выполняет процесс, использующий алгоритм V верифицирующей стороны (операция #2), и передает информацию Т2 доказывающей стороне. Это выполнение процессов и передачи информации Tk успешно проводится для k=3-n (операция #k), и, наконец, выполняется процесс (операция #n+1). Передача и прием информации n раз таким образом называется поэтому "n-проходной" схемой аутентификации открытого ключа.
Таким образом, выше была описана n-проходная схема аутентификации открытого ключа.
2. Структуры алгоритмов, которые относится к 3-проходной схеме аутентификации открытого ключа
Ниже будут описаны алгоритмы, которые относятся к 3-проходной схеме аутентификации открытого ключа. Следует отметить, что в последующем описании, 3-проходная схема аутентификации открытого ключа в некоторых случаях может также называться "3-проходной схемой".
2.1. Пример конкретной структуры алгоритма
Сначала, со ссылкой на фиг.4, будет описан пример конкретной структуры алгоритма, который относится к 3-проходной схеме. На фиг.4 изображена пояснительная схема для описания конкретной структуры алгоритма, которая относится к 3-проходной схеме. Алгоритм 3-проходной схемы состоит из алгоритма Gen генерирования ключей, алгоритма Р доказывающей стороны и алгоритма V верифицирующей стороны. Ниже будет описана каждая структура алгоритма.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует m многомерных полиномов f1(x1, …, xn), fm(x1, …, xn), определенных в кольце k, и вектор s=(s1, …, sn), который является элементом набора Kn. Далее алгоритм Gen генерирования вычисляет y=(y1, …, ym)←(f1(s), …, fm(s)). К тому же, алгоритм Gen генерирования устанавливает (f1(x1, …, xn), …, fm(x1, …, xn), y) в открытом ключе pk и устанавливает s в качестве секретного ключа. Здесь и далее вектор (x1, …, xn) представлен в виде х, и пара многомерных полиномов (f1(x), …, fm(x)) представлена в виде F(x).
Алгоритм Р доказывающей стороны, алгоритм V верифицирующей стороны
Далее, со ссылкой на фиг.4, будет описаны процесс, выполняемый алгоритмом Р доказывающей стороной, и процесс, выполняемый алгоритмом V верифицирующей стороны во время интерактивного протокола.
Во время вышеизложенного интерактивного протокола доказывающая сторона совершенно не дает утечки информации относительно секретного ключа s верифицирующей стороне и представляет верифицирующей стороне то, что "она знает s, удовлетворяющей уравнению y=F(s)". С другой стороны, верифицирующая сторона верифицирует то, знает или нет доказывающая сторона s, удовлетворяющей уравнению y=F(s). Предполагается, что открытый ключ pk становится известным верифицирующей стороне. К тому же, предполагают, что секретный ключ s будет управляться секретным образом посредством доказывающей стороны. Далее приводится описание со ссылкой на последовательность операций, иллюстрированную на фиг.4.
Операция #1:
Сначала, алгоритм Р доказывающей стороны выбирает любое число seed0. Затем алгоритм Р доказывающей стороны генерирует вектор r0, который представляет собой элемент набора Kn, и число seed1 путем применения числа seed0 в генераторе PRNG случайных чисел. То есть алгоритм. Р доказывающей стороны вычисляет (r0, seed1)<-PRNG(seed0). Затем алгоритм Р доказывающей стороны генерирует многомерный полином F1(x)=(f11(x), …, f1m(x)) путем применения числа seed1 в генераторе PRNG случайных чисел. То есть алгоритм Р доказывающей стороны вычисляет F1<-PRNG (seed1).
Операция #1 (продолжение):
Затем алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Это вычисление эквивалентно маскированию секретного ключа s вектором r0. Дополнительно, алгоритм Р доказывающей стороны вычисляет F2(x)<-F(x+r0)+F1(x). Это вычисление эквивалентно маскированию многомерного полинома F(x+r0) для х многомерным полиномом F1(x).
Операция #1 (продолжение):
Затем алгоритм Р доказывающей стороны генерирует значение хэширования с0 для r1 и F1(r1). То есть алгоритм Р доказывающей стороны вычисляет с0<-H(F1(r1), r1). К тому же, алгоритм Р доказывающей стороны генерирует значение хэширования c1 числа seed1. То есть алгоритм Р доказывающей стороны вычисляет c1<-H(seed1). К тому же, алгоритм Р доказывающей стороны генерирует значение хэширования c2 многомерного полинома F2. То есть алгоритм Р доказывающей стороны вычисляет c2<-H(F2). Значения хэширования (с0, c1, c2) отправляются в виде сообщения в алгоритм V верифицирующей стороны. В то же время следует отметить, что совершенно отсутствуют утечки информации относительно s, информации относительно r0 и информации относительно r1 верифицирующей стороне.
Операция #2:
После получения сообщения (с0, c1, c2), алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать среди трех образцов верификации. Например, алгоритм V верифицирующей стороны может выбрать численное значение среди трех численных значений {0, 1, 2}, представляющих собой образцы верификации, и установить численные значения в вызове Ch. Этот вызов Ch отправляется в алгоритм Р доказывающей стороны.
Операция #3:
После получения вызова Ch, алгоритм Р доказывающей стороны генерирует отклик Rsp для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов Ch. В случае когда Ch=0, алгоритм Р доказывающей стороны генерирует отклик Rsp=seed0. В случае когда Ch=1, алгоритм Р доказывающей стороны генерирует отклик Rsp=(seed1, r1). В случае когда Ch=2, алгоритм Р доказывающей стороны генерирует отклик Rsp=(F2, r1). Отклик Rsp, сгенерированный в операции #3, отправляется в алгоритм V верифицирующей стороны. Здесь следует отметить, что совершенно не происходит утечки информации относительно r1 верифицирующей стороне в случае, когда Ch=0, и совершенно не происходит утечки информации относительно r0 верифицирующей стороне в случае, когда Ch=1 или 2.
Операция #4:
После получения отклика Rsp, алгоритм V верифицирующей стороны выполняет следующий процесс верификации с использованием полученного отклика Rsp.
В случае когда Ch=0, алгоритм V верифицирующей стороны вычисляет (r0, seed1)<-PRNG(Rsp). К тому же, алгоритм V верифицирующей стороны вычисляет F1<-PRNG(seed1). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H(seed1). В добавление к этому, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c2=H(F(x+r0)+F1(x)). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда Ch=1, алгоритм V верифицирующей стороны устанавливает (seed1, r1)<-Rsp. К тому же, алгоритм V верифицирующей стороны вычисляет F1<-PRNG(seed1). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство с0=H(F1(r1), r1). В добавление к этому, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H(seed1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда Ch=2, алгоритм V верифицирующей стороны устанавливает (F2, r1)<-Rsp. Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0=H(F2(r1)-y, r1). В добавление к этому, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c2=H(F2). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
(Корректность)
Приведенное здесь описание корректности алгоритмов, которое относится к 3-проходной схеме, будет дополненным. Корректность алгоритмов, которые относятся к 3-проходной схеме, обеспечивается на основании логики того, что F2, F1, r0 и r1, удовлетворяющие следующим формулам (6) и (7), которые представлены ниже, можно вычислить в случае, когда алгоритм Р доказывающей стороны возвращает соответствующий отклик Rsp для всех вызов Ch=0, 1 и 2, выбранный с помощью алгоритма V верифицирующей стороны".
[Формула 6]
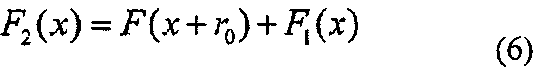
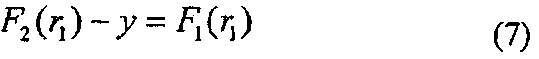
Обеспечив вышеуказанную корректность, тот факт, что успешная подделка с вероятностью более чем 2/3 не возможна, гарантируется до тех пор, пока не будет решена задача решения многостепенной многомерной системы уравнений. То есть чтобы соответствующим образом произвести отклик на все вызовы Ch=0, 1, 2 верифицирующей стороны, фальсификатор должен вычислить F2, F1, r0 и r1, удовлетворяющие формулам (6) и (7), которые приведены выше. Другими словами, фальсификатор должен вычислить s, удовлетворяющий уравнению F(s)=y. Однако остается вероятность того, что фальсификатор производит соответствующие отклики для двух вызовов более высокого порядка среди вызовов Ch=0, 1, 2 верифицирующей стороны. Поэтому вероятность успеха ложной верификации становится равной 2/3. Кроме того, за счет повторного выполнения вышеуказанного интерактивного протокола достаточно большое число раз, вероятность успешной подделки становится пренебрежимо малой.
(Функция Н хеширования)
Ниже приводится дополнительное описание функции Н хеширования. В вышеприведенных алгоритмах, c0, c1, c2 и тому подобное вычисляют с использованием функции Н хеширования. Однако функцию СОМ фиксации можно использовать вместо функции Н хеширования. Функция СОМ фиксации представляет собой функцию, в которой символьная строка S и случайное число ρ представляют собой множители. Пример функции фиксации включает в себя схему, опубликованную на международной конференции CRYPTO 1996 Шаем Халеви (Shai Halevi) и Сильвио Миколи (Silvio Micali).
Например, будет рассмотрен случай, в котором c0, c1 и c2 вычисляют с использованием функция СОМ фиксации. В этом случае случайные числа ρ0, ρ1 и ρ2 подготавливаются перед вычислением c0, c1 и c2, и c0, c1 и c2 генерируются путем применения функций СОМ(·,ρ0), COM(·,ρ1) и COM(·,ρ2) фиксации вместо применения функции Н(·) хеширования. Кроме того, ρi, необходимый для верифицирующей стороны для того, чтобы сгенерировать ci, устанавливается как включенный в отклик Rsp и отправляется.
Выше был представлен пример конкретной структуры алгоритма, который относится к 3-проходной схеме.
2.2. Эффективный алгоритм, основанный на квадратичном многомерном полиноме
Далее будет описан способ построения эффективных алгоритмов, которые относятся к 3-проходной схеме. Здесь будет описан случай, в котором пара квадратичных полиномов (f1(x), …, fm(x)) используется в качестве многомерных полиномов F. Здесь предполагается, что квадратичный полином fi(x) будет выражен в виде следующей формулы (8).
[Формула 7]
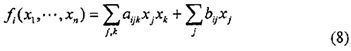
К тому же, пару квадратичных полиномов (f1(x), …, fm(x)) можно представить в виде следующей формулы (9). Здесь х=(х1, …, xn). А1, …, Am представляет собой матрицу размером n×n. Кроме того, каждый из b1, …, bm представляет собой вектор размером n×1.
[Формула 8]
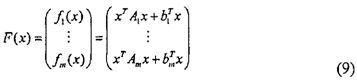
При использовании этого выражения многомерный полином F можно выразить в виде следующих формул (10) и (11). Из следующей формулы (12) можно легко подтвердить, что это выражение удовлетворяется.
[Формула 9]
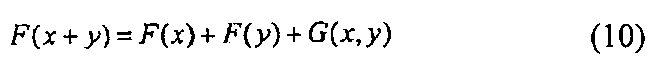
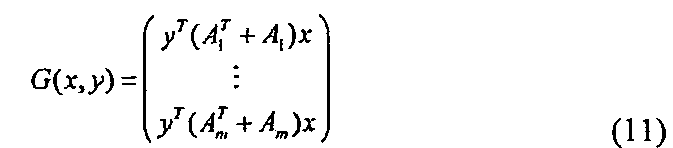
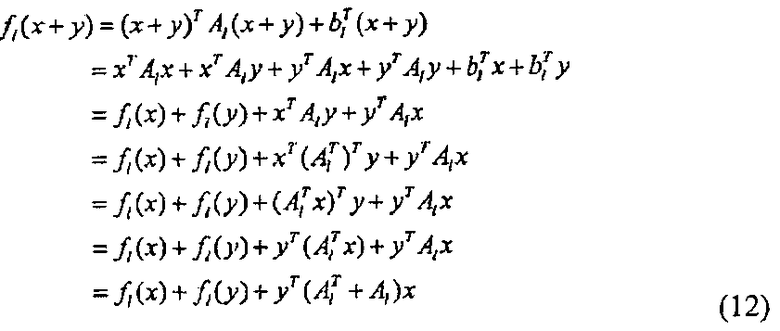
При делении F(x+y) на первую часть, которая зависит от х, вторую часть, которая зависит от y, и третью часть, которая зависит как от х, так и от y таким образом, член G(x, y), соответствующей третьей части, становится билинейным по отношению к х и y. Используя это свойство, можно построить эффективный алгоритм.
Например, вектор t0, который является элементом набора Kn, и вектор е0, который является элементом набора Km, используют для того, чтобы выразить многомерный полином F1(x), который используется для маскирования многомерного полинома F(x+r), as F1(x)=G(x, t0)+е0. В этом случае сумма многомерного полинома F(x+r0) и G(x) выражается в виде формулы (13), представленной ниже.
При этом когда t1=r0+t0, e1=F(r0)+е0, многомерный полином F2(x)=F(x+r0)+F1(x) можно выразить с помощью вектора t1, который представляет собой элемент набора Kn, и вектора е1 который является элементом набора Km. По этой причине, когда "F1(x)=G(x, t0)+е0" установлен, F1 и F2 можно выразить, используя вектор в Kn и вектор в Km, и, таким образом, можно значительно уменьшить объем данных, необходимый для связи. В частности, эффективность связи можно повысить в тысячи или в десятки тысяч раз.
[Формула 10]
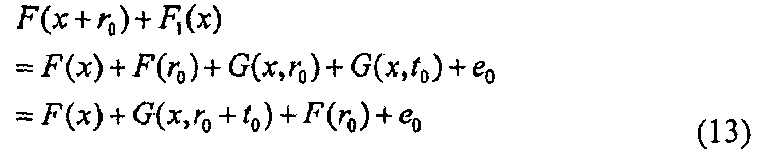
За счет использования вышеуказанной модификации информация относительно r0 совсем не вытекает из F2 (или F1). Например, даже в случае, когда e1 и t1 (или е0 и t0) заданы, информация относительно r0 совсем неизвестна, до тех пор, пока е0 и t0 (или e1 и t1) неизвестны. Соответственно, обеспечивается нулевое знание. Ниже, со ссылкой на фиг.5 и 6, будет описан эффективный алгоритм, который относится к 3-проходной схеме.
2.2.1. Базовая структура (фиг.5)
Сначала, со ссылкой на фиг.5, будет описана базовая структура эффективного алгоритма, который относится к 3-проходной схеме. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Операция #1:
Как показано на фиг.5, алгоритм Р доказывающей стороны сначала произвольно генерирует вектор r0, t0, который является элементом набора Kn и вектор е0, который является элементом набора Km. Затем алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Это вычисление эквивалентно маскированию секретного ключа s вектором r0. Дополнительно, алгоритм Р доказывающей стороны вычисляет t1<-r0-t0. Затем алгоритм Р доказывающей стороны вычисляет e1<-F(r0)-е0.
Операция #1 (продолжение):
Затем алгоритм Р доказывающей стороны вычисляет с0<-H(r1, G(t0, r1)+е0). Затем алгоритм Р доказывающей стороны вычисляет c1<-H(t0, е0). Затем алгоритм Р доказывающей стороны вычисляет с2<-H(t1, e1). Сообщение (с0, c1, с2), сгенерированное в операции #1, отправляется в алгоритм V верифицирующей стороны.
Операция #2:
После получения сообщения (с0, c1, с2) алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать среди трех образцов верификации. Например, алгоритм V верифицирующей стороны может выбрать численное значение среди трех численных значений {0, 1, 2}, представляющих собой образцы верификации и установить выбранное численное значение в вызове Ch. Этот вызов Ch отправляется в алгоритм Р доказывающей стороны.
Операция #3:
После получения вызова Ch, алгоритм Р доказывающей стороны генерирует отклик Rsp для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов Ch. В случае когда Ch=0, алгоритм Р доказывающей стороны генерирует отклик Rsp=(r0, t1, e1). В случае когда Ch=1, алгоритм Р доказывающей стороны генерирует отклик Rsp=(r1, t0, е0). В случае когда Ch=2, алгоритм Р доказывающей стороны генерирует отклик Rsp=(r1, t1, e1). Отклик Rsp, сгенерированный в операции #3, отправляется в алгоритм V верифицирующей стороны.
Операция #4:
После получения отклика Rsp алгоритм V верифицирующей стороны выполняет следующий процесс верификации с использованием полученного отклика Rsp.
В случае когда Ch=0, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H(r0-t1, F(r0)-e1). В добавление к этому, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство с2=H(t1, e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда Ch=1, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0=H(r1, G(t0, r1)+е0). В добавление к этому, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H(t0, е0). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда Ch=2, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0=Н(r1, y-F(r1)-G(t1, r1)-e1). В добавление к этому, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c2=H(t1, e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Выше был описан пример эффективной структуры алгоритма, который относится к 3-проходной схеме. За счет использования алгоритмов, значительно уменьшается размер данных, необходимый для связи.
2.2.2. Распараллеленный алгоритм (фиг.6)
Далее, со ссылкой на фиг.6, будет описан способ распараллеливания алгоритмов, иллюстрированный на фиг.5. Тем не менее, дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Как описано выше, применение вышеописанного протокола сеанса связи делает возможным сохранение вероятности успешной подделки на уровне 2/3 или менее. Следовательно, выполняя протокол сеанса связи дважды, можно сохранить вероятность успешной подделки на уровне (2/3)2 или менее. Более того, если протокол сеанса связи выполняется N раз, вероятность успешной подделки становится равной (2/3)N, и если N устанавливается на достаточно большое число (например, N=140), вероятность успешной подделки становится пренебрежимо малой.
Возможные способы многократного выполнения интерактивного протокола включают в себя последовательный способ, который последовательно повторяет обмен сообщениями, вызовами и отклика много раз, и параллельный способ, который осуществляет обмен многочисленными сообщениями, вызовами и откликами при одном обмене, например. Ниже будут теперь описаны алгоритмы, которые выполняют параллельно вышеупомянутый интерактивный протокол, который относится к 3-проходной схеме (здесь и далее по тексту указаны как распараллеленные алгоритмы).
Операция #1:
Алгоритм Р доказывающей стороны сначала выполняет следующие процессы (1)-(6) для i=1-N.
Процесс (1): Алгоритм Р доказывающей стороны произвольно генерирует векторы r0i, t0i, которые представляют собой элементы набора Kn, и вектор e0i, который является элементом набора Km.
Процесс (2): Алгоритм Р доказывающей стороны вычисляет r1i<-s-r0i. Это вычисление эквивалентно маскированию секретного ключа s вектором r0i. Дополнительно, алгоритм Р доказывающей стороны вычисляет t1i<-r0i+t0i.
Процесс (3): Алгоритм Р доказывающей стороны вычисляет e1i<-F(r0i)-e0i.
Процесс (4): Алгоритм Р доказывающей стороны вычисляет c0i<-Н(r1i, G(r1i, t0i)+e0i).
Процесс (5): Алгоритм Р доказывающей стороны вычисляет c1i<-H(t0i, e0i).
Процесс (6): Алгоритм Р доказывающей стороны вычисляет c2i<-H(t1i, e1i).
Операция #1 (продолжение):
После выполнения описанных выше процессов (1)-(6) для i=1-N, алгоритм Р доказывающей стороны вычисляет Cmt<-H(c01, c11, c21, c0N, c1N, c2N)- Значение Cmt хэширования, сгенерированное в операции #1, отправляется в алгоритм V верифицирующей стороны. Таким образом, сообщение (с01, c11, с21, …, c0N, c1N, c2N) преобразуется в значение хэширования перед отправлением в алгоритм V верифицирующей стороны, тем самым позволяя уменьшить объем связи.
Операция #2:
После получения значения Cmt хэширования алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать среди трех образцов верификации, для каждого i=1-N. Например, алгоритм V верифицирующей стороны может, для каждого i=1-N, выбрать численное значение среди трех численных значений {0, 1, 2}, представляющих собой образцы верификации, и установить выбранное численное значение в вызове Chi. Вызовы Ch1, …, ChN отправляются в алгоритм Р доказывающей стороны.
Операция #3:
После получения вызовов Ch1, …, ChN алгоритм Р доказывающей стороны генерирует отклики Rsp1, …, RspN для отправки в алгоритм V верифицирующей стороны в ответ на каждый принятый вызовы Ch1, …, ChN. В случае когда Chi=0, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r0i, t1i, e1i, c0i). В случае когда Chi=1, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r1i, t0i, e0i, c2i). В случае когда Chi=2, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r1i, t1i, e1i, c1i).
Отклики Rsp1, …, RspN, сгенерированные в операции #3, отправляются в алгоритм V верифицирующей стороны.
Операция #4:
После получения откликов Rsp1, …, RspN алгоритм V верифицирующей стороны выполняет следующий процессы (1)-(3) для i=1-N, используя принятые отклики Rsp1, …, RspN. В данном случае алгоритм V верифицирующей стороны выполняет процесс (1) для случая, где Chi=0, процесс (2) в случае, когда Chi=1, и процесс (3) в случае, когда Chi=2.
Процесс (1): В случае когда Chi=0, алгоритм V верифицирующей стороны отыскивает (r0i, t1i, e1i, c0i) из Rspi. Затем алгоритм V верифицирующей стороны вычисляет c1i=H(r0i-t1i, F(r0i)-e1i). В добавление к этому, алгоритм V верифицирующей стороны вычисляет c2i=H(t1i, e1i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i, c2i).
Процесс (2): В случае когда Chi=1, алгоритм V верифицирующей стороны отыскивает (r1i, t0i, e0i, c2i) из Rspi. Затем алгоритм V верифицирующей стороны вычисляет c0i=Н(r1i, G(r1i, t0i)+e0i). В добавление к этому, алгоритм V верифицирующей стороны вычисляет c1i=H(t0i, e0i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i, c2i).
Процесс (3): В случае когда Chi=2, алгоритм V верифицирующей стороны отыскивает (r1i, t1i, e1i, c1i) из Rspi. Затем алгоритм V верифицирующей стороны вычисляет c0i=Н(r1i, y-F(r1i)-G(t1i, r1i)-e1i). В добавление к этому, алгоритм V верифицирующей стороны вычисляет c2i=H(t1i, e1i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, C1i, c2i).
После выполнения описанных выше процессов (1)-(3) для i=1-N, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство Cmt=Н(с01, с11, с21, …, c0N, c1N, c2N). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда верификация завершается успешно, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Пример структур распараллеленных эффективных алгоритмов, которые относятся к 3-х проходной, схеме был описан выше. К тому же, распараллеленные алгоритмы, показанные на фиг.6, включает в себя ухищрение, в котором сообщение преобразуется хэш-значение перед посылкой. Ухищрение повышает эффективность связи. Аналогично, структуру можно модифицировать таким образом, чтобы вызовы Ch1, …, ChN или отклики Rsp1, …, RspN были преобразованы в хэш-значения перед посылкой. Модификация структуры, выполненная таким образом, позволяет дополнительно повысить ожидаемую эффективность связи.
2.3. Эффективный алгоритм, основанный на многостепенном многомерном полиноме (схема #1)
Вышеизложенные эффективный алгоритмы используют свойство, которые заключаются в том, что полином G, определенный в вышеприведенной формуле (10), становится билинейным в результате выражения многомерного полинома F парой квадратичных полиномов fi, определенных в приведенной выше формуле (8). Однако когда полином G является аддитивно гомоморфным, эффективный алгоритм можно построить подобным образом даже в случае, когда полином G не является билинейным.
Построение эффективного алгоритма с использованием квадратичного полинома fi
Когда полином G является аддитивно гомоморфным, зависимость следующих формул (14)-(16) устанавливается с использованием переменных r0, r1, t0 и е0. К тому же следующая формула (14) представляет собой формулу, полученную путем деления секретного ключа s на s=r0+r1 и разложения открытого ключа F(s). Следующие формулы (14)-(16) можно разделить на первую часть (r1, t0, е0), воспроизводимую с помощью (r0, t1, e1), вторую часть (r1, t1, e1), воспроизводимую с помощью (r1, t0, е0), и третью часть, воспроизводимую с помощью (r1, t1, e1).
Например, "r0, t1", входящий в следующую формулу (15), и "F(r0), e1", входящий в следующую формулу (16), представляют собой первую часть. Дополнительно, "е0, G(t0, r1)", входящий в следующую формулу (14), "t0", входящий в следующую формулу (15), и "е0", входящий в следующую формулу (16), представляют собой вторую часть. Дополнительно, "е1, F(r1), G(t1, r1)", входящий в следующую формулу (14), представляют собой третью часть. Другими словами, следующая формула (14) включает в себя вторую и третью части, следующая формула (15) включает в себя первую и вторую части, и следующая формула (16) включает в себя первую и вторую части.
Как описано выше, каждая из следующих формул (14)-(16) включает в себя два вида частей. Дополнительно, из определения секретного ключа s и зависимости среди следующих формул (14)-(16), гарантируется, что секретный ключ s не доступен даже тогда, когда используется любой один из (r0, t1, e1), (r1, t0, е0) и (r1, t1, e1). Использование этого свойства позволяет, например, построить эффективный алгоритм, который относится к 3-проходной схеме, показанной на фиг.5.
[Формула 11]
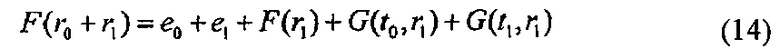


Построение эффективного алгоритма с использованием кубического полинома f1
Способ построения эффективного алгоритма с использованием кубического полинома f1 кольца R, представленный в виде следующей формулы (17), будет рассмотрен путем раскрытия вышеизложенного описание случая, где квадратичный полином fi. Многомерный полином F=(f1, …, fm) выраженный парой кубических полиномов f1 удовлетворяет соотношению следующей формулы (18). Здесь Gx(x, y) представляет собой линейный член для х. Дополнительно, Gy(x, y) представляет собой линейный член для y. Когда Gx=(gx1, gxm) и Gy=(gy1, …, gym) выражены, gx1 и gy1 можно представить в виде следующих формул (19) и (20), соответственно. Поскольку в данном случае правый второй член gx1 является также линейным для одного из х и y, правый второй член может включать в себя gy1.
[Формула 12]
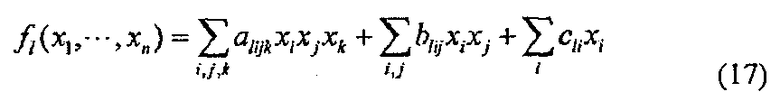
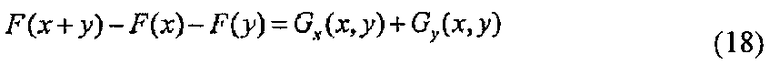
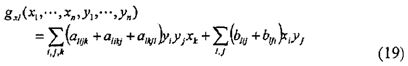
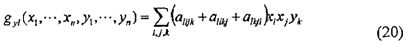
Как понятно из вышеприведенных формул (19) и (20), Gx(x, y) и Gy(x, y) становятся аддитивно гомоморфными для х и y. Таким образом, используя это свойство, открытый ключ F(s) делится путем введения новых переменных r0, r1, t0, u0 и е0, как в способе построения эффективного алгоритма с использованием квадратичного полинома fi.
Поскольку полиномы Gx и Gy являются аддитивно гомоморфными, зависимость среди следующих формул (21)-(24) устанавливается с использованием переменных r0, r1, t0, u0 и е0. Следующие формулы (21)-(24) можно разделить на первую часть, воспроизводимую с помощью (r0, t0, u0, е0), вторую часть, воспроизводимую с помощью (r0, u1, e1), третью часть, воспроизводимую с помощью (r1, t0, е0), и четвертую часть, воспроизводимую с помощью (r1, t1, u1, e1).
Например, "r0, t0", входящий в следующую формулу (22), "u0", входящий в следующую формулу (23), и "F(r0), Gy(r0, u0), е0", входящий в следующую формулу (24), представляют собой первую часть. Дополнительно, "Gy(r0, u1), e1", входящий в следующую формулу (24), представляет собой вторую часть. Дополнительно, "е0, Gx(r0, r1)", входящий в следующую формулу (21), представляет собой третью часть. Дополнительно, "e1, F(r1), Gx(t1, r1)", входящий в следующую формулу (21), "t1", входящий в следующую формулу (22), и "u1", входящий в следующую формулу (23), представляют собой четвертую часть.
Другими словами, следующая формула (21) включает в себя третью и четвертую части, следующие формулы (22) и (23) включают в себя первую и четвертую части, и следующая формула (24) включает в себя первую и вторую части. Таким образом, каждая из следующих формул (21)-(24) включает в себя два вида частей.
Исходя определения секретного ключа s и зависимости среди следующих формул (21)-(24) гарантируется, что секретный ключ s не доступен даже тогда, когда используется любой один из (r0, t0, u0, е0), (r0, u1 e1), (r1, t0, е0) и (r1, t1 u1, e1). Использование этого свойства позволяет, например, построить эффективный алгоритм (здесь и далее расширенный алгоритм), который относится к 3-проходной схеме, с использованием кубического полинома f1 кольца R.
[Формула 13]
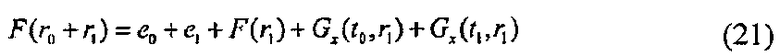


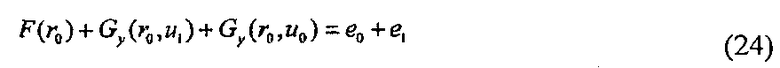
Ниже будет описан пример определенной расширенной структуры алгоритма. Два основных момента, касающихся построения расширенного алгоритма, состоят в том, что сообщение, представленное в виде следующих формул (25)-(27), отправляется верифицирующей стороне, и что одна из первой - четвертой частей верифицируется. Однако только в этой верификации, можно не проверять, что "r1", входящий в третью часть идентичен "r1", входящему в четвертую часть. Аналогично, можно не проверять, что "r0", входящий в первую часть, идентичен "r0", входящему во вторую часть, и что "t0, е0", входящий в первую часть, идентичен "t0, е0", входящему в третью часть. Дополнительно, можно не проверять, что "u1, e1", входящий во вторую часть идентичен "u1, e1", входящему в четвертую часть. Соответственно, пример структуры, обеспечивающий эту верификацию, будет представлен ниже.
[Формула 14]



2.3.1. Базовая структура (фиг.7)
Сначала, со ссылкой на фиг.7, будет описана базовая структура расширенного алгоритма, который относится к 3-проходной схеме. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Операция #1:
Как показано на фиг.7, алгоритм Р доказывающей стороны произвольно генерирует векторы r0, t0, u0, которые представляют собой элементы набора Kn, и вектор е0, который является элементом набора Km. Затем алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Это вычисление эквивалентно маскированию секретного ключа s вектором r0. Затем алгоритм Р доказывающей стороны вычисляет t1<-r0+t0. Затем алгоритм Р доказывающей стороны вычисляет u1<-r1+u0. Затем алгоритм Р доказывающей стороны вычисляет e1<-F(r0)-е0.
Операция #1 (продолжение):
Затем алгоритм Р доказывающей стороны вычисляет с0<-Н(r1, Gx(t0, r1)+е0). Затем алгоритм Р доказывающей стороны вычисляет c1<-H(r0-t0, u0). Затем алгоритм Р доказывающей стороны вычисляет с2<-Н(r0, e1-Gy(r0, u1)). Затем алгоритм Р доказывающей стороны вычисляет с3<-H(t0, e0). Затем алгоритм Р доказывающей стороны вычисляет c4<-H(u1, e1). Сообщения (с0, c1, с2, с3, с4) сгенерированные в операции #1, отправляются в алгоритм V верифицирующей стороны.
Операция #2:
После получения сообщения (с0, c1, с2, c3, c4), алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать среди четырех образцов верификации. Например, алгоритм V верифицирующей стороны может выбрать численное значение четырех численных значений {0, 1, 2, 3}, представляющих собой образцы верификации, и установить выбранное численное значение в вызове Ch. Вызов Ch отправляется в алгоритм Р доказывающей стороны.
Операция #3:
После получения вызова Ch алгоритм Р доказывающей стороны генерирует отклики Rsp для отправки в алгоритм V верифицирующей стороны в ответ на каждый принятый вызов Ch. В случае когда Ch=0, алгоритм Р доказывающей стороны генерирует отклик Rsp=(r0, t0, u0, е0). В случае когда Ch=1, алгоритм Р доказывающей стороны генерирует отклик Rsp=(r0, u1, e1). В случае когда Ch=2, алгоритм Р доказывающей стороны генерирует отклик Rsp=(r1, t0, е0). В случае когда Ch=3, алгоритм Р доказывающей стороны генерирует отклик Rsp=(r1, t1, u1, e1). Отклик Rsp, выработанный в операции #3, отправляется в алгоритм V верифицирующей стороны.
Операция #4:
После получения отклика Rsp алгоритм V верифицирующей стороны выполняет следующий процесс верификации с использованием полученного отклика Rsp.
В случае когда Ch=0, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=Н(r0-t0, u0). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство с2=H(r0, F(r0)+Gy(r0, u0)-е0). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство с3=H(t0, е0). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда Ch=1, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство с2=H(r0, e1-Gy(r0, u1)). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c4=H(u1, e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда Ch=2, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0=H(r1, е0-Gx(t0, r1)). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство с3=H(t0, е0). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда Ch=3, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0=Н(r1, y-F(r1)-e1-Gx(t1, t1)). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H(t1, r1, u1). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c4=H(u1, e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Пример расширенной структуры алгоритма, которая относится к 3-проходной схеме, был описан выше. Благодаря использованию алгоритмов, значительно уменьшается объем данных, необходимый для связи. К тому же, использование кубического полинома позволяет реализовать более высокую безопасность.
2.3.2. Распараллеленный алгоритм (фиг.8)
Далее, со ссылкой на фиг.8, будет описан способ распараллеливания расширенных алгоритмов, который относится к 3-проходной схеме. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Операция #1:
Как показано на фиг.8, алгоритм Р доказывающей стороны выполняет следующие процессы для i=1-N. Сначала, алгоритм Р доказывающей стороны произвольно генерирует векторы r0i, t0i, u0i, которые представляют собой элементы набора Kn, и вектор e0i, который является элементом набора Km. Затем алгоритм Р доказывающей стороны вычисляет r1i<-s-r0i. Это вычисление эквивалентно маскированию секретного ключа s вектором r0i. Затем алгоритм Р доказывающей стороны вычисляет t1i<-r0i-t0i. Затем алгоритм Р доказывающей стороны вычисляет u1i<-r1i-u0i. Затем алгоритм Р доказывающей стороны вычисляет e1i<-F(r0i)-e0i.
Операция #1 (продолжение):
Затем алгоритм Р доказывающей стороны вычисляет c0i<-Н(r1i, Gx(t0i, r1i)+e0i). Затем алгоритм Р доказывающей стороны вычисляет c1i<-H(r0i, -t0i, u0i). Затем алгоритм Р доказывающей стороны вычисляет c2i<-H(r0i, e1i-Gy(r0i, u1i)). Затем алгоритм Р доказывающей стороны вычисляет c3i<-H(t0i, e0i). Затем алгоритм Р доказывающей стороны вычисляет c4i<-Н(u1i, e1i). После генерирования (c0i, с11, c21, c31, c41, …, c0N, c1N, c2N, c3N, c4N) алгоритм P доказывающей стороны вычисляет значение Cmt хэширования <-H(с01, с11, c21, c31, c41, …, c0N, c1N, c2N, c3N, c4N).
Значение Cmt хэширования, сгенерированное в операции #1, отправляется в алгоритм V верифицирующей стороны.
Операция #2:
После получения значения Cmt хэширования алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать из четырех образцов верификации, для каждого i=1-N. Например, алгоритм V верифицирующей стороны может для каждого i=1-N выбрать численное значение четырех численных значений {0, 1, 2, 3}, представляющих собой образцы верификации, и установить выбранное численное значение в вызове Chi. Вызов Chi (i=1-N) отправляется в алгоритм Р доказывающей стороны.
Операция #3:
После получения вызова Chi (i=1-N) алгоритм Р доказывающей стороны генерирует отклики Rspi для каждого i=1-N для отправки в алгоритм V верифицирующей стороны в ответ на каждый принятый вызов Chi. В случае когда Chi=0, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r0i, t0i, u0i, e0i, c0i, c4i). В случае когда Chi=1, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r0i, u1i, e1i, c0i, c1i, c3i). В случае когда Chi=2, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r1i, t0i, e0i, c1i, c2i, c4i). В случае когда Chi=3, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r1i, t1i, u1i, e1i, c2i, c3i). Отклик Rspi (i=1-N), сгенерированный в операции #3, отправляется в алгоритм V верифицирующей стороны.
Операция #4:
После получения отклика Rspi (i=1-N) алгоритм V верифицирующей стороны выполняет следующий процесс для i=1-N с использованием принятого отклика Rsp.
В случае когда Chi=0, алгоритм V верифицирующей стороны вычисляет c1i=H(r0i-t0i, u0i). Затем алгоритм V верифицирующей стороны вычисляет c2i=H(r0i, F(r0i)+Gy(r0i, u0i)-e0i). Затем алгоритм v верифицирующей стороны вычисляет c3i=H(t0i, e0i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i, c2i, c3i, c4i).
В случае когда Chi=1, алгоритм V верифицирующей стороны вычисляет c2i=H(r0i, e1i-Gy(r0i, u1i)). Затем алгоритм V верифицирующей стороны вычисляет c4i=Н(u1i, e1i). Затем алгоритм V верифицирующей стороны вычисляет c3i=H(t0i, e0i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i, c2i, c3i, c4i).
В случае когда Chi=2, алгоритм V верифицирующей стороны вычисляет c0i=H(r1i, Gx(t0i, r1i)+e0i). Затем алгоритм V верифицирующей стороны вычисляет c3i=H(t0i, e0i). Затем алгоритм V верифицирующей стороны вычисляет c3i=H(t0i, e0i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i, c2i, c3i, c4i).
В случае когда Chi=3, алгоритм V верифицирующей стороны вычисляет c0i=Н(r1i, y-F(r1i)-e1i-Gx(t1i, r1i)). Затем алгоритм V верифицирующей стороны вычисляет c1i=H(t1i, r1i-u1i). Затем алгоритм V верифицирующей стороны вычисляет c4i=Н(u1i, e1i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i, c2i, c3i, c4i).
После выполнения описанных выше процессов для i=1-N алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство Cmt=Н(с01, с11, с21, с31, с41, …, c0N, c1N, c2N, c3N, c4N). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда верификация завершается успешно, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Распараллеливание структуры расширенного алгоритма, который относится к 3-проходной схеме, было описано выше. За счет использования алгоритмов, значительно уменьшается объем данных, необходимый для связи. К тому же, использование кубического полинома позволяет реализовать более высокую безопасность.
3. Структура алгоритма, которая относится к 5-проходной схеме аутентификации открытого ключа
Ниже будут описаны алгоритмы, которые относятся к 5-проходной схеме аутентификации открытого ключа. Следует отметить, что в последующем описании 5-проходная схема аутентификации открытого ключа в некоторых случаях может также называться как "5-проходная схема".
В случае 3-проходной схемы вероятность ложной верификации составляет 2/3 в единицу времени интерактивного протокола. Однако в случае 5-проходной схемы, вероятность ложной верификации в единицу времени интерактивного протокола составляет 1/2+1/q. Здесь q - используемый порядок кольца. Соответственно, когда порядок кольца является достаточно большим, вероятность ложной верификации в единицу времени 5-проходной схемы можно уменьшить, и, таким образом, вероятность ложной верификации можно достаточно уменьшить путем выполнения интерактивного протокола маленькое число раз.
Например, когда требуется, чтобы вероятность ложной верификации была равна или менее чем 1/2n, интерактивный протокол должен выполняться n/(log3-1)=1.701n раз или более в 3-проходной схеме. С другой стороны, когда требуется, чтобы вероятность ложной верификации была равна или менее чем 1/2n, интерактивный протокол должен выполняться n/(1-log(1+1/q)) раз или более в 5-проходной схеме. Соответственно, когда q=24, количество передаваемой информации, необходимой для осуществления одинакового уровня безопасности, меньше в 5-проходной схеме, чем в 3-проходной схеме.
3.1. Пример конкретной структуры алгоритма (фиг.9)
Сначала, со ссылкой на фиг.9, будет описан пример конкретной структуры алгоритма, который относится к 5-проходной схеме. На фиг.9 изображена пояснительная схема для описания конкретной структуры алгоритма, который относится к 5-проходной схеме. Алгоритм 5-проходной схемы состоит из алгоритма Gen генерирования ключей, алгоритма Р доказывающей стороны и алгоритма V верифицирующей стороны. Ниже будет описана каждая структура алгоритма.
Алгоритм Gen генерирования ключей
Алгоритм Gen генерирования ключей генерирует многомерные полиномы f1(x1, …, xn), …, fm(x1, xn), определенные в кольце k, и вектор s=(s1, …, sn), который является элементом набора Kn. Далее, алгоритм Gen генерирования ключей вычисляет y=(y1, …, ym)←(f1(s), …, fm(s)). К тому же, алгоритм Gen генерирования ключей устанавливает (f1 …, fm, y) в открытом ключе pk и устанавливает s в качестве секретного ключа. Здесь и далее по тексту вектор (х1, …, xn) представлен в виде х, и пара многомерных полиномов (f1(x), …, fm(x)) представлена в виде F(x).
Алгоритм Р доказывающей стороны, Алгоритм V верифицирующей стороны
Далее, со ссылкой на фиг.9, будут описаны процессы, выполняемые с помощью алгоритма Р доказывающей стороны и алгоритма V верифицирующей стороны во время интерактивного протокола.
Операция #1:
Как показано на фиг.9, алгоритм Р доказывающей стороны произвольно выбирает число seed0. Затем алгоритм Р доказывающей стороны генерирует вектор r0, который представляет собой элемент набора Kn, и пары многомерных полиномов F1(x)=(f11(x), f1m(x)) путем применения числа seed0 в генераторе PRNG случайных чисел. То есть алгоритм Р доказывающей стороны вычисляет (r0, F1)<-G(seed0). Затем алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Это вычисление эквивалентно маскированию секретного ключа s вектором r0.
Операция #1 (продолжение):
Затем алгоритм Р доказывающей стороны генерирует F1(r1) и значение с0 хэширования из r1. То есть алгоритм Р доказывающей стороны вычисляет c0<-H(F1(r1), r1). К тому же, алгоритм Р доказывающей стороны генерирует значение хэширования c1 из числа seed0. То есть алгоритм Р доказывающей стороны вычисляет c1<-H(seed0). Сообщения (с0, c1), выработанные в операции #1, отправляются в алгоритм V верифицирующей стороны.
Операция #2:
После получения сообщения (с0, c1) алгоритм V верифицирующей стороны произвольно выбирает одно число ChA из исходных точек q колец K и посылает выбранное число ChA в алгоритм Р доказывающей стороны.
Операция #3:
После получения числа ChA алгоритм Р доказывающей стороны вычисляет F2(x)<-ChA·F(x+r0)+F1(x). Это вычисление эквивалентно маскированию многомерный полином F(x+r0) для х многомерным полиномом F1(x). Многомерный полином F2, сгенерированный в операции #3, отправляется в алгоритм V верифицирующей стороны.
Операция #4:
После получения многомерного полинома F2 алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать из двух образцов верификации. Например, алгоритм V верифицирующей стороны может выбрать численное значение из двух численных значений {0, 1}, представляющих собой образцы верификации, и установить выбранное численное значение в вызове ChB. Этот вызов ChB отправляется в алгоритм Р доказывающей стороны.
Операция #5:
После получения вызова ChB алгоритм Р доказывающей стороны генерирует отклик Rsp для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов ChB. В случае когда ChB=0, алгоритм Р доказывающей стороны генерирует отклик Rsp=seed0. В случае когда ChB=1, алгоритм Р доказывающей стороны генерирует отклик Rsp=r1. Отклик Rsp, сгенерированный в операции #5 отправляется в алгоритм V верифицирующей стороны.
Операция #6:
После получения отклика Rsp алгоритм V верифицирующей стороны выполняет следующий процесс верификации с использованием полученного отклика Rsp.
В случае когда ChB=0, алгоритм V верифицирующей стороны вычисляет (r0, F1)<-PRNG(Rsp). Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H(Rsp). В добавление к этому, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство F2(x)=ChA·F(F(x+r0)+F1(x). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда ChB=1, алгоритм V верифицирующей стороны устанавливает r1<-Rsp. К тому же, алгоритм V верифицирующей стороны верифицирует, поддерживается ли равенство c0=H(F2(r1)-ChA·y, r1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Корректность
Корректность 5-проходной схемы обеспечивается исходя из того факта, что F1, F2, 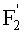
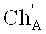
[Формула 15]
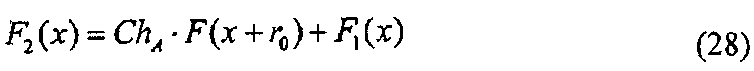
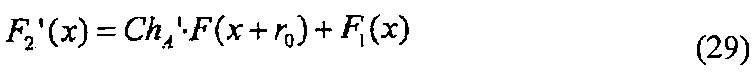
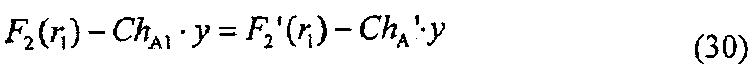
Обеспечив вышеуказанную корректность 5-проходной схемы, тот факт, что подделка с вероятностью выше, чем 1/2+1/q, не возможна, обеспечивается до тех пор, пока не будет решена задача решения многостепенной многомерной системы уравнений. То есть чтобы надлежащим образом произвести отклик на все вызовы ChA=0 и 1 верифицирующей стороны, фальсификатор должен вычислить F1, F2, 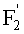
Функция Н хеширования
Ниже приводится дополнительное описание функции Н хеширования. В вышеизложенных алгоритмах, с0, c1 и тому подобное вычисляют с использованием функции Н хеширования. Однако функцию СОМ фиксации можно использовать вместо функции Н хеширования. Функция СОМ фиксации представляет собой функцию, в которой символьная строка S и случайное число ρ представляют собой множители. Пример функции фиксации включает в себя схему, опубликованную на международной конференции CRYPTO 1996 Шаем Халеви (Shai Halevi) и Сильвио Миколи (Silvio Micali).
Например, будет рассмотрен случай, в котором с0 и c1 вычисляют с использованием функция СОМ фиксации. В этом случае случайные числа ρ0 и ρ1 подготавливаются перед вычислением с0 и c1, и с0, c1 генерируются путем применения функций СОМ(·,ρ0) и СОМ(·,ρ1) фиксации вместо применения функции Н(·) хеширования. Кроме того, ρi, необходимый для верифицирующей стороны для того, чтобы сгенерировать ci, устанавливается как включенный в отклик Rsp и отправляется.
Выше был описан пример конкретной структуры алгоритма, который относится к 5-проходной схеме.
3.2. Эффективный алгоритм, основанный на квадратичном многомерном полиноме
Далее будет описан способ создания эффективных алгоритмов, которые относятся к 5-проходной схеме. Здесь будет описан случай, в котором пара квадратичных полиномов (f1(x), …, fm(x)) используется в качестве многомерных полиномов F.
Как и в эффективных алгоритмах, которые относятся к 3-проходной схеме, два вектора, то есть вектор t0, который является элементом набора Kn, и вектор е0, который является элементом набора Km, используются для представления многомерного полинома F1(x), который используется для маскирования многомерного полинома F(x+r0), as F1(x)=G(x, t0)+е0. Когда применяется это выражение, можно получить зависимость, представленную в виде следующей формулы (31), для многомерного полинома F(x+r0).
[Формула 16]
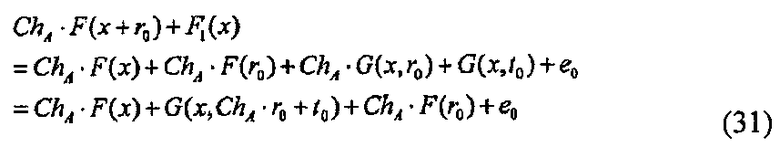
По этой причине, когда t1=ChA·r0+t0, e1=ChA·F(r0)+е0, многомерный полином F2(x)=ChA·F(x+r0)+F1(x) после маскирования можно также представить с помощью двух векторов, то есть вектора t1, который представляет собой элемент набора Kn, и вектора e1, который является элементом набора Km. По этой причине, при установлении "F1(x)=G(x, t0)+е0", F1 и F2 можно представить с использованием вектор в виде Kn и вектора в виде Km, и, таким образом, объем данных, необходимый для связи можно значительно уменьшить. В частности, себестоимость связи можно уменьшить до тысяч и десятков тысяч раз.
За счет использования вышеизложенный модификации информация относительно r0 совершенно не передается из F2 (или F1). Например, даже в том случае, когда e1 и t1 (или е0 и t0) заданы, информация относительно r0 совершенно не известна до тех пор, пока не известны е0 и t0 (или e1 и t1). Соответственно, обеспечивается нулевое знание. Ниже, со ссылкой на фиг.10 и 11, будет описан эффективный алгоритм, который относится к 5-проходной схеме.
3.2.1. Базовая структура (фиг.10)
Сначала, со ссылкой на фиг.10, будет описана базовая структура эффективного алгоритма, который относится к 5-проходной схеме. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Операция #1:
Как показано на фиг.10, алгоритм Р доказывающей стороны произвольно генерирует вектор r0, который является элементом набора Kn, вектор t0, который является элементом набора Kn, и вектор е0, который является элементом набора Km. Затем алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Это вычисление эквивалентно маскированию секретного ключа s вектором r0. Затем алгоритм Р доказывающей стороны вычисляет значение хэширования с0 векторов r0, t0, е0. То есть алгоритм Р доказывающей стороны вычисляет c0<-H(r0, t0, е0). Затем алгоритм Р доказывающей стороны генерирует G(t0, r1)+е0 и значение хэширования c1 из r1. То есть алгоритм Р доказывающей стороны вычисляет с0<-H(r1, G(t0, r1)+е0). Сообщения (с0, c1), сгенерированные в операции #1, отправляются в алгоритм V верифицирующей стороны.
Операция #2:
После получения сообщения (с0, c1), алгоритм V верифицирующей стороны произвольно выбирает одно число ChA из исходных точек q колец K и посылает выбранное число ChA в алгоритм Р доказывающей стороны.
Операция #3:
После получения числа ChA, алгоритм Р доказывающей стороны вычисляет t1<-ChA·r0-t0. Дополнительно, алгоритм Р доказывающей стороны вычисляет e1<-ChA·F(r0)-е0. Алгоритм Р доказывающей стороны отправляет t1 и e1 в алгоритм V верифицирующей стороны.
Операция #4:
После получения t1 и е1 алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать из двух образцов верификации. Например, алгоритм V верифицирующей стороны позволяет выбрать численное значение из двух численных значений {0, 1}, представляющих собой образцы верификации, и установить выбранное численное значение в вызове ChB. Этот вызов ChB отправляется в алгоритм Р доказывающей стороны.
Операция #5:
После получения вызова ChB алгоритм Р доказывающей стороны генерирует отклик Rsp для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов ChB. В случае когда ChB=0, алгоритм Р доказывающей стороны генерирует отклик Rsp=r0. В случае когда ChB=1, алгоритм Р доказывающей стороны генерирует отклик Rsp=r1 Отклик Rsp, сгенерированный в операции #5, отправляется в алгоритм V верифицирующей стороны.
Операция #6:
После получения отклика Rsp алгоритм V верифицирующей стороны выполняет следующий процесс верификации с использованием полученного отклика Rsp.
В случае когда ChB=0, алгоритм V верифицирующей стороны выполняет r0<-Rsp. Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0=Н(r0, ChA·r0-t1, ChA·F(r0)-e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда ChB=1, алгоритм V верифицирующей стороны выполняет r1<-Rsp. Затем алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H1(r1, ChA·(y-F(r1)-G(t1, r1)-e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Выше был описан пример эффективной структуры алгоритма, который относится к 5-проходной схеме. За счет использования алгоритмов, значительно уменьшается объем данных, необходимый для связи.
3.2.2. Распараллеленный алгоритм (фиг.11)
Далее, со ссылкой на фиг.11, будет описан способ распараллеливания эффективных алгоритмов, иллюстрированный на фиг.10. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Как описано выше, применение вышеприведенного интерактивного протокола, который относится к 5-проходной схеме, делает возможным сохранение вероятности успешной подделки на уровне (1/2+1/q) или менее. Следовательно, выполнение интерактивного протокола два раза делает возможным сохранение вероятности успешной подделки на уровне (1/2+1/q)2 или менее. Более того, если интерактивный протокол выполняется N раз, вероятность успешной подделки становится равной (1/2+1/q)N, и если N устанавливается на достаточно большое число (N=80, например), вероятность успешной подделки становится пренебрежимо малой.
Возможные способы выполнения интерактивного протокола много раз включают в себя последовательный способ, в котором обмен сообщением, вызовом и откликом последовательно повторяется много раз, и параллельный способ, в котором обмен многочисленными сообщениями, вызовами и откликами выполняется один раз, например. Ниже будут теперь описаны алгоритмы, которые выполняют вышеприведенный интерактивный протокол, который относится к параллельной 5-проходной схеме (которые в дальнейшем называются как распараллеленные алгоритмы).
Операция #1:
Алгоритм Р доказывающей стороны сначала выполняет следующие процессы (1)-(4) для i=1-N.
Процесс (1): Алгоритм Р доказывающей стороны произвольно генерирует векторы r0i, t0i, которые представляют собой элементы набора Kn, и вектор e0i, который является элементом набора Km.
Процесс (2): Алгоритм Р доказывающей стороны вычисляет r1i<-s-r0i. Это вычисление эквивалентно маскированию секретного ключа s вектором r0i.
Процесс (3): Алгоритм Р доказывающей стороны вычисляет c0i<-H(r0i, t0i, e0i).
Процесс (4): Алгоритм Р доказывающей стороны вычисляет c1i<-Н(r1i, G(t0i, r1i)+e0i).
После выполнения описанных выше процессов (1)-(4) для i=1-N, алгоритм Р доказывающей стороны выполняет значение Cmt хэширования <-Н(с01, с11, …, c0N, c1N). Значение Cmt хэширования, сгенерированное в операции #1, отправляется в алгоритм V верифицирующей стороны.
Операция #2:
После получения значения Cmt хэширования, алгоритм V верифицирующей стороны произвольно выбирает одно число ChAi из исходных точек q колец K для i=1-N и посылает выбранное число ChAi (i=1-N) в алгоритм Р доказывающей стороны.
Операция #3:
После получения числа ChAi (i=1-N) алгоритм Р доказывающей стороны вычисляет t1i<-ChAi·r0i-t0i для i=1-N. Дополнительно, алгоритм Р доказывающей стороны вычисляет e1i<-ChAi·F(r0i)-e0i для i=1-N. Затем алгоритм Р доказывающей стороны отправляет t11, …, t1N и е11, …, e1N в алгоритм V верифицирующей стороны.
Операция #4:
После получения t11, …, t1N и е11, …, e1N алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать из двух образцов верификации для i=1-N. Например, алгоритм V верифицирующей стороны может выбрать численное значение из двух численных значений {0, 1}, представляющих собой образцы верификации, и установить выбранное численное значение в вызове ChBi. Этот вызов ChBi (i=1-N) отправляется в алгоритм Р доказывающей стороны.
Операция #5:
После получения вызова ChBi (i=1-N) алгоритм Р доказывающей стороны генерирует отклик Rspi для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов ChBi для i=1-N. В случае когда ChBi=0, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r0i, c1i). В случае когда ChBi=1, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r1i, c0i). Отклик Rspi (i=1-N), сгенерированный в операции #5, отправляется в алгоритм V верифицирующей стороны.
Операция #6:
После получения отклика Rspi (i=1-N) алгоритм V верифицирующей стороны выполняет следующие процессы (1) и (2) с использованием принятого отклика Rspi (i=1-N).
Процесс (1): В случае когда ChBi=0, алгоритм V верифицирующей стороны выполняет (r0i, c1i)<-Rspi. Затем алгоритм V верифицирующей стороны вычисляет c0i=H(r0i-ChAi·r0i-t1i, ChAi·F(r0i)-e1i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i).
Процесс (2): В случае когда ChBi=1, алгоритм V верифицирующей стороны выполняет (r1i, c0i)<-Rspi. Затем алгоритм V верифицирующей стороны вычисляет c1i=Н(r1i-ChAi·(y-F(r1i))-G(t1i, r1i)-e1i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i).
После выполнение процессов (1) и (2) для i=1-N, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство Cmt=H(c01, с11, …, c0N, c1N). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Пример структур распараллеленных эффективных алгоритмов, которые относятся к 5-проходной схеме, был описан выше. К тому же, распараллеленные алгоритмы, показанные на фиг.11, включают в себя ухищрение, в котором сообщение преобразуется в значение хэширования перед отправкой. Ухищрение повышает эффективность связи. Аналогично, структуру можно модифицировать таким образом, чтобы вызовы ChA1, ChAN, ChB1, ChBN или отклики Rsp1, …, RspN преобразовывались в значения хэширования перед отправкой. Предполагается, что модификация структуры, выполненная таким образом, позволит дополнительно повысить эффективность связи.
3.3. Эффективный алгоритм, основанный на многостепенном многомерном полиноме (схема #1)
Вышеизложенные эффективные алгоритмы используют свойство, которое состоит в том, что полином G, определенный в вышеприведенной формуле (10), становится билинейным за счет представления многомерного полинома F с помощью пары квадратичных полиномов fi, определенных в вышеприведенной формуле (8). Здесь эффективный алгоритм, иллюстрированный на фиг.10, использует тот факт, что открытый ключ F(s) можно разделить на часть, в которой член, который представляет собой ChA раз, зависит от ChA и другой части. Однако даже в случае 5-проходной схемы, когда полином G является линейным, по меньшей мере, для одного из х и y, эффективный алгоритм можно построить подобным образом даже в том случае, когда полином G не является билинейным.
Построение эффективного алгоритма с использованием кубического полинома fi
Способ построения эффективного алгоритма с использованием кубического полинома f1 кольца R будет рассмотрен так, как и в случае 3-проходной схемы. Когда кубический полином f1 представлен в виде вышеприведенной формулы (17), тот факт, что Gx(x, y) и Gy(x, y) становятся линейным для х и y, можно понять из формул (19) и (20).
Таким образом, используя вышеизложенное свойство, открытый ключ F(s) делится на член, который представляет собой ChA раз, путем введения новых переменных r0, r1, t0, u0 и е0. Поскольку полиномы Gx и Gy являются линейными для x и y, зависимость среди следующих формул (32)-(35) устанавливается с использованием переменных r0, r1, t0, u0 и е0. Следующие формулы (32)-(35) можно разделить на первую часть, которая зависит от ChA и вторую часть, которая не зависит от ChA. Здесь первую часть можно воспроизвести с помощью (r1, t1, u1, e1). Вторую часть можно воспроизвести с помощью (r0, t1, u1, e1).
Например, "е0, Gx(t0, r1)", входящий в следующую формулу (32), "t0", входящий в следующую формулу (33), "u0", входящий в следующую формулу (34), и "е0, Gy(r0, u0)", входящий в следующую формулу (35), представляют собой первые части. С другой стороны, "ChAi·F(r0+r1), e1, ChA·F(r1), Gx(t1, r1)", входящий в следующую формулу (32), "ChA·r0, t1", входящий в следующую формулу (33), "ChA·r1, u1", входящий в следующую формулу (34), и “ChA·F(r0), Gy(r0, u1), e1”, входящий в следующую формулу (35), представляют собой вторые части.
Из определения секретного ключа s и зависимости среди следующих формул (32)-(35), обеспечивается тот факт, что секретный ключ s не доступен даже в том случае, когда используется любой один из (r1, t1, u1, e1) и (r0, t1, u1, e1). Использование этого свойства позволяет, например, построить эффективный алгоритм (здесь и далее по тексту расширенный алгоритм), который относится к 5-проходной схеме, с использованием кубического полинома f1 кольца R. [Формула 17]
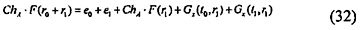


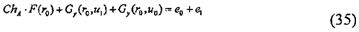
Ниже будет описан пример конкретной расширенной структуры алгоритма. Два основных момента, касающихся построения расширенного алгоритма, состоят в том, что сообщение, представленное в виде следующих формул (36) и (37), отправляется верифицирующей стороне, и что часть (первая часть), которая зависит от ChA, верифицируется для ChA, выбранного верифицирующей стороной. В данном случае поскольку "r0 и r1, используемые во время генерирования сообщения, не допускают замены на другие r0 и r1 во время верификации", пример структуры, в которой добавлена верификация, касающаяся r0 и r1, будет представлен ниже.
[Формула 18]
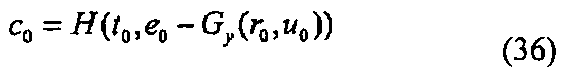
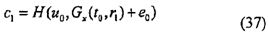
3.3.1. Базовая структура (фиг.12)
Сначала, со ссылкой на фиг.12, будет описана базовая структура расширенного алгоритма, которая относится к 5-проходной схеме. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Операция #1:
Как показано на фиг.12, алгоритм Р доказывающей стороны произвольно генерирует векторы r0, t0, u0, которые представляют собой элементы набора Kn, и вектор е0, который является элементом набора Km. Затем алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Это вычисление эквивалентно маскированию секретного ключа s вектором r0. Затем алгоритм Р доказывающей стороны вычисляет с0<-Н(r0, t0, е0-Gy(r0, u0)). Затем алгоритм Р доказывающей стороны вычисляет c1<-H(r1, u0, Gx(t0, r1)+е0). Сообщения (с0, c1), сгенерированные в операции #1, отправляются в алгоритм V верифицирующей стороны.
Операция #2:
После получения сообщения (с0, c1), алгоритм V верифицирующей стороны произвольно выбирает число ChA. Число ChA отправляется в алгоритм Р доказывающей стороны.
Операция #3:
После получения числа ChA, алгоритм Р доказывающей стороны вычисляет t1<-ChA·r0-t0. Затем алгоритм Р доказывающей стороны вычисляет u1<-ChA·r1-u0. Затем алгоритм Р доказывающей стороны вычисляет e1<-ChA·F(r0)+ChA·Gy(r0, r1)-е0. Затем (t1, u1, e1), сгенерированные в операции #3, отправляются в алгоритм V верифицирующей стороны.
Операция #4:
После получения (t1, u1, e1) алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать из двух образцов верификации. Например, алгоритм V верифицирующей стороны может выбрать численное значение из двух численных значений {0, 1}, представляющих собой образцы верификации, и установить выбранное численное значение в вызове ChB. Этот вызов ChB отправляется в алгоритм Р доказывающей стороны.
Операция #5:
После получения вызова ChB алгоритм Р доказывающей стороны генерирует отклик Rsp для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов ChB. В случае когда ChB=0, алгоритм Р доказывающей стороны генерирует отклик Rsp=r0. В случае когда ChB=1, алгоритм Р доказывающей стороны генерирует отклик Rsp=r1 Отклик Rsp, сгенерированный в операции #5, отправляется в алгоритм V верифицирующей стороны.
Операция #6:
После получения отклика Rsp алгоритм V верифицирующей стороны выполняет следующий процесс верификации с использованием полученного отклика Rsp.
В случае когда ChB=0, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0=Н(r0, ChA·r0-t1, ChA·F(r0)+Gy(r0, u1)-e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда ChB=1, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H(r1, ChA·r1-u1, ChA·(y-F(r1))-Gx(t1, r1)-e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Пример расширенной структуры алгоритма, которая относится к 5-проходной схеме, был описан выше. За счет использования алгоритмов, значительно уменьшается объем данных, необходимый для связи. К тому же, использование кубического полинома позволяет реализовать более высокую безопасность.
3.3.2. Распараллеленный алгоритм (фиг.13)
Далее, со ссылкой на фиг.13, будет описан способ распараллеливания расширенных алгоритмов, которые относятся к 5-проходной схеме. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Операция #1:
Как показано на фиг.13, алгоритм Р доказывающей стороны выполняет следующие процессы для i=1-N. Сначала, алгоритм Р доказывающей стороны произвольно генерирует векторы r0i, t0i, u0i, которые представляют собой элементы набора Kn, и вектор e0i, который является элементом набора Km. Затем алгоритм Р доказывающей стороны вычисляет r1i<-s-r0i. Это вычисление эквивалентно маскированию секретного ключа s вектором r0i Затем алгоритм Р доказывающей стороны вычисляет c0i<-H(r0i, t0i, e0i,-Gy(r0i, u0i). Затем алгоритм P доказывающей стороны вычисляет c1i<-Н(r1i, u0i-Gx(t0i, r1i)+e0i).
Операция #1 (продолжение):
После вычисления (с01 c11, …, c0N, c1N) алгоритм Р доказывающей стороны вычисляет Cmt<-Н(с01, С11, …, C0N, C1N). Значение Cmt хэширования, сгенерированное в операции #1, отправляется в алгоритм V верифицирующей стороны.
Операция #2:
После получения значения Cmt хэширования алгоритм V верифицирующей стороны произвольно выбирает числа ChAi, …, ChAN. Числа ChA1, …, ChAN отправляются в алгоритм Р доказывающей стороны.
Операция #3:
После получения чисел ChAi, …, ChAN алгоритм Р доказывающей стороны выполняет следующий процесс для i=1-N. Сначала, алгоритм Р доказывающей стороны вычисляет t1i<-ChAi·r0i-t0i. Затем алгоритм Р доказывающей стороны вычисляет u1i<-ChAi·r1i-u0i. Затем алгоритм Р доказывающей стороны вычисляет e1i<-ChAi·F(r0i)+ChAi·Gy(r0i, r1i)-e0i.
Затем (t11, u11, е11, …, t1N, u1N, e1N), сгенерированные в операции #3, отправляются в алгоритм V верифицирующей стороны.
Операция #4:
После получения (t11, u11, е11, t1N, u1N, e1N) алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать из двух образцов верификации для i=1-N. Например, алгоритм V верифицирующей стороны может выбрать численное значение среди двух численных значений {0, 1}, представляющих собой образцы верификации для i=1-N, и установить выбранное численное значение в вызове ChBi. Вызовы ChB1-ChBN отправляются в алгоритм Р доказывающей стороны.
Операция #5:
После получения вызовов ChB1-ChBN, алгоритм Р доказывающей стороны генерирует отклик Rspi для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов ChBi для i=1-N. В случае когда ChBi=0, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r0i, c1i). В случае когда GhBi=1, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r1i, C0i). Отклик Rspi, сгенерированный в операции #5, отправляется в алгоритм V верифицирующей стороны.
Операция #6:
После получения отклика Rspi (i=1-N) алгоритм V верифицирующей стороны выполняет следующие процессы с использованием принятого отклика Rspi для i=1-N.
В случае когда ChBi=0, алгоритм V верифицирующей стороны вычисляет c0i=H(r0i-ChAi·r0i-t1i, ChAi·F(r0i)+Gy(r0i, u1i)-e1i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i).
В случае когда ChBi=1, алгоритм V верифицирующей стороны вычисляет c1i=H(r1i, ChAi·r1i-u1i, ChAi·(y-F(r1i))-Gx(t1i, r1i)-e1i). Затем алгоритм V верифицирующей стороны сохраняет (c0i, c1i).
После выполнения вышеизложенных процессов для i=1-N алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство Cmt=H(c01, c11, c0N, c1N). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Распараллеливание структуры расширенного алгоритма, которая относится к 5-проходной схеме, было описано выше. За счет использования алгоритмов значительно уменьшается объем данных, необходимый для связи. К тому же, использование кубического полинома позволяет реализовать более высокую безопасность.
3.4. Эффективный алгоритм, основанный на многостепенном многомерном полиноме (схема #2)
Выше был описан способ построения эффективного алгоритма с использованием кубического полинома f1 кольца R. Здесь будет рассмотрен способ построения расширенного алгоритма с использованием многостепенного полинома f1, определенного в кольце R характеристики q и порядка qk. Многостепенной полином f1 представлен, например, в виде следующей формулы (38). При использовании многостепенного полинома f1 компонент g1 полинома G, определенный как G(x, y)=F(x+y)-F(x)-F(y)=(g1, …, gm), выражен в виде следующей формулы (39).
[Формула 19]
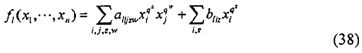
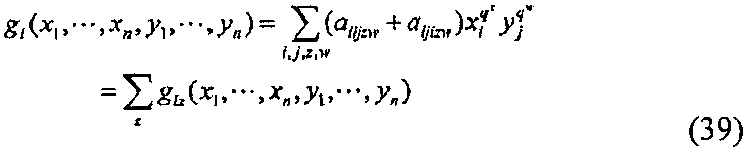
Зависимость, показанная в следующей формуле (40), установлена для ChA, который является элементом набора R. Дополнительно установлена также зависимость, показанная в следующей формуле (41). Таким образом, используя это свойство (здесь и далее по тексту называется как квазилинейность), открытый ключ F(s) делится на член, который представляет собой ChA раз, путем введения новых переменных r0, r1, t0z и е0. Поскольку G имеет квазилинейность, зависимость среди следующих формул (42)-(44) устанавливается с использованием переменных r0, r1, t0z и е0. Следующие формулы (42)-(44) можно разделить на первую часть, которая зависит от ChA, и вторую часть, которая не зависит от ChA. Здесь первую часть можно воспроизвести с помощью (r1, t1z, е1). Вторую часть можно воспроизвести с помощью (r0, t1z, e1).
Например, "е0, ΣGz(t0z, r1)", входящий в следующую формулу (42), "t0z", входящий в следующую формулу (43), и "е0", входящий в следующую формулу (44), представляют собой первые части. С другой стороны, "ChA·F(r0+r1), е1, ChA·F(r1), ΣGz(t1z, r1)", входящий в следующую формулу (42), "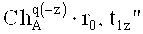
Из определения секретного ключа s и зависимости среди следующих формул (42)-(44), тот факт, что секретный ключ s не доступен, обеспечивается даже в том случае, когда используется любой один из (r1, t1z, e1) и (r0, t1z, e1). Использование этого свойства позволяет, например, построить эффективный алгоритм (здесь и далее по тексту многостепенной расширенный алгоритм), который относится к 5-проходной схеме с использованием многостепенного полинома f1 кольца R.
[Формула 20]
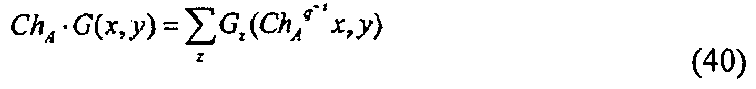
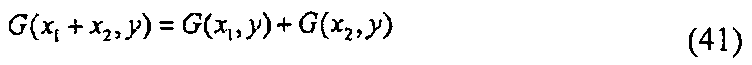
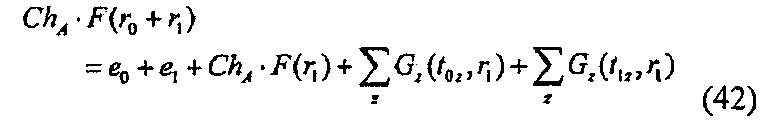


Ниже будет описан пример конкретной многостепенной расширенной структуры алгоритма. Два основных момента, касающихся построения расширенного алгоритма, состоят в том, что сообщение, представленное в виде следующих формул (45) и (46), отправляется верифицирующей стороне, и что часть (первая часть), которая зависит от ChA, верифицируется для ChA, выбранного верифицирующей стороной. Здесь, поскольку "r0 и r1, используемые во время генерирования сообщения, не допускают замены на другие r0 и r1 во время верификации", пример структуры, в которой добавлена верификация, касающаяся r0 и r1 будет представлен ниже.
[Формула 21]

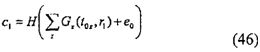
3.4.1. Базовая структура (фиг.14)
Сначала, со ссылкой на фиг.14, будет описана базовая структура многостепенного расширенного алгоритма, которая относится к 5-проходной схеме. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Операция #1:
Как показано на фиг.14, алгоритм Р доказывающей стороны произвольно генерирует векторы r0, t01, t0k, которые представляют собой элементы набора Kn, и вектор e0, который является элементом набора Km. Затем алгоритм Р доказывающей стороны вычисляет r1<-s-r0. Это вычисление эквивалентно маскированию секретного ключа s вектором r0. Затем алгоритм Р доказывающей стороны вычисляет с0<-Н(r0, t01, …, t0k, е0). Затем алгоритм Р доказывающей стороны вычисляет c1<-H(r1, ΣzGz(t0z, r1)+е0) (где Σz представляет собой sum для z=1 to k). Сообщения (с0, c1), сгенерированные в операции #1, отправляются в алгоритм V верифицирующей стороны.
Операция #2:
После получения сообщения (с0, c1) алгоритм V верифицирующей стороны произвольно выбирает число ChA. Число ChA отправляется в алгоритм Р доказывающей стороны.
Операция #3:
После получения числа ChA алгоритм Р доказывающей стороны вычисляет t1z<-(ChA)q(z-1)·r0-t0z для z=1 to k. Затем алгоритм Р доказывающей стороны вычисляет e1<-ChA·F(r0)-е0. Затем (t11, …, t1k, e1), сгенерированные в операции #3, отправляются в алгоритм V верифицирующей стороны.
Операция #4:
После получения (t11, …, t1k, e1) алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать из двух образцов верификации. Например, алгоритм V верифицирующей стороны может выбрать численное значение из двух численных значений {0, 1}, представляющих собой образцы верификации, и установить выбранное численное значение в вызове ChB. Этот вызов ChB отправляется в алгоритм Р доказывающей стороны.
Операция #5:
После получения вызова ChB алгоритм Р доказывающей стороны генерирует отклик Rsp для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов ChB. В случае когда ChB=0, алгоритм Р доказывающей стороны генерирует отклик Rsp=r0. В случае когда ChB=1, алгоритм Р доказывающей стороны генерирует отклик Rsp=r1. Отклик Rsp, сгенерированный в операции #5, отправляется в алгоритм V верифицирующей стороны.
Операция #6:
После получения отклика Rsp алгоритм V верифицирующей стороны выполняет следующий процесс верификации с использованием полученного отклика Rsp.
В случае когда ChB=0, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0=Н(r0, (ChA)q(0)·r0-t11, …, (ChA)q(k-1)·r0-t1k, ChA·F(r0)-e1). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
В случае когда ChB=1, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1=H(r1, ChA·(y-F(r1))-ΣzGz(t1z, r1)). Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Пример многостепенной расширенной структуры алгоритма, которая относится к 5-проходной схеме, был описан выше. За счет использования алгоритмов значительно уменьшается объем данных, необходимый для связи. К тому же, используя многостепенной полином, можно обеспечить более высокую безопасность.
3.4.2. Распараллеленный алгоритм (пример 1 структуры) (фиг.15)
Далее, со ссылкой на фиг.15, будет описан способ распараллеливания многостепенных расширенных алгоритмов, которые относятся к 5-проходной схеме. Однако дополнительное описание структуры алгоритма Gen генерирования ключей будет опущено.
Операция #1:
Как показано на фиг.15, алгоритм Р доказывающей стороны выполняет следующие процессы для i=1-N. Сначала алгоритм Р доказывающей стороны произвольно генерирует векторы r0i, t01i, …, t0ki, которые представляют собой элементы набора Kn, и вектор e0i, который является элементом набора Km. Затем алгоритм Р доказывающей стороны вычисляет r1i<-s-r0i. Это вычисление эквивалентно маскированию секретного ключа s вектором r0i. Затем алгоритм Р доказывающей стороны вычисляет c0i<-Н(r0i, t01i, t0ki, e0i). Затем алгоритм Р доказывающей стороны вычисляет c1i<-Н(r1i, ΣzGz(t0zi, r1i)+e0i) (где Σz представляет собой sum для z=1-k). Сообщения (c0i, c1i) (где i=1-N), сгенерированные в операции #1, отправляются в алгоритм V верифицирующей стороны.
Операция #2:
После получения сообщения (c0i, c1i) (где i=1-N) алгоритм V верифицирующей стороны произвольно выбирает числа ChA1, …, ChAN. Числа ChA1, …, ChAN отправляются в алгоритм Р доказывающей стороны.
Операция #3:
После получения чисел ChA1, …, ChAN алгоритм Р доказывающей стороны вычисляет t1zi<-(ChAi)q(z-1)·r0i-t0zi для i=1-N и z=1-k. Затем алгоритм Р доказывающей стороны вычисляет e1i<-ChAi·F(r0i)-e0i. Затем (t11i, t1ki, e1i) (где i=1-N), сгенерированные в операции #3, отправляются в алгоритм V верифицирующей стороны.
Операция #4:
После получения (t11i, …, t1ki, e1i) (где i=1-N) алгоритм V верифицирующей стороны выбирает, какой образец верификации использовать из двух образцов верификации для i=1-N. Например, алгоритм V верифицирующей стороны может выбрать численное значение из двух численных значений {0, 1}, представляющих собой образцы верификации для i=1-N, и установить выбранное численное значение в вызове ChBi. Вызов ChBi (где i=1-N) отправляется в алгоритм Р доказывающей стороны.
Операция #5:
После получения вызова ChBi (где i=1-N) алгоритм Р доказывающей стороны генерирует отклик Rspi для отправки в алгоритм V верифицирующей стороны в ответ на принятый вызов ChBi для i=1-N. В случае, когда ChBi=0, алгоритм Р доказывающей стороны генерирует отклик Rspi=r0i В случае когда ChBi=1, алгоритм Р доказывающей стороны генерирует отклик Rspi=r1i. Отклик Rspi (где i=1-N), сгенерированный в операции #5, отправляется в алгоритм V верифицирующей стороны.
Операция #6:
После получения отклика Rspi (i=1-N) алгоритм V верифицирующей стороны выполняет следующие процессы верификации с использованием принятого отклика Rspi для i=1-N.
В случае когда ChBi=0, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c0i=H(r0i, (ChAi)q(0)·r0i-t11i, (ChAi)q(k-1)·r0i-t1ki, ChAi·F(r0i-e1i). В случае когда ChBi=1, алгоритм V верифицирующей стороны верифицирует то, соблюдается или нет равенство c1i=Н(r1i, ChAi·(y-F(r1i)-ΣzGz(t1zi, r1i)).
Алгоритм V верифицирующей стороны выводит значение 1, чтобы показать успешное завершение аутентификации в том случае, когда все эти верификации являются успешными, и выводит значение 0, чтобы показать неуспешное завершение аутентификации в том случае, когда верификация завершилась неудачно.
Распараллеливание многостепенного расширенного алгоритма, который относится к 5-проходной схеме, было описано выше. За счет использования алгоритмов, значительно уменьшается объем данных, необходимый для связи. К тому же, используя многостепенной полином, можно обеспечить более высокую безопасность.
3.4.3. Распараллеленный алгоритм (пример 2 структуры: высокая эффективность) (фиг.16)
Однако в распараллеленной структуре многостепенного расширенного алгоритма, иллюстрированного на фиг.15, сообщения (c0i, c1i) (где i=1-N) были отправлены на первом проходе без изменения. Однако, принимая во внимание эффективность связи, предпочтительно, чтобы сообщения (c0i, c1i) (где i=1-N) отправлялись вместе с одним значением хэширования. Для того чтобы отправлять вместе сообщения (c0i, c1i) (где i=1-N) с одним значением хэширования на первом проходе, структуру алгоритма можно модифицировать так, как показано на фиг.16.
В примере структуры фиг.16 алгоритм Р доказывающей стороны вычисляет значение Cmt хэширования <-Н(с01, c11, …, c0N, c1N) в операции #1. После генерирования отклика Rspi в операции #5, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r0i, c1i) в случае, когда ChBi=0 и генерирует отклик Rspi=(r1i, c0i) в случае, когда ChBi=1. С другой стороны, алгоритм V верифицирующей стороны генерирует (c01, с11, …, c0N, c1N) из (ChAi, ChBi, Rspi) (где i=1-N) в операции #6 и верифицирует то, соблюдается или нет равенство Cmt=Н(с01, c11, …, c0N, c1N). Выполняя такую модификацию, можно дополнительное повысить эффективность связи.
Выше был описан эффективный распараллеленный алгоритм, основанный на многостепенных расширенных алгоритмах.
3.4.4. Распараллеленный алгоритм (пример 2 структуры: более высокая эффективность) (фиг.17)
Однако в распараллеленной структуре многостепенного расширенного алгоритма, иллюстрированного на фиг.15, сообщения (c0i, c1i) (где i=1-N) были отправлены на первом проходе без изменения. Дополнительно, (t11i, …, t1ki, e1i) (где i=1-N) были отправлены на третьем проходе без изменения. Однако, принимая во внимание эффективность связи, предпочтительно, чтобы сообщения (c0i, c1i) (где i=1-N) отправлялись вместе с одним значением хэширования. Дополнительно, предпочтительно, чтобы (t11i, …, t1ki, e1i) (где i=1-N) отправлялись вместе с одним значением хэширования. Для того чтобы отправлять вместе сообщения (c0i, c1i) (где i=1-N) с одним значением хэширования на первом проходе и отправлять вместе (t11i, …, t1ki, e1i) (где i=1-N) с одним значением хэширования на третьем проходе, структуру алгоритма можно модифицировать так, как показано на фиг.17.
В примере структуры фиг.17 алгоритм Р доказывающей стороны вычисляет значение Cmt хэширования <-Н(с01, с11, …, c0N, c1N) в операции #1. Алгоритм Р доказывающей стороны вычисляет значение Cmt хэшированияВ <-H(t111, …, t1kN, е11, …, e1N) в операции #3. после генерирования отклика Rspi в операции #5, алгоритм Р доказывающей стороны генерирует отклик Rspi=(r0i, t01i, …, t0ki, e0i, c1i) в случае, когда ChBi=0, и генерирует отклик Rspi=(r1i, t11i, …, t1ki, e1i, c0i) в случае, когда ChBi=1.
С другой стороны, алгоритм V верифицирующей стороны генерирует (c01, с11, …, c0N, c1N) из (ChAi, ChBi, Rspi (где i=1-N) и (t111, …, t1kN, е11, e1N) в операции #6 и верифицирует то, соблюдается или нет равенство CmtA=(с01, с11, …, c0N, c1N) и CmtB=(t111, …, t1kN, е11, e1N). Выполняя такую модификацию, можно дополнительно повысить эффективность связи.
Дополнительный эффективный распараллеленный алгоритм, основанный на многостепенных расширенных алгоритмах, был описан выше.
Применяя многостепенной расширенный алгоритм, описанный выше, можно реализовать эффективную схему аутентификации открытого ключа, имеющую более высокую безопасность. Например, когда (q, n, m, N)=(24, 45, 30, 88) в расширенном алгоритме, который относится к 5-проходной схеме, длина открытого ключа составляет 120 битов, длина секретного ключа составляет 180 битов, и объем данных связи составляет 27512 битов.
Например, когда условие (q, n, m, N)=(22, 42, 40, 118) удовлетворено в случае многостепенного расширенного алгоритма, который относится к 5-проходной схеме, безопасность обеспечивается на одинаковом уровне. При выполнении этого условия, длина открытого ключа составляет 80 битов, длина секретного ключа составляет 84 битов, и объем данных передачи составляет 27814 битов. То есть путем применения многостепенного расширенного алгоритма, объем данных передачи можно поддерживать на том же самом уровне и можно значительно уменьшить длину открытого ключа и длину секретного ключа.
Условие можно модифицировать в (q, n, m, N)=(23, 28, 27, 97). В этом случае длина открытого ключа составляет 81 битов, длина секретного ключа составляет 84 битов, и объем данных передачи составляет 27145 битов. Кроме того, условие можно модифицировать в (q, n, m, N)=(24, 21, 20, 88). В этом случае длина открытого ключа составляет 80 битов, длина секретного ключа составляет 84 битов, и объем данных передачи составляет 28392 битов. При выполнении любого из этих условий достигается значительная эффективность.
4. Модификация схемы цифровой подписи
Ниже будет рассмотрен способ модификации вышеизложенный схемы аутентификации открытого ключа в схеме цифровой подписи.
Когда доказывающая сторона в модели схемы аутентификации открытого ключа совпадает с подписывающей стороной, в схеме цифровой подписи, приближение к модели схемы цифровой подписи можно легко понять в том смысле, что только доказывающая сторона может убедить верифицирующую сторону. На основании этой идеи будет рассмотрен способ модификации вышеописанной схемы аутентификации открытого ключа в схеме цифровой подписи.
4.1. Модификация 3-проходной схемы аутентификации открытого ключа в схеме цифровой подписи
Сначала будет описана модификация схемы аутентификации открытого ключа 3-проходной в схеме цифровой подписи.
4.1.1. Алгоритм цифровой подписи (пример 1 структуры) (фиг.18)
Как показано на фиг.18, эффективный алгоритм (например, смотри фиг.6 и 8), который относится к 3-проходной схеме, представлен с помощью интерактивности три раза и четырех операций, то есть операций #1-#4.
Операция #1 включает в себя процесс (1) генерирования ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i, c2i) и процесс (2) вычисления Cmt<-H(c01, c11, c21, …, c0N, c1N, C2N). Cmt, сгенерированный в операции #1 с помощью алгоритма Р доказывающей стороны, отправляется в алгоритм V верифицирующей стороны.
Операция #2 включает в себя процесс выбора Ch1, …, ChN. Ch1, …, ChN выбранные в операции #2 с помощью алгоритма V верифицирующей стороны, отправляются в алгоритм Р доказывающей стороны.
Операция #3 включает в себя процесс генерирования Rsp1, RspN с использованием Ch1, …, ChN и а1 …, aN. Этот процесс представлен в виде Rspi<-Select(Chi, ai). Rsp1, RspN, сгенерированные в операции #3 с помощью алгоритма Р доказывающей стороны, отправляются в алгоритм V верифицирующей стороны.
Операция #4 включает в себя процесс (1) воспроизведения с01, с11, с21, …, c0N, c1N, c2N с использованием Ch1, …, ChN и Rsp1, …, RspN и процесс (2) верификации Cmt=Н(с01, с11, с21, …, c0N, c1N, c2N) с использованием воспроизведенных с01, c11, c21, …, c0N, c1N, c2N.
Алгоритм схемы аутентификации открытого ключа, представленный с помощью вышеизложенных операций #1-#4, модифицируется в алгоритм Sig генерирования подписи и алгоритм Ver верификации подписи, которые иллюстрированы на фиг.18.
Алгоритм Sig генерирования подписи
Сначала будет описана структура алгоритма Sig генерирования подписи. Алгоритм Sig генерирования подписи включает в себя следующие процессы (1)-(5).
Процесс (1): Алгоритм Sig генерирования подписи генерирует ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i, c2i).
Процесс (2): Алгоритм Sig генерирования подписи вычисляет Cmt<-Н(с01, c11, c21, …, c0N, c1N, c2N).
Процесс (3): Алгоритм Sig генерирования подписи вычисляет (Ch1, …, ChN)<-H(M, Cmt). Здесь M представляет собой документ, к которому прикрепляется подпись.
Процесс (4): Алгоритм Sig генерирования подписи вычисляет Rspi<-Select(Chi, ai).
Процесс (5): Алгоритм Sig генерирования подписи устанавливает (Cmt, Rsp1, …, RspN) в качестве подписи.
Алгоритм Ver верификации подписи
Далее будет описана структура алгоритма Ver верификации подписи. Алгоритм Ver верификации подписи включает в себя следующие процессы (1)-(3).
Процесс (1): Алгоритм Ver верификации подписи вычисляет (Ch1, …, ChN)<-Н(М, Cmt).
Процесс (2): Алгоритм Ver верификации подписи генерирует с01, с11, с21, …, c0N, c1N, c2N с использованием Ch1, …, ChN и Rsp1, …, RspN.
Процесс (3): Алгоритм Ver верификации подписи верифицирует Cmt=Н(с01, c11, с21, …, c0N, c1N, c2N) с использованием воспроизведенных с01, c11, с21, …, c0N, c1N, c2N.
Как описано выше, за счет совпадения доказывающей стороны в модели схемы аутентификации открытого ключа с подписывающей стороной в схеме цифровой подписи алгоритм схемы аутентификации открытого ключа можно модифицировать в алгоритм схемы цифровой подписи.
4.1.2. Алгоритм цифровой подписи (пример 2 структуры: высокая эффективность) (фиг.19)
Однако когда структуре алгоритма Sig генерирования подписи, иллюстрированной на фиг.18, уделяется большое внимание, можно осуществить то, чтобы вычисление значения хэширования выполнялось в процессах (2) и (3). Кроме того, когда структуре алгоритма Ver верификации подписи уделяется большое внимание, можно осуществить то, чтобы то же самое вычисление значения хэширования, как и в процессе (3) алгоритма Sig генерирования подписи, выполнялось в процессе (1). Когда конфигурации алгоритма Sig генерирования подписи и алгоритма Ver верификации подписи усовершенствованы с учетом этих процессов, как показано на фиг.19, можно дополнительно повысить эффективность вычисления.
Алгоритм Sig генерирования подписи
Сначала, со ссылкой на фиг.19, будет описана структура усовершенствованного алгоритма Sig генерирования подписи. Алгоритм Sig генерирования подписи включает в себя следующие процессы (1)-(4).
Процесс (1): Алгоритм Sig генерирования подписи генерирует ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i, c2i).
Процесс (2): Алгоритм Sig генерирования подписи вычисляет (Ch1, …, ChN)<-H(M, с01, c11, с21, …, c0N, c1N, c2N). Здесь M представляет собой документ, к которому прикрепляется подпись.
Процесс (3): Алгоритм Sig генерирования подписи вычисляет Rspi<-Select(Chi, ai).
Процесс (4): Алгоритм Sig генерирования подписи устанавливает (Ch1, …, ChN, Rsp1, …, RspN) в качестве подписи.
Алгоритм Ver верификации подписи
Далее будет описана структура усовершенствованного алгоритма Ver верификации подписи. Алгоритм Ver верификации подписи включает в себя следующие процессы (1) и (2).
Процесс (1): Алгоритм Ver верификации подписи генерирует с01, c11, с21, …, c0N, c1N, c2N с использованием Ch1, …, ChN и Rsp1, …, RspN.
Процесс (2): Алгоритм Ver верификации подписи верифицирует (Ch1, …, ChN)=H(с01, c11, с21, …, c0N, c1N, c2N) с использованием воспроизведенных с01, c11, с21, …, c0N, c1N, c2N.
За счет усовершенствования структур алгоритма Sig генерирования подписи и алгоритма верификации подписи Ve, как описано выше, вычисление значения хэширования в каждом алгоритме уменьшается на один раз и, таким образом, повышается эффективность вычислений.
4.2. Модификация 5-проходной схемы аутентификации открытого ключа в схеме цифровой подписи
Далее будет описана модификация схемы аутентификации открытого ключа, которая относится к 5-проходной схеме в схеме цифровой подписи.
4.2.1. Алгоритм цифровой подписи (пример 1 структуры) (фиг.20)
Как показано на фиг.20, эффективный алгоритм (например, смотри фиг.11, 13, и 16), который относится к 5-проходной схеме, представлен с помощью интерактивности пять раз и шести операций, то есть операций #1-#6.
Операция #1 включает в себя процесс (1) генерирования ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i) для i=1-N и процесс (2) вычисления Cmt<-Н(с01, c11, …, c0N, c1N). Cmt, сгенерированный в операции #1 с помощью алгоритма Р доказывающей стороны, отправляется в алгоритм V верифицирующей стороны.
Операция #2 включает в себя процесс выбора ChA1, …, ChAN. ChA1, …, ChAN, выбранные в операции #2 с помощью алгоритма V верифицирующей стороны, отправляются в алгоритм Р доказывающей стороны.
Операция #3 включает в себя процесс генерирования bi=(t1i, e1i) для i=1-N. Здесь b1, …, bN, сгенерированные в операции #3 с помощью алгоритма Р доказывающей стороны, отправляются в алгоритм V верифицирующей стороны.
Операция #4 включает в себя процесс выбора ChB1, …, ChBN. ChB1, …, ChBN, выбранные в операции #4 с помощью алгоритма V верифицирующей стороны, отправляются в алгоритм Р доказывающей стороны.
Операция #5 включает в себя процесс генерирования Rsp1, …, RspN с использованием ChB1, …, ChBN, a1, …, aN, b1, …, bN. Этот процесс представлен в виде Rspi<-Select(ChBi, ai, bi). Rsp1, …, RspN, сгенерированные в операции #5 с помощью алгоритма Р доказывающей стороны, отправляются в алгоритм V верифицирующей стороны.
Операция #6 включает в себя процесс (1) воспроизведения с01, с11, …, c0N, c1N, с использованием ChA1, …, ChAN, ChB1, …, ChBN, Rsp1, …, RspN и процесс (2) верификации Cmt=H(с01, с11, …, c0N, c1N с использованием воспроизведенных с01, с11, …, c0N, c1N.
Алгоритм схемы аутентификации открытого ключа, представленный с помощью вышеизложенных операций #1-#6, модифицируется в алгоритм Sig генерирования подписи и алгоритм Ver верификации подписи, которые иллюстрированы на фиг.20.
Алгоритм Sig генерирования подписи
Сначала будет описана структура алгоритма Sig генерирования подписи. Алгоритм Sig генерирования подписи включает в себя следующие процессы (1)-(7).
Процесс (1): Алгоритм Sig генерирования подписи генерирует ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i).
Процесс (2): Алгоритм Sig генерирования подписи вычисляет Cmt<-Н(с01, с11, …, c0N, c1N).
Процесс (3): Алгоритм Sig генерирования подписи вычисляет (ChA1, …, ChAN)<-Н(М, Cmt). Здесь М представляет собой документ, к которому прикрепляется подпись.
Процесс (4): Алгоритм Sig генерирования подписи генерирует bi=(t1i, e1i) для i=1-N.
Процесс (5): Алгоритм Sig генерирования подписи вычисляет (ChB1, …, ChBN)<-Н(М, Cmt, ChA1, …, ChAN, b1, …, bN). Дополнительно, можно выполнить модификацию в (ChB1, …, ChBN)<-H(ChA1, …, ChAN, b1, …, bN).
Процесс (6): Алгоритм Sig генерирования подписи вычисляет Rspi<-Select(ChBi, ai, bi).
Процесс (7): Алгоритм Sig генерирования подписи устанавливает (Cmt, b1, …, bN, Rsp1, …, RspN) в качестве цифровой подписи.
Алгоритм Ver верификации подписи
Далее будет описана структура алгоритма Ver верификации подписи. Алгоритм Ver верификации подписи включает в себя следующие процессы (1)-(4).
Процесс (1): Алгоритм Ver верификации подписи вычисляет (ChA1, …, ChAN)=Н(М, Cmt).
Процесс (2): Алгоритм Ver верификации подписи вычисляет (ChB1, …, ChBN)=Н(М, Cmt, ChA1, …, ChAN, b1, bN). Когда модификация в (ChB1, …, ChBN)=H(ChA1, …, ChAN, b1, …, bN) выполняется в процессе (5), выполняемом с помощью алгоритма Ver верификации подписи, алгоритм Ver верификации подписи вычисляет (ChB1, …, ChBN)=H(ChA1, …, ChAN, b1, …, bN).
Процесс (3): Алгоритм Ver верификации подписи генерирует с01, с11, …, c0N, c1N с использованием ChA1, …, ChAN, ChB1, …, ChBN, Rsp1, …, RspN.
Процесс (4): Алгоритм Ver верификации подписи верифицирует Cmt=H(с01, с11, …, c0N, c1N) с использованием воспроизведенных с01, с11, …, c0N, c1N.
Как описано выше, за счет совпадения доказывающей стороны в модели схемы аутентификации открытого ключа с подписывающей стороной, в схеме цифровой подписи, алгоритм схемы аутентификации открытого ключа можно модифицировать в алгоритм схемы цифровой подписи.
4.2.2. Алгоритм цифровой подписи (пример 2 структуры: высокая эффективность) (фиг.21)
Как показано на фиг.21, дополнительный эффективный алгоритм (например, смотри фиг.17), который относится к 5-проходной схеме, представлен с помощью интерактивности пять раз и шести операций #1-#6.
Операция #1 включает в себя процесс (1) генерирования ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i) для i=1-N и процесс (2) вычисления CmtA<-H(с01, с11, …, c0N, c1N). CmtA, сгенерированный в операции #1 с помощью алгоритма Р доказывающей стороны, отправляется в алгоритм V верифицирующей стороны.
Операция #2 включает в себя процесс выбора ChA1, …, ChAN. ChA1, …, ChAN выбранные в операции #2 с помощью алгоритма V верифицирующей стороны, отправляются в алгоритм Р доказывающей стороны.
Операция #3 включает в себя процесс (1) генерирования bi=(t1i, e1i) и процесс (2) вычисления CmtB<-Н(b1, …, bN) для i=1-N. CmtB, сгенерированный в операции #3 с помощью алгоритма Р доказывающей стороны, отправляется в алгоритм V верифицирующей стороны.
Операция #4 включает в себя процесс выбора ChB1, …, ChBN. ChB1, …, GhBN, выбранные в операции #4 с помощью алгоритма V верифицирующей стороны, отправляются в алгоритм Р доказывающей стороны.
Операция #5 включает в себя процесс генерирования Rsp1, …, RspN с использованием ChB1, …, ChBN, a1 …, aN, b1 …, bN. Этот процесс представлен в виде Rspi<-Select(ChBi, ai, bi). Rsp1, …, RspN, сгенерированные в операции #5 с помощью алгоритма Р доказывающей стороны, отправляются в алгоритм V верифицирующей стороны.
Операция #6 включает в себя процесс (1) воспроизведения c01, с11, …, c0N, c1N, b1 …, bN с использованием ChA1, …, ChAN, ChB1, …, ChBN, Rsp1, RspN, процесс (2) верификации CmtA=Н(с01, с11, …, c0N, c1N) с использованием воспроизведенных с01, с11, …, c0N, c1N, и процесс (3) верификации CmtB=H(b1 …, bN) с использованием воспроизведенных b1 …, bN.
Алгоритм схемы аутентификации открытого ключа, представленный с помощью вышеприведенных операций #1-#6, модифицируется в алгоритм Sig генерирования подписи и алгоритм Ver верификации подписи, которые иллюстрированы на фиг.21.
Алгоритм Sig генерирования подписи
Сначала будет описана структура алгоритма Sig генерирования подписи. Алгоритм Sig генерирования подписи включает в себя следующие процессы (1)-(8).
Процесс (1): Алгоритм Sig генерирования подписи генерирует ai=(r0i, t0i, e0i, r1i, t1i, e1i, c0i, c1i).
Процесс (2): Алгоритм Sig генерирования подписи вычисляет CmtA<-H(с01, с11, …, c0N, c1N).
Процесс (3): Алгоритм Sig генерирования подписи вычисляет (ChA1, …, ChAN)<-Н(М, CmtA). Здесь М представляет собой документ, к которому прикрепляется подпись.
Процесс (4): Алгоритм Sig генерирования подписи генерирует bi=(t1i, e1i) для i=1-N.
Процесс (5): Алгоритм Sig генерирования подписи вычисляет CmtB<-H(b1 …, bN).
Процесс (6): Алгоритм Sig генерирования подписи вычисляет (ChB1, …, ChBN)<-Н(М, Cmt, ChA1, …, ChAN, CmtB). Дополнительно, можно выполнить модификацию в (ChB1, …, ChBN)<-H(ChA1, …, ChAN, CmtB).
Процесс (7): Алгоритм Sig генерирования подписи вычисляет Rspi<-Select(ChBi, ai, bi).
Процесс (8): Алгоритм Sig генерирования подписи устанавливает (CmtA, CmtB, Rsp1, …, RspN) в качестве цифровой подписи.
Алгоритм Ver верификации подписи.
Далее будет описана структура алгоритма Ver верификации подписи. Алгоритм Ver верификации подписи включает в себя следующие процессы (1)-(5).
Процесс (1): Алгоритм Ver верификации подписи вычисляет (ChA1, …, ChAN)=H(М, CmtA).
Процесс (2): Алгоритм Ver верификации подписи вычисляет (ChB1, …, ChBN)=H(М, CmtA, ChA1, …, ChAN, b1, bN, CmtB). Когда модификация в (ChB1, …, ChBN)=H(ChA1, …, ChAN, CmtB) выполняется в процессе (6), выполняемом с помощью алгоритма Ver верификации подписи, алгоритм Ver верификации подписи вычисляет (ChB1, …, ChBN)=H(ChA1, …, ChAN, CmtB).
Процесс (3): Алгоритм Ver верификации подписи генерирует с01, с11, …, c0N, c1N с использованием ChA1, …, ChAN, ChB1, …, ChBN, Rsp1, …, RspN.
Процесс (4): Алгоритм Ver верификации подписи верифицирует CmtA=Н(с01, с11, …, c0N, c1N) с использованием воспроизведенных с01, с11, …, c0N, c1N.
Процесс (5): Алгоритм Ver верификации подписи верифицирует CmtB=H(b1, …, bN) с использованием воспроизведенных b1, …, bN.
Как описано выше, за счет совпадения доказывающей стороны в модели схемы аутентификации открытого ключа с подписывающей стороной, в схеме цифровой подписи, алгоритм схемы аутентификации открытого ключа можно модифицировать в алгоритм схемы цифровой подписи.
5. Алгоритм гибридного типа
Необходимость выполнения интерактивного протокола множество раз таким образом, чтобы вероятность успешной подделки становилась пренебрежимо малой, была уже описана. Кроме того, последовательный способ и параллельный способ были представлены в качестве способ выполнения интерактивного протокола множество раз. В частности, параллельный способ был описан на примере специфического распараллеленного алгоритма. Ниже будет представлен алгоритм гибридного типа, в котором объединены последовательный способ и параллельный способ.
5.1. Алгоритм гибридного типа, который относится к 3-проходной схеме аутентификации открытого ключа
Сначала будет описан алгоритм гибридного типа, который относится к 3-проходной схемы аутентификации открытого ключа.
5.1.1. Параллельно-последовательный алгоритм (фиг.22)
Один пример структуры гибридного типа (здесь и далее по тексту называется как параллельно-последовательная структура) будет описан со ссылкой на фиг.22. На фиг.22 изображена схема, иллюстрирующая алгоритм, имеющий базовую структуру, и алгоритм, имеющий параллельно-последовательную структуру.
В случае базовой структуры, сообщение Cmt отправляется из доказывающей стороны верифицирующей стороне на первом проходе. На втором проходе вызов Ch отправляется из верифицирующей стороны доказывающей стороне. На третьем проходе отклик Rsp отправляется из доказывающей стороны верифицирующей стороне.
С другой стороны, в случае параллельно-последовательной структуры, сообщения (Cmt1, …, CmtN) N раз отправляются из доказывающей стороны верифицирующей стороне на первом проходе. На втором проходе вызов Ch1 отправляется один раз из верифицирующей стороны доказывающей стороне. На третьем проходе отклик Rsp1 отправляется один раз из доказывающей стороны верифицирующей стороне. В дальнейшем, вызовы Ch2, …, ChN и отклики Rsp2, RspN обмениваются последовательно между доказывающей стороной и верифицирующей стороной.
В случае параллельно-последовательной структуры основанной на алгоритме схемы аутентификации открытого ключа, описанной выше, обеспечивается безопасность от пассивного прикрепления. Кроме того, число интерактивностей составляет только 2N+1 раз. Кроме того, когда сообщения, отправленные N раз на первом проходе, собираются с одним значением хэширования, можно повысить эффективность связи.
5.1.2. Последовательно-параллельный алгоритм (фиг.23))
Другой пример структуры гибридного типа (здесь и далее по тексту называется как последовательно-параллельная структура) будет описан со ссылкой на фиг.23. На фиг.23 изображена схема, иллюстрирующая алгоритм, имеющий базовую структуру, и алгоритм, имеющий последовательную параллельную структуру.
В случае базовой структуры сообщение Cmt отправляется из доказывающей стороны верифицирующей стороне на первом проходе. На втором проходе вызов Ch отправляется из верифицирующей стороны доказывающей стороне. На третьем проходе отклик Rsp отправляется из доказывающей стороны верифицирующей стороне.
В случае последовательно-параллельной структуры сообщение Cmt1 отправляется один раз из доказывающей стороны верифицирующей стороне на первом проходе. На втором проходе вызов Ch1 отправляется один раз из верифицирующей стороны доказывающей стороне. В дальнейшем сообщения Cmt2, …, CmtN и вызовы Ch2, …, ChN обмениваются последовательно между доказывающей стороной и верифицирующей стороной. После того, как вызов GhN отправляется из верифицирующей стороны доказывающей стороне, отклики Rsp2, RspN N раз отправляются из доказывающей стороны верифицирующей стороне.
В случае последовательно-параллельной структуры, основанной на алгоритме схемы аутентификации открытого ключа, описанной выше, обеспечивается безопасность от активного прикрепления. Кроме того, число интерактивностей составляет только 2N+1 раз.
5.2. Алгоритм гибридного типа, который относится к 5-проходной схеме аутентификации открытого ключа
Далее будет описан алгоритм гибридного типа, который относится к 5-проходной схеме аутентификации открытого ключа.
5.2.1. Параллельно-последовательный алгоритм (пример #1 структуры) (фиг.24))
Сначала, со ссылкой на фиг.24, будет описан один пример структуры гибридного типа (здесь и далее по тексту называется как параллельно-последовательная структура #1). На фиг.24 изображена схема, иллюстрирующая алгоритм, имеющий базовую структуру, и алгоритм, имеющий параллельно-последовательную структуру #1.
В случае базовой структуры сообщение CmtA отправляется из доказывающей стороны верифицирующей стороне на первом проходе. На втором проходе число ChA отправляется из верифицирующей стороны доказывающей стороне. На третьем проходе вектор CmtB отправляется из доказывающей стороны верифицирующей стороне. На четвертом проходе вызов ChB отправляется из верифицирующей стороны доказывающей стороне. На пятом проходе отклик Rsp отправляется из доказывающей стороны верифицирующей стороне.
В случае параллельно-последовательной структуры #1 сообщения (CmtA1, …, CmtAN) N раз отправляются из доказывающей стороны верифицирующей стороне на первом проходе. На втором проходе число ChA1 отправляется один раз из верифицирующей стороны доказывающей стороне. На третьем проходе вектор CmtB1 отправляется один раз из доказывающей стороны верифицирующей стороне. На четвертом проходе вызов ChB1 отправляется один раз из верифицирующей стороны доказывающей стороне. На пятом проходе отклик Rsp1 отправляется один раз из доказывающей стороны верифицирующей стороне. В дальнейшем ChA2, …, ChAN, CmtB2, …, CmtBN, ChB2, …, ChBN и отклики Rsp2, …, RspN обмениваются последовательно между доказывающей стороной и верифицирующей стороной.
В случае параллельно-последовательной структуры #1 обеспечивается безопасность от пассивного прикрепления. Кроме того, число интерактивностей составляет только 4N+1 раз. Кроме того, когда сообщения, отправленные N раз на первом проходе, собираются с одним значением хэширования, можно повысить эффективность связи.
5.2.2. Параллельно-последовательный алгоритм (пример #2 структуры) (фиг.25)
Далее, со ссылкой на фиг.25, будет описан другой пример структуры гибридного типа (здесь и далее по тексту называется как параллельно-последовательная структура #2). На фиг.25 изображена схема, иллюстрирующая алгоритм, имеющий базовую структуру, и алгоритм, имеющий параллельно-последовательную структуру #2.
В случае параллельно-последовательной структуры #2 сообщения (CmtA1, …, CmtAN) N раз отправляются из доказывающей стороны верифицирующей стороне на первом проходе. На втором проходе числа (ChA1, …, ChAN) N раз отправляются из верифицирующей стороны доказывающей стороне. На третьем проходе векторы (CmtB1, …, CmtBN) N раз отправляются из доказывающей стороны верифицирующей стороне. На четвертом проходе вызов ChB1 отправляется один раз из верифицирующей стороны доказывающей стороне. На пятом проходе отклик Rsp1 отправляется один раз из доказывающей стороны верифицирующей стороне. В дальнейшем, ChB2, …, ChBN, отклики Rsp2, RspN обмениваются последовательно между доказывающей стороной и верифицирующей стороной.
В случае параллельно-последовательной структуры #2 обеспечивается безопасность от пассивного прикрепления. Кроме того, число интерактивностей составляет только 2N+3 раз. Кроме того, когда сообщения, отправленные N раз на первом проходе, векторы, отправленные N раз на третьем проходе, и тому подобное собираются с одним значением хэширования, можно повысить эффективность связи.
5.2.3. Последовательно-параллельный алгоритм (пример #1 структуры) (фиг.26)
Далее, со ссылкой на фиг.26, будет описан другой пример структуры гибридного типа (здесь и далее по тексту называется как последовательно-параллельная структура #1). На фиг.26 изображена схема, иллюстрирующая алгоритм, имеющий базовую структуру, и алгоритм, имеющий последовательную параллельную структуру #1.
В случае последовательно-параллельной структуры #1 сообщение CmtA1 на первом проходе отправляется один раз из доказывающей стороны верифицирующей стороне. На втором проходе число ChA1 отправляется один раз из верифицирующей стороны доказывающей стороне. На третьем проходе вектор CmtB1 отправляется один раз из доказывающей стороны верифицирующей стороне. На четвертом проходе вызов ChB1 отправляется один раз из верифицирующей стороны доказывающей стороне. В дальнейшем, CmtA2, …, CmtAN, ChA2, …, GhAN, CmtB2, …, CmtBN, ChB2, …, ChBN обмениваются последовательно между доказывающей стороной и верифицирующей стороной. И, наконец, отклики (Rsp1, …, RspN) N раз отправляются из доказывающей стороны верифицирующей стороне.
В случае последовательно-параллельной структуры #1 обеспечивается безопасность от активного прикрепления. Кроме того, число интерактивностей составляет только 4N+1 раз.
5.2.4. Последовательно-параллельный алгоритм (пример #2 структуры) (фиг.27)
Далее, со ссылкой на фиг.27, будет описан другой пример структуры гибридного типа (здесь и далее по тексту называется как последовательно-параллельная структура #2). На фиг.27 изображена схема, иллюстрирующая алгоритм, имеющий базовую структуру, и алгоритм, имеющий последовательную параллельную структуру #2.
В случае последовательно-параллельной структуры #2 сообщение CmtA1 отправляется один раз из доказывающей стороны верифицирующей стороне на первом проходе. На втором проходе число ChA1 отправляется один раз из верифицирующей стороны доказывающей стороне. В дальнейшем CmtA2, …, CmtAN, ChA2, …, ChAN обмениваются последовательно между доказывающей стороной и верифицирующей стороной. После того как вызов ChAN завершен, векторы (CmtB1, …, CmtBN) N раз отправляются из доказывающей стороны верифицирующей стороне. Затем вызовы (ChB1, …, ChB1) N раз отправляются из верифицирующей стороны доказывающей стороне. И, наконец, отклики (Rsp1, …, RspN) N раз отправляются из доказывающей стороны верифицирующей стороне.
В случае последовательно-параллельной структуры #2 обеспечивается безопасность от активного прикрепления. Кроме того, число интерактивностей составляет только 2N+3 раз.
Алгоритмы гибридного типа, которые относятся к 5-проходной схеме аутентификации открытого ключа, были описаны выше.
6. Приложение
Описание вышеизложенной схемы аутентификации открытого ключа будет приведено здесь в виде приложения.
6.1. Способ установки параметра системы
Приведенное здесь описание способа установки параметра будет дополнительным.
Коэффициенты многомерных полиномов
То, как установить коэффициенты многомерных полиномов и случайное число seed (здесь и далее по тексту называются как коэффициенты и тому подобное многомерных полиномов), которые используются для генерирования коэффициентов, не было описано выше. Коэффициенты и тому подобное многомерных полиномов могут представлять собой параметры, общие для системы, или могут представлять собой параметры, различные для каждого пользователя.
Однако когда коэффициенты и тому подобное многомерных полиномов установлены на параметры, общие для системы, необходимо обновить установку всей системы, если обнаружена неустойчивость многомерных полиномов. Дополнительно, средняя устойчивость (трудности решения) анализируется для многомерных полиномов, имеющих произвольно выбранные коэффициенты, но трудно обеспечить достаточную устойчивость для многомерных полиномов, имеющих некоторые специфические коэффициенты.
Соответственно, изобретатели настоящей технологии разработали структуру, в которой коэффициенты многомерных полиномов генерируют с использованием символьной строки или тому подобного, выбираемой каждым пользователем в виде начального числа генератора псевдослучайных чисел, и генерируют коэффициенты многомерных полиномов. Например, возможные способы включают в себя способ использованием адреса электронной почты пользователя в виде начального числа и способ использования символьной строки, в которой адреса электронной почты, дата обновления и тому подобное объединены в виде начального числа. При использовании таких способов влияние ограничивается только на пользователя, использующего многомерные полиномы, имеющих коэффициенты даже в том случае, если обнаружена неустойчивость многомерных полиномов, имеющих коэффициенты, которые сгенерированы из заданной символьной строки. Дополнительно, поскольку многомерные полиномы изменяются только в результате изменения символьной строки, неустойчивость можно легко исправить.
Способ установки параметров системы был описан выше. В вышеизложенном описании символьная строка была приведена в качестве примера, но для каждого пользователя можно использовать различную строку чисел или различную строку знаков.
Число m полинома и число n переменной
Интерактивный протокол, описанный выше, обеспечивает безопасность от активной атаки. Однако когда интерактивный протокол выполняется повторно и параллельно, условие, которое будет описано ниже, необходимо для того, чтобы доказать, что безопасность от активной атаки надежно обеспечена.
Вышеизложенный интерактивный протокол представляет собой алгоритм верификации для верифицирующей стороны того, что "доказывающая сторона знает s, удовлетворяющий y=F(s) для y" с использованием пары ключей (открытого ключа y и секретного ключа s). По этой причине, когда интерактивность, принятая при верификации выполняется, вероятность того, что информация, которая показывает то, что "доказывающая сторона использует s во время интерактивности" известно верифицирующей стороне, является бесспорной. Дополнительно, устойчивость к коллизиям не обеспечивается для многомерного полинома F. По этой причине, когда вышеизложенный интерактивный протокол выполняется повторно и параллельно, трудно доказать, что безопасность от активной атаки надежно обеспечена без какого-либо условия.
Соответственно, изобретатели настоящей технологии рассмотрели способ побуждения информации показывать то, что "доказывающая сторона использует s во время интерактивности" будет не известно верифицирующей стороне даже при выполнении интерактивности, принятой при верификации. Дополнительно, изобретатели настоящей технологии разработали способ обеспечения безопасности от активной атаки, которая будет обеспечиваться даже в том случае, когда вышеизложенный интерактивный протокол выполняется повторно и параллельно. Этот способ представляет собой способ установки числа m многомерных полиномов f1, …, fm, которые используется в качестве открытых ключей со значением, достаточно меньшим, чем число n переменных. Например, m и n устанавливаются таким образом, чтобы 2m-n<<1 (например, когда n=160 и m=80, 2-80<<1).
В схемах, которые основывают свою безопасность на трудности решения многостепенной многомерной системы уравнений, трудно сгенерировать другой секретный ключ s2, соответствующий открытому ключу pk, даже в том случае, когда секретный ключ s1 и открытый ключ pk, соответствующие ему, заданы. По этой причине, когда гарантируется, что два или более секретных ключей s существуют для открытого ключа pk, информации, показывающая то, что "доказывающая сторона использует s во время интерактивности" можно заставить быть не известной для верифицирующей стороны даже при выполнении интерактивности, принятой при верификации. То есть когда установлена эта гарантия, безопасность от активной атаки можно обеспечить даже в том случае, если интерактивный протокол выполняется повторно и параллельно.
При рассмотрении функции F: Kn->Km включающей в себя число т многостепенных полиномов с п переменными (где n>m), со ссылкой на фиг.29, число элементов области определения, не имеющей по второго прообраза, составляет не более, чем |K|m-1. По этой причине, когда |K|m-n устанавливается достаточно маленьким, вероятность выбора элементов из области определения, не имеющей второго прообраза, можно сделать пренебрежимо малой. То есть когда число m многостепенных полиномов f1, …, fm с n переменными устанавливается на значение, достаточно меньшее, чем число n переменных, можно обеспечить то, что два или более секретных ключей s существуют для открытого ключа pk. Следовательно, даже в том случае, когда интерактивность, принятая при верификации, выполняется, информацию, показывающую то, что "доказывающая сторона использует s во время интерактивности", можно предоставить так, чтобы она была не известной для верифицирующей стороны. Таким образом, безопасность от активной атаки обеспечивается даже в том случае, когда интерактивный протокол выполняется повторно и параллельно.
Как описано выше, за счет наложения условия установки, в котором число m многостепенных полиномов f1, …, fm с n переменными устанавливается на значение, достаточно меньшее, чем число n переменных (где n>m и предпочтительно 2m-n<<1), безопасность можно обеспечить тогда, когда интерактивный протокол выполняется повторно и параллельно.
6.2. Способ реагирования на нерегулярный вызов
Ниже будет рассмотрен способ реагирования на нерегулярный вызов.
6.2.1. Способ реагирования доказывающей стороной
Далее будет рассмотрена вероятность того, что верифицирующая сторона выдает ложный вызов в интерактивном протоколе. Например, в случае 3-проходной схемы, доказывающая сторона отправляет сообщения (с0, c1, с2) верифицирующей стороне и верифицирующая сторона отправляет вызов Ch=0 доказывающей стороне. В дальнейшем отклик Rsp, соответствующий вызову Ch=0, отправляется из доказывающей стороны верифицирующей стороне. До сих пор выполнялась нормальная интерактивность.
После этого предполагается, что верифицирующая сторона в дальнейшем будет оспаривать отклик Rsp, соответствующий вызову Ch=1, на доказывающей стороне. Если доказывающая сторона отправляет отклик Rsp, реагирующий на вызов Ch=1, верифицирующей стороне в ответ на вызов, секретный ключ может подвергаться утечке на верифицирующую сторону. На практике может иметь место утечка секретного ключа. Например, верифицирующая сторона может подделать отправку вызова Ch=0, а не вызов Ch=1 на втором проходе и может, кроме того, оспорить отклик Rsp, реагирующий на вызов Ch=1. С другой стороны, доказывающая сторона может неправильно понять, что биты вызова Ch, отправленные на втором проходе, превращаются в разные биты из-за ошибки связи.
Соответственно, изобретатели настоящей технологии разработали, в качестве способа устранения утечки секретного ключа, способ завершения интерактивности или возобновления интерактивности из первого прохода с использованием нового случайного числа, когда доказывающая сторона оспаривает отклик, соответствующий вызовам Ch из двух или более способов, по отношению к сообщению один раз. При применении этого способа, секретный ключ не подвергается утечке даже в том случае, когда верифицирующая сторона подделывает и оспаривает отклик, соответствующий вызовам Ch из двух или более способов.
6.2.2. Способ реагирования верифицирующей стороной
Далее будет рассмотрена вероятность того, что доказывающая сторона выдает себя за другое лицо и оспаривает повторную отправку вызова Ch. Например, предполагается, что доказывающая сторона отправляет сообщения (с0, c1, с2) верифицирующей стороне в 3-проходной схеме, верифицирующая сторона отправляет вызов Ch=0 доказывающей стороне, и затем доказывающая сторона оспаривает повторную отправку вызова Ch. Когда верифицирующая сторона произвольно повторно выбирает вызов Ch в ответ на вызов, существует вероятность того, что выбран вызов Ch=1, который отличается от ранее отправленного вызова Ch=0. В этом случае вызов Ch=1 отправляется из верифицирующей стороны доказывающей стороне. Предполагается, что доказывающая сторона может отправить отклик Rsp, соответствующий вызову Ch=1, верифицирующей стороне.
В этом случае доказывающая сторона может отреагировать на вызов Ch=1, но может и не отреагировать на вызов Ch=0. То есть вероятность того, что доказывающая сторона вводит в заблуждение верифицирующую сторону, не вызывает сомнений. Например, доказывающая сторона может оспорить повторную отправку этого вызова Ch верифицирующей стороне, поскольку доказывающая сторона теряет вызов Ch. С другой стороны, верифицирующая сторона может рассматривать ранее отправленный вызов как потерянный из-за ошибки связи и повторно отправить вызов Ch в ответ на вызов доказывающей стороны. Затем, когда повторно отправленный вызов Ch отличается от ранее оправленного вызова Ch, подделка может быть успешной.
Как понятно из этого примера, доказывающая сторона может столкнуться с риском подделки, поскольку вызов Ch является произвольно выбранным. Соответственно, чтобы не приводить к риску подделки, изобретатели настоящей технологии разработали способ улучшения интерактивного протокола путем побуждения верифицирующей стороны завершать интерактивность или повторную отправку вызова Ch, который является таким же, как и предыдущий вызов, а не генерировать новое случайное число, когда доказывающая сторона повторно оспаривает отправку вызова Ch по отношению к сообщению один раз. Применение этого способа позволяет устранить риск подделки, использующей вызов для повторной отправки вызова Ch.
Безопасный способ реагирования на нерегулярный вызов был описан выше. В вышеизложенном описании базовая структура 3-проходной была приведена в качестве примера. Однако безопасность можно также повысить путем применения той же самой идеи к последовательной структуре повторения, параллельной структуре повторения или структуре повторения гибридного типа. Конечно, то же самое можно также применить к алгоритмам, которые относятся к 5-проходным алгоритмам.
7. Пример конфигурации аппаратных средств
Каждый алгоритм, описанный выше, можно выполнить с использованием, например, конфигурации аппаратных средств устройства обработки информации, показанной на фиг.28. То есть обработку каждого алгоритма можно осуществить путем управления аппаратными средствами, показанными на фиг.28, с использованием компьютерной программы. Дополнительно, вид этих аппаратных средств является произвольным и может представлять собой персональный компьютер, мобильный информационный терминал, такой как мобильный телефон, PHS или PDA, игровую машину, контактные или бесконтактные микросхемы, контактные или бесконтактные интегральные микросхемы или различные типы информационных бытовых приборов. Более того, PHS - это аббревиатура от словосочетания "personal handy-phone system" (система персональной телефонной связи). К тому же, PDA - это аббревиатура от словосочетания "personal digital assistant" (персональный цифровой ассистент).
Как показано на фиг.28, эти аппаратные средства в основном включают в себя CPU 902, ROM 904, RAM 906, шину 908 главного процессора и мост 910. Более того, эти аппаратные средства включают в себя внешнюю шину 912, интерфейс 914, блок 916 ввода, блок 918 вывода, запоминающее устройство 920, привод 922, соединительный порт 924 и блок 926 связи. Более того, CPU - это аббревиатура от словосочетания центральное процессорное устройство. К тому же, ROM - это аббревиатура от словосочетания постоянное запоминающее устройство. Более того, RAM - это аббревиатура от словосочетания оперативное запоминающее устройство.
CPU 902 функционирует как арифметическое процессорное устройство или блок управления, например, и управляет всей работой или частично каждого структурного элемента на основании различных программ, записанных в ROM 904, RAM 906, запоминающем устройстве 920 или на съемном носителе 928 записи. ROM 904 представляет собой средство для хранения, например, программы, которая загружается в CPU 902, или данных или т.п., которые используются в арифметической операции. RAM 906 временно или постоянно хранит, например, программу, которая загружается в CPU 902 или различные параметры или т.п., которые произвольно изменяются при исполнении программы.
Эти структурные элементы соединены друг с другом с помощью, например, шины 908 главного процессора с возможность выполнения высокоскоростной передачи данных. Со своей стороны, шина 908 главного процессора подсоединена через мост 910 к внешней шине 912, чья скорость передачи данных является, например, относительно низкой. Более того, блок 916 ввода представляет собой, например, мышь, клавиатуру, сенсорную панель, кнопку, переключатель или рычажок. К тому же, блок 916 ввода может представлять собой блок дистанционного управления, который может передавать управляющий сигнал с помощью инфракрасного луча или других радиоволн.
Блок 918 вывода представляет собой, например, устройство отображения, такое как ЭЛТ, ЖКД, ПДП или ЭЛД, устройство вывода аудио, такое как динамик или наушники, принтер, мобильный телефон или устройство для факсимильной связи, который могут визуально или с помощью звука уведомлять пользователя о полученной информации. Более того, ЭЛТ - это аббревиатура от словосочетания электронно-лучевая трубка. ЖКД - это аббревиатура от словосочетания жидкокристаллический дисплей. ПДП - это аббревиатура от словосочетания плазменная дисплейная панель. К тому же, ЭЛД - это аббревиатура от словосочетания электролюминесцентный дисплей.
Запоминающее устройство 920 представляет собой устройство для хранения различных данных. Запоминающее устройство 920 представляет собой, например, магнитное запоминающее устройство, такое как накопитель на жестком диске (HDD), полупроводниковое запоминающее устройство, оптическое запоминающее устройство или магнитооптическое запоминающее устройство. HDD - это аббревиатура от словосочетания "hard disk drive" (накопитель на жестком диске).
Привод 922 представляет собой устройство, которое считывает информацию, записанную на съемном носителе 928 записи, таком как магнитный диск, оптический диск, магнитооптический диск или полупроводниковая память или записывает информацию на съемный носитель 928 записи. Съемный носитель 928 записи представляет собой, например, DVD-носитель, Blu-ray-носитель, HD-DVD-носитель, различные типы полупроводниковых носителей информации или т.п. Конечно, съемный носитель 928 записи может представлять собой, например, электронное устройство или карту с интегральной микросхемой, на которой установлена бесконтактная интегральная микросхема (ИС). ИС - это аббревиатура от словосочетания интегральная схема.
Соединительный порт 924 представляет собой порт, такой как порт USB, порт IEEE1394, SCSI, порт RS-232C или порт для подключения устройства 930, подсоединяемого внешним образом, такого как оптический аудиотерминал. Устройство 930, подсоединяемое внешним образом, представляет собой, например, принтер, мобильный музыкальный плеер, цифровой фотоаппарат, цифровую видеокамеру или цифровой диктофон. Более того, USB - это аббревиатура от словосочетания "universal ser1al bus" (универсальная последовательная шина). К тому же, SCSI - это аббревиатура от словосочетания "small computer system interface" (системный интерфейс малых компьютеров).
Блок 926 связи представляет собой устройство связи, которое будет подсоединяться к сети 932, и представляет собой, например, карту связи для проводной или беспроводной LAN, Bluetooth (зарегистрированный товарный знак) или WUSB, оптический коммуникационный маршрутизатор, маршрутизатор ADSL или устройство для контактной и бесконтактной связи. Сеть 932, подсоединенная к блоку 926 связи, сконфигурирована из сети, подсоединяемой проводным или беспроводным способом, и представляет собой, например, Интернет, LAN для использования в домашних условиях, связь в инфракрасной части спектра, связь в видимой части спектра, широковещание или спутниковую связь. Более того, LAN - это аббревиатура от словосочетания "local area network" (локальная сеть). К тому же, WUSB - это аббревиатура от словосочетания "wireless USB" (беспроводная универсальная последовательная шина). Более того, ADSL - это аббревиатура от словосочетания "asymmetric digital subscriber line" (асимметричная цифровая абонентская линия).
8. Заключение
В заключение будет кратко описано техническое содержание согласно варианту осуществления настоящей технологии. Техническое содержание, изложенное здесь, можно применить к различным устройствам обработки информации, таким как персональный компьютер, мобильный телефон, игровая машина, информационный терминал, информационный бытовой прибор, навигационная система и тому подобное. Кроме того, функцию устройства обработки информации, описанного ниже, можно выполнить с использованием одного устройства обработки информации или с использованием множества устройств обработки информации. Более того, средство для хранения данных и средство для арифметической обработки, которые используются для выполнения процесса с помощью устройства обработки информации, описанного ниже, можно установить на устройстве для обработки информации или можно установить на устройстве, подсоединяемом через сеть.
Функциональная конфигурация вышеизложенного устройства обработки информации реализована следующим образом. Например, устройство обработки информации, описанное ниже в п.(1), имеет функцию выполнения алгоритма, который относится к эффективной схеме аутентификации открытого ключа, который основывает свою безопасность на трудности решения многостепенной многомерной системы уравнений.
(1) Устройство обработки информации, включающее в себя:
блок генерирования сообщения для генерирования сообщения на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, который представляет собой элемент из набора Kn;
блок подачи сообщения для подачи сообщения верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s));
блок генерирования промежуточной информации для генерирования третьей информацию на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения;
блок предоставления промежуточной информации для предоставления третьей информации верифицирующей стороне; и
блок подачи отклика для предоставления верифицирующей стороне информации отклика, соответствующей образцу верификации, выбранного верифицирующей стороной из k (где k≥2) образцов верификации,
причем вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи, при этом
сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и установлены так, что полином G(x1, х2), определенный как G(x1, х2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
(2) Устройство обработки информации по п.(1), в котором
блок генерирования сообщения выполнен с возможностью генерирования сообщения N раз (где N≥2), а
блок подачи сообщения выполнен с возможностью подачи верифицирующей стороне сообщения N раз с интерактивностью один раз; причем
блок генерирования промежуточной информации выполнен с возможностью генерирования третьей информации N раз на основании первой информации, выбранной верифицирующей стороной для сообщений N раз, и второй информации N раз, полученной во время генерирования сообщения, при этом
блок предоставления промежуточной информации выполнен с возможностью предоставления верифицирующей стороне третьей информации N раз с интерактивностью один раз, а
блок подачи отклика выполнен с возможностью подачи верифицирующей стороне информации отклика N раз, соответствующей образцу верификации, выбранному верифицирующей стороной для сообщений N раз, с интерактивностью один раз.
(3) Устройство обработки информации по п.(2), в котором
блок генерирования сообщения выполнен с возможностью генерирования сообщения N раз (где N≥2) и генерирования одного значения хэширования из сообщения N раз, при этом
блок подачи сообщения выполнен с возможностью подачи значения хэширования верифицирующей стороне, а
блок генерирования промежуточной информации выполнен с возможностью генерирования третьей информации N раз на основании первой информации, выбранной верифицирующей стороной для каждого из сообщений N раз, и второй информации N раз, полученной во время генерирования сообщения, причем
блок предоставления промежуточной информации выполнен с возможностью предоставления верифицирующей стороне третьей информации N раз с интерактивностью один раз, а
блок подачи отклика выполнен с возможностью подачи верифицирующей стороне информации отклика N раз, соответствующей образцу верификации, выбранному верифицирующей стороной для каждого из сообщений N раз, и некоторые сообщения, не полученные при выполнении вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей и информации отклика с интерактивностью один раз.
(4) Устройство обработки информации, включающее в себя:
блок хранения информации для хранения пары многостепенных многомерных полиномов F=(f1, …, fm) и векторов y=(y1, …, ym)=(f1(s), …, fm(s));
блок получения сообщения для получения сообщения, сгенерированного на основании пары многостепенных многомерных полиномов F и вектора s, представляющего собой элемент из набора Kn;
блок предоставления информации для предоставления произвольно выбранной первой информации доказывающей стороне, выдающей сообщение;
блок получения промежуточной информации для получения третьей информации, сгенерированной доказывающей стороной на основании первой информации и второй информации, полученной во время генерирования сообщения;
блок предоставления информации об образце, который предоставляет доказывающей стороне информацию относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации;
блок получения отклика для получения информации отклика, соответствующей выбранному образцу верификации, от доказывающей стороны; и
блок верификации для верификации того, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика, причем
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи, при этом
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается так, что полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
(5) Устройство обработки информации по п.(4), в котором
блок получения сообщения выполнен с возможностью получения сообщения N (где N≥2) раз с интерактивностью один раз, при этом
блок предоставления информации выполнен с возможностью произвольного выбора первой информации для каждого из сообщений N раз и предоставления доказывающей стороне выбранной первой информации N раз с интерактивностью один раз, а
блок получения промежуточной информации выполнен с возможностью получения третьей информации N раз, выработанной доказывающей стороной на основании первой информации N раз и второй информации N раз, полученной во время генерирования сообщения N раз,
блок предоставления информации об образце выполнен с возможностью выбора образца верификации для каждого из сообщений N раз и предоставляет доказывающей стороне информацию относительно выбранных образцов верификации N раз с интерактивностью один раз, а
блок получения отклика выполнен с возможностью получения информации отклика N раз, соответствующей выбранным образцам верификации N раз от доказывающей стороны с интерактивностью один раз, при этом
блок верификации выполнен с возможностью определения, что доказывающая сторона сохраняет вектор s, когда верификация завершается успешно, для всех сообщений N раз.
(6) Устройство обработки информации по п.(5), в котором
блок получения сообщения выполнен с возможностью получения одного значения хэширования, сгенерированного из сообщения N раз (где N≥2), а
блок предоставления информации выполнен с возможностью произвольного выбора первой информации для каждого из сообщений N раз и предоставляет доказывающей стороне выбранную первую информацию N раз с интерактивностью один раз, при этом
блок получения промежуточной информации выполнен с возможностью получения третьей информации N раз, сгенерированной доказывающей стороной на основании первой информации N раз и второй информации N раз, которые получены во время генерирования сообщения N раз, а
блок предоставления информации об образце выполнен с возможностью выбора образца верификации для каждого из сообщений N раз и предоставления доказывающей стороне информации относительно выбранных образцов верификации N раз с интерактивностью один раз, причем
блок получения отклика выполнен с возможностью получения, от доказывающей стороны, информацию отклика, соответствующую выбранному образцу верификации, и некоторые сообщения, не полученные при выполнении вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
блок верификации выполнен с возможностью верификации, сохраняет ли доказывающая сторона вектор s на основании значения хэширования, некоторые из сообщений, открытые ключи и информацию отклика, и определения того, что доказывающая сторона выполнен с возможностью сохранения вектора s, когда верификация завершается успешно для всех сообщений N раз.
(7) Способ обработки информации, включающий в себя этапы, на которых:
генерируют сообщение на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, представляющего собой элемент из набора Kn;
подают сообщение верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s));
генерируют третью информации на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения;
предоставляют третью информацию верифицирующей стороне; и
предоставляют верифицирующей стороне информацию отклика, соответствующую образцу верификации, выбираемому верифицирующей стороной из k (где k≥2) образцов верификации, причем
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи, при этом
сообщение представляет собой информацию, полученную путем выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
где пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается так, что полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, x1n) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
(8) Способ обработки информации, включающий в себя этапы, на которых: с помощью устройства обработки информации, хранящего пару многостепенных многомерных полиномов F=(f1, …, fm) и векторы y=(y1, …, ym)=(f1(s), …, fm(s)),
получают сообщение, сгенерированное на основании пары многостепенных многомерных полиномов F и вектора s, представляющего собой элемент из набора Kn;
предоставляют произвольно выбранную первую информацию доказывающей стороне, выдающей сообщение;
получают третью информацию, сгенерированную доказывающей стороной, на основании первой информации и второй информации, полученной во время генерирования сообщения;
предоставляют доказывающей стороне информацию относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации; и
получают информацию отклика, соответствующую выбранному образцу верификации, от доказывающей стороны;
верифицируют, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика, причем
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи, при этом
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается так, что полином G(x1, х2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
(9) Программа, вызывающая выполнение компьютером:
функции генерирования сообщения, выполненной с возможностью генерирования сообщения на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, представляющего собой элемент из набора Kn;
функции подачи сообщения, выполненной с возможностью подачи сообщения верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s));
функции генерирования промежуточной информации, выполненной с возможностью генерирования третьей информации на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения;
функции предоставления промежуточной информации, выполненной с возможностью предоставления третьей информации верифицирующей стороне; и
функции подачи отклика, выполненной с возможностью предоставления верифицирующей стороне информации отклика, соответствующей образцу верификации, выбираемого верифицирующей стороной из k (где k≥2) образцов верификации, причем
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи, при этом
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается таким образом, чтобы полином G(x1, х2), определенный как G(x1, х2)=F(x1+х2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, x1n) (где l=1, 2), был сконфигурирован как член, пропорциональный (xn)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
(10) Программа, вызывающая выполнение компьютером:
функции хранения информации, выполненной с возможностью хранения пары многостепенных многомерных полиномов F=(f1, …, fm) и векторов y=(y1, …, ym)=(f1(s), …, fm(s));
функции получения сообщения, выполненной с возможностью получения сообщения, сгенерированного на основании пары многостепенных многомерных полиномов F и вектора s, который представляет собой элемент из набора Kn;
функции предоставления информации, выполненной с возможностью предоставления произвольно выбранной первой информации доказывающей стороне, выдающей сообщение;
функции получения промежуточной информации, выполненной с возможностью получения третьей информации, сгенерированной доказывающей стороной, на основании первой информации и второй информации, полученной во время генерирования сообщения;
функции предоставления информации об образце, выполненной с возможностью предоставления доказывающей стороне информации относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации; и
функции получения отклика, выполненной с возможностью получения информации отклика, соответствующей выбранному образцу верификации, от доказывающей стороны; и
функции верификации, выполненной с возможностью верификации, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика, при этом
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи, причем
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается так, что полином G(x1, х2), определенный как G(x1, х2)=F(x1+х2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), сконфигурирован как член, пропорциональный (xn)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
(11) Машиночитаемый носитель информации, хранящий программу, вызывающую выполнение компьютером:
функции генерирования сообщения, выполненной с возможностью генерирования сообщения на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, представляющей собой элемент из набора Kn;
функции подачи сообщения, выполненной с возможностью подачи сообщения верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s));
функции генерирования промежуточной информации, выполненной с возможностью генерирования третьей информации на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения;
функции предоставления промежуточной информации, выполненной с возможностью предоставления третьей информации верифицирующей стороне; и
функции подачи отклика, выполненной с возможностью предоставления верифицирующей стороне информации отклика, соответствующей образцу верификации, выбранному верифицирующей стороной из k (где k≥2) образцов верификации, при этом
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи, причем
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается так, что полином G(x1, х2), определенный как G(x1, х2)=F(x1+х2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
(12) Машиночитаемый носитель информации, хранящий программу, вызывающую выполнение компьютером:
функции хранения информации, выполненной с возможностью хранения пары многостепенных многомерных полиномов F=(f1, …, fm) и векторов y=(y1, …, ym)=(f1(s), …, fm(s));
функции получения сообщения, выполненной с возможностью получения сообщения, сгенерированного на основании пары многостепенных многомерных полиномов F и вектора s, представляющего собой элемент из набора Kn;
функции предоставления информации, выполненной с возможностью предоставления произвольно выбранной первой информации доказывающей стороне, выдающей сообщение;
функции получения промежуточной информации, выполненной с возможностью получения третьей информации, сгенерированной доказывающей стороной, на основании первой информации и второй информации, полученной во время генерирования сообщения;
функции предоставления информации об образце, выполненной с возможностью предоставления, доказывающей стороне, информации относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации;
функции получения отклика, выполненной с возможностью получения информации отклика, соответствующей выбранному образцу верификации, от доказывающей стороны; и
функции верификации, выполненной с возможностью верифицирования, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика, при этом
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F и векторы y представляют собой открытые ключи, причем
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и устанавливается так, что полином G(x1, x2), определенный как G(x1, х2)=F(x1+х2)-F(x1)-F(x2) по отношению к векторам x1=(x1l, …, x1n) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
(13) Устройство по любому из пп.(1)-(6), в котором тип, описанные выше, имеют зависимость m<n.
(14) Устройство по п.(13), в котором m и n, описанные выше, имеют зависимость 2m-n<<1.
Примечание
Вышеизложенный алгоритм Р доказывающей стороны представляет собой пример блока генерирования сообщения, блок подачи сообщения, блока подачи отклика, блока генерирования промежуточной информации и блока подачи промежуточной информации. В дополнение к этому вышеизложенный алгоритм V верифицирующей стороны представляет собой пример устройства для хранения информации, блока получения сообщения, блока предоставления информации об образце, блока получения отклика, блока верификации и блока получения промежуточной информации.
Предпочтительные варианты осуществления настоящего изобретения были описаны выше со ссылкой на сопроводительные чертежи, при этом, конечно, настоящее изобретение не ограничено вышеприведенными примерами. Специалисты в данной области техники могут найти различные изменения и модификации в пределах объема прилагаемой формулы изобретения, и следует понимать, что они будут естественным образом подпадать под технической объем настоящего изобретения.
Перечень ссылочных позиций
Gen - алгоритм генерирования ключей
Р - алгоритм доказывающей стороны
V - алгоритм верифицирующей стороны
Sig - алгоритм генерирования подписи
Ver - алгоритм верификации подписи
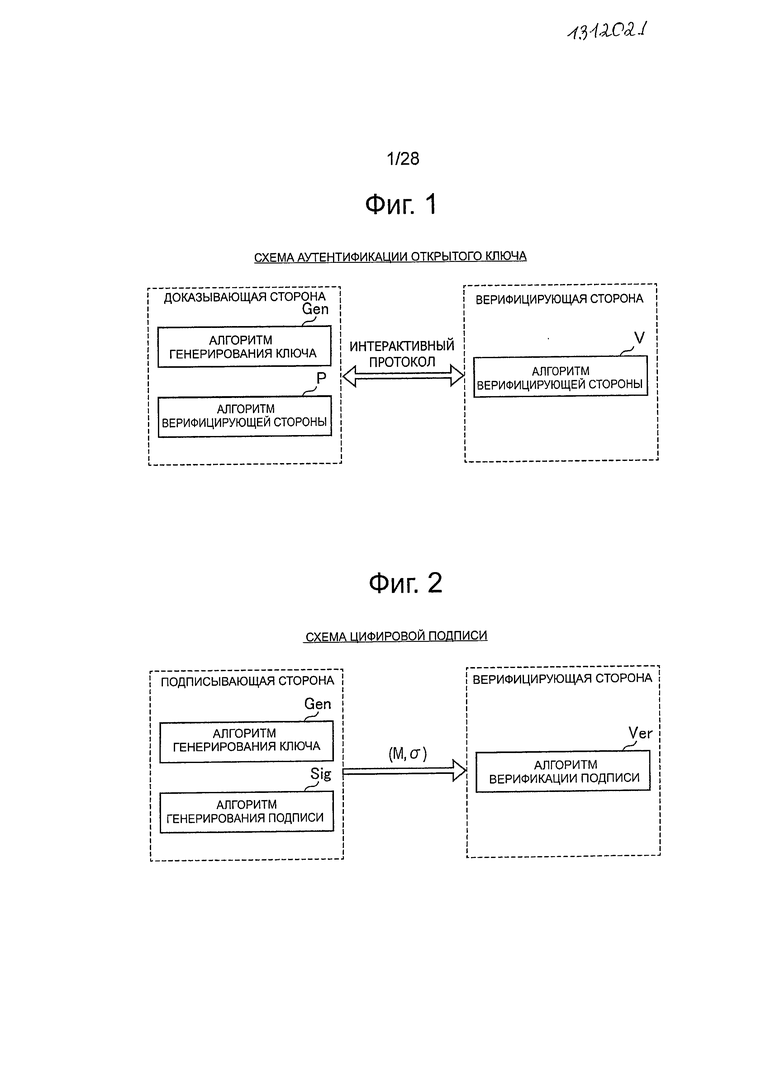
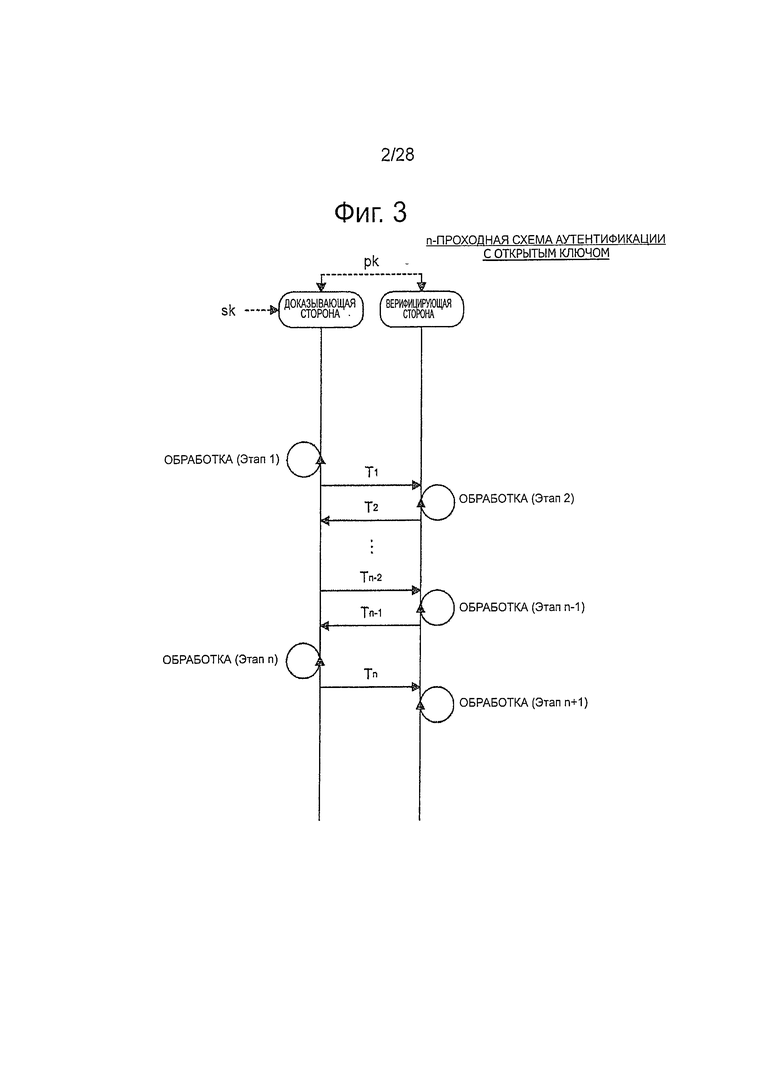
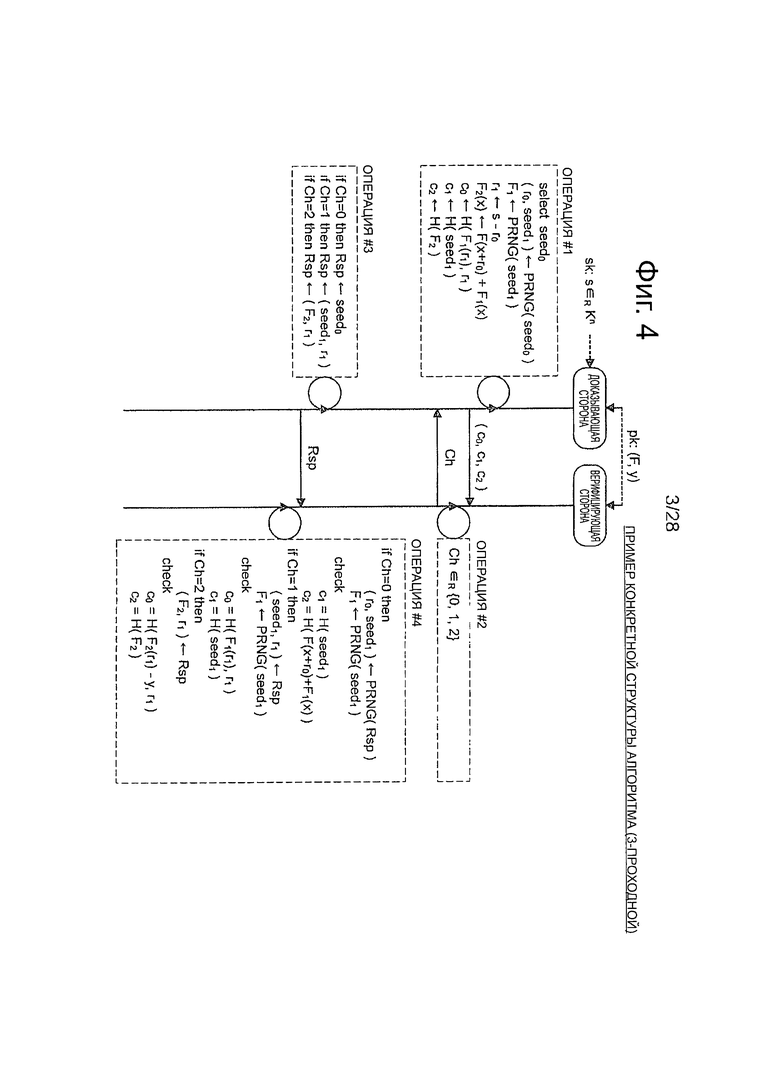
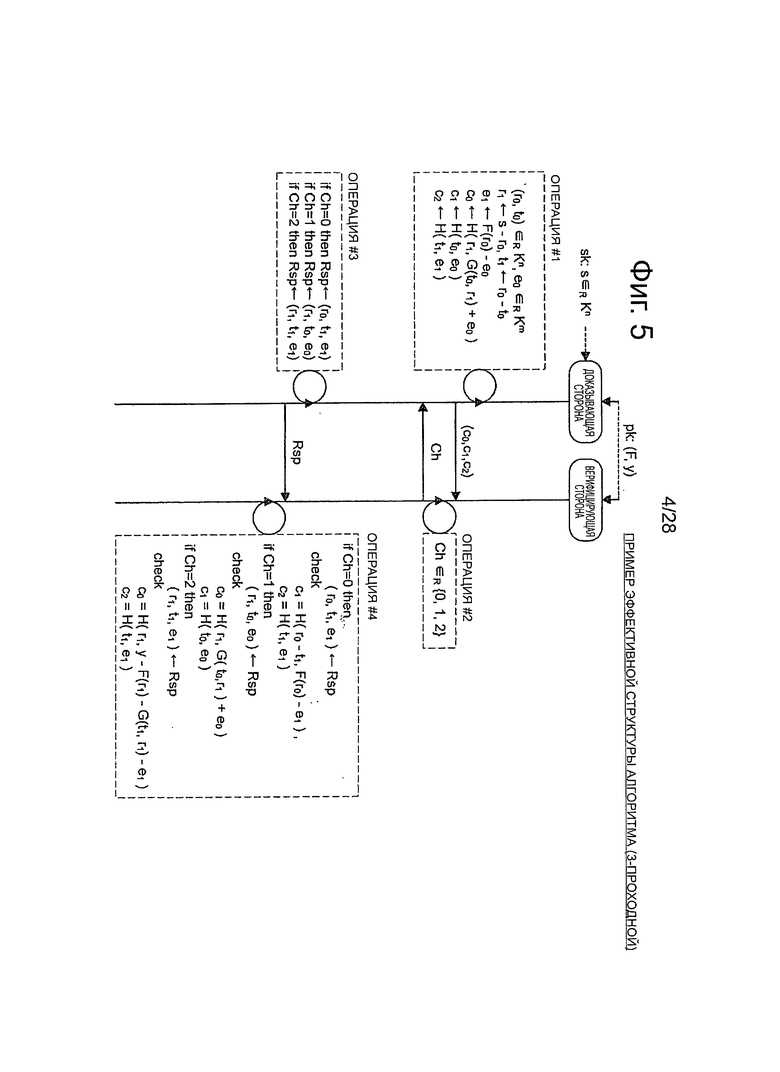
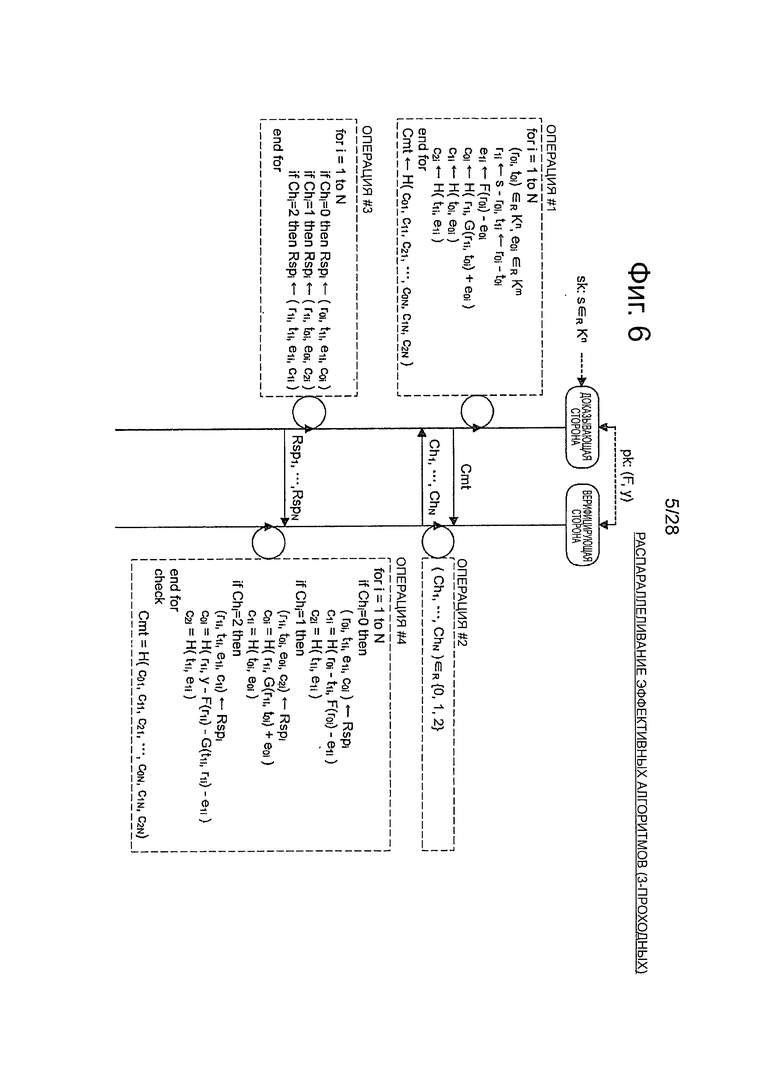
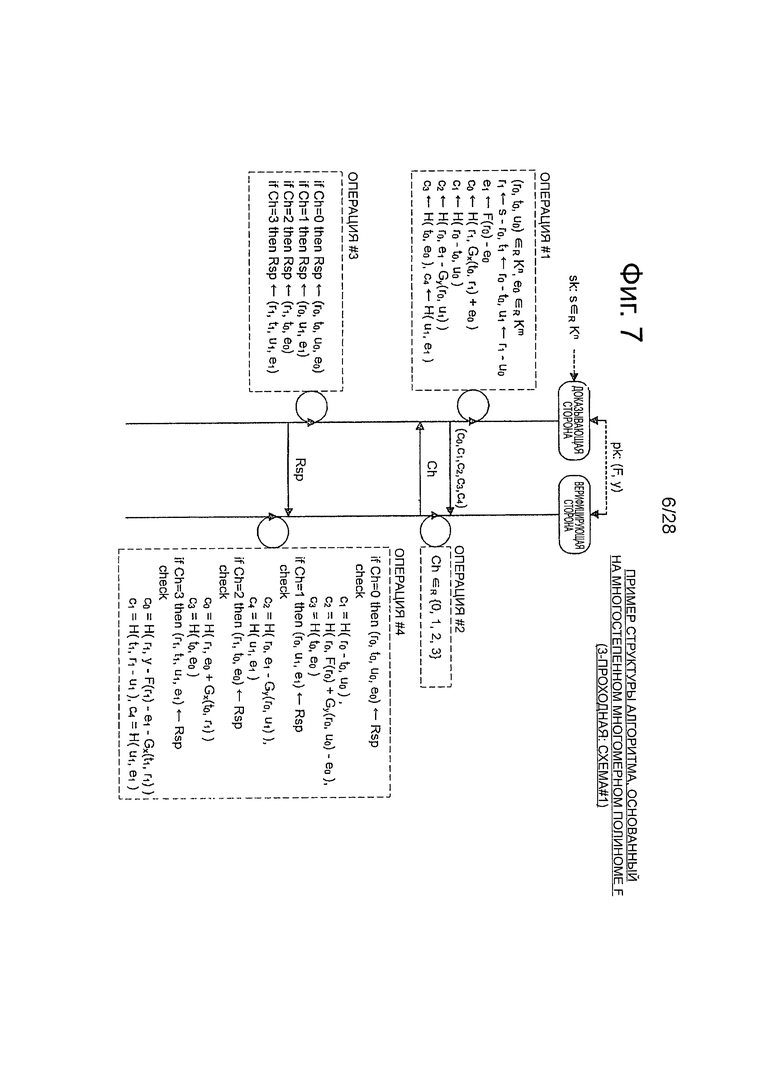
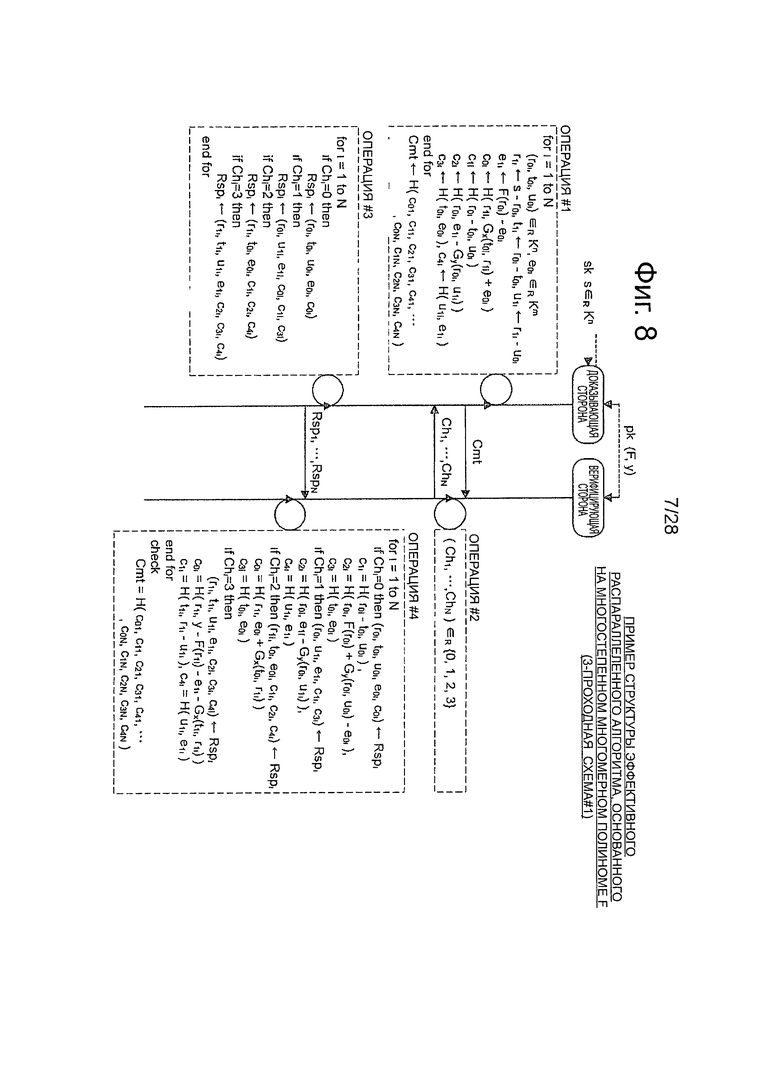
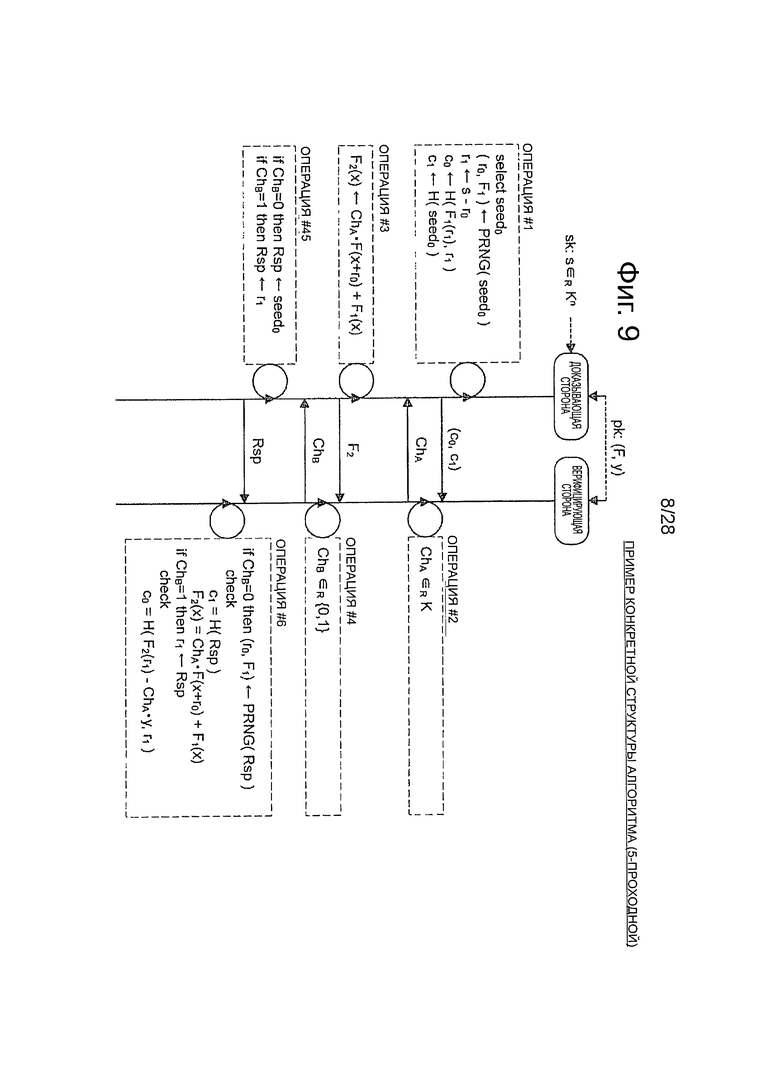
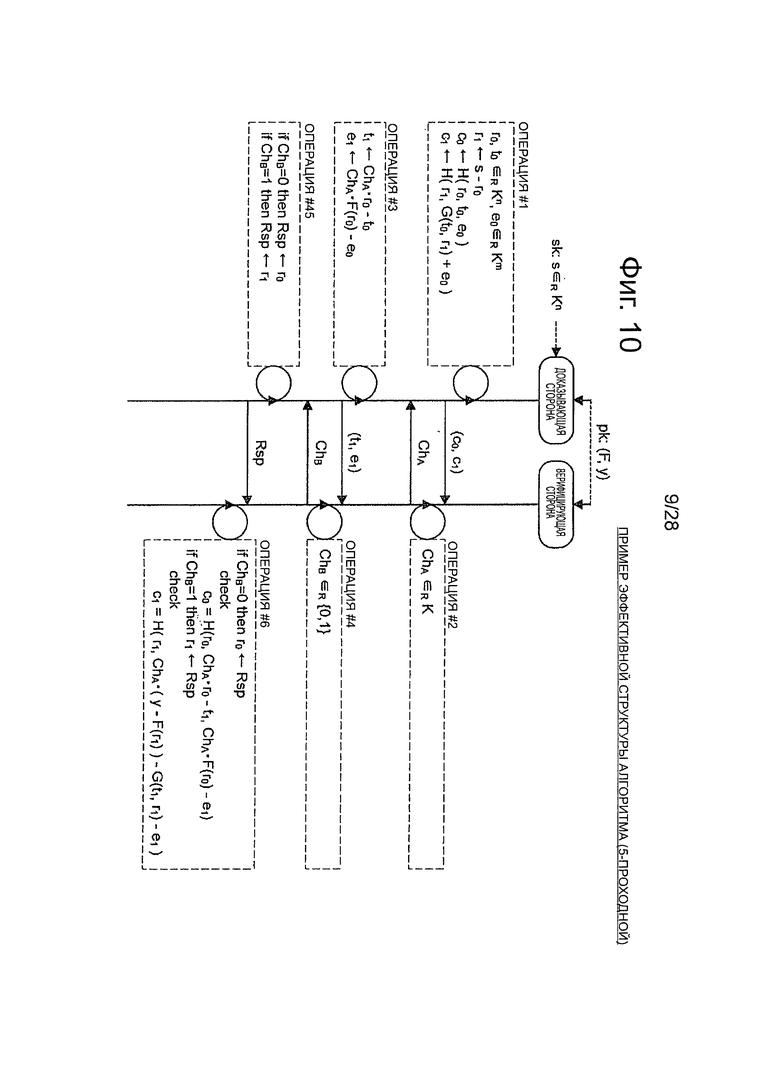
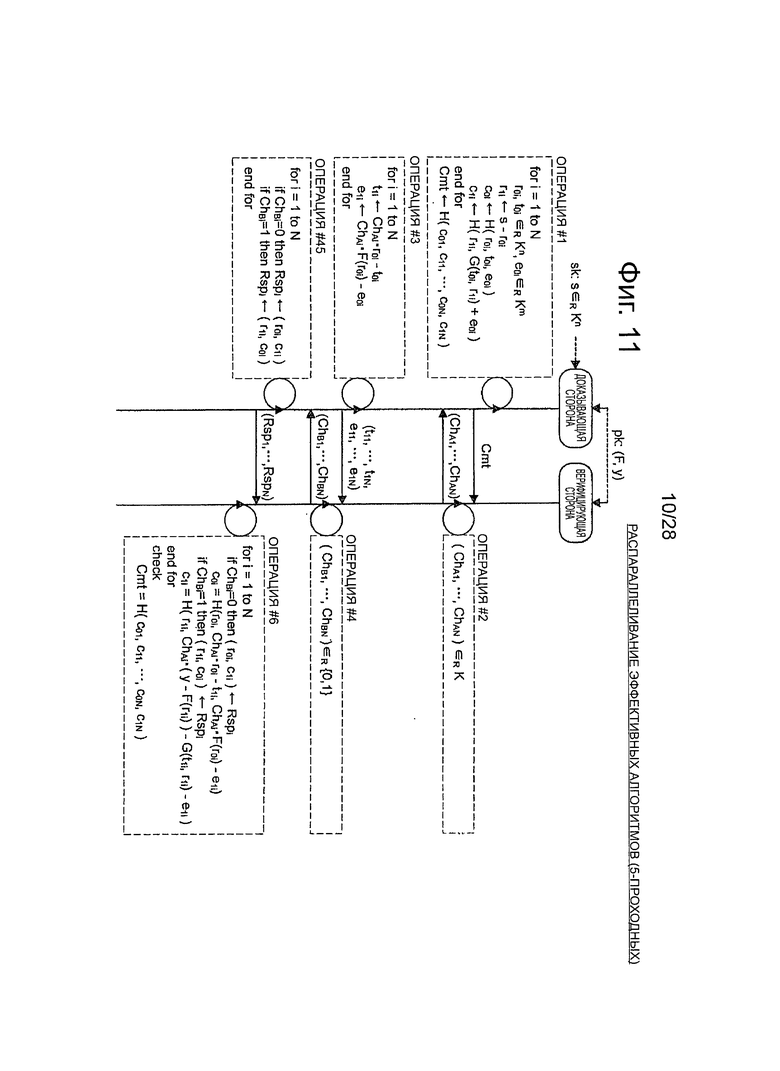
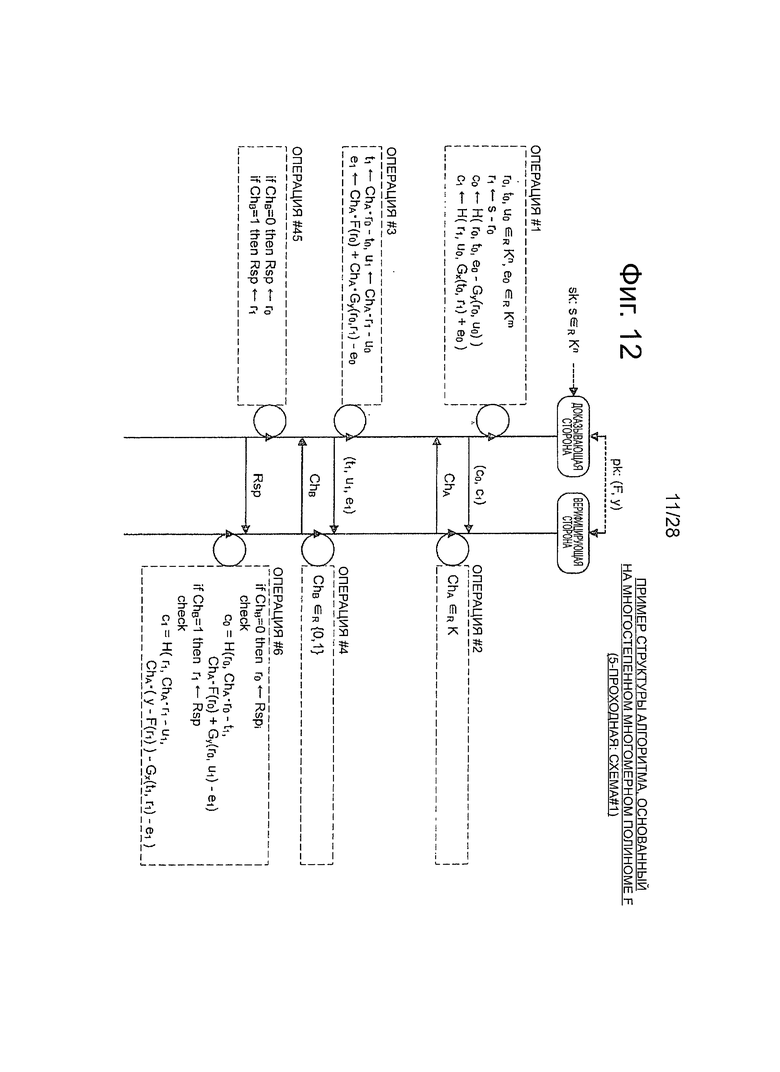
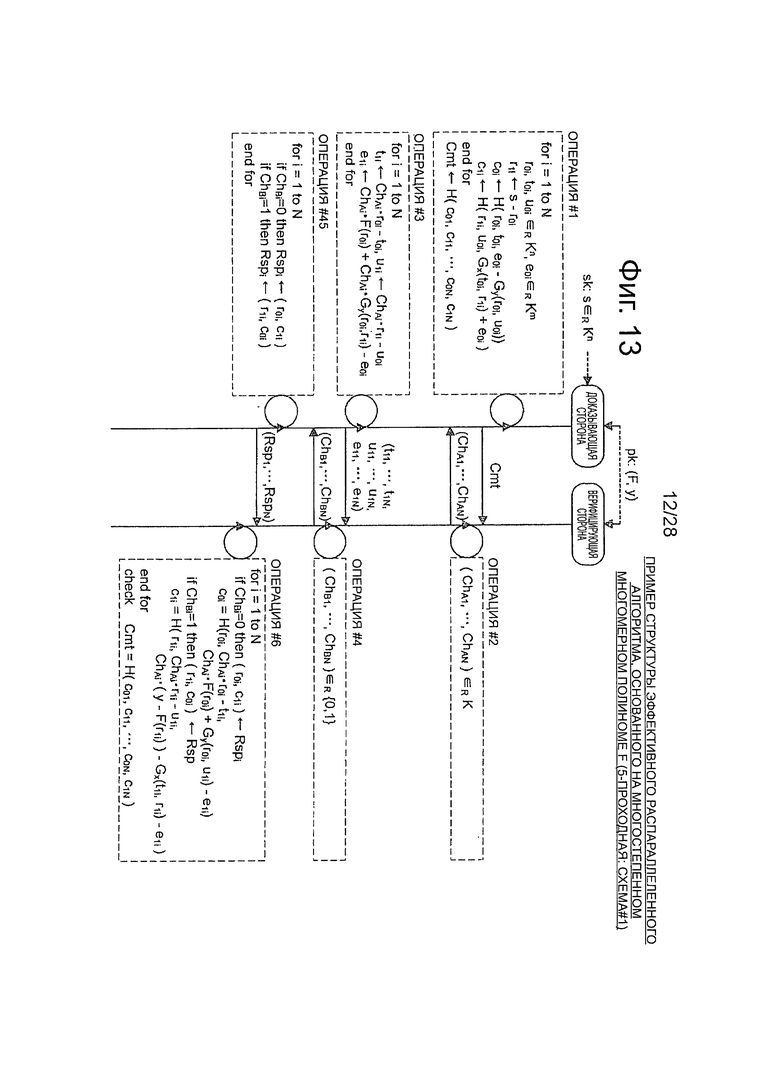
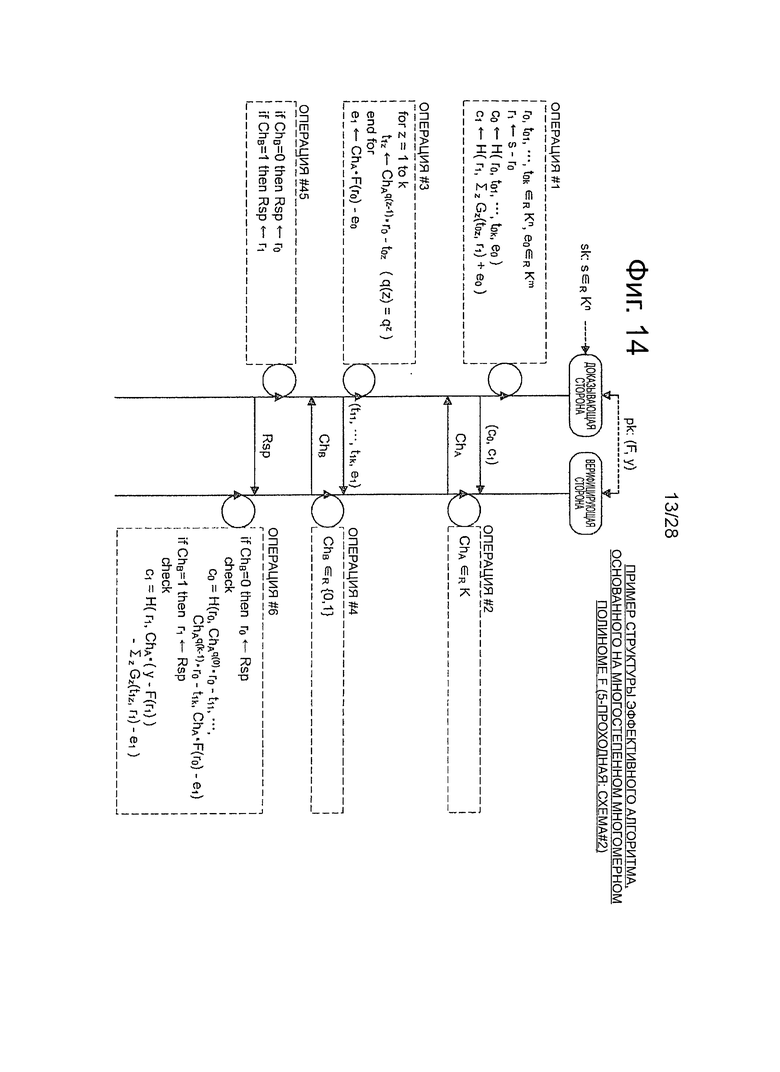
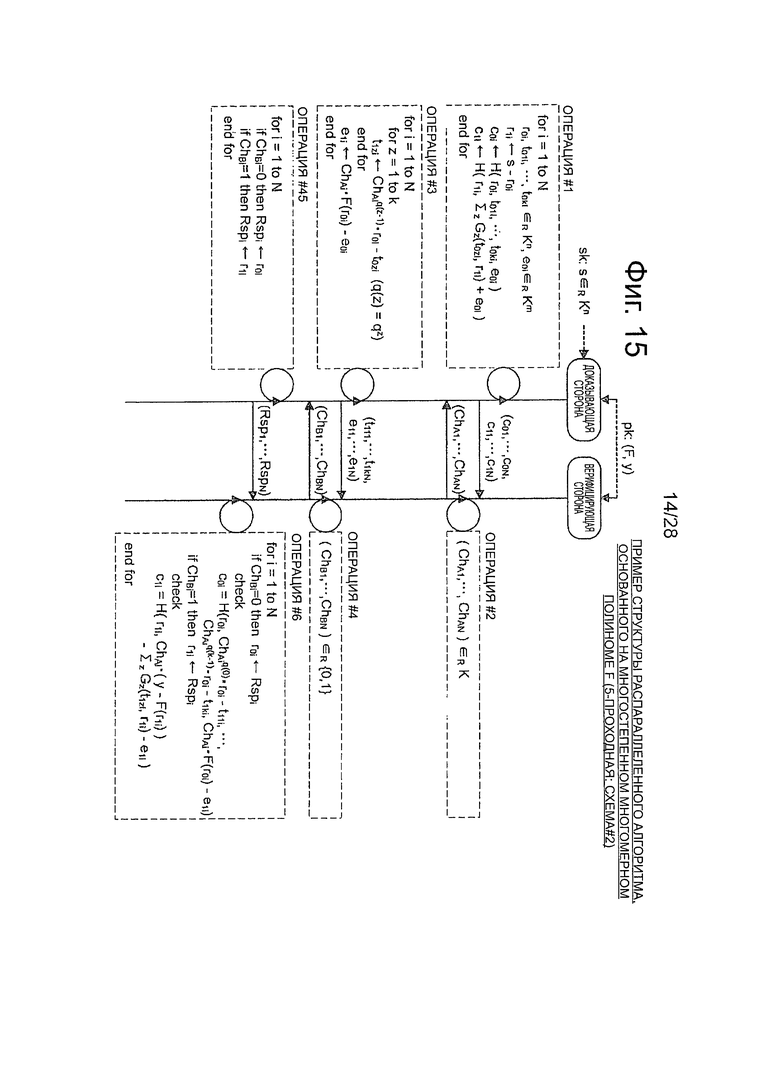
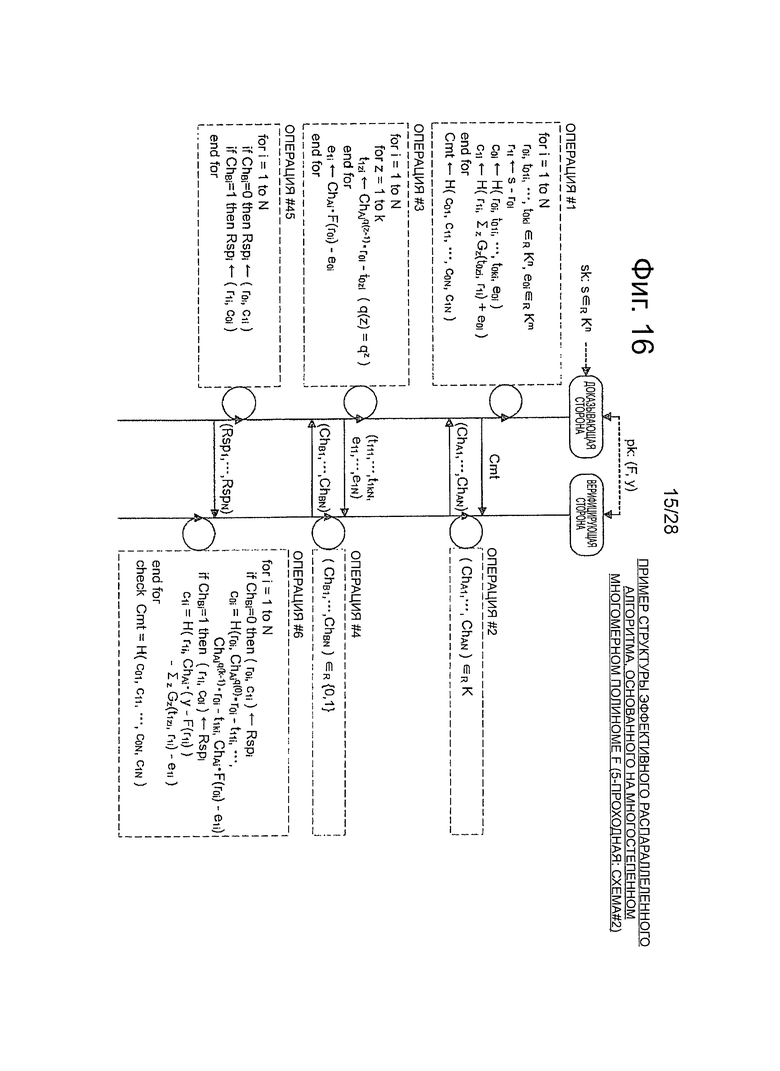
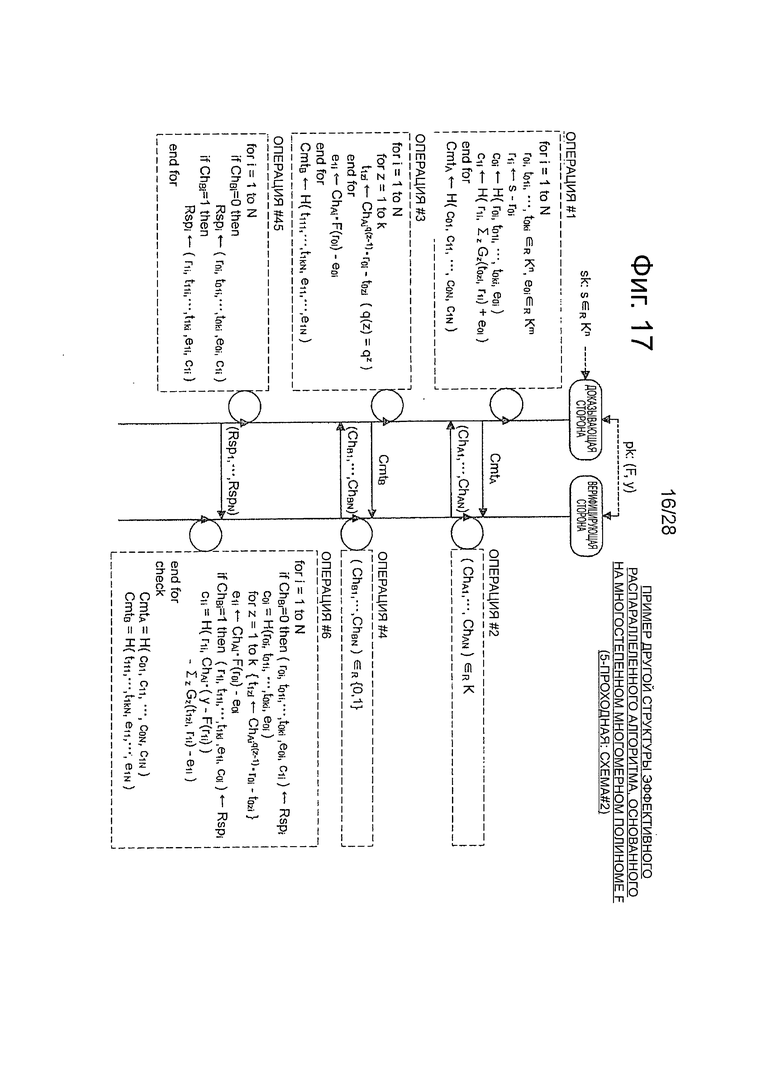
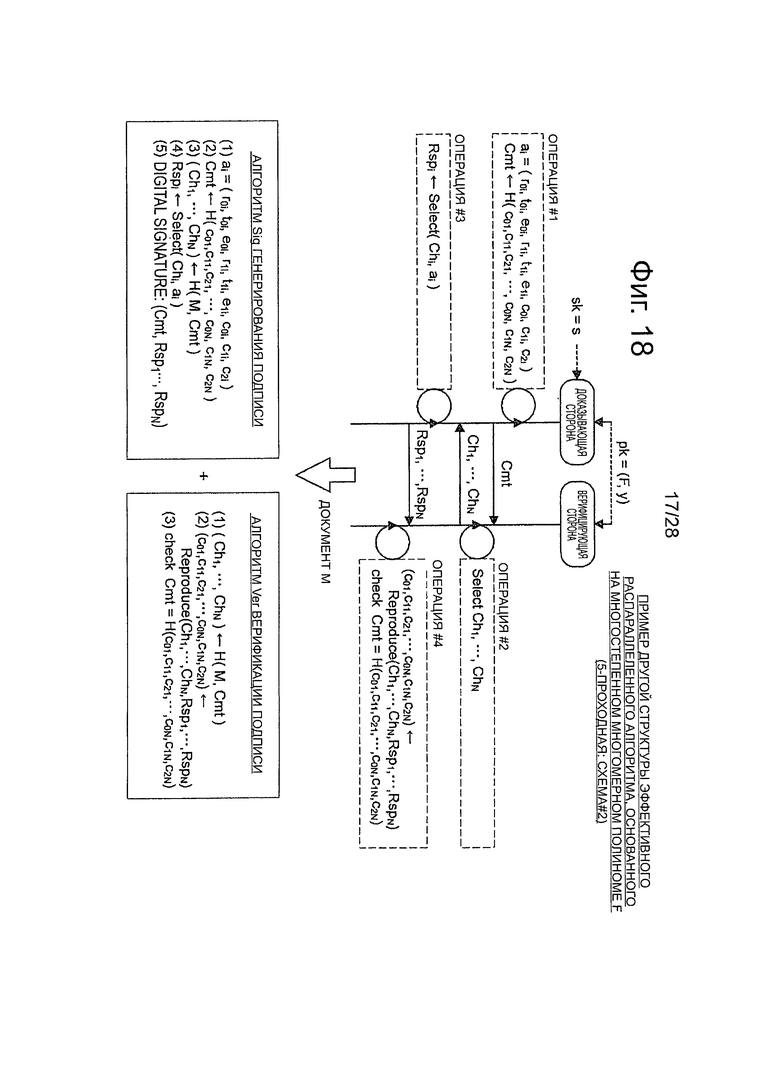
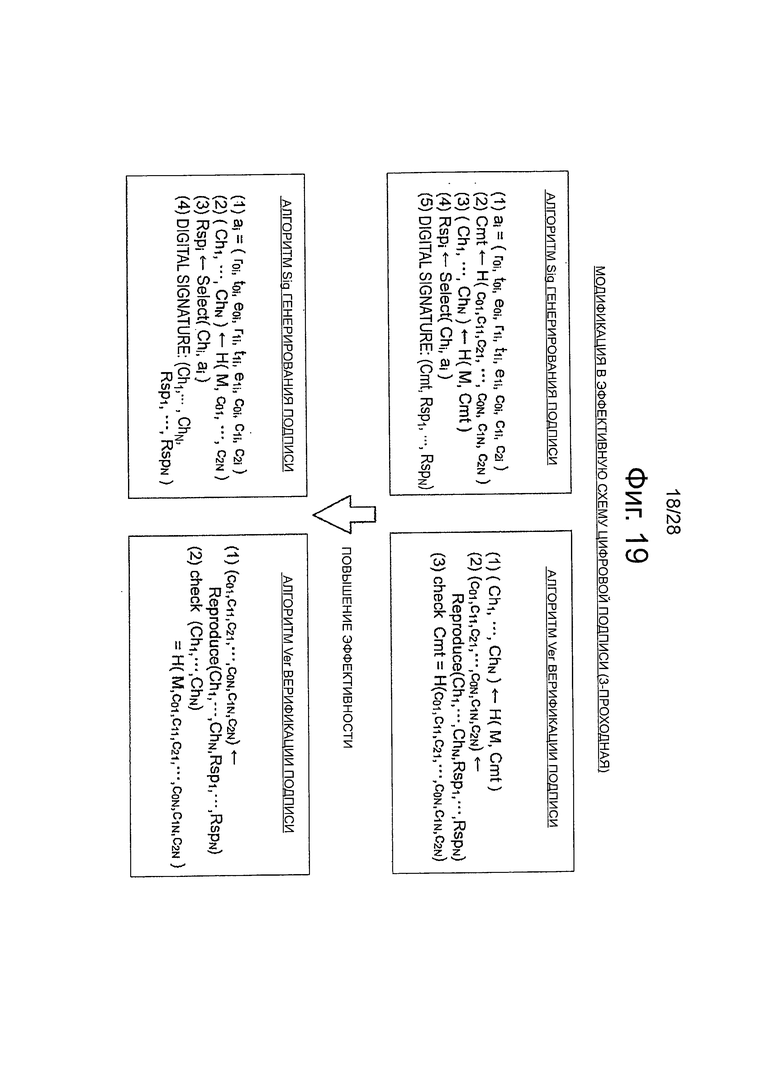
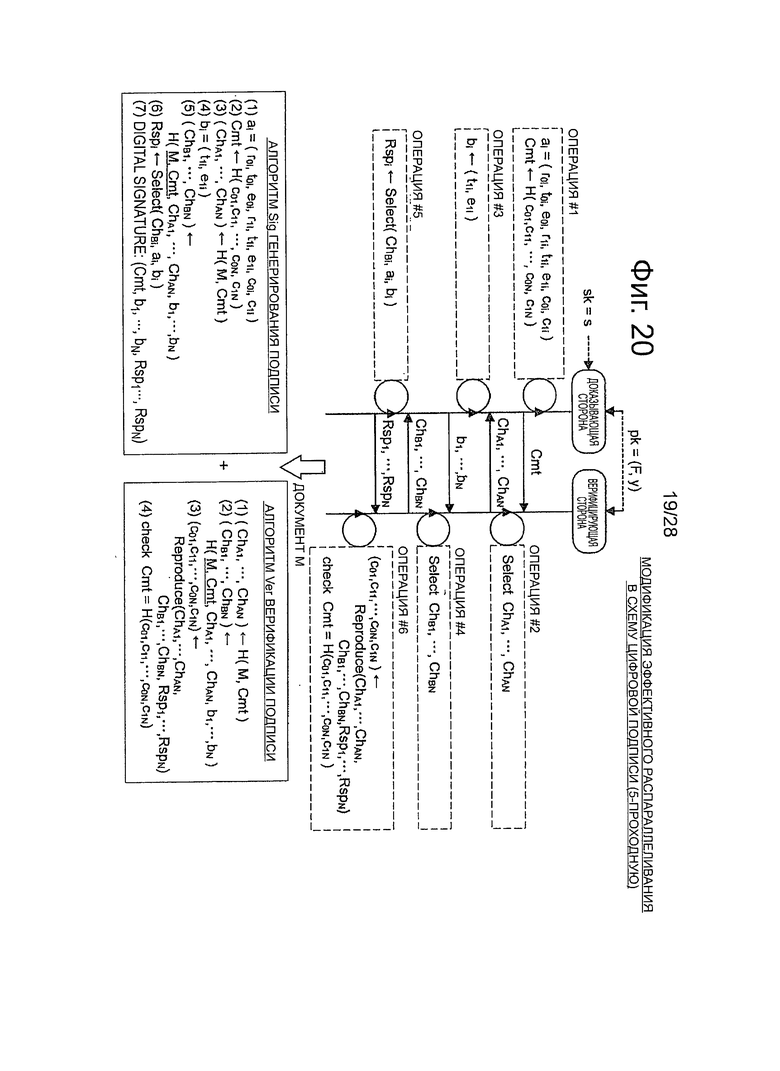
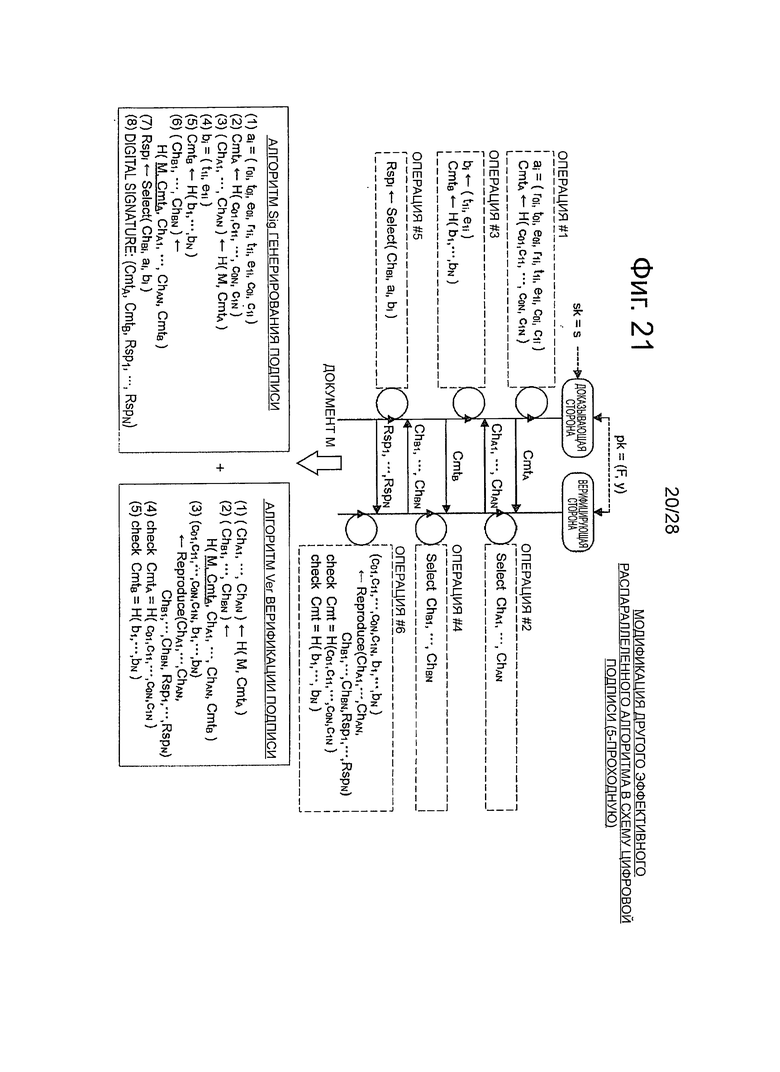
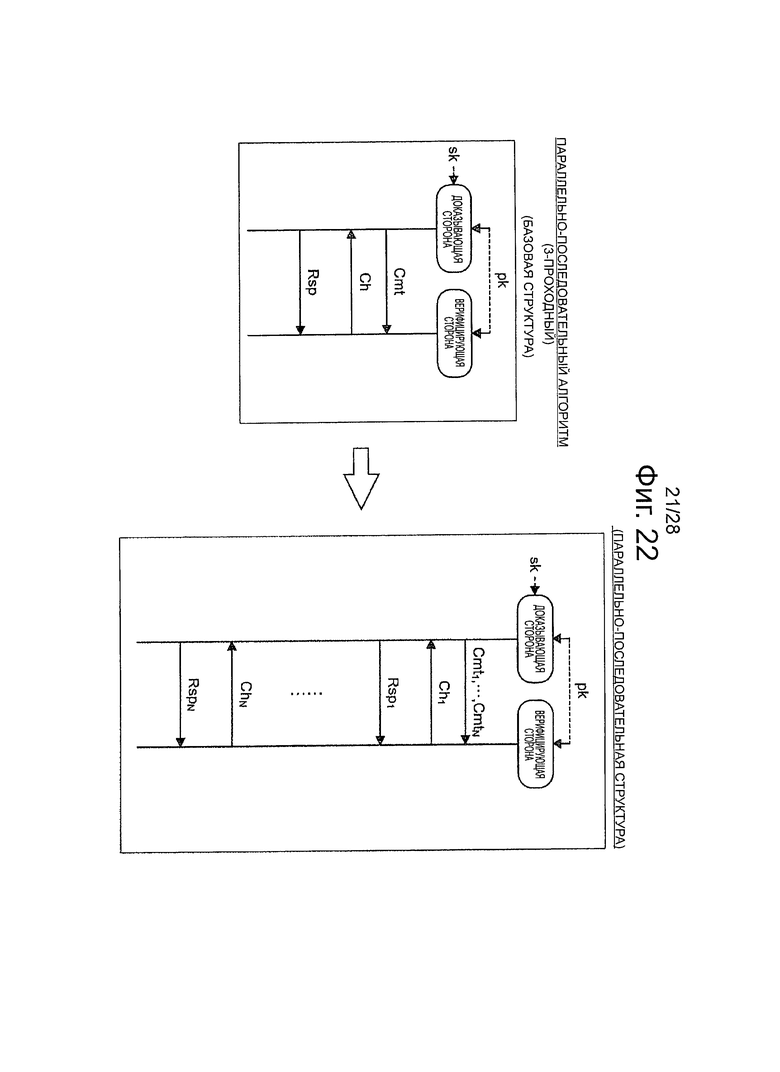
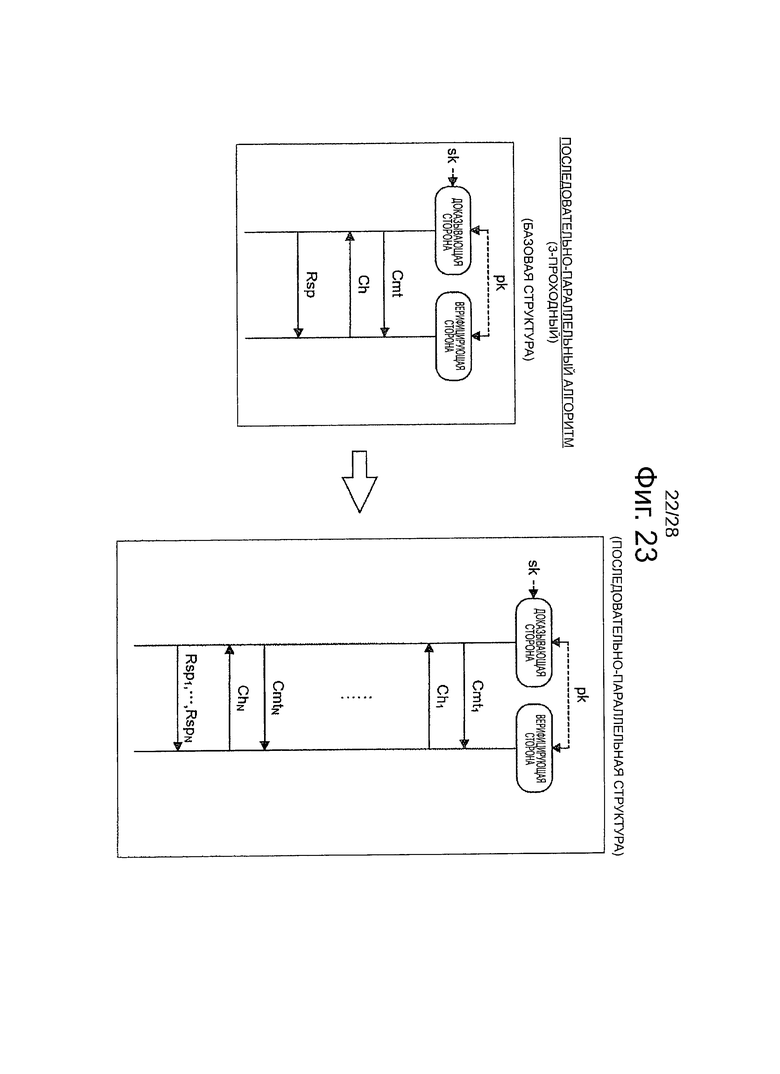
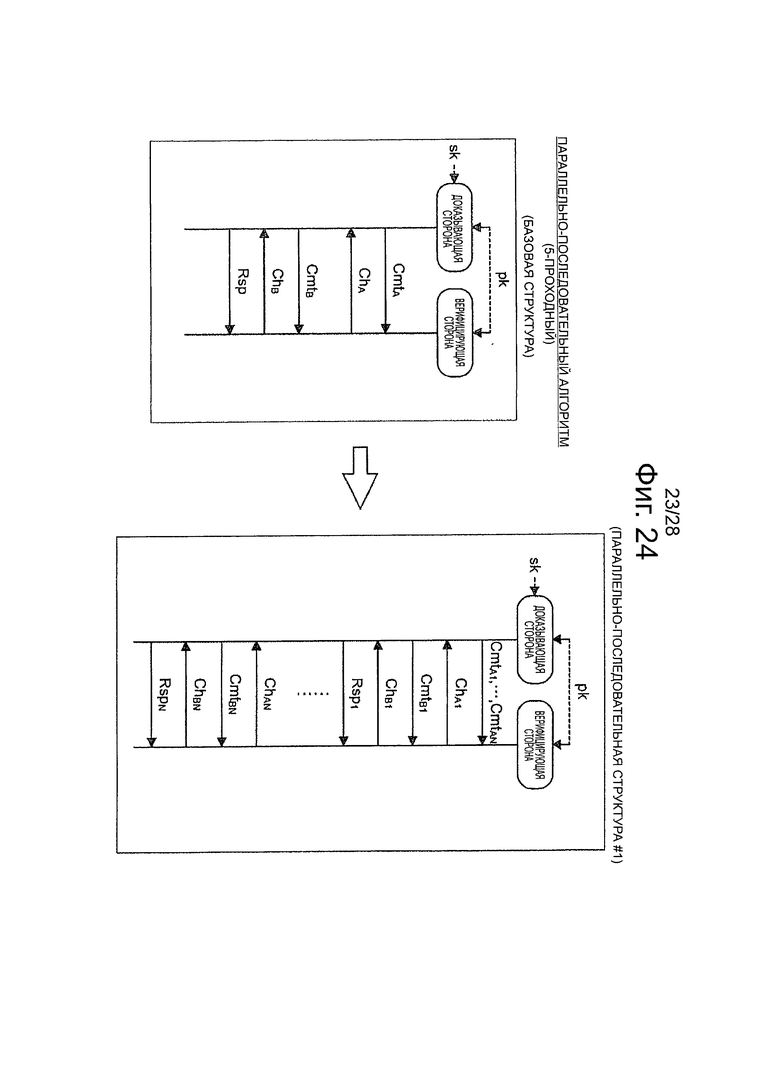
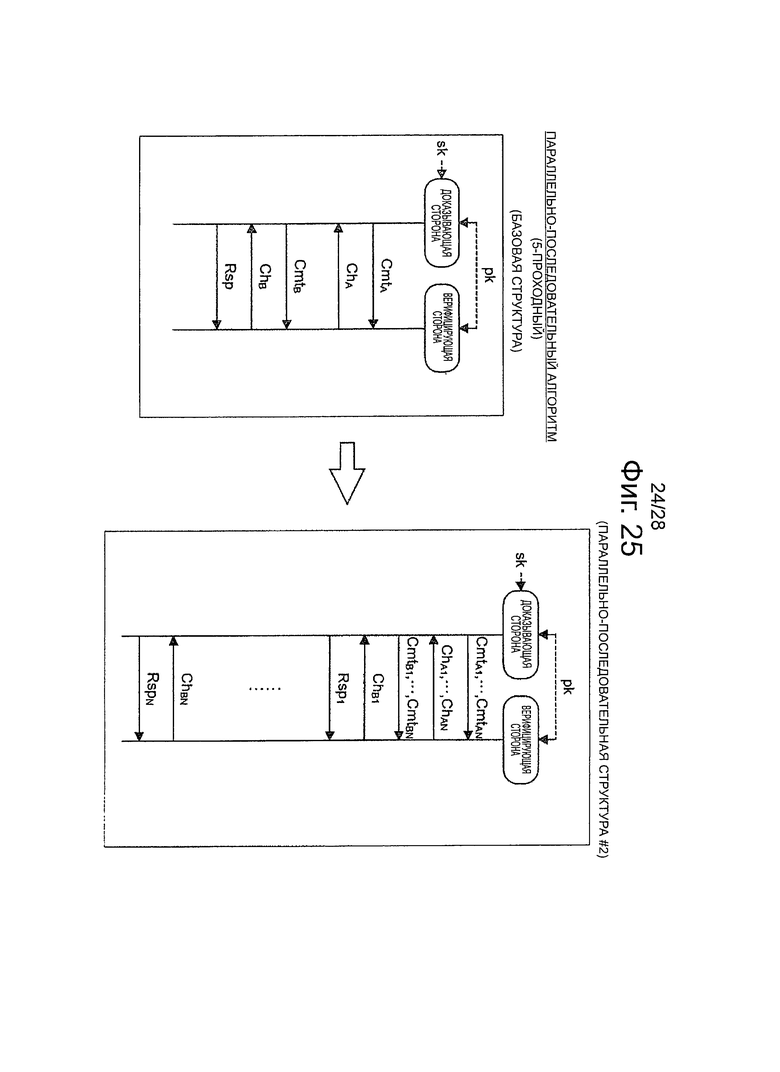
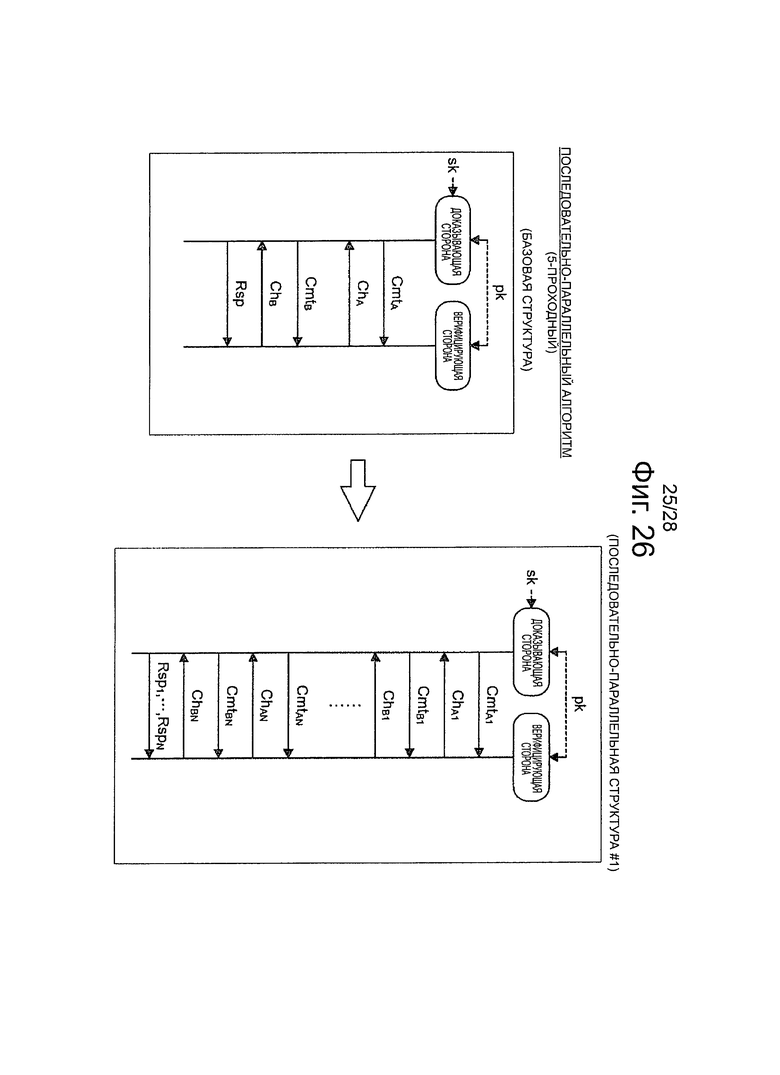
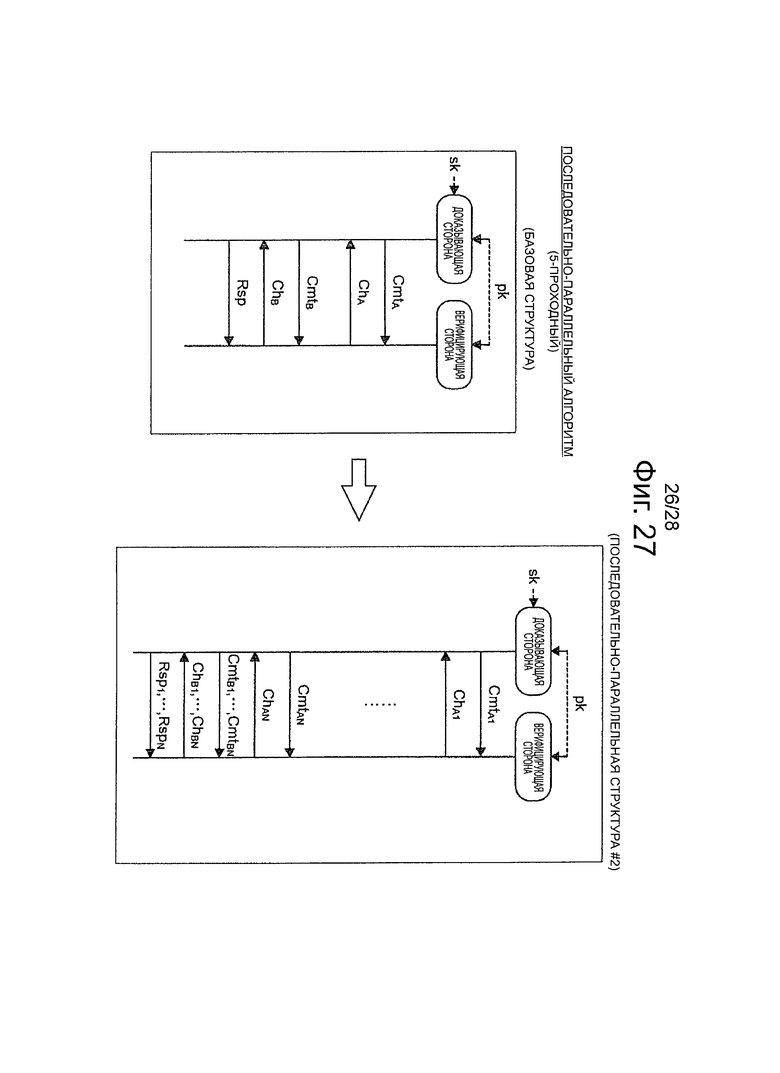
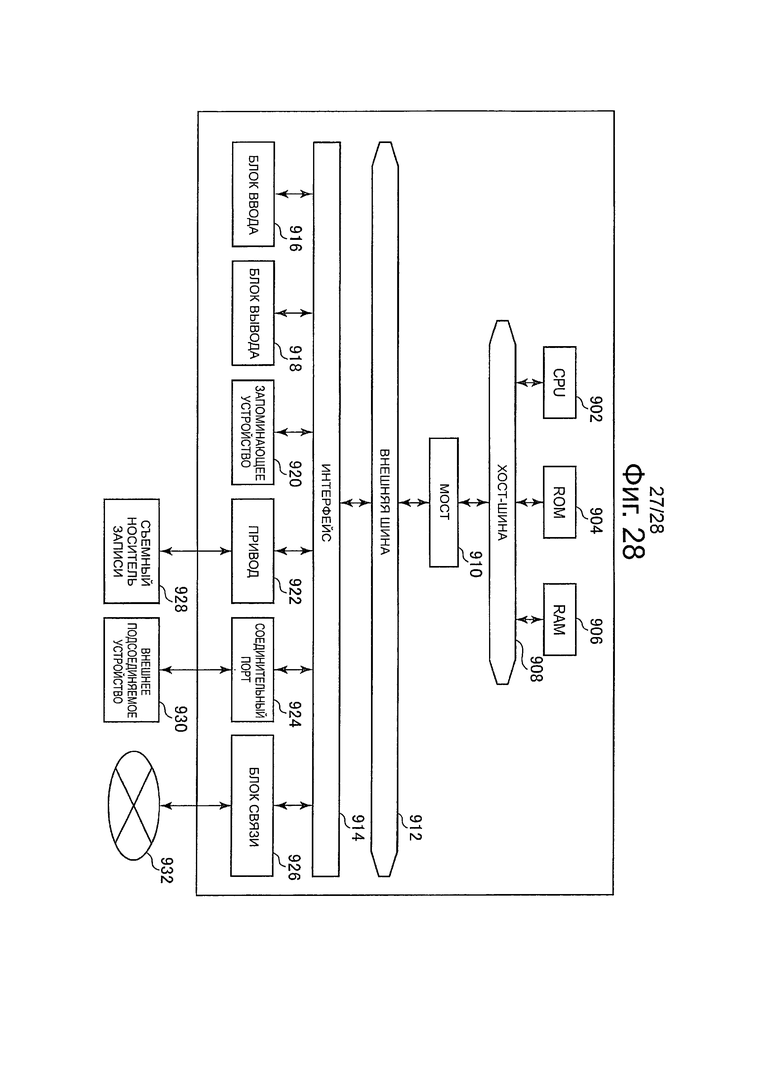
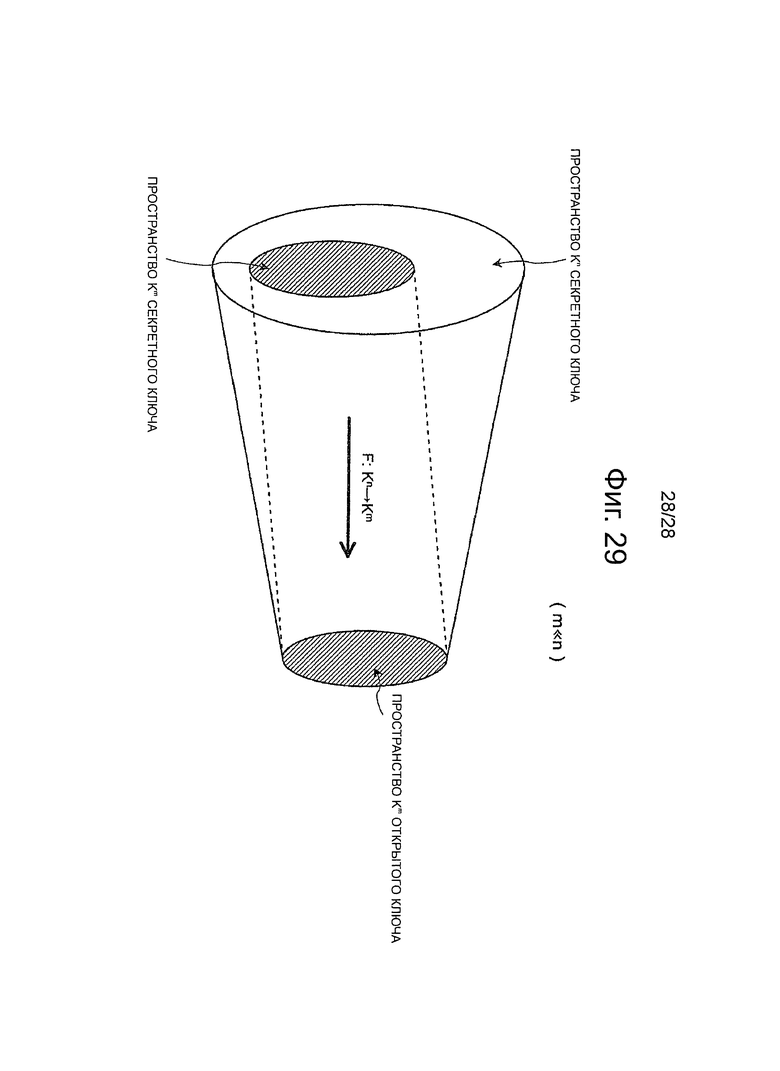
Изобретение относится к области связи. Технический результат - обеспечение высокого уровня надежности и защиты данных. Устройство обработки информации включает в себя блок генерирования сообщения для генерирования сообщения на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, представляющего собой элемент из набора Kn, блок подачи сообщения для подачи сообщения верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы y=(y1, …, ym)=(f1(s), …, fm(s)), блок генерирования промежуточной информации для генерирования третьей информации на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения, блок предоставления промежуточной информации для предоставления третьей информации верифицирующей стороне и блок подачи отклика для предоставления верифицирующей стороне информации отклика, соответствующей образцу верификации, выбираемому верифицирующей стороной из k (где k≥2) образцов верификации. 4 н. и 4 з.п. ф-лы, 29 ил.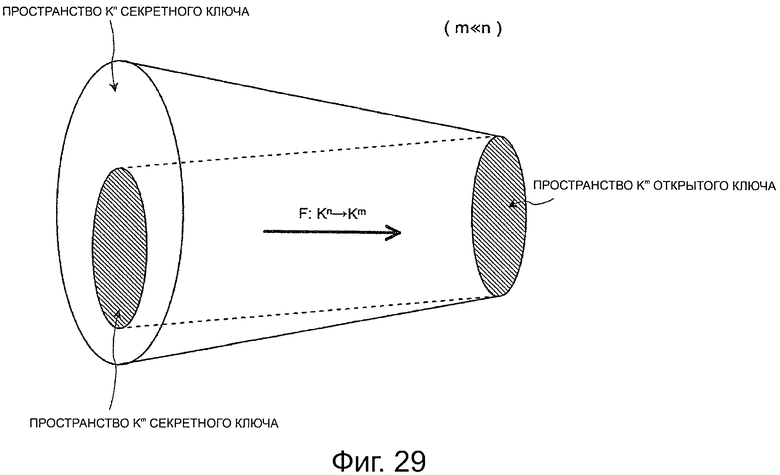
1. Устройство обработки информации, содержащее:
блок генерирования сообщения для генерирования сообщения на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, представляющего собой элемент из набора Kn;
блок подачи сообщения для подачи сообщения верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы у=(у1, …, ym)=(f1(s), …, fm(s));
блок генерирования промежуточной информации для генерирования третьей информации на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения;
блок предоставления промежуточной информации для предоставления третьей информации верифицирующей стороне; и
блок предоставления отклика для предоставления верифицирующей стороне информации отклика, соответствующей образцу верификации, выбранному верифицирующей стороной из k (где k≥2) образцов верификации, при этом
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F являются открытыми ключами или настроечными параметрами системы, и векторы у являются открытыми ключами, причем
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и установлены так, что полином G(x1, x2), определенный как G(x1, х2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(xl1, …, xln) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
2. Устройство обработки информации по п. 1, в котором
блок генерирования сообщения выполнен с возможностью генерирования сообщений N раз (где N≥2), при этом блок подачи сообщения выполнен с возможностью подачи верифицирующей стороне сообщений N раз с интерактивностью один раз; а
блок генерирования промежуточной информации выполнен с возможностью генерирования третьей информации N раз на основании первой информации, выбранной верифицирующей стороной для сообщений N раз, и второй информации, полученной N раз во время генерирования сообщений, причем
блок предоставления промежуточной информации выполнен с возможностью предоставления верифицирующей стороне третьей информации N раз с интерактивностью один раз, а
блок предоставления отклика выполнен с возможностью предоставления верифицирующей стороне информации отклика N раз, соответствующей образцу верификации, выбранному верифицирующей стороной для сообщений N раз, с интерактивностью один раз.
3. Устройство обработки информации по п. 2, в котором
блок генерирования сообщения выполнен с возможностью генерирования сообщений N раз (где N≥2) и генерирования одного значения хэширования из сообщений N раз, а
блок подачи сообщения выполнен с возможностью подачи значения хэширования верифицирующей стороне, причем
блок генерирования промежуточной информации выполнен с возможностью генерирования третьей информации N раз на основании первой информации, выбранной верифицирующей стороной для каждого из сообщений N раз, и второй информации, полученной N раз во время генерирования сообщений, а
блок предоставления промежуточной информации выполнен с возможностью предоставления верифицирующей стороне третьей информации N раз с интерактивностью один раз, при этом
блок предоставления отклика выполнен с возможностью предоставления верифицирующей стороне информации отклика N раз, соответствующей образцу верификации, выбранному верифицирующей стороной для каждого из сообщений N раз, и некоторых сообщений, не полученных при выполнении вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей и информации отклика с интерактивностью один раз.
4. Устройство обработки информации, содержащее:
блок хранения информации для хранения пары многостепенных многомерных полиномов F=(f1, …, fm) и векторов у=(у1, …, ym)=(f1(s), …, fm(s));
блок получения сообщения для получения сообщения, сгенерированного на основании пары многостепенных многомерных полиномов F и вектора s, представляющего собой элемент из набора Kn;
блок предоставления информации для предоставления произвольно выбранной первой информации доказывающей стороне, предоставляющей сообщение;
блок получения промежуточной информации для получения третьей информации, сгенерированной доказывающей стороной на основании первой информации и второй информации, полученной во время генерирования сообщения;
блок предоставления информации об образце для предоставления доказывающей стороне информации об одном образце верификации, произвольно выбранном из k (где k≥3) образцов верификации;
блок получения отклика для получения информации отклика, соответствующей выбранному образцу верификации, от доказывающей стороны; и
блок верификации для верификации, хранит ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика, при этом
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F являются открытыми ключами или настроечными параметрами системы, и векторы у являются открытыми ключами, причем
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и установлены так, что полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(xl1, xln) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
5. Устройство обработки информации по п. 4, в котором:
блок получения сообщения выполнен с возможностью получения сообщений N (где N≥2) раз с интерактивностью один раз, при этом
блок предоставления информации выполнен с возможностью произвольного выбора первой информации для каждого из сообщений N раз и предоставления доказывающей стороне выбранной N раз первой информации с интерактивностью один раз, а
блок получения промежуточной информации выполнен с возможностью получения N раз третьей информации, сгенерированной доказывающей стороной на основании первой информации N раз и второй информации N раз, полученной во время генерирования сообщений N раз, причем
блок предоставления информации об образце выполнен с возможностью выбора образца верификации для каждого из сообщений N раз и предоставления доказывающей стороне информации относительно выбранных N раз образцов верификации с интерактивностью один раз, а
блок получения отклика выполнен с возможностью получения N раз информации отклика, соответствующей выбранным N раз образцам верификации от доказывающей стороны с интерактивностью один раз, при этом
блок верификации выполнен с возможностью определения того, что доказывающая сторона хранит вектор s, когда верификация завершается успешно для всех сообщений N раз.
6. Устройство обработки информации по п. 5, в котором
блок получения сообщения выполнен с возможностью получения одного значения хэширования, сгенерированного из сообщений N раз (где N≥2), при этом
блок предоставления информации выполнен с возможностью произвольного выбора первой информации для каждого из сообщений N раз и предоставления доказывающей стороне выбранной N раз первой информации с интерактивностью один раз, а
блок получения промежуточной информации выполнен с возможностью получения третьей информации N раз, сгенерированной доказывающей стороной на основании первой информации N раз и второй информации N раз, полученной во время генерирования сообщения N раз, причем
блок предоставления информации об образце выполнен с возможностью выбора образца верификации для каждого из сообщений N раз и предоставления доказывающей стороне информации относительно выбранных N раз образцов верификации с интерактивностью один раз, а
блок получения отклика выполнен с возможностью получения от доказывающей стороны информации отклика, соответствующей выбранному образцу верификации и некоторых сообщений, не полученных при выполнении вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, при этом
блок верификации выполнен с возможностью верификации, хранит ли доказывающая сторона вектор s, на основании значения хэширования, некоторых из сообщений, открытых ключей, и информации отклика и определения, что доказывающая сторона хранит вектор s, когда верификация завершается успешно для всех сообщений N раз.
7. Способ обработки информации, содержащий этапы, на которых:
генерируют сообщение на основании пары многостепенных многомерных полиномов F=(f1, …, fm) и вектора s, представляющего собой элемент из набора Kn;
подают сообщение верифицирующей стороне, хранящей пару многостепенных многомерных полиномов F и векторы у=(у1, …, ym)=(f1(s), …, fm(s));
генерируют третью информацию на основании первой информации, произвольно выбранной верифицирующей стороной, и второй информации, полученной во время генерирования сообщения;
предоставляют третью информацию верифицирующей стороне; и
предоставляет верифицирующей стороне информацию отклика, соответствующую образцу верификации, выбираемому верифицирующей стороной из k (где k≥2) образцов верификации, при этом
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F являются открытыми ключами или настроечными параметрами системы, и векторы у являются открытыми ключами, причем
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и установлены так, что полином G(x1, x2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам х1=(xl1, xln) (где l=1, 2), сконфигурирован как член, пропорциональный (xli)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z<k).
8. Способ обработки информации, содержащий этапы, на которых: с помощью устройства обработки информации, хранящего пару многостепенных многомерных полиномов F=(f1, …, fm) и векторы у=(у1, …, ym)=(f1(s), …, fm(s)),
получают сообщение, сгенерированное на основании пары многостепенных многомерных полиномов F и вектора s, представляющего собой элемент из набора Kn;
предоставляют произвольно выбранную первую информацию доказывающей стороне, представляющей сообщение;
получают третью информацию, сгенерированную доказывающей стороной, на основании первой информации и второй информации, полученной во время генерирования сообщения;
предоставляют доказывающей стороне информацию относительно одного образца верификации, произвольно выбранного из k (где k≥3) образцов верификации; и
получают информацию отклика, соответствующую выбранному образцу верификации, от доказывающей стороны;
верифицируют, сохраняет ли доказывающая сторона вектор s на основании сообщения, первой информации, третьей информации, пары многостепенных многомерных полиномов F и информации отклика, при этом
вектор s представляет собой секретный ключ, а
пара многостепенных многомерных полиномов F являются открытыми ключами или настроечными параметрами системы, и векторы у являются открытыми ключами, причем
сообщение представляет собой информацию, полученную посредством выполнения вычисления, подготовленного заранее, для образца верификации, соответствующего информации отклика, на основании открытых ключей, первой информации, третьей информации и информации отклика, а
пара многостепенных многомерных полиномов F включает в себя полиномы f1, …, fm, определенные в кольце R характеристики q и порядка qk, и установлены так, что полином G(x1, х2), определенный как G(x1, x2)=F(x1+x2)-F(x1)-F(x2) по отношению к векторам x1=(xl1, xln) (где l=1, 2), сконфигурирован как член, пропорциональный (x1i)q(z) (где 1≤i≤n, q(z)=qz, и 1≤z≤k).
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Способ приготовления лака | 1924 |
|
SU2011A1 |
Авторы
Даты
2016-11-27—Публикация
2012-06-25—Подача