СПОСОБЫ И СИСТЕМЫ ОБРАБОТКИ ИЗОБРАЖЕНИЙ МАТЕМАТИЧЕСКИХ ВЫРАЖЕНИЙ
ОБЛАСТЬ ТЕХНИКИ
Настоящий документ относится к автоматической обработке изображений отсканированного документа и других содержащих текст изображений, а в частности к способам и системам преобразования изображений и фрагментов изображений документов, содержащих математические выражения, в электронные документы.
УРОВЕНЬ ТЕХНИКИ
Печатные, машинописные и рукописные документы на протяжении долгого времени используются для записи и хранения информации. Несмотря на текущие тенденции отказа от бумажного делопроизводства, печатные документы продолжают широко использоваться в коммерческих организациях, учреждениях и в домашних условиях. С развитием современных компьютерных систем формирование, хранение, поиск и передача электронных документов превратились, наряду с постоянным использованием печатных документов, в чрезвычайно эффективный и экономически рентабельный альтернативный носитель записи информации и хранения информации. Вследствие подавляющих преимуществ в отношении эффективности и экономической рентабельности, обеспечиваемых современными средствами хранения и передачи электронных документов, печатные документы часто преобразуют в электронные документы с помощью многообразия способов и систем, включая конвертацию печатных документов в цифровые изображения отсканированных документов с использованием электронных оптико-механических сканирующих устройств, цифровых камер, а также других устройств и систем, и последующую автоматическую обработку изображений отсканированных документов для получения электронных документов, преобразованных в цифровую форму в соответствии с одним или несколькими стандартами кодирования электронных документов. В качестве одного примера, в настоящее время возможно использовать настольный сканер и сложные программы оптического распознавания символов (OCR), запускаемые на персональном компьютере для преобразования печатного документа на бумажном носителе в соответствующий электронный документ, который можно отображать и редактировать с использованием текстового редактора. Изображения документов также содержатся на веб-страницах и в различных дополнительных источниках. Изображения документов, полученные из этих источников, также преобразуются в электронные документы с использованием OCR-способов.
Хотя современные OCR-программы эволюционировали до такой степени, что позволяют автоматически преобразовывать в электронные документы изображения сложных документов, которые включают картинки, рамки, линии границ и другие нетекстовые элементы, а также текстовые символы любого из множества распространенных алфавитных языков, остаются нерешенными проблемы в отношении преобразования изображений документа, содержащих математические выражения.
В патенте США 7181068 раскрыта система распознавания математических выражений, способ распознавания математических изображений, система распознавания символов и метода распознавания символов. Устройство распознавания математических выражений включает модуль, который распознает символы на изображении документа, словарь, хранящий пару оценочных баллов для каждого типа слова, балл, отображающий вероятность принадлежности к тексту и балл, отражающий вероятность его принадлежность к математическому выражению, оценочный модуль, который получает оценочные баллы, отображающие вероятность принадлежности к тексту и и балл, отражающий вероятность его принадлежность к математическому выражению для каждого из слов, включенных в распознанные символы с ссылкой на словарь, и модуль обнаружения математического выражения, который ищет оптимальный путь, соединяющий слова путем выбора одного из текста и математического выражения на основе формативной грамматики и оценочных баллов, отображающий вероятность принадлежности к тексту и его принадлежности математическому выражению, тем самым детектируя символы, принадлежащие математическому выражению. Элементы математического выражения проверяются на факт того, являются ли они символами на базовой линии, надстрочными символами или подстрочными символами. Диаграмма рассеяния размеров символов, которая предоставляет данные, отображает размер нормализации последовательных символов и распределение их возможных центральных позиций.
В предлагаемом способе происходит итерационное разделение изображения математического выражения документа на составляющие выражения и последующее распознавание этих составляющих. Отличительным признаком является использование рекурсивно-блочного и основанного на графе подхода к распознаванию математических выражений во время OCR-обработки изображения документа, что позволяет выбрать наиболее оптимальный вид компановки результатов распознавания в математическое выражение на основе оценки каждого из путей данного графа, где путь представляет собой группировку символов в строку и учитывает варианты распознавания каждого из символов.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Настоящий документ относится к способам и системам, преобразующим изображения документа, содержащие математическое выражение, в соответствующие электронные документы. В одном из способов реализации изображение или фрагмент изображения, содержащий математическое выражение, рекурсивно разделяют на блоки, отделенные белыми полосами пробелов. К изображению или фрагменту изображения, содержащему математическое выражение, попеременно и рекурсивно применяют горизонтальное и вертикальное разбиение до тех пор, пока полученные при разбиении блоки низшего уровня не будут соответствовать символам, распознаваемым способами распознавания символов. Анализ распознанных символов в виде графа обеспечивает основу для преобразования эквивалентного представления математического выражения, содержащегося на изображении или фрагменте изображения, в цифровую форму.
Техническим результатом работы раскрываемых способа и системы, обрабатывающих при помощи технологии оптического распознавания символов (OCR) изображения и фрагменты изображений документа, содержащих математические выражения, является преобразования изображений математических выражений в электронные представления. В качестве общепринятого электронного представления может быть использования стандарт Юникод. Способы обработки изображений и фрагментов изображений математических выражений, к которым относится настоящий документ, включают рекурсивное попеременное применение методик разбиения изображения на блоки для иерархического разделения изображений или фрагментов изображений, содержащих математическое выражение, на элементарные блоки, каждый из которых соответствует конкретным символам. Рекурсивно-блочный и основанный на графе подход к распознаванию математических выражений во время OCR-обработки изображения документа позволяет выбрать наиболее оптимальный вид компановки результатов распознавания в математическое выражение.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
На Фиг. 1А-В проиллюстрирован печатный документ.
На Фиг. 2 проиллюстрирован типичный настольный сканер и персональный компьютер, которые вместе используются для преобразования печатных документов в оцифрованные электронные документы, хранящиеся на запоминающих устройствах и/или в модулях электронной памяти.
На Фиг. 3 проиллюстрировано функционирование оптических компонентов настольного сканера, изображенного на Фиг. 2.
На Фиг. 4 представлена общая архитектурная схема различных типов компьютеров и других устройств, управляемых процессором.
На Фиг. 5 проиллюстрированное цифровое представление отсканированного документа.
На Фиг. 6А-С проиллюстрирован один подход к преобразованию изображения документа в электронный документ, который используется в некоторых доступных в настоящее время OCR-системах.
На Фиг. 7 альтернативно представлен способ преобразования изображения документа в электронный документ, используемый в различных доступных в настоящее время OCR-способах и системах.
На Фиг. 10А-В проиллюстрирован подход к распознаванию символов, используемый OCR-системой, путем наложения эталона.
На Фиг. 11А-В проиллюстрированы различные аспекты объектов множеств символов для естественных языков.
На Фиг. 12 проиллюстрирован ряд дополнительных типов распознавания символов, который можно использовать для распознавания символов в пределах изображений и фрагментов изображений текстовых документов.
На Фиг. 13А-В проиллюстрирован тип классификатора, который можно использовать для порождения гипотез в отношении разбиения изображения текстовой строки в последовательность изображений символов.
На Фиг. 14А-В представлен ряд примеров математических выражений, а также указаний на элементы в математических выражениях, которые являются сложными и представляют трудности для используемых в настоящее время OCR-способов, применяемых к фрагментам изображений, содержащим математические выражения.
На Фиг. 15A-F проиллюстрирован один из способов разбиения на блоки математического выражения, который разделяет изображение или фрагмент изображения, содержащий математическое выражение, на блоки или разбиения более низкого уровня.
На Фиг. 16А-В проиллюстрированы рекурсивно-блочный и основанный на графе подходы к распознаванию математических формул в процессе OCR-обработки изображения документа.
На Фиг. 17А-С представлены блок-схемы, иллюстрирующие один из способов обработки изображения документа, содержащего математическое выражение, к которому относится настоящий документ.
На Фиг. 18А-С проиллюстрировано применение обработки на основе графа для распознавания фрагментов математических выражений и полных математических выражений.
На Фиг. 19 представлены результаты анализа в форме дерева, сгенерированные с помощью рекурсивно-блочного подхода, исходно представленного на Фиг. 16В, с дугами правильного пути для математического выражения 1406, изображенного на Фиг. 14А.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
Настоящий документ относится к способам и системам, преобразующим изображения документа, содержащие математические выражения, в соответствующие электронные документы. В первом подразделе представленного ниже описания описаны изображения отсканированных документов, электронные документы и доступные в настоящее время OCR-способы и системы. Во втором подразделе описаны проблемы в отношении преобразования изображений документа, содержащих математические выражения. И, наконец, в третьем подразделе представлено подробное описание способов и систем, к которым относится настоящий документ.
Изображения отсканированных документов и электронные документы
На Фиг. 1А-В проиллюстрирован печатный документ. На Фиг. 1А представлен первоначальный документ с текстом на японском языке. Печатный документ 100 включает фотографию 102 и пять разных содержащих текст участков (104-108), включающих японские символы. Данный пример документа используется в представленном ниже описании способа и систем для определения ориентации, к которым относится настоящий документ. Текст на японском языке может быть написан слева направо, вдоль горизонтальных строк, как текст на английском языке, но альтернативно может быть написан способом сверху вниз в пределах вертикальных столбцов. Например, участок 107 явно содержит вертикально написанный текст, тогда как текстовый блок 108 включает текст, написанный горизонтальными строками. На Фиг. 1В печатный документ, проиллюстрированный на Фиг. 1А, показан переведенным на английский язык.
Печатные документы можно преобразовать в оцифрованные изображения отсканированных документов с помощью различных средств, включая электронные оптико-механические устройства сканирования и цифровые камеры. На Фиг. 2 проиллюстрированы типичный настольный сканер и персональный компьютер, которые вместе используются для преобразования печатных документов в оцифрованные электронные документы, которые можно хранить на запоминающих устройствах и/или в модулях электронной памяти. Настольное сканирующее устройство 202 включает прозрачный стеклянный планшет 204, на который лицевой стороной вниз помещают документ 206. Активация сканера приводит к генерированию оцифрованного изображения отсканированного документа, которое можно передать на персональный компьютер (ПК) 208 для хранения на запоминающем устройстве. Программа отображения отсканированного документа может отобразить оцифрованное изображение отсканированного документа на дисплей 210 устройства отображения ПК 212.
На Фиг. 3 проиллюстрировано функционирование оптических компонентов настольного сканера, изображенного на Фиг. 2. Оптические компоненты данного ПЗС-сканера находятся под прозрачным стеклянным планшетом 204. Фронтально перемещаемый источник яркого света 302 освещает фрагмент сканируемого документа 304, свет от которого, в свою очередь, повторно излучается и отражается вниз. Свет повторно излучается и отражается от фронтально перемещаемого зеркала 306 на неподвижное зеркало 308, которое отражает излучаемый свет на массив ПЗС-элементов 310, порождающих электрические сигналы пропорционально интенсивности света, падающего на каждый из ПЗС-элементов. Цветные сканеры могут включать три отдельных строки или массива ПЗС-элементов с красным, зеленым и синим фильтрами. Фронтально перемещаемый источник яркого света и фронтально перемещаемое зеркало перемещаются вместе вдоль документа для генерирования изображения отсканированного документа. Другой тип сканера, в котором используется контактный датчик изображения, называется CIS-сканером. В CIS-сканере подсветка документа осуществляется перемещаемыми цветными светодиодами (LED), причем отраженный свет светодиодов воспринимается массивом фотодиодов, который перемещается вместе с цветными светодиодами.
На Фиг. 4 представлена общая архитектурная схема различных типов компьютеров и других устройств, управляемых процессором. Архитектурная схема высокого уровня может описывать современную компьютерную систему, такую как ПК, изображенный на Фиг. 2, в которой программы отображения отсканированного документа и программы оптического распознавания символов хранятся на запоминающих устройствах для передачи в модуль электронной памяти и исполнения одним или более процессорами. Компьютерная система содержит один или несколько центральных процессоров (ЦП) 402-405, один или более модулей электронной памяти 408, взаимно соединенных с ЦП с помощью шины подсистемы ЦП/память 410 или нескольких шин, первый мост 412, который соединяет шину подсистемы ЦП/память 410 с дополнительными шинами 414 и 416, или другими средствами высокоскоростного взаимодействия, включая несколько высокоскоростных последовательных соединений. Эти шины или последовательные соединения, в свою очередь, соединяют ЦП и модуль памяти со специализированными процессорами, такими как графический процессор 418, а также с одним или более дополнительными мостами 420, взаимно соединенными с высокоскоростными последовательными каналами или с несколькими контроллерами 422-427, такими как контроллер 427, которые обеспечивают доступ к многообразию типов устройств памяти 428, электронным дисплеям, устройствам ввода и другим таким компонентам, подкомпонентам и вычислительным ресурсам.
На Фиг. 5 проиллюстрировано цифровое представление отсканированного документа. На Фиг. 5 небольшой дискообразный фрагмент 502 примера печатного документа 504 представлен в увеличенном виде 506. Соответствующий фрагмент оцифрованного изображения отсканированного документа 508 также представлен на Фиг. 5. Оцифрованный отсканированный документ включает данные, которые представляют двухмерный массив кодировок значений пикселей. В представлении 508 каждая ячейка сетки под символами, такая как ячейка 509, представляет квадратную матрицу пикселей. Небольшой фрагмент 510 сетки представлен с еще большим увеличением (512 на Фиг. 5), на котором отдельные пиксели представлены в виде элементов матрицы, таких как элемент матрицы 514. При таком уровне увеличения края символов кажутся зазубренными, поскольку пиксель является наименьшим элементом детализации, который можно контролировать для излучения света указанной интенсивности. В файле оцифрованного отсканированного документа каждый пиксель представлен фиксированным количеством бит, причем кодирование пикселей осуществляется последовательно. Файл содержит заголовок с информацией, указывающей тип кодирования пикселя, размеры отсканированного изображения и другую информацию, позволяющую программе отображения оцифрованного отсканированного документа извлекать данные кодировки пикселя и отдавать команды на устройство отображения или принтер для воспроизведения кодировок пикселей в виде двухмерного представления первоначального документа. В оцифрованных изображениях отсканированного документа по монохромной шкале оттенков серого широко используют 8-разрядную или 16-разрядную кодировки пикселя, тогда как в цветных изображениях отсканированного документа можно использовать 24 бита или более для кодирования каждого пикселя в соответствии с множеством стандартов кодирования цвета. В качестве одного примера, в широко используемом стандарте RGB для представления интенсивности красного, зеленого и синего света используют три 8-битных значения, закодированных в 24-битном значении. Таким образом, оцифрованное отсканированное изображение по существу представляет документ таким же способом, которым цифровые фотографии представляют визуальные образы. Кодировки пикселей представляют информацию об интенсивности света в конкретных крошечных участках изображения, а в цветных изображениях дополнительно представляет информацию о цвете. В оцифрованном изображении отсканированного документа отсутствует какое-либо указание на значение кодировок пикселей, такое как указания на то, что небольшая двухмерная область смежных пикселей представляет текстовый символ.
В отличие от этого, типичный электронный документ, созданный с помощью текстового редактора, содержит различные типы команд рисования линий, ссылки на представления изображений, такие как оцифрованные фотографии, а также оцифрованные текстовые символы. Одним широко используемым стандартом кодирования текстовых символов является стандарт Юникод. В стандарте Юникод широко используют 8-разрядные байты для кодирования символов Американского стандартного кода для обмена информацией (ASCII) и 16-битный слова для кодирования символов и знаков многих языков. Большая часть вычислительной работы, которую выполняет OCR-программа, представляет собой распознавание изображений текстовых символов, полученных из оцифрованного изображения отсканированного документа, и преобразование изображений символов в соответствующие кодировки Юникод. Очевидно, что для хранения текстовых символов Юникод требуется гораздо меньше места, чем для хранения растровых изображений текстовых символов. Более того, текстовые символы, закодированные по стандарту Юникод, можно редактировать, повторно форматировать с использованием различных шрифтов и обрабатывать множеством дополнительных способов, используемых в текстовых редакторах, тогда как оцифрованные изображения отсканированного документа можно изменять только с помощью специальных программ редактирования изображений.
На исходной стадии преобразования изображения отсканированного документа в электронный документ печатный документ, такой как пример документа 100, представленный на Фиг. 1, анализируется для определения множества участков в пределах документа. Во многих случаях участки могут быть логически упорядочены в виде иерархического нециклического дерева, в котором корень дерева представляет документ как единое целое, промежуточные узлы дерева представляют участки, содержащие меньшие участки, а листья графа представляют наименьшие обнаруженные участки. Участки можно обнаружить, используя на области изображения множество методик, включая множество типов статистического исследования распределений кодировок пикселей или значений пикселей. Например, в цветном документе фотографию можно выделить по большему изменению цвета в области фотографии, а также по более частым изменениям значений интенсивности пикселей по сравнению с участками, содержащими текст. Подробности того, как выполняют анализ изображения отсканированного документа для обнаружения множества участков, таких как участки, изображенные на Фиг. 6, выходят за рамки области настоящего документа.
После того как исходная стадия анализа определила множество участков на изображении отсканированного документа, те участки, которые, вероятно, содержат текст, дополнительно обрабатываются подпрограммами OCR для обнаружения текстовых символов и преобразования текстовых символов в Юникод или любой другой стандарт кодировки символов. Чтобы подпрограммы OCR обработали содержащие текст участки, необходимо определить исходную ориентацию содержащего текст участка, поэтому в подпрограммах OCR могут эффективно использоваться различные способы наложения эталона для обнаружения текстовых символов.
По существу после обнаружения содержащего текст участка изображение участка, содержащего текст, преобразуется из изображения пикселей в растровое изображение в рамках процесса, который называется «бинаризацией», в котором каждый пиксель представлен либо значением бита «0» (указывающим на то, что пиксель отсутствует в пределах фрагмента текстового символа), либо значением бита «1» (указывающим на то, что пиксель присутствует в пределах участка текстового символа). Таким образом, например, на участке черно-белого изображения отсканированного документа, содержащего текст, где текст отпечатан черным цветом на белом фоне, пиксели со значениями менее порогового значения, соответствующими темным участкам изображения, переводятся в биты со значением «1», тогда как пиксели со значениями, меньшими или равными пороговому значению, соответствующему фону, переводятся в биты со значением «0». Условное обозначение значения бита является, конечно же, произвольным, и можно применять противоположные условные обозначения, когда значение «1» указывает на фон, а значение «0» указывает на символ. Растровое изображение можно сжимать с использованием метода кодировки длинами серий для более эффективного хранения.
На Фиг. 6А-С проиллюстрирован один из подходов к преобразованию изображения документа в электронный документ, который используется в некоторых доступных в настоящее время OCR-системах. Данный подход является в сущности иерархическим, и его можно понять и реализовать рекурсивно, нерекурсивно или частично рекурсивно. После исходного определения ориентации изображение документа 602 обрабатывают для разбиения изображения документа на фрагменты или элементы высокого уровня 604-606. В примере, представленном на Фиг. 6А, изображение документа включает картинку 610, первый текстовый блок 612 и второй текстовый блок 614. Это элементы изображения документа высокого уровня, из которых в результате разбиения получают соответствующее изображение первого текстового блока 604, соответствующее изображение второго текстового блока 605 и соответствующую картинку 606. В этом случае картинка является основным элементом изображения документа и не может быть дополнительно разбита. Однако на втором уровне разбиения изображение первого текстового блока 604 разбивается на изображения отдельных текстовых строк 616-620, а изображение второго текстового блока 605 дополнительно разбивается на изображения текстовых строк 622-623. На последнем уровне разбиения каждое изображение текстовой строки, такое как изображение текстовой строки 623, дополнительно разбивается на отдельные символы, такие как изображения символов 626-634, соответствующие изображению текстовой строки 623. В некоторых способах реализации разбиение изображений текстовых строк на изображения символов может включать по меньшей мере частичное исходное разбиение изображений текстовой строки на изображения слов для тех языков, в которых символы алфавита объединяются в слова.
Как проиллюстрировано на Фиг. 6А, в некоторых OCR-способах и системах сначала изображение документа 602 разбивается на изображения символов, такие как изображения символов 626-634, до построения электронного документа, соответствующего изображению документа. Во многих из этих систем изображение символа является наименьшим элементом детализации разбиения, выполняемого OCR-способами и системами в отношении изображений текста.
Затем, как представлено на Фиг. 6В, эти OCR-способы и системы порождают электронный документ, соответствующий изображению документа, обратным иерархическим методом. Изображения символов, такие как изображение символа 640, объединяются в слова, такие как слово 642, для тех языков, в которых символы алфавита объединяются в слова. На следующем уровне построения электронного документа слова объединяются с генерированием текстовых строк, таких как текстовая строка 644, содержащая слово 642. На другом дополнительном уровне построения электронного документа текстовые строки объединяются для генерирования текстовых блоков, таких как текстовый блок 646, содержащий текстовую строку 644. И, наконец, все элементы документа высшего уровня, такие как картинка 606, текстовый блок 648 и текстовый блок 650, объединяются для генерирования электронного документа 652, соответствующего изображению документа 602. Как описано выше, электронный документ по существу содержит представления символов алфавита, знаков и различных типов управляющих последовательностей для порождения рамок, границ и других элементов электронного документа в формате Юникод. Таким образом, символ алфавита 640 по существу представляет оцифрованный символ, такой как символ Юникод, соответствующий изображению символа 633, представленному на Фиг. 6А. Аналогичным образом картинка 645 по существу представляет тип сжатого файла изображения, соответствующего картинке 606, отсканированной в виде части изображения документа. Иными словами, если рассматривать разбиение изображения документа на элементы изображения документа в виде дерева, как показано на Фиг. 6А, то наименьшие возможные элементы дерева преобразуются из отсканированных изображений в соответствующие цифровые представления информации, содержащейся в отсканированных изображениях, а затем цифровые представления повторно объединяются в рамках процесса, представленного на Фиг. 6В, для генерирования оцифрованного электронного документа.
На Фиг. 6А-В разбиение изображения документа на элементы и построение электронного документа из цифровых представлений этих элементов для простоты проиллюстрировано с использованием соответствий типа один-ко-многим от элементов более высокого уровня к элементам более низкого уровня и от элементов более низкого уровня к элементам более высокого уровня. На обеих схемах все элементы заданного уровня объединяются с генерированием одного элемента более высокого уровня на следующем высшем уровне. Однако, как правило, OCR-способы и системы во время обработки изображений документов сталкиваются с разными неоднозначностями и неопределенностями, что приводит к порождению на стадии разбиения нескольких возможных разбиений от элемента более высокого уровня до нескольких множеств элементов более низкого уровня, а на стадии построения электронного документа множество элементов более низкого уровня может объединяться разными способами, что приводит к разным элементам более высокого уровня.
На Фиг. 6С представлен один пример порождения нескольких гипотез во время разбиения изображения документа. На Фиг. 6С исходное изображение документа 602 в соответствии с одной гипотезой, представленной стрелкой 660, разбивается на три компонента 604-606 более низкого уровня, описанных выше со ссылкой на Фиг. 6А. Однако в соответствии со второй гипотезой 662 текстовое изображение может быть альтернативно разбито на один текстовый блок 664 и картинку 606. В этом случае граница между первым текстовым блоком 612 и вторым текстовым блоком 614 может быть нечеткой или может полностью отсутствовать, и в этом случае OCR-способам и системам, возможно, потребуется проверять две альтернативные гипотезы. Порождение ветвления с многовариантной гипотезой как на стадии разбиения, так и на стадии построения при преобразовании изображений документа в электронные документы может приводить к буквально тысячам, десяткам тысяч, сотням тысяч, миллионам или более возможных альтернативных вариантов преобразований. Как правило, для ограничения порождения многовариантных гипотез, обеспечения точной и эффективной навигации по потенциально огромному пространству состояний разбиений и построений электронного документа для определения одного наиболее вероятного электронного документа, соответствующего изображению документа, в OCR-способах и системах используется статистическая оценка, широкое множество типов показателей и широкое множество типов автоматических методик проверки гипотезы.
На Фиг. 7 альтернативно представлен способ преобразования изображения документа в электронный документ, используемый множеством доступных в настоящее время OCR-способов и систем. Изображение документа 702 разбивается на множества элементов высшего уровня изображения 704 и 706 с использованием двух альтернативных гипотез 708 и 710 соответственно. На следующем уровне разбиения изображения текстовых блоков в первом исходном разбиении 704 и изображение единственного тестового блока во втором исходном разбиении 706 разбиваются на изображения текстовых строк в соответствии с тремя гипотезами 712-714 для первого разбиения высшего уровня 704 и двумя гипотезами 716-717 для второго разбиения высшего уровня 706. Затем на следующем уровне разбиения происходит дополнительное разбиение каждого из этих пяти разбиений второго уровня на изображения отдельных символов в соответствии с несколькими гипотезами с порождением в итоге 12 разбиений на наименьшие возможные элементы, таких как разбиение на наименьшие возможные элементы 718. На второй стадии преобразования изображения документа в электронный документ каждое разбиение на наименьшие возможные элементы строит по существу несколько возможных электронных документов, таких как электронные документы 722, соответствующие разбиению на наименьшие возможные элементы 718. На Фиг. 7 проиллюстрировано потенциальное множество электронных документов, которое можно сгенерировать с помощью альтернативных гипотез в рамках способа преобразования, хотя фактически различные альтернативные промежуточные гипотезы и альтернативные электронные документы отфильтровываются в рамках процесса таким образом, что итоговый наиболее высоко оцениваемый электронный документ выбирается среди целесообразного количества альтернатив на итоговых стадиях построения электронного документа. Иными словами, хотя потенциальное пространство состояний возможных электронных документов большое, фильтрация и отсечение происходят на протяжении стадий разбиения и построения так, что в процессе преобразования фактически изучается лишь относительно небольшая часть подпространства.
На Фиг. 8-9 проиллюстрирован один вычислительный подход к определению идентичности и ориентации символа в пределах изображения символа. На Фиг. 8 символ 802 представлен наложенным на прямолинейную сетку 804. Как и на участке 508, изображенном на Фиг. 5, каждый элемент сетки или ячейка представляет собой матрицу пиксельных элементов, в результате чего края символа кажутся гладкими. При большем увеличении, как и на участке 512, изображенном на Фиг. 5, края символа будут казаться зазубренными. Как описано выше, этим пикселям присваивается одно из двух битовых значений - «0» или «1», которые указывают на то, соответствует ли пиксель фрагменту фона или фрагменту символа соответственно. Доля пикселей в пределах каждого столбца элементов сетки представлена на гистограмме 806, показанной поверх прямолинейной сетки 804. На данной гистограмме представлено горизонтальное пространственное распределение пикселей символа в пределах прямолинейной сетки, что представляет фрагмент изображения отсканированного документа, содержащего один символ. Аналогичным образом, на гистограмме 808 представлено пространственное распределение пикселей символа в вертикальном направлении. Гистограмма 810 и гистограмма 806 зеркально симметричны; гистограмма 812 и гистограмма 808 так же зеркально симметричны. Данные гистограммы являются сигнатурами или характерными признаками обнаружения и определения ориентации символа.
На Фиг. 9 проиллюстрирован числовой показатель, который можно вычислить на основе двух из четырех гистограмм, представленных на Фиг. 8. На этом чертеже вычисляется показатель ориентации, называемый «гистограммным показателем», или «h-показателем», по верхней гистограмме и правой гистограмме 806 и 808, вычисляемым для конкретного символа в конкретной ориентации. Каждая гистограмма разделена на четыре участка вертикальными пунктирными линиями, такими как вертикальная пунктирная линия 902. Каждому участку присваивается значение «0» или «1» в зависимости от того, достигает ли столбец гистограммы в пределах участка порогового значения, такое как 0,5. Данные битовые значения упорядочивают таким же способом, что и разбиения. Таким образом, например, в случае гистограммы 806 на разбиениях 904 и 906 отсутствует столбец, который превышает пороговое значение или высоту 0,5, тогда как на разбиениях 908 и 910 присутствует по меньшей мере один столбец гистограммы, который превышает пороговое значение или высоту 0,5. Таким образом, битовые значения, присвоенные разбиениям, порождают четырехбитовый полубайт «0110» 912. Аналогичные вычисления для правой гистограммы 808 порождают четырехбитовый полубайт «0011» 914. Данные два четырехбитовых полубайта можно конкатенировать для порождения восьмибитового h-показателя 916.
Данный h-показатель является примером вычисленной числовой характеристики, которую OCR-система может использовать для сравнения изображений символа с эталонными символами алфавита или множеством символов для обнаружения изображений символа. Существует много примеров таких характеристик элемента или параметров элемента, которые можно вычислить и сравнить с характеристиками элемента или параметрами элемента стандартного множества символов для выбора стандартного символа, наиболее аналогичного изображению символа. Другие примеры включают отношение количества белых пикселей к количеству черных пикселей на участке двоичного изображения символа, относительные длины наиболее длинных вертикальных, горизонтальных и диагональных линий черных пикселей в пределах двоичного изображения символа и другие такие вычисляемые показатели.
На Фиг. 10А-В проиллюстрирован подход к распознаванию символов, используемый в OCR-системе, путем наложения эталона. На Фиг. 10А-В представлен эталонный символ, наложенный на участок двоичного изображения документа 1002, содержащий изображение символа во множестве ориентаций. Для каждой ориентации доля пикселей в эталонном символе, перекрывающихся с черными пикселями на участке двоичного изображения документа, содержащего изображение символа, генерирует показатель перекрывания, или o-показатель. Перед вычислением o-показателей для разных ориентаций эталонного символа в отношении изображения символа выполняют операцию масштабирования, чтобы обеспечить, что эталонный символ и изображение символа имеют приблизительно одинаковый размер. Заданное изображение символа можно сравнить с множеством эталонных символов во множестве ориентаций и выбрать наилучшим образом совпадающий эталонный символ в качестве эталонного символа с наибольшим сгенерированным значением о-показателя. Например, на Фиг. 10В наложение 1004 генерирует перекрывание 100%. Для большей точности можно вычислить двусторонний о-показатель комбинированного перекрывания эталонного символа в отношении изображения символа и для изображения символа в отношении эталонного изображения. Это один пример методик наложения эталона, которые можно использовать для выбора для изображения символа наилучшим образом совпадающего эталона по стандартизованным изображениям символов алфавита или множеству символов.
На Фиг. 11А-В проиллюстрированы различные объекты множества символов для естественных языков. На Фиг. 11А представлен столбец из различных форм символа во множестве символов. В столбце 1104 для первой формы символа 1102 из множества символов представлены разные формы символа в разных стилях текста. Во многих естественных языках могут быть разные стили текста, а также альтернативные письменные формы для заданного символа.
На Фиг. 11В представлено множество концепций, связанных с символами естественного языка. На Фиг. 11В конкретный символ естественного языка представлен узлом 1110 на графе 1112. Конкретный символ может иметь множество общих письменных или печатных форм. Для целей OCR каждая из этих общих форм составляет графему. В некоторых случаях конкретный символ может содержать две или более графем. Например, китайские символы могут содержать комбинацию из двух или более графем, каждая из которых присутствует в дополнительных символах. Корейский язык фактически основан на алфавите, причем в нем используются корейские морфослоговые блоки, содержащие ряд символов алфавита в разных положениях. Таким образом, корейский морфослоговой блок может представлять собой символ более высокого уровня, состоящий из нескольких компонентов графемы. Для символа 1110, представленного на Фиг. 11В, существуют шесть разных графем 1114-1119. Дополнительно существует одно или более разных печатных или письменных отображений графемы, причем каждое отображение представлено эталоном. На Фиг. 11В каждая из графем 1114 и 1116 имеет два альтернативных отображения, представленных эталонами 1120-1121 и 1123-1124 соответственно. Каждая из графем 1115 и 1117-1119 связана с одним эталоном, эталонами 1122 и 1125-1127 соответственно. Например, символ 1102 может быть связан с тремя графемами. Первая из графем охватывает отображения 1102, 1124, 1125 и 1126, вторая - отображения 1128 и 1130, третья - отображение 1132. В этом случае первая графема имеет прямые горизонтальные элементы, вторая графема имеет горизонтальные элементы с короткими вертикальными элементами с правой стороны, а третья графема включает изогнутые, а не прямые, элементы. Альтернативно все отображения символа 1102, 1128, 1124, 1132, 1125, 1126 и 1130 можно представить в виде эталонов, связанных с одной графемой для символа. В некоторой степени выбор графем является несколько условным. В некоторых типах символьно-ориентированных языков может быть тысячи разных графем. Эталоны можно считать альтернативными отображениями или изображениями, и они могут быть представлены множеством пар «параметр/значение параметра», как описано ниже.
Фактически, хотя отношения между символами, графемами и эталонами представлены на Фиг. 11В как строго иерархические, причем каждая графема связана с одним конкретным родительским символом, фактические отношения могут быть не столь просто структурированы. На Фиг. 11С проиллюстрировано несколько более сложное множество отношений, в которых оба из двух символов 1130 и 1132 являются родительским для двух разных графем 1134 и 1136. В качестве одного примера можно привести следующие символы английского языка: строчная буква «о», прописная буква «0», цифровое обозначение нуля «0» и символ градуса «°», все из которых могут быть связаны с кольцеобразной графемой. Отношения альтернативно можно представить в виде графов или сетей. В некоторых случаях графемы (в отличие от или в дополнение к символам) могут быть представлены на высших уровнях в пределах представления. Обнаружение символов, графем, выбор эталонов для конкретного языка, а также обнаружение отношений между ними по существу осуществляются в большой степени произвольно.
На Фиг. 12 проиллюстрирован ряд дополнительных типов распознавания символов, который можно использовать для распознавания символов в пределах изображений и фрагментов изображений текстовых документов. На Фиг. 12 представлено изображение буквы «А» 1202. Описанные выше методики распознавания путем наложения эталона и на основе параметров можно непосредственно применить к изображению 1202. Альтернативно изображение символа 1202 можно исходно обработать с генерированием структуры символа 1204 или контура символа 1206. Структуру символа 1204 можно вычислить как множество прямых и кривых, представляющих своего рода набор локальных центров масс изображения символа. Контур символа 1206 представляет собой набор прямых и кривых, представляющий внешние и внутренние границы символа. Затем методики признакового распознавания или распознавания путем наложения эталона, такие как описанные выше, можно применить либо к структуре символа 1204, либо к контуру символа 1206 с использованием структурных или контурных распознавателей соответственно.
На Фиг. 13А-В проиллюстрирован тип классификатора, который можно использовать для порождения гипотез в отношении разбиения изображения текстовой строки на последовательность изображений символов. Данный тип классификатора абстрактно проиллюстрирован на Фиг. 13А-В. В верхней части Фиг. 13А в виде горизонтальной заштрихованной полосы представлено изображение текстовой строки 1302. На первом этапе, выполняемом классификатором третьего типа, в пределах битовой карты, соответствующей текстовой строке, обнаруживаются смежные не относящиеся к символу биты, выровненные по ширине текстовой строки. Они представлены в виде пробелов 1304-1318. Затем классификатор может рассмотреть все возможные пути, ведущие от начала текстовой строки до конца текстовой строки через обнаруженные пробелы. Например, первый путь, который пересекает все обнаруженные пробелы, проиллюстрирован в отношении текстовой строки 1320, где путь состоит из серии дуг, таких как дуга 1322. Проиллюстрированный применительно к текстовой строке 1320 путь имеет 15 пробелов (1304-1318) и, следовательно, 15 разных дуг. С другой стороны, существует путь, состоящий из одной дуги 1324, проиллюстрированной в отношении текстовой строки 1326. Три дополнительных пути проиллюстрированы в отношении текстовых строк 1328-1330. Каждый возможный путь представляет разную гипотезу в отношении группировки участков изображения текстовой строки в элементы более высокого уровня. Граф, содержащий множество путей пересечения пробелов, называется «графом линейного деления».
Для контроля потенциального комбинаторного взрыва, который может возникнуть, если рассматривать каждую возможную гипотезу, или путь, как отдельное разбиение в процессе преобразования изображения документа, возможным путям по существу присваиваются баллы, а в качестве гипотезы выбирается только путь с наибольшим числом баллов или некоторое количество путей с наибольшим числом баллов. На Фиг. 13В проиллюстрировано присвоение баллов пути. В подходе, представленном на Фиг. 13В, с каждой дугой, такой как дуга 1340, связывают весовое значение, например, с дугой 1340 связано весовое значение 0,28 1342. Существует много способов вычисления весового значения дуги. В одном примере весовое значение дуги 1344 вычисляется как ширина пробела у основания текстовой строки, на которую указывает дуга 1346, умноженная на величину, обратную абсолютному значению разности между интервалом, представленным дугой 1348, и средним значением интервала для текстовой строки, текстового блока, включающего текстовую строку, или какого-либо другого элемента изображения более высокого уровня. В данном конкретном расчете весового значения дуги 1344 предполагается, что чем шире пробел, тем выше вероятность того, что пробел представляет границу между символами или словами и что длины символов или слов попадают в среднюю длину. Данный классификатор третьего типа в одном случае можно использовать для разбиения текстовых строк на символы, а в другом случае - для разбиения текстовых строк на слова. Функция определения весовых значений, определяющая весовые значения дуги, может изменяться в зависимости от того, разбивается ли текстовая строка на символы или на слова. Итоговое число баллов для гипотезы, представленной конкретным путем, пересекающим пробелы, таким как путь, представленный дугами в текстовой строке 1350 на Фиг. 13В, вычисляется как сумма весовых значений отдельных дуг 1352.
Проблемы, связанные с обработкой изображений математических выражений
На Фиг. 14А-В представлен ряд примеров математических выражений, а также указаний элементов в математических выражениях, которые являются сложными и представляют трудности для используемых в настоящее время OCR-способов, применяемых к фрагментам изображений документа, содержащим математические выражения. На Фиг. 11А представлены пять математических уравнений 1402-1410, выбранных из различных учебников по математике. Например, выражение 1402 взято из учебника по математическому анализу, уравнение 1406 взято из учебника по тензорному исчислению, а уравнения 1408 и 1410 взяты из учебника по квантовым вычислениям. Читатель, знакомый с курсами математики и физики на уровне колледжа, легко интерпретирует все уравнения, представленные на Фиг. 14А. Однако с точки зрения автоматических OCR-методологий распознавания этих математических выражений на изображениях и фрагментах изображений документов представляет множество проблем.
На Фиг. 14В проиллюстрированы некоторые из проблем, возникающих при применении автоматических OCR-способов к математическим выражениям, представленным на Фиг. 14А. В качестве одного примера, достаточно часто в математических выражениях заданный тип символа может иметь множество начертаний, или образцов, в разных выражениях. Например, рассмотрим символ интеграла 1412 и символ двойного интеграла 1414 в выражении 1402. Символ интеграла может встречаться один или несколько раз в зависимости от размерности интегрирования, которое представляет символ или символы интеграла. С символом интеграла могут быть связаны нижний и верхний пределы интегрирования, как в случае символа интеграла 1412 в уравнении 1402. Однако положения нижнего и верхнего пределов относительно символа интеграла ∫ в разных выражениях могут различаться.. В некоторых случаях пределы могут быть под и над символом интеграла, а в других случаях они могут появляться справа от верхнего и нижнего фрагментов символа интеграла, как в случае символа интеграла 1412 в выражении 1402. В случае неопределенных интегралов ни нижний, ни верхний пределы интегрирования в символ не включены. В других случаях, таких как двойной интеграл 1414 в выражении 1402, пределы интегрирования представлены более абстрактно, в этом случае - заглавной буквой которая появляется под парой символов интеграла. Как правило, пределы интегрирования выражаются с использованием размеров шрифта, которые существенно меньше размера шрифта символа интеграла, но в разных математических выражениях различие шрифтов может быть разным. Пределы интегрирования могут представлять собой отдельные символы или могут составлять целые математические выражения. Простые способы признакового распознавания и распознавания путем наложения эталона сложно применять к математическим выражениям, в которых используются наборы символов с хорошо определенными значениями, но во множестве разных потенциальных образцов.
Другой проблемой математических выражений является наличие подстрочных и надстрочных символов. Например, обозначение функции 1416 в уравнении 1404 представлено функцией ƒk, которая принимает один параметр z. Однако существуют и дополнительные возможные интерпретации. Например, выражение может означать умножение числа ƒk на заключенное в скобки выражение z или альтернативно оно может быть интерпретировано как произведение трех чисел ƒ, k и z. Во многих случаях разница в размерах шрифта между основным символом и надстрочным написание этого символа в разных выражениях может варьироваться в широких пределах, и это же относится к относительным положениям основного символа и надстрочного символа. Еще большие сложности могут возникать, когда подстрочные и надстрочные написания основных символов сами по себе представляют математические выражения. Например, подстрочный символ «E» 1418 в уравнении 1404 в качестве подстрочного символа имеет выражение qk-1. Однако автоматической OCR-системе может быть неизвестно, является ли все данное выражение подстрочным, или же подстрочным является q, а значение k-1 представляет собой множитель «E» или потенциально каким-либо образом связано со следующим символом (z). Элементы матриц, такие как элемент 1420 в уравнении 1406, также могут создавать проблемы для автоматической OCR-системы. Элемент матрицы 1420 представляет собой дробь и является элементом матрицы 2×2, причем дробь включает знаменатель с надстрочным символом х. Автоматическая OCR-система, неспособная распознать данную дробь как элемент матрицы, вместо этого может учитывать множество возможных ролей этих символов, включая выражение, в котором дробь 1420 умножается на элемент матрицы слева от нее или сама по себе является знаменателем дроби более высокого уровня с числителем «0». В пределах математических выражений может быть произвольное число уровней вложения фрагментов выражений, которые легко интерпретируются людьми, но представляют сложность для анализа автоматическими OCR-способами, которые не могут учитывать полный математический контекст, в котором используются отдельные символы. Другим примером нескольких уровней вложения является подстрочное выражение 1422 числа е в выражении 1408, которое является дробью, содержащей другую дробь в качестве ее знаменателя. Следует отметить, что дробь более высокого уровня имеет горизонтальную черту дроби, тогда как дробь более низкого уровня имеет диагональную черту дроби. В этом уравнении фигурная скобка 1424 появляется без соответствующей закрывающей скобки. Зачастую в математических выражениях фигурные скобки, квадратные скобки и круглые скобки встречаются парами, но иногда это не так. Во многих областях символы могут иметь конкретные специфичные для данной области значения. Например, в уравнении 1410 обозначение 1426 относится к вектору, а обозначение 1428 указывает на побитовое сложение по модулю 2. Без знания контекста выражения автоматическая OCR-система может неверно интерпретировать такие символы.
Указанные выше примеры представляют собой лишь небольшую часть из множества проблем, создаваемых математическими выражениями для OCR-системы. Математические выражения по существу имеют произвольное число уровней вложения, в них используется множество типов специальных символов, имеющих разные значения и использования в разных контекстах, и применяется множество специфических условных обозначений для представления конкретных концепций. Когда математические символы представлены в пределах электронных документов, например, с использованием средств Microsoft Equation Editor, Math Type Equation Editor или LaTeX, необходимо понимать точное значение каждого символа, а также уровни вложения, на которых находятся символы. В качестве одного примера, во многих системах представления математических выражений в цифровом виде парные квадратные, фигурные или круглые скобки указываются путем одного исходного ввода, причем символы появляются в пределах парных квадратных, фигурных или круглых скобок после ввода пары скобок. Чтобы правильно представить символ, OCR-система должна распознать парные фигурные, квадратные или круглые скобки на каждом уровне вложения.
Способы и системы, к которым относится настоящий документ
Настоящий документ относится к способам и системам, включая подсистемы в автоматических OCR-системах, которые обрабатывают изображения и фрагменты изображений документа, содержащие математические выражения, для преобразования изображений математических выражений в электронные представления математических выражений. Как описано выше применительно к Фиг. 11А-С и 12, при OCR-обработке изображений документа изображение документа разбивается на блоки или фрагменты изображений различных типов, которые затем обрабатываются в соответствии со способами обработки подходящими для данных типов. Математические выражения представляют собой еще один тип блока или фрагмента изображения, обрабатываемого описанными здесь способами и системами, которые преобразуют изображения математических выражений в соответствующие электронные представления.
Способы обработки изображений и фрагментов изображений математических выражений, к которым относится настоящий документ, включают рекурсивное попеременное применение методик разбиения изображения на блоки для иерархического разделения изображений или фрагментов изображений, содержащих математическое выражение, на элементарные блоки, каждый из которых соответствует конкретным символам. На Фиг. 15A-F проиллюстрирован один из способов разбиения на блоки математического выражения, который разделяет изображение или фрагмент изображения, содержащий математическое выражение, на блоки или разбиения более низкого уровня. На Фиг. 15А представлено уравнение 1402, изображенное на Фиг. 14А, на которое наложено множество вертикальных параллельных линий. Данные вертикальные линии, такие как вертикальная линия 1502, делят изображение математического выражения 1402 на множество смежных параллельных вертикальных полос. Для ясности иллюстрации степень детализации разбиения на полосы, или ширина полос, в представленном на Фиг. 14А примере относительно большая. Однако в некоторых способах реализации можно использовать полосы шириной в один или два пикселя. В способе разбиения на блоки после разбиения изображения уравнения на вертикальные полосы можно учесть количество пикселей в пределах каждой полосы, соответствующей символам, чтобы построить гистограмму в отношении последовательных интервалов вдоль горизонтальной оси изображения выражения, которая показывает количество пикселей, соответствующих символам для каждого интервала оси x, представляя область пересечения вертикальной полосы с горизонтальной осью или альтернативно долю пикселей, соответствующих символам, в каждой вертикальной полосе. Затем в способе обнаруживаются все одиночные вертикальные полосы и смежные множества вертикальных полос, в которых количество пикселей, соответствующих символам, меньше порогового количества пикселей, в качестве потенциальных границ разбиения. В случае бинарного изображений в одном из способов разбиения на блоки подсчитывается количество пикселей со значением «1» в пределах каждой вертикальной полосы. Вместо вычисления всей гистограммы способ разбиения на блоки может альтернативно подсчитывать количество пикселей, соответствующих символам, в каждой вертикальной полосе относительно порогового значения, обнаруживая те вертикальные полосы, в которых количество пикселей, соответствующих символам, меньше порогового количества символов, как вертикальные полосы со значением «0», а оставшиеся вертикальные полосы - как вертикальные полосы со значением «1». Иными словами, необходимо вычислить не всю гистограмму, а лишь бинарную гистограмму, различающую вертикальные полосы, в которых количество соответствующих символам пикселей меньше порогового количества пикселей, от вертикальных полос, в которых количество соответствующих символам пикселей больше или равно пороговому количеству пикселей. Каждое множество одной или более смежных вертикальных полос, имеющих количество соответствующих символам пикселей меньше порогового количества пикселей, представляет собой потенциальную границу разбиения для разбиения математического выражения на блоки более низкого уровня. Данные потенциальные границы разбиения также называются «вертикальными белыми полосами». Вместо пикселей можно использовать другие методики определения процентного содержания области полосы, соответствующей одному или более символам.
На Фиг. 15А множества смежных вертикальных полос с количеством пикселей, соответствующих символам, меньшим порогового количества пикселей показаны с помощью направленных U-образных меток, таких как U-образная метка 1504. Как показано на Фиг. 15А, разбиение на полосы с крупной детализацией позволяет обнаружить лишь фрагмент потенциальных вертикальных границ разбиения, которые визуально можно обнаружить как разделяющие математическое выражение 1402 на отдельные символы или группы символов вдоль горизонтальной оси. Например, потенциальная вертикальная граница разбиения находится между надстрочной цифрой 2 (1506 на Фиг. 15А) и символом дифференциала 1508, и ее можно было бы обнаружить способами на основе построения гистограммы, в которых сетка параллельных вертикальных линий несколько смещена горизонтально по отношению к математическому выражению. При использовании разбиения на вертикальные полосы с малой детализацией данная и многие дополнительные потенциальные границы разбиения находятся способом на основе построения гистограммы. Альтернативно разбиение на вертикальные полосы с меньшей степенью детализации, как представлено на Фиг. 15А, можно использовать несколько раз со систематическим смещением относительных положений вертикальных линий в отношении математического выражения влево или вправо при каждом использовании. Таким образом, потенциальные вертикальные границы разбиения, такие как потенциальная вертикальная граница разбиения, пролегающая между надстрочной цифрой 2 (1506 на Фиг. 15А) и символом дифференциала 1508, обнаруживаются во время по меньшей мере одного использования способа на основе построения гистограммы. В любом случае использование строго вертикальных линий может не выявить всех возможных логических линий разбиения. Например, было бы логично разделить символ дифференциала 1510 и следующий символ переменной «r» 1511. Однако поскольку основа символа дифференциала 1510 не является вертикальной, верхняя часть основы перекрывается с крайней левой частью символа «r» 1511 в вертикальной проекции на горизонтальную ось. Следовательно, невозможно построить такую вертикальную белую полосу (пробелов) между этими двумя символами, которая не содержала бы пикселей по меньшей мере одного из символов. Для нахождения потенциальных границ разбиения данных типов можно использовать множество параллельных линий под разным наклоном, образующих полосы. На Фиг. 15В линии из множества параллельных линий не перпендикулярны горизонтальной оси, а расположены под некоторым наклоном. В результате этого при несколько меньшей детализации наклонной полосы 1514 полоса не содержит соответствующие символам пиксели и, таким образом, может быть обнаружена как потенциальная граница разбиения.
Следовательно, для проведения разбиения на блоки вдоль горизонтальной оси в способе разбиения на блоки по существу применяется ряд этапов, в каждом из которых на изображение математической формулы в качестве потенциальных границ разбиения накладывают логическое множество параллельных линий, причем на каждом этапе варьируют относительные положения линий и/или их направления. Наложение является логическим в том смысле, что линии представляют собой логические конструкции, определяющие границы потенциальных разбиений, а не фактически рисуются на или включаются в изображение или фрагмент изображения математического выражения. Например, можно использовать ряд этапов с изменением направлений линии от 70° до 110°, с интервалами в пять градусов или десять градусов и со сдвигом относительных положений параллельных линий на небольшую величину на каждом этапе. Потенциальные границы разбиения, обнаруженные на каждом этапе, накапливаются, и из итогового множества границ разбиения выбирается накопленное множество потенциальных границ разбиения.
На Фиг. 15С проиллюстрирован выбор разбиений из множества потенциальных разбиений. В примере, представленном на Фиг. 15С, длинная двусторонняя горизонтальная стрелка 1530 представляет горизонтальную ось, или ось x, изображения математического выражения. Четыре этапа выбора потенциальных границ разбиения представлены четырьмя рядами символов коротких стрелок 1532-1535. Каждый символ короткой стрелки, такой как символ короткой стрелки 1538, включает стрелку, которая указывает направление линий множества параллельных линий, описывающих полосы, логически наложенные на этапе выбора потенциального разбиения на изображение математической формулы, и горизонтальную линию основания, которая указывает на ширину множества одной или более полос, в которых количество соответствующих символам пикселей меньше порогового количества пикселей. Если два или более потенциальных разбиения, такие как потенциальные разбиения 1538-1540, перекрываются вдоль оси x 1530, то сегменты линий основания для всех потенциальных разбиений, имеющих такое же направление, соединяются и после соединения потенциальных разбиений с таким же направлением наиболее широкое соединенное потенциальное разбиение или, иными словами, соединенное потенциальное разбиение с наиболее длинной линией основания, выбирают в качестве разбиения. Потенциальные разбиения, не перекрывающиеся с другими потенциальными разбиениями, также выбираются в качестве разбиений. На Фиг. 15С представленная область изображения математической формулы 1542 разделена разбиениями, выбранными из потенциальных разбиений рядов 1532-1535, в результате чего получается множество блоков 1544-1557, представляющих собой результаты разбиения изображения математического выражения на блоки или разбиения более низкого уровня. В некоторых способах реализации две потенциальные границы разбиения могут быть образованы с перекрыванием, либо когда они физически пересекаются, либо когда линейный сегмент, соединяющий точки на каждой из двух потенциальных границ разбиения, короче порогового расстояния.
На Фиг. 15D проиллюстрировано горизонтальное разбиение первого уровня изображения математического выражения 1402, изображенного на Фиг. 14А, с использованием способа, представленного выше применительно к Фиг. 15А-С. Линии разбиения, такие как линия разбиения 1560, центрированы в пределах фрагментов изображения, через которые можно построить вертикальные или наклонные белые полосы (пробелов). В некоторых случаях, таких как в случае разбиений 1562 и 1564, каждое разбиение, или блок, содержит одиночный символ. В других случаях, например при разбиении 1566, в результате горизонтального разбиения не могут быть получены одиночные символы из-за наличия горизонтальной дробной черты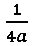 .
.
Как представлено на Фиг. 15Е, аналогичный способ разбиения или разбиения на блоки можно использовать для вертикального разбиения изображения или фрагмента изображения, включающего математическое выражение. На Фиг. 15Е фрагмент изображения 1570, содержащий дробь, 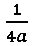 можно вертикально разделить на три разбиения 1572-1574. Применение этапа вертикального разбиения к разбиению 1566, полученному при горизонтальном разбиении первоначального изображения, позволяет образовать разбиения второго уровня, два из которых включают одиночные символы, а один 1574 включает два символа. Затем горизонтальное разбиение разбиения второго уровня 1574 позволяет образовать два разбиения третьего уровня, каждый из которых содержит одиночный символ. Таким образом, попеременное рекурсивное применение горизонтального и вертикального разбиения, или разбиения на блоки, можно использовать для рекурсивного разбиения изображения или фрагмента изображения, содержащего математическое выражение, на иерархическое множество блоков изображения, причем наименьший блок всегда содержит одиночный символ.
можно вертикально разделить на три разбиения 1572-1574. Применение этапа вертикального разбиения к разбиению 1566, полученному при горизонтальном разбиении первоначального изображения, позволяет образовать разбиения второго уровня, два из которых включают одиночные символы, а один 1574 включает два символа. Затем горизонтальное разбиение разбиения второго уровня 1574 позволяет образовать два разбиения третьего уровня, каждый из которых содержит одиночный символ. Таким образом, попеременное рекурсивное применение горизонтального и вертикального разбиения, или разбиения на блоки, можно использовать для рекурсивного разбиения изображения или фрагмента изображения, содержащего математическое выражение, на иерархическое множество блоков изображения, причем наименьший блок всегда содержит одиночный символ.
На Фиг. 15F представлена блок-схема для одного из способов разбиения на блоки, который разделяет изображение, содержащее математическое выражение, на блоки вдоль указанного направления. В способах и системах обработки математического выражения, к которым относится настоящий документ, разбиение на блоки применяется либо в горизонтальном направлении с использованием вертикальных или близких к вертикальным полос, либо в вертикальном направлении с использованием горизонтальных или близких к горизонтальным полос. В блок-схеме, представленной на Фиг. 15F, описано как вертикальное, так и горизонтальное разбиение на блоки. На этапе 1580 подпрограмма «разбиение на блоки» получает в качестве двух аргументов направление разбиения на блоки, либо горизонтальное, либо вертикальное, и изображение или фрагмент изображения, содержащий математическое выражение или формулу. Подпрограмма «разбиение на блоки» инициализирует структуру данных белых полос (пробелов) для хранения указаний всех обнаруженных множеств одной или более смежных полос, перпендикулярных направлению разбиения на блоки, в каждой из которых количество соответствующих символам пикселей в пределах полученного изображения или фрагмента изображения меньше порогового количества пикселей. Во вложенных циклах for на этапах 1582-1586 подпрограмма «разбиение на блоки» выполняет серию этапов по выбору потенциального разбиения, как описано выше применительно к Фиг. 15А-В. Внешний цикл for на этапах 1582-1586 выполняет перебор серий ориентаций параллельных линий от угла -a до +a приблизительно в направлении, перпендикулярном направлению разбиения на блоки. Например, если направление разбиения на блоки является горизонтальным, то серия ориентаций может начинаться от 80° и заканчиваться на 100°, захватывая по 10° с обеих сторон от вертикального направления 90° градусов. Приращение угла может составлять некоторое количество градусов, например, пять градусов, на каждую следующую итерацию внешнего цикла for. Во внутреннем цикле for на этапах 1583-1585 выполняется итерация некоторого количества последовательных изменений положений полос, перпендикулярных или близких к перпендикулярным направлению разбиения на блоки в отношении направления разбиения на блоки. При разбиении на полосы с очень малой детализацией внутренний цикл for может быть необязательным. При разбиении на полосы с более крупной детализацией, как проиллюстрировано на Фиг. 15А-В, ширину полосы можно разделить на целое число, такое как четыре, чтобы получить приращение, и количество итераций внутреннего цикла for равно целому числу, а после каждой итерации будет происходить смещение положений полос на вычисленное значение приращения в выбранном направлении вдоль направления разбиения на блоки. После того как ряд потенциальных разбиений был выбран во вложенных циклах for на этапах 1582-1586 и сохранен в структуре данных белых полос (пробелов), выполняют разбиение перекрывающихся белых (полос) пробелов на этапе 1588, как описано выше применительно к Фиг. 15С, и оставшиеся после разбиения белые (полосы) пробелов используют для разбиения изображения формулы на блоки на этапе 1590, как описано выше применительно к Фиг. 15C-D.
Для обработки математической формулы описанное выше горизонтальное и вертикальное разбиение на блоки применяют рекурсивно до тех пор, пока математическая формула не будет сведена к графемам, распознаваемым как символы описанными выше OCR-подходами. Затем каждое множество распознанных символов, полученное во время рекурсивного разбиения на блоки, обрабатывают, используя этап обработки на основе графа, для преобразования последовательности распознанных символов в представление математической формулы в виде графа.
На Фиг. 16А-В проиллюстрированы рекурсивно-блочный и основанный на графе подход к распознаванию математических формул во время OCR-обработки изображения документа. В верхней части Фиг. 16А повторно представлено выражение 1406, изображенное на Фиг. 14А. На первом этапе, представленном стрелкой 1602 и обозначенном символом «Н», фрагмент изображения документа, содержащего данное выражение, подвергают горизонтальному разбиению на блоки. После горизонтального разбиения на блоки к каждому блоку применяют OCR-способы, такие как описанные выше, для распознавания одного или более символов в пределах блока. На Фиг. 16А в строке 1604 представлены результаты горизонтального разбиения на блоки и применения OCR-способов к каждому блоку. Те блоки, для которых в результате применения OCR-способов были сгенерированы распознанные символы, указаны распознанными символами. Например, при горизонтальном разбиении на блоки сгенерирован блок, содержащий знак равенства 1606. При применении OCR-способов к данному блоку сгенерирован распознанный символ знака равенства. Следовательно, блок представлен на Фиг. 16А знаком равенства 1608. Те блоки, для которых в результате применения OCR-способов не были сгенерированы распознанные символы, представлены в ряду 1604 на Фиг. 16А в виде пунктирных прямоугольников, таких как пунктирный прямоугольник 1610. В случае блока 1610 OCR-способы не позволяют распознать заглавную букву «U» с вертикально расположенной чертой над заглавной буквой «U». Далее те блоки, для которых в результате применения OCR-способов не были сгенерированы распознанные символы, подвергают рекурсивному вертикальному разбиению на блоки, как указано стрелками, обозначенными буквой «V», такими как стрелка 1612. В случае блока 1610 при вертикальном разбиении на блоки были сгенерированы символ штриха, представленный в пунктирном прямоугольнике 1614, и символ U, представленный в прямоугольнике 1616. Однако в случае блока 1618 рекурсивное вертикальное разбиение на блоки генерирует три символа 1620-1622, а также блок 1624, из которого в результате применения OCR-способов не был получен распознанный символ. Таким образом, после вертикального разбиения на блоки к каждому полученному блоку применяются OCR-способы, в результате которых генерируются либо распознанные символы, либо блоки более низкого уровня, к которым затем рекурсивно применяют горизонтальное разбиение на блоки. На Фиг. 16А изогнутые стрелки, обозначенные буквой «Н», такие как стрелка 1626, указывают на рекурсивно применяемое горизонтальное разбиение на блоки к тем блокам, из которых в результате применения OCR-способов не были сгенерированы символы. В итоговом ряду 1630, представленном на Фиг. 16А, каждый отдельный символ в уравнении, содержащийся на изображении уравнения 1406, был распознан путем применения OCR-способов. Таким образом, в случае изображения уравнения 1406 требуется три рекурсивно примененных уровня разбиения на блоки, чтобы разделить изображение уравнения на фрагменты изображения, каждый из которых содержит графему, распознаваемую OCR-способами в качестве символа.
На Фиг. 16В проиллюстрировано рекурсивное применение разбиения на блоки к фрагменту изображения уравнения 1406, представленному на Фиг. 16А, с использованием другого множества иллюстративных условных обозначений. На Фиг. 16В содержащий выражение фрагмент изображения документа, содержащийся на фрагменте изображения 1406 на Фиг. 16А, представлен в виде корневого узла 1640. Рекурсивное применение разбиения на блоки позволяет сгенерировать дерево 1642, в котором листья, такие как лист 1644, соответствуют более мелким фрагментам изображения, каждое из которых содержит графему, распознаваемую OCR-способами в качестве символа.
На Фиг. 17А-С представлены блок-схемы, иллюстрирующие один из способов обработки изображения документа, содержащего математическое выражение, к которому относится настоящий документ. На Фиг. 17А представлена блок-схема для подпрограммы «математическое выражение», которая в качестве аргумента принимает фрагмент изображения документа, содержащего математическое выражение, и в результате генерирует представление математического выражения, содержащегося на фрагменте изображения, в виде графа. На этапе 1702 подпрограмма «математическое выражение» принимает фрагмент изображения, содержащий математическое выражение. Фрагмент изображения может быть указан ссылкой на бинарное изображение документа, а также обозначениями точек в пределах бинарного изображения документа, которые указывают на прямоугольник или многоугольник, содержащий фрагмент изображения, содержащий математическое выражение. На этапе 1704 подпрограмма «математическое выражение» присваивает локальной переменной направление «горизонтальное», а для локальной переменной список - нулевое значение. На этапе 1706 подпрограмма «математическое выражение» вызывает подпрограмму «рекурсивное разбиение на блоки» для выполнения рекурсивного разбиения на блоки полученного фрагмента изображения, как описано выше применительно к Фиг. 16А-В. Подпрограмма «рекурсивное разбиение на блоки» также преобразует списки фрагментов изображений, содержащих символы, в представления в виде графа фрагментов выражения в пределах математического выражения и возвращает итоговое представление в виде графа всего математического выражения. На этапе 1708 представление математического выражения в виде графа, возвращенное подпрограммой «рекурсивное разбиение на блоки», используется для порождения представления математического выражения в цифровом виде, соответствующего математическому выражению, которое содержится в полученном фрагменте изображения.
На Фиг. 17В представлена блок-схема подпрограммы «рекурсивное разбиение на блоки», вызываемой на этапе 1706, представленном на Фиг. 17А. На этапе 1710 подпрограмма «рекурсивное разбиение на блоки» принимает фрагмент изображения s, направление d и ссылку на список l. На этапе 1712 подпрограмма «рекурсивное разбиение на блоки» присваивает локальной переменной localL нуль. На этапе 1714 подпрограмма «рекурсивное разбиение на блоки» вызывает подпрограмму «разбиение на блоки», описанную выше применительно к Фиг. 15F, для проведения разбиения фрагмента изображения на блоки в направлении, указанном полученным аргументом d. Как описано выше, d может указывать либо на горизонтальное, либо на вертикальное разбиение на блоки. Затем в цикле for на этапах 1716-1722 рассматривается каждый блок, сгенерированный подпрограммой «разбиение на блоки». На этапе 1717 текущий рассматриваемый блок b подвергается распознаванию символов с помощью OCR. Если распознавание символов с помощью OCR успешно распознает символ в блоке b, как определено на этапе 1718, то на этапе 1720 подпрограмма «рекурсивное разбиение на блоки» формирует одноэлементный список, который включает один элемент, представляющий распознанный символ. В ином случае на этапе 1719 подпрограмма «рекурсивное разбиение на блоки» рекурсивно вызывает саму себя для проведения следующего уровня разбиения на блоки в направлении разбиения на блоки, противоположном направлению разбиения на блоки, полученном в качестве аргумента d, указанного на Фиг. 17В обозначением 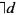 . Иными словами, когда аргумент d имеет значение «горизонтальное», то
. Иными словами, когда аргумент d имеет значение «горизонтальное», то 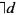 имеет противоположное значение «вертикальное», а когда аргумент d имеет значение «вертикальное», то
имеет противоположное значение «вертикальное», а когда аргумент d имеет значение «вертикальное», то 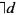 имеет противоположное значение «горизонтальное». Список, сгенерированный на этапе либо 1720, либо 1719, добавляется на этапе 1721 к списку, на который ссылается локальная переменная localL. После того как все блоки, сгенерированные в результате вызова подпрограммы «разбиение на блоки» на этапе 1714, были рассмотрены в циклах for на этапах 1716-1722, подпрограмма «рекурсивное разбиение на блоки» вызывает на этапе 1724 подпрограмму «обработка на основе графа» для проведения на основе графа обработки списка, на который ссылается локальная переменная localL. Наконец, на этапе 1726 список, на который ссылается локальная переменная localL, добавляется к списку, на который ссылается аргумент l.
имеет противоположное значение «горизонтальное». Список, сгенерированный на этапе либо 1720, либо 1719, добавляется на этапе 1721 к списку, на который ссылается локальная переменная localL. После того как все блоки, сгенерированные в результате вызова подпрограммы «разбиение на блоки» на этапе 1714, были рассмотрены в циклах for на этапах 1716-1722, подпрограмма «рекурсивное разбиение на блоки» вызывает на этапе 1724 подпрограмму «обработка на основе графа» для проведения на основе графа обработки списка, на который ссылается локальная переменная localL. Наконец, на этапе 1726 список, на который ссылается локальная переменная localL, добавляется к списку, на который ссылается аргумент l.
На Фиг. 17С представлена блок-схема подпрограммы «обработка на основе графа», вызываемой на этапе 1724 (Фиг. 17В). На этапе 1730 подпрограмма «обработка на основе графа» принимает список l элементов, каждый из которых представляет символ, распознанный во время рекурсивного разбиения на блоки, присваивает локальной переменной best нуль и присваивает локальной переменной bestW большое число. Затем в цикле for на этапах 1732-1737 подпрограмма «обработка на основе графа» рассматривает возможные пути, полученные путем добавления дуг к списку элементов, на который ссылается локальная переменная l. Графы линейного деления описаны ранее в контексте распознавания символа применительно к Фиг. 13А-В. Обработка на основе графа, используемая в подпрограмме «обработка на основе графа», может быть аналогична способам распознавания символа на основе графов линейного деления, описанным ранее, и описана ниже со структурами данных, которые можно использовать для представления списков и путей в некоторых способах реализации. На этапе 1734 текущий рассматриваемый путь оценивается для получения весового значения w для графа. Если w меньше bestW, как определено на этапе 1735, то на этапе 1736 переменной best присваивается значение текущему рассматриваемому пути, а локальной переменной bestW присваивается w. Подпрограмма «обработка на основе графа» возвращает наилучший, или имеющий наименьшее весовое значение, путь, построенный в отношении полученного списка. Не все возможные пути необходимо рассматривать в цикле for на этапах 1732-1737. Можно применять различные эвристические способы для выбора наиболее вероятных потенциальных путей для рассмотрения. Более того, во время оценки потенциального пути на этапе 1734 оценку можно прекратить, как только совокупное весовое значение достигнет текущего значения, сохраненного в локальной переменной bestW.
На Фиг. 18А-С проиллюстрировано применение обработки на основе графа для распознавания фрагментов математических выражений и целых математических выражений. На Фиг. 18А представлено изображение простого математического выражения 1802. Данное выражение может представлять собой фрагмент выражения в пределах более крупного математического выражения. При горизонтальном разбиении на блоки генерируется множество вариантов графемы, причем применение OCR к ним позволяет сгенерировать множество возможных символов 1804, представленное в пределах многорядной структуры данных. Символы, представленные в первом ряду структуры данных, представляют собой символы, которые OCR-способы рассматривают в качестве наиболее вероятных символов, содержащихся на изображении математического выражения 1802. В некоторых случаях вместо одного символа применение OCR-способов позволяет сгенерировать столбец из возможных вариантов символа, такой как столбец 1808. В случае столбца 1808, например, путем применения OCR-способов определяется, что символ 1810 на изображении выражения 1802 может представлять собой либо заглавную букву «S» 1812, либо греческую букву «δ» 1814. Затем множество распознанных символов 1804 преобразуется в структуру данных в виде графа 1816. Структура данных в виде графа включает два типа элементарных структур данных, которые связаны, обеспечивая основу структуры данных для представления одного или более путей.
На Фиг. 18А первый тип элементарной структуры данных 1817 в структуре данных на основе графа проиллюстрирован на вставке 1818. Этот первый тип элементарной структуры данных 1817 включает ссылку на структуру данных 1820, которая связывает элементарную структуру данных с элементарной структурой следующего, второго, типа в пределах структуры данных в виде графа. Первый тип элементарной структуры данных 1817 дополнительно включает несколько подструктур пути, таких как подструктура пути 1822. Каждая подструктура пути включает ссылку на путь 1824, весовое значение дуги 1826 и индекс варианта символа 1828. Значение, хранящееся в ссылке на путь 1824, если оно не нулевое, представляет ссылку на другой из первых типов элементарных структур данных и представляет дугу в пределах пути структуры данных в виде графа. Весовое значение дуги 1826 представляет собой весовое значение, присвоенное дуге, представленной содержимым ссылки на путь 1824. Весовое значение дуги обеспечивает указание на вероятность того, что дуга представляет верную гипотезу группировки символов для математического выражения. В текущем представленном способе реализации чем ниже весовое значение, тем выше вероятность гипотезы. Конечно, в альтернативных способах реализации можно использовать другие условные обозначения. Индекс варианта символа 1828 указывает на то, какой из вариантов символа в столбце вариантов символа, таком как в столбцец 1808, описанном выше, встречается в конкретном пути. Например, индекс варианта символа со значением «0» указывает на то, что в пути встречается символ первого ряда вариантов, представленный одним или более элементарными структурами данных второго типа, как описано ниже. В структуре данных в виде графа 1816, представленной на Фиг. 18А, все верхние элементарные структуры данных 1830-1844 представляют собой элементарную структуру первого типа, проиллюстрированную на вставке 1818. Они представляют возможные узлы и дуги одного или более путей, построенных для множества символов.
Второй тип элементарной структуры данных используется для представления вариантов символа. Например, элементарная структура данных 1846 представляет вариант символа δ 1814. Этот второй тип элементарной структуры данных проиллюстрирован на вставке 1848. Второй тип элементарной структуры данных также включает ссылку на структуру данных 1850, представление знака или символа 1852, весовое значение по OCR 1854, указывающее на вероятность того, что вариант символа фактически представляет соответствующий символ математического выражения или фрагмента выражения, и ссылку на символьную структуру данных, или S-ссылку, 1856, которая позволяет связывать элементарные структуры данных второго типа для образования столбцов, например, связанные структуры данных 1858 и 1846 образуют столбец 1808 в проиллюстрированном выше множестве вариантов символа 1804. Кроме того, во втором типе элементарной структуры данных могут храниться многие другие значения, включая уровень рекурсивного разбиения на блоки, на котором был распознан символ, положение, информацию о типе и размере шрифта символа, а также другую такую информацию, которую можно сделать доступной в процессе применения OCR-способов.
На Фиг. 18В проиллюстрирован первый возможный путь, соответствующий выражению или фрагменту выражения 1802, представленного на Фиг. 18А. Путь указан изогнутыми стрелками, такими как изогнутая стрелка 1860 в выражении в верхней части Фиг. 18В 1802. Каждая дуга отмечена заключенным в кружок целым числом. Каждая дуга представляет группу из одного или более вариантов символа, которые вместе представляют осмысленную группировку символов в пределах математического выражения. Например, первая дуга 1860 указывает на то, что символы «1», «0» и «0» вместе представляют целое число 100. Нижнее выражение 1862 на Фиг. 18В указывает на математическую интерпретацию пути, представленного на Фиг. 18В. Точки, такие как точка 1864, введены для указания на подразумеваемое умножение. Следует отметить, что в пути, представленном на Фиг. 18В, из пути для символов 1866 и 1868 выбраны вторые варианты символов. На Фиг. 18В к подструктурам пути в пределах первого типа элементарных структур данных были добавлены значения, представляющие путь, проиллюстрированный дугами, добавленными к выражению 1802. Например, дуга 1860 представлена ссылкой, которая сохранена в ссылке на путь 1870, на элементарную структуру данных 1833. Весовое значение данной дуги 15 (1872 на Фиг. 18В) сохранено в поле весового значения подструктуры ссылки на путь. Указатель 0 (1874 на Фиг. 18В) указывает на то, что в пути используется первый вариант символа из связанного списка элементарных структур данных второго типа, на который ссылается ссылка на структуру данных. Как представлено выражением 1876 в нижней части Фиг. 18В, весовое значение пути вычисляется как сумма весовых значений дуги для дуг пути и в случае пути, проиллюстрированного на Фиг. 18В, имеет числовое значение 67.
На Фиг. 18С проиллюстрирован второй возможный путь для выражения 1802, изображенного на Фиг. 18А. Данный путь имеет четыре дуги, проиллюстрированные изогнутыми стрелками, такими как изогнутая стрелка 1878. На Фиг. 18С для иллюстрации используются такие же условные обозначения, что и на Фиг. 18В. Полям в пределах подструктур пути в элементарных структурах данных первого типа структуры данных в виде графа 1816 присваиваются значения, представляющие данный второй путь. Весовое значение второго пути представлено выражением 1880 в нижней части Фиг. 18С и имеет значение 36. Следует отметить, что данный второй путь можно считать правильной группировкой символов для математического выражения 1802 на Фиг. 18А. Первая дуга 1878 указывает на группировку символов, представляющих целое число 100, вторая дуга 1882 представляет набор символов «Sin(a+b)», который представляет собой функцию синусаот суммы a+b, третья дуга 1884 представляет собой символ умножения, а четвертая дуга 1886 представляет группу символов «c2».
На Фиг. 19 представлены результаты анализа в форме дерева, сгенерированные при рекурсивном разбиении на блоки, исходно представленном на Фиг. 16В, с дугами корректного пути для математического выражения 1406, изображенного на Фиг. 14А. Корректный путь включает первую дугу 1902 для 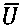 , вторую дугу 1904 для знака равенства, третью дугу 1906 для первой матрицы, четвертую дугу 1908 для второй матрицы и пятую дугу 1910 для третьей матрицы.
, вторую дугу 1904 для знака равенства, третью дугу 1906 для первой матрицы, четвертую дугу 1908 для второй матрицы и пятую дугу 1910 для третьей матрицы.
По заданному выражению можно построить большое количество возможных путей. Однако, как описано выше, можно применять множество типов эвристических способов и способов построения для порождения лишь относительного небольшого числа потенциально возможных путей для последовательности распознанных символов. Например, последовательность десятичных цифр, такая как «100», с высокой вероятностью представляет одно целое число, а не отдельные десятичные цифры. В качестве другого примера последовательность символов «Sin» может быть распознана как распространенное сокращение для функции синуса путем нахождения «Sin» в словаре общеизвестных математических функций. Многие символы могут встречаться парами с заключенными между ними фрагментами выражений, включая круглые скобки и квадратные скобки. Путям, в которых данные пары символов сгруппированы одной дугой, могут присваиваться подходящие весовые значения, поскольку они с высокой вероятностью указывают на вложенные фрагменты выражений. Многие из путей для фрагментов выражений, порожденных во время рекурсивного разбиения на блоки, могут быть напрямую соотнесены с деревьями анализа математического выражения, и такие соотнесения могут обеспечивать основу для мощных эвристических способов выбора корректных потенциально возможных путей. Размер шрифта и положение символа зачастую указывают на подстрочные и надстрочные выражения и обеспечивают дополнительную ценную эвристическую информацию для распознавания надстрочных и подстрочных выражений в математических выражениях. Аналогичные эвристические способы можно использовать для распознавания пределов определенных интегралов и пределов суммирования. Уровень рекурсии при разбиении на блоки, на котором распознан символ, также может служить хорошим указанием на логический уровень фрагмента выражения в пределах математического выражения. Весовые значения, связанные с дугами, вычисляются на основе эвристических способов, использованных для порождения дуг, а также на основе весовых значений, связанных с вариантами символа, охваченными дугами.
Хотя настоящее изобретение описано в отношении конкретных вариантов реализации, предполагается, что настоящее изобретение не ограничено данными вариантами реализации. Специалистам в данной области будут очевидны модификации в пределах сущности настоящего изобретения. Например, любой из множества способов обработки изображений и фрагментов изображений математических выражений, к которым относится настоящий документ, можно получить путем варьирования любого из множества параметров конфигурации и способов реализации, включая язык программирования, аппаратную платформу, операционную систему, структуры управления, модульную организацию, структуры данных и другие такие параметры. В разных способах реализации можно использовать разные типы рекурсивного разложения, генерирующие разные типы структур поддеревьев для различных группировок математических символов. Можно использовать множество типов узловых структур данных и кодировок дерева. В некоторых способах реализации вместо построения иерархического дерева информация, необходимая для порождения гипотезы, может передаваться в качестве параметров в рекурсивные вызовы и, следовательно, может временно храниться в стеке, а не в структуре данных в форме дерева. Для представления в цифровом виде математического выражения, полученного при разложении на символы изображения или фрагмента изображения, содержащего представление математического выражения, можно использовать любую из множества подсистем электронного представления.
Следует понимать, что описанные ранее варианты осуществления предоставлены для того, чтобы позволить любому специалисту в данной области реализовать или использовать настоящее изобретение. Специалистам в данной области будут очевидны различные возможные модификации этих вариантов осуществления, причем общие принципы, описанные в настоящем описании, могут применяться к другим вариантам осуществления без отступления от сущности или объема изобретения. Таким образом, настоящее изобретение не ограничено показанными в настоящем описании вариантами осуществления, но должно соответствовать наиболее широкому объему задач, соответствующих принципам и инновационным элементам, описанным в настоящем документе.


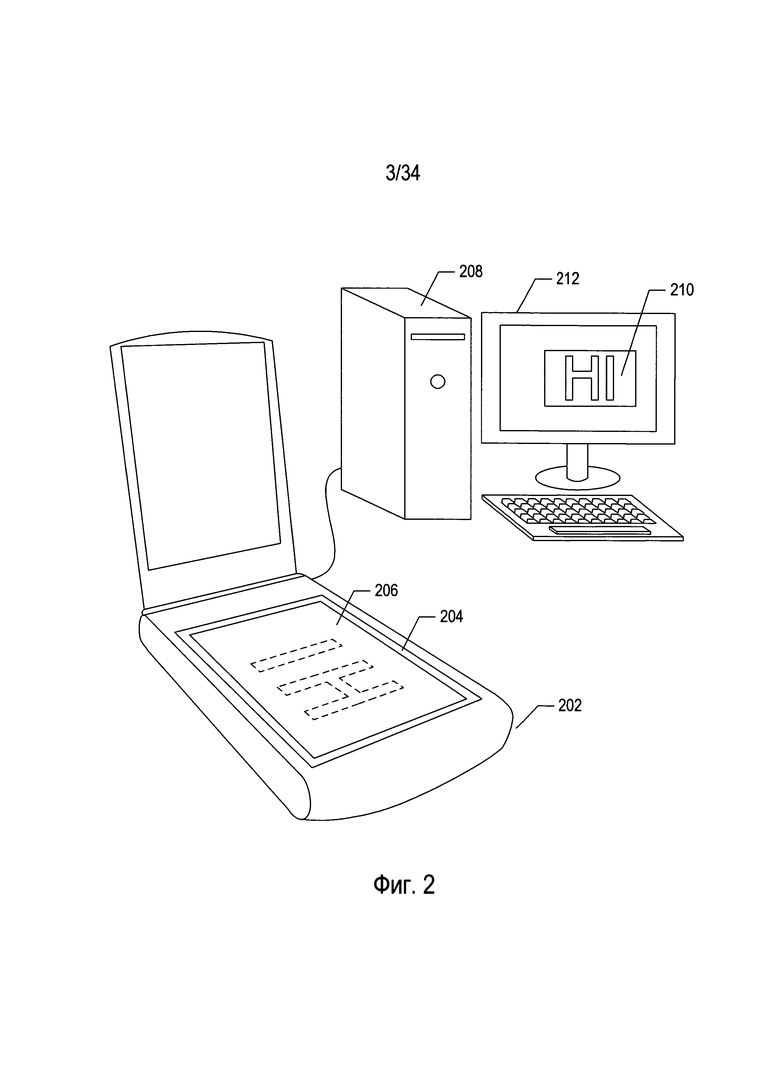
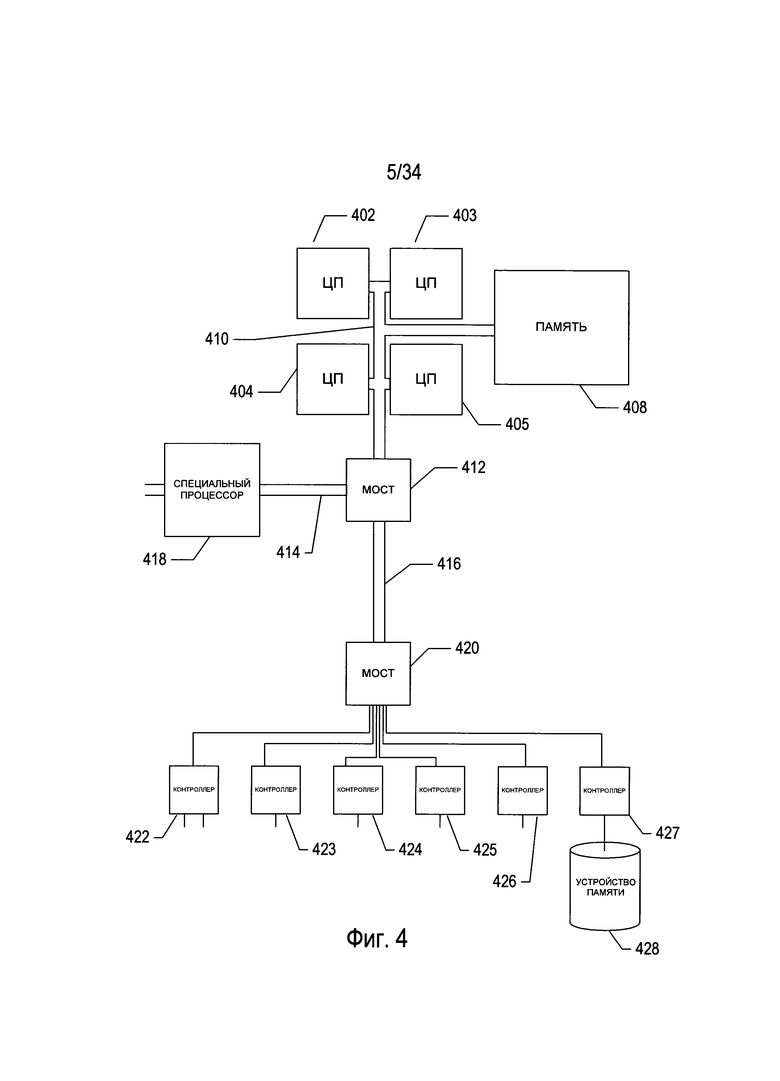
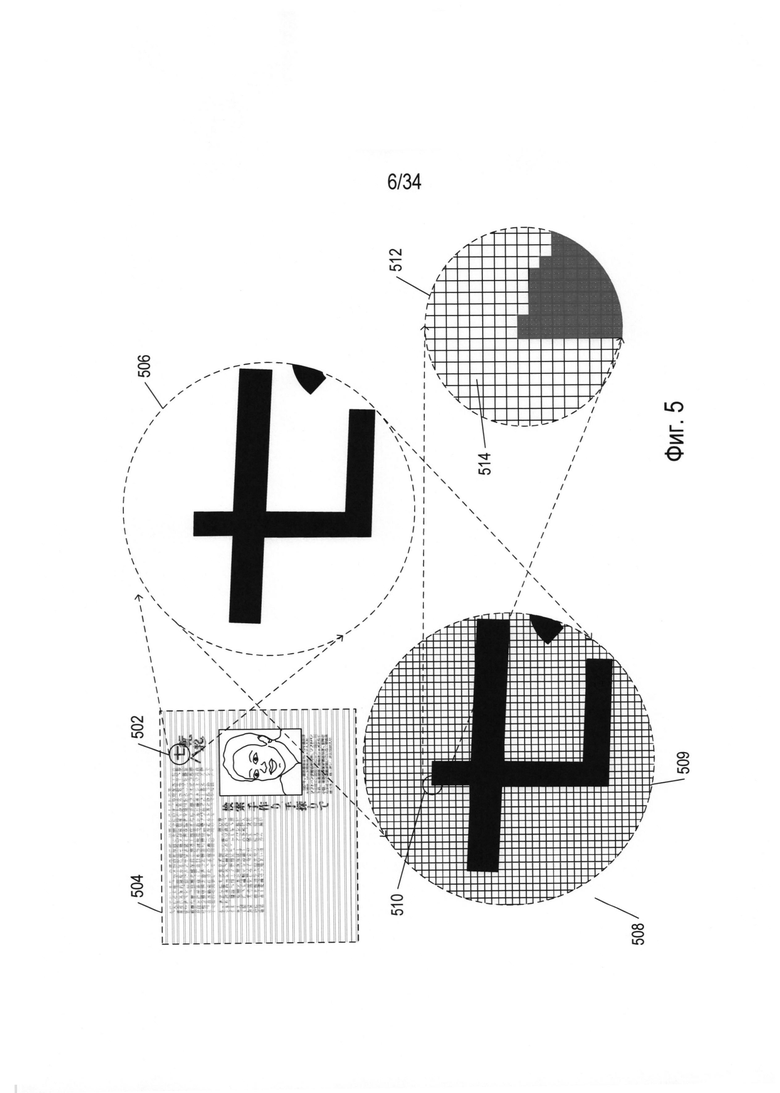
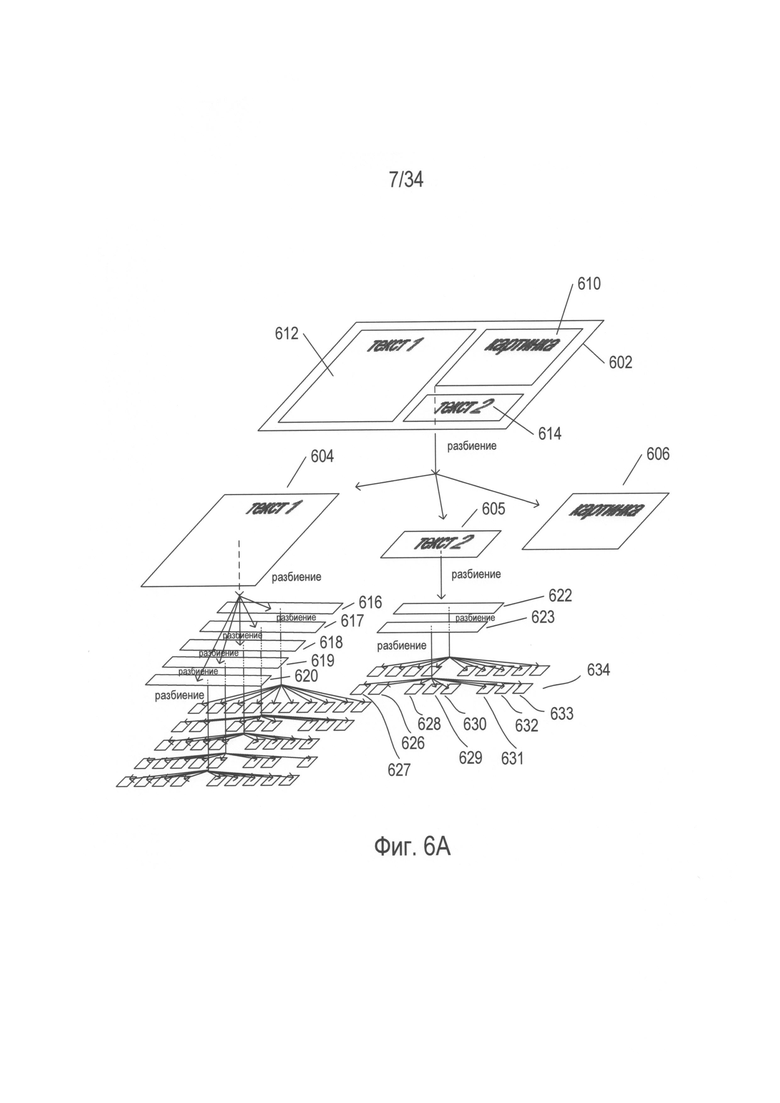
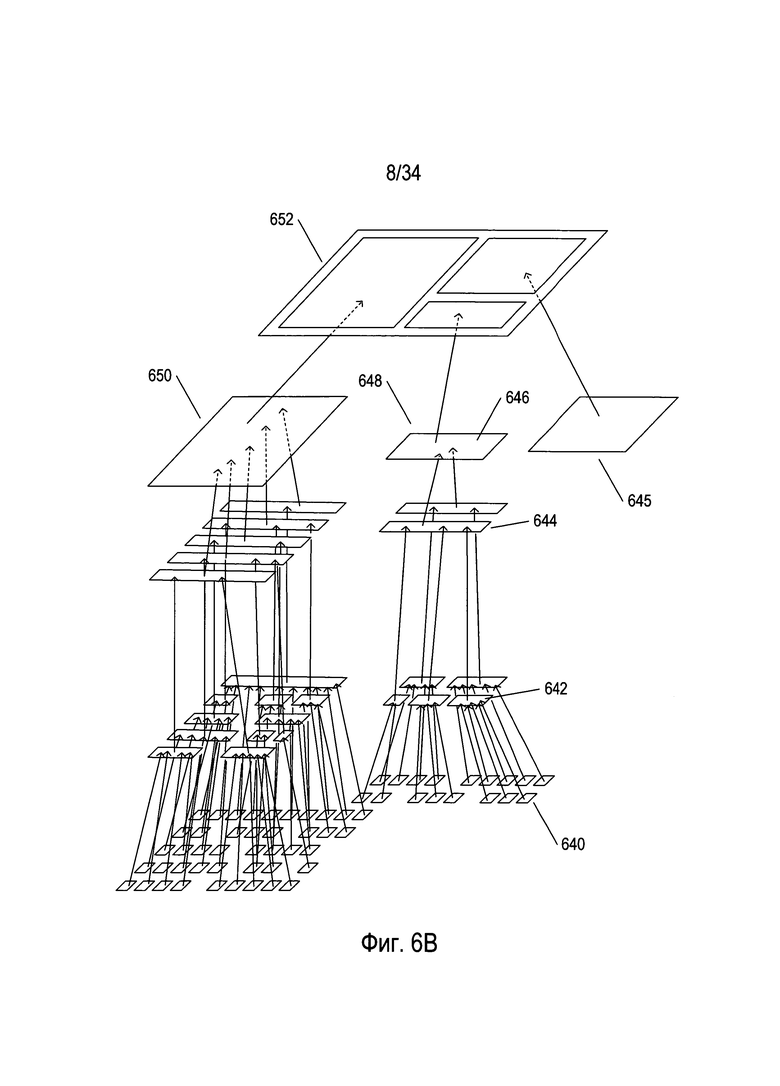
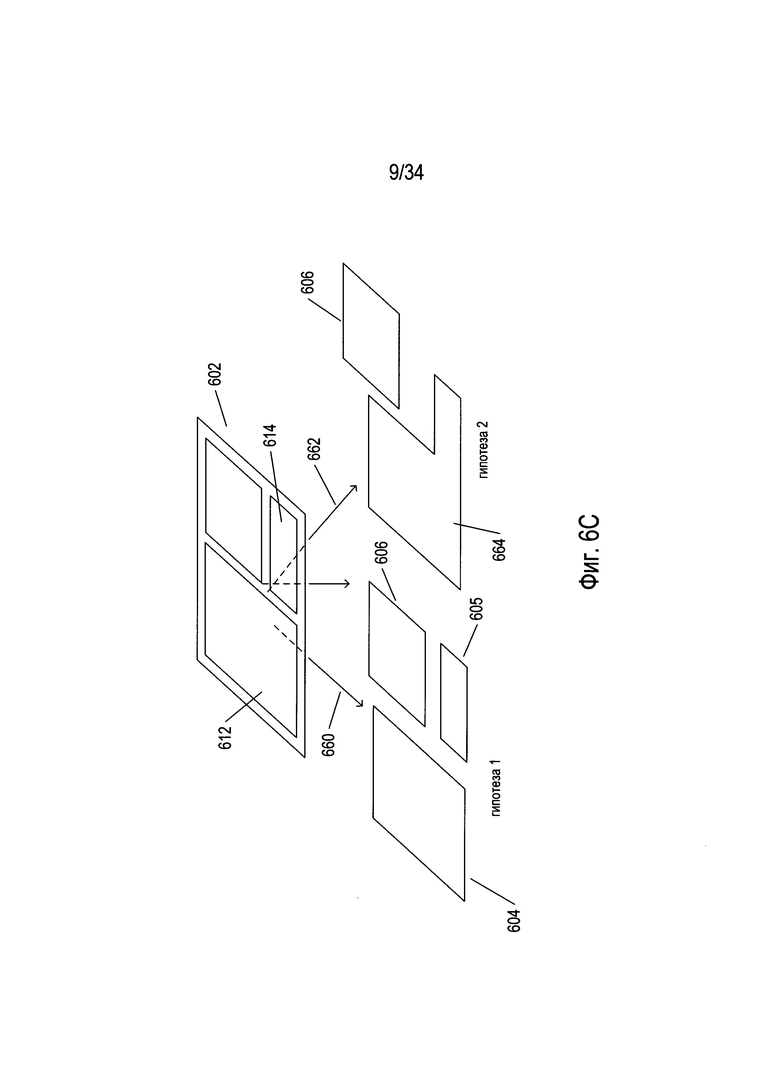
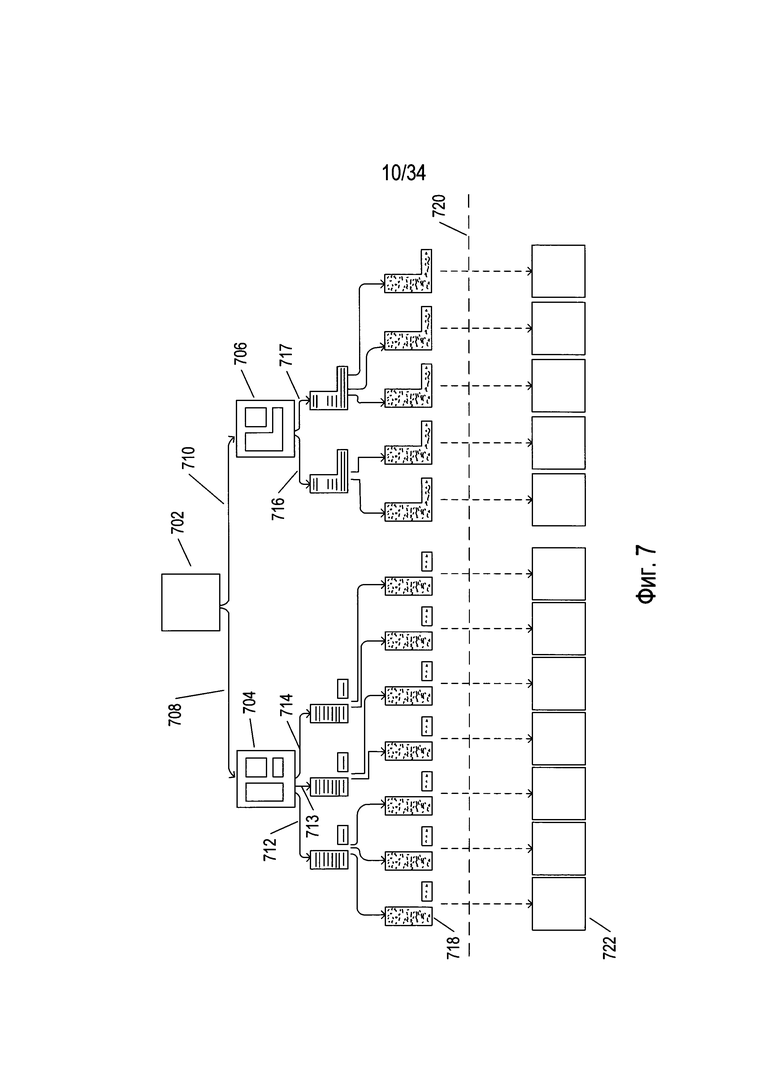
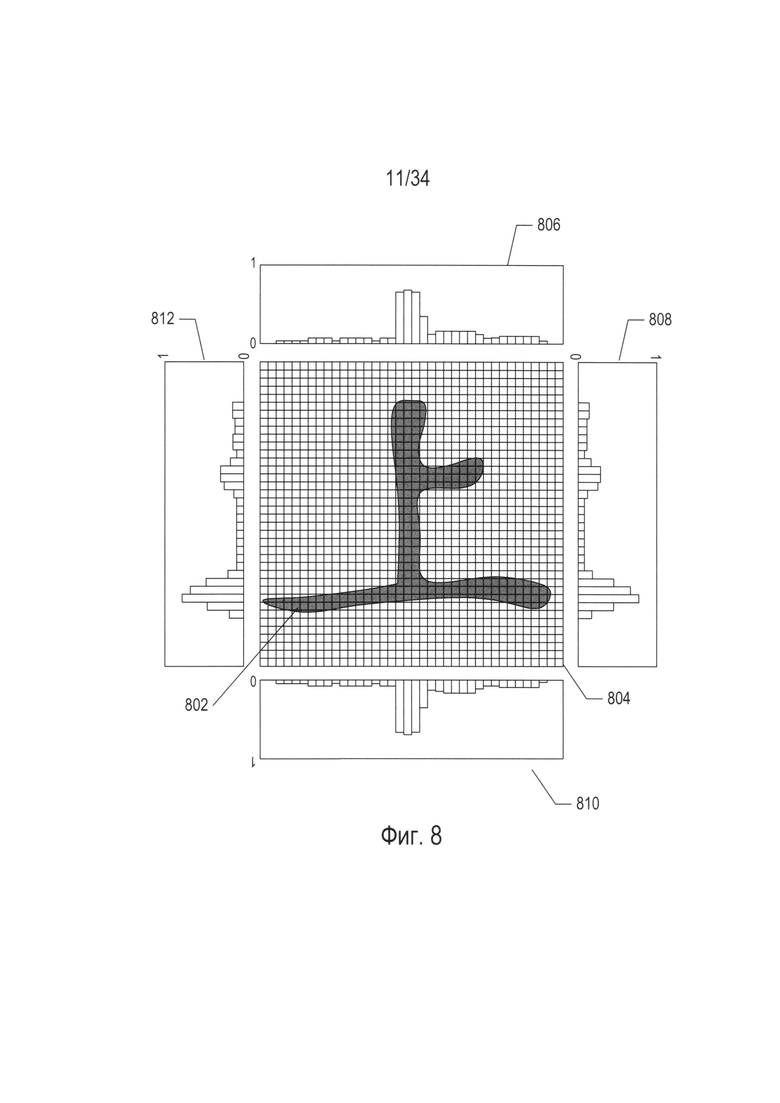
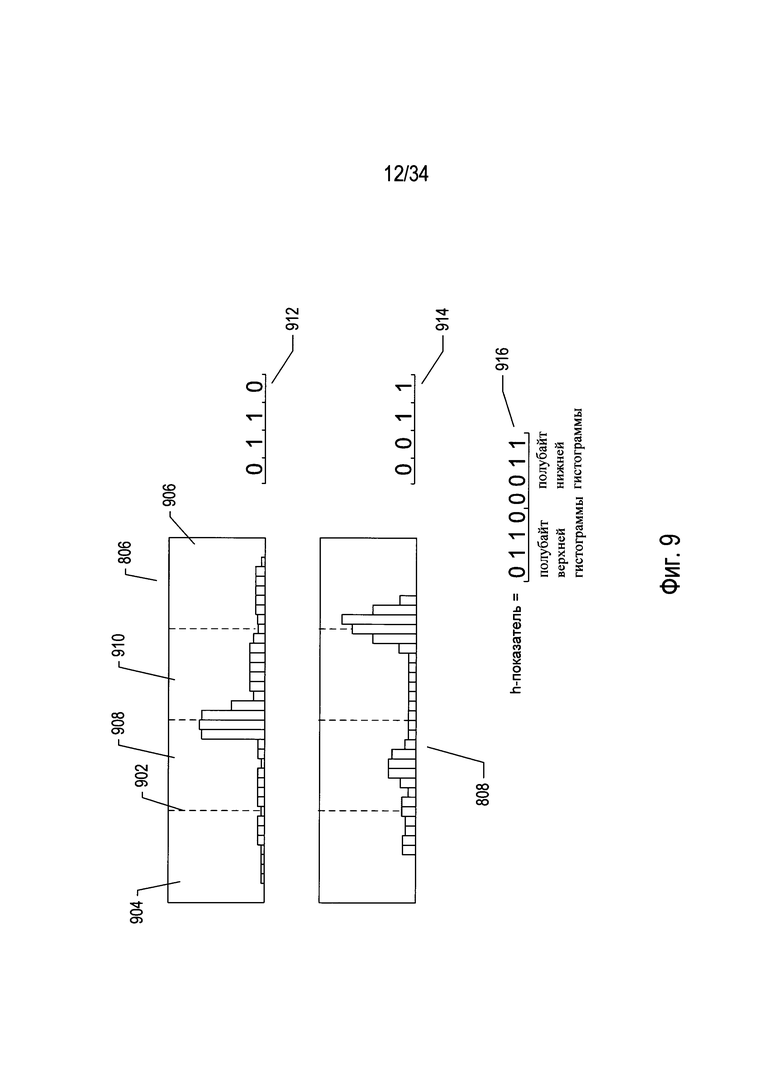
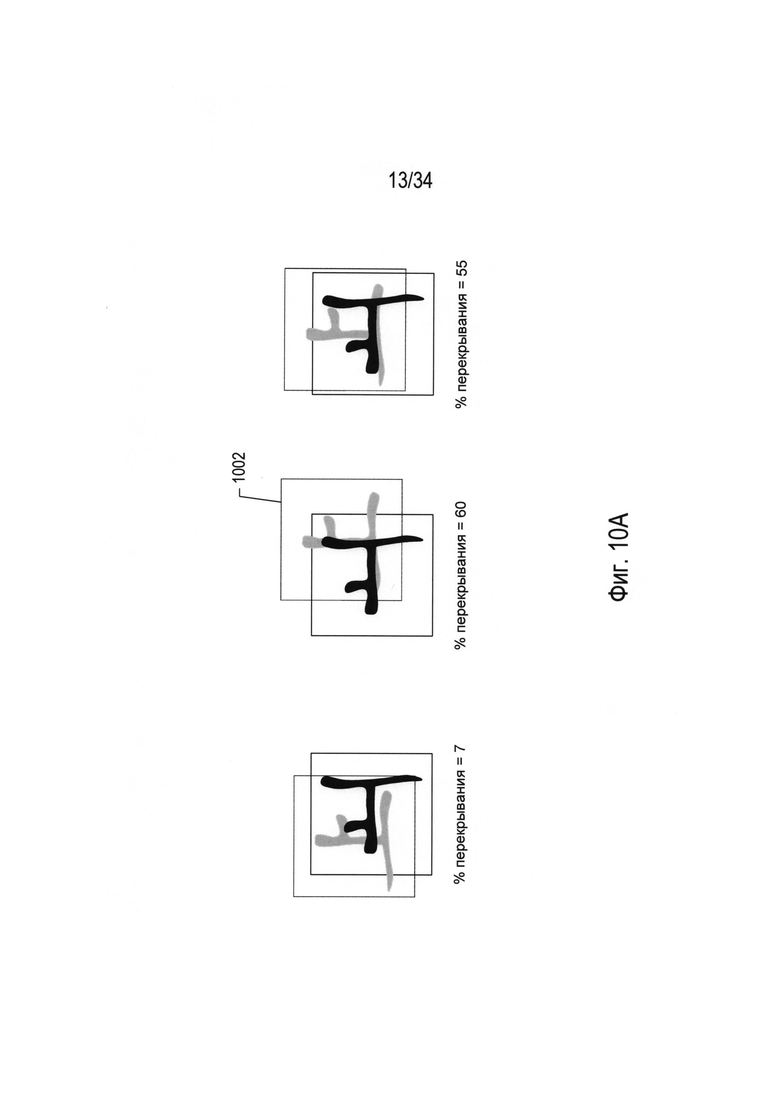
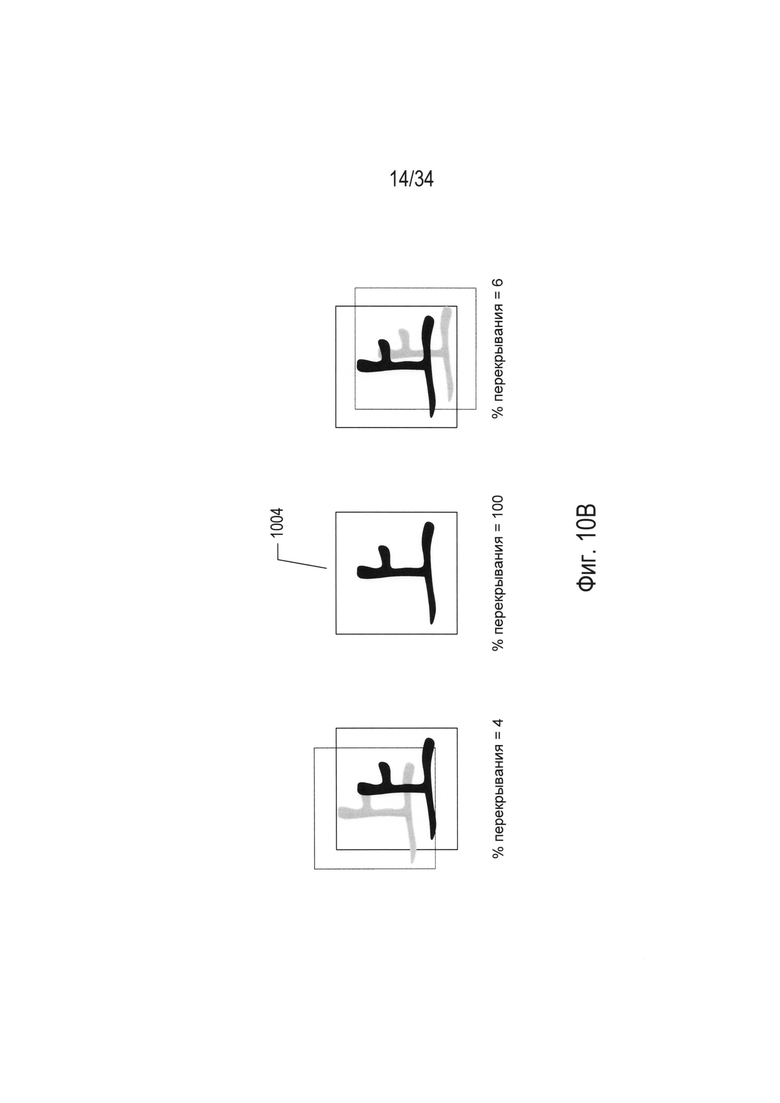
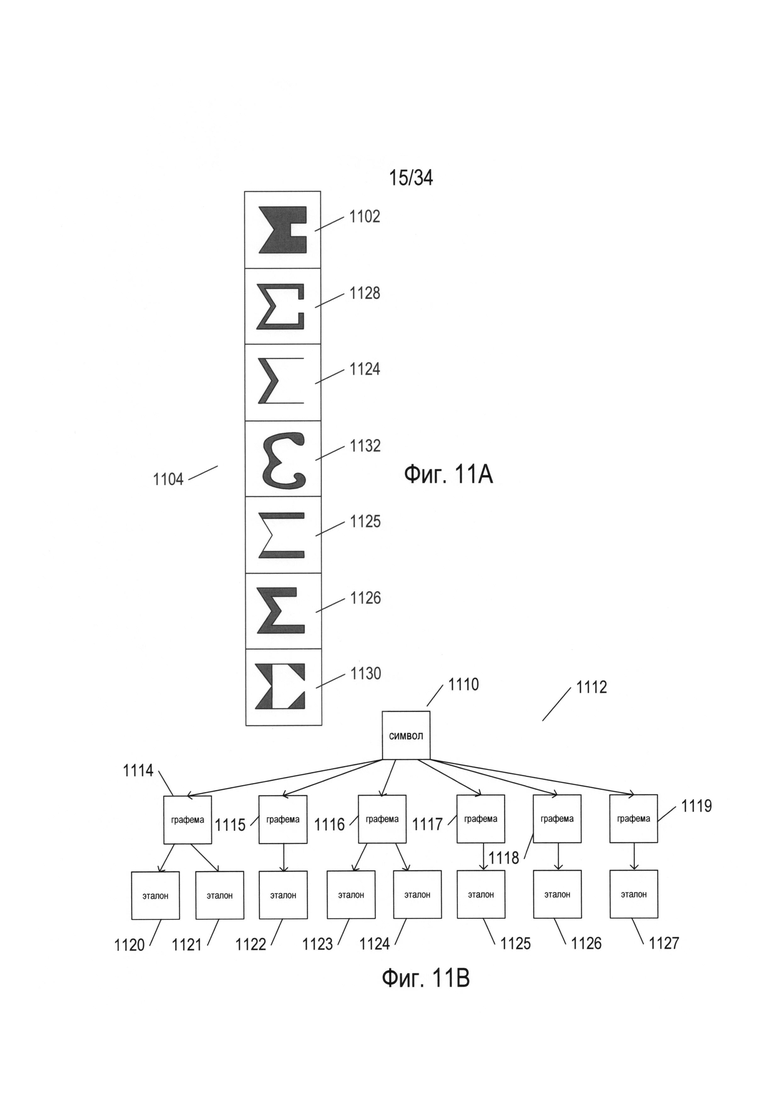
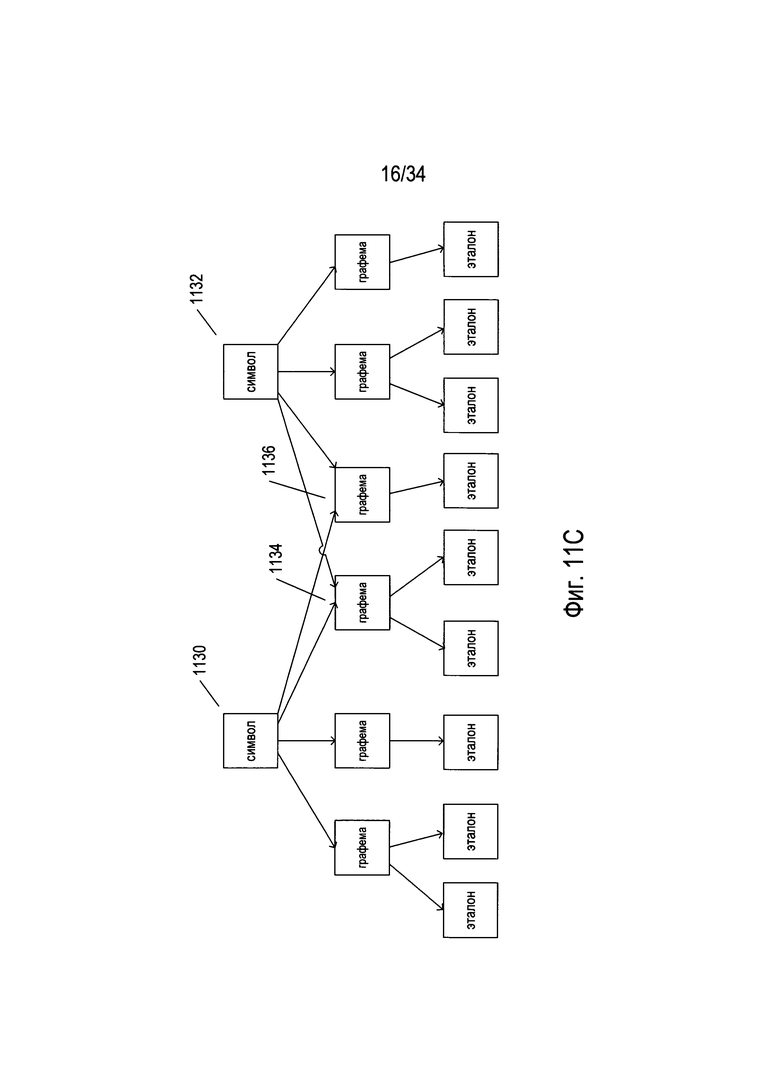

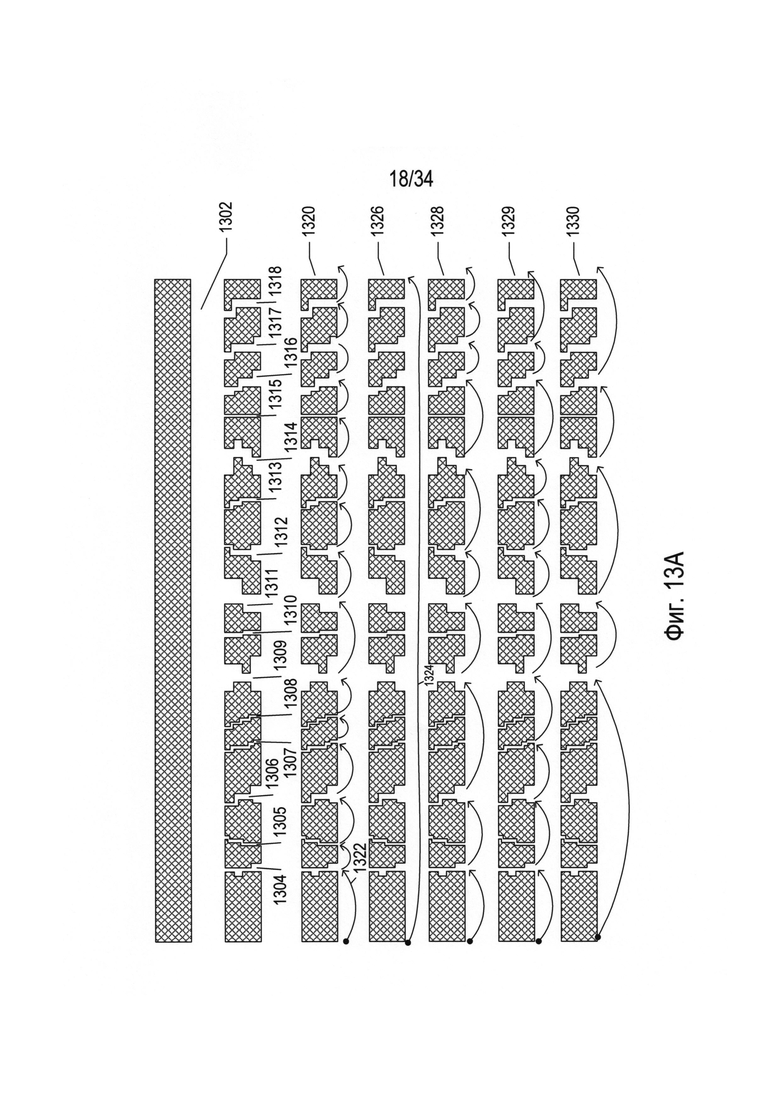
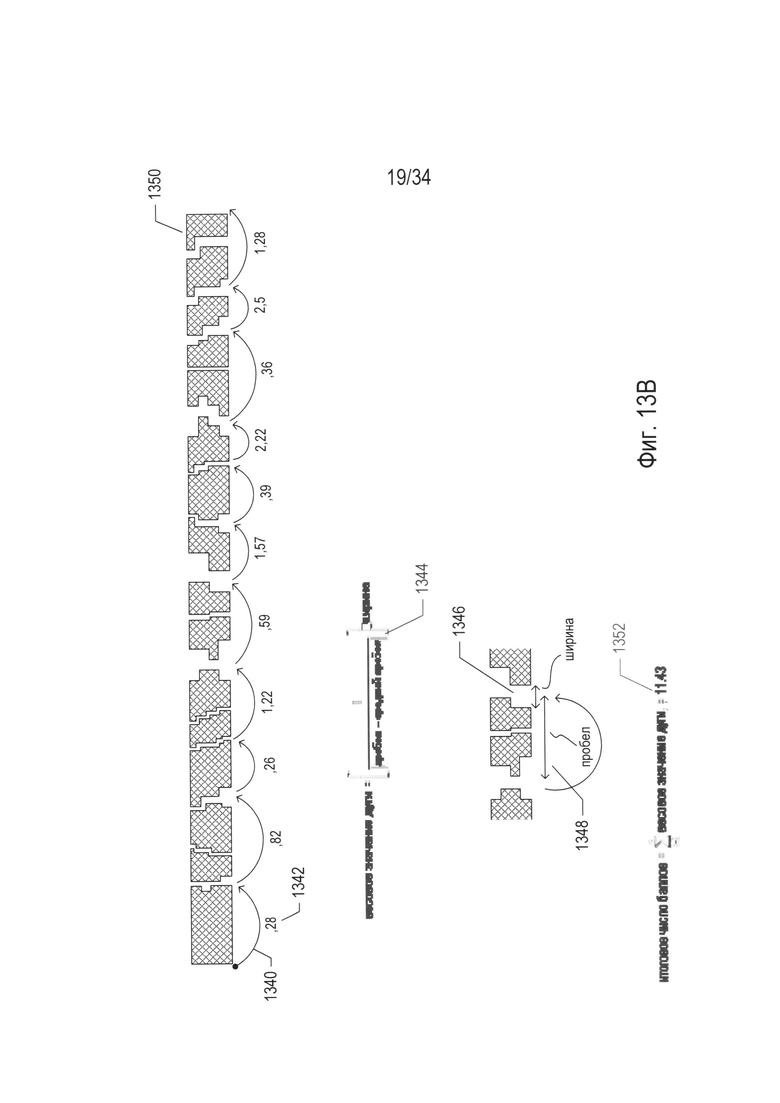
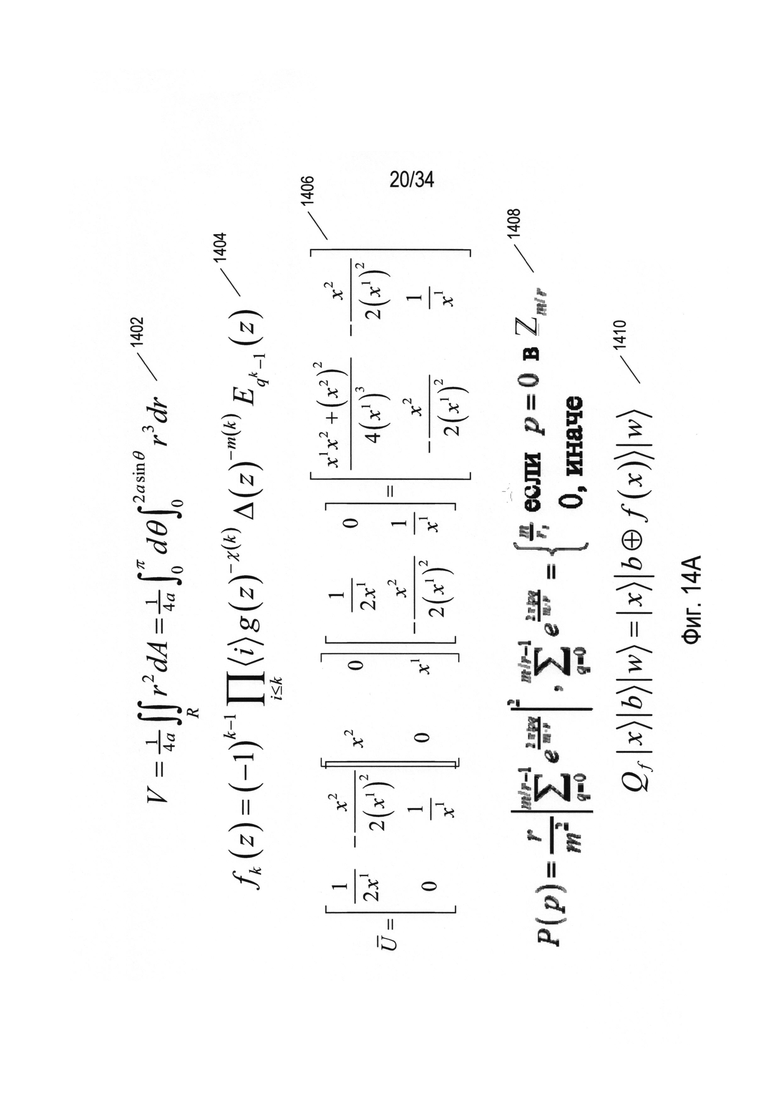

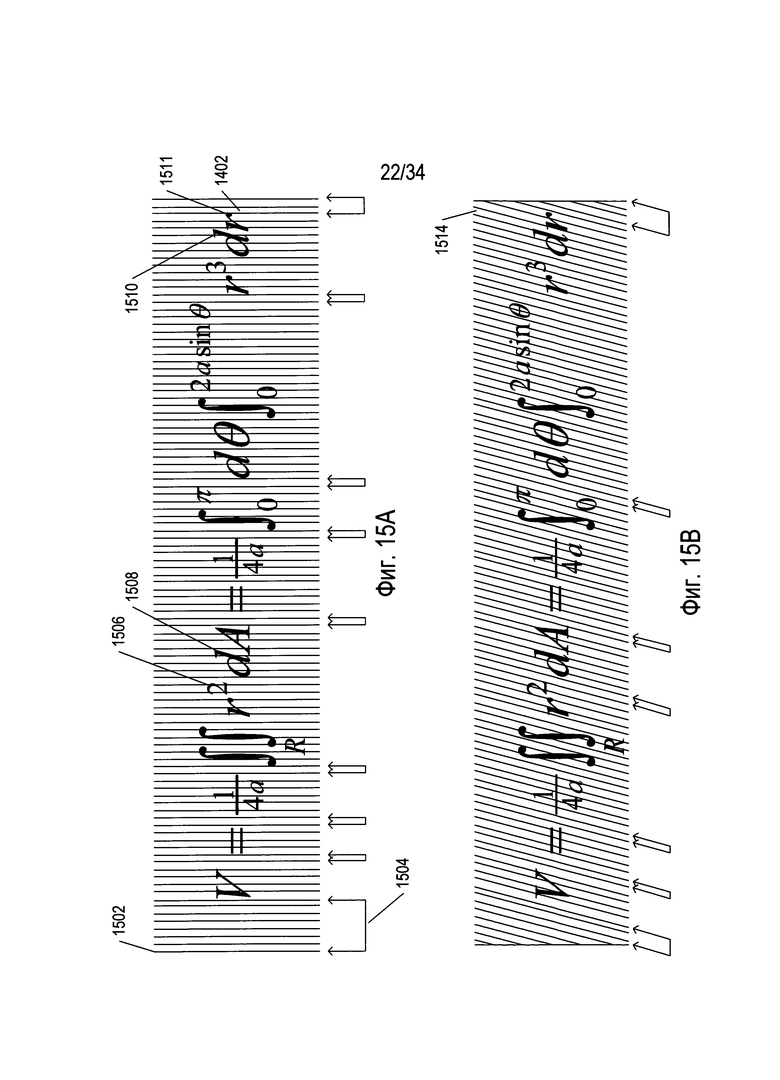
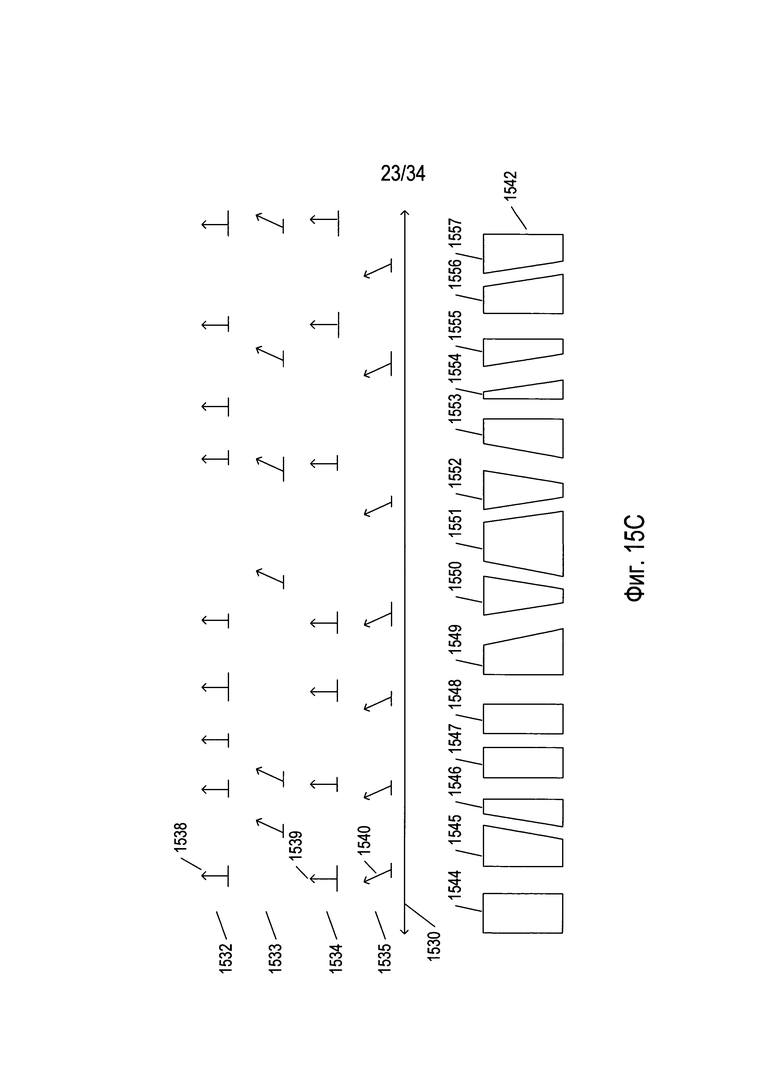
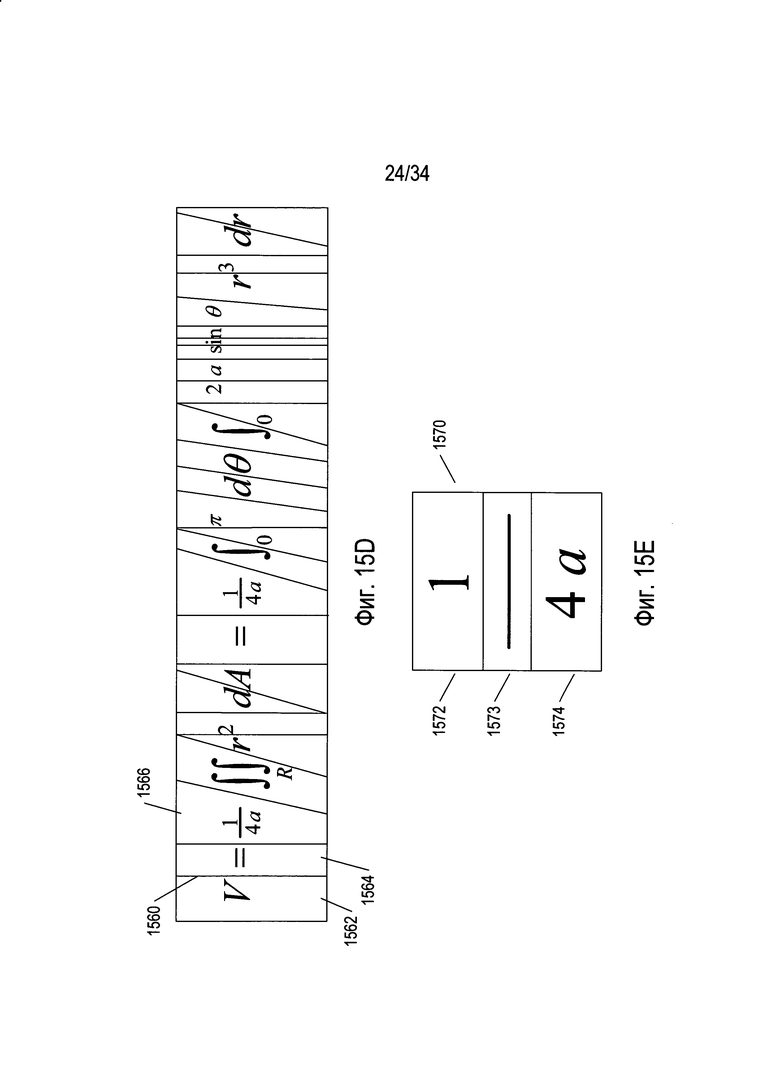
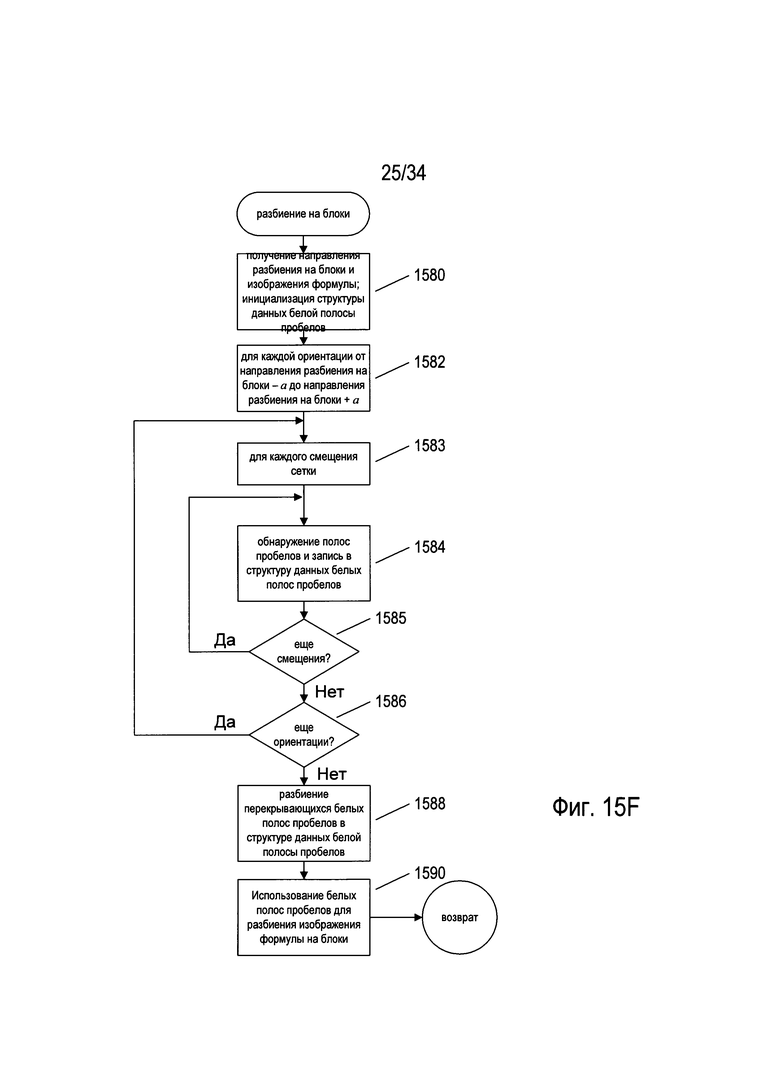
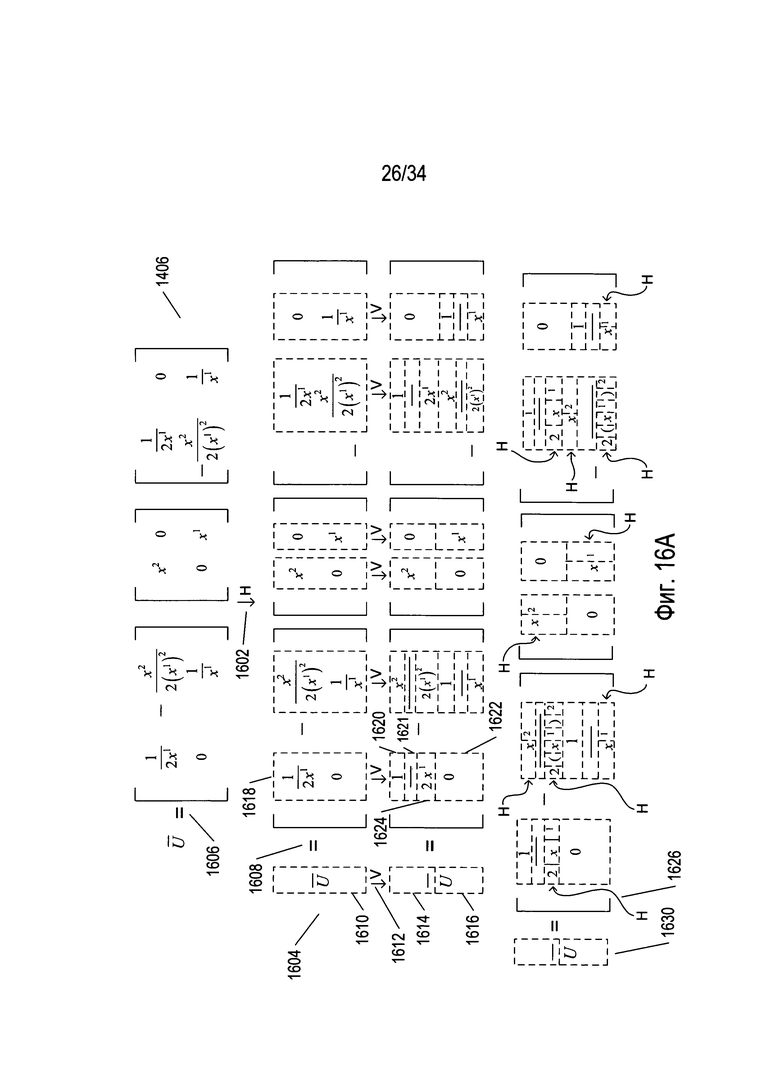
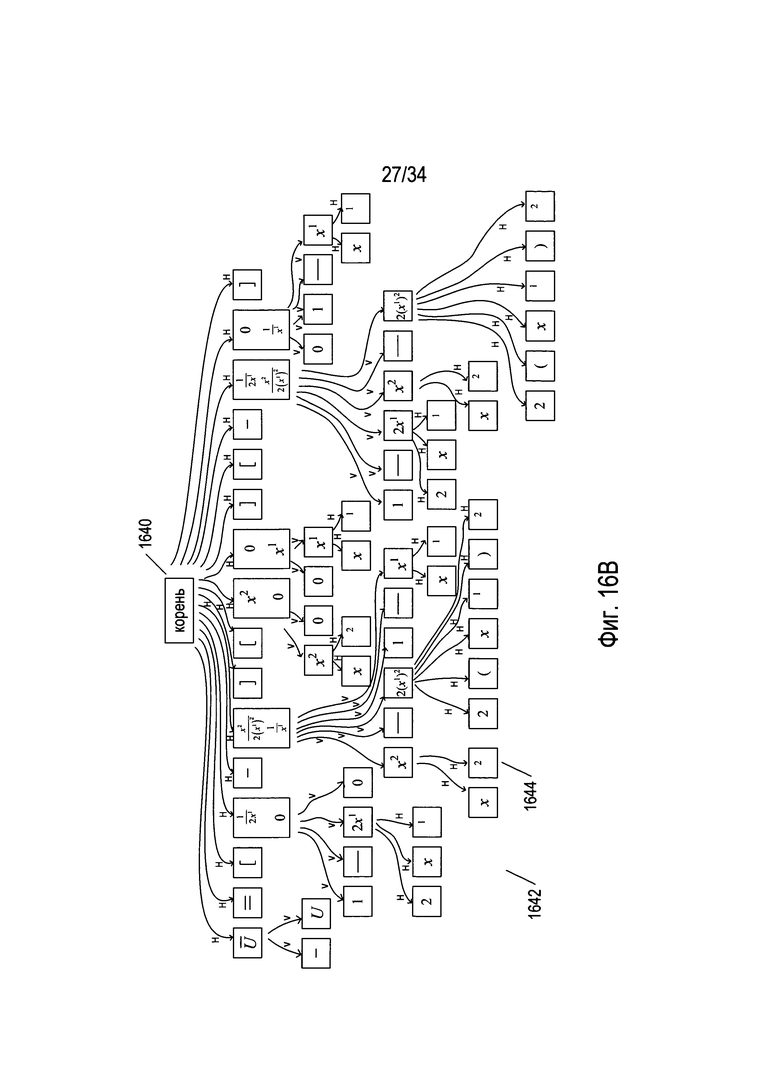
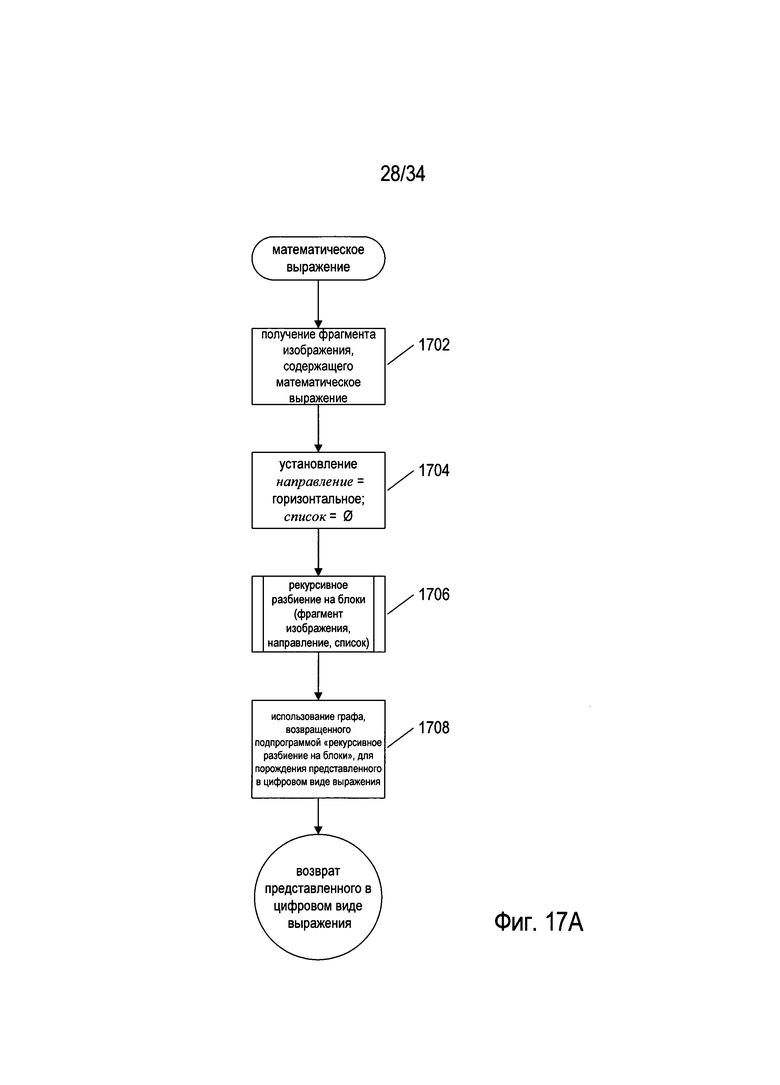
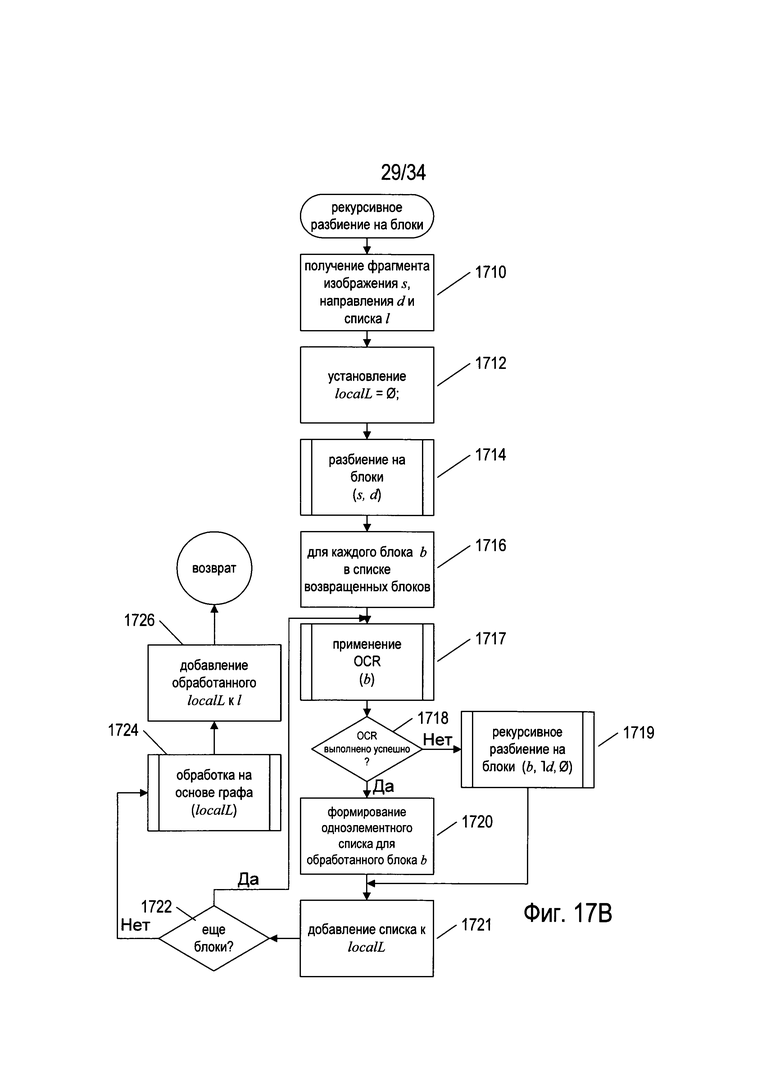
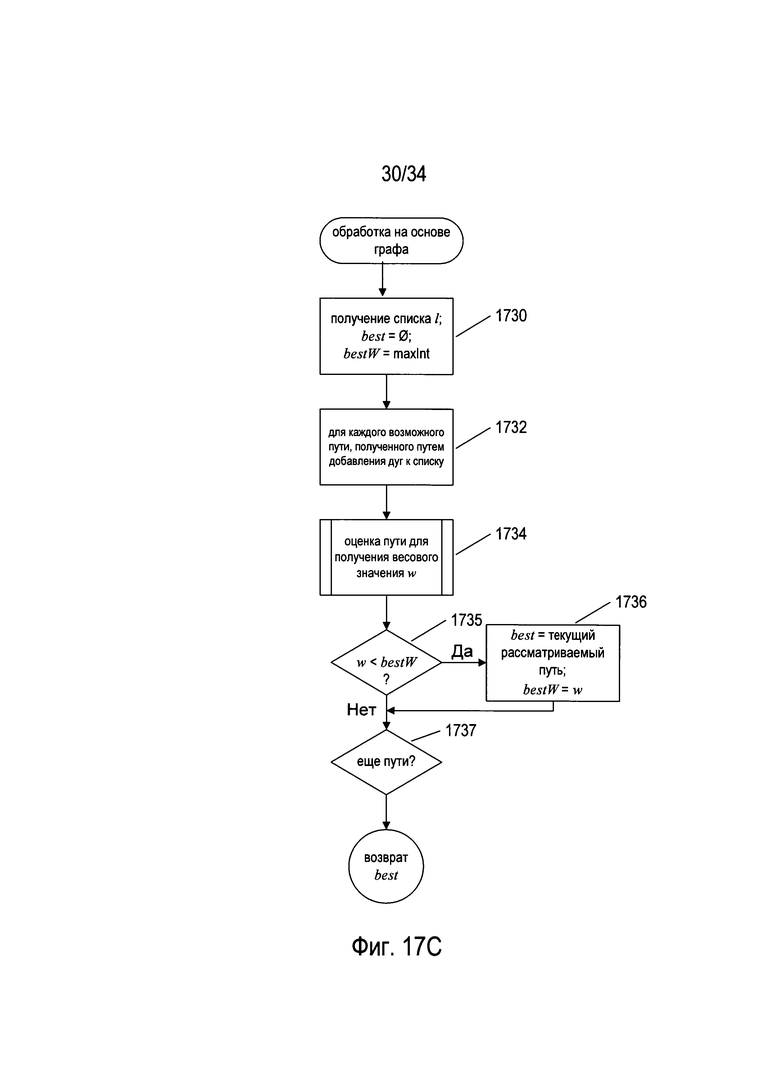
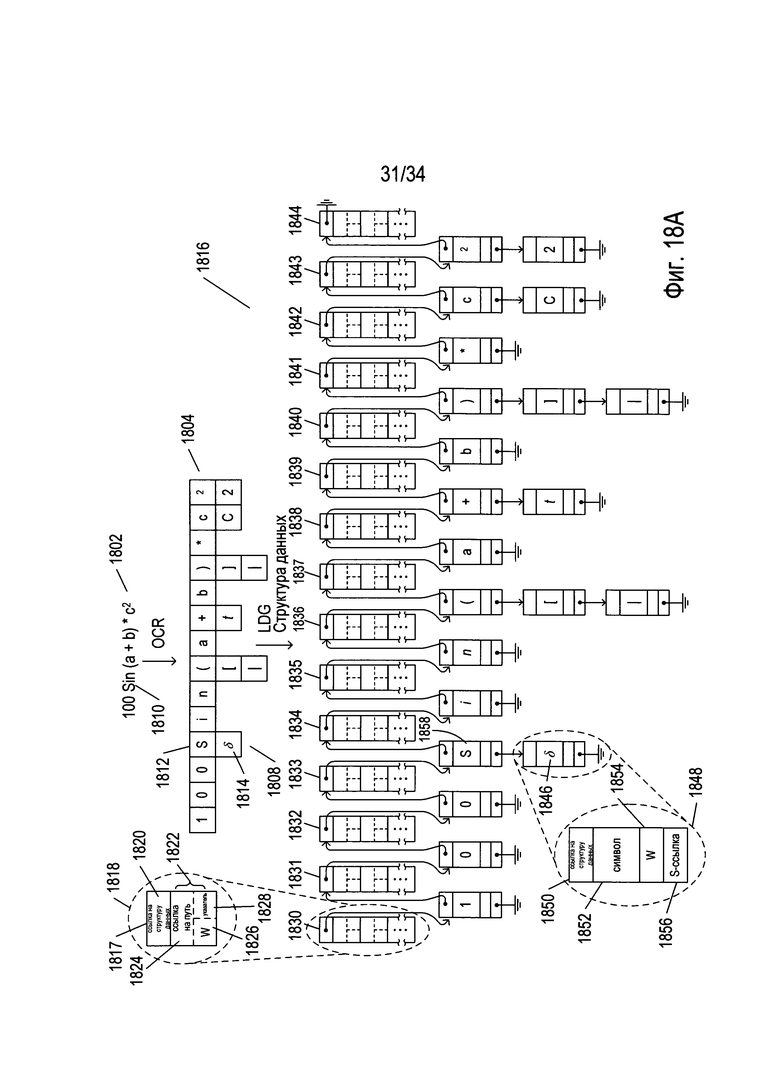
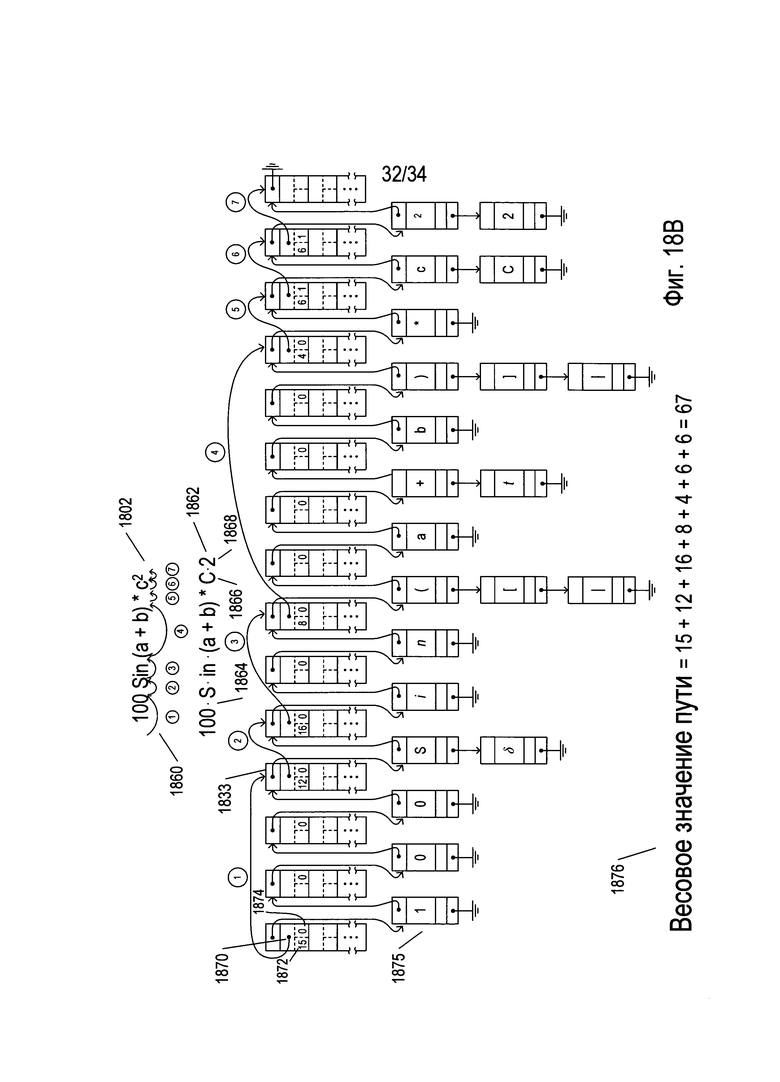
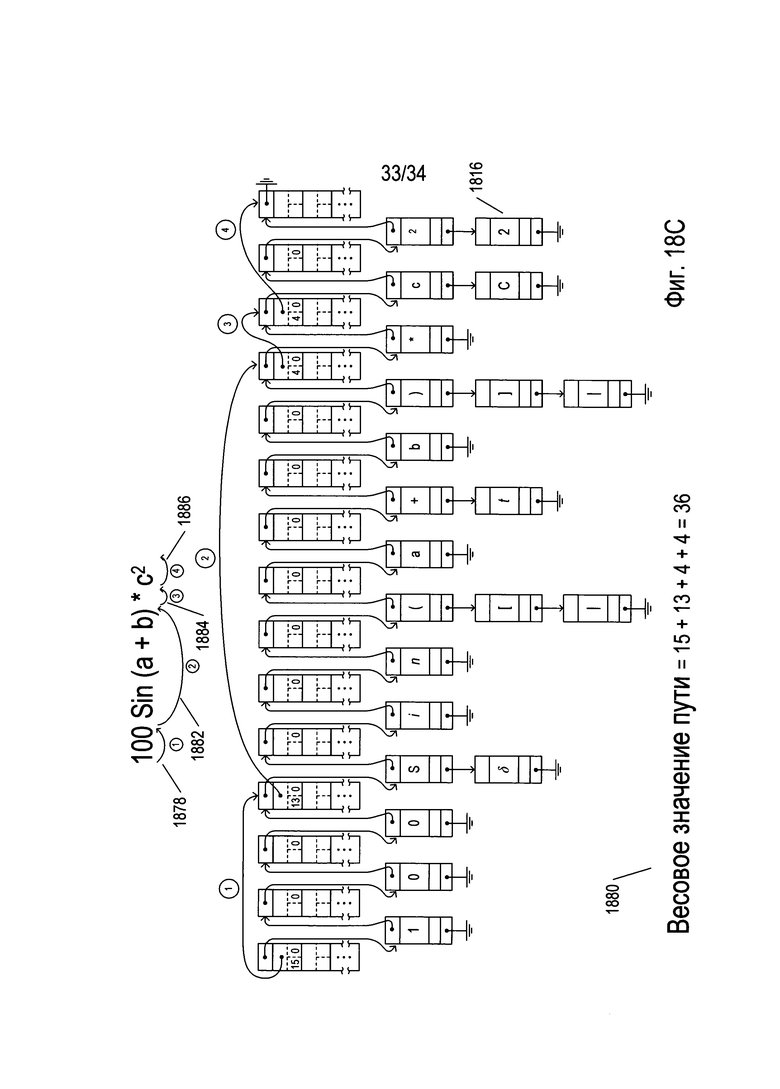

Изобретение относится к системе, способу и модулю памяти для оптического распознавания символов. Технический результат заключается в повышении достоверности оптического распознавания математических выражений. В способе выполняют разбиение на блоки изображения, содержащего математическое выражение, и последующее оптическое распознавание блоков для разложения изображения математического выражения на множество вариантов оптического распознавания символов, упорядоченное согласно весовому значению по OCR, выбор наиболее вероятного пути на основе весового значения для пути среди потенциально возможных путей, где путь соответствует группировке символов на изображении математического выражения и упорядоченному множеству вариантов распознавания символов на данном изображении, использование наиболее вероятного пути и упорядоченного множества вариантов распознавания символов для порождения представления в цифровом виде математического выражения, содержащегося на изображении, где наиболее вероятный путь, отобранный на основе весового значения, содержит информацию о группировке символов и вариантах их распознавания, и сохранение представленного в цифровом виде математического выражения в модуле памяти. 3 н. и 17 з.п. ф-лы, 37 ил.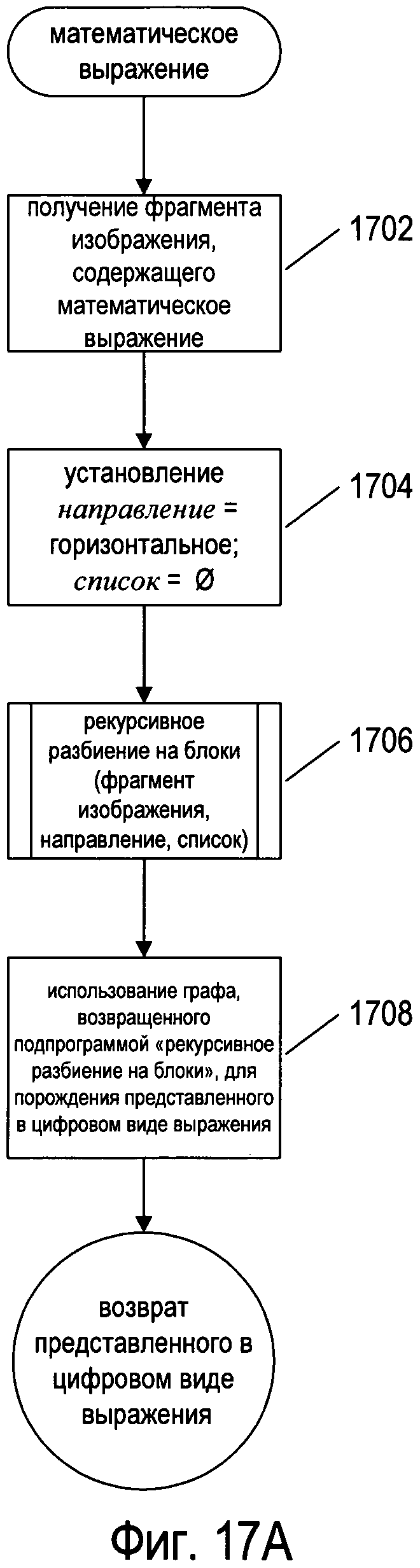
1. Система оптического распознавания символов, содержащая:
один или более процессоров;
один или более модулей памяти; и
компьютерные команды, хранящиеся в одном или более из одного или более модулей памяти, которые, будучи исполненными одним или более из одного или более процессоров, управляют системой оптического распознавания символов для обработки изображения, содержащего математическое выражение, путем
разбиения на блоки изображения, содержащего математическое выражение, и последующего оптического распознавания блоков для разложения изображения математического выражения на упорядоченное множество вариантов оптического распознавания символов, где множество вариантов оптического распознавания символа упорядочено согласно весовому значению по OCR,
выбора наиболее вероятного пути на основе весового значения для пути среди потенциально возможных путей, где путь соответствует группировке символов на изображении математического выражения и упорядоченному множеству вариантов распознавания символов на данном изображении и,
использования наиболее вероятного пути и упорядоченного множества вариантов распознавания символов для порождения представления в цифровом виде математического выражения, эквивалентного математическому выражению, которое содержится на изображении, где наиболее вероятный путь, отобранный на основе весового значения, содержит информацию о группировке символов и вариантах их распознавания, и
сохранения представленного в цифровом виде математического выражения в одном или более из одного или более модулей памяти.
2. Система оптического распознавания символов по п. 1, в которой применение разбиения на блоки к изображению, содержащему математическое выражение, для разложения изображения на упорядоченное множество вариантов распознавания символов дополнительно содержит:
установление указания на направление разбиения изображения на блоки в качестве указания на горизонтальное разбиение на блоки, где установление указания на направления разбиения основано на выборе среди потенциальных границ разбиения с изменением направлений линии потенциальной границы;
горизонтальное разбиение изображения на фрагменты изображения на первом уровне; и
рекурсивно
для каждого фрагмента изображения на текущем уровне
применение одного или более способов распознавания символов к текущему рассматриваемому фрагменту изображения, и,
если с помощью одного или более способов распознавания символов не удается обнаружить фрагмент изображения в качестве фрагмента изображения, содержащего один символ, установление указания на направление разбиения на блоки, противоположное текущему направлению разбиения на блоки, представленному указанием на направление разбиения на блоки, продвижение указания текущего уровня и рекурсивное применение разбиения на блоки к фрагменту изображения с использованием указания на направление разбиения на блоки и указания текущего уровня.
3. Система оптического распознавания символов по п. 1, в которой каждый потенциально возможный путь, соответствующий упорядоченному множеству вариантов распознавания символа, содержит одну или более дуг, причем каждая дуга охватывает подмножество упорядоченного множества вариантов распознавания символа, где подмножество упорядоченного множества вариантов распознавания символа представляет группу из одного или более вариантов символа, которые вместе представляют осмысленную группировку символов в пределах математического выражения.
4. Система оптического распознавания символов по п. 3, в которой с каждой дугой каждого потенциально возможного пути связано весовое значение.
5. Система оптического распознавания символов по п. 4, в которой весовое значение для каждого потенциально возможного пути вычисляется как сумма весовых значений, связанных с дугами потенциально возможного пути.
6. Система оптического распознавания символов по п. 5,
в которой меньшему весовому значению, вычисленному для потенциального пути, соответствует более вероятный потенциально возможный путь; и
в которой выбор наиболее вероятного пути среди потенциально возможных путей, соответствующих упорядоченному множеству вариантов символа, дополнительно включает выбор потенциально возможного пути, имеющего наименьшее вычисленное весовое значение, в качестве наиболее вероятного пути.
7. Система оптического распознавания символов по п. 5,
в которой большему весовому значению, вычисленному для потенциально возможного пути, соответствует более вероятный потенциально возможный путь; и
в которой выбор наиболее вероятного пути среди потенциально возможных путей, соответствующих упорядоченному множеству вариантов символа, дополнительно включает выбор потенциально возможного пути, имеющего наибольшее вычисленное весовое значение, в качестве наиболее вероятного пути.
8. Система оптического распознавания символов по п. 1, в которой разбиение на блоки применяется к изображению или фрагменту изображения путем:
обнаружения белых полос с направлениями, совпадающими с направлением, перпендикулярным направлению разбиения на блоки, или находящимися в пределах порогового углового смещения относительно направления, перпендикулярного направлению разбиения на блоки;
соединения перекрывающихся белых полос во множестве обнаруженных белых полос для генерирования множества неперекрывающихся белых полос; и
использования неперекрывающихся белых полос в качестве границ блока для разбиения изображения или фрагмента изображения на два или более блоков вдоль направления разбиения на блоки.
9. Система оптического распознавания символов по п. 8, в которой каждая белая полоса с направлениями, совпадающими с направлением, перпендикулярным направлению разбиения на блоки, или находящимися в пределах порогового углового смещения относительно направления, перпендикулярного направлению разбиения на блоки, дополнительно содержит:
полосу с параллельными сторонами, причем стороны имеют направления, совпадающие с углом пересечения с указанным направлением разбиения на блоки, которое охватывает изображение или фрагмент изображения, содержащий количество пикселей меньшее порогового количества пикселей или площадь меньшую порогового значения площади, соответствующей символам в пределах изображения.
10. Система оптического распознавания символов по п. 8, в которой соединение перекрывающихся белых полос во множестве обнаруженных белых полос для генерирования множества неперекрывающихся белых полос дополнительно содержит:
обнаружение одной или более групп из двух или более белых полос, которые взаимно пересекаются или каждая из которых отделена от другой белой полосы из группы расстоянием меньше порогового расстояния;
соединение пересекающихся белых полос из каждой группы, имеющих одинаковое направление; и
выбор из каждой группы белой полосы, имеющей направление, совпадающее с направлением одной или более белых полос с наибольшей общей площадью в группе.
11. Способ для обработки изображения документа, содержащего математическое выражение, реализуемый с помощью одного или более процессоров, исполняющих программу, хранящуюся в одном или более модулях памяти системы оптического распознавания символов, которые преобразует изображение или фрагмент изображения, содержащий математическое выражение, в математическое выражение в цифровом виде, эквивалентное математическому выражению, которое содержится на изображении или фрагменте изображения, причем способ включает:
разбиение на блоки изображения, содержащего математическое выражение, и последующее оптическое распознавание блоков для разложения изображения математического выражения на упорядоченное множество вариантов оптического распознавания символов, где множество вариантов оптического распознавания символа упорядочено согласно весовому значению по OCR,
выбор наиболее вероятного пути на основе весового значения для пути среди потенциально возможных путей, где путь соответствует группировке символов на изображении математического выражения и упорядоченному множеству вариантов распознавания символов на данном изображении и,
использование наиболее вероятного пути и упорядоченного множества вариантов распознавания символов для порождения представления в цифровом виде математического выражения, эквивалентного математическому выражению, которое содержится на изображении, где наиболее вероятный путь, отобранный на основе весового значения, содержит информацию о группировке символов и вариантах их распознавания, и
сохранение представленного в цифровом виде математического выражения в одном или более из одного или более модулей памяти.
12. Способ по п. 11, в котором применение разбиения на блоки к изображению, содержащему математическое выражение, для разложения изображения на упорядоченное множество вариантов распознавания символа дополнительно содержит:
установление указания на направление разбиения изображения на блоки в качестве указания на горизонтальное разбиение на блоки, где установление указания на направления разбиения основано на выборе среди потенциальных границ разбиения с изменением направлений линии потенциальной границы;
горизонтальное разбиение изображения на фрагменты изображения на первом уровне; и
рекурсивно
для каждого фрагмента изображения на текущем уровне
применение одного или более способов распознавания символов к текущему рассматриваемому фрагменту изображения, и,
если с помощью одного или более способов распознавания символов не удается обнаружить фрагмент изображения в качестве фрагмента изображения, содержащего один символ, установление указания на направление разбиения на блоки, противоположное текущему направлению разбиения на блоки, представленному указанием на направление разбиения на блоки, продвижение указания текущего уровня и рекурсивное применение разбиения на блоки к фрагменту изображения с использованием указания на направление разбиения на блоки и указания текущего уровня.
13. Способ по п. 11, в котором каждый потенциально возможный путь, соответствующий упорядоченному множеству вариантов распознавания символа, содержит одну или более дуг, причем каждая дуга охватывает подмножество упорядоченного множества вариантов распознавания символа, где подмножество упорядоченного множества вариантов символа представляет группу из одного или более вариантов символа, которые вместе представляют осмысленную группировку символов в пределах математического выражения.
14. Способ по п. 13,
в котором с каждой дугой каждого потенциально возможного пути связано весовое значение; и
в котором весовое значение каждого потенциально возможного пути вычисляется как сумма весовых значений, связанных с дугами потенциально возможного пути.
15. Способ по п. 14,
в котором меньшему весовому значению, вычисленному для потенциально возможного пути, соответствует более вероятный потенциально возможный путь; и
в котором выбор наиболее вероятного пути среди потенциально возможных путей, соответствующих упорядоченному множеству вариантов символа, дополнительно включает выбор потенциально возможного пути, имеющего наименьшее вычисленное весовое значение, в качестве наиболее вероятного пути.
16. Способ по п. 14,
в котором большему весовому значению, вычисленному для потенциально возможного пути, соответствует более вероятный потенциально возможный путь; и
в котором выбор наиболее вероятного пути среди потенциально возможных путей, соответствующих упорядоченному множеству вариантов символа, дополнительно включает выбор потенциально возможного пути, имеющего наибольшее вычисленное весовое значение, в качестве наиболее вероятного пути.
17. Способ по п. 11, в котором разбиение на блоки применяется к изображению или фрагменту изображения путем:
обнаружения белых полос с направлениями, совпадающими с направлением, перпендикулярным направлению разбиения на блоки, или находящимися в пределах порогового углового смещения относительно направления, перпендикулярного направлению разбиения на блоки;
соединения перекрывающихся белых полос во множестве обнаруженных белых полос для генерирования множества неперекрывающихся белых полос; и
использования неперекрывающихся белых полос в качестве границ блока для разбиения изображения или фрагмента изображения на два или более блоков вдоль направления разбиения на блоки.
18. Способ по п. 17, в котором каждая белая полоса с направлениями, совпадающими с направлением, перпендикулярным направлению разбиения на блоки, или находящимися в пределах порогового углового смещения относительно направления, перпендикулярного направлению разбиения на блоки, дополнительно содержит:
полосу с параллельными сторонами, причем стороны имеют направления, совпадающие с углом пересечения с указанным направлением разбиения на блоки, которое охватывает изображение или фрагмент изображения, содержащий количество пикселей меньшее порогового количества пикселей или площадь меньше порогового значения площади, соответствующей символам в пределах изображения.
19. Способ по п. 17, в котором соединение перекрывающихся белых полос во множестве обнаруженных белых полос для генерирования множества неперекрывающихся белых полос дополнительно содержит:
обнаружение одной или более групп из двух или более белых полос, которые взаимно пересекаются или каждая из которых отделена от другой белой полосы из группы расстоянием меньше порогового расстояния;
соединение пересекающихся белых полос из каждой группы, имеющих одинаковое направление; и
выбор из каждой группы белой полосы, имеющей направление, совпадающее с направлением одной или более белых полос с наибольшей общей площадью в группе.
20. Один или более модулей памяти системы оптического распознавания символов, хранящие компьютерные команды,
дополнительно включающей один или более процессоров, которые, будучи исполненными одним или более из одного или более процессоров, преобразуют изображение или фрагмент изображения, содержащий математическое выражение, в представленное в цифровом виде математическое выражение, эквивалентное математическому выражению, которое содержится на изображении или фрагменте изображения, путем:
разбиения на блоки изображения, содержащего математическое выражение, и последующего оптического распознавания блоков для разложения изображения математического выражения на упорядоченное множество вариантов оптического распознавания символов, где множество вариантов оптического распознавания символа упорядочено согласно весовому значению по OCR,
выбора наиболее вероятного пути на основе весового значения для пути среди потенциально возможных путей, где путь соответствует группировке символов на изображении математического выражения и упорядоченному множеству вариантов распознавания символов на данном изображении и,
использования наиболее вероятного пути и упорядоченного множества вариантов распознавания символов для порождения представления в цифровом виде математического выражения, эквивалентного математическому выражению, которое содержится на изображении, где наиболее вероятный путь, отобранный на основе весового значения, содержит информацию о группировке символов и вариантах их распознавания, и
сохранения представленного в цифровом виде математического выражения в одном или более из одного или более модулей памяти.
| US 7181068 B2, 20.02.2007 | |||
| US 7561737 B2, 14.07.2009 | |||
| US 7885456 B2, 08.02.2011 | |||
| ГРАММАТИЧЕСКИЙ РАЗБОР ВИЗУАЛЬНЫХ СТРУКТУР ДОКУМЕНТА | 2006 |
|
RU2421810C2 |
| JP 2003256770 A, 12.09.2003. | |||
Авторы
Даты
2016-09-10—Публикация
2014-09-02—Подача